2.- Funciones de variable compleja.
|
|
|
- Carlos Cárdenas Ojeda
- hace 8 años
- Vistas:
Transcripción
1 2.- Funciones de variable compleja. a) Introducción. Definición de función de variable compleja. b) Mapeos o transformaciones. c) Límites y continuidad de una función. d) Límites y punto al infinito. La esfera de Riemann. a).- Introducción. Definición de función de variable compleja. En el estudio de números reales, una función f asigna a un elemento de su dominio un elemento de su rango acorde a una expresión de la forma x y = f(x) Por ejemplo, la función y = f(x) = 2x + 3 realiza las siguientes asociaciones x y: mientras que su inversa x = f -1 (y) = (y - 3)/2 realiza las asociaciones y x. Para el caso de los números complejos, podemos construir una herramienta similar de asociación entre dos números complejos z y w. Definición. Sea S un conjunto de números complejos. Una función f de variable compleja definida en S es una regla que asigna a cada número complejo z = x + iy de S, algún número complejo w = u + iv. El número complejo w se llama valor de f en z y se denota por f(z), es decir y el conjunto S donde está definida la función f(z) se llama dominio de f. w = f(z), (2.1) 2-1
2 Para representar gráficamente esta asignación o mapeo, se requieren 2 planos complejos: el plano z y el plano w, tal como se muestra en la figura anexa. Dado que z y w son números complejos, relacionados por la función f, es posible escribir donde hemos considerado que y w = f(z) u + iv = f(x + iy) w = u + iv z = x + iy. Lo anterior permite expresar a la función de variable compleja f(z) como la suma f(z) = f(x, y) = u(x, y) + iv(x, y) (2.2) cuando usamos la representación rectangular; mientras que en la representación exponencial podemos escribir donde se ha considerado que f(z) = f(r, ) = u(r, ) + iv(r, ) (2.3) z = re i. Ejemplo. Encuentre las partes real e imaginaria de la función f(z) = 2z 2-8z y expréselas en forma rectangular [u(x, y) y v(x, y)] y forma exponencial [u(r, ) y v(r, )]. Ejercicios. Encuentre las partes real e imaginaria de las funciones indicadas y expréselas en representación rectangular (u(x, y) y v(x, y)) y representación exponencial (u(r, ) y v(r, )). 1. f(z) = zz* 2. f(z) = 1 / z 3. f(z) = (2z - 8)/(z 2 + 1) Si al realizar esta separación, en cualquiera de sus representaciones, resulta que la función v es siempre cero, entonces decimos que la función f(z) es una función real de variable compleja. Un ejemplo de tales funciones es la primera de las listadas en el ejercicio previo, f(z) = zz*. 2-2
3 b).- Mapeos o transformaciones. Como vimos anteriormente, una función compleja de variable compleja f(z) asigna a cada punto z = (x, y) un punto w = (u, v); este tipo de asignación unívoca recibe el nombre de mapeo o transformación. En lo que sigue veremos algunos casos particulares de mapeos que, al aplicarse sobre un conjunto de puntos z k en el plano complejo (ya sean líneas o áreas), nos permite hablar de traslación, rotación, inversión y reflexión. La función Traslación w = f(z) = z + z (2.4) corresponde a una transformación o mapeo que representa una traslación pura del eje de coordenadas, es decir, que traslada al conjunto de puntos z como si el origen se ubicase en z, tal como se muestra en la figura. Por ejemplo, f(z) = z i traslada al segmento de recta que une los puntos z 1 = 1 i y z 2 = 4 + 2i tal como se muestra. 2-3
4 Mientras que g(z) = z + 2-2i traslada al segmento de recta que une los puntos z 1 = -1 +4i y z 2 = 4 + 2i tal como se muestra. Rotación Para analizar la rotación es conveniente retomar la representación exponencial del número complejo z, a saber z = re i Tal como se puede inferir de la figura, rotar al número z un ángulo es equivalente a sumar al argumento de z. Con lo anterior, podemos afirmar que la función w = f(z) = ze i (2.5) corresponde a una transformación o mapeo que representa una rotación pura del eje de coordenadas, es decir, que rota los ejes real e imaginario un ángulo. Si a continuación consideramos el producto w = zz podemos usar la siguiente representación polar de dichos números w = e i, z = re i y z = r e i para tener e i = (re i )(r e i ) de donde vemos que y = rr = Aquí vemos que han ocurrido dos cosas: por una parte, el módulo de z se ha modificado por un factor r ; y por otra parte, el ángulo se ha incrementado una constante, tal como se muestra en la figura. 2-4
5 Con lo anterior, podemos afirmar que la función w = f(z) = zz (2.6) corresponde a una transformación o mapeo que representa, al mismo tiempo, una rotación por un ángulo y una modificación del módulo por un factor r ; en este caso, la transformación dada por la ecuación (2.5) es un caso particular en el que r = 1. Por ejemplo, f(z) = iz = e i/2 z rota /2 al segmento de recta que une los puntos z 1 = 2 - i y z 2 = 3 + i, tal como se muestra. Otro caso interesante es f(z) = -z = (-1)z = e i z. En este caso, se tiene una rotación de alrededor del origen, tal como se muestra para el segmento que va de z 1 = 2 a z 2 = i. 2-5
6 Reflexión Un caso particular de mapeo corresponde a la reflexión del número complejo z, con respecto al eje real, el cual está dado por la función es decir, la función que asigna a un número z su complejo conjugado representa una reflexión en el eje real; mientras que la función f(z) = -z* (2.8) la cual asigna a un número z el inverso aditivo de su complejo conjugado, representa una reflexión en el eje imaginario. Lo mencionado anteriormente puede visualizarse en la figura adjunta. f(z) = z* (2.7) Ejercicio. Represente el mapeo correspondiente a la función f(z) = z* + 4i para el segmento que va del origen al punto z = 3-5i. Inversión Antes de concluir con esta parte del curso, vamos a considerar la función f(z) dada por w = f(z) = 1 / z (2.9) De nueva cuenta, retomamos la representación polar de los números complejos w y z w = e i y z = re i para escribir la expresión (2.9) como e i 1 1 e i re r de donde vemos que =1/r y = - i La primera de las dos últimas expresiones muestra claramente la inversión, el interior de un círculo se mapea en el exterior y el exterior en el interior; mientras que la segunda de ellas muestra que el ángulo se invierte, tal como ocurre con el complejo conjugado. 2-6
7 Gráficamente podemos considerar un semicírculo unitario para mostrar las propiedades de este mapeo, tal como se presenta en la figura. Ejemplo. Encuentre la imagen o mapeo del segmento de recta que une los puntos z 1 = 1 + 2i y z 2 = 3, bajo la transformación (a) f(z) = 3z + 2; y (b) f(z) = z 2. Solución. Una posible parametrización del segmento considerado es z(t) = (t + 1) + i(2 - t), con t 2 así que procedemos a evaluar, para cada inciso, la correspondiente función f(z). (a) f[z(t)] = 3[(t + 1) + i(2 - t)] + 2 = (3t + 5) + i(6-3t) (b) f[z(t)] = [(t + 1) + i(2 - t)] 2 = (6t - 3) + i(4 + 2t - 2t 2 ) En la figura siguiente se muestran, en un mismo Diagrama de Argand, las gráficas correspondientes al segmento de recta en el plano z y su mapeo en el plano w, para la función f(z) = 3z
8 Mientras que en la figura siguiente se muestran las gráficas correspondientes al segmento de recta en el plano z y su mapeo en el plano w, para la función f(z) = z 2. Ejercicios. 1. Para el segmento de recta que va del punto z 1 = x 1 + iy 1 al punto z 2 = x 2 + iy 2, encuentre el mapeo de dicho segmento bajo las siguientes transformaciones: a) f(z) = e z ; y b) f(z) = 1 / (z + 1). 2. Usando los resultados del problema anterior, bosqueje la región del plano w en la que se mapea el rectángulo con vértices en (,), (2,), (2,1) y (,1) del plano z. Solución. 1. Para este problema, la expresión que parametriza al segmento de recta es z(t) = ((x 2 x 1 )t + x 1 ) + i((y 2 y 1 )t + y 1 ), con t 1 y por lo que las expresiones para el mapeo en el plano w son w f z e y t i y t xt () ( ) cos ( ) sin ( ) x( t) 1 y( t) w f () z i x( t) 1 2 y( t) 2 x( t) 1 2 y( t) 2 2. En este caso, lo segmentos son De (,) a (2,): x(t) = 2t, y(t) =. De (2,) a (2,1): x(t) = 2, y(t) = t. De (2,1) a (,1): x(t) =2-2t, y(t) = 1. De (,1) a (,): x(t) =, y(t) = 1 - t. 2-8
9 Los cuales se muestran a continuación. Así que para f(z) = e z, estos segmentos nos llevan al mapeo w = e 2t [cos + i sen ] = (e 2t, ) w = e 2 [cos t + i sen t] = (e 2 cos t, e 2 sen t) w = e 2-2t [cos 1 + i sen 1] = (e 2-2t cos 1, e 2-2t sen 1) w = e [cos(1-t) + i sen(1-t)] = (cos(1-t), sen(1-t)) El mapeo anterior se muestra en la figura siguiente. 2-9
10 Mientras que para f(z) = 1 / (z + 1), los segmentos considerados previamente, nos llevan a 1 w, 2t 1 3 t w, 2 2 t 9 t 9 32t 1 w, t 1 3 2t 1 1 t 1 w, t 1 1 t Este mapeo se muestra en la figura siguiente. c).- Límite y continuidad de una función. Para introducir los conceptos de límite y continuidad de una función vamos a considerar que la función f(z) está definida en un dominio D y que z es un punto de D. A continuación vamos a ver que el límite y la continuidad de la función f(z) se definen de la misma manera que en el caso de variable real. 2-1
11 Definición. Sea f(z) una función definida en todos los puntos de cierta vecindad de z, excepto, posiblemente en el mismo z. Se dice que w es el límite de w = f(z), si para cualquier número positivo, existe un número positivo tal que f () z w, siempre que zz. Se denota el límite de f(z) con la expresión lim f ( z) w (2.1) zz cuando w corresponde al límite de la función f(z) cuando z se aproxima a z ; y significa que la región alrededor de w puede hacerse arbitrariamente pequeña conforme z se aproxima a z sin importar la forma en que lo hace. La definición anterior puede visualizarse en el siguiente esquema. Ejemplo. Demuestre que si f(z) = z / z*, entonces lim f( z) no existe. z Solución. En este caso, basta mostrar que lim f( z) 1 cuando nos acercamos al origen recorriendo el eje real, mientras que lim f( z) 1 cuando lo hacemos recorriendo el eje imaginario. z z Lo anterior muestra que hay dos valores para el límite, pero debido a que el límite debe ser único podemos concluir con la aseveración de que el límite planteado NO existe. A continuación se enuncian una serie de teoremas sobre límites que pueden ser fácilmente demostrado (quedando esto para los estudiantes interesados en tales demostraciones). Separabilidad de las partes real e imaginaria Suponga que f(z) = u(z) + i v(z) y que z = x + i y, entonces lim f ( z) w zz 2-11
12 si y con lo que lim u( z) u ( x, y) ( x, y) lim v( z) v ( x, y) ( x, y) w u iv Supongamos que Teoremas útiles sobre límites entonces i. lim ( ) ( ) zz ii. lim f ( z) g( z) iii. zz zz lim f ( z) A y zz lim g( z) B zz f z g z A B (Suma de límites) AB (Producto de límites) f () z A lim, siempre que B g() z B (Cociente de límites) Continuidad de una función La condición de continuidad para una función de variable compleja w = f(z), en analogía con el caso de funciones reales, se enuncia de la siguiente manera. Definición. La función f(z) es continua en el punto z si se cumple que lo que implica que lim f( z) zz lim f ( z) f ( z ) zz existe, y que f(z ) también existe. Función polinomial P n (z) Las ideas anteriormente desarrolladas nos permiten concluir que una función polinomial P n (z) es continua para todo z, donde P n (z) está definido como donde n es un entero positivo. P n (z) = a n z n + a n-1 z n-1 + a n-2 z n a 1 z + a 2-12
13 Para justificar lo anterior notemos que i. Para toda función constante f(z) = C, el mapeo que se tiene es el siguiente De aquí vemos que es evidente que lim f ( z) lim C C zz zz ii. Para la función identidad f(z) = z, el mapeo que se tiene es el siguiente En este caso, la definición de límite se cumple cuando =, con lo que lim f ( z) lim z z zz zz iii. Para los términos z n con n > 1, basta aplicar los dos resultados anteriores, junto con el límite de un producto, de manera recursiva, para mostrar que los términos a n z n son continuos. Con todo esto, podemos escribir que lim P ( z) P ( z ) zz n n 2-13
14 entonces Límite absoluto Otro resultado de aplicar la definición de límite establece que si lim f ( z) w zz zz lim f ( z) w d).- Límites y el punto al infinito. Plano complejo extendido Hasta el momento el plano complejo, como lo hemos visto, no tiene claramente definido el infinito. Sin embargo, en muchas situaciones es necesario considerar un punto al infinito; cuando esto ocurre, y el plano complejo incluye al infinito, hablamos del plano complejo extendido. En el caso de variables reales, el infinito consta de dos puntos ubicados en los extremos negativo y positivo del eje real, en ambos casos el valor absoluto es el mismo: infinito. Para el caso de los números complejos, si queremos extender la idea nos encontramos con un problema, ya que existe un número infinito de números complejos z tales que su módulo (el análogo al valor absoluto) es infinito, para evitar esta situación trataremos con el llamado punto al infinito. Para visualizar este punto al infinito se utiliza la siguiente idea. Consideremos que el plano complejo pasa por el ecuador de una esfera unitaria centrada en el origen O, tal como se muestra. A cada punto z del plano le corresponde un punto P en la superficie de la esfera. El punto P se determina por la intersección de la recta que va del polo norte N al punto z sobre el plano. 2-14
15 Para puntos z tales que z > 1 el punto P se ubica sobre el hemisferio Norte, para puntos tales que z = 1, el punto P está sobre el ecuador, mientras que para puntos z tales que z < 1 el punto P está sobre el hemisferio Sur; tal como se muestra en la siguiente figura. Al punto P ubicado en el polo Norte le corresponde el punto al infinito representado por. A la esfera unitaria utilizada para desarrollar la idea del punto al infinito se le conoce como esfera de Riemann y a la correspondencia entre puntos P de la esfera y puntos z del plano se le llama proyección estereográfica. Con lo anterior, todos los puntos P de la esfera corresponden con puntos z en el plano complejo extendido, es importante notar que esta correspondencia entre puntos es uno a uno. Límites y punto al infinito Con el esquema anterior, podemos ver que conforme aumenta z, el punto P sobre la esfera se acerca a N, lo que nos permite decir que para positivo y pequeño, los puntos en el plano complejo exteriores al círculo z = 1/ corresponden a puntos sobre la esfera próximos al punto N, con lo que podemos afirmar que el conjunto z > 1/ es un entorno de infinito ( ). Usando la idea anterior, podemos interpretar la expresión lim f( z) zz En este caso, se tiene que para cada número positivo existe un número positivo tal que siempre que f(z) > 1/ < z - z <, es decir, si z está en el entorno de z, entonces f(z) está en el entorno z > 1/ para infinito. 2-15
16 Finalmente, con las ideas desarrolladas anteriormente, resulta válido establecer que si z y w son puntos en los planos complejos z y w, respectivamente, entonces i. lim f( z), zz si y sólo si 1 lim () zz f z 1 ii. lim f ( z) w, si y sólo si lim f w z z z iii. lim f( z) z, si y sólo si z 1 lim 1 f z 2-16
1.- Álgebra de números complejos.
 .- Álgebra de números complejos. a) Definición y representación geométrica. b) Sumas y productos de números complejos. c) Vectores y módulos en el plano complejo. d) Representación en forma exponencial.
.- Álgebra de números complejos. a) Definición y representación geométrica. b) Sumas y productos de números complejos. c) Vectores y módulos en el plano complejo. d) Representación en forma exponencial.
Regiones en el plano complejo
 Regiones en el plano complejo Disco abierto, vecindad o entorno: El conjunto de puntos que satisfacen la desigualdad donde es número real positivo [ : entorno] ====================================== Recordemos
Regiones en el plano complejo Disco abierto, vecindad o entorno: El conjunto de puntos que satisfacen la desigualdad donde es número real positivo [ : entorno] ====================================== Recordemos
Variable Compleja I. Maite Fernández Unzieta Universidad de Guanajuato Enero Junio Eugenio Daniel Flores Alatorre
 Variable Compleja I Maite Fernández Unzieta Universidad de Guanajuato Enero Junio 2012 Eugenio Daniel Flores Alatorre Bibliografía Complex Analysis 3rd ed. Ahlfors Basic Complex Analysis Functions of one
Variable Compleja I Maite Fernández Unzieta Universidad de Guanajuato Enero Junio 2012 Eugenio Daniel Flores Alatorre Bibliografía Complex Analysis 3rd ed. Ahlfors Basic Complex Analysis Functions of one
Puntos y Vectores. 16 de Marzo de 2012
 Geometría en Puntos y Vectores Universidad Autónoma Metropolitana Unidad Iztapalapa 16 de Marzo de 2012 Introducción En Geometría analítica plana las relaciones y las propiedades geométricas se expresan
Geometría en Puntos y Vectores Universidad Autónoma Metropolitana Unidad Iztapalapa 16 de Marzo de 2012 Introducción En Geometría analítica plana las relaciones y las propiedades geométricas se expresan
Integral de Fourier y espectros continuos
 9 2 2 2 Esta expresión se denomina forma de Angulo fase (o forma armónica) de la serie de Fourier. Integral de Fourier y espectros continuos Las series de Fourier son una herramienta útil para representar
9 2 2 2 Esta expresión se denomina forma de Angulo fase (o forma armónica) de la serie de Fourier. Integral de Fourier y espectros continuos Las series de Fourier son una herramienta útil para representar
Números Complejos. Números naturales: útiles para contar cosas N={ 0, 1, 2, } Pero con ellos no podemos resolver la ecuación: X+5=2
 Números Complejos Números naturales: útiles para contar cosas N={ 0, 1, 2, } Pero con ellos no podemos resolver la ecuación: X+5=2 Números Complejos Entonces inventamos los números enteros: Z = { -2, -1,
Números Complejos Números naturales: útiles para contar cosas N={ 0, 1, 2, } Pero con ellos no podemos resolver la ecuación: X+5=2 Números Complejos Entonces inventamos los números enteros: Z = { -2, -1,
Forma polar de números complejos (repaso breve)
 Forma polar de números complejos (repaso breve) Objetivos. pasar la forma polar de números complejos. quisitos. Números complejos, funciones trigonométricas, valor absoluto de números complejos, circunferencia
Forma polar de números complejos (repaso breve) Objetivos. pasar la forma polar de números complejos. quisitos. Números complejos, funciones trigonométricas, valor absoluto de números complejos, circunferencia
UNIDAD 1 NUMEROS COMPLEJOS
 UNIDAD 1 NUMEROS COMPLEJOS El conjunto de los números complejos fue creado para poder resolver algunos problemas matemáticos que no tienen solución dentro del conjunto de los números reales. Por ejemplo
UNIDAD 1 NUMEROS COMPLEJOS El conjunto de los números complejos fue creado para poder resolver algunos problemas matemáticos que no tienen solución dentro del conjunto de los números reales. Por ejemplo
Tema 1. Números Complejos
 Tema 1. Números Complejos Prof. William La Cruz Bastidas 27 de septiembre de 2002 Capítulo 1 Números Complejos Definición 1.1 Un número complejo, z, es un número que se expresa como z = x + iy o, de manera
Tema 1. Números Complejos Prof. William La Cruz Bastidas 27 de septiembre de 2002 Capítulo 1 Números Complejos Definición 1.1 Un número complejo, z, es un número que se expresa como z = x + iy o, de manera
Contenido. Números Complejos 3
 Números Complejos Universidad Central de Venezuela Facultad de Ingeniería Escuela de Ingeniería Eléctrica Departamento de Electrónica, Computación y Control Variable Compleja y Cálculo Operacional Marzo,
Números Complejos Universidad Central de Venezuela Facultad de Ingeniería Escuela de Ingeniería Eléctrica Departamento de Electrónica, Computación y Control Variable Compleja y Cálculo Operacional Marzo,
APUNTES 1 VECTORES M.C. CESAR GUERRA TORRES
 APUNTES 1 VECTORES M.C. CESAR GUERRA TORRES 1. INTRODUCCION Las cantidades físicas en su forma general se dividen en: a) escalares y b) vectores. Un escalar es una cantidad física es utilizada para expresar
APUNTES 1 VECTORES M.C. CESAR GUERRA TORRES 1. INTRODUCCION Las cantidades físicas en su forma general se dividen en: a) escalares y b) vectores. Un escalar es una cantidad física es utilizada para expresar
Raíz cuadrada. Superficies de Riemann
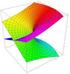 Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
Coordenadas polares. Si P es un punto cualquiera del plano, su posición queda determinada con el par ( r, ), donde: Ejemplo
 Coordenadas polares Sobre el plano elijamos un punto O, que denominamos Polo (u origen) y un rayo con origen O, que denominamos Eje Polar 1 2 Si P es un punto cualquiera del plano, su posición queda determinada
Coordenadas polares Sobre el plano elijamos un punto O, que denominamos Polo (u origen) y un rayo con origen O, que denominamos Eje Polar 1 2 Si P es un punto cualquiera del plano, su posición queda determinada
MATEMATICAS ESPECIALES I PRACTICA 7 CLASE 1. Transformaciones conformes
 MATEMATICAS ESPECIALES I PRACTICA 7 CLASE 1 Transformaciones conformes 1 Determinar donde son conformes las siguientes transformaciones: (a) w() = 2 + 2 (b) w() = 1 + i (c) w() = + 1 (d) w() = En cada
MATEMATICAS ESPECIALES I PRACTICA 7 CLASE 1 Transformaciones conformes 1 Determinar donde son conformes las siguientes transformaciones: (a) w() = 2 + 2 (b) w() = 1 + i (c) w() = + 1 (d) w() = En cada
Familiarizar al alumno con las distintas maneras de expresar números complejos.
 Capítulo 2 Aritmética compleja Objetivos Familiarizar al alumno con las distintas maneras de expresar números complejos. Manejar con soltura las operaciones aritméticas con números complejos. 2.1. Representaciones
Capítulo 2 Aritmética compleja Objetivos Familiarizar al alumno con las distintas maneras de expresar números complejos. Manejar con soltura las operaciones aritméticas con números complejos. 2.1. Representaciones
Análisis Complejo - Primer Cuatrimestre de 2018
 Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Depto. de Matemática Análisis Complejo - Primer Cuatrimestre de 018 Práctica N 1: Números Complejos, Esfera de Riemann y Homografías
Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Depto. de Matemática Análisis Complejo - Primer Cuatrimestre de 018 Práctica N 1: Números Complejos, Esfera de Riemann y Homografías
Funciones continuas. Definición y propiedades
 Funciones continuas. Definición y propiedades Para la lectura de este artículo es recomendable haber leído con anterioridad otros tres artículos relacionados con las sucesiones de números reales y las
Funciones continuas. Definición y propiedades Para la lectura de este artículo es recomendable haber leído con anterioridad otros tres artículos relacionados con las sucesiones de números reales y las
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
DERIVACIÓN COMPLEJA. Sea f definida en todos los puntos z de algún entorno z 0
 1. DERIVACIÓN COMPLEJA Límites Sea f definida en todos los puntos z de algún entorno z 0 f(z) ω 0 es decir, el punto ω f(z) puede quedar próximo a ω 0 si elegimos z suficientemente próximo a z 0, pero
1. DERIVACIÓN COMPLEJA Límites Sea f definida en todos los puntos z de algún entorno z 0 f(z) ω 0 es decir, el punto ω f(z) puede quedar próximo a ω 0 si elegimos z suficientemente próximo a z 0, pero
Curso Propedéutico de Cálculo Sesión 1: Funciones
 Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
Curso Propedéutico de Cálculo Sesión 1: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 Esquema 1 2 El cálculo se basa en las propiedades de los
Profesor: Carlos Arroyave Valencia GUÍA 2 TEMA: VECTORES - OPERACIONES MAGNITUDES FÍSICAS
 INSTITUTO TECNICO INDUSTRIAL PASCUAL BRAVO ÁREA: CIENCIAS NATURALES Y EDUCACIÓN AMBIENTAL (FÍSICA) GRADO: 10 JORNADA: Tarde PERÍODO: II Profesor: Carlos Arroyave Valencia GUÍA 2 TEMA: VECTORES - OPERACIONES
INSTITUTO TECNICO INDUSTRIAL PASCUAL BRAVO ÁREA: CIENCIAS NATURALES Y EDUCACIÓN AMBIENTAL (FÍSICA) GRADO: 10 JORNADA: Tarde PERÍODO: II Profesor: Carlos Arroyave Valencia GUÍA 2 TEMA: VECTORES - OPERACIONES
Ecuaciones de Cauchy-Riemann
 Ecuaciones de Cauchy-Riemann Por lo tanto, si las primeras derivadas parciales son continuas y satisfacen las ecuaciones de Cauchy-Riemann en todos los puntos de la vecindad (entorno), entonces f(z) es
Ecuaciones de Cauchy-Riemann Por lo tanto, si las primeras derivadas parciales son continuas y satisfacen las ecuaciones de Cauchy-Riemann en todos los puntos de la vecindad (entorno), entonces f(z) es
Números Complejos Matemáticas Básicas 2004
 Números Complejos Matemáticas Básicas 2004 21 de Octubre de 2004 Los números complejos de la forma (a, 0) Si hacemos corresponder a cada número real a, el número complejo (a, 0), tenemos una relación biunívoca.
Números Complejos Matemáticas Básicas 2004 21 de Octubre de 2004 Los números complejos de la forma (a, 0) Si hacemos corresponder a cada número real a, el número complejo (a, 0), tenemos una relación biunívoca.
MA3002. Matemáticas Avanzadas para Ingeniería: Funciones de Variable Compleja. Departamento de Matemáticas. Continuidad. Derivada.
 MA3002 variable compleja Cuando el dominio una función f es un conjunto números complejos y cuando los valores que proporciona la función son también números complejos, diremos que f es una función variable
MA3002 variable compleja Cuando el dominio una función f es un conjunto números complejos y cuando los valores que proporciona la función son también números complejos, diremos que f es una función variable
NÚMEROS COMPLEJOS: C
 NÚMEROS COMPLEJOS: C Alejandro Lugon 21 de mayo de 2010 Resumen Este es un pequeño estudio de los números complejos con el objetivo de poder usar las técnicas de solución de ecuaciones y sistemas diferenciales
NÚMEROS COMPLEJOS: C Alejandro Lugon 21 de mayo de 2010 Resumen Este es un pequeño estudio de los números complejos con el objetivo de poder usar las técnicas de solución de ecuaciones y sistemas diferenciales
Números Complejos. Contenido. Definición
 U Contenido Facultad de Ingeniería Escuela de Ingeniería Eléctrica Departamento de Electrónica, Computación y Control Variable Compleja y Cálculo Operacional Números Complejos William La Cruz Números Complejos...3
U Contenido Facultad de Ingeniería Escuela de Ingeniería Eléctrica Departamento de Electrónica, Computación y Control Variable Compleja y Cálculo Operacional Números Complejos William La Cruz Números Complejos...3
Métodos Matemáticos I
 Métodos Matemáticos I Curso 203-4 Hoja de Problemas #2. Dados los siguientes conjuntos: () + 2i (2) 3 + i < 6 (3) + 2i < (4) 0 arg π/3, 0 (5) Re( 2 ) 0 (6) Re( 2 ) < 0 Represéntalos gráficamente. (b) Cuáles
Métodos Matemáticos I Curso 203-4 Hoja de Problemas #2. Dados los siguientes conjuntos: () + 2i (2) 3 + i < 6 (3) + 2i < (4) 0 arg π/3, 0 (5) Re( 2 ) 0 (6) Re( 2 ) < 0 Represéntalos gráficamente. (b) Cuáles
LA FORMA TRIGONOMETRICA DE LOS NUMEROS COMPLEJOS Y EL TEOREMA DE MOIVRE. Capítulo 7 Sec. 7.5 y 7.6
 LA FORMA TRIGONOMETRICA DE LOS NUMEROS COMPLEJOS Y EL TEOREMA DE MOIVRE Capítulo 7 Sec. 7.5 y 7.6 El Plano Complejo Se puede utilizar un plano de coordenadas para representar números complejos. Si cada
LA FORMA TRIGONOMETRICA DE LOS NUMEROS COMPLEJOS Y EL TEOREMA DE MOIVRE Capítulo 7 Sec. 7.5 y 7.6 El Plano Complejo Se puede utilizar un plano de coordenadas para representar números complejos. Si cada
INSTITUCIÓN EDUCATIVA SANTA TERESA DE JESÚS IBAGUÉ - TOLIMA GUIA No.4 ALGEBRA DOCENTE: EDGARD RODRIGUEZ USECHE GRADO : NOVENO
 TEMA: ECUACIÓN DE LA LÍNEA RECTA Las coordenadas cartesianas o coordenadas rectangulares son un ejemplo de coordenadas ortogonales usadas en espacios euclídeos caracterizadas por la existencia de dos ejes
TEMA: ECUACIÓN DE LA LÍNEA RECTA Las coordenadas cartesianas o coordenadas rectangulares son un ejemplo de coordenadas ortogonales usadas en espacios euclídeos caracterizadas por la existencia de dos ejes
Tema 5. Series de Potencias
 Tema 5. Series de Potencias Prof. William La Cruz Bastidas 21 de noviembre de 2002 Tema 5 Series de Potencias Definición 5.1 La sucesión de números complejos {z n } tiene un límite o converge a un número
Tema 5. Series de Potencias Prof. William La Cruz Bastidas 21 de noviembre de 2002 Tema 5 Series de Potencias Definición 5.1 La sucesión de números complejos {z n } tiene un límite o converge a un número
DEFINICIÓN DE LÍMITE Sea una función definida en un intervalo abierto que contiene a (salvo posiblemente en ) y un número real. La afirmación : ( )
 DEFINICIÓN DE LÍMITE Sea una función definida en un intervalo abierto que contiene a (salvo posiblemente en ) y un número real. La afirmación : Significa que para todo existe un tal que si Entonces. TEOREMA
DEFINICIÓN DE LÍMITE Sea una función definida en un intervalo abierto que contiene a (salvo posiblemente en ) y un número real. La afirmación : Significa que para todo existe un tal que si Entonces. TEOREMA
Para entender la diferencia entre una relación y una función primero analizaremos el concepto de cada uno.
 FUNCIONES Diferencia entre relaciones y funciones Para entender la diferencia entre una relación y una función primero analizaremos el concepto de cada uno. Relación Es la correspondencia de un primer
FUNCIONES Diferencia entre relaciones y funciones Para entender la diferencia entre una relación y una función primero analizaremos el concepto de cada uno. Relación Es la correspondencia de un primer
Banco de Ejercicios del Departamental Métodos Matemáticos para Sistemas Lineales Numeros Complejos
 Banco de Ejercicios del Departamental Métodos Matemáticos para Sistemas Lineales Numeros Complejos 1. Efectuar cada una de las operaciones indicadas. a) (35 + 25i) + ( 12 5i) b) ( 75 i) + (34 + 42i) c)
Banco de Ejercicios del Departamental Métodos Matemáticos para Sistemas Lineales Numeros Complejos 1. Efectuar cada una de las operaciones indicadas. a) (35 + 25i) + ( 12 5i) b) ( 75 i) + (34 + 42i) c)
CÁLCULO II Grados en Ingeniería
 CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
Lección 50. Funciones II. Plano cartesiano
 Lección 50 Funciones II Plano cartesiano Un sistema de coordenadas rectangulares o cartesianas, llamado también plano cartesiano o plano xy, está formado por dos rectas coordenadas perpendiculares (rectas
Lección 50 Funciones II Plano cartesiano Un sistema de coordenadas rectangulares o cartesianas, llamado también plano cartesiano o plano xy, está formado por dos rectas coordenadas perpendiculares (rectas
58 7. ESPACIOS COCIENTE
 CAPíULO 7 Espacios cociente En esta sección estudiamos el cociente de un espacio vectorial por un subespacio W. Este cociente se define como el conjunto cociente de por una relación de equivalencia conveniente.
CAPíULO 7 Espacios cociente En esta sección estudiamos el cociente de un espacio vectorial por un subespacio W. Este cociente se define como el conjunto cociente de por una relación de equivalencia conveniente.
y cualquier par (x, y) puede escalarse, multiplicarse por un número real s, para obtener otro vector (sx, sy).
 UNIDAD II: VECTORES EN DOS Y TRES DIMENSIONES Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios
UNIDAD II: VECTORES EN DOS Y TRES DIMENSIONES Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios
MATEMÁTICA D y D 1 Módulo I: Análisis de Variable Compleja
 Matemática D y D MATEMÁTICA D y D Módulo I: Análisis de Variable Compleja Unidad 0 Números Complejos Mag. María Inés Baragatti Números complejos. Generalidades Un número complejo es un par ordenado de
Matemática D y D MATEMÁTICA D y D Módulo I: Análisis de Variable Compleja Unidad 0 Números Complejos Mag. María Inés Baragatti Números complejos. Generalidades Un número complejo es un par ordenado de
Lección 51. Funciones III. Funciones lineales
 Lección 51 Funciones III Funciones lineales Una función lineal es una función de la forma f (x) = mx + b, donde m y b son constantes. Se llama lineal porque su gráfica es una línea recta, en el plano R
Lección 51 Funciones III Funciones lineales Una función lineal es una función de la forma f (x) = mx + b, donde m y b son constantes. Se llama lineal porque su gráfica es una línea recta, en el plano R
(3) Regla del cociente: Si g(z 0 ) 0, f/g es derivable en z 0 y. (z 0 ) = f (z 0 )g(z 0 ) f(z 0 )g (z 0 ) . g
 Funciones holomorfas 2.1. Funciones variable compleja En este capítulo vamos a tratar con funciones f : Ω C C, donde Ω C es el dominio de definición. La forma habitual de expresar estas funciones es como
Funciones holomorfas 2.1. Funciones variable compleja En este capítulo vamos a tratar con funciones f : Ω C C, donde Ω C es el dominio de definición. La forma habitual de expresar estas funciones es como
SISTEMA DE COORDENADAS CARTESIANAS
 SISTEA DE COORDENADAS CARTESIANAS Un par ordenado de números reales (, y) lo podemos representar en el plano en un sistema de coordenadas cartesianas o rectangulares o plano y Este sistema está constituido
SISTEA DE COORDENADAS CARTESIANAS Un par ordenado de números reales (, y) lo podemos representar en el plano en un sistema de coordenadas cartesianas o rectangulares o plano y Este sistema está constituido
ap l i c a c i o n e s d e l a s
 Unidad 9 ap l i c a c i o n e s d e l a s transformaciones lineales Objetivos: Al inalizar la unidad, el alumno: Relacionará algunas transformaciones especiales con movimientos geométricos de vectores
Unidad 9 ap l i c a c i o n e s d e l a s transformaciones lineales Objetivos: Al inalizar la unidad, el alumno: Relacionará algunas transformaciones especiales con movimientos geométricos de vectores
Series de Laurent. R n (z) = (z z 0) n C. ( z. Para probar esta afirmación partimos de la fórmula integral de Cauchy escrita convenientemente = 1
 Semana 3 - lase 37 Series de Laurent. Otra vez Taylor y ahora Laurent Anteriormente consideramos series complejas de potencias. En esta sección revisaremos, desde la perspectiva de haber expresado la derivada
Semana 3 - lase 37 Series de Laurent. Otra vez Taylor y ahora Laurent Anteriormente consideramos series complejas de potencias. En esta sección revisaremos, desde la perspectiva de haber expresado la derivada
Saint Gaspar College MISIONEROS DE LA PRECIOSA SANGRE Formando Personas Integras
 Saint Gaspar College MISIONEROS DE LA PRECIOSA SANGRE Formando Personas Integras DEPARTAMENTO DE CIENCIAS Y TECNOLOGÍA MISS YORMA RIVERA M. V E C T O R E S MAGNITUD FÍSICA Es todo aquello que se puede
Saint Gaspar College MISIONEROS DE LA PRECIOSA SANGRE Formando Personas Integras DEPARTAMENTO DE CIENCIAS Y TECNOLOGÍA MISS YORMA RIVERA M. V E C T O R E S MAGNITUD FÍSICA Es todo aquello que se puede
Fórmula integral de Cauchy
 Fórmula integral de Cauchy Comentario: de acuerdo con esta fórmula, uno puede conocer el valor de f dentro del entorno, conociendo únicamente los valores que toma f en el contorno C! Fórmula integral de
Fórmula integral de Cauchy Comentario: de acuerdo con esta fórmula, uno puede conocer el valor de f dentro del entorno, conociendo únicamente los valores que toma f en el contorno C! Fórmula integral de
Aplicaciones de las derivadas. El teorema del valor medio
 Aplicaciones de las derivadas. El teorema del valor medio Ya hemos hablado en un par de artículos anteriores del concepto de derivada y de su interpretación tanto desde el punto de vista geométrico como
Aplicaciones de las derivadas. El teorema del valor medio Ya hemos hablado en un par de artículos anteriores del concepto de derivada y de su interpretación tanto desde el punto de vista geométrico como
Derivadas Parciales (parte 2)
 40 Derivadas Parciales (parte 2) Ejercicio: Si donde y. Determinar Solución: Consideraremos ahora la situación en la que, pero cada una de las variables e es función de dos variables y. En este caso tiene
40 Derivadas Parciales (parte 2) Ejercicio: Si donde y. Determinar Solución: Consideraremos ahora la situación en la que, pero cada una de las variables e es función de dos variables y. En este caso tiene
Olimpiada Iberoamericana de Matemática Universitaria 2012 Problemas, soluciones y criterios
 Olimpiada Iberoamericana de Matemática Universitaria 202 Problemas, soluciones y criterios. Problemas. (3 puntos) Sea Z el anillo de los enteros. Los conjuntos Z, 2Z y 3Z son semigrupos con respecto a
Olimpiada Iberoamericana de Matemática Universitaria 202 Problemas, soluciones y criterios. Problemas. (3 puntos) Sea Z el anillo de los enteros. Los conjuntos Z, 2Z y 3Z son semigrupos con respecto a
TEMA 7 NÚMEROS COMPLEJOS
 TEMA 7 NÚMEROS COMPLEJOS La unidad imaginaria i. Hay ecuaciones que no se pueden resolver en. Por ejemplo: x + 1 = 0 x = - 1 x = ± -1 En el siglo XVI se inventaron un número para resolver esta i = -1 ecuación.
TEMA 7 NÚMEROS COMPLEJOS La unidad imaginaria i. Hay ecuaciones que no se pueden resolver en. Por ejemplo: x + 1 = 0 x = - 1 x = ± -1 En el siglo XVI se inventaron un número para resolver esta i = -1 ecuación.
LOS NÚMEROS COMPLEJOS
 LOS NÚMEROS COMPLEJOS Para una mirada sobre el origen y desarrollo histórico de los números complejos leer el siguiente documento páginas 8-13 CANTIDADES IMAGINARIAS Definición: Las cantidades imaginarias
LOS NÚMEROS COMPLEJOS Para una mirada sobre el origen y desarrollo histórico de los números complejos leer el siguiente documento páginas 8-13 CANTIDADES IMAGINARIAS Definición: Las cantidades imaginarias
7. Teoría de Cauchy global.
 68 Funciones de variable compleja. Eleonora Catsigeras. 25 Abril 26. 7. Teoría de Cauchy global. 7.. Teorema de Cauchy global. Sea un abierto no vacío Ω C. Teorema 7... Teorema de Cauchy global. Sea f
68 Funciones de variable compleja. Eleonora Catsigeras. 25 Abril 26. 7. Teoría de Cauchy global. 7.. Teorema de Cauchy global. Sea un abierto no vacío Ω C. Teorema 7... Teorema de Cauchy global. Sea f
Capítulo 4 Desarrollos en Serie de Taylor y de Laurent.
 Capítulo 4 Desarrollos en Serie de Taylor y de Laurent. El desarrollo en serie de potencias, que comúnmente se restringe a potencias positivas en el campo real toma forma definitiva en el campo complejo
Capítulo 4 Desarrollos en Serie de Taylor y de Laurent. El desarrollo en serie de potencias, que comúnmente se restringe a potencias positivas en el campo real toma forma definitiva en el campo complejo
La función, definida para toda, es periódica si existe un número positivo tal que
 Métodos con series de Fourier Definición: Función periódica La función, definida para toda, es periódica si existe un número positivo tal que para toda. El número en un periodo de la función. Si existe
Métodos con series de Fourier Definición: Función periódica La función, definida para toda, es periódica si existe un número positivo tal que para toda. El número en un periodo de la función. Si existe
TRIGONOMETRÍA ANALÍTICA
 TRIGONOMETRÍA ANALÍTICA....4 Los alumnos comenzaron a estudiar funciones trigonométricas en el Capítulo 7, cuando aprendieron sobre radianes la transformación de funciones trigonométricas. Aquí aprenderán
TRIGONOMETRÍA ANALÍTICA....4 Los alumnos comenzaron a estudiar funciones trigonométricas en el Capítulo 7, cuando aprendieron sobre radianes la transformación de funciones trigonométricas. Aquí aprenderán
PRACTICO: : LÍMITES DE FUNCIONES
 APUNTE TEORICO-PRACTICO PRACTICO: : LÍMITES DE FUNCIONES UNIVERSIDAD NACIONAL DE RIO NEGRO Asignatura: Matemática 1 Carreras: Lic. en Economía Profesor: Prof. Mabel Chrestia Semestre: 1ero Año: 16 Introducción
APUNTE TEORICO-PRACTICO PRACTICO: : LÍMITES DE FUNCIONES UNIVERSIDAD NACIONAL DE RIO NEGRO Asignatura: Matemática 1 Carreras: Lic. en Economía Profesor: Prof. Mabel Chrestia Semestre: 1ero Año: 16 Introducción
PRACTICO: : LÍMITES DE FUNCIONES
 APUNTE TEORICO-PRACTICO PRACTICO: : LÍMITES DE FUNCIONES UNIVERSIDAD NACIONAL DE RIO NEGRO Asignatura: Matemática 1 Carreras: Lic. en Economía Profesor: Prof. Mabel Chrestia Semestre: 1ero Año: 15 Introducción
APUNTE TEORICO-PRACTICO PRACTICO: : LÍMITES DE FUNCIONES UNIVERSIDAD NACIONAL DE RIO NEGRO Asignatura: Matemática 1 Carreras: Lic. en Economía Profesor: Prof. Mabel Chrestia Semestre: 1ero Año: 15 Introducción
TEMA 3: CONTINUIDAD DE FUNCIONES
 TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Tema 7: Derivada de una función
 Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
1. DEFINICIÓN. ax = b, x 2 = b, 2 + 5i, 0 + ( 2)i, 2 + 3i, 5 + 0i, 1 + 1i. 0 + ( 2)i = 2i, 5 + 0i = 5, 1 + 1i = 1 + i.
 NÚMEROS COMPLEJOS PATRICIA KISBYE 1. DEFINICIÓN En los números reales es posible resolver cualquier ecuación lineal en una variable: ax = b, siempre que a sea distinto de 0. Pero las ecuaciones cuadráticas,
NÚMEROS COMPLEJOS PATRICIA KISBYE 1. DEFINICIÓN En los números reales es posible resolver cualquier ecuación lineal en una variable: ax = b, siempre que a sea distinto de 0. Pero las ecuaciones cuadráticas,
Fórmula integral de Cauchy
 Fórmula integral de Cauchy Comentario: de acuerdo con esta fórmula, uno puede conocer el valor de f dentro del entorno, conociendo únicamente los valores que toma f en el contorno C! Fórmula integral de
Fórmula integral de Cauchy Comentario: de acuerdo con esta fórmula, uno puede conocer el valor de f dentro del entorno, conociendo únicamente los valores que toma f en el contorno C! Fórmula integral de
Unidad III: Curvas en R2 y ecuaciones paramétricas
 Unidad III: Curvas en R2 y ecuaciones paramétricas 2.1 Ecuación paramétrica de la línea recta. La recta constituye una parte fundamental de las matemáticas. Existen numerosas formas de representar una
Unidad III: Curvas en R2 y ecuaciones paramétricas 2.1 Ecuación paramétrica de la línea recta. La recta constituye una parte fundamental de las matemáticas. Existen numerosas formas de representar una
(a, 0) + (b, 0) = (a + b, 0), (a, 0) (b, 0) = (ab, 0),
 NÚMEROS COMPLEJOS 1. Preliminares Definición. Se llama número complejo a todo par ordenado de números reales. Si z = (a, b) es un número complejo, se dice que a es la parte real de z y b es la parte imaginaria
NÚMEROS COMPLEJOS 1. Preliminares Definición. Se llama número complejo a todo par ordenado de números reales. Si z = (a, b) es un número complejo, se dice que a es la parte real de z y b es la parte imaginaria
Así tenemos el siguiente teorema: Sea f una función analítica en un disco Entonces f admite la representación de potencias:
 Así tenemos el siguiente teorema: Sea f una función analítica en un disco Entonces f admite la representación de potencias: donde conocida como serie de Taylor (o serie de Maclaurin cuando ). Además la
Así tenemos el siguiente teorema: Sea f una función analítica en un disco Entonces f admite la representación de potencias: donde conocida como serie de Taylor (o serie de Maclaurin cuando ). Además la
Toda función es una relación, pero no toda relación es una función. Las relaciones multiformes NO son funciones. Relación uno a uno (biunívoca)
 CONCEPTO TRADICIONAL DE FUNCIÓN Cuando dos variables están relacionadas en tal forma que a cada valor de la primera corresponde un valor de la segunda, se dice que la segunda es función de la primera.
CONCEPTO TRADICIONAL DE FUNCIÓN Cuando dos variables están relacionadas en tal forma que a cada valor de la primera corresponde un valor de la segunda, se dice que la segunda es función de la primera.
Problemas de VC para EDVC elaborados por C. Mora, Tema 1. Escribir en forma binómica los siguientes números complejos:, n N; 3 i ; (1+i 3) 20 ; e 1/z
 Problemas de VC para EDVC elaborados por C. Mora, Tema 1 Ejercicio 1 Escribir en forma binómica los siguientes números complejos: i n, n Z; ( 1 + i ) n, n N; ( ) ( ) 4 5 1 + i 3 i ; (1+i 3) 0 ; e 1/z 1
Problemas de VC para EDVC elaborados por C. Mora, Tema 1 Ejercicio 1 Escribir en forma binómica los siguientes números complejos: i n, n Z; ( 1 + i ) n, n N; ( ) ( ) 4 5 1 + i 3 i ; (1+i 3) 0 ; e 1/z 1
Números reales. por. Ramón Espinosa
 Números reales por Ramón Espinosa Existe un conjunto R, cuyos elementos son llamados números reales. Los números reales satisfacen ciertas propiedades algebraicas y de orden que describimos a continuación.
Números reales por Ramón Espinosa Existe un conjunto R, cuyos elementos son llamados números reales. Los números reales satisfacen ciertas propiedades algebraicas y de orden que describimos a continuación.
Esta es la gráfica de la función lineal y = 3x + 2 Vemos que m = 3 y b = 2 (de la forma y = mx + b)
 FUNCIÓN LINEAL Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
FUNCIÓN LINEAL Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
Funciones de Variable Compleja
 U Contenido Facultad de Ingeniería Escuela de Ingeniería Eléctrica Departamento de Electrónica, Computación y Control Variable Compleja y Cálculo Operacional Funciones de Variable Compleja (Continuidad,
U Contenido Facultad de Ingeniería Escuela de Ingeniería Eléctrica Departamento de Electrónica, Computación y Control Variable Compleja y Cálculo Operacional Funciones de Variable Compleja (Continuidad,
FUNCIONES HOLOMORFAS. LAS ECUACIONES DE CAUCHY-RIEMANN Y ALGUNAS DE SUS CONSECUENCIAS
 FUNCIONES HOLOMORFAS. LAS ECUACIONES DE CAUCHY-RIEMANN Y ALGUNAS DE SUS CONSECUENCIAS En este capítulo definiremos las funciones olomorfas como las funciones complejas que son diferenciables en sentido
FUNCIONES HOLOMORFAS. LAS ECUACIONES DE CAUCHY-RIEMANN Y ALGUNAS DE SUS CONSECUENCIAS En este capítulo definiremos las funciones olomorfas como las funciones complejas que son diferenciables en sentido
( + )= ( ) ( ) tiene periodo si es cualquier periodo de ( ). + =cos( +2 )=cos + = ( +2 )=. cosnt+ sinnt) ( )~ Métodos con series de Fourier
 Métodos con series de Fourier Definición: Función periódica La función (), definida para toda, es periódica si existe un número positivo tal que (+)=() para toda. El número en un periodo de la función.
Métodos con series de Fourier Definición: Función periódica La función (), definida para toda, es periódica si existe un número positivo tal que (+)=() para toda. El número en un periodo de la función.
V = v 1 +2v 2 +3v 3. v 2. v 1
 Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
LA CLASE VIRTUAL LOS NUMEROS COMPLEJOS
 LA CLASE VIRTUAL LOS NUMEROS COMPLEJOS La ecuación x 2 +1=0 carece de soluciones en el campo de los números reales. log e (-2) no es un número real. Tampoco es un número real (-2) π Un número complejo
LA CLASE VIRTUAL LOS NUMEROS COMPLEJOS La ecuación x 2 +1=0 carece de soluciones en el campo de los números reales. log e (-2) no es un número real. Tampoco es un número real (-2) π Un número complejo
MA3002. Matemáticas Avanzadas para Ingeniería: Números Complejos. Departamento de Matemáticas. Introducción. Igualdad. Suma y resta.
 MA300 Propiedas Propiedas Los números complejos simbolizados por C son una generalización los números reales. Una generalización algebraica muy interesante: Toda ecuación polinomial c n z n + c n 1 z n
MA300 Propiedas Propiedas Los números complejos simbolizados por C son una generalización los números reales. Una generalización algebraica muy interesante: Toda ecuación polinomial c n z n + c n 1 z n
CASOS DE LA FUNCIÓN AFÍN
 CASOS DE LA FUNCIÓN AFÍN Considera que el precio de un artículo es de Bs 80. Conocido el precio unitario (precio por unidad) es posible calcular fácilmente el precio de varios artículos con solo multiplicar
CASOS DE LA FUNCIÓN AFÍN Considera que el precio de un artículo es de Bs 80. Conocido el precio unitario (precio por unidad) es posible calcular fácilmente el precio de varios artículos con solo multiplicar
ÍNDICE Capítulo 2 La transformada de Laplace 1 Capítulo 2 Series de Fourier 49 Capítulo 3 La integral de Fourier y las transformadas de Fourier 103
 ÍNDICE Capítulo 2 La transformada de Laplace... 1 1.1 Definición y propiedades básicas... 1 1.2 Solución de problemas con valores iniciales usando la transformada de Laplace... 10 1.3 Teoremas de corrimiento
ÍNDICE Capítulo 2 La transformada de Laplace... 1 1.1 Definición y propiedades básicas... 1 1.2 Solución de problemas con valores iniciales usando la transformada de Laplace... 10 1.3 Teoremas de corrimiento
Apéndice A. Vectores: propiedades y operaciones básicas.
 Vectores 145 Apéndice A. Vectores: propiedades y operaciones básicas. Una clasificación básica de las distintas propiedades físicas medibles, establece que estas pueden dividirse en dos tipos: a) Aquellas
Vectores 145 Apéndice A. Vectores: propiedades y operaciones básicas. Una clasificación básica de las distintas propiedades físicas medibles, establece que estas pueden dividirse en dos tipos: a) Aquellas
Funciones reales de variable real.
 CONOCIMIENTOS PREVIOS. Funciones reales de variable real.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
CONOCIMIENTOS PREVIOS. Funciones reales de variable real.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
Números complejos. por. Ramón Espinosa Armenta
 Números complejos por Ramón Espinosa Armenta En el siglo XVI, el matemático italiano Gerolamo Cardano se preguntó si tenía sentido considerar raíces cuadradas de números negativos. Tal raíz cuadrada debería
Números complejos por Ramón Espinosa Armenta En el siglo XVI, el matemático italiano Gerolamo Cardano se preguntó si tenía sentido considerar raíces cuadradas de números negativos. Tal raíz cuadrada debería
VECTORES : Las Cantidades Vectoriales cantidades escalares
 VECTORES En física hay dos tipos de cantidades: Las Cantidades Vectoriales son aquellas que tiene tanto magnitud como dirección y sentido sobre la dirección), mientras que las cantidades escalares son
VECTORES En física hay dos tipos de cantidades: Las Cantidades Vectoriales son aquellas que tiene tanto magnitud como dirección y sentido sobre la dirección), mientras que las cantidades escalares son
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID. PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso )
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 00-003) MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES:
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 00-003) MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES:
INSTITUTO UNIVERSITARIO DE CALDAS GUÍA TALLER GEOMETRÍA ANALÍTICA. GRADO 11-4 DOCENTE: CRISTINA CANO.
 Distancia entre dos puntos del plano INSTITUTO UNIVERSITARIO DE CALDAS Dados dos puntos cualesquiera A(1,y1), B(,y), definimos la distancia entre ellos, d(a,b), como la longitud del segmento que los separa.
Distancia entre dos puntos del plano INSTITUTO UNIVERSITARIO DE CALDAS Dados dos puntos cualesquiera A(1,y1), B(,y), definimos la distancia entre ellos, d(a,b), como la longitud del segmento que los separa.
Laboratorio de Simulación. Trimestre 08P Grupo CC03A Pablo Lonngi. Lección 4
 Laboratorio de Simulación Trimestre 08P Grupo CC03A Pablo Lonngi Lección 4 Números Complejos. IIª parte. Representación polar de un complejo En la forma polar, llamada también forma trigonométrica, un
Laboratorio de Simulación Trimestre 08P Grupo CC03A Pablo Lonngi Lección 4 Números Complejos. IIª parte. Representación polar de un complejo En la forma polar, llamada también forma trigonométrica, un
PAIEP. Valores máximos y mínimos de una función
 Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP Universidad de Santiago de Chile Valores máximos y mínimos de una función Diremos que la función f : D R R, alcanza un máximo absoluto en el punto
Programa de Acceso Inclusivo, Equidad y Permanencia PAIEP Universidad de Santiago de Chile Valores máximos y mínimos de una función Diremos que la función f : D R R, alcanza un máximo absoluto en el punto
01. Dados varios números, los clasifica en los distintos campos numéricos. 02. Interpreta raíces y las relaciona con su notación exponencial.
 2.6 Criterios específicos de evaluación. 01. Dados varios números, los clasifica en los distintos campos numéricos. 02. Interpreta raíces y las relaciona con su notación exponencial. 03. Conoce la definición
2.6 Criterios específicos de evaluación. 01. Dados varios números, los clasifica en los distintos campos numéricos. 02. Interpreta raíces y las relaciona con su notación exponencial. 03. Conoce la definición
PROBLEMA 1 *( ) + SOLUCIÓN: Sea la superficie de la parte esférica superior, parametrizada con coordenadas cilíndricas de la siguiente manera:
 PROBLEMA 1 A una esfera maciza de radio unidad se le hace una perforación cilíndrica siguiendo un eje diametral de la esfera. Suponiendo que el cilindro es circular de radio, con y que el eje que se usa
PROBLEMA 1 A una esfera maciza de radio unidad se le hace una perforación cilíndrica siguiendo un eje diametral de la esfera. Suponiendo que el cilindro es circular de radio, con y que el eje que se usa
PROGRAMA : MATEMÁTICA (Ingeniero Zootecnista)
 PROGRAMA : MATEMÁTICA (Ingeniero Zootecnista) Programa Analítico 1. Nociones de lógica proposicional Oración abierta. Proposición. Variable. Constante. Forma proposicional. Valor de verdad. Negación. Enunciados
PROGRAMA : MATEMÁTICA (Ingeniero Zootecnista) Programa Analítico 1. Nociones de lógica proposicional Oración abierta. Proposición. Variable. Constante. Forma proposicional. Valor de verdad. Negación. Enunciados
6. Teoría de Cauchy local.
 Funciones de variable compleja. Eleonora Catsigeras. 24 Abril 2006. 59 6. Teoría de Cauchy local. Dado un abierto Ω C, se denota con R Ω a un rectángulo contenido en Ω. R indica el conjunto de puntos que
Funciones de variable compleja. Eleonora Catsigeras. 24 Abril 2006. 59 6. Teoría de Cauchy local. Dado un abierto Ω C, se denota con R Ω a un rectángulo contenido en Ω. R indica el conjunto de puntos que
Unidad 2. FUNCIONES Conceptos
 Unidad 2. FUNCIONES Competencia específica a desarrollar Comprender el concepto de función real y tipos de funciones, así como estudiar sus propiedades y operaciones. Función 2.1. Conceptos Se puede considerar
Unidad 2. FUNCIONES Competencia específica a desarrollar Comprender el concepto de función real y tipos de funciones, así como estudiar sus propiedades y operaciones. Función 2.1. Conceptos Se puede considerar
Estructuras Discretas. Conjuntos. Conjuntos & Funciones. Especificación de Conjuntos.
 Estructuras Discretas Conjuntos Conjuntos & Funciones Claudio Lobos [email protected] niversidad Técnica Federico Santa María Estructuras Discretas INF 152 Definición: conjunto n conjunto es una colección
Estructuras Discretas Conjuntos Conjuntos & Funciones Claudio Lobos [email protected] niversidad Técnica Federico Santa María Estructuras Discretas INF 152 Definición: conjunto n conjunto es una colección
