Tema 4 (Resultados).- Espacios vectoriales. Transformaciones lineales.
|
|
|
- Juana Cano Bustos
- hace 6 años
- Vistas:
Transcripción
1 Ingenierías: Aeroespacial, Civil y Química Matemáticas I - Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 4 (Resultados)- Espacios vectoriales Transformaciones lineales Ejercicio Determina cuáles de los siguientes conjuntos de vectores son subespacios vectoriales, cuáles son variadades y cuáles no son ni lo uno ni lo otro, del correspondiente espacio vectorial R n : (a) El conjunto de los vectores (x, x ) R cuyas coordenadas verifican, respectivamente, (a) cos (x ) + sen (x ) = Puesto que para cualquier x R se verifica que cos (x ) + sen (x ) =, el conjunto considerado es R y por tanto, se trata de un subespacio vectorial (a) x x = a (a R) Para a = el conjunto considerado está formado por los vectores (x, x ) que verifican que x = o que x = Es decir se trata de la recta x = y de la recta x = (los vectores determinados por puntos que están en una recta o en la otra) Al sumar un vector de una recta, por ejemplo (, ) con un vector de la otra, por ejemplo (, ) se obtiene el vector (, ) que no está en ninguna de las dos, no verifica la ecuación x x = Por tanto, el conjunto considerado no es subespacio vectorial y es inmediato comprobar que tampoco es una variedad Para a, los puntos (x, x ) R que verifican x x = a determinan una hiprbola equilátera con los ejes coordenados como asíntotas Obviamente un múltiplo de un vector que verifique x x = a no verifica dicha ecuación Por ejemplo (x = a, x = ) verifica dicha ecuación pero (x, x ) = (a, ) no la verifica Por tanto, no se trata de un subespacio vectorial y es fácil comprobar que tampoco se trata de una variedad (a3) x + x = ó x x = Se trata del conjunto de vectores que verifican una ecuación o la otra (o las dos simultáneamente) Cualquier múltiplo de cualesquiera de dichos vectores está en dicho conjunto y pertenece a la misma recta que el primero Sin embargo, al sumar un vector de una recta, por ejemplo (, ) con un vector de la otra, por ejemplo (, ) se obtiene un vector que no está en ninguna de las dos, con los vectores dados, (3, ) Por tanto, el conjunto considerado no es un subespacio 5
2 R-5 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) vectorial De forma análoga puede comprobarse que tampoco es una variedad (al desplazar dos rectas que pasan por el origen se obtienen otras dos rectas) (a4) x + x = a (a R), Para a = el único vector que verifica la ecuación es el vector nulo y por tanto, se trata de un subespacio vectorial Para a <, no hay ningún vector (x, x ) R que verifique la ecuación Por tanto, se trata del conjunto vacío que no es ni un subespacio vectorial ni una variedad Para a >, la ecuación dada determina una la circunferecia de centro el origen de coordenadas y radio a Por tanto, no es ni un subespacio vectorial ni una variedad (a5) x x = a (a R), Si a = se trata de un subespacio vectorial, la recta de ecuación x x = Si a se trata de una variedad, la variedad que pasa por el punto (a, ) y tiene como subespacio director al subespacio vectorial S de ecuación implícita x x = (a6) x + x = a y x x = b, (a, b R) Si a = b =, se trata de un subespacio vectorial puesto que el conjunto considerado está definido como el espacio nulo de una matriz, en concreto se trata de æ Nul Resolviendo el sistema que caracteriza al conjunto tenemos que el único vector que verifica las dos ecuaciones es el vector nulo (el punto de corte de las dos rectas) Si a o b, el conjunto de vectores considerado es una variedad (es un único punto) cuyo subespacio director viene dado por las ecuaciones implícitas x + x = y x x =, es decir el subespacio director es el subespacio nulo (b) El conjunto de los vectores (x, x, x 3 ) R 3 cuyas coordenadas verifican, respectivamente, (b) x + x + x 3 = y x x 3 = a (a R), Si a = es un subespacio vectorial (es una recta que pasa por origen) Matemáticas I Ingenierías: Aeroespacial, Civil y Química
3 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-53 Si a es una variedad (es una recta que no pasa por el origen) (b) x + x = a (a R), Si a =, los vectores que verifican la ecuación dada son los vectores de la forma (x, x, x 3 ) = (,, x 3 ), x 3 R Obviamente dicho conjunto de vectores es un subespacio vectorial de R 3 De hecho, dicho conjunto puede caracterizarse mediante el sistema de ecuaciones lineales homogneas, x =, x = Si a dicha ecuación determina un cilindro (a > ) o el conjunto vacio (a < ) y por tanto no es ni un subespacio ni una variedad (b3) (x + x )(x + x 3 ) =, Es el conjunto formado por dos planos (que no es lo mismo que la recta intersección) Obviamente dicho conjunto no es ni un subespacio ni una variedad, al igual que sucedía con el conjunto de vectores determinados por los puntos de dos rectas) (b4) x = y (x = ó x 3 = ), Se trata de las rectas r x =, x = y s x =, x 3 = Dicho conjunto no es ni un subespacio ni una variedad (b5) Se pueden expresar de la forma x = α, x = α + α, x 3 =, para algún α R Eliminando el parámetro α, el conjunto citado es el de los vectores cuyas coordenadas verifican x = x + x, x 3 = Es decir, se trata de una parábola (en R 3 ) que está contenida en uno de los planos coordenados Obviamente dicho conjunto no es ni un subespacio ni una variedad Matemáticas I -
4 R-54 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) (b6) x + x + x 3 El vector (,, ) verifica la inecuación dada, sin embargo, (,, ) = (,, ) no la verifica Por tanto, no es un subespacio vectorial De la misma forma, tampoco se trata de una variedad (c) El conjunto de los vectores (a, a,,a n ) R n cuyas coordenadas verifican, respectivamente, (c) Cada una de las coordenadas a 3,,a n es la media (aritmtica) de las coordenadas anteriores Las condiciones que caracterizan a los vectores del conjunto considerado vienen dadas por las siguientes ecuaciones, a 3 = (a + a ), a + a a 3 =, a 4 = (a 3 + a + a 3 ), a + a + a 3 4a 4 =, a n = (a n + + a n ), a + + a n (n )a n = Es decir, el conjunto considerado puede caracterizarse como el espacio nulo de una matriz por tanto, es un subespacio vectorial (c) Cada una de las coordenadas a 3,,a n es la media geomtrica de las dos coordenadas anteriores, La media geomtrica de dos números (reales positivos) α y β es γ = αβ Obviamente el conjunto considerado no es un subespacio vectorial puesto que un múltiplo con coeficiente negativo de un elemento del conjunto no está en el conjunto Tampoco es una variedad (c3) La derivada segunda del polinomio se anula para t = a + a t + a 3 t + + a n t n La derivada segunda del polinomio dado es a a 4 t + 4 3a 5 t + + (n )(n )a n t n 3 Matemáticas I Ingenierías: Aeroespacial, Civil y Química
5 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-55 Por tanto, el conjunto de vectores considerado está caracterizado por la ecuación a a a (n )(n )a n = Por tratarse de una ecuación lineal homognea, el conjunto considerado es un subespacio vectorial (c4) La derivada segunda del polinomio vale 3 para t = a + a t + a 3 t + + a n t n Se trata del conjunto de vectores caracterizados por la ecuación implícita no-homognea a a a (n )(n )a n = 3 Por tanto, es una variedad cuyo subespacio dirección es el subespacio dado por la ecuación homognea asociada, a a a (n )(n )a n = Ejercicio Siendo v, v,,v k vectores de R n, demuestra o da un contraejemplo de (cada una) de las siguientes afirmaciones: a) Si v, v,,v k son linealmente independientes, entonces al menos uno de ellos es combinación lineal de los restantes b) Si v, v,,v k son linealmente independientes, entonces cualquiera de ellos es combinación lineal de los restantes Las dos afirmaciones son falsas Ejercicio 3 Determina dos bases distintas de cada uno de los subespacios siguientes así como ecuaciones implícitas independientes para cada uno de ellos: (a) Vectores de R 3 que pueden expresarse como combinación lineal de v = y v = y cuyas coordenadas verifican la ecuación x x + x 3 = Matemáticas I -
6 R-56 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) (b) Subespacio de R 4 generado por los vectores v =, v = 4 v 3 = (c) Subespacio de R 4 definido por las ecuaciones implícitas x x + x 3 x 4 =, x + x + x 3 =, 3x x x 4 = (d) Subespacio de R n definido por las ecuaciones implícitas x + x + + x n =, x + x + + x n =, x + 5x + + 5x n = y v 4 = 3 (a) Vectores de R 3 que pueden expresarse como combinación lineal de v = y v = y cuyas coordenadas verifican, además, la ecuación x x + x 3 = Los vectores x R 3 que se pueden expresar como combinación lineal de los vectores dados son los vectores de la forma x α + β x = α + β = β x 3 α + β Si además sus coordenadas tienen que verificar la ecuación dada tenemos x x + x 3 = α + β β + α + β = β = α Por tanto el subespacio considerado es el formado por los vectores x α x = α α = α = α x 3 α es decir, se trata del subespacio generado por el vector v = [,, ] T (la recta que pasa por el origen de coordenadas y tiene a dicho vector como vector dirección) Matemáticas I Ingenierías: Aeroespacial, Civil y Química
7 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-57 Una base, {v } Otra base, { 3v } Ecuaciones impícitas El sistema x F + F 3 x + x 3 x x + x 3 x 3 F + F 3 x 3 es compatible x + x 3 =, x + x 3 = Observación- El subespacio estaba originalmente definido como la intersección de un plano que venía dado en forma paramtrica con un plano que venía dado en forma implícita Lo único que hemos hecho ha sido expresar la recta intersección en forma paramtrica y en forma implícita (b) Subespacio de R 4 generado por los vectores v =, v = 4, v 3 = y v 4 = 3 x x 4 x 3 x 4 F 3 + F F 3 3F F 4 F 3 3 x x 3 6 x 3 + x x 4-3 x x x 3 + x 3x x 4 x x + x 4 = x 3x Ecuaciones implícitas no redundantes + x 3 = Una base v = Otra base {v, v 3 + v }, v 3 = (c) Subespacio de R 4 definido por las ecuaciones implícitas x x + x 3 x 4 =, x + x + x 3 =, 3x x x 4 = Matemáticas I -
8 R-58 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) 3 F 3 + F = F + F F 3 3F - 3 x = x 3 x 4 x = 3x 3 x F F x x x 3 x 4 = x x 4 Por tanto: El subespacio considerado puede caracterizarse mediante cualesquiera de las siguientes parejas de ecuaciones implícitas no redundantes (y otras muchas), x x + x 3 x 4 = x + 3x 3 x 4 =, y x x 3 + x 4 =, x + 3x 3 x 4 = Una base es v = 3, v = Otra base es {v, v 3v } (d) Subespacio de R n definido por las ecuaciones implícitas x + x + + x n =, x + x + + x n =, x + 5x + + 5x n = Matemáticas I Ingenierías: Aeroespacial, Civil y Química
9 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R F 3 /3 F F = F + F F 3 F x x x n = x 3 x n x 3 x n F 3 F x = x + + x n = = x x n Por tanto, Unas ecuaciones implícitas no redundantes del subespacio dado son x =, x = x 3 x n Una base es v =, v =,,v n = Y otra base es, por ejemplo, {v, v v, v 3 v,, v n v n } Ejercicio 4 Sea V la variedad de R 4 dada por las ecuaciones paramtricas x = + α β + γ, x = + α + β, x 3 = + α 7γ, x 4 = β + γ Determina una base (del subespacio director) y la dimensión de V y halla unas ecuaciones implícitas Matemáticas I -
10 R-6 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) Obtengamos las condiciones para que un vector x R 4 est en V Para que un vector x est en V el sistema anterior, con incóngitas α, β, γ y trmino independiente x, tiene que ser compatible Obtengamos dichas condiciones de compatibilidad x x + 7 x 3 x 4 Por tanto: operaciones fila = x x 4-3 x 3 x x 4 x + 3x 7x 3 5x æ el sistema es compatible x + 3x 7x 3 5x = El subespacio director de V es el subespacio S generado por los tres primeros vectores columna de la matriz ampliada anterior y dicho subespacio está caracterizado por la ecuación implícita (homognea) x + 3x 7x 3 5x 4 = Una base de S viene dada por los tres vectores columna que generan S (que son Linealmente Independientes), v =, v =, v 3 = 7 Ecuación implícita de V : x + 3x 7x 3 5x 4 = 39 dim (V ) = dim (S) = 3 Ejercicio 5 () Determina el rango de las siguientes matrices: A =, B = () Sabiendo que el rango de una matriz A, 3 3, es 3, determina el rango de la matriz æ A A I A (3) Sea A una matriz 5 cuyo rango es rango(a) = Determina la dimensión de los siguientes subespacios vectoriales, Col (A), Nul (A), Col(A T ) y Nul (A T ) Matemáticas I Ingenierías: Aeroespacial, Civil y Química
11 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-6 (4) Sabiendo que una matriz A de orden 4 verifica que A =, (4a) demuestra que Col (A) Nul (A), (4b) demuestra que el rango de A tiene que ser menor o igual y (4c) da ejemplos de matrices A que verifiquen que A = y cuyos rangos respectivos sean, y (a) Determina el rango de las siguientes matrices: A = 3, B = 3 3 Reduciendo a forma escalonada se obtiene rango(a) = rango(b) = 3 (b) Sabiendo que el rango de una matriz A, 3 3, es 3, determina el rango de la matriz æ A A I A Puesto que A es una matriz cuadrada que tiene rango máximo, A tiene inversa y, por tanto, mediante ciertas operaciones elementales (por filas) sobre la matriz A podemos obtener la matriz identidad Al hacer dichas operaciones elementales sobre la matriz [A A ] obtendremos la matriz [I A] puesto que hacer dichas operaciones fila sobre una matriz M es lo mismo que multiplicar dicha matriz, por la izquierda, por la inversa de A dando como resultado A M Por tanto, al hacer las operaciones fila citadas sobre nuestra matriz obtnemos æ A A I A æ A I æ I I I æ æ æ A A I A = A I A = I A I A I A æ I A = I A Por tanto el rango de la matriz dada es 6 æ I A A Trabajando con matrices por bloques es fácil comprobar que la inversa de la matriz de orden 6 dada es æ æ X Y A = I Z T (A ) A Matemáticas I -
12 R-6 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) (c) Sea A una matriz 5 cuyo rango es rango(a) = Determina la dimensión de los siguientes subespacios vectoriales, Col (A), Nul (A), Col (A T ) y Nul (A T ) dim (Col (A)) = dim (Nul (A)) = 5 = 3 dim Col (A T ) = rango(a T ) = rango(a) = dim Nul (A T ) = = 8 (d) Sabiendo que una matriz A de orden 4 verifica que A =, (d) demuestra que Col (A) Nul (A), (d) demuestra que el rango de A tiene que ser menor o igual y (d3) da ejemplos de matrices A que verifiquen que A = y cuyos rangos respectivos sean, y (d) Si un vector y R 4 está en Col(A), se puede expresar como combinación lineal de las columnas de A o lo que es equivalente, existe algún vector x R 4 de forma que Ax = y Por tanto, Es decir, Col (A) Nul (A) Ay = A (Ax) = A x = = y Nul (A) (d) Si llamamos r al rango de A, por el teorema del rango se verifica que dim (Nul (A)) = n r = 4 r Puesto que Col(A) Nul (A), se verifica que dim (Col (A)) = rango(a) = r dim (Nul (A)) = 4 r = r 4 = r (d3) la matriz nula A = (cuadrada de orden 4) tiene rango cero y A =, la matriz A = tiene rango y su cuadrado es la matriz nula la matriz A = tiene rango y su cuadrado es la matriz nula Matemáticas I Ingenierías: Aeroespacial, Civil y Química
13 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-63 Ejercicio 6 Consideremos una transformación lineal T : K n K m y su matriz asociada A, T(x) = Ax, x K n Demuestra que (a) T transforma subespacios vectoriales (de K n ) en subespacios vectoriales (de K m ) Es decir, si S K n es un subespacio vectorial, T(S) = {T(x) : x S} {Ax : x S} es un subespacio vectorial Qu puede afirmarse sobre las dimensiones de S y de T(S)? (b) T transforma variedades de K n en variedades, es decir, si V K n es una variedad, es una variedad T(V ) = {T(x) : x V } {Ax : x V } En qu se puede transformar un plano mediante una transformación lineal? (a) Para comprobar que T(S) = {T(x) : x S} {Ax : x S} es un subespacio vectorial (de K m ) basta con verificar que una combinación lineal arbitraria αy + βy, α, β R de dos vectores y, y de T(S) pertenece a T(S) Puesto que y e y están en T(S), existen x y x en S de forma que y = T(x ), y = T(x ) y, por tanto, αy + βy = αt(x ) + βt(x ) = æ Puesto que Tes lineal = T(αx + βx ) es un vector de T(S) puesto que αx + βx pertenece a S por ser S un subespacio vectorial Qu puede afirmarse sobre las dimensiones de S y de T(S)? Notemos que si tenemos una base {v,,v r } de S, los vectores {T(v ),,T(v r )} = {Av,,Av r } generan el subespacio T(S) puesto que todo vector de T(S) es de la forma T(α v + + α r v r ) = α T(v ) + + α r T(v r ) Suprimiendo vectores que sean combinación lineal de los restantes, del conjunto de vectores {T(v ),, T(v r )} podremos extraer una base que estará formada por a lo sumo r vectores (en caso de que todos los vectores anteriores sean linealmente independientes) Por tanto, se verifica que dim (T(S)) dim (S) Matemáticas I -
14 R-64 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) (b) De forma análoga a lo hecho en el apartado anterior, puede probarse que una transformación lineal transforma una variedad en una variedad Es decir, si V K n es una variedad con subespacio director S y p V, entonces V = p + S y T(V ) = {T(x) : x V } {Ax : x V } = T(p) + T(S) K m es una variedad que pasa por q = T(p) y tiene subespacio director T(S) En este caso hay la posibilidad de que esta última variedad sea de hecho un subespacio vectorial Un ejemplo de sto último viene dado al considerar la proyección ortogonal sobre un plano (que pase por el origen de coordenadas) Por ejemplo, la proyección ortogonal sobre el plano π x 3 = proyecta la recta r x = x + x 3 = sobre el eje OX En qu se puede transformar un plano mediante una transformación lineal? Tanto si se trata de un plano que pasa por el origen de coordenadas (subespacio vectorial de dimensión dos) como si no pasa por el origen de coordenadas (variedad lineal de dimensión dos), mediante una transformación lineal, su transformado será un subespacio o una variedad de dimensión dos (plano) o de dimensión uno (recta) o de dimensión cero (punto) Ejercicio 7 Determina la matriz de una aplicación lineal T : R 4 R 4 sabiendo que T =, T =, T =, T = Sea A la matriz asociada a la transformación lineal T dada Es decir, A es la (única) matriz que verifica que Ax = T(x), x R 4 Siendo A = a a a 3 a 4 sus vectores columna a, a, a 3 y a 4 vienen dados por a = Ae, a = Ae, a 3 = Ae 3, a 4 = Ae 4 donde los vectores e, e, e 3 y e 4 son los vectores canónicos de R 4 Una forma directa de determinar A consiste en expresar las condiciones dadas, A =, A =, A =, A = en forma matricial, A = = A = Matemáticas I Ingenierías: Aeroespacial, Civil y Química
15 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-65 Calculemos la matriz inversa involucrada F 4 F 3 F F 4 F 4 F F 3 F F 3 + F 4 F F 4 F F Por tanto la matriz A es A = = 3 La determinación de la matriz A puede plantearse, a partir de las condiciones dadas, como la resolución de un sistema de ecuaciones en el que las incógnitas son los vectores Matemáticas I -
16 R-66 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) columna de A Tenemos las siguientes igualdades: T = T(e ) + T(e 4 ) = v = a + a 4 = v, T = T(e ) + T(e 3 ) + T(e 4 ) = v = a + a 3 + a 4 = v, T = T(e ) + T(e 3 ) = v 3 = a + a 3 = v 3, T = T(e 4) = v 4 = a 4 = v 4 = e 4 Es decir, tenemos que resolver el sistema a + a 4 = v a + a 3 + a 4 = v a + a 3 = v 3 a 4 = e 4 donde las incógnitas a, a, a 3 y a 4 y los trminos independientes v, v, v 3 y v 4 = e 4 son vectores Resolviendo, directamente, el sistema anterior, tenemos a 4 = e 4 =, a = v a 4 = v e 4 =, a 3 = v a a 4 = v (v e 4 ) e 4 = v v e 4 =, a = v 3 a 3 = v 3 v + v + e 4 = 3 Por tanto, ya tenemos las cuatro columnas de la matriz A pedida Matemáticas I Ingenierías: Aeroespacial, Civil y Química
17 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-67 Ejercicio 8 Determina la matriz A de una transformación lineal T : R 3 R sabiendo que el espacio nulo de A viene dado por la ecuación implícita x x x 3 = y que Ǒ æ T = Teniendo en cuenta las condiciones dadas, tenemos que determinar la única matriz A, 3, que verifica que Av = para cualquier vector v Nul (A) y que A = æ Tomamos vectores linealmente independientes que generen Nul (A), por ejemplo v = y v = Por tanto, A debe verificar A = æ, A = Expresando estas igualdades en forma matricial tenemos A Despejando A, A = æ F + F + F 3 = æ æ y A = = = æ æ æ F F F 3 F Ejercicio 9 Se considera la transformación lineal T cuya matriz asociada es æ A = 4 3 Matemáticas I -
18 R-68 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) (a) Determina el espacio columna de A, Col (A) (b) Calcular los vectores del núcleo de T que, a su vez, verifican el sistema de ecuaciones x + 4x x 3 + x 4 =, x + 6x 4x 3 + x 4 = 4 (c) Sea V el conjunto de los vectores encontrados en el apartado anterior Es V un subespacio vectorial de R 4? Justifica la respuesta (a) Vamos a obtener vectores linealmente independientes que generen Col (A) Si reducimos A a forma escalonada y seleccionamos todas las columnas pivote, de A, tendremos un conjunto de vectores que verifica las dos condiciones anteriores Al reducir A a forma escalonada obtenemos, A = De esto se deduce que: æ el segundo vector-columna de A es un múltiplo del primero, el primer y el tercer vector-columna de A son linealmente independientes, el cuarto vector-columna de A se puede expresar como combinación lineal de la primera y la tercera columnas, cualquier vector y R puede expresarse como combinación lineal de las columnas de A Además, se podrá expresar de infinitas formas distintas puesto que el sistema Ax = y es compatible indeterminado Puesto que las columnas a (primera) y a 3 (tercera) de A son linealmente independientes, el sistema a a 3 æ α β = y es compatible determinado Por tanto cada vector y se podrá expresar de forma única como combinación lineal de a y a 3 Por tanto, el espacio columna de A es Col (A) = R y æ a = æ, a 3 = æ, e = æ, e = son conjuntos de vectores linealmente independientes que generan Col (A) Matemáticas I Ingenierías: Aeroespacial, Civil y Química
19 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-69 (b) Se trata de obtener las soluciones del sistema, no-homogneo, cuya matriz ampliada es Resolvamos el sistema, F 3 F F 4 + F 3 = x x x 3 x 4 F F F 3 F F 4 F = + x 4 x 4 x 4 x = F 4 F 3 x 3 = x 4 x = + 3x 3 + x 4 = x 4 x = x x 3 x 4 = + x 4 + x 4 x 4 = + x 4 + λ, λ R = (c) Obviamente V no es un subespacio vectorial, el vector nulo no está en V Ejercicio Siendo e, e, e 3 los vectores de la base canónica de R 3 y sabiendo que los vectores {u, u, u 3 } verifican e = u +u +u 3, e = u u +u 3, e 3 = u +u +u 3, señala la relación correcta: (a) [e e e 3 ] = (b) [u u u 3 ] = (c) [u u u 3 ] = [u u u 3 ] Ǒ = 9 Ǒ = 9 Matemáticas I -
20 R-7 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) Las relaciones dadas entre los vectores de la base canónica {e, e, e 3 } y los vectores de la base B = {u, u, u 3 } pueden expresarse en forma matricial e e e 3 = u u u 3 = (c) Ejercicio Consideremos los siguientes vectores de R 5, 5 v =, v =, v 3 = 4 3 y v 4 = (a) Son v, v, v 3 y v 4 linealmente independientes? (b) Es v 4 combinación lineal de v, v y v 3? (c) Es v combinación lineal de v, v 3 y v 4? (d) Es v 4 combinación lineal de v y v? (e) Es v 4 combinación lineal de v y v 3? (f) Son v, v y v 3 linealmente independientes? Estudiar si un conjunto de vectores {u,,u p } es linealmente dependiente o independiente es equivalente a estudiar si el sistema homogneo Ax = (siendo A la matriz cuyas columnas son las coordenadas de los vectores dados) es (compatible) indeterminado o determinado En el caso de que el sistema tenga infinitas soluciones, cada una de las soluciones no nulas nos dará una relación de dependencia lineal entre los vectores considerados y podremos determinar qu vectores pueden expresarse como combinación lineal de los demás Todas las preguntas planteadas en el ejercicio pueden responderse reduciendo a forma escalonada la matriz cuyas columnas son los vectores dados, con lo cual podremos discutir el sistema homogneo Ax = operaciones fila Puesto que este sistema homogneo tiene infinitas soluciones (hay una variable libre), los cuatro vectores dados (los cuatro vectores columna de la matriz de los coeficientes de las incógnitas) son Linealmente Dependientes Es decir, Matemáticas I Ingenierías: Aeroespacial, Civil y Química
21 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-7 (a) v, v, v 3 y v 4 no son linealmente independientes Además, todas las posibles relaciones de dependencia lineal de estos vectores vienen dadas por x v + x v + x 3 v 3 + x 4 v 4 = siendo (x, x, x 3, x 4 ) T cualquier solución del sistema homogneo considerado Resolviendo el sistema tenemos operaciones fila x x x 3 x 4 = λ λ λ = λ, λ R Puesto que de las igualdades v + ( λ)v + ( λ)v 3 + λv 4 = (λ R) podemos despejar v 4 para λ, v 4 = v + v 3 = v + v + v 3 tenemos que (b) v 4 es combinación lineal de v y v 3, (e) y de v, v y v 3 Puesto que en todas las relaciones de dependencia lineal obtenidas el coeficiente de v es cero, no podemos despejar v y por tanto (c) v no es combinación lineal de v, v 3 y v 4 Si pudiramos expresar v 4 como combinación lineal de v y v tendríamos v 4 = αv +βv para ciertos valores α, β R y, por tanto, tendríamos αv + βv + v 3 v 4 = Puesto que el sistema homogneo no tiene ningna solución del tipo (x = α, x = β, x 3 =, x 4 =, tenemos que (d) v 4 no es combinación lineal de v y v Si en la matriz ampliada del sistema homogneo suprimimos (antes o despus de hacer las operaciones fila) la columna correspondiente al vector v 4, el sistema correspondiente (equivalente a la ecuación vectorial x v +x v +x 3 v 3 = ) tiene únicamente la solución nula y, por tanto, (f) los vectores {v, v, v 3 } son Linealmente Independientes Ejercicio (Comparar con los resultados obtenidos en el Ejercicio 9 del Tema 3) Sea f : R 3 R 4 la aplicación lineal dada por 3 4 x f(x) = x 3 a x b 4 b 3 Matemáticas I -
22 R-7 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) Determinar las condiciones a satisfacer por a y b para que el vector v = (, 3,, b 4) verifique respectivamente: (a) No pertenezca a la imagen de f (b) Sea la imagen de un único vector de R 3 (c) Sea la imagen de infinitos vectores de R 3 (a) Para un vector v R 3, v / Im (f) f(r 3 ) Ax = v es un sistema incompatible (ver Ejercicio??) (b) Un vector v R 3 es imagen de un único vector de R 3 Ax = v es un sistema compatible determinado (ver Ejercicio??) (c) Un vector v R 3 es imagen de infinitos vectores de R 3 Ax = v es un sistema compatible indeterminado (ver Ejercicio??) Ejercicio 3 Sea T : R R la transformación que hace corresponder al punto P = (x, x ) el punto Q = ( x, x ) Señala la única opción que es correcta es una transformación que no está bien definida X es una aplicación lineal que se representa, respecto de las bases canónicas, por la matriz A = æ es una transformación, pero no es lineal porque tiene por ecuaciones y = x cos π + x sen π, y = x sen π + x cos π Ejercicio 4 (a) Demuestra que para una matriz cuadrada A se verifica que Nul (A) Nul (A ) y Col (A) Col (A ) Matemáticas I Ingenierías: Aeroespacial, Civil y Química
23 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-73 (b) Demuestra que para dos matrices A y B con las dimensiones adecuadas se verifica que Nul (B) Nul (AB) y Col (A) Col (AB) (a) Comprobemos que Nul (A) Nul (A ), las otras inclusiones se pueden obtener de forma análoga, Si x Nul (A) = Ax = = AAx = = x Nul (A ) Comprobemos que Col (A ) Col (A), las otras inclusiones se pueden obtener de forma análoga Puesto que cada columna de A es una combinación lineal de las columnas de A, cualquier cobinación lineal de las columnas de A es combinación lineal de las columnas de A Dicho de otra forma, y Col (A ) = x tal que A x = y = A(Ax) = y = y Col (A) (b) Comprobemos, Si x Nul (B) = Bx = = ABx = = x Nul (AB) Puesto que cada columna de AB es una combinación lineal de las columnas de A, cualquier combinación lineal de las columnas de AB es combinación lineal de las columnas de A Dicho de otra forma, y Col (AB) = x tal que ABx = y = A(Bx) = y = y Col (A)puesto que z = Bx tal que Az = y Ejercicio 5 Dados dos subespacios E y F de R n, hallar las ecuaciones implícitas, las paramtricas y una base del subespacio intersección, E F: (a) E x + x =, F x + x =, en R (b) E x + x =, F x + x =, en R (c) E x + x =, F x + x =, en R 3 (d) E x + x + x 3 =, F x x + x 3 =, en R 3 (e) E = Gen {(,, ), (,, )}, F = Gen {(,, )}, en R 3 (f) E = Gen {(,, ), (,, )}, F = Gen {(,, ), (,, )}, en R 3 Matemáticas I -
24 R-74 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) (g) E = Gen {(,, ), (,, )}, F = Gen {(,, 3), (,, )}, en R 3 (h) E = Gen {(,,, ), (,,, 3)}, F = Gen {(,,, ), (,,, )}, en R 4 (a) E x + x =, F x + x =, en R Intersección de dos rectas distintas que pasan por el origen de coordenadas æ x + x E F = x = = E F = x + x = x = (b) E x + x =, F x + x =, en R Intersección de dos rectas coincidentes que pasan por el origen de coordenadas æ x + x E F = α x x + x = + x = = E F = E = F =, α R α (c) E x + x =, F x + x =, en R 3 E F es la recta intersección de dos planos que pasan por el origen de coordenadas, x + x E F = x = = E F = x + x = x = : α R = Gen α (d) E x + x + x 3 =, F x x + x 3 =, en R 3 E F es la recta intersección de dos planos que pasan por el origen de coordenadas (e) E = Gen {(,, ), (,, )}, F = Gen {(,, )}, en R 3 E F es la intersección de un plano, E, y una recta, F que pasan por el origen de coordenadas Puesto que la recta F está contenida en el plano E, E F = F Matemáticas I Ingenierías: Aeroespacial, Civil y Química
25 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-75 (f) E = Gen {(,, ), (,, )}, F = Gen {(,, ), (,, )}, en R 3 E F es la intersección de dos planos que pasan por el origen de coordenadas (g) E = Gen {(,, ), (,, )}, F = Gen {(,, 3), (,, )}, en R 3 E F es la intersección de dos planos que pasan por el origen de coordenadas E x 3 x = F 3x x 3 = = E F x = x 3 = Es decir, E F es la recta de R 3 dada por E F = Gen x x x 3 = α, α R (h) E = Gen {(,,, ), (,,, 3)}, F = Gen {(,,, ), (,,, )}, en R 4 Pasamos E a forma implícita, E : x x x 3 3 x 4 operaciones fila E x x x x 3 x + x + x 4 x 3 = x + x + x 4 = Pasamos F a forma implícita, F : x x x 3 x 4 operaciones fila F x x x 3 x x x 4 x x x + x x 3 = x + x x 4 = Matemáticas I -
26 R-76 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) Ya tenemos una expresión implíta de E F, x 3 = x E F + x + x 4 = x + x x 3 = x + x x 4 = operaciones fila E F = {} x x x 3 x 4 = Ejercicio 6 Hallar las ecuaciones implícitas, las paramtricas y una base del subespacio suma, E + F, para los siguientes subespacios: (a) E x + x =, F x + x =, en R (b) E x + x =, F x + x =, en R (c) E x + x =, F x + x =, en R 3 (d) E x + x + x 3 =, F x x + x 3 =, en R 3 (e) E = Gen {(,, ), (,, )}, F = Gen {(,, )}, en R 3 (f) E = Gen {(,, ), (,, )}, F = Gen {(,, ), (,, )}, en R 3 (g) E = Gen {(,, ), (,, )}, F = Gen {(,, 3), (,, )}, en R 3 (h) E = Gen {(,,, ), (,,, 3)}, F = Gen {(,,, ), (,,, )}, en R 4 (i) E = Gen {(,, ), (,, )}, F = Gen {(,, )}, en R 3 La relación entre las dimensiones de los subespacios E, F, E F y E + F, dim (E + F) + dim (E F) = dim (E) + dim (F), permite en algunos casos obtener, sin realizar el cálculo directo, el subespacio suma si conocemos el subespacio intersección o viceversa (h) Tenemos dos subespacios E y F de R 4 y según hemos obtenido en el ejercicio anterior Por tanto, E + F R 4, y dim (E) =, dim (F) = y E F = {} dim (E + F) = dim (E) + dim (F) dim (E F) = 4 = E + F = R 4 Matemáticas I Ingenierías: Aeroespacial, Civil y Química
27 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-77 Ejercicio 7 Extender a una base de R n el conjunto linealmente independiente que se da: (a) {v = (,, )} en R 3 (b) {v = (, 3, 4), v = (,, )} en R 3 (c) {v = (,, ), v = (, 3, )} en R 3 (d) {v = (,,, ), v = (,,, 3)} en R 4 (a) Bastará obtener dos vectores lineamente independientes de forma que junto con v formen un conjunto linelamente independiente Esto se puede hacer paso a paso Primero tomamos un vector que no est en la recta generada por v, por ejemplo v = e A continuación tomamos un vector que no est en el plano generado por v y v, por ejemplo v 3 = (,, ) Y ya está x = α + β x = α x 3 = α, α, β R, (b) Basta tomar un vector que no est en el plano determinado por v y v Puesto que la ecuación del plano es 6x + x 3x 3 =, podemos tomar v 3 = e, por ejemplo (c) Basta tomar v 3 = e 3 (d) Para obtener una base de R 4 hacen falta dos vectores linealmente independientes que sean linealmente independientes con v y v Si obtenemos unas ecuaciones implítas del subespacio que generan v y v tendremos dos ecuaciones implítas Si tomamos un vector v 3 que verifique una de dichas ecuaciones y no la otra y un vector v 4 que verifique la otra pero no la primera, ya estará Ejercicio 8 Consideremos la base B = {(, ), ( 3, )} de R (a) Obtener, en dicha base, las ecuaciones implícitas y las paramtricas de los subespacios que en la base canónica vienen definidos mediante: E x + x =, F x x =, G = Gen {(, )}, H = Gen {(3, )} (b) Obtener, en la base canónica, las ecuaciones implícitas y las paramtricas de los subespacios que en la base B vienen definidos mediante: E y + 5y =, F y =, G = Gen {(, ) B }, H = Gen {(, 4) B } Matemáticas I -
28 R-78 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) Denotamos por C la base canónica de R Dado un vector v R consideremos æ x x = [v] C, Tenemos, por tanto, la siguiente relación æ y y = [v] B v = x e + x e = y u + y u que en forma matricial queda æ x x = æ 3 æ y y æ x = y 3y y x = y y y = æ 3 æ x x æ y y = æ 3 æ x x y = x + 3x, y = x + x (a) Expresando, en cada caso, x y x en función de y e y tenemos E x + x =, æ x [ ] x æ 3 = [ ] æ y y = 3y 4y = y = 4 3 α y = α α R F x x =, æ x [ ] x æ 3 = [ ] æ y y = y = H : æ x x æ 3 = æ y y = æ H y = y = α α R (b) Expresando, en cada caso, y e y en función de x y x tenemos æ y E [ 5 ] y æ 3 = [ 5 ] æ x x = 6x + 3x =, æ y F [ ] y æ 3 = [ ] æ x x = x + x = Matemáticas I Ingenierías: Aeroespacial, Civil y Química
29 Tema 4- Espacios vectoriales Transformaciones lineales (Resultados) R-79 G = Gen {u}, u = u + u = u æ x = α G = Gen G x = α α R G x x = Ejercicio 9 Halla las ecuaciones paramtricas de un subespacio F (de R 4 ) complementario de Nul (A), siendo A la matriz 3 3 A = 4 3 Obtengamos una base de Nul (A) :] 3 3 operaciones x fila 3 x 4 x 3 = x 3 4 x 4 = Nul (A) = Gen {e 4 } Tenemos que obtener un subespacio vectorial F que verifique que Nul (A) + F = R 4 y Nul (A) F = {} Obviamente, F = Gen {e, e, e 3 } es un subespacio complementario de Nul (A), F x = α, x = β, x 3 = γ, x 4 = x 4 = Matemáticas I -
Tema 4.- Espacios vectoriales. Transformaciones lineales.
 Ingenierías: Aeroespacial, Civil y Química Matemáticas I - Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 4- Espacios vectoriales Transformaciones lineales
Ingenierías: Aeroespacial, Civil y Química Matemáticas I - Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 4- Espacios vectoriales Transformaciones lineales
Espacios Vectoriales. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21
 Espacios Vectoriales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21 Objetivos Al finalizar este tema tendrás que: Saber si unos vectores son independientes.
Espacios Vectoriales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Espacios Vectoriales 1 / 21 Objetivos Al finalizar este tema tendrás que: Saber si unos vectores son independientes.
2 Espacios vectoriales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
Problemas de Espacios Vectoriales
 Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
SISTEMAS DE ECUACIONES. Un sistema de m ecuaciones lineales con n incógnitas, x 1, x 2,, x n es un conjunto de m igualdades de la forma:
 TEMA Sistemas de ecuaciones SISTEMAS DE ECUACIONES. DEFINICIÓN SISTEMAS DE ECUACIONES Un sistema de m ecuaciones lineales con n incógnitas,,,, n es un conjunto de m igualdades de la forma: a a an n b a
TEMA Sistemas de ecuaciones SISTEMAS DE ECUACIONES. DEFINICIÓN SISTEMAS DE ECUACIONES Un sistema de m ecuaciones lineales con n incógnitas,,,, n es un conjunto de m igualdades de la forma: a a an n b a
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales 1. Estudiar el sistema de ecuaciones según los valores del parámetro a. ax + y + z = a x y + z = a 1 x + (a 1)y + az = a + 3 Resolverlo (si es posible) para a = 1. (Junio
Sistemas de ecuaciones lineales 1. Estudiar el sistema de ecuaciones según los valores del parámetro a. ax + y + z = a x y + z = a 1 x + (a 1)y + az = a + 3 Resolverlo (si es posible) para a = 1. (Junio
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Matrices. Operaciones con matrices.
 Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES MATRICES. SISTEMAS DE ECUACIONES LINEALES Matrices ) Dada la matriz M=, prueba que n n M M, n. ) Demuestra la siguiente implicación: Si I A I AA A
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES MATRICES. SISTEMAS DE ECUACIONES LINEALES Matrices ) Dada la matriz M=, prueba que n n M M, n. ) Demuestra la siguiente implicación: Si I A I AA A
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 1. Espacios Vectoriales Definición de Espacio Vectorial
 Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero
 Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero 11 de Diciembre de 2008 2 B.G.O. 104.- Determina si los siguientes subconjuntos del espacio vectorial correspondiente son subvariedades afines:
Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero 11 de Diciembre de 2008 2 B.G.O. 104.- Determina si los siguientes subconjuntos del espacio vectorial correspondiente son subvariedades afines:
Aplicaciones Lineales. Diagonalización de matrices.
 Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
ÁLGEBRA LINEAL. EXAMEN FINAL 18 de Enero de b) (0, 5 puntos) Estudia si la siguiente afirmación es verdadera o falsa, justificando
 ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
un conjunto cuyos elementos denominaremos vectores y denotaremos por es un espacio vectorial si verifica las siguientes propiedades:
 CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
CAPÍTULO 2: ESPACIOS VECTORIALES 2.1- Definición y propiedades. 2.1.1-Definición: espacio vectorial. Sea un cuerpo conmutativo a cuyos elementos denominaremos escalares o números. No es necesario preocuparse
IES Francisco Ayala Modelo 2 (Septiembre) de 2008 Soluciones Germán Jesús Rubio Luna. Opción A. x - bx - 4 si x > 2
 IES Francisco Ayala Modelo (Septiembre) de 008 Soluciones Germán Jesús Rubio Luna Opción A Ejercicio n 1 de la opción A de septiembre de 008 ax + x si x Sea f: R R la función definida por: f(x). x - bx
IES Francisco Ayala Modelo (Septiembre) de 008 Soluciones Germán Jesús Rubio Luna Opción A Ejercicio n 1 de la opción A de septiembre de 008 ax + x si x Sea f: R R la función definida por: f(x). x - bx
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Ecuaciones de la recta en el espacio
 Ecuaciones de la recta en el espacio Ecuación vectorial de la recta Sea P(x 1, y 1 ) es un punto de la recta r y uu su vector director, el vector PPXX tiene igual dirección que uu, luego es igual a uu
Ecuaciones de la recta en el espacio Ecuación vectorial de la recta Sea P(x 1, y 1 ) es un punto de la recta r y uu su vector director, el vector PPXX tiene igual dirección que uu, luego es igual a uu
RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES
 UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
UNIDD 4 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 00 Resolución de sistemas mediante determinantes x y Resuelve, aplicando x = e y =, los siguientes sistemas de ecuaciones: x 5y = 7 5x + 4y = 6x
3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE
 3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE ECUACIONES LINEALES Y MATRICES COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 3.1.1. Resolución de sistemas de ecuaciones lineales. Método
3. ÁLGEBRA LINEAL // 3.1. SISTEMAS DE ECUACIONES LINEALES Y MATRICES COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 3.1.1. Resolución de sistemas de ecuaciones lineales. Método
Tema 11.- Autovalores y Autovectores.
 Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Espacios Vectoriales
 Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
Espacios Vectoriales Espacios Vectoriales Verónica Briceño V. noviembre 2013 Verónica Briceño V. () Espacios Vectoriales noviembre 2013 1 / 47 En esta Presentación... En esta Presentación veremos: Espacios
f(x, y, z, t) = (x + y t, x + 2y z 3t, 3x + 5y 2z 7t).
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 20 de enero de 20 (2.5 p.) ) Se considera la aplicación lineal f : R 4 R definida por: f(x y
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 20 de enero de 20 (2.5 p.) ) Se considera la aplicación lineal f : R 4 R definida por: f(x y
Tema 4.- Espacios vectoriales. Transformaciones lineales.
 Ingeniería Civil Matemáticas I -3 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 4- Espacios vectoriales Transformaciones lineales 4- Espacios y subespacios
Ingeniería Civil Matemáticas I -3 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 4- Espacios vectoriales Transformaciones lineales 4- Espacios y subespacios
Primer examen parcial Geometría y Álgebra Lineal 1 2 de mayo de 2015 Respuestas y solución
 Primer examen parcial Geometría y Álgebra Lineal 1 2 de mayo de 2015 Respuestas y solución Respuestas a la versión 1: (La versión 1 es aquélla cuyo primer ejercicio dice Un sistema lineal de m ecuaciones
Primer examen parcial Geometría y Álgebra Lineal 1 2 de mayo de 2015 Respuestas y solución Respuestas a la versión 1: (La versión 1 es aquélla cuyo primer ejercicio dice Un sistema lineal de m ecuaciones
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 6 2 Herramientas 8 21 Operaciones
Las variedades lineales en un K-espacio vectorial V pueden definirse como sigue a partir de los subespacios de V.
 Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 13 Capítulo 6 Año 5 6.1. Modelo 5 - Opción A Problema 6.1.1 ( puntos) Justificar razonadamente
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 13 Capítulo 6 Año 5 6.1. Modelo 5 - Opción A Problema 6.1.1 ( puntos) Justificar razonadamente
Departamento de Matemática Aplicada II. Universidad de Sevilla. Solución de la Primera Prueba Alternativa ( )
 MATEMÁTICAS I ( o de GIE y GIERM (Curso - Departamento de Matemática Aplicada II. Universidad de Sevilla Solución de la Primera Prueba Alternativa (-- Ejercicio.. Calcule las raíces cúbicas del número
MATEMÁTICAS I ( o de GIE y GIERM (Curso - Departamento de Matemática Aplicada II. Universidad de Sevilla Solución de la Primera Prueba Alternativa (-- Ejercicio.. Calcule las raíces cúbicas del número
RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES
 3 RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES Página 74 Determinantes de orden 2 Resuelve cada uno de los siguientes sistemas de ecuaciones y calcula el determinante de la matriz de los coeficientes:
3 RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES Página 74 Determinantes de orden 2 Resuelve cada uno de los siguientes sistemas de ecuaciones y calcula el determinante de la matriz de los coeficientes:
Conjuntos y matrices. Sistemas de ecuaciones lineales
 1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
1 Conjuntos y matrices Sistemas de ecuaciones lineales 11 Matrices Nuestro objetivo consiste en estudiar sistemas de ecuaciones del tipo: a 11 x 1 ++ a 1m x m = b 1 a n1 x 1 ++ a nm x m = b n Una solución
102 EJERCICIOS DE ALGEBRA LINEAL por Francisco Rivero Mendoza Ph.D.
 102 EJERCICIOS DE ALGEBRA LINEAL por Francisco Rivero Mendoza Ph.D. Tema 1. Espacios Vectoriales. 1. Dar la definición de cuerpo. Dar tres ejemplos de cuerpos. Dar un ejemplo de un cuerpo finito 2. Defina
102 EJERCICIOS DE ALGEBRA LINEAL por Francisco Rivero Mendoza Ph.D. Tema 1. Espacios Vectoriales. 1. Dar la definición de cuerpo. Dar tres ejemplos de cuerpos. Dar un ejemplo de un cuerpo finito 2. Defina
Tema 3. Matrices, determinantes y sistemas de ecuaciones
 Ingenierías: Aeroespacial, Civil y Química Matemáticas I 2-2 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 3 Matrices, determinantes y sistemas de ecuaciones
Ingenierías: Aeroespacial, Civil y Química Matemáticas I 2-2 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 3 Matrices, determinantes y sistemas de ecuaciones
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Espacios Vectoriales
 Espacios y subespacios vectoriales Espacios Vectoriales 1. Demuestre que con la suma y multiplicación habituales es un espacio vectorial real.. Considere el conjunto C de los números complejos con la suma
Espacios y subespacios vectoriales Espacios Vectoriales 1. Demuestre que con la suma y multiplicación habituales es un espacio vectorial real.. Considere el conjunto C de los números complejos con la suma
Apellidos: Nombre: Curso: 2º Grupo: A Día: 4-X-2015 CURSO ) D = ( 4 2
 EXAMEN DE MATEMATICAS II 1ª EVALUACIÓN Apellidos: Nombre: Curso: 2º Grupo: A Día: 4-X-2015 CURSO 2015-16 Opción A 1.- Considera las matrices A = ( 1 2 2 1 ), B = ( 2 1 0) y C = ( 1 5 0 ) a) [1,5 puntos]
EXAMEN DE MATEMATICAS II 1ª EVALUACIÓN Apellidos: Nombre: Curso: 2º Grupo: A Día: 4-X-2015 CURSO 2015-16 Opción A 1.- Considera las matrices A = ( 1 2 2 1 ), B = ( 2 1 0) y C = ( 1 5 0 ) a) [1,5 puntos]
ELEMENTOS DE GEOMETRÍA. Eduardo P. Serrano
 ELEMENTOS DE GEOMETRÍA Eduardo P. Serrano Este Apunte de Clase está dirigido a los alumnos de la materia Elementos de Cálculo Numérico para Biólogos. Tiene por objeto exponer algunos conceptos básicos
ELEMENTOS DE GEOMETRÍA Eduardo P. Serrano Este Apunte de Clase está dirigido a los alumnos de la materia Elementos de Cálculo Numérico para Biólogos. Tiene por objeto exponer algunos conceptos básicos
Problemas y Ejercicios Resueltos. Tema 4: Sistemas de ecuaciones lineales.
 Problemas y Ejercicios Resueltos. Tema 4: Sistemas de ecuaciones lineales. Ejercicios 1.- Determinar el rango de la siguiente matriz: 0 1 3 4 1 3 5. Solución. 0 1 3 4 1 3 5 AT 1( 1) AT 1 ( 1)T 14 ( 1 )
Problemas y Ejercicios Resueltos. Tema 4: Sistemas de ecuaciones lineales. Ejercicios 1.- Determinar el rango de la siguiente matriz: 0 1 3 4 1 3 5. Solución. 0 1 3 4 1 3 5 AT 1( 1) AT 1 ( 1)T 14 ( 1 )
520142: ALGEBRA y ALGEBRA LINEAL
 520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
Tema 3: Sistemas de ecuaciones lineales
 Tema 3: Sistemas de ecuaciones lineales 1. Introducción Los sistemas de ecuaciones resuelven problemas relacionados con situaciones de la vida cotidiana que tiene que ver con las Ciencias Sociales. Nos
Tema 3: Sistemas de ecuaciones lineales 1. Introducción Los sistemas de ecuaciones resuelven problemas relacionados con situaciones de la vida cotidiana que tiene que ver con las Ciencias Sociales. Nos
ÁLGEBRA LINEAL I Práctica 5
 ÁLGEBRA LINEAL I Práctica 5 Espacios vectoriales (Curso 2014 2015) 1. En el espacio vectorial real IR 2 consideramos los siguientes subconjuntos: (a) A = {(x y) IR 2 x 2 + y 2 = 1}. (b) B = {(x y) IR 2
ÁLGEBRA LINEAL I Práctica 5 Espacios vectoriales (Curso 2014 2015) 1. En el espacio vectorial real IR 2 consideramos los siguientes subconjuntos: (a) A = {(x y) IR 2 x 2 + y 2 = 1}. (b) B = {(x y) IR 2
Capítulo 8: Vectores
 Capítulo 8: Vectores 1. Lección 30. Operaciones con vectores 1.1. Vectores El concepto de vector aparece en Física para describir magnitudes, tales como la fuerza que actúa sobre un punto, en las que no
Capítulo 8: Vectores 1. Lección 30. Operaciones con vectores 1.1. Vectores El concepto de vector aparece en Física para describir magnitudes, tales como la fuerza que actúa sobre un punto, en las que no
1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS
 1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS 1.1 SISTEMAS DE ECUACIONES LINEALES Una ecuación lineal es una ecuación polinómica de grado 1, con una o varias incógnitas. Dos ecuaciones son equivalentes
1 SISTEMAS DE ECUACIONES LINEALES. MÉTODO DE GAUSS 1.1 SISTEMAS DE ECUACIONES LINEALES Una ecuación lineal es una ecuación polinómica de grado 1, con una o varias incógnitas. Dos ecuaciones son equivalentes
Sistemas de Ecuaciones Lineales y Matrices
 Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
es el lugar geométrico de los puntos p tales que p 0 p n o p 0 p o. p x ; y ; z perteneciente a y un vector no
 El Plano y la Recta en el Espacio Matemática 4º Año Cód. 145-15 P r o f. M a r í a d e l L u j á n M a r t í n e z P r o f. J u a n C a r l o s B u e P r o f. M i r t a R o s i t o P r o f. V e r ó n i
El Plano y la Recta en el Espacio Matemática 4º Año Cód. 145-15 P r o f. M a r í a d e l L u j á n M a r t í n e z P r o f. J u a n C a r l o s B u e P r o f. M i r t a R o s i t o P r o f. V e r ó n i
6 Vectores. Dependencia e independencia lineal.
 6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Espacios vectoriales
 Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Espacios vectoriales Sea (K, +,.) un cuerpo con característica 0. Podemos pensar K = Q, R o C. Si V es un conjunto cualquiera en el que
Resumen teoría Prof. Alcón ALGEBRA 1- GRUPO CIENCIAS- TURNO TARDE- Espacios vectoriales Sea (K, +,.) un cuerpo con característica 0. Podemos pensar K = Q, R o C. Si V es un conjunto cualquiera en el que
Matrices y Sistemas de Ecuaciones lineales
 Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León
 Selectividad Septiembre 011 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger
Selectividad Septiembre 011 Pruebas de Acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger
Práctica 1. Espacios vectoriales
 Práctica 1. Espacios vectoriales 1. Demuestre que R n (C n ) es un espacio vectorial sobre R (C) con la suma y el producto por un escalar usuales. Es C n un R-espacio vectorial con la suma y el producto
Práctica 1. Espacios vectoriales 1. Demuestre que R n (C n ) es un espacio vectorial sobre R (C) con la suma y el producto por un escalar usuales. Es C n un R-espacio vectorial con la suma y el producto
Espacio afín. 1. Rectas en el espacio. Piensa y calcula. Aplica la teoría
 6 Espacio afín 1. Rectas en el espacio Piensa y calcula Calcula las coordenadas de un vector que tenga la dirección de la recta que pasa por los puntos A2, 1, 5 y B3, 1, 4 AB 1, 2, 1 Aplica la teoría 1.
6 Espacio afín 1. Rectas en el espacio Piensa y calcula Calcula las coordenadas de un vector que tenga la dirección de la recta que pasa por los puntos A2, 1, 5 y B3, 1, 4 AB 1, 2, 1 Aplica la teoría 1.
Espacios vectoriales
 Espacios vectoriales [Versión preliminar] Prof. Isabel Arratia Z. Algebra Lineal 1 En el estudio de las matrices y, en particular, de los sistemas de ecuaciones lineales realizamos sumas y multiplicación
Espacios vectoriales [Versión preliminar] Prof. Isabel Arratia Z. Algebra Lineal 1 En el estudio de las matrices y, en particular, de los sistemas de ecuaciones lineales realizamos sumas y multiplicación
1 Sistemas de ecuaciones lineales.
 Sistemas de ecuaciones lineales Sistemas de ecuaciones lineales Sea S el siguiente sistema de m ecuaciones lineales y n incógnitas: 9 a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n = b 2 >=
Sistemas de ecuaciones lineales Sistemas de ecuaciones lineales Sea S el siguiente sistema de m ecuaciones lineales y n incógnitas: 9 a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n = b 2 >=
Sistem as de ecuaciones lineales
 Sistem as de ecuaciones lineales. Concepto, clasificación y notación Un sistema de m ecuaciones lineales con n incógnitas se puede escribir del siguiente modo: a x + a 2 x 2 + a 3 x 3 + + a n x n = b a
Sistem as de ecuaciones lineales. Concepto, clasificación y notación Un sistema de m ecuaciones lineales con n incógnitas se puede escribir del siguiente modo: a x + a 2 x 2 + a 3 x 3 + + a n x n = b a
11.SISTEMAS DE ECUACIONES LINEALES DEFINICIÓN DE ECUACIÓN LINEAL DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN
 ÍNDICE 11SISTEMAS DE ECUACIONES LINEALES 219 111 DEFINICIÓN DE ECUACIÓN LINEAL 219 112 DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN 220 113 EQUIVALENCIA Y COMPATIBILIDAD 220 11 REPRESENTACIÓN MATRICIAL
ÍNDICE 11SISTEMAS DE ECUACIONES LINEALES 219 111 DEFINICIÓN DE ECUACIÓN LINEAL 219 112 DEFINICIÓN DE SISTEMA LINEAL Y CONJUNTO SOLUCIÓN 220 113 EQUIVALENCIA Y COMPATIBILIDAD 220 11 REPRESENTACIÓN MATRICIAL
Cuestiones de Álgebra Lineal
 Cuestiones de Álgebra Lineal Algunas de las cuestiones que aparecen en esta relación están pensadas para ser introducidas en un plataforma interactiva de aprendizaje de modo que los parámetros a, b que
Cuestiones de Álgebra Lineal Algunas de las cuestiones que aparecen en esta relación están pensadas para ser introducidas en un plataforma interactiva de aprendizaje de modo que los parámetros a, b que
PAU Madrid. Matemáticas II. Año Examen de junio. Opción A. Ejercicio 1. Valor: 3 puntos.
 Opción A. Ejercicio 1. Valor: 3 puntos. Dado el sistema de ecuaciones lineales: { x ay = 2 se pide: ax y = a + 1 a) (2 puntos) Discutir el sistema según los valores del parámetro a. Resolverlo cuando la
Opción A. Ejercicio 1. Valor: 3 puntos. Dado el sistema de ecuaciones lineales: { x ay = 2 se pide: ax y = a + 1 a) (2 puntos) Discutir el sistema según los valores del parámetro a. Resolverlo cuando la
PROPUESTA A. 3A. a) Despeja X en la ecuación matricial X A B = 2X donde A, B y X son matrices cuadradas
 PROPUESTA A 1A a) Calcula el valor de a R, a > 0, para que la función sea continua en x = 0. b) Calcula el límite 2A. Calcula las siguientes integrales (1 25 puntos por cada integral) Observación: El cambio
PROPUESTA A 1A a) Calcula el valor de a R, a > 0, para que la función sea continua en x = 0. b) Calcula el límite 2A. Calcula las siguientes integrales (1 25 puntos por cada integral) Observación: El cambio
Teoría Tema 9 Ecuaciones del plano
 página 1/11 Teoría Tema 9 Ecuaciones del plano Índice de contenido Determinación lineal de un plano. Ecuación vectorial y paramétrica...2 Ecuación general o implícita del plano...6 Ecuación segmentaria
página 1/11 Teoría Tema 9 Ecuaciones del plano Índice de contenido Determinación lineal de un plano. Ecuación vectorial y paramétrica...2 Ecuación general o implícita del plano...6 Ecuación segmentaria
TEMA 8. GEOMETRÍA ANALÍTICA.
 TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
MATEMÁTICAS I 13 de junio de 2007
 MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Resuelve. Unidad 4. Vectores en el espacio. BACHILLERATO Matemáticas II. Diagonal de un ortoedro y volumen de un paralelepípedo.
 Resuelve Página Diagonal de un ortoedro y volumen de un paralelepípedo. Expresa la diagonal de un ortoedro en función de sus dimensiones, a, b y c. c b a c c b b a Diagonal = a + b + c. Calcula el volumen
Resuelve Página Diagonal de un ortoedro y volumen de un paralelepípedo. Expresa la diagonal de un ortoedro en función de sus dimensiones, a, b y c. c b a c c b b a Diagonal = a + b + c. Calcula el volumen
Ejercicio 2 opción A, modelo 5 Septiembre 2010
 Opción A Ejercicio 1 opción A, modelo 5 Septiembre 2010 [2 5 puntos] Una hoja de papel tiene que contener 18 cm 2 de texto Los márgenes superior e inferior han de ser de 2 cm cada uno y los laterales 1
Opción A Ejercicio 1 opción A, modelo 5 Septiembre 2010 [2 5 puntos] Una hoja de papel tiene que contener 18 cm 2 de texto Los márgenes superior e inferior han de ser de 2 cm cada uno y los laterales 1
Examen de Selectividad Matemáticas JUNIO Andalucía OPCIÓN A
 Eámenes de Matemáticas de Selectividad ndalucía resueltos http://qui-mi.com/ Eamen de Selectividad Matemáticas JUNIO - ndalucía OPCIÓN. Sea f : R R definida por: f ( a b c. a [7 puntos] Halla a b y c para
Eámenes de Matemáticas de Selectividad ndalucía resueltos http://qui-mi.com/ Eamen de Selectividad Matemáticas JUNIO - ndalucía OPCIÓN. Sea f : R R definida por: f ( a b c. a [7 puntos] Halla a b y c para
PAU Madrid. Matemáticas II. Año Examen de septiembre. Opción A. Ejercicio 1. Valor: 2 puntos.
 Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
VECTORES EN EL ESPACIO
 UNIDAD VECTORES EN EL ESPACIO Página 13 Problema 1 Halla el área de este paralelogramo en función del ángulo α: cm Área = 8 sen α = 40 sen α cm α 8 cm Halla el área de este triángulo en función del ángulo
UNIDAD VECTORES EN EL ESPACIO Página 13 Problema 1 Halla el área de este paralelogramo en función del ángulo α: cm Área = 8 sen α = 40 sen α cm α 8 cm Halla el área de este triángulo en función del ángulo
Es decir, det A = producto de diagonal principal producto de diagonal secundaria. Determinante de una matriz cuadrada de orden 3
 1.- DETERMINANTE DE UNA MATRIZ CUADRADA Determinante de una matriz cuadrada de orden 1 Dada una matriz cuadrada de orden 1, A = (a), se define det A = det (a) = a Determinante de una matriz cuadrada de
1.- DETERMINANTE DE UNA MATRIZ CUADRADA Determinante de una matriz cuadrada de orden 1 Dada una matriz cuadrada de orden 1, A = (a), se define det A = det (a) = a Determinante de una matriz cuadrada de
IES Fco Ayala de Granada Junio de 2012 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna
 IES Fco Ayala de Granada Junio de 01 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 01 común Sea f : R R la función definida como f(x) = e x.(x ). [1 punto]
IES Fco Ayala de Granada Junio de 01 (Común Modelo 4) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 01 común Sea f : R R la función definida como f(x) = e x.(x ). [1 punto]
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2005 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA : ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 005 MATEMÁTICAS II TEMA : ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva 1, Ejercicio 4, Opción A Reserva 1, Ejercicio
Sistemas de ecuaciones
 Apuntes Tema 11 Sistemas de ecuaciones 11.1 Definiciones Def.: Se llama sistema de ecuaciones lineales a un conjunto de igualdades dadas de la siguiente forma: a 11 x 1 + a 12 x 2 + a 1n x n = b 1 a 21
Apuntes Tema 11 Sistemas de ecuaciones 11.1 Definiciones Def.: Se llama sistema de ecuaciones lineales a un conjunto de igualdades dadas de la siguiente forma: a 11 x 1 + a 12 x 2 + a 1n x n = b 1 a 21
RESOLUCIÓN DE SISTEMAS MEDIANTE DETERMINANTES
 RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 0 REFLEXION Y RESUELVE Resolución de sistemas Ò mediante determinantes y Resuelve, aplicando x x e y, los siguientes sistemas de ecuaciones: 3x 5y 73 a
RESOLUCIÓN DE SISTEMS MEDINTE DETERMINNTES Página 0 REFLEXION Y RESUELVE Resolución de sistemas Ò mediante determinantes y Resuelve, aplicando x x e y, los siguientes sistemas de ecuaciones: 3x 5y 73 a
Esta expresión polinómica puede expresarse como una expresión matricial de la forma; a 11 a 12 a 1n x 1 x 2 q(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
EJERCICIOS DE SELECTIVIDAD LOGSE en EXTREMADURA MATRICES, DETERMINANTES Y SISTEMAS DE ECUACIONES
 EJERCICIOS DE SELECTIVIDAD LOGSE en EXTREMADURA MATRICES DETERMINANTES Y SISTEMAS DE ECUACIONES JUNIO 06/07. a) Calcula el rango de la matriz A según los valores del parámetro a 3 a A = 4 6 8 3 6 9 b)
EJERCICIOS DE SELECTIVIDAD LOGSE en EXTREMADURA MATRICES DETERMINANTES Y SISTEMAS DE ECUACIONES JUNIO 06/07. a) Calcula el rango de la matriz A según los valores del parámetro a 3 a A = 4 6 8 3 6 9 b)
Introducción a los espacios vectoriales
 1 / 64 Introducción a los espacios vectoriales Pablo Olaso Redondo Informática Universidad Francisco de Vitoria November 19, 2015 2 / 64 Espacios vectoriales 1 Las 10 propiedades de un espacio vectorial
1 / 64 Introducción a los espacios vectoriales Pablo Olaso Redondo Informática Universidad Francisco de Vitoria November 19, 2015 2 / 64 Espacios vectoriales 1 Las 10 propiedades de un espacio vectorial
Aplicaciones Lineales
 Aplicaciones Lineales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Aplicaciones Lineales 1 / 47 Objetivos Al finalizar este tema tendrás que: Saber si una aplicación es
Aplicaciones Lineales AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Aplicaciones Lineales 1 / 47 Objetivos Al finalizar este tema tendrás que: Saber si una aplicación es
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS CC SOCIALES CAPÍTULO 2 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS CC SOCIALES CAPÍTULO 2 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
Trabajo Práctico N 5: ESPACIOS VECTORIALES
 Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio 1: Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
Trabajo Práctico N 5: ESPACIOS VECTORIALES Ejercicio 1: Determine si los siguientes conjuntos con las operaciones definidas en cada caso son o no espacios vectoriales. Para aquellos que no lo sean, indique
Teoría Tema 4 Notación matricial en la resolución de sistemas de ecuaciones por Gauss
 página 1/6 Teoría Tema 4 Notación matricial en la resolución de sistemas de ecuaciones por Gauss Índice de contenido Matriz del sistema y matriz ampliada...2 Método de Gauss...3 Solución única, ausencia
página 1/6 Teoría Tema 4 Notación matricial en la resolución de sistemas de ecuaciones por Gauss Índice de contenido Matriz del sistema y matriz ampliada...2 Método de Gauss...3 Solución única, ausencia
ESPACIOS VECTORIALES
 MATEMÁTICA I - - Capítulo 8 ------------------------------------------------------------------------------------ ESPACIOS VECTORIALES.. Espacios Vectoriales y Subespacios... Definición. Un espacio vectorial
MATEMÁTICA I - - Capítulo 8 ------------------------------------------------------------------------------------ ESPACIOS VECTORIALES.. Espacios Vectoriales y Subespacios... Definición. Un espacio vectorial
APUNTES DE ÁLGEBRA LINEAL TEMA 2. SISTEMAS DE ECUACIONES LINEALES
 APUNTES DE ÁLGEBRA LINEAL TEMA 2. SISTEMAS DE ECUACIONES LINEALES Ignacio López Torres. Reservados todos los derechos. Prohibida la reproducción total o parcial de esta obra, por cualquier medio electrónico
APUNTES DE ÁLGEBRA LINEAL TEMA 2. SISTEMAS DE ECUACIONES LINEALES Ignacio López Torres. Reservados todos los derechos. Prohibida la reproducción total o parcial de esta obra, por cualquier medio electrónico
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales ALBERTO VIGNERON TENORIO Dpto. de Matemáticas Universidad de Cádiz Índice general 1. Sistemas de ecuaciones lineales 1 1.1. Sistemas de ecuaciones lineales. Definiciones..........
Sistemas de ecuaciones lineales ALBERTO VIGNERON TENORIO Dpto. de Matemáticas Universidad de Cádiz Índice general 1. Sistemas de ecuaciones lineales 1 1.1. Sistemas de ecuaciones lineales. Definiciones..........
Tema 2: Espacios Vectoriales
 Tema 2: Espacios Vectoriales José M. Salazar Octubre de 2016 Tema 2: Espacios Vectoriales Lección 2. Espacios vectoriales. Subespacios vectoriales. Bases. Lección 3. Coordenadas respecto de una base. Ecuaciones.
Tema 2: Espacios Vectoriales José M. Salazar Octubre de 2016 Tema 2: Espacios Vectoriales Lección 2. Espacios vectoriales. Subespacios vectoriales. Bases. Lección 3. Coordenadas respecto de una base. Ecuaciones.
ESPACIOS VECTORIALES SUBESPACIOS:
 SUBESPACIOS: Continuación EJEMPLOS: S 2 = {(x 1, x 2 ) / x 2 =x 12 } R 2 es subespacio del espacio vectorial? Interpretación geométrica: Representa una parábola de eje focal el eje de ordenadas, vértice
SUBESPACIOS: Continuación EJEMPLOS: S 2 = {(x 1, x 2 ) / x 2 =x 12 } R 2 es subespacio del espacio vectorial? Interpretación geométrica: Representa una parábola de eje focal el eje de ordenadas, vértice
Tema 2: Espacios vectoriales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 Tema 2: Espacios vectoriales Ejercicios 1. En R 2 se definen las siguientes operaciones: (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 Tema 2: Espacios vectoriales Ejercicios 1. En R 2 se definen las siguientes operaciones: (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
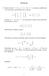 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
ESPACIOS VECTORIALES
 ESPACIOS VECTORIALES Luisa Martín Horcajo U.P.M. Definición: Vector libre. Operaciones Un vector fijo es una segmento orientado, que queda caracterizado por su origen A y su extremo B y se representa por
ESPACIOS VECTORIALES Luisa Martín Horcajo U.P.M. Definición: Vector libre. Operaciones Un vector fijo es una segmento orientado, que queda caracterizado por su origen A y su extremo B y se representa por
Matemática II Tema 3: resolución de sistemas de ecuaciones lineales
 Matemática II Tema 3: resolución de sistemas de ecuaciones lineales 2012 2013 Índice Sistemas de ecuaciones lineales 1 Interpretación geométrica y definición 1 Método de eliminación 4 Resolución de sistemas
Matemática II Tema 3: resolución de sistemas de ecuaciones lineales 2012 2013 Índice Sistemas de ecuaciones lineales 1 Interpretación geométrica y definición 1 Método de eliminación 4 Resolución de sistemas
Sistemas de ecuaciones lineales dependientes de un parámetro
 Vamos a hacer uso del Teorema de Rouché-Frobenius para resolver sistemas de ecuaciones lineales de primer grado. En particular, dedicaremos este artículo a resolver sistemas de ecuaciones lineales que
Vamos a hacer uso del Teorema de Rouché-Frobenius para resolver sistemas de ecuaciones lineales de primer grado. En particular, dedicaremos este artículo a resolver sistemas de ecuaciones lineales que
Opción A Ejercicio 1 opción A, modelo 5 Septiembre Reserva_ tan(x) - sen(x) [2 5 puntos] Calcula lim
![Opción A Ejercicio 1 opción A, modelo 5 Septiembre Reserva_ tan(x) - sen(x) [2 5 puntos] Calcula lim Opción A Ejercicio 1 opción A, modelo 5 Septiembre Reserva_ tan(x) - sen(x) [2 5 puntos] Calcula lim](/thumbs/60/45214373.jpg) IES Fco Ayala de Granada Septiembre de 014 Reserva 1 (Modelo 5) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 5 Septiembre Reserva_1 014 tan(x) - sen(x) [ 5 puntos] Calcula lim
IES Fco Ayala de Granada Septiembre de 014 Reserva 1 (Modelo 5) Soluciones Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo 5 Septiembre Reserva_1 014 tan(x) - sen(x) [ 5 puntos] Calcula lim
Tema 2.- Formas Cuadráticas.
 Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
Álgebra. 004 005. Ingenieros Industriales. Departamento de Matemática Aplicada II. Universidad de Sevilla. Tema.- Formas Cuadráticas. Definición y representación matricial. Clasificación de las formas
ÁLGEBRA LINEAL E.T.S. DE INGENIERÍA INFORMÁTICA INGENIERÍAS TÉCNICAS EN INFORMÁTICA DE SISTEMAS Y GESTIÓN BOLETÍN DE PROBLEMAS DE
 E.T.S. DE INGENIERÍA INFORMÁTICA BOLETÍN DE PROBLEMAS DE ÁLGEBRA LINEAL para las titulaciones de INGENIERÍAS TÉCNICAS EN INFORMÁTICA DE SISTEMAS Y GESTIÓN 1. Matrices y determinantes Ejercicio 1.1 Demostrar
E.T.S. DE INGENIERÍA INFORMÁTICA BOLETÍN DE PROBLEMAS DE ÁLGEBRA LINEAL para las titulaciones de INGENIERÍAS TÉCNICAS EN INFORMÁTICA DE SISTEMAS Y GESTIÓN 1. Matrices y determinantes Ejercicio 1.1 Demostrar
Matrices, Determinantes y Sistemas Lineales.
 12 de octubre de 2014 Matrices Una matriz A m n es una colección de números ordenados en filas y columnas a 11 a 12 a 1n f 1 a 21 a 22 a 2n f 2....... a m1 a m2 a mn f m c 1 c 2 c n Decimos que la dimensión
12 de octubre de 2014 Matrices Una matriz A m n es una colección de números ordenados en filas y columnas a 11 a 12 a 1n f 1 a 21 a 22 a 2n f 2....... a m1 a m2 a mn f m c 1 c 2 c n Decimos que la dimensión
Modelo 4 de Sobrantes de 2004
 Ejercicio n de la opción A del modelo 4 de 24 9 Considera la integral definida I d + [ 5 puntos] Epresa la anterior integral definida aplicando el cambio de variables + t. [ punto] Calcula I. I d + Cambio
Ejercicio n de la opción A del modelo 4 de 24 9 Considera la integral definida I d + [ 5 puntos] Epresa la anterior integral definida aplicando el cambio de variables + t. [ punto] Calcula I. I d + Cambio
UNIVERSIDAD SIMON BOLIVAR MA1116 abril-julio de 2009 Departamento de Matemáticas Puras y Aplicadas. Ejercicios sugeridos para :
 UNIVERSIDAD SIMON BOLIVAR MA6 abril-julio de 29 I / Ejercicios sugeridos para : los temas de las clases del 2 y 23 de abril de 29. Tema : Matrices. Operaciones con matrices. Ejemplos. Operaciones elementales
UNIVERSIDAD SIMON BOLIVAR MA6 abril-julio de 29 I / Ejercicios sugeridos para : los temas de las clases del 2 y 23 de abril de 29. Tema : Matrices. Operaciones con matrices. Ejemplos. Operaciones elementales
Espacios vectoriales. Vectores del espacio.
 Espacios vectoriales. Vectores del espacio. Consideremos un paralelepípedo de bases ABCD y EFGH, siendo A(1,1,1), B(2,1,1), C(2,4,1) y E(1,2,7). Halla: a) el área de una de las bases; b) el volumen del
Espacios vectoriales. Vectores del espacio. Consideremos un paralelepípedo de bases ABCD y EFGH, siendo A(1,1,1), B(2,1,1), C(2,4,1) y E(1,2,7). Halla: a) el área de una de las bases; b) el volumen del
Espacios Vectoriales
 Leandro Marín Octubre 2010 Índice Definición y Ejemplos Paramétricas vs. Impĺıcitas Bases y Coordenadas Para definir un espacio vectorial tenemos que empezar determinando un cuerpo sobre el que esté definido
Leandro Marín Octubre 2010 Índice Definición y Ejemplos Paramétricas vs. Impĺıcitas Bases y Coordenadas Para definir un espacio vectorial tenemos que empezar determinando un cuerpo sobre el que esté definido
ALGUNOS PROBLEMAS DE ÁLGEBRA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 2015
 ÁLGEBRA (Selectividad 015) 1 ALGUNOS PROBLEMAS DE ÁLGEBRA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 015 1 Aragón, junio 15 1 (3 puntos) a) (1,5 puntos) Considera la matriz y los vectores siguientes:
ÁLGEBRA (Selectividad 015) 1 ALGUNOS PROBLEMAS DE ÁLGEBRA PROPUESTOS EN LAS PRUEBAS DE SELECTIVIDAD DE 015 1 Aragón, junio 15 1 (3 puntos) a) (1,5 puntos) Considera la matriz y los vectores siguientes:
EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA
 EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA 2003 (4) Ejercicio 1. Considera los vectores u = (1,1,1), v = (2,2,a) y w = (2,0,0), (a) [1'25 puntos] Halla los valores de a para que los vectores u, v y w sean
EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA 2003 (4) Ejercicio 1. Considera los vectores u = (1,1,1), v = (2,2,a) y w = (2,0,0), (a) [1'25 puntos] Halla los valores de a para que los vectores u, v y w sean
