ELECTRODINÁMICA CLÁSICA FIM 8650 (3)
|
|
|
- Belén Cárdenas San Martín
- hace 5 años
- Vistas:
Transcripción
1 ELECTRODINÁMICA CLÁSICA FIM 8650 (3) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2do. Semestre 2014
2 Resumen de magnetostática ECUACION DE CONTINUIDAD DE LA CARGA ELECTRICA. ρ t + J = 0 En magnetostática, ρ es constante, luego J = 0 FUERZA DE LORENTZ. Fuerza sobre una carga puntual q que se mueve con velocidad v: F = q v B LEY DE BIOT-SAVART. Densidad de flujo magnético (inducción magnética, campo) en r debida a un elemento de circuito dl, ubicado el r, que lleva una corriente I: d B( r) = µ oi 4π dl ( r r ) r r 3
3 Para una partícula con carga q y velocidad v: B( r) = µ o 4π q v ( r r ) r r 3 Para una densidad de corriente J( r ) B( r) = µ o 4π Se concluye que B = 0. J( r ) r r ) r r d 3 r = µ o 3 4π J( r ) r r d 3 r (1) FUERZA DE AMPÈRE. Fuerza entre dos circuitos que llevan corrientes I 1 e I 2. F = µ o 4π I dl1 (dl 2 ( r 1 r 2 ) 1I 2 r 1 r 2 3 o también, la fuerza que el campo magnético externo B ejerce sobre el elemento de circuito dl 1 que lleva una corriente I 1 : d F = I 1 dl 1 B
4 Un elemento que lleva una densidad de corriente J( r ) en una inducción magnética B( r ) queda sometido a una fuerza: F = J( r ) B( r )d 3 r y a un torque N = r [ J( r ) B( r )]d 3 r Partiendo de (1), podemos demostrar que: ya que J = 0 B = µ o µ o J + 4π J( r ) d 3 r = µ r r o J La ecuación B = µ o J se llama Ley de Ampère y vale sólo para magnetostática.
5 POTENCIAL VECTORIAL Se define a través de: B = A De (1) obtenemos una expresión para A A( r) = µ o J( r ) 4π r r d 3 r + Ψ( r) Ya que el rotor de un gradiente es cero, podemos realizar la transformación: A A + Ψ dejando B invariante. Esta es una transformación de calibre. De la ley de Ampère obtenemos: ( A) = ( A) 2 A = µo J
6 Elijiendo un calibre apropiado, podemos imponer A = 0 y encontramos: 2 A = µo J que es reminiscente de la ecuación de Poisson, cuya solución (para cada coordenada cartesiana) se resume en: A( r) = µ o J( r ) 4π r r d 3 r (2)
7 Ejercicio 1.- Una corriente I fluye en un círculo de radio a y una corriente I fluye en un cable rectilíneo muy largo ubicado en el mismo plano. Demostrar que existe una fuerza entre los dos circuitos que vale: F = µ o II (sec α 1) donde α es el ángulo subtendido por el círculo en el punto más cercano del alambre rectilíneo.
8 Ejercicio 2.- Una corriente I fluye en un circuito con forma de elipse de área A y longitud L. Encuentre el campo en el centro de la elipse.
9 Ejercicio 3.- Dos anillos concéntricos tienen radios a y b, llevan corrientes I e I respectivamente. El primero está en el plano x y con su centro en el orígen y el segundo es paralelo al primero y tiene su centro en el eje z a la ditancia c del orígen. Encuentre la fuerza entre los anillos expresada: en términos de integrales elípticas. como una serie de esféricos armónicos.
10 Ejercicio 4.- Dos círculos concéntricos de radios a > b llevan corrientes I e I y sus planos forman un ángulo α. Demuestre que el torque entre los dos circuitos alrededor de la línea de intersección de los dos planos tiene la magnitud, N = µ oπii b 2 2a n=0 [ n + 1 Γ(n ) 2n + 1 Γ(n + 2)Γ( 3 2 ) ] 2 (b a ) 2n P 1 2n+1(cos α)
11 Consideremos ahora una distribución de corriente localizada dentro de un volumen V. Tomamos el orígen dentro de este volumen y buscamos una expresión aproximada para A en un punto alejado del volumen V. Para esto expandimos el denominador de (2). r r o 1 r r = 1 r r + r r 3 Entonces el valor aproximado de la componente cartesiana i de A es [ A i ( r) = µo 1 J i ( r )d 3 r + r ] 4π r r J 3 i ( r ) r d 3 r Ahora utilizaremos la siguiente identidad vectorial, válida para la funciones de posición arbitrarias f ( r), g( r) y u( r), que se anulan en la superficie de una región que contiene V. (f u g + g u f + fg u)d 3 r = 0 (3)
12 Esto se demuestra haciendo una integración por partes: d 3 r g u f = d 3 r f (g u) = d 3 r (fg u + f u g) Ahora si ponemos u = J, con J = 0, tenemos: (f J g + g J fd 3 r ) = 0 (4) Haciendo u = J y f = 1, g = x i, con J = 0, obtenemos: J i ( r )d 3 r = 0 y con f = x i, g = x j nos da: (x i J j + x j J i)d 3 r = 0
13 Entonces el segundo término de (3) r r J i d 3 r = x j x j J id 3 r j = 1 x j (x i 2 J j x j J i)d 3 r j = 1 ɛ ijk x j ( r 2 J) k d 3 r jk = 1 [ ] r ( r 2 J)d 3 r Definimos la densidad de momento magnético como: M( r) = 1 2 [ r J( r)] i
14 y el momento magnético de una densidad de corriente m: m = 1 r 2 J( r )d 3 r (5) Con esto la contribución dipolar al potencial vectorial es: y la inducción magnética, B( r) = µ o 4π V A( r) = µ o m r 4π r 3 [ ] 3ˆn(ˆn m) m donde ˆn es un vector unitario en la dirección de r. Para un circuito confinado a un plano de forma arbitraria el momento magnético es: m = I r d 2 l Es decir m = (corriente) (área), r 3
15 Supongamos ahora que tenemos un conjunto de partículas cargadas con carga q i y masa M i, que tienen velocidades v i y posiciones r i. La densidad de corriente de estas partículas vale: J( r) = q i v i δ( r r i ) Entonces reemplazando en (5) obtenemos: m = 1 q i ( r i v i ) = 2 i i i q i 2M i Li donde L i = M i ( r i v i ) es el momento angular orbital de la partícula i. Ahora si todas las partículas tienen la misma razón q i /M i = e/m, podemos escribir esta relación en términos del moemto angular total; L = M i ( r i v i ): Según la mecánica cuántica: m = e 2M L m = ge 2M L donde el factor g para los electrones vale 2
16 Finalmente, con el mismo procedimiento que se utilizó para el campo eléctrico de un dipolo, se puede demostrar que para la inducción magnética de un dipolo ubicado en el orígen hay una contribución función delta que se expresa como: B = µ o 4π [ 3ˆn(ˆn m) m r 3 + 8π ] mδ( r) 3
17 Fuerza y torque sobre distribución de corrientes localizadas Supongamos una densidad de corriente J( r ), localizada en un volumen V, en presencia de un campo B que varía lentamente dentro de V. Entonces podemos expandir B alrededor de orígen dentro de V, B k ( r) = B k (0) + r B k (0) + (6) Entonces la componente i de la fuerza es: F i = jk ɛ ijk [B k (0) J j ( r )d 3 r + ] J j ( r ) r B k (0)d 3 r + (7) El primer término es cero y siguiendo los pasos para llegar a (5) podemos demostrar que: F i = jk ɛ ijk ( m ) j B k (0) que corresponde a un triple producto vectorial: F = ( m ) B = ( m B) m( B)
18 Como B = 0 obtenemos finalmente: F = ( m B) (8) De aquí encontramos la energía de interacción de un momento magnético en un campo magnético externo: U = m B Con respecto al torque, la contribución más importante está dada por el primer término de (6): N = = r [ J B(0)]d 3 r [( r B) J ( r J) B]d 3 r = m B(0) (9) Este resultado se encuentra aplicando a la primera integral el mismo procedimiento que se utilizó para el segundo término de (7). La segunda integral se anula. Esto se puede ver utilizando (4) con f = g = r
19 Ejercicio 5.- Llene los pasos faltantes y complete la demostración de las ecuaciones (8) y (9).
20 MAGNETISMO EN MATERIALES Empezamos con una definición de magnetización. Consideremos un material donde cada átomo tiene un momento dipolar magnético m i y consideramos un pequeño volumen del material dv, ubicado en la posición definida por r. Dentro de este volumen hay una gran cantidad de átomos, entonces definimos la magnetización en r como: M( r ) = lím dv 0 Ahora utilizamos la expresión para el potencial vectorial magnético en el punto r debido a un momento dipolar magnético ubicado en r : i m i dv A( r) = µ o m ( r r ) 4π r r 3 Entonces si volvemos a nuestro material y queremos calcular el potencial A debido a todos los momentos magnéticos de este material, primero calculamos el potencial debido a los momentos magnéticos en el pequeño volumen dv, i.e. m i.
21 Entonces podemos decir que la contribución a A debido al punto r, donde está ubicado dv, es: da = µ o m i ( r r ) = µ o M( r ) ( r r )d 3 r 4π r r 3 4π r r 3 Ya que m i = M( r )dv = M( r )d 3 r y por lo tanto el potencial A debido a todo el material es: A = µ o M( r ) ( r r ) d 3 r (10) 4π r r 3 Esta integral puede se extendida a todo el espacio y por lo tanto incluir regiones con M = 0 Ahora utilizamos la relación vectorial: ( r r ) r r = 1 3 r r y luego integramos por parte para obtener:
22 A = µ o 4π M( r ) d 3 r r r Nótese que esta expresión es similar a la del potencial vectorial magnético debido a una densidad de corriente J. En realidad si en el punto r hay una densidad de corriente J( r), el potencial A total es: A = µ o 4π J( r ) + M( r ) d 3 r r r Esto implica que en presencia de materiales magnéticos, la relación de Ampère B = µ o J debe ser modificada y escrita así: B = µ o ( J + M) o sea: ( ) 1 B M = µ J o
23 Nótese que el vector entre paréntesis no depende de la magnetización. Sólo depende de la corriente J. Este vector lleva el nombre de campo magnético H : H = 1 µ o B M En analogía con el vector desplazamiento del campo eléctrico. En un número muy grande de materiales es posible de utilizar una aproximación para la relación entre M y H: M = χ m H La cantidad χ m se llama la suscetibilidad magnética del material. Si el material es paramagnético χ m es positiva, mientras que si es diamagnético χ m es negativa. Su valor absoluto para estos materiales es muy pequeño, típicamente < 10 5.
24 Esta relación lineal implica que B y H son proporcionales: B = µ H donde µ se llama permeabilidad del material. Podemos deducir que: µ = µ o (1 + χ m ) La permeabilidad relativa se define como: K m = µ µ o = 1 + χ m Para los materiales paramagnéticos y diamagnéticos K m es muy cercano a 1. Sin embargo para los materiales ferromagnéticos puede tomas valores muy elevados, como para el Permalloy y para el Mumetal.
25 En la ecuación (10) se supone que la integración se realiza en todo el espacio. Si tenemos una magnetización sólo dentro de un volumen finito V, limitado por la superficie S, partiendo de y utilizando: y A = µ o 4π V M( r ) 1 r r d 3 r (u F) = ( u) F + u F V F d 3 r = con u = 1/ r r y F = M obtenemos: S ˆn F d 2 r µ o M A = 4π V r r d 3 r + µo M ˆn 4π S r r d 2 r
26 B en términos de M y φ B = A = µ [ o r r ] M d 3 r 4π V r r 3 Usamos la identidad matemática: ( F G) = ( G) F ( F) G + ( G ) F ( F ) G con F = M y G = ( r r )/ r r 3. Notando que M = 0, obtenemos: [ M r r ] [ = r r ] [ ] M M r r r r 3 r r 3 r r 3 Así podemos expresar B como la suma de dos términos: B = B 1 + B 2
27 donde: Aquí B 1 = µ [ o r r M 4π V r r 3 B 2 = µ o 4π V ] d 3 r [ M ] r r r r 3 d 3 r [ r r ] = 4πδ( r r ) B1 = µ r r 3 om El segundo término se simplifica usando: [ ] M r r [ r r = r r M ] M r r 3 r r 3 r r 3 El segundo término es cero ya que: r r r r 3 = 1 r r
28 Luego: B 2 = µ o 1 M 4π V r r r r 3 d 3 r = µ o φ B = µ o φ + µ o M
29 Condiciones de borde de B y H Consideremos una superficie que separa dos medios magnéticos 1 y 2. A partir de B = 0 y H = J, usando el teorema de la divergencia y el teorema de Stokes, obtenemos ( B 2 B 1 ) ˆn = 0 ˆn ( H 2 H 1 ) = K Donde ˆn es un vector unitario normal a la superficie que va desde ls región 1 a la región 2 y K es la corriente superficial que puede existir en la interfaz y que tiene dimensiones de [A/m]. En el caso de un medio lineal, i.e. donde se cumple B = µ H, y en que K = 0 estas relaciones se reducen a: o B 2 ˆn = B 1 ˆn B2 ˆn = µ 2 µ 1 B1 ˆn H 2 ˆn = µ 1 µ 2 H1 ˆn H2 ˆn = H 1 ˆn Esta situación es ilustrada en la figura siguiente.
30 H 1 H 2 µ >> µ 1 2
31 Ejercicio 6.- Una esfera tiene un alambre aislado muy delgado alrededor de uno de sus diámetros, por donde pasa una corriente. Encuentre la forma en que se debe enrollar el alambre para que el campo magnético sea constante dentro de la esfera.
32 Ejercicio 7.- Una distribución de corriente J( r) existe en un espacio vacío semiinfinito (z > 0) adyacente a un espacio semiinfito (z < 0) que está lleno con un material con permeabilidad µ. a) Demuestre que para z > 0 la inducción magnética puede ser calculada reemplazando el medio de permebilidad µ por una corriente imagen J, con las siguientes componentes: ( µ µo µ + µ o ) J x(x, y, z), ( µ µo µ + µ o ) J y(x, y, z), ( ) µ µo J z(x, y, z) µ + µ o b) Demuestre que para z < 0 la inducción magnética se puede calcular reemplazando J por: en un medio de permeabilidad µ o. 2µ µ + µ o J
33 Métodos para resolver problemas de borde de magnetostática Hay que recordar que las ecuaciones básicas de la magnetostática son: (A) Método general. B = 0 H = J (11) Ya que en general la relación entre H y B es no lineal, partiendo de B = A, tenemos: H( A) = J Esta es la ecuación más general que debe cumplir A en un problema de magnetostática. Para un medio lineal: y si µ es constante: ( 1 µ A) = J ( A) 2 A) = µ J
34 (B) Potencial escalar para J = 0 De (11) podemos escribir: H = Φ M lo que nos da B( Φ M ) = 0. Para un medio lineal, se reduce a (µ Φ M ) y para µ = constante: 2 Φ M = 0 En este último caso también podemos escribir B = Ψ M y por lo tanto: 2 Ψ M = 0
35 (C) Ferromagnetos duros con M dado y J = 0 Estos materiales mantienen M independiente de campo aplicados moderados: Si conocemos M podemos escribir: B = µ o ( H + M) 2 Φ M = M = ρ M cuya solución es: Φ M = 1 4π M( r ) d 3 r r r Si M es distinta de cero dentro del volumen V y cae bruscamente a cero en su superficie, podemos escribir: Φ M = 1 4π V M( r ) d 3 r + 1 r r 4π S ˆn M( r ) d 2 r r r
36 (D) El mismo caso anterior, usando el potencial A De: H = ( 1 µ o B M) = 0 2 A = µo M = µ o JM En un espacio extendido sin límites, la solución de esta ecuación es: A( r) = µ o 4π M( r ) d 3 r r r Nuevamente si M es distinta de cero dentro del volumen V y cae bruscamente a cero en su superficie, podemos escribir: A( r) = µ o 4π V M( r ) d 3 r + µ o r r 4π S M( r ) ˆn d 2 r r r
37 LEY DE INDUCCION DE FARADAY E = C E d l = dφ dt donde φ es el flujo enlazado por el circuito C LEY DE LENZ LA CORRIENTE INDUCIDA TIENE UNA DIRECCION TAL QUE EL CAMPO MAGNÉTICO DEBIDO A ESTA CORRIENTE SE OPONE AL CAMBIO DEL CAMPO MAGNETICO QUE HA INDUCIDO ESTA CORRIENTE Aumento del Campo I Campo producido por la corriente I
38 La Ley de Faraday para circuitos en movimiento. La ley de Faraday dice que: E = E d l = dφ = d dt dt Sea u la velocidad del circuito B ˆndS B t ds 1 u t B t + t pero t B ˆndS = 1 t ds 2 ( Bt+ t ˆnd S 2 B t ˆnd S 1 ) B t+ t ˆnd S 2 B t ˆnd S 1 = B t ˆnd S 2 B t ˆnd S 1 + B t t ˆndS 2
39 Usando el teorema de la divergencia: ( Bt+ t ˆnd S 2 B t ˆnd S ) ( Bt 1 = ˆnd S 2 B t ˆnd S ) 1 + = Luego, haciendo t dt: d dt Bd 3 r + B ˆnd S = B t ( u t d l) + B dv + dt B t u d l + B t t ˆndS 2 B t B t t ˆndS 2 ˆndS donde dv = u ˆndSdt. Ahora B t u d l = B t u d l = ( B u) ˆndS donde usamos el teorema de Stokes. Entonces: d dt B ˆnd S = B u ˆndS + ( B u) ˆndS + B t ˆndS = D B Dt ˆndS
40 donde D B Dt = ( B) u + ( B u) + B t Esta relación es válida para cualquier vector B, pero en nuestro caso es el campo magnético y por lo tanto B = 0. Entonces finalmente, en un sistema móvil: E d l = dφ dt Por lo tanto en un sistema móvil: [ B = ] + ( B t u) ˆndS E = B ( B t u) para en un sistema fijo obtenemos: E = ( E u B) = B t E = E + u B
41 Ejercicio 8.- La figura representa una línea de transmisión constituída por dos conductores paralelos de sección arbitraria pero constante, inmersos en un medio de permitividad ɛ y permeabilidad µ. Demuestre que la inductancia por unidad de largo L y la capacidad por unidad de largo C están relacionadas por: LC = ɛµ
42 Energía del campo magnético Para medios lineales la energía magnética es: W = 1 H 2 Bd 3 r Usando A = B y la identidad: P ( Q) = Q ( P) ( P Q) con P = H y Q = A, tenemos que: W = 1 2 H Ad 3 r = 1 2 A Hd 3 r 1 2 ( H A)d 3 r Para una distribución localizada de corrientes la segunda integral es cero y obtenemos: W = 1 A 2 Jd 3 r (12)
43 Ahora consideremos un medio con permeabilidad µ o en el cual existen los campos B o y H o e introducimos en él un objeto de volumen V y permeabilidad µ 1. Siguiendo un procedimiento similar al utilizado en los dieléctricos, para el cambio de energía obtenemos: W = 1 ( B 2 H o B o H)d 3 r V como los medios son lineales esta relación se puede escribir como: W = 1 (µ 1 µ o ) H 2 H o d 3 r = 1 ( 1 1 ) B V 2 V µ o µ B o d 3 r 1 Si µ o se refiere al vacío, podemos escribir, W = 1 M 2 B o d 3 r V y la fuerza que actúa sobre el cuerpo en la dirección ξ, manteniendo las densidades de corriente constantes está dado por: ( ) W F ξ = ξ J
44 En un sistema con N circuitos que llevan corrientes I i, i = 1... N, la energía total se puede escribir como: W = 1 2 N i=1 L i i 2 i + N i=1 N M ij I i I j (13) j>i Por otra parte si usamos (12) y reemplazamos A por: obtenemos: A( r) = µ o 4π W = µ o 8π d 3 r J( r) r r d 3 r d 3 r J( r) J( r ) r r
45 Ahora podemos pensar que los circuitos no son necesariamente alambres muy delgados, pero que sin embargo, siempre podemos asociar una parte de J a un circuito dado, i.e. por ejemplo el circuito i. De esta manera podemos rescribir la última ecuación como: W = µ o 8π N d 3 r i i=1 N j=1 J( d 3 r i ) r J( r j ) j d 3 r r i r j Entonces esta doble sumatoria se separa en los términos diagonales, en que i = j y los términos no-diagonales i j. Ahora comparamos los términos diagonales con el primer témino de (13) y los no-diagonales con el segundo término. De esta manera podemos definir las inductancias L i y M ij : y L i = µ o 4πIi 2 d 3 r i C i C i d 3 r i J( r i ) J( r i ) r i r i M ij = µ o J( d 3 r i d 3 r i ) r J( r j ) j 4πI i I j C i C j r i r j
46 Estas expresiones pueden ser consideradas como las definiciones más generales de la auto-inductancia y de la inductancia mutua. Campos cuasi estáticos. Difusión magnética Cuasi estático se refiere a un régimen en que las variaciones temporales son suficientemente lentas como para considerar que la velocidad de la luz es infinita. Despreciando la contribución de la corriente de desplazamiento de Maxwell, las ecuaciones relevantes del EM son: H = J; B = 0; E + B t De aquí podemos concluir que: E = A φ t B = µ J = µσe Con φ = 0, 2 A = µσ A t. = 0; J = σ E Ecuación de difusión para A
47 ESTIMACIÓN DEL TIEMPO DE DECAIMIENTO. Para una variación espacial típica L y un tiempo de decaimiento τ, de la última ecuación tenemos: A L 2 A τ τ µσl 2 Ahora si el campo tiene una variación temporal armónica de frecuencia ν = 1/τ, la longitud de decaimiento se puede estimar como: L 1 µνσ
TEORIA ELECTROMAGNETICA FIZ 0321 (6)
 TEORIA ELECTROMAGNETICA FIZ 0321 (6) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2do. Semestre 2006 Fuerza entre cargas en movimiento Fuerza entre cargas q 1 y q 2 que se
TEORIA ELECTROMAGNETICA FIZ 0321 (6) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2do. Semestre 2006 Fuerza entre cargas en movimiento Fuerza entre cargas q 1 y q 2 que se
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (11)
 ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (11) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2006 MAGNETISMO EN LA MATERIA Momento dipolar de electrones y átomos
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (11) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2006 MAGNETISMO EN LA MATERIA Momento dipolar de electrones y átomos
ELECTRODINÁMICA CLÁSICA FIM 8650 (4)
 ELECTRODINÁMICA CLÁSICA FIM 8650 (4) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2do. Semestre 2014 Las cuatro ecuaciones de Maxwell en el vacío son: D = ρ H = J + D B =
ELECTRODINÁMICA CLÁSICA FIM 8650 (4) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2do. Semestre 2014 Las cuatro ecuaciones de Maxwell en el vacío son: D = ρ H = J + D B =
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (9)
 ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (9) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2006 Ejemplo 1 El espectrógrafo de masa fué inventado por Francis
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (9) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2006 Ejemplo 1 El espectrógrafo de masa fué inventado por Francis
TEORIA ELECTROMAGNETICA FIZ 0321 (13)
 TEORIA ELECTROMAGNETICA FIZ 0321 (13) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2do. Semestre 2006 PROBLEMAS Y EJERCICIOS Ejercicio No. 1 Tenemos un circuito no rígido
TEORIA ELECTROMAGNETICA FIZ 0321 (13) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2do. Semestre 2006 PROBLEMAS Y EJERCICIOS Ejercicio No. 1 Tenemos un circuito no rígido
Ingeniería Electrónica ELECTROMAGNETISMO Cátedra Ramos-Lavia Versión
 Versión 2013 1 TRABAJO PRÁCTICO N 0: Modelo Electromagnético 0.1 - Cuáles son las cuatro unidades SI fundamentales del electromagnetismo? 0.2 - Cuáles son las cuatro unidades de campo fundamentales del
Versión 2013 1 TRABAJO PRÁCTICO N 0: Modelo Electromagnético 0.1 - Cuáles son las cuatro unidades SI fundamentales del electromagnetismo? 0.2 - Cuáles son las cuatro unidades de campo fundamentales del
Electromagnetismo II
 Electromagnetismo II Semestre: 2015-1 TAREA 9: Solución Dr. A. Reyes-Coronado Por: Jesús Castrejón Figueroa Problema 1 (10pts) Demuestra que para cualquier vector constante c se cumple que: ( c r)d l =
Electromagnetismo II Semestre: 2015-1 TAREA 9: Solución Dr. A. Reyes-Coronado Por: Jesús Castrejón Figueroa Problema 1 (10pts) Demuestra que para cualquier vector constante c se cumple que: ( c r)d l =
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (10)
 ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (10) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2006 INDUCCION DE FARADAY Al cambiar el flujo magnético enlazado
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (10) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2006 INDUCCION DE FARADAY Al cambiar el flujo magnético enlazado
Guía n 9: Materiales Magnéticos Ecuaciones de Maxwell Ondas Electromagnéticas
 Guía n 9: Materiales Magnéticos Ecuaciones de Maxwell Ondas Electromagnéticas Problema 1 Dos imanes permanentes iguales A y B, cuyo momento magnético es P m están situados como indica la figura. La distancia
Guía n 9: Materiales Magnéticos Ecuaciones de Maxwell Ondas Electromagnéticas Problema 1 Dos imanes permanentes iguales A y B, cuyo momento magnético es P m están situados como indica la figura. La distancia
Unidad Nº 10. Magnetismo
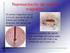 Unidad Nº 10 Magnetismo 10.1. Definición y propiedades del campo magnético. Fuerza magnética en una corriente. Movimiento de cargas en un campo magnético. 10.2. Campos magnéticos creados por corrientes.
Unidad Nº 10 Magnetismo 10.1. Definición y propiedades del campo magnético. Fuerza magnética en una corriente. Movimiento de cargas en un campo magnético. 10.2. Campos magnéticos creados por corrientes.
Método de Separación de Variables.
 FISICA TEORICA 1-2do. Cuatrimestre 2007 Método de Separación de Variables. 1. Se tiene un cubo conductor de lado a conectado a tierra. Calcular el potencial electrostático en todo punto del espacio dividiendo
FISICA TEORICA 1-2do. Cuatrimestre 2007 Método de Separación de Variables. 1. Se tiene un cubo conductor de lado a conectado a tierra. Calcular el potencial electrostático en todo punto del espacio dividiendo
Tema 2: Postulados del Electromagnetismo
 Tema 2: Postulados del Electromagnetismo 1 Índice La carga eléctrica Corriente eléctrica Ecuación de continuidad Ecuaciones de Maxwell en el vacío Fuerza de Lorentz Forma integral de las ecuaciones de
Tema 2: Postulados del Electromagnetismo 1 Índice La carga eléctrica Corriente eléctrica Ecuación de continuidad Ecuaciones de Maxwell en el vacío Fuerza de Lorentz Forma integral de las ecuaciones de
ELECTRICIDAD Y MAGNETISMO FIS 1532 (2)
 ELECTRICIDAD Y MAGNETISMO FIS 1532 (2) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2nd. Semestre 2010 Electrostática, Varias cargas puntuales CAMPO ELECTRICO DE VARIAS CARGAS
ELECTRICIDAD Y MAGNETISMO FIS 1532 (2) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2nd. Semestre 2010 Electrostática, Varias cargas puntuales CAMPO ELECTRICO DE VARIAS CARGAS
Guía de Ejercicios N o 2 FI2A2
 Guía de Ejercicios N o 2 FI2A2 Prof. Auxiliar: Felipe L. Benavides Problema 1 Continuidad de la Corriente y Evolución Temporal de Cargas Libres Considere un sistema formado por dos placas conductoras conectadas
Guía de Ejercicios N o 2 FI2A2 Prof. Auxiliar: Felipe L. Benavides Problema 1 Continuidad de la Corriente y Evolución Temporal de Cargas Libres Considere un sistema formado por dos placas conductoras conectadas
El campo magnético de las corrientes estacionarias
 El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
Electromagnetismo. Dino E.Risso Departamento de Física Universidad del Bío-Bío
 Electromagnetismo Dino E.Risso Departamento de Física Universidad del Bío-Bío 12 de abril de 2010 A nuestros alumnos. Este texto ha sido elaborado bajo el Proyecto de Docencia FDD2001-15 del Fondo de Desarrollo
Electromagnetismo Dino E.Risso Departamento de Física Universidad del Bío-Bío 12 de abril de 2010 A nuestros alumnos. Este texto ha sido elaborado bajo el Proyecto de Docencia FDD2001-15 del Fondo de Desarrollo
Teorema fundamental del cálculo vectorial (a.k.a. Teorema de Helmholtz)
 Teorema fundamental del cálculo vectorial (a.k.a. Teorema de Helmholtz) Brevísima y sesgada introducción para Física 3 Ariel Chernomoretz October 9, 207 El teorema de Helmholtz El siguiente teorema se
Teorema fundamental del cálculo vectorial (a.k.a. Teorema de Helmholtz) Brevísima y sesgada introducción para Física 3 Ariel Chernomoretz October 9, 207 El teorema de Helmholtz El siguiente teorema se
un sistema de conductores cargados. Energía electrostática en función de los vectores de campo. Fuerza electrostática. Presión electrostática.
 11 ÍNDICE GENERAL INTRODUCCIÓN 13 CÁLCULO VECTORIAL 17 Escalares y vectores. Operaciones con vectores. Campos escalares y vectoriales. Sistemas de coordenadas. Transformación de coordenadas. Vector de
11 ÍNDICE GENERAL INTRODUCCIÓN 13 CÁLCULO VECTORIAL 17 Escalares y vectores. Operaciones con vectores. Campos escalares y vectoriales. Sistemas de coordenadas. Transformación de coordenadas. Vector de
Inducción, cuasi-estacionario y leyes de conservación.
 Física Teórica 1 Guia 4 - Inducción y teoremas de conservación 1 cuat. 2014 Inducción, cuasi-estacionario y leyes de conservación. Aproximación cuasi-estacionaria. 1. Se tiene una espira circular de radio
Física Teórica 1 Guia 4 - Inducción y teoremas de conservación 1 cuat. 2014 Inducción, cuasi-estacionario y leyes de conservación. Aproximación cuasi-estacionaria. 1. Se tiene una espira circular de radio
Física 3: Septiembre-Diciembre 2011 Clase 13,Lunes 24 de octubre de 2011
 Clase 13 Potencial Eléctrico Cálculo del potencial eléctrico Ejemplo 35: Efecto punta En un conductor el campo eléctrico es mas intenso cerca de las puntas y protuberancias pues el exceso de carga tiende
Clase 13 Potencial Eléctrico Cálculo del potencial eléctrico Ejemplo 35: Efecto punta En un conductor el campo eléctrico es mas intenso cerca de las puntas y protuberancias pues el exceso de carga tiende
Resumen (i) Introducción. Dinámica del campo magnetostático. Qué es la electrodinámica? Magnetismo y electricidad: cargas en movimiento
 ELECTRODINÁMICA Resumen (i) Introducción Qué es la electrodinámica? Magnetismo y electricidad: cargas en movimiento Dinámica del campo magnetostático Fuentes del campo magnetostático: corrientes estacionarias
ELECTRODINÁMICA Resumen (i) Introducción Qué es la electrodinámica? Magnetismo y electricidad: cargas en movimiento Dinámica del campo magnetostático Fuentes del campo magnetostático: corrientes estacionarias
PROGRAMA DE CURSO. Horas de Trabajo Personal ,0 1,5 5,5. Horas de Cátedra
 Código FI2002 Nombre PROGRAMA DE CURSO Electromagnetismo Nombre en Inglés Electromagnetism SCT Unidades Docentes Horas de Cátedra Horas Docencia Auxiliar Horas de Trabajo Personal 6 10 3,0 1,5 5,5 Requisitos
Código FI2002 Nombre PROGRAMA DE CURSO Electromagnetismo Nombre en Inglés Electromagnetism SCT Unidades Docentes Horas de Cátedra Horas Docencia Auxiliar Horas de Trabajo Personal 6 10 3,0 1,5 5,5 Requisitos
Electromagnetismo. Introducción. Líneas de campo magnético. Experimento de Oersted. El campo magnético de las corrientes estacionarias
 El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (6)
 ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (6) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2008 Michael Faraday realizó el siguiente experimento. Construyó
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (6) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2008 Michael Faraday realizó el siguiente experimento. Construyó
Campo de un hilo infinito. Fuerzas magnéticas. Teorema de Ampère. Campo magnético de una espira circular
 El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
TEORIA ELECTROMAGNETICA FIZ 0321 (2)
 TEORIA ELECTROMAGNETICA FIZ 0321 (2) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2do. Semestre 2006 Solución de problemas de electrostática Ecuación de Laplace Coordenadas
TEORIA ELECTROMAGNETICA FIZ 0321 (2) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 2do. Semestre 2006 Solución de problemas de electrostática Ecuación de Laplace Coordenadas
INDICE 1. Sistemas de Coordenadas e Integrales 2. Gradiente, Divergente y Rotacional 3. Campos Electrostáticos
 INDICE Prefacio XVII 1. Sistemas de Coordenadas e Integrales 1 1.1. Conceptos generales 1 1.2. Coordenadas de un punto 2 1.3. Los campos escalares y cómo se transforman 4 1.4. Campos vectoriales y cómo
INDICE Prefacio XVII 1. Sistemas de Coordenadas e Integrales 1 1.1. Conceptos generales 1 1.2. Coordenadas de un punto 2 1.3. Los campos escalares y cómo se transforman 4 1.4. Campos vectoriales y cómo
Momento angular de una partícula. Momento angular de un sólido rígido
 Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
FISICA 2º BACHILLERATO CAMPO MAGNÉTICO E INDUCCIÓN ELECTROMAGNÉTICA
 A) CAMPO MAGNÉTICO El Campo Magnético es la perturbación que un imán o una corriente eléctrica producen en el espacio que los rodea. Esta perturbación del espacio se manifiesta en la fuerza magnética que
A) CAMPO MAGNÉTICO El Campo Magnético es la perturbación que un imán o una corriente eléctrica producen en el espacio que los rodea. Esta perturbación del espacio se manifiesta en la fuerza magnética que
Unidad Nº 10. Magnetismo
 Unidad Nº 10 Magnetismo 10.1. Definición y propiedades del campo magnético. Fuerza magnética en una corriente. Movimiento de cargas en un campo magnético. 10.2. Campos magnéticos creados por corrientes.
Unidad Nº 10 Magnetismo 10.1. Definición y propiedades del campo magnético. Fuerza magnética en una corriente. Movimiento de cargas en un campo magnético. 10.2. Campos magnéticos creados por corrientes.
Método de Separación de Variables.
 ISICA TEORICA 1 - do c 004 Método de Separación de Variables 1 Se tiene un cubo conductor de lado a conectado a tierra Calcular el potencial electrostático en todo punto del espacio dividiendo la región
ISICA TEORICA 1 - do c 004 Método de Separación de Variables 1 Se tiene un cubo conductor de lado a conectado a tierra Calcular el potencial electrostático en todo punto del espacio dividiendo la región
Cap. 1.- Leyes de Maxwell en forma diferencial e integral
 Asignatura : Teoría Electromagnética CALENDARIZACIÓN DE CONTENIDOS Modalidad Presencial 018 Resultado Aprendizaje la Asignatura: Al finalizar la asignatura, el estudiante será capaz aplicar la ley Maxwell,
Asignatura : Teoría Electromagnética CALENDARIZACIÓN DE CONTENIDOS Modalidad Presencial 018 Resultado Aprendizaje la Asignatura: Al finalizar la asignatura, el estudiante será capaz aplicar la ley Maxwell,
ELECTROMAGNETISMO I El Rotor de H. ELECTROMAGNETISMO I El Rotor de H
 El Rotor de H Escribamos la expresión para Iy.. =? + + + + + + = = esto es igual a la corriente dentro del área analizada 139 El Rotor de H Dividiendo ambos miembros por el área dxdz y tomando el límite
El Rotor de H Escribamos la expresión para Iy.. =? + + + + + + = = esto es igual a la corriente dentro del área analizada 139 El Rotor de H Dividiendo ambos miembros por el área dxdz y tomando el límite
Capítulo 3: Campos Electromagnéticos Estáticos
 Capítulo 3: Campos Electromagnéticos Estáticos Flujo de un campo vectorial Superficie cerrada Ley de Gauss Karl Friedrich Gauss (1777-1855) Flujo de E generado por una carga puntual Superficie arbitraria
Capítulo 3: Campos Electromagnéticos Estáticos Flujo de un campo vectorial Superficie cerrada Ley de Gauss Karl Friedrich Gauss (1777-1855) Flujo de E generado por una carga puntual Superficie arbitraria
Medios materiales y desarrollo multipolar.
 Física Teórica 1 Guia 3 - Medios materiales y multipolos 1 cuat. 2014 Medios materiales y desarrollo multipolar. Medios materiales. 1. Una esfera de radio a está uniformemente magnetizada con densidad
Física Teórica 1 Guia 3 - Medios materiales y multipolos 1 cuat. 2014 Medios materiales y desarrollo multipolar. Medios materiales. 1. Una esfera de radio a está uniformemente magnetizada con densidad
ECUACIONES DE MAXWELL
 ECUACIONE DE MAXWELL Prof. Juan Carlos Muñoz ECUACIONE DE MAXWELL Los fenómenos eléctricos y magnéticos fueron analizados por James Clerk Maxwell en 1864 y comprobado experimentalmente varios años después.
ECUACIONE DE MAXWELL Prof. Juan Carlos Muñoz ECUACIONE DE MAXWELL Los fenómenos eléctricos y magnéticos fueron analizados por James Clerk Maxwell en 1864 y comprobado experimentalmente varios años después.
donde n es un vector unitario normal al área a y dirigido según la regla de mano derecha, con respecto a la dirección de flujo de la corriente I.
 Magnetización. Antes se habló de un dipolo eléctrico una carga positiva +q y una carga negativa -q de igual magnitud separadas por una distancia d. Un dipolo magnético se forma cuando una corriente I circula
Magnetización. Antes se habló de un dipolo eléctrico una carga positiva +q y una carga negativa -q de igual magnitud separadas por una distancia d. Un dipolo magnético se forma cuando una corriente I circula
Tema 8: Magnetostática
 Tema 8: Magnetostática Dr. José Manuel Aller Castro Universidad Politécnica Salesiana Cuenca, Abril 2015 Introducción En este tema se trata con el problema de calcular el campo magnético conocida la densidad
Tema 8: Magnetostática Dr. José Manuel Aller Castro Universidad Politécnica Salesiana Cuenca, Abril 2015 Introducción En este tema se trata con el problema de calcular el campo magnético conocida la densidad
8 Teorema de Ampère, ley de Gauss
 8 Teorema de Ampère, ley de Gauss 3 Teorema de Ampère, ley de Gauss 8.1 Teorema de Ampère 186 La ley de Ampère es una de las leyes fundamentales de la magnetostática, y juega un rol equivalente al de la
8 Teorema de Ampère, ley de Gauss 3 Teorema de Ampère, ley de Gauss 8.1 Teorema de Ampère 186 La ley de Ampère es una de las leyes fundamentales de la magnetostática, y juega un rol equivalente al de la
APUNTES DE FÍSICA II Profesor: José Fernando Pinto Parra UNIDAD 10 EL CAMPO MAGNETICO DEFINICIÓN DEL VECTOR INDUCCIÓN MAGNÉTICA Y DEL CAMPO MAGNÉTICO.
 APUNTES DE FÍSICA II Profesor: José Fernando Pinto Parra UNIDAD 10 EL CAMPO MAGNETICO DEFINICIÓN DEL VECTOR INDUCCIÓN MAGNÉTICA Y DEL CAMPO MAGNÉTICO. Todos hemos observado como un imán atrae objetos de
APUNTES DE FÍSICA II Profesor: José Fernando Pinto Parra UNIDAD 10 EL CAMPO MAGNETICO DEFINICIÓN DEL VECTOR INDUCCIÓN MAGNÉTICA Y DEL CAMPO MAGNÉTICO. Todos hemos observado como un imán atrae objetos de
Sílabo de Teoría electromagnética
 Sílabo de Teoría electromagnética I. Datos generales Código ASUC 01062 Carácter Obligatorio Créditos 2017 Periodo académico 3 Prerrequisito Ninguno Horas Teóricas 2 Prácticas 2 II. Sumilla de la asignatura
Sílabo de Teoría electromagnética I. Datos generales Código ASUC 01062 Carácter Obligatorio Créditos 2017 Periodo académico 3 Prerrequisito Ninguno Horas Teóricas 2 Prácticas 2 II. Sumilla de la asignatura
Análisis II - Análisis matemático II - Matemática 3 2do. cuatrimestre de 2013
 Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Leyes básicas de la teoría electromagética
 Divergencia = xî + y ĵ + z k Rotacional î ĵ k = x y z F x F y F z Leyes básicas de la teoría electromagética Ley de inducción de Faraday C d l =- d S Ley de Gauss d S = 1 ɛ V ρdv Ley de Gauss magnética
Divergencia = xî + y ĵ + z k Rotacional î ĵ k = x y z F x F y F z Leyes básicas de la teoría electromagética Ley de inducción de Faraday C d l =- d S Ley de Gauss d S = 1 ɛ V ρdv Ley de Gauss magnética
FIS1533/FIZ I1
 FIS1533/FIZ0221 - I1 Facultad de Física Pontificia Universidad Católica de Chile Segundo Semestre 2016-16 de Septiembre Tiempo para responder: 120 minutos Nombre: Sección: Buenas Malas Blancas Nota Instrucciones
FIS1533/FIZ0221 - I1 Facultad de Física Pontificia Universidad Católica de Chile Segundo Semestre 2016-16 de Septiembre Tiempo para responder: 120 minutos Nombre: Sección: Buenas Malas Blancas Nota Instrucciones
El campo magnético en los medios materiales. Tema 10 Electromagnetismo Grupo C
 El campo magnético en los medios materiales Tema 10 Electromagnetismo Grupo C El campo magnético y la materia El átomo como un dipolo magnético Imanación y corrientes de imanación Teorema de Àmpere para
El campo magnético en los medios materiales Tema 10 Electromagnetismo Grupo C El campo magnético y la materia El átomo como un dipolo magnético Imanación y corrientes de imanación Teorema de Àmpere para
Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère
 c Rafael R. Boix y Francisco Medina 1 Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère Consideremos un conductor que ocupa un volumen τ. Sea r el vector de posición de
c Rafael R. Boix y Francisco Medina 1 Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère Consideremos un conductor que ocupa un volumen τ. Sea r el vector de posición de
Repaso de electrostática y magnetostática. 1. En cada una de las siguientes distribuciones de carga:
 Física Teórica 1 Guia 1 - Repaso 1 cuat. 2015 Repaso de electrostática y magnetostática. Transformaciones de simetría. Ley de Gauss. Ley de Ampere. 1. En cada una de las siguientes distribuciones de carga:
Física Teórica 1 Guia 1 - Repaso 1 cuat. 2015 Repaso de electrostática y magnetostática. Transformaciones de simetría. Ley de Gauss. Ley de Ampere. 1. En cada una de las siguientes distribuciones de carga:
Pseudo-resumen de Electromagnetismo
 Pseudo-resumen de Electromagnetismo Álvaro Bustos Gajardo Versión 0.6β, al 27 de Octubre de 2011 1. Cargas. Ley de Coulomb 1.1. Carga eléctrica La carga eléctrica es una propiedad cuantitativa de la materia,
Pseudo-resumen de Electromagnetismo Álvaro Bustos Gajardo Versión 0.6β, al 27 de Octubre de 2011 1. Cargas. Ley de Coulomb 1.1. Carga eléctrica La carga eléctrica es una propiedad cuantitativa de la materia,
CAPÍTULO VI Magnetostática
 APÍTULO VI Magnetostática Fundamento teórico I.- Fuerza sobre una carga y movimiento de una carga en un campo magnético Ia.- Fuerza magnética sobre una carga eléctrica Dada una carga eléctrica q que se
APÍTULO VI Magnetostática Fundamento teórico I.- Fuerza sobre una carga y movimiento de una carga en un campo magnético Ia.- Fuerza magnética sobre una carga eléctrica Dada una carga eléctrica q que se
Universidad Nacional Jorge Basadre Grohmann
 Universidad Nacional Jorge Basadre Grohmann Facultad de Ciencias ELECTRICIDAD Y MAGNETISMO Fis. Salvador Eligio del Castillo Lic. Manuel Antonio Tapia Silva Tacna Perú 2003 PROPIEDADES ELÉCTRICAS Y MAGNÉTICAS
Universidad Nacional Jorge Basadre Grohmann Facultad de Ciencias ELECTRICIDAD Y MAGNETISMO Fis. Salvador Eligio del Castillo Lic. Manuel Antonio Tapia Silva Tacna Perú 2003 PROPIEDADES ELÉCTRICAS Y MAGNÉTICAS
Teoremas que se derivan de las ecuaciones de Poisson y Laplace.
 c Rafael R. Boix y Francisco Medina Teoremas que se derivan de las ecuaciones de Poisson y Laplace. Identidades de Green Consideremos dos campos escalares u = u(r) y v = v(r).teniendo en cuenta que se
c Rafael R. Boix y Francisco Medina Teoremas que se derivan de las ecuaciones de Poisson y Laplace. Identidades de Green Consideremos dos campos escalares u = u(r) y v = v(r).teniendo en cuenta que se
Tema 3: Campos estáticos
 Tema 3: Campos estáticos 1 Índice Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
Tema 3: Campos estáticos 1 Índice Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
FÍSICA - 2º BACHILLERATO CAMPO MAGNÉTICO RESUMEN EVIDENCIA EXPERIMENTAL ACERCA DEL MAGNETISMO
 Física 2º Bachillerato Campo Magnético - 1 FÍSICA - 2º BACHILLERATO CAMPO MAGNÉTICO RESUMEN EVIDENCIA EXPERIMENTAL ACERCA DEL MAGNETISMO 1. Existen ciertos cuerpos llamados imanes (naturales y artificiales)
Física 2º Bachillerato Campo Magnético - 1 FÍSICA - 2º BACHILLERATO CAMPO MAGNÉTICO RESUMEN EVIDENCIA EXPERIMENTAL ACERCA DEL MAGNETISMO 1. Existen ciertos cuerpos llamados imanes (naturales y artificiales)
Ayudantía 23. Fuerza magnética sobre conductores, torque magnético y Ley de Ampere 31 de Mayo de 2018 Ayudante: Matías Henríquez -
 Pontificia Universidad Católica de Chile Facultad de Física FIS15 - Electricidad y Magnetismo // 1-2018 Profesor: Giuseppe De Nittis - gidenittis@uc.cl Ayudantía 2 Fuerza magnética sobre conductores, torque
Pontificia Universidad Católica de Chile Facultad de Física FIS15 - Electricidad y Magnetismo // 1-2018 Profesor: Giuseppe De Nittis - gidenittis@uc.cl Ayudantía 2 Fuerza magnética sobre conductores, torque
La Ley de Inducción de Faraday
 La Ley de Inducción de Faraday 1. La Ley de Faraday. Ley de Lenz Consideremos un circuito cerrado C, como el mostrado en Fig. 1, formado por un alambre conductor. Supongamos que existe un campo magnético
La Ley de Inducción de Faraday 1. La Ley de Faraday. Ley de Lenz Consideremos un circuito cerrado C, como el mostrado en Fig. 1, formado por un alambre conductor. Supongamos que existe un campo magnético
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Operadores diferenciales
 Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
Ejercicios resueltos de FISICA II que se incluyen en la Guía de la Asignatura
 Ejercicios resueltos de FISICA II que se incluyen en la Guía de la Asignatura Módulo 2. Campo electrostático 4. Consideremos dos superficies gaussianas esféricas, una de radio r y otra de radio 2r, que
Ejercicios resueltos de FISICA II que se incluyen en la Guía de la Asignatura Módulo 2. Campo electrostático 4. Consideremos dos superficies gaussianas esféricas, una de radio r y otra de radio 2r, que
Lección 3. El campo de las corrientes estacionarias. El campo magnetostático.
 Lección 3. El campo de las corrientes estacionarias. El campo magnetostático. 81. Un campo vectorial está definido por B = B 0 u x (r < a) B r = A cos ϕ ; B r 2 ϕ = C sin ϕ (r > a) r 2 donde r y ϕ son
Lección 3. El campo de las corrientes estacionarias. El campo magnetostático. 81. Un campo vectorial está definido por B = B 0 u x (r < a) B r = A cos ϕ ; B r 2 ϕ = C sin ϕ (r > a) r 2 donde r y ϕ son
FÍSICA GENERAL III - CURSO 2013 Práctica 6: Magnetostática.
 FÍSICA GENERAL III - CURSO 2013 Práctica 6: Magnetostática. 1- Considere un circuito cerrado situado sobre cierta curva C, por el que circula una corriente constante I. En su entorno se genera un campo
FÍSICA GENERAL III - CURSO 2013 Práctica 6: Magnetostática. 1- Considere un circuito cerrado situado sobre cierta curva C, por el que circula una corriente constante I. En su entorno se genera un campo
I. T. Telecomunicaciones Universidad de Alcalá
 I. T. Telecomunicaciones Universidad de Alcalá Soluciones al Examen de Física Septiembre 2006 Departamento de Física P1) La figura muestra una región limitada por los planos x = 0, y = 0, x = 10 cm, y
I. T. Telecomunicaciones Universidad de Alcalá Soluciones al Examen de Física Septiembre 2006 Departamento de Física P1) La figura muestra una región limitada por los planos x = 0, y = 0, x = 10 cm, y
ACTA DE CONSEJO DE FACULTAD/DEPTO./CENTRO: ÁREA/MÓDULO: CIENCIAS BÁSICAS PRERREQUISITOS/CORREQUISITOS: FÍSICA BÁSICA Y LABORATORIO VERSIÓN: UNO
 Página 1 de 6 PROGRAMA: INGENIERÍA DE TELECOMUNICACIONES PLAN DE ESTUDIOS: 4 ACTA DE CONSEJO DE FACULTAD/DEPTO./CENTRO: 68 1. DATOS GENERALES ASIGNATURA/MÓDULO/SEMINARIO: ELECTRICIDAD, MAGNETISMO Y LABORATORIO
Página 1 de 6 PROGRAMA: INGENIERÍA DE TELECOMUNICACIONES PLAN DE ESTUDIOS: 4 ACTA DE CONSEJO DE FACULTAD/DEPTO./CENTRO: 68 1. DATOS GENERALES ASIGNATURA/MÓDULO/SEMINARIO: ELECTRICIDAD, MAGNETISMO Y LABORATORIO
La ley de Biot-Savart
 La ley de Biot-Savart La ley de Biot-Savart calcula el campo producido por un elemento dl de la corriente de intensidad I en un punto P distante r de dicho elemento. La densidad de flujo magnético infinitesimal
La ley de Biot-Savart La ley de Biot-Savart calcula el campo producido por un elemento dl de la corriente de intensidad I en un punto P distante r de dicho elemento. La densidad de flujo magnético infinitesimal
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA AERONÁUTICA Y DEL ESPACIO FÍSICA II
 ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA AERONÁUTICA Y DEL ESPACIO FÍSICA II PROBLEMAS RESUELTOS José Carlos JIMÉNEZ SÁEZ Santiago RAMÍREZ DE LA PISCINA MILLÁN 7.- MAGNETOSTÁTICA DE MEDIOS MATERIALES 7 Magnetostática
ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA AERONÁUTICA Y DEL ESPACIO FÍSICA II PROBLEMAS RESUELTOS José Carlos JIMÉNEZ SÁEZ Santiago RAMÍREZ DE LA PISCINA MILLÁN 7.- MAGNETOSTÁTICA DE MEDIOS MATERIALES 7 Magnetostática
Ayudantía 12. b) La densidad de cargas en la interfaz de los materiales. (Desprecie efectos de borde). Figura 1:
 Pontificia Universidad Católica de Chile Facultad de Física FIS1533 - Electricidad y Magnetismo Profesor: Máximo Bañados Ayudante: Alonso Ruiz (airuiz@uc.cl) Problema 1 Ayudantía 12 Considere 2 placas
Pontificia Universidad Católica de Chile Facultad de Física FIS1533 - Electricidad y Magnetismo Profesor: Máximo Bañados Ayudante: Alonso Ruiz (airuiz@uc.cl) Problema 1 Ayudantía 12 Considere 2 placas
Tema 3: Campos estáticos
 Tema 3: Campos estáticos 1 Índice (I) Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
Tema 3: Campos estáticos 1 Índice (I) Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
LEY DE COULOMB E INTENSIDAD DE CAMPO ELECTRICO
 INDICE Prefacio XIV Visita Guiada 1 Análisis Vectorial 1 2 Ley Coulomb e Intensidad de Campo Eléctrico 26 3 Densidad de Flujo Eléctrico, Ley de Gauss y Divergencia 51 4 Energía y Potencial 80 5 Corriente
INDICE Prefacio XIV Visita Guiada 1 Análisis Vectorial 1 2 Ley Coulomb e Intensidad de Campo Eléctrico 26 3 Densidad de Flujo Eléctrico, Ley de Gauss y Divergencia 51 4 Energía y Potencial 80 5 Corriente
Física 3: Septiembre-Diciembre de 2011 Clase 11, Lunes 17 de octubre de 2011
 Clase 11 Potencial Eléctrico Fuerza y campo eléctrico El campo eléctrico presente en una determinada región del espacio actúa sobre la materia cargada en esa región modificando su comportamiento dinámico.
Clase 11 Potencial Eléctrico Fuerza y campo eléctrico El campo eléctrico presente en una determinada región del espacio actúa sobre la materia cargada en esa región modificando su comportamiento dinámico.
SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN
 SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN Sistemas de coordenadas 3D Transformaciones entre sistemas Integrales de línea y superficie SISTEMA COORDENADO CARTESIANO O RECTANGULAR
SEMINARIO 1: ELEMENTOS DIFERENCIALES DE LÍNEA, SUPERFICIE Y VOLUMEN Sistemas de coordenadas 3D Transformaciones entre sistemas Integrales de línea y superficie SISTEMA COORDENADO CARTESIANO O RECTANGULAR
Repaso de Electromagnetismo (Campos I)
 Repaso de Electromagnetismo (Campos I) RADIOCOMUNICACIÓN-Onda radioeléctrica RADIOCOMUNICACIÓN: Comunicación a distancia por medio de las ondas radioeléctricas Onda radioeléctrica: Ondas electromagnéticas
Repaso de Electromagnetismo (Campos I) RADIOCOMUNICACIÓN-Onda radioeléctrica RADIOCOMUNICACIÓN: Comunicación a distancia por medio de las ondas radioeléctricas Onda radioeléctrica: Ondas electromagnéticas
Electricidad y Magnetismo FIS 1533
 Electricidad y Magnetismo FIS 1533 Benjamin Koch bkoch@fis.puc.cl Pontificia Universidad Católica, Chile 2012 Benjamin Koch (PUC, Chile) EM 2012 1 / 40 Contenido 1 Carga Eléctrica y Campo Eléctrico 2 Ley
Electricidad y Magnetismo FIS 1533 Benjamin Koch bkoch@fis.puc.cl Pontificia Universidad Católica, Chile 2012 Benjamin Koch (PUC, Chile) EM 2012 1 / 40 Contenido 1 Carga Eléctrica y Campo Eléctrico 2 Ley
Figura 1.1 Dos espiras acopladas magnéticamente. Figura 1.2 Dos espiras acopladas magnéticamente.(a) Geometría. (b) Circuito equivalente.
 Inductancia Figura 1.1 Dos espiras acopladas magnéticamente Figura 1.2 Dos espiras acopladas magnéticamente.(a) Geometría. (b) Circuito equivalente. La ley de Faraday predice que un voltaje puede inducirse
Inductancia Figura 1.1 Dos espiras acopladas magnéticamente Figura 1.2 Dos espiras acopladas magnéticamente.(a) Geometría. (b) Circuito equivalente. La ley de Faraday predice que un voltaje puede inducirse
Física 2º Bach. Se calcula la intensidad de campo eléctrico en el punto G debido a cada una de las cargas:
 Física 2º ach. Campos electrostático y magnético 16/03/05 DEPARTAMENTO DE FÍSCA E QUÍMCA Problemas Nombre: [2 PUNTOS /UNO] 1. Calcula: a) la intensidad del campo eléctrico en el centro del lado derecho
Física 2º ach. Campos electrostático y magnético 16/03/05 DEPARTAMENTO DE FÍSCA E QUÍMCA Problemas Nombre: [2 PUNTOS /UNO] 1. Calcula: a) la intensidad del campo eléctrico en el centro del lado derecho
CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA
 CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA Este documento enuncia de forma más detallada la formulación matemática que permite el estudio de campos eléctricos debido a distribuciones
CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA Este documento enuncia de forma más detallada la formulación matemática que permite el estudio de campos eléctricos debido a distribuciones
Cap. 32: Ecuaciones de Maxwell, Magnetismo en la Materia
 Cap. 32: cuaciones de Maxwell, Magnetismo en la Materia n el caso eléctrico, la estructura básica es una carga aislada. Dos cargas de igual magnitud, pero signos opuestos, separadas por una distancia d,
Cap. 32: cuaciones de Maxwell, Magnetismo en la Materia n el caso eléctrico, la estructura básica es una carga aislada. Dos cargas de igual magnitud, pero signos opuestos, separadas por una distancia d,
r = r + a O O y r y r son los vectores de posición de los puntos de la distribución con respecto a cada uno de los orígenes.
 192 5.3. Problemas 5-1. Demuestre: a) Que si la carga total Q de una distribución es nula, el momento dipolar no depende del origen. b) Que si Q = 0 y p = 0, el momento cuadripolar tampoco depende del
192 5.3. Problemas 5-1. Demuestre: a) Que si la carga total Q de una distribución es nula, el momento dipolar no depende del origen. b) Que si Q = 0 y p = 0, el momento cuadripolar tampoco depende del
GRADO: Grado en Ingeniería Electrónica Industrial y Automática CURSO: PRIMERO CUATRIMESTRE: 2º PLANIFICACIÓN SEMANAL DE LA ASIGNATURA
 SESIÓN SEMANA DENOMINACIÓN ASIGNATURA: FISICA II GRADO: Grado en Ingeniería Electrónica Industrial y Automática CURSO: PRIMERO CUATRIMESTRE: 2º PLANIFICACIÓN SEMANAL DE LA ASIGNATURA DESCRIPCIÓN DEL CONTENIDO
SESIÓN SEMANA DENOMINACIÓN ASIGNATURA: FISICA II GRADO: Grado en Ingeniería Electrónica Industrial y Automática CURSO: PRIMERO CUATRIMESTRE: 2º PLANIFICACIÓN SEMANAL DE LA ASIGNATURA DESCRIPCIÓN DEL CONTENIDO
Unidad 20: Campo magnético
 Apoyo para la preparación de los estudios de Ingeniería y Arquitectura Física (Preparación a la Universidad) Unidad 20: Campo magnético Universidad Politécnica de Madrid 13 de mayo de 2010 2 20.1. Planificación
Apoyo para la preparación de los estudios de Ingeniería y Arquitectura Física (Preparación a la Universidad) Unidad 20: Campo magnético Universidad Politécnica de Madrid 13 de mayo de 2010 2 20.1. Planificación
Temario 4.Campo Eléctrico
 Campo Eléctrico 1 1 Temario 4.Campo Eléctrico 4.1 Concepto y definición de campo eléctrico 4.2 Campo eléctrico producido por una y varias cargas puntuales. 4.3 Lineas de Campo 4.4 Un conductor eléctrico
Campo Eléctrico 1 1 Temario 4.Campo Eléctrico 4.1 Concepto y definición de campo eléctrico 4.2 Campo eléctrico producido por una y varias cargas puntuales. 4.3 Lineas de Campo 4.4 Un conductor eléctrico
Capítulo 2: Formulación matemática del problema
 Capítulo : Formulación matemática del problema. Introducción El análisis del comportamiento en régimen permanente o transitorio de una red de puesta a tierra se fundamenta en la teoría electromagnética
Capítulo : Formulación matemática del problema. Introducción El análisis del comportamiento en régimen permanente o transitorio de una red de puesta a tierra se fundamenta en la teoría electromagnética
FUNDAMENTOS DE INGENIERÍA ELÉCTRICA. José Francisco Gómez González Benjamín González Díaz María de la Peña Fabiani Bendicho Ernesto Pereda de Pablo
 FUNDAMENTOS DE INGENIERÍA ELÉCTRICA José Francisco Gómez González Benjamín González Díaz María de la Peña Fabiani Bendicho Ernesto Pereda de Pablo Tema 5: Fundamentos de electrotecnia PUNTOS OBJETO DE
FUNDAMENTOS DE INGENIERÍA ELÉCTRICA José Francisco Gómez González Benjamín González Díaz María de la Peña Fabiani Bendicho Ernesto Pereda de Pablo Tema 5: Fundamentos de electrotecnia PUNTOS OBJETO DE
1.1. Corrientes y resistencias Ecuación de continuidad fem y efecto Joule... 3
 .1 Parte II Magnétostática Índice II Magnétostática 1 1. Corriente eléctrica y ley de Ohm 1 1.1. Corrientes y resistencias....................... 1 1.2. Ecuación de continuidad....................... 2
.1 Parte II Magnétostática Índice II Magnétostática 1 1. Corriente eléctrica y ley de Ohm 1 1.1. Corrientes y resistencias....................... 1 1.2. Ecuación de continuidad....................... 2
TEMA 7 Magnetismo en medios materiales
 TEMA 7 Magnetismo en medios materiales 7. 1 Magnetización, campo H, densidad de corriente de magnetización 7.2 Respuesta a un campo magnético aplicado: susceptibilidad y permeabilidad magnéticas 7.3 Materiales
TEMA 7 Magnetismo en medios materiales 7. 1 Magnetización, campo H, densidad de corriente de magnetización 7.2 Respuesta a un campo magnético aplicado: susceptibilidad y permeabilidad magnéticas 7.3 Materiales
FÍSICA GENERAL II Programación. Contenidos
 UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA 1 er Semestre 2011 FÍSICA GENERAL II Programación 1. Control 1: fecha 01 de abril, contenido: Módulos 1, 2 y 3(parcial: determinar diferencias de potencial a partir
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARIA 1 er Semestre 2011 FÍSICA GENERAL II Programación 1. Control 1: fecha 01 de abril, contenido: Módulos 1, 2 y 3(parcial: determinar diferencias de potencial a partir
Desarrollo multipolar del potencial.
 c Rafael R. Boix y Francisco Medina Desarrollo multipolar del potencial. Consideremos un cuerpo cargado que ocupa una región volumétrica. Sea ρ(r ) la densidad volumétrica de carga del cuerpo cargado.
c Rafael R. Boix y Francisco Medina Desarrollo multipolar del potencial. Consideremos un cuerpo cargado que ocupa una región volumétrica. Sea ρ(r ) la densidad volumétrica de carga del cuerpo cargado.
Período Vigente: 2005
 Tópicos de Física General (0333), Redes Eléctricas I (2107), Cálculo Vectorial (025) PAG.: 1 PROPÓSITO La finalidad de esta asignatura es presentar en una forma clara y directa las leyes generales que
Tópicos de Física General (0333), Redes Eléctricas I (2107), Cálculo Vectorial (025) PAG.: 1 PROPÓSITO La finalidad de esta asignatura es presentar en una forma clara y directa las leyes generales que
Instituto de Física Universidad de Guanajuato Agosto 2007
 Instituto de Física Universidad de Guanajuato Agosto 2007 Física III Capítulo I José Luis Lucio Martínez El material que se presenta en estas notas se encuentra, en su mayor parte, en las referencias que
Instituto de Física Universidad de Guanajuato Agosto 2007 Física III Capítulo I José Luis Lucio Martínez El material que se presenta en estas notas se encuentra, en su mayor parte, en las referencias que
Figura Trabajo de las fuerzas eléctricas al desplazar en Δ la carga q.
 1.4. Trabajo en un campo eléctrico. Potencial Clases de Electromagnetismo. Ariel Becerra Al desplazar una carga de prueba q en un campo eléctrico, las fuerzas eléctricas realizan un trabajo. Este trabajo
1.4. Trabajo en un campo eléctrico. Potencial Clases de Electromagnetismo. Ariel Becerra Al desplazar una carga de prueba q en un campo eléctrico, las fuerzas eléctricas realizan un trabajo. Este trabajo
Ayudantía 13. A = 1, Ωm m = 0,26 Ω 0,26 Ω = 1, W
 Pontificia Universidad Católica de Chile Facultad de Física FIS533 Electricidad y Magnetismo Profesor: Máximo Bañados Ayudante: Felipe Canales, correo: facanales@uc.cl Ayudantía 3 Problema. En el sistema
Pontificia Universidad Católica de Chile Facultad de Física FIS533 Electricidad y Magnetismo Profesor: Máximo Bañados Ayudante: Felipe Canales, correo: facanales@uc.cl Ayudantía 3 Problema. En el sistema
1. INTRODUCCIÓN HISTÓRICA. Gilbert ( ) descubrió que la electrificación era un fenómeno de carácter general.
 ELECTROSTÁTICA 1 Introducción. 2 Carga eléctrica. 3 Ley de Coulomb. 4 Campo eléctrico y principio de superposición. 5 Líneas de campo eléctrico. 6 Flujo eléctrico. 7 Teorema de Gauss. Aplicaciones.. 1.
ELECTROSTÁTICA 1 Introducción. 2 Carga eléctrica. 3 Ley de Coulomb. 4 Campo eléctrico y principio de superposición. 5 Líneas de campo eléctrico. 6 Flujo eléctrico. 7 Teorema de Gauss. Aplicaciones.. 1.
Potencial escalar magnético y cargas de magnetización. Cálculo de la intensidad magnética en ausencia de corrientes libres.
 c Rafael R. Boix y Francisco Medina 1 Potencial escalar magnético y cargas de magnetización. Cálculo de la intensidad magnética en ausencia de corrientes libres. Consideremos un cuerpo magnetizado en ausencia
c Rafael R. Boix y Francisco Medina 1 Potencial escalar magnético y cargas de magnetización. Cálculo de la intensidad magnética en ausencia de corrientes libres. Consideremos un cuerpo magnetizado en ausencia
Electromagnetismo I. 1.- Problema: (25pts)
 Electromagnetismo I emestre: 2015-2 Prof. Alejandro Reyes Coronado Ayud. Carlos Alberto Maciel Escudero Ayud. Christian Esparza López olución del Examen Final olución por Carlos Maciel Escudero 1.- Problema:
Electromagnetismo I emestre: 2015-2 Prof. Alejandro Reyes Coronado Ayud. Carlos Alberto Maciel Escudero Ayud. Christian Esparza López olución del Examen Final olución por Carlos Maciel Escudero 1.- Problema:
Electromagnetismo I. Semestre: TAREA 9 Dr. A. Reyes-Coronado
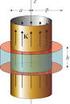
 Electromagnetismo I Semestre: 204-2 TAREA 9 Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruíz.- Problema: (5pts) Un cilindro infinito de radio a posee una magnetización fija paralela a su eje,
Electromagnetismo I Semestre: 204-2 TAREA 9 Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruíz.- Problema: (5pts) Un cilindro infinito de radio a posee una magnetización fija paralela a su eje,
Física II Ecuaciones de Maxwell. Ingeniería Electrónica Departamento de Ciencias Aplicadas y Tecnología Universidad Nacional de Moreno
 Departamento de Ciencias Aplicadas y Tecnología 30 de noviembre de 2015 Índice 1. Repaso de las ecuaciones 1 1.1. ey de Gauss para el campo electrostático....................... 1 1.2. ey de Gauss para
Departamento de Ciencias Aplicadas y Tecnología 30 de noviembre de 2015 Índice 1. Repaso de las ecuaciones 1 1.1. ey de Gauss para el campo electrostático....................... 1 1.2. ey de Gauss para
Física 3. Segundo Cuatrimestre 6 de septiembre de 2017
 Si la aplicación de electricidad a una momia cuya antigüedad se remontaba por lo menos a tres o cuatro mil años no era demasiado sensata, resultaba en cambio lo bastante original como para que todos aprobáramos
Si la aplicación de electricidad a una momia cuya antigüedad se remontaba por lo menos a tres o cuatro mil años no era demasiado sensata, resultaba en cambio lo bastante original como para que todos aprobáramos
