Variables Estadísticas Bidimensionales
|
|
|
- Ignacio Acosta Correa
- hace 7 años
- Vistas:
Transcripción
1 Relación de problemas 3 Variables Estadísticas Bidimensionales 1. En una encuesta realizada a 480 familias se han obtenido los siguientes datos en euros sobre los ingresos mensuales (X) y depósitos de Bancos y Cajas de Ahorros (Y ) X / Y a) Obtener las distribuciones marginales. b) Calcular la media y la varianza de las distribuciones marginales. c) Qué distribución es más homogénea? d) Qué porcentaje de familias poseen unos ingresos mensuales comprendidos entre 1500 y 2500? e) Obtener la distribución de los ingresos mensuales para familias con depósitos superiores a A partir de los siguientes datos: x y a) Representar los datos en una tabla de doble entrada. b) Calcular las medias y varianzas marginales. c) Calcular la covarianza. 3. Se eligen 50 matrimonios al azar y se les pregunta la edad de la mujer al casarse (X) y la del hombre (Y ), obteniendo la siguiente tabla: X / Y
2 12 a) Edad media de los hombres al casarse. b) Edad media de las mujeres al casarse. c) Porcentaje de mujeres que se casaron entre los 18 y 24 años. d) Edad más frecuente a la que los hombres y mujeres se casan. 4. Dada la siguiente distribución de frecuencias: X / Y Calcular la covarianza, son estadísticamente independientes las variables X e Y? 5. En una encuesta realizada a 100 familias en la cual se estudian los ingresos (X) y los gastos (Y ), se obtuvieron los siguientes datos representados en una tabla de doble entrada: X / Y a) En las familias que no superen las 1800 euros de ingresos, calcular qué cantidad se gasta con más frecuencia. b) Una entidad bancaria pretende que el 40% central de las nóminas sea domiciliado. Calcular el valor máximo y el mínimo de este intervalo. c) Si una empresa quiere realizar una campaña con aquellas familias que ingresen más de 1600 euros, qué porcentaje de familias serán objetivo de esta campaña? 6. Los gastos en telefonía fija, móvil e internet de una serie de familias, medidos en euros, durante el invierno (X) y durante el verano (Y ) se indican a continuación: Se pide (X, Y ) [100, 2550] (250, 400] (400, 550] [100,250] (250,400] (400,550] a) Calcular las medias y varianzas marginales de los consumos en invierno y en verano. b) Calcular la distribución condicionada del consumo en los meses de invierno cuando en verano se consume una cantidad igual o menor a 400 euros, así como la media y varianza de esta distribución. c) Cuál es el porcentaje de personas que gastan menos de 300 euros en invierno si en verano han gastado más de 400? 7. Se han medido la capacidad pulmonar (X) y el perímetro torácico (Y ) de 20 atletas obteniéndose los siguientes resultados: Relación de problemas de Estadística Curso
3 13 (X,Y ) [1, 1.10] (1.10, 1.40] (1.4, 1.70] (1.70, 1.80] [1.80,1.85] (1.85,1.90] (1.90,2.00] (2.00,2.30] Se pide a) Obtener la distribución marginal de la variable X. b) Cuántos atletas tienen una capacidad pulmonar mayor de 2 y un perímetro torácico mayor de 1.40? c) Cuál es la capacidad media pulmonar de los atletas que tienen un perímetro torácico inferior a 1.40? d) Calcular la covarianza entre estas variables. 8. Dada la siguiente tabla, donde X representa el peso (en kg) e Y la altura (en cm) de un grupo de niños, se pide: (X, Y ) [60,90] (90, 110] (110,140] [10,15] (15,20] (20,25] (25,30] a) Obtener la altura media de los niños que pesan más de 20 kg. b) Cuál es el peso más frecuente? c) Entre los niños que miden menos de 110 cm, calcular el peso mínimo del 30 % de los niños con más peso. d) Entre los niños que pesan entre 15 y 25 kg, calcular el porcentaje que presentan una altura inferior a 117 cm. 9. Se han obtenido los siguientes datos en una determinada ciudad donde se relaciona la tensión del vapor de agua (Y ), con la temperatura (X) en grados centígrados. (X, Y ) [0.5,1.5] (1.5, 2.5] (2.5, 5.5] [1,1.5] (15,25] (25,30] a) Cuál es la temperatura que con mayor frecuencia se ha alcanzado cuando la tensión de vapor de agua es superior a 1.5? b) Decidir qué variable es más homogénea, la de la tensión de vapor de agua cuando la temperatura es inferior o igual a 15 o C o la de la tensión de vapor de agua cuando la temperatura es superior a 15 o C. c) Cuál es la mínima tensión de vapor de agua del 40 % de las tensiones más altas? d) Son independientes estas variables? Ingeniero Técnico en Informática de Sistemas. Grupo B.
4 En el proceso de manufactura de una prenda de vestir se han controlado dos características: el número de días empleado en la fabricación (Y ) y el número de errores en el acabado (X), obteniéndose la siguiente distribución conjunta sobre una muestra de 120 unidades: (X, Y ) a) Independientemente del tiempo empleado, cuál es el número medio de errores cometidos? y el número más frecuente? b) Cuánto tiempo se dedica por término medio a la manufactura? c) Cuál es el tiempo mínimo que emplea el 30 % de las unidades que más minutos tardan en el proceso de manufactura? 11. En la tabla adjunta se muestran las calificaciones X e Y obtenidas por 200 alumnos en dos asignaturas: Se pide: (X, Y ) [0,2,5) [2,5,5) [5,7) [7,9) [9,10] [0, 2,5) [2,5, 5) [5, 7) [7, 9) [9, 10] a) Representar el histograma para la distribución de las calificaciones de la asignatura correspondientes a Y de los alumnos que han suspendido la asignatura X. b) Qué asignatura tiene las calificaciones más homogéneas? c) Qué porcentaje de alumnos aptos en la asignatura Y obtienen una calificación apta en la asignatura X? d) Cuál es la nota más frecuente en la asignatura X para los alumnos aptos en la asignatura Y? e) Qué nota mínima obtiene el 10% de los alumnos mejores calificados en la asignatura X? 12. En un estudio sobre la resistencia de un cierto tipo de componente se selecciona una muestra de componentes construidas con diferentes concentraciones de un metal y se anota el número de pruebas de resistencia necesarias hasta que se rompen, obteniéndose los siguientes resultados: (X, Y ) donde X representa la concentración del metal e Y el número de pruebas antes de la ruptura. a) Qué distribución es más homogénea con respecto a su valor medio? b) Cuál es el número medio de pruebas necesarias hasta romper las componentes? Y el más frecuente? Relación de problemas de Estadística Curso
5 15 c) Qué número mínimo de pruebas requiere el 50 % de las componentes más resistentes antes de romperse? d) De entre las componentes con una concentración superior a 5, calcular el porcentaje de éstas que necesitan 50 pruebas o menos para romperse. 13. El gerente de una empresa afirma que los empleados jóvenes trabajan más horas extras que los adultos. Según la base de datos, se tiene la siguiente información: (X, Y ) donde X representa el número de horas extra en un determinado mes e Y representa los grupos de edad. a) Cuál es el número total de horas extraordinarias que trabajan los jóvenes de 18 a 35 años en un mes? b) Cuál es el número total de horas extraordinarias que trabajan los adultos de 55 a 70 años en un mes? c) Cuál es el número medio de horas extraordinarias al mes que trabajan los jóvenes de 18 a 35 años? d) Cuál es el número medio de horas extraordinarias al mes que trabajan los adultos de 55 a 70 años? e) Qué grupo de edad trabaja más número de horas extraordinarias en esta empresa? f ) Cuál es el número medio de horas extra que trabaja cualquier trabajador en esta empresa? g) Es cierta la afirmación que hace el gerente de la empresa? 14. Se estudia el número de años (X) de experiencia en cierta empresa y el salario mensual (Y ) que perciben los trabajadores. Los resultados obtenidos son los siguientes: X Y a) Calcular el sueldo medio de los trabajadores que llevan menos de 15 años en la empresa. b) Calcular el sueldo más frecuente de los trabajadores que llevan más de 15 años en esa empresa. c) Calcular el sueldo máximo que perciben el 50% de los trabajadores que menos cobran de esta empresa. d) Calcular el sueldo mínimo que cobra el 20% de los trabajadores que más cobra en la empresa. e) Es más homogénea la distribución de los salarios de los que llevan más de 25 años en la empresa que la distribución de los salarios de los que llevan menos de 10 años? f ) Calcular el salario medio de los trabajadores de la empresa. Ingeniero Técnico en Informática de Sistemas. Grupo B.
6 Dada la siguiente distribución bidimensional: a) Calcular las medias marginales. b) Calcular la covarianza. X Y c) Calcular las medias de Y condicionadas a los distintos valores de X. d) Calcular las medias de X condicionadas a los distintos valores de Y. e) Son X e Y estadísticamente independientes? f ) Hay alguna contradicción entre los tres apartados anteriores? 16. Según un estudio, la distribución de las ventas de cierto artículo según el número de minutos que aparece su publicidad en televisión, es la siguiente: X Y donde Y representa el número de minutos al día que aparece la publicidad en televisión y X representa el número de artículos vendidos en una ciudad. a) Calcular las medias de las ventas para cada uno de los casos de tiempo de publicidad. b) Es independiente el número de ventas de la publicidad en este caso? 17. Dada la siguiente tabla asociada a una variable bidimensional: X Y a) Calcular la media de X condicionada a que Y vale 4 mediante un cambio de origen y escala. b) Calcular la varianza de X condicionada a que Y vale 4 mediante un cambio de origen y escala. c) Calcular la media marginal de Y mediante un cambio de origen y escala. d) Calcular la moda de X dado que Y toma el valor 2. e) Calcular la mediana de Y dado que X toma el valor 20. f ) Calcular la covarianza. Relación de problemas de Estadística Curso
Regresión y Correlación
 Relación de problemas 4 Regresión y Correlación 1. El departamento comercial de una empresa se plantea si resultan rentables los gastos en publicidad de un producto. Los datos de los que dispone son: Beneficios
Relación de problemas 4 Regresión y Correlación 1. El departamento comercial de una empresa se plantea si resultan rentables los gastos en publicidad de un producto. Los datos de los que dispone son: Beneficios
Diplomatura en Ciencias Empresariales
 DEPARTAMENTO DE ESTADÍSTICA E INVESTIGACIÓN OPERATIVA Diplomatura en Ciencias Empresariales ESTADÍSTICA II Relación Tema 7: Variables estadísticas bidimensionales. 1. Se han lanzado dos dados varias veces.
DEPARTAMENTO DE ESTADÍSTICA E INVESTIGACIÓN OPERATIVA Diplomatura en Ciencias Empresariales ESTADÍSTICA II Relación Tema 7: Variables estadísticas bidimensionales. 1. Se han lanzado dos dados varias veces.
RELACIÓN DE EJERCICIOS Y PROBLEMAS SOBRE ANÁLISIS DE DOS VARIABLES (DISTRIBUCIONES BIDIMENSIONALES)
 ESCUELA UNIVERSITARIA DE ESTUDIOS EMPRESARIALES DIPLOMATURA EN CIENCIAS EMPRESARIALES (PRIMER CURSO) RELACIÓN DE EJERCICIOS Y PROBLEMAS SOBRE ANÁLISIS DE DOS VARIABLES (DISTRIBUCIONES BIDIMENSIONALES)
ESCUELA UNIVERSITARIA DE ESTUDIOS EMPRESARIALES DIPLOMATURA EN CIENCIAS EMPRESARIALES (PRIMER CURSO) RELACIÓN DE EJERCICIOS Y PROBLEMAS SOBRE ANÁLISIS DE DOS VARIABLES (DISTRIBUCIONES BIDIMENSIONALES)
RELACIÓN 1. DESCRIPTIVA
 RELACIÓN 1. DESCRIPTIVA 1. En un estudio sobre el número de bacterias que aparecen en determinados cultivos se tomaron 1 de estos cultivos y se contó el número de bacterias que aparecieron en cada uno
RELACIÓN 1. DESCRIPTIVA 1. En un estudio sobre el número de bacterias que aparecen en determinados cultivos se tomaron 1 de estos cultivos y se contó el número de bacterias que aparecieron en cada uno
ESTADÍSTICA. 1.- En una población de 25 familias se ha observado el número de vehículos que tienen obteniéndose los siguientes datos:
 ESTADÍSTICA 1.- En una población de 25 familias se ha observado el número de vehículos que tienen obteniéndose los siguientes datos: 0, 1, 2, 3, 1, 0, 1, 1, 1, 4, 3, 2, 2, 1, 1, 2, 2, 1, 1, 1, 2, 1, 3,
ESTADÍSTICA 1.- En una población de 25 familias se ha observado el número de vehículos que tienen obteniéndose los siguientes datos: 0, 1, 2, 3, 1, 0, 1, 1, 1, 4, 3, 2, 2, 1, 1, 2, 2, 1, 1, 1, 2, 1, 3,
Relación 2: CARACTERÍSTICAS DE UNA DISTRIBUCIÓN DE FRECUENCIAS
 INTRODUCCIÓN A LA ESTADÍSTICA Relación 2: CARACTERÍSTICAS DE UNA DISTRIBUCIÓN DE FRECUENCIAS 1.- Obtener las medias aritmética, geométrica, armónica para la siguiente distribución: SOL: 2,74; 2,544; 2,318
INTRODUCCIÓN A LA ESTADÍSTICA Relación 2: CARACTERÍSTICAS DE UNA DISTRIBUCIÓN DE FRECUENCIAS 1.- Obtener las medias aritmética, geométrica, armónica para la siguiente distribución: SOL: 2,74; 2,544; 2,318
Licenciatura en Administración y Dirección de Empresas INTRODUCCIÓN A LA ESTADÍSTICA EMPRESARIAL
 INTRODUCCIÓN A LA ESTADÍSTICA EMPRESARIAL Relación de Ejercicios nº 1 (Temas 1 4). Curso 2002/2003 1) El aplazamiento en el cobro de las últimas cien ventas facturadas por un establecimiento se había agrupado
INTRODUCCIÓN A LA ESTADÍSTICA EMPRESARIAL Relación de Ejercicios nº 1 (Temas 1 4). Curso 2002/2003 1) El aplazamiento en el cobro de las últimas cien ventas facturadas por un establecimiento se había agrupado
Síntesis Numérica de una Variable
 Relación de problemas 2 Síntesis Numérica de una Variable Estadística 1. En siete momentos del día se observa el número de clientes que hay en un negocio, anotando: 2, 5, 2, 7, 3, 4, 9. Calcular e interpretar
Relación de problemas 2 Síntesis Numérica de una Variable Estadística 1. En siete momentos del día se observa el número de clientes que hay en un negocio, anotando: 2, 5, 2, 7, 3, 4, 9. Calcular e interpretar
Boletín 1. Estadística Descriptiva
 Estadística y metodología de la investigación Curso 2012-2013 Pedro Faraldo, Beatriz Pateiro Boletín 1. Estadística Descriptiva 1. Se desea estimar el porcentaje de albúmina en el suero proteico de personas
Estadística y metodología de la investigación Curso 2012-2013 Pedro Faraldo, Beatriz Pateiro Boletín 1. Estadística Descriptiva 1. Se desea estimar el porcentaje de albúmina en el suero proteico de personas
68 Bioestadística: Métodos y Aplicaciones. curtosis<0 curtosis=0 curtosis>0. Figura 2.10: Apuntamiento de distribuciones de frecuencias
 68 Bioestadística: Métodos y Aplicaciones curtosis0 Figura 2.10: Apuntamiento de distribuciones de frecuencias 2.6. Problemas Ejercicio 2.1. En el siguiente conjunto de números,
68 Bioestadística: Métodos y Aplicaciones curtosis0 Figura 2.10: Apuntamiento de distribuciones de frecuencias 2.6. Problemas Ejercicio 2.1. En el siguiente conjunto de números,
Problemas Estadística Descriptiva
 Problemas Estadística Descriptiva 1. El gasto de dos grupos de familias durante un cierto periodo de tiempo ha sido el siguiente: GRUPO A GRUPO B Gasto Nº familias Gasto Nº familias 10 14 8 5 12 16 10
Problemas Estadística Descriptiva 1. El gasto de dos grupos de familias durante un cierto periodo de tiempo ha sido el siguiente: GRUPO A GRUPO B Gasto Nº familias Gasto Nº familias 10 14 8 5 12 16 10
Nº de litros Nº de automóviles
 1) Se ha realizado una encuesta en 30 hogares en la que se les pregunta el nº de individuos que conviven en el domicilio habitualmente. Las respuestas obtenidas han sido las siguientes: 4, 4, 1, 3, 5,
1) Se ha realizado una encuesta en 30 hogares en la que se les pregunta el nº de individuos que conviven en el domicilio habitualmente. Las respuestas obtenidas han sido las siguientes: 4, 4, 1, 3, 5,
Estadística I Ejercicios Tema 3 Curso 2016/17
 Estadística I Ejercicios Tema 3 Curso 2016/17 1. En la siguiente tabla se representa la distribución conjunta de frecuencias (relativas) de 2 variables: calificación en Estadística I, y número de horas
Estadística I Ejercicios Tema 3 Curso 2016/17 1. En la siguiente tabla se representa la distribución conjunta de frecuencias (relativas) de 2 variables: calificación en Estadística I, y número de horas
RELACIÓN DE EJERCICIOS TEMA 2
 1. Sea una distribución estadística que viene dada por la siguiente tabla: Calcular: x i 61 64 67 70 73 f i 5 18 42 27 8 a) La moda, mediana y media. b) El rango, desviación media, varianza y desviación
1. Sea una distribución estadística que viene dada por la siguiente tabla: Calcular: x i 61 64 67 70 73 f i 5 18 42 27 8 a) La moda, mediana y media. b) El rango, desviación media, varianza y desviación
C7) Dada la distribución bidimensional de las variables "Numero de desplazamientos diarios" y "Medio de transporte utilizado" es cierto que: a) De los
 IS12-Estadística en ITIS Exámen Final Curso 2008-09 Fecha: 28/Enero/09 Nombre alumno: NOTA: MARCAR: (a) Sobre 5 ptos, (b) Sobre 9 ptos C1) Una variable X toma únicamente 4 valores distintos: x1, x2, x3,
IS12-Estadística en ITIS Exámen Final Curso 2008-09 Fecha: 28/Enero/09 Nombre alumno: NOTA: MARCAR: (a) Sobre 5 ptos, (b) Sobre 9 ptos C1) Una variable X toma únicamente 4 valores distintos: x1, x2, x3,
PREGUNTAS APARECIDAS EN EXÁMENES
 PREGUNTAS APARECIDAS EN EXÁMENES 1. a) Utilidad y significado de las medidas de posición central. Defina las que conozca b) Utilidad y significado de las medidas de dispersión. Defina las que conozca 2.
PREGUNTAS APARECIDAS EN EXÁMENES 1. a) Utilidad y significado de las medidas de posición central. Defina las que conozca b) Utilidad y significado de las medidas de dispersión. Defina las que conozca 2.
GUIA N 1: Estadistica descriptiva.
 UNIVERSIDAD DE VALPARAÍSO Ingeniería Civil, primer semestre 2016 GUIA N 1: Estadistica descriptiva. EJERCICIO 1 Clasificar cada una de las siguientes variables: si es cualitativa (nominal u ordinal) o
UNIVERSIDAD DE VALPARAÍSO Ingeniería Civil, primer semestre 2016 GUIA N 1: Estadistica descriptiva. EJERCICIO 1 Clasificar cada una de las siguientes variables: si es cualitativa (nominal u ordinal) o
TEMA 12 INFERENCIA ESTADÍSTICA. ESTIMACIÓN DE LA MEDIA
 Ejercicios Selectividad Tema 12 Inferencia estadística. Matemáticas CCSSII 2º Bachillerato 1 TEMA 12 INFERENCIA ESTADÍSTICA. ESTIMACIÓN DE LA MEDIA LAS MUESTRAS ESTADÍSTICAS EJERCICIO 1 : Septiembre 00-01.
Ejercicios Selectividad Tema 12 Inferencia estadística. Matemáticas CCSSII 2º Bachillerato 1 TEMA 12 INFERENCIA ESTADÍSTICA. ESTIMACIÓN DE LA MEDIA LAS MUESTRAS ESTADÍSTICAS EJERCICIO 1 : Septiembre 00-01.
Problemas del Tema 1
 Estadística 200-20 Problemas del Tema. Se sabe que el 4 % de los días de un mes de 25 días laborables un trabajador de cierta empresa utiliza menos de 5 minutos en salir a fumar. El 40 % de los días este
Estadística 200-20 Problemas del Tema. Se sabe que el 4 % de los días de un mes de 25 días laborables un trabajador de cierta empresa utiliza menos de 5 minutos en salir a fumar. El 40 % de los días este
INFERENCIA ESTADÍSTICA SELECTIVIDAD CyL
 INFERENCIA ESTADÍSTICA SELECTIVIDAD CyL 1. Se quiere estimar la media de la nómina mensual que reciben los directivos de las compañías multinacionales que operan en Europa. a. Si la varianza de la nómina
INFERENCIA ESTADÍSTICA SELECTIVIDAD CyL 1. Se quiere estimar la media de la nómina mensual que reciben los directivos de las compañías multinacionales que operan en Europa. a. Si la varianza de la nómina
EJERCICIOS RECUPERACIÓN MATEMÁTICAS 2º ESO
 NÚMEROS ENTEROS Ejercicio nº 1: EJERCICIOS RECUPERACIÓN MATEMÁTICAS º ESO a Calcula todos los divisores de 46. b Escribe cinco múltiplos consecutivos de 16 comprendidos entre 7 y 10. c Cuándo un número
NÚMEROS ENTEROS Ejercicio nº 1: EJERCICIOS RECUPERACIÓN MATEMÁTICAS º ESO a Calcula todos los divisores de 46. b Escribe cinco múltiplos consecutivos de 16 comprendidos entre 7 y 10. c Cuándo un número
Tabla de frecuencias Los datos obtenidos en estadística se organizan en una tabla, llamada tabla de frecuencias.
 1º BACHILLERATO D MATEMÁTICAS CC SS TEMA 5.- ESTADÍSTICA DESCRIPTIVA PROFESOR: RAFAEL NÚÑEZ NOGALES -------------------------------------------------------------------------------------------------------------
1º BACHILLERATO D MATEMÁTICAS CC SS TEMA 5.- ESTADÍSTICA DESCRIPTIVA PROFESOR: RAFAEL NÚÑEZ NOGALES -------------------------------------------------------------------------------------------------------------
Prueba de evaluación continua Grupo D
 Prueba de evaluación continua Grupo D 23-XI-12 OPCION I 1. En un aparcamiento cobran por cada minuto que está estacionado el vehículo 15 céntimos. El tiempo que los vehículos permanecen estacionados dentro
Prueba de evaluación continua Grupo D 23-XI-12 OPCION I 1. En un aparcamiento cobran por cada minuto que está estacionado el vehículo 15 céntimos. El tiempo que los vehículos permanecen estacionados dentro
x i n i N i f i 1 4? 0,08 2 4?? 3? 16 0,16 4 7? 0, ? 6? 38? ,14 8???
 ESTADÍSTICA Y TÉCNICAS DE MUESTREO RELACIÓN : Estadística Descriptiva (Variables Unidimensionales) Diplomatura de Relaciones Laborales Departamento de Estadística e I.O. Universidad de Sevilla. En el control
ESTADÍSTICA Y TÉCNICAS DE MUESTREO RELACIÓN : Estadística Descriptiva (Variables Unidimensionales) Diplomatura de Relaciones Laborales Departamento de Estadística e I.O. Universidad de Sevilla. En el control
Matemáticas 1º CCSS ESTADÍSTICA BÁSICA
 1 PROBLEMAS RESUELTOS ESTADÍSTICA BÁSICA 1. En la siguiente tabla se dan los datos correspondientes a las notas de Matemáticas de 60 alumnos de 1º Bachillerato. Notas IN: [1, 5) SF: [5, 6) BI: [6, 7) NT:
1 PROBLEMAS RESUELTOS ESTADÍSTICA BÁSICA 1. En la siguiente tabla se dan los datos correspondientes a las notas de Matemáticas de 60 alumnos de 1º Bachillerato. Notas IN: [1, 5) SF: [5, 6) BI: [6, 7) NT:
Problemas de Estadística. 1. Utilizar el gráfico más adecuado para representar cada uno de los siguientes casos:
 Problemas de Estadística 1. Utilizar el gráfico más adecuado para representar cada uno de los siguientes casos: a. En un estudio hecho con 25 varones con objeto de determinar su grupo sanguíneo ha conducido
Problemas de Estadística 1. Utilizar el gráfico más adecuado para representar cada uno de los siguientes casos: a. En un estudio hecho con 25 varones con objeto de determinar su grupo sanguíneo ha conducido
Examen Estadística Descriptiva - Grado ADE Enero 2010
 Examen Estadística Descriptiva - Grado ADE Enero 2010 1.- Se dispone de la renta per capita de la región más rica y más pobre de un determinado país. Año Renta Región rica Renta Región pobre 2003 40 20
Examen Estadística Descriptiva - Grado ADE Enero 2010 1.- Se dispone de la renta per capita de la región más rica y más pobre de un determinado país. Año Renta Región rica Renta Región pobre 2003 40 20
EJERCICIOS DE SELECTIVIDAD
 EJERCICIOS DE SELECTIVIDAD INFERENCIA 1998 JUNIO OPCIÓN A Un fabricante de electrodomésticos sabe que la vida media de éstos sigue una distribución normal con media μ = 100 meses y desviación típica σ
EJERCICIOS DE SELECTIVIDAD INFERENCIA 1998 JUNIO OPCIÓN A Un fabricante de electrodomésticos sabe que la vida media de éstos sigue una distribución normal con media μ = 100 meses y desviación típica σ
Prueba de Evaluación Continua Grupo A 26-XI-14
 Estadística Descriptiva y Regresión y Correlación Prueba de Evaluación Continua Grupo A -XI-1 1.- Los valores de 5 mediciones realizadas con un distanciometro con apreciación en milímetros han sido agrupados
Estadística Descriptiva y Regresión y Correlación Prueba de Evaluación Continua Grupo A -XI-1 1.- Los valores de 5 mediciones realizadas con un distanciometro con apreciación en milímetros han sido agrupados
ESTADÍSTICA DESCRIPTIVA PARA EL TURISMO
 ESTADÍSTICA DESCRIPTIVA PARA EL TURISMO RELACIÓN DE PROBLEMAS PROPUESTOS DE UNA VARIABLE Curso académico 2004-2005 DPTO. ECONOMÍA APLICADA I 1. Obtener las frecuencias acumuladas, las frecuencias relativas
ESTADÍSTICA DESCRIPTIVA PARA EL TURISMO RELACIÓN DE PROBLEMAS PROPUESTOS DE UNA VARIABLE Curso académico 2004-2005 DPTO. ECONOMÍA APLICADA I 1. Obtener las frecuencias acumuladas, las frecuencias relativas
Tema 1. Estadística Descriptiva
 RELACIÓN DE PROBLEMAS MATEMÁTICAS II Curso 2017/2018 Escuela Técnica Superior de Ingeniería Agronómica Departamento de Matemática Aplicada I Tema 1. Estadística Descriptiva 1.1. Consideremos los siguientes
RELACIÓN DE PROBLEMAS MATEMÁTICAS II Curso 2017/2018 Escuela Técnica Superior de Ingeniería Agronómica Departamento de Matemática Aplicada I Tema 1. Estadística Descriptiva 1.1. Consideremos los siguientes
4 Descripción conjunta de varias variables.
 ANÁLISIS EXPLORATORIO DE DATOS 23 ANÁLISIS EXPLORATORIO DE DATOS 2 Descripción conjunta de varias variables..1 Ejemplos Ejemplo.1 La siguiente tabla de frecuencias absolutas corresponde a 200 observaciones
ANÁLISIS EXPLORATORIO DE DATOS 23 ANÁLISIS EXPLORATORIO DE DATOS 2 Descripción conjunta de varias variables..1 Ejemplos Ejemplo.1 La siguiente tabla de frecuencias absolutas corresponde a 200 observaciones
1.- Un estudio estadístico de la superficie de bosque quemada en España desde 1990 hasta el 2001 arroja los siguientes datos, expresados en km 2 :
 Estadística 3º ESO 1.- Un estudio estadístico de la superficie de bosque quemada en España desde 1990 hasta el 2001 arroja los siguientes datos, expresados en km 2 : 250 200 199 145 100 55 140 110 80 60
Estadística 3º ESO 1.- Un estudio estadístico de la superficie de bosque quemada en España desde 1990 hasta el 2001 arroja los siguientes datos, expresados en km 2 : 250 200 199 145 100 55 140 110 80 60
y = 2, entonces: a) x es más dispersa que y. b) son igual de dispersas. 9.- Sean dos variables estadísticas x e y con los siguientes valores x = 5, σ
 VARIABLES ESTADÍSTICAS 1.- Sea X una variable estadística de media 2 metros y desviación típica 5 metros. Sea Y una variable estadística de media 24 cm y desviación típica 60 centímetros. a) Y es más dispersa
VARIABLES ESTADÍSTICAS 1.- Sea X una variable estadística de media 2 metros y desviación típica 5 metros. Sea Y una variable estadística de media 24 cm y desviación típica 60 centímetros. a) Y es más dispersa
ESTADÍSTICA APLICADA A LA COMUNICACIÓN CAMPUS VIRTUAL OCW PRÁCTICA 7: MEDIDAS UNIVARIANTES SOLUCIONES
 ESTADÍSTICA APLICADA A LA COMUNICACIÓN CAMPUS VIRTUAL OCW PRÁCTICA 7: MEDIDAS UNIVARIANTES SOLUCIONES 1. La siguiente tabla presenta la distribución del número de miembros en los hogares de Araba. Contesta
ESTADÍSTICA APLICADA A LA COMUNICACIÓN CAMPUS VIRTUAL OCW PRÁCTICA 7: MEDIDAS UNIVARIANTES SOLUCIONES 1. La siguiente tabla presenta la distribución del número de miembros en los hogares de Araba. Contesta
2 Descripción estadística de una variable. Ejemplos y ejercicios.
 ESTADÍSTICA DESCRIPTIVA Y ANÁLISIS DE DATOS 1 2 Descripción estadística de una variable. Ejemplos y ejercicios. 2.1 Ejemplos. Ejemplo 2.1 Se han medido el grup sanguíneo de 40 individuos y se han observado
ESTADÍSTICA DESCRIPTIVA Y ANÁLISIS DE DATOS 1 2 Descripción estadística de una variable. Ejemplos y ejercicios. 2.1 Ejemplos. Ejemplo 2.1 Se han medido el grup sanguíneo de 40 individuos y se han observado
EJERCICIOS DE RECUPERACIÓN MATEMÁTICAS I (PARTE 4)
 EJERCICIOS DE RECUPERACIÓN MATEMÁTICAS I (PARTE 4) TEMA 13: ESTADÍSTICA UNIDIMENSIONAL 1. El número de fallos en un test que tuvieron 40 personas que se examinaban fue: 1 0 4 2 1 0 2 3 0 1 1 3 1 1 1 4
EJERCICIOS DE RECUPERACIÓN MATEMÁTICAS I (PARTE 4) TEMA 13: ESTADÍSTICA UNIDIMENSIONAL 1. El número de fallos en un test que tuvieron 40 personas que se examinaban fue: 1 0 4 2 1 0 2 3 0 1 1 3 1 1 1 4
3 Número de goles marcados por tu equipo favorito en la última temporada.
 1. Indica que variables son cualitativas y cuales cuantitativas: 1 Comida Favorita. 2 Profesión que te gusta. 3 Número de goles marcados por tu equipo favorito en la última temporada. 4 Número de alumnos
1. Indica que variables son cualitativas y cuales cuantitativas: 1 Comida Favorita. 2 Profesión que te gusta. 3 Número de goles marcados por tu equipo favorito en la última temporada. 4 Número de alumnos
Estadística I Ejercicios Tema 4 Curso 2015/16
 Estadística I Ejercicios Tema 4 Curso 2015/16 1. En una urna hay 15 bolas numeradas de 2 al 16. Extraemos una bola al azar y observamos el número que tiene. a) Describe los sucesos, escribiendo todos sus
Estadística I Ejercicios Tema 4 Curso 2015/16 1. En una urna hay 15 bolas numeradas de 2 al 16. Extraemos una bola al azar y observamos el número que tiene. a) Describe los sucesos, escribiendo todos sus
2. DESCRIPCIÓN ESTADÍSTICA DE UNA VARIABLE. EJEMPLOS Y EJERCICIOS *.
 2. DESCRIPCIÓN ESTADÍSTICA DE UNA VARIABLE. EJEMPLOS Y EJERCICIOS *. 2.1. Ejemplos. Ejemplo 2.1 Se ha medido el grupo sanguíneo de 40 individuos y se han observado las siguientes frecuencias absolutas
2. DESCRIPCIÓN ESTADÍSTICA DE UNA VARIABLE. EJEMPLOS Y EJERCICIOS *. 2.1. Ejemplos. Ejemplo 2.1 Se ha medido el grupo sanguíneo de 40 individuos y se han observado las siguientes frecuencias absolutas
Matemáticas. Selectividad ESTADISTICA COU
 Matemáticas Selectividad ESTADISTICA COU 1. Un dentista observa el Nº de Caries en cada uno de los 100 niños de cierto colegio. La información obtenida aparece resumida en la siguiente tabla. Nº Caries
Matemáticas Selectividad ESTADISTICA COU 1. Un dentista observa el Nº de Caries en cada uno de los 100 niños de cierto colegio. La información obtenida aparece resumida en la siguiente tabla. Nº Caries
Ejercicios Introducción. Capítulo. Estos ejercicios fueron recopilados por los profesores Douglas Rivas, Luis Nava y. Ángel Zambrano.
 Capítulo 1 Ejercicios Estos ejercicios fueron recopilados por los profesores Douglas Rivas, Luis Nava y Ángel Zambrano. 1.1. Introducción 1. Se realiza un estudio en el municipio Libertador del Estado
Capítulo 1 Ejercicios Estos ejercicios fueron recopilados por los profesores Douglas Rivas, Luis Nava y Ángel Zambrano. 1.1. Introducción 1. Se realiza un estudio en el municipio Libertador del Estado
Inferencia estadística en la EBAU de Murcia INFERENCIA ESTADÍSTICA EN LA EBAU DE MURCIA
 INFERENCIA ESTADÍSTICA EN LA EBAU DE MURCIA 1. (Septiembre 2017) El consumo de carne por persona en un año para una población es una variable aleatoria con distribución normal con desviación típica igual
INFERENCIA ESTADÍSTICA EN LA EBAU DE MURCIA 1. (Septiembre 2017) El consumo de carne por persona en un año para una población es una variable aleatoria con distribución normal con desviación típica igual
Estudios estadísticos. a) Crea la tabla de frecuencias absolutas y acumuladas correspondiente. Ten en cuenta
 1 Estadística Qué tienes que saber? 1 QUÉ tienes que saber? Actividades Finales 1 Estudios estadísticos Gráficos estadísticos Un estudio realizado sobre jóvenes con edades comprendidas entre 16 y años
1 Estadística Qué tienes que saber? 1 QUÉ tienes que saber? Actividades Finales 1 Estudios estadísticos Gráficos estadísticos Un estudio realizado sobre jóvenes con edades comprendidas entre 16 y años
Tema 9: Estadística descriptiva
 Tema 9: Estadística descriptiva Matemáticas específicas para maestros Grado en Educación Primaria Matemáticas específicas para maestros Tema 9: Estadística descriptiva Grado en Educación Primaria 1 / 47
Tema 9: Estadística descriptiva Matemáticas específicas para maestros Grado en Educación Primaria Matemáticas específicas para maestros Tema 9: Estadística descriptiva Grado en Educación Primaria 1 / 47
Tema 8: Distribuciones Unidimensionales y Distribuciones Bidimensionales. Consideraciones iniciales:
 Tema 8: Distribuciones Unidimensionales y Distribuciones Bidimensionales. Consideraciones iniciales: - Población: Es el conjunto de todos los elementos que cumplen una determinada característica. Ej.:
Tema 8: Distribuciones Unidimensionales y Distribuciones Bidimensionales. Consideraciones iniciales: - Población: Es el conjunto de todos los elementos que cumplen una determinada característica. Ej.:
MATEMÁTICAS ORIENTADAS A LAS ENSEÑANZAS APLICADAS. 4º ESO ACTIVIDADES DE REPASO. UNIDADES 1, 2 Y 3
 UNIDAD 1. ESTADÍSTICA 1. Clasifica las siguientes variables, marcando con una X donde corresponda: Variable Cuantitativa Variable cualitativa Discreta Número de hijos de una familia Voto político El peso
UNIDAD 1. ESTADÍSTICA 1. Clasifica las siguientes variables, marcando con una X donde corresponda: Variable Cuantitativa Variable cualitativa Discreta Número de hijos de una familia Voto político El peso
Estadística aplicada al Periodismo
 Estadística aplicada al Periodismo Primera prueba parcial (B) Alumno: Grupo: Fecha: Ejercicio. La Encuesta de Pobreza y Desigualdades Sociales (EPDS) realizada por el Gobierno Vasco tiene como objetivo
Estadística aplicada al Periodismo Primera prueba parcial (B) Alumno: Grupo: Fecha: Ejercicio. La Encuesta de Pobreza y Desigualdades Sociales (EPDS) realizada por el Gobierno Vasco tiene como objetivo
(L i 1, L i ] x i n i N i f i F i a i h i (20, 50] 35 2 2 (, 60] 10 0.125 (60, ] 0.425 10 (, ] 75 0.225 (, 100] 28 80 1.4
![(L i 1, L i ] x i n i N i f i F i a i h i (20, 50] 35 2 2 (, 60] 10 0.125 (60, ] 0.425 10 (, ] 75 0.225 (, 100] 28 80 1.4 (L i 1, L i ] x i n i N i f i F i a i h i (20, 50] 35 2 2 (, 60] 10 0.125 (60, ] 0.425 10 (, ] 75 0.225 (, 100] 28 80 1.4](/thumbs/39/19126908.jpg) Problemas Tema 1-I 1. Un gabinete de trabajo ha realizado un estudio sobre la distribución de la renta per cápita por municipio, construyéndose una tabla que posteriormente se extravió, quedando sólo la
Problemas Tema 1-I 1. Un gabinete de trabajo ha realizado un estudio sobre la distribución de la renta per cápita por municipio, construyéndose una tabla que posteriormente se extravió, quedando sólo la
Muestra Una muestra es una parte de la población que elegimos para estudiar la población.
 1.- TERMINOLOGÍA ESTADÍSTICA. TÉCNICAS DE SELECCIÓN DE MUESTRAS Estadística descriptiva Es la ciencia que estudia conjuntos de datos obtenidos de la realidad. Estos datos son interpretados mediante tablas,
1.- TERMINOLOGÍA ESTADÍSTICA. TÉCNICAS DE SELECCIÓN DE MUESTRAS Estadística descriptiva Es la ciencia que estudia conjuntos de datos obtenidos de la realidad. Estos datos son interpretados mediante tablas,
Hoja 6: Estadística descriptiva
 Hoja : Estadística descriptiva Hoja : Estadística descriptiva May Dada la siguiente distribución de frecuencias, halle: a) la mediana; b) la media. Número (x) Frecuencia (y) May De enero a septiembre la
Hoja : Estadística descriptiva Hoja : Estadística descriptiva May Dada la siguiente distribución de frecuencias, halle: a) la mediana; b) la media. Número (x) Frecuencia (y) May De enero a septiembre la
PPTCEG061EM33-A17V1. Distribución normal 1
 PPTCEG061EM33-A17V1 Distribución normal 1 Propiedades distribución normal Distribución normal tipificada Es una distribución estadística continua cuya función de densidad es simétrica, y cuya forma se
PPTCEG061EM33-A17V1 Distribución normal 1 Propiedades distribución normal Distribución normal tipificada Es una distribución estadística continua cuya función de densidad es simétrica, y cuya forma se
ESTADÍSTICA DESCRIPTIVA PARA EL TURISMO
 ESTADÍSTICA DESCRIPTIVA PARA EL TURISMO RELACIÓN DE PROBLEMAS PROPUESTOS DE DOS VARIABLES Curso académico 2004-2005 DPTO. ECONOMÍA APLICADA I 1.- Las calificaciones obtenidas por un grupo de alumnos en
ESTADÍSTICA DESCRIPTIVA PARA EL TURISMO RELACIÓN DE PROBLEMAS PROPUESTOS DE DOS VARIABLES Curso académico 2004-2005 DPTO. ECONOMÍA APLICADA I 1.- Las calificaciones obtenidas por un grupo de alumnos en
4. Expresa como una única potencia de base 2
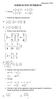 0 9 9 9 0 8 0 : : Matemáticas º ESO EJERCICIOS NÚMEROS. Calcula: 6 : d c b a. Realiza las siguientes operaciones a b. Reduce a una única fracción:. Expresa como una única potencia de base 6 0 d c b a.
0 9 9 9 0 8 0 : : Matemáticas º ESO EJERCICIOS NÚMEROS. Calcula: 6 : d c b a. Realiza las siguientes operaciones a b. Reduce a una única fracción:. Expresa como una única potencia de base 6 0 d c b a.
ESTADÍSTICA Y ANÁLISIS DE DATOS
 ESTADÍSTICA Y ANÁLISIS DE DATOS Práctica del Tema 2. Variables estadísticas bidimensionales Problemas 1. En la siguiente tabla aparecen, según la OIT (Organización Internacional del Trabajo), los parados
ESTADÍSTICA Y ANÁLISIS DE DATOS Práctica del Tema 2. Variables estadísticas bidimensionales Problemas 1. En la siguiente tabla aparecen, según la OIT (Organización Internacional del Trabajo), los parados
Colegio La Inmaculada Misioneras Seculares de Jesús Obrero ACTIVIDADES DEL TEMA 13
 Colegio La Inmaculada Misioneras Seculares de Jesús Obrero Matemáticas º E.S.O. ACTIVIDADES DEL TEMA. Los siguientes datos corresponden a la calificación de alumnos de º ESO A y B en Matemáticas: º A:,,,
Colegio La Inmaculada Misioneras Seculares de Jesús Obrero Matemáticas º E.S.O. ACTIVIDADES DEL TEMA. Los siguientes datos corresponden a la calificación de alumnos de º ESO A y B en Matemáticas: º A:,,,
Estadígrafos de tendencia central
 Estadígrafos de tendencia central Los estadígrafos de tendencia central que estudiaremos son la media, la mediana y la moda. Estos estadígrafos nos dan alguna idea de los datos que estamos estudiando.
Estadígrafos de tendencia central Los estadígrafos de tendencia central que estudiaremos son la media, la mediana y la moda. Estos estadígrafos nos dan alguna idea de los datos que estamos estudiando.
ESTADISTICA APLICADA A LA EDUCACIÒN CODIGO: HOC220 EJERCICIOS SOBRE MEDIDAS DE TENDENCIA CENTRAL, POSICIONAL Y DE DISPERSIÓN
 ESTADISTICA APLICADA A LA EDUCACIÒN CODIGO: HOC220 EJERCICIOS SOBRE MEDIDAS DE TENDENCIA CENTRAL, POSICIONAL Y DE DISPERSIÓN COMPILADOR San Cristóbal, Abril 2011 CODIGO: HOC220 Página 1 1. A un conjunto
ESTADISTICA APLICADA A LA EDUCACIÒN CODIGO: HOC220 EJERCICIOS SOBRE MEDIDAS DE TENDENCIA CENTRAL, POSICIONAL Y DE DISPERSIÓN COMPILADOR San Cristóbal, Abril 2011 CODIGO: HOC220 Página 1 1. A un conjunto
Departamento de Estadística y Econometría. Curso EJERCICIOS DE ESTADÍSTICA APLICADA A LA EMPRESA II. L.A.D.E. TEMA 2
 Departamento de Estadística y Econometría. Curso 2002-2003 EJERCICIOS DE ESTADÍSTICA APLICADA A LA EMPRESA II. L.A.D.E. TEMA 2 1.- Una empresa de elaboración de materiales pone en práctica un nuevo método
Departamento de Estadística y Econometría. Curso 2002-2003 EJERCICIOS DE ESTADÍSTICA APLICADA A LA EMPRESA II. L.A.D.E. TEMA 2 1.- Una empresa de elaboración de materiales pone en práctica un nuevo método
Estadística I Ejercicios de los Temas 1 y 2 Curso 2010/11
 Estadística I Ejercicios de los Temas 1 y 2 Curso 2010/11 1. La siguiente tabla contiene información sobre el número de mujeres activas (en miles) en EEUU, por profesiones y durante 1986. Profesión num.
Estadística I Ejercicios de los Temas 1 y 2 Curso 2010/11 1. La siguiente tabla contiene información sobre el número de mujeres activas (en miles) en EEUU, por profesiones y durante 1986. Profesión num.
1. Una muestra de recibos telefónicos de uso residencial, mostró los siguientes montos a pagar en este mes:
 ACTIVIDADES 1. Una muestra de recibos telefónicos de uso residencial, mostró los siguientes montos a pagar en este mes: 530 462 511 466 382 426 456 449 477 420 462 496 407 425 516 453 473 394 424 414 442
ACTIVIDADES 1. Una muestra de recibos telefónicos de uso residencial, mostró los siguientes montos a pagar en este mes: 530 462 511 466 382 426 456 449 477 420 462 496 407 425 516 453 473 394 424 414 442
Matemáticas Aplicadas a las Ciencias Sociales II Hoja 6: Inferencia Estadística. Estimación de la Media
 Matemáticas Aplicadas a las Ciencias Sociales II Hoja 6: Inferencia Estadística. Estimación de la Media Ejercicio 1: El peso en gramos del contenido de las cajas de cereales de una cierta marca se puede
Matemáticas Aplicadas a las Ciencias Sociales II Hoja 6: Inferencia Estadística. Estimación de la Media Ejercicio 1: El peso en gramos del contenido de las cajas de cereales de una cierta marca se puede
SOLUCIONES AL EXAMEN DE SEPTIEMBRE DE ESTADÍSTICA EXAMEN DE MATEMÁTICAS II
 SOLUCIONES AL EXAMEN DE SEPTIEMBRE DE 4. ESTADÍSTICA EXAMEN DE MATEMÁTICAS II Estadística (primer parcial). Septiembre de 4.- El coeficiente de determinación R nos determina a) el % de la varianza de Y
SOLUCIONES AL EXAMEN DE SEPTIEMBRE DE 4. ESTADÍSTICA EXAMEN DE MATEMÁTICAS II Estadística (primer parcial). Septiembre de 4.- El coeficiente de determinación R nos determina a) el % de la varianza de Y
UNIDAD 6 Medidas de tendencia central
 UNIDAD Medidas de tendencia central UNIDAD MEDIDAS DE TENDENCIA CENTRAL = EJEMPLO. ó Al estudiar la información estadística de los histogramas y los polígonos de frecuencia, se puso en evidencia un significativo
UNIDAD Medidas de tendencia central UNIDAD MEDIDAS DE TENDENCIA CENTRAL = EJEMPLO. ó Al estudiar la información estadística de los histogramas y los polígonos de frecuencia, se puso en evidencia un significativo
ESTADÍSTICA Hoja 2
 Estadística 1 ESTADÍSTICA 0-10. Hoja 1. Sean X e Y variables estadísticas con distribución conjunta: X\Y 0 1-1 1 b 0 c 0 a 0 1 3 1 g 1 d e f a) Completar la tabla y obtener las distribuciones marginales
Estadística 1 ESTADÍSTICA 0-10. Hoja 1. Sean X e Y variables estadísticas con distribución conjunta: X\Y 0 1-1 1 b 0 c 0 a 0 1 3 1 g 1 d e f a) Completar la tabla y obtener las distribuciones marginales
GUIA EXAMEN PARA EXTRAORDINARIO SEGUNDO GRADO. Alumno(a):
 GUIA EXAMEN PARA EXTRAORDINARIO SEGUNDO GRADO Alumno(a): 1. Completa el siguiente cuadrado mágico con la siguiente sucesión numérica: -8, -7, -6, -5, -4, -3, -2, -1, 0, cuya suma horizontal, vertical y
GUIA EXAMEN PARA EXTRAORDINARIO SEGUNDO GRADO Alumno(a): 1. Completa el siguiente cuadrado mágico con la siguiente sucesión numérica: -8, -7, -6, -5, -4, -3, -2, -1, 0, cuya suma horizontal, vertical y
Libro de ejercicios de refuerzo de matemáticas. María de la Rosa Sánchez
 Libro de ejercicios de refuerzo de matemáticas María de la Rosa Sánchez Estadística bidimensional Tema 0 2 Índice general 1. Estadística unidimensional 5 2. Estadística bidimensional 11 3 Tema 1 Estadística
Libro de ejercicios de refuerzo de matemáticas María de la Rosa Sánchez Estadística bidimensional Tema 0 2 Índice general 1. Estadística unidimensional 5 2. Estadística bidimensional 11 3 Tema 1 Estadística
1º BACH CCSS - MATEMÁTICAS - PROBLEMAS DE ANÁLISIS ESTADÍSTICO DE UNA VARIABLE ˆ EJERCICIO 25
 1º BACH CCSS - MATEMÁTICAS - PROBLEMAS DE ANÁLISIS ESTADÍSTICO DE UNA VARIABLE ˆ EJERCICIO 24 Dada la siguiente tabla de ingresos: Ingresos mensuales Frecuencia Menos de 1000 35 [1000, 1100) 70 [1100,
1º BACH CCSS - MATEMÁTICAS - PROBLEMAS DE ANÁLISIS ESTADÍSTICO DE UNA VARIABLE ˆ EJERCICIO 24 Dada la siguiente tabla de ingresos: Ingresos mensuales Frecuencia Menos de 1000 35 [1000, 1100) 70 [1100,
EJERCICIOS ESTADÍSTICA DESCRIPTIVA
 EJERCICIOS ESTADÍSTICA DESCRIPTIVA 1.- Dada la siguiente distribución de frecuencias de variable discreta. Calcular: a) Mediana b) Moda c) Media d) Varianza y desviación típica x i f i 47 1 48 3 49 2 50
EJERCICIOS ESTADÍSTICA DESCRIPTIVA 1.- Dada la siguiente distribución de frecuencias de variable discreta. Calcular: a) Mediana b) Moda c) Media d) Varianza y desviación típica x i f i 47 1 48 3 49 2 50
1. Ejercicios. 2 a parte
 1. Ejercicios. 2 a parte Ejercicio 1 Calcule 1. P (χ 2 9 3 33) 2. P (χ 2 15 7 26). 3. P (15 51 χ 2 8 22). 4. P (χ 2 70 82). Ejercicio 2 Si X χ 2 26, obtenga un intervalo [a, b] que contenga un 95 % de
1. Ejercicios. 2 a parte Ejercicio 1 Calcule 1. P (χ 2 9 3 33) 2. P (χ 2 15 7 26). 3. P (15 51 χ 2 8 22). 4. P (χ 2 70 82). Ejercicio 2 Si X χ 2 26, obtenga un intervalo [a, b] que contenga un 95 % de
Gráficos para variables cuantitativas
 Gráficos para variables cuantitativas Para las variables cuantitativas, consideraremos dos tipos de gráficos, en función de que para realizarlos se usen las frecuencias (absolutas o relativas) o las frecuencias
Gráficos para variables cuantitativas Para las variables cuantitativas, consideraremos dos tipos de gráficos, en función de que para realizarlos se usen las frecuencias (absolutas o relativas) o las frecuencias
Juan José Hernández Ocaña
 Juan José Hernández Ocaña [email protected] Medidas de Posición Divide un conjunto de datos en grupos con la misma cantidad de individuos Percentiles, cuartiles, deciles MEDIDAS DE POSICIÓN Cuartiles
Juan José Hernández Ocaña [email protected] Medidas de Posición Divide un conjunto de datos en grupos con la misma cantidad de individuos Percentiles, cuartiles, deciles MEDIDAS DE POSICIÓN Cuartiles
FUNCIONES Y GRÁFICAS. CARACTERÍSTICAS GENERALES
 FUNCIONES Y GRÁFICAS. CARACTERÍSTICAS GENERALES 1º. La edad de Pedro es el doble de la de Juan. Expresa esta función mediante una fórmula y haz una tabla con algunos de sus puntos. 2º. Relaciona cada texto
FUNCIONES Y GRÁFICAS. CARACTERÍSTICAS GENERALES 1º. La edad de Pedro es el doble de la de Juan. Expresa esta función mediante una fórmula y haz una tabla con algunos de sus puntos. 2º. Relaciona cada texto
GUION DE TRABAJO ESTIVAL
 San Ignacio, - Apartado Correos 1 060 Villafranca de los Barros (Badajoz) Tlf: 9001 - Fax: 9909 A 1. 0A GUION DE TRABAJO ESTIVAL MODALIDAD: REFUERZO ETAPA: E.S.O. ASIGNATURA: MATEMÁTICAS CURSO: º E.S.O.
San Ignacio, - Apartado Correos 1 060 Villafranca de los Barros (Badajoz) Tlf: 9001 - Fax: 9909 A 1. 0A GUION DE TRABAJO ESTIVAL MODALIDAD: REFUERZO ETAPA: E.S.O. ASIGNATURA: MATEMÁTICAS CURSO: º E.S.O.
Muestra Una muestra es una parte de la población que elegimos para estudiar la población.
 1.- TERMINOLOGÍA ESTADÍSTICA. TÉCNICAS DE SELECCIÓN DE MUESTRAS Estadística descriptiva Es la ciencia que estudia conjuntos de datos obtenidos de la realidad. Estos datos son interpretados mediante tablas,
1.- TERMINOLOGÍA ESTADÍSTICA. TÉCNICAS DE SELECCIÓN DE MUESTRAS Estadística descriptiva Es la ciencia que estudia conjuntos de datos obtenidos de la realidad. Estos datos son interpretados mediante tablas,
4 E.M. Curso: Ejercicios de Estadísticas NOMBRE: 4º. Colegio SSCC Concepción - Depto. de Matemáticas. Guía N. Unidad de Aprendizaje: Estadísticas
 Curso: Colegio SSCC Concepción - Depto. de Matemáticas Unidad de Aprendizaje: Estadísticas Capacidades/Destreza/Habilidad: Racionamiento Matemático/ Comprensión, Aplicación/ Valores/ Actitudes: Respeto,
Curso: Colegio SSCC Concepción - Depto. de Matemáticas Unidad de Aprendizaje: Estadísticas Capacidades/Destreza/Habilidad: Racionamiento Matemático/ Comprensión, Aplicación/ Valores/ Actitudes: Respeto,
ESTADÍSTICA Hoja 2
 Estadística 1 ESTADÍSTICA 07-08. Hoja 1. La tabla siguiente muestra la distribución conjunta de las variables X=número de horas semanales de clase e Y=retribución mensual en euros de los profesores de
Estadística 1 ESTADÍSTICA 07-08. Hoja 1. La tabla siguiente muestra la distribución conjunta de las variables X=número de horas semanales de clase e Y=retribución mensual en euros de los profesores de
PROBLEMAS SOBRE V. ESTAD. BIDIMENSIONALES. PROFESOR: ANTONIO PIZARRO.
 1º) (Andalucía, Junio, 98) Se considera la siguiente tabla estadística, donde a es una incógnita: X 2 4 a 3 5 Y 1 2 1 1 3 a) Calcular el valor de a sabiendo que la media de X es 3. b) Mediante la correspondiente
1º) (Andalucía, Junio, 98) Se considera la siguiente tabla estadística, donde a es una incógnita: X 2 4 a 3 5 Y 1 2 1 1 3 a) Calcular el valor de a sabiendo que la media de X es 3. b) Mediante la correspondiente
ESTADÍSTICA. Pruebas de Acceso a la Universidad. Bachillerato de Ciencias Sociales. Departamento de Matemáticas del IES Andalán.
 ESTADÍSTICA Junio 1996. Se sabe que la desviación típica del peso de los individuos de una cierta población es de 6 Kg. Calcula el tamaño de la muestra que se ha de considerar para, con un nivel de confianza
ESTADÍSTICA Junio 1996. Se sabe que la desviación típica del peso de los individuos de una cierta población es de 6 Kg. Calcula el tamaño de la muestra que se ha de considerar para, con un nivel de confianza
PROBLEMAS DE ESTADÍSTICA DESCRIPTIVA
 Prof.: MSc. Julio Rito Vargas A. PROBLEMAS DE ESTADÍSTICA DESCRIPTIVA I. Los datos ordenados de la tabla corresponden a la vida útil (en horas) de una muestra de 40 lámparas de 100 watts producidos por
Prof.: MSc. Julio Rito Vargas A. PROBLEMAS DE ESTADÍSTICA DESCRIPTIVA I. Los datos ordenados de la tabla corresponden a la vida útil (en horas) de una muestra de 40 lámparas de 100 watts producidos por
VARIABLES ESTADÍSTICAS BIDIMENSIONALES
 VARIABLES ESTADÍSTICAS BIDIMENSIONALES 1.- En una variable estadística bidimensional, el diagrama de dispersión representa: a) la nube de puntos. b) las varianzas de las dos variables. c) los coeficientes
VARIABLES ESTADÍSTICAS BIDIMENSIONALES 1.- En una variable estadística bidimensional, el diagrama de dispersión representa: a) la nube de puntos. b) las varianzas de las dos variables. c) los coeficientes
EJERCICIOS DE ESTADÍSTICA DESCRIPTIVA. Prof.: MSc. Julio Rito Vargas A.
 ACTIVIDAD PRÁCTICA #1 EJERCICIOS DE ESTADÍSTICA DESCRIPTIVA Prof.: MSc. Julio Rito Vargas A. IIIC-2017 1.- Dada la siguiente distribución de frecuencias de variable discreta. Calcular: a) Mediana b) Moda
ACTIVIDAD PRÁCTICA #1 EJERCICIOS DE ESTADÍSTICA DESCRIPTIVA Prof.: MSc. Julio Rito Vargas A. IIIC-2017 1.- Dada la siguiente distribución de frecuencias de variable discreta. Calcular: a) Mediana b) Moda
INFERENCIA ESTADÍSTICA CON EL SOFTWARE MINITAB
 UNIVERSIDAD PRIVADA ALAS PERUANAS ESCUELA PROFESIONAL DE INGENIERÍA DE SISTEMAS INFERENCIA ESTADÍSTICA CON EL SOFTWARE MINITAB 15.0 E1) La tabla muestra el tiempo requerido, en días, para determinar auditorias
UNIVERSIDAD PRIVADA ALAS PERUANAS ESCUELA PROFESIONAL DE INGENIERÍA DE SISTEMAS INFERENCIA ESTADÍSTICA CON EL SOFTWARE MINITAB 15.0 E1) La tabla muestra el tiempo requerido, en días, para determinar auditorias
12. (SEPTIEMBRE 2004) Una muestra aleatoria de 9 tarrinas de helado proporciona los siguientes pesos en gramos
 DEPARTAMENTO DE MATEMÁTICAS UNIDAD 5. Estadística IES Galileo Galilei EJERCICIOS DE SELECTIVIDAD 1. (JUNIO 2000) Una variable aleatoria X tiene distribución normal siendo su desviación típica igual a 3.
DEPARTAMENTO DE MATEMÁTICAS UNIDAD 5. Estadística IES Galileo Galilei EJERCICIOS DE SELECTIVIDAD 1. (JUNIO 2000) Una variable aleatoria X tiene distribución normal siendo su desviación típica igual a 3.
Nombre: Solución: a) N(
 1998 JUNIO OPCIÓN A Un fabricante de electrodomésticos sabe que la vida media de éstos sigue una distribución normal con media µ = 100 meses y desviación típica σ = 12 meses. Determínese el mínimo tamaño
1998 JUNIO OPCIÓN A Un fabricante de electrodomésticos sabe que la vida media de éstos sigue una distribución normal con media µ = 100 meses y desviación típica σ = 12 meses. Determínese el mínimo tamaño
Tabla de frecuencias agrupando los datos Cuando hay muchos valores distintos, los agruparemos en intervalos (llamados clases) de la misma amplitud.
 1. TABLAS Y GRÁFICOS ESTADÍSTICOS Estadística Es la ciencia que estudia conjunto de datos obtenidos de la realidad. Estos datos son interpretados mediante tablas, gráficas y otros parámetros tales como
1. TABLAS Y GRÁFICOS ESTADÍSTICOS Estadística Es la ciencia que estudia conjunto de datos obtenidos de la realidad. Estos datos son interpretados mediante tablas, gráficas y otros parámetros tales como
Estadística I Examen Extraordinario, 24 Junio Grados en ADE, DER-ADE, ADE-INF, FICO, ECO, ECO-DER.
 Estadística I Examen Extraordinario, Junio. Grados en ADE, DER-ADE, ADE-INF, FICO, ECO, ECO-DER. REGLAS DEL EXAMEN: Usar cuadernillos separados para cada problema. Hacer los cálculos con al menos dos decimales
Estadística I Examen Extraordinario, Junio. Grados en ADE, DER-ADE, ADE-INF, FICO, ECO, ECO-DER. REGLAS DEL EXAMEN: Usar cuadernillos separados para cada problema. Hacer los cálculos con al menos dos decimales
UNLaM. Estadística. Secretaría de Extensión Universitaria. Trabajo Practico N 4. Medidas de Posición. Agente de Propaganda Médica
 Medidas de Posición Trabajo Practico N El percentil k (P k ) es el valor de la variable tal que el k por ciento de los valores de la muestra son menores o iguales que él. Ej. Si P 35 (el percentil 35)
Medidas de Posición Trabajo Practico N El percentil k (P k ) es el valor de la variable tal que el k por ciento de los valores de la muestra son menores o iguales que él. Ej. Si P 35 (el percentil 35)
RESOLUCIÓN DEL PRACTIQUEMOS DE LA FICHA N 9
 Actúa y piensa matemáticamente en RESOLUCIÓN DEL PRACTIQUEMOS DE LA FICHA N 9 Comunica y representa ideas matemáticas. ITEM 01: La posta médica registró las edades de 30 de sus pacientes adultos mayores.
Actúa y piensa matemáticamente en RESOLUCIÓN DEL PRACTIQUEMOS DE LA FICHA N 9 Comunica y representa ideas matemáticas. ITEM 01: La posta médica registró las edades de 30 de sus pacientes adultos mayores.
Estadística II Ejercicios Tema 4
 Estadística II Ejercicios Tema 4 1. Los siguientes datos muestran la estatura (en cm.) y el peso (en Kg.) para una muestra de cinco alumnos de una clase: estatura (cm.) peso (Kg.) 154 60 158 62 162 61
Estadística II Ejercicios Tema 4 1. Los siguientes datos muestran la estatura (en cm.) y el peso (en Kg.) para una muestra de cinco alumnos de una clase: estatura (cm.) peso (Kg.) 154 60 158 62 162 61
PENDIENTES 3º ESO. Tercer examen DEPARTAMENTO DE MATEMÁTICAS. Preparación del tercer examen de recuperación de MATEMÁTICAS DE 3º ESO Curso
 014 015 Preparación del tercer eamen de recuperación de MATEMÁTICAS DE 3º ESO Curso 013-014 PENDIENTES 3º ESO Tercer eamen DEPARTAMENTO DE MATEMÁTICAS Curso 013-014 1.- Halla los puntos de corte de las
014 015 Preparación del tercer eamen de recuperación de MATEMÁTICAS DE 3º ESO Curso 013-014 PENDIENTES 3º ESO Tercer eamen DEPARTAMENTO DE MATEMÁTICAS Curso 013-014 1.- Halla los puntos de corte de las
QRB501 Métodos cuantitativos para los negocios. MAESTRÍA Proyecto Profesional
 QRB501 Métodos cuantitativos para los negocios MAESTRÍA Proyecto Profesional Proyecto Profesional: Uso de los métodos cuantitativos para la toma de decisiones en. Contenido OBJETIVO DEL PROYECTO TIEMPO
QRB501 Métodos cuantitativos para los negocios MAESTRÍA Proyecto Profesional Proyecto Profesional: Uso de los métodos cuantitativos para la toma de decisiones en. Contenido OBJETIVO DEL PROYECTO TIEMPO
Número de árboles Crecimiento (m)
 UNIVERSIDAD PÚBLICA DE NAVARRA Hoja. Estadística Descriptiva. En un bosque con distintas especies de árboles se anota la longitud en metros que han crecido a lo largo del año, obteniéndose la tabla de
UNIVERSIDAD PÚBLICA DE NAVARRA Hoja. Estadística Descriptiva. En un bosque con distintas especies de árboles se anota la longitud en metros que han crecido a lo largo del año, obteniéndose la tabla de
 Variables aleatòries vectorials Els problemes assenyalats amb un (*) se faran a classe. 1.- Los estudiantes de una universidad se clasifican de acuerdo a sus años en la universidad (X) y el número de visitas
Variables aleatòries vectorials Els problemes assenyalats amb un (*) se faran a classe. 1.- Los estudiantes de una universidad se clasifican de acuerdo a sus años en la universidad (X) y el número de visitas
