4.2. Relaciones de equivalencia
|
|
|
- María Jesús Medina Ortiz
- hace 7 años
- Vistas:
Transcripción
1 Capítulo. Representación de conjuntos mediante árboles Es más, en la aplicación del corrector ortográfico interactivo los tries resultan especialmente interesantes. A medida que el usuario escribe, el programa iría moviéndose por el árbol, de manera que cada pulsación de una tecla correspondería a bajar un nivel en el árbol. Al acabar una palabra, se comprobaría si existe un valor para la etiqueta $. Todas las operaciones tardarían un tiempo constante y muy reducido. El corrector podría incluir otras utilidades, como por ejemplo completar una palabra a medio escribir si a partir de ese prefijo sólo existe una palabra correcta... Relaciones de equivalencia Las relaciones de equivalencia son un concepto matemático definido sobre un conjunto dado cualquiera. Como tantos otros conceptos matemáticos, está basado en una idea intuitiva, la representación de relaciones del tipo: ciudades en una misma región, alumnos de la misma clase, instrucciones dentro del mismo bloque de código, enteros con el mismo valor de módulo P, etc. Definición. Una relación de equivalencia sobre un conjunto C es una relación R que cumple las siguientes propiedades 7 : Reflexiva. a C; ara Simétrica. a, b C; arb bra Transitiva. a, b, c C; (arb) (b Rc) (a Rc) Es fácil comprobar estas propiedades para los ejemplos anteriores. Por ejemplo, la propiedad reflexiva significa que una ciudad está en la misma región que ella misma, obviamente!; la simétrica diría que si la ciudad a está en la misma región que b, entonces b está en la misma región que a; y la transitiva, que si a está en misma región que b, y esta en la misma que c, entonces a y c están en la misma región. Las tres se cumplen de manera trivial. En la figura.7 se muestra un ejemplo particular de relación de equivalencia, definida sobre un conjunto de nueve elementos. Las relaciones de equivalencia dan lugar al concepto de clase de equivalencia. La clase de equivalencia de un elemento a, según una relación R sobre un conjunto C, es el subconjunto de todos los elementos c de C tales que cra. Por ejemplo, en los casos anteriores tendríamos: la clase de las ciudades de la Región de Murcia, la clase de los alumnos de segundo curso, etc. El conjunto de todas las clases de equivalencia definidas sobre C según la relación R, forma una partición de ese conjunto, es decir, son un conjunto de subconjuntos disjuntos y la unión de todos ellos es el conjunto de partida C. Nuestro interés, como programadores, es estudiar la implementación eficiente de relaciones de equivalencia definidas sobre conjuntos finitos. Además, vamos a considerar especialmente relaciones que no pueden ser calculadas mediante una fórmula (como ocurre, por ejemplo, con la igualdad de enteros módulo P ) y que pueden variar en tiempo de ejecución. En otro caso, la implementación sería inmediata. Pero, en primer lugar, vamos a definir un tipo abstracto de datos para el uso de relaciones de equivalencia. 7 La expresión a Rb se lee a está relacionado con b.
2 .. Relaciones de equivalencia C Figura.7: Ejemplo de relación de equivalencia y clases de equivalencia, definidos sobre el conjunto de los enteros del a. Los elementos que están en la misma clase de equivalencia aparecen dibujados dentro del mismo subconjunto del conjunto C. El TAD relación de equivalencia La definición del tipo abstracto debe enumerar las operaciones que se pueden aplicar sobre relaciones de equivalencia y su significado. Existen varias maneras de plantear la utilización del tipo. Una primera forma sería empezar con una relación mínima, vacía, al crearla y tener una operación para unir varias clases de equivalencia en una. Otra posibilidad sería empezar una sola clase de equivalencia al crear e incluir operaciones para partir una clase en dos o más. A lo largo de toda esta sección, trabajaremos exclusivamente con la primera posibilidad. Además de los constructores del tipo que, en este caso, serían la operación Crear para formar una nueva relación vacía y Union para juntar dos clases añadimos una operación Encuentra para consultar la clase de equivalencia de un elemento de C cualquiera. La especificación informal del tipo abstracto es la siguiente. TAD RelacionEquiv[T: tipo] es Crear, Union, Encuentra Requiere El tipo T debe tener definida una operación de comparación Igual (ent T, T; sal boolean). Descripción Los valores de tipo RelacionEquiv[T] son relaciones de equivalencia modificables, definidas sobre conjuntos de elementos del tipo T. En particular, el conjunto de elementos que pueden participar en la relación de equivalencia es indicado en la operación Crear. Para añadir relaciones entre elementos se debe utilizar la operación Union, y para consulta la clase de un elemento se debe usar Encuentra. Operaciones Operación Crear (ent C: Conjunto[T]; sal RelacionEquiv[T]) Requiere: El conjunto C debe ser no vacío. Calcula: Devuelve una relación de equivalencia mínima sobre el conjunto C, donde las clases de equivalencia son los elementos en sí mismos, es decir, para todo a y b de C, a está relacionado con b síysólo si a=b. Operación Union (ent R: RelacionEquiv[T]; a, b: T) Requiere: Los elementos a y b deben pertenecer al conjunto C sobre el que se ha definido la relación de equivalencia R.
3 Capítulo. Representación de conjuntos mediante árboles Modifica: R Calcula: En la nueva relación de equivalencia R, los elementos a y b pertenecen a la misma clase de equivalencia. Además, se mantienen las demás relaciones definidas previamente sobre R. Operación Encuentra (ent R: RelacionEquiv[T]; a: T; sal T) Requiere: El elemento a deben pertenecer al conjunto C sobre el que se ha definido la relación de equivalencia R. Calcula: Devuelve el nombre de la clase de equivalencia a la que pertenece el elemento a dentro de la relación R. Este nombre es un elemento representativo dentro de dicha clase. Fin RelacionEquiv. Para saber si dos elementos x e y están en la misma clase, simplemente comprobamos si Encuentra(x) = Encuentra(y). Como se documenta en la especificación de Encuentra, el resultado es un elemento de los que pertenecen a la clase de x. Este elemento puede ser seleccionado arbitrariamente entre los de dicha clase. Solamente necesitamos que al aplicar Encuentra para dos elementos relacionados, devuelva siempre el mismo valor. Por ejemplo, en la relación de la figura.7, a la clase formada por {,, } se le puede asociar como nombre representativo cualquiera de esos tres valores; pero una vez asociado uno, no puede variar. En definitiva, lo importante no es el valor concreto, sino que Encuentra() = Encuentra() = Encuentra(). Obviamente, el nombre sí que puede cambiar después de una operación Union. Ejemplo de uso de relaciones de equivalencia Un ejemplo de utilización intensiva de las relaciones de equivalencia lo podemos encontrar en el procesamiento de imágenes digitales. Supongamos una imagen en escala de grises, como la de la figura.8, que está compuesta por una matriz de píxeles. En este caso, las clases de equivalencia son las regiones contiguas y del mismo color. Estas clases surgen de la siguiente relación de equivalencia: dos píxeles a y b están relacionados si tienen el mismo color (o nivel de gris) y además son adyacentes en la imagen 8. En esta aplicación, el cálculo y la modificación de las clases de equivalencia puede resultar interesante para diversos propósitos. Por ejemplo, si queremos aplicar la operación rellenar una región de color, tendremos que buscar la clase de equivalencia del punto sobre el que se aplica el rellenado. Tras aplicar la operación, pueden ocurrir cambios en las clases de equivalencia, que se deberán tener en cuenta posteriormente. También podrían resultar interesantes operaciones para contar el número de regiones existentes en la imagen, o saber cuál contiene más píxeles. Por ejemplo, un posible algoritmo de detección de caras humanas en una imagen podría estar basado en buscar una región contigua de color de piel, y que contenga por lo menos dos regiones oscuras correspondientes a los ojos. En todas estas aplicaciones, la relación está definida sobre un conjunto finito, y puede variar dinámicamente a lo largo del tiempo. Si consideremos imágenes con una resolución de píxeles, entonces el conjunto C sobre el que está definida la relación tendrá elementos. Por lo tanto, conseguir una implementación muy eficiente para 8 Es decir, uno se encuentra inmediatamente encima, debajo, a la izquierda o a la derecha del otro.
4 .. Relaciones de equivalencia 5 Región 0 Región Región Región 5 Región Región Región Región Región 6 Figura.8: Ejemplo de aplicación de relaciones y clases de equivalencia, en procesamiento de imágenes. Aparecen señaladas algunas clases (regiones) cuyos píxeles tienen color negro. conocer y manejar las clases de equivalencia resulta fundamental en este caso.... Representaciones sencillas de relaciones de equivalencia La representación de relaciones de equivalencia es un ejemplo típico de problema donde se intuye fácilmente una solución simple y directa. Pero un pequeño e irritante contratiempo hace que esta solución se comporte peor de lo que se esperaba, lo cual obliga a tomar un largo rodeo para alcanzar una representación eficiente. Representación mediante arrays Supongamos, para simplificar el problema, que las relaciones de equivalencia están definidas sobre un tipo enumerado. Es más, supongamos que los elementos del conjunto C sobre el que se definen están numerados desde hasta cierto límite N. Por ejemplo, en el caso de las imágenes, podemos asignar un número consecutivo a cada píxel, de arriba abajo y de izquierda a derecha. Para imágenes de resolución , N= La representación más sencilla podría consistir en un array de tamaño N, donde en cada posición se almacena el nombre de la clase de equivalencia del elemento correspondiente. La definición del tipo sería la siguiente. tipo RelacionEquiv[N] = array [..N] de entero En la figura.a) se muestra un ejemplo de la disposición en memoria de la estructura, para la relación de equivalencia definida en la figura.7. La implementación de las operaciones Crear y Encuentra es inmediata. operación Crear (var R: RelacionEquiv[N])
5 6 Capítulo. Representación de conjuntos mediante árboles (a) R (b) R ultimo primero Figura.: Ejemplo de representaciones sencillas de relaciones de equivalencia, para la relación de la figura.7. a) Representación con arrays. b) Representación con listas. para i:=,..., N hacer R[i]:= i finpara operación Encuentra (R: RelacionEquiv[N]; a: entero): entero devolver R[a] La operación Encuentra está claramente en un O(), lo cual resulta muy interesante. Por otro lado, Crear tarda un O(N), lo cual no es muy preocupante puesto que sólo se aplicará una vez. El problema es, sin embargo, la operación Union que es previsible que aparezca con más frecuencia. Cómo hacer la unión de dos clases? Simplemente cambiando en el array el nombre de una de las clases por la otra. Supongamos que los parámetros que recibe la operación son nombres de clases (y no valores de elementos particulares). La implementación podría ser la siguiente. operación Union (var R: RelacionEquiv[N]; a, b: entero) para i:=,..., N hacer si R[i] =b entonces R[i]:= a finsi finpara Es fácil ver que la operación Union tarda un O(N), en todos los casos. Este coste puede resultar excesivo para muchas aplicaciones. En el ejemplo del procesamiento de imágenes, se aplicará la unión siempre que un píxel tenga a un lado algún otro píxel del mismo color lo cual suele ser muy frecuente. Si tenemos que aplicar Union para cada píxel de una imagen de , el número total de comparaciones dentro del bucle para sería: ( ) = 0 mil millones de comparaciones! Representación mediante listas Para solucionar el problema anterior podemos intentar una representación dinámica mediante listas, al estilo de las representaciones básicas de conjuntos estudiadas en el
6 .. Relaciones de equivalencia 7 capítulo anterior. Para cada clase de equivalencia usamos una lista de elementos, en la que estarán los elementos que pertenecen a la misma. La definición del tipo sería. tipo RelacionEquiv[N] = array [..N] de Lista[entero] Siendo suficientemente cuidadosos, deberíamos usar una estructura que permita concatenar dos listas de forma rápida. Esto se puede conseguir, por ejemplo, usando listas circulares y doblemente enlazadas; o simplemente almacenando en la cabecera de las listas un puntero al primer y al último elemento, como se muestra en la figura.b). Usando la segunda opción, la operación Union se puede conseguir en un tiempo constante, O(), de la siguiente forma. Se supone que el tipo Lista incluye los atributos primero y ultimo, y los nodos de lista tienen siguiente, para enlazar los elementos. operación Union (var R: RelacionEquiv[N]; a, b: entero) R[a].ultimo.siguiente:= R[b].primero R[a].ultimo:= R[b].ultimo R[b]:= NULO El problema surge ahora con la operación Encuentra. Cómo podemos saber la clase a la que pertenece un elemento concreto? Deberíamos recorrer todas las listas hasta encontrarlo en alguna de ellas. operación Encuentra (R: RelacionEquiv[N]; a: entero): entero para i:=,..., N hacer si BuscaLista (R[i], a) entonces devolver i finsi finpara error( El elemento, a, no está en ninguna clase ) Damos por supuesta la operación BuscaLista, que realiza un simple recorrido secuencial en una lista. No siempre tardará el mismo tiempo, pero sabemos que en el peor caso se recorrerán en total todos los elementos de todas las listas, es decir N. En promedio, la operación Encuentra recorrerá la mitad de las listas, tardando un O(N). Si resulta malo que la operación Union estéenuno(n), como ocurría usando arrays, el hecho de que Encuentra tarde un O(N) puede ser aun más desastroso en aplicaciones que requieren un uso intensivo de las relaciones de equivalencia.... Representación mediante punteros al padre El inconveniente último de las dos anteriores representaciones es que utilizan estructuras lineales ya sean enlazadas (listas) o contiguas en memoria (arrays) lo cual ocasiona tiempos lineales, bien para la búsqueda o para la unión de clases de equivalencia. En su lugar vamos a estudiar el uso de estructuras arbóreas. Vamos a disponer de un árbol para cada clase, donde la raíz del árbol será por definición el nombre de esa clase. Básicamente, la unión de dos árboles se puede conseguir en un tiempo constante, colocando un árbol como subárbol del otro. En cuanto a la búsqueda, está claro que necesitamos una operación que dado un elemento del árbol encuentre cuál es la raíz. Por esta razón, usamos una representación de árboles con punteros al nodo padre.
7 8 Capítulo. Representación de conjuntos mediante árboles Árboles de punteros al padre La clave de la representación de árboles con punteros al padre es que para cada nodo del árbol sólo necesitamos conocer un valor: un puntero o referencia a su padre dentro del árbol. Para la raíz del árbol ese valor será nulo o algún otro valor especial. Suponiendo que el número de elementos del árbol es fijo, o limitado por un tamaño reducido, la estructura de punteros al padre se puede almacenar en simple array. tipo ArbolEnteros[N] = array [..N] de entero Si R es un árbol de enteros que usa esta estructura, entonces la posición R[i] indica el padre del nodo i. Un ejemplo de representación de árboles con esta definición se puede ver en la figura.0. En este caso, se usa el valor 0 para indicar que el nodo es la raíz de un árbol. R: array [..0] de entero Figura.0: Ejemplo de representación de árboles mediante punteros al padre. Bosques de relaciones de equivalencia La anterior representación de árboles con punteros al padre se ajusta perfectamente a nuestras necesidades: el número de elementos de la relación de equivalencia es fijo, se define al crear la relación. Realmente, la estructura no almacena un solo árbol sino un conjunto de árboles, lo que normalmente se conoce como un bosque. La definición del tipo sería la siguiente. tipo RelacionEquiv[N] = array [..N] de entero Como ya hemos avanzado, cada árbol del bosque representa una clase de equivalencia, en la cual la raíz es el nombre de esa clase. La implementación de las operaciones es sencilla. La operación Crear crea una relación de equivalencia mínima, donde cada elemento sólo está relacionado consigo mismo. Equivalentemente, cada elemento del conjunto será la raíz de un árbol. Usando el valor 0 para representar las raíces, tenemos. operación Crear (var R: RelacionEquiv[N]) para i:=,..., N hacer R[i]:= 0 El lector podrá apreciar un curioso hecho, la definición es exactamente la misma que en la representación mediante arrays! La diferencia es la forma en la que se maneja el array. Mientras que antes lo usábamos para almacenar las clases de cada elemento, ahora lo usamos para representar árboles. Esto demuestra, una vez más, la estrecha relación existente entre algoritmos y estructuras de datos. La estructura de datos no determina unívocamente un tipo de datos, sino que se deben tener en cuenta también los algoritmos que manipulan esa estructura.
8 .. Relaciones de equivalencia finpara Aunque su tiempo es claramente un O(N), ya hemos visto que en este caso no supone un inconveniente, ya que sólo se hará al principio. Por otro lado, la operación Union simplemente coloca un árbol como subárbol del otro. Igual que antes, suponemos que los parámetros no son elementos sino nombres de clases de equivalencia 0. operación Union (var R: RelacionEquiv[N]; a, b: entero) R[a]:= b // a se coloca como hijo de b Así pues, la operación tarda un interesante O(). Finalmente, la operación Encuentra debe subir por el árbol, hacia sus antecesores, hasta llegar a la raíz de su árbol. Una posible implementación recursiva sería la siguiente. operación Encuentra (R: RelacionEquiv[N]; a: entero): entero si R[a] =0entonces devolver a sino devolver Encuentra(R[a]) finsi El tiempo de la operación Encuentra depende de la profundidad del nodo buscado dentro del árbol. En principio, es de esperar que un árbol de N nodos tenga una profundidad de un orden logarítmico en función de N, con lo cual el tiempo estaría en un O(log n). Sin embargo, en el peor caso el árbol puede adoptar una forma lineal: cualquier nodo sólo tiene un descendiente como máximo. En tal caso, un árbol de N nodos tendrá profundidad N y las operaciones de búsqueda estarán en promedio en O(N). Vamos a ver un ejemplo ilustrativo de una situación de este tipo. Ejemplo. Utilizando la representación de relaciones de equivalencia con punteros al padre, definimos una variable R de tipo RelacionEquiv[], para almacenar relaciones en el conjunto de los naturales de a.sobre esta estructura aplicamos las siguientes operaciones: Crear(R), Union(R,,), Union(R,,8), Union(R,,), Union(R, 5,6), Union(R,, 6) y Encuentra(R, ). El resultado se muestra en la figura..... Equilibrado y compresión de caminos Podemos extraer una conclusión práctica del anterior ejemplo: si queremos conseguir eficiencia en una representación de árboles debemos garantizar que el árbol crecerá a lo ancho, más que a lo largo. Un árbol poco profundo significa pocos pasos en la búsqueda, lo cual se traduce en operaciones más rápidas. Entonces, cómo podemos hacer que el árbol crezca a lo ancho? Supongamos, en primer lugar, que tenemos un árbol a de profundidad 0 y otro árbol b de profundidad. Tenemos dos opciones en principio igual de válidas, colocar a como hijo de b o viceversa. Si hacemos que a sea hijo de b, entonces el nuevo árbol tendrá profundidad. En cambio, si colocamos b como hijo de a, la profundidad del árbol no varía, seguiría siendo 0. El resultado es bastante claro: si queremos que el árbol no crezca en profundidad, debemos colocar el árbol menos profundo como subárbol 0 En caso contrario, habría que aplicar las operaciones de búsqueda correspondientes.
9 50 Capítulo. Representación de conjuntos mediante árboles R Crear(R) R Union(R,, ) Union(R,, 8) R Union(R,, ) R Union(R, 5, 6) R Union (R,, 6) R Encuentra(R, ) = Encuentra(R, ) = Encuentra(R, ) = Encuentra(R, 6) = 6 Figura.: Evolución de la estructura de relaciones de equivalencia, para las operaciones del ejemplo.. del más profundo. Si ambos son igual de profundos, entonces necesariamente el árbol resultante crecerá en profundidad. Calcular la profundidad de los árboles puede resultar de por sí muy costoso, y especialmente con el tipo de representación usado. Pero si se almacena la profundidad y se va actualizando a medida que crece el árbol, podemos lograrlo eficientemente. Para no incurrir en un uso adicional de memoria, vamos a usar la misma definición del tipo que en el anterior apartado, pero cambiando la forma de manejar las operaciones.
10 .. Relaciones de equivalencia 5 En particular, si antes almacenábamos un 0 en el array para las raíces, ahora podemos tener 0 o un número negativo indicando la profundidad de ese árbol. De esta manera, en la operación Union podemos comprobar fácilmente cuál es el árbol más profundo. En caso de que sean iguales, da lo mismo cuál se coloque como hijo y además sabemos que el árbol resultante aumentará de nivel. operación Union (var R: RelacionEquiv[N]; a, b: entero) si R[b] < R[a] entonces // El árbol b es más profundo R[a]:= b sino // El árbol a es más o igual de profundo si R[a] =R[b] entonces R[a]:= R[a]- finsi R[b]:= a finsi Por otro lado, en la operación Encuentra es posible hacer otra modificación interesante conocida como compresión de caminos. Supongamos que sobre una relación de equivalencia aplicamos la operación Encuentra(x), obteniendo como resultado una clase y cualquiera. La operación habrá necesitado un número de pasos que depende de su profundidad en el árbol. Ahora bien, puesto que después de ejecutar la operación sabemos que la clase de x es y, es posible hacer que x apunte directamente a y, esto es R[x]:= y. De esta forma, la próxima vez que se ejecute Encuentra(x) sólo se necesitará un paso para llegar a la raíz del árbol. Es más, la idea de apuntar directamente a la raíz del árbol se puede aplicar a todos los antecesores del nodo x, que se recorren al aplicar la operación de búsqueda. En definitiva, la operación Encuentra con compresión del árbol sería la siguiente. operación Encuentra (var R: RelacionEquiv[N]; a: entero): entero si R[a] 0 entonces devolver a sino R[a]:= Encuentra(R, R[a]) devolver R[a] finsi El objetivo del proceso de compresión de caminos es reducir la profundidad de los nodos sobre los que se aplica la búsqueda. En algún caso, esta reducción puede dar lugar a una disminución en la profundidad total del árbol. Sin embargo, se puede ver que la implementación de la operación Encuentra no actualiza esa profundidad, que es almacenada en las raíces con valores negativos. Esta omisión no es casual, recalcular la profundidad del árbol supondría un coste computacional de O(N) que echaría a perder la eficiencia de tipo sin producir una mejora sustancial posterior. Así pues, podemos decir que la profundidad almacenada en los nodos raíces es realmente un valor de profundidad máxima o profundidad suponiendo que no se aplican búsquedas. Ejemplo. Vamos a analizar la ejecución de las operaciones del ejemplo., con las modificaciones propuestas para Union y Encuentra. Las operaciones aplicadas son :
11 5 Capítulo. Representación de conjuntos mediante árboles Crear(R), Union(R,,), Union(R,,8), Union(R,,), Union(R, 5,6), Union(R,,6)y Encuentra(R, ). El resultado se muestra en la figura.. R Crear(R) R Union(R,, ) Union(R,, 8) R Union(R,, ) R Union(R, 5, 6) R Union (R,, 6) R Encuentra(R, ) = Encuentra(R, ) = Encuentra(R, 6) = 6 R Figura.: Evolución de la estructura de relaciones de equivalencia, para las operaciones del ejemplo., usando la representación de punteros al padre, con equilibrado y compresión de caminos. Como cabía esperar, la profundidad de los árboles obtenidos es menor aplicando
12 .. Relaciones de equivalencia 5 equilibrado y compresión de camino. Esto significa un menor tiempo de ejecución para las operaciones del tipo. Se puede ver que, en el ejemplo, la operación Encuentra(R,,6)ha sido sustituida por Encuentra(R,,6). Recordemos que la operación Encuentra requiere que se aplique sobre raíces de los árboles. Mientras que el nodo es raíz en el ejemplo., en el ejemplo. no lo es. En su lugar, usamos la clase del nodo, es decir. Evaluación de la eficiencia Es evidente que la estructura utilizada para representar relaciones de equivalencia necesita una cantidad de memoria proporcional al tamaño N del conjunto sobre el que se aplica la relación. En el caso de las imágenes, por ejemplo, la memoria podría ser tanta como la utilizada por la imagen en sí. No obstante, este uso es razonable teniendo en cuenta que la relación no puede ser calculada mediante una fórmula. En lo que se refiere al tiempo de ejecución, tenemos por un lado la operación Union que ejecuta siempre como máximo un número fijo de instrucciones, con lo que su tiempo es un O(). Por otro lado, el tiempo de la operación Encuentra es proporcional al nivel del nodo buscado en el árbol, como ya hemos visto. El tiempo necesario dependerá del caso. Mejor caso. Si se aplican las operaciones Union de forma adecuada, el árbol no crece en profundidad más que una cantidad fija y reducida. En esta situación el tiempo de Encuentra sería un O(). Peor caso. El peor caso se dará cuando el árbol crezca en profundidad lo más rápidamente posible. Teniendo en cuenta la estructura del procedimiento Union, elárbol sólo crecerá de nivel cuando los dos árboles unidos tengan la misma altura. Se puede demostrar por inducción que un árbol de profundidad h tiene como mínimo h nodos. Por lo tanto, para N nodos la profundidad máxima sería log N, y el tiempo de ejecución de Encuentra en el peor caso es un O(log N). Caso promedio. El tiempo promedio de Encuentra, incluyendo equilibrado y compresión de caminos, resulta difícil de calcular. Se puede ver intuitivamente que el tiempo será mucho menor que un tiempo logarítmico. En término medio, será muy difícil que el árbol alcance profundidad. Teniendo en cuenta que el árbol de profundidad 5 se forma uniendo dos árboles de profundidad, será mucho más difícil obtener el árbol de profundidad 5, y así sucesivamente. En concreto, el tiempo de ejecución de Encuentra en el caso promedio es un O(α(N)); donde α(n) es una función de crecimiento muy lento, situado entre un O()yunO(log n). La función α(n) se define como la pseudo-inversa de una función A(x) de crecimiento muy rápido, conocida como función de Ackerman. Por ejemplo, los valores iniciales de esta función son: A() =, A() =, A() =, A() =.. donde los puntos significan repetir la operación de elevación veces. A(5) es un valor tan grande que no existe una notación estándar para expresarlo de forma expandida. A efectos prácticos, el tiempo promedio de Encuentra se puede considerar casi un O(). Base de la inducción: un árbol con altura tiene como mínimo nodos. Paso de inducción: suponiendo que los árboles de altura h tienen como mínimo h nodos, un árbol de altura h tendrá como mínimo h nodos. La demostración se deja como ejercicio. Tener en cuenta que un árbol de altura h se forma uniendo dos árboles de altura h.
Conjuntos disjuntos (Relaciones de equivalencia)
 Conjuntos disjuntos (Relaciones de equivalencia) Una relación R se define en un conjunto C si para todo par de elementos (a,b),a,b C,a R b es verdadera o falsa. Una relación de equivalencia es una relación
Conjuntos disjuntos (Relaciones de equivalencia) Una relación R se define en un conjunto C si para todo par de elementos (a,b),a,b C,a R b es verdadera o falsa. Una relación de equivalencia es una relación
Conjuntos finitos y conjuntos numerables
 Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Desde la secundaria estamos acostumbrados a trabajar con polinomios, los cuales identificamos con expresiones de la forma
 Polinomios Desde la secundaria estamos acostumbrados a trabajar con polinomios, los cuales identificamos con expresiones de la forma p(x) = a 0 + a 1 x +... + a n x n (1) donde x es la variable y a 0,
Polinomios Desde la secundaria estamos acostumbrados a trabajar con polinomios, los cuales identificamos con expresiones de la forma p(x) = a 0 + a 1 x +... + a n x n (1) donde x es la variable y a 0,
Matemáticas I: Hoja 1
 Matemáticas I: Hoja 1 1. Números complejos Hasta ahora, hemos visto que los números reales son aquellos que poseen una expresión decimal y que podemos representar en una recta infinita. No obstante, para
Matemáticas I: Hoja 1 1. Números complejos Hasta ahora, hemos visto que los números reales son aquellos que poseen una expresión decimal y que podemos representar en una recta infinita. No obstante, para
Contenido. Página 2 de 8
 RÚBRICA Contenido INTRODUCCIÓN... 3 CONFIGURACIÓN Y GESTIÓN DE UNA RÚBRICA... 3 Definir un nuevo formulario de calificación desde cero, para crear un nuevo formulario desde cero... 4 Crear un nuevo formulario
RÚBRICA Contenido INTRODUCCIÓN... 3 CONFIGURACIÓN Y GESTIÓN DE UNA RÚBRICA... 3 Definir un nuevo formulario de calificación desde cero, para crear un nuevo formulario desde cero... 4 Crear un nuevo formulario
Complejidad algorítmica. Algoritmos y Estructuras de Datos II (Programación I) Mgter. Vallejos, Oscar A.
 Complejidad algorítmica Complejidad Algorítmica En particular, usualmente se estudia la eficiencia de un algoritmo en tiempo (de ejecución), espacio (de memoria) o número de procesadores (en algoritmos
Complejidad algorítmica Complejidad Algorítmica En particular, usualmente se estudia la eficiencia de un algoritmo en tiempo (de ejecución), espacio (de memoria) o número de procesadores (en algoritmos
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Junio 2011 - Propuesta B
 Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Junio 2011 - Propuesta B 1. Queremos invertir una cantidad de dinero en dos tipos
Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG) Matemáticas aplicadas a las Ciencias Sociales II - Junio 2011 - Propuesta B 1. Queremos invertir una cantidad de dinero en dos tipos
TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS.
 TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS. TEORÍA DE CONJUNTOS. Definiciones. Se define un conjunto como una colección de objetos o cosas, se nombran con letras mayúsculas (A, B...). Cada uno de
TEMA 2: TEORÍA DE CONJUNTOS Y CONJUNTOS NUMÉRICOS. TEORÍA DE CONJUNTOS. Definiciones. Se define un conjunto como una colección de objetos o cosas, se nombran con letras mayúsculas (A, B...). Cada uno de
Topología de R n. Beatriz Porras
 Producto escalar, métrica y norma asociada. Topología de R n Beatriz Porras 1 Producto escalar, métrica y norma asociada Consideramos el espacio vectorial R n sobre el cuerpo R; escribimos los vectores
Producto escalar, métrica y norma asociada. Topología de R n Beatriz Porras 1 Producto escalar, métrica y norma asociada Consideramos el espacio vectorial R n sobre el cuerpo R; escribimos los vectores
1. Conocimientos previos. 1 Funciones exponenciales y logarítmicas.
 . Conocimientos previos. Funciones exponenciales y logarítmicas.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
. Conocimientos previos. Funciones exponenciales y logarítmicas.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
Expresiones algebraicas
 Expresiones algebraicas Expresiones algebraicas Las expresiones algebraicas Elementos de una expresión algebraica Números de cualquier tipo Letras Signos de operación: sumas, restas, multiplicaciones y
Expresiones algebraicas Expresiones algebraicas Las expresiones algebraicas Elementos de una expresión algebraica Números de cualquier tipo Letras Signos de operación: sumas, restas, multiplicaciones y
APLICACIÓN DE ÁRBOLES BINARIOS
 PRÁCTICA Nº 6: 2 sesiones (del 22 al 31 de Mayo de 2002) APLICACIÓN DE ÁRBOLES BINARIOS A LA COMPRESIÓN DE FICHEROS DE TEXTO MEDIANTE LA UTILIZACIÓN DE LOS CÓDIGOS DE HUFFMAN 0.- OBJETIVOS El objetivo
PRÁCTICA Nº 6: 2 sesiones (del 22 al 31 de Mayo de 2002) APLICACIÓN DE ÁRBOLES BINARIOS A LA COMPRESIÓN DE FICHEROS DE TEXTO MEDIANTE LA UTILIZACIÓN DE LOS CÓDIGOS DE HUFFMAN 0.- OBJETIVOS El objetivo
GUIA PRACTICA PARA LA APLICACIÓN DE MS EXCEL TECNOLOGIA/ INFORMATICA
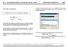 Fórmulas y funciones De la barra de menú seleccionmos la opción insertar y haciendo clic en la opción f x se desplegará el siguiente cuadro de diálogo a partir del cual escogeremos la función adecuada
Fórmulas y funciones De la barra de menú seleccionmos la opción insertar y haciendo clic en la opción f x se desplegará el siguiente cuadro de diálogo a partir del cual escogeremos la función adecuada
Polinomios. 1.- Funciones cuadráticas
 Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Estructuras de datos: Conjuntos disjuntos
 Estructuras de datos: Dep. de Computación - Fac. de Informática Universidad de A Coruña Santiago Jorge sjorge@udc.es Referencias bibliográficas G. Brassard y T. Bratley. Estructura de datos. En Fundamentos
Estructuras de datos: Dep. de Computación - Fac. de Informática Universidad de A Coruña Santiago Jorge sjorge@udc.es Referencias bibliográficas G. Brassard y T. Bratley. Estructura de datos. En Fundamentos
Se utilizarán las letras mayúsculas, tales como A, B y C para nombrar conjuntos. Por ejemplo: a i. o e
 Conjuntos Notación de conjuntos Se utilizarán las letras mayúsculas, tales como A, B y C para nombrar conjuntos. Por ejemplo: A 1,2,3 B 2,5,6 C a, e, i, o, u D #,&,*,@ Es bastante corriente dibujar los
Conjuntos Notación de conjuntos Se utilizarán las letras mayúsculas, tales como A, B y C para nombrar conjuntos. Por ejemplo: A 1,2,3 B 2,5,6 C a, e, i, o, u D #,&,*,@ Es bastante corriente dibujar los
El cuerpo de los números reales
 Capítulo 1 El cuerpo de los números reales 1.1. Introducción Existen diversos enfoques para introducir los números reales: uno de ellos parte de los números naturales 1, 2, 3,... utilizándolos para construir
Capítulo 1 El cuerpo de los números reales 1.1. Introducción Existen diversos enfoques para introducir los números reales: uno de ellos parte de los números naturales 1, 2, 3,... utilizándolos para construir
Dependencia e independencia lineal
 CAPíTULO 3 Dependencia e independencia lineal En este capítulo estudiaremos tres conceptos de gran importancia para el desarrollo del álgebra lineal: el concepto de conjunto generador, el concepto de conjunto
CAPíTULO 3 Dependencia e independencia lineal En este capítulo estudiaremos tres conceptos de gran importancia para el desarrollo del álgebra lineal: el concepto de conjunto generador, el concepto de conjunto
Ejercicio 1: Realiza las siguientes divisiones por el método tradicional y por Ruffini: a)
 Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
VALOR ABSOLUTO. Definición.- El valor absoluto de un número real, x, se define como:
 VALOR ABSOLUTO Cualquier número a tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto a al origen. Observe en el dibujo que la distancia del al origen
VALOR ABSOLUTO Cualquier número a tiene su representación en la recta real. El valor absoluto de un número representa la distancia del punto a al origen. Observe en el dibujo que la distancia del al origen
TEMA 2: EL INTERÉS SIMPLE
 TEMA 2: EL INTERÉS SIMPLE 1.- CAPITALIZACIÓN SIMPLE 1.1.- CÁLCULO DEL INTERÉS: Recibe el nombre de capitalización simple la ley financiera según la cual los intereses de cada periodo de capitalización
TEMA 2: EL INTERÉS SIMPLE 1.- CAPITALIZACIÓN SIMPLE 1.1.- CÁLCULO DEL INTERÉS: Recibe el nombre de capitalización simple la ley financiera según la cual los intereses de cada periodo de capitalización
Práctica 2 Métodos de búsqueda para funciones de una variable
 Práctica 2 Métodos de búsqueda para funciones de una variable Introducción Definición 1. Una función real f se dice que es fuertemente cuasiconvexa en el intervalo (a, b) si para cada par de puntos x 1,
Práctica 2 Métodos de búsqueda para funciones de una variable Introducción Definición 1. Una función real f se dice que es fuertemente cuasiconvexa en el intervalo (a, b) si para cada par de puntos x 1,
3. Métodos clásicos de optimización lineal
 3. Métodos clásicos de optimización lineal Uso del método Simplex El problema que pretende resolverse es un problema de optimización lineal sujeto a restricciones. Para el modelo construido para el problema
3. Métodos clásicos de optimización lineal Uso del método Simplex El problema que pretende resolverse es un problema de optimización lineal sujeto a restricciones. Para el modelo construido para el problema
Construyamos una tabla de valores que incluya valores negativos y positivos de.
 Materia: Matemáticas de 4to año Tema: Representación gráfica de una función exponencial Marco teórico Funciones exponenciales Iniciemos esta sección construyendo las gráficas de algunas funciones exponenciales.
Materia: Matemáticas de 4to año Tema: Representación gráfica de una función exponencial Marco teórico Funciones exponenciales Iniciemos esta sección construyendo las gráficas de algunas funciones exponenciales.
Tema 2. Grupos. 3. El conjunto de matrices de orden 2 con coeficientes enteros (o reales) con la suma es un grupo conmutativo.
 Tema 2. Grupos. 1 Grupos Definición 1 Un grupo es una estructura algebraica (G, ) tal que la operación binaria verifica: 1. * es asociativa 2. * tiene elemento neutro 3. todo elemento de G tiene simétrico.
Tema 2. Grupos. 1 Grupos Definición 1 Un grupo es una estructura algebraica (G, ) tal que la operación binaria verifica: 1. * es asociativa 2. * tiene elemento neutro 3. todo elemento de G tiene simétrico.
Los números naturales
 Los números naturales Los números naturales Los números naturales son aquellos que sirven para contar. Se suelen representar utilizando las cifras del 0 al 9. signo suma o resultado Suma: 9 + 12 = 21 sumandos
Los números naturales Los números naturales Los números naturales son aquellos que sirven para contar. Se suelen representar utilizando las cifras del 0 al 9. signo suma o resultado Suma: 9 + 12 = 21 sumandos
Las listas son una sucesión de cero o más elementos. Esta es una definición muy simple y que no aclara demasiado en términos informáticos.
 LISTAS Las listas son una sucesión de cero o más elementos. Esta es una definición muy simple y que no aclara demasiado en términos informáticos. Hay varios tipos de listas, las hay enlazadas, no enlazadas,
LISTAS Las listas son una sucesión de cero o más elementos. Esta es una definición muy simple y que no aclara demasiado en términos informáticos. Hay varios tipos de listas, las hay enlazadas, no enlazadas,
Algoritmos y Estructuras de Datos Ingeniería en Informática
 2.1.Sean A= {1, 2, 3, 7, 8} y B= {3, 4, 5, 7, 9}, mostrar la ejecución y los resultados de las siguientes operaciones, suponiendo una representación con arrays de booleanos y con listas de elementos (ordenadas
2.1.Sean A= {1, 2, 3, 7, 8} y B= {3, 4, 5, 7, 9}, mostrar la ejecución y los resultados de las siguientes operaciones, suponiendo una representación con arrays de booleanos y con listas de elementos (ordenadas
Tema 1. Álgebra lineal. Matrices
 1 Tema 1. Álgebra lineal. Matrices 0.1 Introducción Los sistemas de ecuaciones lineales aparecen en un gran número de situaciones. Son conocidos los métodos de resolución de los mismos cuando tienen dos
1 Tema 1. Álgebra lineal. Matrices 0.1 Introducción Los sistemas de ecuaciones lineales aparecen en un gran número de situaciones. Son conocidos los métodos de resolución de los mismos cuando tienen dos
Límites e indeterminaciones
 Límites e indeterminaciones La idea de límite de una función no es en sí complicada, pero hubo que esperar hasta el siglo XVII a que los matemáticos Newton 1 y Leibniz 2 le dieran forma y la convirtiesen
Límites e indeterminaciones La idea de límite de una función no es en sí complicada, pero hubo que esperar hasta el siglo XVII a que los matemáticos Newton 1 y Leibniz 2 le dieran forma y la convirtiesen
TEMA I: LOS CONCEPTOS FUNDAMENTALES DE LA TEORÍA DE LA COMPUTABILIDAD
 1 Asignatura: Lógica 3 Curso 2004-2005 Profesor: Juan José Acero 20 25 de Octubre del 2004 TEMA I: LOS CONCEPTOS FUNDAMENTALES DE LA TEORÍA DE LA COMPUTABILIDAD 1. El concepto de algoritmo. Los matemáticos
1 Asignatura: Lógica 3 Curso 2004-2005 Profesor: Juan José Acero 20 25 de Octubre del 2004 TEMA I: LOS CONCEPTOS FUNDAMENTALES DE LA TEORÍA DE LA COMPUTABILIDAD 1. El concepto de algoritmo. Los matemáticos
Problemas de Recursividad
 Problemas de Recursividad Problema 1. El factorial de un número entero n 0, denotado como n!, se define! como!!! i = 1 2 n cuando n > 0, y 0! = 1. Por ejemplo 6! = 1 2 3 4 5 6 = 720 Diseñad una método
Problemas de Recursividad Problema 1. El factorial de un número entero n 0, denotado como n!, se define! como!!! i = 1 2 n cuando n > 0, y 0! = 1. Por ejemplo 6! = 1 2 3 4 5 6 = 720 Diseñad una método
Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas. Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed.
 Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed. Agosto, 00 Notación exponencial La notación exponencial se usa para repetir
Universidad Politécnica de Puerto Rico Departamento de Ciencias y Matemáticas Preparado por: Prof. Manuel Capella-Casellas, M.A.Ed. Agosto, 00 Notación exponencial La notación exponencial se usa para repetir
SISTEMAS DE NUMERACIÓN
 SISTEMAS DE NUMERACIÓN INDICE. 1. DEFINICIÓN DE SISTEMAS DE NUMERACIÓN.... 1 2. TEOREMA FUNDAMENTAL DE LA NUMERACIÓN... 3 3. SISTEMAS DECIMAL, BINARIO, OCTAL Y HEXADECIMAL.... 5 3.1. SISTEMA DECIMAL...
SISTEMAS DE NUMERACIÓN INDICE. 1. DEFINICIÓN DE SISTEMAS DE NUMERACIÓN.... 1 2. TEOREMA FUNDAMENTAL DE LA NUMERACIÓN... 3 3. SISTEMAS DECIMAL, BINARIO, OCTAL Y HEXADECIMAL.... 5 3.1. SISTEMA DECIMAL...
VALORES EXACTOS DE FUNCIONES TRIGONOMÉTRICAS (SENO Y COSENO)
 VALORES EXACTOS DE FUNCIONES TRIGONOMÉTRICAS (SENO Y COSENO) En trigonometría plana, es fácil de encontrar el valor exacto de la función seno y coseno de los ángulos de 30, 5 y 60, gracias a la ayuda de
VALORES EXACTOS DE FUNCIONES TRIGONOMÉTRICAS (SENO Y COSENO) En trigonometría plana, es fácil de encontrar el valor exacto de la función seno y coseno de los ángulos de 30, 5 y 60, gracias a la ayuda de
Algoritmos y Estructuras de Datos Curso 04/05. Ejercicios
 35. Sean A= {1, 2, 3, 7, 8} y B= {3, 4, 5, 7, 9}, mostrar la ejecución y los resultados de las siguientes operaciones, suponiendo una representación con arrays de booleanos y con listas de elementos (ordenadas
35. Sean A= {1, 2, 3, 7, 8} y B= {3, 4, 5, 7, 9}, mostrar la ejecución y los resultados de las siguientes operaciones, suponiendo una representación con arrays de booleanos y con listas de elementos (ordenadas
Sistemas de Ecuaciones Lineales
 Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
Sistemas de Ecuaciones Lineales 1 Sistemas de ecuaciones y matrices Definición 1 Una ecuación lineal en las variables x 1, x 2,..., x n es una ecuación de la forma con a 1, a 2... y b números reales. a
MICROSOFT ACCESS 2007
 MICROSOFT ACCESS 2007 1. AVANZADO Nº Horas: 24 Objetivos: Descripción del funcionamiento del programa de gestión de bases de datos Microsoft Access 2007, estudiando los conceptos fundamentales de las bases
MICROSOFT ACCESS 2007 1. AVANZADO Nº Horas: 24 Objetivos: Descripción del funcionamiento del programa de gestión de bases de datos Microsoft Access 2007, estudiando los conceptos fundamentales de las bases
Determinantes. Primera definición. Consecuencias inmediatas de la definición
 Determinantes Primera definición Para calcular el determinante de una matriz cuadrada de orden n tenemos que saber elegir n elementos de la matriz de forma que tomemos solo un elemento de cada fila y de
Determinantes Primera definición Para calcular el determinante de una matriz cuadrada de orden n tenemos que saber elegir n elementos de la matriz de forma que tomemos solo un elemento de cada fila y de
Tema 05: Tablas hash. M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom
 Tema 05: Tablas hash M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom (Prof. Edgardo A. Franco) 1 Contenido Tablas hash o de dispersión Función
Tema 05: Tablas hash M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom (Prof. Edgardo A. Franco) 1 Contenido Tablas hash o de dispersión Función
f (x) (1+[f (x)] 2 ) 3 2 κ(x) =
![f (x) (1+[f (x)] 2 ) 3 2 κ(x) = f (x) (1+[f (x)] 2 ) 3 2 κ(x) =](/thumbs/40/20918876.jpg) MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
MATEMÁTICAS II - EXAMEN PRIMER PARCIAL - 4/11/11 Grado: Ing. Electrónica Rob. y Mec. Ing. Energía Ing. Organización Ind. Nombre y Apellidos: Ejercicio 1. La curvatura de una función f en un punto x viene
Conjuntos Un conjunto es una colección de objetos. A cada uno de esos objetos se llama elemento del conjunto.
 1 TEORÍA DE CONJUNTOS: IDEAS BÁSICAS Conjuntos Un conjunto es una colección de objetos. A cada uno de esos objetos se llama elemento del conjunto. Un conjunto puede darse enumerando todos y cada uno de
1 TEORÍA DE CONJUNTOS: IDEAS BÁSICAS Conjuntos Un conjunto es una colección de objetos. A cada uno de esos objetos se llama elemento del conjunto. Un conjunto puede darse enumerando todos y cada uno de
FUNCIONES DE UNA VARIABLE Julián de la Horra Departamento de Matemáticas U.A.M.
 FUNCIONES DE UNA VARIABLE Julián de la Horra Departamento de Matemáticas U.A.M. 1 Introducción Una de las primeras necesidades que surgen en las Ciencias Experimentales es la de poder expresar los valores
FUNCIONES DE UNA VARIABLE Julián de la Horra Departamento de Matemáticas U.A.M. 1 Introducción Una de las primeras necesidades que surgen en las Ciencias Experimentales es la de poder expresar los valores
CURSOSO. Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. MATEMÁTICAS. AntonioF.CostaGonzález
 CURSOSO CURSOSO MATEMÁTICAS Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. AntonioF.CostaGonzález DepartamentodeMatemáticasFundamentales FacultaddeCiencias Índice 1 Introducción y objetivos
CURSOSO CURSOSO MATEMÁTICAS Aritmética: Númerosnaturalesyenteros. Númerosracionalesyfraciones. AntonioF.CostaGonzález DepartamentodeMatemáticasFundamentales FacultaddeCiencias Índice 1 Introducción y objetivos
REGLAS DE CODD DEL MODELO RELACIONAL
 REGLAS DE CODD - 1 - REGLAS DE CODD DEL MODELO RELACIONAL En la década de los 80 s comenzaron a aparecer numerosos Sistemas de Gestión de Bases de Datos que se anunciaban como relacionales. Sin embargo
REGLAS DE CODD - 1 - REGLAS DE CODD DEL MODELO RELACIONAL En la década de los 80 s comenzaron a aparecer numerosos Sistemas de Gestión de Bases de Datos que se anunciaban como relacionales. Sin embargo
4. " $#%&' (#) para todo $#* (desigualdad triangular).
 10 Capítulo 2 Espacios Métricos 21 Distancias y espacios métricos Definición 211 (Distancia) Dado un conjunto, una distancia es una aplicación que a cada par le asocia un número real y que cumple los siguientes
10 Capítulo 2 Espacios Métricos 21 Distancias y espacios métricos Definición 211 (Distancia) Dado un conjunto, una distancia es una aplicación que a cada par le asocia un número real y que cumple los siguientes
Curso Completo de Electrónica Digital. 3.7. Simplificación de funciones booleanas
 CURSO Curso Completo de Electrónica Digital Departamento de Electronica y Comunicaciones Universidad Pontifica de Salamanca en Madrid Prof. Juan González Gómez Capítulo 3 ALGEBRA DE BOOLE Continuación...
CURSO Curso Completo de Electrónica Digital Departamento de Electronica y Comunicaciones Universidad Pontifica de Salamanca en Madrid Prof. Juan González Gómez Capítulo 3 ALGEBRA DE BOOLE Continuación...
Representación de números enteros: el convenio complemento a dos
 Representación de números enteros: el convenio complemento a dos Apellidos, nombre Martí Campoy, Antonio (amarti@disca.upv.es) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior
Representación de números enteros: el convenio complemento a dos Apellidos, nombre Martí Campoy, Antonio (amarti@disca.upv.es) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior
MATEMÁTICAS I SUCESIONES Y SERIES
 MATEMÁTICAS I SUCESIONES Y SERIES. Sucesiones En casi cualquier situación de la vida real es muy frecuente encontrar magnitudes que varían cada cierto tiempo. Por ejemplo, el saldo de una cuenta bancaria
MATEMÁTICAS I SUCESIONES Y SERIES. Sucesiones En casi cualquier situación de la vida real es muy frecuente encontrar magnitudes que varían cada cierto tiempo. Por ejemplo, el saldo de una cuenta bancaria
3.3 Funciones crecientes y decrecientes y el criterio de la primera derivada
 SECCIÓN. Funciones crecientes decrecientes el criterio de la primera derivada 79. Funciones crecientes decrecientes el criterio de la primera derivada Determinar los intervalos sobre los cuales una función
SECCIÓN. Funciones crecientes decrecientes el criterio de la primera derivada 79. Funciones crecientes decrecientes el criterio de la primera derivada Determinar los intervalos sobre los cuales una función
Microsoft Access 2003 (Completo)
 Página 1 Horas de teoría: 27 Horas de práctica: 25 Precio del Curso: 167 Descripción del funcionamiento del programa de gestión de bases de datos Microsoft Access 2003, estudiando los conceptos fundamentales
Página 1 Horas de teoría: 27 Horas de práctica: 25 Precio del Curso: 167 Descripción del funcionamiento del programa de gestión de bases de datos Microsoft Access 2003, estudiando los conceptos fundamentales
Representación de números enteros: el convenio complemento a uno
 Representación de números enteros: el convenio complemento a uno Apellidos, nombre Martí Campoy, Antonio (amarti@disca.upv.es) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior
Representación de números enteros: el convenio complemento a uno Apellidos, nombre Martí Campoy, Antonio (amarti@disca.upv.es) Departamento Centro Informàtica de Sistemes i Computadors Escola Tècnica Superior
ALGEBRA Y GEOMETRÍA II 2º semestre Año: 2012. Guía de Estudio y Ejercitación propuesta
 ALGEBRA Y GEOMETRÍA II 2º semestre Año: 2012 1 Guía de Estudio y Ejercitación propuesta Esta selección de Temas y Ejercicios están extraídos del texto FUNDAMENTOS DE ALGEBRA LINEAL de R. Larson y D. Falvo.
ALGEBRA Y GEOMETRÍA II 2º semestre Año: 2012 1 Guía de Estudio y Ejercitación propuesta Esta selección de Temas y Ejercicios están extraídos del texto FUNDAMENTOS DE ALGEBRA LINEAL de R. Larson y D. Falvo.
Herramientas digitales de auto-aprendizaje para Matemáticas
 real de con Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura real de con Índice real de con real de con.
real de con Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura real de con Índice real de con real de con.
TEMA 2. ORGANIZACIONES DE FICHEROS Y ESTRUCTURAS DE ACCESO
 TEMA 2. ORGANIZACIONES DE FICHEROS Y ESTRUCTURAS DE ACCESO 1. Introducción 2. Conceptos fundamentales de organizaciones de ficheros 3. Dispositivos de almacenamiento secundario 4. Ficheros desordenados
TEMA 2. ORGANIZACIONES DE FICHEROS Y ESTRUCTURAS DE ACCESO 1. Introducción 2. Conceptos fundamentales de organizaciones de ficheros 3. Dispositivos de almacenamiento secundario 4. Ficheros desordenados
Conceptos básicos de la matemática
 , 1 2 Contents 1 Conceptos básicos de la matemática 5 1.1 Introducción................................... 5 1.2 Conjuntos.................................... 5 1.2.1 Clases de conjuntos...........................
, 1 2 Contents 1 Conceptos básicos de la matemática 5 1.1 Introducción................................... 5 1.2 Conjuntos.................................... 5 1.2.1 Clases de conjuntos...........................
TEMA 4 El tipo conjunto
 TEMA El tipo conjunto PROGRAMACIÓN Y ESTRUCTURAS DE DATOS Tipo conjunto. Definiciones generales. Diccionario.. Tabla de dispersión.. Trie.. Árboles de búsqueda digitales. Cola de prioridad.. Montículo..
TEMA El tipo conjunto PROGRAMACIÓN Y ESTRUCTURAS DE DATOS Tipo conjunto. Definiciones generales. Diccionario.. Tabla de dispersión.. Trie.. Árboles de búsqueda digitales. Cola de prioridad.. Montículo..
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD = 3 2
 UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
UNIDAD 2: LÍMITES DE FUNCIONES.CONTINUIDAD 1.- Límites en el Infinito: lim x + f(x) = L Se dice que el límite de f (x) cuando x tiende a + es L ϵ Ɽ, si podemos hacer que f(x) se aproxime a L tanto como
Determinante de una matriz
 25 Matemáticas I : Preliminares Tema 3 Determinante de una matriz 31 Determinante de una matriz cuadrada Definición 67- Sea A una matriz cuadrada de orden n Llamaremos producto elemental en A al producto
25 Matemáticas I : Preliminares Tema 3 Determinante de una matriz 31 Determinante de una matriz cuadrada Definición 67- Sea A una matriz cuadrada de orden n Llamaremos producto elemental en A al producto
f n = 0 si n = 0 (ER)
 1. El significado de la recursión La recursión (en particular la iteración) es una componente fundamental de los lenguajes de programación. Vamos aquí a mostrar cuales son las dificultades que surgen al
1. El significado de la recursión La recursión (en particular la iteración) es una componente fundamental de los lenguajes de programación. Vamos aquí a mostrar cuales son las dificultades que surgen al
Robert A. Hanneman. Departmento de Sociología de la Universidad de California Riverside
 INTRODUCCIÓN A LOS MÉTODOS DEL ANÁLISIS DE REDES SOCIALES. CAPÍTULO SEGUNDO Robert A. Hanneman. Departmento de Sociología de la Universidad de California Riverside NOTA PREVIA Este documento está traducido
INTRODUCCIÓN A LOS MÉTODOS DEL ANÁLISIS DE REDES SOCIALES. CAPÍTULO SEGUNDO Robert A. Hanneman. Departmento de Sociología de la Universidad de California Riverside NOTA PREVIA Este documento está traducido
Espacio de Funciones Medibles
 Capítulo 22 Espacio de Funciones Medibles Igual que la σ-álgebra de los conjuntos medibles, la familia de funciones medibles, además de contener a todas las funciones razonables (por supuesto son medibles
Capítulo 22 Espacio de Funciones Medibles Igual que la σ-álgebra de los conjuntos medibles, la familia de funciones medibles, además de contener a todas las funciones razonables (por supuesto son medibles
2.1. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable x)
 Bloque : Cálculo Diferencial Tema : Límite y Continuidad de una función.. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable ) La forma de comportarse una función para valores muy grandes
Bloque : Cálculo Diferencial Tema : Límite y Continuidad de una función.. LÍMITE CUANDO X TIENDE A INFINITO (Valores grandes de la variable ) La forma de comportarse una función para valores muy grandes
Filtros digitales dominio del espacio dominio de la frecuencia
 Tema 3: Filtros 1 Filtros digitales Los filtros digitales constituyen uno de los principales modos de operar en el procesamiento de imágenes digitales. Pueden usarse para distintos fines, pero en todos
Tema 3: Filtros 1 Filtros digitales Los filtros digitales constituyen uno de los principales modos de operar en el procesamiento de imágenes digitales. Pueden usarse para distintos fines, pero en todos
P (X 5) = P (x = 5) + P (X = 6) + P (X = 7) + P (X = 8) = 0.005416467 + 0.051456432 + 0.79334918 + 0.663420431 = 0.999628249
 Hoja 3: robabilidad y variables aleatorias 1. La probabilidad de que un enfermo se recupere tomando un nuevo fármaco es 0.95. Si se les administra a 8 enfermos, hallar: a La probabilidad de que se recuperen
Hoja 3: robabilidad y variables aleatorias 1. La probabilidad de que un enfermo se recupere tomando un nuevo fármaco es 0.95. Si se les administra a 8 enfermos, hallar: a La probabilidad de que se recuperen
TEMA 6 LA EMPRESA: PRODUCCIÓN, COSTES Y BENEFICIOS
 TEMA 6 LA EMPRESA: PRODUCCIÓN, COSTES Y BENEFICIOS 1 Contenido 1. Introducción 2. Conceptos básicos 3. La función de producción y la productividad 3.1. Concepto de función de producción 3.2. Productividad
TEMA 6 LA EMPRESA: PRODUCCIÓN, COSTES Y BENEFICIOS 1 Contenido 1. Introducción 2. Conceptos básicos 3. La función de producción y la productividad 3.1. Concepto de función de producción 3.2. Productividad
si este límite es finito, y en este caso decimos que f es integrable (impropia)
 Capítulo 6 Integrales impropias menudo resulta útil poder integrar funciones que no son acotadas, e incluso integrarlas sobre recintos no acotados. En este capítulo desarrollaremos brevemente una teoría
Capítulo 6 Integrales impropias menudo resulta útil poder integrar funciones que no son acotadas, e incluso integrarlas sobre recintos no acotados. En este capítulo desarrollaremos brevemente una teoría
Conversión de unidades: factores de conversión vs. reglas de tres
 Conversión de unidades: factores de conversión vs. reglas de tres Apellidos, nombre Atarés Huerta, Lorena (loathue@tal.upv.es) Departamento Centro Departamento de Tecnología de Alimentos ETSIAMN (Universidad
Conversión de unidades: factores de conversión vs. reglas de tres Apellidos, nombre Atarés Huerta, Lorena (loathue@tal.upv.es) Departamento Centro Departamento de Tecnología de Alimentos ETSIAMN (Universidad
HOMOGENEIDAD DIMENSIONAL
 HOMOGENEIDAD DIMENSIONAL Los observables que podemos medir se agrupan en conjuntos caracterizados por una propiedad que llamamos magnitud. Existe la magnitud tiempo, la magnitud velocidad, la magnitud
HOMOGENEIDAD DIMENSIONAL Los observables que podemos medir se agrupan en conjuntos caracterizados por una propiedad que llamamos magnitud. Existe la magnitud tiempo, la magnitud velocidad, la magnitud
TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES
 TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES (TALF) BLOQUE II: LENGUAJES REGULARES Tema 2: Autómatas Finitos Parte 2 (de 3). Autómatas Finitos No Deterministas (AFNDs) Grado en Ingeniería Informática URJC
TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES (TALF) BLOQUE II: LENGUAJES REGULARES Tema 2: Autómatas Finitos Parte 2 (de 3). Autómatas Finitos No Deterministas (AFNDs) Grado en Ingeniería Informática URJC
Declaración de variables (integer, single, double, boolean, etc.) en Visual Basic. Dim. Ejemplos. (CU00309A)
 aprenderaprogramar.com Declaración de variables (integer, single, double, boolean, etc.) en Visual Basic. Dim. Ejemplos. (CU00309A) Sección: Cursos Categoría: Curso Visual Basic Nivel I Fecha revisión:
aprenderaprogramar.com Declaración de variables (integer, single, double, boolean, etc.) en Visual Basic. Dim. Ejemplos. (CU00309A) Sección: Cursos Categoría: Curso Visual Basic Nivel I Fecha revisión:
Tema 1 Sistemas de numeración
 Tema 1 Sistemas de numeración 1.1 - Sistema de numeración BINARIO En el sistema binario de numeración existen solamente dos símbolos distintos: el 0 y el 1. A primera vista puede resultar una forma de
Tema 1 Sistemas de numeración 1.1 - Sistema de numeración BINARIO En el sistema binario de numeración existen solamente dos símbolos distintos: el 0 y el 1. A primera vista puede resultar una forma de
Ibero Rubik. Cubo de 5x5x5 Método para principiantes
 Ibero Rubik Cubo de 5x5x5 Método para principiantes 1 Copyright 2013 Ibero Rubik. Esta obra está sujeta a la licencia Reconocimiento-NoComercial-CompartirIgual 3.0 Unported de Creative Commons. Para ver
Ibero Rubik Cubo de 5x5x5 Método para principiantes 1 Copyright 2013 Ibero Rubik. Esta obra está sujeta a la licencia Reconocimiento-NoComercial-CompartirIgual 3.0 Unported de Creative Commons. Para ver
Matrices escalonadas y escalonadas reducidas
 Matrices escalonadas y escalonadas reducidas Objetivos. Estudiar las definiciones formales de matrices escalonadas y escalonadas reducidas. Comprender qué importancia tienen estas matrices para resolver
Matrices escalonadas y escalonadas reducidas Objetivos. Estudiar las definiciones formales de matrices escalonadas y escalonadas reducidas. Comprender qué importancia tienen estas matrices para resolver
Apuntes de Matemática Discreta 2. Operaciones con Conjuntos
 Apuntes de Matemática Discreta 2. Operaciones con Conjuntos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 2 Operaciones con Conjuntos
Apuntes de Matemática Discreta 2. Operaciones con Conjuntos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 2 Operaciones con Conjuntos
Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos:
 1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
Coordenadas polares en el plano. Coordenadas ciĺındricas y esféricas en el espacio. Coordenadas... Coordenadas... Coordenadas...
 En el estudio de los conjuntos y las funciones es fundamental el sistema que se utilize para representar los puntos. Estamos acostumbrados a utilizar la estructura de afín o de vectorial de R n, utilizando
En el estudio de los conjuntos y las funciones es fundamental el sistema que se utilize para representar los puntos. Estamos acostumbrados a utilizar la estructura de afín o de vectorial de R n, utilizando
UNIDAD UNO PROGRAMACIÓN LÍNEAL Parte 3
 UNIDAD UNO PROGRAMACIÓN LÍNEAL Parte 3 Matriz unitaria "I" de base con variables artificiales. Cuando el problema de programación lineal se expresa en la forma canónica de maximizar, las variables de holgura
UNIDAD UNO PROGRAMACIÓN LÍNEAL Parte 3 Matriz unitaria "I" de base con variables artificiales. Cuando el problema de programación lineal se expresa en la forma canónica de maximizar, las variables de holgura
Ecuaciones de primer grado
 Ecuaciones de primer grado º ESO - º ESO Definición, elementos y solución de la ecuación de primer grado Una ecuación de primer grado es una igualdad del tipo a b donde a y b son números reales conocidos,
Ecuaciones de primer grado º ESO - º ESO Definición, elementos y solución de la ecuación de primer grado Una ecuación de primer grado es una igualdad del tipo a b donde a y b son números reales conocidos,
Divisibilidad y congruencias
 Divisibilidad y congruencias Ana Rechtman Bulajich y Carlos Jacob Rubio Barrios Revista Tzaloa, año 1, número 2 Empecemos por explicar el significado de la palabra divisibilidad. En este texto vamos a
Divisibilidad y congruencias Ana Rechtman Bulajich y Carlos Jacob Rubio Barrios Revista Tzaloa, año 1, número 2 Empecemos por explicar el significado de la palabra divisibilidad. En este texto vamos a
CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS. Este capítulo comprende diversas propiedades geométricas de secciones (para casos
 CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS Este capítulo comprende diversas propiedades geométricas de secciones (para casos prácticos, secciones de vigas) siendo la más importante el momento de inercia.
CAPÍTULO III MOMENTO DE INERCIA EN ÁREAS PLANAS Este capítulo comprende diversas propiedades geométricas de secciones (para casos prácticos, secciones de vigas) siendo la más importante el momento de inercia.
Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.2 Determinación aproximada de extremos: Método de Newton-Raphson
 Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.2 Determinación aproximada de extremos: Método de Newton-Raphson Francisco Palacios Escuela Politécnica Superior de Ingeniería
Cálculo científico y técnico con HP49g/49g+/48gII/50g Módulo 3: Aplicaciones Tema 3.2 Determinación aproximada de extremos: Método de Newton-Raphson Francisco Palacios Escuela Politécnica Superior de Ingeniería
MODELO 4. CALCULO DEL VALOR PRESENTE NETO Y LA TASA INTERNA DE RETORNO PARA UN PROYECTO DE INVERSIÓN.
 MODELO 4. CALCULO DEL VALOR PRESENTE NETO Y LA TASA INTERNA DE RETORNO PARA UN PROYECTO DE INVERSIÓN. PROPÓSITO: Diseñar un modelo en hoja de cálculo que permita calcular el Valor Presente Neto (VPN) de
MODELO 4. CALCULO DEL VALOR PRESENTE NETO Y LA TASA INTERNA DE RETORNO PARA UN PROYECTO DE INVERSIÓN. PROPÓSITO: Diseñar un modelo en hoja de cálculo que permita calcular el Valor Presente Neto (VPN) de
2: Autómatas finitos y lenguajes regulares.
 2: Autómatas finitos y lenguajes regulares. Los autómatas finitos son el modelo matemático de los sistemas que presentan las siguientes características: 1) En cada momento el sistema se encuentra en un
2: Autómatas finitos y lenguajes regulares. Los autómatas finitos son el modelo matemático de los sistemas que presentan las siguientes características: 1) En cada momento el sistema se encuentra en un
Divisores de un número y regla del producto
 Divisores de un número y regla del producto Eugenio Flores En estas notas, nuestra intención es llegar a través de varios pasos naturales, a poder ver la fórmula para calcular los divisores de un número
Divisores de un número y regla del producto Eugenio Flores En estas notas, nuestra intención es llegar a través de varios pasos naturales, a poder ver la fórmula para calcular los divisores de un número
Ejercicios resueltos de tiro oblicuo
 Ejercicios resueltos de tiro oblicuo 1) Un arquero dispara una flecha cuya velocidad de salida es de 100m/s y forma un ángulo de 30º con la horizontal. Calcula: a) El tiempo que la flecha está en el aire.
Ejercicios resueltos de tiro oblicuo 1) Un arquero dispara una flecha cuya velocidad de salida es de 100m/s y forma un ángulo de 30º con la horizontal. Calcula: a) El tiempo que la flecha está en el aire.
UNIVERSIDAD SAN MARCOS
 Prof. Edwin Gerardo Acuña Acuña UNIVERSIDAD SAN MARCOS ALGEBRA Este capítulo estudia los conceptos básicos del álgebra, una de las disciplinas de la matemática que tiene más aplicaciones en diversos campos.
Prof. Edwin Gerardo Acuña Acuña UNIVERSIDAD SAN MARCOS ALGEBRA Este capítulo estudia los conceptos básicos del álgebra, una de las disciplinas de la matemática que tiene más aplicaciones en diversos campos.
Probabilidad. La probabilidad mide la frecuencia con la que aparece un resultado determinado cuando se realiza un experimento.
 Matemáticas segundo medio COLEGIO SSCC CONCEPCION NOMBRE: Clase Teórica Práctica Nº 30 Probabilidad Probabilidad: Introducción La probabilidad mide la frecuencia con la que aparece un resultado determinado
Matemáticas segundo medio COLEGIO SSCC CONCEPCION NOMBRE: Clase Teórica Práctica Nº 30 Probabilidad Probabilidad: Introducción La probabilidad mide la frecuencia con la que aparece un resultado determinado
operaciones inversas Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
 Potencias y raíces Potencias y raíces Potencia operaciones inversas Raíz exponente índice 7 = 7 7 7 = 4 4 = 7 base base Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
Potencias y raíces Potencias y raíces Potencia operaciones inversas Raíz exponente índice 7 = 7 7 7 = 4 4 = 7 base base Para unificar ambas operaciones, se define la potencia de exponente fraccionario:
TEMA II TEORÍA INTUITIVA DE CONJUNTOS
 TEMA II TEORÍA INTUITIVA DE CONJUNTOS Policarpo Abascal Fuentes TEMA II Teoría intuitiva de conjuntos p. 1/4 TEMA II 2. TEORÍA INTUITIVA DE CONJUNTOS 2.1 CONJUNTOS 2.1.1 Operaciones con conjuntos 2.2 RELACIONES
TEMA II TEORÍA INTUITIVA DE CONJUNTOS Policarpo Abascal Fuentes TEMA II Teoría intuitiva de conjuntos p. 1/4 TEMA II 2. TEORÍA INTUITIVA DE CONJUNTOS 2.1 CONJUNTOS 2.1.1 Operaciones con conjuntos 2.2 RELACIONES
Sistemas de ecuaciones lineales
 Sistemas de ecuaciones lineales Este tema resulta fundamental en la mayoría de las disciplinas, ya que son muchos los problemas científicos y de la vida cotidiana que requieren resolver simultáneamente
Sistemas de ecuaciones lineales Este tema resulta fundamental en la mayoría de las disciplinas, ya que son muchos los problemas científicos y de la vida cotidiana que requieren resolver simultáneamente
INFORMACIÓN SOBRE LA PRUEBA DE ACCESO (PAU) A LA UNIVERSIDAD DE OVIEDO. CURSO 2015/2016
 INFORMACIÓN SOBRE LA PRUEBA DE ACCESO (PAU) A LA UNIVERSIDAD DE OVIEDO. CURSO 2015/2016 Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II 1. COMENTARIOS Y/O ACOTACIONES RESPECTO AL TEMARIO EN RELACIÓN
INFORMACIÓN SOBRE LA PRUEBA DE ACCESO (PAU) A LA UNIVERSIDAD DE OVIEDO. CURSO 2015/2016 Materia: MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II 1. COMENTARIOS Y/O ACOTACIONES RESPECTO AL TEMARIO EN RELACIÓN
NIVEL 14: ESTRUCTURAS DE ACCESO DIRECTO
 NIVEL 14: ESTRUCTURAS DE ACCESO DIRECTO Tablas de Hashing 2 Tablas de hashing Motivación y definiciones Posibles estructuras de implementación Área primaria y área de desbordamiento Funciones de hashing
NIVEL 14: ESTRUCTURAS DE ACCESO DIRECTO Tablas de Hashing 2 Tablas de hashing Motivación y definiciones Posibles estructuras de implementación Área primaria y área de desbordamiento Funciones de hashing
UNIDAD 3: ANALICEMOS LA FUNCION EXPONENCIAL Y LOGARITMICA.
 UNIDAD 3: ANALICEMOS LA FUNCION EXPONENCIAL Y LOGARITMICA Históricamente, los exponentes fueron introducidos en matemáticas para dar un método corto que indicara el producto de varios factores semejantes,
UNIDAD 3: ANALICEMOS LA FUNCION EXPONENCIAL Y LOGARITMICA Históricamente, los exponentes fueron introducidos en matemáticas para dar un método corto que indicara el producto de varios factores semejantes,
Curvas en paramétricas y polares
 Capítulo 10 Curvas en paramétricas y polares Introducción Después del estudio detallado de funciones reales de variable real expresadas en forma explícita y con coordenadas cartesianas, que se ha hecho
Capítulo 10 Curvas en paramétricas y polares Introducción Después del estudio detallado de funciones reales de variable real expresadas en forma explícita y con coordenadas cartesianas, que se ha hecho
En las figuras anteriores vemos algunos casos (no todos) que pueden presentarse al pasar por un punto x 0. (en este caso, para x 0 =2)
 UNIVERSIDAD DEL VALLE PROFESOR CARLOS IVAN RESTREPO CONTINUIDAD. 1.- Continuidad en un punto. Continuidad lateral..- Continuidad en un intervalo. 3.- Operaciones con funciones continuas 4.- Discontinuidades.
UNIVERSIDAD DEL VALLE PROFESOR CARLOS IVAN RESTREPO CONTINUIDAD. 1.- Continuidad en un punto. Continuidad lateral..- Continuidad en un intervalo. 3.- Operaciones con funciones continuas 4.- Discontinuidades.
La función cuadrática
 La función cuadrática En primer semestre estudiamos las ecuaciones cuadráticas. También resolvimos estas ecuaciones por el método gráfico. Para esto, tuvimos que convertir la ecuación en una función igualándola
La función cuadrática En primer semestre estudiamos las ecuaciones cuadráticas. También resolvimos estas ecuaciones por el método gráfico. Para esto, tuvimos que convertir la ecuación en una función igualándola
La circunferencia y el círculo
 La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
La circunferencia y el círculo Contenidos 1. La circunferencia. La circunferencia Elementos de la circunferencia. 2. Posiciones relativas. Punto y circunferencia. Recta y circunferencia. Dos circunferencias.
Lección 13: Resolución algebraica de sistemas de ecuaciones
 GUÍA DE MATEMÁTICAS III Lección 1: Resolución algebraica de sistemas de ecuaciones En la lección anterior hemos visto cómo resolver gráficamente un sistema de ecuaciones. Si bien ese método es relativamente
GUÍA DE MATEMÁTICAS III Lección 1: Resolución algebraica de sistemas de ecuaciones En la lección anterior hemos visto cómo resolver gráficamente un sistema de ecuaciones. Si bien ese método es relativamente
