Teselaciones y Grafos de Intersección de Segmentos en Superficies no Planas
|
|
|
- Miguel Iglesias Zúñiga
- hace 7 años
- Vistas:
Transcripción
1 Teselaciones y Grafos de Intersección de Segmentos en Superficies no Planas N. de Castro, F.J. Cobos, J.C. Dana y A. Márquez Universidad de Sevilla. Departamento de Matemática Aplicada I. {natalia,cobos,dana,almar}@us.es Resumen En este trabajo se caracterizan aquellos grafos que admiten una teselación en el cilindro y en el toro, en donde la teselación de un grafo es la representación que asocia a cada componente de una inmersión dada (vértices, aristas y caras), baldosas en la superficie de manera que las incidencias topológicas de dicha inmersión se corresponden con adyacencias geométricas entre las baldosas. Como aplicación directa de las teselaciones de grafos, se caracterizan aquellos grafos que admiten una representación en éstas superficies como intersección de segmentos en dos direcciones ortogonales. Palabras Clave: Teselación de grafos, Grafos de intersección. 1 Introducción Recientemente la representación de grafos ha creado un gran interés debido a sus aplicaciones en numerosas áreas como el diseño de circuitos VLSI, arquitectura de computadores y dibujo de grafos [1]. En este trabajo se estudian dos tipos de representaciones de grafos en las superficies del cilindro y del toro. La primera es lo que se conoce como la teselación de un grafo, que asocia a cada grafo inmerso en una superficie una partición de la misma en baldosas, cada una asociada a una componente del grafo (vértices, aristas o caras) de manera que las incidencias topológicas entre las componentes del grafo quedan representadas por adyacencias geométricas entre las baldosas. Tamassia y Tollis introducen esta representación en [6], donde caracterizan los grafos teselables en el plano y la esfera utilizando como baldosas rectángulos (degenerados o no). En un intento de generalizar este resultado, Mohar y Rosenstiehl [5], estudian la teselación de grafos en la superficie del toro, aunque en este caso los vértices y caras de una inmersión tórica del grafo están representados como segmentos en dos direcciones no ortogonales, con lo que las aristas del grafo quedan representadas como cuadriláteros no rectángulos delimitados por dichos segmentos. Estos autores caracterizan aquellos grafos que admiten esta representación, que denominaremos teselación torcida de un grafo en el toro. 1
2 Figura 1: Teselación de un grafo en el plano. Además, los autores en [5] plantean la posibilidad de representar grafos en el toro utilizando direcciones ortogonales para las componentes del grafo. Así, comentan textualmente: Figura 2: Teselación torcida de un grafo en el toro. It would be interensting to know which toroidal maps have a tessellation representation in the square model of the torus with the directions and parallel to the sides of the fundamental square. 1 En la sección 2 completamos este trabajo caracterizando aquellos grafos que admiten una teselación con direcciones ortogonales en el cilindro y el toro. Esta caracterización nos permite representar grafos como intersección de segmentos, es decir, asignarle segmentos a los vértices del grafo y las aristas de éste vienen determinadas por las adyacencias entre dichos segmentos. Diversos autores estudian la representación de grafos bipartitos como intersección de segmentos horizontales y verticales [4, 2, 3] en el plano. En la sección 4 caracterizamos aquellos grafos que admiten este tipo de representación en el cilindro y el toro. 1 Sería interesante saber qué grafos admiten una teselación en el toro con las direcciones y (asociadas a vértices y caras) paralelas a los lados del rectángulo fundamental. 2
3 2 Teselaciones de grafos en el cilindro Consideraremos inmersiones de grafos en el cilindro donde llevamos los vértices a puntos de la superficie cilíndrica y las aristas a arcos de curvas de Jordan que no se intersecan salvo en vértices comunes. Trabajaremos con inmersiones sobre el cilindro con dos caras no acotadas, a las que nos referiremos como la cara izquierda y la cara derecha. Sea G un grafo inmerso en el cilindro, una orientación cilíndrica Γ de G es una orientación de sus aristas de manera que: Γ no tiene fuentes (vértices sin aristas de entrada), ni sumideros (vértices sin aristas de salida). Todo ciclo dirigido rodea al cilindro en la misma dirección (digamos en la dirección de las agujas del reloj). En el siguiente lema [7] se dan dos propiedades muy interesantes sobre las orientaciones cilíndricas: Lema 2.1. Sea Γ una orientación cilíndrica. Se tiene: Para todo vértice v de Γ las aristas de entrada (de salida) aparecen consecutivamente alrededor de v. (Ver Figura 3(a)). El borde de toda cara interna de Γ consiste en dos caminos dirigidos con origen y llegada común. (Ver Figura 3(b)). Figura 3: (a) Aristas alrededor de un vértice. (b) Caminos dirigidos de una cara. Según el Lema 2.1, para cada vértice v de una orientación cilíndrica podemos distinguir dos caras que lo contienen, aquella que separa las aristas entrantes de las salientes en el sentido contrario al de las agujas del reloj, que denotaremos por I(v) y aquella que separa las aristas entrantes de las salientes en el sentido de las agujas del reloj, que denotaremos por D(v) (Ver Figura 3 (a)). 3
4 Por otra parte, para cada cara f de una orientación cilíndrica, también podemos distinguir dos vértices: aquel del que salen los dos caminos dirigidos, que denotaremos por sub(f), y al que llegan, que denotaremos por Sup(f). Esta notación también puede generalizarse a las aristas de la orientación cilíndrica ya que si e = (u; v) es una arista recorrida desde u hasta v, podemos denotar por sub(e) = u y por Sup(e) = v. Análogamente, la orientación de la arista nos permite diferenciar entre la cara a la izquierda de e, y la cara a la derecha de e, que denotaremos por I(e) y D(e), respectivamente. Sea Γ una orientación cilíndrica de G, dicha orientación cilíndrica define también una orientación Γ en el dual G en la que el dual e de una arista e está dirigida desde I(e) hasta D(e) (Ver Figura 4). Figura 4: Orientación cilíndrica de un grafo (vértices negros) y su dual (vértices blancos). Lema 2.2. Sea G un grafo inmerso en el cilindro con distintas caras izquierda y derecha, entonces existe una orientación cilíndrica Γ de G. Una baldosa en el cilindro es un rectángulo delimitado por dos generatrices y dos arcos de circunferencia. Puesto que el cilindro es una superficie no acotada, admitimos baldosas no acotadas y baldosas en el infinito, aunque no admitiremos en ninguna de las superficies baldosas que puedan completar una circunferencia o banda cilíndrica. Dada una orientación cilíndrica de un grafo G. Una teselación de G sobre el cilindro es una aplicación que lleva cada componente c de G (vértices, aristas o caras) en una baldosa rectangular T (c) del cilindro tal que: El interior de las baldosas T (c) y T (d) es disjunto para todo c d. La unión de todas las baldosas T (c) es el cilindro. Para cada arista e G el lado inferior (superior, izquierdo, derecho) de la baldosa T (e) se apoya en el lado superior (inferior, derecho, izquierdo, respectivamente) de la baldosa T (sub(e)), (T (Sup(e)), T (I(e)), T (D(e)), Respectivamente). Ninguna baldosa constituye una circunferencia o banda circular del cilindro. 4
5 Figura 5: Baldosas asociadas a las componentes de un grafo. Dado un digrafo acíclico, un orden topológico τ en sus vértices asocia a cada vértice v un entero no negativo τ(v) tal que τ(u) < τ(v) para cada arista dirigida (u, v). Teorema 2.1. Un grafo es teselable en el cilindro si y sólo si es 2-conexo. Demostración: Si suponemos que el grafo tiene un punto de corte, podemos llegar fácilmente a una contradicción con la hipótesis de que sea teselable, ya que existe una cara que debe estar representada forzosamente por una circunferencia. Figura 6: Teselación de un grafo en el cilindro. Recíprocamente, si suponemos que es 2-conexo, el siguiente algoritmo que es una adaptación del que presentan Tamassia y Tollis en [7], da una teselación del grafo. ALGORITMO TESELACIÓN Entrada: Un grafo plano 2-conexo con n vértices inmerso en el plano con dos caras distinguidas f 1 y f 2. Salida: Una teselación tipo 1 del grafo en el cilindro cuyas caras izquierda y derecha son f 1 y f 2. Paso 1: Construir una orientación cilíndrica γ de G cuya cara izquierda sea f 1 y cuya cara derecha sea f 2. 5
6 Paso 2: Construir el grafo dual Γ de Γ donde las aristas están orientadas de izquierda a derecha. Γ es un digrafo acíclico con exactamente una salida y exactamente una entrada. Paso 3: Computar un orden topológico α en el digrafo obtenido de Γ al eliminar las aristas que intersecan a un camino de desde f 1 a f 2. Paso 4: Computar un orden topológico β en Γ. Paso 5: Sea θ 0 = 2π n, para cada vértice v dibujar un segmento desde el punto (β(i(v)), α(v)θ 0 ) hasta (β(d(v)), α(v)θ 0 ). Paso 6: Para cada arista e dibujar un rectángulo de vértices: (β(i(e)), α(sub(e))θ 0 ), (β(d(e)), α(sub(e))θ 0 ), (β(i(e)), α(sup(e))θ 0 ) y (β(d(e)), α(sup(e))θ 0 ). Paso 7: Para cada cara f dibujar un arco circular desde el punto (β(f), α(sub(f))θ 0 ) hasta el punto (β(f), α(sup(f))θ 0 ). 3 Teselaciones de grafos en el toro Trabajamos en esta sección con inmersiones tóricas de grafos, es decir representaremos los vértices del grafo como puntos del toro y las aristas como arcos de curvas de Jordan que no se intersecan salvo en vértices comunes y de tal forma que todo meridiano y todo paralelo del toro interseca a algún vértice o arista del grafo. Diremos que una inmersión de un grafo en el toro es 2-celular si todas las caras son homeomorfas a discos abiertos. Si el borde de cada cara es un ciclo simple, entonces las caras son homeomorfas a discos cerrados. En ese caso diremos que la inmersión es 2-celular cerrada. Figura 7: Vértice esencial. Es fácil encontrar inmersiones en el toro de grafos 2-conexos con alguna cara cuyo borde no es un ciclo simple (ver Figura 7). En ese caso, denominaremos vértice esencial al vértice que se repite al recorrer el borde de dicha cara. Dado un grafo tórico G, y C un ciclo de G que lo rodea en la dirección de los meridianos, podemos cortar el grafo duplicando los vértices y aristas de C, obteniendo un nuevo grafo en el cilindro G C. 6
7 Podemos obtener una orientación cilíndrica de G C y al identificar nuevamente las aristas y vértices de C y su copia, obtenemos una orientación en las aristas de G que denominaremos orientación tórica de G. Una baldosa en el toro es un rectángulo delimitado por dos meridianos y dos paralelos de manera que ninguna baldosa complete una circunferencia o banda cilíndrica. Partiendo de una orientación tórica de un grafo G, una teselación de G sobre el toro es una aplicación que lleva cada componente c de G (vértices, aristas o caras) a una baldosa rectangular T (c) del toro cumpliendo lo siguiente: El interior de las baldosas T (c) y T (d) es disjunto para todo c d. Las baldosas constituyen una partición del toro. Para cada arista e del grafo G, el lado inferior (superior, izquierdo, derecho) de la baldosa T (e) se apoya en el lado superior (inferior, derecho, izquierdo) de la baldosa T (sub(e)), T (Sup(e)), T (I(e)), T (D(e)), respectivamente). Ninguna baldosa constituye un meridiano completo o banda cilíndrica. Figura 8: Teselación ortogonal de un grafo en el toro. Teorema 3.1. Una inmersión 2-celular de un grafo en el toro es teselable si y sólo si es cerrada. Demostración: La demostración de este Teorema se basa en el Teorema 2.1. Consideramos un ciclo C que rodee al toro en la dirección de los meridianos. Cortando el toro por dicho ciclo, duplicando sus vértices y aristas, obtenemos un nuevo grafo inmerso en el cilindro G C. Podemos obtener una teselación de G C en la que los segmentos asociados a los vértices de C queden a la misma altura. Identificando nuevamente los segmentos y rectángulos asociados a las componentes duplicadas, obtenemos una teselación de G en el toro. 7
8 4 Grafos de intersección de segmentos En esta sección veremos como podemos obtener una representación como intersección de segmentos ortogonales en el cilindro y el toro, aplicando los resultados obtenidos sobre las teselaciones en éstas superficies. Dada una familia de segmentos en una superficie, su grafo de intersección tiene un vértice por cada segmento y dos vértices son adyacentes si y sólo si los correspondientes segmentos se intersecan. En esta sección estudiaremos un tipo particular de grafos de intersección de segmentos, conocidos como grafos de contacto que son aquellos en que los segmentos no se cruzan, sino que el extremo de uno de ellos se apoya en el otro. Dado un grafo G, su representación por segmentos es una familia de segmentos tal que su grafo de contacto es isomorfo a G. Numerosos autores han estudiado la representación de grafos bipartitos en el plano [4, 2, 3], obteniendo que todos los grafos planos bipartitos son representables por segmentos horizontales y verticales en el plano. En este trabajo, completamos dicho resultado estudiando los grafos representables por segmentos en el cilindro y en el toro. Teorema 4.1. Un grafo es representable en S como intersección de segmentos horizontales y verticales (donde S es el cilindro o el toro) si y sólo si es bipartito y no tiene aristas múltiples. Demostración: Dado un grafo G bipartito, inmerso en S (donde S puede ser el cilindro o el toro), supondremos que sus vértices están coloreados con dos colores, blanco y negro, de manera que dos vértices del mismo color no sean adyacentes. Podemos añadir vértices y aristas virtuales de manera que todas las caras del grafo sean cuadriláteros. Si alguna de las aristas que hemos introducido conecta vértices adyacentes, la subdividimos con dos nuevos vértices virtuales. Esta subdivisión trasforma dos caras que eran cuadriláteros en caras de seis vértices, pero podemos añadir nuevas aristas virtuales uniendo los nuevos vértices con los que ya estaban, con la certeza de que no crearemos aristas dobles. Por tanto, podemos suponer que G es un grafo bipartito inmerso en S y que todas sus caras internas son cuadriláteros. Por cada cara interna f conectamos sus dos vértices negros con una arista por el interior de f. Todas estas aristas constituyen un nuevo grafo G N, cuyos vértices son los vértices negros de G y dos vértices son adyacentes si pertenecen a la misma cara en G. De forma análoga podemos definir G B, considerando los vértices blancos de G. Obsérvese G N y G B son grafos duales el uno del otro, ya que cada arista de G N interseca una única arista de G B y viceversa. Es fácil comprobar que el grafo G N es 2-conexo si G está inmerso en el cilindro o que no tiene vértices esenciales si está inmerso en el toro, ya que de ser así G tendría una arista doble. Por tanto, G N es teselable en S, es decir, G N admite una representación en S de manera que sus vértices (los vértices negros de G) quedan representados por segmentos horizontales y sus caras (los vértices blancos de G), quedan representados por segmentos verticales. Obviamente si partimos de una configuración de segmentos horizontales y verticales en S, su grafo de intersección ha de ser bipartito y sin aristas múltiples. 8
9 Figura 9: Referencias [1] G. Di Battista, P. Eades, R. Tamassia and I.G. Tollis. Algorithms for drawing graphs: an annotated bibliography. Computational Geometry: Theory and Applications, 4(5): , [2] J. Czyzowicz, E. Kranakis and J. Urrutia. A simple proof of the representation of bipartite planar graphs as the contact graph of orthgonal straight line segments. Information Processing Letters, 66: , [3] H. de Fraysseix, P.O. de Mendez and J. Pach. Representation of planar graphs by segments. Colloquia Mathematica Societatis János Bolyai, Intuitive Geometry, [4] I. Ben-Arroyo Hartman, I. Newman and R. Ziv. On grid intersection graphs. Discrete Math., 87:41 52, [5] B. Mohar and P. Rosenstiehl. Tessellation and visibility representations of maps on the torus. Discrete Computational Geometry, 19: , [6] R. Tamassia and I.G. Tollis. Tessellation representations of planar graphs. Proc. 27th Annual Allerton Conf., pages 48 57, [7] R. Tamassia and I.G. Tollis. Representations of graphs on a cylinder. SIAM J. Discrete Mathematics, 4(1): ,
Hélices en el cilindro y en el toro y planificación de movimientos de robots
 Hélices en el cilindro y en el toro y planificación de movimientos de robots F.J. Cobos, J.C. Dana 1, A. Márquez 1 y F. Mateos 1 Resumen El motivo de este artículo es la búsqueda del camino más corto entre
Hélices en el cilindro y en el toro y planificación de movimientos de robots F.J. Cobos, J.C. Dana 1, A. Márquez 1 y F. Mateos 1 Resumen El motivo de este artículo es la búsqueda del camino más corto entre
Grafos. Algoritmos y Estructuras de Datos III
 Grafos Algoritmos y Estructuras de Datos III Grafos Un grafo G = (V, X ) es un par de conjuntos, donde V es un conjunto de puntos o nodos o vértices y X es un subconjunto del conjunto de pares no ordenados
Grafos Algoritmos y Estructuras de Datos III Grafos Un grafo G = (V, X ) es un par de conjuntos, donde V es un conjunto de puntos o nodos o vértices y X es un subconjunto del conjunto de pares no ordenados
Teoría de Grafos Introducción Grafos isomorfos
 Capítulo 1 Teoría de Grafos 1.1. Introducción Definición. Denominaremos pseudomultigrafo a una terna (V,E, γ), donde V y E son conjuntos y γ : E {{u,v}: u,v V }. El conjunto V se denomina conjunto de vértices
Capítulo 1 Teoría de Grafos 1.1. Introducción Definición. Denominaremos pseudomultigrafo a una terna (V,E, γ), donde V y E son conjuntos y γ : E {{u,v}: u,v V }. El conjunto V se denomina conjunto de vértices
GRAFOS BIPARTITOS SOBRE CURVAS CONVEXAS PARALELAS MIGUEL GÓMEZ DOMÍNGUEZ JOSÉ LUIS ROSADO OLMO
 GRAFOS BIPARTITOS SOBRE CURVAS CONVEXAS PARALELAS MIGUEL GÓMEZ DOMÍNGUEZ JOSÉ LUIS ROSADO OLMO Introducción Un grafo bipartito es biplanar si admite en un conjunto partito una recta dibujada de tal forma
GRAFOS BIPARTITOS SOBRE CURVAS CONVEXAS PARALELAS MIGUEL GÓMEZ DOMÍNGUEZ JOSÉ LUIS ROSADO OLMO Introducción Un grafo bipartito es biplanar si admite en un conjunto partito una recta dibujada de tal forma
Ampliación de Topología
 Ampliación de Topología Problemas. Curso 2003 04 Homotopía de aplicaciones y tipos de homotopía 1. Sea X un espacio, y sea f: S 1 X una aplicación continua. Demostrar que f es homótopa a una aplicación
Ampliación de Topología Problemas. Curso 2003 04 Homotopía de aplicaciones y tipos de homotopía 1. Sea X un espacio, y sea f: S 1 X una aplicación continua. Demostrar que f es homótopa a una aplicación
INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.
 INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.7 GRAFOS CONEXOS7 ÁRBOLES..7 BOSQUES DE ÁRBOLES...8 RECORRIDO DE UN GRAFO..8
INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.7 GRAFOS CONEXOS7 ÁRBOLES..7 BOSQUES DE ÁRBOLES...8 RECORRIDO DE UN GRAFO..8
Acerca del interior de un polígono
 Acerca del interior de un polígono Mario Ponce PUC-Chile 9 de marzo de 2011 Resumen En esta nota proponemos una demostración elemental del Teorema de la curva de Jordan para polígonos, justificando así
Acerca del interior de un polígono Mario Ponce PUC-Chile 9 de marzo de 2011 Resumen En esta nota proponemos una demostración elemental del Teorema de la curva de Jordan para polígonos, justificando así
Introducción a la Teoría de Grafos
 Introducción a la Teoría de Grafos Conceptos Simples, Problemas Difíciles Héctor Ramírez C. 1 1 Departamento de Ingeniería Matemática Universidad de Chile Curso MA3701: Optimización Héctor Ramírez C. (U.
Introducción a la Teoría de Grafos Conceptos Simples, Problemas Difíciles Héctor Ramírez C. 1 1 Departamento de Ingeniería Matemática Universidad de Chile Curso MA3701: Optimización Héctor Ramírez C. (U.
Curso de Posgrado: Tópicos avanzados en teoría de grafos
 Curso de Posgrado: Tópicos avanzados en teoría de grafos 1. Grafos planares 1.1. Preliminares Recordemos algunos conceptos: Una curva es la imagen de una función contínua f : [0, 1] R 2. Una curva poligonal
Curso de Posgrado: Tópicos avanzados en teoría de grafos 1. Grafos planares 1.1. Preliminares Recordemos algunos conceptos: Una curva es la imagen de una función contínua f : [0, 1] R 2. Una curva poligonal
Grafos. Amalia Duch Brown Octubre de 2007
 Grafos Amalia Duch Brown Octubre de 2007 Índice 1. Definiciones Básicas Intuitivamente un grafo es un conjunto de vértices unidos por un conjunto de líneas o flechas dependiendo de si el grafo es dirigido
Grafos Amalia Duch Brown Octubre de 2007 Índice 1. Definiciones Básicas Intuitivamente un grafo es un conjunto de vértices unidos por un conjunto de líneas o flechas dependiendo de si el grafo es dirigido
1. GRAFOS : CONCEPTOS BASICOS
 1. GRAFOS : CONCEPTOS BASICOS Sea V un conjunto finito no vacio y sea E V x V. El par (V, E) es un grafo no dirigido, donde V es un conjunto de vértices o nodos y E es un conjunto de aristas. Denotaremos
1. GRAFOS : CONCEPTOS BASICOS Sea V un conjunto finito no vacio y sea E V x V. El par (V, E) es un grafo no dirigido, donde V es un conjunto de vértices o nodos y E es un conjunto de aristas. Denotaremos
1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS.
 UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
TEMA IV TEORÍA DE GRAFOS
 TEMA IV TEORÍA DE GRAFOS Poli Abascal Fuentes TEMA IV Teoría de grafos p. 1/? TEMA IV 4. TEORÍA DE GRAFOS 4.1 GRAFOS 4.1.1 Introducción 4.1.2 Definiciones básicas 4.1.3 Caminos y recorridos 4.1.4 Subgrafos,
TEMA IV TEORÍA DE GRAFOS Poli Abascal Fuentes TEMA IV Teoría de grafos p. 1/? TEMA IV 4. TEORÍA DE GRAFOS 4.1 GRAFOS 4.1.1 Introducción 4.1.2 Definiciones básicas 4.1.3 Caminos y recorridos 4.1.4 Subgrafos,
Triangulación de Polígonos: Problema de la Galería de Arte. Geometría Computacional, MAT-125
 http://ilevel.biz/wp-content/uploads/2013/07/riccomaresca-outsider-art-gallery-1024x576.png Triangulación de Polígonos: Problema de la Galería de Arte. Geometría Computacional, MAT-125 Cuántas cámaras
http://ilevel.biz/wp-content/uploads/2013/07/riccomaresca-outsider-art-gallery-1024x576.png Triangulación de Polígonos: Problema de la Galería de Arte. Geometría Computacional, MAT-125 Cuántas cámaras
GRAFOS GEOMÉTRICOS. Introducción. Número de corte. Aplicaciones. Incidencias de puntos y rectas. Distancias unitarias. k-sets.
 GRAFOS GEOMÉTRICOS CROSSING LEMMA Y APLICACIONES GEOMÉTRICAS Introducción. Número de corte. Aplicaciones. Incidencias de puntos y rectas. Distancias unitarias. k-sets. Qué es un grafo geométrico? vi =
GRAFOS GEOMÉTRICOS CROSSING LEMMA Y APLICACIONES GEOMÉTRICAS Introducción. Número de corte. Aplicaciones. Incidencias de puntos y rectas. Distancias unitarias. k-sets. Qué es un grafo geométrico? vi =
Espacios conexos. 6.1 Conexos
 Capítulo 6 Espacios conexos 6.1 Conexos Definición 6.1.1 (Conjuntos separados). Dado un espacio topológico (X, τ) y dos subconjuntos A, B X, diremos que A y B están separados si A B = A B = Es evidente
Capítulo 6 Espacios conexos 6.1 Conexos Definición 6.1.1 (Conjuntos separados). Dado un espacio topológico (X, τ) y dos subconjuntos A, B X, diremos que A y B están separados si A B = A B = Es evidente
Grafos. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Grafos 1 / 30
 Grafos AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Grafos / 0 Objetivos Al finalizar este tema tendréis que: Conocer la terminología básica de la teoría de grafos. Pasar
Grafos AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Grafos / 0 Objetivos Al finalizar este tema tendréis que: Conocer la terminología básica de la teoría de grafos. Pasar
Introducción a la Geometría Computacional. Análisis de Algoritmos
 Introducción a la Geometría Computacional Análisis de Algoritmos Geometría Computacional La Geometría Computacional surgió a finales de los 70s del área de diseño y análisis de algoritmos. Estudio sistemático
Introducción a la Geometría Computacional Análisis de Algoritmos Geometría Computacional La Geometría Computacional surgió a finales de los 70s del área de diseño y análisis de algoritmos. Estudio sistemático
Pruebas de Acceso a las Universidades de Castilla y León
 Pruebas de Acceso a las Universidades de Castilla y León DIBUJO TÉCNICO Texto para los Alumnos 9 páginas Antes de empezar a trabajar has de tener en cuenta lo siguiente: OPTATIVIDAD: Debes escoger una
Pruebas de Acceso a las Universidades de Castilla y León DIBUJO TÉCNICO Texto para los Alumnos 9 páginas Antes de empezar a trabajar has de tener en cuenta lo siguiente: OPTATIVIDAD: Debes escoger una
EL TEOREMA DE LOS CUATRO
 EL TEOREMA DE LOS CUATRO VÉRTICES Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría Diferencial. Curso 1995/96
EL TEOREMA DE LOS CUATRO VÉRTICES Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría Diferencial. Curso 1995/96
UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-RUACS. Investigación de Operaciones
 UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-RUACS Facultad de Ingeniería Industrial Investigación de Operaciones Tema: Teoría de los Grafos Elaborado por: Ing. Carlos Alberto Moreno. Docente: Ing. Pastrana
UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-RUACS Facultad de Ingeniería Industrial Investigación de Operaciones Tema: Teoría de los Grafos Elaborado por: Ing. Carlos Alberto Moreno. Docente: Ing. Pastrana
Espacios topológicos. 3.1 Espacio topológico
 Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Capítulo 3 Espacios topológicos 3.1 Espacio topológico Definición 3.1.1. Un espacio topológico es un par (X, τ), donde X es un conjunto, y τ es una familia de subconjuntos de X que verifica las siguientes
Hamilton, Euler y Dijkstra
 UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE COMPUTACION Matemáticas Discretas III (Cód. 6108) Práctica # 2 Hamilton, Euler y Dijkstra 1. Sea G = un multigrafo no dirigido donde
UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE COMPUTACION Matemáticas Discretas III (Cód. 6108) Práctica # 2 Hamilton, Euler y Dijkstra 1. Sea G = un multigrafo no dirigido donde
Dimensión métrica de grafos infinitos S
 Dimensión métrica de grafos infinitos S J Cáceres a, C Hernando b, M Mora c, A Moreno-González d, I Pelayo e, ML Puertas a, C Seara c (a) Departamento de Estadística y Matemática Aplicada, Universidad
Dimensión métrica de grafos infinitos S J Cáceres a, C Hernando b, M Mora c, A Moreno-González d, I Pelayo e, ML Puertas a, C Seara c (a) Departamento de Estadística y Matemática Aplicada, Universidad
Superficies. Las 2-variedades (o superficies) son espacios topologicos localmente homeomorfos al plano R 2. Esfera Toro Abierto del plano
 Superficies Las 2-variedades (o superficies) son espacios topologicos localmente homeomorfos al plano R 2. Ejemplos: Esfera Toro Abierto del plano Superficies abiertas y cerradas Hay muchas maneras de
Superficies Las 2-variedades (o superficies) son espacios topologicos localmente homeomorfos al plano R 2. Ejemplos: Esfera Toro Abierto del plano Superficies abiertas y cerradas Hay muchas maneras de
ALUMNO: GRUPO: Sean las series de bases r y r' y el haz de vértice V de la figura, todos ellos coplanarios.
 CANALES Y PUERTOS DE GRANADA INGENIERÍA GRÁFICA II. EXAMEN FINAL. 31 DE ENERO DE 2012 EJERCICIO TEÓRICO ALUMNO: GRUPO: NOTAS - El test consta de un total de 40 preguntas que se valorarán con las puntuaciones
CANALES Y PUERTOS DE GRANADA INGENIERÍA GRÁFICA II. EXAMEN FINAL. 31 DE ENERO DE 2012 EJERCICIO TEÓRICO ALUMNO: GRUPO: NOTAS - El test consta de un total de 40 preguntas que se valorarán con las puntuaciones
El origen: Los puentes de Königsberg. Grafos. Algoritmos y Estructuras de Datos III. Leonhard Euler ( )
 El origen: Los puentes de Königsberg Grafos Algoritmos y Estructuras de Datos III Leonhard Euler (1707 1783) El origen: Los puentes de Königsberg La ciudad de Königsberg (hoy Kaliningrado) tenía en el
El origen: Los puentes de Königsberg Grafos Algoritmos y Estructuras de Datos III Leonhard Euler (1707 1783) El origen: Los puentes de Königsberg La ciudad de Königsberg (hoy Kaliningrado) tenía en el
Puntos y Vectores. 16 de Marzo de 2012
 Geometría en Puntos y Vectores Universidad Autónoma Metropolitana Unidad Iztapalapa 16 de Marzo de 2012 Introducción En Geometría analítica plana las relaciones y las propiedades geométricas se expresan
Geometría en Puntos y Vectores Universidad Autónoma Metropolitana Unidad Iztapalapa 16 de Marzo de 2012 Introducción En Geometría analítica plana las relaciones y las propiedades geométricas se expresan
TEMA 7 Las formas y las medidas que nos rodean. 2. Repaso a las figuras planas elementales
 TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
TEMA 7 Las formas y las medidas que nos rodean 1. Introducción 1.1. Qué es la geometría? Es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano
Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton
 Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton I. Fórmula de Euler Ejercicio 1. Considere un cuadrado y escoja arbitrariamente 10 puntos en su interior. Utilizando estos
Taller 6 La fórmula de Euler y los Sólidos Platónicos Profesor: Maximiliano Leyton I. Fórmula de Euler Ejercicio 1. Considere un cuadrado y escoja arbitrariamente 10 puntos en su interior. Utilizando estos
Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler]
![Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler] Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler]](/thumbs/66/55246007.jpg) Matemáticas Discretas L. Enrique Sucar INAOE Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y circuitos Isomorfismo
Matemáticas Discretas L. Enrique Sucar INAOE Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y circuitos Isomorfismo
Conexión Motivación. Lección 10
 Lección 10 Conexión Estudiamos la propiedad topológica que nos va a permitir obtener una versión general para espacios métricos del teorema del valor intermedio que conocemos para funciones reales de variable
Lección 10 Conexión Estudiamos la propiedad topológica que nos va a permitir obtener una versión general para espacios métricos del teorema del valor intermedio que conocemos para funciones reales de variable
MÓDULO Nº 3. Nivelación. Matemática Módulo Nº3. Contenidos. Polígonos Circunferencia y Círculo Volúmenes
 MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
Tema 1: Introducción a la Teoría de Grafos
 Tema 1: Introducción a la Teoría de Grafos MATEMÁTICA A DISCRETA Nociones básicas Subgrafos. Operaciones con grafos Formas de definir un grafo Isomorfismo de grafos Tema 1: 1 Nociones básicas: Grafo: G
Tema 1: Introducción a la Teoría de Grafos MATEMÁTICA A DISCRETA Nociones básicas Subgrafos. Operaciones con grafos Formas de definir un grafo Isomorfismo de grafos Tema 1: 1 Nociones básicas: Grafo: G
Geometría en una retícula
 Geometría en una retícula Pascual Jara Luis Merino 19 de octubre de 2013 * Resumen Vamos a estudiar problemas relativos a polígonos simples (aquellos en los que los lados no se cruzan) cuyos vértices son
Geometría en una retícula Pascual Jara Luis Merino 19 de octubre de 2013 * Resumen Vamos a estudiar problemas relativos a polígonos simples (aquellos en los que los lados no se cruzan) cuyos vértices son
Un GRAFO O GRAFO NO ORIENTADO es una terna G = {V, A,ϕ } conv
 DEFINICIÓN 1: Un GRAFO O GRAFO NO ORIENTADO es una terna G = {V, A,ϕ } conv φ donde: V = {v 1, v 2,, v n }: conjunto finito de vértices o nodos. A = {a 1, a 2,, a n }: conjunto finito de aristas o lados
DEFINICIÓN 1: Un GRAFO O GRAFO NO ORIENTADO es una terna G = {V, A,ϕ } conv φ donde: V = {v 1, v 2,, v n }: conjunto finito de vértices o nodos. A = {a 1, a 2,, a n }: conjunto finito de aristas o lados
Capítulo 3: Grafos Clase 1: Grafos: Modelos, tipos, representación e isomorfismo
 Capítulo 3: Grafos Clase 1: Grafos: Modelos, tipos, representación e isomorfismo Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 4: Grafos 1 / 35 Por qué estudiamos
Capítulo 3: Grafos Clase 1: Grafos: Modelos, tipos, representación e isomorfismo Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 4: Grafos 1 / 35 Por qué estudiamos
Diagrama de Voronoi. Ejemplo de problemas geométricos:
 Diagrama de Voronoi Definición: Sea P={p1,p2,..,pn} un conjunto de puntos en el plano. Estos puntos son llamados sitios. Asignar a cada punto del plano el sitio más cercano. Todos los puntos asignados
Diagrama de Voronoi Definición: Sea P={p1,p2,..,pn} un conjunto de puntos en el plano. Estos puntos son llamados sitios. Asignar a cada punto del plano el sitio más cercano. Todos los puntos asignados
Conceptos iniciales de teoría de nudos. Escuela de Matemáticas. Realizado por: Jefferson Andrés García Ortiz. Profesor: José Gregorio Rodriguez Nieto
 Conceptos iniciales de teoría de nudos Escuela de Matemáticas Realizado por: Jefferson Andrés García Ortiz Profesor: José Gregorio Rodriguez Nieto Universidad Nacional De Colombia 2014 1 2 Resumen En el
Conceptos iniciales de teoría de nudos Escuela de Matemáticas Realizado por: Jefferson Andrés García Ortiz Profesor: José Gregorio Rodriguez Nieto Universidad Nacional De Colombia 2014 1 2 Resumen En el
GRAFOS. 1. La matriz de adyacencia del grafo G es
 GRAFOS. La matriz de adyacencia del grafo G es entonces, A) G es un pseudografo B) G es un grafo completo. G no es conexo Supongamos V={v,v,v,v } son los vértices del grafo. En los pseudografo están permitidas
GRAFOS. La matriz de adyacencia del grafo G es entonces, A) G es un pseudografo B) G es un grafo completo. G no es conexo Supongamos V={v,v,v,v } son los vértices del grafo. En los pseudografo están permitidas
Dibujo Técnico Cuerpos Sólidos Redondos: Desarrollos y Transformadas.
 38. CUERPOS SÓLIDOS REDONDOS: DESARROLLOS Y TRANSFORMADAS. 38.6. Desarrollo del cilindro. 38.6.1. Cilindro recto. En realidad el trabajar con un cilindro es lo mismo que trabajar con un prisma pero este
38. CUERPOS SÓLIDOS REDONDOS: DESARROLLOS Y TRANSFORMADAS. 38.6. Desarrollo del cilindro. 38.6.1. Cilindro recto. En realidad el trabajar con un cilindro es lo mismo que trabajar con un prisma pero este
Centro Asociado Palma de Mallorca. Tutor: Antonio Rivero Cuesta
 Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
Algebra Geometry Glossary Spanish Algebra Geometry Glossary
 1) acute angle / ángulo agudo un ángulo menor de 90 lgebra Geometry Glossary Spanish lgebra Geometry Glossary agudo ángulo ángulo de 90 2) acute triangle / triágulo acutángulo un triángulo en el que los
1) acute angle / ángulo agudo un ángulo menor de 90 lgebra Geometry Glossary Spanish lgebra Geometry Glossary agudo ángulo ángulo de 90 2) acute triangle / triágulo acutángulo un triángulo en el que los
Sobre digrafos adjuntos y (h, j) adjuntos de multidigrafos k regulares
 Revista Colombiana de Matemáticas Volumen 37 (2003), páginas 81 86 Sobre digrafos adjuntos y (h, j) adjuntos de multidigrafos k regulares Elsa Osio Teresa Braicovich Cora Bernardi Cristina Costes Universidad
Revista Colombiana de Matemáticas Volumen 37 (2003), páginas 81 86 Sobre digrafos adjuntos y (h, j) adjuntos de multidigrafos k regulares Elsa Osio Teresa Braicovich Cora Bernardi Cristina Costes Universidad
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema 4: Figuras geométricas
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 4: Figuras geométricas 1 Conceptos geométricos En la clase de matemáticas, y en los textos escolares, encontramos expresiones tales como:
Definiciones: conjuntos, grafos, y árboles. Agustín J. González ELO 320: Estructura de Datos y Algoritmos. 2002
 Definiciones: conjuntos, grafos, y árboles Agustín J. González ELO 320: Estructura de Datos y Algoritmos. 2002 1 Conjuntos (sets) y Grafos (graphs) Un Conjunto es una colección de objetos distintos. No
Definiciones: conjuntos, grafos, y árboles Agustín J. González ELO 320: Estructura de Datos y Algoritmos. 2002 1 Conjuntos (sets) y Grafos (graphs) Un Conjunto es una colección de objetos distintos. No
Coloración de grafos
 Alumno: Grupo: Coloración de grafos Comencemos planteando el problema de dar color a las regiones de un mapa plano de modo que a regiones vecinas se les asigne distinto color. Este problema puede ser resuelto
Alumno: Grupo: Coloración de grafos Comencemos planteando el problema de dar color a las regiones de un mapa plano de modo que a regiones vecinas se les asigne distinto color. Este problema puede ser resuelto
TEMA 1: GEOMETRÍA EN EL ESPACIO
 MATEMÁTICA 2do año A y B Marzo, 2012 TEMA 1: GEOMETRÍA EN EL ESPACIO Ejercicio 1: Indica si cada una de las siguientes proposiciones es verdadera o falsa: Por un punto pasa una recta y una sola Dos puntos
MATEMÁTICA 2do año A y B Marzo, 2012 TEMA 1: GEOMETRÍA EN EL ESPACIO Ejercicio 1: Indica si cada una de las siguientes proposiciones es verdadera o falsa: Por un punto pasa una recta y una sola Dos puntos
SUPERFICIES REGLADAS ALABEADAS
 SUPERFICIES REGLADAS ALABEADAS Las superficies se consideran el lugar geométrico de las sucesivas posiciones de una línea móvil que se mueve en el espacio siguiendo una ley determinada y continua. La línea
SUPERFICIES REGLADAS ALABEADAS Las superficies se consideran el lugar geométrico de las sucesivas posiciones de una línea móvil que se mueve en el espacio siguiendo una ley determinada y continua. La línea
3-variedades. Una 3-variedad es un espacio topologico (hausdorff y segundo numerable) que es localmente homeomorfo a R3.
 3-Variedades 3-variedades Las 3- variedades son espacios que localmente se parecen al espacio euclidiano. Dos variedades son iguales si es posible deformar continuamente a una para obtener la otra Una
3-Variedades 3-variedades Las 3- variedades son espacios que localmente se parecen al espacio euclidiano. Dos variedades son iguales si es posible deformar continuamente a una para obtener la otra Una
INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES. Tema 3 EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS.
 INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES Tema EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS. C.- Qué es cómo se representa un sistema de coordenadas cartesianas rectangulares
INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES Tema EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS. C.- Qué es cómo se representa un sistema de coordenadas cartesianas rectangulares
Las variedades lineales en un K-espacio vectorial V pueden definirse como sigue a partir de los subespacios de V.
 Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
El primer ejercicio se valorará sobre 4 puntos. Los dos restantes sobre 3 puntos cada uno OPCIÓN A
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2010-2011 MATERIA: DIBUJO TÉCNICO II 8 INSTRUCCIONES CRITERIOS GENERALES DE CALIFICACIÓN
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2010-2011 MATERIA: DIBUJO TÉCNICO II 8 INSTRUCCIONES CRITERIOS GENERALES DE CALIFICACIÓN
La Distancia de un Punto a una Recta y de un Punto a un Plano, y un Teorema de Pitágoras en Tres Dimensiones
 58 Sociedad de Matemática de Chile La Distancia de un Punto a una Recta y de un Punto a un Plano, y un Teorema de Pitágoras en Tres Dimensiones Miguel Bustamantes 1 - Alejandro Necochea 2 El propósito
58 Sociedad de Matemática de Chile La Distancia de un Punto a una Recta y de un Punto a un Plano, y un Teorema de Pitágoras en Tres Dimensiones Miguel Bustamantes 1 - Alejandro Necochea 2 El propósito
Capítulo 4: Grafos Clase 2: Caminos, Circuitos Eulerianos y Hamiltonianos
 Capítulo 4: Grafos Clase 2: Caminos, Circuitos Eulerianos y Hamiltonianos Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 4: Grafos 1 / 29 Navegación de grafos
Capítulo 4: Grafos Clase 2: Caminos, Circuitos Eulerianos y Hamiltonianos Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 4: Grafos 1 / 29 Navegación de grafos
Puntos y rectas en el triángulo
 Puntos y rectas en el triángulo En los triángulos hay un conjunto de rectas y puntos importantes. Las rectas son las bisectrices, las mediatrices, las alturas, las medianas y las bisectrices exteriores.
Puntos y rectas en el triángulo En los triángulos hay un conjunto de rectas y puntos importantes. Las rectas son las bisectrices, las mediatrices, las alturas, las medianas y las bisectrices exteriores.
Grafos de orden máximo y mínimo con diámetro y dimensión métrica fijados
 Grafos de orden máximo y mínimo con diámetro y dimensión métrica fijados Carmen Hernando, Mercè Mora, Ignacio M. Pelayo, Carlos Seara, David R. Wood Universitat Politècnica de Catalunya carmen.hernando@upc.edu,
Grafos de orden máximo y mínimo con diámetro y dimensión métrica fijados Carmen Hernando, Mercè Mora, Ignacio M. Pelayo, Carlos Seara, David R. Wood Universitat Politècnica de Catalunya carmen.hernando@upc.edu,
Lámina 1a. Cálculo mental diario
 Lámina 1a Clase: 1 Cálculo mental diario a) 13 13 = b) 10 3 70 = c) 6:2 2 4 = d) 4 4 42:2 = e) -15 + 5 5 = f) 12 6 6 = g) 5 + (3 8) = h) -20 5-10 = i) 8 (6+4) = j) (-40) + (-3) = k) 3 (-13) = l) 143 +
Lámina 1a Clase: 1 Cálculo mental diario a) 13 13 = b) 10 3 70 = c) 6:2 2 4 = d) 4 4 42:2 = e) -15 + 5 5 = f) 12 6 6 = g) 5 + (3 8) = h) -20 5-10 = i) 8 (6+4) = j) (-40) + (-3) = k) 3 (-13) = l) 143 +
EXPRESIÓN GRÁFICA: SISTEMAS DE REPRESENTACIÓN
 EXPRESIÓN GRÁFIC: SISTEMS DE REPRESENTCIÓN Plano de representación Plano de representación Punto de vista V Punto de vista V en el TEM 8 Intersección de superficies. plicaciones al dibujo técnico. El resto
EXPRESIÓN GRÁFIC: SISTEMS DE REPRESENTCIÓN Plano de representación Plano de representación Punto de vista V Punto de vista V en el TEM 8 Intersección de superficies. plicaciones al dibujo técnico. El resto
A RG. Diédrico 22. Sección 3. Cilindro recto por un proyectante Hoja 1/2
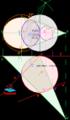 Dibujar la sección producida por el plano α al cilindro recto de base circular y altura 50 mm, obteniendo su verdadera magnitud. en la parte inferior de la lámina obtener el desarrollo del prisma y de
Dibujar la sección producida por el plano α al cilindro recto de base circular y altura 50 mm, obteniendo su verdadera magnitud. en la parte inferior de la lámina obtener el desarrollo del prisma y de
Algebra Matricial y Teoría de Grafos
 Algebra Matricial y Teoría de Grafos Unidad 3: Nociones de teoría de grafos Luis M. Torres Escuela Politécnica del Litoral Quito, Enero 2008 Maestría en Control de Operaciones y Gestión Logística p.1 Contenido
Algebra Matricial y Teoría de Grafos Unidad 3: Nociones de teoría de grafos Luis M. Torres Escuela Politécnica del Litoral Quito, Enero 2008 Maestría en Control de Operaciones y Gestión Logística p.1 Contenido
SUPERFICIES POLIÉDRICAS CONVEXAS
 SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
SUPERFICIES POLIÉDRICAS CONVEXAS OBJETIVOS Conocer las características y relaciones métricas del te tra - edro, hexaedro o cubo y octaedro, para su represen tación en el sistema diédrico en sus múltiples
Sesión 4: Teoría de Grafos
 Modelos Gráficos Probabilistas L. Enrique Sucar INAOE Sesión 4: Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y
Modelos Gráficos Probabilistas L. Enrique Sucar INAOE Sesión 4: Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y
Sistema Diédrico (II). Superficies poliédricas y radiadas. Desarrollos
 Sistema Diédrico (II). Superficies poliédricas y radiadas. Desarrollos Cuando realizamos el desarrollo de una superficie estamos representando la verdadera magnitud de esta, lo que nos permitirá aplicar
Sistema Diédrico (II). Superficies poliédricas y radiadas. Desarrollos Cuando realizamos el desarrollo de una superficie estamos representando la verdadera magnitud de esta, lo que nos permitirá aplicar
2007 Carmen Moreno Valencia
 Tema VIII. Grafos Grafos 1 2007 Carmen Moreno Valencia 1. Grafos, digrafos y multigrafos 2. Grafos eulerianos 3. Matrices de adyacencia e incidencia 4. Exploración de grafos pesados 1. Grafos, digrafos
Tema VIII. Grafos Grafos 1 2007 Carmen Moreno Valencia 1. Grafos, digrafos y multigrafos 2. Grafos eulerianos 3. Matrices de adyacencia e incidencia 4. Exploración de grafos pesados 1. Grafos, digrafos
Secciones Cónicas. 0.1 Parábolas
 Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
1. Dibujar un punto del primer cuadrante y su simétrico respecto del plano vertical de proyección.
 Referencias.- En todos los ejercicios: La primera coordenada representa a la distancia al plano lateral de referencia, la segunda coordenada es el alejamiento y la tercera coordenada es la elevación. [P(x,
Referencias.- En todos los ejercicios: La primera coordenada representa a la distancia al plano lateral de referencia, la segunda coordenada es el alejamiento y la tercera coordenada es la elevación. [P(x,
TOPOLOGÍA SOLUCIONES A LAS RELACIONES DE PROBLEMAS
 TOPOLOGÍA SOLUCIONES A LAS RELACIONES DE PROBLEMAS Ejercicio 4.1.- Relación 4. Compacidad. Conexión Supongamos que A es compacto y sea A α Λ B α un recubrimiento de A por bolas abiertas. Entonces, como
TOPOLOGÍA SOLUCIONES A LAS RELACIONES DE PROBLEMAS Ejercicio 4.1.- Relación 4. Compacidad. Conexión Supongamos que A es compacto y sea A α Λ B α un recubrimiento de A por bolas abiertas. Entonces, como
DIBUJO TÉCNICO. UNIDAD DIDÁCTICA VIII: Geometría 3D (IV)
 UNIDAD DIDÁCTICA VIII: Geometría 3D (IV) ÍNDICE Página: 1 SUPERFICIES DE REVOLUCIÓN 2 2 SUPERFICIE CILÍNDRICA 2 21 CILINDROS 2 22 PROYECCIONES DE UN CILINDRO 3 23 SECCIONES PLANAS 4 3 SUPERFICIES CÓNICAS
UNIDAD DIDÁCTICA VIII: Geometría 3D (IV) ÍNDICE Página: 1 SUPERFICIES DE REVOLUCIÓN 2 2 SUPERFICIE CILÍNDRICA 2 21 CILINDROS 2 22 PROYECCIONES DE UN CILINDRO 3 23 SECCIONES PLANAS 4 3 SUPERFICIES CÓNICAS
A G R. Diédrico 17. Cuerpos 4. Tetraedro
 Dibujar los tetraedros, de igual arista, en las cuatro posiciones siguientes: 1. Apoyado por la cara AB en el PH (la posición de la izquierda). 2. on una arista, la AB en el PH y la opuesta horizontal.
Dibujar los tetraedros, de igual arista, en las cuatro posiciones siguientes: 1. Apoyado por la cara AB en el PH (la posición de la izquierda). 2. on una arista, la AB en el PH y la opuesta horizontal.
UNIDAD 3 LA RECTA Y SU ECUACIÓN CARTESIANA. Dada la ecuación de dos rectas. Determinará si se cortan, si son paralelas o perpendiculares. Y l.
 UNIDAD 3 LA RECTA SU ECUACIÓN CARTESIANA OBJETIVOS ESPECÍFICOS. Al término de la unidad, el alumno: Conocerá las distintas formas de representación de la recta e identificará cuál de ellas conviene usar.
UNIDAD 3 LA RECTA SU ECUACIÓN CARTESIANA OBJETIVOS ESPECÍFICOS. Al término de la unidad, el alumno: Conocerá las distintas formas de representación de la recta e identificará cuál de ellas conviene usar.
Elementos de Geometría
 Elementos de Geometría Manuel Maia 19 de marzo de 2012 1 Puntos, Rectas, Planos y Ángulos Hay cuatro términos o conceptos que aceptaremos sin definición: conjunto, punto recta y plano. Estos se llaman
Elementos de Geometría Manuel Maia 19 de marzo de 2012 1 Puntos, Rectas, Planos y Ángulos Hay cuatro términos o conceptos que aceptaremos sin definición: conjunto, punto recta y plano. Estos se llaman
Tema 2: Figuras geométricas
 Tema 2: Figuras geométricas En este tema empezaremos a estudiar: 1. la circunferencia. 2. los triángulos. 3. los cuadriláteros. 4. los poĺıgonos. 1 2 La circunferencia (p. 31) El cerebro humano es muy
Tema 2: Figuras geométricas En este tema empezaremos a estudiar: 1. la circunferencia. 2. los triángulos. 3. los cuadriláteros. 4. los poĺıgonos. 1 2 La circunferencia (p. 31) El cerebro humano es muy
Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.
![Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos. Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.](/thumbs/54/33802392.jpg) Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
Figuras planas. Definiciones
 Figuras planas Definiciones Polígono: definición Un polígono es una figura plana (yace en un plano) cerrada por tres o más segmentos. Los lados de un polígono son cada uno de los segmentos que delimitan
Figuras planas Definiciones Polígono: definición Un polígono es una figura plana (yace en un plano) cerrada por tres o más segmentos. Los lados de un polígono son cada uno de los segmentos que delimitan
UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE
 UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE CUERPOS: POLIEDROS Se denomina superficie poliédrica aquella que está formada por varios poligonos consecutivos. Estos son las caras de
UNIDAD Nº 6 GEOMETRÍA DESCRIPTIVA PROYECCIÓN DIÉDRICA O DE MONGE CUERPOS: POLIEDROS Se denomina superficie poliédrica aquella que está formada por varios poligonos consecutivos. Estos son las caras de
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE #3
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE #3 ÁREA Y PERÍMETRO DE FIGURAS PLANAS LINEA POLIGONAL: Se llama línea poligonal a la gura formada por la unión de segmentos de
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN CLASE #3 ÁREA Y PERÍMETRO DE FIGURAS PLANAS LINEA POLIGONAL: Se llama línea poligonal a la gura formada por la unión de segmentos de
Figura 1.7 Además, para poliedros específicos puede ser muy fácil establecer una correspondencia adecuada entre sus puntos y los de la esfera. Por eje
 1.2 Equivalencia topológica Existen diversas demostraciones del teorema de Euler. Hemos elegido la anterior por dos razones. La primera, su elegancia; muchas de las restantes demostraciones usan inducción
1.2 Equivalencia topológica Existen diversas demostraciones del teorema de Euler. Hemos elegido la anterior por dos razones. La primera, su elegancia; muchas de las restantes demostraciones usan inducción
REVISIÓN DE ALGUNOS CONCEPTOS DE GEOMETRÍA MÉTRICA
 MAT B Repartido Nº I REVISIÓN DE ALGUNOS CONCEPTOS DE GEOMETRÍA MÉTRICA Conceptos primitivos Partiremos de un conjunto que llamaremos espacio, E, a cuyos elementos llamamos puntos, (a los cuales escribiremos
MAT B Repartido Nº I REVISIÓN DE ALGUNOS CONCEPTOS DE GEOMETRÍA MÉTRICA Conceptos primitivos Partiremos de un conjunto que llamaremos espacio, E, a cuyos elementos llamamos puntos, (a los cuales escribiremos
Modelación de objetos 3D Parte I: Mallas de polígonos y triangulaciones
 Modelación de objetos 3D Parte I: Mallas de polígonos y triangulaciones Contenido Motivación Polígonos simples 3D Almacenamiento de mallas de polígonos OpenGl y mallas de polígonos Triangulaciones Triangulaciones
Modelación de objetos 3D Parte I: Mallas de polígonos y triangulaciones Contenido Motivación Polígonos simples 3D Almacenamiento de mallas de polígonos OpenGl y mallas de polígonos Triangulaciones Triangulaciones
EJERCICIOS DE LOS TEMAS 9 y 10.GEOMETRÍA
 1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
MCRivara/CG2008/1. MCRivara/CG2007/2MCRivara/CG2008/1 1. Modelación de Sólidos. Computación Gráfica. Modelos de sólidos
 Computación Gráfica Modelación de Sólidos Prof. María Cecilia Rivara mcrivara@dcc.uchile.cl Semestre 2009/1 Modelación de Sólidos Objetivo: Modelos matemáticos de objetos del mundo real (automóvil, motor,
Computación Gráfica Modelación de Sólidos Prof. María Cecilia Rivara mcrivara@dcc.uchile.cl Semestre 2009/1 Modelación de Sólidos Objetivo: Modelos matemáticos de objetos del mundo real (automóvil, motor,
Los elementos de V son los vértices (o nodos) de G y los elementos de A son las aristas (o arcos) de G.
 MATERIAL TEÓRICO º Cuatrimestre Año 03 Prof. María Elena Ruiz Prof. Carlos Roberto Pérez Medina UNIDAD III: GRAFOS Definición: Llamaremos grafo a una terna G= (V, A, ϕ), donde V y A son conjuntos finitos,
MATERIAL TEÓRICO º Cuatrimestre Año 03 Prof. María Elena Ruiz Prof. Carlos Roberto Pérez Medina UNIDAD III: GRAFOS Definición: Llamaremos grafo a una terna G= (V, A, ϕ), donde V y A son conjuntos finitos,
Minicurso de Teoría de Gráficas Escuela de Verano 2014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana
 Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
EL TEOREMA DE JORDAN Y LOS GRAFOS PLANARES
 TRABAJO DE FIN DE GRADO, JUNIO 2016 EL TEOREMA DE JORDAN Y LOS GRAFOS PLANARES DEPARTAMENTO DE GEOMETRÍA Y TOPOLOGÍA FACULTAD DE CIENCIAS MATEMÁTICAS, UCM DIRIGIDO POR JESÚS M. RUIZ JAIME DAN PORRAS RHEE
TRABAJO DE FIN DE GRADO, JUNIO 2016 EL TEOREMA DE JORDAN Y LOS GRAFOS PLANARES DEPARTAMENTO DE GEOMETRÍA Y TOPOLOGÍA FACULTAD DE CIENCIAS MATEMÁTICAS, UCM DIRIGIDO POR JESÚS M. RUIZ JAIME DAN PORRAS RHEE
TRIÁNGULOS: RELACIONES DE DESIGUALDAD ENTRE SEGMENTOS Y ÁNGULOS
 TRIÁNGULOS: RELACIONES DE DESIGUALDAD ENTRE SEGMENTOS Y ÁNGULOS Introducción.- Anteriormente, a partir de la congruencia de triángulos, hemos estudiado las condiciones que han de verificarse para que dos
TRIÁNGULOS: RELACIONES DE DESIGUALDAD ENTRE SEGMENTOS Y ÁNGULOS Introducción.- Anteriormente, a partir de la congruencia de triángulos, hemos estudiado las condiciones que han de verificarse para que dos
Sistema axonométrico. Con el estudio de esta Unidad nos proponemos alcanzar los siguientes objetivos:
 UNIDAD 9 Sistema axonométrico E l sistema axonométrico se divide en ortogonal y oblicuo según sea la dirección de proyección. La axonometría ortogonal puede ser isométrica, dimétrica o trimétrica según
UNIDAD 9 Sistema axonométrico E l sistema axonométrico se divide en ortogonal y oblicuo según sea la dirección de proyección. La axonometría ortogonal puede ser isométrica, dimétrica o trimétrica según
10. COLOREADO DE GRAFOS
 10. COLOREADO DE GRAFOS Ejemplo 8. 8 Horario de exámenes finales. Tenemos que hacer un horario para realizar siete exámenes finales, Numeramos las asignaturas de 1 a 7. Hay alumnos matriculados en varias
10. COLOREADO DE GRAFOS Ejemplo 8. 8 Horario de exámenes finales. Tenemos que hacer un horario para realizar siete exámenes finales, Numeramos las asignaturas de 1 a 7. Hay alumnos matriculados en varias
APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS
 APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS 1. Introducción La investigación que se presenta a continuación tiene su origen en mi función de director de trabajos de investigación realizados
APLICACIÓN DE LAS FUNCIONES AL ESTUDIO DE MOSAICOS Y POLIEDROS 1. Introducción La investigación que se presenta a continuación tiene su origen en mi función de director de trabajos de investigación realizados
Sistema diédrico: prisma, cono y cilindro
 UNIDAD 7 Sistema diédrico: prisma, cono y cilindro Capitel basado en el prisma y el cilindro (Modificación de la fotografía de la Mezquita de las Tornerías, Toledo, de Luana Fischer Ferreira, del Banco
UNIDAD 7 Sistema diédrico: prisma, cono y cilindro Capitel basado en el prisma y el cilindro (Modificación de la fotografía de la Mezquita de las Tornerías, Toledo, de Luana Fischer Ferreira, del Banco
18. PERSPECTIVA CABALLERA.
 18. PERSPECTIVA CABALLERA. La perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los
18. PERSPECTIVA CABALLERA. La perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los
INSTITUTO DE FORMACIÓN DOCENTE DE CANELONES MATEMÁTICA 1 GEOMETRÍA EUCLIDIANA
 GEOMETRÍA EUCLIDIANA Axiomas de Pertenencia 1) Existe un conjunto infinito llamado espacio, cuyos elementos se llaman puntos. 2) En el espacio existen subconjuntos estrictos llamados planos, cada uno de
GEOMETRÍA EUCLIDIANA Axiomas de Pertenencia 1) Existe un conjunto infinito llamado espacio, cuyos elementos se llaman puntos. 2) En el espacio existen subconjuntos estrictos llamados planos, cada uno de
XLV Olimpiada Matemática Española Primera Fase Primera y segunda sesión Viernes tarde, 23 de enero de 2008
 XLV Olimpiada Matemática Española Primera Fase Primera y segunda sesión Viernes tarde, 23 de enero de 2008 SOLUCIONES 1 y 4. Dado un triángulo acutángulo ABC, determinar para que puntos de su interior
XLV Olimpiada Matemática Española Primera Fase Primera y segunda sesión Viernes tarde, 23 de enero de 2008 SOLUCIONES 1 y 4. Dado un triángulo acutángulo ABC, determinar para que puntos de su interior
Tema 5 Árboles y Grafos.
 Tema 5 Árboles y Grafos. Definiciones básicas de teoría de grafos. Un grafo consta de un conjunto de nodos, un conjunto de aristas y una correspondencia f del conjunto de aristas al conjunto de nodos.
Tema 5 Árboles y Grafos. Definiciones básicas de teoría de grafos. Un grafo consta de un conjunto de nodos, un conjunto de aristas y una correspondencia f del conjunto de aristas al conjunto de nodos.
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre
 Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Típicamente, un grafo se representa
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Típicamente, un grafo se representa
Observación En algunas fuentes, estas coloraciones se denominan coloraciones admisibles; aquí, por comodidad, las denominamos coloraciones.
 Coloración de grafos Hay muchos problemas, como la asignación de tareas y los problemas de almacenamiento, donde es necesario partir el conjunto de vértices (resp. aristas) de un grafo asociado de tal
Coloración de grafos Hay muchos problemas, como la asignación de tareas y los problemas de almacenamiento, donde es necesario partir el conjunto de vértices (resp. aristas) de un grafo asociado de tal
Conjuntos de nivel, diagramas de contorno, gráficas. Funciones vectoriales de una y dos variables.
 Empezaremos el curso introduciendo algunos conceptos básicos para el estudio de funciones de varias variables, que son el objetivo de la asignatura: Funciones escalares de dos y tres variables. Conjuntos
Empezaremos el curso introduciendo algunos conceptos básicos para el estudio de funciones de varias variables, que son el objetivo de la asignatura: Funciones escalares de dos y tres variables. Conjuntos
Cónicas. Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá. November 27,
 Cónicas Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá November 27, 2013 marcos.marva@uah.es Cómo definir una cónica Como intersección de un plano y un cono recto de doble hoja
Cónicas Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá November 27, 2013 marcos.marva@uah.es Cómo definir una cónica Como intersección de un plano y un cono recto de doble hoja
Computación Geométrica Descomposición en polígonos monótonos
 Computación Geométrica Descomposición en polígonos monótonos Introducción a la Geometría Computacional Copyright 2010-2011 Universidad de Alicante 1 Ejemplos Introducción a la Geometría Computacional Copyright
Computación Geométrica Descomposición en polígonos monótonos Introducción a la Geometría Computacional Copyright 2010-2011 Universidad de Alicante 1 Ejemplos Introducción a la Geometría Computacional Copyright
