UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS
|
|
|
- Francisco José Martín Franco
- hace 6 años
- Vistas:
Transcripción
1 UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS Asignatura : Cálculo Numérico, MAT-113. Profesor : Emilio Cariaga L. Periodo : 1er. Semestre 016. INTRODUCCIÓN A LA SOLUCIÓN NUMÉRICA DE ECUACIONES DIFERENCIALES I 1. Introducción Una ecuación diferencial (ED) es aquella en que la incógnita es una función, y en que además la igualdad involucra la o las derivadas de la función incógnita. Las ED surgen, por ejemplo, como consecuencia de aplicar las leyes de conservación de la masa, del momemtum, y de la energía. Una ED Ordinaria (EDO) es aquella en que la función incógnita depende sólo de una variable, y por lo tanto una EDO involucra sólo derivadas ordinarias. Por ejemplo, para la función incógnita P (t) dp dt = kp. Una ED Parcial (EDP) es aquella en que la función incógnita depende de dos o más variables, y por lo tanto una EDP involucra derivadas parciales. Por ejemplo, para la función incógnita T (x, y) T xx + T yy = f. Existen tres grandes familias de técnicas para resolver una ED: 1. Soluciones Analíticas: una técnica de resolución se dice analítica o exacta si permite obtener una expresión algebraica explícita para la función incógnita.. Soluciones Numéricas: una técnica de resolución se dice numérica si permite obtener una aproximación (en algún sentido) para la función incógnita. 3. Soluciones Cualitativas: una técnica de resolución se dice cualitativa si permite obtener información de la solución a partir de la ED en sí misma. Respecto de la Solución Numérica de una ED en este curso se presentarán métodos para EDO y para EDP. En efecto, para EDO veremos algunos métodos de un paso, tales como Euler, Taylor y Runge-Kutta. Para EDP se expondrán los fundamentos del método de Diferencias Finitas para EDP elípticas y parabólicas. 1
2 . Solución Numérica de EDO Considere el pvi y = f(x, y) y(x 0 ) = y 0, para el cual supondremos, en todo lo que sigue, que está bien definido, esto es, posee solución, esta es única, y además es estable (depende continuamente de las condiciones iniciales). En todo lo que sigue se considera una partición del intervalo [x 0, x M ], esto es, x 0, x 1,..., x i, x i+1,..., x M, denotando h = x i+1 x i, para i = 0, 1,,..., M 1. Por otro lado, si y(x), x [x 0, x M ] denota la solución exacta del pvi, entonces, utilizaremos y i para denotar la aproximación de y(x i ), esto es, y i y(x i ), con i = 1,,..., M. Note que para i = 0 se tiene una igualdad: y 0 = y(x 0 ), esto es, la condición inicial..1. Método de Euler Por definición se sabe que y = lím h y(x + h) y(x). h A partir de lo anterior se puede utilizar la razón y(x + h) y(x) h como una aproximación de y. Luego, podemos plantear la siguiente aproximación y(x + h) y(x) f(x, y), h o sea, y(x + h) y(x) + hf(x, y). Esta última aproximación motiva la definición del método de Euler como con i = 0, 1,..., M 1. y i+1 = y i + hf(x i, y i ),
3 .. Método de Taylor Asumiendo que la solución del pvi es suficientemente diferenciable se puede utilizar un polinomio de Taylor. Para presentar la técnica se utilizará un polinomio de Taylor de segundo grado: y(x + h) = y(x) + h1 1! y(1) (x) + h! y() (x) + h3 3! y(+1) (ɛ), con ɛ entre x y x + h. En esta última igualdad note que y = f. Por otro lado, y se puede calcular como y = (y ) = d dx f(x, y) = f x 1 + f y y = f x + f y f. Por lo tanto, es posible plantear la siguiente aproximación y(x + h) y(x) + hf(x, y) + h (f x(x, y) + f y (x, y)f(x, y)), la cual motiva la definición del método de Taylor de orden y i+1 = y i + hf(x i, y i ) + h (f x(x i, y i ) + f y (x i, y i )f(x i, y i )), para i = 0, 1,,..., M 1. De manera análoga se puede puede definir un método de Taylor de orden 3, 4, o superior..3. Métodos de Runge-Kutta Carl David Tolmé Runge, Martin Wilhelm Kutta, El ahora denominado método de Runge-Kutta fue parte de la tesis doctoral del Profesor Kutta, en la Universidad de Munich, la cual finalizó en 1900, y publicó en ( Tal como se puede apreciar en la deducción del método de Taylor la principal dificultad surge al calcular las derivadas y (n), n = 3, 4,..., a partir de y = f(x, y). En efecto, este enfoque conduce a un número excesivo de evaluaciones funcionales (f, f x, f y, f xx, f yy,...) al momento de ejecutar el respectivo código computacional. Por ejemplo, se puede demostrar que para la derivada de tercer orden y (3) : y (3) = f xx + f xy f + f(f yx + f yy f) + f y (f x + f y f). En base a esto, se puede aseverar que la motivación básica de los así llamados métodos de Runge-Kutta consiste en alcanzar exactitudes de un método de Taylor de orden 4 ó 5, por ejemplo, pero sin calcular derivadas adicionales, esto es, sólo evaluando la función dato f(x, y). Los métodos de Runge-Kutta se pueden motivar como una generalización de la expresión que define el método de Euler, esto es, y i+1 = y i + hf(x i, y i ), 3
4 a través de una relación más general del tipo y i+1 = y i + hφ(x i, y i, h), en donde φ es una función incremento y se interpreta como una pendiente generalizada sobre el respectivo intervalo de solución. Específicamente,se define como una combinación lineal de las pendientes calculadas en diversos puntos vecinos, esto es, φ = a 1 k a n k n, con a i constantes, y k i definida como k 1 = f(x i, y i ) k = f(x i + p 1 h, y i + q 11 k 1 h) k 3 = f(x i + p h, y i + q 1 k 1 h + q k h) k n = f(x i + p n 1 h, y i + q n 1,1 k 1 h + q n 1, k h q n 1,n 1 k n 1 h), siendo p i, y q i constantes adecuadas. Por ejemplo, 1. Runge-Kutta de orden 1. Para n = 1: φ = a 1 k 1, k 1 = f(x i, y i ), con lo cual, y i+1 = y i + a 1 f(x i, y i )h. Note que si se elige a 1 = 1 se obtiene el método de Euler.. Runge-Kutta de orden. Para n = : φ = a 1 k 1 + a k, k 1 = f(x i, y i ), y k = f(x i + p 1 h, y i + q 11 k 1 h), con lo cual, y i+1 = y i + φ(x i, y i, h)h = y i + (a 1 k 1 + a k )h. El problema consiste en determinar las constantes a 1, a, p 1, y q 11. Para tal efecto recordemos que el desarrollo en serie de Taylor para una función en dos variables, está dado por g(x + r, y + s) = g(x, y) + rg x (x, y) + sg y (x, y) +..., en donde se han mencionado explícitamente sólo los términos lineales. Aplicando este último desarrollo a la función en dos variables k podemos escribir k = f(x i + p 1 h, y i + q 11 k 1 h) = f(x i, y i ) + (p 1 h)f x + (q 11 k 1 h)f y +..., con lo cual la expresión de Runge-Kutta se puede escribir como y i+1 = y i + (a 1 + a )fh + (a p 1 f x + a q 11 f y f) h +... Finalmente, comparando esta última expresión con la definición del método de Taylor de orden, esto es, y i+1 = y i + fh + (f x + f y f) h, 4
5 se obtiene el siguiente sistema de 3 ecuaciones con 4 incógnitas (y que por lo tanto, posee infinitas soluciones) a 1 + a = 1 a p 1 = 1 a q 11 = 1. En particular, si se hace a = 1/, se obtiene que a 1 = 1/, p 1 = 1, y q 11 = 1, con lo cual se obtiene un método de Runge-Kutta de orden (para i = 0, 1,, 3,..., M 1): y i+1 = y i + ( k 1 + k )h k 1 = f(x i, y i ) k = f(x i + h, y i + k 1 h) 3. Runge-Kutta de orden 4-Clásico. Siguiendo una argumentación similar al ejemplo anterior se obtiene el método clásico de Runge-Kutta de orden 4: y i+1 = y i + ( k 1 + k + k 3 + k 4 )h 6 k 1 = f(x i, y i ) k = f(x i + h/, y i + k 1 h/) k 3 = f(x i + h/, y i + k h/) k 4 = f(x i + h, y i + k 3 h), para i = 0, 1,, 3,..., M 1. 5
6 .4. EJERCICIOS 1. Para cada uno de los pvi dados a continuación se pide: (i) calcular la solución exacta o analítica, (ii) escribir la expresión algebraica que define los métodos de Euler, Taylor (orden, 3 y 4), y RK-4 clásico, (iii) a partir de la condición inicial dada ejecute, con calculadora, al menos dos pasos con h = 1/100. a) y = cos x, y(0) = 1. b) y tan x = y, y( π ) = π. c) (x + 1)y + 3x 3 y = 6xe 3x /, y(0) = 1. d) (x + 4)y + 3xy = x, y(0) = 1. e) ydx + x(ln x ln y 1)dy = 0, y(1) = e. f ) (x + ye y/x )dx xe y/x dy = 0, y(1) = 0.. Un modelo matemático para el área A que ocupa una colonia de bacterias está dado por da = A(,18 0,043A). dt Suponga que el área inicial es de 0,4cm. Se dispone del siguiente conjunto de datos experimentales, en donde el tiempo t se observó en días: t A Se pide: (i) calcular la solución exacta, (ii) graficar simultáneamente los datos y la curva solución en [0, 5], (iii) construya una tabla con las soluciones numéricas (use h = 1): Euler, Taylor de orden, y RK-4 clásico, y que incluya además, los datos experimentales y los valores numéricos calculados a partir de la solución exacta. Compare y comente. 3. Considere un tanque cónico invertido con un orificio circular en su vértice basal de radio r = 1 10 [pie] por el cual puede fluir un cierto líquido contenido en el tanque. Se sabe que si x denota la altura del nivel del líquido medido desde el vértice, entonces se satisface: A(x) dx dt = 0, 6πr gx, en donde, A(x) es el área de la sección transversal del tanque a una altura x y g = 3, 1[pie/s ]. Sabiendo que el tanque tiene una altura inicial de líquido igual a 10[pie], y un volumen inicial de 51 3 π[pie3 ], se pide: (i) calcular la solución exacta x(t), (ii) aproximar la altura x cuando han transcurrido 0[s] utilizando el método de Taylor de orden 3, con tamaño de paso t = 10[s], (iii) comparar la altura exacta y aproximada, calculando el error absoluto. Ayuda: el volumen de un cono de radio basal R y altura H está dado por V = 1 3 πr H. 6
7 4. Un cultivo de bacterias tiene P 0 > 0 bacterias inicialmente. Al cabo de una hora se determina que el número de bacterias P (t) ha aumentado a 3 P 0. Si la tasa de crecimiento es directamente proporcional al número de bacterias en ese instante, esto es, dp (t) dt = kp (t), k > 0 se pide: (i) resolver la ecuación diferencial dada para demostrar que P (t) = P 0 e kt, con k = ln(3/), (ii) calcular el tiempo que debe transcurrir para que el número de bacterias de triplique, (iii) aproximar el número de bacterias al cabo de dos horas, utilizando el método de Taylor de orden 4, con t = 1[hr] y P 0 = 100[bacterias], (iv) comparar la aproximación obtenida en el punto anterior con el valor exacto. Comentar. 5. En el instante en que se saca un pastel del horno su temperatura es igual a 300 F. Tres minutos después su temperatura es igual a 00 F. Si T (t) denota la temperatura (en F ) del pastel t[min] después de haber sido sacado del horno, la ley de enfriamiento de Newton permite aseverar que existe una constante k > 0 tal que dt dt = k(t 70). Se pide: (i) demostrar que la función T (t) está dada por T (t) = 70+30e kt ; t 0, en donde, k = (1/3) ln(13/3), resolviendo la edo dada, (ii) aproxime (con t = 1[min]) la temperatura del pastel cuendo han transcurrido dos minutos usando el método de Euler (Taylor de Orden 1), (iii) aproxime (con t = 1[min]) la temperatura del pastel cuando han transcurrido dos minutos usando el método de Taylor de Orden 3, (iv) calcule el error relativo de las aproximaciones obtenidas en los puntos (ii) y (iii). Comente sus resultados. 6. Resuelva numéricamente la ecuación de van der Pol dy dx µ(1 y ) dy dx + y = 0, para µ > 0, utilizando el comando ode45 de Matlab, en el intervalo [0, 0]. Solución: a) La edo dada puede ser transformada en el sgte. sistema y 1 = y y = µ(1 y1)y y 1. b) Construya el archivo vdp1.m con el sgte. contenido (µ = 1): function dydt = vdp1(t, y) dydt = [y(); (1 y(1) ) y() y(1)]; c) En la línea de comandos ejecute las siguientes instrucciones: > inter = [0, 0] ; > ci = [, 0] ; > [t, y] = ode45( vdp1, inter, ci); 7
8 d) Ejecute la siguiente instrucción para graficar la solución obtenida: > plot(t, y); 7. Resuelva numéricamente el sistema depredador-presa dx dt dy dt = 1,x 0,6xy = 0,8y + 0,3xy, en el intervalo [0,0] y con condiciones iniciales x(0) =, y(0) = 1. Grafique la solución obtenida. 8. Considere el sgte. sistema de ecuaciones diferenciales ordinarias, el cual surge al realizar un balance de masa sobre cada reactor en un sistema interconectado. Se pide resolver numéricamente y determinar las concentraciones alcanzadas en estado estacionario. dc 1 dt dc dt dc 3 dt dc 4 dt dc 5 dt Grafique la solución obtenida. = 0,1c 1 + 0,0c = 0,15c 1 0,15c = 0,05c 0,5c = 0,1c 3 0,1375c 4 + 0,05c 5 = 0,03c 1 + 0,01c 0,04c 5, Indicación: haga >help ode45 para obtener más información sobre éste y otros comandos de Matlab que permiten resolver numéricamente sistemas de ecuaciones diferenciales ordinarias. 8
9 9. TAREA 3 (Burgen-Faires, Análisis Numérico, 9na. ed., pag. 93, 011.) Considere la reacción química irreversible en la cual moléculas de dicromato de potasio sólido KCrO7, moléculas de agua HO y 3 átomos de azufre sólido S se combinan para producir 3 moléculas de dióxido de azufre gaseoso SO, 4 moléculas de hidróxido de potasio sólido KOH y moléculas de óxido de cromo sólido CrO3. Si originalmente se dispone de n 1 moléculas de KCrO7, n moléculas de HO y n 3 moléculas de S, la siguiente ecuación diferencial describe la cantidad x(t) de KOH después del tiempo t: x = k (n 1 x ) (n x ) (n 3 3x 4 )3, en donde k = 6, es la velocidad de la reacción, n 1 = n = 10 3, y n 3 = Se pide: (a) calcular la solución exacta o analítica (se sugiere el uso de un CAS), (b) aproxime x(t), para t = 1/10, /10,..., 1 segundo, utilizando el método de Euler con h = t = 1/100 (sugerido), (c) repita (b) con Taylor de orden, (d) repita (b) con Runge-Kutta clásico de orden 4, (e) calcule error absoluto y relativo porcentual, (f) grafique la curva exacta y las aproximaciones obtenidas por los tres métodos mencionados. FECHA DE ENTREGA: martes 31 de mayo. Individual. Manuscrito. No se reciben informes después de esta fecha. 9
10 .5. LABORATORIO 1. Considere el PVI y = ty y t y(1) =, cuya Solución Exacta está dada por la función Se pide, t y(t) = ln t + 1, t > 0. a) Graficar la Solución Exacta y(t) = t ln t+ 1 en el intervalo [1, 4]. Solución: construya el correspondiente file.m. Luego use fplot. b) Construir una partición del intervalo [a, b] = [1, 4] que posea N = 10 subintervalos, esto es, que posea N +1 = 11 puntos, los cuales hemos denotado como: t 0, t 1,..., t 9, t 10. Recuerde que t m = t 0 + m h, m = 0, 1,..., N, con h := (b a)/n. Solución: >> h=(4-1)/10 h = >> tt=1:h:4; >> t=tt t = >> c) Evalúe la Solución Exacta en los 11 puntos de la partición anterior. Grafique el conjunto {(t i, y(t i )), i = 0, 1,..., 10}. 10
11 Solución: previamente debe construir el archivo fun.m dado por: function y=fun(t) y=t./(log(t)+0.5); >> t t = >> y=fun(t) y = >> plot(t,y, o ) >> grid on d) Construya la aproximación de Euler de los puntos (t i, y(t i )), i = 0, 1,..., 10, definidos previamente. Solución: recuerde que el método de Euler está definido como, w 0 = α w i+1 = w i + h f(t i, w i ), i = 0, 1,,..,9. function A=euler(a,b,alfa,N) h=(b-a)/n; tt=a:h:b; 11
12 t=tt ; w(1)=alfa; for i=1:n w(i+1)=w(i)+h*gf(t(i),w(i)); end w=w ; A(:,1)=t; A(:,)=w; % % Funcion Auxiliar function u=gf(t,y) u=(t*y-y^)/t^; e) Taylor de Orden function A=taylor(a,b,alfa,N) h=(b-a)/n; tt=a:h:b; t=tt ; w(1)=alfa; for i=1:n aux=(1/)*(h^)*(ft(t(i),w(i))+fy(t(i),w(i))*f(t(i),w(i))); w(i+1)=w(i)+h*f(t(i),w(i))+aux; end w=w ; A(:,1)=t; A(:,)=w; % % Funcion Auxiliar function u=f(t,y) u=(t*y-y^)/(t^); function u=ft(t,y) u=(*(y^)-t*y)/(t^3); function u=fy(t,y) u=(*y+t)/(t^);. Método de Runge-Kutta Clásico de Orden 4. Considere el PVI y = ty y t y(1) =, cuya solución exacta está dada por la función t y(t) = ln t
13 a) Escriba el sgte. programa en un file.m: function A=RK4(a,b,M,yo) h=(b-a)/m; xo=a; Y(1,1)=yo; X(1,1)=xo; x=xo; y=yo; Exac(1,1)=x/(log(x)+0.5); for i=:1:m+1 K1=funD(x,y); K=funD(x+h/,y+h*K1/); K3=funD(x+h/,y+h*K/); K4=funD(x+h,y+K3*h); Y(i,1)=Y(i-1,1)+(h/6)*(K1+*K+*K3+K4); X(i,1)=X(i-1,1)+h; x=x(i,1); y=y(i,1); Exac(i,1)=x/(log(x)+0.5); end A(:,1)=X; A(:,)=Y; A(:,3)=Exac; function z=fund(x,y) z=(x*y-y*y)/(x*x); b) Corra el programa anterior con a = 1, b = 3, yo =, M =, 4, 8, 10, 0, 100, 00, 300. c) Para cada valor de M, ubique en un mismo gráfico, las soluciones exacta y aproximada. Compare y comente. d) Para cada valor de M, grafique el error definido como: Error=Valor Exacto-Valor Aproximado. e) Repita los 3 puntos anteriores con b = 100, esto es, en el intervalo [1, 100]. Cuál es el efecto de ampliar la longitud del intervalo?. f ) Modifique el programa RK4.m dado de modo tal que el tamaño de paso h quede en el input, en vez del número de intervalos, esto es, M. 13
14 UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS Asignatura : Cálculo Numérico, MAT-113. Profesor : Emilio Cariaga L. Periodo : 1er. Semestre 016. INTRODUCCIÓN A LA SOLUCIÓN NUMÉRICA DE ECUACIONES DIFERENCIALES II 3. MÉTODO DE DIFERENCIAS FINITAS (MDF) La mayor parte de esta sección está basada en el texto: Análisis Numérico II, M.C.Bustos, M.Campos, G.Gatica, Universidad de Concepción, El Método de Diferencias Finitas es una técnica de aproximación que se utiliza transversalmente para resolver todo tipo de ecuaciones diferenciales, lo cual se explica en parte por la idea base que le dá origen la cual consiste simplemente en aproximar directamente la(s) derivada(s) presente(s) en la ecuación diferencial, luego de lo cual se obtiene un sistemas algebraico de ecuaciones lineales o no lineales, dependiendo de si la ecuación diferencial original es lineal o no lineal. En el caso de las Ecuaciones en Derivadas Parciales se distinguen tres grandes familias de técnicas de resolución numérica: (i) Método de Diferencias Finitas, (ii) Método de Elementos Finitos, (iii) Método de Volúmenes Finitos. El objetivo de esta sección es presentar las ideas fundamentales del método de diferencias finitas con aplicación a un problema con valores de contorno (pvc) consistente en una ecuación diferencial ordinaria de segundo orden lineal FUNDAMENTOS Sea m = 1,,..., un número natural, sea φ C m [a, b] una función, y sea x ]a, b[ un número real. El desarrollo en serie de Taylor de la función φ, alrededor de x, está dado por φ(y) = φ(x) + φ(1) (x) 1! (y x) 1 + φ() (x)! (y x) φ(m) (ɛ) (y x) m, m! 14
15 con ɛ entre x e y. En particular, si m = φ(y) = φ(x) + φ(1) (x) 1! (y x) 1 + φ() (ɛ) (y x).! Caso 1: Forward Difference para φ. Haciendo y = x + h, h > 0, se obtiene φ(x + h) = φ(x) + hφ (x) + h φ() (ɛ 1 ), con ɛ 1 entre x y x + h. Despejando φ se obtiene ó φ (x) = φ (x) = φ(x + h) φ(x) h φ(x + h) φ(x) h h φ() (ɛ 1 ), + O(h) Caso : Backward Difference para φ. Haciendo y = x h, h > 0, se obtiene φ(x h) = φ(x) hφ (x) + h φ() (ɛ ), con ɛ entre x h y x. Despejando φ se obtiene ó φ (x) = φ (x) = φ(x) φ(x h) h φ(x) φ(x h) h + h φ() (ɛ ), + O(h) Caso 3: Central Difference para φ. Para φ C 3 [a, b] consideramos φ(y) = φ(x) + φ (x)(y x) + φ() (x) (y x) + φ(3) (ɛ) (y x) 3, 6 con ɛ entre x e y. Evaluando en y = x + h, y en y = x h se obtienen y φ(x + h) = φ(x) + φ (x)h + φ() (x) h + φ(3) (ɛ 1 ) h 3, 6 φ(x h) = φ(x) φ (x)h + φ() (x) h φ(3) (ɛ ) h 3, 6 con ɛ 1 entre x y x + h, y con ɛ entre x h y x. Restando estas últimas dos expresiones y despejando φ se obtiene φ (x) = φ(x + h) φ(x h) h 15 + O(h ).
16 Caso 4: Central Difference para φ. Para φ C 4 [a, b] consideramos φ(y) = φ(x)+φ (x)(y x)+ φ() (x) (y x) + φ(3) (ɛ) 6 (y x) 3 + φ(4) (ɛ) (y x) 4 4 con ɛ entre x e y. Evaluando en y = x + h, y en y = x h se obtienen y φ(x + h) = φ(x) + φ (x)h + φ() (x) h + φ(3) (ɛ) 6 h 3 + φ(4) (ɛ 1 ) h 4, 4 φ(x h) = φ(x) φ (x)h + φ() (x) h φ(3) (ɛ) 6 h 3 + φ(4) (ɛ ) h 4, 4 con ɛ 1 entre x y x + h, y con ɛ entre x h y x. Sumando estas últimas dos expresiones y despejando φ () se obtiene φ () (x) = 3.. APLICACIÓN A EDO φ(x + h) φ(x) + φ(x h) h + O(h ). Sean p(x), q(x), r(x), funciones continuas en el intervalo [a, b]. Asumimos que p es estrictamente positiva o negativa sobre ]a, b[, y que existe una constante Q > 0, tal que q(x) Q > 0. Se considera el problema con valores en la frontera o contorno (pvc) u = p(x)u + q(x)u + r(x), x ]a, b[ u(a) = α u(b) = β Sea n = 1,,..., un número natural. Se define la partición del intervalo [a, b]: x 0 = a, x j = a+jh, h = (b a)/n, para j = 1,..., n. La idea base del método de diferencias finitas es reemplazar las derivadas u y u por aproximaciones construidas a partir del polinomio de Taylor. Específicamente, utilizaremos y u (x) = u(x + h) u(x h) h u u(x + h) u(x) + u(x h) (x) = h h 6 u(3) (ɛ 1 ) h 1 u(4) (ɛ ). Remplazando las expresiones anteriores en la ecuación se obtiene luego de reordenar u(x + h) u(x) + u(x h) u(x + h) u(x h) h p(x) q(x)u(x) h + p(x) h 6 u(3) (ɛ 1 ) h 1 u(4) (ɛ ) = r(x) 16
17 ó con L h (u)(x) := L(u)(x) = L h (u)(x) τ(x, h) = r(x), u(x + h) u(x) + u(x h) u(x + h) u(x h) h p(x) q(x)u(x) h τ(x, h) := p(x) h 6 u(3) (ɛ 1 ) + h 1 u(4) (ɛ ), y L definido como L := L h τ. El operador L h se denomina Operador de Diferencias Finitas, mientras que τ es el Error de Truncación de la Discretización de L por L h. Se define como la aproximación por diferencias finitas de la función u, solución del pvc dado, a la función U, que satisface O sea para j = 1,,..., n 1, L h (U)(x j ) = r(x j ); j = 1,,..., n 1. U(x j+1 ) U(x j ) + U(x j 1 ) h p(x j ) U(x j+1) U(x j 1 ) q(x j )U(x j ) = r(x j ). h Denotando U j := U(x j ), p j := p(x j ), q j := q(x j ), r j := r(x j ), y reordenando términos se obtiene 1 (1 + p jh )U j 1 + (1 + q jh )U j 1 (1 p jh )U j+1 = h r j, o equivalentemente para j = 1,,..., n 1, b j U j 1 + a j U j c j U j+1 = h r j, con a j := 1+ qjh, b j := 1 pjh (1+ ), c j := 1 pjh (1 ), U 0 = u(a), U n = u(b). A modo de ilustración suponga n = 4, esto es, se tienen 3 nodos interiores: x 1, x, y x 3, a los cuales se asocian las incógnitas U 1, U, y U 3, respectivamente. Note que para j = 0 y j = 4, los valores de U 0 y U 4 son conocidos por las condiciones de contorno o de borde. Evaluando y reordenando se obtiene que el vector incógnita U = [U 1, U, U 3 ] debe satisfacer el sistema de ecuaciones lineales a 1 c 1 0 b a c 0 b 3 a 3 U 1 U U 3 = h r 1 r r 3 + b 1α 0. c 3 β Tal como se puede apreciar este esquema aplicado a este pvc conduce a una matriz de coeficientes principales tridiagonal. 17
18 3.3. Teorema Base del MDF Sea U = (U(x j )) (n 1) 1 el vector solución aproximada por diferencias finitas, y sea u = (u(x j )) (n 1) 1 el vector solución exacta, a partir de los cuales se define el vector error global e, como e = U u. Se puede mostrar que el vector error global e satisface la ecuación L h (e)(x j ) = τ j, para j = 1,,..., n 1, o equivalentemente b j e j 1 + a j e j c j e j+1 = h τ j, para j = 1,,..., n 1. Matricialmente, con τ = (τ j ) (n 1) 1, ó Ae = h τ e = h A 1 τ. Tomando norma en esta última igualdad, e h A 1 τ. A partir de esta última desigualdad se definen los tres conceptos fundamentales respecto del estudio teórico del método de diferencias finitas: a) Estabilidad: el esquema de discretización se dice estable ssi existe una constante C > 0, que no depende de h, tal que h A 1 C. b) Consistencia: el esquema de discretización se dice consistente ssi lím τ(x, h) = 0. h 0 c) Convergencia: el esquema de discretización se dice convergente ssi lím e(h) = 0. h 0 Tal como puede apreciarse para que el esquema de discretización basado en el método de diferencias finitas sea convergente, es suficiente, que sea estable y consistente. Esta es la aseveración principal del así llamado Teorema Fundamental del Método de Diferencias Finitas. 18
19 3.4. Ejercicios: a) Considere el pvc definido para x [0, 1] por u (x + 1)u (x + 1)u = x(6 3x x 4x 3 ), x ]0, 1[ u(0) = 0 u(1) = 1. Se pide resolver numéricamente utilizando un esquema de DF de orden O(h ), con h = 0,5. Se pide, además, comparar los resultados numéricos obtenidos con la solución exacta u(x) = x 3. b) Considere el pvc definido para x [0, ] por u + 6u u =, x ]0, [ u(0) = 10 u() = 1. Se pide resolver numéricamente utilizando un esquema de DF de orden O(h ), con h = 0,1. Se pide, además, comparar los resultados numéricos obtenidos con la solución exacta. c) Considere el pvc definido para x [0, 10] por T = f(x), x ]0, 10[ T (0) = 40 T (10) = 00. Se pide resolver numéricamente utilizando un esquema de DF de orden O(h ), con h =. Se pide, además, comparar los resultados numéricos obtenidos con la solución exacta. Este pvc (Ecuación de Poisson) modela una barra caliente con una fuente de calor uniforme dada por f(x) = APLICACIÓN A UNA EDP ELÍPTICA En lo que sigue se sigue la presentacion del texto:burgen-faires, Análisis Numérico, 9na. ed., 011, Capítulo Fórmulas de Aproximación Las fórmulas anteriores se pueden aplicar directamente a las derivadas parciales de primer y segundo orden: u u(x + x, y) u(x, y) (x, y) = + O( x) x x u u(x, y) u(x x, y) (x, y) = + O( x) x x u u(x + x, y) u(x x, y) (x, y) = + O( x ) x x 19
20 ó ó u u(x, y + y) u(x, y) (x, y) = + O( y) y y u u(x, y) u(x, y y) (x, y) = + O( y) y y u u(x, y + y) u(x, y y) (x, y) = + O( y ) y y u u(x + x, y) u(x, y) + u(x x, y) (x, y) = x x + O( x ) u u(x, y + y) u(x, y) + u(x, y y) (x, y) = y y + O( y ) Modelo Matemático Consideramos una EDP lineal de orden, definida sobre un dominio rectangular del plano cartesiano XY, S = {(x, y) R : a < x < b, c < y < d} con condiciones su frontera S tipo Dirichlet. El problema consiste en determinar la funcion u = u(x, y) tal que sujeta a la condicion de frontera u xx (x, y) + u yy (x, y) = f(x, y), (x, y) S u(x, y) = g(x, y), (x, y) S en donde, f y g son funciones continuas conocidas. Se puede demostrar que el problema así formulado posee solución, y esta es única Discretizacion de la region S = S S Denotemos por n =, 3,... y m =, 3,... el numero de subintervalos en los que se quieren particionar los intervalos [a, b] y [c, d], respectivamente. Con esto los respectivos tamaños de paso h y k quedan determinados por h := b a n y k := d c m. Por lo tanto, la particion P de la region S esta dada por P := {(x i, y j ) S : x i = a + ih, y j = c + jk, i = 0, n, j = 0, m} Discretización de la ecuación u xx + u yy = f Teniendo presente las discretizaciones de las derivadas de segundo orden ya presentadas, y evaluando en los elementos de la partición P podemos plantear que para i = 1, n 1 y j = 1, m 1: u(x i+1, y j ) u(x i, y j ) + u(x i 1, y j ) h + u(x i, y j+1 ) u(x i, y j ) + u(x i, y j 1 ) k = f(x i, y j ) + O(h, k ), 0
21 y respecto de las condiciones de frontera para i = 1, n 1 y j = 1, m: u(x 0, y j ) = g(x 0, y j ) u(x i, y 0 ) = g(x i, y 0 ) u(x n, y j ) = g(x n, y j ) u(x i, y m ) = g(x i, y m ). Anotando como w i,j u(x i, y j ) el aproximante vía Método de Diferencias Finitas, estos quedan definidos como la solucion del sistema algebraico de ecuaciones lineales w i+1,j w i,j + w i 1,j h + w i,j+1 w i,j + w i 1,j 1 k = f i,j, para i = 1, n 1 y j = 1, m 1, el cual se puede escribir de manera algebraicamente equivalente como [1 + (h/k) ]w i,j (w i+1,j + w i 1,j ) (h/k) (w i,j 1 + w i,j+1 ) = h f ij.[ ] Note que si, en particular h = k la ecuacion anterior queda como OBSERVACIONES: 4w i,j w i+1,j w i 1,j w i,j 1 w i,j+1 = f ij. 1. Este metodo tiene un error de truncamiento local de orden O(h + k ).. Note que la ecuacion [ ] corresponde a un sistema de ecuaciones lineales Ax = b de orden (n 1)(m 1) (n 1)(m 1). 3. Con el objeto de que el sistema Ax = b mencionado posea mejores cualidades se recomienda numerar los nodos (elementos de la particion P ) de izquierda a derecha, y de arriba hacia abajo. Especificamente, P l := (x i, y j ), w l := w i,j, l := i + (m 1 j)(n 1), i = 1, n 1, j = 1, m La discretizacion de las condiciones de frontera quedan tal cual. EJEMPLO RESUELTO: se invita al estudiante a leer con atención el Ejemplo 1 de la página
22 PROYECTO FINAL (Ponderación Semestral: 15 %) (Burden-Faires, 011, Problema 8, página 74-75) Considere una placa rectangular de plata de 6 por 5 centímetros, al interior de la cual se genera calor de manera uniforme en cada uno de sus puntos a una tasa de q = 1,5[cal/cm 3 s]. La temperatura en estado estable u = u(x, y) satisface la ecuacion de Poisson u xx + u yy = q/k, para cada (x, y) S =]0, 6[ ]0, 5[, con K = 1,04[cal/cm g grados]. Además, las condiciones de frontera sobre S están dadas por Se pide: u(x, 0) = x(6 x), u(x, 5) = 0, 0 x 6 u(0, y) = y(5 y), u(6, y) = 0, 0 y Resolver vía MDF con h = k = 1.. Por razones físicas interesa aproximar el valor de la temperatura en el centro de la placa, esto es, en el punto (3, 5/). Se pide construir una aproximación basada en la aplicación del MDF. Debe utilizar h = 1/(d 1 + d ), k = 1/(d 7 + d 8 ), en donde, d i representa el dígito i-ésimo de su RUN. Instrucciones: 1. El método para resolver el sistema de ecuaciones Ax = b es de su elección. Se sugiere Gauss-Seidel, y/o de Relajación para mejorar la convergencia.. El lenguaje y ambiente de cómputo es de libre eleción. Se sugiere Matlab u Octave. 3. El programa computacional para implementar el MDF puede escribirlo usted mismo, o utilizar uno ya construido, en cuyo caso debe informar la fuente exacta. En cualquier caso la escritura y ejecución deben ser suyas. 4. Trabajo individual. 5. Plazo de entrega: VIERNES 17 DE JUNIO. No se recibirán trabajos después de esa fecha. 6. Una vez recibidos los trabajos cada estudiante será interrogado oralmente para que explique con detalle todos los elementos solicitados, incluyendo el programa utilizado y su ejecución.
Métodos en diferencias para problemas de contorno
 Métodos numéricos de resolución de ecs. en derivadas parciales Curso 2006-07. Prácticas 1 y 2 Métodos en diferencias para problemas de contorno 1 Resultados sobre existencia de solución de un problema
Métodos numéricos de resolución de ecs. en derivadas parciales Curso 2006-07. Prácticas 1 y 2 Métodos en diferencias para problemas de contorno 1 Resultados sobre existencia de solución de un problema
Complementos de Matemáticas, ITT Telemática
 Introducción Métodos numéricos para EDOs Complementos de Matemáticas, ITT Telemática Tema 4. Solución numérica de problemas de valor inicial para ecuaciones diferenciales ordinarias Departamento de Matemáticas,
Introducción Métodos numéricos para EDOs Complementos de Matemáticas, ITT Telemática Tema 4. Solución numérica de problemas de valor inicial para ecuaciones diferenciales ordinarias Departamento de Matemáticas,
PRÁCTICA N 3 ECUACIONES DFERENCIALES
 PRÁCTICA N 3 ECUACIONES DFERENCIALES 1. Utiliza el método de Euler para aproximar las soluciones de los problemas de valor inicial siguientes a.,, y b.,, y c.,, y d.,, y e. ( ) ( ),, y f.,, y 2. Las soluciones
PRÁCTICA N 3 ECUACIONES DFERENCIALES 1. Utiliza el método de Euler para aproximar las soluciones de los problemas de valor inicial siguientes a.,, y b.,, y c.,, y d.,, y e. ( ) ( ),, y f.,, y 2. Las soluciones
Métodos numéricos para Ecuaciones Diferenciales Ordinarias. Laboratori de Càlcul Numèric (LaCàN) www-lacan.upc.es
 Métodos numéricos para Ecuaciones Diferenciales Ordinarias Laboratori de Càlcul Numèric (LaCàN) www-lacan.upc.es Ecuación Diferencial Ordinaria (EDO) n Gran cantidad de problemas de la física y la ingeniería
Métodos numéricos para Ecuaciones Diferenciales Ordinarias Laboratori de Càlcul Numèric (LaCàN) www-lacan.upc.es Ecuación Diferencial Ordinaria (EDO) n Gran cantidad de problemas de la física y la ingeniería
Práctica II: Problemas de valor inicial en EDO s.
 AMPLIACIÓN DE MATEMÁTICAS o Ing. de Telecomunicación y Aeronáutica) Departamento de Matemática Aplicada II. Universidad de Sevilla CURSO ACADÉMICO 008-009 Práctica II: Problemas de valor inicial en EDO
AMPLIACIÓN DE MATEMÁTICAS o Ing. de Telecomunicación y Aeronáutica) Departamento de Matemática Aplicada II. Universidad de Sevilla CURSO ACADÉMICO 008-009 Práctica II: Problemas de valor inicial en EDO
Método de diferencias finitas para ecuaciones diferenciales parciales elípticas. (Parte I)
 Método de diferencias finitas para ecuaciones diferenciales parciales elípticas (Parte I) Contenido Ecuaciones en derivadas parciales Ecuaciones en derivadas parciales elípticas Ecuación de Laplace Aproximación
Método de diferencias finitas para ecuaciones diferenciales parciales elípticas (Parte I) Contenido Ecuaciones en derivadas parciales Ecuaciones en derivadas parciales elípticas Ecuación de Laplace Aproximación
Hojas de problemas de interpolación y cuadratura numérica. Ampliación de Matemáticas.
 Hojas de problemas de interpolación y cuadratura numérica. Ampliación de Matemáticas. 1.- El polinomio p 3 (x) = 2 (x + 1) + x(x + 1) 2x(x + 1)(x 1) interpola a los primeros cuatro datos de la tabla x
Hojas de problemas de interpolación y cuadratura numérica. Ampliación de Matemáticas. 1.- El polinomio p 3 (x) = 2 (x + 1) + x(x + 1) 2x(x + 1)(x 1) interpola a los primeros cuatro datos de la tabla x
Ecuaciones diferenciales ordinarias
 Tema 9 Ecuaciones diferenciales ordinarias Versión: 13 de mayo de 29 9.1 Introducción El objetivo de este tema es exponer muy brevemente algunos de los conceptos básicos relacionados con las ecuaciones
Tema 9 Ecuaciones diferenciales ordinarias Versión: 13 de mayo de 29 9.1 Introducción El objetivo de este tema es exponer muy brevemente algunos de los conceptos básicos relacionados con las ecuaciones
Diferenciación numérica: Método de Euler implícito Métodos tipo Runge-Kutta
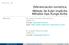 Clase No. 24: Diferenciación numérica: Método de Euler implícito Métodos tipo Runge-Kutta MAT 251 Dr. Alonso Ramírez Manzanares CIMAT A.C. e-mail: alram@ cimat.mx web: http://www.cimat.mx/alram/met_num/
Clase No. 24: Diferenciación numérica: Método de Euler implícito Métodos tipo Runge-Kutta MAT 251 Dr. Alonso Ramírez Manzanares CIMAT A.C. e-mail: alram@ cimat.mx web: http://www.cimat.mx/alram/met_num/
1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: con el método de diferencias centrales, existe y es única.
 I. Resolución numérica de Problemas de Contorno en E.D.O.: Métodos en diferencias finitas 1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: y (x) + 4 sen x y (x) 4
I. Resolución numérica de Problemas de Contorno en E.D.O.: Métodos en diferencias finitas 1) Determinar qué elección de h asegurará, a priori, que la solución numérica del P.C.: y (x) + 4 sen x y (x) 4
Universidad Técnica Federico Santa María Departamento de Matemática Preinforme 2 Laboratorio Mat 270 Análisis Numérico Entrega 4 al 8 junio de 2018
 Universidad Técnica Federico Santa María Departamento de Matemática Preinforme 2 Laboratorio Mat 270 Análisis Numérico Entrega 4 al 8 junio de 2018 Utilice el instructivo para presentar preinformes publicado
Universidad Técnica Federico Santa María Departamento de Matemática Preinforme 2 Laboratorio Mat 270 Análisis Numérico Entrega 4 al 8 junio de 2018 Utilice el instructivo para presentar preinformes publicado
Ecuaciones diferenciales
 Ecuaciones diferenciales 1. Conceptos generales Ecuación diferencial ordinaria. Definición Se llama ecuación diferencial ordinaria (E.D.O.) a una relación entre la variable independiente x, una función
Ecuaciones diferenciales 1. Conceptos generales Ecuación diferencial ordinaria. Definición Se llama ecuación diferencial ordinaria (E.D.O.) a una relación entre la variable independiente x, una función
Ecuaciones Diferenciales Ordinarias y Simulación con Matlab
 Ecuaciones Diferenciales Ordinarias y Simulación con Matlab L. Héctor Juárez Valencia y M a Luisa Sandoval Solís Departamento de Matemáticas, Universidad Autónoma Metropolitana-Iztapalapa, D. F., México
Ecuaciones Diferenciales Ordinarias y Simulación con Matlab L. Héctor Juárez Valencia y M a Luisa Sandoval Solís Departamento de Matemáticas, Universidad Autónoma Metropolitana-Iztapalapa, D. F., México
2 Obtener el término general de las siguientes sucesiones definidas por recurrencia: y0 = a > 0
 CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
CÁLCULO NUMÉRICO I (Ejercicios Temas 1 y ) 1 Cuáles de los siguientes algoritmos son finitos? (a) Cálculo del producto de dos números enteros. (b) Cálculo de la división de dos números enteros. (c) Cálculo
CÁLCULO NUMÉRICO I (Tema 2 - Relación 1)
 CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
CÁLCULO NUMÉRICO I (Tema - Relación 1) 1 Cuáles de los siguientes algoritmos son finitos? a) Cálculo del producto de dos números enteros. b) Cálculo de la división de dos números enteros. c) Cálculo de
Soluciones Numéricas de Modelos Matemáticos
 Cuarta Sesión 9 de febrero de 2011 Contenido Aproximación Numérica 1 Aproximación Numérica 2 3 4 Algunos Métodos Sencillos para EDPs Aproximación numérica a una función por Series de Taylor Serie de Taylor:
Cuarta Sesión 9 de febrero de 2011 Contenido Aproximación Numérica 1 Aproximación Numérica 2 3 4 Algunos Métodos Sencillos para EDPs Aproximación numérica a una función por Series de Taylor Serie de Taylor:
Introducción a los métodos de solución numérica de E.D.P.
 Capítulo 5 Introducción a los métodos de solución numérica de E.D.P. 5.1 Introducción. En lo sucesivo consideramos las notaciones para E.D.P. siguientes: Supongamos una E.D.P. de orden 2 para la función
Capítulo 5 Introducción a los métodos de solución numérica de E.D.P. 5.1 Introducción. En lo sucesivo consideramos las notaciones para E.D.P. siguientes: Supongamos una E.D.P. de orden 2 para la función
MÉTODOS NUMÉRICOS - ALGUNAS INSTRUCCIONES EN DERIVE
 MÉTODOS NUMÉRICOS - ALGUNAS INSTRUCCIONES EN DERIVE Las siguientes instrucciones corresponden, en su mayoría, a funciones definidas por el profesor Julio C. Morales, como complemento a las utilidades del
MÉTODOS NUMÉRICOS - ALGUNAS INSTRUCCIONES EN DERIVE Las siguientes instrucciones corresponden, en su mayoría, a funciones definidas por el profesor Julio C. Morales, como complemento a las utilidades del
Preliminares Problemas de Valor Inicial Problemas de Contorno ECUACIONES DIFERENCIALES ORDINARIAS
 ECUACIONES DIFERENCIALES ORDINARIAS Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Preliminares Las ecuaciones
ECUACIONES DIFERENCIALES ORDINARIAS Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Contenido Preliminares 1 Preliminares 2 3 El Método de Disparo Lineal Preliminares Las ecuaciones
Ecuaciones Diferenciales. Conceptos Generales
 Tema 1 Ecuaciones Diferenciales. Conceptos Generales Introducción La Modelización y Simulación es una área enorme de la ciencia pura y aplicada, a la que intentamos aproximarnos en esta asignatura. Dadas
Tema 1 Ecuaciones Diferenciales. Conceptos Generales Introducción La Modelización y Simulación es una área enorme de la ciencia pura y aplicada, a la que intentamos aproximarnos en esta asignatura. Dadas
ECUACIONES DIFERENCIALES
 ECUACIONES DIFERENCIALES INGENIERÍA (NIVEL LICENCIATURA) Curso Básico - Primavera 2017 Omar De la Peña-Seaman Instituto de Física (IFUAP) Benemérita Universidad Autónoma de Puebla (BUAP) 1 / Omar De la
ECUACIONES DIFERENCIALES INGENIERÍA (NIVEL LICENCIATURA) Curso Básico - Primavera 2017 Omar De la Peña-Seaman Instituto de Física (IFUAP) Benemérita Universidad Autónoma de Puebla (BUAP) 1 / Omar De la
Observación: El método de Euler, es el método de Taylor de orden 1.
 METODO DE TAYLOR TEOREMA DE TAYLOR DE ORDEN N Sea y(t) una función tal que sea n veces continuamente diferenciable en el intervalo [a,b] y existe y (N+1) existe en [a, b] Para todo t k + [a, b] abrá un
METODO DE TAYLOR TEOREMA DE TAYLOR DE ORDEN N Sea y(t) una función tal que sea n veces continuamente diferenciable en el intervalo [a,b] y existe y (N+1) existe en [a, b] Para todo t k + [a, b] abrá un
Lista de ejercicios # 5
 UNIVERSIDAD DE COSTA RICA FACULTAD DE CIENCIAS MA-005 Ecuaciones Diferenciales para Ingeniería ESCUELA DE MATEMÁTICA Segundo Semestre del 206 Lista de ejercicios # 5 Ecuaciones diferenciales en derivadas
UNIVERSIDAD DE COSTA RICA FACULTAD DE CIENCIAS MA-005 Ecuaciones Diferenciales para Ingeniería ESCUELA DE MATEMÁTICA Segundo Semestre del 206 Lista de ejercicios # 5 Ecuaciones diferenciales en derivadas
Análisis Numérico para Ingeniería. Clase Nro. 3
 Análisis Numérico para Ingeniería Clase Nro. 3 Ecuaciones Diferenciales Ordinarias Introducción Problemas de Valores Iniciales Método de la Serie de Taylor Método de Euler Simple Método de Euler Modificado
Análisis Numérico para Ingeniería Clase Nro. 3 Ecuaciones Diferenciales Ordinarias Introducción Problemas de Valores Iniciales Método de la Serie de Taylor Método de Euler Simple Método de Euler Modificado
Ampliación de Matemáticas y Métodos Numéricos
 4. Ampliación de EDP. Resolución numérica Ampliación de Matemáticas y Métodos Numéricos M a Luz Muñoz Ruiz José Manuel González Vida Francisco José Palomo Ruiz Francisco Joaquín Rodríguez Sánchez Departamento
4. Ampliación de EDP. Resolución numérica Ampliación de Matemáticas y Métodos Numéricos M a Luz Muñoz Ruiz José Manuel González Vida Francisco José Palomo Ruiz Francisco Joaquín Rodríguez Sánchez Departamento
Ecuaciones Diferenciales Ordinarias (2)
 MODELACION NUMERICA CON APLICACIONES EN INGENIERIA HIDRAULICA Y AMBIENTAL Ecuaciones Diferenciales Ordinarias (2) Yarko Niño C. y Paulo Herrera R. Departamento de Ingeniería Civil, Universidad de Chile
MODELACION NUMERICA CON APLICACIONES EN INGENIERIA HIDRAULICA Y AMBIENTAL Ecuaciones Diferenciales Ordinarias (2) Yarko Niño C. y Paulo Herrera R. Departamento de Ingeniería Civil, Universidad de Chile
E.T.S. Minas: Métodos Matemáticos Ejercicios Tema 7 Ecuaciones diferenciales de primer orden
 E.T.S. Minas: Métodos Matemáticos Ejercicios Tema 7 Ecuaciones diferenciales de primer orden Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
E.T.S. Minas: Métodos Matemáticos Ejercicios Tema 7 Ecuaciones diferenciales de primer orden Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
Tarea #6. 5. Implemente en Mathematica los algoritmos de integración numérica vistos en clase, se
 MA51 Análisis Numérico I Prof. Oldemar Rodríguez Rojas. Fecha de entrega: Martes 1 de noviembre del 8. Tarea #6 1. Implemente en Mathematica los algoritmos de derivación numérica vistos en clase, se deben
MA51 Análisis Numérico I Prof. Oldemar Rodríguez Rojas. Fecha de entrega: Martes 1 de noviembre del 8. Tarea #6 1. Implemente en Mathematica los algoritmos de derivación numérica vistos en clase, se deben
SISTEMAS DE ECUACIONES
 1 SISTEMAS DE ECUACIONES OBJETIVO: RESOLVER SISTEMAS DE ECUACIONES LINEALES UTILIZANDO DIVERSOS MÉTODOS DE SOLUCIÓN CONTENIDO: Representación matricial de un sistema de ecuaciones. Transformaciones elementales.
1 SISTEMAS DE ECUACIONES OBJETIVO: RESOLVER SISTEMAS DE ECUACIONES LINEALES UTILIZANDO DIVERSOS MÉTODOS DE SOLUCIÓN CONTENIDO: Representación matricial de un sistema de ecuaciones. Transformaciones elementales.
Apellidos:... Nombre:... Examen
 Cálculo Numérico I. Grado en Matemáticas y doble grado Física/Matemáticas. 16 de junio de 017 Curso 016/017. Apellidos:... Nombre:... Examen 1. Explicar razonadamente si las siguientes afirmaciones son
Cálculo Numérico I. Grado en Matemáticas y doble grado Física/Matemáticas. 16 de junio de 017 Curso 016/017. Apellidos:... Nombre:... Examen 1. Explicar razonadamente si las siguientes afirmaciones son
Ecuaciones diferenciales
 de primer orden 21 de noviembre de 2016 de primer orden Introducción Introducción a las ecuaciones diferenciales Las primeras ecuaciones diferenciales surgen al tratar de resolver ciertos problemas de
de primer orden 21 de noviembre de 2016 de primer orden Introducción Introducción a las ecuaciones diferenciales Las primeras ecuaciones diferenciales surgen al tratar de resolver ciertos problemas de
Cálculo Numérico (0258) TEMA 6 SOLUCIÓN NUMÉRICA DE ECUACIONES DIFERENCIALES ORDINARIAS. Semestre
 Cálculo Numérico (58) Semestre - TEMA 6 SOLUCIÓN NUMÉRICA DE ECUACIONES DIFERENCIALES ORDINARIAS Semestre - Septiembre U.C.V. F.I.U.C.V. CÁLCULO NUMÉRICO (58) - TEMA 6 Las notas presentadas a continuación
Cálculo Numérico (58) Semestre - TEMA 6 SOLUCIÓN NUMÉRICA DE ECUACIONES DIFERENCIALES ORDINARIAS Semestre - Septiembre U.C.V. F.I.U.C.V. CÁLCULO NUMÉRICO (58) - TEMA 6 Las notas presentadas a continuación
1.4. El problema de Cauchy. Resolución numérica de E.D.: generalidades.
 36 Prelininares. 1.4. El problema de Cauchy. Resolución numérica de E.D.: generalidades. 1.4.1. El problema de Cauchy. Existencia y unicidad. Aquí, enumeramos los resultados principales de existencia y
36 Prelininares. 1.4. El problema de Cauchy. Resolución numérica de E.D.: generalidades. 1.4.1. El problema de Cauchy. Existencia y unicidad. Aquí, enumeramos los resultados principales de existencia y
Diferenciación numérica: Método de Euler explícito
 Clase No. 21: MAT 251 Diferenciación numérica: Método de Euler explícito Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/
Clase No. 21: MAT 251 Diferenciación numérica: Método de Euler explícito Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/
EJERCICIO COMPUTACIONAL N o 5. CUADRATURA Y DERIVACIÓN NUMÉRICAS
 EJERCICIO COMPUTACIONAL N o 5. CUADRATURA Y DERIVACIÓN NUMÉRICAS Ángel Durán Departamento de Matemática Aplicada Universidad de Valladolid 14 de mayo de 2011 Contenidos 1 Cuadratura numérica Técnicas elementales
EJERCICIO COMPUTACIONAL N o 5. CUADRATURA Y DERIVACIÓN NUMÉRICAS Ángel Durán Departamento de Matemática Aplicada Universidad de Valladolid 14 de mayo de 2011 Contenidos 1 Cuadratura numérica Técnicas elementales
APLICACIONES COMPUTACIONALES
 APLICACIONES COMPUTACIONALES INGENIERÍA EJECUCIÓN MECÁNICA ECUACIONES DIFERENCIALES PARCIALES (EDP) MOTIVACIÓN Una ecuación que tiene derivadas parciales de una función desconocida, de dos o más variables
APLICACIONES COMPUTACIONALES INGENIERÍA EJECUCIÓN MECÁNICA ECUACIONES DIFERENCIALES PARCIALES (EDP) MOTIVACIÓN Una ecuación que tiene derivadas parciales de una función desconocida, de dos o más variables
Ecuaciones Diferenciales y Métodos Numéricos
 NOMBRE...Número... Ecuaciones Diferenciales y Métodos Numéricos 3 er Curso I. Caminos. Ecuaciones en Derivadas Parciales Examen Parcial: 7-XII-2006 Observaciones: Escribir exactamente la solución donde
NOMBRE...Número... Ecuaciones Diferenciales y Métodos Numéricos 3 er Curso I. Caminos. Ecuaciones en Derivadas Parciales Examen Parcial: 7-XII-2006 Observaciones: Escribir exactamente la solución donde
Diferenciación numérica: Método de Euler explícito
 Clase No. 21: MAT 251 Diferenciación numérica: Método de Euler explícito Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/
Clase No. 21: MAT 251 Diferenciación numérica: Método de Euler explícito Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/
Unidad IV: Diferenciación e integración numérica
 Unidad IV: Diferenciación e integración numérica 4.1 Diferenciación numérica El cálculo de la derivada de una función puede ser un proceso "difícil" ya sea por lo complicado de la definición analítica
Unidad IV: Diferenciación e integración numérica 4.1 Diferenciación numérica El cálculo de la derivada de una función puede ser un proceso "difícil" ya sea por lo complicado de la definición analítica
Análisis Matemático I
 Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Universidad Nacional de La Plata Facultad de Ciencias Exactas Departamento de Matemática Análisis Matemático I Evaluación Final - Agosto de 26. Nombre: Dirección correo electrónico: Ejercicio. Sea f una
Métodos numéricos para problemas de contorno
 Métodos numéricos para problemas de contorno Damián Ginestar Peiró Departamento de Matemática Aplicada Universidad Politécnica de Valencia (UPV) Métodos numéricos para PVF 1 / 28 Programa 1 Introducción
Métodos numéricos para problemas de contorno Damián Ginestar Peiró Departamento de Matemática Aplicada Universidad Politécnica de Valencia (UPV) Métodos numéricos para PVF 1 / 28 Programa 1 Introducción
2. Actividad inicial: Crecimiento del dinero.
 Índice 1. Introducción 6 2. Actividad inicial: Crecimiento del dinero. 6 3. EDO de variables separables 7 3.1. Técnica de resolución de una ODE de variables separables........... 8 3.2. Ejemplos desarrollados...............................
Índice 1. Introducción 6 2. Actividad inicial: Crecimiento del dinero. 6 3. EDO de variables separables 7 3.1. Técnica de resolución de una ODE de variables separables........... 8 3.2. Ejemplos desarrollados...............................
Derivada y diferencial
 Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Lista de ejercicios # 4
 UNIVERSIDAD DE COSTA RICA MA-5 FACULTAD DE CIENCIAS Ecuaciones Diferenciales para Ingeniería ESCUELA DE MATEMÁTICA Primer Ciclo del 5 Lista de ejercicios # 4 Sistemas de ecuaciones diferenciales. EPII-II-
UNIVERSIDAD DE COSTA RICA MA-5 FACULTAD DE CIENCIAS Ecuaciones Diferenciales para Ingeniería ESCUELA DE MATEMÁTICA Primer Ciclo del 5 Lista de ejercicios # 4 Sistemas de ecuaciones diferenciales. EPII-II-
CAPÍTULO. 7 Métodos numéricos
 CAPÍTULO 7 Métodos numéricos 7.3 Método de Euler mejorado Consideremos ahora el polinomio de Taylor de orden de y.x/ en x D x 0 para aproximar a la solución del PVI y 0 D f.x; y/, con y.x 0 / D y 0. Esta
CAPÍTULO 7 Métodos numéricos 7.3 Método de Euler mejorado Consideremos ahora el polinomio de Taylor de orden de y.x/ en x D x 0 para aproximar a la solución del PVI y 0 D f.x; y/, con y.x 0 / D y 0. Esta
7.3 Método de Euler mejorado
 43 Ecuaciones diferenciales Ejercicios 7..1 Euler. Soluciones en la página 477 Determine una aproximación lineal de la solución y.x/ de cada una de los siguientes PVI en el punto indicado utilizando el
43 Ecuaciones diferenciales Ejercicios 7..1 Euler. Soluciones en la página 477 Determine una aproximación lineal de la solución y.x/ de cada una de los siguientes PVI en el punto indicado utilizando el
(a) [0,7 puntos] Encuentre los valores de las constantes A y B, y del punto x 2 (0, 1) de modo que la fórmula de cuadratura:
![(a) [0,7 puntos] Encuentre los valores de las constantes A y B, y del punto x 2 (0, 1) de modo que la fórmula de cuadratura: (a) [0,7 puntos] Encuentre los valores de las constantes A y B, y del punto x 2 (0, 1) de modo que la fórmula de cuadratura:](/thumbs/87/96403039.jpg) UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERÍA. INSTITUTO DE CIENCIAS BÁSICAS. Cálculo Numérico, Control 3. Semestre Otoño 7 Problema ( puntos) (a) [,7 puntos] Encuentre los valores de las constantes
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERÍA. INSTITUTO DE CIENCIAS BÁSICAS. Cálculo Numérico, Control 3. Semestre Otoño 7 Problema ( puntos) (a) [,7 puntos] Encuentre los valores de las constantes
Introducción a la resolución numérica de problemas para ecuaciones en derivadas parciales (I)
 Introducción a la resolución numérica de problemas para ecuaciones en derivadas parciales (I) Dpto. EDAN, Universidad de Sevilla Dpto. EDAN, Universidad de Sevilla () Resolución de EDP 1 / 15 Recordatorio
Introducción a la resolución numérica de problemas para ecuaciones en derivadas parciales (I) Dpto. EDAN, Universidad de Sevilla Dpto. EDAN, Universidad de Sevilla () Resolución de EDP 1 / 15 Recordatorio
Métodos Numéricos en Ecuaciones Diferenciales Ordinarias
 Tema 4 Métodos Numéricos en Ecuaciones Diferenciales Ordinarias 4.1 Introducción Estudiaremos en este Tema algunos métodos numéricos para resolver problemas de valor inicial en ecuaciones diferenciales
Tema 4 Métodos Numéricos en Ecuaciones Diferenciales Ordinarias 4.1 Introducción Estudiaremos en este Tema algunos métodos numéricos para resolver problemas de valor inicial en ecuaciones diferenciales
Instituto de Matemática. Agosto de ) Encuentre experimentalmente los siguientes valores de su calculadora:
 Curso de Métodos Numéricos Instituto de Matemática Práctico 1: Errores Agosto de 2005 1) Encuentre experimentalmente los siguientes valores de su calculadora: (a) El valor ɛ mach definido como el minimo
Curso de Métodos Numéricos Instituto de Matemática Práctico 1: Errores Agosto de 2005 1) Encuentre experimentalmente los siguientes valores de su calculadora: (a) El valor ɛ mach definido como el minimo
Apellidos:... Nombre:... Examen
 Cálculo Numérico I. Grado en Matemáticas. Curso 0/0. 0 de Junio de 0 Apellidos:... Nombre:... Examen. Decidir razonadamente si las siguientes afirmaciones son verdaderas o falsas, buscando un contraejemplo
Cálculo Numérico I. Grado en Matemáticas. Curso 0/0. 0 de Junio de 0 Apellidos:... Nombre:... Examen. Decidir razonadamente si las siguientes afirmaciones son verdaderas o falsas, buscando un contraejemplo
Solución de ecuaciones diferenciales por el método de elementos finitos
 Solución de ecuaciones diferenciales por el método de elementos finitos Departamento de Matemáticas Método de elemento finito Un problema del método de diferencias finitas es que al aplicarlo obtenemos
Solución de ecuaciones diferenciales por el método de elementos finitos Departamento de Matemáticas Método de elemento finito Un problema del método de diferencias finitas es que al aplicarlo obtenemos
Teorema de la Función Implícita
 Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
Métodos Numéricos - Cap. 7. Ecuaciones Diferenciales Ordinarias PVI 1/8
 No se puede mostrar la imagen en este momento. Métodos Numéricos - Cap. 7. Ecuaciones Diferenciales Ordinarias PVI 1/8 Ecuaciones Diferenciales Ordinarias (EDO) Una Ecuación Diferencial es aquella ecuación
No se puede mostrar la imagen en este momento. Métodos Numéricos - Cap. 7. Ecuaciones Diferenciales Ordinarias PVI 1/8 Ecuaciones Diferenciales Ordinarias (EDO) Una Ecuación Diferencial es aquella ecuación
UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS SOLUCIÓN NUMÉRICA DE SISTEMAS DE ECUACIONES LINEALES
 UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS Asignatura : Cálculo Numérico, MAT-1123. Profesor : Emilio Cariaga L. Periodo : 1er. Semestre 216. SOLUCIÓN
UNIVERSIDAD CATÓLICA DE TEMUCO FACULTAD DE INGENIERÍA DEPTO. DE CIENCIAS MATEMÁTICAS Y FÍSICAS Asignatura : Cálculo Numérico, MAT-1123. Profesor : Emilio Cariaga L. Periodo : 1er. Semestre 216. SOLUCIÓN
Funciones Reales de Varias Variables
 Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
Métodos en diferencias en regiones irregulares
 Métodos en diferencias en regiones irregulares Pablo Barrera Sánchez, Guilmer González Flores, Francisco Domínguez Mota XXII ENOAN, 19-23.03.2012 Índice 1 Introducción y motivación Introducción y motivación
Métodos en diferencias en regiones irregulares Pablo Barrera Sánchez, Guilmer González Flores, Francisco Domínguez Mota XXII ENOAN, 19-23.03.2012 Índice 1 Introducción y motivación Introducción y motivación
APLICACIONES COMPUTACIONALES INGENIERÍA EJECUCIÓN MECÁNICA
 APLICACIONES COMPUTACIONALES INGENIERÍA EJECUCIÓN MECÁNICA ECUACIONES DIFERENCIALES ORDINARIAS (EDO) MOTIVACIÓN Se llamará ecuación diferencial a aquella ecuación que contiene una variable dependiente
APLICACIONES COMPUTACIONALES INGENIERÍA EJECUCIÓN MECÁNICA ECUACIONES DIFERENCIALES ORDINARIAS (EDO) MOTIVACIÓN Se llamará ecuación diferencial a aquella ecuación que contiene una variable dependiente
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Pauta Examen Final - Ecuaciones Diferenciales
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERIA Y CIENCIAS INSTITUTO DE CIENCIAS BÁSICAS ECUACIONES DIFERENCIALES Pauta Examen Final - Ecuaciones Diferenciales P1.- Indicar el tipo de EDO de las siguientes
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERIA Y CIENCIAS INSTITUTO DE CIENCIAS BÁSICAS ECUACIONES DIFERENCIALES Pauta Examen Final - Ecuaciones Diferenciales P1.- Indicar el tipo de EDO de las siguientes
Ecuaciones Diferenciales Ordinarias
 Nivelación de Matemática MTHA UNLP EDO 1 Ecuaciones Diferenciales Ordinarias 1. Introducción Una ecuación diferencial ordinaria es una ecuación de la forma: F (x, y, y,..., y (n) ) = 0 que expresa una
Nivelación de Matemática MTHA UNLP EDO 1 Ecuaciones Diferenciales Ordinarias 1. Introducción Una ecuación diferencial ordinaria es una ecuación de la forma: F (x, y, y,..., y (n) ) = 0 que expresa una
Las raíces del polinomio característico P (λ) = λ 2 + 4λ + 3 son
 Tiempo total: 2 horas 4 minutos Problema 1 [2 puntos]. Colgamos una masa m de un muelle vertical cuya constante de Hooke es λ. El medio ofrece una resistencia igual a µ veces la velocidad instantánea.
Tiempo total: 2 horas 4 minutos Problema 1 [2 puntos]. Colgamos una masa m de un muelle vertical cuya constante de Hooke es λ. El medio ofrece una resistencia igual a µ veces la velocidad instantánea.
E.T.S. Minas: Métodos Matemáticos Soluciones Tema 2 Aproximación e interpolación
 E.T.S. Minas: Métodos Matemáticos Soluciones Tema 2 Aproximación e interpolación Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Curso 2006/07
E.T.S. Minas: Métodos Matemáticos Soluciones Tema 2 Aproximación e interpolación Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Curso 2006/07
6. Ecuaciones Diferenciales
 6. Ecuaciones Diferenciales La mayor parte de los problemas científicos y tecnológicos que se resuelven por computadora están relacionados con ecuaciones diferenciales, de una u otra forma. Estos pueden
6. Ecuaciones Diferenciales La mayor parte de los problemas científicos y tecnológicos que se resuelven por computadora están relacionados con ecuaciones diferenciales, de una u otra forma. Estos pueden
EJERCICIOS UNIDADES 1, 2 Y 3
 EJERCICIOS UNIDADES 1, Y 3 Nota: En adelante utilizaremos la abreviación ED para ecuación diferencial. TEMAS A EVALUAR Unidad 1 o Clasificación de las ecuaciones diferenciales o Problemas de valor inicial
EJERCICIOS UNIDADES 1, Y 3 Nota: En adelante utilizaremos la abreviación ED para ecuación diferencial. TEMAS A EVALUAR Unidad 1 o Clasificación de las ecuaciones diferenciales o Problemas de valor inicial
Integración Numérica. Hermes Pantoja Carhuavilca. Métodos Computacionales. Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos
 Integración Numérica Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Métodos Computacionales Hermes Pantoja Carhuavilca 1 de 64 CONTENIDO Introducción
Integración Numérica Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Métodos Computacionales Hermes Pantoja Carhuavilca 1 de 64 CONTENIDO Introducción
CAPÍTULO. 7 Métodos numéricos
 CAPÍTULO 7 Métodos numéricos 7.4 Método de Runge-Kutta En las secciones previas se resolvió el PVI y 0 D f.x; y/, con y.x 0 / D y 0 utilizando aproximaciones lineal y cuadrática de la solución y.x/. Observamos
CAPÍTULO 7 Métodos numéricos 7.4 Método de Runge-Kutta En las secciones previas se resolvió el PVI y 0 D f.x; y/, con y.x 0 / D y 0 utilizando aproximaciones lineal y cuadrática de la solución y.x/. Observamos
Cálculo I Aplicaciones de las Derivadas: Linealización y Diferenciales. Julio C. Carrillo E. * 1. Introducción 1. 2.
 4.7. Aplicaciones de las Derivadas: Linealización y Diferenciales Julio C. Carrillo E. * Índice 1. Introducción 1 2. Errores 2 3. Linealización 4 4. Diferenciales 10 A. Teorema de Taylor (Opcional) 17
4.7. Aplicaciones de las Derivadas: Linealización y Diferenciales Julio C. Carrillo E. * Índice 1. Introducción 1 2. Errores 2 3. Linealización 4 4. Diferenciales 10 A. Teorema de Taylor (Opcional) 17
Prácticas de Métodos Numéricos Prof. Tomás Martín
 %%Control 1. Lecciones A-B Tomás Martín Hernández Iniciada: 16 de febrero de 2009 10:49 Preguntas: 5 Prácticas de Métodos Numéricos Prof. Tomás Martín 1. (Puntos: 0,5) Importante: El separador decimal
%%Control 1. Lecciones A-B Tomás Martín Hernández Iniciada: 16 de febrero de 2009 10:49 Preguntas: 5 Prácticas de Métodos Numéricos Prof. Tomás Martín 1. (Puntos: 0,5) Importante: El separador decimal
Matemática IV Taller, Ecuaciones de orden 1. dy dx = y xy2 2. Determine la solución general de la ecuación. (y 4x)dx + (y x)dy = 0.
 Matemática IV - 2000953 Taller, Ecuaciones de orden 1 1. Resuelva R: y 2 x = ln y. dy dx = y 3, y(0) = 1. 1 2xy2 2. Determine la solución general de la ecuación (y 4x)dx + (y x)dy = 0. 3. Una persona tiene
Matemática IV - 2000953 Taller, Ecuaciones de orden 1 1. Resuelva R: y 2 x = ln y. dy dx = y 3, y(0) = 1. 1 2xy2 2. Determine la solución general de la ecuación (y 4x)dx + (y x)dy = 0. 3. Una persona tiene
9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal
 Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
SOLUCIONES NUMÉRICAS DE ECUACIONES DIFERENCIALES ORDINARIAS
 9 SOLUCIONES NUMÉRICAS DE ECUACIONES DIFERENCIALES ORDINARIAS 9 Métodos de Euler y análisis de errores 9 Métodos de Runge-Kutta 93 Métodos multipasos 94 Ecuaciones y sistemas de orden superior 95 Problemas
9 SOLUCIONES NUMÉRICAS DE ECUACIONES DIFERENCIALES ORDINARIAS 9 Métodos de Euler y análisis de errores 9 Métodos de Runge-Kutta 93 Métodos multipasos 94 Ecuaciones y sistemas de orden superior 95 Problemas
= a y t N. = b. En estos puntos es donde se va a obtener la aproximación de la solución.
 Métodos de Runge Kutta Los métodos de Taylor tienen la propiedad de un error local de truncamiento de orden superior, pero la desventaja de requerir el cálculo y la evaluación de las derivadas de f(t,
Métodos de Runge Kutta Los métodos de Taylor tienen la propiedad de un error local de truncamiento de orden superior, pero la desventaja de requerir el cálculo y la evaluación de las derivadas de f(t,
Integración numérica
 Integración numérica Javier Segura Cálculo Numérico I. Tema 4. Javier Segura (Universidad de Cantabria) Integración numérica CNI 1 / 21 Introducción y definiciones Estructura de la presentación: 1 Introducción
Integración numérica Javier Segura Cálculo Numérico I. Tema 4. Javier Segura (Universidad de Cantabria) Integración numérica CNI 1 / 21 Introducción y definiciones Estructura de la presentación: 1 Introducción
Complementos de Análisis. Año 2016
 Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
METODOS DE RUNGE KUTTA
 METODOS DE RUNGE KUTTA Los métodos de Runge-Kutta (RK logran una exactitud del procedimiento de una serie de Taylor, sin requerir el cálculo de derivadas superiores. Probablemente uno de los procedimientos
METODOS DE RUNGE KUTTA Los métodos de Runge-Kutta (RK logran una exactitud del procedimiento de una serie de Taylor, sin requerir el cálculo de derivadas superiores. Probablemente uno de los procedimientos
Problema de convolución y deconvolución Diferencias finitas para EDO
 Clase No. 24: Problema de convolución y deconvolución Diferencias finitas para EDO MAT 251 Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/alram/met_num/
Clase No. 24: Problema de convolución y deconvolución Diferencias finitas para EDO MAT 251 Dr. Alonso Ramírez Manzanares Depto. de Matemáticas Univ. de Guanajuato e-mail: alram@ cimat.mx web: http://www.cimat.mx/alram/met_num/
Tema 8 Ecuaciones diferenciales
 Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Práctico Preparación del Examen
 Cálculo Diferencial e Integral (Áreas Tecnológicas) Segundo Semestre 4 Universidad de la República Práctico Preparación del Examen Límites, funciones y continuidad Ejercicio Sea log(+x ) f(x) =, si x
Cálculo Diferencial e Integral (Áreas Tecnológicas) Segundo Semestre 4 Universidad de la República Práctico Preparación del Examen Límites, funciones y continuidad Ejercicio Sea log(+x ) f(x) =, si x
Profesor Francisco R. Villatoro 13 de Diciembre de 1999 SOLUCIONES. 1. Una matriz A de n n es diagonalmente dominante (estrictamente) por filas si
 Cuarta relación de problemas Técnicas Numéricas Profesor Francisco R. Villatoro 13 de Diciembre de 1999 SOLUCIONES 1. Una matriz A de n n es diagonalmente dominante estrictamente por filas si a ii > a
Cuarta relación de problemas Técnicas Numéricas Profesor Francisco R. Villatoro 13 de Diciembre de 1999 SOLUCIONES 1. Una matriz A de n n es diagonalmente dominante estrictamente por filas si a ii > a
r r a) Clasificar el sistema x = Ax en función del parámetro r R.
 Examen Final de Ecuaciones Diferenciales Fecha: 15 de junio de 2012 3 Problemas (7.5 puntos) Tiempo total: 3 horas Problema 1 [2.5 puntos]. Queremos dibujar el croquis de un sistema lineal 2D y realizar
Examen Final de Ecuaciones Diferenciales Fecha: 15 de junio de 2012 3 Problemas (7.5 puntos) Tiempo total: 3 horas Problema 1 [2.5 puntos]. Queremos dibujar el croquis de un sistema lineal 2D y realizar
A = α cuyos VAPs son λ = 2 y λ ± = α ± i. (No hace falta que comprobeis este dato.) a) Calcular la solución general real del sistema x = Ax.
 Examen Final de Ecuaciones Diferenciales Fecha: 7 de junio de 013 3 Problemas (7.5 puntos) Tiempo total: horas 30 minutos Problema 1 [.5 puntos]. Consideramos la matriz A = α 1 0 1 α 0, α R, 0 0 cuyos
Examen Final de Ecuaciones Diferenciales Fecha: 7 de junio de 013 3 Problemas (7.5 puntos) Tiempo total: horas 30 minutos Problema 1 [.5 puntos]. Consideramos la matriz A = α 1 0 1 α 0, α R, 0 0 cuyos
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E1100
 CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E1100 A) Primer parcial 1) Si se lanza verticalmente un objeto hacia arriba desde el nivel del suelo, con una velocidad inicial de 0 pies/s, entonces
CÁLCULO DIFERENCIAL E INTEGRAL I EVALUACIÓN GLOBAL E1100 A) Primer parcial 1) Si se lanza verticalmente un objeto hacia arriba desde el nivel del suelo, con una velocidad inicial de 0 pies/s, entonces
METODOS NUMERICOS. Curso
 Boletín 1 de prácticas. 1. Localizar las raíces de la ecuación F (x) = 0, para los siguientes casos: (a) F (x) = x + e x. (b) F (x) = 0.5 x + 0.2 sen(x). (c) F (x) = x tg(x). (d) F (x) = x 5 3. (e) F (x)
Boletín 1 de prácticas. 1. Localizar las raíces de la ecuación F (x) = 0, para los siguientes casos: (a) F (x) = x + e x. (b) F (x) = 0.5 x + 0.2 sen(x). (c) F (x) = x tg(x). (d) F (x) = x 5 3. (e) F (x)
Centro. Asignatura. Convocatoria Junio (Curso )
 UNIVERSIDAD DE OVIEDO Fecha Lunes, 6/5/ Página de 9 Centro DEPARTAMENTO DE MATEMÁTICAS Asignatura Análisis Numérico Convocatoria Junio (Curso 9-) Ejercicio.- Dado el problema de valor inicial y y t aty
UNIVERSIDAD DE OVIEDO Fecha Lunes, 6/5/ Página de 9 Centro DEPARTAMENTO DE MATEMÁTICAS Asignatura Análisis Numérico Convocatoria Junio (Curso 9-) Ejercicio.- Dado el problema de valor inicial y y t aty
Análisis Matemático. Convocatoria de enero Prueba Global. Evaluación Continua
 Apellidos y nombre: Análisis Matemático. Convocatoria de enero. 9--26. Prueba Global. Evaluación Continua Instrucciones: No abandonar el examen durante los primeros 3 minutos. Tiempo para esta parte del
Apellidos y nombre: Análisis Matemático. Convocatoria de enero. 9--26. Prueba Global. Evaluación Continua Instrucciones: No abandonar el examen durante los primeros 3 minutos. Tiempo para esta parte del
Métodos Numéricos: Resumen y ejemplos Tema 4: Resolución aproximada de EDO s
 Métodos Numéricos: Resumen y ejemplos Tema 4: Resolución aproximada de EDO s Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Marzo 2008, versión
Métodos Numéricos: Resumen y ejemplos Tema 4: Resolución aproximada de EDO s Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Marzo 2008, versión
FACULTAD DE INGENIERÍA DIVISIÓN DE CIENCIAS BÁSICAS EXAMENFINALDEANÁLISIS NUMÉRICO SEMESTRE
 EXAMENFINALDEANÁLISIS NUMÉRICO SEMESTRE 014- Estudiante: Calificación: INSTRUCCIONES: Este examen es la demostración de su capacidad de trabajo y comprensión de la asignatura, es un documento oficial de
EXAMENFINALDEANÁLISIS NUMÉRICO SEMESTRE 014- Estudiante: Calificación: INSTRUCCIONES: Este examen es la demostración de su capacidad de trabajo y comprensión de la asignatura, es un documento oficial de
Elementos de Cálculo Numérico / Cálculo Numérico Segundo Cuatrimestre 2017
 Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Depto. de Matemática Elementos de Cálculo Numérico / Cálculo Numérico Segundo Cuatrimestre 2017 Práctica N 2: Ecuaciones Diferenciales:
Universidad de Buenos Aires - Facultad de Ciencias Exactas y Naturales - Depto. de Matemática Elementos de Cálculo Numérico / Cálculo Numérico Segundo Cuatrimestre 2017 Práctica N 2: Ecuaciones Diferenciales:
Métodos Numéricos: soluciones Tema 2 Aproximación e interpolación
 Métodos Numéricos: soluciones Tema 2 Aproximación e interpolación Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Febrero 2008, Versión 1.3
Métodos Numéricos: soluciones Tema 2 Aproximación e interpolación Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Febrero 2008, Versión 1.3
Métodos Numéricos para problemas de valor inicial
 Práctica 4 Métodos Numéricos para problemas de valor inicial 4.1. Introducción Los métodos analíticos de integración de ecuaciones diferenciales sólo son útiles para resolver una pequeña parte de las ecuaciones
Práctica 4 Métodos Numéricos para problemas de valor inicial 4.1. Introducción Los métodos analíticos de integración de ecuaciones diferenciales sólo son útiles para resolver una pequeña parte de las ecuaciones
n A 1 = max( j i=1 Ejercicio Deducir del problema anterior que, si A es una matriz de orden n real, Ax 2 2 µ 2 x T x, donde µ = ρ(a T A) 1/2.
 Normas matriciales Cálculo Numérico Normas matriciales 2 Ejercicio..- Sea Hallar: A, A 2 y A. 2 0 0 A = 0 2 2 0 Ejercicio.2.- Probar que en IR n las normas, 2 y son equivalentes. Ejercicio.3.- Probar que.
Normas matriciales Cálculo Numérico Normas matriciales 2 Ejercicio..- Sea Hallar: A, A 2 y A. 2 0 0 A = 0 2 2 0 Ejercicio.2.- Probar que en IR n las normas, 2 y son equivalentes. Ejercicio.3.- Probar que.
9. DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES.
 9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
Ampliación de Matemáticas y Métodos Numéricos
 Ampliación de Matemáticas y Métodos Numéricos Relación de ejercicios. Introducción a los Métodos Numéricos Ej. El problema del cálculo del punto de corte de dos rectas con pendiente similar es un problema
Ampliación de Matemáticas y Métodos Numéricos Relación de ejercicios. Introducción a los Métodos Numéricos Ej. El problema del cálculo del punto de corte de dos rectas con pendiente similar es un problema
2. Métodos analíticos para la resolución de ecuaciones diferenciales de primer orden
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 7: EDO s de primer orden Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Noviembre
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 7: EDO s de primer orden Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Noviembre
(a) (0.5 puntos) Compruebe que esta ecuación tiene exactamente una solución en el intervalo
 UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERÍA. INSTITUTO DE CIENCIAS BÁSICAS. Cálculo Numérico, Control 1. Semestre Otoño 007 Problema 1. Se desea encontrar una raíz de la función f(x) = cos (x) x.
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERÍA. INSTITUTO DE CIENCIAS BÁSICAS. Cálculo Numérico, Control 1. Semestre Otoño 007 Problema 1. Se desea encontrar una raíz de la función f(x) = cos (x) x.
