Cálculo I Aplicaciones de las Derivadas: Linealización y Diferenciales. Julio C. Carrillo E. * 1. Introducción 1. 2.
|
|
|
- Carolina Fidalgo Benítez
- hace 6 años
- Vistas:
Transcripción
1 4.7. Aplicaciones de las Derivadas: Linealización y Diferenciales Julio C. Carrillo E. * Índice 1. Introducción 1 2. Errores 2 3. Linealización 4 4. Diferenciales 10 A. Teorema de Taylor (Opcional) 17 * Profesor Escuela de Matemáticas, UIS.
2 1. Introducción Si una función f(x) es derivable en un número a, entonces y = L(x) =f(a)+f 0 (a)(x a) representa la ecuación de la recta tangente a la gráfica de f en el punto (a, f(a)). Se espera que la gráfica del recta tangente está muy próxima a la gráfica de f en cercanías del punto de tangencia. Por esta razón, se puede esperar que si x está cerca del número a entonces el valor f(x) esté muy cercan del valor L(x) de la recta tangente. De esta manera, los valores L(x) de la recta tangente en (a, f(a)) se pueden usar para aproximar los valores f(x) de la función. El error en esta aproximación, denotado R(x), será R(x) =f(x) L(x). Julio C. Carrillo E. Para uso exclusivo en el salón de clase 1/28
3 2. Errores Definición 1 (Errores en aproximaciones). Sea x un valor aproximado del valor real x. Se define el error en este cálculo como x x, y el error relativo en el mismo cálculo como x x x. El error relativo es un error sin dimensiones, o en tanto por uno. Si se multiplica por 100, el error relativo se convierte en tanto por ciento o error porcentual. En la práctica es más importante el error relativo. Definición 2 (Cifras significativas o dígitos exactos). La cantidad de cifras significativas de un número aproximado es la cantidad de dígitos significativos exactos de dicho número. Definición 3 (Cifras decimales exactas o dígitos decimales correctos). La cantidad de cifras decimales exactas de un número aproximado es la cantidad de cifras exactas que están después de la coma decimal. Por ejemplo, 5,078 tiene 4 cifras significativas, 3 cifras decimales exactas 0, tiene 3 cifras significativas, 6 cifras decimales exactas 4235 tiene 4 cifras significativas, 0 cifras decimales exactas 525,48 tiene 5 cifras significativas, 2 cifras decimales exactas Julio C. Carrillo E. Para uso exclusivo en el salón de clase 2/28
4 Definición 4 (Cifras decimales exactas y cifras significativas). Se dice que el número x aproxima a x con d cifras decimales exactas si d es el mayor entero no negativo para el cual x x < 0,5 10 d. Igualmente, se dice que el número x aproxima a x con k cifras significativas si k es el mayor entero no negativo para el cual x x x < 0, k =5 10 k. Ejemplo 1. Si x =25,3654 es una aproximación de x =25,36536 calcular el número de decimales correctos y el numero de cifras significativas de la aproximación. Solución. Para que la aproximación de x mediante x tenga d cifras decimales exactas, el error relativo x x =0,00004 = debe cumplir con la condición que apple 0,5 10 d =) 10 d 5 apple 1 8 =) d apple 5 log 8 = 4, Es decir la aproximación tiene 4 decimales correctos. Así que x =25,3654. Por otro lado, para que la aproximación de x mediante x tenga d cifras significativas el error relativo x x x =1, Julio C. Carrillo E. Para uso exclusivo en el salón de clase 3/28
5 debe cumplir con la condición que 1, apple 5 10 k =) 10 k 6 apple 5 1, =) k apple 6+log 1,5769 =6, 5 Entonces la aproximación x tiene k =6cifras significativas. Es decir, x =25,3654. Observación 1. Observe que se pueden obtener a d y k de una manera más sencilla, pues apple 0, y dado que 1,5759 < 5 entonces 1, < Linealización Definición 5 (Linealización). Si una función f(x) es derivable en un número a, entonces se dice que la función L(x) =f(a)+f 0 (a)(x a) es una linealización de f en a. Para un número x próximo a a, la aproximación se denomina aproximación lineal local de f en a. f(x) L(x) Según lo expuesto previamente, es posible encontrar el número de cifras decimales exactas y el número de cifras significativas en esta aproximación de f(x) mediante los valores de la recta tangente. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 4/28
6 Ejemplo 2. Encuentre una linealización de f(x) =senx en a =0. Solución. Dado que f(x) =senx y f 0 (x) =cosx entonces f(0) = 0 y f 0 (0) = 1. Entonces la ecuación de la recta tangente a la gráfica de la función f(x) =senx en (0, 0) es y = f(0) + f 0 (0)(x 0) = x. En tal caso, la linealización de f(x) =senx en a =0es L(x) =x. Además la aproximación local de f en a =0es sen x x, lo cual explica porque la gráfica de f(x) =senx y su linealización L(x) son casi la misma cerca del origen. Ejemplo 3. Calcule un valor aproximado de ln1,1 mediante su linealización y determine una cota superior para el valor absoluto del error cometido en la aproximación. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 5/28
7 Solución. Consideremos la linealización de la función f(x) =lnx en a =1. La función y sus derivadas en a =1son: Entonces la linealización de f(x) =lnx en a =1es f(x) =ln1, f(1) = 0, f 0 (x) = 1 x, f0 (1) = 1. L(x) =f(0) + f 0 (0)(x 1) = x 1. Por lo tanto, la aproximación local de f(x) =lnx en a =0es ln x x 1. Al hacer x =1,1 se tiene que el valor aproximado de ln 1,1 mediante su linealización en a =1es ln 1,1 0,1. Una forma de conocer una cota del error en la estimación de f(x) mediante la linealización de f en a cercano a x, se establece mediante el siguiente teorema. Teorema 1 (Teorema de Taylor de primer orden). Sea f(x) una función tal que f 00 (x) existe en un intervalo I. Sia y x con dos números distintos de I entonces existe un c entre a y x tal que f(x) =f(a)+f 0 (a)(x a)+ f 00 (c) (x a) 2. 2! Julio C. Carrillo E. Para uso exclusivo en el salón de clase 6/28
8 Demostración. Se define el error en la aproximación de f(x) mediante su linealización L(x) como R 1 (x). En tal caso, f(x) =f(a)+f 0 (a)(x a)+r 1 (x) (1) En este caso, se busca un número real a 2 de manera que este error sea de la forma Así que, Observe que R 1 (x) =a 2 (x a) 2. f(x) =f(a)+f 0 (a)(x a)+a 2 (x a) 2. f(x) f(a) f 0 (a)(x a) a 2 (x a) 2 =0 (2) Al cambiar en esta ecuación a a por t, no se va a cumplir la ecuación, pero se va poder definir la función donde Según la definición de G(t) y (2) se tiene que G(t) =F (t) a 2 (x t) 2, F (t) =f(x) f(t) f 0 (t)(x t). G(a) =0 F (a) a 2 (x a) 2 =0. Como x 6= a entonces se sigue de este resultado que se pude considerar a 2 = F (a) (x a) 2. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 7/28
9 De esta manera se tiene que la función G(t), que está bien definida en el intervalo cerrado J con extremos a y x, se puede escribir como (x t) 2 G(t) =F (t) (x a) 2F (a). Adicionalmente, G(t) es continua en J, derivable en el interior de J y G(x) =G(a) =0.Porelteorema de Rolle existe un c entre a y x tal que G 0 (c) =0.Como G 0 (c) =G 0 (t) = F 0 2(x t) (t)+ x=c (x a) 2F (a) = f 00 (t)(x t)+ x=c apple = f 00 2(x c) (c)(x c)+ (x a) 2F (a) =(x c) f 00 (c)+ donde x 6= c, pues c está entre a y x, entonces se sigue de G 0 (c) =0que donde a su vez De (1), (3) y (4) se sigue el resultado. 2F (a) (x a) 2 2(x t) (x a) 2F (a) x=c F (a) = f 00 (c) 2 (x a)2, (3) F (a) =f(x) f(a) f 0 (a)(x a) =R 1 (a). (4) Ejemplo 4. Utilice la fórmula de Taylor de primer orden para calcular cos 60,5 y determine el número de cifras decimales exactas en esta aproximación. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 8/28
10 Solución. Como 60,5 está próximo a 60 = rad, y la función coseno y su primera derivada son 3 fáciles de evaluar en este número, se elige a = 3.Paraf(x) =cosx se tiene que f =cos 3 3 = 1 2 y f 0 = sen p =. Entonces la linealización de f es 2 L(x) =f(a)+f 0 (a)(x a) = 1 p 3 x Para poder utilizar esta fórmula se debe convertir el ángulo de 60,5 a radianes: 60,5 =60 +0,5 = 3 +0,5 180 = Por lo tanto, cos 60,5 L 3 + = 1 p =0, Se tiene que f 00 (x) = cos x. Por el teorema de Taylor de primer orden tenemos que el error en esta aproximación es R 1 (x) = f 00 (c) 2 cos c 2 x = x, 2! para algún c entre x y.como cos c < 1, se tiene que 3 R = cos c apple =3, < 0, Julio C. Carrillo E. Para uso exclusivo en el salón de clase 9/28
11 Por lo tanto, con sus cuatro cifras decimales exactas. cos 60,5 0, Diferenciales El error R 1 (x) en la aproximación de f(x) mediante su linealización L(x) =f(a) +f 0 (a)(x a) esta determinado por la cercanía de x a a. Como se vio en la sección anterior, entre más cercano esté x de a más pequeño será el error R 1 (x) en esta estimación. Por tal razón tiene sentido considerar el error relativo R 1 (x) x a = f(x) f(a) f 0 (a)(x a). x a Por ejemplo, en el caso del ejemplo 4 se tiene que este error nos dice que 1 R 1 (x) x a apple = 360 =0,8726 %. Originalmente la idea de linealización de una función fue expresada mediante diferenciales. Si f(x) es una función derivable en un intervalo abierto que contiene al número a. Si x es un número diferente sobre el eje x se definen los incrementos (incertidumbres) x y y mediante las diferencias x = x a, y = f(x) f(a) =f(a + x) f(a). Julio C. Carrillo E. Para uso exclusivo en el salón de clase 10/28
12 Para valores de x que estén próximos a 0, se tiene que el error relativo R 1 (x) x a = f(a + x) f(a) f 0 (a) x x Esto quiere decir que el cociente diferencial = y f 0 (a) x x = y x f 0 (x) 0. y x = f(x) x f(a) a = f(a + x) f(x) x es una aproximación del valor de la derivada de f en a: y x f 0 (a) o bien y f 0 (a) x. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 11/28
13 Las cantidades x y f 0 (a) x se denominan diferenciales y se denotan como dx y dy respectivamente. Es decir, x = dx, dy = f 0 (a)dx. Según la figura, para un cambio dx en x la cantidad dy = f 0 (a)dx representa un cambio en la linealización. Y cuando dx 0, el cambio en el incremento y es aproximadamente el mismo el mismo que el cambio en la linealización dy: y dy. Definición 6 (Diferenciales). La diferencial de la variable independiente x es el número diferente de cero x, y se denota por dx; es decir, dx = x. Si f es una función derivable en x, entonces la diferencial de la variable dependiente y se denota por dy; es decir, dy = f 0 (x) x = f 0 (x)dx. Dado que y dy, el valor y es la cantidad exacta mientras que la cantidad diferencial dy representa su aproximación. El error en esta aproximación es y dy. Ejemplo Encuentre y y dy para f(x) =5x 2 +4x Compare los valores de y y dy para x =6y x = dx =0,002. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 12/28
14 Solución. 1. y = f(x + x) f(x) = 5(x + x) 2 +4(x + x)+1 5x 2 +4x +1 =5 (x + x) 2 x 2 +4((x + x) x) =5 x(2x + x)+4 x = (10x +4) x +5( x) 2. Dado que f 0 (x) =10x +4y dy = f 0 (x)dx entonces dy =(10x +4)dx =(10x +4) x. Por lo tanto, y y dy difieren en 5( x) Cuando x =6y x =0,02: y =(10(6)+4)(0,02) + 5(0,02) 2 =1,282 mientras que dy =(10(6)+4)(0,02) = 1,28. La diferencia en las respuestas es y dy =5( x) 2 =5(0,002) 2 =0,002. En resumen, el valor exacto y =1,28 es aproximado por el valor diferencial dy =1,28 yelerroren esta aproximación es 0,002. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 13/28
15 Otra aplicación de los diferenciales se obtiene al considerar que y = f(x + x) f(x), y f 0 (a) x de lo cual se sigue que f(x + x) f(x)+f 0 (x)dx. (5) Ejemplo 6. Use diferenciales para aproximar (2,01) 3. Solución. Sean f(x) =x 3 y x =2, el cual es el número real más cercano a 2,1. Enestecaso x =0,01. En tal caso, dy = f 0 (x)dx =3x 2 x. Por lo tanto, de (5): (x + x) 3 x 3 +3x 2 x. Al considerar x =2y x =0,01 se tiene que (2,01) (2)(0,01) = 8,12. Ejemplo 7. La arista de un cubo mide 30 cm con un error posible de ±0,02 cm. Cuál es el máximo error posible aproximado en el volumen del cubo? Solución. El volumen del cubo es V = x 3 donde x es la longitud de su arista. Si x es el error en la medida de la longitud de su arista, entonces el error correspondiente en el cálculo del volumen del cubo es V =(x + x) 3 x 3. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 14/28
16 Esta cantidad se puede aproximar por su diferencial: dv = V 0 (x)dx =3x 2 x. Así que para x =30y x = ±0,02 el máximo error aproximado es V dv =3(30) 2 (±0,02) = ±54 cm 2. Para estimar el efecto que un error de medida de alrededor de 0,02 cm produce un error en el cálculo del volumen de alrededor de 54 cm 3, que parece a simple vista considerable, se considera el error relativo. Si V V es el error relativo real, los errores relativo aproximado y relativo aproximado porcentual son: dv V = ±54 (30) 3 = ± =) dv V 100 % = ±1 5 %=0,2%. Es decir, el error relativo porcentual es aproximadamente alrededor del 0,2%, lo cual es muy bajo. Teorema 2 (Reglas de diferenciales). Si u = f(x) y v = g(x), dondef y g son diferenciables en su mismo dominio, entonces d(u + v) =du + dv, d(uv) =udv + vdu u vdu udv d =. v v 2 Julio C. Carrillo E. Para uso exclusivo en el salón de clase 15/28
17 Ejemplo 8. Encuentre dy para y = x 2 cos 3x. Solución. Por las reglas de los diferenciales, dy = x 2 d(cos 3x)+cos3xd(x 2 )= 3x 2 cos 3xdx+2xcos 3xdx=( 3x 2 cos 3x +2xcos 3x)dx. De modo alternativo, como y = x 2 cos 3x es derivable, entonces dy = f 0 (x)dx =( 3x 2 cos 3x +2x cos 3x)dx. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 16/28
18 A. Teorema de Taylor (Opcional) Un primer problema de la teoría de ajuste de funciones f(x) mediante interpolación consiste en encontrar un polinomio p(x), de un cierto grado, el cual coincida con f(x) y sus derivadas hasta un cierto orden en un punto x 0 del dominio de f(x), y que además sea una buena aproximación de f(x) cuando x que esté cerca de x 0. En primer lugar, supongamos que se conoce f(x 0 ). Esta sola condición determina un polinomio p(x) de grado cero que coincide con f en x 0 : p(x) =f(x 0 ). Como p(x) es una función constante, ella no da buenas estimaciones de f(x) cuando la misma función f(x) no sea constante. Consideremos que f tiene derivada de primer orden en x 0. Entonces se busca en polinomio p(x) tal que p(x 0 )=f(x 0 ),p 0 (x 0 )=f 0 (x 0 ). Ahora estas dos condiciones determinan un polinomio de primer grado Por lo tanto, como p(x) =a + bx. p(x 0 )=f(x 0 ) =) a + bx 0 = f(x 0 ) p 0 (x 0 )=f 0 (x 0 ) =) b = f 0 (x 0 ) Julio C. Carrillo E. Para uso exclusivo en el salón de clase 17/28
19 el cual es un sistema de dos ecuaciones en las variables a, b que tiene una única solución: De esto se sigue que a = f(x 0 ) f 0 (x 0 )x 0, b = f 0 (x 0 ). p(x) =f(x 0 )+f 0 (x 0 )(x x 0 ). Igualmente, vamos a tener que p(x) no es una buena aproximación de f(x) para valores de x cercanos a x 0 si f(x) no es una función lineal. Nuevamente, si tenemos que f(x) tiene derivada de segundo orden en x 0 entonces se busca un polinomio p(x) tal que p(x 0 )=f(x 0 ), p 0 (x 0 )=f 0 (x 0 ), p 00 (x 0 )=f 00 (x 0 ). (6) Mediante esta tres condiciones se puede construir un polinomio de segundo grado, p(x) =a + bx + cx 2. En efecto, de las condiciones establecidas tenemos el sistema de ecuaciones lineales p(x 0 )=f(x 0 ) =) a + bx 0 + cx 2 0 = f(x 0 ) p 0 (x 0 )=f 0 (x 0 ) =) b +2cx 0 = f 0 (x 0 ) p 00 (x 0 )=f 00 (x 0 ) =) 2c = f 00 (x 0 ) el cual se puede representar en forma matricial como 2 1 x 0 x a x 0 5 4b5 = c 2 3 f(x 0 ) 4f 0 (x 0 ) 5. f 00 (x 0 ) Julio C. Carrillo E. Para uso exclusivo en el salón de clase 18/28
20 Dado que el determinante de la matriz de los coeficientes de este sistema es diferente de cero, de hecho es 2, tenemos que tal sistema tiene una única solución a, b, c; esto a su vez garantiza la existencia y unicidad el polinomio p(x). Por otro lado, resolviendo este sistema de ecuaciones encontramos que a = f(x 0 ) f 0 (x 0 )x 0 + f 00 (x 0 ) 2 x 2 0, b = f 0 (x 0 ) f 00 (x 0 )x 0, c = f 00 (x 0 ). 2 De acuerdo con esto, encontramos finalmente que el polinomio p(x) lo podemos representar de la forma p(x) =f(x 0 )+f 0 (x 0 )(x x 0 )+ f 00 (x 0 ) (x x 0 ) 2. 2 Recíprocamente, es fácil de comprobar que este polinomio satisface las condiciones dadas en (6). Ejemplo 9. Sea f(x) =e x.entoncesf 0 (x) =e x y f 00 (x) =e x. Entonces la recta tangente a la gráfica de f(x) en el punto (0, 1) es p 1 (x) =f(0) + f 0 (0)(x 0) = 1 + x. Intuitivamente se espera que la recta tangente sea, generalmente, la que mejor aproxima los valores que toma la función en los puntos vecinos al punto de tangencia ya que, además de pasar por el punto, tiene la misma pendiente de la curva. Ahora también se puede encontrar un polinomio de segundo grado que pase también por el punto (0, 1) y tal que sus dos primeras derivadas en x =0coincidan con las de f(x) =e x, que son todas iguales a 1. Lo que se busca con tal polinomio de segundo grado es obtener una curva que tiene en el punto (0,1) la misma ordenada, la misma pendiente y concavidad con el mismo signo de la función que se desea aproximar. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 19/28
21 Por este motivo es de esperar que se haya mejorado la aproximación obtenida con el polinomio de primer grado. En este caso el polinomio es p 2 (x) =f(0) + f 0 (0)(x 0) + f 00 (0) (x 0) 2 =1+x + x2 2! 2. Si se calculan algunas ordenadas para valores de x cercamos a x =0, se encuentra que el polinomio de segundo grado proporciona una aproximación mejor que el de primer grado, tal como se puede apreciar en la siguiente tabla. Se agrega la información del polinomio de Taylor p 3 (x) =1+x + x2 2 + x3 6. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 20/28
22 x e x p 1 (x) p 2 (x) p 3 (x) 0,1 0,9048 0,9000 0,9050 0, ,2 0,8187 0,8000 0,8200 0, ,1 1,1052 1,1000 1,1050 1, ,2 1,2214 1,2000 1,2200 1,22213 Las anteriores aproximaciones se pueden mejorar utilizando los llamados polinomios de Taylor, de tal modo que se puede mejorar la aproximación al aumentar el grado del polinomio. En general, tenemos el siguiente teorema. Teorema 3 (Polinomios de Taylor). Sea f(x) una función tal que f (n) (x 0 ) existe. Entonces existe un único polinomio p n (x) de grado a lo más n que satisface las n +1condiciones: Tal polinomio es obien, p n (x 0 )=f(x 0 ),p 0 (x 0 )=f 0 (x 0 ),...,p (n) (x 0 )=f (n) (x 0 ). p n (x) =f(x 0 )+f 0 (x 0 )(x x 0 )+ f 00 (x 0 ) 2! p n (x) = nx k=0 (x x 0 ) f (n) (x 0 ) (x x 0 ) n, n! f (k) (x 0 ) (x x 0 ) k, k! el cual se llama polinomio de Taylor de grado n de f(x) en x 0. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 21/28
23 Demostración. Las n +1condiciones dadas sobre f(x) determinan un polinomio de grado n, p(x) =a 0 + a 1 x + + a n x n. De las condiciones establecidas tenemos el sistema de ecuaciones lineales p(x 0 )=f(x 0 ) =) a 0 + a 1 x 0 + a 2 x a n x n 0 = f(x 0 ) p 0 (x 0 )=f 0 (x 0 ) =) a 1 +2a 2 x na n x n 1 0 = f 0 (x 0 ) p 00 (x 0 )=f 00 (x 0 ) =) 2a 2 + +(n 1)na n x n 0 = f 00 (x 0 ) p (n) (x 0 )=f (n) (x 0 ) =) 2 3 (n 1)na n x n 0 = f (n) (x 0 ) el cual se puede representar en forma matricial como x 0 x 2 0 x n 0 0 1! 2x 0 nx n ! (n 1)nx n n!x n 0 a 0 a 1 a 2. a n = 2 3 f(x 0 ) f 0 (x 0 ) f 00 (x 0 ) f (n) (x 0 ) Dado que el determinante de la matriz de los coeficientes de este sistema es diferente de cero, de hecho es ny k!, k=1 Julio C. Carrillo E. Para uso exclusivo en el salón de clase 22/28
24 tenemos que tal sistema tiene una única solución a 0,a 1,...a n ; esto a su vez garantiza la existencia y unicidad el polinomio p(x). Ahora bien, para facilitar la obtención del polinomio, éste se considera de la forma Como se tiene que p(x) =a 0 + a 1 (x x 0 )+ + a n (x x 0 ) n. p(x) =a 0 + a 1 (x x 0 )+a 2 (x x 0 ) 2 + a 3 (x x 0 ) a n (x x 0 ) n, p 0 (x) =a 1 +2a 2 (x x 0 )+3a 3 (x x 0 ) na n (x x 0 ) n, p 00 (x) =2a (x x 0 )+ + na n (x x 0 ) n,. p (n) (x) =2 3 (n 1)na n p(x 0 )=f(x 0 )=) a 0 = f(x 0 ) p 0 (x 0 )=f 0 (x 0 )=) a 1 = f 0 (x 0 ) p 000 (x 0 )=f 000 (x 0 )=) 2a 1 = f 00 (x 0 ) De esto se obtiene que p (n) (x 0 )=f (n) (x 0 )=)n!a n = f (n) (x 0 ) a k = f (k) (x 0 ), k =0, 1,...,n. k! Julio C. Carrillo E. Para uso exclusivo en el salón de clase 23/28
25 Ejemplo 10. Si f(x) =cosx entonces f 0 (x) = sen x, f 00 (x) = cos x, f 000 (x) =senx, f 0000 (x) =cosx, y así sucesivamente. Como f(0) = 1, f 0 (0) = 0, f 00 (0) = 1, f 000 (0) = 0, f 0000 (0) = 1, etcétera, entonces el polinomio de Taylor de grado 2n de f(x) en x 0 =0es p 2n (x) =1 x 2 2! + x4 4! + +( 1)n x2n (2n)! = nx ( 1) k x 2k. (2k)! En este caso no aparecen potencias impares. La Figura 1 nos muestra algunas de las gráficas de este polinomio para algunos valores pares de n. k=0 p 0 (x) p 2 (x) p 4 (x) Julio C. Carrillo E. Para uso exclusivo en el salón de clase 24/28
26 p 6 (x) p 8 (x) p 10 (x) Figura 1: Gráficas del polinomio de Taylor p 2n (x) de cos(x) en el intervalo [ 5, 5], para n =0, 1, 2, 3, 4, 5. Si bien la función f(x) en general es desconocida, podemos plantear el problema establecer que tan buena es la aproximación de f(x) mediante los valores del polinomio de Taylor p n (x). Si f(x) tiene derivada de orden n en x 0 yelerror en la aproximación de f(x) mediante el polinomio de Taylor p n (x) se define como R n (x) =f(x) p n (x), que también se llama resto, entonces se tiene que f(x) =p n (x)+r n (x) = nx k=0 f (k) (x 0 ) (x x 0 ) k + R n (x), k! la cual se llama la fórmula de Taylor con resto R n (x). Esta fórmula es útil para estimar el orden de magnitud de R n (x), o lo que es lo mismo, para determinar que tan buena es la aproximación de f(x) mediante p n (x) para un x dado. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 25/28
27 El término del resto explica entonces en que casos los polinomios de Taylor son una buena aproximación de una función dada. Aunque algunos autores llaman también a R n (x) el residuo, generando la noción de residuo de la división, en general se prefiere utilizar la palabra resto para significar que es la parte que se le agrega al polinomio de Taylor para obtener la función. En general, el polinomio de Taylor p n (x) de grado n de una función f(x) en x 0 da mejores aproximación cuando n es suficientemente grande y cuando x esta cerca de x 0. Por lo tanto, si se puede demostrar que el término del resto tiende a 0, entonces se debe tener que el polinomio de Taylor p n (x) es una buena aproximación de la función f(x); ojalá, no solamente en x sino también para los valores de x en un cierto intervalo. La siguiente gráfica nos muestra que p 5 (x) es una mejor aproximación a f(x) que p 3 (x) puesto que R 5 (x) está más cercano a 0 para más valores de x. Figura 2: Gráficas del resto R n (x), n =1, 3, 5, de la función f(x) =senx cuando x 0 =0. El Teorema de Taylor, en su versión implícita, establece que el error R n (x) en la aproximación de f(x) mediante el polinomio de Taylor p n (x) tiende a cero más rápido que cualquier polinomio no nulo de grado n cuando x! x 0. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 26/28
28 Teorema 4 (Teorema de Taylor). Sea f(x) una función tal que f (n+1) (x 0 ) existe para toda x en un intervalo I que contiene a x 0.Entoncesparatodox en I se tiene que existe existen funciones p n (x) y R n (x) tales que f(x) =p n (x)+r n (x), donde p n (x) =f(x 0 )+f 0 (x 0 )(x x 0 )+ f 00 (x 0 ) (x x 0 ) f (n) (x 0 ) (x x 0 ) n 2! n! recibe el nombre de polinomio de Taylor de ƒ en x 0,degradon, y R n (x) = f (n) (c) (x x 0 ) n, n! para algún c entre x 0 y x. AR n (x) se le llama la forma del residuo de Lagrange. Demostración. La demostración de este resultado es similar al caso demostrado para el caso del polinomio y del resto de segundo grado. Ejemplo 11. Sea f(x) =e x y x 0 =0. Como la derivada f (k) (x) =e x para todo entero positivo k yen particular f (k) (0) = 1, entonces tenemos que nx e x x k = k! + R n(x). k=0 Como f (n+1) (x) =e x > 0 para todo x entonces f (n+1) (x) es creciente en cualquier intervalo. En particular, si 0 <xapple b entonces 1 apple e x apple e b. Así que x n+1 (n +1)! apple R n(x) apple e b x n+1 (n +1)! si 0 <xapple b. Julio C. Carrillo E. Para uso exclusivo en el salón de clase 27/28
29 Si se desea calcular el número de Euler e, se puede considerar x = b =1ytener en cuenta que e b = e<3. En tal caso, nx 1 e = k! + R n(1), k=0 donde 1 (n +1)! apple R 3 n(1) < (n +1)!, lo cual permite calcular e con el grado de aproximación que se desee. Si por ejemplo, se desea calcular e con 7 cifras decimales exactas, basta considerar 3 (n +1)! apple () (n +1)! = Mediante cálculo directo se puede obtener que 12! = y 13! = Porlotanto, n 12. Así que para n =12, e = En este caso, X12 k=0 1 k! + R 12(1) donde 1, apple R 12 (1) < 4, (7) e p 12 (1) = X12 K=0 1 k! = =2, Así que el valor de e con siete cifras decimales es e 2, o con ocho cifras decimales es e 2, Esto es consistente con el hecho que de (7) se tiene que 2, <e<2, Julio C. Carrillo E. Para uso exclusivo en el salón de clase 28/28
Derivación. Aproximaciones por polinomios.
 Derivación... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Matemáticas (Grado en Químicas) Contenidos Derivada 1 Derivada 2 3 4 5 6 Outline Derivada 1 Derivada 2 3 4 5 6 Definición
Derivación... 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Matemáticas (Grado en Químicas) Contenidos Derivada 1 Derivada 2 3 4 5 6 Outline Derivada 1 Derivada 2 3 4 5 6 Definición
= f (a) R. f(x) f(a) x a. recta por (a, f(a)) de pendiente f(a+h2) f(a) recta tangente por (a, f(a)) de pendiente f (a)
 1 1. DERIVACIÓN 1.1. DEFINICIONES Y RESULTADOS PRINCIPALES Definición 1.1. Derivada. Sea f una función definida en un intervalo abierto I con a I. Decimos que f es derivable en a si existe y es real el
1 1. DERIVACIÓN 1.1. DEFINICIONES Y RESULTADOS PRINCIPALES Definición 1.1. Derivada. Sea f una función definida en un intervalo abierto I con a I. Decimos que f es derivable en a si existe y es real el
Polinomios de Aproximación (Polinomios de Taylor P n )
 Polinomios de Aproximación ( P n ) Sabemos que la recta tangente a una función en un punto es la mejor aproximación lineal a la gráca de f en las cercanías del punto de tangencia (xo, f(xo)), es aquella
Polinomios de Aproximación ( P n ) Sabemos que la recta tangente a una función en un punto es la mejor aproximación lineal a la gráca de f en las cercanías del punto de tangencia (xo, f(xo)), es aquella
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
Derivada y diferencial
 Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Cálculo I. Índice Continuidad. Julio C. Carrillo E. * 1. Introducción Continuidad puntual Continuidad en un intervalo 8
 2.4. Continuidad Julio C. Carrillo E. * Índice 1. Introducción 1 2. Continuidad puntual 2 3. Continuidad en un intervalo 8 4. Conclusiones 18 * Profesor Escuela de Matemáticas, UIS. 1. Introducción Las
2.4. Continuidad Julio C. Carrillo E. * Índice 1. Introducción 1 2. Continuidad puntual 2 3. Continuidad en un intervalo 8 4. Conclusiones 18 * Profesor Escuela de Matemáticas, UIS. 1. Introducción Las
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Cálculo Diferencial en una variable
 Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
CONTINUIDAD DE FUNCIONES. SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos.
 CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
Tema 1. Cálculo diferencial
 Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Tema 1. Cálculo diferencial 1 / 57 Una función es una herramienta mediante la que expresamos la relación entre una causa (variable independiente) y un efecto (variable dependiente). Las funciones nos permiten
Grado en Química Bloque 1 Funciones de una variable
 Grado en Química Bloque Funciones de una variable Sección.7: Aproximación de funciones. Desarrollo de Taylor. Aproximación lineal. La aproximación lineal de una función y = f(x) en un punto x = a es la
Grado en Química Bloque Funciones de una variable Sección.7: Aproximación de funciones. Desarrollo de Taylor. Aproximación lineal. La aproximación lineal de una función y = f(x) en un punto x = a es la
1. El Teorema de Rolle Generalizado.
 Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
Proyecto III: Los Teoremas de Rolle y del valor Medio Objetivos: Profundizar el estudio de algunos teoremas del cálculo diferencial 1 El Teorema de Rolle Generalizado La formulación más común del Teorema
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 01/02
 Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
DERIVADAS PARCIALES Y APLICACIONES
 CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
CAPITULO IV CALCULO II 4.1 DEFINICIÓN DERIVADAS PARCIALES Y APLICACIONES En cálculo una derivada parcial de una función de diversas variables es su derivada respecto a una de esas variables con las otras
Cálculo I. Índice Aplicaciones de las Derivadas: A Extremos de Funciones. Julio C. Carrillo E. * 1. Introducción 1
 4.2. Aplicaciones de las Derivadas: A Extremos de Funciones Índice Julio C. Carrillo E. * 1. Introducción 1 2. Extremos absolutos, relativos y de frontera 1 3. Existencia de extremos absolutos 4 4. Existencia
4.2. Aplicaciones de las Derivadas: A Extremos de Funciones Índice Julio C. Carrillo E. * 1. Introducción 1 2. Extremos absolutos, relativos y de frontera 1 3. Existencia de extremos absolutos 4 4. Existencia
EL TEOREMA DE TAYLOR INTRODUCCION:
 EL TEOREMA DE TAYLOR INTRODUCCION: Sabemos que la recta tangente, como la mejor aproximación lineal a la gráfica de f en las cercanías del punto de tangencia (x o, f(x o )), es aquella recta que pasa por
EL TEOREMA DE TAYLOR INTRODUCCION: Sabemos que la recta tangente, como la mejor aproximación lineal a la gráfica de f en las cercanías del punto de tangencia (x o, f(x o )), es aquella recta que pasa por
3. Funciones de varias variables
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Cálculo I. Índice Derivada. Julio C. Carrillo E. * 1. Introducción La derivada Derivadas de orden superior
 3.1. Derivada Julio C. Carrillo E. * Índice 1. Introducción 1 2. La derivada 3 3. Derivadas de orden superior 18 4. Conclusiones 19 * Profesor Escuela de Matemáticas, UIS. 1. Introducción El término derivabilidad
3.1. Derivada Julio C. Carrillo E. * Índice 1. Introducción 1 2. La derivada 3 3. Derivadas de orden superior 18 4. Conclusiones 19 * Profesor Escuela de Matemáticas, UIS. 1. Introducción El término derivabilidad
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE
 BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE El concepto de derivada. Relación entre continuidad y derivabilidad. Función derivada. Operaciones con derivadas. Derivación de las funciones
BLOQUE 4. CÁLCULO DIFERENCIAL DE FUNCIONES REALES DE UNA VARIABLE El concepto de derivada. Relación entre continuidad y derivabilidad. Función derivada. Operaciones con derivadas. Derivación de las funciones
Métodos Numéricos en Ecuaciones Diferenciales Ordinarias
 Tema 4 Métodos Numéricos en Ecuaciones Diferenciales Ordinarias 4.1 Introducción Estudiaremos en este Tema algunos métodos numéricos para resolver problemas de valor inicial en ecuaciones diferenciales
Tema 4 Métodos Numéricos en Ecuaciones Diferenciales Ordinarias 4.1 Introducción Estudiaremos en este Tema algunos métodos numéricos para resolver problemas de valor inicial en ecuaciones diferenciales
Capítulo 2: Cálculo diferencial de una y varias variables
 Capítulo 2: Cálculo diferencial de una y varias variables (Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos Límites y continuidad Límites laterales
Capítulo 2: Cálculo diferencial de una y varias variables (Fundamentos Matemáticos de la Biotecnología) Departamento de Matemáticas Universidad de Murcia Contenidos Límites y continuidad Límites laterales
Derivadas de orden superior
 Tema 6 Derivadas de orden superior 6 Polinomios de Taylor Nuestro objetivo es aproimar una función dada mediante funciones polinómicas Resulta conveniente estudiar las funciones polinómicas con más detenimiento
Tema 6 Derivadas de orden superior 6 Polinomios de Taylor Nuestro objetivo es aproimar una función dada mediante funciones polinómicas Resulta conveniente estudiar las funciones polinómicas con más detenimiento
Cálculo Diferencial de una Variable
 Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Esquema Esquema de la exposición Definición. Interpretación geométrica de
Departamento de Matemática Aplicada Universitat Politècnica de València, España Fundamentos Matemáticos para la Ingenieria Civil Esquema Esquema de la exposición Definición. Interpretación geométrica de
Unidad IV. 4.1 Conceptos de incremento y de razón de cambio. La derivada de una función.
 Unidad IV Derivadas 4.1 Conceptos de incremento y de razón de cambio. La derivada de una función. Derivada de una función en un punto. Dada la función f(x) continúa en el intervalo abierto I, se define
Unidad IV Derivadas 4.1 Conceptos de incremento y de razón de cambio. La derivada de una función. Derivada de una función en un punto. Dada la función f(x) continúa en el intervalo abierto I, se define
Cálculo 20. Semestre B-2015 Prof. José Prieto Correo: 1. Teoremas sobre funciones derivables
 Cálculo 20. Semestre B-2015 Prof. José Prieto Correo: prieto@ula.ve 1. Teoremas sobre funciones derivables Problema 1 Determine si la función dada satisface las hipótesis del Teorema de Bolzano sobre el
Cálculo 20. Semestre B-2015 Prof. José Prieto Correo: prieto@ula.ve 1. Teoremas sobre funciones derivables Problema 1 Determine si la función dada satisface las hipótesis del Teorema de Bolzano sobre el
Departamento de Matemáticas
 MA25 Clase 5: Series de potencias. Operaciones con series de potencias. Series de potencias Elaborado por los profesores Edgar Cabello y Marcos González Cuando estudiamos las series geométricas, demostramos
MA25 Clase 5: Series de potencias. Operaciones con series de potencias. Series de potencias Elaborado por los profesores Edgar Cabello y Marcos González Cuando estudiamos las series geométricas, demostramos
EXAMEN DE MATEMÁTICAS I (Primer Parcial) 10 de febrero de 2010
 CUESTIONES TIPO TEST Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0. puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- En un triángulo esférico rectángulo,
CUESTIONES TIPO TEST Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0. puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- En un triángulo esférico rectángulo,
DERIVADAS DE FUNCIONES DE UNA VARIABLE
 DERIVADAS DE FUNCIONES DE UNA VARIABLE DERIVADAS DE FUNCIONES DE UNA VARIABLE [4.] Estudiar la derivabilidad de la función los puntos en los que esté definida. 3 f( ) y obtener f ( ) en En primer lugar
DERIVADAS DE FUNCIONES DE UNA VARIABLE DERIVADAS DE FUNCIONES DE UNA VARIABLE [4.] Estudiar la derivabilidad de la función los puntos en los que esté definida. 3 f( ) y obtener f ( ) en En primer lugar
Funciones de Una Variable Real I. Derivadas
 Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
CONCEPTOS QUE DEBES DOMINAR
 INTERVALOS CONCEPTOS QUE DEBES DOMINAR Un intervalo es un conjunto infinito de números reales comprendidos entre dos extremos, que pueden estar incluidos en él o no. 1. Intervalo abierto (a, b): Comprende
INTERVALOS CONCEPTOS QUE DEBES DOMINAR Un intervalo es un conjunto infinito de números reales comprendidos entre dos extremos, que pueden estar incluidos en él o no. 1. Intervalo abierto (a, b): Comprende
ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 5 - Verano 2009
 ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
MATEMÁTICAS: PAU 2016 JUNIO CASTILLA Y LEÓN
 MATEMÁTICAS: PAU 26 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A 5 a a) Discutir para qué valores de a R la matriz M = ( ) tiene inversa. Calcular M a para a =. ( 5 puntos) Para que exista inversa de una
MATEMÁTICAS: PAU 26 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A 5 a a) Discutir para qué valores de a R la matriz M = ( ) tiene inversa. Calcular M a para a =. ( 5 puntos) Para que exista inversa de una
Derivadas. Jesús García de Jalón de la Fuente. IES Ramiro de Maeztu Madrid
 Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta
Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta tangente a una curva Recta
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática ( )
 Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 4 (APLICACIONES DE LA DERIVADA) Profesora: Yulimar Matute Febrero 2012 RECTA
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 4 (APLICACIONES DE LA DERIVADA) Profesora: Yulimar Matute Febrero 2012 RECTA
CÁLCULO ELEMENTAL PROBLEMAS. Valor absoluto. Funciones y sus gráficas
 CÁLCULO ELEMENTAL PROBLEMAS Valor absoluto - Resolver las ecuaciones siguientes: (i) 2x 6 = x (ii) x + 8 = 3x 4 2- Resolver la inecuación 2x 3 4 Funciones y sus gráficas 3- Dada f(x) = 2x 2 x, hallar f(
CÁLCULO ELEMENTAL PROBLEMAS Valor absoluto - Resolver las ecuaciones siguientes: (i) 2x 6 = x (ii) x + 8 = 3x 4 2- Resolver la inecuación 2x 3 4 Funciones y sus gráficas 3- Dada f(x) = 2x 2 x, hallar f(
Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o
![Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o](/thumbs/74/71098358.jpg) DERIVADAS Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-, 3] hallar x o El teorema de Lagrange dice que: f(3) - f(-) = f
DERIVADAS Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-, 3] hallar x o El teorema de Lagrange dice que: f(3) - f(-) = f
2 x
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08-2 Importante: Visita regularmente ttp://www.dim.ucile.cl/~calculo. Aí encontrarás las guías de ejercicios
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08-2 Importante: Visita regularmente ttp://www.dim.ucile.cl/~calculo. Aí encontrarás las guías de ejercicios
EXAMEN DE MATEMÁTICAS I. Test
 Primer Parcial 16 de febrero de 005 Test Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0. puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Considerando
Primer Parcial 16 de febrero de 005 Test Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0. puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Considerando
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES
 MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
MATEMÁTICAS APLICADAS A LAS C.C. SOCIALES CAPÍTULO 5 Curso preparatorio de la prueba de acceso a la universidad para mayores de 25 años curso 2010/11 Nuria Torrado Robles Departamento de Estadística Universidad
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Tema 5. Aproximación funcional local: Polinomio de Taylor. 5.1 Polinomio de Taylor
 Tema 5 Aproximación funcional local: Polinomio de Taylor Teoría Los polinomios son las funciones reales más fáciles de evaluar; por esta razón, cuando una función resulta difícil de evaluar con exactitud,
Tema 5 Aproximación funcional local: Polinomio de Taylor Teoría Los polinomios son las funciones reales más fáciles de evaluar; por esta razón, cuando una función resulta difícil de evaluar con exactitud,
TEMA 5: LA INTEGRAL DEFINIDA
 Alonso Fernández Galián TEMA 5: LA INTEGRAL DEFINIDA Originalmente el Cálculo Diferencial e Integral estaba fuertemente vinculado a la geometría analítica. Ya vimos la aplicación de las derivadas al cálculo
Alonso Fernández Galián TEMA 5: LA INTEGRAL DEFINIDA Originalmente el Cálculo Diferencial e Integral estaba fuertemente vinculado a la geometría analítica. Ya vimos la aplicación de las derivadas al cálculo
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL
 REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
REPASO DE FUNCIONES FUNCIONES REALES DE VARIABLE REAL CORRESPONDENCIA. Se llama CORRESPONDENCIA entre dos conjuntos A y B a toda ley que asocia elementos del conjunto A con elementos del conjunto B. Se
EJERCICIOS DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 2: Cálculo diferencial de una variable
 EJERCICIOS DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Índice 2. Cálculo diferencial de una variable. 2..
EJERCICIOS DE CÁLCULO I Para Grados en Ingeniería Capítulo 2: Cálculo diferencial de una variable Domingo Pestana Galván José Manuel Rodríguez García Índice 2. Cálculo diferencial de una variable. 2..
DERIVADAS. Problemas con Solución.
 DERIVADAS. Problemas con Solución. Aplica la definición de derivada como un límite, para calcular f siendo fx = x + x +. 4. Sea la función fx = x/x, halla la derivada de f en el punto de abcisa usando
DERIVADAS. Problemas con Solución. Aplica la definición de derivada como un límite, para calcular f siendo fx = x + x +. 4. Sea la función fx = x/x, halla la derivada de f en el punto de abcisa usando
DERIVADA DE UNA FUNCIÓN
 DERIVADA DE UNA FUNCIÓN 3URI/XLV~xH] Se estudia aquí uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. Además de la definición y su interpretación, se allarán las
DERIVADA DE UNA FUNCIÓN 3URI/XLV~xH] Se estudia aquí uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. Además de la definición y su interpretación, se allarán las
Unidad V. 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales.
 Unidad V Aplicaciones de la derivada 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales. Una tangente a una curva es una recta que toca la curva en un solo punto y tiene la misma
Unidad V Aplicaciones de la derivada 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales. Una tangente a una curva es una recta que toca la curva en un solo punto y tiene la misma
Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos
 Análisis I Matemática I Análisis II (C) Cuat II - 2009 Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior 1. Calcular las derivadas
Análisis I Matemática I Análisis II (C) Cuat II - 2009 Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior 1. Calcular las derivadas
DEFINICIÓN : f es una función de R en R si a cada número real, x Dom, le hace corresponder un único número real, f(x):
 1 FUNCIONES ELEMENTALES CONCEPTO DE FUNCIÓN DEFINICIÓN : f es una función de R en R si a cada número real, x Dom, le hace corresponder un único número real, f(x): Lo denotamos por : f : Dom -----> R x
1 FUNCIONES ELEMENTALES CONCEPTO DE FUNCIÓN DEFINICIÓN : f es una función de R en R si a cada número real, x Dom, le hace corresponder un único número real, f(x): Lo denotamos por : f : Dom -----> R x
Universidad Carlos III de Madrid
 Universidad Carlos III de Madrid Ejercicio 1 2 4 5 6 Total Puntos Departamento de Economía Examen Final de Matemáticas I 16 de Enero de 201 APELLIDOS: Duración del Examen: 2 horas. NOMBRE: DNI: Titulación:
Universidad Carlos III de Madrid Ejercicio 1 2 4 5 6 Total Puntos Departamento de Economía Examen Final de Matemáticas I 16 de Enero de 201 APELLIDOS: Duración del Examen: 2 horas. NOMBRE: DNI: Titulación:
Cálculo en varias variables
 Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Lección 3: Aproximación de funciones. por polinomios. Fórmula de Taylor para
 Lección 3: Aproximación de funciones por polinomios. Fórmula de Taylor para funciones escalares 3.1 Introducción Cuando es difícil trabajar con una función complicada, tratamos a veces de hallar una función
Lección 3: Aproximación de funciones por polinomios. Fórmula de Taylor para funciones escalares 3.1 Introducción Cuando es difícil trabajar con una función complicada, tratamos a veces de hallar una función
C alculo Octubre 2010
 Cálculo Octubre 2010 Derivada. Introducción Recordemos la definición de pendiente de una recta: α y 1 y0 x 0 x 1 Pendiente= m = tanα = y 1 y 0 x 1 x 0 Y ahora consideremos las pendientes de las rectas
Cálculo Octubre 2010 Derivada. Introducción Recordemos la definición de pendiente de una recta: α y 1 y0 x 0 x 1 Pendiente= m = tanα = y 1 y 0 x 1 x 0 Y ahora consideremos las pendientes de las rectas
Cuadratura de Newton-Cotes
 Profesor: Jaime Álvarez Maldonado Universidad de Santiago de Chile Facultad de Ciencia Departamento de Matemática y Ciencias de la Computación INTEGRACION NUMERICA Ayudante: Rodrigo Torres Aguirre INTEGRACION
Profesor: Jaime Álvarez Maldonado Universidad de Santiago de Chile Facultad de Ciencia Departamento de Matemática y Ciencias de la Computación INTEGRACION NUMERICA Ayudante: Rodrigo Torres Aguirre INTEGRACION
Cálculo Infinitesimal y Numérico. E.T.S. de Ingeniería Informática. Universidad de Sevilla1
 Cálculo Infinitesimal y Numérico. E.T.S. de Ingeniería Informática. Universidad de Sevilla1 Tema 2: Interpolación. Ejercicios y Problemas 1. Ejercicios Ejercicio 1. 1. Dar, sin desarrollar, los polinomios
Cálculo Infinitesimal y Numérico. E.T.S. de Ingeniería Informática. Universidad de Sevilla1 Tema 2: Interpolación. Ejercicios y Problemas 1. Ejercicios Ejercicio 1. 1. Dar, sin desarrollar, los polinomios
CÁLCULO NUMÉRICO (0258)
 CÁLCULO NUMÉRICO (58) Tema 5. Diferenciación e Integración Numérica Enero 5. Utilice la fórmula para calcular la derivada de f(x) = cos(x) en utilizar la fórmula. f(x + ) f(x) f'(x) x = y con =.. Estime
CÁLCULO NUMÉRICO (58) Tema 5. Diferenciación e Integración Numérica Enero 5. Utilice la fórmula para calcular la derivada de f(x) = cos(x) en utilizar la fórmula. f(x + ) f(x) f'(x) x = y con =.. Estime
1. Para la función f(x) = x sen x, halle su polinomio de Taylor de orden 2 en a = 0. x x3 3!, x x3
 Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
Cálculo I (Grado en Ingeniería Informática) Problemas resueltos, - y -4 (tercera parte) Preparado por los profesores de la asignatura: Pablo Fernández, Dragan Vukotić (coordinadores), Luis Guijarro, Kazaros
EJERCICIOS PROPUESTOS: Interpolación
 EJERCICIOS PROPUESTOS: Interpolación 1º. Determínese el polinomio de primer grado que en x = 1 toma el valor y en x 1 = toma el valor. Para ello: a) Escríbase el sistema de ecuaciones lineales que proporciona
EJERCICIOS PROPUESTOS: Interpolación 1º. Determínese el polinomio de primer grado que en x = 1 toma el valor y en x 1 = toma el valor. Para ello: a) Escríbase el sistema de ecuaciones lineales que proporciona
Apuntes de Funciones
 Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
Apuntes de Funciones El concepto de función es un elemento fundamental dentro del análisis matemático, así como en sus aplicaciones. Esta idea se introdujo con el objetivo de matematizar la transformación
Definición 11.1 Sea f : A E F una aplicación r-veces diferenciable en un punto a A. o
 Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
Análisis Matemático I: Cálculo diferencial
 Contents : Cálculo diferencial Universidad de Murcia Curso 2007-2008 Contents 1 Objetivos Definir, entender y aplicar el concepto de función derivable. Estudiar la relación entre derivabilidad, crecimiento,
Contents : Cálculo diferencial Universidad de Murcia Curso 2007-2008 Contents 1 Objetivos Definir, entender y aplicar el concepto de función derivable. Estudiar la relación entre derivabilidad, crecimiento,
Apuntes. Genius, a good idea in Maths Ximo Beneyto. Tema : Derivabilidad. Teorema de Taylor
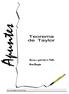 Apuntes Genius, a good idea in Maths Ximo Beneyto 1. Hallar el desarrollo de Taylor y la expresión del resto de Lagrange, para las siguientes funciones. 1.1 f(x) = sen x en a =, n = 3 1.2 f(x) = Ln x en
Apuntes Genius, a good idea in Maths Ximo Beneyto 1. Hallar el desarrollo de Taylor y la expresión del resto de Lagrange, para las siguientes funciones. 1.1 f(x) = sen x en a =, n = 3 1.2 f(x) = Ln x en
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
AYUDA MEMORIA PARA EL ESTUDIO DE MATEMÁTICAS II - SISTEMAS
 AYUDA MEMORIA PARA EL ESTUDIO DE MATEMÁTICAS II - SISTEMAS Potencias de la unidad imaginaria i 0 = 1 i 1 = i i 2 = 1 i 3 = i i 4 = 1 Los valores se repiten de cuatro en cuatro, por eso, para saber cuánto
AYUDA MEMORIA PARA EL ESTUDIO DE MATEMÁTICAS II - SISTEMAS Potencias de la unidad imaginaria i 0 = 1 i 1 = i i 2 = 1 i 3 = i i 4 = 1 Los valores se repiten de cuatro en cuatro, por eso, para saber cuánto
Herramientas digitales de auto-aprendizaje para Matemáticas
 Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura Índice la cadena Tabla de Dada una función f : D R R,
Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura Índice la cadena Tabla de Dada una función f : D R R,
1. Hallar los extremos de las funciones siguientes en las regiones especificadas:
 1 1. DERIVACIÓN 1. Hallar los extremos de las funciones siguientes en las regiones especificadas: b) f(x) x (x 1) en el intervalo [, ] y en su dominio. DOMINIO. D R. CORTES CON LOS EJES. Cortes con el
1 1. DERIVACIÓN 1. Hallar los extremos de las funciones siguientes en las regiones especificadas: b) f(x) x (x 1) en el intervalo [, ] y en su dominio. DOMINIO. D R. CORTES CON LOS EJES. Cortes con el
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE M
 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-6-4-M--00-0 CURSO: Matemática aplicada JORNADA: SEMESTRE: Matutina do. Semestre AÑO: 0 TIPO DE EXAMEN: Examen
UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CLAVE-6-4-M--00-0 CURSO: Matemática aplicada JORNADA: SEMESTRE: Matutina do. Semestre AÑO: 0 TIPO DE EXAMEN: Examen
DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD
 DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3)
DERIVADAS, LÍMITES Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3)
INTERPOLACIÓN: Error en la la interpolación polinómica de Lagrange
 INTERPOLACIÓN: Error en la la interpolación polinómica de Lagrange Arturo Hidalgo LópezL Alfredo López L Benito Carlos Conde LázaroL Marzo, 007 Departamento de Matemática Aplicada y Métodos Informáticos
INTERPOLACIÓN: Error en la la interpolación polinómica de Lagrange Arturo Hidalgo LópezL Alfredo López L Benito Carlos Conde LázaroL Marzo, 007 Departamento de Matemática Aplicada y Métodos Informáticos
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 13 Capítulo 6 Año 5 6.1. Modelo 5 - Opción A Problema 6.1.1 ( puntos) Justificar razonadamente
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 13 Capítulo 6 Año 5 6.1. Modelo 5 - Opción A Problema 6.1.1 ( puntos) Justificar razonadamente
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática ( )
 Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 3 (DERIVADAS) Profesora: Yulimar Matute Febrero 2012 DERIVADAS POR DEFINICIÓN
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 3 (DERIVADAS) Profesora: Yulimar Matute Febrero 2012 DERIVADAS POR DEFINICIÓN
Funciones elementales
 Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
Tema Funciones elementales.1. Función real de variable real Una función real de variable real es cualquier aplicación f : D R! R. Se dice que el conjunto D es el dominio de f. El rango de f es el conjunto
1 Método de la bisección. 1.1 Teorema de Bolzano Teorema 1.1 (Bolzano) Contenido
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
Diferencial de una función 1
 Cálculo _Comisión y Año 7 Diferencial de una función Dada una función y f (, derivable en x, se define: Diferencial de f, en x, al producto de la derivada de la función en dicho punto, por el incremento
Cálculo _Comisión y Año 7 Diferencial de una función Dada una función y f (, derivable en x, se define: Diferencial de f, en x, al producto de la derivada de la función en dicho punto, por el incremento
Universidad de Chile Integración por partes. Ingeniería Matemática SEMANA 6: PRIMITIVAS
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Ingeniería Matemática SEMANA 6: PRIMITIVAS 3.3. Integración por partes Proposición 3. (Fórmula de integración
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 08- Ingeniería Matemática SEMANA 6: PRIMITIVAS 3.3. Integración por partes Proposición 3. (Fórmula de integración
Repaso de Funciones. MATE 3031 Cálculo 1. 01/12/2016 Prof. José G. Rodríguez Ahumada 1 de 26
 Repaso de Funciones MATE 3031 Cálculo 1 01/12/2016 Prof. José G. Rodríguez Ahumada 1 de 26 FUNCIONES 01/12/2016 Prof. José G. Rodríguez Ahumada 2 de 26 Cómo se representa una función? Sea x={1,2,3}, y
Repaso de Funciones MATE 3031 Cálculo 1 01/12/2016 Prof. José G. Rodríguez Ahumada 1 de 26 FUNCIONES 01/12/2016 Prof. José G. Rodríguez Ahumada 2 de 26 Cómo se representa una función? Sea x={1,2,3}, y
Universidad Icesi Departamento de Matemáticas y Estadística
 Universidad Icesi Departamento de Matemáticas y Estadística Solución del primer examen parcial del curso Cálculo de una variable Grupo: Once Período: Inicial del año 000 Prof: Rubén D. Nieto C. PUNTO 1.
Universidad Icesi Departamento de Matemáticas y Estadística Solución del primer examen parcial del curso Cálculo de una variable Grupo: Once Período: Inicial del año 000 Prof: Rubén D. Nieto C. PUNTO 1.
Funciones de una variable real II Fórmula de Taylor y aplicaciones
 Universidad de Murcia Departamento Matemáticas Funciones de una variable real II Fórmula de Taylor y aplicaciones B. Cascales J. M. Mira L. Oncina Departamento de Matemáticas Universidad de Murcia Grado
Universidad de Murcia Departamento Matemáticas Funciones de una variable real II Fórmula de Taylor y aplicaciones B. Cascales J. M. Mira L. Oncina Departamento de Matemáticas Universidad de Murcia Grado
Complementos de Matemáticas, ITT Telemática
 Aproximación de funciones Interpolación Int. Segm. Complementos de Matemáticas, ITT Telemática Tema 2. Departamento de Matemáticas, Universidad de Alcalá Aproximación de funciones Interpolación Int. Segm.
Aproximación de funciones Interpolación Int. Segm. Complementos de Matemáticas, ITT Telemática Tema 2. Departamento de Matemáticas, Universidad de Alcalá Aproximación de funciones Interpolación Int. Segm.
5. ANÁLISIS MATEMÁTICO // 5.2. DERIVADA DE
 5. ANÁLISIS MATEMÁTICO // 5.2. DERIVADA DE UNA FUNCIÓN EN UN PUNTO Y APLICACIONES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2010-2011 5.2.1. El problema de la tangente. Derivada.
5. ANÁLISIS MATEMÁTICO // 5.2. DERIVADA DE UNA FUNCIÓN EN UN PUNTO Y APLICACIONES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2010-2011 5.2.1. El problema de la tangente. Derivada.
CÁLCULO II Funciones de varias variables
 CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
ANÁLISIS MATEMÁTICO IES A SANGRIÑA 2016/2017
 ANÁLISIS MATEMÁTICO 4. INTEGRACIÓN INDEFINIDA UN POCO DE HISTORIA El símbolo de integración fue introducido por el matemático alemán Gottfried Leibniz en 1675, basándose en la palabra latina summa, suma,
ANÁLISIS MATEMÁTICO 4. INTEGRACIÓN INDEFINIDA UN POCO DE HISTORIA El símbolo de integración fue introducido por el matemático alemán Gottfried Leibniz en 1675, basándose en la palabra latina summa, suma,
BORRADOR. Series de potencias y de funciones Sucesiones de funciones
 Capítulo 5 Series de potencias y de funciones 5.1. Sucesiones de funciones En los dos últimos capítulos de la asignatura, deseamos estudiar ciertos tipos de series de funciones, es decir, expresiones sumatorias
Capítulo 5 Series de potencias y de funciones 5.1. Sucesiones de funciones En los dos últimos capítulos de la asignatura, deseamos estudiar ciertos tipos de series de funciones, es decir, expresiones sumatorias
Ejercicios Temas 3 y 4: Interpolación polinomial. Ajuste de curvas.
 Ejercicios Temas 3 y 4: Interpolación polinomial. Ajuste de curvas.. El número de personas afectadas por el virus contagioso que produce la gripe en una determinada población viene dado por la siguiente
Ejercicios Temas 3 y 4: Interpolación polinomial. Ajuste de curvas.. El número de personas afectadas por el virus contagioso que produce la gripe en una determinada población viene dado por la siguiente
2.1.5 Teoremas sobre derivadas
 si x < 0. f(x) = x si x 0 x o = 0 Teoremas sobre derivadas 9 2. f(x) = x 3, x o = 3 a. Determine si f es continua en x o. b. Halle f +(x o ) y f (x o ). c. Determine si f es derivable en x o. d. Haga la
si x < 0. f(x) = x si x 0 x o = 0 Teoremas sobre derivadas 9 2. f(x) = x 3, x o = 3 a. Determine si f es continua en x o. b. Halle f +(x o ) y f (x o ). c. Determine si f es derivable en x o. d. Haga la
MATEMÁTICAS VI. CÁLCULO INTEGRAL UNIDAD I LA INTEGRAL INDEFINIDA
 UNIDAD I LA INTEGRAL INDEFINIDA INTRODUCCIÓN El cálculo diferencial proporciona una regla para obtener la derivada de una función sencilla, con esta regla se obtienen las fórmulas para derivar todo tipo
UNIDAD I LA INTEGRAL INDEFINIDA INTRODUCCIÓN El cálculo diferencial proporciona una regla para obtener la derivada de una función sencilla, con esta regla se obtienen las fórmulas para derivar todo tipo
Práctico 7 - Desarrollo de Taylor. 1. Polinomio de Taylor. Universidad de la República Cálculo 1 Facultad de Ingeniería - IMERL Segundo Semestre 2016
 Universidad de la República Cálculo Facultad de Ingeniería - IMERL Segundo Semestre 206 Práctico 7 - Desarrollo de Taylor. Polinomio de Taylor. El polinomio de Mc Laurin de orden 4 asociado a una cierta
Universidad de la República Cálculo Facultad de Ingeniería - IMERL Segundo Semestre 206 Práctico 7 - Desarrollo de Taylor. Polinomio de Taylor. El polinomio de Mc Laurin de orden 4 asociado a una cierta
Práctico Preparación del Examen
 Cálculo Diferencial e Integral (Áreas Tecnológicas) Segundo Semestre 4 Universidad de la República Práctico Preparación del Examen Límites, funciones y continuidad Ejercicio Sea log(+x ) f(x) =, si x
Cálculo Diferencial e Integral (Áreas Tecnológicas) Segundo Semestre 4 Universidad de la República Práctico Preparación del Examen Límites, funciones y continuidad Ejercicio Sea log(+x ) f(x) =, si x
Derivada de una función en un punto. Función derivada. Diferencial de una función en un punto. dy = f (x) dx. Derivada de la función inversa
 Derivada de una función en un punto Las tres expresiones son equivalentes. En definitiva, la derivada de una función en un punto se obtiene como el límite del cociente incremental: el incremento del valor
Derivada de una función en un punto Las tres expresiones son equivalentes. En definitiva, la derivada de una función en un punto se obtiene como el límite del cociente incremental: el incremento del valor
Funciones Reales de Varias Variables
 Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
a de un conjunto S de R n si
 1 235 Máximos, mínimos y puntos de ensilladura Definición.- Se dice que una función real f( x) tiene un máximo absoluto en un punto a de un conjunto S de R n si f( x) f( a) (2) para todo x S. El número
1 235 Máximos, mínimos y puntos de ensilladura Definición.- Se dice que una función real f( x) tiene un máximo absoluto en un punto a de un conjunto S de R n si f( x) f( a) (2) para todo x S. El número
Derivadas. Derivabilidad
 Apuntes Tema 4 Derivadas. Derivabilidad 4.1 Derivada de una función Llamamos tasa de variación media al cociente entre el incremento que sufre la variable dependiente y el incremento de la variable independiente.
Apuntes Tema 4 Derivadas. Derivabilidad 4.1 Derivada de una función Llamamos tasa de variación media al cociente entre el incremento que sufre la variable dependiente y el incremento de la variable independiente.
DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL
 DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL Definición. Sea f :]a, b[ R y x 0 ]a, b[. Sedicequef es derivable en x 0 si existe f(x lim 0 +h) f(x 0 ) h 0 h yesfinito. En ese caso denotaremos por
DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL Definición. Sea f :]a, b[ R y x 0 ]a, b[. Sedicequef es derivable en x 0 si existe f(x lim 0 +h) f(x 0 ) h 0 h yesfinito. En ese caso denotaremos por
Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o
![Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o](/thumbs/49/25449703.jpg) DERIVADAS Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3) - f(-1) =
DERIVADAS Y TEOREMAS DE DERIVABILIDAD Aplicando el teorema de los incrementos finitos a la función f(x) = x 2 + 4x - 2 en los extremos [-1, 3] hallar x o El teorema de Lagrange dice que: f(3) - f(-1) =
Problemas Ampliación de Matemáticas. Sistemas lineales 1.- Encontrar la factorización L U de las siguientes matrices:
 Problemas Ampliación de Matemáticas. Sistemas lineales 1.- Encontrar la factorización L U de las siguientes matrices: 5 2 1 1 0 3 1 0 3 3 1 6. 3 1 6 5 2 1 2.- Dada la matriz A = 10 7 8 7 5 6, 8 6 10 hallar
Problemas Ampliación de Matemáticas. Sistemas lineales 1.- Encontrar la factorización L U de las siguientes matrices: 5 2 1 1 0 3 1 0 3 3 1 6. 3 1 6 5 2 1 2.- Dada la matriz A = 10 7 8 7 5 6, 8 6 10 hallar
UNIVERSIDAD DE EXTREMADURA Departamento de Matemáticas. Matemáticas. Manuel Fernández García-Hierro Badajoz, Febrero 2008
 UNIVERSIDAD DE EXTREMADURA Departamento de Matemáticas Matemáticas Manuel Fernández García-Hierro Badajoz, Febrero 2008 Capítulo X Integración numérica Introducción La integral definida I(f) = b a f(x)
UNIVERSIDAD DE EXTREMADURA Departamento de Matemáticas Matemáticas Manuel Fernández García-Hierro Badajoz, Febrero 2008 Capítulo X Integración numérica Introducción La integral definida I(f) = b a f(x)
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Métodos Numéricos Cap 5: Interpolación y Aproximación polinomial
 1/12 Aproximación funcional e Interpolación Representación mediante funciones analíticas sencillas de: Información discreta. (Resultante de muestreos). Funciones complicadas. Siendo y k = f(x k ) una cierta
1/12 Aproximación funcional e Interpolación Representación mediante funciones analíticas sencillas de: Información discreta. (Resultante de muestreos). Funciones complicadas. Siendo y k = f(x k ) una cierta
