Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas.
|
|
|
- Roberto Aguirre Carmona
- hace 5 años
- Vistas:
Transcripción
1 Tema 7- Haces de hipercuádricas Clasificación de los haces de cónicas Determinación de cónicas 71 Puntos base y fundamentales de un haz Definición 711 Sea el espacio proyectivo Pn(k) de dimensión n sobre un cuerpo k de característica distinta de dos Sean Q, Q dos hipercuádricas en Pn(k) definidas por las ecuaciones XAX t = 0 y XA X t = 0 respectivamente Se llama haz de hipercuádricas generado por Q y Q a la familia de hipercuádricas definidas por las ecuaciones X(λA + λ A X t = 0 con (λ : λ ) P1(k) Nota 712 Sean Q y Q dos hipercuádricas distintas de Pn(k) Sea H el haz definido por Q y Q Entonces, el haz definido por dos hipercuádricas distintas de H coincide con H Definición 713 Se llama base de un haz H y se representa Base(H) al conjunto de puntos V(Q) Q H Es decir Base(H) es el conjunto de puntos de Pn(k) que pertenecen a todas las hipercuádricas lugar del haz H Nota 714 En adelante diremos que un punto P Pn pertenece a una hipercuádrica si P pertenece a la hipercuádrica lugar correspondiente Lema 715 Si H es un haz de hipercuádricas, se tiene : Base(H) = V(Q) V(Q ) donde Q y Q son dos hipercuádricas cualesquiera (distintas) del haz Demostración: Es obvio que Base(H) = Q H V(Q ) V(Q) V(Q ) Recíprocamente, sea P V(Q) V(Q ) y sea Q una hipercuádrica de H Sean P = (a 0 : : a n ), y A, A, A matrices simétricas tales que Q : XAX t = 0, Q : XA X t = 0, Q : XA X t = 0 Existen λ, λ k, no ambos nulos, tales que A = λa + λ A Entonces (a 0,, a n )A a 0 a n = λ(a 0,, a n )A a 0 a n + λ (a 0,, a n )A a 0 a n = 0 y por tanto P V(Q ) 2 Lema 716 Si P Pn no es un punto base de un haz H, entonces existe una única hipercuádrica Q de H que pasa por P Demostración: Si existiera más de una hipercuádrica del haz pasando por el punto P, éste sería un punto base por 715 Esto prueba la unicidad Veamos la existencia Sean Q, Q H dos hipercuádricas distintas Consideremos P = (a 0 : : a n ) y A, A matrices simétricas tales que Q : XAX t = 0 y Q : XA X t = 0 Podemos suponer (a 0,, a n )A(a 0,, a n ) t 0 La ecuación a 0 a 0 λ(a 0,, a n )A + λ (a 0,, a n )A = 0 a n a n tiene siempre una solución en (λ : λ ) P1(k) En efecto, basta tomar λ = (a 0,, a n )A (a 0,, a n ) t y λ = (a 0,, a n )A(a 0,, a n ) t 2 Nota 717 En resumen, dado un punto P Pn, o está en todas las hipercuádricas de un haz (P es un punto base) o está solamente en una de ellas (P no es un punto base) Definición 718 Un haz se dice degenerado si todas las hipercuádricas que lo componen son degeneradas Lema 719 En un haz no degenerado de Pn(k) existen a lo más n + 1 hipercuádricas degeneradas Si además k es algebraicamente cerrado, existe al menos una degenerada Demostración: Sea H un haz no degenerado y sea Q H una hipercuádrica no degenerada Sea Q H otra hipercuádrica Sean A,A, las matrices de las ecuaciones de Q, Q respectivamente Escribamos a 00 a 0n a 00 a 0n A =, A = a 0n a nn a 0n a nn
2 Entonces una hipercuádrica del haz tiene una matriz de la forma λa 00 + µa 00 λa 0n + µa 0n C (λ:µ) =, (λ : µ) P1(k) λa 0n + µa 0n λa nn + µa nn Calculemos los (λ : µ) tales que det(c (λ:µ) ) = 0 Podemos suponer µ 0 ya que det(c (λ:0) ) 0 (si λ 0) y det(c (λ,µ) ) es un polinomio homogéneo de grado n + 1 en las variables (λ, µ) Obsérvese que el determinante de C (λ:1) es un polinomio, en la variable λ, de la forma det(a)λ n+1 + y este polinomio es de grado n + 1, luego tiene a lo sumo n + 1 raíces en k 2 Definición 7110 Los puntos fundamentales de un haz H son los puntos del conjunto F(H) = Sing(Q) Lema 7111 Sea H un haz no degenerado Sea P un punto de Pn Son equivalentes : 1 P es fundamental Q H 2 pol Q (P ) = pol Q (P ) para cualesquiera dos hipercuádricas Q, Q (distintas) de H tales que P / Sing(Q) y P / Sing(Q ) 3 Existen dos hipercuádricas Q, Q (distintas) de H tales que P / Sing(Q) y P / Sing(Q ) y tales que pol Q (P ) = pol Q (P ) Demostración: Sea R un sistema de referencia en Pn(k) 1) 2) Sea P = (a 0 : : a n ) F(H) Entonces existe Q H tal que P Sing(Q ) (esto es: (a 0,, a n )A = 0, donde Q : XA X t = 0) Sean Q, Q H, (Q Q,) tales que P / Sing(Q) Sing(Q ) y supongamos que A, A son matrices representantes de ecuaciones de Q, Q respectivamente Como Q Q (ya que P es singular para Q y no singular para Q) la matriz A puede escribirse de la forma y por tanto A = λa + µa (a 0,, a n )A = (a 0,, a n )(λa + µa ) = λ(a 0,, a n )A + µ(a 0,, a n )A = λ(a 0,, a n )A Esto prueba que pol Q (P ) = pol Q (P ) ya que λ 0 (si lo fuera, Q sería igual a Q y esto no es posible pues P es singular para Q y no singular para Q ) 2) 3) Es evidente 3) 1) Sean A, A matrices representantes de las ecuaciones de dos hipercuádricas Q, Q Sea λ k (no nulo) tal que (a 0,, a n )A = λ(a 0,, a n )A con (a 0 : : a n ) = P La existencia de λ se deduce de la igualdad pol Q (P ) = pol Q (P ) Sea Q = [A λa ] H Es claro que P es singular para Q ya que (a 0,, a n )(A λa ) = (a 0,, a n )A λ(a 0,, a n )A = 0 Nota 7112 De la prueba del teorema anterior se deduce fácilmente que si un punto P es singular para dos hipercuádricas distintas de un haz H, lo es para todas las hipercuádricas de H y éste es degenerado Es decir, si H es no degenerado, F(H) = Sing(Q 0 ) Q 0 H 2
3 72 Clasificación de los haces de cónicas En lo que sigue trabajaremos en P2(C) Algunos de los resultados enunciados son también válidos en el plano proyectivo real La verificación de la validez es dejada como ejercicio, por ejemplo el lema 719 Proposición 721 Sean Q, Q dos cónicas distintas tales que V(Q) V(Q ) contiene a una recta Entonces el haz H(Q, Q ) es degenerado Demostración: Como la base de H(Q, Q ) contiene una recta, todas las cónicas de este haz contienen una recta, luego son degeneradas y el haz es degenerado 2 Proposición 722 Sean Q, Q dos cónicas degeneradas tales que V(Q) V(Q ) es un punto Entonces el haz H(Q, Q ) es degenerado Demostración: Como antes, hay tres casos posibles: Q es un par de rectas y Q es otro par de rectas En este caso, el punto singular de Q debe coincidir con el de Q (en caso contrario, Q y Q se cortarían en más de un punto) Así, el resultado sigue de 7112 Q es un par de rectas, Q es una recta doble y debe pasar por el punto singular de Q (si no, Q cortaría a Q en más de un punto) El resultado sigue de 7112 Q es una recta doble y Q es otra recta doble Así, existe un punto P singular para ambas cónicas y el resultado es consecuencia de 7112 Veamos ahora los diferentes tipos de haces de cónicas (no degenerados) que pueden presentarse Lo haremos usando el 719 y los dos resultados anteriores, en función del número y tipo de cónicas degeneradas que haya en el haz 721 Tipo 1 Consideremos las cuatro rectas r, r, s, s (en posición general) y los puntos A, B, C, D como en la figura 1 Sea H el haz generado por las cónicas Q 1 y Q 2 tales que V(Q 1 ) = r r y V(Q 2 ) = s s 2 Tomemos R = {A, B, C; D} como sistema de referencia Unas matrices M 1, M 2 representantes de Q 1, Q 2 son: M 1 = 0 0 1, M 2 =
4 Veamos cuáles son las cónicas degeneradas de este haz La matriz de una cónica genérica del haz es de la forma M (λ1 :λ 2 ) = λ 1 M 1 + λ 2 M 2, así, M (λ1 :λ 2 ) = λ 1 M 1 + λ 2 M 2 = 0 λ 1 λ 2 λ 1 λ 1 0 λ 2 λ 2 λ 1 λ 2 0 = λ 1λ 2 (λ 1 λ 2 ) Hay tres cónicas degeneradas en el haz, la correspondiente a (λ 1 : 0) = (1 : 0) que es Q 1, la que corresponde a (0 : λ 2 ) = (0 : 1) que es Q 2 y la que se obtiene para (λ 1 : λ 2 ) = (1 : 1) Esta última cónica es otro par de rectas Q 3 cuyo lugar es t t y cuya clase matriz está definida por M 1 + M 2 = correspondiente a la ecuación x 1 (x 0 x 2 ) = 0 Los puntos base son los puntos de corte de los dos pares de rectas, es decir {A, B, C, D}, y los puntos fundamentales son los puntos singulares de las cónicas degeneradas, es decir los puntos diagonales del cuadrivértice Las polares de estos puntos respecto de las cónicas del haz para las que no son singulares, coinciden Tomemos un punto diagonal del cuadrivértice, por ejemplo R = r r Este punto no es singular para la cónica Q 2 ni para Q 3, luego se tiene la igualdad de rectas pol Q2 (R) = pol Q3 (R) (ver 7111) Esta recta pasa por los otros puntos fundamentales (ya que s s es conjugado con todos los puntos del plano, respecto de Q 2 y análogamente ocurre con t t, respecto de Q 3 ) Así, la recta pol Q2 (R) es la recta diagonal que no pasa por R Un razonamiento análogo se aplica a los otros puntos fundamentales El siguiente teorema es una caracterización de las cónicas del haz H Teorema 723 Una cónica de P2(C) pertenece al haz H si y sólo si pasa por los puntos A, B, C, D Demostración: Si una cónica pertenece al haz, pasa por los puntos base {A, B, C, D} Veamos la otra implicación Consideremos R = {A, B, C, D} como sistema de referencia en P2(C) Como antes, consideremos (con las notaciones anteriores) Q 1 y Q 2 Se tiene desde luego la igualdad H(Q 1, Q 2 ) = H Una matrices representantes de Q 1 y Q 2 son: M 1 = , M 2 = Sea Q una cónica que pasa por los puntos A, B, C, D Vamos a probar que su matriz respecto R es combinación de las dos matrices anteriores En efecto, notemos M una matriz de Q Se tiene: M = a 00 a 01 a 02 a 01 a 11 a 12 a 02 a 12 a 22 como A = (1 : 0 : 0) R V(Q) se tiene que a 00 = 0 Análogamente, como B y C también pertenecen a V(Q), entonces, a 11 = 0 y a 22 = 0 como D = (1 : 1 : 1) R V(Q) se tiene que a 01 + a 02 + a 12 = 0, entonces la matriz M es 0 a 01 a 01 a 12 M = a 01 0 a 12 = a 01 M 1 a 12 M 2 a 01 a 12 a 12 0 Luego Q H(Q 1, Q 2 ) 2 Nota 724 (Construcción geométrica de la polar de un punto respecto de una cónica) Lo anterior proporciona un método geométrico para trazar la polar de un punto respecto a una cónica Sea Q una cónica y sea P un punto no perteneciente a V(Q) Se trazan dos rectas por P cada una de ellas cortando a V(Q) en dos puntos distintos (Q no puede reducirse a una recta doble, caso en el que el cálculo de la polar es trivial) Sean estos puntos A, B, C, D Dichos puntos forman un cuadrivértice Tracemos los tres pares de rectas posibles que los contienen Es decir, (A + B) (C + D), (A + C) (B + D), (B + C) (A + D), uno de esos pares es el par de rectas que trazamos al principio Entonces, por el teorema anterior, Q pertenece al haz formado por dos de esos pares de rectas, y como P es fundamental en ese haz, su polar es la recta que pasa por los otros dos puntos fundamentales, es decir, los otros dos puntos diagonales del cuadrivértice A, B, C, D Nota 725 Como aplicación de lo visto anteriormente se pueden resolver los siguientes problemas de determinación de cónicas
5 1 Dados 5 puntos, 3 a 3 no alineados, existe una única cónica no degenerada que pasa por los 5 puntos dados En efecto: se construye la matriz genérica del haz del tipo 1 con 4 de los puntos dados y se halla la cónica del haz que pasa por el punto restante 2 Dadas 5 rectas, 3 a 3 no concurrentes, existe una única cónica no degenerada tangente a las 5 rectas Se usa la cónica dual en P 2(cf prop??4) 3 Dados 4 puntos, 3 a 3 no alineados, y una recta que no pase por ninguno de ellos, hallar las cónicas no degeneradas que pasan por los cuatro puntos y son tangentes a la recta dada 4 Dadas 4 rectas, 3 a 3 no concurrentes, y un punto de ninguna de las rectas, hallar las cónicas no degeneradas que pasan por el punto y son tangentes a las 4 rectas dadas 722 Tipo 2 Consideremos dos pares de rectas r, r, s, s como en la figura 2 : Los pares de rectas se cortan en tres puntos P, Q, R donde P es singular para la cónica Q 1 cuyo lugar es r r Llamemos Q 2 a la cónica de lugar s s y a su punto singular S = s s Sea H el haz definido por las dos cónicas anteriores Como antes calculemos las cónicas degeneradas de H Empecemos tomando un sistema de referencia adecuado Sea R = {P, Q, R; U}, donde U es un punto cualquiera de s \ {S, P } Entonces, unas matrices representantes de Q 1 y Q 2 son, respectivamente: M 1 = y una matriz de una cónica genérica del haz es: M (λ1:λ 2) =, M 2 = λ 1 λ 1 λ 1 0 λ 2 λ 1 λ 2 0 cuyo determinante es λ 2 1λ 2 Así, hay solamente dos cónicas degeneradas en H Como P es un punto base y fundamental, todas las cónicas no degeneradas del haz tienen la misma tangente en P, a saber, la recta s Teorema 726 Conservamos las notaciones anteriores Sea C una cónica no degenerada en P2(C) Son equivalentes: i) C pertenece a H ii) C pasa por los puntos P, Q, R y es tangente a s en el punto P Demostración: i) ii) Esta parte está probada en lo que antecede al teorema ii) i) Elijamos como antes un sistema de referencia R = {P, Q, R, U} en el plano Sea C una cónica que pasa por P, Q, R y es tangente a s en P Una matriz de C, respecto de R, es de la forma: 0 a 01 a 02 A = a 01 0 a 12 a 02 a 12 0 Por otro lado, s tiene como ecuación x 1 x 2 = 0 respecto R Como C es tangente a s en P debe verificarse que ((1, 0, 0)A(x 0, x 1, x 2 ) t = 0) (x 1 x 2 = 0)
6 Es decir a 01 = a 02 Entonces la matriz A es: 0 a 01 a 01 A = a 01 0 a 12 = a 01 M 1 + a 12 M 2 a 01 a 12 0 Lo que prueba que C está en H 2 Nota 727 Como aplicación de lo visto anteriormente se pueden resolver los siguientes problemas de determinación de cónicas 1 Dados 4 puntos, 3 a 3 no alineados, y una recta que pase por uno de ellos, hallar las cónicas no degeneradas que pasan por los cuatro puntos y son tangentes a la recta dada Se construye el haz del tipo 2 obtenido con 3 de los puntos dados y la recta dada, y se halla la cónica del haz que pasa por el punto restante 2 Dadas 4 rectas, 3 a 3 no concurrentes, y un punto de una de ellas, hallar las cónicas no degeneradas que pasan por el punto y son tangentes a las 4 rectas dadas Es el dual del caso anterior 3 Dados 3 puntos no alineados, una recta que pasa por uno de ellos y otra que no pasa por ninguno de ellos, hallar las cónicas no degeneradas que pasan por los puntos dados y son tangentes a las rectas dadas 4 Dadas 3 rectas no concurrentes, un punto de una de ellas y otro que no está en ninguna de ellas, hallar las cónicas no degeneradas que pasan por los puntos dados y son tangentes a las rectas dadas 723 Tipo 3 Consideremos tres rectas r, r, s como en la figura 3 (la recta s aparece repetida pues representará la cónica degenerada cuya cónica lugar es s) Sea P = r r y sean Q, R los puntos de corte de s con r y r respectivamente Veamos cuáles son las cónicas degeneradas del haz H generado por Q 1, cuyo lugar es r r y Q 2, cuyo lugar es s Tomando R = {P, Q, R; U}, con U cualquier punto en posición general respecto de los otros tres, unas matrices representantes de Q 1 y Q 2 son: M 1 = y la matriz de una cónica genérica del haz es de la forma, M 2 = M (λ1 :λ 2 ) = λ 1 M 1 + λ 2 M 2 = λ λ 1 0 λ 1 0 cuyo determinante es λ 2 λ 2 1 Hay solamente dos cónicas degeneradas, Q 1 y Q 2 Nótese que la polar del punto P, por ser fundamental, es la misma para todas las cónicas de H para las que P es no singular Esta polar es la recta s Lo mismo ocurre con los puntos fundamentales Q y R La polar de Q es la recta r, respecto de toda cónica de H para la que Q es no singular Análogamente, la polar de R es r Teorema 728 Con las notaciones anteriores, sea C una cónica en P2(C) Son equivalentes: i) C está en H
7 ii) C pasa por {Q, R} y es tangente a r en Q y a r en R En este caso se dice que las cónicas del haz H son bitangentes en {Q, R} Demostración: i) ii) Hemos probado esta parte en lo que antecede al teorema ii) i) Sea R = {P, Q, R; U} un sistema de referencia en el plano, con U cualquier punto en posición general respecto de los otros tres Unas matrices de unas ecuaciones de las cónicas Q 1, Q 2, que definen el haz, son, respectivamente: M 1 = 0 0 1, M 2 = Sea A una matriz de una ecuación de C verificando ii), con a 00 a 01 a 02 A = a 01 a 11 a 12 a 02 a 12 a 22 Como Q, R V(C) entonces a 11 = a 22 = 0, como r = pol C (Q) entonces a 01 = 0 y como r = pol C (R) entonces a 02 = 0 Así, la matriz A es de la forma: a a 12 = a 12 M 1 + a 00 M 2 0 a 12 0 Es decir, C está en H 2 Nota 729 Como aplicación de lo visto anteriormente se pueden resolver los siguientes problemas de determinación de cónicas 1 Dados dos rectas y tres puntos, dos de ellos incidentes con una recta dada exactamente, hallar las cónicas no degeneradas que pasan por los puntos dados y son tangentes a las rectas dadas Se resolvería calculando, en el haz de bitangentes definido por el par de puntos y rectas incidentes, la cónica que pasa por el tercer punto 2 Dadas 3 rectas no concurrentes, y dos puntos incidentes con una recta dada exactamente, hallar las cónicas no degeneradas que pasan por los puntos dados y son tangentes a las rectas dadas Es el caso dual del anterior 724 Tipo 4 Sean Q 1 una cónica no degenerada, P un punto de Q 1, t la tangente a Q 1 en P Sea t otra recta pasando por P y Q 2 la cónica cuyo lugar es t t Sea P el otro punto de corte de Q 1 con t (ver figura 4) Sea R = {P, P, P ; U} un sistema de referencia verificando: U V(Q 1 ) P = pol Q1 (P ) t
8 Una matriz de una ecuación de Q 2 será M 2 = Por otra parte, y puesto que, de una parte, P, P, U Q 1 y de otra, pol Q1 (P ) (x 1 = 0) y pol Q1 (P ) (x 0 = 0), una matriz de una ecuación de Q 1 será de la forma M 1 = Entonces, una matriz de una cónica genérica del haz H = H(Q 1, Q 2 ) es 0 λ 2 0 M (λ1:λ 2) = λ 2 0 λ 1 0 λ 1 2λ 2 El determinante de esta matriz es λ 3 2, es decir, H tiene una única cónica degenerada, la propia Q 2 El único punto fundamental es P (que es también un punto base) Toda cónica no degenerada del haz tiene a t como recta tangente en P En cambio, y puesto que P no es fundamental, la tangente a P (respecto de una cónica no degenerada de H, y distinta de Q 1 ) es distinta de pol Q1 (P ) Teorema 7210 Con las notaciones anteriores, sea Q una cónica no degenerada de P2(C) Entonces, son equivalentes: i) Q pertenece a H \ Q 1 ii) V(Q 1 ) V(Q) = {P, P }, las tangentes a Q y Q 1 en P son iguales (a t) y las tangentes a Q y Q 1 en P son distintas Demostración: i) ii) Esto se ha probado en lo que antecede al enunciado del teorema ii) i) Como hemos visto, tomado el sistema de referencia de más arriba, unas matrices representantes de Q 1 y Q 2 son: M 1 = 1 0 0, M 2 = Sea Q una cónica no degenerada verificando ii) Escribamos la matriz A de Q como 0 a 01 0 A = a 01 0 a 12, 0 a 12 a 22 donde hemos utilizado que los puntos P, P están en Q y que pol Q (P ) = t (x 1 = 0) Por otra parte, V(Q) sólo corta a V(Q 1 ) en los puntos {P, P } Escribamos las ecuaciones de V(Q) V(Q ) : { x 0 x 1 x 2 2 = 0 2a 01 x 0 x 1 + 2a 12 x 1 x 2 + a 22 x 2 2 = 0 que es equivalente a: { x 0 x 1 x 2 2 = 0 x 2 (2a 12 x 1 + (2a 01 + a 22 )x 2 ) = 0 Las únicas soluciones (x 0 : x 1 : x 2 ) de este sistema con x 2 = 0 son P = (1 : 0 : 0) y P = (0 : 1 : 0) Supongamos ahora que x 2 0 Debe verificarse entonces, 2a 12 x 1 + (2a 01 + a 22 )x 2 = 0 Por otra parte, como pol Q (P ) (a 01 x 0 + a 12 x 2 = 0) (x 0 = 0), se tiene a 12 0 Si 2a 01 + a 22 0, el punto 4a 2 12 (, 2a 01 + a 22, 2a 12 ) 2a 01 + a 22 está en V(Q 1 ) V(Q) y es distinto de P y de P Así pues, debe verificarse 2a 01 + a 22 = 0 Entonces, se tiene: 0 a 01 0 A = a 01 0 a 12 = a 01 M 1 + a 12 M 2 0 a 12 2a 01
9 Esto prueba que Q está en el haz H 2 Nota 7211 Dos cónicas no degeneradas, Q, Q 1, como en el teorema anterior se dirán osculatrices en el punto P, que es el único punto fundamental del haz definido por ambas Nota 7212 Como aplicación de lo visto anteriormente se pueden resolver los siguientes problemas de determinación de cónicas 1 Dada una cónica no degenerada Q y tres puntos, dos de ellos del lugar de Q, hallar una cónica no degenerada que sea osculatriz con Q en uno de los puntos de su lugar, y pase por los otros dos puntos Se resolvería con el haz de osculatrices definido por Q y la cónica definida por la tangente a Q en el punto osculador y la recta que pasa por los dos puntos del lugar de Q 2 Problema dual del anterior? 725 Tipo 5 Sean Q 1 una cónica no degenerada, P un punto de Q 1, t la tangente a Q 1 en P (Ver figura 5) Consideremos el haz H generado por Q 1 y por Q 2, la cónica cuyo lugar es t Este haz tiene solamente un punto base, P, y, al menos, una recta de puntos fundamentales, t Hallemos las cónicas degeneradas de este haz Si tomamos R = {P, P, P ; U} un sistema de referencia tal que U, P V(Q 1 ) \ {P } y P = pol Q (P ) t, unas matrices M 1, M 2 representantes de Q 1, Q 2 son, respectivamente, M 1 = , M 2 = Una matriz de una cónica genérica de este haz tiene la forma M (λ1 :λ 2 ) = λ 1 M 1 + λ 2 M 2 = λ 1 0 2λ 1 0 λ 1 0 λ 2 cuyo determinante vale 2λ 3 1 Así, la única cónica degenerada del haz es Q 2 El punto P es base y fundamental y todas las cónicas no degeneradas del haz tienen a t como tangente en P Teorema 7213 Con las notaciones anteriores, sea Q una cónica no degenerada de P2(C) Son equivalentes: i) Q está en H \ {Q 1 } ii) V(Q) V(Q 1 ) = {P } Demostración: i) ii) Esto ha sido probado en lo que antecede al enunciado de este teorema ii) i) Sea Q una cónica de P2(C) verificando ii) Tomando el mismo sistema de referencia que más arriba, una matriz de Q tiene la forma 0 a 01 a 02 A = a 01 a 11 a 12 a 02 a 12 a 22
10 puesto que P = (1 : 0 : 0) están en Q Usemos ahora la hipótesis de que V(Q) V(Q 1 ) = {P } El sistema de ecuaciones de V(Q) V(Q 1 ) es { 2a01 x 0 x 1 + 2a 02 x 0 x 2 + a 11 x a 12 x 1 x 2 + a 22 x 2 2 = 0 x 0 x 2 + x 2 1 = 0 o equivalentemente { x2 [(2a 02 + a 11 )x 0 + 2a 12 x 1 + a 22 x 2 ] = 0 x 0 x 2 + x 2 1 = 0 En este sistema, si x 2 = 0 entonces x 1 = 0, y la solución es, en este caso, P = (1 : 0 : 0) Si x 2 0, entonces se pueden dividir las dos ecuaciones del sistema anterior por x 2 2, quedando x 0 x 2 = ( x 1 x 2 ) 2 2a 01 ( x 1 x 2 ) 3 + (2a 02 + a 11 )( x 1 x 2 ) 2 + 2a 12 ( x 1 x 2 ) + a 22 = 0 La ecuación de tercer grado no es idénticamente nula porque si a 22 = 0, entonces P V(Q) V(Q 1 ), contra la hipótesis Por otra parte, si tiene una solución λ C, al ser algebraicamente cerrado, entonces el punto (λ 2 : λ : 1) verifica el sistema de ecuaciones anterior y, por tanto, está en V(Q) V(Q 1 ), contra la hipótesis La única posibilidad restante es que la ecuación anterior de tercer grado tenga todos los términos nulos menos el independiente, es decir: a 01 = 2a 02 + a 11 = a 12 = 0 Entonces, se tiene A = 0 0 a a 02 0 a 02 0 a 22 = a 02 M 1 + a 22 M 2 Y, por tanto, Q está en H 2 Nota 7214 Dos cónicas no degeneradas, Q, Q 1, como en el teorema anterior se dirán superosculatrices en el punto P Nota 7215 Como aplicación de lo visto anteriormente se pueden resolver los siguientes problemas de determinación de cónicas 1 Dada una cónica no degenerada Q y dos puntos, uno de ellos del lugar de Q, hallar una cónica no degenerada que sea superosculatriz con Q en el punto de su lugar, y pase por el otro punto Se resolvería con el haz de superosculatrices definido por Q y la cónica definida por la tangente a Q en el punto superosculador 2 Problema dual del anterior? PARA AMPLIAR: EN LO QUE SIGUE SE ESTUDIA LA EQUIVALENCIA ENTRE HACES 73 Equivalencia proyectiva de haces Definición 731 Sean H y H dos haces de hipercuádricas en Pn(k) Diremos que H es (proyectivamente) equivalente a H si existe un cambio de sistema de referencia que lleva uno en el otro Teorema 732 En P2(C), dos haces no degenerados de cónicas, son equivalentes si y sólo si son del mismo tipo Demostración: El teorema de caracterización del tipo 1, permite asegurar que el cambio de sistema de referencia (que formalmente es análogo a una homografía) que transforma los puntos base de un haz en los del otro, cf??, garantiza que los dos haces son equivalentes Los teoremas de caracterización de los tipos 2 y 3, se harían de un modo análogo La diferencia con el tipo 1 está en que no es único el cambio de sistema de referencia entre dos haces de estos tipos Para el tipo 4 es necesario probar que, dadas dos cónicas no degeneradas y dos puntos en cada uno de sus lugares, existe un cambio de sistema de referencia que lleva una cónica en la otra, y los puntos de una en los de la otra El tipo 5 es más fácil que el anterior 2
Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de
 Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
Polaridad. Tangentes. Estudio geométrico de cónicas y cuádricas
 Tema 6- Polaridad Tangentes Estudio geométrico de cónicas y cuádricas En este tema pretendemos estudiar propiedades de V(Q), especialmente en los casos real y complejo, con n =2,3 Para ello, necesitamos
Tema 6- Polaridad Tangentes Estudio geométrico de cónicas y cuádricas En este tema pretendemos estudiar propiedades de V(Q), especialmente en los casos real y complejo, con n =2,3 Para ello, necesitamos
Hipercuádricas afines. Clasificación. Interpretación proyectiva de propiedades afines.
 Tema 8- Hipercuádricas afines Clasificación Interpretación proyectiva de propiedades afines 81 Hipercuádricas afines Sea k un cuerpo de característica distinta de dos Definición 811 Una hipercuádrica afín
Tema 8- Hipercuádricas afines Clasificación Interpretación proyectiva de propiedades afines 81 Hipercuádricas afines Sea k un cuerpo de característica distinta de dos Definición 811 Una hipercuádrica afín
Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas
 Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
Hipercuádricas afines. Clasificación. Elementos afines y euclídeos.
 Capítulo 6 Hipercuádricas afines. Clasificación. Elementos afines y euclídeos. Sea k un cuerpo de característica distinta de dos. Definición 6.0.1. Una hipercuádrica afín en k n es una ecuación de segundo
Capítulo 6 Hipercuádricas afines. Clasificación. Elementos afines y euclídeos. Sea k un cuerpo de característica distinta de dos. Definición 6.0.1. Una hipercuádrica afín en k n es una ecuación de segundo
Interpretación proyectiva de propiedades euclídeas. Elementos
 Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
El grupo lineal proyectivo. Homologías. Afinidades.
 Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05
 - EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
El espacio proyectivo P n (k). Sistemas de referencia. Dualidad. Departamento de Algebra Septiembre El espacio proyectivo P n (k).
 Notas de la asignatura AMPLIACIÓN DE GEOMETRÍA de la Licenciatura de Matemáticas, Facultad de Matemáticas, Universidad de Sevilla, para el curso 2000-01 Departamento de Algebra Septiembre 2000 Tema 1-
Notas de la asignatura AMPLIACIÓN DE GEOMETRÍA de la Licenciatura de Matemáticas, Facultad de Matemáticas, Universidad de Sevilla, para el curso 2000-01 Departamento de Algebra Septiembre 2000 Tema 1-
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas.
 Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
- EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11
 - EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11 Nota: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura Álgebra Lineal y Geometría I. EJERCICIO 1. Sean P 1,...,
- EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11 Nota: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura Álgebra Lineal y Geometría I. EJERCICIO 1. Sean P 1,...,
Tema 5. Cónicas. Asi, para las identificaciones habituales, (punto proyectivo recta vectorial punto de un plano afín ampliado), RP 2 R3 {0}
 Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Las variedades lineales en un K-espacio vectorial V pueden definirse como sigue a partir de los subespacios de V.
 Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares).
 Capítulo 6 Espacios Vectoriales 6.1 Definiciones Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares). Definición 6.1.1 Se dice que
Capítulo 6 Espacios Vectoriales 6.1 Definiciones Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares). Definición 6.1.1 Se dice que
Funciones convexas Definición de función convexa. Tema 7
 Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Tema 7 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Ejercicios de Ampliación de Geometría. Hoja 2
 Ejercicios de Ampliación de Geometría Licenciatura en Ciencias Matemáticas, 2 Curso 27 de Octubre de 2008 Hoja 2 Dualidad y radiaciones. 1. Formular y resolver en el espacio proyectivo dual los siguientes
Ejercicios de Ampliación de Geometría Licenciatura en Ciencias Matemáticas, 2 Curso 27 de Octubre de 2008 Hoja 2 Dualidad y radiaciones. 1. Formular y resolver en el espacio proyectivo dual los siguientes
+ : X V X. (+) P : V X u P + u. (P + u) + v = P + (u + v). Nota La propiedad 1) de la definición anterior implica, en primer lugar, que
 Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
- RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05
 - RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05 Ejercicio 1. Junio 98 En el espacio proyectivo ordinario de dimensión 4, se consideran dos rectas, r y s, que se cruzan. Probar la verdad
- RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05 Ejercicio 1. Junio 98 En el espacio proyectivo ordinario de dimensión 4, se consideran dos rectas, r y s, que se cruzan. Probar la verdad
Recta en en el plano
 Universidad Nacional de Rosario Facultad de Ciencias Exactas, Ingeniería y Agrimensura Escuela de Ciencias Exactas y Naturales Departamento de Matemática Recta en en el plano Autor: Dr. Francisco Vittone
Universidad Nacional de Rosario Facultad de Ciencias Exactas, Ingeniería y Agrimensura Escuela de Ciencias Exactas y Naturales Departamento de Matemática Recta en en el plano Autor: Dr. Francisco Vittone
1. Espacio vectorial. Subespacios vectoriales
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Sea k un cuerpo. 1. Espacio vectorial. Subespacios vectoriales Definición 1.1. Un k-espacio vectorial o espacio vectorial
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Sea k un cuerpo. 1. Espacio vectorial. Subespacios vectoriales Definición 1.1. Un k-espacio vectorial o espacio vectorial
Tema 11.- Autovalores y Autovectores.
 Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
2 Espacios vectoriales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Teorema del Valor Medio
 Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Tema 6 Teorema del Valor Medio Abordamos en este tema el estudio del resultado más importante del cálculo diferencial en una variable, el Teorema del Valor Medio, debido al matemático italo-francés Joseph
Seis problemas resueltos de geometría
 Problema 1 a) Dados los puntos P(4, 2, 3) y Q(2, 0, 5), da la ecuación implícita del plano π de modo que el punto simétrico de P respecto a π es Q. b) Calcula el valor del parámetro λ R para que el plano
Problema 1 a) Dados los puntos P(4, 2, 3) y Q(2, 0, 5), da la ecuación implícita del plano π de modo que el punto simétrico de P respecto a π es Q. b) Calcula el valor del parámetro λ R para que el plano
6.8. Descomposición mediante valores singulares. v 2 =
 68 Descomposición mediante valores singulares Los valores singulares de una matriz m n Supongamos que A es una matriz real cualquiera Los autovalores de A T A tienen la siguiente propiedad A T Ax = λx
68 Descomposición mediante valores singulares Los valores singulares de una matriz m n Supongamos que A es una matriz real cualquiera Los autovalores de A T A tienen la siguiente propiedad A T Ax = λx
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones
![Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones Semana 09 [1/28] Sucesiones. 29 de abril de Sucesiones](/thumbs/49/25360651.jpg) Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
Semana 09 [1/28] 29 de abril de 2007 Semana 09 [2/28] Definición Sucesión Una sucesión real es una función: f : N R n f (n) Observaciones Para distinguir a una sucesión de las demás funciones, se ocupará
El teorema del valor intermedio
 Ya hemos tratado en un artículo anterior el problema de la continuidad de una función. Ahora nos hemos de preguntar sobre las ventajas que, en análisis matemático, nos proporciona este hecho. Existen una
Ya hemos tratado en un artículo anterior el problema de la continuidad de una función. Ahora nos hemos de preguntar sobre las ventajas que, en análisis matemático, nos proporciona este hecho. Existen una
Estudio proyectivo 23. Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España TEMA II
 Estudio proyectivo 23 Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA II
Estudio proyectivo 23 Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA II
Capítulo 7. Espacios vectoriales. 7.1 Definición y ejemplos
 Capítulo Espacios vectoriales.1 Definición y ejemplos Un espacio vectorial sobre un cuerpo K (que supondremos conmutativo es un conjunto no vacío junto con 1. una operación interna, +, a la que llamaremos
Capítulo Espacios vectoriales.1 Definición y ejemplos Un espacio vectorial sobre un cuerpo K (que supondremos conmutativo es un conjunto no vacío junto con 1. una operación interna, +, a la que llamaremos
Funciones convexas Definición de función convexa. Tema 14
 Tema 14 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Tema 14 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones definidas en intervalos, las funciones
Análisis Matemático I
 Análisis Matemático I Funciones Implícitas Francisco Montalvo Curso 2011/12 Índice 1. Teorema de existencia de Funciones Implícitas 1 1.1. Punto fijo.............................. 1 1.2. Planteamiento............................
Análisis Matemático I Funciones Implícitas Francisco Montalvo Curso 2011/12 Índice 1. Teorema de existencia de Funciones Implícitas 1 1.1. Punto fijo.............................. 1 1.2. Planteamiento............................
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Podemos pues formular los dos problemas anteriores en términos de matrices.
 Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
si existe un entorno V de a contenido en A, tal que la diferencia f(x) f(a) no cambia de signo cuando x V :
 Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Movimientos. Teorema de Cartan-Dieudonné. Semejanzas.
 Capítulo 5 Movimientos. Teorema de Cartan-Dieudonné. Semejanzas. 5.1 Isometrías y movimientos Partimos de un espacio euclídeo (X, V, +) y recordemos que una isometría de V es un elemento ϕ Gl(V ) que conserva
Capítulo 5 Movimientos. Teorema de Cartan-Dieudonné. Semejanzas. 5.1 Isometrías y movimientos Partimos de un espacio euclídeo (X, V, +) y recordemos que una isometría de V es un elemento ϕ Gl(V ) que conserva
La regla de Cramer. a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2... a n1 x 1 + a n2 x
 Consideremos un sistema de n ecuaciones lineales con n incógnitas como el siguiente: a 11 x 1 + a 1 x +. + a 1n x n b 1 a 1 x 1 + a x +. + a n x n b... a n1 x 1 + a n x +. + a nn x n b n La matriz de los
Consideremos un sistema de n ecuaciones lineales con n incógnitas como el siguiente: a 11 x 1 + a 1 x +. + a 1n x n b 1 a 1 x 1 + a x +. + a n x n b... a n1 x 1 + a n x +. + a nn x n b n La matriz de los
ELEMENTOS DE GEOMETRÍA. Eduardo P. Serrano
 ELEMENTOS DE GEOMETRÍA Eduardo P. Serrano Este Apunte de Clase está dirigido a los alumnos de la materia Elementos de Cálculo Numérico para Biólogos. Tiene por objeto exponer algunos conceptos básicos
ELEMENTOS DE GEOMETRÍA Eduardo P. Serrano Este Apunte de Clase está dirigido a los alumnos de la materia Elementos de Cálculo Numérico para Biólogos. Tiene por objeto exponer algunos conceptos básicos
TEMA 4 ESPACIOS VECTORIALES
 TEMA 4 ESPACIOS VECTORIALES Índice 4.1. Definición y propiedades.................. 101 4.1.1. Dependencia e independencia lineal....... 103 4.2. Subespacios vectoriales................... 105 4.2.1. Ecuaciones
TEMA 4 ESPACIOS VECTORIALES Índice 4.1. Definición y propiedades.................. 101 4.1.1. Dependencia e independencia lineal....... 103 4.2. Subespacios vectoriales................... 105 4.2.1. Ecuaciones
ÁLGEBRA LINEAL. EXAMEN EXTRAORDINARIO 2 de julio de 2012 Duración del examen: 3 horas Fecha publicación notas: 11 de julio
 ÁLGEBRA LINEAL EXAMEN EXTRAORDINARIO 2 de julio de 22 Duración del examen: 3 horas Fecha publicación notas: de julio Fecha revisión examen: 3 de julio Apellidos: Nombre: Grupo: Titulación: ESCRIBA EL APELLIDO
ÁLGEBRA LINEAL EXAMEN EXTRAORDINARIO 2 de julio de 22 Duración del examen: 3 horas Fecha publicación notas: de julio Fecha revisión examen: 3 de julio Apellidos: Nombre: Grupo: Titulación: ESCRIBA EL APELLIDO
ÍNDICE INTRODUCCIÓN... 9 INSTRUCCIONES PARA EL LECTOR... 13
 ÍNDICE INTRODUCCIÓN 9 INSTRUCCIONES PARA EL LECTOR 13 CAPÍTULO 1 GENERALIDADES TEOREMA DE LAGRANGE I Grupos 17 II Subgrupos 25 III Orden de un grupo 36 IV Índice de un subgrupo 40 Ejercicios correspondientes
ÍNDICE INTRODUCCIÓN 9 INSTRUCCIONES PARA EL LECTOR 13 CAPÍTULO 1 GENERALIDADES TEOREMA DE LAGRANGE I Grupos 17 II Subgrupos 25 III Orden de un grupo 36 IV Índice de un subgrupo 40 Ejercicios correspondientes
Clasificación Afín de las Cuádricas
 Capítulo VIII Clasificación Afín de las Cuádricas Como no puede ser de otro modo, en este capítulo seguiremos suponiendo que k es un cuerpo conmutativo de característica distinta de 2, que todos los espacios
Capítulo VIII Clasificación Afín de las Cuádricas Como no puede ser de otro modo, en este capítulo seguiremos suponiendo que k es un cuerpo conmutativo de característica distinta de 2, que todos los espacios
3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3]
![3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3] 3. Calcular una base normalizada asociada a esa referencia y las coordenadas en ella del punto [1, 2, 5, 3]](/thumbs/68/59191793.jpg) Ejercicio 0.1 Sea K un cuerpo con q elementos y sea V un espacio vectorial de dimensión n + 1 sobre K. Calcular cuantas bases distintas (como subconjuntos) tiene V, cuantas referencias distintas hay en
Ejercicio 0.1 Sea K un cuerpo con q elementos y sea V un espacio vectorial de dimensión n + 1 sobre K. Calcular cuantas bases distintas (como subconjuntos) tiene V, cuantas referencias distintas hay en
Universidad Nacional de Colombia Departamento de Matemáticas Álgebra Lineal - Grupo 1 Resumen Unidad n 3
 Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 1 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
Universidad Nacional de Colombia Departamento de Matemáticas 1000003-5 Álgebra Lineal - Grupo 1 Resumen Unidad n 3 Vectores en R n Definición. El conjunto de las n-tuplas ordenadas de números reales se
Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero
 Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero 11 de Diciembre de 2008 2 B.G.O. 104.- Determina si los siguientes subconjuntos del espacio vectorial correspondiente son subvariedades afines:
Ejercicios resueltos de Álgebra, hoja 2. Beatriz Graña Otero 11 de Diciembre de 2008 2 B.G.O. 104.- Determina si los siguientes subconjuntos del espacio vectorial correspondiente son subvariedades afines:
11. Cónicas proyectivas
 24 FRANCISCO JAVIER GALLEGO RODRIGO. Cónicas proyectivas Recordemos que una de las razones para construir el espacio proyectivo fue estudiar qué les pasa a los objetos afines cuando nos vamos al infinito.
24 FRANCISCO JAVIER GALLEGO RODRIGO. Cónicas proyectivas Recordemos que una de las razones para construir el espacio proyectivo fue estudiar qué les pasa a los objetos afines cuando nos vamos al infinito.
Selectividad Junio 2007 JUNIO 2007
 Selectividad Junio 7 JUNIO 7 PRUEBA A PROBLEMAS 1.- Sea el plano π + y z 5 = y la recta r = y = z. Se pide: a) Calcular la distancia de la recta al plano. b) Hallar un plano que contenga a r y sea perpendicular
Selectividad Junio 7 JUNIO 7 PRUEBA A PROBLEMAS 1.- Sea el plano π + y z 5 = y la recta r = y = z. Se pide: a) Calcular la distancia de la recta al plano. b) Hallar un plano que contenga a r y sea perpendicular
Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos.
 Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada
Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Funciones convexas Definición de función convexa. Tema 10
 Tema 10 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones reales de variable real definidas en
Tema 10 Funciones convexas Los resultados obtenidos en el desarrollo del cálculo diferencial nos permiten estudiar con facilidad una importante familia de funciones reales de variable real definidas en
Sistemas de Ecuaciones Lineales y Matrices
 Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Capítulo 4 Sistemas de Ecuaciones Lineales y Matrices El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación lineal con n-incógnitas x 1, x 2,, x n es una
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
Unidad 6 Geometría euclídea. Producto escalar
 Unidad 6 Geometría euclídea Producto escalar PÁGINA 131 SOLUCIONES 1 La recta 4 x 3y + 6 = 0 tiene de pendiente 4 m = 3 4 Paralela: y 1 = ( x ) 4x 3y 5 = 0 3 4 Perpendicular: y 1 = ( x ) 3x + 4y 10 = 0
Unidad 6 Geometría euclídea Producto escalar PÁGINA 131 SOLUCIONES 1 La recta 4 x 3y + 6 = 0 tiene de pendiente 4 m = 3 4 Paralela: y 1 = ( x ) 4x 3y 5 = 0 3 4 Perpendicular: y 1 = ( x ) 3x + 4y 10 = 0
x, y = x 0 y 0 + x 1 y 1 + x 2 y 2 + x 3 y 3. Es fácil ver que verifica 1. Es simétrica. x, y = y, x para todo x, y R 4.
 1 Tema 2. Sección 1. Espacio vectorial de Minkowski. Manuel Gutiérrez. Departamento de Álgebra, Geometría y Topología. Universidad de Málaga. 29071-Málaga. Spain. Abril de 2010. En este capítulo se recordará
1 Tema 2. Sección 1. Espacio vectorial de Minkowski. Manuel Gutiérrez. Departamento de Álgebra, Geometría y Topología. Universidad de Málaga. 29071-Málaga. Spain. Abril de 2010. En este capítulo se recordará
1. Producto escalar. Propiedades Norma de un vector. Espacio normado. 1.2.Ortogonalidad. Ángulos. 1.4.Producto escalar en V 3.
 . Producto escalar. Propiedades... Norma de un vector. Espacio normado...ortogonalidad. Ángulos..3.Producto escalar en V..4.Producto escalar en V 3.. Producto vectorial de dos vectores de V 3...Expresión
. Producto escalar. Propiedades... Norma de un vector. Espacio normado...ortogonalidad. Ángulos..3.Producto escalar en V..4.Producto escalar en V 3.. Producto vectorial de dos vectores de V 3...Expresión
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
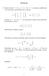 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
Tema 2: Diagonalización
 TEORÍA DE ÁLGEBRA II: Tema 2. DIPLOMATURA DE ESTADÍSTICA 1 Tema 2: Diagonalización 1 Introducción Sea f : R n R n lineal. Dada una base B de R n podemos asociar a f la matriz A 1 = [f, B] M n. Si C es
TEORÍA DE ÁLGEBRA II: Tema 2. DIPLOMATURA DE ESTADÍSTICA 1 Tema 2: Diagonalización 1 Introducción Sea f : R n R n lineal. Dada una base B de R n podemos asociar a f la matriz A 1 = [f, B] M n. Si C es
Breve introducción a Matrices
 1 - Introducción Breve introducción a Matrices Def. 1.1 Llamaremos matriz de orden mxn a la disposición en m filas y n columnas de mxn números 1. Observación 1.1 Convendremos que los números a los que
1 - Introducción Breve introducción a Matrices Def. 1.1 Llamaremos matriz de orden mxn a la disposición en m filas y n columnas de mxn números 1. Observación 1.1 Convendremos que los números a los que
Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León
 Selectividad Junio 14 Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger una de
Selectividad Junio 14 Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº páginas: INDICACIONES: 1.- OPTATIVIDAD: El alumno deberá escoger una de
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
SEPTIEMBRE 2005 PRUEBA A. b) Para a = 1, calcúlese la recta que pasa por (1, 1, 1) y se apoya en r y s.
 Selectividad Septiembre 5 SEPTIEMBRE 5 PRUEBA A PROBLEMAS - a) Calcúlense los valores de a para los cuales las rectas r x = λ y s y = 3+λ son perpendiculares z = + a λ b) Para a =, calcúlese la recta que
Selectividad Septiembre 5 SEPTIEMBRE 5 PRUEBA A PROBLEMAS - a) Calcúlense los valores de a para los cuales las rectas r x = λ y s y = 3+λ son perpendiculares z = + a λ b) Para a =, calcúlese la recta que
Sistemas de Ecuaciones Lineales. Matrices y determinantes.
 Capítulo 3 Sistemas de Ecuaciones Lineales Matrices y determinantes 31 Sistemas de Ecuaciones Lineales El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación
Capítulo 3 Sistemas de Ecuaciones Lineales Matrices y determinantes 31 Sistemas de Ecuaciones Lineales El problema central del Álgebra Lineal es la resolución de ecuaciones lineales simultáneas Una ecuación
Matrices Inversas. Rango Matrices Elementales
 Matrices Inversas. Rango Matrices Elementales Araceli Guzmán y Guillermo Garro Facultad de Ciencias UNAM Semestre 2018-1 doyouwantmektalwar.wordpress.com Matrices Matrices identidad La matriz identidad
Matrices Inversas. Rango Matrices Elementales Araceli Guzmán y Guillermo Garro Facultad de Ciencias UNAM Semestre 2018-1 doyouwantmektalwar.wordpress.com Matrices Matrices identidad La matriz identidad
PAU Madrid. Matemáticas II. Año Examen de septiembre. Opción A. Ejercicio 1. Valor: 2 puntos.
 Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
Matrices y sistemas de ecuaciones
 Matrices y sistemas de ecuaciones María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Matrices y sistemas de ecuaciones Matemáticas I 1 / 59 Definición de Matriz Matrices
Matrices y sistemas de ecuaciones María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Matrices y sistemas de ecuaciones Matemáticas I 1 / 59 Definición de Matriz Matrices
4.2 Producto escalar.
 Producto escalar. 147 Este resultado tiene su recíproco, es decir, cualquier matriz cuadrada A define la forma bilineal b(x, y) =x T Ay Si b es simétrica, la matriz A es simétrica. Si b es definida positiva,
Producto escalar. 147 Este resultado tiene su recíproco, es decir, cualquier matriz cuadrada A define la forma bilineal b(x, y) =x T Ay Si b es simétrica, la matriz A es simétrica. Si b es definida positiva,
ÁLGEBRA II (LSI PI) UNIDAD Nº 2 GEOMETRÍA ANALÍTICA. Facultad de Ciencias Exactas y Tecnologías UNIVERSIDAD NACIONAL DE SANTIAGO DEL ESTERO
 17 ÁLGEBRA II (LSI PI) UNIDAD Nº GEOMETRÍA ANALÍTICA Facultad de Ciencias Exactas y Tecnologías aa Error! No hay texto con el estilo especificado en el documento. 1 UNIVERSIDAD NACIONAL DE SANTIAGO DEL
17 ÁLGEBRA II (LSI PI) UNIDAD Nº GEOMETRÍA ANALÍTICA Facultad de Ciencias Exactas y Tecnologías aa Error! No hay texto con el estilo especificado en el documento. 1 UNIVERSIDAD NACIONAL DE SANTIAGO DEL
ALGEBRA LINEAL Segundo Semestre. Parte II
 1 Universidad Nacional de La Plata Facultad de Ciencias Astronómicas y Geofísicas ALGEBRA LINEAL 2015 Segundo Semestre Parte II 2 1. Valores y Vectores propios. Diagonalización.Forma de Jordan. 1.1. Polinomios
1 Universidad Nacional de La Plata Facultad de Ciencias Astronómicas y Geofísicas ALGEBRA LINEAL 2015 Segundo Semestre Parte II 2 1. Valores y Vectores propios. Diagonalización.Forma de Jordan. 1.1. Polinomios
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones.
 Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Tema 4. Espacio Proyectivo.
 Tema 4. Espacio Proyectivo. Definición y modelos. *) El origen de la geometría proyectiva está relacionado con el estudio de la perspectiva, para conseguir cuadros o planos realistas del mundo 3-dimensional;
Tema 4. Espacio Proyectivo. Definición y modelos. *) El origen de la geometría proyectiva está relacionado con el estudio de la perspectiva, para conseguir cuadros o planos realistas del mundo 3-dimensional;
Conjuntos, relaciones y funciones Susana Puddu
 Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Susana Puddu 1. Repaso sobre la teoría de conjuntos. Denotaremos por IN al conjunto de los números naturales y por ZZ al de los enteros. Dados dos conjuntos A y B decimos que A está contenido en B o también
Transformaciones lineales
 CAPíTULO 4 Transformaciones lineales En este capítulo estudiamos las primeras propiedades de las transformaciones lineales entre espacios vectoriales. 1. Construcciones de transformaciones lineales Lema
CAPíTULO 4 Transformaciones lineales En este capítulo estudiamos las primeras propiedades de las transformaciones lineales entre espacios vectoriales. 1. Construcciones de transformaciones lineales Lema
Autovalores y autovectores Diagonalización y formas canónicas
 Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Autovalores y autovectores Diagonalización y formas canónicas Autovalores y autovectores.propiedades Sea V un espacio vectorial sobre K y f End(V ). Fijada una base de V, existirá una matriz cuadrada A,
Espacios vectoriales
 CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
Problemas de Geometría Proyectiva
 Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
El examen de Geometría afín y proyectiva del 19 de junio del 2006 resuelto por cortesía de Alberto Castellón
 El examen de Geometría afín y proyectiva del 19 de junio del 2006 resuelto por cortesía de Alberto Castellón 1) Considérese un símplex {O 1, O 2, O 3, I} de un plano proyectivo con A y B los puntos diagonales
El examen de Geometría afín y proyectiva del 19 de junio del 2006 resuelto por cortesía de Alberto Castellón 1) Considérese un símplex {O 1, O 2, O 3, I} de un plano proyectivo con A y B los puntos diagonales
Capítulo 2. Determinantes Introducción. Definiciones
 Capítulo 2 Determinantes 2.1. Introducción. Definiciones Si nos centramos en la resolución de un sistema A x = b con A una matriz n n, podemos calcular A 1 y la resolución es inmendiata. El problema es
Capítulo 2 Determinantes 2.1. Introducción. Definiciones Si nos centramos en la resolución de un sistema A x = b con A una matriz n n, podemos calcular A 1 y la resolución es inmendiata. El problema es
Problema a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente.
 Problema 717.- a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente. Hallar el lugar geométrico de los puntos comunes a
Problema 717.- a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente. Hallar el lugar geométrico de los puntos comunes a
4. Aplicaciones: rango de una matriz y ecuaciones de un subespacio
 TEMA 2 ESPACIOS VECTORIALES 35 4 Aplicaciones: rango de una matriz y ecuaciones de un subespacio Terminaremos este tema aprovechando la teoría de espacios vectoriales que hemos estudiado para obtener algunas
TEMA 2 ESPACIOS VECTORIALES 35 4 Aplicaciones: rango de una matriz y ecuaciones de un subespacio Terminaremos este tema aprovechando la teoría de espacios vectoriales que hemos estudiado para obtener algunas
ÁLGEBRA Algunas soluciones a la Práctica 8
 ÁLGEBRA Algunas soluciones a la Práctica 8 Aplicaciones bilineales y formas cuadráticas (Curso 2008 2009 6. Sean a y b dos números reales. En el espacio P 1 de los polinomios de grado menor o igual que
ÁLGEBRA Algunas soluciones a la Práctica 8 Aplicaciones bilineales y formas cuadráticas (Curso 2008 2009 6. Sean a y b dos números reales. En el espacio P 1 de los polinomios de grado menor o igual que
Capítulo V. T 2 (e, e
 Capítulo V Métricas En este capítulo y en los siguientes, el cuerpo base de los espacios vectoriales que se consideren será de característica distinta de 2. Empecemos recordando las nociones básicas que
Capítulo V Métricas En este capítulo y en los siguientes, el cuerpo base de los espacios vectoriales que se consideren será de característica distinta de 2. Empecemos recordando las nociones básicas que
Diagonalización. Tema Valores y vectores propios Planteamiento del problema Valores y vectores propios
 61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
Capítulo V. Valores y vectores propios. Diagonalización de operadores lineales.
 Capítulo V Valores y vectores propios. Diagonalización de operadores lineales. Hemos visto que la aplicaciones lineales de en están definidas a través de una expresión de la forma ; pero esta fórmula puede
Capítulo V Valores y vectores propios. Diagonalización de operadores lineales. Hemos visto que la aplicaciones lineales de en están definidas a través de una expresión de la forma ; pero esta fórmula puede
Sobre vectores y matrices. Independencia lineal. Rango de una matriz
 Espacios vectoriales Llamaremos R 2 al conjunto de todos los pares ordenados de la forma (a 1, a 2 ) tal que a 1, a 2 R. Es decir: R 2 = {(a 1, a 2 ) : a 1, a 2 R} De la misma forma: R 3 = {(a 1, a 2,
Espacios vectoriales Llamaremos R 2 al conjunto de todos los pares ordenados de la forma (a 1, a 2 ) tal que a 1, a 2 R. Es decir: R 2 = {(a 1, a 2 ) : a 1, a 2 R} De la misma forma: R 3 = {(a 1, a 2,
520142: ALGEBRA y ALGEBRA LINEAL
 520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
520142: ALGEBRA y ALGEBRA LINEAL Segundo Semestre 2008, Universidad de Concepción CAPITULO 10: Espacios Vectoriales DEPARTAMENTO DE INGENIERIA MATEMATICA Facultad de Ciencias Físicas y Matemáticas 1 Definición
Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES
 Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES Prof. Rafael López Camino Universidad de Granada 1 Matrices Definición 1.1 Una matriz (real) de n filas y m columnas es una expresión de la forma a 11...
Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES Prof. Rafael López Camino Universidad de Granada 1 Matrices Definición 1.1 Una matriz (real) de n filas y m columnas es una expresión de la forma a 11...
Descomposición en valores singulares Notas para los cursos 21 y 22 (J.L. Mancilla Aguilar)
 Valores Singulares Descomposición en valores singulares Notas para los cursos y (JL Mancilla Aguilar) Tanto los valores singulares como la descomposición en valores singulares de una matriz son conceptos
Valores Singulares Descomposición en valores singulares Notas para los cursos y (JL Mancilla Aguilar) Tanto los valores singulares como la descomposición en valores singulares de una matriz son conceptos
6.6. Diagonalización de matrices simétricas o hermitianas. Ejemplo de una diagonalización de una matriz simétrica
 6.6 Diagonalización de matrices simétricas o hermitianas Ejemplo de una diagonalización de una matriz simétrica Matrices hermitianas Los autovalores de las matrices reales simétricas o complejas hermitianas
6.6 Diagonalización de matrices simétricas o hermitianas Ejemplo de una diagonalización de una matriz simétrica Matrices hermitianas Los autovalores de las matrices reales simétricas o complejas hermitianas
Distancia entre dos rectas que se cruzan Perpendicular común
 Perpendicular común En un espacio de tres dimensiones dos rectas se cruzan cuando no tienen ningún punto en común y no están contenidas en el mismo plano. Si no tienen ningún punto en común pero sí que
Perpendicular común En un espacio de tres dimensiones dos rectas se cruzan cuando no tienen ningún punto en común y no están contenidas en el mismo plano. Si no tienen ningún punto en común pero sí que
Es trivial generalizar la definición al caso de varios conjuntos: A B C, etc.
 Tema 1 Espacios Vectoriales 1.1 Repaso de Estructuras Algebraicas 1. Producto cartesiano de conjuntos. Dados los conjuntos A y B, se llama producto cartesiano de A y B, y se denota por A B al conjunto
Tema 1 Espacios Vectoriales 1.1 Repaso de Estructuras Algebraicas 1. Producto cartesiano de conjuntos. Dados los conjuntos A y B, se llama producto cartesiano de A y B, y se denota por A B al conjunto
Apéndice sobre ecuaciones diferenciales lineales
 Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Álgebra Lineal. Tema 8. Valores y vectores propios. Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas
 Álgebra Lineal Tema 8. Valores y vectores propios Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR
Álgebra Lineal Tema 8. Valores y vectores propios Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR
ALGEBRA LINEAL Y GEOMETRÍA I
 ALGEBRA LINEAL Y GEOMETRÍA I TEMA 3: Autovalores y Autovectores. Introducción Ya conoces que las aplicaciones lineales entre espacios vectoriales, al elegir bases en ellos, las puedes representar por matrices.
ALGEBRA LINEAL Y GEOMETRÍA I TEMA 3: Autovalores y Autovectores. Introducción Ya conoces que las aplicaciones lineales entre espacios vectoriales, al elegir bases en ellos, las puedes representar por matrices.
Ejemplo Considére un sistema de dos ecuaciones con dos incognitas. ax + by = m. acx + ady = n
 Sistemas de dos ecuaciones lineales con dos incognitas Ejemplo Considére un sistema de dos ecuaciones con dos incognitas ax + by = m cx + dy = n (donde a, b, c, d, m, n son números reales dados). Para
Sistemas de dos ecuaciones lineales con dos incognitas Ejemplo Considére un sistema de dos ecuaciones con dos incognitas ax + by = m cx + dy = n (donde a, b, c, d, m, n son números reales dados). Para
Operaciones elementales
 Operaciones elementales Objetivos Conocer y justificar operaciones elementales con ecuaciones de un sistema de ecuaciones lineales, conocer su forma matricial (operaciones elementales con renglones de
Operaciones elementales Objetivos Conocer y justificar operaciones elementales con ecuaciones de un sistema de ecuaciones lineales, conocer su forma matricial (operaciones elementales con renglones de
