Polaridad. Tangentes. Estudio geométrico de cónicas y cuádricas
|
|
|
- Luz Villalba Franco
- hace 7 años
- Vistas:
Transcripción
1 Tema 6- Polaridad Tangentes Estudio geométrico de cónicas y cuádricas En este tema pretendemos estudiar propiedades de V(Q), especialmente en los casos real y complejo, con n =2,3 Para ello, necesitamos introducir el concepto de polaridad, que nos permitirá estudiar secciones lineales de V(Q), es decir V(Q) L con L una variedad lineal proyectiva Hablando en términos médicos, haremos un TAC a V(Q), cuando estudiemos V(Q) L siendo L un plano, o haremos una punción a V(Q), cuando estudiemos V(Q) L siendo L una recta 61 Polaridad Sea Q una hipercuádrica en Pn(k), con ecuación XAX t = 0 en cierto sistema de referencia R Definición 611 Diremos que dos puntos P y P son conjugados respecto de Q, que notaremos P Q P, cuando se verifique: donde P = (a 0 : : a n ) R y P = (a 0 : : a n) R ( ) (a 0,, a n )A a 0 a n = 0, Nota 612 Es preciso observar que la definición anterior no depende del sistema de referencia En efecto, si R es otro sistema de referencia, de modo que λx = Y M representa las ecuaciones del cambio de R a R, según la nota 516, unas ecuaciones de Q respecto de R son Y BY t = 0, con B = MAM t Por tanto,l si P = (b 0 : : b n ) R y P = (b 0 : : b n) R, se tiene que λ(a 0,, a n ) = (b 0,, b n )M y µ(a 0,, a n) = (b 0,, b n)m Por tanto (a 0,, a n )A a 0 b 0 = 0 (b 0,, b n )B = 0 a n b n Por esta razón, para simplificar, la condición ( ) de conjugación la expresaremos por P AP t = 0, siendo conscientes de que estamos abusando del lenguaje, confundiendo con un mismo nombre un punto y sus coordenadas respecto de un sistema de referencia fijo Nota 613 La relación de conjugación respecto de Q es simétrica, pero no es ni transitiva ni reflexiva, en general De hecho, los puntos autoconjugados respecto de Q son, precisamente, los de V(Q) Definición 614 Llamaremos polar de un punto respecto de Q al conjunto {P Pn(k) P Q P }, y lo representaremos por pol Q (P ) Nota 615 pol Q (P ) es una variedad lineal proyectiva de ecuación P AX t = 0 Si P A = 0, entonces pol Q (P ) = Pn(k), diremos que P es un punto singular de Q, y al conjunto de todos ellos lo llamaremos lugar singular de Q: Sing(Q) Si P no es singular, entonces P AX t = 0 es la ecuación de un hiperplano En cualquier caso, dim pol Q (P ) n 1 Por otra parte Sing(Q) es una variedad lineal proyectiva dada por las ecuaciones XA = 0, luego es de dimensión n rango(q) Así, las hipercuádricas no degeneradas se caracterizan por no tener puntos singulares Generalizamos ahora el concepto de polar de una variedad lineal proyectiva cualquiera Definición 616 Si L Pn es una variedad lineal proyectiva, llamaremos polar de L respecto de Q al conjunto de puntos conjugados con todos los de L, es decir pol Q (L) = {P Pn L pol Q (P )} Enumeramos en la proposición siguiente una larga lista de propiedades elementales Proposición 617 Los siguientes resultados se refieren a variedades lineales proyectivas de Pn 1 Si L 1 L 2 entonces pol Q (L 1 ) pol Q (L 2 ) 2 pol Q (L) Sing(Q) = pol Q (Pn) 3 pol Q ( i I L i) = i I pol Q(L i ) 4 pol Q (L) = P L pol Q(P ) y por tanto, pol Q (L) es una variedad lineal proyectiva 5 pol Q ( i I L i) i I pol Q(L i ) 6 pol Q (pol Q (L)) L
2 7 dim pol Q (L) n dim L 1 Demostración: 1 Es consecuencia de la definición 2 Aplicar 1 a L Pn 3 Es consecuencia de la equivalencia pol Q (P ) L i para todo i si y sólo si pol Q (P ) L i 4 Aplicar 3 a L = P L P 5 Es consecuencia de 1 aplicado a L i L i para todo i 6 Primero pol Q (pol Q (P )) P por definición Después aplicar 3 y 5 a L = P L P 7 Tomar una base {P 0,, P r } de L, con dim L = r Por 3 pol Q (L) = pol Q (P 0 ) pol Q (P r ), y cada pol Q (P i ) es un hiperplano o Pn La intersección de un número menor o igual que r + 1 hiperplanos es de dimensión mayor o igual que n (r + 1) 2 Proposición 618 Si Q es no degenerada, las propiedades 5, 6 y 7 anteriores son igualdades Demostración: 7 Sean {P 0,, P r } una base de L Si XAX t = 0 es una ecuación de Q, A 0, y por tanto, {P 0 A,, P r A} son vectores linealmente independientes Luego dim pol Q (P 0 ) pol Q (P r ) = n rango{p 0 A,, P r A} = n r 1 6 Aplicar lo anterior para calcular la dimensión de pol Q (pol Q (L)) que es dim L 5 Se tiene por 6 que L i = pol Q(L i ) si y sólo si L i = pol Q (L i ) Luego pol Q ( L i ) = pol Q ( pol Q (L i)) 3 = pol Q (pol Q ( L i)) 6 = pol Q (L i ) Ejercicio 1 Dar contraejemplos de las igualdades anteriores, en los casos en que Q sea degenerada PARA AMPLIAR: Nota 619 Si Q es una hipercuádrica no degenerada de Pn, la polaridad induce una aplicación Φ Q : Pn P n, que asocia a cada punto P su hiperplano polar De hecho Φ Q es una homografía de matriz A, en sistemas de referencia adecuado El caso más interesante es cuando n = 1, porque componiendo Φ Q con la dualidad, se obtiene una aplicación Φ Q : P1 P1 que denotaremos inv Q, porque es una involución u homografía involutiva En efecto, Φ Q asocia a cada punto P el hiperplano P AX t = 0, cuyo dual es él mismo, pero en dimensión 1, esto es el punto P A ( ) 2 Así la matriz de inv Q es ( 0 1 A 1 0 ), cuyo cuadrado es A I, si A es simétrica, por lo que inv 2 Q =id Por otra parte inv Q(P ) es el único punto de P1 conjugado con P respecto de Q 62 Tangentes Definición 621 Una variedad lineal proyectiva L se dice tangente a Q si L pol Q (L), es decir, si existen puntos P tales que P L pol Q (P ); dichos puntos se dicen puntos de tangencia de L a Q Ejemplo Sea Q : 2x 0 x 1 x 2 2 = 0 en P2(R) La recta x 1 = 0 es tangente a Q en (1 : 0 : 0) La recta x 2 = 0 no es tangente a Q 2 Sea Q : x 2 0 x 2 1 = 0 en P2(R) La recta x 0 = 0 es tangente a Q en (0 : 0 : 1) La recta x 2 = 0 no es tangente a Q La recta x 0 + x 1 = 0 es tangente a Q en todos sus puntos 3 Sea Q : 2x 0 x 1 x 2 2 = 0 en P3(R) La recta x 2 = x 3 = 0 no es tangente a Q La recta x 1 = x 3 = 0 es tangente a Q en (1 : 0 : 0 : 0) La recta x 0 = x 2 = 0 es tangente a Q en todos sus puntos Veamos ahora algunos resultados elementales sobre hiperplanos tangentes Proposición 623 Sea Q un hipercuádrica, L Pn una variedad lineal proyectiva y H Pn un hiperplano
3 1 Si L Sing(Q) entonces L es tangente a Q 2 Si Q es degenerada, H es tangente a Q si y sólo si H Sing(Q) 3 Si Q es no degenerada, H es tangente a Q si y sólo si existe un punto P V(Q) tal que H = pol Q (P ) 4 Si Q es no degenerada, de ecuación XAX t = 0, y H tiene ecuación UX t = 0, entonces H es tangente a Q si y sólo si H V(Q ) con Q una hipercuádrica (dual) de P n de ecuación UA 1 U t = 0 Demostración: 1 Es consecuencia de 2 en la proposición Recíprocamente, sea P H pol Q (H) Si P Sing(Q) ya está Si P / Sing(Q) entonces pol Q (P ) es un hiperplano y, como P pol Q (H), pol Q (P ) H, luego pol Q (P ) = H Por el punto 2 de la proposición 617, H Sing(Q) 3 Análogo a lo anterior 4 Sea H : UX t = 0 tangente a Q Por 3 existe un P V(Q) tal que H : P AX t = 0 Por tanto λp = UA 1 Sustituyendo en la ecuación P AP t = 0 se tiene la condición enunciada 2 Nota 624 Sea Q una hipercuádrica de Pn, R un sistema de referencia fijo en Pn, de modo que la ecuación de Q es XAX t = 0 Sea L una variedad lineal proyectiva de dimensión r 0 Si se fija otro sistema de referencia R L en L, se producen unas ecuaciones paramétricas en L: λ(x 0,, x n ) = (y 0,, y r )M con M una matriz (r+1) (n+1) de rango máximo (cf nota 128) Nótese que (y 0 : : y r ) son las coordenadas respecto de R L del punto (x 0 : : x n ) L respecto de R Definición 625 Llamamos Q L a la hipercuádrica de L, cuya ecuación respecto de R L es (y 0,, y r )MAM t y 0 y r = 0, resultado de sustituir las paramétricas de L en la ecuación de Q Nótese que B = MAM t es una matriz simétrica de orden r + 1 Ejemplo 626 El caso L : x 0 = 0 es muy simple, si tomamos un sistema de referencia R L cómodo (cf ejemplo 129, en donde (0 : x 1 : : x n ) = (x 1 : : x n ) RL ) En ese caso B es la submatriz de A que resulta de eliminar su fila y columna cero Veamos ahora algunas propiedades triviales, pero fundamentales de Q L Proposición 627 Sean Q una hipercuádrica y L una variedad lineal proyectiva no vacía 1 Sean P, P L, entonces P Q L P si y sólo si P Q P 2 Si P L, pol Q L (P ) = pol Q (P ) L 3 Si L L, pol Q L (L ) = pol Q (L ) L 4 V(Q L ) = V(Q) L 5 V(Q) L si y sólo si pol Q (L) L 6 rango(q L ) = r dim L pol Q (L) Por tanto L es tangente a Q si y sólo si Q L es degenerada Demostración: Todas son triviales salvo, quizás, las dos últimas V(Q) L V(Q L = L rango(q L ) = 0 L = pol Q L (L) = L pol Q (L) L pol Q (L) La última se obtiene al observar que Sing(Q L ) = pol Q L (L) = pol Q (L) L, y además por la nota 615 rango(q L ) = r dim Sing(Q L ) 2 Como consecuencia elemental podemos analizar la intersección de una hipercuádrica-lugar real o compleja con una recta Corolario 628 Sea Q una hipercuádrica compleja y L una recta Se tiene que V(Q) L son dos puntos, 1 punto o la propia L El primer caso se produce sólo en el caso no tangente Demostración: Es consecuencia del punto 4 de la proposición anterior y del ejemplo Corolario 629 Sea Q una hipercuádrica real y L una recta Se tiene que V(Q) L son dos puntos, el vacío, 1 punto o la propia L Los dos primeros casos se producen sólo en el caso no tangente Demostración: Es consecuencia del punto 4 de la proposición anterior y del ejemplo
4 En el caso real y no degenerado podemos precisar más que la proposición anterior sobre la intersección de una hipercuádrica-lugar y un hiperplano tangente De hecho, por la proposición anterior el caso no tangente ya está claro: Q H es no degenerada, es decir el rango baja en una unidad Proposición 6210 Sea Q una hipercuádrica real o compleja no degenerada y H un hiperplano tangente 1 Se tiene que rango(q H ) = n 1 2 En el caso real, además sp(q H ) = sp(q) Demostración: Se trata de encontrar un sistema de referencia adecuado Sea P 0 = pol Q (H), como H es tangente a Q, por el punto 3 de la proposición 623 P 0 V(Q) H Sean P 1 / H cualquiera y {P 2,, P n } una base cualquiera de H 1 H, con H 1 = pol Q (P 1 ) Como P 1 / H, entonces P 0 / H 1 ; de aquí se deduce que {P 0, P 2,, P n } es una base de H Por tanto {P 0, P 1, P 2,, P n } son linealmente independientes, y añadiendo un punto unidad conveniente se construye un sistema de referencia R Imponiendo que la polar de P 0 = (1 : 0 : : 0) R es H : x 1 = 0, y que {P 2,, P n } son conjugados con P 1, se tiene que una matriz (simétrica) A de las ecuaciones de Q respecto de R es a 0 0 A = 0 0 A 0 0 Así A es diagonal por cajas, de modo que su rango es la suma de los rangos de sus cajas diagonales, es decir rango(a) = n + 1 = 2+rango(A ), con lo que se tiene que rango(a ) = n 1 También se tiene que los autovalores de A son los de A y los de la caja 2 2, que son uno positivo y otro negativo (su producto es 1) Por tanto, sp(a) = sp(a ) Finalmente, usando un argumento análogo al del ejemplo 626, una matriz de Q H, con H : x 1 = 0, en cierto sistema de referencia es B = A 0 obtenida al quitar en A la fila y columna 1 Queda comprobar que rango(b) = rango(a ) y sp(b) = sp(a ) 2 Obtenemos una aplicación inmediata de este resultado Corolario 6211 Sea Q una hipercuádrica no degenerada real o compleja de Pn con n 2 Su lugar no contiene hiperplanos Demostración: Por reducción al absurdo, si V(Q) H, con H un hiperplano, entonces V(Q H ) = H, por lo que la ecuación de Q H no puede ser otra que 0 = 0 El rango de Q H, por la proposición anterior y por el apartado 5 de la proposición 627 sólo puede ser n o n 1, que nunca puede ser cero 2 A diferencia de las no degeneradas, los lugares de las hipercuádricas degeneradas siempre contienen rectas Proposición 6212 Si Q es una hipercuádrica degenerada, entonces V(Q) es un cono de vértice Sing(Q), ie la recta que pasa por cada punto de V(Q) y por cada punto de Sing(Q) está contenida en V(Q) Demostración: Sea XAX t = 0 una ecuación de Q Si P V(Q), P AP t = 0, y si P 0 Sing(Q), P 0 A = 0; por tanto si P 1 P P 0, recordando que confundimos puntos con sus coordenadas, P 1 = λp + µp 0, y se verifica que P 1 AP t 1 = 0 2, 63 Estudio geométrico de las cónicas Proposición 631 Los lugares de las cónicas reales o complejas no degeneradas no contienen rectas Demostración: Es una consecuencia inmediata del corolario Descripción de los lugares de las cónicas complejas: Como sabemos se clasifican por su rango Sea Q una cónica de P2(C) 1 Si rango(q) = 3, Q se dirá cónica no degenerada compleja, una ecuación reducida es x x x 2 2 = 0 Por la proposición anterior, su lugar no contiene rectas y por el corolario 628, una recta lo corta en un punto (si son tangentes, cf 6210 y 5111) o en dos (si no lo son)
5 2 Si rango(q) = 2, una ecuación reducida es x x 2 1 = (x 0 + ix 1 )(x 0 ix 1 ) = 0 Así V(Q) es la unión de dos rectas distintas que se cortan en el punto (0 : 0 : 1) = Sing(Q) Diremos que Q es un par de rectas complejas 3 Si rango(q) = 1, una ecuación reducida es x 2 0 = 0 Así V(Q) = Sing(Q) es una única recta, que llamaremos recta doble compleja 4 Si rango(q) = 0, su ecuación reducida es 0 = 0 Así V(Q) = P2(C) Descripción de los lugares de las cónicas reales: Como sabemos se clasifican por su rango y su signatura proyectiva Sea Q una cónica de P2(R) 1 Si rango(q) = sp(q) = 3, Q se dirá cónica no degenerada imaginaria, ya que una ecuación reducida es x x x 2 2 = 0 y por tanto su lugar es vacío 2 Si rango(q) = 3, sp(q) = 1, Q se dirá cónica no degenerada real, una ecuación reducida es x x 2 1 x 2 2 = 0 Por la proposición anterior, su lugar no contiene rectas y por el corolario 629, una recta lo corta en un punto (si son tangentes, cf 6210 y 5112) o en dos o el vacío (si no lo son) 3 Si rango(q) = sp(q) = 2, una ecuación reducida es x x 2 1 = (x 0 + ix 1 )(x 0 ix 1 ) = 0 Así V(Q) = (0 : 0 : 1) = Sing(Q) Diremos que Q es un par de rectas imaginarias 4 Si rango(q) = 2, sp(q) = 0, una ecuación reducida es x 2 0 x 2 1 = (x 0 + x 1 )(x 0 x 1 ) = 0 Así V(Q) es la unión de dos rectas distintas que se cortan en el punto (0 : 0 : 1) = Sing(Q) Diremos que Q es un par de rectas reales 5 Si rango(q) = sp(q) = 1, su ecuación reducida es x 2 0 = 0 Así V(Q) = Sing(Q) es una única recta, que llamaremos recta doble real 6 Si rango(q) = 0, su ecuación reducida es 0 = 0 Así V(Q) = P2(R) 64 Estudio geométrico de las cuádricas Proposición 641 Los lugares de las cuádricas reales o complejas de rango 4 o 3 no contienen planos Demostración: El caso no degenerado es una consecuencia inmediata del corolario 6211 Si Q tiene rango 3 podemos suponer que una ecuación es f = XAX t = 0 y no tiene la variable x 3 Si V(Q) π, con π un plano, entonces Q H con H : x 3 = 0, es una cónica de rango 3 en H cuyo lugar contiene a la recta H π, que contradice En la siguiente descripción veremos que, en cambio, todas las cuádricas complejas son regladas, es decir, sus lugares contienen rectas Descripción de los lugares de las cuádricas complejas: Sea Q una cuádrica de P3(C) 1 Si rango(q) = 4, la llamaremos cuádrica no degenerada compleja Una ecuación reducida es x 2 0 +x 2 1 +x 2 2 +x 2 3 = 0 Su lugar contiene, por ejemplo, las rectas de la familia { λ(x0 + ix 1 ) = µ(x 2 + ix 3 ), µ(x 0 ix 1 ) = λ(x 2 ix 3 ) para cada valor (λ : µ) P1(C) Una situación análoga se verá, más adelante, en las cuádricas reales de puntos hiperbólicos, en donde se estudiarán, en detalle, propiedades de estas rectas contenidas en la cuádrica-lugar 2 Si rango(q) = 3, la llamaremos cono complejo Una ecuación reducida es x x x 2 2 = 0 Su lugar no contiene planos (cf 641), pero sí rectas que pasan por el punto Sing(Q) (cf 6212) 3 Si rango(q) = 2, una ecuación reducida es x 2 0 +x 2 1 = (x 0 +ix 1 )(x 0 ix 1 ) = 0 Así V(Q) es la unión de dos planos distintos que se cortan en la recta x 0 = x 1 = 0 que es Sing(Q) Diremos que Q es un par de planos complejos 4 Si rango(q) = 1, una ecuación reducida es x 2 0 = 0 Así V(Q) = Sing(Q) es un único plano, que llamaremos plano doble complejo 5 Si rango(q) = 0, su ecuación reducida es 0 = 0 Así V(Q) = P3(C) Descripción de los lugares de las cuádricas reales: Como sabemos se clasifican por su rango y su signatura proyectiva Sea Q una cuádrica de P3(R) 1 Si rango(q) = sp(q) = 4, Q se dirá cuádrica no degenerada imaginaria, ya que una ecuación reducida es x x x x 2 3 = 0 y por tanto su lugar es vacío
6 2 rango(q) = 4 y sp(q) = 2, Q se dirá cuádrica de puntos elípticos, como justificaremos enseguida Sus planos tangentes, por 6210, cortan a V(Q) en el lugar de una cónica de rango 2 y signatura 2, es decir, en un punto Los planos no tangentes, por 627, cortan a V(Q) en el lugar de una cónica no degenerada, que por lo visto antes, o es una cónica real no degenerada, o es el vacío Lo anterior nos describe completamente, cómo es la sección plana del lugar de una cuádrica de puntos elípticos Una ecuación reducida es x x x 2 2 x 2 3 = 0, y podemos exhibir ejemplos en donde se dan todos los casos anteriores, por ejemplo, x 2 + x 3 = 0, es un plano tangente, x 3 = 0 no corta a V(Q), y x 0 = 0 lo corta en una cónica real no degenerada El lugar V(Q), desde luego, no contiene planos, por 641, pero tampoco contiene rectas En efecto, supongamos que V(Q) L, con L una recta, y tomemos un plano cualquiera H que contenga a L Consideremos la cónica Q H, cuyo lugar es V(Q H ) = V(Q) H L H L, que contradice la descripción de las secciones planas del párrafo anterior De esto se deduce que, por el corolario 629, el corte de una recta con el lugar de una cuádrica de puntos elípticos son dos puntos, el vacío o un punto; el último caso corresponde a una recta tangente 3 rango(q) = 4 y sp(q) = 0, Q se dirá cuádrica de puntos hiperbólicos, como justificaremos enseguida Sus planos tangentes, por 6210, cortan a V(Q) en el lugar de una cónica de rango 2 y signatura 0, es decir, en un par de rectas reales Esto significa que esta cuádrica es reglada Vamos a dar una relación de propiedades sobre las rectas de esta cuádrica Proposición 642 Sea Q una cuádrica de puntos hiperbólicos de P3(R) Se verifica: (a) Por cada punto de V(Q) pasan dos rectas contenidas en V(Q) (b) Existen dos familias de rectas F 1 y F 2 contenidas en V(Q) (c) Dos rectas de la misma familia se cruzan, y de distinta familia se cortan (d) V(Q) = r F i r, para cada i = 1, 2 (e) No hay más rectas en V(Q) que las de las dos familias anteriores Demostración: Aunque hay demostraciones de carácter geométrico, lo más simple es observar que existe un sistema de referencia en el que Q tiene como ecuación: x 0 x 1 x 2 x 3 = 0 Sean F 1 y F 2 las familias de rectas siguientes: { { λx0 = µx F 2 λx0 = µx 1 F 3 µx 1 = λx 2 3 µx 1 = λx 2 para cada (λ : µ) P1(R) Es evidente que todas las rectas de F 1 y F 2 están en V(Q) Si P = (a 0 : a 1 : a 2 : a 3 ) V(Q) las rectas { { a2 x 0 = a 0 x 2 a3 x 0 = a 0 x 3, a 0 x 1 = a 2 x 3 a 0 x 1 = a 3 x 2 pasan por P y son de las familias anteriores, salvo que (a 0, a 2 ) = (0, 0) o (a 0, a 3 ) = (0, 0) En este último caso, considerar las rectas { a1 x 0 = a 3 x 2 a 3 x 1 = a 1 x 3 { a1 x 0 = a 2 x 3 a 2 x 1 = a 1 x 2 Se puede comprobar fácilmente (usando sus ecuaciones) que dos rectas de la misma familia se cruzan y dos rectas de distinta familia se cortan, en efecto, si (λ : µ) (λ : µ ) P1(R) : λ 0 µ 0 0 µ 0 λ λ 0 µ 0 = λ µ 2 λ 0 µ 0 λ µ 0 0 µ 0 λ λ 0 0 µ = 0 0 µ 0 λ 0 µ λ 0 Sólo queda probar la última afirmación Sea t V(Q), y tomamos un P t cualquiera Por el segundo apartado, sea P = r s con r F 1 y s F 2 Entonces el plano tangente a Q en P es H := pol Q (P ) pol Q (t) pol Q (r) pol Q (s) Por la proposición 627, H r s t y, por tanto, H V(Q) r s t Por ser Q una cuádrica de puntos hiperbólicos, debe ser t = r o t = s 2 4 Si rango(q) = sp(q) = 3, Q se dirá cono imaginario, una ecuación reducida es x x x 2 2 = 0 Por tanto V(Q) = Sing(Q) es un único punto 5 Si rango(q) = 3, sp(q) = 1, Q se dirá cono real, una ecuación reducida es x x 2 1 x 2 2 = 0 Por 6212, su lugar se obtiene proyectando desde el punto singular (vértice) una cónica real no degenerada
7 6 Si rango(q) = sp(q) = 2, una ecuación reducida es x x 2 1 = (x 0 + ix 1 )(x 0 ix 1 ) = 0 Así V(Q) = Sing(Q) es una recta Diremos que Q es un par de planos imaginarios 7 Si rango(q) = 2, sp(q) = 0, una ecuación reducida es x 2 0 x 2 1 = (x 0 + x 1 )(x 0 x 1 ) = 0 Así V(Q) es la unión de dos planos distintos que se cortan en la recta {x 0 = x 1 = 0} = Sing(Q) Diremos que Q es un par de planos reales 8 Si rango(q) = sp(q) = 1, su ecuación reducida es x 2 0 = 0 Así V(Q) = Sing(Q) es un único plano, que llamaremos plano doble real 9 Si rango(q) = 0, su ecuación reducida es 0 = 0 Así V(Q) = P3(R)
Hipercuádricas afines. Clasificación. Interpretación proyectiva de propiedades afines.
 Tema 8- Hipercuádricas afines Clasificación Interpretación proyectiva de propiedades afines 81 Hipercuádricas afines Sea k un cuerpo de característica distinta de dos Definición 811 Una hipercuádrica afín
Tema 8- Hipercuádricas afines Clasificación Interpretación proyectiva de propiedades afines 81 Hipercuádricas afines Sea k un cuerpo de característica distinta de dos Definición 811 Una hipercuádrica afín
Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas
 Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
Hipercuádricas afines. Clasificación. Elementos afines y euclídeos.
 Capítulo 6 Hipercuádricas afines. Clasificación. Elementos afines y euclídeos. Sea k un cuerpo de característica distinta de dos. Definición 6.0.1. Una hipercuádrica afín en k n es una ecuación de segundo
Capítulo 6 Hipercuádricas afines. Clasificación. Elementos afines y euclídeos. Sea k un cuerpo de característica distinta de dos. Definición 6.0.1. Una hipercuádrica afín en k n es una ecuación de segundo
Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas.
 Tema 7- Haces de hipercuádricas Clasificación de los haces de cónicas Determinación de cónicas 71 Puntos base y fundamentales de un haz Definición 711 Sea el espacio proyectivo Pn(k) de dimensión n sobre
Tema 7- Haces de hipercuádricas Clasificación de los haces de cónicas Determinación de cónicas 71 Puntos base y fundamentales de un haz Definición 711 Sea el espacio proyectivo Pn(k) de dimensión n sobre
Interpretación proyectiva de propiedades euclídeas. Elementos
 Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05
 - EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
- EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11
 - EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11 Nota: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura Álgebra Lineal y Geometría I. EJERCICIO 1. Sean P 1,...,
- EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11 Nota: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura Álgebra Lineal y Geometría I. EJERCICIO 1. Sean P 1,...,
El espacio proyectivo P n (k). Sistemas de referencia. Dualidad. Departamento de Algebra Septiembre El espacio proyectivo P n (k).
 Notas de la asignatura AMPLIACIÓN DE GEOMETRÍA de la Licenciatura de Matemáticas, Facultad de Matemáticas, Universidad de Sevilla, para el curso 2000-01 Departamento de Algebra Septiembre 2000 Tema 1-
Notas de la asignatura AMPLIACIÓN DE GEOMETRÍA de la Licenciatura de Matemáticas, Facultad de Matemáticas, Universidad de Sevilla, para el curso 2000-01 Departamento de Algebra Septiembre 2000 Tema 1-
El grupo lineal proyectivo. Homologías. Afinidades.
 Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España TEMA IV
 52 Variedades Cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
52 Variedades Cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
Problemas de Geometría Proyectiva
 Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
Distancia entre dos rectas que se cruzan Perpendicular común
 Perpendicular común En un espacio de tres dimensiones dos rectas se cruzan cuando no tienen ningún punto en común y no están contenidas en el mismo plano. Si no tienen ningún punto en común pero sí que
Perpendicular común En un espacio de tres dimensiones dos rectas se cruzan cuando no tienen ningún punto en común y no están contenidas en el mismo plano. Si no tienen ningún punto en común pero sí que
Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de
 Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
Capítulo 5 Haces de hipercuádricas. Clasificación de los haces de cónicas. Determinación de cónicas. 5.1. Definición y ecuaciones Definición 5.1.1. Sea (X, T, π) un espacio proyectivo de dimensión n sobre
Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares).
 Capítulo 6 Espacios Vectoriales 6.1 Definiciones Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares). Definición 6.1.1 Se dice que
Capítulo 6 Espacios Vectoriales 6.1 Definiciones Sea V un conjunto no vacío (cuyos elementos se llamarán vectores) y sea K un cuerpo (cuyos elementos se llamarán escalares). Definición 6.1.1 Se dice que
- RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05
 - RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05 Ejercicio 1. Junio 98 En el espacio proyectivo ordinario de dimensión 4, se consideran dos rectas, r y s, que se cruzan. Probar la verdad
- RELACION COMPLEMENTARIA DE AMPLIACION DE GEOMETRIA - Curso 04-05 Ejercicio 1. Junio 98 En el espacio proyectivo ordinario de dimensión 4, se consideran dos rectas, r y s, que se cruzan. Probar la verdad
Estudio proyectivo 23. Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España TEMA II
 Estudio proyectivo 23 Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA II
Estudio proyectivo 23 Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA II
+ : X V X. (+) P : V X u P + u. (P + u) + v = P + (u + v). Nota La propiedad 1) de la definición anterior implica, en primer lugar, que
 Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
2 Intersección de una recta y una cuádrica. 1 Definición y ecuaciones. ( x y z
 2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas.
 Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Index. Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80
 Index Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80 Adjunto, 14 Aplicación, 2 bilineal, 47 biyectiva, 3 compuesta, 3 identidad, 3 inversa, 3 inyectiva,
Index Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80 Adjunto, 14 Aplicación, 2 bilineal, 47 biyectiva, 3 compuesta, 3 identidad, 3 inversa, 3 inyectiva,
Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España TEMA III
 34 Variedades cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
34 Variedades cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
Seis problemas resueltos de geometría
 Problema 1 a) Dados los puntos P(4, 2, 3) y Q(2, 0, 5), da la ecuación implícita del plano π de modo que el punto simétrico de P respecto a π es Q. b) Calcula el valor del parámetro λ R para que el plano
Problema 1 a) Dados los puntos P(4, 2, 3) y Q(2, 0, 5), da la ecuación implícita del plano π de modo que el punto simétrico de P respecto a π es Q. b) Calcula el valor del parámetro λ R para que el plano
Las variedades lineales en un K-espacio vectorial V pueden definirse como sigue a partir de los subespacios de V.
 Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Capítulo 9 Variedades lineales Al considerar los subespacios de R 2, vimos que éstos son el conjunto {(0, 0)}, el espacio R 2 y las rectas que pasan por el origen. Ahora, en algunos contextos, por ejemplo
Movimientos. Teorema de Cartan-Dieudonné. Semejanzas.
 Capítulo 5 Movimientos. Teorema de Cartan-Dieudonné. Semejanzas. 5.1 Isometrías y movimientos Partimos de un espacio euclídeo (X, V, +) y recordemos que una isometría de V es un elemento ϕ Gl(V ) que conserva
Capítulo 5 Movimientos. Teorema de Cartan-Dieudonné. Semejanzas. 5.1 Isometrías y movimientos Partimos de un espacio euclídeo (X, V, +) y recordemos que una isometría de V es un elemento ϕ Gl(V ) que conserva
Planos y Rectas. 19 de Marzo de 2012
 el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
Tema 5. Cónicas. Asi, para las identificaciones habituales, (punto proyectivo recta vectorial punto de un plano afín ampliado), RP 2 R3 {0}
 Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones.
 Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Podemos pues formular los dos problemas anteriores en términos de matrices.
 Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
+ : X V X. (+) P : V X u P + u. (P + u) + v = P + (u + v). Nota La propiedad 1) de la definición anterior implica, en primer lugar, que
 Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
Capítulo 1 El espacio afín 11 Introducción Dependencia lineal afín La Geometría afín sobre un cuerpo k tiene como objetos básicos los siguientes: un conjunto no vacío X, cuyos elementos serán llamados
Clasificación Afín de las Cuádricas
 Capítulo VIII Clasificación Afín de las Cuádricas Como no puede ser de otro modo, en este capítulo seguiremos suponiendo que k es un cuerpo conmutativo de característica distinta de 2, que todos los espacios
Capítulo VIII Clasificación Afín de las Cuádricas Como no puede ser de otro modo, en este capítulo seguiremos suponiendo que k es un cuerpo conmutativo de característica distinta de 2, que todos los espacios
Espacios vectoriales reales
 140 Fundamentos de Matemáticas : Álgebra Lineal 9.1 Espacios vectoriales Capítulo 9 Espacios vectoriales reales Los conjuntos de vectores del plano, R 2, y del espacio, R 3, son conocidos y estamos acostumbrados
140 Fundamentos de Matemáticas : Álgebra Lineal 9.1 Espacios vectoriales Capítulo 9 Espacios vectoriales reales Los conjuntos de vectores del plano, R 2, y del espacio, R 3, son conocidos y estamos acostumbrados
G. SERRANO SOTELO. H = e 0 + E
 CLASIFICACIÓN AFÍN DE CÓNICAS Y CUÁDRICAS G. SERRANO SOTELO 1. Cuádricas en un hiperplano afín Sea E un R-espacio vectorial de dimensión n +1. Sean E = e 1,...,e n un hiperplano vectorial de E y e un vector
CLASIFICACIÓN AFÍN DE CÓNICAS Y CUÁDRICAS G. SERRANO SOTELO 1. Cuádricas en un hiperplano afín Sea E un R-espacio vectorial de dimensión n +1. Sean E = e 1,...,e n un hiperplano vectorial de E y e un vector
Sobre vectores y matrices. Independencia lineal. Rango de una matriz
 Espacios vectoriales Llamaremos R 2 al conjunto de todos los pares ordenados de la forma (a 1, a 2 ) tal que a 1, a 2 R. Es decir: R 2 = {(a 1, a 2 ) : a 1, a 2 R} De la misma forma: R 3 = {(a 1, a 2,
Espacios vectoriales Llamaremos R 2 al conjunto de todos los pares ordenados de la forma (a 1, a 2 ) tal que a 1, a 2 R. Es decir: R 2 = {(a 1, a 2 ) : a 1, a 2 R} De la misma forma: R 3 = {(a 1, a 2,
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones.
 Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Estudia la posición relativa de los planos siguientes según los distintos valores de m: ; A b = m 1 m 1
 Problema 1 Estudia la posición relativa de los planos siguientes según los distintos valores de m: π 1 x + y + z = m + 1 π 2 mx + y + ) z = m π 3 x + my + z = 1 Si vemos los tres planos como un sistema
Problema 1 Estudia la posición relativa de los planos siguientes según los distintos valores de m: π 1 x + y + z = m + 1 π 2 mx + y + ) z = m π 3 x + my + z = 1 Si vemos los tres planos como un sistema
MATEMÁTICAS: PAU 2016 JUNIO CASTILLA Y LEÓN
 MATEMÁTICAS: PAU 26 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A 5 a a) Discutir para qué valores de a R la matriz M = ( ) tiene inversa. Calcular M a para a =. ( 5 puntos) Para que exista inversa de una
MATEMÁTICAS: PAU 26 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A 5 a a) Discutir para qué valores de a R la matriz M = ( ) tiene inversa. Calcular M a para a =. ( 5 puntos) Para que exista inversa de una
TEMA 12.- RECTAS Y PLANOS EN EL ESPACIO. y una base de vectores de V cualquiera
 TEMA 12.- RECTAS Y PLANOS EN EL ESPACIO 1.- PUNTOS Y VECTORES. ESPACIO AFÍN y una base de vectores de V cualquiera {,, B = u1 u2 u} A cada punto del espacio, P, le asociamos el vector OP, que tendrá unas
TEMA 12.- RECTAS Y PLANOS EN EL ESPACIO 1.- PUNTOS Y VECTORES. ESPACIO AFÍN y una base de vectores de V cualquiera {,, B = u1 u2 u} A cada punto del espacio, P, le asociamos el vector OP, que tendrá unas
Ejercicios de Ampliación de Geometría. Hoja 2
 Ejercicios de Ampliación de Geometría Licenciatura en Ciencias Matemáticas, 2 Curso 27 de Octubre de 2008 Hoja 2 Dualidad y radiaciones. 1. Formular y resolver en el espacio proyectivo dual los siguientes
Ejercicios de Ampliación de Geometría Licenciatura en Ciencias Matemáticas, 2 Curso 27 de Octubre de 2008 Hoja 2 Dualidad y radiaciones. 1. Formular y resolver en el espacio proyectivo dual los siguientes
Temas 4 y 5: El espacio afín. Variedades lineales. Paralelismo.
 ALGEBRA II: Temas 4-5 DIPLOMATURA DE ESTADÍSTICA 1 Temas 4 y 5: El espacio afín Variedades lineales Paralelismo 1 Introducción La Geometría afín sobre R tiene como objetos básicos los siguientes: un conjunto
ALGEBRA II: Temas 4-5 DIPLOMATURA DE ESTADÍSTICA 1 Temas 4 y 5: El espacio afín Variedades lineales Paralelismo 1 Introducción La Geometría afín sobre R tiene como objetos básicos los siguientes: un conjunto
Formas canónicas de Jordan
 Capítulo 6 Formas canónicas de Jordan 61 Subespacios propios generalizados Introducción En el capítulo anterior se han estudiado los endomorfismos diagonalizables y se han dado condiciones necesarias y
Capítulo 6 Formas canónicas de Jordan 61 Subespacios propios generalizados Introducción En el capítulo anterior se han estudiado los endomorfismos diagonalizables y se han dado condiciones necesarias y
Breve introducción a Matrices
 1 - Introducción Breve introducción a Matrices Def. 1.1 Llamaremos matriz de orden mxn a la disposición en m filas y n columnas de mxn números 1. Observación 1.1 Convendremos que los números a los que
1 - Introducción Breve introducción a Matrices Def. 1.1 Llamaremos matriz de orden mxn a la disposición en m filas y n columnas de mxn números 1. Observación 1.1 Convendremos que los números a los que
Formas canónicas reales
 Capítulo 7 Formas canónicas reales Introducción Sea V un espacio vectorial sobre C, f End(V y M B (f = A M(n n Sea λ = a + bi es una autovalor complejo de f de multiplicidad m Para tal autovalor complejo
Capítulo 7 Formas canónicas reales Introducción Sea V un espacio vectorial sobre C, f End(V y M B (f = A M(n n Sea λ = a + bi es una autovalor complejo de f de multiplicidad m Para tal autovalor complejo
Inversa de una matriz
 Capítulo 2 Álgebra matricial 2.1. Inversa de una matriz Inversa de una matriz Para una matriz cuadrada A n n, la matriz B n n que verifica las condiciones AB = I n y B A=I n se denomina inversa de A, y
Capítulo 2 Álgebra matricial 2.1. Inversa de una matriz Inversa de una matriz Para una matriz cuadrada A n n, la matriz B n n que verifica las condiciones AB = I n y B A=I n se denomina inversa de A, y
Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES
 Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES Prof. Rafael López Camino Universidad de Granada 1 Matrices Definición 1.1 Una matriz (real) de n filas y m columnas es una expresión de la forma a 11...
Tema 1 CÁLCULO MATRICIAL y ECUACIONES LINEALES Prof. Rafael López Camino Universidad de Granada 1 Matrices Definición 1.1 Una matriz (real) de n filas y m columnas es una expresión de la forma a 11...
, donde denota la matriz traspuesta de B.
 Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº Páginas: INDICACIONES:.- OPTATIVIDAD: El alumno deberá escoger una de las dos opciones, pudiendo
Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº Páginas: INDICACIONES:.- OPTATIVIDAD: El alumno deberá escoger una de las dos opciones, pudiendo
Tema 3: Espacios vectoriales
 Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
Tema 3: Espacios vectoriales K denotará un cuerpo. Definición. Se dice que un conjunto no vacio V es un espacio vectorial sobre K o que es un K-espacio vectorial si: 1. En V está definida una operación
4. Aplicaciones: rango de una matriz y ecuaciones de un subespacio
 TEMA 2 ESPACIOS VECTORIALES 35 4 Aplicaciones: rango de una matriz y ecuaciones de un subespacio Terminaremos este tema aprovechando la teoría de espacios vectoriales que hemos estudiado para obtener algunas
TEMA 2 ESPACIOS VECTORIALES 35 4 Aplicaciones: rango de una matriz y ecuaciones de un subespacio Terminaremos este tema aprovechando la teoría de espacios vectoriales que hemos estudiado para obtener algunas
6 Vectores. Dependencia e independencia lineal.
 6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
6 Vectores. Dependencia e independencia lineal. Introducción Hay fenómenos reales que se pueden representar adecuadamente mediante un número con su adecuada unidad de medida. Sin embargo para representar
El espacio proyectivo. Sistemas de referencia. Dualidad.
 Capítulo 1 El espacio proyectivo Sistemas de referencia Dualidad En todo lo que sigue k designará un cuerpo arbitrario 11 Espacio afín como subespacio del proyectivo Definición 111 Sea un entero n 0 El
Capítulo 1 El espacio proyectivo Sistemas de referencia Dualidad En todo lo que sigue k designará un cuerpo arbitrario 11 Espacio afín como subespacio del proyectivo Definición 111 Sea un entero n 0 El
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 013 Capítulo 10 Año 009 10.1. Modelo 009 - Opción A Problema 10.1.1 (3 puntos) Dados el plano π
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 013 Capítulo 10 Año 009 10.1. Modelo 009 - Opción A Problema 10.1.1 (3 puntos) Dados el plano π
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Proposición Sea V un espacio vectorial sobre K de dimensión n y B una base de V. Gl(n, K) = {A M(n n, K) A = 0}.
 Tema 6 Formas canónicas 6.1 Introducción Proposición 6.1.1. Sea V un espacio vectorial sobre K de dimensión n y B una base de V. La aplicación Φ B : End(V ) M(n n, K) definida por Φ B (f) = M B (f), es
Tema 6 Formas canónicas 6.1 Introducción Proposición 6.1.1. Sea V un espacio vectorial sobre K de dimensión n y B una base de V. La aplicación Φ B : End(V ) M(n n, K) definida por Φ B (f) = M B (f), es
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
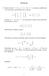 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
Geometría afín y proyectiva, 2016 SEMANA 2
 Geometría afín y proyectiva, 2016 SEMANA 2 Sonia L. Rueda ETS Arquitectura. UPM September 20, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Geometría afín y proyectiva, 2016 SEMANA 2 Sonia L. Rueda ETS Arquitectura. UPM September 20, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Geometría afín y proyectiva, 2016 SEMANA 4
 Geometría afín y proyectiva, 2016 SEMANA 4 Sonia L. Rueda ETS Arquitectura. UPM September 30, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Geometría afín y proyectiva, 2016 SEMANA 4 Sonia L. Rueda ETS Arquitectura. UPM September 30, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Espacios vectoriales reales.
 Capítulo 4 Espacios vectoriales reales. 4.1 Espacios vectoriales. Definición 86.- Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe
Capítulo 4 Espacios vectoriales reales. 4.1 Espacios vectoriales. Definición 86.- Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe
Teorema de Hahn-Banach
 Capítulo 3 Teorema de Hahn-Banach 3.1. Introducción Una vez introducidos los espacios vectoriales más importantes donde se tiene una estructura métrica a saber, los espacios de Hilbert y los espacios de
Capítulo 3 Teorema de Hahn-Banach 3.1. Introducción Una vez introducidos los espacios vectoriales más importantes donde se tiene una estructura métrica a saber, los espacios de Hilbert y los espacios de
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
Matrices y Sistemas de Ecuaciones lineales
 Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
Matrices y Sistemas de Ecuaciones lineales Llamaremos M m n (K) al conjunto de las matrices A = (a ij ) (i = 1, 2,..., m; j = 1, 2,..., n) donde los elementos a ij pertenecen a un cuerpo K. Las matrices,
GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]
![GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos] GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]](/thumbs/86/94405582.jpg) Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
2 Espacios vectoriales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 2 Espacios vectoriales 2.1 Espacio vectorial Un espacio vectorial sobre un cuerpo K (en general R o C) es un conjunto V sobre el que hay
ÁLGEBRA Algunas soluciones a la Práctica 8
 ÁLGEBRA Algunas soluciones a la Práctica 8 Aplicaciones bilineales y formas cuadráticas (Curso 24 25 1. Comprobar si las siguientes aplicaciones son o no bilineales y en las que resulten serlo, dar la
ÁLGEBRA Algunas soluciones a la Práctica 8 Aplicaciones bilineales y formas cuadráticas (Curso 24 25 1. Comprobar si las siguientes aplicaciones son o no bilineales y en las que resulten serlo, dar la
Ejercicio 1 de la Opción A del modelo 1 de Solución
 Ejercicio 1 de la Opción A del modelo 1 de 2008 Sean f : R R y g : R R las funciones definidas por f(x) = x 2 -(x + 1) + ax + b y g(x) = ce Se sabe que las gráficas de f y g se cortan en el punto ( 1,
Ejercicio 1 de la Opción A del modelo 1 de 2008 Sean f : R R y g : R R las funciones definidas por f(x) = x 2 -(x + 1) + ax + b y g(x) = ce Se sabe que las gráficas de f y g se cortan en el punto ( 1,
Cada recta vectorial se llama punto proyectivo. Se llama dimensión del espacio proyectivo a dim P(V ) = dim V 1.
 "Con eso francamente que nunca he sentido gusto por el estudio o la investigación en física o en geometría, a no ser que pudiera servir como medio de llegar a algún tipo de conocimiento de las causas próximas...para
"Con eso francamente que nunca he sentido gusto por el estudio o la investigación en física o en geometría, a no ser que pudiera servir como medio de llegar a algún tipo de conocimiento de las causas próximas...para
Sistemas de ecuaciones lineales
 CAPíTULO 6 Sistemas de ecuaciones lineales 1 Rango de una matriz a 11 a 1n Sea A = M m n (K) El rango por filas de la matriz A es la dimensión del a m1 a mn subespacio vectorial de K n generado por sus
CAPíTULO 6 Sistemas de ecuaciones lineales 1 Rango de una matriz a 11 a 1n Sea A = M m n (K) El rango por filas de la matriz A es la dimensión del a m1 a mn subespacio vectorial de K n generado por sus
SEPTIEMBRE 2005 PRUEBA A. b) Para a = 1, calcúlese la recta que pasa por (1, 1, 1) y se apoya en r y s.
 Selectividad Septiembre 5 SEPTIEMBRE 5 PRUEBA A PROBLEMAS - a) Calcúlense los valores de a para los cuales las rectas r x = λ y s y = 3+λ son perpendiculares z = + a λ b) Para a =, calcúlese la recta que
Selectividad Septiembre 5 SEPTIEMBRE 5 PRUEBA A PROBLEMAS - a) Calcúlense los valores de a para los cuales las rectas r x = λ y s y = 3+λ son perpendiculares z = + a λ b) Para a =, calcúlese la recta que
Capítulo 7. Espacios vectoriales. 7.1 Definición y ejemplos
 Capítulo Espacios vectoriales.1 Definición y ejemplos Un espacio vectorial sobre un cuerpo K (que supondremos conmutativo es un conjunto no vacío junto con 1. una operación interna, +, a la que llamaremos
Capítulo Espacios vectoriales.1 Definición y ejemplos Un espacio vectorial sobre un cuerpo K (que supondremos conmutativo es un conjunto no vacío junto con 1. una operación interna, +, a la que llamaremos
1. Espacio vectorial. Subespacios vectoriales
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Sea k un cuerpo. 1. Espacio vectorial. Subespacios vectoriales Definición 1.1. Un k-espacio vectorial o espacio vectorial
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Sea k un cuerpo. 1. Espacio vectorial. Subespacios vectoriales Definición 1.1. Un k-espacio vectorial o espacio vectorial
Clasificación de Métricas y
 Capítulo VII Clasificación de Métricas y Cuádricas Dada una métrica T 2 sobre un k-espacio vectorial E, para simplificar la notación, y siempre que no haya motivo de confusión, cualesquiera que sean e,
Capítulo VII Clasificación de Métricas y Cuádricas Dada una métrica T 2 sobre un k-espacio vectorial E, para simplificar la notación, y siempre que no haya motivo de confusión, cualesquiera que sean e,
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
La Diferencial de Fréchet
 Capítulo 6 La Diferencial de Fréchet Es bien conocido que una función de una variable f es derivable en un punto a si y sólo si su gráfica admite una recta tangente (no vertical) en el punto (a, f(a)).
Capítulo 6 La Diferencial de Fréchet Es bien conocido que una función de una variable f es derivable en un punto a si y sólo si su gráfica admite una recta tangente (no vertical) en el punto (a, f(a)).
1. DIAGONALIZACIÓN Y FORMAS CANÓNICAS
 1 1. DIAGONALIZACIÓN Y FORMAS CANÓNICAS Sea f : V V un endomorfismo de V, f End(V, con V un K-espacio vectorial de dimensión n, y sean B = {e 1,..., e n } B = {e 1,..., e n} bases de V. La matriz de f
1 1. DIAGONALIZACIÓN Y FORMAS CANÓNICAS Sea f : V V un endomorfismo de V, f End(V, con V un K-espacio vectorial de dimensión n, y sean B = {e 1,..., e n } B = {e 1,..., e n} bases de V. La matriz de f
Afinidades. Movimientos
 Capítulo 3 Afinidades. Movimientos 3.1 Aplicaciones afines Nota En lo que sigue E = (X, V, + es un espacio afín sobre K de dimensión n y R = {O, B} un sistema de referencia de E. Definición 3.1.1 Llamamos
Capítulo 3 Afinidades. Movimientos 3.1 Aplicaciones afines Nota En lo que sigue E = (X, V, + es un espacio afín sobre K de dimensión n y R = {O, B} un sistema de referencia de E. Definición 3.1.1 Llamamos
Espacios vectoriales reales
 144 Matemáticas 1 : Álgebra Lineal Capítulo 9 Espacios vectoriales reales 9.1 Espacios vectoriales Los conjuntos de vectores del plano, R, y del espacio, R 3, son conocidos y estamos acostumbrados a movernos
144 Matemáticas 1 : Álgebra Lineal Capítulo 9 Espacios vectoriales reales 9.1 Espacios vectoriales Los conjuntos de vectores del plano, R, y del espacio, R 3, son conocidos y estamos acostumbrados a movernos
Tema 11.- Autovalores y Autovectores.
 Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Teoría de la Dimensión
 Capítulo II Teoría de la Dimensión En este capítulo introduciremos una de las propiedades más importantes que tienen los espacios vectoriales: la dimensión. Dos son los modos posibles de llegar a la noción
Capítulo II Teoría de la Dimensión En este capítulo introduciremos una de las propiedades más importantes que tienen los espacios vectoriales: la dimensión. Dos son los modos posibles de llegar a la noción
Álgebra lineal y geometría II Tema 7
 Álgebra lineal y geometría II Tema 7 J.M. Aroca M.J. Fernández Bermejo 15 de diciembre de 2013 2 0.1. Homografías Dedicaremos este tema al estudio de las homografías, es decir las rectas de isomorfismos
Álgebra lineal y geometría II Tema 7 J.M. Aroca M.J. Fernández Bermejo 15 de diciembre de 2013 2 0.1. Homografías Dedicaremos este tema al estudio de las homografías, es decir las rectas de isomorfismos
Tema 2: Diagonalización
 TEORÍA DE ÁLGEBRA II: Tema 2. DIPLOMATURA DE ESTADÍSTICA 1 Tema 2: Diagonalización 1 Introducción Sea f : R n R n lineal. Dada una base B de R n podemos asociar a f la matriz A 1 = [f, B] M n. Si C es
TEORÍA DE ÁLGEBRA II: Tema 2. DIPLOMATURA DE ESTADÍSTICA 1 Tema 2: Diagonalización 1 Introducción Sea f : R n R n lineal. Dada una base B de R n podemos asociar a f la matriz A 1 = [f, B] M n. Si C es
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
Mas dimensiones U U-V
 Mas dimensiones Si R 2 ={(x,y) /x,y en R} y R 3 ={(x,y,z) / x,y,z R} son buenos modelos del plano y del espacio euclidianos, entonces parece razonable pensar que R 4 ={(x,y,z,w) / x,y,z,w R} debe ser un
Mas dimensiones Si R 2 ={(x,y) /x,y en R} y R 3 ={(x,y,z) / x,y,z R} son buenos modelos del plano y del espacio euclidianos, entonces parece razonable pensar que R 4 ={(x,y,z,w) / x,y,z,w R} debe ser un
AP = A p 1 p 2 p n = Ap 1 Ap 2. λ 1 p 21 λ 2 p 22 λ n p 2n. .. = λ 1 p 1 λ 2 p 2
 Capítulo 6 Diagonalización 6 Valores y vectores propios 6 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V, nos planteamos el problema
Capítulo 6 Diagonalización 6 Valores y vectores propios 6 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V, nos planteamos el problema
Para localizar un punto o un objeto en el espacio necesitamos un sistema de referencia. R es una cuaterna { O,i, j, k}
 Geometría afín del espacio MATEMÁTICAS II 1 1 SISTEMA DE REFERENCIA. ESPACIO AFÍN Para localizar un punto o un objeto en el espacio necesitamos un sistema de referencia. Definición: Un sistema de referencia
Geometría afín del espacio MATEMÁTICAS II 1 1 SISTEMA DE REFERENCIA. ESPACIO AFÍN Para localizar un punto o un objeto en el espacio necesitamos un sistema de referencia. Definición: Un sistema de referencia
TEMA 4 ESPACIOS VECTORIALES
 TEMA 4 ESPACIOS VECTORIALES Índice 4.1. Definición y propiedades.................. 101 4.1.1. Dependencia e independencia lineal....... 103 4.2. Subespacios vectoriales................... 105 4.2.1. Ecuaciones
TEMA 4 ESPACIOS VECTORIALES Índice 4.1. Definición y propiedades.................. 101 4.1.1. Dependencia e independencia lineal....... 103 4.2. Subespacios vectoriales................... 105 4.2.1. Ecuaciones
GEOMETRÍA. (x 1) 2 +(y 2) 2 =1. Razónalo. x y + z = 2. :3x 3z +1= 0 es doble de la distancia al plano π 2. : x + y 1= 0. Razónalo.
 GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
Espacios vectoriales
 CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
11. Cónicas proyectivas
 24 FRANCISCO JAVIER GALLEGO RODRIGO. Cónicas proyectivas Recordemos que una de las razones para construir el espacio proyectivo fue estudiar qué les pasa a los objetos afines cuando nos vamos al infinito.
24 FRANCISCO JAVIER GALLEGO RODRIGO. Cónicas proyectivas Recordemos que una de las razones para construir el espacio proyectivo fue estudiar qué les pasa a los objetos afines cuando nos vamos al infinito.
El espacio proyectivo
 Capítulo 7 El espacio proyectivo 71 Historia La geometría proyectiva estudia las propiedades de las figuras invariantes por proyección y sección Nace en el renacimiento La cultura medieval basada en el
Capítulo 7 El espacio proyectivo 71 Historia La geometría proyectiva estudia las propiedades de las figuras invariantes por proyección y sección Nace en el renacimiento La cultura medieval basada en el
GEOMETRÍA. que pasa por el punto P y es paralelo a π. (0,9 puntos) b) Determinar la ecuación del plano π
 GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
Sistemas de ecuaciones lineales. Matrices
 Dpto de MATEMÁTICA APLICADA A LOS RECURSOS NATURALES Sección departamental en la ETSI de Montes Algebra Sistemas de ecuaciones lineales Matrices Sistemas lineales Solución de un sistema lineal Sistemas
Dpto de MATEMÁTICA APLICADA A LOS RECURSOS NATURALES Sección departamental en la ETSI de Montes Algebra Sistemas de ecuaciones lineales Matrices Sistemas lineales Solución de un sistema lineal Sistemas
1. Medida Exterior. Medida de Lebesgue en R n
 1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
1. La integral de Lebesgue surge del desarrollo de la integral de Riemann, ante las dificultades encontradas en las propiedades de paso al ĺımite para calcular la integral de una función definida como
Sistemas de ecuaciones lineales
 Tema 1 Sistemas de ecuaciones lineales 11 Definiciones Sea K un cuerpo Una ECUACIÓN LINEAL CON COEFICIENTES EN K es una expresión del tipo a 1 x 1 + + a n x n = b, en la que n es un número natural y a
Tema 1 Sistemas de ecuaciones lineales 11 Definiciones Sea K un cuerpo Una ECUACIÓN LINEAL CON COEFICIENTES EN K es una expresión del tipo a 1 x 1 + + a n x n = b, en la que n es un número natural y a
