Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
|
|
|
- Lucas Martín Romero
- hace 7 años
- Vistas:
Transcripción
1 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio!
2 Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En todo lo que sigue trabajaremos en el espacio euclídeo R 2 y en él supondremos que los sistemas de referencia que se utilicen son métricos Elipse Definición Llamamos elipse al lugar geométrico de los puntos del plano tales que la suma de sus distancias a dos puntos fijos llamados focos es constante (2a > 0). Figura 5.1: x2 a 2 + y2 b 2 = 1 Ecuación reducida Sean F y F los focos y d(f, F ) = 2c y sea O el punto medio del segmento F F. Para calcular la ecuación reducida de la elipse tomaremos el siguiente sistema de referencia: Tomaremos el punto O como origen de coordenadas. El eje X X será la recta F F (si F = F, tomaremos como eje X X cualquier recta que pase por O). Como eje Y Y la perpendicular a XX pasando por O. B = {u 1, u 2 } es una base métrica cuyos vectores se han tomado, respectivamente, en las direcciones de los ejes. 69
3 De este modo, podemos asignar las siguientes coordenadas F = (c, 0), F = ( c, 0). Sea pues, P = (x, y) un punto cualquiera de R 2. Con esta asignación, se tiene: d(p, F ) + d(p, F ) = 2a (x c) 2 + y 2 + (x + c) 2 + y 2 = 2a x 2 + c 2 2cx + y 2 = 4a 2 + x 2 + c 2 + 2cx + y 2 4a (x + c) 2 + y 2 a (x + c) 2 + y 2 = a 2 + cx a 2 x 2 + a 2 c 2 + 2a 2 cx + a 2 y 2 = a 4 + c 2 x 2 + 2a 2 cx (a 2 c 2 )x 2 + a 2 y 2 = a 2 (a 2 c 2 ) Como 2a > 2c, haciendo b 2 = a 2 c 2, obtenemos: y dividiendo por el producto a 2 b 2, resulta que es la ecuación reducida de la elipse. b 2 x 2 + a 2 y 2 = a 2 b 2 x 2 a 2 + y2 b 2 = 1 Elementos geométricos El punto O, centro de simetría de la elipse, recibe el nombre de centro de la misma. los números reales positivos a, b y c se denominan, respectivamente, semieje mayor, semieje menor y semidistancia focal. Reciben el nombre de ejes de la elipse, sus ejes de simetría (y = 0, x = 0, respectivamente, eje mayor y eje menor). A los puntos A = (a, 0), A = ( a, 0), B = (0, b) y B = (0, b) intersección de la elipse con sus ejes se les llama vértices de la elipse. Los lados del triángulo rectángulo F OB, verifican la relación pitagórica a 2 = b 2 + c 2. En el caso particular en que F = F (c = 0), se verifica que a 2 = b 2 con lo que se obtiene la ecuación x 2 + y 2 = a 2 que es una circunferencia de centro O y radio r = a. Excentricidad de la elipse es el número real 0 e < 1 definido por e = c a. dpto. de álgebra
4 Figura 5.2: x2 a 2 y2 b 2 = Hipérbola Definición Llamamos hipérbola al lugar geométrico de los puntos del plano tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos llamados focos es constante (2a > 0). Ecuación reducida Procediendo a tomar un sistema de referencia similar al caso de la elipse, podemos asignar a los focos las siguientes coordenadas F = (c, 0), F = ( c, 0). Sea pues, P = (x, y) un punto cualquiera de R 2. Con esta asignación, se tiene: d(p, F ) d(p, F ) = 2a (x c) 2 + y 2 (x + c) 2 + y 2 = ±2a x 2 + c 2 2cx + y 2 = 4a 2 + x 2 + c 2 + 2cx + y 2 ± 4a (x + c) 2 + y 2 ±a (x + c) 2 + y 2 = a 2 + cx a 2 x 2 + a 2 c 2 + 2a 2 cx + a 2 y 2 = a 4 + c 2 x 2 + 2a 2 cx (c 2 a 2 )x 2 a 2 y 2 = a 2 (c 2 a 2 ) Como 2a < 2c, haciendo b 2 = c 2 a 2, obtenemos: b 2 x 2 a 2 y 2 = a 2 b 2 m. iglesias
5 y dividiendo por el producto a 2 b 2, resulta que es la ecuación reducida de la hipérbola. x 2 a 2 y2 b 2 = 1 Elementos geométricos El punto O, centro de simetría de la hipérbola, recibe el nombre de centro de la misma. los números reales positivos a, b y c se denominan, respectivamente, semieje real, semieje imaginario y semidistancia focal. Reciben el nombre de ejes de la hipérbola, sus ejes de simetría (y = 0, x = 0, llamados, respectivamente, eje real y eje imaginario). La razón de este último nombre es que las soluciones de la intersección del eje x = 0 con la hipérbola son los números complejos (imaginarios puros) ±bi. A los puntos A = (a, 0), A = ( a, 0), B = (0, b) y B = (0, b) se les llama, respectivamente, vértices reales y vértices imaginarios de la hipérbola. Los lados del triángulo rectángulo AOB, verifican la relación pitagórica c 2 = a 2 + b 2. En el caso particular en que a 2 = b 2, la hipérbola recibe el nombre de equilátera y su ecuación es x 2 y 2 = a 2. Las rectas y = ± b x son las asíntotas de la hipérbola. a Llamamos excentricidad de una hipérbola al número real 1 < e < + definido por e = c a Parábola Definición Llamamos parábola al lugar geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco y de una recta fija r, llamada directriz. Figura 5.3: y 2 = 2 p x dpto. de álgebra
6 Ecuación reducida Tomaremos, en este caso como ejes de coordenadas X X la perpendicular a r (directriz) que pase por el foco F. Si R = X X r, tomaremos como eje Y Y la mediatriz del segmento RF. De lo anterior se deduce que el origen O de coordenadas es el punto medio del segmento RF. Por tanto, si d(r, F ) = p, F = ( p 2, 0 ), r x + p 2 = 0 y para que el punto P = (x, y) pertenezca a la parábola se ha de verificar que d(p, r) = d(p, F ) = x + p ( = x p ) 2 + y 2 2 2, de donde, elevando al cuadrado, x 2 + px + p2 4 = x2 px + p2 4 + y2, de donde obtenemos la ecuación reducida de la parábola, Elementos geométricos y 2 = 2 p x. La recta y = 0 (eje de simetría de la parábola), es el eje de la misma. El punto O = (0, 0), intersección de la parábola con su eje, recibe el nombre de vértice. Al número real positivo p = d(f, r), se le suele llamar parámetro de la parábola. 5.2 Cónicas generales: clasificación Definición Llamaremos cónica al conjunto de puntos del plano que satisfagan la ecuación general de segundo grado C a 11 x 2 + a 22 y 2 + 2a 12 xy + 2a 01 x + 2a 02 y + a 00 = 0 ecuación, que puede ser expresada matricialmente del siguiente modo: C ( 1 x y ) a 00 a 01 a 02 1 a 01 a 11 a 12 x = 0. a 02 a 12 a 22 y La matriz A = recibe el nombre de matriz de la cónica C. Si det(a) 0, se dice que C es no degenerada. a 00 a 01 a 02 a 01 a 11 a 12 a 02 a 12 a 22 Si det(a) = 0, se dice que C es una cónica degenerada. Es nuestro objetivo demostrar que toda ecuación general de segundo grado C tal que det(a) 0 es una elipse, una hipérbola o una parábola pero para llegar a este resultado necesitamos una serie de lemas previos, fundamentalmente relacionados con las matrices simétricas., m. iglesias
7 Lema Sea C xax t = 0, x = (1, x, y) la ecuación general de una cónica y sea f MO(E) de ecuación matricial x = xm R (f), x = (1, x, y), x = ( 1, x, y ) y sea M = M R (f) 1. Se verifica que f(c) x MAM t x t = 0. Demostración De x = xm R (f) se deduce que x = x t M R (f) 1 = x t M, de donde sustituyendo este valor en la ecuación de la cónica se tiene que f(c) x MAM t x t = 0. Lema Si se verifica que Demostración ( a11 a A 0 = 12 a 12 a 22 ), det(λi A 0 ) = λ 2 Tr(A 0 )λ + det(a 0 ). En efecto, ( ) λ a11 a det(λi A 0 ) = det 12 = a 12 λ a 22 = λ 2 (a 11 + a 22 )λ + (a 11 a 22 a 2 12) = = λ 2 Tr(A 0 )λ + det(a 0 ). Lema (invariantes métricos) Sea C xax t = 0 una cónica y f(c) x A x t = 0 la cónica obtenida aplicando a C el movimiento f de matriz inversa M. Se verifica que i.1) det(a ) = det(a). i.2) det(a 0 ) = det(a 0). i.3) Tr(A 0 ) = Tr(A 0). Los números det(a), det(a 0 ) y Tr(A 0 ) reciben el nombre de invariantes métricos de la cónica C. Demostración Sean M = 1 α β 0 0 a 11 a 21 a 12 a 22 y M 0 = ( a 11 a 12 a 21 a 22 ), donde M es la inversa de la matriz de un movimiento (se recuerda que M 0 es ortogonal y que, por tanto, M t 0 = M0 1 y que, además, det(m 0 ) = ±1). Del resultado del lema se deduce que de donde A = MAM t = 1 α β 0 0 a 11 a 21 a 12 a 22 a 00 a 01 a 02 a 01 a 11 a 12 a 02 a 12 a α β a 11 a 12 a 21 a 22, (5.1) A 0 = M 0 A 0 M 0 t = M 0 A 0 M 1 0 = A 0 A 0. (5.2) De estos resultados se deducen inmediatamente los tres apartados. En efecto, dpto. de álgebra
8 1. De la igualdad 5.1 se deduce que det(a ) = det(m) det(a) det(m t ) = (±1) det(a)(±1) = det(a), lo que demuestra el apartado i.1) del lema. 2. Como por 5.2, A 0 es semejante a A 0, ambas matrices tienen el mismo polinomio característico. Aplicando pues el resultado del lema 5.2.2, se tiene que y, por tanto, λ 2 Tr(A 0 )λ + det(a 0 ) = λ 2 Tr(A 0)λ + det(a 0) Tr(A 0 ) = Tr(A 0), det(a 0 ) = det(a 0 ). Con lo que quedan demostrados los apartados i.2) e i.3). Lema Sea A 0 la matriz simétrica ( a11 a A 0 = 12 a 12 a 22 ). Se verifica que: 1. Los autovalores de A 0 son reales. 2. Si A 0 tiene dos autovalores distintos λ µ y a y b son autovectores asociados, respectivamente a λ y µ, entonces a b. 3. A 0 es diagonalizable mediante una matriz de paso ortogonal. Demostración 1. De acuerdo con el lema 5.2.2, la ecuación característica de A 0 es λ 2 Tr(A 0 )λ + det(a 0 ) = 0. Es decir una ecuación de segundo grado cuyo discriminante 0. En efecto, Caben pues dos casos: = (a 11 + a 22 ) 2 4(a 11 a 22 a 12 ) 2 = (a 11 a 22 ) 2 + 4a (a) > 0. En este caso la ecuación característica tiene dos raíces reales y distintas, luego A 0 tiene dos autovalores λ y µ reales y distintos. (b) = 0. Entonces (a 11 a 22 ) 2 + 4a 2 12 = 0, de donde 2. En efecto, luego A 0 es de la forma a 11 a 22 = 0, a 12 = 0, ( ) a11 0 A 0 = 0 a 11 y, por tanto, es diagonal y sus autovalores son λ = a 11 = µ. λa b = λa B (b B ) t = a B A 0 (b B ) t = a B (b B A 0 ) t = a B (µb B ) t = µa b, de donde λa b = µa b = (λ µ) a b = 0 = a b = 0 = a b. }{{} 0 m. iglesias
9 3. Sean λ y µ los autovalores de A 0. Caben dos casos: λ = µ. Entonces A 0 es según lo demostrado anteriormente diagonal, luego una matriz de paso es la matriz unidad que es ortogonal. λ µ. En este{ caso, si a y b son autovectores asociados, respectivamente, a λ y µ se a tiene que B 0 = a, b } es una base ortonormal de que diagonaliza A 0. La matriz de b paso sería pues P = M(B 0, B), que es ortogonal. Proposición Si C a 11 x 2 + a 22 y 2 + 2a 12 xy + 2a 01 x + 2a 02 y + a 00 = 0 es una cónica no degenerada (det(a) 0), entonces C es irreducible. contiene rectas. En otras palabras C no Demostración Procedamos al absurdo. Supongamos que Si esto fuese así, se tendría que C (ax + by + c)(a x + b y + c ) = 0. C aa x 2 + bb y 2 + (ab + ba )xy + (ac + ca )x + (bc + ca )y + cc = 0, de donde la matriz de la cónica sería o, lo que es lo mismo, A = A = 1 2 cc 1 2 (ac + ca ) 1 2 (bc + ca ) 1 2 (ac + ca ) aa 1 2 (ab + ba ) 1 2 (bc + ca 1 ) 2 (ab + ba ) bb cc + cc ac + ca bc + ca ac + ca aa + aa ba + ab bc + ca ab + ba bb + bb De donde deducimos que det(a) = 0, en contra de la hipótesis, por ser la suma de ocho determinantes nulos (cada uno de ellos tiene, al menos, dos columnas iguales). Teorema (clasificación de las cónicas) Toda cónica no degenerada es una elipse, una hipérbola o una parábola. Demostración La prueba del teorema consistirá en aplicar uno o más movimientos a la cónica dada de modo que obtengamos la ecuación de la misma referida a sus ejes (ecuación reducida), lo que nos permitirá averiguar fácilmente qué tipo de cónica es. Sea C xax t = 0 una cónica no degenerada (det(a) 0) y B 0 la base de V calculada en el apartado 3 del lema Consideremos el movimiento f cuya matriz inversa es M = = M(B 0 0, B) Por el lema 5.2.1, sabemos que la matriz de f(c) es A = MAM t M 0 0. dpto. de álgebra
10 o sea, A = M 0 0 a 00 a 01 a 02 a 01 a 02 A M t 0 0. Es decir, A es de la forma A = a 00 a 01 a 02 a 01 λ 1 a 02 λ 2, donde λ 1 y λ 2 son los autovalores de A 0. Caben, ahora, dos posibilidades. Caso 1 λ 1 0, λ 2 0. Consideremos en este caso la traslación T cuya matriz es a 01 a 02 1 λ 1 λ 2 La matriz M, inversa, de la anterior es M = 1 a 01 a 02 λ 1 λ 2 ( Tu 1 = T u ), de donde la matriz de T (f(c)) será de la forma A = M A M t = 1 a 01 a 02 λ 1 λ 2 a 00 a 01 a 02 a 01 λ 1 a 02 λ a 01 λ 1 1 a 02 λ 2 1. Es decir, A = a 00 λ 1 λ 2, de donde (g f)(c) λ 1 x 2 + λ 2 y 2 + a 00 = 0. (5.3) Recordando que en todo el proceso (ver lema sobre invariantes métricos de las cónicas), i.1) det(a ) = det(a ) = det(a), i.2) det(a 0 ) = det(a 0 ) = det(a 0), i.3) Tr(A 0 ) = Tr(A 0 ) = Tr(A 0), se tiene que a 00 = A λ 1 λ 2 = A A 00. (5.4) m. iglesias
11 Por otra parte, la ecuación 5.3, es la ecuación reducida de una elipse o una hipérbola, según los signos de λ 1, λ 2 y a 00 y, que podemos resumir en la siguientes tablas.1 ELIPSES (sig(λ 1 ) = sig(λ 2 )) λ 1 λ 2 a 00 A A 00 Tr(A 0 ) TIPO E.I E.R E.R. + E.I. HIPÉRBOLAS (sig(λ 1 ) sig(λ 2 )) λ 1 λ 2 A Caso 2 λ 1 = 0, λ 2 0. En este caso, A = Apliquemos a f(c) la traslación T cuya matriz es a 00 a 01 a 02 a 01 0 a 02 λ 2 1 a a 02 λ 2. Si M es su matriz inversa, la matriz de (T f)(c), será o sea donde A = M A M t = 1 a a 02 λ 2 A = a 00 a 01 a 02 a 01 0 a 02 λ 2 a 00 a 01 0 a λ 2 a 00 = a a a 01 a 02 2 λ a 1 a 02 λ 2 1 Como a 01 0 (ya que si fuese igual a cero det(a ) = det(a) = 0, en contra de la hipótesis), es posible calcular a con la condición de que a 00 = 0 y se tendría que 0 a A 01 0 = a λ 2 Luego que es la ecuación reducida de una parábola. 2 T (f(c)) λ 2 y a 01 x = 0 1 Se recuerda que las ecuaciones reducidas de la elipse real e hipérbola son, respectivamente, b 2 x 2 + a 2 y 2 a 2 b 2 = 0, b 2 x 2 a 2 y 2 a 2 b 2 = 0., 2 Al suponer λ 2 0, se intenta llegar a la forma reducida y 2 = 2 p x dpto. de álgebra
12 Como det(a 0 ) = 0 y det(a 0) = det(a 0 ), se de duce que la condición necesaria y suficiente para que una cónica no degenerada sea una parábola es que det(a 0 ) = 0. Por otra parte, como det(a ) = λ 2 a 01 2 = det(a), se tiene que a 01 = ± A λ 2. Ahora bien, como Tr(A 0 ) = λ 2 = Tr(A 0 ), sustituyendo se tiene: a A 01 = ± Tr(A 0 ). Todos los resultados anteriores se recogen en la siguiente tabla. CLASIFICACIÓN DE LAS CÓNICAS A 0 Cónica Irreducible Ecuaciones reducidas A 00 0 Cónica con centro A 00 = 0 Parábola A 00 > 0 Elipse A 00 < 0 Hipérbola { sig( A ) = sig(tr(a0 )) E.I. sig( A ) sig(tr(a 0 )) E.R. Elipses e hipérbolas: λ 1 x 2 + λ 2 y 2 + b 00 = 0 Donde: b 00 = A A 00 y (λ 1, λ 2 son los autovalores de autovalores de A 0 ). Parábolas: λ 2 y 2 + 2b 01 x = 0 A Donde: b 01 = ± Tr(A 0 ) y λ 2 = Tr(A 0 ), es el autovalor no nulo de A Elementos de las cónicas. Resumen 1. Tangentes t a una cónica C P 0 = (x 0, y 0 ) C = r t (1, x 0, y 0 ) A (1, x, y) t = 0. P = (a, b) / C. Sea P 0 = (x 0, y 0 ) C. De este modo, D(t) = P 0 P. (a) Calculamos el punto P 0 resolviendo el sistema: { (1, x0, y 0 ) A (1, x 0, y 0 ) t = 0 (1, x 0, y 0 ) A (1, a, b) t = 0 donde, en la segunda ecuación se ha impuesto la condición de que P = (a, b) pertenezca a la recta tangente por P 0. m. iglesias
13 (b) Calculamos la ecuación de la recta tangente a C por P 0 por el método del apartado anterior o bien, teniendo en cuenta que t = P + P 0 P. 2. Centro C de una cónica. (Centro de simetría) Basta resolver el sistema, C { a01 + a 11 x + a 12 y = 0 a 02 + a 12 x + a 22 y = 0 donde, como puede observarse, los coeficientes del sistema son, respectivamente, la segunda y tercera filas de A. 3. Ejes (e) de las cónicas. (Ejes de simetría) Elipses e hipérbolas (a) Dirección de los ejes. Se calcula resolviendo la ecuación: (α, β) A 0 ( β, α) t = 0 (b) Se calcula el centro C de la cónica (c) Para cada dirección, se calcula la ecuación del eje e teniendo en cuenta que dicho eje pasa por el centro de la cónica. Es decir: e x = c + λ(α, β) Parábolas La ecuación del eje viene dada por: (0, a 11, a 12 ) A (1, x, y) t = 0 (0, a 12, a 22 ) A (1, x, y) t = 0 Aunque alguna de ellas pudiera dar la identidad 0 = 0. Siempre es válida la fórmula: 4. Asíntotas de la hipérbola (a) Direcciones Asintóticas. Se calculan resolviendo la ecuación: (0, A 02, A 01 ) A (1, x, y) t = 0 (α, β) A 0 (α, β) t = 0 (b) Ecuaciones de las asíntotas (a). Vienen dadas por: a (0, α, β)a(1, x, y)t = 0. Nota Cuando se conocen las coordenadas del centro C de la hipérbola, se tiene que a = C + (α, β), ya que las asíntotas pasan por el centro de la hipérbola. 5. Focos de las cónicas. Elipse (Hipérbola) (a) Se calculan: su ecuación reducida, semidistancia focal (c), centro y ejes de la elipse (hipérbola). dpto. de álgebra
14 (b) Se decide cuál es el eje mayor (eje real). En el caso de la elipse, un procedimiento para determinar el eje mayor es calcular la intersección de uno de los ejes con la elipse con lo cual se calcularán dos vértices opuestos, V y V, de la misma. Si d(v, V ) = 2a el eje elegido es el eje mayor. En el caso de la hipérbola, se calcula la intersección de un eje con dicha hipérbola y si la intersección es real, el eje elegido es el eje real. En caso contrario, hemos elegido el eje imaginario. (c) Los focos son los puntos sobre el eje mayor (eje real) cuya distancia al centro es igual a c. Parábola (P). (a) Se calculan: su ecuación reducida, parámetro p de la parábola, eje y vértice V (V = e P). (b) El foco (F ) es un punto sobre el eje tal que la distancia al vértice es igual a p 2. (c) Se calcula la perpendicular r p, al eje e pasando por F. Caso 1. r p P = = r p es la directriz. Caso 2. r p P = F es el foco de P. 5.4 Ejemplos Ejemplo 1 Dada la cónica Se pide: 1. Clasificarla y hallar su ecuación reducida. C 3x 2 + 2xy y 2 + 2x 4y 5 = La tangente en el punto de ella, P 0 = (1, 0). 3. Las tangentes a la cónica desde el origen de coordenadas. Solución De los datos obtenemos que A = 1 3 1, A 0 = ( Como det(a) = 5 y A 00 = det(a 0 ) = 4, se tiene que C es una hipérbola. 2. La ecuación reducida de las hipérbolas es de la forma, donde λ 1 y λ 2 son los autovalores de A 0. λ 1 x 2 λ 2 y 2 + A A 00 = 0, λi A 0 = 0 = λ 2 2λ 4 = 0, ). de donde λ 1 = 1 + 5, λ 2 = 1 5. Por consiguiente la ecuación reducida de C es (1 + 5) x 2 + (1 5) y = 0. m. iglesias
15 3. Se tiene que P 0 C y O C Como P 0 C, la ecuación de la recta tangente a C por P 0 viene dada por la fórmula Es decir, la ecuación buscada es (1, 1, 0) A (1, x, y) t = 0. 4x y 4 = 0. Como O C tratemos de calcular un punto P = (α, β) C tal que la recta P 0 P sea tangente a C. Se han de cumplir dos condiciones: P C = 3α 2 + 2αβ β 2 + 2α 4β 5 = 0. El punto O debe pertenecer a la tangente a C por el punto P. Dicha tangente tiene por ecuación t 0 (1, α, β) A (1, x, y) t = 0 y, por tanto, se ha de verificar la condición Condición, que es equivalente a (1, α, β) A (1, 0, 0) t = α 2 β = 0. Se trata pues de resolver el sistema formado por ambas ecuaciones. { 3α 2 + 2αβ β 2 + 2α 4β 5 = 0 α 2 β 5 = 0 cuyas soluciones son { α = 1 } 3, β = 8, {α = 1, β = 2}. 3 Calculando las ecuaciones de las rectas OP para las dos soluciones de P, se tiene que las tangentes buscadas son y = 8 x, y = 2 x. Ejemplo 2 Dada la cónica Se pide: 1. Clasificarla. C 7x 2 + 8xy + y x 6y + 3 = 0 2. Calcular se ecuación reducida, semiejes y semidistancia focal. 3. Coordenadas de su centro. 4. Ecuaciones de sus ejes. 5. id. de sus asíntotas. 6. Coordenadas de los focos. dpto. de álgebra
16 Solución 1. Sean A y A 0 las matrices A = , A 0 = ( Como det(a) = 270, A 00 = det(a 0 ) = 9, se deduce que C es una hipérbola. Su ecuación reducida viene dada por λ 1 x 2 λ 2 y 2 + A A 00 = 0, donde λ 1 y λ 2 son los autovalores de A 0. Calculemos pues dichos autovalores. Por tanto, la ecuación reducida de C es x 2 9y 2 = 30 x2 30 y λi A 0 == λ 1 = 1, λ 2 = El centro de la hipérbola se obtiene resolviendo el sistema { 6 + 7x + 4y = 0 C 3 + 4x + y = 0 ). = 1 = a 2 = 30, b 2 = 10 3, c2 = cuya solución es C = (2, 5). 3. Las direcciones de los ejes (e 1, e 2 ) vienen dadas por la ecuación (α, β)a 0 ( β, α) t = 0, de donde obtenemos 6 β α 4 β α 2 = 0 2 α 2 3 α β 2 β 2 = 0, ecuación de segundo grado que resuelta en la incógnita α tiene como soluciones α = β, α = 1 2 β. Dando a β, respectivamente, los valores 1 y 2, obtenemos que D(e 1 ) = (2, 1), D(e 2 ) = (1, 2). Luego las ecuaciones de los ejes son: e 1 = (2, 5) + (2, 1), e 2 = (2, 5) + (1, 2). 4. Sean a 1 y a 2 las asíntotas de la hipérbola. Las direcciones asintóticas vienen dadas por la ecuación (α, β)a 0 (α, β) t = 0, de donde obtenemos 7 α β α + β 2 = 0, m. iglesias
17 ecuación, que resuelta en la incógnita α, tiene como soluciones α = β, α = β 7, de donde y, por tanto, D(a 1 ) = (1, 1), D(a 2 ) = (1, 7) a 1 = (2, 5) + (1, 1), a 2 = (2, 5) + (1, 7). 5. Para calcular los focos hay que decidir, en primer lugar, cuál es el eje real (eje que corta a la hipérbola). Tomemos, por ejemplo, el eje { x = 2 + t e 2 = (2, 5) + (1, 2) y = 5 2t Para averiguar si corta a la hipérbola hay que comprobar que el siguiente sistema tiene soluciones reales. 7x 2 + 8xy + y x 6y + 3 = 0 C e 2 x = 2 + t y = 5 2t Sustituyendo los valores de x e y, dados por las ecuaciones segunda y tercera, en la primera ecuación. se tiene que 30 5t 2 = 0 = t = ± 6, lo que nos indica que C e 2, luego e 2 es el eje real. Nótese que con este resultado podríamos calcular fácilmente los vértices reales de la hipérbola. Hay que hallar, ahora, un punto sobre e 2 tal que su distancia al centro C sea igual a c (semidistancia focal). O, lo que es lo mismo: de donde Ejemplo 3 Dada la cónica se pide: (2 + t 2) 2 + ( 5 2t + 5) 2 = = t = ±2 15, 3 x = 2 ± , y = P x 2 2xy + y 2 + 2x + 1 = 0, 1. Probar que es una parábola y calcular su ecuación reducida. 2. La ecuación de su eje. 3. Las coordenadas del vértice. 4. Las coordenadas del foco y la ecuación de la directriz de dicha parábola. dpto. de álgebra
18 Solución 1. De la ecuación de P deducimos que A = 1 1 1, A 0 = ( Como det(a) = 1, det(a 0 ) = 0, se deduce que P es una parábola. La ecuación reducida de una parábola es λ 2 y 2 A = 2 Tr(A 0 ) x, (λ 2 = Tr(A 0 )). Por tanto, sustituyendo los valores calculados, se tiene la ecuación reducida ). 1 2 y 2 = 2 2 x = y2 = Ahora bien, si p es el parámetro de la parábola, 2 2 x. 2p = 2 2 = p = Este último dato lo utilizaremos más adelante. 2. Calculemos el eje y el vértice de P. La ecuación del eje e de una parábola viene dada por (0, a 11, a 12 )A(1, x, y) t = (5.5) sustituyendo, se tiene que e x 2 y = 0. El vértice V se obtiene resolviendo el sistema { x V = P e 2 2xy + y 2 + 2x + 1 = x 2 y = 0 ( de donde V = 5 ) 8, El foco es un punto sobre el eje e de la parábola tal que su distancia al vértice V es igual a p. Es decir, si F es el foco se ha de verificar que 2 d(f, V ) 2 = p2 4. Como un punto de e es de la forma (t, 12 ) + t, se tiene que ( t ( 1 + 8) 2 + t + 1 ) 2 = 8 ( ) 2 2, 8 de donde 2 ( t + 5 ) 2 = = t = 3 4, t = 1 2. m. iglesias
19 Ahora bien, t = 3 ( 4 = F 1 = 3 ) 4, 1, 4 t = 1 2 = F 2 = ( 12 ), 0. Para decidir cuál de los puntos F 1 o F 2 es el foco, calculamos: la recta r p perpendicular el eje por uno de los puntos. Elijamos, por ejemplo, F 2. ( r p x + 1 ) + y = 0. 2 Si r p P =, r p es la directriz. Si, por el contrario, r p P, F 2 sería el foco. { x 2 + y 2 2xy + 2x + 1 = 0 r p P y = x 1 2 de donde 16 x x + 5 = 0. Como esta ecuación carece de solución real, podemos afirmar que r p es la directriz y F 1 el foco de la parábola. Ejemplo 4 Dada la cónica calcular los focos de la misma. Solución Las matrices de la cónica son: C 6 x x y + 6 y 2 16 x 16 y = 0, A = , A 0 = Para resolver el problema, daremos los siguientes pasos: 1. Clasificación Como ( ). det(a) = 512, A 00 = det(a 0 ) = 32, sig( A ) sig ( Tr(A 0 ) ), se deduce que C es una elipse real. 2. Ecuación reducida λi A 0 = 0 = λ 2 12 λ + 32 = 0 = λ = 8, λ = 4. Luego la ecuación reducida es de donde obtenemos 4 x y 2 16 = 0, a 2 = 4, b 2 = 2 = c 2 = Centro Obtenemos las coordenadas del centro resolviendo el sistema { 8 + 6x + 2y = 0 C 8 + 2x + 6y = 0 cuya solución es C = (1, 1). dpto. de álgebra
20 4. Ejes (e 1, e 2 ) De (α, β)a 0 ( β, α) t = 0 = 2 β α 2 = 0, Ecuación, que resuelta en la incógnita α tiene como soluciones α = ±β = D(e 1 ) = (1, 1), D(e 2 ) = (1, 1). Por tanto, e 1 = (1, 1) + (1, 1), e 2 = (1, 1) + (1, 1). 5. Eje mayor. Para determinar cuál es el eje mayor, podemos aplicar lo expuesto en el apartado 5 (Elipse) de la sección 5.3. Sin embargo es bueno recordar que la dirección del eje mayor es un autovector asociado al menor autovalor (en valor absoluto) de A 0. Esto simplifica mucho los cálculos. En efecto, ( ) 6 2 (1, 1) = (8, 8) = 8(1, 1), 2 6 de donde deducimos que e 1 no es el eje mayor. Pero ( ) 6 2 (1, 1) = (4, 4) = 4(1, 1), 2 6 luego el eje mayor es e 2 = (1, 1) + (1, 1). 6. Focos Recordemos que los focos son dos puntos sobre el eje mayor tal que la distancia de cada uno de ellos al centro de la elipse es igual a c (semidistancia focal). De acuerdo con esto, si F es un foco, tenemos que F e 2 = F = (1 + t, 1 t). d(f, C) 2 = c 2 = (1 + t 1) 2 + (1 t 1) 2 = 2 = t = ±1. Luego,los focos de la elipse son F 1 = (2, 0), F 2 = (0, 2). Ejemplo 5 Dados un punto F, una recta r y el número real e > 0, se pide: 1. Probar que el lugar geométrico de los puntos del plano tales que es una cónica no degenerada. 2. Clasificarla según los valores de e. d(p, F ) d(p, r) = e 3. Calcular la ecuación en la forma polar de dicha cónica. Solución Para mayor sencillez, tomemos la siguiente referencia: Origen de coordenadas: el punto O = F. Eje OX: la perpendicular a r desde el punto F. coordenadas D = (d, 0) con lo cual r x = d, Sea r OX = D asignemos a D las Como es obvio, el eje OY queda determinado trazando la perpendicular a OX por O. m. iglesias
21 1. Si P = (x, y) es un punto cualquiera del plano, teniendo en cuenta lo anterior, se tiene que d(p, F ) = d(p, O) = x 2 + y 2, d(p, r) = x d. Por consiguiente, de donde se obtiene la ecuación d(p, F ) d(p, r) = e = x2 + y 2 (x d) 2 = e2, C (1 e 2 )x 2 + t 2 + 2e 2 dx e 2 d 2 = 0 (5.6) que, evidentemente, es la ecuación de una cónica. Para ver que no es degenerada construyamos la matriz de dicha cónica: e 2 d 2 e 2 d 0 ( ) A = e 2 d 1 e e 2 0 = A 0 =. 0 Como det(a) = e 2 d 2 < 0, la cónica C es no degenerada. 2. Para clasificar la cónica, tengamos en cuenta que por consiguiente, A 00 = det(a 0 ) = 1 e 2, (e > 0), 0 < e < 1 = A 00 > 0, Tr(A 0 ) > 0 = C es una E.R. e = 1 = A 00 = 0 = C es una P. 1 < e = A 00 < 0 = C es una H. El número e > 0 recibe el nombre de excentricidad de la cónica. 3. Haciendo Nota y sustituyendo en 5.6, se tiene x = ρ cos θ, y = ρ sen θ = ρ 2 = x 2 + y 2 ρ = que es la ecuación en la forma polar de C. e d e cos θ 1 No es difícil comprobar que en los casos en que e 1 (elipses e hipérbolas), e = c a. En efecto, calculemos la ecuación reducida de C. En el caso elipse se tiene que y, en el caso hipérbola, y, ambos casos, es a = a = e d 1 e 2, c = e2 d 1 e 2 e d e 2 1, c = e2 d e 2 1 e = c a. dpto. de álgebra
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Bloque 2. Geometría. 4. Iniciación a las Cónicas
 Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
Lugar Geométrico. Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz
 1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
A pesar de la importancia de las cónicas como secciones de una superficie cónica, para estudiar los elementos y propiedades de cada una de ellas en
 SECCIONES CÓNICAS Las secciones cónicas se pueden definir como lugares geométricos en el plano, sin embargo la definición clásica de las cónicas, que se debe a Apolonio de Perga, se hizo mediante un procedimiento
SECCIONES CÓNICAS Las secciones cónicas se pueden definir como lugares geométricos en el plano, sin embargo la definición clásica de las cónicas, que se debe a Apolonio de Perga, se hizo mediante un procedimiento
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
UNI DAD 4 ESPACIO BIDIMENSIONAL: CÓNICAS
 UNI DAD 4 ESPACIO BIDIMENSIONAL: CÓNICAS Objetivos Geometría analítica Introducción L cónica sección cónica Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0 A B C D E F 4.1. Circunferencia Circunferencia es el conjunto
UNI DAD 4 ESPACIO BIDIMENSIONAL: CÓNICAS Objetivos Geometría analítica Introducción L cónica sección cónica Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0 A B C D E F 4.1. Circunferencia Circunferencia es el conjunto
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
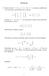 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
Función lineal y cuadrática. Curvas de primer y segundo grado.
 Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Tema 5. Cónicas. Asi, para las identificaciones habituales, (punto proyectivo recta vectorial punto de un plano afín ampliado), RP 2 R3 {0}
 Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
TEMA 9 LUGARES GEOMÉTRICOS. CÓNICAS 1. Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
 TEMA 9 LUGARES GEOMÉTRICOS. CÓNICAS 1 TEMA 9 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(x,) a las
TEMA 9 LUGARES GEOMÉTRICOS. CÓNICAS 1 TEMA 9 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(x,) a las
COLEGIO NUESTRA SEÑORA DEL BUEN CONSEJO. Melilla LUGARES GEOMÉTRICOS Y CÓNICAS
 LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
Facultad de Ingeniería Facultad de Tecnología Informática. Matemática Números reales Elementos de geometría analítica. Profesora: Silvia Mamone
 Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a)
 Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a la recta x + 7y + 1 = 0
 Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Lugares geométricos y cónicas
 Lugares geométricos y cónicas E S Q U E M A D E L A U N I D A D. Lugar geométrico página 6.. Definición página 6. Circunferencia página 6.. Ecuación página 6.. Casos particulares página 67. Elipse página
Lugares geométricos y cónicas E S Q U E M A D E L A U N I D A D. Lugar geométrico página 6.. Definición página 6. Circunferencia página 6.. Ecuación página 6.. Casos particulares página 67. Elipse página
RESUMEN TEÓRICO LUGARES GEÓMETRICOS. CÓNICAS (circunferencia y elipse)
 RESUMEN TEÓRICO LUGARES GEÓMETRICOS. CÓNICAS (circunferencia y elipse) 1. LUGARES GEOMÉTRICOS Definición: Se llama lugar geométrico a la figura que forman un conjunto de puntos que cumplen una determinada
RESUMEN TEÓRICO LUGARES GEÓMETRICOS. CÓNICAS (circunferencia y elipse) 1. LUGARES GEOMÉTRICOS Definición: Se llama lugar geométrico a la figura que forman un conjunto de puntos que cumplen una determinada
Secciones Cónicas. 0.1 Parábolas
 Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
Evaluación NOMBRE APELLIDOS CURSO Y GRUPO FECHA CALIFICACIÓN. 3 b) y 16 x Lugares geométricos y cónicas
 Evaluación NOMBRE APELLIDOS CURSO Y GRUPO FECHA CALIFICACIÓN 4 La ecuación del lugar geométrico de los puntos del plano que equidistan de la recta x y 4, y del punto P (, ) es: a) x y x y 68 0 b) 4x 9y
Evaluación NOMBRE APELLIDOS CURSO Y GRUPO FECHA CALIFICACIÓN 4 La ecuación del lugar geométrico de los puntos del plano que equidistan de la recta x y 4, y del punto P (, ) es: a) x y x y 68 0 b) 4x 9y
TEMA 7: CÓNICAS CIRCUNFERENCIA. A partir de esta ecuación podemos hallar el centro y el radio sin más que deshacer los cambios:
 TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro.
 Cónicas 1.- Circunferencia Definición 1 (Definición geométrica) Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro. Analíticamente la circunferencia
Cónicas 1.- Circunferencia Definición 1 (Definición geométrica) Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro. Analíticamente la circunferencia
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
LUGARES GEOMÉTRICOS. CÓNICAS
 9 LUGARES GEOMÉTRICOS. CÓNICAS Página PARA EMPEZAR, RELEXIONA Y RESUELVE Cónicas abiertas: parábolas e hipérbolas Completa la siguiente tabla, en la que α es el ángulo que forman las generatrices con el
9 LUGARES GEOMÉTRICOS. CÓNICAS Página PARA EMPEZAR, RELEXIONA Y RESUELVE Cónicas abiertas: parábolas e hipérbolas Completa la siguiente tabla, en la que α es el ángulo que forman las generatrices con el
Es la elipse el conjunto de puntos fijos cuya suma de distancias a dos puntos fijos llamados focos es constante.
 ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.
 La Parábola La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz. Características geométricas. a) Vértice. Es el
La Parábola La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz. Características geométricas. a) Vértice. Es el
UNIDAD 3: GEOMETRÍA ANALÍTICA Nociones preliminares, línea recta, estudio de las cónicas
 009 UNIDAD 3: GEOMETRÍA ANALÍTICA Nociones preliminares, línea recta, estudio de las cónicas Se hace referencia a las definiciones, fórmulas y algunos ejemplos sobre los temas indicados Iván Moyota Ch.
009 UNIDAD 3: GEOMETRÍA ANALÍTICA Nociones preliminares, línea recta, estudio de las cónicas Se hace referencia a las definiciones, fórmulas y algunos ejemplos sobre los temas indicados Iván Moyota Ch.
INTRO. ESTUDIO DE LAS CÓNICAS
 INTRO. ESTUDIO DE LAS CÓNICAS Una vez que se han estudiado los sistemas de coordenadas y las ecuaciones de las figuras geométricas más elementales, las rectas, se pasará a hacer un estudio de algunas líneas
INTRO. ESTUDIO DE LAS CÓNICAS Una vez que se han estudiado los sistemas de coordenadas y las ecuaciones de las figuras geométricas más elementales, las rectas, se pasará a hacer un estudio de algunas líneas
Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6
 página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
Cónicas y cuádricas. Circunferencia Elipse Parábola Hipérbola
 Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
PAU Madrid. Matemáticas II. Año Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos.
 PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
B23 Curvas cónicas Curvas cónicas
 Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
3º B.D. opción Físico-Matemática Matemática II. Parábola.
 Parábola. Definición: Lugar geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco y de una recta fija z llamada directriz. Siendo F no perteneciente a z. Entonces siendo P
Parábola. Definición: Lugar geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco y de una recta fija z llamada directriz. Siendo F no perteneciente a z. Entonces siendo P
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas.
 Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1
 ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1 Cónicas (Curso 010 011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.. Dada
ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1 Cónicas (Curso 010 011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.. Dada
ÁLGEBRA Soluciones a la Práctica 15
 ÁLGEBRA Soluciones a la Práctica 15 Cónicas (Curso 008 009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 9. Calcular la ecuación
ÁLGEBRA Soluciones a la Práctica 15 Cónicas (Curso 008 009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 9. Calcular la ecuación
Soluciones. Abril de 2010
 FACULTAD CS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA1001-1 Introducción al Cálculo Semestre 010-01 Profesor: Jorge San Martín Auxiliares: Natalia Ruiz - Alfredo Torrico Soluciones Abril de 010 P1
FACULTAD CS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE MA1001-1 Introducción al Cálculo Semestre 010-01 Profesor: Jorge San Martín Auxiliares: Natalia Ruiz - Alfredo Torrico Soluciones Abril de 010 P1
Parte II - Prácticas 8 a 9. Álgebra A 62 ÁLGEBRA A 62 (INGENIERÍA)
 Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Aquella que tiene nulos los elementos nos situados en la diagonal principal. Los elementos situados por encima de la diagonal principal son nulos.
 Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
Geometría Analítica Enero 2015
 Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. A( 2,, B( 8,, C( 5, 10) R( 6, 5) S( 2, - T(3,- U( -1, - V( 2, - W( 9, 4) II.- Demuestre
Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. A( 2,, B( 8,, C( 5, 10) R( 6, 5) S( 2, - T(3,- U( -1, - V( 2, - W( 9, 4) II.- Demuestre
4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16.
 Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Se quiere instalar un gran depósito de propano para abastecer a una factoría industrial y a dos urbanizaciones.
 Resuelve Página Dónde se situará el depósito? Se quiere instalar un gran depósito de propano para abastecer a una factoría industrial y a dos urbanizaciones. Han de cumplirse las siguientes condiciones:
Resuelve Página Dónde se situará el depósito? Se quiere instalar un gran depósito de propano para abastecer a una factoría industrial y a dos urbanizaciones. Han de cumplirse las siguientes condiciones:
UNIDAD 5: Curvas y superficies 5.A. Cónicas
 UNIDAD 5: Curvas y superficies 5.A. Cónicas En un principio se estudiaron las curvas que quedaban determinadas cuando se cortaba un cono recto con planos en distintas posiciones respecto de la base del
UNIDAD 5: Curvas y superficies 5.A. Cónicas En un principio se estudiaron las curvas que quedaban determinadas cuando se cortaba un cono recto con planos en distintas posiciones respecto de la base del
INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO
 PRIMER EXAMEN PARCIAL INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO GUÍA DE GEOMETRÍA ANALÍTICA 2016-2017A SISTEMA DE COORDENADAS, LUGARES
PRIMER EXAMEN PARCIAL INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO GUÍA DE GEOMETRÍA ANALÍTICA 2016-2017A SISTEMA DE COORDENADAS, LUGARES
PAU Madrid. Matemáticas II. Año Examen de junio. Opción A. Ejercicio 1. Valor: 2 puntos.
 Opción A. Ejercicio 1. Valor: 2 puntos. Calcular las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos en aquel momento,
Opción A. Ejercicio 1. Valor: 2 puntos. Calcular las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos en aquel momento,
Ejercicios 16/17 Lección 5. Geometría. 1. como combinación lineal de u = (2,5), expresa uno de ellos como combinación lineal de los otros dos.
 Ejercicios 16/17 Lección 5. Geometría. 1 1. Expresa el vector u = ( 3, 1) como combinación lineal de los vectores v = ( 3, ) w = ( 4, 1). y. Expresa w = (4, 6) como combinación lineal de u = (,5) y v =
Ejercicios 16/17 Lección 5. Geometría. 1 1. Expresa el vector u = ( 3, 1) como combinación lineal de los vectores v = ( 3, ) w = ( 4, 1). y. Expresa w = (4, 6) como combinación lineal de u = (,5) y v =
Geometría Analítica Agosto 2016
 Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
EXÁMENES DE ALGEBRA Y GEOMETRÍA MATEMÁTICAS II CURSO
 EXÁMENES DE ALGEBRA Y GEOMETRÍA MATEMÁTICAS II CURSO 2016-17 1 2 Ejercicio 1º.- Considera las matrices A 1 1 y B 0 1 1 0 a) (1,25 puntos) Encuentra las matrices X e Y tales que X Y = A T y 2X Y = B. b)
EXÁMENES DE ALGEBRA Y GEOMETRÍA MATEMÁTICAS II CURSO 2016-17 1 2 Ejercicio 1º.- Considera las matrices A 1 1 y B 0 1 1 0 a) (1,25 puntos) Encuentra las matrices X e Y tales que X Y = A T y 2X Y = B. b)
ELIPSE. Muchos cometas tienen órbitas extremadamente excéntricas. Por ejemplo, el cometa Halley, tiene una excentricidad orbital de casi 0.97!
 ELIPSE Las órbitas de los planetas son elípticas. La excentricidad de la órbita de la Tierra es muy pequeña (menor de 0.2), de manera que la órbita es casi circular. La órbita de Plutón es la más excéntrica
ELIPSE Las órbitas de los planetas son elípticas. La excentricidad de la órbita de la Tierra es muy pequeña (menor de 0.2), de manera que la órbita es casi circular. La órbita de Plutón es la más excéntrica
UNPSJB - Facultad Ciencias Naturales - Asignatura: Matemática 1 Ciclo Lectivo: 2014 CONICAS
 Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1
 ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1 Cónicas (Curso 011 01) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 3. Dada
ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1 Cónicas (Curso 011 01) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 3. Dada
GEOMETRÍA. (x 1) 2 +(y 2) 2 =1. Razónalo. x y + z = 2. :3x 3z +1= 0 es doble de la distancia al plano π 2. : x + y 1= 0. Razónalo.
 GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
Podemos pues formular los dos problemas anteriores en términos de matrices.
 Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA
 ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
EJERCICIOS DE GEOMETRÍA PLANA. 1. Hallar las ecuaciones paramétricas de la recta r que pasa por el punto ( 2, 2) tiene como vector director el vector
 EJERCICIOS DE GEOMETRÍA PLANA Hallar las ecuaciones paramétricas de la recta r que pasa por el punto (, ) tiene como vector director el vector v i j A y x a + vt La ecuación paramétrica de una recta es
EJERCICIOS DE GEOMETRÍA PLANA Hallar las ecuaciones paramétricas de la recta r que pasa por el punto (, ) tiene como vector director el vector v i j A y x a + vt La ecuación paramétrica de una recta es
ACADEMIA DE FÍSICO-MATEMÁTICAS MATEMÁTICAS III CICLO ESCOLAR TERCER SEMESTRE G E O M É T R Í A GUÍA A N A L Í T I C A
 CENTRO DE ESTUDIOS DE BACHILLERATO LIC. JESÚS REYES HEROLES ACADEMIA DE FÍSICO-MATEMÁTICAS MATEMÁTICAS III CICLO ESCOLAR TERCER SEMESTRE GEOMETRÍA G E O M É T R Í A GUÍA ANALÍTICA A N A L Í T I C A G U
CENTRO DE ESTUDIOS DE BACHILLERATO LIC. JESÚS REYES HEROLES ACADEMIA DE FÍSICO-MATEMÁTICAS MATEMÁTICAS III CICLO ESCOLAR TERCER SEMESTRE GEOMETRÍA G E O M É T R Í A GUÍA ANALÍTICA A N A L Í T I C A G U
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
TEMA 5. CURVAS CÓNICAS.
 5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
MATEMÁTICAS 1º BACH. C. N. Y S. 25 de enero de 2010 Geometría y Logaritmos
 MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
Ejercicios 17/18 Lección 5. Geometría. 1. como combinación lineal de u = (2,5), expresa uno de ellos como combinación lineal de los otros dos.
 Ejercicios 17/18 Lección 5. Geometría. 1 1. Expresa el vector u = ( 3, 1) como combinación lineal de los vectores v = ( 3, ) w = ( 4, 1). y. Expresa w = (4, 6) como combinación lineal de u = (,5) y v =
Ejercicios 17/18 Lección 5. Geometría. 1 1. Expresa el vector u = ( 3, 1) como combinación lineal de los vectores v = ( 3, ) w = ( 4, 1). y. Expresa w = (4, 6) como combinación lineal de u = (,5) y v =
Introducción La Circunferencia Parábola Elipse Hiperbola. Conicas. Hermes Pantoja Carhuavilca
 Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Contenido 1 Introducción 2 La Circunferencia 3 Parábola 4 Elipse 5 Hiperbola Objetivos Se persigue que el estudiante:
Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica I Contenido 1 Introducción 2 La Circunferencia 3 Parábola 4 Elipse 5 Hiperbola Objetivos Se persigue que el estudiante:
Página 209 PARA RESOLVER. 44 Comprueba que el triángulo de vértices A( 3, 1), B(0, 5) y C(4, 2) es rectángulo
 44 Comprueba que el triángulo de vértices A(, ), B(0, ) y C(4, ) es rectángulo y halla su área. Veamos si se cumple el teorema de Pitágoras: AB = (0 + ) + ( ) = AC = (4 + ) + ( ) = 0 BC = 4 + ( ) = 0 +
44 Comprueba que el triángulo de vértices A(, ), B(0, ) y C(4, ) es rectángulo y halla su área. Veamos si se cumple el teorema de Pitágoras: AB = (0 + ) + ( ) = AC = (4 + ) + ( ) = 0 BC = 4 + ( ) = 0 +
C O N I C A S. Elipse
 C O N I C A S Elipse El primer matemático que inició el estudio de las cónicas fue Apolonio de Perga (6 190 a.c), que enseñó matemáticas en las universidades de Alejandría y Pérgamo. Su estudio lo plamó
C O N I C A S Elipse El primer matemático que inició el estudio de las cónicas fue Apolonio de Perga (6 190 a.c), que enseñó matemáticas en las universidades de Alejandría y Pérgamo. Su estudio lo plamó
PROBLEMARIO DE GEOMETRIA ANALITICA EN EL PLANO.
 PROBLEMARIO DE GEOMETRIA ANALITICA EN EL PLANO. FACULTAD DE MATEMATICAS UNIVERSIDAD VERACRUZANA 2010 Xalapa, Ver. México 1 1. La distancia entre dos puntos en la recta real es 5. Si uno de los puntos
PROBLEMARIO DE GEOMETRIA ANALITICA EN EL PLANO. FACULTAD DE MATEMATICAS UNIVERSIDAD VERACRUZANA 2010 Xalapa, Ver. México 1 1. La distancia entre dos puntos en la recta real es 5. Si uno de los puntos
Colegio Internacional Torrequebrada. Departamento de Matemáticas
 Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
Tema 11.- Autovalores y Autovectores.
 Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
Álgebra 004-005 Ingenieros Industriales Departamento de Matemática Aplicada II Universidad de Sevilla Tema - Autovalores y Autovectores Definición, propiedades e interpretación geométrica La ecuación característica
MATEMÁTICAS I 13 de junio de 2007
 MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
MATEMÁTICAS: PAU 2016 JUNIO CASTILLA Y LEÓN
 MATEMÁTICAS: PAU 26 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A 5 a a) Discutir para qué valores de a R la matriz M = ( ) tiene inversa. Calcular M a para a =. ( 5 puntos) Para que exista inversa de una
MATEMÁTICAS: PAU 26 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A 5 a a) Discutir para qué valores de a R la matriz M = ( ) tiene inversa. Calcular M a para a =. ( 5 puntos) Para que exista inversa de una
FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS LA HIPÉRBOLA
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO 10 TALLER Nº 8 SEMESTRE LA HIPÉRBOLA RESEÑA HISTÓRICA Apolonio de Perge (c. 6 190 a. C.), geómetra griego nacido en Perga (hoy Murtina
FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO 10 TALLER Nº 8 SEMESTRE LA HIPÉRBOLA RESEÑA HISTÓRICA Apolonio de Perge (c. 6 190 a. C.), geómetra griego nacido en Perga (hoy Murtina
Aplicaciones Lineales. Diagonalización de matrices.
 Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 013 Capítulo 1 Año 011 1.1. Modelo 011 - Opción A Problema 1.1.1 (3 puntos) Dado el sistema: λx
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás de mayo de 013 Capítulo 1 Año 011 1.1. Modelo 011 - Opción A Problema 1.1.1 (3 puntos) Dado el sistema: λx
CIRCUNFERENCIA. Ecuación de la circunferencia
 CIRCUNFERENCIA Definición Se llama circunferencia al conjunto de puntos del plano que equidistan de un punto fijo llamado centro. La distancia constante del centro a todos los puntos de la circunferencia
CIRCUNFERENCIA Definición Se llama circunferencia al conjunto de puntos del plano que equidistan de un punto fijo llamado centro. La distancia constante del centro a todos los puntos de la circunferencia
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/2010. Solución al primer examen parcial. x - x 3 1
 UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
INECUACIONES Y VALOR ABSOLUTO
 INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
INECUACIONES Y VALOR ABSOLUTO U.C.V. F.I.U.C.V. CÁLCULO I (051) - TEMA 1 Pág.: 1 de 3 1. Resuelva las siguientes ecuaciones: a. 4 3x = 5 b. x + 1x + = 3 c. x + 1x + 4 = 10 d. x 1 + = 4 e. x + 3 = 4 f.
Docente Matemáticas. Marzo 11 de 2013
 Geometría Analítica Ana María Beltrán Docente Matemáticas Marzo 11 de 2013 1 Geometría Analítica Definición 1. Un lugar geométrico es el conjunto de todos los puntos del plano que tienen una característica
Geometría Analítica Ana María Beltrán Docente Matemáticas Marzo 11 de 2013 1 Geometría Analítica Definición 1. Un lugar geométrico es el conjunto de todos los puntos del plano que tienen una característica
Diagonalización. Tema Valores y vectores propios Planteamiento del problema Valores y vectores propios
 61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
Departamento de Matemática Aplicada II. Universidad de Sevilla. Solución de la Primera Prueba Alternativa ( )
 MATEMÁTICAS I ( o de GIE y GIERM (Curso - Departamento de Matemática Aplicada II. Universidad de Sevilla Solución de la Primera Prueba Alternativa (-- Ejercicio.. Calcule las raíces cúbicas del número
MATEMÁTICAS I ( o de GIE y GIERM (Curso - Departamento de Matemática Aplicada II. Universidad de Sevilla Solución de la Primera Prueba Alternativa (-- Ejercicio.. Calcule las raíces cúbicas del número
1 + r, y = y 1 + ry Si P es el punto medio del segmento P 1 P 2, entonces x = x 1 + x 2 2
 CAPÍTULO 5 Geometría analítica En el tema de Geometría Analítica se asume cierta familiaridad con el plano cartesiano. Se entregan básicamente los conceptos más básicos y los principales resultados (fórmulas)
CAPÍTULO 5 Geometría analítica En el tema de Geometría Analítica se asume cierta familiaridad con el plano cartesiano. Se entregan básicamente los conceptos más básicos y los principales resultados (fórmulas)
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de Circunferencia.
 ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
Indice Elementos de geometr ıa anal ıtica onicas Coordenadas Polares
 Índice 1 Elementos de geometría analítica 2 1.1 Introducción....................................... 2 1.2 Sistema de coordenadas rectangulares......................... 2 1.3 Distancia entre dos puntos...............................
Índice 1 Elementos de geometría analítica 2 1.1 Introducción....................................... 2 1.2 Sistema de coordenadas rectangulares......................... 2 1.3 Distancia entre dos puntos...............................
3.1 DEFINICION. Una elipse E es el conjunto de los puntos del plano euclideano IR2 tales que la suma de sus distancias a dos puntos fijos del plano
 3.1 DEFINICION. Una elipse E es el conjunto de los puntos del plano euclideano IR tales que la suma de sus distancias a dos puntos fijos del plano es una constante. Sean Fl y F, dos puntos del plano ft
3.1 DEFINICION. Una elipse E es el conjunto de los puntos del plano euclideano IR tales que la suma de sus distancias a dos puntos fijos del plano es una constante. Sean Fl y F, dos puntos del plano ft
Proyecto. Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas. Geometría Analítica. Isidro Huesca Zavaleta
 Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
Geometría Analítica Tema 6 sesión 2: Generación de Rectas, Circunferencias y Curvas Isidro Huesca Zavaleta La Integración de dos Ciencias La Geometría Analítica nació de la integración de dos ciencias
TEMA III: DIAGONALIZACIÓN.
 TEMA III: DIAGONALIZACIÓN. OBJETIVOS: Generales: 1. Captar el motivo que justifica el problema de la diagonalización de endomorfismos. 2. Resolver y aplicar dicho problema cuando sea posible. Específicos:
TEMA III: DIAGONALIZACIÓN. OBJETIVOS: Generales: 1. Captar el motivo que justifica el problema de la diagonalización de endomorfismos. 2. Resolver y aplicar dicho problema cuando sea posible. Específicos:
a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2
![a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2 a ij x i x j = [x] t B A+At ) t = At +(A t ) t = At +A x i x j + a ij + a ji x j x i = s ij x i x j + s ji x j x i 2](/thumbs/65/53464617.jpg) 68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
68 Matemáticas I : Álgebra Lineal Tema 7 Formas cuadráticas Aunque, pueda parecernos que vamos a estudiar un nuevo concepto, un caso particular de las formas cudráticas ya ha sido estudiado, pues el cuadrado
Circunferencias. d) A( 1, 5) y d = X = (x, y) punto genérico del lugar geométrico. b) dist (X, A) = d
 Circunferencias 6 Halla, en cada caso, el lugar geométrico de los puntos del plano cuya distancia al punto A es d. a) A(, ) y d = b) A(, ) y d = 1 c) A(, ) y d = 1 d) A( 1, ) y d = X = (x, y) punto genérico
Circunferencias 6 Halla, en cada caso, el lugar geométrico de los puntos del plano cuya distancia al punto A es d. a) A(, ) y d = b) A(, ) y d = 1 c) A(, ) y d = 1 d) A( 1, ) y d = X = (x, y) punto genérico
Problema a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente.
 Problema 717.- a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente. Hallar el lugar geométrico de los puntos comunes a
Problema 717.- a) En un triángulo rectángulo OAB una recta r paralela a la hipotenusa corta a los catetos OA y OB en los puntos A y B respectivamente. Hallar el lugar geométrico de los puntos comunes a
Cónicas. Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá. November 27,
 Cónicas Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá November 27, 2013 marcos.marva@uah.es Cómo definir una cónica Como intersección de un plano y un cono recto de doble hoja
Cónicas Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá November 27, 2013 marcos.marva@uah.es Cómo definir una cónica Como intersección de un plano y un cono recto de doble hoja
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS Álgebra Guía de Ejercicios º Elementos Elementos de Geometría Analítica Plana ELEME TOS DE GEOMETRÍA A ALÍTICA Distancia
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS Álgebra Guía de Ejercicios º Elementos Elementos de Geometría Analítica Plana ELEME TOS DE GEOMETRÍA A ALÍTICA Distancia
UNIDAD 6: CÓNICAS. Carrera: Arquitectura. Asignatura: Matemática. Material de estudio: Cónicas
 UNIDAD 6: CÓNICAS LUGAR GEOMÉTRICO Se denomina así al conjunto de puntos del plano que cumplen con una propiedad métrica determinada. En el caso de las cónicas existe siempre al menos un punto llamado
UNIDAD 6: CÓNICAS LUGAR GEOMÉTRICO Se denomina así al conjunto de puntos del plano que cumplen con una propiedad métrica determinada. En el caso de las cónicas existe siempre al menos un punto llamado
Problemas de Selectividad de Matemáticas II Comunidad de Madrid (Resueltos) Isaac Musat Hervás
 Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos Isaac Musat Hervás 22 de mayo de 203 Capítulo 7 Año 2006 7.. Modelo 2006 - Opción A Problema 7.. 2 puntos Un punto de luz situado
Problemas de Selectividad de Matemáticas II Comunidad de Madrid Resueltos Isaac Musat Hervás 22 de mayo de 203 Capítulo 7 Año 2006 7.. Modelo 2006 - Opción A Problema 7.. 2 puntos Un punto de luz situado
E E V (P, Q) v = P Q AA + AB = AB AA = 0.
 Espacios afines. 1 Definición y propiedades. Definición 1.1 Sea E un conjunto no vacío. Se dice que E está dotado de estructura de espacio afín asociado a un espacio vectorial V, si existe una aplicación:
Espacios afines. 1 Definición y propiedades. Definición 1.1 Sea E un conjunto no vacío. Se dice que E está dotado de estructura de espacio afín asociado a un espacio vectorial V, si existe una aplicación:
