1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
|
|
|
- Rosa María Rivero Caballero
- hace 7 años
- Vistas:
Transcripción
1 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación del tipo: a + a + a + a 0 + a 0 + a 00 0 donde a ij R a, a, a no son los tres nulos. La epresión polinómica de arriba se puede escribir, en forma matricial, del siguiente modo: siendo A la matriz simétrica: ( A A donde a ij a ji para todo i j. a 00 a 0 a 0 a 0 a a a 0 a a 0 Los casos particulares más interesantes son los siguientes: a La ecuación de una elipse en forma canónica es + a b con a, b > 0. La matriz asociada será A /a /b b La ecuación de una hipérbola en forma canónica es a b con a, b > 0. La matriz asociada será
2 CÓNICAS A /a /b c La ecuación de una parábola en forma canónica es p con p > 0. La matriz asociada será 0 p 0 A p Estudiemos cada uno de ellos por separado.... Elipse. Dados dos puntos del plano euclídeo, F F, con distancia de uno a otro d(f, F c, se llama elipse de focos F F semieje a > c al lugar geométrico formado por los puntos X (, del plano tales que d(x, F + d(x, F a. La recta que contiene al segmento F F su mediatriz son los ejes de la elipse. La intersección de los ejes es el centro de simetría los cuatro puntos de corte de los ejes con la elipse (dos por cada eje son los vértices. Si los focos tienen coordenadas F (c, 0 F ( c, 0, no es difícil probar que la ecuación de la elipse es siendo b a c. a + b X d(x, F a b a d(x, F F ( c, 0 a F (c, 0 d(x, F + d(x, F a a + b
3 CÓNICAS 3 Los ejes coordenados son los ejes de la elipse. Proposición.. Dado un punto X de una elipse, la recta tangente a la misma que pasa por X es bisectriz de las rectas R XF R XF que unen X con F X con F respectivamente.... Hipérbola. Dados dos puntos del plano euclídeo, F F, con distancia de uno a otro d(f, F c, se llama hipérbola de focos F F semieje a > 0 ( a < c al lugar geométrico formado por los puntos X (, del plano tales que d(x, F d(x, F a. La recta que contiene al segmento F F su mediatriz son los ejes de la hipérbola. La intersección de los ejes es el centro de simetría los dos puntos de corte de la recta que contiene a F F con la hipérbola son los vértices. Si las coordenadas de los focos son F (c, 0 F ( c, 0, la ecuación de la hipérbola es a b con b c a > 0 Elementos importantes de las hipérbolas son sus asíntotas. La hipérbola tiene por asíntotas a las rectas de la ecuación a b ± b a X b a d(x, F F ( c, 0 d(x, F c a b F (c, 0 b a d(x, F d(x, F a a b
4 CÓNICAS 4 Proposición.. Dado un punto X de una hipérbola, la recta tangente a la misma que pasa por X es bisectriz de las rectas R XF R XF que unen X con F X con F respectivamente...3. Parábola. Es el lugar geométrico de los puntos X (, del plano tales que equidistan de un punto, F, llamado foco de la parábola, de una recta directriz r, situada a distancia p > 0 de F. El eje de la parábola es la recta perpendicular a r que pasa por F. El eje corta a la parábola en un punto al que se llama vértice. Supondremos que F (p/, 0 que r { p/}. Entonces, resulta fácil probar que la ecuación de la parábola es p d(x, r X d(x, F F (p/, 0 r { p/} Proposición.3. Dado un punto X de una parábola, la recta tangente a la misma que pasa por X es bisectriz de la recta R XF, que pasa por X F, la recta S, paralela al eje que pasa por X... Secciones cónicas. El nombre de cónica dado a elipse, hipérbola parábola viene del hecho de que estas curvas se obtienen de la intersección de un plano con un cono. Por ejemplo, el cono C { + z 0} cortado con el plano z da lugar a la elipse + (es una circunferencia. El corte de C con el plano da lugar a la curva z, que es una hipérbola, el corte
5 CÓNICAS 5 de C con el plano + z da lugar a la curva +, que es una parábola. A la elipse, la hipérbola la parábola se las suele llamar cónicas no degeneradas o irreducibles. No obstante, la intersección de un plano con un cono puede dar lugar también a otras situaciones: i C {z 0} da lugar a la ecuación + 0 (un punto. ii C { 0} proporciona la ecuación z 0 ( z( + z 0, que se corresponde con dos rectas que se cortan. iii C { z} da lugar a 0, que es una recta (recta doble. Todas estas cónicas se denominan cónicas degeneradas..3. Ecuación reducida de una cónica. Sea la cónica que, respecto de un sistema de referencia rectangular jo, R {O, u, u }, tiene coordenadas, con epresión polinómica: epresión matricial: donde X a + a + a + a 0 + a 0 + a 00 0 ( ( A A es la matriz simétrica: A a 00 a 0 a 0 a 0 a a a 0 a a con a ij a ji para todo i j, ā 0 ó X t AX 0 ( ( a0 ( a00 ā t ā A 0 ( a a A 0 a 0 a a La matriz A 0 representa los coecientes de los términos cuadráticos del polinomio, la columna ā representa los coecientes de la parte lineal a 00 es el término constante.
6 CÓNICAS 6 Haremos un cambio de coordenadas rectangulares (un giro compuesto con una traslación de ejes de modo que la ecuación polinómica ( sea lo más sencilla posible. Paso. Giro de ejes. La matriz asociada a un giro de ángulo α es ( cos α sen α φ sen α cos α La nueva referencia rectangular obtenida tras el giro es R {O, u, u } con coordenadas,, esto es, ( ( φ u u u O α u R {O, u, u } R {O, u, u } o, de modo equivalente, X GX donde X, X ( 0 Escribiremos G t 0 φ. G cos α sen α 0 sen α cos α Dado que nuestro objetivo es simplicar (, esto se conseguirá diagonalizando la matriz A 0 que aparece en ( mediante la transformación ortogonal que representa el giro. Elegimos φ de modo que
7 CÓNICAS 7 φ A 0 φ φ t A 0 φ D siendo D una matriz diagonal cuas entradas en la diagonal principal son los autovalores (todos reales de la matriz simétrica A 0. Recordemos que las columnas de φ son las coordenadas de los vectores de una base de autovectores (unitarios de A 0 asociados a los respectivos autovalores, cumpliéndose φ. Veamos cuál es la epresión matricial de la cónica respecto de la referencia R : donde X t AX (GX t A(GX X t G t AGX X t A X ( ( A G t a00 ā AG t φ a φ t ā φ t 00 ā t A 0 φ ā A 0 ( a con A 0 D 0 0 a. De este modo, la ecuación matricial ( pasa a ser de la forma X t A X 0 (3 La ecuación de la cónica respecto de la referencia R, (3, es más sencilla que ( (A 0 es diagonal. Obsérvese que al realizar el giro, desaparecen los términos cuadráticos cruzados en el polinomio de la cónica respecto de la nueva referencia R. Queda por hacer una traslación de los ejes de R. Paso. Traslación de ejes. Una traslación de ejes simplicará aún más la epresión (3. Denotamos a la nueva referencia rectangular después de la traslación como R {O, u, u } denotamos por, a las nuevas coordenadas. La matriz de la traslación será con t ( t t Se tiene ( 0 T t t I las coordenadas de O respecto de R e I X T X ( 0 0.
8 CÓNICAS 8 siendo X Entonces, X t A X (T X t A (T X X t T t A T X X t A X con A T t A T (GT t A(GT. La ecuación matricial (3 pasa a ser de la forma X t A X 0 (4 Se prueba fácilmente que la matriz A tiene la forma ( A a00 + ā t t + t t A 0 t (ā + A 0 t t φ φ t (ā + A 0 t φ t A 0 φ con t φ t ( t t son las coordenadas de O respecto de las referencias R R. Ya sabemos que la parte cuadrática asociada a A ( a A 0 φ t A 0 φ 0 0 a es diagonal, su diagonal principal está formada por los autovalores de A 0. Ahora se busca que la parte lineal asociada a A sea lo más sencilla posible (si puede ser, nula para simplicar la ecuación (4. Interesa elegir t para que φ t (ā + A 0 t 0. De ese modo, A sería diagonal. La condición a imponer en la traslación es, pues,, ā + A 0 t 0 (5 u u u O u u O u R {O, u, u } R {O, u, u } R {O, u, u } No siempre será posible encontrar un t solución única de este sistema lineal. De haberlo, esas serán las coordenadas, respecto de R, del centro de
9 CÓNICAS 9 la cónica. Si el sistema es compatible indeterminado, la cónica tendrá innitos centros, si es incompatible, la cónica no tendrá centro (caso de la parábola. Tendremos tres situaciones posibles para la matriz A en función de que eista uno, ninguno o innitos centros: i En caso de que la cónica tenga centro único, esto es, si A 0 A 0 0 o, en otras palabras, si los dos autovalores de A 0 son no nulos, entonces el sistema (5 es compatible determinado. En este caso, tras la traslación, desaparecen los términos en e obteniéndose la matriz reducida A (6 0 0 que da lugar a la ecuación reducida, respecto de R, En función de los signos de los coecientes, los distintos casos posibles son: elipse real, elipse imaginaria (conjunto vacío, hipérbola, un punto (dos rectas imaginarias que se cortan en dicho punto o dos rectas reales que se cortan. ii Si alguno de los autovalores de A 0 es nulo A 0, no se anulan los dos términos lineales e. Ese es el caso de la parábola, para la que el sistema (5 es incompatible. La matriz reducida resultante para la parábola es del tipo A (7 iii Si alguno de los autovalores de A 0 es nulo A 0, la matriz A es A 00 0 donde 0 son los autovalores de A 0 00 (8 puede tomar cualquier valor real. En función del signo de ese valor, tendremos una recta doble, dos rectas paralelas reales o dos rectas paralelas imaginarias.
10 CÓNICAS 0.4. Invariantes métricos de las cónicas. Proposición.4. Invariantes métricos de las cónicas. Las transformaciones rectangulares de coordenadas (giros traslaciones no modican A, A 0 ni tr(a 0. En particular: A A A, A 0 A 0 A 0, tr(a 0 tr(a 0 tr(a 0 Demostración. Dado que T G, A T t A T A G t AG A Por otro lado, como A 0 A 0 φ t A 0 φ φ A 0 φ, podemos armar que las matrices A 0 A 0 A 0 son semejantes, por tanto, tienen el mismo polinomio característico λ a λ + a. Como en el polinomio característico a es la traza a el determinante de la matriz, queda probado que A 0 A 0 A 0 tr(a 0 tr(a 0 tr(a Coecientes de la ecuación reducida en función de los invariantes. i En las cónicas con centro único (con A 0 0, los coecientes de las ecuaciones reducidas son Por otro lado, 00 A A A 0 A 0 a son las raíces de p(λ, el polinomio característico de A 0 siendo p(λ λ tr(a 0 λ + det(a 0. ii En las parábolas (cónicas con vértice, resulta tr(a 0 tr(a 0 A 0 A, de modo que 0 ± A tr(a 0
11 CÓNICAS iii En el resto de casos (rectas paralelas, a sean reales o imaginarias, recta doble, mientras que 0 son los autovalores de A 0 00 A +A siendo A ii el adjunto de a ii en A. A +A tr(a Clasicación de las cónicas en función de los invariantes. En el siguiente esquema encontramos una clasicación de las cónicas en función de los invariantes estudiados: Caso. A 0... Si A 0 0 (cónica con centro único, puede ocurrir:..a A 0 > 0 sig( A sig(tr(a 0. Elipse imaginaria...b A 0 > 0 sig( A sig(tr(a 0. Elipse real...c A 0 < 0. Hipérbola.. Si A 0 0. Parábola. Caso. A 0.. Si A 0 0 (rectas no paralelas, puede ocurrir:..a A 0 > 0 par de rectas imaginarias (un punto...b A 0 < 0 par de rectas reales.. Si A 0 0 (rectas paralelas, puede ocurrir:..a A + A > 0 par de rectas imaginarias distintas...b A + A < 0 par de rectas reales distintas...c A + A 0 recta doble. Ejemplo. Clasicar obtener la ecuación reducida de la cónica
12 CÓNICAS Resulta A 3, A 0 ( Como A 7, A 0 3 tr(a 0 4, tenemos una elipse imaginaria. Calculemos la ecuación reducida. La matriz asociada a dicha ecuación será la matriz diagonal: A 00 Los valores a son los autovalores de A 0. Calculémoslos: p(λ det(a 0 λi (λ (λ 3 Se tiene 3. Además, 00 A 7 A 0 3 La matriz A es A la ecuación reducida será Ejemplo. Clasicar encontrar la ecuación reducida de la cónica ( A, A 0 3 Se tiene A A 0 0, de modo que la cónica es una parábola. Calculemos la ecuación reducida. Téngase en cuenta que la matriz asociada en el caso de la parábola es A El polinomio característico de A 0 es p(λ λ(λ, de modo que los autovalores son 0. Por tanto, (el autovalor no nulo. Únicamente
13 CÓNICAS 3 queda por saber el valor de obtiene a partir de la igualdad esto es, 0 ± A ( A tr(a 0 ±. La ecuación reducida se 0, + 0 ó.5. Cálculo de los elementos de una cónica. Centro ejes de cónicas con centro. Si la cónica tiene centro (o centros, éste se obtiene resolviendo el sistema lineal (5, ā + A 0 t 0. Los ejes se obtienen a partir de los autovectores asociados a los autovalores de A 0 (las columnas de φ apoados en el centro. Obsérvese que, en el caso de la hipérbola, el eje que no la corta es aquel obtenido del autovector asociado al autovalor de signo negativo. Ejemplo 3. Dada la cónica , se pide su clasicación, ecuación reducida los elementos característicos de la misma. Resulta A 3 3 3, A 0 ( Como A A 0, tenemos una hipérbola. Calculemos el centro. Basta resolver el sistema lineal Resulta c ( / 5/ (. ( c c ( 3 Hallemos la ecuación reducida. Para ello debemos obtener la matriz diagonal
14 CÓNICAS 4 A 00 Los valores a son los autovalores de A 0. Calculémoslos: p(λ det(a 0 λi (λ (λ + Se tiene. Además, 00 A A 0 La matriz A es A la ecuación reducida será de modo equivalente, ( + (. Se puede escribir, Los ejes vienen determinados por los autovectores asociados a los autovalores. Debemos calcular los subespacios propios V V. Tras echar cuentas, resultan V L{( +, } V L{(, } (bastaría con calcular uno de los subespacios propios a que sabemos que el otro será perpendicular. Dado que en A 0 hemos elegido como primer autovalor λ como segundo autovalor λ, la primera columna de φ será (+, dividido por su norma la segunda columna de φ será (, dividido por su norma. Los ejes serán Eje X ( ( / 5/ ( + + λ Eje Y ( ( / 5/ ( + λ
15 CÓNICAS 5 Ejemplo 4. Clasicar obtener la ecuación reducida los elementos característicos de la cónica: Resulta A 3, A 0 ( Como A, A 0 3 tr(a 0 4, tenemos una elipse real. Calculemos la ecuación reducida. La matriz asociada a dicha ecuación será la matriz diagonal: A 00 Los valores a son los autovalores de A 0. Calculémoslos: p(λ det(a 0 λi (λ (λ 3 Se tiene 3. Además, 00 A A 0 3 La matriz A es A 3 3 la ecuación reducida será + 3 /3 ó ( /3 + ( /9 Las columnas de la matriz del giro φ se obtienen a partir de una base ortogonal de autovectores unitarios asociados a los autovalores de A 0. Los subespacios propios asociados son V L{(, } V 3 L{(, }. Por tanto,
16 CÓNICAS 6 φ ( / / / / Se tiene el ángulo α arc cos ( / π/4. (0, ( /, / (/, / O π/4 (, 0 El centro de la cónica es la solución c (/3, /3 del sistema ( + ( c 0 Los ejes se obtienen a partir de los autovectores asociados a los autovalores λ λ 3, resultando: Eje X ( ( /3 /3 ( + λ Eje Y ( ( /3 /3 ( + λ
17 CÓNICAS 7 O (/3, /3 Calculemos los vértices. La ecuación reducida indica que a /3 b /9. Además, c (/3, /3 φ ( / / / / Llegamos a la conclusión de que los vértices son v v v 3 v 4 ( /3 /3 ( /3 /3 ( /3 /3 ( /3 /3 + ( / /3 / ( / /3 / + ( / /9 / ( / /9 / Por otro lado, dado que c /3 /9, los focos son 3 F ( /3 /3 + 3 ( / /
18 CÓNICAS 8 F ( /3 /3 3 ( / / v 3 F v (/3, /3 v 4 F v Vértice ejes de la parábola. Si la cónica tiene vértice (parábola, el eje de la misma se obtiene apoando en el vértice el autovector asociado al autovalor 0 (la columna de φ correspondiente a λ 0. El otro eje (secundario se obtiene apoando en el vértice el autovector dado por la otra columna de φ. Para obtener el vértice, se corta la familia de rectas paralelas al eje secundario con la cónica. La recta que corte eactamente en un punto a la cónica será dicho eje, el punto de intersección será el vértice. Ejemplo 5. Dada la parábola del ejemplo, se piden sus elementos característicos. A 3 3 Se tiene A A 0 0., A 0 ( El polinomio característico de A 0 es p(λ λ(λ, de modo que los autovalores son 0. El vector propio asociado al autovalor 0 nos da la dirección del eje de la parábola.
19 CÓNICAS 9 V 0 { : A 0 0} {(, : 0} L{(, } Como V es perpendicular a V 0 (la matriz A 0 es simétrica, es claro que V L{(, }. Si se hacen las cuentas, V { : (A 0 I 0} {(, : + 0} L{(, } La matriz φ asociada al giro será φ ( El eje de la parábola tendrá la dirección del vector (,. Obsérvese que las rectas de la forma + n son perpendiculares a dicho vector. Estamos interesados en encontrar, de entre todas estas rectas, aquella que corta a la párabola en un único punto, que será el vértice. El resto de rectas cortará a la parábola en dos puntos o en ninguno (puntos imaginarios. Despejamos n (podríamos despejar n también sustituímos en la ecuación de la cónica para obtener la intersección, quedando ( + n + ( + n + 4 6( + n + 0 De modo que 4 + ( 4n (n 6n + 0 (4n 0 ± ( 4n + 0 6(n 6n + 8 Dado que la intersección de la recta la cónica debe ser un único punto (el vértice, tendremos que buscar el valor de la n que hace que la obtenida sea única, esto es, buscamos n tal que ( 4n + 0 6(n 6n+ 0. Resolviendo, resulta n, de modo que la coordenada 4 del vértice es 3. La coordenada se obtiene sustituendo el valor 8 de n el de en la ecuación de la recta, quedando El vértice v es, por tanto, el punto de coordenadas
20 CÓNICAS 0 v ( 3/8 /8 Obsérvese que la recta + /4 contiene al vértice es tangente en él a la parábola. Las rectas + k con k < /4 no se cortan con la parábola las rectas + k con k > /4 se cortan en dos puntos con la parábola. Los ejes a están determinados. El eje X (eje de la parábola es ( ( 3/8 /8 ( + λ El eje Y (tangente a la parábola en el vértice es ( ( 3/8 /8 Dado que la ecuación reducida es ( + λ + 0 ó tenemos p con p 4. Como la parábola se encuentra en el semiplano + /4 el foco está en el mismo semiplano, éste será el punto F ( 3/8 /8 + 8 ( / / ( 5/4 5/4
21 CÓNICAS v F Asíntotas de la hipérbola. Si la hipérbola tiene centro (c, c, la ecuación de las asíntotas será del tipo c m( c para dos valores de m que se obtienen de resolver la ecuación ( ( m A0 0 m Esta ecuación proporciona las pendientes de las dos asíntotas buscadas. Ejemplo 6. Obtener los vértices, los focos las asíntotas de la hipérbola del ejemplo 3. Teníamos A 3 3 3, A 0 ( Las asíntotas son rectas que pasan por el centro c (/, 5/ tienen pendiente m, que se obtiene resolviendo la ecuación: ( m A0 ( m 0 Desarrollando, queda m + m + 0, con lo que m ±. Por consiguiente, las asíntotas son
22 CÓNICAS e 5/ ( + ( / 5/ ( ( / Calculemos los vértices. Dado que A, la ecuación reducida es + ó ( + ( La hipérbola se corta con el eje Y, donde están los vértices los focos. Se tiene a b 3/4 c /4. Como los subespacios propios son resulta: V L{( +, } V L{(, }, Eje X ( ( / 5/ ( + + λ Eje Y ( ( / 5/ ( + λ La matriz del giro será φ Por consiguiente, los vértices son v ( / 5/ + 3/4 4 4
23 CÓNICAS 3 Los focos son v F F ( / 5/ ( / 5/ ( / 5/ 3/4 + /4 / F v 5/ ( + ( / (/, 5/ v F 5/ ( ( /
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
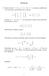 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
1. ESPACIO EUCLÍDEO. ISOMETRÍAS
 . ESPACIO EUCLÍDEO. ISOMETRÍAS. En el espacio euclídeo usual R 4 se consideran los subespacios vectoriales y W = {(x, y, z, t R 4 : x y =, z + t = } Hallar: W 2 = L{(,, 2, 2, (,,, } a Las ecuaciones de
. ESPACIO EUCLÍDEO. ISOMETRÍAS. En el espacio euclídeo usual R 4 se consideran los subespacios vectoriales y W = {(x, y, z, t R 4 : x y =, z + t = } Hallar: W 2 = L{(,, 2, 2, (,,, } a Las ecuaciones de
COLEGIO NUESTRA SEÑORA DEL BUEN CONSEJO. Melilla LUGARES GEOMÉTRICOS Y CÓNICAS
 LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Respuestas ejercicios edición 2007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1
 Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
Lugares geométricos y cónicas
 Lugares geométricos y cónicas E S Q U E M A D E L A U N I D A D. Lugar geométrico página 6.. Definición página 6. Circunferencia página 6.. Ecuación página 6.. Casos particulares página 67. Elipse página
Lugares geométricos y cónicas E S Q U E M A D E L A U N I D A D. Lugar geométrico página 6.. Definición página 6. Circunferencia página 6.. Ecuación página 6.. Casos particulares página 67. Elipse página
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
Lugar Geométrico. Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz
 1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
Tema 5. Cónicas. Asi, para las identificaciones habituales, (punto proyectivo recta vectorial punto de un plano afín ampliado), RP 2 R3 {0}
 Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
Cónicas y cuádricas. Circunferencia Elipse Parábola Hipérbola
 Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
Bloque 2. Geometría. 4. Iniciación a las Cónicas
 Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
22. CURVAS CÓNICAS-ELIPSE
 22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
Geometría Analítica Enero 2015
 Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. A( 2,, B( 8,, C( 5, 10) R( 6, 5) S( 2, - T(3,- U( -1, - V( 2, - W( 9, 4) II.- Demuestre
Laboratorio #1 Distancia entre dos puntos I.- Hallar el perímetro del triángulo, cuyos vértices son los puntos dados. A( 2,, B( 8,, C( 5, 10) R( 6, 5) S( 2, - T(3,- U( -1, - V( 2, - W( 9, 4) II.- Demuestre
Función lineal y cuadrática. Curvas de primer y segundo grado.
 Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Parte II - Prácticas 8 a 9. Álgebra A 62 ÁLGEBRA A 62 (INGENIERÍA)
 Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Aquella que tiene nulos los elementos nos situados en la diagonal principal. Los elementos situados por encima de la diagonal principal son nulos.
 Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
1 + 3(0, 2) = ( 1, 2) + (0, 6) = ( 1, 4) ) ( = arc cos e 5
 utoevaluación Página Dados los vectores uc c, m v (0, ), calcula: a) u b) u + v c) u : ( v) uc c, m v (0, ) a) u c m + ( ) b) u + v c c, m + (0, ) (, ) + (0, 6) (, ) c) u : ( v) () (u v ) c 0 +( m ) (
utoevaluación Página Dados los vectores uc c, m v (0, ), calcula: a) u b) u + v c) u : ( v) uc c, m v (0, ) a) u c m + ( ) b) u + v c c, m + (0, ) (, ) + (0, 6) (, ) c) u : ( v) () (u v ) c 0 +( m ) (
GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA
 ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
MATEMÁTICAS I 13 de junio de 2007
 MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
B23 Curvas cónicas Curvas cónicas
 Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
1. DIAGONALIZACIÓN. FORMAS CANÓNICAS
 1 1. DIAGONALIZACIÓN. FORMAS CANÓNICAS 1. Se considera la matriz: A = ( 2 3 4 13 con coeficientes en R. Hallar los valores propios, los vectores propios y una matriz P que permita la diagonalización de
1 1. DIAGONALIZACIÓN. FORMAS CANÓNICAS 1. Se considera la matriz: A = ( 2 3 4 13 con coeficientes en R. Hallar los valores propios, los vectores propios y una matriz P que permita la diagonalización de
ESTUDIO GRÁFICO DE LA ELIPSE.
 Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Secciones Cónicas. 0.1 Parábolas
 Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
Secciones Cónicas 0.1 Parábolas Las secciones cónicas, también llamadas cónicas, se obtienen cortando un cono circular recto doble con un plano. Al cambiar la posición del plano se tiene un círculo, una
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
TEMA 5. CURVAS CÓNICAS.
 5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
1. DIAGONALIZACIÓN DE ENDOMORFISMOS
 . DIAGONALIZACIÓN DE ENDOMORFISMOS. Se considera la matriz: A ( 2 3 4 3 con coecientes en R. Hallar los valores propios, los vectores propios y una matriz P que permita la diagonalización de A. Calcular
. DIAGONALIZACIÓN DE ENDOMORFISMOS. Se considera la matriz: A ( 2 3 4 3 con coecientes en R. Hallar los valores propios, los vectores propios y una matriz P que permita la diagonalización de A. Calcular
Facultad de Ingeniería Facultad de Tecnología Informática. Matemática Números reales Elementos de geometría analítica. Profesora: Silvia Mamone
 Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6
 página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
CURVAS TÉCNICAS CURVAS CÓNICAS
 2º BACH CURVAS TÉCNICAS CURVAS CÓNICAS ANA BALLESTER JIMÉNEZ CURVAS TÉCNICAS 1. ÓVALOS. El óvalo es una curva cerrada, plana y convexa formada generalmente por cuatro arcos de circunferencia iguales dos
2º BACH CURVAS TÉCNICAS CURVAS CÓNICAS ANA BALLESTER JIMÉNEZ CURVAS TÉCNICAS 1. ÓVALOS. El óvalo es una curva cerrada, plana y convexa formada generalmente por cuatro arcos de circunferencia iguales dos
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
GEOMETRÍA ANALÍTICA LA CIRCUNFERENCIA
 LA CIRCUNFERENCIA CONTENIDO. Ecuación común de la circunferencia Ejemplos. Ecuación general de la circunferencia. Análisis de la ecuación. Ejercicios Estudiaremos cuatro curvas que por su importancia aplicaciones
LA CIRCUNFERENCIA CONTENIDO. Ecuación común de la circunferencia Ejemplos. Ecuación general de la circunferencia. Análisis de la ecuación. Ejercicios Estudiaremos cuatro curvas que por su importancia aplicaciones
4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16.
 Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
22 CURVAS CÓNICAS- HIPÉRBOLAS
 22 CURVAS CÓNICAS- HIPÉRBOLAS 22.1 Características generales. La hipérbola se obtiene al cortar la superficie cónica por un plano paralelo al eje que corta las dos hojas de la cónica. 22.2 Focos y directrices.
22 CURVAS CÓNICAS- HIPÉRBOLAS 22.1 Características generales. La hipérbola se obtiene al cortar la superficie cónica por un plano paralelo al eje que corta las dos hojas de la cónica. 22.2 Focos y directrices.
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO
 PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO 1. Estudiar si la siguiente ecuación matricial corresponde a una homotecia del plano y, en su caso, calcular el centro y la razón: 1 1 1 ' = 3 y' 3 y. Estudiar
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO 1. Estudiar si la siguiente ecuación matricial corresponde a una homotecia del plano y, en su caso, calcular el centro y la razón: 1 1 1 ' = 3 y' 3 y. Estudiar
A pesar de la importancia de las cónicas como secciones de una superficie cónica, para estudiar los elementos y propiedades de cada una de ellas en
 SECCIONES CÓNICAS Las secciones cónicas se pueden definir como lugares geométricos en el plano, sin embargo la definición clásica de las cónicas, que se debe a Apolonio de Perga, se hizo mediante un procedimiento
SECCIONES CÓNICAS Las secciones cónicas se pueden definir como lugares geométricos en el plano, sin embargo la definición clásica de las cónicas, que se debe a Apolonio de Perga, se hizo mediante un procedimiento
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1
 ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1 Cónicas (Curso 011 01) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 3. Dada
ÁLGEBRA LINEAL II Algunas soluciones a la Práctica 4.1 Cónicas (Curso 011 01) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 3. Dada
GEOMETRÍA ANALÍTICA PROBLEMARIO GUÍA DE PROBLEMAS PARA LOS EXÁMENES DEPARTAMENTALES
 PROBLEMARIO GUÍA DE PROBLEMAS PARA LOS EXÁMENES DEPARTAMENTALES CONTENIDO: 1. Conceptos básicos (Problemas 1-18). Línea recta (Problemas 19-6). Circunferencia (Problemas 7-4) 4. Parábola (Problemas 44-6)
PROBLEMARIO GUÍA DE PROBLEMAS PARA LOS EXÁMENES DEPARTAMENTALES CONTENIDO: 1. Conceptos básicos (Problemas 1-18). Línea recta (Problemas 19-6). Circunferencia (Problemas 7-4) 4. Parábola (Problemas 44-6)
PAU Madrid. Matemáticas II. Año Examen de junio. Opción A. Ejercicio 1. Valor: 2 puntos.
 Opción A. Ejercicio 1. Valor: 2 puntos. Calcular las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos en aquel momento,
Opción A. Ejercicio 1. Valor: 2 puntos. Calcular las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos en aquel momento,
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/2010. Solución al primer examen parcial. x - x 3 1
 UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
UCV FACULTAD DE INGENIERIA CALCULO I 16/04/010 Solución al primer eamen parcial 1. Encuentre el conjunto de todos los números reales que satisfacen el sistema de inecuaciones - 3 4 4 0 1 1 1 Solución:
Ejercicios 16/17 Lección 5. Geometría. 1. como combinación lineal de u = (2,5), expresa uno de ellos como combinación lineal de los otros dos.
 Ejercicios 16/17 Lección 5. Geometría. 1 1. Expresa el vector u = ( 3, 1) como combinación lineal de los vectores v = ( 3, ) w = ( 4, 1). y. Expresa w = (4, 6) como combinación lineal de u = (,5) y v =
Ejercicios 16/17 Lección 5. Geometría. 1 1. Expresa el vector u = ( 3, 1) como combinación lineal de los vectores v = ( 3, ) w = ( 4, 1). y. Expresa w = (4, 6) como combinación lineal de u = (,5) y v =
Formulario: Geometría Analítica
 Universidad Autónoma del Estado de México UAEM Facultad de Ingeniería Formulario: Geometría Analítica Elaborado por: Estudiante en Ingeniería en Electrónica Formulario Geometría Analítica 1. VECTORES EN
Universidad Autónoma del Estado de México UAEM Facultad de Ingeniería Formulario: Geometría Analítica Elaborado por: Estudiante en Ingeniería en Electrónica Formulario Geometría Analítica 1. VECTORES EN
GEOMETRÍA. (x 1) 2 +(y 2) 2 =1. Razónalo. x y + z = 2. :3x 3z +1= 0 es doble de la distancia al plano π 2. : x + y 1= 0. Razónalo.
 GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
UNI DAD 4 ESPACIO BIDIMENSIONAL: CÓNICAS
 UNI DAD 4 ESPACIO BIDIMENSIONAL: CÓNICAS Objetivos Geometría analítica Introducción L cónica sección cónica Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0 A B C D E F 4.1. Circunferencia Circunferencia es el conjunto
UNI DAD 4 ESPACIO BIDIMENSIONAL: CÓNICAS Objetivos Geometría analítica Introducción L cónica sección cónica Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0 A B C D E F 4.1. Circunferencia Circunferencia es el conjunto
UNPSJB - Facultad Ciencias Naturales - Asignatura: Matemática 1 Ciclo Lectivo: 2014 CONICAS
 Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
Asignatura: Matemática 1 Ciclo Lectivo: 014 CONICAS La superficie que se muestra en la figura se llama doble cono circular recto, o simplemente cono. Es la superficie tridimensional generada por una recta
INTRO. ESTUDIO DE LAS CÓNICAS
 INTRO. ESTUDIO DE LAS CÓNICAS Una vez que se han estudiado los sistemas de coordenadas y las ecuaciones de las figuras geométricas más elementales, las rectas, se pasará a hacer un estudio de algunas líneas
INTRO. ESTUDIO DE LAS CÓNICAS Una vez que se han estudiado los sistemas de coordenadas y las ecuaciones de las figuras geométricas más elementales, las rectas, se pasará a hacer un estudio de algunas líneas
1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a)
 Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES. Tema 3 EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS.
 INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES Tema EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS. C.- Qué es cómo se representa un sistema de coordenadas cartesianas rectangulares
INTRODUCCIÓN A LAS MATEMÁTICAS SUPERIORES Tema EL PLANO Y LAS GRÁFICAS EL PLANO CARTESIANO. COORDENADAS Y DISTANCIA ENTRE PUNTOS. C.- Qué es cómo se representa un sistema de coordenadas cartesianas rectangulares
Geometría Analítica Agosto 2016
 Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
Laboratorio #1 Distancia entre dos puntos I.- Demostrar que los puntos dados no son colineales. 1) A (0, 5), B(3, 1), C( 11, 27) 2) A (1, 4), B( 2, 10), C(5, 5) II.- Demostrar que los puntos dados forman
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2012 2013) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2012 2013) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
Ejercicios 17/18 Lección 5. Geometría. 1. como combinación lineal de u = (2,5), expresa uno de ellos como combinación lineal de los otros dos.
 Ejercicios 17/18 Lección 5. Geometría. 1 1. Expresa el vector u = ( 3, 1) como combinación lineal de los vectores v = ( 3, ) w = ( 4, 1). y. Expresa w = (4, 6) como combinación lineal de u = (,5) y v =
Ejercicios 17/18 Lección 5. Geometría. 1 1. Expresa el vector u = ( 3, 1) como combinación lineal de los vectores v = ( 3, ) w = ( 4, 1). y. Expresa w = (4, 6) como combinación lineal de u = (,5) y v =
Es la elipse el conjunto de puntos fijos cuya suma de distancias a dos puntos fijos llamados focos es constante.
 ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
ESQUEMA LAS CÓNICAS LA PARÁBOLA ECUACIONES DE LA PARÁBOLA ECUACIÓN DE LA TANGENTE A UNA PARÁBOLA ELIPSE ECUACIONES DE LA ELIPSE PROPIEDADES DE LA ELIPSE LA HIPÉRBOLA ECUACIONES DE LA HIPÉRBOLA 10 ASÍNTOTAS
1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a la recta x + 7y + 1 = 0
 Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS Álgebra Guía de Ejercicios º Elementos Elementos de Geometría Analítica Plana ELEME TOS DE GEOMETRÍA A ALÍTICA Distancia
UNIVERSIDAD DIEGO PORTALES FACULTAD DE INGENIERÍA INSTITUTO DE CIENCIAS BASICAS Álgebra Guía de Ejercicios º Elementos Elementos de Geometría Analítica Plana ELEME TOS DE GEOMETRÍA A ALÍTICA Distancia
Guía de estudio Nº 3: Ejercicios propuestos sobre Lugares geométricos. Secciones cónicas
 U.C.V. Facultad de Ingeniería CÁLCULO I (5) Guía de estudio Nº : Ejercicios propuestos sobre Lugares geométricos. Secciones cónicas.- Determine la ecuación del lugar geométrico de los puntos (, ) del plano
U.C.V. Facultad de Ingeniería CÁLCULO I (5) Guía de estudio Nº : Ejercicios propuestos sobre Lugares geométricos. Secciones cónicas.- Determine la ecuación del lugar geométrico de los puntos (, ) del plano
ESCUELA PREPARATORIA OFICIAL NO.16 MATERÍA: GEOMETRÍA ANALITICA GUÍA DE ESTUDIO PARA LA ÚLTIMA OPORTUNIDAD DE ACREDITAR LA MATERÍA
 Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Geometría analítica 1.- Ecuación de la recta 2.- Cónicas 3.-Ecuación de la parábola UNIDAD II: CONICAS (CIRCUNFERENCIA Y PARABOLAS) Una superficie cónica de revolución está engendrada por la rotación de
Cónicas. Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá. November 27,
 Cónicas Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá November 27, 2013 marcos.marva@uah.es Cómo definir una cónica Como intersección de un plano y un cono recto de doble hoja
Cónicas Marcos Marvá Departamento de Física y Matemáticas, Universidad de Alcalá November 27, 2013 marcos.marva@uah.es Cómo definir una cónica Como intersección de un plano y un cono recto de doble hoja
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2013 2014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2013 2014) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = O, ē 1, ē 2, ē 3 } y R = P, ū 1, ū 2, ū 3 },
TEMA III: DIAGONALIZACIÓN.
 TEMA III: DIAGONALIZACIÓN. OBJETIVOS: Generales: 1. Captar el motivo que justifica el problema de la diagonalización de endomorfismos. 2. Resolver y aplicar dicho problema cuando sea posible. Específicos:
TEMA III: DIAGONALIZACIÓN. OBJETIVOS: Generales: 1. Captar el motivo que justifica el problema de la diagonalización de endomorfismos. 2. Resolver y aplicar dicho problema cuando sea posible. Específicos:
UNIDAD 6: CÓNICAS. Carrera: Arquitectura. Asignatura: Matemática. Material de estudio: Cónicas
 UNIDAD 6: CÓNICAS LUGAR GEOMÉTRICO Se denomina así al conjunto de puntos del plano que cumplen con una propiedad métrica determinada. En el caso de las cónicas existe siempre al menos un punto llamado
UNIDAD 6: CÓNICAS LUGAR GEOMÉTRICO Se denomina así al conjunto de puntos del plano que cumplen con una propiedad métrica determinada. En el caso de las cónicas existe siempre al menos un punto llamado
Departamento de Ingeniería Matemática - Universidad de Chile
 Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Álgebra Lineal 8-7 Formas cuadráticas SEMANA 4: FORMAS CUADRÁTICAS 7 Formas cuadráticas y matrices definidas positivas
Rectas y Cónicas. Sistema de Coordenadas Cartesianas. Guía de Ejercicios # Encuentre las coordenadas de los puntos mostrados en la figura.
 Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
Universidad de Los Andes Facultad de Ciencias Forestales y Ambientales Escuela de ingeniería Forestal Departamento de Botánica y Ciencias Básicas Matemáticas I I 2014 Prof. K. Chang. Rectas y Cónicas Guía
INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO
 PRIMER EXAMEN PARCIAL INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO GUÍA DE GEOMETRÍA ANALÍTICA 2016-2017A SISTEMA DE COORDENADAS, LUGARES
PRIMER EXAMEN PARCIAL INSTITUTO POLITÉCNICO NACIONAL CECYT LÁZARO CÁRDENAS DEL RÍO ÁREA BÁSICA ACADÉMIA DE MATEMÁTICAS TURNO MATUTINO GUÍA DE GEOMETRÍA ANALÍTICA 2016-2017A SISTEMA DE COORDENADAS, LUGARES
1 + r, y = y 1 + ry Si P es el punto medio del segmento P 1 P 2, entonces x = x 1 + x 2 2
 CAPÍTULO 5 Geometría analítica En el tema de Geometría Analítica se asume cierta familiaridad con el plano cartesiano. Se entregan básicamente los conceptos más básicos y los principales resultados (fórmulas)
CAPÍTULO 5 Geometría analítica En el tema de Geometría Analítica se asume cierta familiaridad con el plano cartesiano. Se entregan básicamente los conceptos más básicos y los principales resultados (fórmulas)
Evaluación NOMBRE APELLIDOS CURSO Y GRUPO FECHA CALIFICACIÓN. 3 b) y 16 x Lugares geométricos y cónicas
 Evaluación NOMBRE APELLIDOS CURSO Y GRUPO FECHA CALIFICACIÓN 4 La ecuación del lugar geométrico de los puntos del plano que equidistan de la recta x y 4, y del punto P (, ) es: a) x y x y 68 0 b) 4x 9y
Evaluación NOMBRE APELLIDOS CURSO Y GRUPO FECHA CALIFICACIÓN 4 La ecuación del lugar geométrico de los puntos del plano que equidistan de la recta x y 4, y del punto P (, ) es: a) x y x y 68 0 b) 4x 9y
LUGARES GEOMÉTRICOS. CÓNICAS
 9 LUGARES GEOMÉTRICOS. CÓNICAS Página PARA EMPEZAR, RELEXIONA Y RESUELVE Cónicas abiertas: parábolas e hipérbolas Completa la siguiente tabla, en la que α es el ángulo que forman las generatrices con el
9 LUGARES GEOMÉTRICOS. CÓNICAS Página PARA EMPEZAR, RELEXIONA Y RESUELVE Cónicas abiertas: parábolas e hipérbolas Completa la siguiente tabla, en la que α es el ángulo que forman las generatrices con el
Academia de Matemáticas T.M Geometría Analítica Página 1
 INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
PAU Madrid. Matemáticas II. Año Examen de septiembre. Opción A. Ejercicio 1. Valor: 2 puntos.
 Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
Opción A. Ejercicio. Valor: 2 puntos. Se considera la función real de variable real definida por: f(x) = a) ( punto) Determinar sus máximos y mínimos relativos x x 2 + b) ( punto) Calcular el valor de
DIVISIÓN DE UN SEGMENTO EN UNA RAZÓN DADA
 SISTEMA COORDENADO CARTESIANO, DISTANCIA ENTRE DOS PUNTOS ANGULO ENTRE DOS RECTAS y AREA 1) Transportar a una gráfica los siguientes puntos: a) ( 5, 2 ) b) (0, 0 ) c) ( 1 + 3, 1-3 ) d) ( 0, 3 ) e) ( -
SISTEMA COORDENADO CARTESIANO, DISTANCIA ENTRE DOS PUNTOS ANGULO ENTRE DOS RECTAS y AREA 1) Transportar a una gráfica los siguientes puntos: a) ( 5, 2 ) b) (0, 0 ) c) ( 1 + 3, 1-3 ) d) ( 0, 3 ) e) ( -
Esta expresión polinómica puede expresarse como una expresión matricial de la forma; a 11 a 12 a 1n x 1 x 2 q(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
INDICE. 88 determinante 36. Familias de líneas rectas Resumen de resultados 96
 INDICE Geometría Analítica Plana Capitulo Primero Sistema de Coordenadas Articulo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5
INDICE Geometría Analítica Plana Capitulo Primero Sistema de Coordenadas Articulo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5
UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 02 de 2012
 UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 0 de 0 PARTE I: Ejercicios cortos de selección Múltiple. En cada uno de los siguientes
UNIVERSIDAD CENTROAMERICANA JOSÉ SIMEÓN CAÑAS ALGEBRA VECTORIAL Y MATRICES GUIA DE TRABAJO Secciones Cónicas Ciclo 0 de 0 PARTE I: Ejercicios cortos de selección Múltiple. En cada uno de los siguientes
Cónicas: circunferencia y parábola
 Universidad Nacional de Rosario Facultad de Ciencias Exactas, Ingeniería y Agrimensura Escuela de Formación Básica Departamento de Matemática Álgebra y Geometría Analítica Cónicas: circunferencia y parábola
Universidad Nacional de Rosario Facultad de Ciencias Exactas, Ingeniería y Agrimensura Escuela de Formación Básica Departamento de Matemática Álgebra y Geometría Analítica Cónicas: circunferencia y parábola
2 Intersección de una recta y una cuádrica. 1 Definición y ecuaciones. ( x y z
 2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
RESUMEN TEÓRICO LUGARES GEÓMETRICOS. CÓNICAS (circunferencia y elipse)
 RESUMEN TEÓRICO LUGARES GEÓMETRICOS. CÓNICAS (circunferencia y elipse) 1. LUGARES GEOMÉTRICOS Definición: Se llama lugar geométrico a la figura que forman un conjunto de puntos que cumplen una determinada
RESUMEN TEÓRICO LUGARES GEÓMETRICOS. CÓNICAS (circunferencia y elipse) 1. LUGARES GEOMÉTRICOS Definición: Se llama lugar geométrico a la figura que forman un conjunto de puntos que cumplen una determinada
Departamento de Matemática Aplicada II. Universidad de Sevilla. Solución de la Primera Prueba Alternativa ( )
 MATEMÁTICAS I ( o de GIE y GIERM (Curso - Departamento de Matemática Aplicada II. Universidad de Sevilla Solución de la Primera Prueba Alternativa (-- Ejercicio.. Calcule las raíces cúbicas del número
MATEMÁTICAS I ( o de GIE y GIERM (Curso - Departamento de Matemática Aplicada II. Universidad de Sevilla Solución de la Primera Prueba Alternativa (-- Ejercicio.. Calcule las raíces cúbicas del número
Dibujo Técnico Curvas cónicas-parábola
 22. CURVAS CÓNICAS-PARÁBOLAS 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar
22. CURVAS CÓNICAS-PARÁBOLAS 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar
UNIDAD 5: Curvas y superficies 5.A. Cónicas
 UNIDAD 5: Curvas y superficies 5.A. Cónicas En un principio se estudiaron las curvas que quedaban determinadas cuando se cortaba un cono recto con planos en distintas posiciones respecto de la base del
UNIDAD 5: Curvas y superficies 5.A. Cónicas En un principio se estudiaron las curvas que quedaban determinadas cuando se cortaba un cono recto con planos en distintas posiciones respecto de la base del
Las curvas cónicas son las secciones producidas por un plano secante sobre una superficie cónica de revolución. (Fig. 31)
 Dibujo Trazado de Curvas cónicas Las curvas cónicas son las secciones producidas por un plano secante sobre una superficie cónica de revolución. (Fig. 31) Fig. 31 Una superficie cónica de revolución es
Dibujo Trazado de Curvas cónicas Las curvas cónicas son las secciones producidas por un plano secante sobre una superficie cónica de revolución. (Fig. 31) Fig. 31 Una superficie cónica de revolución es
IES Francico Ayala Examen modelo 1 del Libro 1996_97 con soluciones Germán Jesús Rubio luna. Opción A
 Opción A Ejercicio n 1 de la opción A del modelo 1 del libro 96_97 De una función continua f : R R se sabe que si F : R R es una primitiva suya, entonces también lo es la función G dada por G(x) 3 - F(x).
Opción A Ejercicio n 1 de la opción A del modelo 1 del libro 96_97 De una función continua f : R R se sabe que si F : R R es una primitiva suya, entonces también lo es la función G dada por G(x) 3 - F(x).
IPN CECYT 7 CUAUHTEMOC ACADEMIA DE MATEMÁTICAS GUÍA PARA EL E.T.S GEOMETRÍA ANALÍTICA
 IPN CECYT 7 CUAUHTEMOC ACADEMIA DE MATEMÁTICAS GUÍA PARA EL E.T.S DE GEOMETRÍA ANALÍTICA CONCEPTOS BÁSICOS 1.- Hallar la distancia entre los pares de puntos cuyas coordenadas son: a) A (4, 1), B (3, 2)
IPN CECYT 7 CUAUHTEMOC ACADEMIA DE MATEMÁTICAS GUÍA PARA EL E.T.S DE GEOMETRÍA ANALÍTICA CONCEPTOS BÁSICOS 1.- Hallar la distancia entre los pares de puntos cuyas coordenadas son: a) A (4, 1), B (3, 2)
EJERCICIOS DE GEOMETRÍA PLANA. 1. Hallar las ecuaciones paramétricas de la recta r que pasa por el punto ( 2, 2) tiene como vector director el vector
 EJERCICIOS DE GEOMETRÍA PLANA Hallar las ecuaciones paramétricas de la recta r que pasa por el punto (, ) tiene como vector director el vector v i j A y x a + vt La ecuación paramétrica de una recta es
EJERCICIOS DE GEOMETRÍA PLANA Hallar las ecuaciones paramétricas de la recta r que pasa por el punto (, ) tiene como vector director el vector v i j A y x a + vt La ecuación paramétrica de una recta es
CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos)
 CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos) Ejercicio nº 1.- Escribe la ecuación de la circunferencia con centro en el punto (, 3) que es tangente a la recta 3 4 + 5 = 0. El radio, R, de la circunferencia
CONICAS Y LUGARES GEOMÉTRICOS ( problemas resueltos) Ejercicio nº 1.- Escribe la ecuación de la circunferencia con centro en el punto (, 3) que es tangente a la recta 3 4 + 5 = 0. El radio, R, de la circunferencia
Razonar el trazado de rectas tangentes a la elipse y la hipérbola haciendo uso de las circunferencias focales y, a la
 CURVAS CÓNICAS OBJETIVOS 1 Conocer y/o recordar los elementos y propiedades fundamentales que configuran las tres curvas cónicas, junto a la construcción geométrica de cada una de ellas. 2 Razonar el trazado
CURVAS CÓNICAS OBJETIVOS 1 Conocer y/o recordar los elementos y propiedades fundamentales que configuran las tres curvas cónicas, junto a la construcción geométrica de cada una de ellas. 2 Razonar el trazado
5x + 4y 20 = 0! 5 ( x) + 4 ( y) 20 = 0! 5x 4y 20 = 0. al origen O. En resumen, la ecuación 5x + 4y 20 = 0 no tiene ninguna simetría.
 Geometría Analítica; C. H. Lehmann. Ejercicio, grupo, capítulo II, página 0.. Discute la ecuación + 0 = 0, estudiando las intersecciones, las simetrías la etensión. Después traza la grá ca correspondiente.
Geometría Analítica; C. H. Lehmann. Ejercicio, grupo, capítulo II, página 0.. Discute la ecuación + 0 = 0, estudiando las intersecciones, las simetrías la etensión. Después traza la grá ca correspondiente.
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro.
 Cónicas 1.- Circunferencia Definición 1 (Definición geométrica) Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro. Analíticamente la circunferencia
Cónicas 1.- Circunferencia Definición 1 (Definición geométrica) Se llama Circunferencia al lugar geométrico de los puntos del plano equidistantes de un punto fijo llamado centro. Analíticamente la circunferencia
Docente Matemáticas. Marzo 11 de 2013
 Geometría Analítica Ana María Beltrán Docente Matemáticas Marzo 11 de 2013 1 Geometría Analítica Definición 1. Un lugar geométrico es el conjunto de todos los puntos del plano que tienen una característica
Geometría Analítica Ana María Beltrán Docente Matemáticas Marzo 11 de 2013 1 Geometría Analítica Definición 1. Un lugar geométrico es el conjunto de todos los puntos del plano que tienen una característica
Unidad IV. La parábola
 Unidad IV. La parábola El estudiante, resolverá problemas teóricos o prácticos relativos a la parábola, a través del análisis descriptivo, aplicación y combinación de sus propiedades, gráficas y ecuaciones,
Unidad IV. La parábola El estudiante, resolverá problemas teóricos o prácticos relativos a la parábola, a través del análisis descriptivo, aplicación y combinación de sus propiedades, gráficas y ecuaciones,
TEMA 7: CÓNICAS CIRCUNFERENCIA. A partir de esta ecuación podemos hallar el centro y el radio sin más que deshacer los cambios:
 TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
TEMA 7: CÓNICAS CIRCUNFERENCIA Se define la circunferencia como el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. A dicha distancia se le llama radio de la circunferencia.
INDICE. 88 determinante 36. Familias de líneas rectas Resumen de resultados 96 Capitulo IV
 INDICE Geometría Analítica Plana Capitulo Primero Artículo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5 5. Carácter de la geografía
INDICE Geometría Analítica Plana Capitulo Primero Artículo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5 5. Carácter de la geografía
