MATEMÁTICAS I 13 de junio de 2007
|
|
|
- Héctor Sáez Álvarez
- hace 7 años
- Vistas:
Transcripción
1 MATEMÁTICAS I 13 de junio de º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si la familia de vectores { u,u, } 1 2 u 3 a) u 1 es combinación lineal de u 2 y u 3. b) u1 0 X c) { u,u,u,v} Si G { u,u,..., } 1 2 um de V(R), es ligada, podemos asegurar: es ligada para cualquier vector v del espacio. = es un sistema generador de R 3, podemos asegurar: a) G es una base de R 3 para cualquier número natural m. X b) Si m> 3, entonces G es ligado. c) u Si 0 es un valor propio de la transformación lineal f, se verifica: a) N(f) = { 0 }. X b) dim N(f ) 1 c) Que λ= 0 sea un valor propio de f no proporciona ninguna información acerca del N(f). 4.- Si dos matrices A y B tienen los mismos valores propios podemos afirmar que: a) A y B son semejantes. b) Tienen los mismos subespacios de vectores propios asociados. X c) Tienen el mismo polinomio característico. 5.- En el espacio afín euclídeo se consideran los vectores u = ( 1,0,0) ; v= ( 0,1,0) w = 0,2,0 ( ). Cuál de las siguientes afirmaciones es cierta? X a) ( u v) w = ( 2,0,0) b) u ( v w) = ( 2,0,0) u v w = 2 c) ( ) 6.- Si la ecentricidad de una cónica es 0, la cónica es: a) Degenerada. X b) Una circunferencia. Unidad Docente de la E.T.S.I.T.G.C. 1 ;
2 c) Una parábola. 7.- Si A = 18 y los valores propios de la forma cuadrática de una cónica son 0 y 2, entonces la ecuación reducida es: a) 2( y' ) 2 + 6' = 0 b) 2( y' ) 2 3' = 0 X c) 2( y' ) 2 6' = La simetría aial en el espacio verifica: a) Es un movimiento inverso. b) La única recta invariante es el eje de simetría. X c) Sus puntos dobles son los del eje de simetría. 9.- En el plano euclídeo: X a) Cualquier homotecia conserva la orientación. b) Cualquier semejanza conservan la orientación. c) Ninguna de las anteriores La ecuación de un movimiento T en E n sin puntos dobles es: a) T (X) = A + M AX X b) T(X) = A + M AX+ AA ' c) T (X) + = M AX AA' MATEMÁTICAS I 2º PARCIAL (1ª Parte) Teoría: contestar sólo a una de las dos opciones siguientes A) ó B): A) 1) Sean v 1 y v 2 dos vectores propios de una matriz A, asociados a dos valores propios distintos entre sí, λ 1 y λ 2. Demostrar que v 1 y v 2 son vectores linealmente independientes. 2) Demostrar que dos matrices semejantes de orden 2 tienen la misma traza. B) 1) Demostrar que el conjunto de vectores propios de una matriz A M ( R) asociados a un mismo valor propio, junto con el vector 0, es un subespacio n vectorial de R. 2) Demostrar que dos matrices semejantes tienen el mismo determinante. n (1 punto) Unidad Docente de la E.T.S.I.T.G.C. 2
3 2.- Hallar la ecuación de la semejanza directa que transforma los puntos O(0,0) y P(1,2) en O (15,-1) y P (-7,-5), respectivamente. (1 punto) Ecuación de la semejanza directa: ' = e a b y sustituyendo los puntos y' f b a y S(O) = O ' 15 = e a b 0 a = 6 1 f b a 0 b = 8, obtenemos que:, quedando la ecuación e = 15 S(P) = P ' 7 = e a b 1 f = 1 5 f b a de la semejanza ' = y' 1 8 6y MATEMÁTICAS I 2º PARCIAL (2ª Parte) Dado el espacio vectorial R 3 : a) Hallar una base del subespacio vectorial generado por los vectores: a = 2,4,0,b = 1,2,1,c = 3,2,1,d = 3,4,1 { } S= ( ) ( ) ( ) ( ) y epresar el vector d en dicha base. b) Encontrar un vector común al subespacio E generado por los vectores u 1 = (1,2,3) y u 2 = (3,2,1) y al subespacio F generado por los vectores v 1 = (1,0,1) y v 2 =. ( 3,4,3) c) Indicar si los subespacios vectoriales H = {(,y,z)/2+ y z= 0;+ y= 0} y G={ ( α β+ 2 γ, β α 2 γ, α β+ 2 γ)/ α, β, γ R} son iguales. d) Sean B = { u = ( 2,1,0 ), v = ( 1,0,1 ), w = ( 0,1, 2) } y B' = { u ' = ( 0,1,1 ), v ' = ( 1,0,0 ), w ' = ( 2,0,1) }. Hallar la matriz del cambio de base de B a B. (1.25 puntos) a) Una base #1: ROW_REDUCE = Una base puede ser la canónica {(1,0,0),(0,1,0),(0,0,1)} del espacio Unidad Docente de la E.T.S.I.T.G.C. 3
4 vectorial R^3, puesto que S genera R^3. y epresar el vector d en dicha base. Al escoger la base canónica el vector queda igual (3,4,1) b) Un vector común #2: α [1, 2, 3] + β [3, 2, 1] = λ [1, 0, 1] + µ [3, 4, 3] #3: SOLVE(α [1, 2, 3] + β [3, 2, 1] = λ [1, 0, 1] + µ [3, 4, 3], [α, β, λ], Real) #4: α = µ β = µ λ = µ #5: [4, 4, 4] El vector (1,1,1) o cualquier otro proporcional incluido el vector nulo. c) #6: SOLVE([2 + y - z = 0, + y = 0], [, y]) #7: [ = z y = -z] #8: SOLUTIONS([2 + y - z = 0, + y = 0], [, y, z]) #9: [[@1, Una base de H: {(1,-1,1)} #10: SOLVE([ = α - β + 2 γ, y = β - α - 2 γ, z = α - β + 2 γ], [, y, z, α, β, γ]) #11:[ - α + β - 2 γ = 0 y + α - β + 2 γ = 0 z - α + β - 2 γ = 0] #12: SOLUTIONS([ = α - β + 2 γ, y = β - α - 2 γ, z = α - β + 2 γ], [, y, z, α, β, 2 Una base de G: {(1,-1,1)} Sí H=G son subespacios vectoriales iguales, son de igual dimensión y coinciden las bases. d) Cambio de base de B a B #14: Matriz del cambio de base B a la canónica: #15: Matriz del cambio de base B' a la canónica: ` #16: y = y` z z` ` #17: y = y` z z` Matriz del cambio de base de B a B' #19: = Unidad Docente de la E.T.S.I.T.G.C. 4
5 4.- Dada la transformación lineal f ( ) = A , donde A = 1 3 4, se pide: a) Hallar la dimensión y una base de los subespacios N(f) e Imf, respectivamente. b) Estudiar si f es diagonalizable y, en su caso, calcular una matriz D diagonal semejante a la matriz A y la matriz P que permite la diagonalización. Sea g una transformación lineal de R 3 tal que g( u ) = 6u, ( ) g v = 3 v, ( ) g w 6 w para los vectores u = ( 1, 1,0 ), v = ( 1,1, 1) w = ( 1, 0, 1) =, c) Cómo se denominan los vectores u, v y w? Cómo se denominan los escalares 3 y 6? d) Hallar la matriz M asociada a g respecto de la base canónica. (1.25 puntos) a) Núcleo de f: #1: Cálculo del núcleo: Resolvemos AX= #2: y = z #3: SOLVE y = 0, [, y, z], Real z 0 #4: + 3 y = 0 z = 0 La solución es {(-3λ,λ,0), λεr}, luego la dimn(f)=1 y una base es {(-3,1,0)} Imagen de f: La dim(imf)=3-1=2, y una base está formada por dos columnas de A l.i. por ejemplo la primera y la tercera {(-5,1,0),(-12,4,-2)} no pueden ser la primera y la segunda. b) Valores propios de A: Se obtienen a partir del polinomio característico. Luego #5: CHARPOLY = - w (w + 2) A tiene un valor propio simple λ1=0, y un valor propio doble λ2=-2. Unidad Docente de la E.T.S.I.T.G.C. 5
6 Calculamos los vectores propios asociados #6: EXACT_EIGENVECTOR 1 3 4, 0 = #7: EXACT_EIGENVECTOR 1 3 4, -2 = Luego la dimv0=1, y la dimv(-2)=2, es decir coinciden con el orden de multiplicidad de los valores propios. Por lo tanto A es diagonalizable y como matrices diagonal y P pedidas proponemos #8: y respectivamente c) Los vectores u,v,w son vectores propios de la transformación g y los escalares 3 y 6 son los valores propios asociados a los anteriores valores propios de la siguiente forma: 3 es el valor propio asociado a v y 6 es el valor propio asociado a u y w. d) Tenemos que g tiene un valor propio simple, 3, el cual tiene a v como vector propio asociado y un valor propio doble, 6, que tiene a u,w como vectores propios asociados, luego la matriz diagonal D que escribiremos a continuación es una matriz semejante a M #9: D #10: Las matrices D y M están relacionadas por la epresión D = -1 P M P donde P es la matriz de cambio de la base de vectores -1 propios a la canónica y despejando M = P D P #11: P #12: P D P = Unidad Docente de la E.T.S.I.T.G.C. 6
7 5.- En el espacio afín ordinario, se consideran la referencia: R = { A, { u, v, w }, donde A es el punto de coordenadas A = (1, 2, 3) y los vectores u, v, w tienen por coordenadas u = ( 1,2,0 ), v = ( 3, 7,1) y w = ( 2,0,1 ). Se pide: a) Hallar las ecuaciones del cambio de referencia de la canónica a R. b) Comprobar si eisten puntos del espacio que tienen las mismas coordenadas respecto de la referencia canónica y de R. c) Ecuación, en la referencia R, del plano cuya ecuación en la referencia canónica es z = 0. (1.25 puntos) a) Llamando (,y,z) a las coordenadas de un punto genérico del espacio respecto de la referencia canónica y (,y,z ) a las coordenadas de ese mismo punto respecto de la ' referencia R, se tiene que = [1] y, por y y' z 3 0 tanto, el cambio de la referencia canónica a R, que es lo que se pide en el apartado a) se ' calcula mediante la matriz inversa, es decir, = y' y z b) = y y z 3 0 z Resolviendo el sistema se obtiene un único punto P=(-13,-3,5) c) La epresión matricial [1] puede ponerse como = ' - 3y' - 2z' + 1 y = 2 ' - 7 y' + 2 z = y' + z' + 3 Por tanto, observando la última ecuación, el plano z=0 tendrá por ecuación en la referencia R: y ' + z' + 3=0 Unidad Docente de la E.T.S.I.T.G.C. 7
8 6.- Dadas H 1, homotecia de centro C 1 (1,1,1) y razón k 1 =1/2, y H 2 homotecia de centro C 2 (-1,1,- 1) y razón k 2 = 2. Se pide: a) Hallar las ecuaciones de T = H 2 oh 1, e identificar T. b) Transformada mediante H 1 de la recta de ecuación: +1 = -y = z (1 punto) La ecuación de la homotecia de centro C(a,b,c) y razón k es: ' ( 1 k)a k 0 0 = y' ( 1 k)b 0 k 0y ( 1 k)c 0 0 k z La ecuación de la homotecia H 1 de centro C 1 (1,1,1) y razón k 1 =1/2 es: ' 2 2 = y' 0 0y 2 2 z La ecuación de la homotecia H 2 de centro C 2 (-1,1,-1) y razón k 2 =2 es: ' = y' y z a) T=H 2 oh ' = 2 2 y' = 0 0 y y z z = 1 k C C. T es una TRASLACIÓN de vector (2,0,2) ( ) b) T =H 1 oh ' 2 2 = = y' y y z z = 1 k C C. T es una TRASLACIÓN de vector (1,0,1) ( ) Unidad Docente de la E.T.S.I.T.G.C. 8
9 c) De la ecuación de la homotecia H 1 se despejan las coordenadas, y, z: = 1+ 2' ' = y = 1+ 2y', obsérvese que es la homotecia del mismo y' 0 0y 2 2 z = 1 + 2z' z centro y razón k=2. Se sustituye en la ecuación de la recta r + 1= y = z 1+ 2' + 1 = ( 1+ 2y') = 1+ 2z' r' ' = y' = + z' Dada la cónica de ecuación y + y y + 49 = 0. Se pide: a) Clasificar la cónica Hallar: b) La ecuación reducida. c) La ecentricidad. d) La ecuación del eje focal. e) Las ecuaciones de las asíntotas. (1.25 puntos) a) #1: A #2: DET(A) = -18 #3: Ac MINOR(A, 1, 1) #4: A00 DET(Ac) #5: A00 = -10 ES UNA HIPÉRBOLA DET(A) 0; DET(Ac)<0 b) DET(A) #6: k A00 9 #7: k = 5 valores propios de Ac: #8: EIGENVALUES(Ac) = [-1, 10] Consideramos primero el NEGAtivo, para obtener como eje de abscisas 0X'' el eje focal Ecuación reducida: #9: y + = 0 5 Unidad Docente de la E.T.S.I.T.G.C. 9
10 c) 9 2 #10: - = #11: SOLVE - = 0,, Real #12: = - = #13: 10 y + = #14: SOLVE10 y + = 0, y i 3 2 i #15: y = - y = Semiejes:a=3 5, b=3 2/ #16: a #17: b 10 Semidistancia focal: 2 2 #18: c (a + b ) 3 22 #19: c = 10 Ecentricidad: c 11O #20: e = = a 10 d) Primeramente hallamos el centro de la hipérbola: 1 0 #21: DELETE_ELEMENT(A, 1) = 0 y #22: = y #23: SOLVE =, [, y], Real y #24: = y = A continuación la pendiente del eje focal: Unidad Docente de la E.T.S.I.T.G.C. 10
11 2 - #25: EXACT_EIGENVECTOR(Ac, -1) = = #26: Eje focal #27: y + = e) 1 #28: SOLVE[1, m] Ac = [0], m, Real m #29: m = m = #30: y + = (3 2-10) #31: y + = ( ) Unidad Docente de la E.T.S.I.T.G.C. 11
MATEMÁTICAS I 2º EXAMEN PARCIAL 12 junio de 2009
 Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Un sistema generador G de R 3 : a) Está constituido por
Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Un sistema generador G de R 3 : a) Está constituido por
MATEMÁTICAS I 2º EXAMEN PARCIAL 9 de junio de 2008
 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 Sólo una respuesta a cada cuestión es correcta Respuesta correcta: 0 puntos Respuesta incorrecta: -0 puntos Respuesta en blanco: 0 puntos - Sean F y G dos
MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 Sólo una respuesta a cada cuestión es correcta Respuesta correcta: 0 puntos Respuesta incorrecta: -0 puntos Respuesta en blanco: 0 puntos - Sean F y G dos
ETSI de Topografía, Geodesia y Cartografía
 3ª Prueba de Evaluación Continua 7 05 12 (Grupo C) Espacio vectorial 1. a) Definir vectores linealmente dependientes en un espacio vectorial V. u,u,,u de un espacio vectorial V son b) Demostrar que si
3ª Prueba de Evaluación Continua 7 05 12 (Grupo C) Espacio vectorial 1. a) Definir vectores linealmente dependientes en un espacio vectorial V. u,u,,u de un espacio vectorial V son b) Demostrar que si
Hoja de diagonalización MATEMÁTICAS I
 Hoja de diagonalización MATEMÁTICAS I 8-9.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) Ax así como los subespacios vectoriales
Hoja de diagonalización MATEMÁTICAS I 8-9.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) Ax así como los subespacios vectoriales
Hoja de diagonalización MATEMÁTICAS I
 Hoja de diagonalización MATEMÁTICAS I 007-008 1.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) = Ax, así como los subespacios vectoriales
Hoja de diagonalización MATEMÁTICAS I 007-008 1.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) = Ax, así como los subespacios vectoriales
Hoja de diagonalización MATEMÁTICAS I
 Hoja de diagonalización MATEMÁTICAS I 9- - En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) Ax así como los subespacios vectoriales N(f)
Hoja de diagonalización MATEMÁTICAS I 9- - En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) Ax así como los subespacios vectoriales N(f)
Soluciones de la hoja de diagonalización MATEMÁTICAS I
 Soluciones de la hoja de diagonalización MATEMÁTICAS I 9- - En los siguientes casos estudiar si f es una aplicación lineal y, en caso afirmativo, hallar una matriz A tal que f(x) Ax, así como los subespacios
Soluciones de la hoja de diagonalización MATEMÁTICAS I 9- - En los siguientes casos estudiar si f es una aplicación lineal y, en caso afirmativo, hallar una matriz A tal que f(x) Ax, así como los subespacios
PRUEBA DE DIAGONALIZACIÓN CURSO Apellidos: Nombre: Grupo: Fecha:
 Tipo 1 Apellidos: Nombre: Grupo: Fecha: 1.- Sea f una transformación lineal de un espacio vectorial V de dimensión n. Sea B una base de V. Sea A la matriz asociada a f respecto de la base B. Señala, sin
Tipo 1 Apellidos: Nombre: Grupo: Fecha: 1.- Sea f una transformación lineal de un espacio vectorial V de dimensión n. Sea B una base de V. Sea A la matriz asociada a f respecto de la base B. Señala, sin
Aplicaciones Lineales. Diagonalización de matrices.
 Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
TEMA V. Espacios vectoriales
 TEMA V. Espacios vectoriales 1 1. Demostrar que cada uno de los siguientes conjuntos tiene estructura de espacio vectorial sobre el cuerpo de los reales: a El conjunto (R 2, +,, R. b El conjunto (R 3,
TEMA V. Espacios vectoriales 1 1. Demostrar que cada uno de los siguientes conjuntos tiene estructura de espacio vectorial sobre el cuerpo de los reales: a El conjunto (R 2, +,, R. b El conjunto (R 3,
PROBLEMAS RESUELTOS del espacio vectorial curso
 PROBLEMAS RESUELTOS del espacio vectorial curso - - Consideremos el conjunto R formado por todas las parejas () de números reales Se define en R la operación interna ()( )( ) una de las operaciones eternas
PROBLEMAS RESUELTOS del espacio vectorial curso - - Consideremos el conjunto R formado por todas las parejas () de números reales Se define en R la operación interna ()( )( ) una de las operaciones eternas
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO
 PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO 1. Estudiar si la siguiente ecuación matricial corresponde a una homotecia del plano y, en su caso, calcular el centro y la razón: 1 1 1 ' = 3 y' 3 y. Estudiar
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO 1. Estudiar si la siguiente ecuación matricial corresponde a una homotecia del plano y, en su caso, calcular el centro y la razón: 1 1 1 ' = 3 y' 3 y. Estudiar
DIAGONALIZACIÓN DE MATRICES CUADRADAS
 DIAGONALIZACIÓN DE MATRICES CUADRADAS.- Considerar los vectores u = (, -, ) y v = (, -, ) de : a) Escribir, si es posible, los vectores (, 7, -4) y (, -5, 4) como combinación lineal de u y v. b) Para qué
DIAGONALIZACIÓN DE MATRICES CUADRADAS.- Considerar los vectores u = (, -, ) y v = (, -, ) de : a) Escribir, si es posible, los vectores (, 7, -4) y (, -5, 4) como combinación lineal de u y v. b) Para qué
Álgebra Lineal. Ejercicios de evaluación. Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas
 Álgebra Lineal Ejercicios de evaluación Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR Problema
Álgebra Lineal Ejercicios de evaluación Grado en Ingeniería Informática Doble Grado en Ingeniería Informática y Administración de Empresas AUTORES: J. S ALAS, A. T ORRENTE Y E.J.S. V ILLASEÑOR Problema
A.-TRANSFORMACIONES DEL PLANO
 A.-TRANSFORMACIONES DEL PLANO 1.- Sean los giros G y G, de centros O(0,0) y O (1,0) y ángulos respectivos 120º y α. Hallar las ecuaciones de GoG y sus elementos característicos para: a) α=90º b) α=240º
A.-TRANSFORMACIONES DEL PLANO 1.- Sean los giros G y G, de centros O(0,0) y O (1,0) y ángulos respectivos 120º y α. Hallar las ecuaciones de GoG y sus elementos característicos para: a) α=90º b) α=240º
Soluciones Hoja Problemas Espacio Vectorial 05-06
 Soluciones Hoja Problemas Espacio Vectorial -6.- Se considera R con la suma habitual y con el producto por un escalar que se indica en los casos siguientes. Prueba que en ninguno de ellos, (R,, ) es espacio
Soluciones Hoja Problemas Espacio Vectorial -6.- Se considera R con la suma habitual y con el producto por un escalar que se indica en los casos siguientes. Prueba que en ninguno de ellos, (R,, ) es espacio
ESPACIOS VECTORIALES Y APLICACIONES LINEALES
 Departamento de Matemática Aplicada II E.E.I. ÁLGEBRA Y ESTADÍSTICA Boletín n o (010-011 ESPACIOS VECTORIALES Y APLICACIONES LINEALES 1. En el espacio vectorial ordinario R 4 estudiar cuáles de los siguientes
Departamento de Matemática Aplicada II E.E.I. ÁLGEBRA Y ESTADÍSTICA Boletín n o (010-011 ESPACIOS VECTORIALES Y APLICACIONES LINEALES 1. En el espacio vectorial ordinario R 4 estudiar cuáles de los siguientes
1.- Definir: Vectores linealmente dependientes y Sistemas ligados.
 Prueba de Evaluación Continua Grupo B 23-03-11 1- Definir: Vectores linealmente dependientes Sistemas ligados Demostrar que un conjunto de vectores son linealmente dependientes si sólo si uno de ellos
Prueba de Evaluación Continua Grupo B 23-03-11 1- Definir: Vectores linealmente dependientes Sistemas ligados Demostrar que un conjunto de vectores son linealmente dependientes si sólo si uno de ellos
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
Ejercicios tipo test de las lecciones 1 y El vector e = ( 1, 0, λ) está en el plano generado por los vectores u = (1, 2, 1) y
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Ejercicios tipo test de las lecciones 1 y 2. 1. El vector e = ( 1, 0, λ) está en el plano generado por los vectores u = (1,
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Ejercicios tipo test de las lecciones 1 y 2. 1. El vector e = ( 1, 0, λ) está en el plano generado por los vectores u = (1,
ETSI en Topografía, Geodesia y Cartografía
 4ª Prueba de Evaluación Continua 24-5-17 TRANSFORMACIONES GEOMÉTRICAS DEL ESPACIO EUCLÍDEO (Grupo A) APELLIDOS: NOMBRE: Grupo: 1.- a) Definición de transformación involutiva. b) Demostrar que la matriz
4ª Prueba de Evaluación Continua 24-5-17 TRANSFORMACIONES GEOMÉTRICAS DEL ESPACIO EUCLÍDEO (Grupo A) APELLIDOS: NOMBRE: Grupo: 1.- a) Definición de transformación involutiva. b) Demostrar que la matriz
Tema 1: Espacios vectoriales
 PROBLEMAS DE MATEMÁTICAS Parte I: Álgebra Primero de Químicas FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha Tema 1: Espacios vectoriales 1 Determina si cada
PROBLEMAS DE MATEMÁTICAS Parte I: Álgebra Primero de Químicas FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha Tema 1: Espacios vectoriales 1 Determina si cada
CONJUNTO R n. = (5, 2, 10) de 3, son linealmente. = (2,1,3) y v 3. = (0,1, 1) y u 3. = (2,0,3, 1), u 3. = (1,1, 0,m), v 2
 CONJUNTO R n.- Considerar los vectores u = (, -3, ) y v = (, -, ) de 3 : a) Escribir, si es posible, los vectores (, 7, -4) y (, -5, 4) como combinación lineal de u y v. b) Para qué valores de x es el
CONJUNTO R n.- Considerar los vectores u = (, -3, ) y v = (, -, ) de 3 : a) Escribir, si es posible, los vectores (, 7, -4) y (, -5, 4) como combinación lineal de u y v. b) Para qué valores de x es el
A = [a 1 a 2 a 3. El sistema Ax = c tiene infinitas soluciones N. Existe un único vector x tal que T (x) = c X. T es suprayectiva
 Asignatura: ÁLGEBRA LINEAL Fecha: 6 de Julio de Fecha publicación notas: 6 de Julio de Fecha revisión examen: de Julio de Duración del examen: horas y media APELLIDOS Y NOMBRE: DNI: Titulación:. ( punto:,
Asignatura: ÁLGEBRA LINEAL Fecha: 6 de Julio de Fecha publicación notas: 6 de Julio de Fecha revisión examen: de Julio de Duración del examen: horas y media APELLIDOS Y NOMBRE: DNI: Titulación:. ( punto:,
Matemáticas para la Empresa
 Matemáticas para la Empresa 1 o L. A. D. E. Curso 2008/09 Relación 1. Espacios Vectoriales 1. a) En IR 2 se consideran las operaciones habituales: (x, y) + (x, y ) = (x + x, y + y ) λ(x, y) = (λx, λy)
Matemáticas para la Empresa 1 o L. A. D. E. Curso 2008/09 Relación 1. Espacios Vectoriales 1. a) En IR 2 se consideran las operaciones habituales: (x, y) + (x, y ) = (x + x, y + y ) λ(x, y) = (λx, λy)
TRANSFORMACIONES GEOMÉTRICAS Curso 04-05
 -En el plano vectorial V, con la base ortonormal { i,j } vectores u (, ) v (, ) éstos determinan Hallar en la base { i,j } transformaciones ortogonales tales que f( D ) se consideran los las semirrectas
-En el plano vectorial V, con la base ortonormal { i,j } vectores u (, ) v (, ) éstos determinan Hallar en la base { i,j } transformaciones ortogonales tales que f( D ) se consideran los las semirrectas
ÁLGEBRA LINEAL. EXAMEN EXTRAORDINARIO 2 de julio de 2012 Duración del examen: 3 horas Fecha publicación notas: 11 de julio
 ÁLGEBRA LINEAL EXAMEN EXTRAORDINARIO 2 de julio de 22 Duración del examen: 3 horas Fecha publicación notas: de julio Fecha revisión examen: 3 de julio Apellidos: Nombre: Grupo: Titulación: ESCRIBA EL APELLIDO
ÁLGEBRA LINEAL EXAMEN EXTRAORDINARIO 2 de julio de 22 Duración del examen: 3 horas Fecha publicación notas: de julio Fecha revisión examen: 3 de julio Apellidos: Nombre: Grupo: Titulación: ESCRIBA EL APELLIDO
TRANSFORMACIONES GEOMÉTRICAS Curso 03-04
 .-En el plano vectorial V, con la base ortonormal { i,j } vectores u (, ) y v (, ) éstos determinan. Hallar en la base { i,j } transformaciones ortogonales tales que f( D ) se consideran los y las semirrectas
.-En el plano vectorial V, con la base ortonormal { i,j } vectores u (, ) y v (, ) éstos determinan. Hallar en la base { i,j } transformaciones ortogonales tales que f( D ) se consideran los y las semirrectas
Relación 1. Espacios vectoriales
 MATEMÁTICAS PARA LA EMPRESA Curso 2007/08 Relación 1. Espacios vectoriales 1. (a) En IR 2 se consideran las operaciones habituales: (x, y) + (x, y ) = (x + x, y + y ) λ(x, y) = (λx, λy) Demuestra que IR
MATEMÁTICAS PARA LA EMPRESA Curso 2007/08 Relación 1. Espacios vectoriales 1. (a) En IR 2 se consideran las operaciones habituales: (x, y) + (x, y ) = (x + x, y + y ) λ(x, y) = (λx, λy) Demuestra que IR
1. DIAGONALIZACIÓN DE ENDOMORFISMOS
 . DIAGONALIZACIÓN DE ENDOMORFISMOS. Se considera la matriz: A ( 2 3 4 3 con coecientes en R. Hallar los valores propios, los vectores propios y una matriz P que permita la diagonalización de A. Calcular
. DIAGONALIZACIÓN DE ENDOMORFISMOS. Se considera la matriz: A ( 2 3 4 3 con coecientes en R. Hallar los valores propios, los vectores propios y una matriz P que permita la diagonalización de A. Calcular
f(x, y, z, t) = (x + y t, x + 2y z 3t, 3x + 5y 2z 7t).
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 20 de enero de 20 (2.5 p.) ) Se considera la aplicación lineal f : R 4 R definida por: f(x y
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 20 de enero de 20 (2.5 p.) ) Se considera la aplicación lineal f : R 4 R definida por: f(x y
1. DIAGONALIZACIÓN. FORMAS CANÓNICAS
 1 1. DIAGONALIZACIÓN. FORMAS CANÓNICAS 1. Se considera la matriz: A = ( 2 3 4 13 con coeficientes en R. Hallar los valores propios, los vectores propios y una matriz P que permita la diagonalización de
1 1. DIAGONALIZACIÓN. FORMAS CANÓNICAS 1. Se considera la matriz: A = ( 2 3 4 13 con coeficientes en R. Hallar los valores propios, los vectores propios y una matriz P que permita la diagonalización de
Geometría afín y proyectiva, 2016 SEMANA 4
 Geometría afín y proyectiva, 2016 SEMANA 4 Sonia L. Rueda ETS Arquitectura. UPM September 30, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Geometría afín y proyectiva, 2016 SEMANA 4 Sonia L. Rueda ETS Arquitectura. UPM September 30, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
GEOMETRÍA AFÍN Y PROYECTIVA Espacios Vectoriales.
 Sonia L. Rueda ETS Arquitectura. UPM Año 2016-2017. 1 GEOMETRÍA AFÍN Y PROYECTIVA Espacios Vectoriales. 1. Determinar si los siguientes conjuntos de vectores son subespacios vectoriales de R 4. A = {(x,
Sonia L. Rueda ETS Arquitectura. UPM Año 2016-2017. 1 GEOMETRÍA AFÍN Y PROYECTIVA Espacios Vectoriales. 1. Determinar si los siguientes conjuntos de vectores son subespacios vectoriales de R 4. A = {(x,
Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos.
 Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada
Tema 2. Aplicaciones lineales. Diagonalización de endomorfismos. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada
Examen Final Ejercicio 2 (1 hora y 30 min.) 27 de mayo de 2011
 Álgebra Lineal II Eamen Final Ejercicio 2 ( hora 30 min 27 de mao de 20 En el espacio afín euclideo usual consideramos una pirámide triangular ABCD de la cual sabemos: - A (0, 0, 0, B (, 0, 0, C (0,, -
Álgebra Lineal II Eamen Final Ejercicio 2 ( hora 30 min 27 de mao de 20 En el espacio afín euclideo usual consideramos una pirámide triangular ABCD de la cual sabemos: - A (0, 0, 0, B (, 0, 0, C (0,, -
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS ESPACIOS EUCLÍDEOS ) a) Decir cuál de las siguientes aplicaciones de x de no definir un producto escalar comprobar el axioma que falla: a ) x' x,y,
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS ESPACIOS EUCLÍDEOS ) a) Decir cuál de las siguientes aplicaciones de x de no definir un producto escalar comprobar el axioma que falla: a ) x' x,y,
Examen Final Ejercicio único (3 horas) 20 de enero de n(n 1) 2. C n,3 = n(n 3) n =
 Álgebra Lineal I Examen Final Ejercicio único (3 horas) 0 de enero de 014 1. Sea P un polígono regular de n lados. (i) Cuántas diagonales tiene el polígono?. Las diagonales son segmentos que unen pares
Álgebra Lineal I Examen Final Ejercicio único (3 horas) 0 de enero de 014 1. Sea P un polígono regular de n lados. (i) Cuántas diagonales tiene el polígono?. Las diagonales son segmentos que unen pares
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas
 EXÁMENES DE MATEMÁTICAS Álgebra Primero de Ingeniería Química FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha 5 de julio de 99. Dada la aplicación lineal: T
EXÁMENES DE MATEMÁTICAS Álgebra Primero de Ingeniería Química FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha 5 de julio de 99. Dada la aplicación lineal: T
Problemas de exámenes de Aplicaciones Lineales y Matrices
 1 Problemas de exámenes de Aplicaciones Lineales y Matrices 1. Consideramos f End(R n ), que tiene matriz A respecto la base canónica. Cuál de las siguientes afirmaciones es incorrecta? a) Si v es un vector
1 Problemas de exámenes de Aplicaciones Lineales y Matrices 1. Consideramos f End(R n ), que tiene matriz A respecto la base canónica. Cuál de las siguientes afirmaciones es incorrecta? a) Si v es un vector
MATEMÁTICAS II Examen del 28/06/2007 Solución Importante
 MATEMÁTICAS II Eamen del 8/06/007 Solución Importante Las calificaciones se harán públicas en la página web de la asignatura y en el tablón de anuncios del Dpto. de Métodos Cuantitativos en Economía y
MATEMÁTICAS II Eamen del 8/06/007 Solución Importante Las calificaciones se harán públicas en la página web de la asignatura y en el tablón de anuncios del Dpto. de Métodos Cuantitativos en Economía y
SOLUCIONES DEL SEGUNDO PARCIAL (17/12/2013)
 ÁLGEBRA LINEAL 1S1M-b SOLUCIONES DEL SEGUNDO PARCIAL 17/12/2013 1. Dada una aplicación lineal f : de manera que : Se pide, obtener su matriz con respecto a las bases canónicas. Calculamos =col 2. Calcular
ÁLGEBRA LINEAL 1S1M-b SOLUCIONES DEL SEGUNDO PARCIAL 17/12/2013 1. Dada una aplicación lineal f : de manera que : Se pide, obtener su matriz con respecto a las bases canónicas. Calculamos =col 2. Calcular
PROBLEMAS DE ÁLGEBRA LINEAL INGENIERÍA DE TELECOMUNICACIONES - E.T.S.I.T. CURSO 2005/06
 PROBLEMAS DE ÁLGEBRA LINEAL INGENIERÍA DE TELECOMUNICACIONES - E.T.S.I.T. CURSO 200/06 1. Utilizar el método de eliminación de Gauss para resolver el sistema de ecuaciones lineales siguiente: 2 x 1 2 x
PROBLEMAS DE ÁLGEBRA LINEAL INGENIERÍA DE TELECOMUNICACIONES - E.T.S.I.T. CURSO 200/06 1. Utilizar el método de eliminación de Gauss para resolver el sistema de ecuaciones lineales siguiente: 2 x 1 2 x
Problemas de Espacios Vectoriales
 Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Problemas de Espacios Vectoriales 1. Qué condiciones tiene que cumplir un súbconjunto no vacío de un espacio vectorial para que sea un subespacio vectorial de este? Pon un ejemplo. Sean E un espacio vectorial
Espacios vectoriales.
 Unidad docente de Matemáticas Matemáticas (CC. Químicas) Espacios vectoriales. Si detectas cualquier error o errata por favor, comunicaselo al profesor de la asignatura. El subíndice can significa canónica/o..
Unidad docente de Matemáticas Matemáticas (CC. Químicas) Espacios vectoriales. Si detectas cualquier error o errata por favor, comunicaselo al profesor de la asignatura. El subíndice can significa canónica/o..
ÁLGEBRA LINEAL. EXAMEN FINAL 18 de Enero de b) (0, 5 puntos) Estudia si la siguiente afirmación es verdadera o falsa, justificando
 ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
Matemáticas Empresariales II. Aplicaciones Lineales
 Matemáticas Empresariales II Lección 5 Aplicaciones Lineales Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales II 1 / 34 Definición - Aplicación Lineal Sean
Matemáticas Empresariales II Lección 5 Aplicaciones Lineales Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales II 1 / 34 Definición - Aplicación Lineal Sean
A-PDF Page Cut DEMO: Purchase from to remove the watermark. Ejercicios resueltos 125
 A-PDF Page Cut DEMO: Purchase from www.a-pdf.com to remove the watermark Ejercicios resueltos 125 Las matrices asociadas a g f y f g son, respectivamente 0 3 8 ) 14 13 g f BA = 3 3 1 f g AB = 16 22 7 2
A-PDF Page Cut DEMO: Purchase from www.a-pdf.com to remove the watermark Ejercicios resueltos 125 Las matrices asociadas a g f y f g son, respectivamente 0 3 8 ) 14 13 g f BA = 3 3 1 f g AB = 16 22 7 2
Diagonalización de matrices
 Diagonalización de matrices María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Diagonalización de matrices Matemáticas I 1 / 22 Valores y vectores propios de una matriz Definición
Diagonalización de matrices María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Diagonalización de matrices Matemáticas I 1 / 22 Valores y vectores propios de una matriz Definición
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
SEGUNDO PARCIAL - EJERCICIOS DE REPASO
 Algebra y Geometría 28 SEGUNDO PARCIAL - EJERCICIOS DE REPASO 3-6-8 ESPACIOS VECTORIALES. Construya en R 2 un subconjunto que sea: a cerrado para la suma y resta de vectores, pero no para la multiplicacion
Algebra y Geometría 28 SEGUNDO PARCIAL - EJERCICIOS DE REPASO 3-6-8 ESPACIOS VECTORIALES. Construya en R 2 un subconjunto que sea: a cerrado para la suma y resta de vectores, pero no para la multiplicacion
ÁLGEBRA Práctica Clasificar según los valores de λ IR las cónicas de los siguientes haces: 2. Para las siguientes cónicas
 ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
ÍNDICE NOCIONES BÁSICAS SOBRE TRANSFORMACIONES GEOMÉTRICAS 2 TRANSFORMACIONES GEOMÉTRICAS EN EL ESPACIO 22 PROBLEMAS DE MOVIMIENTOS EN EL PLANO 1
 Índice La belleza está estrechamente relacionada con la simetría Hermann WEYL (885-955) ÍNDICE NOCIONES BÁSICAS SOBRE TRANSFORMACIONES GEOMÉTRICAS TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO 8 TRANSFORMACIONES
Índice La belleza está estrechamente relacionada con la simetría Hermann WEYL (885-955) ÍNDICE NOCIONES BÁSICAS SOBRE TRANSFORMACIONES GEOMÉTRICAS TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO 8 TRANSFORMACIONES
ÁLGEBRA LINEAL. EXAMEN EXTRAORDINARIO 5 de Julio de T (e 1 ) = e 1 e 2 + 2e 3 T (e 2 ) = e 1 + 2e 2 3e 3. [T (e 1 ) T (e 2 )] =
![ÁLGEBRA LINEAL. EXAMEN EXTRAORDINARIO 5 de Julio de T (e 1 ) = e 1 e 2 + 2e 3 T (e 2 ) = e 1 + 2e 2 3e 3. [T (e 1 ) T (e 2 )] = ÁLGEBRA LINEAL. EXAMEN EXTRAORDINARIO 5 de Julio de T (e 1 ) = e 1 e 2 + 2e 3 T (e 2 ) = e 1 + 2e 2 3e 3. [T (e 1 ) T (e 2 )] =](/thumbs/82/86817902.jpg) ÁLGEBRA LINEAL EXAMEN EXTRAORDINARIO 5 de Julio de Apellidos y Nombre: Ejercicio. Sea T : R R 3 una transformación lineal definida como: T (e ) = e e + e 3 T (e ) = e + e 3e 3 donde {e, e }, {e, e, e 3}
ÁLGEBRA LINEAL EXAMEN EXTRAORDINARIO 5 de Julio de Apellidos y Nombre: Ejercicio. Sea T : R R 3 una transformación lineal definida como: T (e ) = e e + e 3 T (e ) = e + e 3e 3 donde {e, e }, {e, e, e 3}
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
1. Ejercicios. Algebra Lineal Problemas del tema 4 Endomorfismos Curso Universidad de Oviedo
 1. Ejercicios Ejercicio 1 En R 2, referido a la base canónica, se consideran los vectores u 1 = (1, 1) y u 2 = (2,). Un endomorfismo de R 2, T los transforma en los vectores v 1 = ( 2,1) y v 2 = (, 1)
1. Ejercicios Ejercicio 1 En R 2, referido a la base canónica, se consideran los vectores u 1 = (1, 1) y u 2 = (2,). Un endomorfismo de R 2, T los transforma en los vectores v 1 = ( 2,1) y v 2 = (, 1)
PAU Madrid. Matemáticas II. Año Examen de junio. Opción A. Ejercicio 1. Valor: 2 puntos.
 Opción A. Ejercicio 1. Valor: 2 puntos. Calcular las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos en aquel momento,
Opción A. Ejercicio 1. Valor: 2 puntos. Calcular las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos en aquel momento,
Diagonalización. Tema Valores y vectores propios Planteamiento del problema Valores y vectores propios
 61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
61 Matemáticas I : Álgebra Lineal Tema 6 Diagonalización 61 Valores y vectores propios 611 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial
Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 2006
 ÁLGEBRA Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 006 1. Calcular la ecuación de una hipérbola que tiene por asíntota a la recta x = y, por eje la recta x+y = 1 y que pasa por el
ÁLGEBRA Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 006 1. Calcular la ecuación de una hipérbola que tiene por asíntota a la recta x = y, por eje la recta x+y = 1 y que pasa por el
EXAMEN JUNIO PP 1A SEMANA
 EXAMEN JUNIO PP A SEMANA XAVI AZNAR Ejercicio. Defina semejanza, razón de semejanza y movimento asociado a una semejanza. Ejercicio. En el espacio vectorial V 3 (R) sea q la forma cuadrática cuya expresión
EXAMEN JUNIO PP A SEMANA XAVI AZNAR Ejercicio. Defina semejanza, razón de semejanza y movimento asociado a una semejanza. Ejercicio. En el espacio vectorial V 3 (R) sea q la forma cuadrática cuya expresión
SOLUCIONES A LA AUTOEVALUACIÓN - Espacios Vectoriales.
 SOLUCIONES A LA AUTOEVALUACIÓN - Espacios Vectoriales. A) Soluciones a las Cuestiones C-1) a) Sí, por ejemplo el eje X, formado por los vectores de la forma (λ, 0), que se identificarían con el número
SOLUCIONES A LA AUTOEVALUACIÓN - Espacios Vectoriales. A) Soluciones a las Cuestiones C-1) a) Sí, por ejemplo el eje X, formado por los vectores de la forma (λ, 0), que se identificarían con el número
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
Podemos pues formular los dos problemas anteriores en términos de matrices.
 Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Tema 5 Diagonalización 51 Introducción Valores y vectores propios 511 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V de dimensión
Geometría afín y proyectiva, 2016 SEMANA 3
 Geometría afín y proyectiva, 2016 SEMANA 3 Sonia L. Rueda ETS Arquitectura. UPM September 20, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Geometría afín y proyectiva, 2016 SEMANA 3 Sonia L. Rueda ETS Arquitectura. UPM September 20, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
TEMA III: DIAGONALIZACIÓN.
 TEMA III: DIAGONALIZACIÓN. OBJETIVOS: Generales: 1. Captar el motivo que justifica el problema de la diagonalización de endomorfismos. 2. Resolver y aplicar dicho problema cuando sea posible. Específicos:
TEMA III: DIAGONALIZACIÓN. OBJETIVOS: Generales: 1. Captar el motivo que justifica el problema de la diagonalización de endomorfismos. 2. Resolver y aplicar dicho problema cuando sea posible. Específicos:
MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-2011 CUESTIONES TIPO TEST
 MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-011 NOTA: CUESTIONES TIPO TEST SOLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTION RESPUESTA CORRECTA: + 0. PUNTOS RESPUESTA INCORRECTA: - 0.1 PUNTOS RESPUESTA
MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-011 NOTA: CUESTIONES TIPO TEST SOLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTION RESPUESTA CORRECTA: + 0. PUNTOS RESPUESTA INCORRECTA: - 0.1 PUNTOS RESPUESTA
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
Capítulo V. Valores y vectores propios. Diagonalización de operadores lineales.
 Capítulo V Valores y vectores propios. Diagonalización de operadores lineales. Hemos visto que la aplicaciones lineales de en están definidas a través de una expresión de la forma ; pero esta fórmula puede
Capítulo V Valores y vectores propios. Diagonalización de operadores lineales. Hemos visto que la aplicaciones lineales de en están definidas a través de una expresión de la forma ; pero esta fórmula puede
{ } { 1, 0, 0, 0, 0,1,1,1,(1,1,1,1)} ( ) ( ) ( )
 .- Se considera R con la suma habitual con el producto por un escalar que se indica en los casos siguientes. Prueba que en ninguno de ellos, (R,+, ) es espacio vectorial señalando alguna propiedad del
.- Se considera R con la suma habitual con el producto por un escalar que se indica en los casos siguientes. Prueba que en ninguno de ellos, (R,+, ) es espacio vectorial señalando alguna propiedad del
TÉCNICA SUPERIOR DE INGENIERÍA INFORMÁTICA
 ESCUELA ESTUDIOS DE TÉCNICA SUPERIOR DE INGENIERÍA INFORMÁTICA DEPARTAMENTO DE INGENIERÍA INFORMÁTICA MATEMÁTICA APLICADA I ÁLGERA LINEAL OLETINES DE PROLEMAS Curso 8-9 Sistemas de ecuaciones lineales.
ESCUELA ESTUDIOS DE TÉCNICA SUPERIOR DE INGENIERÍA INFORMÁTICA DEPARTAMENTO DE INGENIERÍA INFORMÁTICA MATEMÁTICA APLICADA I ÁLGERA LINEAL OLETINES DE PROLEMAS Curso 8-9 Sistemas de ecuaciones lineales.
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 2.1-2.2 Espacios Euclídeos. Ortogonalidad (Curso 2011 2012) 1. Se considera un espacio euclídeo de dimensión 3, y en él una base {ē 1, ē 2, ē 3 } tal que el módulo de ē 1 y el
ÁLGEBRA LINEAL II Práctica 2.1-2.2 Espacios Euclídeos. Ortogonalidad (Curso 2011 2012) 1. Se considera un espacio euclídeo de dimensión 3, y en él una base {ē 1, ē 2, ē 3 } tal que el módulo de ē 1 y el
Tema 1. Espacios Vectoriales Definición de Espacio Vectorial
 Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
Tema 1 Espacios Vectoriales. 1.1. Definición de Espacio Vectorial Notas 1.1.1. Denotaremos por N, Z, Q, R, C, a los conjuntos de los números Naturales, Enteros, Racionales, Reales y Complejos, respectivamente.
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
Matemáticas para la Empresa
 Matemáticas para la Empresa 1 o D.C.E. 1 o L.A.D.E. Curso 2008/09 Relación 2. Aplicaciones Lineales. Diagonalización. Formas Cuadráticas 1. Estudia si son lineales las aplicaciones siguientes: a) La aplicación
Matemáticas para la Empresa 1 o D.C.E. 1 o L.A.D.E. Curso 2008/09 Relación 2. Aplicaciones Lineales. Diagonalización. Formas Cuadráticas 1. Estudia si son lineales las aplicaciones siguientes: a) La aplicación
EXAMEN EXTRAORDINARIO DE MATEMÁTICAS I 9 de septiembre de 2009 PRIMER PARCIAL
 EXAMEN EXTRAORDINARIO DE MATEMÁTICAS I 9 de septiembre de 9 PRIMER PARCIAL CUESTIONES TIPO TEST NOTA: SÓLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTIÓN RESPUESTA CORRECTA: +, PUNTOS RESPUESTA INCORRECTA:
EXAMEN EXTRAORDINARIO DE MATEMÁTICAS I 9 de septiembre de 9 PRIMER PARCIAL CUESTIONES TIPO TEST NOTA: SÓLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTIÓN RESPUESTA CORRECTA: +, PUNTOS RESPUESTA INCORRECTA:
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
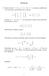 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
Examen Final Soluciones (3 horas) 8 de julio de 2015
 Álgebra Lineal I Examen Final Soluciones (3 horas) 8 de julio de 2015 1. Siete personas suben en un ascensor en la planta baja de un edificio de cinco pisos. Cada una de ellas se apea en alguna de las
Álgebra Lineal I Examen Final Soluciones (3 horas) 8 de julio de 2015 1. Siete personas suben en un ascensor en la planta baja de un edificio de cinco pisos. Cada una de ellas se apea en alguna de las
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo y con respecto
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo y con respecto
Unidad 4 Espacios vectoriales. Aplicaciones lineales
 Unidad 4 Espacios vectoriales. Aplicaciones lineales PÁGINA 8 SOLUCIONES. La solución queda: Operando los vectores e igualando los vectores resultantes, obtenemos:. La solución queda: Sean los polinomios
Unidad 4 Espacios vectoriales. Aplicaciones lineales PÁGINA 8 SOLUCIONES. La solución queda: Operando los vectores e igualando los vectores resultantes, obtenemos:. La solución queda: Sean los polinomios
Tema 3.3. Aplicaciones afines. Cónicas y cuádricas
 Tema 3.3. Aplicaciones afines. Cónicas y cuádricas Definición 1. Sean A = (P, V, f) y A = (P, V, f ) dos espacios afines tales que V y V son espacios vectoriales sobre un mismo cuerpo. Una función θ :
Tema 3.3. Aplicaciones afines. Cónicas y cuádricas Definición 1. Sean A = (P, V, f) y A = (P, V, f ) dos espacios afines tales que V y V son espacios vectoriales sobre un mismo cuerpo. Una función θ :
TEMA 5: Aplicaciones Lineales. Diagonalización.
 TEMA 5: Aplicaciones Lineales. Diagonalización. 1. Aplicaciones Lineales 1.1. Definición, propiedades y ejemplos. Definición 1. Dados dos espacios vectoriales V y V sobre un mismo cuerpo K, una aplicación
TEMA 5: Aplicaciones Lineales. Diagonalización. 1. Aplicaciones Lineales 1.1. Definición, propiedades y ejemplos. Definición 1. Dados dos espacios vectoriales V y V sobre un mismo cuerpo K, una aplicación
AP = A p 1 p 2 p n = Ap 1 Ap 2. λ 1 p 21 λ 2 p 22 λ n p 2n. .. = λ 1 p 1 λ 2 p 2
 Capítulo 6 Diagonalización 6 Valores y vectores propios 6 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V, nos planteamos el problema
Capítulo 6 Diagonalización 6 Valores y vectores propios 6 Planteamiento del problema Problema general de diagonalización Dado un operador lineal f sobre un espacio vectorial V, nos planteamos el problema
TRANSFORMACIONES LINEALES 1. TRANSFORMACIONES NÚCLEO E IMAGEN
 RANSFORMACIONES LINEALES 1 RANSFORMACIONES NÚCLEO E IMAGEN DEFINICION : Sean V W espacios vectoriales Una transformación lineal de V en W es una función que asigna a cada vector v V un único vector v W
RANSFORMACIONES LINEALES 1 RANSFORMACIONES NÚCLEO E IMAGEN DEFINICION : Sean V W espacios vectoriales Una transformación lineal de V en W es una función que asigna a cada vector v V un único vector v W
Tema 7. El espacio vectorial R n Conceptos generales
 Tema 7 El espacio vectorial R n. 7.1. Conceptos generales Un vector es un segmento orientado que queda determinado por su longitud, dirección y sentido. Sin embargo, desde el punto de vista del Álgebra,
Tema 7 El espacio vectorial R n. 7.1. Conceptos generales Un vector es un segmento orientado que queda determinado por su longitud, dirección y sentido. Sin embargo, desde el punto de vista del Álgebra,
Tema 9: Vectores en el Espacio
 9..- Vectores Fijos: Un vector fijo del plano y su extremo en el punto B. Tema 9: Vectores en el Espacio AB es un segmento orientado que tiene su origen en punto A Un vector viene caracterizado por su
9..- Vectores Fijos: Un vector fijo del plano y su extremo en el punto B. Tema 9: Vectores en el Espacio AB es un segmento orientado que tiene su origen en punto A Un vector viene caracterizado por su
FINAL DE ÁLGEBRA Y GEOMETRÍA ANALÍTICA 30 mayo 2006 Tema 1
 FINAL DE ÁLGEBRA Y GEOMETRÍA ANALÍTICA 0 mayo 006 Tema Apellido y nombres:... 4 5 Calificación final ) Dadas las rectas : x y + z = r : r : ( x, y, z) = (,,) + λ(, ) x z + k = 0 k para que las rectas sean
FINAL DE ÁLGEBRA Y GEOMETRÍA ANALÍTICA 0 mayo 006 Tema Apellido y nombres:... 4 5 Calificación final ) Dadas las rectas : x y + z = r : r : ( x, y, z) = (,,) + λ(, ) x z + k = 0 k para que las rectas sean
APUNTES DE MATEMÁTICAS UNIVERSIDAD DE SEVILLA GRADOS EN ECONOMÍA Y ADMINISTRACIÓN DE EMPRESAS PRIMER CURSO
 APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
2.9 Ejercicios resueltos
 86 Sistemas de ecuaciones lineales. Espacios vectoriales. 2.9 Ejercicios resueltos Ejercicio 2. Sea A = ( ) 2. Se pide: 3 m a) Encontrar m para que existan matrices cuadradas B ynonulastalesque A B =0.
86 Sistemas de ecuaciones lineales. Espacios vectoriales. 2.9 Ejercicios resueltos Ejercicio 2. Sea A = ( ) 2. Se pide: 3 m a) Encontrar m para que existan matrices cuadradas B ynonulastalesque A B =0.
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones.
 Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Álgebra Lineal Escuela Politécnica Superior Universidad de Málaga Emilio Muñoz-Velasco (Basado en los apuntes de Jesús Medina e Inmaculada Fortes)
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
ETSI de Topografía, Geodesia y Cartografía
 Prueba de Evaluación Continua Grupo A 9-04-14 ESPACIOS VECTORIALES-DIAGONALIZACIÓN (parte sin DERIVE) 1. a) Definir sistema ligado de vectores de un espacio vectorial V. b) Demostrar que si un sistema
Prueba de Evaluación Continua Grupo A 9-04-14 ESPACIOS VECTORIALES-DIAGONALIZACIÓN (parte sin DERIVE) 1. a) Definir sistema ligado de vectores de un espacio vectorial V. b) Demostrar que si un sistema
Tema 4: Endomorfismos
 Marisa Serrano, Zulima Fernández Universidad de Oviedo 11 de enero de 2010 email: mlserrano@uniovi.es Índice 1 2 3 4 en espacios de dimensión dos en espacios eucĺıdeos de dimensión tres Definición Definición
Marisa Serrano, Zulima Fernández Universidad de Oviedo 11 de enero de 2010 email: mlserrano@uniovi.es Índice 1 2 3 4 en espacios de dimensión dos en espacios eucĺıdeos de dimensión tres Definición Definición
Geometría afín y proyectiva, 2016 SEMANA 2
 Geometría afín y proyectiva, 2016 SEMANA 2 Sonia L. Rueda ETS Arquitectura. UPM September 20, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Geometría afín y proyectiva, 2016 SEMANA 2 Sonia L. Rueda ETS Arquitectura. UPM September 20, 2016 Geometría afín y proyectiva 1. Álgebra Lineal 2. Geometría afín y eucĺıdea 3. Cónicas y cuádricas Álgebra
Tema 1: Espacios vectoriales
 PROBLEMAS DE MATEMÁTICAS Parte I: Álgebra Primero de Ingeniería Química FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha Tema 1: Espacios vectoriales 1 Determina
PROBLEMAS DE MATEMÁTICAS Parte I: Álgebra Primero de Ingeniería Química FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha Tema 1: Espacios vectoriales 1 Determina
1. Espacio vectorial. Subespacios vectoriales
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Sea k un cuerpo. 1. Espacio vectorial. Subespacios vectoriales Definición 1.1. Un k-espacio vectorial o espacio vectorial
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Sea k un cuerpo. 1. Espacio vectorial. Subespacios vectoriales Definición 1.1. Un k-espacio vectorial o espacio vectorial
