MATEMÁTICAS I 2º EXAMEN PARCIAL 9 de junio de 2008
|
|
|
- Natalia Natividad Romero Caballero
- hace 5 años
- Vistas:
Transcripción
1 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 Sólo una respuesta a cada cuestión es correcta Respuesta correcta: 0 puntos Respuesta incorrecta: -0 puntos Respuesta en blanco: 0 puntos - Sean F y G dos subespacios vectoriales de V Se verifica: a) dimf + dimg = dim(f G) dim(f G) b) dimf + dimg = dim(f + G) dim(f G) X c) dimf + dimg = dim(f + G) + dim(f G) n - Si G = { u,u,u, u4} es un sistema generador de R, podemos asegurar: a) n 4 b) n=4 X c) n 4 - Sea (,) un vector propio de la matriz A, tal que: A = Entonces: a) λ= 0 es un valor propio de A asociado a dicho vector propio X b) λ= es un valor propio de A asociado a dicho vector propio c) λ= es un valor propio de A asociado a dicho vector propio 4- Dada la matriz A = 0 Entonces: X a) Es diagonalizable para todo real b) Solamente es diagonalizable si = 0 0 c) No puede ser semejante a la matriz A = 0 5- Una base ortonormal (métrica) del subespacio vectorial y-z=0 de R es: a) {( 0,,), (, 0, 0 )} b) ( 0,-, - ), (,, ) X c) ( 0, -, - ), (, 0, 0 ) ' 6- Sean = las ecuaciones del cambio de sistema de y' y z' z O, A, B, C O ', A', B', C' Se verifica, entonces, que: referencia afín de R { } a R { } a) OO ' = (,, ) X b) OB = O' A' O' B' + O'C' c) O ' A' = (,,) respecto de la base OA, OB, OC 7- En el espacio euclídeo la ecuación matricial de un giro de ángulo α alrededor del eje OY, es: U D de Matemáticas de la ETSI en Topografía, Geodesia y Cartografía
2 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de ' a) = y' 0 0 cosα senαy z' 0 0 senα cosα z ' b) = y ' 0 0 cos α senα y z' 0 0 senα cosα z ' 0 cos 0 sen X c) α α = y' y z' 0 senα 0 cosα z 8- El producto de dos homotecias del plano de distinto centro y razones k y /k es siempre: X a) Una traslación b) Una homotecia c) La identidad 9- La ecuación del haz de cónicas: ( y) = 0 son tipo hiperbólico λ y si: a) λ< b) λ= X c) λ> 0- Si en una cónica se verifica que A00 = Ac < 0 y A = 0, entonces: a) La cónica es una hipérbola X b) La cónica son dos rectas secantes c) La cónica es una elipse imaginaria MATEMÁTICAS I º Parcial ª Parte - Teoría: contestar sólo a una de las dos preguntas siguientes: I) Sean A y A las matrices asociadas a la misma transformación lineal f : V V, respecto de las bases B y B, respectivamente Deducir la relación que eiste entre A y A II) Sean F y G dos subespacios vectoriales de V Se pide: a) Definir F+G b) Son F+G y F G subespacios vectoriales de V? (demostrarlo o poner un contraejemplo, según proceda en cada caso) ( punto) U D de Matemáticas de la ETSI en Topografía, Geodesia y Cartografía
3 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 = e Se considera el subespacio S de ecuación cartesiana en = y z a) Obtener una base de S formada por vectores unitarios b) Si S es el subespacio engendrado por el sistema { e + e - e, e + e }, hallar unas ecuaciones paramétricas y cartesianas del subespacio S c) Hallar una base de cada uno de los subespacios vectoriales S S y S +S (5 puntos) - En un espacio vectorial V, sea la base canónica B { e, e, } - En el espacio vectorial euclídeo tridimensional V, se pide: a) Hallar una base ortonormal del plano vectorial F engendrado por los vectores u = (,,0 ) y v = (,, ) b) Hallar F (subespacio ortogonal de F) c) Ampliar la base encontrada en el apartado a) para obtener una base ortonormal de V (5 puntos) MATEMÁTICAS I º Parcial ª Parte (Aula de Informática) 4- Sean B = u,u, u una base del espacio vectorial R y f la transformación lineal f u = u+ u del mismo tal que f u = u u u Se pide: f u = u a) Matriz A asociada a f respecto de la base B b) Ecuación matricial de f c) Obtener el subespacio Núcleo de f y dar una base de dicho subespacio d) Obtener el subespacio Imagen de f y dar una base de dicho subespacio e) Son los dos subespacios anteriores N(f) e Im(f) suplementarios? f) Hallar los valores propios de A y los subespacios de vectores propios asociados g) Razonar si A es diagonalizable En caso afirmativo, escribir una matriz diagonal D semejante a A y la matriz de paso correspondiente h) Hallar A n, para cualquier número natural n (5 puntos) 5- En el espacio euclídeo tridimensional, se pide: a) Hallar las ecuaciones de la semejanza directa de razón k = 4, centro el punto π C (,, ), ángulo α = y cuyo eje es la recta e (, y, z) = (,, ) + λ(,,0 ) U D de Matemáticas de la ETSI en Topografía, Geodesia y Cartografía
4 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 b) Hallar las ecuaciones de la transformada de la recta: e (, y, z) = (,, ) + λ(,,0 ) c) Hallar la ecuación del transformado del plano z = 0 (75 puntos) 6- Dada la cónica de ecuación y = 0 Se pide: a) Clasificación b) Ecuación reducida c) Semiejes y ecentricidad d) Centro e) Ejes f) Asíntotas, si las tiene (5 puntos) NOTA: Publicación de calificaciones: viernes de junio por la tarde Revisión de eamen: martes 7 a las h en el Laboratorio de Matemáticas SOLUCIONES - En un espacio vectorial V, sea la base canónica B = { e, e, e } Se considera el subespacio S de ecuación cartesiana en = y z a) Obtener una base de S formada por vectores unitarios b) Si S es el subespacio engendrado por el sistema { e + e - e, e + e }, hallar unas ecuaciones paramétricas y cartesianas del subespacio S c) Hallar una base de cada uno de los subespacios vectoriales S S y S +S (5 puntos) SOLUCIÓN a) S Ecuación cartesiana Ec paramétrica = y = z = = y z Dimensión : dim S = -= α β α Base unitaria BS = ( 0,, ), ( 0,, ), β b) S Sistema generador { e e - e, e + } base de S e +, como son linealmente independientes, forman Base de S = {(,, ), (,, 0) } Ec paramétrica = y = z = α + β α + β α Ec cartesiana y = y = 0, para todo valor de z z 0 U D de Matemáticas de la ETSI en Topografía, Geodesia y Cartografía 4
5 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 c) S S y + z = 0 = y Ecuación cartesiana de S S: y = 0 z = 0 Dimensión dim S S=-= Base de S S, {, 0} (, Sistema generador de B + = (,,0 ), (,0, ) (,,, ) (,, 0) S,, y rango de S S S + S S B + =, por tanto,una base de S = e S + es B { e, e, } - En el espacio vectorial euclídeo tridimensional V, se pide: a) Hallar una base ortonormal del plano vectorial F engendrado por los vectores u = (,,0 ) y v = (,, ) b) Hallar F (subespacio ortogonal de F) c) Ampliar la base encontrada en el apartado a) para obtener una base ortonormal de V SOLUCIÓN a) Base ortonormal de F #: u [,, 0] #: u [, -, -] (5 puntos) La base buscada ha de estar formada por dos vectores v y v de F que sean unitarios y ortogonales entre sí u #: v u 5 5 #4: v,, v ha de ser combinación lineal de u y u: #5: v λ u + μ u #6: v [λ + μ, λ - μ, -μ] A su vez v tiene que ser perpendicular a u, luego, el producto escalar u v ha de ser cero: #7: v u = 0 #8: SOLVE(v u = 0, [λ, μ], Real) #9: 5 λ - μ = 0 Si, por ejemplo, λ =, entonces μ = 5: #0: v [6, -, -5] U D de Matemáticas de la ETSI en Topografía, Geodesia y Cartografía 5
6 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 Como además v ha de ser unitario, ya se tiene que: v #: =, -, - v Luego, {v,, 0, v -,, - } es una base ortonormal de F b) Subespacio ortogonal de F: Es la recta vectorial perpendicular a F; está engendrada por el vector u u: #: u u = [-,, -] c) Ampliar la base {v, v} hasta formar una base ortonormal de V, {v, v, v} Basta tomar: [-,, -] #: v = = -,, - [-,, -] ª Parte (Aula de Informática) 4- Sean B = u,u, u una base del espacio vectorial R y f la transformación lineal f u = u+ u del mismo tal que f u = u u u Se pide: f u = u a) Matriz A asociada a f respecto de la base B b) Ecuación matricial de f c) Obtener el subespacio Núcleo de f y dar una base de dicho subespacio d) Obtener el subespacio Imagen de f y dar una base de dicho subespacio e) Son los dos subespacios anteriores N(f) e Im(f) suplementarios? f) Hallar los valores propios de A y los subespacios de vectores propios asociados g) Razonar si A es diagonalizable En caso afirmativo, escribir una matriz diagonal D semejante a A y la matriz de paso correspondiente h) Hallar A n, para cualquier número natural n (5 puntos) SOLUCIÓN a) La matriz asociada o que define f se obtiene mediante las imágenes de los vectores B = u,u, : de la base { } u U D de Matemáticas de la ETSI en Topografía, Geodesia y Cartografía 6
7 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 f ( u) = u+ u = (,0,) B 0 f ( u) = u u u = (,, ) B A= M( f,b) = 0 f ( u) = u = (0,,0) B 0 f(u ) f(u ) f(u ) b) La ecuación matricial o ecuaciones de la transformación lineal es: y 0 Y=AX y = 0 y 0 c) El núcleo es: N(f ) = { R / f () = 0}, luego: 0 0 f(,,) = ( 0,0,0 ) 0 = 0 = = 0 0 siendo la dimensión del núcleo de y una base BN(f) = {(,,) } d) La imagen es: Im(f ) = { y R / R con f () = y}, luego y y = 0 = = 0 α+ β que son las y ecuaciones paramétricas del subespacio imagen, siendo dim(im(f))=r(a)= y una base B =,0,,(0,,0) Im(f ) {( ) } e) No son suplementarios, dado que el vector (,,) del núcleo pertenece al subespacio imagen y por tanto Im(f ) N(f ) { 0 } f) Valores propios: λ 0 ( ) A I 0 0 triple λ = λ = λ λ= 0 λ λ 0 0 Vectores propios: ( A λ I) v= 0 0 λ y = 0 0 λz =α Para λ= y = 0 y=α v = (,,) 0 0z 0 z=α g) No, es diagonalizable, ya que no es posible encontrar una base del espacio vectorial formada por vectores propios de f La dimensión del subespacio propio asociada al valor propio es y no coincide con el orden de multiplicidad que es triple U D de Matemáticas de la ETSI en Topografía, Geodesia y Cartografía 7
8 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 h) A 0 AA A 0 AA Luego A n = En el espacio euclídeo tridimensional, se pide: a) Hallar las ecuaciones de la semejanza directa de razón k = 4, centro el punto C,,, ángulo y cuyo eje es la recta e, y, z,,,,0 e, y, z,,,,0 c) Hallar la ecuación del transformado del plano z = 0 (75 puntos) b) Hallar las ecuaciones de la transformada de la recta: SOLUCIÓN Una semejanza directa es la composición de un giro y una homotecia, así, S(C, k, e, ) H(C, K) G(e, ) con C e z C(,,) e y α=π/ u La ecuación matricial del giro de eje e, y,z (,, ) t(,, 0) y ángulo En el sistema de referencia R' C,u,u,u definido por: C(,,) e, u (,,0)// e,u (0,0,) u,u uu (,,0) La matriz de cambio de la referencia R a la canónica del espacio es P U D de Matemáticas de la ETSI en Topografía, Geodesia y Cartografía 8
9 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 la ecuación del giro en la referencia R es ' G' 0 0 cos sen y' y y y z' z z z 0 0 sen cos Se pasa al sistema de referencia canónica del espacio R definido por R O,e,e,e siendo O(0,0,0), e ( 00,, ),e ( 00,, ),e ( 00,, ) Como la matriz del cambio de referencia es P, queda ' PG'P G y' y y y z' z z z 0 La ecuación de la homotecia de centro C=(,,) y de razón k=4 se conoce directamente en la referencia canónica R puesto que la matriz es: ' kc k H y' y kcy 0 k 0y 0 4 0y z' z kcz 0 0 k z 0 0 4z La composición SGH H G tendrá por ecuación matricial: ' y' y z' z ' y' y z' 0 z ( producto conmutativo) b) Hallar las ecuaciones de la transformada de la recta La transformación inversa es ' y' z' ' y y' y ' y' z' 6 8 z z' 0 z ' y' 8 8 e, y, z (,, ) t(,, 0) como la recta e tiene por ecuaciones y z despejando, ' y ' z ' por tanto, el eje e es invariante respecto de la semejanza U D de Matemáticas de la ETSI en Topografía, Geodesia y Cartografía 9
10 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 Esto se podía haber deducido sin calcular, puesto que el eje es el invariante del giro y el centro de la semejanza pertenece al propio eje c) Hallar la ecuación del transformado del plano z=0 El plano z=0 se transforma en ( ' y' + 8) = 0 ' y' + 8= Dada la cónica de ecuación y = 0 Se pide: a) Clasificación b) Ecuación reducida c) Semiejes y ecentricidad d) Centro e) Ejes f) Asíntotas, si las tiene (5 puntos) SOLUCIÓN #: - y = 0 a) Clasificación: 0 #: A #: MINOR(A,, ) 0 #4: 0-0 #5: Ac 0 - #6: DET(Ac) #7: - Cónica de tipo hiperbólico #8: DET(A) #9: 6 Se trata de una HIPÉRBOLA b) Ecuación reducida: #0: λ + λ y + k = 0 DET(A) #: k DET(Ac) #: - #: EIGENVALUES(Ac) #4: [, -] - y - = 0, es decir: y #5: - = / U D de Matemáticas de la ETSI en Topografía, Geodesia y Cartografía 0
11 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 c) Semiejes y ecentricidad: #6: a = #7: b = #8: c = a + b = + #9: c = #0: e = 6 #: e = d) Centro: #: SOLVE([ + = 0, - y = 0], [, y]) #: [ = - y = 0] e) Ejes: #4: EXACT_EIGENVECTOR(Ac, ) #5: [[@, 0]] Eje focal: Pasa por C(-,0) y es paralelo a (,0) #6: y = 0 Eje no focal: Pasa por C(-,0) y es perpendicular al eje focal #7: = - f) Asíntotas: Las asíntotas son rectas que pasan por el centro y tienen de pendiente m tal que: #8: - m = 0 #9: SOLVE( - m = 0, m) #0: m = - m = Luego, su ecuación es: #: y - 0 = ( + ) #: y - 0 = - ( + ) NOTA: Como la ecuación de la cónica no tiene término en y, se podría haber realizado el estudio completando los cuadrados de la y de la y, obteniéndose una ecuación reducida NOTA: Publicación de calificaciones: viernes de junio por la tarde Revisión de eamen: martes 7 a las h en el Laboratorio de Matemáticas U D de Matemáticas de la ETSI en Topografía, Geodesia y Cartografía
12 Nombre de archivo: Problema de Luisdoc Directorio: C:\Documents and Settings\Administrador\Escritorio Plantilla: Normaldot Título: Asunto: Autor: Matemáticas Palabras clave: Comentarios: Fecha de creación: 04/06/008 6: Cambio número: 7 Guardado el: 08/06/008 6:6 Guardado por: Matemáticas Tiempo de edición: 58 minutos Impreso el: 08/06/008 6:9 Última impresión completa Número de páginas: Número de palabras: 9 (apro) Número de caracteres: 8 (apro)
MATEMÁTICAS I 2º EXAMEN PARCIAL 12 junio de 2009
 Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Un sistema generador G de R 3 : a) Está constituido por
Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Un sistema generador G de R 3 : a) Está constituido por
MATEMÁTICAS I 13 de junio de 2007
 MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
Espacio Euclídeo. a b = a b. a b = b a c)
 .- Un hiperplano de R es: a) Una recta. b) Un plano. c) {0}..- Sean a y b dos vectores de R, si a es ortogonal a b, entonces: a) a b = 0 b) a b = b a c) a b = a b.- Sea F una recta vectorial de R y F un
.- Un hiperplano de R es: a) Una recta. b) Un plano. c) {0}..- Sean a y b dos vectores de R, si a es ortogonal a b, entonces: a) a b = 0 b) a b = b a c) a b = a b.- Sea F una recta vectorial de R y F un
Soluciones Hoja Problemas Espacio Vectorial 05-06
 Soluciones Hoja Problemas Espacio Vectorial -6.- Se considera R con la suma habitual y con el producto por un escalar que se indica en los casos siguientes. Prueba que en ninguno de ellos, (R,, ) es espacio
Soluciones Hoja Problemas Espacio Vectorial -6.- Se considera R con la suma habitual y con el producto por un escalar que se indica en los casos siguientes. Prueba que en ninguno de ellos, (R,, ) es espacio
Soluciones de la hoja de diagonalización MATEMÁTICAS I
 Soluciones de la hoja de diagonalización MATEMÁTICAS I 9- - En los siguientes casos estudiar si f es una aplicación lineal y, en caso afirmativo, hallar una matriz A tal que f(x) Ax, así como los subespacios
Soluciones de la hoja de diagonalización MATEMÁTICAS I 9- - En los siguientes casos estudiar si f es una aplicación lineal y, en caso afirmativo, hallar una matriz A tal que f(x) Ax, así como los subespacios
PRUEBA DE DIAGONALIZACIÓN CURSO Apellidos: Nombre: Grupo: Fecha:
 Tipo 1 Apellidos: Nombre: Grupo: Fecha: 1.- Sea f una transformación lineal de un espacio vectorial V de dimensión n. Sea B una base de V. Sea A la matriz asociada a f respecto de la base B. Señala, sin
Tipo 1 Apellidos: Nombre: Grupo: Fecha: 1.- Sea f una transformación lineal de un espacio vectorial V de dimensión n. Sea B una base de V. Sea A la matriz asociada a f respecto de la base B. Señala, sin
Hoja de diagonalización MATEMÁTICAS I
 Hoja de diagonalización MATEMÁTICAS I 8-9.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) Ax así como los subespacios vectoriales
Hoja de diagonalización MATEMÁTICAS I 8-9.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) Ax así como los subespacios vectoriales
Hoja de diagonalización MATEMÁTICAS I
 Hoja de diagonalización MATEMÁTICAS I 007-008 1.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) = Ax, así como los subespacios vectoriales
Hoja de diagonalización MATEMÁTICAS I 007-008 1.- En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) = Ax, así como los subespacios vectoriales
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO
 PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO 1. Estudiar si la siguiente ecuación matricial corresponde a una homotecia del plano y, en su caso, calcular el centro y la razón: 1 1 1 ' = 3 y' 3 y. Estudiar
PROBLEMAS DE HOMOTECIAS Y SEMEJANZAS EN EL PLANO 1. Estudiar si la siguiente ecuación matricial corresponde a una homotecia del plano y, en su caso, calcular el centro y la razón: 1 1 1 ' = 3 y' 3 y. Estudiar
Hoja de diagonalización MATEMÁTICAS I
 Hoja de diagonalización MATEMÁTICAS I 9- - En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) Ax así como los subespacios vectoriales N(f)
Hoja de diagonalización MATEMÁTICAS I 9- - En los siguientes casos estudiar si f es una aplicación lineal y en caso afirmativo hallar una matriz A tal que f(x) Ax así como los subespacios vectoriales N(f)
ETSI en Topografía, Geodesia y Cartografía
 4ª Prueba de Evaluación Continua 24-5-17 TRANSFORMACIONES GEOMÉTRICAS DEL ESPACIO EUCLÍDEO (Grupo A) APELLIDOS: NOMBRE: Grupo: 1.- a) Definición de transformación involutiva. b) Demostrar que la matriz
4ª Prueba de Evaluación Continua 24-5-17 TRANSFORMACIONES GEOMÉTRICAS DEL ESPACIO EUCLÍDEO (Grupo A) APELLIDOS: NOMBRE: Grupo: 1.- a) Definición de transformación involutiva. b) Demostrar que la matriz
Tema 1: Espacios vectoriales
 PROBLEMAS DE MATEMÁTICAS Parte I: Álgebra Primero de Químicas FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha Tema 1: Espacios vectoriales 1 Determina si cada
PROBLEMAS DE MATEMÁTICAS Parte I: Álgebra Primero de Químicas FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha Tema 1: Espacios vectoriales 1 Determina si cada
EXAMEN EXTRAORDINARIO DE MATEMÁTICAS I 9 de septiembre de 2009 PRIMER PARCIAL
 EXAMEN EXTRAORDINARIO DE MATEMÁTICAS I 9 de septiembre de 9 PRIMER PARCIAL CUESTIONES TIPO TEST NOTA: SÓLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTIÓN RESPUESTA CORRECTA: +, PUNTOS RESPUESTA INCORRECTA:
EXAMEN EXTRAORDINARIO DE MATEMÁTICAS I 9 de septiembre de 9 PRIMER PARCIAL CUESTIONES TIPO TEST NOTA: SÓLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTIÓN RESPUESTA CORRECTA: +, PUNTOS RESPUESTA INCORRECTA:
Se pide: (b) Ecuaciones que permiten obtener las coordenadas cartesianas en R en función de las de R.
 ÁLGEBRA Práctica 13 Espacios afines E 2 y E 3 (Curso 2004 2005) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = {O, ē 1, ē 2, ē 3 } y R = {P, ū 1, ū 2, ū 3 }, donde
ÁLGEBRA Práctica 13 Espacios afines E 2 y E 3 (Curso 2004 2005) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = {O, ē 1, ē 2, ē 3 } y R = {P, ū 1, ū 2, ū 3 }, donde
ETSI de Topografía, Geodesia y Cartografía
 3ª Prueba de Evaluación Continua 7 05 12 (Grupo C) Espacio vectorial 1. a) Definir vectores linealmente dependientes en un espacio vectorial V. u,u,,u de un espacio vectorial V son b) Demostrar que si
3ª Prueba de Evaluación Continua 7 05 12 (Grupo C) Espacio vectorial 1. a) Definir vectores linealmente dependientes en un espacio vectorial V. u,u,,u de un espacio vectorial V son b) Demostrar que si
A.-TRANSFORMACIONES DEL PLANO
 A.-TRANSFORMACIONES DEL PLANO 1.- Sean los giros G y G, de centros O(0,0) y O (1,0) y ángulos respectivos 120º y α. Hallar las ecuaciones de GoG y sus elementos característicos para: a) α=90º b) α=240º
A.-TRANSFORMACIONES DEL PLANO 1.- Sean los giros G y G, de centros O(0,0) y O (1,0) y ángulos respectivos 120º y α. Hallar las ecuaciones de GoG y sus elementos característicos para: a) α=90º b) α=240º
5º Prueba de Evaluación continua (CÓNICAS) 5 de junio de 2012
 Grupo C ETSI de Topografía, Geodesia y Cartografía º Prueba de Evaluación continua (CÓNICAS) de junio de 0.- Clasificar la cónica x y xy x y = 0 A = ; A = 0 Cónica no degenerada. = = = < 0 A c la cónica
Grupo C ETSI de Topografía, Geodesia y Cartografía º Prueba de Evaluación continua (CÓNICAS) de junio de 0.- Clasificar la cónica x y xy x y = 0 A = ; A = 0 Cónica no degenerada. = = = < 0 A c la cónica
referencia ortonormal del espacio que tenga a este vector como primer vector de la base. Los (1, 0,1) 1 1 (1, 0,1) 2 2
 EJERCICIO ENTREGABLE EN CLASE (Tipo A) Obtener las ecuaciones de la transformación geométrica siguiente: GIRO: eje r (1,0,0)+(-1,-1,1)t y ángulo: 120º. Y obtener los transformados de los siguientes elementos:
EJERCICIO ENTREGABLE EN CLASE (Tipo A) Obtener las ecuaciones de la transformación geométrica siguiente: GIRO: eje r (1,0,0)+(-1,-1,1)t y ángulo: 120º. Y obtener los transformados de los siguientes elementos:
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
EJERCICIOS PAU MATEMÁTICAS II ARAGÓN Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.com
 GEOMETRÍA 1- Dados el punto P(1,-1,0) y la recta : 1 0 3 3 0 a) Determine la ecuación general del plano (Ax+By+Cz+D=0) que contiene al punto P y a la recta s. b) Determine el ángulo que forman el plano
GEOMETRÍA 1- Dados el punto P(1,-1,0) y la recta : 1 0 3 3 0 a) Determine la ecuación general del plano (Ax+By+Cz+D=0) que contiene al punto P y a la recta s. b) Determine el ángulo que forman el plano
TÉCNICA SUPERIOR DE INGENIERÍA INFORMÁTICA
 ESCUELA ESTUDIOS DE TÉCNICA SUPERIOR DE INGENIERÍA INFORMÁTICA DEPARTAMENTO DE INGENIERÍA INFORMÁTICA MATEMÁTICA APLICADA I ÁLGERA LINEAL OLETINES DE PROLEMAS Curso 8-9 Sistemas de ecuaciones lineales.
ESCUELA ESTUDIOS DE TÉCNICA SUPERIOR DE INGENIERÍA INFORMÁTICA DEPARTAMENTO DE INGENIERÍA INFORMÁTICA MATEMÁTICA APLICADA I ÁLGERA LINEAL OLETINES DE PROLEMAS Curso 8-9 Sistemas de ecuaciones lineales.
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
TRANSFORMACIONES GEOMÉTRICAS Curso 03-04
 .-En el plano vectorial V, con la base ortonormal { i,j } vectores u (, ) y v (, ) éstos determinan. Hallar en la base { i,j } transformaciones ortogonales tales que f( D ) se consideran los y las semirrectas
.-En el plano vectorial V, con la base ortonormal { i,j } vectores u (, ) y v (, ) éstos determinan. Hallar en la base { i,j } transformaciones ortogonales tales que f( D ) se consideran los y las semirrectas
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS ESPACIOS EUCLÍDEOS ) a) Decir cuál de las siguientes aplicaciones de x de no definir un producto escalar comprobar el axioma que falla: a ) x' x,y,
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS ESPACIOS EUCLÍDEOS ) a) Decir cuál de las siguientes aplicaciones de x de no definir un producto escalar comprobar el axioma que falla: a ) x' x,y,
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
1. Determina cuáles de los siguientes conjuntos son subespacios vectoriales. Para aquellos que lo sean, halla una base.
 EJERCICIOS PROPUESTOS 1. Espacios vectoriales. Sistemas de ecuaciones. 1. Determina cuáles de los siguientes conjuntos son subespacios vectoriales. Para aquellos que lo sean, halla una base. (a) S = {
EJERCICIOS PROPUESTOS 1. Espacios vectoriales. Sistemas de ecuaciones. 1. Determina cuáles de los siguientes conjuntos son subespacios vectoriales. Para aquellos que lo sean, halla una base. (a) S = {
ÁLGEBRA Práctica Clasificar según los valores de λ IR las cónicas de los siguientes haces: 2. Para las siguientes cónicas
 ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
ESPACIO VECTORIAL 12 de marzo de ligado, entonces al menos un vector de H es combinación lineal del resto de ellos.
 ESPACIO VECTORIAL de marzo de 00 PRUEBA Nº - Demostrar que en un espacio vectorial V, si H u, u,, u r es un sistema ligado, entonces al menos un vector de H es combinación lineal del resto de ellos - Si
ESPACIO VECTORIAL de marzo de 00 PRUEBA Nº - Demostrar que en un espacio vectorial V, si H u, u,, u r es un sistema ligado, entonces al menos un vector de H es combinación lineal del resto de ellos - Si
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
Un conjunto E a,b,c, de elementos (llamados vectores) se dice que constituye. (a,b) (a',b') (a a',b b')
 ESPACIOS VECTORIALES Un conjunto E a,b,c, de elementos (llamados vectores) se dice que constituye un espacio vectorial sobre un cuerpo conmutativo K (que generalmente es el cuerpo de los reales) si se
ESPACIOS VECTORIALES Un conjunto E a,b,c, de elementos (llamados vectores) se dice que constituye un espacio vectorial sobre un cuerpo conmutativo K (que generalmente es el cuerpo de los reales) si se
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
Aplicaciones Lineales. Diagonalización de matrices.
 Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
Tema 2 Aplicaciones Lineales. Diagonalización de matrices. 2.1. Definiciones y propiedades Nota 2.1.1. En este tema trabajaremos con los Espacios Vectoriales R n y R m definidos sobre el cuerpo R. Definición
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo y con respecto
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo y con respecto
MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-2011 CUESTIONES TIPO TEST
 MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-011 NOTA: CUESTIONES TIPO TEST SOLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTION RESPUESTA CORRECTA: + 0. PUNTOS RESPUESTA INCORRECTA: - 0.1 PUNTOS RESPUESTA
MATEMÁTICAS I Examen Extraordinario Diciembre 17-I-011 NOTA: CUESTIONES TIPO TEST SOLO HAY UNA RESPUESTA CORRECTA EN CADA CUESTION RESPUESTA CORRECTA: + 0. PUNTOS RESPUESTA INCORRECTA: - 0.1 PUNTOS RESPUESTA
A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES
 RESUMEN DE GEOMETRÍA MATEMÁTICAS II A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES Un vector fijo de origen A y extremo B, siendo A y B puntos del espacio, es un segmento orientado caracterizado por:
RESUMEN DE GEOMETRÍA MATEMÁTICAS II A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES Un vector fijo de origen A y extremo B, siendo A y B puntos del espacio, es un segmento orientado caracterizado por:
Index. Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80
 Index Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80 Adjunto, 14 Aplicación, 2 bilineal, 47 biyectiva, 3 compuesta, 3 identidad, 3 inversa, 3 inyectiva,
Index Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80 Adjunto, 14 Aplicación, 2 bilineal, 47 biyectiva, 3 compuesta, 3 identidad, 3 inversa, 3 inyectiva,
GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]
![GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos] GEOMETRÍA. Septiembre 94. Determinar la ecuación del plano que pasa por el punto M (1, 0, [1,5 puntos]](/thumbs/86/94405582.jpg) Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
Matemáticas II Pruebas de Acceso a la Universidad GEOMETRÍA Junio 94 1 Sin resolver el sistema, determina si la recta x y + 1 = 0 es exterior, secante ó tangente a la circunferencia (x 1) (y ) 1 Razónalo
PROBLEMAS RESUELTOS del espacio vectorial curso
 PROBLEMAS RESUELTOS del espacio vectorial curso - - Consideremos el conjunto R formado por todas las parejas () de números reales Se define en R la operación interna ()( )( ) una de las operaciones eternas
PROBLEMAS RESUELTOS del espacio vectorial curso - - Consideremos el conjunto R formado por todas las parejas () de números reales Se define en R la operación interna ()( )( ) una de las operaciones eternas
Tema 1: Espacios vectoriales
 PROBLEMAS DE MATEMÁTICAS Parte I: Álgebra Primero de Ingeniería Química FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha Tema 1: Espacios vectoriales 1 Determina
PROBLEMAS DE MATEMÁTICAS Parte I: Álgebra Primero de Ingeniería Química FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha Tema 1: Espacios vectoriales 1 Determina
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1. Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 6 Espacios euclídeos 6.1 Producto escalar. Espacio euclídeo Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 6 Espacios euclídeos 6.1 Producto escalar. Espacio euclídeo Se llama producto escalar sobre un espacio vectorial real V a cualquier aplicación
ÍNDICE NOCIONES BÁSICAS SOBRE TRANSFORMACIONES GEOMÉTRICAS 2 TRANSFORMACIONES GEOMÉTRICAS EN EL ESPACIO 22 PROBLEMAS DE MOVIMIENTOS EN EL PLANO 1
 Índice La belleza está estrechamente relacionada con la simetría Hermann WEYL (885-955) ÍNDICE NOCIONES BÁSICAS SOBRE TRANSFORMACIONES GEOMÉTRICAS TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO 8 TRANSFORMACIONES
Índice La belleza está estrechamente relacionada con la simetría Hermann WEYL (885-955) ÍNDICE NOCIONES BÁSICAS SOBRE TRANSFORMACIONES GEOMÉTRICAS TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO 8 TRANSFORMACIONES
ETSI de Topografía, Geodesia y Cartografía
 Prueba de Evaluación Continua Grupo A 9-04-14 ESPACIOS VECTORIALES-DIAGONALIZACIÓN (parte sin DERIVE) 1. a) Definir sistema ligado de vectores de un espacio vectorial V. b) Demostrar que si un sistema
Prueba de Evaluación Continua Grupo A 9-04-14 ESPACIOS VECTORIALES-DIAGONALIZACIÓN (parte sin DERIVE) 1. a) Definir sistema ligado de vectores de un espacio vectorial V. b) Demostrar que si un sistema
UNIVERSIDAD DEL NORTE Departamento de Matemáticas y Estadística Álgebra Lineal Ejercicios resueltos- Mayo de 2018
 UNIVERSIDAD DEL NORTE Departamento de Matemáticas y Estadística Álgebra Lineal Ejercicios resueltos- Mayo de 2018 I. Sistemas homogéneos, subespacios, dependencia e independencia lineal 1. En cada caso
UNIVERSIDAD DEL NORTE Departamento de Matemáticas y Estadística Álgebra Lineal Ejercicios resueltos- Mayo de 2018 I. Sistemas homogéneos, subespacios, dependencia e independencia lineal 1. En cada caso
1. ESPACIO EUCLÍDEO. ISOMETRÍAS
 . ESPACIO EUCLÍDEO. ISOMETRÍAS. En el espacio euclídeo usual R 4 se consideran los subespacios vectoriales y W = {(x, y, z, t R 4 : x y =, z + t = } Hallar: W 2 = L{(,, 2, 2, (,,, } a Las ecuaciones de
. ESPACIO EUCLÍDEO. ISOMETRÍAS. En el espacio euclídeo usual R 4 se consideran los subespacios vectoriales y W = {(x, y, z, t R 4 : x y =, z + t = } Hallar: W 2 = L{(,, 2, 2, (,,, } a Las ecuaciones de
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
Tema 3.3. Aplicaciones afines. Cónicas y cuádricas
 Tema 3.3. Aplicaciones afines. Cónicas y cuádricas Definición 1. Sean A = (P, V, f) y A = (P, V, f ) dos espacios afines tales que V y V son espacios vectoriales sobre un mismo cuerpo. Una función θ :
Tema 3.3. Aplicaciones afines. Cónicas y cuádricas Definición 1. Sean A = (P, V, f) y A = (P, V, f ) dos espacios afines tales que V y V son espacios vectoriales sobre un mismo cuerpo. Una función θ :
EL ESPACIO EUCLÍDEO. 1.- Sean (R 3,R 3,f) el espacio afín usual tridimensional real, R ={P 0, P 1, P 2, P 3 } y R,
 EL ESPACIO EUCLÍDEO 1.- Sean (R,R,f) el espacio afín usual tridimensional real, R {P 0, P 1, P, P } y R, {Q 0, Q 1, Q,Q } dos referencias afines de (R,R,f) de bases asociadas B{ P 0 P 1 P 0 P, P0 P } y
EL ESPACIO EUCLÍDEO 1.- Sean (R,R,f) el espacio afín usual tridimensional real, R {P 0, P 1, P, P } y R, {Q 0, Q 1, Q,Q } dos referencias afines de (R,R,f) de bases asociadas B{ P 0 P 1 P 0 P, P0 P } y
ESPACIOS VECTORIALES Y APLICACIONES LINEALES
 Departamento de Matemática Aplicada II E.E.I. ÁLGEBRA Y ESTADÍSTICA Boletín n o (010-011 ESPACIOS VECTORIALES Y APLICACIONES LINEALES 1. En el espacio vectorial ordinario R 4 estudiar cuáles de los siguientes
Departamento de Matemática Aplicada II E.E.I. ÁLGEBRA Y ESTADÍSTICA Boletín n o (010-011 ESPACIOS VECTORIALES Y APLICACIONES LINEALES 1. En el espacio vectorial ordinario R 4 estudiar cuáles de los siguientes
1. Ejercicios. Algebra Lineal Problemas del tema 4 Endomorfismos Curso Universidad de Oviedo
 1. Ejercicios Ejercicio 1 En R 2, referido a la base canónica, se consideran los vectores u 1 = (1, 1) y u 2 = (2,). Un endomorfismo de R 2, T los transforma en los vectores v 1 = ( 2,1) y v 2 = (, 1)
1. Ejercicios Ejercicio 1 En R 2, referido a la base canónica, se consideran los vectores u 1 = (1, 1) y u 2 = (2,). Un endomorfismo de R 2, T los transforma en los vectores v 1 = ( 2,1) y v 2 = (, 1)
UTN FRBA Final de Álgebra y Geometría Analítica 21/05/2013. Apellido y nombre del alumno: Leg.:.. Corrigió: Revisó:...
 UTN FRBA Final de Álgebra y Geometría Analítica 1/05/01 Apellido y nombre del alumno: Leg.:.. Corrigió: Revisó:... La condición para aprobar esta evaluación es tener bien resueltos como mínimo tres ejercicios.
UTN FRBA Final de Álgebra y Geometría Analítica 1/05/01 Apellido y nombre del alumno: Leg.:.. Corrigió: Revisó:... La condición para aprobar esta evaluación es tener bien resueltos como mínimo tres ejercicios.
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
7 Aplicaciones ortogonales
 Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 7 Aplicaciones ortogonales 7.1 Aplicación ortogonal Se llama aplicación ortogonal a un endomorfismo f : V V sobre un espacio vectorial
Águeda Mata y Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 7 Aplicaciones ortogonales 7.1 Aplicación ortogonal Se llama aplicación ortogonal a un endomorfismo f : V V sobre un espacio vectorial
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
1. Efectuar las siguientes operaciones, expresando el resultado en forma binómica: (1 i)(2 i)(i 3) ; 344 ( i) 231 i(1 + i) 5
 1.5.1 Complejos 1. Efectuar las siguientes operaciones, expresando el resultado en forma binómica: i 1 ; 2 + i ; 2i 2 i 1 + i +i; 5 (1 i)(2 i)(i 3) ; i344 +( i) 231 ; (1 + i) 5 + 1 (1 i) 5 1 ; 2. Usar,
1.5.1 Complejos 1. Efectuar las siguientes operaciones, expresando el resultado en forma binómica: i 1 ; 2 + i ; 2i 2 i 1 + i +i; 5 (1 i)(2 i)(i 3) ; i344 +( i) 231 ; (1 + i) 5 + 1 (1 i) 5 1 ; 2. Usar,
1. ESPACIO EUCLÍDEO. ISOMETRÍAS
 1 1. ESPACIO EUCLÍDEO. ISOMETRÍAS Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos conceptos
1 1. ESPACIO EUCLÍDEO. ISOMETRÍAS Muchos de los fenómenos que se investigan en la geometría utilizan nociones como las de longitud de un vector y ángulo entre vectores. Para introducir estos dos conceptos
FINAL DE ÁLGEBRA Y GEOMETRÍA ANALÍTICA 30 mayo 2006 Tema 1
 FINAL DE ÁLGEBRA Y GEOMETRÍA ANALÍTICA 0 mayo 006 Tema Apellido y nombres:... 4 5 Calificación final ) Dadas las rectas : x y + z = r : r : ( x, y, z) = (,,) + λ(, ) x z + k = 0 k para que las rectas sean
FINAL DE ÁLGEBRA Y GEOMETRÍA ANALÍTICA 0 mayo 006 Tema Apellido y nombres:... 4 5 Calificación final ) Dadas las rectas : x y + z = r : r : ( x, y, z) = (,,) + λ(, ) x z + k = 0 k para que las rectas sean
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
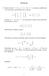 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
TRANSFORMACIONES GEOMÉTRICAS Curso 04-05
 -En el plano vectorial V, con la base ortonormal { i,j } vectores u (, ) v (, ) éstos determinan Hallar en la base { i,j } transformaciones ortogonales tales que f( D ) se consideran los las semirrectas
-En el plano vectorial V, con la base ortonormal { i,j } vectores u (, ) v (, ) éstos determinan Hallar en la base { i,j } transformaciones ortogonales tales que f( D ) se consideran los las semirrectas
Teoría Tema 9 Repaso a la geometría en dos dimensiones de 1ºBachillerato
 página 1/17 Teoría Tema 9 Repaso a la geometría en dos dimensiones de 1ºBachillerato Índice de contenido Ecuación vectorial, paramétrica, cartesiana y general de la recta en dos dimensiones...2 Pendiente
página 1/17 Teoría Tema 9 Repaso a la geometría en dos dimensiones de 1ºBachillerato Índice de contenido Ecuación vectorial, paramétrica, cartesiana y general de la recta en dos dimensiones...2 Pendiente
FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas
 EXÁMENES DE MATEMÁTICAS Álgebra Primero de Ingeniería Química FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha 5 de julio de 99. Dada la aplicación lineal: T
EXÁMENES DE MATEMÁTICAS Álgebra Primero de Ingeniería Química FACULTAD DE CIENCIAS QUÍMICAS Departamento de Matemáticas Universidad de Castilla-La Mancha 5 de julio de 99. Dada la aplicación lineal: T
f(x, y, z, t) = (x + y t, x + 2y z 3t, 3x + 5y 2z 7t).
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 20 de enero de 20 (2.5 p.) ) Se considera la aplicación lineal f : R 4 R definida por: f(x y
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Álgebra Convocatoria de enero de 20 de enero de 20 (2.5 p.) ) Se considera la aplicación lineal f : R 4 R definida por: f(x y
G. SERRANO SOTELO. H = e 0 + E
 CLASIFICACIÓN AFÍN DE CÓNICAS Y CUÁDRICAS G. SERRANO SOTELO 1. Cuádricas en un hiperplano afín Sea E un R-espacio vectorial de dimensión n +1. Sean E = e 1,...,e n un hiperplano vectorial de E y e un vector
CLASIFICACIÓN AFÍN DE CÓNICAS Y CUÁDRICAS G. SERRANO SOTELO 1. Cuádricas en un hiperplano afín Sea E un R-espacio vectorial de dimensión n +1. Sean E = e 1,...,e n un hiperplano vectorial de E y e un vector
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2016 2017) 1. En el espacio afín IR 3 se considera la referencia canónica R y la referencia R = {(1, 0, 1); (1, 1, 0), (1, 1, 1), (1, 0, 0)}. Denotamos
ÁLGEBRA LINEAL II Práctica 3.1-3.2 Geometría afín. (Curso 2016 2017) 1. En el espacio afín IR 3 se considera la referencia canónica R y la referencia R = {(1, 0, 1); (1, 1, 0), (1, 1, 1), (1, 0, 0)}. Denotamos
GUÍA DE APRENDIZAJE ALGEBRA LINEAL Y GEOMETRIA
 GUÍA DE APRENDIZAJE ALGEBRA LINEAL Y GEOMETRIA Datos Descriptivos TITULACIÓN: CENTROS IMPLICADOS: E.T.S. DE INGENIEROS NAVALES CICLO: MÓDULO: MÓDULO 0.1: Asignaturas Formación Básica MATERIA: ASIGNATURA:
GUÍA DE APRENDIZAJE ALGEBRA LINEAL Y GEOMETRIA Datos Descriptivos TITULACIÓN: CENTROS IMPLICADOS: E.T.S. DE INGENIEROS NAVALES CICLO: MÓDULO: MÓDULO 0.1: Asignaturas Formación Básica MATERIA: ASIGNATURA:
Definición 1.28 (Determinación de una recta) Una recta en el plano viene determinada por un punto y un vector libre, no nulo, r (P; u )
 1.3. La recta en el plano afín La recta está formada por puntos del plano en una dirección dada. La ecuación de la recta es la condición necesaria y suficiente que deben cumplir las coordenadas de un punto
1.3. La recta en el plano afín La recta está formada por puntos del plano en una dirección dada. La ecuación de la recta es la condición necesaria y suficiente que deben cumplir las coordenadas de un punto
GEOMETRÍA. (x 1) 2 +(y 2) 2 =1. Razónalo. x y + z = 2. :3x 3z +1= 0 es doble de la distancia al plano π 2. : x + y 1= 0. Razónalo.
 GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
GEOMETRÍA 1. (Junio, 1994) Sin resolver el sistema, determina si la recta x +3y +1= 0 es exterior, secante o tangente a la circunferencia (x 1) +(y ) =1. Razónalo.. (Junio, 1994) Dadas las ecuaciones de
{ } { 1, 0, 0, 0, 0,1,1,1,(1,1,1,1)} ( ) ( ) ( )
 .- Se considera R con la suma habitual con el producto por un escalar que se indica en los casos siguientes. Prueba que en ninguno de ellos, (R,+, ) es espacio vectorial señalando alguna propiedad del
.- Se considera R con la suma habitual con el producto por un escalar que se indica en los casos siguientes. Prueba que en ninguno de ellos, (R,+, ) es espacio vectorial señalando alguna propiedad del
1. Si están situados en rectas paralelas: la recta que une los orígenes, deja sus extremos en un mismo semiplano.
 CAPÍTULO 1 El plano vectorial Consideremos P como el plano intuitivo de puntos: A,B,C... 1.1. El espacio vectorial de los vectores Definición 1.1 Vectores fijos Dado dos puntos cualesquiera A e B del espacio
CAPÍTULO 1 El plano vectorial Consideremos P como el plano intuitivo de puntos: A,B,C... 1.1. El espacio vectorial de los vectores Definición 1.1 Vectores fijos Dado dos puntos cualesquiera A e B del espacio
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2012 2013) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2012 2013) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
Matrices. Operaciones con matrices.
 Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
Matrices. Operaciones con matrices. Ejercicio. Dadas las matrices ( ) ( ) 4 A = B = ( ) C = D = 4 5 ( ) 4 E = F = seleccione las que se pueden sumar y súmelas. Ejercicio. Dadas las matrices ( ) ( ) A =
ÁLGEBRA LINEAL II Práctica
 ÁLGEBRA LINEAL II Práctica 2.1-2.2 Espacios Euclídeos. Ortogonalidad (Curso 2011 2012) 1. Se considera un espacio euclídeo de dimensión 3, y en él una base {ē 1, ē 2, ē 3 } tal que el módulo de ē 1 y el
ÁLGEBRA LINEAL II Práctica 2.1-2.2 Espacios Euclídeos. Ortogonalidad (Curso 2011 2012) 1. Se considera un espacio euclídeo de dimensión 3, y en él una base {ē 1, ē 2, ē 3 } tal que el módulo de ē 1 y el
Teoría Tema 9 Ecuaciones del plano
 página 1/11 Teoría Tema 9 Ecuaciones del plano Índice de contenido Determinación lineal de un plano. Ecuación vectorial y paramétrica...2 Ecuación general o implícita del plano...6 Ecuación segmentaria
página 1/11 Teoría Tema 9 Ecuaciones del plano Índice de contenido Determinación lineal de un plano. Ecuación vectorial y paramétrica...2 Ecuación general o implícita del plano...6 Ecuación segmentaria
Tema 1: Introducción y fundamentos matemáticos. Parte 4/4 Vectores en física II: Coordenadas y componentes
 Tema 1: Introducción y fundamentos matemáticos ntonio González Fernández Departamento de Física plicada III Universidad de Sevilla Parte 4/4 Vectores en física II: Coordenadas y componentes plicaciones
Tema 1: Introducción y fundamentos matemáticos ntonio González Fernández Departamento de Física plicada III Universidad de Sevilla Parte 4/4 Vectores en física II: Coordenadas y componentes plicaciones
Problemas de exámenes de Geometría
 1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
PROBLEMAS DE ÁLGEBRA LINEAL INGENIERÍA DE TELECOMUNICACIONES - E.T.S.I.T. CURSO 2005/06
 PROBLEMAS DE ÁLGEBRA LINEAL INGENIERÍA DE TELECOMUNICACIONES - E.T.S.I.T. CURSO 200/06 1. Utilizar el método de eliminación de Gauss para resolver el sistema de ecuaciones lineales siguiente: 2 x 1 2 x
PROBLEMAS DE ÁLGEBRA LINEAL INGENIERÍA DE TELECOMUNICACIONES - E.T.S.I.T. CURSO 200/06 1. Utilizar el método de eliminación de Gauss para resolver el sistema de ecuaciones lineales siguiente: 2 x 1 2 x
Ejercicios tipo test de las lecciones 1 y El vector e = ( 1, 0, λ) está en el plano generado por los vectores u = (1, 2, 1) y
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Ejercicios tipo test de las lecciones 1 y 2. 1. El vector e = ( 1, 0, λ) está en el plano generado por los vectores u = (1,
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Ejercicios tipo test de las lecciones 1 y 2. 1. El vector e = ( 1, 0, λ) está en el plano generado por los vectores u = (1,
x y z x y z x y z z z z z z z
 . Un vector v tiene módulo 5 y es tal que cos ; siendo α el ángulo que forma el vector con el eje x. 5 Escribir la expresión cartesiana del o los vectores v sabiendo que su segunda y tercera componentes
. Un vector v tiene módulo 5 y es tal que cos ; siendo α el ángulo que forma el vector con el eje x. 5 Escribir la expresión cartesiana del o los vectores v sabiendo que su segunda y tercera componentes
SOLUCIONES A LA AUTOEVALUACIÓN - Espacios Vectoriales.
 SOLUCIONES A LA AUTOEVALUACIÓN - Espacios Vectoriales. A) Soluciones a las Cuestiones C-1) a) Sí, por ejemplo el eje X, formado por los vectores de la forma (λ, 0), que se identificarían con el número
SOLUCIONES A LA AUTOEVALUACIÓN - Espacios Vectoriales. A) Soluciones a las Cuestiones C-1) a) Sí, por ejemplo el eje X, formado por los vectores de la forma (λ, 0), que se identificarían con el número
GUÍA DE APRENDIZAJE ALGEBRA LINEAL Y GEOMETRIA
 GUÍA DE APRENDIZAJE ALGEBRA LINEAL Y GEOMETRIA Datos Descriptivos TITULACIÓN: CENTROS IMPLICADOS: E.T.S. DE INGENIEROS NAVALES CICLO: MÓDULO: MATERIA: ASIGNATURA: CURSO: 1 º SEMESTRE: DEPARTAMENTO RESPONSABLE:
GUÍA DE APRENDIZAJE ALGEBRA LINEAL Y GEOMETRIA Datos Descriptivos TITULACIÓN: CENTROS IMPLICADOS: E.T.S. DE INGENIEROS NAVALES CICLO: MÓDULO: MATERIA: ASIGNATURA: CURSO: 1 º SEMESTRE: DEPARTAMENTO RESPONSABLE:
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 4: Endomorfismos
 Marisa Serrano, Zulima Fernández Universidad de Oviedo 11 de enero de 2010 email: mlserrano@uniovi.es Índice 1 2 3 4 en espacios de dimensión dos en espacios eucĺıdeos de dimensión tres Definición Definición
Marisa Serrano, Zulima Fernández Universidad de Oviedo 11 de enero de 2010 email: mlserrano@uniovi.es Índice 1 2 3 4 en espacios de dimensión dos en espacios eucĺıdeos de dimensión tres Definición Definición
en el espacio queda caracterizado por un par de puntos A y B, o bien por su módulo, dirección y sentido junto con el origen, siendo:
 TEMA 10: VECTORES EN EL ESPACIO. 10.1 Vectores fijos y libres en el espacio vectorial. 10. Operaciones con vectores libres. Bases del espacio vectorial. 10.3 Producto escalar. Módulo y ángulo de vectores.
TEMA 10: VECTORES EN EL ESPACIO. 10.1 Vectores fijos y libres en el espacio vectorial. 10. Operaciones con vectores libres. Bases del espacio vectorial. 10.3 Producto escalar. Módulo y ángulo de vectores.
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
b E: base canónica de R 3, E = {1, x, x 2 } base de P 2 2) Analice la verdad o la falsedad de las siguientes proposiciones. Justifique sus respuestas.
 UTN. FRBA ÁLGEBRA Y GEOMETRÍA ANALÍTICA de Mayo de01 Tema: 1 Apellido y nombres del alumno:...legajo:. 1 4 5 Calificación final La condición para aprobar el examen es tener como mínimo tres ejercicios
UTN. FRBA ÁLGEBRA Y GEOMETRÍA ANALÍTICA de Mayo de01 Tema: 1 Apellido y nombres del alumno:...legajo:. 1 4 5 Calificación final La condición para aprobar el examen es tener como mínimo tres ejercicios
Producto Escalar. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31
 Producto Escalar AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31 Objetivos Al finalizar este tema tendrás que: Saber usar el producto escalar. Calcular
Producto Escalar AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Producto Escalar 1 / 31 Objetivos Al finalizar este tema tendrás que: Saber usar el producto escalar. Calcular
Parte II - Prácticas 8 a 9. Álgebra A 62 ÁLGEBRA A 62 (INGENIERÍA)
 Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Tema 3.2. Espacio afín eucĺıdeo. Problemas métricos
 Tema 3.2. Espacio afín eucĺıdeo. Problemas métricos Definición: Un espacio afín es una terna A = (P, V, f) en la que P es un conjunto no vacío, V un espacio vectorial de dimensión finita sobre un cuerpo
Tema 3.2. Espacio afín eucĺıdeo. Problemas métricos Definición: Un espacio afín es una terna A = (P, V, f) en la que P es un conjunto no vacío, V un espacio vectorial de dimensión finita sobre un cuerpo
Movimientos. Teorema de Cartan-Dieudonné. Semejanzas.
 Capítulo 5 Movimientos. Teorema de Cartan-Dieudonné. Semejanzas. 5.1 Isometrías y movimientos Partimos de un espacio euclídeo (X, V, +) y recordemos que una isometría de V es un elemento ϕ Gl(V ) que conserva
Capítulo 5 Movimientos. Teorema de Cartan-Dieudonné. Semejanzas. 5.1 Isometrías y movimientos Partimos de un espacio euclídeo (X, V, +) y recordemos que una isometría de V es un elemento ϕ Gl(V ) que conserva
EXAMEN JUNIO PP 1A SEMANA
 EXAMEN JUNIO PP A SEMANA XAVI AZNAR Ejercicio. Defina semejanza, razón de semejanza y movimento asociado a una semejanza. Ejercicio. En el espacio vectorial V 3 (R) sea q la forma cuadrática cuya expresión
EXAMEN JUNIO PP A SEMANA XAVI AZNAR Ejercicio. Defina semejanza, razón de semejanza y movimento asociado a una semejanza. Ejercicio. En el espacio vectorial V 3 (R) sea q la forma cuadrática cuya expresión
TEMA 11.- VECTORES EN EL ESPACIO
 TEMA 11.- VECTORES EN EL ESPACIO 1.- INTRODUCCIÓN Un vector fijo AB del espacio (también lo era en el plano) es un segmento orientado que tiene su origen en un punto A y su extremo en otro punto B. Estos
TEMA 11.- VECTORES EN EL ESPACIO 1.- INTRODUCCIÓN Un vector fijo AB del espacio (también lo era en el plano) es un segmento orientado que tiene su origen en un punto A y su extremo en otro punto B. Estos
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID. PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso )
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 00-003) MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES:
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) MODELO DE EXAMEN (Curso 00-003) MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN INSTRUCCIONES:
ÁLGEBRA LINEAL. EXAMEN EXTRAORDINARIO 5 de Julio de T (e 1 ) = e 1 e 2 + 2e 3 T (e 2 ) = e 1 + 2e 2 3e 3. [T (e 1 ) T (e 2 )] =
![ÁLGEBRA LINEAL. EXAMEN EXTRAORDINARIO 5 de Julio de T (e 1 ) = e 1 e 2 + 2e 3 T (e 2 ) = e 1 + 2e 2 3e 3. [T (e 1 ) T (e 2 )] = ÁLGEBRA LINEAL. EXAMEN EXTRAORDINARIO 5 de Julio de T (e 1 ) = e 1 e 2 + 2e 3 T (e 2 ) = e 1 + 2e 2 3e 3. [T (e 1 ) T (e 2 )] =](/thumbs/82/86817902.jpg) ÁLGEBRA LINEAL EXAMEN EXTRAORDINARIO 5 de Julio de Apellidos y Nombre: Ejercicio. Sea T : R R 3 una transformación lineal definida como: T (e ) = e e + e 3 T (e ) = e + e 3e 3 donde {e, e }, {e, e, e 3}
ÁLGEBRA LINEAL EXAMEN EXTRAORDINARIO 5 de Julio de Apellidos y Nombre: Ejercicio. Sea T : R R 3 una transformación lineal definida como: T (e ) = e e + e 3 T (e ) = e + e 3e 3 donde {e, e }, {e, e, e 3}
Tema 6: Espacios euclídeos
 Águeda Mata y Miguel Reyes, Dpto de Matemática Aplicada, FI-UPM 1 Tema 6: Espacios euclídeos Ejercicios 1 Demuestra que la aplicación < A, B >= traza(ab t ), A, B M m n (R), es un producto escalar sobre
Águeda Mata y Miguel Reyes, Dpto de Matemática Aplicada, FI-UPM 1 Tema 6: Espacios euclídeos Ejercicios 1 Demuestra que la aplicación < A, B >= traza(ab t ), A, B M m n (R), es un producto escalar sobre
DIAGONALIZACIÓN DE MATRICES CUADRADAS
 DIAGONALIZACIÓN DE MATRICES CUADRADAS.- Considerar los vectores u = (, -, ) y v = (, -, ) de : a) Escribir, si es posible, los vectores (, 7, -4) y (, -5, 4) como combinación lineal de u y v. b) Para qué
DIAGONALIZACIÓN DE MATRICES CUADRADAS.- Considerar los vectores u = (, -, ) y v = (, -, ) de : a) Escribir, si es posible, los vectores (, 7, -4) y (, -5, 4) como combinación lineal de u y v. b) Para qué
Matemáticas Empresariales II. Aplicaciones Lineales
 Matemáticas Empresariales II Lección 5 Aplicaciones Lineales Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales II 1 / 34 Definición - Aplicación Lineal Sean
Matemáticas Empresariales II Lección 5 Aplicaciones Lineales Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales II 1 / 34 Definición - Aplicación Lineal Sean
ÁLGEBRA LINEAL E.T.S. DE INGENIERÍA INFORMÁTICA INGENIERÍAS TÉCNICAS EN INFORMÁTICA DE SISTEMAS Y GESTIÓN BOLETÍN DE PROBLEMAS DE
 E.T.S. DE INGENIERÍA INFORMÁTICA BOLETÍN DE PROBLEMAS DE ÁLGEBRA LINEAL para las titulaciones de INGENIERÍAS TÉCNICAS EN INFORMÁTICA DE SISTEMAS Y GESTIÓN 1. Matrices y determinantes Ejercicio 1.1 Demostrar
E.T.S. DE INGENIERÍA INFORMÁTICA BOLETÍN DE PROBLEMAS DE ÁLGEBRA LINEAL para las titulaciones de INGENIERÍAS TÉCNICAS EN INFORMÁTICA DE SISTEMAS Y GESTIÓN 1. Matrices y determinantes Ejercicio 1.1 Demostrar
Ejercicio 2 (Examen de septiembre de 2009) Razona cuáles de los siguientes conjuntos son subespacios vectoriales:
 Ejercicio 1 De los siguientes subconjuntos de R 3 decida cuales son subespacios y cuales no: a) U 1 = {(x,y,z) / x = 1 = y+z} b) U 2 = {(x,y,z) / x+3y = 0,z 0} c) U 3 = {(x,y,z) / x+2y+3z= 0 = 2x+y} d)
Ejercicio 1 De los siguientes subconjuntos de R 3 decida cuales son subespacios y cuales no: a) U 1 = {(x,y,z) / x = 1 = y+z} b) U 2 = {(x,y,z) / x+3y = 0,z 0} c) U 3 = {(x,y,z) / x+2y+3z= 0 = 2x+y} d)
