G. SERRANO SOTELO. H = e 0 + E
|
|
|
- Francisco Javier Suárez Carrizo
- hace 5 años
- Vistas:
Transcripción
1 CLASIFICACIÓN AFÍN DE CÓNICAS Y CUÁDRICAS G. SERRANO SOTELO 1. Cuádricas en un hiperplano afín Sea E un R-espacio vectorial de dimensión n +1. Sean E = e 1,...,e n un hiperplano vectorial de E y e un vector de E que no está en E, e / E. Los vectores {e,e 1,...,e n } forman una base de E, y si representamos por (x,x 1,...,x n ) sus funciones coordenadas, el hiperplano afín H definido por H = e + E tiene por ecuación implícita x =1.Enestesistemadecoordenadaslaecuaciónimplícita del hiperplano del infinito E es x =. Definición 1.1. Una cuádrica de H es una familia C = {λt } (λ R), formada por una métrica simétrica T sobre E ytodassusproporcionales. El lugar geométrico definido por la cuádrica C es la intersección del hiperplano afín H con el conjunto de los vectores de E que son isótropos para la métrica T locus de C = {e E : T (e, e) =} H En coordenadas, el locus de C representa la ecuación de una hipersuperficie de grado de H. Enefecto,siG =(g ij )eslamatrizdeunrepresentantet de la cuádrica C respecto de una base {e,e 1,...,e n } de E en la que la ecuación de H es x =1,se tiene g g 1... g n 1 locus de C = (1,x 1,...,x n ) H : g 1 x 1... x n 1 g g 1n x =, g n g n1... g nn x n de donde resulta g 11 x g nn x n +(g 1 x 1 x + + g n 1n x n 1 x n )+(g 1 x g n x n )+g =. Observación 1.. La parte cuadrática, g 11 x 1+ +g nn x n+(g 1 x 1 x + +g n 1n x n 1 x n ), de esta ecuación se corresponde con la matriz de la restricción de la métrica T al hiperplano del infinito E, g g 1n T E =..... g n1... g nn 1
2 G. Serrano Sotelo Ejemplo 1.3. H = {(1,x,y)} R 3, C = {λt }, G = locus de C 1 x y x = 1 y Curva de grado dos del plano xy x +y +xy 6x +4y +1=. Ejemplo H = {(1,x,y,z)} R 4, C = {λt }, G = locus de C 1 x y z x y = 1 z Superficie de grado dos del espacio xyz x y + z +6xy +4yz x +y =. Observación 1.5. Llamaremos cónicas alascuádricassobreunplanoafíndedeun R-espacio vectorial de dimensión 3. Definición 1.6. Una cuádrica C = {λt } es irreducible o no degenerada si lo es cualquiera de sus métricas representantes. Ejemplo 1.7. Las cónicas de ecuaciones (a) x x a +y 1 =, (b) b a y 1 =, b (c) y px =, donde a, b, p R {} son irreducibles pues las métricas representantes, de matrices (a) 1 1/a, (b) 1 1/a, (c) 1 1, 1/b 1/b 1/p son no singulares.. Centros de una cuádrica Sea C = {λt } una cuádrica sobre el hiperplano afín H de E. Definición.1. Un vector e E define un centro de la cuádrica C si e T (e,e)=paratodoe E. / E y Proposición.. Si C = {λt } es una cuádrica irreducible y tiene centro éste es único.
3 Clasificación afín de cónicas y cuádricas 3 Demostración. Sea e E un vector que define un centro de la cuádrica C. Como T es una métrica irreducible el subespacio ortogonal al hiperplano del infinito, E,esunarecta,luegoe es un generador de ella pues es ortogonal a E, y como e / E esta recta e corta a H en un único punto, c = e H, queeselcentrode la cuádrica. Corolario.3. Si C = {λt } es una cuádrica irreducible con centro existe una base {e,e 1,...,e n } de E en la que las coordenadas del centro son c = 1, Adj g 1 Adj g,..., Adj g n Adj g, donde G =(g ij ) es la matriz, respecto de esa base, de una métrica representante de C. Demostración. Respecto de la base {e,e 1,...,e n } de E, enlaquee es el vector que define el centro, E = e,y{e 1,...,e n } una base de E,laecuaciónimplícitade E es x =,luegosusubespacioincidenteestágeneradoporlaformalinealω de coordenadas en la base dual ω =(1,,...,). Si G =(g ij )eslamatrizdet en esta base se tiene que E = G 1 ω = e con luego el centro es e = Adj g G, Adj g 1 G,, Adj g n ), G c = 1, Adj g 1 G,, Adj g n ), G donde Adj g = G es el detreminante de la restricción de G a E. 3. Cuádricas afinmente equivalentes Sea E un espacio vectorial real de dimensión n +1yH un hiperplano afín de E de subespacio director E. Definición 3.1. Sea C = {λt } una cuádrica de H. Sellamanrangor eíndicei de la cuádrica a los de cualquiera de las métricas que la representan. Se llaman rango r e í n d i c e i de la cuádrica en el infinito a los de la restricción a E de cualquiera de las métricas que la representan. r =rg(t ), i =indice(t ); r =rg(t E ), i =indice(t E ) Definición 3.. Dos cuádricas C = {λt } y C = {µt } de H son afínmente equivalentes si existe un automorfismo E f E que deja invariante el hiperplano H y tal que el morfismo inducido T (E) f T (E) transformalafamilia{λt } en la familia {µt }. Teorema 3.3. Si dos cuádricas C = {λt } y C = {µt } de H son afínmente equivalentes, tienen iguales sus rangos, índices, rangos en el infinito e índices en el infinito, r = r, i = i ; r = r, i = i. Demostración. Como C y C son afínmente equivalentes existe un automorfismo f de E tal que f (T )=µt para algún µ R. Además, como f deja invariante H, f restringe f aunautomorfismoe E cuyo morfismo inducido T (E ) f T (E )transforma la métrica T E en la métrica µt E. Puesto que el rango y el índice de una métrica son invariantes por cambio de base se concluye.
4 4 G. Serrano Sotelo Demostraremos que el recíproco de este teorema también es cierto. Para ello obtendremos primero las ecuaciones reducidas afines de las cuádricas. 4. Ecuaciones reducidas afines de las cuádricas 4.1. Ecuaciones reducidas de las cuádricas con centro. Sea e H un centro de la cuádrica C = {λt } y {e 1,...,e n } una base reducida para la métrica T E.Enlabase{e,e 1,...,e n } de E la matriz de la métrica T es T (e,e ) Se presentan pues dos posibilidades, (1) Si T (e,e )=,elcentroe es un vector isótropo para la métrica T,estoes un punto del locus de la cuádrica. En este caso la matriz es , 1... y se deduce que el rango e índice de la cuádrica coinciden con el rango e índice de la cuádrica en el infinito r = r, i = i La ecuación reducida afín de la cuádrica es x x p x p+1 x p+q =, donde los números p y q son respectivamente el número de raíces positivas y el número de raíces negativas de la ecuación secular de la restricción de la métrica al hiperplano del infinito E e i =mín(p, q) yr = n (p + q).
5 Clasificación afín de cónicas y cuádricas 5 () Si T (e,e )=α =, tomando como representante inicial de la cuádrica la métrica 1 α,lamatrizdeestamétricaenlabase{e,e 1,...,e n } de E es , 1... de la que se deducen las relaciones entre los rangos e índices de la cuádrica y los de su restricción al infinito, que dan los dos casos siguientes r = r +1, i = i, si p q r = r +1, i = i +1, si p>q Los números p y q son respectivamente el número de raíces positivas y el número de raíces negativas de la ecuación secular de la restricción de la métrica al hiperplano del infinito E. En ambos casos, la ecuación reducida afín de la cuádrica es x x p x p+1 x p+q =1 4.. Ecuaciones reducidas de las cuádricas sin centro. En este caso, de la definición de centro se sigue que E E,luegoRadT E = E E = E ycomoradt E resulta dim Rad T E =dime =dime dim E +dim(radt E )=1+dimRadT Así pues existen vectores e 1 y v tales que, e 1 Rad T E,e 1 / Rad T y v E E,T (v, e 1 )=β = α β La matriz de la restricción de la métrica T al plano v, e 1, T v,e1 =,es β no singular y de índice uno. Por tanto, v, e 1 define un plano hiperbólico y es posible seleccionar otra base {e,e 1 } de este plano en la que la matriz de la restricción es 1. 1 Elijiendo ahora una base reducida {e,...,e n } para la métrica restricción T e,e 1 se obtiene una base {e,e 1,e,...,e n } de E en la que la matriz de T es
6 6 G. Serrano Sotelo Esto permite obtener la siguiente relación entre los rangos e índices de la cuádrica y los de su restricción al infinito r = r +, i = i +1 En este caso, la ecuación reducida afín de la cuádrica es x + + x p x p+1 x p+q x 1 =, donde los números p y q son respectivamente el número de raíces positivas y el número de raíces negativas de la ecuación secular de la restricción de la métrica al hiperplano del infinito E. 5. Clasificación afín De las ecuaciones reducidas afines del apartado anterior se sigue que si dos cuádricas tienen iguales sus rangos, índices, rangos en el infinito e índices en el infinito son afínmente equivalentes. Combinando este resultado con el teorema?? obtenemos el teorema de clasificación. Teorema 5.1. La condición necesaria y suficiente para que dos cuádricas C = {λt } y C = {µt } de H sean afínmente equivalentes es que tengan iguales sus rangos, índices, rangos en el infinito e índices en el infinito, r = r, i = i ; r = r, i = i. Utilizando este teorema obtenemos los siguientes cuadros de clasificación afín de cónicas y cuádricas.
7 Clasificación afín de cónicas y cuádricas Clasificación afín de cónicas en H R 3. r 3(Irreducibles) 1 r i \i 1 1 Par de rectas 1 Hipérbola reales x y =1 no paralelas Elipse Elipse real imaginaria x + y =1 x + y = 1 x y = Par de rectas imaginarias no paralelas x + y = 1 Par de rectas Par de rectas Parábola reales imaginarias y =x paralelas paralelas x =1 x = 1 Recta real doble x = Recta real Conjunto Plano x = vacío afín Ejemplo 5.. Clasificar afínmente las cónicas siguientes (a) x xy + y +4x 6y +1= (b) x +4xy +4y x 4y 3= (a) Escribamos la matriz G de la métrica T y la matriz G de su restricción al infinito G = ; G = (b) Calculemos el número de raíces nulas r, el número de raíces positivas r + yelnúmero de raíces negativas r de la ecuación secular de la métrica T ydelamétricat E p(x) = xi G = x 3 3x 11x +1, r (p(x)) =, r + (p(x)) =, r (p(x)) = 1 p (x) = xi G = x x, r (p (x)) = 1, r + (p (x)) = 1, r (p (x)) = Luego los rangos y los índices de T y de su restricción al infinito son r =3,i=1; r =1,i = Por tanto, es una cónica irreducible sin centro de matriz reducida 1 1 y 1 ecuación reducida afín y x =, esto es, una Parábola. 3 1 G = ; G = 4 4 p(x) = xi G = x 3 x x, r (p(x)) = 1, r + (p(x)) = 1, r (p(x)) = 1
8 8 G. Serrano Sotelo p (x) = xi G = x 5x, r (p (x)) = 1, r + (p (x)) = 1, r (p (x)) = Los rangos y los índices de la métrica T y de su restricción al infinito son r =,i=1; r =1,i = Es una cónica degenerada con centro, de matriz reducida 1 1 y ecuación reducida afín x 1 =, que representa una Par de rectas reales y paralelas. Ejemplo 5.3. Calcular el centro, los ejes principales y la ecuación reducida métrica de la curva de grado dos del plano real de ecuación 3x +3y xy +x 4y +1= Solución. Sea G la matriz de una métrica T representante de la cónica en H R 3 y G su restricción al infinito. G = ; G = Se tiene xi G = x 3 7x +9x +3 ; xi G =(x )(x 4) r =3 i =1 Cónica irreducible con centro: x + y =1(Elipse real) r = i = (a) Centrodelaelipse= 1 8, 5 8 ) Por el Corolario??, c = 1, Adj g 1 G, Adj g )=(1, 1 G 8, 5 8 ) (b) Calculemos una base ortonormal de diagonalización para G. ker(g I) =(, 1, 1) ; ker(g 4I) =(, 1, 1) {u 1 = 1 (, 1, 1), u = 1 (, 1, 1)} es la base buscada. (c) En la base {c, u 1,u } la matriz de T es T (c, c), con T (c, c) = Luego la ecuación reducida métrica de la elipse es x 3/16 + ȳ 3/3 =1, donde x yȳ son las coordenadas asociadas a la base {u 1,u }. (d) Ecuaciones de la transformación afín efectuada para pasar del sistema de referencia inicial en H, en el que las coordenadas son {x, y}, al sistema de referencia de origen c y ejes las rectas c + u 1, c + u, respecto del que las coordenadas son { x, ȳ}.
9 Clasificación afín de cónicas y cuádricas 9 Si B representa la matriz del cambio de base realizado en E, esto es B = 1 1 1, componiendo el automorfismo de cambio de base con la traslación 1 1 de vector c se obtienen las ecuaciones x = x x 1/5 = B + = y ȳ 1 (x + y 4 8 ) 5/8 ȳ = 1 (x y ) (e) Los ejes principales de la elipse son las rectas c+u 1, c+u de ecuaciones respectivas ȳ = x y = ; x = x + y 4 8 = (f ) Las medidas sobre los semiejes, a y b, la excentricidad y los focos F y F de la elipse, respecto del sistema de referencia inicial, son 3 3 a = ; b = 16 3 c = 3 a b = 3 = Excentricidad = c a = F =(, ) = F =(, ) F =( 3, ) = F =( 3 1, 3+5 ) 8 8 Ejemplo 5.4. Calcular el vértice, los ejes principales, la ecuación reducida métrica, el foco y la directriz de la parábola del ejemplo?? x xy + y +4x 6y +1= Solución. Sean G y G como en el ejemplo anterior. G = ; G = Tenemos que encontrar una base {e, v 1,v } en la que la matriz de T es de la forma α α con α,β =. El vector e define el vértice de la parábola y {v 1,v } es una base β ortonormal de diagonalización para G. (a) Calculemos v 1 y v. xi G = x(x ) Forma diagonal β = ker G x y = v 1 = 1 (, 1, 1) ker(g I) x + y = v = 1 (, 1, 1) (b) Vértice de la parábola V =( 31 8, 11 8 ) El vector e que define el vértice está en H, luego sus coordenadas son de a forma e =(1,x,y), y verifica las condiciones T (e, e) =,T (e, v 1 )=α y T (e, v )=.
10 1 G. Serrano Sotelo Calculemos x e y resolviendo el sistema determinado por la primera y tercera condiciones T (e, e) = x xy + y +4x 6y +1= x = 31 T (e, v )= 5+x y = 8, y = 11 = e =(1, , 11 8 ) (c) En la base {e, v 1,v } la matriz de T es T (e, v 1 ) T (e, v 1 ), con T (e, v 1 )= 1, luego la ecuación reducida métrica de la parábola es ȳ = 1 x, donde x yȳ son las coordenadas asociadas a la base {v 1,v }. (d) Ecuaciones de la transformación afín efectuada para pasar del sistema de referencia inicial en H, en el que las coordenadas son {x, y}, al sistema de referencia de origen e y ejes las rectas e + v 1, e + v, respecto del que las coordenadas son { x, ȳ}. Si B representa la matriz del cambio de base realizado en E, esto es B = 1 1 1, componiendo el automorfismo de cambio de base con la traslación 1 1 de vector e se obtienen las ecuaciones x y x = B + ȳ 31/5 11/8 = x = 1 (x + y ) ȳ = 1 (x y + 1 (e) Los ejes principales de la parábola son las rectas e + v 1, e + v de ecuaciones respectivas Eje de simetría ȳ = x y = ; x = x + y = (f ) Calculemos por último el foco F yladirectrizddelaparábola, respecto de las coordenadas iniciales x e y. Comparando la ecuación reducida métrica ȳ = 1 x con ȳ =px x, resultaque p = 1 y las coordenadas del foco y la ecuación de la directriz son (p/, ) y x = p/. En las coordenadas iniciales se tiene F =( 3 8, 1 8 ) ; d x + y +5= 4 )
11 Clasificación afín de cónicas y cuádricas Clasificación afín de cuádricas en H R 4. r 4 (Irreducibles) 3 (Conos y Cilindros) 1 r i \i Hiperboloide Hiperboloide 1 reglado no reglado x y + z = 1 x y z = 1 Cono real x y + z = Elipsoide Elipsoide Cono real imaginario imaginario x + y + z = 1 x + y + z = 1 x + y + z = Paraboloide Cilindro 1 reglado hiperbólico y z x = x y = 1 Paraboloide Cilindro Cilindro no reglado elíptico imaginario y + z x = x + y = 1 x + y = 1 Par planos reales no paralelos x y = Par planos imaginarios no paralelos x + y = Cilindro 1 parabólico y x = Par planos Par planos Par planos reales imaginarios reales paralelos paralelos coincidentes x = 1 x = 1 x = Plano real Conjunto Espacio x = vacío afín
12 1 G. Serrano Sotelo Ejemplo 5.5. Clasificar afínmente las cuádricas siguientes (a) x +z xy +xz yz 3= (b) y +4xz +x 4y +6z +5= (a) Las matrices G y G son (b) G = ; G = Calculemos los rangos y los índices de la cuádrica y de su restricción al infinito p(x) =x 4 x 3 11x +5x +6, r (p(x)) =, r + (p(x)) =, r (p(x)) = p (x) =x 3 4x + x +, r (p (x)) =, r + (p (x)) =, r (p (x)) = 1 r =4,i=; r =3,i =1 1 Es una cuádrica irreducible con centro, de matriz reducida 1 1 y 1 ecuación reducida afín x y + z = 1. Luego es un Hiperboloide reglado. Calculemos su centro c = 1, Adj g 1 G, Adj g G, Adj g 3 )=(1,,, ), G esto es, el centro es el origen de coordenadas, Centro =(,, ) G = 1 ; G = 3 p(x) =x 4 7x 3 8x + 36x, r (p(x)) = 1, r + (p(x)) =, r (p(x)) = 1 p (x) =x 3 x 4x +8, r (p (x)) =, r + (p (x)) =, r (p (x)) = 1 Los rangos y los índices de la cuádrica y de su restricción al infinito son r =3,i=1; r =3,i =1 Es una cuádrica degenerada con centro, de matriz reducida 1 1 y ecuación reducida afín x y + z =, que representa una Superficie cónica 1 real.
13 Clasificación afín de cónicas y cuádricas Ejercicios. 1. Clasificar afínmente las cónicas siguientes: (a) x +y x +4y += (b) x xy + y +4x 6y +1= (c) 3x 5xy + y x +y +1= (d) x +4xy +4y x 4y =3 (e) x +y +3xy +x +5y 3= (f ) x + y + xy + x + y +1= (g) x + y xy x y +1= (h) x +4y +4xy x 4y +=. Clasificar afínmente según los valores del parámetro λ la familia de cónicas siguiente: x +(λ + 1)y xy =λ 3λ Calcular el centro, los ejes principales, la ecuación reducida métrica y la representación gráfica de las curvas de grado dos siguientes: 3x xy +3y +x 4y +1=, x y +xy 6x +4y +3= 4. Demostar que la curva plana de ecuación 4x + y +4xy +6x +1=, es una parábola. Calcular su vértice, eje principal, ecuación reducida métrica y representación gráfica. 5. Clasificar afínmente las cuádricas siguientes: (a) x +y +z xy +xz yz +1= (b) 6x + y +6z xy + 1xz yz +1= (c) x y z yz x +3y +3z = (d) x +3y z = (e) z xy +xz +yz +x +y 4z =1 6. Representar gráficamente la superficie de grado dos: 3x +y +3z xz x 4y z 5=, calculando previamente su centro, ejes principales y ecuación reducida métrica. 7. Demostrar que las cuádricas: x + y + z 4xz 4y +=, x + y z +xz x +1=, representan hiperboloides reglado y no reglado, respectivamente. Calcular para cada uno de ellos el centro, los ejes principales y la ecuación reducida métrica. 8. Demostrar que la superficie de segundo grado: x +y +4xy +4z +3=, es un paraboloide hiperbólico. Calcular el vértice, eje principal, plano tangente en el vértice y ecuación reducida métrica.
14 14 G. Serrano Sotelo 9. Demostrar que la superficie de segundo grado: y +4xz +x y +6z +5=, es un cono. Calcular el vértice, eje principal y ecuación reducida métrica. 1. Clasificar afínmente según los valores del parámetro λ la familia de cuádricas siguiente: x y + λz xz +yz +x +1=. En cada caso, hacer un estudio lo más completo posible de las superficies de segundo grado resultantes.
CLASIFICACIÓN AFÍN DE CÓNICAS
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS CLASIFICACIÓN AFÍN DE CÓNICAS Sea E un R-espacio vectorial de dimensión. Sean E = e 1, e un plano vectorial de E y e 0 un
Álgebra lineal y Geometría II. Métricas y formas cuadráticas. 1. La matriz de la métrica T 2 ((x, y, z), (x, y, z )) = xx + yy + 3zz 2xz 2zx es:
 Álgebra lineal y Geometría II Gloria Serrano Sotelo Departamento de MATEMÁTICAS ÁLGEBRA LINEAL Y GEOMETRÍA. 0 FÍSICAS Métricas y formas cuadráticas.. La matriz de la métrica T ((x, y, z), (x, y, z )) =
Álgebra lineal y Geometría II Gloria Serrano Sotelo Departamento de MATEMÁTICAS ÁLGEBRA LINEAL Y GEOMETRÍA. 0 FÍSICAS Métricas y formas cuadráticas.. La matriz de la métrica T ((x, y, z), (x, y, z )) =
Clasificación Afín de las Cuádricas
 Capítulo VIII Clasificación Afín de las Cuádricas Como no puede ser de otro modo, en este capítulo seguiremos suponiendo que k es un cuerpo conmutativo de característica distinta de 2, que todos los espacios
Capítulo VIII Clasificación Afín de las Cuádricas Como no puede ser de otro modo, en este capítulo seguiremos suponiendo que k es un cuerpo conmutativo de característica distinta de 2, que todos los espacios
Hipercuádricas afines. Clasificación. Elementos afines y euclídeos.
 Capítulo 6 Hipercuádricas afines. Clasificación. Elementos afines y euclídeos. Sea k un cuerpo de característica distinta de dos. Definición 6.0.1. Una hipercuádrica afín en k n es una ecuación de segundo
Capítulo 6 Hipercuádricas afines. Clasificación. Elementos afines y euclídeos. Sea k un cuerpo de característica distinta de dos. Definición 6.0.1. Una hipercuádrica afín en k n es una ecuación de segundo
Cónicas. Clasificación.
 Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Tema 7 Cónicas. Clasificación. Desde el punto de vista algebraico una cónica es una ecuación de segundo grado en las variables x, y. De ese modo, la ecuación general de una cónica viene dada por una expresión
Hipercuádricas afines. Clasificación. Interpretación proyectiva de propiedades afines.
 Tema 8- Hipercuádricas afines Clasificación Interpretación proyectiva de propiedades afines 81 Hipercuádricas afines Sea k un cuerpo de característica distinta de dos Definición 811 Una hipercuádrica afín
Tema 8- Hipercuádricas afines Clasificación Interpretación proyectiva de propiedades afines 81 Hipercuádricas afines Sea k un cuerpo de característica distinta de dos Definición 811 Una hipercuádrica afín
SERIE SUPERFICIES. 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones:
 SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
SERIE SUPERFICIES 1.- Determinar la ecuación cartesiana del cilindro que contiene a la curva de ecuaciones: 4x C z 0 y que se genera por rectas perpendiculares al plano: x + y + 3z + = 0.-Sea la superficie
Interpretación proyectiva de propiedades euclídeas. Elementos
 Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
Tema 9.- Interpretación proyectiva de propiedades euclídeas. Elementos de las cónicas y cuádricas euclídeas 9.1 El espacio euclídeo como subespacio del proyectivo. Consideramos el espacio euclídeo R n
SOLUCIONES. ÁLGEBRA LINEAL Y GEOMETRÍA (Examen Ordinario : ) Grado en Matemáticas Curso
 ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
ÁLGEBRA LINEAL Y GEOMETRÍA Eamen Ordinario : 6--7 Grado en Matemáticas Curso 6-7 SOLUCIONES Dados tres puntos distintos alineados A, A, A A R, al número real r tal que A A = r A A lo llamaremos raón simple
Tema 5. Cónicas. Asi, para las identificaciones habituales, (punto proyectivo recta vectorial punto de un plano afín ampliado), RP 2 R3 {0}
 Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 5. Cónicas. Introducción. Ejemplos.- El cono C = {(x, y, z) R 3 /x 2 + y 2 = z 2 } está formado por las rectas vectoriales 0 (x 1,x 2, 1) [x 1,x 2, 1] RP 2 con (x 1,x 2, 1) C Π 1 = C 1, circunferencia
Tema 3.3. Aplicaciones afines. Cónicas y cuádricas
 Tema 3.3. Aplicaciones afines. Cónicas y cuádricas Definición 1. Sean A = (P, V, f) y A = (P, V, f ) dos espacios afines tales que V y V son espacios vectoriales sobre un mismo cuerpo. Una función θ :
Tema 3.3. Aplicaciones afines. Cónicas y cuádricas Definición 1. Sean A = (P, V, f) y A = (P, V, f ) dos espacios afines tales que V y V son espacios vectoriales sobre un mismo cuerpo. Una función θ :
Index. Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80
 Index Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80 Adjunto, 14 Aplicación, 2 bilineal, 47 biyectiva, 3 compuesta, 3 identidad, 3 inversa, 3 inyectiva,
Index Ángulo, 80 entre dos planos, 80 entre dos rectas, 80 entre dos vectores, 59 entre recta y plano, 80 Adjunto, 14 Aplicación, 2 bilineal, 47 biyectiva, 3 compuesta, 3 identidad, 3 inversa, 3 inyectiva,
MATEMÁTICAS I 2º EXAMEN PARCIAL 12 junio de 2009
 Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Un sistema generador G de R 3 : a) Está constituido por
Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Un sistema generador G de R 3 : a) Está constituido por
Clasificación Euclídea de las
 Capítulo X Clasificación Euclídea de las Cuádricas Fijemos en todo este capítulo un espacio afín euclídeo (A, V, Ω 2 ) de dimensión n y una métrica euclídea Ω 2 representante del absoluto. Las bases asociadas
Capítulo X Clasificación Euclídea de las Cuádricas Fijemos en todo este capítulo un espacio afín euclídeo (A, V, Ω 2 ) de dimensión n y una métrica euclídea Ω 2 representante del absoluto. Las bases asociadas
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
1 CUÁDRICAS Cuádricas. Estudio particular. 1 x y z. 1 x y z. a 00 a 01 a 02 a 03 a 10 a 11 a 12 a 13 a 20 a 21 a 22 a 23 a 30 a 31 a 32 a 33
 CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
CUÁDRICAS. CUÁDRICAS.. Cuádricas. Estudio particular. Una cuádrica se dene como el lugar geométrico de los puntos del espacio euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen
Superficies cuádricas
 Superficies cuádricas Jana Rodriguez Hertz GAL2 IMERL 9 de noviembre de 2010 definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: definición superficie
Superficies cuádricas Jana Rodriguez Hertz GAL2 IMERL 9 de noviembre de 2010 definición superficie cuádrica definición (forma cuadrática) una superficie cuádrica está dada por la ecuación: definición superficie
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 14 Cónicas (Curso 2007 2008) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
ÁLGEBRA Práctica Clasificar según los valores de λ IR las cónicas de los siguientes haces: 2. Para las siguientes cónicas
 ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
ÁLGEBRA Práctica 14 Cónicas (Curso 2006 2007) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Clasificar según los valores de λ
Respuestas faltantes en ejercicios edición 2007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4-1
 Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
Editorial Mc Graw Hill. Edición 007 Respuestas faltantes en ejercicios edición 007 Sección 4.4: Superficie cuadráticas de revolución Ejercicio 4- R r + x + y Ejercicio 4-3 + R x + y + z Ecuaciones: x +
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. Para las siguientes cónicas (1) 5x
Este documento es de distribución gratuita y llega gracias a El mayor portal de recursos educativos a tu servicio!
 Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Este documento es de distribución gratuita y llega gracias a Ciencia Matemática El mayor portal de recursos educativos a tu servicio! Capítulo 5 Cónicas 5.1 Definiciones y ecuaciones reducidas Nota En
Tema 1 (Resultados).- Cónicas y Cuádricas.
 Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
Ingenierías: Aeroespacial, Civil y Química Matemáticas I 010-011 Departamento de Matemática Aplicada II Escuela Superior de Ingenieros Universidad de Sevilla Tema 1 (Resultados)- Cónicas y Cuádricas Ejercicio
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05
 - EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
- EJERCICIOS DE AMPLIACION DE GEOMETRIA - Curso 04-05 Nota previa: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura GEOMETRIA, que se utilizarán profusamente a lo largo
2 Intersección de una recta y una cuádrica. 1 Definición y ecuaciones. ( x y z
 2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
2. Cuádricas. En todo este capítulo trabajaremos en el espacio afín euclídeo E 3 con respecto a una referencia rectangular {O; ē 1, ē 2, ē 3}. Denotaremos por (x, y, las coordenadas cartesianas respecto
Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España TEMA IV
 52 Variedades Cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
52 Variedades Cuadráticas Autor: Francisco Martín Cabrera, Departamento Matemática Fundamental, Universidad de La Laguna, Islas Canarias, España http://creativecommons.org/licenses/by-nc-sa/2.5/es/ TEMA
Formulario: Geometría Analítica
 Universidad Autónoma del Estado de México UAEM Facultad de Ingeniería Formulario: Geometría Analítica Elaborado por: Estudiante en Ingeniería en Electrónica Formulario Geometría Analítica 1. VECTORES EN
Universidad Autónoma del Estado de México UAEM Facultad de Ingeniería Formulario: Geometría Analítica Elaborado por: Estudiante en Ingeniería en Electrónica Formulario Geometría Analítica 1. VECTORES EN
Tema 1.- Cónicas y Cuádricas.
 Ingeniería Química. Matemáticas I. 013-014. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Tema 1.- Cónicas y Cuádricas. 1.1.- Las cónicas. Ecuaciones reducidas.
Ingeniería Química. Matemáticas I. 013-014. Departamento de Matemática Aplicada II. Escuela Superior de Ingenieros. Universidad de Sevilla. Tema 1.- Cónicas y Cuádricas. 1.1.- Las cónicas. Ecuaciones reducidas.
Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la
 Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 2006
 ÁLGEBRA Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 006 1. Calcular la ecuación de una hipérbola que tiene por asíntota a la recta x = y, por eje la recta x+y = 1 y que pasa por el
ÁLGEBRA Examen extraordinario Ejercicio 4 (55 minutos) 4 de septiembre de 006 1. Calcular la ecuación de una hipérbola que tiene por asíntota a la recta x = y, por eje la recta x+y = 1 y que pasa por el
Cónicas y cuádricas. Circunferencia Elipse Parábola Hipérbola
 Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
Grado en Óptica y Optometría Curso 2009-2010 Cónicas y cuádricas. Curvas cónicas Entre las curvas, quizás más importante y con más renombre, figuran las conocidas como curvas cónicas, cuyo nombre proviene
1. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes (si es posible): (1.d) x 2 + y 2 + 2x + 1 = 0
 Clasificación de cónicas.. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes si es posible:.a x xy + y + x y + 0.b x + xy y 6x + y 0.c x + xy + y x y 0.d x + y + x +
Clasificación de cónicas.. Clasifica las siguientes cónicas dando su ecuación reducida, centro o vértice y ejes si es posible:.a x xy + y + x y + 0.b x + xy y 6x + y 0.c x + xy + y x y 0.d x + y + x +
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2012 2013) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2012 2013) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Parte II - Prácticas 8 a 9. Álgebra A 62 ÁLGEBRA A 62 (INGENIERÍA)
 Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Parte II - Prácticas 8 a 9 Álgebra A 62 Ingeniería 2015 CICLO BÁSICO COMÚN UBA ÁLGEBRA A 62 (INGENIERÍA) Práctica 8 Introducción a las transformaciones lineales Definiciones y propiedades Transformaciones
Problemas de Geometría Proyectiva
 Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
Problemas de Geometría Proyectiva José M. Sánchez Abril José M. Rodríguez-Sanjurjo, Jesús M. Ruiz 1995 * I. VARIEDADES PROYECTIVAS Número 1. Se consideran en el plano proyectivo P 2 los cuatro puntos a
Universidad de Salamanca
 Universidad de Salamanca Gloria Serrano Sotelo Departamento de MATEMÁTICAS 1. Subespacios invariantes por un endomorfismo Sea E un k-espacio vectorial y T un endomorfismo de E. Un subespacio vectorial
Universidad de Salamanca Gloria Serrano Sotelo Departamento de MATEMÁTICAS 1. Subespacios invariantes por un endomorfismo Sea E un k-espacio vectorial y T un endomorfismo de E. Un subespacio vectorial
5º Prueba de Evaluación continua (CÓNICAS) 5 de junio de 2012
 Grupo C ETSI de Topografía, Geodesia y Cartografía º Prueba de Evaluación continua (CÓNICAS) de junio de 0.- Clasificar la cónica x y xy x y = 0 A = ; A = 0 Cónica no degenerada. = = = < 0 A c la cónica
Grupo C ETSI de Topografía, Geodesia y Cartografía º Prueba de Evaluación continua (CÓNICAS) de junio de 0.- Clasificar la cónica x y xy x y = 0 A = ; A = 0 Cónica no degenerada. = = = < 0 A c la cónica
NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular.
 ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo y con respecto
ÁLGEBRA Práctica 15 Cónicas (Curso 2008 2009) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo y con respecto
V = v 1 +2v 2 +3v 3. v 2. v 1
 Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
Coordenadas Hay muchas maneras de darle coordenadas a los puntos del espacio, las ecuaciones de las curvas o superficies dependen de las coordenadas que utilicemos y eligiendo las coordenadas adecuadas
- EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11
 - EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11 Nota: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura Álgebra Lineal y Geometría I. EJERCICIO 1. Sean P 1,...,
- EJERCICIOS - - Álgebra Lineal y Geometría II - Curso 10-11 Nota: Los primeros 18 ejercicios constituyen un repaso de los conceptos de la asignatura Álgebra Lineal y Geometría I. EJERCICIO 1. Sean P 1,...,
7 Superficies cuadráticas
 La esfera Planteamiento de problemas Otras superficies cuadráticas El elipsoide Cilindros Hiperboloides Paraboloides Conos Planteamiento de problemas Problemas y ejercicios del capítulo 7 Superficies cuadráticas
La esfera Planteamiento de problemas Otras superficies cuadráticas El elipsoide Cilindros Hiperboloides Paraboloides Conos Planteamiento de problemas Problemas y ejercicios del capítulo 7 Superficies cuadráticas
Universidad de Salamanca
 Universidad de Salamanca Gloria Serrano Sotelo Departamento de MATEMÁTICAS 1 Espacio vectorial dual Base dual Funciones coordenadas Sea E un k-espacio vectorial El conjunto E de las aplicaciones lineales
Universidad de Salamanca Gloria Serrano Sotelo Departamento de MATEMÁTICAS 1 Espacio vectorial dual Base dual Funciones coordenadas Sea E un k-espacio vectorial El conjunto E de las aplicaciones lineales
Ejercicios y Talleres. puedes enviarlos a
 Ejercicios y Talleres puedes enviarlos a klasesdematematicasymas@gmail.com TALLER-LABORATORIO SUPERFICIES CUADRICAS - CILINDROS APLICACIONES OBJETIVOS Analizar características y propiedades en la representacion
Ejercicios y Talleres puedes enviarlos a klasesdematematicasymas@gmail.com TALLER-LABORATORIO SUPERFICIES CUADRICAS - CILINDROS APLICACIONES OBJETIVOS Analizar características y propiedades en la representacion
Bloque 2. Geometría. 4. Iniciación a las Cónicas
 Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
Bloque 2. Geometría 4. Iniciación a las Cónicas 1. La circunferencia Se llama circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. Elevando al cuadrado
CURVAS Y SUPERFICIES. RELACIÓN 2
 CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
y v 0, 0, 1 y v 1, 0, 1 se tiene la ecuación
 SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
SUPERFICIES Mostraremos varios métodos para generar superficies y encontrar sus ecuaciones. 1. Superficies cilíndricas Dada una curva en el plano de ecuación y un vector con Γ 0, es decir, no horizontal,
IDENTIFICACIÓN DE SUPERFICES CUÁDRICAS
 IDENTIFICACIÓN DE SUPERFICES CUÁDRICAS LUIS HUMBERTO SORIANO SÁNCHE Captura: Hanna Leslye García Guerra Evelyn Salazar Guerrero IDENTIFICACIÓN DE SUPERFICIES CUÁDRICAS Definición. Se llama superficie al
IDENTIFICACIÓN DE SUPERFICES CUÁDRICAS LUIS HUMBERTO SORIANO SÁNCHE Captura: Hanna Leslye García Guerra Evelyn Salazar Guerrero IDENTIFICACIÓN DE SUPERFICIES CUÁDRICAS Definición. Se llama superficie al
Esta expresión polinómica puede expresarse como una expresión matricial de la forma; a 11 a 12 a 1n x 1 x 2 q(x 1, x 2,, x n ) = (x 1, x 2,, x n )
 Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
Tema 3 Formas cuadráticas. 3.1. Definición y expresión matricial Definición 3.1.1. Una forma cuadrática sobre R es una aplicación q : R n R que a cada vector x = (x 1, x 2,, x n ) R n le hace corresponder
( ) 2 +( 1) 2. BLOQUE III Geometría analítica plana. Resoluciones de la autoevaluación del libro de texto
 Pág. de Dados los vectores u, y v0,, calcula: a u b u + v c u v u, v0, 5 a u = = = + b u + v =, + 0, =, + 0, 6 =, c u v = u v = 0 + = Determina el valor de k para que los vectores a, y b6, k sean ortogonales.
Pág. de Dados los vectores u, y v0,, calcula: a u b u + v c u v u, v0, 5 a u = = = + b u + v =, + 0, =, + 0, 6 =, c u v = u v = 0 + = Determina el valor de k para que los vectores a, y b6, k sean ortogonales.
Aplicaciones de la Clasificación de endomorfismos Gloria Serrano Sotelo
 Aplicaciones de la Clasificación de endomorfismos Gloria Serrano Sotelo Potencia y exponencial de una matriz Calculemos A 50 y e A siendo A= 0-3 0. El polinomio característico de T es chxl = Hx + L Hx
Aplicaciones de la Clasificación de endomorfismos Gloria Serrano Sotelo Potencia y exponencial de una matriz Calculemos A 50 y e A siendo A= 0-3 0. El polinomio característico de T es chxl = Hx + L Hx
Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante.
 REPARTIDO IV - CÓNICAS Elipse Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante. Elementos de la elipse Focos Son los puntos fijos F
REPARTIDO IV - CÓNICAS Elipse Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante. Elementos de la elipse Focos Son los puntos fijos F
APUNTES DE MATEMÁTICAS UNIVERSIDAD DE SEVILLA GRADOS EN ECONOMÍA Y ADMINISTRACIÓN DE EMPRESAS PRIMER CURSO
 APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
APUNTES E MATEMÁTICAS EXÁMENES RESUELTOS E MATEMÁTICAS I EPARTAMENTO E ECONOMÍA APLICAA I UNIVERSIA E SEVILLA GRAOS EN ECONOMÍA Y AMINISTRACIÓN E EMPRESAS PRIMER CURSO Jesús Muñoz San Miguel http://www.personal.us.es/jmiguel
CUADERNO XI CÓNICAS Y CUÁDRICAS. Miguel A. Sainz, Joan Serarols, Anna M. Pérez Dep. de Informática y Matemática Aplicada Universidad de Girona
 Capítulo XI : Cónicas y cuádricas 1 CUADERNO XI CÓNICAS Y CUÁDRICAS Miguel A. Sainz, Joan Serarols, Anna M. Pérez Dep. de Informática y Matemática Aplicada Universidad de Girona RESUMEN: Se estudian las
Capítulo XI : Cónicas y cuádricas 1 CUADERNO XI CÓNICAS Y CUÁDRICAS Miguel A. Sainz, Joan Serarols, Anna M. Pérez Dep. de Informática y Matemática Aplicada Universidad de Girona RESUMEN: Se estudian las
Función lineal y cuadrática. Curvas de primer y segundo grado.
 Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
Tema 5 Función lineal y cuadrática. Curvas de primer y segundo grado. 5.0.1 Ecuaciones en dos variables. Una linea del plano es el conjunto de puntos (x, y), cuyas coordenadas satisfacen la ecuación F
x y z x y z x y z z z z z z z
 . Un vector v tiene módulo 5 y es tal que cos ; siendo α el ángulo que forma el vector con el eje x. 5 Escribir la expresión cartesiana del o los vectores v sabiendo que su segunda y tercera componentes
. Un vector v tiene módulo 5 y es tal que cos ; siendo α el ángulo que forma el vector con el eje x. 5 Escribir la expresión cartesiana del o los vectores v sabiendo que su segunda y tercera componentes
ÁLGEBRA LINEAL II Práctica 4.1
 ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
ÁLGEBRA LINEAL II Práctica 4.1 Cónicas (Curso 2010 2011) NOTA: Todos los problemas se suponen planteados en el plano afín euclídeo dotado de un sistema cartesiano rectangular. 1. En el plano afín euclídeo
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas.
 Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Semana 13: Determinación de cónicas. Haces de cónicas proyectivas. Sonia L. Rueda ETS Arquitectura. UPM Geometría afín y proyectiva, 2015 Geometría afín y proyectiva 1. Álgebra lineal 2. Geometría afín
Lección 1: Cónicas y Cuádricas (Secciones 7.4 y 7.5 del temario)
 MATEMÁTICAS I (Curso 2011-2012) Primer Curso del Grado en Ingeniería Electrónica, Robótica y Mecatrónica, Ingeniería de la Energía e Ingeniería de Organización Industrial Departamento de Matemática Aplicada
MATEMÁTICAS I (Curso 2011-2012) Primer Curso del Grado en Ingeniería Electrónica, Robótica y Mecatrónica, Ingeniería de la Energía e Ingeniería de Organización Industrial Departamento de Matemática Aplicada
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
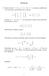 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
MATEMÁTICAS I 13 de junio de 2007
 MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
MATEMÁTICAS I 13 de junio de 2007 2º EXAMEN PARCIAL Sólo una respuesta a cada cuestión es correcta. Respuesta correcta: 0.2 puntos. Respuesta incorrecta: -0.1 puntos Respuesta en blanco: 0 puntos 1.- Si
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 1 ESPACIOS VECTORIALES
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
EJERCICIOS DE ÁLGEBRA LINEAL TEMA ESPACIOS VECTORIALES Formas reducidas y escalonada de una matriz SISTEMAS DE ECUACIONES LINEALES ) Encuentre una sucesión de matrices elementales E, E,..., E k tal que
ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R
 ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R SUPERFICIES ING. RICARDO F. SAGRISTÁ -2006- SUPERFICIES.- 1.- Ecuaciones de superficies. Ya hemos estudiado la superficie
ALGEBRA Y GEOMETRÍA I DPTO. DE MATEMÁTICA ESCUELA DE FORMACIÓN BÁSICA F.C.E.I.A U.N.R SUPERFICIES ING. RICARDO F. SAGRISTÁ -2006- SUPERFICIES.- 1.- Ecuaciones de superficies. Ya hemos estudiado la superficie
GEOMETRIA ANALITICA EN EL ESPACIO
 CAPITULO VII CALCULO II GEOMETRIA ANALITICA EN EL ESPACIO Es el estudio de las formas geométricas en un sistema ordenado. Un sistema de ejes coordenados en el espacio, dividen al espacio en ocho octangulos.
CAPITULO VII CALCULO II GEOMETRIA ANALITICA EN EL ESPACIO Es el estudio de las formas geométricas en un sistema ordenado. Un sistema de ejes coordenados en el espacio, dividen al espacio en ocho octangulos.
MATEMÁTICAS I 2º EXAMEN PARCIAL 9 de junio de 2008
 MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 Sólo una respuesta a cada cuestión es correcta Respuesta correcta: 0 puntos Respuesta incorrecta: -0 puntos Respuesta en blanco: 0 puntos - Sean F y G dos
MATEMÁTICAS I º EXAMEN PARCIAL 9 de junio de 008 Sólo una respuesta a cada cuestión es correcta Respuesta correcta: 0 puntos Respuesta incorrecta: -0 puntos Respuesta en blanco: 0 puntos - Sean F y G dos
Algebra Lineal y Geometría
 Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
Algebra Lineal y Geometría Unidad n 11:Ecuación General de Segundo Grado en Tres Variables. Algebra Lineal y Geometría Esp.Liliana Eva Mata 1 Contenidos Superficies. Relaciones elementales entre propiedades
COLEGIO NUESTRA SEÑORA DEL BUEN CONSEJO. Melilla LUGARES GEOMÉTRICOS Y CÓNICAS
 LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
LUGARES GEOMÉTRICOS Y CÓNICAS 01. Halla la ecuación de la circunferencia de centro ( 5, 12) y radio 13. Comprueba que pasa por el punto (0, 0). 02. Halla las ecuaciones de los siguientes lugares geométricos:
Lugar Geométrico. Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz
 1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
1 Lugar Geométrico Se llama lugar geométrico a un conjunto de puntos que cumplen una determinada propiedad. Mediatriz Mediatriz de un segmento es el lugar geométrico de los puntos del plano que equidistan
Álgebra Lineal UCR. Sétimo tema, 2013
 Álgebra Lineal UCR Sétimo tema, 2013 Presentaciones basadas principalmente en Arce,C, Castillo,W y González, J. (2004) Álgebra lineal. Tercera edición. UCR. San Pedro. Otras fuentes serán mencionadas cuando
Álgebra Lineal UCR Sétimo tema, 2013 Presentaciones basadas principalmente en Arce,C, Castillo,W y González, J. (2004) Álgebra lineal. Tercera edición. UCR. San Pedro. Otras fuentes serán mencionadas cuando
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS
 EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS ESPACIOS EUCLÍDEOS ) a) Decir cuál de las siguientes aplicaciones de x de no definir un producto escalar comprobar el axioma que falla: a ) x' x,y,
EJERCICIOS DE ÁLGEBRA LINEAL TEMA 3 ESPACIOS EUCLÍDEOS ESPACIOS EUCLÍDEOS ) a) Decir cuál de las siguientes aplicaciones de x de no definir un producto escalar comprobar el axioma que falla: a ) x' x,y,
SECCIONES CÓNICAS (1)Determinar y graficar el lugar geométrico de los puntos que equidistan de F(0, 2) y de la recta
 LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
LOS EJERCICIOS DEBEN RESOLVERSE TAMBIÉN USANDO SOFTWARE MATEMÁTICO. LAS ECUACIONES PEDIDAS SON, EN TODOS LOS CASOS, LAS CANÓNICAS Y LAS PARAMÉTRICAS. I) GEOMETRÍA ANALÍTICA EN EL PLANO 1. Determinar y
INDICE. 88 determinante 36. Familias de líneas rectas Resumen de resultados 96
 INDICE Geometría Analítica Plana Capitulo Primero Sistema de Coordenadas Articulo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5
INDICE Geometría Analítica Plana Capitulo Primero Sistema de Coordenadas Articulo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5
Unidad 8 Lugares geométricos. Cónicas
 Unidad 8 Lugares geométricos. Cónicas PÁGINA 75 SOLUCIONES. La elipse es una cónica obtenida al cortar una superficie cónica por un plano oblicuo al eje y que corte a todas las generatrices. La hipérbola
Unidad 8 Lugares geométricos. Cónicas PÁGINA 75 SOLUCIONES. La elipse es una cónica obtenida al cortar una superficie cónica por un plano oblicuo al eje y que corte a todas las generatrices. La hipérbola
Aquella que tiene nulos los elementos nos situados en la diagonal principal. Los elementos situados por encima de la diagonal principal son nulos.
 Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
Álgebra lineal Matrices Rango de una matriz Orden del mayor menor complementario no nulo. Matriz regular det A Diagonal principal Elementos a ii de la matriz. Si la matriz es cuadrado son los elementos
Espacio Euclídeo. a b = a b. a b = b a c)
 .- Un hiperplano de R es: a) Una recta. b) Un plano. c) {0}..- Sean a y b dos vectores de R, si a es ortogonal a b, entonces: a) a b = 0 b) a b = b a c) a b = a b.- Sea F una recta vectorial de R y F un
.- Un hiperplano de R es: a) Una recta. b) Un plano. c) {0}..- Sean a y b dos vectores de R, si a es ortogonal a b, entonces: a) a b = 0 b) a b = b a c) a b = a b.- Sea F una recta vectorial de R y F un
EXAMEN JUNIO PP 1A SEMANA
 EXAMEN JUNIO PP A SEMANA XAVI AZNAR Ejercicio. Defina semejanza, razón de semejanza y movimento asociado a una semejanza. Ejercicio. En el espacio vectorial V 3 (R) sea q la forma cuadrática cuya expresión
EXAMEN JUNIO PP A SEMANA XAVI AZNAR Ejercicio. Defina semejanza, razón de semejanza y movimento asociado a una semejanza. Ejercicio. En el espacio vectorial V 3 (R) sea q la forma cuadrática cuya expresión
Autoevaluación. Bloque III. Geometría. BACHILLERATO Matemáticas I * 8 D = (3, 3) Página Dados los vectores u c1, 1m y v (0, 2), calcula:
 Autoevaluación Página Dados los vectores u c, m y v (0, ), calcula: a) u b) u+ v c) u : ( v) u c, m v (0, ) a) u c m + ( ) b) u+ v c, m + (0, ) (, ) + (0, 6) (, ) c) u :( v) () (u v ) c 0 + ( ) ( ) m 8
Autoevaluación Página Dados los vectores u c, m y v (0, ), calcula: a) u b) u+ v c) u : ( v) u c, m v (0, ) a) u c m + ( ) b) u+ v c, m + (0, ) (, ) + (0, 6) (, ) c) u :( v) () (u v ) c 0 + ( ) ( ) m 8
Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas
 Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
Capítulo 4 Hipercuádricas. Polaridad. Estudio geométrico de las cónicas y cuádricas Comenzamos con el objeto básico de este curso. Hemos estudiado hasta ahora variedades lineales proyectivas, que están
B23 Curvas cónicas Curvas cónicas
 Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Respuestas ejercicios edición 2007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1
 Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
Editorial Mc Graw Hill. Edición 007 Respuestas ejercicios edición 007 Sección 3.3: Transformación de coordenadas Ejercicio 3-1 a) Simetría respecto de ambos ejes y respecto del origen. b) Simetría respecto
Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio.
 SUPERFICIES SUPERFICIES Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio. Una Superficie puede estar engendrada
SUPERFICIES SUPERFICIES Se puede considerar una superficie, como una lámina infinitamente delgada, que recubre un cuerpo, separa dos medios o dos regiones del espacio. Una Superficie puede estar engendrada
INDICE. 88 determinante 36. Familias de líneas rectas Resumen de resultados 96 Capitulo IV
 INDICE Geometría Analítica Plana Capitulo Primero Artículo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5 5. Carácter de la geografía
INDICE Geometría Analítica Plana Capitulo Primero Artículo 1. Introducción 1 2. Segmento rectilíneo dirigido 1 3. Sistema coordenado lineal 3 4. Sistema coordenado en el plano 5 5. Carácter de la geografía
Bioingeniería MATEMÁTICA I. Carreras. Programa Analítico y de Examen de la asignatura: Año: MSc. Ing. Dora A. Christian.
 FACULTAD DE INGENIERÍA Universidad Nacional de San Juan Carreras Bioingeniería Programa Analítico y de Examen de la asignatura: MATEMÁTICA I Año: 2014-... MSc. Ing. Dora A. Christian Profesora Titular...
FACULTAD DE INGENIERÍA Universidad Nacional de San Juan Carreras Bioingeniería Programa Analítico y de Examen de la asignatura: MATEMÁTICA I Año: 2014-... MSc. Ing. Dora A. Christian Profesora Titular...
Clasificación de Métricas y
 Capítulo VII Clasificación de Métricas y Cuádricas Dada una métrica T 2 sobre un k-espacio vectorial E, para simplificar la notación, y siempre que no haya motivo de confusión, cualesquiera que sean e,
Capítulo VII Clasificación de Métricas y Cuádricas Dada una métrica T 2 sobre un k-espacio vectorial E, para simplificar la notación, y siempre que no haya motivo de confusión, cualesquiera que sean e,
ALGEBRA. Escuela Politécnica Superior de Málaga
 ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
ALGEBRA. Escuela Politécnica Superior de Málaga Tema 1. Espacios Vectoriales. Sistemas de ecuaciones. Espacio vectorial. Espacios vectoriales R n. Dependencia e independencia lineal. Base. Matrices y determinantes.
Ejercicios tipo test de las lecciones 1 y El vector e = ( 1, 0, λ) está en el plano generado por los vectores u = (1, 2, 1) y
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Ejercicios tipo test de las lecciones 1 y 2. 1. El vector e = ( 1, 0, λ) está en el plano generado por los vectores u = (1,
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Ejercicios tipo test de las lecciones 1 y 2. 1. El vector e = ( 1, 0, λ) está en el plano generado por los vectores u = (1,
EJERCICIOS PAU MATEMÁTICAS II ARAGÓN Autor: Fernando J. Nora Costa-Ribeiro Más ejercicios y soluciones en fisicaymat.wordpress.com
 GEOMETRÍA 1- Dados el punto P(1,-1,0) y la recta : 1 0 3 3 0 a) Determine la ecuación general del plano (Ax+By+Cz+D=0) que contiene al punto P y a la recta s. b) Determine el ángulo que forman el plano
GEOMETRÍA 1- Dados el punto P(1,-1,0) y la recta : 1 0 3 3 0 a) Determine la ecuación general del plano (Ax+By+Cz+D=0) que contiene al punto P y a la recta s. b) Determine el ángulo que forman el plano
Escuela Universitaria de Ingeniería Técnica Aeronáutica Expresión Gráfica en la Ingeniería INGENIERÍA GRÁFICA
 Escuela Universitaria de Ingeniería Técnica Aeronáutica Expresión Gráfica en la Ingeniería INGENIERÍA GRÁFICA 6. LÍNEAS Y SUPERFICIES. 6.1. Líneas 6.1.1. Generación 6.2 Superficies. 6.2.2 Clasificación
Escuela Universitaria de Ingeniería Técnica Aeronáutica Expresión Gráfica en la Ingeniería INGENIERÍA GRÁFICA 6. LÍNEAS Y SUPERFICIES. 6.1. Líneas 6.1.1. Generación 6.2 Superficies. 6.2.2 Clasificación
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16.
 Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
Problemas de circunferencias 4. Escribe la ecuación de la circunferencia de centro C(-2,3) y radio 4. Sol: (x+2) 2 +(y-3) 2 =16. 10. 5. Calcula la potencia del punto P(-1,2) a la circunferencia: x 2 +y
A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES
 RESUMEN DE GEOMETRÍA MATEMÁTICAS II A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES Un vector fijo de origen A y extremo B, siendo A y B puntos del espacio, es un segmento orientado caracterizado por:
RESUMEN DE GEOMETRÍA MATEMÁTICAS II A. VECTORES 1. VECTORES FIJOS Y VECTORES LIBRES Un vector fijo de origen A y extremo B, siendo A y B puntos del espacio, es un segmento orientado caracterizado por:
Departamento de Matemática Aplicada II. Universidad de Sevilla. Solución de la Primera Prueba Alternativa ( )
 MATEMÁTICAS I ( o de GIE y GIERM (Curso - Departamento de Matemática Aplicada II. Universidad de Sevilla Solución de la Primera Prueba Alternativa (-- Ejercicio.. Calcule las raíces cúbicas del número
MATEMÁTICAS I ( o de GIE y GIERM (Curso - Departamento de Matemática Aplicada II. Universidad de Sevilla Solución de la Primera Prueba Alternativa (-- Ejercicio.. Calcule las raíces cúbicas del número
