Grafos. es un grafo sobre V, donde V es el conjunto de vértices y E el conjunto de aristas. Lo anotaremos G ( V, E) Abierto Cerrado
|
|
|
- Irene Castilla Cano
- hace 7 años
- Vistas:
Transcripción
1 Grafos Sea V un conjunto finito no vacío, y E V V. El par ( V, E) es un grafo sobre V, one V es el conjunto e vértices y E el conjunto e aristas. Lo anotaremos G ( V, E). Vértice(s) repetio(s) Arista(s) repetio(s) Abierto Cerrao Nombre Si Si Si Camino Si Si Si Camino cerrao Si No Si Recorrio Si No Si Circuito No No Si Camino simple No No Si Ciclo Un grafo G es conexo; si existe un camino simple para too par e vértices istintos e G. Un grafo que no es conexo se ice isconexo. Un grafo o multígrafo G (sin vértices aislaos) tiene un circuito euleriano; si existe un circuito en G que recorre caa una e sus arista. Activia Consiere el grafo e la figura y etermine lo inicao en caa caso: a) Un camino e b a que no sea un recorrio b) Un recorrio b- que no sea un camino simple c) Un camino simple e b a. Cuántos existen? ) Un camino cerrao e b a b que no sea un circuito e) Un circuito e b a b que no sea un ciclo f) Un ciclo e b a b
2 Subgrafos e isomorfismos e grafos Activia 1 a) Lee y analiza las siguientes efiniciones. Sea G V, E un grafo (irigio o no) G V, E es un subgrafo e G; si y sólo si E vértices e V 1 G V, E es un subgrafo recubrior e G ; si y solo si V G U, E E, one caa arista e E 1 es inciente con los es un subgrafo inucio por U, si y sólo si U V y E contiene a toas las aristas e G (con ambos vértices en U). Anotaremos G U V b) Consiera los grafos e caa figura y completa caa cela con SI ó NO, según correspona.
3 Activia 2 a) Locura Instantánea: Para el juego e la locura instantánea se requieren cuatro cubos. Caa una e las seis caras e un cubo se pinta e un color: rojo (R), blanco (B), vere (V) o amarillo (A). El objetivo el juego es colocar los cubos en una columna e cuatro, e moo que aparezcan los cuatro colores (iferentes) en caa uno e los cuatro laos e la columna. Consiera los cubos inicaos en la figura y resuelve el acertijo. Utiliza grafos y subgrafos para simplificar la tarea. b) Caa uno e los multígrafos etiquetaos en la siguiente figura surge en el análisis e un conjunto e cuatro bloques para el juego e locura instantánea. Determine en caa caso, si es posible resolver el acertijo. Activia 3 Dos grafos no irigios G1 V1, E1 y G2 V2, E2 f : V V, e forma que si a, b E1, entonces, 1 2 son isomorfos; si existe una función biyectiva f a f b E2 y recíprocamente. Determinar si los siguientes pares e grafos son isomorfos. En caso afirmativo, efinir una tal función f.
4 Grao e un vértice: Recorrios y circuitos eulerianos Sea G V, E un grafo o multigrafo no irigio. Llamaremos grao e un vértice v, al número e aristas que son incientes con v. (Un lazo en un vértice v se consiera como os aristas incientes en v ). Anotaremos gr ( v ). Si toos los vértices tienen el mismo grao, se enomina grafo regular. Si son e grao k se ice k-regular La suma e los graos e toos los vértices el grafo G es igual al oble el número e aristas. gr v E Dem: a cargo el lector vv 2 El número e vértices e grao impar es par. Dem: La iea es agrupar toos los graos e los vértices e grao par y por otro los vértices e grao impar y luego sumarlos. De esta manera se aplica el teorema anterior y se ve que la suma es os veces el numero e aristas. Como la primer sumatoria se suman números pares, se obtiene e resultao un número par. Como la seguna sumatoria tiene que ser un número par, se euce que la cantia e vértices e grao impar tiene que ser par como se quería emostrar. Sea G V, E un grafo o multigrafo no irigio, sin vértices aislaos. Diremos que G tiene un circuito euleriano; si existe un circuito en G que recorre caa una e sus aristas. Si existe un recorrio abierto e u a v en G que recorre toas las aristas, se llama recorrio euleriano. G tiene un circuito euleriano si y solo si G es conexo y too vértice e G tiene grao par. Dem. (Directo) Como G tiene un circuito euleriano, entonces para cualquier par e vértices istintos existe un recorrio entre ellos, por lo tanto existe un camino simple entre ellos por lo que G es Conexo. Si u es el vértice inicial el circuito euleriano. Para cualquier otro vértice v caa vez que el circuito llega a v partirá e este, por lo que caa vez que se pasa por v se contribuye con os uniaes al grao e v y como aemás caa arista el circuito se recorre una sola vez se euce que el grao e v es par. Para el vértice u se realiza un proceimiento similar y se llega a que el grao el vértice u es par. Dem. (Reciproco) Si el grafo G tiene 1 o 2 aristas los grafos son e la siguiente manera Por lo que los circuitos eulerianos son triviales En otro caso se procee por inucción sobre el número e aristas. La iea es partir e que G tiene n aristas y seleccionar un vértice inicial c para construir el circuito euleriano y e esta manera se suponrá que para cualquier subgrafo e G que cumpla las hipótesis
5 verificará el teorema. Como el grafo G es conexo y caa vértice tiene grao par, poemos construir un circuito C que contenga a c. Si el circuito contiene toas las aristas e G, hemos hallao el circuito euleriano, en caso contrario eliminamos las aristas el circuito C, eliminano también los vértices aislaos que puieran haber. El subgrafo restante K, tiene toos los vértices e grao par, pero puee no ser conexo, sin embargo caa componente e K es conexa y tenrá un circuito euleriano. Aemás caa uno e estos circuitos eulerianos tenrá un vértice que esta en c. De esta manera poemos partir e c, recorrer C hasta llegar hasta un vértice e una e las componentes e K, recorrer este circuito euleriano. Luego continuar recorrieno el circuito C hasta llegar a otro vértice e otra componente, recorrer este otro circuito euleriano y luego terminar e recorrer el circuito C. Como el grafo G es finito este proceso se termina, puiénose así construir el circuito euleriano. G tiene un recorrio euleriano sii G es conexo y tiene exactamente os vértices e grao impar Dem: a cargo el lector Activia 1 Los siete puentes e Konigsberg: Es posible recorrer las ciuaes e ambas márgenes el río y e las islas, pasano solo una vez por caa uno e los 7 puentes? Activia 2 Al visitar el museo e ciencias, Pablo y Sebastian intentan resolver si porían pasar por las siete habitaciones y el pasillo que las roea sin cruzar ninguna puerta más e una vez. Si comienzan ese la posición el pasillo marcaa con una estrella pueen lograr su objetivo? Activia 3 a) Encuentre un circuito euleriano para el grafo e la figura b) Si se elimina la arista, e e este grafo, encuentre un recorrio euleriano para el subgrafo resultante
6 Grafos Planos Sea V un conjunto e n vértices. El grafo completo sobre V, es un grafo no irigio sin lazos tal que para toos a, bv, a b, existe una arista a, b. Anotaremos K n Los grafos que se muestran en la siguiente figura, son los únicos grafos completos posibles para el número ao e vértices Un grafo (o multigrafo) G es plano si poemos ibujar G en el plano e moo que sus aristas se intersequen sólo en los vértices e G. Este ibujo e G se conoce como una inmersión e G en el plano. Al igual que K 4 ; K 1, K 2 y K 3 son planos. Un grafo G ( V, E) es bipartito; si V V 1 V2, V 1 V 2 y caa arista e G es e la forma a, b, con a V 1 y b V2. Si caa vértice e V 1 está unio con los vértices e V 2, se tiene un grafo bipartito completo; enotao por K,, con V1 m y V2 n m n Sea G ( V, E) un grafo no irigio sin lazos, tal que E. Una subivisión elemental e G resulta cuano eliminamos una arista e u, w e G y entonces las aristas u, v, v, w se añaen a G e, one v V. Los grafos no irigios sin lazos G1 ( V1, E1 ) y G2 ( V2, E2) son homeomorfos si son isomorfos o si ambos pueen obtenerse el mismo grafo no irigio sin lazos H, por una sucesión e subivisiones elementales. Teorema e Kuratowsky: Un grafo no es plano si y sólo si contiene un subgrafo que es homeomorfo a K 5 o K 3, 3 Teorema e Euler Sea G ( V, E) un grafo o multigrafo plano conexo con V v y E e. Sea r el número e regiones en el plano eterminaas por una inmersión plana e G. Entonces, v e r 2
7 Activia 1 Para caa grafo e la figura, etermine si el grafo es o no bipartito. Activia 2 Determine cuáles e los grafos e la figura son planos. Si un grafo es plano, vuelve a ibujarlo sin aristas solapaas. Si no es plano, encuentre un subgrafo homeomorfo a K 5 o K 3, 3. Activia 3 Determine el número e vértices, aristas y regiones para caa uno e los grafos planos e la figura. Luego muestre que sus respuestas satisfacen el teorema e Euler para grafos planos conexos.
8 Grafo Dual Para construir un grafo ual (respecto a una inmersión particular) e un grafo o multigrafo plano G con V a, b, c,, e, f, colocamos un punto (vértice) entro e caa región, incluyeno la región infinita eterminaa por el grafo. Luego, para caa arista compartia por os regiones, ibujamos una arista que conecte a los vértices ubicaos en ellas. Así se obtiene G. Observaciones Una arista en G correspone a una arista en G, y viceversa. Un vértice e grao 2 en G origina un par e aristas en G que conectan los mismos os vértices Dao un lazo en G origina un vértice colgante en G y viceversa. El grao e un vértice en G es el numero e aristas en la frontera el camino cerrao en torno e la región en G que contiene ese vértice. Por qué se ice un grafo ual y no el grafo ual e G? Si G es un grafo plano, entonces puee que no exista un único grafo ual para G, en el sentio que G puee tener grafos uales no isomorfos, epenieno e la istribución particular e las regiones. En la figura, G y G no son isomorfos porque G tiene un vértice con grao 6 (la región infinita) que G no tiene (ver iagramas). Sólios platónicos y sus grafos Un grafo es regular e oren k si el número e aristas que concurren en caa vértice es k Un grafo es completamente regular si tanto G como G son regulares (no necesariamente = oren) POLIEDRO CUBO TETRAEDRO OCTAEDRO DODECAEDRO ICOSAEDRO CARAS 6 cuaraos 4 triángulos equiláteros 8 triángulos equiláteros 12 pentágonos regulares 20 triángulos equiláteros VÉRTICES ARISTAS
9 G 3- regular G 3- regular G 3- regular G 4- regular G 4- regular G 3- regular G 5- regular G 3- regular G 5- regular G 3- regular Sea G un grafo plano regular e oren k, e manera que su ual G sea un grafo plano regular e oren k. Si k 2 y k 2, solamente hay cinco tipos e grafos completamente regulares. Caa uno e e los grafos obtenios se corresponerá con las versiones planas e los sólios platónicos Como G tiene k aristas en caa vértice y caa arista une os vértices, se tiene: (1) 2e kv Como G es regular e oren k, caa región e G está roeaa e k aristas y caa arista comparte os regiones, entonces: (2) 2 e k r Activia Complete la emostración el teorema enunciao, siguieno lo inicao en caa caso a) Usano (1), (2) y el teorema e Euler, emostrar que: v 2k 2 k kk 4 k (consiere cara exterior) (3) b) A partir e la fórmula (3) y tenieno en cuenta que v y 4 k son números positivos, emostrar que k 2 k 2 4 k k v r e Tipo Cubo c) Utilizano el resultao anterior, eterminar los posibles valores e k, k y completar la siguiente tabla.
Minicurso de Teoría de Gráficas Escuela de Verano 2014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana
 Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
Un grafo G = (V, E) se dice finito si V es un conjunto finito.
 1 Grafos: Primeras definiciones Definición 1.1 Un grafo G se define como un par (V, E), donde V es un conjunto cuyos elementos son denominados vértices o nodos y E es un subconjunto de pares no ordenados
1 Grafos: Primeras definiciones Definición 1.1 Un grafo G se define como un par (V, E), donde V es un conjunto cuyos elementos son denominados vértices o nodos y E es un subconjunto de pares no ordenados
Información importante
 Departamento e Matemática Coorinación e Matemática I (MAT01) 1 er Semestre e 010 Semana 1: Lunes 07 viernes 11 e Junio Información importante Durante esta semana se publicarán las notas el Certamen en
Departamento e Matemática Coorinación e Matemática I (MAT01) 1 er Semestre e 010 Semana 1: Lunes 07 viernes 11 e Junio Información importante Durante esta semana se publicarán las notas el Certamen en
LAS CIENCIAS DE LA PLANIFICACIÓN
 LAS CIENCIAS DE LA PLANIFICACIÓN 5. EL PROBLEMA DEL VIAJANTE (PV) (The Traveling Salesman Problem TSP) Un problema como el de las vacaciones, pero vital para las empresas, es el problema del viajante (PV):
LAS CIENCIAS DE LA PLANIFICACIÓN 5. EL PROBLEMA DEL VIAJANTE (PV) (The Traveling Salesman Problem TSP) Un problema como el de las vacaciones, pero vital para las empresas, es el problema del viajante (PV):
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre
 Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Típicamente, un grafo se representa
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Típicamente, un grafo se representa
( ) 2. Pendiente de una Recta Tangente. Sea f una función que es continua en x. 1. Para definir la pendiente de la recta tangente ( )
 Derivaa e una Función Ínice.. Introucción.. Peniente e una recta tangente.. Derivaa e una función. 4. Derivaas laterales. 5. Derivaa e una función compuesta (Regla e la Caena). 6. Tabla e erivaas usuales.
Derivaa e una Función Ínice.. Introucción.. Peniente e una recta tangente.. Derivaa e una función. 4. Derivaas laterales. 5. Derivaa e una función compuesta (Regla e la Caena). 6. Tabla e erivaas usuales.
2.5 Derivación implícita
 SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
SECCIÓN.5 Derivación implícita 4.5 Derivación implícita Distinguir entre funciones eplícitas e implícitas. Hallar la erivaa e una función por erivación implícita. E X P L O R A C I Ó N Representación gráfica
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
 UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
2.3 Reglas del producto, del cociente y derivadas de orden superior
 SECCIÓN 2.3 Reglas el proucto, el cociente y erivaas e oren superior 119 2.3 Reglas el proucto, el cociente y erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar
SECCIÓN 2.3 Reglas el proucto, el cociente y erivaas e oren superior 119 2.3 Reglas el proucto, el cociente y erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar
SOLUCION DE UN ERROR CON OTRO ERROR
 SOLUCION DE UN ERROR CON OTRO ERROR El matemático, al igual que too ser humano, puee incurrir en errores; en algunos casos sucee que el error no ha sio cometio por el creaor e la obra sino por los encargaos
SOLUCION DE UN ERROR CON OTRO ERROR El matemático, al igual que too ser humano, puee incurrir en errores; en algunos casos sucee que el error no ha sio cometio por el creaor e la obra sino por los encargaos
Un poliedro es un cuerpo geométrico que tiene todas sus caras planas y formadas por polígonos.
 CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
3 DERIVADAS ALGEBRAICAS
 DERIVADAS ALGEBRAICAS DERIVADAS ALGEBRAICAS Entiénase la erivaa como la peniente e la recta tangente a la función en un punto ao, lo anterior implica que la función ebe eistir en ese punto para poer trazar
DERIVADAS ALGEBRAICAS DERIVADAS ALGEBRAICAS Entiénase la erivaa como la peniente e la recta tangente a la función en un punto ao, lo anterior implica que la función ebe eistir en ese punto para poer trazar
Matemática. Desafío. GUÍA DE EJERCITACIÓN AVANZADA Cuerpos geométricos GUICEN032MT22-A16V1
 GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
FUNCIONES TRIGONOMÉTRICAS
 Unia os Geometría Trigonometría 8. FUNCIONES TRIGONOMÉTRICAS 8. El círculo trigonométrico o unitario En temas anteriores, las funciones trigonométricas se asociaron con razones, es ecir con cocientes e
Unia os Geometría Trigonometría 8. FUNCIONES TRIGONOMÉTRICAS 8. El círculo trigonométrico o unitario En temas anteriores, las funciones trigonométricas se asociaron con razones, es ecir con cocientes e
MATEMÁTICAS (GEOMETRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)
![(f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x) (f + g) (x) = f (x) + g (x) (α f) (x) = α f (x) (f g) (x) = f (x) g(x) + f(x) g (x) (x) = f (x) g(x) f(x) g (x) g. [g(x)] 2 (f g) (x) = f (g(x)) g (x)](/thumbs/24/2434623.jpg) Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
Derivaa e una función en un punto: El concepto e erivaa e una función matemática se halla íntimamente relacionao con la noción e límite. Así, la erivaa se entiene como la variación que experimenta la función
Caminos y Flujos optimales. Introducción a la Investigación de Operaciones 2007
 Caminos y Flujos optimales Introducción a la Investigación de Operaciones 2007 Contenido Definiciones básicas. Conexidad. Clausura transitiva. Esqueletos y caminos optimales. Redes. Flujos. Algoritmo de
Caminos y Flujos optimales Introducción a la Investigación de Operaciones 2007 Contenido Definiciones básicas. Conexidad. Clausura transitiva. Esqueletos y caminos optimales. Redes. Flujos. Algoritmo de
Cálculo Diferencial en una variable
 Tema 3 Cálculo Diferencial en una variable 3.1 Introucción Analizaremos en este Tema los conceptos funamentales acerca e las erivaas e las funciones reales e variable real. En el tema siguiente estuiaremos
Tema 3 Cálculo Diferencial en una variable 3.1 Introucción Analizaremos en este Tema los conceptos funamentales acerca e las erivaas e las funciones reales e variable real. En el tema siguiente estuiaremos
Problema nº 1: Dominó/Dominó triangular
 Problema nº 1: Dominó/Dominó triangular Las fichas del juego del dominó son rectángulos formados a partir de la unión de dos cuadrados. En esos cuadrados hay puntos que pueden variar de 0 a 6. Así tenemos
Problema nº 1: Dominó/Dominó triangular Las fichas del juego del dominó son rectángulos formados a partir de la unión de dos cuadrados. En esos cuadrados hay puntos que pueden variar de 0 a 6. Así tenemos
SOLUCIONES MINIMOS 2º ESO TEMA 8 CUERPOS GEOMÉTRICOS
 SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
10- Los poliedros. Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos.
 Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
La capacitancia tiene la unidad del SI coulomb por volt. La unidad de capacitancia del SI es el farad (F), en honor a Michael Faraday.
 1. Qué es capacitancia? Se efine como la razón entre la magnitu e la carga e cualquiera e los conuctores y la magnitu e la iferencia e potencial entre ellos. La capacitancia siempre es una cantia positiva
1. Qué es capacitancia? Se efine como la razón entre la magnitu e la carga e cualquiera e los conuctores y la magnitu e la iferencia e potencial entre ellos. La capacitancia siempre es una cantia positiva
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Un grafo G es un par (V,E) donde V es un conjunto (llamado conjunto de vértices) y E un subconjunto de VxV (conjunto de aristas).
 TEMA 5.- GRAFOS 5.1.- DEFINICIONES BÁSICAS Un grafo G es un par (V,E) donde V es un conjunto (llamado conjunto de vértices) y E un subconjunto de VxV (conjunto de aristas). Gráficamente representaremos
TEMA 5.- GRAFOS 5.1.- DEFINICIONES BÁSICAS Un grafo G es un par (V,E) donde V es un conjunto (llamado conjunto de vértices) y E un subconjunto de VxV (conjunto de aristas). Gráficamente representaremos
Apuntes de Matemática Discreta 14. Grafos
 Apuntes de Matemática Discreta 14. Grafos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 14 Grafos Contenido 14.1 Generalidades.....................................
Apuntes de Matemática Discreta 14. Grafos Francisco José González Gutiérrez Cádiz, Octubre de 2004 Universidad de Cádiz Departamento de Matemáticas ii Lección 14 Grafos Contenido 14.1 Generalidades.....................................
INSTRUCTIVO PARA TUTORÍAS
 INSTRUCTIVO PARA TUTORÍAS Las tutorías corresponen a los espacios acaémicos en los que el estuiante el Politécnico Los Alpes puee profunizar y reforzar sus conocimientos en iferentes temas e cara al eamen
INSTRUCTIVO PARA TUTORÍAS Las tutorías corresponen a los espacios acaémicos en los que el estuiante el Politécnico Los Alpes puee profunizar y reforzar sus conocimientos en iferentes temas e cara al eamen
Introducción a la Teoría de Grafos
 Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Árboles Un árbol es un grafo conexo y acíclico (sin ciclos). Un bosque es un grafo acíclico, o sea, una unión disjunta
Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Árboles Un árbol es un grafo conexo y acíclico (sin ciclos). Un bosque es un grafo acíclico, o sea, una unión disjunta
Poliedros Regulares Convexos
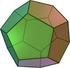 Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Poliedros Regulares
Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 besode@alumni.uv.es Poliedros Regulares
11. MOSAICOS. El ángulo interior de un polígono regular de n lados es
 11. MOSAICOS Cuando una o varias piezas recubren un plano sin solaparse tenemos un recubrimiento o mosaico. Los mosaicos más sencillos son los que solo utilizan una pieza de una única forma y tamaño. Aun
11. MOSAICOS Cuando una o varias piezas recubren un plano sin solaparse tenemos un recubrimiento o mosaico. Los mosaicos más sencillos son los que solo utilizan una pieza de una única forma y tamaño. Aun
CONOCER Y DIFERENCIAR LOS POLIEDROS REGULARES
 OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
Tema: Los Grafos y su importancia para la optimización de redes.
 Tema: Los Grafos y su importancia para la optimización de redes. Qué son los Grafos? Un grafo es una dupla G= {X,U}, donde X es un conjunto finito y no vacio de elementos llamados vértices y U es el conjunto
Tema: Los Grafos y su importancia para la optimización de redes. Qué son los Grafos? Un grafo es una dupla G= {X,U}, donde X es un conjunto finito y no vacio de elementos llamados vértices y U es el conjunto
Planaridad. Algoritmos y Estructuras de Datos III
 Planaridad Algoritmos y Estructuras de Datos III Por qué planares? Por qué planares? Por qué planares? Grafos planares Definiciones: Una representación planar de un grafo G es un conjunto de puntos en
Planaridad Algoritmos y Estructuras de Datos III Por qué planares? Por qué planares? Por qué planares? Grafos planares Definiciones: Una representación planar de un grafo G es un conjunto de puntos en
11 POLIEDROS EJERCICIOS. 6 Cuántas caras, vértices y aristas hay en los siguientes poliedros? a) b) c)
 11 POLIEROS EJERIIOS 1 ibuja una línea recta en tu cuaderno. escribe algún segmento real en el techo de la clase que se cruce con la línea que has dibujado. 6 uántas caras, vértices y aristas hay en los
11 POLIEROS EJERIIOS 1 ibuja una línea recta en tu cuaderno. escribe algún segmento real en el techo de la clase que se cruce con la línea que has dibujado. 6 uántas caras, vértices y aristas hay en los
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
IES CUADERNO Nº 8 NOMBRE: FECHA: / / Cuerpos geométricos
 Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Figura en el espacio o cuerpo geométrico es el conjunto de puntos que no están contenidos en un mismo plano, es la porción de espacio limitado.
 Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuerpos geométricos. Volúmenes
 4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
UCLM - Pruebas de Acceso a Enseñanzas Universitarias Oficiales de Grado (PAEG)
 PAEG Junio 03 Propuesta B Matemáticas aplicaas a las CCSS II º Bachillerato UCLM - Pruebas e Acceso a Enseñanzas Universitarias Oiciales e Grao (PAEG) Matemáticas aplicaas a las Ciencias Sociales II Junio
PAEG Junio 03 Propuesta B Matemáticas aplicaas a las CCSS II º Bachillerato UCLM - Pruebas e Acceso a Enseñanzas Universitarias Oiciales e Grao (PAEG) Matemáticas aplicaas a las Ciencias Sociales II Junio
GRAFOS. LICESIO J. RODRíGUEZ-ARAGÓN
 GRAFOS LICESIO J. RODRíGUEZ-ARAGÓN 1 LEONARD EULER Matemático y físico nacido en 1707 en Basilea (Suiza). Principal matemático del siglo XVIII y uno de los más grandes matemáticos de todos los tiempos.
GRAFOS LICESIO J. RODRíGUEZ-ARAGÓN 1 LEONARD EULER Matemático y físico nacido en 1707 en Basilea (Suiza). Principal matemático del siglo XVIII y uno de los más grandes matemáticos de todos los tiempos.
5º de E. Primaria LOS CUERPOS GEOMÉTRICOS -TEMA 15
 LOS POLIEDROS Los poliedros son cuerpos geométricos que tienen todas sus caras formadas por polígonos. Muchos objetos de nuestro alrededor tienen forma de poliedro: Los elementos de un poliedro son caras,
LOS POLIEDROS Los poliedros son cuerpos geométricos que tienen todas sus caras formadas por polígonos. Muchos objetos de nuestro alrededor tienen forma de poliedro: Los elementos de un poliedro son caras,
a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL
 G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
3.1. DERIVADAS DE SEGUNDO ORDEN
 .. DERIVADAS DE SEGUNDO ORDEN La erivaa y ' f ' es la primera erivaa e y con respecto a, pero igualmente es posible realizar la erivaa e la erivaa, y y '' f ''. Lo que se conoce como la seguna erivaa e
.. DERIVADAS DE SEGUNDO ORDEN La erivaa y ' f ' es la primera erivaa e y con respecto a, pero igualmente es posible realizar la erivaa e la erivaa, y y '' f ''. Lo que se conoce como la seguna erivaa e
Matemáticas Discretas TC1003
 Matemáticas Discretas TC1003 Grafos: Básicos Departamento de Matemáticas / Centro de Sistema Inteligentes ITESM Grafos: Básicos Matemáticas Discretas - p. 1/12 Grafos: El tema de Teoría de Grafos apareció
Matemáticas Discretas TC1003 Grafos: Básicos Departamento de Matemáticas / Centro de Sistema Inteligentes ITESM Grafos: Básicos Matemáticas Discretas - p. 1/12 Grafos: El tema de Teoría de Grafos apareció
CUERPOS GEOMÉTRICOS. Un polígono es una figura compuesta por tres o más segmentos rectos (lados) que cierran una región en el espacio.
 CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
SOLUCIÓN: Sea x la distancia entre A y C. Por el Teorema del coseno tenemos:
 EJERCICIO 30 Dese un punto A se ivisan otros os puntos B y C bajo un ángulo e 5º 9. Se sabe que B y C istan 450 m y que A y B istan 500 m. Averigua la istancia entre A y C. Sea la istancia entre A y C.
EJERCICIO 30 Dese un punto A se ivisan otros os puntos B y C bajo un ángulo e 5º 9. Se sabe que B y C istan 450 m y que A y B istan 500 m. Averigua la istancia entre A y C. Sea la istancia entre A y C.
Síntesis de Imágenes: ray casting básico
 Tema III Síntesis e Imágenes: ray casting básico Ricaro Ramos Colaboraores: Enrique Sierra Blanco, Eloy Álvarez Fernánez, Reyes Berguillos Moretón, Mª el Carmen Suárez Torrente, Mª Sanra García Peláez,
Tema III Síntesis e Imágenes: ray casting básico Ricaro Ramos Colaboraores: Enrique Sierra Blanco, Eloy Álvarez Fernánez, Reyes Berguillos Moretón, Mª el Carmen Suárez Torrente, Mª Sanra García Peláez,
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO
 DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
Diferencias entre Figuras y
 10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
Cuál es el resto? Números en columnas. Con la planilla de cálculo: b) Se escriben los números
 Números en columnas a) Se escriben los números en tres columnas: Encuentra en qué columna se ubican los números: 24; 141; 814; 1721; 10001. b) Se escriben los números en cinco colum- 0 1 2 3 4 5 6 7 8
Números en columnas a) Se escriben los números en tres columnas: Encuentra en qué columna se ubican los números: 24; 141; 814; 1721; 10001. b) Se escriben los números en cinco colum- 0 1 2 3 4 5 6 7 8
4. GEOMETRÍA // 4.4. POLIEDROS.
 4. GEOMETRÍA // 4.4. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 Bibliografía. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas:
4. GEOMETRÍA // 4.4. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 Bibliografía. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas:
La regla de la constante. DEMOSTRACIÓN Sea ƒ(x) c. Entonces, por la definición de derivada mediante el proceso de límite, se deduce que.
 SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
SECCIÓN. Reglas básicas e erivación razón e cambio 07. Reglas básicas e erivación razón e cambio Encontrar la erivaa e una función por la regla e la constante. Encontrar la erivaa e una función por la
Soluciones a algunos ejercicios de Matemática Discreta 1.
 Soluciones a algunos ejercicios de Matemática Discreta 1. Eleonora Catsigeras * 23 de agosto de 2005 Práctico 1.- Ejercicio 5 Cuántos números naturales pares de tres dígitos (en base 10) tienen todos sus
Soluciones a algunos ejercicios de Matemática Discreta 1. Eleonora Catsigeras * 23 de agosto de 2005 Práctico 1.- Ejercicio 5 Cuántos números naturales pares de tres dígitos (en base 10) tienen todos sus
LA DERIVADA POR FÓRMULAS
 CAPÍTULO LA DERIVADA POR FÓRMULAS. FÓRMULAS Obtener la erivaa e cualquier función por alguno e los os métoos vistos anteriormente, el e tabulaciones y el e incrementos, resulta una tarea muy engorrosa,
CAPÍTULO LA DERIVADA POR FÓRMULAS. FÓRMULAS Obtener la erivaa e cualquier función por alguno e los os métoos vistos anteriormente, el e tabulaciones y el e incrementos, resulta una tarea muy engorrosa,
2.3 Reglas del producto, del cociente y derivadas de orden superior
 SECCIÓN.3 Reglas el proucto, el cociente erivaas e oren superior 119.3 Reglas el proucto, el cociente erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar la erivaa
SECCIÓN.3 Reglas el proucto, el cociente erivaas e oren superior 119.3 Reglas el proucto, el cociente erivaas e oren superior Encontrar la erivaa e una función por la regla el proucto. Encontrar la erivaa
TEMA 9 CUERPOS GEOMÉTRICOS
 Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD
 SLUINES LS EJERIIS E L UNI Pág. 1 Página 207 PRTI 1 Reproduce sobre papel cuadriculado el paralelogramo (,,, ). a) Somételo a una traslación de vector t 1. b) Traslada la figura obtenida, ', mediante t
SLUINES LS EJERIIS E L UNI Pág. 1 Página 207 PRTI 1 Reproduce sobre papel cuadriculado el paralelogramo (,,, ). a) Somételo a una traslación de vector t 1. b) Traslada la figura obtenida, ', mediante t
TEMA 4: Transformaciones 3D
 TEMA 4: Transformaciones D Ínice. Sistemas e Coorenaas. Transformaciones Básicas. Traslación. Escalao. Rotación lana 4. Afilamiento 5. Deformaciones. Composición e Transformaciones 4. Rotación General
TEMA 4: Transformaciones D Ínice. Sistemas e Coorenaas. Transformaciones Básicas. Traslación. Escalao. Rotación lana 4. Afilamiento 5. Deformaciones. Composición e Transformaciones 4. Rotación General
TEMA 9 Electrostática
 Bases Físicas y Químicas el Meio Ambiente TMA 9 lectrostática Cargas eléctricas ntre os cuerpos hay siempre fuerzas atractivas ebio a sus respectivas masas y pueen existir otras fuerzas entre ellos si
Bases Físicas y Químicas el Meio Ambiente TMA 9 lectrostática Cargas eléctricas ntre os cuerpos hay siempre fuerzas atractivas ebio a sus respectivas masas y pueen existir otras fuerzas entre ellos si
OPCIONES. c.- Titular o Comprador de la Opción: inversionista que adquiere el derecho a comprar/vender el activo subyacente.
 arlos A. Díaz ontreras 1 OPIONES La opción es "un contrato que a erecho a su poseeor o titular (el que compró la opción), a comprar o vener un activo eterminao y a un precio eterminao, urante un perioo
arlos A. Díaz ontreras 1 OPIONES La opción es "un contrato que a erecho a su poseeor o titular (el que compró la opción), a comprar o vener un activo eterminao y a un precio eterminao, urante un perioo
congruentes es porque tienen la misma longitud AB = CD y, cuando dos ángulos DEF son congruentes es porque tienen la misma medida
 COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES
 TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN...1 2. SUPERFICIES POLIÉDRICAS. POLIEDROS...1 3. FIGURAS DE REVOLUCIÓN...3 4. POLIEDROS
TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN...1 2. SUPERFICIES POLIÉDRICAS. POLIEDROS...1 3. FIGURAS DE REVOLUCIÓN...3 4. POLIEDROS
Potencial eléctrico (V)
 Activia 1 [a] xplica el concepto e potencial electrostático en un punto. [b] Dibuja aproximaamente en un sistema e coorenaas el gráfico ue relaciona el potencial creao por una carga puntual positiva (eje
Activia 1 [a] xplica el concepto e potencial electrostático en un punto. [b] Dibuja aproximaamente en un sistema e coorenaas el gráfico ue relaciona el potencial creao por una carga puntual positiva (eje
Manual de la Práctica 2: Análisis de sistemas discretos
 Control por computaor Manual e la Práctica : Análisis e sistemas iscretos Jorge Pomares Baeza Fracisco Anrés Canelas Herías Grupo e Innovación Eucativa en Automática 009 GITE IEA - - Introucción En la
Control por computaor Manual e la Práctica : Análisis e sistemas iscretos Jorge Pomares Baeza Fracisco Anrés Canelas Herías Grupo e Innovación Eucativa en Automática 009 GITE IEA - - Introucción En la
Conceptos geométricos II
 Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
XXII OLIMPIADA NACIONAL DE FÍSICA Guadalajara, Jal de noviembre de 2011 Prueba teórica
 XXII OLIMPI NIONL E FÍSI Guaalajara, Jal. 0-4 e noviembre e 011 Prueba teórica 1. PROLEM olisión e pieras (8 puntos) Una piera esférica se eja caer ese un eificio alto e altura h (ese la calle) al tiempo
XXII OLIMPI NIONL E FÍSI Guaalajara, Jal. 0-4 e noviembre e 011 Prueba teórica 1. PROLEM olisión e pieras (8 puntos) Una piera esférica se eja caer ese un eificio alto e altura h (ese la calle) al tiempo
Apuntes sobre la Parábola: su medición según Arquímedes y otras propiedades
 Investigación y Docencia por Néstor guilera puntes sobre la Parábola: su meición según rquímees y otras propieaes Introucción (Versión revisaa e mayo e 2001) Muchas veces habrán oío que rquímees fue el
Investigación y Docencia por Néstor guilera puntes sobre la Parábola: su meición según rquímees y otras propieaes Introucción (Versión revisaa e mayo e 2001) Muchas veces habrán oío que rquímees fue el
Cuerpos geométricos OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Elementos de un poliedro y su desarrollo. Los poliedros regulares y sus características.
 826464 _ 0385-0396.qxd /2/07 09:27 Página 385 Cuerpos geométricos INTRODUCCIÓN Esta unidad completa la serie dedicada a la Geometría y afianza su comprensión mediante la descripción y desarrollo de las
826464 _ 0385-0396.qxd /2/07 09:27 Página 385 Cuerpos geométricos INTRODUCCIÓN Esta unidad completa la serie dedicada a la Geometría y afianza su comprensión mediante la descripción y desarrollo de las
6. PROBLEMAS DE MARKETING
 6. PROBLEMAS DE MARKETING PROBLEMA 1 (POSICIONAMIENTO DEL PRODUCTO) Se ha realizao una encuesta sobre un grupo e consumiores e vino tinto e mesa para que, sobre una escala e 0 a 10, califiquen a las iferentes
6. PROBLEMAS DE MARKETING PROBLEMA 1 (POSICIONAMIENTO DEL PRODUCTO) Se ha realizao una encuesta sobre un grupo e consumiores e vino tinto e mesa para que, sobre una escala e 0 a 10, califiquen a las iferentes
x x x x x x qv o B =m v o 2
 ísica e 2º achillerato Activia Una partícula e masa m, carga positiva q y otaa e velocia horizontal, penetra en una región el espacio one hay un campo eléctrico E y un campo magnético. Ambos campos son
ísica e 2º achillerato Activia Una partícula e masa m, carga positiva q y otaa e velocia horizontal, penetra en una región el espacio one hay un campo eléctrico E y un campo magnético. Ambos campos son
1 /13. dictamen 01/13 1. Sobre el Proyecto de Decreto
 ictamen 1 1 /13 Sobre el Proyecto e Decreto sobre el Proyecto e Decreto por el que se crea el Registro Vasco e Certificaos e Profesionalia y Acreitaciones Parciales Acumulables, y se establece el proceimiento
ictamen 1 1 /13 Sobre el Proyecto e Decreto sobre el Proyecto e Decreto por el que se crea el Registro Vasco e Certificaos e Profesionalia y Acreitaciones Parciales Acumulables, y se establece el proceimiento
MÓDULO Nº 3. Nivelación. Matemática Módulo Nº3. Contenidos. Polígonos Circunferencia y Círculo Volúmenes
 MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
DEPARTAMENTO DE INGENIERÍA ELÉCTRICA Y ENERGÉTICA MÁQUINAS SÍNCRONAS: CORTOCIRCUITOS
 UNVERSDAD DE CANTABRA DEPARTAMENTO DE NGENERÍA ELÉCTRCA Y ENERGÉTCA MÁQUNAS SÍNCRONAS: CORTOCRCUTOS Miguel Angel Roríguez Pozueta CORTOCRCUTOS 1. CORTOCRCUTO PERMANENTE TRFÁSCO EN BORNES DEL NDUCDO Se
UNVERSDAD DE CANTABRA DEPARTAMENTO DE NGENERÍA ELÉCTRCA Y ENERGÉTCA MÁQUNAS SÍNCRONAS: CORTOCRCUTOS Miguel Angel Roríguez Pozueta CORTOCRCUTOS 1. CORTOCRCUTO PERMANENTE TRFÁSCO EN BORNES DEL NDUCDO Se
Electromagnetismo Pedagogía en Física R. Lagos. PROBLEMAS RESUELTOS
 PROBLEMAS RESUELTOS. Un capacitor e lleno e aire está compuesto e os placas paralela, caa una con un área e 7 6 [ 2 ], separaas por una istancia e,8 [mm]. Si se aplica una iferencia e potencial e 20 [V]
PROBLEMAS RESUELTOS. Un capacitor e lleno e aire está compuesto e os placas paralela, caa una con un área e 7 6 [ 2 ], separaas por una istancia e,8 [mm]. Si se aplica una iferencia e potencial e 20 [V]
Soluciones oficiales Clasificación Olimpiada Nacional Nivel Mayor
 Soluciones oficiales Clasificación Olimpiada Nacional 009 Comisión Académica Nivel Maor Problema 1. Calcule todas las soluciones m, n de números enteros que satisfacen la ecuación m n = 009 (n + 1) Solución.
Soluciones oficiales Clasificación Olimpiada Nacional 009 Comisión Académica Nivel Maor Problema 1. Calcule todas las soluciones m, n de números enteros que satisfacen la ecuación m n = 009 (n + 1) Solución.
Regla de la cadena. f (x) 1 x 3. d dx x3 1 x 3. (3x 2 ) 3 x. f(x) 3 d dx ln x 3. 1 x. para x70, d dx ln x 1. para x60, d dx ln( x) 1x.
 74 CAPÍTULO 3 La erivaa EJEMPLO 4 Diferencie f ()=ln 3. Regla e la caena Solución Debio a que 3 ebe ser positiva, se entiene que 70. Así, por (3), con u= 3, tenemos Solución alterna: Por iii) e las lees
74 CAPÍTULO 3 La erivaa EJEMPLO 4 Diferencie f ()=ln 3. Regla e la caena Solución Debio a que 3 ebe ser positiva, se entiene que 70. Así, por (3), con u= 3, tenemos Solución alterna: Por iii) e las lees
ELEMENTOS Y CLASES DE ÁNGULOS
 Apellidos: Curso: Grupo: Nombre: Fecha: ELEMENTOS Y CLASES DE ÁNGULOS Dos rectas que se cortan forman 4 regiones llamadas ángulos. Las partes de un ángulo son: los lados: son las semirrectas que lo forman.
Apellidos: Curso: Grupo: Nombre: Fecha: ELEMENTOS Y CLASES DE ÁNGULOS Dos rectas que se cortan forman 4 regiones llamadas ángulos. Las partes de un ángulo son: los lados: son las semirrectas que lo forman.
RADIACIÓN SOLAR. Las características más singulares que presenta la radiación son:
 RADIACIÓN SOLAR El flujo e raiación solar que llega a la tierra es la fuente primaria e toas las formas e energía conocias. La raiación solar es el origen e los movimientos e circulación e la atmósfera
RADIACIÓN SOLAR El flujo e raiación solar que llega a la tierra es la fuente primaria e toas las formas e energía conocias. La raiación solar es el origen e los movimientos e circulación e la atmósfera
RECOMENDACIÓN 326-6. (Cuestión 59/1)
 Rc. 326-6 RECOMENDACIÓN 326-6 DETERMINACIÓN Y MEDICIÓN DE LA POTENCIA DE LOS TRANSMISORES RADIOELÉCTRICOS (Cuestión 59/) Rc. 326-6 (95-959-963-966-974-978-982-986-990) El CCIR, CONSIDERANDO a) que el artículo
Rc. 326-6 RECOMENDACIÓN 326-6 DETERMINACIÓN Y MEDICIÓN DE LA POTENCIA DE LOS TRANSMISORES RADIOELÉCTRICOS (Cuestión 59/) Rc. 326-6 (95-959-963-966-974-978-982-986-990) El CCIR, CONSIDERANDO a) que el artículo
Actividades del final de la unidad
 Activiaes el final e la unia 1. Calcula el flujo magnético a través e una espira cuaraa e 10 cm e lao situaa en un campo magnético e valor 0,2 T cuano la normal a la espira forma con la irección el campo
Activiaes el final e la unia 1. Calcula el flujo magnético a través e una espira cuaraa e 10 cm e lao situaa en un campo magnético e valor 0,2 T cuano la normal a la espira forma con la irección el campo
1. Progresiones aritméticas
 1 PROGRESIONES ARITMÉTICAS 1 1. Progresiones aritméticas Una progresión aritmética es una sucesión en la que cada término es igual al anterior más un número constante llamado diferencia de la progresión.
1 PROGRESIONES ARITMÉTICAS 1 1. Progresiones aritméticas Una progresión aritmética es una sucesión en la que cada término es igual al anterior más un número constante llamado diferencia de la progresión.
Recuerda lo fundamental
 12 Figuras planas y espaciales Recuerda lo fundamental Curso:... Fecha:... TRIÁNGULOS Mediana de un triángulo es un segmento que...... Las tres medianas de un triángulo se cortan en el...... Las mediatrices
12 Figuras planas y espaciales Recuerda lo fundamental Curso:... Fecha:... TRIÁNGULOS Mediana de un triángulo es un segmento que...... Las tres medianas de un triángulo se cortan en el...... Las mediatrices
Problemas y Conjeturas
 U UNIVERSITAT DE BARCELONA B Problemas y Conjeturas de la Teoría de Grafos (Trabajo Académicamente Dirigido) Autora: Cristina Araúz Lombardía Trabajo Académicamente Dirigido por F. Javier Soria de Diego
U UNIVERSITAT DE BARCELONA B Problemas y Conjeturas de la Teoría de Grafos (Trabajo Académicamente Dirigido) Autora: Cristina Araúz Lombardía Trabajo Académicamente Dirigido por F. Javier Soria de Diego
CONJUNTO Y TIPOS DE CONJUNTOS
 CONJUNTO Y TIPOS DE CONJUNTOS Ejemplos 1. Determine cuáles de los siguientes conjuntos corresponden a conjuntos vacíos. a) El conjunto de los números naturales mayores que 3 y menores que 6. b) El conjunto
CONJUNTO Y TIPOS DE CONJUNTOS Ejemplos 1. Determine cuáles de los siguientes conjuntos corresponden a conjuntos vacíos. a) El conjunto de los números naturales mayores que 3 y menores que 6. b) El conjunto
Cálculos de instalaciones de fontanería, gas y calefacción. Volumen 2: métodos de cálculos de calefacción y gas. Santiago Durán Montejano
 Cálculos e instalaciones e fontanería, gas y calefacción. Volumen 2: métoos e cálculos e calefacción y gas. Santiago Durán Montejano 1ª eición: febrero 2008 Santiago Durán Montejano Tornapunta Eiciones,
Cálculos e instalaciones e fontanería, gas y calefacción. Volumen 2: métoos e cálculos e calefacción y gas. Santiago Durán Montejano 1ª eición: febrero 2008 Santiago Durán Montejano Tornapunta Eiciones,
DERIVADAS DE LAS FUNCIONES ELEMENTALES
 Universia Metropolitana Dpto. e Matemáticas Para Ingeniería Cálculo I (FBMI0) Proesora Aia Montezuma Revisión: Proesora Ana María Roríguez Semestre 08-09A DERIVADAS DE LAS FUNCIONES ELEMENTALES DERIVADAS
Universia Metropolitana Dpto. e Matemáticas Para Ingeniería Cálculo I (FBMI0) Proesora Aia Montezuma Revisión: Proesora Ana María Roríguez Semestre 08-09A DERIVADAS DE LAS FUNCIONES ELEMENTALES DERIVADAS
1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS.
 UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
UNIDAD 1.- CONCEPTOS REQUERIDOS CONJUNTOS. AXIOMAS DE PERTENENCIA, PARALELISMO, ORDEN Y PARTICIÓN. 1 NOCIONES BÁSICAS SOBRE CONJUNTOS. SÍMBOLOS. 1.1 Determinaciones de un conjunto. Un conjunto queda determinado
Estructuras Algebraicas
 Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
Tema 1 Estructuras Algebraicas Definición 1 Sea A un conjunto no vacío Una operación binaria (u operación interna) en A es una aplicación : A A A Es decir, tenemos una regla que a cada par de elementos
FUNCIONES TRIGONOMÉTRICAS
 CAPÍTULO 6 FUNCIONES TRIGONOMÉTRICAS 6.1 FUNCIONES TRASCENDENTES (Áreas 1, y ) Las funciones trascenentes se caracterizan por tener lo que se llama argumento. Un argumento es el número o letras que lo
CAPÍTULO 6 FUNCIONES TRIGONOMÉTRICAS 6.1 FUNCIONES TRASCENDENTES (Áreas 1, y ) Las funciones trascenentes se caracterizan por tener lo que se llama argumento. Un argumento es el número o letras que lo
Figura 3.1. Grafo orientado.
 Leyes de Kirchhoff 46. ECUACIONES DE INTERCONEXION. Leyes de Kirchhoff..1. Definiciones. Una red está formada por la interconexión de componentes en sus terminales; y deben cumplirse simultáneamente las
Leyes de Kirchhoff 46. ECUACIONES DE INTERCONEXION. Leyes de Kirchhoff..1. Definiciones. Una red está formada por la interconexión de componentes en sus terminales; y deben cumplirse simultáneamente las
Cuerpos geométricos. Objetivos. Antes de empezar. 1. Poliedros...pág. 138 Definición Elementos de un poliedro
 8 Cuerpos geométricos. Objetivos En esta quincena aprenderás a: Identificar que es un poliedro. Determinar los elementos de un poliedro: Caras, aristas y vértices. Clasificar los poliedros. Especificar
8 Cuerpos geométricos. Objetivos En esta quincena aprenderás a: Identificar que es un poliedro. Determinar los elementos de un poliedro: Caras, aristas y vértices. Clasificar los poliedros. Especificar
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Derivación bajo la integral
 Derivación bajo la integral José Alfreo Cañizo Rincón e julio, 2004. ntroucción Estas notas contienen una presentación e los teoremas usuales e erivación bajo la integral y la regla e Leibniz. El objetivo
Derivación bajo la integral José Alfreo Cañizo Rincón e julio, 2004. ntroucción Estas notas contienen una presentación e los teoremas usuales e erivación bajo la integral y la regla e Leibniz. El objetivo
DESCOMPOSICÓN DE LA LUZ EN DETERMINADAS LONGITUDES DE ONDA MEDIANTE LA RED DE DIFRACCIÓN.
 ESPECTROS DE EMISIÓN DE LUZ EN LOS GASES: DESCOMPOSICÓN DE LA LUZ EN DETERMINADAS LONGITUDES DE ONDA MEDIANTE LA RED DE DIFRACCIÓN. (Práctica nº 14: Espectroscopía) CARLOS HUERTAS BARRA FERNANDO HUESO
ESPECTROS DE EMISIÓN DE LUZ EN LOS GASES: DESCOMPOSICÓN DE LA LUZ EN DETERMINADAS LONGITUDES DE ONDA MEDIANTE LA RED DE DIFRACCIÓN. (Práctica nº 14: Espectroscopía) CARLOS HUERTAS BARRA FERNANDO HUESO
UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS. Métodos multivariantes en control estadístico de la calidad
 UNIVESIDAD NACIONAL MAYO DE SAN MACOS FACULTAD DE CIENCIAS MATEMÁTICAS E.A.P. DE ESTADÍSTICA Métoos multivariantes en control estaístico e la calia Capítulo I. Gráficos e control estaístico univariaa TABAJO
UNIVESIDAD NACIONAL MAYO DE SAN MACOS FACULTAD DE CIENCIAS MATEMÁTICAS E.A.P. DE ESTADÍSTICA Métoos multivariantes en control estaístico e la calia Capítulo I. Gráficos e control estaístico univariaa TABAJO
Qué son los cuerpos geométricos?
 Qué son los cuerpos geométricos? Definición Los cuerpos geométricos son regiones cerradas del espacio. Una caja de tetrabrick es un ejemplo claro de la figura que en matemáticas se conoce con el nombre
Qué son los cuerpos geométricos? Definición Los cuerpos geométricos son regiones cerradas del espacio. Una caja de tetrabrick es un ejemplo claro de la figura que en matemáticas se conoce con el nombre
Ámbito científico tecnológico
 Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
10 FIGURAS Y CUERPOS GEOMÉTRICOS
 10 FIGURS Y UERPOS GEOMÉTRIOS EJERIIOS PR ENTRENRSE Poliedros y cuerpos redondos. Propiedades 10.2 Un poliedro regular tiene 8 vértices y 12 aristas. Utiliza la fórmula de Euler para saber de qué poliedro
10 FIGURS Y UERPOS GEOMÉTRIOS EJERIIOS PR ENTRENRSE Poliedros y cuerpos redondos. Propiedades 10.2 Un poliedro regular tiene 8 vértices y 12 aristas. Utiliza la fórmula de Euler para saber de qué poliedro
