ESTRUCTURAS POLIEDRICAS
|
|
|
- María Dolores Crespo Alcaraz
- hace 9 años
- Vistas:
Transcripción
1 ESTRUCTURAS POLIEDRICAS ELEMENTOS DE DISEÑO TRIDIMENSIONAL Integrante Grupo N 5 Guillermo Alexis Cordova Bonilla
2 ESTRUCTURA Conjunto de piezas o elementos que sirve de soporte rígido de algo, especialmente d e una construcción POLIEDRO Es, en el sentido dado por la geometría clásica al término, un cuerpo geométrico cuyas caras son planas y encierran un volumen finito. La palabra poliedro viene del griego clásico πολύεδρον (polyedron), de la raíz πολύς (polys), "muchas" y de έδρα (edra), "base", "asiento", "cara".conjunto de piezas o elementos que sirve de soporte rígido de algo, especialm ente de una construcción
3 Sólido limitado por superficies planas (polígonos). Sus partes se denominan: caras: polígonos que limitan al poliedro, aristas: lados de las caras del poliedro, vértices: puntos donde concurren varias aristas.
4
5 Prisma triangular Prisma cuadrangular Prisma pentagonal Prisma hexagonal PRISMA En geometría, un prisma es un sólido determinado por dos polígonos paralelos y congruentes que se denominan bases y por tantos paralelogramos como lados tengan las bases, denominados caras
6 Pirámide triangular Pirámide cuadrangular Pirámide pentagonal Pirámide hexagonal PIRAMIDE Una pirámide es un poliedro limitado por una base, que es un polígono con una cara; y por caras, que son triángulos coincidentes en un punto denominado ápice.
7 POLIEDROS REGULARES Poliedro cuyas caras son polígonos regulares iguales y todas sus aristas son de igual longitud; en consecuencia, todos sus vértices están contenidos en una esfera. Los poliedros regulares son cinco y se denominan: tetraedro regular: poliedro regular definido por 4 triángulos equiláteros iguales, hexaedro regular (cubo): poliedro regular definido por 6 cuadrados iguales, octaedro regular: poliedro regular definido por 8 triángulos equiláteros iguales, dodecaedro regular: poliedro regular definido por 12 pentágonos regulares iguales, icosaedro regular: poliedro regular definido por 20 triángulos equiláteros iguales.
8 POLIEDROS IRREGULARES Poliedro definido por polígonos que no son todos iguales. Clasificación de los Poliedros Irregulares Los poliedros irregulares se clasifican básicamente en: tetraedro, pentaedro, hexaedro, heptaedro, octaedro, pirámide prisma
9 POLIEDROS REGULARES FUNDAMENTALES Y/O PLATONICOS POLIEDROS NO REGULARES
10
11 SOLIDOS DE ARQUIMIDES (POLIEDROS IRREGULARES) Por otro lado, existen poliedros que son totalmente irregulares, ya que estos derivan de la combinación o mezcla de 2 o varios poliedros regulares. A este grupo de poliedros irregulares se les conoce como: Sólidos de Arquímedes. La diferencia entre los sólidos de Arquímedes y los sólidos platónicos es que cada sólido platónico se compone de un solo tipo de polígono regular, mientras que cada sólido de Arquímedes se compone de más de un tipo de polígono regular. En realidad, hay 13 sólidos de Arquímedes : Tetraedro truncado (8 caras) Cuboctaedro (14 caras) Cubo truncado (14 caras)
12 Octaedro truncado (14 caras) Rombicuboctaedro (26 caras) Cuboctaedro truncado (26 caras) Cubo romo (38 caras) Icosaedro truncado (32 caras)
13 Icosidodecaedro (32 caras) Rombicosidodecaedro (62 caras) Icosidodecaedro truncado (62 caras) Dodecaedro truncado (32 caras) Dodecaedro romo (92 caras)
14
15 ANTIPRISMAS Todos los prismas se construyen con dos caras paralelas llamadas directrices, que le dan el nombre al prisma, y una serie de paralelogramos, tantos como lados tenga la cara directriz. Los antiprismas tienen una construcción parecida, dos caras paralelas y una serie de triángulos; el número de lados de las cara directriz multiplicado por dos; así, el antiprisma cuadrado se compone de dos cuadrados y ocho triángulos; tiene ocho vértices y 16 aristas.
16 OTRAS FAMILIAS DE POLIEDROS Sólidos de Johnson Son un grupo extenso que contiene los poliedros convexos, de caras regulares restantes; sólo uno de ellos es uniforme y fueron clasificados y ampliamente estudiados por Norman Johnson. Son en total 92 y entre ellos se enumeran: Pirámide triangular elongada. Rotunda pentagonal elongada. Girobifastigium. Girobicupola cuadrangular giroelongada, que es él único cuerpo de este grupo que sigue siendo uniforme. etc.
17 SOLIDOS DE CATALAN Se obtienen logrando el dual de los sólidos de Arquímedes; el dual es básicamente el reemplazo de una cara por un vértice y viceversa. Por ejemplo, el dual del icosaedro (20 caras y 12 vértices) es el dodecaedro (12 caras y 20 vértices) y el dual del dodecaedro es el icosaedro. No son de caras regulares y no todos son de caras uniformes. Trece en total.
18 SOLIDOS DE CATALAN Se obtienen logrando el dual de los sólidos de Arquímedes; el dual es básicamente el reemplazo de una cara por un vértice y viceversa. Por ejemplo, el dual del icosaedro (20 caras y 12 vértices) es el dodecaedro (12 caras y 20 vértices) y el dual del dodecaedro es el icosaedro. No son de caras regulares y no todos son de caras uniformes. Trece en total.
19
20 APLICACIONES EN EDIFICACIONES Edificio de oficinas La Cite des Affaires Arquitectos: Manuelle Gautrand Architecture Ubicación: 106 Rue de la Montat, Saint-Étienne, France Año Proyecto: 2010
21 APLICACIONES EN EDIFICACIONES Biblioteca Nacional de Bielorrusia Arquitectos: Mihail Vinogrdov, Victor Kramarenko Ubicación: Minsk, Bielorrusia Año Proyecto:
22 APLICACIONES EN EDIFICACIONES (Vivienda campestre) Poliedro habitable Ubicación: Bogotá, Bogotá, Colombia Arquitecto: Manuel Villa Área: 75.0 m2 Año Proyecto: 2009
23 APLICACIONES EN EDIFICACIONES En planta arquitectónica Casa Vigo Sundt, Madison, Arquitecto: Frank Lloyd Wright Ubicación: Madison, Wisconsin, Estados Unidos Año Proyecto: 1942
24 APLICACIONES EN EDIFICACIONES En Isometrico Casa Hanselmann, Fort Wayne, Indiana, Arquitecto: Michael Graves Ubicación: Fort Wayne, Indiana, Estados Unidos Año Proyecto: 1967
25 APLICACIONES EN EDIFICACIONES En Seccion e Isometrico Piramide de Keops, Kefren y Micerinos, Ghizeh, Egipto, 2500 a.c.
26 APLICACIONES EN EDIFICACIONES En Planta Arquitectonica y elevacion Casa Bath, Centro de la Comunidad Judia de Trenton, Arquitecto: Louis I. Kahn Ubicación: Trenton, New Jersey, Estados Unidos Año Proyecto:
27 APLICACIONES EN PAISAJISMO (ESTRUCTURA DE TECHO) Bosque Fulleriano Arquitecto: Giancarlo Mazzanti Ubicación: Barrio de Altos de Cazucá en los suburbios de Bogotá, Colombia Año Proyecto: 2012
28 APLICACIONES EN PAISAJISMO Proyecto Base formal estructural Taller Fadua Construyo: Facultad de Arq, diseño, arte y urbanismo de la Universidad de Buenos Aires Ubicación: Universidad de Buenos Aires, Argentina Año de proyecto: 2012
29 APLICACIONES EN PAISAJISMO Jardín Botánico Tropical de Nong Nooch Construyo: Mr. Pisit and Mrs. Nong Nooch Ubicación: Provincia de Chon Buri, Tailandia Año de proyecto: 1954
30 APLICACIONES EN EXTERIOR E INTERIOR El Poliedro de Caracas eventos y espectáculos, Ubicación: Al sur de la ciudad de Caracas, en la zona de La Rinconada, Caracas Venezuela Año de proyecto: 1974 Arquitectos: Héctor Hermidas, Jimmy Alcock, Roberto Andrade
31 APLICACIONES EN EXTERIOR E INTERIOR Bar para exposición de Heineken. Construyo: Ingetec Ingeniería Ubicación: Exposición en Mexico Año del proyecto: 2009.
32 APLICACIONES EN EXTERIOR E INTERIOR Epcot (Prototipo experimental de la comunidad del mañana) es un parque temático Construyo: Walt Disney company Ubicación: Walt Disney World Resort en Florida, Estados Unidos Año del proyecto: 1982
33 APLICACIONES EN MUEBLES Mueble 'Divyna Concurso de diseño en Mexico: Segundo lugar fue para 'Divyna', de Edgar Godínez, de la UAM Azcapotzalco. El Artículo fue fabricada con encino rojo y nogal negro; se basó en poliedros con cortes de ángulos de 60 grados Aggregate Daybed de Hania Stella - Sawicka, Inspirada en las esferas de meditación tailandesas. Es un punto de descanso y plegable portátil dice su autora. $3900
34 APLICACIONES EN MUEBLES Aparador de lujo Diamond La empresa de mobiliario portuguesa Boca do Lobo euros Lámpara de Rasmus Fenhahn en el que un complejo poliedro de madera y papel japonés intenta acercarse a la esfera describiendo con sus figuras geométricas una bonita jaula de luz tamizada.
35 APLICACIONES EN DISEÑO GRAFICO E INDUSTRIAL
36 APLICACIONES EN DISEÑO GRAFICO _PolygonStructure_001_02_f_Pshop
37 APLICACIONES EN ILUSION OPTICA
38 OBJETOS HECHOS CON POLIEDROS
39 TALLER DE POLIEDROS (PAPEL FABRIANO y/o PALILLOS) TALLER :Elija una estructura de edificación (hotel, estadio, museo) que se tenga por base un polígono para formar poliedros en una edificación. El material empleado es hojas de papel fabriano y/o cartón. Palillos de dientes (con punta en ambos lados) opcional Barras de silicón (de las que se colocan en las pistolas de calor) opcional Son 40 módulos en base de 0.40 x 0.40m. Herramientas de dibujo y corte.
40 CONCLUSIONES SOBRE ESTRUCTURAS POLIEDRICAS Las conclusiones que se sacan del tema estructuras poliédricas es que teniendo claro que es un poliedro se puede tener en síntesis su beneficios y/o características, también sus debilidades el poliedro en si (volumen limitado por planos que contienen varias caras según su forma, vértices que son punto de unión de la líneas (aristas) pueden crearse delimitación de espacios para utilización optima de espacio usando las estructuras en los tipos de poliedros estudiados y partiendo de las figuras básicas pueden crearse nuevos poliedros y utilizar materiales innovadores con los que se pueden realizar edificaciones, muebles, objetos internos/externos ocuparlo en paisajismo, ilusiones ópticas, obteniendo muchas formas de aplicación con un sin numero de materiales diferentes y texturas aplicadas usando los elementos de diseño bidimensionales y tridimensionales; en el que los poliedros es mas útil trabajar en modo proceso de abstracción ya que es una forma geométrica muy utilizada como volumen base.
41
42
Figura en el espacio o cuerpo geométrico es el conjunto de puntos que no están contenidos en un mismo plano, es la porción de espacio limitado.
 Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
Cuenca, 11 de noviembre de 2013 Clase 13 Geometría del espacio Figuras geométricas en el espacio Definiciones: Geometría del espacio: Rama de las matemáticas encargada de las propiedades y medida de las
CUERPOS GEOMÉTRICOS. Un polígono es una figura compuesta por tres o más segmentos rectos (lados) que cierran una región en el espacio.
 CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
CUERPOS GEOMÉTRICOS 07 Comprende que son los cuerpos geométricos e identifica las partes que los componen. En Presentación de Contenidos recuerdan qué son los polígonos para comprender cómo se forman los
Cuerpos geométricos son porciones de espacio limitadas por superficies planas o curvas. CUERPOS GEOMÉTRICOS PRISMAS PIRÁMIDES CILINDROS CONOS ESFERAS
 UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
UNIDAD DIDÁCTICA CUERPOS GEOMÉTRICOS 1. CUERPOS GEOMÉTRICOS En nuestro entorno observamos continuamente objetos de diversas formas: pelotas, botes, cajas, pirámides, etc. Todos estos objetos son cuerpos
Punto. Recta. Semirrecta. Segmento. Rectas Secantes. Rectas Paralelas. Rectas Perpendiculares
 Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
Punto El punto es un objeto geométrico que no tiene dimensión y que sirve para indicar una posición. A Recta Es una sucesión continua e indefinida de puntos en una sola dimensión. Semirrecta Es una línea
10- Los poliedros. Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos.
 Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Aprende a reconocer los poliedros en nuestro entorno; identifica sus elementos y aprende a clasificarlos. Impreso por Juan Carlos Vila Vilariño Centro PASTORIZA (Nº 3) Sumario 1 Los poliedros... 3 1.1
Un poliedro es un cuerpo geométrico que tiene todas sus caras planas y formadas por polígonos.
 CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
CUERPOS GEOMÉTRICOS Los cuerpos geométricos son figuras geométricas tridimensionales (tienen alto, ancho y largo) que ocupan un lugar en el espacio. 1. POLIEDROS. 1.1. DEFINICIÓN. Un poliedro es un cuerpo
Diferencias entre Figuras y
 10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
10 Lección Refuerzo Matemáticas Diferencias entre Figuras y Cuerpos Geométricos APRENDO JUGANDO Competencia Aplica conocimientos acerca de las principales características de polígonos y cuerpos geométricos.
SOLUCIONES MINIMOS 2º ESO TEMA 8 CUERPOS GEOMÉTRICOS
 SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
SOLUCIONES MINIMOS º ESO TEMA 8 CUERPOS GEOMÉTRICOS Ejercicio nº 1.- Escribe el nombre de cada uno de los elementos de este poliedro: Ejercicio nº.- Cuáles de las siguientes figuras son poliedros? Por
Conceptos geométricos II
 Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
Conceptos geométricos II Ángulo Ángulos Consecutivos Ángulos Alternos y Ángulos Correspondientes Polígono Polígono Regular Polígono Irregular Triángulo Cuadrilátero Superficie Círculo Superficie reglada
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO
 DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
DE PRISMAS Y POLIEDROS. A LA BÚSQUEDA DEL CUBOIDE PERFECTO De poliedros En el espacio euclídeo tridimensional podemos resumir algunas nociones básicas de geometría clásica Un poliedro es la zona espacial
Diagonal: es un segmento que une dos vértices no consecutivos del poliedro. Puede trazarse en una misma cara o entre distintas caras.
 CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
CLASIFICASION DE CUERPOS GEOMETRICOS 1 2 Cuerpos Geométrico s Ángulo diedro: es el ángulo formado por dos caras del poliedro. El ángulo formado por tres o más caras que concurren en un vértice, se denomina
MATEMÁTICAS (GEOMETRÍA)
 COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
COLEGIO COLOMBO BRITÁNICO Formación en la Libertad y para la Libertad MATEMÁTICAS (GEOMETRÍA) GRADO:7 O DOCENTE: Nubia E. Niño C. FECHA: 8 / 07 / 15 Guía Didáctica 3-2 Desempeños: * Reconoce y clasifica
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA
 RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
RESUMEN DE VARIOS CONCEPTOS BÁSICOS DE GEOMETRÍA 1.- Figuras Congruentes y Semejantes. Teorema de Thales. Escalas. - Se dice que dos figuras geométricas son congruentes si tienen la misma forma y el mismo
MYP (MIDDLE YEARS PROGRAMME)
 MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MYP (MIDDLE YEARS PROGRAMME) 2014-2015 Fecha 19/05/2015 APUNTES DE GEOMETRÍA 2º ESO 1. EL TEOREMA DE PITÁGORAS El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa
MÓDULO Nº 3. Nivelación. Matemática Módulo Nº3. Contenidos. Polígonos Circunferencia y Círculo Volúmenes
 MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
Geometría. Cuerpos Geométricos. Trabajo
 Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
IES CUADERNO Nº 8 NOMBRE: FECHA: / / Cuerpos geométricos
 Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Cuerpos geométricos Contenidos 1. Poliedros Definición Elementos de un poliedro 2. Tipos de poliedros Prismas Prismas regulares Desarrollo de un prisma recto Paralelepípedos Pirámides Pirámides regulares
Matemática. Desafío. GUÍA DE EJERCITACIÓN AVANZADA Cuerpos geométricos GUICEN032MT22-A16V1
 GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
GUÍ DE EJERCITCIÓN VNZD Cuerpos geométricos Programa Entrenamiento Desafío GUICEN02MT22-16V1 Matemática Una semiesfera tiene un área total de 4π cm 2. Si se corta por la mitad, de manera de formar dos
Geometría. Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid
 Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Geometría Jesús García de Jalón de la Fuente IES Ramiro de Maeztu Madrid Ángulos Un ángulo es la región del plano limitada por dos semirrectas con el origen común. Lados Vértice Clasificación de los ángulos
Trabajo de Investigación Cuerpos Geométricos
 Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
Saint George s College Área de Matemáticas y sus Aplicaciones Tercera Unidad Trabajo de Investigación Cuerpos Geométricos Integrantes: -Stefan Jercic -Ignacio Larrain -Cristian Majluf Curso: 10 E Profesora:
SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL
 G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
G3D1: Sólidos convexos y cóncavos SÓLIDOS EN EL ESPACIO TRIDIMENSIONAL Pon tres ejemplos de objetos cotidianos que sean convexos: Pon tres ejemplos de objetos cotidianos que sean cóncavos: G3D2: Caracterización
Circunradio y Volumen de Poliedros
 Circunradio y Volumen de Poliedros Julio Castiñeira Merino. Introducción A mis queridos nietos Santiago, Gonzalo y Nicolás Una parte importante de los poliedros convexos con caras regulares son inscribibles
Circunradio y Volumen de Poliedros Julio Castiñeira Merino. Introducción A mis queridos nietos Santiago, Gonzalo y Nicolás Una parte importante de los poliedros convexos con caras regulares son inscribibles
CONOCER Y DIFERENCIAR LOS POLIEDROS REGULARES
 OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
OJETIVO 1 CONOCER Y DIERENCIR LOS POLIEDROS REGULRES NOMRE: CURSO: ECH: CONCEPTO DE POLIEDRO Vértice Un poliedro es un cuerpo geométrico cuyas caras son polígonos. Los elementos del poliedro son: Caras:
Ámbito científico tecnológico
 Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Dirección Xeral de Educación, Formación Profesional e Innovación Educativa Educación secundaria para personas adultas Ámbito científico tecnológico Educación a distancia semipresencial Módulo Unidad didáctica
Cuerpos geométricos. Volúmenes
 4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
4 uerpos geométricos. Volúmenes. Poliedros Un poliedro es un cuerpo geométrico limitado por cuatro o más polígonos planos. Los elementos de un poliedro son: aras: son los polígonos que lo delimitan. ristas:
Geometría del espacio
 Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
Áreas y volumenes de cuerpos geométricos Un poliedro es un cuerpo geométrico que está limitado por cuatro o más polígonos. Los elementos de un poliedro son: Caras del poliedro: son los polígonos que lo
congruentes es porque tienen la misma longitud AB = CD y, cuando dos ángulos DEF son congruentes es porque tienen la misma medida
 COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
COLEGIO COLMBO BRITÁNICO DEPARTAMENTO DE MATEMÁTICAS GEOMETRÍA NOVENO GRADO PROFESORES: RAÚL MARTÍNEZ, JAVIER MURILLO Y JESÚS VARGAS CONGRUENCIA Y SEMEJANZA Cuando tenemos dos segmentos escribimos AB CD
Los Cuerpos Geométricos
 06 Lección Apertura Matemáticas Los Cuerpos Geométricos APRENDO JUGANDO Competencia Describe qué son e identifica las características de los cuerpos geométricos. Diseño instruccional El maestro comenta
06 Lección Apertura Matemáticas Los Cuerpos Geométricos APRENDO JUGANDO Competencia Describe qué son e identifica las características de los cuerpos geométricos. Diseño instruccional El maestro comenta
MATEMÁTICAS 1º DE ESO
 MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
MATEMÁTICAS 1º DE ESO LOE TEMA XII: POLIEDROS Y CUERPOS DE REDONDOS Poliedros. o Elementos de un poliedro y desarrollo plano. Prismas. o Elementos y tipos de prismas. Pirámides. o Elementos y tipos de
Poliedro cóncavo: es aquel que no cumple la propiedad anterior. Una recta puede cortarlo por más de dos puntos.
 El sistema diédrico D13 El prisma Poliedros Poliedro es un cuerpo geométrico limitado por polígonos. Caras del poliedro son los polígonos que lo limitan. Vértices son los vértices de las caras. Aristas
El sistema diédrico D13 El prisma Poliedros Poliedro es un cuerpo geométrico limitado por polígonos. Caras del poliedro son los polígonos que lo limitan. Vértices son los vértices de las caras. Aristas
Geometría en el espacio. Poliedros
 Geometría en el espacio. Gemma Hermida Granado Trinidad Gómez Ramírez 28 de junio de 2006 Geometría en el espacio. 1 Programación de la unidad Objetivos didácticos Conceptos Procedimientos Actitudes Criterios
Geometría en el espacio. Gemma Hermida Granado Trinidad Gómez Ramírez 28 de junio de 2006 Geometría en el espacio. 1 Programación de la unidad Objetivos didácticos Conceptos Procedimientos Actitudes Criterios
Liceo N 1 Javiera Carrera 8 años 2011
 GUIA DE ESTUDIO : Cuerpos geométricos Prof. Juan Schuchhardt E. DEFINICIÓN: Los poliedros son aquellos cuerpos geométricos que están limitados por superficies planas y de contorno poligonal. Un poliedro
GUIA DE ESTUDIO : Cuerpos geométricos Prof. Juan Schuchhardt E. DEFINICIÓN: Los poliedros son aquellos cuerpos geométricos que están limitados por superficies planas y de contorno poligonal. Un poliedro
Qué son los cuerpos geométricos?
 Qué son los cuerpos geométricos? Definición Los cuerpos geométricos son regiones cerradas del espacio. Una caja de tetrabrick es un ejemplo claro de la figura que en matemáticas se conoce con el nombre
Qué son los cuerpos geométricos? Definición Los cuerpos geométricos son regiones cerradas del espacio. Una caja de tetrabrick es un ejemplo claro de la figura que en matemáticas se conoce con el nombre
a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta.
 POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
POLIEDROS Ejercicio nº 1.- a De los siguientes cuerpos geométricos, di cuáles son poliedros y cuáles no. Razona tu respuesta. b Cuál es la relación llamada fórmula de Euler que hay entre el número de caras,
TEMA 9 CUERPOS GEOMÉTRICOS
 Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Tel: 98 9 6 91 Fax: 98 1 89 96 TEMA 9 CUERPOS GEOMÉTRICOS Objetivos / Criterios de evaluación O.1.1 Conocer las fórmulas de áreas y volúmenes de figuras geométricas sencillas de D. O.1. Resolver problemas
Sistemas de Representación y Dibujo Técnico Año 2015. Geometría Básica
 EL PUNTO Geometría Básica El punto es la entidad geométrica más pequeña y finita. Se puede definir por intersección de 2 rectas. En un plano, se puede definir por medio de 2 coordenadas. En el espacio,
EL PUNTO Geometría Básica El punto es la entidad geométrica más pequeña y finita. Se puede definir por intersección de 2 rectas. En un plano, se puede definir por medio de 2 coordenadas. En el espacio,
5º de E. Primaria LOS CUERPOS GEOMÉTRICOS -TEMA 15
 LOS POLIEDROS Los poliedros son cuerpos geométricos que tienen todas sus caras formadas por polígonos. Muchos objetos de nuestro alrededor tienen forma de poliedro: Los elementos de un poliedro son caras,
LOS POLIEDROS Los poliedros son cuerpos geométricos que tienen todas sus caras formadas por polígonos. Muchos objetos de nuestro alrededor tienen forma de poliedro: Los elementos de un poliedro son caras,
geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia
 geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia CBC TALLER DE DIBUJO Cátedra Arq. VÍCTOR MURGIA 2008 3 INTRODUCCIÓN AL LENGUAJE GEOMÉTRICO línea recta Este texto trata sobre conceptos básicos
geometría 2008 cbc taller de dibujo cátedra arq. víctor murgia CBC TALLER DE DIBUJO Cátedra Arq. VÍCTOR MURGIA 2008 3 INTRODUCCIÓN AL LENGUAJE GEOMÉTRICO línea recta Este texto trata sobre conceptos básicos
III: Geometría para maestros. Capitulo 1: Figuras geométricas
 III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
III: Geometría para maestros. Capitulo : Figuras geométricas SELECCIÓN DE EJERCICIOS RESUELTOS SITUACIONES INTRODUCTORIAS En un libro de primaria encontramos este enunciado: Dibuja un polígono convexo
UNIDAD DIDÁCTICA DE MATEMÁTICAS
 UNIDAD DIDÁCTICA DE MATEMÁTICAS Carnicer, Laura Chulia, Ángela Escudero, Pablo Herrero, Andrea 3º F, grupo tardes. Didáctica de la matemática. Identificación de los cuerpos geométricos: cubos, ortoedros,
UNIDAD DIDÁCTICA DE MATEMÁTICAS Carnicer, Laura Chulia, Ángela Escudero, Pablo Herrero, Andrea 3º F, grupo tardes. Didáctica de la matemática. Identificación de los cuerpos geométricos: cubos, ortoedros,
Cuerpos geométricos OBJETIVOS CONTENIDOS PROCEDIMIENTOS. Elementos de un poliedro y su desarrollo. Los poliedros regulares y sus características.
 826464 _ 0385-0396.qxd /2/07 09:27 Página 385 Cuerpos geométricos INTRODUCCIÓN Esta unidad completa la serie dedicada a la Geometría y afianza su comprensión mediante la descripción y desarrollo de las
826464 _ 0385-0396.qxd /2/07 09:27 Página 385 Cuerpos geométricos INTRODUCCIÓN Esta unidad completa la serie dedicada a la Geometría y afianza su comprensión mediante la descripción y desarrollo de las
11 POLIEDROS EJERCICIOS. 6 Cuántas caras, vértices y aristas hay en los siguientes poliedros? a) b) c)
 11 POLIEROS EJERIIOS 1 ibuja una línea recta en tu cuaderno. escribe algún segmento real en el techo de la clase que se cruce con la línea que has dibujado. 6 uántas caras, vértices y aristas hay en los
11 POLIEROS EJERIIOS 1 ibuja una línea recta en tu cuaderno. escribe algún segmento real en el techo de la clase que se cruce con la línea que has dibujado. 6 uántas caras, vértices y aristas hay en los
CUERPOS GEOMÉTRICOS. POLIEDROS
 INTRODUCCIÓN CUERPOS GEOMÉTRICOS - POLIEDROS Este texto te servirá para que estudies los contenidos sobre poliedros que fueron desarrollados por los distintos grupos en clases y tiene como objetivos que
INTRODUCCIÓN CUERPOS GEOMÉTRICOS - POLIEDROS Este texto te servirá para que estudies los contenidos sobre poliedros que fueron desarrollados por los distintos grupos en clases y tiene como objetivos que
4. GEOMETRÍA // 4.4. POLIEDROS.
 4. GEOMETRÍA // 4.4. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 Bibliografía. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas:
4. GEOMETRÍA // 4.4. POLIEDROS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 Bibliografía. Bibliografía. 1. Alsina, C., Pérez, R., Ruiz, C., Simetría dinámica, Serie Matemáticas:
Los cuerpos geométricos
 Los cuerpos geométricos Los poliedros y sus elementos Clasifica estos cuerpos en poliedros y no poliedros. A B C D E F G poliedros> B, D, E, F A, C, G no poliedros > Cuenta las caras, los vértices y las
Los cuerpos geométricos Los poliedros y sus elementos Clasifica estos cuerpos en poliedros y no poliedros. A B C D E F G poliedros> B, D, E, F A, C, G no poliedros > Cuenta las caras, los vértices y las
Piden: Dato: Piden: Dato: Piden: Dato:
 SEMANA 1 PRISMAS Y PIRÁMIDE 1. Calcule el número de caras de un prisma donde el número de vértices más el número de aristas es 50. A) 10 B) 0 C) 0 D) 1 E) 18 Sea n el número de lados de la base del prisma:
SEMANA 1 PRISMAS Y PIRÁMIDE 1. Calcule el número de caras de un prisma donde el número de vértices más el número de aristas es 50. A) 10 B) 0 C) 0 D) 1 E) 18 Sea n el número de lados de la base del prisma:
INSTITUCION EDUCATIVA DIVERSIFICADO DE CHIA TALLER DE VOLUMENES Y POLIEDROS
 Sep. 18 de 2015 Señores Estudiantes grados Novenos El siguiente trabajo ya lo estamos realizando en clase, pero los datos que a continuación aparecen son refuerzo para terminar las figuras geométricas
Sep. 18 de 2015 Señores Estudiantes grados Novenos El siguiente trabajo ya lo estamos realizando en clase, pero los datos que a continuación aparecen son refuerzo para terminar las figuras geométricas
16. Geometría. con el ordenador
 16. Geometría con el ordenador Ámbito científico 1. Geometría con Cabri 2. Transformaciones geométricas 3. Lugares geométricos y cónicas 4. Poliedros con Poly 310 Geometría con el ordenador 1. Geometría
16. Geometría con el ordenador Ámbito científico 1. Geometría con Cabri 2. Transformaciones geométricas 3. Lugares geométricos y cónicas 4. Poliedros con Poly 310 Geometría con el ordenador 1. Geometría
Recuerda lo fundamental
 12 Figuras planas y espaciales Recuerda lo fundamental Curso:... Fecha:... TRIÁNGULOS Mediana de un triángulo es un segmento que...... Las tres medianas de un triángulo se cortan en el...... Las mediatrices
12 Figuras planas y espaciales Recuerda lo fundamental Curso:... Fecha:... TRIÁNGULOS Mediana de un triángulo es un segmento que...... Las tres medianas de un triángulo se cortan en el...... Las mediatrices
Poliedros Regulares Convexos
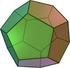 Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 [email protected] Poliedros Regulares
Poliedros Regulares Convexos Características y relaciones entre ellos AUTOR: Begoña Soler de Dios 1 Máster en Profesor de Educación Secundaria Esp. Matemáticas 1 [email protected] Poliedros Regulares
D18 Poliedros regulares
 El sistema diédrico D18 Poliedros regulares Clases de poliedros regulares convexos No pueden existir más de cinco clases de poliedros regulares convexos. Teniendo en cuenta que la suma de las caras de
El sistema diédrico D18 Poliedros regulares Clases de poliedros regulares convexos No pueden existir más de cinco clases de poliedros regulares convexos. Teniendo en cuenta que la suma de las caras de
Cuerpos geométricos. Objetivos. Antes de empezar. 1. Poliedros...pág. 138 Definición Elementos de un poliedro
 8 Cuerpos geométricos. Objetivos En esta quincena aprenderás a: Identificar que es un poliedro. Determinar los elementos de un poliedro: Caras, aristas y vértices. Clasificar los poliedros. Especificar
8 Cuerpos geométricos. Objetivos En esta quincena aprenderás a: Identificar que es un poliedro. Determinar los elementos de un poliedro: Caras, aristas y vértices. Clasificar los poliedros. Especificar
ELEMENTOS Y CLASES DE ÁNGULOS
 Apellidos: Curso: Grupo: Nombre: Fecha: ELEMENTOS Y CLASES DE ÁNGULOS Dos rectas que se cortan forman 4 regiones llamadas ángulos. Las partes de un ángulo son: los lados: son las semirrectas que lo forman.
Apellidos: Curso: Grupo: Nombre: Fecha: ELEMENTOS Y CLASES DE ÁNGULOS Dos rectas que se cortan forman 4 regiones llamadas ángulos. Las partes de un ángulo son: los lados: son las semirrectas que lo forman.
1. ESQUEMA - RESUMEN Página. 2. EJERCICIOS DE INICIACIÓN Página. 3. EJERCICIOS DE DESARROLLO Página. 4. EJERCICIOS DE AMPLIACIÓN Página
 1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 7 3. EJERCICIOS DE DESARROLLO Página 7 4. EJERCICIOS DE AMPLIACIÓN Página 9 5. EJERCICIOS DE REFUERZO Página 12 6. EJERCICIOS RESUELTOS
1. ESQUEMA - RESUMEN Página 2 2. EJERCICIOS DE INICIACIÓN Página 7 3. EJERCICIOS DE DESARROLLO Página 7 4. EJERCICIOS DE AMPLIACIÓN Página 9 5. EJERCICIOS DE REFUERZO Página 12 6. EJERCICIOS RESUELTOS
GEOMETRÍA DE 6º DE E.P. MARISTAS LA INMACULADA.
 GEOMETRÍA DE 6º DE E.P. MARISTAS LA INMACULADA. Profesor: Alumno:. Curso: Sección: 1. LAS FIGURAS PLANAS 2. ÁREA DE LAS FIGURAS PLANAS 3. CUERPOS GEOMÉTRICOS . FIGURAS PLANAS 1. Los polígonos y suss elementos
GEOMETRÍA DE 6º DE E.P. MARISTAS LA INMACULADA. Profesor: Alumno:. Curso: Sección: 1. LAS FIGURAS PLANAS 2. ÁREA DE LAS FIGURAS PLANAS 3. CUERPOS GEOMÉTRICOS . FIGURAS PLANAS 1. Los polígonos y suss elementos
POLÍGONOS POLÍGONOS. APM Página 1
 POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
MÓDULO Nº 4. Nivelación. Matemática 2005. Módulo Nº4. Contenidos. Circunferencia y Círculo Volúmenes
 MÓDULO Nº 4 Nivelación Matemática 2005 Módulo Nº4 Contenidos Circunferencia y Círculo Volúmenes Nivelación Circunferencia y Círculo Circunferencia. Es una línea curva cerrada, cuyos puntos tienen la propiedad
MÓDULO Nº 4 Nivelación Matemática 2005 Módulo Nº4 Contenidos Circunferencia y Círculo Volúmenes Nivelación Circunferencia y Círculo Circunferencia. Es una línea curva cerrada, cuyos puntos tienen la propiedad
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS.
 CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
CUERPOS GEOMÉTRICOS EN EL PLANO Y EN EL ESPACIO: APLICACIONES DIDÁCTICAS. Resumen AUTORIA FERNANDO VALLEJO LÓPEZ TEMÁTICA DIDÁCTICA DE LA MATEMÁTICA ETAPA ESO EN ÉSTE ARTÍCULO, SE ESTUDIAN LOS CUERPOS
Geometría Tridimensional. Capítulo de Preguntas. 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos?
 Geometría Tridimensional. Capítulo de Preguntas 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos? 2. Qué es volumen y cómo lo encontramos? 3. Cómo se relacionan los volúmenes
Geometría Tridimensional. Capítulo de Preguntas 1. Cuáles son las diferencias entre prismas y pirámides, y entre cilindros y conos? 2. Qué es volumen y cómo lo encontramos? 3. Cómo se relacionan los volúmenes
TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES
 TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN...1 2. SUPERFICIES POLIÉDRICAS. POLIEDROS...1 3. FIGURAS DE REVOLUCIÓN...3 4. POLIEDROS
TEMA 9: FIGURAS GEOMÉTRICAS ESPACIALES Matías Arce, Sonsoles Blázquez, Tomás Ortega, Cristina Pecharromán 1. INTRODUCCIÓN...1 2. SUPERFICIES POLIÉDRICAS. POLIEDROS...1 3. FIGURAS DE REVOLUCIÓN...3 4. POLIEDROS
GOBERNACIÓN DEL QUINDÍO SECRETARIA DE EDUCACIÓN DEPARTAMENTAL FICHA TÉCNICA. FABRICACIÓN: poliestireno, plástico, madera o MDF.
 GOBERNACIÓN DEL QUINDÍO SECRETARIA DE EDUCACIÓN DEPARTAMENTAL FICHA TÉCNICA DENOMINACIÓN DEL BIEN O SERVICIO DENOMINACIÓN TÉCNICA DEL BIEN O SERVICIO UNIDAD DE MEDIDA DESCRIPCIÓN 48 figuras distribuidas
GOBERNACIÓN DEL QUINDÍO SECRETARIA DE EDUCACIÓN DEPARTAMENTAL FICHA TÉCNICA DENOMINACIÓN DEL BIEN O SERVICIO DENOMINACIÓN TÉCNICA DEL BIEN O SERVICIO UNIDAD DE MEDIDA DESCRIPCIÓN 48 figuras distribuidas
MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) TALLER DE REPASO PARA EL BIMESTRAL 3P
 COLEGIO COLOMBO BRITANICO Formación en la Libertad y para la Libertad MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) GRADO:7 O DOCENTES: Natalia A. Gil V. Nubia E. Niño C. FECHA: 18 / 08 /15 Taller Adicional
COLEGIO COLOMBO BRITANICO Formación en la Libertad y para la Libertad MATEMÁTICAS (TIC) REPASO BIMESTRAL (3P) GRADO:7 O DOCENTES: Natalia A. Gil V. Nubia E. Niño C. FECHA: 18 / 08 /15 Taller Adicional
TETRAEDRO CUBO OCTAEDRO DODECAEDRO ICOSAEDRO
 6.- SÓLIDOS Al finalizar el sexto curso de Educación Primaria, los estudiantes deben describir cuerpos geométricos usando el vocabulario apropiado con términos como vértices, caras, aristas, planos, diedros,
6.- SÓLIDOS Al finalizar el sexto curso de Educación Primaria, los estudiantes deben describir cuerpos geométricos usando el vocabulario apropiado con términos como vértices, caras, aristas, planos, diedros,
RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS
 RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS. 1.-Calcule la superficie total de un tetraedro cuya arista mide 2 (12 3 ) 2.- Se tiene un tetraedro cuya arista mide 6 3 cm. Calcular.- 2.1.-La superficie
RESUMEN DE FORMULAS EJERCICIOS de APLICACIÓN POLIEDROS. 1.-Calcule la superficie total de un tetraedro cuya arista mide 2 (12 3 ) 2.- Se tiene un tetraedro cuya arista mide 6 3 cm. Calcular.- 2.1.-La superficie
open green road Guía Matemática CUERPOS GEOMÉTRICOS tutora: Jacky Moreno .co
 Guía Matemática CUERPOS GEOMÉTRICOS tutora: Jacky Moreno.co 1. Geometría en el espacio Al observar nuestro alrededor podemos notar una infinidad de objetos que ocupan un lugar en el espacio físico en el
Guía Matemática CUERPOS GEOMÉTRICOS tutora: Jacky Moreno.co 1. Geometría en el espacio Al observar nuestro alrededor podemos notar una infinidad de objetos que ocupan un lugar en el espacio físico en el
Los cuerpos geométricos
 Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Los cuerpos geométricos Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales que existen en la realidad o pueden concebirse mentalmente ocupan un volumen en el espacio desarrollándose
Polígonos y Poliedros
 09 Lección Apertura Matemáticas Polígonos y s Competencia Socializa sus ideas y llega a acuerdos con los que asimila conceptos relacionados con polígonos y poliedros. Diseño instruccional El maestro aclarará
09 Lección Apertura Matemáticas Polígonos y s Competencia Socializa sus ideas y llega a acuerdos con los que asimila conceptos relacionados con polígonos y poliedros. Diseño instruccional El maestro aclarará
Poliedros regulares Cuerpos de revolución
 Poliedros regulares Cuerpos de revolución Poliedro. Un poliedro es un cuerpo limitado por caras poligonales. Ángulo diedro. Ángulo poliedro Se llama ángulo diedro de un poliedro el que está formado por
Poliedros regulares Cuerpos de revolución Poliedro. Un poliedro es un cuerpo limitado por caras poligonales. Ángulo diedro. Ángulo poliedro Se llama ángulo diedro de un poliedro el que está formado por
Districte Universitari de Catalunya
 Proves d accés a la universitat Convocatòria 2014 Dibujo técnico Serie 3 Indique las opciones escogidas: Ejercicio 1: Opción A Opción B Ejercicio 2: Opción A Opción B Ejercicio 3: Opción A Opción B Qualificació
Proves d accés a la universitat Convocatòria 2014 Dibujo técnico Serie 3 Indique las opciones escogidas: Ejercicio 1: Opción A Opción B Ejercicio 2: Opción A Opción B Ejercicio 3: Opción A Opción B Qualificació
11 Cuerpos geométricos
 89485 _ 0369-0418.qxd 1/9/07 15:06 Página 369 Cuerpos geométricos INTRODUCCIÓN Los poliedros, sus elementos y tipos ya son conocidos por los alumnos del curso anterior. Descubrimos y reconocemos de nuevo
89485 _ 0369-0418.qxd 1/9/07 15:06 Página 369 Cuerpos geométricos INTRODUCCIÓN Los poliedros, sus elementos y tipos ya son conocidos por los alumnos del curso anterior. Descubrimos y reconocemos de nuevo
Los poliedros y sus elementos
 Los poliedros y sus elementos De las siguientes figuras, rodea las que sean poliedros o tengan forma de poliedro. Dibuja y escribe el nombre de tres objetos que tengan forma de poliedro. espuesta libre
Los poliedros y sus elementos De las siguientes figuras, rodea las que sean poliedros o tengan forma de poliedro. Dibuja y escribe el nombre de tres objetos que tengan forma de poliedro. espuesta libre
LOS POLIEDROS. Los poliedros se clasifican en prismas y en pirámides.
 LOS POLIEDROS Una caja de zapatos, un dado y muchos otros objetos con superficies planas que ves a tu alrededor, tienen forma poliédrica. Se llaman poliedros a los cuerpos geométricos cuyas caras son polígonos.
LOS POLIEDROS Una caja de zapatos, un dado y muchos otros objetos con superficies planas que ves a tu alrededor, tienen forma poliédrica. Se llaman poliedros a los cuerpos geométricos cuyas caras son polígonos.
EJERCICIOS DE LOS TEMAS 9 y 10.GEOMETRÍA
 1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
Fórmula de Superficie de Área: Si dos sólidos son similares con un factor de. escala de entonces las áreas de superficie están en una relación de.
 Materia: Matemática de Séptimo Tema: Cálculo de Volumen Y si te dieran dos cubos similares y te preguntan cuál es el factor de escala de sus caras? Cómo encontrarías sus áreas de superficie y sus volúmenes?
Materia: Matemática de Séptimo Tema: Cálculo de Volumen Y si te dieran dos cubos similares y te preguntan cuál es el factor de escala de sus caras? Cómo encontrarías sus áreas de superficie y sus volúmenes?
Matemáticas Grado 4 Relacionar figuras bidimensionales y tridimensionales
 Matemáticas Grado 4 Relacionar figuras bidimensionales y tridimensionales Estimado padre o tutor legal: Actualmente su hijo/a está aprendiendo a relacionar figuras bidimensionales a objetos tridimensionales.
Matemáticas Grado 4 Relacionar figuras bidimensionales y tridimensionales Estimado padre o tutor legal: Actualmente su hijo/a está aprendiendo a relacionar figuras bidimensionales a objetos tridimensionales.
CUERPOS GEOMÉTRICOS. Clases de cuerpos geométricos. Los poliedros. Los poliedros regulares.
 CUERPOS GEOMÉTRICOS. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales - que existen en la realidad o pueden concebirse mentalmente - ocupan un volumen en el espacio desarrollándose
CUERPOS GEOMÉTRICOS. Se denominan cuerpos geométricos a aquellos elementos que, ya sean reales o ideales - que existen en la realidad o pueden concebirse mentalmente - ocupan un volumen en el espacio desarrollándose
Indicar y Justificar la verdad (V) o falsedad (F) de las siguientes afirmaciones:
 GEOMETRÍ DEL ESIO ompetencias: Reconoce a la recta y el plano en R. Describir las posiciones relativas entre dos planos y entre una recta y un lano. Describir el Teorema de las tres perpendiculares. Definir
GEOMETRÍ DEL ESIO ompetencias: Reconoce a la recta y el plano en R. Describir las posiciones relativas entre dos planos y entre una recta y un lano. Describir el Teorema de las tres perpendiculares. Definir
POLÍGONO ÁNGULOS DE UN POLÍGONO CLASIFICACIÓN: La denominación de polígono palabra compuesta de poli, del griego: muchos; y gonos del griego: ángulos
 POLÍGONO La denominación de polígono palabra compuesta de poli, del griego: muchos; y gonos del griego: ángulos Un polígono es una porción del plano limitada por una línea poligonal cerrada. Los segmentos
POLÍGONO La denominación de polígono palabra compuesta de poli, del griego: muchos; y gonos del griego: ángulos Un polígono es una porción del plano limitada por una línea poligonal cerrada. Los segmentos
5to Grado - Geometría, Medidas, y Algebra Estándar Básico 3. Evaluación.
 5to Grado - Geometría, Medidas, y Algebra Estándar Básico 3. Evaluación. 5.3.1 Identificar y clasificar triángulos de acuerdo a sus ángulos (agudo, recto, obtuso) y lados (escaleno, isósceles, equilátero).
5to Grado - Geometría, Medidas, y Algebra Estándar Básico 3. Evaluación. 5.3.1 Identificar y clasificar triángulos de acuerdo a sus ángulos (agudo, recto, obtuso) y lados (escaleno, isósceles, equilátero).
Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos
 Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos Cierto, mires por donde mires no podrás dejar de ver cuerpos geométricos de todo tipo. Por eso es importante
Ámbito Científico-Tecnológico Módulo IV Bloque 4 Unidad 4 Estamos rodeados de cuerpos. geométricos Cierto, mires por donde mires no podrás dejar de ver cuerpos geométricos de todo tipo. Por eso es importante
FIGURAS, ÁREAS Y PERÍMETROS
 FIGURAS, ÁREAS Y PERÍMETROS 05 Identifica propiedades de las figuras geométricas, de área y de perímetro y utiliza modelos con los que representa información matemática. Para hablar de áreas y perímetros,
FIGURAS, ÁREAS Y PERÍMETROS 05 Identifica propiedades de las figuras geométricas, de área y de perímetro y utiliza modelos con los que representa información matemática. Para hablar de áreas y perímetros,
CLASIFICACIÓN DE LAS FIGURAS Y CUERPOS GEOMÉTRICOS. Según los lados. Triángulos. Según los ángulos. Paralelogramo. Cuadriláteros.
 CLASIFICACIÓN DE LAS FIGURAS Y CUERPOS GEOMÉTRICOS Equilátero Polígonos Según los lados Isósceles Figuras geometrícas Nombre según los lados 3-Triángulo 4-Cuadrilátero 5-Pentágono 6-Hexágono 7-Heptágono
CLASIFICACIÓN DE LAS FIGURAS Y CUERPOS GEOMÉTRICOS Equilátero Polígonos Según los lados Isósceles Figuras geometrícas Nombre según los lados 3-Triángulo 4-Cuadrilátero 5-Pentágono 6-Hexágono 7-Heptágono
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
 ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO 1. Área y volumen del ortoedro y del cubo. 1.1. Área y volumen del ortoedro. 1.2. Cálculo de la diagonal del ortoedro. 1.3. Área y volumen del cubo. 2. Área y
Cuerpos geométricos: poliedros
 Cuerpos geométricos: poliedros Viajar desde la geometría en el plano hacia un espacio tridimensional, donde se insertan los cuerpos geométricos, nos acerca al mundo real. En el proceso de fabricación de
Cuerpos geométricos: poliedros Viajar desde la geometría en el plano hacia un espacio tridimensional, donde se insertan los cuerpos geométricos, nos acerca al mundo real. En el proceso de fabricación de
Polydrón. (Polígonos que se enganchan) José María Yáñez Sinovas. Ceip Vicente Aleixandre. Valladolid
 Polydrón (Polígonos que se enganchan) José María Yáñez Sinovas Ceip Vicente Aleixandre Valladolid 1-Descripción y posibilidades didácticas Este juego se compone de piezas de plástico que se pueden engarzar
Polydrón (Polígonos que se enganchan) José María Yáñez Sinovas Ceip Vicente Aleixandre Valladolid 1-Descripción y posibilidades didácticas Este juego se compone de piezas de plástico que se pueden engarzar
Ecuaciones: Ejercicios de la 3º Evaluación -- Dtpo de Matemáticas 3º Eso.
 Ecuaciones: Ejercicios de la 3º Evaluación -- Dtpo de Sistemas Ejercicios de a reas y volu menes I 1Calcula el volumen, en centímetros cúbicos, de una habitación que tiene 5 m de largo, 40 dm de ancho
Ecuaciones: Ejercicios de la 3º Evaluación -- Dtpo de Sistemas Ejercicios de a reas y volu menes I 1Calcula el volumen, en centímetros cúbicos, de una habitación que tiene 5 m de largo, 40 dm de ancho
Tema 6: Geometría en dimensión 3
 Tema 6: Geometría en dimensión 3 Contenidos: 1. Introducción. 2. Poliedros. 3. Volumen. Capacidad. Unidades. 4. Volumen de sólidos básicos: prismas y cilindros. 5. Volumen de pirámides y conos. 6. Volumen
Tema 6: Geometría en dimensión 3 Contenidos: 1. Introducción. 2. Poliedros. 3. Volumen. Capacidad. Unidades. 4. Volumen de sólidos básicos: prismas y cilindros. 5. Volumen de pirámides y conos. 6. Volumen
Carrera: Diseño Industrial
 POLÍGONOS 1) Dados los siguientes polígonos se pide determinar cuales de ellos son cóncavos y cuales convexos. Justifique sus respuestas. a) b) c) 2) En los polígonos graficados a continuación indique
POLÍGONOS 1) Dados los siguientes polígonos se pide determinar cuales de ellos son cóncavos y cuales convexos. Justifique sus respuestas. a) b) c) 2) En los polígonos graficados a continuación indique
CENTRO EDUCATIVO PAULO FREIRE TALLER
 CENTRO EDUCATIVO PAULO FREIRE TALLER 1: Una plaza circular está limitada por una circunferencia de longitud 188,4m. Determinar el diámetro y el área de la plaza. 2: Si el área de un círculo es 144 cm 2,
CENTRO EDUCATIVO PAULO FREIRE TALLER 1: Una plaza circular está limitada por una circunferencia de longitud 188,4m. Determinar el diámetro y el área de la plaza. 2: Si el área de un círculo es 144 cm 2,
Triángulos y Cuadriláteros
 04 Lección Apertura Matemáticas Triángulos y Cuadriláteros APRENDO JUGANDO Competencia Identifica las características de los triángulos y los cuadriláteros. Diseño instruccional Por la importancia que
04 Lección Apertura Matemáticas Triángulos y Cuadriláteros APRENDO JUGANDO Competencia Identifica las características de los triángulos y los cuadriláteros. Diseño instruccional Por la importancia que
EJERCICIOS MÓDULO 4. Geometría plana. 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9?
 Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
Seminario Universitario Matemática EJERCICIOS MÓDULO 4 Geometría plana 1) Cuántos vértices tiene un polígono cuyo número total de diagonales es 9? ) Cuántos lados tiene un polígono en el cual la suma de
MATEMÁTICAS Y SU DIDÁCTICA
 MATEMÁTICAS Y SU DIDÁCTICA ESCUELA UNIVERSITARIA DE MAGISTERIO SAGRADO CORAZÓN UNIVERSIDAD DE CÓRDOBA Curso académico: 2011 2012 ACTIVIDADES DE GEOMETRÍA TRABAJO EN GRUPO Las siguientes actividades se
MATEMÁTICAS Y SU DIDÁCTICA ESCUELA UNIVERSITARIA DE MAGISTERIO SAGRADO CORAZÓN UNIVERSIDAD DE CÓRDOBA Curso académico: 2011 2012 ACTIVIDADES DE GEOMETRÍA TRABAJO EN GRUPO Las siguientes actividades se
Estrellas en la Sagrada Familia de Gaudí: Un contexto nuevo para estudiar poliedros.
 Comunicación Estrellas en la Sagrada Familia de Gaudí. Un contexto nuevo para estudiar poliedros. Estrellas en la Sagrada Familia de Gaudí: Un contexto nuevo para estudiar poliedros. María de los Desamparados
Comunicación Estrellas en la Sagrada Familia de Gaudí. Un contexto nuevo para estudiar poliedros. Estrellas en la Sagrada Familia de Gaudí: Un contexto nuevo para estudiar poliedros. María de los Desamparados
Geometría en 3D: Preguntas del Capítulo
 Geometría en 3D: Preguntas del Capítulo 1. Cuáles son las similitudes y las diferencias entre prismas y pirámides? 2. Cómo se nombran los poliedros? 3. Cómo encuentras la sección transversal de una figura
Geometría en 3D: Preguntas del Capítulo 1. Cuáles son las similitudes y las diferencias entre prismas y pirámides? 2. Cómo se nombran los poliedros? 3. Cómo encuentras la sección transversal de una figura
CUADERNO Nº 8 NOMBRE: FECHA: / /
 Cuerpos geométricos Contenidos 1. Poliedros regulares Definiciones Desarrollos Planos de simetría Poliedros duales 2. Otros poliedros Prismas Pirámides Planos de simetría Poliedros semirregulares 3. Cuerpos
Cuerpos geométricos Contenidos 1. Poliedros regulares Definiciones Desarrollos Planos de simetría Poliedros duales 2. Otros poliedros Prismas Pirámides Planos de simetría Poliedros semirregulares 3. Cuerpos
Hay 5 sólidos platónicos
 1 Un sólido es un poliedro, o sea una figura tridimensional conformada por planos de diversas formas (polígonos) que se intersectan. Hay 5 sólidos platónicos Fueron estudiados y descriptos por los geómetras
1 Un sólido es un poliedro, o sea una figura tridimensional conformada por planos de diversas formas (polígonos) que se intersectan. Hay 5 sólidos platónicos Fueron estudiados y descriptos por los geómetras
GEOMETRIA 8 AÑO 2011 1. Nombre:.Curso:
 GEOMETRIA 8 AÑO 2011 1 GUÍA DE APOYO AL TEMA : GEOMETRÍA Prof. Juan Schuchhardt E. Nombre:.Curso: UNIDAD #4 GEOMETRIA Tema # 2: Cuerpos geométricos En esta unidad aprenderás a: Identificar cuerpos poliédricos,
GEOMETRIA 8 AÑO 2011 1 GUÍA DE APOYO AL TEMA : GEOMETRÍA Prof. Juan Schuchhardt E. Nombre:.Curso: UNIDAD #4 GEOMETRIA Tema # 2: Cuerpos geométricos En esta unidad aprenderás a: Identificar cuerpos poliédricos,
10 FIGURAS Y CUERPOS GEOMÉTRICOS
 EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10.2 Completa la siguiente tabla. Caras (C ) Vértices (V ) Aristas (A) C V A 2 Tetraedro 4
EJERCICIOS PROPUESTOS 10.1 Indica cuál de estos poliedros es cóncavo y cuál es convexo. a) Cóncavo b) Convexo 10.2 Completa la siguiente tabla. Caras (C ) Vértices (V ) Aristas (A) C V A 2 Tetraedro 4
Matemáticas UNIDAD 6 CONSIDERACIONES METODOLÓGICAS. Material de apoyo para el docente. Preparado por: Héctor Muñoz
 CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 6 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl SISTEMATIZACIÓN DE CONOCIMIENTOS ACERCA DE FIGURAS Y CUERPOS
CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 6 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl SISTEMATIZACIÓN DE CONOCIMIENTOS ACERCA DE FIGURAS Y CUERPOS
PRIMERO DE ESO Primer trimestre TEMA UNO: LA COMUNICACIÓN VISUAL
 PRIMERO DE ESO Primer trimestre TEMA UNO: LA COMUNICACIÓN VISUAL 1. La comunicación visual y sus tipos. 2. Elementos de la comunicación visual. 3. Principales canales de comunicación: prensa, televisión,
PRIMERO DE ESO Primer trimestre TEMA UNO: LA COMUNICACIÓN VISUAL 1. La comunicación visual y sus tipos. 2. Elementos de la comunicación visual. 3. Principales canales de comunicación: prensa, televisión,
