Ayudantía 2 - Solución
|
|
|
- José Ignacio Toledo Valenzuela
- hace 9 años
- Vistas:
Transcripción
1 Ayudantía - Solución Profesor: Ricardo Ramírez Ayudante: Juan Pablo Garrido L ([email protected]) Problema Un recipiente semihemisferico no conductor de radio a tiene una carga total Q uniformemente distribuida en su supercie interior. Encuentre el campo eléctrico en el punto O. Solución: Este problema lo debemos resolver utilizando la lay de coulomb para distribuciones superciales de carga. Esta ley nos dice para este caso ue kd( r r E( ) = ) r r 3 Como ya hemos visto, el elemento de carga lo podemos escribir como d = σda, donde σ es la densidad de carga supercial en el interior del recipiente (constante). Debemos escribir el elemento de área da de tal manera ue podamos recorrer la supercie y para esto haremos lo siguiente: Considerare una cascara esférica con la siguiente disposición para las variables θ y γ
2 Al hacer una peueña variación del ángulo θ, vemos ue se recorre un peueño arco de longitud ds = R sin(γ)θ. Por otro lado al hacer una peueña variación del ángulo γ se recorre un arco de longitud ds = Rdγ. De esta manera el elemento de área de la circunferencia lo podemos escribir como da = ds ds = R sin(γ)dγdθ De esta manera podemos escribir el elemento de carga como d = σr sin(γ)dγdθ Por otro lado, debemos determinar los vectores r y r. Claramente r = y por otro lado(mirando la gura) veremos ue r = R sin(γ) cos(θ)î + R sin(γ) sin(θ)ĵ + R cos(γ)ˆk No es difícil ver ue r r = R De esta manera especicando los recorridos de las variables para ue recorran el recipiente se tiene ue E( ) = π 3π π kσ( R sin(γ) cos(θ)î R sin(γ) sin(θ)ĵ R cos(γ)ˆk) R 3 R sin(γ)dγdθ Por simetría sabemos ue el campo eléctrico resultante estará en dirección ˆk y por lo tanto, de la integral anterior, no consideramos las componentes restantes: E( ) = π π π De esta manera π π kσ( cos(γ)ˆk) sin(γ)dγdθ = kσ dθ ( cos(γ)ˆk) sin(γ)dγ = πkσ π E( ) = πkσ( π cos(θ) )ˆk = πkσ (cos(π) cos(π))ˆk = (πkσ)ˆk π Finalmente, para escribir este resultado en función de Q, debemos determinar el valor de σ. Esto es fácil sabiendo ue la carga esta uniformemente distribuida en la supercie interior, tendremos ue De esta manera σ = Q πr E( ) = kq R ˆk π π ( sin(θ)ˆk))dγ
3 Problema En la gura, el alambre AB tiene longitud L y es perpendicular al alambre CD, de longitud L. Cada uno de ellos tiene la misma carga Q, distribuida uniformemente. Calcule la magnitud y dirección de la fuerza ue uno de ellos ejerce sobre el otro. Solución: Este problema se resuelve de igual forma ue el problema anterior. Lo primero ue haremos es calcular el campo eléctrico ue produce el alambre vertical sobre un punto de su eje de simetría. Como la carga Q esta uniformemente distribuida, se tendrá ue sobre el eje el campo eléctrico estará en dirección ĵ El campo eléctrico producido por una carga d será de = kd r. Donde r es la distancia desde la carga d ubicada en xî hasta el punto de aplicación dĵ: r = x + d. Al igual como lo hemos hecho antes, la carga d la podemos escribir como d = λ dx donde λ es la densidad lineal de carga y la denimos como λ = Q L. Asi, el campo ueda expresado como de = kλ dx x + d Ya dijimos ue el campo estará en dirección ĵ ya ue las componentes en x se anularan. Las componentes en y las podemos escribir como de y = de cos(θ). Es facil ver ue cos(θ) = d (x + d ) 3
4 De esta manera Integrando desde x = L hasta x = L: L E y = kλ d L de y = kλ ddx (x + d ) 3 x dx = kλ (x + d ) 3 d( (d x + d L L ) = kλ L d L + d De esta manera la fuerza ue ejerce el alambre horizontal sobre una peueña carga d del alambre vertical ue esta a una altura y será kλ L df = de = d d L + y Este alambre tiene distinta densidad de carga ya ue si bien tiene la misma carga total almacenada, tiene la mitad de largo ue el alambre horizontal. De esta manera denimos λ = Q L Asi, d = λ dy y la fuerza ueda expresada como Integrando desde y = L hasta y = L Se tiene ue Por lo tanto Desarrollando kλ L df = λ dy y L + y L F = kλ λ L L y L + y dy y L + y dy = L L ln( + y L ) y F = kλ λ L( L ln( L + y L y 5 F = kλ λ ln( ( ) ) Reemplazando los valores de λ y λ en función de Q: F = kq L 5 ln( ( ) ) ) L L ) 4
5 Problema 3 Considere un alambre rectilíneo innito a una distancia R de un alambre semicircular de radio R como se ve en la gura. Ambos están uniformemente cargados con densidad lineal de carga λ. Encuentre la fuerza de repulsión entre ambas. Solución: Lo primero ue hacemos es calcular el campo eléctrico producido por un alambre innito a una distancia d de él. El campo eléctrico tendrá dirección ĵ ya ue al ser el alambre innitamente largo se anularan las componentes de campo en x. Esto se puede apreciar en la siguiente gura: Comprobemos esto calculando el campo. El campo eléctrico ue produce una peueña carga d ubicada en el punto r = xî del alambre sobre el punto de r = dĵ será: d E = kd( r r ) r r 3 Ahora, se tiene ue d = λdx y por lo tanto: = kd( xî + dĵ) (x + d ) 3 d E = kλdx( xî + dĵ) (x + d ) 3 Integrando desde a + : E = + kλdx( xî + dĵ) (x + d ) 3 + = kλ(( x (x + d ) 3 + )î + ( d )ĵ) (x + d ) 3 5
6 La función f(x) = x (x +d ) 3 par toma valor. Por otro lado, la función g(x) = es impar y por lo tanto la integral de esta función en un intervalo d (x +d ) 3 desde a + será el doble de la integral de g(x) desde a + : + g(x)dx = + Por lo tanto, la expresión para el campo se reduce a Se tiene ue (x +d ) 3 Por lo tanto = x d (x +d ) + E = kdλ x E = kdλ( d (x + d ) 3 g(x)dx ĵ (x + d ) 3 es par y la integral de esta función )ĵ = kλ d ĵ Ahora ue sabemos como es el campo eléctrico generado por un alambre innito podemos calcular la fuerza sobre el alambre semicircular. Para calcular esta fuerza consideraremos peueños trozos de cable con carga d en el cual la fuerza aplicada sobre el será por denición:df = de, donde E es el campo eléctrico producido por el alambre innito a la altura en ue se encuentra la carga d. Recorreré los elementos de carga del alambre en función de un ángulo θ ue recorra el alambra semicircular. Considerare la siguiente gura: El campo eléctrico producido por el alambre innito depende de la distancia a la cual se esta de el, como la altura de cada elemento d de carga varia, la fuerza producida sobre cada una de estas cargas también lo hará. La altura de cada elemento d en función del ángulo θ ueda expresada como d(θ) = R + R sin(θ). Además, el elemento de carga d es por denición igual a λds, donde ds es un peueño trozo de alambre circular el cual podemos escribir en función del ángulo θ como ds = Rdθ. De esta manera la fuerza sobre una carga d será: df = de = λrdθ kλ R + R sin(θ) = kλ dθ + sin(θ) 6
7 Integrando desde θ = a θ = π obtenemos la fuerza total sobre el alambre semicircular. Para esto utilizamos el hecho de ue: Con esto tenemos ue la fuerza resultante es + sin(θ) = sin(θ) cos(θ) F = 4kλ 7
8 Problema 4 Una carga puntual > esta rodeada por una supercie cerrada formada por un manto cónico de radio R y altura H, y una supercie semiesférica concéntrica con la carga, según se observa en la gura. Calcule el ujo de campo eléctrico a través del manto cónico. Solución: La supercie ue rodea a la carga es cerrada. Por la ley de gauss, el ujo a través de la supercie es: φ = S E d S = ɛ () Además, el ujo ue atraviesa la supercie cerrada (ue llamamos S) será igual a la suma de los ujos ue pasen por la semiesfera (ue llamamos S e ) y los ujos ue pasen por el manto cónico(ue llamamos S c ). Esto se puede escribir como: φ = φ e + φ c = φ c = φ + φ e () De esta manera, encontrando el valor de φ e resolvemos el problema inmediatamente. φ e se calcula como: φ e = S e E d S El campo eléctrico producido por la carga es E = 4πɛ R ˆr. Donde ˆr es el vector unitario en dirección radial. El vector ds también esta en dirección radial, ya ue ds = ˆndS y ˆn es paralelo a ˆr como muestra la gura: De esto, se tendrá ue E d S = 4πɛ Integrando se obtiene el ujo para la semiesfera: φ e = E d S = S e S e 4πɛ ˆr ˆndS = R 4πɛ R ds = 4πɛ R ds R ds S e La integral S e ds corresponde al área de la semiesfera. Entonces S e ds = πr. De esta manera el ujo será: φ e = 4πɛ R πr = ɛ (3) 8
9 De (),() y (3) se tiene nalmente ue: φ c = ɛ 9
10 Problema 5 Considere un cilindro muy largo de radio R ue se carga en su interior con una densidad ρ = ρ ( r R ), donde ρ es una constante positiva, siendo r la distancia medida desde el eje del cilindro. Encuentre a ue distancia del eje el campo eléctrico es máximo y calcule esta magnitud máxima. Solución: Dado ue el cilindro es muy largo, el campo eléctrico estará en dirección radial en coordenadas cilíndricas. Con esto podemos considerar como supercie de gauss un cilindro de radio r < R, con igual eje ue el cilindro de radio R. Esto se puede apreciar en la siguiente gura: Podemos entonces escribir el campo eléctrico como E = Eˆr, donde ˆr es el vector unitario radial en coordenadas cilíndricas. Por la ley de gauss se tendrá ue: E ˆndS = E ˆndS + E ˆndS = interior () S tapas manto ɛ El vector normal ˆn de las tapas es perpendicular a ˆr. Con esto se tendrá ue ˆr ˆn = y por lo tanto E ˆndS = Eˆr ˆndS = () tapas tapas El vector ˆn, normal al manto, será paralelo a ˆr y por lo tanto ˆr ˆn = lo ue implica ue: E ˆndS = Eˆr ˆndS = E ds manto manto manto La integral manto ds corresponde al área del manto: manto ds = πrl. Por lo tanto: E ˆndS = E πrl (3) manto Reemplazando () y (3) en () resulta ue: E πrl = interior ɛ (4)
11 Lo ue falta para resolver este problema es calcular la carga ue hay en el interior de la super- cie de gauss. Tenemos una densidad volumétrica de carga eléctrica dentro de esta supercie. Vemos ue se cumplirá la siguiente relación: d = ρ(r ) dv (5) Para calcular dv consideramos el volumen entre dos cilindros de la largo L y mismo eje ue el cilindro del problema, con radios r y r + dr como muestra la gura: Luego, dv será simplemente el volumen entre los dos cilindros, lo ue resulta: dv = πr dr L (6) Reemplazando (6) en (5): Integrando: d = πr dr L p(r ) d = πr dr L ρ ( r R ) = d = πl ρ (r r R )dr De (4) y (7): Despejando E: r = πlρ (r r R )dr = πlρ ( r r r dr r R dr ) = = πlρ ( r r3 3R ) = πlρ ( 3Rr r 3 ) 6R = = πlρ 3R (3Rr r 3 ) (7) E πrl = πlρ 3Rɛ (3Rr r 3 ) E = ρ 6Rɛ (3Rr r ) (8)
12 Queremos saber para ue valor de r el campo eléctrico es maximo. Para esto derivamos E respecto a r: de dr = ρ 6Rɛ (3R 4r) Igualando a se obtiene ue el valor de r buscado es: r = 3R 4 De esta manera E max = 3ρ R 6ɛ
Electromagnetismo I. Semestre: TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado
 Electromagnetismo I Semestre: 01- TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruí 1.- Problema: (5pts) (a) Doce cargas iguales q se encuentran localiadas en los vérices
Electromagnetismo I Semestre: 01- TAREA 1 Y SU SOLUCIÓN Dr. A. Reyes-Coronado Solución por Carlos Andrés Escobar Ruí 1.- Problema: (5pts) (a) Doce cargas iguales q se encuentran localiadas en los vérices
AUXILIAR 1 PROBLEMA 1
 AUXILIAR 1 PROBLEMA 1 Calcular el campo eléctrico en cualquier punto del espacio, producido por una recta de carga infinita (con densidad lineal de carga λ0). Luego, aplicar el teorema de Gauss para obtener
AUXILIAR 1 PROBLEMA 1 Calcular el campo eléctrico en cualquier punto del espacio, producido por una recta de carga infinita (con densidad lineal de carga λ0). Luego, aplicar el teorema de Gauss para obtener
E 1.3. LA LEY DE GAUSS
 E 1.3. LA LEY DE GAUSS E 1.3.1. Calcule el flujo del campo eléctrico producido por un disco circular de radio R [m], uniformemente cargado con una densidad σ [C/m 2 ], a través de la superficie de una
E 1.3. LA LEY DE GAUSS E 1.3.1. Calcule el flujo del campo eléctrico producido por un disco circular de radio R [m], uniformemente cargado con una densidad σ [C/m 2 ], a través de la superficie de una
GUÍA 1: CAMPO ELÉCTRICO Electricidad y Magnetismo
 GUÍA 1: CAMPO ELÉCTRICO Primer Cuatrimestre 2013 Docentes: Dr. Alejandro Gronoskis Lic. María Inés Auliel Andrés Sabater Universidad Nacional de Tres de febrero Depto de Ingeniería Universidad de Tres
GUÍA 1: CAMPO ELÉCTRICO Primer Cuatrimestre 2013 Docentes: Dr. Alejandro Gronoskis Lic. María Inés Auliel Andrés Sabater Universidad Nacional de Tres de febrero Depto de Ingeniería Universidad de Tres
Introducción. Flujo Eléctrico.
 Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
Capítulo 16. Electricidad
 Capítulo 16 Electricidad 1 Carga eléctrica. Ley de Coulomb La carga se mide en culombios (C). La del electrón vale e = 1.6021 10 19 C. La fuerza eléctrica que una partícula con carga Q ejerce sobre otra
Capítulo 16 Electricidad 1 Carga eléctrica. Ley de Coulomb La carga se mide en culombios (C). La del electrón vale e = 1.6021 10 19 C. La fuerza eléctrica que una partícula con carga Q ejerce sobre otra
Calcular la diferencia de potencial entre el centro de la esfera y el infinito.
 Problema 2.1 Carga volumétrica, principio de superpo- sición Figura 2.1. Esfera con distribución de carga no simétrica (Problema 2.1) Una esfera no conductora de radio R está dividida es dos semiesferas.
Problema 2.1 Carga volumétrica, principio de superpo- sición Figura 2.1. Esfera con distribución de carga no simétrica (Problema 2.1) Una esfera no conductora de radio R está dividida es dos semiesferas.
2.1 Introducción. 2.2 Flujo sobre una superficie. 42 Ley de Gauss
 2 Ley de Gauss 42 Ley de Gauss 2.1 Introducción En el capítulo anterior enunciamos las leyes fundamentales de la electrostática. La ley de Coulomb para una carga puntual y el principio de superposición
2 Ley de Gauss 42 Ley de Gauss 2.1 Introducción En el capítulo anterior enunciamos las leyes fundamentales de la electrostática. La ley de Coulomb para una carga puntual y el principio de superposición
1 Funciones de Varias Variables
 EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
EJECICIOS DE FUNDAMENTOS MATEMÁTICOS (DISEO) Funciones de Varias Variables. Dada f(x, y) ln ( x + ln(y) ). a) Calcular la derivada direccional en el punto (x, y) (, e 2 ) en la dirección del vector v (3,
CAPÍTULO III Electrostática
 CAPÍTULO III Electrostática Fundamento teórico I.- Ley de Coulomb Ia.- Ley de Coulomb La fuerza electrostática F que una carga puntual q con vector posición r ejerce sobre una carga puntual q con vector
CAPÍTULO III Electrostática Fundamento teórico I.- Ley de Coulomb Ia.- Ley de Coulomb La fuerza electrostática F que una carga puntual q con vector posición r ejerce sobre una carga puntual q con vector
Tarea 9. H ds = E ds (2)
 Tarea 9. ea una supercie con frontera y suponga que E es un campo eléctrico que es perpendicular a - Muestre que el ujo magnético inducido a través de es constante en el tiempo. (Use la Ley de Faraday)
Tarea 9. ea una supercie con frontera y suponga que E es un campo eléctrico que es perpendicular a - Muestre que el ujo magnético inducido a través de es constante en el tiempo. (Use la Ley de Faraday)
Instituto de Física Universidad de Guanajuato Agosto 2007
 Instituto de Física Universidad de Guanajuato Agosto 2007 Física III Capítulo I José Luis Lucio Martínez El material que se presenta en estas notas se encuentra, en su mayor parte, en las referencias que
Instituto de Física Universidad de Guanajuato Agosto 2007 Física III Capítulo I José Luis Lucio Martínez El material que se presenta en estas notas se encuentra, en su mayor parte, en las referencias que
Ley de Gauss. Ley de Gauss
 Objetivo: Ley de Gauss Hasta ahora, hemos considerado cargas puntuales Cómo podemos tratar distribuciones más complicadas, por ejemplo, el campo de un alambre cargado, una esfera cargada, o un anillo cargado?
Objetivo: Ley de Gauss Hasta ahora, hemos considerado cargas puntuales Cómo podemos tratar distribuciones más complicadas, por ejemplo, el campo de un alambre cargado, una esfera cargada, o un anillo cargado?
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Problemas de Potencial Eléctrico. Boletín 2 Tema 2
 1/22 Problemas de Potencial Eléctrico Boletín 2 Tema 2 Fátima Masot Conde Ing. Industrial 21/11 Problema 1 Ocho partículas con una carga de 2 nc cada una están uniformemente distribuidas sobre el perímetro
1/22 Problemas de Potencial Eléctrico Boletín 2 Tema 2 Fátima Masot Conde Ing. Industrial 21/11 Problema 1 Ocho partículas con una carga de 2 nc cada una están uniformemente distribuidas sobre el perímetro
Departamento de Física Aplicada III
 Departamento de Física Aplicada III Escuela Superior de Ingenieros Camino de los Descubrimientos s/n 4109 Sevilla Examen de Campos electromagnéticos. o Curso de Ingeniería Industrial. Septiembre de 011
Departamento de Física Aplicada III Escuela Superior de Ingenieros Camino de los Descubrimientos s/n 4109 Sevilla Examen de Campos electromagnéticos. o Curso de Ingeniería Industrial. Septiembre de 011
Primer examen parcial del curso Física II, M
 Primer examen parcial del curso Física II, 106015M Prof. Beatriz Londoño 11 de octubre de 2013 Tenga en cuenta: Escriba en todas las hojas adicionales su nombre! Hojas sin nombre no serán corregidas El
Primer examen parcial del curso Física II, 106015M Prof. Beatriz Londoño 11 de octubre de 2013 Tenga en cuenta: Escriba en todas las hojas adicionales su nombre! Hojas sin nombre no serán corregidas El
Electromagnetismo I. 0.5$m$ F q cos θ = F g sin θ, (1)
 Electromagnetismo I Semestre: 2015-2 Prof. Alejandro Reyes Coronado Ayud. Carlos Alberto Maciel Escudero Ayud. Christian Esparza López Solución a la Tarea 2 1.- Problema: (10pts) Solución por Christian
Electromagnetismo I Semestre: 2015-2 Prof. Alejandro Reyes Coronado Ayud. Carlos Alberto Maciel Escudero Ayud. Christian Esparza López Solución a la Tarea 2 1.- Problema: (10pts) Solución por Christian
Universidad de Alcalá. Departamento de Física. Solución del Ejercicio propuesto del Tema 4
 Universidad de Alcalá Departamento de Física Solución del Ejercicio propuesto del Tema 4 1) La figura muestra un condensador esférico, cuyas armaduras interna y externa tienen radios R i 1 cm y R e 2 cm.
Universidad de Alcalá Departamento de Física Solución del Ejercicio propuesto del Tema 4 1) La figura muestra un condensador esférico, cuyas armaduras interna y externa tienen radios R i 1 cm y R e 2 cm.
Flujo Eléctrico. Hemos aprendido a calcular el E establecido por un sistema de cargas puntuales o una distribución de carga uniforme o continua.
 Ley de Gauss Presentación basada en el material contenido en: R. Serway,; Physics for Scientists and Engineers, Saunders College Publishers, 3 rd edition. Flujo Eléctrico Hemos aprendido a calcular el
Ley de Gauss Presentación basada en el material contenido en: R. Serway,; Physics for Scientists and Engineers, Saunders College Publishers, 3 rd edition. Flujo Eléctrico Hemos aprendido a calcular el
FLUJO ELECTRICO Y LA LEY DE GAUSS
 21 UNIVRSIDAD NACIONAL SANTIAGO ANTÚNZ D MAYOLO FACULTAD D INGNIRÍA CIVIL CURSO: FISICA III FLUJO LCTRICO Y LA LY D GAUSS AUTOR: Mag. Optaciano L. Vásquez García HUARAZ - PRÚ I. INTRODUCCIÓN Para realizar
21 UNIVRSIDAD NACIONAL SANTIAGO ANTÚNZ D MAYOLO FACULTAD D INGNIRÍA CIVIL CURSO: FISICA III FLUJO LCTRICO Y LA LY D GAUSS AUTOR: Mag. Optaciano L. Vásquez García HUARAZ - PRÚ I. INTRODUCCIÓN Para realizar
Volumen de Sólidos de Revolución
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
Problemas de electricidad
 Problemas de ectricidad Problema 1 Tenemos una carga de valor 0 = situada en origen de coordenadas y otra carga de valor 1 = situada en (d = a, φ = 45 o ) tal y como muestra figura. 1. Calcur fuerza éctrica
Problemas de ectricidad Problema 1 Tenemos una carga de valor 0 = situada en origen de coordenadas y otra carga de valor 1 = situada en (d = a, φ = 45 o ) tal y como muestra figura. 1. Calcur fuerza éctrica
CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA
 CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA Este documento enuncia de forma más detallada la formulación matemática que permite el estudio de campos eléctricos debido a distribuciones
CAMPOS ELÉCTRICOS DEBIDOS A DISTRIBUCIONES CONTINUAS DE CARGA Este documento enuncia de forma más detallada la formulación matemática que permite el estudio de campos eléctricos debido a distribuciones
Integrales Múltiples.
 CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
EXAMEN DE FÍSICA. 24 DE JUNIO DE TEORÍA. GRUPOS 16(B) Y 17(C)
 Página 1 de 8 Índice de exámenes EXAMEN DE FÍSICA. 24 DE JUNIO DE 1999. TEORÍA. GRUPOS 16(B) Y 17(C) C1. Tenemos una superficie cónica de radio r = 0.5 m y altura h 2 m (ver figura), dentro de un campo
Página 1 de 8 Índice de exámenes EXAMEN DE FÍSICA. 24 DE JUNIO DE 1999. TEORÍA. GRUPOS 16(B) Y 17(C) C1. Tenemos una superficie cónica de radio r = 0.5 m y altura h 2 m (ver figura), dentro de un campo
Figura Trabajo de las fuerzas eléctricas al desplazar en Δ la carga q.
 1.4. Trabajo en un campo eléctrico. Potencial Clases de Electromagnetismo. Ariel Becerra Al desplazar una carga de prueba q en un campo eléctrico, las fuerzas eléctricas realizan un trabajo. Este trabajo
1.4. Trabajo en un campo eléctrico. Potencial Clases de Electromagnetismo. Ariel Becerra Al desplazar una carga de prueba q en un campo eléctrico, las fuerzas eléctricas realizan un trabajo. Este trabajo
Módulo 1: Electrostática Campo eléctrico
 Módulo 1: Electrostática Campo eléctrico 1 Campo eléctrico Cómo puede ejercerse una fuerza a distancia? Para explicarlo se introduce el concepto de campo eléctrico Una carga crea un campo eléctrico E en
Módulo 1: Electrostática Campo eléctrico 1 Campo eléctrico Cómo puede ejercerse una fuerza a distancia? Para explicarlo se introduce el concepto de campo eléctrico Una carga crea un campo eléctrico E en
encuentre la fuerza resultante sobre la carga de 3μC. Ejercicio 3: Determine la fuerza resultante sobre la carga q 1
 1 Ejercicio 1: Dos cargas Puntuales están, separadas por una distancia de 10cm, si q 1 = 2μC y q 2 = 4μC, determine la magnitud de la fuerza que se ejercen entre ellas. Ejercicio 2: Tres cargas de 2μC,
1 Ejercicio 1: Dos cargas Puntuales están, separadas por una distancia de 10cm, si q 1 = 2μC y q 2 = 4μC, determine la magnitud de la fuerza que se ejercen entre ellas. Ejercicio 2: Tres cargas de 2μC,
Los sistemas coordenados sirven para localizar puntos en el espacio. La localización de un punto se obtiene por intersección de tres superficies.
 Los sistemas coordenados sirven para localizar puntos en el espacio. La localización de un punto se obtiene por intersección de tres superficies. La intersección de dos superficies da lugar a una línea.
Los sistemas coordenados sirven para localizar puntos en el espacio. La localización de un punto se obtiene por intersección de tres superficies. La intersección de dos superficies da lugar a una línea.
PROBLEMAS ELECTROESTÁTICA
 POBLEMAS DE ELETOESTÁTIA III ampo electrostático en los conductores Prof. J. Martín ONDUTOES AGADOS EN EL AI O Pr obl e ma alcular : a) la capacidad de una superficie esférica de radio ; b) la capacidad
POBLEMAS DE ELETOESTÁTIA III ampo electrostático en los conductores Prof. J. Martín ONDUTOES AGADOS EN EL AI O Pr obl e ma alcular : a) la capacidad de una superficie esférica de radio ; b) la capacidad
Geometría de masas: Cálculos del tensor de Inercia
 Departamento: Física Aplicada Mecánica acional (ngeniería ndustrial) Curso 007-08 eometría de masas: Cálculos del tensor de nercia Tensor de inercia de una varilla delgada. Calculo del tensor de inercia
Departamento: Física Aplicada Mecánica acional (ngeniería ndustrial) Curso 007-08 eometría de masas: Cálculos del tensor de nercia Tensor de inercia de una varilla delgada. Calculo del tensor de inercia
Sistemas de coordenadas
 Sistemas de coordenadas. Introducción En un sistema de coordenadas un punto se representa como la intersección de tres superficies ortogonales llamadas superficies coordenadas del sistema: u u u = cte
Sistemas de coordenadas. Introducción En un sistema de coordenadas un punto se representa como la intersección de tres superficies ortogonales llamadas superficies coordenadas del sistema: u u u = cte
Áreas entre curvas. Ejercicios resueltos
 Áreas entre curvas Ejercicios resueltos Recordemos que el área encerrada por las gráficas de dos funciones f y g entre las rectas x = a y x = b es dada por Ejercicios resueltos b a f x g x dx Ejercicio
Áreas entre curvas Ejercicios resueltos Recordemos que el área encerrada por las gráficas de dos funciones f y g entre las rectas x = a y x = b es dada por Ejercicios resueltos b a f x g x dx Ejercicio
FÍSICA 2º Bachillerato Ejercicios: Campo magnético y corriente eléctrica
 1(9) Ejercicio nº 1 Una partícula alfa se introduce en un campo cuya inducción magnética es 1200 T con una velocidad de 200 Km/s en dirección perpendicular al campo. Calcular la fuerza qué actúa sobre
1(9) Ejercicio nº 1 Una partícula alfa se introduce en un campo cuya inducción magnética es 1200 T con una velocidad de 200 Km/s en dirección perpendicular al campo. Calcular la fuerza qué actúa sobre
Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo,
 Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 42 Índice. 1. Superficies. 2. El espacio eucĺıdeo tridimensional. Coordenadas Cartesianas. 3. Distancia entre
Geometría del Espacio. Física Geográfica. Licenciatura de Humanidades. Febrero-Mayo, 2007. 42 Índice. 1. Superficies. 2. El espacio eucĺıdeo tridimensional. Coordenadas Cartesianas. 3. Distancia entre
VELOCIDAD Y ACELERACION. RECTA TANGENTE.
 VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
Notas para la asignatura de Electricidad y Magnetismo Unidad 1: Electrostática
 Notas para la asignatura de Electricidad y Magnetismo Unidad 1: Electrostática Presenta: M. I. Ruiz Gasca Marco Antonio Instituto Tecnológico de Tláhuac II Agosto, 2015 Marco Antonio (ITT II) México D.F.,
Notas para la asignatura de Electricidad y Magnetismo Unidad 1: Electrostática Presenta: M. I. Ruiz Gasca Marco Antonio Instituto Tecnológico de Tláhuac II Agosto, 2015 Marco Antonio (ITT II) México D.F.,
y = 2x + 8x 7, y = x 4. y = 4 x, y = x + 2, x = 2, x = 3. x = 16 y, x = 6 y. y = a x, y = x, x y = a. (1 x)dx. y = 9 x, y = 0.
 . Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
. Encuentre el área de la región limitada por las curvas indicadas:.. y = x, y = x +... x = y, x = y +... y = x +, y = x +, y = x....5..6..7..8..9..0....... y = x + 8x 7, y = x. y = x, y = x +, x =, x
Santiago, julio 6 del Tercera Solemne Cálculo Varias Variables. Nombre:
 Nombre: Santiago, julio 6 del 26. Tercera Solemne Cálculo Varias Variables. 1. La temperatura en un punto (x, y) sobre una placa metalica es T (x, y) 4x 2 4xy + y 2. Una hormiga camina sobre la placa alrededor
Nombre: Santiago, julio 6 del 26. Tercera Solemne Cálculo Varias Variables. 1. La temperatura en un punto (x, y) sobre una placa metalica es T (x, y) 4x 2 4xy + y 2. Una hormiga camina sobre la placa alrededor
2 ln x dx. Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = 1 x dx dv = dx v = x y por tanto
 Tema 6 Integración Definida Ejercicios resueltos Ejercicio Calcular la integral definida ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = x dx dv
Tema 6 Integración Definida Ejercicios resueltos Ejercicio Calcular la integral definida ln x dx Solución: Resolvemos la integral por partes. Si hacemos u = ln x y dv = dx, entonces u =ln x du = x dx dv
Campo Eléctrico en el vacío
 Campo Eléctrico en el vacío Electrostática: Interacción entre partículas cargadas q1 q2 Ley de Coulomb En el vacío: K = 8.99 109 N m2/c2 0 = 8.85 10 12 C2/N m2 Balanza de torsión Electrostática: Interacción
Campo Eléctrico en el vacío Electrostática: Interacción entre partículas cargadas q1 q2 Ley de Coulomb En el vacío: K = 8.99 109 N m2/c2 0 = 8.85 10 12 C2/N m2 Balanza de torsión Electrostática: Interacción
CAMPO ELÉCTRICO ÍNDICE
 CAMPO ELÉCTRICO ÍNDICE 1. Introducción 2. Ley de Coulomb 3. Campo eléctrico 4. Líneas de campo eléctrico 5. Distribuciones continuas de carga eléctrica 6. Flujo del campo eléctrico. Ley de Gauss 7. Potencial
CAMPO ELÉCTRICO ÍNDICE 1. Introducción 2. Ley de Coulomb 3. Campo eléctrico 4. Líneas de campo eléctrico 5. Distribuciones continuas de carga eléctrica 6. Flujo del campo eléctrico. Ley de Gauss 7. Potencial
FISICA III - Ejemplo - Primer Parcial
 FSCA - Ejemplo - Primer Parcial 1) En cuatro de los cinco vértices de un pentágono regular de lado a se colocan sendas cargas q. a) Cuál es la magnitud de la carga que deberá colocarse en el quinto vértice
FSCA - Ejemplo - Primer Parcial 1) En cuatro de los cinco vértices de un pentágono regular de lado a se colocan sendas cargas q. a) Cuál es la magnitud de la carga que deberá colocarse en el quinto vértice
FÍSICA 2ºBach CURSO 2014/2015
 PROBLEMAS CAMPO ELÉCTRICO 1.- (Sept 2014) En el plano XY se sitúan tres cargas puntuales iguales de 2 µc en los puntos P 1 (1,-1) mm, P 2 (-1,-1) mm y P 3 (-1,1) mm. Determine el valor que debe tener una
PROBLEMAS CAMPO ELÉCTRICO 1.- (Sept 2014) En el plano XY se sitúan tres cargas puntuales iguales de 2 µc en los puntos P 1 (1,-1) mm, P 2 (-1,-1) mm y P 3 (-1,1) mm. Determine el valor que debe tener una
(Problemas - Parte 2) Prof. Cayetano Di Bartolo Andara
 Física 3 (Problemas - Parte 2) Prof. Cayetano Di Bartolo Andara Ultima actualización: Julio de 2004 Julio de 2004 Física-3 (Problemas - Parte 2) Prof. Cayetano Di Bartolo Andara Departamento de Física
Física 3 (Problemas - Parte 2) Prof. Cayetano Di Bartolo Andara Ultima actualización: Julio de 2004 Julio de 2004 Física-3 (Problemas - Parte 2) Prof. Cayetano Di Bartolo Andara Departamento de Física
Guía n 0: Herramientas de Física y Matemáticas
 Guía n 0: Herramientas de Física y Matemáticas Problema Dadas dos partículas en el espacio ubicadas en los puntos de coordenadas p = (0,5, 2) y p 2 = (2,3,). Hallar el vector posición de la partícula respecto
Guía n 0: Herramientas de Física y Matemáticas Problema Dadas dos partículas en el espacio ubicadas en los puntos de coordenadas p = (0,5, 2) y p 2 = (2,3,). Hallar el vector posición de la partícula respecto
VECTORES. también con letras sobre las cuales se coloca una flechita ( a ). A = módulo de A. modulo o magnitud, dirección y sentido. vector.
 VECTORES Según su naturaleza las cantidades físicas se clasifican en magnitudes escalares y magnitudes vectoriales Las magnitudes como el tiempo, la temperatura, la masa y otras, son magnitudes escalares
VECTORES Según su naturaleza las cantidades físicas se clasifican en magnitudes escalares y magnitudes vectoriales Las magnitudes como el tiempo, la temperatura, la masa y otras, son magnitudes escalares
Campo Magnético en un alambre recto.
 Campo Magnético en un alambre recto. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se hizo pasar
Campo Magnético en un alambre recto. A.M. Velasco (133384) J.P. Soler (133380) O.A. Botina (133268) Departamento de física, facultad de ciencias, Universidad Nacional de Colombia Resumen. Se hizo pasar
CAMPO Y POTENCIAL ELÉCTRICO
 CAMPO Y POTENCIAL ELÉCTRICO PREGUNTAS 1. Cómo se aplica el principio de superposición para las fuerzas entre cargas eléctricas?. Qué le ocurre a una placa sólida, conductora, cuando se coloca en un campo
CAMPO Y POTENCIAL ELÉCTRICO PREGUNTAS 1. Cómo se aplica el principio de superposición para las fuerzas entre cargas eléctricas?. Qué le ocurre a una placa sólida, conductora, cuando se coloca en un campo
Resistencia de Materiales 1A. Profesor Herbert Yépez Castillo
 Resistencia de Materiales 1A Profesor Herbert Yépez Castillo 2014-2 2 Capítulo 5. Torsión 5.4 Ángulo 3 Un par es un momento que tiende a hacer girar respecto a su eje longitudinal. Su efecto es de interés
Resistencia de Materiales 1A Profesor Herbert Yépez Castillo 2014-2 2 Capítulo 5. Torsión 5.4 Ángulo 3 Un par es un momento que tiende a hacer girar respecto a su eje longitudinal. Su efecto es de interés
TEMA PE9. PE.9.2. Tenemos dos espiras planas de la forma y dimensiones que se indican en la Figura, siendo R
 TEMA PE9 PE.9.1. Los campos magnéticos de los que estamos rodeados continuamente representan un riesgo potencial para la salud, en Europa se han establecido recomendaciones para limitar la exposición,
TEMA PE9 PE.9.1. Los campos magnéticos de los que estamos rodeados continuamente representan un riesgo potencial para la salud, en Europa se han establecido recomendaciones para limitar la exposición,
Campo de velocidades se puede representar mediante una función potencial φ, escalar
 Flujo Potencial Campo de velocidades se puede representar mediante una función potencial φ, escalar Condición necesaria flujo irrotacional, V=0. Hipótesis: Flujo irrotacional, incompresible y permanente
Flujo Potencial Campo de velocidades se puede representar mediante una función potencial φ, escalar Condición necesaria flujo irrotacional, V=0. Hipótesis: Flujo irrotacional, incompresible y permanente
Rectas y Planos en el Espacio
 Rectas y Planos en el Espacio Rectas y Planos en el Espacio Verónica Briceño V. septiembre 2012 Verónica Briceño V. () Rectas y Planos en el Espacio septiembre 2012 1 / 20 En esta Presentación... En esta
Rectas y Planos en el Espacio Rectas y Planos en el Espacio Verónica Briceño V. septiembre 2012 Verónica Briceño V. () Rectas y Planos en el Espacio septiembre 2012 1 / 20 En esta Presentación... En esta
( ) m normal. UNIDAD III. DERIVACIÓN Y APLICACIONES FÍSICAS Y GEOMÉTRICAS 3.8. Aplicaciones geométricas de la derivada
 UNIDAD III. DERIVACIÓN Y APLICACIONES FÍSICAS Y GEOMÉTRICAS 3.8. Aplicaciones geométricas de la derivada Dirección de una curva Dado que la derivada de f (x) se define como la pendiente de la recta tangente
UNIDAD III. DERIVACIÓN Y APLICACIONES FÍSICAS Y GEOMÉTRICAS 3.8. Aplicaciones geométricas de la derivada Dirección de una curva Dado que la derivada de f (x) se define como la pendiente de la recta tangente
2- El flujo de un campo vectorial se define para una superficie abierta o cerrada?
 ASIGNATURA FISICA II AÑO 2012 GUIA NRO. 2 LEY DE GAUSS Bibliografía Obligatoria (mínima) Capítulo 24 Física de Serway Tomo II Apunte de la cátedra: Capìtulo III PREGUNTAS SOBRE LA TEORIA Las preguntas
ASIGNATURA FISICA II AÑO 2012 GUIA NRO. 2 LEY DE GAUSS Bibliografía Obligatoria (mínima) Capítulo 24 Física de Serway Tomo II Apunte de la cátedra: Capìtulo III PREGUNTAS SOBRE LA TEORIA Las preguntas
Figura 1. Círculo unidad. Definición. 1. Llamamos número π (pi) al valor de la integral
 ANÁLISIS MATEMÁTICO BÁSICO. LAS FUNCIONES TRIGONOMÉTRICAS. La función f(x) = 1 x 2 es continua en el intervalo [ 1, 1]. Su gráfica como vimos es la semicircunferencia de radio uno centro el origen de coordenadas.
ANÁLISIS MATEMÁTICO BÁSICO. LAS FUNCIONES TRIGONOMÉTRICAS. La función f(x) = 1 x 2 es continua en el intervalo [ 1, 1]. Su gráfica como vimos es la semicircunferencia de radio uno centro el origen de coordenadas.
Si se incrementa el número de elementos en los cuales se ha dividido la placa y simultáneamente se disminuye el tamaño de cada elemento se obtiene
 Capítulo 5 Fuerzas distribuidas. Centroides y centros de gravedad Introducción La acción de la Tierra sobre un cuerpo rígido debe representarse por un gran número de pequeñas fuerzas distribuidas sobre
Capítulo 5 Fuerzas distribuidas. Centroides y centros de gravedad Introducción La acción de la Tierra sobre un cuerpo rígido debe representarse por un gran número de pequeñas fuerzas distribuidas sobre
Carga Eléctrica. Una propiedad fundamental de la materia ya observada desde la antigüedad. Los cuerpos pueden cargarse eléctricamente por frotamiento.
 ELECTROSTATICA Carga Eléctrica Una propiedad fundamental de la materia ya observada desde la antigüedad. Los cuerpos pueden cargarse eléctricamente por frotamiento. Aparecen fuerzas de atracción n o repulsión
ELECTROSTATICA Carga Eléctrica Una propiedad fundamental de la materia ya observada desde la antigüedad. Los cuerpos pueden cargarse eléctricamente por frotamiento. Aparecen fuerzas de atracción n o repulsión
1 Curvas planas. Solución de los ejercicios propuestos.
 1 Curvas planas. Solución de los ejercicios propuestos. 1. Se considera el lugar geométrico de los puntos del plano tales que la suma del cuadrado de las distancias a los puntos P 1 = (, 0) y P = (, 0)
1 Curvas planas. Solución de los ejercicios propuestos. 1. Se considera el lugar geométrico de los puntos del plano tales que la suma del cuadrado de las distancias a los puntos P 1 = (, 0) y P = (, 0)
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (9)
 ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (9) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2006 Ejemplo 1 El espectrógrafo de masa fué inventado por Francis
ELECTRICIDAD Y MAGNETISMO FIZ 1300 FIS 1532 (9) Ricardo Ramírez Facultad de Física, Pontificia Universidad Católica, Chile 1er. Semestre 2006 Ejemplo 1 El espectrógrafo de masa fué inventado por Francis
Superficies Curvas. Guía de clase elaborada por Ing. Guillermo Verger
 Superficies Curvas Guía de clase elaborada por Ing. Guillermo Verger www.ingverger.com.ar Superficie cilíndrica Es aquella generada por una recta llamada generatriz que se mueve en el espacio manteniendose
Superficies Curvas Guía de clase elaborada por Ing. Guillermo Verger www.ingverger.com.ar Superficie cilíndrica Es aquella generada por una recta llamada generatriz que se mueve en el espacio manteniendose
1. INTEGRALES DEFINIDAS E IMPROPIAS
 . INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
. INTEGRALES DEFINIDAS E IMPROPIAS. Hallar el área de la región limitada por la parábola y = y el eje OX. Los cortes de la gráfica de y = con el eje OX son los valores de tales que =, esto es, = y =. El
TEMA 2. CAMPO ELECTROSTÁTICO
 TEMA 2. CAMPO ELECTROSTÁTICO CUESTIONES TEÓRICAS RELACIONADAS CON ESTE TEMA. Ejercicio nº1 Indica qué diferencias respecto al medio tienen las constantes K, de la ley de Coulomb, y G, de la ley de gravitación
TEMA 2. CAMPO ELECTROSTÁTICO CUESTIONES TEÓRICAS RELACIONADAS CON ESTE TEMA. Ejercicio nº1 Indica qué diferencias respecto al medio tienen las constantes K, de la ley de Coulomb, y G, de la ley de gravitación
BACHILLERATO FÍSICA A. HERRAMIENTAS MATEMÁTICAS DE LA FÍSICA. Dpto. de Física y Química. R. Artacho
 BACHILLERATO FÍSICA A. HERRAMIENTAS MATEMÁTICAS DE LA FÍSICA R. Artacho Dpto. de Física y Química ÍNDICE 1. Áreas y volúmenes de figuras geométricas. Funciones trigonométricas 3. Productos de vectores
BACHILLERATO FÍSICA A. HERRAMIENTAS MATEMÁTICAS DE LA FÍSICA R. Artacho Dpto. de Física y Química ÍNDICE 1. Áreas y volúmenes de figuras geométricas. Funciones trigonométricas 3. Productos de vectores
Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99, 01, curso cero de física
 VECTORES: TRIÁNGULOS Demostrar que en una semicircunferencia cualquier triángulo inscrito con el diámetro como uno de sus lados es un triángulo rectángulo. Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99,
VECTORES: TRIÁNGULOS Demostrar que en una semicircunferencia cualquier triángulo inscrito con el diámetro como uno de sus lados es un triángulo rectángulo. Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99,
MATERIALES DIELÉCTRICOS
 MATERIALES DIELÉCTRICOS PREGUNTAS 1. Qué le ocurre a una placa sólida, dieléctrica, cuando se coloca en un campo eléctrico uniforme?. Qué es un material dieléctrico?, argumente. 3. Hay dieléctricos polar
MATERIALES DIELÉCTRICOS PREGUNTAS 1. Qué le ocurre a una placa sólida, dieléctrica, cuando se coloca en un campo eléctrico uniforme?. Qué es un material dieléctrico?, argumente. 3. Hay dieléctricos polar
Apuntes de dibujo de curvas
 Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Apuntes de dibujo de curvas El objetivo de estas notas es dar unas nociones básicas sobre dibujo de curvas definidas por medio de ecuaciones cartesianas explícitas o paramétricas y polares: 1. Curvas en
Integración sobre superficies
 Problemas propuestos con solución Integración sobre superficies IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna [email protected] Índice 1. Parametrizaciones 1 2. Área de una superficie
Problemas propuestos con solución Integración sobre superficies IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna [email protected] Índice 1. Parametrizaciones 1 2. Área de una superficie
FISICA 2º BACHILLERATO CAMPO ELECTRICO
 ) CMPO ELÉCTRICO Cuando en el espacio vacío se introduce una partícula cargada, ésta lo perturba, modifica, haciendo cambiar su geometría, de modo que otra partícula cargada que se sitúa en él, estará
) CMPO ELÉCTRICO Cuando en el espacio vacío se introduce una partícula cargada, ésta lo perturba, modifica, haciendo cambiar su geometría, de modo que otra partícula cargada que se sitúa en él, estará
Interacciones Eléctricas La Ley de Coulomb
 Interacciones Eléctricas La Ley de Coulomb 1. Introducción La Electrostática se ocupa del estudio de las interacciones entre cargas eléctricas en reposo. Las primeras experiencias relativas a los fenómenos
Interacciones Eléctricas La Ley de Coulomb 1. Introducción La Electrostática se ocupa del estudio de las interacciones entre cargas eléctricas en reposo. Las primeras experiencias relativas a los fenómenos
MATEMÁTICAS 1º BACH. C. N. Y S. 25 de enero de 2010 Geometría y Logaritmos
 MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
Ejercicios Resueltos Electromagnetismo Parte 1
 Ejercicios Resueltos Electromagnetismo Parte 1 Diego Andrés Palma Sánchez [email protected] http://www.udec.cl/~dipalma Agosto de 2015 1. Cargas! 1.1. Ejercicio 1 Una vara de teflón se frota con piel de
Ejercicios Resueltos Electromagnetismo Parte 1 Diego Andrés Palma Sánchez [email protected] http://www.udec.cl/~dipalma Agosto de 2015 1. Cargas! 1.1. Ejercicio 1 Una vara de teflón se frota con piel de
GEOMETRÍA. que pasa por el punto P y es paralelo a π. (0,9 puntos) b) Determinar la ecuación del plano π
 GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
CAMPOS: CIRCULACIÓN Y FLUJO
 AMPO: IRULAIÓN Y FLUJO Dado el vector a ( x + y) i ˆ + xy ˆ j calcular su circulación a lo largo de la recta y x+ desde el punto A (, ) al B (, 2). olución: I.T.I. 99, 5, I.T.T. 2 En la trayectoria que
AMPO: IRULAIÓN Y FLUJO Dado el vector a ( x + y) i ˆ + xy ˆ j calcular su circulación a lo largo de la recta y x+ desde el punto A (, ) al B (, 2). olución: I.T.I. 99, 5, I.T.T. 2 En la trayectoria que
UNIVERSIDADES DE ANDALUCÍA PRUEBA DE ACCESO A LA UNIVERSIDAD
 Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Opción A Ejercicio 1.- Sea f : R R definida por f(x) = x 3 +ax 2 +bx+c. a) [1 75 puntos] Halla a,b y c para que la gráfica de f tenga un punto de inflexión de abscisa x = 1 2 y que la recta tangente en
Unidad V. 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales.
 Unidad V Aplicaciones de la derivada 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales. Una tangente a una curva es una recta que toca la curva en un solo punto y tiene la misma
Unidad V Aplicaciones de la derivada 5.1 Recta tangente y recta normal a una curva en un punto. Curvas ortogonales. Una tangente a una curva es una recta que toca la curva en un solo punto y tiene la misma
RESPUESTAS. Examen UNI 2015 I. Matemática
 RESPUESTAS Examen UNI 05 I Matemática Pregunta 0 Semanalmente, un trabajador ahorra cierta cantidad en soles, y durante 0 semanas ahorra las siguientes cantidades: 5 9 8 8 5 6 7 7 7 9 9 6 8 6 6 0 8 9 5
RESPUESTAS Examen UNI 05 I Matemática Pregunta 0 Semanalmente, un trabajador ahorra cierta cantidad en soles, y durante 0 semanas ahorra las siguientes cantidades: 5 9 8 8 5 6 7 7 7 9 9 6 8 6 6 0 8 9 5
TRIGONOMETRÍA DEL CÍRCULO
 TRIGONOMETRÍA DEL CÍRCULO Otra unidad de medida para ángulos: RADIANES 1 Usamos grados para medir ángulos cuando aplicamos trigonometría a los problemas del mundo real. Por ejemplo, en topografía, construcción,
TRIGONOMETRÍA DEL CÍRCULO Otra unidad de medida para ángulos: RADIANES 1 Usamos grados para medir ángulos cuando aplicamos trigonometría a los problemas del mundo real. Por ejemplo, en topografía, construcción,
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN. Tema: LA INTEGRAL DEFINIDA
 UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN Tema: LA INTEGRAL DEFINIDA La integral definida Anteriormente se mencionó que la Integral Indefinida da como resultado una familia de funciones
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN Tema: LA INTEGRAL DEFINIDA La integral definida Anteriormente se mencionó que la Integral Indefinida da como resultado una familia de funciones
Integrales dobles. Integrales dobles
 Integrales dobles Integrales iteradas b g2 (x) a g 1 (x) f(x, y) dydx ó d h2 (y) c h 1 (y) f(x, y) dxdy Los límites interiores de integración pueden ser variables respecto a la variable exterior de integración,
Integrales dobles Integrales iteradas b g2 (x) a g 1 (x) f(x, y) dydx ó d h2 (y) c h 1 (y) f(x, y) dxdy Los límites interiores de integración pueden ser variables respecto a la variable exterior de integración,
3. Si la diferencia de volúmenes de los cilindros A) 2 3 B) En el gráfico se tiene un tronco de cilindro. A) 196p B) 200p C) 250p
 ilindro y tronco de cilindro 1. En el gráfico se muestra un cilindro recto de base circular, además, T es punto de contacto de la recta PT en la superficie cilíndrica. Si PT=15 y P=8, calcule la distancia
ilindro y tronco de cilindro 1. En el gráfico se muestra un cilindro recto de base circular, además, T es punto de contacto de la recta PT en la superficie cilíndrica. Si PT=15 y P=8, calcule la distancia
7. Cambio de variables en integrales triples.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 011 1. Lección. Integrales múltiples. 7. Cambio de variables en integrales triples. El teorema del cambio de variables para integrales triples es análogo al de integrales
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 011 1. Lección. Integrales múltiples. 7. Cambio de variables en integrales triples. El teorema del cambio de variables para integrales triples es análogo al de integrales
Contenido 1. Integrales Dobles 2. Integrales Triples
 Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
Integración Contenido 1. Integrales Dobles 2 1.1. Integrales iteradas............................. 2 1.2. Regiones en R 2.............................. 3 1.3. Volumen..................................
Módulo 7: Fuentes del campo magnético
 7/04/03 Módulo 7: Fuentes del campo magnético Campo magnético creado por cargas puntuales en movimiento Cuando una carga puntual q se mueve con velocidad v, se produce un campo magnético B en el espacio
7/04/03 Módulo 7: Fuentes del campo magnético Campo magnético creado por cargas puntuales en movimiento Cuando una carga puntual q se mueve con velocidad v, se produce un campo magnético B en el espacio
2 Energía electrostática y Capacidad
 2 Energía electrostática y Capacidad M. Mudarra Física III (2A) - M. Mudarra Enginyeria Aeroespacial - p. 1/44 Densidad de energía electrostática 2.2 Campo E en presencia de 2.6 Fuerzas sobre Física III
2 Energía electrostática y Capacidad M. Mudarra Física III (2A) - M. Mudarra Enginyeria Aeroespacial - p. 1/44 Densidad de energía electrostática 2.2 Campo E en presencia de 2.6 Fuerzas sobre Física III
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna [email protected]
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna [email protected]
IES Fco Ayala de Granada Junio de 2011 (Específico Modelo 5) Solución Germán-Jesús Rubio Luna. Opción A
 IES Fco Ayala de Granada Junio de 2011 (Específico Modelo 5) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 2011 específico1 [2'5 puntos] Un alambre de 100 m de longitud se divide
IES Fco Ayala de Granada Junio de 2011 (Específico Modelo 5) Germán-Jesús Rubio Luna Opción A Ejercicio 1 opción A, modelo Junio 2011 específico1 [2'5 puntos] Un alambre de 100 m de longitud se divide
CONTENIDO SÓLIDO RÍGIDO I. CINEMÁTICA. Definición de sólido rígido. Cálculo de la posición del centro de masas. Movimiento de rotación y de traslación
 CONTENIDO Definición de sólido rígido Cálculo de la posición del centro de masas Movimiento de rotación y de traslación Movimiento del sólido rígido en el plano Momento de inercia Teorema de Steiner Tema
CONTENIDO Definición de sólido rígido Cálculo de la posición del centro de masas Movimiento de rotación y de traslación Movimiento del sólido rígido en el plano Momento de inercia Teorema de Steiner Tema
CINEMÁTICA: MOVIMIENTO CIRCULAR, CONCEPTOS BÁSICOS Y GRÁFICAS
 CINEMÁTICA: MOVIMIENTO CIRCULAR, CONCEPTOS BÁSICOS Y GRÁFICAS Un volante cuyo diámetro es de 3 m está girando a 120 r.p.m. Calcular: a) su frecuencia, b) el periodo, c) la velocidad angular, d) la velocidad
CINEMÁTICA: MOVIMIENTO CIRCULAR, CONCEPTOS BÁSICOS Y GRÁFICAS Un volante cuyo diámetro es de 3 m está girando a 120 r.p.m. Calcular: a) su frecuencia, b) el periodo, c) la velocidad angular, d) la velocidad
Capítulo 10. Efectos de superficie. Sistema respiratorio
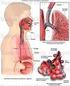 Capítulo 10 Efectos de superficie. Sistema respiratorio 1 Tensión superficial El coeficiente de tensión superficial γ es la fuerza por unidad de longitud que hay que realizar para aumentar una superficie:
Capítulo 10 Efectos de superficie. Sistema respiratorio 1 Tensión superficial El coeficiente de tensión superficial γ es la fuerza por unidad de longitud que hay que realizar para aumentar una superficie:
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de Circunferencia.
 ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
ÁLGEBRA VECTORIAL Y MATRICES. Ciclo 02 de 2012. Circunferencia. Elementos de la circunferencia. El segmento de recta es una cuerda. El segmento de recta es una cuerda que pasa por el centro, por lo tanto
 RELACIÓN DE PROBLEMAS CAMPO ELÉCTRICO 1. Se tienen dos cargas puntuales; q1= 0,2 μc está situada a la derecha del origen de coordenadas y dista de él 3 m y q2= +0,4 μc está a la izquierda del origen y
RELACIÓN DE PROBLEMAS CAMPO ELÉCTRICO 1. Se tienen dos cargas puntuales; q1= 0,2 μc está situada a la derecha del origen de coordenadas y dista de él 3 m y q2= +0,4 μc está a la izquierda del origen y
PAU Madrid. Matemáticas II. Año Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos.
 PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
PAU Madrid. Matemáticas II. Año 22. Examen modelo. Opción A. Ejercicio 1. Valor: 2 puntos. Se considera una varilla AB de longitud 1. El extremo A de esta varilla recorre completamente la circunferencia
FISICA 2º BACHILLERATO CAMPO MAGNÉTICO E INDUCCIÓN ELECTROMAGNÉTICA
 A) CAMPO MAGNÉTICO El Campo Magnético es la perturbación que un imán o una corriente eléctrica producen en el espacio que los rodea. Esta perturbación del espacio se manifiesta en la fuerza magnética que
A) CAMPO MAGNÉTICO El Campo Magnético es la perturbación que un imán o una corriente eléctrica producen en el espacio que los rodea. Esta perturbación del espacio se manifiesta en la fuerza magnética que
Análisis Dinámico: Ecuaciones diferenciales
 Análisis Dinámico: Jesús Getán y Eva Boj Facultat d Economia i Empresa Universitat de Barcelona Marzo de 2014 Jesús Getán y Eva Boj Análisis Dinámico: 1 / 51 Introducción Solución genérica Solución de
Análisis Dinámico: Jesús Getán y Eva Boj Facultat d Economia i Empresa Universitat de Barcelona Marzo de 2014 Jesús Getán y Eva Boj Análisis Dinámico: 1 / 51 Introducción Solución genérica Solución de
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2006 MATEMÁTICAS II TEMA 4: FUNCIONES
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 006 MATEMÁTICAS II TEMA 4: FUNCIONES Junio, Ejercicio, Opción A Junio, Ejercicio, Opción B Reserva, Ejercicio, Opción A Reserva, Ejercicio, Opción B Reserva,
Geometría. Cuerpos Geométricos. Trabajo
 Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
Geometría Cuerpos Geométricos Trabajo CUERPOS GEOMÉTRICOS 1. Clasifique los cuerpos geométricos. Dos grupos de sólidos geométricos del espacio presentan especial interés: 1.1. Poliedros: Aquellos cuerpos
3. Cambio de variables en integrales dobles.
 GADO DE INGENIEÍA AEOESPACIAL. CUSO. Lección. Integrales múltiples. 3. Cambio de variables en integrales dobles. Para calcular integrales dobles eiste, además del teorema de Fubini, otra herramienta fundamental
GADO DE INGENIEÍA AEOESPACIAL. CUSO. Lección. Integrales múltiples. 3. Cambio de variables en integrales dobles. Para calcular integrales dobles eiste, además del teorema de Fubini, otra herramienta fundamental
