NECESIDAD DE RESOLVER UNA ECUACIÓN DIFERENCIAL
|
|
|
- Xavier Valverde Herrera
- hace 6 años
- Vistas:
Transcripción
1 NECESIDAD DE RESOLVER UNA ECUACIÓN DIFERENCIAL Propósito Al terminar esta sección quien imparte el curso habrá logrado que los estudiantes: Sientan la necesidad de resolver una ecuación diferencial. PROBLEMA DEL ENFRIAMIENO DEL CAFÉ Si una taza de café se sirve con una temperatura de 90 C (9 F) y empieza a enfriarse en una habitación que se encuentra a una temperatura constante de 25 C (77 F), qué temperatura tendrá el café después de media hora? Sugerencia para quien imparte el curso. Dada la dificultad que implica el tratamiento de este problema, se proponen algunas preguntas que quien imparte el curso planteará en el momento oportuno, para orientar el avance del grupo hacia los conceptos clave que se pretende alcanzar. Qué le ocurre a un objeto caliente que se deja sobre una mesa en el interior de una habitación que se encuentra a una temperatura menor? En Física se conoce como Ley de enfriamiento de Newton al principio termodinámico que establece que, la rapidez de enfriamiento de un cuerpo en cualquier momento, es directamente proporcional a la diferencia entre la temperatura del cuerpo y la temperatura del medio que lo rodea. Esta ley de enfriamiento se puede expresar con esta ecuación diferencial: k( ) 0, Donde t es el tiempo de enfriamiento, 0 la temperatura del medio que rodea al cuerpo, en grados Fahrenheit, la temperatura del cuerpo en el instante t y k una constante de proporcionalidad positiva. En el caso del café que nos ocupa, en qué unidades se mide el tiempo t? - Unidad Modelos y Predicción
2 Cuál es la temperatura de la habitación donde está el café? 0 = 77 F De modo que la ecuación diferencial se convierte en: k 77 rataremos de resolver esta ecuación, es decir, buscamos la función (t) que satisfaga la ecuación anterior. Sugerencia para quien imparte el curso. Recomendamos de manera muy especial que los estudiantes hagan en su cuaderno el siguiente desarrollo, no bastará con que lo sigan en el pizarrón, deben hacerlo para comprenderlo mejor, tratando de contestar las preguntas que se plantean. Lo primero que podría ocurrírsenos es multiplicar ambos miembros por la diferencial de la variable independiente t, es decir, por : k( 77) Sugerencia para quien imparte el curso. Es conveniente en este momento recordar la definición de diferencial de una función, para que tenga sentido descomponer la expresión cociente de diferenciales. tratándola como un Cómo se define la diferencial de una función? Efectivamente, el producto de la derivada de una función por la diferencial de la variable independiente, corresponde a la diferencial de la función: por lo tanto, de la expresión anterior: = - k( 77). Reunamos en el primer miembro las expresiones que contienen a la variable y en el segundo las que contienen t: 77 k Integremos ambos lados de la igualdad: 77 k Resolvamos por separado cada una de estas integrales: Unidad Modelos y Predicción -
3 77 ln 77 c e k k t c2 De manera que tenemos: ln 77 k t c, donde c es una constante de integración resultante de simplificar, cuyo valor podrá ser determinado a partir de las condiciones iniciales de la situación que estamos tratando. Esta ecuación puede ser resuelta para, a través de la operación contraria o inversa del logaritmo natural: la exponencial de base e, tomando la exponencial a ambos miembros de la igualdad: e ln 77 e k t c Dificultad que pudiera presentarse Es probable que sea necesario recordar las propiedades de los logaritmos que se mencionaron en la Unidad, para que resulte natural su aplicación en este momento. Qué se obtiene con la expresión e ln A? e ln A = A, porque la exponencial y el logaritmo natural son funciones inversas De modo que Por lo que obtenemos: 77 e k t c A qué es igual a n+m? a n + m = a n a m Por lo tanto: 77 e k t c e k t c 77 e e... () Aún no hemos considerado otro dato, cuál es el valor de la temperatura inicial del café,? = 9 F cuando t = 0-5 Unidad Modelos y Predicción
4 Nuestra expresión se convierte en: 9 = 77 + e 0 e c Cuál es el valor de e 0? e 0 = De donde: e c = 9 77 e c = 7 Regresando a la expresión () para, ésta puede escribirse así: = e -kt En este momento no podemos determinar el valor de la constante k, a menos que tuviéramos alguna información adicional, por ejemplo, que después de 5 minutos ( de hora) el café se ha enfriado a 0 C (0 F). Si así fuera: e k k 7e e 27 7 k omando logaritmo natural a ambos miembros. k ln e ln k ln k ln Usando propiedades de los logaritmos, a qué es igual n log a? Es decir: n log a = log a n k ln Por lo tanto, la expresión (), conociendo el valor de k, queda así: 77 7e t ln 77 7e ln t Unidad Modelos y Predicción - 6
5 Finalmente, la Ley de enfriamiento de Newton, para el café en cuestión es: ( t) 77 7 Hemos resuelto la ecuación diferencial planteada, ahora tenemos la función que nos permite resolver el problema del enfriamiento del café. t Cuando t hora, 2 t ( t) 77 7 se convierte en De donde = 8.2 F = 28.6 C A continuación mostramos la gráfica de la función obtenida para el enfriamiento del café, la temperatura en función del tiempo t. Donde se observa que conforme transcurre el tiempo, la temperatura del café se acerca más y más a la temperatura del aire que lo rodea. 77 F t - 7 Unidad Modelos y Predicción
6 Conceptos clave: 0. Ley de enfriamiento de Newton La rapidez de enfriamiento de un cuerpo en cualquier momento, es directamente proporcional a la diferencia entre la temperatura del cuerpo y la temperatura del medio que lo rodea.. Integral indefinida de una función del tipo du u 2. Diferencial de una función du ln u c u La diferencial de una función f(x) es el producto de la derivada de la función por la diferencial de la variable independiente x: df ( x) df dx dx Unidad Modelos y Predicción - 8
SOLUCIÓN GENERAL Y SOLUCIÓN PARTICULAR DE UNA ECUACIÓN DIFERENCIAL
 SOLUCIÓN GENERAL Y SOLUCIÓN PARTICULAR DE UNA ECUACIÓN DIFERENCIAL Propósito Al finalizar esta sección, quien imparte el curso habrá logrado que los estudiantes: Distingan la solución general de una solución
SOLUCIÓN GENERAL Y SOLUCIÓN PARTICULAR DE UNA ECUACIÓN DIFERENCIAL Propósito Al finalizar esta sección, quien imparte el curso habrá logrado que los estudiantes: Distingan la solución general de una solución
Documento 6 : Modelos exponenciales
 Unidad 4: Funciones reales de una variable real Tema: Modelos cuadráticos. Capacidades. C..: Manejar conceptos y propiedades de las funciones exponenciales y logarítmicas y resolver situaciones problemáticas
Unidad 4: Funciones reales de una variable real Tema: Modelos cuadráticos. Capacidades. C..: Manejar conceptos y propiedades de las funciones exponenciales y logarítmicas y resolver situaciones problemáticas
EJERCICIOS UNIDADES 1, 2 Y 3
 EJERCICIOS UNIDADES 1, Y 3 Nota: En adelante utilizaremos la abreviación ED para ecuación diferencial. TEMAS A EVALUAR Unidad 1 o Clasificación de las ecuaciones diferenciales o Problemas de valor inicial
EJERCICIOS UNIDADES 1, Y 3 Nota: En adelante utilizaremos la abreviación ED para ecuación diferencial. TEMAS A EVALUAR Unidad 1 o Clasificación de las ecuaciones diferenciales o Problemas de valor inicial
La función exponencial se define con una base constante cuyo exponente es el valor variable, es decir:
 Función Exponencial La función exponencial se define con una base constante cuyo exponente es el valor variable, es decir: Con Gráfica función exponencial a) Si la función es creciente en. b) Si la función
Función Exponencial La función exponencial se define con una base constante cuyo exponente es el valor variable, es decir: Con Gráfica función exponencial a) Si la función es creciente en. b) Si la función
Ecuaciones diferenciales
 5 Ecuaciones diferenciales 5.1. Qué es una ecuación diferencial Una ecuación diferencial es una ecuación en la que la incógnita a despejar no es un número sino una función. Las operaciones que intervienen
5 Ecuaciones diferenciales 5.1. Qué es una ecuación diferencial Una ecuación diferencial es una ecuación en la que la incógnita a despejar no es un número sino una función. Las operaciones que intervienen
Ecuaciones Diferenciales
 Teóricas de Análisis Matemático (8) Práctica 0 Ecuaciones Diferenciales Práctica 0 Parte Ecuaciones Diferenciales Si un fenómeno está representado por una función f, la derivada de f representa la variación
Teóricas de Análisis Matemático (8) Práctica 0 Ecuaciones Diferenciales Práctica 0 Parte Ecuaciones Diferenciales Si un fenómeno está representado por una función f, la derivada de f representa la variación
Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos:
 1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
1 CONOCIMIENTOS PREVIOS. 1 Logaritmos. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Operaciones básicas con números reales. Propiedades de
Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/ HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5
 Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/2006 - HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5 1) A continuación diremos de qué tipo son las ecuaciones diferenciales ordinarias (e.
Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/2006 - HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5 1) A continuación diremos de qué tipo son las ecuaciones diferenciales ordinarias (e.
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN. Tema: TÉCNICAS DE INTEGRACIÓN
 UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN Tema: TÉCNICAS DE INTEGRACIÓN TÉCNICAS DE INTEGRACIÓN En matemáticas, cada tipo de problema sugiere un tipo de solución. Para calcular la derivada
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN Tema: TÉCNICAS DE INTEGRACIÓN TÉCNICAS DE INTEGRACIÓN En matemáticas, cada tipo de problema sugiere un tipo de solución. Para calcular la derivada
Erika Riveros Morán. Funciones Exponenciales y Logarítmicas. Si, y se llama FUNCION EXPONENCIAL DE BASE a, a la función
 Definición: Funciones Exponenciales y Logarítmicas Si, y se llama FUNCION EXPONENCIAL DE BASE a, a la función Su gráfica queda determinada por los valores de la base a Por ejemplo: Si ( ) 1 Del gráfico
Definición: Funciones Exponenciales y Logarítmicas Si, y se llama FUNCION EXPONENCIAL DE BASE a, a la función Su gráfica queda determinada por los valores de la base a Por ejemplo: Si ( ) 1 Del gráfico
3.4 Ley de Enfriamiento de Newton
 3.4 Ley de Enfriamiento de Newton 139 11 10 9 habitantes, en condiciones de bienestar (es decir, sin desnutrición ni padecimientos por falta de recursos). Considere t D 0 en 1939, P.0/ D 2:3 10 9 y una
3.4 Ley de Enfriamiento de Newton 139 11 10 9 habitantes, en condiciones de bienestar (es decir, sin desnutrición ni padecimientos por falta de recursos). Considere t D 0 en 1939, P.0/ D 2:3 10 9 y una
Funciones exponencial y logarítmica
 Capítulo 5 Funciones exponencial y logarítmica 5.1. Introducción Dos de la funciones más importantes que se presentan en el estudio de las aplicaciones de la matemática son la función exponencial y = a
Capítulo 5 Funciones exponencial y logarítmica 5.1. Introducción Dos de la funciones más importantes que se presentan en el estudio de las aplicaciones de la matemática son la función exponencial y = a
Introducción a Ecuaciones Diferenciales
 Introducción a Ecuaciones Diferenciales Temas Ecuaciones diferenciales que se resuelven directamente aplicando integración. Problemas con condiciones iniciales y soluciones particulares. Problemas aplicados.
Introducción a Ecuaciones Diferenciales Temas Ecuaciones diferenciales que se resuelven directamente aplicando integración. Problemas con condiciones iniciales y soluciones particulares. Problemas aplicados.
Variables separables
 Definición: Variables separables Si el segundo miembro de una ecuación expresada de la forma: puede expresar como una función que depende solamente de x, multiplicada por una función que depende solamente
Definición: Variables separables Si el segundo miembro de una ecuación expresada de la forma: puede expresar como una función que depende solamente de x, multiplicada por una función que depende solamente
Ecuación de calor: Solución con el método de separación de variables y serie de medio rango de Fourier *
 Universidad de San Carlos Departamento de Matemática Facultad de Ingeniería s septiembre/211 Matemática Aplicada 2N Ecuación de calor: Solución con el método de separación de variables y serie de medio
Universidad de San Carlos Departamento de Matemática Facultad de Ingeniería s septiembre/211 Matemática Aplicada 2N Ecuación de calor: Solución con el método de separación de variables y serie de medio
UNIDAD 3 LOGARITMOS EJERCICIOS RESUELTOS. Objetivo general.
 . UNIDAD LOGARITMOS EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad comprenderás la importancia histórica de los logaritmos y resolverás ejercicios y problemas en los que apliques los logaritmos
. UNIDAD LOGARITMOS EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad comprenderás la importancia histórica de los logaritmos y resolverás ejercicios y problemas en los que apliques los logaritmos
INTEGRACIÓN POR PARTES
 INTEGRACIÓN POR PARTES Propósitos Reconocer que el método de integración por partes amplía las posibilidades de integrar productos de funciones y saber que se desprende de la derivada de un producto. Utilizar
INTEGRACIÓN POR PARTES Propósitos Reconocer que el método de integración por partes amplía las posibilidades de integrar productos de funciones y saber que se desprende de la derivada de un producto. Utilizar
Ecuaciones Diferenciales Ordinarias
 Nivelación de Matemática MTHA UNLP EDO 1 Ecuaciones Diferenciales Ordinarias 1. Introducción Una ecuación diferencial ordinaria es una ecuación de la forma: F (x, y, y,..., y (n) ) = 0 que expresa una
Nivelación de Matemática MTHA UNLP EDO 1 Ecuaciones Diferenciales Ordinarias 1. Introducción Una ecuación diferencial ordinaria es una ecuación de la forma: F (x, y, y,..., y (n) ) = 0 que expresa una
Tema 7. Factores de integración
 Tema 7. Factores de integración 7. QUÉ ES UN FACTOR DE INTEGRACIÓN? En general, la ecuación diferencial (7.) M(,)d + N(,)d 0 no es eacta. Ocasionalmente, sin embargo, es posible transformar (7.) en una
Tema 7. Factores de integración 7. QUÉ ES UN FACTOR DE INTEGRACIÓN? En general, la ecuación diferencial (7.) M(,)d + N(,)d 0 no es eacta. Ocasionalmente, sin embargo, es posible transformar (7.) en una
1. Conocimientos previos. 1 Funciones exponenciales y logarítmicas.
 . Conocimientos previos. Funciones exponenciales y logarítmicas.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
. Conocimientos previos. Funciones exponenciales y logarítmicas.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas.
GUÍA N 2 CÁLCULO I. Desigualdades. 1, la expresión anterior, (note el cambio del operador <). 6
 UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS GUÍA N CÁLCULO I Profesor: Carlos Ruz Leiva Desigualdades. Ej. Resuelva la desigualdad x < 9x + 4. Sumar 9x,
UNIVERSIDAD DIEGO PORTALES FACULTAD DE CIENCIAS DE LA INGENIERÍA INSTITUTO DE CIENCIAS BÁSICAS GUÍA N CÁLCULO I Profesor: Carlos Ruz Leiva Desigualdades. Ej. Resuelva la desigualdad x < 9x + 4. Sumar 9x,
Colegio Universitario Boston Función Logarítmica Función Logarítmica 226
 226 Una función logarítmica es una función de la forma representa a la base de la función, y cumple el papel de argumento., donde Para que una función se considere logarítmica se debe cumplir que el valor
226 Una función logarítmica es una función de la forma representa a la base de la función, y cumple el papel de argumento., donde Para que una función se considere logarítmica se debe cumplir que el valor
El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow.
 INTRODUCCION El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de
INTRODUCCION El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de
AMPLIACIÓN DE MATEMÁTICAS Ingeniería Técnica Industrial. Especialidad en Mecánica Boletín n o 1 (Aplicaciones).
 AMPLIACIÓN DE MATEMÁTICAS Ingeniería Técnica Industrial. Especialidad en Mecánica Boletín n o 1 (Aplicaciones). 1. La policía descubre el cuerpo de una profesora de ecuaciones diferenciales. Para resolver
AMPLIACIÓN DE MATEMÁTICAS Ingeniería Técnica Industrial. Especialidad en Mecánica Boletín n o 1 (Aplicaciones). 1. La policía descubre el cuerpo de una profesora de ecuaciones diferenciales. Para resolver
INTRO. LA INTEGRAL INDEFINIDA
 INTRO. LA INTEGRAL INDEFINIDA Se inicia en este tema el estudio de la integral, concepto fundamental de lo que se conoce como cálculo infinitesimal, que alcanzó su auge y desarrollo durante el siglo XVII.
INTRO. LA INTEGRAL INDEFINIDA Se inicia en este tema el estudio de la integral, concepto fundamental de lo que se conoce como cálculo infinitesimal, que alcanzó su auge y desarrollo durante el siglo XVII.
Crecimiento y decaimiento exponencial
 Crecimiento y decaimiento exponencial En general, si y (t) es el valor de una cantidad y en el tiempo t y si la razón de cambio de y con respecto a t es proporcional a su tamaño y (t) en cualquier tiempo,
Crecimiento y decaimiento exponencial En general, si y (t) es el valor de una cantidad y en el tiempo t y si la razón de cambio de y con respecto a t es proporcional a su tamaño y (t) en cualquier tiempo,
ECUACIONES DIFERENCIALES SEPARABLES
 ECUACIONES DIFERENCIALES SEPARABLES Objetivos 1. Modelar situaciones mediante el uso de ecuaciones diferenciales de variables separables. 2. Asociar los resultados del tratamiento matemático del modelo
ECUACIONES DIFERENCIALES SEPARABLES Objetivos 1. Modelar situaciones mediante el uso de ecuaciones diferenciales de variables separables. 2. Asociar los resultados del tratamiento matemático del modelo
Ley de enfriamiento de Newton considerando reservorios finitos
 Ley de enfriamiento de Newton considerando reservorios finitos María ecilia Molas, Florencia Rodriguez Riou y Débora Leibovich Facultad de Ingeniería, iencias Exactas y Naturales Universidad Favaloro,.
Ley de enfriamiento de Newton considerando reservorios finitos María ecilia Molas, Florencia Rodriguez Riou y Débora Leibovich Facultad de Ingeniería, iencias Exactas y Naturales Universidad Favaloro,.
V B. g (1) V B ) g, (2) +ρ B. =( m H. m H (3) ρ 1. ρ B. Aplicando al aire la ecuación de estado de los gases perfectos, en la forma.
 Un globo de aire caliente de volumen =, m 3 está abierto por su parte inferior. La masa de la envoltura es =,87 kg y el volumen de la misma se considera despreciable. La temperatura inicial del aire es
Un globo de aire caliente de volumen =, m 3 está abierto por su parte inferior. La masa de la envoltura es =,87 kg y el volumen de la misma se considera despreciable. La temperatura inicial del aire es
MATEMATICA GRADO 9 II PERIODO PROF. LIC. ESP. BLANCA NIEVES CASTILLO R. CORREO: cel
 GUIA DE TEORIA NO. 1 LO QUE DEBO SABER Regla de Cramer Un sistema de ecuaciones lineales se dice de Cramer cuando cumple las siguientes condiciones: Es un sistema cuadrado, con igual número de ecuaciones
GUIA DE TEORIA NO. 1 LO QUE DEBO SABER Regla de Cramer Un sistema de ecuaciones lineales se dice de Cramer cuando cumple las siguientes condiciones: Es un sistema cuadrado, con igual número de ecuaciones
Análisis gráfico. Enfriamiento de un cuerpo Decaimiento exponencial
 Análisis gráfico Enfriamiento de un cuerpo Decaimiento exponencial Objetivos Representación gráfica de resultados experimentales y análisis de datos. Análisis gráfico de un decaimiento exponencial. Determinación
Análisis gráfico Enfriamiento de un cuerpo Decaimiento exponencial Objetivos Representación gráfica de resultados experimentales y análisis de datos. Análisis gráfico de un decaimiento exponencial. Determinación
Analicemos ahora el siguiente ejemplo: (2x 4y) dx + (12y - 6x + 1) dy = 0. Será ésta una ecuación diferencial reducible a homogénea?
 82 Analicemos ahora el siguiente ejemplo: (2x 4y) dx + (2y - 6x + ) dy = 0 Será ésta una ecuación diferencial reducible a homogénea? Si observamos la ecuación diferencial, tenemos que 2x 4y = 0 2y 6x +
82 Analicemos ahora el siguiente ejemplo: (2x 4y) dx + (2y - 6x + ) dy = 0 Será ésta una ecuación diferencial reducible a homogénea? Si observamos la ecuación diferencial, tenemos que 2x 4y = 0 2y 6x +
* e e Propiedades de la potenciación.
 ECUACIONES DIFERENCIALES 1 REPASO DE ALGUNOS CONCEPTOS PREVIOS AL ESTUDIO DE LAS ECUACIONES DIFERENCIALES 1. Cuando hablamos de una función en una variable escribíamos esta relación como y = f(x), esta
ECUACIONES DIFERENCIALES 1 REPASO DE ALGUNOS CONCEPTOS PREVIOS AL ESTUDIO DE LAS ECUACIONES DIFERENCIALES 1. Cuando hablamos de una función en una variable escribíamos esta relación como y = f(x), esta
1. Introducción. Fundación Uno. Ejercicio Reto. ENCUENTRO # 33 TEMA: Exponenciales y Logaritmos CONTENIDOS: 1. Ecuaciones Exponenciales.
 ENCUENTRO # 33 TEMA: Exponenciales y Logaritmos CONTENIDOS: 1. Ecuaciones Exponenciales. (a) Leyes de los Exponentes (b) Como resolver ecuaciones exponenciales Ejercicio Reto 1. Si a y b las soluciones
ENCUENTRO # 33 TEMA: Exponenciales y Logaritmos CONTENIDOS: 1. Ecuaciones Exponenciales. (a) Leyes de los Exponentes (b) Como resolver ecuaciones exponenciales Ejercicio Reto 1. Si a y b las soluciones
Sistemas de Ecuaciones Exponenciales y Logarítmicas
 Sistemas de Ecuaciones Exponenciales y Logarítmicas Siguiendo con los s de ecuaciones veremos a continuación aquellos que están compuestos por ecuaciones exponenciales y logarítmicas. I. Sistemas de Ecuaciones
Sistemas de Ecuaciones Exponenciales y Logarítmicas Siguiendo con los s de ecuaciones veremos a continuación aquellos que están compuestos por ecuaciones exponenciales y logarítmicas. I. Sistemas de Ecuaciones
INTEGRACIÓN POR CAMBIO DE VARIABLE
 INTEGRACIÓN POR CAMBIO DE VARIABLE Propósitos Identificar las operaciones algebraicas que convierten una integral a una forma inmediata (cambio de variable). Utilizar las tablas de integrales inmediatas
INTEGRACIÓN POR CAMBIO DE VARIABLE Propósitos Identificar las operaciones algebraicas que convierten una integral a una forma inmediata (cambio de variable). Utilizar las tablas de integrales inmediatas
Clase 6 Ecuaciones exponenciales y logarítmicas
 Clase 6 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo, 2014 Función exponencial Recuerde que el gráfico de f(x) = a x, con a > 0 está dado por f(x) = a x con a >
Clase 6 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo, 2014 Función exponencial Recuerde que el gráfico de f(x) = a x, con a > 0 está dado por f(x) = a x con a >
ecuación quede de la forma y' + A(x) y = B(x) 2- Buscar el factor integrante, el cual depende solo de "x" y viene dado por
 76 por el factor integrante resulta donde µ () = e e dy + A () e y d = e B () d e dy + A () e y d = d ( e y) = d (µ () y) Abran sus guías en la página 6 y leamos la información que allí aparece acerca
76 por el factor integrante resulta donde µ () = e e dy + A () e y d = e B () d e dy + A () e y d = d ( e y) = d (µ () y) Abran sus guías en la página 6 y leamos la información que allí aparece acerca
CURSO DE MATEMÁTICA. Repartido Teórico 4
 CURSO DE MATEMÁTICA. Repartido Teórico 4 Mariana Pereira Noviembre, 2007 1. Ecuaciones Diferenciales Una ecuación diferencial es una ecuación donde la incógnita es una fución de una variable, y la ecuación
CURSO DE MATEMÁTICA. Repartido Teórico 4 Mariana Pereira Noviembre, 2007 1. Ecuaciones Diferenciales Una ecuación diferencial es una ecuación donde la incógnita es una fución de una variable, y la ecuación
Unidad II. Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en unaconstante.
 Unidad II Integral indefinida y métodos de integración. 2.1 Definición de integral indefinida. Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones
Unidad II Integral indefinida y métodos de integración. 2.1 Definición de integral indefinida. Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones
Tema 6: Derivada de una función
 Tema 6: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 6: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
ANÁLISIS MATEMÁTICO IES A SANGRIÑA 2016/2017
 ANÁLISIS MATEMÁTICO 4. INTEGRACIÓN INDEFINIDA UN POCO DE HISTORIA El símbolo de integración fue introducido por el matemático alemán Gottfried Leibniz en 1675, basándose en la palabra latina summa, suma,
ANÁLISIS MATEMÁTICO 4. INTEGRACIÓN INDEFINIDA UN POCO DE HISTORIA El símbolo de integración fue introducido por el matemático alemán Gottfried Leibniz en 1675, basándose en la palabra latina summa, suma,
Matemática IV Taller, Ecuaciones de orden 1. dy dx = y xy2 2. Determine la solución general de la ecuación. (y 4x)dx + (y x)dy = 0.
 Matemática IV - 2000953 Taller, Ecuaciones de orden 1 1. Resuelva R: y 2 x = ln y. dy dx = y 3, y(0) = 1. 1 2xy2 2. Determine la solución general de la ecuación (y 4x)dx + (y x)dy = 0. 3. Una persona tiene
Matemática IV - 2000953 Taller, Ecuaciones de orden 1 1. Resuelva R: y 2 x = ln y. dy dx = y 3, y(0) = 1. 1 2xy2 2. Determine la solución general de la ecuación (y 4x)dx + (y x)dy = 0. 3. Una persona tiene
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN
 INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN EJERCICIOS RESUELTOS Calcula una función real f : que cumple las condiciones siguientes: f (0) = 5, f (0) =, f (0) = 0 y f () = + Como f () = +, integremos esta
INTEGRAL INDEFINIDA. MÉTODOS DE INTEGRACIÓN EJERCICIOS RESUELTOS Calcula una función real f : que cumple las condiciones siguientes: f (0) = 5, f (0) =, f (0) = 0 y f () = + Como f () = +, integremos esta
Integral indefinida. Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
 Integral indefinida 1. Integración Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x). Se dice, entonces,
Integral indefinida 1. Integración Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x). Se dice, entonces,
Reacciones Químicas. (molaridad) pues una mol de sustancia química contiene el mismo número de moléculas.
 Reacciones Químicas Consideremos una reacción química que ocurre en una disolución bien mezclada. Se supondrá que la reacción es irreversible y que ningún otro proceso se lleva a cabo para afectar la cantidad
Reacciones Químicas Consideremos una reacción química que ocurre en una disolución bien mezclada. Se supondrá que la reacción es irreversible y que ningún otro proceso se lleva a cabo para afectar la cantidad
2 Métodos de solución de ED de primer orden
 CAPÍTULO Métodos de solución de ED de primer orden.4 Ecuaciones diferenciales de Bernoulli Una ecuación diferencial ordinaria de primer orden de la forma a 0.x/y 0 C a.x/y D f.x/y r ; con r 0; : se denomina
CAPÍTULO Métodos de solución de ED de primer orden.4 Ecuaciones diferenciales de Bernoulli Una ecuación diferencial ordinaria de primer orden de la forma a 0.x/y 0 C a.x/y D f.x/y r ; con r 0; : se denomina
EXAMEN: TEMAS 1 y 2 BCT 1º 4/11/2014 OPCIÓN A. 1. (1 punto) Representa en la recta real (utilizando instrumentos de dibujo) el número:
 EXAMEN: TEMAS 1 y BCT 1º 4/11/014 OPCIÓN A 1. (1 punto) Representa en la recta real (utilizando instrumentos de dibujo) el número: 4+ 3.. (1 punto) Simplifica: x 3 a a x 5 +x factor común factor común
EXAMEN: TEMAS 1 y BCT 1º 4/11/014 OPCIÓN A 1. (1 punto) Representa en la recta real (utilizando instrumentos de dibujo) el número: 4+ 3.. (1 punto) Simplifica: x 3 a a x 5 +x factor común factor común
LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS
 195 LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS JUSTIFICACIÓN En esta lección, basados en la teoría de diferenciales de funciones de dos variables, la cual involucra las derivadas
195 LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS JUSTIFICACIÓN En esta lección, basados en la teoría de diferenciales de funciones de dos variables, la cual involucra las derivadas
Marco Teórico. Materia: Matemáticas de 4to año. Tema: Función logarítmica
 Materia: Matemáticas de 4to año Tema: Función logarítmica Marco Teórico Cada expresión exponencial se puede escribir en forma logarítmica. Por ejemplo, la ecuación x = 2 y se escribe de la siguiente manera:
Materia: Matemáticas de 4to año Tema: Función logarítmica Marco Teórico Cada expresión exponencial se puede escribir en forma logarítmica. Por ejemplo, la ecuación x = 2 y se escribe de la siguiente manera:
Ecuaciones Diferenciales (MA-841)
 Ecuaciones Diferenciales (MA-841) Ecuaciones de Departmento de Matemáticas / CSI ITESM Ecuaciones de Ecuaciones Diferenciales - p. 1/16 Ecuaciones de Iniciaremos nuestras técnicas de solución a ED con
Ecuaciones Diferenciales (MA-841) Ecuaciones de Departmento de Matemáticas / CSI ITESM Ecuaciones de Ecuaciones Diferenciales - p. 1/16 Ecuaciones de Iniciaremos nuestras técnicas de solución a ED con
1. Algunas primitivas inmediatas (o casi inmediatas).
 Cálculo I. o Matemáticas. Curso 00/0. Cálculo de Primitivas. Algunas primitivas inmediatas (o casi inmediatas). (5x 6) = 5 (5x 6) 5 = 5 (5x 6) + C. Nota: Si f(x) = 5x 6 su derivada es 5. En la primera
Cálculo I. o Matemáticas. Curso 00/0. Cálculo de Primitivas. Algunas primitivas inmediatas (o casi inmediatas). (5x 6) = 5 (5x 6) 5 = 5 (5x 6) + C. Nota: Si f(x) = 5x 6 su derivada es 5. En la primera
3 Aplicaciones de primer orden
 CAPÍTULO 3 Aplicaciones de primer orden 3.3 Crecimiento de poblaciones En esta sección veremos dos modelos de ED que sirven para representar la forma en que evoluciona el número P.t/ de habitantes de una
CAPÍTULO 3 Aplicaciones de primer orden 3.3 Crecimiento de poblaciones En esta sección veremos dos modelos de ED que sirven para representar la forma en que evoluciona el número P.t/ de habitantes de una
Problemas Resueltos. 1. La distribución de la temperatura en una placa metálica, viene dada por la función: 70 =
 Problemas Resueltos 1. La distribución de la temperatura en una placa metálica, viene dada por la función: 70 T (, ) =, donde T está medida en grados centígrados,,z en metros. 1+ + + z En qué dirección
Problemas Resueltos 1. La distribución de la temperatura en una placa metálica, viene dada por la función: 70 T (, ) =, donde T está medida en grados centígrados,,z en metros. 1+ + + z En qué dirección
Ecuaciones diferenciales ordinarias de primer orden: problemas resueltos
 Ecuaciones diferenciales ordinarias de primer orden: problemas resueltos BENITO J. GONZÁLEZ RODRÍGUEZ (bjglez@ull.es) DOMINGO HERNÁNDEZ ABREU (dhabreu@ull.es) MATEO M. JIMÉNEZ PAIZ (mjimenez@ull.es) M.
Ecuaciones diferenciales ordinarias de primer orden: problemas resueltos BENITO J. GONZÁLEZ RODRÍGUEZ (bjglez@ull.es) DOMINGO HERNÁNDEZ ABREU (dhabreu@ull.es) MATEO M. JIMÉNEZ PAIZ (mjimenez@ull.es) M.
FUNCIONES EXPONENCIALES y LOGARITMICAS FUNCIONES EXPONENCIALES
 Ingeniería en Sistemas de Información 01 FUNCIONES EXPONENCIALES LOGARITMICAS La función eponencial FUNCIONES EXPONENCIALES La función eponencial es de la forma, siendo a un número real positivo. El dominio
Ingeniería en Sistemas de Información 01 FUNCIONES EXPONENCIALES LOGARITMICAS La función eponencial FUNCIONES EXPONENCIALES La función eponencial es de la forma, siendo a un número real positivo. El dominio
CAPÍTULO 2. INTEGRALES: INTRODUCCIÓN Y PROPIEDADES 2.1. Introducción 2.2. Teorema 2.3. Propiedades 2.4. Ejemplos 2.5. Integración de una función
 CAPÍTULO. INTEGRALES: INTRODUCCIÓN Y PROPIEDADES.. Introducción.. Teorema.. Propiedades.4. Ejemplos.. Integración de una función compuesta Capítulo Integrales: Introducción y propiedades ( f() g() ) (
CAPÍTULO. INTEGRALES: INTRODUCCIÓN Y PROPIEDADES.. Introducción.. Teorema.. Propiedades.4. Ejemplos.. Integración de una función compuesta Capítulo Integrales: Introducción y propiedades ( f() g() ) (
INTEGRACIÓN INDEFINIDA
 1. PRIMITIVA DE UNA FUNCIÓN Definición: Sean F(x) y f(x) dos funciones reales definidas en un mismo dominio D. Se dice, entonces, que F(x) es una primitiva de f(x) si se cumple quef'(x) = f(x), x. Dicho
1. PRIMITIVA DE UNA FUNCIÓN Definición: Sean F(x) y f(x) dos funciones reales definidas en un mismo dominio D. Se dice, entonces, que F(x) es una primitiva de f(x) si se cumple quef'(x) = f(x), x. Dicho
1.3.1 Fundamentos de cálculo vectorial
 131 Fundamentos de cálculo vectorial 1 Función escalar Una función se define como una representación escalar que está dada en términos de un vector Un ejemplo analítico puede darse por la función f(x)
131 Fundamentos de cálculo vectorial 1 Función escalar Una función se define como una representación escalar que está dada en términos de un vector Un ejemplo analítico puede darse por la función f(x)
Ecuaciones diferenciales ordinarias
 Tema 9 Ecuaciones diferenciales ordinarias Versión: 13 de mayo de 29 9.1 Introducción El objetivo de este tema es exponer muy brevemente algunos de los conceptos básicos relacionados con las ecuaciones
Tema 9 Ecuaciones diferenciales ordinarias Versión: 13 de mayo de 29 9.1 Introducción El objetivo de este tema es exponer muy brevemente algunos de los conceptos básicos relacionados con las ecuaciones
Ejercicios Departamental de marzo del 2016
 Ejercicios Departamental 06 Ciro Fabián Bermúez Márquez 7 de marzo del 06 El siguiente documento tiene la finalidad de revisar los ejercicios del eamen departamental de cálculo integral que se llevo acabo
Ejercicios Departamental 06 Ciro Fabián Bermúez Márquez 7 de marzo del 06 El siguiente documento tiene la finalidad de revisar los ejercicios del eamen departamental de cálculo integral que se llevo acabo
log1 Determine: Asíntota Horizontal, Intercepto con los ejes, Dominio y Rango, Grafica.
 EXAMEN III PARCIAL /4/16 Nombre: Número Cuenta: # Lista: PARTE PRÁCTICA: 6) Resuelva utilizando el método grafico Valor 15% F O. Min z= 5x+7y Sujeta a x + 6y 180 x + y 80 x 10 x, y 0 4 x y ( x 1) 7) Aplique
EXAMEN III PARCIAL /4/16 Nombre: Número Cuenta: # Lista: PARTE PRÁCTICA: 6) Resuelva utilizando el método grafico Valor 15% F O. Min z= 5x+7y Sujeta a x + 6y 180 x + y 80 x 10 x, y 0 4 x y ( x 1) 7) Aplique
CONCEPTOS BÁSICOS DE CÁLCULO.
 CONCEPTOS BÁSICOS DE CÁLCULO. Las variables y las funciones Un concepto muy importante en el estudio de la variación es el de variable y función. La conexión entre sus expresiones analíticas y representaciones
CONCEPTOS BÁSICOS DE CÁLCULO. Las variables y las funciones Un concepto muy importante en el estudio de la variación es el de variable y función. La conexión entre sus expresiones analíticas y representaciones
Soluciones de ecuaciones de primer orden
 GUIA 2 Soluciones de ecuaciones de primer orden Dada una ecuación diferencial, la primera pregunta que se presenta es cómo hallar sus soluciones? Por cerca de dos siglos (XVIII y XIX ) el esfuerzo de los
GUIA 2 Soluciones de ecuaciones de primer orden Dada una ecuación diferencial, la primera pregunta que se presenta es cómo hallar sus soluciones? Por cerca de dos siglos (XVIII y XIX ) el esfuerzo de los
2.4 Ecuaciones diferenciales de Bernoulli
 .4 Ecuaciones diferenciales de Bernoulli 3 Ejercicios.3. Ecuaciones diferenciales lineales. Soluciones en la página 4 Resolver las siguientes ecuaciones diferenciales lineales.. y 0 C 00y D 0.. x 0 0x
.4 Ecuaciones diferenciales de Bernoulli 3 Ejercicios.3. Ecuaciones diferenciales lineales. Soluciones en la página 4 Resolver las siguientes ecuaciones diferenciales lineales.. y 0 C 00y D 0.. x 0 0x
log = = Las ecuaciones de cancelación cuando se aplican las funciones f x = a x y f 1 = log a x, se convierten en:
 Función logarítmica Función logarítmica y su representación Si a > 0 y a 0, la función exponencial f x = a x bien se incrementa o disminuye y por eso mediante la prueba de la línea horizontal es uno a
Función logarítmica Función logarítmica y su representación Si a > 0 y a 0, la función exponencial f x = a x bien se incrementa o disminuye y por eso mediante la prueba de la línea horizontal es uno a
Funciones Exponenciales y Logarítmicas
 Funciones Exponenciales y Logarítmicas 0.1 Funciones exponenciales Comencemos por analizar la función f definida por f(x) = x. Enumerando coordenadas de varios puntos racionales, esto es de la forma m,
Funciones Exponenciales y Logarítmicas 0.1 Funciones exponenciales Comencemos por analizar la función f definida por f(x) = x. Enumerando coordenadas de varios puntos racionales, esto es de la forma m,
Guía: Función Exponencial y Logarítmica
 Guía: Función Eponencial Logarítmica Aplicaciones de la Función Logaritmo 1.- Escala de Richter Para saber la magnitud de un sismo se mide su amplitud A (en micrometros) su período p (en segundos), que
Guía: Función Eponencial Logarítmica Aplicaciones de la Función Logaritmo 1.- Escala de Richter Para saber la magnitud de un sismo se mide su amplitud A (en micrometros) su período p (en segundos), que
ECUACIONES NO POLINÓMICAS CON UNA INCÓGNITA
 Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones ECUACIONES NO POLINÓMICAS CON UNA INCÓGNITA Una ecuación no polinómica es, en general, más difícil de resolver que una
Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones ECUACIONES NO POLINÓMICAS CON UNA INCÓGNITA Una ecuación no polinómica es, en general, más difícil de resolver que una
LECCIÓN 7: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN REDUCIBLES A HOMOGÉNEAS.
 160 LECCIÓN 7: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN REDUCIBLES A HOMOGÉNEAS. JUSTIFICACIÓN En esta lección centraremos nuestro estudio en aquellas ecuaciones diferenciales homogéneas mediante
160 LECCIÓN 7: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN REDUCIBLES A HOMOGÉNEAS. JUSTIFICACIÓN En esta lección centraremos nuestro estudio en aquellas ecuaciones diferenciales homogéneas mediante
EJERCICIO 1.a): Obtener la solución general de las siguientes ecuaciones diferenciales: (9) (1 + t)y = y
 EJERIIO.a): Obtener la solución general de las siguientes ecuaciones diferenciales: () y = y t (9) ( + t)y = y (2) y = 3t + (0) y = 4ty (3) y = cos(2t)y () (t 2 + )y + ty = 0 (4) y = ln(3t)y (2) y = y
EJERIIO.a): Obtener la solución general de las siguientes ecuaciones diferenciales: () y = y t (9) ( + t)y = y (2) y = 3t + (0) y = 4ty (3) y = cos(2t)y () (t 2 + )y + ty = 0 (4) y = ln(3t)y (2) y = y
1. dejar a una lado de la igualdad la expresión que contenga una raíz.
 1. Resuelve las siguientes ecuaciones reales: Solución x 1 + x = 0 ; 3 x = 3 ; ln(x 1) + 4 = ln 3 Ecuaciones con raíces: No todas las ecuaciones de este tipo son sencillas de resolver, pero podemos intentar
1. Resuelve las siguientes ecuaciones reales: Solución x 1 + x = 0 ; 3 x = 3 ; ln(x 1) + 4 = ln 3 Ecuaciones con raíces: No todas las ecuaciones de este tipo son sencillas de resolver, pero podemos intentar
Función Logaritmo y exponencial. Función logaritmo natural
 Función Logaritmo y exponencial Función logaritmo natural En términos matemáticos la función logaritmo natural es una herramienta de mayor utilidad que el logaritmo del álgebra elemental, el cual está
Función Logaritmo y exponencial Función logaritmo natural En términos matemáticos la función logaritmo natural es una herramienta de mayor utilidad que el logaritmo del álgebra elemental, el cual está
FUNCIONES EXPONENCIAL Y LOGARÍTMICA
 FUNCIONES EXPONENCIAL Y LOGARÍTMICA 1. Crecimiento exponencial. La función exponencial. 1.1 La Función Exponencial. Una función exponencial es una expresión de la forma siguiente:,,. Donde es una constante
FUNCIONES EXPONENCIAL Y LOGARÍTMICA 1. Crecimiento exponencial. La función exponencial. 1.1 La Función Exponencial. Una función exponencial es una expresión de la forma siguiente:,,. Donde es una constante
Laboratorio Nº 4 Ecuaciones diferenciales de orden n. Ecuación lineal homogénea. Soluciones linealmente independientes
 Universidad Diego Portales Segundo Semestre 2007 Facultad de Ingeniería Instituto de Ciencias Básicas Asignatura: Ecuaciones Diferenciales Laboratorio Nº 4 Ecuaciones diferenciales de orden n. Ecuación
Universidad Diego Portales Segundo Semestre 2007 Facultad de Ingeniería Instituto de Ciencias Básicas Asignatura: Ecuaciones Diferenciales Laboratorio Nº 4 Ecuaciones diferenciales de orden n. Ecuación
ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M.
 Introducción ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M. En diferentes situaciones que aparecen con frecuencia en las Ciencias Experimentales, es complicado poder escribir
Introducción ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M. En diferentes situaciones que aparecen con frecuencia en las Ciencias Experimentales, es complicado poder escribir
Instituto Tecnológico de Saltillo
 Instituto Tecnológico de Saltillo CÁLCULO INTEGRAL Enero-Junio 2012 Programa de Unidades I. Teorema Fundamental del Cálculo (Diferenciales). II. La integral Indefinida. III.Técnicas de Integración Indefinida.
Instituto Tecnológico de Saltillo CÁLCULO INTEGRAL Enero-Junio 2012 Programa de Unidades I. Teorema Fundamental del Cálculo (Diferenciales). II. La integral Indefinida. III.Técnicas de Integración Indefinida.
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
SISTEMAS DE ECUACIONES
 SISTEMS E ECUCIONES Ejemplos 1 Resuelva por el método de sustitución el sistema x 8 16 8x Solución Se despeja de la segunda ecuación 8x 8x Se sustitue la expresión 8x en la x 8 16 primera ecuación x 8
SISTEMS E ECUCIONES Ejemplos 1 Resuelva por el método de sustitución el sistema x 8 16 8x Solución Se despeja de la segunda ecuación 8x 8x Se sustitue la expresión 8x en la x 8 16 primera ecuación x 8
Unidad 3. Ecuaciones lineales, ecuaciones cuadráticas, desigualdades y fracciones parciales.
 Part I Unidad. Ecuaciones lineales, ecuaciones cuadráticas, desigualdades y fracciones parciales. Ecuaciones lineales en una variable Una ecuación lineal en una variable puede de nirse como ax + b = 0
Part I Unidad. Ecuaciones lineales, ecuaciones cuadráticas, desigualdades y fracciones parciales. Ecuaciones lineales en una variable Una ecuación lineal en una variable puede de nirse como ax + b = 0
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN REFLEXIONA Y RESUELVE Tangentes a una curva y = f (x) 5 3 5 3 9 14 Halla, mirando la gráfica y las rectas trazadas, f'(3), f'(9) y f'(14). Di otros tres puntos en los
9 DERIVADAS. TÉCNICAS DE DERIVACIÓN REFLEXIONA Y RESUELVE Tangentes a una curva y = f (x) 5 3 5 3 9 14 Halla, mirando la gráfica y las rectas trazadas, f'(3), f'(9) y f'(14). Di otros tres puntos en los
Matemáticas UNIDAD 5 CONSIDERACIONES METODOLÓGICAS. Material de apoyo para el docente. Preparado por: Héctor Muñoz
 CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 5 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl LA RELACIÓN DE PROPORCIONALIDAD 1. DESCRIPCIÓN GENERAL DE
CONSIDERACIONES METODOLÓGICAS Material de apoyo para el docente UNIDAD 5 Preparado por: Héctor Muñoz Diseño Gráfico por: www.genesisgrafica.cl LA RELACIÓN DE PROPORCIONALIDAD 1. DESCRIPCIÓN GENERAL DE
Transformada de Laplace - Conceptos Básicos. e -st f(t)dt. L { f (t) } = F(s) =
 Transformada de Laplace - Conceptos Básicos Definición: Sea f (t) una función de t definida para t > 0. La Transformada de Laplace de f(t) se define como: L { f (t) } = F(s) = 0 e -st f(t)dt Algunas Propiedades
Transformada de Laplace - Conceptos Básicos Definición: Sea f (t) una función de t definida para t > 0. La Transformada de Laplace de f(t) se define como: L { f (t) } = F(s) = 0 e -st f(t)dt Algunas Propiedades
1. ECUAC. DIFERENCIALES ORDINARIAS
 1 1. ECUAC. DIFERENCIALES ORDINARIAS Variables separables. 1. Hallar la solución general de la ecuación de variables separables (x 2 + 4) dy dx = xy. Al separar variables, queda la expresión 1 y dy = ambos
1 1. ECUAC. DIFERENCIALES ORDINARIAS Variables separables. 1. Hallar la solución general de la ecuación de variables separables (x 2 + 4) dy dx = xy. Al separar variables, queda la expresión 1 y dy = ambos
Áreas entre curvas. Ejercicios resueltos
 Áreas entre curvas Ejercicios resueltos Recordemos que el área encerrada por las gráficas de dos funciones f y g entre las rectas x = a y x = b es dada por Ejercicios resueltos b a f x g x dx Ejercicio
Áreas entre curvas Ejercicios resueltos Recordemos que el área encerrada por las gráficas de dos funciones f y g entre las rectas x = a y x = b es dada por Ejercicios resueltos b a f x g x dx Ejercicio
Cálculo de Derivadas
 Cálculo de Derivadas Sean a, b y k constantes (números reales) y consideremos a: u y v como funciones. Derivada de una constante Derivada de x Derivada de la función lineal Derivada de una potencia Derivada
Cálculo de Derivadas Sean a, b y k constantes (números reales) y consideremos a: u y v como funciones. Derivada de una constante Derivada de x Derivada de la función lineal Derivada de una potencia Derivada
Tema 7: Derivada de una función
 Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Errores frecuentes en las ecuaciones diferenciales
 Errores frecuentes en las ecuaciones diferenciales 1 Preliminares 1. Propiedades elementales de la exponencial el logaritmo. Ejemplos: log(x) = log(x) log(), log(x + ) = log(x) + log(), log(x + ) = log(x)
Errores frecuentes en las ecuaciones diferenciales 1 Preliminares 1. Propiedades elementales de la exponencial el logaritmo. Ejemplos: log(x) = log(x) log(), log(x + ) = log(x) + log(), log(x + ) = log(x)
Práctica 08 Funciones y Ecuaciones Exponenciales y Logarítmicas
 Instituto Tecnológico de Costa Rica Escuela de Matemática Matemática General Práctica 08 Funciones y Ecuaciones Exponenciales y Logarítmicas I. Determine el dominio máximo de las siguientes funciones:
Instituto Tecnológico de Costa Rica Escuela de Matemática Matemática General Práctica 08 Funciones y Ecuaciones Exponenciales y Logarítmicas I. Determine el dominio máximo de las siguientes funciones:
Chapter Audio Summary for McDougal Littell Algebra 2
 Chapter 8 Exponential and Logarithmic Functions Al principio del capítulo 8 representaste gráficamente funciones exponenciales generales. Luego aprendiste sobre la base natural e. Examinaste la relación
Chapter 8 Exponential and Logarithmic Functions Al principio del capítulo 8 representaste gráficamente funciones exponenciales generales. Luego aprendiste sobre la base natural e. Examinaste la relación
INTEGRACION POR PARTES
 INTEGRACION POR PARTES Se basa en la regla de derivación del producto de dos funciones derivables en un dominio común. Sean u(x)y v(x) común. Entonces: dos funciones derivables en un dominio udv = uv vdu
INTEGRACION POR PARTES Se basa en la regla de derivación del producto de dos funciones derivables en un dominio común. Sean u(x)y v(x) común. Entonces: dos funciones derivables en un dominio udv = uv vdu
4 Algunos métodos de resolución de ecuaciones diferenciales ordinarias de primer orden II
 4 Algunos métodos de resolución de ecuaciones diferenciales ordinarias de primer orden II 4.1. Ecuaciones lineales La e.d.o. de primer orden lineal es Si g(x) = 0: ecuación lineal homogénea. a 1 (x) +
4 Algunos métodos de resolución de ecuaciones diferenciales ordinarias de primer orden II 4.1. Ecuaciones lineales La e.d.o. de primer orden lineal es Si g(x) = 0: ecuación lineal homogénea. a 1 (x) +
Sea a un real positivo fijo, y sea x cualquier real positivo, entonces:
 LOGARITMOS Y RADICALES Definición Sea a un real positivo fijo, y sea x cualquier real positivo, entonces: La función que hace corresponder a cada número real positivo su logaritmo en base, denotada por,se
LOGARITMOS Y RADICALES Definición Sea a un real positivo fijo, y sea x cualquier real positivo, entonces: La función que hace corresponder a cada número real positivo su logaritmo en base, denotada por,se
Técnicas de Integración. Integración por Partes (I)
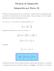 Técnicas de Integración Integración por Partes (I El método de integración por partes es un método que te permite separar una integral (que tiene un producto de dos funciones en una integral simple y lista
Técnicas de Integración Integración por Partes (I El método de integración por partes es un método que te permite separar una integral (que tiene un producto de dos funciones en una integral simple y lista
TEMA 2 ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN
 TEMA ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN 8 INTRODUCCIÓN: Eisten algunos tipos elementales de ecuaciones diferenciales para los cuales se cuenta con procedimientos canónicos que permiten
TEMA ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN 8 INTRODUCCIÓN: Eisten algunos tipos elementales de ecuaciones diferenciales para los cuales se cuenta con procedimientos canónicos que permiten
Integración de funciones trigonométricas
 Integración de funciones trigonométricas Ya vimos las reglas para calcular integrales de funciones trigonométricas. Ahora vamos a considerar productos de funciones trigonométricas y potencias. Para este
Integración de funciones trigonométricas Ya vimos las reglas para calcular integrales de funciones trigonométricas. Ahora vamos a considerar productos de funciones trigonométricas y potencias. Para este
Universidad Nacional Autónoma de México Colegio de Ciencias y Humanidades
 Universidad Nacional Autónoma de México Colegio de Ciencias y Humanidades Área Matemáticas Programas de Estudio de Cálculo Diferencial e Integral II PROGRAMA DE CÁLCULO DIFERENCIAL E INTEGRAL II UBICACIÓN
Universidad Nacional Autónoma de México Colegio de Ciencias y Humanidades Área Matemáticas Programas de Estudio de Cálculo Diferencial e Integral II PROGRAMA DE CÁLCULO DIFERENCIAL E INTEGRAL II UBICACIÓN
ECUACIONES EN Q (NÚMEROS RACIONALES)
 Echa un vistazo a esta situación. ECUACIONES EN Q (NÚMEROS RACIONALES) El domingo, Leonardo caminó 4 unidades. El lunes, Leonardo caminó un tercio de lo que caminó el martes. El caminó un total de 12 unidades
Echa un vistazo a esta situación. ECUACIONES EN Q (NÚMEROS RACIONALES) El domingo, Leonardo caminó 4 unidades. El lunes, Leonardo caminó un tercio de lo que caminó el martes. El caminó un total de 12 unidades
Problemas de enfriamiento
 Problemas de enfriamiento De acuerdo con la ley de enfriamiento de Newton, la tasa de cambio de la temperatura T de un cuerpo respecto del tiempo, en un instante t, en un medio de temperatura constante
Problemas de enfriamiento De acuerdo con la ley de enfriamiento de Newton, la tasa de cambio de la temperatura T de un cuerpo respecto del tiempo, en un instante t, en un medio de temperatura constante
Ecuaciones diferenciales
 de primer orden 21 de noviembre de 2016 de primer orden Introducción Introducción a las ecuaciones diferenciales Las primeras ecuaciones diferenciales surgen al tratar de resolver ciertos problemas de
de primer orden 21 de noviembre de 2016 de primer orden Introducción Introducción a las ecuaciones diferenciales Las primeras ecuaciones diferenciales surgen al tratar de resolver ciertos problemas de
