Capítulo 4: Cálculo en régimen permanente de potenciales en sistemas de puesta a tierra

Transcripción

1 Capítulo 4: Cálculo en régimen permanente de potenciales en sistemas de puesta a tierra 4. ntroducción Las redes de puesta a tierra tienen como uno de sus principales objetivos la reducción de las diferencias de potencial en la superficie de las subestaciones, en sus entornos y en las cercanías de las líneas de transporte. Las normas y recomendaciones para el diseño y operación de redes de puesta a tierra [2,22,99,09,0] utilizan criterios que intentan garantizar la seguridad de las personas. Estos criterios se traducen en especificaciones concretas sobre las diferencias de potencial máximas que pueden aparecer entre dos puntos bien definidos. En particular la bibliografía define las tensiones máximas de paso y de contacto así como los potenciales transferidos en una subestación o en una zona donde se produce una descarga de corriente a tierra [2,22,26,48,90,9, 08,09,0]. En la figura 4. se muestra un diagrama representativo de las tensiones de paso, de contacto y de los potenciales transferidos que pueden aparecer en una subestación. La tensión de paso se define entre los dos pies de una persona, separados.0 m. La tensión de contacto queda determinada entre algún elemento puesto a tierra y los pies unidos de un individuo. Los potenciales transferidos dependen de elementos conductivos que atraviesan los límites de la subestación. Tensión de paso Tensión de contacto m i fallo Subestación 2 Potenciales transferidos Subestación Fig. 4. Tensiones de paso, de contacto y potenciales transferidos en una subestación - -

2 Las recomendaciones utilizadas normalmente para el diseño de las redes de tierra consideran el tiempo de duración de la corriente de falta en la determinación de la tensión de paso y contacto máxima tolerable por el ser humano. Este tiempo depende del retardo en la operación de las protecciones del sistema. Algunos autores [2] incluso han llegado a considerar la resistencia del cuerpo humano, la resistencia de contacto con el suelo y el tiempo de despeje de la falta como variables aleatorias en un modelo probabilístico, con la finalidad de permitir incrementar los límites tolerables de diferencia de potencial aplicados al ser humano debido al riesgo calculado de que puedan ocurrir todos los factores más desfavorables simultáneamente. Antes de los años sesenta [4], se atendía unicamente a que la resistencia de puesta a tierra fuese baja, como criterio de diseño, pero se comprobó que esto puede no ser suficiente para mantener controladas las diferencias de potencial en la subestación y en su entorno, que es el objetivo que se persigue. Para diseñar redes de puesta a tierra que permitan mantener las diferencias de potencial dentro de unos límites que garantice la seguridad de la red tanto para las personas como para los equipos, se han desarrollado diversos métodos. Para determinar las diferencias de potencial se experimentó en los laboratorios durante mucho tiempo un gran número de configuraciones prácticas de redes de puesta a tierra en cubas electrolíticas [4,8,85,3]. Los resultados obtenidos mediante esta técnica pueden ser utilizados por los diseñadores para evaluar los gradientes máximos de potencial mediante algunos métodos aproximados que han sido documentados ampliamente en la literatura especializada [2,27,89,90,0,3,23]. Por otra parte se han realizado modelos matemáticos de la red de puesta a tierra que permiten analizar los potenciales producidos por cualquier configuración electródica compleja, con la ayuda de computadores [23,24,25,54,74,79,87,02 ]. Las técnicas simplificadas para el diseño de redes de puesta a tierra en subestaciones y líneas de transporte permiten que aquellas personas con un entrenamiento básico en el área sean capaces de realizar estos trabajos sin la necesidad de utilizar herramientas complejas de cálculo. Sin embargo en algunos casos particulares los resultados obtenidos por estos métodos no reproducen fielmente la realidad y en general se debe sobredimensionar la red para cumplir con las normas y recomendaciones existentes. En ocasiones los problemas encontrados en la práctica no pueden analizarse mediante técnicas simplificadas sin incurrir en errores importantes, por lo que puede ser necesario utilizar algoritmos de cálculo más complejos

3 En este capítulo se analiza la metodología básica para el desarrollo de herramientas analíticas y numéricas para el cálculo de potenciales producidos por inyecciones de corriente en redes de puesta a tierra complejas en terrenos uniformes y multiestratificados horizontalmente. Se presenta un método original que permite el análisis práctico del comportamiento en régimen permanente de los sistemas de puesta a tierra complejos en terrenos multiestratificados. También se validan los resultados obtenidos mediante los algoritmos que se han desarrollado, con los resultados publicados por autores de otras herramientas semejantes [20]. 4.2 Cálculo de potenciales en terrenos uniformes 4.2. Potencial producido por una inyección puntual de corriente. En la figura 4.2 se presenta el modelo de un subsuelo uniforme. El modelo está formado por dos semiespacios infinitos, el superior que representa el aire y el inferior que representa el subsuelo. La conductividad del aire σ aire se asume nula, y la conductividad del subsuelo se considera uniforme y de valor σ. z > 0 aire σ aire = 0 z=0 r P(r,z) σ subsuelo s R = r 2 + (z+s) 2 Fig. 4.2 Modelo de terreno con resistividad uniforme Si en el modelo de subsuelo uniforme se inyecta una corriente puntual a una profundidad s de la superficie del terreno, los potenciales en el aire y en el subsuelo se pueden determinar a partir de la solución obtenida en la ecuación 2.30, considerando que los potenciales en el infinito deben ser nulos: φ (r,z) = o 4πσ φ (r,z) = 4πσ A o (m) e - m z J o (m.r) dm ; z 0 0 e- m z+s + B (m) e mz J o (m.r) dm ; z Š

4 El término e - m z+s de la ecuación 4.2 representa la inyección de corriente en un medio homogéneo. Este término se superpone a la solución general 2.30 para garantizar que se cumple con la discontinuidad del potencial en el punto de inyección de la corriente. Las condiciones de contorno que deben satisfacer las ecuaciones 4. y 4.2 en la frontera entre el aire y la tierra son la continuidad del potencial φ y la continuidad de la densidad de corriente en la dirección normal J z [07]: de donde se obtiene: σ o φ o (r,0) = φ (r,0) φ o (r,0) = σ z φ (r,0) z A o (m) = 2 e - ms 4.5 B (m) = e - ms 4.6 Sustituyendo las funciones 4.5 y 4.6 en las ecuaciones 4. y 4.2 y utilizando la ecuación 3.8 se determinan los potenciales en el aire y en el subsuelo: φ o (r,z) = 4πσ 2 e - ms e - mz J o (mr) dm = 4πσ 0 φ (r,z) = 4πσ = 4πσ 2 r 2 + (s+z) 2 e - m z+s - m (s-z) + e J o (mr) dm = o r 2 + (z+s) 2 + ; z 0 r 2 + (z-s) 2 ; z Š Tal como demostró Maxwell [7], la solución obtenida en la ecuación 4.8 es idéntica al potencial que produce un par de corrientes inyectadas en un medio infinito y homogéneo, una localizada en la posición z = -s (corriente excitadora) y otra en la posición z = +s (corriente imágen). El potencial en un punto situado en el interior del subsuelo o en la superficie se puede calcular mediante la superposición de los potenciales producidos por una corriente inyectada en el subsuelo y por su respectiva imagen especular calculada mediante un coeficiente de reflexión unitario. Conocida la distribución del potencial φ en todo el espacio de solución, el

5 campo eléctrico E se puede calcular a partir del gradiente negativo del potencial escalar φ (E = - φ). Las líneas de campo eléctrico son normales a las líneas equipotenciales. La densidad de corriente J sigue la misma trayectoria de las líneas de campo eléctrico E debido a que J satisface la ley de Ohm 2.6. Como en el aire la conductividad es despreciable, la corriente en este medio también es practicamente cero y la densidad de corriente en las cercanías de la superficie es tangente a la misma. La densidad de corriente J en las zonas profundas emana radialmente con respecto a la inyección puntual de corriente Potencial producido por un segmento de longitud finita En la figura 4.3 se ha representado un segmento conductor de longitud L orientado según el eje x, y enterrado a la profundidad s en un subsuelo de conductividad uniforme de valor σ. Para calcular el potencial sobre un punto cualquiera del espacio (x,y,z) producido por la corriente drenada a tierra desde un electrodo se divide el segmento en infinitos elementos puntuales de longitud infinitesimal dx y se integran todas las contribuciones parciales. z y x (x,y,z ) so s s s dx s (x,y,z) (x,y,z ) sf s s Fig. 4.3 Potencial producido por un segemento conductor orientado según el eje x Cada uno de los elementos infinitesimales produce un diferencial de potencial dφ ο en un punto de coordenadas (x,y,z) situado en el aire: 2 dφ o (x,y,z) = dx 4πLσ (x-x s ) 2 + (y-y s ) 2 + (z-z s ) o un potencial dφ si el punto está en el subsuelo: - 5 -

6 dφ (x,y,z) = dx 4πLσ [ (x-x s ) 2 + (y-y s ) 2 + (z-z s ) 2 + ] donde : (x-x s ) 2 + (y-y s ) 2 + (z+z s ) 2 es la corriente total drenada a tierra por el electrodo. 4.0 Para determinar la contribución de todos los elementos diferenciales del conductor sobre el punto (x,y,z) se integran las ecuaciones 4.9 y 4.0 con respecto a la variable x entre la coordenada inicial y final del electrodo. Los potenciales en el aire y en la tierra son: 2 φ o (x,y,z) = 4πLσ x sf x so (x-x s ) 2 + (y-y s ) 2 + (z-z s ) 2 dx s 4. φ (x,y,z) = 4πLσ x sf [ x so (x-x s ) 2 + (y-y s ) 2 + (z-z s ) 2 ] dx s + (x-x s ) 2 + (y-y s ) 2 + (z+z s ) Para integrar analíticamente las ecuaciones 4. y 4.2 se utiliza la identidad [34]: dx ln ( x + x 2 + a 2 ) x 2 + a y se obtiene: φ ο (x,y,z) = 2 (x-x ) + (x-x ). 4πLσ [ 2 + (y-y ln ( sf sf s ) 2 + (z-z s ) 2 ) ] (x-x so ) + (x-x so ) 2 + (y-y s ) 2 + (z-z s ) (x-x ) + (x-x ) φ (x,y,z) = 4πLσ [ 2 + (y-y ln ( sf sf s ) 2 + (z-z s ) 2 ) + (x-x so ) + (x-x so ) 2 + (y-y s ) 2 + (z-z s ) 2 (x-x ) + ln ( sf (x-x ) 2 + (y-y sf s ) 2 + (z+z s ) 2 ) ] (x-x so ) + (x-x so ) 2 + (y-y s ) 2 + (z+z s ) Para las orientaciones del conductor según el eje y, los potenciales se - 6 -

7 pueden calcular mediante una transformación de coordenadas del sistema de referencia. Si el conductor está orientado según el eje z, con coordenadas del extremo inicial (x,y,z o ) y coordenadas del extremo final (x,y,z o ), el potencial φ que resulta, es: (z-z )+ (x-x ) φ (x,y,z) = 4πσL [ 2 + (y-y ) 2 + (z-z ) 2 f f ln [ ] + (z-z )+ (x-x ) 2 + (y-y ) 2 + (z-z ) 2 o o ln [ (z+z )+ f (x-x ) 2 + (y-y ) 2 + (z+z ) 2 f ] ] (z+z )+ o (x-x ) 2 + (y-y ) 2 + (z+z ) 2 o 4.6 Las ecuaciones 4.4, 4.5 y 4.6 son de gran utilidad en el análisis del comportamiento de la red de puesta a tierra, debido a que permiten evaluar directamente el potencial que cada electrodo produce sobre un punto determinado, y además son la base para el cálculo de los potenciales propios y mutuos entre los diferentes electrodos de una malla. Mediante los potenciales propios y mutuos entre los electrodos se puede determinar la contribución de la corriente total de falta que se deriva a tierra por cada uno de estos elementos mediante el análisis de circuitos acoplados resistivamente [3] Potencial producido por un segmento orientado según la dirección horizontal, sobre otro segmento orientado en la misma dirección. En la figura 4.4 se muestra una configuración con dos conductores de tierra orientados según la dirección x. Si en el primer electrodo de longitud L se deriva a tierra una corriente de valor, los gradientes de potencial que se establecen en el subsuelo producen un potencial medio sobre el segundo conductor de longitud L 2 con respecto a la referencia de potencial situada en el infinito. El segundo electrodo posee una conductividad muy superior a la del subsuelo y por lo tanto todos los puntos en su superficie o su interior deben permanecer aproximadamente al mismo potencial. Un método aproximado para determinar el potencial que adquiere el conductor consiste en determinar el valor medio de los potenciales que aparecen en el espacio ocupado por el segundo electrodo debido a las corrientes que fluyen a tierra desde el primer electrodo. Para el caso concreto presentado en la figura 4.4 el potencial medio sobre el - 7 -

8 segundo electrodo se puede calcular a partir de: en donde φ viene dada por 4.5. φ = L2 L2 x 2f x 2o φ (x, y 2, z 2 ) dx 4.7 z y x (x,y,z ) o (x,y,z ) 2o 2 2 dx dx 2 L 2 (x,y,z ) L f (x,y,z ) 2f 2 2 Fig. 4.4 Potencial de un electrodo orientado según el eje x, debido a otro electrodo con igual orientación. Para integrar la ecuación 4.7 se utiliza la identidad [34]: ln ( t + t2 + a 2 ) dt t ln ( t + t 2 + a 2 ) - t 2 + a y se obtiene para el potencial medio producido por la corriente que fluye a tierra desde el primer electrodo sobre el segundo electrodo, si ambos electrodos están orientados en la dirección x: donde: φ = L2 4πσL L 2 x 2 =x 2f [ F (x f, u r ) + F (x f, u i ) - F (x o, u r ) - F (x o, u i ) ] x 2 =x 2o 4.9 F (x, u) = (x 2 - x) ln ( (x 2 - x) + (x 2 - x) 2 + u 2 ) - (x 2 - x) 2 + u u r = (y 2 - y ) 2 + (z 2 - z ) u i = (y 2 - y ) 2 + (z 2 + z )

9 z y x s dx 2 r φ(x, y 2, z 2 ) (x, y, z ) dx L Fig. 4.5 Potencial sobre el propio conductor excitador orientado según el eje x Mediante la ecuación 4.9 también se determina el potencial propio del electrodo excitador. Para calcular el potencial propio es necesario considerar las dimensiones finitas del electrodo tal como se muestran en la figura 4.5. El potencial medio del propio conductor que drena la corriente a tierra se puede evaluar integrando los potenciales puntuales en la periferia del electrodo. Si se particulariza la ecuación 4.9 para el cálculo del potencial promedio sobre el propio electrodo excitador, se obtiene la siguiente relación: 2s 2 r φ = L 4πσL [ 2 ( + ( ) + + (L ) ( r + s ) + L L ( + ( 2s 2 ) - ) ( + (L r ) 2 - ) L ln ( ( + ( 2s 2 ) + ) ( + (L r ) 2 + ) L 4.23 La ecuación 4.23 se simplifica considerando que el radio del electrodo es mucho menor que la longitud del conductor L y también mucho menor que su profundidad s: ) ] φ L 4πσL [ ln ( ( r 2L ( + ( 2s 2 ) - ) L ) +2 + ( ) 2 ( + ( 2s 2 ) + ) L 2s L 2 ) + 2-2s L ]

10 En la ecuación 4.24 se observa la dependencia del potencial propio del electrodo excitador con respecto a su radio r. A medida que el radio del conductor aumenta, el potencial medio del electrodo se incrementa logarítmicamente. Se puede demostrar a partir de la expresión 4.9, que los potenciales mutuos dependen débilmente del radio de los electrodos Potencial producido por un segmento orientado según la dirección x sobre otro segmento orientado en la dirección y, o en la dirección z. Si el segundo electrodo está orientado según la dirección del eje y, el potencial sobre este conductor se calcula de forma semejante a la planteada en la ecuación 4.7 pero realizando la integración sobre el eje y, por lo tanto: φ = L2 L2 y 2f φ (x 2, y, z 2 ) dy y 2o 4.25 Para integrar la ecuación 4.25 se utiliza la siguiente identidad [49]: ln ( a + a2 + b 2 + t 2 ) dt = - t + t ln (a + a 2 + b 2 + t 2 ) + a ln ( t + a 2 + b 2 + t 2 ) + 2b tan - ( a + t + a 2 + b 2 + t 2 ) b 4.26 Al integrar según la ecuación 4.25 cada uno de los términos de la ecuación 4.5 se obtiene: 3 φ = L2 4πσL [ L 2 i = y=y 2f (F i (y, x f,z )+F i (y,x f,-z ) - F i (y,x o,z ) - F i (y,x o,-z ) ] y=y2o donde: 4.27 F (y, x, z) = (y - y ) ln [ (x 2 - x) + (x 2 - x) 2 + (y - y ) 2 + (z 2 - z) 2 ] F 2 (y, x, z) = (x 2 - x) ln [ (y - y ) + (x 2 - x) 2 + (y - y ) 2 + (z 2 - z) 2 ] F (y,x,z) = 2 (z - z) tg - (x - x) + (y - y ) + (x - x) 2 + (y - y ) 2 + (z - z) (z - z)

11 F (z) = (z 2 - z) ln ( (z 2 - z) + (z 2 - z) 2 + u 2 ) - (z 2 - z) 2 + u El cálculo de los potenciales sobre conductores orientados en la dirección z producidos por conductores orientados en la dirección x se puede realizar mediante 4.27 intercambiando las coordenadas y por z respectivamente para el electrodo con subíndice Potencial producido por un segmento orientado según la dirección vertical sobre otro segmento orientado en la misma dirección. ntegrando la ecuación 4.6 con respecto a la dirección z a lo largo de la longitud de un conductor paralelo, mediante la identidad 4.8, se obtiene: φ L2 = 4πσL L 2 [ F(z f ) + F(-z f ) - F(z o ) - F(-z o ) ] z = z 2f donde: z = z 2o 4.3 con: u 2 = (x -x ) 2 + (y -y ) Mediante la ecuación 4.3 se determina el potencial mutuo de un electrodo orientado en la dirección z, producido por la corriente que fluye a tierra desde el otro electrodo con la misma orientación. Mediante estas expresiones también es posible calcular el potencial propio sobre el electrodo excitador. Para este fin sólo es necesario asignar convenientemente las coordenadas del propio electrodo de excitación. Meliopoulos[74] presenta una relación completa para el cálculo de los coeficientes de potencial en terreno uniforme, con los electrodos orientados paralelamente a los tres ejes coordenados. Heppe[49] desarrolló las ecuaciones generales que permiten calcular el potencial producido por un segmento sobre otro segmento orientado oblicuamente y en planos paralelos pero con proyecciones oblicuas uno sobre el otro. Este caso se puede analizar a partir de la solución de la integral de Newman. En el presente trabajo, por razones de simplicidad, no se ha considerado la posibilidad de analizar electrodos oblicuos entre si. Sin embargo, esto puede ser extendido sin grandes inconvenientes. - -

12 4.3 Cálculo de potenciales en terrenos multiestratificados 4.3. Potencial producido por una inyección puntual de corriente en uno de los p estratos. En la figura 4.6 se ilustra un modelo del terreno multiestratificado con una inyección de corriente puntual en el estrato j a la profundidad s, y con un número p de capas horizontales. φ o φ φ φ 2 3 σ σ σ 2 3 σ o = 0 z=0 s z r h h 2 h 3 hj φ j φ p σ j σ p h p -z Fig. 4.6 nyección puntual de corriente en un terreno multiestratificado Los potenciales en cada una de las zonas donde no se inyecta la corriente se pueden representar de la siguiente forma: φ (z, r) = k 4πσj o (f (m) e - mz + g (m) e mz ) J k k o (mr) dm ; k j y en el estrato j donde se ha inyectado la corriente : 4.34 φ (z, r) = j 4πσj (e - m z + s + f (m) e - m z + g (m) e mz )J j j o (mr) dm o

13 Recordando que en el aire y en el último estrato el potencial debe ser nulo en el infinito, se determina que los coeficientes funcionales g o (m) y f p (m) deben ser cero para garantizar esta condición. Además se deben satisfacer las condiciones de contorno en los planos que definen las fronteras entre cada estrato, que para los potenciales son: y para las densidades de corriente: φ k (- h k, r ) = φ k+ (- h k, r) ; k=0,, 2,, p φ (- h, r) φ (- h, r) σ k k = σ k+ k ; k = 0,, 2,, p- k z k+ z 4.37 Sustituyendo en las 2p condiciones de contorno representadas por las ecuaciones 4.36 y 4.37, las soluciones generales 4.34 y 4.35, se obtiene un sistema de ecuaciones algebraico que permite determinar los coeficientes funcionales f k (m) y g k (m) para todos los medios considerados. Cuando se evalúan las condiciones de contorno entre dos estratos consecutivos, el estrato k y el k+, se pueden plantear tres situaciones diferentes: a.- k j y k+ j: f k (m) e mhk + g k (m) e - mhk = f k+ (m) e mhk + g k+ (m) e - mh k 4.38 σ k f k (m) emh k - σk g k (m) e- mh k = σk+ f k+ (m) emh k - σk+ g k+ (m) e - mh k 4.39 b.- k = j: k+ - mh k+ - m(h - s) k k+ - mh k f (m) emh gk (m)e e = f (m) emh gk+ e k k k- mh - m(h - s) k k k- - mh k σ f (m) emh σk g (m) e- - σk e = σ f (m)emh σk+ g (m)e k k k k+ k+ k+ c.- k+ = j: mh k k k+ - mh - m (s - h ) k k f (m)emh + gk (m) e- = fk+ (m) emh gk+ (m) e + e k mh k-σk k= k- mh k+ - m(s-h ) k σ f (m)emh g (m)eσk+ f (m)emh σk+ g (m)eσk+ e k k k k+ k

14 El sistema que se obtiene a partir de las 2p ecuaciones determinadas por las condiciones de contorno es disperso, ya que cada una de las ecuaciones del sistema posee a lo sumo cuatro coeficientes. El sistema tiene 2p+2 funciones indeterminadas, pero como ya se ha establecido la necesidad de que g o (m) y f p (m) deben ser nulas para que el potencial sea nulo en el infinito, el resto de las funciones pueden obtenerse del sistema de ecuaciones planteado. El método propuesto para resolver de forma general este sistema consiste en plantear un sitema de dos ecuaciones por cada estrato que liga los coeficientes de un estrato con los del estrato siguiente. De esta forma es posible ir encadenando los subsistemas de ecuaciones hasta que se alcanza el último estrato, donde se conoce uno de los coeficientes. Como también se conoce un coeficiente correspondiente al aire, es posible determinar el resto. Antes de generalizar la solución al cálculo de los coeficientes funcionales indeterminados que ajustan las condiciones de contorno del problema, es conveniente resolver el caso más común que aparece en la práctica, que consiste en analizar un sistema con p estratos donde la inyección de corriente se realiza en el primer estrato. Cuando se aplican las condiciones de contorno en la superficie del terreno se deduce a partir de las ecuaciones 4.42 y 4.43, recordando que g o (m) es nulo y que la conductividad del aire σ o es cero: f (m) f (m) - g (m) = [ -] g (m) = - e- ms 4.44 Entre el primer y segundo estrato se satisface a partir de las ecuaciones 4.42 y 4.43 que: f (m) f (m) g (m) = E 2 g (m) 2-0 ems 4.45 De las ecuaciones en las demás fronteras se establece: f k (m) g (m) k = E k f k+ (m) g k+ (m) donde: E = k + kk ; k = 2, 3,, p k k e- 2mh k k k e 2mh k

15 y: σ - σ k k+ k = k σk + σ k Enlazando la ecuación 4.45 con la sucesión de ecuaciones representada por 4.46, y recordando que el coeficiente f p (m) debe ser nulo se puede escribir la siguiente ecuación: f (m) g (m) que sustituida en 4.44, resulta: p- = 0 E k k= g p (m) - 0 ems 4.49 f (m) [ -] g (m) = [ p- -] k= E k 0 g p (m) + ems = - e - ms 4.50 De la ecuación 4.50 se puede despejar la función g p(m): g p (m) = - ( e - ms + e ms ) [ -] p- E 0 k k= 4.5 Sustituyendo el coeficiente g p(m) obtenido en 4.5 en la ecuación 4.49 se determinan los coeficientes funcionales correspondientes a la primera capa del terreno: p- k= f (m) g (m) = - (e - ms + e ms ) - 0 [ -] p- ems 0 E k k= 4.52 El resto de los coeficientes se puede calcular de forma semejante mediante las expresiones 4.46 y 4.5: E k 0-5 -

16 f k (m) g k (m) p- = E 0 i i = k p- i = k E i 0 g p (m) = - p- [ -] 0 E i i = ( e - ms + e ms ) ; k 4.53 Una vez que se han obtenido los valores de las funciones f k (m) y g k (m) para todos los estratos, y para cada valor de la variable de integración m, es necesario realizar las integrales entre cero e infinito definidas mediante las ecuaciones 4.34 y En el caso biestratificado esta integral puede obtenerse de forma cerrada, realizando una expansión del denominador en serie de términos exponenciales. La evaluación numérica de las expresiones 4.52 y 4.53 presenta problemas numéricos debido a que las matrices E k (m) poseen términos de la forma k k e 2mh k. Estos términos crecen muy rapidamente con el valor de la variable de integración m, pero debe observarse que a medida que crece este, el término k k e-2mh k decrece rápidamente a cero, de tal forma que al multiplicar la última matriz E p- por el vector [0 ] T, el resultado tiende a [0 ] T en el límite cuando el valor de m es muy grande. Por esta razón, para valores grandes de m cuando se integran las expresiones 4.34 y 4.35, se puede emplear las expresiones aproximadas para el cálculo de los coeficientes funcionales, ver Anexo C: f (m) g (m) 0 e- ms ; m f (m) k g (m) k 0 (e- ms + e ms ) k ; m 4.54 Mediante la expresión aproximada 4.54, la ecuación 4.35 y la 3.8, se puede calcular el potencial en un punto cualquiera del primer estrato como: φ (z, r) 4πσ [ r 2 + (z+s) 2 + m max [ [ e - mz e mz] r 2 + (z-s) 2 f (m) g (m) o - e- m(s-z) ] J (mr) dm o ] 4.55 El valor de m max en la ecuación 4.55 es aquel que permite evaluar con la precisión que se desea todos los términos de las matrices E k para cada uno de los valores de k desde el primer estrato hasta el p-. La ecuación 4.55 es exacta si el

17 valor de m max tiende a infinito. Resulta interesante observar en la expresión 4.55 que el potencial producido por la inyección de una corriente en el primer estrato de un terreno multiestratificado se puede calcular mediante la superposición del potencial para un subsuelo homogéneo de conductividad igual a σ y una corrección que depende de la estratificación del medio. En la sección 4.2 se obtuvieron los potenciales para subsuelo uniforme, estos resultados pueden utilizarse para acelerar el cálculo en el caso multiestratificado. El procedimiento consiste en calcular los potenciales considerando que el terreno es uniforme y posteriormente se hace la corrección debida a la estratificación, mediante la evaluación numérica del término integral de la expresión Si la inyección de la corriente es en el estrato j, se pueden generalizar a partir de las expresiones 4.34, 4.35, 4.38, 4.39, 4.40, 4.4, 4.42 y 4.43 para un medio multiestratificado con inyección de corriente en la capa j: f (m) g (m) f k (m) f j (m) g j (m) g (m) k = E k p- = 0 E k f j- (m) k = j f k+ (m) g k+ (m) g (m) j- = E j- g p (m) - 0 ems 4.56 ; k =, 2,, j-2, j+,, p f (m) j g (m) j + E j- 0 e- ms 4.58 j- f (m) j p- = E k g (m) j = 0 j- E k g p (m) - 0 E k k= k= por lo tanto de 4.59 y 4.60 se obtiene: k= ems - 0 e- ms 4.59 f (m) f (m) - g (m) = [ -] g (m) =

18 g p (m) = [ -] j- k= E k 0 [ -] p- ems - ms 0 e- ; j > k= 4.6 Sustituyendo el coeficiente funcional de la última capa g p (m) obtenido en E k 0 4.6, en las expresiones 4.56 y 4.59 se pueden calcular los coeficientes funcionales correspondientes a todos los estratos del subsuelo. Cuando el valor de m tiende a infinito se observa que los coeficientes funcionales f (m) y g (m) tienden a cero, por lo que se puede aproximar la ecuación 4.34 a: m max φ (z, r) [ e 4πσj - mz f (m) + emz g (m) ] J o (mr) dm o 4.62 Mediante la ecuación 4.62 es posible evaluar en forma aproximada, los potenciales en la primera capa de un terreno multiestratificado debido a una inyección en cualquier otra capa. El valor de m max, tal como se ha discutido en el capítulo anterior, debe tener un valor lo suficientemente grande como para que el potencial pueda ser calculado con precisión, pero inferior a los valores que impidan la evaluación de las funciones exponenciales, implícitas y explícitas en el integrando de la ecuación Potencial producido por un electrodo drenando corriente a tierra. Las expresiones 4.5 y 4.6 determinan explicitamente la función g p (m) para el caso de una inyección puntual en el primer estrato o en cualquiera otra capa respectivamente. Una vez conocida esta función se pueden evaluar todos los coeficientes funcionales restantes mediante la sustitución de g p (m) en las ecuaciones 4.46 y 4.49 si la inyección de corriente es en la primera capa, o en las expresiones 4.57 y 4.59 si la inyección es en cualquier otra capa. Generalmente sólo es necesario calcular los coeficientes de las capas donde existen electrodos o donde se desea calcular el potencial. Conocidos los coeficientes funcionales se reemplazan en las ecuaciones 4.34 y Finalmente se realizan las integraciones numéricas tal como se planteó en la sección De esta forma se obtiene el potencial que una inyección puntual de corriente produce en un punto determinado del espacio

19 Para calcular el potencial que produce un electrodo longitudinal en un punto cualquiera del espacio es necesario integrar los potenciales con que contribuye cada uno de los diferenciales del electrodo de forma semejante a como se ha realizado en las ecuaciones 4. y 4.2 para el terreno uniforme o en el Anexo A, ecuación A.33 para un subsuelo con dos estratos. Si el electrodo se encuentra orientado en la dirección x en el primer estrato, el potencial que se produce en un punto (x,y,z) localizado en la primera capa es: φ (x,y,z) = 4πLσ x sf x so o (e - m z-z s + f (m) e - mz + g (m) e mz ) J o (mr) dm dx s donde: r = (x-x s ) 2 + (y-y s ) Como la evaluación numérica de la ecuación 4.63 requiere integrar con respecto a la variable m y con respecto a la dirección x s, es necesario disponer de un método eficiente para realizar esta operación. En la sección se discutió un método que permite obtener la integral entre cero e infinito de funciones que se van alternando positiva y negativamente en tanto que su envolvente decrece monótonamente. Este método puede ser aplicado también en este caso, pero el problema consiste en que la integral longitudinal requiere del conocimiento del valor de la función integrada internamente en m para todos los valores de x s comprendidos entre el extremo origen x so y el extremo final x sf del electrodo. Entre los dos extremos de un electrodo finito existen infinitos puntos y resolver el problema planteado requiere limitar a un valor manejable el número de puntos considerados. Una vez que se ha limitado el número de segmentos, se pueden utilizar algoritmos tales como la regla trapezoidal o el método de Simpson [7] para obtener la solución del potencial en el punto considerado, con la mayor precisión posible y con el menor número de segmentos. El método de Simpson consiste en aproximar la función que se está integrando en arcos de parábola para cada intervalo de integración. Si se divide el electrodo en un número par n de segmentos, la integral según el método de Simpson queda: b y dx h (yo + 4y + 2y + 4y + + 2y + 4y + y n-2 n- n ) a 4.64 el error obtenido al utilizar la ecuación 4.64 para evaluar la integral es aproximadamente [6]: Error h (-yo + 4y - 6y + 4y - - 6y + 4y - y n-2 n- n ) 4.65 A diferencia de lo que sucede con las integrales que involucran funciones de - 9 -

20 Bessel, las funciones generadas por los diferenciales de potencial en la longitud del electrodo poseen un comportamiento relativamente suave y sólo presentan problemas en el proceso de integración para distancias muy pequeñas ya que tienen dependencia inversa con la separación. Por esta razón si los diámetros de los electrodos no son demasiado pequeños, es posible obtener valores muy aproximados a las integrales sin dividir el electrodo en muchos segmentos. Esto se traduce en una reducción considerable de los tiempos de procesamiento requeridos por el algoritmo Potencial sobre un electrodo producido por la corriente drenada a tierra por otro electrodo. Para determinar el potencial medio que produce la corriente drenada a tierra por un electrodo ubicado en el primer estrato y orientado según la dirección x sobre otro electrodo del mismo estrato, se debe integrar el potencial definido en la ecuación 4.63 con respecto a la dirección del segundo electrodo y dividir el resultado por la longitud de este electrodo: φ = L2 L2 (x,y,z ) f2 f2 f2 φ (x,y,z) ds 2 (x,y,z ) o2 o2 o La integral 4.66 puede evaluarse mediante una técnica semejante a la discutida en la sección Se puede dividir el segundo electrodo en un número de segmentos de longitud similar a la del electrodo excitador y en este caso el problema se reduce a evaluar potenciales puntuales entre todos los segmentos de un electrodo con todos los segmentos del otro electrodo. Si se divide cada uno de los electrodos en n segmentos, son necesarias n 2 evaluaciones de las integrales que incluyen funciones de Bessel. Estas integrales son semejantes a las que han sido analizadas en la sección Como cada una de esas evaluaciones requiere un tiempo considerable de cálculo es necesario determinar el menor número de segmentos que permite obtener su valor con la precisión deseada. En general no es necesaria una precisión excesivamente grande en la determinación de los potenciales propios y mutuos entre electrodos de la red debido a que son utilizados únicamente para determinar la distribución de las corrientes en

21 los diferentes electrodos de la red de tierra. En cualquier caso es recomendable dedicar una especial atención a los potenciales mutuos entre electrodos muy cercanos, y en particular al cálculo del potencial medio sobre el propio electrodo excitador ya que en estas condiciones las distancias son reducidas y los potenciales varían inversamente con este parámetro [54]

22 4.4 Cálculo de la distribución de corriente en los electrodos En las secciones 4.2, y 4.3 se presentó una metodología general para la determinación de los potenciales propios y mutuos entre los electrodos de una red de puesta a tierra para terrenos uniformes y multiestratificados. En el Anexo A se particularizan estas ideas a terrenos estratificados en dos capas. El cálculo de estos potenciales es la base para determinar la distribución de corrientes derivadas a tierra por cada uno de los segmentos en que se ha dividido la red. Para el cálculo de los potenciales propios y mutuos de cada electrodo con el resto de los elementos de la red, se inyecta una corriente a un electrodo, mientras que los demás elementos de la red se mantienen en circuito abierto. En estas condiciones se evalúan los potenciales medios sobre la superficie de cada uno de los electrodos. Estos potenciales dependen directamente de la corriente que se ha inyectado en el electrodo de excitación. El cociente entre el potencial medio sobre el electrodo excitador y la corriente inyectada se define como coeficiente de potencial propio del electrodo. Los potenciales sobre el resto de los electrodos de la red debidos a la corriente que circula por el electrodo de excitación definen los coeficientes de potencial mutuos entre los electrodos de la red y el electrodo de excitación. En la figura 4.7 se han representado los coeficientes de potencial propios y mutuos para el caso de tres electrodos inmersos en un terreno de conductividad uniforme σ. = p.u. (b) (a) φ ba (c) φ ca φ aa σ Fig. 4.7 Coeficientes de potencial propios y mutuos del electrodo (a). Debido al principio de reciprocidad en medios homogéneos e isotrópicos, los coeficientes mutuos entre dos conductores cualesquiera de la red deben ser iguales sea quien sea el electrodo de excitación. Se puede demostrar que el principio de

23 reciprocidad se satisface en este caso ya que para evaluar los coeficientes de potencial mutuos es necesario realizar una integral doble a lo largo de la longitud de cada uno de los electrodos. Si se intercambia el orden de la integración no se altera el resultado y por esta razón el coeficiente de potencial entre el electrodo i y j es idéntico al coeficiente obtenido entre los electrodos j e i. Esta simetría permite reducir a la mitad el número de coeficientes de potencial mutuos que deben evaluarse. Si la disposición geométrica de un par de electrodos se repite en la red de tierra, es suficiente con determinar el coeficiente de potencial mutuo de la primera pareja ya que el resto de parejas con la misma distribución espacial poseen el mismo coeficiente de potencial mutuo. Este hecho también es válido para los coeficientes de potencial propios. Todos los coeficientes de potencial propios de los electrodos que poseen la misma orientación, tamaño y profundidad son iguales entre si. Para determinar numéricamente si una pareja de electrodos rectilíneos se encuentran geométricamente en la misma disposición, es suficiente con analizar si las cuatro posibles distancias entre sus extremos coinciden en un orden determinado y si las parejas de electrodos se encuentran a la misma profundidad. Mediante esta idea es posible reducir considerablemente el número de coeficientes de potencial que deben calcularse, con el consiguiente ahorro de tiempo. Como los coeficientes de potencial se han definido a partir de un nivel cero de referencia, y representan el potencial medio que aparece sobre cada electrodo es posible modelar la red mediante una matriz de coeficientes de potencial: donde: V V 2 = V k V n φ φ 2 φ k φ n φ 2 φ 22 φ 2k φ 2n φ φ φ φ k k2 kk kn φ φ φ n n2 nk φ nn Vi es el potencial medio sobre el electrodo i. i es la corriente derivada a tierra por el electrodo i. φii es el coeficiente de potencial propio del electrodo i. φij n 2 k n 4.67 es el coeficiente de potencial mutuo entre el electrodo i y el electrodo j. es el número total de electrodos de la red. El sistema de ecuaciones 4.67 relaciona las n tensiones sobre cada uno de

24 los electrodos con las n corrientes derivadas a tierra por cada uno de esos conductores. Si una red de puesta a tierra tiene todos los electrodos conectados galvánicamente, se puede asumir que las n tensiones de los electrodos son iguales, debido a que en estos no se producen caidas de tensión apreciables por que su conductividad es superior, en varios órdenes de magnitud, a la conductividad del terreno. Conociendo la tensión aplicada a la red de tierra se puede determinar la distribución de corrientes en los electrodos mediante: 2 = k n φ φ 2 φ k φ n φ 2 φ 22 φ 2k φ 2n φ φ φ φ k k2 kk kn φ φ φ φ n n2 nk nn 4.68 La corriente total derivada a tierra se puede calcular sumando todas las corrientes derivadas a tierra por cada uno de los electrodos obtenidas de la ecuación 4.68: n = total = [ ] [ k 2 k n ] t k= V La resistencia de puesta a tierra de la malla se puede calcular a partir de la ecuación 4.69 como: R = V = V total total n k k= 4.70 Si en lugar de conocer la tensión V aplicada a la red de puesta a tierra, se conoce la corriente total inyectada a la malla total, se puede aplicar una tensión de prueba de valor unitario (.0 p.u.) y determinar mediante las ecuaciones 4.68 y 4.69 las corrientes en cada electrodo y la corriente total derivada a tierra. Con la distribución de las corrientes drenadas a tierra calculadas a partir de la aplicación de una tensión unitaria en la red, se determina la distribución de las corrientes debidas a la inyección de la corriente total por linealidad: [ k n = total [ ] k n ] (V=.) V= total total 4.7 El sistema de ecuaciones 4.67 permite calcular la distribución de corrientes

25 derivadas a tierra y las tensiones, en sistemas de puesta a tierra que no están galvánicamente conectados. Un ejemplo clásico está constituido por dos redes independientes de puesta a tierra que se encuentran relativamente cercanas. Si a uno de los dos sistemas se le aplica una tensión V a, las corrientes drenadas a tierra por esta red producen un potencial en la otra malla de tierra independiente galvánicamente. Si se denomina V b al potencial de la segunda red, se puede plantear el siguiente sistema de ecuaciones para el conjunto de las dos redes de tierra: [ V a ] [ V b ] [ φ = aa ] [ φ ab ] [ φ ba ] [ φ bb ] [ a ] [ b ] 4.72 En el sistema 4.72 la suma de los términos del vector de corrientes derivadas a tierra por la red de puesta a tierra - b - es nula, ya que esta malla no está siendo excitada. Si se definen las matrices [U n ] y [U m ] como vectores cuyos elementos son todos unitarios y de dimensión nx y mx respectivamente, donde n es el número de elementos de la malla a y m es el número de elementos de la malla b, aplicando al sistema de ecuaciones 4.72 la reducción de Kronn [05] se puede encontrar el siguiente resultado: [ a ] = [ [ A ] - [ B ] [ D ] - [ C ] ] - [ E ] 4.73 donde: [ A ] = [ φ aa ] [ b ] = - [ D ] - [ C ] [ a ] [ B ] = [ φ ab ] - [ [U n ] t [φ aa ] - [U n ] ] - [U n ] [U n ] t [φ aa ] - [φ ab ] [ C ] = [ φ ba ] - [ [U m ] t [φ bb ] - [U m ] ] - [U m ] [U m ] t [φ bb ] - [φ ba ] [ D ] = [ φ bb ] [ E ] = [ [U n ] t [φ aa ] - [U n ] ] - [U n ] A 4.79 De las ecuaciones 4.73 y 4.74 se obtiene la distribución de corrientes derivadas a tierra por las dos redes. El cálculo de las tensiones que aparecen en cada una de las redes de puesta a tierra se pueden calcular mediante las siguientes expresiones:

26 V a = [ [U n ] t [φ aa ] - [U n ] ] - [ A + [U n ] t [φ aa ] - [φ ab ] [ b ] ] 4.80 V b = [ [U m ] t [φ bb ] - [U m ] ] - [U m ] t [φ bb ] - [φ ba ] [ a ] 4.8 Mediante las ecuaciones 4.73, 4.74, 4.80 y 4.8 es posible calcular potenciales transferidos a los electrodos de una red de puesta a tierra debido a inyecciones de corriente en otra red desacoplada galvánicamente. 4.5 Algoritmo general para el cálculo de potenciales en régimen permanente En las secciones anteriores se ha expuesto una metodología que permite evaluar potenciales en el espacio situado en las cercanías de una configuración electródica compleja que está siendo sometida a una inyección de corriente permanente de muy baja frecuencia. De acuerdo con esa metodología, se ha desarrollado un algoritmo para el cálculo de potenciales en régimen permanente, constituido por los siguientes bloques, ver Fig. 4.8: a. Lectura de los parámetros del modelo del terreno: El modelo del terreno ha sido estudiado en el capítulo tres. En general se pueden considerar tres modelos básicos, el uniforme, el biestratificado y el multiestratificado. Existen otros modelos que pueden ser contemplados tales como el continuamente estratificado y el estratificado verticalmente. En este trabajo solamente se han considerado los tres modelos del subsuelo destacados anteriormente, sin embargo mediante la metodología descrita se podrían incorporar nuevos modelos como por ejemplo, estratificación vertical o variación funcional de la resistividad en el interior del subsuelo. Una vez definido el modelo del terreno, se caracteriza el terreno por sus parámetros. En otras palabras, se especifican las dimensiones de cada capa y su respectiva resistividad. b. Lectura de la topología de red: En este punto se define el número de electrodos, sus dimensiones principales -longitud y radio-, su ubicación en el espacio tridimensional y sus conexiones galvánicas. Se ha desarrollado un editor de la red que permite generar las coordenadas espaciales de los electrodos en forma automática para configuraciones convencionales típicas tales como mallas rectangulares, picas alineadas, etc. Una vez que se introduce la disposición física de los

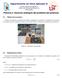
27 electrodos, el algoritmo analiza las simetrías e identifica para qué electrodos se deben calcular los potenciales propios y mutuos. A estos electrodos se les denomina principales. Cada uno de los electrodos restantes se identifica con alguno de los principales. En los cálculos posteriores tan sólo se evaluan los elementos principales. El algoritmo desarrollado no considera elementos que no sean paralelos a uno de los tres ejes coordenados. Sin embargo el editor de topología de la red no esta restringido en este aspecto para permitir futuras extensiones del algoritmo. c. Cálculo de los coeficientes de potencial propios y mutuos: Conocida la topología, las simetrías y el modelo del terreno se calculan los coeficientes de potencial propios y mutuos. Este paso consume el mayor tiempo, particularmente en redes de gran dimensión si se consideran modelos biestratificados o multiestratificados del terreno. Es importante destacar por una parte que es necesario calcular solamente la mitad de los coeficientes mutuos debido a la reciprocidad de la red. Por otro lado existen gran cantidad de electrodos que se encuentran topológicamente en la misma ubicación o simplemente rotados o trasladados, en estos casos es posible reducir aun más el número de coeficientes que deben ser evaluados. Por ejemplo todos los coeficientes de potencial propios de electrodos horizontales, de igual longitud y ubicados a la misma profundidad tienen el mismo valor. Lo mismo ocurre para los electrodos verticales. Si el modelo del terreno es muy complejo y la red muy extensa, resulta muy conveniente utilizar una metodología topológica que evalue el menor número posible de coeficientes. d. Definición de la excitación: Una vez que se han calculado los coeficientes de potencial, el algoritmo requiere la información sobre el tipo de excitación que se aplica a la red. La excitación puede ser aplicada como una fuente de corriente, una fuente de tensión o mediante un equivalente de Thevenin. Dependiendo de la excitación a que se somete la red, quedan definidas las variables independientes y dependientes del sistema y por lo tanto el método de solución que debe utilizarse. e. Cálculo de las corrientes derivadas a tierra: Definida la excitación de la red de puesta a tierra se procede a

28 resolver el sistema de ecuaciones nodales que definen su comportamiento. En este paso se utilizan algoritmos eficientes para la solución de sistemas de ecuaciones lineales. Los métodos de inversión de matrices del tipo LU [92] son convenientes en esta etapa ya que son precisos, rápidos y utilizan poca memoria, ventajas muy atractivas cuando se manejan sistemas de grandes dimensiones. Cuando las redes son muy extensas y en determinados tipos de subsuelo, puede ser que electrodos muy remotos posean acoplamientos muy débiles. Si se aproximan a cero estos términos, puede ser recomendable utilizar técnicas de matrices dispersas para reducir el tiempo de cálculo. En el algoritmo desarrollado no se ha considerado esta posibilidad. f. Cálculo de potenciales en el terreno: Conocidas las corrientes derivadas a tierra por cada uno de los electrodos de la red se calculan por superposición los potenciales que se producen en cualquier punto del espacio. El usuario del programa define los puntos de interés y el algoritmo evalúa para cada punto la sumatoria de todas las contribuciones de cada uno de los electrodos longitudinales. Con los datos obtenidos es posible determinar los potenciales de paso y contacto en la superficie del terreno y los potenciales transferidos por acoplamiento resistivo entre mallas de tierra o entre una malla de tierra y algún electrodo metálico enterrado en las cercanías de la red. g. Salida de resultados y gráficos: La salida del programa presenta en primer lugar aquellos datos de entrada tales como los parámetros del modelo del terreno y la configuración electródica de la red de tierra. En segundo lugar indica el tipo de excitación, su valor, las corrientes derivadas a tierra por cada uno de los electrodos y la resistencia de puesta a tierra de toda la instalación. Finalmente se suministran los potenciales en cada uno de los puntos solicitados por el usuario del programa. Es muy conveniente disponer de rutinas gráficas eficientes que permitan la interpretación rápida de los resultados

29 - Lectura de parámetros del terreno. - Editor de la topología de la red. - Cálculo de los coeficientes de potencial [V ] = [ φ ][ ] V Tipo y valor de la Excitación? Thevenin Cálculo de la distribución de corrientes en los electrodos y resistencia total de puesta a tierra Editor Cálculo de potenciales Salida de resultados Fin Fig. 4.8 Algoritmo general de cálculo de potenciales en régimen permanente. Mediante el método propuesto se puede determinar la distribución de corrientes por todos los electrodos que configuran una red de puesta a tierra, la resistencia total y la distribución de potenciales tanto en la superficie como en cualquier otra zona del espacio cercano a los electrodos. El método de cálculo de la distribución de corrientes en los electrodos de la red y de los potenciales en el terreno se ha desarrollado bajo la hipótesis de que el efecto inductivo de la red de puesta a tierra es despreciable. Esta suposición se puede mantener si la fuente de excitación es de muy baja frecuencia o cuando la red es de pequeñas dimensiones. Redes de tierra de grandes dimensiones o sometidas a perturbaciones transitorias con espectros de alta frecuencia requieren un análisis más completo que implica la solución completa de las ecuaciones de Maxwell en régimen transitorio. El análisis desarrollado en este capítulo, basado en la solución del Laplaciano del potencial escalar ( 2 φ = 0) es de gran utilidad para el diseño en régimen permanente de redes de tierra seguras y económicas en terrenos multiestratificados

30 4.6 Validación del algoritmo de cálculo de potenciales El desarrollo presentado en las secciones anteriores permitió elaborar el programa TERRAM, para el cálculo de sistemas de puesta a tierra en terrenos multiestratificados. Este algoritmo fué realizado en lenguaje Fortran77, para ser ejecutados en ordenadores personales Macintosh, o compatibles BM. Para validar a TERRAM en los casos de terreno uniforme o biestrato, se ha utilizado el programa TERRA [66,67,68] que a su vez se ha validado mediante los resultados publicados por varios autores [8,20,22,23,24,25,27,35,48,54,55,60, 79,02,04,3]. El programa TERRA utiliza el método de las imágenes de Maxwell y la técnica integro-matricial[74] para acelerar el proceso de cálculo. Considera electrodos horizontales o verticales en disposición rectilínea. Calcula la distribución de corrientes drenadas a tierra por cada uno de los subelectrodos que conforman la red, la resistencia de puesta a tierra y las diferencias de potencial en cualquier punto del subsuelo. El programa TERRA se utiliza para el diseño eficiente de sistemas de puesta a tierra reales. El programa TERRAM posee una estructura similar a la de TERRA. Se basa en la evaluación directa de los coeficientes de potencial a partir de las ecuaciones de Maxwell. Permite el análisis de subsuelos multi-estratificados. Este programa en lugar del método de las imágenes, utiliza la técnica descrita en la sección 4.3. También puede calcular la distribución de corrientes drenadas por cada uno de los segmentos en que se ha dividido la red, la resistencia de puesta a tierra y las diferencias de potencial en cualquier punto del subsuelo. En los cálculos con subsuelos de múltiples capas se han utilizado los trabajos realizados por Dawalibi[20], Takahashi[,2] e zzeddine[5] para validar el programa Validación de TERRAM en subsuelos biestratificados Caso : Validación en dos estratos sin picas en la red En la figura 4.9 se presenta una red de tierra cuadrada formada por nueve mallas de 5x5 m cada una. Este sistema de puesta a tierra está constituido por 24 electrodos rectilíneos cuyo diámetro es de.0 cm. La red se encuentra enterrada a una profundida de 50 cm. Se analiza el comportamiento de esta red en dos tipos diferentes de subsuelo