MATEMÁTICAS II Notas de clase
|
|
|
- Esperanza López Rivero
- hace 5 años
- Vistas:
Transcripción
1 MATEMÁTICAS II Notas de clase Ramón Espinosa Departamento de Matemáticas, ITAM Resumen El propósito de estas notas es presentar algunos temas que se ven en el curso de Matemáticas II en el ITAM. En particular se discuten las nociones de continuidad, ites y diferenciación de trayectorias y de funciones de varias variables. El orden de los temas es el orden que se sugiere que se siga en el curso. El material de estas notas suponen que el alumno está familiarizado con vectores y con la geometría en el plano y en el espacio tridimensional. 1. Trayectorias Una trayectoria en el plano es una función g : I R R 2, es decir, g(t) es una función de una variable, definida en un conjunto I (usualmente un intervalo), y cuyos valores son puntos en el plano cartesiano. Podemos escribir g(t) = (x, y), donde x = x(t), y = y(t) son llamadas las funciones componentes de la trayectoria, obsérvese que estas funciones son funciones reales de variable real. El conjunto C = {f(t) t I} es llamado la curva descrita por la trayectoria. Ejemplo 1. La trayectoria tiene componentes g(t) = (1 + 2t, 2 3t), t R, x = 1 + 2t, y = 2 3t, t R, las cuales corresponden a las ecuaciones paramétricas de la recta que pasa por el punto (1, 2) y tiene vector dirección (2, 3). 1
2 Ejemplo 2. Sea a > 0 fijo. La curva descrita por la trayectoria g(t) = (a cos t, a sen t), t R, es un círculo de radio a con centro en el origen, descrito en sentido contrario a las manecillas del reloj. Ejemplo 3. Sean a > 0 y b > 0, fijos. La curva descrita por la trayectoria g(t) = (a cos t, b sen t), t R, es una elipse con semiejes a y b, recorrida en sentido contrario a las manecillas del reloj. Sea g(t) una trayectoria en el plano. Supongamos que g está definida en un intervalo I, excepto posiblemente en t 0 I. Se dice que si t t 0 g(t) = A, ε > 0 δ > 0 tal que 0 < t t 0 < δ g(t) A < ε. El siguiente teorema establece cómo podemos calcular el ite de una trayectoria, calculando el ite de sus componentes. Teorema 1. Sea g(t) = (x, y) una trayectoria en el plano. Entonces si y sólo si Ejemplo 4. Calcular Solución. Como se sigue del teorema anterior que t t 0 g(t) = (a 1, a 2 ), t t 0 x(t) = a 1 y t t0 y(t) = a 2. (sen t/t, 2 cos t). t 0 sen t = 1, 2 cos t = 2, t 0 t t 0 (sen t/t, 2 cos t) = (1, 2). t 0 2
3 Sea g(t) una trayectoria definida en un intervalo I. Se dice que g es continua en t 0 I si t t 0 g(t) = g(t 0 ). El siguiente teorema es una consecuencia inmediata del teorema anterior. Teorema 2. Sea g(t) = (x, y) una trayectoria definida en un intervalo I. Entonces g es continua en t 0 I, si y sólo si x(t) y y(t) son continuas en t 0. Ejemplo 5. La trayectoria g(t) = (cos t, sen t) es continua en R, porque las funciones componentes x = cos t y y = sen t los son. Sea g(t) = (x, y) una trayectoria definida en un intervalo abierto I. Se dice que g es diferenciable en t 0 I si g(t) g(t 0 ) t t 0 t t 0 existe. En este caso el valor ite se denota g (t 0 ) y se le llama la derivada de g en t 0. El siguiente teorema muestra cómo calcular la derivada de una trayectoria. Teorema 3. Sea g(t) = (x, y) una trayectoria definida en un intervalo abierto I. Entonces g es diferenciable en t 0 si y sólo si x(t) y y(t) son diferenciables en t 0. Además g (t 0 ) = (x (t 0 ), y (t 0 )). Ejemplo 6. Si g(t) = (cos t, sen t), entonces g (t) = ( sen t, cos t), para todo t R. Si g(t) es una trayectoria diferenciable en t 0 y además g (t 0 ) (0, 0) se dice que g (t 0 ) es el vector tangente a la curva descrita por la trayectoria en el punto g(t 0 ) = (x 0, y 0 ). En este caso la recta tangente a la trayectoria está descrita por las ecuaciones paramétricas: x = x 0 + (t t 0 )x (t 0 ), y = y 0 + (t t 0 )y (t 0 ). Obsérvese que la recta pasa por (x 0, y 0 ) cuando t = t 0. Ejemplo 7. Determinar la recta tangente a la trayectoria g(t) = (cos t, sen t), cuando t = π/2. 3
4 Solución. g (π/2) = ( sen π/2, cos π/2) = ( 1, 0), por lo que la recta tangente en el punto g(π/2) = (0, 1) es: x = 0 (t π/2)( 1) = π/2 t, y = 1 + (t π/2)0 = 1. Ejemplo 8. Consideremos la trayectoria g(t) = (t sen t, 1 cos t). Obsérvese que g (t) = (1 cos t, sen t), para todo número real t, sin embargo, g (2π) = (0, 0), por lo que no existe la recta tangente en este punto. La razón de esto es que en dicho punto la curva tiene un pico. Análogamente se puede definir la noción de trayectoria en el espacio tridimensional R 3 y en general en R n. Las trayectorias jugarán un papel importante en los siguientes temas. 2. Funciones de varias variables Sea f : Ω R 2 R, es decir, f(x, y) es una función de dos variables, definida en un conjunto Ω, que toma valores reales. Con frecuencia se describe una función f(x, y) a partir de una regla de correspondencia, sin especificar el conjunto donde está definida, en este caso el dominio natural de f(x, y) es el mayor subconjunto de R 2 donde la regla está bien definida. Ejemplo 9. El dominio natural de la función f(x, y) = x + y y x, es el conjunto: {(x, y) y > x}. La gráfica de f(x, y) es el conjunto: {(x, y, z) (x, y) Ω, z = f(x, y)}. Obsérvese que la gráfica de f(x, y) es un subconjunto de R 3. El rango de f(x, y) es el conjunto: {f(x, y) (x, y) Ω}, 4
5 es decir, el rango de una función es el conjunto de todos los posibles valores de la función. Si c es un número real, la curva de nivel c de f(x, y) es el conjunto: N c (f) = {(x, y) Ω f(x, y) = c}. Las curvas de nivel son útiles para describir la gráfica de una función f(x, y), pero a veces éstas no son suficientes, es necesario describir también las intersecciones de la gráfica con los planos xz y yz, estas intersecciones son llamadas las trazas de f(x, y). Más precisamente, la intersección de la gráfica con el plano xz está descrita por la ecuación: z = f(x, 0), análogamente la ecuación z = f(0, y), describe la traza de f(x, y) en el plano yz. Ejemplo 10. Sea f(x, y) = 3 x y. El dominio natural es R 2. La curva de nivel c es el conjunto descrito por la ecuación: 3 x y = c por lo que las curvas de nivel son rectas paralelas. Las trazas están definidas por las ecuaciones: z = 3 x y z = 3 y y corresponden a rectas en los planos xz y yz, respectivamente. Esto es claro si observamos que la gráfica z = 3 x y corresponde al plano x+y +z = 3. 5
6 3 3 3 Ejemplo 11. La función f(x, y) = x 2 + y 2 está definida para todo punto en el plano. La curva de nivel c es el conjunto descrito por la ecuación: x 2 + y 2 = c. Si c > 0 la curva de nivel es el círculo de radio c y centro en el origen. Cuando c tiende a cero por la derecha los círculos son cada vez más pequeños. Si c = 0 la curva de nivel consta solamente del origen, y si c < 0 la curva de nivel es el conjunto vacío. Las trazas están descritas por las ecuaciones z = x 2 y z = y 2 y corresponden a parábolas. En este caso la gráfica es un paraboloide de revolución, obtenido al girar cualquiera de las trazas alrededor del eje z. Obsérvese que el rango es el intervalo [0, ). 6
7 Ejemplo 12. La función f(x, y) = x 2 + y 2 está definida para todo (x, y) R 2. La curva de nivel c es el conjunto descrito por la ecuación: x 2 + y 2 = c. Obsérvese que si c < 0 la curva de nivel es el conjunto vacío. Si c = 0 la curva de nivel consta solamente del origen. Si c > 0 la curva de nivel es el círculo de radio c y centro en el origen. Al igual que en el ejemplo anterior, cuando c tiende a cero por la derecha los círculos son cada vez más pequeños. Las trazas están descritas por las ecuaciones z = x 2 = x y z = x. En este caso la gráfica es un cono. Al igual que en el ejemplo anterior, el rango es el intervalo [0, ). Ejemplo 13. La función f(x, y) = x 2 y 2 está definida para todo punto en el plano. La curva de nivel 0 es el conjunto descrito por la ecuación: x 2 = y 2, equivalentemente y = ±x, es decir, la curva de nivel cero son dos rectas que pasan por el origen. La curva de nivel c = 1 es la hipérbola horizontal: x 2 y 2 = 1, en general las curvas de nivel positivo son hipérbolas horizontales. La curva de nivel c = 1 es la hipérbola vertical: y 2 x 2 = 1, y en general las curvas de nivel negativo son hipérbolas verticales. Las trazas están descritas por las ecuaciones z = x 2 y z = y 2 y corresponden a una parábola hacia arriba y una parábola hacia abajo, respectivamente. La gráfica de esta función es llamada paraboloide hiperbólico, y tiene forma de silla de montar. En este caso el origen es el punto de ensilladura, o punto silla. 7
8 Las curvas de nivel de una función pueden recibir distintos nombres de acuerdo al contexto. Si f(x, y) es una función de producción (que depende de dos insumos), las curvas de nivel se llaman isocuantas. Si f(x, y) es una función de costos las curvas de nivel son llamadas curvas de isocostos. Si f(x, y) es una función de utilidad las curvas de nivel son llamadas curvas de indiferencia. Si f : Ω R 3 R, es una función de tres variables, la gráfica es un subconjunto de R 4, por lo que no podemos visualizarla. Sin embargo tiene sentido definir el análogo a una curva de nivel. La superficie de nivel c de una función f(x, y, z) es el conjunto: N c (f) = {(x, y, z) Ω f(x, y, z) = c}. Ejemplo 14. Sea f(x, y, z) = x 2 + y 2 + z 2. Para cada c > 0 la superficie de nivel c es la esfera de radio c. La superficie de nivel cero es el origen, es decir, N c (f) = {(0, 0, 0)}, y si c < 0 entonces N c (f) =. En general, el conjunto de nivel c de una función f : Ω R n R se define como: N c (f) = {x Ω f(x) = c}. Aquí x = (x 1, x 2,..., x n ) es un vector en R n. 3. Continuidad y ites Una función f : Ω R 2 R se dice que es continua en (x 0, y 0 ) Ω, si f(x, y) está arbitrariamente cerca f(x 0, y 0 ), si (x, y) está suficientemente cerca de (x 0, y 0 ). Formalmente, si para todo ε > 0, existe δ > 0, tal que f(x, y) f(x 0, y 0 ) < ε, si (x x0 ) 2 + (y y 0 ) 2 < δ. Se dice que f es continua en Ω si f es continua en cada punto en Ω. Ejemplo 15. Mostrar que la función constante f(x, y) = c, es continua en R 2. Solución. Sea (x 0, y 0 ) R 2. Obsérvese que f(x, y) f(x 0, y 0 ) = c c = 0, por lo que dado ε > 0, podemos tomar cualquier δ > 0 para asegurar que f(x, y) f(x 0, y 0 ) < ε, si (x x 0 ) 2 + (y y 0 ) 2 < δ. 8
9 Ejemplo 16. Mostrar que la función P 1 (x, y) = x es continua en R 2. Solución. Obsérvese que P 1 (x, y) P 1 (x 0, y 0 ) = x x 0 (x x 0 ) 2 + (y y 0 ) 2, por lo que dado ε > 0, basta tomar δ = ε. La función P 1 (x, y) es llamada la primera proyección. Análogamente se puede probar que la segunda proyección P 2 (x, y) = y es continua en R 2. A partir de la definición formal de continuidad se pueden probar las siguientes propiedades de funciones continuas. Teorema 4. Si f(x, y) y g(x, y) son continuas en (x 0, y 0 ), entonces (1) cf(x, y) es continua en (x 0, y 0 ), para todo c R. (2) f(x, y) + g(x, y) es continua en (x 0, y 0 ). (3) f(x, y)g(x, y) es continua en (x 0, y 0 ). (4) Si g(x 0, y 0 ) 0, entonces f(x, y)/g(x, y) es continua en (x 0, y 0 ). Ejemplo 17. Mostrar que la función f(x, y) = 3 x y es continua en R 2. Solución. Como la función constante 3 es continua en R 2, y también lo son las funciones proyección P 1 (x, y) = x y P 2 (x, y) = y, se sigue de las propiedades (1) y (2) del teorema anterior que f(x, y) = 3 x y es continua en R 2. Ejemplo 18. Mostrar que la función f(x, y) = x 2 + y 2 es continua en R 2. Solución. Hemos visto que la función P 1 (x, y) es continua en R 2, de ahí que, por la propiedad (3) del teorema, x 2 = P 1 (x, y)p 1 (x, y) es continua en R 2. Análogamente la función y 2 es continua en R 2, por lo que, por la propiedad (2), la función f(x, y) = x 2 + y 2 es continua en R 2. Teorema 5. Si f : Ω R 2 R es continua en (x 0, y 0 ) Ω y g : I R R es continua en t 0 = f(x 0, y 0 ) I, entonces g f es continua en (x 0, y 0 ). Ejemplo 19. Mostrar que la función h(x, y) = x 2 + y 2 es continua en R 2. Solución. Hemos visto que la función f(x, y) = x 2 + y 2 es continua en R 2. Además f(x, y) 0 para todo (x, y) R 2. Por otra parte la función g(t) = t es continua en [0, ), de ahí que, por el teorema anterior, la función h(x, y) = (g f)(x, y) = x 2 + y 2 es continua en R 2. 9
10 Ejemplo 20. Mostrar que la función h(x, y) = x 2 x 2 + y 2 es continua si (x, y) (0, 0). Solución. La función f(x, y) = x 2 es continua en R 2. Por el ejemplo anterior, la función g(x, y) = x 2 + y 2 también es continua en R 2. Además si (x, y) (0, 0), entonces g(x, y) > 0, por lo que, por el teorema 4, h(x, y) es continua si (x, y) (0, 0). La función del ejemplo anterior no está definida en el punto (x 0, y 0 ) = (0, 0), sin embargo este punto tiene la propiedad de que podemos acercarnos a él tanto como queramos por puntos en el dominio de la función. Por lo que tiene sentido discutir el comportamiento de la función en este punto. Un punto (x 0, y 0 ) R 2 se dice que es un punto de acumulación de Ω R 2, si existen puntos en Ω distintos de (x 0, y 0 ) que están arbitrariamente cerca de (x 0, y 0 ). Formalmente, si para todo ε > 0 existe (x, y) Ω, tal que 0 < (x x 0 ) 2 + (y y 0 ) 2 < ε. Obsérvese que un punto de acumulación de un conjunto no necesariamente pertenece al conjunto. Ejemplo 21. Consideremos el conjunto Ω = {(x, y) 0 < x 2 + y 2 < 1}. Obsérvese que un punto (x 0, y 0 ) es punto de acumulación de Ω si y sólo si x y Ejemplo 22. Consideremos el conjunto Ω = {(x, y) x + y 0}. Obsérvese que todo punto (x 0, y 0 ) R 2 es punto de acumulación de Ω. Sea f(x, y) una función definida en un conjunto Ω R 2, y sea (x 0, y 0 ) un punto de acumulación de Ω. Se dice que f(x, y) = a, (x,y) (x 0,y 0 ) 10
11 si f(x, y) está arbitrariamente cerca de a cuando (x, y) Ω está suficientemente cerca de (x 0, y 0 ). Formalmente, si para todo ε > 0 existe δ > 0, tal que si (x, y) Ω satisface 0 < (x x 0 ) 2 + (y y 0 ) 2 < ε, entonces f(x, y) a < ε. Obsérvese que si además (x 0, y 0 ) Ω, entonces f(x, y) es continua en (x 0, y 0 ) si y sólo si Ejemplo 23. Calcular Solución. f(x, y) = f(x 0, y 0 ). (x,y) (x 0,y 0 ) (x,y) (2, 1) x2 y 2. La función f(x, y) = x 2 y 2 es continua en R 2, de ahí que Ejemplo 24. Calcular (x,y) (2, 1) x2 y 2 = 2 2 ( 1) 2 = 3. (x,y) (0,0) x 2 x 2 + y 2. Solución. En este caso la función no está definida en (0, 0). Para calcular el ite obsérvese que x 2 x 2 + y 2 x2 + y 2 x 2 + y 2 = x 2 + y 2. Por lo que dado ε > 0, basta tomar δ > 0 para asegurar que f(x, y) 0 = x 2 x 2 + y 2 < ε, si 0 < x 2 + y 2 < δ. El siguiente teorema establece algunas propiedades de ites. Teorema 6. Si f(x, y) = a y g(x, y) = b, (x,y) (x 0,y 0 ) (x,y) (x 0,y 0 ) 11
12 entonces (1) (2) (3) (4) Si b 0, cf(x, y) = ca, c R. (x,y) (x 0,y 0 ) (f(x, y) + g(x, y)) = a + b. (x,y) (x 0,y 0 ) f(x, y)g(x, y) = ab. (x,y) (x 0,y 0 ) f(x, y) (x,y) (x 0,y 0 ) g(x, y) = a b. Ejemplo 25. Calcular Solución. es el conjunto x 2 y 2 (x,y) (1,1) x y. Obsérvese que el dominio natural de la función h(x, y) = x2 y 2 x y Ω = {(x, y) y x}. El punto (1, 1) no pertenece al conjunto, pero es punto de acumulación del mismo. Ahora bien, x 2 y 2 (x,y) (1,1) x y = (x y)(x + y) = (x,y) (1,1) x y x + y = 2. (x,y) (1,1) El siguiente resultado es una extensión del teorema 5. Teorema 7. Sean f : Ω R 2 R y g : I R R, tales que f(x, y) = a, y g(t) = b, (x,y) (x 0,y 0 ) t a entonces g(f(x, y)) = b. (x,y) (x 0,y 0 ) 12
13 Ejemplo 26. Calcular sen(x 2 + y 2 ) (x,y) (0,0) x 2 + y 2. Solución. Sean f(x, y) = x 2 + y 2 y g(t) = sen t/t. Como se sigue del teorema anterior que (x,y) (0,0) x2 + y 2 sen t = 0 y = 1, t 0 t sen(x 2 + y 2 ) (x,y) (0,0) x 2 + y 2 = 1. Se acostumbra simplificar el análisis anterior haciendo t = x 2 + y 2, observando que t 0 si y sólo si (x, y) (0, 0) y escribiendo sen(x 2 + y 2 ) sen t (x,y) (0,0) x 2 + y 2 = = 1. t 0 t Veremos ahora un resultado que nos permitirá determinar si un ite no existe o si una función no es continua en un punto. Teorema 8. Sea f : Ω R 2 R y sea (x 0, y 0 ) punto de acumulación de Ω. Si f(x, y) = a, (x,y) (x 0,y 0 ) entonces para toda trayectoria g : I R R continua en t 0 I, tal que g(t 0 ) = f(x 0, y 0 ), se tiene que f(g(t)) = a. t t 0 Corolario 1. Sea f : Ω R 2 R y sea (x 0, y 0 ) punto de acumulación de Ω. Si g : I R R es una trayectoria continua en t 0 I, tal que g(t 0 ) = f(x 0, y 0 ), y si entonces f(g(t)) t t 0 f(x, y) (x,y) (x 0,y 0 ) no existe, no existe. 13
14 Ejemplo 27. Determinar si existe. (x,y) (0,0) x x 2 + y 2, Solución. Consideremos la trayectoria g(t) = (t, 0). Obsérvese que g(t) es continua, g(0) = (0, 0) y t 0 f(g(t)) = f(t, t) = t 0 t 0 t t 2 = t 0 t t, no existe, pues pero t 0 + t 0 t t = t t 0 + t = 1, t t = t 0 + t t = 1. Corolario 2. Sea f : Ω R 2 R y sea (x 0, y 0 ) un punto de acumulación de Ω. Si g : I R R y h : I R R son trayectorias continuas en t 0 I, tales que g(t 0 ) = f(x 0, y 0 ) = h(t 0 ), y si t t 0 f(g(t)) t t0 f(h(t)), entonces f(x, y) (x,y) (x 0,y 0 ) no existe. Ejemplo 28. Determinar si x y (x,y) (0,0) x + y, existe. Solución. Consideremos la trayectoria continua g(t) = (t, 0). Obsérvese que g(0) = (0, 0) y t 0 t f(g(t)) = f(t, 0) = t 0 t 0 t = 1. 14
15 Si ahora consideramos la trayectoria continua h(t) = (0, t), entonces t 0 t f(h(t)) = f(0, t) = = 1 1, t 0 t 0 t por lo tanto no existe. x y (x,y) (0,0) x + y, Corolario 3. Sea f : Ω R 2 R y sea (x 0, y 0 ) Ω. Si g : I R R es continua en t 0 I, y si t t 0 f(g(t)) f(x 0, y 0 ), entonces f(x, y) no es continua en (x 0, y 0 ). Ejemplo 29. Sea f(x, y) = { 1 si x = 0 o y = 0; 0 en otro caso. Veremos que esta función no es continua en (0, 0). Con este fin consideremos la trayectoria g(t) = (t, t). Es claro que esta trayectoria es continua, además g(0) = (0, 0). Sin embargo, t 0 f(g(t)) = t 0 f(t, t) = 0 = 0 1 = f(0, 0), t 0 por lo tanto f(x, y) no es continua en (0, 0). En general, una función f : Ω R n R se dice que es continua en p 0 Ω, si para todo ε > 0, existe δ > 0, tal que f(x) f(p 0 ) < ε, si x p 0 < δ. Se dice que f es continua en Ω si f es continua en cada punto en Ω. Por otra parte, un punto p 0 R n se dice que es punto de acumulación de Ω R n si para todo ε > 0, existe x Ω tal que 0 < x p 0 < ε. Si f : Ω R n R y p 0 es punto de acumulación de Ω, se dice que f(x) = a, x p 0 15
16 si para todo ε > 0, existe δ > 0, tal que f(x) f(p 0 ) < ε si 0 < x p 0 < δ. Si n = 1 estas definiciones coinciden con las definiciones de continuidad y ite para funciones reales de variable real. Las propiedades de ite y continuidad enunciadas en este trabajo para funciones de dos variables, siguen siendo válidas para funciones de varias variables con valores reales. 4. Derivadas parciales La vecindad de radio r > 0 con centro en (x 0, y 0 ) R 2, es el conjunto: V r (x 0, y 0 ) = {(x, y) R 2 (x x0 ) 2 + (y y 0 ) 2 < r}. Es decir, V r (x 0, y 0 ) es el conjunto de puntos cuya distancia a (x 0, y 0 ) es menor que r. Este conjunto es un disco abierto con centro en p 0 = (x 0, y 0 ) y radio r. r p 0 Sea Ω R 2. Un punto (x 0, y 0 ) Ω se dice que es un punto interior de Ω, si existe r > 0 tal que V r (x 0, y 0 ) Ω, es decir, si decir, si existe un disco abierto con centro en (x 0, y 0 ) que está completamente contenido en el conjunto. Ejemplo 30. Sea Ω = {(x, y) x 0, y 0}. Un punto (x 0, y 0 ) es punto interior de Ω si y sólo si x 0 > 0 y y 0 > 0. 16
17 Ω Un conjunto Ω R 2 se dice que es abierto, si todo punto (x 0, y 0 ) Ω es un punto interior de Ω. Ejemplo 31. El conjunto del ejemplo anterior no es abierto, porque los puntos de la forma (x, 0), con x 0 no son puntos interiores. Tampoco lo son los puntos de la forma (0, y), con y 0. Ejemplo 32. el conjunto Ω = {(x, y) x > 0, y > 0} es abierto. Ω Sea f : Ω R 2 R y sea (x 0, y 0 ) un punto interior de Ω. La derivada parcial de f(x, y) con respecto a x en (x 0, y 0 ) se define como: f x (x f(x 0 + h, y 0 ) f(x 0, y 0 ) 0, y 0 ) =, h 0 h siempre y cuando el ite exista. Obsérvese que si definimos g(x) = f(x, y 0 ), entonces f x (x g(x 0 + h) g(x 0 ) 0, y 0 ) = = g (x 0 ), h 0 h 17
18 en caso de existir, de modo que calcular la derivada parcial de f(x, y) con respecto a x es equivalente a derivar con respecto a x, suponiendo que y es constante. Análogamente la derivada parcial de f(x, y) con respecto a y en p 0 se define como: f y (x f(x 0, y 0 + h) f(x 0, y 0 ) 0, y 0 ) =, h 0 h siempre y cuando el ite exista. También se acostumbra utilizar la notación f x y f y, en lugar de f/ x y f/ y. Obsérvese que al ser (x 0, y 0 ) un punto interior de Ω, podemos asegurar que las rectas x = x 0 + h, y = y 0, y x = x 0, y = y 0 + h, están contenidas en Ω si h es suficientemente pequeño. Ejemplo 33. Sea Entonces f(x, y) = xe 2x 3y. f x = 2xe 2x 3y + e 2x 3y y f y = 3xe 2x 3y, para todo (x, y) R 2. Ejemplo 34. Si entonces f x = f(x, y) = x 2 + y 2, x x 2 + y 2, f y = y x 2 + y 2, para todo (x, y) (0, 0). Para determinar si f x existe en el origen, debemos recurrir a la definición de derivada parcial: f(h, 0) f(0, 0) h = h 0 h h 0 h. Es claro que este ite no existe, por lo tanto la derivada parcial con respecto a x en el origen no existe. Análogamente la derivada parcial con respecto a y en el origen tampoco existe. El ejemplo anterior muestra que una función puede ser continua en un punto, sin que las derivadas parciales existan en dicho punto. 18
19 Ejemplo 35. Sea f(x, y) = { 1 si x = 0 o y = 0; 0 en otro caso. Determinar si las derivadas parciales de la función existen en el punto p 0 = (0, 0). Solución. Obsérvese que (x,y) (0,0) f(h, 0) f(0, 0) h = (x,y) (0,0) por lo tanto f x (0, 0) = 0. Análogamente, f y (0, 0) = h = 0, El ejemplo anterior muestra que las derivadas parciales pueden existir en un punto, sin que la función tenga que ser continua en dicho punto. En general, sea f : Ω R n R y sea p 0 un punto interior de Ω. La derivada parcial de f(x) con respecto a x j en p 0 se define como: f f(p 0 + he j ) f(p (p x 0 ) = 0 ), j h 0 h siempre y cuando el ite exista. Aquí e j = (0,..., 1,..., 0) es el vector que tiene un uno en la posición j y cero en las demás componentes. Si f(x) es una función de producción, las derivadas parciales son llamadas producciones marginales, con respecto al insumo correspondiente. Análogamente, si f(x) es una función de costos, las derivadas parciales son llamadas costos marginales. 5. Diferenciación Recordemos que una función f : I R R es diferenciable en x 0 I, si f(x) f(x 0 ) x x 0 x x 0 existe. En este caso el valor ite se denota f (x 0 ) y es llamado la derivada de f en x 0. Obsérvese que si f es diferenciable en x 0, entonces f(x) f(x 0 ) f (x 0 )(x x 0 ) = 0. x x 0 x x 0 19
20 La recta y = f(x 0 ) + f (x 0 )(x x 0 ) es llamada recta tangente a la gráfica de f en x 0. La última expresión sugiere una manera de extender la noción de diferenciabilidad a funciones de dos variables. Una función f : Ω R 2 R se dice que es diferenciable en un punto interior (x 0, y 0 ) Ω, si f x (x 0, y 0 ) y f y (x 0, y 0 ) existen y además (x,y) (x 0,y 0 ) f(x, y) f(x 0, y 0 ) f x (x 0, y 0 )(x x 0 ) f y (x 0, y 0 )(y y 0 ) (x x0 ) 2 + (y y 0 ) 2 = 0 En este caso se dice que z = f(x 0, y 0 ) + f x (x 0, y 0 )(x x 0 ) + f y (x 0, y 0 )(y y 0 ) es la ecuación del plano tangente a la gráfica de f(x, y) en el punto (x 0, y 0 ). Se dice que f es diferenciable en Ω, si f es diferenciable en cada punto en Ω. Ejemplo 36. Mostrar que la función f(x, y) = 5 + 2x 3y es diferenciable en (2, 1) y obtener la ecuación del plano tangente a la gráfica de f en dicho punto. Solución. bien, En este caso f x = 2 y f y = 3. Además f(2, 1) = 12. Ahora (x,y) (2, 1) 5 + 2x 3y 12 2(x 2) + 3(y + 1) (x 2) 2 + (y + 1) 2 = 0 porque el numerador es igual a cero. La ecuación del plano tangente es: z = (x 2) 3(y + 1). Obsérvese que la gráfica de la función del ejemplo anterior es un plano, en este caso el plano tangente a la gráfica de la función coincide exactamente con la gráfica de la función. 20
21 Ejemplo 37. Consideremos la función f(x, y) = x 2 + y 2. En el ejemplo 34 vimos que las derivadas parciales no existen en el origen, esto muestra que f(x, y) no es diferenciable en el origen. Ejemplo 38. Sea f(x, y) = { 1 si x = 0 o y = 0; 0 en otro caso. En el ejemplo 35 vimos que f x (0, 0) = 0 y f y (0, 0) = 0, sin embargo, (x,y) (0,0) f(x, y) 1 0x 0y x 2 + y 2 no existe, pues si nos acercamos a (0, 0) por medio de la trayectoria y = x, tenemos el ite 1 2x 2 el cual tiende a. x 0 El ejemplo anterior muestra que una función puede tener derivadas parciales en un punto, sin que la función tenga que ser diferenciable en dicho punto. El siguiente teorema relaciona la noción de diferenciabilidad con la noción de continuidad. Teorema 9. Si f : Ω R 2 R es diferenciable en un punto interior (x 0, y 0 ) Ω, entonces f es continua en (x 0, y 0 ). Demostración. Obsérvese que 0 f(x, y) f(x 0, y 0 ) f(x, y) f(x 0, y 0 ) f x (x 0, y 0 )(x x 0 ) f y (x 0, y 0 )(y y 0 ) + f x (x 0, y 0 )(x x 0 ) + f y (x 0, y 0 )(y y 0 ). El primer término del lado derecho corresponde al numerador del ite que aparece en la definición de diferenciabilidad, el cual tiende a cero cuando (x, y) (x 0, y 0 ), pues el denominador tiende a cero. Por otra parte, es claro 21
22 que el segundo término también tiende a cero cuando (x, y) (x 0, y 0 ), de ahí que (x,y) (x 0,y 0 ) f(x, y) = f(x 0, y 0 ) y por lo tanto f es continua en (x 0, y 0 ). Obsérvese que la función f(x, y) = x 2 + y 2 es continua en (0, 0), pero no es diferenciable en dicho punto. Esto muestra que el recíproco del teorema anterior es falso. Mostrar que una función f(x, y) es diferenciable a partir de la definición, puede ser muy difícil. El siguiente teorema, cuya demostración omitimos, establece una manera sencilla de verificar que una función es diferenciable en un conjunto. Teorema 10. Sea f : Ω R 2 R. Si Ω es abierto, y si f x y f y existen y son continuas en Ω, entonces f es diferenciable en cada punto (x 0, y 0 ) Ω. Ejemplo 39. Mostrar que la función f(x, y) = x 2 y 3 es diferenciable en ( 1, 1) y obtener la ecuación del plano tangente a la gráfica de f en dicho punto. Solución. Obsérvese que f x = 2xy 3 y f y = 3x 2 y 2 existen y son continuas en R 2, por lo que, por el teorema anterior, f es diferenciable en R 2. Además f( 1, 1) = 1, f x ( 1, 1) = 2, f y ( 1, 1) = 3, por lo que la ecuación del plano tangente a la gráfica de f en el punto ( 1, 1, 1) es z = 1 2(x + 1) + 3(y 1). Si f(x, y) es diferenciable en un punto interior (x 0, y 0 ) Ω, la función L(x, y) = f(x 0, y 0 ) + f x (x 0, y 0 )(x x 0 ) + f y (x 0, y 0 )(y y 0 ) es llamada la aproximación lineal de f(x, y) alrededor de (x 0, y 0 ). Obsérvese que podemos escribir f(x, y) = L(x, y) + R 1 (x, y), 22
23 donde (x,y) (x 0,y 0 ) R 1 (x, y) (x x0 ) 2 + (y y 0 ) 2 = 0, es decir, L(x, y) aproxima a f(x, y) con un error menor que (x x 0 ) 2 + (y y 0 ) 2. Ejemplo 40. Utilizar una aproximación lineal para estimar el valor de (2.9) 2 + (4.1) 2 Solución. Consideremos la función f(x, y) = x 2 + y 2. Obsérvese que f x = x x 2 + y 2, f y = y x 2 + y 2, son continuas en R 2 \ {(0, 0)}, por lo que f es diferenciable en este conjunto. La aproximación lineal de f alrededor del punto (3, 4) es: L(x, y) = (x 3) + 4 (y 4), 5 de ahí que L(2.9, 4.1) = 5.02 es una aproximación del valor de f(2.9, 4.1) = (2.9) 2 + (4.1) 2. El vector f(x 0, y 0 ) = (f x (x 0, y 0 ), f y (x 0, y 0 )) es llamado el vector gradiente de f(x, y) en el punto (x 0, y 0 ). Con esta notación podemos escribir la aproximación lineal de f alrededor de (x 0, y 0 ) como: L(x, y) = f(x 0, y 0 ) + f(x 0, y 0 ) (x x 0, y y 0 ). En general, una función f : Ω R n R se dice que es diferenciable en un punto interior p 0 Ω, si existe para todo j = 1, 2,..., n, y si f x j (p 0 ) f(x) L(x) = 0, x p 0 x p 0 23
24 donde L(x) = f(p 0 ) + f(p 0 ) (x p 0 ). Aquí f(p 0 ) = ( f (p x 0 ),..., f ) (p 1 x 0 ) n es el vector gradiente de f(x) en el punto p 0. La función L(x) es llamada la aproximación lineal de f alrededor de p 0. Los teoremas 9 y 10 siguen siendo válidos para funciones de más de dos variables, es decir, si f(x) es diferenciable en un punto interior p 0 entonces es continua en p 0, y si las derivadas parciales existen y son continuas en Ω R n, entonces f es diferenciable en Ω. Ejemplo 41. Mostrar que la función f(x, y, z) = 2 + e 3x sen(2y + z) es diferenciable en R 3 y calcular la aproximación lineal de f alrededor del punto p 0 = (0, 1, 2). Solución. Obsérvese que f x = 3e 3x sen(2y + z), f y = 2e 3x cos(2y + z), f z = e 3x cos(2y + z), son continuas en R 3, por lo tanto f es diferenciable en R 3. Además f(p 0 ) = 2, f x (p 0 ) = 0, f y (p 0 ) = 2 y f z (p 0 ) = 1, por lo tanto, L(x, y, z) = 2 + 0(x 0) + 2(y 1) + (z + 2) = 2 + 2(y 1) + (z + 2). Si f(x) es diferenciable en p 0, el vector gradiente también es llamado la derivada de f(x) es p 0 y se denota f (p 0 ). En el caso de funciones de una variable la derivada no es un vector, sino un número, representando la pendiente de la recta tangente a la gráfica de la función en dicho punto. Obsérvese que esta noción de diferenciabilidad de funciones de varias variables generaliza la noción de diferenciabilidad de funciones de una variable. Es posible extender la noción de diferenciabilidad para funciones de varias variables con valores vectoriales, pero esa es otra historia. 24
25 6. Regla de la cadena Veremos a continuación un caso especial de la regla de la cadena, involucrando a los dos tipos de funciones que hemos estudiado hasta el momento: trayectorias y funciones de varias variables. Teorema 11 (Regla de la cadena). Sea g : I R R 2, donde I es un intervalo abierto, y sea f : Ω R 2 R, donde Ω es abierto. Si g(t) es diferenciable en t 0 I, g(t 0 ) Ω y f es diferenciable en (x 0, y 0 ) = g(t 0 ), entonces f g es diferenciable en t 0, además (f g) (t 0 ) = f(g(t 0 )) g (t 0 ), es decir, (f g) (t 0 ) = f x (x 0, y 0 )x (t 0 ) + f y (x 0, y 0 )y (t 0 ). Ejemplo 42. Sean f(x, y) = e x sen(y 1) y g(t) = (t 2, 2t + 1). Utilizar la regla de la cadena para calcular (f g) (0). Solución. f x = e x sen(y 1) y f y = e x cos(y 1), son continuas en R 2, por lo tanto f(x, y) es diferenciable en R 2. Por otra parte, g(t) es diferenciable en R y g (t) = (t 2, 2t + 1). Obsérvese que f(g(0)) = (0, 1) = (0, 1). Por otra parte, g (0) = (0, 2), de ahí que, por la regla de la cadena: (f g) (0) = (0, 1) (0, 2) = 2. Veremos a continuación una aplicación interesante de la regla de la cadena, pero antes necesitamos una definición. Una función f : Ω R 2 R, se dice que es homogénea de grado k si para todo (x, y) Ω. f(tx, ty) = t k f(x, y), Ejemplo 43. Una función de producción de tipo Cobb-Douglas es una función de la forma: f(x, y) = γ x α y β, 25
26 donde α, β, γ son constantes positivas. Obsérvese que f(tx, ty) = γ x α y β = γ t α x α t β y β = γ t α+β x α y β = t α+β f(x, y). Por lo tanto f(x, y) = γ x α y β es homogénenea de grado α + β. Teorema 12 (Euler). Sea f : Ω R 2 R, donde Ω es abierto. Si f(x, y) es homogénea de grado k y además es diferenciable en Ω, entonces para todo (x, y) Ω. kf(x, y) = f x x + f y y, Demostración. Sea (x, y) Ω arbitrario, pero fijo. Sea g : R R 2, definida por: g(t) = (tx, ty), y sea h(t) = f g. Por la regla de la cadena: Por otra parte, h (1) = f(g(1)) g (1) = f(x, y) (x, y). h(t) = f(tx, ty) = t k f(x, y), porque f(x, y) es homogénea de grado k. De ahí que y por lo tanto h (t) = kt k 1 f(x, y), h (1) = kf(x, y). Igualando obtenemos el resultado deseado. En general, sea g : I R R n, donde I es un intervalo abierto, y sea f : Ω R n R, donde Ω es abierto. Si g(t) es diferenciable en t 0 I, g(t 0 ) Ω y f es diferenciable en p 0 = g(t 0 ), entonces f g es diferenciable en t 0, además (f g) (t 0 ) = f(g(t 0 )) g (t 0 ). Obsérvese que si escribimos f en lugar de f, entonces (f g) (t 0 ) = f (g(t 0 )) g (t 0 ). 26
27 De esta manera es claro que la regla de la cadena para trayectorias y funciones de varias variables extiende la regla de la cadena usual que se ve en cursos de Cálculo de una variable. En las siguientes secciones veremos otras aplicaciones importantes de la regla de la cadena. 7. Derivación implícita Consideremos la ecuación x 2 + y 2 = 1. Esta ecuación representa el círculo de radio 1 y centro en el origen. Obsérvese que si (x 0, y 0 ) pertenece al círculo y y 0 > 0, entonces y es función de x cerca de punto. Más precisamente, y = 1 x 2, (x 0, y 0 ) Obsérvese también que dy dx = x = x 1 x 2 y. Análogamente, si y 0 < 0, entonces y = 1 x 2 cerca del punto. En este caso dy dx = x = x 1 x 2 y. 27
28 (x 0, y 0 ) Obsérvese también que en el punto (1, 0) no podemos despejar y como función de x. (1, 0) Una situación similar ocurre en el punto ( 1, 0). En estos casos la recta tangente a la curva es vertical, equivalentemente, el vector gradiente de la función F (x, y) = x 2 + y 2 en el punto (±1, 0) es horizontal, es decir F y = 0. El siguiente teorema, cuya demostración se omite, establece bajo qué condiciones una ecuación define implícitamente una variable como función de otra. Teorema 13 (Función implícita). Sea F : Ω R 2 R, con derivadas parciales continuas en un conjunto abierto Ω. Si (x 0, y 0 ) Ω satisface la ecuación F (x, y) = c, y si F y (x 0, y 0 ) 0, entonces existe un intervalo abierto I tal que x 0 I, y una función f(x) diferenciable en I, tal que si (x, y) satisface la ecuación F (x, y) = c cerca de (x 0, y 0 ), entonces y = f(x). 28
29 El siguiente resultado muestra cómo derivar una función definida implícitamente. Corolario 4 (Diferenciación implícita). Sea F : Ω R 2 R, con derivadas parciales continuas en un conjunto abierto Ω. Si (x 0, y 0 ) Ω satisface la ecuación F (x, y) = c, y si F y (x 0, y 0 ) 0, entonces dy dx = F x F y, x I. Demostración. Consideremos la trayectoria g : I R 2 R, definida por g(x) = (x, f(x)), y sea h(x) = F (g(x)). Por lo tanto h(x) = c, para todo x I, de ahí que h (x) = 0. Por otra parte, por la regla de la cadena, h (x) = F (g(x)) g (x) = F (x, f(x)) (1, dy/dx) = F x + F y dy dx, de ahí que dy F x + F y dx = 0. Como F y (x 0, y 0 ) 0, y F y es continua, se sigue que F y 0 cerca de (x 0, y 0 ), de ahí que dy dx = F x. F y Ejemplo 44. Consideremos de nuevo la ecuación x 2 + y 2 = 1. Aquí F (x, y) = x 2 + y 2, por lo que F y = 2y, de modo que F y 0 si y sólo si y 0. Por el teorema anterior, si (x 0, y 0 ) pertenece al círculo y y 0 0, entonces y es función de x cerca de punto, lo cual coincide con nuestro análisis previo. Obsérvese además que dy dx = F x F y = 2x 2y = x y. Lo que también coincide con los resultados obtenidos previamente. 29
30 Ejemplo 45. Si y está definida implícitamente por la ecuación calcular dy/dx. x 4 x 2 y 2 + y 3 = 1, Solución. Aquí F (x, y) = x 4 x 2 y 2 + y 3, por lo que F x = 4x 3 2xy 2, y F y = 2x 2 y + 3y 2. De ahí que, por el corolario anterior, dy dx = 4x3 + 2xy 2 2x 2 y + 3y 2, si 2x 2 y + 3y Derivadas direccionales Sea f : Ω R 2 R y sea (x 0, y 0 ) un punto interior de Ω. Sea u = (u 1, u 2 ) un vector unitario. La derivada direccional de f(x, y) en la dirección de u en (x 0, y 0 ) se define como: f(x 0 + tu 1, y 0 + tu 2 ) f(x 0, y 0 ) D u f(x 0, y 0 ) =, t 0 t siempre y cuando el ite exista. Obsérvese que D u f(x 0, y 0 ) mide la razón de cambio de f(x, y) en el punto (x 0, y 0 ), en la dirección del vector u = (u 1, u 2 ). El hecho de que u sea unitario asegura que la derivada direccional depende solamente de la dirección del vector u y no de su magnitud. Obsérvese también que si u = (1, 0), entonces D u f(x 0, y 0 ) = f x (x 0, y 0 ) y si u = (0, 1), entonces D u f(x 0, y 0 ) = f y (x 0, y 0 ), de modo que las derivadas parciales son un caso especial de las derivadas direccionales. El siguiente teorema establece cómo calcular las derivadas direccionales cuando la función es diferenciable en el punto en consideración. Teorema 14. Si f : Ω R 2 R es diferenciable en un punto interior (x 0, y 0 ) Ω, entonces D u f(x 0, y 0 ) existe para todo vector unitario u = (u 1, u 2 ). Además D u f(x 0, y 0 ) = f(x 0, y 0 ) (u 1, u 2 ). 30
31 Demostración. Consideremos la trayectoria g(t) = (x 0 + tu 1, y 0 + tu 2 ) y sea h(t) = f(g(t)). Obsérvese que h h(t) h(0) (0) = = D u f(x 0, y 0 ). t 0 t Por otra parte, por la regla de la cadena, h (0) = f(g(0)) g (0) = f(x 0, y 0 ) (u 1, u 2 ). Igualando tenemos que D u f(x 0, y 0 ) = f(x 0, y 0 ) (u 1, u 2 ). Ejemplo 46. Calcular la derivada direccional de f(x, y) = 2x 2 y 3 en el punto p 0 = (2, 1), en la dirección del vector a = (3, 1). Solución. a = 10, por lo que el vector no es unitario. El vector unitario que tiene la misma dirección que a es: ( ) 3 1 u =, Las derivadas parciales de la función son: f x = 4xy 3, f y = 6x 2 y 2, por lo que f(2, 1) = ( 8, 24), de ahí que, por el teorema anterior, ( ) 3 1 D u f(2, 1) = ( 8, 24), = Teorema 15. Si f : Ω R 2 R es diferenciable en un punto interior (x 0, y 0 ) Ω, y f(x 0, y 0 ) (0, 0), entonces f(x 0, y 0 ) apunta en la dirección de máximo crecimiento de f(x, y) a partir de (x 0, y 0 ) y f(x 0, y 0 ) apunta en la dirección en la que f(x, y) decrece más rápidamente a partir de (x 0, y 0 ). Demostración. Sea u un vector unitario. Por el teorema anterior, D u f(x 0, y 0 ) = f(x 0, y 0 ) (u 1, u 2 ) = cos θ f(x 0, y 0 ) u = cos θ f(x 0, y 0 ). 31
32 Este valor es máximo si cos θ = 1, es decir, si el ángulo entre u y f(x 0, y 0 ) es cero, por lo tanto u = f(x 0, y 0 ) f(x 0, y 0 ). Análogamente, D u f(x 0, y 0 ) es mínimo si cos θ = 1, es decir, si el ángulo entre u y f(x 0, y 0 ) es π, de ahí que u = f(x 0, y 0 ) f(x 0, y 0 ). Ejemplo 47. Determinar el vector unitario u para el cual la función f(x, y) = ye 2x crece más rápidamente a partir del punto p 0 = (0, 1) y calcular la tasa máxima de crecimiento. Solución. Las derivadas parciales son: f x = 2ye 2x, f y = ye 2x, por lo tanto f(0, 1) = (2, 1). De ahí que ( ) 2 1 u = 5,. 5 La tasa máxima de crecimiento es: D u f(0, 1) = (2, 1) ( 2 5, 1 5 ) = 5. El siguiente teorema establece que si el gradiente de una función en un punto es distinto de cero, entonces es ortogonal a la curva de nivel que pasa por el punto. Teorema 16. Si f : Ω R 2 R es diferenciable en un punto interior (x 0, y 0 ) Ω, y supongamos que f(x 0, y 0 ) (0, 0). Sea c = f(x 0, y 0 ), y sea g : I R R una trayectoria diferenciable en I tal que g(t 0 ) = (x 0, y 0 ) y f(g(t)) = c para toda c I, entonces f(x 0, y 0 ) g (t 0 ) = 0. Demostración. Sea h(t) = f(g(t)). Por hipótesis h(t) = c para todo t I, de ahí que h (t) = 0 para todo t I. por otra parte, por la regla de la cadena, Por lo tanto f(g(t 0 )) g (t 0 ) = 0. h (t 0 ) = (f g) (t 0 ) = f(g(t 0 )) g (t 0 ). 32
33 Ejemplo 48. Determinar la ecuación de la recta tangente a la curva: en el punto p 0 = (1, 1). xy = 1 Solución. La curva dada es la curva de nivel 1 de la función f(x, y) = xy. Obsérvese que f x = y y f y = x, por lo que f(1, 1) = (1, 1). Por el teorema anterior este vector es ortogonal a la curva de nivel en el punto indicado, de ahí que la ecuación de la recta tangente a la curva es: es decir: (1, 1) (x 1, y 1) = 0, x + y = 2. En general, sea f : Ω R n R y sea p 0 un punto interior de Ω. Sea u R n un vector unitario. La derivada direccional de f(x) en la dirección de u en p 0 se define como: f(p D u f(p 0 ) = 0 + tu) f(p 0 ), t 0 t siempre y cuando el ite exista. Se puede demostrar que si f es diferenciable en p 0, entonces D u f(p 0 ) = f(p 0 ) u, para cualquier vector unitario u. Si f(p 0 ) 0, entonces f(p 0 ) apunta en la dirección donde f crece más rápidamente y f(p 0 ) apunta en la dirección donde f decrece más rápidamente a partir de p 0. El análogo del teorema 16 para funciones de tres variables establece que si f : Ω R 3 R es diferenciable en un punto interior (x 0, y 0, z 0 ) Ω, entonces f(g(t 0 )) g (t 0 ) = 0 para cualquier trayectoria diferenciable g(t) contenida en la superficie de nivel c = f(x 0, y 0, z 0 ), de f(x, y, z). Este hecho justifica la siguiente definición. Sea f : Ω R 3 R, y sea S = {(x, y, z) Ω f(x, y, z) = c}, la superficie de nivel c de f(x, y, z). Si (x 0, y 0, z 0 ) S, f(x, y, z) es diferenciable en (x 0, y 0, z 0 ) y f(x 0, y 0, z 0 ) (0, 0, 0), el plano tangente a la superficie de nivel S en el punto (x 0, y 0, z 0 ), está definido por la ecuación. f(x 0, y 0, z 0 ) (x x 0, y y 0, z z 0 ) = 0. 33
34 Ejemplo 49. Determinar el plano tangente a la superficie de nivel: en el punto p 0 = (1, 1, 2). sen(xz + yz) = 0 Solución. son: Las derivadas parciales de la función f(x, y, z) = sen(xz + yz) f x = z cos(xz + yz), f y = z cos(xz + yz), f z = (x + y) cos(xz + yz), por lo tanto f(1, 1, 2) = (2, 2, 0). De ahí que la ecuación del plano tangente es: 2(x 1) + 2(y + 1) + 0(z 2) = 0, equivalentemente, x + 2y = Polinomio de Taylor Recordemos que si f : I R R es diferenciable en x 0 I, la aproximación lineal de f alrededor de x 0, es la función L(x) = f(x 0 ) + f (x 0 )(x x 0 ). Sin embargo, puede suceder que dos funciones cualitativamente distintas tengan la misma aproximación lineal. Consideremos por ejemplo la función f(x) = x 2 y la función g(x) = x 2 + 4x 2. En el punto x 0 = 1 la aproximación lineal de ambas funciones es: L(x) = 1 + 2(x 1), pero la función f es cóncava hacia arriba y la función g es cóncava hacia abajo. Con el fin de tener una aproximación más precisa de una función f(x) alrededor de un punto x 0, consideremos un polinomio de la forma P (x) = a + b(x x 0 ) + c(x x 0 ) 2 Quisieramos que P (x 0 ) = f(x 0 ), P (x 0 ) = f (x 0 ), P (x 0 ) = f (x 0 ), estas condiciones nos conducen a que a = f(x 0 ), b = f (x 0 ) y c = f (x 0 )/2, de modo que P (x) = f(x 0 ) + f (x 0 )(x x 0 ) + f (x 0 ) (x x 0 )
35 El siguiente teorema, cuya demostración se omite, establece que P (x) es una buena aproximación de f(x) cerca de x 0. Teorema 17. Si f : I R R es una función tal que f es continua en I, entonces para todo x 0 I, donde f(x) = f(x 0 ) + f (x 0 )(x x 0 ) + f (x 0 ) (x x 0 ) 2 + R 2 (x), 2 El polinomio x x 0 R 2 (x) (x x 0 ) 2 = 0. P 2 (x) = f(x 0 ) + f (x 0 )(x x 0 ) + f (x 0 ) (x x 0 ) 2 2 es llamado polinomio de Taylor de orden dos de f(x) alrededor de x 0. Obsérvese que P 2 (x) = L(x) + f (x 0 ) (x x 0 ) 2 2 donde L(x) es la linealización de f(x) alrededor de x 0. La función L(x) también es llamada el polinomio de Taylor de orden uno de f(x) alrededor de x 0. Obsérvese también que cerca de x 0 el error R 2 (x) en la aproximación cuadrática es menor que el error R 1 (x) en la aproximación lineal, pues (x x 0 ) 2 < x x 0 si la distancia al punto es menor que 1. Veremos ahora cómo extender el teorema anterior a funciones de dos variables. Sea f : Ω R 2 R tal que las derivadas parciales de orden dos existen y son continuas en Ω. El Hessiano de f en (x 0, y 0 ) Ω es la función cuadrática: Hf(x 0, y 0 )(x, y) = f xx (x 0, y 0 )x 2 + 2f xy (x 0, y 0 )xy + f yy (x 0, y 0 )y 2. Ejemplo 50. Calcular el Hessiano de en el punto (3, 4). f(x, y) = x 2 + y 2 Solución. Se deja al lector verificar que f xx = y 2 (x 2 + y 2 ) 3/2, f xy = xy (x 2 + y 2 ) 3/2, f yy = 35 x 2 (x 2 + y 2 ) 3/2.
36 Por lo que En conclusión: f xx (3, 4) = , f xy(3, 4) = , f xx(3, 4) = Hf(3, 4) = x xy y2. El siguiente teorema, cuya demostración se omite, extiende el teorema anterior a funciones de dos variables. Teorema 18 (Polinomio de Taylor de orden dos). Si f : Ω R 2 R es tal que las derivadas parciales de orden dos existen y son continuas en Ω, entonces para todo (x 0, y 0 ) Ω, donde f(x, y) = P 2 (x, y) + R 2 (x, y), P 2 (x, y) = f(x 0, y 0 )+ f(x 0, y 0 ) (x x 0, y y 0 )+ 1 2 Hf(x 0, y 0 )(x x 0, y y 0 ), y R 2 (x, y)) (x,y) (x 0,y 0 ) (x x 0 ) 2 + (y y 0 ) 2 = 0. El polinomio P 2 (x, y) que aparece en el teorema anterior es llamado el polinomio de Taylor de orden dos de f(x, y) alrededor de (x 0, y 0 ). Ejemplo 51. Calcular el polinomio de Taylor de orden dos de f(x, y) = x 2 + y 2 alrededor del punto (3, 4), y utilizarlo para aproximar el valor de (2.9) 2 + (4.1) 2. Solución. Utilizando el resultado del ejemplo anterior y la linealización de la función alrededor del punto, tenemos que P 2 (x, y) = (x 3) (y 4) (x 3) (x 3)(y 4) (y 4)2. De ahí que P 2 (2.9, 4.1) = = es una aproximación del valor de f(2.9, 4.1) = (2.9) 2 + (4.1) 2. 36
37 En general, sea f : Ω R n R tal que las derivadas parciales de orden dos existen y son continuas en Ω. El Hessiano de f en p 0 Ω es la función cuadrática: Hf(p 0 )(x) = n i=1 2 f x 2 i x 2 i + 2 p0 n n i=1 j=1 f 2 x i x j x i x j. p0 El polinomio de Taylor de orden dos de f alrededor de p 0 es la función: P 2 (x) = f(p 0 ) + f(p 0 ) (x p 0 ) + Hf(p 0 )(x p 0 ). 10. Máximos y mínimos Sea f : Ω R 2 R. Un punto p 0 = (x 0, y 0 ) Ω se dice que es un máximo local de f, si existe r > 0 tal que f(x, y) f(x 0, y 0 ) para todo (x, y) Ω, tal que (x x 0 ) 2 + (y y 0 ) 2 < r. Análogamente, p 0 es un mínimo local de f, si existe r > 0 tal que f(x 0, y 0 ) f(x, y) para todo (x, y) Ω, tal que (x x 0 ) 2 + (y y 0 ) 2 < r. Un punto p 0 = (x 0, y 0 ) Ω se dice que es un extremo local de f, si p 0 es un máximo o un mínimo local de f. Recordemos que si una función f : I R R tiene un extremo local en x 0 y la función es diferenciable en dicho punto, entonces f (x 0 ) = 0. El siguiente teorema extiende este resultado para funciones de dos variables. Teorema 19. Sea f : Ω R 2 R. Si p 0 = (x 0, y 0 ) Ω es un extremo local de f, y si f es diferenciable en p 0, entonces f(x 0, y 0 ) = (0, 0), es decir, f x (x 0, y 0 ) = 0 y f y (x 0, y 0 ) = 0. 37
38 Demostración. Supongamos que p 0 = (x 0, y 0 ) es un máximo local de f. Sea g(t) = p 0 + t f(x 0, y 0 ) y consideremos la función h(t) = f(g(t)). Obsérvese que h(t) h(0) = f(p 0 ) si t es pequeño, de modo que t 0 = 0 es un máximo local de h, de ahí que h (0) = 0. Por otra parte, por la regla de la cadena tenemos que h (0) = f(x 0, y 0 ) g (0) = f(x 0, y 0 ) f(x 0, y 0 ) = f(x 0, y 0 ) 2. Por lo tanto f(x 0, y 0 ) 2 = 0, y de ahí que f(x 0, y 0 ) = (0, 0). Sea f : Ω R 2 R. Un punto p 0 = (x 0, y 0 ) Ω se dice que es un punto crítico de f si f(x 0, y 0 ) = (0, 0) o si f no es diferenciable en p 0. Un punto crítico que no es ni máximo local ni mínimo local se dice que es un punto silla. Ejemplo 52. La función f(x, y) = 1 x 2 y 2 es diferenciable en R 2. Obsérvese además que f x = 2x y f y = 2y, por lo que el único punto crítico es (0, 0). Este punto corresponde a un máximo local, porque f(x, y) = 1 x 2 y 2 1 = f(0, 0). Ejemplo 53. La función f(x, y) = x 2 + y 2 es diferenciable en R 2 \{(0, 0)}. Obsérvese que f x = x x 2 + y 2, f y = y, (x, y) (0, 0), x 2 + y2 por lo que f(x, y) (0, 0) para todo (x, y) (0, 0). Por lo que el único punto crítico es (0, 0), donde la función no es diferenciable. Este punto corresponde a un mínimo local, porque f(0, 0) = 0 x 2 + y 2 = f(x, y), para todo (x, y) R 2. Ejemplo 54. La función f(x, y) = x 2 y 2 es diferenciable en R 2. Obsérvese que f x = 2x y f y = 2y, por lo que el único punto crítico es (0, 0). Este punto no es máximo local, porque f(0, 0) = 0 < f(x, 0) = x 2, si x 0. Tampoco es mínimo local, porque f(0, y) = y 2 < 0 = f(0, 0), si y 0, por lo tanto (0, 0) es un punto silla. En los ejemplos anteriores fue sencillo determinar por inspección la naturaleza de los puntos críticos, pero no siempre es el caso. Es necesario contar con un criterio que nos permita identificar si un punto crítico es un máximo local, un mínimo local o un punto silla. Recordemos que para funciones de 38
39 una variable una manera de hacer esto era a partir del signo de f (x 0 ). Veremos a continuación cómo tener un criterio similar para funciones de dos variables. Recordemos que si f : Ω R 2 R es tal que las derivadas parciales de orden dos existen y son continuas en Ω, el Hessiano de f en p 0 = (x 0, y 0 ) Ω es la función cuadrática: Hf(x 0, y 0 )(x, y) = f xx (x 0, y 0 )x 2 + 2f xy (x 0, y 0 )xy + f yy (x 0, y 0 )y 2. Se dice que Hf(x 0, y 0 ) es definida positiva, si Hf(x 0, y 0 )(x, y) > 0 para todo (x, y) (0, 0). Análogamente, Hf(x 0, y 0 ) es definida negativa, si Hf(x 0, y 0 )(x, y) < 0 para todo (x, y) (0, 0). El siguiente lema estable condiciones suficientes para asegurar que el Hessiano de una función sea definida positiva o definida negativa. Lema 1. Sea f : Ω R 2 R tal que las derivadas parciales de orden dos existen y son continuas en Ω. Sea p 0 = (x 0, y 0 ) Ω y sea D(p 0 ) = (f xx (p 0 ))(f yy (p 0 )) (f xy (p 0 )) Si D(p 0 ) > 0 y f xx (p 0 ) > 0, entonces Hf(x 0, y 0 ) es definida positiva. 2. Si D(p 0 ) > 0 y f xx (p 0 ) < 0, entonces Hf(x 0, y 0 ) es definida negativa. 3. Si D(p 0 ) < 0 entonces Hf(x 0, y 0 ) no es ni definida positiva ni definida negativa. Demostración. Para simplificar la demostración escribamos: a = f xx (p 0 ), b = f xy (p 0 ), c = f yy (p 0 ), de modo que Hf(x 0, y 0 )(x, y) = ax 2 +2bxy +cy 2. Si además a 0, podemos escribir ( Hf(x 0, y 0 )(x, y) = a x 2 + 2b a xy + b2 y 2 ) ( ) a 2 + c b2 y 2 a ( = a x + by ) + a ( ac b 2 a ) y 2 Obsérvese que si a > 0 y ac b 2 > 0, entonces Hf(x 0, y 0 )(x, 0) 0, además Hf(x 0, y 0 )(x, 0) = 0 si y sólo si x = by/a y y = 0, lo cual se cumple si y sólo 39
40 si (x, y) = (0, 0), de modo que en este caso Hf(x 0, y 0 ) es definida positiva. Análogamente, si a > 0 y ac b 2 > 0, entonces Hf(x 0, y 0 )(x, 0) 0 y además Hf(x 0, y 0 )(x, 0) = 0 si y sólo si (x, y) = (0, 0), por lo que Hf(x 0, y 0 ) es definida negativa. Por último, si ac b 2 < 0, entonces Hf(x 0, y 0 )(x, 0) > 0 y Hf(x 0, y 0 )( by/a, y) > 0, para todo x > 0, y > 0, por lo que Hf(x 0, y 0 ) no es ni definida positiva ni definida negativa. El número D(p 0 ) es llamado el discriminante de f en el punto crítico p 0. Obsérvese que ( ) fxx (p D(p 0 ) = det 0 ) f xy (p 0 ). f xy (p 0 ) f yy (p 0 ) El siguiente teorema establece un criterio de segundas derivadas parciales, para identificar si un punto crítico es un máximo local, un mínimo local o un punto silla. Teorema 20. Sea f : Ω R 2 R tal que las derivadas parciales de orden dos existen y son continuas en Ω. Sea p 0 = (x 0, y 0 ) Ω tal que f(x 0, y 0 ) = (0, 0), entonces 1. Si D(p 0 ) > 0 y f xx (p 0 ) > 0, entonces p 0 es mínimo local. 2. Si D(p 0 ) > 0 y f xx (p 0 ) < 0, entonces p 0 es máximo local. 3. Si D(p 0 ) < 0 entonces p 0 es punto silla. Demostración. Podemos escribir f(x, y) = P 2 (x, y) + R 2 (x, y), donde P 2 (x, y) = f(x 0, y 0 )+ f(x 0, y 0 ) (x x 0, y y 0 )+ 1 2 Hf(x 0, y 0 )(x x 0, y y 0 ), es el polinomio de Taylor de orden dos de f alrededor de p 0. Como además f(x 0, y 0 ) = (0, 0), tenemos que f(x, y) = f(x 0, y 0 ) Hf(x 0, y 0 )(x x 0, y y 0 ) + R 2 (x, y). Si D(p 0 ) > 0 y f xx (p 0 ) > 0, se sigue del lema anterior que Hf(x 0, y 0 ) es definida positiva. Como además R 2 (x, y) es pequeño, se puede demostrar que 1 2 Hf(x 0, y 0 )(x x 0, y y 0 )+R 2 (x, y) > 0, de ahí que f(x, y) > f(x 0, y 0 ), por lo que p 0 es mínimo local. Análogamente se prueba que si D(p 0 ) > 0 y f xx (p 0 ) < 0, entonces Hf(x 0, y 0 ) es definida negativa, y de ahí que f(x, y) < f(x 0, y 0 ), por lo que 40
3. Funciones de varias variables
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Teorema de la Función Implícita
 Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
Teorema de la Función Implícita El círculo de radio 1 con centro en el origen, puede representarse implícitamente mediante la ecuación x 2 + y 2 1 ó explícitamente por las ecuaciones y 1 x 2 y y 1 x 2
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES ) HOJA 3: Derivadas parciales y diferenciación.
 UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
9. DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES.
 9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
CÁLCULO II Funciones de varias variables
 CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
CÁLCULO II Funciones de varias variables Facultad de Informática (UPM) Facultad de Informática (UPM) () CÁLCULO II Funciones de varias variables 1 / 36 Funciones de varias variables Función vectorial de
Práctica 3: Diferenciación
 Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) 1er. Cuatrimestre 2017 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable 1. Vericar que se
Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) 1er. Cuatrimestre 2017 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable 1. Vericar que se
1. Hallar la ecuación paramétrica y las ecuaciones simétricas de la recta en los siguientes casos:
 A. Vectores ANALISIS MATEMATICO II Grupo Ciencias 05 Práctica : Geometría Analítica: Vectores, Rectas y Planos, Superficies en el espacio Para terminar el 3 de septiembre.. Sean v = (0,, ) y w = (,, 4)
A. Vectores ANALISIS MATEMATICO II Grupo Ciencias 05 Práctica : Geometría Analítica: Vectores, Rectas y Planos, Superficies en el espacio Para terminar el 3 de septiembre.. Sean v = (0,, ) y w = (,, 4)
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Práctica 3: Diferenciación
 Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) Primer Cuatrimestre - 03 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable. Vericar que se
Análisis I Matemática I Análisis II (C) Análisis Matemático I (Q) Primer Cuatrimestre - 03 Práctica 3: Diferenciación Aplicación de algunos resultados de diferenciación en una variable. Vericar que se
Práctica 3: Diferenciación I
 Análisis I Matemática I Análisis II (C) Cuat II - 009 Práctica 3: Diferenciación I Derivadas parciales y direccionales. Sea f una función continua en x = a. Probar que f es derivable en x = a si y solo
Análisis I Matemática I Análisis II (C) Cuat II - 009 Práctica 3: Diferenciación I Derivadas parciales y direccionales. Sea f una función continua en x = a. Probar que f es derivable en x = a si y solo
Cálculo en varias variables
 Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
Cálculo en varias variables Dpto. Matemática Aplicada Universidad de Málaga Resumen Límites y continuidad Funciones de varias variables Límites y continuidad en varias variables 1 Límites y continuidad
9. Diferenciación de funciones reales de varias variables reales Diferenciación DERIVADAS PARCIALES
 9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
9.1. Diferenciación 9.1.1. DERIVADAS PARCIALES Derivadas parciales de una función de dos variables Se llaman primeras derivadas parciales de una función f(x, y) respecto de x e y a las funciones: f x (x,
Práctica 3: Diferenciación
 Análisis I Matemática I Análisis II (C) Primer Cuatrimestre - 010 Práctica 3: Diferenciación Derivadas parciales y direccionales 1. Sea f una función continua en x = a. Probar que f es derivable en x =
Análisis I Matemática I Análisis II (C) Primer Cuatrimestre - 010 Práctica 3: Diferenciación Derivadas parciales y direccionales 1. Sea f una función continua en x = a. Probar que f es derivable en x =
Tarea 1 - Vectorial
 Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Tarea - Vectorial 2050. Part :. - 3.2.. Un cerro se queda en las montañas en la altura de 6 mil metros. El cerro tiene la forma del gráfico de la función z = f(x, y) = x 2 y 2. Observamos que plaquitas
Análisis Matemático 2
 Análisis Matemático 2 Una resolución de ejercicios con hipervínculos a videos on-line Autor: Martín Maulhardt Revisión: Fernando Acero y Ricardo Sirne Análisis Matemático II y II A Facultad de Ingeniería
Análisis Matemático 2 Una resolución de ejercicios con hipervínculos a videos on-line Autor: Martín Maulhardt Revisión: Fernando Acero y Ricardo Sirne Análisis Matemático II y II A Facultad de Ingeniería
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Funciones Reales de Varias Variables
 Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 162 CONTENIDO Funciones
x 2 y si x 3y 2 si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.
 FIUBA 07-05-11 Análisis Matemático II Parcial - Tema 1 1. Sea f(x, y) = { x y si x 3y si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.. Sea G(x, y) = (u(x, y),
FIUBA 07-05-11 Análisis Matemático II Parcial - Tema 1 1. Sea f(x, y) = { x y si x 3y si x = 3y Describir el conjunto de los puntos de discontinuidad de f en coordenadas polares.. Sea G(x, y) = (u(x, y),
1. DIFERENCIABILIDAD EN VARIAS VARIABLES
 . DIFERENCIABILIDAD EN VARIAS VARIABLES. Calcular las derivadas direccionales de las siguientes funciones en el punto ā y la dirección definida por v... f(x, y = x + 2xy 3y 2, ā = (, 2, v = ( 3 5, 4 5.
. DIFERENCIABILIDAD EN VARIAS VARIABLES. Calcular las derivadas direccionales de las siguientes funciones en el punto ā y la dirección definida por v... f(x, y = x + 2xy 3y 2, ā = (, 2, v = ( 3 5, 4 5.
CÁLCULO II Grados en Ingeniería
 CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
Extremos Locales. Un punto x 0 es un punto crítico de f si Df(x 0 ) = 0. Un punto crítico que no es un extremo local se llama punto silla.
 Extremos Locales Entre las caracteristicas geometricas básicas de la gráficas de una función estan sus puntos extremos, en los cuales la función alcanza sus valores mayor y menor. Definicón.- Si f : u
Extremos Locales Entre las caracteristicas geometricas básicas de la gráficas de una función estan sus puntos extremos, en los cuales la función alcanza sus valores mayor y menor. Definicón.- Si f : u
CÁLCULO DIFERENCIAL Muestras de examen
 CÁLCULO DIFERENCIAL Muestras de examen Febrero 2012 T1. [2] Demostrar que la imagen continua de un conjunto compacto es compacto. T2. [2.5] Definir la diferencial de una función en un punto y demostrar
CÁLCULO DIFERENCIAL Muestras de examen Febrero 2012 T1. [2] Demostrar que la imagen continua de un conjunto compacto es compacto. T2. [2.5] Definir la diferencial de una función en un punto y demostrar
Diferenciación SEGUNDA PARTE
 ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 4 - Primer Cuatrimestre 009 Diferenciación SEGUNDA PARTE Regla de la Cadena 1 Sean f(u, v, w) = u + v 3 + wu y g(x, y) = x sen(y) Además, tenemos
ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 4 - Primer Cuatrimestre 009 Diferenciación SEGUNDA PARTE Regla de la Cadena 1 Sean f(u, v, w) = u + v 3 + wu y g(x, y) = x sen(y) Además, tenemos
Tema 6: Funciones de varias variables
 Tema 6: Funciones de varias variables de febrero de 6 Preliminares: derivadas parciales. Sea F una función de dos variables, como por ejemplo la función definida por F(x; y) = x y 3 Podemos derivarla con
Tema 6: Funciones de varias variables de febrero de 6 Preliminares: derivadas parciales. Sea F una función de dos variables, como por ejemplo la función definida por F(x; y) = x y 3 Podemos derivarla con
Clase 1: Funciones de Varias Variables
 Clase 1: Funciones de Varias Variables C. J. Vanegas 29 de abril de 2008 1. La geometría de funciones con valores reales Considere la siguiente función f: donde x = (x 1,..., x n ). f : A R n R m x A f(x)
Clase 1: Funciones de Varias Variables C. J. Vanegas 29 de abril de 2008 1. La geometría de funciones con valores reales Considere la siguiente función f: donde x = (x 1,..., x n ). f : A R n R m x A f(x)
1. Funciones de varias variables
 Coordinación de Matemáticas III (MAT 023) 1 er Semestre de 2013 1. Funciones de varias variables 1.1. Definiciones básicas Definición 1.1. Consideremos una función f : U R n R m. Diremos que: 1. f es una
Coordinación de Matemáticas III (MAT 023) 1 er Semestre de 2013 1. Funciones de varias variables 1.1. Definiciones básicas Definición 1.1. Consideremos una función f : U R n R m. Diremos que: 1. f es una
Campos escalares: gráficas, límites y continuidad
 Campos escalares: gráficas, ites y continuidad de febrero de 0 Gráficas de un campo escalar Dominio de un campo escalar Un campo escalar definido sobre un subconjunto U de R n, es una función f con dominio
Campos escalares: gráficas, ites y continuidad de febrero de 0 Gráficas de un campo escalar Dominio de un campo escalar Un campo escalar definido sobre un subconjunto U de R n, es una función f con dominio
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación
 Conocimientos previos Para poder seguir adecuadamente este tema, se requiere que el alumno repase ponga al día sus conocimientos en los siguientes contenidos: Cálculo de derivadas Propiedades de las funciones
Conocimientos previos Para poder seguir adecuadamente este tema, se requiere que el alumno repase ponga al día sus conocimientos en los siguientes contenidos: Cálculo de derivadas Propiedades de las funciones
2. Cálculo diferencial de funciones de varias variables. Mayo, 2009
 Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
Cálculo 2. Cálculo diferencial de funciones de varias variables Mayo, 2009 Definición IR 2 = {(x 1,x 2 )/x 1 IR,x 2 IR} Sean dos puntos a y b, de coordenadas respectivas (a 1,a 2 ) y (b 1,b 2 ). Definición
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
Cálculo Diferencial en una variable
 Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
Funciones de R m R n
 Funciones de R n R m Funciones de R m R n Una funcion f : R n R m es una función cuyo dominio es un subconjunto Ω R n. Denotada por f : Ω R m donde a cada x R n f le asigna un vector f(x) R m. Ejemplo.-
Funciones de R n R m Funciones de R m R n Una funcion f : R n R m es una función cuyo dominio es un subconjunto Ω R n. Denotada por f : Ω R m donde a cada x R n f le asigna un vector f(x) R m. Ejemplo.-
Funciones reales de varias variables.
 Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
Tema 4 Funciones reales de varias variables. 4.1. El espacio euclídeo R n. Definición 4.1.1. Se define el producto escalar entre vectores de R n como la aplicación: ( ) : R n R n R : x y = (x 1, x 2,...,
Curso 2010/ de julio de (2.75 p.) 1) Se considera la función f : (0, ) (0, ) definida por
 Cálculo I Curso 2010/2011 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas 5 de julio de 2011 (275 p) 1) Se considera la función f : (0, ) (0, ) definida por f(x) = 1 + ex x e x a)
Cálculo I Curso 2010/2011 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas 5 de julio de 2011 (275 p) 1) Se considera la función f : (0, ) (0, ) definida por f(x) = 1 + ex x e x a)
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 3 Geometría del plano y del espacio José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es
ANÁLISIS I MATEMÁTICA 1 ANÁLISIS II (Computación) Práctica 5 - Verano 2009
 ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
ANÁLISIS I MATEMÁTICA ANÁLISIS II (Computación) Práctica 5 - Verano 2009 Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior. Calcular las derivadas
Teorema de la Función Implícita
 Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
Teoremas de Taylor. Capítulo 7
 Capítulo 7 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor. Por
Capítulo 7 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor. Por
Soluciones a los ejercicios del examen final
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 201/14 20 de diciembre de 201 Soluciones a los ejercicios del examen final 1) Se considera la función f : R R
a de un conjunto S de R n si
 1 235 Máximos, mínimos y puntos de ensilladura Definición.- Se dice que una función real f( x) tiene un máximo absoluto en un punto a de un conjunto S de R n si f( x) f( a) (2) para todo x S. El número
1 235 Máximos, mínimos y puntos de ensilladura Definición.- Se dice que una función real f( x) tiene un máximo absoluto en un punto a de un conjunto S de R n si f( x) f( a) (2) para todo x S. El número
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
todos los puntos de U, y las funciones df : U R m son continuas en x, entonces F es diferenciable en x.
 clase C 1 clase C p 1. clase C 1 Consideremos U un abierto de R n, y F : U R m. Si para cada x U existe df (x), podemos definir una función df : U R m df (x) = ( 1 (x),..., m (x)) y tiene sentido estudiar
clase C 1 clase C p 1. clase C 1 Consideremos U un abierto de R n, y F : U R m. Si para cada x U existe df (x), podemos definir una función df : U R m df (x) = ( 1 (x),..., m (x)) y tiene sentido estudiar
Problema 1. Calcula las derivadas parciales de las siguientes funciones: (d) f(x, y) = arctan x + y. (e) f(x, y) = cos(3x) sin(3y),
 Problema. Calcula las derivadas parciales de las siguientes funciones: (a) f(x, y) = x + y cos(xy), (b) f(x, y) = x x + y, (c) f(x, y) = log x + y x y, (d) f(x, y) = arctan x + y x y, (e) f(x, y) = cos(3x)
Problema. Calcula las derivadas parciales de las siguientes funciones: (a) f(x, y) = x + y cos(xy), (b) f(x, y) = x x + y, (c) f(x, y) = log x + y x y, (d) f(x, y) = arctan x + y x y, (e) f(x, y) = cos(3x)
x 2 + ln(x + z) y = 0 yz + e xz 1 = 0 define una curva C regular en un entorno de (1, 1, 0) y halle el plano normal a C en dicho punto.
 1 Sea f : R R una función C 3 que satisface f(1, ) = (0, 0), y cuya matriz ( Hessiana ) en (1, ) es: 1 0 H = 0 Hallar todos los b ɛ R de manera que la función: g( = f( + 1 b b (y ) ) tenga extremo en (1,
1 Sea f : R R una función C 3 que satisface f(1, ) = (0, 0), y cuya matriz ( Hessiana ) en (1, ) es: 1 0 H = 0 Hallar todos los b ɛ R de manera que la función: g( = f( + 1 b b (y ) ) tenga extremo en (1,
ANÁLISIS II Computación. Práctica 4. x 3. x 2 + y 2 si (x, y) (0, 0)
 facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
facultad de ciencias exactas y naturales uba primer cuatrimestre 2007 ANÁLISIS II Computación Práctica 4 Derivadas parciales 1. Calcular a) f y (2, 1) para f(x, y) = xy + x y b) f z (1, 1, 1) para f(x,
TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1. CÁLCULO DIFERENCIAL EN VARIAS VARIABLES
 TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1 CÁLCULO DIFERENCIAL EN VARIAS VARIABLES 11 CONCEPTOS BÁSICOS Definición La norma de un vector x =
TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1 CÁLCULO DIFERENCIAL EN VARIAS VARIABLES 11 CONCEPTOS BÁSICOS Definición La norma de un vector x =
UNIVERSIDAD DE SEVILLA. DEPARTAMENTO DE ECONOMÍA APLICADA I. BOLETÍN DE PROBLEMAS DE MATEMÁTICAS I. GRADO EN ECONOMÍA.
 UNIVERSIA E SEVILLA. EPARTAMENTO E ECONOMÍA APLICAA I. BOLETÍN E PROBLEMAS E MATEMÁTICAS I. GRAO EN ECONOMÍA. BLOQUE I: CÁLCULO IFERENCIAL. Tema 1: Funciones de una variable Problema 1 Estudiar la continuidad
UNIVERSIA E SEVILLA. EPARTAMENTO E ECONOMÍA APLICAA I. BOLETÍN E PROBLEMAS E MATEMÁTICAS I. GRAO EN ECONOMÍA. BLOQUE I: CÁLCULO IFERENCIAL. Tema 1: Funciones de una variable Problema 1 Estudiar la continuidad
Fundamentos matemáticos. Tema 5 Derivación de funciones de una y varias variables
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 5 Derivación de funciones de una y varias variables José Barrios García Departamento de Análisis Matemático Universidad de La
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 5 Derivación de funciones de una y varias variables José Barrios García Departamento de Análisis Matemático Universidad de La
Lección 2: Funciones vectoriales: límite y. continuidad. Diferenciabilidad de campos
 Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
Lección 2: Funciones vectoriales: límite y continuidad. Diferenciabilidad de campos vectoriales 1.1 Introducción En economía, frecuentemente, nos interesa explicar la variación de unas magnitudes respecto
Tarea 1 - Vectorial 201420
 Tarea - Vectorial 040. Part :. - 3... Hacer parametrización de la curva de intersección del cilindro x + y = 6 y el plano x + z = 5. Encontrar las coordenadas de los puntos de la curva donde la curvatura
Tarea - Vectorial 040. Part :. - 3... Hacer parametrización de la curva de intersección del cilindro x + y = 6 y el plano x + z = 5. Encontrar las coordenadas de los puntos de la curva donde la curvatura
1. Funciones diferenciables
 1. diferenciables Volvamos sobre el significado de la derivada de una función real de una variable real, Como vimos en el capítulo anterior, f : (a, b) R derivable en x 0, equivale a que f(x) f(x 0 ) =
1. diferenciables Volvamos sobre el significado de la derivada de una función real de una variable real, Como vimos en el capítulo anterior, f : (a, b) R derivable en x 0, equivale a que f(x) f(x 0 ) =
ANALISIS II 12/2/08 COLOQUIO TEMA 1
 ANALISIS II //08 COLOQUIO TEMA Sea f : R R un campo vectorial C y C la curva parametrizada por: γ(t) = (cost, 0, sent) con t ɛ [0, π] Sabiendo que C f ds = 6 y que rot( f( ) = (z, ), calcular la integral
ANALISIS II //08 COLOQUIO TEMA Sea f : R R un campo vectorial C y C la curva parametrizada por: γ(t) = (cost, 0, sent) con t ɛ [0, π] Sabiendo que C f ds = 6 y que rot( f( ) = (z, ), calcular la integral
ANALISIS II Computación. Práctica 4. x 3. x 2 + y 2. x 2 + y 2 si (x, y) (0, 0) 0 si (x, y) = (0, 0)
 facultad de ciencias exactas y naturales uba curso de verano 2006 ANALISIS II Computación Práctica 4 Derivadas parciales 1. Calcular (a) f xy y (2, 1) para f(x, y) = + x y (b) f z (1, 1, 1) para f(x, y,
facultad de ciencias exactas y naturales uba curso de verano 2006 ANALISIS II Computación Práctica 4 Derivadas parciales 1. Calcular (a) f xy y (2, 1) para f(x, y) = + x y (b) f z (1, 1, 1) para f(x, y,
Fundamentos matemáticos. Tema 3 Geometría del plano y del espacio
 Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 3 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Soluciones a los ejercicios propuestos: Matemáticas III. Curso Tema 4. (a) Determinar si f es localmente invertible en (0, 0, 0).
 Soluciones a los ejercicios propuestos: Matemáticas III Curso 08 09 36 Tema 4 1 Sea f : IR 3 IR 3 definida por fx, y, z = e x+y, cosz, e z a Determinar si f es localmente invertible en 0, 0, 0 J fx, y,
Soluciones a los ejercicios propuestos: Matemáticas III Curso 08 09 36 Tema 4 1 Sea f : IR 3 IR 3 definida por fx, y, z = e x+y, cosz, e z a Determinar si f es localmente invertible en 0, 0, 0 J fx, y,
si existe un entorno V de a contenido en A, tal que la diferencia f(x) f(a) no cambia de signo cuando x V :
 Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Capítulo 7 Extremos Relativos Una aplicación clásica del Teorema Local de Taylor es el estudio de los extremos relativos de una función escalar. Aunque la analogía con el caso de una variable es total,
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 01/02
 Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
Escuela Universitaria Politécnica Examen de Cálculo - Febrero - Curso 0/02 x 2 + y 4. (a) Comprueba que el siguiente límite no existe lim (x,y) (0,0) x 2 + y. 2 (b) Busca una trayectoria a través de la
Coordinación de Matemáticas III (MAT 023) x a. Además, diremos que f es continua en U si f es continua en cada punto de U.
 Coordinación de Matemáticas III (MAT 023) 1 er Semestre de 2013 Continuidad de Funciones en Varias Variables 1. Continuidad Definición 1.1. Sean U R n abierto, a U y f : U R una función real de varias
Coordinación de Matemáticas III (MAT 023) 1 er Semestre de 2013 Continuidad de Funciones en Varias Variables 1. Continuidad Definición 1.1. Sean U R n abierto, a U y f : U R una función real de varias
Funciones Diferenciables. Superficies.
 CAPÍTULO 3 Funciones Diferenciables. Superficies. En este importante capítulo presentamos el concepto de diferenciabilidad. Este concepto difiere sustancialmente del de Análisis Matemático I. Estudiamos
CAPÍTULO 3 Funciones Diferenciables. Superficies. En este importante capítulo presentamos el concepto de diferenciabilidad. Este concepto difiere sustancialmente del de Análisis Matemático I. Estudiamos
Tema 6 Funciones reales de varias variables
 Tema 6 Funciones reales de varias variables 6.1 Continuidad y límites 6.1.1 Introducción. Existen muchos procesos en la naturaleza que dependen de dos o más variables. Por ejemplo, el volumen de un sólido
Tema 6 Funciones reales de varias variables 6.1 Continuidad y límites 6.1.1 Introducción. Existen muchos procesos en la naturaleza que dependen de dos o más variables. Por ejemplo, el volumen de un sólido
Funciones Diferenciables. Superficies.
 CAPÍTULO 3 Funciones Diferenciables. Superficies. En este importante capítulo presentamos el concepto de diferenciabilidad. Este concepto difiere del de Análisis Matemático I, porque allí diferenciable
CAPÍTULO 3 Funciones Diferenciables. Superficies. En este importante capítulo presentamos el concepto de diferenciabilidad. Este concepto difiere del de Análisis Matemático I, porque allí diferenciable
Funciones Implícitas.
 CAPÍTULO 5 Funciones Implícitas. En este capítulo presentamos el concepto de función implícita. Esta idea nos ayuda a obtener derivadas de funciones que no podemos conocer explícitamente, pero su aplicación
CAPÍTULO 5 Funciones Implícitas. En este capítulo presentamos el concepto de función implícita. Esta idea nos ayuda a obtener derivadas de funciones que no podemos conocer explícitamente, pero su aplicación
Mini-apunte teoría primer parcial de Análisis Matemático II
 Mini-apunte teoría primer parcial de Análisis Matemático II 1. Ecuaciones Diferenciales Definición 1.1 (ED). Una Ecuación Diferencial es una ecuación en la que intervienen una o más variables independientes,
Mini-apunte teoría primer parcial de Análisis Matemático II 1. Ecuaciones Diferenciales Definición 1.1 (ED). Una Ecuación Diferencial es una ecuación en la que intervienen una o más variables independientes,
Polinomio de Taylor. Extremos.
 CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) x u + f
 1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
1 228 Extensión de la regla de la cadena Funciones diferenciables. z = f(x, y), x = x(u, v, w), y = y(u, v, w) z = f ( x(u, v, w), y(u, v, w) ) z u = f x x u + f y y u z v = f x x v + f y y v z w = f x
Polinomio de Taylor. Extremos.
 CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
CAPÍTULO 6 Polinomio de Taylor. Extremos. En este capítulo trabajamos con el polinomio de Taylor de una función de varias variables y su aplicación al estudio de los extremos de funciones de más de una
Funciones reales de varias variables
 PROBLEMAS DE CÁLCULO II Curso 2-22 2 Funciones reales de varias variables. Dibuja las curvas de niveles,,..., 5 y la representación gráfica de las siguientes funciones a) f(x, y) = 5 x y b) f(x, y) = x
PROBLEMAS DE CÁLCULO II Curso 2-22 2 Funciones reales de varias variables. Dibuja las curvas de niveles,,..., 5 y la representación gráfica de las siguientes funciones a) f(x, y) = 5 x y b) f(x, y) = x
Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad
 Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba, S. 2014. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative
Matemáticas III Tema 1 Funciones de varias variables. Diferenciabilidad Rodríguez Sánchez, F.J. Muñoz Ruiz, M.L. Merino Córdoba, S. 2014. OCW-Universidad de Málaga, http://ocw.uma.es. Bajo licencia Creative
TEORÍA DE CÁLCULO I. Para Grados en Ingeniería. Capítulo 1: Funciones de una variable real. Domingo Pestana Galván José Manuel Rodríguez García
 TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
TEORÍA DE CÁLCULO I Para Grados en Ingeniería Capítulo 1: Funciones de una variable real Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez 1 CAPÍTULO 1.
Extremos de funciones de varias variables
 Capítulo 6 Extremos de funciones de varias variables En este capítulo vamos a considerar la teoría clásica de extremos para funciones diferenciables de varias variables, cuyos dos tópicos habituales son
Capítulo 6 Extremos de funciones de varias variables En este capítulo vamos a considerar la teoría clásica de extremos para funciones diferenciables de varias variables, cuyos dos tópicos habituales son
Análisis Matemático II Curso 2018 Práctica introductoria
 Análisis Matemático II Curso 018 Práctica introductoria Cónicas - Sus ecuaciones y gráficas 1. Encontrar la forma estándar de cada cónica y graficar. a) x + y 6y = 0 b) x + y 1 = 0 c) x(x + 1) y = 4 d)
Análisis Matemático II Curso 018 Práctica introductoria Cónicas - Sus ecuaciones y gráficas 1. Encontrar la forma estándar de cada cónica y graficar. a) x + y 6y = 0 b) x + y 1 = 0 c) x(x + 1) y = 4 d)
(x x 0 ) y 0. O bien z z 0 = x 0. y notamos a este límite ᾱ (t 0 ) = dᾱ dt (t 0).
 O bien z z 0 = x 0 z 0 (x x 0 ) y 0 z 0 (y y 0 ). Para obtener la ecuación cartesiana de este plano hacemos x 0 (x x 0 )+y 0 (y y 0 )+z 0 (z z 0 ) = 0, como x 0 + y0 + z0 = x 0 + y0 + r (x 0 + y0) = r
O bien z z 0 = x 0 z 0 (x x 0 ) y 0 z 0 (y y 0 ). Para obtener la ecuación cartesiana de este plano hacemos x 0 (x x 0 )+y 0 (y y 0 )+z 0 (z z 0 ) = 0, como x 0 + y0 + z0 = x 0 + y0 + r (x 0 + y0) = r
Funciones Reales de Varias Variables
 Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 54 CONTENIDO Funciones
Funciones Reales de Varias Variables Hermes Pantoja Carhuavilca Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Matematica II Hermes Pantoja Carhuavilca 1 de 54 CONTENIDO Funciones
Límites y continuidad. Cálculo 1
 Límites y continuidad Cálculo 1 Razones de cambio y límites La rapidez promedio de un móvil es la distancia recorrida durante un intervalo de tiempo dividida entre la longitud del intervalo. Ejemplo 1
Límites y continuidad Cálculo 1 Razones de cambio y límites La rapidez promedio de un móvil es la distancia recorrida durante un intervalo de tiempo dividida entre la longitud del intervalo. Ejemplo 1
Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos
 Análisis I Matemática I Análisis II (C) Cuat II - 2009 Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior 1. Calcular las derivadas
Análisis I Matemática I Análisis II (C) Cuat II - 2009 Práctica 5: Derivadas parciales de orden superior - Polinomio de Taylor - Convexidad y Extremos Derivadas de orden superior 1. Calcular las derivadas
Derivada y diferencial
 Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Matemáticas III Andalucía-Tech
 Matemáticas III Andalucía-Tech Tema Optimización en campos escalares Índice 1. Formas cuadráticas y matrices simétricas reales 1. Extremos relativos de un campo escalar 3.1. Polinomio de Taylor de un campo
Matemáticas III Andalucía-Tech Tema Optimización en campos escalares Índice 1. Formas cuadráticas y matrices simétricas reales 1. Extremos relativos de un campo escalar 3.1. Polinomio de Taylor de un campo
Derivación de funciones de varias variables.
 Derivación de funciones de varias variables. En este apartado se presentan los conceptos básicos que aparecen en la derivación de funciones de varias variables. La idea es establecer un método para estudiar
Derivación de funciones de varias variables. En este apartado se presentan los conceptos básicos que aparecen en la derivación de funciones de varias variables. La idea es establecer un método para estudiar
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. 2do. cuatrimestre de 2015 Práctica 2 - Integrales de superficie. Definición.1. Una superficie paramétrica (superficie a secas para nosotros) es un conjunto
Análisis II Análisis matemático II Matemática 3. 2do. cuatrimestre de 2015 Práctica 2 - Integrales de superficie. Definición.1. Una superficie paramétrica (superficie a secas para nosotros) es un conjunto
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES ) y = ex cos y. e x cos y e x sin y. y 2.
 UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES HOJA 4: Derivadas de orden superior 4-1. Sea u : R R definida por u(x, y e x sen y. Calcula las cuatro parciales segundas,
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES HOJA 4: Derivadas de orden superior 4-1. Sea u : R R definida por u(x, y e x sen y. Calcula las cuatro parciales segundas,
Funciones de varias variables: continuidad derivadas parciales y optimización
 Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
Titulación: Ingeniero en Telecomunicación. Asignatura: Cálculo. Relación de problemas número 4. Funciones de varias variables: continuidad derivadas parciales y optimización Problema 1. Determinar el dominio
Fundamentos matemáticos. Tema 4 Funciones de una y varias variables
 Grado en Ingeniería agrícola y del medio rural Tema 4 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 4 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative Commons 4.0 Internacional J.
OCW-Universidad de Málaga, (2014). Bajo licencia. Creative Commons Attribution- NonComercial-ShareAlike 3.
 OCW-Universidad de Málaga, http://ocw.uma.es (014). Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3.0 Spain Matemáticas III Relación de ejercicios Tema 1 Ejercicios Ej. 1 Encuentra
OCW-Universidad de Málaga, http://ocw.uma.es (014). Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3.0 Spain Matemáticas III Relación de ejercicios Tema 1 Ejercicios Ej. 1 Encuentra
Cálculo: Notas sobre diferenciabilidad en una variable
 Cálculo: Notas sobre diferenciabilidad en una variable Antonio Garvín Curso 04/05 1 Derivabilidad en una variable 1.1 La derivada de una función en un punto Para una función f: R R tal que todo un intervalo
Cálculo: Notas sobre diferenciabilidad en una variable Antonio Garvín Curso 04/05 1 Derivabilidad en una variable 1.1 La derivada de una función en un punto Para una función f: R R tal que todo un intervalo
1.6 Ejercicios resueltos
 Apuntes de Ampliación de Matemáticas 1.6 Ejercicios resueltos Ejercicio 1.1 En cada uno de los siguientes casos a A {(x,y R : 1 < x < 1, 1 < y < 1}. b A {(x,y R : 1 < x + y < 4}. c A {(x,y R : y > 0}.
Apuntes de Ampliación de Matemáticas 1.6 Ejercicios resueltos Ejercicio 1.1 En cada uno de los siguientes casos a A {(x,y R : 1 < x < 1, 1 < y < 1}. b A {(x,y R : 1 < x + y < 4}. c A {(x,y R : y > 0}.
= f (a) R. f(x) f(a) x a. recta por (a, f(a)) de pendiente f(a+h2) f(a) recta tangente por (a, f(a)) de pendiente f (a)
 1 1. DERIVACIÓN 1.1. DEFINICIONES Y RESULTADOS PRINCIPALES Definición 1.1. Derivada. Sea f una función definida en un intervalo abierto I con a I. Decimos que f es derivable en a si existe y es real el
1 1. DERIVACIÓN 1.1. DEFINICIONES Y RESULTADOS PRINCIPALES Definición 1.1. Derivada. Sea f una función definida en un intervalo abierto I con a I. Decimos que f es derivable en a si existe y es real el
Powered by TCPDF (
 Powered by TCPDF (www.tcpdf.org) Análisis Matemático II - Curso 2018 Nota sobre formas cuadráticas y aplicación al análisis de extremos de una función Breve resumen acerca de las formas cuadráticas Necesitamos
Powered by TCPDF (www.tcpdf.org) Análisis Matemático II - Curso 2018 Nota sobre formas cuadráticas y aplicación al análisis de extremos de una función Breve resumen acerca de las formas cuadráticas Necesitamos
Material para exámen final
 Cálculo 3, FAMAT-UG, aug-dic, 2006 Material para exámen final Fecha del exámen: 5 dic, 2006 Definiciones: Hay que saber las definiciones precisas de todos los siguientes términos, y conocer ejemplos concretos
Cálculo 3, FAMAT-UG, aug-dic, 2006 Material para exámen final Fecha del exámen: 5 dic, 2006 Definiciones: Hay que saber las definiciones precisas de todos los siguientes términos, y conocer ejemplos concretos
Álgebra y Álgebra II - Primer Cuatrimestre 2018 Práctico 4 - Espacios Vectoriales
 Álgebra y Álgebra II - Primer Cuatrimestre 2018 Práctico 4 - Espacios Vectoriales (1) Decidir si los siguientes conjuntos son R-espacios vectoriales con las operaciones abajo denidas. (a) R n con v w =
Álgebra y Álgebra II - Primer Cuatrimestre 2018 Práctico 4 - Espacios Vectoriales (1) Decidir si los siguientes conjuntos son R-espacios vectoriales con las operaciones abajo denidas. (a) R n con v w =
5 Continuidad y derivabilidad de funciones reales de varias variables reales.
 5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
Regla de la Cadena. df(x + tv) t=0
 Regla de la Cadena Teorema: Si f : R R es diferenciable, entonces todas las derivadas direccionales existen. La derivada direccional en x en la dirección v está dada por [ ] [ ] [ ] Df v (x) = gradf(x)
Regla de la Cadena Teorema: Si f : R R es diferenciable, entonces todas las derivadas direccionales existen. La derivada direccional en x en la dirección v está dada por [ ] [ ] [ ] Df v (x) = gradf(x)
CONTINUIDAD DE FUNCIONES. SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos.
 CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
CAPÍTULO IV. CONTINUIDAD DE FUNCIONES SECCIONES A. Definición de función continua. B. Propiedades de las funciones continuas. C. Ejercicios propuestos. 121 A. DEFINICIÓN DE FUNCIÓN CONTINUA. Una función
Continuidad y Continuidad Uniforme. Aplicaciones lineales continuas.
 Continuidad y Continuidad Uniforme. Aplicaciones lineales continuas. Beatriz Porras 1 Límites Las definiciones de ĺımite de funciones de varias variables son similares a las de los ĺımites de funciones
Continuidad y Continuidad Uniforme. Aplicaciones lineales continuas. Beatriz Porras 1 Límites Las definiciones de ĺımite de funciones de varias variables son similares a las de los ĺımites de funciones
Coordinación de Matemática I (MAT021) 1 er Semestre de 2013 Semana 7: Lunes 22 - Viernes 27 de Abril. Contenidos
 Coordinación de Matemática I (MAT01) 1 er Semestre de 013 Semana 7: Lunes - Viernes 7 de Abril Cálculo Contenidos Clase 1: Álgebra de límites. Teorema del Sandwich. Cálculo de límites. Límites trigonométricos.
Coordinación de Matemática I (MAT01) 1 er Semestre de 013 Semana 7: Lunes - Viernes 7 de Abril Cálculo Contenidos Clase 1: Álgebra de límites. Teorema del Sandwich. Cálculo de límites. Límites trigonométricos.
Examen Final de Cálculo Vectorial MATE PREGUNTAS ABIERTAS TEMA A Diciembre 6 de Nombre: Código:
 UNIVERSIDAD DE LOS ANDES DEPARTAMENTO DE MATEMÁTICAS Examen Final de Cálculo Vectorial MATE 1207 PREGUNTAS ABIERTAS TEMA A Diciembre 6 de 2017 Este es un examen individual, no se permite el uso de libros,
UNIVERSIDAD DE LOS ANDES DEPARTAMENTO DE MATEMÁTICAS Examen Final de Cálculo Vectorial MATE 1207 PREGUNTAS ABIERTAS TEMA A Diciembre 6 de 2017 Este es un examen individual, no se permite el uso de libros,
Álgebra y Álgebra II - Segundo Cuatrimestre 2017 Práctico 4 - Espacios Vectoriales
 Álgebra y Álgebra II - Segundo Cuatrimestre 2017 Práctico 4 - Espacios Vectoriales (1) Sea n N. Mostrar que el conjunto de polinomios sobre R de grado menor que n es un subespacio vectorial de R[x]. Este
Álgebra y Álgebra II - Segundo Cuatrimestre 2017 Práctico 4 - Espacios Vectoriales (1) Sea n N. Mostrar que el conjunto de polinomios sobre R de grado menor que n es un subespacio vectorial de R[x]. Este
Ecuaciones Diferenciales Ordinarias Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Matemática Semestre de Otoño, 2012
 Universidad de Chile Ecuaciones Diferenciales Ordinarias Facultad de Ciencias Físicas y Matemáticas Profesora Salomé Martínez Departamento de Ingeniería Matemática Semestre de Otoño, 2012 Pauta: Auxiliar
Universidad de Chile Ecuaciones Diferenciales Ordinarias Facultad de Ciencias Físicas y Matemáticas Profesora Salomé Martínez Departamento de Ingeniería Matemática Semestre de Otoño, 2012 Pauta: Auxiliar
Definición 11.1 Sea f : A E F una aplicación r-veces diferenciable en un punto a A. o
 Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
Capítulo 11 Teoremas de Taylor Una vez más nos disponemos a extender a las funciones de varias variables resultados ya conocidos para funciones de una variable, los teoremas de aproximación de Taylor.
(Polinomio de Taylor en R n )
 APROXIMACIÓN POR POLINOMIOS (Polinomio de Taylor en R n ) MARíA DEL CARMEN CALVO En este trabajo nos ocuparemos de extender a funciones de varias variables los resultados obtenidos para funciones de una
APROXIMACIÓN POR POLINOMIOS (Polinomio de Taylor en R n ) MARíA DEL CARMEN CALVO En este trabajo nos ocuparemos de extender a funciones de varias variables los resultados obtenidos para funciones de una
Función de dos variables
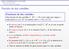 Funciones escalares de dos variables Función de dos variables Funciones de dos variables Una función de dos variables F : R 2 R es una regla que asigna a cada punto (x, y) R 2 un número real z = F (x,
Funciones escalares de dos variables Función de dos variables Funciones de dos variables Una función de dos variables F : R 2 R es una regla que asigna a cada punto (x, y) R 2 un número real z = F (x,
