3 Transformada de Laplace i sèries de Fourier
|
|
|
- Diego Díaz Silva
- hace 5 años
- Vistas:
Transcripción
1 3 Transformada de Laplace i sèries de Fourier Calculeu la de Laplace de les funcions següens: ransformada a f = +, si < <,, si Solució: s e s s s e s b f = sin Solució: s s + c f = 3 Solució: 48 s 4 4 s s s d f = cos Solució: s + ss + 4 e f = sin sin Solució: f f = e sinh Solució: s s + s s s + 9 a Demosreu que exiseix la ransformada de Laplace Lfs, s >, de la funció f = α α > b Demosreu que si α > aleshores L α s = x >, és la funció Γ d Euler c Què podem dir de la funció f = /? d Maeixa preguna per a la funció f = / Γα + s α+, on Γx = 3 Calculeu una aniransformada de Laplace de les funcions següens: a gs = s + s 3 Solució: b gs = 5s Solució: 5 e/5 s + c gs = s 4ss + 5 Solució: e e 5 d gs = s 4 9 Solució: 6 3 sinh sin 3 4 Calculeu la ransformada de Laplace de la funció e 3, si, 5, f =, si = 5 Què podem dir de la unicia de l aniransformada de Laplace d una funció? x e d, 5 Demosreu que sin u cos u du = sin Indicació: feu servir el eorema de con- volució
2 6 Tenin en compe la definició de l exponencial complexa: e iθ = cos θ+i sin θ, calculeu Le ia per a a R i comproveu que s obé el maeix que si s apliqués, formalmen, la ransformada de Laplace a una exponencial real 7 Calculeu la ransformada de Laplace de les funcions següens: e s a f = e U Solució: s + b f = e cos 3 Solució: s + s s + 36 c f = e 3 cos 3 Solució: d f = τe τ dτ Solució: e f = e sin Solució: 9 + s + 3 s ss + s s + s + s + 8 Calculeu una aniransformada de Laplace de les funcions següens: s + 5 a gs = Solució: s e 3 cos s + 34 sin5 b gs = e s s s Solució: + e U 9 Escriviu la funció f =, si < 3π/, sin, si 3π/ en ermes de funcions esgraó uniàries això és, funcions del ipus U a i calculeu la seva ransformada de Laplace Solució: se 3πs/ s + Feu el maeix que al problema anerior amb la funció f = E[] par enera Solució: se s s + Calculeu una aniransformada de Laplace de la funció gs = ln fen servir que s + 4 L n fs = n dn ds Lfs Solució: cos cos n Calculeu una aniransformada de Laplace de la funció gs = a Fen servir la ransformada de Laplace d una convolució b Pels eoremes de ranslació de la forma següen: s + 3 Calculeu la ransformada de Laplace de la funció ona riangular enin en compe que és periòdica Solució: e s s s + e s + e s s + + s s s e s e s
3 4 a Demosreu que si f és coninua a rossos, d ordre exponencial i al que exiseix f lim, aleshores + f + L s = F u du, on F s = Lfs b Calculeu la ransformada de Laplace de la funció Sinus-inegral: c Demosreu que calculeu sin 5 Demosreu que L 6 Calculeu 7 Sigui la funció d f e cos d a Calculeu Lf b Calculeu Lf d = f = sin u u s du := Si F u du si exiseixen les inegrals Com a aplicació fu du d s = Lfs s f =,,, > c Es compleix la fórmula Lf s = slfs f? Què falla? e 8 Calculeu L s Per a quins valors de s exiseix aquesa ransformada? Solució: π, exiseix per s > s + 9 Calculeu L Si Comproveu que e sin d = π Indicació: feu servir l apara 4a 4 Si f és conínua a rossos i d ordre exponencial, demosreu que: L fτ dτ s = Lfs + fτ dτ s s Calculeu L U Solució: e s [ s s + 4 s a ] a 3 Feu servir la ransformada de Laplace per resoldre els següens problemes de Cauchy: a y + y =, y = 3
4 b y 4y + 4y = 3, y =, y = c y + y y y = sin 3, y =, y =, y = d y 5y + 6y = U, y =, y = 4 Resoleu l equació diferencial amb condicions inicials: y + 4y + 3y = δ π + δ 3π, y =, y =, on δ és la dela de Dirac en el pun 5 Resoleu l equació: y + y + y = cosδ 3π, y =, y = 6 Feu servir la ransformada de Laplace per resoldre les equacions inegrals següens: a f + b f = fτ cos τ dτ = 4e + sin Solució: 4e 7e + 4 e e τ e τ f τ dτ Solució: 3 7 Resoleu, fen servir la ransformada de Laplace, el problema de Cauchy y y =, y = Noeu que, en aques cas, no cal conèixer y 8 Considereu l equació inegro-diferencial y x + x yx e d =, y = a Derivan en ambdós membres, deduïu l equació diferencial ordinària de segon ordre que verifica la seva solució Preciseu-ne igualmen les condicions inicials que la deerminen b Alernaivamen, apliqueu direcamen la ransformada de Laplace a l equació inicial 9 a Trobeu la sèrie de Fourier de la funció fx = x + π a l inerval π < x < π Solució: a = π, a n =, b n = n n+ b Useu a per demosrar que 3 a Trobeu la sèrie de Fourier de fx = π 4 = , per π < x <, x, per x < π Solució: a = π 3, a n = n n, b n = π n, b n+ = π n πn + b Useu a per demosrar que π 6 = i que π =
5 c Useu b per robar una sèrie numèrica al que la seva suma sigui π /8 3 a Trobeu la sèrie de Fourier de fx =, si π < x <, x, si x < π a l inerval π < x < π Solució: a = π, a n = n, b πn n = n n b Quan val f a x = 7π 7π? I quan a x = 4π? Solució: f =, f4π = π 3 Trobeu, si és que exiseix, una sèrie de Fourier que convergeix cap a sin x per a o x R Solució: a = 4 π, a n = 4n, a n+ =, b n = 33 Trobeu la sèrie de Fourier de la funció fx = cos x, n=, si π/ x π, si x < π/ 34 Sigui fx coninua a, L i siguin a n i b n els seus coeficiens de Fourier a Proveu que si S M x = a + M a n cos nπ n= L x + b n sin nπ L x, aleshores L a M fxs M x dx = L + a n + b n b Proveu que S Mx dx = L a M + n= a n + b n c Proveu que fxs M x dx SMx dx fx dx d Fen servir els aparas aneriors proveu la anomenada desiguala de Bessel : a + a n + b n L n= fx dx 35 Desenvolupeu la funció fx = x +, per < x <, x, per x < en sèrie de sinus o cosinus, segons convingui Solució: a n =, b n = nπ 36 Desenvolupeu la funció fx =, per < x < /,, per / x < en sèrie de cosinus en mig inerval i en sèrie de sinus en mig inerval 5
6 37 Desenvolupeu la funció fx = x, < x < L a en sèrie de cosinus Solució: L 3 + n 4L nπx n π cos 3 L 4L b en sèrie de sinus Solució: n π 3 n n L nπx sin nπ L c en sèrie de Fourier Solució: L L 3 nπx L nπx 3 + nπ cos L nπ sin L 38 a Trobeu la forma general de la sèrie de Fourier en cosinus i de la sèrie de Fourier en sinus a [, C] per a funcions que compleixen la relació fc x = fx b Maeixa preguna per fc x = fx 39 Desenvolupeu la funció cos xz en sèrie de Fourier en l inerval [ π, π], on z és un paràmere z real Solució: a n = πn z n+ sin z, b n = Proveu les igualas i deduïu que sin πz = z π co πz = π π = + π = 4 z + + z k= k= k= k= k+, k z z k z 4 k+ 4k, 8 6k 6
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
TEMA 5 : Derivades. Tècniques de derivació. Activitats
 TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
Càlcul II / Transformada de Laplace
 Càlcul II / Tranformada de Laplace de eembre de 5 Definicion. bàic Definició Donada f :, + [ R conínua a, + [. ) Se n diu la eva ranformada de Laplace (o L-ranformada) a la funció L[f depenen d un paràmere
Càlcul II / Tranformada de Laplace de eembre de 5 Definicion. bàic Definició Donada f :, + [ R conínua a, + [. ) Se n diu la eva ranformada de Laplace (o L-ranformada) a la funció L[f depenen d un paràmere
x + 2 y = 3 2 x y = 1 4 x + 3 y = k a) Afegiu-hi una equació lineal de manera que el sistema resultant sigui incompatible.
 1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
( 2 3, utilitzeu la matriu inversa B 1 ( 1 4 ( 2 1. Matrius i determinants Sèrie 3 - Qüestió 4. Donada la matriu B =
 1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
Equacions Diferencials 10 de Gener de 2014
 Equacions Diferencials de Gener de 24 243 - Problemes Temps: 2 hores 5 minuts 2,5 punts Contesteu les següents preguntes independents entre sí a Considereu el sistema X α t = AXt amb A =, α R. α a. Classifiqueu-lo.
Equacions Diferencials de Gener de 24 243 - Problemes Temps: 2 hores 5 minuts 2,5 punts Contesteu les següents preguntes independents entre sí a Considereu el sistema X α t = AXt amb A =, α R. α a. Classifiqueu-lo.
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 9 PAU 2006 Pautes de correcció
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Solució de l Examen final 8 de juny de 2015
 ETS d Enginyeria de Telecomunicació de Barcelona PROBABILITAT, PROCESSOS ESTOCÀSTICS I ESTADÍSTICA Solució de l Examen final 8 de juny de 5 Del conjun {,,, n} s escullen succesivamen i de forma aleaòria
ETS d Enginyeria de Telecomunicació de Barcelona PROBABILITAT, PROCESSOS ESTOCÀSTICS I ESTADÍSTICA Solució de l Examen final 8 de juny de 5 Del conjun {,,, n} s escullen succesivamen i de forma aleaòria
Convocatòria Matemàtiques. Proves d accés a la universitat per a més grans de 25 anys. Sèrie 1. Fase específica
 Proves d accés a la universitat per a més grans de 25 anys Matemàtiques Sèrie 1 Fase específica Exercicis Qualificació 1 2 3 Convocatòria 2017 4 5 Problema Suma de notes parcials Qualificació final Qualificació
Proves d accés a la universitat per a més grans de 25 anys Matemàtiques Sèrie 1 Fase específica Exercicis Qualificació 1 2 3 Convocatòria 2017 4 5 Problema Suma de notes parcials Qualificació final Qualificació
EXÀMENS D EQUACIONS DIFERENCIALS 1. x 2x + x = 2e t. (3)
 EXÀMENS D EQUACIONS DIFERENCIALS 1 http://www.ma1.upc.edu/~edos1 Gener 28 1 Considereu el sistema d equacions diferencials lineals ( ( ( x 1 x = y 1 2 y i les condicions de frontera amb α, β R + ( 1 3
EXÀMENS D EQUACIONS DIFERENCIALS 1 http://www.ma1.upc.edu/~edos1 Gener 28 1 Considereu el sistema d equacions diferencials lineals ( ( ( x 1 x = y 1 2 y i les condicions de frontera amb α, β R + ( 1 3
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
1. RECTA TANGENT I NORMAL 2. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS
 APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
MATLAB. 12/1/2017. CNED /2017 Q1
 [MATLAB - % de la nota final de l assignatura] MATLAB. //7. CNED - 6/7 Q. Indiqueu quin resultat retorna Matlab per pantalla en executar les següents comandes. a) [3::9 ; :-3:] 3 5 7 9 7 b) ones(,).*[
[MATLAB - % de la nota final de l assignatura] MATLAB. //7. CNED - 6/7 Q. Indiqueu quin resultat retorna Matlab per pantalla en executar les següents comandes. a) [3::9 ; :-3:] 3 5 7 9 7 b) ones(,).*[
Examen FINAL M2 FIB-UPC 11 de gener de 2017
 Examen FINAL M FIB-UPC 11 de gener de 017 1. (3 punts) Sigui {a n } la successió tal que: a 1 = 56 i a n+1 = a n per a tot n > 1. a) Proveu que 1 a n 56, per a tot n 1. b) Proveu que {a n } és decreixent.
Examen FINAL M FIB-UPC 11 de gener de 017 1. (3 punts) Sigui {a n } la successió tal que: a 1 = 56 i a n+1 = a n per a tot n > 1. a) Proveu que 1 a n 56, per a tot n 1. b) Proveu que {a n } és decreixent.
z 2 4z + 5 = 0, z = x + iy, i 1,
 Àlgebra i Geometria I Tema I NOMBRES COMPLEXOS 1- Necessitat dels nombres complexos i definició (a) Les solucions de les equacions polinòmiques El nombre imaginari i 1 Els enters Z, els racionals Q i els
Àlgebra i Geometria I Tema I NOMBRES COMPLEXOS 1- Necessitat dels nombres complexos i definició (a) Les solucions de les equacions polinòmiques El nombre imaginari i 1 Els enters Z, els racionals Q i els
UIB 2 + f (x) + f(x) ց ց ր ր Per tant, el punt ( 3. Una altra forma de veure-ho és calcular la derivada segona i mirar el signe en x = 3: 2 f (x) =
 El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
+ 1= 0 té alguna arrel real (x en radians).
 Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes. Nom i Cognoms: Grup: Data:
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Examen Final 17 de gener de 2013
 MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
Lista de ejercicios # 2. Uso de series de potencias y de Frobenius
 UNIVERSIDAD DE COSTA RICA FCULTAD DE CIENCIAS MA-15 Ecuaciones Diferenciales ESCUELA DE MATEMÁTICA I Ciclo del 217 Lista de ejercicios # 2 Uso de series de potencias y de Frobenius Uso de series alrededor
UNIVERSIDAD DE COSTA RICA FCULTAD DE CIENCIAS MA-15 Ecuaciones Diferenciales ESCUELA DE MATEMÁTICA I Ciclo del 217 Lista de ejercicios # 2 Uso de series de potencias y de Frobenius Uso de series alrededor
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
P =
 RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
Transformada de Laplace
 Capíulo 7 Tranformada de Laplace En ea ección inroduciremo y eudiaremo la ranformada de Laplace, dearrollaremo alguna de u propiedade ma báica y úile. Depué veremo alguna aplicacione. 7. Definicione y
Capíulo 7 Tranformada de Laplace En ea ección inroduciremo y eudiaremo la ranformada de Laplace, dearrollaremo alguna de u propiedade ma báica y úile. Depué veremo alguna aplicacione. 7. Definicione y
t2 Donat el PVI següent, que depèn d un paràmetre µ R,
 Nom i cognoms: A 1 Equacions Diferencials (40131 Examen Final Juny 018 Temps: 3h... [Test ] [ Nota important: respostes correctes +1 punt incorrectes 0.5 punts ] { t1 x Donat el sistema d EDOs 3x y y y
Nom i cognoms: A 1 Equacions Diferencials (40131 Examen Final Juny 018 Temps: 3h... [Test ] [ Nota important: respostes correctes +1 punt incorrectes 0.5 punts ] { t1 x Donat el sistema d EDOs 3x y y y
TEMA 6 : Geometria en l espai. Activitats
 TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 PAU SÈRIE 3 Pautes de correcció (PAU 2002) MATEMÀTIQUES
 Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 SÈRIE 3 () MATEMÀTIQUES Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 8 SÈRIE 3 () MATEMÀTIQUES Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta
PRIMERA MODEL B Codi B2. A1. C
 TOT n 15-16 -1/1 PRIMERA MODEL B Codi B A1 C1 15-16 1- (1) a) Raoneu que els polinomis són funcions contínues a tots el reals (1) b) Digueu que entenem per discontinuïtat de salt i poseu-ne un exemple
TOT n 15-16 -1/1 PRIMERA MODEL B Codi B A1 C1 15-16 1- (1) a) Raoneu que els polinomis són funcions contínues a tots el reals (1) b) Digueu que entenem per discontinuïtat de salt i poseu-ne un exemple
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2009
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
Nom i cognoms (poseu una al vostre grup)
 Segon Parcial. 16:00h. 14/01/2013. Matemàtiques 3-2012/2013 Q1 Professors: Núria Parés (M1), Yolanda Vidal (M2), Jose J. Muñoz (M3), Francesc Pozo (M4), Silvia Gago (T1), Mireia López (T2) RESPONEU LES
Segon Parcial. 16:00h. 14/01/2013. Matemàtiques 3-2012/2013 Q1 Professors: Núria Parés (M1), Yolanda Vidal (M2), Jose J. Muñoz (M3), Francesc Pozo (M4), Silvia Gago (T1), Mireia López (T2) RESPONEU LES
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
CAPÍTULO 6 TRANSFORMADA DE LAPLACE
 CAPÍTULO 6 TRANSFORMADA DE LAPLACE 6.. INTRODUCCION Definición 6.. Sea f() una función definida para odo ; se define la Transformada de Laplace de f() así: si el límie exise. {f()}(s) = F(s) = = lím b
CAPÍTULO 6 TRANSFORMADA DE LAPLACE 6.. INTRODUCCION Definición 6.. Sea f() una función definida para odo ; se define la Transformada de Laplace de f() así: si el límie exise. {f()}(s) = F(s) = = lím b
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 2015 Criteris de correcció Matemàtiques aplicades a les ciències socials
 Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
Oficina d Accés a la Universitat Pàgina 1 de 7 PAU 015 SÈRIE 1. Un arbre té un volum de 0 m i, per la qualitat de la seva fusta, es ven a 50 per metre cúbic. Cada any l'arbre augmenta el volum en 5 m.
FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. MATEMÀTIQUES-1
 FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. 1. Funcions exponencials. 2. Equacions exponencials. 3. Definició de logaritme. Propietats. 4. Funcions logarítmiques. 5. Equacions logarítmiques. 1. Funcions exponencials.
FUNCIONS EXPONENCIALS I LOGARÍTMIQUES. 1. Funcions exponencials. 2. Equacions exponencials. 3. Definició de logaritme. Propietats. 4. Funcions logarítmiques. 5. Equacions logarítmiques. 1. Funcions exponencials.
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 2008
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 008 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 008 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
SERIE DE ECUACIONES DIFERENCIALES
 SERIE DE ECUACIONES DIFERENCIALES PROFESOR: PEDRO RAMÍREZ MANNY TEMA ) Clasifique cada una de las ecuaciones diferenciales siguienes indicando orden (O), grado (G) y si es lineal (L) o no (NL). a) ( y)
SERIE DE ECUACIONES DIFERENCIALES PROFESOR: PEDRO RAMÍREZ MANNY TEMA ) Clasifique cada una de las ecuaciones diferenciales siguienes indicando orden (O), grado (G) y si es lineal (L) o no (NL). a) ( y)
Matemàtiques 1 - FIB
 Matemàtiques - FI 7--7 Examen Final F Àlgebra lineal JUSTIFIQUEU TOTES LES RESPOSTES. [ punts] Siguin E i F dos espais vectorials, f : E F una aplicació lineal. (a) Digueu què ha de satisfer f per tal
Matemàtiques - FI 7--7 Examen Final F Àlgebra lineal JUSTIFIQUEU TOTES LES RESPOSTES. [ punts] Siguin E i F dos espais vectorials, f : E F una aplicació lineal. (a) Digueu què ha de satisfer f per tal
TEMA 5 : Resolució de sistemes d equacions
 TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
TEMA 5 : Resolució de sistemes d equacions 5.1. EQUACIÓ LINEAL AMB n INCÒGNITES Una equació lineal de n incògnites es qualsevol expressió de la forma: a 1 x 1 + a 2 x 2 +... + a n x n = b, on a i b son
CÁLCULO III. Apuntes
 CÁLCULO III. Apuntes Grado en Ingeniería en Tecnologías Industriales Tema 3 Arturo de Pablo Elena Romera Open Course Ware, UC3M http://ocw.uc3m.es/matematicas 3 TRANSFORMADA DE LAPLACE La transformada
CÁLCULO III. Apuntes Grado en Ingeniería en Tecnologías Industriales Tema 3 Arturo de Pablo Elena Romera Open Course Ware, UC3M http://ocw.uc3m.es/matematicas 3 TRANSFORMADA DE LAPLACE La transformada
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció exponencial
 LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques aplicades a les ciències socials Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques aplicades a les ciències socials Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu
Examen FINAL M2 FIB-UPC 12 de juny de 2015
 Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Introducción a las EDP 17 de Abril de 2015
 7 de Abril de 25 Ejercicio [.5 puntos] Resolver el problema u x (x, ) + u (x, ) + 2u(x, ) = 3, u(x, ϕ(x)) = x 2, en los siguientes casos: ϕ(x) = ϕ(x) =. canónica, haciendo todos los cambios en detalle
7 de Abril de 25 Ejercicio [.5 puntos] Resolver el problema u x (x, ) + u (x, ) + 2u(x, ) = 3, u(x, ϕ(x)) = x 2, en los siguientes casos: ϕ(x) = ϕ(x) =. canónica, haciendo todos los cambios en detalle
SÈRIE 2 Pautes de correcció (PAAU2001) MATEMÀTIQUES
 Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 6 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar altres
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 6 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar altres
PROBLEMES PAU SOBRE SISTEMES D EQUACIONS. 1) PAU 1999 Sèrie 1 Qüestió 1: Resoleu el sistema següent per als valors de k que el facin compatible.
 PROBLEMES PAU SOBRE SISTEMES D EQUACIONS ) PAU 999 Sèrie Qüestió : Resoleu el sistema següent per als valors de k que el facin compatible. x + y 3 x y 4x + 3y k ) PAU 000 Sèrie 5 Qüestió 4: Discutiu el
PROBLEMES PAU SOBRE SISTEMES D EQUACIONS ) PAU 999 Sèrie Qüestió : Resoleu el sistema següent per als valors de k que el facin compatible. x + y 3 x y 4x + 3y k ) PAU 000 Sèrie 5 Qüestió 4: Discutiu el
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2008 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Transformadas de Laplace
 Semana 7 - Clase 9 9// Tema 3: E D O de orden > Algunas definiciones previas Transformadas de Laplace En general vamos a definir una transformación integral, F (s), de una función, f(t) como F (s) = b
Semana 7 - Clase 9 9// Tema 3: E D O de orden > Algunas definiciones previas Transformadas de Laplace En general vamos a definir una transformación integral, F (s), de una función, f(t) como F (s) = b
TEMA 1: Trigonometria
 TEMA 1: Trigonometria La trigonometria, és la part de la geometria dedicada a la resolució de triangles, es a dir, a determinar els valors dels angles i dels costats d un triangle. 1.1 MESURA D ANGLES
TEMA 1: Trigonometria La trigonometria, és la part de la geometria dedicada a la resolució de triangles, es a dir, a determinar els valors dels angles i dels costats d un triangle. 1.1 MESURA D ANGLES
Prova d accés a la Universitat (2013) Matemàtiques II Model 1. (b) Suposant que a = 1, trobau totes les matrius X que satisfan AX + Id = A, on Id
 UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
Tècniques elementals de
 Dept. Matemàtica Aplicada IV Tècniques elementals de Càlcul i Àlgebra Exercicis bàsics Presentació Aquest document va adreçat als estudiants de nou ingrés de les escoles d enginyeria en les quals imparteix
Dept. Matemàtica Aplicada IV Tècniques elementals de Càlcul i Àlgebra Exercicis bàsics Presentació Aquest document va adreçat als estudiants de nou ingrés de les escoles d enginyeria en les quals imparteix
Matemàtiques Sèrie 1
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 013 Matemàtiques Sèrie 1 SOLUCIONS, CRITERIS
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 013 Matemàtiques Sèrie 1 SOLUCIONS, CRITERIS
= 1+ β, essent α i β paràmetres reals. a la recta r 2. i el pla Π d equació
 Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
XXXV OLIMPÍADA MATEMÀTICA
 XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
XXXV OLIMPÍADA MATEMÀTICA Primera fase (Catalunya) 10 de desembre de 1999, de 16 a 0h. 1. Amb quadrats i triangles equilàters de costat unitat es poden construir polígons convexos. Per exemple, es poden
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS
 Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Oficina d'organització de Proves d'accés a la Universitat Pàgina 1 de 8 PAU 2004
 Oficina d'organització de Proves d'accés a la Universitat Pàgina de 8 PAU 004 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar
Oficina d'organització de Proves d'accés a la Universitat Pàgina de 8 PAU 004 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar
Cognoms i Nom: Examen parcial de Física - ELECTRÒNICA 1 de desembre de 2016
 1 de desembre de 016 Model A Qüestions: 50% de l examen A cada qüestió només hi ha una resposta correcta. Encercleu-la de manera clara. Puntuació: correcta = 1 punt, incorrecta = -0.5 punts, en blanc =
1 de desembre de 016 Model A Qüestions: 50% de l examen A cada qüestió només hi ha una resposta correcta. Encercleu-la de manera clara. Puntuació: correcta = 1 punt, incorrecta = -0.5 punts, en blanc =
Criteris generals per a la correcció:
 Oficina d Accés a la Universitat Pàgina 1 de 9 SÈRIE 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 9 SÈRIE 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Transformada de Laplace
 Matemática 4 Segundo Cuatrimestre 2 Transformada de Laplace M. del C. Calvo Dada f G(R ), definimos la transformada de Laplace de f como L(f)(s) = e st f(t) dt para los s R para los cuales converge esta
Matemática 4 Segundo Cuatrimestre 2 Transformada de Laplace M. del C. Calvo Dada f G(R ), definimos la transformada de Laplace de f como L(f)(s) = e st f(t) dt para los s R para los cuales converge esta
Exercicis de trigonometria
 Mesura d'angles 1. En una circumferència de 5 cm de radi, un arc fa 1, m. Troba el seu angle central corresponent en radians i en graus sexagesimals.. Expressa en radians de manera exacta els angles següents,
Mesura d'angles 1. En una circumferència de 5 cm de radi, un arc fa 1, m. Troba el seu angle central corresponent en radians i en graus sexagesimals.. Expressa en radians de manera exacta els angles següents,
Matemàtiques 1 - FIB
 Matemàtiques 1 - FIB 8-1-016 Examen F1 Grafs JUSTIFIQUEU TOTES LES RESPOSTES 1 (a) [05 punts] Doneu la definició de la matriu d incidències d un graf (b) [15 punts] Enuncieu i proveu el Lema de les encaixades
Matemàtiques 1 - FIB 8-1-016 Examen F1 Grafs JUSTIFIQUEU TOTES LES RESPOSTES 1 (a) [05 punts] Doneu la definició de la matriu d incidències d un graf (b) [15 punts] Enuncieu i proveu el Lema de les encaixades
Matemàtiques de la Telecomunicació Definicions i resultats
 Matemàtiques de la Telecomunicació Definicions i resultats apunts per a l assignatura del grau d enginyeria de telecomunicacions de l ETSETB Xavier Gràcia xavier.gracia@upc.edu http://mat-web.upc.edu/people/xavier.gracia/matel
Matemàtiques de la Telecomunicació Definicions i resultats apunts per a l assignatura del grau d enginyeria de telecomunicacions de l ETSETB Xavier Gràcia xavier.gracia@upc.edu http://mat-web.upc.edu/people/xavier.gracia/matel
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
TEMA 4 : Geometria analítica al pla. Vectors i la Recta. Activitats
 TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES B =,
 RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2009
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 0 SÈRIE 4 QÜESTIONS.- Donats el punt P =(,, ) ilarectar : x = y + = z 5 : a) Trobeu l equació cartesiana (és a dir, de la forma Ax +
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 0 SÈRIE 4 QÜESTIONS.- Donats el punt P =(,, ) ilarectar : x = y + = z 5 : a) Trobeu l equació cartesiana (és a dir, de la forma Ax +
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2008-2009 Matemàtiques aplicades a les ciències socials Sèrie 4 Responeu a TRES de les quatre qüestions i resoleu UN dels dos problemes següents. En les respostes,
Proves dʼaccés a la Universitat. Curs 2008-2009 Matemàtiques aplicades a les ciències socials Sèrie 4 Responeu a TRES de les quatre qüestions i resoleu UN dels dos problemes següents. En les respostes,
Oficina d Accés a la Universitat Pàgina 1 de 10 PAU 2014 Criteris específics de correcció i qualificació per ser fets públics un cop finalitzades
 Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 2007
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
x x 1 x 11= 7) y = 6 3x-2 12) y = e 5x (3x 2-6)
 Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
10 Àlgebra vectorial. on 3, -2 i 4 són les projeccions en els eixos x, y, y z respectivament.
 10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
Transformada de Laplace
 Transformada de Laplace Definición: La Transformada de Laplace Dada una función f (t) definida para toda t 0, la transformada de Laplace de f es la función F definida como sigue: { f } 0 st F () s = L
Transformada de Laplace Definición: La Transformada de Laplace Dada una función f (t) definida para toda t 0, la transformada de Laplace de f es la función F definida como sigue: { f } 0 st F () s = L
Universidad de Chile Facultad de Ciencias Departamento de Física. Método de la Física Matemática II
 Universidad de Chile Facultad de Ciencias Departamento de Física Método de la Física Matemática II Problemas Profesor: José Rogan de Agosto 998 Ayudante: Julio Yáñez Considere las funciones ϕ ν (x = x
Universidad de Chile Facultad de Ciencias Departamento de Física Método de la Física Matemática II Problemas Profesor: José Rogan de Agosto 998 Ayudante: Julio Yáñez Considere las funciones ϕ ν (x = x
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 12 PAU 2007
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de PAU 007 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina de PAU 007 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
TOT 1r /15 INDEX PRÈVIA. PRIMERA Global 1a Recuperació 1a. SEGONA Global 2a Recuperació 2a. TERCERA Global 3a JUNY ÍNDEX
 TOT 1r 11-1 -1/15 INDEX PRÈVIA PRIMERA Global 1a Recuperació 1a SEGONA Global a Recuperació a TERCERA Global a JUNY TOT 1r 11-1 -/15 PREVIA MODEL A Codi B1.A0.11-1 1.- Calculeu les següents expressions,
TOT 1r 11-1 -1/15 INDEX PRÈVIA PRIMERA Global 1a Recuperació 1a SEGONA Global a Recuperació a TERCERA Global a JUNY TOT 1r 11-1 -/15 PREVIA MODEL A Codi B1.A0.11-1 1.- Calculeu les següents expressions,
x cos(x t)φ(t)dt φ(x) = sin x + 2 φ(x) = x + 1 2
 Assignatura: Mètodes Matemàtics de la Física II Departament: Física Fonamental Data Examen: 13 juny 2006 1. (3 punts) Una equació integral és una equació en la qual la funció incògnita està sota el signe
Assignatura: Mètodes Matemàtics de la Física II Departament: Física Fonamental Data Examen: 13 juny 2006 1. (3 punts) Una equació integral és una equació en la qual la funció incògnita està sota el signe
RECULL DE PROBLEMES DE SELECTIVITAT SOBRE INTEGRALS. a) Calculeu l'àrea limitada per la gràfica de la funció, l'eix OX i les rectes verticals 0 x = 2.
 RECULL DE PROBLEMES DE SELECTIVITAT SOBRE INTEGRALS ) PAU 999 Sèrie Qüestió: Calcula l àrea determinada per les corbes d equacions el dibui següent: y 4 i y representada en ) PAU 999 Sèrie Qüestió : Calculeu
RECULL DE PROBLEMES DE SELECTIVITAT SOBRE INTEGRALS ) PAU 999 Sèrie Qüestió: Calcula l àrea determinada per les corbes d equacions el dibui següent: y 4 i y representada en ) PAU 999 Sèrie Qüestió : Calculeu
Gràficament: una funció és contínua en un punt si en aquest punt el seu gràfica no es trenca
 Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Oficina d Accés a la Universitat Pàgina 1 de 6 PAU 2016 Criteris de correcció
 Oficina d Accés a la Universitat Pàgina 1 de 6 Criteris de correcció Matemàtiques aplicades a les ciències socials SÈRIE 3 1. Una fàbrica de mobles de cuina ven 1000 unitats mensuals d un model d armari
Oficina d Accés a la Universitat Pàgina 1 de 6 Criteris de correcció Matemàtiques aplicades a les ciències socials SÈRIE 3 1. Una fàbrica de mobles de cuina ven 1000 unitats mensuals d un model d armari
Problemario de la asignatura de Ecuaciones Diferenciales
 Problemario de la asignatura de Ecuaciones Diferenciales Alejandro Hernández Madrigal Maxvell Jiménez Escamilla Academia de Matemáticas y Física Unidad Profesional Interdisciplinaria de Biotecnología,
Problemario de la asignatura de Ecuaciones Diferenciales Alejandro Hernández Madrigal Maxvell Jiménez Escamilla Academia de Matemáticas y Física Unidad Profesional Interdisciplinaria de Biotecnología,
Indiqueu en quins punts Y = f(x) no és contínua, el tipus de discontinuïtats de cada cas i les asímptotes que presenta. (0,1 9 +0,8=1,7 punts)
 Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
Criteris generals per a la correcció:
 Oficina d Accés a la Universitat Pàgina 1 de 13 Sèrie 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 13 Sèrie 2 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts. Podeu utilitzar
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS
 CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
Apunts de Càlcul Tema 2. Derivació de funcions d una variable
 Apunts de Càlcul Tema 2. Derivació de funcions d una variable Lali Barrière, Josep M. Olm Departament de Matemàtica Aplicada 4 - UPC Enginyeria de Sistemes de Telecomunicació Enginyeria Telemàtica EETAC
Apunts de Càlcul Tema 2. Derivació de funcions d una variable Lali Barrière, Josep M. Olm Departament de Matemàtica Aplicada 4 - UPC Enginyeria de Sistemes de Telecomunicació Enginyeria Telemàtica EETAC
A A A A A A A A A A A A A A A A A A A A A A Realitzeu l'operació següent i doneu el resultat el màxim simplificat que pugueu:
 TOT 1r 15-16 -1/10 PRIMERA MODEL A Codi B1A1C115-16 A1- a) Enuncieu i raoneu breument el teorema del residu b) Aplicant el teorema del residu, trobeu els valors de k pels quals el residu de la divisió
TOT 1r 15-16 -1/10 PRIMERA MODEL A Codi B1A1C115-16 A1- a) Enuncieu i raoneu breument el teorema del residu b) Aplicant el teorema del residu, trobeu els valors de k pels quals el residu de la divisió
Tema 11 Funcions inverses. Funcions implícites. Fórmula de Taylor. Extrems.
 Tema 11 Funcions inverses. Funcions implícites. Fórmula de Taylor. Extrems. Objectius: 1. Practicar el Teorema de la Funció Inversa. 2. Practicar el Teorema de la Funció Implícita. 3. Practicar el càlcul
Tema 11 Funcions inverses. Funcions implícites. Fórmula de Taylor. Extrems. Objectius: 1. Practicar el Teorema de la Funció Inversa. 2. Practicar el Teorema de la Funció Implícita. 3. Practicar el càlcul
TEMA 1 : Aplicacions de les derivades
 TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
j Introducció al càlcul vectorial
 FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
FÍSICA 00 9 j Introducció al càlcul vectorial j Activitats finals h Qüestions 1. La suma dels vectors unitaris i, j és un altre vector unitari? Justifiqueu la resposta fent un gràfic. Els vectors unitaris
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
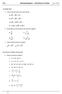 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
Introducción a las EDP A 21 de Abril de 2016
 2 de Abril de 26 Ejercicio [.4 puntos] Resolver el siguiente problema, cuando x >, 2xu x (x, y) + yu y (x, y) + 3u(x, y) = 5x + 2y + 3, u(x, ϕ(x)) = 3x +, en los siguientes casos: ϕ(x) = x y ϕ(x) =. u
2 de Abril de 26 Ejercicio [.4 puntos] Resolver el siguiente problema, cuando x >, 2xu x (x, y) + yu y (x, y) + 3u(x, y) = 5x + 2y + 3, u(x, ϕ(x)) = 3x +, en los siguientes casos: ϕ(x) = x y ϕ(x) =. u
Algunas Aplicaciones de la Transformada de Laplace
 Algunas Aplicaciones de la Transformada de Laplace Dr. Andrés Pérez Escuela de Matemática Facultad de Ciencias Universidad Central de Venezuela 11 de marzo de 2016 A. Pérez Algunas Aplicaciones de la Contenido
Algunas Aplicaciones de la Transformada de Laplace Dr. Andrés Pérez Escuela de Matemática Facultad de Ciencias Universidad Central de Venezuela 11 de marzo de 2016 A. Pérez Algunas Aplicaciones de la Contenido
Solució de l Examen final 14 de juny de que els seus arxius s infectin.
 ETS d Enginyeria de Telecomunicació de Barcelona PROBABILITAT, PROCESSOS ESTOCÀSTICS I ESTADÍSTICA Solució de l Examen final 4 de juny de 2. En un centre de càlcul hi ha ordinadors connectats a una xarxa
ETS d Enginyeria de Telecomunicació de Barcelona PROBABILITAT, PROCESSOS ESTOCÀSTICS I ESTADÍSTICA Solució de l Examen final 4 de juny de 2. En un centre de càlcul hi ha ordinadors connectats a una xarxa
Derivació Funcions Vàries Variables
 Derivació Funcions Vàries Variables Jordi Villanueva Departament de Matemàtica Aplicada I Universitat Politècnica de Catalunya 24 de febrer de 2016 Jordi Villanueva (MA1) Derivació Funcions Vàries Variables
Derivació Funcions Vàries Variables Jordi Villanueva Departament de Matemàtica Aplicada I Universitat Politècnica de Catalunya 24 de febrer de 2016 Jordi Villanueva (MA1) Derivació Funcions Vàries Variables
Col legi Maristes Sants-Les Corts. Departament de matemàtiques. té per asímptotes les rectes =
 Matemàtiques II Propostes recuperació 1a avaluació - 1/5 Col legi Maristes Sants-Les Corts Departament de matemàtiques Matemàtiques II PsPc. B2.A1 Tal i com alguns de vosaltres m heu demanat, us dono una
Matemàtiques II Propostes recuperació 1a avaluació - 1/5 Col legi Maristes Sants-Les Corts Departament de matemàtiques Matemàtiques II PsPc. B2.A1 Tal i com alguns de vosaltres m heu demanat, us dono una
