5.1. Algoritmo en modelos de maximización
|
|
|
- Elvira Maestre Camacho
- hace 5 años
- Vistas:
Transcripción
1 5.1. Algoritmo en modelos de maximización El primer tipo de modelo que vamos a resolver por el método símplex es el que tiene como objetivo maximizar a una función lineal, la cual está sujeta a una serie de restricciones de la forma menor igual que. El modelo tiene la forma: Z c x c x máx cnxn s. a.: a x a x a x b n n 1 a x a x a x b n n 2 a x a x a x b m1 1 m2 2 mn n m x 0 i 1, 2, n Que se representa en forma matricial por: Donde: i Z máx = CX AX < B X > 0 C = (c 1, c 2,...c n ) matriz de costos A = matriz de coeficientes B = matriz columna de términos independientes X = matriz columna de las variables x 1, x 2, x 3,..., x n Algoritmo símplex 1. El primer paso consiste en convertir las desigualdades en igualdades al sumarles una variable de holgura h. Esta variable representa la cantidad que le falta a la desigualdad para ser igualdad. Las variables de holgura son siempre positivas. a x a x a x h b a x a x a x h b a n n n n 2 2 x a x a x h b m1 1 m2 2 mn n m m 180
2 Investigación de operaciones 2. Formamos la tabla símplex. Se construye una tabla como la que se muestra a continuación: En la primera celda escribimos la etiqueta variables básicas, en la siguiente la etiqueta Z, en la última colocamos la etiqueta solución y en las intermedias escribimos los nombres de las variables originales, seguidas de las variables de holgura. El segundo renglón contiene la función objetivo, escrita de la siguiente manera: Z máx c 1 x 1 c 2 x 2... c n x n 0h 1 0h 2 0h 3 =0, esto es, se agregan las variables de holgura h, colocándoles como coeficiente cero ( 0 = +0) y después todas las variables se pasan del lado izquierdo de la igualdad. A partir del tercer renglón escribimos cada una de las restricciones, en la columna de la variable básica colocamos las variables que forman la base ortogonal más simple (las componentes de la matriz identidad) que corresponden a las variables de holgura: 181
3 De esta manera se forma la tabla inicial símplex. La primera solución asociada a esta tabla símplex es: h 1 = b 1 h 2 = b 2... h m = b m Z = 0 Esta solución se obtiene al observar que si en la tabla tomamos las columnas asociadas a las variables básicas, entonces tenemos la matriz identidad aumentada. El valor de Z se lee directamente del coeficiente que está en el renglón de Z, debajo de la columna solución. Una vez que obtuvimos la tabla inicial símplex asociada al modelo de P. L. se continúa para encontrar la solución óptima (si es que existe) o bien determinar que el problema no tiene solución óptima. 3. Verificamos si todos los coeficientes asociados al renglón de Z son mayores o iguales a cero, si es así entonces la solución en la tabla es la óptima. Termina. Si no es así, se continúa con el proceso. 4. Del conjunto de columnas se toma la que tenga el mayor valor negativo (número menor). Ésta es la variable que entra al sistema (pasa a ser básica) de manera que una variable tiene que salir para dar paso a la nueva. 5. Se divide el coeficiente de la columna seleccionada entre los elementos de la columna solución, de la operación se selecciona el menor valor positivo. Ésta es la variable que sale de la base (pasa a ser no básica). Nota. Las divisiones entre cero o entre números negativos no se toman en cuenta. Si todas son negativas o indeterminadas el problema no tiene solución. Termina. 6. La celda que se encuentra en la intersección de la columna seleccionada con el renglón seleccionado contiene al que llamaremos elemento pivote, por medio de operaciones elementales entre columnas el elemento pivote se convierte en 1 y sus elementos restantes en su columna en ceros; se obtiene una nueva columna componente de matriz identidad. 182
4 Investigación de operaciones 7. Se repite el proceso desde el paso 3 operando sobre matrices. Para entender mejor el algoritmo vamos a resolver el siguiente modelo de P. L. Z 3x 5x má x 1 2 s. a.: 3x 2x x x 1 2 x, x Ejemplo 1 1. Lo primero es sumar a cada una de las desigualdades una variable de holgura, lo cual nos permite escribir: 2. Creamos la tabla símplex: Zmáx 3x1 5x2 s. a.: 3x 2x h x h 4 x 1 2 h 2 3 x, x, h, h, h El segundo renglón contiene la función objetivo, escrita como: Z máx 3x 1 5x 2 0h 1 0h 2 0h 3 = 0 183
5 A partir del tercer renglón escribimos cada una de las restricciones, en la columna de las variables básicas colocamos las variables de holgura que aparecen en las restricciones: De la tabla símplex inicial, la solución asociada es: h 1 = 18 h 2 = 4 h 3 = 6 Z = 0 Función objetivo Primera restricción Segunda restricción Tercera restricción Esta solución se obtiene al tomar sólo las columnas asociadas a las variables básicas y los términos independientes que forman una matriz identidad aumentada: 184
6 Investigación de operaciones 3. Observamos que los coeficientes de x 1 y x 2 en el renglón Z son negativos. Se tendrá la solución óptima cuando los valores en Z sean todos positivos. 4. Seleccionamos la columna que tiene como coeficiente a 5, ya que es el mayor valor negativo. Entrará la variable x 2 a formar parte de la base. 5. Realizamos la división de los elementos de la columna solución entre los elementos de la columna seleccionada y se elige el valor menor. El menor de los resultados positivos es 6, por lo tanto la variable que sale es h El elemento pivote es 1 por lo tanto su inverso multiplicativo es 1. Multiplicamos R 3 1 y el resultado lo escribimos en una nueva tabla. 7. Ahora se toma el elemento pivote para hacer cero los coeficientes de su misma columna. Empezamos con R 0. El coeficiente de este renglón en la columna seleccionada es 5, por lo tanto su inverso aditivo es 5, entonces multiplicamos R 3 (actual) por 5 y el resultado se lo sumamos a R
7 Este resultado lo escribimos en la nueva tabla. Continuamos con el renglón R 1, el cual tiene como coeficiente 2, su inverso aditivo es 2. Multiplicamos R 3 por 2 y el resultado se lo sumamos a R 1. Este resultado lo escribimos en la nueva tabla. Como R 2 ya tiene como coeficiente cero en la columna seleccionada, simplemente se transcribe a la nueva tabla: 8. Ésta es la tabla símplex que se obtiene después de una iteración. La solución asociada a esta tabla es: h 1 = 6 h 2 = 4 x 2 = 6 Z =
8 Investigación de operaciones Regresamos al punto El coeficiente asociado a la columna de x 1 es negativo, por lo tanto la solución actual no es óptima y pasamos al punto La columna de x 1 es la única con coeficiente negativo en R 0, por lo tanto, ésta es la variable que pasará a formar parte de la base. 5. Realizamos la división de los elementos de la columna solución entre los elementos de la columna seleccionada. El menor de los resultados positivos es 2, por lo tanto la variable que sale es h El elemento pivote es 3, para convertirlo en 1 multiplicamos por su inverso multiplicativo que es 1/3. Multiplicamos R 1 (1/3) y el resultado lo escribimos en una nueva tabla: 7. Usamos el elemento pivote 1 para hacer cero los coeficientes que están arriba y debajo de él. Empezamos con R 0. El coeficiente de este renglón en la columna seleccionada es 3, por lo tanto su inverso aditivo es 3, entonces multiplicamos R 1 (actual) por 3 y el resultado se lo sumamos a R
9 Este resultado lo escribimos en la nueva tabla. Continuamos con el renglón R 2, el cual tiene como coeficiente 1, su inverso aditivo es 1. Multiplicamos R 1 por 1 y el resultado se lo sumamos a R 2. Este resultado lo escribimos en la nueva tabla: Como R 3 ya tiene como coeficiente cero en la columna seleccionada, simplemente se transcribe a la nueva tabla. 8. Esta es la tabla símplex que se obtiene después de la segunda iteración. La solución asociada a esta tabla es: x 1 = 2, h 2 = 2, x 2 = 6, Z = 36, h 1 = h 3 = 0 (por tener valores múltiples). 188
10 Investigación de operaciones Regresamos al punto 1. Como todos los coeficientes del renglón R 0 son positivos, entonces hemos llegado a la solución óptima del problema donde el valor de z máxima es 36. Ejercicio 1 Selecciona la respuesta que completa de manera correcta los siguientes enunciados: 1. Para poder convertir una desigualdad de la forma menor o igual que en una igualdad, se debe sumar una variable de: a) Superávit. b) Holgura. c) Complementaria. d) Global. 2. La solución del método símplex es óptima si todos los coeficientes del renglón asociado con la función objetivo en la tabla símplex son: a) Cero. b) Negativos. c) Positivos. d) Mayores o iguales a cero. 3. La variable que entra a formar parte de la base es la que en el renglón asociado con la función objetivo en la tabla símplex tiene el coeficiente: a) Positivo. b) Cero. c) Menor negativo. d) Mayor negativo. 4. Para hacer 1 el elemento pivote, multiplicamos por: a) Su inverso aditivo. b) El elemento neutro. c) El mismo. d) Su inverso multiplicativo. 189
11 5. Los elementos que están arriba y abajo del elemento pivote deben convertirse en: a) Positivos. b) Negativos. c) Cero. d) Uno. 6. Resolver por método símplex el siguiente modelo de P. L. Zmá x 5x1 4x2 s. a.: 6x1 4x2 24 x1 2x2 6 x2 2 x, x Soluciones básicas factibles La forma de trabajar del método símplex puede variar en relación con otras lecturas del área, pero los resultados de optimización tendrán que ser siempre iguales para un mismo problema sin importar el método. En este libro tratamos que la enseñanza del algoritmo símplex sea lo más natural posible, partiendo desde la elaboración de la tabla inicial hasta la localización de las variables básicas entrantes y salientes, así como la interpretación de los resultados de la última tabla. En la sección anterior aprendimos el algoritmo del método símplex, el cual es una herramienta poderosa para resolver modelos de programación lineal. En esta sección explicamos cómo es que este método encuentra la solución óptima. Lo primero es escribir las restricciones del modelo en forma de igualdades (sumamos las variables de holgura). Esto se hace porque la solución del modelo (si es que existe) siempre está en un vértice del polígono de soluciones factibles, el cual se forma como la intersección de n restricciones (n es el número de variables del modelo). 190
12 Investigación de operaciones Al convertir todas las restricciones en igualdades, se tiene un sistema de n+m variables con m ecuaciones (m es el número de restricciones sin tomar en cuenta las de no-negatividad). a x a x a x h b a x a x a x h b a n n n n 2 2 m1 x a x a x h b 1 m2 2 mn n m m (1) Los vértices representan las soluciones del sistema anterior. El inconveniente es que como en general n+m > m, entonces el sistema tiene una infinidad de soluciones, ya que tenemos n grados de libertad. Para resolver este problema se divide a las variables en dos grupos: Variables no básicas. De las n+m variables se toman n y se les asigna el valor cero. Variables básicas. El resto de las variables (m) se determinan al resolver el sistema que se obtiene al sustituir el valor de las variables no básicas en el sistema (1). Observamos que existen varias combinaciones para seleccionar cuáles de las variables van a ser básicas y cuáles no básicas. Dependiendo de la combinación que tomemos es el vértice que encontramos, algunos de estos vértices pueden ser factibles (caen dentro de la región factible), no factibles (si alguna o algunas de las variables básicas tienen solución menor a cero) o bien puede ser que el sistema no tenga solución. De los vértices factibles debemos seleccionar aquel que optimice el valor de la función objetivo. Realicemos un ejemplo para comprender mejor estas ideas. 191
13 Ejemplo 2 Tomemos el modelo del ejemplo 1 que resolvimos en la sección anterior. Zmá x 3x1 5x2 s. a.: 3x1 2x2 18 x1 4 x2 6 x1, x2 0 El grupo de restricciones sin tomar en cuenta las de no negatividad son: 3x 1 +2x 2 < 18 x 1 < 4 x 2 < 6 Escritas en forma de igualdad son: 3x 1 + 2x 2 +h 1 = 18 x 1 + h 2 = 4 x 2 + h 3 = 6 Este es un sistema de ecuaciones con 5 variables (2 del modelo y 3 de holgura) y 3 ecuaciones (n = 5, m = 3), por lo tanto tenemos 5 3 = 2 grados de libertad. Esto quiere decir que tenemos 3 variables básicas y 2 no básicas. Debemos seleccionar dos variables no básicas y determinar el valor de las básicas al resolver un sistema de 3 por 3. El número de combinaciones para seleccionar el acomodo de las variables está dado por la fórmula: 5! 5C2 10 2!( 5 2)! Estas combinaciones son: 192
14 Investigación de operaciones Al tomar la primera opción tenemos que x 1 = 0 y x 2 = 0, si sustituimos estos valores en el sistema de ecuaciones obtenemos: 3(0) + 2(0) + h 1 = 18 (0) + h 2 = 4 (0) + h 3 = 6 Al simplificar se tiene un sistema de tres ecuaciones con tres incógnitas cuya solución se obtiene de manera inmediata. h 1 = 18 h 2 = 4 h 3 = 6 Ésta es una solución factible, ya que todas las variables son mayores o iguales a cero. La solución completa es: x 1 = 0, x 2 = 0, h 1 = 18, h 2 = 4, h 3 = 6 Evaluamos la función objetivo en esta solución y obtenemos: Z máx =3x 1 +5x 2 Z=3(0)+5(0) Z=0 Esta solución es justamente con la que empezamos el método símplex al formar la tabla inicial. Al tomar las siguientes combinaciones, obtenemos los otros vértices de la región de soluciones factibles. En la siguiente tabla se resumen estos resultados. 193
15 De la tabla nos damos cuenta que el máximo valor de Z se alcanza en la combinación h 1 = 0, h 3 = 0, x 1 = 2, x 2 = 6, h 2 = 2 con Z = 36. Esta solución coincide con la del método de tablas: El algoritmo del método símplex por tablas tiene la ventaja de que no analiza todas las combinaciones, ya que empezando por una combinación cuya solución sea factible, sólo pasa por las combinaciones que den soluciones factibles y siempre mejorando o manteniendo el valor de la función objetivo. Lo más importante del método símplex por tablas es empezar con una tabla que contenga una solución básica factible; si el modelo tiene todas las restricciones de la forma menor igual que, las variables de holgura nos proporcionan una solución inicial factible, sin embargo, si una o varias de las restricciones son de la forma mayor igual que, tenemos que buscar técnicas que nos permitan obtener una solución inicial básica factible. Una de estas técnicas es ocupando el problema dual, el cual vamos a estudiar en la siguiente sección. 194
16 5.3. Método símplex primal-dual Todo problema de programación lineal de maximización tiene asociado un problema de P. L. de minimización llamado dual y viceversa. Los dos problemas se construyen a partir del mismo problema real, sólo que si en uno de ellos el objetivo es maximizar las utilidades, en el otro el objetivo es minimizar los costos y como resultado el valor de la función objetivo de ambos problemas coincide, es decir, Z máx =Z mín en las soluciones óptimas. Esto significa que hay un equilibrio entre utilidad y costo. El estudio del problema dual se realiza con dos objetivos: Si tenemos un modelo de P. L. cuyo objetivo es minimizar (con restricciones de la forma mayor igual que) llamado modelo primal, entonces el modelo dual asociado será de maximización (con restricciones de la forma menor igual que), el dual se resuelve por el algoritmo descrito en la sección anterior. La solución óptima del modelo dual estará en el valor de las variables de holgura del primal donde se cumple que Z máx =Z mín. Al resolver el problema dual obtenemos un análisis de sensibilidad del modelo calculando los precios sombra Tabla primal-dual Si el problema primal es de maximización, se utiliza el algoritmo descrito directamente. Pero si el modelo por resolver es de minimización se utiliza la llamada tabla primal-dual para trasladar el problema a maximización y volver al uso del mismo algoritmo. Si tenemos el modelo primal de minimización: 196
17 Investigación de operaciones Z c x c x mí n 1 1 n s. a.: a11x1 a1 nxn b1 a21x1 a2nxn b2 ( 2) am 1x1 amnxn bm xi 0 i 1, 2,... n Definimos el modelo dual asociado con el modelo (2), como el modelo de programación lineal que tiene como objetivo maximizar la función objetivo (todas sus restricciones son de la forma menor o igual que): Z b y b y má x 1 1 s. a.: a y a y c m n 11 1 m1 m 1 a y a y c m 12 1 m2 m 2 3 a1 y1 a y c y 0 i 1, 2,... m i n mn m n Observamos que si el modelo dual tiene m variables y n restricciones (sin incluir las de no negatividad), entonces el modelo primal tiene n variables y m restricciones. Las variables y 1 son las variables del problema dual. Para formar la tabla primal-dual se procede como sigue: El tamaño de la tabla es de m + 2 renglones y n + 2 columnas. (m número de variables y n número de restricciones). 1. La celda de la esquina superior izquierda se divide en dos con una diagonal, en la parte superior escribimos la palabra primal (mín) y en la parte inferior dual (máx). 2. En la celda de la esquina superior derecha se escribe el símbolo >, mientras que en la primera columna del último renglón se escribe el símbolo <. () 197
18 3. En la primera columna a partir del segundo renglón se escriben los nombres de las variables del problema dual (m). 4. En el primer renglón se escriben los nombres de las variables del problema primal (n). 5. Se escriben los coeficientes de la función objetivo del modelo dual en la última columna. 6. Se escribe cada una de las restricciones del problema dual en forma vertical, ocupando las columnas de la tabla. 7. En el último renglón se escriben las cantidades limitantes de las restricciones del modelo primal. 8. De esta tabla podemos obtener el modelo dual, lo único que debemos hacer es leer el modelo de manera vertical y los coeficientes de la función objetivo se obtienen de la última columna. Ejemplo 3 Resolver el siguiente modelo de P. L.: Z 4x x x mí n s. a.: 2x x 2x x 3x x x, x, x 0 198
19 Investigación de operaciones Como no tenemos descrito un procedimiento de solución para modelos de minimización usamos una tabla primal-dual para obtener el modelo de maximización asociado y resolvemos por el método visto anteriormente. Creamos la tabla primal-dual, con el procedimiento descrito: De esta tabla podemos obtener el modelo dual, lo único que debemos hacer es leer el modelo de manera vertical y la función objetivo se obtiene de la última columna, es decir: Ymá x 4y1 3y2 s. a.: 2y1 3y2 4 y1 3y2 1 2y1 y2 1 yi 0 i 1, 2 Este es el problema dual asociado al problema primal. Existe una relación importante entre los dos modelos, la última tabla símplex de solución del modelo dual proporciona la solución del primal, debido a la propiedad de soluciones complementarias, la cual damos a continuación. Propiedad de soluciones complementarias En cada iteración el método símplex identifica simultáneamente una solución básica factible para el modelo primal y una solución complementaria para el modelo dual (que se encuentra en el primer renglón de la tabla símplex, como los coeficientes de las variables artificiales). Esto quiere decir que los valores de las variables x i del modelo primal son los valores que se encuentran en el renglón R 0 en las columnas de las variables de holgura de la tabla símplex del modelo dual. 199
20 Ejemplo 4 Continuando con el ejemplo 3 de la sección anterior, el modelo que se obtiene al sumar las variables de holgura es: Y 4y 3y má x 1 2 s. a.: 2y 3y h y2 h2 La tabla inicial que obtenemos es: y 2y1 y2 h3 1 y 0 h 0 i 1, 2 j 1, 2, 3 i j 1 Función objetivo Primera restricción Segunda restricción Tercera restricción La tabla después de la primera iteración es: La tabla después de la segunda iteración es: 200
21 Investigación de operaciones Ésta ya es la tabla óptima, la cual tiene como solución del problema dual la siguiente: y 1 = 0.40 y 2 = 0.20 Z máx = 2.20 Sin embargo, nuestro interés está en la solución del problema primal de minimización, la cual obtenemos del renglón R 0, al tomar los coeficientes de las variables de holgura, es decir: x 1 = h 1 = 0 x 2 = h 2 = 0.40 x 3 = h 3 = 1.80 Al sustituir en la función objetivo, tenemos: Z mín = 4x 1 +x 2 +x 3 Z mín = 4(0) Z mín = 2.20 Se comprueba que efectivamente la función objetivo del problema dual tiene el mismo valor que la función objetivo del primal. Ejemplo 5 Obtener la solución óptima del siguiente modelo de P. L. Z x x 3x 2x mí n s. a.: x 2x 4x x 1 3x x x 4x x x, x, x, x Lo primero es formar la tabla primal-dual, asociada con el modelo: 201
22 De esta tabla obtenemos el modelo dual, el cual es: Zmá x 8y 10y 7y s. a.: y1 y2 1 2y1 3y3 1 4y1 3y2 4y3 3 y2 y3 2 y, y, y Resolvemos este modelo por el método símplex (ya no escribimos detalles). La tabla inicial es: La tabla óptima es: La solución del primal es: x 1 = h 1 = 4.75 x 2 = h 2 = 0 x 3 = h 3 = 1.75 x 4 = h 4 = 0 Z mín =
23 Investigación de operaciones 5.5. Maximización y Minimización (cambios en la función objetivo) Es posible transformar un problema de maximizar a uno de minimizar y viceversa. Para ello analicemos lo siguiente: Supongamos que queremos encontrar el máximo del siguiente conjunto de números: máx{1, 3, 5, 7} Sabemos que el máximo es 7. Ahora multipliquemos los elementos del conjunto por 1, nos queda entonces el conjunto: { 1, 3, 5, 7} Si buscamos el mínimo de este nuevo conjunto obtenemos que es 7. Esto quiere decir que el máx{1, 3, 5, 7} = (mín{ 1, 3, 5, 7}), por lo tanto si queremos cambiar el objetivo de un modelo de P. L. se hace lo siguiente: 1. Se multiplica la función objetivo por Se cambia el objetivo de la función. 3. Se resuelve el modelo. 4. Se multiplica el valor de Z óptimo por 1 y éste es el valor del modelo original. Ejemplo 7 Hallar la solución óptima del siguiente modelo de P. L. Z 5x 10x mí n 1 2 s. a.: 4x 2x x 8x x 2 x, x
24 Este modelo tiene todas las desigualdades de la forma menor igual que, por lo tanto, parece que lo podemos resolver por método símplex, sin embargo, el objetivo de la función es minimizar. Para transformar el problema multiplicamos la función objetivo por 1. Con este cambio nos queda el modelo: 1(Z mín = 5x 1 10x 2 ) Z máx = 5x 1 +10x 2 Zmá x 5x1 10x2 s. a.: 4x1 2x2 10 3x1 8x2 16 x2 5 x1, x2 0 Este modelo ya lo podemos resolver por el método símplex. La tabla inicial es: La tabla final es: Donde obtenemos la solución: x 1 = 0 x 2 = 2 Z máx =
25 Investigación de operaciones Para obtener el valor de Z multiplicamos por 1 de manera que la solución óptima es x 1 = 0 x 2 = 2 con Z mín = 20 Ejercicio 5 Resolver los siguientes modelos utilizando la técnica vista en esta sección. 1. Zmí n 3x1 8x2 x3 s. a.: x x 3x x1 x2 7x3 15 x x x, x, x Z 5x 7x x má x s. a.: 2x 4x x x x, x, x Resumen En esta unidad aprendimos el método símplex y algunas de sus variantes, en la siguiente tabla describimos las características que puede tener un modelo y el método más recomendado para su solución: 211
maximización (con restricciones de la forma menor igual que). asociado al modelo primal de minimización y viceversa.
 UNIDAD 5 MÉTODO SÍMPLEX maximización (con restricciones de la forma menor igual que). asociado al modelo primal de minimización y viceversa. minimización (con restricciones de la forma mayor que). tenga
UNIDAD 5 MÉTODO SÍMPLEX maximización (con restricciones de la forma menor igual que). asociado al modelo primal de minimización y viceversa. minimización (con restricciones de la forma mayor que). tenga
Contenido: Solución algebraica a los problemas de programación lineal con el método simplex.
 Tema II: Programación Lineal Contenido: Solución algebraica a los problemas de programación lineal con el método simplex. Introducción El método simplex resuelve cualquier problema de PL con un conjunto
Tema II: Programación Lineal Contenido: Solución algebraica a los problemas de programación lineal con el método simplex. Introducción El método simplex resuelve cualquier problema de PL con un conjunto
1.Restricciones de Desigualdad 2.Procedimiento algebraico
 Universidad Nacional de Colombia Sede Medellín 1. Restricciones de Desigualdad Clase # 6 EL MÉTODO M SIMPLEX El método m simplex es un procedimiento algebraico: las soluciones se obtienen al resolver un
Universidad Nacional de Colombia Sede Medellín 1. Restricciones de Desigualdad Clase # 6 EL MÉTODO M SIMPLEX El método m simplex es un procedimiento algebraico: las soluciones se obtienen al resolver un
84 Tema 3. Dualidad. todas las restricciones son del tipo, todas las variables son no negativas.
 Tema 3 Dualidad En el desarrollo de la programación lineal la teoria de la dualidad es importante, tanto desde el punto de vista teórico como desde el punto de vista práctico. Para cada modelo lineal se
Tema 3 Dualidad En el desarrollo de la programación lineal la teoria de la dualidad es importante, tanto desde el punto de vista teórico como desde el punto de vista práctico. Para cada modelo lineal se
7. PROGRAMACION LINEAL
 7. PROGRAMACION LINEAL 7.1. INTRODUCCION A LA PROGRMACION LINEAL 7.2. FORMULACION DE UN PROBLEMA LINEAL 7.3. SOLUCION GRAFICA DE UN PROBLEMA LINEAL 7.4. CASOS ESPECIALES DE PROBLEMAS LINEALES 7.4.1. Problemas
7. PROGRAMACION LINEAL 7.1. INTRODUCCION A LA PROGRMACION LINEAL 7.2. FORMULACION DE UN PROBLEMA LINEAL 7.3. SOLUCION GRAFICA DE UN PROBLEMA LINEAL 7.4. CASOS ESPECIALES DE PROBLEMAS LINEALES 7.4.1. Problemas
Dualidad 1. 1 Formas simétricas. 2 Relación primal-dual. 3 Dualidad: el caso general. 4 Teoremas de dualidad. 5 Condiciones de holgura complementaria.
 Dualidad 1 1 Formas simétricas. 2 Relación primal-dual. 3 Dualidad: el caso general. 4 Teoremas de dualidad. Condiciones de holgura complementaria. 6 Solución dual óptima en la tabla. 7 Interpretación
Dualidad 1 1 Formas simétricas. 2 Relación primal-dual. 3 Dualidad: el caso general. 4 Teoremas de dualidad. Condiciones de holgura complementaria. 6 Solución dual óptima en la tabla. 7 Interpretación
Con miras a conocer la metodología que se aplica en el Método SIMPLEX, tenemos a continiacion un ejemplo:
 Método Simplex. Este método fue creado en el año 1947 por el estadounidense George Bernard Dantzig y el ruso Leonid Vitalievich Kantorovich, con el objetivo de crear un algoritmo capaz de crear soluciones
Método Simplex. Este método fue creado en el año 1947 por el estadounidense George Bernard Dantzig y el ruso Leonid Vitalievich Kantorovich, con el objetivo de crear un algoritmo capaz de crear soluciones
Tema 18. Programación lineal Formulación primal de un programa lineal
 Tema 18 Programación lineal 18.1. Formulación primal de un programa lineal Dentro de la programación matemática hablamos de programación lineal (PL) si tanto la función objetivo como las restricciones
Tema 18 Programación lineal 18.1. Formulación primal de un programa lineal Dentro de la programación matemática hablamos de programación lineal (PL) si tanto la función objetivo como las restricciones
Universidad Nacional de Ingeniería UNI-RUACS 01/09/11
 Universidad Nacional de Ingeniería UNI-RUACS 01/09/11 Elaborado por: Deall Daniel Irías Estelí, Nicaragua El método Simplex es un procedimiento iterativo que permite ir mejorando la solución a cada paso.
Universidad Nacional de Ingeniería UNI-RUACS 01/09/11 Elaborado por: Deall Daniel Irías Estelí, Nicaragua El método Simplex es un procedimiento iterativo que permite ir mejorando la solución a cada paso.
METODO SIMPLEX. Paso 1 Se convierte el modelo matemático de Programación Lineal (PL) a su forma estándar.
 METODO SIMPLEX El algoritmo Simplex comprende los siguientes pasos: Paso 1 Se convierte el modelo matemático de Programación Lineal (PL) a su forma estándar. Al elaborar el modelo matemático que representa
METODO SIMPLEX El algoritmo Simplex comprende los siguientes pasos: Paso 1 Se convierte el modelo matemático de Programación Lineal (PL) a su forma estándar. Al elaborar el modelo matemático que representa
Método Simplex. Ing. Ricardo Fernando Otero, MSc
 Método Simplex Ing. Ricardo Fernando Otero, MSc Forma estándar de un modelo de programación lineal Dirección de mejora: Maximizar Todas las restricciones deben ser El lado izquierdo debe contener solo
Método Simplex Ing. Ricardo Fernando Otero, MSc Forma estándar de un modelo de programación lineal Dirección de mejora: Maximizar Todas las restricciones deben ser El lado izquierdo debe contener solo
La Programación Lineal. H. R. Alvarez A., Ph. D. 1
 La Programación Lineal H. R. Alvarez A., Ph. D. 1 El Método Simplex Desarrollado en 1947 por George Dantzig como parte de un proyecto para el Departamento de Defensa Se basa en la propiedad de la solución
La Programación Lineal H. R. Alvarez A., Ph. D. 1 El Método Simplex Desarrollado en 1947 por George Dantzig como parte de un proyecto para el Departamento de Defensa Se basa en la propiedad de la solución
PROBLEMA DE PROGRAMACIÓN LINEAL RESUELTO POR MÉTODO SIMPLEX
 Prof.: MSc. Julio Rito Vargas Avilés Planteamiento del problema: PROBLEMA DE PROGRAMACIÓN LINEAL RESUELTO POR MÉTODO SIMPLEX Una compañía de manufactura se dedica a la fabricación de tres productos: A,
Prof.: MSc. Julio Rito Vargas Avilés Planteamiento del problema: PROBLEMA DE PROGRAMACIÓN LINEAL RESUELTO POR MÉTODO SIMPLEX Una compañía de manufactura se dedica a la fabricación de tres productos: A,
Programación Lineal. Yolanda Hinojosa
 Programación Lineal Yolanda Hinojosa Contenido Formulación primal de un programa lineal. Propiedades Algoritmo del simplex Algoritmo dual del simplex Formulación dual de un programa lineal. Propiedades
Programación Lineal Yolanda Hinojosa Contenido Formulación primal de un programa lineal. Propiedades Algoritmo del simplex Algoritmo dual del simplex Formulación dual de un programa lineal. Propiedades
INGENIERO EN COMPUTACION TEMA: MÉTODO SIMPLEX
 UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACION TEMA: MÉTODO SIMPLEX ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: MARZO DE 2016 UNIDAD DE APRENDIZAJE
UNIVERSIDAD AUTÓNOMA DEL ESTADO DE MÉXICO CENTRO UNIVERSITARIO UAEM ZUMPANGO INGENIERO EN COMPUTACION TEMA: MÉTODO SIMPLEX ELABORÓ: M. EN C. LUIS ENRIQUE KU MOO FECHA: MARZO DE 2016 UNIDAD DE APRENDIZAJE
MÉTODO ALGEBRAICO: Obtención de las soluciones básicas:
 MÉTODO ALGEBRAICO: El método algebraico es una alternativa de solución a problemas de programación lineal. Sin embargo es muy dispendioso, en razón a que trabaja con todos los datos de las ecuaciones,
MÉTODO ALGEBRAICO: El método algebraico es una alternativa de solución a problemas de programación lineal. Sin embargo es muy dispendioso, en razón a que trabaja con todos los datos de las ecuaciones,
Forma estándar de un programa lineal
 Forma estándar de un programa lineal Sin pérdida de generalidad, todo programa lineal se puede escribir como: min cx s.t Ax = b x 0 Objetivo: minimizar Todas las desigualdades como ecuaciones Todas las
Forma estándar de un programa lineal Sin pérdida de generalidad, todo programa lineal se puede escribir como: min cx s.t Ax = b x 0 Objetivo: minimizar Todas las desigualdades como ecuaciones Todas las
Programación Lineal. El método simplex
 Programación Lineal El método simplex El método simplex es una herramienta algebraica que permite localizar de manera eficiente el óptimo entre los puntos extremos de una solución a un problema de programación
Programación Lineal El método simplex El método simplex es una herramienta algebraica que permite localizar de manera eficiente el óptimo entre los puntos extremos de una solución a un problema de programación
Un sistema de ecuaciones diferenciales son aquellas que tienen varias posibilidades para su solución. Estas son:
 Unidad X: Programación lineal (continuación) Objetivo específico: Entender ampliamente el fenómeno del comportamiento de los modelos matemáticos para la resolución de problemas enfocados a las ecuaciones
Unidad X: Programación lineal (continuación) Objetivo específico: Entender ampliamente el fenómeno del comportamiento de los modelos matemáticos para la resolución de problemas enfocados a las ecuaciones
INGENIERÍA DE SISTEMAS INVESTIGACIÓN OPERATIVA
 INGENIERÍA DE SISTEMAS INVESTIGACIÓN OPERATIVA Sesión 4 Objetivos: Aplicar el método simplex a la solución de problemas reales. Contenido: Introducción al método Simplex Requerimiento del método Simplex
INGENIERÍA DE SISTEMAS INVESTIGACIÓN OPERATIVA Sesión 4 Objetivos: Aplicar el método simplex a la solución de problemas reales. Contenido: Introducción al método Simplex Requerimiento del método Simplex
Lo que se hace entonces es introducir variables artificiales ADAPTACIÓN A OTRAS FORMAS DEL MODELO.
 Clase # 8 Hasta el momento sólo se han estudiado problemas en la forma estándar ADAPTACIÓN A OTRAS FORMAS DEL MODELO. Maximizar Z. Restricciones de la forma. Todas las variables no negativas. b i 0 para
Clase # 8 Hasta el momento sólo se han estudiado problemas en la forma estándar ADAPTACIÓN A OTRAS FORMAS DEL MODELO. Maximizar Z. Restricciones de la forma. Todas las variables no negativas. b i 0 para
RESOLVER PROBLEMA DE PROGRAMACIÓN LINEAL POR METODO SIMPLEX
 RESOLVER PROBLEMA DE PROGRAMACIÓN LINEAL POR METODO SIMPLEX Prof. MSc. Julio Rito Vargas Otro ejemplo ================================================================================ Resolver por el método
RESOLVER PROBLEMA DE PROGRAMACIÓN LINEAL POR METODO SIMPLEX Prof. MSc. Julio Rito Vargas Otro ejemplo ================================================================================ Resolver por el método
La Programación Lineal. H. R. Alvarez A., Ph. D. 1
 La Programación Lineal H. R. Alvarez A., Ph. D. 1 Aspectos generales Se considera a George Dantzig el padre de la P. L. Su objetivo es el de asignar recursos escasos a actividades que compiten por ellos.
La Programación Lineal H. R. Alvarez A., Ph. D. 1 Aspectos generales Se considera a George Dantzig el padre de la P. L. Su objetivo es el de asignar recursos escasos a actividades que compiten por ellos.
Universidad Tec Milenio: Profesional HG04002 Análisis de Decisiones I
 Tema # 10 El método de las M s como solución de problemas de programación lineal 1 Objetivo de aprendizaje del tema Al finalizar el tema serás capaz de: Resolver modelos de programación lineal mediante
Tema # 10 El método de las M s como solución de problemas de programación lineal 1 Objetivo de aprendizaje del tema Al finalizar el tema serás capaz de: Resolver modelos de programación lineal mediante
UNIDAD 6 PROGRAMACIÓN LINEAL ENTERA. de programación lineal entera. lineal entera.
 UNIDAD 6 PROGRAMACIÓN LINEAL ENTERA de programación lineal entera. lineal entera. Investigación de operaciones Introducción En la unidad aprendimos a resolver modelos de P. L. por el método símple y el
UNIDAD 6 PROGRAMACIÓN LINEAL ENTERA de programación lineal entera. lineal entera. Investigación de operaciones Introducción En la unidad aprendimos a resolver modelos de P. L. por el método símple y el
Optimización y Programación Lineal
 Optimización y Programación Lineal Método Simplex: Minimización 3 de enero de Método Simplex: Minimización () Optimización y Programación Lineal 3 de enero de / 4 Minimización Minimización En la definición
Optimización y Programación Lineal Método Simplex: Minimización 3 de enero de Método Simplex: Minimización () Optimización y Programación Lineal 3 de enero de / 4 Minimización Minimización En la definición
Forma estándar de un PPL con m restricciones y n variables. (b 0)
 Forma estándar de un PPL con m restricciones y n variables Maximizar (minimizar) Z = c 1 x 1 + c 2 x 2 +... + c n x n a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 +a 22 x 2 +... + a 2n x n = b 2...
Forma estándar de un PPL con m restricciones y n variables Maximizar (minimizar) Z = c 1 x 1 + c 2 x 2 +... + c n x n a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1 a 21 x 1 +a 22 x 2 +... + a 2n x n = b 2...
Después de construir modelos matemáticos de programación
 Introducción Después de construir modelos matemáticos de programación lineal, necesitamos desarrollar métodos que nos permitan encontrar la solución de estos modelos. En esta unidad se resolverán modelos
Introducción Después de construir modelos matemáticos de programación lineal, necesitamos desarrollar métodos que nos permitan encontrar la solución de estos modelos. En esta unidad se resolverán modelos
RESOLVER PROBLEMA DE PROGRAMACIÓN LINEAL POR METODO SIMPLEX
 RESOLVER PROBLEMA DE PROGRAMACIÓN LINEAL POR METODO SIMPLEX Prof. MSc. Julio Rito Vargas ================================================================================ Resolver por el método Simplex,
RESOLVER PROBLEMA DE PROGRAMACIÓN LINEAL POR METODO SIMPLEX Prof. MSc. Julio Rito Vargas ================================================================================ Resolver por el método Simplex,
Formulación del problema de la ruta más corta en programación lineal
 Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Formato para prácticas de laboratorio
 Formato para prácticas de laboratorio CARRERA INGENIERIA INDUSTRIAL PLAN DE ESTUDIO CLAVE DE UNIDAD DE APRENDIZAJE 2007-1 9013 NOMBRE DE LA UNIDAD DE APRENDIZAJE METODOLOGIA PARA LA RESOLUCION DE PROBLEMAS
Formato para prácticas de laboratorio CARRERA INGENIERIA INDUSTRIAL PLAN DE ESTUDIO CLAVE DE UNIDAD DE APRENDIZAJE 2007-1 9013 NOMBRE DE LA UNIDAD DE APRENDIZAJE METODOLOGIA PARA LA RESOLUCION DE PROBLEMAS
Figura 1: Esquema de las tablas simplex de inicio y general.
 RELACIONES PRIMAL-DUAL Los cambios que se hacen en el modelo original de programación lineal afectan a los elementos de la tabla óptima actual el que se tenga en el momento, que a su vez puede afectar
RELACIONES PRIMAL-DUAL Los cambios que se hacen en el modelo original de programación lineal afectan a los elementos de la tabla óptima actual el que se tenga en el momento, que a su vez puede afectar
MÉTODO SIMPLEX. Introducción
 MÉTODO SIMPLEX Introducción El Método Simplex publicado por George Dantzig en 1947 consiste en un algoritmo iterativo que secuencialmente a través de iteraciones se va aproximando al óptimo del problema
MÉTODO SIMPLEX Introducción El Método Simplex publicado por George Dantzig en 1947 consiste en un algoritmo iterativo que secuencialmente a través de iteraciones se va aproximando al óptimo del problema
Sistemas de ecuaciones lineales
 Tema 1 Sistemas de ecuaciones lineales 11 Definiciones Sea K un cuerpo Una ECUACIÓN LINEAL CON COEFICIENTES EN K es una expresión del tipo a 1 x 1 + + a n x n = b, en la que n es un número natural y a
Tema 1 Sistemas de ecuaciones lineales 11 Definiciones Sea K un cuerpo Una ECUACIÓN LINEAL CON COEFICIENTES EN K es una expresión del tipo a 1 x 1 + + a n x n = b, en la que n es un número natural y a
MATE Método Simplex maximización estándar
 MATE 3012 Método Simplex maximización estándar Problema de maximización estándar Un problema de maximización de programación lineal está en la forma estándar, si la función objetiva w = c 1 x 1 + c 2 x
MATE 3012 Método Simplex maximización estándar Problema de maximización estándar Un problema de maximización de programación lineal está en la forma estándar, si la función objetiva w = c 1 x 1 + c 2 x
MÉTODO SIMPLEX. Es un método genérico de solución de problemas lineales, desarrollado por George Dantzig en 1947.
 FUNDACIÓN UNIVERSITARIA DE SAN GIL UNISANGIL UNAB Pág. 1 MÉTODO SIMPLEX Es un método genérico de solución de problemas lineales, desarrollado por George Dantzig en 1947. Matricialmente podemos representar
FUNDACIÓN UNIVERSITARIA DE SAN GIL UNISANGIL UNAB Pág. 1 MÉTODO SIMPLEX Es un método genérico de solución de problemas lineales, desarrollado por George Dantzig en 1947. Matricialmente podemos representar
Facultad de Ciencias Empresariales Escuela de Ingeniería Informática Empresarial Modulo: Matemáticas II
 Integrantes: Daniel Castro Felipe Norambuena Professor : Claudio Enrique Del Pino Ormachea Historia El metodo simplex fue creado en el año de 1947 por el estadounidense George Bernard Dantzig y el ruso
Integrantes: Daniel Castro Felipe Norambuena Professor : Claudio Enrique Del Pino Ormachea Historia El metodo simplex fue creado en el año de 1947 por el estadounidense George Bernard Dantzig y el ruso
ANÁLISIS DE SENSIBILIDAD.
 ANÁLISIS DE SENSIBILIDAD. En la mayoría de las aplicaciones practicas, algunos datos del problema no son conocidos con exactitud y por esto son estimados tan bien como sea posible. Es importante poder
ANÁLISIS DE SENSIBILIDAD. En la mayoría de las aplicaciones practicas, algunos datos del problema no son conocidos con exactitud y por esto son estimados tan bien como sea posible. Es importante poder
Una forma fácil de recordar esta suma (regla de Sarrus): Primero vamos a estudiar algunas propiedades de los determinantes.
 Una forma fácil de recordar esta suma (regla de Sarrus): Ejemplos: Tarea: realizar al menos tres ejercicios de cálculo de determinantes de matrices de 2x2 y otros tres de 3x3. PARA DETERMINANTES DE MATRICES
Una forma fácil de recordar esta suma (regla de Sarrus): Ejemplos: Tarea: realizar al menos tres ejercicios de cálculo de determinantes de matrices de 2x2 y otros tres de 3x3. PARA DETERMINANTES DE MATRICES
Tema 3 Optimización lineal. Algoritmo del simplex
 Tema 3 Optimización lineal. Algoritmo del simplex José R. Berrendero Departamento de Matemáticas Universidad Autónoma de Madrid Contenidos del tema 3 Teorema fundamental de la programación lineal. Algoritmo
Tema 3 Optimización lineal. Algoritmo del simplex José R. Berrendero Departamento de Matemáticas Universidad Autónoma de Madrid Contenidos del tema 3 Teorema fundamental de la programación lineal. Algoritmo
Kg P1 Kg P Unidades Vitamina A
 Dualidad El concepto de dualidad desempeña importantes papeles dentro de la programación lineal (también en la no lineal), tanto desde un punto de vista teórico como práctico. Todo programa lineal lleva
Dualidad El concepto de dualidad desempeña importantes papeles dentro de la programación lineal (también en la no lineal), tanto desde un punto de vista teórico como práctico. Todo programa lineal lleva
METODO SIMPLEX: SOLUCION DE PROBLEMAS DE PROGRAMACION LINEAL.
 METODO SIMPLEX: SOLUCION DE PROBLEMAS DE PROGRAMACION LINEAL. El método Simplex es un procedimiento general para resolver problemas de programación lineal. Desarrollado por George Dantzig en 1947, esta
METODO SIMPLEX: SOLUCION DE PROBLEMAS DE PROGRAMACION LINEAL. El método Simplex es un procedimiento general para resolver problemas de programación lineal. Desarrollado por George Dantzig en 1947, esta
Unidad 2. Matrices Conceptos básicos 2.2. Operaciones con matrices 2.3. Matriz Inversa 2.4. El método de Gauss-Jordan 2.5.
 Unidad. Matrices.. Conceptos básicos.. Operaciones con matrices.. Matriz Inversa.. El método de Gauss-Jordan.. Aplicaciones Objetivos particulares de la unidad Al culminar el aprendizaje de la unidad,
Unidad. Matrices.. Conceptos básicos.. Operaciones con matrices.. Matriz Inversa.. El método de Gauss-Jordan.. Aplicaciones Objetivos particulares de la unidad Al culminar el aprendizaje de la unidad,
INVESTIGACION DE OPERACIONES:
 METODO SIMPLEX El algoritmo símplex fue descubierto por el matemático norteamericano George Bernard Dantzig en 1947, es una técnica para dar soluciones numéricas a problema de programación lineal Un problema
METODO SIMPLEX El algoritmo símplex fue descubierto por el matemático norteamericano George Bernard Dantzig en 1947, es una técnica para dar soluciones numéricas a problema de programación lineal Un problema
Capítulo 4 Método Algebraico
 Capítulo 4 Método Algebraico Introducción En la necesidad de desarrollar un método para resolver problemas de programación lineal de más de dos variables, los matemáticos implementaron el método algebraico,
Capítulo 4 Método Algebraico Introducción En la necesidad de desarrollar un método para resolver problemas de programación lineal de más de dos variables, los matemáticos implementaron el método algebraico,
max c T x s.a. Ax b x 0 y un diccionario general para dicho problema a rs x s, c s x s z = d + b r y r min b T y s.a. A T y c y 0
 CO-34 (S8) 25/3/28 8 Formalizaremos lo visto en la clase anterior. Considere un problema en forma estándar max s.a. c T x Ax b x un diccionario general para dicho problema x r = b r + a rs x s, s NB z
CO-34 (S8) 25/3/28 8 Formalizaremos lo visto en la clase anterior. Considere un problema en forma estándar max s.a. c T x Ax b x un diccionario general para dicho problema x r = b r + a rs x s, s NB z
x 1, x 2 0 Maximizar 3x 1 + x 2 s.a 2x 1 + x 2 4 2x 1 + 3x 2 4 x 1 + 3x 2 3
 EJERCICIOS DE INVESTIGACIÓN OPERATIVA. Hoja. Dado el PL: Maximizar x + x x s.a x + x + x x x x x, x, x Calcula la solución del problema aplicando el algoritmo del Simplex. Existe más de una solución óptima?
EJERCICIOS DE INVESTIGACIÓN OPERATIVA. Hoja. Dado el PL: Maximizar x + x x s.a x + x + x x x x x, x, x Calcula la solución del problema aplicando el algoritmo del Simplex. Existe más de una solución óptima?
UNIDAD 3 MÉTODO SIMPLEX. Fundamentos del método simplex
 UNIDAD 3 MÉTODO SIMPLEX Fundamentos del método simplex Teoría Este método busca la solución, en cada paso, de forma mejorada hasta que no pueda seguir mejorando dicha solución. Al comienzo el vértice principal
UNIDAD 3 MÉTODO SIMPLEX Fundamentos del método simplex Teoría Este método busca la solución, en cada paso, de forma mejorada hasta que no pueda seguir mejorando dicha solución. Al comienzo el vértice principal
Unidad III Teoría de la Dualidad.
 Curso de investigación de operaciones http://www.luciasilva.8k.com/5.5.htm Unidad III Teoría de la Dualidad. III.1 FORMULACIÓN DEL PROBLEMA DUAL La Teoría de la Dualidad es una de las herramientas que
Curso de investigación de operaciones http://www.luciasilva.8k.com/5.5.htm Unidad III Teoría de la Dualidad. III.1 FORMULACIÓN DEL PROBLEMA DUAL La Teoría de la Dualidad es una de las herramientas que
SISTEMAS DE ECUACIONES LINEALES. Método de reducción o de Gauss. 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González.
 SISTEMAS DE ECUACIONES LINEALES Método de reducción o de Gauss 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González. SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS.
SISTEMAS DE ECUACIONES LINEALES Método de reducción o de Gauss 1º DE BACHILLERATO DPTO DE MATEMÁTICAS COLEGIO MARAVILLAS AUTORA: Teresa González. SISTEMAS DE DOS ECUACIONES LINEALES CON DOS INCÓGNITAS.
max z = c T x sujeto a Ax b
 Tema 4 Análisis de sensibilidad El análisis de sensibilidad se realiza después de obtener la solución óptima de un modelo lineal para deteminar como afectan los cambios en los parámetros del modelo a la
Tema 4 Análisis de sensibilidad El análisis de sensibilidad se realiza después de obtener la solución óptima de un modelo lineal para deteminar como afectan los cambios en los parámetros del modelo a la
Repaso del algoritmo SIMPLEX
 Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Industrial IN70K: Clase Auxiliar Repaso del algoritmo SIMPLEX Marcel Goic F. 1 1 Esta es una versión bastante
Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Industrial IN70K: Clase Auxiliar Repaso del algoritmo SIMPLEX Marcel Goic F. 1 1 Esta es una versión bastante
UNIDAD 4 SOLUCIÓN GRÁFICA DE PROBLEMAS DE P. L. de dos dimensiones. especiales.
 UNIDAD 4 SOLUCIÓN GRÁFICA DE PROBLEMAS DE P. L. de dos dimensiones especiales. Investigación de operaciones Introducción Después de construir modelos matemáticos de programación lineal, necesitamos desarrollar
UNIDAD 4 SOLUCIÓN GRÁFICA DE PROBLEMAS DE P. L. de dos dimensiones especiales. Investigación de operaciones Introducción Después de construir modelos matemáticos de programación lineal, necesitamos desarrollar
315 M/R Versión 1 Integral 1/13 2009/1 UNIVERSIDAD NACIONAL ABIERTA VICERRECTORADO ACADÉMICO ÁREA INGENIERÍA
 35 M/R Versión Integral /3 29/ UNIVERSIDAD NACIONAL ABIERTA VICERRECTORADO ACADÉMICO ÁREA INGENIERÍA MODELO DE RESPUESTA (VERSION.2) ASIGNATURA: Investigación de Operaciones I CÓDIGO: 35 MOMENTO: Prueba
35 M/R Versión Integral /3 29/ UNIVERSIDAD NACIONAL ABIERTA VICERRECTORADO ACADÉMICO ÁREA INGENIERÍA MODELO DE RESPUESTA (VERSION.2) ASIGNATURA: Investigación de Operaciones I CÓDIGO: 35 MOMENTO: Prueba
Tema 3. El metodo del Simplex.
 Tema 3. El metodo del Simplex. M a Luisa Carpente Rodrguez Departamento de Matematicas.L. Carpente (Departamento de Matematicas) El metodo del Simplex 2008 1 / 28 Objetivos 1 Conocer el funcionamiento
Tema 3. El metodo del Simplex. M a Luisa Carpente Rodrguez Departamento de Matematicas.L. Carpente (Departamento de Matematicas) El metodo del Simplex 2008 1 / 28 Objetivos 1 Conocer el funcionamiento
4. Métodos de Solución PPL : Solución Algebraica: MÉTODO SIMPLEX Segunda Parte
 4. Métodos de Solución PPL : Solución Algebraica: MÉTODO SIMPLEX Segunda Parte Jorge Eduardo Ortiz Triviño jeortizt@unal.edu.co http:/www.docentes.unal.edu.co MÉTODO SIMPLEX Ejemplo de Simplex: Vamos a
4. Métodos de Solución PPL : Solución Algebraica: MÉTODO SIMPLEX Segunda Parte Jorge Eduardo Ortiz Triviño jeortizt@unal.edu.co http:/www.docentes.unal.edu.co MÉTODO SIMPLEX Ejemplo de Simplex: Vamos a
Para poder elaborar el problema dual a partir del primal, este se debe presentar en su forma canónica de la siguiente forma:
 TEORIA DE LA DUALIDAD. Cada problema de programación lineal tiene un segundo problema asociado con él. Uno se denomina primal y el otro dual. Los 2 poseen propiedades muy relacionadas, de tal manera que
TEORIA DE LA DUALIDAD. Cada problema de programación lineal tiene un segundo problema asociado con él. Uno se denomina primal y el otro dual. Los 2 poseen propiedades muy relacionadas, de tal manera que
Programación Lineal. María Muñoz Guillermo Matemáticas I U.P.C.T. M. Muñoz (U.P.C.T.) Programación Lineal Matemáticas I 1 / 13
 Programación Lineal María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Programación Lineal Matemáticas I 1 / 13 Qué es la Programación Lineal? Introducción La Programación
Programación Lineal María Muñoz Guillermo maria.mg@upct.es U.P.C.T. Matemáticas I M. Muñoz (U.P.C.T.) Programación Lineal Matemáticas I 1 / 13 Qué es la Programación Lineal? Introducción La Programación
Guía de Problemas para el Control 2
 Guía de Problemas para el Control 2 Geometría Problema 1 Demuestre que la intersección de conjuntos convexos es un conjunto convexo. Utilizando esto demuestre que todo poliedro es un conjunto convexo.
Guía de Problemas para el Control 2 Geometría Problema 1 Demuestre que la intersección de conjuntos convexos es un conjunto convexo. Utilizando esto demuestre que todo poliedro es un conjunto convexo.
El Método Simplex. H. R. Alvarez A., Ph. D. 1
 El Método Simplex H. R. Alvarez A., Ph. D. 1 El Método Simplex Desarrollado en 1947 por George Dantzig como parte de un proyecto para el Departamento de Defensa Se basa en la propiedad de la solución esquina
El Método Simplex H. R. Alvarez A., Ph. D. 1 El Método Simplex Desarrollado en 1947 por George Dantzig como parte de un proyecto para el Departamento de Defensa Se basa en la propiedad de la solución esquina
Dirección de operaciones. SESIÓN # 6: Análisis de Sensibilidad. Primera parte.
 Dirección de operaciones SESIÓN # 6: Análisis de Sensibilidad. Primera parte. Contextualización Qué sucede si varía algo en el problema de programación lineal? Ya en este momento tenemos los suficientes
Dirección de operaciones SESIÓN # 6: Análisis de Sensibilidad. Primera parte. Contextualización Qué sucede si varía algo en el problema de programación lineal? Ya en este momento tenemos los suficientes
Programación lineal: Algoritmo del simplex
 Programación lineal: Algoritmo del simplex Se considera la formulación estándar de un problema de programación lineal siguiendo la notación utilizada en las clases teóricas: Minimizar c t x sa: Ax = b
Programación lineal: Algoritmo del simplex Se considera la formulación estándar de un problema de programación lineal siguiendo la notación utilizada en las clases teóricas: Minimizar c t x sa: Ax = b
Matrices. Definiciones básicas de matrices. José de Jesús Angel Angel.
 Matrices Definiciones básicas de matrices wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2009 Contenido 1 Matrices 3 11 Matrices cuadradas 5 12 Matriz transpuesta 5 13 Elementos de
Matrices Definiciones básicas de matrices wwwmathcommx José de Jesús Angel Angel jjaa@mathcommx MathCon c 2007-2009 Contenido 1 Matrices 3 11 Matrices cuadradas 5 12 Matriz transpuesta 5 13 Elementos de
UNIDAD 6.- PROGRAMACIÓN LINEAL
 UNIDAD 6.- PROGRAMACIÓN LINEAL 1. INECUACIONES LINEALES CON DOS INCÓGNITAS Una inecuación de primer grado con dos incógnitas es una inecuación que en forma reducida se puede expresar de la siguiente forma:
UNIDAD 6.- PROGRAMACIÓN LINEAL 1. INECUACIONES LINEALES CON DOS INCÓGNITAS Una inecuación de primer grado con dos incógnitas es una inecuación que en forma reducida se puede expresar de la siguiente forma:
Algoritmo de factorización LU
 Algoritmo de factorización LU Objetivos. Estudiar el algoritmo de la factorización LU de una matriz cuadrada invertible. Requisitos. Matrices elementales y su relación con operaciones elementales, matriz
Algoritmo de factorización LU Objetivos. Estudiar el algoritmo de la factorización LU de una matriz cuadrada invertible. Requisitos. Matrices elementales y su relación con operaciones elementales, matriz
Universidad Tec Milenio: Profesional IO04001 Investigación de Operaciones I. Tema # 9
 IO04001 Investigación de Operaciones I Tema # 9 Otras aplicaciones del método simplex Objetivos de aprendizaje Al finalizar el tema serás capaz de: Distinguir y aplicar la técnica de la variable artificial.
IO04001 Investigación de Operaciones I Tema # 9 Otras aplicaciones del método simplex Objetivos de aprendizaje Al finalizar el tema serás capaz de: Distinguir y aplicar la técnica de la variable artificial.
Tema 3 Algebra. Ecuaciones. Sistemas de ecuaciones: Inecuaciones Índice
 Tema 3 Algebra. Ecuaciones. Sistemas de ecuaciones: Inecuaciones Índice 1. ECUACIONES... 2 1.1. Ecuaciones de primer grado... 2 1.2. Ecuaciones de segundo grado... 3 1.2.1. Ecuación de segundo grado completa...
Tema 3 Algebra. Ecuaciones. Sistemas de ecuaciones: Inecuaciones Índice 1. ECUACIONES... 2 1.1. Ecuaciones de primer grado... 2 1.2. Ecuaciones de segundo grado... 3 1.2.1. Ecuación de segundo grado completa...
1 ÁLGEBRA DE MATRICES
 1 ÁLGEBRA DE MATRICES 1.1 DEFINICIONES Las matrices son tablas numéricas rectangulares. Se dice que una matriz es de dimensión m n si tiene m filas y n columnas. Cada elemento de una matriz se designa
1 ÁLGEBRA DE MATRICES 1.1 DEFINICIONES Las matrices son tablas numéricas rectangulares. Se dice que una matriz es de dimensión m n si tiene m filas y n columnas. Cada elemento de una matriz se designa
La factorización eta CO-3411 (S08) 09/03/
 CO-3411 (S08) 09/03/008 74 La factorización eta Esta factorización es una forma de llevar la matriz A B en cada iteración que evita tener que resolver los sistemas lineales involucrados desde cero, pudiendo
CO-3411 (S08) 09/03/008 74 La factorización eta Esta factorización es una forma de llevar la matriz A B en cada iteración que evita tener que resolver los sistemas lineales involucrados desde cero, pudiendo
Degeneración y ciclaje. Método de las dos fases CO-3411 (S08) 30/03/
 CO-3411 (S08 30/03/2008 98 Degeneración y ciclaje En el caso de problemas generales, una solución será degenerada cuando alguna de las variables básicas se encuentra en una de sus cotas (comparar con el
CO-3411 (S08 30/03/2008 98 Degeneración y ciclaje En el caso de problemas generales, una solución será degenerada cuando alguna de las variables básicas se encuentra en una de sus cotas (comparar con el
UNIDAD UNO PROGRAMACIÓN LÍNEAL Parte 4
 Ing. César Urquizú UNIDAD UNO PROGRAMACIÓN LÍNEAL Parte 4 Ing. César Urquizú Teoría de la dualidad El desarrollo de esta teoría de la dualidad es debido al interés que existe en la interpretación económica
Ing. César Urquizú UNIDAD UNO PROGRAMACIÓN LÍNEAL Parte 4 Ing. César Urquizú Teoría de la dualidad El desarrollo de esta teoría de la dualidad es debido al interés que existe en la interpretación económica
El algoritmo del Simplex. Forma tabular
 El algoritmo del Simplex. Forma tabular 1 Soluciones básicas factibles Consideremos el siguiente poliedro P = {x R n, tal que Ax = b, x } con A M m n, b R m, m n, x y RangoA = RangoA, b = m. Observación
El algoritmo del Simplex. Forma tabular 1 Soluciones básicas factibles Consideremos el siguiente poliedro P = {x R n, tal que Ax = b, x } con A M m n, b R m, m n, x y RangoA = RangoA, b = m. Observación
Introducción.- Problema dual.-
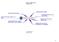 30 Unidad 3 Análisis de dualidad y sensibilidad Competencia-el estudiante debe convertir un modelo estático en dinámico a través del análisis de sensibilidad basado en dos situaciones cambios en la función
30 Unidad 3 Análisis de dualidad y sensibilidad Competencia-el estudiante debe convertir un modelo estático en dinámico a través del análisis de sensibilidad basado en dos situaciones cambios en la función
Sección 1.4 Resolver Equaciones lineales
 Sección 1.4 Resolver Equaciones lineales Copyright 2013, 2009, 2006 Pearson Education, Inc. 1 Ecuación lineal - Definición Una ecuación lineal en una variable, x, es una ecuación que se puede escribir
Sección 1.4 Resolver Equaciones lineales Copyright 2013, 2009, 2006 Pearson Education, Inc. 1 Ecuación lineal - Definición Una ecuación lineal en una variable, x, es una ecuación que se puede escribir
Dirección de Operaciones
 Dirección de Operaciones 1 Sesión No. 6 Nombre: Análisis de sensibilidad. Primera parte. Objetivo: Al finalizar la sesión, el alumno será capaz de identificar la relevancia de la programación lineal en
Dirección de Operaciones 1 Sesión No. 6 Nombre: Análisis de sensibilidad. Primera parte. Objetivo: Al finalizar la sesión, el alumno será capaz de identificar la relevancia de la programación lineal en
Método de eliminación Gaussiana para resolver sistemas de ecuaciones lineales.
 Método de eliminación Gaussiana para resolver sistemas de ecuaciones lineales Consideremos el siguiente sistema de m ecuaciones lineales con n incógnitas con coeficientes reales a 11 x 1 + a 12 x 2 + +
Método de eliminación Gaussiana para resolver sistemas de ecuaciones lineales Consideremos el siguiente sistema de m ecuaciones lineales con n incógnitas con coeficientes reales a 11 x 1 + a 12 x 2 + +
CALCULO I UNIDAD I MATRICES. Instituto Profesional Iplacex
 CALCULO I UNIDAD I MATRICES 1.3 Transformación de matrices A las matrices se les pueden realizar ciertas transformaciones o cambios internos, siempre y cuando no afecten ni el orden ni el rango de la misma.
CALCULO I UNIDAD I MATRICES 1.3 Transformación de matrices A las matrices se les pueden realizar ciertas transformaciones o cambios internos, siempre y cuando no afecten ni el orden ni el rango de la misma.
Matemáticas 2ºBachillerato Aplicadas a las Ciencias Sociales. Un sistema de ecuaciones lineales es un conjunto de ecuaciones lineales de la forma:
 Matemáticas 2ºBachillerato Aplicadas a las Ciencias Sociales 1era evaluación. Sistemas de Ecuaciones Lineales 1) SISTEMAS DE ECUACIONES LINEALES Un sistema de ecuaciones lineales es un conjunto de ecuaciones
Matemáticas 2ºBachillerato Aplicadas a las Ciencias Sociales 1era evaluación. Sistemas de Ecuaciones Lineales 1) SISTEMAS DE ECUACIONES LINEALES Un sistema de ecuaciones lineales es un conjunto de ecuaciones
UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS
 UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS Sistemas de dos ecuaciones con dos incógnitas. Método de igualación. Método de reducción. Método de sustitución Método de eliminación Gaussiana.
UNIDAD I: SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS Sistemas de dos ecuaciones con dos incógnitas. Método de igualación. Método de reducción. Método de sustitución Método de eliminación Gaussiana.
Conversión a la Forma Estándar
 10 de junio de 2014 Introducción Introducción En esta lectura daremos una introducción al método Simplex desarrollado por George Bernard Dantzig (8 de noviembre de 1914 13 de mayo de 2005) en 1947. Este
10 de junio de 2014 Introducción Introducción En esta lectura daremos una introducción al método Simplex desarrollado por George Bernard Dantzig (8 de noviembre de 1914 13 de mayo de 2005) en 1947. Este
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Algoritmo de la factorización LU
 Algoritmo de la factorización LU. Objetivo. Estudiar el algoritmo de la factorización LU de una matriz cuadrada invertible.. Requisitos: Matrices elementales y su relación con operaciones elementales.
Algoritmo de la factorización LU. Objetivo. Estudiar el algoritmo de la factorización LU de una matriz cuadrada invertible.. Requisitos: Matrices elementales y su relación con operaciones elementales.
Optimización de Problemas de Producción
 Optimización de Problemas de Producción Pedro Piñeyro - Luis Stábile Colaboran: Héctor Cancela - Antonio Mauttone - Carlos Testuri Depto. Investigación Operativa. Instituto de Computación. Facultad de
Optimización de Problemas de Producción Pedro Piñeyro - Luis Stábile Colaboran: Héctor Cancela - Antonio Mauttone - Carlos Testuri Depto. Investigación Operativa. Instituto de Computación. Facultad de
ESCUELA DE CIENCIAS CIENCIAS BASICAS TECNOLOGIA E INGENIERIA PROGRAMACION LINEAL Act No. 8. LECTURA LECCION EVALUATIVA 2
 INTRODUCCION AL METODO GRAFICO Antes de entrarnos por completo en los métodos analíticos de la investigación de operaciones es muy conveniente ver un poco acerca de las desigualdades de una ecuación lineal.
INTRODUCCION AL METODO GRAFICO Antes de entrarnos por completo en los métodos analíticos de la investigación de operaciones es muy conveniente ver un poco acerca de las desigualdades de una ecuación lineal.
Colección de Problemas II. mín Z = 8x 1 + 9x 2 + 7x 3 s. a: x 1 + x 2 + x x 1 + 3x 2 + x x 1 + x 2 x 3 30
 1.- Dado el siguiente problema mín Z = 8x 1 + 9x + 7x 3 s. a: x 1 + x + x 3 40 x 1 + 3x + x 3 10 x 1 + x x 3 30 x 1 0, x 0, x 3 0 A) Plantear el problema dual y escribir las condiciones de la holgura complementaria
1.- Dado el siguiente problema mín Z = 8x 1 + 9x + 7x 3 s. a: x 1 + x + x 3 40 x 1 + 3x + x 3 10 x 1 + x x 3 30 x 1 0, x 0, x 3 0 A) Plantear el problema dual y escribir las condiciones de la holgura complementaria
Tema 3: El Método Simplex. Algoritmo de las Dos Fases.
 Tema 3: El Método Simplex Algoritmo de las Dos Fases 31 Motivación Gráfica del método Simplex 32 El método Simplex 33 El método Simplex en Formato Tabla 34 Casos especiales en la aplicación del algoritmo
Tema 3: El Método Simplex Algoritmo de las Dos Fases 31 Motivación Gráfica del método Simplex 32 El método Simplex 33 El método Simplex en Formato Tabla 34 Casos especiales en la aplicación del algoritmo
Integradora 3. Modelos de Programación Lineal
 Métodos Cuantitativos para la Toma de Decisiones Integradora 3. Modelos de Programación Lineal Objetivo Al finalizar la actividad integradora, serás capaz de: R l bl d PL di d l ét d Resolver problemas
Métodos Cuantitativos para la Toma de Decisiones Integradora 3. Modelos de Programación Lineal Objetivo Al finalizar la actividad integradora, serás capaz de: R l bl d PL di d l ét d Resolver problemas
Matrices y Sistemas Lineales
 Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Matrices y Sistemas Lineales Álvarez S, Caballero MV y Sánchez M a M salvarez@umes, mvictori@umes, marvega@umes 1 ÍNDICE Matemáticas Cero Índice 1 Definiciones 3 11 Matrices 3 12 Sistemas lineales 5 2
Sistemas de ecuaciones Ecuaciones lineales con dos incógnitas
 Sistemas de ecuaciones Ecuaciones lineales con dos incógnitas 1. Método de sustitución 1) a + b = 9 a b = 1 } Despejamos cualquiera de las incógnitas que tiene como coeficiente 1, ya que son el caso más
Sistemas de ecuaciones Ecuaciones lineales con dos incógnitas 1. Método de sustitución 1) a + b = 9 a b = 1 } Despejamos cualquiera de las incógnitas que tiene como coeficiente 1, ya que son el caso más
3.1. La Optimización Lineal El Planteamiento
 Gerardo Febres Última revisión: 2016.03.23 3.1. La Optimización Lineal 3.1.1.- El Planteamiento Planteemos un problema extremadamente sencillo. Hacer máximas las ganancias obtenidas al vender tornillos.
Gerardo Febres Última revisión: 2016.03.23 3.1. La Optimización Lineal 3.1.1.- El Planteamiento Planteemos un problema extremadamente sencillo. Hacer máximas las ganancias obtenidas al vender tornillos.
M. En C. Eduardo Bustos as
 PROBLEMS. Hillier, Frederick S. & Hillier, Mark S. Introduction to Management Science.. 2nd. Ed. USA, Mc Graw Hill - Irwin, 2003. 870 pp. M. En C. Eduardo Bustos Farías as 2 3 Software for Solving LP s
PROBLEMS. Hillier, Frederick S. & Hillier, Mark S. Introduction to Management Science.. 2nd. Ed. USA, Mc Graw Hill - Irwin, 2003. 870 pp. M. En C. Eduardo Bustos Farías as 2 3 Software for Solving LP s
Dualidad y postoptimización
 Dualidad y postoptimización José María Ferrer Caja Universidad Pontificia Comillas Definición A cada problema de optimización lineal le corresponde otro que se denomina problema dual En forma canónica
Dualidad y postoptimización José María Ferrer Caja Universidad Pontificia Comillas Definición A cada problema de optimización lineal le corresponde otro que se denomina problema dual En forma canónica
Índice. Funciones de Maple
 INTRODUCCIÓN Con los avances de la tecnología, los cursos de matemáticas en nuestras universidades necesitan el apoyo computacional para la realización de cálculos en diferentes procedimientos, de tal
INTRODUCCIÓN Con los avances de la tecnología, los cursos de matemáticas en nuestras universidades necesitan el apoyo computacional para la realización de cálculos en diferentes procedimientos, de tal
EL MÉTODO SIMPLEX ALGEBRAICO. M. En C. Eduardo Bustos Farías
 EL MÉTODO SIMPLEX ALGEBRAICO M. En C. Eduardo Bustos Farías 1 EL METODO SIMPLEX Es un procedimiento general para resolver problemas de programación lineal. Fue desarrollado en el año de 1947 por George
EL MÉTODO SIMPLEX ALGEBRAICO M. En C. Eduardo Bustos Farías 1 EL METODO SIMPLEX Es un procedimiento general para resolver problemas de programación lineal. Fue desarrollado en el año de 1947 por George
Dirección de Operaciones
 Dirección de Operaciones 1 Sesión No.5 Nombre: El método simplex. Segunda parte. Objetivo Al finalizar la sesión, el alumno será capaz de identificar las herramientas que permiten resolver problemas de
Dirección de Operaciones 1 Sesión No.5 Nombre: El método simplex. Segunda parte. Objetivo Al finalizar la sesión, el alumno será capaz de identificar las herramientas que permiten resolver problemas de
Tema 7: Problemas clásicos de Programación Lineal
 Tema 7: Problemas clásicos de Programación Lineal 1.- Características generales de un problema de transporte y asignación Surgen con frecuencia en diferentes contextos de la vida real. Requieren un número
Tema 7: Problemas clásicos de Programación Lineal 1.- Características generales de un problema de transporte y asignación Surgen con frecuencia en diferentes contextos de la vida real. Requieren un número
