RECULL DE PROBLEMES DE SELECTIVITAT SOBRE INTEGRALS. a) Calculeu l'àrea limitada per la gràfica de la funció, l'eix OX i les rectes verticals 0 x = 2.
|
|
|
- Esther López Aguirre
- hace 5 años
- Vistas:
Transcripción
1 RECULL DE PROBLEMES DE SELECTIVITAT SOBRE INTEGRALS ) PAU 999 Sèrie Qüestió: Calcula l àrea determinada per les corbes d equacions el dibui següent: y 4 i y representada en ) PAU 999 Sèrie Qüestió : Calculeu raonadament l'epressió d'una funció f ( ) tal que f '( ) e i que f ( ). ) PAU 999 Sèrie Problema : 6 Donada la funció f ( ) a) Calculeu l'àrea limitada per la gràfica de la funció, l'ei OX i les rectes verticals. i 4) PAU 999 Sèrie 5 Qüestió : f + k i Trobeu el valor del coeficient k de manera que l'àrea limitada per la funció l'ei d'abscisses sigui igual a 6u. 5) PAU 999 Sèrie 6 Qüestió : f Sigui. Calculeu l'àrea de la regió que limita la gràfica de f d'abscisses i que està representada en el dibui següent: i l'ei Eercicis sobre integrals de les PAU Catalunya
2 6) PAU Sèrie Qüestió : Calculeu l'àrea que té l'únic recinte tancat limitat per les gràfiques de les representat en el dibui següent: y + 7 i 6 y 7) PAU Sèrie Qüestió : Calculeu per integració la superfície del recinte delimitat per les corbes d'equació y 6 representat en el dibui següent: y i la recta 8) PAU Sèrie Qüestió : El polinomi p ( ) + a + b s'anul la per a i complei Calculeu raonadament a i b. p d 4. 9) PAU Sèrie 5 Qüestió : k d Trobeu el valor de k per tal que k + k ) PAU Sèrie Qüestió : π a) Quin és l'angle en radians < < tal que sin ( ) cos ( ) b) Considereu les funcions f ( ) sin ( ) i g ( ) cos ( )?. Calculeu la superfície del recinte delimitat superiorment per les gràfiques d'aquestes funcions, inferiorment per l'ei d'abscisses i π lateralment per les rectes verticals i representat en l'esquema següent: ) PAU Sèrie 4 Qüestió 4: Eercicis sobre integrals de les PAU Catalunya
3 Sabeu que la gràfica de la funció f ( ) passa pel punt (, 4) f '( ). a) Determineu l'epressió de f ( ). b)calculeu l'àrea de la regió limitada per la gràfica de f ( ) i l'ei d'abscissesox. i que la seva funcióderivada és ) PAU Sèrie 5 Qüestió : Teniu una funció f ( ) definida per a (, ), sabeu que el gràfic de f ' forma és dela on f '( ), f '( ), f ' i que f ( ). Dibuieu un gràfic aproimat de f ( ) indicant en quins punts hi ha etremsrelatius. ) PAU Sèrie 5 Qüestió 4: f e Calculeu l'àrea de la regió limitada per la gràfica de la funció d'abscisses i la recta vertical. per a, l'ei 4) PAU Sèrie Qüestió : Calculeu el valor positiu de a que fa que l'àrea compresa entre la recta d'equació la paràbola y a valgui 8. y a + a i 5) PAU Sèrie Qüestió : Calculeu l'àrea compresa entre les gràfiques de les corbes representada en l'esquema següent: y e i y e i la recta y 5 Eercicis sobre integrals de les PAU Catalunya
4 6) PAU Sèrie Qüestió : f Calculeu la primitiva de la funció que s'anul la en el punt d'abscissa. 7) PAU Sèrie Qüestió : e ln ( ) Calculeu d. 8) PAU Sèrie Qüestió : Donada ( f + e + ), determineu la funció g ( ) tal que g '( ) f ( ) una primitiva de f ( )) i que el seu gràfic passa pel punt (, ). (és a dir, 9) PAU Sèrie 5 Qüestió : Considerem la regió S del pla limitada per la paràbola en l'esquema següent: y i la recta y representada Siguin A i B els punts d'intersecció de la recta i la paràbola, i T el triangle que té per vèrtes A, B i l'origen de coordenades (, ). Calculeu l'àrea de la regió que resulta quan es treu el triangle T a la regió S. ) PAU 4 Sèrie Problema : Considereu la funció f ( ) + m +, m. a) Calculeu el valor de m per tal que l àrea del recinte limitat per la gràfica de la funció, l ei OX i les rectes i sigui de unitats quadrades. b) Per a m, indiqueu el punt o els punts on la recta tangent a la gràfica de lafunció forma un angle de 45 amb el semiei positiu de OX. ) PAU 4 Sèrie Qüestió : f cos cos : Donada la funció a) trobeu la seva integral indefinida; π b) quina és la primitiva de f ( ) que passa pel punt,? sin + cos. Indicació: recordeu que ) PAU 4 Sèrie 4 Qüestió : Eercicis sobre integrals de les PAU Catalunya 4
5 Calculeu l àrea del recinte tancat que delimiten la gràfica de la funció y. i la recta y ) PAU 4 Sèrie 4 Qüestió 4: Considereu la funció f ( ) de la figura definida a l interval [, ]. a) Calculeu la funció derivada f '( ) a l interval (, ) b) Hi ha algun punt de (, ) en el qual f ' c) Calculeu f ( ) d. no eisteii? 4) PAU 4 Sèrie 5 Qüestió : Calculeu el valor de la integral següent: d + 5) PAU 5 Sèrie Problema : Considereu la funció f ( ) 4. a) Calculeu l equació de les rectes tangents a la gràfica de f en els punts d abscisses i 4. b) Feu un gràfic dels elements del problema. c) Calculeu l àrea compresa entre la gràfica de f i les rectes tangents que heu trobat a l apartat a). 6) PAU 5 Sèrie Problema : Considereu la funció f ( ) + + b si < ae b si on a i b són nombres reals. a) Quina condició han de complir a i b per tal que f sigui contínua a tot R? b) Trobeu els valors de a i b per als quals f sigui contínua però no derivable a tot R. c) Per a a i b, calculeu. f d 7) PAU 5 Sèrie 4 Qüestió : Eercicis sobre integrals de les PAU Catalunya 5
6 5 4 : f d. Donada la funció: a) Calculeu la integral f F. b) Trobeu la primitiva F de f que compleii 8) PAU 6 Sèrie Qüestió : y f Considereu la funció definida per a [, 5] adjunta. que aparei dibuiada a la figura a) Quina és l epressió de la seva funció derivada quan eistei? b) Calculeu f ( ) d. 9) PAU 6 Sèrie 4 Qüestió : El gràfic de la funció f ( ) +, quan >, és com seguei: a) Trobeu una primitiva de la funció f. b) Calculeu l àrea de la regió ombrejada. ) PAU 6 Sèrie 4 Problema : Considereu la paràbola d equació y +. i a) Calculeu les equacions de les rectes tangents a la paràbola en els punts d abscissa. b) Calculant el mínim de la funció y + trobeu el vèrte de la paràbola. c) Trobeu les interseccions de la paràbola amb els eios i feu una representaciógràfica de la paràbola i de les tangents obtingudes al primer apartat. d) Calculeu l àrea compresa entre la paràbola i les rectes tangents. ) PAU 7 Sèrie Qüestió : Eercicis sobre integrals de les PAU Catalunya 6
7 Busqueu els etrems relatius i els punts de tall amb els eios, i feu una representacióaproimada de la corba d equació delrecinte tancat per aquesta corba i l ei d abscisses. y 4. A continuació, calculeu l àrea ) PAU 7 Sèrie Qüestió 4: La funció derivada ' F d una funció contínua F : R R que passa per l origen és una funció a trossos formada per les semirectes del dibui. Escriviu l epressió de la funció F ( ) com una funció a trossos. ) PAU 7 Sèrie Problema : Donades les funcions f ( ) a 4 i g ( ) + b: a) Calculeu a i b de manera que les gràfiques de f ( ) i de g ( ) siguin tangents en elpunt d abscissa, és a dir, que tinguin lamateia recta tangent en aquest punt. b) Trobeu l equació de la recta tangent esmentada en l apartat anterior. c) Pel valor de a obtingut en el primer apartat, calculeu el valor de l àrea de la regiólimitada per l ei d abscisses OX i la funció f ( ). 4) PAU 8 Sèrie Qüestió : Se sap que certa funció derivable F ( ) verifica les condicions següents: F ' ( ) i 4 F a) Trobeu F ( ). b) Calculeu l àrea compresa entre F ( ) i l ei OX des de fins a. Eercicis sobre integrals de les PAU Catalunya 7
8 5) PAU 9 Sèrie 4 Qüestió : Considereu la funció f ( ) ( ) a, amb a >. a f a) Trobeu els punts de tall de la funció ( ) amb l ei OX. b) Comproveu que l àrea del recinte limitat per la gràfica de la funció f ( ) i l eid abscisses no depèn del valor del paràmetre a. 6) PAU 9 Sèrie Qüestió : Considereu les corbes y 4 i y 6. a) Trobeu-ne els punts d intersecció. b) Representeu les dues corbes en una mateia gràfica, on es vegi clarament el recinte que limiten entre elles. c) Trobeu l àrea d aquest recinte limitat per les dues corbes. 7) PAU 9 Sèrie Problema : 4 b Sigui la funció f ( ) a + +. a) Calculeu els valors de a i b, sabent que la recta + y 4 és tangent a la gràficade la funció f ( ) en el punt d abscissa. Per a la resta d apartats, considereu que a i que b 4. b) Trobeu els intervals de creiement i de decreiement de la funció f ( ). Trobeu iclassifiqueu els etrems relatius que té la funció. f amb l ei OX. c) Calculeu els punts de tall de la funció d) Trobeu l àrea del recinte limitat per la gràfica de la funció f ( ), l ei OX i les rectes i. 8) PAU 9 Sèrie 4 Problema : + La gràfica de la funció f ( ), des de fins a 4, és la següent: i a) Calculeu l equació de les rectes tangents a aquesta funció en els punts d abscissa. Eercicis sobre integrals de les PAU Catalunya 8
9 b) Dibuieu el recinte limitat per la gràfica de la funció i les dues rectes tangentsque heu calculat. c) Trobeu els vèrtes d aquest recinte. d) Calculeu la superfície del recinte damunt dit. 9) PAU Sèrie Qüestió 5: La gràfica de la funció f () sin() és la següent: a) Trobeu-ne una primitiva. b) Aplicant el resultat de l apartat anterior, calculeu l àrea del recinte limitat per la gràfica de la f i l ei d abscisses des de fins a π. funció 4) PAU Sèrie Qüestió 5: Sigui f ( ) 8 + les rectes i.. Trobeu l àrea del recinte limitat per la gràfica d aquesta funció, l ei OX i 4) PAU Sèrie 5 Qüestió 6: y 4 i una recta r que passa per l origen i talla la En la figura es mostra la corba corba en un punt P d abscissa k, amb < k < 4. a) Trobeu l àrea ombrejada, delimitada per la corba i la recta, en funció de k. b) Trobeu per a quin valor de k l àrea de la regió ombrejada és la meitat de l àrea del recinte limitat per la corba i l ei OX. 4) PAU Sèrie Qüestió : Eercicis sobre integrals de les PAU Catalunya 9
10 i g ( ) Definim les funcions f ( ) a ( ), en què a >. a a) Comproveu que l àrea del recinte limitat per les gràfiques de les funcions és b) Calculeu el valor del paràmetre a perquè aquesta àrea sigui mínima. ( + a ) 4 a. 4) PAU Sèrie Qüestió 6: a Sigui ( + ) f a a d per a >. a) Comproveu que f ( a) + a. a b) Calculeu el valor del paràmetre a perquè la funció f (a) tingui un mínim relatiu. 44) PAU Sèrie 4 Qüestió : Calculeu l àrea del recinte limitat per les corbes d equació f ( ) + i g ( ) 5. 45) PAU Sèrie Qüestió : f 9 és la següent: La gràfica de la funció a) Trobeu el punt de tall, (a, ), de la funció amb la part positiva de l ei OX. b) Calculeu l àrea del recinte limitat per la gràfica de f() i l ei OX en el primerquadrant. 46) PAU Sèrie Qüestió : Donada la funció f ( ) i la recta horitzontal y k, amb k >. a)feu un esbós del recinte limitat per les gràfiques de la funció i la recta, i els eios de coordenades. b) Trobeu el valor de k sabent que l àrea d aquest recinte és igual a 4 /. 47) PAU Sèrie 4 Qüestió : La corba y i la recta y k, amb k >, determinen una regió plana. a) Calculeu el valor de l àrea d aquesta regió en funció del paràmetre k. b) Trobeu el valor de k perquè l àrea limitada sigui 6u. Eercicis sobre integrals de les PAU Catalunya
11 48) PAU Sèrie 5 Qüestió 4:(Incomplet) Per a f, considereu la funció +. b) Calculeu l àrea del recinte limitat per la gràfica de f ( ), la recta d equació 5 i l ei OX. 49) PAU Sèrie Qüestió : De la funció polinòmica P ( ) + a + b + sabem que Té un etrem relatiu en el punt d abscissa ; 5 La integral definida en l interval [, ] val. 4 Calculeu el valor dels paràmetres a i b. 5) PAU 4 Sèrie Qüestió 4: Calculeu l àrea de la regió del pla limitada en el primer quadrant per les gràfiques de les funcions y, y 4 i y 9. 5) PAU 4 Sèrie 4 Qüestió 6: Responeu a les qüestions següents: a) La funció f ( ) ( b ) e a, amb a i b constants, té la representació gràfica següent i sabem que passa pels punts A (, ) i B (,) gràfica és horitzontal. Calculeu els valors de a i b. i que en el punt A la recta tangent a la b) Calculeu ln d. 5) PAU 5 Sèrie Qüestió :(Incomplet) b) Calculeu l àrea de la regió plana finita limitada per la corba y i la recta y Eercicis sobre integrals de les PAU Catalunya
12 5) PAU 5 Sèrie 4 Qüestió 4: Sigui f la funció f ( ) sin ( ) π, (unitats en radians).. Calculeu la primitiva de la funció f que passa pel punt 54) PAU 6 Sèrie Qüestió 4: f sin. Sigui la funció a) Calculeu l equació de les rectes tangents a la funció f en els punts d abscissa i π, respectivament. Trobeu les coordenades del punt en què es tallen les dues rectes. b) Calculeu l àrea de la regió limitada per la gràfica de la funció f i les rectes tangents de l apartat anterior (en cas de no haver resolt l apartat anterior, suposeu que les rectes són y i y, respectivament). 55) PAU 6 Sèrie Qüestió 6: Siguin les paràboles f ( ) + k i g ( ) 9k +. a) Calculeu les abscisses, en funció de k, dels punts d intersecció entre les dues paràboles. b) Calculeu el valor del paràmetre k perquè l àrea compresa entre les paràboles sigui de 576 unitats quadrades. 56) PAU 6 Sèrie 5 Qüestió 6: Sabem que una funció f ( ) té per derivada f '( ) ( + ) e i que f ( ). a) Trobeu l equació de la recta tangent a y f ( ) en el punt de la corba d abscissa. b) Calculeu l epressió de f ( ). Eercicis sobre integrals de les PAU Catalunya
13 SOLUCIONARI: ) PAU 999 Sèrie Qüestió : Calcula l àrea determinada per les corbes d equacions el dibui següent: y 4 i y representada en Primer hem de trobar en quin punt es tallen les dues corbes ( ) 4 4 ± 4 Per tant les corbes es tallen en, i. Ara hem de calcular l àrea que hi ha entre la corba inferior i la superior. Al dibui es veu clar que la corba superior és la paràbola, és a dir, la corba y i per tant la inferior és l altra. No cal dir que aiò també ho podíem saber agafant punts, avaluant les dues funcions i fent nosaltres la representació gràfica. Donat que SEMPRE és la mateia funció la que va per dalt no cal separar l interval d integració, en subintervals i per tant el nostre problema es resol mitjançant la integral. [ ] ( ) ( ) d ( 4 ) d k k k ,5u 5 5 ) PAU 999 Sèrie Qüestió : Calculeu raonadament l'epressió d'una funció f ( ) tal que f '( ) e i que f ( ). És evident que ens estan demanant una primitiva. Si agafem la funció G ' e e Aií G e i la derivem utilitzant la Regla de la Cadena tenim que e d e d e d e + k f. És a dir: f e + k De totes les primitives ens demanen la que fa que Sigui Eercicis sobre integrals de les PAU Catalunya
14 f ( ) e + k e + k + k k + k i per f e + tant la solució del problema és ) PAU 999 Sèrie Problema : 6 Donada la funció f ( ) c) Calculeu l'àrea limitada per la gràfica de la funció, l'ei OX i les rectes verticals. Evidentment hem de calcular f ( ) d. D entrada pot ser que aquesta integral funció f ( ) entre els punts f d i i no correspongui amb l àrea per sota de la. Però se suposa que aquest és l apartat c) d un problema on en els dos apartats primers ja ha quedat descartada aquesta possibilitat. f d d d + 4 d + + Però 4 ( 4) ( 4) d + 6 d 4 k 6 ln ( 4 ) k ' k 4 + k + 6( ln ( + 4 ) + k ' ln ( + 4 ) + k ') ( 6) ( ) 6( ln 6 ln 4) 6 6ln ( 6 ) 6 6ln ( ),49u ) PAU 999 Sèrie 5 Qüestió : f + k i Trobeu el valor del coeficient k de manera que l'àrea limitada per la funció l'ei d'abscisses sigui igual a 6u. En aquest cas ens hem de fer un dibui de la funció perquè la regió que ens demanen dependrà del valor del paràmetre k. Dibuiem la funció, per eemple quan k 4 Eercicis sobre integrals de les PAU Catalunya 4
15 En general, els talls de la funció f ( ) + k amb l ei OX seran: f ( ) + k k ± k Per tant ara sabem que l àrea de la regió limitada per la funció f ( ) + k i l ei OX és f d + k d k k ' k + + k k k ( ) k k ( ) k k ' k k k k k k k k ' k k k k k k k k k + 6k k 4k k + k k + k k Finalment: k 4k k f d 6 6 4k k 8 k k 7 k k 7 k k k 79 k 79 k 79 k 9 5) PAU 999 Sèrie 6 Qüestió : f Sigui. Calculeu l'àrea de la regió que limita la gràfica de f d'abscisses i que està representada en el dibui següent: i l'ei Evidentment el problema es resoldrà calculant una integral. Primer de tot anem a calcular els etrems de l interval d integració. Per fer-ho necessitem saber en quins punts la funció f Però talla l ei OX. És a dir, en quins punts f. f ±. Eercicis sobre integrals de les PAU Catalunya 5
16 Per tant el que hem de calcular és: f ( ) d f d d d d d d d d d d [ k] k ' ( + k ) ( + k ) k ' ( ) k ' ) PAU Sèrie Qüestió : Calculeu l'àrea que té l'únic recinte tancat limitat per les gràfiques de les representat en el dibui següent: y + 7 i 6 y Quan ens demanen l àrea compresa entre dues corbes sempre hem de trobar els punts de tall entre les corbes i saber quina va per dalt i quina va per sota. En aquest cas la funció y + 7 és una paràbola invertida i és la que en el gràfic del dibui va per dalt. 6 Calculem ara en quins punts es tallen les dues corbes y + 7 i y per saber els etrems d integració ( + 7) que podem resoldre per Ruffini. (Tot i que es veu clarament que una de les arrels és ) Finalment resolem l equació de n grau que ens dóna com a solucions i. Per tant, el nostre interval d integració serà [, ] i l àrea a calcular serà: (Cal destacar la mala qualitat del dibui que van ficar en aquest eamen de selectiu donat que està totalment deformat) Aquí teniu el dibui de les mateies funcions però una mica millor escalat: Eercicis sobre integrals de les PAU Catalunya 6
17 6 6 + d + d + + k ( 7) 7 7 6ln + 7 6ln + k + 7 6ln + k ln 6 + k k ln,577 7) PAU Sèrie Qüestió : Calculeu per integració la superfície del recinte delimitat per les corbes d'equació y 6 representat en el dibui següent: y i la recta Com sempre, primer hem de calcular on es tallen les dues corbes. y 6 y També cal veure quina és la funció que va per sobre i la que va per sota. Al dibui es veu clar que la recta va per sobre mentre que la paràbola va per sota. Finalment calculem la integral que ens donarà l àrea: ( ) + 6 d + 6 d 6 k + + ( ) ( ) k + 6 ( ) + k k + k u Eercicis sobre integrals de les PAU Catalunya 7
18 8) PAU Sèrie Qüestió : El polinomi p ( ) + a + b s'anul la per a i complei Calculeu raonadament a i b. p d 4. El nostre polinomi depèn de dos paràmetres a i b i ens donen dues condicions, per tant, d entrada, si les dues condicions són independents entre si, el problema tindrà solució única. p ( ) + a + b s anul la per a : p + a + b 4 + a + b a + b 4 a p d 4 + a + b d b + k 4 a a b + k + + b + k 4 + a + b a + b 4 a + b a + b a + b Per tant tenim el sistema: a + b 4 F F 6a + b F F 6a + b 6a + b 4 a a + b a + b a b a 4 4 a 4 6 6a + b 6 + b 8 + b b 6 b 4 6 Per tant la solució al problema és a i b 9) PAU Sèrie 5 Qüestió : k d Trobeu el valor de k per tal que k + k k k+ k d ln ( k ) + a ( ln ( k k ) + a ln ( k + k ) a) k k+ ln ( k ) + a ln a ln ( k ) ln ln ( k ) ln ( k ) k Per tant, k + d k ( k ) ln k e e k e ln ) PAU Sèrie Qüestió : π a) Quin és l'angle en radians < < tal que sin ( ) cos( ) Evidentment és l angle de 45º que correspon a 4 π radians.? (Aiò resulta obvi per definició de sinus i cosinus com a Catet oposat/hipotenusa i Catet contigu/hipotenusa. L angle de 45º fa que els dos catets siguin iguals, és a dir, el triangle és isòsceles i per tant el sinus i el cosinus han de ser el matei.) Eercicis sobre integrals de les PAU Catalunya 8
19 b) Considereu les funcions f ( ) sin ( ) i g ( ) cos( ). Calculeu la superfície del recinte delimitat superiorment per les gràfiques d'aquestes funcions, inferiorment per l'ei d'abscisses i π lateralment per les rectes verticals i representat en l'esquema següent: Resulta evident que el nostre problema es resol mitjançant una integral des de fins π π. Però aquest interval l haurem de dividir en dos subintervals. I, 4 i π π I 4,. f sin g cos. En cadascun d aquests intervals, de les dues funcions i integrarem la funció que va per sota. Evidentment, donat que sin ( ) i cos ( ) π tindrem que en l interval I, 4 la funció que va per sota és f ( ) sin ( ) π π en l interval I 4,, la funció que va per sota és g ( ) cos ( ), mentre que. Per tant, l àrea del nostre problema correspon a la suma de les dues integrals següents: ( ) d ( ) d ( ) ( ) 4 π π 4 π π sin cos cos sin π π π π π cos + cos + sin sin u ) PAU Sèrie 4 Qüestió 4: Sabeu que la gràfica de la funció f ( ) passa pel punt (, 4) f '( ). a) Determineu l'epressió de f ( ). Com f ( ) passa per (, 4) aleshores, f ' f d f + k i que la seva funció derivada és f 4 + k 4 + k 4 + k 4 k i per tant: f b) Calculeu l'àrea de la regió limitada per la gràfica de f ( ) i l'ei d'abscisses OX. Per calcular l àrea de la regió limitada per la gràfica de f ( ) i l ei OX haurem de calcular els punts de tall entre la funció f ( ) i l ei. Per fer-ho resolem l equació f ( ). Eercicis sobre integrals de les PAU Catalunya 9
20 f f d d k + ( ) + k ( ) ( ) + k k + + k Per tant hem de calcular Que el resultat sigui negatiu solament vol dir que la regió que hem integrat està per sota de l ei OX i que té un àrea de u. Per tant, la resposta al problema és u. Aquí tens representada la funció i la regió a integrar: ) PAU Sèrie 5 Qüestió : Teniu una funció f ( ) definida per a (,), sabeu que el gràfic de f ' forma és de la on f '( ), f '( ), f ' i que f ( ). Dibuieu un gràfic aproimat de f ( ) indicant en quins punts hi ha etrems relatius. Podem observar en el gràfic de f '( ) que f '( ) és una funció definida a trossos. En l interval (, ] és una recta de pendent i ordenada a l origen també, mentre que en l interval [, ) f '( ) és una recta de pendent i ordenada a l origen, per tant tenim que: f '( ) si < si < < Ara, integrant en cadascun dels dos intervals tenim que f ( ) + k si < + k ' si < < Eercicis sobre integrals de les PAU Catalunya
21 Com la funció f ( ) és derivable en l interval (, ) (perquè eistei la seva derivada), aleshores f ( ) és continua en aquest interval. En particular ha de ser continua en el punt on es troben els dos intervals i per tant lim f ( ) lim f ( ) f ( ) Però: + lim f lim + k + k + + k k lim f lim + k ' + k ' k ' + + lim f lim f f k k ' i per tant: + f ( ) + si < + si < < En el següent gràfic està representada la funció f ( ) en blau i la seva derivada f ' vermell. en ) PAU Sèrie 5 Qüestió 4: f e Calculeu l'àrea de la regió limitada per la gràfica de la funció d'abscisses i la recta vertical. Evidentment l àrea que ens demanen es resol mitjançant la integral: f d e d f e s ha d integrar per parts. Però la funció Repetirem la demostració de la fórmula de integració per parts: d u v udv + vdu, prenent integrals: d u v udv + vdu u v udv + vdu udv u v vdu En el nostre cas: Agafant u i dv e tenim que: u du d i dv e d v e d e per a Finalment, substituint en la fórmula de la integració per parts tenim: udv u v vdu e d e e d e d e e e Una vegada calcula la integral indefinida, calcular la definida resulta trivial: e e e e e +, l'ei Eercicis sobre integrals de les PAU Catalunya
22 4) PAU Sèrie Qüestió : Calculeu el valor positiu de a que fa que l'àrea compresa entre la recta d'equació la paràbola y a valgui 8. y a + a i Sempre que ens demanin un àrea d un recinte d integració el primer que hem de fer és un dibui del recinte. En la gràfica de la dreta s han representat les gràfiques per al valor a. Evidentment haurem de calcular els punts on les dues corbes es tallen: a a a a a a a + ( a) Per tal de plantejar la integral que correspon a l àrea també hem de saber quina és la funció que va per sobre i quina per sota, en el nostre cas, es veu clarament que la recta per sobre i la paràbola per sota. Aií: (( ) ) ( ) Àrea a + a a d a + a + a d a + + d a + + d a + + ( ) ( ) 8 a ( ) a a a a 9a 8 Àrea 8 8 a a 4 9 5) PAU Sèrie Qüestió : Calculeu l'àrea compresa entre les gràfiques de les corbes representada en l'esquema següent: y e i y e i la recta y 5 Com sempre, el primer que hem de fer es representar el recinte d integració perquè el dibui que donen a la sele tot i que ajuda deia molt que desitjar. Aquí tens el dibui de l eamen de selectivitat i un altra representació realitzada amb el Geogebra. Per plantejar la integral o integrals que corresponen al recinte d integració hem saber on es tallen les diferents corbes. de Eercicis sobre integrals de les PAU Catalunya
23 Aií: f e Tall entre y : i la recta 5 ln 5 f ( ) y e 5 ln ( e ) ln 5 ln e ln 5 ln 5 g e i la recta y 5: Tall entre ln 5 y 5 g ( ) y e 5 ln ( e ) ln 5 ln e ln 5 ln 5 ln 5 Per tant, hem de separar el recinte d integració en dos parts, l interval, on tindrem la funció y 5 que anirà per sobre i la funció g( ) e ln 5 que anirà per sota i l interval, f ( ) e va per sota. on la funció y 5 anirà per sobre i la funció També val a dir que per simetria aquestes dues integrals han de valer el matei, per tant també podem calcular una de les dues i multiplicar el resultat per. ln 5 ln 5 ln 5 A ( 5 e ) d 5 e e 5 e ln 5 5ln 5 5ln 5 5 5ln 5 5ln ln 5 e 5, Per tant, l àrea total serà A A, 4,4 NOTA: També haguéssim pogut calcular l altra integral, seria aquesta: ln 5 ln 5 ln 5 ln 5 A 5 e d 5 e 5 e e 5ln 5 ln 5 5ln 5 5ln 5 e 5 +, 6) PAU Sèrie Qüestió : f Calculeu la primitiva de la funció que s'anul la en el punt d'abscissa. ( ) f d d d d F (*) Sigui un candidat a primitiva, aleshores: F '( ) ( ) ( ) ( ) Per tant, el que necessitem és introduir un dintre de la integral, és a dir, ( ) (*) ( ) d ( ) d + + C + C Eercicis sobre integrals de les PAU Catalunya
24 Com ens demanen la primitiva que s anul la en hem d imposar la condició ( ) F + C + C + C + C C i per tant la primitiva que ens estan demanant és: F ( ) 7) PAU Sèrie Qüestió : e ln ( ) Calculeu d. 4ln 4 Sigui F ( ) ln ( ) un candidat a primitiva, aleshores F '( ) 4ln ( ) Per tant, solament ens cal introduir un dintre de la nostra integral original. Aií: e e e ln ( ) 4ln ( ) 4ln ( ) 4 e 4 4 d d d ln ( ) ( ln e ln ) (( ln e) 4 ( ln) 4 ) ( 4 4 ) ( ) ( ) 8) PAU Sèrie Qüestió : Donada ( f + e + ), determineu la funció g ( ) tal que g '( ) f ( ) una primitiva de f ( )) i que el seu gràfic passa pel punt (, ). Una funció g ( ) tal que g '( ) f ( ) ( ) és una primitiva de f. Per tant: + + g f d + e d e + C Si aquesta primitiva ha de passar pel punt, tenim: + + (és a dir, g e + C e + C + C C g e + 9) PAU Sèrie 5 Qüestió : Considerem la regió S del pla limitada per la paràbola en l'esquema següent: y i la recta y representada Eercicis sobre integrals de les PAU Catalunya 4
25 Siguin A i B els punts d'intersecció de la recta i la paràbola, i T el triangle que té per vèrtes A, B i l'origen de coordenades (, ). Calculeu l'àrea de la regió que resulta quan es treu el triangle T a la regió S. Es pot fer un dibui més acurat del recinte d integració dibuiant també el triangle, seria aií: L àrea que se ns demana és la pintada de color marró. Aquesta àrea es pot calcular de moltes maneres però potser la més intel ligent sigui calcular el recinte entre la recta y i la paràbola i desprès restar-li l àrea del triangle com base altura. Primer de tot necessitem els punts de tall entre la recta i la paràbola. Aií: ± Àrea entre la paràbola i la recta: ( ) d Àrea triangle: base altura AT Àrea recinte: 4 ) PAU 4 Sèrie Problema : Considereu la funció f ( ) + m +, m. a) Calculeu el valor de m per tal que l àrea del recinte limitat per la gràfica de la funció, l ei OX i les rectes i sigui de unitats quadrades. NOTA: La funció f serà sempre positiva en aquest interval, donat que en l interval [, ] la variable és sempre positiva i per tant, donat que m tindrem que tots els termes de f + m +, m seran positius. Aií, una vegada descartats canvis de signe podem assegurar que l àrea demanada coincidirà amb f d f ( ) d ( + m + ) d + m + + m + ( ) 4 + m m 4 4 Eercicis sobre integrals de les PAU Catalunya 5
26 8 8 4 Àrea 6 + m m 4 m m 8 b) Per a m, indiqueu el punt o els punts on la recta tangent a la gràfica de la funció forma un angle de 45 amb el semiei positiu de OX. m f + m + f + + La recta que fa 45º amb el semiei positiu de OX és la diagonal del primer quadrant és a dir, al recta y que té pendent. Per tant, m estan preguntant en quins punts la derivada val. f + + f ' + f '( ) + + Per tant els punts de la funció f on la recta tangent formarà un angle de 45º amb el semiei positiu de OX seran: (, f ( ) ) i (, f ), és a dir, (,) i (, 7 ) ) PAU 4 Sèrie Qüestió : f cos cos : Donada la funció a) trobeu la seva integral indefinida; sin + cos. Indicació: recordeu que ( indicació ) cos cos cos cos cos sin ( ) f d cos cos d cos sin d sin cos d d C sin cos sin + b)quina és la primitiva de F sin C π f que passa pel punt,? π, sin C + π π + passa pel punt F + + C C C F sin F sin ) PAU 4 Sèrie 4 Qüestió : Eercicis sobre integrals de les PAU Catalunya 6
27 Calculeu l àrea del recinte tancat que delimiten la gràfica de la funció y. En qualsevol problema d àrees el primer que hem de fer és dibuiar el recinte. Per poder plantejar la integral caldrà trobar els punts de tall entre les dues gràfiques. Aií: ( ) Finalment plantegem la integral: i la recta y Àrea d d d d d d 8 ) PAU 4 Sèrie 4 Qüestió 4: Considereu la funció f ( ) de la figura definida a l interval [, ]. a) Calculeu la funció derivada f '( ) a l interval (, ) La funció derivada, si eistei coincidei amb la pendent de la recta tangent de la funció. Quan la funció és una recta (polinomi de grau ) la seva derivada és una constant (polinomi de grau ) que coincidei amb la pendent de la recta. En el nostre cas, en l interval (, ) la funció f té una pendent de: y f f Pendent, la funció f té un pendent de: Mentre que en l interval y f f,5,5 Pendent,5 Eercicis sobre integrals de les PAU Catalunya 7
28 Per tant, f ( ) si, ' si (,) Noteu que en el punt la funció f no és derivable!! b) Hi ha algun punt de (, ) en el qual f ' no eistei f ' En no eisteii? perquè la funció f no és derivable donat que no coincideien les derivades laterals per l esquerra i per la dreta. La derivada per l esquerra de seria mentre que per la dreta seria. NOTA: També es podria dir que f no és derivable en el punt argumentant que en aquest punt la gràfica de f no és suau, és a dir, té un pic. c) Calculeu f ( ) d. Per calcular aquesta integral es podria raonar que aquesta integral correspon a l àrea entre la funció f, les rectes, i l ei OX i que per tant es pot calcular com a suma de l àrea de dos triangles i un rectangle o també calculant l epressió analítica de f i integrant-la. Raonant per figures geomètriques tindríem que l àrea és: 7 A AT + A T + A R Raonant calculant la funció f el raonament podria ser el següent: si, + C si, (,) f ( ) f '( ) f ( ) si (,) + C si (,) si, si, f ( ) f ( ) + + si (,) si (,) Finalment integrem la funció: + f ( ) d f ( ) d + f ( ) d d + d ) PAU 4 Sèrie 5 Qüestió : Eercicis sobre integrals de les PAU Catalunya 8
29 Calculeu el valor de la integral següent: d + Podem calcular la primitiva de la funció dividint-la en dos parts d d + d d + d d + d C d ) PAU 5 Sèrie Problema : Considereu la funció f ( ) 4. a) Calculeu l equació de les rectes tangents a la gràfica de f en els punts d abscisses i 4. Sabem que l equació de la recta tangent a la gràfica de la funció f ( ) en el punt a és: y f ( a) f '( a)( a) En el nostre cas: f ' f ( ) 4 f '( ) 4 f ' la recta tangent és: Per tant en el punt y f f ' y 4 y 4 I en el punt 4 la recta tangent és: y f 4 f ' 4 4 y 4 4 y b) Feu un gràfic dels elements del problema. En el gràfic de la dreta estan representats els diferents elements del problema. Eercicis sobre integrals de les PAU Catalunya 9
30 c) Calculeu l àrea compresa entre la gràfica de f i les rectes tangents que heu trobat a l apartat a). Per poder plantejar la integral o les integrals que donen l àrea primer hem de calcular els punts de tall. En el nostre cas no ens cal calcular els talls entre les rectes i la paràbola perquè per construcció la recta y 4 ambdues serà el punt ( ) f es produirà en el punt ( 4, ( 4) ) és tangent a la paràbola en el punt i per tant el tall entre, f. Anàlogament el tall entre la recta y i la paràbola f. Per tant, el únic punt de tall que ens caldrà calcular és el tall entre les dues rectes que segons el dibui ja es veu clar que serà en l abscissa Per tant, l àrea serà: 4 ( 4 ) ( 4 6 ) A f d + + f d 4 ( 4 ( 4 )) 4 6 ( 4 ) d + + d ( 4) 4 4 d + ( 8 + 6) d d + ( 4) d + ( ) ) PAU 5 Sèrie Problema : Considereu la funció f ( ) + + b si < ae b si on a i b són nombres reals. a) Quina condició han de complir a i b per tal que f sigui contínua a tot R? f és una funció definida a trossos, on el primer tros és un polinomi que és una funció continua en tot R i el segon tros és una funció eponencial que també és continua en tot R. Per tant, l únic problema de continuïtat el podem tenir en el punt que és on s uneien els dos trossos de la funció. La funció f serà continua en el punt si els límits laterals coincideien i aquest valor lim f lim + + b + + b b Eercicis sobre integrals de les PAU Catalunya
31 b b lim f lim ae ae ae a a + + b f ae ae a a Per tant, f continua en tot Rsii a b b)trobeu els valors de a i b per als quals f sigui contínua però no derivable a tot R. + + b si < + si < + si < f ( ) f '( ) f '( ) b b b ae si ae b si abe si La funció f serà derivable en els dos trossos, a l igual que abans, el que hem de mirar és el punt on s uneien aquests trossos. + si < + si < si < f '( ) f '( ) b b abe si abe si ab si Per a que no sigui derivable s ha de complir que a b. Per tant hem de resoldre el sistema: a b a a a a a ± a b Per tant per a que la funció sigui continua en tot R però no derivable en tot Rs ha de complir que a b ± c) Per a a i b, calculeu f d. + + b si < si a + + < f ( ) f b ( ) b ae si e si Com en l interval [,] la funció està definida en dos trossos, hem de dividir la integral en dos: f d f d f d d e d e e e e e e ) PAU 5 Sèrie 4 Qüestió : Eercicis sobre integrals de les PAU Catalunya
32 5 4 : f d. Donada la funció: a) Calculeu la integral f f d d d d (*) ( 5 4) F 5 4 un candidat a primitiva, aleshores: Sigui F '( ) ( 5 4) 5 ( 5 4), per tant, necessitem ficar un 5 dintre de la integral. f d d d d (*) ( 5 4) 5 4 (*) 5( 5 4) d 5( 5 4) d ( 5 4) C C b) Trobeu la primitiva F de f que compleii F F + C + C C F ) PAU 6 Sèrie Qüestió : y f Considereu la funció definida per a [, 5] adjunta. que aparei dibuiada a la figura a) Quina és l epressió de la seva funció derivada quan eistei? La derivada en un punt coincidei amb la pendent de la recta tangent en aquest punt. Si la funció és una recta, aleshores la recta tangent en un punt és precisament la funció. Per tant en l interval [, ]: y f f ( ) f '( ) Pendent recta tan gent En l interval [,4 ]: Eercicis sobre integrals de les PAU Catalunya
33 f y f 4 f '( ) 4 4 4,5 : En l interval [ ] y f f f ( ) 5 4 ' Aií: si, f ' si,4 si 4,5 Noteu que en i en 4 la funció no és derivable. b) Calculeu f ( ) d. Com la funció f és estrictament positiva en l interval [, ], és a dir, no canvia de signe en aquest interval, la integral anterior coincidei amb l àrea del recinte format per la funció, l ei OX i les rectes i que podem calcular directament sumant els quadrets, dóna 4. També podríem calcular aquesta àrea trobant l epressió analítica de la funció i desprès integrant-la, en aquest cas el raonament seria: si, + C si, (,) f f f '( ) si,4 f ( ) C si, 4 ( 4,) f f si 4,5 + C si 4,5 [,) [ ) [ ] + C C si C C f ( ) si,4 4 + C C + si 4,5 f ( ) d f ( ) d f ( ) d d d [ ] ) PAU 6 Sèrie 4 Qüestió : El gràfic de la funció f ( ) +, quan >, és com seguei: Eercicis sobre integrals de les PAU Catalunya
34 a) Trobeu una primitiva de la funció f. f d d d d ln ( + ) + C b) Calculeu l àrea de la regió ombrejada f ( ) d d ln ( + ) ln9 ln5 ( ln9 ln5) ln ln 5 ln 9 5 ) PAU 6 Sèrie 4 Problema : Considereu la paràbola d equació y +. i a) Calculeu les equacions de les rectes tangents a la paràbola en els punts d abscissa. Donada una corba f ( ) sabem que l equació de la recta tangent en el punt a és y f ( a) f '( a)( a) En el nostre cas: f ' + + f ( ) + f '( ) + f ' Recta tangent en : ( ) y f f ' y 4 + y + 4 y 4 Recta tangent en : y f f ' y 4 y 4 4 b) Calculant el mínim de la funció y + trobeu el vèrte de la paràbola. Per calcular el mínim hem de fer la derivada: Eercicis sobre integrals de les PAU Catalunya 4
35 y + y ' + y ' + Interval (, ) (, + ) Signe de f '( ) + Monotonia de f ( ) m Per tant, en el punt la funció passa de decreient a creient i per tant té un mínim relatiu., f ( ), 4 c) Trobeu les interseccions de la paràbola amb els eios i feu una representació gràfica de la paràbola i de les tangents obtingudes al primer apartat. Talls amb l ei OX: y + Tall amb l ei OY: (,) (, ) y +, d) Calculeu l àrea compresa entre la paràbola i les rectes tangents. Podem observar que és impossible calcular tot el recinte d integració mitjançant una sola integral. Hem de calcular el punt d intersecció de les dues rectes i integrar els dos recintes. Punt d intersecció de les dues rectes: A A + A on: A ( + ( 4) ) d ( + + ) d + + ( ) + ( ( ) ( 4 4) ) ( ) A + d + d + + ( ) Eercicis sobre integrals de les PAU Catalunya 5
36 A A + A + ) PAU 7 Sèrie Qüestió : Busqueu els etrems relatius i els punts de tall amb els eios, i feu una representació aproimada de la corba d equació per aquesta corba i l ei d abscisses. Etrems relatius: 4 y y' 4 y 4. A continuació, calculeu l àrea del recinte tancat y ' 4 ( ) ± Interval (, ) (, ), (,+ ) Signe de f '( ) + + Monotonia de f ( ) m M m Finalment calculem les dues coordenades d aquests etrems relatius: ( ) ( ) ( ) 4 y A, y B, 4 y C, Punts de tall amb els eios: Talls amb l ei OX: ( ) y Tall amb l ei OY: 4 y, El recinte a integrar, acolorit de color marró coincidirà amb la integral de la funció entre i canviada de signe perquè la funció durant tot aquest interval va per sota de l ei d abscisses. Per tant: 5 4 A f ( ) d ( ) d 5 ± Eercicis sobre integrals de les PAU Catalunya 6
37 ) PAU 7 Sèrie Qüestió 4: F ' d una funció contínua F : La funció derivada funció a trossos formada per les semirectes del dibui. R R que passa per l origen és una Escriviu l epressió de la funció F ( ) com una funció a trossos. Donat que la funció F '( ) és una funció definida en dos trossos (,) i [ ) primitiva F ( ) també serà una funció definida en aquests dos trossos. En l interval (,) la funció F '( ) és la recta de pendent i ordenada en l origen. En l interval [, + ) la funció F '( ) és constant igual a. Aií: si (,) F '( ) si [, + ) I per tant: + C si, F ( ) + C si, + [ ) Donat que la funció passa per l origen tenim: F + C C.,+ la seva Com també ens diuen que la funció és continua en tot Raleshores ha de ser continua en el punt que és on s empalmen els dos trossos que la defineien. Aií: + C + C C I per tant: F si si, + (,) [ ) Eercicis sobre integrals de les PAU Catalunya 7
38 ) PAU 7 Sèrie Problema : Donades les funcions f ( ) a 4 i g ( ) + b: a) Calculeu a i b de manera que les gràfiques de f ( ) i de d abscissa, és a dir, que tinguin la mateia recta tangent en aquest punt. Dues funcions f i g són tangents en un punt funcions i les seves derivades, és a dir, si f ( a) g ( a) g siguin tangents en el punt a si en aquest punt coincideien les i f '( a) g '( a). En el nostre cas: f g a 4 + b a 4 + b a + b 9 4 a + b 6a + b f a 4 f ' a g ( ) + b g '( ) f ' g ' a 6 a 6 a a 6a + b 8 + b b 7 b a a a a 7 b) Trobeu l equació de la recta tangent esmentada en l apartat anterior. Com la recta tangent a les dues funcions és la mateia calcularem la recta tangent a la funció f. Sabem que la recta tangent a la gràfica d una funció f en el punt ' y f a f a a. En el nostre cas, y f ( ) f '( ) f 4 a f ( ) 4 f '( ) f ' y 4 y y a és Eercicis sobre integrals de les PAU Catalunya 8
39 c) Pel valor de a obtingut en el primer apartat, calculeu el valor de l àrea de la regió limitada per l ei d abscisses OX i la funció f ( ). Abans de calcular l àrea ens hem de dibuiar el recinte d integració. Talls de la funció amb l ei OX: y f ( ) 4 4 Com el recinte a integrar queda per sota de l ei OX la integral ens donarà negativa i per tant l àrea coincidirà amb el valor absolut de la integral. 4 4 f ( ) d ( 4) d ( ) ( ) ( ) Per tant: Àrea f ( ) d ) PAU 8 Sèrie Qüestió : Se sap que certa funció derivable F ( ) verifica les condicions següents: a) Trobeu F ( ). F ' ( ) i 4 F Per trobar F ( ) hem de trobar una primitiva de F '( ) F F ' d d d d C C F + C + C C C F ( ) + b) Calculeu l àrea compresa entre F ( ) i l ei OX des de fins a. Si no dibuiem prèviament la funció no podem assegurar que l àrea que ens demanen coincideii amb F d Eercicis sobre integrals de les PAU Catalunya 9
40 perquè podria passar que la funció F ( ) canviés de signe en aquest interval. Però al funció F que: és positiva en aquest interval i no canvia de signe. Aií podem assegurar Àrea F d d d ) PAU 9 Sèrie 4 Qüestió : Considereu la funció f ( ) ( ) a, amb a >. a f a) Trobeu els punts de tall de la funció amb l ei OX. Talls amb l ei OX: ( ) a y f ( ) a a a a Per tant, els punts de tall amb l ei OX són (,) i ( a,) b) Comproveu que l àrea del recinte limitat per la gràfica de la funció f ( ) i l ei d abscisses no depèn del valor del paràmetre a. La funció f ( ) és una paràbola cap a bai donat que el producte ( a ) de segon grau amb el coeficient corresponent a negatiu. és un polinomi a a a a a a Àrea f ( ) d d ( a ) d ( a) d a a a + + a a a a a a a a a a a a a a 6 6a 6 NOTA: Podem observar com el resultat és sempre /6 que no depèn de a. Eercicis sobre integrals de les PAU Catalunya 4
41 6) PAU 9 Sèrie Qüestió : Considereu les corbes y 4 i a) Trobeu-ne els punts d intersecció. y Si volem calcular les dues coordenades dels punts podem triar qualsevol de les funcions. Aií:, 5 B, A ( ) i b) Representeu les dues corbes en una mateia gràfica, on es vegi clarament el recinte que limiten entre elles. c) Trobeu l àrea d aquest recinte limitat per les dues corbes. ( 4 6 ) ( 4 6) ( ) Àrea f g d d + d d ( ) ( ) + 6 ( ) 64 ( ) Eercicis sobre integrals de les PAU Catalunya 4
42 7) PAU 9 Sèrie Problema : 4 b Sigui la funció f ( ) a + +. a) Calculeu els valors de a i b, sabent que la recta + y 4 és tangent a la gràfica de la f en el punt d abscissa. funció 4 + y 4 y 4 y + Per a que una funció f i una recta r siguin tangents en el punt, en aquest punt han de coincidir els seus valors i les seves derivades, és a dir, f r i f '( ) r '. 4 b 4 f ( ) a + + a b f '( ) 4 b f '( ) 4 r ( ) + r '( ) b 4 b 4 4 b 4 b 4 4 f r a a a b b 4 a + + a + a + b b 4 b b 8 f '( ) r ' b 8 b 8 b 6 b 9a + b 9a + 9a 9 a Per tant, a i b Per a la resta d apartats, considereu que a i que b 4. b) Trobeu els intervals de creiement i de decreiement de la funció f ( ). Trobeu i classifiqueu els etrems relatius que té la funció. A partir d aquest apartat ens fan treballar amb la funció f on a i b f ( ) + + Per estudiar els etrems d aquesta funció cal derivar-la i igualar-la a zero., per tant: f ( ) f '( ) 4 8 f '( ) f '( ) Eercicis sobre integrals de les PAU Catalunya 4
43 4 4 ( + ) + Recordem que en la taula següent fiquem els punts on s anul la la derivada i també els punts on la funció és discontinua. f és discontinua en zero. ( ) Interval (, ) (,) (,+ ) Signe de f '( ) + Monotonia de f ( ) m Per tant la funció té un mínim relatiu en el punt f (, ) (, 4) f és estrictament decreient en (, ) (, + ) i estrictament creient en (,) c) Calculeu els punts de tall de la funció f ( ) amb l ei OX. Talls amb l ei OX: 4 4 y f ( ) Per tant els punts de tall amb l ei OX són, i (, ). d) Trobeu l àrea del recinte limitat per la gràfica de la funció f ( ), l ei OX i les rectes i. En el gràfic s ha representat la funció f ( ) i les rectes i. El primer que hem d observar és que la funció f canvia de signe en l interval (, ) per tant, l àrea del recinte no es correspondrà amb el resultat d una única integral sinó la suma de dos. Aií: f ( ) d + + d d d d ln + C Eercicis sobre integrals de les PAU Catalunya 4
44 4 A f ( ) d + 4ln ( 6 + 4ln ) ( + 4ln 4) 8 + 4ln ln, A f ( ) d + 4ln 9+ 4ln ( 6+ 4ln ),7,7 Per tant, A A + A,77 +,7, 48 8) PAU 9 Sèrie 4 Problema : + La gràfica de la funció f ( ), des de fins a 4, és la següent: i a) Calculeu l equació de les rectes tangents a aquesta funció en els punts d abscissa. L equació de la recta tangent a la gràfica d una funció f ( ) en el punt a és y f ( a) f '( a)( a) En el nostre cas f ( ) f '( ) f + ( ) f f ' f ' Rectes tangents: y f f ' y 4 y + 7 y f ( ) f '( ) y ( ) y + y + b) Dibuieu el recinte limitat per la gràfica de la funció i les dues rectes tangents que heu calculat. Eercicis sobre integrals de les PAU Catalunya 44
45 c) Trobeu els vèrtes d aquest recinte. Els vèrtes del recinte seran els punts on les rectes són tangents a la corba, és a dir A (, f ) B 4, f 4 i el punt Con es tallen les dues rectes. Aií: i ( ) (, ( )) (, ) (,4 ) i ( + B (, f ), ) (,) A f + Calculem el punt on es tallen les dues rectes: y C, Eercicis sobre integrals de les PAU Catalunya 45
46 d) Calculeu la superfície del recinte damunt dit. L àrea del recinte no es pot calcular mitjançant una sola integral perquè des de fins a el recinte està limitat per les funcions f i y + 7 mentre que entre i el recinte està limitat per les funcions f ( ) i y +. Per tant: + A ( + 7) d + ( + 7) d d + d + d 7d ln C ln C + ( + ) + A 7 d ln 6,94 A + + d + + d d + d + d d ln C 6 ln + + C 6 + A + d ln ln 6 ln, 44 A A + A,94 +, 44, 958 Eercicis sobre integrals de les PAU Catalunya 46
47 9) PAU Sèrie Qüestió 5: f sin és la següent: La gràfica de la funció a) Trobeu-ne una primitiva. Aquesta integral es fa per parts. Recordem el procediment per treure la fórmula de les integrals per parts: d u v u dv + v du u dv d u v v du u dv u v v du Sigui u i dv sin ( ) d du d i v sin d cos, aleshores: ( ) cos( ) + sin( ) + C sin d cos cos d cos + cos d b) Aplicant el resultat de l apartat anterior, calculeu l àrea del recinte limitat per la gràfica de la f i l ei d abscisses des de fins a π. funció Segons el dibui, la funció no canvia de signe en l interval (,π ) i és positiva en aquest interval, per tant, l àrea del recinte coincidirà amb la integral, aií: π ( π π π ) Àrea sin d sin cos sin cos sin cos ( ) ( ) ( ) ( ) π + π π π 4) PAU Sèrie Qüestió 5: Sigui f ( ) i les rectes 8 + i.. Trobeu l àrea del recinte limitat per la gràfica d aquesta funció, l ei OX Abans de plantejar l àrea mitjançant una integral ens hem d assegurar que la funció no canvia de signe en l interval que estem estudiant. En el nostre cas l interval és [, ] i òbviament el numerador és sempre positiu en aquest interval i no canvia de signe. Per altra banda, el Eercicis sobre integrals de les PAU Catalunya 47
48 denominador tampoc dóna problemes en aquest interval dons l únic punt on s anul la no pertany a [,] perquè + [, ]. Aií, podem assegurar que l àrea del recinte coincidei amb f Procedim ara a calcular la integral: d. Aquesta és una funció racional on el numerador té major grau que el denominador. En aquest cas s ha de fer la divisió dels polinomis ( ) f ( ) d d 4 + d + ln ( + ) + C + + f d + ln ln 5 + ln 4 + ln 5 4) PAU Sèrie 5 Qüestió 6: y 4 i una recta r que passa per l origen i talla la En la figura es mostra la corba corba en un punt P d abscissa k, amb < k < 4. a) Trobeu l àrea ombrejada, delimitada per la corba i la recta, en funció de k. Podem plantejar l àrea del recinte de dues formes diferents: MÈTODE : Plantegem l àrea entre la paràbola, l ei OX i les rectes k, i P. l àrea del triangle de vèrtes (, ), Com el punt P pertany a la gràfica de la corba y ( 4 ) serà P ( k, y ( k )) ( k, k ( 4 k )). i k i li restem i té ordenada k, el punt P Eercicis sobre integrals de les PAU Catalunya 48
49 Per tant el triangle de vèrtes (, ), ( k,) i P tindrà base igual a k i altura igual a k k ( 4 k ) k ( 4 k ) k ( 4 k ), és a dir, Àrea L àrea entre la paràbola, l ei OX i les rectes i kserà k k k k k y d 4 d 4 d k k k ( 4 k ) Àrea recinte Àrea funció - Àrea triangle k k k k k k k k MÈTODE : Calculem l equació de la recta que passa per l origen i per P i calculem l àrea del recinte com l àrea que hi ha entre la paràbola i la recta. Sigui r la recta que busquem. Sabem que r passa per l origen de coordenades és a dir, per O (,) P ( k, y ( k )) de la corba, aquest punt és P ( k, k ( 4 k )) i per un punt Per tant la recta r té ordenada en l origen igual a zero (perquè passa per l origen de coordenades) i té com a pendent: ( ) ( ) k y y k y k 4 k k 4 k 4 k Pendent 4 k k k k Per tant r és la recta de pendent 4 k i ordenada en l origen, és a dir, r : y ( 4 k ) Finalment: k k k ( ( 4 ) ( 4 ) ) ( 4 4 ) ( ) Àrea k d + k d + k d k k k k k k k k b) Trobeu per a quin valor de k l àrea de la regió ombrejada és la meitat de l àrea del recinte limitat per la corba i l ei OX. L àrea del recinte limitat per la corba i l ei OX és: y d 4 d 4 d 4 Si l àrea ombrejada ha de ser la meitat que l àrea anterior tenim que: k k k k k Eercicis sobre integrals de les PAU Catalunya 49
50 4) PAU Sèrie Qüestió : i g ( ) Definim les funcions f ( ) a ( ), en què a >. a a) Comproveu que l àrea del recinte limitat per les gràfiques de les funcions és ( + a ) 4 a. El primer que hem de fer és un dibui de la situació. Per fer-lo és indispensable calcular els punts de tall entre les dues gràfiques. f ( ) g ( ) a( ) a ( ) a ( ) ( ) a a + a + a + ± Àrea ( f ( ) g ( ) ) d a( ) d a a + d a a a a a a a + a + a + + a a a a a a a a 6 6 a a a + a + + a + a + a a a a a a a ( a + ) 4a a a b) Calculeu el valor del paràmetre a perquè aquesta àrea sigui mínima. Ens demanen minimitzar la funció f ( a) 4a + 4. a 4a + 4 8a a ( 4a + 4) 4a a a f ( a) f '( a) a a 9a 9a ( a ) 4a 4 4 a a ( a ) 4 f ( a) a a a a a ' ± Per tant, els candidats a màims o mínims són a i a. Com l enunciat diu que a > hem de descartar el valor a. Per saber que en el punt a de veritat s assolei un mínim es podria fer un estudi del signe de la derivada per intervals. (Solament caldria ficar per a > perquè aií ens ho indica l enunciat) o també estudiant el signe de la segona derivada en aquest punt. Eercicis sobre integrals de les PAU Catalunya 5
51 ( a ) 4a 4 8a a 4a 4 6a 4a 4a + 4a 4a 8 f '( a) f ''( a) a 9a 9a a f '' > és un mínim. 4) PAU Sèrie Qüestió 6: a Sigui ( + ) f a a d per a >. f a + a. a a) Comproveu que a + d a + + C a a a f ( a) ( a + ) d a + a + a + a a b) Calculeu el valor del paràmetre a perquè la funció f ( a) tingui un mínim relatiu. Per a que la funció tingui un mínim relatiu la derivada ha de valer zero. a 9a 9a f a a + f ' a + + a 9a 9a a f '( a) a a a 4 4 a a ± Com l enunciat diu a > ens quedem únicament amb el valor a Caldria demostrar que efectivament a és un mínim. 4 a 4a 4a 4 4 f '( a) f '' 4 ( a) f '' 8 5 > és 4 5 a a a a un mínim. 44) PAU Sèrie 4 Qüestió : Calculeu l àrea del recinte limitat per les corbes d equació f ( ) + i g ( ) 5. Per poder dibuiar el recinte d integració ens va bé calcular primer els punts de tall entre les dues gràfiques. Aií: Eercicis sobre integrals de les PAU Catalunya 5
52 5 f g + + Podem comprovar que en tot l interval [,] tenim que g ( ) f ( ) ( ) > per tant: ( 5 ) ( 5 ) Àrea g f d + d + d ( + ) d + + ( 9 9 9) 45) PAU Sèrie Qüestió : f 9 és la següent: La gràfica de la funció a) Trobeu el punt de tall, (a, ), de la funció amb la part positiva de l ei OX. Talls amb l ei OX: y f ( ) 9 ± Com en l enunciat ens demanen el tall amb la part positiva de l ei OX descartem els valors i i ens quedem únicament amb el valor. Per tant, el punt de tall és (, ) Eercicis sobre integrals de les PAU Catalunya 5
53 b) Calculeu l àrea del recinte limitat per la gràfica de f ( ) i l ei OX en el primer quadrant. Com la funció és positiva en l interval [, ] l àrea coincidirà amb f f d 9 d 9 d (*) F Sigui d. 9 un candidat a primitiva. Aleshores tindríem que: F ' 9 9 integral. (*) per tant, hem de ficar un 9 9 ( 9 ) d d + C ( 9 ) + C dintre de la Àrea f ( ) d ( 9 ) ( 9 ) ( 9 ) ) PAU Sèrie Qüestió : Donada la funció f ( ) i la recta horitzontal y k, amb k >. a)feu un esbós del recinte limitat per les gràfiques de la funció i la recta, i els eios de coordenades. b) Trobeu el valor de k sabent que l àrea d aquest recinte és igual a 4 /. Podem observar que per calcular l àrea del recinte tancat pels eios de coordenades, la recta y k f hem de separar el recinte en dos àrees. De fins a la regió i la funció és un rectangle de base i altura k mentre que de fins l abscissa del punt P la regió Eercicis sobre integrals de les PAU Catalunya 5
54 serà la integral de la recta y k(que va per sobre) menys la funció f ( ) que va per sota. Càlcul del punt P tall entre la recta y k i la funció f ( ) : y f k k k + Aií: k + k + k + k d k d k d k + k + k + k + kd ( ) d [ k] ( ) k + k ( k + ) k ( ) k k k ( k ) ( ) k k + k k + k k k k k k k + k A A + A k + 4 k + k 4 A k + k 4 k + k Per tant, l àrea total serà: Finalment: L equació k no té solucions reals, per tant, l única solució al problema és NOTA: També podem calcular l àrea del recinte com l àrea d un rectangle de base k + i altura k al que se li treu l àrea per sota de la gràfica de la funció f ( ). En aquest cas: A k + k k + k Àrea rectangle: k + k + ( ) k + k 6 k k k + k Finalment calculem l àrea del recinte: A A A ( k + k ) k + k Àrea per sota de la funció: A d ( ) Igualant aquesta epressió a 4 obtenim evidentment el valor k Eercicis sobre integrals de les PAU Catalunya 54
55 47) PAU Sèrie 4 Qüestió : La corba y i la recta y k, amb k >, determinen una regió plana. a)calculeu el valor de l àrea d aquesta regió en funció del paràmetre k. b)trobeu el valor de k perquè l àrea limitada sigui 6u. Al gràfic de la dreta tenim representades les dues funcions i la regió que determinen: Per poder plantejar la integral hem de calcular els punts de tall entre les dues corbes y i y k. k ± k. Finalment plantegem la integral: k ( k ) ( k ) k A k d k k k k k k k k k k k k k k k k k k k k k k k k k k k k k A 6 k k 6 k k k k k k k k Eercicis sobre integrals de les PAU Catalunya 55
56 48) PAU Sèrie 5 Qüestió 4: (Incomplet) Per a, considereu la funció f ( ) +. b) Calculeu l àrea del recinte limitat per la gràfica de f ( ), la recta d equació 5 i l ei OX. Àrea del recinte limitat per f ( ), la recta 5 i l ei OX: 5 5 A f ( ) d d ( ) 5 ( ) ( 5 ) ( ) ) PAU Sèrie Qüestió : De la funció polinòmica P ( ) + a + b + sabem que Té un etrem relatiu en el punt d abscissa ; 5 La integral definida en l interval [, ] val. 4 Calculeu el valor dels paràmetres a i b. Si la funció té un etrem relatiu en el punt d abscissa aleshores en aquest punt s anul larà la seva derivada. Per tant: P + a + b + P ' + a + b ( ) P ' + a + b 7 6a + b 6a + b 7 Si la integral definida en l interval [, ] val 5 4 tindrem que: 5 5 a b 5 P d + a + b + d a b a b 5 a b a b a b a b a b a + b a + b 6 6 Eercicis sobre integrals de les PAU Catalunya 56
57 Per tant tenim el sistema 6a + b 7 que té com a solucions a i b 9. a + b 5) PAU 4 Sèrie Qüestió 4: Calculeu l àrea de la regió del pla limitada en el primer quadrant per les gràfiques de les funcions y, y 4 i y 9. Calculem el punt de tall entre la gràfica recta y 9. Tenim: y 4 i la 4 9 ± > Calculem també el punt de tall entre la paràbola y y : i la recta 9 > 9 9 ± Per tant, per poder calcular l àrea de la regió hem de dividir-la en dos intervals,, i, i plantejar les següents integrals: A ( 4 ) d + ( 9 ) d d + ( 9 ) d ( 7 9) unitats quadrades. 8 8 Eercicis sobre integrals de les PAU Catalunya 57
TEMA 5 : Derivades. Tècniques de derivació. Activitats
 TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
TEMA 5 : Derivades. Tècniques de derivació Activitats. Calculeu, mitjançant la definició de derivada, la derivada de les funcions següents en els punts indicats: a) f() en f() + 4 5 en - c) f() 6 + 5 en
+ 1= 0 té alguna arrel real (x en radians).
 Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
Generalitat de Cataluna Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen r quadrimestre Nom i Cognoms: Grup: Data: ) Calculeu els its següents:
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Districte Universitari de Catalunya
 Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Proves dʼaccés a la Universitat. Curs 2009-2010 Matemàtiques Sèrie 1 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què és el que voleu fer i per què. Cada qüestió val
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2012
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 1 1 k 1.- Determineu el rang de la matriu A = 1 k 1 en funció del valor del paràmetre k. k 1 1 [2 punts] En ser la matriu
La recta. La paràbola
 LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
LA RECTA, LA PARÀBOLA I LA HIPÈRBOLA La recta Una recta és una funció de la forma y = m + n. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall amb
1.- Sabem que el vector (2, 1, 1) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c. . cx by +2z = b
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 5 PAU 0 - Sabem que el vector (,, ) és una solució del sistema ax + by + cz = a + c bx y + bz = a b c cx by +z = b Calculeu el valor
Sèrie 5. Resolució: 1. Siguin i les rectes de d equacions. a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i.
 Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Oficina d Accés a la Universitat Pàgina 1 de 11 Sèrie 5 1. Siguin i les rectes de d equacions : 55 3 2 : 3 2 1 2 3 1 a) Estudieu el paral lelisme i la perpendicularitat entre les rectes i. b) Trobeu l
Districte Universitari de Catalunya
 Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
Proves d Accés a la Universitat. Curs 2012-2013 Matemàtiques Sèrie 4 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val 2 punts.
DERIVADES. TÈCNIQUES DE DERIVACIÓ
 UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
UNITAT 7 DERIVADES. TÈCNIQUES DE DERIVACIÓ Pàgina 56 Tangents a una corba y f (x) 5 5 9 4 Troba, mirant la gràfica i les rectes traçades, f'(), f'(9) i f'(4). f'() 0; f'(9) ; f'(4) 4 Digues uns altres
Problemes d Anàlisi. Problema 4 Un granger desitja tancar en un terreny rectangular adjacent a un riu.
 Problemes d Anàlisi Càlcul diferencial Problema 1 Siga f : R R la funció donada per f() = a + b + c + d Determineu els coeficients a, b, c, d sabent que f té un etrem local en el punt d abscissa = 0, que
Problemes d Anàlisi Càlcul diferencial Problema 1 Siga f : R R la funció donada per f() = a + b + c + d Determineu els coeficients a, b, c, d sabent que f té un etrem local en el punt d abscissa = 0, que
ANÁLISIS. 1 Junio Junio 98. y = 1al dar vuelta
 ANÁLISIS Junio 98 Junio 98 Un punto material recorre la parábola y = 7. Deducir razonadamente la posición, o posiciones, en que la distancia del punto al origen (0, 0) es mínima. Considera la superficie
ANÁLISIS Junio 98 Junio 98 Un punto material recorre la parábola y = 7. Deducir razonadamente la posición, o posiciones, en que la distancia del punto al origen (0, 0) es mínima. Considera la superficie
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes. Nom i Cognoms: Grup: Data:
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques n BATX MA Eamen FINAL Nom i Cognoms: Grup: Data: -5-007 r BLOC: ) Trobeu els límits:
Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra.
 UNITAT 7: FUNCIONS. Definició Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra. Eemple: Completa: f() g() - h() - - (-)
UNITAT 7: FUNCIONS. Definició Una funció és una relació entre dues variables, de tal manera que al variar el valor d'una d'elles va variant el valor de l'altra. Eemple: Completa: f() g() - h() - - (-)
EXERCICIS MATEMÀTIQUES 1r BATXILLERAT
 Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
Treball d estiu/r Batillerat CT EXERCICIS MATEMÀTIQUES r BATXILLERAT. Aquells alumnes que tinguin la matèria de matemàtiques pendent, hauran de presentar els eercicis el dia de la prova de recuperació.
y = m x x f x. Per determinar de totes aquestes rectes quina és la recta tangent, el que es fa és intentar aproximar el pendent m.
 Derivació Objectius: Usar el Maple en el càlcul de derivades i les seves aplicacions Definició de derivada La derivada d'una funció donada f en un punt és el pendent de la recta tangent a la corba 0 y
Derivació Objectius: Usar el Maple en el càlcul de derivades i les seves aplicacions Definició de derivada La derivada d'una funció donada f en un punt és el pendent de la recta tangent a la corba 0 y
DERIVADES: exercicis bàsics ex D.1
 DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
DERIVADES: eercicis bàsics e D.. Estudiar la derivabilitat de les funcions que s indiquen, calculant el seu camp de derivabilitat. Escriure l epressió de la funció derivada corresponent, en el cas de que
Institut Jaume Balmes Aplicacions de les derivades I
 MS 1) Donada la funció y 6 + 8 a) Troba la recta tangent en el seu punt d'infleió. b) Troba la recta normal en el punt de 1 (1+0,5 1,5 punts) ) A la vista de la gràfica d'aquesta funció. a) Estudia la
MS 1) Donada la funció y 6 + 8 a) Troba la recta tangent en el seu punt d'infleió. b) Troba la recta normal en el punt de 1 (1+0,5 1,5 punts) ) A la vista de la gràfica d'aquesta funció. a) Estudia la
x x 1 x 11= 7) y = 6 3x-2 12) y = e 5x (3x 2-6)
 Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Derivació1/ 1.- Calculeu la primera derivada de les funcions següents, simplificant el resultat el màim possible. 1) y = - 4 4 + - ) y 6 4 4 = + 3 3) y = 3 + 4) y = ) 3 y = 6) y = ( + ) 1 + 7) ( 3) y =
Al ser un quocient, el denominador no pot ser 0 i al ser una arrel d index senars no hi ha problema Dom = R\{x 3 +3x 2-6x-8=0}= R\{-4, 2, -1}.
 Col legi Maristes Sants-Les Corts Departament de matemàtiques Codi Sol PsP..- Troba el domini de les següents funcions. d) f ( ) 6 És un quocient de polinomis Dom R\{ -6} R\{,}. f) f ( ) És un quocient
Col legi Maristes Sants-Les Corts Departament de matemàtiques Codi Sol PsP..- Troba el domini de les següents funcions. d) f ( ) 6 És un quocient de polinomis Dom R\{ -6} R\{,}. f) f ( ) És un quocient
f x té màxims o mínims relatius. 6.- Determina els intervals de creixement i decreixement, màxims i mínims de les funcions següents: x
 EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció hi
EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció hi
Prova d accés a la Universitat (2013) Matemàtiques II Model 1. (b) Suposant que a = 1, trobau totes les matrius X que satisfan AX + Id = A, on Id
 UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
UIB Prova d accés a la Universitat () Matemàtiques II Model Contestau de manera clara i raonada una de les dues opcions proposades. Es disposa de 9 minuts. Cada qüestió es puntua sobre punts. La qualificació
11 Límits de funcions. Continuïtat i branques infinites
 Límits de funcions. Continuïtat i branques infinites Pàgina 7 A través d'una lupa a) A = + d " A = " + d A = 0 d "+ Soroll i silenci I = + d " 0 I = 0 d "+ Pàgina 75 a) Cert Cert Cert d) Cert e) Fals f)
Límits de funcions. Continuïtat i branques infinites Pàgina 7 A través d'una lupa a) A = + d " A = " + d A = 0 d "+ Soroll i silenci I = + d " 0 I = 0 d "+ Pàgina 75 a) Cert Cert Cert d) Cert e) Fals f)
SOLUCIONARI Unitat 2. Comencem. Exercicis
 SOLUCIONARI Unitat Comencem Representa en paper mil limetrat la funció f() + 4. Traça amb la màima cura possible la recta tangent a la paràbola en el punt P(, ). Mesura amb un transportador l angle que
SOLUCIONARI Unitat Comencem Representa en paper mil limetrat la funció f() + 4. Traça amb la màima cura possible la recta tangent a la paràbola en el punt P(, ). Mesura amb un transportador l angle que
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2010
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 SÈRIE 1 Pregunta 1 3 1 lim = 3. Per tant, y = 3 és asímptota horitzontal de f. + 3 1 lim =. Per tant, = - és asímptota horitzontal
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 2007
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 7 PAU 007 SÈRIE 3 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Indiqueu en quins punts Y = f(x) no és contínua, el tipus de discontinuïtats de cada cas i les asímptotes que presenta. (0,1 9 +0,8=1,7 punts)
 Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
Generalitat de Catalunya Departament d Ensenyament Institut Jaume Balmes Nom: 1.- Trobeu la funció inversa o recíproca de la funció recorregut de la funció yf(). f ( ) Departament de Matemàtiques 1MA:
f x té màxims o mínims relatius. 6.- Determina els intervals de creixement i decreixement, màxims i mínims de les funcions següents: x
 4- EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció
4- EXERCICIS REPRESENTACIÓ DE FUNCIONS: - Estudia els intervals de monotonia (crei/decrei) de: f - Estudia si la funció f - Determina si la funció 4 té màims o mínims relatius e f té punts on la funció
( 2 3, utilitzeu la matriu inversa B 1 ( 1 4 ( 2 1. Matrius i determinants Sèrie 3 - Qüestió 4. Donada la matriu B =
 1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
Examen Final 17 de gener de 2013
 MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
Col legi Maristes Sants-Les Corts. Departament de matemàtiques. té per asímptotes les rectes =
 Matemàtiques II Propostes recuperació 1a avaluació - 1/5 Col legi Maristes Sants-Les Corts Departament de matemàtiques Matemàtiques II PsPc. B2.A1 Tal i com alguns de vosaltres m heu demanat, us dono una
Matemàtiques II Propostes recuperació 1a avaluació - 1/5 Col legi Maristes Sants-Les Corts Departament de matemàtiques Matemàtiques II PsPc. B2.A1 Tal i com alguns de vosaltres m heu demanat, us dono una
16 febrer 2016 Integrals exercicis. 3 Integrals
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 16 febrer 2016 Integrals exercicis 3 Integrals 28. Troba una funció primitiva de les següents funcions: () = 1/ () = 3 h() = 2 () = 4 () = cos () = sin () =
UIB 2 + f (x) + f(x) ց ց ր ր Per tant, el punt ( 3. Una altra forma de veure-ho és calcular la derivada segona i mirar el signe en x = 3: 2 f (x) =
 El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
El cas positiu no té solució. Si analitzam el cas negatiu, ens surt x = x+, d on x =. A continuació fem la taula següent per veure si el valor obtingut és un màxim, mínim o un punt de sella. x + f (x)
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 2005
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 005 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 11 PAU 005 SÈRIE. Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció exponencial
 LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
LA FUNCIÓ EXPONENCIAL I LA FUNCIÓ LOGARÍTMICA. FUNCIONS DEFINIDES A TROSSOS. Funció eponencial La funció eponencial és de la forma f () = a, on a > 0, a 1 El valor a s anomena base de la funció eponencial.
Equacions i sistemes de segon grau
 Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
x + 2 y = 3 2 x y = 1 4 x + 3 y = k a) Afegiu-hi una equació lineal de manera que el sistema resultant sigui incompatible.
 1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
1998 - Sèrie 3 - Qüestió 4 Discutiu el sistema d'equacions a x y + 2 z = (2 a) 2 x + 3 y z = 3a x + 2 y z = 2a segons els valors del paràmetre a. 1999 - Sèrie 1 - Qüestió 1 Resoleu el sistema següent per
INTEGRALS. 2 a) 3-2 x 2 x 3 dx b) 5-3x 2 dx c) 5 x 2 7 x dx d) x x 4 dx. x x - 2 x2 - x 3 dx c) 1+x 2 dx.
 INTEGRALS a) 3 6 b) 2 2 c) 5 3 2 d) 7 3 e) 2 a) 3-2 2 3 b) 5-3 2 c) 5 2 7 d) 3 a) 5-2 3-7 2 +2-5 3 b) 3 2-3 + 3 +5 2-2 2-3 c) + 2 a) 3-3 2 2 b) -3 2 c) 5-3 2 5 a) 2 +7-6 +3 5 b) 7 3-2+ 3 +3 c) 5+3 7 2
INTEGRALS a) 3 6 b) 2 2 c) 5 3 2 d) 7 3 e) 2 a) 3-2 2 3 b) 5-3 2 c) 5 2 7 d) 3 a) 5-2 3-7 2 +2-5 3 b) 3 2-3 + 3 +5 2-2 2-3 c) + 2 a) 3-3 2 2 b) -3 2 c) 5-3 2 5 a) 2 +7-6 +3 5 b) 7 3-2+ 3 +3 c) 5+3 7 2
FUNCIONS REALS. MATEMÀTIQUES-1
 FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
FUNCIONS REALS. 1. El concepte de funció. 2. Domini i recorregut d una funció. 3. Característiques generals d una funció. 4. Funcions definides a intervals. 5. Operacions amb funcions. 6. Les successions
SOLUCIONARI Unitat 1. Exercicis. Comencem. 1. La gràfica velocitat-temps corresponent a dos mòbils és la que pots veure a la dreta (fig. 1.3).
 SOLUCIONARI Unitat Comencem La funció f() és decreient en l interval (, ). Fes un raonament com el que em fet anteriorment per determinar on decrei amb més rapidesa, si ens movem prop de o si o fem prop
SOLUCIONARI Unitat Comencem La funció f() és decreient en l interval (, ). Fes un raonament com el que em fet anteriorment per determinar on decrei amb més rapidesa, si ens movem prop de o si o fem prop
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
Generalitat de Catalunya. 12 3x. x x x. lim. lim. 2 x. + = e) x +
 1) Una persona va invertir 6 000?comprant accions de dues empreses, A i B. Al cap d un any, el valor de les accions de l empresa A ha pujat un % i, en canvi, el valor de les accions de l empresa B ha baiat
1) Una persona va invertir 6 000?comprant accions de dues empreses, A i B. Al cap d un any, el valor de les accions de l empresa A ha pujat un % i, en canvi, el valor de les accions de l empresa B ha baiat
REPRESENTACIÓ DE FUNCIONS
 1. FUNCIONS PRINCIPALS REPRESENTACIÓ DE FUNCIONS 1.1 Rectes Forma: 4 5 1.2 Paràboles Forma: 1.3 Funcions amb radicals Forma: 1.4 Funcions de proporcionalitat inversa Forma: 1.5 Exponencials Forma: 2 1.6
1. FUNCIONS PRINCIPALS REPRESENTACIÓ DE FUNCIONS 1.1 Rectes Forma: 4 5 1.2 Paràboles Forma: 1.3 Funcions amb radicals Forma: 1.4 Funcions de proporcionalitat inversa Forma: 1.5 Exponencials Forma: 2 1.6
Data de lliurament: divendres 8 d abril de 2016
 INS JÚLIA MINGUELL Matemàtiques 2n BAT. 18 març 2016 Dossier recuperació (2a AVAL.) DOSSIER de RECUPERACIÓ: 2a AVALUACIÓ Data de lliurament: divendres 8 d abril de 2016 Condicions: i) El no lliurament
INS JÚLIA MINGUELL Matemàtiques 2n BAT. 18 març 2016 Dossier recuperació (2a AVAL.) DOSSIER de RECUPERACIÓ: 2a AVALUACIÓ Data de lliurament: divendres 8 d abril de 2016 Condicions: i) El no lliurament
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
1. Què tenen en comú aquestes dues rectes? Com són entre elles? 2. En què es diferencien aquestes dues rectes?
 En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
En la nostra vida diària trobem moltes situacions de relació entre dues variable que es poden interpretar mitjançant una funció de primer grau. La seva expressió algebraica és del tipus f(x)=mx+n. També
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2009
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 1 QÜESTIONS 1.- Considereu la matriu A = ( ) A 2 1 0 =. 2 1 [2 punts] ( ) a 0. Calculeu el valor dels paràmetres a i b perquè
INTEGRACIÓ: resolució exercicis bàsics ex res I.1
 INTEGRACIÓ: resolució exercicis bàsics ex res I. R. Aplicant el teorema d integració per parts, calculeu les següents integrals: (a) π x cos xdx (b) π e x sin xdx eπ + (c) e ln xdx (d) π/ π/ e x cos xdx
INTEGRACIÓ: resolució exercicis bàsics ex res I. R. Aplicant el teorema d integració per parts, calculeu les següents integrals: (a) π x cos xdx (b) π e x sin xdx eπ + (c) e ln xdx (d) π/ π/ e x cos xdx
Exercicis de rectes en el pla
 Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
Equacions de la recta 1. Escriu les diferents equacions de la recta que passa pel punt P(3, 4) i que té com a vector director el vector v = ( 5, 2). 2. Per a la recta d equació director. 6 + y = 1, escriu
TEMA 6 : Geometria en l espai. Activitats
 TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
TEMA 6 : Geometria en l espai Activitats 1. Siguin els punts A(1,2,3), B(0,1,3) i C(2,3,1) a) Trobeu el vector b) Calculeu el mòdul del vector c) Trobeu el vector unitari d igual direcció que el vector
Propietats de les desigualtats.
 Inequacions Desigualtats Direm que a < b a és menor que b si b a és un nombre positiu. Gràficament, a queda a l esquerra de b. Direm que a > b a major que b si a b és un nombre positiu. Gràficament, a
Inequacions Desigualtats Direm que a < b a és menor que b si b a és un nombre positiu. Gràficament, a queda a l esquerra de b. Direm que a > b a major que b si a b és un nombre positiu. Gràficament, a
10 Àlgebra vectorial. on 3, -2 i 4 són les projeccions en els eixos x, y, y z respectivament.
 10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
10 Àlgebra vectorial ÀLGEBR VECTORIL Índe P.1. P.. P.3. P.4. P.5. P.6. Vectors Suma i resta vectorial Producte d un escalar per un vector Vector unitari Producte escalar Producte vectorial P.1. Vectors
LA RECTA. Exercicis d autoaprenentatge 1. Siga la gràfica següent:
 LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
LA RECTA Recordeu: Una recta és una funció de la forma y = mx + n, on m i n són nombres reals. m és el pendent de la recta i n és l ordenada a l origen. L ordenada a l origen ens indica el punt de tall
VECTORS I RECTES AL PLA. Exercici 1 Tenint en compte quin és l'origen i quin és l'extrem, anomena els següents vectors: D
 VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
VECTORS I RECTES AL PLA Un vector és un segment orientat que és determinat per dos punts, A i B, i l'ordre d'aquests. El primer dels punts s'anomena origen i el segons es denomina extrem, i s'escriu AB.
Examen FINAL M2 FIB-UPC 12 de juny de 2015
 Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
Examen FINAL M FIB-UPC 1 de juny de 015 1. ( punts Sigui a R, calculeu els límits següents segons els valors d a: n + n n + a+ a+n a n n n, n n + n!.. ( punts Considereu la integral següent: I = 1.8 1
TEMA 3: Polinomis 3.1 DEFINICIONS:
 TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
SÈRIE 2 Pautes de correcció (PAAU2001) MATEMÀTIQUES
 Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 6 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar altres
Oficina de Coordinació i d'organització de les PAU de Catalunya Pàgina 1 de 6 Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals (ara bé, dins de cada pregunta podeu utilitzar altres
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
TEMA 1 : Aplicacions de les derivades
 TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
TEMA 1 : Aplicacions de les derivades 1.1. INFORMACIÓ EXTRETA DE LA PRIMERA DERIVADA 1.1.1 Creixement i decreixement de funcions Definició: f és creixent en x 0 existeix (x 0 - a, x 0 + a), un entorn del
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES B =,
 RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
RECULL DE PROBLEMES DE VECTORS QUE HAN SORTIR A LES PAU DE MATEMÀTIQUES PAU LOGSE 999 Sèrie Problema : (Incomplet Donats els punts de l'espai A (,,0, B ( 0,,0, C (,0,0 i D ( 0,,0 a Són coplanaris? Formen
= 1+ β, essent α i β paràmetres reals. a la recta r 2. i el pla Π d equació
 Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
Problema A Setembre 0 + y z = En l espai es té la recta r i el pla Π d equacions r x + mz = 0, on x y z = 0 m és un paràmetre real a) Un vector director de la recta r b) El valor de m per al qual la recta
1.- Estudi de funcions Creixement i decreixement de funcions Extrems relatius i absoluts Derivabilitat de funcions
 .- Estudi de funcions..- Creiement i decreiement de funcions..- Etrems relatius i absoluts..- Derivabilitat de funcions.- Representació gràfica de funcions..- Introducció..- Domini de funcions..- Discontinuïtats.4.-
.- Estudi de funcions..- Creiement i decreiement de funcions..- Etrems relatius i absoluts..- Derivabilitat de funcions.- Representació gràfica de funcions..- Introducció..- Domini de funcions..- Discontinuïtats.4.-
Oficina d Accés a la Universitat Pàgina 1 de 10 PAU 2014 Criteris específics de correcció i qualificació per ser fets públics un cop finalitzades
 Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
Oficina d Accés a la Universitat Pàgina 1 de 10 SÈRIE 3 Responeu a CINC de les sis qüestions següents. En les respostes, expliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar
TEMA 4: Equacions exponencials i logarítmiques
 TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
TEMA 4: Equacions exponencials i logarítmiques 4.1. EXPONENCIALS Definim exponencial de base a i exponent n:. Propietats de les exponencials: (1). (2) (3) (4) 1 (5) 4.2. EQUACIONS EXPONENCIALS Anomenarem
UNITAT DIDÀCTICA 10 L ÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES
 7 UNITAT DIDÀCTICA 0 Refleiona i resol Aproimacions successives El valor de la funció f () = + 5 0 per a = 5 no es pot obtenir directament perquè el denominador es fa zero. L obtindrem per aproimacions
7 UNITAT DIDÀCTICA 0 Refleiona i resol Aproimacions successives El valor de la funció f () = + 5 0 per a = 5 no es pot obtenir directament perquè el denominador es fa zero. L obtindrem per aproimacions
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 PAU 2008 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 6 SÈRIE 4 Aquestes pautes no preveuen tots els casos que en la pràctica es poden presentar. Tampoc no pretenen donar totes les possibles
Gràficament: una funció és contínua en un punt si en aquest punt el seu gràfica no es trenca
 Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
Funcions contínues Funcions contínues Continuïtat d una funció Si x 0 és un nombre, la funció f(x) és contínua en aquest punt si el límit de la funció en aquest punt coincideix amb el valor de la funció
PROBLEMES PAU SOBRE SISTEMES D EQUACIONS. 1) PAU 1999 Sèrie 1 Qüestió 1: Resoleu el sistema següent per als valors de k que el facin compatible.
 PROBLEMES PAU SOBRE SISTEMES D EQUACIONS ) PAU 999 Sèrie Qüestió : Resoleu el sistema següent per als valors de k que el facin compatible. x + y 3 x y 4x + 3y k ) PAU 000 Sèrie 5 Qüestió 4: Discutiu el
PROBLEMES PAU SOBRE SISTEMES D EQUACIONS ) PAU 999 Sèrie Qüestió : Resoleu el sistema següent per als valors de k que el facin compatible. x + y 3 x y 4x + 3y k ) PAU 000 Sèrie 5 Qüestió 4: Discutiu el
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS
 CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
CARACTERÍSTIQUES DE FUNCIONS ELEMENTALS 1. FUNCIÓ CONSTANT (document d'ajuda: 1_funcio_constant.html ) Expressió algèbrica: f(x) = n. Gràfica: 2. FUNCIÓ LINEAL (document d'ajuda: 2_funcio_lineal.html )
corresponent de la primera pàgina de l examen.
 Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
Oficina d Accés a la Universitat Pàgina 1 de 5 PAU 017 SÈRIE PAUTES PER ALS CORRECTORS RECORDEU: - Podeu valorar amb tants decimals com considereu convenient, però aconsellem no fer ho amb més de dos.
P =
 RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
RECULL DE PROBLEMES SOBRE MTRIUS I DETERMINNTS QUE HN SORTIT LES PROVES DE SELECTIVITT ) PU LOGSE 004 Sèrie Qüestió 3: Considereu les matrius compleixi X + = B. = i B =. Trobeu una matriu X que ) PU LOGSE
ANÀLISI. MATEMÀTIQUES-2
 1. ANÀLISI. Caldrà repassar alguns temes de cursos anteriors, com el tema de Funcions polinòmiques i, els de Funcions reals i Límits de funcions, caldrà recordar també els gràfics i propietats més importants
1. ANÀLISI. Caldrà repassar alguns temes de cursos anteriors, com el tema de Funcions polinòmiques i, els de Funcions reals i Límits de funcions, caldrà recordar també els gràfics i propietats més importants
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 9 PAU 2006 Pautes de correcció
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 9 PAU 006 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals Ara bé, dins de cada pregunta podeu utilitzar
LÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES
 LÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES Pàgina 7 REFLEIONA I RESOL Aproimacions successives Comprova que: f () = 6,5; f (,9) = 6,95; f (,99) = 6,995 Calcula f (,999); f (,9999); f (,99999);
LÍMITS DE FUNCIONS. CONTINUÏTAT I BRANQUES INFINITES Pàgina 7 REFLEIONA I RESOL Aproimacions successives Comprova que: f () = 6,5; f (,9) = 6,95; f (,99) = 6,995 Calcula f (,999); f (,9999); f (,99999);
Institut d Educació Secundària Funcions IV i estadística d'una variable
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques 1MS Funcions IV i estadística d'una variable Nom: Grup: = a) Trobeu el domini i els
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques 1MS Funcions IV i estadística d'una variable Nom: Grup: = a) Trobeu el domini i els
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 5 PAU 2005 QÜESTIONS
 Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 5 PAU 005 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 5 PAU 005 SÈRIE Avalueu cada pregunta en punts i mitjos punts, però no en altres decimals. Ara bé, dins de cada pregunta podeu utilitzar
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
Oficina d Accés a la Universitat Pàgina 1 de 6 PAU 2016 Criteris de correcció
 Oficina d Accés a la Universitat Pàgina 1 de 6 Criteris de correcció Matemàtiques aplicades a les ciències socials SÈRIE 3 1. Una fàbrica de mobles de cuina ven 1000 unitats mensuals d un model d armari
Oficina d Accés a la Universitat Pàgina 1 de 6 Criteris de correcció Matemàtiques aplicades a les ciències socials SÈRIE 3 1. Una fàbrica de mobles de cuina ven 1000 unitats mensuals d un model d armari
TEMA 4 : Geometria analítica al pla. Vectors i la Recta. Activitats
 TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
TEMA 4 : Geometria analítica al pla. Vectors i la Recta Activitats 1. Donats els punts A(2,1), B(6,5),i C(-1,4): a) Representa els vectors AB i CA i estudia totes les seves característiques b) Calcula
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Àlgebra lineal i equacions diferencials. Curs 2001/02 Exemple de diagonalització.
 Considerem la matriu Àlgebra lineal i equacions diferencials Química Curs 2001/02 Exemple de diagonalització. A = M 3 (R). Calculeu els valors propis de la matriu A. Calculeu els vectors propis pels valors
Considerem la matriu Àlgebra lineal i equacions diferencials Química Curs 2001/02 Exemple de diagonalització. A = M 3 (R). Calculeu els valors propis de la matriu A. Calculeu els vectors propis pels valors
SOLUCIONARI Unitat 3. Comencem. Exercicis
 SOLUCIONARI Unitat Comencem Troba i classifica les discontinuïtats que resenta la funció y. + - + + y la simlificació indica que a hi ha una discontinuïtat - ( + )( -) - evitable. A l eressió y hi trobem
SOLUCIONARI Unitat Comencem Troba i classifica les discontinuïtats que resenta la funció y. + - + + y la simlificació indica que a hi ha una discontinuïtat - ( + )( -) - evitable. A l eressió y hi trobem
Institut d Educació Secundària. x b) A partir de la gràfica d aquesta funció, indica quin és el domini i el recorregut.
 Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques MS Àlgebra i uncions I Nom: Grup: ) Resol les següents equacions: a) 7+ 3+ c) 3 +
Generalitat de Catalunya Departament d Educació Institut d Educació Secundària Jaume Balmes Departament de Matemàtiques MS Àlgebra i uncions I Nom: Grup: ) Resol les següents equacions: a) 7+ 3+ c) 3 +
2 desembre 2015 Límits i número exercicis. 2.1 Límits i número
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
Oficina d Organització de Proves d Accés a la Universitat Pàgina 1 de 10 PAU 2009
 Oficina d Organització de Proves d Accés a la Universitat Pàgina de 0 SÈRIE 4 QÜESTIONS.- Donats el punt P =(,, ) ilarectar : x = y + = z 5 : a) Trobeu l equació cartesiana (és a dir, de la forma Ax +
Oficina d Organització de Proves d Accés a la Universitat Pàgina de 0 SÈRIE 4 QÜESTIONS.- Donats el punt P =(,, ) ilarectar : x = y + = z 5 : a) Trobeu l equació cartesiana (és a dir, de la forma Ax +
ASÍMPTOTES. Les asímptotes a una funció són rectes que donen una idea sobre el comportament de la funció quan les variables s apropen a l'infinit.
 H. Itkur funcions-iii -/ 6 ASÍMPTOTES. Les asímptotes a una funció són rectes que donen una idea sobre el comportament de la funció quan les variables s apropen a l'infinit. Donada la corba y f(, direm
H. Itkur funcions-iii -/ 6 ASÍMPTOTES. Les asímptotes a una funció són rectes que donen una idea sobre el comportament de la funció quan les variables s apropen a l'infinit. Donada la corba y f(, direm
TEMA 6. POLINOMIS II. a n a 2 a 1 a Teorema del residu. 4. Polinomis irreductibles. 6. Fraccions algebraiques
 . REGLA DE RUFFINI És s un mètode m de divisió entre polinomis, més m s senzill que l algoritme l de la divisió i que permet la divisió només quan el divisor és s de la forma Q(x) x b. TEMA 6. S II Professor
. REGLA DE RUFFINI És s un mètode m de divisió entre polinomis, més m s senzill que l algoritme l de la divisió i que permet la divisió només quan el divisor és s de la forma Q(x) x b. TEMA 6. S II Professor
Polinomis i fraccions algèbriques
 Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Unitat 2 EQUACIONS DE PRIMER GRAU. Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 EQUACIONS DE PRIMER GRAU
 Unitat 2 EQUACIONS DE PRIMER GRAU 37 38 Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser capaç
Unitat 2 EQUACIONS DE PRIMER GRAU 37 38 Matemàtiques, Ciència i Tecnologia 5. TRANSFORMACIONS D EXPRESSIONS ALGEBRAIQUES UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser capaç
Problemes de Sistemes de Numeració. Fermín Sánchez Carracedo
 Problemes de Sistemes de Numeració Fermín Sánchez Carracedo 1. Realitzeu els canvis de base que s indiquen a continuació: EF02 16 a binari natural b) 235 10 a hexadecimal c) 0100111 2 a decimal d) FA12
Problemes de Sistemes de Numeració Fermín Sánchez Carracedo 1. Realitzeu els canvis de base que s indiquen a continuació: EF02 16 a binari natural b) 235 10 a hexadecimal c) 0100111 2 a decimal d) FA12
Criteris generals per a la correcció:
 Oficina d Accés a la Universitat Pàgina de Sèrie Responeu a CINC de les sis qüestions següents. En les respostes, epliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar calculadora,
Oficina d Accés a la Universitat Pàgina de Sèrie Responeu a CINC de les sis qüestions següents. En les respostes, epliqueu sempre què voleu fer i per què. Cada qüestió val punts. Podeu utilitzar calculadora,
1. RECTA TANGENT I NORMAL 2. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS
 APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
APLICACIONS DE LA DERIVADA 1. RECTA TANGENT I NORMAL. DETERMINACIÓ DE PARÀMETRES 3. CREIXEMENT I DECREIXEMENT 4. VELOCITAT I ACELERACIÓ - PUNTS SINGULARS 1. RECTA TANGENT I NORMAL 1.1 Trobeu l equació
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
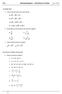 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
TEMES TREBALLATS A 3r d'eso
 TEMES TREBALLATS A r d'eso. Repàs de n d'eso. Nombres racionals. Equacions. Sistemes d'equacions de r grau. Funcions. Geometria en l'espai Recordeu que a part dels apunts teniu d'altres documents per preparar
TEMES TREBALLATS A r d'eso. Repàs de n d'eso. Nombres racionals. Equacions. Sistemes d'equacions de r grau. Funcions. Geometria en l'espai Recordeu que a part dels apunts teniu d'altres documents per preparar
TEMA 4 : Programació lineal
 TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
TEMA 4 : Programació lineal 4.1. SISTEMES D INEQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITA La solució d aquest sistema és l intersecció de les regions que correspon a la solució de cadascuna de les inequacions
Resolucions de l autoavaluació del llibre de text
 Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
Pàg. 1 de 1 Tenim els vectors u(3,, 1), v ( 4, 0, 3) i w (3,, 0): a) Formen una base de Á 3? b) Troba m per tal que el vector (, 6, m) sigui perpendicular a u. c) Calcula u, ì v i ( u, v). a) Per tal que
1.4 Derivades: Unitat de síntesi (i repàs)
 1.4 Derivades: Unitat de síntesi (i repàs) 11. Problemes de: optimització, extrems ( ), punts d inflexió ( ), rectes tangents (T) i interpretació de gràfiques (G): A.- Considereu tots els prismes rectes
1.4 Derivades: Unitat de síntesi (i repàs) 11. Problemes de: optimització, extrems ( ), punts d inflexió ( ), rectes tangents (T) i interpretació de gràfiques (G): A.- Considereu tots els prismes rectes
Matemàtiques Sèrie 1. Instruccions
 Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 0 Matemàtiques Sèrie SOLUCIONS, CRITERIS DE CORRECCIÓ
Proves d accés a cicles formatius de grau superior de formació professional inicial, d ensenyaments d arts plàstiques i disseny, i d ensenyaments esportius 0 Matemàtiques Sèrie SOLUCIONS, CRITERIS DE CORRECCIÓ
