Sea Σ un alfabeto y L el lenguaje de los palíndromos sobre Σ. Sean a, b dos elementos de Σ. Se demuestra por reducción al absurdo que L no es regular:
|
|
|
- Nicolás Gómez Villalobos
- hace 7 años
- Vistas:
Transcripción
1 Universidad Rey Juan Carlos Grado en Ingeniería de Computadores Máquinas Secuenciales, Autómatas y Lenguajes Hoja de Problemas: Propiedades Lenguajes Regulares Nivel del ejercicio : ( ) básico, ( ) medio, ( ) avanzado. 1. ( ) Prueba que el lenguaje de los palíndromos sobre un alfabeto finito con al menos dos elementos no es regular. Sea Σ un alfabeto y L el lenguaje de los palíndromos sobre Σ. Sean a, b dos elementos de Σ. Se demuestra por reducción al absurdo que L no es regular: 1. Supongamos que L es regular. 2. Elegimos n como constante del Lema de Bombeo. 3. Sea x = a n ba n una palabra. Obviamente x pertenece a L y x > n, por tanto, siguiendo el Lema de Bombeo, si L fuese regular, x debería poder componerse de la forma x = u.v.w verificando:. a) u.v n b) v > 0 c) u.v i.w L para todo i Determinamos todas las posibles descomposiciones de x en u.v.w que cumplan las condiciones a) y b). Dado que las primeras n letras de x son a s, para cumplir a), tanto u como v sólo pueden tener letras a. Además, para cumplir la condición b), v tiene que tener por lo menos una a. Resumiendo, podemos especificar las posibles descomposiones de x que cumplan a) y b) de la sigfuiente forma: x = u.v.w = a s.a k.a t ba n (el operador. marca los 3 componentes u, v, y w). Además, se cumple s 0, k 1, t 0 y s + t + k = n. Se puede observar que no hay otra forma de descomponer x en las tres partes, cumpliendo las condiciones a) y b). 5. Podemos demostrar que ninguna de las descomposiciones encontradas en el punto 4 cumple la condición c). Para ello es suficiente encontrar para cada descomposición un número entero i 0 tal que u.v i.w no pertenece a L. En nuestro caso podemos usar i = 2. Para i = 2, se cumple u.v i.w = u.v 2.w = a s.a k.a k.a t ba n. Por s + t + k = n se cumple u.v 2.w = a n+k ba n. Teniendo en cuenta que k 1 (condición que Página 1 de 6
2 hemos establecido antes), observamos que la palabra a n+k ba n no pertenece al lenguaje (pues no es un palíndromo). Por tanto, la palabra x no se puede componer como indica el lema. Eso lleva a una contradicción que indica que nustra supoción inicial: L es regular no es correcta. Y concluimos que L no puede ser regular. 2. ( ) Demuestra o refuta la siguiente afirmación: Todo lenguaje que sea un subconjunto de un lenguaje regular es regular. El lengujae universal sobre un alfabeto es un lenguaje regular, ya que existe un autómata finito que lo acepta (de echo, este autómata sólo requiere un único estado). Por otro lado, hemos demostrado que existen lenguajes que no son regulares (por ejemplo en el ejercicio anterior), dado que qualquier lenguaje es, por definición, un subconjunto del lenguaje universal correspondiente, vemos que la afirmación no es correcta. 3. Sea Σ = {a, b, c} un lenguaje finito. Para cada una de las siguientes definiciones del lenguaje L Σ, demuestra que L no es regular: NOTA: La forma de resolver estos ejercicios es múy similar a lo que se ha especificado en el ejercicio 1. Por ello, sólo se comentan algunos detalles específicos de las soluciones. (a) ( ) L = {a n b n n 1}. Vale elegir la palabra a n b n, donde n es la constante del lema. Al dividir x en u.v.w, v sólo contiene a s. Al bombear v (por ejemplo con i = 2), la palabra que se obtiene tiene más a s que b s, por lo que no pertenece a L. (b) ( ) L = {a n b 2n n 1}. Se puede elegir la palabra a n b 2n. De nuevo, v sólo contiene a s. Al bombear v para i=2, la pabra que se obtiene contiene más a s que b s. (c) ( ) L = {a n b m 0 < n m}. Se puede elegir la palabra a n b n. De nuevo, v sólo contiene a s. Al bombear v para i=2, la pabra que se obtiene contiene más a s que b s. (d) ( ) L = {a n b m n m = 2}. Página 2 de 6
3 Se puede elegir la palabra a n b n +2. Entonces, v sólo contiene a s. Al bombear v hacia abajo (para i=0), la pabra que se obtiene contiene menos que n a s, pero mantiene las n + 2 b s. Por tanto no se cumple que la diferencia entre el número de a s y el número de b s es 2. (e) ( ) L = {a n b m c m m, n 1}. Se puede elegir la palabra x = ab n c n. En este caso, existen varios patrones de descomposición que cumplen las condiciones a) y b) del lema. Analizamos todos los caso posibles y demostramos que ninguno cumple la condición c): u.v.w = λ.a.b n c n : en este caso podemos comprobar que u.v i.w para i = 0 es λ.b n c n = b n c n que no pertenece a L. u.v.w = λ.ab k.b s c n con k +s = n: en este caso podemos comprobar que u.v i.w para i = 0 es λ.b s c n = b s c n que no pertenece a L. u.v.w = ab t.b k.b s c n con k + s + t = n y k > 0: en este caso podemos comprobar que u.v i.w para i = 2 es ab t.b k.b k.b s c n = ab n+k c n que no pertenece a L, ya que k > 0. (f) ( ) L = {a n b m a m+n m, n 1}. (g) ( ) L = {a n b m n, m 0 y n m}. (h) ( ) L = {a n b m a l m, n, l 1 y l m + n}. (i) ( ) L = {w Σ n a (w) = n b (w)}. Supongamos por reducción al absurdo que L es regular. Sea N N la constante del Lema de Bombeo. Sea x = a N b N L una palabra del lenguaje. Además, su longitud verifica x = 2N > N. Por tanto, podemos aplicar el Lema de Bombeo a esta palabra. Aplicándolo, existen tres palabras u, v, w {a, b, c} verificando: Página 3 de 6
4 uv N v > 0 x = uvw uv i w L para todo i 0. Por la forma que tiene x, y usando la propiedad primera y segunda, tenemos que necesariamente u = a j, v = a k, para j 0, k 1, j + k N. Por tanto, w = a N j k b N. Finalmente, aplicando la última propiedad para i = 0 se tendría que uv 0 w L, pero uv 0 w = uw = a j a N j k b N = a N k b N L Esta palabra a N k b N no está en L pues N k N ya que k 1. Por lo tanto, hemos llegado a una contradicción, por lo que se sigue que L no es regular. (j) ( ) L = {w Σ n a (w) < n b (w)}. Podemos considerar la palabra x = a n b n+1. (k) ( ) L = {w Σ n a (w) n b (w)}. Supongamos por reducción al absurdo que L es regular. Entonces su complementario: L c = { } w {a, b, c} n a (w) = n b (w) también debe ser regular. Contradicción. Como hemos demostrado anteriormente (apartado:i), L c no es regular, y por tanto L tampoco lo es. (l) ( ) L = {a n2 n 1}. (m) ( ) L = {a n! n 3}. Página 4 de 6
5 (n) ( ) L = {w 1 cw 2 w 1, w 2 Σ y w 1 = w 2 }. (ñ) ( ) L = {ww w Σ }. (o) ( ) L donde L es el lenguaje del apartado anterior. Por reducción al absurdo podemos demostrar que L no es regular: Suponemos que L es regular. Entonces,. a plicando el teorema que dice que el complemento de un lenguaje regular es regular, L debería ser regular. Pero L = L y ya hemos demostrado en el ejercicio anterior que L no es regular. Por tanto, llegamos a una contradicción que indica que la suposición L es regular. es erronea. Por tanto, L no es regular. 4. ( ) Sea Σ = {., 0, 1, 2, 3, 4, 5, 6, 7, 8, 9} y sea L π Σ el lenguaje de las cadenas que son las truncaciones de la expansión decimal de π. Esto es, Demuestra que L π no es regular. L π = {λ, 3, 3., 3,1, 3,14, 3,141, 3,1415, 3,14159,...}. Esta demostración es más argumental. 5. ( ) Sea Σ = {a, b} un alfabeto finito, y sea L Σ el lenguaje definido por la siguiente igualdad: Es L regular? L = {xwx Σ x, w Σ, x = 2}. Sí lo es. Intenta construir el autómata. 6. ( ) Sea Σ = {0, 1} un alfabeto finito, y sea L Σ el lenguaje definido por la siguiente igualdad: L = {xwx 1 x, w {0, 1} + }. Es L un lenguaje regular? Página 5 de 6
6 Este lenguaje sí es regular. Uno podría argumentar que, por ejemplo con la palabra x = 1 n 01 n no cumple las condiciones del lema de bombeo, porque al bombear 1 s al principio (y no al final), la palabra no pertenece al lenguaje. Por ejemplo para i=2, se obtendría una palabra 1 n+k 01 n con k > 0 y esta palabra no pertenece a L. Analizando bien el lenguaje, esta palabra sí pertenece a L: podemos entender que x = 1 y w = 1 n+k 1 01 n 1 y es obvio que xwx 1 pertenece a L. En realidad, el lenguaje contiene cualquier palabra sobre 0, 1 que empieza y termina en la misma letra. Se puede crear un autómata para este lenguaje. Página 6 de 6
Nivel del ejercicio : ( ) básico, ( ) medio, ( ) avanzado.
 Universidad Rey Juan Carlos Curso 2010 2011 Teoría de Autómatas y Lenguajes Formales Ingeniería Técnica en Informática de Sistemas Hoja de Problemas 12 Propiedades de L.I.C. Nivel del ejercicio : ( ) básico,
Universidad Rey Juan Carlos Curso 2010 2011 Teoría de Autómatas y Lenguajes Formales Ingeniería Técnica en Informática de Sistemas Hoja de Problemas 12 Propiedades de L.I.C. Nivel del ejercicio : ( ) básico,
Lenguaje Regular. Sumario. Lenguaje Regular. Autómatas y Lenguajes Formales. Capítulo 8: Propiedades de los Lenguajes Regulares
 Lenguaje Regular Capítulo 8: Propiedades de los Lenguajes Regulares José Miguel Buenaposada Josemiguel.buenaposada@urjc.es Definición 1 (Lenguaje Regular) Un lenguaje L se denomina regular si y sólo si
Lenguaje Regular Capítulo 8: Propiedades de los Lenguajes Regulares José Miguel Buenaposada Josemiguel.buenaposada@urjc.es Definición 1 (Lenguaje Regular) Un lenguaje L se denomina regular si y sólo si
Propiedades de lenguajes independientes del contexto
 Capítulo 12. Propiedades de lenguajes independientes del contexto 12.1. Identificación de lenguajes independientes del contexto Lema de bombeo. 12.2. Propiedades Cierre, Complemento de lenguajes, Sustitución,
Capítulo 12. Propiedades de lenguajes independientes del contexto 12.1. Identificación de lenguajes independientes del contexto Lema de bombeo. 12.2. Propiedades Cierre, Complemento de lenguajes, Sustitución,
Máquinas Secuenciales, Autómatas y Lenguajes Tema 5: Propiedades de los Lenguajes Regulares. Luis Peña
 Máquinas Secuenciales, Autómatas y Lenguajes Tema 5: Propiedades de los Lenguajes Regulares Luis Peña Lenguaje Regular Definición 1 (Lenguaje Regular) Un lenguaje L se denomina regular si y sólo si existe
Máquinas Secuenciales, Autómatas y Lenguajes Tema 5: Propiedades de los Lenguajes Regulares Luis Peña Lenguaje Regular Definición 1 (Lenguaje Regular) Un lenguaje L se denomina regular si y sólo si existe
1 er Parcial Febrero 2009
 Autómatas y Lenguajes Formales 3 o Ingeniería Informática 1 er Parcial Febrero 2009 Normas : La duración de esta parte del examen es de 2,5 horas. Todos los ejercicios se entregarán en hojas separadas.
Autómatas y Lenguajes Formales 3 o Ingeniería Informática 1 er Parcial Febrero 2009 Normas : La duración de esta parte del examen es de 2,5 horas. Todos los ejercicios se entregarán en hojas separadas.
El lema de bombeo para lenguajes regulares
 El lema de bombeo para lenguajes regulares Lenguajes, Gramáticas y Autómatas, cuarto cuatrimestre (primavera) de Ingeniería en Informática http://webdiis.unizar.es/asignaturas/lga Rubén Béjar Hernández,
El lema de bombeo para lenguajes regulares Lenguajes, Gramáticas y Autómatas, cuarto cuatrimestre (primavera) de Ingeniería en Informática http://webdiis.unizar.es/asignaturas/lga Rubén Béjar Hernández,
TEORÍA DE AUTÓMATAS Y LENGUAJES
 TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES Francisco Vico departamento Lenguajes y Ciencias de la Computación área de conocimiento Ciencias de la Computación e Inteligencia Artificial ETSI Informática Universidad
TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES Francisco Vico departamento Lenguajes y Ciencias de la Computación área de conocimiento Ciencias de la Computación e Inteligencia Artificial ETSI Informática Universidad
Víctor J. Díaz Madrigal y Fernando Enríquez de Salamanca Ros. 2.1 Límites de los lenguajes regulares Teorema de Myhill-Nerode Lema del bombeo
 Guión 2.1 Límites de los lenguajes regulares Teorema de Myhill-Nerode Lema del bombeo Tma. de Myhill-Nerode: Relaciones de equivalencia Una relación de equivalencia sobre Σ es: 1. Invariante por la derecha:
Guión 2.1 Límites de los lenguajes regulares Teorema de Myhill-Nerode Lema del bombeo Tma. de Myhill-Nerode: Relaciones de equivalencia Una relación de equivalencia sobre Σ es: 1. Invariante por la derecha:
Fundamentos de Ciencias de la Computación Trabajo Práctico N 2 Lenguajes Libres del Contexto y Sensibles al Contexto Segundo Cuatrimestre de 2002
 Departamento de Cs. e Ingeniería de la Computación Universidad Nacional del Sur Ejercicios Fundamentos de Ciencias de la Computación Trabajo Práctico N 2 Lenguajes Libres del Contexto y Sensibles al Contexto
Departamento de Cs. e Ingeniería de la Computación Universidad Nacional del Sur Ejercicios Fundamentos de Ciencias de la Computación Trabajo Práctico N 2 Lenguajes Libres del Contexto y Sensibles al Contexto
El lema de bombeo y los lenguajes no regulares
 El lema de bombeo y los lenguajes no regulares Elvira Mayordomo Universidad de Zaragoza 22 de octubre de 202 Contenido de este tema Son todos los lenguajes regulares? El lema de bombeo Cómo aplicar el
El lema de bombeo y los lenguajes no regulares Elvira Mayordomo Universidad de Zaragoza 22 de octubre de 202 Contenido de este tema Son todos los lenguajes regulares? El lema de bombeo Cómo aplicar el
Otras propiedades de los lenguajes regulares
 Capítulo 3 Otras propiedades de los lenguajes regulares En los dos capítulos anteriores hemos presentado las propiedades básicas de los lenguajes regulares pero no hemos visto cómo se puede demostrar que
Capítulo 3 Otras propiedades de los lenguajes regulares En los dos capítulos anteriores hemos presentado las propiedades básicas de los lenguajes regulares pero no hemos visto cómo se puede demostrar que
Teoría de la Computación y Leguajes Formales
 y Leguajes Formales Prof. Hilda Y. Contreras Departamento de Computación hyelitza@ula.ve hildac.teoriadelacomputacion@gmail.com Contenido Tema 0: Introducción y preliminares: Conocimientos matemáticos
y Leguajes Formales Prof. Hilda Y. Contreras Departamento de Computación hyelitza@ula.ve hildac.teoriadelacomputacion@gmail.com Contenido Tema 0: Introducción y preliminares: Conocimientos matemáticos
El ejercicio de la demostración en matemáticas
 El ejercicio de la demostración en matemáticas Demostración directa En el tipo de demostración conocido como demostración directa (hacia adelante) se trata de demostrar que A B partiendo de A y deduciendo
El ejercicio de la demostración en matemáticas Demostración directa En el tipo de demostración conocido como demostración directa (hacia adelante) se trata de demostrar que A B partiendo de A y deduciendo
Teoría de la Computación Lenguajes Regulares (LR) - Propiedades
 Teoría de la Computación Lenguajes Regulares (LR) - Propiedades Prof. Hilda Y. Contreras Departamento de Computación hyelitza@ula.ve http://webdelprofesor.ula.ve/ingenieria/hyelitza Objetivo Lenguajes
Teoría de la Computación Lenguajes Regulares (LR) - Propiedades Prof. Hilda Y. Contreras Departamento de Computación hyelitza@ula.ve http://webdelprofesor.ula.ve/ingenieria/hyelitza Objetivo Lenguajes
Interrogación 2. Pontificia Universidad Católica de Chile Escuela de Ingeniería Departamento de Ciencia de la Computación. Segundo Semestre, 2003
 Pontificia Universidad Católica de Chile Escuela de Ingeniería Departamento de Ciencia de la Computación Interrogación 2 IIC 2222 Teoría de Autómatas y Lenguajes Formales Segundo Semestre, 2003 Esta interrogación
Pontificia Universidad Católica de Chile Escuela de Ingeniería Departamento de Ciencia de la Computación Interrogación 2 IIC 2222 Teoría de Autómatas y Lenguajes Formales Segundo Semestre, 2003 Esta interrogación
Máquinas de Turing IIC3242. IIC3242 Máquinas de Turing 1 / 42
 Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 42 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 42 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Teoría Matemática de la Computación Segundo Problemario Prof. Miguel A. Pizaña 13 de julio de 2016
 Teoría Matemática de la Computación Segundo Problemario Prof. Miguel A. Pizaña 13 de julio de 2016 I Máquinas de Turing. 1. Qué es un a Máquina de Turing? Cómo se define? Cómo se llaman las teorías que
Teoría Matemática de la Computación Segundo Problemario Prof. Miguel A. Pizaña 13 de julio de 2016 I Máquinas de Turing. 1. Qué es un a Máquina de Turing? Cómo se define? Cómo se llaman las teorías que
1. Cadenas EJERCICIO 1
 LENGUAJES FORMALES Y AUTÓMATAS CURSO 2006/2007 - BOLETÍN DE EJERCICIOS Víctor J. Díaz Madrigal y José Miguel Cañete Departamento de Lenguajes y Sistemas Informáticos 1. Cadenas La operación reversa aplicada
LENGUAJES FORMALES Y AUTÓMATAS CURSO 2006/2007 - BOLETÍN DE EJERCICIOS Víctor J. Díaz Madrigal y José Miguel Cañete Departamento de Lenguajes y Sistemas Informáticos 1. Cadenas La operación reversa aplicada
Tema 4: Gramáticas independientes del contexto. Teoría de autómatas y lenguajes formales I
 Tema 4: Gramáticas independientes del contexto Teoría de autómatas y lenguajes formales I Bibliografía Hopcroft, J. E., Motwani, R., y Ullman, J. D. Introducción a la Teoría de Autómatas, Lenguajes y Computación.
Tema 4: Gramáticas independientes del contexto Teoría de autómatas y lenguajes formales I Bibliografía Hopcroft, J. E., Motwani, R., y Ullman, J. D. Introducción a la Teoría de Autómatas, Lenguajes y Computación.
Examen. Pontificia Universidad Católica de Chile Escuela de Ingeniería Departamento de Ciencia de la Computación. Segundo Semestre, 2003.
 Pontificia Universidad Católica de Chile Escuela de Ingeniería Departamento de Ciencia de la Computación Examen IIC 2222 Teoría de Autómatas y Lenguajes Formales Segundo Semestre, 2003 Este examen tiene
Pontificia Universidad Católica de Chile Escuela de Ingeniería Departamento de Ciencia de la Computación Examen IIC 2222 Teoría de Autómatas y Lenguajes Formales Segundo Semestre, 2003 Este examen tiene
Hacia las Gramáticas Propias II
 Hacia las Hacia las II Gramáticas sin Ciclos Universidad de Cantabria Outline Hacia las 1 Hacia las 2 3 Definición Hacia las Definición Diremos que una gramática libre de contexto G := (V, Σ, Q 0, P) es
Hacia las Hacia las II Gramáticas sin Ciclos Universidad de Cantabria Outline Hacia las 1 Hacia las 2 3 Definición Hacia las Definición Diremos que una gramática libre de contexto G := (V, Σ, Q 0, P) es
MODELOS DE COMPUTACION I Preguntas Tipo Test. 1. El lema de bombeo puede usarse para demostrar que un lenguaje determinado es regular.
 MODELOS DE COMPUTACION I Preguntas Tipo Test Indicar si son verdaderas o falsas las siguientes afirmaciones: 1. El lema de bombeo puede usarse para demostrar que un lenguaje determinado es regular. 2.
MODELOS DE COMPUTACION I Preguntas Tipo Test Indicar si son verdaderas o falsas las siguientes afirmaciones: 1. El lema de bombeo puede usarse para demostrar que un lenguaje determinado es regular. 2.
3 Propiedades de los conjuntos regulares 3.1 Lema de Bombeo para conjuntos regulares
 Curso Básico de Computación 3 Propiedades de los conjuntos regulares 3. Lema de Bombeo para conjuntos regulares El lema de bombeo es una herramienta poderosa para probar que ciertos lenguajes son no regulares.
Curso Básico de Computación 3 Propiedades de los conjuntos regulares 3. Lema de Bombeo para conjuntos regulares El lema de bombeo es una herramienta poderosa para probar que ciertos lenguajes son no regulares.
AUTÓMATAS DE ESTADO FINITO
 AUTÓMATAS DE ESTADO FINITO Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 12 de octubre de 2008 Contenido Autómatas de estado finito Concatenación de
AUTÓMATAS DE ESTADO FINITO Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 12 de octubre de 2008 Contenido Autómatas de estado finito Concatenación de
Autómatas de Pila y Lenguajes Incontextuales
 Autómatas de Pila y Lenguajes Incontextuales Elvira Mayordomo Universidad de Zaragoza 5 de noviembre de 2012 Contenido de este tema 1. Introducción a los autómatas de pila 2. Definiciones 3. Equivalencia
Autómatas de Pila y Lenguajes Incontextuales Elvira Mayordomo Universidad de Zaragoza 5 de noviembre de 2012 Contenido de este tema 1. Introducción a los autómatas de pila 2. Definiciones 3. Equivalencia
Terminaremos el capítulo con una breve referencia a la teoría de cardinales.
 TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
TEMA 5. CARDINALES 241 Tema 5. Cardinales Terminaremos el capítulo con una breve referencia a la teoría de cardinales. Definición A.5.1. Diremos que el conjunto X tiene el mismo cardinal que el conjunto
Máquinas de Turing IIC3242. IIC3242 Máquinas de Turing 1 / 45
 Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 45 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Máquinas de Turing IIC3242 IIC3242 Máquinas de Turing 1 / 45 Complejidad Computacional Objetivo: Medir la complejidad computacional de un problema. Vale decir: Medir la cantidad de recursos computacionales
Conjuntos finitos y conjuntos numerables
 Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
1. Lenguajes formales.
 Tema 4: Aplicación de los autómatas: Lenguajes formales 1 Tema 4: Aplicación de los autómatas: Lenguajes formales 1. Lenguajes formales. Como se ha indicado en la introducción del tema, el concepto de
Tema 4: Aplicación de los autómatas: Lenguajes formales 1 Tema 4: Aplicación de los autómatas: Lenguajes formales 1. Lenguajes formales. Como se ha indicado en la introducción del tema, el concepto de
Cuatro Problemas de Algebra en la IMO.
 Cuatro Problemas de Algebra en la IMO. Rafael Sánchez Lamoneda UCV. Escuela de Matemáticas Barquisimeto, 10 de Marzo de 2008 Introducción. El objetivo de esta conferencia es analizar cuatro problemas de
Cuatro Problemas de Algebra en la IMO. Rafael Sánchez Lamoneda UCV. Escuela de Matemáticas Barquisimeto, 10 de Marzo de 2008 Introducción. El objetivo de esta conferencia es analizar cuatro problemas de
Práctica 1: Números reales y sucesiones
 Taller de Cálculo Avanzado - Primer cuatrimestre 2017 Práctica 1: Números reales y sucesiones 1. A partir de los axiomas de cuerpo demostrar las siguientes propiedades cualesquiera sean a, b, c y d en
Taller de Cálculo Avanzado - Primer cuatrimestre 2017 Práctica 1: Números reales y sucesiones 1. A partir de los axiomas de cuerpo demostrar las siguientes propiedades cualesquiera sean a, b, c y d en
Conjuntos finitos y conjuntos numerables
 Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Tema 3 Conjuntos finitos y conjuntos numerables En este tema vamos a usar los números naturales para contar los elementos de un conjunto, o dicho con mayor precisión, para definir los conjuntos finitos
Álgebra. Curso
 Álgebra. Curso 2012-2013 14 de junio de 2013 Resolución Ejercicio. 1. (2 puntos) Utiliza el teorema del descenso (o alternativamente la localización en primos) para probar el siguiente resultado: Sea K
Álgebra. Curso 2012-2013 14 de junio de 2013 Resolución Ejercicio. 1. (2 puntos) Utiliza el teorema del descenso (o alternativamente la localización en primos) para probar el siguiente resultado: Sea K
Aplicaciones de las derivadas. El teorema del valor medio
 Aplicaciones de las derivadas. El teorema del valor medio Ya hemos hablado en un par de artículos anteriores del concepto de derivada y de su interpretación tanto desde el punto de vista geométrico como
Aplicaciones de las derivadas. El teorema del valor medio Ya hemos hablado en un par de artículos anteriores del concepto de derivada y de su interpretación tanto desde el punto de vista geométrico como
Lenguajes No Regulares
 Lenguajes No Regulares Problemas que los Autómatas No Resuelven. Universidad de Cantabria Esquema Lema del Bombeo 1 Lema del Bombeo 2 3 Introducción Todos los lenguajes no son regulares, simplemente hay
Lenguajes No Regulares Problemas que los Autómatas No Resuelven. Universidad de Cantabria Esquema Lema del Bombeo 1 Lema del Bombeo 2 3 Introducción Todos los lenguajes no son regulares, simplemente hay
Introducción. El uso de los símbolos en matemáticas.
 Introducción El uso de los símbolos en matemáticas. En el estudio de las matemáticas lo primero que necesitamos es conocer su lenguaje y, en particular, sus símbolos. Algunos símbolos, que reciben el nombre
Introducción El uso de los símbolos en matemáticas. En el estudio de las matemáticas lo primero que necesitamos es conocer su lenguaje y, en particular, sus símbolos. Algunos símbolos, que reciben el nombre
Álgebra y estructuras finitas/discretas (Grupos A)
 Álgebra y estructuras finitas/discretas (Grupos A) Curso 2007-2008 Soluciones a algunos de los ejercicios propuestos en el Tema 2 Antes de ver la solución de un ejercicio, repase la teoría correspondiente
Álgebra y estructuras finitas/discretas (Grupos A) Curso 2007-2008 Soluciones a algunos de los ejercicios propuestos en el Tema 2 Antes de ver la solución de un ejercicio, repase la teoría correspondiente
Máquina de estado finito con salida sin salida
 Máquina de estado finito con salida sin salida Máquina de estado finito Máquinas de estados finitos se utilizan ampliamente en aplicaciones en ciencias de la computación y redes de datos. Por ejemplo,
Máquina de estado finito con salida sin salida Máquina de estado finito Máquinas de estados finitos se utilizan ampliamente en aplicaciones en ciencias de la computación y redes de datos. Por ejemplo,
TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES Grado en Ingeniería Informática Online, Curso Universidad Rey Juan Carlos
 TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES Grado en Ingeniería Informática Online, Curso 202-203 Universidad Rey Juan Carlos GUÍA PARA LA REALIZACIÓN DE LA HOJA DE PROBLEMAS No 3 (Tema 3: Expresiones Regulares)
TEORÍA DE AUTÓMATAS Y LENGUAJES FORMALES Grado en Ingeniería Informática Online, Curso 202-203 Universidad Rey Juan Carlos GUÍA PARA LA REALIZACIÓN DE LA HOJA DE PROBLEMAS No 3 (Tema 3: Expresiones Regulares)
XVIII Olimpiada Iberoamericana de Matemática Universitaria 2015 Soluciones y Criterios para calicar 24 de noviembre de 2015
 XVIII Olimpiada Iberoamericana de Matemática Universitaria 05 Soluciones y Criterios para calicar 4 de noviembre de 05 Problema Sean a y b números reales tales que a < b y ab > 0. Sea f : [a, b] [a, b]
XVIII Olimpiada Iberoamericana de Matemática Universitaria 05 Soluciones y Criterios para calicar 4 de noviembre de 05 Problema Sean a y b números reales tales que a < b y ab > 0. Sea f : [a, b] [a, b]
Computabilidad y lenguajes formales: Sesión 17. Equivalencia entre Expresiones Regulares y Autómatas Finitos
 Computabilidad y lenguajes formales: Sesión 17. Equivalencia entre Expresiones Regulares y Autómatas Finitos Prof. Gloria Inés Alvarez V. Departamento de Ciencias e Ingeniería de la Computación Pontificia
Computabilidad y lenguajes formales: Sesión 17. Equivalencia entre Expresiones Regulares y Autómatas Finitos Prof. Gloria Inés Alvarez V. Departamento de Ciencias e Ingeniería de la Computación Pontificia
Computabilidad y lenguajes formales: Sesión 18. Lema de bombeo (Pumping lemma)
 Computabilidad y lenguajes formales: Sesión 18. Lema de bombeo (Pumping lemma) Prof. Gloria Inés Alvarez V. Departamento de Ciencias e Ingeniería de la Computación Pontificia Universidad Javeriana Cali
Computabilidad y lenguajes formales: Sesión 18. Lema de bombeo (Pumping lemma) Prof. Gloria Inés Alvarez V. Departamento de Ciencias e Ingeniería de la Computación Pontificia Universidad Javeriana Cali
Operaciones extendidas de conjuntos
 234 A. GENERALIDADES DE TEORÍA DE CONJUNTOS Tema 3. Operaciones extendidas de conjuntos En este tema extenderemos las operaciones de conjuntos anteriormente definidas a familias arbitrarias de conjuntos.
234 A. GENERALIDADES DE TEORÍA DE CONJUNTOS Tema 3. Operaciones extendidas de conjuntos En este tema extenderemos las operaciones de conjuntos anteriormente definidas a familias arbitrarias de conjuntos.
Inducción en definiciones y demostraciones AUTÓMATAS Y LENGUAJES FORMALES PRELIMINARES MATEMÁTICOS. Números naturales. Inducción matemática
 Inducción en definiciones y demostraciones AUTÓMATAS Y LENGUAJES FORMALES PRELIMINARES MATEMÁTICOS Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx
Inducción en definiciones y demostraciones AUTÓMATAS Y LENGUAJES FORMALES PRELIMINARES MATEMÁTICOS Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx
Propiedades de Lenguajes Regulares
 de INAOE (INAOE) 1 / 44 Contenido 1 2 3 4 (INAOE) 2 / 44 Existen diferentes herramientas que se pueden utilizar sobre los lenguajes regulares: El lema de : cualquier lenguaje regular satisface el pumping
de INAOE (INAOE) 1 / 44 Contenido 1 2 3 4 (INAOE) 2 / 44 Existen diferentes herramientas que se pueden utilizar sobre los lenguajes regulares: El lema de : cualquier lenguaje regular satisface el pumping
Sucesiones. Una sucesión de números reales es una tira, o una lista, de nḿeros reales que generalmente denotamos como
 Universidad de la República Facultad de Ingeniería IMERL Sucesiones Curso Cálculo 1 2008 Una sucesión de números reales es una tira, o una lista, de nḿeros reales que generalmente denotamos como a 1, a
Universidad de la República Facultad de Ingeniería IMERL Sucesiones Curso Cálculo 1 2008 Una sucesión de números reales es una tira, o una lista, de nḿeros reales que generalmente denotamos como a 1, a
Ejemplo de demostración de que cierto lenguaje es el lenguaje aceptado por un AFND.
 Ejemplo de demostración de que cierto lenguaje es el lenguaje aceptado por un AFND. Sea el siguiente autómata finito no determinista M: c q0 a b q1 b q2 Sea L = {x {a, b, c} /x es de la forma a(ba) k bc
Ejemplo de demostración de que cierto lenguaje es el lenguaje aceptado por un AFND. Sea el siguiente autómata finito no determinista M: c q0 a b q1 b q2 Sea L = {x {a, b, c} /x es de la forma a(ba) k bc
Introducción. Definición de números primos y compuestos
 en Introducción El presente trabajo expone la solución a uno de los problemas matemáticos que aún después de mucho tiempo no han sido resueltos. Específicamente, en estas páginas se lleva a cabo la tarea
en Introducción El presente trabajo expone la solución a uno de los problemas matemáticos que aún después de mucho tiempo no han sido resueltos. Específicamente, en estas páginas se lleva a cabo la tarea
Examen de Teoría de Autómatas y Lenguajes Formales
 Examen de Teoría de Autómatas y Lenguajes Formales TAL 16 de Septiembre de 2008 (I) CUESTIONES: (Justifique formalmente las respuestas) 1. Pronúnciese acerca de la veracidad o falsedad de los siguientes
Examen de Teoría de Autómatas y Lenguajes Formales TAL 16 de Septiembre de 2008 (I) CUESTIONES: (Justifique formalmente las respuestas) 1. Pronúnciese acerca de la veracidad o falsedad de los siguientes
CLASES DE PROBLEMAS. 1) Introducción 2) Problemas de decisión, Lenguajes, Codificación. y la clase NP-Completa. 6) Otras clases de problemas NP-
 CLASES DE PROBLEMAS 1) Introducción 2) Problemas de decisión, Lenguajes, Codificación. y la clase NP-Completa. 6) Otras clases de problemas Computers and Intractability NP- guide to the theory of 1. Introducción:
CLASES DE PROBLEMAS 1) Introducción 2) Problemas de decisión, Lenguajes, Codificación. y la clase NP-Completa. 6) Otras clases de problemas Computers and Intractability NP- guide to the theory of 1. Introducción:
Seminario de problemas Curso Hoja 3
 Seminario de problemas Curso 207-8. Hoja 3 6. Juanmi quiere invitar a los asistentes al seminario de problemas a pinchos en la Laurel y seguro que le sale por más de 7e. Si suponemos que solo tiene vales
Seminario de problemas Curso 207-8. Hoja 3 6. Juanmi quiere invitar a los asistentes al seminario de problemas a pinchos en la Laurel y seguro que le sale por más de 7e. Si suponemos que solo tiene vales
Teoría de Números. Divisibilidad. Olimpiada de Matemáticas en Tamaulipas
 Teoría de Números Divisibilidad Olimpiada de Matemáticas en Tamaulipas 1. Introducción Divisibilidad es una herramienta de la aritmética que nos permite conocer un poco más la naturaleza de un número,
Teoría de Números Divisibilidad Olimpiada de Matemáticas en Tamaulipas 1. Introducción Divisibilidad es una herramienta de la aritmética que nos permite conocer un poco más la naturaleza de un número,
Números primos y compuestos
 Números primos y compuestos Jorge Tipe Villanueva Sabemos que cualquier entero positivo n tiene como divisores a 1 y n. Si asumimos que n > 1 entonces n tendrá al menos dos divisores pues 1 y n son diferentes.
Números primos y compuestos Jorge Tipe Villanueva Sabemos que cualquier entero positivo n tiene como divisores a 1 y n. Si asumimos que n > 1 entonces n tendrá al menos dos divisores pues 1 y n son diferentes.
Descripción de los Lenguajes Aceptados por Autómatas
 Descripción de los Lenguajes Aceptados por Autómatas Los Teoremas de Kleene Universidad de Cantabria Esquema 1 2 3 Lenguajes Aceptados por Autómatas Como repaso, tenemos un problema de respuesta Si/No
Descripción de los Lenguajes Aceptados por Autómatas Los Teoremas de Kleene Universidad de Cantabria Esquema 1 2 3 Lenguajes Aceptados por Autómatas Como repaso, tenemos un problema de respuesta Si/No
!!! " " # " "!!! $ $ $ % % & % % $ $ $!!! " " # " "!!! $ $ $ % % & % % $ $ $!!! " " # " "!!! $ $ $ % % & % % $ $ $!!! " " # " "!!!!!! " " # " "!!!
 UNIIDAD Nº º NÚMEEROSS REEALLEESS! Resuelve tú ( Pág "# ) Resuelve la ecuación : 9x + 8x 6 ; 9x + 8x 6 ; 9x 8x 8; 9x 8x 8x 8x 8 ; x - 8. Resuelve tú ( Pág "" ) Completa la resolución de 7x 6x + { pasar
UNIIDAD Nº º NÚMEEROSS REEALLEESS! Resuelve tú ( Pág "# ) Resuelve la ecuación : 9x + 8x 6 ; 9x + 8x 6 ; 9x 8x 8; 9x 8x 8x 8x 8 ; x - 8. Resuelve tú ( Pág "" ) Completa la resolución de 7x 6x + { pasar
Máquinas Secuenciales, Autómatas y Lenguajes. Tema 4: Expresiones Regulares. Luis Peña
 Máquinas Secuenciales, Autómatas y Lenguajes Tema 4: Expresiones Regulares Luis Peña Sumario Tema 4: Expresiones Regulares. 1. Concepto de Expresión Regular 2. Teoremas de Equivalencia Curso 2012-2013
Máquinas Secuenciales, Autómatas y Lenguajes Tema 4: Expresiones Regulares Luis Peña Sumario Tema 4: Expresiones Regulares. 1. Concepto de Expresión Regular 2. Teoremas de Equivalencia Curso 2012-2013
Demostración Contraejemplo. Métodos Indirectos
 DEMOSTRACION Una demostración de un teorema es una verificación escrita que muestra que el teorema es verdadero. Informalmente, desde el punto de vista de la lógica, una demostración de un teorema es un
DEMOSTRACION Una demostración de un teorema es una verificación escrita que muestra que el teorema es verdadero. Informalmente, desde el punto de vista de la lógica, una demostración de un teorema es un
Lógica - Conjuntos inductivos
 Lógica - Conjuntos inductivos Matemática discreta y Lógica I Mayo de 2017 Las transparencias son tomadas del curso de Lógica del instituto de computación de Facultad de Ingeniería. Inducción - Plan Conjuntos
Lógica - Conjuntos inductivos Matemática discreta y Lógica I Mayo de 2017 Las transparencias son tomadas del curso de Lógica del instituto de computación de Facultad de Ingeniería. Inducción - Plan Conjuntos
Teoría de Modelos Finitos: Motivación
 Teoría de Modelos Finitos: Motivación IIC3260 IIC3260 Teoría de Modelos Finitos: Motivación 1 / 29 Poder expresivo de una lógica: Caso finito Desde ahora en adelante nos vamos a concentrar en las estructuras
Teoría de Modelos Finitos: Motivación IIC3260 IIC3260 Teoría de Modelos Finitos: Motivación 1 / 29 Poder expresivo de una lógica: Caso finito Desde ahora en adelante nos vamos a concentrar en las estructuras
Expresiones Regulares
 Conjuntos Regulares y Una forma diferente de expresar un lenguaje Universidad de Cantabria Conjuntos Regulares y Esquema 1 Motivación 2 Conjuntos Regulares y 3 4 Conjuntos Regulares y Motivación El problema
Conjuntos Regulares y Una forma diferente de expresar un lenguaje Universidad de Cantabria Conjuntos Regulares y Esquema 1 Motivación 2 Conjuntos Regulares y 3 4 Conjuntos Regulares y Motivación El problema
Los números naturales. Definición y propiedades
 Los números naturales. Definición y propiedades Con la idea de abrir boca para empezar los estudios de matemáticas en bachillerato, en un artículo anterior se hablaba sobre la introducción al número real
Los números naturales. Definición y propiedades Con la idea de abrir boca para empezar los estudios de matemáticas en bachillerato, en un artículo anterior se hablaba sobre la introducción al número real
LENGUAJES Y GRAMÁTICAS
 LENGUAJES Y GRAMÁTICAS Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 20 de septiembre de 2008 Contenido Lenguajes y Gramáticas Gramáticas Gramáticas
LENGUAJES Y GRAMÁTICAS Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 20 de septiembre de 2008 Contenido Lenguajes y Gramáticas Gramáticas Gramáticas
Tema 5: Autómatas a pila. Teoría de autómatas y lenguajes formales I
 Tema 5: Autómatas a pila Teoría de autómatas y lenguajes formales I Bibliografía Hopcroft, J. E., Motwani, R., y Ullman, J. D. Introducción a la Teoría de Autómatas, Lenguajes y Computación. Addison Wesley.
Tema 5: Autómatas a pila Teoría de autómatas y lenguajes formales I Bibliografía Hopcroft, J. E., Motwani, R., y Ullman, J. D. Introducción a la Teoría de Autómatas, Lenguajes y Computación. Addison Wesley.
3. Relacin entre los lenguajes regulares y los autmatas.
 Tema 4: Aplicación de los autómatas: Lenguajes formales 1 Tema 4: Aplicación de los autómatas: Lenguajes formales 3. Relacin entre los lenguajes regulares y los autmatas. Definición. Sea S = (S, E, δ)
Tema 4: Aplicación de los autómatas: Lenguajes formales 1 Tema 4: Aplicación de los autómatas: Lenguajes formales 3. Relacin entre los lenguajes regulares y los autmatas. Definición. Sea S = (S, E, δ)
Clases de complejidad computacional: P y NP
 1er cuatrimestre 2006 La teoría de Se aplica a problemas de decisión, o sea problemas que tienen como respuesta SI o NO (aunque es sencillo ver que sus implicancias pueden extenderse a problemas de optimización).
1er cuatrimestre 2006 La teoría de Se aplica a problemas de decisión, o sea problemas que tienen como respuesta SI o NO (aunque es sencillo ver que sus implicancias pueden extenderse a problemas de optimización).
2do. Parcial. Todos los ejercicios se entregarán en hojas separadas. El examen tipo test cuenta hasta 2 puntos sobre la nota total.
 U.R.J.C. Ingeniera Técnica en Informática de Sistemas Teoría de Autómatas y Lenguajes Formales Junio 2009 2do. Parcial Normas : La duración del examen es de 2 horas. Todos los ejercicios se entregarán
U.R.J.C. Ingeniera Técnica en Informática de Sistemas Teoría de Autómatas y Lenguajes Formales Junio 2009 2do. Parcial Normas : La duración del examen es de 2 horas. Todos los ejercicios se entregarán
Cardinalidad IIC1253. IIC1253 Cardinalidad 1 / 23
 Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. IIC1253
Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. IIC1253
Cardinalidad IIC1253. IIC1253 Cardinalidad 1 / 23
 Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. Ejemplo
Cardinalidad IIC1253 IIC1253 Cardinalidad 1 / 23 Conjuntos con la misma cardinalidad Definición Decimos que dos conjuntos A y B son equinumerosos, denotado como A B, si existe una biyección f : A B. Ejemplo
Tema 3: Gramáticas regulares. Teoría de autómatas y lenguajes formales I
 Tema 3: Gramáticas regulares Teoría de autómatas y lenguajes formales I Bibliografía Hopcroft, J. E., Motwani, R., y Ullman, J. D. Introducción a la Teoría de Autómatas, Lenguajes y Computación. Addison
Tema 3: Gramáticas regulares Teoría de autómatas y lenguajes formales I Bibliografía Hopcroft, J. E., Motwani, R., y Ullman, J. D. Introducción a la Teoría de Autómatas, Lenguajes y Computación. Addison
UNIVERSIDAD NACIONAL DE COLOMBIA DEPARTAMENTO DE MATEMÁTICAS PARCIAL 2 FUNDAMENTOS DE MATEMÁTICAS GRUPO 3
 UNIVERSIDAD NACIONAL DE COLOMBIA DEPARTAMENTO DE MATEMÁTICAS PARCIAL 2 FUNDAMENTOS DE MATEMÁTICAS GRUPO 3 Profesor: Pedro Zambrano abril 20 de 2.017 ESTE DOCUMENTO ES APENAS UNA GUÍA, NO ES LA ÚNICA MAN-
UNIVERSIDAD NACIONAL DE COLOMBIA DEPARTAMENTO DE MATEMÁTICAS PARCIAL 2 FUNDAMENTOS DE MATEMÁTICAS GRUPO 3 Profesor: Pedro Zambrano abril 20 de 2.017 ESTE DOCUMENTO ES APENAS UNA GUÍA, NO ES LA ÚNICA MAN-
El teorema del valor intermedio
 Ya hemos tratado en un artículo anterior el problema de la continuidad de una función. Ahora nos hemos de preguntar sobre las ventajas que, en análisis matemático, nos proporciona este hecho. Existen una
Ya hemos tratado en un artículo anterior el problema de la continuidad de una función. Ahora nos hemos de preguntar sobre las ventajas que, en análisis matemático, nos proporciona este hecho. Existen una
Funciones continuas e inyectivas
 Nuestro último teorema afirmaba que toda función continua en un intervalo cerrado y acotado tiene máximo y mínimo absolutos, pero nada nos informa sobre los puntos en los que se alcanzan. Bajo la hipótesis
Nuestro último teorema afirmaba que toda función continua en un intervalo cerrado y acotado tiene máximo y mínimo absolutos, pero nada nos informa sobre los puntos en los que se alcanzan. Bajo la hipótesis
Memo Garro. A n F. n=1
 σ-álgebra Memo Garro Introducción En este apunte estudiaremos el concepto de σ-álgebra, como un tipo especial de familia de subconjuntos de un espacio Ω, aunque todavía desde un punto de vista puramente
σ-álgebra Memo Garro Introducción En este apunte estudiaremos el concepto de σ-álgebra, como un tipo especial de familia de subconjuntos de un espacio Ω, aunque todavía desde un punto de vista puramente
Teoremas: Condiciones Necesarias, Condiciones Suficientes y Condiciones Necesarias y Suficientes
 FUNCIONES DE VARIABLE COMPLEJA 1 Teoremas: Condiciones Necesarias, Condiciones Suficientes y Condiciones Necesarias y Suficientes Lógica Matemática Una prioridad que tiene la enseñanza de la matemática
FUNCIONES DE VARIABLE COMPLEJA 1 Teoremas: Condiciones Necesarias, Condiciones Suficientes y Condiciones Necesarias y Suficientes Lógica Matemática Una prioridad que tiene la enseñanza de la matemática
Computabilidad y Lenguajes Formales: Teoría de la Computabilidad: Decidibilidad
 300CIG007 Computabilidad y Lenguajes Formales: Teoría de la Computabilidad: Decidibilidad Pontificia Universidad Javeriana Cali Ingenieria de Sistemas y Computación Prof. Gloria Inés Alvarez V. Lo indecidible
300CIG007 Computabilidad y Lenguajes Formales: Teoría de la Computabilidad: Decidibilidad Pontificia Universidad Javeriana Cali Ingenieria de Sistemas y Computación Prof. Gloria Inés Alvarez V. Lo indecidible
300CIG007 Computabilidad y Lenguajes Formales: Autómatas Finitos
 300CIG007 Computabilidad y Lenguajes Formales: Autómatas Finitos Pontificia Universidad Javeriana Cali Ingeniería de Sistemas y Computación Prof. Gloria Inés Alvarez V. Qué es un computador? Todos lo sabemos!!!
300CIG007 Computabilidad y Lenguajes Formales: Autómatas Finitos Pontificia Universidad Javeriana Cali Ingeniería de Sistemas y Computación Prof. Gloria Inés Alvarez V. Qué es un computador? Todos lo sabemos!!!
Teoría de Autómatas y Compiladores [ICI-445] Capítulo 2: Autómatas Finitos
![Teoría de Autómatas y Compiladores [ICI-445] Capítulo 2: Autómatas Finitos Teoría de Autómatas y Compiladores [ICI-445] Capítulo 2: Autómatas Finitos](/thumbs/68/58725388.jpg) Teoría de Autómatas y Compiladores [ICI-445] Capítulo 2: Autómatas Finitos Dr. Ricardo Soto [ricardo.soto@ucv.cl] [http://www.inf.ucv.cl/ rsoto] Escuela de Ingeniería Informática Pontificia Universidad
Teoría de Autómatas y Compiladores [ICI-445] Capítulo 2: Autómatas Finitos Dr. Ricardo Soto [ricardo.soto@ucv.cl] [http://www.inf.ucv.cl/ rsoto] Escuela de Ingeniería Informática Pontificia Universidad
TRADUCTORES E INTERPRETADORES
 TRADUCTORES E INTERPRETADORES Clase 9: Autómatas de Pila Agenda Autómatas de Pila Tipos de Aceptación para Autómatas de Pila Determinismo vs. No Determinismo Equivalencia entre Autómatas de Pila y Gramáticas
TRADUCTORES E INTERPRETADORES Clase 9: Autómatas de Pila Agenda Autómatas de Pila Tipos de Aceptación para Autómatas de Pila Determinismo vs. No Determinismo Equivalencia entre Autómatas de Pila y Gramáticas
Prueba de control Soluciones
 FACULTAD DE MATEMÁTICAS Lenguaje y método matemáticos 30 de septiembre de 011 Prueba de control Soluciones Nombre: 1 Experimente con casos concretos y proponga respuestas para las siguientes preguntas.
FACULTAD DE MATEMÁTICAS Lenguaje y método matemáticos 30 de septiembre de 011 Prueba de control Soluciones Nombre: 1 Experimente con casos concretos y proponga respuestas para las siguientes preguntas.
Cardinalidad. Pablo Verdes. 9 de marzo de 2016 LCC. Pablo Verdes (LCC) Cardinalidad 9 de marzo de / 18
 Cardinalidad Pablo Verdes LCC 9 de marzo de 2016 Pablo Verdes (LCC) Cardinalidad 9 de marzo de 2016 1 / 18 Por qué estudiamos cardinalidad? Recordemos nuestro objetivo: modelar el proceso de cálculo. Cuál
Cardinalidad Pablo Verdes LCC 9 de marzo de 2016 Pablo Verdes (LCC) Cardinalidad 9 de marzo de 2016 1 / 18 Por qué estudiamos cardinalidad? Recordemos nuestro objetivo: modelar el proceso de cálculo. Cuál
Curso Básico de Computación
 Curso Básico de Computación 3 Propiedades de los conjuntos regulares Feliú Sagols Troncoso Matemáticas CINVESTAV-IPN 2010 Curso Básico de Computación (Matemáticas) 3 Propiedades
Curso Básico de Computación 3 Propiedades de los conjuntos regulares Feliú Sagols Troncoso Matemáticas CINVESTAV-IPN 2010 Curso Básico de Computación (Matemáticas) 3 Propiedades
2. El Teorema del Valor Medio
 2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
2.24 45 2. El Teorema del Valor Medio Comenzaremos esta sección recordando dos versiones del teorema del valor medido para funciones de 1-variable y por tanto ya conocidas: 2.22 Sea f : [a, b] R R una
Espacios vectoriales
 CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
CAPíTULO 2 Espacios vectoriales 1. Definición de espacio vectorial Es frecuente representar ciertas magnitudes físicas (velocidad, fuerza,...) mediante segmentos orientados o vectores. Dados dos de tales
Lógica Instituto de Computación. 27 de febrero
 Inducción Lógica 2018 Instituto de Computación 27 de febrero Instituto de Computación (InCo) Inducción Curso 2018 1 / 1 Inducción - Plan Conjuntos inductivos Inducción como mecanismo primitivo para definir
Inducción Lógica 2018 Instituto de Computación 27 de febrero Instituto de Computación (InCo) Inducción Curso 2018 1 / 1 Inducción - Plan Conjuntos inductivos Inducción como mecanismo primitivo para definir
Llamaremos número real a cualquier fracción decimal. Las fracciones decimales periódicas se llaman números racionales, así:
 Capítulo 1 Números Reales 1.1. Introducción Llamaremos número real a cualquier fracción decimal. Ejemplos:, 0;, 3333...;, 5; 0,785; 3, 14159...;,718818...; 1,414136... Las fracciones decimales periódicas
Capítulo 1 Números Reales 1.1. Introducción Llamaremos número real a cualquier fracción decimal. Ejemplos:, 0;, 3333...;, 5; 0,785; 3, 14159...;,718818...; 1,414136... Las fracciones decimales periódicas
Teoremas de Convergencia
 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
El Teorema de Recurrencia de Poincaré
 El Teorema de Recurrencia de Poincaré Pablo Lessa 9 de octubre de 204. Recurrencia de Poincaré.. Fracciones Continuas Supongamos que queremos expresar la relación que existe entre los números 27 y 0. Una
El Teorema de Recurrencia de Poincaré Pablo Lessa 9 de octubre de 204. Recurrencia de Poincaré.. Fracciones Continuas Supongamos que queremos expresar la relación que existe entre los números 27 y 0. Una
Problemas Insolubles Ejemplos
 Problemas Insolubles Ejemplos A continuación enunciaremos una serie de problemas y demostraremos, mediante la técnica de reducibilidad, que los mismos son indecidibles (no solubles a través de una máquina
Problemas Insolubles Ejemplos A continuación enunciaremos una serie de problemas y demostraremos, mediante la técnica de reducibilidad, que los mismos son indecidibles (no solubles a través de una máquina
Teoremas de Tonelli y Fubini
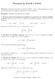 Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I SOLUCIONES
 INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I 19 de Enero de 2009 SOLUCIONES PREGUNTA 1 (2 puntos): Son siete cuestiones que debes responder y entregar en esta misma hoja. 1.1 Considera el
INGENIERÍA EN INFORMÁTICA MODELOS ABSTRACTOS DE COMPUTO I 19 de Enero de 2009 SOLUCIONES PREGUNTA 1 (2 puntos): Son siete cuestiones que debes responder y entregar en esta misma hoja. 1.1 Considera el
Una invitación al estudio de las cadenas de Markov
 Una invitación al estudio de las cadenas de Markov Víctor RIVERO Centro de Investigación en Matemáticas A. C. Taller de solución de problemas de probabilidad, 21-25 de Enero de 2008. 1/ 1 Potencias de
Una invitación al estudio de las cadenas de Markov Víctor RIVERO Centro de Investigación en Matemáticas A. C. Taller de solución de problemas de probabilidad, 21-25 de Enero de 2008. 1/ 1 Potencias de
CONJUNTOS REGULARES. Orlando Arboleda Molina. 19 de Octubre de Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle
 CONJUNTOS REGULARES Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 19 de Octubre de 2008 Contenido Expresiones regulares Teorema de Kleene Autómatas
CONJUNTOS REGULARES Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 19 de Octubre de 2008 Contenido Expresiones regulares Teorema de Kleene Autómatas
Continuidad y monotonía
 Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Tema 14 Continuidad y monotonía Generalizando lo que se hizo en su momento para sucesiones, definiremos la monotonía de una función, en forma bien fácil de adivinar. Probaremos entonces dos resultados
Máquinas de Turing, recordatorio y problemas
 Máquinas de Turing, recordatorio y problemas Elvira Mayordomo, Universidad de Zaragoza 5 de diciembre de 2014 1. Recordatorio de la definición de máquina de Turing Una máquina de Turing, abreviadamente
Máquinas de Turing, recordatorio y problemas Elvira Mayordomo, Universidad de Zaragoza 5 de diciembre de 2014 1. Recordatorio de la definición de máquina de Turing Una máquina de Turing, abreviadamente
a. no (si A entonces B)
 Una tabla de verdad es una tabla que despliega el valor de verdad de una proposición compuesta, para cada combinación de valores de verdad que se pueda asignar a sus componentes. Las tablas de verdad son
Una tabla de verdad es una tabla que despliega el valor de verdad de una proposición compuesta, para cada combinación de valores de verdad que se pueda asignar a sus componentes. Las tablas de verdad son
Introducción TEORÍA DE LA COMPUTACIÓN INTRODUCCIÓN. Lógica
 Introducción TEORÍA DE LA COMPUTACIÓN INTRODUCCIÓN Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx Página Web: www.matematicas.unam.mx/fhq
Introducción TEORÍA DE LA COMPUTACIÓN INTRODUCCIÓN Francisco Hernández Quiroz Departamento de Matemáticas Facultad de Ciencias, UNAM E-mail: fhq@ciencias.unam.mx Página Web: www.matematicas.unam.mx/fhq
Teoría de la Computación y Lenguajes Formales
 Teoría de la Computación y Lenguajes Formales Propiedades de los Lenguajes Libres de Contexto (LLC) Prof. Hilda Y. Contreras Departamento de Computación hyelitza@ula.ve hildac.teoriadelacomputacion@gmail.com
Teoría de la Computación y Lenguajes Formales Propiedades de los Lenguajes Libres de Contexto (LLC) Prof. Hilda Y. Contreras Departamento de Computación hyelitza@ula.ve hildac.teoriadelacomputacion@gmail.com
