Teorema de Karlin - Rubin y ejemplos no
|
|
|
- Miguel Ángel Zúñiga Ávila
- hace 5 años
- Vistas:
Transcripción
1 Teorema de Karlin - Rubin y ejemplos no clásicos E. Nájera Rangel,*, B. G. Peralta Reyes 2, A. Pérez Pérez. División Académica de Ciencias Básicas, Universidad Juárez Autónoma de Tabasco, A.P. 24, C.P , Cunduacán, Tabasco, México *edilberto.najera@ujat.mx 2 Instituto Tecnológico Superior de Comalcalco, carret. vecinal Comalcalco-Paraiso Km 2, Ra. Occidente 3ra. Secc, C.P. 8665, Comalcalco, Tabasco, México El teorema de Karlin - Rubin es una generalización del lema de Neyman - Pearson, de tal forma que bajo ciertas condiciones nos permite obtener los mejores procedimientos para probar hipótesis estadísticas compuestas unilaterales. El propósito de este trabajo es proporcionar una introducción básica de este teorema e ilustrar su aplicación a través de ejemplos no incluídos en los libros de texto más conocidos. The Karlin - Rubin theorem is a generalization of the Neyman-Pearson lemma, so that under certain conditions allows us to obtain the best procedures to test statistical composite one-sided hypotheses. The purpose of this paper is to provide a basic introduction to this theorem and illustrate its application through examples not included in the most popular textbooks. Palabras claves: Estadístico suficiente, prueba de hipótesis, teorema de Karlin-Rubin. Keywords: Sufficient statistic, hypothesis testing, Karlin-Rubin theorem.. Introducción Uno de los objetivos principales de la estadística es el de hacer inferencias respecto a parámetros poblacionales desconocidos a través de la información contenida en una muestra. Estas inferencias pueden interpretarse como estimaciones de los parámetros respectivos o como pruebas de hipótesis relacionadas con sus valores. Específicamente, en este trabajo suponemos un experimento aleatorio para el cual se conoce la forma de su función de densidad o de probabilidad (en el caso discreto) f en algún espacio Euclidiano R k, k, pero que ésta depende de algún parámetro desconocido θ, de modo que f( ) f( ; θ), del cual sólo se sabe que pertenece a cierto conjunto Θ R k, k, llamado el espacio de parámetros. Nuestro interés se centra en probar la hipótesis H 0 : θ Θ 0 versus H : θ Θ c 0, donde Θ 0 Θ y Θ c 0 = Θ Θ 0. A H 0 le llamaremos la hipótesis nula y a H la hipótesis alternativa. Supongamos dada una muestra aleatoria X = (X,..., X n ) de la función de densidad o de probabilidad f(x; θ). Recibido: 5 abril 205. Aceptado: 08 septiembre 205. Publicado: 0 enero 206.
2 2 Definición. Una prueba de hipótesis es una regla que especifica: (a) Los valores de la muestra X para los que se acepta H 0 como cierta. (b) Los valores de la muestra X para los que se rechaza H 0 y se acepta H como cierta. El subconjunto R del rango de X para el cual H 0 se rechaza es llamado la región de rechazo o región crítica. Definición 2. Consideremos el problema de prueba de hipótesis H 0 : θ Θ 0 vs H : θ Θ c 0. Si θ Θ 0 pero la prueba de hipótesis decide incorrectamente rechazar H 0, se dice que se ha cometido un error de tipo I. Si, por otro lado, θ Θ c 0, pero la prueba de hipótesis decide aceptar H 0, se dice que se ha cometido error de tipo II. Denotemos por P θ a la distribución del vector aleatorio X cuando cada X i tiene función de densidad o de probabilidad f(, θ), i =,..., n. Entonces en un problema de prueba de hipótesis H 0 : θ Θ 0 vs H : θ Θ c 0, dada una prueba de hipótesis con región de rechazo R, si θ Θ 0, la probabilidad del error de tipo I es P θ (X R). Si θ Θ c 0, la probabilidad del error de tipo II es P θ (X R c ) = P θ (X R). Definición 3. Dada una prueba de hipótesis con región de rechazo R, la función β : Θ [0, ] dada por β(θ) = P θ (X R) se llama la función potencia de la prueba. Obviamente lo ideal sería que β tomara el valor 0 para todo θ Θ 0 y el valor para todo θ Θ c 0, sin embargo, excepto en situaciones triviales, este ideal no se alcanza. De esta manera, una buena prueba será aquella que toma valores cercanos a 0 para θ Θ 0 y valores cercanos a para θ Θ c 0. Esto conduce a la siguiente definición. Definición 4. Consideremos el problema de prueba de hipótesis H 0 : θ Θ 0 vs H : θ Θ c 0. (a) Para 0 α, una prueba con función potencia β(θ) es una prueba de tamaño α si sup θ Θ0 β(θ) = α. (b) Para 0 α, una prueba con función potencia β(θ) es una prueba de nivel α si sup θ Θ0 β(θ) α. (c) Sea C una clase de pruebas para probar H 0 : θ Θ 0 vs H : θ Θ c 0. Se dice que una prueba en la clase C, con función potencia β(θ), es una prueba uniformemente más potente en la clase C si β(θ) β (θ) para toda θ Θ c 0 y para toda β (θ) que es una función potencia de una prueba en la clase C. En este trabajo, la clase C será la clase de todas las pruebas de nivel α. Es decir, el propósito será encontrar la prueba uniformemente más potente de nivel α. Uno de los resultados más famosos que describe con claridad cuales pruebas son uniformemente más potentes de nivel α cuando tanto H 0 como H son hipótesis Revista de Ciencias Básicas UJAT, ()Junio p
3 3 simples, es decir, cuando H 0 y H especifican cada una sólo una distribución para la muestra X, es el lema de Neyman-Pearson. Este lema puede generalizarse de forma que permita obtener pruebas uniformemente más potentes de nivel α para cuando H 0 y H son hipótesis estadísticas compuestas unilaterales, es decir, pruebas de la forma H 0 : θ θ 0 vs H : θ > θ 0 o H 0 : θ θ 0 vs H : θ < θ 0. Tal generalización es conocida como el teorema de Karlin-Rubin. Por propósitos didácticos hemos decidido incluir en la sección 2 las demostraciones de ambos resultados. Ambas demostraciones están basadas en las demostraciones dadas en [2] (véase también [8] y [9]), pero se hace un desarrollo más detallado. Finalmente, en la sección 3 presentamos dos ejemplos, no incluídos en las referencias más conocidas de la Estadística, sobre el uso del teorema de Karlin-Rubin para determinar pruebas uniformemente más potentes de nivel α. En ambos ejemplos se deben implementar procedimientos numéricos para llevar a cabo las pruebas de hipótesis referidas. 2. Lema de Neyman - Pearson y teorema de Karlin-Rubin Los resultados de teoría de la medida que se usan en las demostraciones dadas en esta sección pueden ser consultados, por ejemplo, en []. Recordemos los siguientes conceptos. Definición 5. Sea X = (X,..., X n ) una muestra aleatoria de la función de densidad o de probabilidad f(x; θ). Un estadístico T = T (X) es suficiente si la distribución condicional de X dado T = t no depende de θ. Así, de acuerdo con esta definición, un estadístico suficiente resume la información que acerca del parámetro θ está contenido en la muestra X (ninguna información adicional en la muestra X, aparte del valor del estadístico T, contiene más información sobre θ). Definición 6. Una familia de funciones de densidad o de probabilidad {g(t; θ) : θ Θ R} de una variable aleatoria T, tiene razón de verosimilitudes monótona si, siempre que θ < θ 2, g(t; θ 2 ) g(t; θ ) es monótona como función de t en {t : g(t; θ ) > 0 o g(t; θ 2 ) > 0}, donde definimos = si c > 0. c 0 Proposición. Sea T una variable aleatoria cuya familia de densidades o de probabilidades es {g(t; θ) : θ Θ R}, tal que para θ < θ 2, es creciente como función de t. Entonces g(t; θ 2 ) g(t; θ ) P θ2 (T t) P θ (T t).
4 4 Prueba. Sean t < t < t 2. De aquí g(t ; θ 2 ) g(t ; θ ) g(t 2; θ 2 ) g(t 2 ; θ ) = g(t ; θ 2 )g(t 2 ; θ ) g(t ; θ )g(t 2 ; θ 2 ). Integrando primero sobre t de a t y después sobre t 2 de t a se tiene P θ2 (T t)( P θ (T t)) P θ (T t)( P θ2 (T t)), de donde, P θ2 (T t) P θ (T t). Teorema. (Lema de Neyman - Pearson) Sea la prueba de hipótesis H 0 : θ = θ 0 vs H : θ = θ, donde f(x; θ i ) es la función de densidad o probabilidad correspondiente a θ i, i =, 2. Consideremos una región de rechazo R tal que x R si f(x; θ ) > kf(x; θ 0 ) y x R c si f(x; θ ) < kf(x; θ 0 ) () para algún k 0, y α = P θ0 (X R). (2) Entonces (a) (Suficiencia) Toda prueba con región de rechazo R que cumple () y (2) es una prueba de nivel α uniformemente más potente. (b) (Necesidad) Si existe una prueba que satisface () y (2) con k > 0, entonces toda prueba de nivel α uniformemente más potente es una prueba de tamaño α, y toda prueba de nivel α uniformemente más potente satisface (), excepto quizá en un conjunto A que satisface P θ0 (X A) = P θ (X A) = 0. Prueba. Probaremos el teorema para el caso en el que f(x; θ 0 ) y f(x; θ ) son funciones de densidad de variables aleatorias (absolutamente) continuas. La demostración para el caso de variables aleatorias discretas es similar; sólo hay que reemplazar las integrales por sumas. Para cualquier prueba con región de rechazo R, definimos una función de prueba φ como sigue: { φ si x R (x) = 0 si x / R. Sea φ la función de prueba de una prueba que satisface () y (2). Sea φ la función de prueba de cualquier otra prueba de nivel α. Sean β(θ) y β (θ) las funciones potencia de las pruebas φ y φ respectivamente. Veamos que (φ(x) φ (x))(f(x; θ ) kf(x; θ 0 )) 0, x R n.
5 5 Si x R, se tiene que φ(x) = y 0 φ (x), por lo que φ(x) φ (x) 0. Por (), f(x; θ ) kf(x; θ 0 ) 0, de donde (φ(x) φ (x))(f(x; θ ) kf(x; θ 0 )) 0. Si x R c, se tiene que φ(x) = 0 por lo que φ(x) φ (x) 0. Por () f(x; θ ) kf(x; θ 0 ) < 0, luego (φ(x) φ (x))(f(x; θ ) kf(x; θ 0 )) 0. Si R es la región de rechazo de φ, [ ] 0 φ(x) φ (x) [f(x; θ ) kf(x; θ 0 )] dx (3) [ ] [ ] = φ(x) φ (x) f(x; θ )dx φ(x) φ (x) kf(x; θ 0 )dx = φ(x)f(x; θ )dx φ (x)f(x; θ )dx k φ(x)f(x; θ 0 )dx +k φ (x)f(x; θ 0 )dx = φ(x)f(x; θ )dx + R φ(x)f(x; θ )dx R c φ (x)f(x; θ )dx R φ (x)f(x; θ )dx (R ) c k φ(x)f(x; θ 0 )dx k R φ(x)f(x; θ 0 )dx + k R c φ (x)f(x; θ 0 )dx R +k = R φ (x)f(x; θ 0 )dx (R ) c f(x; θ )dx f(x; θ )dx k R = β(θ ) β (θ ) k(β(θ 0 ) β (θ 0 )). R f(x; θ 0 )dx + k f(x; θ 0 )dx R La afirmación (a) se demuestra notando que, como φ es una prueba de nivel α y φ es una prueba de tamaño α (sup θ Θ0 P θ (x R) = P θ0 (x R) = α, ya que Θ 0 tiene sólo un punto), entonces β(θ 0 ) β (θ 0 ) = α β (θ 0 ) 0. Por lo tanto, de (3) y como k 0, se tiene 0 β(θ ) β (θ ) k(β(θ 0 ) β (θ 0 )) β(θ ) β (θ ), de donde β(θ ) β (θ ), es decir, φ tiene mayor potencia que φ. Ya que φ fue una prueba arbitraria de nivel α y θ es el único punto en Θ c 0, se concluye que φ es una prueba de nivel α uniformemente más potente. Para probar la afirmación (b), sea ahora φ la función de prueba de cualquier prueba de nivel α uniformemente más potente. Por (a), φ, la prueba que satisface
6 6 () y (2), también es una prueba de nivel α uniformemente más potente, de donde β(θ ) = β (θ ). De (3), y puesto que k > 0, se tiene α β (θ 0 ) = β(θ 0 ) β (θ 0 ) 0, de donde α β (θ 0 ). (4) De (4) y el hecho de que β (θ 0 ) α, se tiene que β (θ 0 ) = α. Así, φ es una prueba de tamaño α; esto también implica que (3) es una igualdad, es decir, se tiene, [ φ(x) φ (x)] [f(x; θ ) kf(x; θ 0 )] dx = 0. Como el integrando es no - negativo, se tiene entonces que [ ] φ(x) φ (x) [f(x; θ ) kf(x; θ 0 )] = 0, excepto en un conjunto A con medida de Lebesgue 0, es decir, excepto en un conjunto A tal que dx = 0. Como f(x; θ ) kf(x; θ 0 ) 0 A x R n, resulta que φ(x) = φ (x) x R n \ A. De aquí se sigue que las regiones de rechazo de φ y φ difieren en un conjunto de medida 0. Así, φ satisface (), excepto en A. Por la continuidad absoluta de f(x; θ i )dx, i =, 2, con respecto a la medida de Lebesgue, se tiene que f(x; θ i )dx = 0, A o sea, P θ0 (X A) = P θ (X A) = 0. Corolario. Consideremos el problema de prueba de hipótesis H 0 : θ = θ 0 vs H : θ = θ. Supongamos que T (X) es un estadístico suficiente del parámetro θ, y que g(t; θ i ), i = 0,, es la función de densidad o de probabilidad de T. Entonces cualquier prueba basada en T con región de rechazo S es una prueba uniformemente más potente de nivel α si satisface t S si g(t; θ ) > kg(t; θ 0 ) y t S c si g(t; θ ) < kg(t; θ 0 ) (5) para algún k 0, donde α = P θ0 (T S). (6)
7 7 Prueba. En términos de la muestra original X, la prueba basada en T tiene región de rechazo R = {x : T (x) S}. Por el teorema de factorización (véase, por ejemplo [2], p. 276) para estadísticos suficientes, la función de densidad o de probabilidad de X se puede escribir como f (x; θ i ) = g (T (x); θ i ) h(x), i = 0,, para alguna función h(x) no negativa. Multiplicando las desigualdades en (5) por esta función no negativa, vemos que R satisface x R si f (x; θ ) = g (T (x); θ ) h(x) > kg (T (x); θ 0 ) h(x) = kf (x; θ 0 ) y x R c si f (x; θ ) = g (T (x); θ ) h(x) < kg (T (x); θ 0 ) h(x) = kf (x; θ 0 ). Además, por (6), P θ0 (X R) = P θ0 (T (X) S) = α. Así, por la parte de suficiencia del teorema de Neyman - Pearson, la prueba basada en T es una prueba uniformemente más potente de nivel α. Teorema 2. (Teorema de Karlin - Rubin) Consideremos el problema de prueba de hipótesis H 0 : θ θ 0 vs H : θ > θ 0. Supongamos que T es un estadístico suficiente de θ, y que la familia de funciones de densidad o de probabilidad de T, {g(t; θ) : θ Θ}, tiene razón de verosimilitudes creciente. Entonces para cualquier t 0, la prueba que rechaza H 0 si y sólo si T > t 0 es una prueba uniformemente más potente de nivel α, donde α = P θ0 (T > t 0 ). Prueba. Sea β(θ) = P θ (T > t 0 ) la función potencia de la prueba. Sea θ > θ 0 y consideremos las pruebas H 0 : θ = θ 0 vs H : θ = θ. Ya que la familia de funciones de densidad o de probabilidad de T tiene razón de verosimilitudes creciente, de la proposición tenemos que si θ 0 < θ, entonces P θ (T t 0 ) P θ0 (T t 0 ), equivalentemente, P θ0 (T t 0 ) P θ (T t 0 ), de donde P θ0 (T > t 0 ) P θ (T > t 0 ), o sea β(θ 0 ) β(θ ) si θ 0 < θ. Así, β(θ) es creciente. Luego, (i) sup θ θ0 β(θ) = β(θ 0 ) = α, por lo que la prueba es de nivel α. (ii) Si definimos k = inf t T g(t;θ ) g(t;θ o), donde T = {t : t > t 0 y g(t; θ ) > 0 o g(t; θ 0 ) > 0}, Revista de Ciencias Básicas UJAT, ()Junio p
8 8 Edilberto Nájera Rangel, Aroldo Pérez Pérez y Braly Guadalupe Peralta Reyes resulta que t > t 0 g(t; θ ) g(t; θ 0 ) > k. Junto con el corolario, (i) y (ii) implican que β(θ ) β (θ ), donde β (θ) es la función potencia de cualquier otra prueba de nivel α de H 0, es decir, cualquier prueba que satisface β (θ 0 ) α. Sin embargo, toda prueba de nivel α de H 0 satisface β (θ 0 ) sup β (θ 0 ) α. Así, β(θ ) β (θ ) para toda prueba de nivel α de H 0. Ya θ Θ 0 que θ fue arbitraria, la prueba es una prueba uniformemente más potente de nivel α. Se puede demostrar, bajo las mismas condiciones del teorema 2, que la prueba que rechaza H 0 : θ θ 0 a favor de H : θ < θ 0 si y sólo si T < t 0 es una prueba uniformemente más potente de nivel α = P θ0 (T < t 0 ). 3. Ejemplos En los dos ejemplos siguientes se aplica el teorema de Karlin - Rubin a dos poblaciones con distribuciones gamma y exponencial truncada, respectivamente. La distribución gamma es muy importante porque, entre otras aplicaciones, se usa en medicina (véase [4]) y en climatología (véase [7]). La distribución exponencial truncada es también muy importante debido a sus aplicaciones en análisis de confiabilidad (véase [5]) y en actuaría (véase [6]), entre otras. Recordemos que un estadístico suficiente T (X) se dice ser un estadístico suficiente minimal si, para cualquier otro estadístico suficiente T (X), T (x) es una función de T (x). Lo cual significa que si T (x) = T (y), entonces T (x) = T (y). Ejemplo. Sea X,..., X n una muestra aleatoria de una población con distribución gamma(α, ), α > 0, es decir, con función de densidad f(x; α) = Γ(α) xα e x, x > 0, donde Γ(α) := 0 t α e t dt es la función gamma. La función de densidad conjunta de X,..., X n es f n (x,..., x n ; α) = de donde se sigue que el estadístico (Γ(α)) n (Πn i=x i ) α exp( Σ n i=x i ), T = log(π n i=x i ) = Σ n i= log(x i ) es un estadístico suficiente minimal (véase por ejemplo, el teorema 6.2.3, p. 28 de [2]) para el parámetro α. Antes de encontrar la densidad de T, primero observemos que si Z tiene distribución exp() = gamma(, ), entonces la densidad de Y = log(z) es h (y) = e y e ey.
9 9 Ahora probemos por inducción sobre el tamaño de muestra n (véase [0]) que la densidad de T es g(t; α) = (Γ (α)) n e (α )t h n (t), (7) donde h n (t) es la densidad de la suma de los logaritmos de una muestra aleatoria de tamaño n de la distribución exp(). (a) Si n =, entonces T = log(x ), de donde se tiene que la densidad de T es g(t; α) = f(e t ; α) dx dt = Γ(α) et(α ) e e t e t = Γ(α) et(α ) h (t), donde h exp(). es la densidad de log(z), con Z una variable aleatoria con distribución (b) Supongamos que la afirmación se cumple para tamaños de muestra n, n 2, y probemos que entonces también se cumple para tamaños de muestra n. Sean T = log(x ), T n = Σ n i=2 log(x i), y g (t ; α) y g n (t n ; α) las densidades de T y T n respectivamente. Entonces la función de densidad de T = T + T n es g(t; α) = = = g (w; α)g n (t w; α)dw Γ(α) e(α )w h (w) (Γ(α)) n e(α )(t w) h n (t w)dw (Γ(α)) n e(α )t h (w)h n (t w)dw. Puesto que h es la densidad de log(z ) y h n es la densidad de Σ n i=2 log(z i), donde las Z i son variables aleatorias independientes con distribución exp(), i =,..., n, entonces la densidad de Y n = Σ n i= log(z i) = log(z ) + Σ n i=2 log(z i) es h n(y n) = Así, la función de densidad de T es g(t; α) = h (w)h n (y n w)dw. (Γ(α)) n e(α )t h n(t), donde h n(t) es la densidad de la suma de los logaritmos de una muestra aleatoria de tamaño n de la distribución exp(). De (a) y (b) se tiene que la densidad de T es la función (7). Además es inmediato comprobar que g(t; α 2 ) g(t; α ) es creciente como función de t si α < α 2. Por lo tanto, si realizamos la prueba de hipótesis H 0 : α α 0 vs H : α > α 0, la prueba que rechaza H 0 si y sólo si T > t 0 es una prueba uniformemente más potente de nivel γ, donde γ = P α0 (T > t 0 ). Ejemplo 2. Sea la función de distribución exponencial truncada F (x; θ) = eθx e θ, x (0, ), θ R.
10 0 Esta familia aparece en Deemer y Votaw [3]. Si X,..., X n es una muestra aleatoria de una población con distribución exponencial truncada, entonces su función de densidad conjunta es ( ) n θ f n (x,..., x n ; θ) = e θσn i= xi, θ luego el estadístico suficiente minimal de θ es T = n X i. O Reilly y Rueda [] obtuvieron la función de densidad de T, la cual es ( ) n θ g(t; θ) = e θ I n (t) e θt, t (0, n), donde I n (t) = (n )! i= n ( n j j=0 ) ( ) j (t j) n + es la función de densidad de la suma de n variables aleatorias independientes con distribución uniforme en (0, ); (t j) + es la parte positiva de (t j). Es directo comprobar que g(t; θ 2 ) g(t; θ ) es creciente como función de t si θ < θ 2. De aquí, si llevamos a cabo la prueba de hipótesis H 0 : θ θ 0 vs H : θ > θ 0, la prueba que rechaza H 0 si y sólo si T > t 0 es una prueba uniformemente más potente de nivel α, donde α = P θ0 (T > t 0 ). Referencias [] Ash, R. B. (2002). Real analysis and probability. Academic Press, New York. [2] Casella, G. and R. L. Berger (2002). Statistical inference. Duxbury, USA. [3] Deemer, W. L. and D. F. Votaw (955). Estimation of parameters of truncated or censored exponential distributions. Annals of Mathematical Statistics, 26, [4] Fay, M. P. and E. J. Feuer (997). Confidence intervals for directly standardized rates: a method based on the gamma distribution. Statistics in Medicine. 6, [5] Gelfand, A. E., A. F. M. Smith and T. Lee (992). Bayesian analysis of constrained parameter and truncated data problems usings Gibbs sampling. Journal of the American Statistical Association, 87(48), [6] Gómez-Déniz, E. y J. M. Sarabia (2008). La distribución binomial exponencial truncada con aplicaciones en el sector del seguro de automóviles. Anales del Instituto de Actuarios Españoles, Tercera Época, 4, [7] Husak, G. J., J. Michaelsen, and C. Funk (2007). Use of the gamma distribution to represent monthly rainfall in Africa for drought monitoring applications. International Journal of Climatology, 27, [8] Lehmann, E. L. (959). Testing statistical hypotheses. Wyley, New York.
11 [9] Mood, A. M., F. A. Graybill and D. C. Boes (974). Introduction to the theory of statistics. McGraw-Hill, Singapore. [0] Nájera, R. E. (204). La distribución fiducial en modelos que no son de grupo. Cómo simular de ella. Tesis de Doctorado en Ciencias. Universidad Nacional Autónoma de México. [] O Reilly, F. and R. Rueda (2007). Fiducial inference for the exponencial distribution. Communications in Statistics-Theory and Methods, 36,
Definición Una hipótesis es una afirmación acerca de un parámetro.
 Capítulo 8 Prueba de hipótesis Existen dos áreas de interés en el proceso de inferencia estadística: la estimación puntual y las pruebas de hipótesis. En este capítulo se presentan algunos métodos para
Capítulo 8 Prueba de hipótesis Existen dos áreas de interés en el proceso de inferencia estadística: la estimación puntual y las pruebas de hipótesis. En este capítulo se presentan algunos métodos para
Inferencia Estadística
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO Facultad de Ciencias Plan de estudios de la Licenciatura en Actuaría Inferencia Estadística Clave 1541 Modalidad Semestre 5 Créditos 10 Área Campo de conocimiento
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO Facultad de Ciencias Plan de estudios de la Licenciatura en Actuaría Inferencia Estadística Clave 1541 Modalidad Semestre 5 Créditos 10 Área Campo de conocimiento
Tests de Hipótesis. Estadística (M)
 Tests de Hipótesis Estadística (M) Ejemplo Una empresa sabe por sus registros históricos que en cada uno de los años anteriores los empleados han faltado un promedio de 6.3 días. Este año la empresa introdujo
Tests de Hipótesis Estadística (M) Ejemplo Una empresa sabe por sus registros históricos que en cada uno de los años anteriores los empleados han faltado un promedio de 6.3 días. Este año la empresa introdujo
CONTRASTE DE HIPÓTESIS
 CONTRASTE DE HIPÓTESIS Antonio Morillas A. Morillas: Contraste de hipótesis 1 CONTRASTE DE HIPÓTESIS 1. Introducción 2. Conceptos básicos 3. Región crítica óptima i. Teorema de Neyman-Pearson ii. Región
CONTRASTE DE HIPÓTESIS Antonio Morillas A. Morillas: Contraste de hipótesis 1 CONTRASTE DE HIPÓTESIS 1. Introducción 2. Conceptos básicos 3. Región crítica óptima i. Teorema de Neyman-Pearson ii. Región
Principios de reducción de la data
 Capítulo 6 Principios de reducción de la data 6.1. Introducción Un experimentador usa la información en una muestra X 1,, X n para realizar el proceso de inferencia sobre algun parámetro desconocido θ.
Capítulo 6 Principios de reducción de la data 6.1. Introducción Un experimentador usa la información en una muestra X 1,, X n para realizar el proceso de inferencia sobre algun parámetro desconocido θ.
INTRODUCCIÓN A LA INFERENCIA ESTADÍSTICA
 UNIVERSIDAD AUTÓNOMA CHAPINGO DIVISIÓN DE CIENCIAS FORESTALES CARRERA DE: Licenciado en Estadística PROGRAMA DE LA ASIGNATURA DE INTRODUCCIÓN A LA INFERENCIA ESTADÍSTICA DATOS GENERALES Departamento (División):
UNIVERSIDAD AUTÓNOMA CHAPINGO DIVISIÓN DE CIENCIAS FORESTALES CARRERA DE: Licenciado en Estadística PROGRAMA DE LA ASIGNATURA DE INTRODUCCIÓN A LA INFERENCIA ESTADÍSTICA DATOS GENERALES Departamento (División):
CONTRASTE DE HIPÓTESIS
 CONTRASTE DE HIPÓTESIS Antonio Morillas A. Morillas: Contraste de hipótesis 1 CONTRASTE DE HIPÓTESIS 1. Introducción 2. Conceptos básicos 3. Región crítica óptima i. Teorema de Neyman-Pearson ii. Región
CONTRASTE DE HIPÓTESIS Antonio Morillas A. Morillas: Contraste de hipótesis 1 CONTRASTE DE HIPÓTESIS 1. Introducción 2. Conceptos básicos 3. Región crítica óptima i. Teorema de Neyman-Pearson ii. Región
Test de Hip otesis 6.3 horarios flexibles un promedio de 5.4 d ıas
 Test de Hipótesis Una firma sabe que en cada uno de los añosanterioreslos empleados han faltado un promedio de 6.3 días (sacando las vacaciones). Este año la firma introdujo el sistema de horarios flexibles
Test de Hipótesis Una firma sabe que en cada uno de los añosanterioreslos empleados han faltado un promedio de 6.3 días (sacando las vacaciones). Este año la firma introdujo el sistema de horarios flexibles
Momentos de Funciones de Vectores Aleatorios
 Capítulo 1 Momentos de Funciones de Vectores Aleatorios 1.1 Esperanza de Funciones de Vectores Aleatorios Definición 1.1 Sea X = (X 1,..., X n ) un vector aleatorio (absolutamente continuo o discreto)
Capítulo 1 Momentos de Funciones de Vectores Aleatorios 1.1 Esperanza de Funciones de Vectores Aleatorios Definición 1.1 Sea X = (X 1,..., X n ) un vector aleatorio (absolutamente continuo o discreto)
Estadística. Tema 2. Variables Aleatorias Funciones de distribución y probabilidad Ejemplos distribuciones discretas y continuas
 Estadística Tema 2 Variables Aleatorias 21 Funciones de distribución y probabilidad 22 Ejemplos distribuciones discretas y continuas 23 Distribuciones conjuntas y marginales 24 Ejemplos distribuciones
Estadística Tema 2 Variables Aleatorias 21 Funciones de distribución y probabilidad 22 Ejemplos distribuciones discretas y continuas 23 Distribuciones conjuntas y marginales 24 Ejemplos distribuciones
Integración de Funciones Reales
 Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Capítulo 20 Integración de Funciones Reales Nos proponemos estudiar en este capítulo las propiedades fundamentales del operador integral. n particular, extenderemos aquí al caso de funciones medibles con
Curso Inferencia. Miguel Ángel Chong R. 24 de septiembre del 2013
 Curso Estadística Miguel Ángel Chong R. miguel@sigma.iimas.unam.mx 24 de septiembre del 2013 Suficiencia Cuando hacemos inferencia sobre un parámetro, usando una muestra aleatoria (X 1,...,X n )yunestadísticoˆ
Curso Estadística Miguel Ángel Chong R. miguel@sigma.iimas.unam.mx 24 de septiembre del 2013 Suficiencia Cuando hacemos inferencia sobre un parámetro, usando una muestra aleatoria (X 1,...,X n )yunestadísticoˆ
Introducción a la Teoría de la Información
 Introducción a la Teoría de la Información Entropía diferencial. Facultad de Ingeniería, UdelaR (Facultad de Ingeniería, UdelaR) Teoría de la Información 1 / 19 Definición Definición (Entropía diferencial)
Introducción a la Teoría de la Información Entropía diferencial. Facultad de Ingeniería, UdelaR (Facultad de Ingeniería, UdelaR) Teoría de la Información 1 / 19 Definición Definición (Entropía diferencial)
Definición 1 (Probabilidad Condicional) Observación 1 Se puede aplicar la definición también a variables discretas o continuas.
 CAPÍTULO 1: ALGUNAS REGLAS DE PROBABILIDAD Para leer Lee: Capítulo 1 Definición 1 (Probabilidad Condicional) Para dos sucesos A y B, P (A B) P (A B) P (B) Observación 1 Se puede aplicar la definición también
CAPÍTULO 1: ALGUNAS REGLAS DE PROBABILIDAD Para leer Lee: Capítulo 1 Definición 1 (Probabilidad Condicional) Para dos sucesos A y B, P (A B) P (A B) P (B) Observación 1 Se puede aplicar la definición también
Estadística Económica y Estadística Empresarial
 Universidad de Valladolid Facultad de Ciencias Económicas y Empresariales Departamento de Estadística y Econometría Licenciatura en Ciencias Económicas Sin docencia. Plan a extinguir Proyecto docente de:
Universidad de Valladolid Facultad de Ciencias Económicas y Empresariales Departamento de Estadística y Econometría Licenciatura en Ciencias Económicas Sin docencia. Plan a extinguir Proyecto docente de:
Teoremas de Convergencia
 Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Capítulo 24 Teoremas de Convergencia El teorema de la convergencia monótona (Lema 21.3) establece ciertas condiciones sobre una sucesión de funciones medibles para que se puedan permutar los símbolos y
Límite superior y límite inferior de una sucesión
 Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Límite superior y límite inferior de una sucesión Objetivos. Definir las nociones de los límites superior e inferior de una sucesión y estudiar sus propiedades básicas. Requisitos. Supremo e ínfimo de
Tema 1: Introducción a la Estadística Bayesiana
 Tema 1: Introducción a la Estadística Bayesiana Introducción En general, se usan probabilidades de modo informal para expresar la información o la incertidumbre que se tiene acerca de observaciones de
Tema 1: Introducción a la Estadística Bayesiana Introducción En general, se usan probabilidades de modo informal para expresar la información o la incertidumbre que se tiene acerca de observaciones de
Suficiencia y Completitud. Estimadores IMVU.
 1 Suficiencia y Completitud. Estimadores IMVU. Graciela Boente 1 1 Universidad de Buenos Aires and CONICET, Argentina 2 Definición X P θ con θ Θ. Se dice que T = t(x) es suficiente para θ si: la distribución
1 Suficiencia y Completitud. Estimadores IMVU. Graciela Boente 1 1 Universidad de Buenos Aires and CONICET, Argentina 2 Definición X P θ con θ Θ. Se dice que T = t(x) es suficiente para θ si: la distribución
TEST DE RAZÓN DE VEROSIMILITUD GENERALIZADA
 TEST DE RAZÓN DE VEROSIMILITUD GENERALIZADA JUAN C. MANRÍQUEZ 1, LUIS CID 2 y MARCELA VALDEZ 3 1 Universidad del Bío Bío, Facultad de Ciencias, Departamento de Matemáticas jcmanriq@ubiobio.cl 2 Universidad
TEST DE RAZÓN DE VEROSIMILITUD GENERALIZADA JUAN C. MANRÍQUEZ 1, LUIS CID 2 y MARCELA VALDEZ 3 1 Universidad del Bío Bío, Facultad de Ciencias, Departamento de Matemáticas jcmanriq@ubiobio.cl 2 Universidad
BLOQUE III: INFERENCIA ESTADISTICA. X, variable aleatoria de interés sobre una determinada población
 BLOQUE III: INFERENCIA ESTADISTICA TEMA 8. MUESTREO Y DISTRIBUCIONES DE MUESTREO 1. Introducción a la Inferencia Estadística X, variable aleatoria de interés sobre una determinada población Observar el
BLOQUE III: INFERENCIA ESTADISTICA TEMA 8. MUESTREO Y DISTRIBUCIONES DE MUESTREO 1. Introducción a la Inferencia Estadística X, variable aleatoria de interés sobre una determinada población Observar el
UNIVERSIDAD DEL CAUCA FACULTAD DE CIENCIAS NATURALES, EXACTAS Y DE LA EDUCACIÓN DEPARTAMENTO DE MATEMÁTICAS
 UNIVERSIDAD DEL CAUCA FACULTAD DE CIENCIAS NATURALES, EXACTAS Y DE LA EDUCACIÓN DEPARTAMENTO DE MATEMÁTICAS ÁREA: PROBABILIDAD Y ESTADÍSITICA ASIGNATURA: INFERENCIA ESTADÍSTICA Código: Mat 331. PERREQUISITO:
UNIVERSIDAD DEL CAUCA FACULTAD DE CIENCIAS NATURALES, EXACTAS Y DE LA EDUCACIÓN DEPARTAMENTO DE MATEMÁTICAS ÁREA: PROBABILIDAD Y ESTADÍSITICA ASIGNATURA: INFERENCIA ESTADÍSTICA Código: Mat 331. PERREQUISITO:
Pruebas de bondad de ajuste para distribuciones con parámetro de forma
 Pruebas de bondad de ajuste para distribuciones con parámetro de forma José A. Villaseñor Alva Colegio de Postgraduados, México ITESM, Monterrey, N.L. 2 de septiembre de 2011 Conferencia Bimestral de la
Pruebas de bondad de ajuste para distribuciones con parámetro de forma José A. Villaseñor Alva Colegio de Postgraduados, México ITESM, Monterrey, N.L. 2 de septiembre de 2011 Conferencia Bimestral de la
Contrastes de hipótesis paramétricos
 Estadística II Universidad de Salamanca Curso 2011/2012 Outline Introducción 1 Introducción 2 Contraste de Neyman-Pearson Sea X f X (x, θ). Desonocemos θ y queremos saber que valor toma este parámetro,
Estadística II Universidad de Salamanca Curso 2011/2012 Outline Introducción 1 Introducción 2 Contraste de Neyman-Pearson Sea X f X (x, θ). Desonocemos θ y queremos saber que valor toma este parámetro,
Tema 5: Funciones medibles. Variables aleatorias. Función de distribución.
 Tema 5: Funciones medibles. Variables aleatorias. Función de distribución. El concepto de variable aleatoria formaliza las magnitudes numéricas asociadas a los resultados de una experimento aleatorio.
Tema 5: Funciones medibles. Variables aleatorias. Función de distribución. El concepto de variable aleatoria formaliza las magnitudes numéricas asociadas a los resultados de una experimento aleatorio.
Integral de Lebesgue
 Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Integral de Lebesgue Problemas para examen n todos los problemas se supone que (, F, µ) es un espacio de medida. Integración de funciones simples positivas. La representación canónica de una función simple
Aplicación de la distribución empírica: Tests de bondad de ajuste
 Aplicación de la distribución empírica: Tests de bondad de ajuste 4 de marzo de 2009 Test de bondad de ajuste Supongamos que se dispone de una m.a.s de tamaño n de una población X con distribución desconocida
Aplicación de la distribución empírica: Tests de bondad de ajuste 4 de marzo de 2009 Test de bondad de ajuste Supongamos que se dispone de una m.a.s de tamaño n de una población X con distribución desconocida
PROGRAMA DE CURSO. Código Nombre MA3403 Probabilidades y Estadística Nombre en Inglés Probability and Statistics SCT
 PROGRAMA DE CURSO Código Nombre MA3403 Probabilidades y Estadística Nombre en Inglés Probability and Statistics SCT Unidades Horas de Horas Docencia Horas de Trabajo Docentes Cátedra Auxiliar Personal
PROGRAMA DE CURSO Código Nombre MA3403 Probabilidades y Estadística Nombre en Inglés Probability and Statistics SCT Unidades Horas de Horas Docencia Horas de Trabajo Docentes Cátedra Auxiliar Personal
Inferencia Estadística.
 Inferencia Estadística. Programa de la Asignatura Facultad Derecho y Ciencias Sociales. Curso 2010-2011. Profesor: Emilio Porcu (http://www.stochastik.math.unigoettingen.de/~eporcu/) Horario Tutorías:
Inferencia Estadística. Programa de la Asignatura Facultad Derecho y Ciencias Sociales. Curso 2010-2011. Profesor: Emilio Porcu (http://www.stochastik.math.unigoettingen.de/~eporcu/) Horario Tutorías:
PROGRAMA DE CURSO. Horas de Trabajo Personal Horas de Cátedra. Básica. Resultados de Aprendizaje
 Código Nombre MA3403 Probabilidades y Estadística Nombre en Inglés Probability and Statistics SCT es Docentes PROGRAMA DE CURSO Horas de Cátedra Horas Docencia Auxiliar Horas de Trabajo Personal 6 10 3
Código Nombre MA3403 Probabilidades y Estadística Nombre en Inglés Probability and Statistics SCT es Docentes PROGRAMA DE CURSO Horas de Cátedra Horas Docencia Auxiliar Horas de Trabajo Personal 6 10 3
Método bayesiano bootstrap y una aplicación en la estimación del percentil 85 en ingeniería de tránsito
 Revista Colombiana de Estadística Volumen 27 N o 2. Págs. 99 a 107. Diciembre 2004 Método bayesiano bootstrap y una aplicación en la estimación del percentil 85 en ingeniería de tránsito Juan Carlos Correa
Revista Colombiana de Estadística Volumen 27 N o 2. Págs. 99 a 107. Diciembre 2004 Método bayesiano bootstrap y una aplicación en la estimación del percentil 85 en ingeniería de tránsito Juan Carlos Correa
Tema 2. Introducción a la Estadística Bayesiana
 2-1 Tema 2 Introducción a la Estadística Bayesiana El teorema de Bayes Ejemplo Interpretación Ejemplo: influencia de la distribución a priori Ejemplo: densidad de flujo Probabilidad bayesiana Ejemplo:
2-1 Tema 2 Introducción a la Estadística Bayesiana El teorema de Bayes Ejemplo Interpretación Ejemplo: influencia de la distribución a priori Ejemplo: densidad de flujo Probabilidad bayesiana Ejemplo:
Teoremas de Tonelli y Fubini
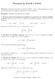 Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Teoremas de Tonelli y Fubini Objetivos. Demostrar teoremas de Tonelli y Fubini, conocer contraejemplos que muestran la importancia de algunas condiciones de estos teoremas. Requisitos. Definición del producto
Profesor/es Nombre Despacho Correo-e Página web Paloma Pérez Fernández
 PLAN DOCENTE DE LA ASIGNATURA Curso académico: 2017-18 Código 502247 Denominación (español) Denominación (inglés) Identificación y características de la asignatura Inferencia Estadística Statistical Inference
PLAN DOCENTE DE LA ASIGNATURA Curso académico: 2017-18 Código 502247 Denominación (español) Denominación (inglés) Identificación y características de la asignatura Inferencia Estadística Statistical Inference
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES ACATLÁN HORAS SEMANA
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES ACATLÁN PLAN DE ESTUDIOS DE LA LICENCIATURA EN MATEMÁTICAS APLICADAS Y COMPUTACIÓN PROGRAMA DE ASIGNATURA SEMESTRE: 5 (QUINTO) Estadística
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES ACATLÁN PLAN DE ESTUDIOS DE LA LICENCIATURA EN MATEMÁTICAS APLICADAS Y COMPUTACIÓN PROGRAMA DE ASIGNATURA SEMESTRE: 5 (QUINTO) Estadística
Soluciones entre ecuaciones diferenciales de orden dos. Solutions between two-order differential equations.
 Universidad del Atlántico Revista Del Programa De Matemáticas Páginas: 16 20 Facultad de Ciencias Básicas c Programa de Matemáticas Vol. IV, No 1, (2017) Soluciones entre ecuaciones diferenciales de orden
Universidad del Atlántico Revista Del Programa De Matemáticas Páginas: 16 20 Facultad de Ciencias Básicas c Programa de Matemáticas Vol. IV, No 1, (2017) Soluciones entre ecuaciones diferenciales de orden
DEFINICIONES BÁSICAS
 1 CLASES DE ESTADÍSTICA II CLASE 14) INTRODUCCIÓN A LAS PRUEBAS DE HIPÓTESIS. A menudo el analista debe tomar decisiones acerca de la investigación que se está desarrollando. En ese proceso de toma de
1 CLASES DE ESTADÍSTICA II CLASE 14) INTRODUCCIÓN A LAS PRUEBAS DE HIPÓTESIS. A menudo el analista debe tomar decisiones acerca de la investigación que se está desarrollando. En ese proceso de toma de
Suficiencia y Completitud. Estimadores IMVU.
 1 Suficiencia y Completitud. Estimadores IMVU. Graciela Boente 1 1 Universidad de Buenos Aires and CONICET, Argentina 2 Definición X P θ con θ Θ. Se dice que T = t(x) es suficiente para θ si: la distribución
1 Suficiencia y Completitud. Estimadores IMVU. Graciela Boente 1 1 Universidad de Buenos Aires and CONICET, Argentina 2 Definición X P θ con θ Θ. Se dice que T = t(x) es suficiente para θ si: la distribución
Inclusión de la igualdad en la hipótesis nula
 Comunicaciones en Estadística Diciembre 2010, Vol. 3, No. 2 Inclusión de la igualdad en la hipótesis nula Including Equal Sign in Null Hypothesis Jorge Ortiz Pinilla a jorgeortiz@usantotomas.edu.co Hanwen
Comunicaciones en Estadística Diciembre 2010, Vol. 3, No. 2 Inclusión de la igualdad en la hipótesis nula Including Equal Sign in Null Hypothesis Jorge Ortiz Pinilla a jorgeortiz@usantotomas.edu.co Hanwen
Notas de clase. Prof. Nora Arnesi
 Notas de clase Este material está sujeto a correcciones, comentarios y demostraciones adicionales durante el dictado de las clases, no se recomienda su uso a aquellos alumnos que no concurran a las mismas
Notas de clase Este material está sujeto a correcciones, comentarios y demostraciones adicionales durante el dictado de las clases, no se recomienda su uso a aquellos alumnos que no concurran a las mismas
Licenciatura en Actuaría PROGRAMA DE ESTUDIO. Integral Profesional Horas teóricas: 3 Horas prácticas: 2 Total de Horas: 5 Confiabilidad
 PROGRAMA DE ESTUDIO Programa Educativo: Licenciatura en Actuaría Área de Formación : Integral Profesional Horas teóricas: 3 Horas prácticas: 2 Total de Horas: 5 Confiabilidad Total de créditos: 8 Clave:
PROGRAMA DE ESTUDIO Programa Educativo: Licenciatura en Actuaría Área de Formación : Integral Profesional Horas teóricas: 3 Horas prácticas: 2 Total de Horas: 5 Confiabilidad Total de créditos: 8 Clave:
Espacios conexos. 6.1 Conexos
 Capítulo 6 Espacios conexos 6.1 Conexos Definición 6.1.1 (Conjuntos separados). Dado un espacio topológico (X, τ) y dos subconjuntos A, B X, diremos que A y B están separados si A B = A B = Es evidente
Capítulo 6 Espacios conexos 6.1 Conexos Definición 6.1.1 (Conjuntos separados). Dado un espacio topológico (X, τ) y dos subconjuntos A, B X, diremos que A y B están separados si A B = A B = Es evidente
El cliente quiere que la probabilidad de seguir comprando a esta empresa cuando las semillas no son de la variedad pedida sea 0.05.
 Estadística (m) Práctica 8 A) Tests de Neyman-Pearson para hipótesis simples. 1. Una empresa vende dos variedades de soja. La variedad 1 tiene un rendimiento por ha. que puede considerarse una variable
Estadística (m) Práctica 8 A) Tests de Neyman-Pearson para hipótesis simples. 1. Una empresa vende dos variedades de soja. La variedad 1 tiene un rendimiento por ha. que puede considerarse una variable
Scientia Et Technica ISSN: Universidad Tecnológica de Pereira Colombia
 Scientia Et Technica ISSN: 0122-1701 scientia@utpeduco Universidad Tecnológica de Pereira Colombia Cifuentes V, Verónica; Marín, Víctor Generalización de la inducción matemática a estructuras inductivas
Scientia Et Technica ISSN: 0122-1701 scientia@utpeduco Universidad Tecnológica de Pereira Colombia Cifuentes V, Verónica; Marín, Víctor Generalización de la inducción matemática a estructuras inductivas
Medidas. Problemas para examen. Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez.
 Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
Medidas Problemas para examen Estos problemas están redactados por Egor Maximenko y Breitner Arley Ocampo Gómez. Sigma-álgebras 1. Propiedades elementales de σ-álgebras. Demuestre que una σ-álgebra es
Generalización de la inducción matemática a estructuras inductivas
 Scientia et Technica Año XVI, No 49, Diciembre de 2011 Universidad Tecnológica de Pereira ISSN 0122-1701 167 Generalización de la inducción matemática a estructuras inductivas Generalization of mathematical
Scientia et Technica Año XVI, No 49, Diciembre de 2011 Universidad Tecnológica de Pereira ISSN 0122-1701 167 Generalización de la inducción matemática a estructuras inductivas Generalization of mathematical
II Verano de las Matemáticas del CIMAT IV Verano de Probabilidad y Estadística
 II Verano de las Matemáticas del CIMAT IV Verano de Probabilidad y Estadística Pruebas Secuenciales de Hipótesis Optimalidad en Estadística: El Caso de Prueba de Hipótesis. Nakamura-Villa-Ramos Guanajuato,
II Verano de las Matemáticas del CIMAT IV Verano de Probabilidad y Estadística Pruebas Secuenciales de Hipótesis Optimalidad en Estadística: El Caso de Prueba de Hipótesis. Nakamura-Villa-Ramos Guanajuato,
INDICE Capítulo I: Conceptos Básicos Capitulo II: Estadística Descriptiva del Proceso
 INDICE Capítulo I: Conceptos Básicos 1.- Introducción 3 2.- Definición de calidad 7 3.- Política de calidad 10 4.- Gestión de la calidad 12 5.- Sistema de calidad 12 6.- Calidad total 13 7.- Aseguramiento
INDICE Capítulo I: Conceptos Básicos 1.- Introducción 3 2.- Definición de calidad 7 3.- Política de calidad 10 4.- Gestión de la calidad 12 5.- Sistema de calidad 12 6.- Calidad total 13 7.- Aseguramiento
Estimación por intervalo del parámetro de la distribución de Poisson con una sola observación
 Revista Colombiana de Estadística Volumen 30 No. 1. pp. 69 a 75. Junio 2007 Estimación por intervalo del parámetro de la distribución de Poisson con una sola observación Interval Estimation for the Poisson
Revista Colombiana de Estadística Volumen 30 No. 1. pp. 69 a 75. Junio 2007 Estimación por intervalo del parámetro de la distribución de Poisson con una sola observación Interval Estimation for the Poisson
Algunas observaciones sobre las inconsistencias del uso de la aproximación normal en intervalos de confianza cuando las observaciones son Bernoullis
 Algunas observaciones sobre las inconsistencias del uso de la aproximación normal en intervalos de confianza cuando las observaciones son Bernoullis Marcos Morales Cortes a, Hortensia J. Reyes Cervantes
Algunas observaciones sobre las inconsistencias del uso de la aproximación normal en intervalos de confianza cuando las observaciones son Bernoullis Marcos Morales Cortes a, Hortensia J. Reyes Cervantes
EXÁMEN INFERENCIA ESTADÍSTICA I Diplomado en Estadística Convocatoria de Febrero 2006
 EXÁMEN INFERENCIA ESTADÍSTICA I Diplomado en Estadística Convocatoria de Febrero 6 Problema ( ptos) Considera un experimento aleatorio con espacio muestral Ω. a) Definir una σ-álgebra A sobre Ω. b) Dar
EXÁMEN INFERENCIA ESTADÍSTICA I Diplomado en Estadística Convocatoria de Febrero 6 Problema ( ptos) Considera un experimento aleatorio con espacio muestral Ω. a) Definir una σ-álgebra A sobre Ω. b) Dar
Conceptos básicos de inferencia estadística (II): Contrastes de hipótesis (repaso)
 Conceptos básicos de inferencia estadística (II): Contrastes de hipótesis (repaso) Tema 1 (II) Estadística 2 Curso 08/09 Tema 1 (II) (Estadística 2) Contrastes de hipótesis Curso 08/09 1 / 21 Contrastes
Conceptos básicos de inferencia estadística (II): Contrastes de hipótesis (repaso) Tema 1 (II) Estadística 2 Curso 08/09 Tema 1 (II) (Estadística 2) Contrastes de hipótesis Curso 08/09 1 / 21 Contrastes
EXAMEN DE ESTADÍSTICA Junio 2011
 EXAMEN DE ESTADÍSTICA Junio 2011 Apellidos: Nombre: DNI: GRUPO: 1. Sea X una variable aleatoria discreta. Determine el valor de k para que la función p(x) { k/x x 1, 2, 3, 4 0 en otro caso sea una función
EXAMEN DE ESTADÍSTICA Junio 2011 Apellidos: Nombre: DNI: GRUPO: 1. Sea X una variable aleatoria discreta. Determine el valor de k para que la función p(x) { k/x x 1, 2, 3, 4 0 en otro caso sea una función
Matemáticas aplicadas a las Ciencias Sociales II
 a la Matemáticas aplicadas a las Ciencias Sociales II a la Manuel Molina Fernández y Jiménez Basado en apuntes del Máster Universitario en Formación del Profesorado en Educación Secundaria CPR Mérida 24
a la Matemáticas aplicadas a las Ciencias Sociales II a la Manuel Molina Fernández y Jiménez Basado en apuntes del Máster Universitario en Formación del Profesorado en Educación Secundaria CPR Mérida 24
Generación de variables aleatorias continuas
 Generación de variables aleatorias continuas Se dice que una variable aleatoria X es continua, o más propiamente, absolutamente continua, si existe f : R R tal que F (x) := P (X x) = x f(t) dt. Al igual
Generación de variables aleatorias continuas Se dice que una variable aleatoria X es continua, o más propiamente, absolutamente continua, si existe f : R R tal que F (x) := P (X x) = x f(t) dt. Al igual
Principio de acotación uniforme
 Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
Capítulo 4 Principio de acotación uniforme 4.1. Introducción. Teorema de Baire En este último capítulo vamos a establecer una serie de resultados sobre aplicaciones lineales y continuas entre espacios
Tema 6: Modelos de probabilidad.
 Estadística 60 Tema 6: Modelos de probabilidad. 6.1 Modelos discretos. (a) Distribución uniforme discreta: La variable aleatoria X tiene una distribución uniforme discreta de parámetro n,que denoteramos
Estadística 60 Tema 6: Modelos de probabilidad. 6.1 Modelos discretos. (a) Distribución uniforme discreta: La variable aleatoria X tiene una distribución uniforme discreta de parámetro n,que denoteramos
Matemáticas aplicadas a las Ciencias Sociales II
 a la Matemáticas aplicadas a las Ciencias Sociales II a la Manuel Molina Fernández y Jiménez Basado en apuntes del Máster Universitario en Formación del Profesorado en Educación Secundaria CPR Mérida 24
a la Matemáticas aplicadas a las Ciencias Sociales II a la Manuel Molina Fernández y Jiménez Basado en apuntes del Máster Universitario en Formación del Profesorado en Educación Secundaria CPR Mérida 24
Tests de Hipótesis. Estadística (M)
 Tests de Hipótesis Estadística (M) Ejemplo Una empresa sabe por sus registros históricos que en cada uno de los años anteriores los empleados han faltado un promedio de 6.3 días. Este año la empresa introdujo
Tests de Hipótesis Estadística (M) Ejemplo Una empresa sabe por sus registros históricos que en cada uno de los años anteriores los empleados han faltado un promedio de 6.3 días. Este año la empresa introdujo
Tema 7. Contrastes de Hipótesis
 7.1. Conceptos básicos Tema 7. Contrastes de Hipótesis Uno de los problemas comunes en inferencia consiste en contrastar una hipótesis estadística. Ejemplo: El fabricante de un determinado tipo de piezas
7.1. Conceptos básicos Tema 7. Contrastes de Hipótesis Uno de los problemas comunes en inferencia consiste en contrastar una hipótesis estadística. Ejemplo: El fabricante de un determinado tipo de piezas
Planificaciones Probabilidad y Estadística B. Docente responsable: GRYNBERG SEBASTIAN PABLO. 1 de 6
 Planificaciones 6109 - Probabilidad y Estadística B Docente responsable: GRYNBERG SEBASTIAN PABLO 1 de 6 OBJETIVOS 1) Que los estudiantes aprendan los elementos básicos del método probabilístico y de la
Planificaciones 6109 - Probabilidad y Estadística B Docente responsable: GRYNBERG SEBASTIAN PABLO 1 de 6 OBJETIVOS 1) Que los estudiantes aprendan los elementos básicos del método probabilístico y de la
Planificaciones Probabilidad y Estadística B. Docente responsable: GRYNBERG SEBASTIAN PABLO. 1 de 6
 Planificaciones 8104 - Probabilidad y Estadística B Docente responsable: GRYNBERG SEBASTIAN PABLO 1 de 6 OBJETIVOS 1) Que los estudiantes aprendan los elementos básicos del método probabilístico y de la
Planificaciones 8104 - Probabilidad y Estadística B Docente responsable: GRYNBERG SEBASTIAN PABLO 1 de 6 OBJETIVOS 1) Que los estudiantes aprendan los elementos básicos del método probabilístico y de la
Clase 1: Simulación de variables aleatorias *
 Clase 1: Simulación de variables aleatorias * Índice 1. Simulación de variables aleatorias 1 1.1. Espacio de Probabilidad. Axiomas de Kolmogorov...... 1 2. Variables aleatorias y distribución de probabilidad
Clase 1: Simulación de variables aleatorias * Índice 1. Simulación de variables aleatorias 1 1.1. Espacio de Probabilidad. Axiomas de Kolmogorov...... 1 2. Variables aleatorias y distribución de probabilidad
Unidad 3. Probabilidad
 Unidad 3. Probabilidad Javier Santibáñez 17 de agosto de 2018 1. Introducción Definición 1. La probabilidad es una medida subjetiva del grado de creencia que se tiene acerca de que algo desconocido sea
Unidad 3. Probabilidad Javier Santibáñez 17 de agosto de 2018 1. Introducción Definición 1. La probabilidad es una medida subjetiva del grado de creencia que se tiene acerca de que algo desconocido sea
Función Característica
 Germán Bassi 21 de marzo de 211 1. Variable Aleatoria Continua Para una variable aleatoria escalar y continua X, la función característica se define como el valor esperado de e jωx, donde j es la unidad
Germán Bassi 21 de marzo de 211 1. Variable Aleatoria Continua Para una variable aleatoria escalar y continua X, la función característica se define como el valor esperado de e jωx, donde j es la unidad
Cálculo de probabilidad. Tema 3: Variables aleatorias continuas
 Cálculo de probabilidad Tema 3: Variables aleatorias continuas Guión Guión 3.1. La función de densidad de probabilidad Definición 3.1 Sea P una medida de probabilidad en un espacio muestral Ω. Se dice
Cálculo de probabilidad Tema 3: Variables aleatorias continuas Guión Guión 3.1. La función de densidad de probabilidad Definición 3.1 Sea P una medida de probabilidad en un espacio muestral Ω. Se dice
Pruebas de bondad de ajuste
 Pruebas de bondad de ajuste Área Académica: Licenciatura en Ingeniería Industrial Profesor(a): Mtra. Ma. Guadalupe Vera Correa Periodo: Julio - diciembre 2017 Pruebas de bondad de ajuste RESUMEN En esta
Pruebas de bondad de ajuste Área Académica: Licenciatura en Ingeniería Industrial Profesor(a): Mtra. Ma. Guadalupe Vera Correa Periodo: Julio - diciembre 2017 Pruebas de bondad de ajuste RESUMEN En esta
Elementos de probabilidad e inferencia estadística en el seguro
 Elementos de probabilidad e inferencia estadística en el seguro Instructor: Act. Erick Mier Moreno. Director general y profesor de AMAT- Applied Mathematics and Actuary Training. Profesor de asignatura
Elementos de probabilidad e inferencia estadística en el seguro Instructor: Act. Erick Mier Moreno. Director general y profesor de AMAT- Applied Mathematics and Actuary Training. Profesor de asignatura
sup si A no es acotado.
 Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
Capítulo 5 Teoría de Baire 1. El teorema de Cantor En este capítulo estudiaremos más a fondo los espacios métricos completos. Lo primero que haremos es establecer la equivalencia entre completitud y la
PROGRAMA DE CURSO. Código Nombre MA3402 Estadística Nombre en Inglés Statistics SCT Requisitos. DIM Resultados de Aprendizaje
 > < ; U Q R ;?C: VT 2 +D :?CB J B > > ; S6D :? < ;? ; C?C : >? ; W( U C > X?2 > R+DE?C : < > ; ; 9 : : R > ; Y < > < ; U Q R ;?C: VT 2 +D :?C B J B > > ; S6D :? < ;? ; C?C : >? ; W( U C > X?2 > R+DE?C
> < ; U Q R ;?C: VT 2 +D :?CB J B > > ; S6D :? < ;? ; C?C : >? ; W( U C > X?2 > R+DE?C : < > ; ; 9 : : R > ; Y < > < ; U Q R ;?C: VT 2 +D :?C B J B > > ; S6D :? < ;? ; C?C : >? ; W( U C > X?2 > R+DE?C
1. MEDIDA E INTEGRACIÓN.
 1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
1. MEDID E INTEGRCIÓN. En este capítulo repasamos algunos conceptos que se vieron en la asignatura mpliación de la Teoría de Funciones de Varias Variables. 1. MEDIDS POSITIVS. (1,1,1) Definición. Una σ-álgebra
Estadística y sus aplicaciones en Ciencias Sociales 6. Prueba de hipótesis. Facultad de Ciencias Sociales, UdelaR
 Estadística y sus aplicaciones en Ciencias Sociales 6. Prueba de hipótesis Facultad de Ciencias Sociales, UdelaR Índice 1. Introducción: hipótesis estadística, tipos de hipótesis, prueba de hipótesis 2.
Estadística y sus aplicaciones en Ciencias Sociales 6. Prueba de hipótesis Facultad de Ciencias Sociales, UdelaR Índice 1. Introducción: hipótesis estadística, tipos de hipótesis, prueba de hipótesis 2.
PRECISIÓN DE SISTEMAS DE MEDICIÓN DESTRUCTIVOS CON MEDICIONES SIMULTÁNEAS.
 PRECISIÓN DE SISTEMAS DE MEDICIÓN DESTRUCTIVOS CON MEDICIONES SIMULTÁNEAS. Américo G. Rivas C Prof. de la Escuela de Ingeniería Industrial. Área de Postgrado. Maestría en Ingeniería Industrial. Universidad
PRECISIÓN DE SISTEMAS DE MEDICIÓN DESTRUCTIVOS CON MEDICIONES SIMULTÁNEAS. Américo G. Rivas C Prof. de la Escuela de Ingeniería Industrial. Área de Postgrado. Maestría en Ingeniería Industrial. Universidad
Práctica 5 Martingalas a tiempo discreto
 Práctica 5 Martingalas a tiempo discreto 1. Tiempos de Parada A lo largo de esta sección vamos a fijar un espacio de probabilidad (Ω, F, P ) junto con una filtración (F n ) n N definida en este espacio.
Práctica 5 Martingalas a tiempo discreto 1. Tiempos de Parada A lo largo de esta sección vamos a fijar un espacio de probabilidad (Ω, F, P ) junto con una filtración (F n ) n N definida en este espacio.
Tema 5: Contraste de hipótesis
 Tema 5: Contraste de hipótesis 1 (a partir del material de A. Jach (http://www.est.uc3m.es/ajach/) y A. Alonso (http://www.est.uc3m.es/amalonso/)) Conceptos fundamentales: hipótesis nula y alternativa,
Tema 5: Contraste de hipótesis 1 (a partir del material de A. Jach (http://www.est.uc3m.es/ajach/) y A. Alonso (http://www.est.uc3m.es/amalonso/)) Conceptos fundamentales: hipótesis nula y alternativa,
Tema1. Modelo Lineal General.
 Tema1. Modelo Lineal General. 1. Si X = (X 1, X 2, X 3, X 4 ) t tiene distribución normal con vector de medias µ = (2, 1, 1, 3) t y matriz de covarianzas 1 0 1 1 V = 0 2 1 1 1 1 3 0 1 1 0 2 Halla: a) La
Tema1. Modelo Lineal General. 1. Si X = (X 1, X 2, X 3, X 4 ) t tiene distribución normal con vector de medias µ = (2, 1, 1, 3) t y matriz de covarianzas 1 0 1 1 V = 0 2 1 1 1 1 3 0 1 1 0 2 Halla: a) La
Tema 1 EL TEOREMA DE PEANO. 1 Compacidad en C(I; R N ): el Teorema de Ascoli-
 Tema 1 EL TEOREMA DE PEANO En este tema vamos a probar que bajo la hipótesis de ser f continua en un entorno del punto (, y 0 ), se puede garantizar la existencia, aunque no necesariamente la unicidad,
Tema 1 EL TEOREMA DE PEANO En este tema vamos a probar que bajo la hipótesis de ser f continua en un entorno del punto (, y 0 ), se puede garantizar la existencia, aunque no necesariamente la unicidad,
Contrastes de Hipótesis paramétricos y no-paramétricos.
 Capítulo 1 Contrastes de Hiptesis paramétricos y no-paramétricos. Estadística Inductiva o Inferencia Estadística: Conjunto de métodos que se fundamentan en la Teoría de la Probabilidad y que tienen por
Capítulo 1 Contrastes de Hiptesis paramétricos y no-paramétricos. Estadística Inductiva o Inferencia Estadística: Conjunto de métodos que se fundamentan en la Teoría de la Probabilidad y que tienen por
j = 1,..., q donde i rs = {I 1 } rs Z j = N p i π i (θ 0 ) θ j
 MLG Ana M. Bianco FCEyN 2008 75 Comenzaremos por probar el siguiente resultado auxiliar. Lema: Supongamos que θ 0, valor verdadero del parámetro, es un punto interior del espacio paramétrico, π i (θ 0
MLG Ana M. Bianco FCEyN 2008 75 Comenzaremos por probar el siguiente resultado auxiliar. Lema: Supongamos que θ 0, valor verdadero del parámetro, es un punto interior del espacio paramétrico, π i (θ 0
La estructura de un cuerpo finito.
 9. CUERPOS FINITOS El objetivo de este capítulo es determinar la estructura de todos los cuerpos finitos. Probaremos en primer lugar que todo cuerpo finito tiene p n elementos, donde p es la característica
9. CUERPOS FINITOS El objetivo de este capítulo es determinar la estructura de todos los cuerpos finitos. Probaremos en primer lugar que todo cuerpo finito tiene p n elementos, donde p es la característica
Generación de variables aleatorias continuas Método de rechazo
 Generación de variables aleatorias continuas Método de rechazo Georgina Flesia FaMAF 18 de abril, 2013 Método de Aceptación y Rechazo Repaso Se desea simular una v. a. X discreta, con probabilidad de masa
Generación de variables aleatorias continuas Método de rechazo Georgina Flesia FaMAF 18 de abril, 2013 Método de Aceptación y Rechazo Repaso Se desea simular una v. a. X discreta, con probabilidad de masa
Selección de distribuciones de probabilidad
 Selección de distribuciones de probabilidad Georgina Flesia FaMAF 3 de mayo, 2012 Análisis estadístico de datos simulados Los sistemas reales tienen fuentes de aleatoriedad: Tipo de sistema Fabricación
Selección de distribuciones de probabilidad Georgina Flesia FaMAF 3 de mayo, 2012 Análisis estadístico de datos simulados Los sistemas reales tienen fuentes de aleatoriedad: Tipo de sistema Fabricación
INFERENCIA BAYESIANA. Antonio López Universitat de València. ESTADÍSTICA ESPACIAL EN EPIDEMIOLOGÍA Y MEDIO AMBIENTE Burjassot, Primavera de 2004
 Antonio López Universitat de València ESTADÍSTICA ESPACIAL EN EPIDEMIOLOGÍA Y MEDIO AMBIENTE Burjassot, Primavera de 2004 - Introducción a la inferencia bayesiana - Análisis bayesiano mediante simulación
Antonio López Universitat de València ESTADÍSTICA ESPACIAL EN EPIDEMIOLOGÍA Y MEDIO AMBIENTE Burjassot, Primavera de 2004 - Introducción a la inferencia bayesiana - Análisis bayesiano mediante simulación
Curso Inferencia. Miguel Ángel Chong R. 17 de septiembre del 2013
 Curso Estadística Miguel Ángel Chong R. miguel@sigma.iimas.unam.mx 17 de septiembre del 2013 Estimador insesgado de minima varianza Definición Estimador insesgado uniformemente de mínima varianza. Diremos
Curso Estadística Miguel Ángel Chong R. miguel@sigma.iimas.unam.mx 17 de septiembre del 2013 Estimador insesgado de minima varianza Definición Estimador insesgado uniformemente de mínima varianza. Diremos
PLAN DE TRABAJO 9 Período 3/09/07 al 28/09/07
 PLAN DE TRABAJO 9 Período 3/09/07 al 28/09/07 TEMAS A ESTUDIAR En esta guía nos dedicaremos a estudiar el tema de Estimación por intervalo y comenzaremos a estudiar las pruebas de hipótesis paramétricas.
PLAN DE TRABAJO 9 Período 3/09/07 al 28/09/07 TEMAS A ESTUDIAR En esta guía nos dedicaremos a estudiar el tema de Estimación por intervalo y comenzaremos a estudiar las pruebas de hipótesis paramétricas.
Teoría de la decisión Estadística
 Pruebas de hìpótesis Unidad 8. Pruebas de hipótesis. Formulación general. Distribución de varianza conocida. Prueba para la bondad del ajuste. Validación de modelos 1 Formulación Una Hipótesis es una proposición
Pruebas de hìpótesis Unidad 8. Pruebas de hipótesis. Formulación general. Distribución de varianza conocida. Prueba para la bondad del ajuste. Validación de modelos 1 Formulación Una Hipótesis es una proposición
Micro currículo OBJETIVO GENERAL. Al finalizar este curso, el alumno estará en capacidad de:
 Micro currículo Materia: ESTADISTICA INFERENCIAL Pensum: Aplica a partir del 2017.1 Resolución: VRA-010 Asignatura Nombre de la materia Código 15034 Créditos 3 Intensidad (H/S) 4 Modalidad PRESENCIAL Prerrequisitos
Micro currículo Materia: ESTADISTICA INFERENCIAL Pensum: Aplica a partir del 2017.1 Resolución: VRA-010 Asignatura Nombre de la materia Código 15034 Créditos 3 Intensidad (H/S) 4 Modalidad PRESENCIAL Prerrequisitos
BIBLIOTECA REMIGIO FIORE FORTEZZA OFM. CAP.
 BIBLIOTECA REMIGIO FIORE FORTEZZA OFM. CAP. CIENCIAS BÁSICAS 2015 2016 www.iucesmag.edu.co/biblioteca/ Contacto: 7216535 7333600 Ext. Jefatura: 248 Secretaria: 326 Circulación y Préstamo: 307 Email: biblioteca@iucesmag.edu.co
BIBLIOTECA REMIGIO FIORE FORTEZZA OFM. CAP. CIENCIAS BÁSICAS 2015 2016 www.iucesmag.edu.co/biblioteca/ Contacto: 7216535 7333600 Ext. Jefatura: 248 Secretaria: 326 Circulación y Préstamo: 307 Email: biblioteca@iucesmag.edu.co
Selección de distribuciones de probabilidad
 Selección de distribuciones de probabilidad Patricia Kisbye FaMAF 6 de mayo, 2010 Análisis estadístico de datos simulados Los sistemas reales tienen fuentes de aleatoriedad: Tipo de sistema Fabricación
Selección de distribuciones de probabilidad Patricia Kisbye FaMAF 6 de mayo, 2010 Análisis estadístico de datos simulados Los sistemas reales tienen fuentes de aleatoriedad: Tipo de sistema Fabricación
UNIVERSIDAD AUTÓNOMA DE ZACATECAS PLAN ANALÍTICO
 ÁREA ACADÉMICA UNIVERSIDAD AUTÓNOMA DE ZACATECAS PLAN ANALÍTICO CIENCIAS BÁSICAS UNIDAD ACADÉMICA MATEMÁTICAS PROGRAMA ACADÉMICO LICENCIATURA EN MATEMÁTICAS CICLO ESCOLAR UNIDAD DIDÁCTICA ESTADÍSTICA I
ÁREA ACADÉMICA UNIVERSIDAD AUTÓNOMA DE ZACATECAS PLAN ANALÍTICO CIENCIAS BÁSICAS UNIDAD ACADÉMICA MATEMÁTICAS PROGRAMA ACADÉMICO LICENCIATURA EN MATEMÁTICAS CICLO ESCOLAR UNIDAD DIDÁCTICA ESTADÍSTICA I
Contrastes basados en el estadístico Ji Cuadrado
 Capítulo 10 Contrastes basados en el estadístico Ji Cuadrado 10.1. Introducción Existen multitud de situaciones en el ámbito de la salud en el que las variables de interés, las cuales no pueden cuantificarse
Capítulo 10 Contrastes basados en el estadístico Ji Cuadrado 10.1. Introducción Existen multitud de situaciones en el ámbito de la salud en el que las variables de interés, las cuales no pueden cuantificarse
Métodos Estadísticos de la Ingeniería Tema 11: Contrastes de Hipótesis Grupo B
 Métodos Estadísticos de la Ingeniería Tema 11: Contrastes de Hipótesis Grupo B Área de Estadística e Investigación Operativa Licesio J. Rodríguez-Aragón Abril 2010 Contenidos...............................................................
Métodos Estadísticos de la Ingeniería Tema 11: Contrastes de Hipótesis Grupo B Área de Estadística e Investigación Operativa Licesio J. Rodríguez-Aragón Abril 2010 Contenidos...............................................................
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES ACATLÁN HORAS SEMANA
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES ACATLÁN PLAN DE ESTUDIOS DE LA LICENCIATURA EN MATEMÁTICAS APLICADAS Y COMPUTACIÓN PROGRAMA DE ASIGNATURA SEMESTRE:4 (CUARTO) Probabilidad
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE ESTUDIOS SUPERIORES ACATLÁN PLAN DE ESTUDIOS DE LA LICENCIATURA EN MATEMÁTICAS APLICADAS Y COMPUTACIÓN PROGRAMA DE ASIGNATURA SEMESTRE:4 (CUARTO) Probabilidad
2 La precisión en los modelos clásicos. estimador por punto para el parámetro e 3θ para una población de Poisson
 POR QUÉ LA INFERENCIA ESTADISTICA BAYESIANA M. A. Gómez Villegas 1 Introducción En este artículo se pretende justificar por qué se debe utilizar la aproximación bayesiana a la inferencia estadística. Como
POR QUÉ LA INFERENCIA ESTADISTICA BAYESIANA M. A. Gómez Villegas 1 Introducción En este artículo se pretende justificar por qué se debe utilizar la aproximación bayesiana a la inferencia estadística. Como
iii. Q es denso en F (para todo par x, y F tal que x < y, existe un r Q tal que x < r < y); v. Para todo a R tal que a < 1, lím n a n = 0.
 LOS TEOREMAS CENTRALES DEL CÁLCULO Y LA COMPLETITUD DE LA RECTA NUMÉRICA: UNA REFLEXIÓN SOBRE LA IMPOSIBILIDAD DE FORMULAR EL CÁLCULO EN EL CONJUNTO DE LOS NÚMEROS RACIONALES JORGE M. LÓPEZ Resumen. En
LOS TEOREMAS CENTRALES DEL CÁLCULO Y LA COMPLETITUD DE LA RECTA NUMÉRICA: UNA REFLEXIÓN SOBRE LA IMPOSIBILIDAD DE FORMULAR EL CÁLCULO EN EL CONJUNTO DE LOS NÚMEROS RACIONALES JORGE M. LÓPEZ Resumen. En
En primer lugar, vamos a precisar un concepto al que ya nos hemos referido anteriormente, el de σ-álgebra.
 Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Capítulo 20 Conjuntos de Borel Hemos demostrado ya que la familia M de los conjuntos medibles contiene a todos los abiertos de R n y, por tanto, a todos los conjuntos que podamos formar a partir de los
Resumen. Recordemos que una cópula es una función C : I 2 I tal que: C(u 2, v 2 ) C(u 2, v 1 ) C(u 1, v 2 ) + C(u 1, v 1 ) 0. (2)
 Contenido 1 2 3 Cópula Empírica Cópula Kernel Resumen Recordemos que una cópula es una función C : I 2 I tal que: 1 Para cualesquiera u, v en I := [0, 1] C(u, 0) = 0 = C(0, v), C(u, 1) = u, C(1, v) = v.
Contenido 1 2 3 Cópula Empírica Cópula Kernel Resumen Recordemos que una cópula es una función C : I 2 I tal que: 1 Para cualesquiera u, v en I := [0, 1] C(u, 0) = 0 = C(0, v), C(u, 1) = u, C(1, v) = v.
Lee, Capítulo 3, Secciones 3.1,3.2,3.4 y 3.5. Gelman et al, Capítulo 2, Secciones
 CAPÍTULO 3: DISTRIBUCIONES CON- JUGADAS Para leer Lee, Capítulo 3, Secciones 3.1,3.2,3.4 y 3.5. Gelman et al, Capítulo 2, Secciones 2.4 2.7. Ejemplo 18 Supongamos que en la situación del Ejemplo 13, se
CAPÍTULO 3: DISTRIBUCIONES CON- JUGADAS Para leer Lee, Capítulo 3, Secciones 3.1,3.2,3.4 y 3.5. Gelman et al, Capítulo 2, Secciones 2.4 2.7. Ejemplo 18 Supongamos que en la situación del Ejemplo 13, se
