Ecuaciones de Maxwell
|
|
|
- Juan Francisco Farías Calderón
- hace 7 años
- Vistas:
Transcripción
1 ANTENAS FUNDAMENTOS DE RADIACIÓN 1 Ecuaciones de Maxwell Ecuaciones diferenciales Los fenómenos electromagnéticos se pueden describir a partir de las cuatro ecuaciones de Maxwell. Ley de Ampère D H= J + t Ley de Faraday B E = t Ley de Gauss D = ρ Ley de Gauss B = Unidades E Campo eléctrico Voltios/m H Intensidad del campo Amperios/m magnético D Desplazamiento del campo Culombios/m eléctrico B Flujo del campo magnético Weber/m =tesla J Densidad de corriente Amperios/m ρ Densidad de carga Culombios/m 3 Ecuación de continuidad De las ecuaciones anteriores se deduce la ecuación de continuidad. Para ello se toma la divergencia de la ley de Ampère. Teniendo en cuenta que la divergencia del rotacional es cero, se obtiene la relación entre las cargas y las corrientes. D = J + t ρ J + = t
2 ANTENAS FUNDAMENTOS DE RADIACIÓN Casos particulares de las Ecuaciones de Maxwell En el espacio libre las corrientes y las cargas son cero y las ecuaciones de Maxwell se pueden simplificar eliminando los términos correspondientes. Asimismo si las fuentes varían armónicamente con el tiempo, las ecuaciones electromagnéticas y sus soluciones se simplifican, utilizando para ello una notación fasorial, de forma que las derivadas respecto al tiempo se transforman en productos por el factor jω. Finalmente para casos sin variación temporal, las ecuaciones toman las formas de electrostática y magnetostática. Ley de Ampère Ley de Diferencial Faraday Caso D B general H= J + E = t t Espacio D B libre H = E = t t Armónica H = J + ( σ + jω ) E E = jωµ H Estacionario H = J E = Ley de Gauss D = ρ D = D = ρ D = ρ Ley de Gauss B = B = B = B = Ecuaciones en forma integral Las ecuaciones de Maxwell se pueden escribir en forma integral, aplicando para ello los teoremas de Stokes y de la divergencia D H dl = J + ds t B E dl = ds t D ds= B ds = ρdv
3 ANTENAS FUNDAMENTOS DE RADIACIÓN 3 En medios materiales hay que considerar la relación entre los vectores intensidad EH, e inducción DB, utilizando la permitividad eléctrica y la permeabilidad magnética, que en el espacio libre toman los valores = 1-9/36p F/m µ = 4p1-7 H/m En general D= E = r E B= µ H = µµ H r Los valores relativos de la permitividad y permeabilidad pueden ser reales o complejos, escalares o matrices, constantes o variables(dependientes de la posición). En cada caso los medios se denominan como: Permitividad, permeabilidad Real Compleja Escalar Matriz Constante Variable Tipo de medio Sin pérdidas Con pérdidas Isótropo Anisótropo Homogéneo Inhomogéneo Finalmente, las antenas se estudiarán en medios homogéneos e isótropos. lineales, En este caso las ecuaciones de Maxwell para campos variables sinusoidalmente se pueden escribir como ρ E = H = E = jωµ H H= J+ jω E
4 ANTENAS FUNDAMENTOS DE RADIACIÓN 4 Ecuaciones de Onda para los Campos Ecuaciones de Maxwell (variación armónica ) ρ E = H = E = jωµ H H= J+ jω E Ecuación de continuidad De las ecuaciones anteriores se deduce la ecuación de continuidad, tomando para ello la divergencia de la Ley de Ampère, y teniendo en cuenta que la divergencia del rotacional es cero. H = J + jω E H = J + jω E ρ = J + jω( ) J + jωρ = Las ecuaciones de Maxwell, desde un punto de vista matemático son un sistema de ecuaciones diferenciales vectoriales de primer orden, apareciendo entremezclados los campos eléctricos y magnéticos. A continuación se van a obtener unas nuevas ecuaciones diferenciales, de segundo orden donde se encuentren separados los campos. Ecuación de onda para el campo eléctrico Tomando el rotacional de la Ley de Faraday se obtiene la ecuación de onda para el campo eléctrico E = jωµ H E = jωµ H E E = jωµ ( J + jωe) ρ E+ ωµe = jωµ J + ( )
5 ANTENAS FUNDAMENTOS DE RADIACIÓN 5 Ecuación de onda para el campo magnético Tomando el rotacional de la Ley de Ampère se obtiene la ecuación de onda para el campo magnético. H= J+ jω E H = J + jω E = + ωµ H + ωµh = J H H J H Definición de los potenciales Para simplificar el cálculo de los campos eléctricos y magnéticos se puede recurrir a una funciones potenciales escalar y vector, que simplifiquen los cálculos. Definición del potencial vector El potencial vector se puede definir teniendo en cuenta la ley de Gauss para el flujo magnético. Si se define B como el rotacional de un vector, automáticamente se cumple que la divergencia es cero. B = B= A Definición del potencial escalar El potencial escalar se puede definir a partir de la Ley de Faraday y de la definición del potencial vector. Teniendo en cuenta que el rotacional del gradiente de una función es cero, se puede definir el potencial escalar como: E = jωµ H E = jω ( A) ( E jω A) = E jω A= Φ E = jω A Φ
6 ANTENAS FUNDAMENTOS DE RADIACIÓN 6 Ecuación de onda para el potencial vector eléctrico La ley de Ampère y las definiciones anteriores nos permiten obtener la siguiente ecuación de onda para el potencial vector eléctrico. H = J + jω E A= µ J + jωµ( Φ jωa) A A= µ J + jωµ( Φ jωa) A+ ωµ A= µ J + ( A+ jωµφ) Ecuación de onda para el potencial escalar eléctrico Utilizando la Ley de Gauss para el campo eléctrico se obtiene la ecuación de onda para el potencia escalar ρ E = ρ ( jω A Φ ) = ρ ( ) Φ+ ωµφ= + jω A+ ωµφ Definición de la condición de Lorentz Se ha definido el campo magnético a partir del rotacional del potencial vector, pero es necesario definir también su divergencia. Esta relación se denomina condición de Lorentz. A+ jωµφ= Es posible simplificar las expresiones de las ecuaciones de onda para los potenciales. Ecuaciones de onda de los potenciales ρ Φ+ k Φ= A+ k A= µ J
7 ANTENAS FUNDAMENTOS DE RADIACIÓN 7 Ondas planas, cilíndricas y esféricas Los campos eléctricos y magnéticos y los potenciales están relacionados mediante la ecuación de onda vectorial inhomogénea. La ecuación de onda escalar homogénea, (en ausencia de fuentes) se puede escribir como Ω+ k Ω= La ecuación de onda se puede resolver de forma analítica en diversos sistemas de coordenadas (cartesianas, cilíndricas, esféricas, etc). Se puede resolver mediante el método de separación de variables, en forma de productos de series. Los coeficientes de las series se determinan a partir de las condiciones de contorno del problema. Ondas planas En algunos casos la ecuación de onda se puede resolver directamente. Por ejemplo en coordenadas cartesianas, cuando no existe variación respecto a x e y la ecuación de onda tiene la solución conocida de ondas planas unidimensionales. Ω+ Ω= k Ω = x Ω = y Ω k + Ω= z jkz Ω= Ae + Be jkz Ondas cilíndricas La solución de la ecuación de onda en coordenadas cilíndricas, con la condición de no variación en las direcciones f,z se puede obtener fácilmente a partir de la expresión de en cilíndricas y de las soluciones de la ecuación diferencial de Bessel.
8 ANTENAS FUNDAMENTOS DE RADIACIÓN 8 Ω+ k Ω= Ω = z Ω = φ 1 ρ ρ ρ Ω Ω + + k Ω= Ω= AH ( kρ) + BH ( kρ) (1) () Las funciones H que se obtienen son las funciones de Hankel modificadas de primera y segunda especie, que tienen un comportamiento asintótico como H H () (1) e ( kρ) ρ jk ρ jk ρ e ( kρ) ρ Representan ondas cilíndricas que se propagan en la dirección radial en el sentido de radios crecientes y decrecientes Ondas esféricas En coordenadas esféricas en el caso de que haya simetría en trono al origen, sin variación respecto a las variables angulares, la solución de la ecuación de onda en con la condición de no variación en las direcciones q,f es Ω+ k Ω= Ω = φ Ω = θ r r r jkr jkr e e Ω= A + B r r Ω Ω + + k Ω=
9 ANTENAS FUNDAMENTOS DE RADIACIÓN 9 La solución se obtiene como superposición de dos ondas esféricas, progresiva (desde el origen a infinito) y regresiva, en sentido contrario. Función de Green de la Ecuación de Onda La ecuación de onda en coordenadas esféricas, con una fuente puntual en el origen de coordenadas se puede resolver teniendo en cuenta que la solución debe ser en forma de ondas progresivas. + = G kg () r G+ kg= () r jkr e G = A r Para determinar el valor de la constante A, se puede integrar en una esfera que encierre el origen de coordenadas, teniendo en cuenta que la superficie de la esfera es proporcional a r, mientras que el volumen es proporcional a r 3. Calculando la divergencia de la solución e integrando se obtiene A=1. s v ˆ sin( θ) θ φ 1 G rr d d + k Gdv = Gdv jkr e Gr () = r v Si las fuentes están situadas en un punto distinto del origen, definido por el vector r ', la solución es la misma que en el caso anterior, con un cambio en el sistema de referencia. jk r r' e Grr (, ') = 4 π r r '
10 ANTENAS FUNDAMENTOS DE RADIACIÓN 1 Soluciones Integrales para los Potenciales Una vez obtenida la solución de la ecuación de onda para una fuente puntual, para obtener la solución general se puede aplicar el principio de superposición, integrando el conjunto de todas las fuentes. Potencial escalar La ecuación de onda para el potencial escalar es ρ Φ+ k Φ= La función de Green para la ecuación de onda en coordenadas esféricas es jk r r' e Grr (, ') = 4 π r r ' La solución para el potencial se puede obtener como la convolución de la respuesta impulsional (función de Green) con las fuentes (distribución volumétrica de cargas). 1 Φ= 1 Φ= Grr (, ') ρ( r ') d jkr r' e ρ( r ') d 4 π r r' Potencial vector Para obtener la solución para el potencial vector eléctrico, se puede partir de la ecuación de onda A k A J + = µ La ecuación de onda anterior se puede descomponer en tres ecuaciones escalares, correspondientes a cada una de las componentes cartesianas del vector. La solución se obtiene sumando las soluciones escalares.
11 ANTENAS FUNDAMENTOS DE RADIACIÓN 11 A + k A = µ J x x x A + k A = µ J y y y A + k A = µ J z z z Solución integral para la ecuación de onda del potencial vector A= µ Grr (, ') Jr ( ') d A= µ jk r r ' e Jr ( ') d 4 π r r' Soluciones Temporales de los Potenciales La solución de la ecuación de onda para variación armónica es jk r r' e Grr (, ') = e 4 π r r ' jωt Teniendo en cuenta que la transformada de Fourier de una función de módulo constante y fase lineal se puede escribir como un delta en el dominio del tiempo. r r' jkr r ' ( t ) 1 e jω t e dω c π = 4 π r r ' 4 π r r ' El potencial escalar se puede obtener a partir de la convolución de la respuesta impulsional con la distribución de cargas. r r ' ρ( r ', t ) Φ (,) rt = c d 4 π r r' El potencial vector de una distribución de corrientes, en el dominio temporal es de la forma r r ' µ J( r ', t ) Art (,) = c d 4 π r r '
12 ANTENAS FUNDAMENTOS DE RADIACIÓN 1 Expresiones generales de los campos Los campos eléctricos y magnéticos se pueden obtener a partir de los potenciales mediante las expresiones siguientes 1 H = A µ E = jω A Φ Las soluciones que se han obtenido para los potenciales en forma integral son 1 Φ= Grr (, ') ρ( r') d A= µ Grr (, ') J( r') d jk r r ' e Grr (, ') = 4 π r r ' R= r r' jkr e GR ( ) = R Para calcular los campos es necesario calcular los gradientes y rotacionales de los potenciales. 1 Φ ( r) = Grr (, ') ρ( r ') d jkr e dg( R) Grr (, ') = ( ) = R ˆ R dr jkr 1 e Grr (, ') = ( jk ) Rˆ R 4 π R A= µ Grr (, ') Jr ( ') d = µ Grr (, ') J( r') d Finalmente, simplificando las anteriores expresiones se obtiene el campo eléctrico, válido en todos los puntos del espacio. jkr jkr 1 ˆ e jk ( ') ' ( ') ˆ ωµ e E = Rρ r dv + ρ r R J d R k R
13 ANTENAS FUNDAMENTOS DE RADIACIÓN 13 El campo magnético es 1 jkr jkr ˆ e jk ( ') ' ( ˆ e H = R Jr dv R Jr ( ')) d π R R 4 A distancias muy cercanas a las fuentes predominan los campos que son proporcionales a 1/r, mientras que a grandes distancias predominan los proporcionales a 1/r Campos inducidos Son proporcionales a 1/r y corresponden a las leyes de Coulomb y Biot y Savart, con un término adicional de fase. Si k= se obtienen las expresiones conocidas de los campos de una distribución de cargas y de corrientes. jkr 1 ˆ e Ei = Rρ( r ') d R 1 jkr ˆ e Hi = R J( r') d R Campos radiados Los campos radiados son proporcionales a 1/r y son los que contribuyen a la radiación a grandes distancias de las fuentes. jkr jk ωµ e Er = r R J d R ( ') ˆ ρ k jkr jk ( ˆ e Hr = R J( r')) d R Los campos magnéticos inducidos y radiados son iguales cuando se cumple la condición 1 k = R R λ R = π
14 ANTENAS FUNDAMENTOS DE RADIACIÓN 14 Campos radiados Los campos radiados se pueden calcular a partir de las expresiones generales de los campos, realizando las correspondientes integrales. Si estamos a una distancia suficientemente grande de la antena, podemos hacer una serie de aproximaciones que nos simplificarán los cálculos. Se puede considerar que todas las ondas originadas en la antena siguen trayectorias paralelas hasta el punto de campo, es decir Al ser las trayectorias de los rayos paralelas, la diferencia de caminos recorridos por las diferentes ondas se puede calcular como R r rˆ r ' Las ondas producidas en cada punto se pueden aproximar por una onda centrada en el origen de coordenadas con un desfase adicional equivalente a la diferencia de caminos. Función de Green aproximada jkr jkr e e Grr (, ') = e R r jkrˆ r' El potencial vector eléctrico a grandes distancias se puede calcular a partir de la función de Green aproximada a grandes distancias Potencial vector Campo magnético A= µ Grr (, ') J( r') d jkr e µ e A= µ J r dv = J r e dv R r jkr jkr rˆ' ( ') ' ( ') ' El campo magnético radiado se obtiene a partir de la expresión anterior, junto con la expresión aproximada del potencial.
15 ANTENAS FUNDAMENTOS DE RADIACIÓN 15 jkr jk ( ˆ e H = R J( r')) d R jk e H = r Jr r e dv jk H = rˆ A µ jkr jkrˆ r ' ( ˆ ( ')) ' Se puede observar que el campo magnético es perpendicular a la dirección radial y al potencial vector. Campo eléctrico El campo eléctrico radiado se puede calcular a partir de los potenciales y la condición de Lorentz j E = jωa Φ= jωa A ωµ El gradiente y la divergencia en coordenadas esféricas es ψ ˆ1 ψ ˆ 1 ψ ψ = rˆ + θ + φ r r θ rsinθ φ Aφ = ra r + ( Aθ sinθ ) + r r rsinθ θ rsinθ φ Se puede observar que todos los términos de la divergencia son proporcionales a la distancia, excepto el primero, la divergencia se puede aproximar por A A r r Tomando el gradiente de la divergencia se llega a Ar ˆ1 Ar ˆ 1 Ar A= rˆ + θ + φ r r r θ rsinθ r φ Efectuando las operaciones indicadas, el sumando que decrece menos con las distancia es el debido a la componente radial
16 ANTENAS FUNDAMENTOS DE RADIACIÓN 16 A r = k r Ar r A ˆ r ( ˆ ) ˆ Finalmente nos queda una expresión muy simple para el campo eléctrico radiado a grandes distancias E = jω( A ( rˆ Ar ) ˆ) = jω( rˆ ( rˆ A)) El campo eléctrico es perpendicular a la dirección radial (sólo tiene componentes tangenciales). Expresiones aproximadas para los campos radiados Los campos eléctricos y magnéticos son perpendiculares entre sí y sólo tienen componentes tangenciales. La relación entre sus módulos es la impedancia característica del medio, que no debe confundirse con la eficiencia. jk H = rˆ A µ E = jω( A rˆ A) = jω( rˆ ( r A)) E = η( H rˆ ) Desarrollando los productos vectoriales, se pueden obtener las componentes de los campos radiados E r = E = jω A θ θ E = jω A φ φ H r H H θ φ = Eφ = η Eθ = η
17 ANTENAS FUNDAMENTOS DE RADIACIÓN 17 El vector de radiación Definición del vector de radiación El potencial vector es el producto de dos términos, por una parte tenemos una onda esférica centrada en el origen de coordenadas, y por otra parte una integral que vamos a denominar vector de radiación N. jkr µ e A= Jr e dv r jkr µ e A= N r N = J r e dv jkrˆ r' ( ') ' jkrˆ r' ( ') ' El vector de radiación se puede considerar como la suma vectorial de todas las corrientes multiplicadas por un término que representa la diferencia de fase entre la onda que produce y la que tendría si la onda estuviera situada en el origen de coordenadas. Interpretación como Transformada de Fourier tridimensional El término de fase depende de la dirección del espacio que se esté considerando y de la distancia al origen. Descomponiendo el vector distancia en sus tres componentes krˆ= k = kxˆ ˆ x + kyy+ kz zˆ r' = xx ' ˆ + y' yˆ + zz ' ˆ Vemos que el vector de radiación se puede interpretar como una integral tridimensional. jkrˆ r' jkx x' jky y' jkzz' N = J( r ') e d = Jr ( ') e e e d
18 ANTENAS FUNDAMENTOS DE RADIACIÓN 18 La integral se puede interpretar como una transformada de Fourier tridimensional entre las posiciones de las fuentes (x,y,z ) y las frecuencias espaciales (kx,ky,kz). El vector k depende de la longitud θφ,. de onda y de las direcciones del espacio ( ) Si las corrientes se distribuyen a lo largo del eje z, la interpretación es más simple. Vector de radiación de un hilo de corriente N = J r e e e dv jkxx' jky y' jkzz' ( ') ' J( x', y', z') = I( z') ( x') ( y') zˆ N = z e x dx e y dy I z e dz jkzz' N = zˆ I( z') e dz ' jk ' ' xx jky y jkzz' ˆ ( ') ' ( ') ' ( ') ' El vector de radiación se puede interpretar como la transformada de Fourier unidimensional de las corrientes. Si el hilo de corriente uniforme, el vector de radiación se calcula como. N = z I z e dz I( z') = I jkzz' ˆ ( ') ' h z Nk z Ie dz h ( jkzz' z ) = ˆ h ' h sin( kz ) Nk ( ) ˆ z = zih h kz k = kcos( θ) z
Figura 1.3.1. Sobre la definición de flujo ΔΦ.
 1.3. Teorema de Gauss Clases de Electromagnetismo. Ariel Becerra La ley de Coulomb y el principio de superposición permiten de una manera completa describir el campo electrostático de un sistema dado de
1.3. Teorema de Gauss Clases de Electromagnetismo. Ariel Becerra La ley de Coulomb y el principio de superposición permiten de una manera completa describir el campo electrostático de un sistema dado de
2.1 Las ecuaciones de Maxwell en el espacio libre. Llamaremos «espacio libre» a todo medio que satisfaga las siguientes propiedades
 Capítulo 2 Leyes básicas de la teoría electromagnética. Ondas electromagnéticas 2.1 Las ecuaciones de Maxwell en el espacio libre 2.1.1 El espacio libre Llamaremos «espacio libre» a todo medio que satisfaga
Capítulo 2 Leyes básicas de la teoría electromagnética. Ondas electromagnéticas 2.1 Las ecuaciones de Maxwell en el espacio libre 2.1.1 El espacio libre Llamaremos «espacio libre» a todo medio que satisfaga
Ecuaciones de Maxwell y Ondas Electromagnéticas
 Capítulo 7: Ecuaciones de Maxwell y Ondas Electromagnéticas Hasta ahora: Ley de Gauss Ley de Faraday-Henry Ley de Gauss para el magnetismo Ley de Ampere Veremos que la Ley de Ampere presenta problemas
Capítulo 7: Ecuaciones de Maxwell y Ondas Electromagnéticas Hasta ahora: Ley de Gauss Ley de Faraday-Henry Ley de Gauss para el magnetismo Ley de Ampere Veremos que la Ley de Ampere presenta problemas
LEY DE NEWTON DE LA VISCOSIDAD
 LEY DE NEWTON DE LA VISCOSIDAD Supongamos un fluido contenido entre dos grandes láminas planas y paralelas de área A separadas entre sí por una pequeña distancia Y. Fig. 1 Fluido contenido entre los láminas
LEY DE NEWTON DE LA VISCOSIDAD Supongamos un fluido contenido entre dos grandes láminas planas y paralelas de área A separadas entre sí por una pequeña distancia Y. Fig. 1 Fluido contenido entre los láminas
Campos Electromagnéticos Estáticos
 Capítulo 3: Campos Electromagnéticos Estáticos Flujo de un campo vectorial Superficie cerrada Ley de Gauss Karl Friedrich Gauss (1777-1855) Flujo de E generado por una carga puntual Superficie arbitraria
Capítulo 3: Campos Electromagnéticos Estáticos Flujo de un campo vectorial Superficie cerrada Ley de Gauss Karl Friedrich Gauss (1777-1855) Flujo de E generado por una carga puntual Superficie arbitraria
Teorema de reciprocidad
 ANTENAS nteracción entre antenas. mpedancias Teorema de reciprocidad Los parámetros de las antenas (directividad, ancho de ha, impedancia, resistencia de radiación, etc. ) son idénticos en transmisión
ANTENAS nteracción entre antenas. mpedancias Teorema de reciprocidad Los parámetros de las antenas (directividad, ancho de ha, impedancia, resistencia de radiación, etc. ) son idénticos en transmisión
CORRIENTES Y LEYES DE CONSERVACIÓN Y OBTENCIÓN DE LAS ECUACIONES PRINCIPALES DEL ELECTROMAGNETISMO.
 CORRIENTES Y LEYES DE CONSERVACIÓN Y OBTENCIÓN DE LAS ECUACIONES PRINCIPALES DEL ELECTROMAGNETISMO. José Manuel Gómez Vega. (mayo 2.002) IngeMek Ingenieros www.ingemek.es CORRIENTES Y LEYES DE CONSERVACIÓN
CORRIENTES Y LEYES DE CONSERVACIÓN Y OBTENCIÓN DE LAS ECUACIONES PRINCIPALES DEL ELECTROMAGNETISMO. José Manuel Gómez Vega. (mayo 2.002) IngeMek Ingenieros www.ingemek.es CORRIENTES Y LEYES DE CONSERVACIÓN
EL CAMPO ELÉCTRICO. Física de 2º de Bachillerato
 EL CAMPO ELÉCTRICO Física de 2º de Bachillerato Los efectos eléctricos y magnéticos son producidos por la misma propiedad de la materia: la carga. Interacción electrostática: Ley de Coulomb Concepto de
EL CAMPO ELÉCTRICO Física de 2º de Bachillerato Los efectos eléctricos y magnéticos son producidos por la misma propiedad de la materia: la carga. Interacción electrostática: Ley de Coulomb Concepto de
Campo Eléctrico. Fig. 1. Problema número 1.
 Campo Eléctrico 1. Cuatro cargas del mismo valor están dispuestas en los vértices de un cuadrado de lado L, tal como se indica en la figura 1. a) Hallar el módulo, dirección y sentido de la fuerza eléctrica
Campo Eléctrico 1. Cuatro cargas del mismo valor están dispuestas en los vértices de un cuadrado de lado L, tal como se indica en la figura 1. a) Hallar el módulo, dirección y sentido de la fuerza eléctrica
El campo magnético de las corrientes estacionarias
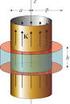 El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
Figura 3.-(a) Movimiento curvilíneo. (b) Concepto de radio de curvatura
 Componentes intrínsecas de la aceleración: Componentes tangencial y normal Alfonso Calera Departamento de Física Aplicada. ETSIA. Albacete. UCLM En muchas ocasiones el análisis del movimiento es más sencillo
Componentes intrínsecas de la aceleración: Componentes tangencial y normal Alfonso Calera Departamento de Física Aplicada. ETSIA. Albacete. UCLM En muchas ocasiones el análisis del movimiento es más sencillo
TEMA 0: Herramientas matemáticas
 1 TEMA 0: Herramientas matemáticas Tema 0: Herramientas matemáticas 1. Campos escalares y vectoriales 2. Gradiente 3. Divergencia 4. Rotacional 5. Teoremas de Gauss y de Stokes 5. Representación gráfica
1 TEMA 0: Herramientas matemáticas Tema 0: Herramientas matemáticas 1. Campos escalares y vectoriales 2. Gradiente 3. Divergencia 4. Rotacional 5. Teoremas de Gauss y de Stokes 5. Representación gráfica
4.2. Ecuaciones de onda para los campos y los potenciales
 4.2. Ecuaciones de onda para los campos y los potenciales Veremos en esta sección que los campos y los potenciales cumplen ecuaciones de onda. Parte de las soluciones de estas ecuaciones tienen caracter
4.2. Ecuaciones de onda para los campos y los potenciales Veremos en esta sección que los campos y los potenciales cumplen ecuaciones de onda. Parte de las soluciones de estas ecuaciones tienen caracter
Última modificación: 1 de agosto de 2010. www.coimbraweb.com
 Contenido ECUACIONES DE MAXWELL 1.- Ecuaciones Maxwell. 2.- La contribución de Hertz. 3.- Campo electromagnético. Objetivo.- Al finalizar el tema, el estudiante será capaz de interpretar las ecuaciones
Contenido ECUACIONES DE MAXWELL 1.- Ecuaciones Maxwell. 2.- La contribución de Hertz. 3.- Campo electromagnético. Objetivo.- Al finalizar el tema, el estudiante será capaz de interpretar las ecuaciones
Campo de un hilo infinito. Fuerzas magnéticas. Teorema de Ampère. Campo magnético de una espira circular
 El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
CAMPOS ELÉCTRICOS Y MAGNÉTICOS EN LA MATERIA
 CAMPOS ELÉCTRICOS Y MAGNÉTICOS EN LA MATERIA Prof O Contreras Al considerar campos dentro de materiales, el campo Eléctrico induce a nivel atómico, Dipolos de Momento Dipolar Eléctrico Si el número de
CAMPOS ELÉCTRICOS Y MAGNÉTICOS EN LA MATERIA Prof O Contreras Al considerar campos dentro de materiales, el campo Eléctrico induce a nivel atómico, Dipolos de Momento Dipolar Eléctrico Si el número de
Electromagnetismo. Introducción. Líneas de campo magnético. Experimento de Oersted. El campo magnético de las corrientes estacionarias
 El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
1. V F La fem inducida en un circuito es proporcional al flujo magnético que atraviesa el circuito.
 Eng. Tèc. Telecom. So i Imatge TEORIA TEST (30 %) 16-gener-2006 PERM: 2 Indique si las siguientes propuestas son VERDADERAS o FALSAS encerrando con un círculo la opción que crea correcta. Acierto=1 punto;
Eng. Tèc. Telecom. So i Imatge TEORIA TEST (30 %) 16-gener-2006 PERM: 2 Indique si las siguientes propuestas son VERDADERAS o FALSAS encerrando con un círculo la opción que crea correcta. Acierto=1 punto;
CAPÍTULO IV Dieléctricos
 Fundamento teórico CAPÍTULO IV Dieléctricos I.- l dipolo Ia.- Momento dipolar Un sistema formado por dos cargas iguales en módulo y de signo opuesto, +q y q, con vectores posición r + y r respectivamente,
Fundamento teórico CAPÍTULO IV Dieléctricos I.- l dipolo Ia.- Momento dipolar Un sistema formado por dos cargas iguales en módulo y de signo opuesto, +q y q, con vectores posición r + y r respectivamente,
INDICE 1. Sistemas de Coordenadas e Integrales 2. Gradiente, Divergente y Rotacional 3. Campos Electrostáticos
 INDICE Prefacio XVII 1. Sistemas de Coordenadas e Integrales 1 1.1. Conceptos generales 1 1.2. Coordenadas de un punto 2 1.3. Los campos escalares y cómo se transforman 4 1.4. Campos vectoriales y cómo
INDICE Prefacio XVII 1. Sistemas de Coordenadas e Integrales 1 1.1. Conceptos generales 1 1.2. Coordenadas de un punto 2 1.3. Los campos escalares y cómo se transforman 4 1.4. Campos vectoriales y cómo
Capítulo 2: Formulación matemática del problema
 Capítulo : Formulación matemática del problema. Introducción El análisis del comportamiento en régimen permanente o transitorio de una red de puesta a tierra se fundamenta en la teoría electromagnética
Capítulo : Formulación matemática del problema. Introducción El análisis del comportamiento en régimen permanente o transitorio de una red de puesta a tierra se fundamenta en la teoría electromagnética
Soluciones de la ecuación de onda ( ) ( ) ( ) ONDAS PLANAS. Ecuación de onda en coordenadas cartesianas. Separación de variables.
 ONDAS PLANAS Soluciones de la ecuación de onda cuación de onda en coordenadas cartesianas Ω+ Ω Ω Ω Ω + + + Ω Separación de variables Ω X Y Z d X dy dz + + + X d Y d Z d X d Y d d X dy Z d dz + + cuaciones
ONDAS PLANAS Soluciones de la ecuación de onda cuación de onda en coordenadas cartesianas Ω+ Ω Ω Ω Ω + + + Ω Separación de variables Ω X Y Z d X dy dz + + + X d Y d Z d X d Y d d X dy Z d dz + + cuaciones
un sistema de conductores cargados. Energía electrostática en función de los vectores de campo. Fuerza electrostática. Presión electrostática.
 11 ÍNDICE GENERAL INTRODUCCIÓN 13 CÁLCULO VECTORIAL 17 Escalares y vectores. Operaciones con vectores. Campos escalares y vectoriales. Sistemas de coordenadas. Transformación de coordenadas. Vector de
11 ÍNDICE GENERAL INTRODUCCIÓN 13 CÁLCULO VECTORIAL 17 Escalares y vectores. Operaciones con vectores. Campos escalares y vectoriales. Sistemas de coordenadas. Transformación de coordenadas. Vector de
INTERACCIÓN ELÉCTRICA
 INTERACCIÓN ELÉCTRICA 1. La carga eléctrica. 2. La ley de Coulomb. 3. El campo eléctrico. 4. La energía potencial. 5. El potencial electroestático. 6. El campo eléctrico uniforme. 7. El flujo de campo
INTERACCIÓN ELÉCTRICA 1. La carga eléctrica. 2. La ley de Coulomb. 3. El campo eléctrico. 4. La energía potencial. 5. El potencial electroestático. 6. El campo eléctrico uniforme. 7. El flujo de campo
ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250)
 Universidad Central de Venezuela Facultad de Ingeniería Ciclo Básico Departamento de Matemática Aplicada ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250) Semestre 1-2011 Mayo 2011 Álgebra Lineal y Geometría
Universidad Central de Venezuela Facultad de Ingeniería Ciclo Básico Departamento de Matemática Aplicada ÁLGEBRA LINEAL Y GEOMETRÍA ANALÍTICA (0250) Semestre 1-2011 Mayo 2011 Álgebra Lineal y Geometría
Coordenadas polares en el plano. Coordenadas ciĺındricas y esféricas en el espacio. Coordenadas... Coordenadas... Coordenadas...
 En el estudio de los conjuntos y las funciones es fundamental el sistema que se utilize para representar los puntos. Estamos acostumbrados a utilizar la estructura de afín o de vectorial de R n, utilizando
En el estudio de los conjuntos y las funciones es fundamental el sistema que se utilize para representar los puntos. Estamos acostumbrados a utilizar la estructura de afín o de vectorial de R n, utilizando
Tema 1: ELECTROSTÁTICA EN EL VACÍO. 2.- Ley de Coulomb. Campo de una carga puntual.
 1.- Carga eléctrica. Propiedades. 2.- Ley de Coulomb. Campo de una carga puntual. 3.- Principio de superposición. 4.- Distribuciones continuas de carga. 5.- Ley de Gauss. Aplicaciones. 6.- Potencial electrostático.
1.- Carga eléctrica. Propiedades. 2.- Ley de Coulomb. Campo de una carga puntual. 3.- Principio de superposición. 4.- Distribuciones continuas de carga. 5.- Ley de Gauss. Aplicaciones. 6.- Potencial electrostático.
LEY DE COULOMB E INTENSIDAD DE CAMPO ELECTRICO
 INDICE Prefacio XIV Visita Guiada 1 Análisis Vectorial 1 2 Ley Coulomb e Intensidad de Campo Eléctrico 26 3 Densidad de Flujo Eléctrico, Ley de Gauss y Divergencia 51 4 Energía y Potencial 80 5 Corriente
INDICE Prefacio XIV Visita Guiada 1 Análisis Vectorial 1 2 Ley Coulomb e Intensidad de Campo Eléctrico 26 3 Densidad de Flujo Eléctrico, Ley de Gauss y Divergencia 51 4 Energía y Potencial 80 5 Corriente
Tema 2: Potencial Eléctrico
 1/41 Tema 2: Potencial Eléctrico Fátima Masot Conde Ing. Industrial 2010/11 Tema 2: Potencial Eléctrico 2/41 Índice: 1. Introducción 2. Energía potencial eléctrica 1. de dos cargas puntuales 2. de un sistema
1/41 Tema 2: Potencial Eléctrico Fátima Masot Conde Ing. Industrial 2010/11 Tema 2: Potencial Eléctrico 2/41 Índice: 1. Introducción 2. Energía potencial eléctrica 1. de dos cargas puntuales 2. de un sistema
Productos diádicos, diadas y tensores
 Productos diádicos, diadas y tensores Lo que sigue es una introducción, bastante poco rigurosa, del concepto de producto diádico y sus posibles aplicaciones al cálculo tensorial. Al final figuran una serie
Productos diádicos, diadas y tensores Lo que sigue es una introducción, bastante poco rigurosa, del concepto de producto diádico y sus posibles aplicaciones al cálculo tensorial. Al final figuran una serie
Dpto. Física y Mecánica. Sistemas de coordenadas y sistemas de referencia
 Dpto. Física y Mecánica Sistemas de coordenadas y sistemas de referencia La descripción del movimiento de un cuerpo requiere la introducción de un sistema de coordenadas espaciales que identifiquen unívocamente
Dpto. Física y Mecánica Sistemas de coordenadas y sistemas de referencia La descripción del movimiento de un cuerpo requiere la introducción de un sistema de coordenadas espaciales que identifiquen unívocamente
Expresiones de velocidad y aceleración en distintas coordenadas
 Apéndice B Expresiones de velocidad y aceleración en distintas coordenadas Índice B.1. Coordenadas cartesianas............... B.1 B.2. Coordenadas cilíndricas y polares......... B.2 B.3. Coordenadas esféricas................
Apéndice B Expresiones de velocidad y aceleración en distintas coordenadas Índice B.1. Coordenadas cartesianas............... B.1 B.2. Coordenadas cilíndricas y polares......... B.2 B.3. Coordenadas esféricas................
Ix ʹ = 8 mb 2, I. c) El momento de inercia respecto de un eje perpendicular al plano de la figura y que pase por una de las masas (eje z ʹ ) será:
 CALCULO DE MOMENTOS DE INECIA Se unen cuatro partículas de masa m mediante varillas sin masa, formando un rectángulo de lados a b. El sistema gira alrededor de un eje en el plano de la figura que pasa
CALCULO DE MOMENTOS DE INECIA Se unen cuatro partículas de masa m mediante varillas sin masa, formando un rectángulo de lados a b. El sistema gira alrededor de un eje en el plano de la figura que pasa
Diseño y Ejecución de una Puesta a Tierra de Baja Resistencia. Qqueshuayllo Cancha, Wilbert Rene.
 CAPITULO 1: FUNDAMENTO FISICO DE UNA PUESTA A TIERRA 1.1 Introducción Por puesta a tierra se entiende como la conexión de un conductor eléctrico (electrodo) enterrado en el suelo con la finalidad de dispersar
CAPITULO 1: FUNDAMENTO FISICO DE UNA PUESTA A TIERRA 1.1 Introducción Por puesta a tierra se entiende como la conexión de un conductor eléctrico (electrodo) enterrado en el suelo con la finalidad de dispersar
ECUACIONES DE MAXWELL
 ECUACIONE DE MAXWELL Prof. Juan Carlos Muñoz ECUACIONE DE MAXWELL Los fenómenos eléctricos y magnéticos fueron analizados por James Clerk Maxwell en 1864 y comprobado experimentalmente varios años después.
ECUACIONE DE MAXWELL Prof. Juan Carlos Muñoz ECUACIONE DE MAXWELL Los fenómenos eléctricos y magnéticos fueron analizados por James Clerk Maxwell en 1864 y comprobado experimentalmente varios años después.
GEOMETRÍA EN EL ESPACIO.
 GEOMETRÍA EN EL ESPACIO. Un sistema de coordenadas tridimensional se construye trazando un eje Z, perpendicular en el origen de coordenadas a los ejes X e Y. Cada punto viene determinado por tres coordenadas
GEOMETRÍA EN EL ESPACIO. Un sistema de coordenadas tridimensional se construye trazando un eje Z, perpendicular en el origen de coordenadas a los ejes X e Y. Cada punto viene determinado por tres coordenadas
Ejercicios resueltos de FISICA II que se incluyen en la Guía de la Asignatura
 Ejercicios resueltos de FISICA II que se incluyen en la Guía de la Asignatura Módulo 2. Campo electrostático 4. Consideremos dos superficies gaussianas esféricas, una de radio r y otra de radio 2r, que
Ejercicios resueltos de FISICA II que se incluyen en la Guía de la Asignatura Módulo 2. Campo electrostático 4. Consideremos dos superficies gaussianas esféricas, una de radio r y otra de radio 2r, que
Campo magnético creado por cargas puntuales móviles.
 Introducción Volvamos ahora considerar los orígenes del campo magnético B. Las primeras fuentes conocidas del magnetismo fueron los imanes permanentes. Un mes después de que Oersted anunciarse su descubrimiento
Introducción Volvamos ahora considerar los orígenes del campo magnético B. Las primeras fuentes conocidas del magnetismo fueron los imanes permanentes. Un mes después de que Oersted anunciarse su descubrimiento
Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère
 c Rafael R. Boix y Francisco Medina 1 Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère Consideremos un conductor que ocupa un volumen τ. Sea r el vector de posición de
c Rafael R. Boix y Francisco Medina 1 Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère Consideremos un conductor que ocupa un volumen τ. Sea r el vector de posición de
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Analicemos ahora el siguiente ejemplo: (2x 4y) dx + (12y - 6x + 1) dy = 0. Será ésta una ecuación diferencial reducible a homogénea?
 82 Analicemos ahora el siguiente ejemplo: (2x 4y) dx + (2y - 6x + ) dy = 0 Será ésta una ecuación diferencial reducible a homogénea? Si observamos la ecuación diferencial, tenemos que 2x 4y = 0 2y 6x +
82 Analicemos ahora el siguiente ejemplo: (2x 4y) dx + (2y - 6x + ) dy = 0 Será ésta una ecuación diferencial reducible a homogénea? Si observamos la ecuación diferencial, tenemos que 2x 4y = 0 2y 6x +
Banco de Ejercicios del Departamental Métodos Matemáticos para Sistemas Lineales Numeros Complejos
 Banco de Ejercicios del Departamental Métodos Matemáticos para Sistemas Lineales Numeros Complejos 1. Efectuar cada una de las operaciones indicadas. a) (35 + 25i) + ( 12 5i) b) ( 75 i) + (34 + 42i) c)
Banco de Ejercicios del Departamental Métodos Matemáticos para Sistemas Lineales Numeros Complejos 1. Efectuar cada una de las operaciones indicadas. a) (35 + 25i) + ( 12 5i) b) ( 75 i) + (34 + 42i) c)
AGRUPACIONES DE ANTENAS. (ARRAYS) MICROONDAS 2009-2010 1
 MICROONDAS 009-010 1 MICROONDAS 009-010 MICROONDAS 009-010 3 Very Large Array at NRAO MICROONDAS 009-010 4 Array de antenas Vivaldi (4-6 GHz) 15 Mhz Antenna Array MICROONDAS 009-010 5 Un array es una antena
MICROONDAS 009-010 1 MICROONDAS 009-010 MICROONDAS 009-010 3 Very Large Array at NRAO MICROONDAS 009-010 4 Array de antenas Vivaldi (4-6 GHz) 15 Mhz Antenna Array MICROONDAS 009-010 5 Un array es una antena
ley de Gauss interpretación física ecuación de Poisson Ley de Gauss Jana Rodriguez Hertz Cálculo 3 IMERL 2 de junio de 2015
 Ley de Gauss Jana Rodriguez Hertz Cálculo 3 IMERL 2 de junio de 2015 enunciado ley de Gauss ley de Gauss S superficie cerrada en R 3 entonces S S r r 3.n ds = 0 si 0 / int S r r 3.n ds = 4π si 0 int S
Ley de Gauss Jana Rodriguez Hertz Cálculo 3 IMERL 2 de junio de 2015 enunciado ley de Gauss ley de Gauss S superficie cerrada en R 3 entonces S S r r 3.n ds = 0 si 0 / int S r r 3.n ds = 4π si 0 int S
Análisis II - Análisis matemático II - Matemática 3 2do. cuatrimestre de 2013
 Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Ejercicios Propuestos Campos en la materia.
 Ejercicios Propuestos Campos en la materia. 1. Un dipolo eléctrico es un par de cargas de la misma magnitud y signos opuestos, situadas en puntos diferentes. Así, la carga total del dipolo es cero. (a)
Ejercicios Propuestos Campos en la materia. 1. Un dipolo eléctrico es un par de cargas de la misma magnitud y signos opuestos, situadas en puntos diferentes. Así, la carga total del dipolo es cero. (a)
12. Campos e.m. clásicos. Acoplamiento mínimo.
 Mecánica Cuántica Avanzada Carlos Pena 12-1 12. Campos e.m. clásicos. Acoplamiento mínimo. [Gre 1.1-1.2] Dinámica del campo electromagnético clásico Ecuaciones de Maxwell. Potenciales. Las ecuaciones de
Mecánica Cuántica Avanzada Carlos Pena 12-1 12. Campos e.m. clásicos. Acoplamiento mínimo. [Gre 1.1-1.2] Dinámica del campo electromagnético clásico Ecuaciones de Maxwell. Potenciales. Las ecuaciones de
Tema 5: Sistemas de Ecuaciones Lineales
 Tema 5: Sistemas de Ecuaciones Lineales Eva Ascarza-Mondragón Helio Catalán-Mogorrón Manuel Vega-Gordillo Índice 1 Definición 3 2 Solución de un sistema de ecuaciones lineales 4 21 Tipos de sistemas ecuaciones
Tema 5: Sistemas de Ecuaciones Lineales Eva Ascarza-Mondragón Helio Catalán-Mogorrón Manuel Vega-Gordillo Índice 1 Definición 3 2 Solución de un sistema de ecuaciones lineales 4 21 Tipos de sistemas ecuaciones
Matemáticas I: Hoja 1
 Matemáticas I: Hoja 1 1. Números complejos Hasta ahora, hemos visto que los números reales son aquellos que poseen una expresión decimal y que podemos representar en una recta infinita. No obstante, para
Matemáticas I: Hoja 1 1. Números complejos Hasta ahora, hemos visto que los números reales son aquellos que poseen una expresión decimal y que podemos representar en una recta infinita. No obstante, para
1. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado:
 CAPÍTULO. GEOMETRÍA AFÍN.. Problemas. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado: a) A(,, ), v = (,, ) ; b) A(0,
CAPÍTULO. GEOMETRÍA AFÍN.. Problemas. Determinar las ecuaciones paramétricas y la ecuación continua de las rectas que pasan por el punto A y con el vector de dirección dado: a) A(,, ), v = (,, ) ; b) A(0,
Curvas en paramétricas y polares
 Capítulo 10 Curvas en paramétricas y polares Introducción Después del estudio detallado de funciones reales de variable real expresadas en forma explícita y con coordenadas cartesianas, que se ha hecho
Capítulo 10 Curvas en paramétricas y polares Introducción Después del estudio detallado de funciones reales de variable real expresadas en forma explícita y con coordenadas cartesianas, que se ha hecho
Herramientas digitales de auto-aprendizaje para Matemáticas
 real de con Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura real de con Índice real de con real de con.
real de con Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura real de con Índice real de con real de con.
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS DE TRAYECTORIAS
 APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS DE TRAYECTORIAS 5 TRAYECTORIAS DE UN HAZ DE CURVAS: Se dice que una familia de curvas T(,, k) 0 (k una constante arbitraria)
APLICACIONES DE LAS ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN A PROBLEMAS DE TRAYECTORIAS 5 TRAYECTORIAS DE UN HAZ DE CURVAS: Se dice que una familia de curvas T(,, k) 0 (k una constante arbitraria)
Los potenciales electromagnéticos. Tema 8 Electromagnetismo
 Los potenciales electromagnéticos Tema 8 Electromagnetismo Los potenciales electromagnéticos Los potenciales electromagnéticos. Transformaciones de contraste. Ecuación de ondas para los potenciales. Soluciones
Los potenciales electromagnéticos Tema 8 Electromagnetismo Los potenciales electromagnéticos Los potenciales electromagnéticos. Transformaciones de contraste. Ecuación de ondas para los potenciales. Soluciones
Aplicaciones de las integrales dobles
 Aplicaciones de las integrales dobles Las integrales dobles tienen multiples aplicaciones en física en geometría. A continuación damos una relación de alguna de ellas.. El área de una región plana R en
Aplicaciones de las integrales dobles Las integrales dobles tienen multiples aplicaciones en física en geometría. A continuación damos una relación de alguna de ellas.. El área de una región plana R en
Tema 3: Campos estáticos
 Tema 3: Campos estáticos 1 Índice Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
Tema 3: Campos estáticos 1 Índice Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
Definición de vectores
 Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen O también denominado Punto de aplicación. Es el punto exacto sobre
Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen O también denominado Punto de aplicación. Es el punto exacto sobre
PROGRAMA DETALLADO DE LA ASIGNATURA MATEMÁTICA III (transición)
 PROGRAMA DETALLADO DE LA ASIGNATURA MATEMÁTICA III (transición) UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA DE LA FUERZA ARMADA CICLO BÁSICO DE INGENIERÍA SEMESTRE ASIGNATURA 4 to. MATEMÁTICA III CÓDIGO
PROGRAMA DETALLADO DE LA ASIGNATURA MATEMÁTICA III (transición) UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA DE LA FUERZA ARMADA CICLO BÁSICO DE INGENIERÍA SEMESTRE ASIGNATURA 4 to. MATEMÁTICA III CÓDIGO
5. INTEGRALES MULTIPLES
 5. INTEGRALES MULTIPLES INDICE 5 5.. Integrales iteradas. 5.. Definición de integral doble: áreas y volúmenes..3 5.3. Integral doble en coordenadas polares 5 5.4. Aplicaciones de la integral doble (geométricas
5. INTEGRALES MULTIPLES INDICE 5 5.. Integrales iteradas. 5.. Definición de integral doble: áreas y volúmenes..3 5.3. Integral doble en coordenadas polares 5 5.4. Aplicaciones de la integral doble (geométricas
El sonido dejará de ser audible cuando su intensidad sea menor o igual a la intensidad umbral:
 P.A.U. MADRID JUNIO 2005 Cuestión 1.- El nivel de intensidad sonora de la sirena de un barco es de 60 db a 10 m de distancia. Suponiendo que la sirena es un foco emisor puntual, calcule: a) El nivel de
P.A.U. MADRID JUNIO 2005 Cuestión 1.- El nivel de intensidad sonora de la sirena de un barco es de 60 db a 10 m de distancia. Suponiendo que la sirena es un foco emisor puntual, calcule: a) El nivel de
Tema Contenido Contenidos Mínimos
 1 Números racionales - Fracciones equivalentes. - Simplificación de fracciones. - Representación y comparación de los números fraccionarios. - Operaciones con números fraccionarios. - Ordenación de los
1 Números racionales - Fracciones equivalentes. - Simplificación de fracciones. - Representación y comparación de los números fraccionarios. - Operaciones con números fraccionarios. - Ordenación de los
Electromagnetismo Radiación electromagnética 1 Introducción. Generalidades
 Electromagnetismo 18 Introducción. Generalidades Plan de la clase: Electromagnetismo 18 1 Ecuaciones de Maxwell en un recinto con fuentes Calibración 3 Ecuación de ondas para los potenciales electrodinámicos
Electromagnetismo 18 Introducción. Generalidades Plan de la clase: Electromagnetismo 18 1 Ecuaciones de Maxwell en un recinto con fuentes Calibración 3 Ecuación de ondas para los potenciales electrodinámicos
3. Resolver triángulos rectángulos utilizando las definiciones de las razones trigonométricas.
 Contenidos mínimos MI. 1. Contenidos. Bloque I: Aritmética y Álgebra. 1. Conocer las clases de números, los conjuntos numéricos: naturales, enteros, racionales, reales y complejos y las propiedades que
Contenidos mínimos MI. 1. Contenidos. Bloque I: Aritmética y Álgebra. 1. Conocer las clases de números, los conjuntos numéricos: naturales, enteros, racionales, reales y complejos y las propiedades que
Tema 3: Campos estáticos
 Tema 3: Campos estáticos 1 Índice (I) Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
Tema 3: Campos estáticos 1 Índice (I) Ecuaciones en el caso estacionario Electrostática Solución del problema electrostático Cálculo de campos mediante Ley de Gauss Energía electrostática Desarrollo multipolar
TEMA 11. Autovalores y autovectores. Diagonalización y formas canónicas.
 TEMA 11 F MATEMÁTICOS TEMA 11 Autovalores y autovectores Diagonalización y formas canónicas 1 Introducción Definición 1 (Matrices semejantes) Sean A y B dos matrices cuadradas de orden n Decimos que A
TEMA 11 F MATEMÁTICOS TEMA 11 Autovalores y autovectores Diagonalización y formas canónicas 1 Introducción Definición 1 (Matrices semejantes) Sean A y B dos matrices cuadradas de orden n Decimos que A
Capítulo 18. Biomagnetismo
 Capítulo 18 Biomagnetismo 1 Fuerza magnética sobre una carga La fuerza que un campo magnético B ejerce sobre una partícula con velocidad v y carga Q es: F = Q v B El campo magnético se mide en teslas,
Capítulo 18 Biomagnetismo 1 Fuerza magnética sobre una carga La fuerza que un campo magnético B ejerce sobre una partícula con velocidad v y carga Q es: F = Q v B El campo magnético se mide en teslas,
I - ACCIÓN DEL CAMPO SOBRE CARGAS MÓVILES
 I - ACCIÓN DEL CAMPO SOBRE CARGAS MÓVILES 1.- Un conductor rectilíneo indefinido transporta una corriente de 10 A en el sentido positivo del eje Z. Un protón que se mueve a 2 105 m/s, se encuentra a 50
I - ACCIÓN DEL CAMPO SOBRE CARGAS MÓVILES 1.- Un conductor rectilíneo indefinido transporta una corriente de 10 A en el sentido positivo del eje Z. Un protón que se mueve a 2 105 m/s, se encuentra a 50
Interacciones electromagnéticas 1. I.H.Hutchinson
 Interacciones electromagnéticas 1 I.H.Hutchinson 1 I.H.Hutchinson 1999 Capítulo 1 Ecuaciones de Maxwell y campos electromagnéticos 1.1 Introducción 1.1.1 Ecuaciones de Maxwell (1865) Ecuaciones de gobierno
Interacciones electromagnéticas 1 I.H.Hutchinson 1 I.H.Hutchinson 1999 Capítulo 1 Ecuaciones de Maxwell y campos electromagnéticos 1.1 Introducción 1.1.1 Ecuaciones de Maxwell (1865) Ecuaciones de gobierno
Ejercicios de M.A.S y Movimiento Ondulatorio de PAU
 1. En el laboratorio del instituto medimos cinco veces el tiempo que un péndulo simple de 1m de longitud tarda en describir 45 oscilaciones de pequeña amplitud. Los resultados de la medición se muestran
1. En el laboratorio del instituto medimos cinco veces el tiempo que un péndulo simple de 1m de longitud tarda en describir 45 oscilaciones de pequeña amplitud. Los resultados de la medición se muestran
Cargas puntuales en movimiento
 Cargas puntuales en movimiento manuel fernández guasti 8 de agosto de 009 1. potenciales ardados Se debe evaluar el campo o los potenciales tomando en cuenta el tiempo de ardo de la distancia que deben
Cargas puntuales en movimiento manuel fernández guasti 8 de agosto de 009 1. potenciales ardados Se debe evaluar el campo o los potenciales tomando en cuenta el tiempo de ardo de la distancia que deben
Bolilla 10: Magnetismo
 Bolilla 10: Magnetismo 1 Bolilla 10: Magnetismo La fuerza magnética es una de las fuerzas fundamentales de la naturaleza. Si bien algunos efectos magnéticos simples fueron observados y descriptos desde
Bolilla 10: Magnetismo 1 Bolilla 10: Magnetismo La fuerza magnética es una de las fuerzas fundamentales de la naturaleza. Si bien algunos efectos magnéticos simples fueron observados y descriptos desde
Temario 4.Campo Eléctrico
 Campo Eléctrico 1 1 Temario 4.Campo Eléctrico 4.1 Concepto y definición de campo eléctrico 4.2 Campo eléctrico producido por una y varias cargas puntuales. 4.3 Lineas de Campo 4.4 Un conductor eléctrico
Campo Eléctrico 1 1 Temario 4.Campo Eléctrico 4.1 Concepto y definición de campo eléctrico 4.2 Campo eléctrico producido por una y varias cargas puntuales. 4.3 Lineas de Campo 4.4 Un conductor eléctrico
Seminario de Física. 2º bachillerato LOGSE. Unidad 3. Campo magnético e Inducción magnética
 A) Interacción Magnética sobre cargas puntuales. 1.- Determina la fuerza que actúa sobre un electrón situado en un campo de inducción magnética B = -2 10-2 k T cuando su velocidad v = 2 10 7 i m/s. Datos:
A) Interacción Magnética sobre cargas puntuales. 1.- Determina la fuerza que actúa sobre un electrón situado en un campo de inducción magnética B = -2 10-2 k T cuando su velocidad v = 2 10 7 i m/s. Datos:
1. Area de una Superficie
 1. Area de una Superficie Integrales de La idea para calcular el área de una superficie es sub-dividirla en regiones bastante pequeñas como para suponer que son planas, y aproximar el valor del área como
1. Area de una Superficie Integrales de La idea para calcular el área de una superficie es sub-dividirla en regiones bastante pequeñas como para suponer que son planas, y aproximar el valor del área como
EJERCICIOS DEL CAPÍTULO 9 - ELECTROMAGNETISMO
 EJERCICIOS DEL CAPÍTULO 9 - ELECTROMAGNETISMO C9. 1 Aceleramos iones de los isótopos C-12, C-13 y C-14 con una d.d.p. de 100 kv y los hacemos llegar a un espectrógrafo de masas perpendicularmente a la
EJERCICIOS DEL CAPÍTULO 9 - ELECTROMAGNETISMO C9. 1 Aceleramos iones de los isótopos C-12, C-13 y C-14 con una d.d.p. de 100 kv y los hacemos llegar a un espectrógrafo de masas perpendicularmente a la
Facultad de Ciencias Curso 2010-2011 Grado de Óptica y Optometría SOLUCIONES PROBLEMAS FÍSICA. TEMA 4: CAMPO MAGNÉTICO
 SOLUCIONES PROLEMAS FÍSICA. TEMA 4: CAMPO MAGNÉTICO. Dos conductores rectilíneos, paralelos mu largos transportan corrientes de sentidos contrarios e iguales a,5 A. Los conductores son perpendiculares
SOLUCIONES PROLEMAS FÍSICA. TEMA 4: CAMPO MAGNÉTICO. Dos conductores rectilíneos, paralelos mu largos transportan corrientes de sentidos contrarios e iguales a,5 A. Los conductores son perpendiculares
Los lugares geométricos de todos los puntos del espacio en los cuales la magnitud escalar tiene un mismo valor.
 2. 2. Introducción A lo largo del estudio de la Física surgen una serie de propiedades, tanto de magnitudes escalares como vectoriales, que se expresan por medio de nuevos conceptos tales como gradiente,
2. 2. Introducción A lo largo del estudio de la Física surgen una serie de propiedades, tanto de magnitudes escalares como vectoriales, que se expresan por medio de nuevos conceptos tales como gradiente,
A modo de prólogo La Física como ciencia La Física y la técnica Justificación de la elección de temas...
 ÍNDICE A modo de prólogo...11 1. La Física como ciencia...11 2. La Física y la técnica... 12 3. Justificación de la elección de temas... 12 Tema I: Campos escalares y vectoriales... 13 1. Introducción:
ÍNDICE A modo de prólogo...11 1. La Física como ciencia...11 2. La Física y la técnica... 12 3. Justificación de la elección de temas... 12 Tema I: Campos escalares y vectoriales... 13 1. Introducción:
IES Fco Ayala de Granada Junio de 2011 (Específico 2 Modelo 1) Soluciones Germán-Jesús Rubio Luna
 PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 010-011 Opción A Ejercicio 1, Opción A, Modelo especifico de Junio de 011 [ 5 puntos] Una ventana normanda consiste en un rectángulo
PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 010-011 Opción A Ejercicio 1, Opción A, Modelo especifico de Junio de 011 [ 5 puntos] Una ventana normanda consiste en un rectángulo
Ecuación de la Recta en el Espacio
 PreUnAB Clase # 21 Octubre 2014 Definición Un sistema de coordenadas rectangulares en el espacio está determinado por tres planos mutuamente perpendiculares, Los ejes generalmente son identificados por
PreUnAB Clase # 21 Octubre 2014 Definición Un sistema de coordenadas rectangulares en el espacio está determinado por tres planos mutuamente perpendiculares, Los ejes generalmente son identificados por
1. SISTEMAS DE ECUACIONES DIFERENCIALES
 1 1 SISTEMAS DE ECUACIONES DIFERENCIALES 11 SISTEMAS LINEALES DE PRIMER ORDEN Un sistema de ecuaciones diferenciales del tipo dx 1 dt a 11 tx 1 + a 1n tx n + f 1 t dx n dt a n1 tx 1 + a nn tx n + f n t
1 1 SISTEMAS DE ECUACIONES DIFERENCIALES 11 SISTEMAS LINEALES DE PRIMER ORDEN Un sistema de ecuaciones diferenciales del tipo dx 1 dt a 11 tx 1 + a 1n tx n + f 1 t dx n dt a n1 tx 1 + a nn tx n + f n t
Herramientas digitales de auto-aprendizaje para Matemáticas
 Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de innovación didáctica Departamento de Matemáticas Universidad de Extremadura Índice Puntos y vectores en En R 3, conviene distinguir
Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de innovación didáctica Departamento de Matemáticas Universidad de Extremadura Índice Puntos y vectores en En R 3, conviene distinguir
índice analítico Prólogo a la segunda edición del volumen II Prólogo a la primera edición del volumen II Prólogo al Berkeley Physics Course
 índice analítico Prólogo a la segunda edición del volumen II Prólogo a la primera edición del volumen II Prólogo al Berkeley Physics Course V VII IX Capítulo 1 Electrostática: cargas y campos 1 1.1 Carga
índice analítico Prólogo a la segunda edición del volumen II Prólogo a la primera edición del volumen II Prólogo al Berkeley Physics Course V VII IX Capítulo 1 Electrostática: cargas y campos 1 1.1 Carga
Capítulo II. Ecuaciones de los circuitos magnéticos
 Capítulo II. Ecuaciones de los circuitos magnéticos 2.1. Intensidad de Campo magnético Los campos magnéticos son el mecanismo fundamental para convertir energía eléctrica de corriente alterna de un nivel
Capítulo II. Ecuaciones de los circuitos magnéticos 2.1. Intensidad de Campo magnético Los campos magnéticos son el mecanismo fundamental para convertir energía eléctrica de corriente alterna de un nivel
Anejo 1. Teoría de Airy. Solución lineal de la ecuación de ondas.
 Anejo 1. Teoría de Airy. Solución lineal de la ecuación de ondas. Introducción y ecuaciones que rigen la propagación del oleaje. La propagación de oleaje en un fluido es un proceso no lineal. Podemos tratar
Anejo 1. Teoría de Airy. Solución lineal de la ecuación de ondas. Introducción y ecuaciones que rigen la propagación del oleaje. La propagación de oleaje en un fluido es un proceso no lineal. Podemos tratar
Cinemática en 2D: Movimiento Circular.
 Cinemática en 2D: Movimiento Circular. Movimiento circular uniforme Otro caso particular de movimiento en dos dimensiones es el de una partícula que se mueve describiendo una trayectoria circular, con
Cinemática en 2D: Movimiento Circular. Movimiento circular uniforme Otro caso particular de movimiento en dos dimensiones es el de una partícula que se mueve describiendo una trayectoria circular, con
5. Campo gravitatorio
 5. Campo gravitatorio Interacción a distancia: concepto de campo Campo gravitatorio Campo de fuerzas Líneas de campo Intensidad del campo gravitatorio Potencial del campo gravitatorio: flujo gravitatorio
5. Campo gravitatorio Interacción a distancia: concepto de campo Campo gravitatorio Campo de fuerzas Líneas de campo Intensidad del campo gravitatorio Potencial del campo gravitatorio: flujo gravitatorio
4.1. Movimiento oscilatorio: el movimiento vibratorio armónico simple.
 4.1. Movimiento oscilatorio: el movimiento vibratorio armónico simple. 4.1.1. Movimiento oscilatorio características. 4.1.2. Movimiento periódico: período. 4.1.3. Movimiento armónico simple: características
4.1. Movimiento oscilatorio: el movimiento vibratorio armónico simple. 4.1.1. Movimiento oscilatorio características. 4.1.2. Movimiento periódico: período. 4.1.3. Movimiento armónico simple: características
Concepto de espacio vectorial. Propiedades. Distintos espacios vectoriales. El espacio real tridimensional.
 Otras páginas Matemáticas 2º MATEMÁTICAS II Álgebra: Espacios Vectoriales Concepto de espacio vectorial. Propiedades. Distintos espacios vectoriales. El espacio real tridimensional. Combinación lineal.
Otras páginas Matemáticas 2º MATEMÁTICAS II Álgebra: Espacios Vectoriales Concepto de espacio vectorial. Propiedades. Distintos espacios vectoriales. El espacio real tridimensional. Combinación lineal.
Ejercicios de M.A.S y Movimiento Ondulatorio de PAU
 1. En el laboratorio del instituto medimos cinco veces el tiempo que un péndulo simple de 1m de longitud tarda en describir 45 oscilaciones de pequeña amplitud. Los resultados de la medición se muestran
1. En el laboratorio del instituto medimos cinco veces el tiempo que un péndulo simple de 1m de longitud tarda en describir 45 oscilaciones de pequeña amplitud. Los resultados de la medición se muestran
Física 3: Septiembre-Diciembre 2011 Clase 13,Lunes 24 de octubre de 2011
 Clase 13 Potencial Eléctrico Cálculo del potencial eléctrico Ejemplo 35: Efecto punta En un conductor el campo eléctrico es mas intenso cerca de las puntas y protuberancias pues el exceso de carga tiende
Clase 13 Potencial Eléctrico Cálculo del potencial eléctrico Ejemplo 35: Efecto punta En un conductor el campo eléctrico es mas intenso cerca de las puntas y protuberancias pues el exceso de carga tiende
Tema 3.-Fuerzas eléctricas
 Tema 3: Fuerzas eléctricas y campo eléctrico Fundamentos Físicos de la Ingeniería Ingeniería Industrial Primer curso Curso 009/010 Dpto. Física Aplicada III Universidad de Sevilla 1 Índice Introducción
Tema 3: Fuerzas eléctricas y campo eléctrico Fundamentos Físicos de la Ingeniería Ingeniería Industrial Primer curso Curso 009/010 Dpto. Física Aplicada III Universidad de Sevilla 1 Índice Introducción
, Ind ice general. 1-1 Descripción general El modelo electromagnético Unidades en el SI y constantes universales 8 Resumen 10
 , Ind ice general CAPíTULO1 EL MODELO ELECTROMAGNÉTICO 2 1-1 Descripción general 2 1-2 El modelo electromagnético 4 1-3 Unidades en el SI y constantes universales 8 Resumen 10 CAPíTULO2 ANÁLISIS VECTORIAL
, Ind ice general CAPíTULO1 EL MODELO ELECTROMAGNÉTICO 2 1-1 Descripción general 2 1-2 El modelo electromagnético 4 1-3 Unidades en el SI y constantes universales 8 Resumen 10 CAPíTULO2 ANÁLISIS VECTORIAL
Curso de Álgebra Lineal
 Curso de Álgebra Lineal 1. NÚMEROS COMPLEJOS 1.1 Definición, origen y operaciones fundamentales con números complejos Definición. Un número complejo, z, es una pareja ordenada (a, b) de números reales
Curso de Álgebra Lineal 1. NÚMEROS COMPLEJOS 1.1 Definición, origen y operaciones fundamentales con números complejos Definición. Un número complejo, z, es una pareja ordenada (a, b) de números reales
AUXILIAR 1 PROBLEMA 1
 AUXILIAR 1 PROBLEMA 1 Calcular el campo eléctrico en cualquier punto del espacio, producido por una recta de carga infinita (con densidad lineal de carga λ0). Luego, aplicar el teorema de Gauss para obtener
AUXILIAR 1 PROBLEMA 1 Calcular el campo eléctrico en cualquier punto del espacio, producido por una recta de carga infinita (con densidad lineal de carga λ0). Luego, aplicar el teorema de Gauss para obtener
Problemas de Electromagnetismo I 2º Grado de Física. L. Soriano
 Problemas de Electromagnetismo I 2º Grado de Física Tema 1.- CALCULO VECTORIAL 1.1 Usar métodos vectoriales para determinar la ecuación de la recta que pasa por (-1,1,0) y (0,0,1). 1.2 Un ave va volando
Problemas de Electromagnetismo I 2º Grado de Física Tema 1.- CALCULO VECTORIAL 1.1 Usar métodos vectoriales para determinar la ecuación de la recta que pasa por (-1,1,0) y (0,0,1). 1.2 Un ave va volando
Figura Trabajo de las fuerzas eléctricas al desplazar en Δ la carga q.
 1.4. Trabajo en un campo eléctrico. Potencial Clases de Electromagnetismo. Ariel Becerra Al desplazar una carga de prueba q en un campo eléctrico, las fuerzas eléctricas realizan un trabajo. Este trabajo
1.4. Trabajo en un campo eléctrico. Potencial Clases de Electromagnetismo. Ariel Becerra Al desplazar una carga de prueba q en un campo eléctrico, las fuerzas eléctricas realizan un trabajo. Este trabajo
EXPRESIÓN PARA LA DIVERGENCIA EN COORDENADAS CARTESIANAS.
 c Rafael R. Boix y Francisco Medina 1 EXPRESIÓN PARA LA DIVERGENCIA EN COORDENADAS CARTESIANAS. Consideremos un punto P 0 del espacio tridimensional de coordenadas cartesianas (x 0, y 0, z 0 ). Consideremos
c Rafael R. Boix y Francisco Medina 1 EXPRESIÓN PARA LA DIVERGENCIA EN COORDENADAS CARTESIANAS. Consideremos un punto P 0 del espacio tridimensional de coordenadas cartesianas (x 0, y 0, z 0 ). Consideremos
