5 DIVISIÓN DE POLINOMIOS. RAÍCES
|
|
|
- Lucía Chávez Henríquez
- hace 9 años
- Vistas:
Transcripción
1 EJERCICIOS PROPUESTOS 5.1 Divide los siguientes monomios. a) 54x 5 9x 2 b) 63x 12 3x 5 c) 35xy 6 7y 3 d) 121x 2 y 6 11yx 4 a) 54x 5 9x x x 5 9x 9 x 2 6x 3 c) 35xy 6 7y xy x y 6 7y 7 y 3 5xy 3 b) 63x 12 3x 5 21x 7 d) 121x 2 y 6 11yx 4 11x 2 y Efectúa estas divisiones. a) (60x 3 75x 2 ) 15x b) (121x 2 55x) 11x 2 a) (60x 3 75x 2 ) 15x 60x 3 75x 2 15x 6 0x x 7 2 5x 1 4x 5x 2 5x b) (121x 2 55x) 11x 2 121x 2 55x x 55x 11x x x x 5.3 Completa estas divisiones de monomios. a) 36xy 3 2x b) 7x 3 11x 2 c) 15x 2 yz 3yz d) ab a 2 b 3 a) 18y 3 b) 77x 5 c) 5x 2 d) a 3 b Realiza las siguientes divisiones. a) (26x 3 z 52x 5 z) 13x 2 b) (26x 3 z 39x 4 z) 13x 4 z a) (26x 3 z 52x 5 z) 13x 2 26x 3 z 52x 5 z 2 3 6x z 13x x z 2 2xz 4x 13x 13x 3 z b) (26x 3 z 39x 4 z) 13x 4 z 26x 3 z 13x 39x 4 z 4 z 2 3 6x z x z 4 2 3x z 13x z x Realiza estas divisiones. a) (x 3 6x 2 6x 5) (x 2 x 1) b) (x 4 5x 3 11x 2 12x 6) (x 2 x 2) c) (x 5 2x 4 3x 2 5x 6) (x 2 3x 2) d) (x 6 3x 4 2x 2 5x 7) (x 4 3x 1) a) x 3 6x 2 6x 5 x 2 x 1 x 3 6x 2 6x x 5 5x 2 5x 5x 2 5x 5 0 b) C(x) x 2 4x 5 R(x) x 4 c) C(x) x 3 5x 2 17x 58 R(x) 203x 110 d) C(x) x 2 3 R(x) 3x 3 3x 2 14x 10
2 5.6 Efectúa la siguiente división de polinomios. (6x 4 7x 3 2x 2 8x 3) (2x 2 3x 1) 6x 4 7x 3 2x 2 8x 3 2x 2 3x 1 6x 4 9x 3 3x 2 3x 2 x 1 6x 4 2x 3 3x 2 6x 4 2x 3 3x 2 x 6x 4 2x 3 2x 2 7x 6x 4 2x 3 2x 2 3x 1 6x 4 2x 3 2x 2 4x Escribe el dividendo de una división de polinomios en la que el divisor es x 2 1, el cociente x 3 3, y el resto 2x. D(x) d(x) C(x) R(x) (x 2 1) (x 3 3) 2x x 5 3x 2 x 3 3 2x Realiza estas divisiones aplicando la regla de Ruffini, y escribe el cociente y el resto de la división. a) (4x 3 8x 2 9x 7) (x 3) c) (5x 5 7x 4 3x 3 5x 2 3x 1) (x 1) b) (2x 3 5x 2 4x 2) (x 3) d) (6x 4 9x 3 10x 2 8x 2) (x 2) a) C(x) 4x 2 4x 3 R(x) 16 b) C(x) 2x 2 x 1 R(x) 5 c) C(x) 5x 4 12x 3 15x 2 20x 23 d) R(x) 24 C(x) 6x 3 21x 2 32x 72 R(x) Averigua el cociente y resto de estas divisiones mediante la regla de Ruffini. a) (2x 3 x 2 5) (x 3) b) (3x 5 3x 2 4) (x 1) a) C(x) 2x 2 5x 15 R(x) 50 b) C(x) 3x 4 3x 3 3x 2 R(x) 4
3 5.10 Efectúa las siguientes divisiones aplicando la regla de Ruffini. a) (x 3 1) (x 1) b) (x 4 1) (x 1) a) b) C(x) x 2 x 1 R(x) 0 C(x) x 3 x 2 x 1 R(x) Utiliza el teorema del resto para calcular el resto de estas divisiones. a) (x 11 2x 2 ) (x 1) c) (x 12 81) (x 1) b) (x 7 1) (x 1) d) ( x ) (x 1) a) R P(1) b) R P(1) c) R P( 1) ( 1) d) R P( 1) ( 1) La división de P(x) x 3 2x 2 k por x 3 da resto 0. Cuánto vale k? Usando el teorema del resto, sabemos que P(3) R. Así, P(3) k 45 k 0. De modo que k Comprueba si x 1 es un factor de estos polinomios. a) A(x) 3x 4 2x 2 x c) C(x) x 7 1 b) B(x) 2x 2 3x d) D(x) 2x 3 3x 1 Aplicamos el teorema del factor, así que será factor si el valor numérico del polinomio en 1 es 0. a) A( 1) 3 ( 1) 4 2 ( 1) 2 ( 1) Sí es factor de A(x). b) B( 1) 2 ( 1) 2 3 ( 1) No es factor de B(x). c) C( 1) ( 1) Sí es factor de C(x). d) D( 1) 2 ( 1) 3 3 ( 1) No es factor de D(x) Encuentra entre los siguientes factores los del polinomio P(x) x 3 3x 2 6x 8. a) x 1 c) x 1 b) x 3 d) x 2 a) P(1) b) P(3) c) P( 1) ( 1) 3 3 ( 1) 2 6 ( 1) 8 10 d) P( 2) ( 2) 3 3 ( 2) 2 6 ( 2) 8 0 Usando el teorema del factor, afirmamos que los factores de P(x) son x 1 y x 2.
4 5.15 Comprueba si 5 y 5 son raíces del siguiente polinomio P(x) x 3 5x 2 5x 5. P(5) ; P( 5) ( 5) 3 5 ( 5) 2 5 ( 5) Ni 5 ni 5 son raíces de P(x) Entre estos valores, indica el posible número de raíces del polinomio P(x) x 3 3x 5 8x 15. a) 5 c) 6 b) 3 d) 1 Al ser un polinomio de grado 5, no puede tener 6 raíces, las otras opciones pueden ser válidas Completa la tabla indicando el grado de cada polinomio y si cada uno de los números indicados es raíz del polinomio. Grado x 1 1 Sí No No x 2 x 2 2 No Sí No x 3 5x 2 5x 5 3 No No No 5.18 Halla las raíces enteras de estos polinomios. a) x 2 7x 10 b) x 2 8x 15 a) Las posibles raíces son: 1, 1, 2, 2, 5, 5, 10, 10. P(1) P( 1) ( 1) 2 7 ( 1) P(2) P( 2) ( 2) 2 7 ( 2) P(5) Por el teorema fundamental del álgebra sabemos que no puede haber más de dos raíces en un polinomio de grado 2, así las raíces del polinomio son 2 y 5. b) Las posibles raíces son: 1, 1, 3, 3, 5, 5, 15, 15. P(1) P( 1) ( 1) 2 8 ( 1) P(3) P( 3) ( 3) 2 8 ( 3) P(5) Por el teorema fundamental del álgebra sabemos que no puede haber más de dos raíces en un polinomio de grado 2, así las raíces del polinomio son 3 y 5.
5 5.19 Determina las raíces enteras de los siguientes polinomios. a) x 3 x 2 9x 9 b) x 3 x 2 25x 25 a) Las posibles raíces son 1, 1, 3, 3, 9, 9. P(1) P( 1) ( 1) 3 ( 1) 2 9 ( 1) 9 0 P(3) P( 3) ( 3) 3 ( 3) 2 9 ( 3) 9 0 Por el teorema fundamental del álgebra sabemos que no puede haber más de tres raíces en un polinomio de grado 3, así las raíces del polinomio son 1, 3 y 3. b) Las posibles raíces son 1, 1, 5, 5, 25, 25. P(1) P( 1) ( 1) 3 ( 1) 2 25 ( 1) P(5) P( 5) ( 5) 3 ( 5) 2 25 ( 5) 25 0 Por el teorema fundamental del álgebra sabemos que no puede haber más de tres raíces en un polinomio de grado 3, así las raíces del polinomio son 1, 5 y Averigua las raíces de estos polinomios. a) x 3 x 2 4x 4 b) x 2 x 1 a) Las posibles raíces del polinomio son 1, 1, 2, 2, 4, 4. P(1) P( 1) ( 1) 3 ( 1) 2 4 ( 1) 4 10 P(2) P( 2) ( 2) 3 ( 2) 2 4 ( 2) 4 24 P(4) P( 4) ( 4) 3 ( 4) 2 4 ( 4) Este polinomio sólo tiene una raíz real, que es 1. b) Las posibles raíces del polinomio son 1, 1. P(1) P( 1) ( 1) 2 ( 1) 1 1 Este polinomio no tiene raíces enteras Se sabe que los siguientes polinomios tienen alguna raíz entera. Indica una de ellas. a) x 2 12x 35 b) x 3 8 a) Por ejemplo, 5; b) Por ejemplo, 2;
6 5.22 a) Descompón en factores estos polinomios. a) x 2 6x 8 b) x 2 14x 33 c) x 3 2x 2 5x 6 d) x 3 4x 2 4x x 2 6x 8 (x 4)(x 2) b) x 2 14x 33 (x 11)(x 3) c) x 3 2x 2 5x 6 (x 2)(x 1)(x 3) d) x 3 4x 2 4x 16 (x 4)(x 2)(x 2) 5.23 Factoriza los siguientes polinomios. a) x 4 x 2 c) x 3 x 2 9x 9 b) x 3 1 d) x 4 6x 3 7x 2 a) x 4 x 2 x 2 (x 2 1) x 2 (x 1)(x 1) b) x 3 1 (x 1)(x 2 x 1) c) x 3 x 2 9x 9 (x 1)(x 2 9) d) x 4 6x 3 7x 2 x 2 (x 2 6x 7) x 2 (x 1)(x 7)
7 RESOLUCIÓN DE PROBLEMAS 5.24 Expresa el polinomio x 2 ax como una diferencia de cuadrados. Puede tratarse de dos figuras geométricas de área x 2 y ax. a 2 a 2 a2 x x = x x a x a x 2 ax a x 2 a Demuestra geométricamente que es cierta la siguiente igualdad. (x 1) 2 (x 1) 2 2(x ) Tenemos un cuadrado de lado x 1 y otro de lado x 1. 1 x x 1 x x 1 x = x + x x x Al final nos quedan dos cuadrados de lado x y dos de lado 1: 2x 2 2 2(x 2 1) 2(x ).
8 EJERCICIOS PARA ENTRENARSE División y regla de Ruffini 5.26 Realiza estas divisiones. a) (12x 2 yz 6xy 3 8xyz 2 ) (2xy) b) (15x 4 3x 3 9x 2 ) (3x 2 ) c) (5a 3 b 2 10ab 2 15a 3 b 4 ) (5ab 2 ) a) (12x 2 yz 6xy 3 8xyz 2 ) (2xy) 1 2 x 2 y 3 12x 2 yz 6xy 3 8xyz 2 2 x y z 6 2 x x y 8 y 2 x x y y z2 6xz 3y 2 4z 2 2xy b) (15x 4 3x 3 9x 2 ) (3x 2 ) 5x 2 x 3 c) (5a 3 b 2 10ab 2 15a 3 b 4 ) (5ab 2 ) a 2 2 3a 2 b Efectúa cada división indicando el polinomio cociente y el polinomio resto. a) x 5 3x 4 x 3 2x 2 x) (x 2 x 1) b) 2x 4 2x 2 3) (x 2 x 1) c) (x 6 x 3 x 1) (x 3 x 2) a) C(x) x 3 4x 2 4x 2 R(x) 5x 2 b) C(x) 2x 2 2x 6 R(x) 8x 9 c) C(x) x 3 x 3 R(x) x 2 4x 5 De una división entera, conocemos que el dividendo es D (x ) x 4 x 3 3x 3, el cociente es C(x) x 2 x 3 5, y el resto es R(x) 4x 2 Cuál es el divisor? D(x) d(x) C(x) R(x) D(x) R(x) d(x) C(x) En nuestro caso: (x 4 x 3 3x 3) ( 4x 2) x 2 3x 5 Haciendo los cálculos tenemos que d(x) x 2 2x 1. x 4 x 2 x 3 7x 5 3x 5 Sabiendo que el polinomio P(x) x 4 4x 3 11x 2 14x k es divisible por el polinomio x 2 2x 4, calcula cuál ha de ser el valor de k. Si hacemos la división de polinomios P(x) (x 2 2x 4), tenemos que el resto es R(x) k 12. Para que sea divisible, el resto tiene que ser 0, así tenemos que k 12 0, de donde k 12. El polinomio P(x) x 5 x 4 x 3 4x 2 4x 2 es múltiplo del polinomio Q(x) x 3 2x a. Averigua los posibles valores de a. Como son múltiplos, tenemos que R(x) 0. Así que P(x) C(x) Q(x). C(x) será de la forma bx 2 cx d; x 5 x 4 x 3 4x 2 4x 2 (bx 2 cx d)(x 3 2x a) De donde tomamos los términos del producto que tienen a: (ab 2c)x 2,(ac 2d)x, ad, y los igualamos a los coeficientes que corresponden: ab 2c 4 ac 2d 4 ad 2 Como a y d son enteros, por la última ecuación tenemos que a es 1, 1, 2 ó 2. Sabemos que b 1, porque es el coeficiente en el producto de x 5. Así que haciendo pruebas para los diferentes valores de a tendremos que a 2.
9 5.31 Realiza las siguientes divisiones aplicando la regla de Ruffini, e indica el cociente y el resto de cada división. a) (x 3 2x 2 x 3) (x 1) b) (x 5 3x 2 x 1) (x 2) c) (x 3 3x 2 x 3) (x 3) a) C(x) x 2 3x 4 R(x) 7 b) C(x) x 4 2x 3 4x 2 11x 23 R(x) 47 c) C(x) x 2 1 R(x) Mediante la regla de Ruffini, calcula el valor que debe tomar m para que se cumpla esta relación. 3x 3 2x m (3x 2 3x 5) (x 1) m m 5 Como el resto es 1, m 5 1 m 6. Completa las siguientes divisiones de polinomios en las que se ha aplicado la regla de Ruffini. a) 1 2 b) a) b) Teoremas y raíces de un polinomio 5.34 Halla el resto de estas divisiones sin llegar a realizarlas. a) (x 3 x 2) (x 2) b) (x 101 1) (x 1) c) (x 4 x 3 x 2 x 1) (x 1) Usamos para ello el teorema del resto: a) P( 2) ( 2) 3 ( 2) b) P( 1) ( 1) c) P(1) Comprueba si las siguientes afirmaciones son correctas. a) P(x) x 2 x 2 tiene por factor a x 2. b) Q(x) x 6 x 3 2 tiene por factor a x 1. c) R(x) x 3 1 tiene por factor a x 1. Vamos a usar el teorema del factor: a) P( 2) ( 2) 2 ( 2) 2 0. Sí es factor. b) Q(1) Sí es factor. c) R( 1) ( 1) No es factor.
10 5.36 Halla los restantes factores de estos polinomios. a) P(x) x 2 x 6, que tiene por factor a x 2. b) Q(x) x 3 2x 2 4x 3, que tiene por factor a x 1. c) R(x) x 3 7x 6, que tiene por factor a x 3. a) P(x) (x 2)(x 3) b) Si hacemos la división, vemos que nos queda de cociente x 2 x 3, que podemos comprobar que no tiene raíces enteras. Así, Q(x) (x 1)(x 2 x 3). c) Aplicando sucesivamente la regla de Ruffini tenemos que R(x) (x 3)(x 1)(x 2) Aplicando el teorema del resto, halla en cada caso el valor que debe tomar k. a) P(x) x 4 x 3 kx 2 10x 3 es divisible por x 3. b) Q(x) 2x 3 7x 2 kx 6 tiene por resto 20 al dividirlo por x 1. c) R(x) 2x 2 kx 15 es divisible por x 5. a) P( 3) ( 3) 4 ( 3) 3 k( 3) 2 10( 3) k 0 k 3 b) Q(1) k 1 6 k k 5 c) R( 5) 2( 5) 2 k( 5) k 0 k Escribe las raíces enteras de estos polinomios. a) P(x) x 2 2x 15 b) Q(x) x 3 6x 2 6x 7 c) R(x) x 4 x a) Las posibles raíces son 1, 1, 3, 3, 5, 5, 15, 15. P( 3) ( 3) 2 2( 3) 15 0 P(5) Como es de grado 2, como máximo tiene 2 raíces. De modo que las raíces de P(x) son 3 y 5. b) Las posibles raíces son 1, 1, 7, 7. Q(7) Si comprobamos con las otras posibles raíces, vemos que para ninguna más Q(x) es 0. De modo que Q(x) sólo tiene una raíz entera que es 7. c) Las posibles raíces son 1, 1, 2, 2, 3, 3, 6, 6. Si comprobamos todos los valores, vemos que nunca se anula R(x). No haría falta comprobarlo si nos fijamos en que los exponentes de x son siempre pares, con lo cual su resultado nunca va a ser negativo; x 4 x 2 0, y sumando 6 resulta que R(x) siempre es mayor que 0. De modo que R(x) no tiene ninguna raíz real. Encuentra un polinomio P(x) de grado tres, cuyas raíces enteras sean 2, 1 y 4, y que, además, verifique que P( 1) 20. P (x) (x 2)(x 1)(x 4) tiene grado 3. P ( 1) 10; 2 P ( 1) 20 P(x) 2P (x) sigue teniendo grado 3 y verifica que P( 1) 20. Así que el polinomio que buscamos es P(x) 2(x 2)(x 1)(x 4).
11 5.40 Calcula a sabiendo que el resto obtenido al dividir x 2 ax 2 por x 1 es 6 unidades inferior al obtenido al dividir x 2 ax 2 por x 5. Usamos el teorema del resto: P(1) 1 2 a 1 2 a 1 Q( 5) ( 5) 2 a( 5) 2 5a 23 Con la condición del enunciado tenemos que a 1 5a 23 6 a 9 2. Factorización de polinomios 5.41 Factoriza estas expresiones sacando factor común. a) 2x 2 yz 2xy 2 z 2x 2 y 2 b) 8x 4 4x 3 6x 2 c) 2x 3 (x 2) 4x 4 (x 2) 2 a) 2x 2 yz 2xy 2 z 2x 2 y 2 2xy(xz yz xy) b) 8x 4 4x 3 6x 2 2x 2 (4x 2 2x 3) c) 2x 3 (x 2) 4x 4 (x 2) 2 2x 3 (x 2)[1 2x(x 2)] 5.42 Factoriza al máximo los siguientes polinomios. a) P(x) x 4 5x 2 4 c) R(x) x 3 19x 30 b) Q(x) x 3 4x 2 7x 10 d) S(x) x 4 x 3 9x 2 9x a) c) x 3 19x 30 (x 2)(x 5)(x 3) x 4 5x 2 4 (x 1)(x 2)(x 1)(x 2) b) d) x 3 4x 2 7x 10 (x 1)(x 2)(x 5) x 4 x 3 9x 2 9x (x 1)(x 3)(x 2 3x) x(x 1)(x 3)(x 3) 5.43 Indica cuáles son las raíces de estos polinomios, sin desarrollar dichas expresiones. a) P(x) 3 (x 2) (x 3) (x 2) b) Q(x) 2x (x 2) (x 3) c) R(x) 4x 2 (x 1) (x 2) Qué grado tiene cada uno de estos polinomios? Puesto que los polinomios están factorizados, las raíces serán cada uno de los valores que anulan los factores. a) Raíces: 2, 3, 2. Grado 3. b) Raíces: 0, 2, 3. Grado 3. c) Raíces: 0, 1, 2. Grado 4.
12 5.44 Halla un polinomio de grado tres, cuyos factores sean x 1, x 1 y x 4, y cuyo término independiente sea 8. P (x) (x 1)(x 1)(x 4), tiene grado 3 y el término independiente es el que resulta de multiplicar los tres términos independientes de cada uno de los factores: 1 ( 1) 4 4. P(x) 2P (x) tiene grado 3 y término independiente Descompón en factores la siguiente expresión, hallando previamente el área de las figuras geométricas. 2x y + + xy 2y x 2 2 y 2xy (xy) 2 2x 2xy x 2 2 y 2 x 2 y xy(2 xy x) 5.46 Factoriza al máximo estos polinomios. a) P(x) x 3 2x 2 9 c) R(x) x 4 2x 3 3x 2 4x 4 b) Q(x) 2x 3 2x 2 10x 6 d) S(x) x 4 x 3 13x 15 Usamos el teorema de Ruffini y llegamos a las siguientes factorizaciones: a) P(x) (x 3)(x 2 x 3) c) R(x) (x 1) 2 (x 2) 2 b) Q(x) (x 3)(x 1)(2x 2) d) S(x) (x 1)(x 3)(x 2 x 5)
13 CUESTIONES PARA ACLARARSE 5.47 De cierto polinomio de grado tres, conocemos sus tres raíces enteras. Existe un único polinomio de grado tres que tenga como raíces a esas tres? Justifica tu respuesta con algún ejemplo. No, si multiplicamos por un entero el polinomio, tiene las mismas raíces. Por ejemplo: (x 1)(x 2)(x 3) tiene las mismas raíces que 2(x 1)(x 2)(x 3) Explica si son ciertas o falsas estas afirmaciones. a) Un polinomio con coeficientes enteros tiene, al menos, una raíz entera. b) Todo divisor del término independiente de un polinomio es una raíz de dicho polinomio. c) Un polinomio de grado n tiene n 1 raíces. Justifica tus respuestas con ejemplos. a) Falso, el polinomio x 2 1 tiene todos sus coeficientes enteros y ninguna raíz entera. b) Falso, el 1 es divisor del término independiente de x 2 1, pero no es raíz del polinomio. c) Falso, el polinomio x 2 1 tiene 2 raíces, 1 y 1, que es el grado del polinomio, y no puede tener más porque estaría en contradicción con el teorema fundamental del álgebra Qué verifica siempre el resto que resulta de dividir un polinomio por un binomio del tipo x a? Justifica tu respuesta y pon algún ejemplo para explicarlo. El resto va a ser un número entero, ya que su grado tiene que ser menor que el del divisor, y además, por el teorema del resto va a ser el valor del polinomio dividendo en a. x 2 1, si lo dividimos por x 1, podemos comprobar usando Ruffini que tiene resto 2, que es un número entero, y además Encuentra un polinomio P(x) de grado dos que verifique las tres condiciones siguientes. x 5 sea factor suyo. P(3) 0. Su coeficiente principal sea 4. La segunda condición nos indica que x 3 es factor del polinomio también. Como un polinomio de grado 2 solo puede tener 2 raíces a lo sumo, pues (x 5)(x 3) tiene grado 2 y cumple las dos primeras condiciones. El coeficiente principal de este producto es 1, así que si multiplicamos por 4 tendremos el polinomio que buscábamos. P(x) 4(x 5)(x 3) Qué le ha de ocurrir a un polinomio de grado tres para que tenga una sola raíz entera? Explícalo con un ejemplo. Que uno de sus factores sea un polinomio de grado 2 que no tenga raíces enteras. Por ejemplo, el polinomio de grado 3 podría ser el resultante de x(x 2 1). Cuál es la relación existente entre los grados del dividendo, divisor, cociente y resto de una división entera de polinomios? Grado (R(x)) Grado (d(x)) Grado (D(x)) Grado (d(x)) Grado (C(x)) 5.53 Existe algún número n para el cual el polinomio x n 1 se anule para algún valor real de x? Si n es impar, se anula para x Qué condición debe verificar n para que el polinomio x n a n sea divisible por el binomio x a? Tiene que ser n par, para que así ( a) n a n y x n a n 0.
14 PROBLEMAS PARA APLICAR 5.55 Un alumno de 3.º de ESO está empeñado en transformar los polinomios x 3 9x 2 27x 27 y x 2 6x 9 en potencias del polinomio x 3. Ayúdale en su tarea. Aplicamos la regla de Ruffini al polinomio de grado 3: Tenemos entonces que x 3 9x 2 27x 27 (x 3)(x 2 6x 9). Este segundo factor resulta ser el polinomio de grado 2 del enunciado, que es un cuadrado perfecto, el cuadrado de una diferencia, x 2 6x 9 (x 3) 2. Y entonces x 3 9x 2 27x 27 (x 3) Al salir de un examen de polinomios quiero contrastar con mis compañeros los resultados que hemos obtenido, pero se han emborronado dos coeficientes y no puedo distinguirlos. 2x 3 5x 2 x Tan solo recuerdo que el polinomio era divisible por x 2 4. Cuál es el polinomio que había escrito en el examen? 2x 3 5x 2 ax (b - 20) x 2 4 2x 3 9x 3 8x 2x 5 6x 4 5x 2 (8 a)x 6x 4 5x 2 (8 a)x (b 20 6x 4 5x 3 (8 a)x (b 20) 6x 4 Por ser divisible (8 a)x (b 20) 0. Esto quiere decir que: 8 a 0 b 20 0 El polinomio es 2x 3 5x 2 8x 20. a 8 b Un alumno ha confundido los números en una división de Ruffini y le ha quedado el siguiente resultado Ayuda al alumno a reconstruir la división, sabiendo que el divisor y el resto están bien, pero que los demás números están desordenados
15 5.58 Una división enlazada de Ruffini, es decir, una división en la que cada cociente obtenido lo utilizamos como nuevo dividendo, nos ha quedado de la siguiente forma Averigua todos los coeficientes que faltan si todos los 1 pertenecen a los polinomios divisores y todos los ceros a los restos. Vamos haciendo los cálculos desde la parte de abajo El departamento de Matemáticas de mi centro ha instalado un factorizador de polinomios. Se trata de una máquina que proporciona un polinomio al azar y, continuación, imprime una tarjeta con los posibles factores del polinomio. Si la persona que juega encuentra los factores del polinomio en la tarjeta obtiene un premio. Jugamos una vez y aparece en la pantalla el polinomio 2x 3 3x 2 8x 12, y nos imprime una tarjeta como esta. x 2 2x 1 x 5 x 6 x 1 x 2 2x 3 x 4 x 3 Qué combinación me proporciona el premio? Vamos probando con cada uno de los posibles factores y tenemos que: P( 2) 2 ( 2) 3 3 ( 2) 2 8 ( 2) P(2) x 3 3x 2 8x (12 2x 3 2x 3 3x 2 8x (12 x 2 4 0x 3 0x 2 8x (12 2x 3 3x 2 8x (12 2x 3 3x 2 8x (10 6x 4 Por el teorema del factor podemos decir entonces que (x 2) y (x 2) son factores. También 2x 3 lo es porque al dividir el polinomio por este binomio nos da resto 0. La combinación correcta es x 2, x 2, 2x 3.
16 5.60 Mi hermano mayor estudia Matemáticas, y practica polinomios conmigo tapándome polinomios y jugando a que adivine lo que oculta Encuentra los polinomios que ha tapado. P(x)(2x 5) 4x 3 18x 2 22x 5. El grado de P(x) tiene que ser 2, para que ambos lados de la igualdad tengan el mismo grado. P(x) será de la forma ax 2 bx c. (ax 2 bx c)(2x 5) 2ax 3 5ax 2 2bx 2 5bx 2cx 5c 4x 3 18x 2 22x 5, igualando coeficientes y resolviendo el sistema obtenemos las incógnitas, y así, P(x) 2x 2 4x 1. Q(x)(x 2) 5x 4 10x 3 6x 12. El grado de Q (x ) tiene que ser 3, para que ambos lados de la igualdad tengan el mismo grado. Q (x ) será de la forma ax 3 bx 2 cx d. (ax 3 bx 2 cx d)(x 2) ax 4 (2a b)x 3 (2b c)x 2 (2c d) 2d 5x 4 10x 3 6x 12, igualando coeficientes y resolviendo el sistema obtenemos las incógnitas. Tenemos entonces que Q(x) 5x 3 6. La parte del ejercicio referente a Q(x) también podríamos resolverla dividiendo por Ruffini. Explica cómo variando simplemente el valor de k el polinomio 2x 3 4x 3k cumple las siguientes condiciones. a) Tiene como factor x 3. b) Al dividirlo por x 2, tiene como resto 5. c) Es divisible por x 1. d) Tiene como raíz 4. e) Es igual al polinomio Q(x) 2(x 3 2x 7). a) Aplicando el teorema del factor, 3k 42 0 k 14. b) k k k k 8 Aplicando el teorema del resto, 3k 8 5 k 1. c) Dividiendo por Ruffini y aplicando el teorema del factor tenemos que k d) Dividiendo por Ruffini y aplicando el teorema del factor tenemos que k. 3 e) En este caso, 3k 14 k 1 4 3
17 REFUERZO División y regla de Ruffini Realiza las siguientes divisiones de un polinomio por un monomio. a) (9xy 3xy 2 3x 2 y) (3xy) b) (5x 2 3x 4 2x) x 2 a) (9xy 3xy 2 3x 2 y) (3xy) 9xy 3 xy 2 3x 2 3x y y x x y y 3 3 x x y y 3 3 b) (5x 2 3x 4 2x) x 2 5 3x x x 2 y x y 3 y x Efectúa estas divisiones de polinomios. a) (3x 4 5x 3 3x 2 6x 1) (x 2 x 2) b) (2x 4 4x 3 3x 2 6x 3) (x 2 1) a) 3x 4 5x 3 3x 2 6x 1 x x 2 3x 4 3x 3 6x 2 6x 1 3x 2 8x 1 3x 4 8x 3 9x 2 3x 4 8x 3 8x 2 16x 3x 4 5x 3 3x 2 10x 3x 4 5x 3 3x 2 10x 2 3x 4 5x 3 x 2 11x 1 b) (2x 4 4x 3 3x 2 6x 3) (x 2 1); C(x) 2x 2 4x 1 y R(x) 2x Mediante la regla de Ruffini, realiza las siguientes divisiones, e indica el cociente y el resto. a) (x 4 x 2 1) (x 2) b) (x 7 2x 4 x 1) (x 1) 5.65 a) b) C(x) x 3 2x 2 5x 10; R(x) C(x) x 6 x 5 x 4 x 3 x 2 x; R(x) 1 Utilizando la regla de Ruffini, calcula el número que se ha de sumar al polinomio para que sea divisible por x k k 9 Como tiene que ser divisible, k 9 0, así que k 9. Teoremas y raíces de un polinomio 5.66 Comprueba si son exactas las siguientes divisiones sin llegar a realizarlas. a) (x 4 81) (x 3) b) (x ) (x 1) Aplicamos el teorema del resto, y si el resto es 0, es porque la división es exacta. a) P(3) Sí es exacta la división. b) P( 1) ( 1) No es división exacta.
18 5.67 Determina, sin realizar ninguna operación, si 3 es una raíz de este polinomio. P(x) 3x 7 5x 5 3x 4 2x 2 x 7 No, 3 no es raíz de P(x), ya que no es divisor del término independiente, Halla las raíces enteras de los siguientes polinomios. a) A(x) x 4 5x 2 4 b) B(x) x 3 3x 2 x 3 a) Las posibles raíces de A(x) son 1, 1, 2, 2, 4, 4. A(1) A( 1) ( 1) 4 5 ( 1) A(2) A( 2) ( 2) 4 5 ( 2) Por el teorema fundamental del álgebra, un polinomio de grado 4 no puede tener más de cuatro raíces. De modo que las raíces del polinomio son 1, 1, 2 y 2. b) Las posibles raíces de B(x) son 1, 1, 3, 3. B(1) B( 1) ( 1) 3 3 ( 1) 2 ( 1) 3 0 B(3) Por el teorema fundamental del álgebra, un polinomio de grado 3 no puede tener más de tres raíces. De modo que las raíces del polinomio son 1, 1 y Sin efectuar el producto de factores, identifica el polinomio P(x) x 4 2x 3 16x 2 2x 15 con alguna de las siguientes factorizaciones. a) (x 3) (x 2) (x 1) (x 1) b) (x 2) (x 2) (x 1) (x 1) c) (x 1) (x 1) (x 3) (x 5) Las respuestas a y b no pueden ser porque dan como raíz 2, que no es un divisor del término independiente de P(x). Además, en c, cada uno de esos factores cumple que P(a) 0. Factorización de polinomios 5.70 Factoriza cada uno de los siguientes polinomios sacando factor común. a) 5x 7 6x 6 3x 5 b) 5xy 3x 2 2xy 2 a) x 5 (5x 2 6x 3) b) x(5y 3x 2y 2 ) 5.71 Factoriza al máximo estos polinomios. a) x 3 3x 2 6x 8 b) x 4 x 3 11x 2 9x 18 Con las posibles raíces del polinomio por Ruffini obtengo la factorización. a) La factorización es (x 2)(x 1)(x 4). c) La factorización es (x 2)(x 1)(x 3)(x 3).
19 5.72 Factoriza la siguiente expresión; determina previamente el área de las figuras geométricas. 2ab 3b 3a 4b 3ab Las tres áreas son 9a 2 b 2,6ab 2,6ab. Factorizamos la suma de las tres y nos queda: 3ab(3ab 2b 2) 5.73 Halla un polinomio de grado cuatro cuyos factores sean x 2 x 1, x 1 y x 3; y cuyo término independiente sea 9. El producto de x 2 x 1, x 1 y x 3, (x 2 x 1)(x 1)(x 3), tiene grado 4, su término independiente sería 3. Así que el polinomio buscado es P(x) 3(x 2 x 1)(x 1)(x 3).
20 AMPLIACIÓN 5.74 Halla los valores que han de tomar m y n, para que el polinomio P(x) 2x 5 x 4 x 3 mx 2 nx 2 sea divisible por x x 5 x 4 3x 3 (m 1mx 2 (3 )nx 2(m x 2 1 2x 5 x 3 2x 3 6x 1 2x 3 x 2 3x (m 1) 2x 5 x 4 3x 3 2x 5 x 4 3x 3 (m 1)x 2 2x 5 x 4 3x 3 (m 1)x 2 2x 5 x 4 3x 3 (m 1)x 2 3x 3 3x 2x 5 x 4 3x 3 (m 1)x 2 (3 n)x 2x 5 x 4 3x 3 (m 1)x 2 (3 n)x (m 1) 2x 5 x 4 3x 3 (m 1)x 2 (3 n)x (m 3) 3 n 0 El resto tiene que ser 0, así que: m 3 0 n 3 m La descomposición factorial de un polinomio P(x) es (x 1) (x 1) (x 3) 2. Escribe un polinomio de tercer grado que, siendo divisor de P(x) sea, a la vez, divisible por x 1 y por x 3, siendo su coeficiente principal 3. Buscamos Q(x) tal que el resto de P(x) Q(x) sea 0. Y además, Q(x) divisible por x 1 y x 3, es decir, que ambos sean factores de Q(x). Le falta un factor más al polinomio para que sea de grado 3, y como tiene que dividir a P(x), este tendrá que ser alguno de los factores de P(x). De modo que Q(x) (x 1) (x 1) (x 3) o Q(x) (x 1) (x 3) Si tenemos el polinomio P(x) x 2 4x c, para qué valores de c se tienen estas factorizaciones? a) (x a) (x b) b) (x a) 2 c) Irreducible a) (x a) (x b) x 2 (a b)x ab. Tenemos que: a b 4 ab c. De donde hay dos posibles soluciones (a, b) (3, 1) ó (2, 2). a, b, c Z c 0 Por tanto, c 3 ó 4 b) (x a) 2 x 2 2ax a 2 2a 4 a 2 c a 2 c 4 c) Para esto tiene que cumplirse que la ecuación de segundo grado no tenga raíces reales. Para ello, b 2 4ac 0. En nuestro caso, c c 0 4 c.
21 5.77 Tres amigos piensan una condición para un polinomio. Escribe el polinomio de grado tres que cumpla las tres condiciones. El coeficiente principal es 2. Tiene que ser divisible por el polinomio x 2 10x 24. Una raíz es la media de las dos raíces del polinomio que ha dicho María. Vamos a ver cuáles son las tres raíces del polinomio x 2 10x x 2 10x 24 (x 4)(x 6) La media de 6 y 4 es 5. El polinomio buscado es 2(x 4)(x 6)(x 5).
22 PARA INTERPRETAR Y RESOLVER 5.78 El puzle Se cuenta con las expresiones polinómicas: (x 3) ( x 2 x 3) 2x 3 11x 2 12x Y las tarjetas: Coloca las tarjetas en los huecos de las expresiones de forma que se obtenga una identidad algebraica. El valor numérico de la primera expresión en x 0 es 9. Por tanto, la tarjeta correspondiente a la segunda expresión es la que tiene marcada el número nueve. Realizando la división 2x 3 11x 2 12x 9 x 3 con el dos y el cinco, en este orden, son las correspondientes a la primera expresión. se obtiene el cociente exacto 2x 2 5x 3 por lo que las tarjetas marcadas 5.79 Aproximaciones sucesivas Se considera el polinomio P(x) x 3 x 3. a) Calcula P(0) y P(2), y comprueba que tienen diferente signo. b) El punto medio del intervalo [0, 2] es 1. Calcula P(1) y comprueba si tiene signo positivo o negativo. c) Elige entre los intervalos [0, 1] y [1, 2] aquel en el que el polinomio cambia de signo en sus extremos y calcula su punto medio y el valor del polinomio en él. d) Realiza la operación anterior cinco veces y da un valor aproximado de una raíz del polinomio P. Punto P(a) [a, b] medio P(c) Nuevo segmento c P(b) P(0) 3 [0, 2] 1 P(1) 1 [1, 2] P(2) 7 P(1) 1 [1, 2] 1,5 P(1,5) 1,875 [1; 1,5] P(2) 7 P(1) 1 [1; 1,5] 1,25 P(1,25) 0,203 [1; 1,25] P(1,5) 1,875 P(1) 1 [1; 1,25] 1,125 P(1,125) 0,451 [1,125; 1,25] P(1,25) 0,203 P(1,125) 0,451 [1,125; 1,25] 1,1875 P(1,1875) 0,138 [1,1875; 1,25] P(1,25) 0,203 El polinomio tendrá una raíz comprendida entre 1,1875 y 1,25.
23 AUTOEVALUACIÓN 5.A1 Al dividir dos polinomios, hemos obtenido como cociente el polinomio C(x) 3x 7, y como resto R(x) 19x 10. Si el divisor es d(x) x 2 2x 1, cuál es el dividendo D(x)? D(x) d(x) C(x) R(x) D(x) (x 2 2x 1)(3x 7) (19x 10) 3x 3 x 2 2x 3 5.A2 Calcula esta división de polinomios. (x 4 x 3 2x 2 x 3) (x 2 x 1) x 4 3x 3 2x 2 3x 3 x 2 x 1 x 4 3x 3 2x 2 3x 3 3 x 2 2x 3 x 4 2x 3 2x 2 x 4 2x 3 2x 2 2x x 4 2x 3 3x 2 3x x 4 2x 3 3x 2 3x 3 x 4 2x 3 3x 2 3x 6 C(x) x 2 2x 3 R(x) 6 5.A3 Completa estos esquemas aplicando la regla de Ruffini. a) b) a) b) A4 Utilizando la regla de Ruffini, realiza cada división, e indica el polinomio cociente y el resto. a) (x 3 3x 2 4) (x 2) b) (x 4 5x 2 4) (x 2) a) b) C(x) x 2 5x 10 R(x) 16 C(x) x 3 2x 2 x 2 R(x) 0 5.A5 5.A6 Averigua qué valor tiene que tomar m, para que el resto obtenido al dividir 2x 3 mx 2 x 6 entre x 1 sea 12. Usamos el teorema del resto para saberlo: C( 1) 2 ( 1) 3 m ( 1) 2 ( 1) 6 9 m 12. Entonces, m 3. Sin efectuar el producto, halla las raíces de estos polinomios. a) (x 1) (x 2) (x 3) b) x (x 7) (x 3) a) Las raíces son 1, 2, 3. b) Las raíces son 0, 7, 3.
24 5.A7 Utilizando el valor numérico, calcula las raíces de estos polinomios. a) x 2 3x 28 b) x 3 x 2 36x 36 a) Las posibles raíces son 1, 1, 2, 2, 4, 4, 7, 7, 14, 14, 28, 28. Como P( 4) 0 y P(7) 0 Y el polinomio es de grado 2, no puede tener más de dos raíces, y son 4 y 7. b) Las posibles raíces son 1, 1, 2, 2, 3, 3, 4, 4, 6, 6, 9, 9, 12, 12, 18, 18. Como P( 1) 0, P(6) 6 0 y P( 6) 0 Y el polinomio es de grado 3, no puede tener más de tres raíces, y son 1, 6 y 6. 5.A8 Completa las siguientes divisiones entre monomios. a) 15x 2 yz 3 3xz 2 b) 8a 2 b 2 c 2 bc 3 a) 5xyz b) 8a 2 b 3 c 5 5.A9 5.A10 5.A11 Factoriza al máximo estos polinomios. a) 6x 3 12x 2 90x 216 b) 2x 4 3x 3 x 6 a) 6x 3 12x 2 90x 216 6(x 3) 2 (x 4) b) 2x 4 3x 3 x 6 (x 1)(x 2)(2x 2 x 3) Factoriza al máximo las siguientes expresiones. a) 3a 2 bc 6abc 3 12a 3 b 2 c b) 9x 4 12x 2 y 3 4y 6 a) 3abc (a 2c 2 4a 2 b) b) (3x 2 2y 3 ) 2 Factoriza al máximo estas expresiones. a) x 3 2x 2 11x 12 b) x 3 5x 2 8x 12 a) x 3 2x 2 11x 12 (x 1)(x 4)(x 3) b) x 3 5x 2 8x 12 (x 6)(x 1)(x 2)
5 DIVISIÓN DE POLINOMIOS. RAÍCES
 AMPLIACIÓN 5.74 Halla los valores que han de tomar m y n, para que el polinomio P(x) 2x 5 x 4 x 3 mx 2 nx 2 sea divisible por x 2 1. 2x 5 x 4 3x 3 (m 1mx 2 (3 )nx 2(m x 2 1 2x 5 x 3 2x 3 6x 1 2x 3 x 2
AMPLIACIÓN 5.74 Halla los valores que han de tomar m y n, para que el polinomio P(x) 2x 5 x 4 x 3 mx 2 nx 2 sea divisible por x 2 1. 2x 5 x 4 3x 3 (m 1mx 2 (3 )nx 2(m x 2 1 2x 5 x 3 2x 3 6x 1 2x 3 x 2
5 DIVISIÓN DE POLINOMIOS. RAÍCES
 EJERCICIOS PARA ENTRENARSE División y regla de Ruffini 5.26 Realiza estas divisiones. a) (12x 2 yz 6xy 3 8xyz 2 ) (2xy) b) (15x 4 3x 3 9x 2 ) (3x 2 ) c) (5a 3 b 2 10ab 2 15a 3 b 4 ) (5ab 2 ) a) (12x 2
EJERCICIOS PARA ENTRENARSE División y regla de Ruffini 5.26 Realiza estas divisiones. a) (12x 2 yz 6xy 3 8xyz 2 ) (2xy) b) (15x 4 3x 3 9x 2 ) (3x 2 ) c) (5a 3 b 2 10ab 2 15a 3 b 4 ) (5ab 2 ) a) (12x 2
Polinomios Primero que todo vamos a definirlos como aquella expresión algebraica de la forma: P(x) = a n x n + a n - 1 x n - 1 + a n - 2 x n - 2 +...
 Polinomios Primero que todo vamos a definirlos como aquella expresión algebraica de la forma: P(x) = a n x n + a n - 1 x n - 1 + a n - 2 x n - 2 +... + a 1 x 1 + a 0 Siendo a n, a n -1... a 1, a o números,
Polinomios Primero que todo vamos a definirlos como aquella expresión algebraica de la forma: P(x) = a n x n + a n - 1 x n - 1 + a n - 2 x n - 2 +... + a 1 x 1 + a 0 Siendo a n, a n -1... a 1, a o números,
Expresiones algebraicas
 Expresiones algebraicas Una expresión algebraica es una combinación de letras y números relacionadas por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación. Las
Expresiones algebraicas Una expresión algebraica es una combinación de letras y números relacionadas por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación. Las
Ejercicio 1: Realiza las siguientes divisiones por el método tradicional y por Ruffini: a)
 Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
Tema 2: Ecuaciones, Sistemas e Inecuaciones. 2.1 División de polinomios. Regla de Ruffini. Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Terminología: o Grado del polinomio:
PARA EMPEZAR. Un cuadrado tiene de lado x centímetros. Escribe la expresión algebraica correspondiente a su área.
 4 POLINOMIOS PARA EMPEZAR Un cuadrado tiene de lado x centímetros. Escribe la expresión algebraica correspondiente a su área. Expresión algebraica: A x Cuáles de las siguientes expresiones algebraicas
4 POLINOMIOS PARA EMPEZAR Un cuadrado tiene de lado x centímetros. Escribe la expresión algebraica correspondiente a su área. Expresión algebraica: A x Cuáles de las siguientes expresiones algebraicas
POLINOMIOS Y FRACCIONES ALGEBRAICAS
 POLINOMIOS Y FRACCIONES ALGEBRAICAS Definición de monomio. Expresión algebraica formada por el producto de un número finito de constantes y variables con exponente natural. Al producto de las constantes
POLINOMIOS Y FRACCIONES ALGEBRAICAS Definición de monomio. Expresión algebraica formada por el producto de un número finito de constantes y variables con exponente natural. Al producto de las constantes
EJERCICIOS PROPUESTOS. La única expresión que indica la suma de varios monomios no semejantes es la d: x 2 y 2.
 3 POLINOMIOS EJERCICIOS PROPUESTOS 3.1 Cuáles de las siguientes expresiones algebraicas son polinomios? a) 1 3 x b) abc c) 1 x d) x y La única expresión que indica la suma de varios monomios no semejantes
3 POLINOMIOS EJERCICIOS PROPUESTOS 3.1 Cuáles de las siguientes expresiones algebraicas son polinomios? a) 1 3 x b) abc c) 1 x d) x y La única expresión que indica la suma de varios monomios no semejantes
5.- Calcula el cociente y el resto de las divisiones siguientes:
 1.- Opera y simplifica las siguientes expresiones: 2.- Efectúa las siguientes operaciones y simplifica el resultado: 3º.- Multiplica cada expresión por el mín.c.m. de los denominadores y simplifica: 4.-
1.- Opera y simplifica las siguientes expresiones: 2.- Efectúa las siguientes operaciones y simplifica el resultado: 3º.- Multiplica cada expresión por el mín.c.m. de los denominadores y simplifica: 4.-
EXPRESIONES ALGEBRAICAS. El tripe de un número menos «cinco» en lenguaje algebraico se escribe
 1 Álgebral EXPRESIONES ALGEBRAICAS El tripe de un número menos «cinco» en lenguaje algebraico se escribe 3x 5: 3x 5 es una expresión algebraica donde x es la incógnita. La letra x representa un número
1 Álgebral EXPRESIONES ALGEBRAICAS El tripe de un número menos «cinco» en lenguaje algebraico se escribe 3x 5: 3x 5 es una expresión algebraica donde x es la incógnita. La letra x representa un número
TEMA 2: POLINOMIOS IDENTIDADES NOTABLES. Ejercicios: 1. Desarrolla las siguientes identidades: 2. Expresa como producto de factores:
 IDENTIDADES NOTABLES TEMA : POLINOMIOS a b a b ab a b a b ab a ba b a b Ejercicios:. Desarrolla las siguientes identidades: a y 5 b 5 4y c 5 5. Epresa como producto de factores: 4 a 9 0 0 b 9 6 c 5 9y
IDENTIDADES NOTABLES TEMA : POLINOMIOS a b a b ab a b a b ab a ba b a b Ejercicios:. Desarrolla las siguientes identidades: a y 5 b 5 4y c 5 5. Epresa como producto de factores: 4 a 9 0 0 b 9 6 c 5 9y
TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS
 TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.- POLINOMIOS Recordemos que un monomio es una expresión algebraica (combinación de letras y números) en la que las únicas operaciones que aparecen entre las
TEMA 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.- POLINOMIOS Recordemos que un monomio es una expresión algebraica (combinación de letras y números) en la que las únicas operaciones que aparecen entre las
lasmatemáticas.eu Pedro Castro Ortega materiales de matemáticas
 º ESO 1. Expresiones algebraicas En matemáticas es muy común utilizar letras para expresar un resultado general. Por ejemplo, el área de un b h triángulo es base por altura dividido por dos y se expresa
º ESO 1. Expresiones algebraicas En matemáticas es muy común utilizar letras para expresar un resultado general. Por ejemplo, el área de un b h triángulo es base por altura dividido por dos y se expresa
Se dice que dos monomios son semejantes cuando tienen la misma parte literal
 Expresiones algebraicas 1 MONOMIOS Conceptos Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural.
Expresiones algebraicas 1 MONOMIOS Conceptos Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural.
3. POLINOMIOS, ECUACIONES E INECUACIONES
 3. POLINOMIOS, ECUACIONES E INECUACIONES 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.1.- POLINOMIOS FACTORIZACIÓN. REGLA DE RUFFINI Un polinomio con indeterminada x es una expresión de la forma: Los números
3. POLINOMIOS, ECUACIONES E INECUACIONES 1.- POLINOMIOS Y FRACCIONES ALGEBRAICAS 1.1.- POLINOMIOS FACTORIZACIÓN. REGLA DE RUFFINI Un polinomio con indeterminada x es una expresión de la forma: Los números
La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes.
 Suma de monomios Sólo podemos sumar monomios semejantes. La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes. ax n + bx n = (a + b)x
Suma de monomios Sólo podemos sumar monomios semejantes. La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes. ax n + bx n = (a + b)x
5 REPASO Y APOYO OBJETIVO 1
 5 REPASO Y APOYO OBJETIVO 1 RECONOCER EL GRADO, LOS TÉRMINOS Y EL TÉRMINO INDEPENDIENTE DE UN POLINOMIO Nombre: Curso: echa: Un monomio es una expresión algebraica formada por el producto de un número,
5 REPASO Y APOYO OBJETIVO 1 RECONOCER EL GRADO, LOS TÉRMINOS Y EL TÉRMINO INDEPENDIENTE DE UN POLINOMIO Nombre: Curso: echa: Un monomio es una expresión algebraica formada por el producto de un número,
83 ESO. 6x 4. «La clave de todo es la paciencia. Un pollo se obtiene empollando el huevo, no rompiéndolo.»
 83 ESO «La clave de todo es la paciencia. Un pollo se obtiene empollando el huevo, no rompiéndolo.» 6 4 10 ÍNDICE: 1. DIVISIÓN DE POLINOMIOS POR MONOMIOS. DIVISIÓN ENTERA DE POLINOMIOS 3. REGLA DE RUFFINI
83 ESO «La clave de todo es la paciencia. Un pollo se obtiene empollando el huevo, no rompiéndolo.» 6 4 10 ÍNDICE: 1. DIVISIÓN DE POLINOMIOS POR MONOMIOS. DIVISIÓN ENTERA DE POLINOMIOS 3. REGLA DE RUFFINI
Definición 3 (Polinomio) Se llama polinomio a la suma algebraica de varios monomios de distinto grado:
 Polinomios Definición 1 (Expresión algebraica) Una expresión algebraica es una expresión con números y letras (que representan números) en la que aparecen las operaciones usuales: suma, resta, multiplicación,
Polinomios Definición 1 (Expresión algebraica) Una expresión algebraica es una expresión con números y letras (que representan números) en la que aparecen las operaciones usuales: suma, resta, multiplicación,
Recordar las principales operaciones con expresiones algebraicas.
 Capítulo 1 Álgebra Objetivos Recordar las principales operaciones con expresiones algebraicas. 1.1. Números Los números naturales se denotarán por N y están constituidos por 0, 1, 2, 3... Con estos números
Capítulo 1 Álgebra Objetivos Recordar las principales operaciones con expresiones algebraicas. 1.1. Números Los números naturales se denotarán por N y están constituidos por 0, 1, 2, 3... Con estos números
TEMA 5. FACTORIZACIÓN DE POLINOMIOS.
 TEMA 5. FACTORIZACIÓN DE POLINOMIOS. 1. SACAR FACTOR COMÚN Cuando todos los términos de un polinomio, P(x), son múltiplos de un mismo monomio, M(x), podemos extraer M(x) como factor común. Por ejemplo:
TEMA 5. FACTORIZACIÓN DE POLINOMIOS. 1. SACAR FACTOR COMÚN Cuando todos los términos de un polinomio, P(x), son múltiplos de un mismo monomio, M(x), podemos extraer M(x) como factor común. Por ejemplo:
Un monomio es el producto indicado de un número por una o varias letras GRADO 4º
 TEMA. POLINOMIOS OPERACIONES. MONOMIOS Un monomio es el producto indicado de un número por una o varias letras GRADO º COEFICIENTE PARTE LITERAL. VALOR NUMÉRICO DE UN MONOMIO Es el resultado que se obtiene
TEMA. POLINOMIOS OPERACIONES. MONOMIOS Un monomio es el producto indicado de un número por una o varias letras GRADO º COEFICIENTE PARTE LITERAL. VALOR NUMÉRICO DE UN MONOMIO Es el resultado que se obtiene
POLINOMIOS. El grado de un polinomio P(x) es el mayor exponente al que se encuentra elevada la variable x.
 POLINOMIOS Un POLINOMIO es una expresión algebraica de la forma: x 1 + a 0 P(x) = a n x n + a n - 1 x n - 1 + a n - 2 x n - 2 +... + a 1 Siendo a n, a n - 1... a 1, a o números, llamados coeficientes.
POLINOMIOS Un POLINOMIO es una expresión algebraica de la forma: x 1 + a 0 P(x) = a n x n + a n - 1 x n - 1 + a n - 2 x n - 2 +... + a 1 Siendo a n, a n - 1... a 1, a o números, llamados coeficientes.
Tema 6 Lenguaje Algebraico. Ecuaciones
 Tema 6 Lenguaje Algebraico. Ecuaciones 1. El álgebra El álgebra es una rama de las matemáticas que emplea números y letras con las operaciones aritméticas de sumar, restar, multiplicar, dividir, potencias
Tema 6 Lenguaje Algebraico. Ecuaciones 1. El álgebra El álgebra es una rama de las matemáticas que emplea números y letras con las operaciones aritméticas de sumar, restar, multiplicar, dividir, potencias
Polinomios. 1.- Funciones cuadráticas
 Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
Polinomios 1.- Funciones cuadráticas Definición 1 (Función polinomial) Sea n un entero no negativo y sean a n, a n 1,..., a, a 1, a 0 número s reales con a n 0. La función se denomina función polinomial
SOLUCIONES A LOS EJERCICIOS DE LA UNIDAD. a) Grado 2 b) Grado 3 c) Grado 2 d)grado 1 e) Grado 1 f) Grado 3 g) Grado 0 h) Grado 2 i) Grado 0
 Pág. Página 8 PRACTICA Monomios Indica cuál es el grado de los siguientes monomios y di cuáles son semejantes: a) x b) x c) x d) x e) x f) x g) h) x i) a) Grado b) Grado c) Grado d)grado e) Grado f) Grado
Pág. Página 8 PRACTICA Monomios Indica cuál es el grado de los siguientes monomios y di cuáles son semejantes: a) x b) x c) x d) x e) x f) x g) h) x i) a) Grado b) Grado c) Grado d)grado e) Grado f) Grado
5. Producto de dos binomios de la forma: ( ax + c)( bx d )
 PRODUCTOS NOTABLES Y FACTORIZACIÓN. Productos Notables: Son polinomios que se obtienen de la multiplicación entre dos o más polinomios que poseen características especiales o expresiones particulares,
PRODUCTOS NOTABLES Y FACTORIZACIÓN. Productos Notables: Son polinomios que se obtienen de la multiplicación entre dos o más polinomios que poseen características especiales o expresiones particulares,
3.2 DIVIDIR UN POLINOMIO POR x a. REGLA DE RUFFINI
 TEMA 3 ÁLGEBRA MATEMÁTICAS CCSSI 1º BACH 1 TEMA 3 ÁLGEBRA 3.1 DIVISIÓN DE POLINOMIOS COCIENTE DE MONOMIOS El cociente de un monomio por otro monomio de grado inferior es un nuevo monomio cuyo grado es
TEMA 3 ÁLGEBRA MATEMÁTICAS CCSSI 1º BACH 1 TEMA 3 ÁLGEBRA 3.1 DIVISIÓN DE POLINOMIOS COCIENTE DE MONOMIOS El cociente de un monomio por otro monomio de grado inferior es un nuevo monomio cuyo grado es
OPERACIONES CON MONOMIOS Y POLINOMIOS. Suma de monomios
 OPERACIONES CON MONOMIOS Y POLINOMIOS Suma de monomios Sólo podemos sumar monomios semejantes. La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de
OPERACIONES CON MONOMIOS Y POLINOMIOS Suma de monomios Sólo podemos sumar monomios semejantes. La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de
, 5m2 + n 1 son expresiones algebraicas. Hay diversidad de situaciones que se pueden expresar mediante expresiones algebraicas.
 1.- POLINOMIOS Y OPERACIONES Expresiones algebraicas Una expresión algebraica está formada por números y letras relacionados por operaciones aritméticas. Por ejemplo, 3x 3x1 x +, a 3 b, y 3, 5m + n 1 son
1.- POLINOMIOS Y OPERACIONES Expresiones algebraicas Una expresión algebraica está formada por números y letras relacionados por operaciones aritméticas. Por ejemplo, 3x 3x1 x +, a 3 b, y 3, 5m + n 1 son
x= 1± 1 24 = 1±5 = 6 0 = 6 18 18 = 1 3 x= 7± 49 60 = 7± 11 10
 1.- Ecuaciones de segundo grado. Resolver las siguientes ecuaciones. a) 5x 2 45 = 0, despejando x 2 = 9, y despejando x (3 y 3 son los únicos números que al elevarlo al cuadrado dan 9) obtengo que x1 =
1.- Ecuaciones de segundo grado. Resolver las siguientes ecuaciones. a) 5x 2 45 = 0, despejando x 2 = 9, y despejando x (3 y 3 son los únicos números que al elevarlo al cuadrado dan 9) obtengo que x1 =
POLINOMIOS. Un polinomio es una expresión algebraica (conjunto de. números y letras que representan números, conectados por las
 POLINOMIOS Teoría 1.- Qué es un polinomio? Un polinomio es una expresión algebraica (conjunto de números y letras que representan números, conectados por las operaciones de suma, resta, multiplicación,
POLINOMIOS Teoría 1.- Qué es un polinomio? Un polinomio es una expresión algebraica (conjunto de números y letras que representan números, conectados por las operaciones de suma, resta, multiplicación,
2. Calcula cociente y resto en la siguiente división de polinomios: (x 5 32) : (x 1)
 1. Un polinomio con raíces únicas 1, 0, 2, 2, 3 es: a) x 4 + 4x 3 + x 2 6x b) x 4 + 6x 3 + 9x 2 4x 12 c) x 5 6x 4 + 9x 3 + 4x 2 12x d) x 5 + 6x 4 + 9x 3 4x 2 12x e) x 4 4x 3 + x 2 + 6x 2. Calcula cociente
1. Un polinomio con raíces únicas 1, 0, 2, 2, 3 es: a) x 4 + 4x 3 + x 2 6x b) x 4 + 6x 3 + 9x 2 4x 12 c) x 5 6x 4 + 9x 3 + 4x 2 12x d) x 5 + 6x 4 + 9x 3 4x 2 12x e) x 4 4x 3 + x 2 + 6x 2. Calcula cociente
Colegio San Patricio A Incorporado a la Enseñanza Oficial Fundación Educativa San Patricio
 TRABAJO PRÁCTICO Nº 5. MONOMIOS Y POLINOMIOS TEORÍA Y PRÁCTICA Monomios Un monomio es una expresión algebraica formada por: - una parte numérica, llamada coeficiente, y - una parte literal, formada por
TRABAJO PRÁCTICO Nº 5. MONOMIOS Y POLINOMIOS TEORÍA Y PRÁCTICA Monomios Un monomio es una expresión algebraica formada por: - una parte numérica, llamada coeficiente, y - una parte literal, formada por
Lección 3: Introducción a la Factorización y Factorización por Factor Común y Agrupación. Dra. Noemí L. Ruiz Limardo 2009
 Lección 3: Introducción a la Factorización y Factorización por Factor Común y Agrupación Dra. Noemí L. Ruiz Limardo 2009 Objetivos de la Lección Al finalizar esta lección los estudiantes: Conocerán el
Lección 3: Introducción a la Factorización y Factorización por Factor Común y Agrupación Dra. Noemí L. Ruiz Limardo 2009 Objetivos de la Lección Al finalizar esta lección los estudiantes: Conocerán el
Suma, diferencia y producto de polinomios
 I, Polinomios Suma, diferencia y producto de polinomios Un monomio es una expresión algebraica donde los números (coeficientes) y las letras (parte literal) están separados por el signo de la multiplicación.
I, Polinomios Suma, diferencia y producto de polinomios Un monomio es una expresión algebraica donde los números (coeficientes) y las letras (parte literal) están separados por el signo de la multiplicación.
TEMA 2. POLINOMIOS Y FRACCIONES ALGEBRAICAS
 TEMA. POLINOMIOS Y FRACCIONES ALGEBRAICAS.. Repaso de polinomios - Epresión algebraica. Valor numérico - Polinomios. Operaciones con polinomios.. Identidades notables - Cuadrado de una suma de una diferencia
TEMA. POLINOMIOS Y FRACCIONES ALGEBRAICAS.. Repaso de polinomios - Epresión algebraica. Valor numérico - Polinomios. Operaciones con polinomios.. Identidades notables - Cuadrado de una suma de una diferencia
RECONOCER EL GRADO, EL TÉRMINO Y LOS COEFICIENTES DE UN POLINOMIO
 OBJETIVO RECONOCER EL GRADO, EL TÉRMINO Y LOS COEICIENTES DE UN POLINOMIO NOMBRE: CURSO: ECHA: Un polinomio es una expresión algebraica formada por la suma de monomios, que son los términos del polinomio.
OBJETIVO RECONOCER EL GRADO, EL TÉRMINO Y LOS COEICIENTES DE UN POLINOMIO NOMBRE: CURSO: ECHA: Un polinomio es una expresión algebraica formada por la suma de monomios, que son los términos del polinomio.
Coeficiente Parte literal Coeficiente Parte literal 5 x 6 am 2. El grado de un monomio es la suma de los exponentes de las letras que lo forman:
 1 Monomios Un monomio es una expresión algebraica formada por: - una parte numérica, llamada coeficiente, y - una parte literal, formada por letras y sus exponentes. Coeficiente Parte literal Coeficiente
1 Monomios Un monomio es una expresión algebraica formada por: - una parte numérica, llamada coeficiente, y - una parte literal, formada por letras y sus exponentes. Coeficiente Parte literal Coeficiente
2 POTENCIAS Y RAÍCES CUADRADAS
 2 POTENCIAS Y RAÍCES CUADRADAS EJERCICIOS PROPUESTOS 2.1 Escribe cada potencia como producto y calcula su valor. a) ( 7) 3 b) 4 5 c) ( 8) 3 d) ( 3) 4 a) ( 7) 3 ( 7) ( 7) ( 7) 343 c) ( 8) 3 ( 8) ( 8) (
2 POTENCIAS Y RAÍCES CUADRADAS EJERCICIOS PROPUESTOS 2.1 Escribe cada potencia como producto y calcula su valor. a) ( 7) 3 b) 4 5 c) ( 8) 3 d) ( 3) 4 a) ( 7) 3 ( 7) ( 7) ( 7) 343 c) ( 8) 3 ( 8) ( 8) (
POLINOMIOS Y DIVISIÓN DE POLINOMIOS MATEMÁTICAS 3º ESO
 POLINOMIOS Y DIVISIÓN DE POLINOMIOS MATEMÁTICAS 3º ESO Dado que los polinomios se utilizan para describir curvas de diferentes tipos, la gente los utiliza en el mundo real para dibujar curvas. Por ejemplo,
POLINOMIOS Y DIVISIÓN DE POLINOMIOS MATEMÁTICAS 3º ESO Dado que los polinomios se utilizan para describir curvas de diferentes tipos, la gente los utiliza en el mundo real para dibujar curvas. Por ejemplo,
6. Usa el teorema del resto para comprobar si los siguientes polinomios son divisibles por (x 2)
 1. Halla el cociente y el resto de la división: (3x 2 7x + 5) : (x 2 ) 2. Halla el cociente y el resto de la división: (x 3 3x 2 2) : (x 2 + 1) 3. Calcula y simplifica: a) 3x(x + 7) 2 + (2x 1)( 3x + 2)
1. Halla el cociente y el resto de la división: (3x 2 7x + 5) : (x 2 ) 2. Halla el cociente y el resto de la división: (x 3 3x 2 2) : (x 2 + 1) 3. Calcula y simplifica: a) 3x(x + 7) 2 + (2x 1)( 3x + 2)
DESCOMPOSICIÓN FACTORIAL
 6. 1 UNIDAD 6 DESCOMPOSICIÓN FACTORIAL Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques la factorización de polinomios cuyos términos tienen coeficientes
6. 1 UNIDAD 6 DESCOMPOSICIÓN FACTORIAL Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques la factorización de polinomios cuyos términos tienen coeficientes
MATEMÁTICAS 5º PRIMARIA DIVISIBILIDAD: MÚLTIPLOS Y DIVISORES
 MATEMÁTICAS 5º PRIMARIA DIVISIBILIDAD: MÚLTIPLOS Y DIVISORES 1 2 MÚLTIPLOS DE UN NÚMERO Un número es múltiplo de otro si se obtiene multiplicando este número por otro número natural. Ejemplo: 12 es múltiplo
MATEMÁTICAS 5º PRIMARIA DIVISIBILIDAD: MÚLTIPLOS Y DIVISORES 1 2 MÚLTIPLOS DE UN NÚMERO Un número es múltiplo de otro si se obtiene multiplicando este número por otro número natural. Ejemplo: 12 es múltiplo
3.1 Polinomios Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios.
 Tema : Polinomios, Ecuaciones y Sistemas de ecuaciones..1 Polinomios Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Ejemplo: P(x) = x 4 x + x + 5 Terminología: Ejemplo:
Tema : Polinomios, Ecuaciones y Sistemas de ecuaciones..1 Polinomios Polinomio: Expresión algebraica formada por la suma y/o resta de varios monomios. Ejemplo: P(x) = x 4 x + x + 5 Terminología: Ejemplo:
Multiplicación y división de polinomios
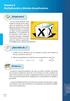 Semana 4 4 Empecemos! En esta sesión daremos continuidad al estudio de las operaciones de polinomios, la multiplicación y división. Para avanzar satisfactoriamente en este tópico debes recordar la propiedad
Semana 4 4 Empecemos! En esta sesión daremos continuidad al estudio de las operaciones de polinomios, la multiplicación y división. Para avanzar satisfactoriamente en este tópico debes recordar la propiedad
TEMA 3. POLINOMIOS Y FRACCIONES ALGEBRAICAS. Ficha 0
 Ficha 0 Un monomio es una expresión algebraica formada por el producto de un número, llamado coeficiente, por una o más variables con exponente natural o cero, llamadas parte literal. El grado es la suma
Ficha 0 Un monomio es una expresión algebraica formada por el producto de un número, llamado coeficiente, por una o más variables con exponente natural o cero, llamadas parte literal. El grado es la suma
5 REPASO Y APOYO OBJETIVO 1
 5 REPASO Y APOYO OBJETIVO 1 RECONOCER EL GRADO, LOS TÉRMINOS Y EL TÉRMINO INDEPENDIENTE DE UN POLINOMIO Nombre: Curso: echa: monomio coeficiente parte literal grado monomios semejantes ACTIVIDADES 1 Completa
5 REPASO Y APOYO OBJETIVO 1 RECONOCER EL GRADO, LOS TÉRMINOS Y EL TÉRMINO INDEPENDIENTE DE UN POLINOMIO Nombre: Curso: echa: monomio coeficiente parte literal grado monomios semejantes ACTIVIDADES 1 Completa
3 POTENCIAS Y RAÍZ CUADRADA
 EJERCICIOS PROPUESTOS 3.1 Indica la base y el exponente de las siguientes potencias y calcula su valor. a) 2 4 c) 4 3 e) 3 5 g) ( 10) 4 b) 3 4 d) 5 3 f) ( 2) 5 h) (6 2 ) a) Base 2, exponente 4; 2 4 16
EJERCICIOS PROPUESTOS 3.1 Indica la base y el exponente de las siguientes potencias y calcula su valor. a) 2 4 c) 4 3 e) 3 5 g) ( 10) 4 b) 3 4 d) 5 3 f) ( 2) 5 h) (6 2 ) a) Base 2, exponente 4; 2 4 16
Expresiones algebraicas
 Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas
Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas
Se llama factores o divisores, a las expresiones algebraicas que multiplicadas entre sí, dan como producto la primera expresión.
 FACTORIZACION Se llama factores o divisores, a las expresiones algebraicas que multiplicadas entre sí, dan como producto la primera expresión. Al proceso de encontrar los factores o divisores a partir
FACTORIZACION Se llama factores o divisores, a las expresiones algebraicas que multiplicadas entre sí, dan como producto la primera expresión. Al proceso de encontrar los factores o divisores a partir
Apuntes de matemáticas 2º ESO Curso 2013-2014. Lenguaje algebraico.
 Lenguaje algebraico. Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas
Lenguaje algebraico. Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas
POLINOMIOS. OPERACIONES CON POLINOMIOS: 1.- Suma y resta de polinomios: Sumando o restando los monomios que sean semejantes.
 Recordemos previamente algunos conceptos: POLINOMIOS MONOMIO: expresión algebraica de la forma a x n, siendo a un número real y n un número natural. ( a se llama coeficiente, x n es la parte literal y
Recordemos previamente algunos conceptos: POLINOMIOS MONOMIO: expresión algebraica de la forma a x n, siendo a un número real y n un número natural. ( a se llama coeficiente, x n es la parte literal y
6 EXPRESIONES FRACCIONARIAS Y RADICALES
 EJERCICIOS PROPUESTOS. Halla el valor numérico de la fracción 7 0 para los valores, 0 y. 8 Para : Para 0: 0 0 Para : 7 0 0. Valor indeterminado. 8 0 7 0 0 0 5 0 8 8. 7 0. No eiste valor numérico. 8 0.
EJERCICIOS PROPUESTOS. Halla el valor numérico de la fracción 7 0 para los valores, 0 y. 8 Para : Para 0: 0 0 Para : 7 0 0. Valor indeterminado. 8 0 7 0 0 0 5 0 8 8. 7 0. No eiste valor numérico. 8 0.
Notas teóricas. a) Suma y resta Se agrupan los monomios del mismo grado y se opera.
 MATEMÁTICAS EJERCICIOS RESUELTOS DE POLINOMIOS POLINOMIOS A. Introducción Teoría B. Ejercicios resueltos B.. Sumas y restas B.. Multiplicación B.3. División B.4. Sacar factor común B.5. Simplificar fracciones
MATEMÁTICAS EJERCICIOS RESUELTOS DE POLINOMIOS POLINOMIOS A. Introducción Teoría B. Ejercicios resueltos B.. Sumas y restas B.. Multiplicación B.3. División B.4. Sacar factor común B.5. Simplificar fracciones
Q(x,t) = -2x 2 t 3 - xt x 5-3x 3 + 4x 2 +2x- 7 22/03/2016. División de polinomios. P(x) = -x 4 + 3x 2-5 R(x) = 5x 4-2x 3 + 3x
 S Escribe un polinomio que cumpla las siguientes condiciones: A)Se llama P(x, y) B)Tiene 5 términos C)Es de grado seis D)No tiene término independiente S Escribe un polinomio que cumpla las siguientes
S Escribe un polinomio que cumpla las siguientes condiciones: A)Se llama P(x, y) B)Tiene 5 términos C)Es de grado seis D)No tiene término independiente S Escribe un polinomio que cumpla las siguientes
Cuando p(a) = 0 decimos que el valor a, que hemos sustituido, es una raíz del polinomio.
 Regla de Ruffini Teorema del resto Polinomios y fracciones algebraicas Dividir un polinomio por -a Regla de Ruffini Factorización de polinomios Divisibilidad de polinomios Fracciones algebraicas Operaciones
Regla de Ruffini Teorema del resto Polinomios y fracciones algebraicas Dividir un polinomio por -a Regla de Ruffini Factorización de polinomios Divisibilidad de polinomios Fracciones algebraicas Operaciones
MÚLTIPLOS Y DIVISORES DIVISIBILIDAD M.C.D. y M.C.M. Un número es múltiplo de otro si se obtiene multiplicando este último por un número natural.
 MÚLTIPLOS Y DIVISORES DIVISIBILIDAD M.C.D. y M.C.M. Múltiplos de un número Un número es múltiplo de otro si se obtiene multiplicando este último por un número natural. Por ejemplo, si multiplicamos 9x2
MÚLTIPLOS Y DIVISORES DIVISIBILIDAD M.C.D. y M.C.M. Múltiplos de un número Un número es múltiplo de otro si se obtiene multiplicando este último por un número natural. Por ejemplo, si multiplicamos 9x2
EXPRESIÓN ALGEBRAICA Monomios, Polinomios
 EXPRESIÓN ALGEBRAICA Monomios, Polinomios CPR. JORGE JUAN Xuvia-Narón Se denomina expresión algebraica a toda combinación de números reales y letras ligadas por las operaciones aritméticas de, adición,
EXPRESIÓN ALGEBRAICA Monomios, Polinomios CPR. JORGE JUAN Xuvia-Narón Se denomina expresión algebraica a toda combinación de números reales y letras ligadas por las operaciones aritméticas de, adición,
Factorización de polinomios FACTORIZACIÓN DE POLINOMIOS
 FACTORIZACIÓN DE POLINOMIOS 1. Polinomios Un monomio es el producto de un número real por una o más letras que pueden estar elevadas a exponentes que sean números naturales. La suma de los exponentes de
FACTORIZACIÓN DE POLINOMIOS 1. Polinomios Un monomio es el producto de un número real por una o más letras que pueden estar elevadas a exponentes que sean números naturales. La suma de los exponentes de
Monomios. Monomios 75. 9x 4. 5x 2. x 11. a) x 8 c)
 Polinomios Qué tienes que saber? 58 QUÉ tienes que saber? Ten en cuenta Un monomio es una epresión algebraica formada por el producto de un número, llamado coeficiente, y una o más variables con eponente
Polinomios Qué tienes que saber? 58 QUÉ tienes que saber? Ten en cuenta Un monomio es una epresión algebraica formada por el producto de un número, llamado coeficiente, y una o más variables con eponente
TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO
 TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO 1. División de polinomios Dados dos polinomios P (el dividendo) y D (el divisor), dividir P entre D es encontrar dos polinomios Q (el cociente)
TEMA 6: DIVISIÓN DE POLINOMIOS RAÍCES MATEMÁTICAS 3º ESO 1. División de polinomios Dados dos polinomios P (el dividendo) y D (el divisor), dividir P entre D es encontrar dos polinomios Q (el cociente)
EJERCICIOS DE POLINOMIOS
 EJERCICIOS DE POLINOMIOS NOMBRE:... Nº:... º....- Escribe el grado, el número de términos y el nombre (monomio, binomio, trinomio, polinomio) que recibe cada una de las siguientes expresiones algebraicas:
EJERCICIOS DE POLINOMIOS NOMBRE:... Nº:... º....- Escribe el grado, el número de términos y el nombre (monomio, binomio, trinomio, polinomio) que recibe cada una de las siguientes expresiones algebraicas:
1. EXPRESIONES ALGEBRAICAS.
 TEMA 3: POLINOMIOS 1. EXPRESIONES ALGEBRAICAS. Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas
TEMA 3: POLINOMIOS 1. EXPRESIONES ALGEBRAICAS. Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES
 Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
Unidad didáctica. Ecuaciones, inecuaciones y sistemas de ecuaciones e inecuaciones CONCEPTOS ECUACIONES Una ecuación es una igualdad entre dos epresiones en las que aparece una o varias incógnitas. En
TEMA 5: ÁLGEBRA EXPRESIONES ALGEBRAICAS
 1 TEMA 5: ÁLGEBRA EXPRESIONES ALGEBRAICAS Una expresión algebraica es un conjunto de números y letras unidos entre sí por las operaciones de sumar, restar, multiplicar, dividir y/o por paréntesis. Las
1 TEMA 5: ÁLGEBRA EXPRESIONES ALGEBRAICAS Una expresión algebraica es un conjunto de números y letras unidos entre sí por las operaciones de sumar, restar, multiplicar, dividir y/o por paréntesis. Las
UNIDAD 1: NÚMEROS NATURALES
 UNIDAD 1: NÚMEROS NATURALES 1. Calcula: Ya conoces las cuatro operaciones básicas, la suma, la resta, multiplicación y división. Cuando te aparezcan varias operaciones para realizar debes saber la siguiente
UNIDAD 1: NÚMEROS NATURALES 1. Calcula: Ya conoces las cuatro operaciones básicas, la suma, la resta, multiplicación y división. Cuando te aparezcan varias operaciones para realizar debes saber la siguiente
Expresiones algebraicas y ecuaciones. Qué es una expresión algebraica? Valor numérico de una expresión algebraica. Algebra
 Expresiones algebraicas y ecuaciones Melilla Qué es una expresión algebraica? Los padres de Iván le han encargado que vaya al mercado a comprar 4 kg de naranjas y 5 kg de manzanas. Pero no saben lo que
Expresiones algebraicas y ecuaciones Melilla Qué es una expresión algebraica? Los padres de Iván le han encargado que vaya al mercado a comprar 4 kg de naranjas y 5 kg de manzanas. Pero no saben lo que
Tema 2 Algebra. Expresiones algebraicas Índice
 Tema 2 Algebra. Expresiones algebraicas Índice 1. Expresiones algebraicas comunes... 2 2. Valor numérico de una expresión algebraica... 2 3. Tipos de expresiones algebraicas... 2 4. Monomios... 2 4.1.
Tema 2 Algebra. Expresiones algebraicas Índice 1. Expresiones algebraicas comunes... 2 2. Valor numérico de una expresión algebraica... 2 3. Tipos de expresiones algebraicas... 2 4. Monomios... 2 4.1.
1º) x³ x² x x⁰ 1-3 0 5-2. 3º) x³ x² x x⁰ 1-3 0 5 -2-2 -2 (-5) 1-5 0+[-2 (-5)] 4º) x³ x² x x⁰ 1-3 0 5-2-2 10-20 1-5 10-15. 2º) x³ x² x x⁰ 1-3 0 5
![1º) x³ x² x x⁰ 1-3 0 5-2. 3º) x³ x² x x⁰ 1-3 0 5 -2-2 -2 (-5) 1-5 0+[-2 (-5)] 4º) x³ x² x x⁰ 1-3 0 5-2-2 10-20 1-5 10-15. 2º) x³ x² x x⁰ 1-3 0 5 1º) x³ x² x x⁰ 1-3 0 5-2. 3º) x³ x² x x⁰ 1-3 0 5 -2-2 -2 (-5) 1-5 0+[-2 (-5)] 4º) x³ x² x x⁰ 1-3 0 5-2-2 10-20 1-5 10-15. 2º) x³ x² x x⁰ 1-3 0 5](/thumbs/42/22841915.jpg) 1. OPERACIONES BÁSICAS Monomio: Producto de números y letras. Ej: 3x²y a) Suma: Se pueden sumar los que tengan las mismas letras elevadas a los mismos exponentes. Ej: 3x²y xy + 4x²y = 7x² xy b) Producto:
1. OPERACIONES BÁSICAS Monomio: Producto de números y letras. Ej: 3x²y a) Suma: Se pueden sumar los que tengan las mismas letras elevadas a los mismos exponentes. Ej: 3x²y xy + 4x²y = 7x² xy b) Producto:
MATEMÁTICAS 2º E.S.O. TEMA 4 ÁLGEBRA
 MATEMÁTICAS º E.S.O. TEMA 4 ÁLGEBRA 4.1. Expresión algebraica. Valor numérico. 4.. Monomios. Operaciones con monomios. 4.3. Polinomios. Operaciones con polinomios. 4.4. Extracción de factor común. 4.5.
MATEMÁTICAS º E.S.O. TEMA 4 ÁLGEBRA 4.1. Expresión algebraica. Valor numérico. 4.. Monomios. Operaciones con monomios. 4.3. Polinomios. Operaciones con polinomios. 4.4. Extracción de factor común. 4.5.
Ecuaciones. 3º de ESO
 Ecuaciones 3º de ESO El signo igual El signo igual se utiliza en: Igualdades numéricas: 2 + 3 = 5 Identidades algebraicas: (x + 4) x = x 2 + 4 4x Fórmulas: El área, A,, de un círculo de radio r es: A =
Ecuaciones 3º de ESO El signo igual El signo igual se utiliza en: Igualdades numéricas: 2 + 3 = 5 Identidades algebraicas: (x + 4) x = x 2 + 4 4x Fórmulas: El área, A,, de un círculo de radio r es: A =
Hallar las raíces enteras de los siguientes polinomios:
 Hallar las raíces enteras de los siguientes polinomios: 1) x 3 + 2x 2 - x - 2 Las raíces enteras se encuentran entre los divisores del término independiente del polinomio: ±1 y ±2. P(1) = 1 3 + 2 1 2-1
Hallar las raíces enteras de los siguientes polinomios: 1) x 3 + 2x 2 - x - 2 Las raíces enteras se encuentran entre los divisores del término independiente del polinomio: ±1 y ±2. P(1) = 1 3 + 2 1 2-1
UNIDAD IV CONTENIDO TEMÁTICO
 UNIDAD IV CONTENIDO TEMÁTICO OPERACIONES CON FRACCIONES ALGEBRAICAS I.S.C. Alejandro de Fuentes Martínez 1 ESQUEMA-RESUMEN RESUMEN DE LA UNIDAD IV Conceptos Mínimo común múltiplo OPERACIONES CON FRACCIONES
UNIDAD IV CONTENIDO TEMÁTICO OPERACIONES CON FRACCIONES ALGEBRAICAS I.S.C. Alejandro de Fuentes Martínez 1 ESQUEMA-RESUMEN RESUMEN DE LA UNIDAD IV Conceptos Mínimo común múltiplo OPERACIONES CON FRACCIONES
UNA ECUACIÓN, SU GRADO Y SU SOLUCIÓN
 86 _ 087-098.qxd 7//07 : Página 88 IDENTIICAR OBJETIVO UNA ECUACIÓN, SU GRADO Y SU SOLUCIÓN NOMBRE: CURSO: ECHA: Dado el polinomio P(x) x +, ya sabemos cómo se calcula su valor numérico: x P() + x P( )
86 _ 087-098.qxd 7//07 : Página 88 IDENTIICAR OBJETIVO UNA ECUACIÓN, SU GRADO Y SU SOLUCIÓN NOMBRE: CURSO: ECHA: Dado el polinomio P(x) x +, ya sabemos cómo se calcula su valor numérico: x P() + x P( )
Unidad 1: Números reales.
 Unidad 1: Números reales. 1 Unidad 1: Números reales. 1.- Números racionales e irracionales Números racionales: Son aquellos que se pueden escribir como una fracción. 1. Números enteros 2. Números decimales
Unidad 1: Números reales. 1 Unidad 1: Números reales. 1.- Números racionales e irracionales Números racionales: Son aquellos que se pueden escribir como una fracción. 1. Números enteros 2. Números decimales
3º ESO POLINOMIOS DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa POLINOMIOS
 º ESO POLINOMIOS DEPARTAMENTO DE MATEMÁTICAS. POLINOMIOS 1.- POLINOMIOS Una expresión algebraica está formada por números y letras asociados por medio de las operaciones aritméticas (suma, resta, multiplicación,
º ESO POLINOMIOS DEPARTAMENTO DE MATEMÁTICAS. POLINOMIOS 1.- POLINOMIOS Una expresión algebraica está formada por números y letras asociados por medio de las operaciones aritméticas (suma, resta, multiplicación,
Comprueba que 5 2 es una raíz del polinomio 2x3 9x x 5. EJERCICIO RESUELTO. Entonces: x 3 + 2x x + 3 = ( x + 1) ( x 2 + x + 3)
 Polinomios 7. Teorema del resto. Factorización Polinomios Actividades Aprenderás a Identificar el resto de la división de un polinomio por un binomio de la forma a como el valor numérico para = a. Aplicar
Polinomios 7. Teorema del resto. Factorización Polinomios Actividades Aprenderás a Identificar el resto de la división de un polinomio por un binomio de la forma a como el valor numérico para = a. Aplicar
PRODUCTOS NOTABLES. Definición: son aquellos productos cuyo desarrollo se conocen fácilmente por simple observación. Y son:
 PRODUCTOS NOTABLES Definición: son aquellos productos cuyo desarrollo se conocen fácilmente por simple observación. Y son: Cuadrado de la suma de dos cantidades Cuadrado de la diferencia de dos cantidades
PRODUCTOS NOTABLES Definición: son aquellos productos cuyo desarrollo se conocen fácilmente por simple observación. Y son: Cuadrado de la suma de dos cantidades Cuadrado de la diferencia de dos cantidades
Polinomios. Cajón de Ciencias. Qué es un polinomio?
 Polinomios Qué es un polinomio? Si ya sabes lo que es un monomio, poco más hay que explicar: un polinomio es un conjunto de varios monomios que no pueden operarse entre sí. Si aún no sabes lo que es un
Polinomios Qué es un polinomio? Si ya sabes lo que es un monomio, poco más hay que explicar: un polinomio es un conjunto de varios monomios que no pueden operarse entre sí. Si aún no sabes lo que es un
POLINOMIOS. El grado de un monomio es la suma de todos los exponentes de las letras o variables.
 RESUMEN Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas
RESUMEN Expresiones algebraicas Trabajar en álgebra consiste en manejar relaciones numéricas en las que una o más cantidades son desconocidas. Estas cantidades se llaman variables, incógnitas o indeterminadas
Ejercicio 1 Completa: Monomio Coeficiente Parte literal Grado
 Soluciones a los ejercicios de Álgebra, primera parte: Ejercicio 1 Completa: Monomio Coeficiente Parte literal Grado 3xz 3 xz 3 1x zy 1 4 abc 1 5 x 5 3 x zy 6 4 abc 6 x 1 Ejercicio Halla el valor numérico
Soluciones a los ejercicios de Álgebra, primera parte: Ejercicio 1 Completa: Monomio Coeficiente Parte literal Grado 3xz 3 xz 3 1x zy 1 4 abc 1 5 x 5 3 x zy 6 4 abc 6 x 1 Ejercicio Halla el valor numérico
4º ESO POLINOMIOS DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa POLINOMIOS
 POLINOMIOS 1.- POLINOMIOS Una epresión algebraica está formada por números y letras asociados por medio de las operaciones aritméticas (suma, resta, multiplicación, división y potenciación). 1 t Ejemplo:
POLINOMIOS 1.- POLINOMIOS Una epresión algebraica está formada por números y letras asociados por medio de las operaciones aritméticas (suma, resta, multiplicación, división y potenciación). 1 t Ejemplo:
INSTITUCION EDUCATIVA LA PRESENTACION
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA Y LUIS LOPEZ TIPO DE GUIA: NIVELACION PERIODO GRADO FECHA DURACION 8 A/B Abril
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMATICAS ASIGNATURA: MATEMATICAS DOCENTE: HUGO HERNAN BEDOYA Y LUIS LOPEZ TIPO DE GUIA: NIVELACION PERIODO GRADO FECHA DURACION 8 A/B Abril
Tema 2: Polinomios. factorización de polinomios y algunas aplicaciones de dicha factorización.
 Tema 2: Polinomios. En este tema trabajaremos el álgebra y estudiaremos las expresiones algebraicas que son combinaciones de letras y números junto a los signos de las distintas operaciones que conocemos.
Tema 2: Polinomios. En este tema trabajaremos el álgebra y estudiaremos las expresiones algebraicas que son combinaciones de letras y números junto a los signos de las distintas operaciones que conocemos.
TEMA 3. POLINOMIOS Y FRACCIONES ALGEBRAICAS. Ficha 1. P x
 Ficha. Dados los siguientes polinomios, ordenarlos en orden decreciente, indicar cuál es su grado, decir cuántos términos tiene, señalar cuál es el término independiente, calcular su valor numérico para
Ficha. Dados los siguientes polinomios, ordenarlos en orden decreciente, indicar cuál es su grado, decir cuántos términos tiene, señalar cuál es el término independiente, calcular su valor numérico para
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo
 Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
Polinomios: Definición: Se llama polinomio en "x" de grado "n" a una expresión del tipo P (x) = a 0 x n + a 1 x n 1 +... + a n Donde n N (número natural) ; a 0, a 1, a 2,..., a n son coeficientes reales
Valor numérico de una expresión algebraica: Es el que se obtiene al sustituir las letras por números y calcular la operación resultante.
 POLIINOMIIOS.. OPERACIIONES.. RUFFIINII Expresión algebraica: Expresión en la que se operan números conocidos y desconocidos, representados por letras, a, b, c, x, y, z,..., que se denominan indeterminadas.
POLIINOMIIOS.. OPERACIIONES.. RUFFIINII Expresión algebraica: Expresión en la que se operan números conocidos y desconocidos, representados por letras, a, b, c, x, y, z,..., que se denominan indeterminadas.
TRABAJO PRÁCTICO Nº 4: POLINOMIOS
 TRABAJO PRÁCTICO Nº : POLINOMIOS EJERCICIOS A DESARROLLAR Clase ) Dados los polinomios reales P(x) =.x ; Q(x) = 3x3 x + y los polinomios complejos R(x) = i.x ; S(x) = x + ( + i).x i, calcular: a) 3x. P(x)
TRABAJO PRÁCTICO Nº : POLINOMIOS EJERCICIOS A DESARROLLAR Clase ) Dados los polinomios reales P(x) =.x ; Q(x) = 3x3 x + y los polinomios complejos R(x) = i.x ; S(x) = x + ( + i).x i, calcular: a) 3x. P(x)
3º ESO PMAR POLINOMIOS DEPARTAMENTO DE MATEMÁTICAS. SAGRADO CORAZÓN COPIRRAI_Julio César Abad Martínez-Losa POLINOMIOS
 º ESO PMAR POLINOMIOS DEPARTAMENTO DE MATEMÁTICAS. POLINOMIOS 1.- POLINOMIOS Una expresión algebraica está formada por números y letras asociados por medio de las operaciones aritméticas (suma, resta,
º ESO PMAR POLINOMIOS DEPARTAMENTO DE MATEMÁTICAS. POLINOMIOS 1.- POLINOMIOS Una expresión algebraica está formada por números y letras asociados por medio de las operaciones aritméticas (suma, resta,
BOLETÍN REPASO MATEMÁTICAS 3º ESO - 2ª PARTE
 BOLETÍN REPASO MATEMÁTICAS 3º ESO - ª PARTE Una expresión algebraica es toda combinación de números y letras unidos por los signos de las operaciones aritméticas: adición, sustracción, multiplicación,
BOLETÍN REPASO MATEMÁTICAS 3º ESO - ª PARTE Una expresión algebraica es toda combinación de números y letras unidos por los signos de las operaciones aritméticas: adición, sustracción, multiplicación,
TEMA 4. POLINOMIOS. Los números reales son polinomios de grado 0.
 TEMA 4. POLINOMIOS. ACCESO CICLO SUPERIOR 1) INTRODUCCIÓN. CONJUNTOS NUMÉRICOS. El concepto de número es tan antiguo o más que la propia civilización. El primer conjunto del que se tiene conocimiento es
TEMA 4. POLINOMIOS. ACCESO CICLO SUPERIOR 1) INTRODUCCIÓN. CONJUNTOS NUMÉRICOS. El concepto de número es tan antiguo o más que la propia civilización. El primer conjunto del que se tiene conocimiento es
TEMA: 5 ÁLGEBRA 3º ESO
 TEMA: 5 ÁLGEBRA 3º ESO 1. MONOMIO Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural. Ejemplo: x
TEMA: 5 ÁLGEBRA 3º ESO 1. MONOMIO Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural. Ejemplo: x
LA DIVISIBILIDAD. Luego, 24 es divisible entre 3. CÓMO SABER SI UN NÚMERO ES DIVISIBLE ENTRE OTRO, SIN HACER LA DIVISIÓN?
 LA DIVISIBILIDAD Qué entendemos por divisibilidad? Es la propiedad de que un número pueda ser dividido por otro un número exacto de veces o que el resto sea cero. Luego, 24 es divisible entre 3. CÓMO SABER
LA DIVISIBILIDAD Qué entendemos por divisibilidad? Es la propiedad de que un número pueda ser dividido por otro un número exacto de veces o que el resto sea cero. Luego, 24 es divisible entre 3. CÓMO SABER
1 x 5. Actividad nº1. Indique cuáles de estas expresiones son polinomios reales (con coeficientes reales) c) 5x 1 + x 4
 POLINOMIOS Alguna vez en la escuela media, en clases de Física, hemos visto expresiones tales como s t = v t + s 0 que representa la relación posición (s) de un móvil, que se desplaza en movimiento rectilíneo
POLINOMIOS Alguna vez en la escuela media, en clases de Física, hemos visto expresiones tales como s t = v t + s 0 que representa la relación posición (s) de un móvil, que se desplaza en movimiento rectilíneo
Desde la secundaria estamos acostumbrados a trabajar con polinomios, los cuales identificamos con expresiones de la forma
 Polinomios Desde la secundaria estamos acostumbrados a trabajar con polinomios, los cuales identificamos con expresiones de la forma p(x) = a 0 + a 1 x +... + a n x n (1) donde x es la variable y a 0,
Polinomios Desde la secundaria estamos acostumbrados a trabajar con polinomios, los cuales identificamos con expresiones de la forma p(x) = a 0 + a 1 x +... + a n x n (1) donde x es la variable y a 0,
