COMPENSACIÓN EN ADELANTO
|
|
|
- Esperanza Ayala Calderón
- hace 9 años
- Vistas:
Transcripción
1
2 COMPENSACIÓN EN ADELANTO Produce un mejoramiento razonable en la respuesta transitoria y un cambio pequeño en la precisión en estado estable. Puede acentuar los efectos del ruido de alta frecuencia. Aumenta el orden del sistema en (a menos que haya una cancelación entre el cero del compensador y un polo de la función de transferencia en lazo abierto no compensada).
3 CARACTERÍSTICAS DE LOS COMPENSADORES EN ADELANTO Considere un compensador de adelanto que tiene la función de transferencia: s + Ts + Kcα = K T c (0 < α < ) αts + s + αt Tiene un cero en s = /T y un polo en s = /(α T). Dado que 0 < α <, vemos que el cero siempre se ubica a la derecha del polo en el plano complejo. Para un valor pequeño de α, el polo se localiza lejos hacia la izquierda. Su valor mínimo se ubica, por lo general, cerca de Entonces, el adelanto de fase máximo que produce el compensador es de alrededor de 65º.
4 CARACTERÍSTICAS DE LOS COMPENSADORES EN ADELANTO En la figura se observa un compensador en adelanto cuando Kc = y α = 0.. Las frecuencias de esquina son ω = /T y ω = /(αt). De la figura se observa que ω m es la media geométrica de las dos frecuencias de esquina, o: logωm = log + log ωm = 2 T αt αt Por lo tanto, se concluye que el compensador en adelanto es básicamente un filtro paso altas.
5 DISEÑO DE COMPENSADORES DE ADELANTO BASADO EN EL ENFOQUE DE LA RESPUESTA EN FRECUENCIA. FUNCIÓN PRINCIPAL DEL COMPENSADOR DE ADELANTO: Volver a dar forma a la curva de respuesta en frecuencia a fin de ofrecer un ángulo de adelanto de fase suficiente para compensar el atraso de fase excesivo asociado con los componentes del sistema fijo. PROCEDIMIENTO Considere el sistema Suponiendo además que las especificaciones del desempeño se dan en términos del margen de fase, del margen de ganancia, de las constantes de error estático de velocidad, etc.
6 DISEÑO DE COMPENSADORES DE ADELANTO BASADO EN EL ENFOQUE DE LA RESPUESTA EN FRECUENCIA. PROCEDIMIENTO. Suponga el siguiente compensador de adelanto: s + Ts + G' () s = K T cα = Kc (0< α < ) Defina αts + s + αt Ts + Así, Gc () s = K α Ts + K α = K La función de transferencia en lazo abierto del sistema compensado es Ts + Ts + Ts + Gc () sgs () = K Gs () = KGs () = G () s αts + αts + αts + donde G () s = KG() s c
7 DISEÑO DE COMPENSADORES DE ADELANTO BASADO EN EL ENFOQUE DE LA RESPUESTA EN FRECUENCIA. PROCEDIMIENTO Determine la ganancia K que satisfaga el requerimiento sobre la constante estática de error determinada. 2. Usando la ganancia K determinada, dibuje las trazas de Bode de G (jω), el sistema con la ganancia ajustada pero sin compensar. Calcule el valor del margen de fase. 3. Determinar el ángulo de adelanto de fase φ necesario que se agregará al sistema. α 2 α 4. Determine el factor de atenuación α a partir de la ecuación: sinφm = = + α + α Establezca la frecuencia a la cual la magnitud del sistema no 2 Compensado G (jω) es igual a 20log(/ α). Seleccione ésta como la nueva frecuencia de cruce de ganancia. Esta frecuencia corresponde a ω m = /( α T), y el cambio de fase máximo φ m ocurre en ella.
8 DISEÑO DE COMPENSADORES DE ADELANTO BASADO EN EL ENFOQUE DE LA RESPUESTA EN FRECUENCIA. PROCEDIMIENTO 5. Determine las frecuencias de esquina del compensador de adelanto del modo siguiente: Cero del compensador de adelanto: ω = T Polo del compensador de adelanto: ω = αt 6. Usando el valor de K determinado en el paso y el de α establecido en el paso 4, calcule la constante Kc a partir de: K c K = α 7. Verifique el margen de ganancia para asegurarse de que es satisfactorio. De no serlo, repita el proceso de diseño modificando la ubicación de los polos y ceros del compensador hasta obtener un resultado satisfactorio.
9 EJEMPLO:
10
11
12
13
14
15
16
17 COMPENSACIÓN DE ATRASO La compensación de atraso produce un mejoramiento notable en la precisión en estado estable a costa de aumentar el tiempo de respuesta transitoria. Suprime los efectos de las señales de ruido a altas frecuencias. Aumenta el orden del sistema en (a menos que haya una cancelación entre el cero del compensador y un polo de la función de transferencia en lazo abierto no compensada). CARACTERÍSTICAS DE LOS COMPENSADORES DE ATRASO Considere un compensador de atraso que tiene la siguiente función de transferencia: s + Ts + Gc() s = K T cβ = Kc ( β > ) βts + s + βt
18 En el plano complejo, un compensador de atraso tiene un cero en s = /T y un polo en s = /(βt). El polo está a la derecha del cero. DISEÑO DE COMPENSADORES DE ATRASO BASADO EN EL ENFOQUE DE LA RESPUESTA EN FRECUENCIA. FUNCIÓN PRINCIPAL DEL COMPENSADOR DE ATRASO: La función principal de un compensador de atraso es proporcionar una atenuación en el rango de las frecuencias altas a fin de aportar un margen de fase suficiente al sistema. La característica de atraso de fase no afecta la compensación de atraso. PROCEDIMIENTO Considere el sistema Suponga además que Kc = y β = 0. Las frecuencias de esquina del compensador de atraso están en ω = /T y ω = /(βt).
19 DISEÑO DE COMPENSADORES DE ATRASO BASADO EN EL ENFOQUE DE LA RESPUESTA EN FRECUENCIA. PROCEDIMIENTO La magnitud del compensador de atraso se vuelve 0 (o 20dB) en frecuencias bajas y (o 0dB) en frecuencias altas. Por lo tanto, el compensador de atraso se comporta como un filtro pasa bajas.. Suponga el compensador de atraso: s + Ts + Gc() s = K T cβ = Kc ( β > ) βts + s + βt Defina K c β = K Gc () s = K Ts De modo que Ts + β +
20 DISEÑO DE COMPENSADORES DE ATRASO BASADO EN EL ENFOQUE DE LA RESPUESTA EN FRECUENCIA. PROCEDIMIENTO La función de transferencia del sistema compensado es: En donde: G () s = KG () s Ts + Ts + Ts + Gc () sgs () = K Gs () = KGs () = G () s βts + βts + βts + Determine la ganancia K que satisfaga el requerimiento en la constante de error estático establecida. Si el sistema no compensado G (jω) = KG(jω) no satisface las especificaciones en los márgenes de fase y de ganancia, encuentre el punto de frecuencia en el cual el ángulo de fase de la función de transferencia en lazo abierto sea igual a 80 más el margen de fase requerido. Éste es el margen de fase especificado entre 5 y 2. (La adición de entre 5 y 2 compensa el atraso de fase del compensador de atraso). Seleccione esta como la nueva frecuencia de cruce de ganancia.
21 DISEÑO DE COMPENSADORES DE ATRASO BASADO EN EL ENFOQUE DE LA RESPUESTA EN FRECUENCIA. PROCEDIMIENTO 3. Para evitar los efectos nocivos del atraso de fase producido por el compensador de atraso, el polo y el cero del compensador de atraso deben ubicarse mucho más abajo que la nueva frecuencia de cruce de ganancia. Por tanto, seleccione la frecuencia de esquina ω = /T (que corresponde al cero del compensador de atraso) entre una octava y una década por debajo de la nueva frecuencia de cruce de ganancia. (Si las constantes de tiempo del compensador de atraso no se vuelven demasiado grandes, se selecciona la esquina de frecuencia ω = /T una década por debajo de la nueva frecuencia de cruce de ganancia). 4. Determine la atenuación necesaria para disminuir la curva de magnitud a 0dB en la nueva frecuencia de cruce de ganancia. Considerando que esta atenuación es de 20log β, determine el valor de β. Luego se obtiene la otra frecuencia de esquina (que corresponde al polo del compensador de atraso) a partir de ω = /(β/t).
22 DISEÑO DE COMPENSADORES DE ATRASO BASADO EN EL ENFOQUE DE LA RESPUESTA EN FRECUENCIA. PROCEDIMIENTO 5. Usando el valor de K determinado en el paso y el de β obtenido en el paso 5, calcule la constante Kc a partir de K c = K β Los compensadores de atraso son, en esencia, filtros paso bajas. Por tanto, la compensación de atraso permite una ganancia alta en las frecuencias bajas (lo cual mejora el desempeño en estado estable) y reduce la ganancia en el rango de las frecuencias críticas más altas, a fin de mejorar el margen de fase.
23 EJEMPLO:
24
25
26
27
28
29 COMPENSACIÓN DE ATRASO-ADELANTO CARACTERÍSTICAS La compensación de atraso adelanto combina las características de la compensación de adelanto con las de la compensación de atraso. El uso de un compensador de atraso adelanto eleva el orden del sistema en 2 (a menos que haya una cancelación entre el cero, o los ceros, del compensador de atraso adelanto y el polo, o los polos, de la función de transferencia en lazo abierto no compensada) El sistema se vuelve más complejo Más difícil controlar el comportamiento de la respuesta transitoria
30 COMPENSACIÓN DE ATRASO-ADELANTO CARACTERÍSTICAS Considere el compensador de atraso adelanto obtenido mediante: G () s = K c El término: s+ s T + T γ s s + T + βt 2 c 2 s + T Ts + = ( γ > ) γ T s + γ s T + γ Produce el efecto de una red de adelanto. En donde γ > y β >. El término: s + T 2 T2s+ = β ( > ) β s + βts 2 + βt 2 Produce el efecto de una red de atraso.
31 Al diseñar un compensador de atraso adelanto es común seleccionar γ = β, más no es necesario. En general γ β. DISEÑO DE COMPENSADORES DE ATRASO-ADELANTO BASADO EN EL ENFOQUE DE LA RESPUESTA EN FRECUENCIA. Combinación de las técnicas de diseño analizadas en la compensación de adelanto y la compensación de atraso. Supongamos que el compensador de atraso adelanto tiene la forma siguiente: s+ s+ ( Ts + )( Ts 2 + ) T T2 Gc() s = Kc = K c T β s + ( β T 2 s ) s s β T βt2 Donde β >. s + T β s + T adelanto Añade un ángulo de adelanto de fase e incrementa el margen de fase en la frecuencia de cruce de ganancia. s + T2 s + βt 2 atraso Proporciona una atenuación cercana y por arriba de la frecuencia de cruce de ganancia y permite incremento de la ganancia en el rango de frecuencias bajas, mejorando el desempeño en estado estable.
32 DISEÑO DE COMPENSADORES DE ATRASO-ADELANTO BASADO EN EL ENFOQUE DE LA RESPUESTA EN FRECUENCIA. s+ s+ ( Ts + )( Ts 2 + ) T T2 Gc() s = Kc = K c T β s + ( β T 2 s ) s s β T βt2 Donde β >.
33 Ejemplo: Considere el sistema de realimentación unitaria cuya función de transferencia en lazo abierto es: K Gs () = ss ( + )( s+ 2) Se quiere que la constante de error estático de velocidad sea de 0seg Que el margen de fase sea de 50 y que el margen de ganancia sea de 0dB o más. Utilizando el compensador de atraso adelanto obtenido mediante: s+ s+ ( Ts + )( Ts 2 + ) T T2 Gc() s = Kc = K c T β s + ( β T 2 s ) s s β T βt2 La función de transferencia en lazo abierto del sistema compensado es G c (s)g(s). Dado que la ganancia K de la planta es ajustable, suponemos que Kc =. En este caso lim G ( s) = s 0 C
34 A partir del requerimiento en la constante de error estático de velocidad, obtenemos: K K Kv = lim sgc( s) G( s) = lim sgc( s) = = 0 s 0 s 0 ss ( + )( s + 2) 2 Por tanto, K = 20. A continuación se dibujan las trazas de Bode del sistema no compensado con K = 20. El margen del sistema no compensado es de 32, lo cual indica que el sistema es inestable.
35 El paso siguiente consiste en seleccionar una nueva frecuencia de cruce de ganancia. A partir de la curva del ángulo de fase para G(jω), observamos que en ω =.5 rad/seg. G( jω) = 80º Es conveniente elegir la nueva frecuencia de cruce de ganancia como de.5rad/seg, a fin de que el adelanto de ángulo de fase requerido en ω =.5 sea de alrededor de 50º, lo cual es muy posible mediante una sola red de atraso adelanto. Una vez seleccionada la frecuencia de cruce de ganancia como.5rad/seg determinamos la frecuencia de esquina de la parte de atraso de fase del compensador de atraso adelanto. Seleccionamos la frecuencia de esquina ω = /T2 que corresponde al cero de la parte de atraso de fase del compensador que se encuentra una década abajo de la nueva frecuencia de cruce de ganancia, o en ω = 0.5rad/seg. Para el compensador de adelanto, el máximo adelanto de ángulo de fase φm se obtiene mediante la ecuación: Observe que β = 0 corresponde a φm = Dado que β β sinφm = = necesitamos un margen de fase de 50, seleccionamos β + β + = 0. β
36 Así la frecuencia de esquina ω = /βt2 (que corresponde al polo de la parte de atraso de fase del compensador) se vuelve ω = 0.05 rad/seg. La función de transferencia de la parte de atraso de fase del compensador de atraso adelanto se vuelve por tanto: La parte de adelanto de fase se determina del modo s s+ = 0 siguiente: dado que la nueva frecuencia de cruce de s s+ ganancia es ω =.5rad/seg, a partir de las trazas de Bode G(j.5) es de 3 db. Por tanto si el compensador de atraso adelanto contribuye con 3dB en w =.5rad/seg, la nueva frecuencia de cruce de ganancia es la que se busca. A partir de este requerimiento, es posible dibujar una recta con una pendiente de 20dB/década y que pase por el punto ( 3dB,.5 rad/seg). Las intersecciones de esta línea y la línea 0dB con la línea 20dB determinan las frecuencias de esquina. Por tanto las frecuencias de esquina para la parte de adelanto son ω = 0.7rad/seg y ω = 7rad/seg. En este caso la función de transferencia de la parte de adelanto del compensador de atraso adelanto se vuelve: s s+ = s s+
37 Si combinamos las funciones de transferencia de las partes de atraso y de adelanto del compensador, obtenemos la función de transferencia del compensador de atraso adelanto. Dado que elegimos Kc =, tenemos que: G () s c s+ 0.7 s s+ 6.67s+ = = s+ 7 s s+ 66.7s+ Las curvas de magnitud y de ángulo de fase del compensador de atraso adelanto recién diseñado aparecen en la figura. La función de transferencia en lazo abierto del sistema compensado es: G () s G() s = c = ( s+ 0.7)( s+ 0.5) 20 ( s+ 7)( s+ 0.05) s( s+ )( s+ 2) 0(.43s+ )( 6.67s+ ) ( )( )( + )( ) s s s s s Las curvas de magnitud y de ángulo de fase del sistema anterior también aparecen en la figura.
38 El margen de fase del sistema compensado es de 50, el margen de ganancia es de 6dB y la constante de error estático de velocidad es de 0/seg, por tanto, se cumplen todos los requerimientos y el diseño queda terminado.
Tipos de Compensación
 - CONTROL DE PROCESOS (segundo cuatrimestre) - CONTROL AVANZADO y AUTOMATISMO Facultad de Ingeniería UNER Carrera: Bioingeniería Planes de estudios: 993 y 2008 Tipos de Compensación + Gc( Gp( + G ( + -
- CONTROL DE PROCESOS (segundo cuatrimestre) - CONTROL AVANZADO y AUTOMATISMO Facultad de Ingeniería UNER Carrera: Bioingeniería Planes de estudios: 993 y 2008 Tipos de Compensación + Gc( Gp( + G ( + -
Lectura 2: Diseño de Sistemas de Control mediante la Respuesta de Frecuencia
 SISEMAS DE ONROL AUOMÁIO DAI-EPN Lectura 2: Diseño de Sistemas de ontrol mediante la Respuesta de Frecuencia Lecturas recomendadas ap., pags. 74-759, Sistemas de ontrol Automático, KUO Benjamín, Séptima
SISEMAS DE ONROL AUOMÁIO DAI-EPN Lectura 2: Diseño de Sistemas de ontrol mediante la Respuesta de Frecuencia Lecturas recomendadas ap., pags. 74-759, Sistemas de ontrol Automático, KUO Benjamín, Séptima
CONTROL DIGITAL Catedrático: Dr. Manuel Adam Medina Alumno: Ing. Jaimes Maldonado José Luis
 Diseño de controladores por el método de respuesta en frecuencia de sistemas discretos. (método gráfico) CONTROL DIGITAL 07--0 Catedrático: Dr. Manuel Adam Medina Alumno: Ing. Jaimes Maldonado José Luis
Diseño de controladores por el método de respuesta en frecuencia de sistemas discretos. (método gráfico) CONTROL DIGITAL 07--0 Catedrático: Dr. Manuel Adam Medina Alumno: Ing. Jaimes Maldonado José Luis
TECNICAS DE DISEÑO Y COMPENSACION
 TECNICAS DE DISEÑO Y COMPENSACION Técnicas para sistemas SISO invariantes en el tiempo Basadas en el lugar de las raices y respuesta en frecuencia Especificaciones de funcionamiento Exactitud o precisión
TECNICAS DE DISEÑO Y COMPENSACION Técnicas para sistemas SISO invariantes en el tiempo Basadas en el lugar de las raices y respuesta en frecuencia Especificaciones de funcionamiento Exactitud o precisión
Autómatas y Sistemas de Control
 Autómatas y Sistemas de Control 3 o Ingeniería Industrial Soluciones problemas propuestos sobre diseño en el dominio de la frecuencia. PROBLEMA (Problema, apartado a), del examen de Junio de 2004) Dado
Autómatas y Sistemas de Control 3 o Ingeniería Industrial Soluciones problemas propuestos sobre diseño en el dominio de la frecuencia. PROBLEMA (Problema, apartado a), del examen de Junio de 2004) Dado
Tema 5 Acciones básicas de control. Controlador PID.
 Tema 5 Acciones básicas de control. Controlador PID. 1. Control en el dominio del tiempo. PID 2. Estudio del Lugar de las raíces 3. Control en el dominio de la frecuencia. Compensadores Control en el dominio
Tema 5 Acciones básicas de control. Controlador PID. 1. Control en el dominio del tiempo. PID 2. Estudio del Lugar de las raíces 3. Control en el dominio de la frecuencia. Compensadores Control en el dominio
1. Diseño de un compensador de adelanto de fase
 COMPENSADORES DE ADELANTO Y RETARDO 1 1. Diseño de un compensador de adelanto de fase El compensador de adelanto de fase persigue el aumento del margen de fase mediante la superposición de la curva de
COMPENSADORES DE ADELANTO Y RETARDO 1 1. Diseño de un compensador de adelanto de fase El compensador de adelanto de fase persigue el aumento del margen de fase mediante la superposición de la curva de
R. Alzate Universidad Industrial de Santander Bucaramanga, marzo de 2012
 Resumen de las Reglas de Diseño de Compensadores R. Alzate Universidad Industrial de Santander Buaramanga, marzo de 202 Sistemas de Control - 23358 Esuela de Ingenierías Elétria, Eletrónia y Teleomuniaiones
Resumen de las Reglas de Diseño de Compensadores R. Alzate Universidad Industrial de Santander Buaramanga, marzo de 202 Sistemas de Control - 23358 Esuela de Ingenierías Elétria, Eletrónia y Teleomuniaiones
Control Automático. Compensadores de adelanto en el dominio de la frecuencia
 Control Automático Compensadores de adelanto en el dominio de la frecuencia Contenido Introducción Estrategia Ecuaciones del compensador de adelanto Cálculo de un compensador de adelanto para corrección
Control Automático Compensadores de adelanto en el dominio de la frecuencia Contenido Introducción Estrategia Ecuaciones del compensador de adelanto Cálculo de un compensador de adelanto para corrección
Tema 5. Análisis de la Respuesta Frecuencial de Sistemas LTI. Automática. 2º Curso del Grado en Ingeniería en Tecnología Industrial
 Tema 5. Análisis de la Respuesta Frecuencial de Sistemas LTI Automática 2º Curso del Grado en Ingeniería en Tecnología Industrial Contenido TEMA 5.- Análisis de respuesta en frecuencia 5.1. Análisis de
Tema 5. Análisis de la Respuesta Frecuencial de Sistemas LTI Automática 2º Curso del Grado en Ingeniería en Tecnología Industrial Contenido TEMA 5.- Análisis de respuesta en frecuencia 5.1. Análisis de
LABORATORIO DE SISTEMAS DE CONTROL AUTOMÁTICO PRÁCTICA N 10
 ESCUELA POLITÉCNICA NACIONAL Campus Politécnico "J. Rubén Orellana R." FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA Carrera de Ingeniería Electrónica y Control 1. TEMA LABORATORIO DE SISTEMAS DE CONTROL
ESCUELA POLITÉCNICA NACIONAL Campus Politécnico "J. Rubén Orellana R." FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA Carrera de Ingeniería Electrónica y Control 1. TEMA LABORATORIO DE SISTEMAS DE CONTROL
Lugar Geométrico de las Raíces
 ELC-33103 Teoría de Control Lugar Geométrico de las Raíces Prof. Francisco M. Gonzalez-Longatt [email protected] http://www.giaelec.org/fglongatt/sp.htm 1. Introducción La característica básica de la
ELC-33103 Teoría de Control Lugar Geométrico de las Raíces Prof. Francisco M. Gonzalez-Longatt [email protected] http://www.giaelec.org/fglongatt/sp.htm 1. Introducción La característica básica de la
Tecnicas de diseño y compensación
 Capítulo 8 Tecnicas de diseño y compensación El objetivo primordial de esta sección es presentar algunos procedimientos para el diseño y compensación de sistemas de control lineales, invariantes en el
Capítulo 8 Tecnicas de diseño y compensación El objetivo primordial de esta sección es presentar algunos procedimientos para el diseño y compensación de sistemas de control lineales, invariantes en el
Departamento de Ingenierías Eléctrica y Electrónica Universidad del Norte
 [email protected] Departamento de Ingenierías Eléctrica y Electrónica Universidad del Norte La respuesta transitoria de un sistema en lazo cerrado se relaciona estrechamente con la localización
[email protected] Departamento de Ingenierías Eléctrica y Electrónica Universidad del Norte La respuesta transitoria de un sistema en lazo cerrado se relaciona estrechamente con la localización
SISTEMAS DE CONTROL ANÁLISIS Y DISEÑO DE SISTEMAS DE CONTROL EN EL DOMINIO DE LA FRECUENCIA. Profesor: Adrián Peidró
 SISTEMAS DE CONTROL PRÁCTICAS DE SISTEMAS DE CONTROL ANÁLISIS Y DISEÑO DE SISTEMAS DE CONTROL EN EL DOMINIO DE LA FRECUENCIA Profesor: Adrián Peidró ([email protected]) OBJETIVOS Afianzar los conocimientos
SISTEMAS DE CONTROL PRÁCTICAS DE SISTEMAS DE CONTROL ANÁLISIS Y DISEÑO DE SISTEMAS DE CONTROL EN EL DOMINIO DE LA FRECUENCIA Profesor: Adrián Peidró ([email protected]) OBJETIVOS Afianzar los conocimientos
Diseño de Compensadores utilizando L.G.R.
 Diseño de omensadores utilizando L..R. omensadores en Atraso Un comensador en atraso aumenta la ganancia del lazo cerrado sin modificar areciablemente el lugar geométrico de las raíces y tiene la siguiente
Diseño de omensadores utilizando L..R. omensadores en Atraso Un comensador en atraso aumenta la ganancia del lazo cerrado sin modificar areciablemente el lugar geométrico de las raíces y tiene la siguiente
Un sistema con realimentación unitaria tiene una función de transferencia en lazo abierto
 Un sistema con realimentación unitaria tiene una función de transferencia en lazo abierto G p ( s) k s( s + )( s + 5) a)para el sistema en lazo abierto, y suponiendo el valor k : Obtener la expresión analítica
Un sistema con realimentación unitaria tiene una función de transferencia en lazo abierto G p ( s) k s( s + )( s + 5) a)para el sistema en lazo abierto, y suponiendo el valor k : Obtener la expresión analítica
1. Método del Lugar de las Raíces
 . Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA... 3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES... 0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
. Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA... 3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES... 0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
1 Problemas Resueltos
 1) Para un sistema de control de retroaliementación unitaria se conoce el diagrama de bode de la función de transferencia a lazo abierto, la cual se muestra en la Fig. 1.1. A partir esta información se
1) Para un sistema de control de retroaliementación unitaria se conoce el diagrama de bode de la función de transferencia a lazo abierto, la cual se muestra en la Fig. 1.1. A partir esta información se
Tema 6 Control de sistemas de orientación de antenas y de telescopios
 Tema 6 Control de sistemas de orientación de antenas y de telescopios. Métodos de control de sistemas de orientación 2. Métodos de ajuste de PIDs 3. Estudio de las perturbaciones 4. Técnicas y diseño de
Tema 6 Control de sistemas de orientación de antenas y de telescopios. Métodos de control de sistemas de orientación 2. Métodos de ajuste de PIDs 3. Estudio de las perturbaciones 4. Técnicas y diseño de
Método aproximado para conocer la localización de las raíces de la ecuación característica con respecto a los semiplanos izquierdo y derecho. (12.
 1. Criterio de estabilidad de Nyquist 1.1 Gráfica de Nyquist Gráfica de L(jω) G(jω)H(jω) en coordenadas polares de Im[L(jω)], Re[L(jω)] con ω variando desde hasta 0. Características: provee información
1. Criterio de estabilidad de Nyquist 1.1 Gráfica de Nyquist Gráfica de L(jω) G(jω)H(jω) en coordenadas polares de Im[L(jω)], Re[L(jω)] con ω variando desde hasta 0. Características: provee información
Como ejemplo, consideremos la función compleja P(s)= s 2 +1.
 Criterio de Estabilidad de Nyquist El criterio de Estabilidad de Nyquist está basado en un teorema de la variable compleja. Para entender este criterio primero se utilizarán los conceptos de transferencia
Criterio de Estabilidad de Nyquist El criterio de Estabilidad de Nyquist está basado en un teorema de la variable compleja. Para entender este criterio primero se utilizarán los conceptos de transferencia
Ejercicios de examen: frecuencial
 EJERCICIO 1 Los diagramas mostrados en la hoja adjunta representan respectivamente el modelo de un sistema que se pretende controlar y el correspondiente a dicho sistema con el regulador. Se pide: a) Qué
EJERCICIO 1 Los diagramas mostrados en la hoja adjunta representan respectivamente el modelo de un sistema que se pretende controlar y el correspondiente a dicho sistema con el regulador. Se pide: a) Qué
Respuesta en frecuencia. Elizabeth Villota
 Elizabeth Villota 1 Desempeño en el dominio de la frecuencia SLIT 2do orden (masa-resorte-amortiguador) Forma espacio de estados Forma función de transferencia respuesta a un escalón diagramas de Bode
Elizabeth Villota 1 Desempeño en el dominio de la frecuencia SLIT 2do orden (masa-resorte-amortiguador) Forma espacio de estados Forma función de transferencia respuesta a un escalón diagramas de Bode
Automá ca. Ejercicios Capítulo7.1.AnálisisFrecuencial(Parte1)
 Automáca Ejercicios Capítulo7.1.AnálisisFrecuencial(Parte1) JoséRamónLlataGarcía EstherGonzálezSarabia DámasoFernándezPérez CarlosToreFerero MaríaSandraRoblaGómez DepartamentodeTecnologíaElectrónica eingenieríadesistemasyautomáca
Automáca Ejercicios Capítulo7.1.AnálisisFrecuencial(Parte1) JoséRamónLlataGarcía EstherGonzálezSarabia DámasoFernándezPérez CarlosToreFerero MaríaSandraRoblaGómez DepartamentodeTecnologíaElectrónica eingenieríadesistemasyautomáca
Sistemas Control Embebidos e Instrumentación Electrónica UNIVERSIDAD EAFIT Semestre 2010/2 2009/2
 DIAGRAMA DE BODE Semestre 2010/2 El Diagrama de BODE se conforma por dos gráficas logarítmicas de: La magnitud de una función de transferencia senoidal: 20log G(jw) ; La unidad de medida que se usa, es
DIAGRAMA DE BODE Semestre 2010/2 El Diagrama de BODE se conforma por dos gráficas logarítmicas de: La magnitud de una función de transferencia senoidal: 20log G(jw) ; La unidad de medida que se usa, es
Unidad V Respuesta de los sistemas de control
 Unidad V Respuesta de los sistemas de control MC Nicolás Quiroz Hernández Un controlador automático compara el valor real de la salida de una planta con la entrada de referencia (el valor deseado), determina
Unidad V Respuesta de los sistemas de control MC Nicolás Quiroz Hernández Un controlador automático compara el valor real de la salida de una planta con la entrada de referencia (el valor deseado), determina
= = Amplificador inversor. Considere el amplificador operacional de la figura Obtengamos el voltaje de salida
 Amplificadores operacionales. Los amplificadores operacionales, también conocidos como amp ops, se usan con frecuencia para amplificar las señales de los circuitos Los amp ops también se usan con frecuencia
Amplificadores operacionales. Los amplificadores operacionales, también conocidos como amp ops, se usan con frecuencia para amplificar las señales de los circuitos Los amp ops también se usan con frecuencia
Nombre: Carné Ordinal. Parte I preguntas (1 punto c/u) Escriba la respuesta en el espacio indicado o encierre en un círculo la respuesta correcta:
 INSTITUTO TECNOLÓGICO DE COSTA RICA II SEMESTRE 2013 ESCUELA DE INGENIERIA EN ELECTRÓNICA CURSO: EL-5408 CONTROL AUTOMÁTICO MEDIO: Examen 3 PROF: ING. EDUARDO INTERIANO Nombre: Carné Ordinal Parte I preguntas
INSTITUTO TECNOLÓGICO DE COSTA RICA II SEMESTRE 2013 ESCUELA DE INGENIERIA EN ELECTRÓNICA CURSO: EL-5408 CONTROL AUTOMÁTICO MEDIO: Examen 3 PROF: ING. EDUARDO INTERIANO Nombre: Carné Ordinal Parte I preguntas
Sistemas Realimentados Simples Estabilidad de Sistemas Contínuos Diagramas de Bode
 Sistemas Realimentados Simples Estabilidad de Sistemas Contínuos Diagramas de Bode p.1/40 Sistema Contínuo U(s) E(s) K G(s) Y + (s) H(s) Figura 1: Sistema contínuo retroalimentado simple F (s) = Y (s)
Sistemas Realimentados Simples Estabilidad de Sistemas Contínuos Diagramas de Bode p.1/40 Sistema Contínuo U(s) E(s) K G(s) Y + (s) H(s) Figura 1: Sistema contínuo retroalimentado simple F (s) = Y (s)
Control Automático. Regulador PID y ajuste del PID. Eduardo Interiano
 Control Automático Regulador PID y ajuste del PID Eduardo Interiano Contenido Regulador PID PID ideal PID real Ajuste empírico del PID (Ziegler-Nichol Ejemplos Ejercicios Referencias 2 El PID ideal El
Control Automático Regulador PID y ajuste del PID Eduardo Interiano Contenido Regulador PID PID ideal PID real Ajuste empírico del PID (Ziegler-Nichol Ejemplos Ejercicios Referencias 2 El PID ideal El
Diseño de Controladores I.
 Departamento de Ingeniería Eléctrica Universidad de Magallanes. Apuntes del curso de Control Automático Roberto Cárdenas Dobson Ingeniero Electricista Msc. Ph.D. Profesor de la asignatura Este apunte se
Departamento de Ingeniería Eléctrica Universidad de Magallanes. Apuntes del curso de Control Automático Roberto Cárdenas Dobson Ingeniero Electricista Msc. Ph.D. Profesor de la asignatura Este apunte se
PROBLEMAS TEMA 2 TEORÍA DE LA APROXIMACIÓN
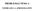 PROBLEMAS TEMA TEORÍA DE LA APROXIMACIÓN PROBLEMA : Determinar la función de transferencia de un filtro paso bajo máximamente plano que cumplan las especificaciones de la figura: a) Determinar el orden
PROBLEMAS TEMA TEORÍA DE LA APROXIMACIÓN PROBLEMA : Determinar la función de transferencia de un filtro paso bajo máximamente plano que cumplan las especificaciones de la figura: a) Determinar el orden
CURSO CONTROL APLICADO- MARCELA VALLEJO VALENCIA-ITM RESPUESTA EN EL TIEMPO
 RESPUESTA EN EL TIEMPO BUENO, YA TENGO UN MODELO MATEMÁTICO. Y AHORA QUÉ? Vamos a analizar el comportamiento del sistema. ENTRADA PLANTA SALIDA NO SE COMO VA A SER. NO LO PUEDO PREDECIR. NO LA PUEDO DESCRIBIR
RESPUESTA EN EL TIEMPO BUENO, YA TENGO UN MODELO MATEMÁTICO. Y AHORA QUÉ? Vamos a analizar el comportamiento del sistema. ENTRADA PLANTA SALIDA NO SE COMO VA A SER. NO LO PUEDO PREDECIR. NO LA PUEDO DESCRIBIR
Análisis de la Estabilidad de un Sistema Realimentado Se trata de analizar la estabilidad del sistema realimentado neativamente, M(, a partir de la re
 Tema 7 Análisis Frecuencial de los Sistemas Realimentados Gijón - Junio 5 1 Indice 7.1. Análisis de la estabilidad de un sistemas realimentado 7.. Maren de ase y de anancia 7..1. Diarama de Bode 7... Diarama
Tema 7 Análisis Frecuencial de los Sistemas Realimentados Gijón - Junio 5 1 Indice 7.1. Análisis de la estabilidad de un sistemas realimentado 7.. Maren de ase y de anancia 7..1. Diarama de Bode 7... Diarama
Caso Resuelto 4 Análisis en el Dominio de la Frecuencia realizado con Excel
 Caso Resuelto 4 Para realizar un análisis completo en el dominio de la frecuencia se necesita construir las gráficas: Polar de Nyquist, Diagramas de Bode de Lazo Abierto, Diagramas de Bode de Lazo Cerrado,
Caso Resuelto 4 Para realizar un análisis completo en el dominio de la frecuencia se necesita construir las gráficas: Polar de Nyquist, Diagramas de Bode de Lazo Abierto, Diagramas de Bode de Lazo Cerrado,
Introducción al control de fuentes conmutadas.
 Introducción al control de fuentes conmutadas. En una fuente conmutada ideal la tensión de salida es una función de la tensión de entrada y del valor del ciclo de trabajo definido. En la práctica existirán
Introducción al control de fuentes conmutadas. En una fuente conmutada ideal la tensión de salida es una función de la tensión de entrada y del valor del ciclo de trabajo definido. En la práctica existirán
Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control
 Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control Elizabeth Villota Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 1 Modelado Modelo: representación
Lugar Geométrico de las Raíces Herramienta para diseño de sistemas de control Elizabeth Villota Curso: Ingeniería de Control (MT221) Facultad de Ingeniería Mecánica UNI-FIM 1 Modelado Modelo: representación
Ingeniería de Control I Tema 11. Reguladores PID
 Ingeniería de Control I Tema 11 Reguladores PID 1 Tema 11. Reguladores PID Introducción Especificaciones de funcionamiento Acciones básicas de control Ajuste empírico de reguladores. Métodos de Ziegler-
Ingeniería de Control I Tema 11 Reguladores PID 1 Tema 11. Reguladores PID Introducción Especificaciones de funcionamiento Acciones básicas de control Ajuste empírico de reguladores. Métodos de Ziegler-
Escuela de Ingeniería Eléctrica. Materia: Teoría de Control (E )
 Escuela de Ingeniería Eléctrica Departamento de electricidad aplicada Materia: Teoría de Control (E-4.26.1) Síntesis de Correctores en Reacción Publicación E.4.26.1-TE-03B-0 Marzo de 2013 Carrera: Ingeniería
Escuela de Ingeniería Eléctrica Departamento de electricidad aplicada Materia: Teoría de Control (E-4.26.1) Síntesis de Correctores en Reacción Publicación E.4.26.1-TE-03B-0 Marzo de 2013 Carrera: Ingeniería
1 Problemas Resueltos
 1) Con la intención de plantear mejoras en un sistema de control de composición, se realizaron experiencias sobre el sistema a lazo abierto y se obtuvo su respuesta frecuencial, la cual se muestra en la
1) Con la intención de plantear mejoras en un sistema de control de composición, se realizaron experiencias sobre el sistema a lazo abierto y se obtuvo su respuesta frecuencial, la cual se muestra en la
6.1. Condición de magnitud y ángulo
 Capítulo 6 Lugar de las raíces La respuesta transitoria de un sistema en lazo cerrado, está ligada con la ubicación de los polos de lazo cerrado en el plano complejo S. Si el sistema tiene una ganancia
Capítulo 6 Lugar de las raíces La respuesta transitoria de un sistema en lazo cerrado, está ligada con la ubicación de los polos de lazo cerrado en el plano complejo S. Si el sistema tiene una ganancia
10. Diseño avanzado de controladores SISO
 10. Diseño avanzado de controladores SISO Parte 2 Panorama de la Clase: Repaso: Parametrización Afín (PA) Consideraciones de diseño: grado relativo rechazo de perturbaciones esfuerzo de control robustez
10. Diseño avanzado de controladores SISO Parte 2 Panorama de la Clase: Repaso: Parametrización Afín (PA) Consideraciones de diseño: grado relativo rechazo de perturbaciones esfuerzo de control robustez
Tema 5 Estabilidad y Compensación
 CIRCUITOS ANALÓGICOS (SEGUNDO CURSO) Tema 5 Estabilidad y Compensación Sebastián López y José Fco. López Instituto Universitario de Microelectrónica Aplicada (IUMA) Universidad de Las Palmas de Gran Canaria
CIRCUITOS ANALÓGICOS (SEGUNDO CURSO) Tema 5 Estabilidad y Compensación Sebastián López y José Fco. López Instituto Universitario de Microelectrónica Aplicada (IUMA) Universidad de Las Palmas de Gran Canaria
Análisis y diseño de sistemas de control por el método de la respuesta en frecuencia
 Análisis y diseño de sistemas de control por el método de la respuesta en frecuencia 7-1 Introducción Con el término respuesta en frecuencia, se quiere hacer referencia a la respuesta de un sistema en
Análisis y diseño de sistemas de control por el método de la respuesta en frecuencia 7-1 Introducción Con el término respuesta en frecuencia, se quiere hacer referencia a la respuesta de un sistema en
COLECCIÓN DE PROBLEMAS DE EXÁMENES DE INGENIERÍA DE CONTROL
 COLECCIÓN DE PROBLEMAS DE EXÁMENES DE INGENIERÍA DE CONTROL A continuación se incluyen preguntas de examen de los últimos años, tanto de teoría como de problemas. Lo indicado entre paréntesis es la puntuación
COLECCIÓN DE PROBLEMAS DE EXÁMENES DE INGENIERÍA DE CONTROL A continuación se incluyen preguntas de examen de los últimos años, tanto de teoría como de problemas. Lo indicado entre paréntesis es la puntuación
ANALISIS EN FRECUENCIA
 ANALISIS EN FRECUENCIA Con el término respuesta en frecuencia, nos referimos a la respuesta de un sistema en estado estable a una entrada senoidal. En los métodos de la respuesta en frecuencia, la frecuencia
ANALISIS EN FRECUENCIA Con el término respuesta en frecuencia, nos referimos a la respuesta de un sistema en estado estable a una entrada senoidal. En los métodos de la respuesta en frecuencia, la frecuencia
Orden de un sistema. El orden de un sistema está definido por el grado de su ecuación característica
 ORDEN DE UN SISTEMA Orden de un sistema El orden de un sistema está definido por el grado de su ecuación característica Normalmente la ecuación característica (denominador) de un sistema tiene mayor grado
ORDEN DE UN SISTEMA Orden de un sistema El orden de un sistema está definido por el grado de su ecuación característica Normalmente la ecuación característica (denominador) de un sistema tiene mayor grado
Control Automático I - Certamen 2 Pauta de Correción
 Control Automático I - Certamen 2 Pauta de Correción 7 de Septiembre 215 1. 1.1. Un sistema electro-mecánico tiene el modelo nominal G (s) = 1 (s+2), cuya salida es la velocidad angular de un eje. Los
Control Automático I - Certamen 2 Pauta de Correción 7 de Septiembre 215 1. 1.1. Un sistema electro-mecánico tiene el modelo nominal G (s) = 1 (s+2), cuya salida es la velocidad angular de un eje. Los
4. Análisis de Sistemas Realimentados
 4. Análisis de Sistemas Realimentados Parte 2 Panorama: Estabilidad y respuesta en frecuencia El criterio de estabilidad de Nyquist Márgenes de estabilidad Robustez CAUT1 Clase 6 1 Estabilidad y respuesta
4. Análisis de Sistemas Realimentados Parte 2 Panorama: Estabilidad y respuesta en frecuencia El criterio de estabilidad de Nyquist Márgenes de estabilidad Robustez CAUT1 Clase 6 1 Estabilidad y respuesta
INSTITUTO POLITÉCNICO NACIONAL Escuela Superior de Ingeniería Mecánica y Eléctrica
 INSTITUTO POLITÉCNICO NACIONAL Escuela Superior de Ingeniería Mecánica y Eléctrica Ingeniería en Control y Automatización TEORÍA DE CONTROL 1: GUÍA PARA EL EXAMEN EXTRAORDINARIO (TEORÍA) Nombre: Grupo
INSTITUTO POLITÉCNICO NACIONAL Escuela Superior de Ingeniería Mecánica y Eléctrica Ingeniería en Control y Automatización TEORÍA DE CONTROL 1: GUÍA PARA EL EXAMEN EXTRAORDINARIO (TEORÍA) Nombre: Grupo
4.3 Respuesta en frecuencia de los sistemas lineales de segundo orden de tiempo continuo sin ceros
 4.3 Respuesta en frecuencia de los sistemas lineales de segundo orden de tiempo continuo sin ceros 93 4.3 Respuesta en frecuencia de los sistemas lineales de segundo orden de tiempo continuo sin ceros
4.3 Respuesta en frecuencia de los sistemas lineales de segundo orden de tiempo continuo sin ceros 93 4.3 Respuesta en frecuencia de los sistemas lineales de segundo orden de tiempo continuo sin ceros
Sintonización de controladores por ubicación de polos y ceros
 Sintonización de controladores por ubicación de polos y ceros Leonardo J. Marín, Víctor M. Alfaro Departamento de Automática, Escuela de Ingeniería Eléctrica, Universidad de Costa Rica Apartado postal
Sintonización de controladores por ubicación de polos y ceros Leonardo J. Marín, Víctor M. Alfaro Departamento de Automática, Escuela de Ingeniería Eléctrica, Universidad de Costa Rica Apartado postal
1. Compensación com PI
 CESÁREO RAIMÚNDEZ.. Ejemplo -. La planta. Compensación com PI G p (s) = (s + 3) 2 + 2 2 debe compensarse de modo que en lazo cerrado exhiba las características:. Error nulo en régimen permanente para entrada
CESÁREO RAIMÚNDEZ.. Ejemplo -. La planta. Compensación com PI G p (s) = (s + 3) 2 + 2 2 debe compensarse de modo que en lazo cerrado exhiba las características:. Error nulo en régimen permanente para entrada
Automá ca. Ejercicios Capítulo7.2.AnálisisFrecuencial(Parte2)
 Automáca Ejercicios Capítulo7..AnálisisFrecuencial(Parte) JoséRamónLlataGarcía EstherGonzálezSarabia DámasoFernándezPérez CarlosToreFerero MaríaSandraRoblaGómez DepartamentodeTecnologíaElectrónica eingenieríadesistemasyautomáca
Automáca Ejercicios Capítulo7..AnálisisFrecuencial(Parte) JoséRamónLlataGarcía EstherGonzálezSarabia DámasoFernándezPérez CarlosToreFerero MaríaSandraRoblaGómez DepartamentodeTecnologíaElectrónica eingenieríadesistemasyautomáca
Determinar el comportamiento transitorio y estacionario del sistema. Especificar e identificar las condiciones de operación
 Análisis de estabilidad Determinar el comportamiento transitorio y estacionario del sistema Especificar e identificar las condiciones de operación El primer paso al analizar un sistema de control es establecer
Análisis de estabilidad Determinar el comportamiento transitorio y estacionario del sistema Especificar e identificar las condiciones de operación El primer paso al analizar un sistema de control es establecer
Serie 10 ESTABILIDAD
 Serie 0 ESTABILIDAD Condición de estabilidad U u Gu U R r + + - Gc Gv Gp C G V G P + c C H G( G (. G (. G (. H ( C V P + G( 0 G( G φ 80 Localización de las raíces Plano s E S T A B L E I N E S T A B L
Serie 0 ESTABILIDAD Condición de estabilidad U u Gu U R r + + - Gc Gv Gp C G V G P + c C H G( G (. G (. G (. H ( C V P + G( 0 G( G φ 80 Localización de las raíces Plano s E S T A B L E I N E S T A B L
19. DISEÑO DE CONTROLADORES
 381 19. DISEÑO DE CONTROLADORES 19.1. INTRODUCCION Con los diagramas de Bode de la respuesta de un lazo abierto se pueden diseñar controladores con las especificaciones del margen de ganancia, el margen
381 19. DISEÑO DE CONTROLADORES 19.1. INTRODUCCION Con los diagramas de Bode de la respuesta de un lazo abierto se pueden diseñar controladores con las especificaciones del margen de ganancia, el margen
Sistemas de Control. UNIVERSIDAD NACIONAL DE INGENIERIA Facultad de Electrotecnia y Computación. Docente: Alejandro A Méndez T
 UNIVERSIDAD NACIONAL DE INGENIERIA Facultad de Electrotecnia y Computación Docente: Alejandro T 009 Prof. Titular FEC - UNI Sistemas de Control Asistente: Yamil O Jiménez L Programa PIED VRAC - UNI Diseño
UNIVERSIDAD NACIONAL DE INGENIERIA Facultad de Electrotecnia y Computación Docente: Alejandro T 009 Prof. Titular FEC - UNI Sistemas de Control Asistente: Yamil O Jiménez L Programa PIED VRAC - UNI Diseño
Control Automático Introducción
 Control Automático Introducción Contenido Qué es control automático? Tareas y objetivos del control automático Estructuras de los circuitos de regulación Tipos de regulación Efecto de las perturbaciones
Control Automático Introducción Contenido Qué es control automático? Tareas y objetivos del control automático Estructuras de los circuitos de regulación Tipos de regulación Efecto de las perturbaciones
Kindergarten de Diseño de Controladores
 Departamento de Ingeniería Eléctrica Universidad de Magallanes Apuntes del curso de Control Automático Roberto Cárdenas Dobson Ingeniero Electricista Msc. Ph.D. Profesor de la asignatura Este apunte se
Departamento de Ingeniería Eléctrica Universidad de Magallanes Apuntes del curso de Control Automático Roberto Cárdenas Dobson Ingeniero Electricista Msc. Ph.D. Profesor de la asignatura Este apunte se
0.1. Error en Estado Estacionario
 0. Error en Estado Estacionario 0.. Error en Estado Estacionario La respuesta permanente es aquella que se alcanza cuando el sistema se establece y es muy importante su estudio pues informa lo que sucede
0. Error en Estado Estacionario 0.. Error en Estado Estacionario La respuesta permanente es aquella que se alcanza cuando el sistema se establece y es muy importante su estudio pues informa lo que sucede
Escuela de Ingeniería Eléctrica. Departamento de electricidad aplicada. Materia: Teoría de Control (E )
 Escuela de Ingeniería Eléctrica Departamento de electricidad aplicada Materia: Teoría de Control (E-4.26.1) Publicación E.4.26.1-TE-02-0 Marzo de 2012 CONTENIDO TEMÁTICO 1. INTRODUCCIÓN:... 3 2. CLASIFICACIÓN
Escuela de Ingeniería Eléctrica Departamento de electricidad aplicada Materia: Teoría de Control (E-4.26.1) Publicación E.4.26.1-TE-02-0 Marzo de 2012 CONTENIDO TEMÁTICO 1. INTRODUCCIÓN:... 3 2. CLASIFICACIÓN
6. Análisis en el dominio de la frecuencia. Teoría de Control
 6. Análisis en el dominio de la frecuencia Teoría de Control Introducción El término respuesta en frecuencia, indica la respuesta en estado estacionario de un sistema a una entrada senoidal. La respuesta
6. Análisis en el dominio de la frecuencia Teoría de Control Introducción El término respuesta en frecuencia, indica la respuesta en estado estacionario de un sistema a una entrada senoidal. La respuesta
CONTROL BÁSICO. Sistemas de Control Realimentados. Coeficientes estáticos de error. Facultad de Ingeniería - UNER. Asignaturas: Control Básico 1
 CONTROL BÁSICO TEMAS: - Diseño de reguladores en bucle cerrado or método frecuencial Facultad de Ingeniería UNER Carrera: Bioingeniería Planes de estudios: 2008 y 993 Sistemas de Control Realimentados
CONTROL BÁSICO TEMAS: - Diseño de reguladores en bucle cerrado or método frecuencial Facultad de Ingeniería UNER Carrera: Bioingeniería Planes de estudios: 2008 y 993 Sistemas de Control Realimentados
Lugar Geométrico de las Raíces o Método de Evans
 Lugar Geométrico de las Raíces o Método de Evans Lugar de la Raíz El lugar de la raíz (root locus es un método gráfico de encontrar la posición de los polos de lazo cerrado de la función de transferencia:
Lugar Geométrico de las Raíces o Método de Evans Lugar de la Raíz El lugar de la raíz (root locus es un método gráfico de encontrar la posición de los polos de lazo cerrado de la función de transferencia:
3. Modelos, señales y sistemas. Panorama Obtención experimental de modelos Respuesta en frecuencia Diagramas de Bode
 3. Modelos, señales y sistemas Panorama Obtención experimental de modelos Respuesta en frecuencia Diagramas de Bode CAUT1 Clase 4 1 Obtención experimental de modelos Muchos sistemas en la práctica pueden
3. Modelos, señales y sistemas Panorama Obtención experimental de modelos Respuesta en frecuencia Diagramas de Bode CAUT1 Clase 4 1 Obtención experimental de modelos Muchos sistemas en la práctica pueden
Unidad Temática 9: Análisis y Diseño de Sistemas de Control a Lazo Cerrado
 Control Automático Ing. Eléctrica Página 1 de 17 Unidad Temática 9: Análisis y Diseño de Sistemas de Control a Lazo Cerrado Algoritmos de Control: Un algoritmo de control se encarga de monitorear el valor
Control Automático Ing. Eléctrica Página 1 de 17 Unidad Temática 9: Análisis y Diseño de Sistemas de Control a Lazo Cerrado Algoritmos de Control: Un algoritmo de control se encarga de monitorear el valor
Dominio de la Frecuencia
 Dominio de la Frecuencia Álvaro Gutiérrez & Félix Monasterio-Huelin 3 de enero de 205 Índice. Introducción 2 2. Representaciones Gráficas 5 2.. Diagrama de Bode........................ 5 2.2. Diagrama
Dominio de la Frecuencia Álvaro Gutiérrez & Félix Monasterio-Huelin 3 de enero de 205 Índice. Introducción 2 2. Representaciones Gráficas 5 2.. Diagrama de Bode........................ 5 2.2. Diagrama
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA LABORATORIO DE CONTROL CLÁSICO PRACTICA N 2 LUGAR DE LAS RAICES OBJETIVO: Hacer uso del comando rltool de matlab para analizar
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA LABORATORIO DE CONTROL CLÁSICO PRACTICA N 2 LUGAR DE LAS RAICES OBJETIVO: Hacer uso del comando rltool de matlab para analizar
Seminario de Procesamiento Digital de Señales
 Seminario de Procesamiento Digital de Señales Unidad 5: Diseño de Filtros Digitales - Parte I Marcelo A. Pérez Departamento Electrónica Universidad Técnica Federico Santa María Contenidos 1 Conceptos Básicos
Seminario de Procesamiento Digital de Señales Unidad 5: Diseño de Filtros Digitales - Parte I Marcelo A. Pérez Departamento Electrónica Universidad Técnica Federico Santa María Contenidos 1 Conceptos Básicos
Sistemas Control Embebidos e Instrumentación Electrónica UNIVERSIDAD EAFIT Semestre 2010/2 2009/2
 DIAGRAMA DE NYQUIST Semestre 2010/2 La respuesta en frecuencia se basa en la respuesta en estado estacionario de un sistema ante una entrada senoidal. Un sistema lineal invariante en el tiempo, si es afectado
DIAGRAMA DE NYQUIST Semestre 2010/2 La respuesta en frecuencia se basa en la respuesta en estado estacionario de un sistema ante una entrada senoidal. Un sistema lineal invariante en el tiempo, si es afectado
Ejercicios resueltos 2: Horno de Carbón Cátedra de Control y Servomecanismos
 Ejercicios resueltos : Horno de Carbón Cátedra de Control y Servomecanismos Idea y desarrollo: Ing. Cristian Zujew Corregido por el Dr. Ing. Cristian Kunusch Objetivo: en esta guía práctica se presenta
Ejercicios resueltos : Horno de Carbón Cátedra de Control y Servomecanismos Idea y desarrollo: Ing. Cristian Zujew Corregido por el Dr. Ing. Cristian Kunusch Objetivo: en esta guía práctica se presenta
El método del lugar de las raíces.
 El método del lugar de las raíces. Las características de un sistema de lazo cerrado son determinadas por los polos de lazo cerrado. Los polos de lazo cerrado son las raíces de la ecuación característica.
El método del lugar de las raíces. Las características de un sistema de lazo cerrado son determinadas por los polos de lazo cerrado. Los polos de lazo cerrado son las raíces de la ecuación característica.
Universidad Simón Bolívar Departamento de Procesos y Sistemas
 Universidad Simón Bolívar Departamento de Procesos y Sistemas Guía de Ejercicios de Sistemas de Control I PS-3 Prof. Alexander Hoyo Junio 00 http://prof.usb.ve/ahoyo [email protected] ÍNDICE Pág. Modelaje Matemático
Universidad Simón Bolívar Departamento de Procesos y Sistemas Guía de Ejercicios de Sistemas de Control I PS-3 Prof. Alexander Hoyo Junio 00 http://prof.usb.ve/ahoyo [email protected] ÍNDICE Pág. Modelaje Matemático
SISTEMAS ELECTRÓNICOS DE CONTROL
 SISTEMAS ELECTRÓNICOS DE CONTROL PRÁCTICA 4: Diseño de Reguladores PID Discretos Objetivos Conocer los comandos de Matlab para discretizar sistemas continuos. Realizar simulaciones de sistemas discretos
SISTEMAS ELECTRÓNICOS DE CONTROL PRÁCTICA 4: Diseño de Reguladores PID Discretos Objetivos Conocer los comandos de Matlab para discretizar sistemas continuos. Realizar simulaciones de sistemas discretos
CONTROL BÁSICO CONTROL de PROCESOS
 CONRO BÁSICO CONRO de PROCESOS EMA: - Diseño de reguladores PID Facultad de Ingeniería UNER Carrera: Bioingeniería Planes de estudio: 1993/008 Integral - Derivativo (PID Consideramos el lazo básico de
CONRO BÁSICO CONRO de PROCESOS EMA: - Diseño de reguladores PID Facultad de Ingeniería UNER Carrera: Bioingeniería Planes de estudio: 1993/008 Integral - Derivativo (PID Consideramos el lazo básico de
4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO
 ANALISIS DE SISTEMAS EN TIEMPO CONTINUO Dinámica de Sistemas 4. 4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO 4..- Efecto de los polos en el comportamiento del sistema. 4..- Estabilidad. 4.3.- Análisis de
ANALISIS DE SISTEMAS EN TIEMPO CONTINUO Dinámica de Sistemas 4. 4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO 4..- Efecto de los polos en el comportamiento del sistema. 4..- Estabilidad. 4.3.- Análisis de
- VI - Filtros Activos. Soluciones
 - VI - Filtros Activos. Soluciones Elaborado por: Ing. Fco. Navarro H. 1 Ejemplo: Diseño de Filtro Activo. - Especificaciones Respuesta de Frecuencia - Diseñe un filtro activo Paso Bajo con las siguientes
- VI - Filtros Activos. Soluciones Elaborado por: Ing. Fco. Navarro H. 1 Ejemplo: Diseño de Filtro Activo. - Especificaciones Respuesta de Frecuencia - Diseñe un filtro activo Paso Bajo con las siguientes
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA DEPARTAMENTO DE CONTROL
 1 0 0 1 2 3 4 5 6 7-1 2 0 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8-2 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA DEPARTAMENTO DE CONTROL OBJETIVO Práctica N
1 0 0 1 2 3 4 5 6 7-1 2 0 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8-2 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA DEPARTAMENTO DE CONTROL OBJETIVO Práctica N
U.T.N. FAC. REG. CBA. - TEORÍA DE LOS CIRCUITOS II - JTP: ING. JUAN JOSÉ GARCIA ABAD GUÍA PARA TRAZAR DIAGRAMAS DE BODE MEDIANTE MÉTODO ASINTÓTICO
 GUÍA PARA TRAZAR DIAGRAMAS DE BODE MEDIANTE MÉTODO ASINTÓTICO Para obtener el diagrama de BODE de amplitud y fase de una función de transferencia F (P), la misma deberá tener el formato expresado en la
GUÍA PARA TRAZAR DIAGRAMAS DE BODE MEDIANTE MÉTODO ASINTÓTICO Para obtener el diagrama de BODE de amplitud y fase de una función de transferencia F (P), la misma deberá tener el formato expresado en la
ESTUDIO DE LA ESTABILIDAD EN EL DOMINIO FRECUENCIAL
 ESTUDIO DE LA ESTABILIDAD EN EL DOMINIO FRECUENCIAL 1.-Introducción. 2.-Criterio de estabilidad de Nyquist. 3.-Estabilidad relativa. 3.1.-Margen de ganancia. 3.2.-Margen de fase. 4.-Estabilidad mediante
ESTUDIO DE LA ESTABILIDAD EN EL DOMINIO FRECUENCIAL 1.-Introducción. 2.-Criterio de estabilidad de Nyquist. 3.-Estabilidad relativa. 3.1.-Margen de ganancia. 3.2.-Margen de fase. 4.-Estabilidad mediante
. (4.5) 3. Obtener el módulo de G(jω): . (4.6) 4. Calcular el ángulo de fase : (4.7)
 Problemas Resueltos de Análisis de Sistemas Lineales Continuos m j A 1 i1 ( ) zi j (45) r n j ( j) 1 j1 p j 3 Obtener el módulo de (jω): ( j) Aj 1 j 1 j 1 z z z 1 2 r ( j) j 1 j 1 j 1 p p p 1 2 m n (46)
Problemas Resueltos de Análisis de Sistemas Lineales Continuos m j A 1 i1 ( ) zi j (45) r n j ( j) 1 j1 p j 3 Obtener el módulo de (jω): ( j) Aj 1 j 1 j 1 z z z 1 2 r ( j) j 1 j 1 j 1 p p p 1 2 m n (46)
CUESTIONES DEL TEMA - V
 Presentación El tema 5 está dedicado al análisis y diseño de filtros activos. Inicialmente se realiza una clasificación de los filtros. Posteriormente se propone el uso de filtros prototipos y el escalado
Presentación El tema 5 está dedicado al análisis y diseño de filtros activos. Inicialmente se realiza una clasificación de los filtros. Posteriormente se propone el uso de filtros prototipos y el escalado
G(S) H(S) La Función de Transferencia de Lazo Cerrado de este sistema de control sería:
 UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA DEPARTAMENTO DE CONTROL Práctica N 7 Laboratorio de Ingeniería de Control Análisis de Sistemas de Control por Lugar Geométrico
UNIVERSIDAD AUTÓNOMA DE NUEVO LEÓN FACULTAD DE INGENIERÍA MECÁNICA Y ELÉCTRICA DEPARTAMENTO DE CONTROL Práctica N 7 Laboratorio de Ingeniería de Control Análisis de Sistemas de Control por Lugar Geométrico
Ejercicio 3 Un sistema de control de velocidad de un motor de corriente continua se modela mediante la ecuación
 Trabajo práctico Nº 4 Fundamentos de control realimentado - Segundo cuatrimestre 2017 Ejercicio 1 Aplicando el criterio de estabilidad de Routh: i) Determine la cantidad de raíces en el semiplano derecho
Trabajo práctico Nº 4 Fundamentos de control realimentado - Segundo cuatrimestre 2017 Ejercicio 1 Aplicando el criterio de estabilidad de Routh: i) Determine la cantidad de raíces en el semiplano derecho
ELECTRÓNICA DE POTENCIA
 ELECTRÓNICA DE POTENCIA Curso 2017 Práctica Nº5 Control de Motores de CC Nota: En todos los ejercicios se utiliza la siguiente nomenclatura, donde I a e I f son las corrientes de armadura y de campo respectivamente:
ELECTRÓNICA DE POTENCIA Curso 2017 Práctica Nº5 Control de Motores de CC Nota: En todos los ejercicios se utiliza la siguiente nomenclatura, donde I a e I f son las corrientes de armadura y de campo respectivamente:
REPRESENTACIONES GRÁFICAS
 REPRESENTACIONES GRÁFICAS 1. Qué son? Son gráficos que permiten mostrar la respuesta en frecuencia de un sistema lineal. Son herramientas útiles para el análisis, síntesis y diseño. 2. Diagrama de Bode
REPRESENTACIONES GRÁFICAS 1. Qué son? Son gráficos que permiten mostrar la respuesta en frecuencia de un sistema lineal. Son herramientas útiles para el análisis, síntesis y diseño. 2. Diagrama de Bode
PS Respuesta Temporal de Sistemas La Función de Transferencia
 PS35 - Respuesta Temporal de Sistemas La Función de Transferencia William Colmenares 4 de junio de 006 Índice. Respuesta Temporal. Polos y Ceros.. ejemplos numéricos.......................... 3 3. Señales
PS35 - Respuesta Temporal de Sistemas La Función de Transferencia William Colmenares 4 de junio de 006 Índice. Respuesta Temporal. Polos y Ceros.. ejemplos numéricos.......................... 3 3. Señales
EJERCICIOS PROPUESTOS SOBRE SISTEMAS DE 1er y 2do ORDEN
 EJERCICIOS PROPUESTOS SOBRE SISTEMAS DE 1er y 2do ORDEN 1. Para la función de transferencia G(s), cuya entrada proviene de un controlador proporcional de ganancia A, y que se encuentran en lazo cerrado
EJERCICIOS PROPUESTOS SOBRE SISTEMAS DE 1er y 2do ORDEN 1. Para la función de transferencia G(s), cuya entrada proviene de un controlador proporcional de ganancia A, y que se encuentran en lazo cerrado
GRAFICA DE LUGAR GEOMETRICO DE LAS RAICES
 GRAFICA DE LUGAR GEOMETRICO DE LAS RAICES La idea básica detrás del método del lugar geométrico de las raíces es que los valores de s que hacen que la función de transferencia alrededor del lazo sea igual
GRAFICA DE LUGAR GEOMETRICO DE LAS RAICES La idea básica detrás del método del lugar geométrico de las raíces es que los valores de s que hacen que la función de transferencia alrededor del lazo sea igual
FILTROS ACTIVOS FILTROS ACTIVOS
 Basados en AO. FILTROS ACTIVOS VENTAJAS: La señal de entrada no se ve atenuada => ganancia. Flexibilidad en el ajuste de ganancia y frecuencia. Habilidad de multiplicar funciones de transferencia en cascada
Basados en AO. FILTROS ACTIVOS VENTAJAS: La señal de entrada no se ve atenuada => ganancia. Flexibilidad en el ajuste de ganancia y frecuencia. Habilidad de multiplicar funciones de transferencia en cascada
REGULACIÓN AUTOMATICA (7)
 REGULACIÓN AUTOMATICA (7) (Respuesta en frecuencia Bode) Escuela Politécnica Superior Profesor: Darío García Rodríguez CONCEPTOS UTILES Definición de Decibelios.- La necesidad de comparar magnitudes en
REGULACIÓN AUTOMATICA (7) (Respuesta en frecuencia Bode) Escuela Politécnica Superior Profesor: Darío García Rodríguez CONCEPTOS UTILES Definición de Decibelios.- La necesidad de comparar magnitudes en
