Universidad Técnica Federico Santa María
|
|
|
- Adrián Silva Rey
- hace 7 años
- Vistas:
Transcripción
1 3. Comportamiento cualitativo de las EDO Hasta aquí, hemos estudiado algunas técnicas que nos permiten resolver analíticamente algunos tipos de ecuaciones diferenciales. Sin embargo, es importante tener presente que la mayoría de las ED no puede resolverse explícitamente, ó, como sucede en muchas aplicaciones, la solución general importa menos que la solución particular que satisface una determinada condición inicial. Interesa, no obstante, describir cómo se comportan las soluciones; por ejemplo al aumentar t crecen sin cota las soluciones? 2. tienden las soluciones a algún valor (0 por ejemplo)? 3. oscilan entre ciertos valores? Para comprender mejor la situación, consideremos el siguiente ejemplo: = 4y(1 y) = / 4y(1 y) = Podríamos encontrar la solución tras la integración, pero las fórmulas obtenidas no son fáciles de interpretar. Por ello, los métodos geométricos y cualitativos permiten obtener mucha información con poco trabajo. Esto es importante sobre todo para ED «difíciles»; considerar la ecuación: = = /10 ey2 sen 2 y ( 1 e y2 /10 sen y) 2 = La integral del lado izquierdo es complicada, sin embargo, cualitativamente, notamos que excepto para y = nπ; f(y) = e y2 /10 sen 2 y > 0 veremos en esta sección que esta información es suficientemente útil. Otra relación que es importante considerar cuando se trata de modelos cuya información, por tanto, puede provenir de mediciones ó datos aproximados, es la dependencia (continua) de las soluciones respecto de las condiciones iniciales, ya que si éstas cambian ligeramente, es deseable que la solución no varíe mucho. Observación. Sea F : D R, donde D R R. Por lo tanto, es posible expresar una EDO de primer orden en la forma dx = F (t, x) ó ẋ = F (t, x) Si F (t, x) = F (x), i.e., si F depende sólo de la variable x, entonces ẋ = F (x), y en este caso la ecuación se dice autonóma. MAT023 (2 sem. 2011) 33
2 Nótese que si en (2), F es un polinomio en la variable x, entonces la ED admite solución única (t, x) R 2. En lo que sigue, siempre supondremos existencia y unicidad de los problemas de Cauchy. Para Una el estudio solución cualitativo, x(t) de ẋ una = F solución (t, x) se x(t) representa de ẋ = geométricamente F (t, x) se representa en el geométricamente plano en el plano t x. t x. Como Como dado dado cualquier cualquier (t 0,x (t 0,) x 0 ) D existe D existe una una solución única que solución pasa que por pasa (t 0,xpor 0 ), (t 0, x 0 ), (por los teoremas ello quiere de existencia decir que ylas unicidad soluciones de soluciones); de la ED seello representan quiere decir porque unalasfamilia soluciones de de la ED (el conjunto curvas de solución todas ellas) en Dse yque representan! curva porsolución una familia que de pasa curvas por un solución punto en determi- curva solución que pasa por un punto D y que existe una únicanado. determinado. 1. ẋ = 1) Estudie ẋ = } x x t }{{ t {{}} f(x,t) f(x,t) dx = 0Cualitativamente x(t) alcanza =0 sus puntos x(t) críticos alcanza sus puntos críticos en x t =0 Método 1 ẋ x = t ED lineal Analíticamente x t = 0 Cualitativamente: Analíticamente: ( x(t) =e ) Método1 ẋ tx e = t ED+ lineal C =e t ( ( t e t +e t +C ) x(t) = e ) t e + C 2 = t +1+C t = e t ( t e t + e t +C ) = t C e t Método 2 u x t 1 2 Método 2 du u = x dx t du +1=u du du = dx u 1 =0 1 ln(u 1) = t + k u 1 = 2 u(t) 1=C ln(u e t 1) = t + k x(t) t = u(t) C e t +11 = C e t x(t) t = C e t ẋ = x t,t 0 dx x = 2) Estudiar ẋ = x t t, t 0. ln x dx = ln t + C Claramente, lo anterior implica x(t) = k 1 que dx t =0 x x = t. Luego: =0 x =0(solución trivial) ln t x = ln t + C de donde Pero x(t) = k 1 t. Además: dx = 0 x t = 0 x = 0 (solución trivial) Pero x>0 t>0 ẋ<0 x>0 t<0 ẋ>0 x<0x > 0 t>0 t > 0 ẋ>0 ẋ < 0 x<0x > 0 t<0 t < 0 ẋ<0 ẋ > 0 x < 0 t > 0 ẋ > 0 x < 0 t < 0 ẋ < MAT023 (2 sem. 2011) 34
3 Así, gráficamente, las soluciones son de la forma: ẋ = t,x 0 xdx= t x2 + t 2 = C 3) ẋ = t 3. ẋ x, = x t 0 = x dx = t x2 + t 2 = C x,x 0 xdx= t x2 + t 2 = C 4. Autónoma: ẋ = 4. Autónoma: ẋ = (x2 1) ẋ =0 x(t) =1o x = ± 4) Consideremos ahora un par de ecuaciones autónomas: 1+c 2 (x2 1) ẋ =0 x(t) =1o x = ± e t 1+ce t ẋ = 1 2 (x2 1) ẋ = 0 x(t) = 1 ó x(t) = 1 x(t) = x(t) =1 Vemos entonces que no es necesario tener ni la solución explícita ni un dibujo exacto para poder describir cualitativamente el comportamiento de la solución de una ED. Más aún, si dx = F (x) es una ED autónoma, las soluciones de ella tienen la siguiente propiedad: Si ξ : R R es una solución, entonces cualquier traslación de la gráfica de ξ en la dirección del eje t es la gráfica de otra solución de la ecuación. En efecto, sea η : R R con η(t) =ξ(t c),c R constante MAT023 (2 sem. 2011) 35 η = ξ(t c) F (ξ(t c)) F (η(t)) η también es una solución
4 tienen la siguiente propiedad: Si ξ : R R es una solución, entonces cualquier traslación de la gráfica de ξ en la dirección del eje t es la gráfica de otra solución de la ecuación. Universidad En efecto, sea Técnica η : R R Federico con η(t) =ξ(t Santa c),c María R constante η = ξ(t c) F (ξ(t c)) F (η(t)) η también es una solución 5) ẋ Ejemplo = x ẋ = x Observación 2. Notemos que el comportamiento está determinado por f(x) 1. Vemos Si centonces R : f(c) que =0, noentonces es necesario x(t) =c tener es una ni lasolución explícita ni un dibujo exacto para poder describir cualitativamente el comportamiento de la solución de una ED. Más aún, si dx = F (x) es 4 una ED autónoma, las soluciones de ella tienen la siguiente propiedad: Proposición 1. Si ξ : R R es una solución, entonces cualquier traslación de la gráfica de ξ en la dirección del eje t es la gráfica de otra solución de la ecuación. En efecto: sea η : R R con η(t) = ξ(t c), c R constante. Entonces: η también es una solución. η = ξ(t c) F (ξ(t c)) F (η(t)) Observación. Notamos que el comportamiento de la solución de las ecuaciones diferenciales autónomas está determinado por f(x). Específicamente: 1. Si c R : f(c) = 0, entonces x(t) = c es una solución. 2. Si f(x) 0, entonces x(t) es creciente o decreciente, dependiendo del signo de f(x). Esta información puede representarse en una recta real que representa a x. MAT023 (2 sem. 2011) 36
5 2. Si f(x) 0, entonces x(t) es creciente o decreciente, dependiendo del sgnf(x) Esta información puede representarse en una recta real que representa a x. Para ver esto, considere 2. Análisis analítico vs cualitativo =4y(1 y) 4y(1 y) = / Podríamos encontrar la solución tras la integración, pero las fórmulas obtenidas no son fáciles de interpretar. Por ello, los métodos = geométricos y cualitativa permiten obtener mucha información con poco trabajo. Esto es importante sobre todo para ED «difíciles». = /10 ey2 sen 2 y ( 1 e y2 /10 sen y) 2 = La integral del lado izquierdo es complicada, sin embargo, cualitativamente, notamos que Considerar /10 =ey2 sen 2 y ( ) 1 e y2 /10 sen 2 y = f(y) = e y2 /10 sen 2 y > 0 excepto para y = nπ, n Z, que nos dan las soluciones de equilibrio. Gráficamente: Pero cualitativamente 37 f(y) =e y2 /10 sen 2 y>0 excepto para y = nπ que nos dan las soluciones de equilibrio La ecuación del ejemplo tiene sólo tres soluciones esencialmente diferentes: Escrecientes, posible «resumir» decreciente yelconstante. comportamiento cualitativo de las soluciones en las llamadas líneas de fase, queeste describimos resumen de decomportamientos la siguiente manera: cualitativos se puede ilustrar geométricamente definiendo una «línea de fases» decre. x 0 crece Definición 2. Sea ẋ = F (x), yseax 0 R : F (x 0 )=0. Entonces diremos que x 0 es una singularidad ounpunto de equilibrio de la ED Definición 3.1. Sea ẋ = F (x), y sea x 0 R : F (x 0 ) = 0. Entonces diremos que x 0 es una singularidad Notaro que un x(t) punto =xde 0 esequilibrio una solución de (cte.) la EDde la ED, pues ẋ(t) =0y F (x 0 )=0 Notar que x(t) = x 0 es una solución (cte.) de la ED, pues Observación 3. La línea de fase se puede obtener directamente de ẋ(t) =F (x), simplemente mirando cuando F (x) ẋ(t) 0. = 0 y F (x 0 ) = 0 Ejemplo Supongamos que Gr F viene dado por Observación. La línea de fase se puede obtener directamente de ẋ(t) = F (x), simplemente mirando cuando F (x) 0. Ejemplo. Supongamos que Gr (F ) viene dado por MAT023 (2 sem. 2011) 37 Entonces, la línea de fase
6 Definición 2. Sea ẋ = F (x), yseax 0 R : F (x 0 )=0. Entonces diremos ẋ(t) que =0y F (x 0 )=0 x 0 es una singularidad ounpunto de equilibrio de la ED Observación 3. La línea de fase se puede obtener directamente de ẋ(t) =F (x), Notar que x(t) =x 0 es una solución (cte.) de la ED, pues simplemente mirando cuando F (x) 0. ẋ(t) =0y F (x 0 )=0 Ejemplo Supongamos que Gr F viene dado por Observación 3. La línea de fase se puede obtener directamente de ẋ(t) =F (x), simplemente mirando cuando F (x) 0. Ejemplo Supongamos que Gr F viene dado por Entonces, la línea de de fasefases esentonces, la línea de fase 38 a b c d a b c d en donde la dirección de la flecha indica si la función crece ( ) o decrece ( ) en donde la dirección de la flecha indica si la función crece ( ) o decrece ( ) en donde la dirección de la flecha en cada intervalo indica si la función crece ( ) o decrece ( ) en dicho intervalo. Escribimos la línea de fase de manera vertical, al lado del gráfico en el plano t x que representa las soluciones, de manera de simplificar su interpretación: d c b a d c b a 6 Observación 4. Dependiendo del comportamiento local de las soluciones de la ecuación de una singularidad aislada en la Línea de Fases, se distinguen los Observación. Dependiendo siguientes tipos del comportamiento de singularidadeslocal de las soluciones de la ecuación en una singularidad aislada en la Línea Observación de Fase, 4. Dependiendo se distinguen del comportamiento (y definen) local delos las soluciones siguientes de la tipos de singularidades: 1. Repulsor ecuación de una o fuente singularidad aislada en la Línea de Fases, se distinguen los siguientes tipos de singularidades 1. Repulsor o fuente: 1. Repulsor o fuente Atractor oo sumidero MAT023 (2 sem. 2011) Atractor-repulsor 3. Atractor-repulsor
7 a siguientes tipos de singularidades Observación 4. Dependiendo del comportamiento local de las soluciones de la ecuación de una singularidad aislada en la Línea de Fases, se distinguen los Observación 4. Dependiendo del comportamiento local de las soluciones de la ecuación 1. Repulsor de unao singularidad fuente aislada en la Línea de Fases, se distinguen los siguientes tipos de singularidades 2. Atractor o sumidero: 1. Repulsor o fuente 2. Atractor o sumidero 2. Atractor o sumidero 3. Atractor-repulsor: 3. Atractor-repulsor 3. Atractor-repulsor Repulsor-atractor 4. Repulsor-atractor: 4. Repulsor-atractor 7 7 Ejemplo. Describir cualitativamente los tipos de soluciones que admite la EDO ẋ =(x 1) 3 e cos(x4 1). Solución. Es inmediato que x =1es la única singularidad (aislada) de la EDO. Como e cos(x4 1) > 0, x R, lagráficadef (x) =(x 1) e cos(x4 1),la línea de fases y los tipos de soluciones de la EDO, son como ilustra la figura, respectivamente. 2 Ejemplo. Describir cualitativamente los tipos de soluciones que admite la EDO ẋ = (x 1) 3 e cos(x4 1) 1 1 Ejemplo. Describir cualitativamente los tipos de soluciones que admite la EDO ẋ =(x 1) 3 e cos(x4 1). Solución. Es inmediato que x =1es La ecuación del ejercicio anterior, es muy1 la única fácil de 2 singularidad integrar 3 bajo 4 (aislada) de la el punto de EDO. vista Como del ecálculo. cos(x4 1) En consecuencia > 0, x esr, difícil lagráficadef conocer explícitamente (x) =(x las ecuaciones 1) e cos(x4 1),la línea de las fases soluciones y los que tipos indica de la soluciones figura. Sin embargo, de la EDO, la líneason de fases como permite ilustra darla figura, una descripción cualitativa del tipo de soluciones y punto de equilibrio. respectivamente. Definición 3. Dos ecuaciones diferenciales 2 autónomas, se dicen cualitativamente equivalentes si, y sólo si, tienen la misma línea de fases, en el sentido del mismo número de puntos singulares, de la misma naturaleza y distribuidos en el mismo orden. 1 1 Solución. Es inmediato que x = 1 es la única singularidad (aislada) de la EDO. Como e cos(x4 1) > 0, x R, la gráfica de F (x) = (x 1) 3 e cos(x4 1), la línea de fases y los tipos de soluciones de la EDO, son como ilustra la figura, en cada subintervalo respectivo. 1. Las ED ẋ = x, ẋ =(x 1) e cos(x4 1), son equivalentes, pues solo tiene un La ecuación del ejercicio anterior, es muy1fácil de 2 integrar 3 bajo 4 el punto de único punto atractor en sus respectivas líneas de fases. vista del cálculo. En consecuencia es difícil conocer explícitamente las ecuaciones 2. ẋ =(x+2)(x+1) ẋ = 1 2 (x2 1).Peroẋ = (x+2)(x+1) ẋ = 1 2 (x2 1) de las soluciones que indica la figura. Sin embargo, la línea de fases permite dar (pues en este último caso el atractor y el repulsor se encuentran en distinto una descripción orden). cualitativa del tipo de soluciones y punto de equilibrio. Definición 3. Dos ecuaciones diferenciales autónomas, se dicen cualitativamente3. equivalentes Sistemas si, yde sóloed si, tienen de primer la misma orden línea (en de fases, el plano) en el sentido del mismo número de puntos singulares, de la misma naturaleza y distribuidos en Consideremos el sistema el mismo orden. La ecuación del ejercicio anterior, es muy difícil de integrar, desde el punto de vista del cálculo. En consecuencia, es difícil conocer explícitamente las expresiones de las soluciones que indica la figura. Sin embargo, la línea de fases permite dar una descripción cualitativa del tipo de soluciones y sus puntos de equilibrio. ẋ = f(t, x, y) ẏ = g(t, x, y) Definición 3.2. Dos ecuaciones diferenciales autónomas, se dicen cualitativamente equivalentes si, y sólo si, tienen la misma línea de fases, en el sentido del mismo número de puntos singulares, de la misma naturaleza y distribuidos en el mismo orden. que podemos expresar matricialmente en la forma 1. Las ED ẋ = x, ẋ =(x 1) e cos(x4 1), son equivalentes, pues solo tiene un único punto atractor en sus dyrespectivas líneas de fases. = F (t, Y ), 2. ẋ =(x+2)(x+1) ẋ = 1 2 (x2 1).Peroẋ = (x+2)(x+1) ẋ = 1 2 (x2 1) (pues en este último caso el atractor y el repulsor se encuentran en distinto 8 orden). 1) Las ED ẋ = x, ẋ = (x 1) e cos(x4 1), son equivalentes, pues cada una de ellas tiene un único punto atractor en sus respectivas líneas de fases. 3. Sistemas de ED de primer orden (en el plano) 2) ẋ = (x + 2)(x + 1) ẋ = 1 2 (x2 1). Pero ẋ = (x + 2)(x + 1) ẋ = 1 2 (x2 1) (pues en este último caso el atractorconsideremos y el repulsorelse sistema encuentran en distinto orden). ẋ = f(t, x, y) ẏ = g(t, x, y) MAT023 (2 sem. 2011) 39 que podemos expresar matricialmente en la forma dy = F (t, Y ),
8 3.1. Algunos Modelos Sencillos Para ilustrar de mejor manera cómo se utilizan las ecuaciones diferenciales para modelar, consideremos algunos modelos sencillos, y comenzaremos con algunos modelos clásicos de crecimiento de población. 1) Crecimiento ilimitado de Poblaciones Este modelo se basa en el supuesto que la velocidad de crecimiento de la población es proporcional al tamaño de la misma. Las variables implicadas en este modelo son: t: tiempo, que es la variable independiente P : número de sujetos de la población, que es la variable dependiente k: constante de proporcionalidad (ó parámetro), que se denomina a veces «coeficiente de velocidad del crecimiento» Así, la hipótesis de que la variación del tamaño de la población es proporcional a ella se escribe como: 2) Modelo logístico de población dp = kp Claramente, el modelo anterior no considera las condiciones del entorno y la cantidad de recursos disponibles. Para considerar estos factores, agregamos a la hipótesis anterior, las siguientes: Si la población es pequeña, la tasa de crecimiento de ella es proporcional a su tamaño. Si la población es grande con respecto a la capacidad de soporte del entorno y de los recursos disponibles, la población disminuirá; es decir, en este caso la tasa de crecimiento es negativa. Usamos los mismos parámetros anteriores, sólo que en este caso la constante k es la razón de cambio de la población en el caso en que ésta sea pequeña. Debemos introducir un nuevo parámetro que dé cuenta de la «capacidad de soporte» del entorno. Es decir, necesitamos un parámetro N que permita modelar la situación: Si P (t) < N, entonces la población P crece. Si P (t) > N, entonces la población P decrece. Luego, el modelo puede ser expresado como dp = k P ( 1 P ) N 40 MAT023 (2 sem. 2011) 40
9 3.2. Ejercicios 1. Obtenga la solución de los siguientes problemas de valores iniciales a) xy = x 2 + y 2 + y, y(3) = 0 b) xy y y = ln(y) ln(x), y(1) = e c) y y = 2e 4x, y(0) = 3 d) y + 5y 9x = 3x3 + x, y( 1) = 4 e) y + 2 x + 1 y = 3, y(0) = Determine los puntos de equilibrio de las siguientes ecuaciones autonomas: a) x = x + 1 b) x = x x 3 c) x = sinh x 2 d) x = x 4 x 3 2x 2 e) x = sen x f) x = sen x x y clasifique la naturaleza (atractor, repulsor, atractor-repulsor) de cada punto de equilibrio. Construya el retrato de fase de cada ecuación. 3. Determine todos los posibles retratos de fases y los respectivos intervalos para λ en la siguiente ecuación diferencial dependiente del parámetro λ: ˆx = (x λ)(x 2 λ), λ R 4. Para las siguientes EDO, encuentre la solución general y esboce las gráficas de varios elementos de la familia de curvas solución. Muestre que no hay soluciones que satisfagan las condiciones iniciales dadas. Por qué no contradice esto el teorema de existencia de soluciones? a) tx x = t 2 cos t, x(0) = 3 b) tx = 2x t, x(0) = 2 5. Suponga que x es una solución del problema de v.i. x = x cos 2 t, x(0) = 1. Pruebe que x(t) > 0 para todos los t para los que x está definido. 6. Suponga que y es una solución del problema de v.i. y = (y 2 1)e ty, y(1) = 0. Pruebe que 1 < y < 1, t para los que y está definido. 7. Suponga que x es una solución del problema de v.i. x = x3 x 1 + t 2 x 2, x(0) = 1 2. Pruebe que 0 < x(t) < 1, t para los que x está definido. 8. Cuál(es) de los siguientes problemas de valor inicial tienen garantizada una única solución, por el teorema de unicidad de soluciones de ED? Justifique. a) y = 4 + y 2, y(0) = 1 b) y = y, y(4) = 0 MAT023 (2 sem. 2011) 41
10 c) y = t arctan y, y(0) = 2 d) y = y sin y + s, y(0) = 1 e) x = t x + 1, x(0) = 0 f) y = 1 y + 2, y(0) = 1 x 9. Considere la ecuación diferencial x (t) = x3 4x 1 + e 3x. a) Describa las singularidades de la ecuación diferencial. b) Encuentre lím t x(t), donde x(t) es la solución que satisface x(0) = Considere la ecuación = a[(y 1)(y 4) b] Determine todos los valores de a y b tales que y 0 = 5 sea un punto de equilibrio atractor para la ecuación. 42 MAT023 (2 sem. 2011) 42
Sistemas autónomos. Introducción a la teoría cualitativa.
 Lección 4 Sistemas autónomos. Introducción a la teoría cualitativa. 4.1 Sistemas autónomos. Mapas de fase. En esta lección nos centraremos en el estudio de sistemas autónomos, es decir, aquellos que pueden
Lección 4 Sistemas autónomos. Introducción a la teoría cualitativa. 4.1 Sistemas autónomos. Mapas de fase. En esta lección nos centraremos en el estudio de sistemas autónomos, es decir, aquellos que pueden
x (0) si f (x) = 2s 1, s > 1 d) f 3. Analizar la existencia de derivadas laterales y de derivada en a = 0, para las siguientes funciones:
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
FACULTAD DE CIENCIAS EXACTAS Y NATURALES UNIVERSIDAD DE BUENOS AIRES COMPLEMENTOS DE ANÁLISIS MAESTRíA EN ESTADíSTICA MATEMÁTICA SEGUNDO CUATRIMESTRE 2007 PRÁCTICA 7 1. Usando sólo la definición de derivada,
Tema 8 Ecuaciones diferenciales
 Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Tema 8 Ecuaciones diferenciales 1. ECUACIONES DIFERENCIALES ORDINARIAS Definición 1.1: Ecuación diferencial Se llama ecuación diferencial de orden n a una ecuación que relaciona la variable independiente
Técnicas cualitativas para las Ecuaciones diferenciales de primer orden: Existencia y Unicidad de soluciones
 Lección 4 Técnicas cualitativas para las Ecuaciones diferenciales de primer orden: Existencia y Unicidad de soluciones 4.1. Introducción Cuando aplicamos técnicas cualitativas para estudiar los problemas
Lección 4 Técnicas cualitativas para las Ecuaciones diferenciales de primer orden: Existencia y Unicidad de soluciones 4.1. Introducción Cuando aplicamos técnicas cualitativas para estudiar los problemas
Derivada y diferencial
 Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
Derivada y diferencial Una cuestión, que aparece en cualquier disciplina científica, es la necesidad de obtener información sobre el cambio o la variación de determinadas cantidades con respecto al tiempo
127. Resolver los siguientes problemas de valor inicial determinando el intervalo maximal de existencia de la solución:
 10. Existencia y unicidad 125. Para las siguientes funciones, halla una constante de Lipschitz o prueba que no existe. 1. f(t, x) = x, D = R R. 2. f(t, x) =tx 1/3, D =[ 10, 10] [ 1, 1]. 3. f(t, x) =1/(tx),
10. Existencia y unicidad 125. Para las siguientes funciones, halla una constante de Lipschitz o prueba que no existe. 1. f(t, x) = x, D = R R. 2. f(t, x) =tx 1/3, D =[ 10, 10] [ 1, 1]. 3. f(t, x) =1/(tx),
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Ecuaciones Diferenciales: Teoría Unidimensional
 Ecuaciones Diferenciales: Teoría Unidimensional M. Fernández Universidad de Extremadura 1 / 49 Campo de pendientes El problema de valor inicial Una ecuación diferencial (abreviadamente ED) es una ecuación
Ecuaciones Diferenciales: Teoría Unidimensional M. Fernández Universidad de Extremadura 1 / 49 Campo de pendientes El problema de valor inicial Una ecuación diferencial (abreviadamente ED) es una ecuación
Ecuaciones diferenciales ordinarias
 Tema 9 Ecuaciones diferenciales ordinarias Versión: 13 de mayo de 29 9.1 Introducción El objetivo de este tema es exponer muy brevemente algunos de los conceptos básicos relacionados con las ecuaciones
Tema 9 Ecuaciones diferenciales ordinarias Versión: 13 de mayo de 29 9.1 Introducción El objetivo de este tema es exponer muy brevemente algunos de los conceptos básicos relacionados con las ecuaciones
Soluciones de ecuaciones de primer orden
 GUIA 2 Soluciones de ecuaciones de primer orden Dada una ecuación diferencial, la primera pregunta que se presenta es cómo hallar sus soluciones? Por cerca de dos siglos (XVIII y XIX ) el esfuerzo de los
GUIA 2 Soluciones de ecuaciones de primer orden Dada una ecuación diferencial, la primera pregunta que se presenta es cómo hallar sus soluciones? Por cerca de dos siglos (XVIII y XIX ) el esfuerzo de los
Fundamentos matemáticos. Tema 8 Ecuaciones diferenciales
 Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
Grado en Ingeniería agrícola y del medio rural Tema 8 José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2016 Licencia Creative Commons 4.0 Internacional J.
UNA INTERPRETACIÓN CUALITATIVA DE LOS DIAGRAMAS DE FASE EN UN CONTEXTO ECONÓMICO RESUMEN. x = f (x,y) ɺ ɺ
 UNA INTERPRETACIÓN CUALITATIVA DE LOS DIAGRAMAS DE FASE EN UN CONTEXTO ECONÓMICO RESUMEN Las soluciones a un sistema de ecuaciones del tipo = f (,) = g(, ) puede representarse de manera gráfica de distintas
UNA INTERPRETACIÓN CUALITATIVA DE LOS DIAGRAMAS DE FASE EN UN CONTEXTO ECONÓMICO RESUMEN Las soluciones a un sistema de ecuaciones del tipo = f (,) = g(, ) puede representarse de manera gráfica de distintas
Aplicaciones de la DERIVADA
 Teorema (criterio de la segunda derivada para extremos relativos) Sea c un número crítico de una función f en el que f ( c ) = 0, suponiendo que existe f (x) para todos los valores de x en un intervalo
Teorema (criterio de la segunda derivada para extremos relativos) Sea c un número crítico de una función f en el que f ( c ) = 0, suponiendo que existe f (x) para todos los valores de x en un intervalo
Técnicas numéricas para las Ecuaciones diferenciales de primer orden: Método de Euler
 Lección 6 Técnicas numéricas para las Ecuaciones diferenciales de primer orden: Método de Euler 61 Introducción a los métodos numéricos En este capítulo y en los anteriores estamos estudiado algunas técnicas
Lección 6 Técnicas numéricas para las Ecuaciones diferenciales de primer orden: Método de Euler 61 Introducción a los métodos numéricos En este capítulo y en los anteriores estamos estudiado algunas técnicas
Ecuaciones Diferenciales Ordinarias
 Ecuaciones Diferenciales Ordinarias (Métodos de Solución) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Primavera 2008, Clase 3 Julio López EDO 1/18 1) Ecuaciones
Ecuaciones Diferenciales Ordinarias (Métodos de Solución) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Primavera 2008, Clase 3 Julio López EDO 1/18 1) Ecuaciones
Ecuaciones lineales de orden superior
 ANEXO GUIA 5 Ecuaciones lineales de orden superior Las ideas presentadas para ecuaciones lineales de segundo orden se pueden generalizar a ecuaciones lineales de orden n d n x n + a n 1(t) dn 1 x n 1 +
ANEXO GUIA 5 Ecuaciones lineales de orden superior Las ideas presentadas para ecuaciones lineales de segundo orden se pueden generalizar a ecuaciones lineales de orden n d n x n + a n 1(t) dn 1 x n 1 +
Introducción al plano de fase
 Universidad Nacional de Colombia Departamento de Matemáticas 1000007 Ecuaciones diferenciales - Grupos 12 y 18 Introducción al plano de fase Existen ecuaciones diferenciales que no pueden ser resueltas
Universidad Nacional de Colombia Departamento de Matemáticas 1000007 Ecuaciones diferenciales - Grupos 12 y 18 Introducción al plano de fase Existen ecuaciones diferenciales que no pueden ser resueltas
= f (a) R. f(x) f(a) x a. recta por (a, f(a)) de pendiente f(a+h2) f(a) recta tangente por (a, f(a)) de pendiente f (a)
 1 1. DERIVACIÓN 1.1. DEFINICIONES Y RESULTADOS PRINCIPALES Definición 1.1. Derivada. Sea f una función definida en un intervalo abierto I con a I. Decimos que f es derivable en a si existe y es real el
1 1. DERIVACIÓN 1.1. DEFINICIONES Y RESULTADOS PRINCIPALES Definición 1.1. Derivada. Sea f una función definida en un intervalo abierto I con a I. Decimos que f es derivable en a si existe y es real el
1. Introducción a las ecuaciones diferenciales. ( Chema Madoz, VEGAP, Madrid 2009)
 1. Introducción a las ecuaciones diferenciales ( Chema Madoz, VEGAP, Madrid 009) 1 Profesores: Manuel Abejón (grupos A y B) Bartolo Luque (grupos C y D) Página del departamento de Matemática Aplicada y
1. Introducción a las ecuaciones diferenciales ( Chema Madoz, VEGAP, Madrid 009) 1 Profesores: Manuel Abejón (grupos A y B) Bartolo Luque (grupos C y D) Página del departamento de Matemática Aplicada y
DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL
 DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL Definición. Sea f :]a, b[ R y x 0 ]a, b[. Sedicequef es derivable en x 0 si existe f(x lim 0 +h) f(x 0 ) h 0 h yesfinito. En ese caso denotaremos por
DERIVABILIDAD DE FUNCIONES REALES DE VARIABLE REAL Definición. Sea f :]a, b[ R y x 0 ]a, b[. Sedicequef es derivable en x 0 si existe f(x lim 0 +h) f(x 0 ) h 0 h yesfinito. En ese caso denotaremos por
Métodos Numéricos en Ecuaciones Diferenciales Ordinarias
 Tema 4 Métodos Numéricos en Ecuaciones Diferenciales Ordinarias 4.1 Introducción Estudiaremos en este Tema algunos métodos numéricos para resolver problemas de valor inicial en ecuaciones diferenciales
Tema 4 Métodos Numéricos en Ecuaciones Diferenciales Ordinarias 4.1 Introducción Estudiaremos en este Tema algunos métodos numéricos para resolver problemas de valor inicial en ecuaciones diferenciales
ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M.
 Introducción ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M. En diferentes situaciones que aparecen con frecuencia en las Ciencias Experimentales, es complicado poder escribir
Introducción ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M. En diferentes situaciones que aparecen con frecuencia en las Ciencias Experimentales, es complicado poder escribir
Ecuaciones diferenciales
 Ecuaciones diferenciales 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos 1 Introducción 2 3 4 5 Definición de solución general y solución particular 6 Solución de una ecuación
Ecuaciones diferenciales 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos 1 Introducción 2 3 4 5 Definición de solución general y solución particular 6 Solución de una ecuación
Aplicaciones de los S.E.D.O.
 Tema 7 Aplicaciones de los S.E.D.O. 7. Introducción Nota: APUNTES INCOMPLETOS Estudiaremos en este Tema algunos modelos de interés en las Ciencias Naturales que utilizan para su modelización sistemas de
Tema 7 Aplicaciones de los S.E.D.O. 7. Introducción Nota: APUNTES INCOMPLETOS Estudiaremos en este Tema algunos modelos de interés en las Ciencias Naturales que utilizan para su modelización sistemas de
Cálculo. Licenciatura en CC. Químicas Tema n o 5 Resultados teóricos. Ecuaciones diferenciales ordinarias
 Cálculo. Licenciatura en CC. Químicas Tema n o 5 Resultados teóricos Ecuaciones diferenciales ordinarias 1. Ecuaciones diferenciales lineales de orden n Considera un número n de funcines de una variable
Cálculo. Licenciatura en CC. Químicas Tema n o 5 Resultados teóricos Ecuaciones diferenciales ordinarias 1. Ecuaciones diferenciales lineales de orden n Considera un número n de funcines de una variable
x = t 3 (x t) 2 + x t. (1)
 Problema 1 - Considera la siguiente ecuación de primer orden: x = t 3 (x t + x t (1 (a Comprueba que x(t = t es solución de la ecuación (b Demuestra que si x = x(t es la solución que pasa por el punto
Problema 1 - Considera la siguiente ecuación de primer orden: x = t 3 (x t + x t (1 (a Comprueba que x(t = t es solución de la ecuación (b Demuestra que si x = x(t es la solución que pasa por el punto
Complementos de Análisis. Año 2016
 Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
Complementos de Análisis. Año 2016 Práctica 8. Ecuaciones diferenciales ordinarias. 1 Modelando con ecuaciones diferenciales Modelar con ecuaciones diferenciales las siguientes situaciones. Intentar resolver
Ecuaciones Diferenciales Ordinarias de Primer Orden
 Tema 2 Ecuaciones Diferenciales Ordinarias de Primer Orden Introducción Estudiaremos en este tema varios tipos de E.D.O. de primer orden que es posible resolver de forma exacta. 2.1 Ecuaciones en variables
Tema 2 Ecuaciones Diferenciales Ordinarias de Primer Orden Introducción Estudiaremos en este tema varios tipos de E.D.O. de primer orden que es posible resolver de forma exacta. 2.1 Ecuaciones en variables
Una metodología para el estudio de la frecuencia de ciclos ĺımite en ecuaciones diferenciales con retardo
 Una metodología para el estudio de la frecuencia de ciclos ĺımite en ecuaciones diferenciales con retardo Romina Cobiaga y Walter Reartes Universidad Nacional del Sur Junio 2017 1 / 16 Introducción Se
Una metodología para el estudio de la frecuencia de ciclos ĺımite en ecuaciones diferenciales con retardo Romina Cobiaga y Walter Reartes Universidad Nacional del Sur Junio 2017 1 / 16 Introducción Se
1. Ecuaciones lineales con coeficientes constantes. Ecuaciones de primer orden. 2. Encontrar la solución de los siguientes problemas de valor inicial.
 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes problemas de valor inicial. ẋ =5x, x0) =.. ẋ + x =0, x) =.. ẋ + x = te t, x0) =. si
. Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes problemas de valor inicial. ẋ =5x, x0) =.. ẋ + x =0, x) =.. ẋ + x = te t, x0) =. si
Ecuaciones Diferenciales. Conceptos Generales
 Tema 1 Ecuaciones Diferenciales. Conceptos Generales Introducción La Modelización y Simulación es una área enorme de la ciencia pura y aplicada, a la que intentamos aproximarnos en esta asignatura. Dadas
Tema 1 Ecuaciones Diferenciales. Conceptos Generales Introducción La Modelización y Simulación es una área enorme de la ciencia pura y aplicada, a la que intentamos aproximarnos en esta asignatura. Dadas
Derivada de una función en un punto. Función derivada. Diferencial de una función en un punto. dy = f (x) dx. Derivada de la función inversa
 Derivada de una función en un punto Las tres expresiones son equivalentes. En definitiva, la derivada de una función en un punto se obtiene como el límite del cociente incremental: el incremento del valor
Derivada de una función en un punto Las tres expresiones son equivalentes. En definitiva, la derivada de una función en un punto se obtiene como el límite del cociente incremental: el incremento del valor
TEMA 5: LA INTEGRAL DEFINIDA
 Alonso Fernández Galián TEMA 5: LA INTEGRAL DEFINIDA Originalmente el Cálculo Diferencial e Integral estaba fuertemente vinculado a la geometría analítica. Ya vimos la aplicación de las derivadas al cálculo
Alonso Fernández Galián TEMA 5: LA INTEGRAL DEFINIDA Originalmente el Cálculo Diferencial e Integral estaba fuertemente vinculado a la geometría analítica. Ya vimos la aplicación de las derivadas al cálculo
Apéndice sobre ecuaciones diferenciales lineales
 Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Apéndice sobre ecuaciones diferenciales lineales Juan-Miguel Gracia 10 de febrero de 2008 Índice 2 Determinante wronskiano. Wronskiano de f 1 (t), f 2 (t),..., f n (t). Derivada de un determinante de funciones.
Contenidos. Grupo EDUMATICUS. Departamento de Matemática Aplicada. Universidad de Málaga 2
 Tema 2 Ecuaciones diferenciales ordinarias de primer orden Definiciones generales Problema de Cauchy Contenidos Resolución de ecuaciones diferenciales ordinarias de primer orden Resolución de ecuaciones
Tema 2 Ecuaciones diferenciales ordinarias de primer orden Definiciones generales Problema de Cauchy Contenidos Resolución de ecuaciones diferenciales ordinarias de primer orden Resolución de ecuaciones
Ecuaciones lineales de segundo orden
 Ecuaciones lineales de segundo orden Considere la ecuación lineal general de segundo orden A( xy ) + Bxy ( ) + Cxy ( ) = Fx ( ) donde las funciones coeficientes A, B, C y abierto I. F son continuas en
Ecuaciones lineales de segundo orden Considere la ecuación lineal general de segundo orden A( xy ) + Bxy ( ) + Cxy ( ) = Fx ( ) donde las funciones coeficientes A, B, C y abierto I. F son continuas en
Ecuaciones Diferenciales Ordinarias
 Ecuaciones Diferenciales Ordinarias (Ecuaciones de 2do Orden) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Otoño 2011, Resumen clases Julio López EDO 1/20 Operadores
Ecuaciones Diferenciales Ordinarias (Ecuaciones de 2do Orden) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Otoño 2011, Resumen clases Julio López EDO 1/20 Operadores
FUNCIONES y = f(x) ESO3
 Las correspondencias entre conjunto de valores o magnitudes se pueden expresar de varias formas: con un enunciado, con una tabla, con una gráfica, o con una fórmula o expresión algebraica o analítica.
Las correspondencias entre conjunto de valores o magnitudes se pueden expresar de varias formas: con un enunciado, con una tabla, con una gráfica, o con una fórmula o expresión algebraica o analítica.
CAPÍTULO 1 INTRODUCCION
 CAPÍTULO 1 INTRODUCCION Definición 1.1. Si una ecuación contiene las derivadas o las diferenciales de una o más variables dependientes con respecto a una o más variables independientes, se dice que es
CAPÍTULO 1 INTRODUCCION Definición 1.1. Si una ecuación contiene las derivadas o las diferenciales de una o más variables dependientes con respecto a una o más variables independientes, se dice que es
a de un conjunto S de R n si
 1 235 Máximos, mínimos y puntos de ensilladura Definición.- Se dice que una función real f( x) tiene un máximo absoluto en un punto a de un conjunto S de R n si f( x) f( a) (2) para todo x S. El número
1 235 Máximos, mínimos y puntos de ensilladura Definición.- Se dice que una función real f( x) tiene un máximo absoluto en un punto a de un conjunto S de R n si f( x) f( a) (2) para todo x S. El número
Ecuaciones diferenciales
 de primer orden 21 de noviembre de 2016 de primer orden Introducción Introducción a las ecuaciones diferenciales Las primeras ecuaciones diferenciales surgen al tratar de resolver ciertos problemas de
de primer orden 21 de noviembre de 2016 de primer orden Introducción Introducción a las ecuaciones diferenciales Las primeras ecuaciones diferenciales surgen al tratar de resolver ciertos problemas de
Ecuaciones Diferenciales Ordinarias
 Nivelación de Matemática MTHA UNLP EDO 1 Ecuaciones Diferenciales Ordinarias 1. Introducción Una ecuación diferencial ordinaria es una ecuación de la forma: F (x, y, y,..., y (n) ) = 0 que expresa una
Nivelación de Matemática MTHA UNLP EDO 1 Ecuaciones Diferenciales Ordinarias 1. Introducción Una ecuación diferencial ordinaria es una ecuación de la forma: F (x, y, y,..., y (n) ) = 0 que expresa una
9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal
 Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
Miguel Reyes, Dpto. de Matemática Aplicada, FI-UPM 1 9 Ecuaciones diferenciales ordinarias. Ecuaciones diferenciales de primer orden en forma normal 9.1 Definición Se llama ecuación diferencial ordinaria
Termodinámica. 1. Introducción. Transformaciones de Legendre Potenciales Termodinámicos
 Termodinámica 2 o curso de la Licenciatura de Físicas Lección 3 Introducción Transformaciones de Legendre Potenciales Termodinámicos 1. Introducción El estado de equilibrio está caracterizado las variables
Termodinámica 2 o curso de la Licenciatura de Físicas Lección 3 Introducción Transformaciones de Legendre Potenciales Termodinámicos 1. Introducción El estado de equilibrio está caracterizado las variables
Ecuaciones Diferenciales
 Ecuaciones Diferenciales Definición de Ecuación diferencial. A toda igualdad que relaciona a una función desconocida o variable dependiente con sus variables independientes y sus derivadas se le conoce
Ecuaciones Diferenciales Definición de Ecuación diferencial. A toda igualdad que relaciona a una función desconocida o variable dependiente con sus variables independientes y sus derivadas se le conoce
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS
 Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
3. Ecuaciones Diferenciales Lineales Homogéneas de Orden Superior con Coeficientes Constantes. Ecuaciones Diferenciales de Segundo Orden
 3. Lineales Homogéneas de de Segundo Orden Sabemos que la solución general de una ecuación diferencial lineal homogénea de segundo orden está dada por por lo que se tiene dos soluciones no triviales, en
3. Lineales Homogéneas de de Segundo Orden Sabemos que la solución general de una ecuación diferencial lineal homogénea de segundo orden está dada por por lo que se tiene dos soluciones no triviales, en
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: MATEMÁTICAS II INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a
Cálculo Diferencial en una variable
 Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
Tema 2 Cálculo Diferencial en una variable 2.1. Derivadas La derivada nos proporciona una manera de calcular la tasa de cambio de una función Calculamos la velocidad media como la razón entre la distancia
Sistemas de ecuaciones diferenciales y el uso de operadores
 Sistemas de ecuaciones diferenciales y el uso de operadores En la clase anterior resolvimos algunos sistemas de ecuaciones diferenciales sacándole provecho a la notación matricial. Sin embrago, algunos
Sistemas de ecuaciones diferenciales y el uso de operadores En la clase anterior resolvimos algunos sistemas de ecuaciones diferenciales sacándole provecho a la notación matricial. Sin embrago, algunos
Ecuaciones Diferenciales Ordinarias
 Ecuaciones Diferenciales Ordinarias (Coeficientes Indeterminados y Variación de Parámetros) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Otoño 2011, Resumen clases
Ecuaciones Diferenciales Ordinarias (Coeficientes Indeterminados y Variación de Parámetros) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Otoño 2011, Resumen clases
1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello
![1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello 1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello](/thumbs/73/68677028.jpg) 1. Enunciados 1.1. Primer ejercicio Sea f(x := e x, x R. 1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello a Asegurar que existe probando que la función f es absolutamente
1. Enunciados 1.1. Primer ejercicio Sea f(x := e x, x R. 1. Se trata en primer lugar de calcular la transformada de Fourier F[f]. Para ello a Asegurar que existe probando que la función f es absolutamente
2.1 Descripción en espacio de estado de sistemas dinámicos
 2 Análisis de sistemas lineales 2.1 Descripción en espacio de estado de sistemas dinámicos El objetivo de este capítulo es formular una teoría general de describir los sistemas dinámicos en funcion de
2 Análisis de sistemas lineales 2.1 Descripción en espacio de estado de sistemas dinámicos El objetivo de este capítulo es formular una teoría general de describir los sistemas dinámicos en funcion de
May 4, 2012 CAPÍTULO 5: OPTIMIZACIÓN
 May 4, 2012 1. Optimización Sin Restricciones En toda esta sección D denota un subconjunto abierto de R n. 1.1. Condiciones Necesarias de Primer Orden. Proposición 1.1. Sea f : D R diferenciable. Si p
May 4, 2012 1. Optimización Sin Restricciones En toda esta sección D denota un subconjunto abierto de R n. 1.1. Condiciones Necesarias de Primer Orden. Proposición 1.1. Sea f : D R diferenciable. Si p
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS (SOLUCIONES ) HOJA 3: Derivadas parciales y diferenciación.
 UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
UNIVERSIDAD CARLOS III DE MADRID MATEMÁTICAS PARA LA ECONOMÍA II PROBLEMAS SOLUCIONES ) 3-1. Calcular, para las siguientes funciones. a) fx, y) x cos x sen y b) fx, y) e xy c) fx, y) x + y ) lnx + y )
Integración indefinida y definida. Aplicaciones de la integral: valor medio de una función continua.
 Integración indefinida y definida. Aplicaciones de la integral: valor medio de una función continua. 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos 1 Introducción 2 3 4 5
Integración indefinida y definida. Aplicaciones de la integral: valor medio de una función continua. 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos 1 Introducción 2 3 4 5
1 Método de la bisección. 1.1 Teorema de Bolzano Teorema 1.1 (Bolzano) Contenido
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
Sistemas de Ecuaciones Diferenciales
 Lección 8 Sistemas de ecuaciones diferenciales lineales 1 Sistemas de Ecuaciones Diferenciales Consideremos el sistema A + S X + S k 1 k 2 Inicialmente se añaden 2 moles de S y 1 mol de A d[a] dt = k 1
Lección 8 Sistemas de ecuaciones diferenciales lineales 1 Sistemas de Ecuaciones Diferenciales Consideremos el sistema A + S X + S k 1 k 2 Inicialmente se añaden 2 moles de S y 1 mol de A d[a] dt = k 1
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
Ecuaciones diferenciales de orden superior
 CAPÍTULO 4 Ecuaciones diferenciales de orden superior OBJETIVOS PARTICULARES Describir los conceptos de combinación lineal, dependencia e independencia lineal, conjunto fundamental de soluciones y solución
CAPÍTULO 4 Ecuaciones diferenciales de orden superior OBJETIVOS PARTICULARES Describir los conceptos de combinación lineal, dependencia e independencia lineal, conjunto fundamental de soluciones y solución
Funciones de Una Variable Real I. Derivadas
 Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
Contents : Derivadas Universidad de Murcia Curso 2010-2011 Contents 1 Funciones derivables Contents 1 Funciones derivables 2 Contents 1 Funciones derivables 2 3 Objetivos Funciones derivables Definir,
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
Cuando una función es derivable en un punto, podemos conocer si es creciente o decreciente en dicho punto:
 1 LA DERIVADA EN EL TRAZADO DE CURVAS Significados de los signos de la Primera y Segunda derivada. Plantearemos a través del estudio del signo de la primera derivada, las condiciones que debe cumplir una
1 LA DERIVADA EN EL TRAZADO DE CURVAS Significados de los signos de la Primera y Segunda derivada. Plantearemos a través del estudio del signo de la primera derivada, las condiciones que debe cumplir una
Modelización por medio de sistemas
 SISTEMAS DE ECUACIONES DIFERENCIALES LINEALES. Modelización por medio de sistemas d y dy Ecuaciones autónomas de segundo orden: = f ( y, ) Una variable independiente. Una variable dependiente. La variable
SISTEMAS DE ECUACIONES DIFERENCIALES LINEALES. Modelización por medio de sistemas d y dy Ecuaciones autónomas de segundo orden: = f ( y, ) Una variable independiente. Una variable dependiente. La variable
March 25, 2010 CAPÍTULO 2: LÍMITES Y CONTINUIDAD DE FUNCIONES EN EL ESPACIO EUCLÍDEO
 March 25, 2010 CAPÍTULO 2: LÍMITE Y CONTINUIDAD DE FUNCIONE EN EL EPACIO EUCLÍDEO 1. Producto Escalar en R n Definición 1.1. Dado x = (x 1,..., x n ), y = (y 1,..., y n ) R n, su producto escalar está
March 25, 2010 CAPÍTULO 2: LÍMITE Y CONTINUIDAD DE FUNCIONE EN EL EPACIO EUCLÍDEO 1. Producto Escalar en R n Definición 1.1. Dado x = (x 1,..., x n ), y = (y 1,..., y n ) R n, su producto escalar está
Lista de ejercicios # 4
 UNIVERSIDAD DE COSTA RICA MA-5 FACULTAD DE CIENCIAS Ecuaciones Diferenciales para Ingeniería ESCUELA DE MATEMÁTICA Primer Ciclo del 5 Lista de ejercicios # 4 Sistemas de ecuaciones diferenciales. EPII-II-
UNIVERSIDAD DE COSTA RICA MA-5 FACULTAD DE CIENCIAS Ecuaciones Diferenciales para Ingeniería ESCUELA DE MATEMÁTICA Primer Ciclo del 5 Lista de ejercicios # 4 Sistemas de ecuaciones diferenciales. EPII-II-
Tema 2 Resolución de EcuacionesNo Lineales
 Tema 2 Resolución de Ecuaciones No Lineales E.T.S.I. Informática Indice Introducción 1 Introducción 2 Algoritmo del método de Bisección Análisis del 3 4 5 6 Algoritmo de los métodos iterativos Interpretación
Tema 2 Resolución de Ecuaciones No Lineales E.T.S.I. Informática Indice Introducción 1 Introducción 2 Algoritmo del método de Bisección Análisis del 3 4 5 6 Algoritmo de los métodos iterativos Interpretación
r r a) Clasificar el sistema x = Ax en función del parámetro r R.
 Examen Final de Ecuaciones Diferenciales Fecha: 15 de junio de 2012 3 Problemas (7.5 puntos) Tiempo total: 3 horas Problema 1 [2.5 puntos]. Queremos dibujar el croquis de un sistema lineal 2D y realizar
Examen Final de Ecuaciones Diferenciales Fecha: 15 de junio de 2012 3 Problemas (7.5 puntos) Tiempo total: 3 horas Problema 1 [2.5 puntos]. Queremos dibujar el croquis de un sistema lineal 2D y realizar
Fundamentos matemáticos. Tema 5 Derivación de funciones de una y varias variables
 Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 5 Derivación de funciones de una y varias variables José Barrios García Departamento de Análisis Matemático Universidad de La
Fundamentos matemáticos Grado en Ingeniería agrícola y del medio rural Tema 5 Derivación de funciones de una y varias variables José Barrios García Departamento de Análisis Matemático Universidad de La
2.2 Rectas en el plano
 2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
La Diferencial de Fréchet
 Capítulo 6 La Diferencial de Fréchet Es bien conocido que una función de una variable f es derivable en un punto a si y sólo si su gráfica admite una recta tangente (no vertical) en el punto (a, f(a)).
Capítulo 6 La Diferencial de Fréchet Es bien conocido que una función de una variable f es derivable en un punto a si y sólo si su gráfica admite una recta tangente (no vertical) en el punto (a, f(a)).
Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/ HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5
 Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/2006 - HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5 1) A continuación diremos de qué tipo son las ecuaciones diferenciales ordinarias (e.
Matemática Aplicada - Licenciatura de Farmacia - Curso 2005/2006 - HOJA 5 1 SOLUCIONES DE LOS EJERCICIOS DE LA HOJA 5 1) A continuación diremos de qué tipo son las ecuaciones diferenciales ordinarias (e.
TEMA 3: CONTINUIDAD DE FUNCIONES
 TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
TEMA 3: CONTINUIDAD DE FUNCIONES. Valor Absoluto Trabajaremos en el campo de los números reales, R. Para el estudio de las propiedades de las funciones necesitamos el concepto de valor absoluto de un número
Funciones reales de variable real
 Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
Tema Funciones reales de variable real Introducción El objetivo fundamental de este tema es recordar conceptos ya conocidos acerca de las funciones reales de variable real.. Conceptos Generales Definición.
2 Deniciones y soluciones
 Deniciones y soluciones Sabemos que la derivada de una función y(x) es otra función y (x) que se determina aplicando una regla adecuada. Por ejemplo, la derivada de y = e 3x es dx = 6xe3x. Si en la última
Deniciones y soluciones Sabemos que la derivada de una función y(x) es otra función y (x) que se determina aplicando una regla adecuada. Por ejemplo, la derivada de y = e 3x es dx = 6xe3x. Si en la última
Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como:
![Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como: Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como:](/thumbs/71/66199093.jpg) Derivadas Antes de dar la definición de derivada de una función en un punto, vamos a introducir el concepto de tasa de variación media y dos ejemplos o motivaciones iniciales que nos van a dar la medida
Derivadas Antes de dar la definición de derivada de una función en un punto, vamos a introducir el concepto de tasa de variación media y dos ejemplos o motivaciones iniciales que nos van a dar la medida
C alculo Octubre 2010
 Cálculo Octubre 2010 Derivada. Introducción Recordemos la definición de pendiente de una recta: α y 1 y0 x 0 x 1 Pendiente= m = tanα = y 1 y 0 x 1 x 0 Y ahora consideremos las pendientes de las rectas
Cálculo Octubre 2010 Derivada. Introducción Recordemos la definición de pendiente de una recta: α y 1 y0 x 0 x 1 Pendiente= m = tanα = y 1 y 0 x 1 x 0 Y ahora consideremos las pendientes de las rectas
Información importante
 Coordinación de Matemática I (MAT021) 1 er Semestre de 2010 Semana 8: Lunes 10 viernes 14 de Mayo Información importante El viernes 14 ser publicada la tarea preparatoria de Taller de Sala. Durante la
Coordinación de Matemática I (MAT021) 1 er Semestre de 2010 Semana 8: Lunes 10 viernes 14 de Mayo Información importante El viernes 14 ser publicada la tarea preparatoria de Taller de Sala. Durante la
2. Método de separación de variables
 APUNTES DE AMPIACIÓN DE MATEMÁTICAS II PARA INGENIEROS DE TEECOMUNICACIONES Elaborados por Arturo de Pablo, Domingo Pestana y José Manuel Rodríguez 2. Método de separación de variables 2.1. Separación
APUNTES DE AMPIACIÓN DE MATEMÁTICAS II PARA INGENIEROS DE TEECOMUNICACIONES Elaborados por Arturo de Pablo, Domingo Pestana y José Manuel Rodríguez 2. Método de separación de variables 2.1. Separación
Teóricas de Análisis Matemático (28) - Práctica 8 - Polinomio de Taylor
 Práctica 8 Polinomio de Taylor. Polinomio de Taylor El análisis completo de una función puede resultar muy difícil. Una forma de abordar este problema es aproximar la función por una más sencilla. En este
Práctica 8 Polinomio de Taylor. Polinomio de Taylor El análisis completo de una función puede resultar muy difícil. Una forma de abordar este problema es aproximar la función por una más sencilla. En este
Semana 2 [1/24] Derivadas. August 16, Derivadas
![Semana 2 [1/24] Derivadas. August 16, Derivadas Semana 2 [1/24] Derivadas. August 16, Derivadas](/thumbs/49/25449732.jpg) Semana 2 [1/24] August 16, 2007 Máximos y mínimos: la regla de Fermat Semana 2 [2/24] Máximos y mínimos locales Mínimo local x es un mínimo local de la función f si existe ε > 0 tal que f( x) f(x) x (
Semana 2 [1/24] August 16, 2007 Máximos y mínimos: la regla de Fermat Semana 2 [2/24] Máximos y mínimos locales Mínimo local x es un mínimo local de la función f si existe ε > 0 tal que f( x) f(x) x (
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática ( )
 Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 4 (APLICACIONES DE LA DERIVADA) Profesora: Yulimar Matute Febrero 2012 RECTA
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 4 (APLICACIONES DE LA DERIVADA) Profesora: Yulimar Matute Febrero 2012 RECTA
Ecuaciones Diferenciales
 UNIVERSIDAD DIEGO PORTALES Ecuaciones Diferenciales 1 ECUACIONES DIFERENCIALES Una ecuación diferencial contiene una función desconocida y algunas de sus derivadas. He aquí algunos ejemplos: (1) y ' =
UNIVERSIDAD DIEGO PORTALES Ecuaciones Diferenciales 1 ECUACIONES DIFERENCIALES Una ecuación diferencial contiene una función desconocida y algunas de sus derivadas. He aquí algunos ejemplos: (1) y ' =
1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS
 1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS 1 1.- LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función f por la izquierda de un punto x = a. Es el valor al
1º BACHILLERATO MATEMÁTICAS CIENCIAS SOCIALES TEMA 4.- LÍMITES, CONTINUIDAD Y DERIVADAS 1 1.- LÍMITE DE UNA FUNCIÓN EN UN PUNTO Límite de una función f por la izquierda de un punto x = a. Es el valor al
Matemática IV Taller, Ecuaciones de orden 1. dy dx = y xy2 2. Determine la solución general de la ecuación. (y 4x)dx + (y x)dy = 0.
 Matemática IV - 2000953 Taller, Ecuaciones de orden 1 1. Resuelva R: y 2 x = ln y. dy dx = y 3, y(0) = 1. 1 2xy2 2. Determine la solución general de la ecuación (y 4x)dx + (y x)dy = 0. 3. Una persona tiene
Matemática IV - 2000953 Taller, Ecuaciones de orden 1 1. Resuelva R: y 2 x = ln y. dy dx = y 3, y(0) = 1. 1 2xy2 2. Determine la solución general de la ecuación (y 4x)dx + (y x)dy = 0. 3. Una persona tiene
(Límites y continuidad, derivadas, estudio y representación de funciones)
 ANÁLISIS I: CÁLCULO DIFERENCIAL (Límites y continuidad, derivadas, estudio y representación de funciones) Curso 009-010 -Enunciados: pg -Soluciones: pg 3 Curso 010-011 -Enunciados: pg 5 -Soluciones: pg
ANÁLISIS I: CÁLCULO DIFERENCIAL (Límites y continuidad, derivadas, estudio y representación de funciones) Curso 009-010 -Enunciados: pg -Soluciones: pg 3 Curso 010-011 -Enunciados: pg 5 -Soluciones: pg
Tema 6: Ecuaciones diferenciales lineales.
 Tema 6: Ecuaciones diferenciales lineales Una ecuación diferencial lineal de orden n es una ecuación que se puede escribir de la siguiente forma: a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x)
Tema 6: Ecuaciones diferenciales lineales Una ecuación diferencial lineal de orden n es una ecuación que se puede escribir de la siguiente forma: a n (x)y (n) (x) + a n 1 (x)y (n 1) (x) + + a 0 (x)y(x)
02. Resolver sistemas de ecuaciones lineales por el método de Gauss.
 3.6 Criterios específicos de evaluación. 01. Conocer lo que significa que un sistema sea incompatible o compatible, determinado o indeterminado, y aplicar este conocimiento para formar un sistema de un
3.6 Criterios específicos de evaluación. 01. Conocer lo que significa que un sistema sea incompatible o compatible, determinado o indeterminado, y aplicar este conocimiento para formar un sistema de un
Ecuaciones Diferenciales Ordinarias
 Ecuaciones Diferenciales Ordinarias (Teoremas de Existencia y Unicidad) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Otoño 2011, Resumen clases Julio López EDO 1/15
Ecuaciones Diferenciales Ordinarias (Teoremas de Existencia y Unicidad) Julio López jclopez@dim.uchile.cl Depto Ingeniería Matemática, Universidad de Chile Otoño 2011, Resumen clases Julio López EDO 1/15
CLASE 1: Funciones y Gráficas
 CLASE 1: Funciones y Gráficas Sergio Stive Solano Sabié Agosto de 2011 CLASE 1: Funciones y Gráficas Sergio Stive Solano Sabié Agosto de 2011 Cuatro maneras de representar una función Definición 1.1 Una
CLASE 1: Funciones y Gráficas Sergio Stive Solano Sabié Agosto de 2011 CLASE 1: Funciones y Gráficas Sergio Stive Solano Sabié Agosto de 2011 Cuatro maneras de representar una función Definición 1.1 Una
Funciones de varias variables. Continuidad
 Capítulo 1 Funciones de varias variables. Continuidad 1. Topología en R n Definición (Norma, espacio vectorial normado). Una norma sobre R n es una aplicación: : R n [0,+ [ x x, que satisface las siguientes
Capítulo 1 Funciones de varias variables. Continuidad 1. Topología en R n Definición (Norma, espacio vectorial normado). Una norma sobre R n es una aplicación: : R n [0,+ [ x x, que satisface las siguientes
Teorema de la Función Implícita
 Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
Teorema de la Función Implícita Sea F : U R p+1 R U abierto F (x 1, x 2,..., x q, y) y un punto a (a 1, a 2,..., a q, b) en U tal que i)f (a 1, a 2,..., a q, b) 0 ii) 0 y continua, existe entonces una
TEMA 6: GEOMETRÍA ANALÍTICA EN EL PLANO
 Alonso Fernández Galián Tema 6: Geometría analítica en el plano TEMA 6: GEOMETRÍA ANALÍTICA EN EL PLANO La geometría analítica es el estudio de objetos geométricos (rectas, circunferencias, ) por medio
Alonso Fernández Galián Tema 6: Geometría analítica en el plano TEMA 6: GEOMETRÍA ANALÍTICA EN EL PLANO La geometría analítica es el estudio de objetos geométricos (rectas, circunferencias, ) por medio
Raíz cuadrada. Superficies de Riemann
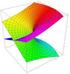 Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática ( )
 Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 3 (DERIVADAS) Profesora: Yulimar Matute Febrero 2012 DERIVADAS POR DEFINICIÓN
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 3 (DERIVADAS) Profesora: Yulimar Matute Febrero 2012 DERIVADAS POR DEFINICIÓN
Métodos de solución de ED de primer orden
 CAPÍTULO Métodos de solución de ED de primer orden.3 Ecuaciones diferenciales lineales Las ecuaciones diferenciales ordinarias de primer orden pueden ser lineales o no lineales. En esta sección centraremos
CAPÍTULO Métodos de solución de ED de primer orden.3 Ecuaciones diferenciales lineales Las ecuaciones diferenciales ordinarias de primer orden pueden ser lineales o no lineales. En esta sección centraremos
2.3 Ecuaciones diferenciales lineales
 .3 Ecuaciones diferenciales lineales 45.3 Ecuaciones diferenciales lineales Las ecuaciones diferenciales ordinarias de primer orden pueden ser lineales o no lineales. En esta sección centraremos la atención
.3 Ecuaciones diferenciales lineales 45.3 Ecuaciones diferenciales lineales Las ecuaciones diferenciales ordinarias de primer orden pueden ser lineales o no lineales. En esta sección centraremos la atención
Criterio 1: Sea f una función derivable en (a,b). f es estrictamente creciente en el intervalo abierto (a, b) si f es positiva en dicho intervalo.
 UNIDAD. APLICACIONES DE LAS DERIVADAS.. Información etraída de la primera derivada.. Información etraída de la segunda derivada.. Derivabilidad en intervalos: Teorema de Rolle, del valor medio y Caucy..4
UNIDAD. APLICACIONES DE LAS DERIVADAS.. Información etraída de la primera derivada.. Información etraída de la segunda derivada.. Derivabilidad en intervalos: Teorema de Rolle, del valor medio y Caucy..4
Ecuación Diferenciales Homogéneas de Primer Orden
 Ecuación Diferenciales Homogéneas de Primer Orden 1. Funciones Homogéneas de grado n Definicion: Diremos que una función f(, y) es homogénea de grado n si f(t, ty) = t n f(, y) si w = y f(, y) = n g(w)
Ecuación Diferenciales Homogéneas de Primer Orden 1. Funciones Homogéneas de grado n Definicion: Diremos que una función f(, y) es homogénea de grado n si f(t, ty) = t n f(, y) si w = y f(, y) = n g(w)
