SOLUCIONARI Unitat 1
|
|
|
- Gloria Murillo Cabrera
- hace 9 años
- Vistas:
Transcripción
1 SOLUCIONARI Unitat Comencem En un problema de física es demana el temps que triga una pilota a assolir una certa altura. Un estudiant, que ha resolt el problema correctament, arriba a la solució t s. La resposta que dóna és t,00808 s. Et sembla que és correcta aquesta resposta? No té cap sentit expressar el resultat amb tantes xifres decimals, ja que no hi ha cap aparell de mesura de temps que pugui apreciar fins a la milionèsima de segon. Si a, i b,, calcula a b i ab i indica en cada cas les xifres decimals correctes. a, b,, a,, b,,80 a b,600 a b, Si en lloc de sumar multipliquem ordenadament, s obté:,90 a b,9699 Per tant, a b,9. Exercicis. Calcula la longitud dels segments indicats a continuació. Expressa n el resultat de manera exacta i utilitza la calculadora per obtenir-ne una aproximació arrodonida a les centèsimes: a) La diagonal d un rectangle de costats i cm. Diagonal: d d 9 cm,8 cm b) El diàmetre d una circumferència la longitud de la qual és 0 cm. Diàmetre: d L 0 d cm,8 cm c) L altura d un triangle equilàter de cm de costat. Altura: h h cm cm,6 cm d) L altura d un con que mesura 6 cm de radi i 9 cm de generatriu. Altura: h h 9 6 cm cm 6, cm. El costat més petit d un rectangle auri mesura cm. Quant mesura l altre costat? Expressa n el resultat de manera exacta i amb una aproximació arrodonida a les dècimes. Mesura, és a dir, cm, cm. Sabent que PQ PS dm, demostra que el segment QR mesura dm fig..). R QO dm QR QO OR dm. Classifica els nombres següents en racionals i irracionals: a),0 b), S P O Matemàtiques. Batxillerat Q
2 c),9 d) e),... f ) 0,8. Indica quins d aquests nombres són irracionals: a) b) c) d) e e) 9 f ) g) 6 9 h) 6 i) 6 9), 0, 6. Per què el número no pot ser 0,6 irracional? No pot ser irracional perquè és el resultat de sumar i dividir nombres que són racionals.. Calcula l àrea d un cercle de cm de radi prenent els següents valors de : a) L aproximació per defecte,. A r, 0,6 cm b) L aproximació per excés,6. A r,6 0,66 cm En quin dels dos casos has obtingut una millor aproximació a la mesura real de la superfície d aquest cercle? Per què? La segona aproximació és més bona que la primera, ja que l aproximació per excès del nombre és millor que l aproximació per defecte. 8. Expressa de manera exacta: a) La longitud d una circumferència de 6 cm de diàmetre. L 6 cm b) L àrea lateral d un cilindre de cm de radi i cm de generatriu. A lat rg 0 cm c) El volum d un con de cm de radi i cm de generatriu. L altura del con mesura: h g r cm r h V 00 cm 9. S ha aconseguit determinar que el radi d una circumferència mesura cm. Es pot conèixer amb exactitud la seva longitud? I l àrea del cercle que limita? Justifica la resposta fent els càlculs corresponents. La longitud de la circumferència es pot conèixer amb exactitud, perquè: L r 8 cm En canvi, només podem saber un valor aproximat de l àrea del cercle corresponent, ja que 6 A r cm 6 i és un nombre irracional. 6 A cm,09 cm Matemàtiques. Batxillerat
3 0. Quant mesura la diagonal d un cub de cm d aresta? Expressa n el resultat de manera exacta i aproxima l a les centèsimes. Diagonal: D D cm,6 cm. La longitud d una circumferència mesura 0 cm. a) Expressa n el resultat aproximat a les centèsimes. L,6 cm b) Quant mesura el radi d aquesta circumferència? L r cm c) Calcula l àrea del cercle que limita i expressa-la de manera exacta. A r cm. Troba cinc nombres racionals compresos entre i, i ordena ls del més petit al més gran. Resposta oberta. Per exemple: 0, 0, 0,6 0,6 0,6. Entre quins nombres enters consecutius es troba cadascun d aquests nombres irracionals? a) i g) 6 h) i) e i 6 i 8 i 9. Representa a la recta numèrica els nombres irracionals següents: a) b) c) 9 d) 8 e) f ) g) h) i) 0 j) k) 8 l) c. Compara aquests parells de nombres reals: a) i g i k l j h e d b a f b) i 0, 0, b) c) d) e) f ) 8 i i i 8 i i c) i 0 0 d),9 i e) 6 i,9 6 f ),9 i,9 0 0 g) i Matemàtiques. Batxillerat
4 h),9 i,,9, 9. Aproxima per defecte i per excés fins a les mil. lèsimes cadascun dels nombres irracionals següents: 6. Ordena del més petit al més gran els nombres reals següents i col. loca el signe de desigualtat que correspongui:,;,99;,9; ;,; 0;, 0,,99,9. Escriu dos nombres racionals compresos entre: Resposta oberta. Per exemple: a) i 6 b) i, i,, i,6 c) i,0 i, d) e i,9 i 8. Expressa de manera exacta: a) L àrea d un triangle equilàter de cm de costat. c 6 A cm b) La longitud de la diagonal d un rectangle els costats del qual mesuren i 6 cm. d a b 6 6 cm cm c) El volum d un cilindre de cm de radi i cm d altura. V r g cm d) L àrea d un hexàgon regular inscrit en una circumferència de 8 cm de diàmetre. d Costat de l hexàgon: c cm c A cm a) Resposta oberta. Per exemple, prenent xifres decimals per a cada nombre: 0. Extreu factor comú de: a) b) Per defecte c) a a a ) ) ) a d) a b c a b c). Les operacions amb nombres irracionals que s indiquen a continuació donen com a resultat un nombre racional. Calcula l en cada cas. a) 0 ) 0 ) 0 b) ) ) ) ) c) ) ) 9 6 d) ) : b) e c) Per excés,0, e,8,8,,6 ) : : e) 6) 6 6) 6 Matemàtiques. Batxillerat
5 f ) ) ) ) ) Si x, y, z i t representen quatre nombres reals, escriu cadascuna d aquestes expressions com un producte de dos factors: a) x y xy x y xy xyx y) b) x y z) t y z) x y z) t y z) y z)x t) c) z z z z z z z z z ) d) x xy y t x y) x xy y t x y) x y) t x y) x y)x y t) e) z x t) x xt t z x t) x xt t z x t) x t) x t)z x t). Calcula sense utilitzar la calculadora: a) b) 96 6 c) 8 9 d) e) 0,00 0, f ). Tot i que a primer cop d ull no ho sembli, els resultats de les arrels següents són tots racionals. Calcula ls. 8 a) b) c) d) 8 8. Expressa en forma de potència: a) b) a c) 0 d) a ) e) 6 a 0 a ) 6 6 f ) 6 6. Expressa en forma d arrel: a) b) c) a a Matemàtiques. Batxillerat
6 d) e) b b 9. Per simplificar una arrel del tipus n a m, cal aconseguir que m i n siguin nombres primers entre ells. Simplifica: a) b) a 0 6 a a a. Les potències d exponent fraccionari verifiquen totes i cadascuna de les propietats de les potències d exponent enter. Aplica aquestes propietats per expressar en funció d una sola potència: a) b) : c) : 6 d) Utilitza la calculadora i aproxima fins a les centèsimes aquests nombres irracionals: a) b) c) 0,,6 d) 0 e) f ),,,68,9,9 c) 0 d) Esbrina quina de les igualtats següents és incorrecta: a) a b) a b b) a b a b c) a ab b a b La de l apartat b), ja que a b) a b.. Expressa en forma d una sola arrel: a) b) c) 0 6 d) e) ) f ) g) a b) a b h) a a b) a b b) 0 Matemàtiques. Batxillerat
7 i) j) a a a 6 a. Expressa de la manera més senzilla possible: a) b) ) c) 000 d) Racionalitza les expressions fraccionàries següents: a) b) c) 6 d) ) 6 ) ). Efectua les operacions indicades racionalitzant prèviament cada expressió fraccionària: a) ; ) 6 b) ) 6 6 ) ) 6. Representa a la recta real els conjunts de nombres següents. Després, defineix-los mitjançant desigualtats: a) [, ) b), ) 0 x x Matemàtiques. Batxillerat 0
8 c) [, ] d), ) e) [, 0) f ) 0, ] g), ) h) [, ) i), 0) 0 x 0 x 0 x x 0 x 0 x d) x e) x 6 f ) x, ) x 6 x. Les inequacions x i x tenen solucions comunes. Troba-les, representa-les gràficament i expressa-les de dues maneres diferents. x 6 x x x x x x, o també, x [, ). 8. Efectua aquestes operacions amb l ajut de la calculadora. Expressa n els resultats utilitzant la notació científica: a), 0 0 6, 0,8 0 b) 0 6 : 0 ) : 0, 0 0 c) ,6 0 0 x 0 0 d) 0 0 ) 9,98 0 j), ] 6. Expressa utilitzant la nova notació els conjunts de nombres reals que verifiquen: a) x b) x 0 x [, ), ) 9. Una estrella es troba a anys llum de la Terra. Quina es la distància en quilòmetres que la separa del nostre planeta? Un any llum és la distància que recorre la llum en un any a la velocitat de km/s. 6 dies h 600 s any any dia h s km any llum s s 9,608 0 km c) x [, ] anys llum 9,608 0,8 0 km Matemàtiques. Batxillerat
9 0. Sabent que un mol d àtoms de ferro conté 6,0 0 àtoms d aquest metall i que té una massa de,8 g, esbrina: a) La massa en grams d un àtom de ferro. mol àtom Fe àtom Fe 6,0 0 átom Fe,8 g Fe 9,0 g Fe mol àtom Fe b) El nombre d àtoms continguts en g de ferro. mol àtom Fe g Fe,8 g Fe Acabem 6,0 0 àtom Fe mol àtom Fe,08 0 àtom Fe. Calcula el costat, el perímetre i l àrea d un quadrat inscrit en una circumferència de cm de radi. Quina de les tres mesures s expressa mitjançant un nombre racional? Expressa les altres dues de manera exacta i amb una aproximació fins a les centèsimes. El diàmetre de la circumferència coincideix amb la diagonal del quadrat i mesura cm. Si representen per c el costat del quadrat, es verifica: c c c 6 c 8 c cm,8 cm El perímetre p del quadrat mesura:. Representa a la recta numèrica els nombres reals següents: a) b),6 c) d) 8 Representació aproximada: d a b c 0. Calcula: a) ) ) 9 b) 0) 0) 0 00 c) ) ) ) ) d) ) ) ) ). Demostra, sense utilitzar la calculadora, que el número 6 és racional. Realitza prèviament la descomposició en factors primers de Dibuixa un quadrat de cm de costat. Determina els punts mitjans dels seus costats i uneix-los successivament. Quina figura n obtens? Per què? Calcula n l àrea i el perímetre. 6 8 p c 8 cm, cm i l àrea A del quadrat és: A c 8 cm L única mesura que s expressa mitjançant un nombre racional és la superficie del quadrat.. Troba quatre nombres racionals compresos entre i 6. Resposta oberta. Per exemple:,;,;,;,. S obtè un altre quadrat: els seus costats són iguals i els quatre angles són rectes. Àrea: A ) cm Perímetre: P cm Matemàtiques. Batxillerat
10 . Considera un nombre positiu, eleva l al quadrat, multiplica l per i, finalment, extreu-ne l arrel quadrada. Demostra que el quocient de la divisió entre l últim nombre i el primer és igual a. x x x x L últim pas és possible perquè x Calcula: a) ) ) b) ) ) c) ) ) 0 d) ) ) En quins casos el resultat d una potència de base és més petit que? Justifica n la resposta amb exemples. Sempre que l exponent és més petit que. Per exemple:,; 0 ;. 0. Expressa com una sola potència: a) b) c) : : : a d) b ) a a b ) b 6 b. Escriu com una única arrel: a) b b) : 0, c) d) : 0, : 6. Expressa de la manera més senzilla possible el resultat de les operacions següents: a) ) 0 b) c) a a a a a a a 6 6 a a 6 a d) b : b b : b b : b Matemàtiques. Batxillerat b b. L arrel quadrada de l arrel cúbica d un nombre positiu x té dos possibles resultats. Per què? Si un d aquests és, quin és l altre? Calcula x. Perquè es tracta d una arrel d índex parell índex 6) x 6 x L altre resultat és, l oposat de.. Racionalitza: 0 6 x x ) 6 6 a) b) 0
11 6 6 c) Quina condició han de verificar els coeficients a, b i c de l equació de segon grau ax bx c 0, per tal que les seves solucions siguin nombres reals? Les solucions de l equació ax bx c 0 són de la forma: b b ac x a Per tant, perquè aquestes solucions siguin nombres reals s ha de verificar que: b ac 0 6. El perímetre d un rectangle mesura 6 cm i una de les seves diagonals, 0 cm. Calcula n l àrea. Anomenem x i y les dimensions del rectangle expressades en centímetres. Es verifica: x y 6 x y 8 x y 0) x y 0 x 8 y 8 y) y y y y 0 y 6 y 0 y 8 y y 6 y y Si y 6 x, i si y, x 6. En qualsevol cas, l àrea del rectangle és A cm. Justifica aquestes igualtats: a) b) 0 0 c) d) a n a n a n a n a n a n n a a n 8. Les solucions d una inequació es troben a l interval [, ], i les d una altra inequació, a l interval [0, ). Expressa mitjançant un interval les solucions comunes a totes dues inequacions. Ajuda t d un gràfic. Les solucions comunes són les que es troben a l interval: [0, ]. 9. Calcula: 00 a) b) 9 c) Quines de les desigualtats següents no són certes? Per què? a) 9 b) 6 6 c) a b a b d) a) Perquè 8 c) Perquè a b a b) 0 Matemàtiques. Batxillerat
NOMBRES REALS: EXERCICIS
 NOMBRES REALS: EXERCICIS. Calcula la longitud dels segments indicats a continuació. Epressa n el resultat de manera eacta i utilitza la calculadora per obtenir-ne una aproimació arrodonida als centèsims:
NOMBRES REALS: EXERCICIS. Calcula la longitud dels segments indicats a continuació. Epressa n el resultat de manera eacta i utilitza la calculadora per obtenir-ne una aproimació arrodonida als centèsims:
SOLUCIONARI Unitat 5
 SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
SOLUCIONARI Unitat 5 Comencem Escriu tres equacions que no tinguin solució en el conjunt. Resposta oberta. Per exemple: a) x b) 5x 0 c) x Estableix tres equacions que no tinguin solució en el conjunt.
NOMBRES REALS. Pàgina 27 REFLEXIONA I RESOL. El pas de Z a Q. El pas de Q a Á
 NOMBRES REALS Pàgina 7 REFLEXIONA I RESOL El pas de Z a Q Digues quines de les equacions següents es poden resoldre en Z i per a quines és necessari el conjunt dels nombres racionals, Q. a) x 0 b) 7x c)
NOMBRES REALS Pàgina 7 REFLEXIONA I RESOL El pas de Z a Q Digues quines de les equacions següents es poden resoldre en Z i per a quines és necessari el conjunt dels nombres racionals, Q. a) x 0 b) 7x c)
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 85 Activitat 1 Calcula l àrea de la figura prenent com a unitat d àrea la quadrícula que hi ha indicada: Activitat Ens referirem a la unitat d àrea amb el símbol
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 85 Activitat 1 Calcula l àrea de la figura prenent com a unitat d àrea la quadrícula que hi ha indicada: Activitat Ens referirem a la unitat d àrea amb el símbol
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS
 Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Unitat 2. POLINOMIS, EQUACIONS I INEQUACIONS 2.1. Divisió de polinomis. Podem fer la divisió entre dos monomis, sempre que m > n. Si hem de fer una divisió de dos polinomis, anirem calculant les divisions
Generalitat de Catalunya Departament d Educació Institut El Palau. Nivell: 1r ESO. Matèria: Matemàtiques. Nom:
 Nivell: 1r ESO Matèria: Matemàtiques Nom: Unitat 1: Divisibilitat Múltiples i divisors 1. Digues si són certes o falses les frases següents i el perquè: a) 4 és divisor de 32 b) 12 és un divisor de 4.
Nivell: 1r ESO Matèria: Matemàtiques Nom: Unitat 1: Divisibilitat Múltiples i divisors 1. Digues si són certes o falses les frases següents i el perquè: a) 4 és divisor de 32 b) 12 és un divisor de 4.
Generalitat de Catalunya Departament d Educació Institut El Palau. Nivell: 1r ESO. Matèria: Matemàtiques. Nom:
 Nivell: 1r ESO Matèria: Matemàtiques Nom: Unitat 1: Divisibilitat Múltiples i divisors 1. Digues si són certes o falses les frases següents i el perquè: a) 4 és divisor de 32 b) 12 és un divisor de 4.
Nivell: 1r ESO Matèria: Matemàtiques Nom: Unitat 1: Divisibilitat Múltiples i divisors 1. Digues si són certes o falses les frases següents i el perquè: a) 4 és divisor de 32 b) 12 és un divisor de 4.
EXERCICIS PROPOSATS. 3 cm
 EXERCICIS PROPOSATS 1.1 Calcula el perímetre de les figures següents. a), b) cm cm cm a) p,5 8 5 1 b) p 9 cm 1. Calcula el perímetre d aquestes figures. a) Un quadrat de 6 centímetres de costat. b) Un
EXERCICIS PROPOSATS 1.1 Calcula el perímetre de les figures següents. a), b) cm cm cm a) p,5 8 5 1 b) p 9 cm 1. Calcula el perímetre d aquestes figures. a) Un quadrat de 6 centímetres de costat. b) Un
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
30 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE Activitat 1 Completa la taula següent: Graus Minuts Segons 30º 30 x 60 = 1.800 1.800 x 60 = 108.000 45º 2.700 162.000 120º 7.200 432.000 270º 16.200 972.000
La porció limitada per una línia poligonal tancada és un
 PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
PLA Si n és el nombre de costats del polígon: El nombre de diagonals és La suma dels seus angles és 180º ( n 2 ). La porció limitada per una línia poligonal tancada és un Entre les seves propietats destaquem
Àmbit de les matemàtiques, de la ciència i de la tecnologia M14 Operacions numèriques UNITAT 2 LES FRACCIONS
 M1 Operacions numèriques Unitat Les fraccions UNITAT LES FRACCIONS 1 M1 Operacions numèriques Unitat Les fraccions 1. Concepte de fracció La fracció es representa per dos nombres enters que s anomenen
M1 Operacions numèriques Unitat Les fraccions UNITAT LES FRACCIONS 1 M1 Operacions numèriques Unitat Les fraccions 1. Concepte de fracció La fracció es representa per dos nombres enters que s anomenen
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 59 Activitat 1 Llegeix atentament el teorema de Tales. Creus que també és certa la proporció següent? Per què? AB CD A B C D El teorema de Tales diu: AB (A B
6. Potències i arrel quadrada
 43 6. Potències i arrel quadrada 1. POTÈNCIES Completa la taula següent en el quadern: 1 2 3 4 5 6 7 8 9 10 1 4 49 1 2 3 4 5 6 7 8 9 10 1 4 9 16 25 36 49 64 81 100 a) 5 600 b) 0,00795 11. Tenim una finca
43 6. Potències i arrel quadrada 1. POTÈNCIES Completa la taula següent en el quadern: 1 2 3 4 5 6 7 8 9 10 1 4 49 1 2 3 4 5 6 7 8 9 10 1 4 9 16 25 36 49 64 81 100 a) 5 600 b) 0,00795 11. Tenim una finca
2n ESO A TREBALL D'ESTIU - MATEMÀTIQUES CURS
 INS PERE BORRELL C. Escoles Pies, 46 17520 PUIGCERDÂ Tel. 972880275 Fax 972141049 Departament de Matemàtiques 2n ESO A TREBALL D'ESTIU - MATEMÀTIQUES CURS 2015-2016 Exercicis que cal fer per preparar la
INS PERE BORRELL C. Escoles Pies, 46 17520 PUIGCERDÂ Tel. 972880275 Fax 972141049 Departament de Matemàtiques 2n ESO A TREBALL D'ESTIU - MATEMÀTIQUES CURS 2015-2016 Exercicis que cal fer per preparar la
7. Calcula P (x ) Q (x ): P (x ) = 5x 4 + x 3 2x 2 5 Q (x ) = 7x 4 5x 2 + 3x + 2 P (x ) Q (x ) = 2x 4 + x 3 + 3x 2 3x 7
 50 SOLUCIONARI 5. Operacions amb polinomis 1. POLINOMIS. SUMA I RESTA PENSA I CALCULA Donat el cub de la figura, calcula en funció de : a) L àrea. b) El volum. a) A ( ) = 6 2 b) V ( ) = 3 CARNET CALCULISTA
50 SOLUCIONARI 5. Operacions amb polinomis 1. POLINOMIS. SUMA I RESTA PENSA I CALCULA Donat el cub de la figura, calcula en funció de : a) L àrea. b) El volum. a) A ( ) = 6 2 b) V ( ) = 3 CARNET CALCULISTA
Unitat 1. Nombres reals.
 Unitat 1. Nombres reals. Conjunts numèrics: - N = Naturals - Z = Enters - Q = Racionals: Són els nombres que es poden expressar com a quocient de dos nombres enters. El conjunt dels nombres racionals,
Unitat 1. Nombres reals. Conjunts numèrics: - N = Naturals - Z = Enters - Q = Racionals: Són els nombres que es poden expressar com a quocient de dos nombres enters. El conjunt dels nombres racionals,
FITXA 1: Angles consecutius i adjacents
 FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
FITXA 1: Angles consecutius i adjacents A.1. OBSERVA AQUESTES FIGURES I FES EL QUE S INDICA: Consecutius Adjacents Oposats 1. Col loca aquests noms en la figura corresponent: angles adjacents, angles oposats
Equacions i sistemes de segon grau
 Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
Equacions i sistemes de segon grau 3 Equacions de segon grau. Resolució. a) L àrea del pati d una escola és quadrada i fa 0,5 m. Per calcular el perímetre del pati seguei els passos següents: Escriu l
FITXA 1: Angles rectes, aguts i obtusos
 FITXA 1: Angles rectes, aguts i obtusos A.1. OBSERVA AQUESTA FIGURA I FES EL QUE S INDICA: Pinta n de blau els costats. Assenyala n de vermell el vèrtex. Pinta n de groc l obertura. A.2. DIBUIXA EL QUE
FITXA 1: Angles rectes, aguts i obtusos A.1. OBSERVA AQUESTA FIGURA I FES EL QUE S INDICA: Pinta n de blau els costats. Assenyala n de vermell el vèrtex. Pinta n de groc l obertura. A.2. DIBUIXA EL QUE
TEMES TREBALLATS A 3r d'eso
 TEMES TREBALLATS A r d'eso. Repàs de n d'eso. Nombres racionals. Equacions. Sistemes d'equacions de r grau. Funcions. Geometria en l'espai Recordeu que a part dels apunts teniu d'altres documents per preparar
TEMES TREBALLATS A r d'eso. Repàs de n d'eso. Nombres racionals. Equacions. Sistemes d'equacions de r grau. Funcions. Geometria en l'espai Recordeu que a part dels apunts teniu d'altres documents per preparar
DOSSIER ESTIU 2018 MATEMÀTIQUES
 DOSSIER ESTIU 2018 MATEMÀTIQUES ELS ALUMNES AMB L ASSIGNATURA SUSPESA HAN D ENTREGAR EL DOSSIER CORRECTAMENT PER PODER REALITZAR L EXAMEN DE SETEMBRE. Has de presentar el dossier en fulls apart. S han
DOSSIER ESTIU 2018 MATEMÀTIQUES ELS ALUMNES AMB L ASSIGNATURA SUSPESA HAN D ENTREGAR EL DOSSIER CORRECTAMENT PER PODER REALITZAR L EXAMEN DE SETEMBRE. Has de presentar el dossier en fulls apart. S han
3. Potències i arrels
 . POTÈNCIES I ARRELS. Potències i arrels. POTÈNCIES D EXPONENT ENTER Calcula mentalment les potències següents: a) 5 b) 4 c) 0 6 d) ( ) e) ( ) 4 f) g) 4 a) 5 b) 8 c) 000 000 d) 8 e) 6 f) 8 g) 6 849 : 4
. POTÈNCIES I ARRELS. Potències i arrels. POTÈNCIES D EXPONENT ENTER Calcula mentalment les potències següents: a) 5 b) 4 c) 0 6 d) ( ) e) ( ) 4 f) g) 4 a) 5 b) 8 c) 000 000 d) 8 e) 6 f) 8 g) 6 849 : 4
FITXA 1: Angles rectes, aguts i obtusos
 FITXA 1: Angles rectes, aguts i obtusos A.1. OBSERVA AQUESTA FIGURA I FES EL QUE S INDICA: Pinta n de blau els costats. Assenyala n de vermell el vèrtex. Pinta n de groc l obertura. A.2. DIBUIXA EL QUE
FITXA 1: Angles rectes, aguts i obtusos A.1. OBSERVA AQUESTA FIGURA I FES EL QUE S INDICA: Pinta n de blau els costats. Assenyala n de vermell el vèrtex. Pinta n de groc l obertura. A.2. DIBUIXA EL QUE
Dossier d estiu de Matemàtiques. 6è d Educació Primària.
 1. Completa les operacions següents: 6 5 4 1 2 x x 9 4 4 5 7 8 5 2 1 9 6 2 1 1 8 2. Quin nombre hem de multiplicar per 537 per obtenir 9.666? 3. Subratlla els nombres que siguin múltiples de 2 i encercla
1. Completa les operacions següents: 6 5 4 1 2 x x 9 4 4 5 7 8 5 2 1 9 6 2 1 1 8 2. Quin nombre hem de multiplicar per 537 per obtenir 9.666? 3. Subratlla els nombres que siguin múltiples de 2 i encercla
Nombres reals Recordes la tècnica d arrodoniment de nombres decimals?
 es ill. w -h ra.m cg w w w Nombres reals Recordes la tècnica d arrodoniment de nombres decimals? Aquests són els nombres decimals successius que resulten d arrodonir el nombre decimal 7,45766 8 fins a
es ill. w -h ra.m cg w w w Nombres reals Recordes la tècnica d arrodoniment de nombres decimals? Aquests són els nombres decimals successius que resulten d arrodonir el nombre decimal 7,45766 8 fins a
TEMA 2: Múltiples i Divisors
 TEMA 2: Múltiples i Divisors 4tESO CB Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per 3
TEMA 2: Múltiples i Divisors 4tESO CB Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per 3
Pauta d estiu matemàtiques 2on E.S.O. curs
 Continguts: Pauta d estiu matemàtiques on E.S.O. curs 00-. Fraccions: suma, resta, producte, divisió, castells, operacions combinades i fracció generatriu.. Álgebra: suma, resta, producte i operacions
Continguts: Pauta d estiu matemàtiques on E.S.O. curs 00-. Fraccions: suma, resta, producte, divisió, castells, operacions combinades i fracció generatriu.. Álgebra: suma, resta, producte i operacions
Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 3 ÀREES I VOLUMS. Unitat 3 ÀREES I VOLUMS
 70 Unitat 3 ÀREES I VOLUMS què treballaràs? En acabar la unitat has de ser capaç de: Reconèixer unitats de mesura d una àrea. Interpretar fórmules d àrees de figures planes. Aplicar fórmules d àrees de
70 Unitat 3 ÀREES I VOLUMS què treballaràs? En acabar la unitat has de ser capaç de: Reconèixer unitats de mesura d una àrea. Interpretar fórmules d àrees de figures planes. Aplicar fórmules d àrees de
UN POLÍGON és una superficie plana
 UNITAT 10 - FIGURES PLANES RECORDA 4t. Primària UN POLÍGON és una superficie plana limitada per segments rectes. Cadascún d aquests segments és un COSTAT i cada punt on s uneixen dos costats forman un
UNITAT 10 - FIGURES PLANES RECORDA 4t. Primària UN POLÍGON és una superficie plana limitada per segments rectes. Cadascún d aquests segments és un COSTAT i cada punt on s uneixen dos costats forman un
MATEMÀTIQUES. DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E. Nom i Cognoms (alumne):... Nom professor:...
 zz Curs: Departament d Educació Generalitat de Catalunya MATEMÀTIQUES DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E CURS 20-20 INS.PUIG CASTELLAR DATA: Nom i Cognoms (alumne):... Nom professor:...
zz Curs: Departament d Educació Generalitat de Catalunya MATEMÀTIQUES DOSSIER DE RECUPERACIÓ MATEMÀTIQUES 2n ESO. GRUP:2E CURS 20-20 INS.PUIG CASTELLAR DATA: Nom i Cognoms (alumne):... Nom professor:...
c) C = (c ij ) de tres files i tres columnes per a) u r = (1, 2, 3, 4), c) u r = (1, 1, 1), v r = (2, 4, 8) i w r = (3, 9, 27)
 SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
SOLUCONAR Unitat 8 Comencem Cada 100 g de producte d un determinat aliment conté 0,06 g de vitamina A, 0,3 g de vitamina B i 0, g de calci. Anàlogament, un altre aliment conté 0,1 g de vitamina A, 0, g
operacions inverses índex base Per a unificar ambdues operacions, es defineix la potència d'exponent fraccionari:
 Potències i arrels Potències i arrels Potència operacions inverses Arrel exponent índex 7 = 7 7 7 = 4 4 = 7 base Per a unificar ambdues operacions, es defineix la potència d'exponent fraccionari: base
Potències i arrels Potències i arrels Potència operacions inverses Arrel exponent índex 7 = 7 7 7 = 4 4 = 7 base Per a unificar ambdues operacions, es defineix la potència d'exponent fraccionari: base
= 25 = 15 =3. FITXA 1: Nombres A.1. ESCRIU AMB XIFRES AQUESTS NOMBRES: A.2. ESCRIU EL NOM D'AQUESTES QUANTITATS: A.3. COMPLETA LA TAULA:
 FITXA 1: Nombres A.1. ESCRIU AMB XIFRES AQUESTS NOMBRES: a) Cent mil dos-cents deu. b) Un milió cent mil dos-cents. c) Mil milions vuitanta mil vuit-cents. d) Nou-cents trenta mil vuitanta. e) Tres mil
FITXA 1: Nombres A.1. ESCRIU AMB XIFRES AQUESTS NOMBRES: a) Cent mil dos-cents deu. b) Un milió cent mil dos-cents. c) Mil milions vuitanta mil vuit-cents. d) Nou-cents trenta mil vuitanta. e) Tres mil
Exercicis de trigonometria
 Mesura d'angles 1. En una circumferència de 5 cm de radi, un arc fa 1, m. Troba el seu angle central corresponent en radians i en graus sexagesimals.. Expressa en radians de manera exacta els angles següents,
Mesura d'angles 1. En una circumferència de 5 cm de radi, un arc fa 1, m. Troba el seu angle central corresponent en radians i en graus sexagesimals.. Expressa en radians de manera exacta els angles següents,
j Unitat 6. Rectes en el pla
 MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
MATEMÀTIQUES 9 4. Calcula a a sabent que a b, b b 4 i que l angle que formen els vectors a i b mesura 0º. b b 4 b 4 b a b a b cos a a cos 0º a cos 0º a a a 9. Els punts A(, ), B(, ) i C(, ) són tres vèrtexs
POLÍGONS, CIRCUMFERÈNCIA I CERCLE
 POLÍGONS, CIRCUMFERÈNCIA I CERCLE POLÍGONS Polígon és la figura plana tancada formada per n segments P 1P,PP3,P3P4,...,Pn P1 ( n 3 ) anomenats costats, essent els punts P,P,... els vèrtexs. 1 Pn L angle
POLÍGONS, CIRCUMFERÈNCIA I CERCLE POLÍGONS Polígon és la figura plana tancada formada per n segments P 1P,PP3,P3P4,...,Pn P1 ( n 3 ) anomenats costats, essent els punts P,P,... els vèrtexs. 1 Pn L angle
Nombres reals. Recordes la tècnica d arrodoniment de nombres decimals?
 es ill. w -h ra cg.m w w w Nombres reals Recordes la tècnica d arrodoniment de nombres decimals? Aquests són els nombres decimals successius que resulten d arrodonir el nombre decimal 7,45766 8 fins a
es ill. w -h ra cg.m w w w Nombres reals Recordes la tècnica d arrodoniment de nombres decimals? Aquests són els nombres decimals successius que resulten d arrodonir el nombre decimal 7,45766 8 fins a
FITXA 1: Polígons. Conceptes
 FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
FITXA 1: Polígons. Conceptes A.1. REPASSA ELS TEUS CONEIXEMENTS. 1. Escriu la lletra de les figures equilàteres. A, D 2. Escriu el nom de les figures equiangulars. A, D 3. Anomena les figures que tenen
Generalitat de Catalunya Departament d Educació Departament de Matemàtiques. Curs SES Pla Marcell. L àlgebra: nombres i lletres
 2 Full de treball A Màgia i matemàtiques? Li has demanat alguna vegada a un amic que li pots endevinar un nombre fen diverses operacions? A.1 Comencem amb un exemple, agafa la calculadora i: a) Pensa un
2 Full de treball A Màgia i matemàtiques? Li has demanat alguna vegada a un amic que li pots endevinar un nombre fen diverses operacions? A.1 Comencem amb un exemple, agafa la calculadora i: a) Pensa un
TEMA 2: Múltiples i Divisors. Activitats. 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per 3 ens doni 25
 TEMA 2: Múltiples i Divisors Activitats Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per
TEMA 2: Múltiples i Divisors Activitats Concepte de múltiple 6 és múltiple de 2 perquè 2 3 = 6 24 és múltiple de 8 perquè 8 3 = 24 25 NO és múltiple de 3 perquè no hi ha cap nombre que multiplicat per
SOLUCIONARI. matemàtiques. Autors del llibre de l alumne Àngela Jané i Sanahuja Jordi Besora i Torradeflot Josep M.
 matemàtiques SOLUCIONARI Autors del llibre de l alumne Àngela Jané i Sanahuja Jordi Besora i Torradeflot Josep M. Guiteras i Piella BARCELONA MADRID BOGOTÀ BUENOS AIRES CARACAS GUATEMALA MÈXIC NOVA YORK
matemàtiques SOLUCIONARI Autors del llibre de l alumne Àngela Jané i Sanahuja Jordi Besora i Torradeflot Josep M. Guiteras i Piella BARCELONA MADRID BOGOTÀ BUENOS AIRES CARACAS GUATEMALA MÈXIC NOVA YORK
RECONÈIXER ELS PRISMES I PIRÀMIDES PRINCIPALS. CALCULAR-NE LES ÀREES
 OBJECTIU RECONÈIXER ELS PRISMES I PIRÀMIDES PRINCIPALS. CALCULAR-NE LES ÀREES 10 NOM: CURS: DATA: CONCEPTE DE PRISMA Un prisma és un poliedre format per dues bases iguals i paral leles, les cares laterals
OBJECTIU RECONÈIXER ELS PRISMES I PIRÀMIDES PRINCIPALS. CALCULAR-NE LES ÀREES 10 NOM: CURS: DATA: CONCEPTE DE PRISMA Un prisma és un poliedre format per dues bases iguals i paral leles, les cares laterals
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera:
 Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
Un sistema lineal de dues equacions amb dues incògnites és un conjunt de dues equacions que podem representar de la manera: ax + by = k a x + b y = k Coeficients de les incògnites: a, a, b, b. Termes independents:
MÍNIM COMÚ MULTIPLE m.c.m
 MÍNIM COMÚ MULTIPLE m.c.m Al calcular el mínim comú múltiple de dos o més nombres el que estem fent és quedar-nos amb el valor més petit de tots els múltiples que són comuns a aquests nombres. És a dir,
MÍNIM COMÚ MULTIPLE m.c.m Al calcular el mínim comú múltiple de dos o més nombres el que estem fent és quedar-nos amb el valor més petit de tots els múltiples que són comuns a aquests nombres. És a dir,
DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO
 Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
Generalitat de Catalunya Departament d Ensenyament Institut Pompeu Fabra DOSSIER PREPARACIÓ RECUPERACIÓ MATEMÀTIQUES Setembre 3r ESO Nom i Cognoms:... INSTRUCCIONS: - Aquest dossier serveix per a preparar
Propietats de les desigualtats.
 Inequacions Desigualtats Direm que a < b a és menor que b si b a és un nombre positiu. Gràficament, a queda a l esquerra de b. Direm que a > b a major que b si a b és un nombre positiu. Gràficament, a
Inequacions Desigualtats Direm que a < b a és menor que b si b a és un nombre positiu. Gràficament, a queda a l esquerra de b. Direm que a > b a major que b si a b és un nombre positiu. Gràficament, a
420 MATEMÀTIQUES 1r ESO MATERIAL FOTOCOPIABLE GRUP PROMOTOR / SANTILLANA EDUCACIÓN, S. L. AVALUACIÓ INICIAL
 NOMBRES NATURALS Escriu en xifres i lletres. a) Un nombre que sigui deu mil unitats més gran que.08.7. b) Un nombre que sigui un milió d unitats més petit que 0.0.. Troba el valor posicional de la xifra.
NOMBRES NATURALS Escriu en xifres i lletres. a) Un nombre que sigui deu mil unitats més gran que.08.7. b) Un nombre que sigui un milió d unitats més petit que 0.0.. Troba el valor posicional de la xifra.
1. Indica si les següents expressions són equacions o identitats: a. b. c. d.
 Dossier d equacions de primer grau 1. Indica si les següents expressions són equacions o identitats: Solucions: Equació / Identitat / Identitat / Identitat 2. Indica els elements d aquestes equacions (membres,
Dossier d equacions de primer grau 1. Indica si les següents expressions són equacions o identitats: Solucions: Equació / Identitat / Identitat / Identitat 2. Indica els elements d aquestes equacions (membres,
TEMA 10: Cossos geomètrics
 TEMA 10: Cossos geomètrics 4tESO CB Cossos geomètrics: podem diferenciar poliedres i cossos de revolució I. Poliedre És una figura tridimensional limitat per cares que tenen forma de polígon: triangles,
TEMA 10: Cossos geomètrics 4tESO CB Cossos geomètrics: podem diferenciar poliedres i cossos de revolució I. Poliedre És una figura tridimensional limitat per cares que tenen forma de polígon: triangles,
TEMA 3: Polinomis 3.1 DEFINICIONS:
 TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
TEMA 3: Polinomis 3.1 DEFINICIONS: Anomenarem monomi qualsevol expressió algèbrica formada per la multiplicació d un nombre real i d una variable elevada a un exponent natural. El nombre es diu coeficient
Activitats de repàs DIVISIBILITAT
 Autor: Enric Seguró i Capa 1 CRITERIS DE DIVISIBILITAT Un nombre és divisible per 2 si acaba en 0 o parell (2,4,6,8). Ex: 10, 24, 62, 5.256, 90.070,... Un nombre és divisible per 3 si la suma de les seves
Autor: Enric Seguró i Capa 1 CRITERIS DE DIVISIBILITAT Un nombre és divisible per 2 si acaba en 0 o parell (2,4,6,8). Ex: 10, 24, 62, 5.256, 90.070,... Un nombre és divisible per 3 si la suma de les seves
Tema 1: TRIGONOMETRIA
 Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Tema : TRIGONOMETRIA Raons trigonomètriques d un angle - sinus ( projecció sobre l eix y ) sin α sin α [, ] - cosinus ( projecció sobre l eix x ) cos α cos α [ -, ] - tangent tan α sin α / cos α tan α
Polinomis i fraccions algèbriques
 Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Tema 2: Divisivilitat. Descomposició factorial. 2.1. Múltiples i divisors. Cal recordar que: Si al dividir dos nombres enters a i b trobem un altre nombre enter k tal que a = k b, aleshores diem que a
Tema 3: EQUACIONS I INEQUACIONS
 Tema 3: EQUACIONS I INEQUACIONS Igualtats algebraiques Es poden diferenciar: identitats i equacions a) Identitats Són igualtats que sempre es compleixen, per qualsevol valor numèric que donem a les lletres.
Tema 3: EQUACIONS I INEQUACIONS Igualtats algebraiques Es poden diferenciar: identitats i equacions a) Identitats Són igualtats que sempre es compleixen, per qualsevol valor numèric que donem a les lletres.
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 55 Activitat 1 Dels nombres següents, indica quins són enters. a) 4 b) 0,25 c) 2 d) 3/5 e) 0 f) 1/2 g) 9 Els nombres enters són: 4, 2, 0 i 9. Activitat 2 Si la
Proves d accés a la Universitat per a més grans de 25 anys Convocatòria 2013
 Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
Pàgina 1 de 5 Sèrie 3 Opció A A1.- Digueu de quin tipus és la progressió numèrica següent i calculeu la suma dels seus termes La progressió és geomètrica de raó 2 ja que cada terme s obté multiplicant
GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ 1.2. CLASSIFICACIÓ
 GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ Representem un punt A en un pla i tracem dues semirectes amb origen en aquest punt. El punt A serà el vèrtex de l angle i cada semirecta serà el costat. 1..
GEOMETRIA PLANA 1. ELS ANGLES 1.1. DEFINICIÓ Representem un punt A en un pla i tracem dues semirectes amb origen en aquest punt. El punt A serà el vèrtex de l angle i cada semirecta serà el costat. 1..
( b) ( a) Matemàtiques - Activitats d estiu 4t ESO + = NOMBRES REALS. 1. Calcula, extraient factors fora dels radicals:
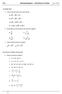 NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
NOMBRES REALS 1. Calcula, extraient factors fora dels radicals: a) 0 45 + 5 = b) 7 + 48 75 = c) 4 7 5 18 + 3 8 = d) 5 1 + 4 48 7 =. Racionalitza els denominadors dels quocients següents: a) 5 c) 6 b) 7
Unitat didàctica 2. Polinomis i fraccions algebraiques
 Unitat didàctica. Polinomis i fraccions algebraiques Refleiona L Andrea té una bona col lecció d espelmes que decoren la seva habitació. Totes les espelmes cilíndriques tenen la mateia alçària: cm. Epressa,
Unitat didàctica. Polinomis i fraccions algebraiques Refleiona L Andrea té una bona col lecció d espelmes que decoren la seva habitació. Totes les espelmes cilíndriques tenen la mateia alçària: cm. Epressa,
SOLUCIONARI Unitat 8. a) De tercer grau i amb dos termes. Comencem. b) De quart grau i amb cinc termes. c) De segon grau i amb un terme.
 SOLUCIONARI Unitat 8 Comencem Utilitza les potències de base 0 per descompondre aqests nombres: 56;,05;,; 005 i tres milions i mig. 56 0 5 0 6 0,05 0 5 0 0, 0 005 0 5 milions i mig 0 6 5 0 5 Troba el valor
SOLUCIONARI Unitat 8 Comencem Utilitza les potències de base 0 per descompondre aqests nombres: 56;,05;,; 005 i tres milions i mig. 56 0 5 0 6 0,05 0 5 0 0, 0 005 0 5 milions i mig 0 6 5 0 5 Troba el valor
ACTIVITATS. a) b) c) d) INS JÚLIA MINGUELL 2n Batxillerat. dv, 18 de març Alumne:
 INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
INS JÚLIA MINGUELL 2n Batxillerat Matemàtiques Tasca Continuada 4 «Matrius i Sistemes d equacions lineals» Alumne: dv, 18 de març 2016 LLIURAMENT: dm, 5 d abril 2016 NOTA: cal justificar matemàticament
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA
 DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
DIBUIX TÈCNIC PER A CICLE SUPERIOR DE PRIMÀRIA Abans de començar cal tenir uns coneixements bàsics que estudiareu a partir d ara. PUNT: No es pot definir, però podem dir que és la marca més petita que
NOMBRES COMPLEXOS. Pàgina 147 REFLEXIONA I RESOL. Extraure fora de l arrel. Potències de. Com es treballa k 1? Trau fora de l arrel:
 NOMBRES COMPLEXOS Pàgina 7 REFLEXIONA I RESOL Extraure fora de l arrel Trau fora de l arrel: a) b) 00 a) b) 00 0 Potències de Calcula les successives potències de : a) ( ) ( ) ( ) b) ( ) c) ( ) 5 a) (
NOMBRES COMPLEXOS Pàgina 7 REFLEXIONA I RESOL Extraure fora de l arrel Trau fora de l arrel: a) b) 00 a) b) 00 0 Potències de Calcula les successives potències de : a) ( ) ( ) ( ) b) ( ) c) ( ) 5 a) (
TRIANGLES. TEOREMA DE PITÀGORES.
 TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
TRIANGLES. TEOREMA DE PITÀGORES. Un triangle ABC és la figura geomètrica del plànol formada per 3 segments anomenats costats els extrems dels quals es tallen a en 3 punts anomenats vèrtexs. Els vèrtexs
4.- Expressa en forma de potència única indicant el signe resultant.
 Pàgina 1 de 8 EXERCICIS PER LA RECUPARACIÓ 1A Avaluació 1.- Calcula de dues maneres (TP i RP): a) 25 + (-1+7) (18 9 + 15)= TP= RP= 9 (-12 + 5 8 = TP= RP= 2.- Treu factor comú i calcula: a) 5.(-3) + (-7).
Pàgina 1 de 8 EXERCICIS PER LA RECUPARACIÓ 1A Avaluació 1.- Calcula de dues maneres (TP i RP): a) 25 + (-1+7) (18 9 + 15)= TP= RP= 9 (-12 + 5 8 = TP= RP= 2.- Treu factor comú i calcula: a) 5.(-3) + (-7).
TEMA 1: EXPRESSIONS ALGEBRAIQUES. Activitats
 TEMA 1: EXPRESSIONS ALGEBRAIQUES Activitats 1.- Expressa en llenguatge algebraic: a) El doble d un nombre. b) El doble d un nombre menys tres unitats. c) El doble d un nombre menys tres unitats, més un
TEMA 1: EXPRESSIONS ALGEBRAIQUES Activitats 1.- Expressa en llenguatge algebraic: a) El doble d un nombre. b) El doble d un nombre menys tres unitats. c) El doble d un nombre menys tres unitats, més un
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE
 SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
SOLUCIONS DE LES ACTIVITATS D APRENENTATGE 3 Activitat Completa els productes següents. a) 0 = 5... e) 0 = 5... b)... = 5 3 f) 25 =... 5 c) 5 =... g) 55 = 5... d) 30 = 5... h) 40 =...... a) 0 = 5 0 e)
Els catets d un triangle rectangle mesuren 5 i 13 centímetres. Calcula n el valor de la hipotenusa.
 1 LONGITUDS I ÀREES EXERCICIS PER A ENTRENAR-SE Teorema de Pitàgores 1.8 Els catets d un triangle rectangle mesuren i 1 centímetres. Calcula n el valor de la hipotenusa. Si fem servir el teorema de Pitàgores:
1 LONGITUDS I ÀREES EXERCICIS PER A ENTRENAR-SE Teorema de Pitàgores 1.8 Els catets d un triangle rectangle mesuren i 1 centímetres. Calcula n el valor de la hipotenusa. Si fem servir el teorema de Pitàgores:
Semblança. Teorema de Tales
 Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
Semblança. Teorema de Tales Dos polígons són semblants si el angles corresponents són iguals i els costats corresponents són proporcionals. ABCDE A'B'C'D'E' si: Â = Â',Bˆ = Bˆ', Ĉ = Ĉ', Dˆ = Dˆ', Ê = Ê'
Les Arcades. Molló del terme. Ermita la Xara. Esglèsia Sant Pere
 Les Arcades Molló del terme Ermita la Xara Esglèsia Sant Pere Pàg. 2 Monomi Un monomi (mono=uno) és una expressió algebraica de la forma: *+,-=/, 1 on R N., rep el nom d indeterminada o variable del monomi,
Les Arcades Molló del terme Ermita la Xara Esglèsia Sant Pere Pàg. 2 Monomi Un monomi (mono=uno) és una expressió algebraica de la forma: *+,-=/, 1 on R N., rep el nom d indeterminada o variable del monomi,
Examen Final 17 de gener de 2013
 MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
MATEMÀTIQUES FIB-UPC Examen Final 7 de gener de 03 a) Representeu gràficament la corba definida per l equació y = x 5x. b) Determineu si el conjunt C = { x R x 5x 6 } és fitat superiorment inferiorment)
quaderns de matemàtiques
 1 quaderns de matemàtiques trigonometria 2 AUTOR / RECOPILADOR: Xavier Vilardell Bascompte [email protected] CURS: 2007-2008 ÚLTIMA REVISIÓ: 22 de gener de 2008 Aquests quaderns de matemàtiques han estat
1 quaderns de matemàtiques trigonometria 2 AUTOR / RECOPILADOR: Xavier Vilardell Bascompte [email protected] CURS: 2007-2008 ÚLTIMA REVISIÓ: 22 de gener de 2008 Aquests quaderns de matemàtiques han estat
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES UNITAT 2 TEOREMA DE TALES.
 Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
Unitat 2 TEOREMA DE TALES. TEOREMA DE PITÀGORES. RAONS TRIGONOMÈTRIQUES 41 42 Matemàtiques, Ciència i Tecnologia 8. TRIGONOMETRIA UNITAT 2 QUÈ TREBALLARÀS? què treballaràs? En acabar la unitat has de ser
DOSSIER DE RECUPERACIÓ 3r ESO
 DOSSIER DE RECUPERACIÓ 3r ESO INS MARIANAO. Departament de matemàtiques La correcta realització d aquest dossier, i la posterior entrega el dia de l examen puntuarà un 20% de la nota total. Les activitats
DOSSIER DE RECUPERACIÓ 3r ESO INS MARIANAO. Departament de matemàtiques La correcta realització d aquest dossier, i la posterior entrega el dia de l examen puntuarà un 20% de la nota total. Les activitats
Aproximar un nombre decimal consisteix a reduir-lo a un altre nombre decimal exacte el valor del qual sigui molt pròxim al seu.
 Aproximar un nombre decimal consisteix a reduir-lo a un altre nombre decimal exacte el valor del qual sigui molt pròxim al seu. El nombre π és un nombre que té infinites xifres decimals. Sabem que aquest
Aproximar un nombre decimal consisteix a reduir-lo a un altre nombre decimal exacte el valor del qual sigui molt pròxim al seu. El nombre π és un nombre que té infinites xifres decimals. Sabem que aquest
UNITAT 3: TRIGONOMETRIA
 UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
UNITAT 3: TRIGONOMETRIA 1. Angles Anomenem angle a l'espai del pla tancat per dues semirectes que tenen un mateix origen. Podem classificar els angles segons la seva obertura en tres tipus: agut, recte
NO, la divisió no és exacta. SI, la divisió és exacta. SI, la divisió és exacta. NO, la divisió no és exacta. NO, la divisió no és exacta.
 1. Comprova si hi ha relació de divibilitat entre aquestos nombres. a) 224 i 40 1 NO, la divisió no és exacta. b) 450 i 50 c) 400 i 16 d) 654 i 32 NO, la divisió no és exacta. e) 568 i 46 NO, la divisió
1. Comprova si hi ha relació de divibilitat entre aquestos nombres. a) 224 i 40 1 NO, la divisió no és exacta. b) 450 i 50 c) 400 i 16 d) 654 i 32 NO, la divisió no és exacta. e) 568 i 46 NO, la divisió
2 desembre 2015 Límits i número exercicis. 2.1 Límits i número
 I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
I. E. S. JÚLIA MINGUELL Matemàtiques 2n BAT. 2 desembre 205 Límits i número exercicis 2. Límits i número 4. Repàs de logaritmes i exponencials: troba totes les solucions de cadascuna de les següents equacions:
UNITAT 8. FIGURES PLANES
 1. Fes servir aquests punts per traçar dues línies poligonals més de cada tipus, apart de les dels exemples: Línia poligonal oberta Línia poligonal oberta creuada Línia poligonal tancada Línia poligonal
1. Fes servir aquests punts per traçar dues línies poligonals més de cada tipus, apart de les dels exemples: Línia poligonal oberta Línia poligonal oberta creuada Línia poligonal tancada Línia poligonal
Sector circular i Segment circular.
 Tema: poligons, circumferència i cercle Activitats de consolidació Pàgina 1 de 8 1. Explica quines són les semblances i diferències entre: Línia poligonal i polígon. Circumferència i cercle. Sector circular
Tema: poligons, circumferència i cercle Activitats de consolidació Pàgina 1 de 8 1. Explica quines són les semblances i diferències entre: Línia poligonal i polígon. Circumferència i cercle. Sector circular
SOLUCIONS DE LES ACTIVITATS D AMPLIACIÓ
 SOLUCIONS DE LES ACTIVITATS D AMPLIACIÓ Unitat 11. Ampliació 1. Fes les operacions següents i ordena n els resultats, expressats en segons, del més gran al més xicotet. 34º 56 43 + 14º 32 29 = 48º 88 72
SOLUCIONS DE LES ACTIVITATS D AMPLIACIÓ Unitat 11. Ampliació 1. Fes les operacions següents i ordena n els resultats, expressats en segons, del més gran al més xicotet. 34º 56 43 + 14º 32 29 = 48º 88 72
DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 2n d ESO
 Institut Galileo Galilei Departament de Matemàtiques Curs 015-16 DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES n d ESO A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats
Institut Galileo Galilei Departament de Matemàtiques Curs 015-16 DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES n d ESO A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats
Feina d estiu Matemàtiques 4 rt eso
 1 TRIGONOMETRIA Feina d estiu Matemàtiques 4 rt eso Els alumnes que tinguin suspesa l assignatura de matemàtiques de 4art d ESO hauran de fer els exercicis que venen en aquest dossier. INDICACIONS Els
1 TRIGONOMETRIA Feina d estiu Matemàtiques 4 rt eso Els alumnes que tinguin suspesa l assignatura de matemàtiques de 4art d ESO hauran de fer els exercicis que venen en aquest dossier. INDICACIONS Els
Equacions de segon grau
 3 Equacions de segon grau Objectius En aquesta quinzena aprendràs a: Identificar les solucions d una equació. Reconèixer i obtenir equacions equivalents. Resoldre equacions de primer grau. Resoldre equacions
3 Equacions de segon grau Objectius En aquesta quinzena aprendràs a: Identificar les solucions d una equació. Reconèixer i obtenir equacions equivalents. Resoldre equacions de primer grau. Resoldre equacions
Proporcionalitat i percentatges
 Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
Proporcionalitat i percentatges Proporcions... 2 Propietats de les proporcions... 2 Càlul del quart proporcional... 3 Proporcionalitat directa... 3 Proporcionalitat inversa... 5 El tant per cent... 6 Coneixement
MATEMÀTIQUES ÀREES I VOLUMS
 materials del curs de: MATEMÀTIQUES ÀREES I VOLUMS EXERCICIS RECULL D APUNTS I EXERCICIS D INTERNET FET PER: Xavier Vilardell Bascompte [email protected] ÚLTIMA REVISIÓ: 08 de febrer de 2010 Aquests materials
materials del curs de: MATEMÀTIQUES ÀREES I VOLUMS EXERCICIS RECULL D APUNTS I EXERCICIS D INTERNET FET PER: Xavier Vilardell Bascompte [email protected] ÚLTIMA REVISIÓ: 08 de febrer de 2010 Aquests materials
Quadern de matemàtiques Decimals1
 Quadern de matemàtiques Decimals CENTENES DESENES UNITATS DECIMES CENTÈSIMES 3,5 Busca les vuit diferències que hi ha en aquests dos dibuixos Curs i grup: Data inici quadern Data acabament Seguiment Data
Quadern de matemàtiques Decimals CENTENES DESENES UNITATS DECIMES CENTÈSIMES 3,5 Busca les vuit diferències que hi ha en aquests dos dibuixos Curs i grup: Data inici quadern Data acabament Seguiment Data
POLINOMIS. Divisió. Regla de Ruffini.
 POLINOMIS. Divisió. Regla de Ruffini. Recordeu: n Un monomi en x és una expressió algebraica de la forma a x on a és un nombre real i n és un nombre natural. A s anomena coeficient i n s anomena grau del
POLINOMIS. Divisió. Regla de Ruffini. Recordeu: n Un monomi en x és una expressió algebraica de la forma a x on a és un nombre real i n és un nombre natural. A s anomena coeficient i n s anomena grau del
PER ALS ALUMNES QUE HAN FET 2n D ESO EL CURS I PER ALS SEUS PARES
 PER ALS ALUMNES QUE HAN FET n D ESO EL CURS 0-07 I PER ALS SEUS PARES INSTITUT GORGS Dept. de Matemàtiques Juny 07 Benvolguts pares i alumnes de l institut Gorgs, Els professors del departament de matemàtiques
PER ALS ALUMNES QUE HAN FET n D ESO EL CURS 0-07 I PER ALS SEUS PARES INSTITUT GORGS Dept. de Matemàtiques Juny 07 Benvolguts pares i alumnes de l institut Gorgs, Els professors del departament de matemàtiques
Tema 2: Equacions i problemes de segon grau.
 Tema : Equacions i problemes de segon grau..1. Les equacions de n grau. Equacions del tipus x + 5x - 3 0, on la incògnita x es troba elevada al quadrat, diem que són equacions de segon grau. Exemples:
Tema : Equacions i problemes de segon grau..1. Les equacions de n grau. Equacions del tipus x + 5x - 3 0, on la incògnita x es troba elevada al quadrat, diem que són equacions de segon grau. Exemples:
6, 1 20, Ordena les fraccions de l exercici 2 de menor a major posant enmig de cada parell el símbol <.
 1. Escriu una fracció a sota de cada dibuix que representi la part acolorida : 2. Col loca les següents fraccions dins la taula de sota, on les has de classificar en Pròpies i Impròpies i també segons
1. Escriu una fracció a sota de cada dibuix que representi la part acolorida : 2. Col loca les següents fraccions dins la taula de sota, on les has de classificar en Pròpies i Impròpies i també segons
Tema 2: GEOMETRIA ANALÍTICA AL PLA
 Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
Tema : GEOMETRIA ANALÍTICA AL PLA Vector El vector AB és el segment orientat amb origen al punt A i extrem al punt B b a A B Les projeccions del vector sobre els eixos són les components del vector: a
FITXA 1: Lectura i descomposició de nombres
 FITXA 1: Lectura i descomposició de nombres 1. ESCRIU AQUESTS NOMBRES: a) Tres mil dos-cents milions cent vuitanta mil. b) Sis-cents noranta mil noranta-set. c) Tres mil dos-cents milions cinc-cents cinquanta
FITXA 1: Lectura i descomposició de nombres 1. ESCRIU AQUESTS NOMBRES: a) Tres mil dos-cents milions cent vuitanta mil. b) Sis-cents noranta mil noranta-set. c) Tres mil dos-cents milions cinc-cents cinquanta
UNITAT 3: SISTEMES D EQUACIONS
 UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
UNITAT 3: SISTEMES D EQUACIONS 1. EQUACIONS DE PRIMER GRAU AMB DUES INCÒGNITES L equació x + y = 3 és una equació de primer grau amb dues incògnites : x i y. Per calcular les solucions escollim un valor
MÚLTIPLES I DIVISORS
 MÚLTIPLES I DIVISORS DETERMINACIÓ DE MÚLTIPLES Múltiple d un nombre és el resultat de multiplicar aquest nombre per un altre nombre natural qualsevol. 2 x 0 = 0 2 x 1 = 2 2 x 2 = 4 2 x 3 = 6 2 x 4 = 8
MÚLTIPLES I DIVISORS DETERMINACIÓ DE MÚLTIPLES Múltiple d un nombre és el resultat de multiplicar aquest nombre per un altre nombre natural qualsevol. 2 x 0 = 0 2 x 1 = 2 2 x 2 = 4 2 x 3 = 6 2 x 4 = 8
( 2 3, utilitzeu la matriu inversa B 1 ( 1 4 ( 2 1. Matrius i determinants Sèrie 3 - Qüestió 4. Donada la matriu B =
 1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
1998 - Sèrie 3 - Qüestió 4 Donada la matriu B = ( 2 3, utilitzeu la matriu inversa B 1 1 1) B X B = ( 1 4 3 2). per trobar una matriu X tal que 2004 - Sèrie 1 - Qüestió 3 Considereu les matrius Trobeu
DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 2n d ESO Adaptació
 DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 2n d ESO Adaptació A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats durant el curs. El dossier s ha de presentar
DOSSIER D ACTIVITATS D ESTIU MATEMÀTIQUES 2n d ESO Adaptació A continuació tens una sèrie d'exercicis i activitats relacionats amb els continguts treballats durant el curs. El dossier s ha de presentar
