UNIVERSIDAD DE MANAGUA
|
|
|
- Ana Belén Castillo Fernández
- hace 8 años
- Vistas:
Transcripción
1 UNIVERSIDAD DE MANAGUA PROBLEMAS RESUELTOS DE PROGRAMACIÒN LINEAL POR METODO GRAFICO CON POM-QM. Profesor: MSc. Julio Rito Vargas Avilés Elaborado por: Yucep Gutiérrez Baltodano. Carlos Reynaldo Guevara. Managua 13 de junio Investigación de Operaciones I
2 Programación Lineal: UNIVERSIDAD DE MANAGUA 1) La fábrica de Hilados y Tejidos Salazar requiere fabricar dos tejidos de calidad diferente T y T 1 ; se dispone de 500 Kg de hilo A, 300 Kg de hilo B y 108 Kg de hilo C. Para obtener un metro de T diariamente se necesitan 125 gr de A, 150 gr de B y 72 gr de C; para producir un metro de T 1 por día se necesitan 200 gr de A, 100 gr de B y 27 de C. El T se vende a $400 el metro y el T 1 se vende a $500 el metro. Si se debe obtener el máximo del beneficio, Cuántos metros de T y T 1 se deben fabricar? 1) Definición del Problema: Objetivo: Maximizar ventas. Restricciones: 500 Kg de hilo A 300 Kg de hilo B 108 Kg de hilo C Produce dos tipos T y T 1 Requerimiento de T 125 gr de A 150 gr de B 72 gr de C 2 Investigación de Operaciones I
3 Venta: UNIVERSIDAD DE MANAGUA equerimiento de T gr de A 100 gr de B 27 gr de C T $400 T 1..$500 Concepto T T 1 Disponible Hilo A 125 gr 200 gr 500,000 gr Hilo B 150 gr 100 gr 300,000 gr Hilo C 72 gr 27 gr 108,000 gr Ventas $400 $500 2) Formulación del modelo matemático Lineal: F.O Max. Z= 400x x2 Sujeto a: 125x x2 500, x x2 300,000 72x x2 108,000 x1 0 x2 0 3 Investigación de Operaciones I
4 3) Solución del modelo: 4 Investigación de Operaciones I
5 2) La empresa Whitt Windows tiene solo tres empleados que hacen dos tipos de ventanas: Con marco de madera y con marco de aluminio, la ganancia es de $60 por cada ventana con marco de madera y de $30 por cada una con marca de aluminio. Doug hace marcos de madera, y puede terminar 6 al día, Linda hace 4 marcos de aluminio al día. Bob forma y corta el vidrio y puede hacer 48 pies cuadrados de vidrio por día, cada ventana con marco de madera usa 6 pies cuadrados de vidrio y cada de aluminio usa 8 pies cuadrados de vidrio. La compañía desea determinar: Cuántas ventanas de cada tipo debe producir al día para maximizar la ganancia total. a. Formule el modelo de programación lineal. b. Use el método grafico para resolver el modelo. 1. Definición del Problema: Objetivo: Maximizar ganancia total Restricciones: Solamente tiene tres empleados. Doug hace marcos de madera 6 al día. Linda hace marcos de aluminio 4 al día. Bob forma y corta el vidrio. (48 pies cuadrados de vidrio por Día). Cada ventana con marco de madera usa 6 pies cuadrados de vidrio Cada de aluminio usa 8 pies cuadrados de vidrio Produce dos tipos de ventana marco de madera y marco de aluminio. Requerimiento de ventana de madera 6 pies cuadrados de vidrio 5 Investigación de Operaciones I
6 Requerimiento de ventana de aluminio 8 pies cuadrados de vidrio Ganancia: Marco de madera $60 Marco de Aluminio..$30 Concepto Madera Aluminio Disponible Madera marcos Aluminio marcos Vidrio pies 2 Ventas $60 $30 2. Formulación del modelo matemático Lineal: F.O Max. Z= 60x1 + 30x2 Sujeto a: x1 6 + x2 4 x1 + x2 48 x1 0 x2 0 6 Investigación de Operaciones I
7 3. Solución del modelo: 7 Investigación de Operaciones I
8 3) En una granja agrícola se desea criar conejos y pollos como complemento en su economía, de forma que no se superen en conjunto las 180 horas mensuales destinadas a esta actividad. Su almacén solo puede albergar un máximo de 1,000 kilogramos de heno. Si se supone que un conejo necesita 20 kilogramos de heno al mes y un pollo 10 kilogramos al mes, que las horas mensuales de cuidado requeridos por un conejo son 3 y por un pollo 2 y que los beneficios que reportaría su venta asciende a C$90 y C$60 por cabeza respectivamente, hallar el número de animales que deben criarse para que el beneficio sea máximo. 1. Definición del Problema: Objetivo: Maximizar ventas por crianza de animales. Restricciones: Su almacén solo puede almacenar como máximo 1,000 kg de heno. No se superen en conjunto 180 horas mensuales. Cría Conejos y pollos. Venta: Requerimiento del Conejo: 20 kg de heno al mes. 3 horas mensuales de cuido al mes. Requerimiento del pollo: 10 kg de heno al mes. 2 horas de cuido al mes. Conejo $90 Pollo..$60 8 Investigación de Operaciones I
9 Concepto Conejo Pollos Disponible Heno 20 gr 10 gr 1000 Kg Horas de cuido 3 horas 2 horas 180 horas Ventas $90 $60 2. Formulación del modelo matemático Lineal: F.O Max. Z= 90x1 + 60x2 Sujeto a: 20x1 + 10x x1 + 2x2 180 x1 0 x2 0 9 Investigación de Operaciones I
10 3. Solución del modelo: UNIVERSIDAD DE MANAGUA 10 Investigación de Operaciones I
11 4) En una fábrica de dulces navideños se preparan dos surtidos para lanzarlos al mercado. El primero deja una utilidad de C$45.00 y contiene 150 gr de polvorones, 100 gramos de mantecado y 80 gr de roscos de vino. El segundo deja una utilidad de C$56.00 y contiene 200 gramos de polvorones, 100 gramos de mantecados y 100 gr de roscos de vino. Se dispone de un total de 200 kg de polvorones, 130 kg de mantecados y 104 kg de roscos de vino. La empresa de embalaje solo le puede suministrar 1200 cajas. Cuántos surtidos de cada tipo convendría fabricar para que el beneficio sea máximo? 1) Definición del Problema: Objetivo: Maximizar ventas de dulces. Restricciones: 200 Kg de polvorones = 200,000 gr 130 Kg de mantecados = 130,000 gr 104 Kg de roscos de vino = 104,000 gr La empresa solo pude suministrar 1,200 cajas. Produce dos tipos de surtidos: Requerimiento de 1er surtido. 150 gr de polvorones. 100 gr de mantecado. 80 gr de roscos vino. Requerimiento de 2do surtido. 200 gr de polvorones 100 gr de mantecado 100 gr de roscos vino Venta: 1er surtido C$ do surtido....c$ Investigación de Operaciones I
12 Concepto 1er Surtido 2do Surtido Disponible Polvorones 150 gr 200 gr 200,000 gr Mantecados 100 gr 100 gr 130,000 gr Roscos de vino 80 gr 100gr 104,000 gr Cajas ,000 Ventas C$45 C$56 2) Formulación del modelo matemático Lineal: F.O Max. Z= 45x1 + 56x2 Sujeto a: 150x x2 200, x x2 130,000 80x x2 104,000 x1 +x2 12,000 x1 0 x Investigación de Operaciones I
13 3) Solución del modelo: UNIVERSIDAD DE MANAGUA 13 Investigación de Operaciones I
14 5) Cierto fabricante produce sillas y mesas para las que requiere la utilización de dos secciones de producción: la sección de montaje y la sección de pintura. La producción de una silla requiere 1 hora de trabajo en la sección de montaje y de 2 horas en la de pintura. Por su parte, la fabricación de una mesa precisa de 3 horas en la sección de montaje y de 1 hora en la de pintura. La sección de montaje sólo puede estar 9 horas diarias en funcionamiento, mientras que la de pintura sólo 8 horas. El beneficio produciendo mesas es doble que el de sillas. Cuál ha de ser la producción diaria de mesas y sillas para que el beneficio sea máximo? 1. Definición del Problema: Objetivo: Maximizar ventas. Restricciones: La producción de una silla requiere 1 hora de montaje y de 2 horas de pinturas. La fabricación de una mesa requiere 3 horas de montaje y 1 de pintura. La sección de montaje solo funciona 9 horas La sección de pintura solo 8 horas El beneficio de mesas es doble que el de sillas. Dos tipos de productos Sillas y mesas. Concepto Silla(X1) Mesa(X2) Disponible Montaje Pintura Formulación del modelo matemático Lineal: F.O Max. Z= x1 + 2x2 Sujeto a: x1 + 3x2 9 2x1 + x2 8 x Investigación de Operaciones I
15 x Solución del modelo: 15 Investigación de Operaciones I
16 6) En una fábrica se elaboran dos tipos de herramientas A y B. En la fábrica trabajan 2 obreros durante 8 horas diarias y un supervisor, para comprobar las herramientas una vez construidas, que trabaja 1 hora diaria. Para la construcción de A se emplean 3 horas diarias de mano de obra y precisa de 4 minutos de revisión, para B es necesaria 1 hora diaria de mano de obra y 3 minutos de revisión. Por problemas de producción en la fábrica no se pueden fabricar más de 12 herramientas A y B es de C$400, C$200 respectivamente. Hallar cuantas unidades se deben elaborar cada día de cada una de ellas para obtener un beneficio máximo. 1. Definición del problema: Objetivo: Maximizar ventas de herramientas. Restricciones: Trabajan 2 obreros 8 horas diarias. Trabaja 1 supervisor para comprobar las herramientas La herramienta trabajan 1 hora diaria. No se pueden fabricar más de 12 herramientas diarias, Dos tipos de Herramientas A Y B Requerimiento de A: 3 horas diarias de mano de obra. 4 minutos de revisión. Requerimiento para B: 1 hora diaria de mano de obra. 3 minutos de revisión. Venta: A=C$400 B=C$ Investigación de Operaciones I
17 Concepto Herramienta A Herramienta B Disponible Mano de obra horas Tiempo de revis min # De Herramien herram Ventas C$400 C$200 2) Formulación del modelo matemático Lineal: F.O Max. Z= 400x x2 Sujeto a: 3x1 + x2 16 4x1 + 3x2 60 x1 + x2 12 x1 0 x Investigación de Operaciones I
18 3) Solución del modelo: 18 Investigación de Operaciones I
19 7. Una empresa produce dos tipos de mesas: un estilo colonial y otro estilo nórdico. Las utilidades que se obtienen de su venta son de $20 por la colonial y $22 por la nórdica. Para esta semana ya hay un pedido de 10 mesas de tipo nórdico. El gerente de producción quiere realizar la planeación de su producción semanal sabiendo que solamente cuenta con 450 horas para la construcción y 200 horas para barnizarlas. En el siguiente cuadro se indican las horas necesarias para realizar cada una de las tareas y la utilidad para ambas mesas. 1) Definición del Problema: Objetivo: Maximizar utilidad de venta de producción. X1: cantidad de mesas de tipo colonial a producir X2: cantidad de mesas de tipo nórdico a producir Restricciones: Pedido: 10 mesas nórdico 450 horas de construcción 200 horas de barnizado. Venta: Colonial.. $20 Nórdica...$22 19 Investigación de Operaciones I
20 Concepto Colonial Nórdica Disponible Pedido Construcción Barnizado Ventas $20 $22 2) Formulación del modelo matemático Lineal: F.O Max. Z= 20x1 + 22x2 Sujeto a: + x2 10 6x1 + 8x x1 + 2x2 200 x1 0 x Investigación de Operaciones I
21 3) Solución del modelo: 21 Investigación de Operaciones I
22 8. Una empresa ensambladora de productos de comunicación debe programar su producción semanal. Debido a problemas de liquidez, le interesa minimizar sus costos semanales, ya que le pagan la producción 20 días después de entregada. Actualmente está armando dos artículos diferentes, el T14 y el B2; ambos artículos deben ser armados y probados por personal especializado. La empresa compradora requiere no menos de 100 aparatos semanales; del modelo B2 debe entregar no menos que la cuarta parte de los que entregue del T14, pero en ningún caso deben superar en más de 150 al número de equipos T14. En el cuadro se indica el tiempo que requieren los especialistas para armar y probar cada equipo, expresado en minutos, así como la disponibilidad de tiempo. 1) Definición del Problema: Objetivo: Minimizar costos mensuales. Restricciones: Pedido: T 14 + B2 100 mínimo de equipos Mínimo de B2: B ¼ T mínimo de equipos B2 Máximo de B2: B T máximo de equipos B2 Armado:10 T + 12 B 55 (60) minutos 22 Investigación de Operaciones I
23 Pruebas: 30 T + 6 B 100 (60) minutos Costos: T: número de artículos T14 a producir B: número de artículos B2 a producir T14.. $100 B2...$60 Equipos T14 B2 Disponible Pedido Mínimo de B -1/4 1 0 Máximo de B Armados 10 min 12 min 3,300 min Pruebas 30 min 6 min 6,000 min Costos $100 $60 2) Formulación del modelo matemático Lineal: F.O Min. Z= 100x1 + 60x2 Sujeto a: x1 + x /4 x1 + x2 0 -x1 + x x x2 3,300 30x1 + 6 x2 6,000 x1 0 x Investigación de Operaciones I
24 3) Solución del modelo: UNIVERSIDAD DE MANAGUA 24 Investigación de Operaciones I
25 9. Un pastelero tiene 150 kg de harina, 22 kg de azúcar y 27.5 kg de mantequilla para hacer dos tipos de pasteles P y Q. Para hacer una docena de pasteles de tipo P necesita 3 kg de harina, 1 kg de azúcar y 1 de mantequilla y para hacer una docena de tipo Q necesita 6 kg de harina, 0 5 kg de azúcar y 1 kg de mantequilla. El beneficio que obtiene por una docena de tipo P es $20 y por una docena de tipo Q es $30. Halla, utilizando las técnicas de programación lineal, el número de docenas que tiene que hacer de cada clase para que el beneficio sea máximo. 1) Definición del Problema: Objetivo: Maximizar beneficio total. Restricciones: 150 kg de harina 22 kg de azúcar 27.5 kg de mantequilla Dos tipos de pasteles P y Q Requerimientos de P 3 kg de harina 1 kg de azúcar 1 kg de mantequilla Requerimientos de Q 6 kg de harina 0.5 kg de azúcar 1 kg de mantequilla 25 Investigación de Operaciones I
26 Beneficio: P.. $20 Q $30 Equipos P Q Disponible Harina Azúcar Mantequilla Beneficio $20 $30 2) Formulación del modelo matemático Lineal: F.O Max. Z= 20x x 2 Sujeto a: 3x 1 + 6x x 1 + ½ x 2 22 x 1 + x x 1 0 x Investigación de Operaciones I
27 3) Solución del modelo: 27 Investigación de Operaciones I
28 10. Una compañía fabrica dos modelos de sombrero: Bae y Viz. La fabricación de los sombreros se realiza en las secciones de moldeado, pintura y montaje. La fabricación de cada modelo Bae requiere 2 horas de moldeado, 3 de pintura y una de montaje. La fabricación del modelo Viz requiere tres horas de moldeado, 2 de pintura y una de montaje. Las secciones de moldeado y pintura disponen, cada una, de un máximo de horas cada mes, y la de montaje de 600.Si el modelo Bae se vende a $100 y el modelo Viz a 120, qué cantidad de sombreros de cada tipo ha de fabricar para maximizar las ventas mensual? 1) Definición del Problema: Objetivo: Maximizar ventas mensuales. Restricciones: Moldeado y pintura 1500 horas como máximo Montaje 600 horas como máximo. Dos tipos de sombreros Bae y Viz Requerimientos de Bae 2 horas de moldeado 3 horas de pintura 1 hora de montaje Requerimientos de Viz Ventas: 3 horas de moldeado 2 horas de pintura 1 hora de montaje 28 Investigación de Operaciones I
29 Bae. $100 Viz $120 Equipos Bae Viz Disponible Moldeado Pintura Montaje Ventas $100 $120 2) Formulación del modelo matemático Lineal: F.O Max. Z= 100x x 2 Sujeto a: 2x 1 + 3x x x x 1 + x x 1 0 x Investigación de Operaciones I
30 3) Solución del modelo: UNIVERSIDAD DE MANAGUA 30 Investigación de Operaciones I
31 11. Una industria vinícola produce vino y vinagre. El doble de la producción de vino es siempre menor o igual que la producción de vinagre más cuatro unidades. Por otra parte, el triple de la producción de vinagre sumado con cuatro veces la producción de vino se mantiene siempre menor o igual a 18 unidades. Halla el número de unidades de cada producto que se deben producir para alcanzar un beneficio máximo, sabiendo que cada unidad de vino deja un beneficio de $80. y cada unidad de vinagre de $40. 1) Definición del Problema: Objetivo: Maximizar beneficio. X1= unidades de vino. X2= unidades de vinagre. Restricciones: Ventas: Vino. $80 Vinagre $40 El doble de la producción de vino es siempre menor o igual que la producción de vinagre más cuatro unidades. El triple de la producción de vinagre sumado con cuatro veces la producción de vino se mantiene siempre menor o igual a 18 unidades. 31 Investigación de Operaciones I
32 Productos Vino Vinagre Disponible Producción vino Producción vinagre Ventas $80 $40 2) Formulación del modelo matemático Lineal: F.O Max. Z= 80x x 2 Sujeto a: 2x 1 - x 2 4 4x x 2 18 x 1 0 x Investigación de Operaciones I
33 3) Solución del modelo: 33 Investigación de Operaciones I
34 12. Una empresa fabrica dos tipos de colonia: A y B. La primera contiene un 15% de extracto de jazmín, un 20% de alcohol y el resto es agua y la segunda lleva un 30% de extracto de jazmín, un 15% de alcohol y el resto es agua. Diariamente se dispone de 60 litros de extracto de jazmín y de 50 litros de alcohol. Cada día se pueden producir como máximo 150 litros de la colonia B. El precio de venta por litro de la colonia A es de $50 y el de la colonia B es $60. Hallar los litros de cada tipo que deben producirse diariamente para que el beneficio sea máximo 1) Definición del Problema: Objetivo: Maximizar beneficio. X1= # de litros de colonia A X2= # de colonia B Restricciones: Diariamente se dispone de 60 litros de extracto de jazmín y de 50 litros de alcohol. Cada día se pueden producir como máximo 150 litros de la colonia B Ventas: Colonia A. $50 Colonia B $60 Productos Colonia A Colonia B Disponible Jazmín 15% 30% 60 Alcohol 20% 15% 50 Producción máxima B Ventas $50 $60 34 Investigación de Operaciones I
35 2) Formulación del modelo matemático Lineal: F.O Max. Z= 50x x 2 Sujeto a: 0.15 x x x x 2 50 X x 1 0 x Investigación de Operaciones I
36 3) Solución del modelo: 36 Investigación de Operaciones I
EJEMPLO 1. Solución: Definimos las variables originales como: = número de conejos. x = número de pollos.
 EJEMPLO. En una granja agrícola se desea criar conejos y pollos como complemento en su economía de forma que no se superen en conjunto las 8 horas mensuales destinadas a esta actividad. Su almacén sólo
EJEMPLO. En una granja agrícola se desea criar conejos y pollos como complemento en su economía de forma que no se superen en conjunto las 8 horas mensuales destinadas a esta actividad. Su almacén sólo
UNIVERSIDAD DE MANAGUA
 UNIVERSIDAD DE MANAGUA PROBLEMAS DE PROGRAMACIÓN LINEAL METODO GRÁFICO y ANALITICO Prof. MSc. Ing. Julio Rito Vargas Avilés Sept. 2014 Resolver los problemas de PL por el método gráfico. Puede usar el
UNIVERSIDAD DE MANAGUA PROBLEMAS DE PROGRAMACIÓN LINEAL METODO GRÁFICO y ANALITICO Prof. MSc. Ing. Julio Rito Vargas Avilés Sept. 2014 Resolver los problemas de PL por el método gráfico. Puede usar el
UNIVERSIDAD DE MANAGUA
 UNIVERSIDAD DE MANAGUA Investigación de Operaciones I Problemas de Programación Lineal (Solución Gráfica, Analítica, Sensibilidad Y Método Simplex Prof. MSc. Ing. Julio Rito Vargas Avilés IIC- 2016 Resolver
UNIVERSIDAD DE MANAGUA Investigación de Operaciones I Problemas de Programación Lineal (Solución Gráfica, Analítica, Sensibilidad Y Método Simplex Prof. MSc. Ing. Julio Rito Vargas Avilés IIC- 2016 Resolver
UNIVERSIDAD DE MANAGUA
 UNIVERSIDAD DE MANAGUA Optimización Problemas de Programación Lineal: Solución Gráfica, Analítica, Sensibilidad y Método Simplex Prof. MSc. Ing. Julio Rito Vargas Avilés Ingeniería/IC- 2018 Resolver los
UNIVERSIDAD DE MANAGUA Optimización Problemas de Programación Lineal: Solución Gráfica, Analítica, Sensibilidad y Método Simplex Prof. MSc. Ing. Julio Rito Vargas Avilés Ingeniería/IC- 2018 Resolver los
1Elección de las incógnitas. x = nº de lotes de A y = nº de lotes de B 2Función objetivo f(x, y) = 20x + 40y 3Restricciones. Página 1.
 EJERCICIOS RESUELTOS 1) Entre impresoras y escáneres de segunda mano se tiene establecido que un pequeño comercio venda como máximo 100 unidades al mes. Dispone de 60 impresoras, lo que le reporta un beneficio
EJERCICIOS RESUELTOS 1) Entre impresoras y escáneres de segunda mano se tiene establecido que un pequeño comercio venda como máximo 100 unidades al mes. Dispone de 60 impresoras, lo que le reporta un beneficio
Suscripciones Administración Reclamos Formule un modelo de programación lineal.
 EJERCICIOS DE APLICACIÓN 1) Par, Inc. es un pequeño fabricante de equipo y material de golf. El distribuidor de Par cree que existe un mercado tanto para una bolsa de golf de precio moderado, llamada modelo
EJERCICIOS DE APLICACIÓN 1) Par, Inc. es un pequeño fabricante de equipo y material de golf. El distribuidor de Par cree que existe un mercado tanto para una bolsa de golf de precio moderado, llamada modelo
PLANTEAMIENTO DE MODELOS
 PLANTEAMIENTO DE MODELOS ITM INSTITUTO TECNOLÓGICO METROPOLITANO Ingenieria de Producción Investigacion de operaciones I profesor: Wbaldo Londoño 19 de febrero de 2016 Contenido 1 2 3 Problema de Producción
PLANTEAMIENTO DE MODELOS ITM INSTITUTO TECNOLÓGICO METROPOLITANO Ingenieria de Producción Investigacion de operaciones I profesor: Wbaldo Londoño 19 de febrero de 2016 Contenido 1 2 3 Problema de Producción
INVESTIGACION DE OPERACIONES (HAMDY A. TAHA) PROBLEMAS DE PLANTEAMIENTO DEL CAPITULO II
 INVESTIGACION DE OPERACIONES (HAMDY A. TAHA) PROBLEMAS DE PLANTEAMIENTO DEL CAPITULO II (TAHA) 2.2-1 Se procesan tres productos a través de tres opciones diferentes. Los tiempos en minutos requeridos por
INVESTIGACION DE OPERACIONES (HAMDY A. TAHA) PROBLEMAS DE PLANTEAMIENTO DEL CAPITULO II (TAHA) 2.2-1 Se procesan tres productos a través de tres opciones diferentes. Los tiempos en minutos requeridos por
EJEMPLO 1. Solución: Definimos las variables originales como: = número de conejos. x = número de pollos.
 EJEMPLO. En una granja agrícola se desea criar conejos y pollos como complemento en su economía, de forma que no se superen en conjunto las 8 horas mensuales destinadas a esta actividad. Su almacén sólo
EJEMPLO. En una granja agrícola se desea criar conejos y pollos como complemento en su economía, de forma que no se superen en conjunto las 8 horas mensuales destinadas a esta actividad. Su almacén sólo
UTALCA IMAFI. Resolver los siguientes ejercicios utilizando el método gráfico. Para ello:
 Resolver los siguientes ejercicios utilizando el método gráfico. Para ello: (a). Modelar matemáticamente la situación planteada. (b). Graficar, en un mismo sistema de coordenadas, todas las restricciones
Resolver los siguientes ejercicios utilizando el método gráfico. Para ello: (a). Modelar matemáticamente la situación planteada. (b). Graficar, en un mismo sistema de coordenadas, todas las restricciones
Tema 6. Programación Lineal
 RELACIÓN DE PROBLEMAS MATEMÁTICAS II Curso 2017/2018 Escuela Técnica Superior de Ingeniería Agronómica Departamento de Matemática Aplicada I Tema 6. Programación Lineal 6.1. Hallar el máximo de la función
RELACIÓN DE PROBLEMAS MATEMÁTICAS II Curso 2017/2018 Escuela Técnica Superior de Ingeniería Agronómica Departamento de Matemática Aplicada I Tema 6. Programación Lineal 6.1. Hallar el máximo de la función
UNIVERSIDAD DE MANAGUA Asignatura: Investigación de Operaciones I. Prof.: MSc. Ing. Julio Rito Vargas Avilés junio 2012
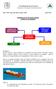 UNIVERSIDAD DE MANAGUA Asignatura: Investigación de Operaciones I Prof.: MSc. Ing. Julio Rito Vargas Avilés junio 2012 Problemas de PL con varias variables Análisis de Sensibilidad Problema 1: Ken & Larry
UNIVERSIDAD DE MANAGUA Asignatura: Investigación de Operaciones I Prof.: MSc. Ing. Julio Rito Vargas Avilés junio 2012 Problemas de PL con varias variables Análisis de Sensibilidad Problema 1: Ken & Larry
EJERCICIOS UNIDAD 4: PROGRAMACIÓN LINEAL
 EJERCICIOS UNIDAD 4: PROGRAMACIÓN LINEAL 1. (011-M-B-1) Se considera el recinto R del plano determinado por las siguientes inecuaciones: 1x + 8y 600; ( x ) ( y ); x 4y 0. a) (1.75 punto) Represente gráficamente
EJERCICIOS UNIDAD 4: PROGRAMACIÓN LINEAL 1. (011-M-B-1) Se considera el recinto R del plano determinado por las siguientes inecuaciones: 1x + 8y 600; ( x ) ( y ); x 4y 0. a) (1.75 punto) Represente gráficamente
Con (0,0 ) no podem os probar porque es tá en la pr opia recta, por lo que probamos con (1,0) 1-0 = 1>0. Obteniendo la nueva zona coloreada.
 Ejercicios resueltos Bloque V. Programación Lineal Tema 4: Resolución gráfica V.4-1 Resolver gráficamente el siguiente modelo de Programación Lineal: Maximizar f ( xy, ) = - y 6 x - y ³ 0 xy, ³ 0 Representamos
Ejercicios resueltos Bloque V. Programación Lineal Tema 4: Resolución gráfica V.4-1 Resolver gráficamente el siguiente modelo de Programación Lineal: Maximizar f ( xy, ) = - y 6 x - y ³ 0 xy, ³ 0 Representamos
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2016 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2016 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción B Reserva 2, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2016 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción B Reserva 2, Ejercicio
EJERCICIOS: TEMA 4: PROGRAMACIÓN LINEAL.
 EJERCICIOS: TEMA 4: PROGRAMACIÓN LINEAL. 1º/ Un taller de fabricación de muebles de oficina dispone de 700 kg de hierro y 1000 kg de alumnio para la producción de sillas y sillones metálicos. Cada silla
EJERCICIOS: TEMA 4: PROGRAMACIÓN LINEAL. 1º/ Un taller de fabricación de muebles de oficina dispone de 700 kg de hierro y 1000 kg de alumnio para la producción de sillas y sillones metálicos. Cada silla
Relación de Ejercicios: Programación Lineal. Modelos para la Prueba de Selectividad de a
 Relación de Ejercicios: Programación Lineal. Modelos para la Prueba de Selectividad de 2 005 a 2 008. EJERCICIO 1.- (3 puntos) Un pastelero dispone de 150 kg de harina, 22 kg de azúcar y 26 kg de mantequilla
Relación de Ejercicios: Programación Lineal. Modelos para la Prueba de Selectividad de 2 005 a 2 008. EJERCICIO 1.- (3 puntos) Un pastelero dispone de 150 kg de harina, 22 kg de azúcar y 26 kg de mantequilla
Tema 4. Programación lineal
 Tema 4. Programación lineal x + y 5 x + 3y 9 1. Representa la región factible que determina el conjunto R { de restricciones y halla de x 0 y 0 forma razonada el punto o puntos de la región factible donde
Tema 4. Programación lineal x + y 5 x + 3y 9 1. Representa la región factible que determina el conjunto R { de restricciones y halla de x 0 y 0 forma razonada el punto o puntos de la región factible donde
UNIVERSIDAD DE MANAGUA Al más alto nivel
 UNIVERSIDAD DE MANAGUA Al más alto nivel Programación Lineal Encuentro #2 Tema: Introducción a la programación lineal Prof.: MSc. Julio Rito Vargas A. Grupos: CCEE y ADMVA /2016 Objetivos: Conocer los
UNIVERSIDAD DE MANAGUA Al más alto nivel Programación Lineal Encuentro #2 Tema: Introducción a la programación lineal Prof.: MSc. Julio Rito Vargas A. Grupos: CCEE y ADMVA /2016 Objetivos: Conocer los
Programación Lineal y Optimización Primer Examen Parcial :Solución Profr. Eduardo Uresti, Enero-Mayo 2010
 Programación Lineal y Optimización Primer Examen Parcial : Profr. Eduardo Uresti, Enero-Mayo 200 Matrícula: Nombre:. Una pequeña empresa fabrica artículos de dos tipos a partir de tres materias primas,
Programación Lineal y Optimización Primer Examen Parcial : Profr. Eduardo Uresti, Enero-Mayo 200 Matrícula: Nombre:. Una pequeña empresa fabrica artículos de dos tipos a partir de tres materias primas,
se trata de un problema de PROGRAMACIÓN LINEAL. Al conjunto de todas las soluciones del problema se le llama conjunto de soluciones factibles.
 TEMA 11: PROGRAMACIÓN LINEAL Ciertos problemas que se plantean en la economía, en la industria, en la medicina, tienen como objeto MAXIMIZAR O MINIMIZAR una función llamada FUNCIÓN OBJETIVO, sujeta a varias
TEMA 11: PROGRAMACIÓN LINEAL Ciertos problemas que se plantean en la economía, en la industria, en la medicina, tienen como objeto MAXIMIZAR O MINIMIZAR una función llamada FUNCIÓN OBJETIVO, sujeta a varias
PROGRAMACIÓN LINEAL. 3) a) (1 punto) Represente gráficamente el recinto definido por el siguiente sistema de inecuaciones:
 PROGRAMACIÓN LINEAL 1) (3 puntos) Cierta sala de espectáculos tiene una capacidad máxima de 1500 personas, entre adultos y niños; el número de niños asistentes no puede superar los 600. El precio de la
PROGRAMACIÓN LINEAL 1) (3 puntos) Cierta sala de espectáculos tiene una capacidad máxima de 1500 personas, entre adultos y niños; el número de niños asistentes no puede superar los 600. El precio de la
2º BACHILLERATO MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II TEMA 4.- PROGRAMACIÓN LINEAL ACTIVIDADES PROPUESTAS PROFESOR: RAFAEL NÚÑEZ NOGALES
 1.- INECUACIONES LINEALES Y SISTEMAS CON DOS INCÓGNITAS. PROGRAMACIÓN LINEAL 1 Sea la región factible definida por las siguientes inecuaciones: x + y 20 ; x y 0 ; 5x 13y + 8 0 a) Represéntela gráficamente
1.- INECUACIONES LINEALES Y SISTEMAS CON DOS INCÓGNITAS. PROGRAMACIÓN LINEAL 1 Sea la región factible definida por las siguientes inecuaciones: x + y 20 ; x y 0 ; 5x 13y + 8 0 a) Represéntela gráficamente
encuentre la matriz A. Valor 10% 4.- Dada la Matriz A 1 2 Valor 10% 5.- Resuelva la siguiente ecuación matricial.
 UNIVERSIDAD NACIONAL AUTÓNOMA DE HONDURAS FACULTAD DE CIENCIAS ECONÓMICAS, CONTABLES Y ADMINISTRATIVAS METODOS CUANTITATIVOS II PRIMER EXAMEN PARCIAL 5/1/9 Valor del examen 1% NOTA Nombre: Número Cuenta:
UNIVERSIDAD NACIONAL AUTÓNOMA DE HONDURAS FACULTAD DE CIENCIAS ECONÓMICAS, CONTABLES Y ADMINISTRATIVAS METODOS CUANTITATIVOS II PRIMER EXAMEN PARCIAL 5/1/9 Valor del examen 1% NOTA Nombre: Número Cuenta:
EJERCICIOS UNIDAD 4: PROGRAMACIÓN LINEAL
 EJERCICIOS UNIDAD 4: PROGRAMACIÓN LINEAL 1. (011-M-B-1) Se considera el recinto R del plano determinado por las siguientes inecuaciones: 1x + 8y 600; ( x ) ( y ); x 4y 0. a) (1.75 punto) Represente gráficamente
EJERCICIOS UNIDAD 4: PROGRAMACIÓN LINEAL 1. (011-M-B-1) Se considera el recinto R del plano determinado por las siguientes inecuaciones: 1x + 8y 600; ( x ) ( y ); x 4y 0. a) (1.75 punto) Represente gráficamente
Dakota quiere maximizar el ingreso total por que se han comprado ya los recursos. Definiendo las variables de decisión como:
 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA UNAN-MANAGUA FAREM - CARAZO Teléfono 2532-2668/Telefax 2532-2684 INVESTIGACIÓN DE OPERACIONES LABORATORIO #7 ANALISIS DE SENSIBILIDAD Y DUALIDAD DE UN PPL I.
UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA UNAN-MANAGUA FAREM - CARAZO Teléfono 2532-2668/Telefax 2532-2684 INVESTIGACIÓN DE OPERACIONES LABORATORIO #7 ANALISIS DE SENSIBILIDAD Y DUALIDAD DE UN PPL I.
UNIVERSIDAD DE MANAGUA
 UNIVERSIDAD DE MANAGUA Sistemático de Programación Lineal Problemas de Programación Lineal: Solución Gráfica, Analítica, Sensibilidad y Método Simplex Prof. MSc. Ing. Julio Rito Vargas Avilés IIIC- 2016
UNIVERSIDAD DE MANAGUA Sistemático de Programación Lineal Problemas de Programación Lineal: Solución Gráfica, Analítica, Sensibilidad y Método Simplex Prof. MSc. Ing. Julio Rito Vargas Avilés IIIC- 2016
Trabajo Práctico Nº 8: Programación Lineal
 Trabajo Práctico Nº 8: Programación Lineal 1. Utilice el método gráfico para resolver los siguientes problemas: a. Maximizar Z = x1 + x2 x 1 + 5x 2 = 0 b. Maximizar
Trabajo Práctico Nº 8: Programación Lineal 1. Utilice el método gráfico para resolver los siguientes problemas: a. Maximizar Z = x1 + x2 x 1 + 5x 2 = 0 b. Maximizar
PROGRAMACIÓN LINEAL PROBLEMAS PARA PLANTEAR
 PROBLEMAS PARA PLANTEAR PROGRAMACIÓN LINEAL 1. Una compañía tiene dos minas. La mina A produce diariamente una tonelada de carbón de antracita de alta calidad, 2 toneladas de carbón de calidad media y
PROBLEMAS PARA PLANTEAR PROGRAMACIÓN LINEAL 1. Una compañía tiene dos minas. La mina A produce diariamente una tonelada de carbón de antracita de alta calidad, 2 toneladas de carbón de calidad media y
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción A Reserva 2, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2003 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción A Reserva 2, Ejercicio
Horas requeridas producto B
 1. J&M Winery fabrica dos tipos de Chardonnay, uno con etiqueta económica y otro con etiqueta especial. Han firmado un contrato de venta de 30.000 cajas de Chardonnay y están seguros que podrán vender
1. J&M Winery fabrica dos tipos de Chardonnay, uno con etiqueta económica y otro con etiqueta especial. Han firmado un contrato de venta de 30.000 cajas de Chardonnay y están seguros que podrán vender
UNIVERSIDAD NACIONAL DE SALTA Facultad de Ciencias Económicas, Jurídicas y Sociales Cátedra: Métodos Cuantitativos para los Negocios
 PROBLEMA Nº 1: FÁBRICA DE BOMBONES Una fábrica de bombones entrega sus productos en cajas de un kilogramo en dos variedades A y B. La caja tipo A contiene trescientos gramos de bombones de licor, quinientos
PROBLEMA Nº 1: FÁBRICA DE BOMBONES Una fábrica de bombones entrega sus productos en cajas de un kilogramo en dos variedades A y B. La caja tipo A contiene trescientos gramos de bombones de licor, quinientos
Fundamentos de la programación lineal. Función Objetivo (F.O.): Para seleccionar qué función objetivo debe elegirse se toma en cuenta lo siguiente:
 Fundamentos de la programación lineal Se llama programación lineal al conjunto de técnicas matemáticas que pretenden resolver la situación siguiente: Optimizar (maximizar o minimizar) una función objetivo,
Fundamentos de la programación lineal Se llama programación lineal al conjunto de técnicas matemáticas que pretenden resolver la situación siguiente: Optimizar (maximizar o minimizar) una función objetivo,
PROBLEMAS DE PROGRAMACIÓN LINEAL (SELECTIVIDAD)
 (3 puntos) Una fábrica produce dos tipos de relojes: de pulsera, que vende a 90 euros la unidad, y de bolsillo, que vende a 120 euros cada uno. La capacidad máxima diaria de fabricación es de 1000 relojes,
(3 puntos) Una fábrica produce dos tipos de relojes: de pulsera, que vende a 90 euros la unidad, y de bolsillo, que vende a 120 euros cada uno. La capacidad máxima diaria de fabricación es de 1000 relojes,
UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA UNAN-MANAGUA FAREM - CARAZO
 UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA UNAN-MANAGUA FAREM - CARAZO INVESTIGACIÓN DE OPERACIONES Laboratorio #1 GRAFICA DE REGIONES CONVEXAS Y SOLUCIÓN POR MÉTODO GRÁFICO DE UN PROBLEMA DE PROGRAMACIÓN
UNIVERSIDAD NACIONAL AUTONOMA DE NICARAGUA UNAN-MANAGUA FAREM - CARAZO INVESTIGACIÓN DE OPERACIONES Laboratorio #1 GRAFICA DE REGIONES CONVEXAS Y SOLUCIÓN POR MÉTODO GRÁFICO DE UN PROBLEMA DE PROGRAMACIÓN
Colegio Portocarrero. Curso Departamento de matemáticas. Matrices y programación lineal
 Matrices y programación lineal Problema 1: En una confiteria se dispone de 24 kg de polvorones y 15 kg de mantecados, que se envasan en dos tipos de caja del modo siguiente: Caja tipo 1: 200 g de polvorones
Matrices y programación lineal Problema 1: En una confiteria se dispone de 24 kg de polvorones y 15 kg de mantecados, que se envasan en dos tipos de caja del modo siguiente: Caja tipo 1: 200 g de polvorones
Universidad Nacional Autónoma de Nicaragua UNAN-Managua. Curso de Investigación de Operaciones
 Universidad Nacional Autónoma de Nicaragua UNAN-Managua Curso de Investigación de Operaciones Profesor: MSc. Julio Rito Vargas Avilés. Estudiantes: FAREM-Carazo Unidad II Modelos de Programación Lineal
Universidad Nacional Autónoma de Nicaragua UNAN-Managua Curso de Investigación de Operaciones Profesor: MSc. Julio Rito Vargas Avilés. Estudiantes: FAREM-Carazo Unidad II Modelos de Programación Lineal
PROGRAMACIÓN LINEAL MÉTODO GRÁFICO
 1 PROGRAMACIÓN LINEAL MÉTODO GRÁFICO Dado un problema de programación lineal se debe: 1. Graficar cada una de las restricciones. 2. Encontrar el Polígono de factibilidad, que es la intersección de los
1 PROGRAMACIÓN LINEAL MÉTODO GRÁFICO Dado un problema de programación lineal se debe: 1. Graficar cada una de las restricciones. 2. Encontrar el Polígono de factibilidad, que es la intersección de los
a) LLamamos x al número de collares e y al número de pulseras. Las restricciones son: x + y 50 2x + y 80 x, y 0
 Nuria Torrado Robles Departamento de Estadística Universidad Carlos III de Madrid Hoja, ejercicios de programación lineal, curso 2010 2011. 1. Un artesano fabrica collares y pulseras. Hacer un collar le
Nuria Torrado Robles Departamento de Estadística Universidad Carlos III de Madrid Hoja, ejercicios de programación lineal, curso 2010 2011. 1. Un artesano fabrica collares y pulseras. Hacer un collar le
SOLUCIONES EJERCICIOS PROGRAMACIÓN LINEAL
 SOLUCIONES EJERCICIOS PROGRAMACIÓN LINEAL Ejercicio nº 1. a) Dibuja el recinto formado por los puntos que cumplen las siguientes condiciones: 1 0 b) Indica si los puntos (0, 0), (, 1) (1, ) forman parte
SOLUCIONES EJERCICIOS PROGRAMACIÓN LINEAL Ejercicio nº 1. a) Dibuja el recinto formado por los puntos que cumplen las siguientes condiciones: 1 0 b) Indica si los puntos (0, 0), (, 1) (1, ) forman parte
Inecuaciones y sistemas de inecuaciones
 6 Inecuaciones y sistemas de inecuaciones 1. Inecuaciones de 1 er grado Escribe todos los números enteros que verifiquen a la vez: 5 < x Ì 6 P I E N S A C A L C U L A 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, 6 1
6 Inecuaciones y sistemas de inecuaciones 1. Inecuaciones de 1 er grado Escribe todos los números enteros que verifiquen a la vez: 5 < x Ì 6 P I E N S A C A L C U L A 4, 3, 2, 1, 0, 1, 2, 3, 4, 5, 6 1
EJERCICIOS PROGRAMACIÓN LINEAL
 EJERCICIOS PROGRAMACIÓN LINEAL 1.- Una compañía fabrica y venden dos modelos de lámpara L 1 y L 2. Para su fabricación se necesita un trabajo manual de 20 minutos para el modelo L 1 y de 30 minutos para
EJERCICIOS PROGRAMACIÓN LINEAL 1.- Una compañía fabrica y venden dos modelos de lámpara L 1 y L 2. Para su fabricación se necesita un trabajo manual de 20 minutos para el modelo L 1 y de 30 minutos para
a) Represente el recinto definido por las siguientes inecuaciones: x + y 3 ; 2x + y 4 ; y 1 Solución
 1.- INECUACIONES LINEALES Y SISTEMAS CON DOS INCÓGNITAS. PROGRAMACIÓN LINEAL Ejercicio de clase 1 : a) Represente gráficamente la región determinada por las siguientes restricciones: 2x + y 6 ; 4x + y
1.- INECUACIONES LINEALES Y SISTEMAS CON DOS INCÓGNITAS. PROGRAMACIÓN LINEAL Ejercicio de clase 1 : a) Represente gráficamente la región determinada por las siguientes restricciones: 2x + y 6 ; 4x + y
Problemas de PL con varias variables Análisis de Sensibilidad
 UNIVERSIDAD NACIONAL DE INGENIERIA UN-NORTE SEDE-ESTELI Asignatura: Investigación de Operaciones I Problemas de PL con varias variables Análisis de Sensibilidad M.C. Ing. Julio Rito Vargas Avilés 1 P.
UNIVERSIDAD NACIONAL DE INGENIERIA UN-NORTE SEDE-ESTELI Asignatura: Investigación de Operaciones I Problemas de PL con varias variables Análisis de Sensibilidad M.C. Ing. Julio Rito Vargas Avilés 1 P.
Programación Lineal MARCAS GRADO I GRADO II UTILIDAD REGULAR 50% 50% $ 5 SÚPER 75% 25% $ 6
 Programación Lineal 1. Una compañía destiladora tiene dos grados de güisqui en bruto (sin mezclar), I y II, de los cuales produce dos marcas diferentes. La marca regular contiene un 0% de cada uno de los
Programación Lineal 1. Una compañía destiladora tiene dos grados de güisqui en bruto (sin mezclar), I y II, de los cuales produce dos marcas diferentes. La marca regular contiene un 0% de cada uno de los
Planteamiento de problemas de programación lineal. M. En C. Eduardo Bustos Farías
 Planteamiento de problemas de programación lineal M. En C. Eduardo Bustos Farías 1 Objetivo Analizar diferentes ejemplos del uso de la metodología de la Investigación de Operaciones para el planteamiento
Planteamiento de problemas de programación lineal M. En C. Eduardo Bustos Farías 1 Objetivo Analizar diferentes ejemplos del uso de la metodología de la Investigación de Operaciones para el planteamiento
PROGRAMACIÓN LINEAL. FUNCIÓN OBJETIVO (Beneficio (en euros) obtenido por la venta de los dos tipos de cable):
 Ejercicio 159 Para fabricar 2 tipos de cable, A y B, que se venderán a 1,50 y 1 el metro, respectivamente, se emplean 16Kg de plástico y 4Kg de cobre para cada hectómetro del tipo A y 6Kg de plástico y
Ejercicio 159 Para fabricar 2 tipos de cable, A y B, que se venderán a 1,50 y 1 el metro, respectivamente, se emplean 16Kg de plástico y 4Kg de cobre para cada hectómetro del tipo A y 6Kg de plástico y
Problemas de programación lineal.
 Matemáticas 2º Bach CCSS. Problemas Tema 2. Programación Lineal. Pág 1/12 Problemas de programación lineal. 1. Unos grandes almacenes encargan a un fabricante pantalones y chaquetas deportivas. El fabricante
Matemáticas 2º Bach CCSS. Problemas Tema 2. Programación Lineal. Pág 1/12 Problemas de programación lineal. 1. Unos grandes almacenes encargan a un fabricante pantalones y chaquetas deportivas. El fabricante
PROGRAMACIÓN LINEAL (Selectividad) 2ºBachillerato C.C.S.S. Noviembre 2015
 PROGRAMACIÓN LINEAL (Selectividad) 2ºBachillerato C.C.S.S. Noviembre 2015 1. (S2015) Un heladero artesano elabora dos tipos de helados A y B que vende cada día. Los helados tipo A llevan 1 gramo de nata
PROGRAMACIÓN LINEAL (Selectividad) 2ºBachillerato C.C.S.S. Noviembre 2015 1. (S2015) Un heladero artesano elabora dos tipos de helados A y B que vende cada día. Los helados tipo A llevan 1 gramo de nata
FACULTAD DE INGENIERÍA DEPARTAMENTO DE SISTEMAS DE PRODUCCIÓN
 FACULTAD DE INGENIERÍA DEPARTAMENTO DE SISTEMAS DE PRODUCCIÓN Asignatura: Investigación de Operaciones 1 Periodo Académico: Julio - Diciembre de 2009 TALLER MÉTODO GRÁFICO 1. PROBLEMA DE PLANEACIÓN DE
FACULTAD DE INGENIERÍA DEPARTAMENTO DE SISTEMAS DE PRODUCCIÓN Asignatura: Investigación de Operaciones 1 Periodo Académico: Julio - Diciembre de 2009 TALLER MÉTODO GRÁFICO 1. PROBLEMA DE PLANEACIÓN DE
EJERCICIOS DE PROGRAMACIÓN LINEAL. RECUPERACIÓN
 EJERCICIOS DE PROGRAMACIÓN LINEAL. RECUPERACIÓN 1.- Ejemplo resuelto Un herrero dispone de 80 kg. de acero y 120 kg. de aluminio quiere hacer bicicletas de paseo y de montaña que quiere vender, respectivamente
EJERCICIOS DE PROGRAMACIÓN LINEAL. RECUPERACIÓN 1.- Ejemplo resuelto Un herrero dispone de 80 kg. de acero y 120 kg. de aluminio quiere hacer bicicletas de paseo y de montaña que quiere vender, respectivamente
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2004 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2004 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción B Reserva 2, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2004 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción B Reserva 2, Ejercicio
La función alcanza el máximo en el punto (10, 3).
 b) f(x, y) = 4x + y + f(0, 0) = f(, 8) = 8 f(0, ) = La función alcanza el máximo en el punto (0, ). PARA RESOLVER 0 Un estudiante reparte propaganda publicitaria en su tiempo libre. La empresa A le paga
b) f(x, y) = 4x + y + f(0, 0) = f(, 8) = 8 f(0, ) = La función alcanza el máximo en el punto (0, ). PARA RESOLVER 0 Un estudiante reparte propaganda publicitaria en su tiempo libre. La empresa A le paga
Ejemplos a resolver en clases-metodo grafico
 Ejemplos a resolver en clases-metodo grafico 1) Una compañía tiene dos minas: la mina A produce diariamente 1 tonelada de carbón de antracita de alta calidad, 2 toneladas de carbón de calidad media y 4
Ejemplos a resolver en clases-metodo grafico 1) Una compañía tiene dos minas: la mina A produce diariamente 1 tonelada de carbón de antracita de alta calidad, 2 toneladas de carbón de calidad media y 4
ASIGNATURA: MATEMÁTICAS CCSS 2º BACHILLERATO. ÁLGEBRA Boletín 3 PROGRAMACIÓN LINEAL
 ASIGNATURA: MATEMÁTICAS CCSS 2º BACHILLERATO TEMA: ÁLGEBRA Boletín 3 PROGRAMACIÓN LINEAL 1) Un taller fabrica y vende dos tipos de alfombras, de seda y de lana. Para la elaboración de una unidad se necesita
ASIGNATURA: MATEMÁTICAS CCSS 2º BACHILLERATO TEMA: ÁLGEBRA Boletín 3 PROGRAMACIÓN LINEAL 1) Un taller fabrica y vende dos tipos de alfombras, de seda y de lana. Para la elaboración de una unidad se necesita
Pogramación Lineal. Matemáticas Aplicadas Ciencias Sociales II. José Manuel del Toro Programación Lineal - 1
 Pogramación Lineal 1) (Junio-00) Una empresa, especializada en la fabricación de mobiliario para casas de muñecas, produce cierto tipo de mesas y sillas que vende a 2000 pts y 3000 pts por unidad, respectivamente.
Pogramación Lineal 1) (Junio-00) Una empresa, especializada en la fabricación de mobiliario para casas de muñecas, produce cierto tipo de mesas y sillas que vende a 2000 pts y 3000 pts por unidad, respectivamente.
PROBLEMA DE FLUJO DE COSTO MINIMO.
 PROBLEMA DE FLUJO DE COSTO MINIMO. EL PROBLEMA DE TRANSPORTE 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y
PROBLEMA DE FLUJO DE COSTO MINIMO. EL PROBLEMA DE TRANSPORTE 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y
PHPSimplex es una herramienta online para resolver problemas de programación lineal. Su uso es libre y gratuito. http://www.phpsimplex.
 IES de MOS Ejercicios Programación Lineal PHPSimplex es una herramienta online para resolver problemas de programación lineal. Su uso es libre y gratuito. http://www.phpsimplex.com 1. Dada la región del
IES de MOS Ejercicios Programación Lineal PHPSimplex es una herramienta online para resolver problemas de programación lineal. Su uso es libre y gratuito. http://www.phpsimplex.com 1. Dada la región del
Producto Maquina A Maquina B Acabado Muñecas 2 hr 1 hr 1 hr Soldados 1 hr 1 hr 3 hr
 Nombre: UNIVERSIDAD NACIONAL AUTONOMA DE HONDURAS METODOS CUANTITATIVOS II EXAMEN PARCIAL I /3/7 Sección # Cuenta: Catedrático: Desarrolle en forma clara y ordenada lo que a continuación se le pide:.-
Nombre: UNIVERSIDAD NACIONAL AUTONOMA DE HONDURAS METODOS CUANTITATIVOS II EXAMEN PARCIAL I /3/7 Sección # Cuenta: Catedrático: Desarrolle en forma clara y ordenada lo que a continuación se le pide:.-
Investigación de Operaciones 1
 Investigación de Operaciones 1 Clase 4 Pablo Andrés Maya Mayo, 2014 Pablo Andrés Maya () Investigación de Operaciones 1 Mayo, 2014 1 / 10 Problema de portafolio La Universidad dispone de un presupuesto
Investigación de Operaciones 1 Clase 4 Pablo Andrés Maya Mayo, 2014 Pablo Andrés Maya () Investigación de Operaciones 1 Mayo, 2014 1 / 10 Problema de portafolio La Universidad dispone de un presupuesto
Investigacion de operaciones 1 Wbaldo Londoño
 Investigacion de operaciones 1 Wbaldo Londoño Instituto Tecnologico Metropolitano ITM 9 de octubre de 2015 Contenido 1 Zapatos S.A 2 Marpo S.A 3 Dynamix Zapatos S.A Al realizar una inspección en una fábrica
Investigacion de operaciones 1 Wbaldo Londoño Instituto Tecnologico Metropolitano ITM 9 de octubre de 2015 Contenido 1 Zapatos S.A 2 Marpo S.A 3 Dynamix Zapatos S.A Al realizar una inspección en una fábrica
PROBLEMAS DEPROGRAMACION LINEAL RESUELTOS
 PROBLEMAS DEPROGRAMACION LINEAL RESUELTOS 1) Se considera la región del plano determinada por las inecuaciones:x + 3 y ; 8 x + y ; y x - 3 ; x 0; y 0 a) Dibujar la región del plano que definen, y calcular
PROBLEMAS DEPROGRAMACION LINEAL RESUELTOS 1) Se considera la región del plano determinada por las inecuaciones:x + 3 y ; 8 x + y ; y x - 3 ; x 0; y 0 a) Dibujar la región del plano que definen, y calcular
El planteamiento y la solución obtenidos por medio del WINQSB son:
 Ejemplos sobre la Regla del 100% 1. Mi alimentación requiere que todo lo que coma pertenezca a uno de los cuatro grupos básicos de alimentos (pastel de chocolate, helado, refrescos y pastel de queso).
Ejemplos sobre la Regla del 100% 1. Mi alimentación requiere que todo lo que coma pertenezca a uno de los cuatro grupos básicos de alimentos (pastel de chocolate, helado, refrescos y pastel de queso).
Matemáticas aplicadas a las CC.SS. II 2º Bachillerato
 4. PROGRAMACIÓN LINEAL 4.1. Introducción 1. Determina las variables, la función objetivo y el conjunto de restricciones de los siguientes problemas de programación lineal: a) En una empresa de alimentación
4. PROGRAMACIÓN LINEAL 4.1. Introducción 1. Determina las variables, la función objetivo y el conjunto de restricciones de los siguientes problemas de programación lineal: a) En una empresa de alimentación
Universidad Nacional De Ingeniería
 Universidad Nacional De Ingeniería UNI-RUACS Investigación de Operaciones I Elaborado por: Rosa Emilia Miranda López Karla Vanessa Guevara ElingJunieth Salguera Docente. IngMario Pastrana Moreno Grupo:
Universidad Nacional De Ingeniería UNI-RUACS Investigación de Operaciones I Elaborado por: Rosa Emilia Miranda López Karla Vanessa Guevara ElingJunieth Salguera Docente. IngMario Pastrana Moreno Grupo:
Colegio Portocarrero. Departamento de matemáticas. PL con solución
 PL con solución Problema 1: Un mayorista de frutos secos tiene almacenados 1800 kg de avellanas y 420 kg de almendras para hacer dos tipos de mezclas que embala en cajas como se indica a continuación:
PL con solución Problema 1: Un mayorista de frutos secos tiene almacenados 1800 kg de avellanas y 420 kg de almendras para hacer dos tipos de mezclas que embala en cajas como se indica a continuación:
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción B Reserva 2, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2012 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción A Reserva 1, Ejercicio 1, Opción B Reserva 2, Ejercicio
Programación lineal. 1. Resolver cada inecuación grá camente por separado indicando mediante echas o sombreando, el semiplano solución.
 I.E.S. CASTILLO DE LUNA Programación lineal En un problema de programación lineal con dos variables x; y, se trata de optimizar (hacer máximo o mínimo, según los casos) una función, llamada función objetivo
I.E.S. CASTILLO DE LUNA Programación lineal En un problema de programación lineal con dos variables x; y, se trata de optimizar (hacer máximo o mínimo, según los casos) una función, llamada función objetivo
Universidad Nacional de Ingeniería
 Universidad Nacional de Ingeniería Recinto Universitario Augusto Cesar Sandino Uní - RUACS Trabajo de Investigación de Operaciones I Orientado Por: Ing. Mario Pastrana Carrera: Ingeniería de Sistemas Año:
Universidad Nacional de Ingeniería Recinto Universitario Augusto Cesar Sandino Uní - RUACS Trabajo de Investigación de Operaciones I Orientado Por: Ing. Mario Pastrana Carrera: Ingeniería de Sistemas Año:
3. Reserva Opción B a) (2 puntos) Represente gráficamente la región factible definida por las siguientes restricciones:
 Enunciados Ejercicio 1 Programación Lineal Selectividad 1. Junio 2015 Opción A (2.5 puntos) Con motivo de su inauguración, una heladería quiere repartir dos tipos de tarrinas de helados. El primer tipo
Enunciados Ejercicio 1 Programación Lineal Selectividad 1. Junio 2015 Opción A (2.5 puntos) Con motivo de su inauguración, una heladería quiere repartir dos tipos de tarrinas de helados. El primer tipo
Análisis de sensibilidad en Modelos lineales:
 Universidad de Managua Curso de Optimización Análisis de sensibilidad en Modelos lineales: CAMBIOS EN LOS COEFICIENTES TECNOLÓGICOS CAMBIOS EN LOS COSTOS/UTILIDADES CAMBIOS EN LOS RECURSOS NUEVO PRODUCTO
Universidad de Managua Curso de Optimización Análisis de sensibilidad en Modelos lineales: CAMBIOS EN LOS COEFICIENTES TECNOLÓGICOS CAMBIOS EN LOS COSTOS/UTILIDADES CAMBIOS EN LOS RECURSOS NUEVO PRODUCTO
George Bernard Dantzig
 PROBLEMAS RESUELTOS DE PROGRAMACION LINEAL George Bernard Dantzig (8 de noviembre de 1914 13 de mayo de 2005) fue un matemático reconocido por desarrollar el método simplex y es considerado como el "padre
PROBLEMAS RESUELTOS DE PROGRAMACION LINEAL George Bernard Dantzig (8 de noviembre de 1914 13 de mayo de 2005) fue un matemático reconocido por desarrollar el método simplex y es considerado como el "padre
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2013 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2013 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción A Reserva 2, Ejercicio
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2013 MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES TEMA 3: PROGRAMACIÓN LINEAL Junio, Ejercicio 1, Opción B Reserva 1, Ejercicio 1, Opción A Reserva 2, Ejercicio
Colegio Portocarrero. Curso Departamento de matemáticas. Matrices, programación lineal, límites, asíntotas, continuidad.
 Matrices, programación lineal, límites, asíntotas, continuidad. Problema 1: Sean A y B dos matrices de tamaño 2 x 2. Es cierta la igualdad (A + B)(A B) = A 2 B 2? Pruébalo si es cierto o busca un contraejemplo
Matrices, programación lineal, límites, asíntotas, continuidad. Problema 1: Sean A y B dos matrices de tamaño 2 x 2. Es cierta la igualdad (A + B)(A B) = A 2 B 2? Pruébalo si es cierto o busca un contraejemplo
EJERCICIOS DE PROGRAMACIÓN LINEAL
 EJERCICIOS DE PROGRAMACIÓN LINEAL 1 Un fabricante desea encontrar la producción semanal óptima de los artículos A, B y C para maximizar sus beneficios. Las ganancias por unidad de estos artículos son:
EJERCICIOS DE PROGRAMACIÓN LINEAL 1 Un fabricante desea encontrar la producción semanal óptima de los artículos A, B y C para maximizar sus beneficios. Las ganancias por unidad de estos artículos son:
MATEMÁTICAS II. Interpretación LINGO
 MATEMÁTICAS II Interpretación LINGO 1 1. Una cadena de hipermercados ha propuesto a una empresa de productos plásticos comercializar en exclusiva tres de sus artículos (A 1, A 2 y A 3 ) con las siguientes
MATEMÁTICAS II Interpretación LINGO 1 1. Una cadena de hipermercados ha propuesto a una empresa de productos plásticos comercializar en exclusiva tres de sus artículos (A 1, A 2 y A 3 ) con las siguientes
Colegio Portocarrero. Curso Departamento de matemáticas. Sistemas, matrices, programación lineal resueltos.
 Sistemas, matrices, programación lineal resueltos. Problema 1: Sean las matrices Encuentra el valor o valores de x de forma que B 2 = A Problema 2: En la remodelación de un centro de enseñanza se quiera
Sistemas, matrices, programación lineal resueltos. Problema 1: Sean las matrices Encuentra el valor o valores de x de forma que B 2 = A Problema 2: En la remodelación de un centro de enseñanza se quiera
PROBLEMA DE FLUJO DE COSTO MINIMO.
 PROBLEMA DE FLUJO DE COSTO MINIMO. EL PROBLEMA DE TRANSPORTE 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y
PROBLEMA DE FLUJO DE COSTO MINIMO. EL PROBLEMA DE TRANSPORTE 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y
Depto. Matemáticas IES Elaios. Tema: Programación Lineal
 Depto. Matemáticas IES Elaios Tema: Programación Lineal Presentación elaborada por el profesor José Mª Sorando, ampliando y adaptando las diapositivas de la Editorial SM Inecuaciones lineales. Interpretación
Depto. Matemáticas IES Elaios Tema: Programación Lineal Presentación elaborada por el profesor José Mª Sorando, ampliando y adaptando las diapositivas de la Editorial SM Inecuaciones lineales. Interpretación
Curso COLEGIO SANTÍSIMA TRINIDAD. Dpto de Matemáticas. Sevilla
 COLEGIO SANTÍSIMA TRINIDAD Sevilla Dpto de Matemáticas Curso 2009-10 Boletín de Programación Lineal Matemáticas 2º Bach CC.SS. 1. Un frutero necesita 16 cajas de naranjas, 5 de plátanos y 20 de manzanas.
COLEGIO SANTÍSIMA TRINIDAD Sevilla Dpto de Matemáticas Curso 2009-10 Boletín de Programación Lineal Matemáticas 2º Bach CC.SS. 1. Un frutero necesita 16 cajas de naranjas, 5 de plátanos y 20 de manzanas.
Programación Lineal y Optimización Primer Examen Parcial :Solución Profr. Eduardo Uresti, Enero-Mayo 2011
 Programación Lineal y Optimización Primer Examen Parcial : Profr. Eduardo Uresti, Enero-Mayo 2011 Matrícula: Nombre: 1. Una pequeña empresa fabrica sustancias de dos tipos a partir de tres materias primas,
Programación Lineal y Optimización Primer Examen Parcial : Profr. Eduardo Uresti, Enero-Mayo 2011 Matrícula: Nombre: 1. Una pequeña empresa fabrica sustancias de dos tipos a partir de tres materias primas,
EJERCICIOS Y PROBLEMAS RESUELTOS
 EJERIIOS PROLEMS RESUELTOS 1. Se tiene una región factible determinada por el polígono de vértices: (2, 1), (, 0), (6, 2), (, ) y E(0, 4) a) Representa gráficamente dicha región, así como las rectas de
EJERIIOS PROLEMS RESUELTOS 1. Se tiene una región factible determinada por el polígono de vértices: (2, 1), (, 0), (6, 2), (, ) y E(0, 4) a) Representa gráficamente dicha región, así como las rectas de
Programación lineal. 1. Dibuja la región del plano definida por las siguientes inecuaciones: x 0, 0 y 2, y + 2x 4. Solución:
 1 LRJS05 1. Dibuja la región del plano definida por las siguientes inecuaciones: 0, 0 y 2, y + 2 4 Representando las rectas asociadas a cada una de las inecuaciones dadas se obtiene la región sombreada
1 LRJS05 1. Dibuja la región del plano definida por las siguientes inecuaciones: 0, 0 y 2, y + 2 4 Representando las rectas asociadas a cada una de las inecuaciones dadas se obtiene la región sombreada
UNIVERSIDAD NACIONAL DE INGENIERÍA Recinto Universitario Augusto C. Sandino.
 UNIVERSIDAD NACIONAL DE INGENIERÍA Recinto Universitario Augusto C. Sandino. Problemas de Costo Minimo Trabajo presentado por: Victor Celis Hecht Ortega Gelmer Castillo Davila Christian Palacios Preza
UNIVERSIDAD NACIONAL DE INGENIERÍA Recinto Universitario Augusto C. Sandino. Problemas de Costo Minimo Trabajo presentado por: Victor Celis Hecht Ortega Gelmer Castillo Davila Christian Palacios Preza
{x 3 y 3. Ejercicios. y la función objetivo que hay que maximizar es
 Ejercicios 1. [S/97]Cada mes una empresa puede gastar, como máximo, un millón de pesetas en salarios y un millón ochocientas mil pesetas en energía (electricidad y gasóleo). La empresa sólo elabora dos
Ejercicios 1. [S/97]Cada mes una empresa puede gastar, como máximo, un millón de pesetas en salarios y un millón ochocientas mil pesetas en energía (electricidad y gasóleo). La empresa sólo elabora dos
Planteamiento de problemas de programación lineal. M. En C. Eduardo Bustos Farías
 Planteamiento de problemas de programación lineal M. En C. Eduardo Bustos Farías 1 Objetivo Analizar diferentes ejemplos del uso de la metodología de la Investigación de Operaciones para el planteamiento
Planteamiento de problemas de programación lineal M. En C. Eduardo Bustos Farías 1 Objetivo Analizar diferentes ejemplos del uso de la metodología de la Investigación de Operaciones para el planteamiento
Ejemplo 1: Programación Entera
 Repaso Prueba 2 Ejemplo 1: Programación Entera Supongamos que una persona está interesada en elegir entre un conjunto de inversiones {1,,7} y quiere hacer un modelo 0,1 para tomar la decisión. Modelar
Repaso Prueba 2 Ejemplo 1: Programación Entera Supongamos que una persona está interesada en elegir entre un conjunto de inversiones {1,,7} y quiere hacer un modelo 0,1 para tomar la decisión. Modelar
Problemas de I.O. con mas de dos variables
 UNIVERSIDAD NACIONAL DE INGENIERIA UN-NORTE SEDE-ESTELI Curso de Investigación de Operaciones I Problemas de I.O. con mas de dos variables M.C. Ing. Julio Rito Vargas Avilés 1 1. Orsini. Fabrica tres tipos
UNIVERSIDAD NACIONAL DE INGENIERIA UN-NORTE SEDE-ESTELI Curso de Investigación de Operaciones I Problemas de I.O. con mas de dos variables M.C. Ing. Julio Rito Vargas Avilés 1 1. Orsini. Fabrica tres tipos
GUIA DE EJERCICIOS - TEORIA DE DECISIONES
 GUIA DE EJERCICIOS - TEORIA DE DECISIONES PROBLEMAS EN SITUACION DE CERTIDUMBRE: 1 Un estudiante de Administración de Empresas en la UNAP necesita completar un total de 65 cursos para obtener su licenciatura.
GUIA DE EJERCICIOS - TEORIA DE DECISIONES PROBLEMAS EN SITUACION DE CERTIDUMBRE: 1 Un estudiante de Administración de Empresas en la UNAP necesita completar un total de 65 cursos para obtener su licenciatura.
x y 3 5 (b) Calcula los valores extremos de la función F(x,y ) = 5x + 15y en dicha región e indica dónde se alcanzan.
 ÁLGEBRA CIENCIAS SOCIALES (Selectividad) (a) Representa la región definida por las siguientes inecuaciones determina sus vértices: + + 0 (b) Calcula los valores etremos de la función F(, ) = + en dicha
ÁLGEBRA CIENCIAS SOCIALES (Selectividad) (a) Representa la región definida por las siguientes inecuaciones determina sus vértices: + + 0 (b) Calcula los valores etremos de la función F(, ) = + en dicha
Xochilth Castillo Palacios
 Xochilth Castillo Palacios PROBLEMAS: 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y 3 pueden satisfacer 35,
Xochilth Castillo Palacios PROBLEMAS: 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y 3 pueden satisfacer 35,
Universidad de Managua Al más alto nivel Facultad de Ciencias Económicas y Administrativas. Curso de Programación Unidad IV Lineal Tema.
 Universidad de Managua Al más alto nivel Facultad de Ciencias Económicas y Administrativas Profesor: MSc. Julio Rito Vargas Avilés. Estudiantes: F.C.E.A Curso de Programación Unidad IV Lineal Tema Análisis
Universidad de Managua Al más alto nivel Facultad de Ciencias Económicas y Administrativas Profesor: MSc. Julio Rito Vargas Avilés. Estudiantes: F.C.E.A Curso de Programación Unidad IV Lineal Tema Análisis
Problema 1. Oferta /15/ /20/0 5 40/30/0. Demanda 45/30/10/0 20/0 30/0 30/
 Problema 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y 3 pueden satisfacer 35, 50 y 40 millones de [kwh] respectivamente.
Problema 1. Una empresa energética dispone de tres plantas de generación para satisfacer la demanda eléctrica de cuatro ciudades. Las plantas 1, 2 y 3 pueden satisfacer 35, 50 y 40 millones de [kwh] respectivamente.
