MATEMÁTICAS BÁSICAS. Universidad Nacional de Colombia Sede Bogotá. 24 de julio de Departamento de Matemáticas
|
|
|
- Encarnación Agüero Rojas
- hace 5 años
- Vistas:
Transcripción
1 MATEMÁTICAS BÁSICAS Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas 24 de julio de 2012
2 Parte I Ecuaciones lineales
3 ECUACIONES Una ecuación es una igualdad entre dos expresiones algebraicas que involucra variables. Ejemplos Ecuaciones en una variable Ecuaciones en varias variables 3x 2 = 7 3x 2y = 1 4x 1 lnx = 0 x 2 + y 2 = 25 cos x sen x = 1 x 3x 2 5x = 2.
4 Ecuaciones lineales Solución de una ecuación: Es el conjunto de valores de la variable (o variables) que hacen cierta la igualdad. Ejemplos (A) 3 es solución de 3x 2 = 7, pues es el único valor real que hace verdadera la igualdad. El conjunto solución es {3}. (B) Dada la ecuación x 2 5x + 6 = 0. La transformamos en (x 2)(x 3) = 0 y observamos que el conjunto solución es {2, 3}. (C) (3, 4) es una solución de la ecuación x 2 + y 2 = 25 pero hay muchas más, por ejemplo ( 3, 4),(0, 5),( 5, 0), etc.
5 Ecuaciones equivalentes Dos ecuaciones son equivalentes si tienen el mismo conjunto solución. Para encontrar el conjunto solución de una ecuación muchas veces la transformamos en una equivalente que sea fácil de solucionar; para ello utilizamos las propiedades de la igualdad. Si a = b entonces para cualquier c tenemos: a + c = b + c, a c = b c, a.c = b.c y si además c 0, a/c = b/c.
6 Ecuaciones lineales Son de la forma ax + b = c con a, b y c números reales. Claramente se tiene la siguiente cadena de ecuaciones equivalentes: ax + b = c ax = c b x = c b a { c b y el conjunto solución es a }.
7 Ecuaciones lineales Ejercicio Resolver las siguientes ecuaciones 3x 2(2x 5) = 2(x 3) 8 x+1 3 x 4 = 1 2 3x 4 = 5 + 3(x 3) 2x 3 x = x + 5 5t 22 t 2 6t+9 11 t 2 3t 5 t = 0
8 Ecuaciones lineales Ejercicio Hallar cuatro enteros pares consecutivos, tales que la suma de los tres primeros exceda al cuarto en 8.
9 Ecuaciones lineales Solución Sea n el primer entero par, entonces los otros pares siguientes son n + 2, n + 4 y n + 6. De acuerdo con las condiciones del problema, tenemos n + (n + 2) + (n + 4) = (n + 6) + 8, luego, n = 4.
10 Ecuaciones lineales Ejercicio Si un lado de un triángulo es la tercera parte del perímetro, el segundo lado mide 7 cm y el tercer lado es un quinto del perímetro, Cuál es el perímetro del triángulo?
11 Ecuaciones lineales Ejercicio Un rectángulo cuyo largo es de 24 cm tiene la misma superficie que un cuadrado de 12 cm de lado. Cuáles son las dimensiones del rectángulo?
12 Ecuaciones lineales Ejercicio La distancia marítima entre San Francisco y Honolulú es de millas náuticas. Si un barco sale de San Francisco al mismo tiempo que otro sale de Honolulú, y si el primero viaja a 15 millas náuticas por hora y el segundo a 20 millas náuticas por hora, Cuánto tardarán los barcos en encontrarse? A qué distancia se encontrarán de San Francisco y de Honolulú en ese momento?
13 Ecuaciones lineales Ejercicio Una lancha tarda 1,5 veces más al remontar un río y recorrer 360 millas contra la corriente, que al regreso. Si navega a una velocidad de 15 millas por hora en agua tranquila, Cuál es la velocidad de la corriente?
14 Ecuaciones lineales Solución Sea x la velocidad de la corriente, 15 x la velocidad de la lancha contra la corriente, 15 + x la velocidad de la lancha a favor de la corriente.
15 Ecuaciones lineales Tenemos además que Tiempo contra la corriente = (1,5)(Tiempo con la corriente a favor) Distancia contra la corriente Velocidad contra la corriente x x = 3 = (1,5) Distancia a favor de la corriente Velocidad a favor de la corriente = (1,5) x La velocidad de la corriente del río es 3 millas náuticas por hora.
16 Ecuaciones lineales Ejercicio Cuántos litros de una mezcla que contiene 80 % de alcohol se deben agregar a 5 litros de una solución que está al 20 % para producir una solución al 30 %?
17 Parte II Ecuaciones cuadráticas
18 Ecuación de segundo grado Ejercicio Un rectángulo tiene un perímetro de 20 metros. Expresar el área del rectángulo en función de uno de sus lados.
19 Ecuación de segundo grado Cuántas y cuáles son las soluciones de la ecuación ax 2 + bx + c = 0?
20 Ecuación de segundo grado ax 2 + bx + c = 0 a (x 2 + ba ) x = c a (x 2 ba b2 + x + 4a 2 ( a x + b 2a ( x + b 2a ) = c + b2 4a ) 2 4ac + b2 = 4a ) 2 = b2 4ac 4a 2
21 Ecuación de segundo grado x + b 2a = ± b 2 4ac 4a 2 x = b 2a ± b 2 4ac 2a x = b ± b 2 4ac 2a
22 Ecuación de segundo grado La expresión b 2 4ac se denomina discriminante de la ecuación cuadrática. El signo de dicho número nos proporciona información sobre el número de soluciones así: Discriminante Positivo Cero Negativo Soluciones Dos soluciones distintas Una solución doble No tiene solución
23 Ecuación de segundo grado Ejercicio Resolver 6x 2 19x 7 = 0 (a) Factorizando si es posible, (b) Usando la fórmula cuadrática
24 Ecuación de segundo grado Ejercicio Resolver 2x 2 3x = 0 (a) Factorizando si es posible, (b) Usando la fórmula cuadrática
25 Ecuación de segundo grado Ejercicio Resolver 3x = 0 (a) Factorizando si es posible, (b) Usando la fórmula cuadrática
26 Ecuación de segundo grado Ejercicio Resolver x 2 + 6x 2 = 0 (a) Completando cuadrados, (b) Usando la fórmula cuadrática
27 Ecuación de segundo grado Ejercicio Resolver (a) x 1 = 2x 3 (b) x + x 4 = 4 (c) x x 5 16 = 0 (d) x x = 2 x (e) x+2 4 x+1 = 2 x+2 x (f) 2x = 7 2x 3x 6 (g) 1 3 s 2 2s+4 = s+2 3s+6
28 Ecuación de segundo grado Ejercicio La suma de dos números es 23 y su producto es 132. Hallar los números.
29 Ecuación de segundo grado Ejercicio La suma de un número con su recíproco es Hallar el número.
30 Ecuación de segundo grado Ejercicio Al mismo tiempo, dos automóviles abandonan una intersección, uno hacia el norte y otro al oeste. Poco tiempo después, están separados exactamente por 100 millas. El que iba al norte ha avanzado 20 millas más que el que se dirigía al oeste. Cuánto ha viajado cada vehículo?
31 Parte III Desigualdades
32 Desigualdades lineales Una inecuación es una desigualdad que involucra variables. El conjunto solución de una inecuación es el conjunto de valores para la variable (o variables) que hacen verdadera la desigualdad. Algunos autores llaman simplemente Desigualdades a las inecuaciones y hablan del conjunto solución de la desigualdad.
33 Desigualdades lineales Ejemplos 2 es una solución a la inecuación 5x NO es una solución a la inecuación 5x π es una solución a la inecuación cos x 1
34 Desigualdades cuadráticas En forma análoga a las ecuaciones definimos las inecuaciones o desigualdades lineales y cuadráticas. Ejemplos: 5x x 7 x + 2 x 2 5x También pueden involucrar expresiones racionales como: x 2 5x x 2 < 0
35 Desigualdades Para encontrar el conjunto solución de una inecuación la transformamos en una equivalente utilizando las siguientes propiedades de las desigualdades:
36 Propiedades de las desigualdades Sean a, b, c números reales Si a < b y b < c, entonces a < c. Si a < b, entonces a + c < b + c. Si a < b y c > 0, entonces ac < bc. Si a < b y c < 0, entonces ac > bc. Si 0 < a < b, entonces 1 a > 1 b. Si 0 < a < b, entonces 0 < a 2 < b 2. Si 0 < a < b, entonces 0 < a < b.
37 Propiedades de las desigualdades Sean a, b, c números reales Si a < b y b < c, entonces a < c. Si a < b, entonces a + c < b + c. Si a < b y c > 0, entonces ac < bc. Si a < b y c < 0, entonces ac > bc. Si 0 < a < b, entonces 1 a > 1 b. Si 0 < a < b, entonces 0 < a 2 < b 2. Si 0 < a < b, entonces 0 < a < b.
38 Propiedades de las desigualdades Sean a, b, c números reales Si a < b y b < c, entonces a < c. Si a < b, entonces a + c < b + c. Si a < b y c > 0, entonces ac < bc. Si a < b y c < 0, entonces ac > bc. Si 0 < a < b, entonces 1 a > 1 b. Si 0 < a < b, entonces 0 < a 2 < b 2. Si 0 < a < b, entonces 0 < a < b.
39 Propiedades de las desigualdades Sean a, b, c números reales Si a < b y b < c, entonces a < c. Si a < b, entonces a + c < b + c. Si a < b y c > 0, entonces ac < bc. Si a < b y c < 0, entonces ac > bc. Si 0 < a < b, entonces 1 a > 1 b. Si 0 < a < b, entonces 0 < a 2 < b 2. Si 0 < a < b, entonces 0 < a < b.
40 Propiedades de las desigualdades Sean a, b, c números reales Si a < b y b < c, entonces a < c. Si a < b, entonces a + c < b + c. Si a < b y c > 0, entonces ac < bc. Si a < b y c < 0, entonces ac > bc. Si 0 < a < b, entonces 1 a > 1 b. Si 0 < a < b, entonces 0 < a 2 < b 2. Si 0 < a < b, entonces 0 < a < b.
41 Propiedades de las desigualdades Sean a, b, c números reales Si a < b y b < c, entonces a < c. Si a < b, entonces a + c < b + c. Si a < b y c > 0, entonces ac < bc. Si a < b y c < 0, entonces ac > bc. Si 0 < a < b, entonces 1 a > 1 b. Si 0 < a < b, entonces 0 < a 2 < b 2. Si 0 < a < b, entonces 0 < a < b.
42 Propiedades de las desigualdades Sean a, b, c números reales Si a < b y b < c, entonces a < c. Si a < b, entonces a + c < b + c. Si a < b y c > 0, entonces ac < bc. Si a < b y c < 0, entonces ac > bc. Si 0 < a < b, entonces 1 a > 1 b. Si 0 < a < b, entonces 0 < a 2 < b 2. Si 0 < a < b, entonces 0 < a < b.
43 Solución de una desigualdad lineal Para resolver 2x + 3 < 6 7x procedemos como en una ecuación, teniendo en cuenta las propiedades anteriores. 2x + 3 < 6 7x 2x x < 6 7x + 7x 9x + 3 < 6 9x < 6 3 9x < x < x < 1 3
44 Solución de una desigualdad lineal Para resolver 2x + 3 < 6 7x procedemos como en una ecuación, teniendo en cuenta las propiedades anteriores. 2x + 3 < 6 7x 2x x < 6 7x + 7x 9x + 3 < 6 9x < 6 3 9x < x < x < 1 3
45 Solución de una desigualdad lineal Para resolver 2x + 3 < 6 7x procedemos como en una ecuación, teniendo en cuenta las propiedades anteriores. 2x + 3 < 6 7x 2x x < 6 7x + 7x 9x + 3 < 6 9x < 6 3 9x < x < x < 1 3
46 Solución de una desigualdad lineal Para resolver 2x + 3 < 6 7x procedemos como en una ecuación, teniendo en cuenta las propiedades anteriores. 2x + 3 < 6 7x 2x x < 6 7x + 7x 9x + 3 < 6 9x < 6 3 9x < x < x < 1 3
47 Solución de una desigualdad lineal Para resolver 2x + 3 < 6 7x procedemos como en una ecuación, teniendo en cuenta las propiedades anteriores. 2x + 3 < 6 7x 2x x < 6 7x + 7x 9x + 3 < 6 9x < 6 3 9x < x < x < 1 3
48 Solución de una desigualdad lineal Para resolver 2x + 3 < 6 7x procedemos como en una ecuación, teniendo en cuenta las propiedades anteriores. 2x + 3 < 6 7x 2x x < 6 7x + 7x 9x + 3 < 6 9x < 6 3 9x < x < x < 1 3
49 Solución de una desigualdad lineal Para resolver 2x + 3 < 6 7x procedemos como en una ecuación, teniendo en cuenta las propiedades anteriores. 2x + 3 < 6 7x 2x x < 6 7x + 7x 9x + 3 < 6 9x < 6 3 9x < x < x < 1 3
50 Solución de una desigualdad lineal El conjunto de todos los x < 1 3 puede escribirse como un intervalo, así que la solución de esta desigualdad es ( Solución :, 1 ) 3
51 Solución de una desigualdad lineal El conjunto de todos los x < 1 3 puede escribirse como un intervalo, así que la solución de esta desigualdad es ( Solución :, 1 ) 3
52 Solución de una desigualdad lineal Resolver 4 2x x. 4 2x x 2x 3x x ( 5x) 1 5 (8) x 8 5 Solución: (, 8 ]. 5
53 Solución de una desigualdad lineal Resolver 4 2x x. 4 2x x 2x 3x x ( 5x) 1 5 (8) x 8 5 Solución: (, 8 ]. 5
54 Solución de una desigualdad lineal Resolver 4 2x x. 4 2x x 2x 3x x ( 5x) 1 5 (8) x 8 5 Solución: (, 8 ]. 5
55 Solución de una desigualdad lineal Resolver 4 2x x. 4 2x x 2x 3x x ( 5x) 1 5 (8) x 8 5 Solución: (, 8 ]. 5
56 Solución de una desigualdad lineal Resolver 4 2x x. 4 2x x 2x 3x x ( 5x) 1 5 (8) x 8 5 Solución: (, 8 ]. 5
57 Solución de una desigualdad lineal Resolver 4 2x x. 4 2x x 2x 3x x ( 5x) 1 5 (8) x 8 5 Solución: (, 8 ]. 5
58 Solución de una desigualdad lineal Resolver 4 2x x. 4 2x x 2x 3x x ( 5x) 1 5 (8) x 8 5 Solución: (, 8 ]. 5
59 Solución de una desigualdad lineal Resolver 14 7x x. 14 7x x 7x 10x x ( 17x) 1 17 ( 6) x 6 17 Solución: [ ) 6 17,.
60 Solución de una desigualdad lineal Resolver 14 7x x. 14 7x x 7x 10x x ( 17x) 1 17 ( 6) x 6 17 Solución: [ ) 6 17,.
61 Solución de una desigualdad lineal Resolver 14 7x x. 14 7x x 7x 10x x ( 17x) 1 17 ( 6) x 6 17 Solución: [ ) 6 17,.
62 Solución de una desigualdad lineal Resolver 14 7x x. 14 7x x 7x 10x x ( 17x) 1 17 ( 6) x 6 17 Solución: [ ) 6 17,.
63 Solución de una desigualdad lineal Resolver 14 7x x. 14 7x x 7x 10x x ( 17x) 1 17 ( 6) x 6 17 Solución: [ ) 6 17,.
64 Solución de una desigualdad lineal Resolver 14 7x x. 14 7x x 7x 10x x ( 17x) 1 17 ( 6) x 6 17 Solución: [ ) 6 17,.
65 Solución de una desigualdad lineal Resolver 14 7x x. 14 7x x 7x 10x x ( 17x) 1 17 ( 6) x 6 17 Solución: [ ) 6 17,.
66 Solución de una desigualdad lineal Resolver 2 < 15 8x < 15 8x < 15 8x < 8x ( 13) > 1 8 ( 8x) 1 8 (9) 13 8 > x 9 8 Solución: [ 9 8, 13 ). 8
67 Solución de una desigualdad lineal Resolver 2 < 15 8x < 15 8x < 15 8x < 8x ( 13) > 1 8 ( 8x) 1 8 (9) 13 8 > x 9 8 Solución: [ 9 8, 13 ). 8
68 Solución de una desigualdad lineal Resolver 2 < 15 8x < 15 8x < 15 8x < 8x ( 13) > 1 8 ( 8x) 1 8 (9) 13 8 > x 9 8 Solución: [ 9 8, 13 ). 8
69 Solución de una desigualdad lineal Resolver 2 < 15 8x < 15 8x < 15 8x < 8x ( 13) > 1 8 ( 8x) 1 8 (9) 13 8 > x 9 8 Solución: [ 9 8, 13 ). 8
70 Solución de una desigualdad lineal Resolver 2 < 15 8x < 15 8x < 15 8x < 8x ( 13) > 1 8 ( 8x) 1 8 (9) 13 8 > x 9 8 Solución: [ 9 8, 13 ). 8
71 Solución de una desigualdad lineal Resolver 2 < 15 8x < 15 8x < 15 8x < 8x ( 13) > 1 8 ( 8x) 1 8 (9) 13 8 > x 9 8 Solución: [ 9 8, 13 ). 8
72 Solución de una desigualdad lineal Resolver 2 < 15 8x < 15 8x < 15 8x < 8x ( 13) > 1 8 ( 8x) 1 8 (9) 13 8 > x 9 8 Solución: [ 9 8, 13 ). 8
73 Solución de una desigualdad lineal Resolver 48 > 12x > 12x > 12x > 12x (18) > 1 12 (12x) 1 12 (12) 3 2 > x 1 Solución: [ 1, 3 ). 2
74 Solución de una desigualdad lineal Resolver 48 > 12x > 12x > 12x > 12x (18) > 1 12 (12x) 1 12 (12) 3 2 > x 1 Solución: [ 1, 3 ). 2
75 Solución de una desigualdad lineal Resolver 48 > 12x > 12x > 12x > 12x (18) > 1 12 (12x) 1 12 (12) 3 2 > x 1 Solución: [ 1, 3 ). 2
76 Solución de una desigualdad lineal Resolver 48 > 12x > 12x > 12x > 12x (18) > 1 12 (12x) 1 12 (12) 3 2 > x 1 Solución: [ 1, 3 ). 2
77 Solución de una desigualdad lineal Resolver 48 > 12x > 12x > 12x > 12x (18) > 1 12 (12x) 1 12 (12) 3 2 > x 1 Solución: [ 1, 3 ). 2
78 Solución de una desigualdad lineal Resolver 48 > 12x > 12x > 12x > 12x (18) > 1 12 (12x) 1 12 (12) 3 2 > x 1 Solución: [ 1, 3 ). 2
79 Solución de una desigualdad lineal Resolver 48 > 12x > 12x > 12x > 12x (18) > 1 12 (12x) 1 12 (12) 3 2 > x 1 Solución: [ 1, 3 ). 2
80 Desigualdades lineales Ejercicio Encontrar el conjunto solución de las siguientes desigualdades x 6 + 3x x > 45 9x 3 8x + 6 < x 4 3x 5 2 5x 10
81 Solución de una desigualdad cuadrática. Resolver x 2 + 4x Resolver x 2 + 4x x 2 + 4x (x + 3)(x + 1) 0 Los factores x + 3 y x + 1 se anulan en los puntos 3 y 1 respectivamente, así que dividimos la recta real como sigue 3 1 0
82 Solución de una desigualdad cuadrática. Resolver x 2 + 4x Resolver x 2 + 4x x 2 + 4x (x + 3)(x + 1) 0 Los factores x + 3 y x + 1 se anulan en los puntos 3 y 1 respectivamente, así que dividimos la recta real como sigue 3 1 0
83 Solución de una desigualdad cuadrática. Resolver x 2 + 4x Resolver x 2 + 4x x 2 + 4x (x + 3)(x + 1) 0 Los factores x + 3 y x + 1 se anulan en los puntos 3 y 1 respectivamente, así que dividimos la recta real como sigue 3 1 0
84 Solución de una desigualdad cuadrática. Resolver x 2 + 4x Resolver x 2 + 4x x 2 + 4x (x + 3)(x + 1) 0 Los factores x + 3 y x + 1 se anulan en los puntos 3 y 1 respectivamente, así que dividimos la recta real como sigue 3 1 0
85 Solución de una desigualdad cuadrática. Resolver x 2 + 4x Intervalo (, 3) ( 3, 1) ( 1, ) Signo de (x + 3) + + Signo de (x + 1) + Signo resultante + + Solución: (, 3] [ 1, ).
86 Solución de una desigualdad cuadrática. Resolver x 2 + 4x Intervalo (, 3) ( 3, 1) ( 1, ) Signo de (x + 3) + + Signo de (x + 1) + Signo resultante + + Solución: (, 3] [ 1, ).
87 Solución de una desigualdad cuadrática. Resolver x 2 + 4x Intervalo (, 3) ( 3, 1) ( 1, ) Signo de (x + 3) + + Signo de (x + 1) + Signo resultante + + Solución: (, 3] [ 1, ).
88 Solución de una desigualdad cuadrática. Resolver x 2 + 4x Intervalo (, 3) ( 3, 1) ( 1, ) Signo de (x + 3) + + Signo de (x + 1) + Signo resultante + + Solución: (, 3] [ 1, ).
89 Solución de una desigualdad cuadrática. Resolver x 2 + 4x Intervalo (, 3) ( 3, 1) ( 1, ) Signo de (x + 3) + + Signo de (x + 1) + Signo resultante + + Solución: (, 3] [ 1, ).
90 Solución de una desigualdad cuadrática. Resolver 2x 2 2x 12 < 0. Resolver 2x 2 2x 12 < 0. 2x 2 2x 12 < 0 2(x + 2)(x 3) < 0 Los factores x + 2 y x 3 se anulan en los puntos 2 y 3 respectivamente, así que dividimos la recta real así: 2 0 3
91 Solución de una desigualdad cuadrática. Resolver 2x 2 2x 12 < 0. Resolver 2x 2 2x 12 < 0. 2x 2 2x 12 < 0 2(x + 2)(x 3) < 0 Los factores x + 2 y x 3 se anulan en los puntos 2 y 3 respectivamente, así que dividimos la recta real así: 2 0 3
92 Solución de una desigualdad cuadrática. Resolver 2x 2 2x 12 < 0. Resolver 2x 2 2x 12 < 0. 2x 2 2x 12 < 0 2(x + 2)(x 3) < 0 Los factores x + 2 y x 3 se anulan en los puntos 2 y 3 respectivamente, así que dividimos la recta real así: 2 0 3
93 Solución de una desigualdad cuadrática. Resolver 2x 2 2x 12 < 0. Intervalo (, 2) ( 2, 3) (3, ) Signo de (x + 2) + + Signo de (x 3) + Signo resultante + + Solución: ( 2, 3).
94 Solución de una desigualdad cuadrática. Resolver 2x 2 2x 12 < 0. Intervalo (, 2) ( 2, 3) (3, ) Signo de (x + 2) + + Signo de (x 3) + Signo resultante + + Solución: ( 2, 3).
95 Solución de una desigualdad cuadrática. Resolver 2x 2 2x 12 < 0. Intervalo (, 2) ( 2, 3) (3, ) Signo de (x + 2) + + Signo de (x 3) + Signo resultante + + Solución: ( 2, 3).
96 Solución de una desigualdad cuadrática. Resolver 2x 2 2x 12 < 0. Intervalo (, 2) ( 2, 3) (3, ) Signo de (x + 2) + + Signo de (x 3) + Signo resultante + + Solución: ( 2, 3).
97 Solución de una desigualdad cuadrática. Resolver 2x 2 2x 12 < 0. Intervalo (, 2) ( 2, 3) (3, ) Signo de (x + 2) + + Signo de (x 3) + Signo resultante + + Solución: ( 2, 3).
98 Resolver (x+2)(4 x) (x 1) 0. Resolver (x+2)(4 x) (x 1) 0. Los factores x + 2, 4 x y x 1 se anulan en los puntos 2, 4 y 1 respectivamente, así que dividimos la recta real así:
99 Resolver (x+2)(4 x) (x 1) 0. Resolver (x+2)(4 x) (x 1) 0. Los factores x + 2, 4 x y x 1 se anulan en los puntos 2, 4 y 1 respectivamente, así que dividimos la recta real así:
100 Resolver (x+2)(4 x) (x 1) 0. Intervalo (, 2) ( 2, 1) (1, 4) (4, ) Signo de (x + 2) Signo de (4 x) Signo de (x 1) + + Signo resultante + + Solución: (, 2] (1, 4]. Por qué el intervalo es cerrado en 2 y en 4 y abierto en 1?
101 Resolver (x+2)(4 x) (x 1) 0. Intervalo (, 2) ( 2, 1) (1, 4) (4, ) Signo de (x + 2) Signo de (4 x) Signo de (x 1) + + Signo resultante + + Solución: (, 2] (1, 4]. Por qué el intervalo es cerrado en 2 y en 4 y abierto en 1?
102 Resolver (x+2)(4 x) (x 1) 0. Intervalo (, 2) ( 2, 1) (1, 4) (4, ) Signo de (x + 2) Signo de (4 x) Signo de (x 1) + + Signo resultante + + Solución: (, 2] (1, 4]. Por qué el intervalo es cerrado en 2 y en 4 y abierto en 1?
103 Resolver (x+2)(4 x) (x 1) 0. Intervalo (, 2) ( 2, 1) (1, 4) (4, ) Signo de (x + 2) Signo de (4 x) Signo de (x 1) + + Signo resultante + + Solución: (, 2] (1, 4]. Por qué el intervalo es cerrado en 2 y en 4 y abierto en 1?
104 Resolver (x+2)(4 x) (x 1) 0. Intervalo (, 2) ( 2, 1) (1, 4) (4, ) Signo de (x + 2) Signo de (4 x) Signo de (x 1) + + Signo resultante + + Solución: (, 2] (1, 4]. Por qué el intervalo es cerrado en 2 y en 4 y abierto en 1?
105 Resolver (x+2)(4 x) (x 1) 0. Intervalo (, 2) ( 2, 1) (1, 4) (4, ) Signo de (x + 2) Signo de (4 x) Signo de (x 1) + + Signo resultante + + Solución: (, 2] (1, 4]. Por qué el intervalo es cerrado en 2 y en 4 y abierto en 1?
106 Resolver (x+2)(4 x) (x 1) 0. Intervalo (, 2) ( 2, 1) (1, 4) (4, ) Signo de (x + 2) Signo de (4 x) Signo de (x 1) + + Signo resultante + + Solución: (, 2] (1, 4]. Por qué el intervalo es cerrado en 2 y en 4 y abierto en 1?
107 Resolver 4(x 2)(3 x) x 2 (x+1) 0. Resolver 4(x 2)(3 x) 0. Los factores x 2, 3 x, x 2 y x + 1 x 2 (x+1) se anulan en los puntos 2, 3, 0 y 1 respectivamente
108 Resolver 4(x 2)(3 x) x 2 (x+1) 0. Resolver 4(x 2)(3 x) 0. Los factores x 2, 3 x, x 2 y x + 1 x 2 (x+1) se anulan en los puntos 2, 3, 0 y 1 respectivamente
109 Resolver 4(x 2)(3 x) x 2 (x+1) 0. Intervalo (, 1) ( 1, 0) (0, 2) (2, 3) (3, ) Signo de (x 2) + + Signo de (3 x) Signo de x Signo de (x + 1) Signo resultante + + Solución: ( 1, 0) (0, 2] [3, ). Puede escribirse ( 1, 2] en lugar de ( 1, 0) (0, 2]?
110 Resolver 4(x 2)(3 x) x 2 (x+1) 0. Intervalo (, 1) ( 1, 0) (0, 2) (2, 3) (3, ) Signo de (x 2) + + Signo de (3 x) Signo de x Signo de (x + 1) Signo resultante + + Solución: ( 1, 0) (0, 2] [3, ). Puede escribirse ( 1, 2] en lugar de ( 1, 0) (0, 2]?
111 Resolver 4(x 2)(3 x) x 2 (x+1) 0. Intervalo (, 1) ( 1, 0) (0, 2) (2, 3) (3, ) Signo de (x 2) + + Signo de (3 x) Signo de x Signo de (x + 1) Signo resultante + + Solución: ( 1, 0) (0, 2] [3, ). Puede escribirse ( 1, 2] en lugar de ( 1, 0) (0, 2]?
112 Resolver 4(x 2)(3 x) x 2 (x+1) 0. Intervalo (, 1) ( 1, 0) (0, 2) (2, 3) (3, ) Signo de (x 2) + + Signo de (3 x) Signo de x Signo de (x + 1) Signo resultante + + Solución: ( 1, 0) (0, 2] [3, ). Puede escribirse ( 1, 2] en lugar de ( 1, 0) (0, 2]?
113 Resolver 4(x 2)(3 x) x 2 (x+1) 0. Intervalo (, 1) ( 1, 0) (0, 2) (2, 3) (3, ) Signo de (x 2) + + Signo de (3 x) Signo de x Signo de (x + 1) Signo resultante + + Solución: ( 1, 0) (0, 2] [3, ). Puede escribirse ( 1, 2] en lugar de ( 1, 0) (0, 2]?
114 Resolver 4(x 2)(3 x) x 2 (x+1) 0. Intervalo (, 1) ( 1, 0) (0, 2) (2, 3) (3, ) Signo de (x 2) + + Signo de (3 x) Signo de x Signo de (x + 1) Signo resultante + + Solución: ( 1, 0) (0, 2] [3, ). Puede escribirse ( 1, 2] en lugar de ( 1, 0) (0, 2]?
115 Resolver 4(x 2)(3 x) x 2 (x+1) 0. Intervalo (, 1) ( 1, 0) (0, 2) (2, 3) (3, ) Signo de (x 2) + + Signo de (3 x) Signo de x Signo de (x + 1) Signo resultante + + Solución: ( 1, 0) (0, 2] [3, ). Puede escribirse ( 1, 2] en lugar de ( 1, 0) (0, 2]?
116 Resolver 4(x 2)(3 x) x 2 (x+1) 0. Intervalo (, 1) ( 1, 0) (0, 2) (2, 3) (3, ) Signo de (x 2) + + Signo de (3 x) Signo de x Signo de (x + 1) Signo resultante + + Solución: ( 1, 0) (0, 2] [3, ). Puede escribirse ( 1, 2] en lugar de ( 1, 0) (0, 2]?
117 Ejercicios Encontrar todas las soluciones de las siguientes desigualdades Ejercicio (2x+1)(4 x) x 2 +2x 0 (x+3) 2 (x 3) x 2 7x+12 0 (x 2 x)(3x 1) x 2 3x x x 2 < 16
118 Parte IV Desigualdades con valor absoluto
119 Valor Absoluto Recordemos que el valor absoluto de un número real corresponde a la distancia que hay entre él y el origen. Definición Sea x un número real, x = { x si x 0, x si x < 0.
120 Valor Absoluto x a equivale a a x a, si a 0 a 0 a x a equivale a x a o x a, si a 0 a 0 a
121 Valor Absoluto x a equivale a a x a, si a 0 a 0 a x a equivale a x a o x a, si a 0 a 0 a
122 Desigualdades con valor absoluto Resolver 2x x x x x x 3 2 Solución: [ 5 2, 3 ]. 2
123 Desigualdades con valor absoluto Resolver 2x x x x x x 3 2 Solución: [ 5 2, 3 ]. 2
124 Desigualdades con valor absoluto Resolver 2x x x x x x 3 2 Solución: [ 5 2, 3 ]. 2
125 Desigualdades con valor absoluto Resolver 2x x x x x x 3 2 Solución: [ 5 2, 3 ]. 2
126 Desigualdades con valor absoluto Resolver 2x x x x x x 3 2 Solución: [ 5 2, 3 ]. 2
127 Desigualdades con valor absoluto Resolver 2x x x x x x 3 2 Solución: [ 5 2, 3 ]. 2
128 Desigualdades con valor absoluto Resolver 8 3x x x x x ( 13) x 1 3 ( 3) 13 3 x 1 Solución: [ 1, 13 ]. 3
129 Desigualdades con valor absoluto Resolver 8 3x x x x x ( 13) x 1 3 ( 3) 13 3 x 1 Solución: [ 1, 13 ]. 3
130 Desigualdades con valor absoluto Resolver 8 3x x x x x ( 13) x 1 3 ( 3) 13 3 x 1 Solución: [ 1, 13 ]. 3
131 Desigualdades con valor absoluto Resolver 8 3x x x x x ( 13) x 1 3 ( 3) 13 3 x 1 Solución: [ 1, 13 ]. 3
132 Desigualdades con valor absoluto Resolver 8 3x x x x x ( 13) x 1 3 ( 3) 13 3 x 1 Solución: [ 1, 13 ]. 3
133 Desigualdades con valor absoluto Resolver 8 3x x x x x ( 13) x 1 3 ( 3) 13 3 x 1 Solución: [ 1, 13 ]. 3
134 Desigualdades con valor absoluto Resolver 8 3x x x x x ( 13) x 1 3 ( 3) 13 3 x 1 Solución: [ 1, 13 ]. 3
135 Desigualdades con valor absoluto Resolver x 6. Por la propiedad tenemos que, x 6 o x x 6 4x x 18 x x 6 4x x 6 x 3 2 Solución: (, 9 ] [ 32 ) 2,.
136 Desigualdades con valor absoluto Resolver x 6. Por la propiedad tenemos que, x 6 o x x 6 4x x 18 x x 6 4x x 6 x 3 2 Solución: (, 9 ] [ 32 ) 2,.
137 Desigualdades con valor absoluto Resolver x 6. Por la propiedad tenemos que, x 6 o x x 6 4x x 18 x x 6 4x x 6 x 3 2 Solución: (, 9 ] [ 32 ) 2,.
138 Desigualdades con valor absoluto Resolver x 6. Por la propiedad tenemos que, x 6 o x x 6 4x x 18 x x 6 4x x 6 x 3 2 Solución: (, 9 ] [ 32 ) 2,.
139 Desigualdades con valor absoluto Resolver x 6. Por la propiedad tenemos que, x 6 o x x 6 4x x 18 x x 6 4x x 6 x 3 2 Solución: (, 9 ] [ 32 ) 2,.
140 Desigualdades con valor absoluto Resolver x 6. Por la propiedad tenemos que, x 6 o x x 6 4x x 18 x x 6 4x x 6 x 3 2 Solución: (, 9 ] [ 32 ) 2,.
141 Desigualdades con valor absoluto Resolver x 6. Por la propiedad tenemos que, x 6 o x x 6 4x x 18 x x 6 4x x 6 x 3 2 Solución: (, 9 ] [ 32 ) 2,.
142 Desigualdades con valor absoluto Resolver x 6. Por la propiedad tenemos que, x 6 o x x 6 4x x 18 x x 6 4x x 6 x 3 2 Solución: (, 9 ] [ 32 ) 2,.
143 Desigualdades con valor absoluto Resolver x 6. Por la propiedad tenemos que, x 6 o x x 6 4x x 18 x x 6 4x x 6 x 3 2 Solución: (, 9 ] [ 32 ) 2,.
144 Desigualdades con valor absoluto Resolver x 6. Por la propiedad tenemos que, x 6 o x x 6 4x x 18 x x 6 4x x 6 x 3 2 Solución: (, 9 ] [ 32 ) 2,.
145 Desigualdades con valor absoluto Resolver 25 7x 8. Por la propiedad tenemos que, 25 7x 8 o 25 7x x 8 7x x 33 x x 8 7x x 17 x 17 7 Solución: (, 17 ] [ ) ,.
146 Desigualdades con valor absoluto Resolver 25 7x 8. Por la propiedad tenemos que, 25 7x 8 o 25 7x x 8 7x x 33 x x 8 7x x 17 x 17 7 Solución: (, 17 ] [ ) ,.
147 Desigualdades con valor absoluto Resolver 25 7x 8. Por la propiedad tenemos que, 25 7x 8 o 25 7x x 8 7x x 33 x x 8 7x x 17 x 17 7 Solución: (, 17 ] [ ) ,.
148 Desigualdades con valor absoluto Resolver 25 7x 8. Por la propiedad tenemos que, 25 7x 8 o 25 7x x 8 7x x 33 x x 8 7x x 17 x 17 7 Solución: (, 17 ] [ ) ,.
149 Desigualdades con valor absoluto Resolver 25 7x 8. Por la propiedad tenemos que, 25 7x 8 o 25 7x x 8 7x x 33 x x 8 7x x 17 x 17 7 Solución: (, 17 ] [ ) ,.
150 Desigualdades con valor absoluto Resolver 25 7x 8. Por la propiedad tenemos que, 25 7x 8 o 25 7x x 8 7x x 33 x x 8 7x x 17 x 17 7 Solución: (, 17 ] [ ) ,.
151 Desigualdades con valor absoluto Resolver 25 7x 8. Por la propiedad tenemos que, 25 7x 8 o 25 7x x 8 7x x 33 x x 8 7x x 17 x 17 7 Solución: (, 17 ] [ ) ,.
152 Desigualdades con valor absoluto Resolver 25 7x 8. Por la propiedad tenemos que, 25 7x 8 o 25 7x x 8 7x x 33 x x 8 7x x 17 x 17 7 Solución: (, 17 ] [ ) ,.
153 Desigualdades con valor absoluto Resolver 25 7x 8. Por la propiedad tenemos que, 25 7x 8 o 25 7x x 8 7x x 33 x x 8 7x x 17 x 17 7 Solución: (, 17 ] [ ) ,.
154 Desigualdades con valor absoluto Resolver 25 7x 8. Por la propiedad tenemos que, 25 7x 8 o 25 7x x 8 7x x 33 x x 8 7x x 17 x 17 7 Solución: (, 17 ] [ ) ,.
155 Desigualdades con valor absoluto Para resolver x + 2 x 1 > 2 usamos la definición, { x + 2 si x x + 2 = (x + 2) si x + 2 < 0 { x + 2 si x 2 = x 2 si x < 2 { x 1 si x 1 0 x 1 = (x 1) si x 1 < 0 { x 1 si x 1 = x + 1 si x < 1
156 Desigualdades con valor absoluto Para resolver x + 2 x 1 > 2 usamos la definición, { x + 2 si x x + 2 = (x + 2) si x + 2 < 0 { x + 2 si x 2 = x 2 si x < 2 { x 1 si x 1 0 x 1 = (x 1) si x 1 < 0 { x 1 si x 1 = x + 1 si x < 1
157 Desigualdades con valor absoluto Para resolver x + 2 x 1 > 2 usamos la definición, { x + 2 si x x + 2 = (x + 2) si x + 2 < 0 { x + 2 si x 2 = x 2 si x < 2 { x 1 si x 1 0 x 1 = (x 1) si x 1 < 0 { x 1 si x 1 = x + 1 si x < 1
158 Desigualdades con valor absoluto Para resolver x + 2 x 1 > 2 usamos la definición, { x + 2 si x x + 2 = (x + 2) si x + 2 < 0 { x + 2 si x 2 = x 2 si x < 2 { x 1 si x 1 0 x 1 = (x 1) si x 1 < 0 { x 1 si x 1 = x + 1 si x < 1
159 Desigualdades con valor absoluto La recta real se divide en tres sub-intervalos: (, 2) [ 2, 1) [1, + ) 2 0 1
160 Desigualdades con valor absoluto En (, 2) En [ 2, 1) x + 2 x 1 > 2 ( x 2) ( x + 1) > 2 x + 2 x 1 > 2 (x + 2) ( x + 1) > 2 2x + 1 > 2 3 > 2 Falso S 1 = x > 1/2 ( ) 1 S 2 = 2, [ 2, 1)
161 Desigualdades con valor absoluto En (, 2) En [ 2, 1) x + 2 x 1 > 2 ( x 2) ( x + 1) > 2 x + 2 x 1 > 2 (x + 2) ( x + 1) > 2 2x + 1 > 2 3 > 2 Falso S 1 = x > 1/2 ( ) 1 S 2 = 2, [ 2, 1)
162 Desigualdades con valor absoluto En (, 2) En [ 2, 1) x + 2 x 1 > 2 ( x 2) ( x + 1) > 2 x + 2 x 1 > 2 (x + 2) ( x + 1) > 2 2x + 1 > 2 3 > 2 Falso S 1 = x > 1/2 ( ) 1 S 2 = 2, [ 2, 1)
163 Desigualdades con valor absoluto En (, 2) En [ 2, 1) x + 2 x 1 > 2 ( x 2) ( x + 1) > 2 x + 2 x 1 > 2 (x + 2) ( x + 1) > 2 2x + 1 > 2 3 > 2 Falso S 1 = x > 1/2 ( ) 1 S 2 = 2, [ 2, 1)
164 Desigualdades con valor absoluto En (, 2) En [ 2, 1) x + 2 x 1 > 2 ( x 2) ( x + 1) > 2 x + 2 x 1 > 2 (x + 2) ( x + 1) > 2 2x + 1 > 2 3 > 2 Falso S 1 = x > 1/2 ( ) 1 S 2 = 2, [ 2, 1)
165 Desigualdades con valor absoluto En (, 2) En [ 2, 1) x + 2 x 1 > 2 ( x 2) ( x + 1) > 2 x + 2 x 1 > 2 (x + 2) ( x + 1) > 2 2x + 1 > 2 3 > 2 Falso S 1 = x > 1/2 ( ) 1 S 2 = 2, [ 2, 1)
166 Desigualdades con valor absoluto En (, 2) En [ 2, 1) x + 2 x 1 > 2 ( x 2) ( x + 1) > 2 x + 2 x 1 > 2 (x + 2) ( x + 1) > 2 2x + 1 > 2 3 > 2 Falso S 1 = x > 1/2 ( ) 1 S 2 = 2, [ 2, 1)
167 Desigualdades con valor absoluto En (, 2) En [ 2, 1) x + 2 x 1 > 2 ( x 2) ( x + 1) > 2 x + 2 x 1 > 2 (x + 2) ( x + 1) > 2 2x + 1 > 2 3 > 2 Falso S 1 = x > 1/2 ( ) 1 S 2 = 2, [ 2, 1)
168 Desigualdades con valor absoluto En (, 2) En [ 2, 1) x + 2 x 1 > 2 ( x 2) ( x + 1) > 2 x + 2 x 1 > 2 (x + 2) ( x + 1) > 2 2x + 1 > 2 3 > 2 Falso S 1 = x > 1/2 ( ) 1 S 2 = 2, [ 2, 1)
169 Desigualdades con valor absoluto En [1, ) x + 2 x 1 > 2 (x + 2) (x 1) > 2 Solución S = ( 1 2, 1) [1,+ ). 3 > 2 S 1 = R [1, ) = [1, )
170 Desigualdades con valor absoluto En [1, ) x + 2 x 1 > 2 (x + 2) (x 1) > 2 Solución S = ( 1 2, 1) [1,+ ). 3 > 2 S 1 = R [1, ) = [1, )
171 Desigualdades con valor absoluto En [1, ) x + 2 x 1 > 2 (x + 2) (x 1) > 2 Solución S = ( 1 2, 1) [1,+ ). 3 > 2 S 1 = R [1, ) = [1, )
172 Desigualdades con valor absoluto En [1, ) x + 2 x 1 > 2 (x + 2) (x 1) > 2 Solución S = ( 1 2, 1) [1,+ ). 3 > 2 S 1 = R [1, ) = [1, )
173 Desigualdades con valor absoluto En [1, ) x + 2 x 1 > 2 (x + 2) (x 1) > 2 Solución S = ( 1 2, 1) [1,+ ). 3 > 2 S 1 = R [1, ) = [1, )
174 Desigualdades con valor absoluto Ejercicio Encuentre el conjunto solución de las siguientes desigualdades: 1 2 5x 4 3x 2 12x 8 > x < 2x 5 < 8
MATEMÁTICAS BÁSICAS. Autora: Jeanneth Galeano Peñaloza Edición: Oscar Guillermo Riaño
 MATEMÁTICAS BÁSICAS Autora: Jeanneth Galeano Peñaloza Edición: Oscar Guillermo Riaño Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad Nacional de Colombia
MATEMÁTICAS BÁSICAS Autora: Jeanneth Galeano Peñaloza Edición: Oscar Guillermo Riaño Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad Nacional de Colombia
ECUACIONES. Sergio Stive Solano Sabié 1. Julio de 2013 MATEMÁTICA. Sergio Solano. Ecuaciones. Clases de ecuaciones
 ECUACIONES Sergio Stive Solano 1 Julio de 2013 1 Visita http://sergiosolanosabie.wikispaces.com ECUACIONES Sergio Stive Solano 1 Julio de 2013 1 Visita http://sergiosolanosabie.wikispaces.com Una ecuación
ECUACIONES Sergio Stive Solano 1 Julio de 2013 1 Visita http://sergiosolanosabie.wikispaces.com ECUACIONES Sergio Stive Solano 1 Julio de 2013 1 Visita http://sergiosolanosabie.wikispaces.com Una ecuación
Guía de Matemática NM 3: Inecuaciones
 Centro Educacional San Carlos de Aragón. Coordinación Académica Enseñanza Media. Sector: Matemática. Nivel: NM Prof.: Ximena Gallegos H. Guía de Matemática NM : Inecuaciones Nombre(s): Curso: Fecha. Contenido:
Centro Educacional San Carlos de Aragón. Coordinación Académica Enseñanza Media. Sector: Matemática. Nivel: NM Prof.: Ximena Gallegos H. Guía de Matemática NM : Inecuaciones Nombre(s): Curso: Fecha. Contenido:
Ejemplo.- La desigualdad: 2x + 1 > x + 5, es una inecuación por que tiene una incógnita x que se verifica para valores mayores que 4.
 INECUACIONES.- DEFINICION.- Una inecuación es una desigualdad en las que hay una o más cantidades desconocidas (incógnita) y que solo se verifica para determinados valores de la incógnita o incógnitas.
INECUACIONES.- DEFINICION.- Una inecuación es una desigualdad en las que hay una o más cantidades desconocidas (incógnita) y que solo se verifica para determinados valores de la incógnita o incógnitas.
Práctica Examen 1 Métodos Cuantitativos I
 Práctica Examen 1 Métodos Cuantitativos I A. Comprobación de conceptos: 1. Defina cada concepto en sus propias palabras. Compruebe la respuesta refiriéndose a la definición del texto. a. número entero
Práctica Examen 1 Métodos Cuantitativos I A. Comprobación de conceptos: 1. Defina cada concepto en sus propias palabras. Compruebe la respuesta refiriéndose a la definición del texto. a. número entero
GUIA DE MATEMÁTICA. ECUACIÓN DE 2 GRADO. I. ITEM DE VERDADERO Y FALSO. Indica si las siguientes proposiciones son verdaderas o falsas.
 GUIA DE MATEMÁTICA. ECUACIÓN DE GRADO. Nombre: Curso: 3 medio Fecha: I. ITEM DE VERDADERO Y FALSO. Indica si las siguientes proposiciones son verdaderas o falsas.. La fórmula general de la ecuación de
GUIA DE MATEMÁTICA. ECUACIÓN DE GRADO. Nombre: Curso: 3 medio Fecha: I. ITEM DE VERDADERO Y FALSO. Indica si las siguientes proposiciones son verdaderas o falsas.. La fórmula general de la ecuación de
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN DESIGUALDADES
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN DESIGUALDADES Al inicio del Capítulo, estudiamos las relaciones de orden en los número reales y el signi cado de expresiones como a
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN DESIGUALDADES Al inicio del Capítulo, estudiamos las relaciones de orden en los número reales y el signi cado de expresiones como a
Clase 9 Sistemas de ecuaciones no lineales
 Clase 9 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo, 2014 con dos incógnitas Un sistema de dos ecuaciones en el que al menos una ecuación es no lineal, se llama
Clase 9 Instituto de Ciencias Básicas Facultad de Ingeniería Universidad Diego Portales Marzo, 2014 con dos incógnitas Un sistema de dos ecuaciones en el que al menos una ecuación es no lineal, se llama
Repaso de Álgebra. Colegio Molière. Repasaremos algunas reglas y procedimientos básicos que te serán útiles a lo largo del curso
 Repaso de Álgebra Colegio Molière Repasaremos algunas reglas y procedimientos básicos que te serán útiles a lo largo del curso Operaciones aritméticas a + b b + a ab ba (Ley Conmutativa) (a + b) + c a
Repaso de Álgebra Colegio Molière Repasaremos algunas reglas y procedimientos básicos que te serán útiles a lo largo del curso Operaciones aritméticas a + b b + a ab ba (Ley Conmutativa) (a + b) + c a
ECUACIONES E INECUACIONES.
 CAPÍTULO 3 ECUACIONES E INECUACIONES www.mathspace.jimdo.com mathspace.jimdo@gmail.com 3.1. ECUACIONES Una ecuación es una igualdad donde por lo menos hay un número desconocido, llamado incógnita o variable,
CAPÍTULO 3 ECUACIONES E INECUACIONES www.mathspace.jimdo.com mathspace.jimdo@gmail.com 3.1. ECUACIONES Una ecuación es una igualdad donde por lo menos hay un número desconocido, llamado incógnita o variable,
(Facultades de Ciencias, Ciencias Económicas, Ingeniería y Zootecnia) Coordinadora: Margarita Ospina
 Universidad Nacional de Colombia -Sede Bogotá- Departamento de Matemáticas Segundo semestre de 00 - Matemáticas Básicas PRECÁLCULO- Grupos, 4, 5, 6, 7 y 9. (Facultades de Ciencias, Ciencias Económicas,
Universidad Nacional de Colombia -Sede Bogotá- Departamento de Matemáticas Segundo semestre de 00 - Matemáticas Básicas PRECÁLCULO- Grupos, 4, 5, 6, 7 y 9. (Facultades de Ciencias, Ciencias Económicas,
INECUACIONES LINEALES
 INECUACIONES POLINÓMICAS EN UNA VARIABLE Las inecuaciones en general, son desigualdades entre epresiones algebraicas en las que intervienen una o más variables. Cuando las epresiones algebraicas de cada
INECUACIONES POLINÓMICAS EN UNA VARIABLE Las inecuaciones en general, son desigualdades entre epresiones algebraicas en las que intervienen una o más variables. Cuando las epresiones algebraicas de cada
Matemáticas 3. ax + by + c = 0
 Matemáticas 3 Ecuaciones Lineales Una ecuación lineal es una ecuación de primer grado con 2 incógnitas cuya forma general es: ax + by + c = 0 a, b, c son constantes reales, X, Y" son variables. Toda ecuación
Matemáticas 3 Ecuaciones Lineales Una ecuación lineal es una ecuación de primer grado con 2 incógnitas cuya forma general es: ax + by + c = 0 a, b, c son constantes reales, X, Y" son variables. Toda ecuación
LA ECUACIÓN CUADRÁTICA
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMÁTICAS ASIGNATURA: MATEMÁTICAS DOCENTE: EDISON MEJIA MONSALVE TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N 0 FECHA DURACION 3
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : MATEMÁTICAS ASIGNATURA: MATEMÁTICAS DOCENTE: EDISON MEJIA MONSALVE TIPO DE GUIA: CONCEPTUAL - EJERCITACION PERIODO GRADO N 0 FECHA DURACION 3
Matemáticas Universitarias
 Matemáticas Universitarias 1 Sesión No. 5 Nombre: Desigualdades lineales, cuadráticas y valor absoluto Objetivo de la asignatura: En esta sesión el estudiante conocerá las características y métodos de
Matemáticas Universitarias 1 Sesión No. 5 Nombre: Desigualdades lineales, cuadráticas y valor absoluto Objetivo de la asignatura: En esta sesión el estudiante conocerá las características y métodos de
TEMARIO PRESENTACIÓN 7 MÓDULO I 17 EXPRESIONES ALGEBRAICAS 19
 TEMARIO PRESENTACIÓN 7 MÓDULO I 17 EXPRESIONES ALGEBRAICAS 19 Introducción 19 Lenguaje común y lenguaje algebraico 22 Actividad 1 (Lenguaje común y lenguaje algebraico) 23 Actividad 2 (Lenguaje común y
TEMARIO PRESENTACIÓN 7 MÓDULO I 17 EXPRESIONES ALGEBRAICAS 19 Introducción 19 Lenguaje común y lenguaje algebraico 22 Actividad 1 (Lenguaje común y lenguaje algebraico) 23 Actividad 2 (Lenguaje común y
MATE Dr. Pedro Vásquez UPRM. P. Vásquez (UPRM) Conferencia 1 / 15
 Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia 1 / 15 Modelando con ecuaciones Guías para resolver problemas verbales 1 Identi car la(s) variable(s) 2 Transformar la parte verbal a símbolos matemáticos
Dr. Pedro Vásquez UPRM P. Vásquez (UPRM) Conferencia 1 / 15 Modelando con ecuaciones Guías para resolver problemas verbales 1 Identi car la(s) variable(s) 2 Transformar la parte verbal a símbolos matemáticos
Ecuaciones cuadráticas Resolver ecuaciones cuadráticas fórmula cuadrática y casos especiales
 Ecuaciones cuadráticas Resolver ecuaciones cuadráticas fórmula cuadrática y casos especiales Departamento de Matemáticas Universidad de Puerto Rico - Arecibo Ecuación cuadrática en forma general Una ecuación
Ecuaciones cuadráticas Resolver ecuaciones cuadráticas fórmula cuadrática y casos especiales Departamento de Matemáticas Universidad de Puerto Rico - Arecibo Ecuación cuadrática en forma general Una ecuación
Revisora: María Molero
 57 Capítulo 5: INECUACIONES. Matemáticas 4ºB ESO 1. INTERVALOS 1.1. Tipos de intervalos Intervalo abierto: I = (a, b) = {x a < x < b}. Intervalo cerrado: I = [a, b] = {x a x b}. Intervalo semiabierto por
57 Capítulo 5: INECUACIONES. Matemáticas 4ºB ESO 1. INTERVALOS 1.1. Tipos de intervalos Intervalo abierto: I = (a, b) = {x a < x < b}. Intervalo cerrado: I = [a, b] = {x a x b}. Intervalo semiabierto por
Ecuaciones. 2x + 3 = 5x 2. 2x + 1 = 2 (x + 1) 2x + 1 = 2x x + 2 = 2 (x + 1) 2x + 2 = 2x = 2. x + 1 = 2 x = 1
 Ecuaciones Igualdad Una IGUALDAD se compone de dos expresiones unidas por el signo igual. 2x + 3 = 5x 2 Una igualdad puede ser: Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2 1 2. Cierta 2x + 2 = 2 (x + 1)
Ecuaciones Igualdad Una IGUALDAD se compone de dos expresiones unidas por el signo igual. 2x + 3 = 5x 2 Una igualdad puede ser: Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2 1 2. Cierta 2x + 2 = 2 (x + 1)
Práctica Examen 1 Precálculo 1
 Práctica Eamen 1 Precálculo 1 A. Comprobación de conceptos: 1. Defina cada concepto en sus propias palabras. Compruebe la respuesta refiriéndose a la definición del teto. a. número entero b. número racional
Práctica Eamen 1 Precálculo 1 A. Comprobación de conceptos: 1. Defina cada concepto en sus propias palabras. Compruebe la respuesta refiriéndose a la definición del teto. a. número entero b. número racional
UNPAZ - APU - Algebra y Análisis I 1er cuatrimestre 2017
 UNPAZ - APU - Algebra y Análisis I 1er cuatrimestre 017 Práctica 1- Números Reales Entre los conjuntos numéricos más conocidos con los que trabajaremos en esta práctica se encuentran los Naturales (N),
UNPAZ - APU - Algebra y Análisis I 1er cuatrimestre 017 Práctica 1- Números Reales Entre los conjuntos numéricos más conocidos con los que trabajaremos en esta práctica se encuentran los Naturales (N),
27 de febrero de 2013
 1 / 52 Autoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá 27 de febrero de 2013 2 / 52 Razones trigonométricas Considere
1 / 52 Autoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá 27 de febrero de 2013 2 / 52 Razones trigonométricas Considere
Inecuaciones: Actividades de recuperación.
 Inecuaciones: Actividades de recuperación. 1.- Escribe la inecuación que corresponde a los siguientes enunciados: a) El perímetro de un triángulo equilátero es menor que 4. (x = lado del triángulo) b)
Inecuaciones: Actividades de recuperación. 1.- Escribe la inecuación que corresponde a los siguientes enunciados: a) El perímetro de un triángulo equilátero es menor que 4. (x = lado del triángulo) b)
MATEMÁTICAS BÁSICAS. Profesoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza
 Profesoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas 15 de junio de 2009 Razones trigonométricas Considere los triángulos
Profesoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Universidad Nacional de Colombia Sede Bogotá Departamento de Matemáticas 15 de junio de 2009 Razones trigonométricas Considere los triángulos
Resolver ecuaciones cuadráticas. Departamento de Matemáticas Universidad de Puerto Rico - Arecibo
 Resolver ecuaciones cuadráticas Departamento de Matemáticas Universidad de Puerto Rico - Arecibo Ecuación cuadrática en forma general Una ecuación cuadrática tiene una forma general como sigue ax + bx
Resolver ecuaciones cuadráticas Departamento de Matemáticas Universidad de Puerto Rico - Arecibo Ecuación cuadrática en forma general Una ecuación cuadrática tiene una forma general como sigue ax + bx
Fabio Prieto Ingreso 2003
 Fabio Prieto Ingreso 00. INECUACIONES CON UNA VARIABLE.. Inecuación lineal Llamaremos desigualdad lineal de una variable a cualquier epresión de la forma: a + b > 0 o bien a + b < 0 o bien a + b 0 o bien
Fabio Prieto Ingreso 00. INECUACIONES CON UNA VARIABLE.. Inecuación lineal Llamaremos desigualdad lineal de una variable a cualquier epresión de la forma: a + b > 0 o bien a + b < 0 o bien a + b 0 o bien
Carpeta de TRABAJOS PRÁCTICOS de MATEMÁTICA para 4 Año Automotores
 ESCUELA TÉCNICA N 6 D.E. 6 Confederación Suiza GUIA DE VERANO: Carpeta de TRABAJOS PRÁCTICOS de MATEMÁTICA para 4 Año Automotores APELLIDO Y NOMBRE DEL ALUMNO:... PROFESOR:... DIVISIÓN:... Página Para
ESCUELA TÉCNICA N 6 D.E. 6 Confederación Suiza GUIA DE VERANO: Carpeta de TRABAJOS PRÁCTICOS de MATEMÁTICA para 4 Año Automotores APELLIDO Y NOMBRE DEL ALUMNO:... PROFESOR:... DIVISIÓN:... Página Para
Escuela de Ciencias Básicas Tecnologías e Ingeniería. Algebra Trigonometría y Geometría Analítica
 Guía No 1 Algebra y Trigonometría Grupo: 1 UNAD Escuela de Ciencias Básicas Tecnologías e Ingeniería Algebra Trigonometría y Geometría Analítica ECUACIONES DE PRIMER GRADO EN UNA VARIABLE Ecuación Una
Guía No 1 Algebra y Trigonometría Grupo: 1 UNAD Escuela de Ciencias Básicas Tecnologías e Ingeniería Algebra Trigonometría y Geometría Analítica ECUACIONES DE PRIMER GRADO EN UNA VARIABLE Ecuación Una
PREPARADURÍA INTRODUCTORIA (Semana 1)
 Universidad Simón Bolívar Preparadurías de Matemáticas I (MA1111) Preparador: Ricardo J. Fernández Terán ( RicharOrange@hotmail.com ) PREPARADURÍA INTRODUCTORIA (Semana 1) Contenidos: Propiedades de los
Universidad Simón Bolívar Preparadurías de Matemáticas I (MA1111) Preparador: Ricardo J. Fernández Terán ( RicharOrange@hotmail.com ) PREPARADURÍA INTRODUCTORIA (Semana 1) Contenidos: Propiedades de los
Repaso Prueba Nivel Matemática
 Centro Educacional San Carlos de Aragón. Coordinación Académica Enseñanza Media. Sector: Matemática. Nivel: NM Prof.: Ximena Gallegos H. Repaso Prueba Nivel Matemática Nombre: Curso: Fecha. Contenidos:
Centro Educacional San Carlos de Aragón. Coordinación Académica Enseñanza Media. Sector: Matemática. Nivel: NM Prof.: Ximena Gallegos H. Repaso Prueba Nivel Matemática Nombre: Curso: Fecha. Contenidos:
Inecuaciones: son desigualdades en las que se encuentra presente en uno cualquiera de los miembros, o en ambos, una o más variables, o incógnitas.
 TEMA: INECUACIONES Desigualdad: se llama desigualdad a toda relación entre epresiones numéricas o algebraicas unidas por uno de los cuatro signos de desigualdad,,,, Por ejemplo: 6 0 ; 0 ; 8, etc.... Las
TEMA: INECUACIONES Desigualdad: se llama desigualdad a toda relación entre epresiones numéricas o algebraicas unidas por uno de los cuatro signos de desigualdad,,,, Por ejemplo: 6 0 ; 0 ; 8, etc.... Las
4º ESO TEMA 3: ECUACIONES E INECUACIONES; SISTEMAS MATEMÁTICAS-OPCIÓN B TEMA3: ECUACIONES E INECUACIONES; SISTEMAS DE ECUACIONES Y DE INECUACIONES
 TEMA3: ECUACIONES E INECUACIONES; SISTEMAS DE ECUACIONES Y DE INECUACIONES REPASO DE ECUACIONES DE PRIMER Y SEGUNDO GRADO 1- Resuelve las siguientes ecuaciones: a) (4x + 3)(4x 3) 4(3 2x) 2 = 3x b) 2x +
TEMA3: ECUACIONES E INECUACIONES; SISTEMAS DE ECUACIONES Y DE INECUACIONES REPASO DE ECUACIONES DE PRIMER Y SEGUNDO GRADO 1- Resuelve las siguientes ecuaciones: a) (4x + 3)(4x 3) 4(3 2x) 2 = 3x b) 2x +
Álgebra y trigonometría: Ecuaciones y desigualdades
 Álgebra y trigonometría: Ecuaciones y desigualdades CNM-108 Instituto de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Este documento es distribuido bajo una licencia Creative
Álgebra y trigonometría: Ecuaciones y desigualdades CNM-108 Instituto de Matemáticas Facultad de Ciencias Exactas y Naturales Universidad de Antioquia Este documento es distribuido bajo una licencia Creative
La ecuación de segundo grado.
 La ecuación de segundo grado. Sean números reales Se denomina ecuación de segundo grado (o ecuación cuadrática) en la variable a la ecuación cuya forma canónica es Ejemplos. Son ecuaciones cuadráticas:
La ecuación de segundo grado. Sean números reales Se denomina ecuación de segundo grado (o ecuación cuadrática) en la variable a la ecuación cuya forma canónica es Ejemplos. Son ecuaciones cuadráticas:
Relación Ecuaciones. Ecuaciones de primer grado. Matemáticas. Resolver las siguientes ecuaciones: 5(x + 1) [1] = x + 3 5x x + 2 [2] 3 {3
![Relación Ecuaciones. Ecuaciones de primer grado. Matemáticas. Resolver las siguientes ecuaciones: 5(x + 1) [1] = x + 3 5x x + 2 [2] 3 {3 Relación Ecuaciones. Ecuaciones de primer grado. Matemáticas. Resolver las siguientes ecuaciones: 5(x + 1) [1] = x + 3 5x x + 2 [2] 3 {3](/thumbs/74/71283356.jpg) Relación Ecuaciones Matemáticas Ecuaciones de primer grado Resolver las siguientes ecuaciones: 5(x + 1) [1] = x + 5x + 9 + x + 8 [] [(x ) ] } = 1 [] x + 1 x + x + 5 7 [] 5x (x 8) = (x + ) [5] x + [] 5x
Relación Ecuaciones Matemáticas Ecuaciones de primer grado Resolver las siguientes ecuaciones: 5(x + 1) [1] = x + 5x + 9 + x + 8 [] [(x ) ] } = 1 [] x + 1 x + x + 5 7 [] 5x (x 8) = (x + ) [5] x + [] 5x
Matemáticas. Sesión #3. Ecuaciones cuadráticas y desigualdades.
 Matemáticas Sesión #3. Ecuaciones cuadráticas y desigualdades. Contextualización Ahora nos toca estudiar las ecuaciones de segundo grado también conocida por ecuaciones cuadráticas. Las ecuaciones cuadráticas
Matemáticas Sesión #3. Ecuaciones cuadráticas y desigualdades. Contextualización Ahora nos toca estudiar las ecuaciones de segundo grado también conocida por ecuaciones cuadráticas. Las ecuaciones cuadráticas
1 Profesor: Aquilino Miranda I TRIMESTRE - UNIDAD DE APRENDIZAJE #1 (DESIGUALDADES) PROFESOR: AQUILINO MIRANDA (COLEGIO DANIEL O.
 1 Profesor: Aquilino Miranda I TRIMESTRE - UNIDAD DE APRENDIZAJE #1 (DESIGUALDADES) PROFESOR: AQUILINO MIRANDA (COLEGIO DANIEL O. CRESPO) Resuelve desigualdades lineales enteras y fraccionarias. Resuelve
1 Profesor: Aquilino Miranda I TRIMESTRE - UNIDAD DE APRENDIZAJE #1 (DESIGUALDADES) PROFESOR: AQUILINO MIRANDA (COLEGIO DANIEL O. CRESPO) Resuelve desigualdades lineales enteras y fraccionarias. Resuelve
Segundo caso. Tercer caso. Resolviendo cada una de las desigualdades: d. (x - 5) 2 0. Si: < 0; (a > 0), el polinomio: ax 2 + bx + c, se transforma
 Inecuaciones Cuadráticas Inecuación cuadrática Forma general: Donde: {a; b; c} IR Del rectángulo se obtiene: P () = a 2 + b + c > < 0 ; a 0 a 2 + b + c > 0; a 2 + b + c < 0 a 2 + b + c 0; a 2 + b + c 0
Inecuaciones Cuadráticas Inecuación cuadrática Forma general: Donde: {a; b; c} IR Del rectángulo se obtiene: P () = a 2 + b + c > < 0 ; a 0 a 2 + b + c > 0; a 2 + b + c < 0 a 2 + b + c 0; a 2 + b + c 0
Preparación para Álgebra universitaria con trigonometría
 Preparación para Álgebra universitaria con trigonometría Este curso cubre los siguientes temas. Usted puede personalizar la gama y la secuencia de este curso para satisfacer sus necesidades curriculares.
Preparación para Álgebra universitaria con trigonometría Este curso cubre los siguientes temas. Usted puede personalizar la gama y la secuencia de este curso para satisfacer sus necesidades curriculares.
Ecuaciones de Primer Grado
 Ecuaciones de Primer Grado Definiciones Igualdad : Una igualdad se compone de dos expresiones unidas por el signo igual. Una igualdad puede ser: 2x + 3 = 5x 2 Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2
Ecuaciones de Primer Grado Definiciones Igualdad : Una igualdad se compone de dos expresiones unidas por el signo igual. Una igualdad puede ser: 2x + 3 = 5x 2 Falsa: 2x + 1 = 2 (x + 1) 2x + 1 = 2x + 2
1 - Ecuaciones. Sistemas de Ecuaciones Mixtos
 Nivelación de Matemática MTHA UNLP 1 1 - Ecuaciones. Sistemas de Ecuaciones Mixtos 1. Conjuntos numéricos Los números mas comunes son los llamados NATURALES O ENTEROS POSI- TIVOS: 1,, 3,... Para designar
Nivelación de Matemática MTHA UNLP 1 1 - Ecuaciones. Sistemas de Ecuaciones Mixtos 1. Conjuntos numéricos Los números mas comunes son los llamados NATURALES O ENTEROS POSI- TIVOS: 1,, 3,... Para designar
Inecuaciones lineales y cuadráticas
 Inecuaciones lineales y cuadráticas 0.1. Inecuaciones lineales Una inecuación lineal tiene la forma ax + b < 0 ó ax + b > 0 ó ax + b 0 ó ax + b 0. El objetivo consiste en hallar el conjunto solución de
Inecuaciones lineales y cuadráticas 0.1. Inecuaciones lineales Una inecuación lineal tiene la forma ax + b < 0 ó ax + b > 0 ó ax + b 0 ó ax + b 0. El objetivo consiste en hallar el conjunto solución de
Ecuaciones de segundo grado con una incógnita
 Instituto Dr. Juan Segundo Fernández Área y curso: Matemática 4º año. Profesora: Graciela Bejar TRABAJO PRÁCTICO Nº 6 Ecuaciones de segundo grado con una incógnita Las ecuaciones de segundo grado o cuadráticas
Instituto Dr. Juan Segundo Fernández Área y curso: Matemática 4º año. Profesora: Graciela Bejar TRABAJO PRÁCTICO Nº 6 Ecuaciones de segundo grado con una incógnita Las ecuaciones de segundo grado o cuadráticas
UNIDAD 5. responde razonadamente: Comprueba si x 1 es solución de alguna de las siguientes ecuaciones. Razona tu respuesta:
 UNIDAD 5 Comprueba si x 1 es solución de alguna de las siguientes ecuaciones. Razona tu respuesta: x x 4 3 4 a) x 3 7 7 7 x 3x b) 1 c) x 5 x 5 1 0 responde razonadamente: a Es cierta si sustituimos la
UNIDAD 5 Comprueba si x 1 es solución de alguna de las siguientes ecuaciones. Razona tu respuesta: x x 4 3 4 a) x 3 7 7 7 x 3x b) 1 c) x 5 x 5 1 0 responde razonadamente: a Es cierta si sustituimos la
Inecuaciones. Inecuaciones polinómicas de 1º grado, con una incógnita. Estas inecuaciones, se pueden llegar a escribir de la forma:
 Inecuaciones Una inecuación es una desigualdad matemática que presenta al menos una variable en alguno de sus miembros, por eso también se le conoce como desigualdad algebraica. Los signos de desigualdad
Inecuaciones Una inecuación es una desigualdad matemática que presenta al menos una variable en alguno de sus miembros, por eso también se le conoce como desigualdad algebraica. Los signos de desigualdad
Fundamentos matemáticos. Tema 1 Números reales. Polinomios
 Grado en Ingeniería agrícola y del medio rural Tema 1 Números reales. Polinomios José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative
Grado en Ingeniería agrícola y del medio rural Tema 1 Números reales. Polinomios José Barrios García Departamento de Análisis Matemático Universidad de La Laguna jbarrios@ull.es 2017 Licencia Creative
INSTEC PENSAMIENTO NUMERICO VARIACIONAL GUIA 1 - GRADO 11
 1.. LOS NUMEROS REALES CONDUCTA DE ENTRADA La figura muestra una recta real -1 0 1 Teniendo en cuenta la Figura responde en minutos a. Cuantos números Reales hay entre -1 y 1. b. Cuantos números naturales
1.. LOS NUMEROS REALES CONDUCTA DE ENTRADA La figura muestra una recta real -1 0 1 Teniendo en cuenta la Figura responde en minutos a. Cuantos números Reales hay entre -1 y 1. b. Cuantos números naturales
1) El producto de dos naturales consecutivos equivale a la suma de esos números aumentada en 19. De ellos, cuál es el número mayor?
 Escuela Conciente de Matemática GAUSS 550 1) El producto de dos naturales consecutivos equivale a la suma de esos números aumentada en 19. De ellos, cuál es el número mayor? A) 4 6 10 0 ) Considere el
Escuela Conciente de Matemática GAUSS 550 1) El producto de dos naturales consecutivos equivale a la suma de esos números aumentada en 19. De ellos, cuál es el número mayor? A) 4 6 10 0 ) Considere el
GOBIERNO DEL ESTADO DE MÉXICO SECRETARÍA DE EDUCACIÓN SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR Y SUPERIOR DIRECCIÓN DE EDUCACIÓN MEDIA SUPERIOR
 GOBIERNO DEL ESTADO DE MÉXICO SECRETARÍA DE EDUCACIÓN SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR Y SUPERIOR DIRECCIÓN DE EDUCACIÓN MEDIA SUPERIOR ESCUELA PREPARATORIA OFICIAL No. 5 EMILIANO ZAPATA GUIA
GOBIERNO DEL ESTADO DE MÉXICO SECRETARÍA DE EDUCACIÓN SUBSECRETARÍA DE EDUCACIÓN MEDIA SUPERIOR Y SUPERIOR DIRECCIÓN DE EDUCACIÓN MEDIA SUPERIOR ESCUELA PREPARATORIA OFICIAL No. 5 EMILIANO ZAPATA GUIA
5. Función cuadrática y ecuación de segundo grado
 Nivelación en Matemática 2010 46 5 Función cuadrática y ecuación de segundo grado 51 Funciones cuadráticas Definición: Una función cuadrática es una función f : R R definida por la fórmula f(x) =ax 2 +
Nivelación en Matemática 2010 46 5 Función cuadrática y ecuación de segundo grado 51 Funciones cuadráticas Definición: Una función cuadrática es una función f : R R definida por la fórmula f(x) =ax 2 +
Resuelva las siguientes desigualdades justificando solo los pasos en que aplique postulados o teoremas de este modulo.
 Ejercicios de autoevaluación Matemáticas II MODULO I CUESTIONARIO Resuelva las siguientes desigualdades justificando solo los pasos en que aplique postulados o teoremas de este modulo. 10. 12. - 4x < 3x
Ejercicios de autoevaluación Matemáticas II MODULO I CUESTIONARIO Resuelva las siguientes desigualdades justificando solo los pasos en que aplique postulados o teoremas de este modulo. 10. 12. - 4x < 3x
f (x) = 3(1 + x2 cos x)(x sin x 1) 2 x ( x + 7x) 2/3 cos 4 (tan x) ) 1/5 f (x) = 3x4 + 6x 3 9x 2 + 3x + 3 x(x 3 + 3x 1)
 1. Derivar las siguientes funciones: ( ) 3 1 a. f(x) = x sin x f (x) = 3(1 + x cos x)(x sin x 1) x 4 b. f(x) = ( ln[(x cos x) 4 ] ) 7 7 (ln(x cos x)) 6 sec x (cos x x sin x) x 1 + tan x c. f(x) = f (x)
1. Derivar las siguientes funciones: ( ) 3 1 a. f(x) = x sin x f (x) = 3(1 + x cos x)(x sin x 1) x 4 b. f(x) = ( ln[(x cos x) 4 ] ) 7 7 (ln(x cos x)) 6 sec x (cos x x sin x) x 1 + tan x c. f(x) = f (x)
C U R S O : MATEMÁTICA
 C U R S O : MATEMÁTICA GUÍA TEÓRICO PRÁCTICA Nº 27 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Una ecuación de segundo grado es una ecuación susceptible de llevar a la forma ax 2 + bx + c = 0,
C U R S O : MATEMÁTICA GUÍA TEÓRICO PRÁCTICA Nº 27 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE SEGUNDO GRADO Una ecuación de segundo grado es una ecuación susceptible de llevar a la forma ax 2 + bx + c = 0,
LA ECUACIÓN CUADRÁTICA
 INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : ASIGNATURA: DOCENTE: TIPO DE GUIA: MATEMÁTICAS MATEMÁTICAS EDISON MEJIA MONSALVE CONCEPTUAL - EJERCITACION PERIODO GRADO 9 N 0 4 FECHA 7 DE ABRIL
INSTITUCION EDUCATIVA LA PRESENTACION NOMBRE ALUMNA: AREA : ASIGNATURA: DOCENTE: TIPO DE GUIA: MATEMÁTICAS MATEMÁTICAS EDISON MEJIA MONSALVE CONCEPTUAL - EJERCITACION PERIODO GRADO 9 N 0 4 FECHA 7 DE ABRIL
Ejercicio nº 1.-Dada la ecuación: responde razonadamente: a) Qué valor obtienes si sustituyes x = 3 en el primer miembro?
 WORKSHEET: UNIT 5. EQUATIONS YEAR: 3 DATE: NAME AND SURNAME: Ejercicio nº 1.-Dada la ecuación: responde razonadamente: a) Qué valor obtienes si sustituyes x = 3 en el primer miembro? b) Qué obtienes si
WORKSHEET: UNIT 5. EQUATIONS YEAR: 3 DATE: NAME AND SURNAME: Ejercicio nº 1.-Dada la ecuación: responde razonadamente: a) Qué valor obtienes si sustituyes x = 3 en el primer miembro? b) Qué obtienes si
Unidad #1: DESIGUALDAD o inecuaciones COLEGIO BENIGNO TOMÁS ARGOTE UNIDAD # 1
 ÁREA: Algebra COLEGIO BENIGNO TOMÁS ARGOTE UNIDAD # 1 ASIGNATURA: Matemática. NIVEL: Duodécimo grado ( CIENCIAS ) PROFESOR: José Alexander Echeverría Ruiz TRIMESTRE: I TÍTULO DE LA UNIDAD DIDÁCTICA: 1.
ÁREA: Algebra COLEGIO BENIGNO TOMÁS ARGOTE UNIDAD # 1 ASIGNATURA: Matemática. NIVEL: Duodécimo grado ( CIENCIAS ) PROFESOR: José Alexander Echeverría Ruiz TRIMESTRE: I TÍTULO DE LA UNIDAD DIDÁCTICA: 1.
Desigualdades o inecuaciones lineales en una variable. Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo
 Desigualdades o inecuaciones lineales en una variable Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades Una desigualdad o inecuación usa símbolos como ,, para representar
Desigualdades o inecuaciones lineales en una variable Prof. Caroline Rodriguez Departamento de Matemáticas UPR - Arecibo Desigualdades Una desigualdad o inecuación usa símbolos como ,, para representar
Semana 8 Bimestre I Número de clases 36 40
 Semana 8 Bimestre I Número de clases 36 40 Clase 36 Tema: Valor numérico de una expresión algebraica Actividad 1 1 Lea el ejemplo que se presenta a continuación y observe el proceso que se emplea para
Semana 8 Bimestre I Número de clases 36 40 Clase 36 Tema: Valor numérico de una expresión algebraica Actividad 1 1 Lea el ejemplo que se presenta a continuación y observe el proceso que se emplea para
EJE N 3 : ECUACION LINEAL, CUADRATICA Y SISTEMA DE ECUACIONES
 TALLER DE INGRESO 018 EJE N : ECUACION LINEAL, CUADRATICA Y SISTEMA DE ECUACIONES ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA 1) Halla el valor de x a) b) c) d) e) f) g) h) i) j) k) l) m) n) ) Resolver
TALLER DE INGRESO 018 EJE N : ECUACION LINEAL, CUADRATICA Y SISTEMA DE ECUACIONES ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA 1) Halla el valor de x a) b) c) d) e) f) g) h) i) j) k) l) m) n) ) Resolver
1. Halle un número entero sabiendo que la suma con el doble de su inverso es 19
 SOLUCIONES Resolver los siguientes problemas:. Halle un número entero sabiendo que la suma con el doble de su inverso es 9. b. Sea x el número entero, entonces su recíproco es x d. x 9 x x 6 9 x x 9x 6
SOLUCIONES Resolver los siguientes problemas:. Halle un número entero sabiendo que la suma con el doble de su inverso es 9. b. Sea x el número entero, entonces su recíproco es x d. x 9 x x 6 9 x x 9x 6
ECUACIONES. Resuelve, con sentido común, las siguientes ecuaciones... 3º ESO. PARA PRACTICAR : LIBRO [ PÁG. 102 / Nº 2, 3, 4 ] mn
![ECUACIONES. Resuelve, con sentido común, las siguientes ecuaciones... 3º ESO. PARA PRACTICAR : LIBRO [ PÁG. 102 / Nº 2, 3, 4 ] mn ECUACIONES. Resuelve, con sentido común, las siguientes ecuaciones... 3º ESO. PARA PRACTICAR : LIBRO [ PÁG. 102 / Nº 2, 3, 4 ] mn](/thumbs/54/33804112.jpg) ECUACIONES Comprender el lenguaje algebraico para resolver ecuaciones Resuelve, con sentido común, las siguientes ecuaciones... 3º ESO. PARA PRACTICAR : LIBRO [ PÁG. 102 / Nº 2, 3, 4 ] mn Estudiar en el
ECUACIONES Comprender el lenguaje algebraico para resolver ecuaciones Resuelve, con sentido común, las siguientes ecuaciones... 3º ESO. PARA PRACTICAR : LIBRO [ PÁG. 102 / Nº 2, 3, 4 ] mn Estudiar en el
1. Ejercicios propuestos
 Coordinación de Matemática I (MAT0) er Semestre de 05 Semana : Guía de Ejercicios de Cálculo, lunes 6 viernes 0 de Marzo Contenidos Clase : La Ecuación Cuadrática. Inecuaciones de grado, con y sin valor
Coordinación de Matemática I (MAT0) er Semestre de 05 Semana : Guía de Ejercicios de Cálculo, lunes 6 viernes 0 de Marzo Contenidos Clase : La Ecuación Cuadrática. Inecuaciones de grado, con y sin valor
ECUACIONES E INECUACIONES (MATEMÁTICAS A) (SOLUCIÓN)
 Examen de ECUACIONES E INECUACIONES (MATEMÁTICAS A) 9.0.1 (SOLUCIÓN) : 1. Resuelve las siguientes ecuaciones: a. x + 3-10 x : x 4 : x + 10 + x : x : 8x + 1 x + 8x 1 + 10 10x 0 x 0 10 b. x + 4 x 4 + x 4
Examen de ECUACIONES E INECUACIONES (MATEMÁTICAS A) 9.0.1 (SOLUCIÓN) : 1. Resuelve las siguientes ecuaciones: a. x + 3-10 x : x 4 : x + 10 + x : x : 8x + 1 x + 8x 1 + 10 10x 0 x 0 10 b. x + 4 x 4 + x 4
Capitulo IV - Inecuaciones
 Capitulo IV - Inecuaciones Definición: Una inecuación es una desigualdad en las que hay una o más cantidades desconocidas (incógnita) y que sólo se verifica para determinados valores de la incógnita o
Capitulo IV - Inecuaciones Definición: Una inecuación es una desigualdad en las que hay una o más cantidades desconocidas (incógnita) y que sólo se verifica para determinados valores de la incógnita o
TEMA 2.- ECUACIONES E INECUACIONES
 TEMA.- ECUACIONES E INECUACIONES 1.- INECUACIONES 1.1.- Repaso De Ecuaciones De Primer Y Segundo Grado Ecuaciones de primer grado x 3 4x 4x 3 x 6 4x 4x 1 x 4 x 5x 7 x 7 3x 14 35x 7 x 7 6 3x 14 3 15x 1
TEMA.- ECUACIONES E INECUACIONES 1.- INECUACIONES 1.1.- Repaso De Ecuaciones De Primer Y Segundo Grado Ecuaciones de primer grado x 3 4x 4x 3 x 6 4x 4x 1 x 4 x 5x 7 x 7 3x 14 35x 7 x 7 6 3x 14 3 15x 1
TEMA 5 - ECUACIONES DE SEGUNDO GRADO Ejercicios Resueltos
 TEMA 5 - ECUACIONES DE SEGUNDO GRADO Ejercicios Resueltos Resuelve mentalmente las siguientes ecuaciones: 1 5 5, 5 9 7, 7 4 5 5 1, 1 Resuelve las siguientes ecuaciones: 6 6, 6 7 16 4, 8 7 9 5 + 6, 10 +
TEMA 5 - ECUACIONES DE SEGUNDO GRADO Ejercicios Resueltos Resuelve mentalmente las siguientes ecuaciones: 1 5 5, 5 9 7, 7 4 5 5 1, 1 Resuelve las siguientes ecuaciones: 6 6, 6 7 16 4, 8 7 9 5 + 6, 10 +
INTERVALOS Y SEMIRRECTAS.
 el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
el blog de mate de aida CSI: Inecuaciones pág 1 INTERVALOS Y SEMIRRECTAS La ordenación de números permite definir algunos conjuntos de números que tienen una representación geométrica en la recta real
INSTITUTO TECNICO MARIA INMACULADA Formando líderes estudiantiles para un futuro mejor
 INSTITUTO TECNICO MARIA INMACULADA Formando líderes estudiantiles para un futuro mejor Coordinación Vo. Bo. Eje temático: METODOS COMPLETACION CUADRADO PERFECTO Y FORMULA GENERAL Área: MATEMÁTICAS Asignatura:
INSTITUTO TECNICO MARIA INMACULADA Formando líderes estudiantiles para un futuro mejor Coordinación Vo. Bo. Eje temático: METODOS COMPLETACION CUADRADO PERFECTO Y FORMULA GENERAL Área: MATEMÁTICAS Asignatura:
10.4 Sistemas de ecuaciones lineales
 Programa Inmersión, Verano 2016 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 001 y MATE 02 Clase #11: martes, 14 de junio de 2016. 10.4 Sistemas de ecuaciones lineales
Programa Inmersión, Verano 2016 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 001 y MATE 02 Clase #11: martes, 14 de junio de 2016. 10.4 Sistemas de ecuaciones lineales
ECUACIONES. Ejercicio nº 1.- Dada la ecuación: responde razonadamente:
 ECUACIONES Ejercicio nº 1.- Dada la ecuación: x 1 x 1 5 3x 7 responde razonadamente: a Qué valor obtienes si sustituyes x 3 en el primer miembro? b Qué obtienes si sustituyes x 3 en el segundo miembro?
ECUACIONES Ejercicio nº 1.- Dada la ecuación: x 1 x 1 5 3x 7 responde razonadamente: a Qué valor obtienes si sustituyes x 3 en el primer miembro? b Qué obtienes si sustituyes x 3 en el segundo miembro?
MATEMÁTICAS B 4º ESO
 MATEMÁTICAS B 4º ESO Las unidades trabajadas durante el curso han sido: UNIDAD 1: NÚMEROS REALES UNIDAD : POTENCIAS Y RADICALES UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS UNIDAD 4: ECUACIONES E INECUACIONES
MATEMÁTICAS B 4º ESO Las unidades trabajadas durante el curso han sido: UNIDAD 1: NÚMEROS REALES UNIDAD : POTENCIAS Y RADICALES UNIDAD : POLINOMIOS Y FRACCIONES ALGEBRAICAS UNIDAD 4: ECUACIONES E INECUACIONES
DESIGUALDADES. AXIOMA 1.- Tricotomía de los números reales. Si a y b son números reales entonces se cumple una y solo una de las relaciones
 DESIGUALDADES 4.1.- AXIOMAS DE ORDEN. Cualquier conjunto o Campo de números que satisface los siguientes 4 Axiomas se dice que es un conjunto de números ORDENADO. El conjunto o Campo de los números reales
DESIGUALDADES 4.1.- AXIOMAS DE ORDEN. Cualquier conjunto o Campo de números que satisface los siguientes 4 Axiomas se dice que es un conjunto de números ORDENADO. El conjunto o Campo de los números reales
Números Complejos. Presentación 1 Precalculus Sec. 1.5
 Números Complejos Presentación 1 Precalculus Sec. 1.5 Tipos de números reales Enteros positivos o números naturales: Enteros no-negativos: 1,, 3, 4,... Enteros 0, 1,, 3, 4,......, 4, 3,, 1, 0, 1,, 3, 4,...
Números Complejos Presentación 1 Precalculus Sec. 1.5 Tipos de números reales Enteros positivos o números naturales: Enteros no-negativos: 1,, 3, 4,... Enteros 0, 1,, 3, 4,......, 4, 3,, 1, 0, 1,, 3, 4,...
FACULTAD DE MATEMÁTICAS XLIII CONCURSO ANUAL DE MATEMÁTICAS DEL SURESTE FASE ABIERTA ÁLGEBRA
 ÁLGEBRA Determinar el más grande de tres enteros impares consecutivos tales que el producto del primer entero y el segundo es más que el tercer entero. (2.5 minutos) Sean y tres enteros consecutivos impares.
ÁLGEBRA Determinar el más grande de tres enteros impares consecutivos tales que el producto del primer entero y el segundo es más que el tercer entero. (2.5 minutos) Sean y tres enteros consecutivos impares.
ACTIVIDADES RECUPERACIÓN VERANO x +1. x Resuelve las siguientes inecuaciones, dando la solución en forma de intervalos:
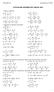 ACTIVIDADES RECUPERACIÓN VERANO 0. Opera y simplifica: 7 e) : f) : 5 0 8 g) + + + + h) +. 6 6 i). +. k). + 5 7 5. Resuelve las siguientes ecuaciones: + + 5 b) 5 + 5 + + + c) + d) 6 6 5 + 7 9 + e) + 5 +
ACTIVIDADES RECUPERACIÓN VERANO 0. Opera y simplifica: 7 e) : f) : 5 0 8 g) + + + + h) +. 6 6 i). +. k). + 5 7 5. Resuelve las siguientes ecuaciones: + + 5 b) 5 + 5 + + + c) + d) 6 6 5 + 7 9 + e) + 5 +
Problemas de fases nacionales e internacionales
 Problemas de fases nacionales e internacionales 1.- (China 1993). Dado el paralelogramo ABCD, se consideran dos puntos E, F sobre la diagonal AC e interiores al paralelogramo. Demostrar que si existe una
Problemas de fases nacionales e internacionales 1.- (China 1993). Dado el paralelogramo ABCD, se consideran dos puntos E, F sobre la diagonal AC e interiores al paralelogramo. Demostrar que si existe una
CAPÍTULO 7: TASAS Y OPERACIONES
 CAPÍTULO 7: TASAS Y OPERACIONES Fecha: 6 2014 CPM Educational Program. All rights reserved. Core Connections en español, Curso 2 Fecha: Caja de herramientas 2014 CPM Educational Program. All rights reserved.
CAPÍTULO 7: TASAS Y OPERACIONES Fecha: 6 2014 CPM Educational Program. All rights reserved. Core Connections en español, Curso 2 Fecha: Caja de herramientas 2014 CPM Educational Program. All rights reserved.
MATEMÁTICAS BÁSICAS. Autoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano
 MATEMÁTICAS BÁSICAS Autoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad
MATEMÁTICAS BÁSICAS Autoras: Margarita Ospina Pulido Jeanneth Galeano Peñaloza Edición: Rafael Ballestas Rojano Universidad Nacional de Colombia Departamento de Matemáticas Sede Bogotá Enero de 2015 Universidad
GUÍAS DE ESTUDIO. Programa de alfabetización, educación básica y media para jóvenes y adultos
 GUÍAS DE ESTUDIO Código PGA-02-R02 1 INSTITUCIÓN EDUCATIVA CASD Programa de alfabetización, educación básica y media para jóvenes y adultos UNIDAD DE TRABAJO Nº 1 PERIODO 1 1. ÁREA INTEGRADA: MATEMÁTICAS
GUÍAS DE ESTUDIO Código PGA-02-R02 1 INSTITUCIÓN EDUCATIVA CASD Programa de alfabetización, educación básica y media para jóvenes y adultos UNIDAD DE TRABAJO Nº 1 PERIODO 1 1. ÁREA INTEGRADA: MATEMÁTICAS
Intervalos semicerrados o semiabiertos se definen de la manera siguiente: (a, b] = {x l a < x b} [a, b) = {x l a x < b}
![Intervalos semicerrados o semiabiertos se definen de la manera siguiente: (a, b] = {x l a < x b} [a, b) = {x l a x < b} Intervalos semicerrados o semiabiertos se definen de la manera siguiente: (a, b] = {x l a < x b} [a, b) = {x l a x < b}](/thumbs/82/87031551.jpg) DESIGUALDADES Intervalos Sean a y b dos números reales tales que a < b. entonces el intervalo abierto de a a b, denotado por (a, b), es en conjunto de todos los números reales x situados entre a y b. (a,
DESIGUALDADES Intervalos Sean a y b dos números reales tales que a < b. entonces el intervalo abierto de a a b, denotado por (a, b), es en conjunto de todos los números reales x situados entre a y b. (a,
FUNCIONES PRÁCTICA N 2
 Capitulo II FUNCIONES PRÁCTICA N. En cada uno de los siguientes casos dar la ley de la función descripta: a) El área de un rectángulo es de 0 cm². Epresar el perímetro del mismo en función de la longitud
Capitulo II FUNCIONES PRÁCTICA N. En cada uno de los siguientes casos dar la ley de la función descripta: a) El área de un rectángulo es de 0 cm². Epresar el perímetro del mismo en función de la longitud
1 Ecuaciones, desigualdades y modelaje
 Programa Inmersión, Verano 07 Notas escritas por Dr M Notas del cursos Basadas en los prontuarios de MATE 300 y MATE 303 Clase #: jueves, 7 de agosto de 07 Ecuaciones, desigualdades y modelaje 7 Ecuaciones
Programa Inmersión, Verano 07 Notas escritas por Dr M Notas del cursos Basadas en los prontuarios de MATE 300 y MATE 303 Clase #: jueves, 7 de agosto de 07 Ecuaciones, desigualdades y modelaje 7 Ecuaciones
TEMA 2. Álgebra. Si la ecuación es del tipo, sacamos factor común x:
 TEMA. Álgebra Ecuaciones de segundo grado. Dada la ecuación de segundo grado incompleta incógnita despejamos de la siguiente forma:, para hallar el valor de la Si la ecuación es del tipo, sacamos factor
TEMA. Álgebra Ecuaciones de segundo grado. Dada la ecuación de segundo grado incompleta incógnita despejamos de la siguiente forma:, para hallar el valor de la Si la ecuación es del tipo, sacamos factor
DESIGUALDAD E INECUACIONES. Sean a, b, c y d números reales cualesquiera. Para ellos valen las siguientes propiedades:
 DESIGUALDAD E INECUACIONES PROPIEDADES DE LA RELACION MAYOR QUE. Sean a, b, c y d números reales cualesquiera. Para ellos valen las siguientes propiedades: ) Ley de tricotomía: Para dos números reales
DESIGUALDAD E INECUACIONES PROPIEDADES DE LA RELACION MAYOR QUE. Sean a, b, c y d números reales cualesquiera. Para ellos valen las siguientes propiedades: ) Ley de tricotomía: Para dos números reales
REACTIVOS MATEMÁTICAS I. Unidad I Introducción al Álgebra. Indica la respuesta correcta a los siguientes planteamientos,
 REACTIVOS MATEMÁTICAS I Unidad I Introducción al Álgebra Indica la respuesta correcta a los siguientes planteamientos, 0.- En un puesto de verduras del mercado, un cliente realizó la siguiente compra:.5
REACTIVOS MATEMÁTICAS I Unidad I Introducción al Álgebra Indica la respuesta correcta a los siguientes planteamientos, 0.- En un puesto de verduras del mercado, un cliente realizó la siguiente compra:.5
Facultad de Ingeniería Facultad de Tecnología Informática. Matemática Números reales Elementos de geometría analítica. Profesora: Silvia Mamone
 Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
Facultad de Ingeniería Facultad de Tecnología Informática Matemática Números reales Elementos de geometría analítica 0 03936 Profesora: Silvia Mamone UB Facultad de Ingeniería Facultad de Tecnología Informática
MATEMÁTICA CPU MÓDULO 1. Números reales Ecuaciones e inecuaciones. Representaciones en la recta y en el plano.
 MATEMÁTICA CPU MÓDULO Números reales. Ecuaciones e inecuaciones. Representaciones en la recta y en el plano.. Marcar con una cruz los conjuntos a los cuales pertenecen los siguientes números: N Z Q R 8
MATEMÁTICA CPU MÓDULO Números reales. Ecuaciones e inecuaciones. Representaciones en la recta y en el plano.. Marcar con una cruz los conjuntos a los cuales pertenecen los siguientes números: N Z Q R 8
CURSO CERO DE MATEMATICAS. Apuntes elaborados por Domingo Pestana Galván. y José Manuel Rodríguez García
 INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
INGENIEROS INDUSTRIALES Y DE TELECOMUNICACIONES CURSO CERO DE MATEMATICAS Apuntes elaborados por Domingo Pestana Galván y José Manuel Rodríguez García UNIVERSIDAD CARLOS III DE MADRID Escuela Politécnica
GUIA DE CATEDRA Matemática Empresarial Guía N.3 F. Elaboración 09 abril /11 F. 1 Revisión 09/04/11 Pagina 1 de 8
 Plan de Estudios: Semestre 1 Área: Matemática 1 Nº Créditos: Intensidad horaria semanal: 3 Hrs T Hrs P Total horas: 6 Tema: Desigualdades 1. OBJETIVO Apropiar los conceptos de desigualdades y establecer
Plan de Estudios: Semestre 1 Área: Matemática 1 Nº Créditos: Intensidad horaria semanal: 3 Hrs T Hrs P Total horas: 6 Tema: Desigualdades 1. OBJETIVO Apropiar los conceptos de desigualdades y establecer
para todo a, Ejemplo No. 57 Resuelva las siguientes ecuaciones lineales: d. x Solución: 4 x x c. x 4
 UNIDAD : ECUACIONES, INECUACIONES Y SISTEMAS DE ECUACIONES Una ecuación es una igualdad entre dos epresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos o datos, desconocidos
UNIDAD : ECUACIONES, INECUACIONES Y SISTEMAS DE ECUACIONES Una ecuación es una igualdad entre dos epresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos o datos, desconocidos
UNIDAD 8 INECUACIONES. Objetivo general.
 8. 1 UNIDAD 8 INECUACIONES Objetivo general. Al terminar esta Unidad resolverás inecuaciones lineales y cuadráticas e inecuaciones que incluyan valores absolutos, identificarás sus conjuntos solución en
8. 1 UNIDAD 8 INECUACIONES Objetivo general. Al terminar esta Unidad resolverás inecuaciones lineales y cuadráticas e inecuaciones que incluyan valores absolutos, identificarás sus conjuntos solución en
OLIMPIADAS COSTARRICENSES DE MATEMÁTICAS
 OLIMPIADAS COSTARRICENSES DE MATEMÁTICAS UNA - UCR - TEC - UNED - MEP - MICITT Álgebra e iπ + φ φ 0 III Nivel I Eliminatoria Marzo 06 Índice. Presentación. Contenidos 3. Algunos consejos útiles 4. Problemas
OLIMPIADAS COSTARRICENSES DE MATEMÁTICAS UNA - UCR - TEC - UNED - MEP - MICITT Álgebra e iπ + φ φ 0 III Nivel I Eliminatoria Marzo 06 Índice. Presentación. Contenidos 3. Algunos consejos útiles 4. Problemas
TEMA 6 ECUACIONES E INECUACIONES
 6.1 Ecuación. Soluciones TEMA 6 ECUACINES E INECUACINES Ejemplo Resuelve por tanteo las siguientes ecuaciones. 1. x 1 7 La solución es x, pues de esa forma al sustituir nos queda: 1 1 7. x 1 5 La solución
6.1 Ecuación. Soluciones TEMA 6 ECUACINES E INECUACINES Ejemplo Resuelve por tanteo las siguientes ecuaciones. 1. x 1 7 La solución es x, pues de esa forma al sustituir nos queda: 1 1 7. x 1 5 La solución
Matemáticas III. Geometría analítica
 Matemáticas III. Geometría analítica Este curso cubre los conceptos mostrados a continuación. El estudiante navega por trayectos de aprendizaje basados en su nivel de preparación. Usuarios institucionales
Matemáticas III. Geometría analítica Este curso cubre los conceptos mostrados a continuación. El estudiante navega por trayectos de aprendizaje basados en su nivel de preparación. Usuarios institucionales
