MECÁNICA CUÁNTICA AVANZADA 2013 Resonancias en el potencial de caparazón
|
|
|
- Inés Salazar Maldonado
- hace 5 años
- Vistas:
Transcripción
1 MECÁNICA CUÁNTICA AVANZADA 2013 esonancias en el potencial de caparazón 1. Desplazamiento de fase y amplitud de dispersión en onda S Consideremos la dispersión en un potencial de caparazón repulsivo: V (r) = γ 2 2m δ(r ) ; γ > 0, γ 1, k, (1.1) donde k es el módulo del vector número de ondas de la onda plana incidente. La fase de dispersión en onda S δ 0 exacta ( γ) fue determinada en clase; el resultado es cot δ 0 (k) = k γ (1 + cot2 k) cot k. (1.2) La correspondiente amplitud de dispersión en onda S es, por lo tanto, f 0 (k) = {k[cot δ 0 (k) i]} 1 { [ = k [i + cot k] 1 ik γ + k ]} 1 γ cot k. (1.3) La factorización es particularmente útil para estudiar los polos no triviales (k 0) de f 0, que como sabemos están relacionados con estados ligados y resonancias. 2. Posición de las resonancias: análisis a partir del desplazamiento de fase Las resonancias aparecen en valores de k tales que δ 0 (k) = π/2, i.e. cot δ 0 (k) = 0. De (1.2) se sigue que esta condición se cumple cuando Las dos soluciones de esta ecuación cuadrática son [ cot 2 k + γ cot k + 1 = 0. (2.1) k cot k = γ 2k 1 ± 1 4k2 γ 2 ], (2.2) 1
2 y cada una de ellas da lugar a una serie infinita de valores de k que satisfacen la ecuación (2.1), debido a la periodicidad de la cotangente. En el límite γ k el factor 4k 2 /γ 2 dentro de la raíz cuadrada se puede despreciar, y se obtienen expresiones sencillas para las dos familias de soluciones: (I) cot k 0 k (2n + 1) π 2 (n Z), (II) cot k γ k. (2.3) Nótese que γ k puede interpretarse como un límite de baja energía, en el sentido de que γ 1 tiene dimensiones de longitud y corresponde a la magnitud del potencial (i.e. 2 γ 2 2m se puede interpretar como una energía típica asociada al potencial). La segunda condición para la aparición de una resonancia es que la pendiente de cot δ 0 (k) sea negativa ( δ 0 (k) > 0) en el punto en que la función se anula. Partiendo de la ecuación (2.1) se encuentra [cot δ 0 (k)] ( = 1 1 γ + 2k ) cot k (1 + cot 2 k). (2.4) γ Sustituyendo las soluciones aproximadas (2.3) se obtiene (I) [cot δ 0(k)] (II) [cot δ 0(k)] = 1 1 γ 1, ( = ) (1 + γ2 γ k 2 ) γ2 k 2, (2.5) donde se ha usado tanto γ k como γ 1. Por lo tanto, las soluciones aproximadas de tipo (II) satisfacen la condición de resonancia, mientras que las de tipo (I) no lo hacen. Un estudio analítico más detallado, que tenga en cuenta las correcciones en k/γ y (γ) 1, es delicado: como se verá más adelante de manera explícita, alrededor de las resonancias δ 0 tiene una dependencia muy fuerte de la energía, y no es fácil controlar las aproximaciones al resultado exacto. Por este motivo, a menudo es más simple utilizar las técnicas asociadas a la presencia de polos en la amplitud de dispersión, que aíslan las resonancias de forma robusta. 3. Posición de las resonancias: análisis a partir de los polos de la amplitud de dispersión Dado que i + cot z 0 z C, los únicos polos no triviales corresponden a 1 ik γ + k γ cot k = 0 cot k = i γ k. (3.1) 2
3 Las soluciones de la ecuación (3.1) son, en general, complejas; por ejemplo, para γ = 3 se puede verificar numéricamente 1 que k i es una solución. 2 Dada una solución k, la parte real de k 2 está asociada a la energía E de una resonancia, y su parte imaginaria a la anchura Γ de la misma: 2 k 2 2m = E + iγ 2, (3.2) e.g. E /(m 2 ) con anchura Γ /(m 2 ) para la solución mencionada. Si utilizamos γ k la condición (3.1) se convierte en cot k γ k k cot k γ, (3.3) es decir, hemos encontrado sólo las soluciones de tipo (II) en (2.3) lo cual es consistente con el análisis anterior, ya que las de tipo (I) no tenían el signo correcto en la derivada de δ 0. Además, dado que la solución es real en este límite, las resonancias resultan ser infinitamente estrechas (Γ = 0); la primera contribución a la parte imaginaria de la solución es O((γ) 1 ). 4. elación de las resonancias con estados ligados de un pozo infinito Es fácil encontrar soluciones aproximadas en k de la ecuación (3.3): para γ 1 γ 1 las soluciones de (3.3) deben estar cerca de k = nπ, con n {1, 2, 3,...} basta dibujar la función k cot k para que resulte evidente: k cot k Es fácil encontrar soluciones exactas e.g. utilizando la función Findoot de Mathematica. 2 Existe también la solución k i, que sigue estando en la hoja no física Im k < 0; sin embargo, e k > 0 implica Γ < 0, i.e. el signo incorrecto de la anchura. 3
4 Ahora bien, cerca de k = nπ es posible expandir la cotangente en serie de Laurent: cot k = 1 k nπ 1 3 (k nπ) + O((k nπ)3 ), (4.1) y si mantenemos sólo el primer término y lo sustituimos en (3.3) se obtiene precisamente k nπγ nπ, (4.2) 1 + γ donde en el último paso hemos usado γ 1. Por lo tanto, tenemos para las localizaciones de las resonancias k (n) nπ y las energías correspondientes son, n {1, 2, 3,...}, (4.3) E (n) 2 π 2 n 2 2m 2. (4.4) Estos son precisamente los niveles de energía de una partícula de masa m confinada en un pozo infinito de radio. Si queremos calcular la primera corrección en γ, podríamos expandir en serie de Taylor en (4.2) y quedarnos con k nπ ( 1 1 (γ) 2 ) E (n) 2 π 2 n 2 2m 2 ( 1 2 (γ) 2 ). (4.5) Esta es una aproximación mejor que (4.4) de la energía real de la resonancia, aunque usar esta fórmula no sería completamente consistente para calcular la corrección completa habría que incluir términos subdominantes también en las ecs. (3.3) y (4.1). 5. Anchuras de las resonancias Ahora examinamos las anchuras de las resonancias. Para ello, en primer lugar introducimos la ecuación (1.2) en la fórmula para Γ { 1 { 1 d(cot δ 0 ) Γ = 2 dk d(cot δ 0 ) de = 2 E=E} de dk = k=k} { 1 (5.1) m d(cot δ 0 ) = 2 2 k dk. k=k} La derivada relevante es d dk cot δ 0(k) = ( 1 γ 2k ) (1 cot k + cot 2 k ), (5.2) γ 4
5 y como en la resonancia cot k γ/k (ecuación (3.3)) nos queda d ( ) ) dk cot δ 0(k) 1 (1 res γ + + γ2, (5.3) donde k es el número de ondas de la resonancia. Usando las condiciones γ, γ/k 1 para despreciar γ 1 en el primer paréntesis y 1 γ 2 /k 2 en el segundo,3 y sustituyendo k = nπ/, resulta k 2 y por lo tanto d dk cot δ 0(k) γ2 3 n 2 π 2, (5.4) Γ (n) 2π3 2 n 3 mγ 2 4 = 4πn (γ) 2 E(n). (5.5) Como habíamos deducido, las anchuras están controladas por el parámetro (γ) 1 : a medida que γ aumenta, la resonancia se hace más estrecha. Nótese, por otra parte, que la condición γ k nos ha llevado, consistentemente, a la aproximación γ nπ la aproximación funcionará mejor para las resonancias a baja energía. 6. Comparación con resultados exactos Es instructivo estudiar hasta qué punto nuestras aproximaciones funcionan bien desde el punto de vista cuantitativo, comparando resultados exactos con los que se obtienen al orden dominante de la expansión en γ y γ/k. Por ejemplo, para γ = 20 y γ = 100 las posiciones exactas de la primera resonancia son k i y k i, respectivamente, mientras que la predicción aproximada era k π. En términos de energías y anchuras, se tiene: γ m2 E (approx) 2 m 2 Γ (approx) m2 E (exact) 2 2 m 2 Γ (exact) También para Γ se confirma que la aproximación funciona mejor para el valor de γ más alto. La teoría general de dispersión nos dice que alrededor de estas resonancias estrechas la sección eficaz total será aproximadamente un pico lorentziano dado por la fórmula de Breit-Wigner; así, usando los valores exactos de (E, Γ) las resonancias apenas discutidas tendrán el siguiente aspecto: 3 Mantener estos términos generaría parte de las correcciones subdominantes, pero se aplica un comentario similar al realizado antes sobre las correcciones a las energías de resonancia aproximadas. 5
6 En este plot la energía está normalizada al valor del estado fundamental del pozo infinito E (0) = 2 π 2, así que el pico aparece cerca del valor 1 de la abscisa predicho 2m 2 por la aproximación (4.4). Obviamente, la aproximación es mejor para el valor mayor de γ, que corresponde también a la resonancia más estrecha. 7. Interpretación y manifestaciones experimentales La conclusión final de este análisis es que para γ muy grande (medido en términos de y k) el potencial se convierte en una barrera impenetrable, y las resonancias tienden a localizarse en las energías de los estados ligados confinados en su interior, haciéndose cada vez más estables (Γ más pequeña vida media τ = /Γ mayor) a medida que γ aumenta. Desde este punto de vista, la aproximación hecha para obtener expresiones analíticas para las resonancias ha resultado ser muy útil, porque nos ha proporcionado una interpretación física interesante del problema sin necesidad de analizar todos los detalles de la solución exacta para cot δ 0. Veamos cómo se manifiestan estas propiedades en el resultado exacto para la sección eficaz, fácilmente obtenible con programas de manipulación algebraica como Mathematica o Maple. Si usamos la expresión de la amplitud de dispersión (1.3) para calcular la sección total eficaz en onda S σ = 4π 2 f 0 2, y la dibujamos e.g. para γ = 100 6
7 Σ 2 Π vemos claramente los picos de resonancia que hemos predicho, situados cerca de los valores {1, 4, 9,...} de la abscisa. Dichos picos aparecen superpuestos a una dependencia no trivial de σ de la energía, caracterizada por una oscilación cuyos máximos presentan alturas similares a las de las resonancias. Finalmente, en los valles entre dichos picos, justo en los valores {1, 4, 9,...} y, por lo tanto, muy cerca de las resonancias, la sección eficaz se anula (efecto amsauer-townsend). Evidentemente, cuando γ disminuye y la anchura de las resonancias aumenta los dos tipos de picos se solapan, y la estructura de la sección eficaz total es menos nítida por ejemplo, para γ = 20: Σ 2 Π El origen de estas tres características prominentes de la sección eficaz (ceros, oscilaciones entre ceros, resonancias) se entiende fácilmente mirando el correspondiente gráfico de cot δ 0, e.g. para γ = 100: 7
8 Los puntos en los que σ = 0 corresponden a las divergencias de cot δ 0 a k = nπ/, mientras que los máximos locales de σ corresponden a los ceros de cot δ 0. Las resonancias, por definición, son los ceros con pendiente de cot δ 0 negativa (lo que hace que a) Γ, dada por la ecuación (5.1), sea positiva; b) la sección eficaz presente una forma de Breit-Wigner a la correspondiente energía; y c) la amplitud de dispersión presente un polo). Los ceros con pendiente positiva, que no generan polos en la amplitud de dispersión y no son resonancias, corresponden a las soluciones (I) de (2.1). 4 Este modelo proporciona un laboratorio teórico simple para entender fenómenos como la interacción de electrones libres con las capas electrónicas en orbital S de gases nobles, o la dispersión de núcleos atómicos con capas cerradas; de hecho, no es casual que la estructura de la serie de resonancias recuerde la de las líneas que aparecen en espectroscopía atómica. Es notable que sea posible generar una estructura tan rica con un potencial que depende sólo de dos parámetros, γ y. La sección 4.4(c) del libro de Gottfried y Yan contiene una discusión mucho más detallada de este problema, con algunas pequeñas diferencias técnicas debidas a que los autores consideran la versión en una dimensión (que por otra parte es totalmente equivalente al sector en onda S del problema tridimensional). 4 La fuerte dependencia de la energía de cot δ 0 cerca de k = nπ/, donde pasa de anularse a divergir en un intervalo pequeño, se ve explícitamente en la ecuación (5.4): la derivada de la cotangente es proporcional a (γ) 2 1. Como se mencionó anteriormente, esta estructura complicada de cot δ 0 hace que el análisis de las resonancias sea delicado. En este sentido, la identificación no ambigua de las resonancias a partir de los polos de la amplitud evita el farragoso trabajo de estudiar todos los ceros de cot δ 0 y el signo de la pendiente en los mismos cerca de una divergencia. 8
Para ilustrar las ideas básicas, supongamos un ejemplo simple de potencial
 Mecánica Cuántica Avanzada Carlos Pena 5-5. Resonancias. [Ros XVI.5, Sak 7.7-8, Ynd.7] Motivación El concepto de resonancia es una pieza clave en el uso de los procesos de dispersión cuántica para el estudio
Mecánica Cuántica Avanzada Carlos Pena 5-5. Resonancias. [Ros XVI.5, Sak 7.7-8, Ynd.7] Motivación El concepto de resonancia es una pieza clave en el uso de los procesos de dispersión cuántica para el estudio
9. Observables de dispersión en el formalismo de matriz S.
 Mecánica Cuántica Avanzada Carlos Pena 9-9. Observables de dispersión en el formalismo de matriz S. [Ros XI.7, Sch 8.2, Ynd 22.3] Probabilidades de transición: regla de oro de Fermi generalizada En términos
Mecánica Cuántica Avanzada Carlos Pena 9-9. Observables de dispersión en el formalismo de matriz S. [Ros XI.7, Sch 8.2, Ynd 22.3] Probabilidades de transición: regla de oro de Fermi generalizada En términos
Mecánica cuántica avanzada - Curso 2011/2012 Problemas - Hoja 2: Teoría de colisiones
 UNIVERSIDAD COMPLUTENSE DE MADRID DEPARTAMENTO DE FÍSICA TEÓRICA I Mecánica cuántica avanzada - Curso 11/1 Problemas - Hoja : Teoría de colisiones 1. Se considera el potencial V (r) = V e αr, donde V y
UNIVERSIDAD COMPLUTENSE DE MADRID DEPARTAMENTO DE FÍSICA TEÓRICA I Mecánica cuántica avanzada - Curso 11/1 Problemas - Hoja : Teoría de colisiones 1. Se considera el potencial V (r) = V e αr, donde V y
21. Efecto fotoeléctrico.
 Mecánica Cuántica Avanzada Carlos Pena 21-1 21. Efecto fotoeléctrico. [Ynd 22.6; premio Nobel 1921 (Einstein)] Concepto. Ionización del hidrógeno. Se llama efecto fotoeléctrico a la emisión de electrones
Mecánica Cuántica Avanzada Carlos Pena 21-1 21. Efecto fotoeléctrico. [Ynd 22.6; premio Nobel 1921 (Einstein)] Concepto. Ionización del hidrógeno. Se llama efecto fotoeléctrico a la emisión de electrones
CAPÍTULO 6 CONCLUSIONES GENERALES
 CAPÍTULO 6: CONCLUSIONES GENERALES 66 CAPÍTULO 6 CONCLUSIONES GENERALES 6. Resumen Esta última parte tiene como objetivo buscar puntos de convergencia entre los métodos antes usados, así como dar un breve
CAPÍTULO 6: CONCLUSIONES GENERALES 66 CAPÍTULO 6 CONCLUSIONES GENERALES 6. Resumen Esta última parte tiene como objetivo buscar puntos de convergencia entre los métodos antes usados, así como dar un breve
Tema 4. Oscilaciones pequeñas
 Mecánica teórica Tema 4. Oscilaciones pequeñas Tema 4A Universidad de Sevilla - Facultad de Física cotrino@us.es 24 de octubre de 2017 Tema 4A (Grupo 2) Mecánica Teórica (2017-2018) 24 de octubre de 2017
Mecánica teórica Tema 4. Oscilaciones pequeñas Tema 4A Universidad de Sevilla - Facultad de Física cotrino@us.es 24 de octubre de 2017 Tema 4A (Grupo 2) Mecánica Teórica (2017-2018) 24 de octubre de 2017
La producción de acero en Monterrey N.L. (México) en millones de toneladas, durante el año de 1992 a partir del mes de enero se muestra en la tabla:
 El objetivo al estudiar el concepto razón de cambio, es analizar tanto cuantitativa como cualitativamente las razones de cambio instantáneo y promedio de un fenómeno, lo cual nos permite dar solución a
El objetivo al estudiar el concepto razón de cambio, es analizar tanto cuantitativa como cualitativamente las razones de cambio instantáneo y promedio de un fenómeno, lo cual nos permite dar solución a
20. Absorción y emisión estimulada de fotones por electrones ligados. Coeficientes de Einstein.
 Mecánica Cuántica Avanzada Carlos Pena 20-1 20. Absorción y emisión estimulada de fotones por electrones ligados. Coeficientes de Einstein. [Gre 2.1,2.3; passim] Absorción de fotones en un átomo El proceso
Mecánica Cuántica Avanzada Carlos Pena 20-1 20. Absorción y emisión estimulada de fotones por electrones ligados. Coeficientes de Einstein. [Gre 2.1,2.3; passim] Absorción de fotones en un átomo El proceso
XI. COMPENSACIÓN UTILIZANDO EL LUGAR GEOMÉTRICO DE LAS RAÍCES
 XI. COMPENSACIÓN UTILIZANDO EL LUGAR GEOMÉTRICO DE LAS RAÍCES El lugar geométrico de las raíces representa la ubicación de las raíces de la ecuación característica a lazo cerrado cuando se varía un parámetro
XI. COMPENSACIÓN UTILIZANDO EL LUGAR GEOMÉTRICO DE LAS RAÍCES El lugar geométrico de las raíces representa la ubicación de las raíces de la ecuación característica a lazo cerrado cuando se varía un parámetro
Departamento de Ingenierías Eléctrica y Electrónica Universidad del Norte
 christianq@uninorte.edu.co Departamento de Ingenierías Eléctrica y Electrónica Universidad del Norte Ejemplo: Considere el sistema de la figura: G(s) tiene un par de polos complejos conjugados en s = 1
christianq@uninorte.edu.co Departamento de Ingenierías Eléctrica y Electrónica Universidad del Norte Ejemplo: Considere el sistema de la figura: G(s) tiene un par de polos complejos conjugados en s = 1
Integral de Fourier y espectros continuos
 9 2 2 2 Esta expresión se denomina forma de Angulo fase (o forma armónica) de la serie de Fourier. Integral de Fourier y espectros continuos Las series de Fourier son una herramienta útil para representar
9 2 2 2 Esta expresión se denomina forma de Angulo fase (o forma armónica) de la serie de Fourier. Integral de Fourier y espectros continuos Las series de Fourier son una herramienta útil para representar
OBJETIVO FUNDAMENTACIÓN. Medida de la permitividad dieléctrica compleja del agua y del alcohol.
 Laboratorio_Electromagnetismo Medida de la Permitividad Dieléctrica de Líquidos Polares Francisco Camarena Femenía Miguel Ángel Ballesteros Velasco OBJETIVO Medida de la permitividad dieléctrica compleja
Laboratorio_Electromagnetismo Medida de la Permitividad Dieléctrica de Líquidos Polares Francisco Camarena Femenía Miguel Ángel Ballesteros Velasco OBJETIVO Medida de la permitividad dieléctrica compleja
Teóricas de Análisis Matemático (28) - Práctica 8 - Polinomio de Taylor
 Práctica 8 Polinomio de Taylor. Polinomio de Taylor El análisis completo de una función puede resultar muy difícil. Una forma de abordar este problema es aproximar la función por una más sencilla. En este
Práctica 8 Polinomio de Taylor. Polinomio de Taylor El análisis completo de una función puede resultar muy difícil. Una forma de abordar este problema es aproximar la función por una más sencilla. En este
1 Separación de fases en el fluido de van der Waals
 1 Separación de fases en el fluido de van der Waals La energía libre de van der Waals está dada por [ ( ) ] V Nb F (N, V, ) = N ln + 1 an N Nλ 3 V. (1) donde λ = h/ πm es la longitud de onda de Broglie.
1 Separación de fases en el fluido de van der Waals La energía libre de van der Waals está dada por [ ( ) ] V Nb F (N, V, ) = N ln + 1 an N Nλ 3 V. (1) donde λ = h/ πm es la longitud de onda de Broglie.
SECO 2014-V ([1, 2, 3, 4])
![SECO 2014-V ([1, 2, 3, 4]) SECO 2014-V ([1, 2, 3, 4])](/thumbs/55/36666723.jpg) SECO 214-V ([1, 2, 3, 4]) Félix Monasterio-Huelin y Álvaro Gutiérrez 2 de mayo de 214 Índice Índice 19 Índice de Figuras 19 Índice de Tablas 11 26.Lugar de Raíces: Introducción 111 26.1. Ejemplo de semiasíntotas
SECO 214-V ([1, 2, 3, 4]) Félix Monasterio-Huelin y Álvaro Gutiérrez 2 de mayo de 214 Índice Índice 19 Índice de Figuras 19 Índice de Tablas 11 26.Lugar de Raíces: Introducción 111 26.1. Ejemplo de semiasíntotas
Los pasos que se dan son:
 Hasta ahora hemos admitido que podemos trabajar con la red de cores de nuestro sólido usando una aproximación clásica lo que nos ha permitido determinar los «modos normales de vibración» en el sentido
Hasta ahora hemos admitido que podemos trabajar con la red de cores de nuestro sólido usando una aproximación clásica lo que nos ha permitido determinar los «modos normales de vibración» en el sentido
UNIVERSIDAD CENTRAL DEL ECUADOR FACULTAD DE CIENCIAS QUÍMICAS FUNDAMENTOS DE LA ESPECTROSCOPIA
 Integrantes: Ipiales Gabriela Química de Alimentos Olmos Wendy Química Farmacéutica Día: Miércoles 9-11 Fecha: 05/07/2011 DEFINICIÓN DE ORBITALES ATÓMICOS Un orbital atómico representa una región del espacio
Integrantes: Ipiales Gabriela Química de Alimentos Olmos Wendy Química Farmacéutica Día: Miércoles 9-11 Fecha: 05/07/2011 DEFINICIÓN DE ORBITALES ATÓMICOS Un orbital atómico representa una región del espacio
Capítulo I Óptica lineal, no-lineal y generación de segundo armónico
 Capítulo I Óptica lineal, no-lineal y generación de segundo armónico 1.1 Óptica lineal La óptica es la rama de la física que estudia el comportamiento de luz y su interacción con la materia, la cual la
Capítulo I Óptica lineal, no-lineal y generación de segundo armónico 1.1 Óptica lineal La óptica es la rama de la física que estudia el comportamiento de luz y su interacción con la materia, la cual la
PROBLEMAS FISICA III- Hoja 5
 PROBLEMAS FISICA III- Hoja 5 Problema 1 Una onda es de la forma y = Acos(2πx/λ + π/3) para x < 0. Sabemos que para x > 0 su longitud de onda se reduce a la mitad.aplicando requisitos de continuidad en
PROBLEMAS FISICA III- Hoja 5 Problema 1 Una onda es de la forma y = Acos(2πx/λ + π/3) para x < 0. Sabemos que para x > 0 su longitud de onda se reduce a la mitad.aplicando requisitos de continuidad en
TI 89. Cómo sobrevivir en Precálculo
 TI 89 Cómo sobrevivir en Precálculo TI-89 Menús que más utilizaremos: Operaciones Numéricas Simplificar: 3 + 1 5 ( 4)2 9 3 4 Notar la diferencia entre el símbolo de resta y el signo negativo. Notar el
TI 89 Cómo sobrevivir en Precálculo TI-89 Menús que más utilizaremos: Operaciones Numéricas Simplificar: 3 + 1 5 ( 4)2 9 3 4 Notar la diferencia entre el símbolo de resta y el signo negativo. Notar el
Serie de problemas para el curso. Química Cuantica I
 erie de problemas para el curso Química Cuantica I Matemáticas Tema Resuelva todos los problemas del capítulo de la referencia B6 y compare sus resultados con las soluciones que se incluyen al final de
erie de problemas para el curso Química Cuantica I Matemáticas Tema Resuelva todos los problemas del capítulo de la referencia B6 y compare sus resultados con las soluciones que se incluyen al final de
2 Ecuaciones Algebraicas y Trascendentes
 2 Ecuaciones Algebraicas y Trascendentes 2.1 Introducción Las sucesiones asintóticas son una herramienta usada en el análisis de las soluciones de problemas que surgen en la Teoría de Perturbaciones. En
2 Ecuaciones Algebraicas y Trascendentes 2.1 Introducción Las sucesiones asintóticas son una herramienta usada en el análisis de las soluciones de problemas que surgen en la Teoría de Perturbaciones. En
Física Estadística. A entregar: Viernes 25 de febrero de 2011.
 Física Estadística A entregar: Viernes 25 de febrero de 2011. Prob. 4. El caminante al azar... o borracho Suponga un borracho que acaba de salir de una cantina y que sólo puede caminar hacia su derecha
Física Estadística A entregar: Viernes 25 de febrero de 2011. Prob. 4. El caminante al azar... o borracho Suponga un borracho que acaba de salir de una cantina y que sólo puede caminar hacia su derecha
Física del Estado Sólido Práctico 2 Red Recíproca y Difracción de Rayos X
 Física del Estado Sólido Práctico Red Recíproca y Difracción de Rayos X 1. Considere una red de Bravais con los tres vectores primitivos { a 1, a, a 3 } (figura 1). Un plano de una red cristalina queda
Física del Estado Sólido Práctico Red Recíproca y Difracción de Rayos X 1. Considere una red de Bravais con los tres vectores primitivos { a 1, a, a 3 } (figura 1). Un plano de una red cristalina queda
Un i d a d 5. d i fe r e n C i a L es d e o r d e n s U pe r i o r. Objetivos. Al inalizar la unidad, el alumno:
 Un i d a d 5 má x i m o s, mínimos y d i fe r e n C i a L es d e o r d e n s U pe r i o r Objetivos Al inalizar la unidad, el alumno: Identificará los puntos críticos, máximos y mínimos absolutos y relativos
Un i d a d 5 má x i m o s, mínimos y d i fe r e n C i a L es d e o r d e n s U pe r i o r Objetivos Al inalizar la unidad, el alumno: Identificará los puntos críticos, máximos y mínimos absolutos y relativos
6.1. Condición de magnitud y ángulo
 Capítulo 6 Lugar de las raíces La respuesta transitoria de un sistema en lazo cerrado, está ligada con la ubicación de los polos de lazo cerrado en el plano complejo S. Si el sistema tiene una ganancia
Capítulo 6 Lugar de las raíces La respuesta transitoria de un sistema en lazo cerrado, está ligada con la ubicación de los polos de lazo cerrado en el plano complejo S. Si el sistema tiene una ganancia
2. Obtener la posicion x desde la que se ha emitido la señal Resp : :::::::::::::
 EXAMEN 2 o PARCIAL DE MECANICA Y ONDAS (Teoria) 6 Julio de 2005 _ Apellidos: Nombre: Grupo: _ Instrucciones : Cada cuestión se puntuará con 10=14 puntos, si la respuesta es completamente correcta. Y entre
EXAMEN 2 o PARCIAL DE MECANICA Y ONDAS (Teoria) 6 Julio de 2005 _ Apellidos: Nombre: Grupo: _ Instrucciones : Cada cuestión se puntuará con 10=14 puntos, si la respuesta es completamente correcta. Y entre
MDOF. Dinámica Estructural Aplicada II C 2012 UCA
 MDOF Dinámica Estructural Aplicada II C 2012 UCA Desde el punto de vista dinámico, interesan los grados de libertad en los que se generan fuerzas generalizadas de inercia significativas; es decir, fuerzas
MDOF Dinámica Estructural Aplicada II C 2012 UCA Desde el punto de vista dinámico, interesan los grados de libertad en los que se generan fuerzas generalizadas de inercia significativas; es decir, fuerzas
FIZ Física Contemporánea
 FIZ1111 - Física Contemporánea Interrogación N o 2 13 de Mayo de 2008, 18 a 20 hs Nombre completo: hrulefill Sección: centering Buenas Malas Blancas Nota Table 1. Instrucciones - Marque con X el casillero
FIZ1111 - Física Contemporánea Interrogación N o 2 13 de Mayo de 2008, 18 a 20 hs Nombre completo: hrulefill Sección: centering Buenas Malas Blancas Nota Table 1. Instrucciones - Marque con X el casillero
Resolución de la ecuación de Schrödinger monodimensional
 Resolución de la ecuación de Schrödinger monodimensional I. FUNDAMENTO TEÓRICO En Mecánica cuántica, el estado físico de un sistema unidimensional de una partícula viene descrito completamente por una
Resolución de la ecuación de Schrödinger monodimensional I. FUNDAMENTO TEÓRICO En Mecánica cuántica, el estado físico de un sistema unidimensional de una partícula viene descrito completamente por una
7.- Teorema integral de Fourier. Transformada de Fourier
 7.- Teorema integral de Fourier. Transformada de Fourier a) Introducción. b) Transformada de Fourier. c) Teorema integral de Fourier. d) Propiedades de la Transformada de Fourier. e) Teorema de Convolución.
7.- Teorema integral de Fourier. Transformada de Fourier a) Introducción. b) Transformada de Fourier. c) Teorema integral de Fourier. d) Propiedades de la Transformada de Fourier. e) Teorema de Convolución.
Pozos y Barreras en Mecánica Cuántica: Retraso
 Pozos y Barreras en Mecánica Cuántica: Retraso Temporal Alfonso Isaac Jaimes Nájera Cinvestav 10 de diciembre de 2012 Alfonso Isaac Jaimes Nájera (Cinvestav) Pozos y Barreras: Retraso Temporal 10 de diciembre
Pozos y Barreras en Mecánica Cuántica: Retraso Temporal Alfonso Isaac Jaimes Nájera Cinvestav 10 de diciembre de 2012 Alfonso Isaac Jaimes Nájera (Cinvestav) Pozos y Barreras: Retraso Temporal 10 de diciembre
TEMA 6: GEOMETRÍA ANALÍTICA EN EL PLANO
 Alonso Fernández Galián Tema 6: Geometría analítica en el plano TEMA 6: GEOMETRÍA ANALÍTICA EN EL PLANO La geometría analítica es el estudio de objetos geométricos (rectas, circunferencias, ) por medio
Alonso Fernández Galián Tema 6: Geometría analítica en el plano TEMA 6: GEOMETRÍA ANALÍTICA EN EL PLANO La geometría analítica es el estudio de objetos geométricos (rectas, circunferencias, ) por medio
Últimas notas de SVD
 Últimas notas de SVD MAT-251 Dr. CIMAT A.C. e-mail: alram@cimat.mx web: http://www.cimat.mx/~alram/met_num/ Dr. Salvador Botello CIMAT A.C. e-mail: botello@cimat.mx Relación entre los valores singulares
Últimas notas de SVD MAT-251 Dr. CIMAT A.C. e-mail: alram@cimat.mx web: http://www.cimat.mx/~alram/met_num/ Dr. Salvador Botello CIMAT A.C. e-mail: botello@cimat.mx Relación entre los valores singulares
1. Método del Lugar de las Raíces
 . Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA... 3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES... 0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
. Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA... 3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES... 0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
5. Propagación en un cristal fotónico unidimensional
 5. Propagación en un cristal fotónico unidimensional En este capítulo analizamos la evolución de una onda electromagnética al propagarse a través de un cristal fotónico unidimensional de longitud finita
5. Propagación en un cristal fotónico unidimensional En este capítulo analizamos la evolución de una onda electromagnética al propagarse a través de un cristal fotónico unidimensional de longitud finita
1. Método del Lugar de las Raíces
 . Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA...3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES...0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
. Método del Lugar de las Raíces. MÉTODO DEL LUGAR DE LAS RAÍCES..... IDEA BÁSICA...3.. LUGAR DE LAS RAÍCES DE SISTEMAS SIMPLES...0.3. LUGAR DE GANANCIA CONSTANTE....4. REGLAS PARA LA CONSTRUCCIÓN DEL
7.- Teorema integral de Fourier. Transformada de Fourier
 7.- Teorema integral de Fourier. Transformada de Fourier a) Introducción. b) Transformada de Fourier. c) Teorema integral de Fourier. d) Propiedades de la Transformada de Fourier. e) Teorema de Convolución.
7.- Teorema integral de Fourier. Transformada de Fourier a) Introducción. b) Transformada de Fourier. c) Teorema integral de Fourier. d) Propiedades de la Transformada de Fourier. e) Teorema de Convolución.
Hoja de Problemas 4. Mecánica Cuántica II.
 Hoja de Problemas 4. Mecánica Cuántica II. Fundamentos de Física III. Grado en Física. Curso 15/16. Grupo 516. UAM. 9-3-16 Problema 1 Una partícula de masa m y energía total cero se encuentra en una región
Hoja de Problemas 4. Mecánica Cuántica II. Fundamentos de Física III. Grado en Física. Curso 15/16. Grupo 516. UAM. 9-3-16 Problema 1 Una partícula de masa m y energía total cero se encuentra en una región
1. Propagación de ondas en los sólidos. 2. Interacción de los sólidos iónicos con la radiación IR 3. Calor específico. 4. Temperatura de fusión.
 La aproximación armónica ha permitido predecir alguno de los comportamientos característicos de los sólidos. En los apartados previos hemos visto que esta aproximación permite entender fenómenos como:
La aproximación armónica ha permitido predecir alguno de los comportamientos característicos de los sólidos. En los apartados previos hemos visto que esta aproximación permite entender fenómenos como:
Fundamentos de Espectroscopía Prof. Jesús Hernández Trujillo Fac. Química, UNAM
 Fundamentos de Espectroscopía Prof. Jesús Hernández Trujillo Fac. Química, UNAM Se utiliza el potencial de Morse para describir la interacción entre los átomos en una molécula diatómica. Las gráficas que
Fundamentos de Espectroscopía Prof. Jesús Hernández Trujillo Fac. Química, UNAM Se utiliza el potencial de Morse para describir la interacción entre los átomos en una molécula diatómica. Las gráficas que
Fundamentos Físicos de la Ingeniería. Ingeniería Industrial. Prácticas de Laboratorio
 Fundamentos Físicos de la Ingeniería Ingeniería Industrial Prácticas de Laboratorio Práctica 16 Ley de Hooke 1 Objetivos El objetivo fundamental de esta práctica es medir la constante elástica de un muelle.
Fundamentos Físicos de la Ingeniería Ingeniería Industrial Prácticas de Laboratorio Práctica 16 Ley de Hooke 1 Objetivos El objetivo fundamental de esta práctica es medir la constante elástica de un muelle.
Práctica Nº 7: Red de difracción
 Práctica Nº 7: Red de difracción 1.- INTRODUCCIÓN. INTERFERENCIA o DIFRACCIÓN? Desde el punto de vista físico ambos fenómenos son equivalentes. En general se utiliza el término INTERFERENCIA, para designar
Práctica Nº 7: Red de difracción 1.- INTRODUCCIÓN. INTERFERENCIA o DIFRACCIÓN? Desde el punto de vista físico ambos fenómenos son equivalentes. En general se utiliza el término INTERFERENCIA, para designar
Problemas de Partículas 2011
 Problemas de Partículas 2011 Serie 1 1. Se acelera un protón en un acelerador lineal a 0.5 GV. Calcular la longitud de onda asociada al mismo utilizando el sistema de unidades naturales. cuánto valdrá
Problemas de Partículas 2011 Serie 1 1. Se acelera un protón en un acelerador lineal a 0.5 GV. Calcular la longitud de onda asociada al mismo utilizando el sistema de unidades naturales. cuánto valdrá
Movimiento Browniano Comentarios históricos
 Capítulo 2 Movimiento Browniano En este capítulo presentamos los conceptos básicos asociados al movimiento Browniano. Estos conceptos van a ser útiles para el desarrollo de los capítulos posteriores. 2.1.
Capítulo 2 Movimiento Browniano En este capítulo presentamos los conceptos básicos asociados al movimiento Browniano. Estos conceptos van a ser útiles para el desarrollo de los capítulos posteriores. 2.1.
LA PUNTUACIÓN DE LA PRUEBA SERÁ LA SIGUIENTE: Números... 3 puntos. BLOQUE II El lenguaje algebraico,ecuaciones y sistemas...
 TERCERO DE E.S.O. MATEMÁTICAS ACADÉMICAS BLOQUE I. NÚMEROS. U. D. 1. NÚMEROS RACIONALES. 1.1. Repaso de números naturales y enteros. 1.2. Introducción al número fraccionario como parte de la unidad. 1.3.
TERCERO DE E.S.O. MATEMÁTICAS ACADÉMICAS BLOQUE I. NÚMEROS. U. D. 1. NÚMEROS RACIONALES. 1.1. Repaso de números naturales y enteros. 1.2. Introducción al número fraccionario como parte de la unidad. 1.3.
Funciones de varias variables
 Tema 5 Funciones de varias variables 5.1. Introducción Supongamos que tenemos una placa rectangular R y necesitamos conocer la temperatura T en cada uno de sus puntos. T es una función que depende de las
Tema 5 Funciones de varias variables 5.1. Introducción Supongamos que tenemos una placa rectangular R y necesitamos conocer la temperatura T en cada uno de sus puntos. T es una función que depende de las
PRIMERA PARTE. F roz 1 K Ms
 Universidad de Navarra Nafarroako Unibertsitatea Escuela Superior de Ingenieros Ingeniarien Goi Mailako Eskola ASIGNATURA GAIA Ingeniería de Control I 4º NOMBRE IZENA CURSO KURTSOA FECHA DATA 6 de septiembre
Universidad de Navarra Nafarroako Unibertsitatea Escuela Superior de Ingenieros Ingeniarien Goi Mailako Eskola ASIGNATURA GAIA Ingeniería de Control I 4º NOMBRE IZENA CURSO KURTSOA FECHA DATA 6 de septiembre
LEY DE HOOKE: CONSTANTE ELÁSTICA DE UN MUELLE
 Grupo de prácticas Fecha de sesión Departamento de Física Laboratorio Mecánica Alumnos que realizaron la práctica Sello de control Fecha de entrega LEY DE HOOKE: CONSTANTE ELÁSTICA DE UN MUELLE IMPORTANTE:
Grupo de prácticas Fecha de sesión Departamento de Física Laboratorio Mecánica Alumnos que realizaron la práctica Sello de control Fecha de entrega LEY DE HOOKE: CONSTANTE ELÁSTICA DE UN MUELLE IMPORTANTE:
1. INTRODUCCIÓN A LA COMPUTACIÓN NUMÉRICA: Segunda parte: Teoría de Errores
 1. INTRODUCCIÓN A LA COMPUTACIÓN NUMÉRICA: Segunda parte: Teoría de Errores Jorge Eduardo Ortiz Triviño jeortizt@unal.edu.co http://www.docentes.unal.edu.co/jeortizt/ Objetivos de la sección Exponer los
1. INTRODUCCIÓN A LA COMPUTACIÓN NUMÉRICA: Segunda parte: Teoría de Errores Jorge Eduardo Ortiz Triviño jeortizt@unal.edu.co http://www.docentes.unal.edu.co/jeortizt/ Objetivos de la sección Exponer los
1.- Álgebra de números complejos.
 .- Álgebra de números complejos. a) Definición y representación geométrica. b) Sumas y productos de números complejos. c) Vectores y módulos en el plano complejo. d) Representación en forma exponencial.
.- Álgebra de números complejos. a) Definición y representación geométrica. b) Sumas y productos de números complejos. c) Vectores y módulos en el plano complejo. d) Representación en forma exponencial.
Introducción. Flujo Eléctrico.
 Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
Introducción La descripción cualitativa del campo eléctrico mediante las líneas de fuerza, está relacionada con una ecuación matemática llamada Ley de Gauss, que relaciona el campo eléctrico sobre una
7. Formalismo de matriz S: generalidades.
 Mecánica Cuántica Avanzada Carlos Pena 7-1 7. Formalismo de matriz S: generalidades. [Ros XVI.7, Ynd 22.2] Motivación El formalismo visto hasta ahora es aplicable, en su mayor parte, a la dispersión elástica
Mecánica Cuántica Avanzada Carlos Pena 7-1 7. Formalismo de matriz S: generalidades. [Ros XVI.7, Ynd 22.2] Motivación El formalismo visto hasta ahora es aplicable, en su mayor parte, a la dispersión elástica
DESCRIPCIÓN DEL PRINCIPIO BÁSICO
 TEMA 4. MÉTODO DE LOCALIZACIÓN DE LAS RAÍCES CONTENIDO DESCRIPCIÓN DEL PRINCIPIO BÁSICO LOCALIZACIÓN DE LAS RAÍCES REGLAS PARA DIBUJAR LA LOCALIZACIÓN DE LAS RAÍCES DE EVANS CONSTRUCCIÓN TÍPICA DE ADELANTO
TEMA 4. MÉTODO DE LOCALIZACIÓN DE LAS RAÍCES CONTENIDO DESCRIPCIÓN DEL PRINCIPIO BÁSICO LOCALIZACIÓN DE LAS RAÍCES REGLAS PARA DIBUJAR LA LOCALIZACIÓN DE LAS RAÍCES DE EVANS CONSTRUCCIÓN TÍPICA DE ADELANTO
19. Interacción de fotones con partículas cargadas. Desintegración de niveles atómicos.
 Mecánica Cuántica Avanzada Carlos Pena 19-1 19. Interacción de fotones con partículas cargadas. Desintegración de niveles atómicos. [Ynd 0.5, Gre.1-] Interacción radiación materia no relativista Acoplamiento
Mecánica Cuántica Avanzada Carlos Pena 19-1 19. Interacción de fotones con partículas cargadas. Desintegración de niveles atómicos. [Ynd 0.5, Gre.1-] Interacción radiación materia no relativista Acoplamiento
1.5 Construcción de funcionales Método de Rayleigh-Ritz para la aproximación de funcionales
 .5.8. Método de Rayleigh-Ritz para la aproximación de funcionales La idea de este método consiste en que al buscar el extremo de un funcional: () = ( ) considerando sólo las combinaciones lineales posibles
.5.8. Método de Rayleigh-Ritz para la aproximación de funcionales La idea de este método consiste en que al buscar el extremo de un funcional: () = ( ) considerando sólo las combinaciones lineales posibles
Física y Química 1º Bachillerato LOMCE. Bloque 3: Trabajo y Energía. Trabajo y Energía
 Física y Química 1º Bachillerato LOMCE Bloque 3: Trabajo y Energía Trabajo y Energía 1 El Trabajo Mecánico El trabajo mecánico, realizado por una fuerza que actúa sobre un cuerpo que experimenta un desplazamiento,
Física y Química 1º Bachillerato LOMCE Bloque 3: Trabajo y Energía Trabajo y Energía 1 El Trabajo Mecánico El trabajo mecánico, realizado por una fuerza que actúa sobre un cuerpo que experimenta un desplazamiento,
Profesorado de Nivel Medio y Superior en Biología Matemática - 1º Cuatrimestre Año 2013 FUNCIÓN CUADRÁTICA
 Matemática - º Cuatrimestre Año 0 FUNCIÓN CUADRÁTICA Hemos definido anteriormente la función lineal como una función f: R R de la forma f()a+b con a R y b R, que se representa en el plano mediante una
Matemática - º Cuatrimestre Año 0 FUNCIÓN CUADRÁTICA Hemos definido anteriormente la función lineal como una función f: R R de la forma f()a+b con a R y b R, que se representa en el plano mediante una
2.2 Rectas en el plano
 2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
2.2 Al igual que ocurre con el punto, en geometría intrínseca, el concepto de recta no tiene definición, sino que constituye otro de sus conceptos iniciales, indefinibles. Desde luego se trata de un conjunto
ÍNDICE El movimiento del péndulo físico Objetivos Objetivos parciales. Hitos... 2
 ÍNDICE 1 Proyectos de Computación Algunos ejemplos de posibles proyectos para la asignatura de Computación. Los objetivos nales y parciales se indican a modo de ejemplo y se pueden redenir, modicar etc.
ÍNDICE 1 Proyectos de Computación Algunos ejemplos de posibles proyectos para la asignatura de Computación. Los objetivos nales y parciales se indican a modo de ejemplo y se pueden redenir, modicar etc.
CAPÍTULO. 7 Métodos numéricos
 CAPÍTULO 7 Métodos numéricos 7.3 Método de Euler mejorado Consideremos ahora el polinomio de Taylor de orden de y.x/ en x D x 0 para aproximar a la solución del PVI y 0 D f.x; y/, con y.x 0 / D y 0. Esta
CAPÍTULO 7 Métodos numéricos 7.3 Método de Euler mejorado Consideremos ahora el polinomio de Taylor de orden de y.x/ en x D x 0 para aproximar a la solución del PVI y 0 D f.x; y/, con y.x 0 / D y 0. Esta
ε = = d σ (2) I. INTRODUCCIÓN
 Estudio del comportamiento de un material piezoeléctrico en un campo eléctrico alterno. Eduardo Misael Honoré, Pablo Daniel Mininni Laboratorio - Dpto. de Física -FCEyN- UBA-996. Un material piezoeléctrico
Estudio del comportamiento de un material piezoeléctrico en un campo eléctrico alterno. Eduardo Misael Honoré, Pablo Daniel Mininni Laboratorio - Dpto. de Física -FCEyN- UBA-996. Un material piezoeléctrico
Tema 2 Resolución de EcuacionesNo Lineales
 Tema 2 Resolución de Ecuaciones No Lineales E.T.S.I. Informática Indice Introducción 1 Introducción 2 Algoritmo del método de Bisección Análisis del 3 4 5 6 Algoritmo de los métodos iterativos Interpretación
Tema 2 Resolución de Ecuaciones No Lineales E.T.S.I. Informática Indice Introducción 1 Introducción 2 Algoritmo del método de Bisección Análisis del 3 4 5 6 Algoritmo de los métodos iterativos Interpretación
Raíz cuadrada. Superficies de Riemann
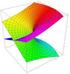 Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
Raíz cuadrada Superficies de Riemann Aplicación: Circuito RLC (a) (b) Aplicación: Circuito RLC Para el circuito (a): De la ley de Ohm con Aplicación: Circuito RLC Es más conveniente utilizar un voltaje
Cálculo Numérico (0258) TEMA 6 SOLUCIÓN NUMÉRICA DE ECUACIONES DIFERENCIALES ORDINARIAS. Semestre
 Cálculo Numérico (58) Semestre - TEMA 6 SOLUCIÓN NUMÉRICA DE ECUACIONES DIFERENCIALES ORDINARIAS Semestre - Septiembre U.C.V. F.I.U.C.V. CÁLCULO NUMÉRICO (58) - TEMA 6 Las notas presentadas a continuación
Cálculo Numérico (58) Semestre - TEMA 6 SOLUCIÓN NUMÉRICA DE ECUACIONES DIFERENCIALES ORDINARIAS Semestre - Septiembre U.C.V. F.I.U.C.V. CÁLCULO NUMÉRICO (58) - TEMA 6 Las notas presentadas a continuación
MECÁNICA CUÁNTICA AVANZADA 2013 Selección de problemas n.2
 MECÁNICA CUÁNTICA AVANZADA 2013 Selección de problemas n.2 I. Consolidación de conceptos y aplicaciones 1. Considérese una interacción de corto alcance entre dos partículas controlada por un parámetro
MECÁNICA CUÁNTICA AVANZADA 2013 Selección de problemas n.2 I. Consolidación de conceptos y aplicaciones 1. Considérese una interacción de corto alcance entre dos partículas controlada por un parámetro
4 Métodos analíticos para el cálculo de tensiones y deformaciones plásticas
 +3Δ =3 = 3( Δ) Ec. 3.10 Ahora bien, como una vez iniciada la plastificación debe cumplirse el criterio de Von Mises debido a la condición de consistencia, se tiene: = =0 = 3( Δ) 3( Δ) = 0 Ec. 3.11 Qué
+3Δ =3 = 3( Δ) Ec. 3.10 Ahora bien, como una vez iniciada la plastificación debe cumplirse el criterio de Von Mises debido a la condición de consistencia, se tiene: = =0 = 3( Δ) 3( Δ) = 0 Ec. 3.11 Qué
ECUACIONES EMPÍRICAS
 17 ECUACIONES EMPÍRICAS 1. OBJETIVOS 1.1 Determinar la ecuación empírica del periodo del péndulo simple 1. Desarrollar métodos gráficos analíticos para tener información del eperimento en estudio.. FUNDAMENTO
17 ECUACIONES EMPÍRICAS 1. OBJETIVOS 1.1 Determinar la ecuación empírica del periodo del péndulo simple 1. Desarrollar métodos gráficos analíticos para tener información del eperimento en estudio.. FUNDAMENTO
Problemas adicionales de Física Cuántica (2010/2011)
 Problemas adicionales de Física Cuántica (2010/2011) Mª del Rocío Calero Fernández-Cortés María Jesús Jiménez Donaire Ejercicio 3.- La potencia (en forma de ondas gravitacionales) emitida por un sistema
Problemas adicionales de Física Cuántica (2010/2011) Mª del Rocío Calero Fernández-Cortés María Jesús Jiménez Donaire Ejercicio 3.- La potencia (en forma de ondas gravitacionales) emitida por un sistema
22. Ecuaciones de onda relativistas: Klein-Gordon
 Mecánica Cuántica Avanzada Carlos Pena 22-1 22. Ecuaciones de onda relativistas: Klein-Gordon [Sch 5.1-2 Ecuaciones de onda relativistas En el momento actual tenemos dos formalismos cualitativamente diferentes,
Mecánica Cuántica Avanzada Carlos Pena 22-1 22. Ecuaciones de onda relativistas: Klein-Gordon [Sch 5.1-2 Ecuaciones de onda relativistas En el momento actual tenemos dos formalismos cualitativamente diferentes,
Capítulo 4. Introducción a la Formulación Lagrangiana y Hamiltoniana para Sistemas Continuos. 4.1 Transición de un sistema discreto a uno continúo
 Capítulo 4 Introducción a la Formulación Lagrangiana y Hamiltoniana para Sistemas Continuos Hay algunos problemas de la mecánica que implican sistemas continuos, como, el problema de un sólido elástico
Capítulo 4 Introducción a la Formulación Lagrangiana y Hamiltoniana para Sistemas Continuos Hay algunos problemas de la mecánica que implican sistemas continuos, como, el problema de un sólido elástico
Ecuaciones No-Lineales y raices polinomiales
 Universidad Nacional de Ingeniería Facultad de Ciencias Física Computacional CC063 Ecuaciones No-Lineales y raices polinomiales Prof: J. Solano 2012-I Introduccion En Física a menudo nos encontramos con
Universidad Nacional de Ingeniería Facultad de Ciencias Física Computacional CC063 Ecuaciones No-Lineales y raices polinomiales Prof: J. Solano 2012-I Introduccion En Física a menudo nos encontramos con
Solución a la Ecuación de Schrödinger para el Oscilador Armónico Cuántico.
 Hurtado Balcazar Diego Alejandro. Martínez Díaz José Rodrigo Alejandro. Méndez Díaz Francisco Antonio. Solución a la Ecuación de Schrödinger para el Oscilador Armónico Cuántico. Introducción. El movimiento
Hurtado Balcazar Diego Alejandro. Martínez Díaz José Rodrigo Alejandro. Méndez Díaz Francisco Antonio. Solución a la Ecuación de Schrödinger para el Oscilador Armónico Cuántico. Introducción. El movimiento
1 Método de la bisección. 1.1 Teorema de Bolzano Teorema 1.1 (Bolzano) Contenido
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 3: Solución aproximada de ecuaciones Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña
DEPARTAMENTO DE MATEMÁTICAS 1
 2.8. MATEMÁTICAS ACADÉMICAS 3º ESO: CONTENIDOS. Bloque 1. Contenidos comunes. Planificación del proceso de resolución de problemas: análisis de la situación, selección y relación entre los datos, selección
2.8. MATEMÁTICAS ACADÉMICAS 3º ESO: CONTENIDOS. Bloque 1. Contenidos comunes. Planificación del proceso de resolución de problemas: análisis de la situación, selección y relación entre los datos, selección
Electrodinámica 2 Soluciones a Exámen 1
 Electrodinámica 2 Soluciones a Exámen 1 José Andrés Sepúlveda Quiroz Facultad de Ciencias Universidad de Colima. 7 de marzo de 2009 1. Problemas del Exámen Primera Parcial Problema 1 Ondas TM y polarización.
Electrodinámica 2 Soluciones a Exámen 1 José Andrés Sepúlveda Quiroz Facultad de Ciencias Universidad de Colima. 7 de marzo de 2009 1. Problemas del Exámen Primera Parcial Problema 1 Ondas TM y polarización.
Mapa Curricular: Funciones y Modelos
 A.PR.11.2.1 Determina el dominio y el alcance de las funciones a partir de sus diferentes representaciones. A.PR.11.2.2 Identifica y aplica las relaciones entre los puntos importantes de una función (ceros,
A.PR.11.2.1 Determina el dominio y el alcance de las funciones a partir de sus diferentes representaciones. A.PR.11.2.2 Identifica y aplica las relaciones entre los puntos importantes de una función (ceros,
7. Forma de Lagrange para el polinomio interpolador. 9. Forma de Newton para el polinomio interpolador
 E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 2: Aproximación e interpolación Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Septiembre
E.T.S. Minas: Métodos Matemáticos Resumen y ejemplos Tema 2: Aproximación e interpolación Francisco Palacios Escuela Politécnica Superior de Ingeniería de Manresa Universidad Politécnica de Cataluña Septiembre
Estructura estelar estática
 Estructura estelar estática Introducción A lo largo de su existencia, una estrella se encuentra en un estado de equilibrio delicado. Pequeños cambios pueden provocar inestabilidades locales o globales.
Estructura estelar estática Introducción A lo largo de su existencia, una estrella se encuentra en un estado de equilibrio delicado. Pequeños cambios pueden provocar inestabilidades locales o globales.
VALOR MEDIO Y DESVIACION ESTANDAR DE UNA SERIE DE MEDIDAS. x 1, x 2, x 3,..., x N. La media aritmética de las N medidas (valor medio o promedio) será:
 VALOR MEDIO Y DESVIACION ESTANDAR DE UNA SERIE DE MEDIDAS Si medimos N veces la magnitud de interés obtendremos los N datos eperimentales: 1, 2, 3,..., N La media aritmética de las N medidas (valor medio
VALOR MEDIO Y DESVIACION ESTANDAR DE UNA SERIE DE MEDIDAS Si medimos N veces la magnitud de interés obtendremos los N datos eperimentales: 1, 2, 3,..., N La media aritmética de las N medidas (valor medio
Física del Estado Sólido I. Tema 2: Enlace y propiedades de los materiales
 Física del Estado Sólido I Tema : Enlace y propiedades de los materiales Tema : Enlace y propiedades de los materiales Introducción Qué interacción es responsable de la cohesión en los cristales? - La
Física del Estado Sólido I Tema : Enlace y propiedades de los materiales Tema : Enlace y propiedades de los materiales Introducción Qué interacción es responsable de la cohesión en los cristales? - La
D TL. Luna Tierra. P Q Luna Tierra
 Problema 1: El origen de la fuerza de marea a) Dibujamos en color rojo las fuerzas de atracción que ejerce la Luna sobre un objeto de masa m situado en los puntos P, Q y S, y en azul la fuerza sobre dicho
Problema 1: El origen de la fuerza de marea a) Dibujamos en color rojo las fuerzas de atracción que ejerce la Luna sobre un objeto de masa m situado en los puntos P, Q y S, y en azul la fuerza sobre dicho
Tema 2: Enlace y propiedades de los materiales
 En la mayoría de moléculas, los enlaces entre los átomos que las constituyen no es mediante la interacción coulombiana que hemos analizado en el caso del enlace iónico. Se necesita tener en cuenta el llamado
En la mayoría de moléculas, los enlaces entre los átomos que las constituyen no es mediante la interacción coulombiana que hemos analizado en el caso del enlace iónico. Se necesita tener en cuenta el llamado
Ecuaciones en Derivadas Parciales y Análisis Numérico
 Ecuaciones en Derivadas Parciales y Análisis Numérico Prácticas Capítulo 4. Series de Fourier. 4.1 Serie de Fourier Vamos a intentar representar algunas funciones por su serie de Fourier de senos. Tomamos
Ecuaciones en Derivadas Parciales y Análisis Numérico Prácticas Capítulo 4. Series de Fourier. 4.1 Serie de Fourier Vamos a intentar representar algunas funciones por su serie de Fourier de senos. Tomamos
Física 2º Bach. Ondas 10/12/04
 Física º Bach. Ondas 10/1/04 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [6 PTOS.] 1. Una partícula de 600 g oscila con M.A.S. Se toma como origen de tiempos el instante en que pasa por el origen
Física º Bach. Ondas 10/1/04 DEPARTAMENTO DE FÍSICA E QUÍMICA Problemas Nombre: [6 PTOS.] 1. Una partícula de 600 g oscila con M.A.S. Se toma como origen de tiempos el instante en que pasa por el origen
ÁTOMO ~ m NÚCLEO ~ mnucleón < m. MATERIA ~ 10-9 m. Átomo FÍSICA MATERIALES PARTÍCULAS
 ESTRUCTURA DE LA MATERIA Grupo D CURSO 20011 2012 EL NÚCLEO ATÓMICO DE QUÉ ESTÁN HECHAS LAS COSAS? MATERIA ~ 10-9 m Átomo FÍSICA MATERIALES ÁTOMO ~ 10-10 m NÚCLEO ~ 10-14 mnucleón < 10-15 m Electrón Protón
ESTRUCTURA DE LA MATERIA Grupo D CURSO 20011 2012 EL NÚCLEO ATÓMICO DE QUÉ ESTÁN HECHAS LAS COSAS? MATERIA ~ 10-9 m Átomo FÍSICA MATERIALES ÁTOMO ~ 10-10 m NÚCLEO ~ 10-14 mnucleón < 10-15 m Electrón Protón
Resolución de Ecuaciones No Lineales
 Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Métodos Computacionales Contenido 1 Introducción Introducción 2 Localización de Raíces Localización de Raíces 3 Métodos Iterativos
Facultad de Ingeniería Industrial Universidad Nacional Mayor de San Marcos Métodos Computacionales Contenido 1 Introducción Introducción 2 Localización de Raíces Localización de Raíces 3 Métodos Iterativos
MÀSTER UNIVERSITARI EN ENGINYERIA AERONÀUTICA SISTEMES DE RADIOFREQÜÈNCIA I COMUNICACIÓ LÍNEAS DE TRANSMISIÓN
 Miembros grupo: Lluís Amat Olóndriz, Valentín Valhondo Pascual Instrumental y equipos necesarios 1 generador de funciones 1 osciloscopio 1 T BNC 3 cables coaxiales: 1 corto y otro largo (12 m), ambos RG-58
Miembros grupo: Lluís Amat Olóndriz, Valentín Valhondo Pascual Instrumental y equipos necesarios 1 generador de funciones 1 osciloscopio 1 T BNC 3 cables coaxiales: 1 corto y otro largo (12 m), ambos RG-58
tiene por límite L cuando la variable independiente x tiende a x , y se nota por L, cuando al acercarnos todo lo que queramos a x lím( x
 UNIDAD 8: LÍMITES DE FUNCIONES. CONTINUIDAD. LÍMITE DE UNA FUNCIÓN Diremos que una función y f () tiene por ite L cuando la variable independiente tiende a, y se nota por f ( ) L, cuando al acercarnos
UNIDAD 8: LÍMITES DE FUNCIONES. CONTINUIDAD. LÍMITE DE UNA FUNCIÓN Diremos que una función y f () tiene por ite L cuando la variable independiente tiende a, y se nota por f ( ) L, cuando al acercarnos
Hoja de Problemas 5. Física Atómica.
 Hoja de Problemas 5. Física Atómica. Fundamentos de Física III. Grado en Física. Curso 25/26. Grupo 56. UAM. 3-3-26 Problema En 896 el astrónomo americano Edward Charles Pickering observó unas misteriosas
Hoja de Problemas 5. Física Atómica. Fundamentos de Física III. Grado en Física. Curso 25/26. Grupo 56. UAM. 3-3-26 Problema En 896 el astrónomo americano Edward Charles Pickering observó unas misteriosas
Series de Laurent. En la práctica, los coeficientes de una serie de Laurent se obtienen por métodos distintos a las expresiones integrales a n
 Series de Laurent En la práctica, los coeficientes de una serie de Laurent se obtienen por métodos distintos a las expresiones integrales a n y b n dadas anteriormente. Además se puede demostrar que la
Series de Laurent En la práctica, los coeficientes de una serie de Laurent se obtienen por métodos distintos a las expresiones integrales a n y b n dadas anteriormente. Además se puede demostrar que la
3º E.S.O. II.- ÁLGEBRA
 3º E.S.O. Se consideran mínimos exigibles para el tercer curso de E.S.O. todos los del segundo curso y los siguientes: I.- NÚMEROS Números racionales - Definir (no de forma rigurosa ) y distinguir los
3º E.S.O. Se consideran mínimos exigibles para el tercer curso de E.S.O. todos los del segundo curso y los siguientes: I.- NÚMEROS Números racionales - Definir (no de forma rigurosa ) y distinguir los
FUNCIONES ANALITICAS (Curso 2011) Práctica 7. Clase 1 - Desarrollo de Laurent - Clasificación de singularidades aisladas
 FUNCIONES ANALITICAS (Curso 2) Práctica 7 Clase - Desarrollo de Laurent - Clasificación de singularidades aisladas. Hallar los desarrollos de Laurent de + en > en las distintas coronas alrededor del origen
FUNCIONES ANALITICAS (Curso 2) Práctica 7 Clase - Desarrollo de Laurent - Clasificación de singularidades aisladas. Hallar los desarrollos de Laurent de + en > en las distintas coronas alrededor del origen
Física Ondas 10/11/06
 Física Ondas 10/11/06 I.E.S. Elviña DEPARTAMENTO DE FÍSICA E QUÍMICA Nombre Problemas [5 Ptos.] 1. Para el proyectil de la figura, calcula: (a) El vector velocidad con que se incrusta en el suelo. [1]
Física Ondas 10/11/06 I.E.S. Elviña DEPARTAMENTO DE FÍSICA E QUÍMICA Nombre Problemas [5 Ptos.] 1. Para el proyectil de la figura, calcula: (a) El vector velocidad con que se incrusta en el suelo. [1]
MATERIAL 06. TEMA: MÉTODOS ESPECTROSCÓPICOS DE ANÁLISIS
 MATERIAL 06. TEMA: MÉTODOS ESPECTROSCÓPICOS DE ANÁLISIS La espectroscopia es el estudio de las interacciones de las radiaciones electromagnéticas con la materia (átomos y moléculas). Los métodos analíticos
MATERIAL 06. TEMA: MÉTODOS ESPECTROSCÓPICOS DE ANÁLISIS La espectroscopia es el estudio de las interacciones de las radiaciones electromagnéticas con la materia (átomos y moléculas). Los métodos analíticos
UNIVERSIDAD NACIONAL DE EDUCACIÓN A DISTANCIA
 UNIVERSIDAD NACIONAL DE EDUCACIÓN A DISTANCIA NOMBRE... APELLIDOS... CALLE... POBLACIÓN... PROVINCIA...C.P... QUÍMICA CUÁNTICA PRUEBA DE EVALUACIÓN A DISTANCIA Número de expediente 09534 09534 Química
UNIVERSIDAD NACIONAL DE EDUCACIÓN A DISTANCIA NOMBRE... APELLIDOS... CALLE... POBLACIÓN... PROVINCIA...C.P... QUÍMICA CUÁNTICA PRUEBA DE EVALUACIÓN A DISTANCIA Número de expediente 09534 09534 Química
CRITERIOS DE EVALUACIÓN DE 4º ESO- Opción B
 CRITERIOS DE EVALUACIÓN DE 4º ESO- Opción B 1. Resolver problemas relacionados con la vida diaria y otras materias del ámbito académico utilizando los distintos tipos de números y operaciones, junto con
CRITERIOS DE EVALUACIÓN DE 4º ESO- Opción B 1. Resolver problemas relacionados con la vida diaria y otras materias del ámbito académico utilizando los distintos tipos de números y operaciones, junto con
Síntesis de problemas con simetría esférica.
 Síntesis de problemas con simetría esférica. 1. Ondas esféricas. Supongamos que tenemos la ecuación de ondas en d = 3 u tt = c u (1) y vamos a buscar soluciones que espacialmente, solo dependen de la variable
Síntesis de problemas con simetría esférica. 1. Ondas esféricas. Supongamos que tenemos la ecuación de ondas en d = 3 u tt = c u (1) y vamos a buscar soluciones que espacialmente, solo dependen de la variable
Aritmética del Computador
 Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Métodos Numéricos Contenido 1 Introducción 2 Teoria de Errores 3 Aritmetica del computador Introducción al estudio de métodos computacionales
Facultad de Ingeniería Mecánica Universidad Nacional de Ingeniería Métodos Numéricos Contenido 1 Introducción 2 Teoria de Errores 3 Aritmetica del computador Introducción al estudio de métodos computacionales
CBC. Matemática (51) universoexacto.com 1
 CBC Matemática (51) universoexacto.com 1 PROGRAMA ANALÍTICO 1 :: UNIDAD 1 Números Reales y Coordenadas Cartesianas Representación de los números reales en una recta. Intervalos de Distancia en la recta
CBC Matemática (51) universoexacto.com 1 PROGRAMA ANALÍTICO 1 :: UNIDAD 1 Números Reales y Coordenadas Cartesianas Representación de los números reales en una recta. Intervalos de Distancia en la recta
