Estructura de Datos. Grafos. Primer Semestre, Grafos. Grafos
|
|
|
- Trinidad Mendoza Roldán
- hace 5 años
- Vistas:
Transcripción
1 Estructura de Datos Grafos Prof.: Mauricio Solar Prof.: Lorna Figueroa Primer Semestre, Grafos Árboles: generalización del concepto de lista, permiten que un elemento tenga más de un sucesor. Grafos: extensión del concepto de árbol, cada elemento puede tener, además de más de un sucesor, varios elementos predecesores. Esta propiedad hace que los grafos sean un TAD adecuado para representar situaciones de relación arbitraria entre los elementos: mapas de carreteras, sistemas de telecomunicaciones, circuitos impresos, redes de computadores, etc. Grafos Ampliamente utilizados en computación, ya que permiten resolver problemas complejos. Grafo de transiciones (AFD):
2 Grafos Planificación de tareas (Pert/CPM) Grafo asociado a un dibujo de líneas (visión artificial) Grafos Tiempos de vuelo entre ciudades Grafos Un grafo G = (V, A) consiste de un conjunto finito o vacío de vértices (o nodos) V y un conjunto de arcos (o aristas) A. V es el conjunto de nodos o vértices. V ={v, v,, v n } A es el conjunto de aristas o arcos, que son las conexiones que se encargan de relacionar los nodos para formar el grafo. A = { (v i, v k, c ik ) / v i, v k V, v i v k, v i, v k están relacionados con un valor c }
3 Grafos Los vértices suelen usarse para representar información. Los arcos para representar la relación entre ellos. Ejemplo: vértices representan ciudades los arcos las carreteras. Ejemplo Red de vuelos de una compañía aérea entre diferentes ciudades, se tiene el grafo G = {V, A}: V = {Concepción, Temuco, Pucón, Santiago, La Serena, Arica}; A = {(Santiago, Concepción), (Santiago, Temuco), (Santiago, Pucón), (Santiago, La Serena), (Santiago, Arica)}. Concepción La Serena Santiago Temuco Arica Pucón Ejemplo: La red de metro de Santiago Los mapas de las líneas del metro de Santiago son grafos que muestran la conectividad de las estaciones. Fuente: ck.us/i/metro6n i6rt7.jpg/
4 Grafos - Clasificación Los grafos se pueden clasificar en diferentes tipos dependiendo de cómo se defina la relación entre los elementos: grafos dirigidos o no dirigidos etiquetados o no etiquetados. También se pueden combinar ambas categorías. Grafos Dirigidos Si los arcos son pares ordenados (v, w) VxV, el grafo es dirigido. En un grafo dirigido los arcos tienen un único sentido. En el ejemplo, V = {a,b,c} A = {(a,b), (a,c), (b,c), (c,a)} b a c Grafos Dirigidos Un grafo dirigido se puede usar para representar bloques de un programa mediante los nodos y la transferencia del flujo de control mediante los arcos. Grafo que representa el sentido del tráfico entre diferentes plazas: Vicuña Constitución Mackenna Plaza de Armas Brasil Almagro Yungay
5 Grafos No Dirigidos Si los arcos son pares no ordenados (v, w) V, v w, el grafo es no dirigido. En un grafo no dirigido los arcos conectan a los vértices en ambos sentidos. En el ejemplo, V = {a,b,c} A = {(a,b), (a,c), (b,a), (b,c), (c,a), (c,b)} b a c Grafos Etiquetados En ciertas aplicaciones es necesario asociar información a los arcos. Esto se logra agregando una etiqueta que contenga cualquier información útil relativa al arco: nombre, peso, costo o un valor de cualquier tipo de datos dado. Esta etiqueta puede representar el tiempo de vuelo entre dos ciudades o indicar cuáles son los parámetros de entrada y de salida en la llamada a un subprograma. Grafos Etiquetados a d c b En el ejemplo, V = {a,b,c,d} A ={(a,b,),(a,c,),(a,d,),(b,a,),(b,c,),(c,a,),(c,b,),(d,a,)}
6 Grafos no Etiquetados En un grafo no etiquetado los arcos no tienen etiquetas. En el caso de un grafo que representa el sentido del tráfico se pueden etiquetar los arcos con el nombre de las calles. Dos vértices son adyacentes o vecinos si hay un arco que los conecta. Los nodos adyacentes pueden ser representados por pares (a, b). b a c d a es adyacente con b, c, d b es adyacente con a y c c es adyacente con a y b d es adyacente con a A = {{a,b}, {a,c}, {a,d}, {b,a}, {b,c}, {c,a}, {c,b}, {d,a}} Camino: secuencia de nodos n, n,..., n m tal que i, i (m-), cada par de nodos (n i, n i+ ) son adyacentes. Camino cerrado: si el primer y último vértice de la sucesión de vértices son el mismo. Camino simple: cada uno de sus nodos, excepto el primero y el último, aparece sólo una vez en la secuencia. Longitud de un camino: número de arcos de ese camino. Un camino es de largo n-, n = nº de nodos. Costo de un camino: la suma de los valores asociados con los arcos que lo componen.
7 Camino(a,c) = Largo del camino(a,d) = Camino simple = c a d b Costo(a,c) = Camino(a,c) = { {a,c} }; {{a,b}, {b, c} } } Largo del camino(a,d) = Camino simple = c a d b Costo(a,c) = Camino(a,c) = { {a,c} }; {{a,b}, {b, c} } } Largo del camino(a,d) = Camino simple = c a d b Costo(a,c) =
8 Camino(a,c) = { {a,c} }; {{a,b}, {b, c} } } Largo del camino(a,d) = Camino simple = {a,b} c a d b Costo(a,c) = Camino(a,c) = { {a,c} }; {{a,b}, {b, c} } } Largo del camino(a,d) = Camino simple = {a,b} c a d b Costo(a,c) = o 9 En los caminos se permite la repetición de aristas, b-a-b-e-f-a-a-b es un camino. La longitud del camino b-a-b-e-f-a-a-b es la cantidad de aristas que tiene: El número de elementos de V es el orden del grafo G, En el ejemplo, el orden es 4.
9 Las aristas adyacentes en un camino tienen un vértice común. Por lo tanto, un camino determina una sucesión de vértices. Ciclo: camino simple en el que el primer y último nodo es el mismo (n = n m ). Un grafo sin ciclos se dice acíclico. El problema de los puentes de Königsberg
10 El problema de los puentes de Königsberg Esta ciudad esta recorrida por el río Pregel que crea dos islas. Se puede recorrer toda la ciudad pasando una sola vez por todos y cada uno de los 7 puentes que unen la parte insular de la ciudad con el resto? El problema de los puentes de Königsberg En 76 el matemático suizo Leonhard Euler resolvió el problema. Abstrajo los detalles de la forma de la ciudad y sus puentes para quedarse con la conectividad. El orden de todos los vértices es impar, lo que implica que es imposible recorrerlos pasando una sola vez por cada uno. Construyó el grafo reemplazando la tierra firme por vértices y los puentes por aristas; es decir Tierra es el vértice a, Tierra es b, la Isla es el vértice c y la Isla es el vértice d. La pregunta es: existe un camino cerrado que contenga exactamente cada una de las aristas? Este camino se llama circuito de Euler o euleriano. Un camino simple que contiene todas las aristas de un grafo G se llama camino euleriano de G, o de otra manera se dice que un grafo conexo no vacío es un camino Euleriano si y solo si no tiene vértices de grado impar. Un camino euleriano cerrado se llama circuito euleriano.
11 Un camino euleriano en un grafo es un camino que contiene a todas las aristas del grafo exactamente una vez. Un grafo es euleriano si contiene un camino euleriano cerrado. Intuitivamente un camino es Euleriano si se puede recorrer el grafo de un solo trazo sin levantar el lápiz del papel. La valencia de un vértice en un grafo es el número de aristas que confluyen en él. Teorema : En un grafo que tiene un circuito euleriano todos los vértices deben tener valencia par. Corolario : Un grafo que tenga un camino euleriano tiene vértices de valencia impar, o no tiene vértices de valencia impar. Este grafo no tiene circuito euleriano ya que aunque u y v tienen valencia impar, pero b-a-c-d-g-f-e es un camino euleriano
12 En este grafo todos los vértices tienen valencia par y de hecho hay un circuito euleriano. En este grafo todos los vértices tienen valencia par pero no hay un circuito euleriano, la razón obvia es que está formada por dos subgrafos que no están conectados entre sí. Sin embargo, cada uno de los subgrafos tiene su propio circuito euleriano. Camino hamiltoniano: sucesión de aristas adyacentes, que visita todos los vértices del grafo una sola vez, (salvo v = v n, si el camino es cerrado). Ciclo hamiltoniano: camino hamiltoniano en que el último vértice visitado es adyacente al primero. Un grafo es hamiltoniano si tiene un ciclo hamiltoniano. Un ciclo es hamiltoniano si pasa por todos los vértices solo una vez.
13 Grafo Hamiltoniano del dodecaedro: Grafo no hamiltoniano de Herschel: Grafo desconectado o inconexo: si en un grafo G = {V,A}, V está formado por dos o más subconjuntos disjuntos de nodos (no hay arcos que conecten nodos de un subconjunto con nodos de otro subconjunto): Grafo es conectado o conexo si: todos los pares de vértices distintos están conectados por un camino en el grafo. grafo conectado o conexo : 4 grafo desconectado o inconexo : 6 4 6
14 El grado de un vértice es el número de vértices adyacentes a él. a d grado (a) = grado (b) = b c grado (c) = grado (d) = Un subgrafo G = (V, A ) de un grafo G=(V,A) es un grafo tal que V V, A A. Ejemplo: si un grafo representa las ciudades y las carreteras de un país, un subgrafo es el grafo de las carreteras de una comuna. Representaciones para Grafos Matriz de Adyacencia. Es una matriz A de V V tal que, A[ i, j ] = Ejemplo : si v j es adyacente a v i en caso contrario a b c d a b c d c a d b
15 Representaciones para Grafos Lista de Adyacencia de un vértice v, es la lista de todos los vértices adyacentes a él. Ejemplo: a b c d b c a d a b c c a d b Recorridos Muchos algoritmos de recorridos se implementan recursivamente Surge un problema de control de la recursión, debido a que los ciclos de un grafo pueden generar llamadas recursivas infinitas. Ejemplo: Se desea ir desde el vértice a, al vértice d. Es necesario recordar los puntos por los cuales ya se ha pasado para evitar hacer nuevamente una llamada recursiva desde ese punto. a Se corre el peligro de quedarse en el ciclo a-b-c. Solución: marcar los vértices por donde se va pasando. b c d Recorridos Recorrer un grafo consiste en pasar una vez por cada vértice de la estructura. Existen varias maneras de realizar este proceso: Recorrido en profundidad. (Es equivalente a un recorrido en preorden de un árbol) Recorrido por amplitud. (Es equivalente a recorrer un árbol por niveles)
16 Recorrido en Profundidad Se procesa un nodo inicial n. Después se procesa uno de los nodos adyacentes que no haya sido previamente visitado iniciando un recorrido en profundidad desde él. Cuando se alcanza un nodo cuyos nodos adyacentes han sido todos visitados el algoritmo vuelve atrás al último nodo visitado al que le quede aún algún sucesor por procesar. Finalmente, se llega a un punto donde todos los nodos alcanzables habrán sido visitados. Un nodo N se dice alcanzable desde un nodo M si y sólo si existe un camino desde M hasta N. Recorridos en Profundidad - Ejemplo Recorrer todos los vértices del siguiente grafo: a c b e d Visitar el nodo a, marcar Recorrido : a c a b e d Recorridos en Profundidad - Ejemplo Localizar sucesores de a: b y c Recorrido en profundidad del vértice b, marcarlo. Recorrido : a b Pendientes : c e c a b d e c a b d Localizar sucesores de b: d y e Recorrido en profundidad del vértice d, marcarlo. Recorrido : a b - d Pendientes : c, e
17 Recorridos en Profundidad - Ejemplo e c a b d Localizar sucesores de d: no tiene Se saca de la pila de pendientes: e Recorrido en profundidad del vértice e, marcarlo. Recorrido : a b d -e Pendientes : c e c a b d Localizar sucesores de c: b Como el sucesor del vértice está marcado y no existen pendientes finaliza el recorrido. Luego, el recorrido del grafo es: a b d e c Recorrido en Profundidad - Algoritmo Algoritmo PrimeroEnProfundidad(G: Grafo; n: Elemento) { Marcar n como visitado; MIENTRAS quede algún nodo m adyacente a n sin visitar PrimeroEnProfundidad(G, m); } Ejemplo Suponiendo que el orden en que están almacenados los nodos en la estructura de datos correspondiente es A-B-C-D-E-F... (el orden alfabético), el orden que seguiría el recorrido en profundidad es: A-B-E-I-F-C-G-J-K-H-D Se exploran primero los verdes y luego los marrones, pasando primero por los de mayor intensidad de color. El nodo D es el último en explorarse en la búsqueda en profundidad pese a ser adyacente al nodo de origen (el A). Esto es debido a que primero se explora la rama del nodo C, que también conduce al nodo D.
18 Recorrido en Amplitud Similar al recorrido por niveles de un árbol, si se considera como un nivel el conjunto de los nodos adyacentes. En este recorrido, tras visitar un nodo, se visitan todos sus nodos adyacentes. Una vez visitados todos los nodos de este primer nivel, se repite el proceso visitando todos los nodos adyacentes del primer vecino de nivel recién recorrido y repitiéndolo para todos los nodos hasta que no quede ninguno por visitar. Ejemplo Para el grafo del ejemplo, el orden del recorrido en amplitud es: A-B-C-D-E-G-H-I-J-K-F Se exploran primero los verdes, después los rojos, los naranjas y, por último, el rosa. Árboles de extensión de costo mínimo En un grafo es habitual encontrar caminos redundantes. Es decir, es posible llegar de un nodo a otro a través de diferentes caminos. Si en un grafo conexo se eliminan los caminos redundantes, seguirá siendo conexo, se podrá llegar de cualquier nodo a cualquier otro.
19 Árboles de extensión de costo mínimo Dado un grafo G = (V, A), conexo con los arcos etiquetados con su costo, un árbol de extensión asociado a G es un árbol libre que conecta todos los vértices de V. El costo del árbol es la suma de los costos de todos los arcos del árbol libre. un árbol libre es un grafo conexo acíclico no dirigido. Árboles de extensión de costo mínimo Aplicación típica: diseño de una red de comunicaciones (telefónica o de Internet, por ejemplo). El árbol de extensión de costo mínimo da la opción de conexión de todas las ciudades al menor costo, ya sea éste el precio del tendido de los cables, el mantenimiento, etc. Árboles de extensión de costo mínimo Grafo etiquetado y su árbol de expansión de costo mínimo:
20 Árboles de extensión de costo mínimo La representación del árbol de expansión no es única. Cada árbol abarcador muestra una manera de planear las rutas de transporte de tal forma que cada ciudad pueda ser atendida. Ejemplo : Costo 64 millas Árboles de extensión de costo mínimo Ejemplo : Costo 667 millas Árboles de extensión de costo mínimo Ejemplo : Arbol de expansión mínima. Costo 479 millas.
21 El algoritmo de Kruskal Algoritmo de tipo "voraz" o "greedy. Construir un árbol generador de peso mínimo Estrategia: añadir aristas de mínimo peso hasta conseguir un árbol generador En cada paso, al incorporar una nueva arista, se debe comprobar que no se forme ningún ciclo con las aristas previamente introducidas no están permitidos en un árbol de expansión. Cuando todos los subgrafos estén unidos, se habrá encontrado el árbol de expansión de costo mínimo. El algoritmo de Kruskal Para añadir los arcos se examina el conjunto de arcos en orden creciente según su costo. Si el arco inspeccionado conecta dos nodos de subgrafos diferentes, se añade al conjunto de nodos, formará parte del árbol de extensión considerándolos como un subgrafo conexo. Si los dos nodos pertenecen al mismo subgrafo, no se añade para evitar la aparición de ciclos en el árbol de extensión. Cuando todos los nodos estén conectados, se habrá encontrado el árbol de extensión buscado. El algoritmo de Kruskal Paso. Se elige la arista de mínimo peso e y se considera S= {e}. Paso. Sea e' la arista de peso mínimo tal que e' no pertenezca a S y S+e' es un grafo acíclico. Se hace S=S+e. Paso. Si S tiene n- aristas, el algoritmo termina. En caso contrario se vuelve al paso.
22 El algoritmo de Kruskal Ejemplo Secuencia de aristas añadidas por el algoritmo de Kruskal. S = {} S = {,} S = {,,4} El algoritmo de Kruskal Secuencia de aristas añadidas por el algoritmo de Kruskal. S = {,,4,} S = {,,4,,6} El algoritmo de Prim Fue diseñado en 9 por el matemático Vojtech Jarnik y luego de manera independiente por el científico computacional Robert C. Prim en 97 y redescubierto por Dijkstra en 99. Por esta razón, el algoritmo es también conocido como algoritmo DJP o algoritmo de Jarnik.
23 El algoritmo de Prim Encuentra un árbol recubridor mínimo en un grafo conexo, no dirigido y cuyas aristas están etiquetadas. Idea básica: añadir, en cada paso, un nuevo vértice a un árbol previamente construido. Este nuevo vértice se une al árbol anterior con la arista de menor peso: el algoritmo encuentra un subconjunto de aristas que forman un árbol con todos los vértices, donde el peso total de todas las aristas en el árbol es el mínimo posible. Si el grafo no es conexo, entonces el algoritmo encontrará el árbol recubridor mínimo para uno de los componentes conexos que forman ese grafo no conexo. El algoritmo de Prim Suponga un grafo G = (V, A), con los arcos etiquetados con su costo. El algoritmo de Prim va construyendo un subconjunto de nodos U, aumentándolo hasta que contenga todos los nodos de V. Inicialmente, U contiene un único nodo de V, que puede ser cualquiera. En cada paso, se localiza el arco más corto (u, n) tal que u U y n V, repitiendo el proceso hasta que U = V. El algoritmo de Prim Algoritmo Prim(Grafo G; Conjunto_de_Arcos *T) { Conjunto_de_arcos U; arcos u, v; T = {}; U = {Cualquier v V}; MIENTRAS U <> V { Sea (u, v) el arco de costo mínimo tal que u U y v V T = T {(u, v)} U = U {v} } }
24 El algoritmo de Prim Ejemplo Secuencia de aristas añadidas por el algoritmo de Prim. El algoritmo de Prim Secuencia de aristas añadidas por el algoritmo de Prim. Algoritmo de Dijkstra Problema: Determinar el costo del camino más corto del origen a todos los demás vértices de V, donde la longitud de un camino es la suma de los costos de los arcos del camino. Solución : Algoritmo de Dijkstra. Este es un algoritmo iterativo, para encontrar los caminos de costo mínimo que parten de un vértice dado y terminan en cada uno de los demás vértices del grafo.
25 Algoritmo de Dijkstra Ejemplo: para el siguiente grafo, encontrar el camino de costo mínimo, que lleva del vértice a todos los demás vértices Algoritmo de Dijkstra Se anotan los costos de ir desde el nodo a sus nodos adyacentes : Se escoge el que tiene el costo menor, y se marca : 4 9 Algoritmo de Dijkstra Se anotan los costos de ir desde el nodo pasando por el vértice a los nodos adyacentes (al ) : Costo(--) = + = 6 Se escoge el que tiene el costo menor, y se marca : 4 6 9
26 Algoritmo de Dijkstra Se anotan los costos de ir desde el nodo pasando por el vértice 4 a los nodos adyacentes (al 4); en caso que tenga un costo menor, se reemplaza : Costo(-4-) = + = Costo(-4-) = + 6 = Se escoge el que tiene el costo menor, y se marca : 4 9 Algoritmo de Dijkstra Se anotan los costos de ir desde el nodo pasando por el vértice a los nodos adyacentes (al ); en caso que tenga un costo menor, se reemplaza : Costo(---) = ++=7 Costo(-4--)=++=6 4 6 Dado que ya se han visitado todos los nodos, se termina el recorrido de Dijkstra. Algoritmo de Dijkstra G = (V, E) V = {,,..., n} origen = S = conjunto de vértices cuya distancia más corta desde el origen ya es conocida C = arreglo bidimensional de costos C[ i, j ] = costo de ir del vértice vi al vértice vj por el arco i j D[ i ] = longitud del camino especial más corto actual para v i camino especial = camino más corto entre el origen y v que pasa sólo a través de los vértices de S D = contendrá la distancia más corta del origen a cada vértice
27 Algoritmo de Dijkstra Dijkstra( ) { S = { }; for( i = ; i n, i++) D[ i ] = C[, i ] ; // asigna valor inicial a D for( i = ; i n -, i++) { elegir un vértice w en V - S tal que D[ w ] sea mínimo ; agregar w a S ; for( cada vértice v en V - S ) D[ v ] = mín(d[ v ], D[ w ] + C[ w, v ]); } } Tiempo de Ejecución de Dijkstra Suponiendo que G = (V, E) es un grafo dirigido con n vértices y a aristas. Si se usa una matriz de adyacencia para representar el grafo dirigido : O(n ). Si se usa una lista de adyacencia para representar el grafo dirigido : O(a log n) ; a es el número de actualizaciones (de las distancias en la cola de prioridad). Algoritmo de Floyd Problema : Determinar el tiempo de vuelo menor entre dos ciudades cualquiera. Se tiene un grafo dirigido etiquetado que da el tiempo de vuelo para ciertas rutas entre ciudades. Se quiere encontrar el camino más corto entre todos los pares. Solución: Algoritmo de Floyd. Se aplica el algoritmo de Dijkstra para cada vértice, como vértice de origen cada vez, por turno.
28 Algoritmo de Floyd Ejemplo: S NY BA Algoritmo de Floyd S NY Matriz inicial de costo: BA A = S BA NY S BA NY Algoritmo de Floyd S NY Reemplazar por los que van a sí mismos: BA A = S BA NY S BA NY
29 Algoritmo de Floyd S NY Pasando por el vértice S: BA A = S BA NY S BA NY Algoritmo de Floyd S NY Pasando por los vértice S y BA : S BA NY BA A = S BA NY Algoritmo de Floyd S NY Pasando por los vértice S, BA y NY : BA A = S BA NY S 7 BA NY
30 Algoritmo de Floyd Floyd ( int *A[n,n]; int c[n,n] ) { int i, j, k; for (i = ; i <= n; i++) for (j = ; i <= n; j++) Vértices numerado : n A[i, j] nxn = se calculan las longitudes de los caminos más cortos. C[ i, j ] = matriz de costos de arcos. A[i, j] = C[i, j] ; // se iniciliza A con todos los costos for (i = ; i <= n;i++) A[ i, i ] = ; for (k = ; k <= n; k++) for (i = ; i <= n; i++) for (j = ; j <= n; j++) if ( (A[i, k] + A[k, j])< A[i, j] ) A[i, j] = A[i, k] + A[k, j]; } Ejercicios Determinar la matriz de adyacencia para el siguiente grafo: Solución : Ejercicios Determinar el camino mínimo (de menor peso) usando el algoritmo de Dijkstra, usando como nodo inicial el nodo N Nodo marca distancia N true N true N true N 4 true N true N 6 true 4 N 7 true
31 Solución : El nodo N será el primer nodo seleccionado. En la tabla se marca como visitado y se inspeccionan los nodos adyacentes, N y N 4. En ambos casos el costo mínimo hasta ese momento es infinito, por lo que se encontró un camino mejor pasando por N. Solución : El costo de este camino es el costo del camino a N más el del arco que los une. Para N es d = d + c, = + =. Para N 4 es d 4 = d + c, 4 = + =. En ambos casos, el campo camino se actualiza a N. De estos dos nodos, se selecciona N 4 por ser el que tiene del camino de menor costo. Se marca y se analizan los nodos adyacentes a N 4, que son N, N, N 6 y N 7. En todos los casos, como no había un camino previo, se toma como mejor camino de forma provisional el camino a través de N 4, actualizándose los campos distancia y camino. Solución : El siguiente nodo seleccionado en N, que tiene como nodos adyacentes N 4 y N. Como N 4 está marcado como visitado, y tiene por tanto un camino mejor que N, no se trabaja con él. El camino a N a través de N tiene peso d = d + c, = + = no es mejor que el que ya tenía N, por lo que no se modifica. El resto de los nodos se escogen en el siguiente orden: N, N, N 7 y N 6
32 Solución : La tabla queda con los siguientes valores finales: Nodo marca distancia camino N true - N true N N true N 4 N 4 true N N true N 4 N 6 true 6 N 7 N 7 true N 4 Ejercicios Dado el siguiente grafo, indicar la secuencia que se obtiene con: en el recorrido suponer un. Recorrido en profundidad. orden alfabético entre los. Recorrido en amplitud. nodos adyacentes a uno dado. el elemento inicial es el nodo a Solución:. a, d, g, e, f, c, b. a, b, e, f, g, d, c Ejercicios El siguiente grafo representa la conexión de una red : Completar la traza de la aplicación del algoritmo de Dijkstra al grafo anterior.
33 Solución Iteración 4 S {} {,} {,,} {,,,} {,,,,4} - n D[] P[] D[] 6 P[] D[] P[] D[4] P[4] Ejercicios El siguiente grafo representa la conexión de una red : Hacer la traza de la aplicación del algoritmo de Dijkstra al grafo Ejercicios Aplicar Floyd al siguiente grafo: A B C
34 Solución: A B C A [i][j] A [i][j] A [i][j] A [i][j] - - C - B A C B A C B A 7 C B A C B A Solución: A B C A [i][j] A [i][j] A [i][j] A [i][j] - - C - B A C B A C B A 7 C B A C B A Fuente: Los grafos como modelos matemáticos: ejemplos históricos y aplicaciones actuales. web.udl.es/usuaris/p4/teaching/grafos_modelos.pdf El problema de los siete puentes de Königsberg (Euler, 76) El problema del cartero chino (Kwan Mei-Ko, 96) El juego del dodecaedro (Hamilton, 7) El problema del vendedor viajero. (Primeras referencias datan de ; J.B. Robinson, On the Hamiltonian game (a traveling-salesman problem), 949. Es la primera referencia del problema tal como es conocido actualmente). Algunas Aplicaciones
35 Algunas Aplicaciones Análisis de redes eléctricas (Kirchho, 47). Enumeración de isómeros químicos (Cayley, 7). El problema del conector mínimo. El problema de los de cuatro colores (Appel y Haken 976) El problema de los horarios. El problema de la asignación de frecuencias en una red celular de telefonía móvil. El problema del camino mínimo (Dijkstra, 99) Análisis del camino crítico. El problema del flujo máximo (Ford y Fulkerson, 96) Modelización de la World-Wide Web El problema de los siete puentes de Königsberg Se puede recorrer toda la ciudad pasando una sola vez por todos y cada uno de los 7 puentes que unen la parte insular de la ciudad con el resto? El problema del cartero chino Un cartero debe repartir la correspondencia a cada una de las manzanas de casas de su distrito siendo la oficina de correos su punto de partida y fin. Encontrar una ruta optima (distancia total recorrida mínima).
36 El problema del cartero chino Situaciones reales : ruta óptima para un camión de basuras para un inspector de contadores de luz, etc., trazado óptimo de un grafo mediante un plotter. El juego del dodecaedro Buscar un recorrido que dé la vuelta al mundo, representado por un dodecaedro, visitando cada ciudad, correspondiente a un vértice del dodecaedro, una sola vez. Solamente se puede desplazar de una ciudad a otra si los vértices correspondientes del dodecaedro están unidos por una arista. El problema del vendedor viajero Un representante de una editorial, con sede en la ciudad A, debe visitar una serie de clientes establecidos en distintas ciudades de manera que su itinerario tenga como principio y n A. Qué ruta deberá seguir con el fin de minimizar costos? Modelización: Dado un grafo completo y ponderado (grafo de distancias), hallar un ciclo hamiltoniano de costo mínimo (longitud total mínima).
37 El problema del vendedor viajero; Aplicaciones Ruta Vehicular Bus Escolar. Atención de Llamadas de Emergencia. Servicio de Correo Expreso. El problema del vendedor viajero, Aplicaciones Secuenciamiento de genes. Ordenamiento de observaciones en telescopios (NASA). El problema del vendedor viajero; Aplicaciones Diseño de chips. Tour Mundial.
38 El problema del vendedor viajero Aplicaciones: El problema del Viejo Pascuero Análisis de redes eléctricas Método efectivo para el análisis de redes eléctricas entendido dicho análisis como el cálculo de la intensidad y la diferencia de potencial de cada elemento de la red (resistencia, bobina, condensador, fuente de tensión, etc.). Enumeración de isómeros químicos Método efectivo para el análisis de redes eléctricas entendido dicho análisis como el cálculo de la intensidad y la diferencia de potencial de cada elemento de la red (resistencia, bobina, condensador, fuente de tensión, etc.).
39 El problema del conector mínimo Dado un conjunto de ciudades se desea construir una red de carreteras, que conecte a todas entre sí. Cual es la red de costo mínimo? Modelización: Dado un grafo conexo y ponderado, hallar un árbol generador de peso mínimo. El problema de los cuatro colores Conjetura (Francis Guthrie, ): Todo mapa trazado sobre una hoja de papel puede colorearse usando solamente cuatro tintas de manera que países" con frontera común" tengan colores diferentes. El problema de los cuatro colores Aplicaciones: El problema de los horarios: Confeccionar un calendario de exámenes, que comprenda el mínimo numero de días, teniendo en cuenta que un estudiante no puede realizar más de un examen en un mismo día. El problema de la asignación de frecuencias en una red celular de telefonía móvil: Asignar a cada celda un rango de frecuencias de manera que celdas contiguas tengan rangos disjuntos. Cómo debe hacerse dicha asignación con el fín de minimizar el total de frecuencias usadas? Modelización: Dado el grafo de incompatibilidades, hallar una vértice coloración del mismo utilizando el menor numero de colores posible.
40 El problema del camino mínimo Dada una red de transporte hallar la ruta óptima entre cada par de elementos de la misma. Modelización: Calcular la distancia y encontrar un camino mínimo entre cada par de vértices de un grafo conexo y ponderado. Análisis del camino crítico Planificar las actividades de un proyecto de forma que el tiempo total para realizarlo sea el menor posible. Modelización: Dado el correspondiente grafo de actividades, hallar el camino mas largo entre los vértices que representan los estados inicio y fín. El problema del flujo máximo Hallar el flujo máximo que fluye a través de una red, desde un nodo fuente hasta un nodo sumidero, cuando sus enlaces tienen una capacidad limitada de transporte.
41 Modelización de la World-Wide Web Estudio de la topología de la Web (conectividad, diámetro, ). Formulación de algoritmos de valoración de las páginas web (algoritmo PageRank de Google, ). Bibliografía Webgrafía. Cormen, Leiserson, Rivest: Introducción a la Algorítmica, The MIT Press-Mc Graw Hill, Aho A. V., Hopcroft J.E., Ullman J.D.; Estructuras de Datos y Algoritmos. Ed. Addison-Wesley, web.udl.es/usuaris/p4/teaching/grafos_modelos.pdf. users.dsic.upv.es/asignaturas/facultad/eda/teoria/tema4/t4eda. pdf 6. rua.ua.es/dspace/bitstream/4/44//ped-6_7- tema.pdf 7. EL Problema del Vendedor Viajero (TSP) y Programación Entera (IP). Daniel Espinoza, U.Ch., Fac.Cs Fís y Mat.,Depto Ing.Ind., 4 de julio de 6
Tema 5 Árboles y Grafos.
 Tema 5 Árboles y Grafos. Definiciones básicas de teoría de grafos. Un grafo consta de un conjunto de nodos, un conjunto de aristas y una correspondencia f del conjunto de aristas al conjunto de nodos.
Tema 5 Árboles y Grafos. Definiciones básicas de teoría de grafos. Un grafo consta de un conjunto de nodos, un conjunto de aristas y una correspondencia f del conjunto de aristas al conjunto de nodos.
Taller de Grafos: Rutas, Mapas y Redes Sociales
 Taller de Grafos: Rutas, Mapas y Redes Sociales Cristina Chiralt y Fernando Hernando Universidad Jaume I e Instituto Universitario de Matemáticas y sus Aplicaciones de Castellón Grado de Matemática Computacional
Taller de Grafos: Rutas, Mapas y Redes Sociales Cristina Chiralt y Fernando Hernando Universidad Jaume I e Instituto Universitario de Matemáticas y sus Aplicaciones de Castellón Grado de Matemática Computacional
INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.
 INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.7 GRAFOS CONEXOS7 ÁRBOLES..7 BOSQUES DE ÁRBOLES...8 RECORRIDO DE UN GRAFO..8
INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.7 GRAFOS CONEXOS7 ÁRBOLES..7 BOSQUES DE ÁRBOLES...8 RECORRIDO DE UN GRAFO..8
Matemáticas Discretas
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2011 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2011 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
Centro Asociado Palma de Mallorca. Tutor: Antonio Rivero Cuesta
 Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
Matemáticas Discretas
 Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2016 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
Coordinación de Ciencias Computacionales - INAOE Matemáticas Discretas Cursos Propedéuticos 2016 Ciencias Computacionales INAOE Dr. Enrique Muñoz de Cote jemc@inaoep.mx http://ccc.inaoep.mx/~jemc Oficina
ARBOLES GENERADORES. Orlando Arboleda Molina. 16 de septiembre de Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle
 ARBOLES GENERADORES Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 16 de septiembre de 2008 Contenido Árboles generadores Algoritmo búsqueda por profundidad
ARBOLES GENERADORES Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 16 de septiembre de 2008 Contenido Árboles generadores Algoritmo búsqueda por profundidad
Representación y manipulación de grafos: caminos, expansión, cortes y flujos
 Un grafo G es un par de conjuntos G =(V,E) Representación y manipulación de grafos: caminos, expansión, cortes y flujos V = un conjunto de n vértices u, v, w V E = un conjunto de m aristas V = n, E = m
Un grafo G es un par de conjuntos G =(V,E) Representación y manipulación de grafos: caminos, expansión, cortes y flujos V = un conjunto de n vértices u, v, w V E = un conjunto de m aristas V = n, E = m
Algebra Matricial y Teoría de Grafos
 Algebra Matricial y Teoría de Grafos Unidad 3: Nociones de teoría de grafos Luis M. Torres Escuela Politécnica del Litoral Quito, Enero 2008 Maestría en Control de Operaciones y Gestión Logística p.1 Contenido
Algebra Matricial y Teoría de Grafos Unidad 3: Nociones de teoría de grafos Luis M. Torres Escuela Politécnica del Litoral Quito, Enero 2008 Maestría en Control de Operaciones y Gestión Logística p.1 Contenido
Estructura de Datos Página 1 de 13 ESTRUCTURA DE DATOS
 Estructura de Datos Página 1 de 13 ESTRUCTURA DE DATOS Contenido TEMA 4. Grafos 4.1. Grafos 4.1.1. Definición 4.1.2.Conceptos 4.2. Modelado de problemas típicos 4.3. Representación de un grafo a través
Estructura de Datos Página 1 de 13 ESTRUCTURA DE DATOS Contenido TEMA 4. Grafos 4.1. Grafos 4.1.1. Definición 4.1.2.Conceptos 4.2. Modelado de problemas típicos 4.3. Representación de un grafo a través
Los elementos de V son los vértices (o nodos) de G y los elementos de A son las aristas (o arcos) de G.
 MATERIAL TEÓRICO º Cuatrimestre Año 03 Prof. María Elena Ruiz Prof. Carlos Roberto Pérez Medina UNIDAD III: GRAFOS Definición: Llamaremos grafo a una terna G= (V, A, ϕ), donde V y A son conjuntos finitos,
MATERIAL TEÓRICO º Cuatrimestre Año 03 Prof. María Elena Ruiz Prof. Carlos Roberto Pérez Medina UNIDAD III: GRAFOS Definición: Llamaremos grafo a una terna G= (V, A, ϕ), donde V y A son conjuntos finitos,
Grafos. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Grafos 1 / 30
 Grafos AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Grafos / 0 Objetivos Al finalizar este tema tendréis que: Conocer la terminología básica de la teoría de grafos. Pasar
Grafos AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Grafos / 0 Objetivos Al finalizar este tema tendréis que: Conocer la terminología básica de la teoría de grafos. Pasar
NIVEL 17: ESTRUCTURAS NO LINEALES
 1 NIVEL 17: ESTRUCTURAS NO LINEALES Recorridos y Algorítmica de Grafos 2 Agenda Recorridos de grafos Recorridos Planos Recorridos en profundidad Recorridos por niveles Recorridos Heurísticos Algorítmica
1 NIVEL 17: ESTRUCTURAS NO LINEALES Recorridos y Algorítmica de Grafos 2 Agenda Recorridos de grafos Recorridos Planos Recorridos en profundidad Recorridos por niveles Recorridos Heurísticos Algorítmica
TEMA IV TEORÍA DE GRAFOS
 TEMA IV TEORÍA DE GRAFOS Poli Abascal Fuentes TEMA IV Teoría de grafos p. 1/? TEMA IV 4. TEORÍA DE GRAFOS 4.1 GRAFOS 4.1.1 Introducción 4.1.2 Definiciones básicas 4.1.3 Caminos y recorridos 4.1.4 Subgrafos,
TEMA IV TEORÍA DE GRAFOS Poli Abascal Fuentes TEMA IV Teoría de grafos p. 1/? TEMA IV 4. TEORÍA DE GRAFOS 4.1 GRAFOS 4.1.1 Introducción 4.1.2 Definiciones básicas 4.1.3 Caminos y recorridos 4.1.4 Subgrafos,
Modelos de Redes: Árbol. M. En C. Eduardo Bustos Farías
 Modelos de Redes: Árbol de expansión n mínimam M. En C. Eduardo Bustos Farías as Objetivos Conceptos y definiciones de redes. Importancia de los modelos de redes Modelos de programación n lineal, representación
Modelos de Redes: Árbol de expansión n mínimam M. En C. Eduardo Bustos Farías as Objetivos Conceptos y definiciones de redes. Importancia de los modelos de redes Modelos de programación n lineal, representación
Francisco J. Hernández López
 Francisco J. Hernández López fcoj23@cimat.mx Estructura de datos no lineales donde cada componente o nodo puede tener uno o más predecesores (a diferencia de los árboles) y sucesores Un grafo esta formado
Francisco J. Hernández López fcoj23@cimat.mx Estructura de datos no lineales donde cada componente o nodo puede tener uno o más predecesores (a diferencia de los árboles) y sucesores Un grafo esta formado
Taller de grafs: rutes, mapes i xarxes socials
 Taller de grafs: rutes, mapes i xarxes socials Cristina Chiralt y Fernando Hernando Universidad Jaume I e Instituto Universitario de Matemáticas y sus Aplicaciones de Castellón Grado de Matemática Computacional
Taller de grafs: rutes, mapes i xarxes socials Cristina Chiralt y Fernando Hernando Universidad Jaume I e Instituto Universitario de Matemáticas y sus Aplicaciones de Castellón Grado de Matemática Computacional
Algoritmos voraces (greedy)
 Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 21 de marzo de 2018 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) Algoritmos voraces 21 de marzo de 2018 1 / 45 1 Algoritmos voraces (greedy) Aplicaciones de
Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 21 de marzo de 2018 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) Algoritmos voraces 21 de marzo de 2018 1 / 45 1 Algoritmos voraces (greedy) Aplicaciones de
Tema: Recorrido de Grafos. Ruta más corta
 PED104. Guía N 12 Página 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación con Estructuras de Datos Tema: Recorrido de Grafos. Ruta más corta Competencia Desarrolla sistemas de información
PED104. Guía N 12 Página 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación con Estructuras de Datos Tema: Recorrido de Grafos. Ruta más corta Competencia Desarrolla sistemas de información
Un grafo G = (V, E) se dice finito si V es un conjunto finito.
 1 Grafos: Primeras definiciones Definición 1.1 Un grafo G se define como un par (V, E), donde V es un conjunto cuyos elementos son denominados vértices o nodos y E es un subconjunto de pares no ordenados
1 Grafos: Primeras definiciones Definición 1.1 Un grafo G se define como un par (V, E), donde V es un conjunto cuyos elementos son denominados vértices o nodos y E es un subconjunto de pares no ordenados
LAS CIENCIAS DE LA PLANIFICACIÓN
 LAS CIENCIAS DE LA PLANIFICACIÓN 1. MODELIZACIÓN CON GRAFOS El objetivo de las ciencias de la planificación es encontrar el mejor método para resolver un problema, y si es posible encontrar la solución
LAS CIENCIAS DE LA PLANIFICACIÓN 1. MODELIZACIÓN CON GRAFOS El objetivo de las ciencias de la planificación es encontrar el mejor método para resolver un problema, y si es posible encontrar la solución
UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-RUACS. Investigación de Operaciones
 UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-RUACS Facultad de Ingeniería Industrial Investigación de Operaciones Tema: Teoría de los Grafos Elaborado por: Ing. Carlos Alberto Moreno. Docente: Ing. Pastrana
UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-RUACS Facultad de Ingeniería Industrial Investigación de Operaciones Tema: Teoría de los Grafos Elaborado por: Ing. Carlos Alberto Moreno. Docente: Ing. Pastrana
3.0.-ARBOLES ABARCADORES Y COMPONENTES CONEXOS CONCEPTO DE ARBOL ABARCADOR Y SU RELACION CON LOS RECORRIDOS.
 3.0.-ARBOLES ABARCADORES Y COMPONENTES CONEXOS 3.1.- CONCEPTO DE ARBOL ABARCADOR Y SU RELACION CON LOS RECORRIDOS. 3.2.- BOSQUES Y COMPONENTES CONEXOS. NEXON LENIN CEFERINO POMPOSO Los árboles son particularmente
3.0.-ARBOLES ABARCADORES Y COMPONENTES CONEXOS 3.1.- CONCEPTO DE ARBOL ABARCADOR Y SU RELACION CON LOS RECORRIDOS. 3.2.- BOSQUES Y COMPONENTES CONEXOS. NEXON LENIN CEFERINO POMPOSO Los árboles son particularmente
LAS CIENCIAS DE LA PLANIFICACIÓN
 LAS CIENCIAS DE LA PLANIFICACIÓN 5. EL PROBLEMA DEL VIAJANTE (PV) (The Traveling Salesman Problem TSP) Un problema como el de las vacaciones, pero vital para las empresas, es el problema del viajante (PV):
LAS CIENCIAS DE LA PLANIFICACIÓN 5. EL PROBLEMA DEL VIAJANTE (PV) (The Traveling Salesman Problem TSP) Un problema como el de las vacaciones, pero vital para las empresas, es el problema del viajante (PV):
Tema 5: Grafos. CIS - UABJB - Estructura de Datos II Ing. Freddy Melgar Algarañaz 1
 Tema 5: Grafos 1 Indice 1. Tipos de grafos 2. Conceptos Básicos 3. Representación de grafos 4. Caminos y conectividad 5. Grafos Bipartitos 6. Recorridos, eulerianos 2 Tipos de Grafos Un grafo G es un par
Tema 5: Grafos 1 Indice 1. Tipos de grafos 2. Conceptos Básicos 3. Representación de grafos 4. Caminos y conectividad 5. Grafos Bipartitos 6. Recorridos, eulerianos 2 Tipos de Grafos Un grafo G es un par
Estructuras de Datos y Algoritmos. Grafos
 Estructuras de Datos y Algoritmos Grafos Definiciones Grafo modelo para representar relaciones entre elementos de un conjunto. Grafo: (V,E), V es un conjunto de vértices o nodos, con una relación entre
Estructuras de Datos y Algoritmos Grafos Definiciones Grafo modelo para representar relaciones entre elementos de un conjunto. Grafo: (V,E), V es un conjunto de vértices o nodos, con una relación entre
Tema: Algoritmos para la ruta más corta en un Grafo.
 Programación IV. Guía No. 10 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos para la ruta más corta en un Grafo. Objetivos Específicos Definir el concepto de camino
Programación IV. Guía No. 10 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos para la ruta más corta en un Grafo. Objetivos Específicos Definir el concepto de camino
Grafos Los siete puentes de Königsberg: Teoría de Grafos
 Grafos Los siete puentes de Königsberg: Un ciudadano de Königsberg (Prusia) se propuso dar un paseo cruzando cada uno de los siete puentes que existen sobre el río Pregel una sola vez. Los dos brazos del
Grafos Los siete puentes de Königsberg: Un ciudadano de Königsberg (Prusia) se propuso dar un paseo cruzando cada uno de los siete puentes que existen sobre el río Pregel una sola vez. Los dos brazos del
Programación Lineal. Modelo de Redes. Alcance de las aplicaciones. Curso: Investigación de Operaciones Ing. Javier Villatoro
 Programación Lineal Modelo de Redes Alcance de las aplicaciones Curso: Investigación de Operaciones Ing. Javier Villatoro ALCANCE DE LAS APLICACONES DE REDES ALCANCE DE LAS APLICACIONES Muchas situaciones
Programación Lineal Modelo de Redes Alcance de las aplicaciones Curso: Investigación de Operaciones Ing. Javier Villatoro ALCANCE DE LAS APLICACONES DE REDES ALCANCE DE LAS APLICACIONES Muchas situaciones
Fundamentos y aplicaciones de la teoría de grafos. Grafos eulerianos y hamiltonianos. Diagramas en árbol. (2ª Parte)
 Fundamentos y aplicaciones de la teoría de grafos. Grafos eulerianos y hamiltonianos. Diagramas en árbol. (2ª Parte) Título: Fundamentos y aplicaciones de la teoría de grafos. Grafos eulerianos y hamiltonianos.
Fundamentos y aplicaciones de la teoría de grafos. Grafos eulerianos y hamiltonianos. Diagramas en árbol. (2ª Parte) Título: Fundamentos y aplicaciones de la teoría de grafos. Grafos eulerianos y hamiltonianos.
Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler]
![Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler] Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler]](/thumbs/66/55246007.jpg) Matemáticas Discretas L. Enrique Sucar INAOE Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y circuitos Isomorfismo
Matemáticas Discretas L. Enrique Sucar INAOE Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y circuitos Isomorfismo
Tema: Recorrido de Grafos
 PED104. Guía N 11 Página 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación con Estructuras de Datos Tema: Recorrido de Grafos Competencia Desarrolla sistemas de información informáticos
PED104. Guía N 11 Página 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación con Estructuras de Datos Tema: Recorrido de Grafos Competencia Desarrolla sistemas de información informáticos
Teoría de Grafos. Herramientas de programación para procesamiento de señales
 Teoría de Grafos Herramientas de programación para procesamiento de señales Indice Nociones básicas: Definiciones Ejemplos Propiedades Nociones avanzadas: Grafos planares Árboles Representación en computadora
Teoría de Grafos Herramientas de programación para procesamiento de señales Indice Nociones básicas: Definiciones Ejemplos Propiedades Nociones avanzadas: Grafos planares Árboles Representación en computadora
Trayectorias y circuitos Eulerianos y Hamiltonianos,
 Trayectorias y circuitos Eulerianos y Hamiltonianos, Eulerianos Trayectoria de Euler: recorrer una gráfica G utilizando cada arista de la gráfica sólo una vez, puede ser necesario o no comenzar y terminar
Trayectorias y circuitos Eulerianos y Hamiltonianos, Eulerianos Trayectoria de Euler: recorrer una gráfica G utilizando cada arista de la gráfica sólo una vez, puede ser necesario o no comenzar y terminar
Tema: Algoritmos para la ruta más corta en un Grafo.
 Programación IV. Guía 10 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos para la ruta más corta en un Grafo. Objetivos Específicos Definir el concepto de camino
Programación IV. Guía 10 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos para la ruta más corta en un Grafo. Objetivos Específicos Definir el concepto de camino
Capítulo 7. Grafos. Continuar
 Capítulo 7. Grafos Continuar Introducción Uno de los primeros resultados de la teoría de grafos fue el que obtuvo Leonhard Euler en el siglo XVIII al resolver el problema de los puentes de Königsberg.
Capítulo 7. Grafos Continuar Introducción Uno de los primeros resultados de la teoría de grafos fue el que obtuvo Leonhard Euler en el siglo XVIII al resolver el problema de los puentes de Königsberg.
5.6 Árbol generador de un grafo
 88 5.6 Árbol generador de un grafo Definición 5.59. Sea G un grafo simple. Un árbol generador de G es un subgrafo de G que es un árbol y contiene todos los vértices de G. Ejemplo 5.60. Un grafo y algunos
88 5.6 Árbol generador de un grafo Definición 5.59. Sea G un grafo simple. Un árbol generador de G es un subgrafo de G que es un árbol y contiene todos los vértices de G. Ejemplo 5.60. Un grafo y algunos
Grafos y Redes. 3. Resolución: Dibujar el camino sin levantar el lápiz y pasando sólo una vez por cada arco o arista.
 Grafos y Redes. Nodos: vértices, 2, 3 2. Arcos: aristas, conexión entre nodos. 2, 54, etc. 3. Resolución: Dibujar el camino sin levantar el lápiz y pasando sólo una vez por cada arco o arista. 4. Grado
Grafos y Redes. Nodos: vértices, 2, 3 2. Arcos: aristas, conexión entre nodos. 2, 54, etc. 3. Resolución: Dibujar el camino sin levantar el lápiz y pasando sólo una vez por cada arco o arista. 4. Grado
Estructuras de Datos ARBOLES Y GRAFOS
 Estructuras de Datos ARBOLES Y GRAFOS Rosa Barrera Capot rosa.barrera@usach.cl Grafo? Características Permiten Modelar un problema Aplicaciones: Ingeniería de Sistemas Modelado de Redes Ingeniería Industrial
Estructuras de Datos ARBOLES Y GRAFOS Rosa Barrera Capot rosa.barrera@usach.cl Grafo? Características Permiten Modelar un problema Aplicaciones: Ingeniería de Sistemas Modelado de Redes Ingeniería Industrial
Algoritmos Voraces. Diseño y Análisis de Algoritmos
 Algoritmos Voraces Diseño y Análisis de Algoritmos Contenidos Contenidos 1 Introducción 2 Ejemplos básicos 3 Cambio de monedas 4 Problema de la mochila 5 Problemas de planificación de tareas 6 Patrones
Algoritmos Voraces Diseño y Análisis de Algoritmos Contenidos Contenidos 1 Introducción 2 Ejemplos básicos 3 Cambio de monedas 4 Problema de la mochila 5 Problemas de planificación de tareas 6 Patrones
AnAnálisis de redes de transporte Tr. Muchas veces se utiliza en aplicaciones que nada tienen que ver con el transporte
 AnAnálisis de redes de transporte Tr Muchas veces se utiliza en aplicaciones que nada tienen que ver con el transporte Resumen Antecedentes y definiciones El camino más corto Árbol de expansión mínima
AnAnálisis de redes de transporte Tr Muchas veces se utiliza en aplicaciones que nada tienen que ver con el transporte Resumen Antecedentes y definiciones El camino más corto Árbol de expansión mínima
2007 Carmen Moreno Valencia
 Tema VIII. Grafos Grafos 1 2007 Carmen Moreno Valencia 1. Grafos, digrafos y multigrafos 2. Grafos eulerianos 3. Matrices de adyacencia e incidencia 4. Exploración de grafos pesados 1. Grafos, digrafos
Tema VIII. Grafos Grafos 1 2007 Carmen Moreno Valencia 1. Grafos, digrafos y multigrafos 2. Grafos eulerianos 3. Matrices de adyacencia e incidencia 4. Exploración de grafos pesados 1. Grafos, digrafos
Teoría de grafos y optimización en redes
 Teoría de grafos y optimización en redes José María Ferrer Caja Universidad Pontificia Comillas Definiciones básicas Grafo: Conjunto de nodos (o vértices) unidos por aristas G = (V,E) Ejemplo V = {,,,,
Teoría de grafos y optimización en redes José María Ferrer Caja Universidad Pontificia Comillas Definiciones básicas Grafo: Conjunto de nodos (o vértices) unidos por aristas G = (V,E) Ejemplo V = {,,,,
Indice. 1. Tipos de grafos. 2. Conceptos Básicos 3. Representación de grafos 4. Subgrafos. Grafos complementarios
 Teoría de Grafos 1 1. Tipos de grafos Indice 2. Conceptos Básicos 3. Representación de grafos 4. Subgrafos. Grafos complementarios 5. Caminos y conectividad 6. Grafos Bipartitos 2 Tipos de Grafos Un grafo
Teoría de Grafos 1 1. Tipos de grafos Indice 2. Conceptos Básicos 3. Representación de grafos 4. Subgrafos. Grafos complementarios 5. Caminos y conectividad 6. Grafos Bipartitos 2 Tipos de Grafos Un grafo
Hamilton, Euler y Dijkstra
 UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE COMPUTACION Matemáticas Discretas III (Cód. 6108) Práctica # 2 Hamilton, Euler y Dijkstra 1. Sea G = un multigrafo no dirigido donde
UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE COMPUTACION Matemáticas Discretas III (Cód. 6108) Práctica # 2 Hamilton, Euler y Dijkstra 1. Sea G = un multigrafo no dirigido donde
Tema 2.TEORIA Y APLICACIONES DE LA TEORÍA DE GRAFOS.
 Tema 2.Fundamentos y aplicaciones de la teoría de grafos. 1 Tema 2.TEORIA Y APLICACIONES DE LA TEORÍA DE GRAFOS. 1. Introducción. Teoría de grafos en una rama de la Topología Surge de los estudios de Euler
Tema 2.Fundamentos y aplicaciones de la teoría de grafos. 1 Tema 2.TEORIA Y APLICACIONES DE LA TEORÍA DE GRAFOS. 1. Introducción. Teoría de grafos en una rama de la Topología Surge de los estudios de Euler
Teoría de redes y optimización en redes
 Teoría de redes y optimización en redes Pedro Sánchez Martín Contenidos Definiciones básicas Árbol generador mínimo de expansión Camino mínimo Algoritmo Dkstra Algoritmo Bellman-Ford Fluo máximo Fluo de
Teoría de redes y optimización en redes Pedro Sánchez Martín Contenidos Definiciones básicas Árbol generador mínimo de expansión Camino mínimo Algoritmo Dkstra Algoritmo Bellman-Ford Fluo máximo Fluo de
5.4 Caminos mínimos: Algoritmo de Dijkstra
 81 5.4 Caminos mínimos: Algoritmo de Dijkstra Al observar nuestro mapa de carreteras se pueden considerar las distancias en km que hay entre las ciudades, a cada arista se le asigna el valor correspondiente
81 5.4 Caminos mínimos: Algoritmo de Dijkstra Al observar nuestro mapa de carreteras se pueden considerar las distancias en km que hay entre las ciudades, a cada arista se le asigna el valor correspondiente
Flujos de redes (Network Flows NF)
 Fluos de redes (Network Flows NF). Terminología. Árbol generador mínimo. Camino mínimo 4. Fluo máximo 5. Fluo de coste mínimo TEORÍA DE GRAFOS. OPTIMIZACIÓN EN REDES Terminología Red o grafo (G) Nodos
Fluos de redes (Network Flows NF). Terminología. Árbol generador mínimo. Camino mínimo 4. Fluo máximo 5. Fluo de coste mínimo TEORÍA DE GRAFOS. OPTIMIZACIÓN EN REDES Terminología Red o grafo (G) Nodos
ÁRBOLES CRISTIAN ALFREDO MUÑOZ ÁLVAREZ JUAN DAVID LONDOÑO CASTRO JUAN PABLO CHACÓN PEÑA EDUARDO GONZALES
 ÁRBOLES CRISTIAN ALFREDO MUÑOZ ÁLVAREZ JUAN DAVID LONDOÑO CASTRO JUAN PABLO CHACÓN PEÑA EDUARDO GONZALES ÁRBOL Un árbol es un grafo no dirigido, conexo, sin ciclos (acíclico), y que no contiene aristas
ÁRBOLES CRISTIAN ALFREDO MUÑOZ ÁLVAREZ JUAN DAVID LONDOÑO CASTRO JUAN PABLO CHACÓN PEÑA EDUARDO GONZALES ÁRBOL Un árbol es un grafo no dirigido, conexo, sin ciclos (acíclico), y que no contiene aristas
Capítulo 5 Introducción a la teoría de grafos
 Capítulo 5 Introducción a la teoría de grafos 5.1. Terminología básica y tipos de grafos Una primera aproximación a la teoría de grafos la tenemos cuando observamos un mapa de carreteras: ciudades (vértices)
Capítulo 5 Introducción a la teoría de grafos 5.1. Terminología básica y tipos de grafos Una primera aproximación a la teoría de grafos la tenemos cuando observamos un mapa de carreteras: ciudades (vértices)
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática. Grafos
 Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Grafos Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias preparadas a partir
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Grafos Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias preparadas a partir
TEMA 5 El tipo grafo. Tipo grafo
 TEMA 5 El tipo grafo PROGRAMACIÓN Y ESTRUCTURAS DE DATOS Tipo grafo 1. Concepto de grafo y terminología 2. Especificación algebraica. Representación de grafos.1. Recorrido en profundidad o DFS.2. Recorrido
TEMA 5 El tipo grafo PROGRAMACIÓN Y ESTRUCTURAS DE DATOS Tipo grafo 1. Concepto de grafo y terminología 2. Especificación algebraica. Representación de grafos.1. Recorrido en profundidad o DFS.2. Recorrido
Sesión 4: Teoría de Grafos
 Modelos Gráficos Probabilistas L. Enrique Sucar INAOE Sesión 4: Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y
Modelos Gráficos Probabilistas L. Enrique Sucar INAOE Sesión 4: Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y
El origen: Los puentes de Königsberg. Grafos. Algoritmos y Estructuras de Datos III. Leonhard Euler ( )
 El origen: Los puentes de Königsberg Grafos Algoritmos y Estructuras de Datos III Leonhard Euler (1707 1783) El origen: Los puentes de Königsberg La ciudad de Königsberg (hoy Kaliningrado) tenía en el
El origen: Los puentes de Königsberg Grafos Algoritmos y Estructuras de Datos III Leonhard Euler (1707 1783) El origen: Los puentes de Königsberg La ciudad de Königsberg (hoy Kaliningrado) tenía en el
Tema 2: Grafos y Árboles. Algoritmos y Estructuras de Datos 3
 Tema 2: Grafos y Árboles Algoritmos y Estructuras de Datos 3 1 ÍNDICE 2.1 Definiciones básicas: grafos y árboles 2.2 Representaciones de árboles y grafos 2.3 Algoritmos de recorrido de árboles binarios
Tema 2: Grafos y Árboles Algoritmos y Estructuras de Datos 3 1 ÍNDICE 2.1 Definiciones básicas: grafos y árboles 2.2 Representaciones de árboles y grafos 2.3 Algoritmos de recorrido de árboles binarios
Francis Guthrie Planteo el problema de los cuatro colores, después de colorear el mapa de Inglaterra 9/15/2015 3
 INTRODUCCION GRAFOS La Teoria de Grafos nace del análisis sobre una inquietud presentada en la isla Kueiphof en Koenigsberg (Pomerania) ya que el río que la rodea se divide en dos brazos. Sobre los brazos
INTRODUCCION GRAFOS La Teoria de Grafos nace del análisis sobre una inquietud presentada en la isla Kueiphof en Koenigsberg (Pomerania) ya que el río que la rodea se divide en dos brazos. Sobre los brazos
Teoría de Grafos Introducción Grafos isomorfos
 Capítulo 1 Teoría de Grafos 1.1. Introducción Definición. Denominaremos pseudomultigrafo a una terna (V,E, γ), donde V y E son conjuntos y γ : E {{u,v}: u,v V }. El conjunto V se denomina conjunto de vértices
Capítulo 1 Teoría de Grafos 1.1. Introducción Definición. Denominaremos pseudomultigrafo a una terna (V,E, γ), donde V y E son conjuntos y γ : E {{u,v}: u,v V }. El conjunto V se denomina conjunto de vértices
Francisco J. Hernández López
 Francisco J. Hernández López fcoj23@cimat.mx Sus aristas son pares de vértices no ordenados, es decir si hay un camino del vértice i al vértice j, será exactamente el mismo camino del vértice j al vértice
Francisco J. Hernández López fcoj23@cimat.mx Sus aristas son pares de vértices no ordenados, es decir si hay un camino del vértice i al vértice j, será exactamente el mismo camino del vértice j al vértice
Guía práctica de estudio 7
 Guía práctica de estudio 7 Algoritmos de Grafos. Parte 2. Elaborado por: Revisión: Ing. Laura Sandoval Montaño Facultad de Ingeniería U.N.A.M. Guía Práctica 7 Estructura de datos y Algoritmos II Algoritmos
Guía práctica de estudio 7 Algoritmos de Grafos. Parte 2. Elaborado por: Revisión: Ing. Laura Sandoval Montaño Facultad de Ingeniería U.N.A.M. Guía Práctica 7 Estructura de datos y Algoritmos II Algoritmos
OBJETIVOS ÍNDICE BIBLIOGRAFÍA
 OBJETIVOS Tema 9: GRAFOS Primera Parte Estructuras de Datos y Algoritmos Curso 2002/03 Definiciones formales de grafo y conceptos relacionados Estructuras de datos para representar grafos Algoritmos para
OBJETIVOS Tema 9: GRAFOS Primera Parte Estructuras de Datos y Algoritmos Curso 2002/03 Definiciones formales de grafo y conceptos relacionados Estructuras de datos para representar grafos Algoritmos para
Estructuras de Datos y Algoritmos: Boletín de Problemas del segundo parcial
 Estructuras de Datos y Algoritmos: Boletín de Problemas del segundo parcial (Facultad de Informática) Curso 00 0 Estructuras de Datos y Algoritmos (FI-UPV) Curso 00 0 Árboles. Si la acción P fuera escribir
Estructuras de Datos y Algoritmos: Boletín de Problemas del segundo parcial (Facultad de Informática) Curso 00 0 Estructuras de Datos y Algoritmos (FI-UPV) Curso 00 0 Árboles. Si la acción P fuera escribir
Capítulo 4: Grafos Clase 2: Caminos, Circuitos Eulerianos y Hamiltonianos
 Capítulo 4: Grafos Clase 2: Caminos, Circuitos Eulerianos y Hamiltonianos Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 4: Grafos 1 / 29 Navegación de grafos
Capítulo 4: Grafos Clase 2: Caminos, Circuitos Eulerianos y Hamiltonianos Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 4: Grafos 1 / 29 Navegación de grafos
1. Conceptos básicos sobre el problema en cuestión y cuestiones afines. 2. Formulación de los correspondientes algoritmos y su pseudocódigo.
 Análisis de Algoritmos Ingeniería Informática, EPS-UAM Información general Organización del curso: 13-15 (mínimo-máximo) semanas docentes: 30-33 clases teóricas. 9-12 clases de problemas 26-30 clases prácticas
Análisis de Algoritmos Ingeniería Informática, EPS-UAM Información general Organización del curso: 13-15 (mínimo-máximo) semanas docentes: 30-33 clases teóricas. 9-12 clases de problemas 26-30 clases prácticas
Apuntes de Teórico de Programación 3. Apuntes de Teórico PROGRAMACIÓN 3. Greedy. Versión 1.1
 Apuntes de Teórico PROGRAMACIÓN 3 Greedy Versión 1.1 1 Índice Índice... Introducción... 3 Ejemplo 1 (problema de las monedas)... 3 Ejemplo (problema de la mochila)... 4 Aplicaciones del método Greedy a
Apuntes de Teórico PROGRAMACIÓN 3 Greedy Versión 1.1 1 Índice Índice... Introducción... 3 Ejemplo 1 (problema de las monedas)... 3 Ejemplo (problema de la mochila)... 4 Aplicaciones del método Greedy a
Unidad 2: Problemas de camino mínimo
 Representación Recorrido de grafos Camino mínimo Unidad 2: Problemas de camino mínimo Representación Matriz de adyacencia Matriz de incidencia Listas de vecinos Recorrido de grafos Estructuras de datos
Representación Recorrido de grafos Camino mínimo Unidad 2: Problemas de camino mínimo Representación Matriz de adyacencia Matriz de incidencia Listas de vecinos Recorrido de grafos Estructuras de datos
Algoritmos y Estructuras de Datos III
 Árboles Algoritmos y Estructuras de Datos III Árboles Definición: Un árbol es un grafo conexo sin circuitos simples. Árboles Teorema: Dado un grafo G = (V, X ) son equivalentes: 1. G es un árbol. 2. G
Árboles Algoritmos y Estructuras de Datos III Árboles Definición: Un árbol es un grafo conexo sin circuitos simples. Árboles Teorema: Dado un grafo G = (V, X ) son equivalentes: 1. G es un árbol. 2. G
Grafos: algunas definiciones
 Grafos: algunas definiciones Un grafo dirigido G es un par (V, E), donde V es un conjunto finito de nodos (o vértices) y E es una relación binaria sobre V. Un grafo no dirigido G es un par (V, E), donde
Grafos: algunas definiciones Un grafo dirigido G es un par (V, E), donde V es un conjunto finito de nodos (o vértices) y E es una relación binaria sobre V. Un grafo no dirigido G es un par (V, E), donde
Conceptos básicos en la Teoría de Grafos
 Conceptos básicos en la Teoría de Grafos Cristina Jordán Lluch Instituto de Matemáticas Multidisciplinar Grupo de Modelización Físico-Matemática Conceptos básicos Subgrafos Caminos, cadenas y ciclos Represetación
Conceptos básicos en la Teoría de Grafos Cristina Jordán Lluch Instituto de Matemáticas Multidisciplinar Grupo de Modelización Físico-Matemática Conceptos básicos Subgrafos Caminos, cadenas y ciclos Represetación
Algoritmos para determinar Caminos Mínimos en Grafos
 Problemas de camino mínimo Algoritmos para determinar Caminos Mínimos en Grafos Algoritmos y Estructuras de Datos III DC, FCEN, UBA, C 202 Problemas de camino mínimo Dado un grafo orientado G = (V, E)
Problemas de camino mínimo Algoritmos para determinar Caminos Mínimos en Grafos Algoritmos y Estructuras de Datos III DC, FCEN, UBA, C 202 Problemas de camino mínimo Dado un grafo orientado G = (V, E)
Un GRAFO O GRAFO NO ORIENTADO es una terna G = {V, A,ϕ } conv
 DEFINICIÓN 1: Un GRAFO O GRAFO NO ORIENTADO es una terna G = {V, A,ϕ } conv φ donde: V = {v 1, v 2,, v n }: conjunto finito de vértices o nodos. A = {a 1, a 2,, a n }: conjunto finito de aristas o lados
DEFINICIÓN 1: Un GRAFO O GRAFO NO ORIENTADO es una terna G = {V, A,ϕ } conv φ donde: V = {v 1, v 2,, v n }: conjunto finito de vértices o nodos. A = {a 1, a 2,, a n }: conjunto finito de aristas o lados
Ejercicios de Grafos Hoja 1 2 curso I.T.I.S. Universidad de Salamanca 2009/10
 Ejercicios de Grafos Hoja 1 2 curso I.T.I.S. Universidad de Salamanca 2009/10 1. Dibujar los grafos, la rueda W 3, el cubo Q 3, los grafos completos K 3, K 4 y los grafos bipartitos completos K 2,5, K
Ejercicios de Grafos Hoja 1 2 curso I.T.I.S. Universidad de Salamanca 2009/10 1. Dibujar los grafos, la rueda W 3, el cubo Q 3, los grafos completos K 3, K 4 y los grafos bipartitos completos K 2,5, K
Instituto de Matemática y Física Taller de Matemática 2009 Estudiantes de Enseñanza Media
 Taller 6 Introducción Desde niños (as) sabemos como dibujar una estrella sin levantar el lápiz ni pasar dos veces por el mismo trazo. Si no la han hecho nunca vean que es posible. Un desafío que muchas
Taller 6 Introducción Desde niños (as) sabemos como dibujar una estrella sin levantar el lápiz ni pasar dos veces por el mismo trazo. Si no la han hecho nunca vean que es posible. Un desafío que muchas
Se puede dibujar la siguiente figura, empezando y terminando en el mismo punto, sin levantar e lápiz del papel?
 Se puede dibujar la siguiente figura, empezando y terminando en el mismo punto, sin levantar e lápiz del papel? Y esta otra? Los puentes de Königsberg Königsberg es famosa por ser la ciudad natal de Immanuel
Se puede dibujar la siguiente figura, empezando y terminando en el mismo punto, sin levantar e lápiz del papel? Y esta otra? Los puentes de Königsberg Königsberg es famosa por ser la ciudad natal de Immanuel
Estructura de Datos. Temario Unidad VI. Árboles Árboles Binarios
 Estructura de Datos Árboles Árboles Binarios Temario Unidad VI 6.1 Definición y operaciones 6.2 Implementación 6.3 Recorrido en Árboles Binarios 6.4 Árboles AVL y su implementación 6.5 Árboles n-arios
Estructura de Datos Árboles Árboles Binarios Temario Unidad VI 6.1 Definición y operaciones 6.2 Implementación 6.3 Recorrido en Árboles Binarios 6.4 Árboles AVL y su implementación 6.5 Árboles n-arios
A5 Introducción a la optimización en redes
 48 Materials David Pujolar Morales A5 Introducción a la optimización en redes Definición 1. Grafo finito. Sea un V un conjunto no vacío con un número finito de elementos y E una familia finita de pares
48 Materials David Pujolar Morales A5 Introducción a la optimización en redes Definición 1. Grafo finito. Sea un V un conjunto no vacío con un número finito de elementos y E una familia finita de pares
Grafos. Amalia Duch Brown Octubre de 2007
 Grafos Amalia Duch Brown Octubre de 2007 Índice 1. Definiciones Básicas Intuitivamente un grafo es un conjunto de vértices unidos por un conjunto de líneas o flechas dependiendo de si el grafo es dirigido
Grafos Amalia Duch Brown Octubre de 2007 Índice 1. Definiciones Básicas Intuitivamente un grafo es un conjunto de vértices unidos por un conjunto de líneas o flechas dependiendo de si el grafo es dirigido
Tema 4y 5. Algoritmos voraces. Algoritmos sobre grafos
 Tema 4y 5. Algoritmos voraces. Algoritmos sobre grafos Objetivos: Estudio de la técnica de diseño de algoritmos voraces Estudio de algunos problemas clásicos: Indice: Mochila con fraccionamiento Algoritmos
Tema 4y 5. Algoritmos voraces. Algoritmos sobre grafos Objetivos: Estudio de la técnica de diseño de algoritmos voraces Estudio de algunos problemas clásicos: Indice: Mochila con fraccionamiento Algoritmos
TEORIA DE GRAFOS. Estructuras Discretas Ing. Jenny Paredes Aguilar
 TEORIA DE GRAFOS Estructuras Discretas Ing. Jenny Paredes Aguilar INTRODUCCION Teoria de grafos se usa en numerosos problemas cuantificables, en las organizaciones, intervienen una serie de elementos entre
TEORIA DE GRAFOS Estructuras Discretas Ing. Jenny Paredes Aguilar INTRODUCCION Teoria de grafos se usa en numerosos problemas cuantificables, en las organizaciones, intervienen una serie de elementos entre
Se puede dibujar la siguiente figura, empezando y terminando en el mismo punto, sin levantar e lápiz del papel?
 Se puede dibujar la siguiente figura, empezando y terminando en el mismo punto, sin levantar e lápiz del papel? Y esta otra? Los puentes de Königsberg Königsberg es famosa por ser la ciudad natal de Immanuel
Se puede dibujar la siguiente figura, empezando y terminando en el mismo punto, sin levantar e lápiz del papel? Y esta otra? Los puentes de Königsberg Königsberg es famosa por ser la ciudad natal de Immanuel
Análisis de algoritmos
 Tema 10: Algoritmos ávidos M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido Introducción Algoritmos ávidos Forma general de un
Tema 10: Algoritmos ávidos M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido Introducción Algoritmos ávidos Forma general de un
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre
 Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Típicamente, un grafo se representa
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Típicamente, un grafo se representa
Estructura de Datos. Códigos de Huffman. Primer Semestre, Compresión de Archivos. Compresión de Archivos
 Estructura de Datos Códigos de Huffman Prof.: Mauricio Solar Prof.: Lorna Figueroa Primer Semestre, 2 Los algoritmos estudiados hasta ahora han sido diseñados, en general, para que utilicen el menor tiempo
Estructura de Datos Códigos de Huffman Prof.: Mauricio Solar Prof.: Lorna Figueroa Primer Semestre, 2 Los algoritmos estudiados hasta ahora han sido diseñados, en general, para que utilicen el menor tiempo
Estructuras de Datos y Algoritmos
 Estructuras de Datos y Algoritmos Práctico 3: Grafos (Finalización: 06/09) Ing. en Computación - Ing. en Informática - Prof. en Computación Año 2018 Ejercicio 1: Dado el siguiente p-digrafo: 5 b 6 d 11
Estructuras de Datos y Algoritmos Práctico 3: Grafos (Finalización: 06/09) Ing. en Computación - Ing. en Informática - Prof. en Computación Año 2018 Ejercicio 1: Dado el siguiente p-digrafo: 5 b 6 d 11
CIRCUITOS DE EULER Y HAMILTON
 CIRCUITOS DE EULER Y HAMILTON Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 8 de septiembre de 2008 Contenido Circuitos de Euler Definición Algoritmo
CIRCUITOS DE EULER Y HAMILTON Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 8 de septiembre de 2008 Contenido Circuitos de Euler Definición Algoritmo
Tema 11. Estructura de datos Grafo
 Tema 11. Estructura de datos Grafo http://aulavirtual.uji.es José M. Badía, Begoña Martínez, Antonio Morales y José M. Sanchiz {badia, bmartine, morales}@icc.uji.es Estructuras de datos y de la información
Tema 11. Estructura de datos Grafo http://aulavirtual.uji.es José M. Badía, Begoña Martínez, Antonio Morales y José M. Sanchiz {badia, bmartine, morales}@icc.uji.es Estructuras de datos y de la información
Este material es de uso exclusivo para clase de algoritmos y estructura de datos, la información de este documento fue tomada textualmente de varios
 CLASE GRAFOS Este material es de uso exclusivo para clase de algoritmos y estructura de datos, la información de este documento fue tomada textualmente de varios libros por lo que está prohibida su impresión
CLASE GRAFOS Este material es de uso exclusivo para clase de algoritmos y estructura de datos, la información de este documento fue tomada textualmente de varios libros por lo que está prohibida su impresión
Caminos y Flujos optimales. Introducción a la Investigación de Operaciones 2007
 Caminos y Flujos optimales Introducción a la Investigación de Operaciones 2007 Contenido Definiciones básicas. Conexidad. Clausura transitiva. Esqueletos y caminos optimales. Redes. Flujos. Algoritmo de
Caminos y Flujos optimales Introducción a la Investigación de Operaciones 2007 Contenido Definiciones básicas. Conexidad. Clausura transitiva. Esqueletos y caminos optimales. Redes. Flujos. Algoritmo de
TIPOS ABSTRACTOS DE DATOS EN HASKELL
 TIPOS ABSTRACTOS DE DATOS EN HASKELL ÍNDICE GENERAL 1. Introducción a Haskell 2. Tipos abstractos de datos en Haskell 3. TAD Grafo 4. TAD Montículos 5. Bibliografía INTRODUCCIÓN A HASKELL 1. Introducción
TIPOS ABSTRACTOS DE DATOS EN HASKELL ÍNDICE GENERAL 1. Introducción a Haskell 2. Tipos abstractos de datos en Haskell 3. TAD Grafo 4. TAD Montículos 5. Bibliografía INTRODUCCIÓN A HASKELL 1. Introducción
Introducción. Königsberg, s.xviii A
 Teoría de Grafos Introducción Königsberg, s.xviii A B C D Euler resuelve este problema mediante la teoría de grafos: sólo puede haber un ciclo euleriano cuando todos los nodos tienen un número par de aristas
Teoría de Grafos Introducción Königsberg, s.xviii A B C D Euler resuelve este problema mediante la teoría de grafos: sólo puede haber un ciclo euleriano cuando todos los nodos tienen un número par de aristas
Análisis y Diseño de Algoritmos. Teoría de Gráficas
 Teoría de Gráficas Arturo Díaz Pérez Sección de Computación Departamento de Ingeniería Eléctrica CINVESTAV-IPN Av. Instituto Politécnico Nacional No. 2508 Col. San Pedro Zacatenco México, D. F. CP 07300
Teoría de Gráficas Arturo Díaz Pérez Sección de Computación Departamento de Ingeniería Eléctrica CINVESTAV-IPN Av. Instituto Politécnico Nacional No. 2508 Col. San Pedro Zacatenco México, D. F. CP 07300
Teoría de Grafos I. 2. Describa tres situaciones prácticas en las cuales un grafo pueda ser útil.
 UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE COMPUTACION Matemáticas Discretas III (Cód. 6108) Práctica # 1 Teoría de Grafos I 1. Defina y de ejemplos de cada uno de los siguientes
UNIVERSIDAD CENTRAL DE VENEZUELA FACULTAD DE CIENCIAS ESCUELA DE COMPUTACION Matemáticas Discretas III (Cód. 6108) Práctica # 1 Teoría de Grafos I 1. Defina y de ejemplos de cada uno de los siguientes
Algoritmos y Estructuras de Datos III
 Árboles Algoritmos y Estructuras de Datos III Árboles Definición: Un árbol es un grafo conexo sin circuitos simples. Árboles Teorema: Dado un grafo G = (V, X ) son equivalentes: 1. G es un árbol. 2. G
Árboles Algoritmos y Estructuras de Datos III Árboles Definición: Un árbol es un grafo conexo sin circuitos simples. Árboles Teorema: Dado un grafo G = (V, X ) son equivalentes: 1. G es un árbol. 2. G
Ciclos Hamiltonianos Algoritmo de la Ruta Más Corta. Matemática Discreta. Agustín G. Bonifacio UNSL. Teoría de Grafos II
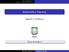 UNSL Teoría de Grafos II y Ejemplos Un ciclo en un grafo que contiene cada vértice justo una vez, excepto por el vértice inicial y el final que aparece dos veces, recibe el nombre de ciclo de Hamilton.
UNSL Teoría de Grafos II y Ejemplos Un ciclo en un grafo que contiene cada vértice justo una vez, excepto por el vértice inicial y el final que aparece dos veces, recibe el nombre de ciclo de Hamilton.
Matemáticas Básicas para Computación
 Matemáticas Básicas para Computación MATEMÁTICAS BÁSICAS PARA COMPUTACIÓN 1 Sesión No. 10 Nombre: Grafos Objetivo: Al término de la sesión el participante conocerá los elementos que integran los grafos,
Matemáticas Básicas para Computación MATEMÁTICAS BÁSICAS PARA COMPUTACIÓN 1 Sesión No. 10 Nombre: Grafos Objetivo: Al término de la sesión el participante conocerá los elementos que integran los grafos,
CLAVE V
 CLAVE-962-2-V-2-00 -2017 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CURSO: Matemática para computación 2 SEMESTRE: Segundo CÓDIGO DEL CURSO: 962 TIPO DE EXAMEN:
CLAVE-962-2-V-2-00 -2017 UNIVERSIDAD DE SAN CARLOS DE GUATEMALA FACULTAD DE INGENIERÍA DEPARTAMENTO DE MATEMÁTICA CURSO: Matemática para computación 2 SEMESTRE: Segundo CÓDIGO DEL CURSO: 962 TIPO DE EXAMEN:
GRAFOS. Tomado de: Joyanes Aguilar Luis, Estructuras de datos en Java. CASOS
 GRAFOS Tomado de: Joyanes Aguilar Luis, Estructuras de datos en Java. CASOS 1.4 El recorrido del cartero Imaginemos un grafo que representa el mapa de las calles de un barrio. Una calle va de una esquina
GRAFOS Tomado de: Joyanes Aguilar Luis, Estructuras de datos en Java. CASOS 1.4 El recorrido del cartero Imaginemos un grafo que representa el mapa de las calles de un barrio. Una calle va de una esquina
Grafos: Fundamentos Representaciones, etc. Jose Aguilar
 Grafos: Fundamentos Representaciones, etc. Jose Aguilar Introducción Las estructura de datos no lineales se caracterizan por tener una relación de adyacencia genérica entre sus elementos, es decir, un
Grafos: Fundamentos Representaciones, etc. Jose Aguilar Introducción Las estructura de datos no lineales se caracterizan por tener una relación de adyacencia genérica entre sus elementos, es decir, un
