ARBOLES GENERADORES. Orlando Arboleda Molina. 16 de septiembre de Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle
|
|
|
- Alberto Vega Carrizo
- hace 6 años
- Vistas:
Transcripción
1 ARBOLES GENERADORES Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 16 de septiembre de 2008
2 Contenido Árboles generadores Algoritmo búsqueda por profundidad Algoritmo búsqueda en anchura Árboles generadores mínimos Algoritmo de Prim Algoritmo de Kruskal
3 Contenido Árboles generadores Algoritmo búsqueda por profundidad Algoritmo búsqueda en anchura Árboles generadores mínimos Algoritmo de Prim Algoritmo de Kruskal
4 Figura: Ejemplo de un grafo Problema: Que rutas pueden ser cerradas de tal manera que se pueda seguir viajando entre cualquier par de ciudades?.
5 Árboles generadores (o recubridor) Árboles generadores (o recubridor) Sea G un grafo simple. Un árbol generador (o recubridor) de G es un subgrafo de G que es un árbol y contiene todos los vértice de G. Figura: Ejemplo de un árbol generador Ejemplo: El árbol anterior es un árbol generador del problema original.
6 Árboles generadores (2) Nota: Un grafo simple con un árbol cobertor debe ser conexo, puesto que hay un camino en el árbol cobertor entre cualquier par de vértices. Teorema 1 Un grafo simple es conexo si y solo si admite un árbol cobertor. Los algoritmos mas usados para construir arboles generadores son: Búsqueda en profundidad y Búsqueda en amplitud.
7 Contenido Árboles generadores Algoritmo búsqueda por profundidad Algoritmo búsqueda en anchura Árboles generadores mínimos Algoritmo de Prim Algoritmo de Kruskal
8 Algoritmo búsqueda por profundidad Idea: Elegir un vértice arbitrario como raíz del árbol. Formar un camino que comienza en ese vértice añadiendo sucesivamente vértices y aristas, siendo cada nueva arista incidente con el último vértice del camino y un vértice que no está en el camino. Si el camino no pasa por todos los vértices del grafo, retroceder al penúltimo vértice e intentar un nuevo camino iniciando en él. También llamado de vuelta atrás o retroceso (en inglés, backtacking) puesto que el algoritmo retorna a los vértices visitados previamente para adicionarlos al camino.
9 Algoritmo búsqueda por profundidad (2) Procedimiento Profundidad ( G: grafo conexo de vertices v 1, v 2,..., v n ) T := arbol que consta solo del vertice v 1 visitar(v 1 ) Fin Procedimiento Procedimiento visitar (v: vertice de G) Para cada vertice w adyacente a v y aun no en T Adicionar vertice w y arista {v, w} a T visitar (w) Fin Para Fin Procedimiento
10 Algoritmo búsqueda por profundidad (3) Figura: Ejemplo de un árbol generador Ejercicio: Construir un árbol generador usando el algoritmo de búsqueda por profundidad, a partir del grafo anterior iniciando en el vertice a.
11 Contenido Árboles generadores Algoritmo búsqueda por profundidad Algoritmo búsqueda en anchura Árboles generadores mínimos Algoritmo de Prim Algoritmo de Kruskal
12 Algoritmo búsqueda en anchura Idea: Elegir un vértice arbitrario como raíz del árbol. Luego añadir todas las aristas incidentes con ese vértice (nivel 1 del árbol). Para cada vértice del nivel 1, visitados en orden, añadir todos los vertices incidentes con él siempre que no formen ciclos. El procedimiento se repite hasta que se adicionen todos los vértices.
13 Algoritmo búsqueda en anchura (2) Procedimiento Anchura ( G: grafo conexo de vertices v 1, v 2,..., v n ) T := arbol que consta solo del vertice v 1 L := lista vacia Mientras L no este vacia borrar el primer vertice v de L Para cada vertice w adyacente a v Si w no esta en L y no esta en T añadir el vertice w al final de la lista L añadir el vertice w y la arista {v, w} a T Fin Si Fin Para Fin Mientras Fin Procedimiento
14 Algoritmo búsqueda en anchura (3) Figura: Ejemplo de un árbol generador Ejercicio: Construir un árbol generador usando el algoritmo de búsqueda en anchura, a partir del grafo anterior iniciando en el vertice a.
15 Figura: Ejemplo de un grafo ponderado Problema: Que aristas deberían mantenerse, para asegurar que hay un camino entre cualquier par de ciudades y el costo total sea el menor posible?.
16 Árboles generadores mínimos Un árbol generador mínimo de un grafo ponderado es un árbol generador tal que la suma de los pesos de sus aristas es la mínima posible de entre todos los árboles generadores. Existen dos algoritmos voraces (procedimientos que realizan una elección óptima en cada uno de sus pasos. La optimización de cada paso no garantiza una solución final optima) a saber: algoritmo de Prim algoritmo de Kruskal
17 Contenido Árboles generadores Algoritmo búsqueda por profundidad Algoritmo búsqueda en anchura Árboles generadores mínimos Algoritmo de Prim Algoritmo de Kruskal
18 Algoritmo de Prim Algoritmo propuesto por Robert Prim en Idea: Elegir cualquier arista de peso mínimo y seleccionarla para el árbol (generador). Luego añadir sucesivamente aristas de peso mínimo que sean incidentes con un vértice que ya está en el árbol y que no formen ciclos con las que ya han sido incorporadas. El algoritmo se ha de detener cuando hayamos añadido n 1 aristas.
19 Algoritmo de Prim (2) Procedimiento Prim ( G: grafo ponderado conexo y no dirigido de n vertices) T := una arista de peso minimo Para i = 1 Hasta n 2 e := una arista de peso minimo incidente con un vertice de T que no forme un ciclo en T cuando se añada T := T con e añadida Fin Para Fin Procedimiento (T es un arbol generador minimo de G)
20 Contenido Árboles generadores Algoritmo búsqueda por profundidad Algoritmo búsqueda en anchura Árboles generadores mínimos Algoritmo de Prim Algoritmo de Kruskal
21 Algoritmo de Kruskal Algoritmo descubierto por Joseph kruskal en en Idea: Elegir cualquier arista de peso mínimo y seleccionarla para el árbol (generador). Luego añadir sucesivamente aristas de peso mínimo que no formen ciclos con las que ya han sido incorporadas. El algoritmo se ha de detener cuando hayamos añadido n 1 aristas.
22 Algoritmo de Kruskal (2) Procedimiento Kruskal ( G: grafo ponderado conexo y no dirigido de n vertices) T := grafo vacio Para i = 1 Hasta n 1 e := una arista de peso minimo de G que no forme un ciclo cuando se añada a T T := T con e añadida Fin Para Fin Procedimiento (T es un arbol generador minimo de G)
Grafos. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Grafos 1 / 30
Grafos AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Grafos / 0 Objetivos Al finalizar este tema tendréis que: Conocer la terminología básica de la teoría de grafos. Pasar
Centro Asociado Palma de Mallorca. Tutor: Antonio Rivero Cuesta
Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
Definición 1.1 Sea G = (V, A) un grafo no dirigido. G se denomina árbol si es conexo y no contiene ciclos.
Matemática Discreta y Lógica 2 1. Árboles Árboles Definición 1.1 Sea G = (V, A) un grafo no dirigido. G se denomina árbol si es conexo y no contiene ciclos. Como un lazo es un ciclo de longitud 1, un árbol
Grafos. Amalia Duch Brown Octubre de 2007
Grafos Amalia Duch Brown Octubre de 2007 Índice 1. Definiciones Básicas Intuitivamente un grafo es un conjunto de vértices unidos por un conjunto de líneas o flechas dependiendo de si el grafo es dirigido
Árboles. Un grafo no dirigido es un árbol si y sólo si existe una ruta unica simple entre cualquiera dos de sus vértices.
ÁRBOLES Árboles Un grafo conectado que no contiene circuitos simples. Utilizados desde 1857, por el matemático Ingles Arthur Cayley para contar ciertos tipos de componentes químicos. Un árbol es un grafo
LAS CIENCIAS DE LA PLANIFICACIÓN
LAS CIENCIAS DE LA PLANIFICACIÓN 5. EL PROBLEMA DEL VIAJANTE (PV) (The Traveling Salesman Problem TSP) Un problema como el de las vacaciones, pero vital para las empresas, es el problema del viajante (PV):
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto. Típicamente, un grafo se representa
Introducción a la Teoría de Grafos
Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Árboles Un árbol es un grafo conexo y acíclico (sin ciclos). Un bosque es un grafo acíclico, o sea, una unión disjunta
Un grafo G = (V, E) se dice finito si V es un conjunto finito.
1 Grafos: Primeras definiciones Definición 1.1 Un grafo G se define como un par (V, E), donde V es un conjunto cuyos elementos son denominados vértices o nodos y E es un subconjunto de pares no ordenados
Teoría de grafos y optimización en redes
Teoría de grafos y optimización en redes José María Ferrer Caja Universidad Pontificia Comillas Definiciones básicas Grafo: Conjunto de nodos (o vértices) unidos por aristas G = (V,E) Ejemplo V = {,,,,
El TAD Grafo. El TAD Grafo
! Esta representación resulta útil cuando el número de vértices se conoce previamente y permanecerá fijo durante la resolución del problema, pero resulta ineficiente si necesitamos añadir o eliminar vértices
Árboles abarcadores mínimos: algoritmo de Prim y algoritmo de Kruskal.
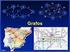Árboles abarcadores mínimos: algoritmo de Prim y algoritmo de Kruskal. Jose Aguilar 1 Grafo de carreteras entre ciudades Mcbo Coro Pto. Cabello Valera Bqto Valencia Maracay Caracas Acarigua Barinas San
Un grafo G es un par (V,E) donde V es un conjunto (llamado conjunto de vértices) y E un subconjunto de VxV (conjunto de aristas).
TEMA 5.- GRAFOS 5.1.- DEFINICIONES BÁSICAS Un grafo G es un par (V,E) donde V es un conjunto (llamado conjunto de vértices) y E un subconjunto de VxV (conjunto de aristas). Gráficamente representaremos
Algoritmos sobre Grafos
Sexta Sesión 27 de febrero de 2010 Contenido Deniciones 1 Deniciones 2 3 4 Deniciones sobre Grafos Par de una lista de nodos y una lista de enlaces, denidos a su vez como pares del conjunto de nodos.
Tema: Los Grafos y su importancia para la optimización de redes.
Tema: Los Grafos y su importancia para la optimización de redes. Qué son los Grafos? Un grafo es una dupla G= {X,U}, donde X es un conjunto finito y no vacio de elementos llamados vértices y U es el conjunto
Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.
![Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.](/thumbs/54/33802392.jpg "Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.")
Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
2007 Carmen Moreno Valencia
Tema VIII. Grafos Grafos 1 2007 Carmen Moreno Valencia 1. Grafos, digrafos y multigrafos 2. Grafos eulerianos 3. Matrices de adyacencia e incidencia 4. Exploración de grafos pesados 1. Grafos, digrafos
LAS CIENCIAS DE LA PLANIFICACIÓN
LAS CIENCIAS DE LA PLANIFICACIÓN 1. MODELIZACIÓN CON GRAFOS El objetivo de las ciencias de la planificación es encontrar el mejor método para resolver un problema, y si es posible encontrar la solución
Caminos y Flujos optimales. Introducción a la Investigación de Operaciones 2007
Caminos y Flujos optimales Introducción a la Investigación de Operaciones 2007 Contenido Definiciones básicas. Conexidad. Clausura transitiva. Esqueletos y caminos optimales. Redes. Flujos. Algoritmo de
Objetivos formativos de Matemática Discreta. Tema 1: Conjuntos, aplicaciones y relaciones
Objetivos formativos de Matemática Discreta Para cada uno de los temas el alumno debe ser capaz de hacer lo que se indica en cada bloque. Además de los objetivos que se señalan en cada tema, se considera
Introducción a la Teoría de Grafos
Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Programa Introducción a la teoría de grafos Problemas de camino mínimo Problemas de flujo máximo Programación lineal
Ruta más Corta con una sóla Fuente de Inicio (Single-Source Shortest Paths) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE
Ruta más Corta con una sóla Fuente de Inicio (Single-Source Shortest Paths) 1 DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Problema de Encontrar la Ruta más Corta 2 Se requiere llegar de
Algoritmos para determinar Caminos Mínimos en Grafos
Problemas de camino mínimo Algoritmos para determinar Caminos Mínimos en Grafos Algoritmos y Estructuras de Datos III DC, FCEN, UBA, C 202 Problemas de camino mínimo Dado un grafo orientado G = (V, E)
Flujos de redes (Network Flows NF)
Fluos de redes (Network Flows NF). Terminología. Árbol generador mínimo. Camino mínimo 4. Fluo máximo 5. Fluo de coste mínimo TEORÍA DE GRAFOS. OPTIMIZACIÓN EN REDES Terminología Red o grafo (G) Nodos
Grafos. Algoritmos y Estructuras de Datos III
Grafos Algoritmos y Estructuras de Datos III Grafos Un grafo G = (V, X ) es un par de conjuntos, donde V es un conjunto de puntos o nodos o vértices y X es un subconjunto del conjunto de pares no ordenados
El TAD Grafo. El TAD Grafo
Objetivos! Estudiar la especificación del TAD Grafo! Presentar diferentes alternativas de implementación! Conocer los algoritmos más importantes de manipulación de grafos Contenidos.1 Conceptos. Especificación
En la fig. 1 se representa el grafo, G=(V,A) donde: V = {1, 2, 3, 4, 5, 6} A = { {1,2}, {1,3}, {1,5}, {3}, {3,4}, {4,5}, {5,6} }
Unidad 1 Parte 1 - Teoría de Grafos Introducción En este capítulo veremos la noción matemática de grafo y propiedades de los mismos. En capítulos subsiguientes veremos las estructuras de datos utilizadas
GRAFOS. Prof. Ing. M.Sc. Fulbia Torres
ESTRUCTURAS DE DATOS 2006 Prof. DEFINICIÓN Un grafo consta de un conjunto de nodos(o vértices) y un conjunto de arcos (o aristas). Cada arco de un grafo se especifica mediante un par de nodos. Denotemos
Introducción a la teoría de grafos
Capítulo 5 Introducción a la teoría de grafos 5.1. Terminología básica y tipos de grafos Una primera aproximación a la teoría de grafos la tenemos cuando observamos un mapa de carreteras: ciudades (vértices)
Coloración de grafos
Alumno: Grupo: Coloración de grafos Comencemos planteando el problema de dar color a las regiones de un mapa plano de modo que a regiones vecinas se les asigne distinto color. Este problema puede ser resuelto
Teorema de Hoffman-Singleton.
Teorema de Hoffman-Singleton. Felipe Negreira. 18 de junio de 01. Sea X un grafo regular de grado, conexo y de diámetro. Cuál es la cantidad máxima de vértices que puede tener X bajo estas condiciones?
GRAFOS CREACIÓN DE ÍNDICES EN GOOGLE DE LOS SITIOS DE LA RED DE INTERNET
GRAFOS CREACIÓN DE ÍNDICES EN GOOGLE DE LOS SITIOS DE LA RED DE INTERNET INDICE 1. Introducción 2. Conceptos matemáticos con ejemplos 3. Resolución de ejercicios 4. Ejercicios con Maxima 5. Explicación
Algoritmos y estructuras de datos
Algoritmos y estructuras de datos Dr. Eduardo A. Rodríguez Tello Laboratorio de Tecnologías de Información Cinvestav Tamaulipas ertello@tamps.cinvestav.mx Cursos de inducción a la MCC Cinvestav Tamaulipas
MATEMÁTICAS PARA LA COMPUTACIÓN
MATEMÁTICAS PARA LA COMPUTACIÓN CAPÍTULO RELACIONES RELACIONES COMO LISTAS ENLAZADAS AUTOR: JOSÉ ALFREDO JIMÉNEZ MURILLO AVC APOYO VIRTUAL PARA EL CONOCIMIENTO RELACIONES COMO LISTAS ENLAZADAS Algunas
(d) Puede haber estrategias que funcionan mejor que Minimax si el contrincante es
Universidad Rey Juan Carlos Curso 2014 2015 Hoja de Problemas Tema 5 1. Cuáles de las siguientes afirmaciones acerca del algoritmo Minimax son ciertas (a) El algoritmo Minimax realiza una exploración primero
Computabilidad y Lenguajes Formales: Autómatas Finitos
300CIG007 Computabilidad y Lenguajes Formales: Autómatas Finitos Pontificia Universidad Javeriana Cali Ingeniería de Sistemas y Computación Prof. Gloria Inés Alvarez V. No Determinismo Hasta ahora cada
OPTIMIZACIÓN VECTORIAL
OPTIMIZACIÓN VECTORIAL Métodos de Búsqueda Directa Utilizan sólo valores de la función Métodos del Gradiente Métodos de Segundo Orden Requieren valores aproimados de la primera derivada de f) Además de
Minicurso de Teoría de Gráficas Escuela de Verano 2014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana
Minicurso de Teoría de Gráficas Escuela de Verano 014 por María Luisa Pérez Seguí Facultad de Ciencias Físico-Matemáticas, Universidad Michoacana Índice 1. Conceptos básicos 1 1.1. Nomenclatura...................................
Proyecto 2: recorridos sobre grafos y componentes conexas
Universidad Simón Bolívar Departamento de Computación y Tecnología de la Información CI-2693. Laboratorio de Algoritmos y Estructuras III Trimestre Abril-Julio 2015 1. Introducción Proyecto 2: recorridos
MODELOS MATEMÁTICOS PARA LA TOMA DE DECISIONES
Facultad Programa Asignatura Administración e Ingenierías Ingeniería de Sistemas MODELOS MATEMÁTICOS PARA LA TOMA DE DECISIONES Problema? Cómo resolver problemas de la vida cotidiana mediante la aplicación
1. Conceptos básicos sobre el problema en cuestión y cuestiones afines. 2. Formulación de los correspondientes algoritmos y su pseudocódigo.
Análisis de Algoritmos Ingeniería Informática, EPS-UAM Información general Organización del curso: 13-15 (mínimo-máximo) semanas docentes: 30-33 clases teóricas. 9-12 clases de problemas 26-30 clases prácticas
(e) Con la poda alfa-beta se eliminan nodos que nunca serán alcanzados
Universidad Rey Juan Carlos Curso 2014 2015 Hoja de Problemas Tema 5 1. Cuáles de las siguientes afirmaciones acerca del algoritmo Minimax son ciertas (a) El algoritmo Minimax realiza una exploración primero
Programa de teoría. Algoritmos y Estructuras de Datos II. 3. Algoritmos voraces. 1. Análisis de algoritmos 2. Divide y vencerás
Programa de teoría Algoritmos y Estructuras de Datos II 1. Análisis de algoritmos 2. Divide y vencerás 3. Algoritmos voraces 4. Programación dinámica 5. Backtracking 6. Ramificación y poda A.E.D. II 1
RELACIÓN DE PROBLEMAS DE CLASE DE PROGRAMACIÓN LINEAL ENTERA
RELACIÓN DE PROBLEMAS DE CLASE DE PROGRAMACIÓN LINEAL ENTERA SIMPLEX Y LINEAL ENTERA a Resuelve el siguiente problema con variables continuas positivas utilizando el método simple a partir del vértice
Grafos y Redes. 3. Resolución: Dibujar el camino sin levantar el lápiz y pasando sólo una vez por cada arco o arista.
Grafos y Redes. Nodos: vértices, 2, 3 2. Arcos: aristas, conexión entre nodos. 2, 54, etc. 3. Resolución: Dibujar el camino sin levantar el lápiz y pasando sólo una vez por cada arco o arista. 4. Grado
Programación Lineal. Modelo de Redes. Alcance de las aplicaciones. Curso: Investigación de Operaciones Ing. Javier Villatoro
Programación Lineal Modelo de Redes Alcance de las aplicaciones Curso: Investigación de Operaciones Ing. Javier Villatoro ALCANCE DE LAS APLICACONES DE REDES ALCANCE DE LAS APLICACIONES Muchas situaciones
I. Complejidad de Problemas
I. Complejidad de Problemas 1. Complejidad de Problemas Tópicos Clasificación de Problemas Clasificación por su Naturaleza Clasificación por su Tratabilidad Clasificación por el tipo de Respuesta 1.1 Clasificación
Apuntes elaborados por: Aaron Asencio, Eduardo Quevedo, Raquel López Revisado por: Javier Miranda el???
Apuntes elaborados por: Aaron Asencio, duardo Quevedo, Raquel López Revisado por: Javier Miranda el??? Tema 9: rafos Los grafos no son más que la versión general de un árbol, es decir, cualquier nodo de
TÓPICOS AVANZADOS EN TEORÍA DE GRAFOS. F.C.E.I.A. - Universidad Nacional de Rosario Escuela de Posgrado y Ed. Continua
TÓPICOS AVANZADOS EN TEORÍA DE GRAFOS F.C.E.I.A. - Universidad Nacional de Rosario Escuela de Posgrado y Ed. Continua 2016 UNA APLICACIÓN Problema: Cubrir (realizar) ciertos trabajos con personas (aspirantes).
Transparencias de Matemática Discreta Doble Grado en Ingeniería en Informática y. Administración de Empresas Curso 2013 2014
ESCUELA POLITÈCNICA SUPERIOR UNIVERSIDAD CARLOS III DE MADRID Transparencias de Matemática Discreta Grado en Ingeniería en Informática Doble Grado en Ingeniería en Informática y Administración de Empresas
Jesús Getán y Eva Boj. Marzo de 2014
Jesús Getán y Eva Boj Facultat d Economia i Empresa Universitat de Barcelona Marzo de 2014 Jesús Getán y Eva Boj 1 / 18 Jesús Getán y Eva Boj 2 / 18 Un Programa lineal consta de: Función objetivo. Modeliza
Una Interfaz Grafo-Matriz
Una Interfaz Grafo-Matriz R. Carballo, C. Escribano, M.A. Asunción Sastre Dept. Matemática Aplicada F.Informática. U.P.M. Boadilla del Monte Madrid, 28660-Madrid e-mail: cescribano@fi.uib.es Resumen. El
Tema 5: Grafos. Índice. E. Martín, A. Méndez, C. Ortiz y J. Sendra. Febrero de Guía del tema. 1. Grafos 1
Tema 5: Grafos E. Martín, A. Méndez, C. Ortiz y J. Sendra Febrero de 2011 Índice Guía del tema II 1. Grafos 1 2. Pseudografos, Multigrafos, Digrafos 3 3. Isomorfismos entre grafos 4 4. Primer teorema de
Introducción a la Teoría de Grafos
Introducción a la Teoría de Grafos Flavia Bonomo fbonomo@dc.uba.ar do. Cuatrimestre 009 Programa Introducción a la teoría de grafos Problemas de camino mínimo Problemas de flujo máximo Clases de complejidad
ÍNDICE INTRODUCCIÓN...13
ÍNDICE INTRODUCCIÓN...13 CAPÍTULO 1. LENGUAJE ALGORÍTMICO...15 1.1 DEFINICIÓN DE ALGORITMO...16 1.2 LA ROTACIÓN DE UNA LISTA DE NÚMEROS NATURALES...20 1.3 CUESTIONES...23 1.3.1 Dos comerciales en el restaurante...23
Planaridad. Algoritmos y Estructuras de Datos III
Planaridad Algoritmos y Estructuras de Datos III Por qué planares? Por qué planares? Por qué planares? Grafos planares Definiciones: Una representación planar de un grafo G es un conjunto de puntos en
TEORÍA DE GRAFOS Ingeniería de Sistemas
TEORÍA DE GRAFOS Ingeniería de Sistemas Código: MAT-31114 AUTORES Ing. Daniel Zambrano Ing. Viviana Semprún UNIDADES DE LA ASIGNATURA» UNIDAD I. Relaciones» UNIDAD II. Estructuras Algebraicas» UNIDAD III.
TEORIA DE GRAFOS. Estructuras Discretas Ing. Jenny Paredes Aguilar
TEORIA DE GRAFOS Estructuras Discretas Ing. Jenny Paredes Aguilar INTRODUCCION Teoria de grafos se usa en numerosos problemas cuantificables, en las organizaciones, intervienen una serie de elementos entre
Estructuras de Datos. Estructuras de Datos para Conjuntos Disjuntos
Estructuras de Datos. Estructuras de Datos para Conjuntos Disjuntos Santiago Zanella 2008 1 Introducción Para ciertas aplicaciones se requiere mantener n elementos distintos agrupándolos en una colección
Coloración. Unos cuantos problemas. Asignación de frecuencias de radio. Gregorio Hernández Peñalver. Unos cuantos problemas. Unos cuantos problemas
Unos cuantos problemas Coloración Gregorio Hernández Peñalver Matemática Discreta Asignación de frecuencias de radio G=(V, A) V={emisoras}, dos emisoras son adyacentes si sus emisiones se solapan elementos
Utiliza más de un procedimiento en la construcción de un teselado; identifica que un teselado es un principio de orden.
TESELADO 14 Utiliza más de un procedimiento en la construcción de un teselado; identifica que un teselado es un principio de orden. El Profesor explica qué es el teselado, sus características y sus aplicaciones.
Complejidad computacional (Análisis de Algoritmos)
Definición. Complejidad computacional (Análisis de Algoritmos) Es la rama de las ciencias de la computación que estudia, de manera teórica, la optimización de los recursos requeridos durante la ejecución
PROGRAMACIÓN LINEAL PROGRAMACIÓN LINEAL.
PROGRAMACIÓN LINEAL. La programación lineal es una técnica de modelado (construcción de modelos). La programación lineal (PL) es una técnica matemática de optimización, es decir, un método que trata de
greedy (adj): avaricioso, voraz, ávido, codicioso, glotón
Algoritmos Greedy Análisis y Diseño de Algoritmos Algoritmos Greedy Características generales Elementos de un algoritmo greedy Esquema de un algoritmo greedy s Almacenamiento óptimo en cintas Problema
Búsqueda en e.e. --> reglas para elegir entre las ramas que con más probabilidad lleven a la solución.
BÚSQUEDA HEURÍSTICA estudio de los métodos y reglas del descubrimiento y la invención. Búsqueda en e.e. --> reglas para elegir entre las ramas que con más probabilidad lleven a la solución. Situaciones
Cualquier vértice que esté en un ciclo tiene al menos grado 2 (el recíproco no es cierto).
.4 Grafos no dirigidos acíclicos: Árboles.4 Grafos no dirigidos acíclicos: Árboles Hasta ahora hemos buscado caminos y estudiado la conexión de un grafo, sin entrar en el estudio de los ciclos y la aciclicidad.
Tema 7: Optimización sobre Redes Muchos de los problemas de Investigación Operativa pueden modelizarse y resolverse sobre un grafo: conjunto de
Tema 7: Optimización sobre Redes Muchos de los problemas de Investigación Operativa pueden modelizarse y resolverse sobre un grafo: conjunto de vértices o nodos conectados con arcos y/o aristas. Diseñar
Sistemas de producción y búsqueda de soluciones. Area de Computación e Inteligencia Artificial 1
Sistemas de producción y búsqueda de soluciones Area de Computación e Inteligencia Artificial 1 Técnicas de búsqueda Resolución de problemas en Inteligencia Artificial. En general, podemos afirmar que
Estructuras de datos Árboles B
Estructuras de datos Árboles B Dra. Elisa Schaeffer elisa.schaeffer@gmail.com PISIS / FIME / UANL Árboles B p. 1 Árboles B Árboles B son árboles balanceados que no son binarios. Todos los vértices contienen
Prueba de optimalidad con. Métodos de Transporte. Autor : Ing. Germán D. Mendoza R.
Prueba de optimalidad con algoritmo STEPPING-STONE en Métodos de Transporte Autor : Ing. Germán D. Mendoza R. PROBLEMAS DE TRANSPORTE FASE 1: Algoritmos de solución básica Inicial: Método de la esquina
Introducción a la programación lineal
Introducción a la programación lineal La programación lineal se aplica a modelos de optimización en los que las funciones objetivo y restricción son estrictamente lineales. La técnica se aplica en una
EL PROBLEMA DE TRANSPORTE
1 EL PROBLEMA DE TRANSPORTE La TÉCNICA DE TRANSPORTE se puede aplicar a todo problema físico compatible con el siguiente esquema: FUENTES DESTINOS TRANSPORTE DE UNIDADES Donde transporte de unidades puede
Modulo del Domo Geodésico
Modulo del Domo Geodésico Resumen: Este modulo es una practica de ingeniería que prueba las habilidades de los estudiantes para construir un Domo Geodésico hecho con rollos de papel periódico. Los estudiantes
APUNTADORES. Un apuntador es un objeto que apunta a otro objeto. Es decir, una variable cuyo valor es la dirección de memoria de otra variable.
APUNTADORES Un apuntador es un objeto que apunta a otro objeto. Es decir, una variable cuyo valor es la dirección de memoria de otra variable. No hay que confundir una dirección de memoria con el contenido
Guía de Modelo Relacional y Conversión de Entidad-Relación a Relacional
Guía de Modelo Relacional y Conversión de Entidad-Relación a Relacional Prof. Claudio Gutiérrez, Aux. Mauricio Monsalve Primavera de 2007 1. Problemas conceptuales 1. Qué es una relación? Qué es un esquema
Descripción inicial del sistema. Descripción final del sistema. Estado 1 Estado 2 Estado n
Búsqueda en Inteligencia Artificial Fernando Berzal, berzal@acm.org Búsqueda en I.A. Introducción Espacios de búsqueda Agentes de búsqueda Uso de información en el proceso de búsqueda Búsqueda sin información
Separadores minimales de vértices de grafos dualmente cordales y caracterizaciones
Separadores minimales de vértices de grafos dualmente cordales y caracterizaciones Mar del Plata, septiembre de 2009 Definiciones rápidas Un uv-separador de G es un conjunto S V (G) tal que G S es no conexo
Convertir un AFND a un AFD
Convertir un AFND a un AFD Existe una equivalencia entre los AFD y AFN, de forma que un autómata M es equivalente a un autómata M' si L(M) ) L(M'). Ejemplo: Los autómatas de la siguiente figura son equivalentes.
Los grafos estrella extendida: reconocimiento y propiedades estructurales
Los grafos estrella extendida: reconocimiento y propiedades estructurales CONICET/ Departamento de Matemática, Universidad Nacional de La Plata LXV Reunión Anual de Comunicaciones Científicas de la UMA,
Planificaciones Algoritmos y Programación II. Docente responsable: CALVO PATRICIA MABEL. 1 de 6
Planificaciones 7504 - Algoritmos y Programación II Docente responsable: CALVO PATRICIA MABEL 1 de 6 OBJETIVOS Que el alumno maneje de modo correcto el diseño de un TDA de acuerdo a las exigencias de una
Soluciones oficiales Clasificación Olimpiada Nacional Nivel Mayor
Soluciones oficiales Clasificación Olimpiada Nacional 009 Comisión Académica Nivel Maor Problema 1. Calcule todas las soluciones m, n de números enteros que satisfacen la ecuación m n = 009 (n + 1) Solución.
4.1. Polinomios y teoría de ecuaciones
CAPÍTULO 4 Polinomios y teoría de ecuaciones 4.1. Polinomios y teoría de ecuaciones Un polinomio real en x, o simplemente polinomio en x es una expresión algebraica de la forma a n x n + a n 1 x n 1 +
Relaciones. Estructuras Discretas. Relaciones. Relaciones en un Conjunto. Propiedades de Relaciones en A Reflexividad
Estructuras Discretas Relaciones Definición: relación Relaciones Claudio Lobos, Jocelyn Simmonds clobos,jsimmond@inf.utfsm.cl Universidad Técnica Federico Santa María Estructuras Discretas INF 152 Sean
Figura 3.1. Grafo orientado.
Leyes de Kirchhoff 46. ECUACIONES DE INTERCONEXION. Leyes de Kirchhoff..1. Definiciones. Una red está formada por la interconexión de componentes en sus terminales; y deben cumplirse simultáneamente las
ÁRBOLES GENERALES Y Y ESTRUCTURAS DE ÍNDICES DEFINICIONES Y REPRESENTACIONES DEFINICIONES Y REPRESENTACIONES. NOMENCLATURA SOBRE ÁRBOLES. DECLARACIÓN Y REPRESENTACIÓN.. CONSTRUCCIÓN.. ÁRBOLES 2-3-4. ÁRBOLES
UNIVERSIDAD MAYOR DE SAN SIMÓN FACULTAD DE CIENCIAS Y TECNOLOGÍA INGENIERÍA DE SISTEMAS BÚSQUEDA PRIMERO EL MEJOR
UNIVERSIDAD MAYOR DE SAN SIMÓN FACULTAD DE CIENCIAS Y TECNOLOGÍA INGENIERÍA DE SISTEMAS BÚSQUEDA PRIMERO EL MEJOR INTEGRANTES: Caricari Cala Aquilardo Villarroel Fernandez Fructuoso DOCENTE: Lic. Garcia
(b) Cuál es la desventaja principal de una heurística con aprendizaje? es más informada que otra función heurística optimista h 2 *?
UNIVERIDD REY JUN CRLO CURO 0-0 INTELIGENCI RTIFICIL Hoja de Problemas Tema Ejercicio : Conteste a las siguientes preguntas: (a) Cómo funciona una heurística con aprendizaje? olución: Una heurística con
DIRECCIÓN TÉCNICO ELECTORAL - DIRECCION GENERAL ELECTORAL - SECRETARIA DE ACTUACIÓN - JUNTA ELECTORAL DE LA PROVINCIA DE BUENOS AIRES
Complejidad - Problemas NP-Completos. Algoritmos y Estructuras de Datos III
Complejidad - Problemas NP-Completos Algoritmos y Estructuras de Datos III Teoría de Complejidad Un algoritmo eficiente es un algoritmo de complejidad polinomial. Un problema está bien resuelto si se conocen
Estrategias de Diseño de Algoritmos
Estrategias de Diseño de Algoritmos Introducción A través de los años, los científicos de la computación han identificado diversas técnicas generales que a menudo producen algorit mos eficientes para la
SWITCH ETHERNET CAPA 2. Justo Ramírez Martínez
SWITCH ETHERNET CAPA 2 Justo Ramírez Martínez ÍNDICE (I) Introducción Ethernet Bridging and Switching Dispositivos de conexión de redes Tipos de dispositivos Dispositivos de conexión de nivel 2 Puentes
Una actividad muy relacionada con la anterior consiste en la generación de mosaicos por medio de polígonos regulares.
Una actividad muy relacionada con la anterior consiste en la generación de mosaicos por medio de polígonos regulares. Actividad 1 (Polígonos regulares): En esta primera actividad los y las estudiantes
Índice Unidad 1: Lógica y teoría de conjuntos... 2
MATEMÁTICA DISCRETA Índice Unidad 1: Lógica y teoría de conjuntos... 2 1. Definiciones... 2 2. Leyes de la lógica... 2 3. Reglas de inferencia... 3 4. Lógica de predicados... 3 5. Teoría de conjuntos...
Soluciones a algunos ejercicios de Matemática Discreta 1.
Soluciones a algunos ejercicios de Matemática Discreta 1. Eleonora Catsigeras * 23 de agosto de 2005 Práctico 1.- Ejercicio 5 Cuántos números naturales pares de tres dígitos (en base 10) tienen todos sus
JUEGOS. Área de aplicación de los algoritmos heurísticos Juegos bi-personales: oponente hostil
JUEGOS Área de aplicación de los algoritmos heurísticos Juegos bi-personales: oponente hostil I Oponente: Jugador: intenta mover a un estado que es el peor para Etiquetar cada nivel del espacio de búsqueda
UNIVERSIDAD DE GUADALAJARA
UNIVERSIDAD DE GUADALAJARA CENTRO UNIVERSITARIO DE LOS ALTOS DIVISIÓN DE ESTUDIOS EN FORMACIONES SOCIALES LICENCIATURA: INGENIERÍA EN COMPUTACIÓN UNIDAD DE APRENDIZAJE POR OBJETIVOS TALLER DE ESTRUCTURA
ESCUELA SUPERIOR POLITECNICA DEL LITORAL Facultad de Ciencias Naturales y Matematicas SYLLABUS DEL CURSO Matematicas Discretas
1. CODIGO Y NUMERO DE CREDITOS ESCUELA SUPERIOR POLITECNICA DEL LITORAL Facultad de Ciencias Naturales y Matematicas SYLLABUS DEL CURSO CODIGO ICM00901 NUMERO DE CREDITOS Teoricos: 4 Practicos: 0 2. DESCRIPCIoN
Tema 4: Búsqueda informada mediante técnicas heurísticas
Tema 4: Búsqueda informada mediante técnicas heurísticas José Luis Ruiz Reina José Antonio Alonso Franciso J. Martín Mateos 1 Departamento de Ciencias de la Computación e Inteligencia Artificial Universidad
4 SCT UPLA = 108 Horas Cronológicas Semestrales Presencialidad (41,67%)
CARRERA NOMBRE DEL PROGRAMA FORMATIVO TOTAL DE CRÉDITOS Pedagogía en Matemática / Licenciatura en Educación CPM 4331 Matemática Discreta 4 SCT UPLA = 108 Horas Cronológicas Semestrales Presencialidad (41,67%)
MANUAL DE USUARIO NOTAS PARCIALES MODULO CONFIGUARACION DE NOTAS -288
MANUAL DE USUARIO NOTAS PARCIALES MODULO CONFIGUARACION DE NOTAS -288 Manual Notas Parciales Página 1 de 39 Tabla de contenido Cómo usar el manual de usuario 4 Inicio 5 Notas Parciales: 6 Profesores (Listados