Modelos de Redes: Árbol. M. En C. Eduardo Bustos Farías
|
|
|
- Juan Castro Farías
- hace 7 años
- Vistas:
Transcripción
1 Modelos de Redes: Árbol de expansión n mínimam M. En C. Eduardo Bustos Farías as
2 Objetivos Conceptos y definiciones de redes. Importancia de los modelos de redes Modelos de programación n lineal, representación n en redes y soluciones usando el computador para: * Modelos de asignación * Modelo del vendedor viajero * Modelos de la ruta mas corta * Modelos de la rama mas corta Y otros.
3 Un problema de redes es aquel que puede representarse por: Nodos 7 Arcos 10 Funciones en los arcos
4 Introducción La importancia de los modelos de redes: * Muchos problemas comerciales pueden ser resueltos a través de modelos redes * El resultado de un problema de redes garantiza una solución entera, dada su estructura matemática. tica. No se necesitan restricciones adicionales para obtener este tipo de solución. * Problemas de redes pueden ser resueltos por pequeños algoritmos, no importando el tamaño o del problema, dada su estructura matemática. tica.
5 Terminología a de Redes * Flujo: Corresponde a la cantidad que debe transportarse desde un nodo i a un nodo j a través s de un arco que los conecta. La siguiente notación n es usada: X ij = cantidad de flujo U ij = cota mínima m de flujo que se debe transportar L ij = cota maxíma de flujo que se puede transportar. * Arcos dirigidos /no dirigidos: Cuando el flujo puede transportarse en una sola dirección n se tiene un arco dirigido (la flecha indica la dirección). Si el flujo puede transportarse en ambas direcciones existe un arco no dirigido (sin flecha). * Nodos adyacentes: Un nodo j es adyacente con un nodo i si existe un arco que une el nodo j con el nodo i.
6 Rutas/Conexión n entre nodos *Ruta: Una colección n de arcos formados por una serie de nodos adyacentes * Los nodos están n conectados si existe una ruta entre ellos. Ciclos / Arboles /Arboles expandidos * Ciclos : Un ciclo se produce cuando al partir de un nodo por un cierto camino se vuelve al mismo nodo por otra ruta. * Arbol : Una serie de nodos que no contienen ciclos. *Arbol expandido: Es un árbol que conecta todos lo nodos de la red (contiene n-1 n 1 arcos).
7 Árbol de expansión n mínimam 7
8 Árbol de expansión n mínimam Este problema surge cuando todos los nodos de una red deben conectar entre ellos, sin formar un loop. El árbol de expansión n mínima m es apropiado para problemas en los cuales la redundancia es expansiva, o el flujo a lo largo de los arcos se considera instantáneo. neo. 8
9 Árbol de expansión n mínimam Este problema se refiere a utilizar las ramas o arcos de la red para llegar a todos los nodos de la red, de manera tal que se minimiza la longitud total. La aplicación n de estos problemas de optimización n se ubica en las redes de comunicación n eléctrica, telefónica, carretera, ferroviaria, aérea, a marítima, etc.; donde los nodos representan puntos de consumo eléctrico, teléfonos, aeropuertos, computadoras. Y los arcos podrían ser de alta tensión, n, cable de fibra óptica, rutas aéreas, a etc. Si n = numero de nodos, entonces la solución óptima debe incluir n-1 n 1 arcos. 9
10 Algoritmo de Kruskal 10
11 Algoritmo de Kruskal 1. Comenzar en forma arbitraria en cualquier nodo y conectarlo con el mas próximo (menos distante o costoso). 2. Identificar el nodo no conectado que esta más m cera o menos costoso de alguno de los nodos conectados. Deshacer los empates de forma arbitraria. Agregar este nodo al conjunto de nodos conectado. 3. Repartir este aso hasta que se hayan conectado todos los nodos. 11
12 EJEMPLO 1 EL TRANSITO DEL DISTRITO METROPOLITANO Árbol de expansión n mínimam 12
13 EL TRANSITO DEL DISTRITO METROPOLITANO La ciudad de Vancouver esta planificando el desarrollo de una nueva línea l en sistemas de tránsito. El sistema debe unir 8 residencias y centros comerciales. El distrito metropolitano de transito necesita seleccionar un conjunto de líneas l que conecten todos los centros a un mínimo m costo. La red seleccionada debe permitir: - Factibilidad de las líneas l que deban ser construídas das. - Mínimo costo posible por línea. l 13
14 RED QUE REPRESENTA EL ARBOL EXPANDIDO. Zona Oeste Zona Norte 3 34 Zona Centro Distrito Comercial Universidad Shopping Center Zona Este Zona Sur 14
15 Solución - Analogía a con un problema de redes - El algoritmo que resuelve este problema es un procedimiento muy fácil f ( trivial( trivial ). - Corresponde a una categoría a de algoritmos ávidos vidos. - Algoritmo: * Comience seleccionando el arco de menor longitud. * En cada iteración, agregue el siguiente arco de menor longitud del conjunto de arcos disponibles, tomando la precaución n de no formar ningún loop. * El algoritmo finaliza cuando todos los nodos están conectados. Solución n mediante el computador - Los entrada consiste en el número n de nodos, el largo de los arcos y la descripción n de la red. 15
16 Solución óptima mediante WINQSB 16
17 RED QU E REPRESENTA LA SOLUCIÓN ÓPTIMA Zona Oeste 1 Zona Norte Loop Zona Centror Distrito Comercial Universidad Shopping Center Zona Este Costo Total = $236 millones 7 Zona Sur 17
18 EJEMPLO 2 RED DE COMUNICACIONES ÀRBOL DE EXPANSIÓN N MÍNIMAM 18
19 Ejemplo 1 Se va a instalar una red de comunicación entre 12 ciudades. Los costos de los posibles enlaces directos entre pares permisibles es el que se muestra en la figura. Cada unidad de costo representa $10,000 dólares. 19
20
21 SOLUCIÓN N CON WINQSB 21
22 22
23 23
24 24
25 25
26 26
27 27
28 28
29 29
30 30
31 31
32 32
33 33
34 34
35 35
36 Solución Interacción Nodo Con nodo Costo ($) SUMA $33 36
37 Método Tabular
38 EJEMPLO 3 winqsb 38
39 Solucione el siguiente árbol de extensión n mínima m para la red de comunicaciones de emergencia usando el método tabular. Las unidades son distancias en kms. 39
40 SOLUCIÓN 40
41 USANDO EL WINQSB 41
42 42
43 43
44 44
45 45
46 46
47 47
48 48
49 49
50 50
51 51
52 52
53 53
54 54
55 55
56 56
57 ITERACIÓN DEL NODO AL NODO SUMA 129 DISTANCIA 57
58 EJEMPLO 4 CENTRO REGIONAL DE CÓMPUTO Árbol de expansión n mínimam 58
59 Un centro regional de cómputo c (C.R.C( C.R.C.),.), debe instalar líneas l especiales para comunicación, n, a fin de conectar a cinco usuarios satélite con una nueva computadora central, la compañí ñía telefónica local es la que instalará la nueva red de comunicaciones, pero es una operación costosa. Con el propósito de reducir costos, se busca que la longitud total (Kms( Kms.) de estas líneas l sea la menor posible. La red para este problema es la siguiente: 59
60 60
61 SOLUCIÓN 61
62 Desarrollo del algoritmo: Ubicarse en el nodo 3 (puede ser en cualquier otro nodo) y se encuentra que el nodo más m s próximo es el 4 (10 Kms.) El siguiente nodo más m s cercano al 3 o 4 es el nodo 6 (20 Kms). Repitiendo el paso anterior tenemos el siguiente árbol de extensión n mínima: m 62
63 Con una extensión de 110 Kms. 63
64 Interacción Nodos Distancia (Km.) Km. 64
65 MÉTODO TABULAR
66 PROBLEMA PARA RESOLVER CAMINOS EN EL PARQUE RUTA MÁS M S CORTA 66
67 67
68 SOLUCIÓN 68
69 69
70 70
71 71
72 72
73 73
74 74
75 EJERCICIO PARA RESOLVER 75
76 La cía. c MCC acaba de obtener la aprobación para ofrecer el servicio de televisión n por cable en una zona metropolitana. Los nodos de la red que aparece en seguida representan los puntos de distribución n a los que deben llegar las líneas l primarias del cable. Los arcos de la red muestran el número n de millas que existen entre los puntos de distribución. Determine la solución n que permitirá a la compañí ñía a llegar a todos los puntos de distribución n con una longitud mínima m de la línea l del cable primario. 76
77 77
78 SOLUCIÓN 78
79 79
80 EJERCICIO PARA RESOLVER 80
81 1. TV Cable Visión n desea establecer una red de comunicación n para brindar el servicio de cable que permita enlazar las 14 ciudades de la República Mexicana. Determinar cómo c se conectarían an dichos 14 ciudades de forma que la longitud de cable a utilizarse sea mínima. m El nodo 1 constituye la estación n de reparto. Los números n expresados en cada rama expresan las distancias entre las ciudades. A través s de la aplicación n de este algoritmo, podemos calcular la cantidad mínima m de cable a ser utilizadas en la red de comunicación n por cable (expresado en metros) 81
82 250 82
83 SOLUCIÓN 83
84 Usando TORA 84
85 1 A = {1} B = {2,3,4,5,6,7,8,9,10,11,12,13,14,15} Min = {(1,2)(1,3)(1,4)} = (1,2) = A = {1,2} B = {3,4,5,6,7,8,9,10,11,12,13,14,15} Min = {(1,3)(1,4)(2,3)(2,5)(2,6)} = (2,3) = A = {1,2,3} B = {4,5,6,7,8,9,10,11,12,13,14,15} Min = {(1,4)(2,5)(2,6)(3,4)(3,5)} = (3,4) = A = {1,2,3,4} B = {5,6,7,8,9,10,11,12,13,14,15} Min = {(2,5)(2,6)(3,5)(4,5)(4,9)} = (4,5) = A = {1,2,3,4,5} B = {6,7,8,9,10,11,12,13,14,15} Min = {(2,6)(4,9)(5,6)(5,7)(5,9)} = (5,6) = A = {1,2,3,4,5,6} B = {7,8,9,10,11,12,13,14,15} Min = {(4,9)(5,7)(5,9)(6,7)(6,8)(6,12)} = (6,7) = A = {1,2,3,4,5,6,7} B = {8,9,10,11,12,13,14,15} Min = {(4,9)(5,9)(6,8)(6,12)(7,8)(7,9)} = (7,8) =
86 8 A = {1,2,3,4,5,6,7,8} B = {9,10,11,12,13,14,15} Min = {(4,9)(5,9)(6,12)(7,9)(8,9)(8,11)(8,12)} = (8,9) = A = {1,2,3,4,5,6,7,8,9} B = {10,11,12,13,14,15} Min = {(6,12)(8,11)(8,12)(9,10)} = (9,10) = A = {1,2,3,4,5,6,7,8,9,10} B = {11,12,13,14,15} Min = {(6,12)(8,11)(8,12)(10,11)(10,15)} = (10,11) = A = {1,2,3,4,5,6,7,8,9,10,11} B = {12,13,14,15} Min = {(6,12)(8,12)(10,15)(11,13)(11,14)(11,15)} = (11,13) = A = {1,2,3,4,5,6,7,8,9,10,11,13} B = {12,14,15} Min = {(6,12)(8,12)(10,15)(11,13)(11,14)(11,15)(13,14)} = (13,14) = A = {1,2,3,4,5,6,7,8,9,10,11,13,14} B = {15} Min = {(6,12)(8,12)(10,15)(11,15)(14,15)} = (14,15) =
87 EJERCICIO PARA RESOLVER 87
88 Una compañí ñía a desea anunciar su producto a las 12 principales estaciones de radio locales. La red de comunicaciones por cable que enlaza a las estaciones de radio se indica en la figura. Determine como se conecta las 12 estaciones de radio de modo que se minimice la longitud total del cable que se utilizó (Kms). 88
89 89
90 SOLUCIÓN 90
91 SOLUCION EN EL TORA : ARBOL *** MINIMAL SPANNING TREE SOLUTION *** Minimal spanning tree length =
92 From To Arc Length N1 N N2 N N4 N N6 N N6 N N10 N N4 N N8 N N10 N N9 N N7 N
93 EJERCICIO PARA RESOLVER ÁRBOL DE EXPANSIÓN N MÍNIMAM 93
94 Una empresa de paquetería a ha iniciado sus labores, repartiendo paquetes por toda la ciudad, pero tiene clientes principales, los cuales necesitan sus paquetes lo más m s pronto posible. La empresa necesita saber cual es el camino más m s rápido r para que sus enviados lleguen a su destino para hacer la entrega a tiempo. 94
95 Distancia en Kms. 95
96 SOLUCIÓN 96
97 Paso 0: A = 0 B = {1,2,3,4,5,6,7,8,9,10,11,12,13} Paso 1: A = {1} B = {2,3,4,5,6,7,8,9,10,11,12,13} Min = {(1,2 1,2)(1,3)(1,5)} = 1 Nodo = 2 Paso 2: A = {1,2} B = {3,4,5,6,7,8,9,10,11,12,13} Min = {(1,3)(1,5)(2,4)(2,5 2,5)}= 2 Nodo = 5 Paso 3: A = {1,2,5} B = {3,4,6,7,8,9,10,11,12,13} Min = {(1,3)(1,5)(2,4 2,4)(5,7)(5,8)}= 3 Nodo = 4 Paso 4: A = {1,2,4,5} B = {3,6,7,8,9,10,11,12,13} Min = {(1,3)(1,5)(5,7)(5,8)(4,3 4,3)(4,7)}= 2 Nodo = 3 Paso 5: A = {1,2,3,4,5} B = {6,7,8,9,10,11,12,13} Min = {(1,3)(1,5)(5,7)(5,8)(4,7)(3,6 3,6)(3,7)}= 1 Nodo = 6 97
98 Paso 6: A = {1,2,3,4,5,6} B = {7,8,9,10,11,12,13} Min = {(1,3)(1,5)(5,7)(5,8)(4,7)(3,7)(6,9)(6,11 6,11)}= 1 Nodo = 11 Paso 7: A = {1,2,3,4,5,6,11} B = {7,8,9,10,12,13} Min = {(1,3)(1,5)(5,7)(5,8)(4,7)(3,7)(6,9)(11,12)(11,13 11,13)}= 1 Nodo = 13 Paso 8: A = {1,2,3,4,5,6,11,13} B = {7,8,9,10,12} Min = {(1,3)(1,5)(5,7)(5,8)(4,7)(3,7)(6,9 6,9)(11,12)(13,12)}= 2 Nodo = 9 Paso 9: A = {1,2,3,4,5,6,9,11,13} B = {7,8,10,12} Min = {(1,3)(1,5)(5,7)(5,8)(4,7)(3,7)(6,9)(9,10)(9,13)(11,12)(13,12 13,12)}= 2 Nodo = 12 Paso 10: A = {1,2,3,4,5,6,9,11,12,13} B = {7,8,9,10} Min = {(1,3)(1,5)(5,7)(5,8)(4,7)(3,7)(6,9)(9,10 9,10)(9,13)(11,12)}= 3 Nodo = 10 98
99 Paso 11: A = {1,2,3,4,5,6,9,10,11,12,13} B = {7,8,9} Min = {(1,3)(1,5)(5,7)(5,8)(4,7)(3,7)(6,9)(9,13)(11,12)(10,7 10,7)(10,8)}= 2 Nodo = 7 Paso 12: A = {1,2,3,4,5,6,7,9,10,11,12,13} B = {8,9} Min = {(1,3)(1,5)(5,7)(5,8)(4,7)(3,7)(6,9)(9,13)(11,12)(10,8)(7,8 7,8)}= 3 Nodo = 8 Resultado final: = 23 99
100 100
101 EJERCICIO PARA RESOLVER 101
102 18 11 Desarrolle la solución n del árbol de extensión mínima (Kms( Kms.) para la siguiente red de comunicaciones de emergencia:
103 ANEXO ALGORITMO DE KRUSKAL GRAFOS 103
104 Algoritmo de Kruskal Dado un grafo ponderado G=(V, A), el algoritmo parte de un grafo G = = (V, Ø). Cada nodo es una componente conexa en sís misma. En cada paso de ejecución n se elige la arista de menor costo de A. Si une dos nodos que pertenecen a distintas componentes conexas entonces se añade a ade al árbol de expansión n G. G En otro caso no se coge, ya que formaría a un ciclo en G. G Acabar cuando G G sea conexo: cuando tengamos n-1 n 1 aristas. Estructura del algoritmo de Kruskal Sea T de tipo Conjunto de aristas, el lugar donde se guardarán n las aristas del árbol de expansión. n. Asignar T a Ø. Mientras T contenga menos de n-1 n 1 aristas hacer: Elegir la arista (v, w) de A con menor costo. Borrar (v, w) de A (para no volver a cogerla). Si v, w están n en distintos componentes conexos entonces añadir a adir (v, w) a T. En otro caso, descartar (v, w). 104
105 Árboles de expansión. n. Algoritmo de Kruskal Ejemplo. Mostrar la ejecución n del algoritmo de Kruskal Necesidades del algoritmo: Las aristas deben ser ordenadas, según n el costo. Necesitamos operaciones para saber si dos nodos están n en la misma componente conexa y para unir componentes. Relación n dos nodos pertenecen a una componente conexa: es una relación n binaria de equivalencia podemos usar la estructura de representación n para relaciones de equivalencia (con operaciones Inicia, Encuentra y Unión). n)
UNIVERSIDAD DE MANAGUA Al más alto nivel
 UNIVERSIDAD DE MANAGUA Al más alto nivel Investigación de Operaciones Encuentro #3 Tema: Optimización de Redes: El problema del árbol de expansión mínima y el problema de costo mínimo Prof.: MSc. Julio
UNIVERSIDAD DE MANAGUA Al más alto nivel Investigación de Operaciones Encuentro #3 Tema: Optimización de Redes: El problema del árbol de expansión mínima y el problema de costo mínimo Prof.: MSc. Julio
Optimización de redes
 UNIVERSIDAD DE MANAGUA Al más alto nivel Optimización de redes Problema de la Ruta más corta Problema del Árbol de expansión mínima Problema del Flujo máximo Problema de Flujo de costo mínimo Maestro Ing.
UNIVERSIDAD DE MANAGUA Al más alto nivel Optimización de redes Problema de la Ruta más corta Problema del Árbol de expansión mínima Problema del Flujo máximo Problema de Flujo de costo mínimo Maestro Ing.
Modelos de Redes: Árbol. M. En C. Eduardo Bustos Farías
 Modelos de Redes: Árbol de expansión n mínimam M. En C. Eduardo Bustos Farías as Objetivos Conceptos y definiciones de redes. Importancia de los modelos de redes Modelos de programación n lineal, representación
Modelos de Redes: Árbol de expansión n mínimam M. En C. Eduardo Bustos Farías as Objetivos Conceptos y definiciones de redes. Importancia de los modelos de redes Modelos de programación n lineal, representación
UNIVERSIDAD NACIONAL DE INGENIERÍA Sede UNI-NORTE
 UNIVERSIDAD NACIONAL DE INGENIERÍA Sede UNI-NORTE Teoría de redes Problema de la Ruta más corta Problema del Árbol de expansión mínima Problema del Flujo máximo Problema de Flujo de costo mínimo Maestro
UNIVERSIDAD NACIONAL DE INGENIERÍA Sede UNI-NORTE Teoría de redes Problema de la Ruta más corta Problema del Árbol de expansión mínima Problema del Flujo máximo Problema de Flujo de costo mínimo Maestro
UNIVERSIDAD NACIONAL DE INGENIERÍA Sede UNI-NORTE
 UNIVERSIDAD NACIONAL DE INGENIERÍA Sede UNI-NORTE Teoría de redes Problema de la Ruta más corta Problema del Árbol de expansión mínima Problema del Flujo máximo Problema de Flujo de costo mínimo Introducción
UNIVERSIDAD NACIONAL DE INGENIERÍA Sede UNI-NORTE Teoría de redes Problema de la Ruta más corta Problema del Árbol de expansión mínima Problema del Flujo máximo Problema de Flujo de costo mínimo Introducción
Modelos de Redes: Problema del flujo máximom. M. En C. Eduardo Bustos Farías
 Modelos de Redes: Problema del flujo máimom M. En C. Eduardo Bustos Farías as Problema del flujo máimom Problema del flujo máimom Este modelo se utiliza para reducir los embotellamientos entre ciertos
Modelos de Redes: Problema del flujo máimom M. En C. Eduardo Bustos Farías as Problema del flujo máimom Problema del flujo máimom Este modelo se utiliza para reducir los embotellamientos entre ciertos
Problemas de la Ruta más m s corta
 Modelos de Redes: Problemas de la Ruta más m s corta M. En C. Eduardo Bustos Farías as Problemas de la Ruta más m s corta Problemas de la Ruta más m s corta Se trata de encontrar la ruta de menor distancia,
Modelos de Redes: Problemas de la Ruta más m s corta M. En C. Eduardo Bustos Farías as Problemas de la Ruta más m s corta Problemas de la Ruta más m s corta Se trata de encontrar la ruta de menor distancia,
Teoría de grafos y optimización en redes
 Teoría de grafos y optimización en redes José María Ferrer Caja Universidad Pontificia Comillas Definiciones básicas Grafo: Conjunto de nodos (o vértices) unidos por aristas G = (V,E) Ejemplo V = {,,,,
Teoría de grafos y optimización en redes José María Ferrer Caja Universidad Pontificia Comillas Definiciones básicas Grafo: Conjunto de nodos (o vértices) unidos por aristas G = (V,E) Ejemplo V = {,,,,
Análisis de algoritmos
 Tema 10: Algoritmos ávidos M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido Introducción Algoritmos ávidos Forma general de un
Tema 10: Algoritmos ávidos M. en C. Edgardo Adrián Franco Martínez http://www.eafranco.com edfrancom@ipn.mx @edfrancom edgardoadrianfrancom 1 Contenido Introducción Algoritmos ávidos Forma general de un
Modelos de Redes: Problemas de la Ruta más m s corta. M. En C. Eduardo Bustos Farías
 Modelos de Redes: Problemas de la Ruta más m s corta M. En C. Eduardo Bustos Farías as Problemas de la Ruta más m s corta 2 Problemas de la Ruta más m s corta Se trata de encontrar la ruta de menor distancia,
Modelos de Redes: Problemas de la Ruta más m s corta M. En C. Eduardo Bustos Farías as Problemas de la Ruta más m s corta 2 Problemas de la Ruta más m s corta Se trata de encontrar la ruta de menor distancia,
Distribución Física y Transporte. Diseño de Rutas para Los Vehículos (Shortes Path) Giancarlo Salazar P
 Distribución Física y Transporte Diseño de Rutas para Los Vehículos (Shortes Path) Giancarlo Salazar P Un problema frecuente en el diseño de rutas, es reducir los costos de transporte y mejorar el servicio
Distribución Física y Transporte Diseño de Rutas para Los Vehículos (Shortes Path) Giancarlo Salazar P Un problema frecuente en el diseño de rutas, es reducir los costos de transporte y mejorar el servicio
Tema 5 Árboles y Grafos.
 Tema 5 Árboles y Grafos. Definiciones básicas de teoría de grafos. Un grafo consta de un conjunto de nodos, un conjunto de aristas y una correspondencia f del conjunto de aristas al conjunto de nodos.
Tema 5 Árboles y Grafos. Definiciones básicas de teoría de grafos. Un grafo consta de un conjunto de nodos, un conjunto de aristas y una correspondencia f del conjunto de aristas al conjunto de nodos.
UNIVERSIDAD DE MANAGUA
 UNIVERSIDAD DE MANAGUA INVESTIGACIÓN DE OPERACIONES Prof.: MSc. Julio Rito Vargas A. Tarea Práctica # Puede hacer uso del software WinQSB (Network Modeling). Encuentre la ruta más corta de la siguiente
UNIVERSIDAD DE MANAGUA INVESTIGACIÓN DE OPERACIONES Prof.: MSc. Julio Rito Vargas A. Tarea Práctica # Puede hacer uso del software WinQSB (Network Modeling). Encuentre la ruta más corta de la siguiente
Flujos de redes (Network Flows NF)
 Fluos de redes (Network Flows NF). Terminología. Árbol generador mínimo. Camino mínimo 4. Fluo máximo 5. Fluo de coste mínimo TEORÍA DE GRAFOS. OPTIMIZACIÓN EN REDES Terminología Red o grafo (G) Nodos
Fluos de redes (Network Flows NF). Terminología. Árbol generador mínimo. Camino mínimo 4. Fluo máximo 5. Fluo de coste mínimo TEORÍA DE GRAFOS. OPTIMIZACIÓN EN REDES Terminología Red o grafo (G) Nodos
Tema: Algoritmos para la ruta más corta en un Grafo.
 Programación IV. Guía No. 10 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos para la ruta más corta en un Grafo. Objetivos Específicos Definir el concepto de camino
Programación IV. Guía No. 10 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos para la ruta más corta en un Grafo. Objetivos Específicos Definir el concepto de camino
CONTENIDO MODELOS PARA LA LOCALIZACION DE PLANTA
 MODELOS PARA LA LOCALIZACION DE PLANTA PROFESOR: DR. JORGE ACUÑA A. 1 CONTENIDO Modelos de localización Modelos de optimización Modelo del centro de gravedad Modelo de distancias (Ardalan) Trayectorias
MODELOS PARA LA LOCALIZACION DE PLANTA PROFESOR: DR. JORGE ACUÑA A. 1 CONTENIDO Modelos de localización Modelos de optimización Modelo del centro de gravedad Modelo de distancias (Ardalan) Trayectorias
20/11/2012 OPTIMIZACION DE REDES. Optimización de Redes
 0//0 PIMIZIN RS ptimización de Redes omponentes Nodos eropuertos odegas Puntos de comunicacion staciones de bombeo entros de rabajo Rutas Líneas ereas Rutas anales ó cables uberías Rutas de manejo de materiales
0//0 PIMIZIN RS ptimización de Redes omponentes Nodos eropuertos odegas Puntos de comunicacion staciones de bombeo entros de rabajo Rutas Líneas ereas Rutas anales ó cables uberías Rutas de manejo de materiales
Prácticas de IO con POM-QM 2014
 PROBLEMAS DE OPTIMIZACIÓN DE REDES (Puede hacer uso del software POM-QM) 1. Encuentre la ruta más corta de la siguiente red. Los números representan las distancias correspondientes reales entre los nodos.
PROBLEMAS DE OPTIMIZACIÓN DE REDES (Puede hacer uso del software POM-QM) 1. Encuentre la ruta más corta de la siguiente red. Los números representan las distancias correspondientes reales entre los nodos.
Algebra Matricial y Teoría de Grafos
 Algebra Matricial y Teoría de Grafos Unidad 3: Nociones de teoría de grafos Luis M. Torres Escuela Politécnica del Litoral Quito, Enero 2008 Maestría en Control de Operaciones y Gestión Logística p.1 Contenido
Algebra Matricial y Teoría de Grafos Unidad 3: Nociones de teoría de grafos Luis M. Torres Escuela Politécnica del Litoral Quito, Enero 2008 Maestría en Control de Operaciones y Gestión Logística p.1 Contenido
Práctica N o 8 Desigualdades Válidas - Algoritmos de Planos de Corte - Algoritmos Branch & Cut
 Práctica N o 8 Desigualdades Válidas - Algoritmos de Planos de Corte - Algoritmos Branch & Cut 8.1 Para cada uno de los siguientes conjuntos, encontrar una desigualdad válida que agregada a la formulación
Práctica N o 8 Desigualdades Válidas - Algoritmos de Planos de Corte - Algoritmos Branch & Cut 8.1 Para cada uno de los siguientes conjuntos, encontrar una desigualdad válida que agregada a la formulación
Apuntes de Teórico de Programación 3. Apuntes de Teórico PROGRAMACIÓN 3. Greedy. Versión 1.1
 Apuntes de Teórico PROGRAMACIÓN 3 Greedy Versión 1.1 1 Índice Índice... Introducción... 3 Ejemplo 1 (problema de las monedas)... 3 Ejemplo (problema de la mochila)... 4 Aplicaciones del método Greedy a
Apuntes de Teórico PROGRAMACIÓN 3 Greedy Versión 1.1 1 Índice Índice... Introducción... 3 Ejemplo 1 (problema de las monedas)... 3 Ejemplo (problema de la mochila)... 4 Aplicaciones del método Greedy a
Programación Lineal. Modelo de Redes. Alcance de las aplicaciones. Curso: Investigación de Operaciones Ing. Javier Villatoro
 Programación Lineal Modelo de Redes Alcance de las aplicaciones Curso: Investigación de Operaciones Ing. Javier Villatoro ALCANCE DE LAS APLICACONES DE REDES ALCANCE DE LAS APLICACIONES Muchas situaciones
Programación Lineal Modelo de Redes Alcance de las aplicaciones Curso: Investigación de Operaciones Ing. Javier Villatoro ALCANCE DE LAS APLICACONES DE REDES ALCANCE DE LAS APLICACIONES Muchas situaciones
Fundamentos de Investigación de Operaciones Modelos de Grafos
 Fundamentos de Investigación de Operaciones de junio de 00 Muchos problemas de optimización puedes ser analizados y resueltos a través de representaciones gráficas. Tal es el caso de los problemas de planificación
Fundamentos de Investigación de Operaciones de junio de 00 Muchos problemas de optimización puedes ser analizados y resueltos a través de representaciones gráficas. Tal es el caso de los problemas de planificación
Este material es de uso exclusivo para clase de algoritmos y estructura de datos, la información de este documento fue tomada textualmente de varios
 CLASE GRAFOS Este material es de uso exclusivo para clase de algoritmos y estructura de datos, la información de este documento fue tomada textualmente de varios libros por lo que está prohibida su impresión
CLASE GRAFOS Este material es de uso exclusivo para clase de algoritmos y estructura de datos, la información de este documento fue tomada textualmente de varios libros por lo que está prohibida su impresión
INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.
 INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.7 GRAFOS CONEXOS7 ÁRBOLES..7 BOSQUES DE ÁRBOLES...8 RECORRIDO DE UN GRAFO..8
INDICE INTRODUCCION1 DESARROLLO2 GRAFOS (CONCEPTO).2 ARISTAS...2 VERTICES2 CAMINOS.3 CLASIFICACION DE GRAFOS...3 GRAFOS EULERIANOS.7 GRAFOS CONEXOS7 ÁRBOLES..7 BOSQUES DE ÁRBOLES...8 RECORRIDO DE UN GRAFO..8
TEORIA DE REDES. Ing. Lino Martin Quispe Tincopa
 TORI S Ing. Lino Martin Quispe Tincopa NLISIS FLUJO S Las técnicas de flujo de redes están orientadas a optimizar situaciones vinculadas a las redes de transporte, redes de comunicación, sistema de vuelos
TORI S Ing. Lino Martin Quispe Tincopa NLISIS FLUJO S Las técnicas de flujo de redes están orientadas a optimizar situaciones vinculadas a las redes de transporte, redes de comunicación, sistema de vuelos
Unidad II: Análisis de Redes
 Unidad II: Análisis de Redes 2.1 Conceptos Básicos Un problema de redes es aquel que puede representarse por: LA IMPORTANCIA DE LOS MODELOS DE REDES: Muchos problemas comerciales pueden ser resueltos a
Unidad II: Análisis de Redes 2.1 Conceptos Básicos Un problema de redes es aquel que puede representarse por: LA IMPORTANCIA DE LOS MODELOS DE REDES: Muchos problemas comerciales pueden ser resueltos a
Tema 7: Problemas clásicos de Programación Lineal
 Tema 7: Problemas clásicos de Programación Lineal 1.- Características generales de un problema de transporte y asignación Surgen con frecuencia en diferentes contextos de la vida real. Requieren un número
Tema 7: Problemas clásicos de Programación Lineal 1.- Características generales de un problema de transporte y asignación Surgen con frecuencia en diferentes contextos de la vida real. Requieren un número
Método simplex para redes (representaciones gráficas) Cálculo del flujo de un árbol de expansión
 . 7 Árbol con ofertas y demandas. (Suponemos que el flujo de los demás arcos es igual a ) Método simplex para redes (representaciones gráficas) 6 - flujo en el arco (,)? Método simplex para redes (representaciones
. 7 Árbol con ofertas y demandas. (Suponemos que el flujo de los demás arcos es igual a ) Método simplex para redes (representaciones gráficas) 6 - flujo en el arco (,)? Método simplex para redes (representaciones
Resuelva los siguientes problemas según el método que se le indique.
 UNIVERSIDAD NACIONAL DE INGENIERIA UNI-NORTE INGENIERÍA INDUSTRIAL E INGENIERÍA DE SISTEMAS INVESTIGACIÓN DE OPERACIONES II Clase Práctica #1 Resuelva los siguientes problemas según el método que se le
UNIVERSIDAD NACIONAL DE INGENIERIA UNI-NORTE INGENIERÍA INDUSTRIAL E INGENIERÍA DE SISTEMAS INVESTIGACIÓN DE OPERACIONES II Clase Práctica #1 Resuelva los siguientes problemas según el método que se le
ARBOLES GENERADORES. Orlando Arboleda Molina. 16 de septiembre de Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle
 ARBOLES GENERADORES Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 16 de septiembre de 2008 Contenido Árboles generadores Algoritmo búsqueda por profundidad
ARBOLES GENERADORES Orlando Arboleda Molina Escuela de Ingeniería de Sistemas y Computación de La Universidad del Valle 16 de septiembre de 2008 Contenido Árboles generadores Algoritmo búsqueda por profundidad
Formulando con modelos lineales enteros
 Universidad de Chile 19 de marzo de 2012 Contenidos 1 Forma de un problema Lineal Entero 2 Modelando con variables binarias 3 Tipos de Problemas Forma General de un MILP Problema de optimización lineal
Universidad de Chile 19 de marzo de 2012 Contenidos 1 Forma de un problema Lineal Entero 2 Modelando con variables binarias 3 Tipos de Problemas Forma General de un MILP Problema de optimización lineal
LAS CIENCIAS DE LA PLANIFICACIÓN
 LAS CIENCIAS DE LA PLANIFICACIÓN 5. EL PROBLEMA DEL VIAJANTE (PV) (The Traveling Salesman Problem TSP) Un problema como el de las vacaciones, pero vital para las empresas, es el problema del viajante (PV):
LAS CIENCIAS DE LA PLANIFICACIÓN 5. EL PROBLEMA DEL VIAJANTE (PV) (The Traveling Salesman Problem TSP) Un problema como el de las vacaciones, pero vital para las empresas, es el problema del viajante (PV):
Caminos y Flujos optimales. 2da y 3er clase 2007
 Caminos y Flujos optimales 2da y 3er clase 2007 ESQUELETOS OPTIMALES (mínimo) Esqueleto de G =(X,U) es un subgrafo que es un árbol y que contiene todos los vértices de G. Esqueleto Mínimo de G = (X, U,
Caminos y Flujos optimales 2da y 3er clase 2007 ESQUELETOS OPTIMALES (mínimo) Esqueleto de G =(X,U) es un subgrafo que es un árbol y que contiene todos los vértices de G. Esqueleto Mínimo de G = (X, U,
Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler]
![Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler] Matemáticas Discretas L. Enrique Sucar INAOE. Teoría de Grafos. Problema de los puentes de Königsberg [Euler]](/thumbs/66/55246007.jpg) Matemáticas Discretas L. Enrique Sucar INAOE Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y circuitos Isomorfismo
Matemáticas Discretas L. Enrique Sucar INAOE Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y circuitos Isomorfismo
A5 Introducción a la optimización en redes
 48 Materials David Pujolar Morales A5 Introducción a la optimización en redes Definición 1. Grafo finito. Sea un V un conjunto no vacío con un número finito de elementos y E una familia finita de pares
48 Materials David Pujolar Morales A5 Introducción a la optimización en redes Definición 1. Grafo finito. Sea un V un conjunto no vacío con un número finito de elementos y E una familia finita de pares
Tema: Algoritmos para la ruta más corta en un Grafo.
 Programación IV. Guía 10 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos para la ruta más corta en un Grafo. Objetivos Específicos Definir el concepto de camino
Programación IV. Guía 10 1 Facultad: Ingeniería Escuela: Computación Asignatura: Programación IV Tema: Algoritmos para la ruta más corta en un Grafo. Objetivos Específicos Definir el concepto de camino
Los grafos son estructuras de datos Representan relaciones entre objetos. Son aplicables en. Relaciones arbitrarias, es decir No jerárquicas.
 ESTRUCTURA DE DATOS Los grafos son estructuras de datos Representan relaciones entre objetos Relaciones arbitrarias, es decir No jerárquicas Son aplicables en Química Modem Geografía Ing. Eléctrica e Industrial,
ESTRUCTURA DE DATOS Los grafos son estructuras de datos Representan relaciones entre objetos Relaciones arbitrarias, es decir No jerárquicas Son aplicables en Química Modem Geografía Ing. Eléctrica e Industrial,
Estimar la adecuación de un nodo para ser expandido.
 Universidad Rey Juan Carlos Curso 2014 2015 Hoja de Problemas Tema 3 - Solución 1. Contesta a las siguientes preguntas: (a) Cuál es el objetivo de una función heurística aplicada a la búsqueda en el espacio
Universidad Rey Juan Carlos Curso 2014 2015 Hoja de Problemas Tema 3 - Solución 1. Contesta a las siguientes preguntas: (a) Cuál es el objetivo de una función heurística aplicada a la búsqueda en el espacio
Análisis y Diseño de Algoritmos Árboles de Mínima Expansión (Minimum Spanning Trees) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE
 Análisis y Diseño de Algoritmos Árboles de Mínima Expansión (Minimum Spanning Trees) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Problema de Cableado de Circuitos Electrónicos 2 Diseño
Análisis y Diseño de Algoritmos Árboles de Mínima Expansión (Minimum Spanning Trees) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Problema de Cableado de Circuitos Electrónicos 2 Diseño
AnAnálisis de redes de transporte Tr. Muchas veces se utiliza en aplicaciones que nada tienen que ver con el transporte
 AnAnálisis de redes de transporte Tr Muchas veces se utiliza en aplicaciones que nada tienen que ver con el transporte Resumen Antecedentes y definiciones El camino más corto Árbol de expansión mínima
AnAnálisis de redes de transporte Tr Muchas veces se utiliza en aplicaciones que nada tienen que ver con el transporte Resumen Antecedentes y definiciones El camino más corto Árbol de expansión mínima
Flujo en Redes. IN34A: Clase Auxiliar. Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Industrial
 Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Industrial IN34A: Clase Auxiliar Flujo en Redes Marcel Goic F. 1 1 Esta es una versión bastante preliminar por
Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Industrial IN34A: Clase Auxiliar Flujo en Redes Marcel Goic F. 1 1 Esta es una versión bastante preliminar por
UNIDAD DOS MODELOS DE TRANSPORTE
 Ing. César Urquizú UNIDAD DOS MODELOS DE TRANSPORTE Ing. César Urquizú Modelos de Transporte Método de la Esquina Noroeste Método del Costo Mínimo o Menor Método de Aproximación de Vogel (MAV) Método del
Ing. César Urquizú UNIDAD DOS MODELOS DE TRANSPORTE Ing. César Urquizú Modelos de Transporte Método de la Esquina Noroeste Método del Costo Mínimo o Menor Método de Aproximación de Vogel (MAV) Método del
ÁRBOLES CRISTIAN ALFREDO MUÑOZ ÁLVAREZ JUAN DAVID LONDOÑO CASTRO JUAN PABLO CHACÓN PEÑA EDUARDO GONZALES
 ÁRBOLES CRISTIAN ALFREDO MUÑOZ ÁLVAREZ JUAN DAVID LONDOÑO CASTRO JUAN PABLO CHACÓN PEÑA EDUARDO GONZALES ÁRBOL Un árbol es un grafo no dirigido, conexo, sin ciclos (acíclico), y que no contiene aristas
ÁRBOLES CRISTIAN ALFREDO MUÑOZ ÁLVAREZ JUAN DAVID LONDOÑO CASTRO JUAN PABLO CHACÓN PEÑA EDUARDO GONZALES ÁRBOL Un árbol es un grafo no dirigido, conexo, sin ciclos (acíclico), y que no contiene aristas
Taller de grafs: rutes, mapes i xarxes socials
 Taller de grafs: rutes, mapes i xarxes socials Cristina Chiralt y Fernando Hernando Universidad Jaume I e Instituto Universitario de Matemáticas y sus Aplicaciones de Castellón Grado de Matemática Computacional
Taller de grafs: rutes, mapes i xarxes socials Cristina Chiralt y Fernando Hernando Universidad Jaume I e Instituto Universitario de Matemáticas y sus Aplicaciones de Castellón Grado de Matemática Computacional
Grafos. AMD Grado en Ingeniería Informática. AMD Grado en Ingeniería Informática (UM) Grafos 1 / 30
 Grafos AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Grafos / 0 Objetivos Al finalizar este tema tendréis que: Conocer la terminología básica de la teoría de grafos. Pasar
Grafos AMD Grado en Ingeniería Informática AMD Grado en Ingeniería Informática (UM) Grafos / 0 Objetivos Al finalizar este tema tendréis que: Conocer la terminología básica de la teoría de grafos. Pasar
Árboles abarcadores mínimos: algoritmo de Prim y algoritmo de Kruskal.
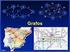 Árboles abarcadores mínimos: algoritmo de Prim y algoritmo de Kruskal. Jose Aguilar 1 Grafo de carreteras entre ciudades Mcbo Coro Pto. Cabello Valera Bqto Valencia Maracay Caracas Acarigua Barinas San
Árboles abarcadores mínimos: algoritmo de Prim y algoritmo de Kruskal. Jose Aguilar 1 Grafo de carreteras entre ciudades Mcbo Coro Pto. Cabello Valera Bqto Valencia Maracay Caracas Acarigua Barinas San
INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE CÓMPUTO ÁRBOLES DE DECISIÓN. M. En C. Eduardo Bustos Farías
 INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE CÓMPUTO ÁRBOLES DE DECISIÓN M. En C. Eduardo Bustos Farías 1 Árboles de decisión La Matriz de Ganancias es conveniente de utilizar para la toma de decisiones
INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE CÓMPUTO ÁRBOLES DE DECISIÓN M. En C. Eduardo Bustos Farías 1 Árboles de decisión La Matriz de Ganancias es conveniente de utilizar para la toma de decisiones
1. Diseñe algoritmos que permitan resolver eficientemente el problema de la mochila 0/1 para los siguientes casos:
 PROGRAMACIÓN DINÁMICA RELACIÓN DE EJERCICIOS Y PROBLEMAS 1. Diseñe algoritmos que permitan resolver eficientemente el problema de la mochila /1 para los siguientes casos: a. Mochila de capacidad W=15:
PROGRAMACIÓN DINÁMICA RELACIÓN DE EJERCICIOS Y PROBLEMAS 1. Diseñe algoritmos que permitan resolver eficientemente el problema de la mochila /1 para los siguientes casos: a. Mochila de capacidad W=15:
Teoría de Grafos. Herramientas de programación para procesamiento de señales
 Teoría de Grafos Herramientas de programación para procesamiento de señales Indice Nociones básicas: Definiciones Ejemplos Propiedades Nociones avanzadas: Grafos planares Árboles Representación en computadora
Teoría de Grafos Herramientas de programación para procesamiento de señales Indice Nociones básicas: Definiciones Ejemplos Propiedades Nociones avanzadas: Grafos planares Árboles Representación en computadora
IN34A - Optimización
 IN34A - Optimización Complejidad Leonardo López H. lelopez@ing.uchile.cl Primavera 2008 1 / 33 Contenidos Problemas y Procedimientos de solución Problemas de optimización v/s problemas de decisión Métodos,
IN34A - Optimización Complejidad Leonardo López H. lelopez@ing.uchile.cl Primavera 2008 1 / 33 Contenidos Problemas y Procedimientos de solución Problemas de optimización v/s problemas de decisión Métodos,
Ejemplo: ubicación de estación de bomberos
 15.053 Jueves, 11 de abril Más aplicaciones de la programación entera. Técnicas de plano de corte para obtener mejores cotas. Ejemplo: ubicación de estación de bomberos Considere la ubicación de estaciones
15.053 Jueves, 11 de abril Más aplicaciones de la programación entera. Técnicas de plano de corte para obtener mejores cotas. Ejemplo: ubicación de estación de bomberos Considere la ubicación de estaciones
El problema del agente viajero
 CO- (F0) //00 El problema del agente viajero Un vendedor tiene que visitar n + ciudades, cada una exactamente una vez. La distancia entre cada par de ciudades viene dada por d ij (en general d ij d ji
CO- (F0) //00 El problema del agente viajero Un vendedor tiene que visitar n + ciudades, cada una exactamente una vez. La distancia entre cada par de ciudades viene dada por d ij (en general d ij d ji
Árboles. Un grafo no dirigido es un árbol si y sólo si existe una ruta unica simple entre cualquiera dos de sus vértices.
 ÁRBOLES Árboles Un grafo conectado que no contiene circuitos simples. Utilizados desde 1857, por el matemático Ingles Arthur Cayley para contar ciertos tipos de componentes químicos. Un árbol es un grafo
ÁRBOLES Árboles Un grafo conectado que no contiene circuitos simples. Utilizados desde 1857, por el matemático Ingles Arthur Cayley para contar ciertos tipos de componentes químicos. Un árbol es un grafo
Programación entera 1
 Programación entera 1 1. El modelo de programación entera. 2. Aplicaciones de la programación entera. 3. Solución gráfica de problemas enteros. 4. El algoritmo de ramificación y acotación. 5. El algoritmo
Programación entera 1 1. El modelo de programación entera. 2. Aplicaciones de la programación entera. 3. Solución gráfica de problemas enteros. 4. El algoritmo de ramificación y acotación. 5. El algoritmo
Sesión 4: Teoría de Grafos
 Modelos Gráficos Probabilistas L. Enrique Sucar INAOE Sesión 4: Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y
Modelos Gráficos Probabilistas L. Enrique Sucar INAOE Sesión 4: Teoría de Grafos Problema de los puentes de Königsberg [Euler] Teoría de Grafos Definición y terminología Tipos de grafos Trayectorias y
Modelos de Transporte: método de la esquina noroeste. M. En C. Eduardo Bustos Farías
 Modelos de Transporte: método de la esquina noroeste M. En C. Eduardo Bustos Farías as Problemas de transporte Surge cuando se necesita un modelo costo-efectividad que permita transportar ciertos bienes
Modelos de Transporte: método de la esquina noroeste M. En C. Eduardo Bustos Farías as Problemas de transporte Surge cuando se necesita un modelo costo-efectividad que permita transportar ciertos bienes
Formulación del problema de la ruta más corta en programación lineal
 Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Formulación del problema de la ruta más corta en programación lineal En esta sección se describen dos formulaciones de programación lineal para el problema de la ruta más corta. Las formulaciones son generales,
Tema: Los Grafos y su importancia para la optimización de redes.
 Tema: Los Grafos y su importancia para la optimización de redes. Qué son los Grafos? Un grafo es una dupla G= {X,U}, donde X es un conjunto finito y no vacio de elementos llamados vértices y U es el conjunto
Tema: Los Grafos y su importancia para la optimización de redes. Qué son los Grafos? Un grafo es una dupla G= {X,U}, donde X es un conjunto finito y no vacio de elementos llamados vértices y U es el conjunto
2007 Carmen Moreno Valencia
 Tema VIII. Grafos Grafos 1 2007 Carmen Moreno Valencia 1. Grafos, digrafos y multigrafos 2. Grafos eulerianos 3. Matrices de adyacencia e incidencia 4. Exploración de grafos pesados 1. Grafos, digrafos
Tema VIII. Grafos Grafos 1 2007 Carmen Moreno Valencia 1. Grafos, digrafos y multigrafos 2. Grafos eulerianos 3. Matrices de adyacencia e incidencia 4. Exploración de grafos pesados 1. Grafos, digrafos
Ruta más Corta con una sóla Fuente de Inicio (Single-Source Shortest Paths) DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE
 Ruta más Corta con una sóla Fuente de Inicio (Single-Source Shortest Paths) 1 DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Problema de Encontrar la Ruta más Corta 2 Se requiere llegar de
Ruta más Corta con una sóla Fuente de Inicio (Single-Source Shortest Paths) 1 DR. JESÚS A. GONZÁLEZ BERNAL CIENCIAS COMPUTACIONALES INAOE Problema de Encontrar la Ruta más Corta 2 Se requiere llegar de
Modelos de Transporte: Problemas de Asignación. M. En C. Eduardo Bustos Farías
 Modelos de Transporte: Problemas de asignación M. En C. Eduardo Bustos Farías as Problemas de Asignación Problemas de Asignación: Son problemas balanceados de transporte en los cuales todas las ofertas
Modelos de Transporte: Problemas de asignación M. En C. Eduardo Bustos Farías as Problemas de Asignación Problemas de Asignación: Son problemas balanceados de transporte en los cuales todas las ofertas
Apellidos:... Nombre:...
 Apellidos:....................................... Nombre:........................................ Introducción a la Inteligencia Artificial 1 er Parcial de Teoría 12 Noviembre 2004 Ejercicio 1: Responder
Apellidos:....................................... Nombre:........................................ Introducción a la Inteligencia Artificial 1 er Parcial de Teoría 12 Noviembre 2004 Ejercicio 1: Responder
Conmutación y Re-envío Parte 1 Switching y Forwarding
 Conmutación y Re-envío Parte 1 Switching y Forwarding Contenido Switches de Almacenamiento y re-envío Repetidores (siempre re-envían) Bridges y LAN Extendidas ELO322 1 Redes Escalables Conmutadores (Switches)
Conmutación y Re-envío Parte 1 Switching y Forwarding Contenido Switches de Almacenamiento y re-envío Repetidores (siempre re-envían) Bridges y LAN Extendidas ELO322 1 Redes Escalables Conmutadores (Switches)
Coloreo de vértices Definiciones: Coloreo de Grafos. Cotas para χ Proposición: Si H es un subgrafo de G entonces χ(h) χ(g).
 Coloreo de vértices Definiciones: Coloreo de Grafos Algoritmos y Estructuras de Datos III Un coloreo (válido) de los vértices de un grafo G = (V, X ) es una asignación f : V C, tal que f (v) f (u) (u,
Coloreo de vértices Definiciones: Coloreo de Grafos Algoritmos y Estructuras de Datos III Un coloreo (válido) de los vértices de un grafo G = (V, X ) es una asignación f : V C, tal que f (v) f (u) (u,
Capítulo 3: Grafos Clase 1: Grafos: Modelos, tipos, representación e isomorfismo
 Capítulo 3: Grafos Clase 1: Grafos: Modelos, tipos, representación e isomorfismo Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 4: Grafos 1 / 35 Por qué estudiamos
Capítulo 3: Grafos Clase 1: Grafos: Modelos, tipos, representación e isomorfismo Matemática Discreta - CC3101 Profesor: Pablo Barceló P. Barceló Matemática Discreta - Cap. 4: Grafos 1 / 35 Por qué estudiamos
Tema 7: Optimización sobre Redes Muchos de los problemas de Investigación Operativa pueden modelizarse y resolverse sobre un grafo: conjunto de
 Tema 7: Optimización sobre Redes Muchos de los problemas de Investigación Operativa pueden modelizarse y resolverse sobre un grafo: conjunto de vértices o nodos conectados con arcos y/o aristas. Diseñar
Tema 7: Optimización sobre Redes Muchos de los problemas de Investigación Operativa pueden modelizarse y resolverse sobre un grafo: conjunto de vértices o nodos conectados con arcos y/o aristas. Diseñar
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática. Búsqueda exhaustiva
 Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Búsqueda exhaustiva Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias preparadas
Parte de Algoritmos de la asignatura de Programación Master de Bioinformática Búsqueda exhaustiva Web asignatura: http://dis.um.es/~domingo/algbio.html E-mail profesor: domingo@um.es Transparencias preparadas
III Unidad Planificación y diseño de una red (LAN)
 Recordemos: Una red de área local, Es un conjunto de Equipos y dispositivos de hardware unidos entre sí con el fin de compartir recursos en una zona geográfica limitada. Planificación y diseño de la red.
Recordemos: Una red de área local, Es un conjunto de Equipos y dispositivos de hardware unidos entre sí con el fin de compartir recursos en una zona geográfica limitada. Planificación y diseño de la red.
Algoritmos y Estructuras de Datos III
 Árboles Algoritmos y Estructuras de Datos III Árboles Definición: Un árbol es un grafo conexo sin circuitos simples. Árboles Teorema: Dado un grafo G = (V, X ) son equivalentes: 1. G es un árbol. 2. G
Árboles Algoritmos y Estructuras de Datos III Árboles Definición: Un árbol es un grafo conexo sin circuitos simples. Árboles Teorema: Dado un grafo G = (V, X ) son equivalentes: 1. G es un árbol. 2. G
UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-RUACS. Investigación de Operaciones
 UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-RUACS Facultad de Ingeniería Industrial Investigación de Operaciones Tema: Teoría de los Grafos Elaborado por: Ing. Carlos Alberto Moreno. Docente: Ing. Pastrana
UNIVERSIDAD NACIONAL DE INGENIERÍA UNI-RUACS Facultad de Ingeniería Industrial Investigación de Operaciones Tema: Teoría de los Grafos Elaborado por: Ing. Carlos Alberto Moreno. Docente: Ing. Pastrana
Grafos y Redes. 3. Resolución: Dibujar el camino sin levantar el lápiz y pasando sólo una vez por cada arco o arista.
 Grafos y Redes. Nodos: vértices, 2, 3 2. Arcos: aristas, conexión entre nodos. 2, 54, etc. 3. Resolución: Dibujar el camino sin levantar el lápiz y pasando sólo una vez por cada arco o arista. 4. Grado
Grafos y Redes. Nodos: vértices, 2, 3 2. Arcos: aristas, conexión entre nodos. 2, 54, etc. 3. Resolución: Dibujar el camino sin levantar el lápiz y pasando sólo una vez por cada arco o arista. 4. Grado
Diagramas de Bloques
 1! Diagrama de Bloques y Grafos Juan Antonio Hernández Tamames, Susana Borromeo Curso 2014-2015 Diagramas de Bloques 2! Representación en Diagramas de Bloques Álgebra de Bloques 1 Ideas Básicas 3! Los
1! Diagrama de Bloques y Grafos Juan Antonio Hernández Tamames, Susana Borromeo Curso 2014-2015 Diagramas de Bloques 2! Representación en Diagramas de Bloques Álgebra de Bloques 1 Ideas Básicas 3! Los
1. GRAFOS : CONCEPTOS BASICOS
 1. GRAFOS : CONCEPTOS BASICOS Sea V un conjunto finito no vacio y sea E V x V. El par (V, E) es un grafo no dirigido, donde V es un conjunto de vértices o nodos y E es un conjunto de aristas. Denotaremos
1. GRAFOS : CONCEPTOS BASICOS Sea V un conjunto finito no vacio y sea E V x V. El par (V, E) es un grafo no dirigido, donde V es un conjunto de vértices o nodos y E es un conjunto de aristas. Denotaremos
CONCEPTOS BÁSICOS DE UNA RED.
 CONCEPTOS BÁSICOS DE UNA RED. 1 Que es una red? Es un conjunto de equipos informáticos y software conectados entre sí por medio de dispositivos físicos que envían y reciben impulsos eléctricos, ondas electromagnéticas
CONCEPTOS BÁSICOS DE UNA RED. 1 Que es una red? Es un conjunto de equipos informáticos y software conectados entre sí por medio de dispositivos físicos que envían y reciben impulsos eléctricos, ondas electromagnéticas
Introducción a la programación lineal
 Introducción a la programación lineal La programación lineal se aplica a modelos de optimización en los que las funciones objetivo y restricción son estrictamente lineales. La técnica se aplica en una
Introducción a la programación lineal La programación lineal se aplica a modelos de optimización en los que las funciones objetivo y restricción son estrictamente lineales. La técnica se aplica en una
GRAFOS. Prof. Ing. M.Sc. Fulbia Torres
 ESTRUCTURAS DE DATOS 2006 Prof. DEFINICIÓN Un grafo consta de un conjunto de nodos(o vértices) y un conjunto de arcos (o aristas). Cada arco de un grafo se especifica mediante un par de nodos. Denotemos
ESTRUCTURAS DE DATOS 2006 Prof. DEFINICIÓN Un grafo consta de un conjunto de nodos(o vértices) y un conjunto de arcos (o aristas). Cada arco de un grafo se especifica mediante un par de nodos. Denotemos
Algoritmos sobre Grafos
 Sexta Sesión 27 de febrero de 2010 Contenido Deniciones 1 Deniciones 2 3 4 Deniciones sobre Grafos Par de una lista de nodos y una lista de enlaces, denidos a su vez como pares del conjunto de nodos.
Sexta Sesión 27 de febrero de 2010 Contenido Deniciones 1 Deniciones 2 3 4 Deniciones sobre Grafos Par de una lista de nodos y una lista de enlaces, denidos a su vez como pares del conjunto de nodos.
Centro Asociado Palma de Mallorca. Tutor: Antonio Rivero Cuesta
 Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
Centro Asociado Palma de Mallorca Lógica y Estructuras Discretas Tutor: Antonio Rivero Cuesta Tema 5 Teoría de Grafos Conceptos Básicos Un grafo consta de: Grafo Un conjunto de nodos, Un conjunto de aristas
Implementación de un Algoritmo para optimizar el flujo en una Red
 Implementación de un Algoritmo para optimizar el flujo en una Red Carlos Aníbal Suárez Hernández 1, Fernando Sandoya 1 Ingeniero en Estadística Informática 00 Director de Tesis, Matemático, Escuela Politécnica
Implementación de un Algoritmo para optimizar el flujo en una Red Carlos Aníbal Suárez Hernández 1, Fernando Sandoya 1 Ingeniero en Estadística Informática 00 Director de Tesis, Matemático, Escuela Politécnica
Grafos. Algoritmos y Estructuras de Datos III
 Grafos Algoritmos y Estructuras de Datos III Grafos Un grafo G = (V, X ) es un par de conjuntos, donde V es un conjunto de puntos o nodos o vértices y X es un subconjunto del conjunto de pares no ordenados
Grafos Algoritmos y Estructuras de Datos III Grafos Un grafo G = (V, X ) es un par de conjuntos, donde V es un conjunto de puntos o nodos o vértices y X es un subconjunto del conjunto de pares no ordenados
Segundo parcial. Martes, 23 de abril de 2003
 5.053 Segundo parcial Martes, 3 de abril de 003 Se permite traer una hoja de papel con anotaciones por una cara. Responda a todas las preguntas en los cuadernillos de examen.. Controle el tiempo. Si un
5.053 Segundo parcial Martes, 3 de abril de 003 Se permite traer una hoja de papel con anotaciones por una cara. Responda a todas las preguntas en los cuadernillos de examen.. Controle el tiempo. Si un
Matemáticas Básicas para Computación
 Matemáticas Básicas para Computación MATEMÁTICAS BÁSICAS PARA COMPUTACIÓN 1 Sesión No. 11 Nombre: Árboles Objetivo: Al término de la sesión el participante conocerá los tipos de grafos específicamente
Matemáticas Básicas para Computación MATEMÁTICAS BÁSICAS PARA COMPUTACIÓN 1 Sesión No. 11 Nombre: Árboles Objetivo: Al término de la sesión el participante conocerá los tipos de grafos específicamente
Práctica 2. Algoritmos de búsqueda local (local search algorithms) y algoritmos avariciosos (greedy algorithms)
 PLANIFICACIÓN Y GESTIÓN DE REDES Grado en Ingeniería Telemática Curso 2012-2013 Práctica 2. Algoritmos de búsqueda local (local search algorithms) y algoritmos avariciosos (greedy algorithms) Autor: Pablo
PLANIFICACIÓN Y GESTIÓN DE REDES Grado en Ingeniería Telemática Curso 2012-2013 Práctica 2. Algoritmos de búsqueda local (local search algorithms) y algoritmos avariciosos (greedy algorithms) Autor: Pablo
Modelos de Inventarios
 Modelos de Inventarios 1. Qué significa PERT? Program Evaluation Review Technique Técnica de Revisión de Evaluación de Programa 2. Qué significa las siglas C.E.P Cantidad Económica de Pedidos 3. Para qué
Modelos de Inventarios 1. Qué significa PERT? Program Evaluation Review Technique Técnica de Revisión de Evaluación de Programa 2. Qué significa las siglas C.E.P Cantidad Económica de Pedidos 3. Para qué
Modelos de Redes: Problema del flujo máximom. M. En C. Eduardo Bustos Farías
 Modelos de Redes: Problema del flujo máimom M. En C. Eduardo Bustos Farías as Problema del flujo máimom Problema del flujo máimom Este modelo se utiliza para reducir los embotellamientos entre ciertos
Modelos de Redes: Problema del flujo máimom M. En C. Eduardo Bustos Farías as Problema del flujo máimom Problema del flujo máimom Este modelo se utiliza para reducir los embotellamientos entre ciertos
Algoritmos Codiciosos y problemas de Optimización en Grafos
 Algoritmos odiciosos y problemas de Optimización en Grafos B10 onceptos Un árbol es un grafo conexo y sin circuitos. Un árbol trivial es un grafo que consiste de un solo vértice. Un grafo sin circuitos
Algoritmos odiciosos y problemas de Optimización en Grafos B10 onceptos Un árbol es un grafo conexo y sin circuitos. Un árbol trivial es un grafo que consiste de un solo vértice. Un grafo sin circuitos
Tema 4y 5. Algoritmos voraces. Algoritmos sobre grafos
 Tema 4y 5. Algoritmos voraces. Algoritmos sobre grafos Objetivos: Estudio de la técnica de diseño de algoritmos voraces Estudio de algunos problemas clásicos: Indice: Mochila con fraccionamiento Algoritmos
Tema 4y 5. Algoritmos voraces. Algoritmos sobre grafos Objetivos: Estudio de la técnica de diseño de algoritmos voraces Estudio de algunos problemas clásicos: Indice: Mochila con fraccionamiento Algoritmos
Caminos y Flujos optimales. Introducción a la Investigación de Operaciones 2007
 Caminos y Flujos optimales Introducción a la Investigación de Operaciones 2007 Contenido Definiciones básicas. Conexidad. Clausura transitiva. Esqueletos y caminos optimales. Redes. Flujos. Algoritmo de
Caminos y Flujos optimales Introducción a la Investigación de Operaciones 2007 Contenido Definiciones básicas. Conexidad. Clausura transitiva. Esqueletos y caminos optimales. Redes. Flujos. Algoritmo de
TEMA IV TEORÍA DE GRAFOS
 TEMA IV TEORÍA DE GRAFOS Poli Abascal Fuentes TEMA IV Teoría de grafos p. 1/? TEMA IV 4. TEORÍA DE GRAFOS 4.1 GRAFOS 4.1.1 Introducción 4.1.2 Definiciones básicas 4.1.3 Caminos y recorridos 4.1.4 Subgrafos,
TEMA IV TEORÍA DE GRAFOS Poli Abascal Fuentes TEMA IV Teoría de grafos p. 1/? TEMA IV 4. TEORÍA DE GRAFOS 4.1 GRAFOS 4.1.1 Introducción 4.1.2 Definiciones básicas 4.1.3 Caminos y recorridos 4.1.4 Subgrafos,
TEMA 5 El tipo grafo. Tipo grafo
 TEMA 5 El tipo grafo PROGRAMACIÓN Y ESTRUCTURAS DE DATOS Tipo grafo 1. Concepto de grafo y terminología 2. Especificación algebraica. Representación de grafos.1. Recorrido en profundidad o DFS.2. Recorrido
TEMA 5 El tipo grafo PROGRAMACIÓN Y ESTRUCTURAS DE DATOS Tipo grafo 1. Concepto de grafo y terminología 2. Especificación algebraica. Representación de grafos.1. Recorrido en profundidad o DFS.2. Recorrido
Arboles Binarios de Búsqueda en C++
 Arboles Binarios de Búsqueda en C++ por CCG/Mayo-2014 Tema de Arboles Binarios de Búsqueda, como un poco de teoría para su mejor entendimiento seguidamente mostrare la implementación en lenguaje de programación
Arboles Binarios de Búsqueda en C++ por CCG/Mayo-2014 Tema de Arboles Binarios de Búsqueda, como un poco de teoría para su mejor entendimiento seguidamente mostrare la implementación en lenguaje de programación
Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.
![Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos. Grafos. Suponiendo que e = [u, v]. Entonces los nodos u y v se llaman extremos de e y u y v se dice que son nodos adyacentes o vecinos.](/thumbs/54/33802392.jpg) Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
Grafos Los grafos son estructuras que constan de vértices o nodos y de aristas o arcos que conectan los vértices entre sí. Un grafo G consiste en dos cosas: 1. Un conjunto V de elementos llamados nodos
CONTENIDO SEMBLANZA DE LOS AUTORES DE LOS ESCRITORES DE CASOS..
 CONTENIDO SEMBLANZA DE LOS AUTORES DE LOS ESCRITORES DE CASOS.. PREFACIO. xix xxi xxiii CAPITULO I Introducción. 1 1.1 Orígenes de la investigación de operaciones. 1 1.2 Naturaleza de la investigación
CONTENIDO SEMBLANZA DE LOS AUTORES DE LOS ESCRITORES DE CASOS.. PREFACIO. xix xxi xxiii CAPITULO I Introducción. 1 1.1 Orígenes de la investigación de operaciones. 1 1.2 Naturaleza de la investigación
Técnicas de planificación y control de proyectos Andrés Ramos Universidad Pontificia Comillas
 Técnicas de planificación y control de proyectos Andrés Ramos Universidad Pontificia Comillas http://www.iit.upcomillas.es/aramos/ Andres.Ramos@upcomillas.es TÉCNICAS DE PLANIFICACIÓN Y CONTROL DE PROYECTOS
Técnicas de planificación y control de proyectos Andrés Ramos Universidad Pontificia Comillas http://www.iit.upcomillas.es/aramos/ Andres.Ramos@upcomillas.es TÉCNICAS DE PLANIFICACIÓN Y CONTROL DE PROYECTOS
Caminos. Sobre los problemas de encontrar caminos en grafos. Complexity D.Moshkovitz
 Caminos Sobre los problemas de encontrar caminos en grafos 1 Introdución Objetivos: Introducir más problemas sobre grafos. Resumen: Caminos Hamiltonianos Caminos Eulerianos 2 Camino Hamiltoniano Entrada:
Caminos Sobre los problemas de encontrar caminos en grafos 1 Introdución Objetivos: Introducir más problemas sobre grafos. Resumen: Caminos Hamiltonianos Caminos Eulerianos 2 Camino Hamiltoniano Entrada:
Introducción. Königsberg, s.xviii A
 Teoría de Grafos Introducción Königsberg, s.xviii A B C D Euler resuelve este problema mediante la teoría de grafos: sólo puede haber un ciclo euleriano cuando todos los nodos tienen un número par de aristas
Teoría de Grafos Introducción Königsberg, s.xviii A B C D Euler resuelve este problema mediante la teoría de grafos: sólo puede haber un ciclo euleriano cuando todos los nodos tienen un número par de aristas
Tema 1. Conceptos básicos
 Tema 1. Conceptos básicos 1. Introducción... 1 2. Conceptos básicos... 2 2.1. Circuito eléctrico... 2 2.2. Teoría de Circuitos... 2 3. Magnitudes de un circuito: Tensión e intensidad... 3 3.1. Carga y
Tema 1. Conceptos básicos 1. Introducción... 1 2. Conceptos básicos... 2 2.1. Circuito eléctrico... 2 2.2. Teoría de Circuitos... 2 3. Magnitudes de un circuito: Tensión e intensidad... 3 3.1. Carga y
Grafos Los siete puentes de Königsberg: Teoría de Grafos
 Grafos Los siete puentes de Königsberg: Un ciudadano de Königsberg (Prusia) se propuso dar un paseo cruzando cada uno de los siete puentes que existen sobre el río Pregel una sola vez. Los dos brazos del
Grafos Los siete puentes de Königsberg: Un ciudadano de Königsberg (Prusia) se propuso dar un paseo cruzando cada uno de los siete puentes que existen sobre el río Pregel una sola vez. Los dos brazos del
ARBOLES ARBOLES COMPUTACIONALES MATEMATICAS DISCRETAS II
 ARBOLES ARBOLES COMPUTACIONALES MATEMATICAS DISCRETAS II Contenido Concepto Características y Propiedades Tipos de Arboles 1. Libres 2. Binarios 3. Expansión Mínima Algoritmo de Kruskal Algoritmo Prim
ARBOLES ARBOLES COMPUTACIONALES MATEMATICAS DISCRETAS II Contenido Concepto Características y Propiedades Tipos de Arboles 1. Libres 2. Binarios 3. Expansión Mínima Algoritmo de Kruskal Algoritmo Prim
