CONCEPTOS BÁSICOS DE CÁLCULO.
|
|
|
- Ángeles Caballero Cuenca
- hace 7 años
- Vistas:
Transcripción
1
2 CONCEPTOS BÁSICOS DE CÁLCULO. Las variables y las funciones Un concepto muy importante en el estudio de la variación es el de variable y función. La conexión entre sus expresiones analíticas y representaciones gráficas es utilizada para manipular los procesos de cambio, pues se considera que es muy difícil realizar operaciones con los cambios si no se cuenta con una fórmula matemática y una gráfica que ayude a representar el comportamiento de esos cambios. Sobre esta base se aborda el cambio y su medición. Es necesario enfatizar que la noción de función no siempre es comprendida por el alumno, y es necesario conseguir una comprensión total de este concepto fundamental. La tabulación como tal debe ser utilizada para registrar datos numéricos experimentales para estudiar la variación, esto con el fin de recalcar el papel de las variables dependientes y las independientes. Un rasgo importante que debe estudiarse en lo referente a las funciones y sus gráficas es el comportamiento cualitativo de la función; Para cuantificar cuanto cambia una función utilizamos el método de la variación; esto es un procedimiento que nos permite saber cuánto aumenta o disminuye en función de la variación de cualquiera de las variables involucradas. Sobra decir la gran importancia que tienen las variables y funciones en la descripción del mundo que nos rodea, ya que existe infinidad de fenómenos naturales, en donde se encuentran involucradas dos o más variables entre sí. Nos introducimos pues al estudio de la variación por medio de modelos matemáticos simples para determinar cuánto cambia una variable en un fenómeno dado en un instante inicial y en uno posterior utilizando la expresión de diferencias: Podemos encontrar en la naturaleza diferentes fenómenos y problemas en donde se presenta una relación entre variables, por ejemplo podemos decir que el área de un círculo es una función de su radio: A= f(r), Al cambiar el valor de éste, en consecuencia habrá también un cambio en el área. Es decir: el incremento del radio repercutirá en un incremento del área: NOTA: El símbolo se emplea para indicar un incremento de la variable 1
3 Otro caso es el que la distancia recorrida por un atleta es una función del tiempo: d = f(t) ; al cambiar la variable tiempo también se verá modificada la variable distancia. Podemos citar una cantidad enorme de problemas donde se puede observar la relación entre dos variables, pero cabe señalar sin embargo que existe una infinidad de fenómenos en donde las variables no son únicamente dos, sino 3 o más; por ejemplo si deseamos estudiar el crecimiento de una planta podemos decir por simple inspección que depende de muchos factores (variables) entre los que podemos mencionar al clima, el tipo de suelo, la cantidad de agua, la cantidad de fertilizante, el tiempo de exposición al sol, la genética de la planta entre otros factores más. Puede verse a simple vista que este es tan solo un ejemplo de la cantidad de variables que implica el estudio de un fenómeno, lo que en consecuencia aumenta el nivel de complejidad en el análisis. Este tipo de fenómenos que presentan muchas variables, se conoce como calculo de varias variables y el tipo de problemas que se abordan en donde solo hay dos de ellas, se conoce como calculo de una variable, que como ya es de tu conocimiento es muy común representar matemáticamente mediante: y = f (x). En el curso se estudiaran por lo tanto, las relaciones entre los cambios de las variables de una función considerando que estos cambios (que pueden ser incrementos o decrementos) en los valores de las variables se dan en términos muy pequeños (infinitesimales) y el cociente de la relación que hay entre estos cambios de cada variable es lo que conocemos como derivada. En términos matemáticos esto es:.. que se lee como: El límite del incremento de la variable dependiente (y) con respecto a la variable independiente (x) cuando el incremento de la variable independiente tiende a ser cero es equivalente a la derivada. 2
4 Los cambios relativos se miden por medio de razones o cocientes entre cambios. Este es un concepto fundamental en el Cálculo Diferencial, ya que siempre que se estudia un fenómeno de la variación lo importante no es sólo determinar los cambios, sino determinar qué tan rápido cambia lo que está cambiando, y la mejor forma de averiguarlo es por medio de las razones entre los cambios. LA DERIVADA. El cálculo se fortaleció a raíz de cuatro clásicos problemas sobre los que los matemáticos europeos trabajaron durante el siglo XVII. Estos problemas fueron: (1) El problema de la recta tangente. (2) El problema de la velocidad y la aceleración. (3) El problema de los máximos y mínimos. (4) El problema del área. Conceptos básicos. Derivada de una función El concepto de derivada no implica un término difícil de comprender, dado lo que ya se ha explicado al inicio del curso en cuanto a sucesiones, límites y la misma derivada que son términos intrínsecamente relacionados entre sí. Explícitamente tenemos que: dada una función y = f(x), la derivada mide la variación de y, cuando hay una pequeña variación de x. Esto es, dada una función y = f (x), si hallamos su derivada se obtiene una nueva función llamada derivada de la anterior. Es decir: Función: y = f (x) Operación derivada: dy Función derivada: y = f (x) 3
5 El procedimiento para obtener dicha derivada se llama derivación. Por otro lado es importante mencionar que: para que exista la derivada de una función en un punto, tiene que existir ese límite. Cuando no existe este límite, se dice que la función no es derivable en ese punto. Para representar la derivada de una función se utilizan los símbolos: y', f '(x) y Es muy importante darse cuenta que en ésta notación: es un símbolo y no una fracción. Los otros símbolos que también se usan para denotar una derivada fueron introducidos por algunos matemáticos que también hicieron aportaciones muy importantes a esta ciencia del cálculo. La notación de la derivada, se llama notación de Leibniz quien la utilizó para indicar simbólicamente el paso al límite de cambiando por d. Para hallar el resultado de la función derivada basta con aplicar la definición del concepto derivada que es: La derivada de una función es el límite de la razón del incremento de la función al incremento de la variable independiente cuando este tiende a cero. Matemáticamente se representa por: Hay una fórmula que se conoce como regla general ó de los 4 pasos para obtener dicha derivada de acuerdo con la definición dada anteriormente. La aplicación de esta fórmula se observa a continuación, hay que poner espacial atención a cada uno de los pasos. EJEMPLO. Obtener por medio de la definición, la derivada de la función y = x 2 4
6 PASO 1 : se sustituye en la función x por x + x, como también y por y + y. PASO 2 : se resta el valor dado de la función del nuevo valor y se obtiene la función. y (que es el incremento de PASO 3 : se divide y (incremento de la función) entre x (incremento de la variable independiente). PASO 4 : se calcula el límite del cociente cuando x tiende a cero, y el límite que se ha obtenido es la derivada que se estaba buscando. MATEMÁTICAMENTE ESTO ES: Sea la función y= x 2 Paso 1: suma de incrementos: Y + y = ( x + x) 2 = x 2 + 2x x + x 2 Paso 2: resta de la función: - Y + y = x 2 + 2x x + x 2 y = x 2 y = 2x x + x 2 Paso 3 división entre el incremento de la variable independiente: y = 2x x + x 2 es decir: y = 2x x + x 2 o sea: y = 2x + x x x x x x x Paso 4: calculo del límite cuando x tiende a cero: Lim y = lim (2x + x) = lim (2x + 0) = 2x x 0 x x 0 x 0 5
7 Por lo que finalmente La función derivada es: Ahora veamos gráficamente el resultado obtenido. Sabemos que la grafica de la función a derivar y = x 2 es una parábola. Asimismo la grafica de la función derivada f (x) o bien Es una recta, que observamos a continuación. Podemos interpretar con estos datos como se ve en la figura, que la derivada representa una recta secante, la cual al tomar el límite cuando Δ x 0, se viene a transformar en una recta tangente debido a que como se ha de recordar del tema de geometría analítica, el cociente que estamos analizando: y es una diferencia de coordenadas y 2 y 1 que representa como ya sabemos x x 2 x 1 La pendiente m de una recta. Ahora bien, si nos proponemos sustituir el valor de x=3 en la función derivada nuestro resultado es: es decir queda: m= 6 que viene a ser el valor de la pendiente de la recta que pasa por este punto. 6
8 SIGNIFICADO GEOMÉTRICO DE LA DERIVADA. Finalmente podemos concluir que la tangente en un punto de una curva se obtiene como límite de la secante en ese punto. En la siguiente figura se observa el ejemplo resuelto: la función a derivar, la derivada y la recta tangente en el punto x=3 Recta secante: Derivada: dy = 2x y = x 2 Recta tangente: límite de la recta secante (derivada en x = 3). Como hemos podido darnos cuenta, hemos llegado a definir matemáticamente y demostrar el significado de la derivada. Y esto fue lo que por mucho tiempo así como procedimos, según se dice es lo que llevó a Leibniz al descubrimiento del cálculo diferencial. Otros matemáticos como por ejemplo Newton, definen la derivada desde otra perspectiva, con relación al cambio en las variables del movimiento de un cuerpo, lo que permite determinar la rapidez o posición de un objeto por medio de la aplicación de la derivada. Nosotros nos enfocaremos a usar desde la perspectiva geométrica de Leibniz su significado de este concepto fundamental del cálculo. La regla general para derivación es fundamental, puesto que se deduce directamente de la definición de derivada, y es muy importante familiarizarse con ella. 7
9 Sin embargo, el procedimiento de aplicar la regla en la resolución de problemas es largo o difícil; por consiguiente, se han deducido de la regla general, a fin de facilitar la tarea, reglas especiales o fórmulas para derivar ciertas formas normales que se presentan con frecuencia. ( Es importante no solo aprender de memoria cada formula sino también poder enunciar en palabras la regla correspondiente ). FORMULAS DE DERIVACIÓN De acuerdo a las clasificaciones de funciones, se han agrupado estas formulas en: Algebraicas y Trascendentes (trigonométricas, exponenciales y logarítmicas.). Una vez que las hayas revisado y analizado, elabora un formulario para que lo tengas a la mano y lo uses cuando estés resolviendo los ejemplos propuestos por el asesor. Derivadas Algebraicas: dc I. = 0...la derivada de una constante es cero II. = 1... la derivada de x respecto de sí misma es igual a 1 III.... la derivada de una suma de funciones es igual a la suma de las derivadas de cada función d IV. ( cv) dv = c... la derivada de una constante por la función es igual a la constante multiplicada por la derivada de la función. d n n 1 V. ( ) x d VI. ( v ) = nx = nv n n 1 dv 8
10 d VII. ( uv) = dv u + v du VIII. d du v u u = 2 v v dv Derivadas trascendentes: logarítmicas y exponenciales d u IX. ( e ) d X. ( ln u) = e u 1 =. u dv du = dv u d u XI. ( a ) v dv = a.lna. d XII. ( v) log = loge dv. v Derivadas trigonométricas (directas e inversas): d XIII. ( senu) d XIV. ( cosu) d XV. ( tan u) dv = cosu. dv = senu. = sec 2 dv u. XVI d (ctg u ) = - csc 2 u du XVII d (sec u ) = sec u. tg u du 9
11 XVIII d (csc u ) = - csc u. ctg u du A continuación se presenta una serie de ejercicios resueltos de derivadas, indicando las formulas que se emplean y el procedimiento usado. Recuerda tener a la mano tu formulario e identificar la formula aplicada: EJERCICIOS RESUELTOS. Hallar la derivada de las siguientes funciones: 1. y = x 4 Utilizando d (x n ) = nx n-1 Obtenemos que: d ( x 4 ) = 4 ( x 4-1 ) = 4 x 3 2. y = x 3 Utilizando d (x n ) = nx n-1 Obtenemos que: d ( x 3 ) = 3 ( x 3-1 ) = 3 x 2 3. y = 3x 6 Utilizando d (x n ) = nx n-1 Obtenemos que: d ( x 6 ) = 6(3) ( x 6-1 ) = 18 x 5 10
12 Cuando se tienen ejemplos de funciones en las que se tienen exponentes negativos, se aplica de manera semejante los procedimientos descritos como se observa a continuación: 4. y = x -3 Utilizando d (x n ) = nx n-1 Obtenemos que: d ( -3x -3-1 ) = -3 ( x -4 ) = -3x y = 4x -2 Utilizando d (x n ) = nx n-1 Obtenemos que: d ( (-2)(4) x -2-1 ) = -8 ( x -3 ) = -8x - 3 Es importante mencionar que en el caso de resultados que se obtengan con exponentes negativos, hay que transformarlos a exponentes positivos, por ello primero debes tener en cuenta el conocimiento de este tema y se te sugiere practiques con los ejercicios propuestos en la presentación electrónica de conceptos básicos Cuando se tienen casos en existen términos radicales, entonces primero se transforman los radicales a exponentes fraccionarios y se procede posteriormente a determinar la derivada como se ve en los siguientes ejemplos. Calcula la derivada de la función:!! =! Primero convertimos la expresión radical a y= x 1/6 11
13 luego Utilizando d (x n ) = nx n-1 Obtenemos que: d (x 1/6 ) = 1/6x 1/6-1 = 1/6X -5/6 = 1 6X 5/6 Pasemos a hora a la aplicación de otra formula: 6. y = 2x Utilizando d (cx ) = c Obtenemos que: d ( 2x) = 2 7. y = -1/2 x Utilizando d (cx ) = c Obtenemos que: d ( -1/2x) = -1/2 SI SE TIENEN CASOS EN DONDE HAY VARIOS TERMINOS EN LA FUNCION A DERIVAR, ENTONCES LA FORMULA QUE SE APLICA, ES COMO SE MUESTRA A CONTINUACION: y = 6 x 2 + 3x 1 Utilizando d (u+v-w) = du + dv dw Obtenemos que: = d ( 6x 2 ) + d ( 3x ) d ( 1 ) =6( 2x 2-1 ) + 3( 1 ) 0 = 12x
14 PUEDE VERSE QUE EL TERCER TERMINO DE LA EXPRESION, ES UN VALOR QUE NO TIENE VARIABLE, ES DECIR ES UN TERMINO CONOCIDO COMO CONSTANTE, POR ELLO COMO LA FORMULA INDICA, LA DERIVADA DE UNA CONSTANTE ES IGUAL A CERO, POR ELLO SE ELIMNA. LO MISMO SUCEDE EN EL SIGUIENTE CASO DONDE EL CUARTO TERMINO NO TIENE VARIABLE Y POR CONSECUENCIA SU DERIVADA ES CERO. y = 6x 3 5x 2 + x + 9 Utilizando d (u+v-w) = du + dv dw Obtenemos que: = d ( 6x 3 ) - d ( 5x 2 ) + d ( x ) +d ( 9 ) =6 ( 3x 3-1 ) -5 ( 2x 2-1 ) = 18x 2 10x + 1 Ahora procedemos a resolver ejercicios de la formula de la derivada del producto y cociente de 2 funciones, hay que poner especial atención al procedimiento con sus respectivos pasos. Ejemplo 1 y = ( x 3 7) (2x 2 + 3) Utilizando d (uv ) = u dv + v du Obtenemos que: dy =( x 3 7 ) d ( 2x ) + ( 2x ) d ( x 3 7 ) luego procedemos a realizar las operaciones indicadas quedando: 13
15 ( x 3 7 ) ( 4x +0 ) + ( 2x ) ( 3x 2-0 ) = 4x 4-28x + 6x 4 + 9x 2 = 10x 4 + 9x 2-28x que es la derivada Ejemplo 2 Calcula la derivada de: Y= (x 2 )( 3x 4 7x) Utilizando d (uv ) = u dv + v du Obtenemos que: d (uv)= ( x 2 ) d ( 3x 4 7x ) + ( 3x 4 7x ) d ( x 2 ) = ( x 2 ) ( 12x 3-7 ) + ( 3x 4 7x ) ( 2x ) = 12x 5 7x 2 + 6x 5 14x 2 = 18x 5 21x 2 Ejemplo 3 y = ( x 3 5x +9) (2x + 1) Utilizando d (uv ) = u dv + v du Obtenemos que: d (uv ) = ( x 3 5x +9 ) d ( 2x + 1 ) + ( 2x + 1 ) d ( x 3 5x +9 ) = ( x 3 5x + 9 ) ( ) + ( 2x + 1 ) ( 3x ) = 2x 3 10x x 3 + 3x 2 10x - 5 = 8x 3 + 3x 2 20x
16 Ahora se procede a la aplicación de la formula 8 de la derivada de un cociente de 2 funciones: y = 8 x +3x 2 x 9x Utilizando d u = v du u dv Obtenemos que: v v 2 ( x 9x ) d ( 8 x +3x 2 ) - ( 8 x + 3x 2 ) d ( x 9x ) (x 9x) 2 = ( x 9x ) ( x ) - ( 8 x + 3x 2 ) ( 1-9 ) (x 9x) 2 = -x + 9x + 6x 2-54x x 3x x + 27x 2 (x 9x) 2 = -24 x = -24 x = 64 24x 2 (x 9x) 2 x 2 18x x 2 64x 2 y = 1 - x 3 x Utilizando d u = v du u dv Obtenemos que: v v 2 15
17 dy= ( x ) d ( 1 - x 3 ) - ( 1 - x 3 ) d ( x ) dv dv ( v ) 2 =( x ) ( 0 3x 2 ) - ( 1 - x 3 ) ( 2x + 0 ) ( v ) 2 = -3x 4 12x 2 2x + 2x 4 ( x ) 2 = - x 4 +12x 2-2x (x 2 + 4) 2 y = 10 x Utilizando d u = v du u dv Obtenemos que: v v 2 dy= (x 2 + 1) d (10) - (10) d (x 2 + 1) (x 2 + 1) 2 =( x 2 + 1) ( 0 ) - (10) (2x + 0 ) = 0 20x (x 2 + 1) 2 (x 2 + 1) 2 = - 20 x (x 2 + 1) 2 VI: Procedemos ahora a mostrar la aplicación de la formula numero Ejemplo: calcula la derivada de la función: 16
18 y = (x 2 + 4x ) 3 Utilizando d (v n ) = nv n-1 dv Obtenemos que: dy= 3 ( x 2 +4x) 3-1 d ( x 2 +4x) 2 = 3 ( x 2 +4x) 2 ( 2x +4 ) = (6x +12) ( x 2 +4x) 2 Ejemplo: y = (8x -7) -5 Utilizando d (v n ) = nv n-1 dv Obtenemos que: dy= -5 ( 8x 7 ) -5-1 d ( 8x 7 ) -6 = -5 ( 8x 7 ) -6 ( 8 ) que al realizar las operaciones y pasamos a exponente positivo queda: = -40 ( 8x 7 ) 6 = = - 40 ( 8x 7 ) 6 Observa ahora que en el siguiente ejemplo la variable independiente es t, es decir la derivada se calcula respecto a t, y se trabaja igual, observa el procedimiento, nota cual es la notación de la derivada: Ejemplo: calcula la derivada de: y = (4t 5 3t 3 + 2t ) -2 Utilizando d (v n ) = nv n-1 dv Obtenemos que: 17
19 dy= -2 ( 4t 5 3t 3 + 2t ) -2-1 d ( 4t 5 3t 3 + 2t ) dt = -2 ( 4t 5 3t 3 + 2t ) -3 ( 20t 4 9t ) = (-40t t 2 4)( 4t 5 3t 3 + 2t ) -3 que de igual manera una vez realizadas las operaciones y pasando el exponente negativo a positivo resulta: = -40t t 2-4 (4t 5 3t 3 + 2t ) 3 y = (4 9x) 1/3 Utilizando d (v n ) = nv n-1 dv Obtenemos que: dy= 1 (4 9x ) 1/3 1 d ( 4-9x ) = 1 (4 9x) 2/3 ( -9 ) 3 3 = -9 ( 4 9x ) 2/3 = -3 3 (4 9x) 2/3 EJERCICIOS de derivadas y graficas: 18
20 Aunque es importante aprender a resolver derivadas, también se requiere para tener una comprensión eficiente del tema, el poder comprender el significado y la representación geométrica ya que ello será de gran utilidad en los siguientes temas de aplicación de la derivada, por ello en los siguientes casos, se explica el resultado de la derivada de una función y su representación grafica. Hallar la derivada de cada una de las siguientes funciones y representa su grafica. a) y = 3x 2 4x + 8 su derivada es: dy = 6x -4 ahora sus graficas respectivas se representan en la siguiente tabla: Función: Primitiva: Y= 3x 2 4x + 8 grafica Derivada: dy = 6x -4 19
21 b) y = 2x + 1 su derivada es: dy = 6x -4 Función: Primitiva: Y= 2x+1 grafica Derivada: dy = 2 ahora es momento que practiques de manera integral tus conocimientos de graficacion de funciones, así como lo aprendido de calculo de derivadas en los siguientes ejemplos. Derivadas logarítmicas y exponenciales. Ejercicios resueltos. 20
22 Observación: habrá que tener especial atención en los ejemplos 2,4, 6 y 7 donde se han empleado las propiedades de los logaritmos. HAY QUE RECORDAR QUE LA FORMA DE EXPRESAR UN LOGARITMO ES EN EL CASO DE: Logaritmo natural: Ln, por ejemplo: algunas funciones como: y= Ln 3x, y= Ln x y= Ln (2x-1) Para el caso de logaritmos de base 10 u otra se entenderá que se usa un subíndice, sin embargo de no escribir el subíndice, se dará por hecho que se trata de un logaritmo de base 10 como por ejemplo: y= Log (x+2 y= Log (1/2x) Una vez explicado y aclarado estos conceptos procedemos a resolver algunos ejemplos de la aplicación de formulas para la derivada de funciones logarítmicas y exponenciales, hay que tener en cuenta lo que se había dicho anteriormente de tener el formulario de derivadas a la mano para que se facilite la observación de la formula. ejemplo: Hallarla derivada de las siguientes funciones: 1. y = Ln (3x + 4) Utilizando d ( ln v ) = 1 dv Obtenemos que: v dy = 1 d ( 3x + 4 ) = 1 ( 3 ) = 3 (3x + 4) (3x + 4) 3x y = Ln x 3 que escribimos como: y = 3 ln x Utilizando d ( ln v ) = 1 dv y la derivada del producto, Obtenemos que: v 21
23 dy = 3d ( Ln x ) = (3) 1 d( x) = = 3 (1) = 3 x x x 3. y = Ln (2x 3 3x 2 + 4) Utilizando d ( ln v ) = 1 dv Obtenemos que: v dy = 1 d ( 2x 3 3x ) ( 2x 3 3x ) = 1 ( 6x 2 6x + 0 ) = 6x 2 6x ( 2x 3 3x ) ( 2x 3 3x ) 4. y = log 2 que escribimos como y = log 2 log x x Utilizando d ( log v ) = log e dv Obtenemos que: v dy = d (log 2) - d(log (x)) = log e d(2) log e d(x) = 0 log e (1) = d x 2 x x - log e x 5. y = log (4x 3) Utilizando d ( log v ) = log e dv Obtenemos que: v dy = log e d (4x 3) = 4 log e 4x 3 4x 3 22
24 = 4 log e 4x 3 6. y = Ln (25 4x) 1/2 = 1 Ln (25-4x) 2 Utilizando d ( ln v ) = l dv y la derivada de un producto, Obtenemos que: v dy = 1 d(ln (25-4x) = 1 1 d( 25 4x) = 1 (-4) = x 2(25-4x) 2 (25-4x) = x 7. log (3x x 2 ) 1/2 = 1 log( 3x x 2 ) 2 Utilizando d ( log v ) = log e dv y la derivada de un producto, Obtenemos que: v dy = 1 d ( log (3x-x 2 ) =1 log e d(3x x 2 ) = log e (3-2x) 2 2 3x x 2 2(3x-x 2 ) = (3-2x) log e 6x- 2x 2 Funciones exponenciales: 8. y = e 3x Utilizando d ( e v ) = e v dv Obtenemos que: dy = e 3x d (3x) = e 3x (3 ) = 3 e 3x 23
25 9. y = 2 e x Utilizando d u = v du u dv Obtenemos que: v v 2 dy = e x d ( 2 ) - 2 d ( e x ) = e x ( 0 ) 2 ( e x ( 1 ) ) = -2e x = -2 e 2x e x ( e x ) y = e 5x Utilizando d ( e v ) = e v dv Obtenemos que: dy = e 5x d (5x ) = e 5x ( 5) = 5e 5x 11. y = x 2 e -x en este caso se aplica la derivada de un producto (u* v) Utilizando d (uv ) = u dv + v du Obtenemos que: dy = x 2 d ( e -x ) + e -x d ( x 2 ) = x 2 ( e -x d ( -x ) ) + e -x ( 2x ) = x 2 ( -e -x ) + e -x ( 2x ) 24
26 = -x 2 e -x + 2x e -x = e -x (- x 2 + 2x ) Derivadas Trigonométricas Ejercicios resueltos. Hallar la derivada de las siguientes funciones: 1. y = Sen 4x Utilizando d (sen u ) = cos u du Obtenemos que: dy= cos 4x d ( 4x ) = cos 4x ( 4 ) = 4 cos 4x la grafica de la función se muestra a continuación. La grafica de la derivada es la siguiente: 25
27 2. S = tang 2t Utilizando d (tang u ) = sec 2 u du Obtenemos que: ds= sec 2 2t d ( 2t ) = sec 2 2t ( 2 ) = dt dt 2 sec 2 2t 3. y = sec 3x Utilizando d (sec u ) = sec u. tg u du Obtenemos que: dy= (sec 3x) ( tg 3x) d ( 3x ) = sec 3x tg 3x ( 3 ) = 3 sec 3x tg 3x 4. y = 3 cos 2x aplicar la derivada de un producto : (u* v) 26
28 Utilizando d (uv ) = u dv + v du Obtenemos que: (0) dy= 3 d(cos 2x) + cos 2x d (3) = 3( sen 2x) d ( 2x ) + cos 2x = -3 sen 2x ( 2 ) = -6 sen 2x DERIVADAS SUCESIVAS DE UNA FUNCIÓN. Derivadas de orden superior: Una función f(x), tiene una derivada f (x) conocida como primera derivada, la cual como ya se ha mencionado se escribe como:!" siendo a su vez esta nueva expresión una nueva!" función a la cual también se le puede calcular su derivada, llamándose entonces segunda derivada, y escribiéndose como f (x), o también!!! EN LA SIGUIENTE TABLA SE MUESTRAN funciones donde se presenta la primera derivada y su segunda derivada:!!! Función primitiva Primera derivada Segunda derivada!" Y= x 3!" =!!! 3!!!!! = 6! Y= x 2!"!" = 2!!!!!!! = 2 Y=2 x - 3!"!" = 6!!!!!!!!! = 24!!! Y= 3x 2 4x + 5!!!!!! = 6 27
29 !"!" = 6! 4 Y= 4x 2!"!" = 8!!!!!!! = 8 Y= e 2x!"!" = 2!!!!!!!!! = 4!!! Y= e - 3x!"!" = 3!!!!!!!!!! = 9!!!! Entonces se puede definir que dada una función f(x), se obtiene a partir de un primer proceso una nueva función que es la derivada, denotándose como f (x). A su vez se denomina segunda derivada f (x) de la función f(x) a aquella que resulta de derivar por segunda vez ésta primera. A continuación se muestran algunos ejemplos donde se observan los procedimientos aplicados. Ejemplo 1. Obtener la derivada de la función y = 5x 2 +3x +1 la primera derivada es: dy = 10x + 3 Ahora la segunda derivada es: d2 y = d (10x + 3 ) = 10 2 d x Por lo que la función con sus respectivas derivadas sucesivas son: 28
30 Función: y = 5x 2 +3x +1 Primera derivada : dy = 10x +3 Segunda derivada: d 2 y = 10 2 Resumiendo entonces una función tiene una ó más derivadas que se denominan derivadas sucesivas o de orden superior. Estas derivadas se conocen como primera, segunda, tercera derivada,... etc y su notación es: Primera derivada: y (x) o bien dy Segunda derivada: y (x) o bien d 2 y 2 tercera derivada: y (x) o bien d 3 y 3 EJERCICIOS RESUELTOS: Hallar las segundas derivadas de las siguientes funciones. A) Y= x 3 + 2x +4 La primera derivada es: dy = d( x 3 +2x +1) = 3x 2 +2 Y la segunda derivada es: d 2 y = d(3x 2 +2) = 6x +0 = 6x 2 29
31 B ) Y= Ln (5x 2 +1) La primera derivada es: dy = d ln ( 5x 2 +1) = 1 d (5x 2 +1) = 1 10x = 10x 5x x x 2 +1 Y la segunda derivada es: d 2 y = d 10x = (5x 2 +1) d(10x) - 10x d(5x 2 +1) = (5x 2 +1)(10) 10X(10X) 2 5x 2 +1 ( 5x 2 +1) 2 ( 5x 2 +1) 2 = 50x x 2 = -50X ( 5x 2 +1) 2 ( 5x 2 +1) 2 c) y = sen 3x primera derivada: dy = cos 3x d (3X) = cos 3x (3) = 3cos 3x segunda derivada: d 2 y = d(3cos 3x) = 3 d(cos 3x) + cos 3x d(3) = 3 (-sen 3x)(3)+cos 3x (0) 2 = -9 sen 3x Referencias. Ayres F. (2010.) Calculo diferencial e integral. Editorial Mc Graw Hill. México D. F. 30
32
El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow.
 INTRODUCCION El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de
INTRODUCCION El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de
MATEMÁTICA - 6 A C y D - Prof. Sandra M. Corti
 TEMA: Derivada La derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente Sea f(x) una función continua
TEMA: Derivada La derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente Sea f(x) una función continua
Cuarto examen parcial Ejercicios resueltos
 Cálculo I Cuarto examen parcial Ejercicios resueltos Hora de inicio: 8:00. Hora de entrega: :00.. Derivar las siguientes funciones usando la definición: (i) f(x) x+. (ii) g(x) x +. (i) f(x) x+ y f(x +
Cálculo I Cuarto examen parcial Ejercicios resueltos Hora de inicio: 8:00. Hora de entrega: :00.. Derivar las siguientes funciones usando la definición: (i) f(x) x+. (ii) g(x) x +. (i) f(x) x+ y f(x +
El proceso de calcular la derivada se denomina derivación. Se dice que ( ) es derivable en c si existe ( ), es decir, lim. existe
 DEFINICIÓN DE LA DERIVADA DE UNA FUNCIÓN La derivada de una función () respecto de (x) es la función () (se lee f prima de (x) y está dada por: ()=lim (+h) () h El proceso de calcular la derivada se denomina
DEFINICIÓN DE LA DERIVADA DE UNA FUNCIÓN La derivada de una función () respecto de (x) es la función () (se lee f prima de (x) y está dada por: ()=lim (+h) () h El proceso de calcular la derivada se denomina
Universidad Nacional Experimental Sur del Lago Jesús María Semprum Programa de Contaduría Pública Prof. Pedro Quintela Matemática II
 Universidad Nacional Experimental Sur del Lago Jesús María Semprum Programa de Contaduría Pública Prof. Pedro Quintela Matemática II Ejercicios Resueltos Ejercicio : Encontrar la pendiente de la recta
Universidad Nacional Experimental Sur del Lago Jesús María Semprum Programa de Contaduría Pública Prof. Pedro Quintela Matemática II Ejercicios Resueltos Ejercicio : Encontrar la pendiente de la recta
Tema 6. Cálculo diferencial de funciones de una variable
 Tema 6 Cálculo diferencial de funciones de una variable Índice Esquema 3 Ideas clave 4 6.1. Introducción y objetivos 4 6.2. Conceptos previos 5 6.3. Función derivada 8 6.4. Cálculo de derivadas 12 6.5.
Tema 6 Cálculo diferencial de funciones de una variable Índice Esquema 3 Ideas clave 4 6.1. Introducción y objetivos 4 6.2. Conceptos previos 5 6.3. Función derivada 8 6.4. Cálculo de derivadas 12 6.5.
(Apuntes en revisión para orientar el aprendizaje) Capítulo III La derivada y algunas aplicaciones
 (Apuntes en revisión para orientar el aprendizaje) Capítulo III La derivada y algunas aplicaciones INTRODUCCIÓN Uno de los problemas fundamentales del Cálculo Diferencial se refiere a la determinación
(Apuntes en revisión para orientar el aprendizaje) Capítulo III La derivada y algunas aplicaciones INTRODUCCIÓN Uno de los problemas fundamentales del Cálculo Diferencial se refiere a la determinación
* e e Propiedades de la potenciación.
 ECUACIONES DIFERENCIALES 1 REPASO DE ALGUNOS CONCEPTOS PREVIOS AL ESTUDIO DE LAS ECUACIONES DIFERENCIALES 1. Cuando hablamos de una función en una variable escribíamos esta relación como y = f(x), esta
ECUACIONES DIFERENCIALES 1 REPASO DE ALGUNOS CONCEPTOS PREVIOS AL ESTUDIO DE LAS ECUACIONES DIFERENCIALES 1. Cuando hablamos de una función en una variable escribíamos esta relación como y = f(x), esta
Ejercicios de Funciones: derivadas y derivabilidad
 Matemáticas 2ºBach CNyT. Ejercicios Funciones: Derivadas, derivabilidad. Pág 1/15 Ejercicios de Funciones: derivadas y derivabilidad 1. Calcular las derivadas en los puntos que se indica: 1., en x = 5.
Matemáticas 2ºBach CNyT. Ejercicios Funciones: Derivadas, derivabilidad. Pág 1/15 Ejercicios de Funciones: derivadas y derivabilidad 1. Calcular las derivadas en los puntos que se indica: 1., en x = 5.
LA DERIVADA DE UNA FUNCIÓN
 LA DERIVADA DE UNA FUNCIÓN f(x + ) f(x) www.cedicaped.com LA DERIVADA DE UNA FUNCION 1. VARIACIONES E INCREMENTOS DE LAS VARIACIONES DEUNA FUNCION Sea f(x) una función, se trata de estudiar las variaciones
LA DERIVADA DE UNA FUNCIÓN f(x + ) f(x) www.cedicaped.com LA DERIVADA DE UNA FUNCION 1. VARIACIONES E INCREMENTOS DE LAS VARIACIONES DEUNA FUNCION Sea f(x) una función, se trata de estudiar las variaciones
Derivada. 1. Pendiente de la recta tangente a una curva
 Nivelación de Matemática MTHA UNLP Derivada Pendiente de la recta tangente a una curva Definiciones básicas Dada una curva que es la gráfica de una función y = f() y sea P un punto sobre la curva La pendiente
Nivelación de Matemática MTHA UNLP Derivada Pendiente de la recta tangente a una curva Definiciones básicas Dada una curva que es la gráfica de una función y = f() y sea P un punto sobre la curva La pendiente
El proceso de calcular la derivada se denomina derivación. Se dice que es derivable en c si existe, es decir, existe
 DEFINICIÓN DE LA DERIVADA DE UNA FUNCIÓN La derivada de una función respecto de (x) es la función (se lee f prima de (x) y está dada por: lim El proceso de calcular la derivada se denomina derivación.
DEFINICIÓN DE LA DERIVADA DE UNA FUNCIÓN La derivada de una función respecto de (x) es la función (se lee f prima de (x) y está dada por: lim El proceso de calcular la derivada se denomina derivación.
UNIDAD 3. La derivada. Objetivos. Al terminar la unidad, el alumno:
 UNIDAD La derivada Objetivos Al terminar la unidad, el alumno: Calculará la derivada de funciones utilizando el álgebra de derivadas. Determinará la relación entre derivación y continuidad. Aplicará la
UNIDAD La derivada Objetivos Al terminar la unidad, el alumno: Calculará la derivada de funciones utilizando el álgebra de derivadas. Determinará la relación entre derivación y continuidad. Aplicará la
= x x x. v p Este cociente indica cómo desciende las ventas al aumentar el precio en una unidad.
 TASA DE VARIACIÓN MEDIA La tasa de variación media de una función nos da una idea de la rapidez con que crece o decrece en un intervalo. Sea y f() una función que relaciona la variable dependiente (y)
TASA DE VARIACIÓN MEDIA La tasa de variación media de una función nos da una idea de la rapidez con que crece o decrece en un intervalo. Sea y f() una función que relaciona la variable dependiente (y)
Cálculo diferencial. Se dice que una función es diferenciable o derivable cuando es posible hallar su derivada.
 Cálculo diferencial I n t r o d u c c i ó n Cuando surgen cuestiones concernientes a la razón entre dos cantidades variables, entramos en los dominios del Cálculo Diferencial. Son por tanto objeto de estudio
Cálculo diferencial I n t r o d u c c i ó n Cuando surgen cuestiones concernientes a la razón entre dos cantidades variables, entramos en los dominios del Cálculo Diferencial. Son por tanto objeto de estudio
TEMA 1: INTRODUCCIÓN AL CÁLCULO
 TEMA 1: INTRODUCCIÓN AL CÁLCULO FMIBII Biomedical engineering degree Cristina Sánchez López de Pablo Universidad San Pablo CEU Madrid Índice de contenidos TEMA 1: INTRODUCCIÓN AL CÁLCULO 1. Gráficas La
TEMA 1: INTRODUCCIÓN AL CÁLCULO FMIBII Biomedical engineering degree Cristina Sánchez López de Pablo Universidad San Pablo CEU Madrid Índice de contenidos TEMA 1: INTRODUCCIÓN AL CÁLCULO 1. Gráficas La
Cálculo I. Índice Motivación al Concepto de Límite. Julio C. Carrillo E. * 1. Introducción Motivación del concepto de límite 1
 2.0. Motivación al Concepto de Límite Julio C. Carrillo E. * Índice 1. Introducción 1 2. Motivación del concepto de límite 1 3. Conclusiones 15 * Profesor Escuela de Matemáticas, UIS. 1. Introducción La
2.0. Motivación al Concepto de Límite Julio C. Carrillo E. * Índice 1. Introducción 1 2. Motivación del concepto de límite 1 3. Conclusiones 15 * Profesor Escuela de Matemáticas, UIS. 1. Introducción La
RELACIONES Y FUNCIONES
 RELACIONES Y FUNCIONES Variables Independiente: Aquella que puede tomar cualquier valor. Dependiente: Depende del valor que tome la variable independiente. Pares ordenados Se representan (a,b) donde: a:
RELACIONES Y FUNCIONES Variables Independiente: Aquella que puede tomar cualquier valor. Dependiente: Depende del valor que tome la variable independiente. Pares ordenados Se representan (a,b) donde: a:
Longitud, áreas y volúmenes. Trigonometría. Circunferencia de radio R Círculo de radio R. 1 Triángulo de base B y altura H A = (BH ) 2
 Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
TEORIA. Indique si es Falso/verdadero
 Universidad Nacional Autónoma de México Facultad de Estudios Superiores Zaragoza Guía para presentar el Examen de Recuperación de Matemáticas I Correspondiente a la carrera de Biología ÁREA: Matemáticas,
Universidad Nacional Autónoma de México Facultad de Estudios Superiores Zaragoza Guía para presentar el Examen de Recuperación de Matemáticas I Correspondiente a la carrera de Biología ÁREA: Matemáticas,
Curso Propedéutico de Cálculo Sesión 3: Derivadas
 Curso Propedéutico de Cálculo Sesión 3: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 5 6 7 Esquema 1 2 3 4 5 6 7 Introducción La derivada
Curso Propedéutico de Cálculo Sesión 3: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 5 6 7 Esquema 1 2 3 4 5 6 7 Introducción La derivada
Límite de funciones. Por otra parte se dice que una función es discontínua si para algún (os) valor (es) de x no existe valor de y.
 Límite de funciones El concepto de límite se explica y define desde diferentes perspectivas en los libros de cálculo. Se habla por ejemplo del límite de una sucesión (como ya se explicó), o bien del límite
Límite de funciones El concepto de límite se explica y define desde diferentes perspectivas en los libros de cálculo. Se habla por ejemplo del límite de una sucesión (como ya se explicó), o bien del límite
DERIVADA DE UNA FUNCIÓN
 DERIVADA DE UNA FUNCIÓN 3URI/XLV~xH] Se estudia aquí uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. Además de la definición y su interpretación, se allarán las
DERIVADA DE UNA FUNCIÓN 3URI/XLV~xH] Se estudia aquí uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. Además de la definición y su interpretación, se allarán las
Cociente incremental. Mide la variación media de f(x) en (x 0, x 0 + x)
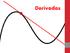 Derivadas Cociente incremental Sea y= f(x) continua en x=x 0 x: incremento de la variable independiente y: incremento de la variable dependiente Se llama cociente incremental al cociente y f ( x x f xo
Derivadas Cociente incremental Sea y= f(x) continua en x=x 0 x: incremento de la variable independiente y: incremento de la variable dependiente Se llama cociente incremental al cociente y f ( x x f xo
DERIVADAS. TÉCNICAS DE DERIVACIÓN
 9 DERIVADAS. TÉCNICAS DE DERIVACIÓN REFLEXIONA Y RESUELVE Tangentes a una curva y = f (x) 5 3 5 3 9 14 Halla, mirando la gráfica y las rectas trazadas, f'(3), f'(9) y f'(14). Di otros tres puntos en los
9 DERIVADAS. TÉCNICAS DE DERIVACIÓN REFLEXIONA Y RESUELVE Tangentes a una curva y = f (x) 5 3 5 3 9 14 Halla, mirando la gráfica y las rectas trazadas, f'(3), f'(9) y f'(14). Di otros tres puntos en los
DERIV. DE UNA FUNC. EN UN PUNTO
 DERIVADA DE UNA FUNCIÓN Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. En este tema, además de definir tal concepto, se mostrará su significado
DERIVADA DE UNA FUNCIÓN Se abre aquí el estudio de uno de los conceptos fundamentales del cálculo diferencial: la derivada de una función. En este tema, además de definir tal concepto, se mostrará su significado
CONCEPTOS QUE DEBES DOMINAR
 INTERVALOS CONCEPTOS QUE DEBES DOMINAR Un intervalo es un conjunto infinito de números reales comprendidos entre dos extremos, que pueden estar incluidos en él o no. 1. Intervalo abierto (a, b): Comprende
INTERVALOS CONCEPTOS QUE DEBES DOMINAR Un intervalo es un conjunto infinito de números reales comprendidos entre dos extremos, que pueden estar incluidos en él o no. 1. Intervalo abierto (a, b): Comprende
Propedéutico de Matemáticas
 Propedéutico de Matemáticas TEMARIO DEL MODULO I, ARITMÉTICA Y ALGEBRA CAPÍTULO 1: CONCEPTOS ELEMENTALES DE ARITMÉTICA Número primo absoluto o simple. Número compuesto. Múltiplo. Submúltiplo, factor o
Propedéutico de Matemáticas TEMARIO DEL MODULO I, ARITMÉTICA Y ALGEBRA CAPÍTULO 1: CONCEPTOS ELEMENTALES DE ARITMÉTICA Número primo absoluto o simple. Número compuesto. Múltiplo. Submúltiplo, factor o
Tema 6: Derivada de una función
 Tema 6: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 6: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 7: Derivada de una función
 Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
UNIVERSIDAD NACIONAL DE ITAPÚA FACULTAD DE HUMANIDADES, CIENCIAS SOCIALES Y CULTURA GUARANÍ Encarnación Paraguay
 PROGRAMA DE ESTUDIOS I - IDENTIFICACIÓN CARRERA: Licenciatura en Ciencias de la Educación con mención en Matemática ASIGNATURA: Matemática VI (Calculo Infinitesimal) CURSO: Tercero CARGA HORARIA: Semanales:
PROGRAMA DE ESTUDIOS I - IDENTIFICACIÓN CARRERA: Licenciatura en Ciencias de la Educación con mención en Matemática ASIGNATURA: Matemática VI (Calculo Infinitesimal) CURSO: Tercero CARGA HORARIA: Semanales:
Cálculo Integral Agosto 2015
 Cálculo Integral Agosto 5 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) (x 5 8x + 3x 3 ) ) (y 3 6y 6 5 + 8) dy 3) (y 3 + 5)(y + 3) dy 4) (t 3 + 3t + ) (t 3 + 5) dt 5) (3y
Cálculo Integral Agosto 5 Laboratorio # Antiderivadas I.- Halle las siguientes integrales indefinidas. ) (x 5 8x + 3x 3 ) ) (y 3 6y 6 5 + 8) dy 3) (y 3 + 5)(y + 3) dy 4) (t 3 + 3t + ) (t 3 + 5) dt 5) (3y
DERIVADAS 1.- TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN. Antes de dar la definición veamos unos ejemplos:
 DERIVADAS 1.- TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN. Antes de dar la definición veamos unos ejemplos: Definición: 2.- TASA DE VARIACIÓN INSTANTÁNEA. DEFINICIÓN DE DERIVADA DE UNA FUNCIÓN EN UN PUNTO.
DERIVADAS 1.- TASA DE VARIACIÓN MEDIA DE UNA FUNCIÓN. Antes de dar la definición veamos unos ejemplos: Definición: 2.- TASA DE VARIACIÓN INSTANTÁNEA. DEFINICIÓN DE DERIVADA DE UNA FUNCIÓN EN UN PUNTO.
0ºK= -273ºC (inicio de la escala absoluta de temperatura)
 LÍMITE: muchos fenómenos de la naturaleza tienen un punto límite, que no es posible traspasar con los conocimientos actuales. uno de estos puntos es el cero absoluto de la temperatura. 0ºK= -273ºC (inicio
LÍMITE: muchos fenómenos de la naturaleza tienen un punto límite, que no es posible traspasar con los conocimientos actuales. uno de estos puntos es el cero absoluto de la temperatura. 0ºK= -273ºC (inicio
INTRO. LA INTEGRAL INDEFINIDA
 INTRO. LA INTEGRAL INDEFINIDA Se inicia en este tema el estudio de la integral, concepto fundamental de lo que se conoce como cálculo infinitesimal, que alcanzó su auge y desarrollo durante el siglo XVII.
INTRO. LA INTEGRAL INDEFINIDA Se inicia en este tema el estudio de la integral, concepto fundamental de lo que se conoce como cálculo infinitesimal, que alcanzó su auge y desarrollo durante el siglo XVII.
LA DERIVADA DEFINICIÓN
 LA DERIVADA DEFINICIÓN La definición más común hace referencia a que la derivada es el límite del cociente entre el incremento de una función y el de la variable cuando este último tiende a cero. Definición
LA DERIVADA DEFINICIÓN La definición más común hace referencia a que la derivada es el límite del cociente entre el incremento de una función y el de la variable cuando este último tiende a cero. Definición
CÁLCULO DE DERIVADAS
 TEMA 4 CÁLCULO DE DERIVADAS Contenidos Criterios de Evaluación 1. Función derivada.. Derivadas sucesivas. 3. Derivadas elementales. 4. Álgebra de derivadas. 5. La Regla de la Cadena. 6. Continuidad y derivabilidad.
TEMA 4 CÁLCULO DE DERIVADAS Contenidos Criterios de Evaluación 1. Función derivada.. Derivadas sucesivas. 3. Derivadas elementales. 4. Álgebra de derivadas. 5. La Regla de la Cadena. 6. Continuidad y derivabilidad.
1 El número x = 0, es irracional. Encontrar una sucesión de números racionales x n cuyo límite sea x.
 El número x =,... es irracional. Encontrar una sucesión de números racionales x n cuyo límite sea x. Si x =, x =, x 3 =, x 4 =,... entonces cada x n es racional y (x x n ) n tiende a cero, es decir, lim
El número x =,... es irracional. Encontrar una sucesión de números racionales x n cuyo límite sea x. Si x =, x =, x 3 =, x 4 =,... entonces cada x n es racional y (x x n ) n tiende a cero, es decir, lim
T2. Teorema fundamental del cálculo Parte II. Regla de Barrow. Enunciar y demostrar.
 EXAMEN TEÓRICO FINAL I T1. Dado y = f(x). Definir función continua en un punto, en un intervalo abierto y en un intervalo cerrado. T2. Teorema fundamental del cálculo Parte II. Regla de Barrow. Enunciar
EXAMEN TEÓRICO FINAL I T1. Dado y = f(x). Definir función continua en un punto, en un intervalo abierto y en un intervalo cerrado. T2. Teorema fundamental del cálculo Parte II. Regla de Barrow. Enunciar
Unidad IV. 4.1 Conceptos de incremento y de razón de cambio. La derivada de una función.
 Unidad IV Derivadas 4.1 Conceptos de incremento y de razón de cambio. La derivada de una función. Derivada de una función en un punto. Dada la función f(x) continúa en el intervalo abierto I, se define
Unidad IV Derivadas 4.1 Conceptos de incremento y de razón de cambio. La derivada de una función. Derivada de una función en un punto. Dada la función f(x) continúa en el intervalo abierto I, se define
UNIDAD DE APRENDIZAJE II
 UNIDAD DE APRENDIZAJE II Saberes procedimentales 1. Interpreta adecuadamente la relación de dependencia que se establece entre dos variables, así como la razón de cambio entre sus valores. 2. Define en
UNIDAD DE APRENDIZAJE II Saberes procedimentales 1. Interpreta adecuadamente la relación de dependencia que se establece entre dos variables, así como la razón de cambio entre sus valores. 2. Define en
ÍNDICE CALCULO DIFERENCIAL CAPITULO I. Resumen de fórmulas
 ÍNDICE CALCULO DIFERENCIAL CAPITULO I Resumen de fórmulas Fórmulas de Algebra y de Geometría elementales, 3. Fórmulas de Trigonometría plana, 4. Fórmulas de Geometría analítica plana, 6. Fórmulas de Geometría
ÍNDICE CALCULO DIFERENCIAL CAPITULO I Resumen de fórmulas Fórmulas de Algebra y de Geometría elementales, 3. Fórmulas de Trigonometría plana, 4. Fórmulas de Geometría analítica plana, 6. Fórmulas de Geometría
Derivadas En este tema, además de definir tal concepto, se mostrará su significado y se hallarán las derivadas de las funciones más usuales.
 Derivadas En este tema, además de deinir tal concepto, se mostrará su signiicado y se hallarán las derivadas de las unciones más usuales. Es de capital importancia dominar la derivación para después poder
Derivadas En este tema, además de deinir tal concepto, se mostrará su signiicado y se hallarán las derivadas de las unciones más usuales. Es de capital importancia dominar la derivación para después poder
Tema 7: Derivada de una función
 Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
Tema 7: Derivada de una función Antes de dar la definición de derivada de una función en un punto, vamos a introducir dos ejemplos o motivaciones iniciales que nos van a dar la medida de la importancia
INTERPRETACION GEOMETRICA DE LA DERIVADA
 INTRODUCCIÓN A LAS DERIVADAS CON ESTA EXPRESIÓN SE CALCULA: a) La pendiente ( m ) de la recta secante a la función al cambiar. b) La velocidad o cambio promedio de la función al cambiar. c) El cociente
INTRODUCCIÓN A LAS DERIVADAS CON ESTA EXPRESIÓN SE CALCULA: a) La pendiente ( m ) de la recta secante a la función al cambiar. b) La velocidad o cambio promedio de la función al cambiar. c) El cociente
CÁLCULO DE PRIMITIVAS
 2 CÁLCULO DE PRIMITIVAS REFLEXIONA Y RESUELVE Concepto de primitiva NÚMEROS Y POTENCIAS SENCILLAS a) b) 2 c) 2 a) 2x b) x c) 3x 3 a) 7x b) c) x 4 a) 3x2 b) x2 c) 2x2 5 a) 6x 5 b) x5 c) 3x5 x 3 2 2 POTENCIAS
2 CÁLCULO DE PRIMITIVAS REFLEXIONA Y RESUELVE Concepto de primitiva NÚMEROS Y POTENCIAS SENCILLAS a) b) 2 c) 2 a) 2x b) x c) 3x 3 a) 7x b) c) x 4 a) 3x2 b) x2 c) 2x2 5 a) 6x 5 b) x5 c) 3x5 x 3 2 2 POTENCIAS
3.1 INTERPRETACION GEOMETRICA 3.2 DEFINICIÓN
 Cap. La derivada. INTERPRETACION GEOMETRICA. DEFINICIÓN. NOTACIÓN. FORMA ALTERNATIVA.5 DIFERENCIABILIDAD.6 DERIVACIÓN.6. FORMULAS DE DERIVACIÓN..6. REGLAS DE DERIVACIÓN.6. DERIVADAS DE ORDEN SUPERIOR.6.
Cap. La derivada. INTERPRETACION GEOMETRICA. DEFINICIÓN. NOTACIÓN. FORMA ALTERNATIVA.5 DIFERENCIABILIDAD.6 DERIVACIÓN.6. FORMULAS DE DERIVACIÓN..6. REGLAS DE DERIVACIÓN.6. DERIVADAS DE ORDEN SUPERIOR.6.
Matemáticas I. Carrera: AGM Participantes Representante de las academias de Ingeniería Agronomía de los Institutos Tecnológicos.
 1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Matemáticas I Ingeniería en Agronomía AGM - 0626 3 2 8 2. HISTORIA DEL PROGRAMA
1.- DATOS DE LA ASIGNATURA Nombre de la asignatura: Carrera: Clave de la asignatura: Horas teoría-horas práctica-créditos Matemáticas I Ingeniería en Agronomía AGM - 0626 3 2 8 2. HISTORIA DEL PROGRAMA
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Capítulo 4: Derivada de una función
 Capítulo 4: Derivada de una función Geovany Sanabria Contenido Razones de cambio 57 Definición de derivada 59 3 Cálculo de derivadas 64 3. Propiedadesdederivadas... 64 3.. Ejercicios... 68 3. Derivadasdefuncionestrigonométricas...
Capítulo 4: Derivada de una función Geovany Sanabria Contenido Razones de cambio 57 Definición de derivada 59 3 Cálculo de derivadas 64 3. Propiedadesdederivadas... 64 3.. Ejercicios... 68 3. Derivadasdefuncionestrigonométricas...
Esta es la gráfica de la función lineal y = 3x + 2 Vemos que m = 3 y b = 2 (de la forma y = mx + b)
 FUNCIÓN LINEAL Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
FUNCIÓN LINEAL Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.
Unidad II. 2.1 Concepto de variable, función, dominio, condominio y recorrido de una función.
 Unidad II Funciones 2.1 Concepto de variable, función, dominio, condominio y recorrido de una función. Función En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio)
Unidad II Funciones 2.1 Concepto de variable, función, dominio, condominio y recorrido de una función. Función En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio)
DERIVADAS DERIVADAS. La siguiente tabla muestra el número de nacimientos en cada mes a lo largo de un año en una determinada población:
 DERIVADAS INTRODUCCIÓN Una recta es tangente a una curva en un punto si solo tiene en común con la curva dicho punto. y 5 4 Recta tangente en (,) La pendiente de una recta es la tangente del ángulo que
DERIVADAS INTRODUCCIÓN Una recta es tangente a una curva en un punto si solo tiene en común con la curva dicho punto. y 5 4 Recta tangente en (,) La pendiente de una recta es la tangente del ángulo que
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (1085) GUÍA DE MATEMÁTICAS VI (1600) I. RELACIONES Y FUNCIONES
 INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (085) GUÍA DE MATEMÁTICAS VI (600) I. RELACIONES Y FUNCIONES Funciones y relaciones. Dominio y rango. Determinar si es función o relación
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (085) GUÍA DE MATEMÁTICAS VI (600) I. RELACIONES Y FUNCIONES Funciones y relaciones. Dominio y rango. Determinar si es función o relación
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática ( )
 Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 3 (DERIVADAS) Profesora: Yulimar Matute Febrero 2012 DERIVADAS POR DEFINICIÓN
Universidad de Oriente Núcleo de Bolívar Departamento de Ciencias Área de Matemática Asignatura: Matemática (0081714) UNIDAD N 3 (DERIVADAS) Profesora: Yulimar Matute Febrero 2012 DERIVADAS POR DEFINICIÓN
Bienvenidos al Maravilloso mundo de los Principia. Philosophiae naturalis Principia mathematica DERIVADAS
 UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 00 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-) Fecha de publicación: 0-0-00 Bienvenidos al Maravilloso mundo de los Principia Contenido Tercer
UNIVERSIDAD SIMÓN BOLÍVAR Enero-Marzo 00 DEPARTAMENTO DE MATEMÁTICAS PURAS Y APLICADAS MATEMÁTICA I (MA-) Fecha de publicación: 0-0-00 Bienvenidos al Maravilloso mundo de los Principia Contenido Tercer
CÁLCULO DIFERENCIAL. b) Al darle a x valores suficientemente grandes, los valores de f(x) crecen cada vez más
 1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO: CÁLCULO DIFERENCIAL Una función f(x) tiene por límite L en el número real x = c, si para toda sucesión de valores x n c del dominio que tenga por límite c, la sucesión
1. LÍMITE DE UNA FUNCIÓN EN UN PUNTO: CÁLCULO DIFERENCIAL Una función f(x) tiene por límite L en el número real x = c, si para toda sucesión de valores x n c del dominio que tenga por límite c, la sucesión
4 DERIVADAS - Trabajo Práctico
 4 DERIVADAS - Trabajo Práctico El concepto de derivada fue desarrollado en el siglo XVII simultáneamente por dos matemáticos: Isaac Newton (Inglaterra, 164-177) y Gottfried Leibniz (Alemania, 1646- ),
4 DERIVADAS - Trabajo Práctico El concepto de derivada fue desarrollado en el siglo XVII simultáneamente por dos matemáticos: Isaac Newton (Inglaterra, 164-177) y Gottfried Leibniz (Alemania, 1646- ),
Determine la razón de cambio promedio de la función en cada intervalo.
 Trabajo Práctico N 3 DERIVADA Y DIFERENCIAL Ejercicio 1: Halle la pendiente de la gráfica de las funciones en los puntos dados aplicando la definición de derivada de la función en un punto. Después halle
Trabajo Práctico N 3 DERIVADA Y DIFERENCIAL Ejercicio 1: Halle la pendiente de la gráfica de las funciones en los puntos dados aplicando la definición de derivada de la función en un punto. Después halle
DERIVADAS DERIVADAS. La siguiente tabla muestra el número de nacimientos en cada mes a lo largo de un año en una determinada población:
 DERIVADAS INTRODUCCIÓN Una recta es tangente a una curva en un punto si solo tiene en común con la curva dicho punto. y 5 4 Recta tangente en (,) La pendiente de una recta es la tangente del ángulo que
DERIVADAS INTRODUCCIÓN Una recta es tangente a una curva en un punto si solo tiene en común con la curva dicho punto. y 5 4 Recta tangente en (,) La pendiente de una recta es la tangente del ángulo que
Nueva creación Reestructuración Ajuste
 1) NOMBRE DE CADA CURSO O ACTIVIDAD CURRICULAR A) NOMBRE DEL CURSO CÁLCULO A B) DATOS BÁSICOS DEL CURSO Tipo de propuesta curricular: Nueva creación Reestructuración Ajuste Tipo de materia: Obligatoria
1) NOMBRE DE CADA CURSO O ACTIVIDAD CURRICULAR A) NOMBRE DEL CURSO CÁLCULO A B) DATOS BÁSICOS DEL CURSO Tipo de propuesta curricular: Nueva creación Reestructuración Ajuste Tipo de materia: Obligatoria
MATEMÁTICAS VI. CÁLCULO INTEGRAL UNIDAD I LA INTEGRAL INDEFINIDA
 UNIDAD I LA INTEGRAL INDEFINIDA INTRODUCCIÓN El cálculo diferencial proporciona una regla para obtener la derivada de una función sencilla, con esta regla se obtienen las fórmulas para derivar todo tipo
UNIDAD I LA INTEGRAL INDEFINIDA INTRODUCCIÓN El cálculo diferencial proporciona una regla para obtener la derivada de una función sencilla, con esta regla se obtienen las fórmulas para derivar todo tipo
CONTINUIDAD Y DERIVADA CONCEPTO DE DERIVADA DE UNA FUNCIÓN. REGLAS DE DERIVACIÓN
 Índice Presentación... 3 Concepto de derivada de una función en un punto... 4 La derivada como un límite... 5 Derivada y continuidad. Funciones no derivables... 6 Función derivada. Reglas para derivar...
Índice Presentación... 3 Concepto de derivada de una función en un punto... 4 La derivada como un límite... 5 Derivada y continuidad. Funciones no derivables... 6 Función derivada. Reglas para derivar...
DERIVADAS. Para hallar la pendiente de una curva en algún punto hacemos uso de la recta tangente de una curva en un punto.
 DERIVADAS Tema: La derivada como pendiente de una curva Para hallar la pendiente de una curva en algún punto hacemos uso de la recta tangente de una curva en un punto. La pendiente de la curva en el punto
DERIVADAS Tema: La derivada como pendiente de una curva Para hallar la pendiente de una curva en algún punto hacemos uso de la recta tangente de una curva en un punto. La pendiente de la curva en el punto
Cálculo Integral Enero 2015
 Cálculo Integral Enero 015 Laboratorio # 1 Antiderivadas I.- Halle las siguientes integrales indefinidas. 10) ) 6) 1 1 1 1 16) 1 8) 9) 18) II.- Calcule 1.. 1 Cálculo Integral Enero 015 Laboratorio # Aplicaciones
Cálculo Integral Enero 015 Laboratorio # 1 Antiderivadas I.- Halle las siguientes integrales indefinidas. 10) ) 6) 1 1 1 1 16) 1 8) 9) 18) II.- Calcule 1.. 1 Cálculo Integral Enero 015 Laboratorio # Aplicaciones
INSTITUTO FRANCISCO POSSENTI A.C. PREPARATORIA (1085) GUÍA DE MATEMÁTICAS V (1500)
 INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (1085) GUÍA DE MATEMÁTICAS V (1500) UNIDAD I: RELACIONES Y FUNCIONES. Considera las siguientes funciones y gráficas para determinar en
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (1085) GUÍA DE MATEMÁTICAS V (1500) UNIDAD I: RELACIONES Y FUNCIONES. Considera las siguientes funciones y gráficas para determinar en
, se denomina primitiva de esta función a otra F(x)
 1. CONCEPTO DE INTEGRAL INDEFINIDA Definición: Dada una función f (x), se denomina primitiva de esta función a otra F(x) tal que F '( x) = f ( x) Esta definición indica que el cálculo de primitivas constituye
1. CONCEPTO DE INTEGRAL INDEFINIDA Definición: Dada una función f (x), se denomina primitiva de esta función a otra F(x) tal que F '( x) = f ( x) Esta definición indica que el cálculo de primitivas constituye
ANÁLISIS MATEMÁTICO, LA PENDIENTE Y LA VELOCIDAD
 ANÁLISIS MATEMÁTICO, LA PENDIENTE Y LA VELOCIDAD Joaquín González Álvarez Con este trabajo nos proponemos mostrar un método didáctico elemental de Análisis Matemático que hemos ideado como alternativa
ANÁLISIS MATEMÁTICO, LA PENDIENTE Y LA VELOCIDAD Joaquín González Álvarez Con este trabajo nos proponemos mostrar un método didáctico elemental de Análisis Matemático que hemos ideado como alternativa
5.1 DISTINTOS TIPOS DE FUNCIONES LINEALES
 Tema 5 : Funciones elementales - Matemáticas B 4º E.S.O. 1 TEMA 5 FUNCIONES ELEMENTALES 5.1 DISTINTOS TIPOS DE FUNCIONES LINEALES 3º 5.1.1 - FUNCIONES DE PROPORCIONALIDAD: y = mx Las funciones de proporcionalidad
Tema 5 : Funciones elementales - Matemáticas B 4º E.S.O. 1 TEMA 5 FUNCIONES ELEMENTALES 5.1 DISTINTOS TIPOS DE FUNCIONES LINEALES 3º 5.1.1 - FUNCIONES DE PROPORCIONALIDAD: y = mx Las funciones de proporcionalidad
UNIDAD 10. DERIVADAS. APLICACIONES DE LAS DERIVADAS
 Unidad 0. Derivadas. Aplicaciones de las derivadas UNIDAD 0. DERIVADAS. APLICACIONES DE LAS DERIVADAS. TASA DE VARIACIÓN MEDIA. Se llama TASA DE VARIACIÓN MEDIA (TVM) de una función () f en un intervalo
Unidad 0. Derivadas. Aplicaciones de las derivadas UNIDAD 0. DERIVADAS. APLICACIONES DE LAS DERIVADAS. TASA DE VARIACIÓN MEDIA. Se llama TASA DE VARIACIÓN MEDIA (TVM) de una función () f en un intervalo
Instituto Tecnológico de Saltillo
 Instituto Tecnológico de Saltillo CÁLCULO INTEGRAL Enero-Junio 2012 Programa de Unidades I. Teorema Fundamental del Cálculo (Diferenciales). II. La integral Indefinida. III.Técnicas de Integración Indefinida.
Instituto Tecnológico de Saltillo CÁLCULO INTEGRAL Enero-Junio 2012 Programa de Unidades I. Teorema Fundamental del Cálculo (Diferenciales). II. La integral Indefinida. III.Técnicas de Integración Indefinida.
Funciones. 1. Funciones. Ecuaciones. Curvas. 2. Función lineal. La recta
 Funciones 1 Funciones Ecuaciones Curvas Una función es una correspondencia entre números Mediante la función f a cada número x se le hace corresponder un solo número que se representa por f(x) Puesto que
Funciones 1 Funciones Ecuaciones Curvas Una función es una correspondencia entre números Mediante la función f a cada número x se le hace corresponder un solo número que se representa por f(x) Puesto que
UNIDAD I MATEMÁTICA 3 A
 UNIDAD I MATEMÁTICA 3 A NÚMEROS REALES (R) Números Racionales Expresiones Decimales El Conjunto Q de los números racionales está formado por todos aquellos números que pueden expresarse en forma de fracción,
UNIDAD I MATEMÁTICA 3 A NÚMEROS REALES (R) Números Racionales Expresiones Decimales El Conjunto Q de los números racionales está formado por todos aquellos números que pueden expresarse en forma de fracción,
Constante de integración
 Constante de integración Cuando impongamos una condición que deba satisfacer la antiderivada de la función dada, por ejemplo, que pase por un punto dado, tendremos la posibilidad de reducir toda una familia
Constante de integración Cuando impongamos una condición que deba satisfacer la antiderivada de la función dada, por ejemplo, que pase por un punto dado, tendremos la posibilidad de reducir toda una familia
UNIDAD EDUCATIVA SAGRADOS CORAZONES CENTRO
 UNIDAD EDUCATIVA SAGRADOS CORAZONES CENTRO Contemplar, vivir y anunciar el amor redentor de Cristo CIENCIAS EXACTAS SUPLETORIO - Matemáticas Tercer Año de Bachillerato 07 08 Dirección: Calles Sucre Oe
UNIDAD EDUCATIVA SAGRADOS CORAZONES CENTRO Contemplar, vivir y anunciar el amor redentor de Cristo CIENCIAS EXACTAS SUPLETORIO - Matemáticas Tercer Año de Bachillerato 07 08 Dirección: Calles Sucre Oe
Tema Contenido Contenidos Mínimos
 1 Estadística unidimensional - Variable estadística. - Tipos de variables estadísticas: cualitativas, cuantitativas discretas y cuantitativas continuas. - Variable cualitativa. Distribución de frecuencias.
1 Estadística unidimensional - Variable estadística. - Tipos de variables estadísticas: cualitativas, cuantitativas discretas y cuantitativas continuas. - Variable cualitativa. Distribución de frecuencias.
FUNCIONES DE PROPORCIONALIDAD: y = mx. Su pendiente es 0. La recta y = 0 coincide con el eje
 Funciones elementales - Matemáticas B 4º E.S.O. FUNCIONES ELEMENTALES DISTINTOS TIPOS DE FUNCIONES LINEALES FUNCIONES DE PROPORCIONALIDAD: y = mx FUNCIÓN CONSTANTE: y = n Las funciones de proporcionalidad
Funciones elementales - Matemáticas B 4º E.S.O. FUNCIONES ELEMENTALES DISTINTOS TIPOS DE FUNCIONES LINEALES FUNCIONES DE PROPORCIONALIDAD: y = mx FUNCIÓN CONSTANTE: y = n Las funciones de proporcionalidad
Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como:
![Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como: Derivadas. 1. Tasa de variación media La tasa de variación media de una función f(t) en un intervalo [a, b] se define como:](/thumbs/71/66199093.jpg) Derivadas Antes de dar la definición de derivada de una función en un punto, vamos a introducir el concepto de tasa de variación media y dos ejemplos o motivaciones iniciales que nos van a dar la medida
Derivadas Antes de dar la definición de derivada de una función en un punto, vamos a introducir el concepto de tasa de variación media y dos ejemplos o motivaciones iniciales que nos van a dar la medida
MATEMÁTICAS BÁSICAS DIFERENCIAL DEFINICIÓN DE DIFERENCIAL
 MATEMÁTICAS BÁSICAS DIFERENCIAL DEFINICIÓN DE DIFERENCIAL Sea una función f ( ). d Se define como la diferencial de la variable independiente a: Se define como la diferencial de la variable dependiente
MATEMÁTICAS BÁSICAS DIFERENCIAL DEFINICIÓN DE DIFERENCIAL Sea una función f ( ). d Se define como la diferencial de la variable independiente a: Se define como la diferencial de la variable dependiente
CÁLCULO ELEMENTAL PROBLEMAS. Valor absoluto. Funciones y sus gráficas
 CÁLCULO ELEMENTAL PROBLEMAS Valor absoluto - Resolver las ecuaciones siguientes: (i) 2x 6 = x (ii) x + 8 = 3x 4 2- Resolver la inecuación 2x 3 4 Funciones y sus gráficas 3- Dada f(x) = 2x 2 x, hallar f(
CÁLCULO ELEMENTAL PROBLEMAS Valor absoluto - Resolver las ecuaciones siguientes: (i) 2x 6 = x (ii) x + 8 = 3x 4 2- Resolver la inecuación 2x 3 4 Funciones y sus gráficas 3- Dada f(x) = 2x 2 x, hallar f(
UNIDAD 1 NUMEROS COMPLEJOS
 UNIDAD 1 NUMEROS COMPLEJOS El conjunto de los números complejos fue creado para poder resolver algunos problemas matemáticos que no tienen solución dentro del conjunto de los números reales. Por ejemplo
UNIDAD 1 NUMEROS COMPLEJOS El conjunto de los números complejos fue creado para poder resolver algunos problemas matemáticos que no tienen solución dentro del conjunto de los números reales. Por ejemplo
ANÁLISIS MATEMÁTICO IES A SANGRIÑA 2016/2017
 ANÁLISIS MATEMÁTICO 4. INTEGRACIÓN INDEFINIDA UN POCO DE HISTORIA El símbolo de integración fue introducido por el matemático alemán Gottfried Leibniz en 1675, basándose en la palabra latina summa, suma,
ANÁLISIS MATEMÁTICO 4. INTEGRACIÓN INDEFINIDA UN POCO DE HISTORIA El símbolo de integración fue introducido por el matemático alemán Gottfried Leibniz en 1675, basándose en la palabra latina summa, suma,
. Manual General para el Uso del Software Graphmatica.
 1. Manual General para el Uso del Software Graphmatica. http://www.graphmatica.com/espanol/grmat0n.html Graphmatica es un software de uso libre muy fácil de utilizar y que puede ser descargado de Internet
1. Manual General para el Uso del Software Graphmatica. http://www.graphmatica.com/espanol/grmat0n.html Graphmatica es un software de uso libre muy fácil de utilizar y que puede ser descargado de Internet
Si la variable independiente x con un valor inicial a que le da un valor final b a la diferencia b-a se le llama incremento de la variable y se
 Si la variable independiente x con un valor inicial a que le da un valor final b a la diferencia b-a se le llama incremento de la variable y se simboliza con la letra delta. La derivada de la función con
Si la variable independiente x con un valor inicial a que le da un valor final b a la diferencia b-a se le llama incremento de la variable y se simboliza con la letra delta. La derivada de la función con
Colegio San Agustín (Santander) Página 1
 Matemáticas 1ºBachillerato Aplicadas a las Ciencias Sociales 1era evaluación. Teoría de las funciones 1) Teoría de funciones Una función (f) es la relación entre un conjunto de elementos dado X (llamado
Matemáticas 1ºBachillerato Aplicadas a las Ciencias Sociales 1era evaluación. Teoría de las funciones 1) Teoría de funciones Una función (f) es la relación entre un conjunto de elementos dado X (llamado
Análisis Matemático I (Lic. en Cs. Biológicas)
 Análisis Matemático I (Lic. en Cs. Biológicas) Segundo Cuatrimestre 25 Práctica 6: Integración Ejercicio. Hallar en cada caso una función g : R R que cumpla (i) g (x) = 2. (ii) g (x) = x. (iii) g (x) =
Análisis Matemático I (Lic. en Cs. Biológicas) Segundo Cuatrimestre 25 Práctica 6: Integración Ejercicio. Hallar en cada caso una función g : R R que cumpla (i) g (x) = 2. (ii) g (x) = x. (iii) g (x) =
Elementos de cálculo usando mathematica
 Tlamati Sabiduría Volumen 7 Número Especial 1, Septiembre 2016 3 er. Encuentro de Jóvenes en la Investigación de Bachillerato-CONACYT Elementos de cálculo usando mathematica Memorias Alejandra Cano Calleja
Tlamati Sabiduría Volumen 7 Número Especial 1, Septiembre 2016 3 er. Encuentro de Jóvenes en la Investigación de Bachillerato-CONACYT Elementos de cálculo usando mathematica Memorias Alejandra Cano Calleja
SESIÓN 6 INTERPRETACION GEOMETRICA DE LA DERIVADA, REGLA GENERAL PARA DERIVACIÓN, REGLAS PARA DERIVAR FUNCIONES ALGEBRAICAS.
 SESIÓN 6 INTERPRETACION GEOMETRICA DE LA DERIVADA, REGLA GENERAL PARA DERIVACIÓN, REGLAS PARA DERIVAR FUNCIONES ALGEBRAICAS. I. CONTENIDOS: 1. Interpretación geométrica de la derivada 2. Regla general
SESIÓN 6 INTERPRETACION GEOMETRICA DE LA DERIVADA, REGLA GENERAL PARA DERIVACIÓN, REGLAS PARA DERIVAR FUNCIONES ALGEBRAICAS. I. CONTENIDOS: 1. Interpretación geométrica de la derivada 2. Regla general
I Al finalizar el curso el estudiante será capaz de:
 A) Nombre del Curso 2 CÁLCULO I B) Datos básicos del curso Semestre Horas de teoría por semana Horas de práctica por semana Horas trabajo adicional estudiante Créditos I 3 2 3 8 C) Objetivos del curso
A) Nombre del Curso 2 CÁLCULO I B) Datos básicos del curso Semestre Horas de teoría por semana Horas de práctica por semana Horas trabajo adicional estudiante Créditos I 3 2 3 8 C) Objetivos del curso
S O L U C I Ó N y R Ú B R I C A
 ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO 08 PERÍODO PRIMER TÉRMINO MATERIA Cálculo de una variable PROFESORES EVALUACIÓN SEGUNDA
ESCUELA SUPERIOR POLITÉCNICA DEL LITORAL FACULTAD DE CIENCIAS NATURALES Y MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICAS AÑO 08 PERÍODO PRIMER TÉRMINO MATERIA Cálculo de una variable PROFESORES EVALUACIÓN SEGUNDA
DEPARTAMENTO DE MATEMÁTICAS. IES GALLICUM
 UNIDAD I: REPASO de NÚMEROS (7 Horas) 1.- Conocer los conceptos básicos del campo numérico: recta real, potencias, raíces, intervalos, etc. 2.- Dominar las técnicas básicas del cálculo en el campo de los
UNIDAD I: REPASO de NÚMEROS (7 Horas) 1.- Conocer los conceptos básicos del campo numérico: recta real, potencias, raíces, intervalos, etc. 2.- Dominar las técnicas básicas del cálculo en el campo de los
PLANTEL 15 CONTRERAS GUÍA PARA EL EXAMEN EXTRAORDINARIO DE MATEMÁTICAS V (504) QUINTO SEMESTRE CICLO LECTIVO: 2016-B
 PLANTEL 15 CONTRERAS GUÍA PARA EL EXAMEN EXTRAORDINARIO DE MATEMÁTICAS V (504) QUINTO SEMESTRE CICLO LECTIVO: 2016-B EMPLEA LA DEFINICIÓN Y TEOREMAS DE LÍMITES EN LA CONTINUIDAD Y DISCONTINUIDAD DE LAS
PLANTEL 15 CONTRERAS GUÍA PARA EL EXAMEN EXTRAORDINARIO DE MATEMÁTICAS V (504) QUINTO SEMESTRE CICLO LECTIVO: 2016-B EMPLEA LA DEFINICIÓN Y TEOREMAS DE LÍMITES EN LA CONTINUIDAD Y DISCONTINUIDAD DE LAS
1 LIMITES Y DERIVADAS
 1 LIMITES Y DERIVADAS 2.1 LA TANGENTE Y PROBLEMAS DE LA VELOCIDAD Problema de la tangente Se dice que la pendiente de la recta tangente a una curva en el punto P es el ite de las rectas secantes PQ a medida
1 LIMITES Y DERIVADAS 2.1 LA TANGENTE Y PROBLEMAS DE LA VELOCIDAD Problema de la tangente Se dice que la pendiente de la recta tangente a una curva en el punto P es el ite de las rectas secantes PQ a medida
Unidad 2. FUNCIONES Conceptos
 Unidad 2. FUNCIONES Competencia específica a desarrollar Comprender el concepto de función real y tipos de funciones, así como estudiar sus propiedades y operaciones. Función 2.1. Conceptos Se puede considerar
Unidad 2. FUNCIONES Competencia específica a desarrollar Comprender el concepto de función real y tipos de funciones, así como estudiar sus propiedades y operaciones. Función 2.1. Conceptos Se puede considerar
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (1085) GUÍA DE MATEMÁTICAS VI (1600 ) I. RELACIONES Y FUNCIONES
 INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (085) GUÍA DE MATEMÁTICAS VI (600 ) I. RELACIONES Y FUNCIONES Funciones y relaciones. Dominio y rango. Determinar si es función o relación
INSTITUTO FRANCISCO POSSENTI A.C. Per crucem ad lucem PREPARATORIA (085) GUÍA DE MATEMÁTICAS VI (600 ) I. RELACIONES Y FUNCIONES Funciones y relaciones. Dominio y rango. Determinar si es función o relación
UNIDAD 2: ANALICEMOS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA
 UNIDAD 2: ANALICEMOS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA FUNCIÓN EXPONENCIAL. Se llama función exponencial a la función de la forma y = a x en donde a R +, a y x es una variable. Existen muchos fenómenos
UNIDAD 2: ANALICEMOS LA FUNCIÓN EXPONENCIAL Y LOGARÍTMICA FUNCIÓN EXPONENCIAL. Se llama función exponencial a la función de la forma y = a x en donde a R +, a y x es una variable. Existen muchos fenómenos
5. ANÁLISIS MATEMÁTICO // 5.1. DERIVADAS Y
 5. ANÁLISIS MATEMÁTICO // 5.1. DERIVADAS Y APLICACIONES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2017-2018 5.1.1. El problema de la tangente. Derivada. Pierre de Fermat tenía una
5. ANÁLISIS MATEMÁTICO // 5.1. DERIVADAS Y APLICACIONES. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2017-2018 5.1.1. El problema de la tangente. Derivada. Pierre de Fermat tenía una
Diferencial de una función 1
 Cálculo _Comisión y Año 7 Diferencial de una función Dada una función y f (, derivable en x, se define: Diferencial de f, en x, al producto de la derivada de la función en dicho punto, por el incremento
Cálculo _Comisión y Año 7 Diferencial de una función Dada una función y f (, derivable en x, se define: Diferencial de f, en x, al producto de la derivada de la función en dicho punto, por el incremento
