EL TRIMESTRE ECONÓMICO, vol. LXXXI (4), núm. 324, octubre-diciembre de 2014, pp
|
|
|
- Ernesto Moreno Maldonado
- hace 6 años
- Vistas:
Transcripción
1 EL TRIMESTRE ECONÓMICO, vol. LXXXI (4), núm. 34, octubre-diciembre de 014, pp VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX-V Y GMEXICO-B Calibración de parámetros de volatilidad estocástica con funciones cuadráticas de pérdida* Ambrosio Ortiz-Ramírez, Francisco Venegas-Martínez y Mario Durán-Bustamante** RESUMEN Esta investigación propone una metodología para estimar los parámetros del modelo de volatilidad estocástica de Heston (1993) por medio de funciones cuadráticas de pérdida, las cuales minimizan el error entre precios de mercado y precios teóricos. Para ello se plantean tres clases de funciones de pérdida, de las cuales dos están asociadas a precios y otra a volatilidades implícitas. La metodología propuesta se aplica a un conjunto de precios de opciones sobre AMX-L, WALMEX-V y GMEXICO-B. Los resultados indican que para opciones de compra sobre AMX-L se generan volatilidades implícitas consistentes con las observadas con base en el criterio de la raíz de la pérdida del error cuadrático medio, mientras que para opciones de compra sobre WALMEX-V y GMEXICO-B se generan volatilidades implícitas consistentes con las observadas con base en el criterio de la raíz de la pérdida relativa del error cuadrático medio. * Palabras clave: opciones financieras, volatilidad estocástica, modelos de calibración, estimación de parámetros. Clasificación JEL: C8, G13, G17. Artículo recibido el 3 de junio de 013 y aceptado el 15 de enero de 014. ** Profesores-investigadores de la Escuela Superior de Economía del Instituto Politécnico Nacional (IPN) (correos electrónicos: amortiz@ipn.mx, fvenegas1111@yahoo.com.mx y mario.d.bustamante@ gmail.com). 943
2 944 EL TRIMESTRE ECONÓMICO ABSTRACT This paper proposes a methodology to estimate the parameters of the stochastic volatility model from Heston (1993) through quadratic loss functions, which minimize the error between market prices and theoretical prices. To do this, three classes of loss functions are stated, two of which correspond to prices and the other one to implied volatilities. The proposed methodology is applied to a set of option prices on AMX-L, WALMEX-V, and GMEXICO-B. The results indicate that for call options on AMX-L the generated implied volatilities are consistent with observed data under the criterion of the root of the mean quadratic error, while for call options on WALMEX-V and GMEXICO-B the generated implied volatilities are consistent with observed data under the criterion of the root of the mean quadratic relative error. INTRODUCCIÓN A pesar de su popularidad entre practicantes e investigadores, el modelo de Black, Scholes y Merton (BSM) refleja sólo una pequeña parte de la complejidad de los mercados de derivados, produciendo un sesgo persistente en la determinación de las primas de las opciones. De hecho, el supuesto de volatilidad constante es una de las limitantes más drásticas por su contraste con las sonrisas de volatilidad (volatility smile) y las muecas de volatilidad (smirk) implícitas en los precios de opciones que se negocian en los mercados de derivados. En las últimas décadas, la investigación ha sido pródiga debido a los cientos de contribuciones que descansan en supuestos más realistas que los del modelo de BSM. Al respecto, se han propuesto muchos y diversos modelos, algunos muy sofisticados, que suponen diferentes procesos estocásticos para conducir la dinámica de los activos subyacentes y su correspondiente prima de riesgo; véase, al respecto, Gatheral (006). No obstante, un inconveniente de estos modelos es que pocas veces ofrecen fórmulas cerradas. Así, la ventaja de contar con supuestos más realistas se compensa con una implementación y calibración más compleja. Entre dichos modelos alternativos, se encuentran los de volatilidad estocástica (VE). En este enfoque la volatilidad cambia en el tiempo de acuerdo con un proceso estocástico, usualmente especificado mediante una ecuación diferencial estocástica que acompaña la dinámica del precio del activo subyacente.
3 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 945 Los trabajos seminales de Hull y White (1987), Stein y Stein (1991) y Heston (1993) motivaron, sin duda, el desarrollo de los modelos de volatilidad estocástica; estos modelos tienen dos factores, y uno de ellos conduce la dinámica estocástica de la volatilidad. Dentro de este enfoque se han propuesto diferentes modelos para el proceso de volatilidad, particularmente los procesos con reversión a la media del tipo Ornstein-Uhlenbeck, como en Schöbel y Zhu (1999), que suponen dos movimientos brownianos correlacionados y obtienen la función característica del logaritmo del precio con una expresión compuesta por un sistema de ecuaciones diferenciales estocásticas. Asimismo, Zhu (010) propone un modelo de volatilidad estocástica de doble raíz en el contexto Longstaff (1989). Para resumir, en el cuadro 1, se muestra un resumen de modelos de volatilidad estocástica de dos factores. CUADRO 1. Resumen de modelos de volatilidad estocástica de dos factores Modelo Autor dvt = κ vdt + σdwt Johnson/Shano (1987) d ln vt = κ ( θ ln v) dt + σdwt Wiggins (1987) dvt = κ v dt + σ v dwt Hull/White (1987) dvt = ( a + β vt ) dt + σ vt dwt Hull/White (1988) dst = ( r δ ) dt + vt dw1, t + dzt St dvt = κ ( θ vt ) dt + σ vt dw, t Bates (1996) dvt = κ ( θ v) dt + σdw Stein/Stein (1991) t Schöbel/Zhu (1999) dvt = κ ( θ vt ) dt + σ vt dwt Heston (1993) / dvt = κ ( θ vt ) dt + σ vt 3 dwt Lewis (000) dvt = κ ( θ vt λvt ) dt + σ vt dwt Zhu (010) Es importante destacar otros modelos de volatilidad estocástica que consideran saltos en la dinámica del subyacente, como son los de Bates (1996) y Bakshi, Cao, y Chen (1997). Estos modelos son una extensión con volatilidad estocástica del modelo de difusión con saltos de Merton (1976). Evi-
4 946 EL TRIMESTRE ECONÓMICO dentemente, la lista en el cuadro 1 no es exhaustiva; lo realmente interesante en esta lista es cómo elegir uno u otro modelo con base en criterios de ajuste con los precios de mercado. En conclusión, muchos de estos modelos de valuación de opciones se definen por lo general mediante dos procesos: uno para el precio del activo subyacente y otro para la dinámica de la volatilidad, y lo importante es cuál de ellos se ajusta mejor a un conjunto de datos. 1 Es importante mencionar que el modelo de Heston (1993) ha sido objeto de varias críticas, una de ellas es la dificultad de estimar sus parámetros para calibrar smiles de corto plazo. El presente trabajo propone una metodología para la estimación de los parámetros del modelo de Heston mediante funciones de pérdida cuadráticas. La metodología consiste en minimizar una medida del error entre los precios observados y los precios teóricos. Para ello, se utiliza la transformada fundamental de Lewis (000) y, posteriormente, se desarrolla un algoritmo de calibración que minimiza el error, dado un conjunto de parámetros iniciales asociado a la transformada de Lewis. La metodología se aplica a la valuación de opciones europeas sobre acciones de América Móvil, S.A.B. de C.V, serie L (AMX-L), Wal-Mart de México, S.A.B. de C.V., serie V (WALMEX-V) y Grupo México, S.A.B. de C.V., serie B (GMEXICO-B), que se negocian en el MexDer (Mercado Mexicano de Derivados). Este trabajo está organizado como sigue: en la primera sección se plantea el marco general de los modelos de volatilidad estocástica; en la segunda se discuten, brevemente, las características teóricas del modelo de Heston junto con su función de densidad marginal para diferentes valores de los parámetros de correlación y volatilidad de la varianza; en el transcurso de la tercera sección se presenta la transformada fundamental de Lewis (000) y la fórmula general para calcular el precio de una opción bajo una clase general de modelos de volatilidad estocástica; a través de la cuarta sección se desarrolla la metodología de calibración de parámetros del modelo de Heston con funciones cuadráticas de pérdida, el algoritmo de calibración propuesto minimiza el error dado un conjunto de parámetros iniciales asociado a la transformada de Lewis; en la quinta sección se presentan y analizan los resultados obtenidos después de aplicar la metodología para valuar opciones sobre acciones de AMX-L, WALMEX-V y GMEXICO-B; por último, se presentan las conclusiones. 1 Varios modelos de volatilidad estocástica y su estimación econométrica puede consultarse en Shephard (005).
5 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 947 I. EL MARCO TEÓRICO DE VOLATILIDAD ESTOCÁSTICA Los modelos de volatilidad estocástica con sus respectivas extensiones, en general, han resultado ser más apropiados, con cierta reserva, para la valuación de opciones en tiempo continuo que otras alternativas con volatilidad constante. Usualmente, estos modelos son planteados en tiempo continuo aunque también se encuentran en la bibliografía en tiempo discreto mediante modelos GARCH y sus extensiones, como se hace en Harvey, Ruiz y Shepard (1994). Un modelo general de volatilidad estocástica es comúnmente planteado como un sistema de dos ecuaciones diferenciales estocásticas: ds = μ S dt + v S dw t t t t t t v t t t t dv = α( v ) dt + β( v ) dw Para generar el efecto de apalancamiento se supone que el rendimiento de activo y las innovaciones de la volatilidad están correlacionadas de tal forma que: E( dw dw tv t ) = ρdt De esta manera el precio del derivado depende ahora del tiempo, del precio del activo subyacente y de la volatilidad: P = P( t, S, v ) t t t Cuando se considera volatilidad estocástica se relajan dos de los supuestos del modelo de Black, Scholes y Merton; el primero es que un solo movimiento browniano genera incertidumbre (riesgo de mercado) y el segundo, relacionado con el anterior, es que los mercados son completos. Los modelos de volatilidad estocástica consideran, en general, dos movimientos brownianos, y es por ello que el precio del derivado no se puede replicar, por lo que el mercado no es completo. Esto significa que existe un número infinito de precios que invalidan el supuesto de no arbitraje. Si se incluye otro instrumento de cobertura con un derivado, entonces el mercado es completo y, en consecuencia, los derivados ahora deberán valuarse relacionando unos con otros, así como el activo subyacente. Ésta es una de las razones de que los modelos de volatilidad estocástica se puedan calibrar dado un conjunto de precios de mercado de las opciones, es decir, dado un conjunto de pará-
6 948 EL TRIMESTRE ECONÓMICO metros iniciales y mediante la implementación de un algoritmo numérico se pueden estimar los parámetros del modelo, minimizando la distancia entre los precios de mercado y los obtenidos con el modelo teórico. Para modelar el riesgo de volatilidad es común introducir otro movimiento browniano W t que representa la parte de W v t que es ortogonal a W t, v por lo que se puede escribir Wt = ρwt + 1 ρ W t. En este caso, el activo subyacente no depende de W t y, por lo tanto, el riesgo generado por este browniano no está incluido en el precio del activo. Por otro lado, el riesgo de W t está incrustado en la prima de riesgo μ t r t. En consecuencia, un inversionista podría ser adverso al riesgo y, aunque su aversión no se observa en el mercado del activo subyacente, aparecerá en el mercado de opciones, ya que estos contratos dependen implícitamente de v t. Así, mediante un derivado se puede identificar la prima de riesgo, y entonces se pueden obtener precios de otros derivados. II. MODELO DE VOLATILIDAD ESTOCÁSTICA DE HESTON Heston (1993) valúa una opción sobre una acción con volatilidad estocástica, y un rasgo relevante de su trabajo es que obtiene las funciones características de las probabilidades neutrales al riesgo como soluciones de una ecuación diferencial parcial de segundo orden. Posteriormente, por medio de estas probabilidades neutrales al riesgo obtiene una fórmula similar a la de Black, Scholes y Merton para valuar una opción europea de compra; el precio de la opción de venta se puede obtener con la paridad put-call. Otra característica esencial del modelo de Heston (1993) es que proporciona una fórmula cerrada (en términos de integrales de variables complejas) para el precio de una opción con el supuesto de correlación entre el precio del activo subyacente y su volatilidad. Aunque la fórmula es cerrada, su cálculo es usualmente complicado por incluir variables complejas. Así, el precio de la opción se obtiene al calcular la probabilidad de que una opción de compra expire dentro del dinero; aunque dicha probabilidad no se puede calcular directamente, ésta se puede calcular a través de la inversión de la función característica del logaritmo del precio del subyacente. A continuación se plantea la dinámica estocástica que conduce la volatilidad. Supongamos que el precio actual, S t de una acción es conducido por: dst = μdt + vt dw1, t S t
7 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 949 donde μ es el parámetro de tendencia y W 1, t es un proceso de Wiener. La volatilidad v t es conducida por el proceso: d v = β v dt + δ dw, t t t donde W, t es un proceso de Wiener correlacionado con W 1, t, i.e., Cov( dw1, t, dw, t) = ρ. Para simplificar el modelo, se aplica el lema de Itô con el fin de obtener el proceso para la varianza v t, el cual se puede expresar como un proceso del tipo Cox, Ingersoll y Ross (1985), es decir, ( ) + dv = κ θ v dt σ v dw, (1) t t t t En el contexto de los modelos de volatilidad estocástica, los parámetros θ, κ y σ, se interpretan como la varianza de largo plazo, la tasa de reversión a la varianza de largo plazo y la volatilidad de la varianza (a menudo denominada como la volatilidad de la volatilidad), respectivamente. Heston muestra que el precio al tiempo t de una opción de compra con tiempo un vencimiento T t (como proporción de año), denotado por c( S, v, t), está dada por: c( S, v, t) = St P1 KP( t, T ) P () donde S t es el precio spot del activo, K el precio de ejercicio de la opción y, P( t, T ) es un factor de descuento. Por ejemplo, si r es una tasa de interés constante y continuamente capitalizable, entonces se puede tomar P t T e r ( (, ) T t ) =. El precio de una opción de venta europea al tiempo t, se obtiene con la paridad put-call como sigue: p( S, v, t) = c( S, v, t) + KP( t, T ) S t (3) Las cantidades P 1 y P son las probabilidades de que la opción expire dentro del dinero, condicionales al logaritmo del precio del subyacente, xt = ln( St) = x, y a la volatilidad, vt = v, ambas al tiempo t. Para valuar opciones es necesaria una dinámica neutral al riesgo, que en este caso está expresada en términos de los parámetros neutrales al riesgo κ y θ como sigue: 1 dxt = r vt dt vt dw t + * 1, (4) dvt = κ ( θ vt ) dt + σ vt dw *, t
8 950 EL TRIMESTRE ECONÓMICO A continuación, se obtiene el proceso neutral al riesgo para el precio del subyacente y la varianza expresados en la ecuación anterior. Supongamos que el precio de la acción es conducido por: ds = μdt + vdw1 S donde S = St, v = v y dw dw t 1 = 1, t. Después de aplicar el lema de Itô al proceso x = ln S, se sigue que 1 dx = v dt vdw μ + σ 1 (5) Por otra parte, el proceso para la raíz cuadrada de la varianza v satisface: d v = β vdt + δdw (6) donde β y δ son parámetros y dw = dw, t. Al aplicar el lema de Itô, se tiene que el proceso para la varianza v es el proceso de Cox, Ingersoll y Ross (1985), es decir, dv = κ ( θ v) dt + σ vdw (7) donde κ = β, θ = δ / β y σ = δ. Si κ, θ y σ satisfacen las condiciones κθ > σ y v 0 > 0, se puede demostrar que la varianza v t es siempre positiva y su proceso dado en (7) está bien definido en estas condiciones, esa propiedad se conoce como condición de proceso de raíz cuadrada de Feller. Si se expresa (5) como el proceso neutral al riesgo: 1 d ln S = r v dt ( r) dt vdw + μ + σ 1 1 = r v dt + σ vdw * 1 donde r es la tasa de interés libre de riesgo y r W1 * = W1 μ v t (8) entonces la versión neutral al riesgo del proceso en (7) para v está dada por
9 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 951 ( ) + dv = κ θ v dt λdt σdw * (9) donde λ = λ( t, St, vt ) es el premio al riesgo por volatilidad, y λ W *= W t σ (10) Por lo tanto, los procesos para el precio de la acción y para la varianza son, respectivamente, 1 d ln S = r v dt vdw * + σ 1 (11) y donde ( ) + dv = κ θ v dt λdt σdw * (1) μ r W W* 1 + v t 1 W* = λ W + t σ (13) Bajo la medida de probabilidad P se tiene que W1 N( 0, T ) y W N( 0, T ), es necesaria una nueva medida Q tal que W * 1 N( 0, T ) y W * N( 0, T ) bajo Q. Por el teorema de Girsanov, la medida Q existe si λ( t, St, vt ) y ( μ r) t/ v satisfacen la condición de Novikov. Como se explica en Heston (1993), el modelo de consumo de Breeden (1979), aplicado al proceso CIR, produce un premio al riesgo por volatilidad de la forma λ( t, St, vt ) = λv. En este caso, el proceso para la varianza en (1) se transforma en: ( ) + dv = κ θ v dt λvdt σdw κθ = + v dt dw + ( κ λ) + σ * κ λ ( ) + * * v dt dw * = κ θ σ * (14) donde κ * = κ + λ y θ * = κθ /( κ + λ ) son los parámetros neutrales al riesgo. Si se omite el asterisco de κ * y θ *, los procesos para el precio de la acción y la varianza son:
10 95 EL TRIMESTRE ECONÓMICO 1 dxt = r vt dt vt dw t + * 1, dvt = ( vt ) (15) κ θ dt + σ vt dw *, t las cuales coinciden con las ecuaciones en (4). De acuerdo con la dinámica anterior, las probabilidades P 1 y P se interpretan como las probabilidades ajustadas al riesgo o neutrales al riesgo. Por lo tanto, ( ) P = P x ln K x = x, v = v (16) j T t t para j = 1,. Las probabilidades P j se obtienen al invertir las funciones características f j en donde: 1 1 Pj = + π 0 e Re iφ ln( K ) fj iφ ( ) = f = exp C + D v + iφx, con v v j j j t κθ Cj = rφiτ + bj ρσφi σ D = b d j ρσφi + d j j 1 e j σ 1 gje bj ρσφi + dj gj = b ρσφi d j ( dj ) τ + τ djτ ( ) d = ρσφi b σ ( u φi φ ) j j j j d φ (17) 1 gje ln 1 g En las ecuaciones anteriores τ = T t es el plazo al vencimiento, i = 1 es la unidad imaginaria, u1 = 1/, u = 1/, b1 = κ + λ ρσ y b = κ + λ. El parámetro λ representa la prima al riesgo por volatilidad como función del precio del activo, el tiempo y la volatilidad. Aunque () y (3) se consideran soluciones en forma cerrada, cada una requiere calcular dos integrales complejas, como se observa en (17), por lo que es necesario recurrir a un método numérico para aproximar las integrales y obtener el precio de la opción. djτ j
11 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 953 Por otro lado, si se escribe xt = ln( St / S 0 ) μ t, entonces se puede expresar el modelo de Heston en (1) en términos del rendimiento centrado x t y de v t (véase Čivžek et al., 011). De esta manera, el proceso es caracterizado por la transición Pt ( x, v v0 ) del rendimiento x y la varianza v al tiempo t dado un rendimiento inicial x = 0 y varianza v 0 al tiempo t = 0. La dinámica temporal de P ( x, v v ) es conducida por la siguiente ecuación de Fokkert 0 Planck (o forward Kolmogorov): = {( ) } + + t P v v P 1 κ θ ( x vp ) ρσ ( x v vp ) + 1 x ( vp ) + σ v ( vp) (18) Al resolver esta ecuación se obtiene la siguiente fórmula semianalítica para la densidad de los rendimientos centrados de x, dado un cambio en el precio en un intervalo de tiempo t, de acuerdo con Dragulescu y Yakovenko (00): donde: 1 + i x F Pt ( x ) ξ + e t ( ) = π ξ d ξ (19) t t Ft ( ξ κθ ) t ln cosh sinh σ γ κθ Ω Ω γ + κγ Ω = + σ κ Ω γ = κ + iρσξ, y Ω = γ + σ ( ξ iξ) A continuación, se muestra gráficamente la densidad marginal del modelo de Heston dada por (19) para diferentes valores de ρ, con parámetros dados por: CUADRO. Parámetros de la densidad marginal de Heston con diferentes valores de ρ κ θ σ ρ x , 0, +0.5 (-0.5, 0.5) La gráfica 1 muestra la función de densidad marginal del modelo de Heston para diferentes valores de ρ. y se compara con la densidad de una distribución normal ~ ( 0, ). Obsérvese que el parámetro de correlación controla, en efecto, el sesgo de la densidad. En efecto, si ρ = 0.5, la densi-
12 954 EL TRIMESTRE ECONÓMICO GRÁFICA 1. Función de densidad marginal del modelo de Heston para diferentes valores de ρ ρ = 0.5 ρ = 0 ρ = dad muestra sesgo negativo, mientras que si ρ = +0.5, la densidad muestra sesgo positivo, en el caso de ρ = 0, la densidad es simétrica. De la misma manera, se muestra la densidad del modelo de Heston para diferentes valores del parámetro de volatilidad de la varianza σ, con parámetros dados el siguiente cuadro. CUADRO 3. Parámetros de la densidad marginal de Heston con diferentes valores de σ κ θ σ ρ x , 0.3, (-0.5, 0.5) La gráfica muestra la función de densidad marginal del modelo de Heston para diferentes valores de σ y se compara con la densidad de una distribución normal ~ ( 0, ). Obsérvese que el parámetro de volatilidad de la volatilidad controla la curtosis de la densidad; por lo tanto, si σ es relativamente alta, entonces la densidad presenta exceso de curtosis con su correspondiente efecto en las colas (colas pesadas). III. CÁLCULO DE LA PRIMA DE LA OPCIÓN POR MEDIO DE LA TRANSFORMACIÓN DE LEWIS El cálculo del precio de la opción con el modelo de Heston tiene algunos detalles técnicos, un tanto complejos, que hay que tomar en cuenta, ya
13 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 955 GRÁFICA. Función de densidad marginal del modelo de Heston para diferentes valores de σ σ = 0.15 σ = 0.3 σ = que es necesario evaluar las integrales complejas en (17). La forma cerrada requiere los siguientes parámetros: el precio spot del activo S = S t, el precio de ejercicio K, el tiempo al vencimiento τ = T t, y la tasa de interés libre de riesgo y constante r, además de estimaciones para los parámetros que conducen el proceso de tendencia, como son: la varianza de largo plazo θ, la varianza actual v i, el premio al riesgo por volatilidad λ, el parámetro de reversión a la media κ, la volatilidad de la varianza σ, y la correlación entre los procesos que conducen el precio del activo y la volatilidad, ρ. Lewis (000) muestra que el precio de la opción c( S, V, τ ) en el modelo de Heston (1993) se puede expresar en términos de la transformada fundamental H ˆ ( k, V, τ ), donde k = k r ik i es un número complejo, V la volatilidad y τ = T t, el plazo al vencimiento. Con esta transformación se obtienen precios de opciones de manera más sencilla, ya que sólo se necesita evaluar una integral. La fórmula general para el precio de una opción de compra bajo una clase general de modelos de volatilidad estocástica está dada por: Hˆ δτ rτ 1 + ikx ( k, V, τ ) c( S, V, τ ) = Se Ke e k π ik i d ik i k ik (0) donde X = ln S/ K + ( r δ ) τ, k i = 1/ y δ es la tasa de dividendos. Para el modelo de Heston la transformada fundamental es de la forma:
14 956 EL TRIMESTRE ECONÓMICO donde: [ ] H ˆ ( k, V, τ ) = exp f 1 ( t) + f ( t) Vt (1) 1 hexp( td) f1( t) = ω tg ln 1 h f t g 1 exp( td) ( ) = 1 hexp( td) () d = ( ˆ 1/ θ + 4c ), 1 g = g ( θ ˆ + d ), h = θˆ + d θˆ d (3) ˆ θ = ( 1 γ ik) ρσ + k γ ( 1 γ ) σ para γ < 1 (4) σ y además: t = σ τ /, ω = kθ / σ, c = c( k) / σ y c( k) = k ik/. En este caso, γ es un parámetro de aversión al riesgo, y se restringe a γ 1. Ésta es otra manera de representar la prima al riesgo por volatilidad, la cual supone neutralidad al riesgo y proporciona una expresión de la prima al riesgo ajustada por volatilidad dada por λ, con λ proporcional a la varianza, λ( t, St, vt ) = λv. En la gráfica 3 se muestra una superficie de precios de opciones de compra y en la gráfica 4 una superficie de precios de opciones de venta, los precios de las opciones se calculan con la transformada fundamental de Lewis y parámetros dados por: GRÁFICA 3. Superficie de precios opciones de compra con el modelo de Heston 40 C, (S, τ) τ S
15 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 957 GRÁFICA 4. Superficie de precios opciones de venta con el modelo de Heston P (S, τ) S τ CUADRO 4. Parámetros empleados para calcular precios de opciones del modelo de Heston con la transformada de Lewis v κ θ λ σ ρ K r δ k i γ El plazo al vencimiento es desde T t = τ = 0. 1,, 1 y el precio del subyacente varía dentro del rango: S t = 50,, 150. IV. ESTIMACIÓN DE PARÁMETROS DEL MODELO DE HESTON CON FUNCIONES DE PÉRDIDA CUADRÁTICAS Si se estiman los parámetros de un modelo de volatilidad estocástica mediante series históricas de rendimientos de los activos, no todos los parámetros serían útiles para efectos de valuación de derivados, ya que los parámetros estimados estarían bajo una medida de probabilidad verdadera, mientras que los negociadores de derivados ajustan tales parámetros para la determinación de precios de derivados. En particular, para los modelos de volatilidad estocástica el coeficiente de la varianza es una modificación del valor verdadero, lo cual es resultado del supuesto de que la prima de riesgo de volatilidad es independiente del precio del subyacente y del tiempo,
16 958 EL TRIMESTRE ECONÓMICO además de ser proporcional a la volatilidad, es decir: λ( t, v, S) = λv. Para recuperar tal prima de riesgo, es necesario consultar precios de algunos derivados que se negocien en el mercado. Por esa razón, en la industria y en la investigación (Bakshi, Cao y Chen, 1997) cada vez hay más preferencia por utilizar únicamente precios de derivados y calibrar un modelo en base a un conjunto de opciones líquidas. Un procedimiento estándar es el siguiente: una mesa de derivados planea vender una opción exótica y a la vez cubrir su exposición, además se supone que se emplea un modelo de volatilidad estocástica. La primera etapa consiste en obtener un conjunto de precios de mercado de opciones europeas líquidas, para después calibrar el modelo. Los parámetros calibrados son los neutrales al riesgo, y por lo tanto se pueden utilizar sin modificaciones para valuar y cubrir la opción exótica. En cierto sentido, es una generalización de la metodología para obtener las volatilidades implícitas bajo el modelo de Black, Scholes y Merton, el propósito de la calibración es valuar la opción exótica de tal manera que sea consistente con los precios de mercado de las europeas. Si el modelo calibrado genera precios consistentes con el mercado, entonces los parámetros estimados deberían ser estacionarios a través del tiempo, y su variabilidad se debe sólo a errores de medición. En la práctica, por supuesto, esto no sucede así, y se tiene que recalibrar los parámetros diariamente o con mayor frecuencia si es necesario. Para la calibración se debe minimizar una cierta medida de distancia entre los precios de mercado y los precios teóricos dados por el modelo. Es decir, se determinan parámetros tales que el error entre los precios de mercado y los precios del modelo teórico sea el mínimo posible, tal error es medido por una función de pérdida. Supongamos que se cuenta con un conjunto N de precios de mercado de opciones denotados por Pi ( i = 1,,, N ) y que los precios del modelo dependen de un conjunto de parámetros Θ { ρ, κ, θ, σ, v( 0 ), k i, γ } que en este caso son los de la transformada fundamental de Lewis. De acuerdo con Bakshi et al. (1997) se pueden construir tres funciones de pérdida: iii) Función de pérdida del error cuadrático medio: $FEM; iii) Función de pérdida relativa del error cuadrático medio: %FEM; iii) Función de pérdida del error cuadrático medio de volatilidad implícita: FEMVI. Veáse Heston (1993), p. 39.
17 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 959 La función de pérdida del error cuadrático medio es el promedio de los cuadrados de los errores estimados: $FEM Θ N 1 ( ) = ( Θ) N e i i = 1 (5) donde ei ( Θ) = Pi Pi ( Θ) son los errores de estimación para i = 1,,, N. La función de pérdida relativa del error cuadrático medio está definida por: % FEM Θ ( ) = 1 N N i = 1 ei ( Θ) P i (6) La función de pérdida del error cuadrático medio de volatilidad implícita se define por: FEMVI Θ N 1 ( ) = N i = 1 ( σ i σ i ( Θ) ) (7) Con el propósito de encontrar los parámetros que minimicen las funciones en (5) y (6) se plantean como: y RFEM = e i ( Θ) $ Min Θ N 1 N i = 1 (8) % RFEM = Min Θ 1 N N i = 1 ei ( Θ) P i (9) A diferencia de la raíz cuadrada de la función de pérdida del error cuadrático medio $RFEM que minimiza el promedio de la raíz cuadrada de la diferencia entre precios de mercado y precios del modelo teórico, la raíz función de pérdida relativa del error cuadrático medio $RFEM en (8) minimiza el porcentaje o diferencia relativa entre tales precios, Bakshi et al. (1997) y Heston y Nandi (000) estiman parámetros con este enfoque. $RFEM y $RFEM arrojan parámetros que minimizan la distancia entre precios de mercado y precios del modelo teórico. También se pueden determinar parámetros que mini-
18 960 EL TRIMESTRE ECONÓMICO micen la distancia entre volatilidades implícitas obtenidas a partir de precios de mercado y las volatilidades implícitas obtenidas a partir de precios del modelo teórico, por medio de la raíz de la función de pérdida de volatilidad implícita del error cuadrático medio RFEMIV definida por: RFEMIV = N 1 Min ( σ i σ i ( Θ) ) (30) Θ N i = 1 En la expresión anterior σ i es la volatilidad implícita de Black, Scholes y Merton, que se obtiene al invertir la fórmula de BSM e igualarla a precios de mercado, y σ i ( Θ ) es la volatilidad implícita de BSM obtenida al invertir la fórmula de BSM e igualarla a precios obtenidos con el modelo teórico. Los parámetros estimados obtenidos de la función de pérdida en (30) pueden utilizarse para modelar algunas propiedades de la distribución de los rendimientos del activo subyacente, ya que la forma de la curva de volatilidad implícita representa la distribución de rendimientos del activo subyacente en estudio. Una mueca de volatilidad (volatility smirk) implica un sesgo o asimetría en la distribución, mientras que una sonrisa de volatilidad (volatility smile) implica curtosis. Cada una de las funciones de pérdida descritas asigna una ponderación diferente a las opciones. La raíz de la función de pérdida del error cuadrático medio $RFEM asigna más peso a opciones dentro-del-dinero, lo cual se debe a que dichas opciones son más caras. Cualquier error en la estimación dado por una diferencia entre los precios de mercado y los precios ajustados es causado por estas opciones, la raíz de la función de pérdida del error cuadrático medio $RFEM tenderá a producir parámetros que conducen a errores pequeños de valuación para opciones dentro-del-dinero. Por su parte, la raíz de la función de pérdida relativa del error cuadrático medio %RFEM asigna más peso a opciones muy fuera del dinero, debido a que estas opciones tienen poco valor. Por último la raíz de la función de pérdida del error cuadrático medio de volatilidad implícita RFEMVI asigna una ponderación similar a todas las opciones. V. CALIBRACIÓN Y ANÁLISIS DE RESULTADOS Con el propósito de aplicar la metodología descrita en la sección anterior, se tomaron los datos del Boletín del Resumen del Mercado de Opciones
19 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 961 (BRMO) del día 5/10/013 de MexDer. Este resumen contiene las opciones que tienen contratos abiertos, es decir, que tienen operación y cierta liquidez. En este trabajo se consideran opciones europeas sobre acciones de América Móvil, S.A.B. de C.V. serie L (AMX-L), Wal-Mart de México, S.A.B. de C.V. serie V (WALMEX-V) y Grupo México, S.A.B. de C.V. serie B (GMEXICO-B) con un plazo al vencimiento de 56 días; asimismo, se obtuvieron del proveedor de precios (vendor) la curva TIIE8-IRS para la tasa libre de riesgo, las volatilidades implícitas y la delta de todas las opciones negociadas en ese día. 1. Calibración para opciones sobre AMX-L El cuadro 5 muestra datos relevantes para la calibración de los parámetros para opciones sobre AMX-L: Fecha actual t Fecha de vencimiento T CUADRO 5. Parámetros relevantes Plazo al vencimiento t = T - t Tasa libre de riesgo r Precio spot AMX-L S t 5/10/013 0/1/ El cuadro 6 muestra un resumen de los valores de las funciones de pérdida y los valores estimados de los parámetros del modelo de Heston para cada función de pérdida. En la calibración 3 se utilizó la transformada fundamental de Lewis. CUADRO 6. Resumen de las funciones de pérdida con los correspondientes valores de los parámetros estimados del modelo de Heston con la transformada de Lewis $RFEM %RFEM RFEMVI Valor de la función de pérdida Rho ( ρ) Kappa ( κ ) Theta ( θ) Volatilidad de la varianza ( σ ) Varianza actual ( V 0 ) Parte imaginaria de k( k i ) Gamma ( γ ) Para la calibración se utilizó el algoritmo de Nelder-Mead, descrito en Lagarias, Reeds, Wright y Wright (1999).
20 CUADRO 7. Precios estimados con el modelo de Heston con las funciones de pérdida y volatilidades implícitas Tipo de opción Precio de ejercicio Moneyness (K/S) Precio de cierre Vol. imp. B.S. $RFEM-V.I. %RFEM-V.I. RFEMVI-V.I. Vol. imp. Precios σ vi Precios σ vi Precios σ vi mdo. Put Put Call Call Call Call Call
21 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 963 La interpretación de los valores de las funciones de pérdida es la siguiente. El valor de $RFEM es de , el cual corresponde a un error de aproximadamente 5.9 centavos, en promedio, entre los precios de mercado y los precios producidos por el modelo de Heston. Por su parte, el valor de %RFEM es de , que corresponde a un error de aproximadamente 5.53% en promedio entre los precios de mercado y los precios producidos por el modelo de Heston. Por último, el valor de RFEMIV es de corresponde a una diferencia de.53% entre las volatilidades implícitas obtenidas de los precios de mercado y las volatilidades implícitas obtenidas con el modelo de Heston. El cuadro 7 muestra los precios de cierre de opciones de compra y venta AMX-L obtenidos del boletín, la volatilidad implícita calculada con el método de bisección y los correspondientes precios estimados con el modelo de Heston junto con las volatilidades implícitas y los valores de las funciones de pérdida, además de las volatilidades implícitas que reporta el boletín. En las gráficas 5 y 6 se muestran los resultados obtenidos en el cuadro 7. Obsérvese que los valores estimados por $RFEM y %RFEM para opciones de compra producen volatilidades implícitas que en su mayoría están alejadas de las volatilidades del mercado. Por su parte, los valores estimados por RFEMVI para opciones de compra producen volatilidades implícitas que están GRÁFICA 5. Volatilidades implícitas de opciones de compra obtenidas de las funciones de pérdida 0.5 Volatilidad implícita Calls Moneyness (K/S) Vol. imp. B.S. $RFEM-V.I. %RFEM-V.I. RFEMVI-V.I. V.I.M.
22 964 EL TRIMESTRE ECONÓMICO 0.37 GRÁFICA 6. Volatilidades implícitas de opciones de venta obtenidas de las funciones de pérdida 0.36 Volatilidad implícita puts Moneyness (K/S) Vol. imp. B.S. $RFEM-V.I. %RFEM-V.I. RFEMVI-V.I. V.I.M. razonablemente cerca de las volatilidades del mercado en todos los niveles de moneyness. Para opciones de venta, el mejor ajuste corresponde a %RFEM. En las gráficas 7 y 8 se muestran las comparaciones entre los precios de mercado teóricos a través de las funciones de pérdida. Obsérvese que los valores estimados por RFEMVI para opciones de compra son muy cercanos a los publicados por el boletín de MexDer. Para opciones de venta, los valores estimados de $RFEM y RFEMVI son mayores a los publicados en el boletín, lo anterior se debe a que para opciones de compra se cuenta con cinco precios, de los cuales tres son de opciones que están dentro-del-dinero y los dos precios restantes son de opciones fuera-del-dinero. Para opciones de venta sólo hay dos precios de mercado y ambos están fuera-del-dinero. Una vez que se han calibrado los parámetros del modelo es deseable examinar la eficiencia de la calibración con las tres funciones de pérdida. Para ello se determinan los precios de todas las opciones de compra y de venta que forman parte del boletín de opciones y sus volatilidades implícitas con los parámetros estimados, pero con la particularidad de que, para el caso de %RFEM, se hace la valuación sólo para opciones cuyo precio de liquidación es mayor a $0.50, como lo sugiere Bakshi et al. (1997). Los resultados se muestran en el cuadro 8.
23 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 965 GRÁFICA 7. Comparación entre precios estimados de opciones de compra y precios de mercado 1.4 Precios ajustados Calls Moneyness (K/S) Precios-$RFEM Precios-%RFEM Precios-RFEMVI Precio de cierre GRÁFICA 8. Comparación entre precios estimados de opciones de venta y precios de mercado 0.40 Precios ajustados Puts Moneyness (K/S) Precios-$RFEM Precios-%RFEM Precios-RFEMVI Precio de cierre
24 966 EL TRIMESTRE ECONÓMICO CUADRO 8. Resumen de las funciones de pérdida con los correspondientes valores ajustados de los parámetros estimados del modelo de Heston con la transformada de Lewis $RFEM %RFEM RFEMVI Valor de la función de pérdida Rho ( ρ) Kappa ( κ ) Theta ( θ) Volatilidad de la varianza ( σ ) Varianza actual ( V 0 ) Parte imaginaria de k( k i ) Gamma ( γ ) En el cuadro anterior se observa que el valor de $RFEM es de , lo que corresponde a un error de aproximadamente 5 centavos en promedio entre los precios de mercado y los precios producidos por el modelo de Heston. Por su parte, el valor de %RFEM es de 0.047, lo que corresponde a un error de aproximadamente 4.7% en promedio entre los precios de mercado y los precios producidos por el modelo de Heston. Por último, el valor de RFEMIV es de , el cual corresponde a una diferencia de 30.5% entre las volatilidades implícitas obtenidas de los precios de mercado y las volatilidades implícitas obtenidas del modelo de Heston. Los cuadros 9 y 10 muestran, respectivamente, los precios de cierre de opciones de compra y de venta de AMX-L obtenidos del boletín para cada precio de ejercicio reportado, la volatilidad implícita calculada con el método de bisección y los correspondientes precios estimados con el modelo de Heston junto con las volatilidades implícitas y los valores de las funciones de pérdida, además de las volatilidades implícitas provenientes del boletín. En las gráficas 9 y 10 se muestran los resultados obtenidos en los cuadros 9 y 10. Obsérvese que, para opciones de compra, los valores estimados por $RFEM, %RFEM y RFEMIV producen volatilidades implícitas que están alejadas de las volatilidades implícitas del mercado en todos los niveles de moneyness. Para opciones de venta y fuera del dinero, el mejor ajuste se obtiene con %RFEM. Por último, el parámetro de correlación resultó negativo en todos los casos, lo cual implica que la densidad del subyacente tiene sesgo negativo.
25 CUADRO 9. Precios estimados de opciones de compra con el modelo de Heston con funciones de pérdida para cada precio de ejercicio (K) y sus volatilidades implícitas, y las volatilidades implícitas de mercado Tipo de opción Precio de ejercicio Moneyness (K/S) Precio de cierre Vol. imp. B.S. $RFEM-V.I. %RFEM-V.I. RFEMVI-V.I. Vol. imp. Precios σ vi Precios σ vi Precios σ vi mdo. Call NA 3.14 NA 3.05 NA 3.14 NA Call NA.67 NA.59 NA.66 NA Call NA.13 NA.0 NA 0.10 Call NA Call Call Call Call Call Call Call Call Call Call Call Call NA: no aplica.
26 CUADRO 10. Precios estimados de opciones de venta con el modelo de Heston con funciones de pérdida para cada precio de ejercicio (K) y sus volatilidades implícitas, y las volatilidades implícitas de mercado Tipo de opción Precio de ejercicio Moneyness (K/S) Precio de cierre Vol. imp. B.S. $RFEM-V.I. %RFEM-V.I. RFEMVI-V.I. Vol. imp. Precios σ vi Precios σ vi Precios σ vi mdo. Put Put Put Put Put Put Put Put Put Put Put Put Put Put Put Put
27 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 969 GRÁFICA 9. Comparación entre volatilidades implícitas estimadas para opciones de compra y volatilidades implícitas de mercado Volatilidad implícita Calls Vol. imp. B.S. $RFEM-V.I. %RFEM-V.I. RFEMVI-V.I. V.I.M Moneyness (K/S) GRÁFICA 10. Comparación entre volatilidades implícitas estimadas para opciones de venta y volatilidades implícitas de mercado Volatilidad implícita Puts Vol. imp. B.S. $RFEM-V.I. %RFEM-V.I. RFEMVI-V.I. V.I.M Moneyness (K/S)
28 970 EL TRIMESTRE ECONÓMICO. Calibración para opciones sobre WALMEX-V El cuadro 11 muestra datos relevantes para la calibración de los parámetros para opciones sobre WALMEX-V: Fecha actual t Fecha de vencimiento T Cuadro 11. Parámetros relevantes Plazo al vencimiento t = T - t Tasa libre de riesgo r Precio spot WALMEX-V S t 5/10/013 0/1/ El cuadro 1 muestra un resumen de los valores de las funciones de pérdida y los valores estimados de los parámetros del modelo de Heston para cada función de pérdida. CUADRO 1. Resumen de las funciones de pérdida con los correspondientes valores de los parámetros estimados del modelo de Heston con la transformada de Lewis $RFEM %RFEM RFEMVI Valor de la función de pérdida Rho ( ρ) Kappa ( κ ) Theta ( θ) Volatilidad de la varianza ( σ ) Varianza actual ( V 0 ) Parte imaginaria de k( k i ) Gamma ( γ ) A continuación se proporciona la interpretación de los valores de las funciones de pérdida del cuadro 1. El valor de $RFEM es de , lo que corresponde a un error de aproximadamente 5 centavos en promedio entre los precios de mercado y los precios producidos por el modelo de Heston. Por su parte, el valor de %RFEM es de 0.046, lo que conduce a un error de aproximadamente 4.3%, en promedio, entre los precios de mercado y los precios producidos por el modelo de Heston. Por último, el valor de RFEMIV es de , el cual corresponde a una diferencia de 1.4% entre las volatilidades implícitas obtenidas de los precios de mercado y las volatilidades implícitas obtenidas con el modelo de Heston. El cuadro 13 muestra los precios de cierre de opciones de compra y venta de WALMEX-V obtenidos del BRMO, la volatilidad implícita calculada con
29 Tipo de opción VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 971 CUADRO 13. Precios estimados con el modelo de Heston con las funciones de pérdida y volatilidades implícitas Precio de ejercicio Moneyness (K/S) Precio de cierre Vol. imp. B.S. $RFEM-V.I. %RFEM-V.I. RFEMVI-V.I. Vol. imp. Precios σ vi Precios σ vi Precios σ vi mdo. Put Put Put Put Call Call Call Call Call Call Call el método de bisección, y los correspondientes precios estimados con el modelo de Heston junto con las volatilidades implícitas y los valores de las funciones de pérdida, además de las volatilidades implícitas que reporta el boletín. Los resultados obtenidos en el cuadro 13 se muestran en las gráficas 11 y 1. Obsérvese que, para opciones de compra, los valores estimados de %RFEM producen volatilidades implícitas que están cerca de las volatilidades implícitas del mercado en todos los niveles de moneyness, mientras que los valores estimados por $RFEM y RFEMVI producen volatilidades implícitas que están alejadas de las volatilidades implícitas del mercado. Para opciones de venta en-el-dinero, el ajuste más próximo es para $RFEM y RFEMVI. Para opciones de venta muy dentro-del-dinero, las volatilidades implícitas generadas por %RFEM son las más cercanas a las del mercado. En las gráficas 13 y 14 se presentan los precios de mercado en comparación con los obtenidos teóricamente y, en cada caso, se muestran las funciones de pérdida. Obsérvese que para opciones de compra los valores estimados por %RFEM son los más cercanos a los publicados por el boletín de Mex- Der. Para opciones de venta, los valores estimados para las tres funciones, en general, producen precios muy cercanos a los publicados en el boletín. Cabe mencionar que en el caso de opciones de compra todas están fueradel-dinero y de los cuatro precios de opciones de venta tres están dentro-deldinero.
30 97 EL TRIMESTRE ECONÓMICO GRÁFICA 11. Volatilidades implícitas de opciones de compra obtenidas de las funciones de pérdida Volatilidad implícita Calls Vol. imp. B.S. $RFEM-V.I. %RFEM-V.I. RFEMVI-V.I. V.I.M Moneyness (K/S) GRÁFICA 1. Volatilidades implícitas de opciones de venta obtenidas de las funciones de pérdida Volatilidad implícita Puts Vol. imp. B.S. $RFEM-V.I. %RFEM-V.I. RFEMVI-V.I. V.I.M Moneyness (K/S)
31 VALUACIÓN DE OPCIONES EUROPEAS SOBRE AMX-L, WALMEX Y GMEXICO-B 973 GRÁFICA 13. Comparación entre precios estimados de opciones de compra y precios de mercado Precios ajustados Calls Precios-$RFEM Precios-%RFEM Precios-RFEMVI Precio de cierre Moneyness (K/S) GRÁFICA 14. Comparación entre precios estimados de opciones de venta y precios de mercado Precios-$RFEM Precios-%RFEM Precios-RFEMVI Precio de cierre Precios ajustados Puts Moneyness (K/S)
32 974 EL TRIMESTRE ECONÓMICO Con el propósito de analizar la eficiencia de la calibración de %RFEM se hace la valuación pero sólo para opciones cuyo precio de liquidación es mayor a $0.50, esto con el fin de reducir las diferencias en precios al excluir opciones con primas con poco valor. En el boletín se verifica que para el caso de las opciones de compra todas están fuera-del-dinero y para opciones de venta tres de las cuatro están dentro-del-dinero. Los resultados se muestran a continuación: CUADRO 14. Resumen de las funciones de pérdida con los correspcondientes valores ajustados de los parámetros estimados del modelo de Heston con la transformada de Lewis $RFEM %RFEM RFEMVI Valor de la función de pérdida Rho ( ρ) Kappa ( κ ) Theta ( θ) Volatilidad de la varianza ( σ ) Varianza actual ( V 0 ) Parte imaginaria de k( k i ) Gamma ( γ ) En este caso, el valor de $RFEM es de 0.103, lo que corresponde a un error de aproximadamente $1, en promedio, entre los precios de mercado y los precios producidos por el modelo de Heston. El valor de %RFEM es de , lo que corresponde a un error de aproximadamente 4.4%, en promedio, entre los precios de mercado y los precios producidos por el modelo de Heston. Por último, el valor de RFEMIV es de 0.391, el cual corresponde a una diferencia de 39% entre las volatilidades implícitas obtenidas de los precios de mercado y las volatilidades implícitas obtenidas del modelo de Heston. Los cuadros 15 y 16 presentan, respectivamente, los precios de cierre de opciones de compra y de venta de WALMEX-V obtenidos del boletín para cada precio de ejercicio reportado, la volatilidad implícita calculada con el método de bisección y los correspondientes precios estimados con el modelo de Heston junto con las volatilidades implícitas y los valores de cada función de pérdida, además de las volatilidades implícitas que reporta el boletín. En las gráficas 15 y 16 se examinan los resultados de los cuadros 15 y 16. Nótese que, para opciones de compra, los valores estimados por $RFEM,
Ingeniería en Instrumentos Derivados. Opciones 1
 Ingeniería en Instrumentos Derivados Opciones 1 Alvaro Díaz Valenzuela Dottore in Matematica Magíster en Ciencias de la Ingeniería 12 de noviembre de 2010 Índice Opciones Definiciones Estrategias con Opciones
Ingeniería en Instrumentos Derivados Opciones 1 Alvaro Díaz Valenzuela Dottore in Matematica Magíster en Ciencias de la Ingeniería 12 de noviembre de 2010 Índice Opciones Definiciones Estrategias con Opciones
Cálculo estocástico: una introducción
 Departamento de Matemática y Estadística Universidad Politécnica de Cartagena Murcia, Marzo 2010 Guión 1 Movimiento Browniano Reseñas históricas Modelización y propiedades básicas. 2 Integrales estocásticas
Departamento de Matemática y Estadística Universidad Politécnica de Cartagena Murcia, Marzo 2010 Guión 1 Movimiento Browniano Reseñas históricas Modelización y propiedades básicas. 2 Integrales estocásticas
Deducción de las fórmulas de Black-Scholes mediante valor esperado del pago futuro
 Deducción de las fórmulas de Black-Scholes mediante valor esperado del pago futuro Alexis Sánchez Tello de Meneses 4 Septiembre 04 Abstract Se desarrollará a partir del modelo de evolución log-normal para
Deducción de las fórmulas de Black-Scholes mediante valor esperado del pago futuro Alexis Sánchez Tello de Meneses 4 Septiembre 04 Abstract Se desarrollará a partir del modelo de evolución log-normal para
ESTIMACIÓN DE LOS PARÁMETROS DEL MODELO DE HESTON. UNA APLICACIÓN AL ÍNDICE IBEX 35
 Revista Electrónica de Comunicaciones y Trabajos de ASEPUMA. Rect@. Volumen 11. Páginas 197 214 ESTIMACIÓN DE LOS PARÁMETROS DEL MODELO DE HESTON. UNA APLICACIÓN AL ÍNDICE IBEX 35 JOSÉ LUIS CRESPO ESPERT
Revista Electrónica de Comunicaciones y Trabajos de ASEPUMA. Rect@. Volumen 11. Páginas 197 214 ESTIMACIÓN DE LOS PARÁMETROS DEL MODELO DE HESTON. UNA APLICACIÓN AL ÍNDICE IBEX 35 JOSÉ LUIS CRESPO ESPERT
Replicación aproximada de derivados de electricidad en mercados incompletos
 Replicación aproximada de derivados de electricidad en mercados incompletos Seminario DERIVEX Alvaro J. Riascos Villegas Universidad de los Andes y Quantil Octubre 24 de 2012 Alvaro J. Riascos Villegas
Replicación aproximada de derivados de electricidad en mercados incompletos Seminario DERIVEX Alvaro J. Riascos Villegas Universidad de los Andes y Quantil Octubre 24 de 2012 Alvaro J. Riascos Villegas
METODOS ESTADÍSTICOS
 METODOS ESTADÍSTICOS Introducción. Uno de los objetivos de la asignatura de Hidrología, es mostrar a los alumnos, las herramientas de cálculo utilizadas en Hidrología Aplicada para diseño de Obras Hidráulicas.
METODOS ESTADÍSTICOS Introducción. Uno de los objetivos de la asignatura de Hidrología, es mostrar a los alumnos, las herramientas de cálculo utilizadas en Hidrología Aplicada para diseño de Obras Hidráulicas.
Caracterización de la incertidumbre del precio futuro del cobre
 USc/lb Caracterización de la incertidumbre del precio futuro del cobre La incertidumbre en un modelo de programación estocástica debe tener la estructura de árbol de escenarios, como se muestra en la Figura
USc/lb Caracterización de la incertidumbre del precio futuro del cobre La incertidumbre en un modelo de programación estocástica debe tener la estructura de árbol de escenarios, como se muestra en la Figura
Modelo de cambios de régimen en el traspaso de las tasas de interés
 Modelo de cambios de régimen en el traspaso de las tasas de interés (Regime switching in interest rate pass-through and dynamic bank modelling with risks) Alberto Humala XXIII Encuentro de Economistas
Modelo de cambios de régimen en el traspaso de las tasas de interés (Regime switching in interest rate pass-through and dynamic bank modelling with risks) Alberto Humala XXIII Encuentro de Economistas
Procesos polinomiales y sus aplicaciones en matemáticas financieras 1/22
 Procesos polinomiales y sus aplicaciones en matemáticas financieras II-ConMate-P Sergio Pulido LaMME ENSIIE/ Université d Evry Val d Essonne 15 de abril, 2016 Procesos polinomiales y sus aplicaciones en
Procesos polinomiales y sus aplicaciones en matemáticas financieras II-ConMate-P Sergio Pulido LaMME ENSIIE/ Université d Evry Val d Essonne 15 de abril, 2016 Procesos polinomiales y sus aplicaciones en
Introducción a modelos matemáticos aplicados a finanzas cuantitativas
 Introducción a modelos matemáticos aplicados a finanzas cuantitativas Clase 3: Opciones americanas. La fórmula de Black-Scholes Patricia Kisbye 12, 14 y 15 de diciembre de 2017 Encuentro de Estudiantes
Introducción a modelos matemáticos aplicados a finanzas cuantitativas Clase 3: Opciones americanas. La fórmula de Black-Scholes Patricia Kisbye 12, 14 y 15 de diciembre de 2017 Encuentro de Estudiantes
Estimación de variables no observables para la economía peruana
 Estimación de variables no observables para la economía peruana XXX Encuentro de Investigación del BCRP Ismael Ignacio Mendoza Mogollón imendoza@mef.gob.pe Octubre 2012 XXX Encuentro de Economistas (Institute)
Estimación de variables no observables para la economía peruana XXX Encuentro de Investigación del BCRP Ismael Ignacio Mendoza Mogollón imendoza@mef.gob.pe Octubre 2012 XXX Encuentro de Economistas (Institute)
Valoración de opciones mediante el modelo de Black-Scholes
 Valoración de opciones mediante el modelo de Black-Scholes José Luis Alcaraz Aunión 3 de diciembre de 2010 Resumen Este trabajo presenta la valoración de opciones usando el modelo de Black- Scholes (BS).
Valoración de opciones mediante el modelo de Black-Scholes José Luis Alcaraz Aunión 3 de diciembre de 2010 Resumen Este trabajo presenta la valoración de opciones usando el modelo de Black- Scholes (BS).
UNIVERSIDAD AUTO NOMA METROPOLITANA
 UNIVERSIDAD AUTO NOMA METROPOLITANA UNIDAD IZTAPALAPA DIVISIO N DE CIENCIAS BA SICAS E INGENIERI A DEPARTAMENTO DE MATEMA TICAS POSGRADO EN MATEMA TICAS Robustez de la distribucio n del precio de un activo
UNIVERSIDAD AUTO NOMA METROPOLITANA UNIDAD IZTAPALAPA DIVISIO N DE CIENCIAS BA SICAS E INGENIERI A DEPARTAMENTO DE MATEMA TICAS POSGRADO EN MATEMA TICAS Robustez de la distribucio n del precio de un activo
Estocástica: FINANZAS Y RIESGO
 Modelación de Medidas y Norma en finanzas Modelación de Medidas y Norma en finanzas Estocástica: Gauge Theory on Financial Modeling Guillermo Sierra Juárez* Fecha de recepción: 6 de enero de 2015 Fecha
Modelación de Medidas y Norma en finanzas Modelación de Medidas y Norma en finanzas Estocástica: Gauge Theory on Financial Modeling Guillermo Sierra Juárez* Fecha de recepción: 6 de enero de 2015 Fecha
Algunas Distribuciones Continuas de Probabilidad. UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
Algunas Distribuciones Continuas de Probabilidad UCR ECCI CI-1352 Probabilidad y Estadística Prof. M.Sc. Kryscia Daviana Ramírez Benavides Introducción El comportamiento de una variable aleatoria queda
Secuencias Aleatorias
 Caminantes aleatorios. Secuencias Aleatorias Contenidos. Secuencias aleatorias. Caminantes aleatorios. Movimiento Browniano. La hipótesis de eficiencia de los mercados implica que la cotización de un título
Caminantes aleatorios. Secuencias Aleatorias Contenidos. Secuencias aleatorias. Caminantes aleatorios. Movimiento Browniano. La hipótesis de eficiencia de los mercados implica que la cotización de un título
Aplicaciones de Cálculo Estocástico
 Aplicaciones de Cálculo Estocástico en la gestión de productos financieros Manuel Menéndez Sánchez (mmenensa@banesto.es) Jueves, 11 de Marzo de 2010 Índice 1. Introducción...3 1.1 Productos financieros...4
Aplicaciones de Cálculo Estocástico en la gestión de productos financieros Manuel Menéndez Sánchez (mmenensa@banesto.es) Jueves, 11 de Marzo de 2010 Índice 1. Introducción...3 1.1 Productos financieros...4
AVISO A LOS SOCIOS LIQUIDADORES, OPERADORES Y PÚBLICO EN GENERAL CÁLCULO DEL PRECIO O PRIMA DE LIQUIDACIÓN DIARIA PARA OPCIONES.
 México, D.F., a 10 de marzo de 2008. AVISO A LOS SOCIOS LIQUIDADORES, OPERADORES Y PÚBLICO EN GENERAL CÁLCULO DEL PRECIO O PRIMA DE LIQUIDACIÓN DIARIA PARA OPCIONES. A continuación se da a conocer el nuevo
México, D.F., a 10 de marzo de 2008. AVISO A LOS SOCIOS LIQUIDADORES, OPERADORES Y PÚBLICO EN GENERAL CÁLCULO DEL PRECIO O PRIMA DE LIQUIDACIÓN DIARIA PARA OPCIONES. A continuación se da a conocer el nuevo
Valuación de opciones asiáticas versus opciones europeas con tasa de interés estocástica
 Disponible en www.sciencedirect.com www.cya.unam.mx/index.php/cya Contaduría y Administración 61 (2016) 629 648 Valuación de opciones asiáticas versus opciones europeas con tasa de interés estocástica
Disponible en www.sciencedirect.com www.cya.unam.mx/index.php/cya Contaduría y Administración 61 (2016) 629 648 Valuación de opciones asiáticas versus opciones europeas con tasa de interés estocástica
Superficies de volatilidad: Evidencia empírica del cálculo de la volatilidad implícita de la opción sobre el ETF QQQ
 Superficies de volatilidad: Evidencia empírica del cálculo de la volatilidad implícita de la opción sobre el ETF QQQ Luis Gonzalo Reyes Meza* Pablo Santin Filloy** Fecha de recepción: 27 de junio de 2011
Superficies de volatilidad: Evidencia empírica del cálculo de la volatilidad implícita de la opción sobre el ETF QQQ Luis Gonzalo Reyes Meza* Pablo Santin Filloy** Fecha de recepción: 27 de junio de 2011
PASEO ALEATORIO. MOVIMIENTO BROWNIANO
 PASEO ALEATORIO. MOVIMIENTO BROWNIANO Jorge Estévez Grupo ER El movimiento browniano es el movimiento aleatorio que se observa en algunas partículas microscópicas que se hallan en un medio fluido (por
PASEO ALEATORIO. MOVIMIENTO BROWNIANO Jorge Estévez Grupo ER El movimiento browniano es el movimiento aleatorio que se observa en algunas partículas microscópicas que se hallan en un medio fluido (por
Procesos de Lévy y transformada de Fourier aplicados a la valoración de opciones financieras
 Procesos de Lévy y transformada de Fourier aplicados a la valoración de opciones financieras John Freddy Moreno Trujillo* Docente investigador Universidad Externado de Colombia Magister en matemática aplicada.
Procesos de Lévy y transformada de Fourier aplicados a la valoración de opciones financieras John Freddy Moreno Trujillo* Docente investigador Universidad Externado de Colombia Magister en matemática aplicada.
Tema1. Modelo Lineal General.
 Tema1. Modelo Lineal General. 1. Si X = (X 1, X 2, X 3, X 4 ) t tiene distribución normal con vector de medias µ = (2, 1, 1, 3) t y matriz de covarianzas 1 0 1 1 V = 0 2 1 1 1 1 3 0 1 1 0 2 Halla: a) La
Tema1. Modelo Lineal General. 1. Si X = (X 1, X 2, X 3, X 4 ) t tiene distribución normal con vector de medias µ = (2, 1, 1, 3) t y matriz de covarianzas 1 0 1 1 V = 0 2 1 1 1 1 3 0 1 1 0 2 Halla: a) La
Tema 3: VARIABLE ALEATORIA BIDIMENSIONAL
 Tema 3: VARIABLE ALEATORIA BIDIMENSIONAL Carlos Alberola López Lab. Procesado de Imagen, ETSI Telecomunicación Despacho 2D014 caralb@tel.uva.es, jcasasec@tel.uva.es, http://www.lpi.tel.uva.es/sar Concepto
Tema 3: VARIABLE ALEATORIA BIDIMENSIONAL Carlos Alberola López Lab. Procesado de Imagen, ETSI Telecomunicación Despacho 2D014 caralb@tel.uva.es, jcasasec@tel.uva.es, http://www.lpi.tel.uva.es/sar Concepto
TEMA 5. PROCESOS ESTOCÁSTICOS.-CURSO 2017/18
 TEMA 5. PROCESOS ESTOCÁSTICOS.-CURSO 2017/18 5.1. Concepto de proceso estocástico. Tipos de procesos. Realización de un proceso. 5.2. Características de un proceso estocástico. 5.3. Ejemplos de procesos
TEMA 5. PROCESOS ESTOCÁSTICOS.-CURSO 2017/18 5.1. Concepto de proceso estocástico. Tipos de procesos. Realización de un proceso. 5.2. Características de un proceso estocástico. 5.3. Ejemplos de procesos
Tópicos avanzados en Finanzas Empíricas I. Curso para Central Bankers - Febrero 2005 Centro de estudios Gerzensee - Suiza
 ópicos avanzados en Finanzas Empíricas I urso para entral Bankers - Febrero 005 entro de estudios Gerzensee - uiza emario ontenido informacional de productos derivados: distribuciones neutrales al riesgo
ópicos avanzados en Finanzas Empíricas I urso para entral Bankers - Febrero 005 entro de estudios Gerzensee - uiza emario ontenido informacional de productos derivados: distribuciones neutrales al riesgo
Teoría de las Finanzas Opciones Americanas. Introducción. Introducción(1/2) Introducción (1/2)
 Teoría de las Finanzas Opciones Americanas Introducción Alejandro Mosiño Universidad de Guanajuato v.2014 Introducción (1/2) Introducción(1/2) Como hemos visto, una opción es americana si el propietario
Teoría de las Finanzas Opciones Americanas Introducción Alejandro Mosiño Universidad de Guanajuato v.2014 Introducción (1/2) Introducción(1/2) Como hemos visto, una opción es americana si el propietario
MODELO MULTICOMMODITY CON VOLATILIDAD ESTOCÁSTICA - ESTIMACIÓN EN AUSENCIA DE PRECIOS DE OPCIONES
 PONTIFICIA UNIVERSIDAD CATOLICA DE CHILE ESCUELA DE INGENIERIA MODELO MULTICOMMODITY CON VOLATILIDAD ESTOCÁSTICA - ESTIMACIÓN EN AUSENCIA DE PRECIOS DE OPCIONES FEDERICO ANTONIO ALONSO SOTO-LUQUE Tesis
PONTIFICIA UNIVERSIDAD CATOLICA DE CHILE ESCUELA DE INGENIERIA MODELO MULTICOMMODITY CON VOLATILIDAD ESTOCÁSTICA - ESTIMACIÓN EN AUSENCIA DE PRECIOS DE OPCIONES FEDERICO ANTONIO ALONSO SOTO-LUQUE Tesis
Ejercicio 1. Ejercicio 2
 Guía de Ejercicios Ejercicio. Calcular los momentos de primer y segundo orden (media y varianza) de una variable aleatoria continua con distribución uniforme entre los límites a y b.. Sabiendo que la función
Guía de Ejercicios Ejercicio. Calcular los momentos de primer y segundo orden (media y varianza) de una variable aleatoria continua con distribución uniforme entre los límites a y b.. Sabiendo que la función
7. REGRESIÓN POR MÍNIMOS CUADRADOS: REGRESIÓN POLINOMIAL. Jorge Eduardo Ortiz Triviño
 7. REGRESIÓN POR MÍNIMOS CUADRADOS: REGRESIÓN POLINOMIAL Jorge Eduardo Ortiz Triviño jeortizt@unal.edu.co http:/www.docentes.unal.edu.co/jeortizt/ Introducción Los datos frecuentemente son dados para valores
7. REGRESIÓN POR MÍNIMOS CUADRADOS: REGRESIÓN POLINOMIAL Jorge Eduardo Ortiz Triviño jeortizt@unal.edu.co http:/www.docentes.unal.edu.co/jeortizt/ Introducción Los datos frecuentemente son dados para valores
Las Matemáticas para la Gestión del Riesgo en Carteras Financieras. Carteras compuestas por dos activos con correlaciones estadísticas arbitrarias
 Las Matemáticas para la Gestión del Riesgo en Carteras Financieras Carteras compuestas por dos activos con correlaciones estadísticas arbitrarias Apellidos, nombre Departamento Centro Cortés López, Juan
Las Matemáticas para la Gestión del Riesgo en Carteras Financieras Carteras compuestas por dos activos con correlaciones estadísticas arbitrarias Apellidos, nombre Departamento Centro Cortés López, Juan
Estadística Bayesiana y Riesgos
 Estadística Bayesiana y Riesgos Manuel Mendoza Ramírez Instituto Tecnológico Autónomo de México Seminario Aleatorio. Contribuciones Recientes de la Estadística a la Actuaría en México. ITAM. México, D.F.
Estadística Bayesiana y Riesgos Manuel Mendoza Ramírez Instituto Tecnológico Autónomo de México Seminario Aleatorio. Contribuciones Recientes de la Estadística a la Actuaría en México. ITAM. México, D.F.
Daniel Arrieta Rodríguez #"$#"$!# $#%$&
 !"# Daniel Arrieta Rodríguez #"$#"$!# $#%$& Introducción Hasta el crash de 1987 metodología BSM estándar de mercado en valoración de derivados. BSM explicaba cómo eliminar el riesgo asociado a las posiciones
!"# Daniel Arrieta Rodríguez #"$#"$!# $#%$& Introducción Hasta el crash de 1987 metodología BSM estándar de mercado en valoración de derivados. BSM explicaba cómo eliminar el riesgo asociado a las posiciones
Ecuaciones diferenciales estocásticas: ejemplos
 Ecuaciones diferenciales estocásticas: ejemplos Curso Procesos Estocásticos Programa de Doctorado de Sistemas Complejos Juan M.R. Parrondo Dept. Física Atómica, Molecular y Nuclear, Universidad Complutense
Ecuaciones diferenciales estocásticas: ejemplos Curso Procesos Estocásticos Programa de Doctorado de Sistemas Complejos Juan M.R. Parrondo Dept. Física Atómica, Molecular y Nuclear, Universidad Complutense
Concepto de VA bidimensional. Tema 3: VARIABLE ALEATORIA BIDIMENSIONAL. Concepto de VA bidimensional. Concepto de VA bidimensional
 Concepto de VA bidimensional Tema 3: VARIABLE ALEATORIA BIDIMENSIONAL Carlos Alberola López Lab. rocesado de Imagen, ETSI Telecomunicación Despacho D04 caralb@tel.uva.es, jcasasec@tel.uva.es, http://www.lpi.tel.uva.es/sar
Concepto de VA bidimensional Tema 3: VARIABLE ALEATORIA BIDIMENSIONAL Carlos Alberola López Lab. rocesado de Imagen, ETSI Telecomunicación Despacho D04 caralb@tel.uva.es, jcasasec@tel.uva.es, http://www.lpi.tel.uva.es/sar
LADE y DER-LADE. Primer evaluación parcial
 ECONOMETRÍA II CURSO 2007 LADE y DER-LADE Primer evaluación parcial 1. Considere la variable y t para el proceso y t = c + φ y t 1 + a t, donde a t es un ruido blanco. Suponga para φ los valores φ = 0.3
ECONOMETRÍA II CURSO 2007 LADE y DER-LADE Primer evaluación parcial 1. Considere la variable y t para el proceso y t = c + φ y t 1 + a t, donde a t es un ruido blanco. Suponga para φ los valores φ = 0.3
Valoración del riesgo de demanda. Expositor: Ec. Marcelo Pérez
 Valoración del riesgo de demanda Expositor: Ec. Marcelo Pérez México DF, Abril 2014 CONTENIDO Procesos estocásticos Valoración del riesgo de demanda Análisis de demanda 2 PROCESOS ESTOCÁSTICOS 5 0 Ruido
Valoración del riesgo de demanda Expositor: Ec. Marcelo Pérez México DF, Abril 2014 CONTENIDO Procesos estocásticos Valoración del riesgo de demanda Análisis de demanda 2 PROCESOS ESTOCÁSTICOS 5 0 Ruido
Econometría dinámica y financiera
 Econometría dinámica y financiera Introducción a la econometría financiera. Modelos ARCH Profesora: Dolores García Martos E-mail:mdgmarto@est-econ.uc3m.es Introducción Los modelos que hemos visto son lineales
Econometría dinámica y financiera Introducción a la econometría financiera. Modelos ARCH Profesora: Dolores García Martos E-mail:mdgmarto@est-econ.uc3m.es Introducción Los modelos que hemos visto son lineales
Estimación de Parámetros
 Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: p Estimación de Parámetros Prueba de Hipótesis Estimación
Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: p Estimación de Parámetros Prueba de Hipótesis Estimación
Rodolfo Oconitrillo Brenes. Riesgo de Mercado
 Rodolfo Oconitrillo Brenes Riesgo de Mercado Prob(Xt
Rodolfo Oconitrillo Brenes Riesgo de Mercado Prob(Xt
Instituto de Matemática Aplicada del Litoral
 PROBLEMAS DE BARRERA EN PROCESOS ESTOCÁSTICOS Ernesto Mordecki http://www.cmat.edu.uy/ mordecki mordecki@cmat.edu.uy Facultad de Ciencias Montevideo, Uruguay. Instituto de Matemática Aplicada del Litoral
PROBLEMAS DE BARRERA EN PROCESOS ESTOCÁSTICOS Ernesto Mordecki http://www.cmat.edu.uy/ mordecki mordecki@cmat.edu.uy Facultad de Ciencias Montevideo, Uruguay. Instituto de Matemática Aplicada del Litoral
Valuación de garantías del Estado a concesiones con ingresos estocásticos. Francisco Velásquez y Víctor del Carpio
 Valuación de garantías del Estado a concesiones con ingresos estocásticos Diciembre 14, 2006 Contenido Planteamiento del problema Alternativas de solución Aplicación Conclusiones y agenda pendiente 1 Planteamiento
Valuación de garantías del Estado a concesiones con ingresos estocásticos Diciembre 14, 2006 Contenido Planteamiento del problema Alternativas de solución Aplicación Conclusiones y agenda pendiente 1 Planteamiento
TESIS INSTITUTO POLITÉCNICO NACIONAL VALUACIÓN DE OPCIONES EUROPEAS CON EL MODELO DE VOLATILIDAD DE HESTON ESCUELA SUPERIOR DE ECONOMÍA
 INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE ECONOMÍA SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN VALUACIÓN DE OPCIONES EUROPEAS CON EL MODELO DE VOLATILIDAD DE HESTON TESIS QUE PARA OBTENER
INSTITUTO POLITÉCNICO NACIONAL ESCUELA SUPERIOR DE ECONOMÍA SECCIÓN DE ESTUDIOS DE POSGRADO E INVESTIGACIÓN VALUACIÓN DE OPCIONES EUROPEAS CON EL MODELO DE VOLATILIDAD DE HESTON TESIS QUE PARA OBTENER
Movimiento Browniano o proceso de Wiener
 1 Movimiento Browniano o proceso de Wiener Se dice que Z [ ] es un proceso de Wiener o movimiento Browniano si Z es una función definida en algún intervalo I = [, T ] (eventualmente puede ser T = + ),
1 Movimiento Browniano o proceso de Wiener Se dice que Z [ ] es un proceso de Wiener o movimiento Browniano si Z es una función definida en algún intervalo I = [, T ] (eventualmente puede ser T = + ),
Estimación de Parámetros. Jhon Jairo Padilla A., PhD.
 Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: Estimación de Parámetros Prueba de Hipótesis Estimación de
Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: Estimación de Parámetros Prueba de Hipótesis Estimación de
Estimación de Parámetros. Jhon Jairo Padilla A., PhD.
 Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: Estimación de Parámetros Prueba de Hipótesis Estimación de
Estimación de Parámetros Jhon Jairo Padilla A., PhD. Inferencia Estadística La inferencia estadística puede dividirse en dos áreas principales: Estimación de Parámetros Prueba de Hipótesis Estimación de
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS
 Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
Ejercicios de ECUACIONES DIFERENCIALES ORDINARIAS Grado en Matemáticas Curso 203-204 . Ecuaciones lineales con coeficientes constantes Ecuaciones de primer orden. Encontrar la solución de los siguientes
UNIVERSIDAD DE ATACAMA
 UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDAD GUÍA DE TRABAJO 3 Profesor: Hugo S. Salinas. Primer Semestre 2010 1. Sea X 1,..., X n una muestra aleatoria
UNIVERSIDAD DE ATACAMA FACULTAD DE INGENIERÍA / DEPARTAMENTO DE MATEMÁTICA ESTADÍSTICA Y PROBABILIDAD GUÍA DE TRABAJO 3 Profesor: Hugo S. Salinas. Primer Semestre 2010 1. Sea X 1,..., X n una muestra aleatoria
Part I. Momentos de una variable aleatoria. Esperanza y varianza. Modelos de Probabilidad. Mario Francisco. Esperanza de una variable aleatoria
 una una típica Part I Momentos. Esperanza y varianza Esperanza una una típica Definición Sea X una discreta que toma los valores x i con probabilidades p i. Supuesto que i x i p i
una una típica Part I Momentos. Esperanza y varianza Esperanza una una típica Definición Sea X una discreta que toma los valores x i con probabilidades p i. Supuesto que i x i p i
CIMPA Summer School on Inverse Problems on its Application ECUACIÓN DIFERENCIAL PARCIAL QUE ORIGINA EL MODELO DE BLACK - SCHOLES
 CIMPA Summer School on Inverse Problems on its Applications ECUACIÓN DIFERENCIAL PARCIAL QUE ORIGINA EL MODELO DE BLACK - SCHOLES 11 de enero de 2010 El modelo de Black -Scholes, permite la valoración
CIMPA Summer School on Inverse Problems on its Applications ECUACIÓN DIFERENCIAL PARCIAL QUE ORIGINA EL MODELO DE BLACK - SCHOLES 11 de enero de 2010 El modelo de Black -Scholes, permite la valoración
Econometría II Grado en finanzas y contabilidad
 Econometría II Grado en finanzas y contabilidad Procesos autorregresivos Profesora: Dolores García Martos E-mail:mdgmarto@est-econ.uc3m.es Este documento es un resumen/modificación de la documentación
Econometría II Grado en finanzas y contabilidad Procesos autorregresivos Profesora: Dolores García Martos E-mail:mdgmarto@est-econ.uc3m.es Este documento es un resumen/modificación de la documentación
5. Distribuciones de probabilidad multivariadas
 5. Distribuciones de probabilidad multivariadas Sobre un dado espacio muestral podemos definir diferentes variables aleatorias. Por ejemplo, en un experimento binomial, X 1 podría ser la variable binomial
5. Distribuciones de probabilidad multivariadas Sobre un dado espacio muestral podemos definir diferentes variables aleatorias. Por ejemplo, en un experimento binomial, X 1 podría ser la variable binomial
Descomposición Factorial de la In ación en Perú
 Descomposición Factorial de la n ación en Perú Alberto Humala (BCRP) Gabriel Rodríguez (BCRP) XXV Encuentro de Economistas Banco Central de Reserva del Perú 26-28/11/2008 Humala-Rodríguez () n ación 26-28/11/2008
Descomposición Factorial de la n ación en Perú Alberto Humala (BCRP) Gabriel Rodríguez (BCRP) XXV Encuentro de Economistas Banco Central de Reserva del Perú 26-28/11/2008 Humala-Rodríguez () n ación 26-28/11/2008
DEPARTAMENTO ECONOMIA FINANCIERA Y CONTABILIDAD I
 1 DEPARTAMENTO ECONOMIA FINANCIERA Y CONTABILIDAD I LICENCIATURA EN CIENCIAS ACTUARIALES Y FINANCIERAS Plan 2001 METODOS Y MODELOS DE LOS SISTEMAS DINAMICOS 4,5 Créditos Código 208 Profesores : Dr. Jose
1 DEPARTAMENTO ECONOMIA FINANCIERA Y CONTABILIDAD I LICENCIATURA EN CIENCIAS ACTUARIALES Y FINANCIERAS Plan 2001 METODOS Y MODELOS DE LOS SISTEMAS DINAMICOS 4,5 Créditos Código 208 Profesores : Dr. Jose
Capacitación Opciones Valoración
 Capacitación Opciones Valoración Juego de Probabilidades En el juego de la Roulette, el derecho de escoger un número cuesta $1. Existen 38 números disponibles, es decir 38 oportunidades. Si al jugar, mi
Capacitación Opciones Valoración Juego de Probabilidades En el juego de la Roulette, el derecho de escoger un número cuesta $1. Existen 38 números disponibles, es decir 38 oportunidades. Si al jugar, mi
Part I. Variables aleatorias unidimensionales. Estadística I. Mario Francisco. Definición de variable aleatoria. Variables aleatorias discretas
 Part I unidimensionales de s de s Definición Dado un experimento aleatorio, con espacio muestral asociado Ω, una es cualquier función, X, X : Ω R que asocia a cada suceso elemental un número real, verificando
Part I unidimensionales de s de s Definición Dado un experimento aleatorio, con espacio muestral asociado Ω, una es cualquier función, X, X : Ω R que asocia a cada suceso elemental un número real, verificando
ANALISIS DE FRECUENCIA EN HIDROLOGIA JULIAN DAVID ROJO HERNANDEZ
 ANALISIS DE FRECUENCIA EN HIDROLOGIA JULIAN DAVID ROJO HERNANDEZ Probabilidad - Período de retorno y riesgo La probabilidad de ocurrencia de un fenómeno en hidrología puede citarse de varias Formas: El
ANALISIS DE FRECUENCIA EN HIDROLOGIA JULIAN DAVID ROJO HERNANDEZ Probabilidad - Período de retorno y riesgo La probabilidad de ocurrencia de un fenómeno en hidrología puede citarse de varias Formas: El
Estadística. Tema 2. Variables Aleatorias Funciones de distribución y probabilidad Ejemplos distribuciones discretas y continuas
 Estadística Tema 2 Variables Aleatorias 21 Funciones de distribución y probabilidad 22 Ejemplos distribuciones discretas y continuas 23 Distribuciones conjuntas y marginales 24 Ejemplos distribuciones
Estadística Tema 2 Variables Aleatorias 21 Funciones de distribución y probabilidad 22 Ejemplos distribuciones discretas y continuas 23 Distribuciones conjuntas y marginales 24 Ejemplos distribuciones
Momentos de una variable
 Momentos de una variable Momentos respecto del origen Dada una variable aleatoria X con función de probabilidad o densidad f(x) podemos definir una función de X que sea igual a la variable elevada a un
Momentos de una variable Momentos respecto del origen Dada una variable aleatoria X con función de probabilidad o densidad f(x) podemos definir una función de X que sea igual a la variable elevada a un
AVISO A LOS SOCIOS LIQUIDADORES, OPERADORES Y PÚBLICO EN GENERAL CALCULO DEL PRECIO O PRIMA DE LIQUIDACIÓN DIARIA PARA OPCIONES.
 México, D.F., a 9 de junio de 2006. AVISO A LOS SOCIOS LIQUIDADORES, OPERADORES Y PÚBLICO EN GENERAL CALCULO DEL PRECIO O PRIMA DE LIQUIDACIÓN DIARIA PARA OPCIONES. A continuación se da a conocer el nuevo
México, D.F., a 9 de junio de 2006. AVISO A LOS SOCIOS LIQUIDADORES, OPERADORES Y PÚBLICO EN GENERAL CALCULO DEL PRECIO O PRIMA DE LIQUIDACIÓN DIARIA PARA OPCIONES. A continuación se da a conocer el nuevo
Selección de distribuciones de probabilidad
 Selección de distribuciones de probabilidad Georgina Flesia FaMAF 3 de mayo, 2012 Análisis estadístico de datos simulados Los sistemas reales tienen fuentes de aleatoriedad: Tipo de sistema Fabricación
Selección de distribuciones de probabilidad Georgina Flesia FaMAF 3 de mayo, 2012 Análisis estadístico de datos simulados Los sistemas reales tienen fuentes de aleatoriedad: Tipo de sistema Fabricación
Conceptos de Probabilidad y estadística. Jhon Jairo Padilla A., PhD
 Conceptos de Probabilidad y estadística Jhon Jairo Padilla A., PhD Introducción La ingeniería de tráfico está soportada sobre conceptos de probabilidad y estadística como: Probabilidad Variable aleatoria
Conceptos de Probabilidad y estadística Jhon Jairo Padilla A., PhD Introducción La ingeniería de tráfico está soportada sobre conceptos de probabilidad y estadística como: Probabilidad Variable aleatoria
Licenciatura en Actuaría PROGRAMA DE ESTUDIO
 PROGRAMA DE ESTUDIO Productos Financieros Derivados II Programa Educativo: Área de Formación : Licenciatura en Actuaría Transversal Horas teóricas: 3 Horas prácticas: 2 Total de Horas: 5 Total de créditos:
PROGRAMA DE ESTUDIO Productos Financieros Derivados II Programa Educativo: Área de Formación : Licenciatura en Actuaría Transversal Horas teóricas: 3 Horas prácticas: 2 Total de Horas: 5 Total de créditos:
Transformaciones y esperanza
 Capítulo 3 Transformaciones y esperanza 3.1. Introducción Por lo general estamos en condiciones de modelar un fenómeno en términos de una variable aleatoria X cuya función de distribución acumulada es
Capítulo 3 Transformaciones y esperanza 3.1. Introducción Por lo general estamos en condiciones de modelar un fenómeno en términos de una variable aleatoria X cuya función de distribución acumulada es
La economía y las ecuaciones diferenciales: La fórmula de Black-Scholes. David Torcal y Andrea Santamaría 16 de Diciembre 2010
 La economía y las ecuaciones diferenciales: La fórmula de Black-Scholes David Torcal y Andrea Santamaría 16 de Diciembre 2010 Objetivo del estudio Extender los conceptos aprendidos sobre la resolución
La economía y las ecuaciones diferenciales: La fórmula de Black-Scholes David Torcal y Andrea Santamaría 16 de Diciembre 2010 Objetivo del estudio Extender los conceptos aprendidos sobre la resolución
MASTER FINANZAS DE EMPRESA
 MASTER FINANZAS DE EMPRESA Materia Carácter Créditos 4 Matemáticas de los derivados financieros Optativa Código 607640 Presenciales 4 No presenciales Curso Segundo Trimestre 5 y 6 Idioma Español 0 Departamento
MASTER FINANZAS DE EMPRESA Materia Carácter Créditos 4 Matemáticas de los derivados financieros Optativa Código 607640 Presenciales 4 No presenciales Curso Segundo Trimestre 5 y 6 Idioma Español 0 Departamento
Análisis Económico y Financiero
 Valuación, Análisis y Riesgo 01 Enero 2014 Análisis Económico y Financiero Estimación dinámica de la curva de rendimiento en México Carlos Sánchez Cerón Carlos Sánchez Cerón Análisis Económico y Financiero
Valuación, Análisis y Riesgo 01 Enero 2014 Análisis Económico y Financiero Estimación dinámica de la curva de rendimiento en México Carlos Sánchez Cerón Carlos Sánchez Cerón Análisis Económico y Financiero
Volatilidad estocástica y la ecuación de Fokker-Planck: parámetros dependientes del tiempo y filtro de Kalman
 Revista de Administración, Finanzas Economía (Journal of Management, Finance and Economics), vol. 4, núm. 1 (010), pp. 64-75. Volatilidad estocástica la ecuación de Fokker-Planck: parámetros dependientes
Revista de Administración, Finanzas Economía (Journal of Management, Finance and Economics), vol. 4, núm. 1 (010), pp. 64-75. Volatilidad estocástica la ecuación de Fokker-Planck: parámetros dependientes
EL PRINCIPIO DE MÁXIMA VEROSIMILITUD (LIKELIHOOD)
 EL PRINCIPIO DE MÁXIMA VEROSIMILITUD (LIKELIHOOD) Fortino Vela Peón fvela@correo.xoc.uam.mx FVela-0 Objetivo Introducir las ideas básicas del principio de máxima verosimilitud. Problema Considere el experimento
EL PRINCIPIO DE MÁXIMA VEROSIMILITUD (LIKELIHOOD) Fortino Vela Peón fvela@correo.xoc.uam.mx FVela-0 Objetivo Introducir las ideas básicas del principio de máxima verosimilitud. Problema Considere el experimento
Diseños D-óptimos bayesianos para modelos lineales heteroscedásticos
 XXVI Simposio Internacional de Estadística 2016 Sincelejo, Sucre, Colombia, 8 al 12 de Agosto de 2016 Diseños D-óptimos bayesianos para modelos lineales heteroscedásticos Catalina Patiño Bustamante 1,a,
XXVI Simposio Internacional de Estadística 2016 Sincelejo, Sucre, Colombia, 8 al 12 de Agosto de 2016 Diseños D-óptimos bayesianos para modelos lineales heteroscedásticos Catalina Patiño Bustamante 1,a,
ESTIMACIÓN DE FUNCIONES DE DENSIDAD DE DATOS CORRELACIONADOS Y/O CON VALORES ATÍPICOS
 Servy, Elsa Cuesta, Cristina Marí, Gonzalo Instituto de Investigaciones Teóricas y Aplicadas, Escuela de Estadística ESTIMACIÓN DE FUNCIONES DE DENSIDAD DE DATOS CORRELACIONADOS Y/O CON VALORES ATÍPICOS
Servy, Elsa Cuesta, Cristina Marí, Gonzalo Instituto de Investigaciones Teóricas y Aplicadas, Escuela de Estadística ESTIMACIÓN DE FUNCIONES DE DENSIDAD DE DATOS CORRELACIONADOS Y/O CON VALORES ATÍPICOS
Kolmogorov y la teoría de la la probabilidad. David Nualart. Academia de Ciencias y Universidad de Barcelona
 Kolmogorov y la teoría de la la probabilidad David Nualart Academia de Ciencias y Universidad de Barcelona 1 La axiomatización del cálculo de probabilidades A. N. Kolmogorov: Grundbegriffe des Wahrscheinlichkeitsrechnung
Kolmogorov y la teoría de la la probabilidad David Nualart Academia de Ciencias y Universidad de Barcelona 1 La axiomatización del cálculo de probabilidades A. N. Kolmogorov: Grundbegriffe des Wahrscheinlichkeitsrechnung
Paul Malliavin: Un matemático excepcional Liliana Blanco Castañeda Universidad Nacional de Colombia (Sede Bogotá)
 aul Malliavin: Un matemático excepcional Liliana Blanco Castañeda Universidad Nacional de Colombia (Sede Bogotá) El matemático francés aul Malliavin pertenece al grupo de matemáticos entre los que podemos
aul Malliavin: Un matemático excepcional Liliana Blanco Castañeda Universidad Nacional de Colombia (Sede Bogotá) El matemático francés aul Malliavin pertenece al grupo de matemáticos entre los que podemos
diseminación de los patrones de masa de alta exactitud y validación de la incertidumbre estimada mediante simulación numérica
 Comparación de los métodos utilizados para la diseminación de los patrones de masa de alta exactitud validación de la incertidumbre estimada mediante simulación numérica Lautaro Ramírez Varas Luis Omar
Comparación de los métodos utilizados para la diseminación de los patrones de masa de alta exactitud validación de la incertidumbre estimada mediante simulación numérica Lautaro Ramírez Varas Luis Omar
Regresión múltiple. Demostraciones. Elisa Mª Molanes López
 Regresión múltiple Demostraciones Elisa Mª Molanes López El modelo de regresión múltiple El modelo que se plantea en regresión múltiple es el siguiente: y i = β 0 + β 1 x 1i + β 2 x 2i +...+ β k x ki +
Regresión múltiple Demostraciones Elisa Mª Molanes López El modelo de regresión múltiple El modelo que se plantea en regresión múltiple es el siguiente: y i = β 0 + β 1 x 1i + β 2 x 2i +...+ β k x ki +
Econometría II Grado en finanzas y contabilidad
 Econometría II Grado en finanzas y contabilidad Metodología Box-Jenkins Profesora: Dolores García Martos E-mail:mdgmarto@est-econ.uc3m.es Este documento es un resumen/modificación de la documentación elaborada
Econometría II Grado en finanzas y contabilidad Metodología Box-Jenkins Profesora: Dolores García Martos E-mail:mdgmarto@est-econ.uc3m.es Este documento es un resumen/modificación de la documentación elaborada
Regresión Lineal Múltiple
 Unidad 4 Regresión Lineal Múltiple Javier Santibáñez (IIMAS, UNAM) Regresión Semestre 2017-2 1 / 35 Introducción La idea de la regresión lineal múltiple es modelar el valor esperado de la variable respuesta
Unidad 4 Regresión Lineal Múltiple Javier Santibáñez (IIMAS, UNAM) Regresión Semestre 2017-2 1 / 35 Introducción La idea de la regresión lineal múltiple es modelar el valor esperado de la variable respuesta
SOBRE LA INTRODUCCIÓN DE INCERTIDUMBRE EN UN MODELO DE CRECIMIENTO ECONÓMICO
 V JORNADAS ASEPMA SOBRE LA INTRODCCIÓN DE INCERTIDMBRE EN N MODELO DE CRECIMIENTO ECONÓMICO Álvarez López Alberto A Resumen Presentamos una manera de incorporar incertidumbre en un modelo de crecimiento
V JORNADAS ASEPMA SOBRE LA INTRODCCIÓN DE INCERTIDMBRE EN N MODELO DE CRECIMIENTO ECONÓMICO Álvarez López Alberto A Resumen Presentamos una manera de incorporar incertidumbre en un modelo de crecimiento
Departamento de Matemática Aplicada a las T.I.C. SOLUCIONES
 Departamento de Matemática Aplicada a las T.I.C. ASIGNATURA: ESTADÍSTICA Y PROCESOS ESTOCÁSTICOS EAMEN FINAL Otoño 25-6 FECHA: 5 de Enero de 26 Fecha publicación notas: 22 de Enero de 26 Fecha revisión
Departamento de Matemática Aplicada a las T.I.C. ASIGNATURA: ESTADÍSTICA Y PROCESOS ESTOCÁSTICOS EAMEN FINAL Otoño 25-6 FECHA: 5 de Enero de 26 Fecha publicación notas: 22 de Enero de 26 Fecha revisión
Distribuciones de probabilidad multivariadas
 Capítulo 3 Distribuciones de probabilidad multivariadas Sobre un dado espacio muestral podemos definir diferentes variables aleatorias. Por ejemplo, en un experimento binomial, X 1 podría ser la variable
Capítulo 3 Distribuciones de probabilidad multivariadas Sobre un dado espacio muestral podemos definir diferentes variables aleatorias. Por ejemplo, en un experimento binomial, X 1 podría ser la variable
Apuntes de Series Temporales
 Apuntes de Series Temporales David Rodríguez 7 de Noviembre de 2009. Modelos de Series Temporales Modelo AR() El modelo AutoRegresivo AR() es un proceso aleatorio de la forma X t = ϕx t + σϵ t, ϵ t N (0,
Apuntes de Series Temporales David Rodríguez 7 de Noviembre de 2009. Modelos de Series Temporales Modelo AR() El modelo AutoRegresivo AR() es un proceso aleatorio de la forma X t = ϕx t + σϵ t, ϵ t N (0,
Ciencia y Sociedad ISSN: Instituto Tecnológico de Santo Domingo República Dominicana
 Ciencia y Sociedad ISSN: 0378-7680 dpc@mail.intec.edu.do Instituto Tecnológico de Santo Domingo República Dominicana Sukhomlin, N. Estudio de simetría y de posibilidades de la resolución exacta de las
Ciencia y Sociedad ISSN: 0378-7680 dpc@mail.intec.edu.do Instituto Tecnológico de Santo Domingo República Dominicana Sukhomlin, N. Estudio de simetría y de posibilidades de la resolución exacta de las
Procesos estocásticos
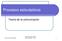 Teoría de la comunicación Comunicaciones - U.A.H. Indice Probabilidad. Variables Aleatorias. Procesos Estocásticos. Comunicaciones - U.A.H. Probabilidad Probabilidad. Dado un experimento ε del tipo que
Teoría de la comunicación Comunicaciones - U.A.H. Indice Probabilidad. Variables Aleatorias. Procesos Estocásticos. Comunicaciones - U.A.H. Probabilidad Probabilidad. Dado un experimento ε del tipo que
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Distribuciones de probabilidad Discretas
 Distribuciones de probabilidad Discretas Distribución Uniforme Discreta Definición Una variable aleatoria X, tiene una distribución uniforme discreta, si cada uno de los valores x 1, x 2,.. x n, tiene
Distribuciones de probabilidad Discretas Distribución Uniforme Discreta Definición Una variable aleatoria X, tiene una distribución uniforme discreta, si cada uno de los valores x 1, x 2,.. x n, tiene
ESTADÍSTICA I Tema 2: Algunas ideas básicas sobre inferencia estadística. Muestreo aleatorio
 ESTADÍSTICA I Tema 2: Algunas ideas básicas sobre inferencia estadística. Muestreo aleatorio Muestra aleatoria Conceptos probabiĺısticos básicos El problema de inferencia Estadísticos. Media y varianza
ESTADÍSTICA I Tema 2: Algunas ideas básicas sobre inferencia estadística. Muestreo aleatorio Muestra aleatoria Conceptos probabiĺısticos básicos El problema de inferencia Estadísticos. Media y varianza
Conceptos de Probabilidad y estadística. Jhon Jairo Padilla A., PhD
 Conceptos de Probabilidad y estadística Jhon Jairo Padilla A., PhD Introducción La ingeniería de tráfico está soportada sobre conceptos de probabilidad y estadística como: Probabilidad Variable aleatoria
Conceptos de Probabilidad y estadística Jhon Jairo Padilla A., PhD Introducción La ingeniería de tráfico está soportada sobre conceptos de probabilidad y estadística como: Probabilidad Variable aleatoria
Unidad 3. Probabilidad. Javier Santibáñez (IIMAS, UNAM) Inferencia Estadística Semestre / 22
 Unidad 3. Probabilidad Javier Santibáñez (IIMAS, UNAM) Inferencia Estadística Semestre 2018-1 1 / 22 Espacios de probabilidad El modelo matemático para estudiar la probabilidad se conoce como espacio de
Unidad 3. Probabilidad Javier Santibáñez (IIMAS, UNAM) Inferencia Estadística Semestre 2018-1 1 / 22 Espacios de probabilidad El modelo matemático para estudiar la probabilidad se conoce como espacio de
Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación. Facultad de Ciencias Sociales, UdelaR
 Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación Facultad de Ciencias Sociales, UdelaR Índice 1. Repaso: estimadores y estimaciones. Propiedades de los estimadores. 2. Estimación puntual.
Estadística y sus aplicaciones en Ciencias Sociales 5. Estimación Facultad de Ciencias Sociales, UdelaR Índice 1. Repaso: estimadores y estimaciones. Propiedades de los estimadores. 2. Estimación puntual.
Pérdida Esperada. Pérdida Esperada (PE): Valor esperado de pérdida por riesgo crediticio en un horizonte de tiempo determinado.
 Pérdida Esperada Uno de los objetivos de este estudio es construir una función de pérdidas para el portafolio de la cartera de préstamos que ofrece la entidad G&T Continental, basados en el comportamiento
Pérdida Esperada Uno de los objetivos de este estudio es construir una función de pérdidas para el portafolio de la cartera de préstamos que ofrece la entidad G&T Continental, basados en el comportamiento
Capítulo 9 Estructura y Administración de Portafolios de Inversión
 Capítulo 9 Estructura y Administración de Portafolios de Inversión Objetivo Presentar los conceptos básicos y el proceso vinculado a la administración de portafolios de inversión Parte I CONCEPTOS BÁSICOS
Capítulo 9 Estructura y Administración de Portafolios de Inversión Objetivo Presentar los conceptos básicos y el proceso vinculado a la administración de portafolios de inversión Parte I CONCEPTOS BÁSICOS
Nombre y Apellidos:... EXAMEN ECONOMETRÍA II (Enero 2010)
 Nombre y Apellidos:... NIU:... Grupo:... EXAMEN ECONOMETRÍA II (Enero 2010) Lea cuidadosamente cada pregunta. Marque muy claramente la respuesta de cada pregunta en la hoja de respuestas. Observe que los
Nombre y Apellidos:... NIU:... Grupo:... EXAMEN ECONOMETRÍA II (Enero 2010) Lea cuidadosamente cada pregunta. Marque muy claramente la respuesta de cada pregunta en la hoja de respuestas. Observe que los
Probabilidad de Default en el Area Euro : Evidencia en los mercados de deuda soberana
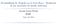 Probabilidad de Default en el Area Euro : Evidencia en los mercados de deuda soberana Gonzalo Lezma Florida BCRP Lima, Oct 2012 Outline 1 Objetivo 2 Introducción 3 Resumen Teórico 4 Datos 5 Trabajo Exploratorio
Probabilidad de Default en el Area Euro : Evidencia en los mercados de deuda soberana Gonzalo Lezma Florida BCRP Lima, Oct 2012 Outline 1 Objetivo 2 Introducción 3 Resumen Teórico 4 Datos 5 Trabajo Exploratorio
Métodos de gradiente. Métodos de Krylov
 Métodos de gradiente. Métodos de Krylov Damián Ginestar Peiró Departamento de Matemática Aplicada Universidad Politécnica de Valencia Curso 2012-2013 (UPV) Métodos de gradiente. Métodos de Krylov Curso
Métodos de gradiente. Métodos de Krylov Damián Ginestar Peiró Departamento de Matemática Aplicada Universidad Politécnica de Valencia Curso 2012-2013 (UPV) Métodos de gradiente. Métodos de Krylov Curso
