Para aprender Termodinámica resolviendo problemas GASES REALES.
|
|
|
- Mercedes Segura Iglesias
- hace 7 años
- Vistas:
Transcripción
1 Fato de ompesibilidad. GASES REAES. El fato de ompesibilidad se define omo ( ) ( ) la pesión, la tempeatua y la natualeza de ada gas. Euaión de van de Waals. ( ) z = eal = eal y es funión de a euaión de van de Waals modifia a la euaión de los gases ideales tomando en uenta el volumen oupado po las moléulas a 0K, epesentado po la onstante b ; y las ataiones moleulaes epesentadas po la onstante a : a + ( b) = RT Constantes de van de Waals paa vaias substanias. ideal RT substania a/dm 6 ba mol - a/dm 6 atm mol - b/dm mol -1 Helio Neón Agón Kiptón Hidógeno Nitógeno Oxígeno Monóxido de abono Dióxido de abono Amoniao Metano Etano Eteno opano Butano Mateial didátio en evisión 19
2 -metil popano entano Beneno a euaión de van de Waals es una euaión úbia on espeto al volumen y al númeo de moles. Todas las euaiones de este tipo pesentan un punto de inflexión uyas oodenadas epesentan el punto ítio. Este punto de inflexión se puede obtene a pati del iteio de las deivadas, es dei, igualamos la pimea deivada y la segunda deivada a eo y junto on la euaión oiginal esolvemos el sistema de tes euaiones on tes inógnitas y obtenemos las oodenadas del punto de inflexión. De la euaión de van del Waals se obtienen: a 8a = b ; = ; T = 7b 7bR inipio de los estados oespondientes. Si dos o más gases tiene dos de sus vaiables eduidas iguales, se enuentan en estados oespondientes. Esto signifia que su teea vaiable eduida es la misma y po lo tanto tienen el mismo fato de ompesibilidad. T as pesión eduida se define omo = ; la tempeatua eduida omo T = T y el volumen eduido omo =. A ontinuaión se pesenta una tabla on las vaiables ítias de difeentes gases. Constantes ítias expeimentales paa divesas substanias substania T /K /ba /atm / mol -1 /RT Helio Neón Agón Kiptón Mateial didátio en evisión 0
3 Hidógeno Nitógeno Oxígeno Monóxido de abono Cloo Dióxido de abono Agua Amoniao Metano Etano Eteno opano Butano metil popano entano Beneno odemos esibi la euaión de van de Waals intoduiendo las vaiables eduidas y obtenemos una euaión genealizada donde han desapaeido los paámetos que dependen de la natualeza de ada gas: 8T = 1 Se puede segui el mismo poedimiento on otas euaiones de estado que ontengan dos onstantes Otas euaiones de estado. Existen muhas otas euaiones de estado, algunas de las uales se pesentan a ontinuaión, así omo su expesión de la ley de estados oespondientes: Mateial didátio en evisión 1
4 Euaión Su expesión en estados oespondientes Dieteii RTe = b art / Bethelot a + ( b) = RT T Euaión viial B C D = RT Euaión viial en funión de la pesión ( 1 ' ' '... ) = RT + B + C + D + ( / T Te ) = 1 8 = 1 T oblemas esueltos. 1. aa el helio, = y =.45atm. Calula las onstantes mol a y bde van de Waals y el adio de las moléulas onsideándolas esféias. Soluión. = b mol b = = = mol a = 7b atm 7b atm=0.051 a = = mol mol Mateial didátio en evisión
5 a onstante b de van de Waals es el volumen de 1 mol de moléulas a 0K, po lo ual el volumen de una moléula de helio seía moleula 4 = π 1m mol 10 m 10 m = =. 10 =. 10 moleulas moleula 1m mol 4π 0 8 = = m= 1.97 A 6 9 m El esultado no es bueno poque la euaión de van de Waals no es muy peisa alededo del punto ítio, sin embago, tiene la gan vitud de pedei la existenia del punto ítio y además nos pemite entende un poo más el poeso de liuefaión de los gases. egunta: Si se tataa de moléulas de butano, seía oeto onsidealas omo esféias?. aa el agón las onstantes de van de Waals son 1 a = 1.6 atm mol y b = mol. Elaboa la gáfia vs a 50 K, 75 K, 100 K, 150 K y 00 K paa moles de agón en el intevalo de volúmenes de a 0. usando la euaión de van de Waals. Soluión os álulos se muestan en la siguiente tabla ealizada en Exel y las gáfias se muestan adelante ealizadas on Oigin. Obsevamos que la euaión de van de Waals paa el agón a bajas tempeatuas no pedie adeuadamente el ompotamiento del agón pues: a) obtenemos pesiones negativas, b) en una egión se pedie que el volumen aumenta al aumenta la pesión. Mateial didátio en evisión
6 / /atm a 50K /atm a 100 K /atm a 150 K /atm a 00K Mateial didátio en evisión 4
7 600 Isotemas de van de Waals paa el Agón K /atm K 150 K K K / egunta: Dado que la euaión de van de Waals es úbia on espeto al volumen, tiene tes aíes. Qué suede a altas tempeatuas on estas tes aíes?. Utiliza la euaión de van de Waals paa elaboa la gáfia de Z vs paa el CO ente 0 y 1000 atm a 00K, 500 K y a 000 K. aa el CO a =.64atm mol y b = mol Soluión. o definiión 1 Z =. Calulamos la pesión a difeentes volúmenes (omo lo RT hiimos en el poblema anteio utilizando la euaión de van de Waals) y obtenemos Z. o ejemplo, tomamos =0.081 mol -1 y alulamos : Mateial didátio en evisión 5
8 atm K atm.64 Kmol = mol = atm mol mol mol Z ( ) ( ) ( ) van dewaals vandewaals = = = ideal RT y luego alulamos atm0.081 mol = atm K Kmol A ontinuaión se muesta una pate de la hoja de álulo heha en exel paa la tempeatua de 1000 K y posteiomente las gáfias en oigin a todas las tempeatuas que se desea hae el álulo. / mol -1 dado /atm alulada Z = alulado on RT dado y alulada Obsevamos que la euaión de van de Waals epodue ualitativamente el ompotamiento de un gas eal. A bajas pesiones, el fato de ompesibilidad tiende a la unidad. A bajas tempeatuas (en este aso po ejemplo 00 K) y Mateial didátio en evisión 6
9 bajas pesiones, el fato de ompesibilidad es meno que la unidad, lo ual india que el efeto que detemina el ompotamiento del gas son las ataiones moleulaes. Al aumenta la pesión, entan en juego las epulsiones moleulaes y el fato de ompesibilidad ee y llega a se mayo que la unidad. Si la tempeatua aumenta, las ataiones moleulaes son venidas po la enegía témia y el fato de ompesibilidad ee más ápidamente e inluso habá tempeatuas a las uales el fato de ompesibilidad sea siempe mayo que la unidad (en este aso 000K) K K Z K /atm egunta: esentaán todos los gases un ompotamiento simila al del CO? 4. Calula el volumen que oupa un mol de oxígeno a 100 atm y 98 K onsideando que se ompota omo un gas de van de Waals. a= 1.6 amt mol - ; b= mol -1. Soluión: a euaión de van de Waals es úbia on espeto al volumen. aa esolve este poblema utilizamos los métodos numéios. El objetivo del análisis numéio es esolve poblemas numéios omplejos utilizando solamente Mateial didátio en evisión 7
10 opeaiones simples de la aitmétia, on el fin de desaolla y evalua métodos paa alula esultados numéios a pati de los datos popoionados. os métodos de álulo se llaman algoitmos. El método que vamos a utiliza paa obtene el volumen de un gas de van de Waals es el Método de Newton Raphson. a) Esibimos la euaión de van de Waals de la siguiente manea: RT a = b a + ( b) = RT a ab b + = RT b + a ab = RT ( ) b + RT + a ab = 0 esta última euaión la tomamos omo f ( x ) = 0 b) Obtenemos: T ) Apliamos: f xi = xi 1 f ( ) = b RT + a = 0 ( xi ) '( x ) i d) odemos empeza a poba on el volumen que queamos, peo es más onveniente hae una estimaión utilizando la euaión del gas ideal: RT 1 = = i = i 1 ( i ) '( i ) f f.0168 = = e) Calulamos la toleania omo Mateial didátio en evisión 8
11 1 = = 0.10 f) Seguimos apliando el algoitmo hasta umpli on la toleania fijada = = = = = = = = = g) Si estamos onfomes on esta toleania, podemos dei que el volumen oupado po este gas de van de Waals en las ondiiones dadas es = 0.04 mol 1 egunta: Qué oto método numéio se eomendaía paa esolve este poblema? 5. Una muesta de hidógeno se enuenta a 5.4 atm y K. a) En qué ondiiones de tempeatua y pesión debe esta una muesta de loo paa esta en estados oespondientes on el hidógeno? b) Cuál es el fato de ompesibilidad de ada uno de estos gases? ) Cuál es el volumen mola de ada uno de estos gases? d) Cuál es el volumen eduido de ada uno de estos gases? Soluión. a) aa que dos o mas gases se enuenten en estados oespondientes, deben esta en las mismas ondiiones eduidas. aa el hidógeno: 5.4atm = = = y 1.67 atm T K T = = = T.98 K o lo tanto, el loo debe tene la misma pesión eduida y la misma tempeatua eduida que el hidógeno paa esta en estados oespondientes, es dei, la pesión y la tempeatua a las que debe esta el loo son: Mateial didátio en evisión 9
12 = = 78.87atm= atm T = TT = K= K b) El fato de ompesibilidad ( Z ) puede obtenese de la gáfia del fato de ompesibilidad genealizado omo se muesta en la figua siguiente, de donde Z = 0.5 y po lo tanto ) el volumen mola de ada uno de los gases es: hidogeno K ZRT Kmol = = = 0.09 mol 5.4atm 1 Mateial didátio en evisión 0
13 loo K ZRT Kmol = = = mol atm 1 d) y sus volúmenes eduidos pueden obtenese omo: hidogeno 0.09 = = mol = mol loo = = mol mol os esultados se esumen en la siguiente tabla: / atm T / K / mol -1 T Hidógeno Cloo Z Conluimos diiendo que el hidógeno (a 5.4 atm y K) y el loo (a atm y K) se enuentan en estados oespondientes, es dei, tienen la misma teea vaiable eduida ( ) y po lo tanto el mismo fato de ompesibilidad. egunta: Qué ventaja tiene el heho de que los gases sigan el inipio de los Estados Coespondientes? Mateial didátio en evisión 1
Para aprender Termodinámica resolviendo problemas
 GASES REAES. Fator de ompresibilidad. El fator de ompresibilidad se define omo ( ) ( ) ( ) z = real = real y es funión de la presión, la temperatura y la naturaleza de ada gas. Euaión de van der Waals.
GASES REAES. Fator de ompresibilidad. El fator de ompresibilidad se define omo ( ) ( ) ( ) z = real = real y es funión de la presión, la temperatura y la naturaleza de ada gas. Euaión de van der Waals.
Pman = cmhg= atm
 emodinámia eoía (11) oblemas esueltos Semeste: 014-1 1. Una masa de 0 g de SO se enuenta almaenada en un tanque on un volumen de 50 dm a una tempeatua de 800 R. La pesión baométia loal es de 700 mm Hg.
emodinámia eoía (11) oblemas esueltos Semeste: 014-1 1. Una masa de 0 g de SO se enuenta almaenada en un tanque on un volumen de 50 dm a una tempeatua de 800 R. La pesión baométia loal es de 700 mm Hg.
Fórmulas de Diseño para Columnas
 Fómulas de Diseño paa Columnas 15 de noviembe de 2017 En las seiones peedentes hemos disutido la apaidad teóia de aga de las olumnas ante pandeo tanto elástio omo inelástio. Con esta idea en mente, estamos
Fómulas de Diseño paa Columnas 15 de noviembe de 2017 En las seiones peedentes hemos disutido la apaidad teóia de aga de las olumnas ante pandeo tanto elástio omo inelástio. Con esta idea en mente, estamos
Recursión y Relaciones de Recurrencia. UCR ECCI CI-1204 Matemáticas Discretas Prof. M.Sc. Kryscia Daviana Ramírez Benavides
 Reusión y Relaiones de Reuenia UCR ECCI CI-04 Matemátias Disetas Pof. M.S. Kysia Daviana Ramíez Benavides Pogesión Geométia Es una suesión infinita de númeos donde el oiente de ualquie témino (distinto
Reusión y Relaiones de Reuenia UCR ECCI CI-04 Matemátias Disetas Pof. M.S. Kysia Daviana Ramíez Benavides Pogesión Geométia Es una suesión infinita de númeos donde el oiente de ualquie témino (distinto
Física General 1 Proyecto PMME - Curso 2007 Instituto de Física Facultad de Ingeniería UdelaR
 ísia Geneal 1 Poyeto PMME - Cuso 007 Instituto de ísia aultad de Ingenieía UdelaR DINÁMICA DE LA PARTÍCULA MOVIMIENTO CIRCULAR EN UN PLANO VERTICAL abiana Andade Juan Pablo Balaini Pablo Doglio Intoduión:
ísia Geneal 1 Poyeto PMME - Cuso 007 Instituto de ísia aultad de Ingenieía UdelaR DINÁMICA DE LA PARTÍCULA MOVIMIENTO CIRCULAR EN UN PLANO VERTICAL abiana Andade Juan Pablo Balaini Pablo Doglio Intoduión:
Problema encadenado 1. Apartado 1
 Poblema enadenado 1. 1. Dibuja dos iunfeenias de igual adio tangentes ente si y tangentes a los lados del tiángulo del que se onoe: el lado = 120 mm, el ángulo = 700 y la mediana m = 85 mm. De las posibles
Poblema enadenado 1. 1. Dibuja dos iunfeenias de igual adio tangentes ente si y tangentes a los lados del tiángulo del que se onoe: el lado = 120 mm, el ángulo = 700 y la mediana m = 85 mm. De las posibles
SOFTWARE EDUCATIVO PARA EL ANÁLISIS Y DISEÑO DE ELEMENTOS DE CONCRETO REFORZADO. Delma V. Almada Navarro y Humberto López Salgado
 SOFTWARE EDUCATIVO PARA EL ANÁLISIS Y DISEÑO DE ELEMENTOS DE CONCRETO REFORZADO Delma V. Almada Navao y Humbeto López Salgado Depto. de Ingenieía Civil, ITESM Ave. Eugenio Gaza Sada Su 50 Aulas IV, e piso.
SOFTWARE EDUCATIVO PARA EL ANÁLISIS Y DISEÑO DE ELEMENTOS DE CONCRETO REFORZADO Delma V. Almada Navao y Humbeto López Salgado Depto. de Ingenieía Civil, ITESM Ave. Eugenio Gaza Sada Su 50 Aulas IV, e piso.
Medición de la conductividad térmica de materiales aislantes en el CENAM Dr. Leonel Lira Cortés Dr. Edgar Mendez Lango
 Medición de la conductividad témica de mateiales aislantes en el CENAM D. Leonel Lia Cotés D. Edga Mendez Lango ÁREA DE METROLOGÍA ELECTRÍCA DIVISIÓN DE TERMOMETRÍA CONTENIDO INTRODUCCION ECUACION DE CONDUCCION
Medición de la conductividad témica de mateiales aislantes en el CENAM D. Leonel Lia Cotés D. Edga Mendez Lango ÁREA DE METROLOGÍA ELECTRÍCA DIVISIÓN DE TERMOMETRÍA CONTENIDO INTRODUCCION ECUACION DE CONDUCCION
5 El colectivo macrocanónico.
 5 El colectivo macocanónico. Vesión boado. En el colectivo macocanónico, el sistema se encuenta en equilibio con un baño témico exteno a tempeatua ( ja) T, y con un baño o foco de patículas cuyo potencial
5 El colectivo macocanónico. Vesión boado. En el colectivo macocanónico, el sistema se encuenta en equilibio con un baño témico exteno a tempeatua ( ja) T, y con un baño o foco de patículas cuyo potencial
TRANSFORMACIONES GEOMÉTRICAS: Inversión.
 PRFESR: FRNCISC MNUEL GLÁN SN JSÉ. TRNSFRMCINES GEMÉTRICS: Invesión. INVERSIÓN siguientes leyes: La invesión es una tansfomaión que se ige po las M' ' 1. Dos puntos invesos y están alineados on un punto
PRFESR: FRNCISC MNUEL GLÁN SN JSÉ. TRNSFRMCINES GEMÉTRICS: Invesión. INVERSIÓN siguientes leyes: La invesión es una tansfomaión que se ige po las M' ' 1. Dos puntos invesos y están alineados on un punto
Tema 6 Puntos, rectas y planos en el espacio
 Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
Tema 6 Puntos, ectas planos en el espacio. Punto medio. Los puntos A (,, ) B (-,, -) son vétices de un paalelogamo cuo cento es el punto M (,, ). Halla Los otos dos vétices las ecuaciones del lado AB.
Transferencia de Energía. Grupo ª
 Tansfeencia de Enegía 547 Gupo 3. 204-08-25 6ª 204-08-25 ontenido El 204-08-20 no hubo clase. Ejemplo de tansfeencia de enegía po difusión a tavés de mateiales compuestos. A 0 T 0 M M 2 A 2L T 2L B T B
Tansfeencia de Enegía 547 Gupo 3. 204-08-25 6ª 204-08-25 ontenido El 204-08-20 no hubo clase. Ejemplo de tansfeencia de enegía po difusión a tavés de mateiales compuestos. A 0 T 0 M M 2 A 2L T 2L B T B
Resolución de triángulos rectángulos
 Resolución de tiángulos ectángulos Ahoa vamos a aplica las funciones tigonométicas paa esolve tiángulos ectángulos. Resuelve el siguiente tiángulo ectángulo: Ejemplo y 60 Empezamos notando que podemos
Resolución de tiángulos ectángulos Ahoa vamos a aplica las funciones tigonométicas paa esolve tiángulos ectángulos. Resuelve el siguiente tiángulo ectángulo: Ejemplo y 60 Empezamos notando que podemos
RECTAS EN EL PLANO. r datos, podemos dar la ecuación de dicha recta de varias P o Ecuación vectorial
 RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
Práctica 2: Modulaciones analógicas lineales
 TEORÍA DE LA COMUNICACIÓN 2009/10 - EPS-UAM Pátia 2: Modulaiones analógias lineales Gupo Puesto Apellidos, nombe Apellidos, nombe Feha El objetivo de esta pátia es familiaiza al alumno on divesas modulaiones
TEORÍA DE LA COMUNICACIÓN 2009/10 - EPS-UAM Pátia 2: Modulaiones analógias lineales Gupo Puesto Apellidos, nombe Apellidos, nombe Feha El objetivo de esta pátia es familiaiza al alumno on divesas modulaiones
TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1
 TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1 página 2 SEGUNDO BIMESTRE 1 FUNCIONES DE MAS DE 90 GRADOS 1.1 CONCEPTOS Y DEFINICIONES Los valoes de las funciones tigonométicas solamente eisten paa
TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1 página 2 SEGUNDO BIMESTRE 1 FUNCIONES DE MAS DE 90 GRADOS 1.1 CONCEPTOS Y DEFINICIONES Los valoes de las funciones tigonométicas solamente eisten paa
VECTORES EN TRES DIMENSIONES
 FÍSIC PR TODOS 1 CRLOS JIMENEZ HURNG VECTORES EN TRES DIMENSIONES Los vetoes pueden epesase en funión de oodenadas, de la siguiente manea: a; b; ) o de ota foma: a i + b j + k donde: i, j, k, son vetoes
FÍSIC PR TODOS 1 CRLOS JIMENEZ HURNG VECTORES EN TRES DIMENSIONES Los vetoes pueden epesase en funión de oodenadas, de la siguiente manea: a; b; ) o de ota foma: a i + b j + k donde: i, j, k, son vetoes
ALGORITMO PROPUESTO PARA DETECCIÓN DE FALLAS
 CAPÍTULO 5 ALGORITMO PROPUESTO PARA DETECCIÓN DE FALLAS Los notables avances en la capacidad de manejo de datos po las PC están siendo apovechados en el pocesamiento de señales. Ahoa es posible escudiña
CAPÍTULO 5 ALGORITMO PROPUESTO PARA DETECCIÓN DE FALLAS Los notables avances en la capacidad de manejo de datos po las PC están siendo apovechados en el pocesamiento de señales. Ahoa es posible escudiña
INSTRUCCIONES GENERALES Y VALORACIÓN
 UNIVERSIDAD DE ALCALÁ PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (Mayoes 5 años) Cuso 009-010 MATERIA: FÍSICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates: La pimea pate consiste en
UNIVERSIDAD DE ALCALÁ PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (Mayoes 5 años) Cuso 009-010 MATERIA: FÍSICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates: La pimea pate consiste en
El método de las imágenes
 El método de las imágenes Antonio González Fenández Dpto. de Física Aplicada III Univesidad de Sevilla Sinopsis de la pesentación El teoema de unicidad pemite enconta soluciones po analogías con poblemas
El método de las imágenes Antonio González Fenández Dpto. de Física Aplicada III Univesidad de Sevilla Sinopsis de la pesentación El teoema de unicidad pemite enconta soluciones po analogías con poblemas
Tema 3. Reacción sólido-fluido no catalitica
 Tema 3. eaión sólido-fluido no atalitia (fluido) + b (sólido) podutos fluidos podutos sólidos podutos fluidos y sólidos Modelo de eaión: NS on despendimiento enizas y adheentes Patíula que ha eaionado
Tema 3. eaión sólido-fluido no atalitia (fluido) + b (sólido) podutos fluidos podutos sólidos podutos fluidos y sólidos Modelo de eaión: NS on despendimiento enizas y adheentes Patíula que ha eaionado
Derivadas de funciones trigonométricas y sus inversas
 Deivadas de funciones tigonométicas y sus invesas Las funciones tigonométicas se definen a pati de un tiángulo ectángulo como sigue: sin α y csc α y y cos α x sec α x α x tan α y x cot α x y Como puedes
Deivadas de funciones tigonométicas y sus invesas Las funciones tigonométicas se definen a pati de un tiángulo ectángulo como sigue: sin α y csc α y y cos α x sec α x α x tan α y x cot α x y Como puedes
PROBLEMAS DE OPTIMIZACIÓN (1)
 PROBLEMAS DE OPTIMIZACIÓN (1) Sugeencia paa el pofeso Hace énfasis ante los estudiantes aceca de la siguiente impotante aplicación del Cálculo Difeencial, pues la esolución de polemas de optimización es
PROBLEMAS DE OPTIMIZACIÓN (1) Sugeencia paa el pofeso Hace énfasis ante los estudiantes aceca de la siguiente impotante aplicación del Cálculo Difeencial, pues la esolución de polemas de optimización es
UNIVERSIDAD NACIONAL EXPERIMENTAL FRANCISCO DE MIRANDA COMPLEJO ACADÉMICO PUNTO FIJO PROGRAMA DE INGENIERÍA MECÁNICA CÁTEDRA: TERMODINÁMICA APLICADA
 UEFM UIVERSIDAD ACIOAL EXPERIMETAL FRACISCO DE MIRADA COMPLEJO ACADÉMICO PUTO FIJO PROGRAMA DE IGEIERÍA MECÁICA CÁTEDRA: TERMODIÁMICA APLICADA TEMA 8: COMBUSTIÓ. Combustibles y Combustión. Combustión completa
UEFM UIVERSIDAD ACIOAL EXPERIMETAL FRACISCO DE MIRADA COMPLEJO ACADÉMICO PUTO FIJO PROGRAMA DE IGEIERÍA MECÁICA CÁTEDRA: TERMODIÁMICA APLICADA TEMA 8: COMBUSTIÓ. Combustibles y Combustión. Combustión completa
EQUILIBRIO QUÍMICO QCA 01
 1.- En un reiiente de 1L, a 000, se introduen 6 1 10-3 moles de CO y una ierta antidad de H, roduiéndose la reaión: H (g) + CO (g) H O(g) + CO(g) Si uando se alanza el equilibrio, la resión total es de
1.- En un reiiente de 1L, a 000, se introduen 6 1 10-3 moles de CO y una ierta antidad de H, roduiéndose la reaión: H (g) + CO (g) H O(g) + CO(g) Si uando se alanza el equilibrio, la resión total es de
MAGNITUDES ESCALARES Y VECTORIALES
 U R S O: FÍSI OMÚN MTERIL: F-01 Sistema intenacional de medidas MGNITUDES ESLRES VETORILES En 1960, un comité intenacional estableció un conjunto de patones paa estas magnitudes fundamentales. El sistema
U R S O: FÍSI OMÚN MTERIL: F-01 Sistema intenacional de medidas MGNITUDES ESLRES VETORILES En 1960, un comité intenacional estableció un conjunto de patones paa estas magnitudes fundamentales. El sistema
Práctica 8: Carta de Smith
 Páctica 8: Cata de Smith Objetivo Familiaización con el manejo de la Cata de Smith. Contenidos Repesentación de impedancias y admitancias. Obtención de paámetos de las líneas empleando la Cata de Smith.
Páctica 8: Cata de Smith Objetivo Familiaización con el manejo de la Cata de Smith. Contenidos Repesentación de impedancias y admitancias. Obtención de paámetos de las líneas empleando la Cata de Smith.
Capa límite laminar incompresible. Soluciones de semejanza
 Capa límite lamina incompesible. Soluciones de semejanza M. Rodíguez 1 Solución de Blasius (198) Las ecuaciones de la capa límite paa una placa plana son u x + v y = a intega con las condiciones u u x
Capa límite lamina incompesible. Soluciones de semejanza M. Rodíguez 1 Solución de Blasius (198) Las ecuaciones de la capa límite paa una placa plana son u x + v y = a intega con las condiciones u u x
Aplicación de los Residuos al cálculo de Integrales Reales
 Aplicación de los Residuos al cálculo de Integales Reales A continuación, se haá un estudio sobe cietos tipos de integales eales que pesentan una equivalencia con las integales complejas sobe caminos ceados,
Aplicación de los Residuos al cálculo de Integales Reales A continuación, se haá un estudio sobe cietos tipos de integales eales que pesentan una equivalencia con las integales complejas sobe caminos ceados,
Segunda ley de Newton
 Segunda ley de Newton Fundamento La segunda ley de la mecánica de Newton se expesa matemáticamente. F = ext m a El sumatoio se efiee a las fuezas exteioes. En la páctica, dento de las fuezas exteioes que
Segunda ley de Newton Fundamento La segunda ley de la mecánica de Newton se expesa matemáticamente. F = ext m a El sumatoio se efiee a las fuezas exteioes. En la páctica, dento de las fuezas exteioes que
Trabajo Práctico Nº 12: Pandeo. Determinación de Cargas Criticas. Diseño y verificación de Secciones
 Tabajo átio Nº 1: andeo. Deteminaión de agas itias. Diseño veifiaión de Seiones Nota: la longitud de pandeo equivalente Lp se suele epesa omo Lp k. L donde L es la longitud eal de la olumna el oefiiente
Tabajo átio Nº 1: andeo. Deteminaión de agas itias. Diseño veifiaión de Seiones Nota: la longitud de pandeo equivalente Lp se suele epesa omo Lp k. L donde L es la longitud eal de la olumna el oefiiente
INGENIERIA DE EJECUCIÓN EN MECANICA PROGRAMA DE PROSECUCION DE ESTUDIOS VESPERTINO GUIA DE LABORATORIO ASIGNATURA NIVEL 02
 INGENIERIA DE EJEUIÓN EN MEANIA PROGRAMA DE PROSEUION DE ESTUDIOS VESPERTINO GUIA DE LABORATORIO ASIGNATURA 955 MATERIALES. NIVEL E3 Popiedades de Mateiales Líquidos y Solidos onductividad HORARIO: VIERNES:
INGENIERIA DE EJEUIÓN EN MEANIA PROGRAMA DE PROSEUION DE ESTUDIOS VESPERTINO GUIA DE LABORATORIO ASIGNATURA 955 MATERIALES. NIVEL E3 Popiedades de Mateiales Líquidos y Solidos onductividad HORARIO: VIERNES:
Si se denotan en color azul los parámetros conocidos y en rojo los desconocidos, el Formulario 1 quedaría como sigue:
 Ejecicios esueltos: Tomando como base el Fomulaio y los Consideandos, se plantea a continuación la esolución de divesos ejecicios.. El único electón de un átomo hidogenoide tiene una enegía potencial de
Ejecicios esueltos: Tomando como base el Fomulaio y los Consideandos, se plantea a continuación la esolución de divesos ejecicios.. El único electón de un átomo hidogenoide tiene una enegía potencial de
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Cuso 007-008 MATERIA: QUÍMICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates. En
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBAS DE ACCESO A ESTUDIOS UNIVERSITARIOS (LOGSE) Cuso 007-008 MATERIA: QUÍMICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates. En
Tensor de inercia. Tensor de inercia. I pzx. I pxx. I pxy. = I pyz. I pxz. I. Leyes de Newton. II. Cinemática
 Univesidad Simón Bolíva. ees de Newton. Cinemátia. Dinámia Sist. de atíulas Definiiones a le da le Tenso de ineia a le Es. de agange Tenso de ineia ( + ) Momentos de ineia: (Sieme ositivos) ( + ) Poiedades
Univesidad Simón Bolíva. ees de Newton. Cinemátia. Dinámia Sist. de atíulas Definiiones a le da le Tenso de ineia a le Es. de agange Tenso de ineia ( + ) Momentos de ineia: (Sieme ositivos) ( + ) Poiedades
En relación con los problemas 12, 13 y 14 Partícula en una caja unidimensional de lado L: V=0 dentro de la caja e infinito en las paredes.
 En elación con los poblemas 1, 1 14 Patícula en una caja unidimensional de lado : V0 dento de la caja e infinito en las paedes. Una dimensión: HΨ( EΨ( paa siendo contono: p H m m m Ψ( 0 0 a solución es:
En elación con los poblemas 1, 1 14 Patícula en una caja unidimensional de lado : V0 dento de la caja e infinito en las paedes. Una dimensión: HΨ( EΨ( paa siendo contono: p H m m m Ψ( 0 0 a solución es:
OPCIÓN A FÍSICA. 30/11/2010. E r
 OPCIÓN A FÍSICA. 0//00 PROBLEMA EXPERIMENTAL (.5 p). En el laboatoio de física se ealiza un expeimento paa medi la densidad de un sólido y de una disolución. Paa ello se utiliza un dinamómeto, se pesa
OPCIÓN A FÍSICA. 0//00 PROBLEMA EXPERIMENTAL (.5 p). En el laboatoio de física se ealiza un expeimento paa medi la densidad de un sólido y de una disolución. Paa ello se utiliza un dinamómeto, se pesa
Tema 7 Problemas métricos
 Tema 7 Poblemas méticos. Plano pependicula. Halla la ecuación del plano que contiene a los puntos A (- -) B ( -) es pependicula al plano. Los vectoes AB n (vecto nomal del plano ) uno de los puntos A o
Tema 7 Poblemas méticos. Plano pependicula. Halla la ecuación del plano que contiene a los puntos A (- -) B ( -) es pependicula al plano. Los vectoes AB n (vecto nomal del plano ) uno de los puntos A o
SOLUCIONES DE LOS EJERCICIOS DE APLICACIÓN II TEMA 4
 SOLUCIONES DE LOS EJERCICIOS DE APLICACIÓN II TEMA 4 Ejecicio de aplicación 44 (Deivación) Se desea obtene una viga ectangula a pati de un tonco cilíndico de 6 cm de diámeto a) Demosta que la viga con
SOLUCIONES DE LOS EJERCICIOS DE APLICACIÓN II TEMA 4 Ejecicio de aplicación 44 (Deivación) Se desea obtene una viga ectangula a pati de un tonco cilíndico de 6 cm de diámeto a) Demosta que la viga con
Diferencia de potencial y potencial eléctricos. En el campo gravitatorio.
 Difeencia de potencial y potencial elécticos En el campo gavitatoio. Difeencia de potencial y potencial elécticos El tabajo se cuantifica po la fueza que ejece el campo y la distancia ecoida. W F d Difeencia
Difeencia de potencial y potencial elécticos En el campo gavitatoio. Difeencia de potencial y potencial elécticos El tabajo se cuantifica po la fueza que ejece el campo y la distancia ecoida. W F d Difeencia
Elementos de una TEORIA RELATIVISTA DE LA GRAVITACION
 Elementos de una TEORIA RELATIVISTA DE LA GRAVITACION po Rodolfo CARABIO. CONCEPTO DE INTERACCION GRAVITATORIA En este tabajo se mostaa ómo es posible establee una teoía de la gavitaión a pati de los postulados
Elementos de una TEORIA RELATIVISTA DE LA GRAVITACION po Rodolfo CARABIO. CONCEPTO DE INTERACCION GRAVITATORIA En este tabajo se mostaa ómo es posible establee una teoía de la gavitaión a pati de los postulados
Capítulo 8. Sistemas de partículas idénticas
 Capítulo 8 Sistemas de patículas idénticas 8 Indistinguibilidad 8 Funciones popias del opeado de pemutación 8 Átomo de helio 83 spín total 8 Sistemas de patículas idénticas n la mecánica clásica en una
Capítulo 8 Sistemas de patículas idénticas 8 Indistinguibilidad 8 Funciones popias del opeado de pemutación 8 Átomo de helio 83 spín total 8 Sistemas de patículas idénticas n la mecánica clásica en una
Modelo de Programación Matemática del Problema de Equilibrado de Líneas con Subgrafos de Montaje Alternativos *
 IX Congeso de Ingenieía de Oganización Gión, 8 y 9 de septiembe de 2005 Modelo de Pogamación Matemática del Poblema de Equilibado de Líneas con Subgafos de Montae Altenativos * Liliana Capacho Betancout
IX Congeso de Ingenieía de Oganización Gión, 8 y 9 de septiembe de 2005 Modelo de Pogamación Matemática del Poblema de Equilibado de Líneas con Subgafos de Montae Altenativos * Liliana Capacho Betancout
Fig. 1 Esquema para el cálculo de B
 P1- CAMPO DE UN AAMRE (EY DE OT-SAVART). Considee una poción de un alambe ecto de longitud po el que cicula una coiente constante. (a) Calcule la inducción magnética paa puntos sobe el plano que divide
P1- CAMPO DE UN AAMRE (EY DE OT-SAVART). Considee una poción de un alambe ecto de longitud po el que cicula una coiente constante. (a) Calcule la inducción magnética paa puntos sobe el plano que divide
CURSO 2004-2005 - CONVOCATORIA: Junio
 ubomisión de mateia de Físia de º De ahilleato Coodinaión P..U. 005-006 PU D CCO L UNIVIDD. LOG L.O.G... FÍIC CUO 00-005 - CONVOCOI: Junio OLUCION De las dos opiones popuestas, sólo hay que desaolla una
ubomisión de mateia de Físia de º De ahilleato Coodinaión P..U. 005-006 PU D CCO L UNIVIDD. LOG L.O.G... FÍIC CUO 00-005 - CONVOCOI: Junio OLUCION De las dos opiones popuestas, sólo hay que desaolla una
Sistemas de comunicación
 Sistemas de comunicación Páctico Intefeencia Intesimbólica y Pulsos de Nyqvist Cada ejecicio comienza con un símbolo el cuál indica su dificultad de acuedo a la siguiente escala: básica, media, avanzada,
Sistemas de comunicación Páctico Intefeencia Intesimbólica y Pulsos de Nyqvist Cada ejecicio comienza con un símbolo el cuál indica su dificultad de acuedo a la siguiente escala: básica, media, avanzada,
2.5 Vectores cartesianos
 .5 VECTORES CRTESINOS 43.5 Vectoes catesianos Las opeaciones del álgeba vectoial, cuando se aplican a la esolución de poblemas en tes dimensiones, se simplifican consideablemente si pimeo se epesentan
.5 VECTORES CRTESINOS 43.5 Vectoes catesianos Las opeaciones del álgeba vectoial, cuando se aplican a la esolución de poblemas en tes dimensiones, se simplifican consideablemente si pimeo se epesentan
CAPITULO 3 MÉTODO DE RESOLUCIÓN MEDIANTE INTEGRALES
 CAPÍTULO : METODO DE RESOLUCIÓN MEDIANTE INTEGRALES CAPITULO MÉTODO DE RESOLUCIÓN MEDIANTE INTEGRALES. Resumen En este capítulo se encuenta solución analítica mediante el método de sepaación de vaiables
CAPÍTULO : METODO DE RESOLUCIÓN MEDIANTE INTEGRALES CAPITULO MÉTODO DE RESOLUCIÓN MEDIANTE INTEGRALES. Resumen En este capítulo se encuenta solución analítica mediante el método de sepaación de vaiables
CROMATOGRAFIA DE GASES INDICE
 CROMATOGRAFIA DE GASES INDICE I. Genealidades, definiciones básicas. II. Fundamentos Retención Eficiencia Resolución Poblema geneal de la elución III. Elución pogamada IV. Instumentación paa comatogafía
CROMATOGRAFIA DE GASES INDICE I. Genealidades, definiciones básicas. II. Fundamentos Retención Eficiencia Resolución Poblema geneal de la elución III. Elución pogamada IV. Instumentación paa comatogafía
Potencial Eléctrico, Capacitores y Dieléctricos
 Pauta o Cetamen CONSIDERACIONES GENERALES: Cada pegunta tiene como nota máxima un 7.. La nota final se tomaá como el pomedio ente las notas de cada pegunta. Poblema En los puntos A, B, C que coesponden
Pauta o Cetamen CONSIDERACIONES GENERALES: Cada pegunta tiene como nota máxima un 7.. La nota final se tomaá como el pomedio ente las notas de cada pegunta. Poblema En los puntos A, B, C que coesponden
ELIMINATORIA, 14 de abril de 2007 PROBLEMAS
 ELIMINATORIA, 14 de abil de 007 PROBLEMAS 1) Un númeo positivo tiene la popiedad de que su doble es una unidad más gande que él, cuántos divisoes positivos tiene? a) 1 b) c) 3 d) No se puede detemina )
ELIMINATORIA, 14 de abil de 007 PROBLEMAS 1) Un númeo positivo tiene la popiedad de que su doble es una unidad más gande que él, cuántos divisoes positivos tiene? a) 1 b) c) 3 d) No se puede detemina )
Selectividad Septiembre 2009 SEPTIEMBRE 2009
 Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Tema 2. Sistemas conservativos
 Tema. Sistemas consevativos Cuata pate: Movimiento planetaio. Satélites A) Ecuaciones del movimiento Suponemos que uno de los cuepos, de masa M mucho mayo que m, se encuenta en eposo en el oigen de coodenadas
Tema. Sistemas consevativos Cuata pate: Movimiento planetaio. Satélites A) Ecuaciones del movimiento Suponemos que uno de los cuepos, de masa M mucho mayo que m, se encuenta en eposo en el oigen de coodenadas
CASTILLA Y LEÓN / SEPTIEMBRE 02. LOGSE / MATEMÁTICAS II / EXAMEN COMPLETO PRUEBA A
 CASTILLA Y LEÓN / SEPTIEMBRE. LOGSE / MATEMÁTICAS II / EXAMEN CRITERIOS GENERALES DE EVALUACIÓN DE LA PRUEBA: Se obsevaán fundamentalmente los siguientes aspectos: coecta utilización de los conceptos,
CASTILLA Y LEÓN / SEPTIEMBRE. LOGSE / MATEMÁTICAS II / EXAMEN CRITERIOS GENERALES DE EVALUACIÓN DE LA PRUEBA: Se obsevaán fundamentalmente los siguientes aspectos: coecta utilización de los conceptos,
Potencia máxima en derivación
 Potencia máxima en deivación ntoducción La Física tiene dos amas, que no son independientes y que podamos considea como complementaias, son la teóica y la expeimental. La expeimental compueba las deducciones
Potencia máxima en deivación ntoducción La Física tiene dos amas, que no son independientes y que podamos considea como complementaias, son la teóica y la expeimental. La expeimental compueba las deducciones
SUPERPOSICIÓN DE M. A.S.
 SUPERPOSICIÓN DE M. A.S. Enconta la ecuación del movimiento que esulta de la supeposición de dos movimientos amónicos simples paalelos cuas ecuaciones son sen t + π A sen t + π con m A m. Hace un gáfico
SUPERPOSICIÓN DE M. A.S. Enconta la ecuación del movimiento que esulta de la supeposición de dos movimientos amónicos simples paalelos cuas ecuaciones son sen t + π A sen t + π con m A m. Hace un gáfico
3.3.- Cálculo del campo eléctrico mediante la Ley de Gauss
 Lección 1. Campo Electostático en el vacío: Conceptos y esultados fundamentales 17..- Cálculo del campo eléctico mediante la Ley de Gauss La Ley de Gauss pemite calcula de foma sencilla el campo eléctico
Lección 1. Campo Electostático en el vacío: Conceptos y esultados fundamentales 17..- Cálculo del campo eléctico mediante la Ley de Gauss La Ley de Gauss pemite calcula de foma sencilla el campo eléctico
Objetivos El alumno conocerá y aplicará diferentes métodos de solución numérica para la resolución de sistemas de ecuaciones lineales.
 PÁCTICA SOLUCIÓN NUMÉICA DE SISTEMAS DE ECUACIONES LINEALES (PATE I) Objetivos El alumno conoceá aplicaá difeentes métodos de solución numéica paa la esolución de sistemas de ecuaciones lineales. Elaboada
PÁCTICA SOLUCIÓN NUMÉICA DE SISTEMAS DE ECUACIONES LINEALES (PATE I) Objetivos El alumno conoceá aplicaá difeentes métodos de solución numéica paa la esolución de sistemas de ecuaciones lineales. Elaboada
PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES
 PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES. Halla las dimensiones del ectángulo de áea máima que se puede inscibi en una cicunfeencia de adio 5 cm. A máima 5cm Po el teoema de Pitágoas: 0 de donde 0cm 00 La
PROBLEMAS DE OPTIMIZACIÓN DE FUNCIONES. Halla las dimensiones del ectángulo de áea máima que se puede inscibi en una cicunfeencia de adio 5 cm. A máima 5cm Po el teoema de Pitágoas: 0 de donde 0cm 00 La
ECUACIONES DE LA RECTA
 Tema 6 Rectas y planos en el espacio- Matemáticas II º Bachilleato TEMA 6 y 7 - RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA Paa halla la ecuación de una ecta en el espacio necesito: Dos puntos
Tema 6 Rectas y planos en el espacio- Matemáticas II º Bachilleato TEMA 6 y 7 - RECTAS Y PLANOS EN EL ESPACIO ECUACIONES DE LA RECTA Paa halla la ecuación de una ecta en el espacio necesito: Dos puntos
y F 2 F 2 F 1 i (ma) i (ma) V (mv) V (mv) 1 6,1 0, ,9 0, ,0 0, ,6 0,
 FÍSICA APLICADA A FARMACIA. CURSO 0-0. FIAL EXTRAORDIARIO. 8 JUIO Poblema (expeimental,.5 p). Un hilo conducto de cobe de (7.9±0.) metos de longitud y diámeto (0.9±0.0) mm se conecta a una fuente de voltaje
FÍSICA APLICADA A FARMACIA. CURSO 0-0. FIAL EXTRAORDIARIO. 8 JUIO Poblema (expeimental,.5 p). Un hilo conducto de cobe de (7.9±0.) metos de longitud y diámeto (0.9±0.0) mm se conecta a una fuente de voltaje
Ejemplo 6-3. Tema 2. Electrocinética V =IR. Resolver circuitos simples. Resistencias Ley de Ohm: I, intensidad de corriente eléctrica.
 Tema 2. Electocinética Ojetivos: Defini los conceptos intensidad de coiente eléctica, velocidad de aaste, densidad de coiente y esistencia. Estalece la ley de Ohm. Defini la esistividad, y conoce su dependencia
Tema 2. Electocinética Ojetivos: Defini los conceptos intensidad de coiente eléctica, velocidad de aaste, densidad de coiente y esistencia. Estalece la ley de Ohm. Defini la esistividad, y conoce su dependencia
EQUILIBRIO QUÍMICO QCA 07
 1.- Dado el equilibrio: N (g) + 3 H (g) NH 3 (g) Justifique la influenia sobre el mismo de: a) Un aumento de la resión total. b) Una disminuión de la onentraión de N. ) Una disminuión de la temeratura.
1.- Dado el equilibrio: N (g) + 3 H (g) NH 3 (g) Justifique la influenia sobre el mismo de: a) Un aumento de la resión total. b) Una disminuión de la onentraión de N. ) Una disminuión de la temeratura.
ANALISIS DE RIESGO E INCERTIDUMBRE. Evaluacion de Proyectos Jose Fuentes Valdes
 ANALISIS DE RIESGO E INCERTIDUMBRE Análisis Deteministico V/S Análisis de Riesgo e Incetidumbe Valoes Únicos y Conocidos Valoes Vaiables y Desconocidos ANALISIS DETERMINISTICO Pecio Cantidad Invesión EVALUACION
ANALISIS DE RIESGO E INCERTIDUMBRE Análisis Deteministico V/S Análisis de Riesgo e Incetidumbe Valoes Únicos y Conocidos Valoes Vaiables y Desconocidos ANALISIS DETERMINISTICO Pecio Cantidad Invesión EVALUACION
EQUILIBRIO QUÍMICO QCA 04 ANDALUCÍA
 1.- Considérese el siguiente sistema en equilibrio: SO 3 (g) SO (g) + 1/ O (g) H > 0 Justifique la veraidad o falsedad de las siguientes afirmaiones: a) Al aumentar la onentraión de oxígeno, el equilibrio
1.- Considérese el siguiente sistema en equilibrio: SO 3 (g) SO (g) + 1/ O (g) H > 0 Justifique la veraidad o falsedad de las siguientes afirmaiones: a) Al aumentar la onentraión de oxígeno, el equilibrio
FRANCISCO JAVIER GARCÍA CAPITÁN
 MÁXIMOS SIN DERIVDS FRNCISCO JVIER GRCÍ CPITÁN Resumen Este atículo eune vaios ejemplos de cómo calcula extemos sin necesidad de usa el cálculo difeencial Solo usaemos conocidas desigualdades ente las
MÁXIMOS SIN DERIVDS FRNCISCO JVIER GRCÍ CPITÁN Resumen Este atículo eune vaios ejemplos de cómo calcula extemos sin necesidad de usa el cálculo difeencial Solo usaemos conocidas desigualdades ente las
SERIE # 3 CÁLCULO VECTORIAL
 SERIE # 3 ÁLULO VETORIAL ÁLULO VETORIAL Página 1 1) Sea el campo vectoial F (x,y,)=( 3x+ y)i+( x+ y ) j ( x) k. alcula lago de la cuva : 4 5 x = + y y =, del punto A ( 3, 1, 1) al punto B ( 3, 1, -1).
SERIE # 3 ÁLULO VETORIAL ÁLULO VETORIAL Página 1 1) Sea el campo vectoial F (x,y,)=( 3x+ y)i+( x+ y ) j ( x) k. alcula lago de la cuva : 4 5 x = + y y =, del punto A ( 3, 1, 1) al punto B ( 3, 1, -1).
A continuación obligamos, aplicando el producto escalar, a que los vectores:
 G1.- Se sabe que el tiángulo ABC es ectángulo en el vétice C, que petenece a la ecta intesección de los planos y + z = 1 e y 3z + 3 = 0, y que sus otos dos vétices son A( 2, 0, 1 ) y B ( 0, -3, 0 ). Halla
G1.- Se sabe que el tiángulo ABC es ectángulo en el vétice C, que petenece a la ecta intesección de los planos y + z = 1 e y 3z + 3 = 0, y que sus otos dos vétices son A( 2, 0, 1 ) y B ( 0, -3, 0 ). Halla
Cálculo diferencial e integral en una variable. Examen Febrero de 2018
 Cálculo difeencial e integal en una vaiable 2do semeste de 207 Examen Febeo de 208 Ejecicios: Múltiple opción (Total: 6 puntos) Ejecicio Sea f : [, + ) R una función continua tal que x R. Indique la opción
Cálculo difeencial e integal en una vaiable 2do semeste de 207 Examen Febeo de 208 Ejecicios: Múltiple opción (Total: 6 puntos) Ejecicio Sea f : [, + ) R una función continua tal que x R. Indique la opción
CATALUÑA / JUNIO 02. LOGSE / FÍSICA / EXAMEN COMPLETO
 Resuelva el poblema P1 y esponda a las uestiones C1 y C Esoja una de las opiones (A o B) y esuelva el poblema P y onteste a las uestiones C3 y C4 de la opión esogida (En total hay que esolve dos poblemas
Resuelva el poblema P1 y esponda a las uestiones C1 y C Esoja una de las opiones (A o B) y esuelva el poblema P y onteste a las uestiones C3 y C4 de la opión esogida (En total hay que esolve dos poblemas
Ingeniería en Alimentos - Fenómenos de Transporte Difusión Molecular de Masa Parte II
 Ingenieía en limentos - Fenómenos de Tanspote ifusión oleula de asa ate II IFUSIO E U GS TRVES E U GS ESTCIORIO Y QUE O SE IFUE Supuestos: estado estable difusión unidieional áea de flujo onstante sistema
Ingenieía en limentos - Fenómenos de Tanspote ifusión oleula de asa ate II IFUSIO E U GS TRVES E U GS ESTCIORIO Y QUE O SE IFUE Supuestos: estado estable difusión unidieional áea de flujo onstante sistema
Esta guía es una herramienta que usted debe usar para lograr los siguientes objetivos:
 FÍSICA GENERAL II GUÍA - Campo eléctico: Ley de Gauss Objetivos de apendizaje Esta guía es una heamienta que usted debe usa paa loga los siguientes objetivos: Defini el concepto de Flujo de Campo Eléctico.
FÍSICA GENERAL II GUÍA - Campo eléctico: Ley de Gauss Objetivos de apendizaje Esta guía es una heamienta que usted debe usa paa loga los siguientes objetivos: Defini el concepto de Flujo de Campo Eléctico.
Aplicaciones de la Optimización Convexa al análisis de redes
 Aplicaciones de la Optimización Convea al análisis de edes Intoducción Repaso de conceptos básicos de unciones de vaias vaiables y conveidad Repaso : Función deivada pacial La deivada pacial de con especto
Aplicaciones de la Optimización Convea al análisis de edes Intoducción Repaso de conceptos básicos de unciones de vaias vaiables y conveidad Repaso : Función deivada pacial La deivada pacial de con especto
INTRODUCCIÓN AL ANÁLISIS DE LA VARIANZA
 -1- T 1 T T x 11 x 1 x 1 x 1n1 x n x n INTRODUCCIÓN AL ANÁLISIS DE LA VARIANZA José Luis Vicente Villadón Depatamento de Estadística -- ANALISIS DE LA VARIANZA DISEÑO DE UNA VIA Disponemos de poblaciones,
-1- T 1 T T x 11 x 1 x 1 x 1n1 x n x n INTRODUCCIÓN AL ANÁLISIS DE LA VARIANZA José Luis Vicente Villadón Depatamento de Estadística -- ANALISIS DE LA VARIANZA DISEÑO DE UNA VIA Disponemos de poblaciones,
Figura 1. Viscosímetro de Ostwald.
 FISICA GENEAL II 01 Guía de Tabajo Patio N o Deteminaión de visosidades C.L. Di Pinzio, amia Máximo, Comes aú Intoduión: E visosímeto de Ostwad E visosímeto de Ostwad (Fig.1) es un apaato eativamente simpe
FISICA GENEAL II 01 Guía de Tabajo Patio N o Deteminaión de visosidades C.L. Di Pinzio, amia Máximo, Comes aú Intoduión: E visosímeto de Ostwad E visosímeto de Ostwad (Fig.1) es un apaato eativamente simpe
OTRAS APLICACIONES DE LA APROXIMACIÓN DE CAPA LÍMITE LAMINAR. CORRIENTES LIBRES.
 OTRAS APLICACIONES DE LA APROXIMACIÓN DE CAPA LÍMITE LAMINAR. CORRIENTES LIBRES. 1 Intoducción Los movimientos de choos de líquido en el seno del mismo líquido, la estela de cuepos en el seno de una coiente
OTRAS APLICACIONES DE LA APROXIMACIÓN DE CAPA LÍMITE LAMINAR. CORRIENTES LIBRES. 1 Intoducción Los movimientos de choos de líquido en el seno del mismo líquido, la estela de cuepos en el seno de una coiente
de perfil, y se halla la tercera proyección tanto del punto P como de la recta r. La proyección r corta a los planos de proyección en H r
 Actividad SISTEMA IÉRICO II TEMA 9 Paa eolve eta actividad, emo de tene en cuenta lo iguiente: o ecta on paalela en el epacio, i u poyeccione obe lo do plano de poyección también lo on.. Sea el punto P(-P
Actividad SISTEMA IÉRICO II TEMA 9 Paa eolve eta actividad, emo de tene en cuenta lo iguiente: o ecta on paalela en el epacio, i u poyeccione obe lo do plano de poyección también lo on.. Sea el punto P(-P
5.2 PROBLEMAS PRACTICOS DE MÁXIMOS Y MINIMOS
 8. Un avión que vuela a velocidad constante de Km/h pasa sobe una estación teeste de ada a una altua de 1 Km. Y se eleva a un ángulo de º. qué velocidad aumenta la distancia ente el avión la estación de
8. Un avión que vuela a velocidad constante de Km/h pasa sobe una estación teeste de ada a una altua de 1 Km. Y se eleva a un ángulo de º. qué velocidad aumenta la distancia ente el avión la estación de
ESTÁTICA. El Centro de Gravedad (CG) de un cuerpo es el punto donde se considera aplicado el peso.
 C U R S O: FÍSICA COMÚN MATERIAL: FC-08 ESTÁTICA En esta unidad analizaemos el equilibio de un cuepo gande, que no puede considease como una patícula. Además, vamos a considea dicho cuepo como un cuepo
C U R S O: FÍSICA COMÚN MATERIAL: FC-08 ESTÁTICA En esta unidad analizaemos el equilibio de un cuepo gande, que no puede considease como una patícula. Además, vamos a considea dicho cuepo como un cuepo
Puntos, rectas y planos en el espacio. Problemas métricos en el espacio
 1. Estudia la posición elativa de las ectas y s: x = 2t 1 x + 3y + 4z 6 = 0 : ; s : y = t + 1 2x + y 3z + 2 = 0 z = 3t + 2 Calcula la distancia ente ambas ectas (Junio 1997) Obtengamos un vecto diecto
1. Estudia la posición elativa de las ectas y s: x = 2t 1 x + 3y + 4z 6 = 0 : ; s : y = t + 1 2x + y 3z + 2 = 0 z = 3t + 2 Calcula la distancia ente ambas ectas (Junio 1997) Obtengamos un vecto diecto
Ejercicios resueltos: Tomando como base los Considerandos y el Formulario 3, se plantea a continuación la resolución de diversos ejercicios.
 Ejecicios esueltos: Tomando como base los Consideandos y el Fomulaio 3, se plantea a continuación la esolución de diesos ejecicios. 1. Cuando un electón pasa pependiculamente a taés de las líneas de flujo
Ejecicios esueltos: Tomando como base los Consideandos y el Fomulaio 3, se plantea a continuación la esolución de diesos ejecicios. 1. Cuando un electón pasa pependiculamente a taés de las líneas de flujo
9 Cuerpos geométricos
 865 _ 045-056.qxd 7/4/07 1:0 Página 45 Cuepos geométicos INTRODUCCIÓN Los cuepos geométicos están pesentes en múltiples contextos de la vida eal, de aí la impotancia de estudialos. Es inteesante constui
865 _ 045-056.qxd 7/4/07 1:0 Página 45 Cuepos geométicos INTRODUCCIÓN Los cuepos geométicos están pesentes en múltiples contextos de la vida eal, de aí la impotancia de estudialos. Es inteesante constui
TEMA 9: FORMAS GEOMÉTRICAS. Primer Curso de Educación Secundaria Obligatoria. I.e.s. Fuentesaúco.
 2009 TEMA 9: FORMAS GEOMÉTRICAS. Pime Cuso de Educación Secundaia Obligatoia. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 09: FORMAS GEOMÉTRICAS. 1. Ideas Elementales de Geometía
2009 TEMA 9: FORMAS GEOMÉTRICAS. Pime Cuso de Educación Secundaia Obligatoia. I.e.s. Fuentesaúco. Manuel González de León. mgdl 01/01/2009 TEMA 09: FORMAS GEOMÉTRICAS. 1. Ideas Elementales de Geometía
FÓRMULAS Y DEDUCCIONES QUE HAY QUE SABER. Mm v GM
 CLASE : LEY DE LA GRAVIACIÓN UNIVERSAL. SAÉLIES I FÓRMULAS Y DEDUCCIONES QUE HAY QUE SABER VELOCIDAD ORBIAL DE UN SAÉLIE: g c gr Mm v 0 F F G m v PERIODO DE UN SAÉLIE: v g0r PESO DE UN SAÉLIE EN UNA ÓRBIA:
CLASE : LEY DE LA GRAVIACIÓN UNIVERSAL. SAÉLIES I FÓRMULAS Y DEDUCCIONES QUE HAY QUE SABER VELOCIDAD ORBIAL DE UN SAÉLIE: g c gr Mm v 0 F F G m v PERIODO DE UN SAÉLIE: v g0r PESO DE UN SAÉLIE EN UNA ÓRBIA:
Física General 1 Proyecto PMME - Curso 2007 Instituto de Física Facultad de Ingeniería UdelaR
 Física Geneal Poyecto PMME - Cuso 007 Instituto de Física Facultad de Ingenieía UdelaR TITULO DINÁMICA DEL RÍGIDO. AUTORES Emiliano Gacía, Juan Manuel Galasso, Valeia Rey INTRODUCCIÓN El siguiente ejecicio,
Física Geneal Poyecto PMME - Cuso 007 Instituto de Física Facultad de Ingenieía UdelaR TITULO DINÁMICA DEL RÍGIDO. AUTORES Emiliano Gacía, Juan Manuel Galasso, Valeia Rey INTRODUCCIÓN El siguiente ejecicio,
ESTÁTICA. El Centro de Gravedad (CG) de un cuerpo es el punto donde se considera aplicado el peso.
 C U R S O: FÍSICA MENCIÓN MATERIAL: FM- 09 ESTÁTICA En esta unidad analizaemos el equilibio de un cuepo gande, que no puede considease como una patícula. Además, vamos a considea dicho cuepo como un cuepo
C U R S O: FÍSICA MENCIÓN MATERIAL: FM- 09 ESTÁTICA En esta unidad analizaemos el equilibio de un cuepo gande, que no puede considease como una patícula. Además, vamos a considea dicho cuepo como un cuepo
CÁLCULO Primer curso de Ingeniero de Telecomunicación Segundo Examen Parcial. 13 de Junio de 2001 Primera parte. ; y = u v ; z = u2 v 2
 CÁLCULO Pime cuso de Ingenieo de Telecomunicación Segundo Examen Pacial. 1 de Junio de 1 Pimea pate Ejecicio 1. Obtene la expesión en que se tansfoma z xx +z xy +z yy ; al cambia las vaiables independientes
CÁLCULO Pime cuso de Ingenieo de Telecomunicación Segundo Examen Pacial. 1 de Junio de 1 Pimea pate Ejecicio 1. Obtene la expesión en que se tansfoma z xx +z xy +z yy ; al cambia las vaiables independientes
MAGNITUDES ESCALARES Y VECTORIALES
 C U R S O: FÍSIC Mención MTERIL: FM-01 MGNITUDES ESCLRES VECTORILES Sistema intenacional de medidas En 1960, un comité intenacional estableció un conjunto de patones paa estas magnitudes fundamentales.
C U R S O: FÍSIC Mención MTERIL: FM-01 MGNITUDES ESCLRES VECTORILES Sistema intenacional de medidas En 1960, un comité intenacional estableció un conjunto de patones paa estas magnitudes fundamentales.
SECCIÓN 2: GEOMETRÍA EN LAS SECCIONES DE SANEAMIENTO
 El diseño de las edes de Saneamiento: Estuctua Básica de la Red SECCIÓN 2: GEOMETRÍA EN LAS SECCIONES DE SANEAMIENTO INTRODUCCIÓN Conociendo el caudal a evacua, coesponde detemina la sección más adecuada
El diseño de las edes de Saneamiento: Estuctua Básica de la Red SECCIÓN 2: GEOMETRÍA EN LAS SECCIONES DE SANEAMIENTO INTRODUCCIÓN Conociendo el caudal a evacua, coesponde detemina la sección más adecuada
CARACTERISTICAS DE LOS CAMPOS CONSERVATIVOS
 CARACTERISTICAS DE LOS CAMPOS CONSERVATIVOS Paa los inteeses de la Física, los Campos Vectoiales se clasifican en dos gupos: -CAMPOS VECTORIALES CONSERVATIVOS.CAMPOS VECTORIALES NO CONSERVATIVOS Los de
CARACTERISTICAS DE LOS CAMPOS CONSERVATIVOS Paa los inteeses de la Física, los Campos Vectoiales se clasifican en dos gupos: -CAMPOS VECTORIALES CONSERVATIVOS.CAMPOS VECTORIALES NO CONSERVATIVOS Los de
TRANSICIONES DE FASE.
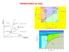 RANSCONES DE FASE. Qué podemos deci de estos diagamas (Diagamas de Fase)? Una misma sustancia (agua en este caso) puede pesentase en muchas fomas posible (Fases: Gas o vapo líquida o solida y esta a su
RANSCONES DE FASE. Qué podemos deci de estos diagamas (Diagamas de Fase)? Una misma sustancia (agua en este caso) puede pesentase en muchas fomas posible (Fases: Gas o vapo líquida o solida y esta a su
UNIDAD Nº 2 VECTORES Y FUERZAS
 UNIVERSIDAD DE SANTIAGO DE CHILE DEPARTAMENTO DE FISICA FISICA EXPERIMENTAL PLAN ANUAL INGENIERIA FISICA 1 e SEMESTRE 2012 UNIDAD Nº 2 VECTORES Y FUERZAS OBJETIVOS Medi el módulo de un vecto fueza usando
UNIVERSIDAD DE SANTIAGO DE CHILE DEPARTAMENTO DE FISICA FISICA EXPERIMENTAL PLAN ANUAL INGENIERIA FISICA 1 e SEMESTRE 2012 UNIDAD Nº 2 VECTORES Y FUERZAS OBJETIVOS Medi el módulo de un vecto fueza usando
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables (x 0 ). x ik. x ik 1
 1. RESUMEN Ingenieía Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Vaias Vaiables 08-1 Ingenieía Matemática Univesidad de Chile Guía Semana 5 Teoema del valo medio.
1. RESUMEN Ingenieía Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Vaias Vaiables 08-1 Ingenieía Matemática Univesidad de Chile Guía Semana 5 Teoema del valo medio.
226 Capítulo 4: Aplicaciones de las derivadas
 4.6 Método de Newton 5 6. La deivada dtd del ejemplo 4 a. Demueste que es una función ceciente de. b. Puebe que es una función dececiente de. c. Demueste que dt d = ƒsd = gsd = c a + - es una función ceciente
4.6 Método de Newton 5 6. La deivada dtd del ejemplo 4 a. Demueste que es una función ceciente de. b. Puebe que es una función dececiente de. c. Demueste que dt d = ƒsd = gsd = c a + - es una función ceciente
Potencial Eléctrico y Diferencia de Potencial
 Potenial létrio y iferenia de Potenial Potenial létrio: se llama potenial elétrio en un punto A de un ampo elétrio al trabajo () neesario para transportar la unidad de arga positiva ( ) desde fuera del
Potenial létrio y iferenia de Potenial Potenial létrio: se llama potenial elétrio en un punto A de un ampo elétrio al trabajo () neesario para transportar la unidad de arga positiva ( ) desde fuera del
Primer parcial de Química Física. 11de Mayo de 2007 (Examen de Repesca)
 Pime pacial de Química Física. de Mayo de 7 (Examen de Repesca) ) a) Indica, azonando lo más bevemente posible las espuestas, si son vedadeas o falsas las siguientes afimaciones. iet / I) La función de
Pime pacial de Química Física. de Mayo de 7 (Examen de Repesca) ) a) Indica, azonando lo más bevemente posible las espuestas, si son vedadeas o falsas las siguientes afimaciones. iet / I) La función de
Adaptación de impedancias
 .- El tansfomado ideal Adaptación de impedancias I +V +V TI Tansfomado ideal V elaciones V-I: V = I = a. I, válidas paa cualquie fecuencia. a Si se conecta una esistencia al secundaio, ente el nodo +V
.- El tansfomado ideal Adaptación de impedancias I +V +V TI Tansfomado ideal V elaciones V-I: V = I = a. I, válidas paa cualquie fecuencia. a Si se conecta una esistencia al secundaio, ente el nodo +V
EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES
 EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES De su cota y espectacula existencia (1911-1927 el átomo de Boh dejó una imagen simple del átomo y vaios conceptos nuevos y fundamentales, como el de númeos
EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES De su cota y espectacula existencia (1911-1927 el átomo de Boh dejó una imagen simple del átomo y vaios conceptos nuevos y fundamentales, como el de númeos
Campos eléctricos y Magnéticos
 Campos elécticos y Magnéticos Fueza eléctica: es la fueza de atacción ejecida ente dos o más patículas cagadas. La fueza eléctica no sólo mantiene al electón ceca del núcleo, también mantiene a los átomos
Campos elécticos y Magnéticos Fueza eléctica: es la fueza de atacción ejecida ente dos o más patículas cagadas. La fueza eléctica no sólo mantiene al electón ceca del núcleo, también mantiene a los átomos
