Recursión y Relaciones de Recurrencia. UCR ECCI CI-1204 Matemáticas Discretas Prof. M.Sc. Kryscia Daviana Ramírez Benavides
|
|
|
- Gustavo Ortega Paz
- hace 5 años
- Vistas:
Transcripción
1 Reusión y Relaiones de Reuenia UCR ECCI CI-04 Matemátias Disetas Pof. M.S. Kysia Daviana Ramíez Benavides
2 Pogesión Geométia Es una suesión infinita de númeos donde el oiente de ualquie témino (distinto del pimeo) ente su pedeeso es una onstante llamada azón omún. Ejemplos: 5, 5, 45, 35, 5/5 = 3, 45/5 = 3, 35/45 = 3, 5 = 3*5, 45 = 3*5, 35 = 3*45, 7,, 63, 89, /7 = 3, 63/ = 3, 89/63 = 3, = 3*7, 63 = 3*, 89 = 3*63, UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia
3 Relaión de Reuenia Es una euaión en donde paa obtene el valo atual se depende de uno o más valoes pedeesoes inmediatos a él. e0 e e ek a + a + a a = f n, n k n n a0 = A Donde: 0, a n = n A,..., a n k n = A k k Z +, detemina el oden de la elaión y debe se n k. e i Z +, i = 0,,,..., k, detemina si la elaión es lineal o no. f(n) es una funión dada, n N y de oden k. Cada n i R, i = 0,,,..., k y n 0. Son los oefiientes de la elaión. Cada a j R, j = 0,,,..., k-. Son las ondiiones fontea o iniiales. n k n k ( ) UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 3
4 Relaión de Reuenia (ont.) Una elaión de euenia paa una suesión {a 0, a, a, a 3, } es una fómula que expesa ada témino a n, a pati de ieto n N, en funión de uno o más de los téminos que le peeden. Los valoes de los téminos neesaios paa empeza a alula se llaman ondiiones iniiales. Se die que una suesión es una soluión de la elaión de euenia si su témino geneal veifia diha elaión. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 4
5 Relaión de Reuenia (ont.) Las elaiones de euenia pueden onsidease omo ténias avanzadas de onteo. Resuelve poblemas uya soluión no puede obtenese usando vaiaiones, pemutaiones, ombinaiones o on las ténias deivadas del pinipio de inlusión-exlusión. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 5
6 Relaión de Reuenia (ont.) Ejemplos: 5, 5, 45, 35, a n+ = 3a n, a 0 = 5, n 0 7,, 63, 89, a n+ = 3a n, a 0 = 7, n 0 UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 6
7 Relaión de Reuenia (ont.) Toda elaión de euenia tiene: Coefiientes, pueden se onstantes o vaiables, que son valoes que están multipliando ada témino on subíndie de la elaión de euenia. Condiiones fontea o iniiales, que son los valoes iniiales que se neesitan paa esolve la elaión de euenia, y se denotan omo a 0, a,, a k-. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 7
8 Relaión de Reuenia (ont.) Una elaión de euenia puede se: Pime Oden: Cuando la elaión de euenia sólo depende de su pedeeso inmediato. Ejemplo: a n+ = 3a n, a 0 = 5, n 0. Segundo Oden: Cuando la elaión de euenia depende de sus dos pedeesoes inmediatos. Ejemplo: a n = a n- + 5a n-, a 0 = 0, a =, n. Lineal: Cuando ada témino on subíndie de la elaión de euenia apaee elevado a la pimea potenia. Ejemplo: a n+ = 3a n, a 0 = 5, n 0. No Lineal: Cuando algún témino on subíndie de la elaión de euenia apaee elevado a una potenia difeente a la pimea potenia. Ejemplo: a n+ = 3a n, a 0 = 5, n 0. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 8
9 Relaión de Reuenia (ont.) Una elaión de euenia puede se: Homogénea: Cuando f(n) = 0 paa todo n N. Ejemplo: a n+ = 3a n a n+ 3a n = 0, a 0 = 5, n 0. No Homogénea: Cuando f(n) 0 paa todo n N. Ejemplo: a n+ = 3a n + n a n+ 3a n = n, a 0 = 5, n 0. Coefiientes Constantes: Cuando ada témino on subíndie de la elaión de euenia está multipliado po una onstante. Ejemplo: a n+ = 3a n, a 0 = 5, n 0. Coefiientes Vaiables: Cuando algún témino on subíndie de la elaión de euenia está multipliado po una valo vaiable. Ejemplo: a n = na n-, a 0 =, n. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 9
10 Relaiones de Reuenia (ont.) La soluión geneal de una elaión de euenia es el valo de a n es una funión de n que no depende de los téminos anteioes de la suesión, una vez definido las ondiiones fontea o iniiales, que se obtiene a pati de la elaión de euenia. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 0
11 Soluión Geneal: Relaiones de Reuenia de Pime Oden, Lineales, Homogéneas y on Coefiientes Constantes La elaión de euenia a n+ = a n, a 0 = A 0, n 0 Donde: es una onstante difeente de eo. a 0 = A 0 es únia. La soluión geneal de diha elaión está dada po a n = A 0 n, n 0. Está última euaión es una funión diseta uyo dominio es el onjunto N de los enteos no negativos. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia
12 Soluión Geneal: Relaiones de Reuenia de Segundo Oden, Lineales, Homogéneas y on Coefiientes Constantes La elaión de euenia n+ a n+ + n+ a n+ + n a n = 0, a 0 = A 0, a = A, n 0 Donde: n+, n+ y n son onstantes difeentes de eo. a 0 = A 0 y a = A son únias. Paa obtene la soluión geneal de diha elaión: Se sustituye a n = d n, donde d 0 y 0, se obtiene: n+ d n+ + n+ d n+ + n d n = 0. Se saa omo fato omún d n, se obtiene una euaión uadátia llamada euaión aateístia: n+ + n+ + n = 0. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia
13 Soluión Geneal: Relaiones de Reuenia de Segundo Oden, Lineales, Homogéneas y on Coefiientes Constantes (ont.) Paa obtene la soluión geneal de diha elaión: Se esuelve la euaión uadátia y se obtiene las aíes de esa euaión y, estas son llamadas aíes aateístias. Estas aíes pueden se: númeos eales distintos, númeos eales iguales y númeos omplejos onjugados. Sólo se analizaá los dos pimeos asos. Si las aíes obtenidas son númeos eales distintos se va fomando la soluión geneal de la siguiente manea: a n = n + n. Si las aíes obtenidas son númeos eales iguales se va fomando la soluión geneal de la siguiente manea: a n = n + n n. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 3
14 UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 4 Soluión Geneal: Relaiones de Reuenia de Segundo Oden, Lineales, Homogéneas y on Coefiientes Constantes (ont.) Paa obtene la soluión geneal de diha elaión: Una vez que se tiene este avane de la soluión geneal on las ondiiones fontea o iniiales se foma un sistema de euaiones y se halla y. Con los valoes que se obtengan de las aíes y, y las onstantes y se obtiene la soluión geneal de la elaión de euenia: a n = n + n, n 0 Raíes difeentes. a n = n + n n, n 0 Raíes iguales. Raíes eales iguales 0 Raíes eales difeentes = + = = + = + = + = + = + = A a A a A a A a
15 Soluión Geneal: Relaiones de Reuenia de Pime o Segundo Oden, Lineales, No Homogéneas y on Coefiientes Constantes La elaión de euenia n+ a n+ + n+ a n+ + n a n =f(n), a 0 = A 0, a = A, n 0 Donde: f(n) 0. n+, n+ y n son onstantes difeentes de eo. a 0 = A 0 y a = A son únias. Paa obtene la soluión geneal de diha elaión se suma la soluión homogénea asoiada a nh y la soluión patiula a np. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 5
16 Soluión Geneal: Relaiones de Reuenia de Pime o Segundo Oden, Lineales, No Homogéneas y on Coefiientes Constantes (ont.) Paa obtene la soluión geneal de diha elaión se ealiza lo siguiente: Se esuelve la elaión homogénea asoiada omo se onoe sin saa las onstantes, on los pasos anteiomente dados, y así se obtendá la soluión homogénea asoiada a nh. Luego, se obtiene la soluión patiula a np obsevando la funión dada f(n) y busando en la tabla. Si a np ontiene aíes distintas a las obtenidas en a nh, entones se pasa al siguiente paso. Si ontiene una aíz igual a las obtenidas en a nh, entones a np = na np y se pasa al siguiente paso. Si ontiene dos aíes iguales a las obtenidas en a nh, entones a np = n a np y se pasa al siguiente paso. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 6
17 Soluión Geneal: Relaiones de Reuenia de Pime o Segundo Oden, Lineales, No Homogéneas y on Coefiientes Constantes (ont.) f(n), onstante n n n t, t Z+ n, R n t n a n p A, onstante A n + A 0 A n + A n + A 0 A t n t + A t- n t- + + A n + A 0 A n n (A t n t + A t- n t- + + A n + A 0 ) Tabla UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 7
18 Soluión Geneal: Relaiones de Reuenia de Pime o Segundo Oden, Lineales, No Homogéneas y on Coefiientes Constantes (ont.) Paa obtene la soluión geneal de diha elaión se ealiza lo siguiente: Se obtiene el valo de ada onstante de la a np, o sea, las onstantes A t, A t-,..., A, A 0 ; lo ual se loga sustituyendo ada témino a n de la elaión de euenia dada po la a np y esolviendo la euaión. Po ejemplo: f(n) = n, po lo tanto a np = A n, entones se obtiene algo así: n+ A n+ + n+ A n+ + n A n = n Con la soluión homogénea asoiada a nh y la soluión patiula a p n obtenidas se tiene la soluión geneal de la elaión de euenia a n = a nh + a np. Po último, se alula los valoes y de la soluión homogénea asoiada, mediante un sistema de euaiones, sustituyendo on las ondiiones iniiales dadas. Con esto se obtiene la soluión geneal de la elaión de euenia. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 8
19 Tansfomaión de una Relaión de Reuenia No Lineal a Lineal Se puede tansfoma una elaión de euenia no lineal a lineal paa pode esolvela mediante una sustituión algebaia b n = a n. Ejemplo: a n+ = 3a n, a 0 = 3, n 0 b n+ = 3b n, b 0 = 9, n 0 Una vez heho esto se puede esolve omo una elaión de euenia lineal, paa este ejemplo oesponde a una elaión de pime oden, homogénea y on oefiientes onstantes. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 9
20 Tansfomaión de una Relaión de Reuenia No Lineal a Lineal Después de esolvela se saa la aíz a ada númeo obtenido en la soluión geneal paa tene la soluión geneal de la elaión de euenia no lineal. Ejemplo: b n = 9*3 n, n 0 a n = 3* 3 n, n 0 UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia 0
21 Refeenias Bibliogáfias Jonnsonbaugh, Rihad. Matemátias Disetas. Pentie Hall, Méxio. Sexta Ediión, 005. Gimaldi, Ralph P. Matemátia Diseta y Combinatoia. Addison Wesley Longman de Méxio, S.A. Teea Ediión, 998. UCR-ECCI CI-04 Matemátias Disetas Reusión y Relaiones de Reuenia
Recursión y Relaciones de Recurrencia. UCR ECCI CI-1204 Matemáticas Discretas M.Sc. Kryscia Daviana Ramírez Benavides
 Reursión y Relaiones de Reurrenia UCR ECCI CI-04 Matemátias Disretas M.S. Krysia Daviana Ramírez Benavides Algoritmos Reursivos Un algoritmo es reursivo si se soluiona un problema reduiéndolo a una instania
Reursión y Relaiones de Reurrenia UCR ECCI CI-04 Matemátias Disretas M.S. Krysia Daviana Ramírez Benavides Algoritmos Reursivos Un algoritmo es reursivo si se soluiona un problema reduiéndolo a una instania
Recursión y Relaciones de Recurrencia. UCR ECCI CI-0111 Estructuras Discretas Prof. Kryscia Daviana Ramírez Benavides
 Reursión y Relaiones de Reurrenia UCR ECCI CI-0 Estruturas Disretas Prof. Krysia Daviana Ramírez Benavides Algoritmos Reursivos Un algoritmo es reursivo si se soluiona un problema reduiéndolo a una instania
Reursión y Relaiones de Reurrenia UCR ECCI CI-0 Estruturas Disretas Prof. Krysia Daviana Ramírez Benavides Algoritmos Reursivos Un algoritmo es reursivo si se soluiona un problema reduiéndolo a una instania
Fórmulas de Diseño para Columnas
 Fómulas de Diseño paa Columnas 15 de noviembe de 2017 En las seiones peedentes hemos disutido la apaidad teóia de aga de las olumnas ante pandeo tanto elástio omo inelástio. Con esta idea en mente, estamos
Fómulas de Diseño paa Columnas 15 de noviembe de 2017 En las seiones peedentes hemos disutido la apaidad teóia de aga de las olumnas ante pandeo tanto elástio omo inelástio. Con esta idea en mente, estamos
MICROECONOMÍA. EQUILIBRIO GENERAL Y ECONOMÍA DE LA INFORMACIÓN. Tema 1 EQUILIBRIO GENERAL Y FALLOS DE MERCADO
 MICROECONOMÍA. EQUIIBRIO GENERA Y ECONOMÍA DE A INORMACIÓN Tema EQUIIBRIO GENERA Y AOS DE MERCADO enando Peea Tallo Olga Maía Rodíguez Rodíguez htt://bit.l/8l8ddu Un Modelo de Euilibio Geneal: Dos fatoes
MICROECONOMÍA. EQUIIBRIO GENERA Y ECONOMÍA DE A INORMACIÓN Tema EQUIIBRIO GENERA Y AOS DE MERCADO enando Peea Tallo Olga Maía Rodíguez Rodíguez htt://bit.l/8l8ddu Un Modelo de Euilibio Geneal: Dos fatoes
RECTAS EN EL PLANO. r datos, podemos dar la ecuación de dicha recta de varias P o Ecuación vectorial
 RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
RECTAS EN EL PLANO Ecuación de la ecta La ecuación de una ecta puede dase de difeentes fomas, que veemos a continuación. Conocidos un punto P(p 1, p ) y un vecto de diección d = (d 1, d ) (o sea, un vecto
Propagación de las ondas
 Popagaión de las ondas Popagaión de las ondas 1.1.pdf Fabie Lengonne, 2008-2013 Medios de popagaión Condiiones neesaias Medio mateial Paa popaga una onda sonoa, el medio debe se ompuesto de patíulas mateiales.
Popagaión de las ondas Popagaión de las ondas 1.1.pdf Fabie Lengonne, 2008-2013 Medios de popagaión Condiiones neesaias Medio mateial Paa popaga una onda sonoa, el medio debe se ompuesto de patíulas mateiales.
Pman = cmhg= atm
 emodinámia eoía (11) oblemas esueltos Semeste: 014-1 1. Una masa de 0 g de SO se enuenta almaenada en un tanque on un volumen de 50 dm a una tempeatua de 800 R. La pesión baométia loal es de 700 mm Hg.
emodinámia eoía (11) oblemas esueltos Semeste: 014-1 1. Una masa de 0 g de SO se enuenta almaenada en un tanque on un volumen de 50 dm a una tempeatua de 800 R. La pesión baométia loal es de 700 mm Hg.
Tema 3. Reacción sólido-fluido no catalitica
 Tema 3. eaión sólido-fluido no atalitia (fluido) + b (sólido) podutos fluidos podutos sólidos podutos fluidos y sólidos Modelo de eaión: NS on despendimiento enizas y adheentes Patíula que ha eaionado
Tema 3. eaión sólido-fluido no atalitia (fluido) + b (sólido) podutos fluidos podutos sólidos podutos fluidos y sólidos Modelo de eaión: NS on despendimiento enizas y adheentes Patíula que ha eaionado
SOLUCIONES rectas-planos
 SOLUCIONES ectas-planos x + y z. Ecuación de la ecta que pasa po A(,, ) y se apoya en las ectas x y + z x z + s y 4 y. Ecuación de la ecta que pasa po (,, ) es paalela al plano π x + y 4z + y está en x
SOLUCIONES ectas-planos x + y z. Ecuación de la ecta que pasa po A(,, ) y se apoya en las ectas x y + z x z + s y 4 y. Ecuación de la ecta que pasa po (,, ) es paalela al plano π x + y 4z + y está en x
El método de Descartes para trazar normales a curvas
 47 Noviembe 004, pp.41-46 El método de Desates paa taza nomales a uvas El tabajo que hemos desaollado en este atíulo es un estudio de un método históio desaollado po Desates paa alula la eta nomal a una
47 Noviembe 004, pp.41-46 El método de Desates paa taza nomales a uvas El tabajo que hemos desaollado en este atíulo es un estudio de un método históio desaollado po Desates paa alula la eta nomal a una
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS Tipos de Discontinuidades en un Punto 1 - Tiene ramas infinitas en un punto
 LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS Tipos de Disontinuidades en un Punto - Tiene ramas infinitas en un punto y 5 La reta 5 es una asíntota vertial - Presenta un salto en un punto, si y
LÍMITES DE FUNCIONES. CONTINUIDAD Y RAMAS INFINITAS Tipos de Disontinuidades en un Punto - Tiene ramas infinitas en un punto y 5 La reta 5 es una asíntota vertial - Presenta un salto en un punto, si y
Práctica 2: Modulaciones analógicas lineales
 TEORÍA DE LA COMUNICACIÓN 2009/10 - EPS-UAM Pátia 2: Modulaiones analógias lineales Gupo Puesto Apellidos, nombe Apellidos, nombe Feha El objetivo de esta pátia es familiaiza al alumno on divesas modulaiones
TEORÍA DE LA COMUNICACIÓN 2009/10 - EPS-UAM Pátia 2: Modulaiones analógias lineales Gupo Puesto Apellidos, nombe Apellidos, nombe Feha El objetivo de esta pátia es familiaiza al alumno on divesas modulaiones
RESOLUCIÓN DE ACTIVIDADES
 RESOLUCIÓN DE ACTIVIDADES Atividades iniiales. Expresa en notaión matriial y resuelve por el método de Gauss los sistemas de euaiones siguientes: Las resoluión de los sistemas puede expresarse de la forma
RESOLUCIÓN DE ACTIVIDADES Atividades iniiales. Expresa en notaión matriial y resuelve por el método de Gauss los sistemas de euaiones siguientes: Las resoluión de los sistemas puede expresarse de la forma
Segunda ley de Newton
 Segunda ley de Newton Fundamento La segunda ley de la mecánica de Newton se expesa matemáticamente. F = ext m a El sumatoio se efiee a las fuezas exteioes. En la páctica, dento de las fuezas exteioes que
Segunda ley de Newton Fundamento La segunda ley de la mecánica de Newton se expesa matemáticamente. F = ext m a El sumatoio se efiee a las fuezas exteioes. En la páctica, dento de las fuezas exteioes que
CINEMÁTICA Y DINÁMICA DEL MOTOR
 CINEMÁTICA Y DINÁMICA DEL MOTOR CINEMÁTICA DEL MOTOR Como ha sido expuesto, el movimiento del pistón se tansfoma en movimiento iula del igüeñal gaias a un sistema biela - manivela. Se puede obtene obsevando
CINEMÁTICA Y DINÁMICA DEL MOTOR CINEMÁTICA DEL MOTOR Como ha sido expuesto, el movimiento del pistón se tansfoma en movimiento iula del igüeñal gaias a un sistema biela - manivela. Se puede obtene obsevando
2.1. Potencia. cc A. Potencia de un punto respecto. de una circunferencia. 2. Potencia 2.1. Potencia. ccc Definición
 02 otenia Existen oneptos geométios, que eniean un ieto gado de omplejidad si se ven sólo desde su intepetaión matemátia, y que sin embago, mediante su apliaión y tazado sobe el plano, posibilitan una
02 otenia Existen oneptos geométios, que eniean un ieto gado de omplejidad si se ven sólo desde su intepetaión matemátia, y que sin embago, mediante su apliaión y tazado sobe el plano, posibilitan una
Trabajo Práctico Nº 12: Pandeo. Determinación de Cargas Criticas. Diseño y verificación de Secciones
 Tabajo átio Nº 1: andeo. Deteminaión de agas itias. Diseño veifiaión de Seiones Nota: la longitud de pandeo equivalente Lp se suele epesa omo Lp k. L donde L es la longitud eal de la olumna el oefiiente
Tabajo átio Nº 1: andeo. Deteminaión de agas itias. Diseño veifiaión de Seiones Nota: la longitud de pandeo equivalente Lp se suele epesa omo Lp k. L donde L es la longitud eal de la olumna el oefiiente
TRIGONOMETRÍA 1 (Resumen) cotg. Definiciones generales (válidas para cualquier ángulo de cualquier cuadrante) y r. cosec. sec.
 Tignometía Resumen TRIGONOMETRÍA (Resumen) Definiiones en tiángulos etángulos ateto opuesto sen ateto ontiguo os ateto opuesto tg ateto ontiguo ose ateto opuesto se ateto ontiguo ateto ontiguo otg ateto
Tignometía Resumen TRIGONOMETRÍA (Resumen) Definiiones en tiángulos etángulos ateto opuesto sen ateto ontiguo os ateto opuesto tg ateto ontiguo ose ateto opuesto se ateto ontiguo ateto ontiguo otg ateto
Física General 1 Proyecto PMME - Curso 2007 Instituto de Física Facultad de Ingeniería UdelaR
 ísia Geneal 1 Poyeto PMME - Cuso 007 Instituto de ísia aultad de Ingenieía UdelaR DINÁMICA DE LA PARTÍCULA MOVIMIENTO CIRCULAR EN UN PLANO VERTICAL abiana Andade Juan Pablo Balaini Pablo Doglio Intoduión:
ísia Geneal 1 Poyeto PMME - Cuso 007 Instituto de ísia aultad de Ingenieía UdelaR DINÁMICA DE LA PARTÍCULA MOVIMIENTO CIRCULAR EN UN PLANO VERTICAL abiana Andade Juan Pablo Balaini Pablo Doglio Intoduión:
VECTORES EN TRES DIMENSIONES
 FÍSIC PR TODOS 1 CRLOS JIMENEZ HURNG VECTORES EN TRES DIMENSIONES Los vetoes pueden epesase en funión de oodenadas, de la siguiente manea: a; b; ) o de ota foma: a i + b j + k donde: i, j, k, son vetoes
FÍSIC PR TODOS 1 CRLOS JIMENEZ HURNG VECTORES EN TRES DIMENSIONES Los vetoes pueden epesase en funión de oodenadas, de la siguiente manea: a; b; ) o de ota foma: a i + b j + k donde: i, j, k, son vetoes
TRIGONOMETRÍA (Resumen) Definiciones generales (válidas para cualquier ángulo de cualquier cuadrante) y r. cosec. sec. cotg x +
 TRIGONOMETRÍA (Resumen) Definiiones en tiángulos etángulos ateto opuesto sen ateto ontiguo os ateto opuesto tg ateto ontiguo ose ateto opuesto se ateto ontiguo ateto ontiguo otg ateto opuesto Razones de
TRIGONOMETRÍA (Resumen) Definiiones en tiángulos etángulos ateto opuesto sen ateto ontiguo os ateto opuesto tg ateto ontiguo ose ateto opuesto se ateto ontiguo ateto ontiguo otg ateto opuesto Razones de
2 2 2 x. Solución: Ya que la integración es una curva cerrada y la integral esta representada por funciones reales, empleamos el teorema de Green
 Elaborado por: Jhonny hoquehuana Lizarraga Variable ompleja Exámenes esueltos Segundo Parial. alular x y { xln( y ) x ( y) } dx y ( x ) dy y, donde es el uadrado de vérties ± i ± i. Soluión: Ya que la
Elaborado por: Jhonny hoquehuana Lizarraga Variable ompleja Exámenes esueltos Segundo Parial. alular x y { xln( y ) x ( y) } dx y ( x ) dy y, donde es el uadrado de vérties ± i ± i. Soluión: Ya que la
Pruebas de Acceso a Ensen anzas Universitarias Oficiales de Grado (PAEG)
 PAEG junio 016 Propuesta B Matemátias II º Bahillerato Pruebas de Aeso a Ensen anzas Universitarias Oiiales de Grado (PAEG) Matemátias II (Universidad de Castilla-La Manha) junio 016 Propuesta B EJERCICIO
PAEG junio 016 Propuesta B Matemátias II º Bahillerato Pruebas de Aeso a Ensen anzas Universitarias Oiiales de Grado (PAEG) Matemátias II (Universidad de Castilla-La Manha) junio 016 Propuesta B EJERCICIO
DIMENSIONAMIENTO DE CONDUCTORES SECUNDARIOS 1 DE LOS TRANSFORMADORES DE CORRIENTE Y POTENCIAL
 ELT 60 DIMENSIONAMIENTO DE CONDCTORES SECNDARIOS DE LOS TRANSFORMADORES DE MEDIDA DIMENSIONAMIENTO DE CONDCTORES SECNDARIOS DE LOS TRANSFORMADORES DE CORRIENTE Y POTENCIAL - INTRODCCION Todas las empesas
ELT 60 DIMENSIONAMIENTO DE CONDCTORES SECNDARIOS DE LOS TRANSFORMADORES DE MEDIDA DIMENSIONAMIENTO DE CONDCTORES SECNDARIOS DE LOS TRANSFORMADORES DE CORRIENTE Y POTENCIAL - INTRODCCION Todas las empesas
Resolviendo la Ecuación de Schrodinger en 1-D
 Resolvieno la Ecación e Schoinge en -D D. Hécto René VEGA-ARRILLO so e Física Moena Unia Acaémica e Ingenieía Eléctica Univesia Atónoma e Zacatecas Docmento: FM/Notas/RES/070309 Domingo/-Mazo/009 ontenio
Resolvieno la Ecación e Schoinge en -D D. Hécto René VEGA-ARRILLO so e Física Moena Unia Acaémica e Ingenieía Eléctica Univesia Atónoma e Zacatecas Docmento: FM/Notas/RES/070309 Domingo/-Mazo/009 ontenio
Selectividad Septiembre 2009 SEPTIEMBRE 2009
 Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
CATALUÑA / JUNIO 02. LOGSE / FÍSICA / EXAMEN COMPLETO
 Resuelva el poblema P1 y esponda a las uestiones C1 y C Esoja una de las opiones (A o B) y esuelva el poblema P y onteste a las uestiones C3 y C4 de la opión esogida (En total hay que esolve dos poblemas
Resuelva el poblema P1 y esponda a las uestiones C1 y C Esoja una de las opiones (A o B) y esuelva el poblema P y onteste a las uestiones C3 y C4 de la opión esogida (En total hay que esolve dos poblemas
2.1 ECUACIONES DIFERENCIALES DE SEGUNDO ORDEN CON COEFICIENTES CONSTANTES.
 . ECUACIONES DIFERENCIALES DE SEGUNDO ORDEN CON COEFICIENTES CONSTANTES. Una uaión difnial d sgundo odn s d la foma: p( q( g( Si g ( s llama E ua ió n ho m o g é n a aso ontaio; s di, si g ( s llama E
. ECUACIONES DIFERENCIALES DE SEGUNDO ORDEN CON COEFICIENTES CONSTANTES. Una uaión difnial d sgundo odn s d la foma: p( q( g( Si g ( s llama E ua ió n ho m o g é n a aso ontaio; s di, si g ( s llama E
Problema encadenado 1. Apartado 1
 Poblema enadenado 1. 1. Dibuja dos iunfeenias de igual adio tangentes ente si y tangentes a los lados del tiángulo del que se onoe: el lado = 120 mm, el ángulo = 700 y la mediana m = 85 mm. De las posibles
Poblema enadenado 1. 1. Dibuja dos iunfeenias de igual adio tangentes ente si y tangentes a los lados del tiángulo del que se onoe: el lado = 120 mm, el ángulo = 700 y la mediana m = 85 mm. De las posibles
. Esta segunda función es posible que no pueda explicitarse: no pueda encontrarse la fórmula y f (x)
 1 FUNCIONES DE DOS VARIABLES DERIVACIÓN IMPLÍCITA (Tangente a una cuva de nivel); FUNCIONES HOMOGÉNEAS Deivación implícita ecta tangente a una cuva de nivel Si (a, b) es un punto que cumple la ecuación
1 FUNCIONES DE DOS VARIABLES DERIVACIÓN IMPLÍCITA (Tangente a una cuva de nivel); FUNCIONES HOMOGÉNEAS Deivación implícita ecta tangente a una cuva de nivel Si (a, b) es un punto que cumple la ecuación
Introducción a la Química Computacional
 Introduión a la Químia Computaional MÉTODO D LA VARIACION PARA ROLVR APROXIMADAMNT LA CUACIÓN D CRÖDINGR Reservados todos los derehos de reproduión. Luis A. Montero Cabrera y Rahel Crespo Otero, Universidad
Introduión a la Químia Computaional MÉTODO D LA VARIACION PARA ROLVR APROXIMADAMNT LA CUACIÓN D CRÖDINGR Reservados todos los derehos de reproduión. Luis A. Montero Cabrera y Rahel Crespo Otero, Universidad
Sistemas de comunicación
 Sistemas de comunicación Páctico Intefeencia Intesimbólica y Pulsos de Nyqvist Cada ejecicio comienza con un símbolo el cuál indica su dificultad de acuedo a la siguiente escala: básica, media, avanzada,
Sistemas de comunicación Páctico Intefeencia Intesimbólica y Pulsos de Nyqvist Cada ejecicio comienza con un símbolo el cuál indica su dificultad de acuedo a la siguiente escala: básica, media, avanzada,
Supercies Regladas. Ejemplo El cilíndro y el cono circular son ejemplos de supercies regladas
 Unidad 1. Superies Cuádrias 1.6 Superies Regladas Superies Regladas Deniión 1. Una superie on la propiedad de que para ada punto en ella hay toda una reta que está ontenida en la superie y que pasa por
Unidad 1. Superies Cuádrias 1.6 Superies Regladas Superies Regladas Deniión 1. Una superie on la propiedad de que para ada punto en ella hay toda una reta que está ontenida en la superie y que pasa por
MATEMÁTICAS II TEMA 6 Planos y rectas en el espacio. Problemas de ángulos, paralelismo y perpendicularidad, simetrías y distancias
 Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Ecuaciones de Máxwell y ondas electromagnéticas
 Zero Order of Magnitude ZOoM)-PID 13-28 Euaiones de Máxwell y ondas eletromagnétias 1. Estímese la intensidad y la potenia total de un láser neesario para elevar una pequeña esfera de plástio de 15 µm
Zero Order of Magnitude ZOoM)-PID 13-28 Euaiones de Máxwell y ondas eletromagnétias 1. Estímese la intensidad y la potenia total de un láser neesario para elevar una pequeña esfera de plástio de 15 µm
PROBLEMAS DEL TEMA 1: CIRCUITOS ELÉCTRICOS EN AC. Problemas de reactancias
 ey Juan Carlos POBEMAS DE TEMA : CICUITOS EÉCTICOS EN AC Problemas de reatanias Problema 4. Una bobina on = 5 mh se oneta a un generador de tensión alterna sinusoidal de V ef = 80 V. Calula la reatania
ey Juan Carlos POBEMAS DE TEMA : CICUITOS EÉCTICOS EN AC Problemas de reatanias Problema 4. Una bobina on = 5 mh se oneta a un generador de tensión alterna sinusoidal de V ef = 80 V. Calula la reatania
TRANSFORMACIONES GEOMÉTRICAS: Inversión.
 PRFESR: FRNCISC MNUEL GLÁN SN JSÉ. TRNSFRMCINES GEMÉTRICS: Invesión. INVERSIÓN siguientes leyes: La invesión es una tansfomaión que se ige po las M' ' 1. Dos puntos invesos y están alineados on un punto
PRFESR: FRNCISC MNUEL GLÁN SN JSÉ. TRNSFRMCINES GEMÉTRICS: Invesión. INVERSIÓN siguientes leyes: La invesión es una tansfomaión que se ige po las M' ' 1. Dos puntos invesos y están alineados on un punto
MMII_L1_c3: Clasificación de las ecuaciones. Formas Canónicas
 MMII_L_c3: Clasificación de las ecaciones. Fomas Canónicas Gión: En esta clase nos basamos en la definición de las Cvas Caacteísticas CC de la anteio paa intodci la clasificación de las ecaciones el tipo
MMII_L_c3: Clasificación de las ecaciones. Fomas Canónicas Gión: En esta clase nos basamos en la definición de las Cvas Caacteísticas CC de la anteio paa intodci la clasificación de las ecaciones el tipo
Seminario de problemas. Curso Hoja 18
 Seminario de problemas. Curso 016-17. Hoja 18 111. Demuestra que una ondiión neesaria y sufiiente para que un triángulo sea isóseles es que tenga dos medianas iguales. Soluión: Vamos a utilizar un resultado
Seminario de problemas. Curso 016-17. Hoja 18 111. Demuestra que una ondiión neesaria y sufiiente para que un triángulo sea isóseles es que tenga dos medianas iguales. Soluión: Vamos a utilizar un resultado
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables (x 0 ). x ik. x ik 1
 1. RESUMEN Ingenieía Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Vaias Vaiables 08-1 Ingenieía Matemática Univesidad de Chile Guía Semana 5 Teoema del valo medio.
1. RESUMEN Ingenieía Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Vaias Vaiables 08-1 Ingenieía Matemática Univesidad de Chile Guía Semana 5 Teoema del valo medio.
SOLUCIÓN DE LA PRUEBA DE ACCESO
 Físia Físia COMUNIDAD DE MADRID CONVOCATORIA JUNIO 008 SOLUCIÓN DE LA RUEBA DE ACCESO AUTOR: Tomás Caballeo Rodíguez imea pate Expeienia : Expeienia : A x A x a) En el MAS: x A sen(t 0 ) dx v A os(t 0
Físia Físia COMUNIDAD DE MADRID CONVOCATORIA JUNIO 008 SOLUCIÓN DE LA RUEBA DE ACCESO AUTOR: Tomás Caballeo Rodíguez imea pate Expeienia : Expeienia : A x A x a) En el MAS: x A sen(t 0 ) dx v A os(t 0
Lección 4. Ecuaciones diferenciales. 4. Propiedades algebraicas de las soluciones. Fórmulas de Abel y Liouville.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0. 4. Proiedades algebraias de las soluiones. Fórmulas de Abel y Liouville. A lo largo de esta seión suondremos que P, Q y R son funiones ontinuas en un intervalo
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0. 4. Proiedades algebraias de las soluiones. Fórmulas de Abel y Liouville. A lo largo de esta seión suondremos que P, Q y R son funiones ontinuas en un intervalo
DIVISIBILIDAD DE POLINOMIOS
 DIVISIÓN DE OLINOMIOS.- DIVISIBILIDAD DE OLINOMIOS Dados dos polinomios, D ( ) y d ( ) con d ( ) 0, llamados dividendo y diviso, con g( D( ) ) g( d( ) ), dividi el pimeo D ( ) ente (:) el segundo ( ) (que
DIVISIÓN DE OLINOMIOS.- DIVISIBILIDAD DE OLINOMIOS Dados dos polinomios, D ( ) y d ( ) con d ( ) 0, llamados dividendo y diviso, con g( D( ) ) g( d( ) ), dividi el pimeo D ( ) ente (:) el segundo ( ) (que
PRUEBA DE ACCESO (LOGSE) UNIVERSIDAD DE EXTREMADURA JUNIO 2012 (GENERAL) (RESUELTOS por Antonio Menguiano) Tiempo máximo: 1 hora y 30 minutos OPCIÓN A
 IES STER DJOZ PRUE DE ESO (OGSE) UNIVERSIDD DE EXTREMDUR JUNIO (GENER) (RESUETOS po ntonio Menguiano) MTEMÁTIS II Tiempo máimo: hoa y minutos Instucciones: El alumno elegiá una de las dos opciones popuestas
IES STER DJOZ PRUE DE ESO (OGSE) UNIVERSIDD DE EXTREMDUR JUNIO (GENER) (RESUETOS po ntonio Menguiano) MTEMÁTIS II Tiempo máimo: hoa y minutos Instucciones: El alumno elegiá una de las dos opciones popuestas
Ecuaciones de primer grado
 Euaiones de primer grado. Resuelve las siguientes euaiones de primer grado on paréntesis. 3( + ) + ( 3 ) = 7 3( ) ( 3 ) ( + ) = 3( ) ( + ) ( + 3) = 3 + = 5 ( 7 ). Resuelve las siguientes euaiones de primer
Euaiones de primer grado. Resuelve las siguientes euaiones de primer grado on paréntesis. 3( + ) + ( 3 ) = 7 3( ) ( 3 ) ( + ) = 3( ) ( + ) ( + 3) = 3 + = 5 ( 7 ). Resuelve las siguientes euaiones de primer
Primer parcial de Química Física. 11de Mayo de 2007 (Examen de Repesca)
 Pime pacial de Química Física. de Mayo de 7 (Examen de Repesca) ) a) Indica, azonando lo más bevemente posible las espuestas, si son vedadeas o falsas las siguientes afimaciones. iet / I) La función de
Pime pacial de Química Física. de Mayo de 7 (Examen de Repesca) ) a) Indica, azonando lo más bevemente posible las espuestas, si son vedadeas o falsas las siguientes afimaciones. iet / I) La función de
UNIVERSIDAD NACIONAL DEL CALLAO
 UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA ESCUELA PROFESIONAL DE INGENIERÍA ELÉCTRICA Cuso: TEORÍA DE CAMPOS ELECTROMAGNÉTICOS PROFESOR: ING. JORGE MONTAÑO PISFIL TEORÍA
UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA ESCUELA PROFESIONAL DE INGENIERÍA ELÉCTRICA Cuso: TEORÍA DE CAMPOS ELECTROMAGNÉTICOS PROFESOR: ING. JORGE MONTAÑO PISFIL TEORÍA
Adenda Electrones en potencial periódico
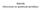 Adenda Electones en potencial peiódico Bandas en potencial peiódico Banda de conducción niveles atómicos Electones en un potencial peiódico ed simetía taslacional R = n1 a1 + n2a2 + n3a3; n1, n2, n3 enteos
Adenda Electones en potencial peiódico Bandas en potencial peiódico Banda de conducción niveles atómicos Electones en un potencial peiódico ed simetía taslacional R = n1 a1 + n2a2 + n3a3; n1, n2, n3 enteos
Guía Regla de la Cadena(1 er Orden)
 UNIVERSIDAD DE CHILE CÁLCULO EN VARIAS VARIABLES PROFESOR: MARCELO LESEIGNEUR AUXILIARES: ALFONSO TORO - SEBASTIÁN COURT Guía Regla de la Cadena1 e Oden 1. Sean f : R R y g : R R dos funciones difeenciables.
UNIVERSIDAD DE CHILE CÁLCULO EN VARIAS VARIABLES PROFESOR: MARCELO LESEIGNEUR AUXILIARES: ALFONSO TORO - SEBASTIÁN COURT Guía Regla de la Cadena1 e Oden 1. Sean f : R R y g : R R dos funciones difeenciables.
CÁLCULO VECTORIAL. Operaciones con vectores libres. , siendo las componentes de ( )
 CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
CÁLCULO VECTOIAL Opeaciones con vectoes libes Suma de vectoes libes La suma de n vectoes libes P P P n es un vecto libe llamado esultante = i j k la suma de las componentes espectivas, siendo las componentes
Elementos de una TEORIA RELATIVISTA DE LA GRAVITACION
 Elementos de una TEORIA RELATIVISTA DE LA GRAVITACION po Rodolfo CARABIO. CONCEPTO DE INTERACCION GRAVITATORIA En este tabajo se mostaa ómo es posible establee una teoía de la gavitaión a pati de los postulados
Elementos de una TEORIA RELATIVISTA DE LA GRAVITACION po Rodolfo CARABIO. CONCEPTO DE INTERACCION GRAVITATORIA En este tabajo se mostaa ómo es posible establee una teoía de la gavitaión a pati de los postulados
Núcleo e Imagen de una Transformación Lineal
 Núleo e Imagen de una Transformaión Lineal Departamento de Matemátias CCIR/ITESM 8 de junio de Índie 7.. Núleo de una transformaión lineal................................. 7.. El núleo de una matri la
Núleo e Imagen de una Transformaión Lineal Departamento de Matemátias CCIR/ITESM 8 de junio de Índie 7.. Núleo de una transformaión lineal................................. 7.. El núleo de una matri la
Método de Separación de Variables
 Método de Separaión de Variables Este método se emplea para resolver euaiones de la forma: f g d 0. Para hallar la soluión de este tipo de euaiones se proede a separar las variables agrupando de un lado
Método de Separaión de Variables Este método se emplea para resolver euaiones de la forma: f g d 0. Para hallar la soluión de este tipo de euaiones se proede a separar las variables agrupando de un lado
CAPÍTULO II Teoremas de conservación
 eoeas de onsevaión CPÍULO II eoeas de onsevaión Fundaento teóio I.- Leyes de ewton Ia.- Piea ley Un uepo soetido a una fueza neta nula, F n 0, se ueve de foa que su antidad de oviiento, p v, peanee onstante
eoeas de onsevaión CPÍULO II eoeas de onsevaión Fundaento teóio I.- Leyes de ewton Ia.- Piea ley Un uepo soetido a una fueza neta nula, F n 0, se ueve de foa que su antidad de oviiento, p v, peanee onstante
Ecuación Solución o raíces de una ecuación.
 Euaión Igualdad que ontiene una o más inógnitas Soluión o raíes de una euaión. Valores de las inógnitas que umplen la igualdad. 15 = 3x + 6 15 6 = 3x 9 = 3x 3 = x on Existen diversos métodos de hallar
Euaión Igualdad que ontiene una o más inógnitas Soluión o raíes de una euaión. Valores de las inógnitas que umplen la igualdad. 15 = 3x + 6 15 6 = 3x 9 = 3x 3 = x on Existen diversos métodos de hallar
ÁLGEBRA LINEAL I LISTA DE EJERCICIOS 3. Página para el curso:
 ÁLGEBRA LINEAL I LISTA DE EJERCICIOS 3 DANIEL LABARDINI FRAGOSO DANIEL BALAM CRUZ HUITRÓN Página paa el cuso: www.matem.unam.mx/labadini/teaching.html A lo lago de los siguientes ejecicios, seá un campo.
ÁLGEBRA LINEAL I LISTA DE EJERCICIOS 3 DANIEL LABARDINI FRAGOSO DANIEL BALAM CRUZ HUITRÓN Página paa el cuso: www.matem.unam.mx/labadini/teaching.html A lo lago de los siguientes ejecicios, seá un campo.
OPERACIONES CON FUNCIONES
 . SUMA Y RESTA DE FUNCIONES OPERACIONES CON FUNCIONES Dadas g unciones eales de vaiable eal se deine la unción suma + g como: g g con Dom g Dom Dom g Es deci, la unción g hace coesponde a cada númeo eal
. SUMA Y RESTA DE FUNCIONES OPERACIONES CON FUNCIONES Dadas g unciones eales de vaiable eal se deine la unción suma + g como: g g con Dom g Dom Dom g Es deci, la unción g hace coesponde a cada númeo eal
SOLUCIONES DE LOS EJERCICIOS DE APLICACIÓN II TEMA 4
 SOLUCIONES DE LOS EJERCICIOS DE APLICACIÓN II TEMA 4 Ejecicio de aplicación 44 (Deivación) Se desea obtene una viga ectangula a pati de un tonco cilíndico de 6 cm de diámeto a) Demosta que la viga con
SOLUCIONES DE LOS EJERCICIOS DE APLICACIÓN II TEMA 4 Ejecicio de aplicación 44 (Deivación) Se desea obtene una viga ectangula a pati de un tonco cilíndico de 6 cm de diámeto a) Demosta que la viga con
DETERMINACIÓN DE LAS CORRIENTES DE INSERCIÓN EN SISTEMAS DE DISTRIBUCIÓN DE n TRANSFORMADORES.
 ng. Horaio Salvañá HS ngeniería - www.hsingenieria.om.ar DETERMNACÓN DE LAS CORRENTES DE NSERCÓN EN SSTEMAS DE DSTRBUCÓN DE n TRANSFORMADORES. Autor: ng. Horaio Salvañá Objetivo: El objeto de este trabajo
ng. Horaio Salvañá HS ngeniería - www.hsingenieria.om.ar DETERMNACÓN DE LAS CORRENTES DE NSERCÓN EN SSTEMAS DE DSTRBUCÓN DE n TRANSFORMADORES. Autor: ng. Horaio Salvañá Objetivo: El objeto de este trabajo
ˆk, donde f 1. son funciones escalares, entonces su producto cruz o vectorial del operador con la función es: y f 2
 Rotacional de una función vectoial Si una función vectoial es f = f 1 î + f 2 ĵ + f 3 ˆk, donde f 1, f 2, f 3 son funciones escalaes, entonces su poducto cuz o vectoial del opeado con la función es: f
Rotacional de una función vectoial Si una función vectoial es f = f 1 î + f 2 ĵ + f 3 ˆk, donde f 1, f 2, f 3 son funciones escalaes, entonces su poducto cuz o vectoial del opeado con la función es: f
LECCIÓN 5: CINEMÁTICA DEL PUNTO
 LECCIÓN 5: CINEMÁTICA DEL PUNTO 5.1.Punto mateial. 5.. Vecto de posición. Tayectoia. 5.3. Vecto velocidad. 5.4. Vecto aceleación. 5.5. Algunos tipos de movimientos. 5.1. PUNTO MATERIAL. Un punto mateial
LECCIÓN 5: CINEMÁTICA DEL PUNTO 5.1.Punto mateial. 5.. Vecto de posición. Tayectoia. 5.3. Vecto velocidad. 5.4. Vecto aceleación. 5.5. Algunos tipos de movimientos. 5.1. PUNTO MATERIAL. Un punto mateial
UNIVERSIDAD NACIONAL EXPERIMENTAL POLITECNICA ANTONIO JOSÉ DE SUCRE VICERRECTORADO BARQUISIMETO DEPARTAMENTO DE INGENIERÍA QUÍMICA. Ingeniería Química
 UNIVERSIDAD NACIONAL EXERIMENTAL OLITECNICA ANTONIO JOSÉ DE SUCRE VICERRECTORADO BARQUISIMETO DEARTAMENTO DE INGENIERÍA QUÍMICA Ingeniería Químia Unidad III. Balane de materia Sistemas Monofásios Clase
UNIVERSIDAD NACIONAL EXERIMENTAL OLITECNICA ANTONIO JOSÉ DE SUCRE VICERRECTORADO BARQUISIMETO DEARTAMENTO DE INGENIERÍA QUÍMICA Ingeniería Químia Unidad III. Balane de materia Sistemas Monofásios Clase
2. CURVAS EN EL SISTEMA POLAR
 2. CURVAS EN EL SISTEMA POLAR Objetivo: El alumno obtendá ecuaciones en foma pola de cuvas en el plano y deteminaá las caacteísticas de éstas a pati de su ecuación en foma pola. Contenido: 2.1 Sistema
2. CURVAS EN EL SISTEMA POLAR Objetivo: El alumno obtendá ecuaciones en foma pola de cuvas en el plano y deteminaá las caacteísticas de éstas a pati de su ecuación en foma pola. Contenido: 2.1 Sistema
RECTAS EN EL ESPACIO
 IES Pade Poeda (Guadi UNIDAD 9 GEOMETRÍA AFÍN RETAS EN EL ESPAIO. EUAIONES DE LA RETA Una ecta queda deteminada po Un punto A ( a a a Un ecto de diección ( A ( A; se le llama deteminación lineal de la
IES Pade Poeda (Guadi UNIDAD 9 GEOMETRÍA AFÍN RETAS EN EL ESPAIO. EUAIONES DE LA RETA Una ecta queda deteminada po Un punto A ( a a a Un ecto de diección ( A ( A; se le llama deteminación lineal de la
Una función es creciente en un intervalo [a,b] si dados dos puntos cualesquiera del intervalo, x 1, x 2, x 1 < x 2 se cumple que f(x 1 ) < f(x 2 )
![Una función es creciente en un intervalo [a,b] si dados dos puntos cualesquiera del intervalo, x 1, x 2, x 1 < x 2 se cumple que f(x 1 ) < f(x 2 ) Una función es creciente en un intervalo [a,b] si dados dos puntos cualesquiera del intervalo, x 1, x 2, x 1 < x 2 se cumple que f(x 1 ) < f(x 2 )](/thumbs/84/91222313.jpg) Aplicaciones de la deivada MATEMÁTICAS II CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN.. Definiciones Se dice que una función f es ceciente en un punto si paa cualquie punto de un entono de, (, + ) se veifica:
Aplicaciones de la deivada MATEMÁTICAS II CRECIMIENTO Y DECRECIMIENTO DE UNA FUNCIÓN.. Definiciones Se dice que una función f es ceciente en un punto si paa cualquie punto de un entono de, (, + ) se veifica:
UNIDAD 11: PUNTOS, RECTAS Y PLANOS EN EL ESPACIO
 I.E.. Isabel Peillán y Quiós Matemáticas Depatamento de Matemáticas UNIDAD : Puntos, ectas y planos en el espacio UNIDAD : PUNTO, RECTA Y PLANO EN EL EPACIO Ecuaciones de la ecta Ecuaciones del plano Posiciones
I.E.. Isabel Peillán y Quiós Matemáticas Depatamento de Matemáticas UNIDAD : Puntos, ectas y planos en el espacio UNIDAD : PUNTO, RECTA Y PLANO EN EL EPACIO Ecuaciones de la ecta Ecuaciones del plano Posiciones
m lnq = ln e n ( α +βε r ) ( ) = a 1(1 r n ) 1 r
 Antonio Castaño Tieno Vícto Pablo Galván Chacón Abil 200 Ejecicio Imaginemos un gas cuántico ideal de patículas idénticas y supongamos que el númeo máximo de patículas que pueden esta en el mismo estado
Antonio Castaño Tieno Vícto Pablo Galván Chacón Abil 200 Ejecicio Imaginemos un gas cuántico ideal de patículas idénticas y supongamos que el númeo máximo de patículas que pueden esta en el mismo estado
Para aprender Termodinámica resolviendo problemas GASES REALES.
 Fato de ompesibilidad. GASES REAES. El fato de ompesibilidad se define omo ( ) ( ) la pesión, la tempeatua y la natualeza de ada gas. Euaión de van de Waals. ( ) z = eal = eal y es funión de a euaión de
Fato de ompesibilidad. GASES REAES. El fato de ompesibilidad se define omo ( ) ( ) la pesión, la tempeatua y la natualeza de ada gas. Euaión de van de Waals. ( ) z = eal = eal y es funión de a euaión de
Adaptación de impedancias
 .- El tansfomado ideal Adaptación de impedancias I +V +V TI Tansfomado ideal V elaciones V-I: V = I = a. I, válidas paa cualquie fecuencia. a Si se conecta una esistencia al secundaio, ente el nodo +V
.- El tansfomado ideal Adaptación de impedancias I +V +V TI Tansfomado ideal V elaciones V-I: V = I = a. I, válidas paa cualquie fecuencia. a Si se conecta una esistencia al secundaio, ente el nodo +V
Singularidades. Una serie de Laurent es una serie de potencias que pueden ser positivas y/o negativas: a n (z z 0 ) n =
 Singularidades Hay muhas funiones que son analítias en una región on exepión de algunos puntos aislados donde no están definidas. Por ejemplo, /z es analítia en C {0} y os(z) es analítia en C {0, ±π, ±π,
Singularidades Hay muhas funiones que son analítias en una región on exepión de algunos puntos aislados donde no están definidas. Por ejemplo, /z es analítia en C {0} y os(z) es analítia en C {0, ±π, ±π,
5 El colectivo macrocanónico.
 5 El colectivo macocanónico. Vesión boado. En el colectivo macocanónico, el sistema se encuenta en equilibio con un baño témico exteno a tempeatua ( ja) T, y con un baño o foco de patículas cuyo potencial
5 El colectivo macocanónico. Vesión boado. En el colectivo macocanónico, el sistema se encuenta en equilibio con un baño témico exteno a tempeatua ( ja) T, y con un baño o foco de patículas cuyo potencial
TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES
 TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES La técnica del desaollo de facciones paciales es establecida paa cuida todos los casos sistemáticamente. Hay 4 clases de poblemas, dependiendo
TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES La técnica del desaollo de facciones paciales es establecida paa cuida todos los casos sistemáticamente. Hay 4 clases de poblemas, dependiendo
EJERCITACIÓN PARA EXAMEN DE MATEMATICA MAYORES DE 25 AÑOS SIN CICLO MEDIO COMPLETO. PRACTICO 3 Función Lineal Rectas Noviembre 2011
 EJERCITACIÓN PARA EXAMEN DE MATEMATICA MAYORES DE 5 AÑOS SIN CICLO MEDIO COMPLETO PRACTICO Función Lineal Rectas Noviembe RECORDAR: Una unción lineal es de la oma popiedad que los cocientes incementales:
EJERCITACIÓN PARA EXAMEN DE MATEMATICA MAYORES DE 5 AÑOS SIN CICLO MEDIO COMPLETO PRACTICO Función Lineal Rectas Noviembe RECORDAR: Una unción lineal es de la oma popiedad que los cocientes incementales:
Cónicas. = 0 son rectas que pasan por su centro y tienen de pendiente m tal que: a) m = a
 .- Las asíntotas de la hipérbola a x + a y + axy + a 0x + a 0y + a 00 = 0 son retas que pasan por su entro y tienen de pendiente m tal que: a a) m = a b) m es raíz de m + a m + a 0 a = a + am + a m = )
.- Las asíntotas de la hipérbola a x + a y + axy + a 0x + a 0y + a 00 = 0 son retas que pasan por su entro y tienen de pendiente m tal que: a a) m = a b) m es raíz de m + a m + a 0 a = a + am + a m = )
6. GEOMETRIA ANALÍTICA
 Geometía Heamientas infomáticas paa el ingenieo en el estudio del algeba lineal 6. GEOMETRIA ANALÍTICA 6.. VARIEDAD LINEAL AFIN 6... DEFINICION 6... ECUACIONES PARAMETRICAS 6... ECUACIONES IMPLICITAS 6..4.
Geometía Heamientas infomáticas paa el ingenieo en el estudio del algeba lineal 6. GEOMETRIA ANALÍTICA 6.. VARIEDAD LINEAL AFIN 6... DEFINICION 6... ECUACIONES PARAMETRICAS 6... ECUACIONES IMPLICITAS 6..4.
Temas Teóricos. puesto que ambas implican condiciones geométricas y no de movimiento.
 Temas Teóios Eletomagnetismo Es. de Mawell paa uepos en Movimiento. Lino pagnolo. Einstein fue uno de los pimeos en analia la Eletodinámia uando los ondutoes u objetos agados tienen un movimiento mu ápido
Temas Teóios Eletomagnetismo Es. de Mawell paa uepos en Movimiento. Lino pagnolo. Einstein fue uno de los pimeos en analia la Eletodinámia uando los ondutoes u objetos agados tienen un movimiento mu ápido
Lección 3.1. Antiderivadas y La Integral Indefinida. 02/03/2016 Prof. José G. Rodríguez Ahumada 1 de 20
 Leión. Antiderivadas y La Integral Indefinida 0/0/06 de 0 Atividades. Referenia del Teto: Seión. Antiderivadas y la Integral Indefinida, Ver ejemplos al 9 Ejeriios de Prátia: Impares Asignaión.: Seión.
Leión. Antiderivadas y La Integral Indefinida 0/0/06 de 0 Atividades. Referenia del Teto: Seión. Antiderivadas y la Integral Indefinida, Ver ejemplos al 9 Ejeriios de Prátia: Impares Asignaión.: Seión.
DISEÑO Y ANÁLISIS DE DATOS EN PSICOLOGÍA II
 DISEÑO Y ANÁLISIS DE DATOS EN PSICOLOGÍA II PRÁCTICA 9 Problema.- En una determinada investigaión se estudia en diferentes estados amerianos la relaión entre varias variables soiodemográfias y el índie
DISEÑO Y ANÁLISIS DE DATOS EN PSICOLOGÍA II PRÁCTICA 9 Problema.- En una determinada investigaión se estudia en diferentes estados amerianos la relaión entre varias variables soiodemográfias y el índie
0 1 a 1. a a = a + 2a a = 2a = 0 a = a = 2 0 Sistema incompatible a 1 1 a a a 2a 2a. a a.
 Pueba de Acceso a la Univesidad. SEPTIEMBRE 00. Instucciones: Se poponen dos opciones A y B. Hay que elegi una de las dos opciones y contesta a sus cuestiones. La puntuación está detallada en cada una
Pueba de Acceso a la Univesidad. SEPTIEMBRE 00. Instucciones: Se poponen dos opciones A y B. Hay que elegi una de las dos opciones y contesta a sus cuestiones. La puntuación está detallada en cada una
Chapter 1 Integrales irracionales
 Chapte Integales iacionales. Del tipo R R(, (a + b) m,..., (a + b) y z )d Se esuelven mediante el siguiente cambio de vaiable a + b = t n donde n = m.c.m(,,..., z) Difeenciando tendemos ad = nt n dt d
Chapte Integales iacionales. Del tipo R R(, (a + b) m,..., (a + b) y z )d Se esuelven mediante el siguiente cambio de vaiable a + b = t n donde n = m.c.m(,,..., z) Difeenciando tendemos ad = nt n dt d
SOFTWARE EDUCATIVO PARA EL ANÁLISIS Y DISEÑO DE ELEMENTOS DE CONCRETO REFORZADO. Delma V. Almada Navarro y Humberto López Salgado
 SOFTWARE EDUCATIVO PARA EL ANÁLISIS Y DISEÑO DE ELEMENTOS DE CONCRETO REFORZADO Delma V. Almada Navao y Humbeto López Salgado Depto. de Ingenieía Civil, ITESM Ave. Eugenio Gaza Sada Su 50 Aulas IV, e piso.
SOFTWARE EDUCATIVO PARA EL ANÁLISIS Y DISEÑO DE ELEMENTOS DE CONCRETO REFORZADO Delma V. Almada Navao y Humbeto López Salgado Depto. de Ingenieía Civil, ITESM Ave. Eugenio Gaza Sada Su 50 Aulas IV, e piso.
I = de orden 2. Hallar la relación entre los parámetros a, b c, a 4 ab 2a ac ab ac + + ac = 0
 Puebas de Aptitud paa el Acceso a la Univesidad SEPTIEMBRE 9 Matemáticas II ÁLGEBRA a [,5 puntos] Sean las matices A = b c, I = de oden Halla la elación ente los paámetos a, b y c paa que se veifique que
Puebas de Aptitud paa el Acceso a la Univesidad SEPTIEMBRE 9 Matemáticas II ÁLGEBRA a [,5 puntos] Sean las matices A = b c, I = de oden Halla la elación ente los paámetos a, b y c paa que se veifique que
SESIÓN DE APRENDIZAJE
 INSTITUCIÓN EDUCATIVA INMACULADA DE LA MERCED SESIÓN DE APRENDIZAJE APRENDIZAJE ESPERADO Determina la regla de orrespondenia de una funión Representa e Identifia funiones Resuelve operaiones on funiones
INSTITUCIÓN EDUCATIVA INMACULADA DE LA MERCED SESIÓN DE APRENDIZAJE APRENDIZAJE ESPERADO Determina la regla de orrespondenia de una funión Representa e Identifia funiones Resuelve operaiones on funiones
Modulo de Desigualdades e Inecuaciones. 3º Medio
 Modulo de Desigualdades e Ineuaiones. º Medio TEMA : Orden, Valor Absoluto y sus propiedades Definiión : La desigualdad a < b es una relaión de orden en el universo de los números reales. Por lo tanto
Modulo de Desigualdades e Ineuaiones. º Medio TEMA : Orden, Valor Absoluto y sus propiedades Definiión : La desigualdad a < b es una relaión de orden en el universo de los números reales. Por lo tanto
REPARTIDO III CIRCUNFERENCIA
 Pof.: Lucia Tafenabe Ecuación Geneal REPRTIDO III IRUNFERENI B B cento, Ecuación de la icunfeencia conociendo cento (α, β) adio. adio B MN ( - α) ( - β) Deteminación de la ecuación de la cicunfeencia conociendo:
Pof.: Lucia Tafenabe Ecuación Geneal REPRTIDO III IRUNFERENI B B cento, Ecuación de la icunfeencia conociendo cento (α, β) adio. adio B MN ( - α) ( - β) Deteminación de la ecuación de la cicunfeencia conociendo:
Sistemas homogéneos multicomponentes 24 de marzo de 2009 Cuestiones y problemas: C: 7.3, 5
 Índie 5 CELINA GONZÁLEZ ÁNGEL JIMÉNEZ IGNACIO LÓPEZ RAFAEL NIETO Sistemas homogéneos multiomponentes 24 de marzo de 2009 Cuestiones y problemas: C: 7.3, 5 subrayados y en negrita para voluntarios punto
Índie 5 CELINA GONZÁLEZ ÁNGEL JIMÉNEZ IGNACIO LÓPEZ RAFAEL NIETO Sistemas homogéneos multiomponentes 24 de marzo de 2009 Cuestiones y problemas: C: 7.3, 5 subrayados y en negrita para voluntarios punto
Examen de Física-1, 1 Ingeniería Química Diciembre de 2010 Cuestiones (Un punto por cuestión).
 Examen de Física-, Ingenieía Química Diciembe de Cuestiones (Un punto po cuestión). Cuestión : Los vectoes (,, ), (,, 5) y (,, ), están aplicados en los puntos A (,, ), B (,, ) y C (,, ) espectivamente.
Examen de Física-, Ingenieía Química Diciembe de Cuestiones (Un punto po cuestión). Cuestión : Los vectoes (,, ), (,, 5) y (,, ), están aplicados en los puntos A (,, ), B (,, ) y C (,, ) espectivamente.
Tensor de inercia. Tensor de inercia. I pzx. I pxx. I pxy. = I pyz. I pxz. I. Leyes de Newton. II. Cinemática
 Univesidad Simón Bolíva. ees de Newton. Cinemátia. Dinámia Sist. de atíulas Definiiones a le da le Tenso de ineia a le Es. de agange Tenso de ineia ( + ) Momentos de ineia: (Sieme ositivos) ( + ) Poiedades
Univesidad Simón Bolíva. ees de Newton. Cinemátia. Dinámia Sist. de atíulas Definiiones a le da le Tenso de ineia a le Es. de agange Tenso de ineia ( + ) Momentos de ineia: (Sieme ositivos) ( + ) Poiedades
Examen Final Tema A Cálculo Vectorial Mayo 23 de 2017
 Examen Final Tema A Cálulo Vetorial Mayo 3 de 17 Este es un examen individual, no se permite el uso de libros, apuntes, aluladoras o ualquier otro medio eletrónio. Reuerde apagar y guardar su teléfono
Examen Final Tema A Cálulo Vetorial Mayo 3 de 17 Este es un examen individual, no se permite el uso de libros, apuntes, aluladoras o ualquier otro medio eletrónio. Reuerde apagar y guardar su teléfono
4. Soluciones de ecuaciones lineales en series de potencias. ( Chema Madoz, VEGAP, Madrid 2009)
 Soluioes de euaioes lieales e seies de poteias Chema Madoz, VEGAP, Madid 9 Repaso de Seies de Poteias Reueda de álulo que ua seie de poteias e a es ua seie de la foma a a a Se die que es ua seie de poteias
Soluioes de euaioes lieales e seies de poteias Chema Madoz, VEGAP, Madid 9 Repaso de Seies de Poteias Reueda de álulo que ua seie de poteias e a es ua seie de la foma a a a Se die que es ua seie de poteias
La ecuación lineal de primer grado con tres incógnitas. El plano en el espacio afín
 La euaión lineal de primer grado on tres inógnitas. El plano en el espaio afín En un artíulo anterior habíamos hablado sobre la euaión lineal de primer grado on dos inógnitas y sobre la reta en el plano
La euaión lineal de primer grado on tres inógnitas. El plano en el espaio afín En un artíulo anterior habíamos hablado sobre la euaión lineal de primer grado on dos inógnitas y sobre la reta en el plano
r 2 F 2 E = E C +V = 1 2 mv 2 GMm J O = mr 2 dθ dt = mr 2 ω = mrv θ v θ = J O mr E = O 2mr GMm 2 r
 Física paa Ciencias e Ingenieía 18.1 18.1 Leyes de Keple Supongamos que se ha lanzado un satélite atificial de masa m, sometido al campo gavitatoio teeste, de tal manea que su enegía mecánica sea negativa.
Física paa Ciencias e Ingenieía 18.1 18.1 Leyes de Keple Supongamos que se ha lanzado un satélite atificial de masa m, sometido al campo gavitatoio teeste, de tal manea que su enegía mecánica sea negativa.
Corrección examen PAU. Junio OPCIÓN A. Realizando la multiplicación e igualando a B, obtenemos el sistema:
 Coección eamen PU. Junio 4. OPCIÓN a) Debemos enconta los valoes de, y que veifiquen: 3, Realizando la multiplicación e igualando a B, obtenemos el sistema: 3 Debemos esolve dicho sistema y paa ello antes
Coección eamen PU. Junio 4. OPCIÓN a) Debemos enconta los valoes de, y que veifiquen: 3, Realizando la multiplicación e igualando a B, obtenemos el sistema: 3 Debemos esolve dicho sistema y paa ello antes
Capítulo 1: Ondas Electromagnéticas. Parte I Revisión Electromagnetismo Ecuaciones de Maxwell Relaciones Constitutivas
 Capítulo : Ondas letomagnétias Pate I Revisión letomagnetismo uaiones de Maxwell Relaiones Constitutivas Gupo de Radiofeuenia, UC3M Tema : Ondas letomagnétias Mioondas-- Revisión letomagnetismo Idea intuitiva
Capítulo : Ondas letomagnétias Pate I Revisión letomagnetismo uaiones de Maxwell Relaiones Constitutivas Gupo de Radiofeuenia, UC3M Tema : Ondas letomagnétias Mioondas-- Revisión letomagnetismo Idea intuitiva
Teoria y Cuestiones. [a n cos (nx)+b n sin (nx)]
![Teoria y Cuestiones. [a n cos (nx)+b n sin (nx)] Teoria y Cuestiones. [a n cos (nx)+b n sin (nx)]](/thumbs/80/81469262.jpg) Ingeniero Industrial Asignatura: Transformadas Integrales y Euaiones en Derivadas Pariales Convoatoria de Febrero del 2004 Teoria y Cuestiones 1. Consideremos la funión ½ 0 si
Ingeniero Industrial Asignatura: Transformadas Integrales y Euaiones en Derivadas Pariales Convoatoria de Febrero del 2004 Teoria y Cuestiones 1. Consideremos la funión ½ 0 si
a) Estudiar su posición relativa en el espacio. b) Calcular las distancias entre ellas. c) Trazar una recta que corte perpendicularmente a ambas.
 º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
RECTAS EN EL ESPACIO.
 IES Pade Poeda (Guadi UNI 9 GEOETRÍ FÍN RETS EN EL ESPIO EUIONES E L RET Una ecta queda deteminada po Un punto ( a a a Un ecto de diección ( ( ; se le llama deteminación lineal de la ecta Si X ( es un
IES Pade Poeda (Guadi UNI 9 GEOETRÍ FÍN RETS EN EL ESPIO EUIONES E L RET Una ecta queda deteminada po Un punto ( a a a Un ecto de diección ( ( ; se le llama deteminación lineal de la ecta Si X ( es un
Ortogonalización. Dr. Luis Javier Morales Mendoza. FIEC Universidad Veracruzana Poza Rica Tuxpan
 Ooonalizaión D. Luis Javie Moales Mendoza FIEC Univesidad Veauzana Poza Ria Tuxpan Índie.. Veoes en D y 3D.. El Eo Cuadáio Medio (MSE).3. Funiones Ooonales.. MSE paa -señales.5. Taea D. Luis Javie Moales
Ooonalizaión D. Luis Javie Moales Mendoza FIEC Univesidad Veauzana Poza Ria Tuxpan Índie.. Veoes en D y 3D.. El Eo Cuadáio Medio (MSE).3. Funiones Ooonales.. MSE paa -señales.5. Taea D. Luis Javie Moales
RELACION DE ORDEN: PRINCIPALES TEOREMAS
 RELACION DE ORDEN: PRINCIPALES TEOREMAS Sean a, b, c y d númeos eales; se tiene que:. Si a < b c < d a + c < b + d. Si a 0 a > 0 3. Si a < b -a > -b 4. Si a > 0 a - > 0 ; si a < 0 a - < 0 5. Si 0 < a
RELACION DE ORDEN: PRINCIPALES TEOREMAS Sean a, b, c y d númeos eales; se tiene que:. Si a < b c < d a + c < b + d. Si a 0 a > 0 3. Si a < b -a > -b 4. Si a > 0 a - > 0 ; si a < 0 a - < 0 5. Si 0 < a
