TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES
|
|
|
- Cristina Carrasco Castellanos
- hace 6 años
- Vistas:
Transcripción
1 TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES La técnica del desaollo de facciones paciales es establecida paa cuida todos los casos sistemáticamente. Hay 4 clases de poblemas, dependiendo del denominado D(s): Caso : C(s) tiene polos eales de e oden. Caso 2: C(s) tiene polos eales epetidos de pime oden. Caso 3: C(s) tiene un pa de polos complejos conjugados (un facto cuadático en el denominado). Caso 4: C(s) tiene paes epetidos de polos complejos conjugados (un facto cuadático epetido en el denominado). CASO : POLOS REALES DE ER ORDEN. La posición de estos polos eales dec(s) en el plano s se muesta en la figua. Los polos pueden se positivos ceos o negativos y ellos están situados en el eje eal en el plano s. En este ejemplo s₁ es positivo, s₀ es ceo, s₂ es negativo. Paa los polos mostados en la figua, la tansfomada F(s) y sus facciones paciales son: D(s) = s (s s ) (s + s 2 ) A 0 s + A s s + A 2 s + s 2 Jw plano s X x x -s₂ s₀ s₁ Figua. Localización de los polos eales en el plano s Hay tantas facciones como hay factoes en el denominado de C(s), ya que s₀=0, el facto s-s₀ es escito simplemente como s. la tansfomada invesa paa C(s) es: c(t) = A 0 + A e s t + A 2 e s 2t
2 El polo s₁ es positivo, po lo tanto el témino A e s t es un incemento exponencial y el sistema es inestable. El polo s₂ es negativo, y el témino A 2 e s 2t es una caída exponencial con valo final de ceo. Po lo tanto, paa que un sistema sea estable, todos los polos eales que contibuyen a complementa la solución deben esta en la mitad izquieda del plano s.(ve figua A) Figua A. Compotamiento de los polos: positivo y negativo. Paa evalua un típico coeficiente A k, multiplicando ambos lados de la ecuación po el facto (s s k ). El esultado es: (s s k ) (s s k ) D(s) = A s s k s s k s s k + A s s A s s k + + A v 2 s s v La multiplicación del facto s s k sobe el lado izquiedo del a ecuación. Y el mismo facto D(s) debeá dividise fuea. Si s = s k, todos los téminos en el lado deecho de la ecuación son ceo excepto A k. Así, una egla geneal paa evalua las constantes paa polos eales de oden simple es: A k [(s s k ) D(s) ] s=s k = [ D (s) ] s=s k Donde D (s) es dd(s) ds polos coespondientes. Paa el caso de: Las constantes son: = D(s) (s s k). Los coeficientes A k son llamados los esiduos de C(s) de los s + 2 s(s + )(s + 3) = A 0 s + A (s + ) + A 2 (s + 3) s + 2 A 0 = [s C(s)] s=0 = [ (s + )(s + 3) ] s=0 = 2 3
3 A = [(s + )C(s)] s= = [ s + 2 s(s + 3) ] s= = 2 A 2 = [(s + 3)C(s)] s= 3 = [ s + 2 s(s + ) ] s= 3 = 6 La solución de c(t) es: c(t) = 2 3 e t 2 e 3t 6 CASO 2: POLOS REALES DE ORDEN MÚLTIPLE. La posición de los polos eales de F(s), algunos de los cuales son epetidos, se muesta en la figua 2. El símbolo ] es poyectado paa indica un polo de oden. Jw plano s X x 0 s₁ ] 3 s₁ Figua 2. Localización de polos eales en el plano s. Todos los polos eales están situados sobe el eje eal del plano s. paa los polos mostados en la figua 2, la tansfomada de C(s) y sus facciones paciales son: D(s) = (s s ) 3 (s + s 2 ) A 3 (s s ) 3 + A 2 (s s ) 2 + A s s + A 2 s + s 2 El oden de D(s) en este caso es cuato, y hay cuato facciones. Note que el polo múltiplo s, el cual es de oden 3, tiene esultados en tes facciones en el lado deecho de la ecuación C(s). Paa designa las constantes en las facciones paciales, un solo subíndice es usado paa un polo de pime oden. Paa polos de oden múltiplo, una notación de doble subíndice es usada. El pime subíndice designa el polo, y el segundo subíndice designa el oden del polo en la facción pacial. Los constantes asociados con los denominadoes de pime oden en el desaollo de las
4 facciones paciales son denominados esiduos; po lo tanto únicamente las constantes A y A 2 son esiduos de la ecuación C(s). La tansfomada invesa de C(s) es: Como calcula las constantes del oden múltiplo: c(t) = A 3 t 2 2 es t + A 2 te s t + A e s t + A 2 e s 2t Paa la tansfomada geneal con aíces eales epetidas: D(s) = (s s q ) (s + s ) A q A q( ) A q( k) (s s q ) + (s s q ) ( ) + + (s s q ) ( k) + + A q s s q + A s s + La constante A q puede evaluase simplemente, multiplicando ambos lados de la ecuación C(s) po (s s q ) obtendemos: (s s q ) (s s q ) D(s) = (s s ) = A q + A q( ) (s s q ) + + A q (s s q ) (s s q ) + A s s Nótese que el facto (s s q ) es dividido fuea de la pate izquieda de la ecuación Paa s = s q todos los téminos en el lado deecho de la ecuación son ceos excepto paa A q : A q = [ (s s q ) D(s) ] s=s q La evaluación de A q( ) no puede ealizase en una manea simila. Multiplicando ambos lados de la ecuación C(s) po (s s q ) ( k) y haciendo s = s q esultando en ambos lados su estado infinito, lo cual hace que A q( ) sea indeteminable. Si el témino A q queda eliminado en la ecuación (s s q ) C(s), A q( ) puede evaluase. Así puede ealizase po difeenciación de la ecuación (s s q ) C(s) con especto a s: Haciendo s = s q : d ds [ (s s q) D(s) ] = A q( ) + 2A q( 2) (s s q ) + d ds [ (s s q) D(s) ] s=s q +
5 Repitiendo la deivación obtenemos el coeficiente A q( z) d 2 A q( z) = 2 ds 2 [ (s s q) D(s) ] s=s q Este poceso puede epetise hasta que cada constante sea deteminada. Una fómula geneal paa descubi esos coeficientes asociados con el polo eal epetido de oden, es: A q( k) = k! d k ds k [ (s s q) D(s) ] s=s q Paa el caso de: (s + 2) 3 (s + 3) = A 3 (s + 2) 3 + A 2 (s + 2) 2 + A s A 2 s + 3 Las constantes son: A 3 = [ (s + 2) 3 C(s)] s= 2 = [ s + 3 ] s= 2 = A 2 = d ds [ (s + 2)3 C(s)] s= 2 = d ds [ s + 3 ] = [ () s= 2 (s + 3) 2] = s= 2 d 2 A = 2! ds 2 [(s + 2)3 C(s)] s= 2 = 2 d 2 ds 2 [ s + 3 ] = d s= 2 2 ds [ () (s + 3) 2] = s= 2 A = 2 [+(2)(s+3) (s+3) 4 ]s= 2 = 2 [2 ]= A 2 = [(s + 3)C(s)] s= 3 = [ (s + 2) 3] = s= 3 Y la solución como una función de tiempo es c (t) = t2 2 e 2t te 2t + e 2t e 3t
6 CASO N 3. POLOS COMPLEJOS CONJUGADOS. La posición de los polos complejos de F(s) en el plano s se muesta en la figua 3. Figua 3. Localizaciones de los polos complejos conjugados en el plano s. Los polos complejos siempe son pesentados en paes complejos conjugados; su pate eal puede se positivo o negativo. Paa los polos mostados en la figua 3 la tansfomada F(s) y sus facciones paciales son: D(s) = (s 2 + 2δw n s + w 2 n )(s s 3 ) = A (s s ) + A 2 (s s 2 ) + A 3 (s s 3 ) A = + A 2 + A 3 (s+δw n jw n s 2 ) (s+δw n jw n s 2 ) (s s 3 ) La tansfomada invesa de C(s) es: f(t)=a e ( δw n+jw n δ 2) + A 2 e ( δw n+jw n δ 2) + A e (s 3t) Entonces los polos S y S 2 son complejos conjugados y entonces f(t) es una cantidad eal, los coefiientes A y A 2 tienen también que se complejos conjugados. La ecuación puede escibise con los pimeos téminos combinados paa una más usual foma senosoidal amotiguada: c(t) = 2 A e δw nt sen (w n δ 2 t + ) + A 3 e s 3t c(t) = 2 A e σt sen(w d t + ) + A 3 e s 3t
7 Donde el ángulo: = angulo de A Los valoes de A y A 3, del mismo modo que se fundamenta en la manea peviamente mostada, son: A = (s s )C(s) s=s A 2 = (s s 3 )C(s) s=s3 Así como s es complejo, la constante A es también compleja. Recuédese que A 3 está asociada con el polo complejo con la pate imaginaia positiva. En la figua 3, los polos complejos tienen una pate eal negativa, σ = δw n, donde la azón de amotiguamiento δ es positiva. Paa este caso la coespondiente espuesta tansitoia es conocida como una sinusoidal de amotiguada y se muesta en la figua 4. Su valo final es ceo. El ángulo mostado en la figua 4, es medido del eje eal negativo y se elaciona a la azón de amotiguamiento po : Cos n = δ Figua 4. Bosquejo de una senoide exponencial amotiguada. Si el polo complejo tiene una pate eal positiva, la espuesta con especto al tiempo se incementa exponencialmente con el tiempo y el sistema es inestable. Si las aíces complejas son en la mitad deecha del plano s, la azón del amotiguamiento es negativa. El ángulo n paa este caso es medido paa el eje eal positivo y está dado po: Paa el caso de: cos n = δ (s 2 +6s+25)(s+2) = A s+3 j4 + A 2 s+3+j4 + A 3 s+2 Las constantes son:
8 A (s + 3 j4) (s+6s+25)(s+2) s= 3+j4 = (s+3+j4)(s+2) s= 3+j4 = = = ( 3+j4+3+j4)( 3+j4+2) (j8)( +j4) ( )( ) = ( ( ) A 3 (s + 2) = = (s 2 +6s+25)(s+2) s= 2 = (s 2 +6s+25)(s+2) s= 2 = = La solución es: c(t)=0.06e 3t sen (4t ) e 2t Este ejemplo es usado paa ilusta las técnicas en facciones paciales de expansión. C(s) c(t) 0 t (s + c)[(s + a) 2 + b 2 ] e ct (c a) 2 + b 2 + e at sen(bt ) b (c a) 2 + b 2 = tan b c a El ángulo de fase en el témino sinusoidal amotiguada es: = tan b = = c a tan 4 = Esto es impotante paa hace nota que: tan 4 tan 4 Paa obtene el valo coecto paa el ángulo de, es útil taza un esquema, como el mostado e la figua 5. Esto evita ambigüedades y confima que es evaluado coectamente.
9 Figua 5. Calculo del ángulo θ. POLOS IMAGINARIOS. La posición de los polos imaginaios de C(s) en el plano s se muesta en la figua 6. Como la pate eal de los polos es ceo, los polos se poyectan sobe los ejes imaginaios. Esta situación es un caso especial de polos complejos, u,g, la azón de amotiguamiento δ = 0. Paa los polos mostados en la figua 4-5, la tansfomada f(s) y sus facciones paciales son: = = A + D(s) (s 2 +w 2 n )(s s 3 ) s s A 2 s s 2 + A 3 s s 3 Figua 6. Polos de C(s) contienen dos polos imaginaios complejos en el plano s. La cuadática puede facto izase en témino de los polos s y s 2 ; asi: s 2 + w 2 n = (s jw n )(s + jw n )=( s s )( s + s 2 ) La tansfomada invesa de la ecuación (4-57) es: c(t)= A e jw nt +A 2 e jw nt +A 3 e s 3t como c(t)es una cantidad eal, los coeficientes A y A 2 son complejos conjugados. Los teminos de la ecuación pueden combinase paa una foma mas usual. c(t)=2 A sen (w n t + ) + A 3 e s 3t
10 Ya que no hay téminos de amotiguamiento multiplicando la senoide, esos téminos epesentan un valo de estado estable. El ángulo es: =angulo de A +90 Los valoes de A y A 2, establecidos de la manea convencional son: A = [(s s )C(s)] s=s Paa el caso donde A 2 = [(s + s 2 )C(s)] s= s2 00 (s )(s + 2) = A (s j5) + A 2 (s + j5) + A 2 (s + 2) Los valoes de los coeficientes son A = [(s j5)c(s)] s=j5 = [ 00 ] 00 (s+j5)(s+2) s=j5= = 00 = (j5+j5)(j5+2) (j0)(j5+2) 00 = 00 = (0 90 )( ) ( ) La solución es: 00 A 3 = [(s + 2)C(s)] s= 2 = [ ] (s 2 +25) s= 2 = 00 c(t)= 3.72 sen (5t-68.2 )+3.45e 2t φ = = 68.2 ( ) = 00 (29) = 3.45 CASO 4: POLOS COMPLEJOS DE ORDEN MÚLTIPLE. Aunque los polos conjugados complejos de oden múltiple no ocuen muy fecuentemente, es impotante conoce de qué modo pocede si se pesentaan. Ellos pueden tatase en la misma manea como los polos eales epetidos. La expansión de la facción pacial de la tansfomada C(s) con polos complejos múltiples es.
11 C(s)= + (s 2 +2δw n s+w n 2 ) Q (s) = A A (s+δw n +jw n δ 2 ) A (s+δw n +jw n δ 2 ) + (s+δw n +jw n δ 2 ) + + A (s+δw n +jw n δ 2 ) + A (s+δw n +jw n δ 2 ) + A (s+δw n +jw n δ 2 ) Las constantes son evaluadas en la misma manea como paa aíces eales epetidas, la tansfomada invesa es de la foma: c(t)= 2 A t ( )! e δw nt sen(w n δ 2 t + ) + 2 A t 2 ( 2)! e δw nt sen(w n δ 2 t + ) +
TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES
 TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES La técnica del desarrollo de fracciones parciales es establecida para cuidar todos los casos sistemáticamente. Hay 4 clases de problemas, dependiendo
TEOREMA DE DESARROLLO DE HEAVISIDE EN FRACCIONES PARCIALES La técnica del desarrollo de fracciones parciales es establecida para cuidar todos los casos sistemáticamente. Hay 4 clases de problemas, dependiendo
TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1
 TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1 página 2 SEGUNDO BIMESTRE 1 FUNCIONES DE MAS DE 90 GRADOS 1.1 CONCEPTOS Y DEFINICIONES Los valoes de las funciones tigonométicas solamente eisten paa
TRIGONOMETRÍA FUNCIONES DE MÁS DE 90 GRADOS página 1 página 2 SEGUNDO BIMESTRE 1 FUNCIONES DE MAS DE 90 GRADOS 1.1 CONCEPTOS Y DEFINICIONES Los valoes de las funciones tigonométicas solamente eisten paa
Análisis de respuesta en frecuencia
 Análisis de espuesta en fecuencia Con el témino espuesta en fecuencia, nos efeimos a la espuesta de un sistema en estado estable a una entada senoidal. En los métodos de la espuesta en fecuencia, la fecuencia
Análisis de espuesta en fecuencia Con el témino espuesta en fecuencia, nos efeimos a la espuesta de un sistema en estado estable a una entada senoidal. En los métodos de la espuesta en fecuencia, la fecuencia
SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO
 SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO Sugeencias paa quien impate el cuso: Se espea que con la popuesta didáctica pesentada en conjunción con los apendizajes que sobe el estudio de la tigonometía
SENO Y COSENO PARA UN ÁNGULO EN EL PLANO CARTESIANO Sugeencias paa quien impate el cuso: Se espea que con la popuesta didáctica pesentada en conjunción con los apendizajes que sobe el estudio de la tigonometía
Aplicación de los Residuos al cálculo de Integrales Reales
 Aplicación de los Residuos al cálculo de Integales Reales A continuación, se haá un estudio sobe cietos tipos de integales eales que pesentan una equivalencia con las integales complejas sobe caminos ceados,
Aplicación de los Residuos al cálculo de Integales Reales A continuación, se haá un estudio sobe cietos tipos de integales eales que pesentan una equivalencia con las integales complejas sobe caminos ceados,
CAPÍTULO II LEY DE GAUSS
 Tópicos de lecticidad y Magnetismo J.Pozo y R.M. Chobadjian. CAPÍTULO II LY D GAUSS La Ley de Gauss pemite detemina el campo eléctico cuando las distibuciones de cagas pesentan simetía, en caso contaio
Tópicos de lecticidad y Magnetismo J.Pozo y R.M. Chobadjian. CAPÍTULO II LY D GAUSS La Ley de Gauss pemite detemina el campo eléctico cuando las distibuciones de cagas pesentan simetía, en caso contaio
Capítulo 8. Sistemas de partículas idénticas
 Capítulo 8 Sistemas de patículas idénticas 8 Indistinguibilidad 8 Funciones popias del opeado de pemutación 8 Átomo de helio 83 spín total 8 Sistemas de patículas idénticas n la mecánica clásica en una
Capítulo 8 Sistemas de patículas idénticas 8 Indistinguibilidad 8 Funciones popias del opeado de pemutación 8 Átomo de helio 83 spín total 8 Sistemas de patículas idénticas n la mecánica clásica en una
( ) y ( ) = CAMPOS: OPERADOR NABLA ( ) ( )
 CAMPOS: OPERADOR NABLA Repesenta los campos vectoiales A i + j, B i j. Halla la divegencia el otacional de cada uno de ellos eplica el significado físico de los esultados obtenidos. Solución: I.T.I., 3,
CAMPOS: OPERADOR NABLA Repesenta los campos vectoiales A i + j, B i j. Halla la divegencia el otacional de cada uno de ellos eplica el significado físico de los esultados obtenidos. Solución: I.T.I., 3,
EJERCITACIÓN PARA EXAMEN DE MATEMATICA MAYORES DE 25 AÑOS SIN CICLO MEDIO COMPLETO. PRACTICO 3 Función Lineal Rectas Noviembre 2011
 EJERCITACIÓN PARA EXAMEN DE MATEMATICA MAYORES DE 5 AÑOS SIN CICLO MEDIO COMPLETO PRACTICO Función Lineal Rectas Noviembe RECORDAR: Una unción lineal es de la oma popiedad que los cocientes incementales:
EJERCITACIÓN PARA EXAMEN DE MATEMATICA MAYORES DE 5 AÑOS SIN CICLO MEDIO COMPLETO PRACTICO Función Lineal Rectas Noviembe RECORDAR: Una unción lineal es de la oma popiedad que los cocientes incementales:
MATEMÁTICAS II TEMA 6 Planos y rectas en el espacio. Problemas de ángulos, paralelismo y perpendicularidad, simetrías y distancias
 Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Geometía del espacio: poblemas de ángulos y distancias; simetías MATEMÁTICAS II TEMA 6 Planos y ectas en el espacio Poblemas de ángulos, paalelismo y pependiculaidad, simetías y distancias Ángulos ente
Fuerza magnética sobre conductores.
 Fueza magnética sobe conductoes. Peviamente se analizó el compotamiento de una caga q que se mueve con una velocidad dento de un campo magnético B, la cual expeimenta una fueza dada po la expesión: F q(v
Fueza magnética sobe conductoes. Peviamente se analizó el compotamiento de una caga q que se mueve con una velocidad dento de un campo magnético B, la cual expeimenta una fueza dada po la expesión: F q(v
Práctica 8: Carta de Smith
 Páctica 8: Cata de Smith Objetivo Familiaización con el manejo de la Cata de Smith. Contenidos Repesentación de impedancias y admitancias. Obtención de paámetos de las líneas empleando la Cata de Smith.
Páctica 8: Cata de Smith Objetivo Familiaización con el manejo de la Cata de Smith. Contenidos Repesentación de impedancias y admitancias. Obtención de paámetos de las líneas empleando la Cata de Smith.
Coordenadas homogéneas
 Coodenadas homogéneas Una matiz de otación 3 x 3 no nos da ninguna posibilidad paa la taslación y el escalado. Intoducimos una cuata coodenada p(x,y,z) p(wx,wy,wz,w), donde w tiene un valo abitaio y epesenta
Coodenadas homogéneas Una matiz de otación 3 x 3 no nos da ninguna posibilidad paa la taslación y el escalado. Intoducimos una cuata coodenada p(x,y,z) p(wx,wy,wz,w), donde w tiene un valo abitaio y epesenta
GRÁFICA DE LAS FUNCIONES TRIGONOMÉTRICAS
 FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO: 10 TALLER Nº: 6 SEMESTRE 1 GRÁFICA DE LAS FUNCIONES TRIGONOMÉTRICAS RESEÑA HISTÓRICA Leonhad Eule, (1707-1783) Fue un matemático
FACULTAD DE CIENCIAS EXACTAS Y NATURALES SEMILLERO DE MATEMÁTICAS GRADO: 10 TALLER Nº: 6 SEMESTRE 1 GRÁFICA DE LAS FUNCIONES TRIGONOMÉTRICAS RESEÑA HISTÓRICA Leonhad Eule, (1707-1783) Fue un matemático
DIVISIBILIDAD DE POLINOMIOS
 DIVISIÓN DE OLINOMIOS.- DIVISIBILIDAD DE OLINOMIOS Dados dos polinomios, D ( ) y d ( ) con d ( ) 0, llamados dividendo y diviso, con g( D( ) ) g( d( ) ), dividi el pimeo D ( ) ente (:) el segundo ( ) (que
DIVISIÓN DE OLINOMIOS.- DIVISIBILIDAD DE OLINOMIOS Dados dos polinomios, D ( ) y d ( ) con d ( ) 0, llamados dividendo y diviso, con g( D( ) ) g( d( ) ), dividi el pimeo D ( ) ente (:) el segundo ( ) (que
Vectores Presentanción basada en el material contenido en: Serway, R. Physics for Scientists and Engineers. Saunders College Pub. 3rd edition.
 Vectoes Pesentanción basada en el mateial contenido en: Seway, R. Physics fo Scientists and Enginees. Saundes College Pub. 3d edition. Sistemas de Coodenadas Se usan paa descibi la posición de un punto
Vectoes Pesentanción basada en el mateial contenido en: Seway, R. Physics fo Scientists and Enginees. Saundes College Pub. 3d edition. Sistemas de Coodenadas Se usan paa descibi la posición de un punto
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables (x 0 ). x ik. x ik 1
 1. RESUMEN Ingenieía Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Vaias Vaiables 08-1 Ingenieía Matemática Univesidad de Chile Guía Semana 5 Teoema del valo medio.
1. RESUMEN Ingenieía Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Vaias Vaiables 08-1 Ingenieía Matemática Univesidad de Chile Guía Semana 5 Teoema del valo medio.
4 Parte. Tiempo límite: 20 min.
 4 Pate IV O-PAEP Tiempo límite: 0 min. Instucciones: Resuelva cada poblema de esta sección usando cualquie espacio disponible de la página paa hace cálculos y anotaciones. Maque luego la única contestación
4 Pate IV O-PAEP Tiempo límite: 0 min. Instucciones: Resuelva cada poblema de esta sección usando cualquie espacio disponible de la página paa hace cálculos y anotaciones. Maque luego la única contestación
. Esta segunda función es posible que no pueda explicitarse: no pueda encontrarse la fórmula y f (x)
 1 FUNCIONES DE DOS VARIABLES DERIVACIÓN IMPLÍCITA (Tangente a una cuva de nivel); FUNCIONES HOMOGÉNEAS Deivación implícita ecta tangente a una cuva de nivel Si (a, b) es un punto que cumple la ecuación
1 FUNCIONES DE DOS VARIABLES DERIVACIÓN IMPLÍCITA (Tangente a una cuva de nivel); FUNCIONES HOMOGÉNEAS Deivación implícita ecta tangente a una cuva de nivel Si (a, b) es un punto que cumple la ecuación
ÓPTICA GEOMÉTRICA: REFLEXIÓN, REFRACCIÓN Y LENTES
 PRÁCTICA ÓPTICA GEOMÉTRICA: REFLEXIÓN, REFRACCIÓN Y LENTES A) MATERIAL Fuente de luz, banco óptico, lente delgada convegente, pantalla. B) OBJETIVO Intoduci los conceptos de ayo luminoso y de índice de
PRÁCTICA ÓPTICA GEOMÉTRICA: REFLEXIÓN, REFRACCIÓN Y LENTES A) MATERIAL Fuente de luz, banco óptico, lente delgada convegente, pantalla. B) OBJETIVO Intoduci los conceptos de ayo luminoso y de índice de
Esta guía es una herramienta que usted debe usar para lograr los siguientes objetivos:
 FÍSICA GENERAL II GUÍA - Campo eléctico: Ley de Gauss Objetivos de apendizaje Esta guía es una heamienta que usted debe usa paa loga los siguientes objetivos: Defini el concepto de Flujo de Campo Eléctico.
FÍSICA GENERAL II GUÍA - Campo eléctico: Ley de Gauss Objetivos de apendizaje Esta guía es una heamienta que usted debe usa paa loga los siguientes objetivos: Defini el concepto de Flujo de Campo Eléctico.
Diferencia de potencial y potencial eléctricos. En el campo gravitatorio.
 Difeencia de potencial y potencial elécticos En el campo gavitatoio. Difeencia de potencial y potencial elécticos El tabajo se cuantifica po la fueza que ejece el campo y la distancia ecoida. W F d Difeencia
Difeencia de potencial y potencial elécticos En el campo gavitatoio. Difeencia de potencial y potencial elécticos El tabajo se cuantifica po la fueza que ejece el campo y la distancia ecoida. W F d Difeencia
Derivadas de funciones trigonométricas y sus inversas
 Deivadas de funciones tigonométicas y sus invesas Las funciones tigonométicas se definen a pati de un tiángulo ectángulo como sigue: sin α y csc α y y cos α x sec α x α x tan α y x cot α x y Como puedes
Deivadas de funciones tigonométicas y sus invesas Las funciones tigonométicas se definen a pati de un tiángulo ectángulo como sigue: sin α y csc α y y cos α x sec α x α x tan α y x cot α x y Como puedes
Junio 2010 OPCIÓN A. A vemos que se diferencian en el cuadrado de la matriz unitaria. Dado que en este caso. por ser la matriz nula.
 Junio OPCÓN Poblema. a) Si obsevamos los desaollos de ) ( y ) ( vemos que se difeencian en el cuadado de la matiz unitaia. Dado que en este caso se veifica: ) ( ) ( ) ( ) ( + + ) ( ) ( ) ( b) b.) Paa que
Junio OPCÓN Poblema. a) Si obsevamos los desaollos de ) ( y ) ( vemos que se difeencian en el cuadado de la matiz unitaia. Dado que en este caso se veifica: ) ( ) ( ) ( ) ( + + ) ( ) ( ) ( b) b.) Paa que
FUERZA ELECTRO MOTRIZ Y RESISTENCIA INTERNA DE UNA PILA
 FUEZA ELECTO MOTIZ Y ESISTENCIA INTENA DE UNA ILA Intoducción: En la figua 1 se muesta un cicuito de dos esistencias 1 y 2 conectadas en seie, este gupo a su vez está conectado en seie con una pila ideal
FUEZA ELECTO MOTIZ Y ESISTENCIA INTENA DE UNA ILA Intoducción: En la figua 1 se muesta un cicuito de dos esistencias 1 y 2 conectadas en seie, este gupo a su vez está conectado en seie con una pila ideal
Apuntes de Trigonometría Elemental
 Apuntes de Tigonometía Elemental José Antonio Salgueio González IES Bajo Guadalquivi - ebija ii Agadecimientos A Rocío, que con su apoyo hace posible la ealización de este poyecto 1 Índice geneal Agadecimientos
Apuntes de Tigonometía Elemental José Antonio Salgueio González IES Bajo Guadalquivi - ebija ii Agadecimientos A Rocío, que con su apoyo hace posible la ealización de este poyecto 1 Índice geneal Agadecimientos
Cinemática Cuerpos en caída libre PRIMERA PARTE
 CORPORACIÓN UNIVERSITARIA MINUTO DE DIOS FACULTAD DE INGENIERIA RESPUESTAS DEL PIRATA Cinemática Cuepos en caída libe PRIMERA PARTE ) Las gotas de lluvia caen desde una nube situada a 700 m sobe la supeficie
CORPORACIÓN UNIVERSITARIA MINUTO DE DIOS FACULTAD DE INGENIERIA RESPUESTAS DEL PIRATA Cinemática Cuepos en caída libe PRIMERA PARTE ) Las gotas de lluvia caen desde una nube situada a 700 m sobe la supeficie
Apuntes de Electrostática Prof. J. Martín ETSEIT ELECTROESTÁTICA I CAMPO ELECTRICO EN EL ESPACIO LIBRE
 LCTROSTÁTICA I CAMPO LCTRICO N L SPACIO LIBR. Le de Coulomb. Cagas puntuales 3. Distibuciones de caga 4. Campo eléctico 5. cuaciones de campo 6. Le de Gauss 7. Potencial eléctico 8. negía potencial 9.
LCTROSTÁTICA I CAMPO LCTRICO N L SPACIO LIBR. Le de Coulomb. Cagas puntuales 3. Distibuciones de caga 4. Campo eléctico 5. cuaciones de campo 6. Le de Gauss 7. Potencial eléctico 8. negía potencial 9.
UNIVERSIDAD POLITÉCNICA DE MADRID
 UNIVERSIDAD POLITÉCNICA DE MADRID ESCUELA DE INGENIERÍA AERONÁUTICA Y DEL ESPACIO (EIAE) Mecánica de Fluidos I Poblema de ecuaciones geneales Un cilindo de adio R 0 y una cacasa concéntica con el cilindo
UNIVERSIDAD POLITÉCNICA DE MADRID ESCUELA DE INGENIERÍA AERONÁUTICA Y DEL ESPACIO (EIAE) Mecánica de Fluidos I Poblema de ecuaciones geneales Un cilindo de adio R 0 y una cacasa concéntica con el cilindo
V = R 2 2 EJERCICIOS DE POTENCIAS EN CIRCUITOS MONOFASICOS
 EJERIIOS DE POENIAS EN IRUIOS MONOFASIOS EJERIIO 1.- En el cicuito de la figua, la esistencia consume 300 W, los dos condensadoes 300 VAR cada uno y la bobina 1.000 VAR. Se pide, calcula: a) El valo de
EJERIIOS DE POENIAS EN IRUIOS MONOFASIOS EJERIIO 1.- En el cicuito de la figua, la esistencia consume 300 W, los dos condensadoes 300 VAR cada uno y la bobina 1.000 VAR. Se pide, calcula: a) El valo de
Guía Regla de la Cadena(1 er Orden)
 UNIVERSIDAD DE CHILE CÁLCULO EN VARIAS VARIABLES PROFESOR: MARCELO LESEIGNEUR AUXILIARES: ALFONSO TORO - SEBASTIÁN COURT Guía Regla de la Cadena1 e Oden 1. Sean f : R R y g : R R dos funciones difeenciables.
UNIVERSIDAD DE CHILE CÁLCULO EN VARIAS VARIABLES PROFESOR: MARCELO LESEIGNEUR AUXILIARES: ALFONSO TORO - SEBASTIÁN COURT Guía Regla de la Cadena1 e Oden 1. Sean f : R R y g : R R dos funciones difeenciables.
Series de Polinomios Ortogonales
 Semana - Clase 6 9/0/0 Tema : Seies Seies de Polinomios Otogonales Enunciaemos un teoema debido a Weiestass el cual gaantiza que una función contínua en un intevalo [a, b puede se apoximada unifomemente
Semana - Clase 6 9/0/0 Tema : Seies Seies de Polinomios Otogonales Enunciaemos un teoema debido a Weiestass el cual gaantiza que una función contínua en un intevalo [a, b puede se apoximada unifomemente
UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA ESCUELA PROFESIONAL DE INGENIERÍA ELÉCTRICA ESTÁTICA
 UNIVESIDD NCINL DEL CLL CULTD DE INGENIEÍ ELÉCTIC Y ELECTÓNIC ESCUEL PESINL DE INGENIEÍ ELÉCTIC ESTÁTIC * Equilibio de cuepos ígidos ING. JGE MNTÑ PISIL CLL, 2010 EQUILIBI DE CUEPS ÍGIDS CNCEPTS PEVIS
UNIVESIDD NCINL DEL CLL CULTD DE INGENIEÍ ELÉCTIC Y ELECTÓNIC ESCUEL PESINL DE INGENIEÍ ELÉCTIC ESTÁTIC * Equilibio de cuepos ígidos ING. JGE MNTÑ PISIL CLL, 2010 EQUILIBI DE CUEPS ÍGIDS CNCEPTS PEVIS
LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA
 LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA OBJETIVOS I.- Loga el equilibio estático de objetos que pueden ota en tono a un eje, po medio de la aplicación de fuezas y toques. INTRODUCCIÓN
LABORATORIO DE FISICA Nº 1 MAQUINAS SIMPLES PALANCA-POLEA OBJETIVOS I.- Loga el equilibio estático de objetos que pueden ota en tono a un eje, po medio de la aplicación de fuezas y toques. INTRODUCCIÓN
9. NÚMEROS COMPLEJOS EN FORMA POLAR
 Númeos Complejos en Foma Pola 9. NÚMEROS COMPLEJOS EN FORMA POLAR Recodemos que en la Unidad vimos que a un númeo complejo podemos expesalo en foma inómica z = a + i donde a, son númeos eales, que se epesenta
Númeos Complejos en Foma Pola 9. NÚMEROS COMPLEJOS EN FORMA POLAR Recodemos que en la Unidad vimos que a un númeo complejo podemos expesalo en foma inómica z = a + i donde a, son númeos eales, que se epesenta
9. NÚMEROS COMPLEJOS EN FORMA POLAR
 9. NÚMEROS COMPLEJOS EN FORMA POLAR Recodemos que en la Unidad vimos que a un númeo complejo podemos expesalo en foma inómica z = a + i donde a, son númeos eales, que se epesenta gáficamente mediante un
9. NÚMEROS COMPLEJOS EN FORMA POLAR Recodemos que en la Unidad vimos que a un númeo complejo podemos expesalo en foma inómica z = a + i donde a, son númeos eales, que se epesenta gáficamente mediante un
BOLILLA 3 DESPLAZAMIENTO, VELOCIDAD Y ACELERACION
 FACULTAD DE CIENCIAS CURSO DE INTRODUCCION A LA METEOROLOGIA 11 BOLILLA 3 DESPLAZAMIENTO, VELOCIDAD Y ACELERACION 1. INTRODUCCION A LA CINEMATICA El oigen de la dinámica se emonta a los pimeos expeimentos
FACULTAD DE CIENCIAS CURSO DE INTRODUCCION A LA METEOROLOGIA 11 BOLILLA 3 DESPLAZAMIENTO, VELOCIDAD Y ACELERACION 1. INTRODUCCION A LA CINEMATICA El oigen de la dinámica se emonta a los pimeos expeimentos
CLASE #2 de Bessel: Modos normales de una membrana circular (Continuación):
 CLASE #2 de Bessel: Modos nomales de una membana cicula (Continuación): Intoducción En la clase anteio esolvimos usando el Método de Sepaación de Vaiables, la ecuación de ondas paa una membana cicula de
CLASE #2 de Bessel: Modos nomales de una membana cicula (Continuación): Intoducción En la clase anteio esolvimos usando el Método de Sepaación de Vaiables, la ecuación de ondas paa una membana cicula de
SERIE # 3 CÁLCULO VECTORIAL
 SERIE # 3 ÁLULO VETORIAL ÁLULO VETORIAL Página 1 1) Sea el campo vectoial F (x,y,)=( 3x+ y)i+( x+ y ) j ( x) k. alcula lago de la cuva : 4 5 x = + y y =, del punto A ( 3, 1, 1) al punto B ( 3, 1, -1).
SERIE # 3 ÁLULO VETORIAL ÁLULO VETORIAL Página 1 1) Sea el campo vectoial F (x,y,)=( 3x+ y)i+( x+ y ) j ( x) k. alcula lago de la cuva : 4 5 x = + y y =, del punto A ( 3, 1, 1) al punto B ( 3, 1, -1).
REPARTIDO III CIRCUNFERENCIA
 Pof.: Lucia Tafenabe Ecuación Geneal REPRTIDO III IRUNFERENI B B cento, Ecuación de la icunfeencia conociendo cento (α, β) adio. adio B MN ( - α) ( - β) Deteminación de la ecuación de la cicunfeencia conociendo:
Pof.: Lucia Tafenabe Ecuación Geneal REPRTIDO III IRUNFERENI B B cento, Ecuación de la icunfeencia conociendo cento (α, β) adio. adio B MN ( - α) ( - β) Deteminación de la ecuación de la cicunfeencia conociendo:
LEY DE GAUSS. Este enunciado constituye en realidad una de las principales leyes del Electromagnetismo.
 LY D GAU La ley de Gauss es un enunciado ue es deivable de las popiedades matemáticas ue tiene el Vecto de intensidad de Campo léctico con especto a las supeficies en el espacio. ste enunciado constituye
LY D GAU La ley de Gauss es un enunciado ue es deivable de las popiedades matemáticas ue tiene el Vecto de intensidad de Campo léctico con especto a las supeficies en el espacio. ste enunciado constituye
Conceptos centrales. Tema 1. Cadenas. Alfabetos. Cadenas. Cadenas. Nociones Preliminares y Lenguajes. Dr. Luis A. Pineda ISBN:
 Tema Nociones Peliminaes y Lenguajes D. Luis A. Pineda ISBN: 0--- Alfabetos Lenguajes Repesentación Intepetación Poblemas Conceptos centales Funciones, algoitmos y fómulas Alfabetos Conjunto finito (no
Tema Nociones Peliminaes y Lenguajes D. Luis A. Pineda ISBN: 0--- Alfabetos Lenguajes Repesentación Intepetación Poblemas Conceptos centales Funciones, algoitmos y fómulas Alfabetos Conjunto finito (no
Solución al examen de Física
 Solución al examen de Física Campos gavitatoio y eléctico 14 de diciembe de 010 1. Si se mantuviea constante la densidad de la Tiea: a) Cómo vaiaía el peso de los cuepos en su supeficie si su adio se duplicaa?
Solución al examen de Física Campos gavitatoio y eléctico 14 de diciembe de 010 1. Si se mantuviea constante la densidad de la Tiea: a) Cómo vaiaía el peso de los cuepos en su supeficie si su adio se duplicaa?
200. Hallar la ecuación de la simetría ortogonal respecto de la recta:
 Hoja de Poblemas Geometía IX 200 Halla la ecuación de la simetía otogonal especto de la ecta: SOLUCIÓN n( x a) Sean: - S la simetía otogonal especto de la ecta n ( x a) - P un punto cualquiea cuyo vecto
Hoja de Poblemas Geometía IX 200 Halla la ecuación de la simetía otogonal especto de la ecta: SOLUCIÓN n( x a) Sean: - S la simetía otogonal especto de la ecta n ( x a) - P un punto cualquiea cuyo vecto
Selectividad Septiembre 2009 SEPTIEMBRE 2009
 Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Selectividad Septiembe 9 OPCIÓN A PROBLEMAS SEPTIEMBRE 9 1.- Sea la función f () =. + 1 a) Halla el dominio, intevalos de cecimiento y dececimiento, etemos elativos, intevalos de concavidad y conveidad,
Capitulo III. Capítulo III
 Cinemática y Dinámica de Máquinas. III. Métodos analíti de análisis cinemático Capitulo III Métodos analíti de análisis cinemático. 1 R Sancibián y. de Juan. Ing. Mecánica Cinemática y Dinámica de Máquinas.
Cinemática y Dinámica de Máquinas. III. Métodos analíti de análisis cinemático Capitulo III Métodos analíti de análisis cinemático. 1 R Sancibián y. de Juan. Ing. Mecánica Cinemática y Dinámica de Máquinas.
GALICIA / JUNIO 03. LOGSE / FÍSICA / EXAMEN COMPLETO
 GALICIA / JUNIO 3. LOGSE / FÍSICA / EXAMEN COMPLEO El examen de física de las P.A.U. pesenta dos opciones de semejante nivel de dificultad. Cada opción consta de tes pates difeentes(poblemas, cuestiones
GALICIA / JUNIO 3. LOGSE / FÍSICA / EXAMEN COMPLEO El examen de física de las P.A.U. pesenta dos opciones de semejante nivel de dificultad. Cada opción consta de tes pates difeentes(poblemas, cuestiones
CÁLCULO Primer curso de Ingeniero de Telecomunicación Segundo Examen Parcial. 13 de Junio de 2001 Primera parte. ; y = u v ; z = u2 v 2
 CÁLCULO Pime cuso de Ingenieo de Telecomunicación Segundo Examen Pacial. 1 de Junio de 1 Pimea pate Ejecicio 1. Obtene la expesión en que se tansfoma z xx +z xy +z yy ; al cambia las vaiables independientes
CÁLCULO Pime cuso de Ingenieo de Telecomunicación Segundo Examen Pacial. 1 de Junio de 1 Pimea pate Ejecicio 1. Obtene la expesión en que se tansfoma z xx +z xy +z yy ; al cambia las vaiables independientes
Ecuación de Laplace y Ecuación de Poisson Teorema de Unicidad. Métodos de las Imágenes. Campos y Ondas UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA
 Electostática táti Clase 3 Ecuación de Laplace y Ecuación de Poisson Teoema de Unicidad. Métodos de las Imágenes Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA 2 E V m
Electostática táti Clase 3 Ecuación de Laplace y Ecuación de Poisson Teoema de Unicidad. Métodos de las Imágenes Campos y Ondas FACULTAD DE INGENIERÍA UNIVERSIDAD NACIONAL DE LA PLATA ARGENTINA 2 E V m
CI52R: ESTRUCTURAS DE ACERO
 CI5R: ESTRUCTURAS DE ACERO of.: Ricado Heea. Aux.: hillipo Coea. Capítulo 7: Diseño paa Esfuezos Combinados ogama CI5R NÚERO NOBRE DE LA UNIDAD OBJETIVOS Diseño paa esfuezos combinados 7 DURACIÓN semana
CI5R: ESTRUCTURAS DE ACERO of.: Ricado Heea. Aux.: hillipo Coea. Capítulo 7: Diseño paa Esfuezos Combinados ogama CI5R NÚERO NOBRE DE LA UNIDAD OBJETIVOS Diseño paa esfuezos combinados 7 DURACIÓN semana
MECANICA APLICADA I. EXAMEN PARCIAL PRIMER EJERCICIO TIEMPO: 75. cuando
 MECNIC PLICD I. EXMEN PCIL. 17-04-99. PIME EJECICI TIEMP: 75 1. btene la expesión de la velocidad de ω V s ω V s sucesión del cento instantáneo de otación cuando =. 2 2. Indica qué afimaciones son cietas
MECNIC PLICD I. EXMEN PCIL. 17-04-99. PIME EJECICI TIEMP: 75 1. btene la expesión de la velocidad de ω V s ω V s sucesión del cento instantáneo de otación cuando =. 2 2. Indica qué afimaciones son cietas
EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES
 EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES De su cota y espectacula existencia (1911-1927 el átomo de Boh dejó una imagen simple del átomo y vaios conceptos nuevos y fundamentales, como el de númeos
EL MODELO CUÁNTICO PARA ÁTOMOS HIDROGENOIDES De su cota y espectacula existencia (1911-1927 el átomo de Boh dejó una imagen simple del átomo y vaios conceptos nuevos y fundamentales, como el de númeos
INSTRUCCIONES GENERALES Y VALORACIÓN
 UNIVERSIDAD DE ALCALÁ PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (Mayoes 5 años) Cuso 009-010 MATERIA: FÍSICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates: La pimea pate consiste en
UNIVERSIDAD DE ALCALÁ PRUEBA DE ACCESO A ESTUDIOS UNIVERSITARIOS (Mayoes 5 años) Cuso 009-010 MATERIA: FÍSICA INSTRUCCIONES GENERALES Y VALORACIÓN La pueba consta de dos pates: La pimea pate consiste en
z a3 Ecuaciones continuas de la recta: eliminando el parámetro de (2) = = u u u
 Geometía. Puntos, ectas y planos en el espacio. Poblemas méticos en el espacio Pedo Casto Otega. Coodenadas o componentes de un vecto Sean dos puntos ( a, a ) y ( ) uuu uuu vecto son: = ( b a, b a, b a
Geometía. Puntos, ectas y planos en el espacio. Poblemas méticos en el espacio Pedo Casto Otega. Coodenadas o componentes de un vecto Sean dos puntos ( a, a ) y ( ) uuu uuu vecto son: = ( b a, b a, b a
Cátedra de Física 1. Autor: Ing. Ricardo Minniti. Sábado 10 de Febrero de 2007 Página 1 de 14. Índice
 Cáteda de Física Índice Figua - Enunciado Solución Ecuación - Momento de inecia definición Figua - Sistema de estudio 3 Ecuación - Descomposición del momento de inecia3 Figua 3 - Cálculo del momento de
Cáteda de Física Índice Figua - Enunciado Solución Ecuación - Momento de inecia definición Figua - Sistema de estudio 3 Ecuación - Descomposición del momento de inecia3 Figua 3 - Cálculo del momento de
( ) CIRCUNFERENCIA UNIDAD VIII VIII.1 DEFINICIÓN DE CIRCUNFERENCIA
 CIRCUNRNCIA UNIA III III. INICIÓN CIRCUNRNCIA Una cicunfeencia se define como el luga geomético de los puntos P, que equidistan de un punto fijo en el plano llamado cento. La distancia que eiste de cualquiea
CIRCUNRNCIA UNIA III III. INICIÓN CIRCUNRNCIA Una cicunfeencia se define como el luga geomético de los puntos P, que equidistan de un punto fijo en el plano llamado cento. La distancia que eiste de cualquiea
Una nueva teoría electromagnetica I. Propiedades del electrón en reposo: masa, carga, spin y estabilidad.
 Una nueva teoía electomagnetica I. Popiedades del electón en eposo: masa, caga, spin y estabilidad. Manuel Henández Rosales. 18 de Junio de 215 Abstact En este atículo a pati de nuevas ecuaciones paa el
Una nueva teoía electomagnetica I. Popiedades del electón en eposo: masa, caga, spin y estabilidad. Manuel Henández Rosales. 18 de Junio de 215 Abstact En este atículo a pati de nuevas ecuaciones paa el
Sistemas de coordenadas
 Electicidad Magnetismo - Gpo. Cso / Tema : Intodcción Concepto de campo Repaso de álgeba vectoial Sistemas de coodenadas Catesiano Cvilíneas genealiadas: cilíndico esféico. Opeadoes vectoiales. Gadiente
Electicidad Magnetismo - Gpo. Cso / Tema : Intodcción Concepto de campo Repaso de álgeba vectoial Sistemas de coodenadas Catesiano Cvilíneas genealiadas: cilíndico esféico. Opeadoes vectoiales. Gadiente
Ejemplos 2. Cinemática de los Cuerpos Rígidos
 Ejemplos. Cinemática de los Cuepos Rígidos.1. Rotación alededo de un eje fijo.1.** El bloque ectangula ota alededo de la ecta definida po los puntos O con una velocidad angula de 6,76ad/s. Si la otación,
Ejemplos. Cinemática de los Cuepos Rígidos.1. Rotación alededo de un eje fijo.1.** El bloque ectangula ota alededo de la ecta definida po los puntos O con una velocidad angula de 6,76ad/s. Si la otación,
Prof. Nathaly Moreno Salas Ing. Víctor Trejo. Turbomáquinas Térmicas CT-3412
 7. OMPRESORES AXIALES Pof. Nathal Moeno Salas Ing. Vícto Tejo Tubomáquinas Témicas T-34 ompesoes Aiales ontenido Pemisas paa el estudio de un compeso aial Etapa de un compeso aial Tiángulo de velocidad
7. OMPRESORES AXIALES Pof. Nathal Moeno Salas Ing. Vícto Tejo Tubomáquinas Témicas T-34 ompesoes Aiales ontenido Pemisas paa el estudio de un compeso aial Etapa de un compeso aial Tiángulo de velocidad
Leyes de Kepler. Antes de demostrar las tres leyes de Kepler, haré un análisis matemático de lo que es una elipse.
 Leyes de Keple. Antes de demosta las tes leyes de Keple, haé un análisis matemático de lo que es una elipse. Una elipse (Fig.) es el luga geomético de un punto que se mueve en un plano de tal manea que
Leyes de Keple. Antes de demosta las tes leyes de Keple, haé un análisis matemático de lo que es una elipse. Una elipse (Fig.) es el luga geomético de un punto que se mueve en un plano de tal manea que
GRADO GRATUITAS. Matemáticas DESCARGAS GRATUITAS GRADO 11 MATEMÁTICAS
 DESCARGAS GRATUITAS GRADO Matemáticas DESCARGAS GRATUITAS GRADO MATEMÁTICAS RESPONDE LAS PREGUNTAS Las funciones tigonométicas de un ángulo en posición nomal están definidas así: Paa el cálculo de los
DESCARGAS GRATUITAS GRADO Matemáticas DESCARGAS GRATUITAS GRADO MATEMÁTICAS RESPONDE LAS PREGUNTAS Las funciones tigonométicas de un ángulo en posición nomal están definidas así: Paa el cálculo de los
Cálculo de integrales reales impropias mediante teoría de residuos
 Análisis III B - Tuno mañana - Integales impopias 1 Cálculo de integales eales impopias mediante teoía de esiduos Teoema 1. Sea f : C C tal que a) f es holomofa en Im(z) > salvo en un númeo finito de puntos
Análisis III B - Tuno mañana - Integales impopias 1 Cálculo de integales eales impopias mediante teoía de esiduos Teoema 1. Sea f : C C tal que a) f es holomofa en Im(z) > salvo en un númeo finito de puntos
FUERZA SOBRE UNA CARGA ELECTRICA DEBIDA A UN CAMPO MAGNETICO
 FUERZA SOBRE UNA CARGA ELECTRICA DEBIDA A UN CAMPO MAGNETICO Los campos magnéticos pueden genease po imanes pemanentes, imanes inducidos y po coientes elécticas. Ahoa inteesaá enconta la fueza sobe una
FUERZA SOBRE UNA CARGA ELECTRICA DEBIDA A UN CAMPO MAGNETICO Los campos magnéticos pueden genease po imanes pemanentes, imanes inducidos y po coientes elécticas. Ahoa inteesaá enconta la fueza sobe una
Elementos no-lineales en circuitos eléctricos y procesos iterativos
 Elementos no-lineales en cicuitos elécticos y pocesos iteatios Salado Acha Daza* Resumen Este documento tata sobe la solución iteatia equeida en poblemas donde se tienen elementos no-lineales en una ed
Elementos no-lineales en cicuitos elécticos y pocesos iteatios Salado Acha Daza* Resumen Este documento tata sobe la solución iteatia equeida en poblemas donde se tienen elementos no-lineales en una ed
Examen de Física-1, 1 Ingeniería Química Diciembre de 2010 Cuestiones (Un punto por cuestión).
 Examen de Física-, Ingenieía Química Diciembe de Cuestiones (Un punto po cuestión). Cuestión : Los vectoes (,, ), (,, 5) y (,, ), están aplicados en los puntos A (,, ), B (,, ) y C (,, ) espectivamente.
Examen de Física-, Ingenieía Química Diciembe de Cuestiones (Un punto po cuestión). Cuestión : Los vectoes (,, ), (,, 5) y (,, ), están aplicados en los puntos A (,, ), B (,, ) y C (,, ) espectivamente.
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES
 VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
VECTORES 7.1 LOS VECTORES Y SUS OPERACIONES DEFINICIÓN Un vecto es un segmento oientado. Un vecto AB queda deteminado po dos puntos, oigen A y extemo B. Elementos de un vecto: Módulo de un vecto es la
a) Estudiar su posición relativa en el espacio. b) Calcular las distancias entre ellas. c) Trazar una recta que corte perpendicularmente a ambas.
 º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
º-Halla a y b paa que las ectas siguientes sean paalelas: x+ay - z s 4x y +6 z a ; b- x+y +bz º-Dadas las ectas de ecuaciones x z - y - (x, y,z) (,0,)+ (,,-) a) Estudia su posición elativa en el espacio.
MOVIMIENTO DE LA PELOTA
 MOVIMIENTO DE LA PELOTA Un niño golpea una pelota de 5 gamos de manea que, sale despedida con una elocidad de 12 m/s desde una altua de 1 5 m sobe el suelo. Se pide : a) Fueza o fuezas que actúan sobe
MOVIMIENTO DE LA PELOTA Un niño golpea una pelota de 5 gamos de manea que, sale despedida con una elocidad de 12 m/s desde una altua de 1 5 m sobe el suelo. Se pide : a) Fueza o fuezas que actúan sobe
MANTENIMIENTO DE INVENTARIOS OPTIMIZACIÓN POR DIFERENCIACIÓN Autor: Germán Méndez Giraldo Universidad Distrital Francisco José de Caldas
 MANENIMIENO DE INVENARIOS OPIMIZACIÓN POR DIFERENCIACIÓN Auto: Gemán Méndez Gialdo Univesidad Distital Fancisco José de Caldas Como consulto administativo se le esta cuestionando paa que ecomiende sobe
MANENIMIENO DE INVENARIOS OPIMIZACIÓN POR DIFERENCIACIÓN Auto: Gemán Méndez Gialdo Univesidad Distital Fancisco José de Caldas Como consulto administativo se le esta cuestionando paa que ecomiende sobe
Laboratorio de Técnicas Experimentales II - 2º Física Laboratorio L1 - "Osciloscopio"
 Laboatoio de Técnicas Expeimentales II - º Física Laboatoio L - "Osciloscopio" Páctica L- - Estudio de un cicuito : estado de caga de un condensado y filtos de fecuencia - Inducción electomagnética Objetivo
Laboatoio de Técnicas Expeimentales II - º Física Laboatoio L - "Osciloscopio" Páctica L- - Estudio de un cicuito : estado de caga de un condensado y filtos de fecuencia - Inducción electomagnética Objetivo
2. CURVAS EN EL SISTEMA POLAR
 2. CURVAS EN EL SISTEMA POLAR Objetivo: El alumno obtendá ecuaciones en foma pola de cuvas en el plano y deteminaá las caacteísticas de éstas a pati de su ecuación en foma pola. Contenido: 2.1 Sistema
2. CURVAS EN EL SISTEMA POLAR Objetivo: El alumno obtendá ecuaciones en foma pola de cuvas en el plano y deteminaá las caacteísticas de éstas a pati de su ecuación en foma pola. Contenido: 2.1 Sistema
Física General 1 Proyecto PMME - Curso 2007 Instituto de Física Facultad de Ingeniería UdelaR
 Física Geneal Poyecto PMME - Cuso 007 Instituto de Física Facultad de Ingenieía UdelaR TITULO DINÁMICA DEL RÍGIDO. AUTORES Emiliano Gacía, Juan Manuel Galasso, Valeia Rey INTRODUCCIÓN El siguiente ejecicio,
Física Geneal Poyecto PMME - Cuso 007 Instituto de Física Facultad de Ingenieía UdelaR TITULO DINÁMICA DEL RÍGIDO. AUTORES Emiliano Gacía, Juan Manuel Galasso, Valeia Rey INTRODUCCIÓN El siguiente ejecicio,
DESARROLLO de Unidad VIII: Movimiento Potencial Bidimensional
 Depatamento de Aeonáutica : Mecánica de los Fluidos IA 7 DESARROLLO de Unidad VIII: Movimiento Potencial Bidimensional Poblema 6 : Una fuente bidimensional de intensidad q está ubicada en una esquina ectangula
Depatamento de Aeonáutica : Mecánica de los Fluidos IA 7 DESARROLLO de Unidad VIII: Movimiento Potencial Bidimensional Poblema 6 : Una fuente bidimensional de intensidad q está ubicada en una esquina ectangula
En relación con los problemas 12, 13 y 14 Partícula en una caja unidimensional de lado L: V=0 dentro de la caja e infinito en las paredes.
 En elación con los poblemas 1, 1 14 Patícula en una caja unidimensional de lado : V0 dento de la caja e infinito en las paedes. Una dimensión: HΨ( EΨ( paa siendo contono: p H m m m Ψ( 0 0 a solución es:
En elación con los poblemas 1, 1 14 Patícula en una caja unidimensional de lado : V0 dento de la caja e infinito en las paedes. Una dimensión: HΨ( EΨ( paa siendo contono: p H m m m Ψ( 0 0 a solución es:
A r. 1.5 Tipos de magnitudes
 1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
1.5 Tipos de magnitudes Ente las distintas popiedades medibles puede establecese una clasificación básica. Un gupo impotante de ellas quedan pefectamente deteminadas cuando se expesa su cantidad mediante
TALLER VERTICAL 3 DE MATEMÁTICA MASSUCCO ARRARAS - MARAÑON DI LEO Geometría lineal Recta y Plano
 LA LINEA RECTA: DEFINICIÓN. TALLER VERTICAL DE MATEMÁTICA Recibe el nombe de línea ecta el luga geomético de los puntos tales que, tomados dos puntos cualesquiea distintos P, ) P, ) el valo de la epesión:
LA LINEA RECTA: DEFINICIÓN. TALLER VERTICAL DE MATEMÁTICA Recibe el nombe de línea ecta el luga geomético de los puntos tales que, tomados dos puntos cualesquiea distintos P, ) P, ) el valo de la epesión:
MMII_L1_c3: Clasificación de las ecuaciones. Formas Canónicas
 MMII_L_c3: Clasificación de las ecaciones. Fomas Canónicas Gión: En esta clase nos basamos en la definición de las Cvas Caacteísticas CC de la anteio paa intodci la clasificación de las ecaciones el tipo
MMII_L_c3: Clasificación de las ecaciones. Fomas Canónicas Gión: En esta clase nos basamos en la definición de las Cvas Caacteísticas CC de la anteio paa intodci la clasificación de las ecaciones el tipo
6: PROBLEMAS METRICOS
 Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
Unidad 6: PROBLEMAS METRICOS 6.1.- DIRECCIONES DE RECTAS Y PLANOS Los poblemas afines tatan de incidencias (ve si un punto está contenido en una ecta o en un plano y ve si una ecta está contenida en un
ESTÁTICA. El Centro de Gravedad (CG) de un cuerpo es el punto donde se considera aplicado el peso.
 C U R S O: FÍSICA MENCIÓN MATERIAL: FM- 09 ESTÁTICA En esta unidad analizaemos el equilibio de un cuepo gande, que no puede considease como una patícula. Además, vamos a considea dicho cuepo como un cuepo
C U R S O: FÍSICA MENCIÓN MATERIAL: FM- 09 ESTÁTICA En esta unidad analizaemos el equilibio de un cuepo gande, que no puede considease como una patícula. Además, vamos a considea dicho cuepo como un cuepo
z Región III Región II Región I
 Capacito de placas ciculaes - solución completa amos a calcula el potencial electostático en todo el espacio paa un capacito de placas ciculaes y paalelas. Las placas conductoas están ubicadas en z = ±l/2,
Capacito de placas ciculaes - solución completa amos a calcula el potencial electostático en todo el espacio paa un capacito de placas ciculaes y paalelas. Las placas conductoas están ubicadas en z = ±l/2,
Lección 2. El campo de las cargas en reposo: campo electrostático.
 Lección 2. El campo de las cagas en eposo: campo electostático. 41. Sea el campo vectoial E = x x 2 + y u y 2 x + x 2 + y u 2 y. Puede tatase de un campo electostático? Cuánto vale el flujo de E a tavés
Lección 2. El campo de las cagas en eposo: campo electostático. 41. Sea el campo vectoial E = x x 2 + y u y 2 x + x 2 + y u 2 y. Puede tatase de un campo electostático? Cuánto vale el flujo de E a tavés
TEORÍA DE CAMPOS Y OPERADORES DIFERENCIALES. PROBLEMAS RESUELTOS
 TEORÍA DE CAMPOS Y OPERADORES DIFERENCIALES. PROBLEMAS RESUELTOS 1. Dado un campo vectoial v = ( x + y ) i + xy j + ϕ( x, y, k en donde ϕ es una función tal que sus deivadas paciales son las funciones
TEORÍA DE CAMPOS Y OPERADORES DIFERENCIALES. PROBLEMAS RESUELTOS 1. Dado un campo vectoial v = ( x + y ) i + xy j + ϕ( x, y, k en donde ϕ es una función tal que sus deivadas paciales son las funciones
Ejemplos Ley de Gauss, Fundamentos Físicos y Tecnológicos de la Informática, P. Gomez et al., pp
 Ejemplos Ley de Gauss, Fundamentos Físicos y Tecnológicos de la Infomática, P. Gomez et al., pp. 5-. Ejemplo 1º. Aplicando el teoema de Gauss halla el campo eléctico ceado po una distibución esféica de
Ejemplos Ley de Gauss, Fundamentos Físicos y Tecnológicos de la Infomática, P. Gomez et al., pp. 5-. Ejemplo 1º. Aplicando el teoema de Gauss halla el campo eléctico ceado po una distibución esféica de
v L G M m =m v2 r D M S r D
 Poblemas de Campo Gavitatoio 1 Calcula la velocidad media de la iea en su óbita alededo del ol y la de la luna en su óbita alededo de la iea, sabiendo que el adio medio de la óbita luna es 400 veces meno
Poblemas de Campo Gavitatoio 1 Calcula la velocidad media de la iea en su óbita alededo del ol y la de la luna en su óbita alededo de la iea, sabiendo que el adio medio de la óbita luna es 400 veces meno
4 ta OLIMPIADA CIENTIFICA ESTUDIANTIL PLURINACIONAL BOLIVIANA OLIMPIADA BOLIVIANA DE MATEMATICA ra Etapa (Examen Simultáneo) 1º SECUNDARIA
 OLIMPI OLIVIN E MTEMTI 0 a Etapa (Examen Simultáneo) º SEUNRI PELLIO PTERNO PELLIO MTERNO NOMRES TELÉFONO E ONTTO ISTRITO EUTIVO UNI EUTIV Fiscal Paticula onvenio PREGUNTS E OPION MULTIPLE (Enciee en un
OLIMPI OLIVIN E MTEMTI 0 a Etapa (Examen Simultáneo) º SEUNRI PELLIO PTERNO PELLIO MTERNO NOMRES TELÉFONO E ONTTO ISTRITO EUTIVO UNI EUTIV Fiscal Paticula onvenio PREGUNTS E OPION MULTIPLE (Enciee en un
4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO
 ANALISIS DE SISTEMAS EN TIEMPO CONTINUO Dinámica de Sistemas 4. 4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO 4..- Efecto de los polos en el comportamiento del sistema. 4..- Estabilidad. 4.3.- Análisis de
ANALISIS DE SISTEMAS EN TIEMPO CONTINUO Dinámica de Sistemas 4. 4.- ANALISIS DE SISTEMAS EN TIEMPO CONTINUO 4..- Efecto de los polos en el comportamiento del sistema. 4..- Estabilidad. 4.3.- Análisis de
CATALUÑA / SEPTIEMBRE 02. LOGSE / FÍSICA / EXAMEN COMPLETO
 CATALUÑA / SEPTIEMBRE 0. LOGSE / FÍSICA / EXAMEN COMPLETO Resuelva el poblema P1 y esponde a las cuestiones C1 y C Escoge una de las opciones (A o B) y esuelva el poblema P y esponda a las cuestiones C3
CATALUÑA / SEPTIEMBRE 0. LOGSE / FÍSICA / EXAMEN COMPLETO Resuelva el poblema P1 y esponde a las cuestiones C1 y C Escoge una de las opciones (A o B) y esuelva el poblema P y esponda a las cuestiones C3
TRANSICIONES DE FASE.
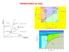 RANSCONES DE FASE. Qué podemos deci de estos diagamas (Diagamas de Fase)? Una misma sustancia (agua en este caso) puede pesentase en muchas fomas posible (Fases: Gas o vapo líquida o solida y esta a su
RANSCONES DE FASE. Qué podemos deci de estos diagamas (Diagamas de Fase)? Una misma sustancia (agua en este caso) puede pesentase en muchas fomas posible (Fases: Gas o vapo líquida o solida y esta a su
XIII.- TEOREMA DEL IMPULSO
 XIII.- TEOREMA DEL IMPULSO http://libos.edsauce.net/ XIII.1.- REACCIÓN DE UN FLUIDO EN MOVIMIENTO SOBRE UN CANAL GUÍA El cálculo de la fueza ejecida po un fluido en movimiento sobe el canal que foman los
XIII.- TEOREMA DEL IMPULSO http://libos.edsauce.net/ XIII.1.- REACCIÓN DE UN FLUIDO EN MOVIMIENTO SOBRE UN CANAL GUÍA El cálculo de la fueza ejecida po un fluido en movimiento sobe el canal que foman los
Fundamentos de Química Terma3 2
 Tema 3: Estuctua atómica (II): Estuctua electónica del átomo 3.1 Intoducción a la mecanica cuántica 3. Ecuación de Schödinge. 3.3 Modelo mecanocuántico del átomo 3.4 Átomos polielectónicos y configuación
Tema 3: Estuctua atómica (II): Estuctua electónica del átomo 3.1 Intoducción a la mecanica cuántica 3. Ecuación de Schödinge. 3.3 Modelo mecanocuántico del átomo 3.4 Átomos polielectónicos y configuación
PRÁCTICA 7. b) Elabore un archivo de Excel que calcule la cantidad que va a producir esta empresa (no es obligatorio).
 1.- Suponga una empesa que actúa como competitiva a pesa de que es la única empesa del secto. A coto plazo, tiene la siguiente función de costes totales (donde epesenta la cantidad de bien): 56 a) Si la
1.- Suponga una empesa que actúa como competitiva a pesa de que es la única empesa del secto. A coto plazo, tiene la siguiente función de costes totales (donde epesenta la cantidad de bien): 56 a) Si la
Semana 6. Razones trigonométricas. Semana Ángulos: Grados 7 y radianes. Empecemos! Qué sabes de...? El reto es...
 Semana Ángulos: Gados 7 adianes Razones tigonométicas Semana 6 Empecemos! Continuamos en el estudio de la tigonometía. Esta semana nos dedicaemos a conoce halla las azones tigonométicas: seno, coseno tangente,
Semana Ángulos: Gados 7 adianes Razones tigonométicas Semana 6 Empecemos! Continuamos en el estudio de la tigonometía. Esta semana nos dedicaemos a conoce halla las azones tigonométicas: seno, coseno tangente,
Facultad de Ciencias Curso Grado de Óptica y Optometría SOLUCIONES PROBLEMAS FÍSICA. TEMA 3: CAMPO ELÉCTRICO
 Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
Facultad de iencias uso - SOLUIOS ROLMAS FÍSIA. TMA : AMO LÉTRIO. n los puntos (; ) y (-; ) de un sistema de coodenadas donde las distancias se miden en cm, se sitúan dos cagas puntuales de valoes, y -,
Adaptación de impedancias
 .- El tansfomado ideal Adaptación de impedancias I +V +V TI Tansfomado ideal V elaciones V-I: V = I = a. I, válidas paa cualquie fecuencia. a Si se conecta una esistencia al secundaio, ente el nodo +V
.- El tansfomado ideal Adaptación de impedancias I +V +V TI Tansfomado ideal V elaciones V-I: V = I = a. I, válidas paa cualquie fecuencia. a Si se conecta una esistencia al secundaio, ente el nodo +V
Ondas y Rotaciones. Leyes de Newton. III. Jaime Feliciano Hernández Universidad Autónoma Metropolitana - Iztapalapa México, D. F. 15 de agosto de 2012
 Ondas y Rotaciones Leyes de Newton. III Jaime Feliciano Henández Univesidad Autónoma Metopolitana - Iztapalapa México, D. F. 15 de agosto de 2012 INTRODUCCIÓN. La pimea Ley de Newton explica qué le sucede
Ondas y Rotaciones Leyes de Newton. III Jaime Feliciano Henández Univesidad Autónoma Metopolitana - Iztapalapa México, D. F. 15 de agosto de 2012 INTRODUCCIÓN. La pimea Ley de Newton explica qué le sucede
TEMA I. Un espacio vectorial es una estructura algebraica que se compone de dos conjuntos y de dos operaciones que cumplen 8 propiedades.
 1 Espacios vectoiales 2 Combinaciones lineales 3 Dependencia e independencia lineal 4 Bases 5 Rango de un conjunto de vectoes 6 Tansfomaciones elementales 7 Método de Gauss TEMA I 1 Espacios vectoiales
1 Espacios vectoiales 2 Combinaciones lineales 3 Dependencia e independencia lineal 4 Bases 5 Rango de un conjunto de vectoes 6 Tansfomaciones elementales 7 Método de Gauss TEMA I 1 Espacios vectoiales
PAUTA CONTROL 3 CÁLCULO EN VARIAS VARIABLES, 2014/1
 PAUTA CONTROL CÁLCULO EN VARIAS VARIABLES, 14/1 (1) (a) Demueste que el máximo de la función x y z sobe la esfea x + y + z = a es (a /) y que el mínimo de la función x + y + z sobe la supeficie x y z =
PAUTA CONTROL CÁLCULO EN VARIAS VARIABLES, 14/1 (1) (a) Demueste que el máximo de la función x y z sobe la esfea x + y + z = a es (a /) y que el mínimo de la función x + y + z sobe la supeficie x y z =
El método del lugar de las raíces.
 El método del lugar de las raíces. Las características de un sistema de lazo cerrado son determinadas por los polos de lazo cerrado. Los polos de lazo cerrado son las raíces de la ecuación característica.
El método del lugar de las raíces. Las características de un sistema de lazo cerrado son determinadas por los polos de lazo cerrado. Los polos de lazo cerrado son las raíces de la ecuación característica.
TRIGONOMETRÍA IDENTIDADES TRIGONOMÉTRICAS página 39
 TRIGONOMETRÍA IDENTIDADES TRIGONOMÉTRICAS página 39 página 40 INSTITUTO VALLADOLID PREPARATORIA SEGUNDO SEMESTRE 3 IDENTIDADES TRIGONOMÉTRICAS 3. FÓRMULAS FUNDAMENTALES La base del estudio de este inciso
TRIGONOMETRÍA IDENTIDADES TRIGONOMÉTRICAS página 39 página 40 INSTITUTO VALLADOLID PREPARATORIA SEGUNDO SEMESTRE 3 IDENTIDADES TRIGONOMÉTRICAS 3. FÓRMULAS FUNDAMENTALES La base del estudio de este inciso
