EL PROBLEMA DE APOLONIO 1
|
|
|
- Sara Pérez Hidalgo
- hace 9 años
- Vistas:
Transcripción
1 EL PROBLEMA DE APOLONIO 1 Benjamín R. Sarmiento Lugo 2 Universidad Pedagógica Nacional Profesor de Planta Bogotá Colombia [email protected] RESUMEN El objetivo de este cursillo es reconstruir el problema planteado por Apolonio de Perga en su tratado sobre tangencias, el cual es uno de los problemas más famosos de la geometría euclidiana por cuanto da lugar a diez problemas sobre tangencias. Se usará el software de geometría dinámica Regla y Compás para hacer las construcciones y se abordarán los diferentes casos que se pueden presentar en cada uno de los nueve primeros problemas que resolvió Apolonio. El décimo problema de Apolonio, muy relacionado con los centros de Soddy y del que se cree que fue resuelto por primera vez por Newton, no se presentará en este cursillo. INTRODUCCIÓN El problema de Apolonio (Apolonio de Perga, a.c.), se plantea en el tratado sobre tangencias y se enuncia de la siguiente forma: Dados tres objetos, cada uno de los cuales puede ser punto, recta o circunferencia, construir una circunferencia que sea tangente a los tres objetos dados. (o que los contenga en el caso de los puntos) Al hacer las combinaciones de tres objetos, puntos, rectas o circunferencias, resultan los casos siguientes: 1. Tres puntos 2. Tres rectas 3. Dos puntos y una recta 4. Dos rectas y un punto 5. Dos puntos y una circunferencia 6. Dos circunferencias y un punto 7. Dos rectas y una circunferencia 8. Dos circunferencias y una recta 9. Un punto, una recta y una circunferencia 10. Tres circunferencias Los dos primeros casos aparecen en el Libro IV de los Elementos de Euclides; los casos 3, 4, 5, 6, 8 y 9 están en el Libro I de la obra Tangencias (o Contactos) de Apolonio, y los casos 7 y 10 se encuentran en el Libro II de la misma obra. 1 Cursillo presentado en el Encuentro de Geometría y Aritmética Licenciado en Matemáticas Magíster en Educación Matemática Universidad Pedagógica Nacional 1
2 PROBLEMA 1: Dados tres puntos no colineales, construir una circunferencia que los contenga. Pasos para la construcción: 1) Trazar los segmentos AB y BC. 2) Trazar las mediatrices de los segmentos AB y BC. (M1 y M2) 3) Señalar la intersección de las mediatrices M1 y M2. (Circuncentro P) 4) Dibujar la circunferencia de centro P y radio PA. Figura 1 PROBLEMA 2: Dadas tres rectas, construir una circunferencia que sea tangente a las tres rectas. Caso 1: Si dos de las rectas son paralelas. 1) Sean R1 y R2 las rectas paralelas, y T1 la recta transversal. 2) Trazar la recta media paralela a R1 y R2. (Ya que los centros de las circunferencias tangentes estarán en esta recta) 3) Trazar la bisectriz del ángulo formado por R1 y T1. (Ya que en la bisectriz estará el centro de una de las circunferencias tangentes). 4) Trazar la bisectriz del ángulo formado por R2 y T1. (Ya que en la bisectriz estará el centro de una de las circunferencias tangentes) 5) Señalar la intersección de R1 y T1, y la intersección de R2 y T1. (Puntos P y Q) 6) Trazar segmentos que pasen por P y Q perpendiculares respectivamente a R1. (Aquí se determinan los radios de las circunferencias) 2
3 7) Trazar las circunferencias con centros en P y Q, respectivamente. Figura 2. Caso 2: Si las tres rectas se cortan entre sí. Figura 3. PROBLEMA 3: Dados dos puntos y una recta, construir una circunferencia tangente a la recta y que contenga a los dos puntos. Caso 1: Si los dos puntos dados A y B están en una recta paralela a la recta L dada. 1) Se construye un punto C sobre la recta L. 2) Se traza la mediatriz del segmento AB 3
4 3) C es la intersección de la mediatriz y la recta dada. 4) Se construye la circunferencia que contiene a los puntos A, B y C. Figura 4. Figura 5. Caso 2: Si los puntos A y B no están en una recta paralela a la recta L. 1) Trazamos la recta AB. 2) Hallamos la intersección de AB y la recta L. (El punto de intersección es M). 3) Trazar la circunferencia C1 de diámetro AB. Figura 6. Figura 7. 4) Desde M trazar una tangente a la circunferencia C1. 5) Marcar el punto de tangencia T. 6) Trazar circunferencia con centro M y radio MT. 7) Hallar intersecciones entre la recta L y la circunferencia C2. (P y Q) 8) Construir las circunferencias que pasan por A,B,P y A,B,Q. 4
5 Figura 8. Figura 9. Caso 3: Cuando uno de los puntos está sobre la recta L. 1) Trazar el segmento AB. 2) Trazar la mediatriz del segmento AB. 3) Trazar perpendicular a la recta L, que pase por B. 4) Hallar intersección de la mediatriz y la perpendicular a L. ( Punto C ) 5) Trazar circunferencia con centro C y radio BC: Figura 10. Caso 4: Cuando los puntos están sobre una recta perpendicular a la recta L. 1. Trazar la recta AB. 2. Señalar la intersección de las recta L y AB. (punto P). 5
6 3. Hallar el punto medio M1 entre los puntos A y B. (La distancia PM1 es el radio de la circunferencia buscada). 4. Trazar la perpendicular a la recta AB que pase por M1. (Sobre esta perpendicular estará el centro de la circunferencia buscada). 5. Trazar la circunferencia con centro Ay radio PM1. 6. Marcar la intersección entre la perpendicular 1 y la circunferencia C A. (punto C, será el centro de la circunferencia buscada. 7. Trazar circunferencia con centro C y radio CA. Figura 11. PROBLEMA 4: Dadas dos rectas y un punto, construir una circunferencia que sea tangente a las dos rectas y que contenga al punto. Caso 1: Si las rectas se cortan y el punto queda comprendido entre ellas. 1) Trazar la bisectriz del ángulo formado por las rectas L y M. 2) Hallar simétrico del punto A respecto a la bisectriz. (Simétrico de A es B) 3) Realizar la construcción del problema 3: (P P R). 6
7 Figura 12. Figura 13. Caso 2: Si el punto dado A pertenece a una de las rectas dadas. 1) Trazar perpendicular P a la recta L por el punto A. 2) Trazar las bisectrices de los ángulos determinados por las dos rectas. 3) Hallar intersecciones entre la perpendicular y las bisectrices. ( P y Q ) 4) P y Q son los centros de las circunferencias buscadas. 7
8 Figura 14. Figura 15. Caso 3: El punto A está comprendido entre dos rectas que son paralelas. 1) Trazar circunferencia con centro A y diámetro igual a distancia entre las rectas. 2) Trazar la paralela media M. 3) Hallar intersecciones entre la circunferencia y la paralela media. ( P y Q ). 4) P y Q son los centros de las circunferencias buscadas y los radio son AP y AQ. Si el punto B está en una de las dos rectas dadas, la construcción se reduce a encontrar el centro, que es la intersección entre la media paralela y la recta que pasa por B y es perpendicular a la media paralela. 8
9 Figura 16. PROBLEMA 5: Dados dos puntos y una circunferencia, construir una circunferencia que contenga a los dos puntos y sea tangente a la circunferencia dada. Caso 1: Si los puntos A y B son exteriores a la circunferencia dada. 1) Trazar la mediatriz del segmento AB y la recta AB. 2) Construir circunferencia que pase por A y B, que corte a la circunferencia C. 3) Trazar eje radical de las circunferencias. 4) Hallar intersección entre eje radical y la recta AB. (Punto M) 5) Desde M, trazar tangentes a la circunferencia C. 6) Marcar los puntos de tangencia P y Q. 7) Trazar las circunferencias que pasan por A,B,P y A,B,Q. (Centros C1 y C2) Figura 17. 9
10 Caso 2: Si los puntos A y B son interiores a la circunferencia dada. La construcción es similar a la anterior: 1) Trazar la mediatriz del segmento AB y la recta AB. 2) Construir circunferencia que pase por A y B, que corte a la circunferencia C. 3) Trazar eje radical de las circunferencias. 4) Hallar intersección entre eje radical y la recta AB. (Punto M) 5) Desde M, trazar tangentes a la circunferencia C. 6) Marcar los puntos de tangencia P y Q. 7) Trazar las circunferencias que pasan por A,B,P y A,B,Q. (Centros C1 y C2) Figura 18. Caso 3: Si uno de los puntos (A) está sobre la circunferencia dada y el otro punto (B) es exterior (o interior) a la circunferencia C. 1) Trazar la recta AC. 2) Trazar el segmento AB. 3) Trazar la mediatriz del segmento AB. 4) Hallar intersección de la AC y la mediatriz de AB (punto C1, que será el centro de la circunferencia pedida. 5) Construir la circunferencia de centro C1 radio AC1. 10
11 Figura 19. Figura 20. PROBLEMA 6: Dadas dos circunferencias y un punto, construir una circunferencia que contenga al punto y que sea tangente a las dos circunferencias dadas. Caso 1: Cuando el punto P es exterior a ambas circunferencias. 1) Hallar los centros de homotecia directo e inverso. (directo H, inverso K) 2) Trazar el segmento C 1 C 2 (Que uno los centros de las circunferencias dadas) 3) Hallar las intersecciones del segmento C 1 C 2 con las circunferencias dadas. 4) Trazar la circunferencia que pasa por los puntos A, B y P. 5) Trazar el segmento PH. (Une el punto P con el centro de homotecia H). 6) Hallar la intersección entre el segmento PH y la circunferencia ABP. (punto M). 7) Ocultar las rectas tangentes, el segmento C1C2, los puntos A, B, H y K. 8) Para desarrollar el paso (9), seguir el problema 5 (P-P-C). 9) Construir la circunferencia que pasa por P y M, tangente a la circunferencia C 1. (Resultan dos circunferencias rojas que son las circunferencias pedidas). 10) Se pueden obtener dos circunferencias más, repitiendo los pasos anteriores para el centro de homotecia inverso K. 11
12 Figura 21. Figura 22. Figura
13 Caso 2: Cuando el punto P pertenece a una de las circunferencias (C2). 1) Hallar los centros de homotecia directo e inverso. (directo H, inverso K) 2) Trazar la recta PH. (del punto P al centro de homotecia H). 3) Hallar la intersección de la recta PH con la circunferencia C 1 (punto Q). 4) P y Q son los puntos de tangencia para una de las circunferencias buscadas. 5) Trazar las semirrectas C 1 Q y C 2 P. 6) Hallar la intersección entre las rectas C 1 Q y C 2 P. (punto T 1, este es el centro de una de las circunferencias buscadas). 7) Trazar la circunferencia de centro T 1 y radio T 1 P. (circunferencia roja). 8) Ahora, trazar la recta PK. (del punto P al centro de homotecia inverso K). 9) Hallar la intersección entre la recta PK y la circunferencia C 1. (punto R) 10) P y R son los puntos de tangencia para otra de las circunferencias buscadas. 11) Trazar las semirrectas C 1 R y C 2 P. 12) Hallar la intersección entre las rectas C 1 R y C 2 P. (punto T 2, este es el centro de otra de las circunferencias buscadas). 13) Trazar la circunferencia de centro T 2 y radio T 2 P. (circunferencia roja). Figura 24. PROBLEMA 7: Dadas dos rectas y una circunferencia, construir una circunferencia que sea tangente a las rectas y a la circunferencia dada. 13
14 Caso 1: Cuando las rectas son paralelas y la circunferencia es tangente a las dos rectas. Figura 25. Caso 2: Cuando la circunferencia está comprendida entre dos rectas L y M. 1) Determinar el radio de la circunferencia dada O. 2) Trazar paralelas a cada lado de la recta L, a una distancia igual al radio de la circunferencia O. (Rectas L 1 y L 2 ). 3) Trazar la bisectriz del ángulo formado por las rectas L y M. 4) Hallar el simétrico del centro O respecto a la bisectriz. (punto O ) 5) Trazar la recta OO. 6) Señalar la intersección entre la recta OO y la recta paralela L 1. (punto M). 7) Desde M, trazar tangentes a la circunferencia de diámetro OO. Marcar los puntos de tangencia D y E. 8) Trazar la circunferencia con centro en M y radio MD. 9) Hallar las intersecciones de la paralela L 1 con la circunferencia C M de centro M. (puntos A y B). 10) Trazar perpendiculares a la paralela L 1 por los puntos A y B. 11) Hallar las intersecciones de las perpendiculares halladas con la bisectriz. (puntos P y Q). 12) Los puntos P y Q son los centros de las circunferencias buscadas. Trazar circunferencias con centros en P y Q tangentes a las rectas L y M. 14
15 13) Si se siguen estos pasos para la recta paralela L 2, se obtienen otras dos circunferencias. Figura
EL PROBLEMA DE APOLONIO
 EL PROBLEMA DE APOLONIO Benjamín Sarmiento Lugo Profesor Universidad Pedagógica Nacional Bogotá D.C, Colombia [email protected] Resumen El objetivo de este cursillo es presentar uno de los problemas
EL PROBLEMA DE APOLONIO Benjamín Sarmiento Lugo Profesor Universidad Pedagógica Nacional Bogotá D.C, Colombia [email protected] Resumen El objetivo de este cursillo es presentar uno de los problemas
Tangencias usando potencia y eje radical IES BELLAVISTA
 Tangencias usando potencia y eje radical IES BELLAVISTA Potencia Se define la potencia de un punto con respecto a una circunferencia como el producto de los segmentos comprendidos entre dicho punto y la
Tangencias usando potencia y eje radical IES BELLAVISTA Potencia Se define la potencia de un punto con respecto a una circunferencia como el producto de los segmentos comprendidos entre dicho punto y la
EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 2: TANGENCIAS EN LAS CIRCUNFERENCIAS
 EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 2: TANGENCIAS EN LAS CIRCUNFERENCIAS 1. TANGENCIAS EN LAS CIRCUNFERENCIAS Decimos que dos elementos geométricos son tangentes cuando tienen un punto en común. Las tangencias
EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 2: TANGENCIAS EN LAS CIRCUNFERENCIAS 1. TANGENCIAS EN LAS CIRCUNFERENCIAS Decimos que dos elementos geométricos son tangentes cuando tienen un punto en común. Las tangencias
GEOMETRÍA TANGENCIAS - 1
 GEOMETRÍA TANGENCIAS - 1 TANGENCIAS BÁSICAS Recordemos que dos líneas se dice que son tangentes cuando tienen un solo punto común sin cortarse. Para resolver cualquier problema de tangencias de rectas
GEOMETRÍA TANGENCIAS - 1 TANGENCIAS BÁSICAS Recordemos que dos líneas se dice que son tangentes cuando tienen un solo punto común sin cortarse. Para resolver cualquier problema de tangencias de rectas
1. Lugar geométrico de los centros de las circunferencias que pasen por un punto fijo
 Unidad 1. Dibujo Geométrico 1. Lugar geométrico de los centros de las circunferencias que pasen por un punto fijo 2. Circunferencia que pasa por dos o tres puntos 1.5. Circunferencia que pasa por dos puntos
Unidad 1. Dibujo Geométrico 1. Lugar geométrico de los centros de las circunferencias que pasen por un punto fijo 2. Circunferencia que pasa por dos o tres puntos 1.5. Circunferencia que pasa por dos puntos
8. UNIDAD DIDACTICA 8: TANGENCIAS Y ENLACES
 8. UNIDAD DIDACTICA 8: TANGENCIAS Y ENLACES 8.1. TANGENCIAS Se dice que dos figuras planas son tangentes cuando tienen un solo punto en común, al que se conoce como punto de tangencia. Las tangencias pueden
8. UNIDAD DIDACTICA 8: TANGENCIAS Y ENLACES 8.1. TANGENCIAS Se dice que dos figuras planas son tangentes cuando tienen un solo punto en común, al que se conoce como punto de tangencia. Las tangencias pueden
GEOMETRÍA TANGENCIAS - 1
 GEOMETRÍA TANGENCIAS - 1 TANGENCIAS BÁSICAS Recordemos que dos líneas se dice que son tangentes cuando tienen un solo punto común sin cortarse. Para resolver cualquier problema de tangencias de rectas
GEOMETRÍA TANGENCIAS - 1 TANGENCIAS BÁSICAS Recordemos que dos líneas se dice que son tangentes cuando tienen un solo punto común sin cortarse. Para resolver cualquier problema de tangencias de rectas
TANGENCIAS. En general, las tangencias tienen por objeto unir circunferencias y rectas mediante otras circunferencias y
 Apuntes TANGENCIAS. Problemas de tangencias: rectas tangentes a circunferencias y circunferencias entre sí, conociendo el radio. Aplicación del eje y centro radical en problemas de tangencias: recta y
Apuntes TANGENCIAS. Problemas de tangencias: rectas tangentes a circunferencias y circunferencias entre sí, conociendo el radio. Aplicación del eje y centro radical en problemas de tangencias: recta y
11. ALGUNOS PROBLEMAS CON TRIÁNGULOS
 11. ALGUNOS PROBLEMAS CON TRIÁNGULOS Estos problemas son ejemplos de aplicación de las propiedades estudiadas. 11.1. Determinar la posición de un topógrafo que tiene tres vértices geodésicos A,B,C, si
11. ALGUNOS PROBLEMAS CON TRIÁNGULOS Estos problemas son ejemplos de aplicación de las propiedades estudiadas. 11.1. Determinar la posición de un topógrafo que tiene tres vértices geodésicos A,B,C, si
18. TANGENCIAS Características generales Rectas tangentes a una circunferencia desde un punto exterior.
 18. TANGENCIAS 18.1. Características generales. Tangencia entre recta y circunferencia: una recta t es tangente a una circunferencia de centro O en un punto T cuando es perpendicular en T al radio OT.
18. TANGENCIAS 18.1. Características generales. Tangencia entre recta y circunferencia: una recta t es tangente a una circunferencia de centro O en un punto T cuando es perpendicular en T al radio OT.
Tangencias IES BELLAVISTA
 Tangencias IES BELLAVISTA Posiciones relativas entre recta y circunferencia Posiciones relativas entre dos circunferencias Consideraciones sobre tangencias Si dos circunferencias son tangentes, el punto
Tangencias IES BELLAVISTA Posiciones relativas entre recta y circunferencia Posiciones relativas entre dos circunferencias Consideraciones sobre tangencias Si dos circunferencias son tangentes, el punto
Geometría Moderna II
 Ma. Guadalupe Lucio Gómez Maqueo Facultad de Ciencias, UNAM Geometría Moderna II Estas notas se desarrollaron para cubrir los temas del programa de Geometría Moderna II que se imparte en la Facultad de
Ma. Guadalupe Lucio Gómez Maqueo Facultad de Ciencias, UNAM Geometría Moderna II Estas notas se desarrollaron para cubrir los temas del programa de Geometría Moderna II que se imparte en la Facultad de
Una recta y una circunferencia, o dos circunferencias, son exteriores si no tienen ningún punto común, y secantes si tienen dos puntos comunes.
 Geometría plana B19 Tangencias Tangencias y enlaces Conceptos básicos Una recta y una circunferencia, o dos circunferencias, son tangentes entre sí, si tienen un único punto común, llamado punto de tangencia.
Geometría plana B19 Tangencias Tangencias y enlaces Conceptos básicos Una recta y una circunferencia, o dos circunferencias, son tangentes entre sí, si tienen un único punto común, llamado punto de tangencia.
NOMBRE Y APELLIDOS : 1.- Hallar el ejer radical de las circunferencia c1 y c2 en los tres casos siguientes.
 NMBRE Y AELLIDS : 1.- Hallar el ejer radical de las circunferencia c1 y c2 en los tres casos siguientes. 1 2 c2 c1 1 2 c1 1 2 c2 c1 c2 2.- Hallar el centro radical de las circunferencias c1, c2 y c3 en
NMBRE Y AELLIDS : 1.- Hallar el ejer radical de las circunferencia c1 y c2 en los tres casos siguientes. 1 2 c2 c1 1 2 c1 1 2 c2 c1 c2 2.- Hallar el centro radical de las circunferencias c1, c2 y c3 en
3 reglas básicas que se cumplen SIEMPRE
 3 reglas básicas que se cumplen SIEMPRE 1.En todo ejercicio de Tangencias deberás indicar SIEMPRE indicar el Punto de Tangencia y el Centro de las Circunferencias tangentes. Un ejercicio de tangencias
3 reglas básicas que se cumplen SIEMPRE 1.En todo ejercicio de Tangencias deberás indicar SIEMPRE indicar el Punto de Tangencia y el Centro de las Circunferencias tangentes. Un ejercicio de tangencias
ECUACIÓN DE LA RECTA. 6. Hallar la ecuación de la recta que pase por el punto A ( 1, 2) y que determina en el eje X un segmento de longitud 6.
 ECUACIÓN DE LA RECTA 1. El ángulo de inclinación de una recta mide 53º y pasa por los puntos ( 3, n) y ( 5, 4). Hallar el valor de n. A) 1 /5 B) 8 /5 C) 1 /5 D) 8 /5 E) 7 /3. Qué tipo de triángulo es el
ECUACIÓN DE LA RECTA 1. El ángulo de inclinación de una recta mide 53º y pasa por los puntos ( 3, n) y ( 5, 4). Hallar el valor de n. A) 1 /5 B) 8 /5 C) 1 /5 D) 8 /5 E) 7 /3. Qué tipo de triángulo es el
B5 Lugares geométricos
 Geometría plana B5 Lugares geométricos Lugar geométrico Se llama así a la figura que forman todos los puntos que tienen una misma propiedad. Los lugares geométricos pueden ser del plano o del espacio,
Geometría plana B5 Lugares geométricos Lugar geométrico Se llama así a la figura que forman todos los puntos que tienen una misma propiedad. Los lugares geométricos pueden ser del plano o del espacio,
CURVAS CÓNICAS-TANGENCIAS:
 CURVAS CÓNICAS-TANGENCIAS: ELIPSE Recta tangente por un punto de la elipse 1.Se hallan los focos. 2.Se traza la Circunferencia focal correspondiente a uno de los focos.(f2) 3.Averiguar el simétrico de
CURVAS CÓNICAS-TANGENCIAS: ELIPSE Recta tangente por un punto de la elipse 1.Se hallan los focos. 2.Se traza la Circunferencia focal correspondiente a uno de los focos.(f2) 3.Averiguar el simétrico de
TEMA 5. CURVAS CÓNICAS.
 5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
5.1. GENERALIDADES. TEMA 5. CURVAS CÓNICAS. Se denominan secciones cónicas a aquellas superficies que son producidas por la intersección de un plano con una superficie cónica de revolución (una superficie
UNIDAD 6. CIRCUNFERENCIA
 UNIDAD 6. CIRCUNFERENCIA DEFINICIONES CIRCUNFERENCIA: Dados un plano, un punto O en dicho plano y un número real positivo r, (r > 0), se llama Circunferencia de centro O y radio r, C(O; r), al conjunto
UNIDAD 6. CIRCUNFERENCIA DEFINICIONES CIRCUNFERENCIA: Dados un plano, un punto O en dicho plano y un número real positivo r, (r > 0), se llama Circunferencia de centro O y radio r, C(O; r), al conjunto
B23 Curvas cónicas Curvas cónicas
 Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
Geometría plana B23 Curvas cónicas Curvas cónicas Superficie cónica de revolución es la engendrada por una recta que gira alrededor de otra a la que corta. Curvas cónicas son las que resultan de la intersección
22 CURVAS CÓNICAS- HIPÉRBOLAS
 22 CURVAS CÓNICAS- HIPÉRBOLAS 22.1 Características generales. La hipérbola se obtiene al cortar la superficie cónica por un plano paralelo al eje que corta las dos hojas de la cónica. 22.2 Focos y directrices.
22 CURVAS CÓNICAS- HIPÉRBOLAS 22.1 Características generales. La hipérbola se obtiene al cortar la superficie cónica por un plano paralelo al eje que corta las dos hojas de la cónica. 22.2 Focos y directrices.
21.3. Rectas tangentes exteriores a dos circunferencias.
 21. TANGENCIAS 21.1. Características generales. Tangencia entre recta y circunferencia: una recta t es tangente a una circunferencia de centro O en un punto T cuando es perpendicular en T al radio OT.
21. TANGENCIAS 21.1. Características generales. Tangencia entre recta y circunferencia: una recta t es tangente a una circunferencia de centro O en un punto T cuando es perpendicular en T al radio OT.
CONSTRUCCIONES Y LUGARES GEOMÉTRICOS. Matemáticas 1º Educación Secundaria Obligatoria
 CONSTRUCCIONES Y LUGARES GEOMÉTRICOS Matemáticas 1º Educación Secundaria Obligatoria Consideraciones metodológicas Los conceptos de mediatriz y bisectriz permitirán introducir el concepto de lugar geométrico
CONSTRUCCIONES Y LUGARES GEOMÉTRICOS Matemáticas 1º Educación Secundaria Obligatoria Consideraciones metodológicas Los conceptos de mediatriz y bisectriz permitirán introducir el concepto de lugar geométrico
Cabri-geométrico en un problema de Apolonio
 Cabri-geométrico en un problema de Apolonio Juana Contreras S. Instituto de Matemática y Física Universidad de Talca El clásico problema atribuido al gran geómetra Apolonio de Perga (siglo III A.C.), conocido
Cabri-geométrico en un problema de Apolonio Juana Contreras S. Instituto de Matemática y Física Universidad de Talca El clásico problema atribuido al gran geómetra Apolonio de Perga (siglo III A.C.), conocido
LA GEOMETRÍA PLANA. Llanos: Si su medida es de 180º. Agudos: Si su medida esta comprendida entre 0 y 90. Rectos: si su medida es 90
 LA GEOMETRÍA PLANA La geometría plana trata de aquellos elementos que solo tienen dos dimensiones y, que por lo tanto, se encuentran y operan en un plano. Los elementos básicos con los que se suele trabajar
LA GEOMETRÍA PLANA La geometría plana trata de aquellos elementos que solo tienen dos dimensiones y, que por lo tanto, se encuentran y operan en un plano. Los elementos básicos con los que se suele trabajar
2º BACH TANGENCIAS ANA BALLESTER JIMÉNEZ
 2º BACH TANGENCIAS ANA BALLESTER JIMÉNEZ TANGENCIAS Propiedades: Si dos circunferencias son tangentes, el punto de tangencia se encuentra en la recta que une los centros (fig.1) Si una recta es tangente
2º BACH TANGENCIAS ANA BALLESTER JIMÉNEZ TANGENCIAS Propiedades: Si dos circunferencias son tangentes, el punto de tangencia se encuentra en la recta que une los centros (fig.1) Si una recta es tangente
TEMA 4. TRANSFORMACIONES EN EL PLANO
 TEMA 4. TRANSFORMACIONES EN EL PLANO HERRAMIENTAS PARA TRANSFORMACIONES En este bloque encontramos las siguientes herramientas: Simetría axial La herramienta Refleja objeto en recta dibuja la figura simétrica
TEMA 4. TRANSFORMACIONES EN EL PLANO HERRAMIENTAS PARA TRANSFORMACIONES En este bloque encontramos las siguientes herramientas: Simetría axial La herramienta Refleja objeto en recta dibuja la figura simétrica
MATHEMATICA. Geometría - Recta. Ricardo Villafaña Figueroa. Material realizado con Mathematica. Ricardo Villafaña Figueroa
 MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
MATHEMATICA Geometría - Recta Material realizado con Mathematica 2 Contenido Sistema de Coordenadas... 3 Distancia entre dos puntos... 3 Punto Medio... 5 La Recta... 8 Definición de recta... 8 Pendiente
1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a la recta x + 7y + 1 = 0
 Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Universidad Técnica Federico Santa María Departamento de Matemática Campus Santiago Geometría Analítica 1. Determine el valor de la constante k para que la recta kx + (3 k)y + 7 = 0 sea perpendicular a
Circunferencias. d) A( 1, 5) y d = X = (x, y) punto genérico del lugar geométrico. b) dist (X, A) = d
 Circunferencias 6 Halla, en cada caso, el lugar geométrico de los puntos del plano cuya distancia al punto A es d. a) A(, ) y d = b) A(, ) y d = 1 c) A(, ) y d = 1 d) A( 1, ) y d = X = (x, y) punto genérico
Circunferencias 6 Halla, en cada caso, el lugar geométrico de los puntos del plano cuya distancia al punto A es d. a) A(, ) y d = b) A(, ) y d = 1 c) A(, ) y d = 1 d) A( 1, ) y d = X = (x, y) punto genérico
2.-GEOMETRÍA PLANA O EUCLIDIANA
 2.-GEOMETRÍA PLANA O EUCLIDIANA 2.2.-Cuadriláteros. Definición, clasificación y notación. Clasificación de los cuadriláteros: Paralelogramos y no paralelogramos. Los cuadriláteros son los polígonos de
2.-GEOMETRÍA PLANA O EUCLIDIANA 2.2.-Cuadriláteros. Definición, clasificación y notación. Clasificación de los cuadriláteros: Paralelogramos y no paralelogramos. Los cuadriláteros son los polígonos de
Academia de Matemáticas T.M Geometría Analítica Página 1
 INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
INSTITUTO POLITECNICO NACIONAL CENTRO DE ESTUDIOS CIENTIFICOS Y TECNOLOGICOS 10. CARLOS VALLEJO MÁRQUEZ PROBLEMARIO DE GEOMETRIA ANALITICA Distancia entre puntos 1.- Determina la distancia entre los puntos
Tema 6 Tangencias, Enlaces y Polaridad
 Tema 6 Tangencias, Enlaces y Polaridad En este tema revisaremos la unión de curvas y líneas mediante tangencias, además de introducir el concepto de polaridad. Las tangencias es un campo extensísimo, del
Tema 6 Tangencias, Enlaces y Polaridad En este tema revisaremos la unión de curvas y líneas mediante tangencias, además de introducir el concepto de polaridad. Las tangencias es un campo extensísimo, del
ESTUDIO GRÁFICO DE LA ELIPSE.
 Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Curvas Cónicas para Dibujo y Matemáticas. Aplicación web Dibujo Técnico para ESO y Bachillerato Matemáticas para Bachillerato Educación Plástica y Visual Autor: José Antonio Cuadrado Vicente. ESTUDIO GRÁFICO
Se llama potencia de inversión a la constante k² y circunferencia fundamental de inversión a la de centro O y radio k.
 Geometría plana B18 Inversión Inversión gráfica Considerando un punto fijo O en un plano, llamado centro o polo de inversión y una constante k², se llama inversión a una correspondencia en la que a cada
Geometría plana B18 Inversión Inversión gráfica Considerando un punto fijo O en un plano, llamado centro o polo de inversión y una constante k², se llama inversión a una correspondencia en la que a cada
Dibujo Técnico Curvas cónicas-parábola
 22. CURVAS CÓNICAS-PARÁBOLAS 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar
22. CURVAS CÓNICAS-PARÁBOLAS 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar
ACTIVIDADES PROPUESTAS
 GEOMETRÍA DINÁMICA ACTIVIDADES PROPUESTAS 1. Dibujar un pentágono y trazar sus diagonales. 2. A partir de una circunferencia c y de un punto exterior A, trazar la circunferencia que tiene centro en el
GEOMETRÍA DINÁMICA ACTIVIDADES PROPUESTAS 1. Dibujar un pentágono y trazar sus diagonales. 2. A partir de una circunferencia c y de un punto exterior A, trazar la circunferencia que tiene centro en el
NIVEL : 1er. AÑO PROF. L. ALTIMIRAS R. CARRERA : GEOGRAFÍA AYUD. C. ESCOBEDO C. AÑO : 2009 GEOMETRÍA ANALÍTICA
 UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
UNIVERSIDAD DE CHILE FACULTAD DE ARQUITECTURA Y URBANISMO ESCUELA DE GEOGRAFÍA DEPARTAMENTO DE CIENCIAS DE LA CONSTRUCCIÓN ASIGNATURA : MATEMATICAS MATERIAL DE APOYO NIVEL : 1er. AÑO PROF. L. ALTIMIRAS
Unidad 8 Lugares geométricos. Cónicas
 Unidad 8 Lugares geométricos. Cónicas PÁGINA 75 SOLUCIONES. La elipse es una cónica obtenida al cortar una superficie cónica por un plano oblicuo al eje y que corte a todas las generatrices. La hipérbola
Unidad 8 Lugares geométricos. Cónicas PÁGINA 75 SOLUCIONES. La elipse es una cónica obtenida al cortar una superficie cónica por un plano oblicuo al eje y que corte a todas las generatrices. La hipérbola
Unidad Didáctica 8. Dibujo Geométrico
 Unidad Didáctica 8 Dibujo Geométrico 1.- Tazados Geométricos Básicos Trazados Rectas Paralelas Rectas paralelas. Las que no llegan nunca a cortarse, o se cortan en el infinito. Con Escuadra y Cartabón:
Unidad Didáctica 8 Dibujo Geométrico 1.- Tazados Geométricos Básicos Trazados Rectas Paralelas Rectas paralelas. Las que no llegan nunca a cortarse, o se cortan en el infinito. Con Escuadra y Cartabón:
LUGARES GEOMÉTRICOS.
 9 LUGARES GEOMÉTRICOS. Página. Halla las ecuaciones de los siguientes lugares geométricos: a) Mediatriz del segmento de extremos A(, ), B(7, ). Comprueba que es una recta perpendicular al segmento en su
9 LUGARES GEOMÉTRICOS. Página. Halla las ecuaciones de los siguientes lugares geométricos: a) Mediatriz del segmento de extremos A(, ), B(7, ). Comprueba que es una recta perpendicular al segmento en su
Cuerpo de Profesores de Enseñanza Secundaria. Dibujo. Pr Práctica Tema 33
 Cuerpo de Profesores de Enseñanza Secundaria Dibujo Pr - 33 Práctica Tema 33 PRÁCTICA TEMA 33 CONSTRUCCIONES GEOMÉTRICAS FUNDAMENTALES. ANGULOS EN LA CIRCUNFERENCIA. POTENCIA, EJE Y CENTRO RADICAL. ARCO
Cuerpo de Profesores de Enseñanza Secundaria Dibujo Pr - 33 Práctica Tema 33 PRÁCTICA TEMA 33 CONSTRUCCIONES GEOMÉTRICAS FUNDAMENTALES. ANGULOS EN LA CIRCUNFERENCIA. POTENCIA, EJE Y CENTRO RADICAL. ARCO
Tema 6 Tangencias y polaridad
 Tema 6 Tangencias y polaridad Tema 6 Tangencias y polaridad...1 Tangencias... 2 Propiedades... 2 Enlaces... 3 Definición... 3 Construcción de enlaces... 3 Enlace de dos rectas oblicuas mediante dos arcos
Tema 6 Tangencias y polaridad Tema 6 Tangencias y polaridad...1 Tangencias... 2 Propiedades... 2 Enlaces... 3 Definición... 3 Construcción de enlaces... 3 Enlace de dos rectas oblicuas mediante dos arcos
Ejercicios resueltos
 Ejercicios resueltos.- Comprueba que las rectas r x + y y s x y + 4 son secantes y halla el punto de intersección de las mismas., es decir, los coeficientes de las incógnitas no son proporcionales, por
Ejercicios resueltos.- Comprueba que las rectas r x + y y s x y + 4 son secantes y halla el punto de intersección de las mismas., es decir, los coeficientes de las incógnitas no son proporcionales, por
TEMA 1. TRAZADOS GEOMÉTRICOS ELEMENTALES
 TEMA 1. TRAZADOS GEOMÉTRICOS ELEMENTALES GEOMETRÍA: Rama de las matemáticas que se ocupa del estudio de las figuras geométricas, incluyendo puntos, rectas, planos Proviene del Griego GEO (tierra) METRÍA
TEMA 1. TRAZADOS GEOMÉTRICOS ELEMENTALES GEOMETRÍA: Rama de las matemáticas que se ocupa del estudio de las figuras geométricas, incluyendo puntos, rectas, planos Proviene del Griego GEO (tierra) METRÍA
Matemáticas II. d) Perpendicular al plano π: 2x y + 3z 1 = 0, paralelo a la recta r : x 1 2 = y 3 = z 8
 I.E.S. Juan Carlos I Ciempozuelos (Madrid) Matemáticas II * Geometría analítica en R 3 * 1. Determina cuáles de las siguientes ternas de puntos son puntos alineados. Encuentra la ecuación de la recta que
I.E.S. Juan Carlos I Ciempozuelos (Madrid) Matemáticas II * Geometría analítica en R 3 * 1. Determina cuáles de las siguientes ternas de puntos son puntos alineados. Encuentra la ecuación de la recta que
Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6
 página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
página 1/13 Problemas Tema 7 Enunciados de problemas ampliación Temas 5 y 6 Hoja 1 1. Dado el segmento de extremos A( 7,3) y B(5,11), halla la ecuación de su mediatriz. 2. Halla la distancia del punto
16 PROPORCIONALIDAD INVERSA.-POTENCIA
 16 PROPORCIONALIDAD INVERSA.-POTENCIA 16.1 Características generales. Consideramos que una variable x puede adquirir los valores a, b, c, d,.. y otra variable y los valores a, b, c, d, x e y son inversamente
16 PROPORCIONALIDAD INVERSA.-POTENCIA 16.1 Características generales. Consideramos que una variable x puede adquirir los valores a, b, c, d,.. y otra variable y los valores a, b, c, d, x e y son inversamente
Ejercicios resueltos
 ECUACIÓN DE LA RECTA.- PRIMERO DE BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. Ejercicios resueltos.- Comprueba que las rectas r x + y y s x y + 4 son secantes y halla el punto de intersección de las mismas.,
ECUACIÓN DE LA RECTA.- PRIMERO DE BACHILLERATO.- TEORÍA Y EJERCICIOS. Pág. Ejercicios resueltos.- Comprueba que las rectas r x + y y s x y + 4 son secantes y halla el punto de intersección de las mismas.,
22. CURVAS CÓNICAS-ELIPSE
 22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
22. CURVAS CÓNICAS-ELIPSE 22.1. Características generales. Las curvas cónicas son las secciones planas de un cono de revolución. El cono de revolución es la superficie que genera una recta r al girar alrededor
Triángulo equilátero. Dibuja una circunferencia
 Triángulo equilátero Dibuja una circunferencia Traza una diagonal de la circunferencia que corte a ésta en los puntos A y B. Con centro en B y radio BO, traza un arco que corte a la circunferencia en los
Triángulo equilátero Dibuja una circunferencia Traza una diagonal de la circunferencia que corte a ésta en los puntos A y B. Con centro en B y radio BO, traza un arco que corte a la circunferencia en los
Láminas para hacer durante las vacaciones
 Diseño Equipacional Dibujo Técnico 1 Comisión 1 C Prof. Sanchez Láminas para hacer durante las vacaciones Se trabaja en hojas A4, con el mismo formato y rótulo que el resto de las láminas. En cada hoja
Diseño Equipacional Dibujo Técnico 1 Comisión 1 C Prof. Sanchez Láminas para hacer durante las vacaciones Se trabaja en hojas A4, con el mismo formato y rótulo que el resto de las láminas. En cada hoja
2º BACH TANGENCIAS ANA BALLESTER JIMÉNEZ
 2º BACH TANGENCIAS ANA BALLESTER JIMÉNEZ TANGENCIAS Propiedades: Si dos circunferencias son tangentes, el punto de tangencia se encuentra en la recta que une los centros (fig.1) Si una recta es tangente
2º BACH TANGENCIAS ANA BALLESTER JIMÉNEZ TANGENCIAS Propiedades: Si dos circunferencias son tangentes, el punto de tangencia se encuentra en la recta que une los centros (fig.1) Si una recta es tangente
CONSTRUCCIÓN GEOMÉTRICA DE LAS CÓNICAS
 CONSTRUCCIÓN GEOMÉTRICA DE LAS CÓNICAS Yuli Andrea Rodríguez Rodríguez 1 Universidad Pedagógica Nacional [email protected] Benjamin R. Sarmiento Lugo 2 Universidad Pedagógica Nacional [email protected]
CONSTRUCCIÓN GEOMÉTRICA DE LAS CÓNICAS Yuli Andrea Rodríguez Rodríguez 1 Universidad Pedagógica Nacional [email protected] Benjamin R. Sarmiento Lugo 2 Universidad Pedagógica Nacional [email protected]
Geometría Analítica. GEOMETRÍA ANALÍTICA PLANA SISTEMA DE COORDENADAS RECTANGULARES 1. DE UN PUNTO 2. DISTANCIA ENTRE DOS PUNTOS
 Geometría Analítica GEOMETRÍA ANALÍTICA PLANA René Descartes, matemático francés, en 67 define una ecuación algebraica para cada figura geométrica; es decir, un conjunto de pares ordenados de números reales
Geometría Analítica GEOMETRÍA ANALÍTICA PLANA René Descartes, matemático francés, en 67 define una ecuación algebraica para cada figura geométrica; es decir, un conjunto de pares ordenados de números reales
1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a)
 Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
Ejercicios de cónicas 1º bachillerato C 1) Clasifica las siguientes cónicas y expresa sus focos y su excentricidad: a) b) c) d) e) f) g) h) i) Soluciones: a) Circunferencia de centro ( y radio 3. Excentricidad
PAUTA ACTIVIDADES: CONSTRUYENDO RECTAS CON REGLA Y COMPÁS
 PAUTA ACTIVIDADES: CONSTRUYENDO RECTAS CON REGLA Y COMPÁS Antes de partir el trabajo con la guía, debe contar con los siguientes materiales: I. Construcción de rectas paralelas 1. Dibuje una recta. 2.
PAUTA ACTIVIDADES: CONSTRUYENDO RECTAS CON REGLA Y COMPÁS Antes de partir el trabajo con la guía, debe contar con los siguientes materiales: I. Construcción de rectas paralelas 1. Dibuje una recta. 2.
Tema 3. GEOMETRIA ANALITICA.
 Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
Álgebra lineal. Curso 087-009. Tema. Hoja 1 Tema. GEOMETRIA ANALITICA. 1. Hallar la ecuación de la recta: a) que pase por ( 4, ) y tenga pendiente 1. b) que pase por (0, 5) y tenga pendiente. c) que pase
TEMA VI: ÁNGULOS ENTRE ELEMENTOS
 TEMA VI: ÁNGULOS ENTRE ELEMENTOS 6.1.D Ángulo entre dos rectas El cálculo del ángulo de dos rectas que se cortan es sencillo. Si las rectas se cruzan, el ángulo es el formado entre una de las rectas y
TEMA VI: ÁNGULOS ENTRE ELEMENTOS 6.1.D Ángulo entre dos rectas El cálculo del ángulo de dos rectas que se cortan es sencillo. Si las rectas se cruzan, el ángulo es el formado entre una de las rectas y
TEMA 3. LUGARES GEOMÉTRICOS
 TEMA 3. LUGARES GEOMÉTRICOS LA HERRAMIENTA LUGAR GEOMÉTRICO Para construir un lugar geométrico necesitaremos dos objetos: un punto que será el que describirá el lugar geométrico, y otro que será el punto
TEMA 3. LUGARES GEOMÉTRICOS LA HERRAMIENTA LUGAR GEOMÉTRICO Para construir un lugar geométrico necesitaremos dos objetos: un punto que será el que describirá el lugar geométrico, y otro que será el punto
TANGENCIAS. Tangencias como aplicación de los conceptos de potencia e inversión TEMAR. Objetivos y orientaciones metodológicas. t.
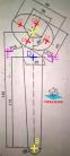 TANGENCIAS Tangencias como aplicación de los conceptos de potencia e inversión TEMAR Objetivos y orientaciones metodológicas El objetivo de este tema es hacer aplicación de los conceptos de "potencia"
TANGENCIAS Tangencias como aplicación de los conceptos de potencia e inversión TEMAR Objetivos y orientaciones metodológicas El objetivo de este tema es hacer aplicación de los conceptos de "potencia"
UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA
 C u r s o : Matemática Material N 8 GUÍA TEÓRICO PRÁCTICA Nº 5 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
C u r s o : Matemática Material N 8 GUÍA TEÓRICO PRÁCTICA Nº 5 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA
 C u r s o : Matemática Material N 18 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA GUÍA TEÓRICO PRÁCTICA Nº 15 SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
C u r s o : Matemática Material N 18 UNIDAD: ÁLGEBRA Y FUNCIONES ECUACIÓN DE LA RECTA GUÍA TEÓRICO PRÁCTICA Nº 15 SISTEMA CARTESIANO ORTOGONAL Para determinar la posición de los puntos de un plano usando
1.3.-Trazados geométricos básicos.
 1.3.-Trazados geométricos básicos. 1.3.1.-Notaciones Los elementos básicos del dibujo técnico son el punto, la recta y el plano. El punto no tiene dimensión, podemos considerarlo como una posición del
1.3.-Trazados geométricos básicos. 1.3.1.-Notaciones Los elementos básicos del dibujo técnico son el punto, la recta y el plano. El punto no tiene dimensión, podemos considerarlo como una posición del
EJERCICIOS DE DISTANCIAS PROCEDIMIENTOS DE EJECUCIÓN
 EJERCICIOS DE DISTANCIAS PROCEDIMIENTOS DE EJECUCIÓN 1-2-3.- Procedimiento: - Explicados en teoría 1) 2) 3) 4.- Procedimiento: - Trazar el plano P perpendicular a la recta R, pasando por el punto A, ayudándome
EJERCICIOS DE DISTANCIAS PROCEDIMIENTOS DE EJECUCIÓN 1-2-3.- Procedimiento: - Explicados en teoría 1) 2) 3) 4.- Procedimiento: - Trazar el plano P perpendicular a la recta R, pasando por el punto A, ayudándome
CAPÍTULO 3. COORDENADAS CARTESIANAS EN EL PLANO. RECTAS Y CIRCUNFERENCIAS.
 CAPÍTULO 3. COORDENADAS CARTESIANAS EN EL PLANO. RECTAS CIRCUNFERENCIAS. Ejercicios E1. Sean r la recta que pasa por los puntos. A(1, 2), B(3, 1), s la recta que pasa por el punto C(2, 2) y tiene pendiente
CAPÍTULO 3. COORDENADAS CARTESIANAS EN EL PLANO. RECTAS CIRCUNFERENCIAS. Ejercicios E1. Sean r la recta que pasa por los puntos. A(1, 2), B(3, 1), s la recta que pasa por el punto C(2, 2) y tiene pendiente
CURSO DE GEOMETRÍA 2º EMT
 CURSO DE GEOMETRÍA 2º EMT UNIDAD 0 REPASO 1º CIRCUNFERENCIA Y ANGULOS INSCRIPTOS Ángulos en la circunferencia 1. La circunferencia. 1.1. Elementos de una circunferencia Definición 1. Se llama circunferencia
CURSO DE GEOMETRÍA 2º EMT UNIDAD 0 REPASO 1º CIRCUNFERENCIA Y ANGULOS INSCRIPTOS Ángulos en la circunferencia 1. La circunferencia. 1.1. Elementos de una circunferencia Definición 1. Se llama circunferencia
GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA
 ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
ESCUELA PREPARATORIA OFICIAL No. 268 GUÍA DE ESTUDIO PARA EL EXAMEN EXTRAORDINARIO DE GEOMETRÍA ANALÍTICA Profra: Citlalli Artemisa García García 1) Qué es la pendiente? 2) Cómo es la pendiente de rectas
1. Halla la ecuación de la recta r, sabiendo que pasa por A(1,-2) y B(-1,2)
 1. Halla la ecuación de la recta r, sabiendo que pasa por A(1,-2) y B(-1,2) 2. Halla la ecuación de la recta r, sabiendo que es paralela a y=2x-3 y pasa por el punto (1,3). 3. Halla la ecuación de la recta
1. Halla la ecuación de la recta r, sabiendo que pasa por A(1,-2) y B(-1,2) 2. Halla la ecuación de la recta r, sabiendo que es paralela a y=2x-3 y pasa por el punto (1,3). 3. Halla la ecuación de la recta
Dibujo Técnico Curvas técnicas
 22 CURVAS TÉCNICAS En la actualidad, una parte importante de los objetos que se fabrican están realizados bajo algún tipo de forma curva geométrica. Si prestamos atención a nuestro entorno, nos damos cuenta
22 CURVAS TÉCNICAS En la actualidad, una parte importante de los objetos que se fabrican están realizados bajo algún tipo de forma curva geométrica. Si prestamos atención a nuestro entorno, nos damos cuenta
Relaciones geométricas IES BELLAVISTA
 Relaciones geométricas IES BELLAVISTA Igualdad y semejanza Dos figuras son iguales cuando sus lados y sus ángulos son iguales y están igualmente dispuestos. Dos figuras son semejantes cuando sus ángulos
Relaciones geométricas IES BELLAVISTA Igualdad y semejanza Dos figuras son iguales cuando sus lados y sus ángulos son iguales y están igualmente dispuestos. Dos figuras son semejantes cuando sus ángulos
A IES La Asunción. Elx. Mario Ortega González.
 1 2 3 4 5 6 C A 1 2 3 4 5 r1 6 F' M r2 B D IES La Asunción. Elx. Mario Ortega González. Trazamos los radios vectores r1 y r2, los sumamos y ya tenemos lo que mide el eje mayor A,B. La distancia desde el
1 2 3 4 5 6 C A 1 2 3 4 5 r1 6 F' M r2 B D IES La Asunción. Elx. Mario Ortega González. Trazamos los radios vectores r1 y r2, los sumamos y ya tenemos lo que mide el eje mayor A,B. La distancia desde el
Manejo de las herramientas de Dibujo
 Manejo de las herramientas de Dibujo Una vez aprendidos los instrumentos de dibujo más básicos, en la siguiente ficha, vas a descubrir para que sirven en la práctica, y vas a poder adquirir soltura en
Manejo de las herramientas de Dibujo Una vez aprendidos los instrumentos de dibujo más básicos, en la siguiente ficha, vas a descubrir para que sirven en la práctica, y vas a poder adquirir soltura en
2º BACH TANGENCIAS ANA BALLESTER JIMÉNEZ
 2º BACH TANGENCIAS ANA BALLESTER JIMÉNEZ TANGENCIAS Propiedades: Si dos circunferencias son tangentes, el punto de tangencia se encuentra en la recta que une los centros (fig.1) Si una recta es tangente
2º BACH TANGENCIAS ANA BALLESTER JIMÉNEZ TANGENCIAS Propiedades: Si dos circunferencias son tangentes, el punto de tangencia se encuentra en la recta que une los centros (fig.1) Si una recta es tangente
11. CURVAS TÉCNICAS ÓVALO Definición Construcción de óvalos
 11. CURVAS TÉCNICAS Las curvas técnicas tienen muchas aplicaciones en la resolución de problemas de dibujo técnico, ya sean éstos provenientes del ámbito del diseño industrial, arquitectónico o gráfico.
11. CURVAS TÉCNICAS Las curvas técnicas tienen muchas aplicaciones en la resolución de problemas de dibujo técnico, ya sean éstos provenientes del ámbito del diseño industrial, arquitectónico o gráfico.
2. Enlace de puntos que no están en línea recta por medio de arcos que sean tangentes entre sí
 Unidad Nº 2. Dibujo Geométrico 1. Enlace de puntos y de líneas. Introducción 2. Enlace de puntos que no están en línea recta por medio de arcos que sean tangentes entre sí 3. Empalmar dos rectas perpendiculares
Unidad Nº 2. Dibujo Geométrico 1. Enlace de puntos y de líneas. Introducción 2. Enlace de puntos que no están en línea recta por medio de arcos que sean tangentes entre sí 3. Empalmar dos rectas perpendiculares
Lugares geométricos y cónicas
 Lugares geométricos y cónicas E S Q U E M A D E L A U N I D A D. Lugar geométrico página 6.. Definición página 6. Circunferencia página 6.. Ecuación página 6.. Casos particulares página 67. Elipse página
Lugares geométricos y cónicas E S Q U E M A D E L A U N I D A D. Lugar geométrico página 6.. Definición página 6. Circunferencia página 6.. Ecuación página 6.. Casos particulares página 67. Elipse página
n Por ejemplo, en un pentágono tenemos que saber que sus ángulos suman 540º y cada ángulo del pentágono son 108º.
 MATEMÁTICAS 3º ESO TEMA 10 PROBLEMAS MÉTRICOS EM EL PLANO- 1. ÁNGULOS EN LOS POLÍGONOS La suma de los ángulos de un polígono de n lados es: 180º (n-2) 180º(n - 2) La medida de cada ángulo de un polígono
MATEMÁTICAS 3º ESO TEMA 10 PROBLEMAS MÉTRICOS EM EL PLANO- 1. ÁNGULOS EN LOS POLÍGONOS La suma de los ángulos de un polígono de n lados es: 180º (n-2) 180º(n - 2) La medida de cada ángulo de un polígono
TEMA 1. ELEMENTOS DE GEOMETRIA EN EL PLANO
 2ª EVALUACIÓN AMPLIACIÓN MATEMÁTICAS TEMA 1. ELEMENTOS DE GEOMETRIA EN EL PLANO 1. EL PUNTO El punto es uno de los conceptos primarios de geometría. El punto no es un objeto físico y no tiene dimensiones
2ª EVALUACIÓN AMPLIACIÓN MATEMÁTICAS TEMA 1. ELEMENTOS DE GEOMETRIA EN EL PLANO 1. EL PUNTO El punto es uno de los conceptos primarios de geometría. El punto no es un objeto físico y no tiene dimensiones
( ) 2 +( 1) 2. BLOQUE III Geometría analítica plana. Resoluciones de la autoevaluación del libro de texto
 Pág. de Dados los vectores u, y v0,, calcula: a u b u + v c u v u, v0, 5 a u = = = + b u + v =, + 0, =, + 0, 6 =, c u v = u v = 0 + = Determina el valor de k para que los vectores a, y b6, k sean ortogonales.
Pág. de Dados los vectores u, y v0,, calcula: a u b u + v c u v u, v0, 5 a u = = = + b u + v =, + 0, =, + 0, 6 =, c u v = u v = 0 + = Determina el valor de k para que los vectores a, y b6, k sean ortogonales.
TEMA 3 TRAZADO GEOMETRICO. CONICAS
 TEM 3 TRZDO GEOMETRICO. CONICS 1. CIRCUNFERENCIS...2 1.1 TNGENCIS...2 2. DIVISION DE CIRCUNFERENCIS...9 2.1 EN TRES Y SEIS PRTES IGULES...9 2.2 EN CUTRO Y OCHO PRTES IGULES...10 2.3 EN CINCO Y DIEZ PRTES
TEM 3 TRZDO GEOMETRICO. CONICS 1. CIRCUNFERENCIS...2 1.1 TNGENCIS...2 2. DIVISION DE CIRCUNFERENCIS...9 2.1 EN TRES Y SEIS PRTES IGULES...9 2.2 EN CUTRO Y OCHO PRTES IGULES...10 2.3 EN CINCO Y DIEZ PRTES
Matemáticas II. Grupos: 2 B, C y E. Escuela Secundaria Diurna No. 264 Miguel Servet. Alumno (a): Actividades extraescolares
 Escuela Secundaria Diurna No. 264 Miguel Servet Jornada Ampliada Matemáticas II Actividades extraescolares Profra. Gisel M. Leal Martínez Grupos: 2 B, C y E. Alumno (a): octubre, 2017 ACTIVIDAD II Tema:
Escuela Secundaria Diurna No. 264 Miguel Servet Jornada Ampliada Matemáticas II Actividades extraescolares Profra. Gisel M. Leal Martínez Grupos: 2 B, C y E. Alumno (a): octubre, 2017 ACTIVIDAD II Tema:
RESUMEN DE GEOMETRIA EUCLIDIANA. Profesor: Manuel J. Salazar Jiménez. Relaciones no definidas: pertenecer a, estar entre, congruente a, equidistar
 RESUMEN DE GEOMETRIA EUCLIDIANA Profesor: Manuel J. Salazar Jiménez Nociones no definidas o nociones primitivas: Punto, recta, plano, espacio, distancia. Relaciones no definidas: pertenecer a, estar entre,
RESUMEN DE GEOMETRIA EUCLIDIANA Profesor: Manuel J. Salazar Jiménez Nociones no definidas o nociones primitivas: Punto, recta, plano, espacio, distancia. Relaciones no definidas: pertenecer a, estar entre,
Primera edición INVERSIÓN DT2
 Primera edición INVERSIÓN DT2 Inversión 1 La Inversión en Dibujo Técnico es una transformación geométrica en la que a una figura corresponde otra. Sección 1 Introducción Definición La Inversión en Dibujo
Primera edición INVERSIÓN DT2 Inversión 1 La Inversión en Dibujo Técnico es una transformación geométrica en la que a una figura corresponde otra. Sección 1 Introducción Definición La Inversión en Dibujo
BLOQUE 1: Para entrar en calor.
 BLOQUE 1: Para entrar en calor. Actividad 1: Teorema de Viviani. En un triángulo equilátero la suma de distancias, desde un punto interior, a los tres lados se mantiene constante. Qué mide esa constante
BLOQUE 1: Para entrar en calor. Actividad 1: Teorema de Viviani. En un triángulo equilátero la suma de distancias, desde un punto interior, a los tres lados se mantiene constante. Qué mide esa constante
PUNTO, RECTA, SEMIRECTA Y SEGMENTO. SEMIRECTA: Una semirecta es una porción de recta delimitada por un punto.
 2ºESO Definiciones importantes de Geometría INTRODUCCIÓN A LA GEOMETRÍA GEOMETRÍA: Es una rama de las matemáticas que se ocupa del estudio de propiedades de puntos, rectas. polígonos,etc. Proviene del
2ºESO Definiciones importantes de Geometría INTRODUCCIÓN A LA GEOMETRÍA GEOMETRÍA: Es una rama de las matemáticas que se ocupa del estudio de propiedades de puntos, rectas. polígonos,etc. Proviene del
Unidad 4Transformaciones geométricas
 4.1. Dados los puntos A, B y C sobre una recta r, de manera que AB = 20 mm y BC = 20 mm, determina sobre r el punto D para que la razón doble (ABCD) = 19/14. 1. Por los puntos A y B de la recta r se trazan
4.1. Dados los puntos A, B y C sobre una recta r, de manera que AB = 20 mm y BC = 20 mm, determina sobre r el punto D para que la razón doble (ABCD) = 19/14. 1. Por los puntos A y B de la recta r se trazan
DIBUJO TÉCNICO II EJERCICIOS DE APOYO. Prof. Jesús Macho Martínez
 DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
DIBUJO TÉCNICO II EJERCICIOS DE APOYO Esta obra de Jesús Macho Martínez está bajo una Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported 1º.- Deducir razonadamente el valor del ángulo α marcado
1º BACH TANGENCIAS CURVAS TÉCNICAS CURVAS CÓNICAS ANA BALLESTER JIMÉNEZ
 1º BACH TANGENCIAS CURVAS TÉCNICAS CURVAS CÓNICAS ANA BALLESTER JIMÉNEZ TANGENCIAS Propiedades: Si dos circunferencias son tangentes, el punto de tangencia se encuentra en la recta que une los centros
1º BACH TANGENCIAS CURVAS TÉCNICAS CURVAS CÓNICAS ANA BALLESTER JIMÉNEZ TANGENCIAS Propiedades: Si dos circunferencias son tangentes, el punto de tangencia se encuentra en la recta que une los centros
TALLER # 4 DE GEOMETRÍA EUCLIDIANA SEMEJANZAS Y RELACIONES MÉTRICAS. Universidad de Antioquia
 TALLER # 4 DE GEOMETRÍA EUCLIDIANA SEMEJANZAS Y RELACIONES MÉTRICAS Universidad de Antioquia Profesor: Manuel J. Salazar J. 1. El producto de las medidas de las diagonales de un cuadrilátero inscrito es
TALLER # 4 DE GEOMETRÍA EUCLIDIANA SEMEJANZAS Y RELACIONES MÉTRICAS Universidad de Antioquia Profesor: Manuel J. Salazar J. 1. El producto de las medidas de las diagonales de un cuadrilátero inscrito es
ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos:
 ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos: Curso: TEMA 1: TRAZADOS BÁSICOS. 1. RECTAS PARALELAS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar.
ACTIVIDADES DE GEOMETRÍA PARA 4º ESO DE EPV Nombre y apellidos: Curso: TEMA 1: TRAZADOS BÁSICOS. 1. RECTAS PARALELAS Las rectas paralelas son aquellas que por mucho que las prolongues nunca se van a cortar.
Lámina 1: Rectas paralelas horizontales, verticales, inclinadas y cruzadas.
 Lámina 1: Rectas paralelas horizontales, verticales, inclinadas y cruzadas. Lámina 2: Realiza los siguientes patrones Traza un segmento de 50 mm por el punto R paralelo a la recta r. Divide el segmento
Lámina 1: Rectas paralelas horizontales, verticales, inclinadas y cruzadas. Lámina 2: Realiza los siguientes patrones Traza un segmento de 50 mm por el punto R paralelo a la recta r. Divide el segmento
UNIDAD 8 Geometría analítica
 Pág. 1 de 5 I. Sabes hallar puntos medios de segmentos, puntos simétricos de otros y ver si varios puntos están alineados? 1 Los puntos A( 1, 3), B(2, 6), C (7, 2) y D( 5, 3) son vértices de un cuadrilátero.
Pág. 1 de 5 I. Sabes hallar puntos medios de segmentos, puntos simétricos de otros y ver si varios puntos están alineados? 1 Los puntos A( 1, 3), B(2, 6), C (7, 2) y D( 5, 3) son vértices de un cuadrilátero.
