Ampli cadores de Potencia, Conceptos básicos
|
|
|
- Alba Ortiz de Zárate Macías
- hace 8 años
- Vistas:
Transcripción
1 Ampl cadores de otenca, onceptos báscos 1 J.. Hurcan Abstract Los ampl cadores de potenca son conertdores que transforman la energía de la fuente en señal de potenca de salda. Estos pueden ser tpo clase A, AB, B y. Los cuales tenen dstntos parámetros de e cenca y uso. ndex Terms ower Ampl ers.. ntroducton Un ampl cador de potenca conerte la potenca de una fuente de corrente contnua (olarzacón de un crcuto con transtores) a potenca de salda en forma de señal, lo cual es controlado usando una señal de entrada. S sobre la carga se desarrolla una gran cantdad de potenca, el dsposto deberá manejar una gran excursón en oltaje y corrente. Los puntos de operacón deben estar en un área permtda de oltaje y corrente que asegure la máxma dspacón, (SOA, Safe Operatng Area). Se deben consderar los oltajes de ruptura y efectos térmcos permtdos en los dspostos de estado sóldo, las característcas no lneales en el funconamento y usar los parámetros para gran señal del dsposto. La cura de la Fg. 1 muestra las caracterstcas de emsor y colector de un transstor delmtada por el SOA, que está de ndo por la EMAX. [1]. AB, la polarzacón del ampl cador es de tal forma que la corrente de colector solamente uye para un lapso menor a los 36 o y mayor a los 18 o de la onda correspondente. ara el funconamento en clase B, la corrente urá solo durante 18 o de la onda de entrada. Fnalmente, para funconamento en clase, el dsposto conducrá durante un perodo nferor a los 18 o correspondente a la onda de entrada. La Fg., muestra el comportamento del dsposto en las dstntas clases. BE lase A lase B lase AB lase π π π π π π onduccón > π onduccón < π Max SOA Fg.. omportamento para clase A, AB, B,. Los ampl cadores tpo AB y B usan con guracones transstorzadas llamadas push-pull. ada uno de estos ampl cadores posee característcas de e cenca y dstorsón dstntos, por lo cual, sus aplcacón será a dstntas áreas. Fg. 1. Area Segura de Operacón del Transstor. B E La corrente y el oltaje E no podrán sobrepasar los máxmos ndcados.. lasfcacón de los amplfcadores de potenca Exsten cuatro clas cacones báscas de ampl cadores de potenca: A, AB, B y. En clase A, el ampl cador está polarzado de tal forma que la corrente por el colector uye durante el cclo completo de la señal de entrada. ara clase Documento preprarado en el DE, Unersdad de la Frontera 4.. Relacones báscas en los amplfcadores de potenca ara analzar los ampl cadores de potenca se requere de certas cantdades y relacones asocadas a su funconamento y desempeño. omo el ampl cador de pontenca conerte la potenca de de la fuente de almentacón en una señal de potenca en la carga, la e cenca de este proceso está dada por L(A) (1) Donde es la e cenca, L(A), es la potenca meda de señal en la carga y, la potenca meda de salda en la fuente de almentacón. La potenca meda dspada en el dsposto de ampl- cacón, consderando un transstor bpolar como dsposto de potenca, será E L ()
2 Donde E es la dspacón meda de colector, L es la potenca total, es decr, L() más L(A) en la carga. ara la ealuacón de las dstntas cantdades de potenca, se usa la relacón básca dada por (3), donde p es la potenca nstantánea, e son el oltaje y la corrente nstantáneos. p (3) Sean e formas de onda perodca, con componente contnua (la cual puede ser cero) y una componente de corrente alterna, no necesaramente snusodal dc ac (4) dc ac (5) Luego la potenca meda en un perodo será 1 Z p d!t dc dc 1 Z " " A ac ac d!t (6) Donde, es la contrbucón de la componente contnua y A es la contrbucón de la componente alterna a la potenca meda. S las componentes de corrente alterna son tpo snusodal, se tene ac m cos!t (7) ac m cos!t (8) Reemplazando en la ecuacón (6), se tene dc dc 1 Z dc dc m m [( m cos!t) ( m cos!t)] d!t Z cos!t d!t dc dc m m dc dc m m omo p p ; entonces (9) armónco de la señal. ara el caso de una señal snusodal con componente contnua será q rms D rms. El amplfcador lase A En operacón clase A, el ampl cador reproduce toda la señal de entrada, la corrente de colector es dstnta de cero todo el tempo, lo cual se consdera muy ne cente, ya que para señal cero en la entrada, se tene un >, luego el transstor dspa potenca. A. Ampl cador Emsor común Sea la con guracón de emsor común de la Fg. 3, la cual funcona en clase A. or smplccdad se hace la resstenca de emsor R E. Se seleccona para máxma potenca de salda, lo que mplca que la recta de carga de A debe pasar por la cura EMAX. Fg. 3. R B (a) Emsor omún. En la Fg. 4, se muestra las rectas de carga para dos puntos del ampl cador, las cuales se ntersectan con la cura E. Se obsera que será la máxma corrente permtda para y E1 será el máxmo oltaje permtdo para E, para el transstor en cuestón. El óptmo elegdo será el punto de reposo, debdo a que 1 <, lo cual mplca una dsmnusón en la corrente de colector, lo que trae consgo una dsmnusón en la dstorsón y una menor corrente de base requerda para obtener 1. (b) dc dc m m p p dc dc rms rms (1) 1 uando la señal de corrente peródca tene componente contnua se expresa el alor rms de la forma de onda como rms q D 1 rms rms ::: n rms (11) Fg. 4. Dstntos puntos. E E 1 E Donde D, es la componente contnua de la señal, 1rms es el prmer armónco de la señal, nrms es el n ésmo ara que la realzacón sea factble, E1 debe ser menor que EO, así se tomará que E1. Lo cual puede
3 AMLFADORES DE OTENA, ONETOS BÁSOS 3 no ser necesaramente efecto para otras con guracones en clase A. ara alores arbtraros Max y EMax, el punto estará dado por la tangente a la cura EMax, dado por las coordenadas Max y E EMax como se ndca en la Fg. 5. Se asume que la señal de entrada puede manejar el transstor entre el corte y la saturacón, de esta forma para una aracón en la corrente de base, se tene la aracón en la corrente de colector, y una aracón en la potenca. Note que la recta de carga de A tene la msma pendente que la recta de carga de. Max Max E p E Max Fg. 7. uras de, E y p. E E Luego de acuerdo a (11), consderando que la corrente tene componente contnua y alterna, se tene Fg. 5. unto. para máxma excusón smétrca. Trazando la onda de corrente, como se ndca en la Fg. 6,se obtene la onda del E. Note que la excursón será smétrca. Max L s 4 max p 3 5 R L max (13) 8 De la cura se determna, entonces Max EMax E E L (14) 4 8 L() " " L(A) or otro lado, la potenca promedo entregada por la fuente será Fg. 6. Excursón de la corrente y el oltaje. La Fg. 7, muestra las formas de onda a traés del tempo, E, p, E y L. La onda de potenca nstantánea de la fuente p, estará dada por el producto y tene la msma forma que. E c E. Note que la forma de onda de E tene una frecuenca el doble de las otras formas de onda. (15) omo la potenca dspada en el transstor debe ser la potenca de la fuente menos la potenca en la carga (total, es decr la A y la ), se tene que A.1 Determnacón de la E cenca La potenca en la carga será L rms (1) E L Fnalmente, la e cenca estará dada por 8 (16)
4 4 8 :5 (17) La e cenca de este ampl cador es baja, 5%, esto debdo prncpalmente a que se mantene una corrente de reposo en la carga, la cual no es usada (desperdcada). Max B. on guracón emsor común con transformador de acoplo Sea el crcuto de la Fg. 8a. Una forma de mejorar la e cenca del ampl cador clase A es usar el acoplo de la carga medante un transformador. ómo es eso? Fg. 1. E Rectas de carga de y A. E N s N s L Max p R L (19) Debdo a que E, se tene que EMax, por lo tanto, de la cura se determna que Max, así (a) Fg. 8. (a) Ampl cador acoplado por transformador. (b) Equalente. ara y A se obtenen los crcutos equalentes de la Fg.9. E E (b) E E L L(A) RL () Dado que la potenca meda de la fuente es, entonces Max EMax Fnalmente, la e cenca de la conersón será L(A) :5 Fnalmente, la potenca dspada por el transstor será (1) () Fg. 9. (a) Equalentes de y A (b) E L Al consderar el acoplamento la recta de carga en pasa por E, pues R, luego la recta de carga de A corta el eje del oltaje en un alor. omo consecuenca de esto, cuando no hay señal, no exstrá corrente por el colector. B.1 Determnacón de la E cenca La potenca en la carga será L rms (18) omo sólo la carga recbe componente alterna, la corrente efecta será la ampltud sobre p ; luego Note que solo exste L LA. Example 1: Sea el ampl cador clase A de la Fg.8, sabendo que a la carga se le entrega una potenca de [W ] :onsdere la realcón de transformacón n:1. alcular: La potenca de la fuente para que el transstor trabaje en clase A: Dado que el rendmento es el 5%, se tene :5 L(A) [W ] 4 [W ]
5 AMLFADORES DE OTENA, ONETOS BÁSOS 5 omo L(A) RL [W ], entonces 1[] 1 [] : Además, como L p R L ; R 1 n:1 [W ] p 1 [] : [A]. Ampl cador con resstenca de emsor Una aracón del ampl cador es consderar R E 6 : ara este caso se tene el crcuto de la Fg. 11. R R E E Fg. 13. Ampl cador con R E y E. La maxma excursón se dará cuando cuando R 1 N s E R A Luego reemplazando en la recta de carga de, se tene 1 [ ] E R 1 [] L E ; así se obtene R R E Fg. 11. Ampl cador con R E : ara esta stuacón se tene que la recta de no es del todo n nta dado el alor de R E como se ndca en la Fg. 1. La recta de A será léemente mod cada. Sn embargo, el rendmento permanece gual. Max E Recta de carga de Recta de carga de A E E 1 [ ] 1 [ ] 8:88 [ ] 1 1 1[] [ ] 1 [ ] 1 [] RL 1:11 [A] 8 [] 1 [] ara el cálculo de las potencas se tene L(A) rmsr L p RL R L 4:93 [W ] 1 [ ] 1:11 [A] 11:11 [W ] La potenca dspada por el transstor será E 6:5 [W ]. El amplfcador lase B En esta operacón, se usa un transstor para ampl car el cclo posto de la señal de entrada, mentras un segundo dsposto se preocupa del cclo negato. La con guracón se conoce como push-pull. Fg. 1. Rectas de carga ampl cador clase A mod cado. Example : Sea el ampl cador de la Fg.13, determne la potenca en la carga, la potenca entregada por la fuente y la potenca dspada por el transstor. onsdere la relacón de transformacón n : 1, R E 1 [] ; 8 [] : ara, se tene 1 N s ara A, 1 [ ] [] E E E E ( ) E E Fg. 14. Ampl cador clase B. Se requeren dos transstores para producr la onda completa. ada transstor se polarza en al punto de corte en lugar del punto medo del nteralo de operacón. S el oltaje de entrada es posto, de acuerdo a la conexón del transformador se tene que conduce y está en
6 6 corte. S el oltaje de entrada es negato no conduce y conduce. Esto permtrá obtener la onda de salda de acuerdo a la Fg.15. Max Esta cura corr esponde a un tr ansstor (1) Max 1 N s E (a) 1 N s Fg. 17. aracón en torno al punto de operacón 1 Max Fg. 15. (b) onduccón de los transstores. Max La corrente de colector es cero cuando la señal de entrada es cero, por lo tanto el transstor no dspa potenca en reposo. En, el E, y en A, la aracón de será solo posta, consderando que la recta de carga es E R E L R L ; de la cura se tene que, luego para, la recta corta en E, de acuerdo a la Fg.16. Fg. 18. Max uras de corrente. romedo Max Max : Así, la potenca total en la carga por cada transstor será Max L Max R L R L E Fg. 16. Rectas de arga A y del ampl cador clase B. 4 (3) Luego, la potenca total en la carga sumnstrada por ambos transstores Al consderar señal posta en la base, el E dsmnuye a partr de como se muestra en la Fg.17. De la cura dada en la Fg. 16, se obtene Max EMax Luego, la potenca en la carga será nueamente la ndcada en (1). En este caso, cada transstor opera durante un sem-cclo, por lo tanto, el alor efecto de la onda será L(A) (4) ara determnar la potenca entregada por la fuente, se requere determnar la corrente meda consumda, la cual se llamará. De acuerdo a la Fg. 18, la onda de corrente producda sera la superposcón de los dos semcclos aportados por la conduccón de los dos transstores.
7 AMLFADORES DE OTENA, ONETOS BÁSOS 7 1 Z Max Así se tene que Max Max sn (!t) d!t Z sn (!t) d!t Max o o Max RL Fg Funconamento del smetría complementara. :636 Fnalmente, se tene el redmento (5) :785 (6) 4 Lo que corresponde a un 78.5% de e cenca en la conersón. or otro lado, la potenca dspada por el colector será E A. Ampl cador de Smetría omplementara Sea el crcuto de la Fg. 19 que corresponde a un ampl cador de smetra complementara. La carga será de acoplamento drecto. Fg. 1. Ampl cador de smetría complementara con acoplamento capacto. 4 o L 8 E 4 - Fg. 19. Ampl cador de smetría complementara, con acoplamento drecto. uando la señal de entrada es posta, el oltaje en el emsor de es leemente menor que en la entrada, hacendo conducr este y dejando en corte. uando el oltaje de entrada es negato, conduce, quedando en corte, como se muestra en la Fg.. El crcuto de la Fg.1 será un ampl cador de smetría complementara con acoplamento capacto. ara este caso se tene que la almentacón de cada transstor es y la carga será. De esta forma a partr de las relacones del clase B pushpull, (4), (5) y (6), reeemplazando por y RL por, se puede determnar o Luego el rendmento será 8 4 :785 4 Example 3: Sea el ampl cador de smetría complementara que excta una carga de 1 [] : S los transstores tenen alores nomnales de 1A, 4 y 4W, determne el que produce la maxma potenca en la carga para entrada snusodal. 1Ω
8 8. El problema de la dstorsón El problema de la con guracón es que la onda de salda tene dstorsón debdo a que los transstores no empezan a conducr nmedatamente, dado que la señal en la base debe sobrepasar el umbral BE : El sem-cclo de la salda no es una snusode perfecta. o(t) References [1] uttler,. (197). Lnear Electroncs rcuts, McGraw-Hll. [] Saant, Roden, arpenter (1993). Dseño Electrónco. Addson- Wesley. [3] Rashd, M. (). rcutos Mcroelectróncos, Análss y Dseño. Thomson. [4] roc, M, Harter, J.(1987) Electroncs Deces, rcuts and Systemas, Englewood l s, N.J. : rentce-hall [5] Dede, E, Esp, J (1983) Dseño de rcutos y Sstemas Electróncos, Marcombo Fg.. Dstorsón de la onda de salda. ara el ampl cador de la Fg.3 se consdera que R 1 R entregan un oltaje en la base en torno a BEON. Lo cual permte la conduccón del transstor al nco de la onda de entrada. R 1 N s R 1 Fg. 3. Dsmnucón de la dstorsón. ara este caso, la conduccón de ambos transstores será mayor a 18 ; lo que hace que su funconamento sea llamado lase AB. BB R 1 R 1 R B BB BE R 1 jjr. El amplfcador lase AB Se dce que este ampl cador posee un comportamento en clase A y clase B []. En este ampl cador, el funconamento del dsposto de potenca es mayor a los 18 y menor a 36 : Sea el crcuto de la Fg. 3, se muestra una aracón propuesta en [], la cual susttuye el transformador en a entrada por dos señales proenentes de una etapa anteror, la cual asegura el desfaces de las ondas para la conduccón de uno u otro transstor.. onclusones Se han planteado algunos conceptos báscos de ampl - cadores de potenca. Las magntudes más mportantes a consderar son la e cenca, la potenca en la carga y la potenca dspada en el transstor.
Respuesta A.C. del FET 1/14
 espuesta A.C. del FET 1/14 1. Introduccón Una ez que se ubca al transstor dentro de la zona saturada o de corrente de salda constante, se puede utlzar como amplfcador de señales. En base a un FET canal
espuesta A.C. del FET 1/14 1. Introduccón Una ez que se ubca al transstor dentro de la zona saturada o de corrente de salda constante, se puede utlzar como amplfcador de señales. En base a un FET canal
Circuito Monoestable
 NGENEÍA ELETÓNA ELETONA (A-0 00 rcuto Monoestable rcuto Monoestable ng. María sabel Schaon, ng. aúl Lsandro Martín Este crcuto se caracterza por presentar un únco estado estable en régmen permanente, y
NGENEÍA ELETÓNA ELETONA (A-0 00 rcuto Monoestable rcuto Monoestable ng. María sabel Schaon, ng. aúl Lsandro Martín Este crcuto se caracterza por presentar un únco estado estable en régmen permanente, y
R L C. v i. dv dt. i x. v x V/R. recta de carga estática. V+V im. V-V im. Recta de carga dinámica: i vx R = C = L =
 R = R L C R R C = C d C dt L = d L L dt R x x /R recta de carga estátca x = ( ) R x x _ x = M senωt M ( ) Recta de carga dnámca: x x = R M x x R /R x Q _ x elemento no lneal x x = 0 s = k 2 ( ) x T s s
R = R L C R R C = C d C dt L = d L L dt R x x /R recta de carga estátca x = ( ) R x x _ x = M senωt M ( ) Recta de carga dnámca: x x = R M x x R /R x Q _ x elemento no lneal x x = 0 s = k 2 ( ) x T s s
COMPARADOR CON AMPLIFICADOR OPERACIONAL
 COMAADO CON AMLIFICADO OEACIONAL COMAADO INESO, COMAADO NO INESO Tenen como msón comparar una tensón arable con otra, normalmente constante, denomnada tensón de referenca, dándonos a la salda una tensón
COMAADO CON AMLIFICADO OEACIONAL COMAADO INESO, COMAADO NO INESO Tenen como msón comparar una tensón arable con otra, normalmente constante, denomnada tensón de referenca, dándonos a la salda una tensón
EL AMPLIFICADOR OPERACIONAL.
 Tema 6. El mplfcador peraconal. Tema 6 EL MPLIFICD PECINL.. Introduccón... Símbolos y termnales del amplfcador operaconal... El amplfcador operaconal como amplfcador de tensón..3. Conceptos báscos de realmentacón..4.
Tema 6. El mplfcador peraconal. Tema 6 EL MPLIFICD PECINL.. Introduccón... Símbolos y termnales del amplfcador operaconal... El amplfcador operaconal como amplfcador de tensón..3. Conceptos báscos de realmentacón..4.
DEPARTAMENTO DE INDUSTRIA Y NEGOCIO UNIVERSIDAD DE ATACAMA COPIAPO - CHILE
 DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
DEPATAMENTO DE NDUSTA Y NEGOCO UNESDAD DE ATACAMA COPAPO - CHLE ESSTENCA EN SEE, PAALELO, MXTO Y SUPEPOSCÓN En los sguentes 8 crcutos calcule todas las correntes y ajes presentes, para ello consdere los
Guía de ejercicios #1
 Unversdad Técnca Federco Santa María Departamento de Electrónca Fundamentos de Electrónca Guía de ejerccos # Ejercco Ω v (t) V 3V Ω v0 v 6 3 t[mseg] 6 Suponendo el modelo deal para los dodos, a) Dbuje
Unversdad Técnca Federco Santa María Departamento de Electrónca Fundamentos de Electrónca Guía de ejerccos # Ejercco Ω v (t) V 3V Ω v0 v 6 3 t[mseg] 6 Suponendo el modelo deal para los dodos, a) Dbuje
PROBLEMAS DE ELECTRÓNICA ANALÓGICA (Diodos)
 PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
PROBLEMAS DE ELECTRÓNCA ANALÓGCA (Dodos) Escuela Poltécnca Superor Profesor. Darío García Rodríguez . En el crcuto de la fgura los dodos son deales, calcular la ntensdad que crcula por la fuente V en funcón
TEMA 4 Amplificadores realimentados
 TEM 4 mplfcadores realmentados 4.1.- Introduccón La realmentacón (feedback en nglés) negata es amplamente utlzada en el dseño de amplfcadores ya que presenta múltples e mportantes benefcos. Uno de estos
TEM 4 mplfcadores realmentados 4.1.- Introduccón La realmentacón (feedback en nglés) negata es amplamente utlzada en el dseño de amplfcadores ya que presenta múltples e mportantes benefcos. Uno de estos
EBAS Exámenes resueltos
 www.smplyjarod.com EAS Exámenes resueltos -9 pto. de Electrónca Físca Examen de: ELETÓNA ÁSA(Feb/) PÁGNA N o APELLOS NOME N o N ALFAÓN ANTES E EMPEZA lea atentamente estas NSTUONES Mantenga en lugar SLE
www.smplyjarod.com EAS Exámenes resueltos -9 pto. de Electrónca Físca Examen de: ELETÓNA ÁSA(Feb/) PÁGNA N o APELLOS NOME N o N ALFAÓN ANTES E EMPEZA lea atentamente estas NSTUONES Mantenga en lugar SLE
Tema 4. Transistor Bipolar (BJT)
 Tema 4. Transstor polar (JT) Joaquín aquero López lectrónca, 2007 Joaquín aquero López 1 Transstor polar (JT): Índce 4.1) Introduccón a los elementos de 3 termnales 4.2) Transstor polar JT (polar Juncton
Tema 4. Transstor polar (JT) Joaquín aquero López lectrónca, 2007 Joaquín aquero López 1 Transstor polar (JT): Índce 4.1) Introduccón a los elementos de 3 termnales 4.2) Transstor polar JT (polar Juncton
DELTA MASTER FORMACIÓN UNIVERSITARIA C/ Gral. Ampudia, 16 Teléf.: 91 533 38 42-91 535 19 32 28003 MADRID
 DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
DELTA MATE OMAÓN UNETAA / Gral. Ampuda, 6 8003 MADD EXÁMEN NTODUÓN A LA ELETÓNA UM JUNO 008 El examen consta de ses preguntas. Lea detendamente los enuncados. tene cualquer duda consulte al profesor. Todas
TEMA 6 AMPLIFICADORES OPERACIONALES
 Tema 6 Amplfcadores peraconales ev 4 TEMA 6 AMPLIFICADES PEACINALES Profesores: Germán llalba Madrd Mguel A. Zamora Izquerdo Tema 6 Amplfcadores peraconales ev 4 CNTENID Introduccón El amplfcador dferencal
Tema 6 Amplfcadores peraconales ev 4 TEMA 6 AMPLIFICADES PEACINALES Profesores: Germán llalba Madrd Mguel A. Zamora Izquerdo Tema 6 Amplfcadores peraconales ev 4 CNTENID Introduccón El amplfcador dferencal
AMPLIFICADORES CON BJT.
 Tema 5 MPLIFICDORES CON BJT..- Introduccón...- Prncpo de Superposcón...- Nomenclatura..3.- Recta de Carga Estátca..4.- Recta de Carga Dnámca..- Modelo de pequeña señal del BJT...- El cuadrpolo y el modelo
Tema 5 MPLIFICDORES CON BJT..- Introduccón...- Prncpo de Superposcón...- Nomenclatura..3.- Recta de Carga Estátca..4.- Recta de Carga Dnámca..- Modelo de pequeña señal del BJT...- El cuadrpolo y el modelo
5. LNAs y Mezcladores
 5. Ns y Mezcladores 5.1 Característcas de los N El N (ow Nose mplfer es el prmer eslabón de la cadena del receptor. En el caso de un transceptor (transmsor-receptor que use FDD (frequency-dson duplexng
5. Ns y Mezcladores 5.1 Característcas de los N El N (ow Nose mplfer es el prmer eslabón de la cadena del receptor. En el caso de un transceptor (transmsor-receptor que use FDD (frequency-dson duplexng
Problemas donde intervienen dos o más variables numéricas
 Análss de Regresón y Correlacón Lneal Problemas donde ntervenen dos o más varables numércas Estudaremos el tpo de relacones que exsten entre ellas, y de que forma se asocan Ejemplos: La presón de una masa
Análss de Regresón y Correlacón Lneal Problemas donde ntervenen dos o más varables numércas Estudaremos el tpo de relacones que exsten entre ellas, y de que forma se asocan Ejemplos: La presón de una masa
v i CIRCUITOS ELÉCTRICOS (apuntes para el curso de Electrónica)
 IUITOS EÉTIOS (apuntes para el curso de Electrónca) os crcutos eléctrcos están compuestos por: fuentes de energía: generadores de tensón y generadores de corrente y elementos pasos: resstores, nductores
IUITOS EÉTIOS (apuntes para el curso de Electrónca) os crcutos eléctrcos están compuestos por: fuentes de energía: generadores de tensón y generadores de corrente y elementos pasos: resstores, nductores
Simulador Convertidores DC-DC
 Dept d'eng. Electrònca, Elèctrca, Automàtca (DEEEA) Escola Tècnca Superor d'engnyera (ETSE) Unverstat ovra rgl (U) Proyecto Fnal de arrera Smulador onvertdores D-D AUTO: íctor Galera Ortega DIETO: Abdelal
Dept d'eng. Electrònca, Elèctrca, Automàtca (DEEEA) Escola Tècnca Superor d'engnyera (ETSE) Unverstat ovra rgl (U) Proyecto Fnal de arrera Smulador onvertdores D-D AUTO: íctor Galera Ortega DIETO: Abdelal
Tema 1. Conceptos Básicos de la Teoría de Circuitos
 Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades.3 Carga y corrente.4 Tensón.5 Potenca y energía.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de tensón
Tema. Conceptos Báscos de la Teoría de Crcutos. Introduccón. Sstema de undades.3 Carga y corrente.4 Tensón.5 Potenca y energía.6 Ley de Ohm.7 Fuentes ndependentes.8 Leyes de Krchhoff.9 Dsores de tensón
PROPORCIONAR RESERVA ROTANTE PARA EFECTUAR LA REGULACIÓN PRIMARIA DE FRECUENCIA ( RPF)
 ANEXO I EVALUACIÓN DE LA ENERGIA REGULANTE COMENSABLE (RRmj) OR ROORCIONAR RESERVA ROTANTE ARA EFECTUAR LA REGULACIÓN RIMARIA DE FRECUENCIA ( RF) REMISAS DE LA METODOLOGÍA Las pruebas dnámcas para la Regulacón
ANEXO I EVALUACIÓN DE LA ENERGIA REGULANTE COMENSABLE (RRmj) OR ROORCIONAR RESERVA ROTANTE ARA EFECTUAR LA REGULACIÓN RIMARIA DE FRECUENCIA ( RF) REMISAS DE LA METODOLOGÍA Las pruebas dnámcas para la Regulacón
UNIVERSIDAD DE GUADALAJARA, CUCEI DEPARTAMENTO DE ELECTRÓNICA LABORATORIO DE ELECTRÓNICA II
 UNIVERSIDAD DE GUADALAJARA, CUCEI DEPARTAMENTO DE ELECTRÓNICA LABORATORIO DE ELECTRÓNICA II PRACTICA 11: Crcutos no lneales elementales con el amplfcador operaconal OBJETIVO: El alumno se famlarzará con
UNIVERSIDAD DE GUADALAJARA, CUCEI DEPARTAMENTO DE ELECTRÓNICA LABORATORIO DE ELECTRÓNICA II PRACTICA 11: Crcutos no lneales elementales con el amplfcador operaconal OBJETIVO: El alumno se famlarzará con
AMPLIFICADOR OPERACIONAL
 apítulo MPLFDO OPEONL El mplfcador Operaconal es un amplfcador con realmentacón que se encuentra en el mercado como una pastlla de crcuto ntegrado. Es dfícl enumerar la totaldad de las aplcacones de este
apítulo MPLFDO OPEONL El mplfcador Operaconal es un amplfcador con realmentacón que se encuentra en el mercado como una pastlla de crcuto ntegrado. Es dfícl enumerar la totaldad de las aplcacones de este
AMPLIFICADOR OPERACIONAL
 Fundamentos de Electrónca Amplfcador Operaconal 4 1 CAPÍTULO 4 AMPLIFICADO OPEACIONAL 4.1 PESENTACIÓN El amplfcador operaconal (A.O.) se puede consderar como un amplfcador unersal debdo a su gran ersatldad
Fundamentos de Electrónca Amplfcador Operaconal 4 1 CAPÍTULO 4 AMPLIFICADO OPEACIONAL 4.1 PESENTACIÓN El amplfcador operaconal (A.O.) se puede consderar como un amplfcador unersal debdo a su gran ersatldad
LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA
 LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA. LA MEDIANA: Es una medda de tendenca central que dvde al total de n observacones debdamente ordenadas
LECTURA 07: MEDIDAS DE TENDENCIA CENTRAL (PARTE II) LA MEDIANA Y LA MODA TEMA 17: LA MEDIANA Y LA MODA. LA MEDIANA: Es una medda de tendenca central que dvde al total de n observacones debdamente ordenadas
Convertidores Digital-Analógico y Analógico-Digital
 Convertdores Dgtal-Analógco y Analógco-Dgtal Conversón Dgtal-Analógca y Analógca-Dgtal Con estos crcutos se trata de consegur una relacón bunívoca entre una señal analógca y una dgtal o vceversa. Las magntudes
Convertdores Dgtal-Analógco y Analógco-Dgtal Conversón Dgtal-Analógca y Analógca-Dgtal Con estos crcutos se trata de consegur una relacón bunívoca entre una señal analógca y una dgtal o vceversa. Las magntudes
Guía de Electrodinámica
 INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
INSTITITO NACIONAL Dpto. de Físca 4 plan electvo Marcel López U. 05 Guía de Electrodnámca Objetvo: - econocer la fuerza eléctrca, campo eléctrco y potencal eléctrco generado por cargas puntuales. - Calculan
1 Aplicaciones básicas del amplificador operacional
 1 Aplcacones báscas del amplfcador operaconal 15 1 Aplcacones báscas del amplfcador operaconal El objeto prncpal de esta práctca es la presentacón y expermentacón del amplfcador operaconal (AO) en confguracones
1 Aplcacones báscas del amplfcador operaconal 15 1 Aplcacones báscas del amplfcador operaconal El objeto prncpal de esta práctca es la presentacón y expermentacón del amplfcador operaconal (AO) en confguracones
GUIAS DE ACTIVIDADES Y TRABAJO PRACTICO Nº 22
 DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
DOCENTE: LIC.GUSTO DOLFO JUEZ GUI DE TJO PCTICO Nº 22 CES: POFESODO Y LICENCITU EN IOLOGI PGIN Nº 132 GUIS DE CTIIDDES Y TJO PCTICO Nº 22 OJETIOS: Lograr que el lumno: Interprete la nformacón de un vector.
Solución: Se denomina malla en un circuito eléctrico a todas las trayectorias cerradas que se pueden seguir dentro del mismo.
 1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
1 A qué se denomna malla en un crcuto eléctrco? Solucón: Se denomna malla en un crcuto eléctrco a todas las trayectoras cerradas que se pueden segur dentro del msmo. En un nudo de un crcuto eléctrco concurren
IES Menéndez Tolosa (La Línea) Física y Química - 1º Bach - Gráficas
 IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
IES Menéndez Tolosa (La Línea) Físca y Químca - 1º Bach - Gráfcas 1 Indca qué tpo de relacón exste entre las magntudes representadas en la sguente gráfca: La gráfca es una línea recta que no pasa por el
Capitalización y descuento simple
 Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
Undad 2 Captalzacón y descuento smple 2.1. Captalzacón smple o nterés smple 2.1.1. Magntudes dervadas 2.2. Intereses antcpados 2.3. Cálculo de los ntereses smples. Métodos abrevados 2.3.1. Método de los
CARTAS DE CONTROL. Han sido difundidas exitosamente en varios países dentro de una amplia variedad de situaciones para el control del proceso.
 CARTAS DE CONTROL Las cartas de control son la herramenta más poderosa para analzar la varacón en la mayoría de los procesos. Han sdo dfunddas extosamente en varos países dentro de una ampla varedad de
CARTAS DE CONTROL Las cartas de control son la herramenta más poderosa para analzar la varacón en la mayoría de los procesos. Han sdo dfunddas extosamente en varos países dentro de una ampla varedad de
3. VARIABLES ALEATORIAS.
 3. VARIABLES ALEATORIAS. Una varable aleatora es una varable que toma valores numércos determnados por el resultado de un epermento aleatoro (no hay que confundr la varable aleatora con sus posbles valores)
3. VARIABLES ALEATORIAS. Una varable aleatora es una varable que toma valores numércos determnados por el resultado de un epermento aleatoro (no hay que confundr la varable aleatora con sus posbles valores)
EL AMPLIFICADOR OPERACIONAL
 Tema 6 EL AMPLIFICAD PEACINAL.- Introduccón...- Símbolos y termnales del amplfcador operaconal...- El amplfcador operaconal como amplfcador de tensón..3.- Conceptos báscos de realmentacón..4.- El amplfcador
Tema 6 EL AMPLIFICAD PEACINAL.- Introduccón...- Símbolos y termnales del amplfcador operaconal...- El amplfcador operaconal como amplfcador de tensón..3.- Conceptos báscos de realmentacón..4.- El amplfcador
Medidas de centralización
 1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
1 Meddas de centralzacón Meda Datos no agrupados = x X = n = 0 Datos agrupados = x X = n = 0 Medana Ordenamos la varable de menor a mayor. Calculamos la columna de la frecuenca relatva acumulada F. Buscamos
RESISTENCIAS EN SERIE Y LEY DE LAS MALLAS V 1 V 2 V 3 A B C
 RESISTENCIS EN SERIE Y LEY DE LS MLLS V V 2 V 3 C D Fgura R R 2 R 3 Nomenclatura: Suponemos que el potencal en es mayor que el potencal en, por lo tanto la ntensdad de la corrente se mueve haca la derecha.
RESISTENCIS EN SERIE Y LEY DE LS MLLS V V 2 V 3 C D Fgura R R 2 R 3 Nomenclatura: Suponemos que el potencal en es mayor que el potencal en, por lo tanto la ntensdad de la corrente se mueve haca la derecha.
TEMA 2 Amplificadores con transistores: Modelos de pequeña señal
 Tema 2 TMA 2 Amplfcadores con transstores: Modelos de pequeña señal 2..- Introduccón La polarzacón de un transstor es la responsable de establecer las correntes y tensones que fjan su punto de trabajo
Tema 2 TMA 2 Amplfcadores con transstores: Modelos de pequeña señal 2..- Introduccón La polarzacón de un transstor es la responsable de establecer las correntes y tensones que fjan su punto de trabajo
1. Lección 7 - Rentas - Valoración (Continuación)
 Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
Apuntes: Matemátcas Fnanceras 1. Leccón 7 - Rentas - Valoracón (Contnuacón) 1.1. Valoracón de Rentas: Constantes y Dferdas 1.1.1. Renta Temporal y Pospagable En este caso, el orgen de la renta es un momento
ECUALIZADORES. 1. Introducción
 ECUALIADOES Federco Myara. Introduccón Un ecualzador permte aumentar o reducr la gananca selectamente en tres o más frecuencas para corregr defcencas en la respuesta frecuencal de un sstema (generalmente
ECUALIADOES Federco Myara. Introduccón Un ecualzador permte aumentar o reducr la gananca selectamente en tres o más frecuencas para corregr defcencas en la respuesta frecuencal de un sstema (generalmente
Tema 3. Teoremas de la Teoría de Circuitos
 Tema 3. Teoremas de la Teoría de Crcutos 3.1 Introduccón 3. Superposcón 3.3 Transformacón de fuentes 3.4 Teorema de Theenn 3.5 Teorema de Norton V Th Th L 3.6 Máxma transferenca de potenca José. Pereda,
Tema 3. Teoremas de la Teoría de Crcutos 3.1 Introduccón 3. Superposcón 3.3 Transformacón de fuentes 3.4 Teorema de Theenn 3.5 Teorema de Norton V Th Th L 3.6 Máxma transferenca de potenca José. Pereda,
Relaciones entre variables
 Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
Relacones entre varables Las técncas de regresón permten hacer predccones sobre los valores de certa varable Y (dependente), a partr de los de otra (ndependente), entre las que se ntuye que exste una relacón.
OPERACIONES ARMONIZACION DE CRITERIOS EN CALCULO DE PRECIOS Y RENDIMIENTOS
 P L V S V LT R A BANCO DE ESPAÑA OPERACIONES Gestón de la Informacón ARMONIZACION DE CRITERIOS EN CALCULO DE PRECIOS Y RENDIMIENTOS El proceso de ntegracón fnancera dervado de la Unón Monetara exge la
P L V S V LT R A BANCO DE ESPAÑA OPERACIONES Gestón de la Informacón ARMONIZACION DE CRITERIOS EN CALCULO DE PRECIOS Y RENDIMIENTOS El proceso de ntegracón fnancera dervado de la Unón Monetara exge la
Tema 4: Variables aleatorias
 Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Estadístca 46 Tema 4: Varables aleatoras El concepto de varable aleatora surge de la necesdad de hacer más manejables matemátcamente los resultados de los expermentos aleatoros, que en muchos casos son
Análisis Matemático en la Economía: Optimización y Programación. Augusto Rufasto
 Análss Matemátco en la Economía: Optmzacón y Programacón [email protected]@lycos.com www.geoctes.com/arufast-http://rufasto.trpod.com La optmzacón y la programacón están en el corazón del problema
Análss Matemátco en la Economía: Optmzacón y Programacón [email protected]@lycos.com www.geoctes.com/arufast-http://rufasto.trpod.com La optmzacón y la programacón están en el corazón del problema
Es el movimiento periódico de un punto material a un lado y a otro de su posición en equilibrio.
 1 Movmento Vbratoro Tema 8.- Ondas, Sondo y Luz Movmento Peródco Un móvl posee un movmento peródco cuando en ntervalos de tempo guales pasa por el msmo punto del espaco sempre con las msmas característcas
1 Movmento Vbratoro Tema 8.- Ondas, Sondo y Luz Movmento Peródco Un móvl posee un movmento peródco cuando en ntervalos de tempo guales pasa por el msmo punto del espaco sempre con las msmas característcas
Facultad de Ingeniería División de Ciencias Básicas Coordinación de Ciencias Aplicadas Departamento de Probabilidad y Estadística
 Facultad de Ingenería Dvsón de Cencas Báscas Coordnacón de Cencas Aplcadas Departamento de Probabldad y Estadístca Probabldad y Estadístca Prmer Eamen Fnal Tpo A Semestre: 00- Duracón máma:. h. Consderar
Facultad de Ingenería Dvsón de Cencas Báscas Coordnacón de Cencas Aplcadas Departamento de Probabldad y Estadístca Probabldad y Estadístca Prmer Eamen Fnal Tpo A Semestre: 00- Duracón máma:. h. Consderar
1.- Una empresa se plantea una inversión cuyas características financieras son:
 ESCUELA UNIVERSITARIA DE ESTUDIOS EMPRESARIALES. Departamento de Economía Aplcada (Matemátcas). Matemátcas Fnanceras. Relacón de Problemas. Rentas. 1.- Una empresa se plantea una nversón cuyas característcas
ESCUELA UNIVERSITARIA DE ESTUDIOS EMPRESARIALES. Departamento de Economía Aplcada (Matemátcas). Matemátcas Fnanceras. Relacón de Problemas. Rentas. 1.- Una empresa se plantea una nversón cuyas característcas
TEMA 4. TRABAJO Y ENERGIA.
 TMA 4. TRABAJO Y NRGIA. l problema undamental de la Mecánca es descrbr como se moverán los cuerpos s se conocen las uerzas aplcadas sobre él. La orma de hacerlo es aplcando la segunda Ley de Newton, pero
TMA 4. TRABAJO Y NRGIA. l problema undamental de la Mecánca es descrbr como se moverán los cuerpos s se conocen las uerzas aplcadas sobre él. La orma de hacerlo es aplcando la segunda Ley de Newton, pero
TEMA 10. OPERACIONES PASIVAS Y OPERACIONES ACTIVAS.
 GESTIÓN FINANCIERA. TEMA 10. OPERACIONES PASIVAS Y OPERACIONES ACTIVAS. 1.- Funconamento de las cuentas bancaras. FUNCIONAMIENTO DE LAS CUENTAS BANCARIAS. Las cuentas bancaras se dvden en tres partes:
GESTIÓN FINANCIERA. TEMA 10. OPERACIONES PASIVAS Y OPERACIONES ACTIVAS. 1.- Funconamento de las cuentas bancaras. FUNCIONAMIENTO DE LAS CUENTAS BANCARIAS. Las cuentas bancaras se dvden en tres partes:
Unidad temática 2: AMPLIFICADORES DE AUDIOFRECUENCIAS DE GRAN SEÑAL
 Undad temátca : AMPLIFICADOES DE AUDIOFECUENCIAS DE GAN SEÑAL Profeor: Ing. Aníbal Laqudara. J..P.: Ing. Idoro Pablo Perez. Ay. Dplomado: Ing. Carlo Díaz. Ay. Dplomado: Ing. Alejandro Gordana Ay. Alumno:
Undad temátca : AMPLIFICADOES DE AUDIOFECUENCIAS DE GAN SEÑAL Profeor: Ing. Aníbal Laqudara. J..P.: Ing. Idoro Pablo Perez. Ay. Dplomado: Ing. Carlo Díaz. Ay. Dplomado: Ing. Alejandro Gordana Ay. Alumno:
TERMODINÁMICA DEL EQUILIBRIO CAPÍTULO V. EQUILIBRIO DE REACCIÓN QUÍMICA
 Ing. Federco G. Salazar Termodnámca del Equlbro TERMODINÁMICA DEL EQUILIBRIO CAPÍTULO V. EQUILIBRIO DE REACCIÓN QUÍMICA Contendo 1. Conversón y Coordenada de Reaccón. 2. Ecuacones Independentes y Regla
Ing. Federco G. Salazar Termodnámca del Equlbro TERMODINÁMICA DEL EQUILIBRIO CAPÍTULO V. EQUILIBRIO DE REACCIÓN QUÍMICA Contendo 1. Conversón y Coordenada de Reaccón. 2. Ecuacones Independentes y Regla
Trabajo y Energía Cinética
 Trabajo y Energía Cnétca Objetvo General Estudar el teorema de la varacón de la energía. Objetvos Partculares 1. Determnar el trabajo realzado por una fuerza constante sobre un objeto en movmento rectlíneo..
Trabajo y Energía Cnétca Objetvo General Estudar el teorema de la varacón de la energía. Objetvos Partculares 1. Determnar el trabajo realzado por una fuerza constante sobre un objeto en movmento rectlíneo..
7. Máquinas Síncrónicas
 7. Máqunas Síncróncas 7.1 Introduccón Las máqunas sncróncas (o sncróncas) son maqunas cuyo estator se encuentra almentado por corrente alterna, en tanto el rotor tene almentacón contnua ya sea a través
7. Máqunas Síncróncas 7.1 Introduccón Las máqunas sncróncas (o sncróncas) son maqunas cuyo estator se encuentra almentado por corrente alterna, en tanto el rotor tene almentacón contnua ya sea a través
Electricidad y calor. Un repaso... Temas. 4. Primera ley de la Termodinámica. Webpage: Algunas definiciones
 Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
Electrcdad y calor Webpage: http://pagnas.sca.uson.mx/qb 2007 Departamento de Físca Unversdad de Sonora Temas 4. Prmera ley de la Termodnámca.. Concepto de Trabajo aplcado a gases.. Trabajo hecho por un
E0601 y E0602 ELECTRÓNICA DE POTENCIA MANUAL DE PRACTICAS (SIMULACIÓN/EXPERIMENTAL) Facultad de Ciencias UASLP
 E61 y E62 ELECTRÓNICA DE POTENCIA MANUAL DE PRACTICAS (SIMULACIÓN/EXPERIMENTAL) Facultad de Cencas UASLP ProfesorInestgador VI Facultad de Cencas UASLP 25 I 1. Presentacón La electrónca de potenca ha tendo
E61 y E62 ELECTRÓNICA DE POTENCIA MANUAL DE PRACTICAS (SIMULACIÓN/EXPERIMENTAL) Facultad de Cencas UASLP ProfesorInestgador VI Facultad de Cencas UASLP 25 I 1. Presentacón La electrónca de potenca ha tendo
OP-AMP ideal. Circuito equivalente. R o. i o. R i. v o. i 2 + v 2. A(v 1 v 2 )
 El amplfcador operaconal Símbolos y termnales El amplfcador operaconal op amp es un crcuto ntegrado básco utlzado en crcutos analógcos. Aplcacones: amplfcacón/escalamento de señales de entrada nversón
El amplfcador operaconal Símbolos y termnales El amplfcador operaconal op amp es un crcuto ntegrado básco utlzado en crcutos analógcos. Aplcacones: amplfcacón/escalamento de señales de entrada nversón
Leyes de tensión y de corriente
 hay6611x_ch03.qxd 1/4/07 5:07 PM Page 35 CAPÍTULO 3 Leyes de tensón y de corrente CONCEPTOS CLAVE INTRODUCCIÓN En el capítulo 2 se presentaron la resstenca así como varos tpos de fuentes. Después de defnr
hay6611x_ch03.qxd 1/4/07 5:07 PM Page 35 CAPÍTULO 3 Leyes de tensón y de corrente CONCEPTOS CLAVE INTRODUCCIÓN En el capítulo 2 se presentaron la resstenca así como varos tpos de fuentes. Después de defnr
Tema 3: Adaptadores de Señal
 Tema 3: Adaptadores de Señal Sstema GENERAL de nstrumentacón (bloques( funconales): Señal sensor Fltrado, A/D Amplfcacón Rado, nternet bus de datos Medo Sensor prmaro Transductor de entrada Adaptacón de
Tema 3: Adaptadores de Señal Sstema GENERAL de nstrumentacón (bloques( funconales): Señal sensor Fltrado, A/D Amplfcacón Rado, nternet bus de datos Medo Sensor prmaro Transductor de entrada Adaptacón de
ACTIVIDADES INICIALES
 Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Soluconaro 7 Números complejos ACTIVIDADES INICIALES 7.I. Clasfca los sguentes números, dcendo a cuál de los conjuntos numércos pertenece (entendendo como tal el menor conjunto). a) 0 b) 6 c) d) e) 0 f)
Comparación entre distintos Criterios de decisión (VAN, TIR y PRI) Por: Pablo Lledó
 Comparacón entre dstntos Crteros de decsón (, TIR y PRI) Por: Pablo Lledó Master of Scence en Evaluacón de Proyectos (Unversty of York) Project Management Professonal (PMP certfed by the PMI) Profesor
Comparacón entre dstntos Crteros de decsón (, TIR y PRI) Por: Pablo Lledó Master of Scence en Evaluacón de Proyectos (Unversty of York) Project Management Professonal (PMP certfed by the PMI) Profesor
8 MECANICA Y FLUIDOS: Calorimetría
 8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
8 MECANICA Y FLUIDOS: Calormetría CONTENIDOS Dencones. Capacdad caloríca. Calor especíco. Equlbro térmco. Calormetría. Calorímetro de las mezclas. Marcha del calorímetro. Propagacón de Errores. OBJETIVOS
TEMA 8: PRÉSTAMOS ÍNDICE
 TEM 8: PRÉSTMOS ÍNDICE 1. CONCEPTO DE PRÉSTMO: SISTEMS DE MORTIZCIÓN DE PRÉSTMOS... 1 2. NOMENCLTUR PR PRÉSTMOS DE MORTIZCIÓN FRCCIOND... 3 3. CUDRO DE MORTIZCIÓN GENERL... 3 4. MORTIZCIÓN DE PRÉSTMO MEDINTE
TEM 8: PRÉSTMOS ÍNDICE 1. CONCEPTO DE PRÉSTMO: SISTEMS DE MORTIZCIÓN DE PRÉSTMOS... 1 2. NOMENCLTUR PR PRÉSTMOS DE MORTIZCIÓN FRCCIOND... 3 3. CUDRO DE MORTIZCIÓN GENERL... 3 4. MORTIZCIÓN DE PRÉSTMO MEDINTE
Amplificadores operacionales con diodos
 5 Amplfcadres peracnales cn dds 5.1 Intrduccón En este capítul se estudan ls crcuts amplfcadres peracnales que ncrpran dds. Ests cmpnentes n lneales hacen que la característca de transferenca del crcut
5 Amplfcadres peracnales cn dds 5.1 Intrduccón En este capítul se estudan ls crcuts amplfcadres peracnales que ncrpran dds. Ests cmpnentes n lneales hacen que la característca de transferenca del crcut
FUNDAMENTOS QUIMICOS DE LA INGENIERIA
 FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
FUNDAMENTOS QUIMICOS DE LA INGENIERIA (BLOQUE DE INGENIERIA QUIMICA) GUION DE PRACTICAS DE LABORATORIO ANTONIO DURÁN SEGOVIA JOSÉ MARÍA MONTEAGUDO MARTÍNEZ INDICE PRACTICA PAGINA BALANCE MACROSCÓPICO DE
Población: Es el conjunto de todos los elementos cuyo conocimiento nos interesa y serán objeto de nuestro estudio.
 Tema 9 - Estadístca - Matemátcas B 4º E.S.O. 1 TEMA 9 - ESTADÍSTICA 9.1 DOS RAMAS DE LA ESTADÍSTICA 9.1.1 - INTRODUCCIÓN La estadístca tene por objeto el desarrollo de técncas para el conocmento numérco
Tema 9 - Estadístca - Matemátcas B 4º E.S.O. 1 TEMA 9 - ESTADÍSTICA 9.1 DOS RAMAS DE LA ESTADÍSTICA 9.1.1 - INTRODUCCIÓN La estadístca tene por objeto el desarrollo de técncas para el conocmento numérco
Módulo 3. OPTIMIZACION MULTIOBJETIVO DIFUSA (Fuzzy Multiobjective Optimization)
 Módulo 3. OPTIMIZACION MULTIOBJETIVO DIFUSA (Fuzzy Multobjectve Optmzaton) Patrca Jaramllo A. y Rcardo Smth Q. Insttuto de Sstemas y Cencas de la Decsón Facultad de Mnas Unversdad Naconal de Colomba, Medellín,
Módulo 3. OPTIMIZACION MULTIOBJETIVO DIFUSA (Fuzzy Multobjectve Optmzaton) Patrca Jaramllo A. y Rcardo Smth Q. Insttuto de Sstemas y Cencas de la Decsón Facultad de Mnas Unversdad Naconal de Colomba, Medellín,
Análisis de Regresión y Correlación
 1 Análss de Regresón y Correlacón El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes (o relaconadas). El análss de correlacón
1 Análss de Regresón y Correlacón El análss de regresón consste en emplear métodos que permtan determnar la mejor relacón funconal entre dos o más varables concomtantes (o relaconadas). El análss de correlacón
Capítulo 8. Ruido. Introducción
 55 Capítulo 8 Rudo Introduccón En prncpo, puede defnrse como rudo a cualquer señal ndeseable en un sstema de telecomuncacones. Sn embargo, tal defncón resultaría ambgua, ya que permte nterpretar como rudo
55 Capítulo 8 Rudo Introduccón En prncpo, puede defnrse como rudo a cualquer señal ndeseable en un sstema de telecomuncacones. Sn embargo, tal defncón resultaría ambgua, ya que permte nterpretar como rudo
ELEMENTOS DE ELECTRICIDAD BASICA
 MODULO 1 ELEMENTOS DE ELECTRICIDAD BASICA A contnuacón se resumen algunos elementos de Electrcdad Básca que se supone son conocdos por los estudantes al ngresar a la Unversdad DESCUBRIMIENTO DE LA ELECTRICIDAD:
MODULO 1 ELEMENTOS DE ELECTRICIDAD BASICA A contnuacón se resumen algunos elementos de Electrcdad Básca que se supone son conocdos por los estudantes al ngresar a la Unversdad DESCUBRIMIENTO DE LA ELECTRICIDAD:
Tema 1.3_A La media y la desviación estándar
 Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
Curso 0-03 Grado en Físca Herramentas Computaconales Tema.3_A La meda y la desvacón estándar Dónde estudar el tema.3_a: Capítulo 4. J.R. Taylor, Error Analyss. Unv. cence Books, ausalto, Calforna 997.
Técnico. Capítulo. Indice. Aclaraciones y consideraciones para usar este catálogo. Como identificar un buen cable
 Técnco Indce 1 4 6 7 10 7 Aclaracones y consderacones para usar este catálogo Como dentfcar un buen cable Característcas de aslantes y vanas: PVC PVC/Nylon Santoprene (EPDM) XLPE Poletleno - Pololefna
Técnco Indce 1 4 6 7 10 7 Aclaracones y consderacones para usar este catálogo Como dentfcar un buen cable Característcas de aslantes y vanas: PVC PVC/Nylon Santoprene (EPDM) XLPE Poletleno - Pololefna
Disipación de energía mecánica
 Laboratoro de Mecáa. Expermento 13 Versón para el alumno Dspacón de energía mecáa Objetvo general El estudante medrá la energía que se perde por la accón de la uerza de rozamento. Objetvos partculares
Laboratoro de Mecáa. Expermento 13 Versón para el alumno Dspacón de energía mecáa Objetvo general El estudante medrá la energía que se perde por la accón de la uerza de rozamento. Objetvos partculares
Maestría en Administración. Medidas Descriptivas. Formulario e Interpretación. Dr. Francisco Javier Cruz Ariza
 Maestría en Admnstracón Meddas Descrptvas Formularo e Interpretacón Dr. Francsco Javer Cruz Arza A contnuacón mostramos el foco de atencón de las dstntas meddas que abordaremos en el presente manual. El
Maestría en Admnstracón Meddas Descrptvas Formularo e Interpretacón Dr. Francsco Javer Cruz Arza A contnuacón mostramos el foco de atencón de las dstntas meddas que abordaremos en el presente manual. El
1. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA. Definición del álgebra geométrica del espacio-tiempo
 EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO. GENERALIDADES DEL ÁLGEBRA GEOMÉTRICA Defncón del álgebra geométrca del espaco-tempo Defno el álgebra geométrca del espaco y tempo como el álgebra de las matrces
Resumen TEMA 1: Teoremas fundamentales de la dinámica y ecuaciones de Lagrange
 TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange Mecánca 2 Resumen TEMA : Teoremas fundamentales de la dnámca y ecuacones de Lagrange. Prncpos de dnámca clásca.. Leyes de ewton a) Ley
REGULACION No. CONELEC 004/01 CALIDAD DEL SERVICIO ELECTRICO DE DISTRIBUCION EL DIRECTORIO DEL CONSEJO NACIONAL DE ELECTRICIDAD CONELEC.
 REGULACION No. CONELEC 004/01 CALIDAD DEL SERVICIO ELECTRICO DE DISTRIBUCION EL DIRECTORIO DEL CONSEJO NACIONAL DE ELECTRICIDAD CONELEC Consderando: Que, es necesaro asegurar un nvel satsfactoro de la
REGULACION No. CONELEC 004/01 CALIDAD DEL SERVICIO ELECTRICO DE DISTRIBUCION EL DIRECTORIO DEL CONSEJO NACIONAL DE ELECTRICIDAD CONELEC Consderando: Que, es necesaro asegurar un nvel satsfactoro de la
Fisicoquímica CIBEX Guía de Trabajos Prácticos 2010. Trabajo Práctico N 7. - Medida de la Fuerza Electromotriz por el Método de Oposición-
 Fscoquímca CIBX Guía de Trabajos Práctcos 2010 Trabajo Práctco N 7 - Medda de la Fuerza lectromotrz por el Método de Oposcón- Objetvo: Medr la fuerza electromotrz (FM) de la pla medante el método de oposcón
Fscoquímca CIBX Guía de Trabajos Práctcos 2010 Trabajo Práctco N 7 - Medda de la Fuerza lectromotrz por el Método de Oposcón- Objetvo: Medr la fuerza electromotrz (FM) de la pla medante el método de oposcón
Aplicación de la termodinámica a las reacciones químicas Andrés Cedillo Departamento de Química Universidad Autónoma Metropolitana-Iztapalapa
 Aplcacón de la termodnámca a las reaccones químcas Andrés Cedllo Departamento de Químca Unversdad Autónoma Metropoltana-Iztapalapa Introduccón Las leyes de la termodnámca, así como todas las ecuacones
Aplcacón de la termodnámca a las reaccones químcas Andrés Cedllo Departamento de Químca Unversdad Autónoma Metropoltana-Iztapalapa Introduccón Las leyes de la termodnámca, así como todas las ecuacones
Transformación de Park o D-Q
 Apénce B ransformacón e Park o D-Q B.. Expresón e la matrz e transformacón La transformacón e Park o D-Q conerte las componentes 'abc' el sstema trfásco a otro sstema e referenca 'q'. El objeto e la transformacón
Apénce B ransformacón e Park o D-Q B.. Expresón e la matrz e transformacón La transformacón e Park o D-Q conerte las componentes 'abc' el sstema trfásco a otro sstema e referenca 'q'. El objeto e la transformacón
ONDAS ESFÉRICAS RADIACIÓN ACÚSTICA
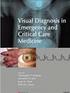 ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
ONDAS ESFÉRCAS RADACÓN ACÚSTCA.- SEA UN MEDO FLUDO LMTADO SÓTROPO Y HOMOGÉNEO. CONSDEREMOS EN SU NTEROR UNA ESFERA DE RADO QUE SE HNCHA RÁPDAMENTE HASTA LOGRAR UN VALOR DE RADO. EL FLUDO ALREDEDOR DE LA
TRABAJO 1: Variables Estadísticas Unidimensionales (Tema 1).
 TRABAJO 1: Varables Estadístcas Undmensonales (Tema 1). Técncas Cuanttatvas I. Curso 2016/2017. APELLIDOS: NOMBRE: GRADO: GRUPO: DNI (o NIE): A: B: C: D: En los enuncados de los ejerccos que sguen aparecen
TRABAJO 1: Varables Estadístcas Undmensonales (Tema 1). Técncas Cuanttatvas I. Curso 2016/2017. APELLIDOS: NOMBRE: GRADO: GRUPO: DNI (o NIE): A: B: C: D: En los enuncados de los ejerccos que sguen aparecen
CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS
 CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS Edgar Acuña Fernández Departamento de Matemátcas Unversdad de Puerto Rco Recnto Unverstaro de Mayagüez Edgar Acuña Analss de Regreson Regresón con varables
CAPÍTULO 5 REGRESIÓN CON VARIABLES CUALITATIVAS Edgar Acuña Fernández Departamento de Matemátcas Unversdad de Puerto Rco Recnto Unverstaro de Mayagüez Edgar Acuña Analss de Regreson Regresón con varables
