Laboratorio N 10, Operaciones diferenciales. Gradiente, divergencia y rotacional. Introducción.
|
|
|
- Mariano Salazar Tebar
- hace 7 años
- Vistas:
Transcripción
1 Universidad Diego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Asignatura: Cálculo III Laboratorio N 10, Operaciones diferenciales. Gradiente, divergencia y rotacional. Introducción. n El gradiente es una operación que se aplica sobre una función real f : R R y su resultado es una función vectorial (campo vectorial) cuyos componentes son las derivadas parciales de la función f. En particular para funciones f : R R tenemos que: f f f f ( x, y, z) grad ( f ) =,,. x y z n n La divergencia es una operación que se aplica sobre una función vectorial F : R R y su resultado es una función real formada por la suma de las derivadas parciales: n Fi F div( F) =. i= 1 dxi El rotacional es una operación que se aplica sobre una función vectorial y el resultado es otra función vectorial. En particular, para funciones F : R R tenemos: iˆ ˆj kˆ F F rot ( ) ˆ F F 1 ˆ F F F F = = i j 1 kˆ + +. x y z y z z x x y F1 F F Las funciones vectoriales F, tales que F = 0 se denominan campos potenciales o conservativos. Como se verá en el ejercicio resuelto (a), deberá existir una función real f, que habitualmente se le denomina potencial escalar, tal que F = f. Un campo de divergencia nula se denomina campo solenoidal. Ejemplos Resueltos: 1. Defina funciones de usuario para calcular las operaciones diferenciales básicas, es decir para el gradiente, la divergencia y el rotacional.. Denominamos grad a la función de usuario que permite calcular el gradiente de funciones f : R R: Define library\grad(a,b,c,e)=[diff(a,b),diff(a,c),diff(a,e)] Debemos hacer notar que el gradiente, también puede calcularse usando la función de usuario Df_m aplicada sobre funciones definidas en la forma {f} m, es decir, suponiendo que las funciones reales (campos escalares) son funciones vectoriales con un solo componente y escribiendo el comando Df_m( m,x,y,z)
2 Denominamos div a la función de usuario que calcula la divergencia de una función vectorial: Define library\div(a,b,c,e)=diff(a[1],b)+diff(a[],c)+diff(a[],e) Otra manera de calcular la divergencia es tomando la traza de la matriz de derivadas parciales, es decir aplicando el comando traza(df_m(f,x,y,z)). Recuerde que la traza es una función de usuario que se define de la siguiente manera: Define library\traza(a)=sum(mattolist(trn(diag(a)),1)) Denominamos rot a la función de usuario que calcula el rotacional de una función vectorial: Define library\rot(a,b,c,e)=[diff(a[],c)-diff(a[],e),diff(a[1],e)-diff(a[],b),diff(a[],b)-diff(a[1],c)]. Empleando las funciones de usuario arriba definidas calcule la divergencia y el rotacional de las siguientes funciones vectoriales: a. F = ( xy, yz, zx) x b. ( ) ˆ x F = e sen y i + e cos( y) ˆj+ zkˆ a. Los cálculos se muestran en la figura 1 b. Los cálculos se muestran en la figura Figura 1 Figura Figura. Con ayuda de la calculadora demuestre que: a. ( f ) = 0, el rotacional del gradiente es cero b. ( F ) = 0, la divergencia del rotacional es cero. a. Al aplicar la función de usuario grad sobre la función general f (,, ) f ( xyz,, ) f( xyz,, ) f( xyz,, ) xyz se obtiene un vector en la forma,,. Por otro lado la función de x y z usuario rot se aplica sobre una lista por lo que primeramente debemos convertir este vector a una lista mediante el siguiente comando: mattolist(trn(grad(f(x,y,z),x,y,z)),1) m
3 Aplicamos ahora la función rot sobre la lista m. El resultado se muestra en la figura. Resumimos aquí los resultados obtenidos: = f( xyz,, ) + f( xyz,, ) = 0 1 z y y z = f( xyz,, ) f( xyz,, ) = 0 z x x z = f( xyz,, ) + f( xyz,, ) = 0 y x x y Vemos que cada componente esta compuesto por la resta de las derivadas cruzadas, como estas derivadas son iguales cada componente se anula. b. Definimos un campo vectorial general: {P(x,y,z),Q(x,y,z),R(x,y,z)} F Calculamos su rotacional, lo escribimos como una lista y la almacenamos en m mattolist(trn(rot(f,x,y,z)),1) m Aplicamos la función de usuario div sobre m (ver figura 4) y obtenemos el siguiente resultado: divmxyz (,,, ) = Pxyz (,, ) + Pxyz (,, ) z y y z + Q( x, y, z) Q( x, y, z) z x x z R( xyz,, ) + R( xyz,, ) = 0 y x x y En esta expresión se observa claramente que las derivadas cruzadas de una misma función aparecen con distintos signos y por lo tanto se cancelan. 4. Cree un programa que permita determinar si un campo vectorial es conservativo o no y en caso de que sea conservativo calcule el potencial escalar correspondiente. a. Utilice el programa creado para encontrar el potencial escalar del campo: F = yi ˆ + z cos yz + x ˆ j+ ycos yz k ( ( ) ) ( ) ˆ En el recuadro se muestra en programa Pot_f que permite calcular el potencial escalar (salvo constante numérica) en caso de que la función vectorial sea un campo conservativo. a. La utilización del programa Pot_f para determinar el potencial escalar del campo: F = yi ˆ + z( cos( yz) + x) ˆ j+ ycos( yz) k ˆ Se muestra en las figuras 5 y 6 Programa Pot_f DelVar F,h,g,C Input F, "{P(x,y,z),Q(x,y,z),R(x,y,z)}" If norm(rot(f,x,y,z))=0 Then (F[1],x) h (simplify(f[]-diff(h,y)),y) g (simplify(f[]-diff(h,z)-diff(g,z)),z) C PrintNatural h+g+c, El potencial es: Else Print "No es conservativo" IfEnd
4 5. Construya una función de usuario para calcular factores de escala de coordenadas curvilíneas. a. Utilice la función de usuario para calcular los factores de escala de las coordenadas i. Cilíndricas. ii. Esféricas. Los factores de escala correspondientes a las coordenadas curvilíneas (,, ) u1 u u se denotan por r h 1, h y h respectivamente y se calculan mediante las fórmulas h i =, con i = 1,,. ui Definimos función de usuario FactEsc : a-i La figura 7 muestra el cálculo de los factores de escala para las coordenadas cilíndricas r, θ, z. ( ) Figura 4 Figura 5 Figura 6 Define library\factesc(a,b)= (simplify(dotp(listtomat(diff(a,b)),listtomat(diff(a,b))))) Figura 7 Figura 8 Figura 9 a-ii Para calcular los factores de escala para las coordenadas esféricas ( r, θ, φ ) construimos la función: { rcosφsin θ, rsinφsin θ, rcosθ} m La figura 8 muestra el cálculo para los correspondientes factores de escala. Hacemos notar que los factores de escala calculados son esencialmente correctos. Sin embargo, el factor h φ puede simplificarse aún más y quedar en la forma hφ = rsenθ 6. Construya una función de usuario para calcular el gradiente en coordenadas curvilíneas.
5 : La fórmula del gradiente en coordenadas curvilíneas: 1 f 1 f 1 f f = eˆ ˆ ˆ 1+ e + e, donde h 1, h y h son los factores de escala h1 du1 h du h du correspondientes a las coordenadas ( u1, u, u ) ê, 1 ê y ê son los vectores unitarios correspondientes. La función de usurario gradcurv permite calcular el gradiente en coordenadas curvilíneas. Para poder utilizarlo es necesario calcular antes los factores de escala Define library\gradcurv(a,b,c,e,f)= diff ( ab, ), diff ( ac, ), diff ( ae, ) f [] 1 f [ ] f [ ] Un ejemplo de aplicación de este gradiente para coordenadas esféricas está dado en la figura 9.
si existen las derivadas parciales en r 0 lim = 0
 Universidad Diego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Asignatura: Cálculo III Laboratorio N 6, nciones de varias variables, Derivadas. Introducción. En este laboratorio vamos
Universidad Diego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Asignatura: Cálculo III Laboratorio N 6, nciones de varias variables, Derivadas. Introducción. En este laboratorio vamos
Laboratorio N 8, Extremos condicionados, Multiplicadores de Lagrange.
 Universidad Diego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Asignatura: Cálculo III Laboratorio N 8, Extremos condicionados, Multiplicadores de Lagrange. Introducción. En este laboratorio
Universidad Diego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Asignatura: Cálculo III Laboratorio N 8, Extremos condicionados, Multiplicadores de Lagrange. Introducción. En este laboratorio
Campos Vectoriales y Operadores Diferenciales
 Campos Vectoriales y Operadores Diferenciales 1 Campos Vectoriales y Operadores Diferenciales Opcional Un en R n es una función (continua) F : D R n R n. Una (línea de corriente o también curva integral)
Campos Vectoriales y Operadores Diferenciales 1 Campos Vectoriales y Operadores Diferenciales Opcional Un en R n es una función (continua) F : D R n R n. Una (línea de corriente o también curva integral)
SERIE # 2 CÁLCULO VECTORIAL
 SERIE # CÁLCULO VECTORIAL SERIE 1) Calcular las coordenadas del punto P de la curva: en el que el vector P 1, 1, r t es paralelo a r t Página 1 t1 r t 1 t i ( t ) j e k ) Una partícula se mueve a lo largo
SERIE # CÁLCULO VECTORIAL SERIE 1) Calcular las coordenadas del punto P de la curva: en el que el vector P 1, 1, r t es paralelo a r t Página 1 t1 r t 1 t i ( t ) j e k ) Una partícula se mueve a lo largo
Primer Examen Parcial Tema A Cálculo Vectorial Marzo 5 de 2016
 rimer Examen arcial Tema A Cálculo Vectorial Marzo 5 de 016 Este es un examen individual, no se permite el uso de libros, apuntes, calculadoras o cualquier otro medio electrónico. Recuerde apagar y guardar
rimer Examen arcial Tema A Cálculo Vectorial Marzo 5 de 016 Este es un examen individual, no se permite el uso de libros, apuntes, calculadoras o cualquier otro medio electrónico. Recuerde apagar y guardar
Operadores diferenciales
 Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
( ) () i ( ) ( ) ( ) cálculos. Por ejemplo, dada una región de integración D de la forma indicada en la figura (i) tenemos:
 Universidad iego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Asignatura: Cálculo III Laboratorio N 9, Integrales Multiples. Introducción. En este laboratorio estudiamos las integrales
Universidad iego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Asignatura: Cálculo III Laboratorio N 9, Integrales Multiples. Introducción. En este laboratorio estudiamos las integrales
6. El teorema de la divergencia.
 GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0. Lección. Cálculo vectorial. 6. El teorema de la divergencia. Ya vimos una versión del teorema de Green en el plano que expresa la igualdad entre la integral doble
GRADO DE INGENIERÍA AEROESPACIAL. CURSO 0. Lección. Cálculo vectorial. 6. El teorema de la divergencia. Ya vimos una versión del teorema de Green en el plano que expresa la igualdad entre la integral doble
Ejercicios del Tema 5
 Ejercicios del Tema 5 En este documento encontrará cómo se puede emplear el programa Maxima para resolver o apoyar algunos pasos de la resolución de varios de los ejercicios del tema. Debe tener en cuenta
Ejercicios del Tema 5 En este documento encontrará cómo se puede emplear el programa Maxima para resolver o apoyar algunos pasos de la resolución de varios de los ejercicios del tema. Debe tener en cuenta
Capítulo 5. Integrales sobre curvas y superficies
 Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
Dpto. Física y Mecánica. Operadores diferenciales
 Dpto. Física y Mecánica Operadores diferenciales Se denominan líneas coordenadas de un espacio euclídeo tridimensional a aquellas que se obtienen partiendo un punto dado P de coordenadas (q 1, q 2, q 3
Dpto. Física y Mecánica Operadores diferenciales Se denominan líneas coordenadas de un espacio euclídeo tridimensional a aquellas que se obtienen partiendo un punto dado P de coordenadas (q 1, q 2, q 3
Gradiente, divergencia y rotacional. Matemá4cas para Ingeniería I Lilia Meza Montes 2017
 Gradiente, divergencia y rotacional Matemá4cas para Ingeniería I Lilia Meza Montes 017 Definición A par4r de una función escalar f(x,y,z) obtenemos otra función vectorial llamada gradiente f ( x, y, z)
Gradiente, divergencia y rotacional Matemá4cas para Ingeniería I Lilia Meza Montes 017 Definición A par4r de una función escalar f(x,y,z) obtenemos otra función vectorial llamada gradiente f ( x, y, z)
CÁLCULO II Grados en Ingeniería
 CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
CÁLCULO II Grados en Ingeniería Domingo Pestana Galván José Manuel Rodríguez García Figuras realizadas con Arturo de Pablo Martínez Capítulo 1. Cálculo diferencial 1.1 Funciones. Límites y continuidad
Matemáticas III Andalucía-Tech
 Matemáticas III Andalucía-Tech Tema Optimización en campos escalares Índice 1. Formas cuadráticas y matrices simétricas reales 1. Extremos relativos de un campo escalar 3.1. Polinomio de Taylor de un campo
Matemáticas III Andalucía-Tech Tema Optimización en campos escalares Índice 1. Formas cuadráticas y matrices simétricas reales 1. Extremos relativos de un campo escalar 3.1. Polinomio de Taylor de un campo
1. Lección 9 - Continuidad y Derivabilidad
 1. Lección 9 - Continuidad y Derivabilidad 1.1. Continuidad El concepto de continuación es el mismo que el visto en el primer cuatrimestre pero generalizado al caso de los campos escalares. Así, sea la
1. Lección 9 - Continuidad y Derivabilidad 1.1. Continuidad El concepto de continuación es el mismo que el visto en el primer cuatrimestre pero generalizado al caso de los campos escalares. Así, sea la
Diferenciación de funciones f : R n R m. f(x, y) = ( e xy, x 2 + y, 2x 3 y 2) r(h) (h 1, h 2 ) e. 2(1 + h 1 ) 3 (3 + h 2 ) h 1 12h 2
 Funciones de R n en R m Diferenciación de funciones f : R n R m Definición. Considere la función f : A R n R m definida en un conjunto abierto A de R n y sea x 0 A. Se dice que esta función es diferenciable
Funciones de R n en R m Diferenciación de funciones f : R n R m Definición. Considere la función f : A R n R m definida en un conjunto abierto A de R n y sea x 0 A. Se dice que esta función es diferenciable
Laboratorio Nº 6 Sistema de ecuaciones diferenciales
 Universidad Diego Portales Primer Semestre 007 Facultad de Ingeniería Instituto de Ciencias Básicas Asignatura: Ecuaciones Diferenciales Objetivo general Laboratorio Nº 6 Sistema de ecuaciones diferenciales
Universidad Diego Portales Primer Semestre 007 Facultad de Ingeniería Instituto de Ciencias Básicas Asignatura: Ecuaciones Diferenciales Objetivo general Laboratorio Nº 6 Sistema de ecuaciones diferenciales
UNIVERSIDAD NACIONAL AUTÓNOMA DE HONDURAS
 UNIVERSIDAD NACIONAL AUTÓNOMA DE HONDURAS FACULTAD DE CIENCIAS ESCUELA DE FÍSICA Laboratorios virtuales: Electricidad y Magnetismo I Uso de Mathematica: Campos Vectoriales y Sistemas de Coordenadas ELABORADO
UNIVERSIDAD NACIONAL AUTÓNOMA DE HONDURAS FACULTAD DE CIENCIAS ESCUELA DE FÍSICA Laboratorios virtuales: Electricidad y Magnetismo I Uso de Mathematica: Campos Vectoriales y Sistemas de Coordenadas ELABORADO
CAMPOS: CIRCULACIÓN Y FLUJO
 AMPO: IRULAIÓN Y FLUJO Dado el vector a ( x + y) i ˆ + xy ˆ j calcular su circulación a lo largo de la recta y x+ desde el punto A (, ) al B (, 2). olución: I.T.I. 99, 5, I.T.T. 2 En la trayectoria que
AMPO: IRULAIÓN Y FLUJO Dado el vector a ( x + y) i ˆ + xy ˆ j calcular su circulación a lo largo de la recta y x+ desde el punto A (, ) al B (, 2). olución: I.T.I. 99, 5, I.T.T. 2 En la trayectoria que
Examen final de Cálculo Integral
 Examen final de Cálculo Integral 8 de junio de (Soluciones) Cuestiones C Sí se puede asegurar que es integrable, como consecuencia del teorema 4. de los apuntes: Llamamos W y f : W R a la esfera y a la
Examen final de Cálculo Integral 8 de junio de (Soluciones) Cuestiones C Sí se puede asegurar que es integrable, como consecuencia del teorema 4. de los apuntes: Llamamos W y f : W R a la esfera y a la
Sistemas de coordenadas
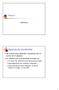 Tema 2 Vectores Sistemas de coordenadas Se utilizan para describir la posición de un punto en el espacio Un sistema de coordenadas consiste en un punto de referencia que llamaremos origen ejes específicos
Tema 2 Vectores Sistemas de coordenadas Se utilizan para describir la posición de un punto en el espacio Un sistema de coordenadas consiste en un punto de referencia que llamaremos origen ejes específicos
ANALISIS MATEMATICO II (Ciencias- 2011) Trabajo Práctico 8
 ANALISIS MATEMATIO II (iencias- 2011) Integrales sobre curvas (o de línea) Trabajo Práctico 8 1. Evaluar las siguientes integrales curvilíneas γ f ds. (a) f(x, y, z) = x + y + z ; r(t) = (sen t, cos t,
ANALISIS MATEMATIO II (iencias- 2011) Integrales sobre curvas (o de línea) Trabajo Práctico 8 1. Evaluar las siguientes integrales curvilíneas γ f ds. (a) f(x, y, z) = x + y + z ; r(t) = (sen t, cos t,
CÁLCULO VECTORIAL I. B, es un nuevo vector que se define del siguiente modo: Si A ybson (LI), entonces el vector A. B se caracteriza por:
 PRODUCTO VECTORIAL DE DOS VECTORES El producto vectorial de dos vectores A y, y escribimos A, es un nuevo vector que se define del siguiente modo: Si A yson (LI), entonces el vector A se caracteriza por:
PRODUCTO VECTORIAL DE DOS VECTORES El producto vectorial de dos vectores A y, y escribimos A, es un nuevo vector que se define del siguiente modo: Si A yson (LI), entonces el vector A se caracteriza por:
IES Fco Ayala de Granada ( Modelo 6) Soluciones Germán-Jesús Rubio Luna
 PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 011-01 Opción A Ejercicio 1, Opción A, Modelo 6 de 01 a 1+ si x 1 x- ['5 puntos] Se considera la función derivable f : R R definida por
PRUEBA DE ACCESO A LA UNIVERSIDAD MATEMÁTICAS II DE ANDALUCÍA CURSO 011-01 Opción A Ejercicio 1, Opción A, Modelo 6 de 01 a 1+ si x 1 x- ['5 puntos] Se considera la función derivable f : R R definida por
NOCIONES DE CALCULO VECTORIAL
 NOCIONES DE CALCULO VECTORIAL ANÁLISIS VECTORIAL o ÁLGEBRA VECTORIAL: Suma, resta y multiplicación de vectores. o CÁLCULO VECTORIAL: Gradiente, divergencia y rotacional. Teorema de la Divergencia. Teorema
NOCIONES DE CALCULO VECTORIAL ANÁLISIS VECTORIAL o ÁLGEBRA VECTORIAL: Suma, resta y multiplicación de vectores. o CÁLCULO VECTORIAL: Gradiente, divergencia y rotacional. Teorema de la Divergencia. Teorema
3. Expresar las siguientes figuras en (i) coordenadas cilíndricas (ii) coordenadas esféricas (a) x 2 + y 2 + z 2 = 25 (b) z 2 = 2(x 2 + y 2 ) B + 3
 ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA DEPARTAMENTO ACADÉMICO DE INGENIERÍA ELÉCTRICA ACADEMIA DE MATEMÁTICAS GUÍA DE LA MATERIA DE CÁLCULO VECTORIAL TURNO VESPERTINO Junio 2011 I. SISTEMAS
ESCUELA SUPERIOR DE INGENIERÍA MECÁNICA Y ELÉCTRICA DEPARTAMENTO ACADÉMICO DE INGENIERÍA ELÉCTRICA ACADEMIA DE MATEMÁTICAS GUÍA DE LA MATERIA DE CÁLCULO VECTORIAL TURNO VESPERTINO Junio 2011 I. SISTEMAS
Definición. Tema 12: Teoremas de Integración del Cálculo Vectorial. Gradiente de un campo escalar. Rotacional de un campo vectorial.
 Tema 12: Teoremas de Integración del Cálculo Vectorial El operador nabla e conoce como operador nabla al pseudo-vector = ( x, y, ) Juan Ignacio Del Valle Gamboa ede de Guanacaste Universidad de Costa Rica
Tema 12: Teoremas de Integración del Cálculo Vectorial El operador nabla e conoce como operador nabla al pseudo-vector = ( x, y, ) Juan Ignacio Del Valle Gamboa ede de Guanacaste Universidad de Costa Rica
FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 8. SISTEMAS DE ECUACIONES LINEALES
 FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 8. SISTEMAS DE ECUACIONES LINEALES 1.- Discusión de sistemas lineales: Teorema de Rouché-Fröbenius. En este apartado trataremos la discusión
FUNDAMENTOS MATEMÁTICOS (Grado en Ingeniería Informática) Práctica 8. SISTEMAS DE ECUACIONES LINEALES 1.- Discusión de sistemas lineales: Teorema de Rouché-Fröbenius. En este apartado trataremos la discusión
Coordenadas Generalizadas en el Espacio
 Capítulo 3 Coordenadas Generalizadas en el Espacio Las coordenadas cartesianas usuales en R 3 pueden verse también como un sistema de tres familias de superficies en el espacio, de modo que cada punto
Capítulo 3 Coordenadas Generalizadas en el Espacio Las coordenadas cartesianas usuales en R 3 pueden verse también como un sistema de tres familias de superficies en el espacio, de modo que cada punto
Análisis II - Análisis matemático II - Matemática 3 2do. cuatrimestre de 2013
 Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Análisis II - Análisis matemático II - Matemática 3 do. cuatrimestre de 3 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones.. Verificar el teorema de Stokes para el hemisferio
Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal.
 Concepto de Campo Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal. El concepto de campo se introdujo en el estudio de la electricidad para
Concepto de Campo Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal. El concepto de campo se introdujo en el estudio de la electricidad para
Guía n 0: Herramientas de Física y Matemáticas
 Guía n 0: Herramientas de Física y Matemáticas Problema Dadas dos partículas en el espacio ubicadas en los puntos de coordenadas p = (0,5, 2) y p 2 = (2,3,). Hallar el vector posición de la partícula respecto
Guía n 0: Herramientas de Física y Matemáticas Problema Dadas dos partículas en el espacio ubicadas en los puntos de coordenadas p = (0,5, 2) y p 2 = (2,3,). Hallar el vector posición de la partícula respecto
TENSIONES. 1. El estado de tensiones de un punto viene dado por el siguiente tensor de segundo orden: es efectivamente un tensor de segundo orden.
 TENSIONES. El estado de tensiones de un punto viene dado por el siguiente tensor de segundo orden: 500 500 800 = 500 000 750 MPa 800 750 00 r Calcule el vector de tensiones T n en el plano definido por
TENSIONES. El estado de tensiones de un punto viene dado por el siguiente tensor de segundo orden: 500 500 800 = 500 000 750 MPa 800 750 00 r Calcule el vector de tensiones T n en el plano definido por
gradiente de una función? Para esos valores, calcule la función potencial.
 CAMPOS CONSERVATIVOS. FUNCIÓN POTENCIAL 1. Sea F = 4xy 3x ( z (, 2x (, 2x, z. Demuestre que Fdl trayectoria C. es independiente de la 2. Dado el campo vectorial F = 3x ( + 2y y ( e 3, 2x 2ye 3. Es posible
CAMPOS CONSERVATIVOS. FUNCIÓN POTENCIAL 1. Sea F = 4xy 3x ( z (, 2x (, 2x, z. Demuestre que Fdl trayectoria C. es independiente de la 2. Dado el campo vectorial F = 3x ( + 2y y ( e 3, 2x 2ye 3. Es posible
(3 p.) 3) Se considera la superficie z = z(x, y) definida implícitamente por la ecuación. 3x 2 z x 2 y 2 + 2z 3 3yz = 15.
 Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 2012/2013 21 de junio de 2013 4 p.) 1) Se considera la función fx) = x 4 e 1 x 2. a) Calcular los intervalos de
Universidade de Vigo Departamento de Matemática Aplicada II E.T.S.I. Minas Cálculo I Curso 2012/2013 21 de junio de 2013 4 p.) 1) Se considera la función fx) = x 4 e 1 x 2. a) Calcular los intervalos de
GUIA Hallar el módulo del vector de origen en (20,-5,8) y extremo en (-4,-3,2).
 GUIA 0 1 - Hallar el módulo del vector de origen en (20,-5,8) etremo en (-4,-3,2). 2 - a) Hallar las componentes cartesianas de los siguientes vectores: (i) (ii) A A A = 4 A = θ =30º 4 θ =135º (iii) (iv)
GUIA 0 1 - Hallar el módulo del vector de origen en (20,-5,8) etremo en (-4,-3,2). 2 - a) Hallar las componentes cartesianas de los siguientes vectores: (i) (ii) A A A = 4 A = θ =30º 4 θ =135º (iii) (iv)
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2011 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción A Reserva, Ejercicio 4,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción A Reserva, Ejercicio 4,
Examen Final de Cálculo Vectorial MATE PREGUNTAS ABIERTAS TEMA A Diciembre 6 de Nombre: Código:
 UNIVERSIDAD DE LOS ANDES DEPARTAMENTO DE MATEMÁTICAS Examen Final de Cálculo Vectorial MATE 1207 PREGUNTAS ABIERTAS TEMA A Diciembre 6 de 2017 Este es un examen individual, no se permite el uso de libros,
UNIVERSIDAD DE LOS ANDES DEPARTAMENTO DE MATEMÁTICAS Examen Final de Cálculo Vectorial MATE 1207 PREGUNTAS ABIERTAS TEMA A Diciembre 6 de 2017 Este es un examen individual, no se permite el uso de libros,
[ ] 2, 2, 3 [ ( )] 2, 2, 3 CAMPOS: SUPERFICIES ( ) Hallar un vector unitario normal a la superficie x 2 y + 2xz = 4 en el punto (2, 2,3).
![[ ] 2, 2, 3 [ ( )] 2, 2, 3 CAMPOS: SUPERFICIES ( ) Hallar un vector unitario normal a la superficie x 2 y + 2xz = 4 en el punto (2, 2,3). [ ] 2, 2, 3 [ ( )] 2, 2, 3 CAMPOS: SUPERFICIES ( ) Hallar un vector unitario normal a la superficie x 2 y + 2xz = 4 en el punto (2, 2,3).](/thumbs/57/41080540.jpg) CAMPOS SUPERFICIES Hallar un vector unitario normal a la superficie x 2 y + 2xz 4 en el punto (2, 2,3). Solución I.T.I. 98, I.T.T. 99, 02 En primer lugar deberíamos verificar que el punto (2, 2,3) pertenece
CAMPOS SUPERFICIES Hallar un vector unitario normal a la superficie x 2 y + 2xz 4 en el punto (2, 2,3). Solución I.T.I. 98, I.T.T. 99, 02 En primer lugar deberíamos verificar que el punto (2, 2,3) pertenece
Se define la derivada de f en el punto c, según el vector u, al ĺımite, que denominamos f (c; u) ó D u f (c), si existe: f (c; u) = D u f (c) = lim
 Derivada direccional (1) Sea f : D Rn R m x = (x 1,, x i,, x n ) y = f (x) = (y 1,, y j,, y m ). Siendo y j = f j (x) = f j (x 1,, x i,, x n ), j = 1, 2,, m f (x) = (f 1 (x),, f j (x),, f m (x)) Sea c
Derivada direccional (1) Sea f : D Rn R m x = (x 1,, x i,, x n ) y = f (x) = (y 1,, y j,, y m ). Siendo y j = f j (x) = f j (x 1,, x i,, x n ), j = 1, 2,, m f (x) = (f 1 (x),, f j (x),, f m (x)) Sea c
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Cálculo diferencial e integral 4
 álculo diferencial e integral 4 Guía 4 1. alcular la divergencia y el rotacional de los siguientes campos vectoriales: a) V (x, y, z) = yzi + xzj + xyk. b) V (x, y, z) = x 2 i + (x + y) 2 j + (x + y +
álculo diferencial e integral 4 Guía 4 1. alcular la divergencia y el rotacional de los siguientes campos vectoriales: a) V (x, y, z) = yzi + xzj + xyk. b) V (x, y, z) = x 2 i + (x + y) 2 j + (x + y +
Para las siguientes funciones obtenga los puntos críticos y establezca la naturaleza de cada uno de ellos. Solución: ( )
 SERIE DE ÁLULO VETORIAL 1 PROFESOR: PEDRO RAMÍREZ MANNY TEMA 1 Para las siguientes funciones obtenga los puntos críticos y establezca la naturaleza de cada uno de ellos. f x, y = x + y 6x + 6y + 8 1) (
SERIE DE ÁLULO VETORIAL 1 PROFESOR: PEDRO RAMÍREZ MANNY TEMA 1 Para las siguientes funciones obtenga los puntos críticos y establezca la naturaleza de cada uno de ellos. f x, y = x + y 6x + 6y + 8 1) (
Observaciones del profesor:
 INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a los cuatro ejercicios de una de las dos opciones (A o B) que se le ofrecen. Nunca deberá contestar a unos ejercicios de una opción y a otros
INSTRUCCIONES GENERALES Y VALORACIÓN El alumno contestará a los cuatro ejercicios de una de las dos opciones (A o B) que se le ofrecen. Nunca deberá contestar a unos ejercicios de una opción y a otros
Matemáticas Empresariales II. Continuidad y Derivabilidad
 Matemáticas Empresariales II Lección 9 Continuidad y Derivabilidad Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales II 1 / 25 Continuidad Sea la función f :
Matemáticas Empresariales II Lección 9 Continuidad y Derivabilidad Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales II 1 / 25 Continuidad Sea la función f :
MODELACION EN VARIABLES DE ESTADO
 CAPÍTULO VIII INGENIERÍA DE SISTEMAS I MODELACION EN VARIABLES DE ESTADO 8.1. DEFINICIONES Estado: El estado de un sistema dinámico es el conjunto más pequeño de variables de modo que el conocimiento de
CAPÍTULO VIII INGENIERÍA DE SISTEMAS I MODELACION EN VARIABLES DE ESTADO 8.1. DEFINICIONES Estado: El estado de un sistema dinámico es el conjunto más pequeño de variables de modo que el conocimiento de
Capítulo 3. Funciones con valores vectoriales
 Capítulo 3. Funciones con valores vectoriales 3.1. Curvas: recta tangente y longitud de arco 3.2. Superficies parametrizadas 3.3. Campos vectoriales, campos conservativos Capítulo 3. Funciones con valores
Capítulo 3. Funciones con valores vectoriales 3.1. Curvas: recta tangente y longitud de arco 3.2. Superficies parametrizadas 3.3. Campos vectoriales, campos conservativos Capítulo 3. Funciones con valores
Lección 3. Cálculo vectorial. 5. El teorema de Stokes.
 GRADO DE INGENIERÍA AEROESPAIAL. URSO. 5. El teorema de Stokes. En esta sección estudiaremos otro de los teoremas clásicos del análisis vectorial: el teorema de Stokes. Esencialmente se trata de una generalización
GRADO DE INGENIERÍA AEROESPAIAL. URSO. 5. El teorema de Stokes. En esta sección estudiaremos otro de los teoremas clásicos del análisis vectorial: el teorema de Stokes. Esencialmente se trata de una generalización
SERIE # 4 CÁLCULO VECTORIAL
 SERIE # 4 CÁLCULO VECTORIAL Página 1 1) Calcular 1 x y dy dx. 0 0 1 ) Evaluar la integral doble circunferencia x y 9. x 9 x da R, donde R es la región circular limitada por la 648 15 x y ) Calcular el
SERIE # 4 CÁLCULO VECTORIAL Página 1 1) Calcular 1 x y dy dx. 0 0 1 ) Evaluar la integral doble circunferencia x y 9. x 9 x da R, donde R es la región circular limitada por la 648 15 x y ) Calcular el
VECTORES. BIDIMENSIONAL
 VETORES. IDIMENSIONL 1. Dado los vectores,,, D, E, F y G que se muestran en la figura, determinar el modulo del vector resultante si = 5N y F = 4N. Rpta. R = 17,35N. 2. En el primer cuadrante de un sistema
VETORES. IDIMENSIONL 1. Dado los vectores,,, D, E, F y G que se muestran en la figura, determinar el modulo del vector resultante si = 5N y F = 4N. Rpta. R = 17,35N. 2. En el primer cuadrante de un sistema
E.T.S.I. Industriales y Telecomunicación Curso Grados E.T.S.I. Industriales y Telecomunicación
 E.T.S.I. Industriales Telecomunicación Curso 010-011 Grados E.T.S.I. Industriales Telecomunicación Ejercicios resueltos 1 f x, x e Representar el dominio de la función x x El dominio es el conjunto de
E.T.S.I. Industriales Telecomunicación Curso 010-011 Grados E.T.S.I. Industriales Telecomunicación Ejercicios resueltos 1 f x, x e Representar el dominio de la función x x El dominio es el conjunto de
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
c) Calcular las asíntotas horizontales y verticales de f y representar de forma aproximada
 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas Cálculo I Curso 2011/2012 2 de julio de 2012 (75 p) 1) Se considera la función f : R R definida por f(x) = ex 2 e x + 1 a) Determinar
Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas Cálculo I Curso 2011/2012 2 de julio de 2012 (75 p) 1) Se considera la función f : R R definida por f(x) = ex 2 e x + 1 a) Determinar
2.3. Plano tangente a una superficie paramétrica. Sea la superficie paramétrica S determinada por la función vectorial
 .3. Plano tanente a na sperficie paramétrica. Sea la sperficie paramétrica S determinada por la fnción ectorial ( ) R R en el pnto P, cyo ector posición 3 : /, x,, y,, z, es (, ). Si se mantiene a constante
.3. Plano tanente a na sperficie paramétrica. Sea la sperficie paramétrica S determinada por la fnción ectorial ( ) R R en el pnto P, cyo ector posición 3 : /, x,, y,, z, es (, ). Si se mantiene a constante
Soluciones de los ejercicios del primer examen parcial
 Matemáticas III (GIC, curso 2015 2016) Soluciones de los ejercicios del primer examen parcial EJERCICIO 1. Determina en qué ecuación se transforma la ecuación en derivadas parciales z yy + 3z xy + 2z xx
Matemáticas III (GIC, curso 2015 2016) Soluciones de los ejercicios del primer examen parcial EJERCICIO 1. Determina en qué ecuación se transforma la ecuación en derivadas parciales z yy + 3z xy + 2z xx
INTEGRALES CURVILÍNEAS
 (Apuntes sin revisión para orientar el aprendizaje) INTEGRALES URVILÍNEAS (Material de apoyo y orientación para preparar el tema) Las integrales curvilíneas constituyen el estudio de funciones sobre curvas.
(Apuntes sin revisión para orientar el aprendizaje) INTEGRALES URVILÍNEAS (Material de apoyo y orientación para preparar el tema) Las integrales curvilíneas constituyen el estudio de funciones sobre curvas.
TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1. CÁLCULO DIFERENCIAL EN VARIAS VARIABLES
 TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1 CÁLCULO DIFERENCIAL EN VARIAS VARIABLES 11 CONCEPTOS BÁSICOS Definición La norma de un vector x =
TEORÍA DE CÁLCULO II PARA GRADOS DE INGENIERÍA Elaborada por Domingo Pestana y José Manuel Rodríguez 1 CÁLCULO DIFERENCIAL EN VARIAS VARIABLES 11 CONCEPTOS BÁSICOS Definición La norma de un vector x =
DEPARTAMENTO DE FISICA DOCENTE: ING. JOEL PACO S.
 .1.- INTRODUCION Las propiedades físicas en la mecánica deben expresarse por una magnitud y una cierta unidad que las permita medir y comparar entre si, sin embargo debido a que en algunos casos esa información
.1.- INTRODUCION Las propiedades físicas en la mecánica deben expresarse por una magnitud y una cierta unidad que las permita medir y comparar entre si, sin embargo debido a que en algunos casos esa información
OCW-Universidad de Málaga, (2014). Bajo licencia. Creative Commons Attribution- NonComercial-ShareAlike 3.
 OCW-Universidad de Málaga, http://ocw.uma.es (014). Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3.0 Spain Matemáticas III Relación de ejercicios Tema 1 Ejercicios Ej. 1 Encuentra
OCW-Universidad de Málaga, http://ocw.uma.es (014). Bajo licencia Creative Commons Attribution- NonComercial-ShareAlike 3.0 Spain Matemáticas III Relación de ejercicios Tema 1 Ejercicios Ej. 1 Encuentra
Conjuntos de Vectores y Matrices Ortogonales
 Conjuntos de Vectores y Matrices Ortogonales Departamento de Matemáticas, CCIR/ITESM 28 de junio de 2011 Índice 21.1.Introducción............................................... 1 21.2.Producto interno............................................
Conjuntos de Vectores y Matrices Ortogonales Departamento de Matemáticas, CCIR/ITESM 28 de junio de 2011 Índice 21.1.Introducción............................................... 1 21.2.Producto interno............................................
Problemas resueltos del Boletín 4
 Boletines de problemas de Matemáticas II Problemas resueltos del Boletín 4 Problema 1. Resolver el siguiente sistema de ecuaciones diferenciales: { y = 1 z, z = 1 } y Solución: Lo transformamos como sigue:
Boletines de problemas de Matemáticas II Problemas resueltos del Boletín 4 Problema 1. Resolver el siguiente sistema de ecuaciones diferenciales: { y = 1 z, z = 1 } y Solución: Lo transformamos como sigue:
Derivación numérica. h 0 h. f)(x) =
 Derivación numérica Contenidos Derivada primera de funciones de una variable Derivada segunda de funciones de una variable Derivadas de funciones de dos variables Derivada primera de funciones de una variable
Derivación numérica Contenidos Derivada primera de funciones de una variable Derivada segunda de funciones de una variable Derivadas de funciones de dos variables Derivada primera de funciones de una variable
CAPÍTULO 10. Teoremas Integrales.
 CAPÍTULO 10 Teoremas Integrales. Este capítulo final contiene los teoremas integrales del análisis vectorial, de amplia aplicación a la física y a la ingeniería. Los anteriores capítulos han preparado
CAPÍTULO 10 Teoremas Integrales. Este capítulo final contiene los teoremas integrales del análisis vectorial, de amplia aplicación a la física y a la ingeniería. Los anteriores capítulos han preparado
Necesitamos tener los vectores de dirección de ambas rectas. Para calcular el ángulo que forman, aplicamos la siguiente fórmula:
 PROBLEMAS MÉTRICOS ÁNGULOS ÁNGULO QUE FORMAN DOS RECTAS Necesitamos tener los vectores de dirección de ambas rectas. Para calcular el ángulo que forman, aplicamos la siguiente fórmula: cos α = ÁNGULO QUE
PROBLEMAS MÉTRICOS ÁNGULOS ÁNGULO QUE FORMAN DOS RECTAS Necesitamos tener los vectores de dirección de ambas rectas. Para calcular el ángulo que forman, aplicamos la siguiente fórmula: cos α = ÁNGULO QUE
Ejercicios de Fundamentos Matemáticos I. Rafael Payá Albert. Ingeniería de Telecomunicaciones. Departamento de Análisis Matemático
 Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
Teoría Electromagnética. Escalar: Número, cantidad: masa, carga, temperatura, volumen, edad, altura, etc.
 Apéndice A: Cálculo Vectorial Escalar: Número, cantidad: masa, carga, temperatura, volumen, edad, altura, etc. Vector: Número + Dirección: velocidad, aceleración, desplazamiento, fuerza, campos, etc. F
Apéndice A: Cálculo Vectorial Escalar: Número, cantidad: masa, carga, temperatura, volumen, edad, altura, etc. Vector: Número + Dirección: velocidad, aceleración, desplazamiento, fuerza, campos, etc. F
A) Hallar el volumen del sólido formado cuando la región del primer cuadrante limitada por Z 4. 1 x 4 1 dx. Z b. p (x) h (x) dx.
 ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA I.T.I. Especialidad en Electricidad. Curso 4-5. Soluciones al Segundo Parcial de Fundamentos Matemáticos de la Ingeniería. PROBLEMA.- A) Hallar el volumen del
ESCUELA UNIVERSITARIA POLITÉCNICA DE SEVILLA I.T.I. Especialidad en Electricidad. Curso 4-5. Soluciones al Segundo Parcial de Fundamentos Matemáticos de la Ingeniería. PROBLEMA.- A) Hallar el volumen del
Webpage: Departamento de Física Universidad de Sonora
 Mecánica y fluidos Webpage: http://paginas.fisica.uson.mx/qb 2007 Departamento de Física Universidad de Sonora Temario III.- VECTORES. 1. Clasificación de cantidades físicas: Escalares y vectores. 2.
Mecánica y fluidos Webpage: http://paginas.fisica.uson.mx/qb 2007 Departamento de Física Universidad de Sonora Temario III.- VECTORES. 1. Clasificación de cantidades físicas: Escalares y vectores. 2.
Problemas de Análisis Vectorial y Estadístico
 Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
Relación 1. Funciones Γ y β 1. Función Gamma Definimos la función gamma Γ(p) como: Demostrar que: Γ(p) = t (p 1) e t dt para p> a) Γ(1) = 1 b) Integrando por partes, ver que Γ(p) = (p 1)Γ(p 1) para p>1
Álgebra Lineal Ma1010
 Álgebra Lineal Ma1010 s de Vectores y Matrices es Departamento de Matemáticas ITESM s de Vectores y Matrices es Álgebra Lineal - p. 1/44 En esta lectura veremos conjuntos y matrices ortogonales. Primero
Álgebra Lineal Ma1010 s de Vectores y Matrices es Departamento de Matemáticas ITESM s de Vectores y Matrices es Álgebra Lineal - p. 1/44 En esta lectura veremos conjuntos y matrices ortogonales. Primero
Universidad Diego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Laboratorio Nº 12 Cálculo I Extremos locales y Anàlisis de curvas
 Universidad Diego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Laboratorio Nº 12 Cálculo I Extremos locales y Anàlisis de curvas Contenidos : Puntos crìticos Intervalos de Crecimiento
Universidad Diego Portales Facultad de Ingeniería. Instituto de Ciencias Básicas Laboratorio Nº 12 Cálculo I Extremos locales y Anàlisis de curvas Contenidos : Puntos crìticos Intervalos de Crecimiento
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS.
 UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
MATEMÁTICAS 1º BACH. C. N. Y S. 25 de enero de 2010 Geometría y Logaritmos
 MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
Tema 1. Introducción
 Grado en Ingeniería Aeroespacial en Aeronavegación Tema 1. Introducción Felipe Alonso Atienza felipe.alonso@urjc.es @FelipeURJC Escuela Técnica Superior de Ingeniería de Telecomunicación Universidad Rey
Grado en Ingeniería Aeroespacial en Aeronavegación Tema 1. Introducción Felipe Alonso Atienza felipe.alonso@urjc.es @FelipeURJC Escuela Técnica Superior de Ingeniería de Telecomunicación Universidad Rey
EXPRESIÓN PARA LA DIVERGENCIA EN COORDENADAS CARTESIANAS.
 c Rafael R. Boix y Francisco Medina 1 EXPRESIÓN PARA LA DIVERGENCIA EN COORDENADAS CARTESIANAS. Consideremos un punto P 0 del espacio tridimensional de coordenadas cartesianas (x 0, y 0, z 0 ). Consideremos
c Rafael R. Boix y Francisco Medina 1 EXPRESIÓN PARA LA DIVERGENCIA EN COORDENADAS CARTESIANAS. Consideremos un punto P 0 del espacio tridimensional de coordenadas cartesianas (x 0, y 0, z 0 ). Consideremos
Materia: Matemática de 5to Tema: Producto Punto. Marco Teórico
 Materia: Matemática de 5to Tema: Producto Punto Marco Teórico En términos comunes, el producto punto de dos vectores es un número que describe la cantidad de fuerza que dos vectores diferentes contribuyen
Materia: Matemática de 5to Tema: Producto Punto Marco Teórico En términos comunes, el producto punto de dos vectores es un número que describe la cantidad de fuerza que dos vectores diferentes contribuyen
Tema 1: Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla. Parte 5/7 Circulación, rotacional y teorema de Stokes
 Tema 1: Fundamentos Matemáticos Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla Parte 5/7 Circulación, rotacional y teorema de Stokes La circulación es una integral
Tema 1: Fundamentos Matemáticos Antonio González Fernández Departamento de Física Aplicada III Universidad de Sevilla Parte 5/7 Circulación, rotacional y teorema de Stokes La circulación es una integral
TEMAS DE FÍSICA I VECTORES Profr. Abelardo Rodríguez Soria et al TRIMESTRE 11 P
 TEMAS DE FÍSICA I VECTORES Profr. Abelardo Rodríguez Soria et al TRIMESTRE 11 P PRELIMINARES. Un vector se representa gráficamente en el papel mediante una flecha. La longitud de la flecha representa la
TEMAS DE FÍSICA I VECTORES Profr. Abelardo Rodríguez Soria et al TRIMESTRE 11 P PRELIMINARES. Un vector se representa gráficamente en el papel mediante una flecha. La longitud de la flecha representa la
Ejercicios Resueltos (Espacios Vectoriales) Mat156 2 do Semestre de 2012
 Ejercicios Resueltos (Espacios Vectoriales) Mat156 do Semestre de 01 1. Determinar si los siguientes conjuntos son subespacios: a) {(0,y) : y R} de R. b) {(x,y,z) R 3 : x+y 3z = 0} de R 3. c) {p(x) R [x]
Ejercicios Resueltos (Espacios Vectoriales) Mat156 do Semestre de 01 1. Determinar si los siguientes conjuntos son subespacios: a) {(0,y) : y R} de R. b) {(x,y,z) R 3 : x+y 3z = 0} de R 3. c) {p(x) R [x]
A. Espacios vectoriales y TLs: Práctica 1 (2018)
 Es paci cios Vectoria iales De finic ici i ión on Conv enci cióóóóón de E inst stei ein para a la sumatoria Tran ansf sforma maci ciones Line neal es Cambio de base y cambio de coo rden adasa A. Espacios
Es paci cios Vectoria iales De finic ici i ión on Conv enci cióóóóón de E inst stei ein para a la sumatoria Tran ansf sforma maci ciones Line neal es Cambio de base y cambio de coo rden adasa A. Espacios
Movimiento curvilíneo. Magnitudes cinemáticas
 Movimiento curvilíneo. Magnitudes cinemáticas Movimiento curvilíneo Supongamos que el movimiento tiene lugar en el plano XY, Situamos un origen, y unos ejes, y representamos la trayectoria del móvil, es
Movimiento curvilíneo. Magnitudes cinemáticas Movimiento curvilíneo Supongamos que el movimiento tiene lugar en el plano XY, Situamos un origen, y unos ejes, y representamos la trayectoria del móvil, es
Soluciones de los ejercicios del examen final de la primera convocatoria
 Matemáticas III GI, curso 2015 2016 oluciones de los ejercicios del examen final de la primera convocatoria EJERIIO 1. De un campo escalar fx, y, z se sabe que es de clase R 3 y que su gradiente en el
Matemáticas III GI, curso 2015 2016 oluciones de los ejercicios del examen final de la primera convocatoria EJERIIO 1. De un campo escalar fx, y, z se sabe que es de clase R 3 y que su gradiente en el
División Departamento Licenciatura. Asignatura: Horas/semana: Horas/semestre: Obligatoria X Teóricas 4.0 Teóricas 64.0
 UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA PROGRAMA DE ESTUDIO CÁLCULO VECTORIAL CIENCIAS BÁSICAS 3 8 Asignatura Clave Semestre Créditos COORDINACIÓN DE MATEMÁTICAS INGENIERÍA CIVIL
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO FACULTAD DE INGENIERÍA PROGRAMA DE ESTUDIO CÁLCULO VECTORIAL CIENCIAS BÁSICAS 3 8 Asignatura Clave Semestre Créditos COORDINACIÓN DE MATEMÁTICAS INGENIERÍA CIVIL
Los lugares geométricos de todos los puntos del espacio en los cuales la magnitud escalar tiene un mismo valor.
 Física para iencias e Ingeniería ÁLGEBRA ETORIAL 2.1 2.1 Introducción A lo largo del estudio de la Física surgen una serie de propiedades, tanto de magnitudes escalares como vectoriales, que se epresan
Física para iencias e Ingeniería ÁLGEBRA ETORIAL 2.1 2.1 Introducción A lo largo del estudio de la Física surgen una serie de propiedades, tanto de magnitudes escalares como vectoriales, que se epresan
Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena
 1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
2. Sea f(x, y) = x 2 2xy+y 2. Aquí el discriminante es igual a cero. Qué son los puntos críticos: mínimos locales, máximos locales o puntos silla?
 1. Sea f(x, y) = Ax 2 + B con A 0. Cuáles son los puntos críticos de f? Son máximos locales o mínimos locales? Solución. Los puntos críticos son aquellos en los que las derivadas parciales son iguales
1. Sea f(x, y) = Ax 2 + B con A 0. Cuáles son los puntos críticos de f? Son máximos locales o mínimos locales? Solución. Los puntos críticos son aquellos en los que las derivadas parciales son iguales
Integrales de Superficie
 Capítulo 12 Integrales de uperficie 12.1. Definiciones Básicas Nuestro porpóstito en esta sección es el definir el concepto de integral de una función f : M R sobre una superficie M en el espacio. Para
Capítulo 12 Integrales de uperficie 12.1. Definiciones Básicas Nuestro porpóstito en esta sección es el definir el concepto de integral de una función f : M R sobre una superficie M en el espacio. Para
9. DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES.
 9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
9 DIFERENCIACIÓN DE FUNCIONES DE VARIAS VARIABLES 91 Derivadas parciales y direccionales de un campo escalar La noción de derivada intenta describir cómo resulta afectada una función y = f(x) por un cambio
Mecánica y fluidos. Temario. Webpage:
 Mecánica fluidos Webpage: http://paginas.fisica.uson.m/qb 2007 Departamento de Física Universidad de Sonora Temario III.- VECTORES. 1. Clasificación de cantidades físicas: Escalares vectores. 2. Representación
Mecánica fluidos Webpage: http://paginas.fisica.uson.m/qb 2007 Departamento de Física Universidad de Sonora Temario III.- VECTORES. 1. Clasificación de cantidades físicas: Escalares vectores. 2. Representación
Universidad Diego Portales Segundo Semestre 2007 Facultad de Ingeniería
 Universidad Diego Portales Segundo Semestre 007 Facultad de Ingeniería Instituto de Ciencias Básicas Asignatura: Ecuaciones Diferenciales Laboratorio Nº Ecuaciones Diferenciales Eactas, Lineales de Primer
Universidad Diego Portales Segundo Semestre 007 Facultad de Ingeniería Instituto de Ciencias Básicas Asignatura: Ecuaciones Diferenciales Laboratorio Nº Ecuaciones Diferenciales Eactas, Lineales de Primer
U n i v e r s i d a d A u t ó n o m a d e S a n L u i s P o t o s í F a c u l t a d d e I n g e n i e r í a Programa analítico
 1) NOMBRE DE CADA CURSO O ACTIVIDAD CURRICULAR Se debe abrir una sección como ésta para cada curso. A) NOMBRE DEL CURSO: CÁLCULO C B) DATOS BÁSICOS DEL CURSO Tipo de propuesta curricular: Nueva creación
1) NOMBRE DE CADA CURSO O ACTIVIDAD CURRICULAR Se debe abrir una sección como ésta para cada curso. A) NOMBRE DEL CURSO: CÁLCULO C B) DATOS BÁSICOS DEL CURSO Tipo de propuesta curricular: Nueva creación
SERIE ÁLGEBRA VECTORIAL
 SERIE ÁLGEBRA VECTORIAL 1.-Sea C(2, -3, 5) el punto medio del segmento dirigido AB. Empleando álgebra vectorial, determinar las coordenadas de los puntos A y B, si las componentes escalares de AB sobre
SERIE ÁLGEBRA VECTORIAL 1.-Sea C(2, -3, 5) el punto medio del segmento dirigido AB. Empleando álgebra vectorial, determinar las coordenadas de los puntos A y B, si las componentes escalares de AB sobre
ANÁLISIS MATEMÁTICO II - Grupo Ciencias 2018 Práctica 9 Campos conservativos - Teorema de Green
 ANÁLISIS MATEMÁTIO II - Grupo iencias 018 Práctica 9 ampos conservativos - Teorema de Green A. ampos conservativos 1. Mostrar que F x, y) = y cos x) i + x sen y) j no es un campo vectorial gradiente..
ANÁLISIS MATEMÁTIO II - Grupo iencias 018 Práctica 9 ampos conservativos - Teorema de Green A. ampos conservativos 1. Mostrar que F x, y) = y cos x) i + x sen y) j no es un campo vectorial gradiente..
VECTORES. también con letras sobre las cuales se coloca una flechita ( a ). A = módulo de A. modulo o magnitud, dirección y sentido. vector.
 VECTORES Según su naturaleza las cantidades físicas se clasifican en magnitudes escalares y magnitudes vectoriales Las magnitudes como el tiempo, la temperatura, la masa y otras, son magnitudes escalares
VECTORES Según su naturaleza las cantidades físicas se clasifican en magnitudes escalares y magnitudes vectoriales Las magnitudes como el tiempo, la temperatura, la masa y otras, son magnitudes escalares
EJERCICIOS VECTORES EN EL ESPACIO 1. Dados los vectores A = 2î - 4 ĵ + 6 kˆ y B = î + 5 ĵ 9 kˆ, encontrar un vector c tal que 3 a + 2b + 4 c
 EJERCICIOS VECTORES EN EL ESPACIO 1. Dados los vectores A = î - 4 ĵ + 6 kˆ y B = î + 5 ĵ 9 kˆ, encontrar un vector c tal que 3 a + b + 4 c 1 = 0. RESPUESTA: i+ j. Dados los vectores A = î - ĵ + 3 kˆ y
EJERCICIOS VECTORES EN EL ESPACIO 1. Dados los vectores A = î - 4 ĵ + 6 kˆ y B = î + 5 ĵ 9 kˆ, encontrar un vector c tal que 3 a + b + 4 c 1 = 0. RESPUESTA: i+ j. Dados los vectores A = î - ĵ + 3 kˆ y
Instituto Politécnico Nacional Escuela Superior de Ingeniería Mecánica y Eléctrica Departamento de Ingeniería Eléctrica Academia de Matemáticas
 Escuela Superior de Ingeniería Mecánica Eléctrica. Efectúe las operaciones grafique.. ( - i ( i. ( i ( - i Guía para el E.T.S. de Fundamentos de Álgebra Números Complejos. Efectúe cada una de las operaciones
Escuela Superior de Ingeniería Mecánica Eléctrica. Efectúe las operaciones grafique.. ( - i ( i. ( i ( - i Guía para el E.T.S. de Fundamentos de Álgebra Números Complejos. Efectúe cada una de las operaciones
