Los lugares geométricos de todos los puntos del espacio en los cuales la magnitud escalar tiene un mismo valor.
|
|
|
- Vanesa Méndez Mendoza
- hace 6 años
- Vistas:
Transcripción
1 Física para iencias e Ingeniería ÁLGEBRA ETORIAL Introducción A lo largo del estudio de la Física surgen una serie de propiedades, tanto de magnitudes escalares como vectoriales, que se epresan por medio de nuevos conceptos tales como gradiente, divergencia, laplaciana, rota - cional, sus relaciones con nuevas definiciones tales como flujo circulación de un vector, así como ciertos teoremas transformaciones de vectores. 2.2 oncepto de campo escalar campo vectorial. Representación gráfica. En general, se llama campo a una magnitud física cuo valor es función del punto del espacio que se considere del instante en que se mida. i la magnitud es función solamente el punto del espacio que se considere,, por tanto, independiente del tiempo, se dice que es un campo estacionario. egún la naturalea de la magnitud física puede ser un campo escalar, o un campo vectorial. ampo escalar i se trata de un campo escalar estacionario de una cierta magnitud, será, en general, función de las coordenadas de cada punto del espacio: = (,, ). Las representaciones geométricas audan a tener una idea clara de cómo varían ciertas magnitudes físicas. Los campos escalares estacionarios suelen representarse por medio de las llamadas superficies de nivel, o superficies equipotenciales, que se definen como: Los lugares geométricos de todos los puntos del espacio en los cuales la magnitud escalar tiene un mismo valor. En la práctica, se dibujan las superficies de nivel que corresponden a valores de la magnitud escalar, que se diferencian en una cantidad constante. De esta forma se conoce el valor de en los diferentes puntos del espacio, además, se visualia rápidamente en qué regiones eperimenta la maor rapide de variación, que son aquéllas donde las superficies de nivel se encuentran más próimas unas a otras. Las superficies de nivel en el espacio forman un sistema de capas envolventes sin ningún punto de contacto, a que dos superficies de nivel correspondientes a valores distintos de la magnitud escalar no pueden cortarse. i lo hicieran, la magnitud tendría a la ve dos valores distintos en los puntos de intersección, lo cual es absurdo. Un ejemplo sencillo de representación gráfica de un campo escalar estacionario es el de las superficies de nivel utiliadas en la confección de mapas en los cuales la cota de cada punto es función de su posición en el plano de dibujo: = (, ). [Fig. 2-1]. e dibujan las curvas de nivel (, ) = cte. a intervalos constantes. Las regiones del mapa donde se aproiman las curvas de nivel son aquéllas donde la pendiente es maor. FIG. 2-1 ampo vectorial e denomina campo vectorial a una magnitud física de carácter vectorial que es, en general, función de cada punto del espacio del instante que se considere. on ejemplos de campos vectoriales: los campos de fueras gravitatorias, electrostáticas, magnéticas, los campos de velocidades en el seno de un fluido en movimiento, etc. i la magnitud vectorial es solamente función de cada punto del espacio, pero no es función del tiempo, se dice que es un campo estacionario. Los campos vectoriales se representan por medio de las llamadas líneas de fuera, que se obtienen traando, a partir de cada punto del espacio, un pequeño segmento en la dirección del vector correspondiente a dicho punto. El etremo de dicho segmento sirve de origen para traar otro segmento en la nueva dirección que tenga la magnitud vectorial, así sucesivamente. De esta forma se obtiene una línea poligonal. i se dibuja nuevamente esta línea poligonal, tomando los puntos más próimos entre sí, los segmentos que determinan serán más pequeños, en el límite, cuando las longitudes de estos segmentos tiendan a cero, la línea poligonal se convertirá en una línea curva, denominada línea de fuera del campo vectorial. FIG. 2-2
2 2.2 ÁLGEBRA ETORIAL aletos Física para iencias e Ingeniería Por la forma en que se ha dibujado, se deduce que la línea de fuera tiene la propiedad de ser tangente en cada punto al vector campo que eiste en dicho punto, su sentido es el de dicho vector campo. Para que las líneas de fuera indiquen en cada punto el módulo, además de la dirección sentido del vector campo, se conviene en dibujarlas de la siguiente forma: En cada punto se toma una pequeña superficie de área da, perpendicular a la dirección del vector en dicho punto, se dibujan, a partir de los puntos de dicha superficie un número de líneas de fuera, dn, uniformemente distribuidas, igual al producto del módulo del vector por el área da del elemento de superficie. De esta forma queda determinado el módulo del vector en dicho punto, por la densidad, De forma que en aquellas regiones en las que las líneas de fuera estén más próimas entre sí el módulo del vector campo tendrá un maor valor. Y por el contrario, el módulo será menor en aquellas regiones donde las líneas de fuera estén más separadas. 2.3 Gradiente de un magnitud escalar Una magnitud escalar se modifica, en general, de un punto a otro la variación que eperimenta al pasar del punto (,, ) al (+d, +d, +d) es dn da d = d + d + d d d d Esta epresión se puede considerar como el producto de los vectores i + j + k d d d dl = d i +d j +d k de modo que podemos conocer la variación de la magnitud escalar en todo el campo si conocemos el vector definido por la relación [2.2]. Un vector cuas componentes son las derivadas de una magnitud escalar respecto a las coordenadas respectivas se define como gradiente de dicha magnitud. 2.4 OPerador nabla grad = d i + d j + d [2.1] [2.2] [2.3] k [2.4] e puede representar simbólicamente el vector [2.4] introduciendo el operador denominado nabla = i + j + k [2.5] d d d que indica una operación a realiar con la magnitud a la que se aplique. En este caso, indica la derivada parcial de una magnitud respecto a la coordenada correspondiente = grad = d i + d j + d k [2.6] 2.5 Flujo de un vector e llama flujo de un vector E a través de un elemento de superficie ds a la epresión dφ = E.ds [2.7] siendo ds un vector normal al elemento de superficie cuo módulo es igual a su área. i el elemento pertenece a una superficie que encierra un volumen, dicho vector se toma en el sentido de la normal hacia el eterior del volumen encerrado por la superficie. Puesto que el flujo es una magnitud escalar, el flujo a través de toda la superficie será Φ = E.ds [2.8]
3 Física para iencias e Ingeniería ÁLGEBRA ETORIAL Divergencia de un vector e puede hallar una epresión mu útil del flujo de un vector a través de una superficie si se divide el volumen encerrado por dicha superficie en paralelepípedos elementales, por medio de tres series de planos infinitamente próimos paralelos a los coordenados. El flujo es igual a la suma de los flujos a través de la superficie de cada paralelepípedo, pues cualquier cara interior al volumen pertenece a dos paralelepípedos consecutivos,, en consecuencia, el flujo a través de ella interviene dos veces con signos opuestos, a que uno de ellos es entrante, el otro, saliente, quedando solamente los flujos a través de las caras que forman la superficie. X Z O A D FIG. 2-3 E H B F G Y i consideramos uno de los paralelepípedos de aristas d, d, d, el flujo, por ejemplo, a través de la cara ABD paralela al plano YZ es igual al producto de la componente E del vector E por el área dd de dicha cara. i en el centro del paralelepípedo el vector es E, su componente E en el centro de la cara ABD es E + 1 E 2 d d el flujo a través de ella E + 1 E 2 d d dd iguiendo el mismo raonamiento, el flujo a través de la cara opuesta EFGH, es, teniendo en cuenta el cambio de sentido de la normal, E 1 E 2 d d d d Procediendo de la misma forma para los otros dos pares de caras sumando todas las epresiones, se obtiene para el flujo total a través del paralelepípedo de volumen dv = ddd dφ 1 = E d + E d + E d d d d La epresión entre corchetes se denomina, divergencia del vector E según [2.5] [2.9] div E = E d + E d + E d = E [2.10] es decir, su epresión es el producto escalar del operador nabla por el vector. 2.7 Teorema de Green egún [2.9], el flujo del vector E a través de la superficie es igual a la suma de las epresiones [2.8] etendida a todo el volumen encerrado por dicha superficie E.da = div E dv epresión que constitue el enunciado del teorema de Green. 2.8 Operador laplaciana i el vector E deriva de un potencial, es decir, si el vector se puede epresar a partir de una función escalar, por medio de la relación E = grad = [2.12] la divergencia del vector es [2.11]
4 2.4 ÁLGEBRA ETORIAL aletos Física para iencias e Ingeniería div E = div grad = ( ) = = i + j + k i + j + k = 2 d d d d d d d d + 2 [2.13] 2 d 2 La epresión [2.12] 2.9 irculación de un vector 2 d d d 2 se representa simbólicamente introduciendo el operador denominado laplaciana, que indica que ha que calcular las derivadas parciales segundas de la magnitud a la que se aplique respecto a la coordenada correspondiente: 2 d d d = Δ [2.14] 2 El operador laplaciana se puede aplicar igualmente a un vector en ese caso representa un vector cuas componentes son las laplacianas de las componentes del vector ΔE = i ΔE + j ΔE + k ΔE [2.15] e denomina circulación de un vector a lo largo de una línea a la integral L E dl [2.16] amos a calcular la circulación de un vector a lo largo de un rectángulo de lados d, d, paralelos a los ejes OY OZ, contenido en el plano YZ, siguiendo el sentido ABD. i en el centro del rectángulo el vector es E, la circulación es X Z O D A ds FIG. 2-4 a lo largo de DA B La circulación total es Y a lo largo de AB a lo largo de B a lo largo de D E + E 1 2 d d E E 1 2 d d E E dd E E 1 2 d d E E 1 2 d d iguiendo el mismo raonamiento, si el rectángulo estuviera situado en el plano XY o en el XZ las circulaciones serían E E d d o E E d d
5 Física para iencias e Ingeniería ÁLGEBRA ETORIAL Rotacional de un vector e puede obtener una epresión general definiendo un vector denominado rotacional cua epresión es rot E = E E i + E E j + E E k omparando [2.16] la epresión [2.5] del operador nabla[2.17], teniendo en cuenta la epresión del producto vectorial de dos vectores, se deduce inmediatamente que [2.17] rot E = E = E E i + E E j + E E k [2.18] De modo que, si definimos otro vector ds normal al elemento de superficie, de módulo igual a su área, cuo sentido sea el correspondiente a aquel en que se recorre la línea, cua epresión es ds = d d i +d d j +d d k [2.19] se puede considerar que la circulación a lo largo de un rectángulo elemental orientado de cualquier modo con respecto a los ejes de coordenadas tiene por epresión E dl = rot E ds = E ds 2.11 Teorema de tokes = E E dd i + E E d d j + E E d d k onsideremos ahora una curva cerrada [Fig. 2.5], situada en una región del espacio en el que eiste un campo vectorial. Imaginemos una superficie cualquiera limitada por dicha curva dividimos esa superficie en rectángulos infinitesimales por intersección de dos series de planos infinitamente próimos perpendiculares entre sí. [2.20] La circulación a lo largo de la curva es, evidentemente, la suma de las circulaciones a lo largo de cada uno de los infinitos rectángulos elementales recorridos en el mismo sentido que la curva, pues cada lado de cada rectángulo es recorrido dos veces en sentidos contrarios queda como resultado de dicha suma la circulación a lo largo de los lados eteriores que forman la periferia o contorno de la curva. Por tanto, según lo indicado anteriormente, E dl = rot E ds = E ds [2.21] FIG. 2-5 relación que epresa el llamado teorema de tokes, según el cual La circulación de un vector a lo largo de una curva cerrada es igual al flujo del rotacional de dicho vector a través de una superficie cualquiera limitada por la curva. i el vector E deriva de un potencial, es decir, si el vector se puede epresar a partir de una función escalar, por medio de la relación E = grad = [2.11] el rotacional del vector es rot E = E = ( ) = por consiguiente, una cualquiera de sus componentes, por ejemplo la componente es ( ) = 2 2 = 0
6 2.6 ÁLGEBRA ETORIAL aletos Física para iencias e Ingeniería otro tanto ocurre con las otras componentes, de modo que, De forma análoga, es fácil comprobar que rot grad = = 0 [2.22] div rot E = E = 0 [2.23] 2.12 Relaciones importantes de álgebra vectorial a) i se aplica el rotacional a un vector, que es a su ve, el rotacional de otro vector, entonces rot rot E = rot 2 E = ( E) teniendo en cuenta la propiedad del doble producto vectorial rot rot E = rot 2 E = ( E) = E ( )E Desarrollando el último término ( )E = 2 E d 2 sustituendo en [2.23] queda + 2 E d E i + 2 E d 2 d E d E d 2 = grad dive ( )E j + 2 E d 2 rot rot E = rot 2 E = grad dive ΔE + 2 E d E k = ΔE d 2 [2.24] [2.25] b) i calculamos la divergencia del producto vectorial de dos vectores desarrollando, ordenando términos se obtiene div ( a b ) = (a b a b )+ (a b a b )+ (a b a b ) div ( a b a ) =b a +b a a +b a a a b b +a b b +a b b teniendo en cuenta la epresión del rotacional de un vector, queda c) En algunos casos es útil transformar una integral del tipo dl grad ϕ div ( a b ) = b rot a a rot b [2.26] etendida a una curva cerrada, siendo ϕ una función que cumple con la condición Δϕ = 0, en una integral de superficie. Para ello, si consideramos la componente del producto vectorial del integrando siendo el vector a haciendo uso del teorema de tokes (dl grad ϕ ϕ ϕ d d ) = = (dl grad ϕ ) = ( 2 ϕ a = 0i + ϕ j ϕ k a dl + 2 ϕ 2 )ds + 2 ϕ 2 ds + 2 ϕ ds
7 Física para iencias e Ingeniería ÁLGEBRA ETORIAL 2.7 según la condición impuesta a la función ϕ, queda (dl grad ϕ ) = 2 ϕ ds + 2 ϕ 2 ds + 2 ϕ ds = (grad ϕ ds) Para las componentes, se pueden escribir relaciones análogas, de modo que resulta finalmente dl grad ϕ = grad (grad ϕ ds) [2.27] d) Para concluir este grupo de relaciones vamos a analiar dos transformaciones que se deducen directamente del teorema de Green. onsideremos el vector a = b siendo una función escalar. i calculamos la divergencia de dicho vector div a = div ( b ) = b d + b d + b d +b d +b d +b d recordando las definiciones de gradiente de una magnitud escalar, de la divergencia de un vector, resulta div a = div ( b ) = div b + b grad aplicando el teorema de Green ( b ) ds = ( div b + b grad )dv = div b dv + e) upongamos un vector definido por la epresión a =U grad siendo U dos funciones escalares. i consideramos el producto escalar b grad dv ( b ) ds = div b dv + b grad dv [2.28] a ds = (U grad ) ds =U n ds donde representa la derivada respecto a la normal al elemento de superficie, calculamos la divergencia n cia del vector a div a = div(u grad ) = U + U + U +U que, teniendo en cuenta la definición de gradiente el producto escalar de dos vectores, queda div a = div(u grad ) = grad U grad +U Δ i ahora aplicamos el teorema de Green [2.10] al vector a a ds = (grad U grad +U Δ )dv = (grad U grad dv +U Δ + U Δ dv si escribimos esta última relación permutando entre sí las funciones U, restamos las dos ecuaciones obtenemos el denominado lema de Green. (U Δ ΔU )dv = (U U n n )dv [2.29]
Los lugares geométricos de todos los puntos del espacio en los cuales la magnitud escalar tiene un mismo valor.
 2. 2. Introducción A lo largo del estudio de la Física surgen una serie de propiedades, tanto de magnitudes escalares como vectoriales, que se expresan por medio de nuevos conceptos tales como gradiente,
2. 2. Introducción A lo largo del estudio de la Física surgen una serie de propiedades, tanto de magnitudes escalares como vectoriales, que se expresan por medio de nuevos conceptos tales como gradiente,
Los lugares geométricos de todos los puntos del espacio en los cuales la magnitud escalar tiene un mismo valor.
 Física para iencias e Ingeniería ÁLGEBRA ETORIAL 7.2- Introdcción A lo largo del estdio de la Física srgen na serie de propiedades, tanto de magnitdes escalares como vectoriales, qe se epresan por medio
Física para iencias e Ingeniería ÁLGEBRA ETORIAL 7.2- Introdcción A lo largo del estdio de la Física srgen na serie de propiedades, tanto de magnitdes escalares como vectoriales, qe se epresan por medio
Definición. Tema 12: Teoremas de Integración del Cálculo Vectorial. Gradiente de un campo escalar. Rotacional de un campo vectorial.
 Tema 12: Teoremas de Integración del Cálculo Vectorial El operador nabla e conoce como operador nabla al pseudo-vector = ( x, y, ) Juan Ignacio Del Valle Gamboa ede de Guanacaste Universidad de Costa Rica
Tema 12: Teoremas de Integración del Cálculo Vectorial El operador nabla e conoce como operador nabla al pseudo-vector = ( x, y, ) Juan Ignacio Del Valle Gamboa ede de Guanacaste Universidad de Costa Rica
Operadores diferenciales
 Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
Apéndice A Operadores diferenciales A.1. Los conceptos de gradiente, divergencia y rotor Sobre el concepto de gradiente. Si f r) es una función escalar, entonces su gradiente, en coordenadas cartesianas
CAPÍTULO I Campos escalares y vectoriales
 ampos escalares ectoriales APÍTULO I ampos escalares ectoriales undamento teórico I- Operaciones básicas con ectores El módulo de un ector donde Ia- Módulo de un ector ( ) i j k iene dado por son las componentes
ampos escalares ectoriales APÍTULO I ampos escalares ectoriales undamento teórico I- Operaciones básicas con ectores El módulo de un ector donde Ia- Módulo de un ector ( ) i j k iene dado por son las componentes
Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal.
 Concepto de Campo Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal. El concepto de campo se introdujo en el estudio de la electricidad para
Concepto de Campo Un campo es toda magnitud física definida en una cierta región del espacio y para un cierto intervalo temporal. El concepto de campo se introdujo en el estudio de la electricidad para
UNIVERSIDAD AUTÓNOMA DE SINALOA FACULTAD DE AGRONOMÍA HIDRÁULICA
 UNIVERSIDAD AUTÓNOMA DE SINALOA FACULTAD DE AGRONOMÍA HIDRÁULICA UNIDAD III. HIDROCINEMÁTICA Introducción. La hidrocinemática o cinemática de los líquidos se ocupa del estudio de las partículas que integran
UNIVERSIDAD AUTÓNOMA DE SINALOA FACULTAD DE AGRONOMÍA HIDRÁULICA UNIDAD III. HIDROCINEMÁTICA Introducción. La hidrocinemática o cinemática de los líquidos se ocupa del estudio de las partículas que integran
Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos:
 CONOCIMIENTOS PREVIOS. Vectores.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Trigonometría. Resolución de ecuaciones de primer grado. Sería
CONOCIMIENTOS PREVIOS. Vectores.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Trigonometría. Resolución de ecuaciones de primer grado. Sería
Volumen de Sólidos de Revolución
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
Ejercicios resueltos de FISICA II que se incluyen en la Guía de la Asignatura
 Ejercicios resueltos de FISICA II que se incluyen en la Guía de la Asignatura Módulo 2. Campo electrostático 4. Consideremos dos superficies gaussianas esféricas, una de radio r y otra de radio 2r, que
Ejercicios resueltos de FISICA II que se incluyen en la Guía de la Asignatura Módulo 2. Campo electrostático 4. Consideremos dos superficies gaussianas esféricas, una de radio r y otra de radio 2r, que
INTRODUCCIÓN AL CONCEPTO DE CAMPOS
 1. CONCEPTO DE CAMPO. INTRODUCCIÓN AL CONCEPTO DE CAMPOS Una magnitud definida en un cierto espacio (p.ej. el euclídeo) y que pueda expresarse analíticamente como una función de las coordenadas espaciales
1. CONCEPTO DE CAMPO. INTRODUCCIÓN AL CONCEPTO DE CAMPOS Una magnitud definida en un cierto espacio (p.ej. el euclídeo) y que pueda expresarse analíticamente como una función de las coordenadas espaciales
Programa de Acceso Inclusivo, Equidad y Permanencia. PAIEP, Universidad de Santiago
 Guía de vectores. Vectores En matemática, un vector es una herramienta geométrica utilizada para representar una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo
Guía de vectores. Vectores En matemática, un vector es una herramienta geométrica utilizada para representar una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
MAGNITUDES VECTORIALES
 MGNITUDES VECTORILES ÍNDICE 1. Magnitudes escalares y magnitudes vectoriales 2. Componentes de un vector 3. Coordenadas polares 4. Clasificación de los vectores 5. Suma y resta de vectores 6. Producto
MGNITUDES VECTORILES ÍNDICE 1. Magnitudes escalares y magnitudes vectoriales 2. Componentes de un vector 3. Coordenadas polares 4. Clasificación de los vectores 5. Suma y resta de vectores 6. Producto
Ejercicios de Fundamentos Matemáticos I. Rafael Payá Albert. Ingeniería de Telecomunicaciones. Departamento de Análisis Matemático
 Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
CARÁCTER DE LA GEOMETRÍA ANALÍTICA
 CARÁCTER DE LA GEOMETRÍA ANALÍTICA La Geometría Elemental, conocida a por el estudiante, se denomina también Geometría PURA para distinguirla del presente estudio. Recordaremos que por medio de un sistema
CARÁCTER DE LA GEOMETRÍA ANALÍTICA La Geometría Elemental, conocida a por el estudiante, se denomina también Geometría PURA para distinguirla del presente estudio. Recordaremos que por medio de un sistema
El campo magnético de las corrientes estacionarias
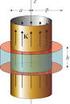 El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias Introducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
ROTACIONAL y DIVERGENCIA Campos vectoriales: Campo escalar: Campo vectorial: Campo vectorial:
 ROTACIONAL DIVERGENCIA Campos vectoriales: Los campos vectoriales son uno de los conceptos fundamentales de la física. Sin ellos es imposible entender el electromagnetismo, la óptica, o ramas más avanzadas
ROTACIONAL DIVERGENCIA Campos vectoriales: Los campos vectoriales son uno de los conceptos fundamentales de la física. Sin ellos es imposible entender el electromagnetismo, la óptica, o ramas más avanzadas
CALCULO VECTORIAL GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES
 GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES 1.- En cada uno de los siguientes casos calcular la integral de línea dada a) + +, donde C es el segmento de recta que une el punto O(0,0)
GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES 1.- En cada uno de los siguientes casos calcular la integral de línea dada a) + +, donde C es el segmento de recta que une el punto O(0,0)
Temario 4.Campo Eléctrico
 Campo Eléctrico 1 1 Temario 4.Campo Eléctrico 4.1 Concepto y definición de campo eléctrico 4.2 Campo eléctrico producido por una y varias cargas puntuales. 4.3 Lineas de Campo 4.4 Un conductor eléctrico
Campo Eléctrico 1 1 Temario 4.Campo Eléctrico 4.1 Concepto y definición de campo eléctrico 4.2 Campo eléctrico producido por una y varias cargas puntuales. 4.3 Lineas de Campo 4.4 Un conductor eléctrico
Campo de un hilo infinito. Fuerzas magnéticas. Teorema de Ampère. Campo magnético de una espira circular
 El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
El campo magnético de las corrientes estacionarias ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo magnético Teorema de Ampère El potencial vector Ecuaciones
Longitud, áreas y volúmenes. Trigonometría. Circunferencia de radio R Círculo de radio R. 1 Triángulo de base B y altura H A = (BH ) 2
 Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
Longitud, áreas y volúmenes Circunferencia de radio R Círculo de radio R A πr L πr Triángulo de base B y altura H A (BH ) Cuadrado de lado L A L Rectángulo de base B y altura H Superficie esférica A 4πR
GEOMETRÍA ANALÍTICA LA CIRCUNFERENCIA
 LA CIRCUNFERENCIA CONTENIDO. Ecuación común de la circunferencia Ejemplos. Ecuación general de la circunferencia. Análisis de la ecuación. Ejercicios Estudiaremos cuatro curvas que por su importancia aplicaciones
LA CIRCUNFERENCIA CONTENIDO. Ecuación común de la circunferencia Ejemplos. Ecuación general de la circunferencia. Análisis de la ecuación. Ejercicios Estudiaremos cuatro curvas que por su importancia aplicaciones
Lección 3. Cálculo vectorial. 5. El teorema de Stokes.
 GRADO DE INGENIERÍA AEROESPAIAL. URSO. 5. El teorema de Stokes. En esta sección estudiaremos otro de los teoremas clásicos del análisis vectorial: el teorema de Stokes. Esencialmente se trata de una generalización
GRADO DE INGENIERÍA AEROESPAIAL. URSO. 5. El teorema de Stokes. En esta sección estudiaremos otro de los teoremas clásicos del análisis vectorial: el teorema de Stokes. Esencialmente se trata de una generalización
[ ] 2, 2, 3 [ ( )] 2, 2, 3 CAMPOS: SUPERFICIES ( ) Hallar un vector unitario normal a la superficie x 2 y + 2xz = 4 en el punto (2, 2,3).
![[ ] 2, 2, 3 [ ( )] 2, 2, 3 CAMPOS: SUPERFICIES ( ) Hallar un vector unitario normal a la superficie x 2 y + 2xz = 4 en el punto (2, 2,3). [ ] 2, 2, 3 [ ( )] 2, 2, 3 CAMPOS: SUPERFICIES ( ) Hallar un vector unitario normal a la superficie x 2 y + 2xz = 4 en el punto (2, 2,3).](/thumbs/57/41080540.jpg) CAMPOS SUPERFICIES Hallar un vector unitario normal a la superficie x 2 y + 2xz 4 en el punto (2, 2,3). Solución I.T.I. 98, I.T.T. 99, 02 En primer lugar deberíamos verificar que el punto (2, 2,3) pertenece
CAMPOS SUPERFICIES Hallar un vector unitario normal a la superficie x 2 y + 2xz 4 en el punto (2, 2,3). Solución I.T.I. 98, I.T.T. 99, 02 En primer lugar deberíamos verificar que el punto (2, 2,3) pertenece
Electromagnetismo. Introducción. Líneas de campo magnético. Experimento de Oersted. El campo magnético de las corrientes estacionarias
 El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
El campo magnético de las corrientes estacionarias Electromagnetismo Andrés Cantarero Sáez Curso 25-26 Grupo C ntroducción Propiedades diferenciales del campo magnético Propiedades integrales del campo
. Universidad Tecnológica Nacional - Facultad Regional Rosario. Álgebra y Geometría Analítica EL PLANO
 . Universidad Tecnológica Nacional - Facultad Regional Rosario Álgebra y Geometría Analítica EL PLANO Autores: Lic. Martha Fascella Ing. Ricardo F. Sagristá 0 Contenido EL PLANO... 3.- Definición del plano
. Universidad Tecnológica Nacional - Facultad Regional Rosario Álgebra y Geometría Analítica EL PLANO Autores: Lic. Martha Fascella Ing. Ricardo F. Sagristá 0 Contenido EL PLANO... 3.- Definición del plano
a) Analice la continuidad en (1,0). E1) Dada F : IR 2 π g : D IR 2 I R 2 2 2
 Ejemplos de parcial de Análisis Matemático II Los ítems E1, E, E3 E4 corresponden a la parte práctica Los ítems T1 T son teóricos (sólo para promoción) T1) Sea F : IR IR diferenciable tal que F(,) 00 =
Ejemplos de parcial de Análisis Matemático II Los ítems E1, E, E3 E4 corresponden a la parte práctica Los ítems T1 T son teóricos (sólo para promoción) T1) Sea F : IR IR diferenciable tal que F(,) 00 =
Integral definida. dx es diferencial de x, e indica cuál es la variable de la función que se integra.
 Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Integral definida Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x =
Puntos y Vectores. 16 de Marzo de 2012
 Geometría en Puntos y Vectores Universidad Autónoma Metropolitana Unidad Iztapalapa 16 de Marzo de 2012 Introducción En Geometría analítica plana las relaciones y las propiedades geométricas se expresan
Geometría en Puntos y Vectores Universidad Autónoma Metropolitana Unidad Iztapalapa 16 de Marzo de 2012 Introducción En Geometría analítica plana las relaciones y las propiedades geométricas se expresan
Física II Ecuaciones de Maxwell. Ingeniería Electrónica Departamento de Ciencias Aplicadas y Tecnología Universidad Nacional de Moreno
 Departamento de Ciencias Aplicadas y Tecnología 30 de noviembre de 2015 Índice 1. Repaso de las ecuaciones 1 1.1. ey de Gauss para el campo electrostático....................... 1 1.2. ey de Gauss para
Departamento de Ciencias Aplicadas y Tecnología 30 de noviembre de 2015 Índice 1. Repaso de las ecuaciones 1 1.1. ey de Gauss para el campo electrostático....................... 1 1.2. ey de Gauss para
TEMA 0: Herramientas matemáticas
 1 TEMA 0: Herramientas matemáticas Tema 0: Herramientas matemáticas 1. Campos escalares y vectoriales 2. Gradiente 3. Divergencia 4. Rotacional 5. Teoremas de Gauss y de Stokes 5. Representación gráfica
1 TEMA 0: Herramientas matemáticas Tema 0: Herramientas matemáticas 1. Campos escalares y vectoriales 2. Gradiente 3. Divergencia 4. Rotacional 5. Teoremas de Gauss y de Stokes 5. Representación gráfica
Tema 6. Planos y rectas en el espacio. Problemas métricos (Ángulos, paralelismo y perpendicularidad, simetrías, distancias )
 Matemáticas II (Bachillerato de Ciencias) Geometría del espacio: Problemas métricos 7 Tema 6 Planos rectas en el espacio Problemas métricos (Ángulos, paralelismo perpendicularidad, simetrías, distancias
Matemáticas II (Bachillerato de Ciencias) Geometría del espacio: Problemas métricos 7 Tema 6 Planos rectas en el espacio Problemas métricos (Ángulos, paralelismo perpendicularidad, simetrías, distancias
Espacios vectoriales. Vectores del espacio.
 Espacios vectoriales. Vectores del espacio. Consideremos un paralelepípedo de bases ABCD y EFGH, siendo A(1,1,1), B(2,1,1), C(2,4,1) y E(1,2,7). Halla: a) el área de una de las bases; b) el volumen del
Espacios vectoriales. Vectores del espacio. Consideremos un paralelepípedo de bases ABCD y EFGH, siendo A(1,1,1), B(2,1,1), C(2,4,1) y E(1,2,7). Halla: a) el área de una de las bases; b) el volumen del
Figura Trabajo de las fuerzas eléctricas al desplazar en Δ la carga q.
 1.4. Trabajo en un campo eléctrico. Potencial Clases de Electromagnetismo. Ariel Becerra Al desplazar una carga de prueba q en un campo eléctrico, las fuerzas eléctricas realizan un trabajo. Este trabajo
1.4. Trabajo en un campo eléctrico. Potencial Clases de Electromagnetismo. Ariel Becerra Al desplazar una carga de prueba q en un campo eléctrico, las fuerzas eléctricas realizan un trabajo. Este trabajo
2- El flujo de un campo vectorial se define para una superficie abierta o cerrada?
 ASIGNATURA FISICA II AÑO 2012 GUIA NRO. 2 LEY DE GAUSS Bibliografía Obligatoria (mínima) Capítulo 24 Física de Serway Tomo II Apunte de la cátedra: Capìtulo III PREGUNTAS SOBRE LA TEORIA Las preguntas
ASIGNATURA FISICA II AÑO 2012 GUIA NRO. 2 LEY DE GAUSS Bibliografía Obligatoria (mínima) Capítulo 24 Física de Serway Tomo II Apunte de la cátedra: Capìtulo III PREGUNTAS SOBRE LA TEORIA Las preguntas
Ejercicios típicos del segundo parcial
 Ejercicios típicos del segundo parcial El segundo examen parcial consiste en tres ejercicios prácticos y dos teóricos, aunque esta frontera es muy difusa. Por ejemplo, el primer ejercicio de esta serie,
Ejercicios típicos del segundo parcial El segundo examen parcial consiste en tres ejercicios prácticos y dos teóricos, aunque esta frontera es muy difusa. Por ejemplo, el primer ejercicio de esta serie,
son dos elementos de Rⁿ, definimos su suma, denotada por
 1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
Planos y Rectas. 19 de Marzo de 2012
 el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
el Geometría en el Planos y Rectas Universidad Autónoma Metropolitana Unidad Iztapalapa 19 de Marzo de 2012 el Anteriormente vimos que es posible encontrar un número infinito de vectores, no paralelos
Tema 5: Energía y Leyes de Conservación*
 Tema 5: Energía y Leyes de Conservación* Física I Grado en Ingeniería Electrónica, Robótica y Mecatrónica (GIERM) Primer Curso *Prof.Dr. Joaquín Bernal Méndez y Prof.Dra. Ana Mª Marco Ramírez 1 Índice
Tema 5: Energía y Leyes de Conservación* Física I Grado en Ingeniería Electrónica, Robótica y Mecatrónica (GIERM) Primer Curso *Prof.Dr. Joaquín Bernal Méndez y Prof.Dra. Ana Mª Marco Ramírez 1 Índice
PROBLEMAS DE OPTIMIZACIÓN
 1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
1 PROBLEMAS DE OPTIMIZACIÓN Planteamiento y resolución de los problemas de optimización Se quiere construir una caja, sin tapa, partiendo de una lámina rectangular de cm de larga por de ancha. Para ello
a y Para aplicar el teorema de Stokes, calculamos en primer lugar el rotacional del campo vectorial: i j k / x / y / z
 TEOREMA E TOKE. 1. Usar el teorema de tokes para calcular la integral de línea ( ) d + ( ) d + ( ) d, donde es la curva intersección de la superficie del cubo a, a, a el plano + + 3a/, recorrida en sentido
TEOREMA E TOKE. 1. Usar el teorema de tokes para calcular la integral de línea ( ) d + ( ) d + ( ) d, donde es la curva intersección de la superficie del cubo a, a, a el plano + + 3a/, recorrida en sentido
Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère
 c Rafael R. Boix y Francisco Medina 1 Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère Consideremos un conductor que ocupa un volumen τ. Sea r el vector de posición de
c Rafael R. Boix y Francisco Medina 1 Rotacional del campo magnético creado por corrientes estacionarias. Ley de Ampère Consideremos un conductor que ocupa un volumen τ. Sea r el vector de posición de
EXAMEN PARCIAL DE FÍSICA DE PRIMER CURSO. 7 DE FEBRERO DE GRUPOS C Y D.
 Página 1 de 14 Al índice de exámenes EXAMEN PARCIAL DE FÍSICA DE PRIMER CURSO. 7 DE FEBRERO DE 1994. GRUPOS C Y D. E1. Deducir la ecuación de dimensiones de las siguientes magnitudes: 1- velocidad; 2-
Página 1 de 14 Al índice de exámenes EXAMEN PARCIAL DE FÍSICA DE PRIMER CURSO. 7 DE FEBRERO DE 1994. GRUPOS C Y D. E1. Deducir la ecuación de dimensiones de las siguientes magnitudes: 1- velocidad; 2-
Funciones de varias variables
 Funciones de varias variables 1. Conceptos elementales Funciones IR n IR m. Definición Una función f (también f o f): A IR n IR m es una aplicación que a cada x (también x o x) A IR n le hace corresponder
Funciones de varias variables 1. Conceptos elementales Funciones IR n IR m. Definición Una función f (también f o f): A IR n IR m es una aplicación que a cada x (también x o x) A IR n le hace corresponder
DINAMICA DEL PUNTO. Es el momento con respecto a un punto O de la cantidad de movimiento de una partícula móvil.
 DINMIC DEL PUNTO Leyes de Newton Primera ley o ley de inercia: si sobre un sistema material no actúa fuerza alguna sigue en reposo o movimiento rectilíneo uniforme si inicialmente lo estaba. Segunda ley
DINMIC DEL PUNTO Leyes de Newton Primera ley o ley de inercia: si sobre un sistema material no actúa fuerza alguna sigue en reposo o movimiento rectilíneo uniforme si inicialmente lo estaba. Segunda ley
Movimiento curvilíneo. Magnitudes cinemáticas
 Movimiento curvilíneo. Magnitudes cinemáticas Movimiento curvilíneo Supongamos que el movimiento tiene lugar en el plano XY, Situamos un origen, y unos ejes, y representamos la trayectoria del móvil, es
Movimiento curvilíneo. Magnitudes cinemáticas Movimiento curvilíneo Supongamos que el movimiento tiene lugar en el plano XY, Situamos un origen, y unos ejes, y representamos la trayectoria del móvil, es
3.1. Distancia entre dos puntos. Definición 3.1. Sean a, b e, se llama distancia entre los números a y b que se denota por d (a, b), a la cantidad:
 III. UNIDAD: GEOMETRIA ANALITICA LANA. La Geometría Analítica permite usar los métodos algebraicos en la solución de problemas geométricos, recíprocamente, los métodos de la geometría analítica pueden
III. UNIDAD: GEOMETRIA ANALITICA LANA. La Geometría Analítica permite usar los métodos algebraicos en la solución de problemas geométricos, recíprocamente, los métodos de la geometría analítica pueden
en dos dimensiones como objetos que tienen magnitud, dirección y su representación geométrica.
 1 N.SN.11.1.1 Define vectores en dos dimensiones como objetos que tienen magnitud, dirección y su representación geométrica. Vectores Unidad 4: Vectores Tema 1: Vectores Lección 1: Definición 11 Introducción
1 N.SN.11.1.1 Define vectores en dos dimensiones como objetos que tienen magnitud, dirección y su representación geométrica. Vectores Unidad 4: Vectores Tema 1: Vectores Lección 1: Definición 11 Introducción
ELECTROMAGNETISMO PARA INGENIERÍA ELECTRÓNICA. CAMPOS Y ONDAS
 ELECTROMAGNETISMO PARA INGENIERÍA ELECTRÓNICA. CAMPOS Y ONDAS Introducción a la Teoría de Campos Introducción Capítulo 2 El modelo de campos eléctricos magnéticos es un derivado formal de la Teoría de
ELECTROMAGNETISMO PARA INGENIERÍA ELECTRÓNICA. CAMPOS Y ONDAS Introducción a la Teoría de Campos Introducción Capítulo 2 El modelo de campos eléctricos magnéticos es un derivado formal de la Teoría de
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
 LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
LUGARES GEOMÉTRICOS. CÓNICAS. 9.1 LUGARES GEOMÉTRICOS Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad. Llamando X(,) a las coordenadas del punto genérico aplicando analíticamente
TEMA 8. GEOMETRÍA ANALÍTICA.
 TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
VECTORES 1.2 CONCEPTOS Y DEFINICIONES FUNDAMENTALES. En este capítulo estudiaremos los vectores y su álgebra.
 CAPITULO I CALCULO II VECTORES 1.1 INTRODUCCIÓN Los vectores son un auxiliar utilísimo para la geometría del espacio. En esta unidad partiendo de lo que ya se sabe de vectores en el plano, se contemplan
CAPITULO I CALCULO II VECTORES 1.1 INTRODUCCIÓN Los vectores son un auxiliar utilísimo para la geometría del espacio. En esta unidad partiendo de lo que ya se sabe de vectores en el plano, se contemplan
CINEMÁTICA. Introducción
 CINEMÁTICA 1- MAGNITUDES ESCALARES Y VECTORIALES. 2- CINEMÁTICA. MAGNITUDES FUNDAMENTALES PARA EL ESTUDIO DEL MOVIMIENTO. 3- CLASIFICACIÓN DE MOVIMIENTOS. Introducción La cinemática es una parte de la
CINEMÁTICA 1- MAGNITUDES ESCALARES Y VECTORIALES. 2- CINEMÁTICA. MAGNITUDES FUNDAMENTALES PARA EL ESTUDIO DEL MOVIMIENTO. 3- CLASIFICACIÓN DE MOVIMIENTOS. Introducción La cinemática es una parte de la
Examen de Selectividad Matemáticas JUNIO Andalucía OPCIÓN A
 Eámenes de Matemáticas de Selectividad ndalucía resueltos http://qui-mi.com/ Eamen de Selectividad Matemáticas JUNIO - ndalucía OPCIÓN. Sea f : R R definida por: f ( a b c. a [7 puntos] Halla a b y c para
Eámenes de Matemáticas de Selectividad ndalucía resueltos http://qui-mi.com/ Eamen de Selectividad Matemáticas JUNIO - ndalucía OPCIÓN. Sea f : R R definida por: f ( a b c. a [7 puntos] Halla a b y c para
Bloque 2. Geometría. 3. La recta. 1. Definición de recta
 Bloque 2. Geometría 3. La recta 1. Definición de recta Para representar puntos en un plano (superficie de dos dimensiones) utilizamos dos rectas graduadas y perpendiculares, cuyo corte es el punto 0 de
Bloque 2. Geometría 3. La recta 1. Definición de recta Para representar puntos en un plano (superficie de dos dimensiones) utilizamos dos rectas graduadas y perpendiculares, cuyo corte es el punto 0 de
La integral doble sobre recintos no rectangulares
 La integral doble sobre recintos no rectangulares IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Conjuntos de tipos I II 2 3. Aplicaciones
La integral doble sobre recintos no rectangulares IABEL MARRERO Departamento de Análisis Matemático Universidad de La Laguna imarrero@ull.es Índice 1. Introducción 1 2. Conjuntos de tipos I II 2 3. Aplicaciones
1. Cinemática: Elementos del movimiento
 1. Cinemática: Elementos del movimiento 1. Una partícula con velocidad cero, puede tener aceleración distinta de cero? Y si su aceleración es cero, puede cambiar el módulo de la velocidad? 2. La ecuación
1. Cinemática: Elementos del movimiento 1. Una partícula con velocidad cero, puede tener aceleración distinta de cero? Y si su aceleración es cero, puede cambiar el módulo de la velocidad? 2. La ecuación
Cinemática del sólido rígido
 Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
Cinemática del sólido rígido Teoría básica para el curso Cinemática del sólido rígido, ejercicios comentados α δ ω B B A A P r B AB A ω α O Ramírez López-Para, Pilar Loizaga Garmendia, Maider López Soto,
CAPÍTULO 10. Teoremas Integrales.
 CAPÍTULO 10 Teoremas Integrales. Este capítulo final contiene los teoremas integrales del análisis vectorial, de amplia aplicación a la física y a la ingeniería. Los anteriores capítulos han preparado
CAPÍTULO 10 Teoremas Integrales. Este capítulo final contiene los teoremas integrales del análisis vectorial, de amplia aplicación a la física y a la ingeniería. Los anteriores capítulos han preparado
Problemas métricos. 1. Problemas afines y problemas métricos
 . Problemas afines y problemas métricos Al trabajar en el espacio (o análogamente en el plano) se nos pueden presentar dos tipos de problemas con los elementos habituales (puntos, rectas y planos): Problemas
. Problemas afines y problemas métricos Al trabajar en el espacio (o análogamente en el plano) se nos pueden presentar dos tipos de problemas con los elementos habituales (puntos, rectas y planos): Problemas
1. INTRODUCCIÓN HISTÓRICA. Gilbert ( ) descubrió que la electrificación era un fenómeno de carácter general.
 ELECTROSTÁTICA 1 Introducción. 2 Carga eléctrica. 3 Ley de Coulomb. 4 Campo eléctrico y principio de superposición. 5 Líneas de campo eléctrico. 6 Flujo eléctrico. 7 Teorema de Gauss. Aplicaciones.. 1.
ELECTROSTÁTICA 1 Introducción. 2 Carga eléctrica. 3 Ley de Coulomb. 4 Campo eléctrico y principio de superposición. 5 Líneas de campo eléctrico. 6 Flujo eléctrico. 7 Teorema de Gauss. Aplicaciones.. 1.
2. Distancia entre dos puntos. Punto medio de un segmento
 Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
Geometría 1 Geometría anaĺıtica Una ecuación de primer grado con dos incógnitas x e y tiene infinitas soluciones Por ejemplo x + y = 3 tiene como soluciones (0, 3), (1, ), ( 1, 4), etc Hasta ahora se han
ds = ds = 4πr2 Kq r 2 φ = q ε
 1 El teorema de Gauss. Supongamos una superficie que es atravesada por las líneas de fuerza de un campo eléctrico. Definimos flujo de dicho campo eléctrico a través de la superficie como φ = E S = E S
1 El teorema de Gauss. Supongamos una superficie que es atravesada por las líneas de fuerza de un campo eléctrico. Definimos flujo de dicho campo eléctrico a través de la superficie como φ = E S = E S
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 26 de Junio de 2008 Primera parte. =1, a,b > 0.
 ÁLULO Primer curso de ngeniero de Telecomunicación Examen Final. 6 de Junio de 8 Primera parte Ejercicio. onsideremos los rectángulos de lados paralelos a los ejes que pueden inscribirse en la elipse x
ÁLULO Primer curso de ngeniero de Telecomunicación Examen Final. 6 de Junio de 8 Primera parte Ejercicio. onsideremos los rectángulos de lados paralelos a los ejes que pueden inscribirse en la elipse x
MATEMÁTICAS 1º BACH. C. N. Y S. 25 de enero de 2010 Geometría y Logaritmos
 MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
MATEMÁTICAS 1º BACH. C. N. Y S. 5 de enero de 010 Geometría y Logaritmos x yz 1) Tomar logaritmos, y desarrollar, en la siguiente expresión: A 4 ab log x log b 4log a log y ) Quitar logaritmos: log A )
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 2011 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO
 PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción A Reserva, Ejercicio 4,
PROBLEMAS RESUELTOS SELECTIVIDAD ANDALUCÍA 0 MATEMÁTICAS II TEMA 3: ESPACIO AFIN Y EUCLIDEO Junio, Ejercicio 4, Opción A Junio, Ejercicio 4, Opción B Reserva, Ejercicio 4, Opción A Reserva, Ejercicio 4,
APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 2 ÁLGEBRA VECTORIAL
 Vectores y escalares. REPÚBLICA BOLIVARIANA DE VENEZUELA APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 2 ÁLGEBRA VECTORIAL Las magnitudes escalares son aquellas magnitudes físicas que
Vectores y escalares. REPÚBLICA BOLIVARIANA DE VENEZUELA APUNTES DE FÍSICA I Profesor: José Fernando Pinto Parra UNIDAD 2 ÁLGEBRA VECTORIAL Las magnitudes escalares son aquellas magnitudes físicas que
1. Características del movimiento
 CINEMÁTICA TEMA 1 1. Características del movimiento En el universo todo está en continuo movimiento. Movimiento es el cambio de posición de un cuerpo a lo largo del tiempo respecto a un sistema de referencia
CINEMÁTICA TEMA 1 1. Características del movimiento En el universo todo está en continuo movimiento. Movimiento es el cambio de posición de un cuerpo a lo largo del tiempo respecto a un sistema de referencia
Tema 3 : Campo Eléctrico
 Tema 3 : Campo Eléctrico Esquema de trabajo: 1.- Carga eléctrica 2.- Ley de Colulomb 3.- Campo eléctrico. Intensidad de campo eléctrico. 4.- Energía potencial eléctrica. 5.- Potencial eléctrico. Superficies
Tema 3 : Campo Eléctrico Esquema de trabajo: 1.- Carga eléctrica 2.- Ley de Colulomb 3.- Campo eléctrico. Intensidad de campo eléctrico. 4.- Energía potencial eléctrica. 5.- Potencial eléctrico. Superficies
EJERCICIOS RESUELTOS. x + ; a = 1; b = 1. x x x. x x
 B7_9 //9 : Página EJERIIOS RESUELTOS alcula las funciones primitivas, que toman el valor b cuando a, de las funciones f definidas por: f() + 7; a ; b. 7 f() + ; a ; b. F ( ) ( + 7 ) d + 7 + c omo debe
B7_9 //9 : Página EJERIIOS RESUELTOS alcula las funciones primitivas, que toman el valor b cuando a, de las funciones f definidas por: f() + 7; a ; b. 7 f() + ; a ; b. F ( ) ( + 7 ) d + 7 + c omo debe
. Por ejemplo, para ubicar los puntos, simplemente se localiza su respectivo valor en la numeración y se le marca.
 MATEMÁTICAS BÁSICAS SISTEMAS COORDENADOS SISTEMA COORDENADO UNIDIMENSIONAL Eiste una correspondencia biectiva o biunívoca entre el conjunto de los números reales el de los puntos de una recta. A esta recta
MATEMÁTICAS BÁSICAS SISTEMAS COORDENADOS SISTEMA COORDENADO UNIDIMENSIONAL Eiste una correspondencia biectiva o biunívoca entre el conjunto de los números reales el de los puntos de una recta. A esta recta
Problemas de exámenes de Geometría
 1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
CAMPOS: CIRCULACIÓN Y FLUJO
 AMPO: IRULAIÓN Y FLUJO Dado el vector a ( x + y) i ˆ + xy ˆ j calcular su circulación a lo largo de la recta y x+ desde el punto A (, ) al B (, 2). olución: I.T.I. 99, 5, I.T.T. 2 En la trayectoria que
AMPO: IRULAIÓN Y FLUJO Dado el vector a ( x + y) i ˆ + xy ˆ j calcular su circulación a lo largo de la recta y x+ desde el punto A (, ) al B (, 2). olución: I.T.I. 99, 5, I.T.T. 2 En la trayectoria que
FISICA 2º BACHILLERATO CAMPO ELECTRICO
 ) CMPO ELÉCTRICO Cuando en el espacio vacío se introduce una partícula cargada, ésta lo perturba, modifica, haciendo cambiar su geometría, de modo que otra partícula cargada que se sitúa en él, estará
) CMPO ELÉCTRICO Cuando en el espacio vacío se introduce una partícula cargada, ésta lo perturba, modifica, haciendo cambiar su geometría, de modo que otra partícula cargada que se sitúa en él, estará
Mecánica y fluidos. Temario. Webpage:
 Mecánica fluidos Webpage: http://paginas.fisica.uson.m/qb 2007 Departamento de Física Universidad de Sonora Temario III.- VECTORES. 1. Clasificación de cantidades físicas: Escalares vectores. 2. Representación
Mecánica fluidos Webpage: http://paginas.fisica.uson.m/qb 2007 Departamento de Física Universidad de Sonora Temario III.- VECTORES. 1. Clasificación de cantidades físicas: Escalares vectores. 2. Representación
únicamente un valor de y. Además, el domino serán todos los valores de x excepto x = 3, puesto que anula el denominador. Eso se expresa Domf(x)
 Tema 1: Funciones elementales 1.0 INTRODUCCIÓN: Las distintas ciencias conocen, desde hace tiempo, lees que describen relaciones entre magnitudes, de tal manera que conociendo el valore de algunas de ellas,
Tema 1: Funciones elementales 1.0 INTRODUCCIÓN: Las distintas ciencias conocen, desde hace tiempo, lees que describen relaciones entre magnitudes, de tal manera que conociendo el valore de algunas de ellas,
Cálculo I (Grado en Ingeniería Informática) Problemas adicionales resueltos
 Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
Cálculo I (Grado en Ingeniería Informática) - Problemas adicionales resueltos Calcula el ĺımite lím ( n + n + n + ) n Racionalizando el numerador, obtenemos L lím ( n + n + n (n + n + ) (n + ) + ) lím
1. Funciones de varias variables
 Coordinación de Matemáticas III (MAT 023) 1 er Semestre de 2013 1. Funciones de varias variables 1.1. Definiciones básicas Definición 1.1. Consideremos una función f : U R n R m. Diremos que: 1. f es una
Coordinación de Matemáticas III (MAT 023) 1 er Semestre de 2013 1. Funciones de varias variables 1.1. Definiciones básicas Definición 1.1. Consideremos una función f : U R n R m. Diremos que: 1. f es una
Unidad 5: Geometría analítica del plano.
 Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
Geometría analítica del plano 1 Unidad 5: Geometría analítica del plano. 1.- Vectores. Operaciones con vectores. Un vector fijo es un segmento entre dos puntos, A y B del plano, al que se le da una orientación
x-z = 0 x+y+2 = [2012] [EXT-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por
![x-z = 0 x+y+2 = [2012] [EXT-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por x-z = 0 x+y+2 = [2012] [EXT-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por](/thumbs/55/35462313.jpg) x = 1+t 1. [014] [EXT-A] Considera los puntos A(1,1,) y B(1,-1,-) y la recta dada por y = t. z = 1 a) Halla la ecuación general del plano que que contiene a r y es paralelo a la recta que pasa por A y
x = 1+t 1. [014] [EXT-A] Considera los puntos A(1,1,) y B(1,-1,-) y la recta dada por y = t. z = 1 a) Halla la ecuación general del plano que que contiene a r y es paralelo a la recta que pasa por A y
VECTORES. también con letras sobre las cuales se coloca una flechita ( a ). A = módulo de A. modulo o magnitud, dirección y sentido. vector.
 VECTORES Según su naturaleza las cantidades físicas se clasifican en magnitudes escalares y magnitudes vectoriales Las magnitudes como el tiempo, la temperatura, la masa y otras, son magnitudes escalares
VECTORES Según su naturaleza las cantidades físicas se clasifican en magnitudes escalares y magnitudes vectoriales Las magnitudes como el tiempo, la temperatura, la masa y otras, son magnitudes escalares
3. Funciones de varias variables
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 17 3. Funciones de varias variables Función real de varias variables reales Sea f una función cuyo dominio es un subconjunto D de R n
UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA II
 C u r s o : Matemática 3º Medio Material Nº MT-11 UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA II INTERSECCIÓN CON EL EJE Y La parábola asociada a la función = a + b + c siempre intersecta al eje de
C u r s o : Matemática 3º Medio Material Nº MT-11 UNIDAD: ÁLGEBRA Y FUNCIONES FUNCIÓN CUADRÁTICA II INTERSECCIÓN CON EL EJE Y La parábola asociada a la función = a + b + c siempre intersecta al eje de
5 Rectas y planos en el espacio
 5 Rectas planos en el espacio A B AB v A cada par de puntos A B del plano o del espacio tridimensional, hemos asociado en un vector AB como se muestra en la figura contigua; de manera que si conocemos
5 Rectas planos en el espacio A B AB v A cada par de puntos A B del plano o del espacio tridimensional, hemos asociado en un vector AB como se muestra en la figura contigua; de manera que si conocemos
Coordinación de Matemática IV Guía-Apunte de Preparación del CAR. 2 do Semestre Contenidos del Certamen
 Universidad Técnica Federico anta aría Coordinación de atemática IV Guía-Apunte de Preparación del CAR 2 do emestre 2011 Información Contenidos del Certamen Teorema de Green, Teorema de Green para Regiones
Universidad Técnica Federico anta aría Coordinación de atemática IV Guía-Apunte de Preparación del CAR 2 do emestre 2011 Información Contenidos del Certamen Teorema de Green, Teorema de Green para Regiones
Julio C. Carrillo E. Profesor Escuela de Matemáticas Universidad Industrial de Santander. Monday, November 5, 2007 at 8:44 am (FA07.
 Julio C. Carrillo E. Profesor Escuela de Matemáticas Universidad Industrial de Santander Monday, November 5, 2007 at 8:44 am (FA07.01,02) Para uso exclusivo en el salón de clase. 2007 c Julio C. Carrillo
Julio C. Carrillo E. Profesor Escuela de Matemáticas Universidad Industrial de Santander Monday, November 5, 2007 at 8:44 am (FA07.01,02) Para uso exclusivo en el salón de clase. 2007 c Julio C. Carrillo
5 Continuidad y derivabilidad de funciones reales de varias variables reales.
 5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
5 Continuidad y derivabilidad de funciones reales de varias variables reales. 5.1 Funciones reales de varias variables reales. Curvas de nivel. Continuidad. 5.1.1 Introducción al Análisis Matemático. El
Unidad 5: Geometría Analítica
 Unidad 5 Geometría Analítica 5. Ecuaciones de una recta Los planos y las rectas son objetos geométricos que se pueden representar mediante ecuaciones. Encontraremos la ecuación vectorial de una recta r
Unidad 5 Geometría Analítica 5. Ecuaciones de una recta Los planos y las rectas son objetos geométricos que se pueden representar mediante ecuaciones. Encontraremos la ecuación vectorial de una recta r
Física 2º Bacharelato
 Física 2º Bacharelato DPARTAMNTO D FÍSICA QUÍMICA lectrostática 11/02/08 Nombre: Problemas 1. n la región comprendida entre dos placas cargadas, x véase la figura, existe un campo eléctrico uniforme de
Física 2º Bacharelato DPARTAMNTO D FÍSICA QUÍMICA lectrostática 11/02/08 Nombre: Problemas 1. n la región comprendida entre dos placas cargadas, x véase la figura, existe un campo eléctrico uniforme de
I. T. Telecomunicaciones Universidad de Alcalá Soluciones a los ejercicios propuestos Tema 1
 I. T. Telecomunicaciones Universidad de Alcalá Soluciones a los ejercicios propuestos 28-9-Tema 1 Departamento de Física 1) Dado el campo vectorial F = y i+x j, calcule su circulación desde (2,1, 1) hasta
I. T. Telecomunicaciones Universidad de Alcalá Soluciones a los ejercicios propuestos 28-9-Tema 1 Departamento de Física 1) Dado el campo vectorial F = y i+x j, calcule su circulación desde (2,1, 1) hasta
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
(Apuntes sin revisión para orientar el aprendizaje) CÁLCULO VECTORIAL EXTREMOS DE FUNCIONES ESCALARES DE VARIABLE VECTORIAL
 (Apuntes sin revisión para orientar el aprendizaje) CÁLCULO VECTORIAL EXTREMOS DE FUNCIONES ESCALARES DE VARIABLE VECTORIAL En numerosas aplicaciones de la ingeniería se presentan problemas de optimización,
(Apuntes sin revisión para orientar el aprendizaje) CÁLCULO VECTORIAL EXTREMOS DE FUNCIONES ESCALARES DE VARIABLE VECTORIAL En numerosas aplicaciones de la ingeniería se presentan problemas de optimización,
Vectores. 1) Magnitudes físicas
 Vectores 1) Magnitudes físicas Eisten magnitudes físicas que quedan perfectamente definidas mediante un número epresado en sus unidades correspondientes. Ejemplos de este tipo de magnitud son: la masa
Vectores 1) Magnitudes físicas Eisten magnitudes físicas que quedan perfectamente definidas mediante un número epresado en sus unidades correspondientes. Ejemplos de este tipo de magnitud son: la masa
Integrales Múltiples.
 CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
CAPÍTULO 8 Integrales Múltiples. En este capítulo generalizamos las integrales definidas de una variable a dos y tres variables. La interpretación geométrica de las integrales definidas de una variable
Momento angular de una partícula. Momento angular de un sólido rígido
 Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
Momento angular de una partícula Se define momento angular de una partícula respecto de del punto O, como el producto vectorial del vector posición r por el vector momento lineal mv L=r mv Momento angular
TEMA 11. VECTORES EN EL ESPACIO
 TEMA 11. VECTORES EN EL ESPACIO Dados dos puntos y, se define el vector como el segmento orientado caracterizado por su módulo, su dirección y su sentido. Dos vectores son equipolentes si tienen el mismo
TEMA 11. VECTORES EN EL ESPACIO Dados dos puntos y, se define el vector como el segmento orientado caracterizado por su módulo, su dirección y su sentido. Dos vectores son equipolentes si tienen el mismo
Definición de vectores
 Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen O también denominado Punto de aplicación. Es el punto exacto sobre
Definición de vectores Un vector es todo segmento de recta dirigido en el espacio. Cada vector posee unas características que son: Origen O también denominado Punto de aplicación. Es el punto exacto sobre
TEMA 6 Ejercicios / 3
 TEMA 6 Ejercicios / 1 TEMA 6: RECTAS Y PLANOS EN EL ESPACIO 1. Ecuaciones de los planos cartesianos en forma vectorial, paramétrica e implícita. Ecuaciones del plano XY: Punto del plano P 0, 0, 0 Vectores
TEMA 6 Ejercicios / 1 TEMA 6: RECTAS Y PLANOS EN EL ESPACIO 1. Ecuaciones de los planos cartesianos en forma vectorial, paramétrica e implícita. Ecuaciones del plano XY: Punto del plano P 0, 0, 0 Vectores
