ANTIDERIVADAS. Pues... si es tan simple así significa que ya soy capaz de hacerlo. Lo intentaré. Quiero encontrar la antiderivada de 2x.
|
|
|
- Margarita Velázquez Luna
- hace 6 años
- Vistas:
Transcripción
1 ANTIDERIVADAS Qué es una antiderivada? La respuesta es muy simple. Una antiderivada es la operación inversa a la derivada. Pero qué significa ser la operación inversa de la derivada? Significa que la antiderivada va a deshacer lo que la derivada se encargó de hacer. El método más básico para resolver una antiderivada es adivinar. Lo que harás es pensar en una posible respuesta, derivarla y ver si da! Las antiderivadas también son llamadas Integrales Indefinidas. Pues... si es tan simple así significa que ya soy capaz de hacerlo. Lo intentaré. Quiero encontrar la antiderivada de 2x. Objetivo: Encontrar la antiderivada de 2x Me guiaré por lo que dije arriba. Necesito deshacer lo que una derivada hizo. Debo devolver la función f(x) = 2x a su forma antes de derivar. Sencillo! Si derivo F (x) = x 2 obtengo 2x! Lo primero que harás al momento de hacer una antiderivada es preguntarte Qué función debo derivar para que me dé 2x? (2x para este caso). Ahora si me fijo con cuidado me puedo dar cuenta que si derivo F (x) = x 2 + también obtengo 2x... y si derivo F (x) = x también obtengo 2x. Cada vez que le sumo una constante a F (x) y derivo eso, sigo obteniendo 2x. Así que realmente la antiderivada de mi función f(x) = 2x es F (x) = x 2 + C, donde C representa cualquier constante. Eso no fue tan difícil. Lo intentaré de nuevo! Objetivo: Encontrar la antiderivada de f(x) = x 2 Me hago la pregunta Qué función debo derivar para obtener x 2? De ahora en adelante le llamaré a esa función F (x). Puedo encontrar F (x) en este caso? Claro que sí! Si digo F (x) = x + C al momento de derivar encuentro que F (x) = x 2 y esto es igual a f(x).
2 Intentemos con una un poco más difícil. Objetivo: Encuentra la antiderivada de f(x) = x 4 Qué función debo derivar para que me de x 4? Puedes pensar un poco y decir, si derivo F (x) = x 5 +C entonces F (x) = 5x 4... Casi! Estoy cerca! Tengo un 5 que no quiero ahí... Intentaré esto, diré que F (x) = x5 5 + C. Si derivo F (x) = x5 5 + C entonces F (x) = 5x4 5 = x4 = f(x) La función F (x) que encontré funciona. Como sé que funciona? Al derivar F (x) obtengo f(x). En notación F (x) = f(x). Haré una más! Objetivo: Encuentra la antiderivada de f(x) = x Qué función debo derivar para que me de x? Intentaré usando F (x) = x4 4 + C F (x) = (4)x 4 = x = f(x) Funciona. La F (x) que encontré es correcta. Es hora de formalizar un par de cosas. Debemos comenzar por encontrar una notación para la operación de la antiderivada. Otra! Objetivo: Encuentra la antiderivada de f(x) = x 2/ Qué función debo derivar para obtener x 2/? Esta es un poco más difícil que las demás... Intentaré F (x) = x 5/. Elegí 5/ por qué al derivar yo le resto al exponente así que si estoy aplicando la operación inversa por que no sumarle... F (x) = 5x2/ 2
3 Derivé mi F (x) pero no me dio lo que tenía que dar! multiplicaré eso por /5. Mi nueva F (x) será x5/. 5 Para quitarle el 5/ que está al frente, F (x) = 5x 2/ = x 2/ 5 Funciona! Uno más... Objetivo: Encuentra la antiderivada de f(x) = x 4 Igual que cuando calculaba derivadas, escribiré x 4 como x 4. Veré si F (x) = x funciona. F (x) = (x 4 ) Casi... intentaré con F (x) = x. F (x) = ( x 4 ) = x 4 Si funciona! Para avanzar debo introducir la notación para la operación antiderivar. Anteriormente utilizábamos la operación de la derivada y decíamos por ejemplo... derivar(x ) = x 2 Luego introdujimos esta notación d dx (x ) = x 2 Qué notación debería usar para la antiderivada? Como símbolo utilizo para expresar antiderivar(x 2 ) = x + C
4 Para antiderivada usare la siguiente notación x 2 dx = x + C EXPLICACIÓN DE LA SIMBOLOGÍA DE LA ANTIDERIVADA Cuando usábamos la derivada teníamos dos notaciones: dy dx Donde dy dx es la notación de Leibniz y y es la notación de Newton. Para la antiderivada usaremos esta notación y f(x) dx = F (x) + C F (x) es la antiderivada de f(x); recuerda que eso significa qué al derivar F (x) obtienes f(x). La C es para hacer la antiderivada más general (pero necesaria). El símbolo es una S alargada, la razón de eso lo verás más adelante. Lo que haré ahora será intentar encontrar un patrón en las antiderivadas que encontré anteriormente. Cuando busco la antiderivada de x n el resultado tiene exponente n + (le sumo al exponente). Esto tiene sentido dado que d dx (xn ) = nx n La derivada le quita y la antiderivada le suma (SON INVERSAS!). Al mirar nuevamente los ejemplos, veo que el número que tengo en el exponente en el resultado de la antiderivada aparece en el denominador. En el primer ejemplo tengo x 5 en el numerador y 5 en el denominador. Lo que 4
5 significa que si antiderivo x n mi resultado será una fracción en donde el numerador será x n+ y el denominador será n +, con ese patrón reconocido puedo escribir una fórmula general para este caso. x n dx = xn+ n + + C Observa que también funciona para los últimos ejemplos! CUIDADO: Qué sucede si tengo esta integral? dx x = x dx Aplicando la fórmula te encontrarás un inconveniente... Cuál es? Al aplicar la fórmula cuando n = obtengo,. Esto no puede ser... Cuál es la integral 0 entonces? Esto lo veremos más adelante! Con eso, puedo decir que mi fórmula es x 0 5
6 (F.) x n dx = xn+ + C; n n + Recuerda que la constante C es para generalizar la antiderivada! A esta se le llama constante de integración. Integración? Eso también lo veremos después! De cierta manera, la antiderivada y la derivada son hermanas, es posible que la antiderivada herede propiedades de la derivada. Objetivo: Encuentra la antiderivada de x 2 + 2x. Usando los símbolos, evalúa (x 2 + 2x) dx Recuerda hacerte la pregunta Qué debo derivar para obtener x 2 +2x? Si derivo la expresión x + x 2 + C obtengo x 2 + 2x. Si ves es como si hubiese antiderivado x 2 primero y luego 2x. Al tener ambas antiderivadas simplemente las sumo y obtengo mi respuesta. Puedo decir entonces que la antiderivada de una suma es la suma de las antiderivadas de cada función. Tomaré dos funciones f(x), g(x), sus antiderivadas serán F (x) y G(x) respectivamente. Para mi ejemplo puedo escribir (x 2 + 2x)dx = x 2 dx + 2x dx = x + x 2 + C Después te demostraré que poner una sola constante de integración es suficiente. Con eso listo, puedo escribir mi propiedad 6
7 (P.) [f(x) + g(x)]dx = f(x) dx + g(x) dx = F (x) + G(x) + C Objetivo: Evalúa dx Cuando ves solamente el diferencial se da por entendido que es dx Qué derivo para obtener? Simple, x + C. 4x Como evalúo dx? Si derivo, x + C obtengo, listo. Y si evalúo dx? En este caso la 5 respuesta es x4 5 + C. En los últimos dos casos puedo escribir las antiderivadas así 4x dx = 5 dx = 5 dx 4x dx Si saco alguna constante de la antiderivada el resultado es el mismo! (Siempre y cuando multiplique la constante de vuelta). Escribiré mi otra propiedad. Si k es una constante y F (x) es la antiderivada de f(x), (P.2) kf(x)dx = k f(x) dx = kf (x) + C Las propiedades P. y P.2 muestran la linealidad de una antiderivada (busca más información de esto en otros documentos). 7
8 Curiosidad: Te he dicho que las derivadas y las antiderivadas son operaciones inversas. Se que son inversas pero de alguna manera, muy en el fondo, son hermanas. Linealidad de una derivada: d d [f(x) + g(x)] = dx dx (f(x)) + d dx (g(x)) d dx [kf(x)] = k d dx [f(x)] EJEMPLOS Ejemplo : Calcula la antiderivada 9 x 8 dx a.) Primer acercamiento: En vez de aplicar la fórmula y memorizar todo, puedes piensa: Qué puedo derivar para conseguir la función que está dentro de la integral? Digamos que la respuesta a la integral es f(x). La misma puede ser f(x) = x 9 + o incluso f(x) = x , por eso la respuesta mas general es: f(x) = x 9 + C. b.) Segundo Acercamiento: Aplicando la fórmula F., el procedimiento será el siguiente... Para este caso (y usando la propiedad P.) n = 8. Por eso: 9 x 8 dx = 9 x 8 dx = 9 x C = x9 + C Listo! Toma en cuenta que según el diferencial (dx) me dice que integre x, por eso lo hice. No olvides, nunca, la constante de integración. Ejemplo 2: Evalúa u du En problemas que se ven como este, pensar en una solución directa (como se hizo en el primer acercamiento del primer ejemplo) puede resultar complicado. Por eso, después de modificar un par de cosas utilizaré, las fórmulas. Solución: 8
9 Antes de comenzar a resolver, puedo usar varias propiedades de exponentes para volver a escribir lo que está dentro de la integral de manera que pueda aplicar una de las fórmulas mencionadas. Para esto digo: u = (u ) /2 (escribo la raíz como exponente), luego (u ) /2 = u /2 (propiedad de exponenciación), finalmente = u /2 (propiedad de exponenciación, la u sube al numerador u /2 con exponente negativo). Haciendo esto, puedes aplicar la fórmula F.: du = u u /2 du = u( /2)+ ( /2) + + C = u /2 /2 + C Recuerda que se ve mejor hacer que la respuesta se vea como la función que está dentro de la antiderivada por eso; el /2 sube al numerador como 2 y el u /2 baja al denominador con exponente positivo y cambiado a raíz cuadrada. Por eso la respuesta es: u du = 2 u + C No olvides la constante de integración, y observa que antiderivé con respecto a u por que el diferencial du me lo dijo! Ejemplo : Integra ( 2t 7t 2 t ) dt Para poder resolver la integral lo ideal es separar la fracción en varias partes: 2t 7t 2 t 2 = 2t t 2 7t2 t 2 = 2t 7 Mira que puedo sumar el 7 y el 25 antes de hacer la antiderivada: ( 2t 7t 2 t ) dt = (2t ) dt = (2t + 8) dt Puedo separar, usando la propiedad P., esta antiderivada en varias partes: = 2t dt + 8 dt 9
10 Un dato interesante, para estas dos antiderivadas no es necesario escribir una constante de integración para cada una; puedes escribir una sola para todas las antiderivadas, ya te lo demostraré. Observa que ambas antiderivadas se pueden resolver de manera directa haciendo la pregunta: Qué debo derivar para que me resulte lo que tengo dentro de la integral? Si derivo t 2 + C donde C es una constante, obtengo 2t, si derivo 8t + C 2 donde C 2 es una constante obtengo 8. Por eso: 2t dt + 2 dt = t 2 + C + 2t + C 2 Con esto hecho, la respuesta debe ser: ( 2t 7t 2 t ) dt = t 2 + 8t + C + C 2 Pero como C y C 2 son constantes, las puedo sumar para hacer una sola constante C. Por eso la respuesta es: ( 2t + 7t 2 t ) dt = t 2 + 8t + C Ya te demostré que puedes usar una sola constante de integración. Terminó el problema. No olvides: Nunca dejes la constante de integración, no olvides ver el diferencial antes de integrar. Ejemplo 4: Calcula la antiderivada ( a y/4 a2 + b ) dy donde a y b son constantes. 2 ab2 a.) Recuerda que a y b son constantes, por eso las puedes sacar de la antiderivada (propiedad P.2). Aplica la fórmula F.. a y /4 a2 + b dy = a 2 a2 + b 2 y /4 dy = a y (/4)+ a2 + b 2 (/4) + = a y 7/4 a2 + b 2 7/4 = 4 a y7/4 7 a 2 + b 2 b.) Constantes fuera de la antiderivada y luego efectuó la operación. ab 2 dy = ab 2 dy = ab 2 y = y ab 2 0
11 d.) Combinando todo y agregando la constante de integración: ( a y/4 a2 + b 4 a y7/4 ) dy = 2 ab2 7 a 2 + b y 2 ab 2 + C
Integrales que producen Funciones Trigonométricas Inversas
 Integrales que procen Funciones Trigonométricas Inversas Veremos un grupo de funciones cuyas antiderivadas son funciones trigonométricas inversas. Para comenzar, recuerda que d (sen (x = x Si al derivar
Integrales que procen Funciones Trigonométricas Inversas Veremos un grupo de funciones cuyas antiderivadas son funciones trigonométricas inversas. Para comenzar, recuerda que d (sen (x = x Si al derivar
Técnicas de Integración. Integración por Partes (I)
 Técnicas de Integración Integración por Partes (I El método de integración por partes es un método que te permite separar una integral (que tiene un producto de dos funciones en una integral simple y lista
Técnicas de Integración Integración por Partes (I El método de integración por partes es un método que te permite separar una integral (que tiene un producto de dos funciones en una integral simple y lista
Técnicas de Integración. Fracciones Parciales (III)
 Técnicas de Integración Fracciones Parciales (III) En los documentos anteriores mencioné que cuando teníamos un denominador de la forma (ax+b) n o que el numerador fuera de mayor exponente que el denominador,
Técnicas de Integración Fracciones Parciales (III) En los documentos anteriores mencioné que cuando teníamos un denominador de la forma (ax+b) n o que el numerador fuera de mayor exponente que el denominador,
Técnicas de Integración. Fracciones Parciales (I)
 Técnicas de Integración Fracciones Parciales (I) Hay ciertas integrales que no lucen muy bien al momento de trabajarlas. Muchas veces nos encontraremos con una rama de estas integrales, las integrales
Técnicas de Integración Fracciones Parciales (I) Hay ciertas integrales que no lucen muy bien al momento de trabajarlas. Muchas veces nos encontraremos con una rama de estas integrales, las integrales
INTEGRALES. EL PROBLEMA DEL ÁREA I
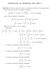 INTEGRALES. EL PROBLEMA DEL ÁREA I Ejercicio : En este ejercicio vamos a practicar el cálculo de la integral indefinida haciendo uso de la integral inmediata: (f(x)) n f (x)dx n = (f(x))n+ + K (K constante)
INTEGRALES. EL PROBLEMA DEL ÁREA I Ejercicio : En este ejercicio vamos a practicar el cálculo de la integral indefinida haciendo uso de la integral inmediata: (f(x)) n f (x)dx n = (f(x))n+ + K (K constante)
5.1. Primitiva de una función. Reglas básicas
 Tema 5 Integración Indefinida 5.1. Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
Tema 5 Integración Indefinida 5.1. Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
Sucesiones. Límite de una sucesión.
 1 CONOCIMIENTOS PREVIOS. 1 Sucesiones. Límite de una sucesión. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Repasar las operaciones básicas
1 CONOCIMIENTOS PREVIOS. 1 Sucesiones. Límite de una sucesión. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Repasar las operaciones básicas
UNIVERSIDAD ARTURO PRAT IQUIQUE CHILE DEPARTAMENTO DE CIENCIAS FISICAS Y MATEMATICAS INTEGRALES
 DEPARTAMENTO DE CIENCIAS FISICAS Y MATEMATICAS INTEGRALES MARIA ELISA VODNIZZA LIRA e-mail : mvodnizz@cec.unap.cl url : www.unap.cl/~mvodnizz SEPTIEMBRE - 00 INTEGRALES Uno de los problemas importantes
DEPARTAMENTO DE CIENCIAS FISICAS Y MATEMATICAS INTEGRALES MARIA ELISA VODNIZZA LIRA e-mail : mvodnizz@cec.unap.cl url : www.unap.cl/~mvodnizz SEPTIEMBRE - 00 INTEGRALES Uno de los problemas importantes
Integrales indenidas
 Integrales indenidas Adriana G. Duarte 7 de agosto de 04 Resumen Antiderivación. Integrales indenidas, propiedades. Técnicas de integración: inmediatas,por sustitución, por partes. Ejemplos y ejercicios.
Integrales indenidas Adriana G. Duarte 7 de agosto de 04 Resumen Antiderivación. Integrales indenidas, propiedades. Técnicas de integración: inmediatas,por sustitución, por partes. Ejemplos y ejercicios.
Radicales y sus operaciones MATEMÁTICAS 2º CICLO E.S.O.
 Radicales y sus operaciones MATEMÁTICAS º CICLO E.S.O. Objetivos: Simplificar radicales Efectuar operaciones de suma, resta, multiplicación y división con radicales Racionalizar parte de una fracción Notación:
Radicales y sus operaciones MATEMÁTICAS º CICLO E.S.O. Objetivos: Simplificar radicales Efectuar operaciones de suma, resta, multiplicación y división con radicales Racionalizar parte de una fracción Notación:
Unidad II. Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en unaconstante.
 Unidad II Integral indefinida y métodos de integración. 2.1 Definición de integral indefinida. Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones
Unidad II Integral indefinida y métodos de integración. 2.1 Definición de integral indefinida. Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones
Operatoria con Potencias y Raíces
 PreUnAB Clase # 3 Junio 2014 Definición Se llama potencia a una expresiń de la forma, donde a es la base y n es el exponente. Potencia de Exponente Entero a n = a a a... a Cuando el exponente es un número
PreUnAB Clase # 3 Junio 2014 Definición Se llama potencia a una expresiń de la forma, donde a es la base y n es el exponente. Potencia de Exponente Entero a n = a a a... a Cuando el exponente es un número
INTRO. LA INTEGRAL INDEFINIDA
 INTRO. LA INTEGRAL INDEFINIDA Se inicia en este tema el estudio de la integral, concepto fundamental de lo que se conoce como cálculo infinitesimal, que alcanzó su auge y desarrollo durante el siglo XVII.
INTRO. LA INTEGRAL INDEFINIDA Se inicia en este tema el estudio de la integral, concepto fundamental de lo que se conoce como cálculo infinitesimal, que alcanzó su auge y desarrollo durante el siglo XVII.
Matemáticas Empresariales I. Cálculo de Primitivas
 Matemáticas Empresariales I Lección 7 Cálculo de Primitivas Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales I 1 / 45 Concepto de Integral Indefinida Definición
Matemáticas Empresariales I Lección 7 Cálculo de Primitivas Manuel León Navarro Colegio Universitario Cardenal Cisneros M. León Matemáticas Empresariales I 1 / 45 Concepto de Integral Indefinida Definición
Integración por Partes III. Método Tabular
 Integración por Partes III Método Tabular I.) INTEGRALES NO CÍCLICAS El método tabular te va a permitir desarrollar cierto tipo de integrales sin tener que utilizar todos los pasos de la integración por
Integración por Partes III Método Tabular I.) INTEGRALES NO CÍCLICAS El método tabular te va a permitir desarrollar cierto tipo de integrales sin tener que utilizar todos los pasos de la integración por
Módulo 8. Simplificación de radicales
 Módulo 8 Simplificación de radicales OBJETIVO Simplificar expresiones algebraicas con radicales. La simplificación de radicales tiene su principal aplicación en las operaciones con radicales. Estas operaciones
Módulo 8 Simplificación de radicales OBJETIVO Simplificar expresiones algebraicas con radicales. La simplificación de radicales tiene su principal aplicación en las operaciones con radicales. Estas operaciones
ene 5 12:59 Está basado en la regla de la cadena. Si F(x) y g(x) son funciones derivables, la regla de la cadena nos dice que:
 Métodos de integración: 1) Método de descomposición Para calcular una integral indefinida, usamos las propiedades de las integrales y las igualdades que conozcamos para descomponer la integral en otras
Métodos de integración: 1) Método de descomposición Para calcular una integral indefinida, usamos las propiedades de las integrales y las igualdades que conozcamos para descomponer la integral en otras
El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow.
 INTRODUCCION El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de
INTRODUCCION El cálculo integral fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de
Herramientas digitales de auto-aprendizaje para Matemáticas
 ir Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura ir ir Índice. Definiciones y propiedades Método de por
ir Herramientas digitales de auto-aprendizaje para Matemáticas, Grupo de Innovación Didáctica Departamento de Matemáticas Universidad de Extremadura ir ir Índice. Definiciones y propiedades Método de por
Integración indefinida y definida. Aplicaciones de la integral: valor medio de una función continua.
 Integración indefinida y definida. Aplicaciones de la integral: valor medio de una función continua. 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos 1 Introducción 2 3 4 5
Integración indefinida y definida. Aplicaciones de la integral: valor medio de una función continua. 1 1 Departamento de Matemáticas. Universidad de Alcalá de Henares. Contenidos 1 Introducción 2 3 4 5
Las operaciones con números irracionales
 Las operaciones con números irracionales Antes de empezar a sumar, restar, multiplicar, y realizar cualquier tipo de las operaciones con números irracionales, debemos comprender como extraer, e introducir
Las operaciones con números irracionales Antes de empezar a sumar, restar, multiplicar, y realizar cualquier tipo de las operaciones con números irracionales, debemos comprender como extraer, e introducir
(6x + 8) + (4x + 2) (6x + 8) + (4x + 2) = 10x + 10
 Operaciones con números complejos Objetivos de aprendizaje Sumar números complejos. Restar números complejos. Multiplicar números complejos. Encontrar conjugados de números complejos. Dividir números complejos.
Operaciones con números complejos Objetivos de aprendizaje Sumar números complejos. Restar números complejos. Multiplicar números complejos. Encontrar conjugados de números complejos. Dividir números complejos.
ANÁLISIS MATEMÁTICO IES A SANGRIÑA 2016/2017
 ANÁLISIS MATEMÁTICO 4. INTEGRACIÓN INDEFINIDA UN POCO DE HISTORIA El símbolo de integración fue introducido por el matemático alemán Gottfried Leibniz en 1675, basándose en la palabra latina summa, suma,
ANÁLISIS MATEMÁTICO 4. INTEGRACIÓN INDEFINIDA UN POCO DE HISTORIA El símbolo de integración fue introducido por el matemático alemán Gottfried Leibniz en 1675, basándose en la palabra latina summa, suma,
Unidad 5 - Trabajo Práctico 5 Parte 1 Elementos de Matemática
 06 Unidad 5 - Trabajo Práctico 5 Parte Unidad 5 Integral indefinida. Primitivas inmediatas. Uso de tablas de integrales. Integración por descomposición, por sustitución y por partes. Integral definida:
06 Unidad 5 - Trabajo Práctico 5 Parte Unidad 5 Integral indefinida. Primitivas inmediatas. Uso de tablas de integrales. Integración por descomposición, por sustitución y por partes. Integral definida:
DERIVADA E INTEGRAL CÁLCULO INTEGRAL
 Índice Presentación... 3 El cálculo del área... 4 La integral como un área... 5 Propiedades... 6 Funciones definidas a través de una integral... 7 Regla de Barrow... 8 Integrales indefinidas... 9 Reglas
Índice Presentación... 3 El cálculo del área... 4 La integral como un área... 5 Propiedades... 6 Funciones definidas a través de una integral... 7 Regla de Barrow... 8 Integrales indefinidas... 9 Reglas
Integral indefinida. Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
 Integral indefinida 1. Integración Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x). Se dice, entonces,
Integral indefinida 1. Integración Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x). Se dice, entonces,
OPERACIONES CON POLINOMIOS
 4. 1 UNIDAD 4 OPERACIONES CON POLINOMIOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques las operaciones de suma, resta, multiplicación y división de polinomios.
4. 1 UNIDAD 4 OPERACIONES CON POLINOMIOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas en los que apliques las operaciones de suma, resta, multiplicación y división de polinomios.
La integral indefinida
 La integral indefinida por Iván Cruz Cuando hablamos de cálculo integral, es común hacer referencia a operaciones inversas, por ejemplo: Tiene como su operación inversa a: En cálculo diferencial se resuelven
La integral indefinida por Iván Cruz Cuando hablamos de cálculo integral, es común hacer referencia a operaciones inversas, por ejemplo: Tiene como su operación inversa a: En cálculo diferencial se resuelven
INTEGRACIÓN DE RACIONALES. Siendo p(x) y q(x) dos polinomios. Nos podemos encontrar dos casos:
 INTEGRACIÓN DE RACIONALES Nos hallamos ante una racional cuando estamos atacando un problema y nos encontramos con un cociente de polinomios que tenemos que integrar. Hemos de resolver: f(x) = p(x) q(x)
INTEGRACIÓN DE RACIONALES Nos hallamos ante una racional cuando estamos atacando un problema y nos encontramos con un cociente de polinomios que tenemos que integrar. Hemos de resolver: f(x) = p(x) q(x)
Tema 10: Cálculo integral
 Tema 0: Cálculo integral. Introducción El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
Tema 0: Cálculo integral. Introducción El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
Tema 10: Cálculo Integral
 . Introducción Tema 0: Cálculo Integral El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
. Introducción Tema 0: Cálculo Integral El matemático inglés Isaac Barrow (60-677) fue el precursor del cálculo de integrales definidas, enunciando la regla que lleva su nombre y que conecta la integral
1. Función primitiva e integral indefinida
 Entrenamiento Matemático Sesión 0 (4 -Octubre-00) Cálculo elemental de Primitivas GRUPO:. Función primitiva e integral indefinida Dada una función f: R-->R, se dice que una función derivable F es primitiva
Entrenamiento Matemático Sesión 0 (4 -Octubre-00) Cálculo elemental de Primitivas GRUPO:. Función primitiva e integral indefinida Dada una función f: R-->R, se dice que una función derivable F es primitiva
OPERAR CON POTENCIAS: MULTIPLICACIÓN, DIVISIÓN Y POTENCIA DE POTENCIA
 OPERAR CON POTENCIAS: MULTIPLICACIÓN, DIVISIÓN Y POTENCIA DE POTENCIA OBJETIVO MULTIPLICACIÓN DE POTENCIAS Como las potencias son multiplicaciones, se va a trabajar con ellas cuando multiplicamos o dividimos:
OPERAR CON POTENCIAS: MULTIPLICACIÓN, DIVISIÓN Y POTENCIA DE POTENCIA OBJETIVO MULTIPLICACIÓN DE POTENCIAS Como las potencias son multiplicaciones, se va a trabajar con ellas cuando multiplicamos o dividimos:
FUNDAMENTOS NUMÉRICOS
 SEMANA 3 ÍNDICE ECUACIONES... 3 APRENDIZAJES ESPERADOS... 3 INTRODUCCIÓN... 3 PROPIEDADES DE LA IGUALDAD... 4 ECUACIONES... 4 ECUACIONES LINEALES... 4 ECUACIONES CUADRÁTICAS... 5 RESOLUCIÓN DE UNA ECUACIÓN
SEMANA 3 ÍNDICE ECUACIONES... 3 APRENDIZAJES ESPERADOS... 3 INTRODUCCIÓN... 3 PROPIEDADES DE LA IGUALDAD... 4 ECUACIONES... 4 ECUACIONES LINEALES... 4 ECUACIONES CUADRÁTICAS... 5 RESOLUCIÓN DE UNA ECUACIÓN
1. Conocimientos previos. 2. Sucesión Progresiones aritméticas. 1 CONOCIMIENTOS PREVIOS. 1
 CONOCIMIENTOS PREVIOS. Límites.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Repasar las operaciones básicas con expresiones algebraicas. Repasar
CONOCIMIENTOS PREVIOS. Límites.. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Repasar las operaciones básicas con expresiones algebraicas. Repasar
2. Continuidad y derivabilidad. Aplicaciones
 Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
Métodos Matemáticos (Curso 2013 2014) Grado en Óptica y Optometría 7 2. Continuidad y derivabilidad. Aplicaciones Límite de una función en un punto Sea una función f(x) definida en el entorno de un punto
INTEGRACIÓN INDEFINIDA
 1. PRIMITIVA DE UNA FUNCIÓN Definición: Sean F(x) y f(x) dos funciones reales definidas en un mismo dominio D. Se dice, entonces, que F(x) es una primitiva de f(x) si se cumple quef'(x) = f(x), x. Dicho
1. PRIMITIVA DE UNA FUNCIÓN Definición: Sean F(x) y f(x) dos funciones reales definidas en un mismo dominio D. Se dice, entonces, que F(x) es una primitiva de f(x) si se cumple quef'(x) = f(x), x. Dicho
Si f es derivable, definimos al diferencial de una función (df), como el producto de la derivada de f por un incremento de la variable ( x).
 2 Integrales Indefinidas y Métodos de Integración La integral Indefinida o antiderivada es el nombre que recibe la operación inversa a la derivada. Es decir, dada una función F aquella consiste en encontrar
2 Integrales Indefinidas y Métodos de Integración La integral Indefinida o antiderivada es el nombre que recibe la operación inversa a la derivada. Es decir, dada una función F aquella consiste en encontrar
Unidad IV. 4.1 Conceptos de incremento y de razón de cambio. La derivada de una función.
 Unidad IV Derivadas 4.1 Conceptos de incremento y de razón de cambio. La derivada de una función. Derivada de una función en un punto. Dada la función f(x) continúa en el intervalo abierto I, se define
Unidad IV Derivadas 4.1 Conceptos de incremento y de razón de cambio. La derivada de una función. Derivada de una función en un punto. Dada la función f(x) continúa en el intervalo abierto I, se define
La integral indefinida. Formulas y ejemplos Autor: jose maria guzman perez
 La integral indefinida. Formulas y ejemplos Autor: jose maria guzman perez 1 Presentación del curso En el siguiente curso que te presentamos a continuación tendrás la posibilidad de tener una guía sobre
La integral indefinida. Formulas y ejemplos Autor: jose maria guzman perez 1 Presentación del curso En el siguiente curso que te presentamos a continuación tendrás la posibilidad de tener una guía sobre
FISICA MECANICA DOCUMENTO DE CONTENIDO MATEMATICAS PARA FISICOS
 FISICA MECANICA DOCUMENTO DE CONTENIDO MATEMATICAS PARA FISICOS Objetivo general: Brindar algunas herramientas matemáticas que los estudiantes de física necesitan para su buen desempeño en el curso de
FISICA MECANICA DOCUMENTO DE CONTENIDO MATEMATICAS PARA FISICOS Objetivo general: Brindar algunas herramientas matemáticas que los estudiantes de física necesitan para su buen desempeño en el curso de
La raíz n-ésima de un número, es. Y, al igual que la simplificación de las raíces cuadradas, podemos simplificar las raíces n-ésimas.
 RAÍZ ENÉSIMA Hasta ahora, hemos visto exponentes con números enteros y raíz cuadrada. En esta guía, vamos a vincular las raíces y exponentes. En primer lugar, vamos a definir raíces adicionales. Al igual
RAÍZ ENÉSIMA Hasta ahora, hemos visto exponentes con números enteros y raíz cuadrada. En esta guía, vamos a vincular las raíces y exponentes. En primer lugar, vamos a definir raíces adicionales. Al igual
Métodos de integración
 Teóricas de Análisis Matemático (8) - Práctica 9 - Métodos de integración Práctica 9 - Parte Métodos de integración Esta parte de la materia está dedicada a estudiar distintos métodos que nos resultarán
Teóricas de Análisis Matemático (8) - Práctica 9 - Métodos de integración Práctica 9 - Parte Métodos de integración Esta parte de la materia está dedicada a estudiar distintos métodos que nos resultarán
ÁREA: BÁSICA CLAVE DE LA ASIGNATURA: LA 102
 MATEMÁTICAS ÁREA: BÁSICA CLAVE DE LA ASIGNATURA: LA 102 OBJETIVO(S) GENERAL(ES) DE LA ASIGNATURA: Al término del curso, el alumno analizará los principios de las matemáticas; aplicará los mismos como herramientas
MATEMÁTICAS ÁREA: BÁSICA CLAVE DE LA ASIGNATURA: LA 102 OBJETIVO(S) GENERAL(ES) DE LA ASIGNATURA: Al término del curso, el alumno analizará los principios de las matemáticas; aplicará los mismos como herramientas
RADICALES. Un radical es una expresión de la forma, en la que n y ; con tal que cuando a sea negativo, n ha de ser impar.
 RADICALES Un radical es una expresión de la forma, en la que n y a ; con tal que cuando a sea negativo, n ha de ser impar. Se puede expresar un radical en forma de potencia: Radicales equivalentes Utilizando
RADICALES Un radical es una expresión de la forma, en la que n y a ; con tal que cuando a sea negativo, n ha de ser impar. Se puede expresar un radical en forma de potencia: Radicales equivalentes Utilizando
Números. Índice del libro. 1. Los números reales. 2. Operaciones con números enteros y racionales. 3. Números decimales
 1. Los números reales 2. Operaciones con números enteros y racionales 3. decimales 4. Potencias de exponente entero 5. Radicales 6. Notación científica y unidades de medida 7. Errores Índice del libro
1. Los números reales 2. Operaciones con números enteros y racionales 3. decimales 4. Potencias de exponente entero 5. Radicales 6. Notación científica y unidades de medida 7. Errores Índice del libro
5. INTEGRALES. 5.1 Integral indefinida
 5. INTEGRALES 5.1 Integral indefinida Al igual que la derivada, el concepto de integral surge como una herramienta de la mecánica clásica desarrollada fundamentalmente por Newton y Leibnitz. La aplicación
5. INTEGRALES 5.1 Integral indefinida Al igual que la derivada, el concepto de integral surge como una herramienta de la mecánica clásica desarrollada fundamentalmente por Newton y Leibnitz. La aplicación
Integración por fracción parcial -Caso Lineal
 * Método de integración por fracción parcial Caso lineal Recordemos que una función racional h es la forma: Px ( ) hx ( ) Qx ( ) Donde P(x) y Q(x) son polinomios y Q(x) no es el polinomio nulo.pues veremos
* Método de integración por fracción parcial Caso lineal Recordemos que una función racional h es la forma: Px ( ) hx ( ) Qx ( ) Donde P(x) y Q(x) son polinomios y Q(x) no es el polinomio nulo.pues veremos
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es Índice 1. Definiciones 3 2. Herramientas 5 2.1. Reglas de derivación............................
Clase 1. Tema: Simplificación de fracciones algebraicas. Matemáticas 8. Bimestre: IV Número de clase: 1. Esta clase tiene video.
 Bimestre: IV Número de clase: Clase Esta clase tiene video Tema: Simplificación de fracciones algebraicas Actividad Lea la siguiente información. Una fracción algebraica es el cociente entre dos expresiones
Bimestre: IV Número de clase: Clase Esta clase tiene video Tema: Simplificación de fracciones algebraicas Actividad Lea la siguiente información. Una fracción algebraica es el cociente entre dos expresiones
Derivadas e integrales
 Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
Derivadas e integrales Álvarez S., Caballero M.V. y Sánchez M a M salvarez@um.es, m.victori@um.es, marvega@um.es ÍNDICE Matemáticas Cero Índice. Definiciones 3. Herramientas 4.. Reglas de derivación.......................
Antiderivada o Primitiva
 Octubre 2013 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada En esta Presentación... En esta Presentación veremos: Definición de Antiderivada Ejemplos En esta Presentación...
Octubre 2013 En esta Presentación... En esta Presentación veremos: Definición de Antiderivada En esta Presentación... En esta Presentación veremos: Definición de Antiderivada Ejemplos En esta Presentación...
CURSO BÁSICO DE MATEMÁTICAS PARA ESTUDIANTES DE ECONÓMICAS Y EMPRESARIALES. Unidad didáctica 8. Introducción a la integración INTEGRAL INDEFINIDA
 INTEGRAL INDEFINIDA CONCEPTOS BÁSICOS: PRIMITIVA E INTEGRAL INDEFINIDA El cálculo de integrales indefinidas de una función es un proceso inverso del cálculo de derivadas ya que se trata de encontrar una
INTEGRAL INDEFINIDA CONCEPTOS BÁSICOS: PRIMITIVA E INTEGRAL INDEFINIDA El cálculo de integrales indefinidas de una función es un proceso inverso del cálculo de derivadas ya que se trata de encontrar una
10. Ecuaciones, parte IV
 Matemáticas I, 01-I Variables y Constantes, Incógnitas y Parámteros En una ecuación como E = mc hay tres letras: E, my c. En este caso E representa la energía, m la masa y c la velocidad de la luz (en
Matemáticas I, 01-I Variables y Constantes, Incógnitas y Parámteros En una ecuación como E = mc hay tres letras: E, my c. En este caso E representa la energía, m la masa y c la velocidad de la luz (en
5.1 Primitiva de una función. Reglas básicas
 Tema 5 Integración Indefinida 5.1 Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
Tema 5 Integración Indefinida 5.1 Primitiva de una función. Reglas básicas En este tema estudiaremos lo que podríamos llamar el problema inverso de la derivación, es decir, dada una función f hallar otra
f(x) = x + 2 x 2 4 f(x) = x 2 2x 4
 Tu pregunta es Obtén el dominio de las siguiente funciones, f(x) = x 1 x + 1 f(x) = x + 1 x 1 f(x) = x + 1 x + 1 f(x) = x 4 x + x 3 f(x) = x + x 4 f(x) = x x 4 f(x) = 1 x 3 + 3 x 1 f(x) = x 3 Bien, el
Tu pregunta es Obtén el dominio de las siguiente funciones, f(x) = x 1 x + 1 f(x) = x + 1 x 1 f(x) = x + 1 x + 1 f(x) = x 4 x + x 3 f(x) = x + x 4 f(x) = x x 4 f(x) = 1 x 3 + 3 x 1 f(x) = x 3 Bien, el
La Lección de hoy es sobre Simplificar Fracciones y Radicales. El cuál es la expectativa para el aprendizaje del estudiante LA.1.A1.
 Simplifying Radical Fractions-LA.1.A1.8-Beach Pam. La Lección de hoy es sobre Simplificar Fracciones y Radicales. El cuál es la expectativa para el aprendizaje del estudiante LA.1.A1.8 Una fracción no
Simplifying Radical Fractions-LA.1.A1.8-Beach Pam. La Lección de hoy es sobre Simplificar Fracciones y Radicales. El cuál es la expectativa para el aprendizaje del estudiante LA.1.A1.8 Una fracción no
Semana02[1/33] Números Reales. March 9, Números Reales
![Semana02[1/33] Números Reales. March 9, Números Reales Semana02[1/33] Números Reales. March 9, Números Reales](/thumbs/57/41059919.jpg) Semana02[1/33] March 9, 2007 Axiomas de R en torno a la desigualdad Números reales positivos Semana02[2/33] Para introducir la idea de orden en los reales y poder trabajar con desigualdades, existen diversas
Semana02[1/33] March 9, 2007 Axiomas de R en torno a la desigualdad Números reales positivos Semana02[2/33] Para introducir la idea de orden en los reales y poder trabajar con desigualdades, existen diversas
INTEGRACIÓN Julián de la Horra Departamento de Matemáticas U.A.M.
 INTEGRACIÓN Julián de la Horra Departamento de Matemáticas U.A.M. 1 Introducción En este capítulo vamos a abordar y estudiar el concepto de integral definida. Empezaremos planteando algunos ejemplos sencillos
INTEGRACIÓN Julián de la Horra Departamento de Matemáticas U.A.M. 1 Introducción En este capítulo vamos a abordar y estudiar el concepto de integral definida. Empezaremos planteando algunos ejemplos sencillos
Teoría Tema 3 Derivabilidad - Aplicación a funciones
 Asignatura: Matemáticas II 2ºBacillerato página 1/16 Teoría Tema 3 Derivabilidad - Aplicación a funciones Derivada de una función constante f(x) = k Vamos a aplicar la definición analítica de derivada
Asignatura: Matemáticas II 2ºBacillerato página 1/16 Teoría Tema 3 Derivabilidad - Aplicación a funciones Derivada de una función constante f(x) = k Vamos a aplicar la definición analítica de derivada
Resolver las siguientes integrales aplicando fracciones parciales,
 Tu pregunta es, Resolver las siguientes integrales aplicando fracciones parciales, 1- x+1 (x 3) 2 dx 2- x+1 (x 1) 2 dx 3- x (x 3) 2 dx 4- x 2 dx (x 3)(x+2) 2 Bien, para la primera, x + 1 (x 3) 2 dx Ésta
Tu pregunta es, Resolver las siguientes integrales aplicando fracciones parciales, 1- x+1 (x 3) 2 dx 2- x+1 (x 1) 2 dx 3- x (x 3) 2 dx 4- x 2 dx (x 3)(x+2) 2 Bien, para la primera, x + 1 (x 3) 2 dx Ésta
1. PRIMITIVA DE UNA FUNCIÓN 2. PROPIEDADES DE LA INTEGRAL INDEFINIDA 3. INTEGRALES INMEDIATAS Ejemplos de integrales inmediatas tipo potencia
 Cálculo de primitivas MATEMÁTICAS II. PRIMITIVA DE UNA FUNCIÓN. PROPIEDADES DE LA INTEGRAL INDEFINIDA. INTEGRALES INMEDIATAS.. Ejemplos de integrales inmediatas tipo potencia.. Ejemplos de integrales inmediatas
Cálculo de primitivas MATEMÁTICAS II. PRIMITIVA DE UNA FUNCIÓN. PROPIEDADES DE LA INTEGRAL INDEFINIDA. INTEGRALES INMEDIATAS.. Ejemplos de integrales inmediatas tipo potencia.. Ejemplos de integrales inmediatas
INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES
 INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES INTEGRACIÓN POR PARTES Este método permite resolver un gran número de integrales no inmediatas. 1. Sean u y v dos funciones dependientes
INTEGRACIÓN POR PARTES Y POR DESCOMPOSICIÓN EN FRACCIONES SIMPLES INTEGRACIÓN POR PARTES Este método permite resolver un gran número de integrales no inmediatas. 1. Sean u y v dos funciones dependientes
OBJETIVOS CONTENIDOS PROCEDIMIENTOS
 8 _ 0-0.qxd //0 : Página Números reales INTRODUCCIÓN Los alumnos han trabajado en cursos anteriores con las potencias, y conocen el significado de las potencias de exponente natural y de las partes que
8 _ 0-0.qxd //0 : Página Números reales INTRODUCCIÓN Los alumnos han trabajado en cursos anteriores con las potencias, y conocen el significado de las potencias de exponente natural y de las partes que
Unidad 1 Integrales Indefinidas 1.1 Diferenciales Aproximaciones Anti derivada
 Unidad 1 Integrales Indefinidas 1.1 Diferenciales 1.1.1 Aproximaciones 1.1. Anti derivada 1. Integración 1..1 Formulas 1.. Integrales Inmediatas 1..3 Cambio de variable 1.3 Métodos de integración 1.3.1
Unidad 1 Integrales Indefinidas 1.1 Diferenciales 1.1.1 Aproximaciones 1.1. Anti derivada 1. Integración 1..1 Formulas 1.. Integrales Inmediatas 1..3 Cambio de variable 1.3 Métodos de integración 1.3.1
2. La fórmula de la derivada de un producto de dos funciones, aplicada a f(x) g(x), permite escribir,
 INTRO. MÉTODOS DE INTEGR. ( II ) En este tema se continúa con los métodos de integración iniciados en el capítulo anterior, en el que a partir del concepto de primitiva y de las derivadas de las funciones
INTRO. MÉTODOS DE INTEGR. ( II ) En este tema se continúa con los métodos de integración iniciados en el capítulo anterior, en el que a partir del concepto de primitiva y de las derivadas de las funciones
CAPITULO 5. Integral Indefinida. Licda. Elsie Hernández Saborío. Instituto Tecnológico de Costa Rica Escuela de Matemática
 CAPITULO 5 Integral Indefinida 1 Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Revista digital Matemática, educación e internet (www.cidse.itcr.ac.cr) Créditos
CAPITULO 5 Integral Indefinida 1 Licda. Elsie Hernández Saborío Instituto Tecnológico de Costa Rica Escuela de Matemática Revista digital Matemática, educación e internet (www.cidse.itcr.ac.cr) Créditos
Tabla de Contenidos. Resolviendo Ecuaciones. Operaciones Inversas. Slide 1 / 107. Slide 2 / 107. Slide 4 / 107. Slide 3 / 107.
 Slide 1 / 107 Slide 2 / 107 Tabla de Contenidos Resolviendo Ecuaciones Operaciones Inversas Ecuaciones de un paso Ecuaciones de dos pasos Ecuaciones de Multi-pasos Variables en ambos lados Más Ecuaciones
Slide 1 / 107 Slide 2 / 107 Tabla de Contenidos Resolviendo Ecuaciones Operaciones Inversas Ecuaciones de un paso Ecuaciones de dos pasos Ecuaciones de Multi-pasos Variables en ambos lados Más Ecuaciones
Slide 1 / 107. Resolviendo Ecuaciones
 Slide 1 / 107 Resolviendo Ecuaciones Slide 2 / 107 Tabla de Contenidos Operaciones Inversas Ecuaciones de un paso Click on a topic to go to that section. Ecuaciones de dos pasos Ecuaciones de Multi-pasos
Slide 1 / 107 Resolviendo Ecuaciones Slide 2 / 107 Tabla de Contenidos Operaciones Inversas Ecuaciones de un paso Click on a topic to go to that section. Ecuaciones de dos pasos Ecuaciones de Multi-pasos
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN. Tema: TÉCNICAS DE INTEGRACIÓN
 UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN Tema: TÉCNICAS DE INTEGRACIÓN TÉCNICAS DE INTEGRACIÓN En matemáticas, cada tipo de problema sugiere un tipo de solución. Para calcular la derivada
UNIDAD II. INTEGRAL DEFINIDA Y LOS MÉTODOS DE INTEGRACIÓN Tema: TÉCNICAS DE INTEGRACIÓN TÉCNICAS DE INTEGRACIÓN En matemáticas, cada tipo de problema sugiere un tipo de solución. Para calcular la derivada
MÉTODOS DE INTEGRACION
 MÉTODOS DE INTEGRACION En este tema se continúa con los métodos de integración iniciados en el capítulo anterior, en el que a partir del concepto de primitiva y de las derivadas de las funciones elementales
MÉTODOS DE INTEGRACION En este tema se continúa con los métodos de integración iniciados en el capítulo anterior, en el que a partir del concepto de primitiva y de las derivadas de las funciones elementales
Operador Diferencial y Ecuaciones Diferenciales
 Operador Diferencial y Ecuaciones Diferenciales. Operador Diferencial Un operador es un objeto matemático que convierte una función en otra, por ejemplo, el operador derivada convierte una función en una
Operador Diferencial y Ecuaciones Diferenciales. Operador Diferencial Un operador es un objeto matemático que convierte una función en otra, por ejemplo, el operador derivada convierte una función en una
LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS
 195 LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS JUSTIFICACIÓN En esta lección, basados en la teoría de diferenciales de funciones de dos variables, la cual involucra las derivadas
195 LECCIÓN 8: ECUACIONES DIFERENCIALES ORDINARIAS DE PRIMER ORDEN EXACTAS JUSTIFICACIÓN En esta lección, basados en la teoría de diferenciales de funciones de dos variables, la cual involucra las derivadas
1. Algunas primitivas inmediatas (o casi inmediatas).
 Cálculo I. o Matemáticas. Curso 00/0. Cálculo de Primitivas. Algunas primitivas inmediatas (o casi inmediatas). (5x 6) = 5 (5x 6) 5 = 5 (5x 6) + C. Nota: Si f(x) = 5x 6 su derivada es 5. En la primera
Cálculo I. o Matemáticas. Curso 00/0. Cálculo de Primitivas. Algunas primitivas inmediatas (o casi inmediatas). (5x 6) = 5 (5x 6) 5 = 5 (5x 6) + C. Nota: Si f(x) = 5x 6 su derivada es 5. En la primera
INTEGRACION POR PARTES
 INTEGRACION POR PARTES Se basa en la regla de derivación del producto de dos funciones derivables en un dominio común. Sean u(x)y v(x) común. Entonces: dos funciones derivables en un dominio udv = uv vdu
INTEGRACION POR PARTES Se basa en la regla de derivación del producto de dos funciones derivables en un dominio común. Sean u(x)y v(x) común. Entonces: dos funciones derivables en un dominio udv = uv vdu
ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M.
 Introducción ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M. En diferentes situaciones que aparecen con frecuencia en las Ciencias Experimentales, es complicado poder escribir
Introducción ECUACIONES DIFERENCIALES Julián de la Horra Departamento de Matemáticas U.A.M. En diferentes situaciones que aparecen con frecuencia en las Ciencias Experimentales, es complicado poder escribir
open green road Guía Matemática POTENCIAS DE EXPONENTE RACIONAL profesor: Nicolás Melgarejo .cl
 Guía Matemática POTENCIAS DE EXPONENTE RACIONAL profesor: Nicolás Melgarejo.cl . Introducción Hemos escuchado muchas veces que una potencia es la multiplicación abreviada de un término por sí mismo un
Guía Matemática POTENCIAS DE EXPONENTE RACIONAL profesor: Nicolás Melgarejo.cl . Introducción Hemos escuchado muchas veces que una potencia es la multiplicación abreviada de un término por sí mismo un
2.1 Reglas básicas de derivación y ritmos o velocidades de cambio
 PRIMER BIMESTRE Guía didáctica: Cálculo La ecuación de la velocidad instantánea es la derivada de la función posición: La velocidad instantánea para t = 2s, es 8 m/s Esperamos, que con los ejemplos resueltos
PRIMER BIMESTRE Guía didáctica: Cálculo La ecuación de la velocidad instantánea es la derivada de la función posición: La velocidad instantánea para t = 2s, es 8 m/s Esperamos, que con los ejemplos resueltos
Lección 5: Ecuaciones con números naturales
 GUÍA DE MATEMÁTICAS I Lección 5: Ecuaciones con números naturales Observe la siguiente tabla y diga cuáles son los números que faltan. 1 2 3 4 5 6 7 8 9 10 11 12 3 6 9 12 Es sencillo encontrar la regla
GUÍA DE MATEMÁTICAS I Lección 5: Ecuaciones con números naturales Observe la siguiente tabla y diga cuáles son los números que faltan. 1 2 3 4 5 6 7 8 9 10 11 12 3 6 9 12 Es sencillo encontrar la regla
2 Unidad II: Ecuaciones Diferenciales de Orden Superior
 ITESM, Campus Monterrey Departamento de Matemáticas MA-41: Ecuaciones Diferenciales Lectura # Profesor: Victor Segura Flores Unidad II: Ecuaciones Diferenciales de Orden Superior.1 Ecuaciones Diferenciales
ITESM, Campus Monterrey Departamento de Matemáticas MA-41: Ecuaciones Diferenciales Lectura # Profesor: Victor Segura Flores Unidad II: Ecuaciones Diferenciales de Orden Superior.1 Ecuaciones Diferenciales
Introducción a las Funciones Logarítmicas MATE 3171
 Introducción a las Funciones Logarítmicas MATE 3171 Logaritmos de base a Anteriormente repasamos que para 0 < a < 1 o a > 1, la función exponencial f(x) = a x es uno-a-uno, y por lo tanto tiene una función
Introducción a las Funciones Logarítmicas MATE 3171 Logaritmos de base a Anteriormente repasamos que para 0 < a < 1 o a > 1, la función exponencial f(x) = a x es uno-a-uno, y por lo tanto tiene una función
Teoría Tema 8 Indeterminaciones
 página /7 Teoría Tema 8 Indeterminaciones Índice de contenido Qué es una indeterminación?...2 Tipos de indeterminaciones y ejemplos...3 página 2/7 Qué es una indeterminación? Hasta ahora hemos calculado
página /7 Teoría Tema 8 Indeterminaciones Índice de contenido Qué es una indeterminación?...2 Tipos de indeterminaciones y ejemplos...3 página 2/7 Qué es una indeterminación? Hasta ahora hemos calculado
RADICALES. CONCEPTO Y OPERACIONES. Concepto de raíz. - La raíz cuadrada de un número a es otro número b, que al elevarlo al cuadrado te da a
 UD : Los números reales RADICALES. CONCEPTO Y OPERACIONES. Concepto de raíz. - La raíz cuadrada de un número a es otro número b, que al elevarlo al cuadrado te da a (que es lo mismo que decir que a b si
UD : Los números reales RADICALES. CONCEPTO Y OPERACIONES. Concepto de raíz. - La raíz cuadrada de un número a es otro número b, que al elevarlo al cuadrado te da a (que es lo mismo que decir que a b si
REPASO ALGEBRA ELEMENTAL
 REPASO ALGEBRA ELEMENTAL OPERACIONES MATEMÁTICAS POR: DRA. KARILUZ DÁVILA DÍAZ Operaciones matemáticas comunes Operaciones matemáticas comunes que se utilizan en el curso de Química General son: Operación
REPASO ALGEBRA ELEMENTAL OPERACIONES MATEMÁTICAS POR: DRA. KARILUZ DÁVILA DÍAZ Operaciones matemáticas comunes Operaciones matemáticas comunes que se utilizan en el curso de Química General son: Operación
T0. TRANSFORMADAS DE LAPLACE
 ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA MATEMATICAS T0. TRANSFORMADAS DE LAPLACE Mediante transformadas de Laplace (por Pierre-Simon
ESCUELA TÉCNICA SUPERIOR DE NÁUTICA Y MÁQUINAS NAVALES / NAUTIKAKO ETA ITSASONTZI MAKINETAKO GOI ESKOLA TEKNIKOA MATEMATICAS T0. TRANSFORMADAS DE LAPLACE Mediante transformadas de Laplace (por Pierre-Simon
5. Métodos de integración y aplicaciones de la integral denida 5.5 Fracciones parciales. Métodos de Integración. Integración por fracciones parciales
 Métodos de Integración Integración por fracciones parciales P x) Consideremos la función racional donde P, Q son polinomios. Si derivamos una función racional Qx) obtenemos una funciòn racional. Si integramos
Métodos de Integración Integración por fracciones parciales P x) Consideremos la función racional donde P, Q son polinomios. Si derivamos una función racional Qx) obtenemos una funciòn racional. Si integramos
ENTEROS. Definición de Enteros. Slide 1 / 239. Slide 2 / 239. Slide 3 / 239. Temas a desarrollar
 Slide 1 / 239 ENTEROS Temas a desarrollar Definición de N Enteros Valor Absoluto Comparación y Orden de los N Enteros Suma de Enteros Convertir la Resta en Suma Revisión de Sumas y Restas con Enteros Multiplicando
Slide 1 / 239 ENTEROS Temas a desarrollar Definición de N Enteros Valor Absoluto Comparación y Orden de los N Enteros Suma de Enteros Convertir la Resta en Suma Revisión de Sumas y Restas con Enteros Multiplicando
GUÍA DE EJERCICIOS: MATEMÁTICAS
 GUÍA DE EJERCICIOS: MATEMÁTICAS Matrices Esta guía de estudio está diseñada con ejercicios resueltos paso a paso con el fin de mostrar los procedimientos detallados para abordar cada uno de ellos. Las
GUÍA DE EJERCICIOS: MATEMÁTICAS Matrices Esta guía de estudio está diseñada con ejercicios resueltos paso a paso con el fin de mostrar los procedimientos detallados para abordar cada uno de ellos. Las
ENTEROS. Definición de Enteros. Slide 2 / 239. Slide 1 / 239. Slide 3 / 239. Slide 4 / 239. Slide 6 / 239. Slide 5 / 239. Temas a desarrollar
 Slide 1 / 239 ENTEROS Slide 2 / 239 Temas a desarrollar Definición de N Enteros Valor Absoluto Comparación y Orden de los N Enteros Suma de Enteros Convertir la Resta en Suma Revisión de Sumas y Restas
Slide 1 / 239 ENTEROS Slide 2 / 239 Temas a desarrollar Definición de N Enteros Valor Absoluto Comparación y Orden de los N Enteros Suma de Enteros Convertir la Resta en Suma Revisión de Sumas y Restas
Tema 3. Calculo de primitivas (2ª parte)
 Tema 3. Calculo de primitivas (2ª parte) Este tema es una continuación del anterior y está dedicado al estudio de los métodos de integración adecuados a la resolución de dos tipos de integrales concretas:
Tema 3. Calculo de primitivas (2ª parte) Este tema es una continuación del anterior y está dedicado al estudio de los métodos de integración adecuados a la resolución de dos tipos de integrales concretas:
* e e Propiedades de la potenciación.
 ECUACIONES DIFERENCIALES 1 REPASO DE ALGUNOS CONCEPTOS PREVIOS AL ESTUDIO DE LAS ECUACIONES DIFERENCIALES 1. Cuando hablamos de una función en una variable escribíamos esta relación como y = f(x), esta
ECUACIONES DIFERENCIALES 1 REPASO DE ALGUNOS CONCEPTOS PREVIOS AL ESTUDIO DE LAS ECUACIONES DIFERENCIALES 1. Cuando hablamos de una función en una variable escribíamos esta relación como y = f(x), esta
ûintroducción ûintegración Inmediata ûajustar una Integral ûpropiedades : * * Genius, el secreto de los mejores. Ximo Beneyto
 ûintroducción ûintegración Inmediata ûajustar una Integral ûpropiedades : * * Genius, el secreto de los mejores. Ximo Beneyto ADVERTENCIA! En casi todos los CUADERNOS GÈNIUS hay problemas INSERTADOS que
ûintroducción ûintegración Inmediata ûajustar una Integral ûpropiedades : * * Genius, el secreto de los mejores. Ximo Beneyto ADVERTENCIA! En casi todos los CUADERNOS GÈNIUS hay problemas INSERTADOS que
TEMA 2 POTENCIAS NOMBRE Y APELLIDOS... HOJA 1 - FECHA...
 Nueva del Carmen,. 011 Valladolid. Tel: 1 Fax: 1 Matemáticas º ESO TEMA POTENCIAS NOMBRE Y APELLIDOS... HOJA 1 - FECHA... Comenzamos a trabajar con potencias. Son muy fáciles si las cogemos el tranquillo
Nueva del Carmen,. 011 Valladolid. Tel: 1 Fax: 1 Matemáticas º ESO TEMA POTENCIAS NOMBRE Y APELLIDOS... HOJA 1 - FECHA... Comenzamos a trabajar con potencias. Son muy fáciles si las cogemos el tranquillo
MULTIPLICACIÓN DE POTENCIAS DE IGUAL BASE
 MULTIPLICACIÓN DE POTENCIAS DE IGUAL BASE Ejemplos 1. Resuelva la operación 9. 1 Solución En esta operación hay tres factores. Dos de esos factores tienen la misma base que es base. y el tercer factor
MULTIPLICACIÓN DE POTENCIAS DE IGUAL BASE Ejemplos 1. Resuelva la operación 9. 1 Solución En esta operación hay tres factores. Dos de esos factores tienen la misma base que es base. y el tercer factor
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias.
 Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
Teorema de Existencia y Unicidad Ecuaciones Diferenciales Ordinarias. Dr. Rafael Morones E. Dept. de Matemáticas ITAM August 5, 2002 1 Contenido 1 Preliminares. 3 1.1 Sucesiones...............................
4 Conjunto de los números reales
 Programa Inmersión, Verano 2016 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 3001 y MATE 3023 Clase #4: viernes, 3 de junio de 2016. 4 Conjunto de los números reales 4.1
Programa Inmersión, Verano 2016 Notas escritas por Dr. M Notas del cursos. Basadas en los prontuarios de MATE 3001 y MATE 3023 Clase #4: viernes, 3 de junio de 2016. 4 Conjunto de los números reales 4.1
Por qué expresar de manera algebraica?
 Álgebra 1 Sesión No. 2 Nombre: Fundamentos de álgebra. Parte II. Objetivo: al finalizar la sesión, el estudiante conocerá e identificará las expresiones racionales, las diferentes formas de representar
Álgebra 1 Sesión No. 2 Nombre: Fundamentos de álgebra. Parte II. Objetivo: al finalizar la sesión, el estudiante conocerá e identificará las expresiones racionales, las diferentes formas de representar
METODOS DE INTEGRACION IV FRACCIONES PARCIALES
 METODOS DE INTEGRACION IV FRACCIONES PARCIALES Una función racional es una función de la forma En la que f(x) y g(x) son polinomios. Si el frado de f(x) es menor que el de g(x), F(x) se denomina fracción
METODOS DE INTEGRACION IV FRACCIONES PARCIALES Una función racional es una función de la forma En la que f(x) y g(x) son polinomios. Si el frado de f(x) es menor que el de g(x), F(x) se denomina fracción
GUÍA DE EJERCICIOS: MATEMÁTICAS
 GUÍA DE EJERCICIOS: MATEMÁTICAS Matrices Esta guía de estudio está diseñada con ejercicios resueltos paso a paso con el fin de mostrar los procedimientos detallados para abordar cada uno de ellos. Las
GUÍA DE EJERCICIOS: MATEMÁTICAS Matrices Esta guía de estudio está diseñada con ejercicios resueltos paso a paso con el fin de mostrar los procedimientos detallados para abordar cada uno de ellos. Las
ECUACIONES EN Q (NÚMEROS RACIONALES)
 Echa un vistazo a esta situación. ECUACIONES EN Q (NÚMEROS RACIONALES) El domingo, Leonardo caminó 4 unidades. El lunes, Leonardo caminó un tercio de lo que caminó el martes. El caminó un total de 12 unidades
Echa un vistazo a esta situación. ECUACIONES EN Q (NÚMEROS RACIONALES) El domingo, Leonardo caminó 4 unidades. El lunes, Leonardo caminó un tercio de lo que caminó el martes. El caminó un total de 12 unidades
