Ejemplo Curvas Principales Definiciones Algoritmo. Ejemplo Tortugas. En este ejemplo se miden la dimensiones del caparazón de las tortugas siendo
|
|
|
- Irene Macías Padilla
- hace 5 años
- Vistas:
Transcripción
1 Ejemplo Tortugas En este ejemplo se miden la dimensiones del caparazón de las tortugas siendo x 1 = 10 log(longitud del caparazón), x 2 = 10 log(ancho del caparazón) Se estudiaron 24 machos y 24 hembras. ( ) x m = x h = ( ) y γ 1,m = (0.7996, ) t γ 1,h = (0.7892, ) t 1/49
2 Hembras 10 log(ancho) log(largo) 2/49
3 Ejemplo Tortugas Hembras v v 1 3/49
4 Ejemplo Tortugas Hembras 10 log(ancho) log(largo) 4/49
5 Ejemplo Tortugas Hembras 10 log(ancho) log(largo) 5/49
6 y Regresión noparamétrica {(t i, y i ) : 1 i n} vectores aleatorios independientes y i = η (t i ) + ɛ i t ɛ i i.i.d. variables aleatorias, independientes de {t i, i 1}, E (ɛ i ) = 0 and Eɛ 2 i < 6/49
7 Regresión noparamétrica η(t 0 ) se obtiene minimizando n (y i a) 2 w i (t 0 ) i=1 w i (t) = K h n (t t i ) n K hn (t t j ) j=1 K hn (u) = 1 ( ) u K h n h n K 0, K(u) du = 1 7/49
8 Regresión noparamétrica y t 8/49
9 Regresión noparamétrica y t 9/49
10 Curvas principales x Definimos las curvas principales como aquellas curvas que son auto consistentes para la distribución de x or para un conjunto de observaciones x 1,..., x n. Es decir, que si agarramos un punto de la curva z y todos los datos x i que se proyectan sobre z, el promedio de esas observaciones es z. x 1 10/49
11 x 1,..., x n R p independientes Observación x i = µ + ν i γ + e i E(e i ) = 0 Cov(e i ) = I p entonces el estimador de mínimos cuadrados de γ es la primer componente principal, o sea, γ 1 = argmin a n x i µ ν i a 2 i=1 11/49
12 Observación x 1,..., x n R p independientes Una generalización del problema anterior es considerar el modelo x i = f(ν i ) + e i donde f(ν) = (f 1 (ν),..., f p (ν)) t con f j funciones suaves. 12/49
13 f 1 (ν) = cos(ν), f 2 (ν) = sin(ν), ν [0, 2π] x x 1 Ajuste no paramétrico 13/49
14 Curvas principales x x 1 14/49
15 Curvas principales x x 1 15/49
16 Curvas principales x x 1 16/49
17 Curvas principales periódicas x x 1 17/49
18 Curvas principales periódicas x x 1 18/49
19 Curvas principales periódicas x x 1 19/49
20 Preliminares Una curva unidimensional en R p es un vector f(ν) de p funciones f 1 (ν),..., f p (ν) que dependen de una variable ν I R. f j (ν) se llaman las funciones coordenadas ν provee un orden a lo largo de la curva. Si h : I J es monótona podemos transformar ν por λ = h(ν) Las funciones f j (ν) se transforman como f j (h 1 (λ)) Existe una parametrización natural dada por el arco de curva 20/49
21 Preliminares El arco de una curva f de ν 0 a ν 1 se define como l = f (ν) es la tangente en ν ν1 ν 0 f (z) dz Una curva tal que f (ν) 1 se dice una curva parametrizada con unidad de velocidad 1. Suavidad de la curva en tal caso se traduce en el aspecto visual de {f(ν) : ν I} ya que no debe haber picos. 21/49
22 Preliminares El vector f (ν) es la aceleración de la curva. Si la curva tiene unidad de velocidad 1 entonces f (ν) es ortogonal al vector tangente f (ν). En ese caso, f (ν) f (ν) se llama la normal principal de la curva en ν. 22/49
23 Preliminares Los vectores f (ν) y f (ν) generan un plano. Hay un único círculo de velocidad 1 en ese plano que pasa por f(ν) y que tiene la misma velocidad y aceleración en f(ν) que la curva. El radio r f (ν) de ese círculo se llama el radio de curvatura de la curva f en ν. 1 r f (ν) = f (ν) El centro c f (ν) del círculo se llama el centro de curvatura de la curva f en ν. 23/49
24 Definición Sea x R p un vector aleatorio con densidad y tal que E(x) = 0, Var(x) = Σ existe. Sea f una curva suave (C ) de unidad de velocidad 1 parametrizada sobre I R Supondremos que I es cerrado (puede ser infinito) la curva no se interseca, o sea, ν 1 ν 2 = f(ν 1 ) f(ν 2 ) 24/49
25 Definición Definimos el índice de proyección ν f : R p R como ν f (x) = sup{ν : ν = argmin x f(λ) } λ El índice de proyección de x es el valor de ν para el cual f(ν) está lo más cerca de x. Si hay varios valores elegimos el mayor. ν f (x) está bien definido y es medible Definición 1. La curva se dice auto consistente o curva principal de x si ( ) E x ν f (x) = ν = f(ν) p.p. ν. 25/49
26 Definición x x 1 26/49
27 Preguntas Para qué tipo de distribuciones existen las curvas principales? Cuántas curvas principales hay para una distribución dad? Cuáles son sus propiedades? Delicado, P. (2001). Another Look at Principal Curves and Surfaces. Journal of Multivariate Analysis, 77, Hastie, T. and W. Stuetzle (1989) Principal curves. Journal of the American Statistical Association, 84, Sea x R p, E(x) = µ, Var(x) = Σ. Sea a = 1, x 0 R p es un punto fijo y definamos y = x 0 + a a t (x x 0 ). Si y es auto consistente para x entonces es una curva principal. 27/49
28 Preguntas Para distribuciones eĺıpticas las componentes principales son curvas principales Para distribuciones esféricas E(µ, I p ), o sea, su densidad es a h( x µ ) Cualquier recta que pasa por µ es una curva principal Si p = 2 y µ = 0, el círculo de centro en el origen y radio E( x ) es una curva principal. Si x N 2 (0, I 2 ), el círculo de centro en el origen y radio π/2 es una curva principal. Si x = f(ν) + e con E(e) = 0, puede haber casos en los que la curva principal no sea f. 28/49
29 Una propiedad de distancias Sea d(x, ) la distancia de x a su proyección en la curva f d(x, ) = x f(ν f (x) Si x P, definamos D 2 (P, f) = Ed 2 (x, f) Consideremos la recta f(ν) = x 0 + ν v y recordemos que E(x) = 0 La distancia D 2 (P, ) = D 2 (P, x 0, v) El gradiente de D 2 (P, x 0, v) = 0 si y sólo si u = 0 y v es un autovector de Σ, o sea, la recta es la asociada a una componente principal. 29/49
30 Una propiedad de distancias Sea v R p, v = 1 y supongamos que x t 0 v = 0 sin pérdida de generalidad. Entonces, D 2 (P, x 0, v) = tr(σ)+ x 0 2 v t Σv (x t 0 v) 2 = tr(σ)+ x 0 2 v t Σv Luego, para calcular el gradiente tenemos que agregar los vínculos v = 1 y x t 0 v = 0 es decir, debemos derivar Λ(x 0, v) = D 2 (P, x 0, v) + λ 1 (v t v 1) + λ 2 x t 0 v 30/49
31 Una propiedad de distancias Λ(x 0, v) x 0 = 2x 0 + λ 2 v (1) v Λ(x 0, v) = 2Σv + λ 1 v (2) Multiplicando (1) por v t e igualando a 0 obtenemos que λ 2 = 0 pues x t 0 v = 0, de donde por (1) se deduce que x 0 = 0 La ecuación (2) implica que si v Λ(x 0, v) = 0 entonces Σv = cv, o sea v es un autovector de Σ. 31/49
32 Una propiedad de distancias Para extenderlo a curvas principales, sea G = el conjunto de las curvas parametrizadas sobre I Para g G sea f t = f + tg Definición 2. La curva f se dice un punto crítico de la distancia de variación en la clase G si D 2 (P, f t ) t = 0 t=0 g G 32/49
33 Una propiedad de distancias Sea G B la clase de las funciones suaves (C ) parametrizadas sobre I tales que g 2 = sup ν p j=1 g 2 j (ν) 1 g 2 1. Entonces, f es una curva principal para x si y sólo si f es un punto crítico de la distancia de variación en la clase G B. La demostración se basa en probar que se puede intercambiar la derivada con la esperanza y usar que D 2 (P, f t ) = 2 E {[E (x ν f (x)) f (ν f (x))] g (ν f (x))} t t=0 33/49
34 Algoritmo Estamos interesados en encontrar curvas suaves asociadas a puntos críticos de D 2 (P, f t ). La estrategia del algoritmo consiste en tomar una curva suave inicial, que será la asociada a la mayor componente principal lineal chequear si es una curva principal. Para ello, se proyectan los datos sobre la curva y evaluamos la esperanza condicional sobre los puntos proyectados. Si la esperanza condicional coincide con la curva, ya está. Sino, buscamos una nueva curva y seguimos. 34/49
35 Algoritmo Sea f (0) (ν) = µ + ν γ 1 donde µ = E(x) y γ 1 es el autovector de Σ asociado a su mayor autovalor. Sea ν (0) (x) = ν f (0)(x). Repita sobre el índice de iteración j los pasos a) a d) ( ) a) Sea f (j) (ν) = E x ν f (j 1)(x) = ν b) Defina ν (j) (x) = ν f (j)(x) c) Transforme ν (j) (x) de modo que f (j) sea de velocidad unitaria. d) Calcule { ( )} D 2 (P, f (j) ) = E x f (j) (ν (j) (x) 2 = E E x f (j) (ν (j) (x) 2 ν (j) (x) Hasta que la variación en D 2 (P, f (j) ) esté por debajo de un umbral. 35/49
36 Algoritmo Si x 1,..., x n son i.i.d., se reemplaza P por la empírica y la esperanza condicional por un suavizado, resultando el algoritmo. Sea f (0) (ν) = x + ν γ 1 donde γ 1 es el autovector de S asociado a su mayor autovalor. Sea ν (0) (x) = ν f (0)(x). Repita sobre el índice de iteración j los pasos a) a d) a) Sea f (j) (ν) un smoother (puede ser un polinomio local o basado en splines) de las respuestas x 1,..., x n versus los valores observados de la covariable ν f (j 1)(x 1),..., ν f (j 1)(x n) b) Defina ν (j) (x) = ν f (j)(x) c) Transforme ν (j) (x) de modo que f (j) sea de velocidad unitaria. 36/49
37 Algoritmo d) Calcule D 2 (P, f (j) ) = 1 n n x i f (j) (ν (j) (x i ) 2 i=1 Hasta que la variación en D 2 (P, f (j) ), es decir, D 2 (P, f (j 1) ) D 2 (P, f (j) ) D 2 (P, f (j 1) ) esté por debajo de un umbral que en el algorimto por default es /49
38 Algoritmo Un punto clave en el algoritmo es el calculo de ν f (x i ) para f( ) = f (j) ( ) fija. Queremos buscar para cada 1 i n, el valor ν i = ν f (x i ) = ν f (j)(x i ). En la iteración j 1 calculamos ν (j 1) i calcular f(ν (j 1) i ). = ν f (j 1)(x i ) y podemos Definamos d ik como la distancia entre x i y su punto más cercano en el segmento que une f(ν (j 1) k ) con f(ν (j 1) k+1 ). 38/49
39 Algoritmo Asociado a d ik existe un valor ν ik [ν (j 1) k, ν (j 1) k+1 ] Definimos ν i = ν ik donde d ik = min 1 k n 1 d ik 39/49
40 x 1,..., x n i.i.d. x i x donde ( sin(ν) x = 5 cos(ν) con ν U[0, 2π) y e N(0, I 2 ). ) + e 40/49
41 x x 1 41/49
42 x x 1 Resultado de 10 iteraciones 42/49
43 x x 1 Resultado de 10 iteraciones 43/49
44 x x 1 Resultado de 10 iteraciones 44/49
45 x 1,..., x n i.i.d. x i x donde ( sin(ν) x = 5 cos(ν) con ν U[0, π/2) y e N(0, I 2 ). ) + e 45/49
46 x x 1 46/49
47 x x 1 Resultado de 10 iteraciones 47/49
48 x x 1 Resultado de 10 iteraciones 48/49
49 Ejercicio: Repetir los ejemplos anteriores con 20, 100 y 200 iteraciones. Qué observa? 49/49
MAT 1102 Geometría Solución Control N 5
 Pontificia Universidad Católica de Chile Facultad de Matemáticas Departamento de Matemática Primer Semestre de 2001 MAT 1102 Geometría Solución Control N 5 Versión A 1. Dadas las rectas l 1 : 2x y = 0,
Pontificia Universidad Católica de Chile Facultad de Matemáticas Departamento de Matemática Primer Semestre de 2001 MAT 1102 Geometría Solución Control N 5 Versión A 1. Dadas las rectas l 1 : 2x y = 0,
EXAMEN A PP 1A SEMANA
 EXAMEN A PP A SEMANA XAVI AZNAR Ejercicio. Defina. Simetría. Proyección. Homotecia vectorial y escriba sus polinomios mínimos. Demostración.. Una simetría σ de base B y dirección D es un endomorfismo tal
EXAMEN A PP A SEMANA XAVI AZNAR Ejercicio. Defina. Simetría. Proyección. Homotecia vectorial y escriba sus polinomios mínimos. Demostración.. Una simetría σ de base B y dirección D es un endomorfismo tal
SUPERFICIES. 2.2 Plano tangente y recta normal. 2.3 Métrica sobre una superficie: Primera forma fundamental y aplicaciones.
 SUPERFICIES. 2.2 Plano tangente y recta normal. 2.3 Métrica sobre una superficie: Primera forma fundamental y aplicaciones. 2.1 Superficie parametrizacida. Ecuaciones implícitas. Curvas paramétricas. 2.2
SUPERFICIES. 2.2 Plano tangente y recta normal. 2.3 Métrica sobre una superficie: Primera forma fundamental y aplicaciones. 2.1 Superficie parametrizacida. Ecuaciones implícitas. Curvas paramétricas. 2.2
MATEMÁTICAS: PAU 2016 JUNIO CASTILLA Y LEÓN
 MATEMÁTICAS: PAU 26 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A 5 a a) Discutir para qué valores de a R la matriz M = ( ) tiene inversa. Calcular M a para a =. ( 5 puntos) Para que exista inversa de una
MATEMÁTICAS: PAU 26 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A 5 a a) Discutir para qué valores de a R la matriz M = ( ) tiene inversa. Calcular M a para a =. ( 5 puntos) Para que exista inversa de una
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS.
 UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
UNIVERSIDAD DIEGO PORTALES. FACULTAD DE INGENIERIA. INSTITUTO DE CIENCIAS BASICAS. Cálculo III, Examen Final. Semestre Primavera 1 Tiempo: 11 min. Problema 1 [1,5 puntos] La curvatura de una trayectoria
Descomposición en valores singulares Notas para los cursos 21 y 22 (J.L. Mancilla Aguilar)
 Valores Singulares Descomposición en valores singulares Notas para los cursos y (JL Mancilla Aguilar) Tanto los valores singulares como la descomposición en valores singulares de una matriz son conceptos
Valores Singulares Descomposición en valores singulares Notas para los cursos y (JL Mancilla Aguilar) Tanto los valores singulares como la descomposición en valores singulares de una matriz son conceptos
, donde denota la matriz traspuesta de B.
 Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº Páginas: INDICACIONES:.- OPTATIVIDAD: El alumno deberá escoger una de las dos opciones, pudiendo
Pruebas de acceso a enseñanzas universitarias oficiales de grado Castilla y León MATEMÁTICAS II EJERCICIO Nº Páginas: INDICACIONES:.- OPTATIVIDAD: El alumno deberá escoger una de las dos opciones, pudiendo
VELOCIDAD Y ACELERACION. RECTA TANGENTE.
 VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
VELOCIDAD Y ACELERACION. RECTA TANGENTE. 3. Describir la trayectoria y determinar la velocidad y aceleración del movimiento descrito por las curvas siguientes: (a) r (t) = i 4t 2 j + 3t 2 k. (b) r (t)
Tema 3: Cinemática del punto
 Tema 3: Cinemática del punto FISICA I, 1º Grado en Ingeniería Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla 1 Índice Introducción Ecuaciones de una curva Velocidad y aceleración Movimientos
Tema 3: Cinemática del punto FISICA I, 1º Grado en Ingeniería Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla 1 Índice Introducción Ecuaciones de una curva Velocidad y aceleración Movimientos
Estimación de homografías
 Estimación de homografías Visión en Robótica 1er cuatrimestre de 2013 1 Introducción del problema Una homografía es una transformación proyectiva que determina una correspondencia entre puntos El problema
Estimación de homografías Visión en Robótica 1er cuatrimestre de 2013 1 Introducción del problema Una homografía es una transformación proyectiva que determina una correspondencia entre puntos El problema
Estadística para la Economía y la Gestión IN 3401
 Estadística para la Economía y la Gestión IN 3401 3 de junio de 2010 1 Modelo de Regresión con 2 Variables Método de Mínimos Cuadrados Ordinarios Supuestos detrás del método MCO Errores estándar de los
Estadística para la Economía y la Gestión IN 3401 3 de junio de 2010 1 Modelo de Regresión con 2 Variables Método de Mínimos Cuadrados Ordinarios Supuestos detrás del método MCO Errores estándar de los
SEPTIEMBRE 2003 PRUEBA A
 PROBLEMAS SEPTIEMBRE 003 PRUEBA A 1.- a) Discutir en función de los valores de m: x 3y 0 x y+ z 0 x + y + mz m b) Resolver en los casos de compatibilidad el sistema anterior..- Calcular el área de la región
PROBLEMAS SEPTIEMBRE 003 PRUEBA A 1.- a) Discutir en función de los valores de m: x 3y 0 x y+ z 0 x + y + mz m b) Resolver en los casos de compatibilidad el sistema anterior..- Calcular el área de la región
Distancia entre dos rectas que se cruzan Perpendicular común
 Perpendicular común En un espacio de tres dimensiones dos rectas se cruzan cuando no tienen ningún punto en común y no están contenidas en el mismo plano. Si no tienen ningún punto en común pero sí que
Perpendicular común En un espacio de tres dimensiones dos rectas se cruzan cuando no tienen ningún punto en común y no están contenidas en el mismo plano. Si no tienen ningún punto en común pero sí que
Superficies. Primera Forma Fundamental
 Tema Superficies. Primera Forma Fundamental Dpto. Matemática Aplicada I E.T.S. de Arquitectura Universidad de Sevilla Curso 005 006 Tema. Superficies. Primera Forma Fundamental 1. Curvas sobre superficies
Tema Superficies. Primera Forma Fundamental Dpto. Matemática Aplicada I E.T.S. de Arquitectura Universidad de Sevilla Curso 005 006 Tema. Superficies. Primera Forma Fundamental 1. Curvas sobre superficies
Acerca del Teorema de Gershgorin
 Acerca del Teorema de Gershgorin La siguiente nota se refiere al Teorema de Gershgorin y está motivada parcialmente por la parte c) de dicho teorema que puede verse en las notas de Geometría y Algebra
Acerca del Teorema de Gershgorin La siguiente nota se refiere al Teorema de Gershgorin y está motivada parcialmente por la parte c) de dicho teorema que puede verse en las notas de Geometría y Algebra
Problemas resueltos del Boletín 1
 Boletines de problemas de Matemáticas II Problemas resueltos del Boletín Problema. Dada la curva r (t) = t [0, π], parametrizarla naturalmente. ( (cos t + t sen t), (sen t t cos t), t ), con En primer
Boletines de problemas de Matemáticas II Problemas resueltos del Boletín Problema. Dada la curva r (t) = t [0, π], parametrizarla naturalmente. ( (cos t + t sen t), (sen t t cos t), t ), con En primer
Estadística Diplomado
 Diplomado HRB UNAM 1 / 25 1 Estimación Puntual Momentos Máxima Verosimiltud Propiedades 2 / 25 1 Estimación Puntual Momentos Máxima Verosimiltud Propiedades 2 Estimación por Intervalos Cantidades Pivotales
Diplomado HRB UNAM 1 / 25 1 Estimación Puntual Momentos Máxima Verosimiltud Propiedades 2 / 25 1 Estimación Puntual Momentos Máxima Verosimiltud Propiedades 2 Estimación por Intervalos Cantidades Pivotales
CURVAS Y SUPERFICIES. RELACIÓN 2
 CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
CURVAS Y SUPERFICIES. RELACIÓN 2 SUPERFICIES EN EL ESPACIO Curso 2015-16 1. Demostrar que las siguientes cuádricas reales son superficies. Obtener una parametrización de cada una de ellas. En cada caso,
Extremos Restringidos (Multiplicadores de Lagrange)
 Extremos Restringidos (Multiplicadores de Lagrange) Dada la curva en el plano (x h) a + (y k) b = 1. Esta es una elipse con centro en (h,k) y queremos encontrar qué punto de esta elipse se encuentra más
Extremos Restringidos (Multiplicadores de Lagrange) Dada la curva en el plano (x h) a + (y k) b = 1. Esta es una elipse con centro en (h,k) y queremos encontrar qué punto de esta elipse se encuentra más
Tema 4: Movimiento en 2D y 3D
 Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla Física I, GIC, Dpto. Física Aplicada III, ETSI, Universidad de Sevilla, 2017/18 1
Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Civil Escuela Técnica Superior de Ingeniería Universidad de Sevilla Física I, GIC, Dpto. Física Aplicada III, ETSI, Universidad de Sevilla, 2017/18 1
SEMANA 12: CURVAS EN EL ESPACIO. ds v(t) = d r (t) =
 FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 8-2 Basado en el apunte del ramo Matemáticas Aplicadas, de Felipe Álvarez, Juan Diego Dávila, Roberto Cominetti
FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo Diferencial e Integral 8-2 Basado en el apunte del ramo Matemáticas Aplicadas, de Felipe Álvarez, Juan Diego Dávila, Roberto Cominetti
ANALISIS II 12/2/08 COLOQUIO TEMA 1
 ANALISIS II //08 COLOQUIO TEMA Sea f : R R un campo vectorial C y C la curva parametrizada por: γ(t) = (cost, 0, sent) con t ɛ [0, π] Sabiendo que C f ds = 6 y que rot( f( ) = (z, ), calcular la integral
ANALISIS II //08 COLOQUIO TEMA Sea f : R R un campo vectorial C y C la curva parametrizada por: γ(t) = (cost, 0, sent) con t ɛ [0, π] Sabiendo que C f ds = 6 y que rot( f( ) = (z, ), calcular la integral
Clasificación Supervisada
 Clasificación Supervisada Ricardo Fraiman 26 de abril de 2010 Resumen Reglas de Clasificación Resumen Reglas de Clasificación Descripción del problema Muestra de entrenamiento (X 1, Y 1 ),..., (X n, Y
Clasificación Supervisada Ricardo Fraiman 26 de abril de 2010 Resumen Reglas de Clasificación Resumen Reglas de Clasificación Descripción del problema Muestra de entrenamiento (X 1, Y 1 ),..., (X n, Y
Guía Semanas 13 y RESUMEN. Universidad de Chile. Ingeniería Matemática. Triedro de vectores y factores escalares. Supongamos que r.
 1. RESUMEN Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08-1 Ingeniería Matemática Guía Semanas 13 y 14 Triedro de vectores y factores
1. RESUMEN Ingeniería Matemática FACULTAD DE CIENCIAS FÍSICAS Y MATEMÁTICAS UNIVERSIDAD DE CHILE Cálculo en Varias Variables 08-1 Ingeniería Matemática Guía Semanas 13 y 14 Triedro de vectores y factores
Tema 6: Ángulos y distancias en el espacio
 Tema 6: Ángulos y distancias en el espacio February, 017 1 Ángulos entre elementos del espacio Los ángulos entre elementos del espacio, es una aplicación sencilla del producto escalar. Recuerdo las condiciones
Tema 6: Ángulos y distancias en el espacio February, 017 1 Ángulos entre elementos del espacio Los ángulos entre elementos del espacio, es una aplicación sencilla del producto escalar. Recuerdo las condiciones
Guía realizada por: Pimentel Yender.
 REPÚBLICA BOLIVARIANA DE VENEZUELA MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN U.E. COLEGIO DON CESAR ACOSTA BARINAS. ESTADO, BARINAS. PROFESOR: PIMENTEL YENDER. FÍSICA 4TO AÑO. MOVIMIENTO CIRCULAR
REPÚBLICA BOLIVARIANA DE VENEZUELA MINISTERIO DEL PODER POPULAR PARA LA EDUCACIÓN U.E. COLEGIO DON CESAR ACOSTA BARINAS. ESTADO, BARINAS. PROFESOR: PIMENTEL YENDER. FÍSICA 4TO AÑO. MOVIMIENTO CIRCULAR
Capítulo VI. Diferenciabilidad de funciones de varias variables
 Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Capítulo VI Diferenciabilidad de funciones de varias variables La definición de diferenciabilidad para funciones el cociente no tiene sentido, puesto que no está definido, porque el cociente entre el vector
Análisis Multivariado 2 - Práctica 1. 1 Componentes principales y autoconsistencia
 Análisis Multivariado 2 - Práctica 1 1 Componentes principales y autoconsistencia 1. Sea Σ R p p una matriz de covarianza definida positiva. Considere el problema de aproximar Σ por una matriz Γ R p p
Análisis Multivariado 2 - Práctica 1 1 Componentes principales y autoconsistencia 1. Sea Σ R p p una matriz de covarianza definida positiva. Considere el problema de aproximar Σ por una matriz Γ R p p
MATEMÁTICA AGRONOMÍA RESPUESTAS AL SEGUNDO PARCIAL Primer Cuatrimestre Tema 1
 Ejercicio Considerando la recta R que pasa por los puntos A = (; 0; ) y B = (2; ; 5) y el punto P = (2; ; ), hallar la ecuación implícita del plano π que es perpendicular a la recta R y contiene al punto
Ejercicio Considerando la recta R que pasa por los puntos A = (; 0; ) y B = (2; ; 5) y el punto P = (2; ; ), hallar la ecuación implícita del plano π que es perpendicular a la recta R y contiene al punto
Tema 4: Movimiento en 2D y 3D
 Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Ingeniería Electrónica, Robótica y Mecatrónica Departamento de Física Aplicada III Escuela Técnica Superior de Ingeniería Universidad de Sevilla Índice
Tema 4: Movimiento en 2D y 3D FISICA I, 1º Grado en Ingeniería Electrónica, Robótica y Mecatrónica Departamento de Física Aplicada III Escuela Técnica Superior de Ingeniería Universidad de Sevilla Índice
x 2 + ln(x + z) y = 0 yz + e xz 1 = 0 define una curva C regular en un entorno de (1, 1, 0) y halle el plano normal a C en dicho punto.
 1 Sea f : R R una función C 3 que satisface f(1, ) = (0, 0), y cuya matriz ( Hessiana ) en (1, ) es: 1 0 H = 0 Hallar todos los b ɛ R de manera que la función: g( = f( + 1 b b (y ) ) tenga extremo en (1,
1 Sea f : R R una función C 3 que satisface f(1, ) = (0, 0), y cuya matriz ( Hessiana ) en (1, ) es: 1 0 H = 0 Hallar todos los b ɛ R de manera que la función: g( = f( + 1 b b (y ) ) tenga extremo en (1,
Capítulo 5. Integrales sobre curvas y superficies
 Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
Capítulo 5. Integrales sobre curvas y superficies 5.1. Integrales de funciones escalares sobre curvas 5.2. Integrales de campos vectoriales sobre curvas 5.3. Teorema de Green 5.4. Integrales sobre superficies
Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena
 1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
1 Universidad Simón Bolívar. Preparaduría nº 3. christianlaya@hotmail.com ; @ChristianLaya Plano tangente a una superficie y a una superficie de nivel, derivada direccional y regla de la cadena Derivada
Clase 10: Extremos condicionados y multiplicadores de Lagrange
 Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
Clase 10: Extremos condicionados y multiplicadores de Lagrange C.J. Vanegas 7 de abril de 008 1. Extremos condicionados y multiplicadores de Lagrange Estamos interesados en maximizar o minimizar una función
Tema 4 - Introducción
 Tema 4 - Introducción 1 Tema 3. Estimación puntual Criterios de comparación de estimadores: Insesgadez. Estimadores de mínima varianza. Error cuadrático medio. Consistencia. Cómo obtener estimadores? Tema
Tema 4 - Introducción 1 Tema 3. Estimación puntual Criterios de comparación de estimadores: Insesgadez. Estimadores de mínima varianza. Error cuadrático medio. Consistencia. Cómo obtener estimadores? Tema
Julio C. Carrillo E. Profesor Escuela de Matemáticas Universidad Industrial de Santander. Monday, November 5, 2007 at 8:44 am (FA07.
 Julio C. Carrillo E. Profesor Escuela de Matemáticas Universidad Industrial de Santander Monday, November 5, 2007 at 8:44 am (FA07.01,02) Para uso exclusivo en el salón de clase. 2007 c Julio C. Carrillo
Julio C. Carrillo E. Profesor Escuela de Matemáticas Universidad Industrial de Santander Monday, November 5, 2007 at 8:44 am (FA07.01,02) Para uso exclusivo en el salón de clase. 2007 c Julio C. Carrillo
1 CÓNICAS Cónicas. Estudio particular. 1 x y. 1 x y. a 00 a 01 a 02 a 10 a 11 a 12 a 20 a 21 a 22
 CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
CÓNICAS. CÓNICAS.. Cónicas. Estudio particular. Una cónica se dene como el lugar geométrico de los puntos del plano euclídeo que, respecto de una referencia cartesiana rectangular, satisfacen una ecuación
2.5 Teorema de Jordan
 Capítulo 2/ Forma canónica de Jordan (Versión 13-03-2015) 15 2.5 Teorema de Jordan En esta sección queremos abordar ya el caso general de un endomorfismo f : V V cualquiera (no necesariamente con un único
Capítulo 2/ Forma canónica de Jordan (Versión 13-03-2015) 15 2.5 Teorema de Jordan En esta sección queremos abordar ya el caso general de un endomorfismo f : V V cualquiera (no necesariamente con un único
Vectores. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo equivalente a QP.
 Wilson Herrera 1 Vectores 1. Dados los puntos P (1, 2), Q( 2, 2) y R(1, 6): a) Representarlos en el plano XOY. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo
Wilson Herrera 1 Vectores 1. Dados los puntos P (1, 2), Q( 2, 2) y R(1, 6): a) Representarlos en el plano XOY. b) Hallar la magnitud de cada uno de los vectores P Q, QRy P R. c) Encontrar el vector fijo
Seis problemas resueltos de geometría
 Problema 1 a) Dados los puntos P(4, 2, 3) y Q(2, 0, 5), da la ecuación implícita del plano π de modo que el punto simétrico de P respecto a π es Q. b) Calcula el valor del parámetro λ R para que el plano
Problema 1 a) Dados los puntos P(4, 2, 3) y Q(2, 0, 5), da la ecuación implícita del plano π de modo que el punto simétrico de P respecto a π es Q. b) Calcula el valor del parámetro λ R para que el plano
CÁLCULO Primer curso de Ingeniero de Telecomunicación Examen Final. 7 de Julio de 2000 Primera parte
 ÁLULO Primer curso de Ingeniero de Telecomunicación Examen Final. 7 de Julio de 000 Primera parte Ejercicio 1. Entre todos los rectángulos del plano YOZ,inscritos en la parábola z = a y (siendo a>0) yconbaseenelejeoy
ÁLULO Primer curso de Ingeniero de Telecomunicación Examen Final. 7 de Julio de 000 Primera parte Ejercicio 1. Entre todos los rectángulos del plano YOZ,inscritos en la parábola z = a y (siendo a>0) yconbaseenelejeoy
Curso 2010/ de julio de (2.75 p.) 1) Se considera la función f : (0, ) (0, ) definida por
 Cálculo I Curso 2010/2011 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas 5 de julio de 2011 (275 p) 1) Se considera la función f : (0, ) (0, ) definida por f(x) = 1 + ex x e x a)
Cálculo I Curso 2010/2011 Universidade de Vigo Departamento de Matemática Aplicada II ETSI Minas 5 de julio de 2011 (275 p) 1) Se considera la función f : (0, ) (0, ) definida por f(x) = 1 + ex x e x a)
Tema1. Modelo Lineal General.
 Tema1. Modelo Lineal General. 1. Si X = (X 1, X 2, X 3, X 4 ) t tiene distribución normal con vector de medias µ = (2, 1, 1, 3) t y matriz de covarianzas 1 0 1 1 V = 0 2 1 1 1 1 3 0 1 1 0 2 Halla: a) La
Tema1. Modelo Lineal General. 1. Si X = (X 1, X 2, X 3, X 4 ) t tiene distribución normal con vector de medias µ = (2, 1, 1, 3) t y matriz de covarianzas 1 0 1 1 V = 0 2 1 1 1 1 3 0 1 1 0 2 Halla: a) La
Planteamiento del problema
 Planteamiento del problema La interpolación consiste en construir una función (o una curva) que pase por una serie de puntos prefijados. Interpolación polinomial: el conjunto de datos observados se interpola
Planteamiento del problema La interpolación consiste en construir una función (o una curva) que pase por una serie de puntos prefijados. Interpolación polinomial: el conjunto de datos observados se interpola
Superficies parametrizadas
 1 Universidad Simón Bolívar.. Preparaduría nº 1. christianlaya@hotmail.com ; @ChristianLaya Superficies parametrizadas Superficies parametrizadas: Una superficie parametrizada es una función donde D es
1 Universidad Simón Bolívar.. Preparaduría nº 1. christianlaya@hotmail.com ; @ChristianLaya Superficies parametrizadas Superficies parametrizadas: Una superficie parametrizada es una función donde D es
1. Curvas Regulares y Simples
 1. Regulares y Simples en R n. Vamos a estudiar algunas aplicaciones del calculo diferencial e integral a funciones que están definidas sobre los puntos de una curva del plano o del espacio, como por ejemplo
1. Regulares y Simples en R n. Vamos a estudiar algunas aplicaciones del calculo diferencial e integral a funciones que están definidas sobre los puntos de una curva del plano o del espacio, como por ejemplo
Soluciones Hoja Problemas Espacio Vectorial 05-06
 Soluciones Hoja Problemas Espacio Vectorial -6.- Se considera R con la suma habitual y con el producto por un escalar que se indica en los casos siguientes. Prueba que en ninguno de ellos, (R,, ) es espacio
Soluciones Hoja Problemas Espacio Vectorial -6.- Se considera R con la suma habitual y con el producto por un escalar que se indica en los casos siguientes. Prueba que en ninguno de ellos, (R,, ) es espacio
EL TEOREMA DE LOS CUATRO
 EL TEOREMA DE LOS CUATRO VÉRTICES Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría Diferencial. Curso 1995/96
EL TEOREMA DE LOS CUATRO VÉRTICES Prof. Rafael López Camino Departamento de Geometría y Topología Universidad de Granada Material docente para el alumno Asignatura: Geometría Diferencial. Curso 1995/96
El teorema de Stokes. 1. Integración de formas en variedades
 Capítulo 12 El teorema de Stokes 1. Integración de formas en variedades En esta sección definimos la integral de una k-forma diferencial ω definida en una variedad diferenciable en R n de dimensión k,
Capítulo 12 El teorema de Stokes 1. Integración de formas en variedades En esta sección definimos la integral de una k-forma diferencial ω definida en una variedad diferenciable en R n de dimensión k,
Ejercicios de Fundamentos Matemáticos I. Rafael Payá Albert. Ingeniería de Telecomunicaciones. Departamento de Análisis Matemático
 Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
Ejercicios de Fundamentos Matemáticos I Ingeniería de Telecomunicaciones Rafael Payá Albert Departamento de Análisis Matemático Universidad de Granada FUNDAMENTO MATEMÁTICO I Relación de Ejercicios N o
Curvas. Definición 6. Una curva cerrada simple o una curva de Jordan es una curva cerrada con la propiedad de que f(t 1 ) = f(t 2 ) t 1 = t 2
 Introducción a las Funciones Vectoriales (Funciones de R R n ) Curvas Definición. Una función vectorial f : I R R 2 continua en I = [a, b] se llama trayectoria ó camino. Definición 2. A la imagen de una
Introducción a las Funciones Vectoriales (Funciones de R R n ) Curvas Definición. Una función vectorial f : I R R 2 continua en I = [a, b] se llama trayectoria ó camino. Definición 2. A la imagen de una
1 Espacios de Banach:
 Ecuaciones Diferenciales - 2 cuatrimestre 2003 Resultados preliminares parte II Espacios de Banach: Sea X un IR-espacio vectorial. Definición. Una función : X [0, + ) se dice una norma si. x + y x + y
Ecuaciones Diferenciales - 2 cuatrimestre 2003 Resultados preliminares parte II Espacios de Banach: Sea X un IR-espacio vectorial. Definición. Una función : X [0, + ) se dice una norma si. x + y x + y
Curso Propedéutico de Cálculo Sesión 7:
 Curso Propedéutico de Cálculo Sesión 7: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 Esquema 1 2 3 4 Hasta ahora nos hemos enfocado en funciones
Curso Propedéutico de Cálculo Sesión 7: Joaquín Ortega Sánchez Centro de Investigación en Matemáticas, CIMAT Guanajuato, Gto., Mexico Esquema 1 2 3 4 Esquema 1 2 3 4 Hasta ahora nos hemos enfocado en funciones
Se pide: (b) Ecuaciones que permiten obtener las coordenadas cartesianas en R en función de las de R.
 ÁLGEBRA Práctica 13 Espacios afines E 2 y E 3 (Curso 2004 2005) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = {O, ē 1, ē 2, ē 3 } y R = {P, ū 1, ū 2, ū 3 }, donde
ÁLGEBRA Práctica 13 Espacios afines E 2 y E 3 (Curso 2004 2005) 1. En un espacio afín real de dimensión 3, se consideran dos sistemas de referencia R = {O, ē 1, ē 2, ē 3 } y R = {P, ū 1, ū 2, ū 3 }, donde
1.4. Teoría local de curvas en el espacio.
 18 1.4. Teoría local de curvas en el espacio. En esta sección vamos a hacer un estudio similar al realizado en la sección anterior, pero en el caso de que α : I R 3 es una curva parametrizada diferenciable
18 1.4. Teoría local de curvas en el espacio. En esta sección vamos a hacer un estudio similar al realizado en la sección anterior, pero en el caso de que α : I R 3 es una curva parametrizada diferenciable
6.8. Descomposición mediante valores singulares. v 2 =
 68 Descomposición mediante valores singulares Los valores singulares de una matriz m n Supongamos que A es una matriz real cualquiera Los autovalores de A T A tienen la siguiente propiedad A T Ax = λx
68 Descomposición mediante valores singulares Los valores singulares de una matriz m n Supongamos que A es una matriz real cualquiera Los autovalores de A T A tienen la siguiente propiedad A T Ax = λx
Problemas Tema 3 Solución a problemas de Derivabilidad - Hoja 01 - Problemas 1, 3, 4, 6, 7
 página 1/6 Problemas Tema 3 Solución a problemas de Derivabilidad - Hoja 01 - Problemas 1, 3, 4, 6, 7 Hoja 1. Problema 1 Resuelto por Curro García Olmedo (noviembre 2014) 1. Obtener la derivada de f (
página 1/6 Problemas Tema 3 Solución a problemas de Derivabilidad - Hoja 01 - Problemas 1, 3, 4, 6, 7 Hoja 1. Problema 1 Resuelto por Curro García Olmedo (noviembre 2014) 1. Obtener la derivada de f (
Métodos Estadísticos Multivariados
 Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre 2011 1 / 20 Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre
Métodos Estadísticos Multivariados Victor Muñiz ITESM Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre 2011 1 / 20 Victor Muñiz (ITESM) Métodos Estadísticos Multivariados Agosto-Diciembre
1 Estudio local de curvas
 E.T.S. Arquitectura. Curvas y Super cies.1 1 Estudio local de curvas Sea una curva C R 3 con representación paramétrica regular ~r(t), t 2 I R, de clase mayor o igual a 3 y sea s = s(t) = Z t t 0 k~r 0
E.T.S. Arquitectura. Curvas y Super cies.1 1 Estudio local de curvas Sea una curva C R 3 con representación paramétrica regular ~r(t), t 2 I R, de clase mayor o igual a 3 y sea s = s(t) = Z t t 0 k~r 0
Capítulo 3. Funciones con valores vectoriales
 Capítulo 3. Funciones con valores vectoriales 3.1. Curvas: recta tangente y longitud de arco 3.2. Superficies parametrizadas 3.3. Campos vectoriales, campos conservativos Capítulo 3. Funciones con valores
Capítulo 3. Funciones con valores vectoriales 3.1. Curvas: recta tangente y longitud de arco 3.2. Superficies parametrizadas 3.3. Campos vectoriales, campos conservativos Capítulo 3. Funciones con valores
1. Límites de sucesiones en R n
 1. Límites de sucesiones en R n Definición 1 (Límite de una sucesión). Dada {A k } k=1 = {a1 k,... an k } Rn decimos que el límite de A k cuando k tiende a infinito es L si: lím A k = L ε > 0, N N : A
1. Límites de sucesiones en R n Definición 1 (Límite de una sucesión). Dada {A k } k=1 = {a1 k,... an k } Rn decimos que el límite de A k cuando k tiende a infinito es L si: lím A k = L ε > 0, N N : A
Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la
 Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
Geometría Analítica Preliminares Identidades Trigonométricas Definición: Se llama pendiente de una recta a la tangente de un ángulo de inclinación formado por el eje X y la recta, tal que, esto es Recta
Cálculo de Probabilidades y Estadística. Segunda prueba. 1
 08231. Cálculo de Probabilidades y Estadística. Segunda prueba. 1 Problema 1. Se eligen tres puntos A, B y C, al azar e independientemente, sobre una circunferencia. Determinar la distribución del valor
08231. Cálculo de Probabilidades y Estadística. Segunda prueba. 1 Problema 1. Se eligen tres puntos A, B y C, al azar e independientemente, sobre una circunferencia. Determinar la distribución del valor
Multiplicadores de Lagrange
 Funciones de R n en R 1 Multiplicadores de Lagrange Para entender el método de los multiplicadores de Lagrange ilustraremos las ideas con un ejemplo Ejemplo Sea f : R 2 R dada por fx, y) = x + 1) 2 + y
Funciones de R n en R 1 Multiplicadores de Lagrange Para entender el método de los multiplicadores de Lagrange ilustraremos las ideas con un ejemplo Ejemplo Sea f : R 2 R dada por fx, y) = x + 1) 2 + y
1. Espacio vectorial. Subespacios vectoriales
 Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Sea k un cuerpo. 1. Espacio vectorial. Subespacios vectoriales Definición 1.1. Un k-espacio vectorial o espacio vectorial
Álgebra lineal y Geometría I Gloria Serrano Sotelo Departamento de MATEMÁTICAS Sea k un cuerpo. 1. Espacio vectorial. Subespacios vectoriales Definición 1.1. Un k-espacio vectorial o espacio vectorial
El grupo lineal proyectivo. Homologías. Afinidades.
 Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
Tema 3- El grupo lineal proyectivo Homologías Afinidades 31 El grupo lineal proyectivo Recordamos que en el tema anterior hemos definido, para una variedad lineal proyectiva L P n no vacía, el grupo lineal
Método de mínimos cuadrados (Continuación)
 Clase No. 11: MAT 251 Método de mínimos cuadrados (Continuación) Dr. Alonso Ramírez Manzanares CIMAT A.C. e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/ Dr. Joaquín Peña Acevedo CIMAT
Clase No. 11: MAT 251 Método de mínimos cuadrados (Continuación) Dr. Alonso Ramírez Manzanares CIMAT A.C. e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/ Dr. Joaquín Peña Acevedo CIMAT
MATEMÁTICAS: EBAU 2017 JUNIO CASTILLA Y LEÓN
 MATEMÁTICAS: EBAU 7 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A Sean A = ( 4 ) y B = ( 3 ), a) Estudiar si A y B tienen inversa y calcularla cuando sea posible. ( punto) Una matriz cuadrada M tiene inversa
MATEMÁTICAS: EBAU 7 JUNIO CASTILLA Y LEÓN Opción A Ejercicio A Sean A = ( 4 ) y B = ( 3 ), a) Estudiar si A y B tienen inversa y calcularla cuando sea posible. ( punto) Una matriz cuadrada M tiene inversa
Relación de ejercicios del tema 1
 Relación de ejercicios del tema Asignatura: Curvas y Superficies. Grado en Matemáticas. Grupo: 2 0 -B Profesor: Rafael López Camino. Encontrar una parametrización α(t) de la curva cuya traza es la circunferencia
Relación de ejercicios del tema Asignatura: Curvas y Superficies. Grado en Matemáticas. Grupo: 2 0 -B Profesor: Rafael López Camino. Encontrar una parametrización α(t) de la curva cuya traza es la circunferencia
Si cálculamos el límite de estas pendiente cuando t tiende a t 0 f 2 (t) f 2 (t 0 )
 ANÁLISIS MATEMÁTICO BÁSICO. TANGENTES A CURVAS PARAMÉTRICAS. La forma más general de representar un curva en el plano no es a través de una gráfica sino de una curva paramétrica (ver Apéndice al tema de
ANÁLISIS MATEMÁTICO BÁSICO. TANGENTES A CURVAS PARAMÉTRICAS. La forma más general de representar un curva en el plano no es a través de una gráfica sino de una curva paramétrica (ver Apéndice al tema de
EL ESPACIO EUCLÍDEO. 1.- Sean (R 3,R 3,f) el espacio afín usual tridimensional real, R ={P 0, P 1, P 2, P 3 } y R,
 EL ESPACIO EUCLÍDEO 1.- Sean (R,R,f) el espacio afín usual tridimensional real, R {P 0, P 1, P, P } y R, {Q 0, Q 1, Q,Q } dos referencias afines de (R,R,f) de bases asociadas B{ P 0 P 1 P 0 P, P0 P } y
EL ESPACIO EUCLÍDEO 1.- Sean (R,R,f) el espacio afín usual tridimensional real, R {P 0, P 1, P, P } y R, {Q 0, Q 1, Q,Q } dos referencias afines de (R,R,f) de bases asociadas B{ P 0 P 1 P 0 P, P0 P } y
ANALISIS MATEMATICO II (Ciencias- 2011) Trabajo Práctico 8
 ANALISIS MATEMATIO II (iencias- 2011) Integrales sobre curvas (o de línea) Trabajo Práctico 8 1. Evaluar las siguientes integrales curvilíneas γ f ds. (a) f(x, y, z) = x + y + z ; r(t) = (sen t, cos t,
ANALISIS MATEMATIO II (iencias- 2011) Integrales sobre curvas (o de línea) Trabajo Práctico 8 1. Evaluar las siguientes integrales curvilíneas γ f ds. (a) f(x, y, z) = x + y + z ; r(t) = (sen t, cos t,
1. INTRODUCCIÓN. MOVIMIENTO Y SISTEMA DE REFERENCIA.
 TEMA 1 CINEMÁTICA 1. INTRODUCCIÓN. MOVIMIENTO Y SISTEMA DE REFERENCIA. Un cuerpo está en movimiento cuando cambia de lugar respecto a un punto que se considera fijo, a medida que pasa el tiempo. En todo
TEMA 1 CINEMÁTICA 1. INTRODUCCIÓN. MOVIMIENTO Y SISTEMA DE REFERENCIA. Un cuerpo está en movimiento cuando cambia de lugar respecto a un punto que se considera fijo, a medida que pasa el tiempo. En todo
Optimización de Problemas no lineales.
 Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Industrial IN34A: Clase Auxiliar Optimización de Problemas no lineales. Marcel Goic F. Esta es una versión bastante
Universidad de Chile Facultad de Ciencias Físicas y Matemáticas Departamento de Ingeniería Industrial IN34A: Clase Auxiliar Optimización de Problemas no lineales. Marcel Goic F. Esta es una versión bastante
Problemas métricos. 1. Problemas afines y problemas métricos
 . Problemas afines y problemas métricos Al trabajar en el espacio (o análogamente en el plano) se nos pueden presentar dos tipos de problemas con los elementos habituales (puntos, rectas y planos): Problemas
. Problemas afines y problemas métricos Al trabajar en el espacio (o análogamente en el plano) se nos pueden presentar dos tipos de problemas con los elementos habituales (puntos, rectas y planos): Problemas
CALCULO VECTORIAL GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES
 GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES 1.- En cada uno de los siguientes casos calcular la integral de línea dada a) + +, donde C es el segmento de recta que une el punto O(0,0)
GUÍA DE EJERCICIOS N 1 INTEGRALES DE LINEA Y SUS APLICACIONES 1.- En cada uno de los siguientes casos calcular la integral de línea dada a) + +, donde C es el segmento de recta que une el punto O(0,0)
Tema 11: Diferenciabilidad en varias variables.
 Tema 11: Diferenciabilidad en varias variables. José M. Salazar Noviembre de 2016 Tema 11: Diferenciabilidad en varias variables. Lección 14. Diferenciabilidad en varias variables. Lección 15. Aplicaciones
Tema 11: Diferenciabilidad en varias variables. José M. Salazar Noviembre de 2016 Tema 11: Diferenciabilidad en varias variables. Lección 14. Diferenciabilidad en varias variables. Lección 15. Aplicaciones
Pseudo-resumen de Electromagnetismo
 Pseudo-resumen de Electromagnetismo Álvaro Bustos Gajardo Versión 0.6β, al 27 de Octubre de 2011 1. Cargas. Ley de Coulomb 1.1. Carga eléctrica La carga eléctrica es una propiedad cuantitativa de la materia,
Pseudo-resumen de Electromagnetismo Álvaro Bustos Gajardo Versión 0.6β, al 27 de Octubre de 2011 1. Cargas. Ley de Coulomb 1.1. Carga eléctrica La carga eléctrica es una propiedad cuantitativa de la materia,
Análisis Matemático I (Ing. de Telecomunicación), Examen final, 26 de enero de 2010 RESPUESTAS A AMBOS MODELOS
 Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Análisis Matemático I (Ing. de Telecomunicación), 29-1 Examen final, 26 de enero de 21 RESPUESTAS A AMBOS MODELOS Primera Parte Las preguntas 1 14 son de tipo test. Se pide elegir una única respuesta en
Primer Examen Parcial Tema A Cálculo Vectorial Marzo 5 de 2016
 rimer Examen arcial Tema A Cálculo Vectorial Marzo 5 de 016 Este es un examen individual, no se permite el uso de libros, apuntes, calculadoras o cualquier otro medio electrónico. Recuerde apagar y guardar
rimer Examen arcial Tema A Cálculo Vectorial Marzo 5 de 016 Este es un examen individual, no se permite el uso de libros, apuntes, calculadoras o cualquier otro medio electrónico. Recuerde apagar y guardar
Diferenciciación en R n
 Diferenciciación en R n R. Álvarez-Nodarse Universidad de Sevilla Cómo definir la derivada? Definición Sea A un abierto de R n, a A y f : A R n R m. La derivada parcial i-ésima (1 i n) de f en a se define
Diferenciciación en R n R. Álvarez-Nodarse Universidad de Sevilla Cómo definir la derivada? Definición Sea A un abierto de R n, a A y f : A R n R m. La derivada parcial i-ésima (1 i n) de f en a se define
Tema 6. Apéndice: La esfera
 Matemáticas II (Bachillerato de Ciencias) Geometría del espacio: La esfera (Apéndice del TEMA 6) 141 Tema 6 Apéndice: La esfera La superficie esférica (la esfera) es el conjunto de puntos del espacio que
Matemáticas II (Bachillerato de Ciencias) Geometría del espacio: La esfera (Apéndice del TEMA 6) 141 Tema 6 Apéndice: La esfera La superficie esférica (la esfera) es el conjunto de puntos del espacio que
Clase 7 Herramientas de Álgebra Lineal
 Clase 7 Herramientas de Álgebra Lineal 1 Formas cuadráticas La descomposición en valores singulares 3 Normas de matrices 4 Ejercicios Dada una matriz M R n n, la función escalar x T Mx, donde x R n, es
Clase 7 Herramientas de Álgebra Lineal 1 Formas cuadráticas La descomposición en valores singulares 3 Normas de matrices 4 Ejercicios Dada una matriz M R n n, la función escalar x T Mx, donde x R n, es
ÁLGEBRA LINEAL. EXAMEN FINAL 18 de Enero de b) (0, 5 puntos) Estudia si la siguiente afirmación es verdadera o falsa, justificando
 ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
ÁLGEBRA LINEAL EXAMEN FINAL 8 de Enero de Apellidos y Nombre: Duración del examen: 3 horas Publicación de notas: enero Revisión de Examen: feb Ejercicio. ( puntos a (, puntos Estudia si la siguiente afirmación
CÓNICAS. 1. Dada la cónica x 2 + 2xy y 2 2x 2y + 4 = 0, se pide su clasicación y los elementos característicos de la misma. = 1
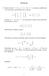 CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
CÓNICAS. Dada la cónica x + x x + 4, se pide su clasicación los elementos característicos de la misma. A 4 A Se tiene A 6 A, de modo que la cónica es una hipérbola. Calculemos su centro. A c c Resolviendo
Soluciones a los ejercicios del examen final C =. 1 0
 Universidade de Vigo Departamento de Matemática Aplicada II E T S E de Minas Álgebra Lineal Curso 205/6 de enero de 206 Soluciones a los ejercicios del examen final Se considera el subespacio U {X M 2
Universidade de Vigo Departamento de Matemática Aplicada II E T S E de Minas Álgebra Lineal Curso 205/6 de enero de 206 Soluciones a los ejercicios del examen final Se considera el subespacio U {X M 2
Análisis II Análisis matemático II Matemática 3.
 1 Análisis II Análisis matemático II Matemática 3. 1er. cuatrimestre de 2008 Práctica 1 - urvas, integral de longitud de arco e integrales curvilíneas. urvas Definición 1. Una curva R 3 es un conjunto
1 Análisis II Análisis matemático II Matemática 3. 1er. cuatrimestre de 2008 Práctica 1 - urvas, integral de longitud de arco e integrales curvilíneas. urvas Definición 1. Una curva R 3 es un conjunto
Espacios vectoriales reales.
 Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Tema 3 Espacios vectoriales reales. 3.1 Espacios vectoriales. Definición 3.1 Un espacio vectorial real V es un conjunto de elementos denominados vectores, junto con dos operaciones, una que recibe el nombre
Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados
 Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
Capítulo 5 Espacios Vectoriales Euclídeos. Métodos de los mínimos cuadrados En este tema iniciamos el estudio de los conceptos geométricos de distancia y perpendicularidad en K n. Empezaremos con las definiciones
IX CONGRESO INTERNACIONAL DE CIENCIAS DE LA TIERRA ( SANTIAGO DE CHILE, 6 10 NOVIEMBRE, 2006 )
 IX CONGRESO INTERNACIONAL DE CIENCIAS DE LA TIERRA ( SANTIAGO DE CHILE, 6 1 NOVIEMBRE, 6 ) PONENCIA: REDUCCIÓN Y AJUSTE POR MINIMOS CUADRADOS DE DISTANCIAS APLICANDO EL ANALISIS VECTORIAL AUTOR: FIS MARIO
IX CONGRESO INTERNACIONAL DE CIENCIAS DE LA TIERRA ( SANTIAGO DE CHILE, 6 1 NOVIEMBRE, 6 ) PONENCIA: REDUCCIÓN Y AJUSTE POR MINIMOS CUADRADOS DE DISTANCIAS APLICANDO EL ANALISIS VECTORIAL AUTOR: FIS MARIO
Indice de contenido. Ecuaciones de los círculos / Ecuación estándar de un círculo. Problemas complementarios
 l' Indice de contenido Un sistema de coordenadas lineales / Intervalos finitos / Intervalos infinitos / Desigualdades Ejes de coordenadas / Coordenadas / Cuadrantes / Fórmula de la distancia / Fórmulas
l' Indice de contenido Un sistema de coordenadas lineales / Intervalos finitos / Intervalos infinitos / Desigualdades Ejes de coordenadas / Coordenadas / Cuadrantes / Fórmula de la distancia / Fórmulas
ANÁLISIS MATEMÁTICO II - Grupo Ciencias 2018 Comentarios y ejemplos - Práctica 10
 ANÁLII MATEMÁTICO II - Grupo Ciencias 218 Comentarios y ejemplos - Práctica 1 A. Parametrizaciones de superficies El concepto de parametrización de una superficie es análogo al de parametrización de una
ANÁLII MATEMÁTICO II - Grupo Ciencias 218 Comentarios y ejemplos - Práctica 1 A. Parametrizaciones de superficies El concepto de parametrización de una superficie es análogo al de parametrización de una
Problemas de Geometría Analítica del Espacio
 1) Dados los vectores u(4, 4, 8), v( 2,, 5), w(3, 5, 8) y a(22,, 11). Hallar los valores de x, y, z que verifican la combinación lineal a = x u + y v + z w. 2) Dados los vectores a( 5, 19, n) y b( h, 3,
1) Dados los vectores u(4, 4, 8), v( 2,, 5), w(3, 5, 8) y a(22,, 11). Hallar los valores de x, y, z que verifican la combinación lineal a = x u + y v + z w. 2) Dados los vectores a( 5, 19, n) y b( h, 3,
GEOMETRÍA. que pasa por el punto P y es paralelo a π. (0,9 puntos) b) Determinar la ecuación del plano π
 GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
GEOMETRÍA 1.- Se considera la recta r : ( x, y, z) = ( t + 1, t,3 t), el plano π: x y z = 0y el punto P (1,1,1). Se pide: a) Determinar la ecuación del plano π 1 que pasa por el punto P y es paralelo a
1. ESPACIO EUCLÍDEO. ISOMETRÍAS
 . ESPACIO EUCLÍDEO. ISOMETRÍAS. En el espacio euclídeo usual R 4 se consideran los subespacios vectoriales y W = {(x, y, z, t R 4 : x y =, z + t = } Hallar: W 2 = L{(,, 2, 2, (,,, } a Las ecuaciones de
. ESPACIO EUCLÍDEO. ISOMETRÍAS. En el espacio euclídeo usual R 4 se consideran los subespacios vectoriales y W = {(x, y, z, t R 4 : x y =, z + t = } Hallar: W 2 = L{(,, 2, 2, (,,, } a Las ecuaciones de
Factorización QR Método iterativo de Jacobi
 Clase No. 13: MAT 251 Factorización QR Método iterativo de Jacobi Dr. Alonso Ramírez Manzanares CIMAT A.C. e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/ Dr. Joaquín Peña Acevedo CIMAT
Clase No. 13: MAT 251 Factorización QR Método iterativo de Jacobi Dr. Alonso Ramírez Manzanares CIMAT A.C. e-mail: alram@ cimat.mx web: http://www.cimat.mx/ alram/met_num/ Dr. Joaquín Peña Acevedo CIMAT
Ejercicios Resueltos de Cálculo III.
 Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
Ejercicios Resueltos de Cálculo III. 1.- Considere y. a) Demuestre que las rectas dadas se cortan. Encuentre el punto de intersección. b) Encuentre una ecuación del plano que contiene a esas rectas. Como
TEMA 8 REGRESIÓN Y CORRELACIÓN
 /7 TEMA 8 REGRESIÓN Y CORRELACIÓN Dada una variable aleatoria bidimensional (, ) supongamos que las variables no sean independientes, es decir, que eista cierta relación entre ellas. Nos planteamos entonces
/7 TEMA 8 REGRESIÓN Y CORRELACIÓN Dada una variable aleatoria bidimensional (, ) supongamos que las variables no sean independientes, es decir, que eista cierta relación entre ellas. Nos planteamos entonces
Análisis II Análisis matemático II Matemática 3.
 Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
Análisis II Análisis matemático II Matemática 3. er. cuatrimestre de 8 Práctica 4 - Teoremas de Stokes y de Gauss. Campos conservativos. Aplicaciones. Ejercicio. Verificar el teorema de Stokes para el
