SOLUCIONES ENERO 2018
|
|
|
- Asunción Villalba Olivares
- hace 5 años
- Vistas:
Transcripción
1 Página 1 de 9 SOLUCIONES ENERO 018 Soluciones extraídas del libro: XVIII CONCURSO DE PRIMAVERA 014 Obtenibles en NIVEL: Segundo ciclo de la E. S. O. AUTORES: Colectivo Concurso de Primavera. Comunidad de Madrid Enero 1: Sea n un natural. Cuál es el natural más cercano al cuadrado de n + 1? Solución: Puesto que: (n + 1 ) = n + n El natural más cercano al cuadrado de n + 1 es n + n. Enero -3: En dos lados consecutivos de un hexágono regular se han dibujado cuatro triángulos equiláteros. Con los centros de los polígonos regulares se ha construido un pentágono. Calcular el área del pentágono Solución: El pentágono se compone de una pieza roja y 4 piezas amarillas. La pieza roja es la sexta parte del hexágono. La pieza amarilla es la tercera parte de un triángulo equilátero, que es la sexta parte del hexágono. Por lo tanto, cuatro de estas piezas equivalen a 4/18 del hexágono. El pentágono corresponde a (1/6 + 4/18 =) 7/18 del hexágono Enero 4: Calcular el valor del producto: 017 (1 1 i ) i=
2 Página de 9 Solución: Tenemos: 017 (1 1 i ) i= = (1 1 ) (1 1 3 ) ( ). (1 016) (1 017 ) = ( 1 ) ( ) ( ).. ( ) ( ) ( 1) ( + 1) (3 1) (3 + 1) (4 1) (4 + 1) = (017 1) ( ) = (016 1) ( ) Notemos que (salvo en la primera y última fracción) el primer factor del denominador es el segundo factor del numerador de la fracción anterior y que el segundo factor del denominador es el primer factor del numerador de la fracción siguiente. Al simplificar queda pues: 017 (1 1 i ) i= = = = Enero 5-6: En un triángulo equilátero ABC de lado 4, se toma D en CB. Si S 1 es el área del triángulo ADB y S es el área del triángulo ADC, cuál es el mayor valor del producto S 1 S? Solución: Sea h la altura por el vértice A. Por Pitágoras: h = 16 4 = 3 Tendremos, al calcular áreas: ( + x) 3 ( x) 3 S 1 = ; S = S 1 S = 3 (4 x ) Obviamente el producto S 1 S es máximo cuando x=0, en cuyo caso el producto vale 1 Enero 7: Si el número de nueve cifras: N = d es primo, qué dígito es el representado por d? Nivel: A partir de 1ESO. Solución: Desde luego d {0,, 4, 6, 8}, pues en caso contrario sería par y por tanto divisible por y de aquí, no primo. Debe cumplirse, pues, que d {1, 3, 5, 7, 9}. Pero si d = 5 el número es múltiplo de 5.
3 Página 3 de 9 Además la suma de las cifras del número es 7 + d. De aquí, si d = 3 el número es múltiplo de 3 y si d = 9, el número es múltiplo de 9. Si d = 7 tenemos: = = 197 ( ) = y el número debería ser múltiplo de 197. Sólo que da la posibilidad de que d = 1. Enero 8-9: Hace dos años el número de estudiantes de mi centro era un cuadrado perfecto. El año pasado se matricularon 100 estudiantes más que el anterior y el nuevo número resultó ser un cuadrado perfecto más uno. Este año se matricularon 100 estudiantes más que el año anterior y de nuevo el número de estudiantes es un cuadrado perfecto. Cuántos estudiantes se matricularon este año? Solución: Sea N el número de estudiantes matriculados el primer año. Tendremos pasando la información del enunciado a ecuaciones: N = x N = y + 1 N + 00 = z } x = y + 1 x + 00 = z } 100 = z y = (z + y) (z y) Y como 101 es primo y z + y > z y, la ecuación última es equivalente al sistema de dos ecuaciones con dos incógnitas: z + y = 101 z y = 1 } Fácilmente resoluble y que aporta la solución N = x = 401. Enero 10: Cuál es el mayor resto posible cuando divides un número de dos cifras entre la suma de estas? Solución: En una división entera el resto siempre ha de ser menor que el divisor. Como se pide el mayor resto, vamos a comenzar probando con el mayor divisor posible: = 18. El resto de la división de 99 entre 18 es 9. El siguiente divisor posible es: = 17. El resto de la división de 98 (89) entre 17 es 13 (4). El siguiente divisor posible es = = 16. El resto de la división de 97 (88, 79) entre 16 es 1 (8, 15). El siguiente divisor posible es 15. Pero ya no se necesario seguir: El resto de las divisiones por números menores o iguales a 15 son menores que 15. En definitiva, el mayor resto posible al dividir un número de dos cifras por la suma de las cifras es 15 que sale al dividir 79 entre 16.
4 Página 4 de 9 Enero 11-1: En un cuadrado ABCD de m de lado, M es el punto medio del lado AB y P es un punto cualquiera del lado CB. Hallar el menor valor posible de DP + PM. Solución: Dibujamos el simétrico del cuadrado ABCD respecto de la arista CB. Sea M el simétrico de M respecto de CB. El menor valor de DP + DM sale cuando P está en el segmento que une D y M. Aplicando Pitágoras, tenemos que el menor valor posible de DP + PM es: + 3 = 13 Enero 13: La suma de los m primeros impares es 1 más la suma de los n primeros pares. Cuál es la suma de todos los valores que puede tomar n? Solución: La suma de los primeros m impares es: (m 1) = 1+m 1 m = m. La suma de los primeros n pares es: n = +n n = n + n. Por lo tanto, debe cumplirse m = 1 + n + n. Si definimos d ( N) como m = n + d, tenemos: (n + d) = 1 + n + n dn + d = 1 + n n = 1 d Dando valores a d, tenemos: d = 1 n = d = 3 n = d = 5 n = d = 7 n = d = 9 n = d = 11 n = d = 13 n = = 11 1 = 11; d = n = 1 1 = 08 3 N = N; d = 4 n = = = = N; d = 6 n = = = = N; d = 8 n = = N = N; d = 10 n = = N = N; d = 1 n = = 68 3 N = N; d = 14 n = = 16 7 N d 1
5 Página 5 de 9 No hace falta seguir, valores más grandes de d aportan menor numerador y mayor denominador y por tanto valores de n < 1, que no son admisibles. Hay únicamente tres valores de n: 11, 8 y 16 cuya suma es 55. Enero 14: En un triángulo rectángulo de hipotenusa 4 cm, la suma de sus catetos es 18 cm. Calcular el área del triángulo Nivel: Preparación OMS de primer ciclo. Solución: Sean x e y los catetos del triángulo rectángulo. Al aplicar Pitágoras tendremos x + y = 16. Por otra parte, del enunciado, x + y = 18. Tenemos formado el sistema: x + y = 16 x + y = 18 } que no es necesario resolver, pues, elevando al cuadrado la segunda ecuación tenemos: 18 = (x + y) = x + y + xy = 16 + xy área = x y = = 1 Enero 15: Al sumar 39 al número de tres cifras A4 obtenemos 5B3. Si 5B3 es múltiplo de 3, cuál es el mayor valor posible de A? Nivel: A partir de 1ESO. Solución 1: Puesto que 5B3 es múltiplo de 3, la suma de sus cifras debe ser múltiplo de 3. La suma de cifras es 8 + B, por lo que B puede ser 1, 4 o 7. Si B = 1 A4 = = 184 = 1 (al comparar las centenas). Por lo tanto, B 1 Si B = 4 A4 = = 14 A = 1. Si B = 7 A4 = = 44 A = 4. El mayor posible valor de A es 4. Solución : Al tenerse: A 4 5 B 3 debe de cumplirse que 3 + A = B. Como el valor más grande de B es 7, el valor más grande de A es 4. Enero 16-17: En la figura adjunta, cuál es el valor del ángulo x? Nivel: A partir de ESO. Solución: Aplicamos que la suma de los
6 Página 6 de 9 tres ángulos de un triángulo es 180. Tendremos de derecha a izquierda Enero 18: Hallar el menor y mayor valor posible de n, tal que n (n+1) da resto 1 al dividirlo por 3 Nivel: Preparación OMS de primer ciclo. Solución: Si n es múltiplo de 3 n (n + 1) es múltiplo de 3 y no puede dar de resto 1. Si n da resto 1 al dividirlo por 3 (n + 1) da resto al dividirlo por 3 n (n + 1) da resto (1 =) al dividirlo por 3, luego tampoco puede dar resto 1. Si n da resto al dividirlo por 3 (n + 1) es múltiplo de 3 n (n + 1) es múltiplo de 3 y no puede dar de resto 1. Por tanto, n (n + 1) nunca da resto 1 al ser dividido por 3 Enero 19-0: De cuantas maneras podemos añadir un cuadrado igual a los cuatro de la figura para que la figura resultante tenga al menos un eje de simetría? Solución: Hay tres maneras de añadir un cuadrado idéntico a los de la figura para que se tenga al menos un eje de simetría
7 Página 7 de 9 Enero 1: Hallar el mayor natural que divida a todos los términos de la sucesión a n = n 5 n Solución: Tenemos n 5 n = (n 1) n (n + 1) (n + 1). Por tanto, cada término de la sucesión es múltiplo del producto de tres naturales consecutivos. Por tanto, cada término de la sucesión es múltiplo de 3 (ya que en tres naturales consecutivos hay uno que es múltiplo de 3). Además, tenemos: n acaba en n 5 acaba en por lo que n 5 n acaba en 0. O en otras palabras cada término es múltiplo de 10. Tenemos, pues, que cada término es múltiplo de 30. Como, además, el segundo término es 30, no puede haber un divisor mayor. Enero -3: En la figura, ABE = EBC y ACE = ECD. Si = CEB, hallar el ángulo BAC =. Solución: Llamamos x a la mitad del ángulo verde e y a la mitad del ángulo rojo. Tendremos, en el triángulo ABC: x y = 180 x y + = 0 (*) y en el triángulo BCE: x y + y =180 x y + = 0 x y + = 0 (**) De las ecuaciones (*) y (**) tenemos: = Enero 4: Hallar el máximo de la expresión x x cuando x es un real cualquiera Solución: y = x x es una parábola invertida (a = - 1 < 0), y por tanto x x y V (= la ordenada del vértice de la parábola). Como x V = b a = 1 ( 1) = 1 y V = 1 (1 ) = 1 4
8 Página 8 de 9 Enero 5-6: En la figura se tiene una circunferencia de radio 1 y los rectángulos dibujados son todos iguales con un lado doble de otro. Cuál es el área de cada rectángulo? Nivel: A partir de ESO. Solución: Dibujamos el diámetro de la figura de abajo y, al aplicar Pitágoras al triángulo rectángulo generado, tenemos: = (x) + (4x), 4 = 4x + 16x = 0x x = 4 0 = 1 5 Área = x = 1 5 = 5 Enero 7: Cuántos números de 5 cifras, todas distintas, cumplen que la cifra de las unidades es la suma de las restantes? Solución: Veamos las diferentes posibilidades que hay en la cifra de las unidades y en las restantes cifras. cifra en las unidades cifras en las demás posiciones 6 0, 1,, 3 7 0, 1,, 4 8 0, 1,, 5, 0, 1, 3, 4 9 0, 1,, 6 0, 1, 3, 5 0,, 3, 4 Veamos los que terminan en 6: Para la primera posición tenemos 3 candidatos (no participa la cifra 0, pues el número no tendría cinco cifras). Para la segunda posición tenemos otros tres candidatos (pues ahora no participa la cifra elegida en la primera posición y si participa el 0). Para la tercera posición tenemos dos candidatos. Para la cuarta posición tenemos un candidato y `para las unidades sólo tenemos a la cifra 6. En total: ( =) 18 números. Lo mismo ocurre con cada grupo asociado a cada una de las posibles unidades (7, 8, 9). En total salen (18 7 =) 16 números que cumplen el requisito exigido en el enunciado. Enero 8: En el triángulo ABC, con BC=13, CA=14 y AB=15, hallar la altura por B
9 Página 9 de 9 Solución: Sea h la altura por B. Quedan definidos dos triángulos rectángulos. Al aplicar sobre ellos el teorema de Pitágoras, tenemos: 15 = h + (14 x) 13 = x + h } h = 15 (14 x) h = 13 x } x = 169 8x = 140 x = 5; h = 13 5 = 1 Enero 9: En una circunferencia de centro O y diámetro AB, se tiene una cuerda BC. Si OBC=58 o, cuánto mide el ángulo OCA? Solución: Como OB = OC (= radio circunferencia) tenemos que OCB = CBO = 58 Por otra parte (ángulo central = AOB = ACB ) ACB = 90. De aquí: ACO = ACB - OCB = = 3 Enero 30-31: Ordena los cinco segmentos de la figura por su longitud. Solución: Aplicaremos que en un triángulo a mayor ángulo se le opone mayor lado. En ACD, tenemos que D = (180 - ( )=) 55, y aplicando lo anterior: AC < CD < AD. En ABC, tenemos B = (180 - ( )=) 70, y aplicando lo anterior: AB < BC < AC. Y en definitiva: AB < BC < AC < CD < AD
SOLUCIONES MARZO 2017
 Página 1 de 0 SOLUCIONES MARZO 017 Autor: Rafael Martínez Calafat. Profesor jubilado de Matemáticas Marzo 1: Hallar los valores de k de manera que 5n 3 +4n+k sea múltiplo de 3 para todo n natural Nivel:
Página 1 de 0 SOLUCIONES MARZO 017 Autor: Rafael Martínez Calafat. Profesor jubilado de Matemáticas Marzo 1: Hallar los valores de k de manera que 5n 3 +4n+k sea múltiplo de 3 para todo n natural Nivel:
Nivel: A partir de 4ESO. Solución: La relación entre la apotema y el lado del hexágono es la misma que entre la altura y
 Página 1 de 9 SOLUCIONES MAYO 2017 Soluciones extraídas de los libros: XVI CONCURSO DE PRIMAVERA 2012 XVII CONCURSO DE PRIMAVERA 2013 Obtenibles en http://www.concursoprimavera.es#libros AUTORES: Colectivo
Página 1 de 9 SOLUCIONES MAYO 2017 Soluciones extraídas de los libros: XVI CONCURSO DE PRIMAVERA 2012 XVII CONCURSO DE PRIMAVERA 2013 Obtenibles en http://www.concursoprimavera.es#libros AUTORES: Colectivo
SOLUCIONES SEPTIEMBRE 2016
 Página de 9 SOLUCIONES SEPTIEMBRE 206 Soluciones extraídas de los libros: XII CONCURSO DE PRIMAVERA 2008 XV CONCURSO DE PRIMAVERA 20 XVI CONCURSO DE PRIMAVERA 202 Obtenibles en http://www.concursoprimavera.es#libros
Página de 9 SOLUCIONES SEPTIEMBRE 206 Soluciones extraídas de los libros: XII CONCURSO DE PRIMAVERA 2008 XV CONCURSO DE PRIMAVERA 20 XVI CONCURSO DE PRIMAVERA 202 Obtenibles en http://www.concursoprimavera.es#libros
donde n es el numero de lados. n APOTEMA: Es la altura de un triangulo formado por el centro del polígono regular y dos vértices consecutivos.
 Polígonos regulares 1 POLIGONOS REGULARES DEFINICION: Un polígono regular es el que tiene todos sus lados y sus ángulos congruentes. DEFINICION: Un polígono esta inscrito en una circunferencia si sus vértices
Polígonos regulares 1 POLIGONOS REGULARES DEFINICION: Un polígono regular es el que tiene todos sus lados y sus ángulos congruentes. DEFINICION: Un polígono esta inscrito en una circunferencia si sus vértices
Tema 10: Problemas métricos en el plano
 Tema 10: Problemas métricos en el plano 10.1 Relaciones angulares Construye un polígono de cinco lados, divídelo en triángulos para averiguar la suma de los ángulos interiores del pentágono. Nuestro pentágono
Tema 10: Problemas métricos en el plano 10.1 Relaciones angulares Construye un polígono de cinco lados, divídelo en triángulos para averiguar la suma de los ángulos interiores del pentágono. Nuestro pentágono
SOLUCIONES JUNIO 2018
 Página 1 de 11 SOLUCIONES JUNIO 018 Soluciones extraídas del libro: XVIII CONCURSO DE PRIMAVERA 014 Obtenibles en http://www.concursoprimavera.es#libros NIVEL: Bachillerato y preparación OME AUTORES: Colectivo
Página 1 de 11 SOLUCIONES JUNIO 018 Soluciones extraídas del libro: XVIII CONCURSO DE PRIMAVERA 014 Obtenibles en http://www.concursoprimavera.es#libros NIVEL: Bachillerato y preparación OME AUTORES: Colectivo
SOLUCIÓN PRIMERA ELIMINATORIA NACIONAL NIVEL C
 XXIV OLIMPIADA COSTARRICENSE DE MATEMÁTICA MEP ITCR UCR UNA UNED - MICIT SOLUCIÓN PRIMERA ELIMINATORIA NACIONAL NIVEL C 01 1. Un factor de la factorización completa de corresponde a mx y + 9y m x y x 4
XXIV OLIMPIADA COSTARRICENSE DE MATEMÁTICA MEP ITCR UCR UNA UNED - MICIT SOLUCIÓN PRIMERA ELIMINATORIA NACIONAL NIVEL C 01 1. Un factor de la factorización completa de corresponde a mx y + 9y m x y x 4
SOLUCIONES FEBRERO 2018
 Página 1 de 18 SOLUCIONES FEBRERO 018 AUTOR: Rafael Martínez Calafat. Profesor jubilado de Matemáticas Nivel: PROBLEMAS PARA PREPARACIÓN OME. Febrero 1: Cuáles son los más pequeños subconjuntos de A {1,,..,
Página 1 de 18 SOLUCIONES FEBRERO 018 AUTOR: Rafael Martínez Calafat. Profesor jubilado de Matemáticas Nivel: PROBLEMAS PARA PREPARACIÓN OME. Febrero 1: Cuáles son los más pequeños subconjuntos de A {1,,..,
SOLUCIONES SEPTIEMBRE 2017
 Página 1 de 7 SOLUCIONES SEPTIEMBRE 2017 Soluciones extraídas del libro: XVIII CONCURSO DE PRIMAVERA 2014 Obtenibles en http://www.concursoprimavera.es#libros NIVEL: Primer ciclo de la E. S. O. AUTORES:
Página 1 de 7 SOLUCIONES SEPTIEMBRE 2017 Soluciones extraídas del libro: XVIII CONCURSO DE PRIMAVERA 2014 Obtenibles en http://www.concursoprimavera.es#libros NIVEL: Primer ciclo de la E. S. O. AUTORES:
Bloque 33 Guía: Ubicación de puntos, distancia y longitudes en el plano cartesiano SGUICEG047EM33-A17V1
 SGUICEG047EM33-A17V1 Bloque 33 Guía: Ubicación de puntos, distancia longitudes en el plano cartesiano TABLA DE CORRECCIÓN UBICACIÓN DE PUNTOS, DISTANCIAS Y LONGITUDES EN EL PLANO CARTESIANO N Clave Dificultad
SGUICEG047EM33-A17V1 Bloque 33 Guía: Ubicación de puntos, distancia longitudes en el plano cartesiano TABLA DE CORRECCIÓN UBICACIÓN DE PUNTOS, DISTANCIAS Y LONGITUDES EN EL PLANO CARTESIANO N Clave Dificultad
4. Resolver un triángulo rectángulo e isósceles en el que la hipotenusa tiene 9 pies de longitud.
 7 CAPÍTULO SIETE Ejercicios propuestos 7.5 Triángulos 1. Construya de ser posible los siguientes triángulos ABC. En caso de que existan, determine sus cuatro puntos característicos empleando regla y compás.
7 CAPÍTULO SIETE Ejercicios propuestos 7.5 Triángulos 1. Construya de ser posible los siguientes triángulos ABC. En caso de que existan, determine sus cuatro puntos característicos empleando regla y compás.
OLCOMA En un triángulo rectángulo la hipotenusa mide 6cm y el perímetro 14 cm. Entonces el área del triángulo es
 OLCOMA 1 PARTE I: SELECCIÓN ÚNICA 1 Si x 2 + y 2 = 6xy, con x > 0, y > 0 y x > y entonces el valor de la razón x+y x y corresponde a (a) 2 (b) 3 (c) 5 (d) 6 Partiendo, x 2 + y 2 = 6xy y completando cuadrados
OLCOMA 1 PARTE I: SELECCIÓN ÚNICA 1 Si x 2 + y 2 = 6xy, con x > 0, y > 0 y x > y entonces el valor de la razón x+y x y corresponde a (a) 2 (b) 3 (c) 5 (d) 6 Partiendo, x 2 + y 2 = 6xy y completando cuadrados
EJERCICIOS DE VERANO MATEMÁTICAS 3º ESO
 EJERCICIOS DE VERANO MATEMÁTICAS 3º ESO Página 1 de 14 Entregar el día del examen de recuperación de matemáticas. Será condición indispensable para aprobar la asignatura. 1. Calcula: NUMEROS ENTEROS. FRACCIONES.
EJERCICIOS DE VERANO MATEMÁTICAS 3º ESO Página 1 de 14 Entregar el día del examen de recuperación de matemáticas. Será condición indispensable para aprobar la asignatura. 1. Calcula: NUMEROS ENTEROS. FRACCIONES.
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales.
 Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Los segmentos se determinan por su longitud. Supongamos que tenemos dos
Este documento ha sido generado para facilitar la impresión de los contenidos. Los enlaces a otras páginas no serán funcionales. Los segmentos se determinan por su longitud. Supongamos que tenemos dos
Triángulos (Parte 2)
 Triángulos (Parte 2) APRENDIZAJES ESPERADOS Analizar en el triángulo rectángulo, los teoremas de Pitágoras y Euclides. Aplicar los diferentes teoremas y propiedades de los triángulos rectángulos, equiláteros
Triángulos (Parte 2) APRENDIZAJES ESPERADOS Analizar en el triángulo rectángulo, los teoremas de Pitágoras y Euclides. Aplicar los diferentes teoremas y propiedades de los triángulos rectángulos, equiláteros
RAZONAMIENTO GEOMÉTRICO
 RAZONAMIENTO GEOMÉTRICO Fundamentos de Matemáticas I Razonamiento geométrico Video Previo a la actividad: Áreas y perímetros de cuerpos y figuras planas Video Previo a la actividad: Áreas y perímetros
RAZONAMIENTO GEOMÉTRICO Fundamentos de Matemáticas I Razonamiento geométrico Video Previo a la actividad: Áreas y perímetros de cuerpos y figuras planas Video Previo a la actividad: Áreas y perímetros
OLIMPÍADA POPULAR ESTUDIANTIL DE MATEMÁTICA TEMARIO DE ENSEÑANZA PREUNIVERSITARIA CURSO
 OLIMPÍADA POPULAR ESTUDIANTIL DE MATEMÁTICA TEMARIO DE ENSEÑANZA PREUNIVERSITARIA CURSO 00 00 Los estudiantes de 0mo grado deben resolver los problemas al 4 Los estudiantes de no grado deben resolver los
OLIMPÍADA POPULAR ESTUDIANTIL DE MATEMÁTICA TEMARIO DE ENSEÑANZA PREUNIVERSITARIA CURSO 00 00 Los estudiantes de 0mo grado deben resolver los problemas al 4 Los estudiantes de no grado deben resolver los
SOLUCIONES DICIEMBRE 2016
 Página 1 de 8 SOLUCIONES DICIEMBRE 2016 Soluciones extraídas del libro: XVII CONCURSO DE PRIMAVERA 2013 Obtenible en http://www.concursoprimavera.es#libros Autores: Colectivo Concurso de primavera. Comunidad
Página 1 de 8 SOLUCIONES DICIEMBRE 2016 Soluciones extraídas del libro: XVII CONCURSO DE PRIMAVERA 2013 Obtenible en http://www.concursoprimavera.es#libros Autores: Colectivo Concurso de primavera. Comunidad
PÁGINA 88. Pág. 1. Unidad 9. Problemas métricos en el plano
 Soluciones a las actividades de cada epígrafe PÁGINA 88 1 En los siguientes triángulos rectángulos, se dan dos catetos y se pide la hipotenusa (si su medida no es eacta, dala con una cifra decimal): a)
Soluciones a las actividades de cada epígrafe PÁGINA 88 1 En los siguientes triángulos rectángulos, se dan dos catetos y se pide la hipotenusa (si su medida no es eacta, dala con una cifra decimal): a)
RESOLUCIÓN DE TRIÁNGULOS
 RESOLUCIÓN DE TRIÁNGULOS Resolver un triángulo consiste en determinar la longitud de sus tres lados y la amplitud de sus tres ángulos. Vamos a recordar primero la resolución para triángulos rectángulos
RESOLUCIÓN DE TRIÁNGULOS Resolver un triángulo consiste en determinar la longitud de sus tres lados y la amplitud de sus tres ángulos. Vamos a recordar primero la resolución para triángulos rectángulos
SEGUNDA OLIMPIADA ESTATAL DE MATEMÁTICAS
 PROBLEMAS PROPUESTOS PARA LA ETAPA DE ZONA TERCER GRADO 1. Cuánto mide el área sombreada A entre el área sombreada B en la siguiente figura? Para referenciar las argumentaciones se le inscriben letras
PROBLEMAS PROPUESTOS PARA LA ETAPA DE ZONA TERCER GRADO 1. Cuánto mide el área sombreada A entre el área sombreada B en la siguiente figura? Para referenciar las argumentaciones se le inscriben letras
1. Teoremas válidos para triángulos rectángulos
 1. Teoremas válidos para triángulos rectángulos Sea ABC triángulo rectángulo en C, entonces: El lado opuesto al ángulo recto, AB, es llamado HIPOTENUSA, y los lados AC y BC, CATETOS. cateto hipotenusa
1. Teoremas válidos para triángulos rectángulos Sea ABC triángulo rectángulo en C, entonces: El lado opuesto al ángulo recto, AB, es llamado HIPOTENUSA, y los lados AC y BC, CATETOS. cateto hipotenusa
1. Encuentra cuánto vale el ángulo exterior θ en la siguiente figura si son conocidos los ángulos α y β. El ángulo θ se llama ángulo exterior en C.
 1. Encuentra cuánto vale el ángulo exterior θ en la siguiente figura si son conocidos los ángulos α y β. El ángulo θ se llama ángulo exterior en C. 2. En un triángulo rectángulo, los ángulos agudos están
1. Encuentra cuánto vale el ángulo exterior θ en la siguiente figura si son conocidos los ángulos α y β. El ángulo θ se llama ángulo exterior en C. 2. En un triángulo rectángulo, los ángulos agudos están
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN ÁREA Y PERÍMETRO DE FIGURAS PLANAS Y TEOREMA DE PITÁGORAS
 MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN ÁREA Y PERÍMETRO DE FIGURAS PLANAS Y TEOREMA DE PITÁGORAS ÁREA Y PERÍMETRO DE FIGURAS PLANAS LINEA POLIGONAL: Se llama línea poligonal
MATEMÁTICAS BÁSICAS UNIVERSIDAD NACIONAL DE COLOMBIA - SEDE MEDELLÍN ÁREA Y PERÍMETRO DE FIGURAS PLANAS Y TEOREMA DE PITÁGORAS ÁREA Y PERÍMETRO DE FIGURAS PLANAS LINEA POLIGONAL: Se llama línea poligonal
Soluciones Nota nº 1
 Soluciones Nota nº 1 Problemas Propuestos 1- En el paralelogramo ABCD el ángulo en el vértice A es 30º Cuánto miden los ángulos en los vértices restantes? Solución: En un paralelogramo, los ángulos contiguos
Soluciones Nota nº 1 Problemas Propuestos 1- En el paralelogramo ABCD el ángulo en el vértice A es 30º Cuánto miden los ángulos en los vértices restantes? Solución: En un paralelogramo, los ángulos contiguos
XVI. Cuarta Fecha. Primer Nivel. = 3 3 r 2. 4 de Agosto de 2018 Soluciones. Individual
 XVI Cuarta Fecha 4 de Agosto de 018 Soluciones Individual Primer Nivel 1 En una circunferencia de radio r se inscribe un triángulo equilátero (es decir, los tres vértices del triángulo pertenecen a la
XVI Cuarta Fecha 4 de Agosto de 018 Soluciones Individual Primer Nivel 1 En una circunferencia de radio r se inscribe un triángulo equilátero (es decir, los tres vértices del triángulo pertenecen a la
INSTITUTO DE FORMACIÓN DOCENTE DE CANELONES REPARTIDO Nº 6. 3) Calcular la diagonal de un cuadrado de 7 cm de lado.
 REPARTIDO Nº 6 1) Calcular la hipotenusa de un triángulo rectángulo sabiendo que los catetos miden 6 cm y 8 cm respectivamente. 2) Si la hipotenusa de un triángulo rectángulo mide 13 cm y uno de sus catetos
REPARTIDO Nº 6 1) Calcular la hipotenusa de un triángulo rectángulo sabiendo que los catetos miden 6 cm y 8 cm respectivamente. 2) Si la hipotenusa de un triángulo rectángulo mide 13 cm y uno de sus catetos
Seminario de problemas. Curso Hoja 5
 Seminario de problemas. Curso 2014-15. Hoja 5 29. Encuentra los números naturales N que cumplen las siguientes condiciones: sus únicos divisores primos son 2 y 3, y el número de divisores de N 2 es el
Seminario de problemas. Curso 2014-15. Hoja 5 29. Encuentra los números naturales N que cumplen las siguientes condiciones: sus únicos divisores primos son 2 y 3, y el número de divisores de N 2 es el
Cuadriláteros y circunferencia
 CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
CLAVES PARA EMPEZAR Un triángulo isósceles tiene dos lados iguales: b c. Como es rectángulo, se cumple el teorema de Pitágoras: 10 2 b 2 b 2 100 2b 2 b 7,07. Los dos lados miden 7,07 cm cada uno. r A C
13Soluciones a los ejercicios y problemas PÁGINA 250
 PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 5 dm b) 8 8 cm P 5 4 0
PÁGINA 50 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm cm 5 cm 8 cm a) 5 5 dm b) 8 8 cm P 5 4 0
FORMAS POLIGONALES TEMA 8
 FORMAS POLIGONALES TEMA 8 1. LOS POLÍGONOS DEFINICIÓN: Un polígono es una figura geométrica plana limitada por segmentos llamados lados, y por vértices. A B C A Lado D Clasificación de los polígonos:
FORMAS POLIGONALES TEMA 8 1. LOS POLÍGONOS DEFINICIÓN: Un polígono es una figura geométrica plana limitada por segmentos llamados lados, y por vértices. A B C A Lado D Clasificación de los polígonos:
ELEMENTOS DE GEOMETRÍA
 LONGITUDES Y ÁREAS. 1. Perímetro y área. 1.1. Medidas del rectángulo. 1.2. Medidas del cuadrado. 1.3. Medidas del rombo. 1.4. Medidas del romboide. 1.5. Medidas de un paralelogramo cualquiera. 1.6. Medidas
LONGITUDES Y ÁREAS. 1. Perímetro y área. 1.1. Medidas del rectángulo. 1.2. Medidas del cuadrado. 1.3. Medidas del rombo. 1.4. Medidas del romboide. 1.5. Medidas de un paralelogramo cualquiera. 1.6. Medidas
Unidad 8 Áreas y Volúmenes
 Unidad 8 Áreas y Volúmenes PÁGINA 132 SOLUCIONES Unidades de medida. Pasa a centímetros cuadrados las siguientes cantidades. a) b) c) Pasa a metros cúbicos las siguientes unidades. a) b) c) Cuántos litros
Unidad 8 Áreas y Volúmenes PÁGINA 132 SOLUCIONES Unidades de medida. Pasa a centímetros cuadrados las siguientes cantidades. a) b) c) Pasa a metros cúbicos las siguientes unidades. a) b) c) Cuántos litros
25.º OLIMPIADA NACIONAL JUVENIL DE MATEMÁTICA CUARTA RONDA DEPARTAMENTAL NIVEL 1 17 de agosto de 2013
 CUARTA RONDA DEPARTAMENTAL NIVEL 1 Nombre y Apellido:............................................... Colegio:............................. Grado/Curso:...... Sección:..... Ciudad:................................
CUARTA RONDA DEPARTAMENTAL NIVEL 1 Nombre y Apellido:............................................... Colegio:............................. Grado/Curso:...... Sección:..... Ciudad:................................
= =. Cuál es el valor de (b a)?
 TERCERA RONDA - REGIONAL - 6 DE SETIEMBRE DE 2003 - NIVEL 1 Nombre y Apellido:................................. Grado:....... Sección:...... Puntaje:.......... Los dibujos correspondientes a problemas
TERCERA RONDA - REGIONAL - 6 DE SETIEMBRE DE 2003 - NIVEL 1 Nombre y Apellido:................................. Grado:....... Sección:...... Puntaje:.......... Los dibujos correspondientes a problemas
Halla los siguientes perímetros y áreas:
 73 CAPÍTULO 9: LONGITUDES Y ÁREAS.. Matemáticas 1º y º de ESO 1. TEOREMA DE PITÁGORAS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes
73 CAPÍTULO 9: LONGITUDES Y ÁREAS.. Matemáticas 1º y º de ESO 1. TEOREMA DE PITÁGORAS 1.1. Concepto de perímetro y de área de una figura plana El perímetro de una figura plana es la suma de las longitudes
NIVEL 6 CÓDIGO SECCIÓN 1: ALTERNATIVA MÚLTIPLE. Cuántos números de 4 dígitos hay de la forma a99b que sean divisibles entre 54?
 Problema 1. Cuántos números de 4 dígitos hay de la forma a99b que sean divisibles entre 54? A. 3 B. 4 C. 5 6 Como 54 = 2 27 = 2 3 3, 9 tiene que dividir a a99b, luego 9 divide a a + b. Además 2 divide
Problema 1. Cuántos números de 4 dígitos hay de la forma a99b que sean divisibles entre 54? A. 3 B. 4 C. 5 6 Como 54 = 2 27 = 2 3 3, 9 tiene que dividir a a99b, luego 9 divide a a + b. Además 2 divide
Unidad nº 6 Figuras planas 13
 Unidad nº 6 Figuras planas 13 Cuestiones 3 1 Puede ser que la suma de los ángulos de un polígono sea 40º Justifica tu respuesta. Debería cumplirse 180º (n ) = 40º, que no se cumple para ningún valor entero
Unidad nº 6 Figuras planas 13 Cuestiones 3 1 Puede ser que la suma de los ángulos de un polígono sea 40º Justifica tu respuesta. Debería cumplirse 180º (n ) = 40º, que no se cumple para ningún valor entero
4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES
 4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES Y EL TEOREMA DE PITÁGORAS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS. 4.1.1. El teorema de Thales y consecuencias. Thales de Mileto vivió hacia
4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES Y EL TEOREMA DE PITÁGORAS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS. 4.1.1. El teorema de Thales y consecuencias. Thales de Mileto vivió hacia
MÓDULO Nº 3. Nivelación. Matemática Módulo Nº3. Contenidos. Polígonos Circunferencia y Círculo Volúmenes
 MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
MÓDULO Nº 3 Nivelación Matemática 2005 Módulo Nº3 Contenidos Polígonos Circunferencia y Círculo Volúmenes Nivelación Polígonos Polígono Regular: Son aquellos polígonos que tienen todos sus lados y ángulos
OLIMPÍADA JUVENIL DE MATEMÁTICA 2013 CANGURO MATEMÁTICO CUARTO AÑO
 OLIMPÍADA JUVENIL DE MATEMÁTICA 2013 CANGURO MATEMÁTICO CUARTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. El número 200013 2013 no es divisible entre A 2; B 3; C 5; D 7; E 11. 2. María dibujó
OLIMPÍADA JUVENIL DE MATEMÁTICA 2013 CANGURO MATEMÁTICO CUARTO AÑO RESPONDE LA PRUEBA EN LA HOJA DE RESPUESTA ANEXA 1. El número 200013 2013 no es divisible entre A 2; B 3; C 5; D 7; E 11. 2. María dibujó
4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES
 4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES Y EL TEOREMA DE PITÁGORAS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 4.1.1. El teorema de Thales y consecuencias. 4.1.1. El teorema
4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES Y EL TEOREMA DE PITÁGORAS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS Curso 2011-2012 4.1.1. El teorema de Thales y consecuencias. 4.1.1. El teorema
Cuadratura. Cuadratura del Rectángulo
 Introducción 1 Cuadratura Denición 1. Cuadratura: en Geometría, determinación de un cuadrado equivalente en supercie a una gura geométrica dada. Cuadratura del Rectángulo Lema 1. el segmento CD de la gura
Introducción 1 Cuadratura Denición 1. Cuadratura: en Geometría, determinación de un cuadrado equivalente en supercie a una gura geométrica dada. Cuadratura del Rectángulo Lema 1. el segmento CD de la gura
Lugares geométricos. Áreas y perímetros
 Lugares geométricos. Áreas y perímetros CLAVES PARA EMPEZAR A r B r a r a Triángulo equilátero Cuadrado VIDA COTIDIANA Del centro del rectángulo al punto medio de los lados habrá al largo 2 m y al ancho,5
Lugares geométricos. Áreas y perímetros CLAVES PARA EMPEZAR A r B r a r a Triángulo equilátero Cuadrado VIDA COTIDIANA Del centro del rectángulo al punto medio de los lados habrá al largo 2 m y al ancho,5
REAL SOCIEDAD MATEMÁTICA ESPAÑOLA. XLIII OLIMPIADA MATEMÁTICA ESPAÑOLA Comunidad de Madrid. Primera sesión, viernes 24 de noviembre de 2006
 REAL SOCIEDAD MATEMÁTICA ESPAÑOLA XLIII OLIMPIADA MATEMÁTICA ESPAÑOLA Comunidad de Madrid Primera sesión, viernes 4 de noviembre de 006 En la hoja de respuestas, rodea con un círculo la opción que creas
REAL SOCIEDAD MATEMÁTICA ESPAÑOLA XLIII OLIMPIADA MATEMÁTICA ESPAÑOLA Comunidad de Madrid Primera sesión, viernes 4 de noviembre de 006 En la hoja de respuestas, rodea con un círculo la opción que creas
4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES
 4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES Y EL TEOREMA DE PITÁGORAS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS 4.1.1. El teorema de Thales y consecuencias. Thales de Mileto vivió hacia
4. GEOMETRÍA // 4.1. EL TEOREMA DE THALES Y EL TEOREMA DE PITÁGORAS. COMPLEMENTOS PARA LA FORMACIÓN DISCIPLINAR EN MATEMÁTICAS 4.1.1. El teorema de Thales y consecuencias. Thales de Mileto vivió hacia
Soluciones Primer Nivel
 Soluciones Primer Nivel Torneos Geométricos 2017 2º Ronda 1. En un papel cuadriculado con cuadrados de un centímetro de lado, se ha dibujado un cuadrilátero con vértices en los nodos del mismo (vértices
Soluciones Primer Nivel Torneos Geométricos 2017 2º Ronda 1. En un papel cuadriculado con cuadrados de un centímetro de lado, se ha dibujado un cuadrilátero con vértices en los nodos del mismo (vértices
TORNEOS GEOMÉTRICOS Primera Ronda Primer Nivel - 5º Año de Escolaridad
 TORNEOS GEOMÉTRICOS 2017. Primera Ronda Primer Nivel - 5º Año de Escolaridad Problema 1. El hexágono regular de la figura tiene área 6cm 2. Halla el área de la región sombreada. Solución: El triángulo
TORNEOS GEOMÉTRICOS 2017. Primera Ronda Primer Nivel - 5º Año de Escolaridad Problema 1. El hexágono regular de la figura tiene área 6cm 2. Halla el área de la región sombreada. Solución: El triángulo
Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS
 Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm 2 cm 5 cm 8 cm 2 a) b) 5 m 8 m 17 m 15 m 3 a) b) 5
Pág. 1 Á REAS Y PERÍMETROS DE FIGURAS SENCILLAS Halla el área y el perímetro de las figuras coloreadas de los siguientes ejercicios: 1 a) b) 5 dm 4 cm 2 cm 5 cm 8 cm 2 a) b) 5 m 8 m 17 m 15 m 3 a) b) 5
Trabajo Práctico de Orientación Segundo año (2012)
 COLEGIO SECUNDARIO LA PLATA Colegio Secundario La Plata Educar para un mundo mejor Trabajo Práctico de Orientación Segundo año (01) 1) Resolver el siguiente ejercicio combinado con potencias y raíces:
COLEGIO SECUNDARIO LA PLATA Colegio Secundario La Plata Educar para un mundo mejor Trabajo Práctico de Orientación Segundo año (01) 1) Resolver el siguiente ejercicio combinado con potencias y raíces:
SGUICEG024MT22-A16V1. SOLUCIONARIO Ubicación de puntos, distancia y longitudes en el plano cartesiano
 SGUICEG04MT-A16V1 SOLUCIONARIO Ubicación de puntos, distancia longitudes en el plano cartesiano 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA UBICACIÓN DE PUNTOS, DISTANCIA Y LONGITUDES EN EL PLANO CARTESIANO Ítem
SGUICEG04MT-A16V1 SOLUCIONARIO Ubicación de puntos, distancia longitudes en el plano cartesiano 1 TABLA DE CORRECCIÓN GUÍA PRÁCTICA UBICACIÓN DE PUNTOS, DISTANCIA Y LONGITUDES EN EL PLANO CARTESIANO Ítem
El ejercicio de la demostración en matemáticas
 El ejercicio de la demostración en matemáticas Demostración directa En el tipo de demostración conocido como demostración directa (hacia adelante) se trata de demostrar que A B partiendo de A y deduciendo
El ejercicio de la demostración en matemáticas Demostración directa En el tipo de demostración conocido como demostración directa (hacia adelante) se trata de demostrar que A B partiendo de A y deduciendo
open green road Guía Matemática tutora: Jacky Moreno .co
 Guía Matemática PERÍMETRO Y ÁREA tutora: Jacky Moreno.co 1. Perímetro y área de figuras planas Los registros más antiguos que se tienen del campo de la geometría corresponden a la cultura mesopotámica,
Guía Matemática PERÍMETRO Y ÁREA tutora: Jacky Moreno.co 1. Perímetro y área de figuras planas Los registros más antiguos que se tienen del campo de la geometría corresponden a la cultura mesopotámica,
EJERCICIOS ÁREAS DE REGIONES PLANAS
 EJERCICIOS ÁREAS DE REGIONES PLANAS 1. En un triángulo equilátero se inscribe una circunferencia de radio R y otra de radio r tangente a dos de los lados y a la primera circunferencia, hallar el área que
EJERCICIOS ÁREAS DE REGIONES PLANAS 1. En un triángulo equilátero se inscribe una circunferencia de radio R y otra de radio r tangente a dos de los lados y a la primera circunferencia, hallar el área que
XIV Concurso Intercentros de Matemáticas de la Comunidad de Madrid
 PRUE POR EQUIPOS 1º y 2º de E.S.O. (45 minutos) 1. Si x e y representan cifras distintas de cero, encuentra todos los números de siete cifras de la forma yxyxyxy divisibles por 18 y que verifican que el
PRUE POR EQUIPOS 1º y 2º de E.S.O. (45 minutos) 1. Si x e y representan cifras distintas de cero, encuentra todos los números de siete cifras de la forma yxyxyxy divisibles por 18 y que verifican que el
Ángulo inscrito es aquel cuyo vértice está en la circunferencia. Todos los ángulos inscritos que compartan el mismo arco son iguales.
 TEMA 8: PROBLEMAS MÉTRICOS EN EL PLANO ÁNGULOS EN LA CIRCUNFERENCIA Ángulo central es aquel cuyo vértice está en el centro de la circunferencia. Ángulo inscrito es aquel cuyo vértice está en la circunferencia.
TEMA 8: PROBLEMAS MÉTRICOS EN EL PLANO ÁNGULOS EN LA CIRCUNFERENCIA Ángulo central es aquel cuyo vértice está en el centro de la circunferencia. Ángulo inscrito es aquel cuyo vértice está en la circunferencia.
A) 7 B) 111 C) 567 D) 722 E) 728. El número que desconoce Sara se representa por la variable x, estableciendo la siguiente ecuación:
 CANGURO MATEMÁTICO Portal Fuenterrebollo 1. Sara escoge un número, lo divide por 7, al resultado le suma 7 y finalmente multiplica la suma por 7. De esta manera consigue el número 777. Cuál número fue
CANGURO MATEMÁTICO Portal Fuenterrebollo 1. Sara escoge un número, lo divide por 7, al resultado le suma 7 y finalmente multiplica la suma por 7. De esta manera consigue el número 777. Cuál número fue
GUIA DE TRABAJO Materia: Matemáticas. Tema: Geometría-8a- Soluciones de relaciones métricas en los triángulos Fecha: Profesor: Fernando Viso
 GUIA DE TRAJO Materia: Matemáticas. Tema: Geometría-8a- Soluciones de relaciones métricas en los triángulos Fecha: Profesor: Fernando Viso Nombre del alumno: Sección del alumno: CONDICIONES: Trabajo individual.
GUIA DE TRAJO Materia: Matemáticas. Tema: Geometría-8a- Soluciones de relaciones métricas en los triángulos Fecha: Profesor: Fernando Viso Nombre del alumno: Sección del alumno: CONDICIONES: Trabajo individual.
EXAMEN SEGUNDO NIVEL SOLUCIONARIO
 XXVI OLIMPIADA COSTARRICENSE DE MATEMÁTICA UCR-UN A-IT CR-UN ED-MEP-MICIT SEGUNDA ELIMINATORIA NACIONAL EXAMEN SEGUNDO NIVEL SOLUCIONARIO 2014 SOLUCIONARIO EXAMEN SEGUNDO NIVEL SEGUNDA ELIMINATORIA 2014
XXVI OLIMPIADA COSTARRICENSE DE MATEMÁTICA UCR-UN A-IT CR-UN ED-MEP-MICIT SEGUNDA ELIMINATORIA NACIONAL EXAMEN SEGUNDO NIVEL SOLUCIONARIO 2014 SOLUCIONARIO EXAMEN SEGUNDO NIVEL SEGUNDA ELIMINATORIA 2014
XXIV OLIMPIADA NACIONAL DE MATEMATICA Nivel Menor
 XXIV OLIMPIADA NACIONAL DE MATEMATICA Nivel Menor Primera prueba de clasificación, 5 de Agosto de 01 SOLUCIONES, Comisión Académica Problema 1. La figura muestra al triángulo ABC, rectángulo en C, su circunferencia
XXIV OLIMPIADA NACIONAL DE MATEMATICA Nivel Menor Primera prueba de clasificación, 5 de Agosto de 01 SOLUCIONES, Comisión Académica Problema 1. La figura muestra al triángulo ABC, rectángulo en C, su circunferencia
Cuadratura. Cuadratura del Rectángulo
 Denición 1. : en Geometría, determinación de un cuadrado equivalente en supercie a una gura geométrica dada. del Rectángulo Lema 1. el segmento CD de la gura es la media geométrica de AC y CB, es decir
Denición 1. : en Geometría, determinación de un cuadrado equivalente en supercie a una gura geométrica dada. del Rectángulo Lema 1. el segmento CD de la gura es la media geométrica de AC y CB, es decir
Soluciones oficiales de los problemas de la Final de la XXI Olimpiada Nacional de Matemática 2009
 Soluciones oficiales de los problemas de la Final de la XXI Olimpiada Nacional de Matemática 009 Comisión Académica 1 Nivel Menor Problema 1. Considere un triángulo cuyos lados miden 1, r y r. Determine
Soluciones oficiales de los problemas de la Final de la XXI Olimpiada Nacional de Matemática 009 Comisión Académica 1 Nivel Menor Problema 1. Considere un triángulo cuyos lados miden 1, r y r. Determine
Departamento de Educación Plástica y Visual. Unidad 3: Polígonos. 3º ESO EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 3: POLÍGONOS.
 EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 3: POLÍGONOS Página 1 de 15 1. POLÍGONOS 1.1. Conocimiento de los polígonos regulares Polígono: Proviene de la palabra compuesta de Poli (muchos) Gonos (ángulos). Se
EDUCACIÓN PLÁSTICA Y VISUAL UNIDAD 3: POLÍGONOS Página 1 de 15 1. POLÍGONOS 1.1. Conocimiento de los polígonos regulares Polígono: Proviene de la palabra compuesta de Poli (muchos) Gonos (ángulos). Se
4, halla sen x y tg x. 5
 TRIGONOMETRÍA 1º.- Sabiendo que 90 º < x < 70 º y que 4, halla sen x y tg x. 5 a) sen x? ; de la fórmula fundamental sen x + cos x 1 se obtiene sen x 1 - cos x. 9 5 de donde sen x 5 3, solución positiva
TRIGONOMETRÍA 1º.- Sabiendo que 90 º < x < 70 º y que 4, halla sen x y tg x. 5 a) sen x? ; de la fórmula fundamental sen x + cos x 1 se obtiene sen x 1 - cos x. 9 5 de donde sen x 5 3, solución positiva
SOLUCIONES PRIMER NIVEL
 SOLUCIONES PRIMER NIVEL 1. Los cuatro polígonos de la figura son regulares. Halla los valores de los tres ángulos, de vértice A limitados por dos lados de los polígonos dados, indicados en la figura. Solución:
SOLUCIONES PRIMER NIVEL 1. Los cuatro polígonos de la figura son regulares. Halla los valores de los tres ángulos, de vértice A limitados por dos lados de los polígonos dados, indicados en la figura. Solución:
PERÍMETRO Y ÁREA DE UN POLÍGONO
 PERÍMETRO Y ÁREA DE UN POLÍGONO - Área y perímetro del triángulo - Cálculo del perímetro Es la longitud de su contorno ó la suma de sus lados. P = a + b + c Recuerda: - El perímetro de un triángulo escaleno
PERÍMETRO Y ÁREA DE UN POLÍGONO - Área y perímetro del triángulo - Cálculo del perímetro Es la longitud de su contorno ó la suma de sus lados. P = a + b + c Recuerda: - El perímetro de un triángulo escaleno
A 2 TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO TEOREMA DE PITÁGORAS:
 TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS ELEMENTOS CLASIFICACIÓN TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO A b h A b a A perímetro apotema A r TEOREMA DE PITÁGORAS: a b c 1 POLÍGONOS
TEMA 10. POLÍGONOS ÁREAS Y PERÍMETROS ELEMENTOS CLASIFICACIÓN TRIÁNGULOS CUADRILÁTEROS POLÍGONOS REGULARES CIRCUNFERENCIA CÍRCULO A b h A b a A perímetro apotema A r TEOREMA DE PITÁGORAS: a b c 1 POLÍGONOS
Lección 6: EXPRESIONES ALGEBRAICAS: MONOMIOS
 Lección 6: EXPRESIONES ALGEBRAICAS: MONOMIOS 1.- ÁLGEBRA. EXPRESIONES ALGEBRAICAS Y LENGUAJE ALGEBRAICO ÁLGEBRA es la parte de las matemáticas que estudia las expresiones algebraicas. EXPRESIÓN ALGEBRAICA
Lección 6: EXPRESIONES ALGEBRAICAS: MONOMIOS 1.- ÁLGEBRA. EXPRESIONES ALGEBRAICAS Y LENGUAJE ALGEBRAICO ÁLGEBRA es la parte de las matemáticas que estudia las expresiones algebraicas. EXPRESIÓN ALGEBRAICA
Polígonos. Triángulos
 CLAVES PARA EMPEZAR Cada hora equivale a una abertura de 360 o : 12 30 o A las 12 h: ángulo 0 o A las 11 h y a la 1 h: ángulo 30 o A las 9 h y a las 3 h: ángulo 90 o A las 7 h y a las 5 h: ángulo 150 o
CLAVES PARA EMPEZAR Cada hora equivale a una abertura de 360 o : 12 30 o A las 12 h: ángulo 0 o A las 11 h y a la 1 h: ángulo 30 o A las 9 h y a las 3 h: ángulo 90 o A las 7 h y a las 5 h: ángulo 150 o
EJERCICIOS DE LOS TEMAS 9 y 10.GEOMETRÍA
 1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
1.- Dos triángulos ABC y A C son semejantes y la razón de semejanza entre el primero y el segundo es,4. Calcula las longitudes de los lados que faltan sabiendo que AB = 0 cm, BC = 15 cm y A C = 10 cm.
ARITMÉTICA. 1. Resolver las siguientes ecuaciones en Q. 2 x + 5. d) ( ) 2. g) 0,86 x 0,73 = 1. x = 1 4 3x. = x + + l) ( ) ( )( ) m) ( )( ) ( ) 2
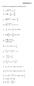 1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 x + 3 1 + 4 = x + 1 d) ( ) e) f) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 g) 0,86 x 0,73
1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 x + 3 1 + 4 = x + 1 d) ( ) e) f) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 g) 0,86 x 0,73
Guía College Board 2012 Rev 28 Página 48 de 120. NOTA: La figura no está dibujada a escala.
 Conceptos de geometría Las figuras que acompañan a los ejercicios en la prueba tienen el propósito de proveerle información útil para resolver los problemas. Las figuras están dibujadas con la mayor precisión
Conceptos de geometría Las figuras que acompañan a los ejercicios en la prueba tienen el propósito de proveerle información útil para resolver los problemas. Las figuras están dibujadas con la mayor precisión
Unidad didáctica 9 Geometría plana
 Unidad didáctica 9 Geometría plana 1.- Ángulos Un ángulo es la porción de plano limitada por dos semirrectas que tienen el mismo origen. Los lados del ángulo son las semirrectas que lo forman. El vértice
Unidad didáctica 9 Geometría plana 1.- Ángulos Un ángulo es la porción de plano limitada por dos semirrectas que tienen el mismo origen. Los lados del ángulo son las semirrectas que lo forman. El vértice
Universidad del istmo INGENIERÍA EN SISTEMAS CON ÉNFASIS EN SEGURIDAD INFORMATICA
 Universidad del istmo INGENIERÍA EN SISTEMAS CON ÉNFASIS EN SEGURIDAD INFORMATICA ASIGNATURA: Cálculo Diferencial e Integral I PROFESOR: José Alexander Echeverría Ruiz CUATRIMESTRE: Segundo TÍTULO DE LA
Universidad del istmo INGENIERÍA EN SISTEMAS CON ÉNFASIS EN SEGURIDAD INFORMATICA ASIGNATURA: Cálculo Diferencial e Integral I PROFESOR: José Alexander Echeverría Ruiz CUATRIMESTRE: Segundo TÍTULO DE LA
FORMULARIO (ÁREAS DE FIGURAS PLANAS)
 FORMULARIO (ÁREAS DE FIGURAS PLANAS) Rectángulo Triángulo Paralelogramo Cuadrado Cuadrilátero cuyos lados forman ángulos de 90º. Es la porción de plano limitada por tres segmentos de recta. Cuadrilátero
FORMULARIO (ÁREAS DE FIGURAS PLANAS) Rectángulo Triángulo Paralelogramo Cuadrado Cuadrilátero cuyos lados forman ángulos de 90º. Es la porción de plano limitada por tres segmentos de recta. Cuadrilátero
SOLUCIONES OCTUBRE 2017
 Página 1 de 15 SOLUCIONES OCTUBRE 2017 AUTOR: Mario Mestre. INS Pont de Suert. L Alta Ribagorça Octubre 1-8: En un hexágono regular hemos inscrito y circunscrito dos circunferencias. Si el área de la corona
Página 1 de 15 SOLUCIONES OCTUBRE 2017 AUTOR: Mario Mestre. INS Pont de Suert. L Alta Ribagorça Octubre 1-8: En un hexágono regular hemos inscrito y circunscrito dos circunferencias. Si el área de la corona
ARITMÉTICA. 1. Resolver las siguientes ecuaciones en Q. 2 x + 5. d) ( x ) ( x ) x = x + = x. l) ( ) ( )( ) + = + + o) ( x ) 2.
 1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 d) ( x ) ( x ) + 3 1 = + 1 4 e) f) g) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 0,86x 0,73
1. Resolver las siguientes ecuaciones en Q. ARITMÉTICA a) b) 3. x + 1 = 3 83 3,90x x = 3 31 c) 0,x + x 4,16 = 6 d) ( x ) ( x ) + 3 1 = + 1 4 e) f) g) x x + = 0,3 0, 6x 3 0, 6 1x + 6x = 0,3 8 0,86x 0,73
Desafío 77. Epi, Blas y el triángulo de la rima
 Desafío 77. Epi, Blas y el triángulo de la rima Siendo ABC un triángulo rectángulo cuya hipotenusa es BC, y F la intersección de la bisectriz por B con la mediana por A, hallar que dimensiones debe tener
Desafío 77. Epi, Blas y el triángulo de la rima Siendo ABC un triángulo rectángulo cuya hipotenusa es BC, y F la intersección de la bisectriz por B con la mediana por A, hallar que dimensiones debe tener
Curso Curso
 Problema 77. Se considera un triángulo equilátero de lado 1 y centro O, y vértices A, B y C. Un rayo luminoso parte de O, se refleja una vez en cada uno de los tres lados, AB, AC y BC (en el orden dado)
Problema 77. Se considera un triángulo equilátero de lado 1 y centro O, y vértices A, B y C. Un rayo luminoso parte de O, se refleja una vez en cada uno de los tres lados, AB, AC y BC (en el orden dado)
lado s, entonces DA=s, ED=s/2 y AE Entonces, por semejanza tenemos que
 PROBLEMA Dado un cuadrado ABCD, llamamos E al punto medio del lado CD. Unimos A con E; desde B trazamos la perpendicular a AE y esta corta a AE en F. Probar que CF=CD. Solución 1 Como ABCD es un cuadrado,
PROBLEMA Dado un cuadrado ABCD, llamamos E al punto medio del lado CD. Unimos A con E; desde B trazamos la perpendicular a AE y esta corta a AE en F. Probar que CF=CD. Solución 1 Como ABCD es un cuadrado,
EDUCACIÓN PLÁSTICA Y VISUAL. Trabajo de Recuperación de Pendientes Para 3º ESO. Geometría. IES Ramón Menéndez Pidal DPTO. DE DIBUJO 3º ESO 1
 EDUCACIÓN PLÁSTICA Y VISUAL Trabajo de Recuperación de Pendientes Para 3º ESO Geometría IES Ramón Menéndez Pidal DPTO. DE DIBUJO 3º ESO 1 TEOREMA DE THALES El Teorema de Thales sirve para dividir un segmento
EDUCACIÓN PLÁSTICA Y VISUAL Trabajo de Recuperación de Pendientes Para 3º ESO Geometría IES Ramón Menéndez Pidal DPTO. DE DIBUJO 3º ESO 1 TEOREMA DE THALES El Teorema de Thales sirve para dividir un segmento
Figuras planas. Definiciones
 Figuras planas Definiciones Polígono: definición Un polígono es una figura plana (yace en un plano) cerrada por tres o más segmentos. Los lados de un polígono son cada uno de los segmentos que delimitan
Figuras planas Definiciones Polígono: definición Un polígono es una figura plana (yace en un plano) cerrada por tres o más segmentos. Los lados de un polígono son cada uno de los segmentos que delimitan
TORNEOS GEOMÉTRICOS 2016 Primera Ronda. Primer Nivel - 5º Año de Escolaridad
 TORNEOS GEOMÉTRICOS 2016 Primera Ronda Primer Nivel - 5º Año de Escolaridad 1- En el triángulo rectángulo ABC cuyo ángulo en C mide 48º se trazan la bisectrices de los ángulos B y C, que se cortan en O.
TORNEOS GEOMÉTRICOS 2016 Primera Ronda Primer Nivel - 5º Año de Escolaridad 1- En el triángulo rectángulo ABC cuyo ángulo en C mide 48º se trazan la bisectrices de los ángulos B y C, que se cortan en O.
2. El menor número que se le debe sumar a 2553 para que desaparezca el dígito 5 es: a) 550 c) 150 e) 50 b) 510 d) 110 f) n.d.l.a.
 XIV OLIMPIADA NACIONAL DE MATEMÁTICA SEGUNDA RONDA COLEGIAL - DE AGOSTO DE 00 - NIVEL Nombre y Apellido:... Curso/Grado:...Sección:... Puntaje:... Tienes 80 minutos para resolver los problemas. Escribe
XIV OLIMPIADA NACIONAL DE MATEMÁTICA SEGUNDA RONDA COLEGIAL - DE AGOSTO DE 00 - NIVEL Nombre y Apellido:... Curso/Grado:...Sección:... Puntaje:... Tienes 80 minutos para resolver los problemas. Escribe
Viernes mañana Problema 1. Sean a 1, b 1 números naturales cuyo máximo común divisor y mínimo común múltiplo designamos por D y M, respectivamente.
 Soluciones Viernes mañana Problema 1. Sean a 1, b 1 números naturales cuo máximo común divisor mínimo común múltiplo designamos por D M, respectivamente. Si a b son los respectivos cocientes obtenidos
Soluciones Viernes mañana Problema 1. Sean a 1, b 1 números naturales cuo máximo común divisor mínimo común múltiplo designamos por D M, respectivamente. Si a b son los respectivos cocientes obtenidos
Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja?
 Nota4: Soluciones problemas propuestos Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja? Solución: Consideremos primero todos aquellos triángulos
Nota4: Soluciones problemas propuestos Problema 1. Cuántos triángulos rectángulos se pueden formar que tengan sus vértices en vértices de una caja? Solución: Consideremos primero todos aquellos triángulos
ÁNGULOS EN POLÍGONOS. Ejercicio nº 1.- En los siguientes polígonos, halla la media del ángulo : Ejercicio nº 2.-
 ÁNGULOS EN POLÍGONOS Ejercicio nº 1.- En los siguientes polígonos, halla la media del ángulo : a b c Ejercicio nº.- Halla el valor del ángulo en cada uno de estos casos: a b c Ejercicio nº 3.- Halla el
ÁNGULOS EN POLÍGONOS Ejercicio nº 1.- En los siguientes polígonos, halla la media del ángulo : a b c Ejercicio nº.- Halla el valor del ángulo en cada uno de estos casos: a b c Ejercicio nº 3.- Halla el
POLÍGONOS POLÍGONOS. APM Página 1
 POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
POLÍGONOS 1. Polígonos. 1.1. Elementos de un polígono. 1.2. Suma de los ángulos interiores de un polígono. 1.3. Diagonales de un polígono. 1.4. Clasificación de los polígonos. 2. Polígonos regulares. Elementos.
IES LOS PEDROCHES. Geométrico
 Geométrico Relaciones Trazar y acotar en mm. sobre cada uno de los segmentos correspondientes, la distancia entre cada par de elementos dados: Puntos P y Q, rectas r y s y circunferencia de centro O. +Q
Geométrico Relaciones Trazar y acotar en mm. sobre cada uno de los segmentos correspondientes, la distancia entre cada par de elementos dados: Puntos P y Q, rectas r y s y circunferencia de centro O. +Q
XIII OLIMPIADA HONDUREÑA DE MATEMÁTICAS Gracias, Lempira, 31 de octubre de 2015
 XIII OLIMPIADA HONDUREÑA DE MATEMÁTICAS Gracias, Lempira, 31 de octubre de 2015 SOLUCIONES DEL NIVEL I Problema 1. Encuentre un número de dos cifras, tal que al intercambiar sus cifras se forma un nuevo
XIII OLIMPIADA HONDUREÑA DE MATEMÁTICAS Gracias, Lempira, 31 de octubre de 2015 SOLUCIONES DEL NIVEL I Problema 1. Encuentre un número de dos cifras, tal que al intercambiar sus cifras se forma un nuevo
PRIMERA ELIMINATORIA NACIONAL
 XXIV OLIMPIADA COSTARRICENSE DE MATEMÁTICA MEP ITCR UCR UNA UNED - MICIT PRIMERA ELIMINATORIA NACIONAL NIVEL C 01 Estimado ( estudiante: La Comisión de las Olimpiadas Costarricenses de Matemática 01 le
XXIV OLIMPIADA COSTARRICENSE DE MATEMÁTICA MEP ITCR UCR UNA UNED - MICIT PRIMERA ELIMINATORIA NACIONAL NIVEL C 01 Estimado ( estudiante: La Comisión de las Olimpiadas Costarricenses de Matemática 01 le
XX OLIMPIADA NACIONAL DE MATEMÁTICA TERCERA RONDA REGIONAL - 6 DE SETIEMBRE DE NIVEL 1. Nombre y Apellido:... Puntaje:...
 TERCERA RONDA REGIONAL - 6 DE SETIEMBRE DE 2008 - NIVEL 1 Nombre y Apellido:................................. Puntaje:.................... Colegio:................................... Grado:...........
TERCERA RONDA REGIONAL - 6 DE SETIEMBRE DE 2008 - NIVEL 1 Nombre y Apellido:................................. Puntaje:.................... Colegio:................................... Grado:...........
14. PROPORCIONALIDAD DIRECTA
 14. PROPORCIONALIDAD DIRECTA 14.1. Características generales Consideramos que una variable x puede adquirir los valores a,b,c,d, y otra variable los valores a, b, c, d, x e y son directamente proporcionales
14. PROPORCIONALIDAD DIRECTA 14.1. Características generales Consideramos que una variable x puede adquirir los valores a,b,c,d, y otra variable los valores a, b, c, d, x e y son directamente proporcionales
Seminario de problemas-eso. Curso Hoja 14
 Seminario de problemas-eso. Curso 011-1. Hoja 14 6. Determina el valor de m tal que la ecuación en x x 4 (3m + )x + m = 0 tenga cuatro raíces en progresión aritmética. Como la suma de las cuatro raíces
Seminario de problemas-eso. Curso 011-1. Hoja 14 6. Determina el valor de m tal que la ecuación en x x 4 (3m + )x + m = 0 tenga cuatro raíces en progresión aritmética. Como la suma de las cuatro raíces
