SIMETRÍA INFINITA. nt = kt
|
|
|
- Luis Vicente Villalba Herrero
- hace 6 años
- Vistas:
Transcripción
1 SIMETRÍA INFINITA Al considerar el cristal como un medio periódico en el cual un grupo de átomos (el motivo) se repite en las tres dimensiones del espacio, de manera que entre dos puntos homólogos de dos motivos cualesquiera es posible imaginar un vector traslación, se ha considerado el cristal como un medio infinito. La simetría de este medio, periódico e infinito ha de ser necesariamente diferente de la que se ha estudiado para el cristal considerado como una masa homogénea (de propiedades vectoriales discontinúas, hay que recordarlo), por bien que compatibles entre ellas. En este apartado se estudiará la simetría del modelo microscópico del cristal, es decir la simetría de las posiciones de los átomos. Traslación Entre los elementos de simetría de este medio aparece inmediatamente la traslación como característica del propio medio. Y como tal ha de ser considerada uno de los elementos de simetría. Este se representa por un vector (recordad los primeros capítulos) que indican la dirección, el sentido y la magnitud de la traslación. Si el vector traslación tiene por coordenadas (m,n,p), al aplicar este a un punto (x,y,z) quedará como: ( m, n, p t ) ( x, y, z) ( x + m, y + n, z + p) Ejes helicoidales Son elementos compuestos de simetría resultado de combinar un eje de rotación con una traslación paralela al eje, la operación de los cuales consiste en un giro seguido de una traslación. Obviamente, la traslación asociada al eje helicoidal ha de ser compatible con la traslación del cristal paralela al eje (que es, hay que recordarlo, elemento de simetría del cristal). Esto implica que para un eje helicoidal de orden n, después de n operaciones sobre un punto, este quede como si se le hubiera aplicado la traslación del cristal paralela al eje (o un múltiplo de esta). Es decir, que se ha de cumplir que nt = kt siendo n el orden del eje, t la traslación asociada al eje, k un número entero y T la traslación del cristal paralela al eje. Gráficamente se puede representar de la siguiente manera: En la siguiente figura se han representado los movimientos sobre un punto 1 de un eje helicoidal de orden 4, con una traslación asociada t. Del punto 1 se pasa al 2, y de este al 3, y así sucesivamente, de manera que después de cuatro operaciones, los puntos 1 y 5 están (1)
2 relacionados por la traslación del cristal T, paralela al eje. Se ha de cumplir que t sea más pequeña que T. Si fuese t > T, y se admite que T es un elemento de simetría del retículo, se genera una traslación t < T, como se demuestra en la siguiente figura. Sea T la traslación del cristal paralela al eje helicoidal, y se supone una traslación asociada al eje t>t. Si se aplica la operación del eje al punto P0, el simétrico es el P1. Como T es un elemento de simetría del cristal, a P1 se le puede aplicar T -1, y aparece el punto P 1, que está relacionado con el P0 por el eje helicoidal con una traslación t <T. Por tanto, de la expresión (1), si t<t, se deduce que 0 k < n, y por tanto quedan limitados los posibles ejes helicoidales, la notación de los cuales es, según la siguiente tabla: n k
3 orden (n) k t notación T , T, 3 T 4 1, 2, T, 4 T, 4 T 6 1, 2, 3, 4, T, 6 T, 6 T, 6 T, 6 T, 31, 32 41, 42, 43 61, 62, 63, 64, 65 Planos de deslizamiento Son operaciones complejas de simetría que implican una reflexión en un plano, seguida de una traslación paralela al plano, que es ½ o 1/4 de alguna de las traslaciones paralelas al plano. Las notaciones que se utilizan hacen referencia a la dirección de la traslación asociada al plano, como se indica en la tabla siguiente. notación t orientación posible a a/2 (001), (010) b b/2 (001), (100) c c/2 (100), (010)
4 n (a/2+b/2), (a/2+c/2), (b/2+c/2) (001), (010) y (100), respectivamente d a/4+b/4, a/4+c/4, c/4+b/4 Representación gráfica En simetría espacial se suele proyectar el contenido (real -átomos- y ideal - simetría-) de la celda fundamental sobre una de las caras de esta, normalmente la (001), es decir la formada por a y b, siguiendo la dirección de c. De esta manera todo el volumen de la celda queda proyectado en el interior del paralelogramo que definen a y b, mientras que el vector c queda proyectado como un punto. Las coordenadas que se utilizan son parciales, es decir, las coordenadas relativas tomando a, b y c como unidad en cada caso. Así, un punto de coordenadas (0.3, 0.5, 0.45) como el que se ha proyectado en la figura está en 0.30a, 0.50b, y 0.45c. En la proyección las coordenadas x e y se pueden leer sobre los ejes, la coordenada z hay que especificarla al lado del elemento proyectado. Normalmente, si es cero no se indica y se da por sobreentendido. Para proyectar un eje, si está en la dirección de c se representa como un punto, en el cual se ha de indicar el tipo de eje de acuerdo con las notaciones normalmente utilizadas. Si el eje es paralelo al plano de proyección, queda como una línea, en la cual se indica el tipo de eje y la altura (la coordenada z) a la que se encuentra el eje. Los planos de simetría se proyectan de la misma
5 paralelos a (100), (010) y (001), respectivamente. manera, pero el resultado es, o bien una línea, o bien ocupan la totalidad del paralelogramo de proyección (la cara a-b). En cada caso hay que utilizar una simbología que indique clara e inequívocamente cual es la traslación asociada al plano. Es decir, hay que indicar si se trata de un plano a, b, c o n. Por eso se unen los símbolos tal como se indica en las siguientes figuras, en las que se han representado las proyecciones imaginarias (los planos no pueden tener existencia tal como han sido representados) de diversos planos de simetría (reflexión y deslizamiento) Los planos m siempre se representan con una línea continúa, excepto cuando se proyectan sobre la totalidad del plano de proyección, mientras que los otros se representan de manera diversa según sea el plano en el cual se proyectan. En las figuras siguientes está la proyección de planos con orientaciones diversas sobre diversos planos de la celda fundamental. Proyección de planos de simetría orientados paralelamente a (100) sobre los planos (001) y (010). Proyección de los planos de simetría orientados paralelamente a (010), sobre los planos (100) y (001).
6 Proyección de planos de simetría orientados paralelamente a (001) sobre los tres planos fundamentales de la celda, (100), (010) y (001). En la proyección sobre (001) hay que anotar las correspondientes coordenadas de altura z. RETÍCULOS Al definir microscópicamente el cristal se dedujeron unos vectores fundamentales (los más pequeños posibles que permiten expresar cualquier otro como combinación lineal de ellos), que a la vez configuraban una celda fundamental (ver capítulo de periodicidad). Las celdas fundamentales pueden tener diversas formas y tamaños, y se caracterizan por tres vectores fundamentales a, b y c, y los ángulos que forman entre ellos α, β y γ. Según los módulos relativos de los tres vectores y de los ángulos entre ellos, la celda tiene una u otro simetría. Seguidamente se estudiarán las posibles celdas fundamentales en función de estos parámetros y se clasificaran de acuerdo con su simetría en alguno de los siete sistemas cristalinos. Además, hay que señalar la posibilidad de utilizar celdas múltiples cuando la distribución de nudos así lo aconseja, especialmente para una mejor claridad de visualización de su simetría. La celda, tal como se ha definido hasta ahora es una celda simple, formada por nudos en cada uno de sus vértices y por tanto con una multiplicidad igual a uno. Si se evalúa cuantos nudos hay en el interior de la celda representada en la figura, se llegará a la conclusión que la
7 contribución de cada uno de los ocho que hay en los vértices suma la unidad. Pero se admitirá la existencia de celdas múltiples, es decir celdas que contienen más de un nudo, y que por tanto, los vectores que las definen no son necesariamente los más pequeños posibles, la cual cosa lleva a la existencia de vectores traslación del retículo en el interior de la celda. Estos son algunos ejemplos. Celda C: Esta celda tiene nudos en los vértices, pero también en las posiciones (0.5, 0.5, 0), es decir en el centre de la cara definida por a y b, (001). Esta es una celda múltiple, que se llama C, y su multiplicidad es dos: un nudo correspondiente a las fracciones de los que ocupan los vértices, y otro en las dos mitades de los que centran las caras (001) de la celda. Igualmente se podrían definir celdas múltiples A y B, con nudos en los centros de las caras correspondientes. Celda I Celda con nudos en los vértices y otro nudo en posición (0.5, 0.5, 0.5), la cual cosa implica la existencia de un vector traslación del retículo que va desde (0,0,0) a (0,5, 0.5, 0.5). Su multiplicidad es dos, las fracciones de nudos de los vértices (81/8) y el nudo central. Celda F Celda múltiple con nudos en los vértices y en el centro de todas las caras de la celda fundamental, es decir en posiciones (0.5, 0, 0.5), (0, 0.5, 0.5) i (0.5, 0.5, 0),
8 la cual cosa implica la existencia de tres vectores del retículo menores que los fundamentales de esta celda. Igualmente, en dos dimensiones se pueden definir las celdas simples y una múltiple con un nudo en el centro del paralelogramo. Tipos de retículos El conjunto de nudos que definen un retículo posee cierta simetría, por tanto, las posibles combinaciones de los vectores fundamentales y de los ángulos entre ellos dan lugar a distribución de nudos con diversas simetrías, que han de permitir su clasificación en sistemas cristalinos. De esta manera es posible deducir la existencia de cinco retículos bidimensionales y 14 en tres dimensiones (que son los llamados retículos de Bravais). Retículos bidimensionales En este caso la deducción es sencilla porqué solo se dispone de dos vectores (a y b) y el ángulo que forman entre ellos (γ). Esto limita extraordinariamente las posibilidades. Los vectores a y b pueden tener módulos iguales o diferentes, mientras que al ángulo γ se le puede dar cualquier valor o los que tienen significación especial en Cristalografía, es decir los ángulos de giro de los ejes posibles. Estos son 180º, 90º, 120º y 60º. Por razones evidentes se ha de descartar el ángulo de 180º (daría vectores en la misma dirección), mientras que 120º y 60º son suplementarios y hace falta seleccionar únicamente uno (60º). Por tanto, las posibles redes han de salir de la tabla siguiente: Vectores Ángulo Simetría Celda Retículo a b a a γ sin limitaciones 2 p oblicuo b γ = 90º 2mm p ortogonal b γ = 60º 2
9 a = b γ sin limitaciones 2mm c ortogonal a a = b γ = 90º 4mm p cuadrado = b γ = 60º 6mm p hexagonal a b Se puede ver fácilmente que el retículo con y γ = 60º no tiene más simetría que el primer caso en que γ puede tener cualquier valor, por tanto, el caos con γ = 60º es un caso particular del primero y no representa un retículo nuevo, de nuevas características y simetría. La cual cosa limita los posibles retículos diferentes en dos dimensiones a cinco. En la siguiente figura se han representado las seis posibilidades, señalando la que no representa una nueva celda, y dibujando diversas celdas en el caso del ortogonal centrada y del hexagonal, a fin de facilitar la comprensión de la simetría del conjunto de nudos. En el caso del retículo ortogonal centrado, se definen unos nuevos vectores fundamentales a y b, y por tanto se definen como a b; γ = 90º, aunque existe una traslación interna del retículo T=a/2+b/2.
10
11 Retículos tridimensionales o de Bravais Por razones de espacio y oportunidad no se hace la deducción de las 14 posibilidades de retículos en tres dimensiones, y se anima al estudiante a leer los correspondientes capítulos de algunos de los libros de Cristalografía sugeridos en la bibliografía de la asignatura. En todo caso, a continuación se hace una lista de los 14 retículos de Bravais, con sus características, simetría y sistema cristalino al cual pertenecen. SISTEMA SIMETRÍA RETÍCULO(S) vectores fundamentales ángulos entre vectores Triclínico 1 P a b c sin restricciones Monoclínico 2/m P, C a b c α = γ β > 90º Rómbico mmm P, C, I, F a b c α = β = γ = 90º Tetragonal 4/mmm P, I a = b c α = β = γ = 90º Trigonal 3m R a = b = c α = β = γ Hexagonal 6/mmm P a = b c α = β = 90º γ = 120º Cúbico m3m P, I, F a = b = c α = γ = β = 90º Hay que resaltar que el signo diferente significa que no hay limitaciones, es decir que en estos casos, el ángulo puede tener cualquier valor, incluyendo los especiales. Esto quiere decir que puede existir una celda triclínica ortogonal, no obstante, la simetría del cristal seguirá siendo triclínica porqué el contenido de la celda tendrá esta simetría, independientemente de la forma del retículo. Hace falta que las simetrías del retículo (distribución de nudos) y del contenido (distribución de átomos) sean compatibles, y eso quiere decir que la simetría del retículo ha de incluir la de los átomos, no al revés.
CONDUCTIVIDAD ELÉCTRICA I E
 CONDUCTVDAD LÉCTRCA La conductividad eléctrica de una substancia se define como la relación entre la intensidad de corriente eléctrica producida y el campo eléctrico que la produce: = el campo eléctrico
CONDUCTVDAD LÉCTRCA La conductividad eléctrica de una substancia se define como la relación entre la intensidad de corriente eléctrica producida y el campo eléctrico que la produce: = el campo eléctrico
EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA
 EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA 2003 (4) Ejercicio 1. Considera los vectores u = (1,1,1), v = (2,2,a) y w = (2,0,0), (a) [1'25 puntos] Halla los valores de a para que los vectores u, v y w sean
EJERCICIOS DE SELECTIVIDAD DE GEOMETRIA 2003 (4) Ejercicio 1. Considera los vectores u = (1,1,1), v = (2,2,a) y w = (2,0,0), (a) [1'25 puntos] Halla los valores de a para que los vectores u, v y w sean
CRISTALOFÍSICA. Isotropía y anisotropía
 CRISTALOFÍSICA Las propiedades físicas de un cristal se pueden definir como la relación entre dos cantidades medibles. Así por ejemplo, la densidad es la relación entre la masa y el volumen. Isotropía
CRISTALOFÍSICA Las propiedades físicas de un cristal se pueden definir como la relación entre dos cantidades medibles. Así por ejemplo, la densidad es la relación entre la masa y el volumen. Isotropía
Módulo 3. Introducción a la cristalografía
 Módulo 3. Introducción a la cristalografía Poliedros cristalográficos recortables Un método muy recomendable para estudiar la forma y simetría de los cristales consiste en construir poliedros recortables.
Módulo 3. Introducción a la cristalografía Poliedros cristalográficos recortables Un método muy recomendable para estudiar la forma y simetría de los cristales consiste en construir poliedros recortables.
UNIDAD 1: LA MATERIA CRISTALINA
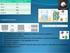 UNIDAD 1: LA MATERIA CRISTALINA CONCEPTOS MATERIA CRISTALINA: Aquella cuyas partículas están perfectamente ordenadas en el espacio, ocupando posiciones fijas y a distancias regulares unas de otras, formando
UNIDAD 1: LA MATERIA CRISTALINA CONCEPTOS MATERIA CRISTALINA: Aquella cuyas partículas están perfectamente ordenadas en el espacio, ocupando posiciones fijas y a distancias regulares unas de otras, formando
CRISTALOGRAFIA. Es un sólido compuesto de átomos, iones o moléculas ordenados de una cierta forma y que se repite en tres dimensiones.
 CRISTALOGRAFIA CRISTAL SÓLIDO MONOCRISTALINO SÓLIDO POLICRISTALINO Es un sólido compuesto de átomos, iones o moléculas ordenados de una cierta forma y que se repite en tres dimensiones. Región donde el
CRISTALOGRAFIA CRISTAL SÓLIDO MONOCRISTALINO SÓLIDO POLICRISTALINO Es un sólido compuesto de átomos, iones o moléculas ordenados de una cierta forma y que se repite en tres dimensiones. Región donde el
x-z = 0 x+y+2 = [2012] [EXT-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por
![x-z = 0 x+y+2 = [2012] [EXT-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por x-z = 0 x+y+2 = [2012] [EXT-B] Halla el punto simétrico del P(2,1,-5) respecto de la recta r definida por](/thumbs/55/35462313.jpg) x = 1+t 1. [014] [EXT-A] Considera los puntos A(1,1,) y B(1,-1,-) y la recta dada por y = t. z = 1 a) Halla la ecuación general del plano que que contiene a r y es paralelo a la recta que pasa por A y
x = 1+t 1. [014] [EXT-A] Considera los puntos A(1,1,) y B(1,-1,-) y la recta dada por y = t. z = 1 a) Halla la ecuación general del plano que que contiene a r y es paralelo a la recta que pasa por A y
Estructura cristalina: Índices de Miller. Y en términos de grado de compacidad? Volumen de átomos= Volumen de la celda= ( ) 3
 1 Cuántos átomos hay en una celda unidad? Vértices 1/8 Caras 1/2 Número total de átomos en la celda unidad: 8 en los vértices: 8 x 1/8 = 1 6 en las caras: 6 x 1/2 = 3 Total: 4 átomos Y en términos de grado
1 Cuántos átomos hay en una celda unidad? Vértices 1/8 Caras 1/2 Número total de átomos en la celda unidad: 8 en los vértices: 8 x 1/8 = 1 6 en las caras: 6 x 1/2 = 3 Total: 4 átomos Y en términos de grado
Siete sistemas y catorce retículos
 ESTRUCTURA CRISTALINA - PERFECCION Siete sistemas y catorce retículos Celda unitaria c a b Constantes reticulares o parámetros reticulares Longitud de los bordes Ángulos entre los ejes cristalográficos
ESTRUCTURA CRISTALINA - PERFECCION Siete sistemas y catorce retículos Celda unitaria c a b Constantes reticulares o parámetros reticulares Longitud de los bordes Ángulos entre los ejes cristalográficos
TEMA 8. GEOMETRÍA ANALÍTICA.
 TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
TEMA 8. GEOMETRÍA ANALÍTICA. 8..- El plano. Definimos el plano euclideo como el conjunto de puntos ( x, y) R. Así, cada punto del plano posee dos coordenadas. Para representar puntos del plano utilizaremos
Física del Estado Sólido REDES CRISTALINAS. Dr. Andrés Ozols. Facultad de Ingeniería Universidad de Buenos Aires. Dr. A. Ozols 1
 Física del Estado Sólido REDES CRISTALINAS Dr. Andrés Ozols Facultad de Ingeniería Universidad de Buenos Aires 2009 Dr. A. Ozols 1 ÁTOMOS EN SÓLIDOS Dr. A. Ozols 2 ORDEN CRISTALINO y FORMA René Just Hauy
Física del Estado Sólido REDES CRISTALINAS Dr. Andrés Ozols Facultad de Ingeniería Universidad de Buenos Aires 2009 Dr. A. Ozols 1 ÁTOMOS EN SÓLIDOS Dr. A. Ozols 2 ORDEN CRISTALINO y FORMA René Just Hauy
Álgebra y Geometría Analítica I - LF 2016 Práctica 1: Algunos elementos de la Geometría Analítica
 Álgebra y Geometría Analítica I - LF 2016 Práctica 1: Algunos elementos de la Geometría Analítica 1. a) Marcar en un eje los puntos a(1);b( 2) y c(4). b) Hallar los puntos simétricos respecto al origen
Álgebra y Geometría Analítica I - LF 2016 Práctica 1: Algunos elementos de la Geometría Analítica 1. a) Marcar en un eje los puntos a(1);b( 2) y c(4). b) Hallar los puntos simétricos respecto al origen
y cualquier par (x, y) puede escalarse, multiplicarse por un número real s, para obtener otro vector (sx, sy).
 UNIDAD II: VECTORES EN DOS Y TRES DIMENSIONES Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios
UNIDAD II: VECTORES EN DOS Y TRES DIMENSIONES Un espacio vectorial (o espacio lineal) es el objeto básico de estudio en la rama de la matemática llamada álgebra lineal. A los elementos de los espacios
LA CIRCUNFERENCIA. La circunferencia es la sección producida por un plano perpendicular al eje.
 LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
LA CIRCUNFERENCIA La circunferencia es la sección producida por un plano perpendicular al eje. β = 90º La circunferencia es un caso particular de elipse. Se llama circunferencia al lugar geométrico de
EJERCICIOS DE GEOMETRÍA
 EJERCICIOS DE GEOMETRÍA 1. Se consideran las rectas r x 2 = 0 x 2z = 1, s y + 3 = 0 y + z = 3 a) Estudiar la posición relativa de r y s. b) Hallar la mínima distancia entre ambas. Se pide: Sol: Se cruzan
EJERCICIOS DE GEOMETRÍA 1. Se consideran las rectas r x 2 = 0 x 2z = 1, s y + 3 = 0 y + z = 3 a) Estudiar la posición relativa de r y s. b) Hallar la mínima distancia entre ambas. Se pide: Sol: Se cruzan
CÁLCULO VECTORIAL I. B, es un nuevo vector que se define del siguiente modo: Si A ybson (LI), entonces el vector A. B se caracteriza por:
 PRODUCTO VECTORIAL DE DOS VECTORES El producto vectorial de dos vectores A y, y escribimos A, es un nuevo vector que se define del siguiente modo: Si A yson (LI), entonces el vector A se caracteriza por:
PRODUCTO VECTORIAL DE DOS VECTORES El producto vectorial de dos vectores A y, y escribimos A, es un nuevo vector que se define del siguiente modo: Si A yson (LI), entonces el vector A se caracteriza por:
EJERCICIOS DE GEOMETRÍA
 1) Sean las rectas EJERCICIOS DE GEOMETRÍA x 2y 6z 1 r : x y 0 x y 1 s: z 2 a a) Determinar la posición relativa de r y s según los valores de a. b) Calcular la distancia entre las rectas r y s cuando
1) Sean las rectas EJERCICIOS DE GEOMETRÍA x 2y 6z 1 r : x y 0 x y 1 s: z 2 a a) Determinar la posición relativa de r y s según los valores de a. b) Calcular la distancia entre las rectas r y s cuando
CÁLCULO II ESCUELA MILITAR DE INGENIERÍA MISCELÁNEAS DE PROBLEMAS VECTORES. 1. Sean A = (1, 2), B = ( 1, 3) y C = (0, 4); hallar: a) A + B
 ESCUELA MILITAR DE INGENIERÍA MISCELÁNEAS DE PROBLEMAS CÁLCULO II VECTORES. 1. Sean A = (1, 2), B = ( 1, 3) y C = (0, 4); hallar: a) A + B b) A B + C c) 4A 3B d) 4(A + B) 5C e) 1 2 (A B) + 1 4 C 2. Sean
ESCUELA MILITAR DE INGENIERÍA MISCELÁNEAS DE PROBLEMAS CÁLCULO II VECTORES. 1. Sean A = (1, 2), B = ( 1, 3) y C = (0, 4); hallar: a) A + B b) A B + C c) 4A 3B d) 4(A + B) 5C e) 1 2 (A B) + 1 4 C 2. Sean
2. El conjunto de los números complejos
 Números complejos 1 Introducción El nacimiento de los números complejos se debió a la necesidad de dar solución a un problema: no todas las ecuaciones polinómicas poseen una solución real El ejemplo más
Números complejos 1 Introducción El nacimiento de los números complejos se debió a la necesidad de dar solución a un problema: no todas las ecuaciones polinómicas poseen una solución real El ejemplo más
TEMA 10 SISTEMAS DE REPRESENTACIÓN
 TEMA 10 SISTEMAS DE REPRESENTACIÓN La geometría descriptiva estudia la representación geométrica de objetos tridimensionales sobre el plano. Un sistema de representación es un conjunto de reglas y procedimientos
TEMA 10 SISTEMAS DE REPRESENTACIÓN La geometría descriptiva estudia la representación geométrica de objetos tridimensionales sobre el plano. Un sistema de representación es un conjunto de reglas y procedimientos
Problemas de exámenes de Geometría
 1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
1 Problemas de exámenes de Geometría 1. Consideramos los planos π 1 : X = P+λ 1 u 1 +λ 2 u 2 y π 2 : X = Q+µ 1 v 1 +µ 2 v 2. Cuál de las siguientes afirmaciones es incorrecta? a) Si π 1 π 2 Ø, entonces
Síntesis y Caracterización Estructural de los Materiales Ángel Carmelo Prieto Colorado
 Síntesis y Caracterización Estructural de los Materiales Ángel Carmelo Prieto Colorado Física de la Materia Condensada, Cristalografía y Mineralogía. Facultad de Ciencias. Universidad de Valladolid. Estructura
Síntesis y Caracterización Estructural de los Materiales Ángel Carmelo Prieto Colorado Física de la Materia Condensada, Cristalografía y Mineralogía. Facultad de Ciencias. Universidad de Valladolid. Estructura
33. SISTEMA PLANOS ACOTADOS
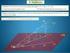 33. SISTEMA PLANOS ACOTADOS 33.1. Elementos del sistema. En el sistema de planos acotados o sistema acotado solo interviene un solo elemento el plano de proyección π. Como en los otros sistemas de representación
33. SISTEMA PLANOS ACOTADOS 33.1. Elementos del sistema. En el sistema de planos acotados o sistema acotado solo interviene un solo elemento el plano de proyección π. Como en los otros sistemas de representación
TEMAS 6 Y 7 RECTAS Y PLANOS EN EL ESPACIO
 Temas 6 y 7 Rectas y planos en el espacio Matemáticas II - 2º Bachillerato 1 TEMAS 6 Y 7 RECTAS Y PLANOS EN EL ESPACIO RECTAS Y PLANOS EJERCICIO 1 : Halla el volumen del tetraedro determinado por los ejes
Temas 6 y 7 Rectas y planos en el espacio Matemáticas II - 2º Bachillerato 1 TEMAS 6 Y 7 RECTAS Y PLANOS EN EL ESPACIO RECTAS Y PLANOS EJERCICIO 1 : Halla el volumen del tetraedro determinado por los ejes
6. Mosaicos y movimientos. en el plano
 6. Mosaicos y movimientos en el plano Ámbito científico 1. Mosaicos 2. Módulos planos 3. Diseña mosaicos 4. Ejemplos de mosaicos 5. Ejemplos de tramas 6. Mosaicos semiregulares I 7. Libro de espejos 8.
6. Mosaicos y movimientos en el plano Ámbito científico 1. Mosaicos 2. Módulos planos 3. Diseña mosaicos 4. Ejemplos de mosaicos 5. Ejemplos de tramas 6. Mosaicos semiregulares I 7. Libro de espejos 8.
CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS
 CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS U.T. 4.- ESTATICA. 3.1.- Centro de gravedad de un cuerpo. Un cuerpo de masa M, se puede considerar compuesto por multitud de partículas
CFGS CONSTRUCCION METALICA MODULO 246 DISEÑO DE CONSTRUCCIONES METALICAS U.T. 4.- ESTATICA. 3.1.- Centro de gravedad de un cuerpo. Un cuerpo de masa M, se puede considerar compuesto por multitud de partículas
GEOMETRÍA ANALÍTICA EJERCITARIO DE FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) UNIVERSIDAD NACIONAL DE ASUNCIÓN
 UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) EJERCITARIO DE GEOMETRÍA ANALÍTICA (ÁLGEBRA VECTORIAL - PRÁCTICA) AÑO 2014 ÁLGEBRA VECTORIAL - EJERCICIOS
UNIVERSIDAD NACIONAL DE ASUNCIÓN FACULTAD DE INGENIERÍA CURSO PREPARATORIO DE INGENIERÍA (CPI) EJERCITARIO DE GEOMETRÍA ANALÍTICA (ÁLGEBRA VECTORIAL - PRÁCTICA) AÑO 2014 ÁLGEBRA VECTORIAL - EJERCICIOS
Verifique los resultados analíticos mediante la resolución gráfica usando un software de Matemática.
 Álgebra Geometría Analítica Prof. Gisela Saslavsk Vectores en R en R 3. Rectas planos en el espacio Verifique los resultados analíticos mediante la resolución gráfica usando un software de Matemática..
Álgebra Geometría Analítica Prof. Gisela Saslavsk Vectores en R en R 3. Rectas planos en el espacio Verifique los resultados analíticos mediante la resolución gráfica usando un software de Matemática..
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO
 31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Tenemos la recta
31. SISTEMA AXONOMÉTRICO. LA RECTA Y EL PLANO 31.1. Representación de la recta. Si un punto se representaba por cuatro proyecciones, la recta se representa igual por cuatro proyecciones. Tenemos la recta
4. El ClNa cristaliza en el sistema cúbico con parámetro [a]=5.631å. Calcular su densidad sabiendo que su masa molecular es 58.45 uma.
![4. El ClNa cristaliza en el sistema cúbico con parámetro [a]=5.631å. Calcular su densidad sabiendo que su masa molecular es 58.45 uma. 4. El ClNa cristaliza en el sistema cúbico con parámetro [a]=5.631å. Calcular su densidad sabiendo que su masa molecular es 58.45 uma.](/thumbs/28/12696458.jpg) Síntesis y Caracterización Estructural de los Materiales: Bases Cristalográficas. 1. Dibuje en las celdas fundamentales cúbicas adjuntas (a = 3 Å): a. Las filas reticulares de índices de Weiss [02-1],
Síntesis y Caracterización Estructural de los Materiales: Bases Cristalográficas. 1. Dibuje en las celdas fundamentales cúbicas adjuntas (a = 3 Å): a. Las filas reticulares de índices de Weiss [02-1],
VECTORES. también con letras sobre las cuales se coloca una flechita ( a ). A = módulo de A. modulo o magnitud, dirección y sentido. vector.
 VECTORES Según su naturaleza las cantidades físicas se clasifican en magnitudes escalares y magnitudes vectoriales Las magnitudes como el tiempo, la temperatura, la masa y otras, son magnitudes escalares
VECTORES Según su naturaleza las cantidades físicas se clasifican en magnitudes escalares y magnitudes vectoriales Las magnitudes como el tiempo, la temperatura, la masa y otras, son magnitudes escalares
1.-La Cristalografía. 2.-Simetría
 1.-La Cristalografía La Cristalografía es la ciencia que se ocupa de los sólidos cristalinos y describe su estructura interna, es decir, como están distribuidos los átomos en su interior. También estudia
1.-La Cristalografía La Cristalografía es la ciencia que se ocupa de los sólidos cristalinos y describe su estructura interna, es decir, como están distribuidos los átomos en su interior. También estudia
LA RECTA Y SUS ECUACIONES
 UNIDAD LA RECTA Y SUS ECUACIONES EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivo. Recordarás
UNIDAD LA RECTA Y SUS ECUACIONES EJERCICIOS RESUELTOS Objetivo general. Al terminar esta Unidad resolverás ejercicios y problemas correspondientes a las rectas en el plano y sus ecuaciones. Objetivo. Recordarás
The problem of the structural biologist
 The problem of the structural biologist Biological function 3d structure of bio-molecules Structure and basic knowledge? Pure carbon: diamond Pure carbon: graphite The role of Crystallography Crystallography
The problem of the structural biologist Biological function 3d structure of bio-molecules Structure and basic knowledge? Pure carbon: diamond Pure carbon: graphite The role of Crystallography Crystallography
Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99, 01, curso cero de física
 VECTORES: TRIÁNGULOS Demostrar que en una semicircunferencia cualquier triángulo inscrito con el diámetro como uno de sus lados es un triángulo rectángulo. Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99,
VECTORES: TRIÁNGULOS Demostrar que en una semicircunferencia cualquier triángulo inscrito con el diámetro como uno de sus lados es un triángulo rectángulo. Solución: I.T.I. 96, 98, 02, 05, I.T.T. 96, 99,
Contenido. 5. Estructura cristalina. Omar De la Peña-Seaman IFUAP Física del Estado Sólido Maestría (Física) 1/51 51
 Contenido 5. Estructura cristalina 1 / Omar De la Peña-Seaman IFUAP Física del Estado Sólido Maestría (Física) 1/51 51 Contenido: Tema 05 5. Estructura cristalina 5.1 Arreglo periódico de átomos: bases,
Contenido 5. Estructura cristalina 1 / Omar De la Peña-Seaman IFUAP Física del Estado Sólido Maestría (Física) 1/51 51 Contenido: Tema 05 5. Estructura cristalina 5.1 Arreglo periódico de átomos: bases,
El pipeline de visualización es el conjunto de
 Sistemas de Visualización Pipeline de visualización 3D Definición del modelo geométrico Transformaciones geométricas Transformaciones de visualización Volumen de visualización Proyecciones Pipeline de
Sistemas de Visualización Pipeline de visualización 3D Definición del modelo geométrico Transformaciones geométricas Transformaciones de visualización Volumen de visualización Proyecciones Pipeline de
No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano.
 FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
FUNCIONES GRAFICAS No es otra cosa, que la representación de los resultados de una función sobre el plano carteciano. INTÉRVALOS Un intervalo es el conjunto de todos los números reales entre dos números
ESTÁTICA 3 3 VECTORES
 ESTÁTICA Sesión 3 3 VECTORES 3.1. Componentes en dos dimensiones 3.1.1. Operación con vectores por sus componentes 3.1.2. Vectores de posición por sus componentes 3.2. Componentes en tres dimensiones 3.2.1.
ESTÁTICA Sesión 3 3 VECTORES 3.1. Componentes en dos dimensiones 3.1.1. Operación con vectores por sus componentes 3.1.2. Vectores de posición por sus componentes 3.2. Componentes en tres dimensiones 3.2.1.
LABORATORIO DE ESTADO SÓLIDO Y SEMICONDUCTORES 1.1. PRÁCTICA N o 1 REDES DE BRAVAIS Y ESTRUCTURAS CRISTALINAS
 LABORATORIO DE ESTADO SÓLIDO Y SEMICONDUCTORES 1.1 PRÁCTICA N o 1 REDES DE BRAVAIS Y ESTRUCTURAS CRISTALINAS 1. INTRODUCCIÓN 1.1 Red de Bravais y celda primitiva unidad Uno de los conceptos fundamentales
LABORATORIO DE ESTADO SÓLIDO Y SEMICONDUCTORES 1.1 PRÁCTICA N o 1 REDES DE BRAVAIS Y ESTRUCTURAS CRISTALINAS 1. INTRODUCCIÓN 1.1 Red de Bravais y celda primitiva unidad Uno de los conceptos fundamentales
son dos elementos de Rⁿ, definimos su suma, denotada por
 1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
1.1 Definición de un vector en R², R³ y su Interpretación geométrica. 1.2 Introducción a los campos escalares y vectoriales. 1.3 La geometría de las operaciones vectoriales. 1.4 Operaciones con vectores
TEMA 11. VECTORES EN EL ESPACIO
 TEMA 11. VECTORES EN EL ESPACIO Dados dos puntos y, se define el vector como el segmento orientado caracterizado por su módulo, su dirección y su sentido. Dos vectores son equipolentes si tienen el mismo
TEMA 11. VECTORES EN EL ESPACIO Dados dos puntos y, se define el vector como el segmento orientado caracterizado por su módulo, su dirección y su sentido. Dos vectores son equipolentes si tienen el mismo
GRUPOS PUNTUALES. 4.- Si un plano de simetría contiene un eje de orden n, existen n planos que contienen el eje. formando entre ellos ángulos de
 GRUPOS PUNTUALES Existen algunas relaciones entre elementos de simetría que pueden ser útiles a la hora de deducir cuales son los conjuntos de estos que forman grupo. 1.- Todos los elementos de simetría
GRUPOS PUNTUALES Existen algunas relaciones entre elementos de simetría que pueden ser útiles a la hora de deducir cuales son los conjuntos de estos que forman grupo. 1.- Todos los elementos de simetría
Capítulo 1 Vectores. 26 Problemas de selección - página 13 (soluciones en la página 99)
 Capítulo 1 Vectores 26 Problemas de selección - página 13 (soluciones en la página 99) 21 Problemas de desarrollo - página 22 (soluciones en la página 100) 11 1.A PROBLEMAS DE SELECCIÓN Sección 1.A Problemas
Capítulo 1 Vectores 26 Problemas de selección - página 13 (soluciones en la página 99) 21 Problemas de desarrollo - página 22 (soluciones en la página 100) 11 1.A PROBLEMAS DE SELECCIÓN Sección 1.A Problemas
TEMA 2 SISTEMAS DE REPRESENTACIÓN
 TEMA 2 SISTEMAS DE REPRESENTACIÓN 1. SISTEMAS DE REPRESENTACIÓN Todos los sistemas de representación, tienen como objetivo representar sobre una superficie bidimensional, como es una hoja de papel, los
TEMA 2 SISTEMAS DE REPRESENTACIÓN 1. SISTEMAS DE REPRESENTACIÓN Todos los sistemas de representación, tienen como objetivo representar sobre una superficie bidimensional, como es una hoja de papel, los
Matemáticas. Si un error simple ha llevado a un problema más sencillo se disminuirá la puntuación.
 UNIVERSIDAD POLITÉCNICA DE CARTAGENA PRUEBAS DE ACCESO A LA UNIVERSIDAD DE LOS MAYORES DE 25 AÑOS CONVOCATORIA 2014 CRITERIOS DE EVALUACIÓN Matemáticas GENERALES: El examen constará de dos opciones (dos
UNIVERSIDAD POLITÉCNICA DE CARTAGENA PRUEBAS DE ACCESO A LA UNIVERSIDAD DE LOS MAYORES DE 25 AÑOS CONVOCATORIA 2014 CRITERIOS DE EVALUACIÓN Matemáticas GENERALES: El examen constará de dos opciones (dos
Translaciones, giros, simetrías.
 Translaciones, giros, simetrías. Transformaciones geométricas Transformación geométrica es una aplicación del plano en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo
Translaciones, giros, simetrías. Transformaciones geométricas Transformación geométrica es una aplicación del plano en el plano tal que a cada punto de un plano le hace corresponder otro punto del mismo
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO MATERIA: DIBUJO TÉCNICO II
 UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
UNIVERSIDADES PÚBLICAS DE LA COMUNIDAD DE MADRID PRUEBA DE ACCESO A LAS ENSEÑANZAS UNIVERSITARIAS OFICIALES DE GRADO Curso 2014-2015 MATERIA: DIBUJO TÉCNICO II INSTRUCCIONES GENERALES Y CALIFICACIÓN Después
TECNOLOGÍA. 4º E.S.O. DIBUJO TÉCNICO -.DIBUJO TÉCNICO.-
 Introducción. -.DIBUJO TÉCNICO.- El objetivo del dibujo técnico y del dibujo en general es poder plasmar en dos dimensiones (las de una hoja de papel) objetos, es decir, cuerpos con tres dimensiones. Para
Introducción. -.DIBUJO TÉCNICO.- El objetivo del dibujo técnico y del dibujo en general es poder plasmar en dos dimensiones (las de una hoja de papel) objetos, es decir, cuerpos con tres dimensiones. Para
TECNOLOGÍA. 1º E.S.O. DIBUJO TÉCNICO -.DIBUJO TÉCNICO.-
 Introducción. -.DIBUJO TÉCNICO.- El objetivo del dibujo técnico y del dibujo en general es poder plasmar en dos dimensiones (las de una hoja de papel) objetos, es decir, cuerpos con tres dimensiones. Para
Introducción. -.DIBUJO TÉCNICO.- El objetivo del dibujo técnico y del dibujo en general es poder plasmar en dos dimensiones (las de una hoja de papel) objetos, es decir, cuerpos con tres dimensiones. Para
Problemas métricos. Ángulo entre rectas y planos
 Problemas métricos Ángulo entre rectas y planos Ángulo entre dos rectas El ángulo que forman dos rectas es el ángulo agudo que determinan entre sí sus vectores directores. Dos rectas son perpendiculares
Problemas métricos Ángulo entre rectas y planos Ángulo entre dos rectas El ángulo que forman dos rectas es el ángulo agudo que determinan entre sí sus vectores directores. Dos rectas son perpendiculares
INTRODUCCIÓN A LA NORMALIZACION
 INTRODUCCIÓN A LA NORMALIZACION INTRODUCCIÓN A LA NORMALIZACION -. INTRODUCCION -. TIPOS DE DIBUJOS TÉCNICOS -. ELEMENTOS QUE COMPONEN UN DIBUJO TÉCNICO -. CLASES Y GRUPOS DE LÍNEAS -. NORMAS A TENER EN
INTRODUCCIÓN A LA NORMALIZACION INTRODUCCIÓN A LA NORMALIZACION -. INTRODUCCION -. TIPOS DE DIBUJOS TÉCNICOS -. ELEMENTOS QUE COMPONEN UN DIBUJO TÉCNICO -. CLASES Y GRUPOS DE LÍNEAS -. NORMAS A TENER EN
Dibujo Técnico Sistema diédrico.- Cambios de plano, giros y ángulos. ÁNGULOS.
 30. SISTEMA DIÉDRICO.- CAMBIOS DE PLANO, GIROS Y ÁNGULOS. 30.1. Cambios de plano. Los cambios de planos de proyección consisten en tomar o elegir otros planos de proyección de forma que los elementos que
30. SISTEMA DIÉDRICO.- CAMBIOS DE PLANO, GIROS Y ÁNGULOS. 30.1. Cambios de plano. Los cambios de planos de proyección consisten en tomar o elegir otros planos de proyección de forma que los elementos que
Movimientos en el plano y mosaicos
 Matemáticas de Nivel II de ESPA: Movimientos en el plano - 1 Movimientos en el plano y mosaicos En esta unidad se presenta la utilidad de la geometría para ornamentar objetos y espacios en las actividades
Matemáticas de Nivel II de ESPA: Movimientos en el plano - 1 Movimientos en el plano y mosaicos En esta unidad se presenta la utilidad de la geometría para ornamentar objetos y espacios en las actividades
Profesor: Fernando Ureña Portero
 Curso 13-14 1.-Los puntos A(1,3,1) y B(2,1,3) son vértices consecutivos de un cuadrado. Los otros dos vértices pertenecen a una recta r que pasa por el punto P(2,7,0). a) (3p) Hallar la ecuación de la
Curso 13-14 1.-Los puntos A(1,3,1) y B(2,1,3) son vértices consecutivos de un cuadrado. Los otros dos vértices pertenecen a una recta r que pasa por el punto P(2,7,0). a) (3p) Hallar la ecuación de la
TRIGONOMETRÍA. 1. Ángulos. 2. Razones trigonométricas de ángulos agudos
 TRIGONOMETRÍA 1 Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, el ángulo está comprendido entre 0 y 360
TRIGONOMETRÍA 1 Ángulos Hasta ahora se han considerado los ángulos como la porción del plano comprendida entre dos semirrectas con el origen común De esta manera, el ángulo está comprendido entre 0 y 360
1. Curvas Regulares y Simples
 1. Regulares y Simples en R n. Vamos a estudiar algunas aplicaciones del calculo diferencial e integral a funciones que están definidas sobre los puntos de una curva del plano o del espacio, como por ejemplo
1. Regulares y Simples en R n. Vamos a estudiar algunas aplicaciones del calculo diferencial e integral a funciones que están definidas sobre los puntos de una curva del plano o del espacio, como por ejemplo
Ecuaciones de la forma. y se sabe que pasa por el punto ( 4 ;16 ), cuál es la ecuación de la recta? con m > 0. contenga los puntos ( 2;? por qué?
 Ecuaciones de la forma y = m. Haga las gráficas de y = y = y = y = y y y y y y a. Como son las rectas b. Cuales son simétricas respecto al origen c. La recta y que tipo de simetría presenta respecto a
Ecuaciones de la forma y = m. Haga las gráficas de y = y = y = y = y y y y y y a. Como son las rectas b. Cuales son simétricas respecto al origen c. La recta y que tipo de simetría presenta respecto a
x+2y = 6 z = [C-LE] [JUN-A] Calcúlese la distancia del origen al plano que pasa por A(1,2,0) y contiene a la recta r x+2 2 = y-1
![x+2y = 6 z = [C-LE] [JUN-A] Calcúlese la distancia del origen al plano que pasa por A(1,2,0) y contiene a la recta r x+2 2 = y-1 x+2y = 6 z = [C-LE] [JUN-A] Calcúlese la distancia del origen al plano que pasa por A(1,2,0) y contiene a la recta r x+2 2 = y-1](/thumbs/52/30710835.jpg) 1. [ANDA] [JUN-A] Considera el punto P(2,0,1) y la recta r a) Halla la ecuación del plano que contiene a P y a r. b) Calcula el punto simétrico de P respecto de la recta r. x+2y = 6 z = 2. 2. [ANDA] [SEP-A]
1. [ANDA] [JUN-A] Considera el punto P(2,0,1) y la recta r a) Halla la ecuación del plano que contiene a P y a r. b) Calcula el punto simétrico de P respecto de la recta r. x+2y = 6 z = 2. 2. [ANDA] [SEP-A]
Un ángulo mide y otro Cuánto mide la suma de estos ángulos?
 Los Ángulos Qué es un ángulo y su notación? Son dos rayos cualesquiera que determinan dos regiones del plano. Su notación: Para nombrar los ángulos, utilizaremos los símbolos
Los Ángulos Qué es un ángulo y su notación? Son dos rayos cualesquiera que determinan dos regiones del plano. Su notación: Para nombrar los ángulos, utilizaremos los símbolos
Anexo 1 ( Momentos de segundo orden )
 .1 neo 1 ( Momentos de segundo orden ) 1. Momento de inercia En muchas de las fórmulas empleadas en ingeniería aparecen epresiones analíticas de la forma ρ d, siendo ρ la distancia de un elemento diferencial
.1 neo 1 ( Momentos de segundo orden ) 1. Momento de inercia En muchas de las fórmulas empleadas en ingeniería aparecen epresiones analíticas de la forma ρ d, siendo ρ la distancia de un elemento diferencial
TEMA 6. Ángulos, distancias, simetrías Problemas Resueltos
 Matemáticas II (Bachillerato de Ciencias) Soluciones de los problemas propuestos Tema 6 88 Ángulos entre rectas y planos TEMA 6 Ángulos, distancias, simetrías Problemas Resueltos Dadas las rectas r y s
Matemáticas II (Bachillerato de Ciencias) Soluciones de los problemas propuestos Tema 6 88 Ángulos entre rectas y planos TEMA 6 Ángulos, distancias, simetrías Problemas Resueltos Dadas las rectas r y s
Teoría Tema 6 Ecuaciones de la recta
 página 1/14 Teoría Tema 6 Ecuaciones de la recta Índice de contenido Base canónica en dos dimensiones como sistema referencial...2 Ecuación vectorial de la recta...4 Ecuación paramétrica de la recta...6
página 1/14 Teoría Tema 6 Ecuaciones de la recta Índice de contenido Base canónica en dos dimensiones como sistema referencial...2 Ecuación vectorial de la recta...4 Ecuación paramétrica de la recta...6
La recta en el plano.
 1 CONOCIMIENTOS PREVIOS. 1 La recta en el plano. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas. Representación
1 CONOCIMIENTOS PREVIOS. 1 La recta en el plano. 1. Conocimientos previos. Antes de iniciar el tema se deben de tener los siguientes conocimientos básicos: Intervalos y sus definiciones básicas. Representación
TEMA 1. Números Reales. Teoría. Matemáticas
 1 1.- Los números reales Cuáles son los números reales? Los números reales son todos los números racionales y todos los números irracionales. El conjunto de los números reales se designa con el símbolo
1 1.- Los números reales Cuáles son los números reales? Los números reales son todos los números racionales y todos los números irracionales. El conjunto de los números reales se designa con el símbolo
BLOQUE 2 : GEOMETRÍA
 BLOQUE 2 : GEOMETRÍA EJERCICIO 1 Dado el plano Л : x + 2y z = 2, el punto P( 2,3,2) perteneciente al plano Л y la recta r de ecuación:, a) Determina la posición relativa de r y Л. b) Calcula la ecuación
BLOQUE 2 : GEOMETRÍA EJERCICIO 1 Dado el plano Л : x + 2y z = 2, el punto P( 2,3,2) perteneciente al plano Л y la recta r de ecuación:, a) Determina la posición relativa de r y Л. b) Calcula la ecuación
 Caso de varios vectores primitivos de un mismo arreglo. Base o Motivo: Átomo o conjunto de átomos que se asocian con un punto de la malla Malla o Lattice: Es un arreglo infinito de puntos en el espacio,
Caso de varios vectores primitivos de un mismo arreglo. Base o Motivo: Átomo o conjunto de átomos que se asocian con un punto de la malla Malla o Lattice: Es un arreglo infinito de puntos en el espacio,
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS DE GRANADA
 ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS DE GRANADA EXAMEN GEOMETRÍA APLICADA. EXAMEN FINAL DE JUNIO EJERCICIO PROYECCIÓN DIÉDRICA. Un plano P tiene su traza horizontal formando
ESCUELA TÉCNICA SUPERIOR DE INGENIEROS DE CAMINOS, CANALES Y PUERTOS DE GRANADA EXAMEN GEOMETRÍA APLICADA. EXAMEN FINAL DE JUNIO EJERCICIO PROYECCIÓN DIÉDRICA. Un plano P tiene su traza horizontal formando
PSU Matemática NM-4 Guía 23: Isometrías. Nombre: Curso: Fecha: -
 Centro Educacional San Carlos de Aragón. Dpto. Matemática. Prof. Ximena Gallegos H. PSU Matemática NM- Guía : Isometrías Nombre: Curso: Fecha: - Contenido: Isometrías. Aprendizaje Esperado: Analiza traslaciones
Centro Educacional San Carlos de Aragón. Dpto. Matemática. Prof. Ximena Gallegos H. PSU Matemática NM- Guía : Isometrías Nombre: Curso: Fecha: - Contenido: Isometrías. Aprendizaje Esperado: Analiza traslaciones
Algebra lineal y conjuntos convexos
 Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
Apéndice A Algebra lineal y conjuntos convexos El método simplex que se describirá en el Tema 2 es de naturaleza algebraica y consiste en calcular soluciones de sistemas de ecuaciones lineales y determinar
. De R (Reales) a C (Complejos)
 INTRODUCCIÓN Los números complejos se introducen para dar sentido a la raíz cuadrada de números negativos. Así se abre la puerta a un curioso y sorprendente mundo en el que todas las operaciones (salvo
INTRODUCCIÓN Los números complejos se introducen para dar sentido a la raíz cuadrada de números negativos. Así se abre la puerta a un curioso y sorprendente mundo en el que todas las operaciones (salvo
Dibujo Técnico Triángulos
 12. TRIÁNGULOS 12.1. Características generales Un triángulo ABC es una figura plana limitada por tres rectas que se cortan dos a dos, determinando los segmentos AB, AC y BC que son los lados del triángulo.
12. TRIÁNGULOS 12.1. Características generales Un triángulo ABC es una figura plana limitada por tres rectas que se cortan dos a dos, determinando los segmentos AB, AC y BC que son los lados del triángulo.
Estructura de los Sólidos
 Estructura de los Sólidos Estructura Cristalina OBJETIVOS a) Definir sólidos cristalinos y amorfos b) Definir estructura cristalina c) Describir las diferentes estructuras cristalinas d) Utilizar índices
Estructura de los Sólidos Estructura Cristalina OBJETIVOS a) Definir sólidos cristalinos y amorfos b) Definir estructura cristalina c) Describir las diferentes estructuras cristalinas d) Utilizar índices
Instituto de Física Universidad de Guanajuato Agosto 2007
 Instituto de Física Universidad de Guanajuato Agosto 2007 Física III Capítulo I José Luis Lucio Martínez El material que se presenta en estas notas se encuentra, en su mayor parte, en las referencias que
Instituto de Física Universidad de Guanajuato Agosto 2007 Física III Capítulo I José Luis Lucio Martínez El material que se presenta en estas notas se encuentra, en su mayor parte, en las referencias que
ejerciciosyexamenes.com GEOMETRIA
 GEOMETRIA 1.- Dado el vector AB= (2,-1,3) y el punto B(3,1,2) halla las coordenadas del punto A. Sol: A =(1,2,-1) 2.- Comprobar si los vectores AB y CD son equipolentes, siendo A(1,2,-1), B(0,3,1), C(1,1,1)
GEOMETRIA 1.- Dado el vector AB= (2,-1,3) y el punto B(3,1,2) halla las coordenadas del punto A. Sol: A =(1,2,-1) 2.- Comprobar si los vectores AB y CD son equipolentes, siendo A(1,2,-1), B(0,3,1), C(1,1,1)
Conceptos básicos de Geometría
 Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 15 de enero del 2013 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) 15 de enero del 2013 1 / 25 1 Geometría Afín Geometría Euclidiana Áreas y ángulos Dr. Eduardo
Dr. Eduardo A. RODRÍGUEZ TELLO CINVESTAV-Tamaulipas 15 de enero del 2013 Dr. Eduardo RODRÍGUEZ T. (CINVESTAV) 15 de enero del 2013 1 / 25 1 Geometría Afín Geometría Euclidiana Áreas y ángulos Dr. Eduardo
MATEMÁTICAS II TEMA 6 Planos y rectas en el espacio. Problemas de ángulos, paralelismo y perpendicularidad, simetrías y distancias
 Geometría del espacio: problemas de ángulos y distancias; simetrías MATEMÁTICAS II TEMA 6 Planos y rectas en el espacio Problemas de ángulos, paralelismo y perpendicularidad, simetrías y distancias Ángulos
Geometría del espacio: problemas de ángulos y distancias; simetrías MATEMÁTICAS II TEMA 6 Planos y rectas en el espacio Problemas de ángulos, paralelismo y perpendicularidad, simetrías y distancias Ángulos
Colegio Internacional Torrequebrada. Departamento de Matemáticas
 Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
Geometría. Problema 1: Calcula la distancia del punto P(1, 1, 1) a la recta Problema 2: Dadas las rectas, se pide: a) Analiza su posición relativa. b) Halla la ecuación general del plano π que contiene
METODOS DE REPRESENTACIÓN
 METODOS DE REPRESENTACIÓN PROYECCIONES: A efectos de describir una pieza o maquinaria, lo más preciso es la representación gráfica de la misma. El criterio fundamental que se sigue en la representación
METODOS DE REPRESENTACIÓN PROYECCIONES: A efectos de describir una pieza o maquinaria, lo más preciso es la representación gráfica de la misma. El criterio fundamental que se sigue en la representación
Tema 7: Superficies regladas desarrollables. Pirámide-cono, prisma-cilindro.
 Tema 7: Superficies regladas desarrollables. Pirámide-cono, prisma-cilindro. Definición y representación diédrica. Las superficies regladas están generadas por el movimiento de una recta. En las superficies
Tema 7: Superficies regladas desarrollables. Pirámide-cono, prisma-cilindro. Definición y representación diédrica. Las superficies regladas están generadas por el movimiento de una recta. En las superficies
Si se pueden obtener las imágenes de x por simple sustitución.
 TEMA 0: REPASO DE FUNCIONES FUNCIONES: TIPOS DE FUNCIONES Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción,
TEMA 0: REPASO DE FUNCIONES FUNCIONES: TIPOS DE FUNCIONES Funciones algebraicas En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción,
CUERPOS. Poliedros: Aquellos cuerpos geométricos totalmente limitados por polígonos, como por ejemplo, el prisma, la pirámide; etc.
 CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
CUERPOS Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede calcular el volumen del mismo
Algunos conceptos básicos de Trigonometría DEFINICIÓN FIGURA OBSERVACIONES. Nombre y definición Figura Característica
 Ángulos. DEFINICIÓN FIGURA OBSERVACIONES Ángulo. Es la abertura formada por dos semirrectas unidas en un solo punto llamado vértice. Donde: α = Ángulo O = Vértice OA = Lado inicial OB = Lado terminal Un
Ángulos. DEFINICIÓN FIGURA OBSERVACIONES Ángulo. Es la abertura formada por dos semirrectas unidas en un solo punto llamado vértice. Donde: α = Ángulo O = Vértice OA = Lado inicial OB = Lado terminal Un
DIBUJO MECÁNICO TEMA 4 : ACOTACIÓN
 DIBUJO MECÁNICO TEMA 4 : ACOTACIÓN Prof. Andrés Meléndez Tema 4: Contenido. Definiciones. Tipos de cota: Cota Funcional, Cota no funcional Cota auxiliar. Aplicaciones; Elementos de cota, Línea de cota,
DIBUJO MECÁNICO TEMA 4 : ACOTACIÓN Prof. Andrés Meléndez Tema 4: Contenido. Definiciones. Tipos de cota: Cota Funcional, Cota no funcional Cota auxiliar. Aplicaciones; Elementos de cota, Línea de cota,
MATEMÁTICASII Curso académico BLOQUE GEOMETRÍA. TEMA 1: VECTORES
 MATEMÁTICASII Curso académico 2015-2016 BLOQUE GEOMETRÍA. TEMA 1: VECTORES 1.1 VECTORES DEL ESPACIO. VECTORES LIBRES DEL ESPACIO Sean y dos puntos del espacio. Llamaremos vector (fijo) a un segmento orientado
MATEMÁTICASII Curso académico 2015-2016 BLOQUE GEOMETRÍA. TEMA 1: VECTORES 1.1 VECTORES DEL ESPACIO. VECTORES LIBRES DEL ESPACIO Sean y dos puntos del espacio. Llamaremos vector (fijo) a un segmento orientado
Bases Matemáticas para la Educación Primaria. Guía de Estudio. Tema 5: Transformaciones geométricas planas. Orientación espacial
 Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 5: Transformaciones geométricas planas. Orientación espacial 1 Transformaciones geométricas 2 ISOMETRÍAS EN LIBROS DE PRIMARIA Cuáles de
Bases Matemáticas para la Educación Primaria Guía de Estudio Tema 5: Transformaciones geométricas planas. Orientación espacial 1 Transformaciones geométricas 2 ISOMETRÍAS EN LIBROS DE PRIMARIA Cuáles de
Espacios Vectoriales
 Leandro Marín Octubre 2010 Índice Definición y Ejemplos Paramétricas vs. Impĺıcitas Bases y Coordenadas Para definir un espacio vectorial tenemos que empezar determinando un cuerpo sobre el que esté definido
Leandro Marín Octubre 2010 Índice Definición y Ejemplos Paramétricas vs. Impĺıcitas Bases y Coordenadas Para definir un espacio vectorial tenemos que empezar determinando un cuerpo sobre el que esté definido
El medir y las Cantidades Físicas escalares y vectores en física. Prof. R. Nitsche C. Física Medica UDO Bolívar
 El medir y las Cantidades Físicas escalares y vectores en física Prof. R. Nitsche C. Física Medica UDO Bolívar Medir Medir es el requisito de toda ciencia empírica (experimental); medir significa simplemente
El medir y las Cantidades Físicas escalares y vectores en física Prof. R. Nitsche C. Física Medica UDO Bolívar Medir Medir es el requisito de toda ciencia empírica (experimental); medir significa simplemente
Mecánica de Fluidos. Análisis Diferencial
 Mecánica de Fluidos Análisis Diferencial Análisis Diferencial: Descripción y caracterización del flujo en función de la descripción de una partícula genérica del flujo. 1. Introducción 2. Movimiento de
Mecánica de Fluidos Análisis Diferencial Análisis Diferencial: Descripción y caracterización del flujo en función de la descripción de una partícula genérica del flujo. 1. Introducción 2. Movimiento de
TEMA 9: SISTEMA DIÉDRICO: VISTAS PRINCIPALES. DIBUJO EN PERSPECTIVA. ACOTACIÓN
 TEMA 9: SISTEMA DIÉDRICO: VISTAS PRINCIPALES. DIBUJO EN PERSPECTIVA. ACOTACIÓN 1 TEMA 9: SISTEMA DIÉDRICO: VISTAS PRINCIPALES. DIBUJO EN PERSPECTIVA. ACOTACIÓN 9.1.- DIBUJO EN PERSPECTIVA Los objetos que
TEMA 9: SISTEMA DIÉDRICO: VISTAS PRINCIPALES. DIBUJO EN PERSPECTIVA. ACOTACIÓN 1 TEMA 9: SISTEMA DIÉDRICO: VISTAS PRINCIPALES. DIBUJO EN PERSPECTIVA. ACOTACIÓN 9.1.- DIBUJO EN PERSPECTIVA Los objetos que
VECTORES vector Vector posición par ordenado A(a, b) representa geométricamente segmento de recta dirigido componentes del vector
 VECTORES Un vector (Vector posición) en el plano es un par ordenado de números reales A(a, b). Se representa geométricamente por un segmento de recta dirigido, cuyo punto inicial es el origen del sistema
VECTORES Un vector (Vector posición) en el plano es un par ordenado de números reales A(a, b). Se representa geométricamente por un segmento de recta dirigido, cuyo punto inicial es el origen del sistema
Volumen de Sólidos de Revolución
 60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
60 CAPÍTULO 4 Volumen de Sólidos de Revolución 6 Volumen de sólidos de revolución Cuando una región del plano de coordenadas gira alrededor de una recta l, se genera un cuerpo geométrico denominado sólido
GEOMETRÍA DE LOS CRISTALES I
 CAPÍTULO 4 GEOMETRÍA DE LOS CRISTALES I 4.1 REDES Conjuntos de puntos imaginarios que tienen una relación fija en el espacio constituyendo un armazón sobre el cual el cristal se construye. En la Figura
CAPÍTULO 4 GEOMETRÍA DE LOS CRISTALES I 4.1 REDES Conjuntos de puntos imaginarios que tienen una relación fija en el espacio constituyendo un armazón sobre el cual el cristal se construye. En la Figura
UNIDAD 7: PROGRESIONES OBJETIVOS
 UNIDAD 7: PROGRESIONES Reconocer sucesiones y deducir su regla de formación en los casos en que sea posible. Obtener distintos términos en sucesiones recurrentes. Distinguir si una sucesión es una progresión
UNIDAD 7: PROGRESIONES Reconocer sucesiones y deducir su regla de formación en los casos en que sea posible. Obtener distintos términos en sucesiones recurrentes. Distinguir si una sucesión es una progresión
La prueba extraordinaria de septiembre está descrita en los criterios y procedimientos de evaluación.
 La prueba extraordinaria de septiembre está descrita en los criterios y procedimientos de evaluación. Los contenidos mínimos de la materia son los que aparecen con un * UNIDAD 1: LOS NÚMEROS NATURALES
La prueba extraordinaria de septiembre está descrita en los criterios y procedimientos de evaluación. Los contenidos mínimos de la materia son los que aparecen con un * UNIDAD 1: LOS NÚMEROS NATURALES
Universidad de Murcia
 Universidad de Murcia CRISTALOGRAFÍA Control MURCIA 2011 2012 Francisco Cánovas Picón Índice Índice.............................................. 2 1. Problema 1.......................................
Universidad de Murcia CRISTALOGRAFÍA Control MURCIA 2011 2012 Francisco Cánovas Picón Índice Índice.............................................. 2 1. Problema 1.......................................
MÓDULO 8: VECTORES. Física
 MÓDULO 8: VECTORES Física Magnitud vectorial. Elementos. Producto de un vector por un escalar. Operaciones vectoriales. Vector unitario. Suma de vectores por el método de componentes rectangulares. UTN
MÓDULO 8: VECTORES Física Magnitud vectorial. Elementos. Producto de un vector por un escalar. Operaciones vectoriales. Vector unitario. Suma de vectores por el método de componentes rectangulares. UTN
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS)
 CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
CUERPOS GEOMÉTRICOS (CONCEPTOS BÁSICOS) Los cuerpos geométricos ocupan un lugar en el espacio. Hay cuerpos de forma regular, en los que pueden medirse 3 dimensiones: largo, ancho y alto. Con estas se puede
MATERIAS DE MODALIDAD: FASES GENERAL Y ESPECÍFICA CURSO JUNIO
 PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASES GENERAL Y ESPECÍFICA CURSO 2015 2016 MATERIA: DIBUJO TÉCNICO II (2) Convocatoria: JUNIO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE,
PRUEBAS DE ACCESO A LA UNIVERSIDAD MATERIAS DE MODALIDAD: FASES GENERAL Y ESPECÍFICA CURSO 2015 2016 MATERIA: DIBUJO TÉCNICO II (2) Convocatoria: JUNIO EL ALUMNO DEBE ELEGIR Y DESARROLLAR, OBLIGATORIAMENTE,

 ᒬ 01) En el triángulo ABC de la figura AD = BD;
ᒬ 01) En el triángulo ABC de la figura AD = BD;